Сайт викладача фізики

·                                       АСТРОНОМІЯ

Зміст.

§1. Загальні відомості про астрономію та ті об’єкти, що є предметом її вивчення.

Тема 1. Загальні відомості про закономірності видимого руху Сонця, Місяця, зірок та планет.

§2. Закономірності видимого руху Сонця.

§3. Закономірності видимого руху Місяця.

§4. Сонячні і місячні затемнення. Припливи та відпливи.

§5. Сузір’я. Зоряні величини.

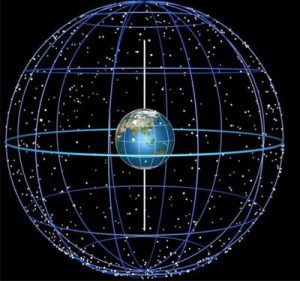
§6. Система зоряних координат. Закономірності видимого руху зірок. Прецесійне обертання Землі.

§7. Закономірності видимого руху планет.

§8. Закони Кеплера.

§9. Про теорію Ньютона та про те, як вона пояснює загальний устрій Сонячної системи.

Тема 2. Загальні відомості про методи та засоби  астрономічних досліджень.

§10. Визначення відстаней до космічних об’єктів. Одиниці вимірювання космічних відстаней.

§11. Спектральний аналіз – базовий метод космічних досліджень.

§12. Про прямі та непрямі вимірювання, або про те як зважують планети зірки і галактики.

§13. Сучасні наземні та орбітальні телескопи.

Тема 3. Загальні відомості про об’єкти Сонячної системи.

§14. Загальні відомості про Сонце.

§15. Загальні відомості про Землю.

§16. Місяць – природний супутник Землі.

§17. Планети земної групи.

§18. Планети-гіганти.

§19. Карликові планети та малі тіла Сонячної системи.

Тема 4. Загальні відомості про зірка та галактики.

§20. Спектральна класифікація зірок.

§21. Еволюційна класифікація зірок.

§22. Загальні відомості про галактики та квазари.

Тема 5. Космологія – наука про Всесвіт.

§23. З історії наукових поглядів на устрій Всесвіту.

§24. З історії становлення сучасної теорії еволюційного Всесвіту та про філософські аспекти цієї теорії.

§25. Основи сучасної теорії еволюційного Всесвіту (теорії Великого Вибуху).

§26. Про докази того, що сучасна теорія еволюційного Всесвіту є правильною.

§27. Про еволюцію зірок.

§28. Про еволюцію Сонячної системи.

§29. Геологічна історія Землі.

§30. Про еволюційну теорію Дарвіна, або про те, що з’явилось раніше, яйце чи курка.

§31. Про енергетичні передумови еволюційного самозародження та саморозвитку життя на Землі.

§32. Чи одинокі ми у Всесвіті?

§33. Про НЛО, інопланетян та позаземні цивілізації.

§34. Про дикунські теорії, чорні дірки, паралельні світи та розумну сутність Землі.

.

§1. Загальні відомості про астрономію та ті об’єкти, що є предметом її вивчення.

Астрономія (від грец. astron – зоря, nomos – закон) – це наука, яка вивчає загальний устрій, параметри, закономірності руху та еволюційного саморозвитку, всієї сукупності космічних об’єктів і Всесвіту загалом. Предметом вивчення астрономії є вся сукупність космічних об’єктів, основними з яких є Сонце та його планетарна система, все різноманіття зірок, наша та інші галактики, системи галактик і Всесвіт загалом. Гранично стисло про ці об’єкти, можна сказати наступне.

Найпомітнішими макрооб’єктами Всесвіту є зірки. Зірка (зоря) – це самосвітній космічний макрооб’єкт, в надрах якого відбуваються або відбувалися термоядерні реакції. Зірки як і люди, народжуються, живуть, старіють і помирають. Просто зірки живуть набагато довше. Про те, як народжуються, живуть, старіють і помирають зірки, ми поговоримо дещо пізніше, а точніше, в тому розділі який називається космологією – наукою про Всесвіт (від грец. kosmos – Всесвіт, logos – наука, вчення). Наразі ж просто зауважимо, що у своєму еволюційному розвитку, зірка проживає декілька стадій: стадію народження (протозоряна туманність) → стадію активного життя (звичайна зірка) → стадію старіння (червоний гігант) → стадію смерті, а точніше стадію переходу до якісно нового стану, яким в залежності від маси зірки може бути білий карлик (для М < 7М_☼), нейтронна зірка (для 7М_☼ < М < 16М_☼) або чорна діра (М > 16М_☼).

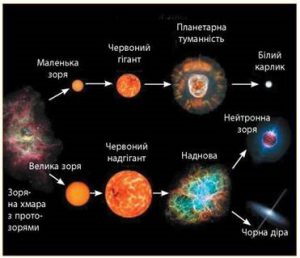
Мал.1. Загальна картина етапів життя зірки.

Найважливішим параметром зірки, параметром від якого визначально залежить тривалість життя, променева активність (світність) та кінцева доля зірки, є її маса. А ця маса може знаходитись в межах від 0,05М_☼ до тисяч сонячних мас. Якщо ж говорити про геометричні розміри зірок і зокрема про їх діаметр, то він може становити від десятка кілометрів – для нейтронних зірок, до тисяч діаметрів Сонця – для червоних надгігантів. При цьому, якщо мова йде про так звані чорні діри, то їх геометричні розміри не перевищують розмірів горошини. Втім, для чорної діри, терміни: геометричні розміри, густина, хімічний склад, тощо – втрачають сенс. Не менш разючими є і відмінності в світності зірок: від практично невидимих чорних карликів (згаслих білих карликів), нейтронних зірок та чорних дір, до над яскравих спалахів наднових зірок, світність яких в мільярди разів перевищує світність Сонця.

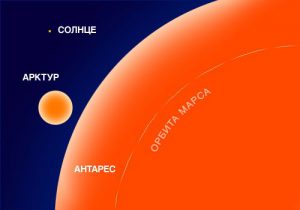
Мал.2. Порівняльні розміри деяких зірок.

Однією з незлічених зірок Всесвіту, є Сонце. За мірками сучасного Всесвіту, Сонце є активною зіркою середніх розмірів, середньої маси, середнього віку та середньої світності (енергетичної потужності). Сонце представляє собою розжарену газоподібну кулю, температура поверхні якої близька до 6000К. Радіус цієї кулі 695∙10⁶м, що в 109 разів перевищує радіус Землі. При цьому маса Сонця в 330 000 разів перевищує масу Землі і в 750 разів – загальну масу всіх планет Сонячної системи. Сонце, на 73% складається з водню, на 25% – з гелію і на 2% – з інших хімічних елементів. Джерелом тієї енергії яку постійно випромінює Сонце, є термоядерні реакції які відбуваються в розжарених до 13,5∙10⁶К надрах Сонця, і в процесі яких ядра атомів водню перетворюються на ядра атомів гелію.

Сонце належить до числа тих не надто розповсюджених зірок, які мають планетарні системи. При цьому основними складовими планетарної системи Сонця (Сонячної системи) є: Сонце, вісім планет (Меркурій, Венера, Земля, Марс, Юпітер, Сатурн, Уран, Нептун) та понад 100 супутників цих планет, п’ять карликових планет, пояс астероїдів і пояс Койпера, комети, метеороїди та космічний пил.

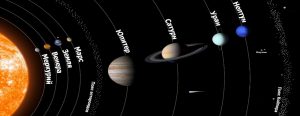
Мал.3. Сонячна система – це сукупність гравітаційно пов’язаних космічних об’єктів, які обертаються навколо Сонця.

Наймасивнішими та найпомітнішими елементами планетарної системи Сонця (звичайно окрім самого Сонця), є планети. Планета (від грец. planetes – блукаюча) – це масивне космічне тіло, яке обертається навколо зірки, гравітаційне поле якого є достатнім для того щоб надати цьому тілу кулястої форми, але не достатнім, щоб генерувати термоядерні реакції, і яке шляхом приєднання до себе дрібніших тіл, очистило околиці своєї орбіти.

Планети Сонячної системи обертаються по слабо видовженим еліптичним (майже круговим) орбітам, які знаходяться в межах майже плоского диску – площині екліптики. Чотири внутрішні планети Сонячної системи (Меркурій, Венера, Земля, Марс), прийнято називати планетами земної групи. Ці планети мають відносно малі розміри, відносно малі маси, і складаються з відносно важких хімічних елементів. Планети земної групи мають тверду поверхню, яка оточена газоподібною атмосферою (Окрім Меркурія, який атмосфери не має).  Чотири зовнішні планети Сонячної системи (Юпітер, Сатурн, Уран, Плутон), прийнято називати планетами-гігантами. Ці планети мають відносно великі розміри та маси, і складаються головним чином з водню та гелію. Планети-гіганти не мають чітко вираженої твердої чи рідкої поверхні. Атмосфери цих планет, являють собою безпосереднє продовження їх надр.

Шість із восьми планет Сонячної системи мають природні супутники, тобто достатньо масивні космічні тіла, які обертаються навколо відповідної планети. Крім цього, всі планети-гіганти мають безліч дрібних супутників (дрібних камінців, крижинок та пилу) які обертаються в екваторіальній площині планети та утворюють характерне кільце. Особливо помітним та ефектним це планетарне кільце є у Сатурна.

В Сонячній системі є дві ділянки заповнені малими тілами: пояс астероїдів і пояс Койпера. Пояс астероїдів розташований між орбітами Марса та Юпітера і складається з величезної кількості кам’янистих брил, загальна маса яких співрозмірна з масою Місяця. При цьому четверта частина цієї маси зосереджена в найбільшому астероїді (Церера), який за сучасною класифікацією відноситься до так званих карликових планет. Пояс Койпера (названо на честь нідерландського астронома Джерарда Койпера) знаходиться за орбітою планети Нептун і представляє собою сукупність величезної кількості льодяних брил, складовими частинами яких є вода, аміак та метан. Найбільші об’єкти поясу Койпера (Плутон, Макемаке, Ерида, Хаумеа) прийнято вважати карликовими планетами.

Карликова планета – це таке космічне тіло, яке обертається навколо Сонця (тобто не є супутником іншої планети), маса якого є достатньою для того щоб надати цьому тілу кулястої форми, але не достатньою для того, щоб очистити околиці своєї орбіти від інших подібних тіл. Карликові планети значно менші за Місяць. Але якщо говорити про визначальну відмінність карликової планети від звичайної (великої) планети, то вона полягає в тому, що карликова планета не є гравітаційною домінантою на траєкторії свого руху. Це означає, що разом з карликовою планетою, приблизно такими ж орбітами навколо Сонця обертається багато інших масивних тіл поясу астероїдів або поясу Койпера.  На сьогоднішній день, астрономи налічують п’ять карликових планет. При цьому ще п’ять об’єктів Сонячної системи претендують на це звання.

Мал.4. Загальний вигляд та співвідношення розмірів карликових планет.

Важливими та помітними складовими Сонячної системи є комети і метеороїди. Кометами (від грец. kometes – довговолосий) називають ті об’єкти Сонячної системи, які рухаються по сильно витягнутим еліптичним орбітам і які представляють собою відносно невеликі (діаметром від десятків метрів до десятків кілометрів) крижані тіла з вкрапленнями дрібних твердих частинок. В процесі наближення до Сонця, зовнішні шари криги випаровуються. При цьому, навколо ядра комети утворюється пароподібна атмосфера (кома) та довгий хвіст, які на фоні зоряного неба світяться відбитим сонячним світлом.

Поява комети на фоні зоряного неба не є надто частим явищем. Достатньо сказати, що за всю історію спостережень зафіксовано не більше 500 комет, з яких лише близько 200 спостерігалися більше одного разу. Найвідомішою з комет є комета Галлея, яка з періодичністю 75 років обертається навколо Сонця і перші згадки про яку датовані початком нашої ери.

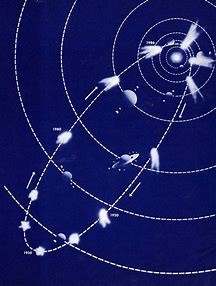
Мал.5. Вигляд комети Галлея на фоні зоряного неба. Схема руху комети Галлея.

         Метеороїдами називають дрібні тверді тіла, що рухаються в міжпланетному просторі і розміри яких значно менші за розміри дрібних астероїдів (d<10м), але значно більші за розміри космічного пилу (d>0,1мм). Ті метеороїди, які потрапляючи в атмосферу Землі, повністю згорають в ній, називаються метеорами. А ті, які падають на поверхню Землі – метеоритами. Видимими проявами падіння метеорів є короткотривалі спалахи, які ми часто називаємо «падінням зірки».

Мал.6. Ті короткотривалі спалахи, які ми часто спостерігаємо на фоні зоряного неба і зазвичай називаємо «падінням зірки», є видимими проявами падіння метеорів.

Сонячна система, є маленьким фрагментом величезної зіркової системи, яку називають Чумацьким Шляхом, Молочним Шляхом, або просто – наша Галактика. Дані назви походять від факту того, що в ясну безмісячну ніч, на фоні зоряного неба, можна побачити широку сріблясту смугу (мал.7). Цю зоряну смугу, наші прадіди називали Чумацьким Шляхом. Напевно тому, що вона нагадувала їм ту чумацьку дорогу, якою вони ходили в далекі мандри. Ті ж хто не чумакував, називали цю зоряну смугу Молочним Шляхом. Можливо тому, що вона їм нагадувала смужку густо розбризканих крапель молока. Та як би там не було, а на сьогоднішній день достовірно відомо, що та срібляста смуга яка опоясує зоряне небо, є видимою частиною величезної зоряної системи (галактики), яку називають по різному: Чумацьким Шляхом, Молочним Шляхом, чи просто – наша Галактика (з великої літери Г). До речі, слово «галактика» походить від грецького  galakticos, що означає «молочний».

Мал.7. Та срібляста смуга, що опоясує зоряне небо, є видимою частиною нашої Галактики (Чумацького Шляху, Молочного Шляху).

         Галактика – велетенська космічна система, яка складається з зірок та їх скупчень, міжзоряної речовини, хмар газу та пилу, різноманітних випромінювань, і можливо з того, що прийнято називати чорною матерією. При цьому всі речовинні складові галактики, так чи інакше обертаються навколо спільного центру мас, та утворюють цілісну систему гравітаційно пов’язаних об’єктів. Маси галактик варіюються від 10⁶ до 10¹³ мас Сонця. А їх діаметри – від десятків до сотень тисяч світлових років.

Наприклад наша Галактика (Чумацький Шлях) – це велика спіральна галактика, до складу якої входить близько 250∙10⁹ найрізноманітніших зірок. Загальна маса Галактики, близька до 600∙10⁹М_☼. Діаметр галактичного диску, близький до 100 000 світлових років, а його товщина за межами ядра Галактики близька до 1 000 св.р. Сонце знаходиться на відстані 30 000 св.р. від центру галактичного диску і обертається навколо цього центру з швидкістю 220 км/с. При цьому період обертання Сонця близький до 200 мільйонів років.

Мал.8. Загальний вигляд нашої Галактики.

Галактики рідко бувають поодинокими. Зазвичай вони об’єднані в невеликі групи, або входять до складу величезних скупчень які налічують сотні, а іноді і тисячі галактик. Скажімо Чумацький шлях входить до складу галактичного скупчення, яке називають Місцевою групою. Ця група складається з трьох великих галактик (Чумацький Шлях, Туманність Андромеди, Галактика Трикутника), та більш як 50, дрібних карликових галактик, найвідомішими з яких є Велика і Мала Магелланові Хмари. Потрібно зауважити, що з Землі, неозброєним оком, можна побачити лише три галактики: Туманність Андромеди, Велику та Малу Магелланові Хмари (дві останні видно лише в південних широтах Землі).

За сучасними уявленнями Всесвіт являє собою сукупність так званих галактичних ниток (стінів) розділених великими проміжками міжгалактичної порожнечі (войдами). Це означає, що Всесвіт має сіткоподібну структуру в якій речовинні об’єкти у вигляді скупчень галактик, розділені великими проміжками так званої темної матерії. При цьому в мега масштабах розмірів (понад 10⁹св.р.) Всесвіт є практично ізотропним, тобто таким, усереднений розподіл речовини (мас-енергії) в якому є однаковим в усіх напрямках.

Мал.9. Загальна картина великомасштабної структури Всесвіту.

На завершення додамо, що сучасна астрономія нерозривно пов’язана з фізикою. Цей нерозривний зв’язок полягає не лише в тому, що астрономічні дослідження цілком і повністю базуються на застосуванні фізичних законів, фізичних методів вимірювань та фізичному методі досліджень. Нерозривний взаємозв’язок астрономії і фізики з усією очевидністю ілюструє факт того, що той базовий розділ сучасної астрономії який називається космологією – наукою про Всесвіт, одночасно є і певним розділом сучасної фізики – науки про Природу. Не будемо забувати і про те, що за сучасною науковою термінологією, термін «Природа», є більш загальним аніж термін «Всесвіт».

Контрольні запитання.

1. Що є предметом вивчення астрономії?
2. Які космічні об’єкти називають зірками (зорями)?
3. Які стадії проживає зірка в процесі своєї еволюції?
4. Від чого залежить тривалість життя та еволюційна доля зівки?
5. Опишіть загальний устрій Сонячної системи.
6. Які космічні об’єкти називають карликовими планетами і чим вони відрізняються від звичайних планет?
7. Які космічні об’єкти називають метеороїдами; метеорами; метеоритами?
8. Які космічні об’єкти називаються галактиками?
9. Опишіть загальний устрій нашої Галактики.
10. Що означає твердження: в мега масштабах, Всесвіт практично ізотропний?

.

Тема 1. Загальні відомості про закономірності видимого руху Сонця, Місяця, зірок та планет.

.

§2. Закономірності видимого руху Сонця.

Сьогодні загально відомо, що Земля обертається навколо Сонця та своєї осі, і що це обертання спричиняє як зміну дня і ночі, так і зміну пір року на Землі. Однак жителі Землі, у повній відповідності з законами Природи і зокрема тим, який називається принципом відносності, не відчувають ані добового, ані річного обертання Землі. Натомість вони бачать, що не Земля обертається навколо Сонця та своєї осі, а Сонце певним чином обертається навколо Землі. Власне про закономірності цього видимого обертання ми і поговоримо.

Спостерігаючи за поведінкою Сонця в наших широтах, не важко констатувати факт того, що вранці воно поступово виринає із-за лінії східної частини горизонту, повільно піднімається над цим горизонтом, і опівдні досягає найвищої висоти. Потім Сонце поступово опускається і у вечірній час заходить за лінію західної частини горизонту. При цьому через певний проміжок часу, який ми називаємо ніччю, Сонце знову виринає на сході.

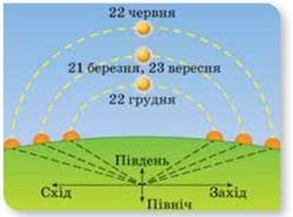
Побутує думка, що саме ті точки в яких Сонце з’являється над горизонтом та зникає за нам, і є тими орієнтирами, які точно вказують на східний та західний напрямки. Ця думка не є безумовно правильною. Адже не важко переконатися в тому, що зимою, весною і літом, Сонце сходить і заходить в суттєво в різних місцях. При цьому вимірювання показують, що кутова різниця між напрямками на точку сходу (заходу) Сонця 22 грудня та його сходу (заходу) 22 червня, становить 2∙23,5° = 47°. І як ви розумієте, ця різниця є не просто суттєвою, а досить великою.

.

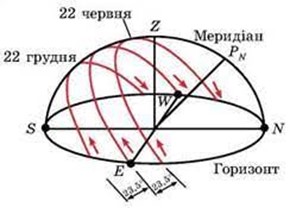
Мал.10. В різні пори року, Сонце сходить та заходить в суттєво різних точках лінії горизонту.

Детальніше описуючи видимий рух Сонця можна сказати наступне. По суті, траєкторія видимого руху Сонця навколо Землі, має вигляд щільної спіралі. Рухаючись цією спіраллю, Сонце поступово зміщується таким чином, що з 22 грудня по 22 червня, точки сходу і заходу Сонця поступово зміщуються в північному напрямку. При цьому кожного наступного дня, висота підйому Сонця над лінією горизонту та тривалість дня, стають все більшими і більшими. Нарешті 22 червня настає так званий день літнього сонцестояння. В цей день Сонце сходить в гранично північно-східній точці горизонту, а заходить в гранично північно-західній точці. При цьому опівдні, Сонце піднімається на гранично велику річну висоту, тривалість дня стає найбільшою, а тривалість ночі – найменшою.

Після дня літнього сонцестояння, Сонце вирушає у зворотну дорогу. З 22 червня по 22 грудня, точки сходу і заходу Сонця поступово зміщуються в південному напрямку. При цьому кожного наступного дня, висота Сонця над лінією горизонту та тривалість дня, стають все меншими і меншими. Нарешті 22 грудня настає так званий день зимового сонцестояння. Цього дня Сонце сходить в гранично південно-східній точці горизонту, а заходить в гранично південно-західній точці. При цьому опівдні, Сонце піднімається на гранично низьку річну висоту, тривалість дня є гранично малою, а тривалість ночі – гранично великою.

Потрібно зауважити, що двічі на рік, а саме 21 березня і 23 вересня, настають дні відповідно весняного та осіннього рівнодення, тобто ті дні в які тривалість дня і ночі є однаковою. Характерним є те, що саме в ці дні, Сонце сходить точно на Сході, а заходить точно на Заході. Тому, якщо ви за точками сходу та заходу Сонця захочите точно визначити де Схід а де Захід, то визначайте ці точки 21 березня або 23 вересня.

Вище описана видима поведінка Сонця та факт періодичності зміни пір року на Землі, є результатом поєднання трьох фактів. 1) Земля з періодичністю 1доба = 24 години обертається навколо своєї осі. 2) Земля з періодичністю 1 рік = 365 діб обертається навколо Сонця, 3) Кут нахилу між віссю обертання Землі та перпендикуляром до площини її обертання навколо Сонця (площини екліптики), становить 23,5°.

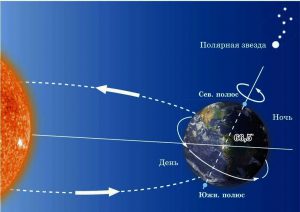
Мал.11. Земля з певною періодичністю обертається як навколо своєї осі так і навколо Сонця. При цьому кут нахилу між віссю обертання Землі та перпендикуляром до площини екліптики, становить 23,5°.

Факт того, що вісь обертання Землі не є перпендикулярною до площини екліптики, тобто тієї площини в якій Земля обертається навколо Сонця, визначальним чином впливає як на зміну пір року на Землі, так і на те, що в різних місцях Землі тривалість дня і ночі є різною і такою, що змінюється протягом року. Дійсно, якби вісь обертання Землі була перпендикулярною до площини екліптики, то в будь якій тоці Землі тривалість дня і ночі була б однаковою (12год 00хв) і не змінною протягом року. При цьому кількість того сонячного світла яке потрапляє в ту чи іншу точку Землі, протягом року залишалась би незмінною. А це означає, що на Землі були б відсутні зміни пір року.

Інша справа, що на різних широтах кліматичні умови були б суттєво різними. Різними тому, що Земля кругла і тому величина того кута під яким сонячні промені падають на її поверхню в різних широтах є різною. Скажімо в екваторіальних широтах сонячне проміння падає на поверхню Землі під кутом близьким до 90° і тому гранично сильно нагріває відповідну поверхню. В середніх широта, сонячне проміння падає на поверхню Землі під значно меншим кутом і тому відповідно менше нагріває цю поверхню. Якщо ж мова йде про приполярні широти, то в них кут падіння променів на поверхню Землі близький до 0° і тому відповідні поверхні нагріваються гранично мало. Умовно кажучи, в екваторіальних широтах Землі було б вічне літо, в середніх широтах – вічна весна-осінь, а в приполярних широтах – вічна зима.

Звісно, вище описана картина є гранично спрощеною і досить умовною. Адже в реальності на клімат тієї чи іншої ділянки Землі впливає не лише те під яким кутом сонячне проміння падає на відповідну ділянку, а й багато інших обставин, зокрема рельєф місцевості, близькості до вод океанів і морів, роза вітрів, наявність океанічних течій, тощо. Однак в загальних рисах, ця картина відповідала б дійсності. Адже якби вісь обертання Землі була перпендикулярною до площини її обертання навколо Сонця, то в усіх точках Землі тривалість дня і ночі дійсно була б однаковою, а кліматичні умови протягом року залишались би практично незмінними.

Та як би там не було, а фактом є те, що в реальності вісь обертання Землі  не є перпендикулярною до площини екліптики і утворює з цією площиною кут 66,5°. В такій ситуації, в різних широтах Землі картина зміни дня і ночі є суттєво різною. Наприклад в зображеній на мал.12 ситуації, на Південному полюсі Землі буде полярний день, а на Північному полюсі – полярна ніч. Це означає, що протягом доби, тобто того проміжку часу за який Земля робить один оберт навколо своєї осі, на Південному полюсі, Сонце не буде заходити за лінію горизонту і тому там буде цілодобовий день. Натомість на Північному полюсі, Сонце протягом доби не буде з’являтись над лінією горизонту і тому там буде цілодобова ніч.

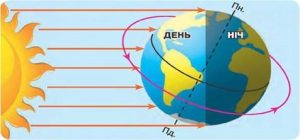
Мал.12. В різних широтах Землі тривалість дня і ночі є різною і такою, що протягом року змінюється.

Факт того, що вісь добового обертання Землі не є перпендикулярною до площини її річного обертання навколо Сонця (площини екліптики), пояснює не лише періодичність зміни тривалості дня і ночі, а й періодичність зміни пір року. Дійсно, в грудні (див. мал.13), нахил осі обертання Землі відносно Сонця такий, що її південна півкуля освітлюється Сонцем набагато сильніше та під більш прямим кутом ніж північна. А це означає, що в грудні, в північній півкулі буде зима, а в південній – літо. Через три місяці, тобто у березні, освітленість північної і південної півкуль стає практично однаковою. При цьому, в північній півкулі на зміну холодної зими, приходить помірно тепла весна. А в південній півкулі, на зміну спекотному літу приходить помірно тепла осінь. Через наступні три місяці, тобто в червні, Земля буде повернута до Сонця таким чином, що її північна півкуля буде освітлена набагато сильніше за південну. При цьому в північній півкулі на зміну помірно теплій весні прийде жарке літо. А в південній півкулі, помірно теплу осінь змінить холодна зима. І як ви розумієте, ще через три місяці, зима південної півкулі зміниться весною, а літо північної – осінню.

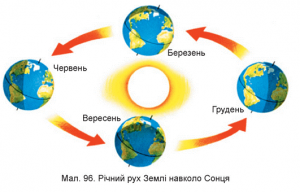
Мал.13. Зміна пір року на Землі, пояснюється тим, що вісь добового обертання Землі не є перпендикулярною до площини її річного обертання навколо Сонця.

Потрібно зауважити, що на різних географічних широтах видимий рух Сонця виглядає суттєво по різному. Скажімо на Північному полюсі, Сонце з’являється над лінією горизонту 21 березня (мал.14а) і на полюсі настає полярний день. Рухаючись над лінією горизонту щільною спіралеподібною траєкторією (один оберт за 24 години), Сонце поступово піднімається до тих пір, поки 22 червня не досягне кута підйому 23,5º. Після цього, рухаючись аналогічною спіральною кривою, Сонце поступово опускається і 23 вересня заходить за лінію горизонту. Заходить, щоб знову з’явитись над цією лінією через півроку.

По мірі віддалення від географічного полюса Землі, тривалість полярного дня, тобто того проміжку часу протягом якого Сонце не заходить за лінію горизонту стає все меншою і меншою. При цьому тією межею яка відділяє ту частину Землі де тривалість полярного дня більша 24 годин, від тієї частини де ця тривалість менша 24 годин, є так зване полярне коло. І це коло віддалене від географічного полюса Землі на 23,5º, тобто має широту 65,5º.

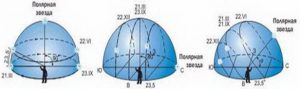
Мал.14. Картина видимого річного руху Сонця при спостереженні: а) з географічного полюса Землі; б) з екватора; в) з середніх широт.

Якщо ж говорити про той рух Сонця який спостерігається в околицях географічного екватора Землі, то він характеризується тим, що на екваторі тривалості дня і ночі протягом року залишаються незмінними і чисельно рівними (12 годин – день, 12 годин – ніч). При цьому Сонце обертається навколо Землі щільною спіральною кривою, витки якої практично перпендикулярні до лінії горизонту (мал.14б). В процесі цього руху, Сонце поступово зміщується з півдня на північ і навпаки. Кут же цього зміщення відносно лінії схід-захід, як і в інших місцях Землі становить 23,5º.

Не важко бачити, що параметри видимого руху Сонця, є результатом певної комбінації трьох базових фактів:

1. Земля з періодичністю 1доба = 24 години обертається навколо своєї осі.
2. Земля з періодичністю 1 рік = 365 діб обертається навколо Сонця,
3. Кут нахилу між віссю обертання Землі та перпендикуляром до площини її обертання навколо Сонця (площини екліптики), становить 23,5°.

Контрольні запитання.

1. Чи правильне твердження: «Та точка в якій Сонце заходить за лінію горизонту, безумовно вказує на західний напрямок»? Чому?
2. В які дні точки сходу та заходу Сонця, точно вказують на східний та західний напрямки?
3. Які дні називаються днями літнього та зимового сонцестояння; днями весняного та осіннього рівнодення? Що характерно для цих днів?
4. Опишіть видимий рух Сонця від дня зимового сонцестояння до дня літнього сонцестояння і навпаки (для середніх широт).
5. Що називають площиною екліптики? Під яким кутом вісь обертання Землі нахилена до площини екліптики?
6. Які факти визначають параметри видимого з Землі руху Сонця?
7. Які факти вказують на те, що кут нахилу між віссю обертання Землі та перпендикуляром до площини екліптики, становить 23,5°.
8. Поясніть чому на географічних полюсах Землі півроку триває полярний день, а наступні півроку – полярна ніч?
9. Чому для різних широт, в один і той же день висота максимального підйому Сонця над лінією горизонту є різною?
10. Як пояснюється періодичність змін пір року на Землі?
11. В яких місцях земної кулі можна спостерігати факт того, що видимий рух Сонця представляє собою неперервну спіральну криву?

.

§3. Закономірності видимого руху Місяця.

На відміну від Сонця, Місяць дійсно обертається навколо Землі. І період цього обертання 27,32 доби. При цьому, дослідження показують, що та площина в якій Місяць обертається навколо Землі, нахилена до тієї площини в якій Земля обертається навколо Сонця (площини екліптики) під кутом 5°.

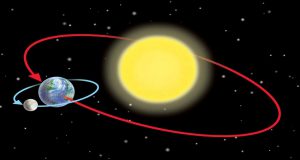
Мал.15. Площина обертання Місяця навколо Землі, нахилена до площини екліптики під кутом 5°.

Питання про періодичність обертання Місяця навколо Землі є досить заплутаним. Адже є одного боку вимірювання показують, що період обертання Місяця навколо Землі дорівнює  27,32 доби. З іншого боку, видима періодичність обертання Місяця навколо Землі становить 24год 52хв, а видима періодичність зміни фаз Місяця дорівнює 29,53 доби. Втім, різноманіття цих періодичностей має своє наукове пояснення. І це пояснення грунтується на сукупності трьох фактів:

1. Земля з періодичністю 1 доба = 24 години обертається навколо своєї осі;
2. Місяць з періодичністю 27,32 доби обертається навколо Землі;
3. Земля разом з Місяцем з періодичністю 1 рік = 365 діб обертається навколо Сонця.

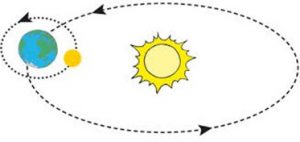
Мал.16. В реальності, Місяць з періодичністю 27,32 доби обертається навколо Землі. При цьому Земля з періодичністю 1,00 доби обертається навколо своєї осі і з періодичністю 365 діб обертається навколо Сонця.

Перш ніж пояснити різноманіття тих періодичностей які характеризують рух Місяця, пояснимо видиму з Землі періодичність змін фаз Місяця. А це пояснення є наступним. Оскільки Місяць не є самосвітнім тілом, то він видимий лише тому, що його поверхня відбиває сонячне світло. Як і будь яка планета, Місяць завжди освітлюється Сонцем лише з одного боку. А оскільки Місяць обертається навколо Землі, то з Землі, в різні періоди цього обертання, освітлена частина Місяця виглядає по різному. А це означає, що в процесі обертання навколо Землі, видима форма місяця має періодично змінюватись. Власне ці зміни, які прийнято називати фазами Місяця, ми і спостерігаємо.

Розрізняють чотири основні фази Місяця (мал.16): новий місяць (1) – фаза темного місяця; перша чверть (3) – фаза повного півмісяця при збільшенні цієї повноти); повний місяць (повня 5) – фаза повного місяця; третя чверть (7) – фаза повного півмісяця при зменшенні цієї повноти).

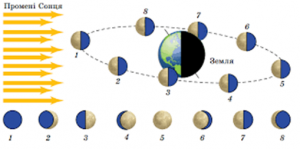
Мал.17. В процесі обертання Місяця навколо Землі, його освітлена Сонцем половина виглядає по різному.

Новий місяць, це фаза темного, невидимого Місяця. Ця фаза обумовлена тим, що Місяць перебуває між Землею і Сонцем. А це означає, що Місяць повернутий до Землі своєю неосвітленою (темною) стороною і тому є невидимим з Землі. Крім цього, новий місяць ніколи не буває на фоні нічного неба. Адже за визначенням він знаходиться з боку освітленої Сонцем, а отже денної сторони Землі. З точки зору астрономічної науки, фаза нового місяця є досить короткотривалою. Однак в побутовій практиці прийнято вважати, що фаза нового місяця триває декілька (не більше трьох) діб і закінчується тим, що відразу ж після заходу Сонця, на фоні вечірнього неба з’являється тоненький серп так званого молодика.

Протягом наступного тижня, серп молодого місяця поступово округлюється і у підсумку перетворюється на повну півкулю. Момент цього перетворення прийнято називати фазою першої чверті. В наступні сім днів,  Місяць продовжує поступово округлюватись допоки не досягне фази повного місяця, яку прийнято називати повня. Повня, це фаза повного місяця, яка є протилежною до фази нового місяця, і яка характеризується тим, що з Землі освітлену Сонцем півкулю Місяця видно у вигляді правильного яскравого диска. В астрономії, момент повні визначається досить точно. В побутовій же практиці повним місяцем зазвичай називають період у декілька діб, протягом яких Місяць візуально майже не відрізняється від повного. Під час повні, протягом декількох годин спостерігається так званий опозиційний ефект – помітне зростання яскравості місячного диска. Це зростання пояснюється тим, що у відповідний момент, сонячне світло падає на поверхню Місяця таким чином, що практично не створює видимих з Землі тіней. Власне середину того проміжку часу протягом якого спостерігається опозиційний ефект, в астрономії і вважається моментом максимально повного місяця.

Після повні, видима частина Місяця починає поступово зменшуватись. Спочатку до півкола (третя чверть), а потім до вузького серпа, повернутого опуклою стороною до Сонця що сходить. В наступні дні, тоненький серп Місяця зникає в променях вранішнього Сонця і настає фаза нового місяця, після якої цикл фазових змін Місяця в точності повторюється. При цьому вимірювання показують, що повний цикл змін фаз Місяця відбувається за 29,53 доби.

Потрібно зауважити, що коли Місяць знаходиться в фазі вузького серпа, іноді можна побачити тьмяне світіння неосвітленої Сонцем частини місячного диска. Це явище називають попелястим світінням Місяця. Попелясте світіння є наслідком того, що Земля у відповідний час повернута до Місяця своєю освітленою Сонцем поверхнею. При цьому, відбите від Землі сонячне світло, освітлює нічний бік Місяця.

Важливим та не простим питанням, є питання про періодичність обертання Місяця навколо Землі. Адже з одного боку, ми бачимо, що Місяць з періодичністю 24 доби 52 хвилини видимо обертається навколо Землі. З іншого боку ми бачимо, що фази Місяця змінюються з періодичністю 29,53 доби. З третьої сторони нам кажуть, що період обертання Місяця навколо Землі становить 27,32 доби. Пояснюючи всі ці періодичності та зв’язки між ними, можна сказати наступне.

Як відомо, Земля з періодичністю 24 год обертається навколо своєї осі. Якби Місяць не обертався навколо Землі, то мешканці Землі бачили б, що за 24 год, Місяць робить один оберт навколо будь-якої точки земної поверхні. При цьому ми б говорили, що період видимого добового обертання Місяця в точності дорівнює 24 год. Однак Місяць, з періодичністю 27,32 доби обертається навколо Землі. При цьому обертається в тому ж напрямку що і Земля. Тому, за той час, поки певна точка поверхні Землі зробить один оберт, Місяць встигне зробити 1/27,32 оберту в тому ж напрямку. А це означає, що для того щоб відповідній точці земної поверхні, знову опинитись під Місяцем, вона має обертатись певний додатковий час. І цей час становить 52 хв: ∆t=(1/27,32)∙1добу= (1/27,32)∙24∙60хв = 52 хв.

Тепер стосовно того зв’язку який існує між періодом обертання Місяця навколо Землі (27,32 доби) та періодом тих фазових змін Місяця, які ми бачимо з Землі (29,53 доби). Пояснюючи факт не співпадіння цих двох періодичносте можна сказати наступне. Припустимо, що в початковий момент часу, Місяць перебуває у повні. Це означає, що Земля, Місяць і Сонце знаходяться на одній лінії (мал.18). Якби Земля не оберталась навколо Сонця, то через 27,32 доби, тобто через один повний оберт Місяця навколо Землі, Земля, Місяць і Сонце, знову опинилися б на одній лінії і Місяць знову був би у повні. Однак в реальності Земля, з періодичністю 365 днів (точніше 365,24 доби) обертається навколо Сонця. А це означає, що за той час, поки Місяць робить один повний оберт навколо Землі (27,32 доби), Земля встигне повернутись на кут (360º/365)∙27,32 = 27º. В такій ситуації, для того щоб Місяць знову опинився у повні, Місяць має певний додатковий час обертатися навколо Землі. І величина цього додаткового часу ∆t = 27,32∙27°/(360º–27º) = 2,21 доби. А це означає, що видима з Землі періодичність змін фаз Місяця має становити 27,32 + 2,21 = 29,53 доби, що в точності відповідає реальній періодичності цих змін.

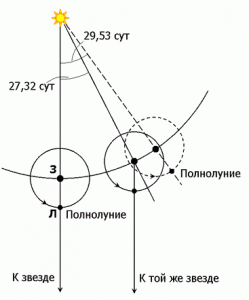
Мал.18. Повний цикл зміни фаз Місяця відбувається за 29,53 доби, що на 2,21 доби більше за період його обертання навколо Землі.

Таким чином, періодичність обертання Місяця навколо Землі можна охарактеризувати трьома величинами:

1. Той період, який характеризує реальну періодичність обертання Місяця навколо Землі і який дорівнює 27,32 доби. Цей період зазвичай називають періодом обертання Місяця навколо Землі. Однак в астрономії його часто називають сидеричним або зоряним місяцем (від лат. sidus – зоря).
2. Той період, який характеризує видиму з Землі періодичність змін фаз Місяця і який дорівнює 29,53 доби. Цей період прийнято називати синодичним місяцем (від грец. synodos – з’єднання).
3. Той період, який характеризує періодичність видимого з Землі добового обертання Місяця і який дорівнює 24 год. 52 хв.

Потрібно зауважити, що подібно до того як реальна періодичність обертання Місяця навколо Землі (27,32 доби) не співпадає з видимою періодичністю цього обертання (29,53 доби), реальна періодичність обертання Землі навколо своєї осі (23год 56хв 4,1с) також не співпадає з тією видимою періодичністю яка називається добою і яка дорівнює 24год 00хв 00с. Це пояснюється тим, що Земля обертається не лише навколо власної осі, а і навколо Сонця, і що ці обертання є співнаправленими.

Дійсно, за той час поки певна точка поверхні Землі зробить повний оберт навколо своєї осі (23год 56хв 4,1с = 1436,07хв), Земля встигне зробити 1/365,24 = 0,002738 оберту в тому ж напрямку навколо Сонця. А це означає, що для видимого завершення повного добового оберту Землі, вона має обертатись певний додатковий час. І величина цього часу 1436,07хв∙0,002738 = 3хв 55,9с.

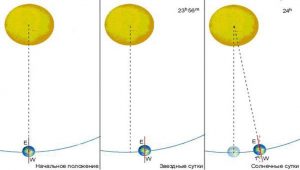
Мал.19. Оскільки Земля обертається не лише навколо власної осі а й навколо Сонця, то та періодичність яку називають добою (24год 00хв 00с) на 3хв 55,9с більша за реальний період обертання Землі навколо своєї осі.

На завершення зауважимо, що з точки зору фізичної суті тих процесів які відбуваються у Всесвіті, безумовно основною характеристикою періодичності обертання Місяця навколо Землі, є той реальний період обертання, який дорівнює 27,32 доби. Наприклад якщо описуючи механіку обертання Місяця навколо Землі, ми визначаємо величину тієї відцентрової сили інерції (F_і = ma_д = mv²/ℓ = (m/ℓ)(L/t)² = (m/ℓ)(2πℓ/T)² = 4mπ²ℓ/T²) яка динамічно зрівноважує силу гравітаційного притягування Місяця до Землі (F = GMm/ℓ²), то в цьому випадку Т = 27,32 доби.

Однак, з точки зору земного спостерігача і тих процесів які відбуваються на Землі набагато важливішою є та періодичність з якою Місяць видимо обертається навколо Землі (24год 52хв). Скажімо періодичність наявних на Землі океанічних припливів і відпливів, визначальним чином залежить не від реальної періодичності обертання Місяця навколо Землі (27,32 доби), а від періодичності його видимого обертання (24год 52хв). Або наприклад, візуальним відображенням факту обертання Місяця навколо Землі, є не реальний період цього обертання (27,32 доби), а періодичність зміни фаз Місяця, яка називається синодичним місяцем і яка дорівнює 29,53 доби. Ця періодичність і визначає тривалість того проміжку часу яку ми називаємо календарним місяцем.

Аналогічне можна сказати і про реальну (23год 56хв) та видиму (24год 00хв) періодичності обертання Землі навколо власної осі. Адже для земного спостерігача саме видима періодичність обертання Сонця навколо Землі, яка є результатом обертання Землі навколо своєї осі та навколо Сонця, визначає ту періодичність яка називається добою. Власне сучасний календар, тобто сучасна система відліку часу, базується на періодичності обертання Землі навколо Сонця (рік), періодичності видимого обертання Землі навколо своєї осі (доба), та на періодичності змін фаз Місяця (синодичний місяць).

Контрольні запитання.

1. Як пояснюється факт того, що в різні моменти часу освітлена частина Місяця виглядає по різному?
2. Чи означає факт зміни фаз Місяця, що в різні моменти часу Місяць по різному освітлюється Сонцем?
3. Яка фаза Місяця є невидимою з Землі? Чому?
4. Що називають опозиційним ефектом?
5. Як визначають точний момент повні?
6. Відомо, що реальний період обертання Місяця навколо Землі 27,32 доби, видимий період цього обертання 24год 52хв, а видима період зміни фаз Місяця 29,53 доби. Сукупністю яких фактів пояснюється різноманіття цих періодів?
7. Чому період обертання Місяця навколо Землі (27,32 доби) не співпадає з періодичністю зміни фаз Місяця (29,53 доби)?
8. Чому період видимого обертання Місяця навколо Землі (24год 52хв) не співпадає з періодом обертання Землі навколо своєї осі (24год 00хв)?
9. Чому та періодичність яка називається доба (24год 00хв) не співпадає з реальним періодом обертання Землі навколо своєї осі?
10. На сукупності яких періодичностей побудована сучасна система відліку часу?

Вправа 3.

1. Обертання Землі навколо своєї осі і Місяця навколо Землі відбувається в одному напрямку. При цьому тривалість доби на Землі 24год 00хв, а період обертання Місяця 27,32 доби. Визначити видимий з Землі період обертання Місяця.
2. Обертання планети навколо своєї осі і супутника навколо планети відбувається в одному напрямку. При цьому тривалість доби на планети 20год 00хв, а період обертання супутника 30,00 доби. Визначити видимий з планети період обертання супутника.
3. Тривалість доби на планеті 20год 00хв, а період її обертання навколо зірки 300 діб. Визначити період обертання планети навколо своєї осі. Обертання планети навколо своєї осі і навколо зірки відбувається в одному напрямку.
4. Відомо, що період обертання Місяця навколо Землі становить 27,32 доби, а відстань між центрами Землі і Місяця дорівнює 3,84∙10⁸м. Визначити масу Землі.
5. Відомо, що період обертання Землі навколо Сонця 365 діб, а відстань між центрами Землі і Сонця 1,49∙10¹¹м. Визначити масу Сонця.

.

§4. Сонячні і місячні затемнення. Припливи та відпливи.

До числа загально відомих, але не надто частих явищ, відносяться сонячні і місячні затемнення. Причина цих явищ очевидна. В потоці сонячного проміння, як Земля так і Місяць залишають певну світлову тінь. Тому коли в процесі обертання навколо Землі, Місяць опиняється між Землею і Сонцем, то певна ділянка Землі опиняється в тіні Місяця і на цій ділянці спостерігається сонячне затемнення (мал.20а). Коли ж Земля опиняється між Місяцем і Сонцем, то Місяць потрапляє в тінь Землі і відбувається місячне затемнення (мал.20б).

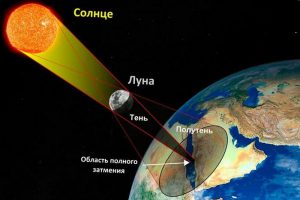
Мал.20. а) Коли певна ділянка Землі опиняється в тіні Місяця, то на цій ділянці спостерігається сонячне затемнення. б) Коли Місяць опиняється в тіні Землі, то відбувається місячне затемнення.

Оскільки за той проміжок часу який називається синодичним місяцем (29,53доби), Місяць двічі перебуває на лінії Сонце – Земля, то логічно передбачити, що протягом кожного місяця, з Землі можна спостерігати два затемнення – одне місячне і одне сонячне. Фактично ж нічого подібного не відбувається. В реальності на Землі протягом року можна спостерігати від двох до п’яти сонячних затемнень і від нуля до трьох – затемнень місячних. При цьому якщо мова йде про певну точку Землі, то в ній повне сонячне затемнення спостерігається приблизно раз на 300 років, а часткове – раз на 30 років. Натомість місячні затемнення спостерігаються практично з усієї нічної півкулі Землі. Пояснюючи дані факти можна сказати наступне.

Основна причина факту того, що сонячні і місячні затемнення відбуваються не з періодичністю 29,53 доби а значно рідше і за складною схемою повторюваності, полягає в тому, що площина обертання Місяця навколо Землі, нахилена до площини обертання Землі навколо Сонця (площини екліптики), під кутом 5º. Результатом цього нахилу є те, що місячні і сонячні затемнення відбуваються лише в тих не надто частих випадках, коли Місяць не лише перебуваю в фазі повного чи нового місяця, а й в так званих вузлах місячної орбіти. Тобто в тих точках, де орбіта Місяця перетинається з площиною екліптики. До речі, термін «екліптика» в перекладі з грецької означає «затемнення». Така назва пов’язана з тим, що сонячні і місячні затемнення відбуваються лише тоді, коли Місяць у своєму русі небосхилом перетинає ту площину в якій Сонце видимо обертається навколо Землі, а в реальності – Земля обертається навколо Сонця.

Мал.21. Місячні і сонячні затемнення відбуваються за виконання двох умов: 1) Місяць знаходиться в фазі повного або нового місяця; 2) Місяць знаходиться в точці перетину його траєкторії з площиною екліптики.

Оскільки лінійні розміри (діаметр) Місяця значно менші за лінійні розміри Землі, а їх відстані до Сонця приблизно однакові, то величина тієї тіні яку в потоці сонячного світла створює Місяць є значно меншою за ту тінь яку створює Земля. Тому повне сонячне затемнення, можуть бачити лише ті спостерігачі які знаходяться в межах тієї невеликої ділянки Землі на яку падає повна місячна тінь. Зазвичай, діаметр цієї ділянки близький до 200км. На тих же ділянках земної поверхні, куди падає напівтінь від Місяця, спостерігається часткове сонячне затемнення. Зазвичай діаметр цієї ділянки близький до 2000км.

На відміну від затемнень сонячних, місячні затемнення спостерігаються з усіх точок нічної півкулі Землі. При цьому як і сонячні, місячні затемнення можуть бути як повними, так і частковими. Характерною особливістю повних та часткових місячних затемнень є факт того, що при цих затемненнях, Місяць не зникає повністю, а набуває темно-червоного забарвлення. Даний факт пояснюється двома обставинами. Перша полягає в тому, що проходячи через атмосферу Землі, сонячне світло частково поглинається її атомами (розсіюється) і набуває червонуватого відтінку. Друга обставина полягає в тому, що подібно до збиральної лінзи, атмосфера Землі певним чином заломлює світло, тобто змінює напрям його розповсюдження. При цьому частина сонячного світла потрапляє на затінену Землею поверхню Місяця і надає цій поверхні темно-червоного забарвлення.

Мал.22. При повному місячному затемненні, Місяць повністю не зникає в тіні Землі, а набуває темно-червоного забарвлення.

Таким чином, періодичність сонячних і місячних затемнень складним чином залежить від великої кількості обставин, зокрема: 1. Періодичності обертання Землі навколо Сонця; періодичності обертання Місяця навколо Землі; періодичності обертання Землі навколо своєї осі; 2. Лінійних розмірів Сонця, Землі і Місяця та відстаней між цими об’єктами; 3. Факту того, що площина обертання Місяця навколо Землі, нахилена до площини обертання Землі навколо Сонця (площини екліптики) під кутом 5°.

Важливим проявом взаємопов’язаності Землі і Місяця є явище, яке називається припливами і відпливами. На узбережжях океанів і відкритих морів можна спостерігати наступне: в певні проміжки часу, а точніше з періодичністю 12год 26хв, рівень прибережної води сильно підвищується, а потім відповідно знижується. Це явище називають припливами і відпливами. З прадавніх часів, люди звернули увагу на те, що приливи і відпливи певним чином пов’язані з добовим обертанням Місяця навколо Землі. І це відповідає дійсності. Адже обертаючись навколо Землі, Місяць, у повній відповідності з законом всесвітнього тяжіння, притягує ту воду що знаходиться під ним, та змушує її рухатись за собою. А потрібно зауважити, що добове обертання Місяця навколо Землі, по суті є не стільки результатом обертання самого Місяця, скільки результатом обертання Землі навколо своєї осі. Втім, це не має суттєвого значення. Адже фактом залишається те, що Місяць з періодичністю 24 год 52 хв обертається над поверхнею Землі.

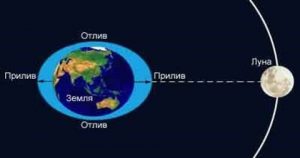
Мал.23. Припливи і відпливи є результатом обертання Землі навколо своєї осі та йому відповідного добового обертання Місяця навколо Землі.

Виникає питання: якщо Місяць з періодичністю 24год 52хв обертається над поверхнею Землі, то чому спричинені цим обертанням припливи і відпливи мають періодичність 12год 26хв? Адже за 24год 52хв Місяць робить навколо Землі лише один оберт, і тому періодичність припливної хвилі має становити 24год 52хв, а не половину від цього часу. Відповідь на це не просте запитання полягає в факті обертання Землі навколо своєї осі, та в розумінні суті того, що називається силою інерції.

Дійсно. Якби Земля не оберталась навколо своєї осі, то створювана обертальним рухом Місяця припливна хвиля, обходила Землю за 24 год 52 хв. Однак, як відомо, Земля все таки обертається. А це означає, що на всі точки земної кулі, діє певна відцентрова сила інерції, яка прагне надати цій кулі форму еліпсоїда. Власне ця сили інерції і є основною причиною того, що створюване гравітаційною дією Місяця припливне збурення води, практично рівномірно розподіляється між двома діаметрально протилежними сторонами Землі. Адже сила інерції, це та сила яка завжди прагне перерозподілити речовину того тіла що обертається, симетрично осі його обертання. Результатом цього перерозподілу і є дві симетричні припливні хвилі.

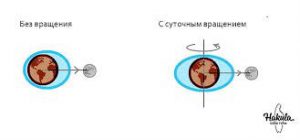
Мал.24. Факт обертання Землі навколо своєї осі, спричиняє симетричний перерозподіл припливної води.

Таким чином, факт того що створюване гравітаційною дією Місяця припливне збурення води, практично рівномірно розподіляється між діаметрально протилежними частинами Землі, є прямим наслідком дії тієї сили інерції, поява якої обумовлена обертанням Землі навколо своєї осі. А ця сила завжди прагне до того, щоб всю наявну на Землі речовину симетрично розподілити відносно осі обертання Землі. Саме такий інерційний перерозподіл приливної води і відбувається.

Дослідження показують, що у відкритому океані, висота тієї гігантської за площею припливної хвилі, поява якої обумовлена певною сукупністю гравітаційно-інерційних взаємодій, приблизно дорівнює 20см. А це означає, що для тих човнів, яхт та кораблів які мандрують просторами океанів і морів, припливна хвиля є практично непомітною. Чому ж набігаючи на берегову лінію материків, ця непомітна хвиля створює такі величезні підйоми прибережної води, висота яких в середньому дорівнює 4–5 метрів?

Гранично стисло та спрощено відповідаючи на це запитання, можна сказати наступне. Оскільки відносно не значна за висотою підйому води, океанічна припливна хвиля, має величезну площу поверхні, то кількість зосередженої в ній води, є надзвичайно великою. А враховуючи величезну швидкість руху цієї хвилі (близько 800 км/год), не важко збагнути, що кількість зосередженої в ній кінетичної енергії є фантастично великою. І от коли ця низька але надпотужна океанічна припливна хвиля, стикається з материковим підйомом океанічного дна, наявна в ній кінетична енергія, перетворюється на енергію потенціальну. При цьому швидкість хвилі зменшується, а висота води в ній – збільшується. Власне ця сповільнена але висока приливна хвиля і створює ті припливи, а за ними і відпливи які спостерігаються на берегах океанів та відкритих морів. Простіше кажучи, та величезна кількість води, що зосереджена в непомітно низькій океанічній припливній хвилі, стикаючись з материковим підйомом океанічного дна, стає відповідно більш високою.

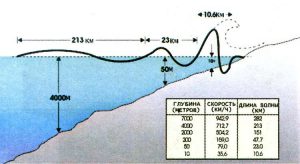
Мал.25.  Коли океанічна припливна хвиля, стикається з підйомом океанічного дна, наявна в ній кінетична енергія, перетворюється на енергію потенціальну. При цьому швидкість хвилі зменшується, а висота води в ній – збільшується.

У внутрішніх морях, наприклад у Чорному морі, припливи і відпливи є малопомітними. І це закономірно. Адже в такі моря припливна океанічна хвиля майже не потрапляє. Що правда, в кожному закритому морі, ба навіть озері, виникають власні припливні хвилі. Однак масштаби цих хвиль зазвичай є не значними. Скажімо у Чорному морі, середня висота прибережних припливних хвиль не перевищує 20 см. Втім, за певних обставин, наприклад у вузьких та не надто глибоких бухтах, висота припливної хвилі може бути суттєво більшою.

Контрольні запитання.

1. Якщо протягом 29,53 доби Місяць двічі перебуває на лінії Сонце – Земля, то чому у відповідні моменти ми частіш за все не спостерігаємо відповідних затемнень?
2. За виконання яких умов відбуваються сонячні та місячні затемнення?
3. Чому ту площину в якій Сонце видимо обертається навколо Землі, назвали «екліптикою» і з чим пов’язана така назва?
4. Як часто складаються ті умови за яких відбуваються сонячні і місячні затемнення?
5. З яких точок Землі можна бачити: а) повне сонячне затемнення; б) повне місячне затемнення?
6. Чому при повному затемненні Місяця, Місяць не зникає повністю, а надуває темно-червоного забарвлення?
7. Якщо реальний період обертання Місяця навколо Землі 27,32 доби, то чому період його видимого з Землі обертання дорівнює 24год 52хв?
8. Якщо період видимого обертання Місяця навколо Землі 24год 52хв, то чому створювані цим обертанням припливи відбуваються з періодичністю 12год 26хв?
9. Чому та припливна хвиля висота якої у відкритому океані близька до 20см, створює прибережні підйоми води висотою 4 – 5 метрів?

.

§5. Сузір’я. Зоряні величини.

В ясну безмісячну ніч, та вдалині від міських вогнів, погляду спостерігача відкривається велична картина зоряного неба. Побутує думка, що кількість зірок на зоряному небі є незліченно великою. Насправді ж, неозброєним оком в безмісячну ніч можна побачити та розрізнити не більше 5000 зірок. Втім, якщо мова йде про наукові спостереження, то на теперішній час, астрономи визначили точні координати кількох мільйонів зірок.

Аналізуючи картину зоряного неба, люди з прадавніх часів, виділяли на ньому найяскравіші зірки, подумки об’єднували ці зірки в певні фігури та надавали їм певні назви. Ці умовні фігури та їм відповідні ділянки зоряного неба, прийнято називати сузір’ями. Сузір’я – це певна умовна ділянка зоряного неба з чітко окресленими межами, яка охоплює всі приналежні цій ділянці світила та має власну назву.

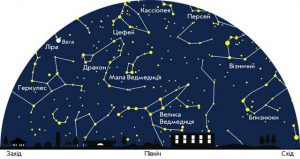
Мал.26. З незапам’ятних часів, люди виділяли на зоряному небі певні комбінації зірок (сузір’я) та надавали їм відповідні імена.

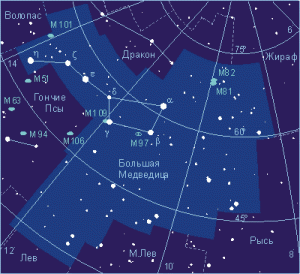
Зоряне небо, а відповідно і ті його зображення які представляють у вигляді небесних сфер та зоряних мап, умовно розділяють на 88 сузір’їв. Звісно, поділ цілісного зоряного неба на сузір’я є досить умовним і таким, що відображає не певні реальні властивості навколишнього світу, а певні суб’єктивні, історично обумовлені традиції. При цьому назви сузір’їв зазвичай відображають не певну реальну схожість того що можна побачити на зоряному небі, а певні історично обумовлені міфи, легенди, тощо. Скажімо в обрисах того сузір’я яке називають Великою Ведмедицею (мал.27а) і найяскравіші зірки якого розташовані у вигляді чи то ковша, чи то воза, важко розгледіти обриси реальної ведмедиці. Або наприклад, в сукупності тих зірок які знаходяться в сузір’ї Діви (мал.27б), навіть за наявності фантазії, важко побачити обриси реальної діви.

Потрібно зауважити, що до певного сузір’я належать не лише ті найбільш яскраві зірки за якими люди впізнають це сузір’я, а й все різноманіття видимих та невидимих зірок, що знаходяться в загально прийнятих межах відповідного сузір’я. Тому наприклад, до сузір’я Великої Ведмедиці (мал.26), належать не лише ті сім яскравих зірок за якими люди власне й впізнають це сузір’я, а й все різноманіття інших зірок, які знаходяться у визначених околицях цих зірок.

.

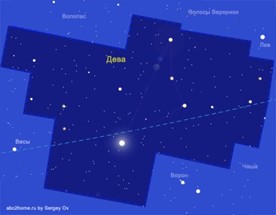
Мал.27. Поділ цілісного зоряного неба на сузір’я є досить умовним і таким, що відображає не певні реальні властивості навколишнього світу, а певні суб’єктивні, історично обумовлені традиції.

Потрібно мати на увазі і те, що багато з тих зірок які на зоряному небі виглядають близькими сусідами і належать до одного сузір’я, часто-густо віддалені одна від одної набагато більше, аніж від тих зірок що знаходяться на протилежній стороні зоряного неба. Адже картина зоряного неба практично не відображає глибину цього неба. Тому ті зірки які є візуально близькими, в реальності можуть виявитися надзвичайно далекими і навпаки. Скажімо за космічними мірками ті яскраві зірки які називаються Альфа Центавра, Сиріус та Альтаїр є над близькими сусідами. І це при тому що вони знаходяться не просто в різних, а в діаметрально протилежних сузір’ях: Альфа Центавра – в сузір’ї Центавр, Сиріус – в сузір’ї Великого Пса, Альтаїр – в сузір’ї Орла.

Важливим сузір’ям північної півкулі зоряного неба, є сузір’я Малої Ведмедиці. Це сузір’я не вирізняється яскравими зірками і не є надто помітним на фоні інших зірок. Особливість і важливість Малої Ведмедиці полягає в тому, що серед її визначальних семи зірок, загальне розташування яких схоже на розташування базових зірок сузір’я Великої Ведмедиці, є одна зірка, навколо якої обертаються всі зірки північної півкулі зоряного неба. Ця зівка називається Полярною.

Полярна зірка практично в точності знаходиться на тій осі, яка співпадає з віссю добового обертання Землі і навколо якої обертається зоряне небо. Це означає, що в процесі добового обертання зоряного неба (а фактично, в процесі обертання Землі навколо своєї осі), місцезнаходження Полярної зірки залишається незмінним і таким яке вказує на напрям Північного полюса Землі. Тому якщо в нічний час вам потрібно визначити географічні напрямки сторін світу, то станьте обличчям в напрямку Полярної зірки, і цей напрямок буде напрямком на Північ. При цьому протилежний напрямок буде Півднем, напрямок праворуч – Сходом, а напрямок ліворуч – Заходом.

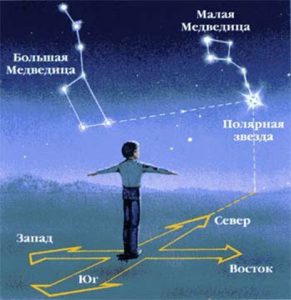
Мал.28. Якщо в нічний час ви втратили просторові орієнтири, то вчиніть так, як показано на цьому малюнку.

Зірки Малої Ведмедиці, в тому числі і та, яка називається Полярною, не є надто яскравими. Тому на практиці місцезнаходження Полярної зірки визначають за допомогою зірок того сузір’я, яке називається Велика Ведмедиця. Загальні обриси Великої Ведмедиці як і обриси Малої Ведмедиці визначаються сімома зірками, які у своїй сукупності утворюють фігуру схожу на чумацький віз. До речі, в Україні Велику і Малу Ведмедиці з прадавніх часів називали Великим і Малим Возом. На відміну від не надто яскравих зірок Малої Ведмедиці, зірки Великої Ведмедиці є  набагато яскравішими, і тому відповідне сузір’є легко ідентифікується. А знаючи розташування зірок Великої Ведмедиці, не важко визначити місцезнаходження Полярної зірки. З цією метою, на продовженні тієї лінії яка з’єднує зірки задньої стінки Великого Воза (мал.28) відкладають приблизно 5 відстаней між цими зірками і отримують практично точну координату Полярної зірки.

Оскільки зоряне небо неперервно видимо обертається навколо Землі (обертається в результаті реального добового обертання самої Землі), то видима з Землі картина зоряного неба поступово змінюється. При цьому з плином часу, певні зірки і сузір’я з’являються над лінією горизонту, а певні – зникають за горизонтом.

.

Мал.29. З плином часу картина зоряного неба поступово змінюється.

Варто зауважити, що протягом тисячоліть картина видимого розташування зірок в сузір’ях, може суттєво змінюватись. Ці зміни обумовлені тим, що видима картина зоряного неба не відображає глибину цього неба (космосу), та фактом обертання зірок навколо центру Галактики. Періодичність цього обертання вимірюється сотнями мільйонів років. Тому протягом нашого життя, зміни у видимому розташуванні зірок є практично не помітними. Однак, якщо мова йде про десятки і сотні тисячоліть, то зміни в розташуванні зірок стають очевидними. Ілюстрацією цієї очевидності, є представлена на мал.30 часова трансформація зовнішнього вигляду загально відомого сузір’я Великої Ведмедиці.

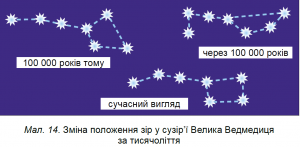
Мал.30. Зміна видимого з Землі розташування зірок в сузір’ї Великої Ведмедиці за 200 тисячоліть.

Найбільш яскраві зорі кожного сузір’я позначають буквами грецького алфавіту: α (альфа) – найяскравіша зірка сузір’я, β (бета) – друга за яскравістю, γ (гама) – третя, δ (дельта) – четверта, ε (епсилон) – п’ята, і т.д. При цьому деякі зорі мають  власні імена. Наприклад  α Малої Ведмедиці називається Полярною, α Великої Ведмедиці називається Дубхе,  β Великої Ведмедиці називається Мерак,  α Ліри – Вега, α Великого Пса – Сіріус, α Тельця – Альдебаран, α Оріона – Бетельгейзе, α Центавр – Альфа Центавра …

В ті далекі часи, коли люди ще нічого не знали ні про реальні розміри зірок, ні про їх реальну світлову потужність, ні про відстані до них, параметри зірок оцінювали за величиною їх видимої яскравості (видимого блиску), тобто за кількістю того світла, що потрапляє в око спостерігача від даної зірки. В астрономії величину яка оцінює порівняльну яскравість зірки за зоровими відчуттями людини, називають видимою зоряною величиною. Видима зоряна величина, це безрозмірна величина, яка характеризує порівняльну яскравість небесного тіла і яка оцінюється за зоровими відчуттями земного спостерігача (позначається m – від англ. magnitude, що в змістовному перекладі означає «зоряна величина»).

Першу систему класифікації зірок за їх зоряною величиною, було запроваджено ще у другому сторіччі до нашої ери, давньогрецьким астрономом Гіппархом. Гіппарх розділив усі видимі неозброєним оком зорі, на шість зоряних величин. При цьому, найбільш яскраві зірки, стали називати зірками першої величини (позначаються 1^m), менш яскраві – зірками другої величини (позн. 2^m) і т.д. Найменш яскраві, ледь помітні неозброєним оком зірки, були віднесені до розряду зірок шостої величини (позн. 6^m). Згодом, для більш точної оцінки яскравості тієї чи іншої зірки, почали використовувати не лише цілі, а й дробові  значення зоряної величини (1,3^m; 2,7^m; 3,2^m; тощо). Прийнято вважати, що яскравість зірки шостої зоряної величини (6^m) у 100 разів менша за яскравість зірки першої величини (1^m). А це означає, що яскравості двох сусідніх зоряних величин відрізняються  у ⁵√100=2,512≈2,5 рази.

В подальшому, вище описану класифікаційну схему суттєво розширили. Ті світила, яскравість яких у відповідне число разів перевищувала яскравість зірок першої зоряної величини (1^m), отримували відповідно менші за 1^m величини: 0^m;–1^m; –2^m і т.д. Наприклад Вега (α Ліри), має зоряну величину +0,03^m. Найяскравіша зоря нічного неба Сіріус, має зоряну величину –1,43^m. Усереднена зоряна величина Венери –4,5^m; зоряна величина Місяця у повні –13^m; Сонця –26,8^m. Ті ж візуально не видимі зірки яскравість яких була меншою за 6^m, отримували відповідно більші значення зоряної величини. Тому є зорі 7^m; 8^m; 9^m і т.д. Скажімо орбітальний телескоп «Хабл» дозволяє спостерігати за зірками, зоряна величина яких 31,5^m. Це означає, що даний телескоп дозволяє бачити ті зірки, яскравість яких у 2,512^{(31,5 – 6)} = 2,512^26,5 = 4∙10¹⁰ рази менша за яскравість тих зірок, які ледь помітні неозброєним оком людини.

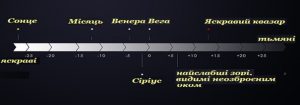
Мал.31. Ту порівняльну яскравість небесного тіла яка оцінюється за зоровими відчуттями земного спостерігача, називають видимою зоряною величиною.

Звісно, видима зоряна величина не відображає ані реальні розміри зірки, ані її реальну світлову потужність, ані її реальну яскравість. Наприклад на фоні зоряного неба, Венера виглядає набагато яскравішою за будь яку зірку. Однак це зовсім не означає, що ця планета випромінює більше світла ніж зірки. Видима зоряна величина, це лише міра тієї порівняльної яскравості, яку створює відповідна зірка і яка оцінюється за зоровими відчуттями земного спостерігача. Втім, якщо мова йде про реальну яскравість зірки, а по суті про її реальну потужність випромінювання, то в сучасній астрономії мірою цієї яскравості є абсолютна зоряна величина.

Абсолютна зоряна величина (М), це безрозмірна величина, яка характеризує порівняльну яскравість небесного тіла, і яка показує яку видиму зоряну величину мало б небесне тіло в тому випадку, якби відстань до нього становила 10 парсеків (Про ту позасистемну одиницю вимірювання космічних відстаней яка називається парсек (пк), ми поговоримо в §10. На разі ж просто зауважимо 1пк = 3,26св.р = 3,086·10¹⁶м). Абсолютна зоряна величина окремих зірок лежить в діапазоні від –10^m для так званих нових зірок, до +15^m для тих зірок які називаються коричневими карликами. Наприклад абсолютна зоряна величина Сонця +4,79^m.

Можна довести, що між видимою (m) та абсолютною (М) зоряними величинами існує співвідношення М = m – 5(lgd – 1),  d – відстань до відповідної зірки виміряна в парсеках. Наприклад видима зоряна величина Сіріуса –1,43^m, а Полярної +1,97^m. Це означає, що з точки зору земного спостерігача, яскравість Сіріуса більша за яскравість Полярної у 2,512^∆m = 2,512^{(1,97 – (– 1,43))} = 2,512^3,4 = 23 рази. З іншого боку, відстань до Полярної зірки 133пк, а до Сіріуса 2,63пк. При цьому абсолютні зоряні величини цих зірок відповідно дорівнюють:

М (Полярна) = m – 5(lgd – 1) = +1,97 – 5(lg133 – 1) = +1,97 – 5(2,12 – 1) = –3,64;

М (Сіріус) = m – 5(lgd – 1) = –1,43 – 5(lg2,63 – 1) = –1,43 – 5(0,42 – 1) = +1,47.

А це означає, що якби Сіріус і Полярна були на однаковій відстані від Землі то видима яскравість Полярної була б більшою за яскравість Сіріуса у 2,512^∆М = 2,512^1,47+3,64 = 2,512^5,11 = 110 разів. До речі, за однакових умов, видима яскравість Полярної (М = –3,64^m) була б більшою за видиму яскравість Сонця (М = +4,79^m) у 2,512^∆М = 2,512^4,79+3,64 = 2,512^8,43 = 2350 разів.

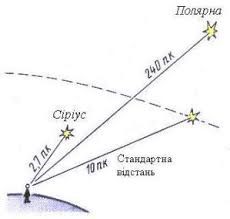
Мал.32. З точки зору земного спостерігача яскравість Сіріуса більша за яскравість Полярної у 23 рази. В реальності ж Поляна яскравіша за Сіріус в 110 разів.

Таким чином, визначивши видиму зоряну величину (m) космічного об’єкту та відстань до нього (d), можна визначити його абсолютну (реальну) зоряну величину (М). А ця абсолютна (реальна) зоряна величина, по суті є мірою світлової потужності (світності L) космічного об’єкту. Світність (світлова потужність) космічного об’єкту – це фізична величина яка характеризує кількість тієї світлової енергії, що випромінюється космічним об’єктом (зорею, галактикою, тощо) за одиницю часу.

Позначається: L

Визначальне рівняння: L=E/t, де Е – загальна кількість тієї світлової енергії яку випромінює космічний об’єкт за час t;

Одиниця вимірювання: [L] = Дж/с = Вт.

На практиці світність космічного об’єкту часто вимірюють не в ватах, а в одиницях світності Сонця, яка дорівнює L_☼=3,86·10²⁶Вт.

Можна довести, що абсолютна зоряна величина (М) та світність (L) космічного об’єкту зв’язані співвідношенням L = 10^{0,4(5 –М)}, де L – світність об’єкту в одиницях світності Сонця. Наприклад для Полярної L = 10^{0,4(5 –(–3,64)} = 10^3,45 = 2800L_☼. Це означає, що Полярна за одиницю часу випромінює світлової енергії в 2800 разів більше ніж Сонце.

Зорі характеризуються не лише певною зоряною величиною, а й певним кольором. Вони можуть бути голубими, білими, жовтими, червоними.  Колір зірки певним чином залежить від температури її поверхні. При цьому найгарячіші зірки є голубими, а найхолодніші – червоними. Сонце належить до класу жовтих, а точніше жовто-білих зірок, тобто зірок класу G.

Мал.33. Дослідження показують, що колір зірки визначеним чином залежить від температури її поверхні.

Колір зірки є надзвичайно важливою, об’єктивною характеристикою базових параметрів відповідної зірки. Достатньо сказати, що на основі аналізу кольору зірки, в тому числі і спектрального аналізу її світла, можна достатньо точно визначити не лише температуру поверхні цієї зірки, а і її масу, хімічний склад, тиск випромінювання, швидкість осьового обертання, тощо. Про те, як вище згадані та інші параметри зірки пов’язані з параметрами того світла яке вона випромінює, ми поговоримо в §12 (Спектральний аналіз – базовий метод космічних досліджень) і §20 (Спектральна класифікація зірок).

Контрольні запитання.

1. Що називають сузір’ям? Чи відображає поділ зоряного неба на сузір’я, певні об’єктивні параметри цього неба?
2. Як позначають найбільш яскраві зірки сузір’я?
3. Чому ті зірки які є видимо близькими сусідами, в реальності можуть бути більш віддаленими аніж зірки з діаметрально протилежних сторін зоряного неба?
4. Як в зоряну ніч визначають географічні напрямки світу?
5. Як на практиці визначають місцезнаходження полярної зірки?
6. Чому з плином часу видиме розташування зірок може змінюватись?
7. Що характеризує видима зоряна величина зірки?
8. Зоряні величини зірок А і Б відповідно дорівнюють 2^m і 5^m. Яка з цих зірок є більш яскравою і у скільки разів?
9. Чим абсолютна зоряна величина відрізняється від видимої зоряної величини? Яка з цих величин є більш об’єктивною?
10. Який зв’язок між видимою та абсолютною зоряними величинами?
11. Що характеризує світність зірки?
12. Який зв’язок між абсолютною зоряною величиною та світністю зірки?

Вправа 5.

1. Відомо, що видима зоряна величина п’ятої за яскравістю зорі неба (Вега) +0,03^m, а відстань до неї 7,75пк. Визначити абсолютну зоряну величину та світність Веги (в ватах і в одиницях світності Сонця).
2. Відомо, що видима зоряна величина найближчої до Сонячної системи зірки (Проксима Центавра) +11,1^m, а відстань до неї 1,3пк. Визначити абсолютну зоряну величину та світність (в ватах і в одиницях світності Сонця) Проксима Центаври.
3. Відомо, що видима зоряна величина найближчої до Чумацького Шляху великої галактики (Андромеда) +3,4^m, а відстань до неї 7,7·10⁵пк. Визначити абсолютну зоряну величину та світність (в ватах і в одиницях світності Сонця) Андромеди.

.

§6. Небесна сфера. Система зоряних координат. Закономірності видимого руху зірок. Прецесійне обертання Землі.

Подібно до того як Землю представляють у вигляді глобуса, видиме з Землі зоряне небо, також можна представити у вигляді відповідної небесної сфери. Небесна сфера – це уявна, умовна сфера довільного радіусу, в центрі якої знаходиться Земля і на яку спроектовані всі видимі об’єкти навколоземного простору так, як їх бачить земний спостерігач. По суті центром небесної сфери є центр Землі, однак в астрономічній практиці, центром небесної сфери прийнято вважати ту точку в якій знаходиться спостерігач.

Подібно до того як координати певної точки земної поверхні задаються її географічною широтою і довготою, координати космічного об’єкту на небесній сфері також визначаються його небесною широтою і довготою. Різниця лише в тому, що в астрономії небесну широту зазвичай називають азимутом або схиленням, а небесну довготу – висотою або сходженням.

.

Мал.34. Координати тіла як на Землі так і на небесній сфері задають певною широтою і довготою.

В астрономічній практиці, на небесній сфері виділяють велике різноманіття ліній, точок та площин. Ми не будемо розглядати все різноманіття. Зупинимся лише на мінімально необхідних, базових елементах небесної сфери. А цими елементами є: вісь світу, полюси світу, небесний екватор, небесний меридіан. Вісь світу – це та уявна лінія, навколо якої обертається небесна сфера (зоряне небо) і яка співпадає з віссю добового обертання Землі. Полюсами світу – називають ті точки, в яких вісь світу перетинається з небесною сферою. Площина, яка перпендикулярна до осі світу і проходить через центр небесної сфери, називається площиною небесного екватора, а лінія перетину цієї площини з небесною сферою, називається небесним екватором. Небесний екватор ділить небесну сферу на дві півкулі: північну і південну. Те коло, яке проходить через полюси світу і в площині якого знаходиться спостерігач, називають небесним меридіаном. Небесний меридіан ділить небесну сферу на західну і східну півсфери.

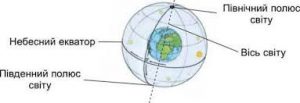
Мал.35. Небесна сфера та її основні елементи.

Оскільки на практиці за об’єктами небесної сфери спостерігає конкретний спостерігач який знаходиться в певній точці поверхні Землі, то практично важливою є та система небесних координат яка прив’язана до конкретного спостерігача. Цю систему називають горизонтальною системою небесних координат. Базовими елементами цієї системи є: прямовисна лінія, площина та лінія математичного горизонту, площина та лінія небесного меридіану.

Прямовисна лінія (вертикаль) – це лінія яка проходить через центр Землі та ту точку в якій знаходиться спостерігач (лінія напрям якої збігається з напрямком нитки виска в тій точці де знаходиться спостерігач). Ту точку над головою спостерігача, в якій небесна сфера перетинається з відповідною прямовисною лінією (з вертикаллю) називають зенітом. А ту невидиму точку небесної сфери яка є діаметрально протилежна до зеніту називається надир.

Площиною математичного горизонту називають ту умовну площину яка перпендикулярна до прямовисної лінії і проходить через ту точку в якій знаходиться спостерігач. На площині математичного горизонту позначають напрямки географічних сторін світу: Північ (N), Південь (S), Схід (Е), Захід (W). Лінію перетину площини математичного горизонту з небесною сферою називають лінією математичного горизонту. Лінія математичного горизонту ділить небесну сферу на дві половини: видиму для спостерігача, з вершиною в зеніті, і невидиму – з вершиною в надирі.

Потрібно зауважити, що лінія математичного горизонту, не завжди співпадає з лінією реально видимого горизонту. Адже якщо наприклад, ви будите знаходитись в точці заглиблення рельєфу, то лінія вами видимого горизонту буде знаходитись над лінією математичного горизонту. Якщо ж ви будите знаходитися на певному пагорбі, то лінія реально видимого горизонту буде під лінією математичного горизонту.

Площиною небесного меридіану називають ту площину яка перпендикулярна до площини математичного горизонту, і яка проходить через прямовисну лінію та вісь Північ – Південь (N–S).  Лінію перетину площини небесного меридіану з небесною сферою називають лінією небесного меридіану. Ця лінія ділить небесну сферу на східну (праворуч від напрямку на північ) та західну (ліворуч від напрямку на північ).

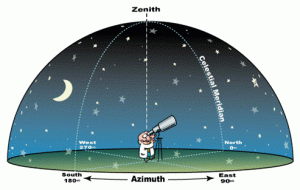
Мал.36. Основними елементами горизонтальної системи координат є: прямовисна лінія, площина математичного горизонту і площина небесного меридіану.

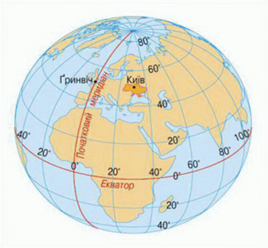
Як відомо, місцезнаходження тіла на поверхні Землі, а відповідно і на глобусі, визначається двома географічними координатами: географічною широтою та географічною довготою. При цьому, географічна широта визначається кутовою координатою тієї кругової лінії, що є паралельною лінії географічного екватора Землі і яка називається паралеллю. А географічна довгота, визначається кутовою координатою тієї кругової лінії що проходить через географічні полюси Землі і яка називається меридіаном. Наприклад географічні координати Києва 50º27ʹ16ʺ північної широти і 30º31ʹ25ʺ східної довготи. Це означає, що Київ заходиться на перетині тієї паралелі координата якої 50º27ʹ16ʺ на північ від екватора та тієї меридіана, координата якого 30º31ʹ25ʺ на схід від того меридіану який проходить через розташовану в околицях Лондона Гринвіцьку королівську обсерваторію, і який за домовленістю вважається нульовим меридіаном.

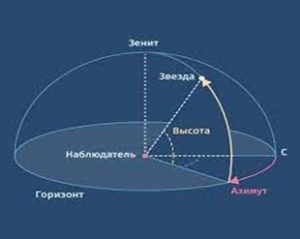
Місцезнаходження космічного об’єкту на небесній сфері, також визначається певною широтою і довготою. Різниця лише в тому, що в горизонтальній системі небесних координат, небесну широту називають не паралеллю, а азимутом (від арабського «ас-сумут» – напрямок), а небесну довготу називають не меридіаном, а висотою (висотою над горизонтом). При цьому азимут (А) світила дорівнює тому куту на який має повернутись спостерігач за годинниковою стрілкою, від тієї лінії яка вказує на Північ. Наприклад азимут Півночі 0º, азимут Сходу 90º, азимут Півдня 180º, а азимут Заходу 270º. Висота (h) світила дорівнює куту між площиною горизонту та напрямком на відповідне світило. Наприклад якщо світило знаходиться на лінії математичного горизонту, то його висота 0º, а якщо прямо над головою спостерігача, то висота світила 90º.

.

Мал.37. Місцезнаходження космічного об’єкту на небесній сфері визначається двома кутовими координатами: азимутом і висотою.

Таким чином, в горизонтальній системі координат, положення космічного об’єкту на небесній сфері визначається двома кутовими координатами: азимутом (А) і висотою (h). При цьому, для того щоб за заданим азимутом (А) і висотою (h), визначити місцезнаходження об’єкту на небесній сфері, необхідно: 1) стати обличчям в напрямку півночі; 2) повернутися на кут А (азимут) за годинниковою стрілкою (направо); 3) підняти свій погляд на кут h (висота). Відповідна точка на небесній сфері (на небі) і буде тим об’єктом небесні координати якого А і h.

Малоприємною особливістю астрономії є факт того, що в ній в залежності від тих задач які вирішуються, застосовують різні системи координат, зокрема: горизонтальна система координат, екваторіальна система координат, екліптична система координат, галактична система координат, міжнародна небесна система координат. Тому не дивуйтесь якщо в тому чи іншому науковому або навчальному джерелі, координати космічного об’єкту будуть визначатися не його азимутом (А) і висотою (h), а схиленням (δ) і прямим піднесенням (α), або схиленням (δ) і годинниковим кутом (t), або екліптичною широтою (β) і екліптичною довготою (λ), або галактичною широтою (b) і галактичною довготою (ℓ), або …

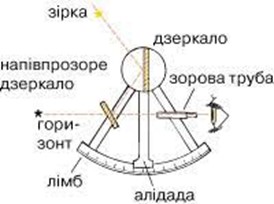
Той прилад за допомогою якого визначають кутові координати небесних світил і загалом кути між двома видимими об’єктами, називається секстантом (мал.38). Базова деталь цього приладу виготовлена у вигляді сектора кола, дугою якого є кутова шкала (лімб). Зазвичай цією деталлю є сектор величиною 1/6 кола, звідси і назва sextantis – одна шоста. На секторальній основі приладу жорстко закріплені зорова труба та напівпрозоре дзеркало, а у вершині конуса на осі обертання закріплено рухомий важіль (алідада) і основне дзеркало.

. 

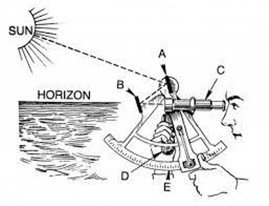
Мал.38. Схема загального устрою та принципу дії секстанту.

Принцип дії цієї системи полягає в наступному. Спостерігач, дивлячись через зорову трубу та напівпрозоре дзеркало, орієнтує прилад таким чином, щоб лінія зору була направлена на лінію математичного горизонту. Обертаючи алідаду, спостерігач добивається того, щоб світло від об’єкту вимірювання, відбиваючись від рухомого і нерухомого дзеркал, потрапляло в зорову трубу (промінь від зірки має співпадати з променем від лінії математичного горизонту). При цьому вісь алідади вкаже на вимірювальній шкалі (лімбу) кут нахилу світила над лінією цього горизонту. Сучасні астрономічні секстанти дозволяють вимірювати кутові величини з точністю до однієї кутової секунди (1ʺ=1º/3600).

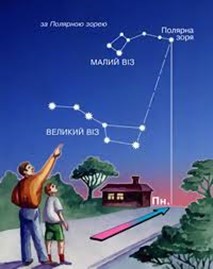
Застосовуючи секстант можна точно визначити кутову висоту того чи іншого космічного об’єкту, а й ту географічну широту на якій знаходиться спостерігач. Для цього вище описаним способом визначають кут нахилу Полярної зірки над математичним горизонтом даної місцевості. Величина цього кута і є відповідною географічною широтою. Наприклад для Києва, кут нахилу Полярної зірки над математичним горизонтом 50°27’16”. Це означає, що Київ знаходиться на широті 50°27’16” північної півкулі Землі.

 .

Мал.39. Кут нахилу Полярної зірки над математичним горизонтом даної місцевості і є тією географічною широтою на якій знаходиться спостерігач.

Спостерігаючи за зоряним небом (небесною сферою) бодай декілька годин, не важко помітити, що вся сукупність зірок, як єдине ціле, обертається навколо Землі, а точніше навколо тієї осі, яку прийнято називати віссю світу. При цьому період обертання небесної сфери навколо Землі становить 24год 00хв. І це закономірно, адже видиме з Землі обертання фактично нерухомої небесної сфери, обумовлене добовим обертанням Землі. А період цього обертання 24год 00хв.

В північній півкулі, тією видимою точкою навколо якої обертаються зірки і сузір’я, є α Малої Ведмедиці, яку називають Полярною. Адже саме Полярна зірка розташована в безпосередній близькості від північного полюса світу.

Мал.40. Зірки і сузір’я небесної сфери, обертаються навколо осі, яка проходить через центр Землі та Полярну зірку.

Подібно до того, як на різних географічних широтах видимий рух Сонця виглядає по різному (мал.14), по різному виглядає і добовий рух зірок. Скажімо, на північному полюсі Землі, Полярна зірка знаходиться в зеніті, тобто на лінії земної вертикалі. При цьому, в процесі свого добового руху, всі зорі північної півкулі, описують кола, які є паралельними лінії горизонту (мал.41а). А це означає, що на полюсі, зірки не сходять і не заходять, а їх висота над лінією горизонту залишається незмінною. Якщо ж говорити про зоряне небо екватора, то на ньому Поляра зірка знаходиться практично на лінії горизонту (мал.41б). При цьому, зорі сходять і заходять в площині, що є перпендикулярною до лінії горизонту. В середніх же широтах, Полярна зірка знаходиться над лінією горизонту, а її кут нахилу до цієї лінії дорівнює географічній широті того місця де знаходиться спостерігач. При цьому, деякі зірки сходять і заходять, а деякі ніколи не опускаються за лінію горизонту(мал.40в).

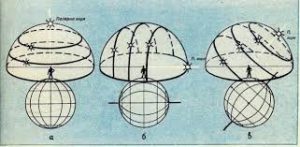
Мал.41. В різних місцях Землі, а точніше, на її різних географічних широтах, добовий рух зірок виглядає суттєво по різному.

Завершуючи розмову про розташування та видимий рух зірок, потрібно зауважити, що з плиним часу, просторова орієнтація осі обертання Землі, а отже і тієї осі світу навколо якої видимо обертається небесна сфера, періодично змінюється. Скажімо на теперішній час, напрям осі обертання Землі проходить через близькі околиці Полярної зірки. А от через 12000 років, цей напрям буде близьким до тієї яскравої зірки яка знаходиться в сузір’ї Ліри і називається Вега. Даний факт пояснюється так званою прецесією осі обертання Землі.

Прецесією називають повільне порівняно з періодом обертання тіла навколо своєї осі, зміщення (обертання) цієї осі в процесі якого вісь обертання тіла описує конус. Наприклад Земля, одночасно з відносно швидким добовим обертанням навколо своєї осі (Т=1доба) та річним обертанням навколо Сонця (Т=1рік), здійснює повільне прецесійне обертання навколо осі, яка є перпендикулярною до площини екліптики, і період якого Т=25796±2,5 років (цей період часто називають платонівським роком). При цьому кут прецесійного обертання Землі (23,5º), практично дорівнює куту нахилу площини екліптики до площини екватору Землі (площини небесного екватора).

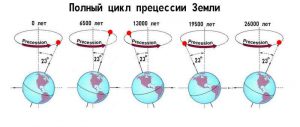
Мал.42. Земля не лише обертається навколо Сонця та своєї осі, а й здійснює певні прецесійні коливання.

За певних умов явище прецесії притаманне будь яким тілам що обертаються навколо своєї осі. Класичною ілюстрацією цього явища є механічна поведінка тієї загально відомої іграшки, яка називається дзиґою. Не важко переконатися в тому, що та дзиґа яка швидко обертається навколо своєї осі, в ситуації коли ця вісь нахилена до горизонтальної площини опори, прецесійно обертається навколо тієї осі що є перпендикулярною до опори. Це прецесійне обертання обумовлено низкою причин і зокрема фактом того, що на дзиґу діють дві рівні за величиною і протилежні за напрямком сили (сила тяжіння і реакція опори) які не лежать на одній прямій та створюють певний обертальний момент. Власне цей обертальний момент, у поєднанні з фактом осьового обертання дзиги та законом збереження моменту імпульсу і є основними причинами прецесійного обертання дзиги.

Планета Земля по суті і є величезною дзиґою яка обертається як навколо своєї осі так і навколо Сонця. При цьому тією «опорою» на яку спирається «земна дзиґа» є площина екліптики, тією віссю навколо якої прецесійно обертається «дзиґа» є перпендикуляр до площини екліптики кут нахилу якого до осі обертання Землі 23,5º, а тими силами які створюють певний обертальний момент, є та різниця гравітаційних сил, поява якої обумовлена різницею відстаней від полюсів Землі до Сонця.

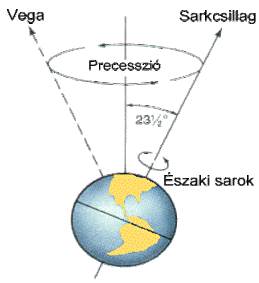
Мал.43. Прецесійне обертання дзиги і Землі має різні масштаби, але однакову фізичну суть.

Контрольні запитання.

1. Що називають небесною сферою? Чи має ця сфера певний радіус та об’єм?
2. Назвіть базові елементи горизонтальної системи небесних координат.
3. Яку лінію називають лінією математичного горизонту? Чи співпадає ця лінія з лінією видимого горизонту?
4. Які величини характеризують координати об’єкту на поверхні Землі?
5. Які величини характеризують координати об’єкту на небесній сфері? Як визначаються ці координати?
6. Уявно визначте місцезнаходження об’єкту азимут якого 60º, а його висота 45º.
7. Поясніть загальний устрій та принцип дії секстанта.
8. Як за допомогою секстанта визначається та географічна широта певної місцевості?
9. Чим відрізняється видимий рух зірок при спостереженні за ними з географічного полюса та екватора?
10. Де побачить Полярну зірку той спостерігач який знаходиться: а) на полюсі; б) на екваторі; в) в середніх широтах?
11. Що називають прецесією осі обертання Землі?
12. Які силові причини прецесійного обертання Землі?
13. Чому кут прецесійного обертання земної осі дорівнює 23,5°?

.

§7. Закономірності видимого руху планет.

З незапам’ятних часів, люди звернули увагу на факт того, що поведінка  п’яти яскравих зірок, сильно відрізняється від поведінки всієї сукупності інших зірок. Відрізняється тим, що вони не належать певним сузір’ям, а мандрують між ними. Ці особливі зірки назвали планетами, що в буквальному перекладі означає «блукаючі» (грец. planetes – блукати). В часи Римської імперії планети отримали назви провідних давньоримських богів:  Меркурій – бог торгівлі, Венера – богиня кохання, Марс – бог війни, Юпітер – верховний бог громовержець, Сатурн – бог землеробства. В наші дні, було відкрито ще дві, невидимі неозброєним оком планети: Уран – названо на честь бога неба та Нептун – названо на честь бога морів.

Загальною закономірністю видимого з Землі руху планет, є факт того, що вони рухаються в близьких околицях площини екліптики, тобто тієї площини в якій Сонце видимо обертається навколо Землі, а в реальності – Земля обертається навколо Сонця.

Мал.44. Планети Сонячної системи обертаються в близьких околицях площини екліптики.

Видима з Землі поведінка тієї чи іншої планети, по суті є результуючою чотирьох обставин: 1) періодичності обертання Землі навколо своєї осі; 2) періодичності обертання Землі навколо Сонця; 3) періодичності обертання планети навколо Сонця; 4) розташування планети відносно Землі і Сонця. Скажімо видима поведінка тих планет які розташовані між Землею і Сонцем (Меркурій і Венера), суттєво відрізняється від видимої поведінки тих планет які знаходяться за Землею (Марс, Юпітер, Сатурн). Гранично стисло і спрощено, описуючи та пояснюючи цю поведінку можна сказати наступне.

Найближчою до Сонця планетою є Меркурій. Серед видимих з Землі планет, Меркурій найменш пристосований для візуальних спостережень. Адже більшу частину часу, він знаходиться або за Сонцем, або в його яскравому світлі. Над лінією горизонту, Меркурій можна побачити лише в періоди так званої елонгації (від лат. elongo – віддаляюся), тобто періоди найбільшого кутового відхилення планети відносно лінії Земля – Сонце. Для Меркурія величина цього максимального відхилення не перевищує 28°. А зважаючи на суттєву еліптичність орбіти Меркурія, реальна величина максимального кута його елонгації змінюється від 18° до 28°.

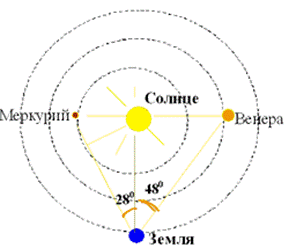
Мал.45. Кут максимальної елонгації Меркурія не перевищує 28°.

Найбільш сприятливими для візуального спостереження Меркурія є близькі до екватора широти. Якщо ж мова йде про середні широти Землі, то в них візуальне спостереження Меркурія можливе лише протягом декількох тижнів на рік і тривалостями лише лічені десятки хвилин після заходу Сонця, або перед його сходом. При цьому навіть в періоди максимальної елонгації, побачити Меркурій на фоні достатньо світлого вечірнього або вранішнього неба, не просто. А тим більше в ситуаціях, коли в багатьох місцевостях, лінія математичного горизонту закрита навколишнім рельєфом

Значно простіше спостерігати та аналізувати поведінку другої за віддаленістю від Сонця планети, Венери. Як і Меркурій, Венеру можна побачити на вечірньому або перед вранішньому небі. Але на відміну від Меркурія, на фоні зоряного неба, Венера перебуває набагато довше і світить набагато яскравіше. Достатньо сказати, що Венера це третій за яскравістю (після Сонця і Місяця) об’єкт небесної сфери, зоряна величина якого в найбільш сприятливі дні становить –4,8^m. А це в 20 разів більше за яскравість найбільш яскравої зірки північної зоряної півкулі – Сіріуса (–1,46^m) та більш як в 100 разів перевищує яскравість Полярної зірки (1,97^m).

Коли відразу ж після заходу Сонця, Венера вперше з’являється над лінією горизонту, то перебуває над цією лінією лічені десятки хвилин. Проте, кожного наступного дня, вона з’являється все вище і вище, та прямуючи за Сонцем, ховається за лінією горизонту, через все більшу і більшу кількість часу. Через декілька тижнів, Венера досягає так званої точки східної елонгації, тобто точки максимального віддалення від Сонця в східному напрямку. Побувши в околицях цієї точки декілька днів, Венера відправляється у зворотній шлях і приблизно через той же час (декілька тижнів) ховається в променях Сонця що заходить.

Через певний час (приблизно через два місяці), Венера знову з’являється над лінією горизонту, але вже в променях Сонця що сходить. Кожного наступного дня, вона з’являється все раніше і раніше, та все вище і вище над лінією горизонту. Нарешті, досягнувши точки західної елонгації, Венера на декілька днів зупиняється, а потім вирушає у зворотній шлях, тобто в напрямку Сонця що сходить.

Гранично стисле та спрощене пояснення видимої з Землі поведінки Венери, полягає в наступному. Оскільки Венера з періодичністю 226 земних діб обертається навколо Сонця, то земний спостерігач бачить, що в періоди елонгації, Венера спочатку віддаляється від Сонця, а потім – наближається до нього. З іншого боку, земний спостерігач бачить, що Сонце, а разом з ним і Венера, з періодичністю одна доба, обертаються навколо Землі. Власне результатом накладання цих двох періодичностей і є видима з Землі кінематична поведінка Венери.

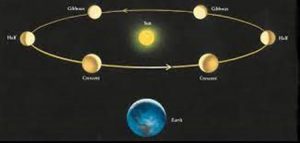
Мал.46. З погляду земного спостерігача, Венера в періоди елонгації спочатку віддаляється від Сонця, а потім – наближається до нього.

Потрібно зауважити, що з Землі можна спостерігати не лише різні фази Місяця, а й різні фази Венери. (Щоправда, фази Венери можна побачити лише за допомогою телескопа). Це означає, що при погляді з Землі, освітлена Сонцем частина Венери в різні часові проміжки виглядає по різному (мал.47). Наприклад, якщо Венера знаходиться між Сонцем і Землею, то земний спостерігач бачитиме тонкий серп молодої Венери. А зважаючи на факт наявності у Венери потужної атмосфери, молода серповидна Венера буде оточена характерним світловим обрамленням (гало), яке є результатом заломлення світла атмосферою планети. Якщо ж Венера буде знаходитись за Сонцем, то з Землі її освітлена частина буде видимою максимально повно. При цьому Венера буде знаходитись у фазі повні. Зважаючи на факт того, що навколо Сонця в одному і тому ж напрямку обертаються як Земля так і Венера, повний цикл змін фаз Венери (від повні до повні) становить 584 дні.

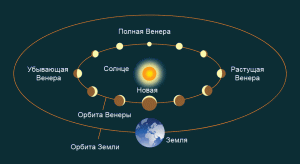
Мал.47. З Землі можна спостерігати не лише різні фази Місяця, а й різні фази Венери.

Ясно, коли Венера знаходиться у фазі повні, то кількість того світла яке відбиває її поверхня в напрямку Землі є максимально великою. Звідси можна зробити висновок про те, що на нічному небі саме у повні Венера має бути максимально яскравою. Однак з іншого боку, у повні Венера знаходиться на максимально великій відстані від Землі, і тому відсоток того світла яке потрапляє на Землю від Венери є мінімальним. Якщо ж Венера знаходиться у фазі молодика, то кількість того світла яке вона відбиває в напрямку Землі є мінімальною, але відсоток його потрапляння на Землю є максимально великим.

При цьому потрібно мати на увазі, що співвідношення між максимальною (258млн.км) та мінімальною (38млн.км) відстанями від Землі до Венери, близьке до 6,8. А це означає, що співвідношення між кількістю того світла яке потрапляє на Землю від Венери у повні та від Венери молодика становить 1/(6,8)²=1/46. Зважаючи на сукупність вище згаданих та інших обставин, максимальна яскравість Венери (–4,8^m) спостерігається в тих випадках, коли відстань до неї близька до 68млн.км, а видима освітленість її диску, близька до 28%. Загалом же, видима зоряна величина Венери коливається в межах від –3,8^m до –4,8^m.

Меркурій і Венеру часто називають внутрішніми планетами, тобто такими, орбіти яких знаходяться між Сонцем та орбітою Землі. Натомість Марс, Юпітер, Сатурн, Уран і Нептун, називають планетами зовнішніми, тобто такими, орбіти яких знаходяться за орбітою Землі. (Нагадаємо, що з Землі, неозброєним оком видно лише три зовнішні планети: Марс, Юпітер і Сатурн). Видима кінематична поведінка зовнішніх планет, суттєво відрізняється від аналогічної поведінки планет внутрішніх. Відрізняється по-перше тим, що тривалість та періодичність появи зовнішніх планет на нічному небі, визначається не видимою з Землі віддаленістю планети від Сонця, а тим, на денній чи нічній стороні неба перебуває дана планета. При цьому, приблизно половину земного року, кожна з зовнішніх планет перебуває на нічній стороні неба і тому є видимою, а іншу половину року, вона перебуває на денній стороні неба і тому є невидимою. Скажімо, в зображеній на мал.48 ситуації, Марс перебуває на нічній стороні неба і тому в нічний час є видимим на фоні зоряного неба. Коли ж через пів року, Земля опиниться на протилежній стороні своєї орбіти, то за такого ж розташування Марса, він буде знаходитись на денній стороні неба і тому в нічний час не буде видимим.

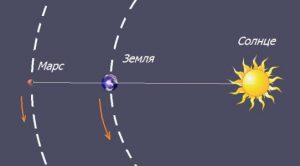
Мал.48. За даного розташування Сонця, Землі та Марса, Марс відносно Землі перебуває на нічній стороні неба і тому в нічний час є видимим.

Другою характерною особливістю зовнішніх планет є факт того, що в процесі свого видимого обертання навколо Землі, вони з певною періодичністю описують характерні петлі. Це звичайно не означає, що протягом однієї ночі, планета на фоні зоряного неба описує певну петлю. Мова йде про наступне. Якщо щоденно та в один і той же час, фіксувати координати зовнішньої планети, то можна зробити висновок про те, що в певні проміжки часу планета з певною приблизно постійною швидкістю рухається вздовж екліптики. Однак, на певному етапі спостережень з’ясовується, що швидкість руху планети вздовж екліптики починає знижуватися, і що через деякий час планета зупиняється. При цьому в наступні дні, планета починає рухатись в зворотному напрямку. Через певний час, планета знову поступово сповільнюючи свій видимий рух зупиняється і знову починає рухатись в правильному напрямку. Пояснюючи цю дивну поведінку зовнішніх планет, розглянемо та проаналізуємо видимий рух Марса.

На фоні зоряного неба, Марс виглядає яскравою, червонуватою зіркою, видима зоряна величина якої –2,9^m (в момент максимального зближення з Землею). Червоне забарвлення Марса, пояснюється наявністю на його поверхні великої кількості червонуватого оксиду заліза. Період обертання Марса навколо Сонця 687 земних діб, що майже в два рази перевищує період річного обертання Землі. А це означає, що в процесі свого обертального руху навколо Сонця, Земля приблизно два рази на рік обганяє Марс. Власне в момент цього обгону і створюється візуальна ілюзія того, що на фоні зоряного неба Марс описує характерну петлю (мал.48).

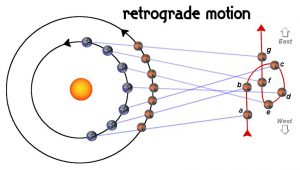
Мал.49. В процесі «обгону» Землею зовнішньої планети, ця планета, на фоні видимого з Землі зоряного неба, описує характерну петлю.

Дійсно. Припустимо, що протягом тих днів коли Земля, в процесі свого обертального руху навколо Сонця «обганятиме» Марс, ми в певні моменти часу будемо фіксувати видиме положення Марса на фоні зоряного неба. Проводячи такі спостереження ви з’ясуєте, що на відрізку а – b планета рухається в звичному для себе напрямку і з практично незмінною швидкістю. На відрізку b – c планета, продовжуючи рухатись в звичному напрямку, поступово зменшує швидкість свого видимого руху до нуля. На відрізку с – d, напрям руху планети змінюється на протилежний, а її видима швидкість поступово збільшується від нуля, до певної максимальної величини. На відрізку d – e, Марс рухаючись в зворотному напрямку поступово зменшує швидкість видимого руху і знову «зупиняється». На відрізку е – f, правильний напрям руху Марса відновлюється, а його видима швидкість поступово збільшується до звичної величини.

Характеризуючи вище описаний рух планети, часто говорять, що в процесі видимого обертання навколо Землі, зовнішні планети описують певні характерні петлі. Подібним чином видимо рухаються всі зовнішні планети. Різниця лише в тому, що періоди обертання цих планет навколо Сонця значно більші ніж у Марса. Наприклад для Юпітер Т=11,86 земних років, а для Сатурн Т=29,46 земних років. А це означає, що протягом того часу який називається періодом обертання планети навколо Сонця, Земля обганятиме цю планету більше число разів і тому на відповідній траєкторії буде більше число петель.

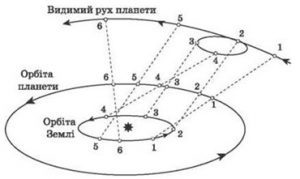
Мал.50. Видимий з Землі рух зовнішніх планет, характеризується наявністю певних, циклічних змін величини і напрямку цього руху.

Та яким би «блукаючим» не був видимий з Землі рух тієї чи іншої планети, а нічого незвичного та надприродного в цьому русі нема. Адже різноманіття «блукаючих» рухів планет, є результатом певної комбінації чотирьох базових обставин (фактів): 1) періодичності обертання Землі навколо своєї осі; 2) періодичності обертання Землі навколо Сонця; 3) періодичності обертання планети навколо Сонця; 4) розташування планети відносно Землі і Сонця.

Завершуючи розмову про закономірності видимого руху планет, ще раз наголосимо на тому, що видимий рух планет Сонячної системи, відбувається в близьких околицях площини екліптики, тобто тієї площини в якій Сонце видимо обертається навколо Землі, а фактично Земля обертається навколо Сонця. Власне в околицях цієї площини рухаються не лише планети, а й Місяць. Тому, якщо в просторах зоряного неба, ви захочите відшукати ту чи іншу планету, шукайте її вздовж траєкторії руху Місяця. Тільки не забувайте про те, що площина обертання Місяця навколо Землі, дещо нахилена до площина екліптики. А це означає, що за певних умов, планети можуть знаходитись як значно вище так і значно нижче Місяця.

Мал.51. Видимий рух планет, Сонця та Місяця відбувається в близьких околицях площини екліптики.

Контрольні запитання.

1. На зоряному небі планети виглядають як звичайні зірки. Чому ці зірки назвали блукаючими?
2. Які факти визначально впливають на видимий рух планет сонячної системи?
3. Який кут називають кутом максимальної елонгації планети? Для яких планет є сенс говорити про такий кут?
4. Чому кут максимальної елонгації Меркурія змінюється від 18° до 28°?
5. Чому Меркурій можна побачити лише в лічені дні та в короткі проміжки часу?
6. Опишіть видиму поведінку Венери як вечірньої зірки.
7. Поясніть видиму поведінку Венери як вечірньої зірки.
8. Чому видима зоряна величина Венери коливається в межах від –3,8^m до –4,8^m?
9. Чому в процесі свого видимого руху, Марс, Юпітер і Сатурн описують характерні петлі?
10. На основі аналізу мал.50 опишіть видимий рух зовнішньої планети.
11. Чому зовнішні планети приблизно півроку спостерігаються на фоні зоряного неба, а півроку не спостерігаються?
12. В якій частині зоряного неба потрібно шукати планети?

.

§8. Закони Кеплера.

З прадавніх часів вважалося, що світ небесних тіл є ідеальним, і що тому ці тіла можуть рухатися лише ідеальними траєкторіями. А цими ідеальними траєкторіями було прийнято вважати кола, а в об’ємному сенсі – сфери. Стародавні вчені створили велику кількість теорії (а точніше науково подібних гіпотез), які пояснювали закономірності видимого руху Сонця, Місяця, планет та зірок. При цьому пояснювали виходячи з того, що видима поведінка всіх небесних тіл, є результатом їх руху певними коловими орбітами, або орбітами які є певними комбінаціями декількох колових рухів. І в цьому сенсі, практично сучасна теорія Миколи Коперника (1473–1543) не була винятком. Адже згідно з цією теорією, планети обертались навколо Сонця по ідеально круглим орбітам.

Однак, на початку 17-го століття, німецький астроном і математик Йоганн Кеплер, на основі аналізу тих даних які за 38 років досліджень зібрав данський астроном Тихо Браге (1546–1601), дійшов висновку: пояснити реальні закономірності руху планет виходячи з того, що ці планети обертаються навколо Сонця по ідеально круглим орбітам – неможливо. Аналізуючи наявні факти, та проводячи власні дослідження, Кеплер в 1618–1621 роках сформулював три закони (закони Кеплера), які не лише кількісно пояснили кінематичну поведінку всіх планет Сонячної системи, а й суттєво вплинули на подальший розвиток не лише астрономії, а й фізики. Що ж, давайте сформулюємо та проаналізуємо ці закони.

Перший закон Кеплера: кожна планета обертається навколо Сонця по еліптичній орбіті, в одному з фокусів якої знаходиться Сонце.

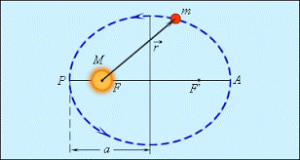
Мал.52. Кожна планета обертається навколо Сонця по еліптичній орбіті, в одному з фокусів якої знаходиться Сонце (перший закон Кеплера).

Нагадаємо. Еліпс – це замкнута крива на площині, яка проведена навколо двох базових точок F₁ і F₂ (фокусів еліпса) таким чином, що сума відстаней від цих точок до будь якої точки еліпса залишається незмінною і чисельно рівною довжині великої осі еліпса. Іншими словами: для будь-якої точки Р еліпса (мал.53) виконується співвідношення |F₁P| + |F₂P| = 2а. Намалювати еліпс, а заодно й переконатися в тому, що для будь якої його точки Р, виконується співвідношення |F₁P| + |F₂P| = const, не складно. Для цього візьміть два маленькі цвяхи (булавки, шурупи, тощо) та надійно зафіксуйте їх на рівній поверхні. Ці цвяхи будуть фокусами вашого еліпса. Тепер візьміть нитку, подвійна довжина якої дещо більша за відстань між цвяхами. Зв’яжіть  кінці нитки та накиньте отриману петлю на цвяхи. Натягнувши нитку осердям олівця чи ручки, плавно опишіть замкнуту лінію. Ця лінія і буде еліпсом.

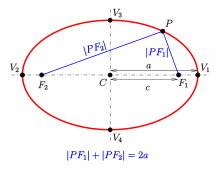
Мал.53. Загальний вигляд та основні параметри еліпса.

До числа основних параметрів еліпса відносяться. Центр еліпса (С) – середина того відрізку що з’єднує фокуси еліпса. Фокусна відстань еліпса (с)– відстань від фокуса еліпса (F₁ чи F₂) до його центру (С). Головна вісь еліпса – пряма що проходить через фокуси еліпса. Мала вісь еліпса – пряма що проходить через центр еліпса та є перпендикулярною до його головної осі. Головні вершини еліпса (V₁, V₂) – точки перетину еліпса з його головною віссю. Довжина великої піввісі еліпса (а) – відстань від центру еліпса (С) до його головної вершина (V₁ чи V₂).

Однією з основних характеристик еліпса, є його ексцентриситет. Ексцентриситет еліпса (е) – це величина, що характеризує ступінь витягнутості еліпса і яка дорівнює відношенню фокусної відстані еліпса (с) до довжини його великої піввісі (а): е = с/а. Ексцентриситет еліпса знаходиться в межах 0 < е < 1. Еліпс, ексцентриситет якого дорівнює нулю (е = 0), називається колом. Дійсно, для кола с=0, а=R, тому е=с/а=0/R=0. Якщо ж еліпс гранично видовжений, то його фокусна відстань не набагато менша за довжину великої піввісі (с → а) і тому ексцентриситет такого еліпса є близьким до 1 (оскільки с → а, то е=с/а → 1). Наочні уявлення про реальну ступінь витягнутості еліпса для певних значень його ексцентриситету, можна почерпнути на основі аналізу мал.54.

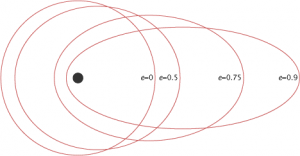
Мал.54. Ступені витягнутості еліпса для різних значень його ексцентриситету.

За винятком Меркурія, ексцентриситети орбіт планет Сонячної системи, є досить малими: Меркурій е=0,2056; Венера е=0,0068; Земля е=0,0167; Марс=0,0933; Юпітер е=0,0484; Сатурн е=0,0557; Уран е=0,0444; Нептун е=0,0112. Це означає що орбіти більшості планет, зокрема Венери, Землі і Нептуна, не надто відрізняються від колових. Однак, якщо мова йде про комети, то ексцентриситет їх орбіт є надзвичайно великим. Скажімо для комети Галлея е=0,967. Окрім Меркурія планетою з відносно великим ексцентриситетом її орбіти (е=0,093) є Марс. Власне досліджуючи траєкторію руху Марса, Кеплер і з’ясував, що планети обертаються навколо Сонця не по ідеально круговим орбітам, а по певним еліптичним орбітам.

Потрібно зауважити, що найближчу до Сонця точку еліптичної орбіти планети називають перигелієм, а найбільш віддалену – афелієм. Наприклад Земля, в перигелії віддалена від Сонця на 147∙10⁶ км, а в афелії – на 152∙10⁶ км. Зверніть увагу на факт того, що в літні місяці, Земля віддалена від Сонця на суттєво більшу відстань аніж у зимові. Даний факт вказує на те, що температурний режим на Землі, визначально залежить не стільки від відстані до Сонця, скільки від того, під яким кутом сонячне проміння падає на поверхню Землі.

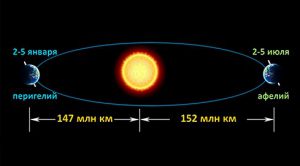
Мал.55. В процесі обертання навколо Сонця, відстань між Землею і Сонцем періодично змінюється.

Аналізуючи швидкісні параметри руху Марса, Кеплер звернув увагу на факт того, що в процесі наближення до Сонця, швидкість планети збільшується, а в процесі віддалення від Сонця – зменшується. Намагаючись кількісно оцінити величину цього збільшення та зменшення, Кеплер математично вивів цікаву закономірність, яку і сформулював у вигляді свого другого закону. Другий закон Кеплера: радіус-вектор планети, в процесі її обертального руху навколо Сонця, за однакові проміжки часу описує однакові площі.

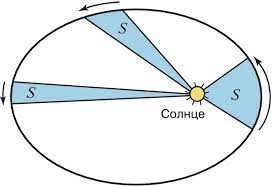
Мал.56. Радіус-вектор планети, в процесі її обертального руху навколо Сонця, за однакові проміжки часу описує однакові площі (другий закон Кеплера).

Спрощено пояснюючи той зв’язок який існує між другим законом Кеплера та фактом того, що при наближенні до Сонця швидкість планети збільшується, а при віддаленні зменшується, можна сказати наступне. Швидкість руху планети на будь якій ділянці траєкторії визначається за формулою v=ℓ/t, де ℓ – довжина відповідної ділянки, t – час руху планети цією ділянкою. За умовою закону t₁=t₂, S₁=S₂ («за однакові проміжки часу описує однакові площі»). Із аналізу мал.56 ясно, що площа того сектору S який за час t описує радіус-вектор планети (r), пропорційна усередненій довжині цього радіус-вектора та довжині того фрагменту траєкторії (ℓ) яка обмежує цей сектор: S ~ r·ℓ. Іншими словами, S₁ ~ r₁·ℓ₁; S₂ ~ r₂·ℓ₂. А зважаючи на те, що S₁=S₂, r₁ < r₂, можна стверджувати, що ℓ₁ > ℓ₂. А це означає, що швидкість руху планети на першій ділянці (v₁=ℓ₁/t₁), більша за її швидкість на другій ділянці (v₁=ℓ₁/t₁): v₁ > v₂.

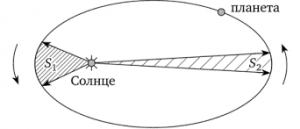
Мал.57. Другий закон Кеплера, є геометричним відображенням факту того, що при наближені до Сонця, швидкість руху планети збільшується, а при віддалені – зменшується.

Наступне математичне узагальнення, Кеплер зробив на основі аналізу відомих  періодів обертання планет навколо Сонця та параметрів їх орбіт. При цьому він з’ясував, що періоди обертання планет навколо Сонця (Т), певним чином зв’язані з тією відстанню, яка називається довжиною великої піввісі еліпса (а). Цей зв’язок Кеплер сформулював у вигляді свого третього закону. Третій закон Кеплера: квадрати періодів обертань планет, відносяться як куби великих півосей їх орбіт, тобто (Т₁/Т₂)² = (а₁/а₂)³.

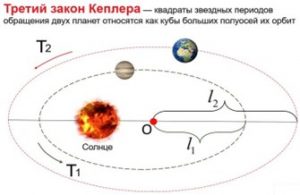
Мал.58. Квадрати періодів обертань планет, відносяться як куби великих півосей їх орбіт: (Т₁/Т₂)² = (ℓ₁/ℓ₂)³ (третій закон Кеплера).

По суті третій закон Кеплера є відображенням факту того, що для всіх планет, відношення квадрату періоду їх обертання (Т²) до кубу довжини великої піввісі орбіти (а³), є постійною величиною. Дійсно, якщо Т₁²/Т₂² = а₁³/а₂³, то Т₁²/а₁³ = Т₂²/а₂³ = const. В цьому не важко переконатися, якщо періоди обертання планет виразити в періодах обертання Землі, а довжини їх великих півосей виразити в довжинах великої піввісі Землі, а фактично в астрономічних одиницях (астрономічна одиниця – середня відстань від Землі до Сонця). В цьому випадку, у відповідності з третім законом Кеплера Т²/а³=1. Дійсно:

для Меркурія: Т = 0,241Т_з; а = 0,387а.о; Т²/а³ = 1,00;

для Венери: Т = 0,615Т_з; а = 0,723а.о;  Т²/а³ = 1,00;

для Землі: Т = 1,000Т_з; а = 1,000а.о;  Т²/а³ = 1,00;

для Марса: Т = 1,881Т_з; а = 1,524а.о;  Т²/а³ = 1,00;

для Юпітера: Т = 11,862Т_з; а = 5,204а.о;  Т²/а³ = 1,00;

для Сатурна: Т = 29,457Т_з; а = 9,582а.о;  Т²/а³ = 0,99;

Закони Кеплера відіграли значну роль в становленні сучасної астрономічної науки. Однак, ці закони ще не були тією цілісною системою знань, яка б дозволяла не просто констатувати певні факти і співвідношення, а пояснювати всю сукупність цих фактів та співвідношень. Адже закони Кеплера не пояснювали, чому планети обертаються певними еліптичними орбітами? Не пояснювали, чому при наближенні до Сонця швидкість планети збільшується, а при віддаленні – зменшується? Не пояснювала, чому між періодами обертання планет навколо Сонця та довжинами їх великих півосей, існують певні співвідношення? Відповіді на ці, та безліч інших запитань, дала теорія, яку прийнято називати ньютонівською механікою. Автором цієї видатної теорії був геніальний англійський фізик і математик Ісаак Ньютон (1642–1727). Втім, про те як теорія Ньютона пояснює загальний устрій Сонячної системи, ми поговоримо в наступному параграфі.

Контрольні запитання.

1. Що стверджується в першому законі Кеплера?
2. Яку криву називають еліпсом?
3. Що характеризує ексцентриситет еліпса?
4. Доведіть що ексцентриситет кола дорівнює нулю.
5. Яка з планет Сонячної системи має найбільший ексцентриситет, а яка найменший? Що це означає?
6. Що називають перигелієм та афелієм орбіти планети?
7. Що стверджується в другому законі Кеплера? Яка фізична суть цього закону?
8. Доведіть, що твердження радіус-вектор планети за однакові проміжки часу описує однакові площі, по суті означає, що при наближенні до Сонця швидкість планети збільшується, а при віддаленні – зменшується.
9. Що стверджується в третьому законі Кеплера? Як можна сформулювати цей закон по іншому?

.

§9. Про теорію Ньютона і про те, як вона пояснює загальний устрій Сонячної системи.

Як не парадоксально, а великі теорії вирізняються не своєю складністю, а геніальною простотою. Скажімо, яких тільки чудернадських та надскладних механізмів не придумували вчені стародавньої Греції, намагаючись пояснити видимі рухи об’єктів навколоземного простору. Тут і рухомі та нерухомі кришталеві сфери та півсфери, і осі та півосі, і цикли та епіцикли. Тут і складні системи цих сфер, осей, циклів та епіциклів. Ну а про надскладні системи механічних приводів цих сфер, півсфер і осей, годі й говорити. Однак, всі ці надскладні теорії не пояснювали наявного різноманіття механічних рухів навколоземних об’єктів. А головне, вони навіть не намагались пояснити, а яким же чином всі ці надскладні механізми працюють. І лише після того, як геніальний Ньютон створив свою знамениту механіку, все стало зрозумілим та очевидним. В основі ж ньютонівської механіки лежать три прості базові твердження, які називаються законами Ньютона:

Перший закон Ньютона: Тіло буде знаходитись в стані механічного спокою, або в стані прямолінійного рівномірного руху, до тих пір поки на нього не подіє зовнішня сила, яка і змусить тіло змінити цей стан. По суті це означає, шо безпричинної зміни швидкості руху тіла не буває, і що цією причиною є дія на тіло зовнішньої сили F. Іншими словами:  F → a.

Другий закон Ньютона: Під дією зовнішньої сили F, тіло масою m отримує прискорення а, величина якого прямо пропорційна діючій на тіло силі і обернено пропорційна масі тіла. Іншими словами: F → a = F/m.

Третій закон Ньютона: Діюча на тіло зовнішня сила F, завжди породжує рівну їй за величиною і протилежну за напрямком протидіючу силу Fꞌ.  Іншими словами: F → Fꞌ = – F.

Не важко бачити, що закони Ньютона є очевидно простими і представляють собою цілісну систему взаємо пов’язаних та взаємо доповнюючих тверджень. Власне на основі цих тверджень, та відкритого ним закону всесвітнього тяжіння, Ньютон пояснив не лише все різноманіття тих механічних рухів які відбуваються на Землі, а й практично все різноманіття тих механічних процесів які відбуваються у Всесвіті. А оскільки ті процеси що відбуваються у Всесвіті, визначальним чином підпорядковані закону всесвітнього тяжіння, то буде не зайвим згадати і цей закон.

Закон всесвітнього тяжіння – це закон, в якому стверджується: два тіла  маси яких m₁ і m₂ взаємно притягуються з гравітаційною силою F_гр, величина якої прямо пропорційна добутку взаємодіючих мас (m₁∙m₂) і обернено пропорційна квадрату відстані між центрами цих мас (r²). Іншими словами: F_гр=G(m₁m₂/r²), де G=6,67∙10^–11Н∙кг²/м² – постійна величина, яка називається гравітаційною сталою і значення якої визначається експериментально.

Потрібно зауважити, що питома величина гравітаційної сили є надзвичайно малою. Адже гравітаційна стала G=6,67∙10^–11Н∙кг²/м², по суті дорівнює тій гравітаційній силі, з якою взаємно притягуються два тіла масою по 1кг кожне, будучи розташованими на відстані 1м одне від одного. Іншими словами: якщо m₁=m₂=1кг; r=1м, то F_гр=6,67∙10^–11Н=0,0000000000667Н, а це в мільярди разів менше за ту силу яку ви відчуваєте, тримаючи в руці вантаж масою 102г і яка дорівнює 1Н. Звідси ясно, чому у повсякденному житті, ми практично не зустрічаємся з проявами гравітаційних сил. За винятком того випадку, коли ми та всі наземні тіла притягуємся до того надмасивного тіла, яким є наша Земля.

Інша справа, об’єкти космічні. Адже для них, питомо непомітні гравітаційні сили, набувають фантастично великих величин. Наприклад Місяць (m=7,33∙10²²кг) перебуваючи на відстані r=3,84∙10⁸м від Землі (M=5,98∙10²⁴кг), притягується до цієї Землі з гравітаційною силою F_гр=G(Мm/r²)=2∙10²⁰Н. Щоб уявити величину цієї сили, уявіть надміцний сталевий трос, діаметр якого дорівнює діаметру Місяця (3500км). Так от, цей трос, кожний сантиметр квадратний якого здатен підняти вантаж масою в декілька тон, ледь-ледь спроможний витримати вище згадану силу.

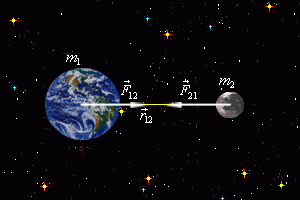
Мал.59. Місяць і Земля взаємно притягуються з силою: F_гр= 2∙10²⁰Н.

Ви можете запитати: а якщо Місяць з такою фантастично великою силою притягується до Землі, то чому ж він не падає на Землю? Відповідаючи на це слушне запитання, ньютонівська механіка стверджує: Місяць не падає на Землю тому, що на нього, окрім гравітаційної сили (F_гр), діє рівна їй за величиною але протилежна за напрямком сила інерції (F_i). Сила, поява якої обумовлена тим, що обертаючись навколо Землі, Місяць рухається з певним доцентровим прискоренням. А це означає, що на нього неминуче діє певна відцентрова сила, яку і називають силою інерції. Нагадаємо:

Сила інерції – це така сила, поява якої обумовлена прискореним рухом тіла і яка завжди протидіє появі та зростанню цього прискорення.

Позначається: F_i

Визначальне рівняння: F_i = – ma

Одиниця вимірювання: [F_i] = кг∙м/с² = Н  (ньютон).

Звичайно, якби Місяць з певною, строго визначеною швидкістю не обертався навколо Землі, то під дією гравітаційної сили, неминуче падав би на неї. Однак, фактом залишається те, що Місяць з періодичністю Т=27,3 доби обертається навколо Землі, а отже рухається з певним доцентровим прискоренням, величина якого визначається за формулою а_д=v²/r. В такій ситуації на Місяць неминуче діє відцентрова сила інерції, величина якої визначається за формулою F_i=ma_д=mv²/r, де m = 7,33∙10²²кг – маса Місяця, v – лінійна швидкість його орбітального руху, r = 3,84∙10⁸м   – відстань між центрами мас Землі і Місяця.

Таким чином, на Місяць діють дві сили: сила гравітаційної взаємодії з Землею (F_гр=GМm/r²=2∙10²⁰Н) та обумовлена обертальним рухом Місяця, сила інерції (F_i=ma_д=mv²/r). І не важко довести, що величина діючої на Місяць сили інерції в точності дорівнює величині гравітаційної сили, тобто 2∙10²⁰Н. Дійсно. Оскільки за один оберт навколо Землі, тобто за час t = Т =27,3 доби = 2,36∙10⁶с, Місяць проходить відстань ℓ = 2πr = 2∙3,14∙3,84∙10⁸м = 24,12∙10⁸м, то швидкість його обертального руху v = ℓ/Т = 1020м/с. При цьому, величина діючої на Місяць сили інерції становить  F_i = ma_д = mv²/r = 7,33∙10²²кг∙(1022м/с)²/3,84∙10⁸м = 2∙10²⁰Н.

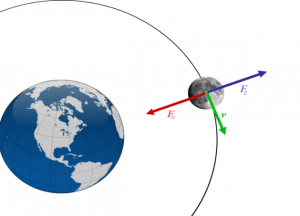
Мал.60. У повній відповідності з законами ньютонівської механіки, Місяць обертається навколо Землі певною майже коловою  орбітою.

Тепер, коли ви знаєте як влаштована, та як працює система Земля – Місяць, не важко погодитись з тим, що аналогічним чином влаштована і працює вся Сонячна система. Різниця лише в тому, що ця система складається не з двох об’єктів, а з величезної їх кількості. Адже Сонячна система, це не лише Сонце та вісім великих планет, а й 173 супутників цих планет, 5 карликових планет та 8 їх супутників, величезна кількість астероїдів і комет, незліченна кількість метеороїдів та дрібних і не надто дрібних об’єктів поясу Койпера. І всі ці об’єкти, у повній відповідності з законами ньютонівської механіки обертаються навколо Сонця та інших масивних тіл Сонячної системи, утворюючи надзвичайно гармонічну, саморегульовану систему. І динамічна рівновага цієї системи, її саморегульованість та самодостатність, забезпечується сукупністю лише двох силових чинників: сили гравітаційної взаємодії між тілами та сили інерції, яка по суті є силою взаємодії прискорено рухомого тіла з тим фізичним об’єктом який називається простором Всесвіту.

Мал.61. Всі об’єкти Сонячної системи обертаються навколо Сонця у повній відповідності з законами ньютонівської механіки.

В свій час, ми поговоримо про те як і коли виникла Сонячної системи. Сьогодні ж, просто констатуємо факт того, що сучасна Сонячна система, це злагоджений цілісний механізм, який сформувався приблизно 4,5 мільярдів років тому і який з тих пір бездоганно працює. Центральним об’єктом цього механізму є зірка середніх розмірів, яку ми називаємо Сонцем і навколо якої обертаються її великі та малі природні супутники: планети, астероїди, комети та інші тіла При цьому, більшість планет мають свої супутникові системи. Загальний же принцип дії цієї надскладної механічної системи надзвичайно простий, і полягає в наступному. Кожен елемент системи, під дією сили гравітаційної взаємодії та сили інерції, обертається навколо центрального тіла, при цьому швидкість його обертання є такою, що забезпечує динамічну рівновагу між силою гравітаційної взаємодії та силою інерції.

Звісно, кількісно описати найдрібніші деталі механічної поведінки кожного об’єкту Сонячної системи, надзвичайно складно. Адже ця поведінка визначається не лише взаємодією цього об’єкту з Сонцем, а й з усіма іншими об’єктами Сонячної системи. Однак, якщо застосовуючи закони ньютонівської механіки, ви дійсно врахуєте всі ці взаємодії, то безумовно отримаєте результат, який практично співпадає з реальністю.

Втім, не варто думати, що ньютонівська механіка є тією супер теорією яка може пояснити все і вся. Скажімо ця механіка не може пояснити деякі нюанси механічної поведінки тієї найближчої до Сонця планети яку називають Меркурієм. Ці пояснення дає теорія відносності, яка по суті є уточненим варіантом ньютонівської механіки. До речі, в теорії відносності аргументовано стверджується і доводиться, що ті сили які прийнято називати силою гравітаційної взаємодії (F_гр=Gm₁m₂/r²) та силою інерції (F_i=–ma), є різними проявами однієї і тієї ж фундаментальної сили. І що ці прояви відрізняються лише тим, що гравітаційна сила є результатом взаємодії тіла з тими об’єктами які представляють собою згустки сконденсованої (явної) мас-енергії, а сила інерції є результатом взаємодії тіла з тим об’єктом який називається простором-часом і який є носієм та джерелом прихованої мас-енергія.

Варто зауважити, що відкриттю закону всесвітнього тяжіння, значною мірою сприяли раніше сформульовані закони Кеплера. Власне на основі аналізу цих законів та трьох базових законів механіки, Ньютон математично довів, що масивні земні і космічні тіла взаємодіють з силою, величина якої визначається за формулою F_гр=Gm₁m₂/r². Створена ж на основі трьох законів Ньютона та закону всесвітнього тяжіння цілісна система знань (ньютонівська механіка), дозволила пояснити практично все різноманіття відомих механічних явищ та закономірностей, в тому числі і ті закони які називаються законами Кеплера.

Ілюструючи можливості ньютонівської механіки, «відкриємо» та уточнимо третій закон Кеплера. Нагадаємо, в цьому законі стверджується: для всіх планет Сонячної системи, відношення квадрату періоду їх обертання (Т²) до кубу довжини великої піввісі їх орбіт (а³), є постійною величиною. Іншими словами: Т²/а³=const. Оскільки в реальності траєкторії руху планет навколо Сонця мало відрізняються від колових, то для спрощення математичних пояснень, розглянемо ситуацію в якій малий космічний об’єкт масою m (наприклад Місяць), обертається навколо великого космічного об’єкту масою М (наприклад Землі), коловою орбітою радіусом r.

Оскільки в процесі колового обертання, малий об’єкт не наближається до великого і не віддаляється від нього, то діючі на цей об’єкт гравітаційна сила F_гр=GМm/r² та сила інерції F_i=ma_д=mv²/r, динамічно зрівноважують одна одну: GМm/r² = mv²/r, звідси GМ/r = v². Виходячи з того, що за той час який називається періодом обертання (t=Т), малий об’єкт робить один повний оберт навколо великого, тобто проходить шлях ℓ=2πr, можна записати v=ℓ/t=2πr/T. А це означає, що GМ/r = v²= (2πr/T)²= 4π²r²/T², звідси М(Т²/r³)= 4π²/G. А враховуючи, що 4, π, G, M – величини постійні, можна записати Т²/r³ = const.

Таким чином, у повній відповідності з законами ньютонівської механіки, в тій системі де малий (малий за відносною масою) космічний об’єкт обертається навколо великого (великого за відносною масою) об’єкту, відношення квадрату періоду обертання малого об’єкту Т², до кубу довжини великої піввісі його орбіти а³ (для колової орбіти ця довжина дорівнює радіусу орбіти а³=r³), є постійною величиною: Т²/а³=const.

Ньютонівська механіка не лише підтверджує достовірність того експериментально встановленого співвідношення, яке називається третім законом Кеплера (Т²/а³=const), а й суттєво уточнює цей закон. Адже у відповідності з ньютонівською механікою власне постійною величиною є М(Т²/а³) = 4π²/G = const, де М – загальна маса системи тіл (М+m). Іншими словами, у відповідності з законами ньютонівської механіки, уточненим варіантом третього закону Кеплера є формула (М+m)(Т²/r³) =4π²/G =const.

По суті це означає, що в системі Сонце – планети (планета – її супутники, Земля – Місяць, тощо), всі об’єкти певним чином обертаються навколо спільного центру мас. Інша справа, що цей центр мас дуже близький до центру мас Сонця і тому обертання Сонця навколо спільного центру мас Сонячної системи є практично непомітним. А тим більше в ситуації коли навколо Сонця обертається не одна планета, а певна збалансована сукупність планет та інших космічних об’єктів.

Певною ілюстрацією факту того, що в системі гравітаційно пов’язаних космічних об’єктів, навколо спільного центру мас певними комбінаціями еліптично кругових траєкторій, рухаються всі об’єкти системи, є траєкторія руху системи Земля – Місяць навколо Сонця. Бо коли ми стверджуємо, що Земля певною еліптичною орбітою обертається навколо Сонця, а Місяць обертається навколо Землі, то це не зовсім відповідає дійсності. Адже фактично і Земля і Місяць певним чином обертаються навколо центру мас системи Земля – Місяць. А цей центр знаходиться на відстані х_с = mr/(M+m) = 4650 км від центру Землі. По суті це означає, що траєкторія руху Землі навколо Сонця не є строго еліптичною, а представляє собою певну комбінацію еліпса та кругових коливань, радіус яких 4650 км, а періодичність 27,3 доби (мал.62). Інша справа, що в масштабі руху Землі навколо Сонця, місячні коливання траєкторії цього руху є мізерно малими. Однак ви маєте знати, що такі коливання існують і що за певних обставин мають бути врахованими.

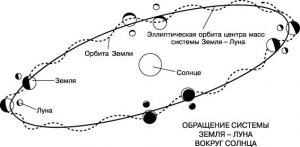
Мал.62. Загальна картина траєкторії руху системи Земля – Місяць навколо Сонця.

Завершуючи розмову про ньютонівську механіку і про те, як вона пояснює загальний устрій Сонячної системи, важливо ще раз наголосити на тому, що ньютонівська механіка є класичним прикладом наукової теорії, тобто такої цілісної системи знань, яка на основі малої кількості достовірних базових тверджень, пояснює незліченну кількість споріднених явищ. Скажімо закони Кеплера визначали декілька конкретних співвідношень які характеризують рух планет Сонячної системи навколо Сонця. При цьому визначали без пояснення того, чому ці співвідношення існують. Ньютонівська ж механіка не лише кількісно описала механічну поведінку цих планет, а й пояснила причини такої поведінки. Більше того, ньютонівська механіка описувала і пояснювала механічну поведінку незліченної кількості об’єктів та їх систем починаючи від атомів, молекул, піщинок, камінців та м’ячів, і закінчуючи планетами, кометами, астероїдами, зірками і галактиками. Починаючи від простих механізмів як то важелі, шківи та похилі площини, і закінчуючи механікою автомобілів, літаків та океанських лайнерів. Починаючи від механіки дитячих іграшок і закінчуючи механікою планетарних систем, галактик та систем галактик. І все це різноманіття пояснювалось на основі декількох простих базових тверджень: трьох законів Ньютона та закону всесвітнього тяжіння.

Контрольні запитання.

1. Чому ми стверджуємо, що три закони Ньютона це система взаємопов’язаних та взаємодоповнюючих тверджень?
2. Що стверджується в законі всесвітнього тяжіння?
3. Що показує гравітаційна стала (G=6,67∙10^–11Н∙кг²/м²)?
4. Чому в побутовій практиці гравітаційні сили є мізерно малими, а в масштабах космічних взаємодій – фантастично великими?
5. Яку силу називають силою інерції?
6. Відомо, що Місяць з величезною гравітаційною силою притягується до Землі. Чому ж він не падає на Землю?
7. Поясніть загальний устрій та «принцип дії» Сонячної системи.
8. Поясніть чому в процесі обертання навколо Сонця, Земля здійснює певні коливання відносно еліптичної траєкторії руху? Який період цих коливань?
9. Що відбуватиметься з Місяцем при: а) збільшенні швидкості його руху; б) зменшенні цієї швидкості?
10. Поясніть в чому відмінність між законами Кеплера та теорією Ньютона?

Вправа 9.

1. Визначте силу гравітаційної взаємодії між Землею та Сонцем, якщо відомо що відстань між ними 1,5∙10¹¹м, а їх маси відповідно 6∙10²⁴кг і 2∙10³⁰кг.
2. Знаючи період обертання Землі навколо Сонця (365 діб) та відстань до нього (1,49∙10¹¹м), визначити масу Сонця.
3. Знаючи період обертання Місяця (27,3доби) та відстань до нього (3,84∙10⁸м), визначити масу Землі.
4. Знаючи радіус Землі (6,37·10⁶м) та прискорення вільного падіння на ній (9,8м/с²) визначте масу Землі. Порівняйте отриманий результат з результатом попередньої задачі. Зробіть висновок.
5. Знаючи прискорення вільного падіння (g=1,6м/с²) та радіус (R=1,74∙10⁶м) Місяця, визначити масу Місяця та його середню густину.
6. На якій відстані від поверхні Землі сила притягування космічного корабля до Землі буде у 100 разів меншою ніж на її поверхні?
7. При якій тривалості доби, вага тіла на екваторі Землі буде у два рази менше ніж на полюсі?

.

Тема 2. Загальні відомості про методи та засоби астрономічних досліджень.

§10. Визначення відстаней до космічних об’єктів. Одиниці вимірювання космічних відстаней.

Планети, зірки і галактики, знаходяться на таких недосяжно великих відстанях від Землі, що мимоволі виникає питання: «А яким чином вчені вимірюють ці відстані?» Що ж, давайте поговоримо про те, як вимірюються космічно великі відстані.

Найбільш очевидні, прості та достовірні методи вимірювання відстаней до космічних об’єктів, базуються на застосуванні загальновідомих геометричних співвідношень. Наприклад загальновідомо, що в прямокутному трикутнику (мал.63а), синусом кута α називають відношення протилежного цьому куту катета (а) до гіпотенузи (с), тобто sinα=а/с. Звідси випливає, що с=а/sinα. Власне на застосуванні цього простого співвідношення і побудовані найбільш прості та достовірні методи вимірювання відстаней до недосяжних космічних об’єктів. Дійсно, спостерігаючи за далеким космічним об’єктом S з точок Т і С відстань між якими (а) є відомою (мал.63б), та вимірявши величина того кута π який утворюють відповідні лінії зору, можна визначити відстань до цього об’єкту: r=а/sinπ.

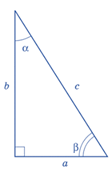
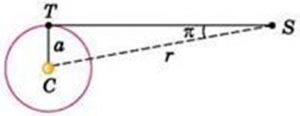
Мал.63. Вимірявши відстань (а) між точками Т і С, та величину кута π між тими лініями вздовж яких об’єкт S видно з точок Т і С, відстань до цього об’єкту  визначають за формулою r=а/sinπ.

Таким чином, визначення відстані до недосяжно далекого об’єкту, зводиться до вимірювання величини того кута під яким цей об’єкт видно з двох базових точок, відстань між якими є відомою. В астрономічній практиці, величину того кута під яким космічний об’єкт видно з двох базових точок, прийнято називати паралактичним зміщенням об’єкту, або паралаксом (від грец. parallaxis – відхилення, зміщення), позначається π (р).

Варто зауважити, що в реальних астрономічних вимірюваннях, величина паралаксу значно менша одного кутового градуса і вимірюється в кутових хвилинах 1ʹ=1º/60, або в кутових секундах 1ʺ=1ʹ/60=1º/3600. Ясно, що для таких мізерних кутів, відстані ТS і СS (мал.63б) є практично однаковими. Важливим є лише те, щоб той базовий відрізок (а) на основі якого визначається відстань до космічного об’єкту (r=а/sinπ), був перпендикулярним до того напрямку в якому знаходиться об’єкт.

Зазвичай відстані до відносно не далеких космічних об’єктів, зокрема планет Сонячної системи, визначають наступним чином. Спостерігаючи за цим об’єктом з двох віддалених обсерваторій А і В (наприклад таких, відстань між якими дорівнює усередненому радіусу Землі а=R=6,37∙10⁶м), вимірюють кут паралактичного зміщення цього об’єкту π. При цьому відстань до об’єкту, визначається за формулою  ℓ=R/sinπ.

Той кут паралактичного зміщення (паралакс) під яким видно космічний об’єкт з двох точок відстань між якими дорівнює радіусу Землі, а напрям між ними є перпендикулярним до напрямку на даний об’єкт, називають геоцентричним (добовим, горизонтальним)  паралаксом (від грецького, geos – Земля). Наприклад геоцентричний паралакс Місяця 57ʹ = 3420”, а Сонця 8,8ʺ.

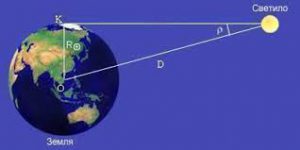
Мал.64. Визначаючи відстань до планет Сонячної системи, в якості базової відстані, обирають відстань, яка дорівнює радіусу Землі (6,37∙10⁶м)

Для визначення геоцентричного (добового) паралаксу певного космічного об’єкту, зовсім не обов’язково узгоджено спостерігати за цим об’єктом з двох різних точок Землі. Достатньо використати факт добового обертання Землі і для різних моментів доби визначати паралактичне зміщення відповідного об’єкту.

Власне до створення системи взаємопов’язаних обсерваторій, геоцентричні (добові) паралакси космічних об’єктів  визначали саме шляхом вимірювання їх паралактичного зміщення для різних моментів доби. А це вимірювання полягало в наступному. Кутовий напрямок на відповідний об’єкт визначали двічі на добу, наприклад опівночі і через шість годин. За цей час (чверть доби), Земля робить чверть оберту і тому відстань між точками спостережень фактично дорівнює радіусу Землі. Визначивши різницю між напрямками виміряними опівночі і через шість годин, отримували той добовий паралакс (π), базовою відстанню для якого є радіус Землі (R=6,37∙10⁶м). При цьому відстань до космічного об’єкту визначалася за формулою ℓ=R/sinπ.

Можна довести, що для гранично малих та виміряних в кутових секундах кутів, виконується співвідношення sinπ = πʺsin1ʺ. А зважаючи на те, що sin1ʺ=1/206265 можна записати ℓ = R/sinπ = 206265∙R/πʺ, де R = 6,37·10⁶м – радіус Землі, πʺ – виміряний в кутових секундах геоцентричний (добовий) паралакс відповідного космічного об’єкту. Наприклад, якщо добовий паралакс Місяця 57ʹ = 3420”, а Сонця 8,8ʺ, то відстань від центру Землі до центру Місяця дорівнює ℓ=(206265/3420)R = 60,3R = 384·10⁶м= 3,84·10⁸м, а відстань від центру Землі до центру Сонця ℓ = (206265/8,8)R = 23439R = 1,5·10¹¹м.

Потрібно зауважити, що той кут який називають геоцентричним (добовим) паралаксом, не є тим кутом який характеризує видимі розміри космічного об’єкту і який називається кутовим розміром (діаметром) цього об’єкту. Кутовим розміром (діаметром) космічного об’єкту, називають той кут вершиною якого є очі спостерігача і який знаходиться між тими прямими які проходять через крайні точки об’єкту спостережень (мал.65). Наприклад вимірювання показують, що усереднені кутові розміри Сонця і Місяця є майже однаковими: для Сонця 32′, для Місяця 31′.

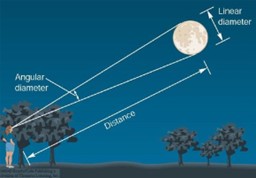
Мал.65. Видимі з Землі розміри космічного об’єкту характеризує величина яка називається кутовим розміром (діаметром) цього об’єкту.

Добовий (геоцентричний)  паралакс застосовується для вимірювання відстаней в межах Сонячної системи. Якщо ж мова йде про ті об’єкти які знаходяться за межами Сонячної системи, то їх добовий паралакс такий мізерно малий, що практично не підлягає експериментальному вимірюванню. Для визначення відстаней до тих космічних об’єктів які знаходяться за межами Сонячної системи, застосовують метод так званого річного (геліоцентричного) паралаксу. В цьому методі, базовою довжиною є не радіус Землі (а = R = 6,37∙10⁶м), а усереднена відстань між центрами Землі і Сонця (а = 1,5∙10¹¹м), цю відстань називають астрономічною одиницею. Астрономічна одиниця – це позасистемна одиниця вимірювання довжини, яка дорівнює усередненій відстані між центрами мас Сонця та Землі: 1а.о.=1,49597870∙10¹¹м = 1,5∙10¹¹м.

Той кут паралактичного зміщення (паралакс) під яким видно космічний об’єкт з тих точок відстань між якими дорівнює одній астрономічній одиниці, а напрям між ними є перпендикулярним до напрямку на даний об’єкт, називають річним (геліоцентричним) паралаксом (від грецького, helios – Сонце).

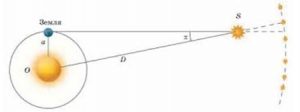
Мал.66. Визначаючи відстань до зірок нашої Галактики, в якості базової відстані обирають усереднену відстань між центрами Землі і Сонця (1,5∙10¹¹м)

Технологія вимірювання відстані до космічного об’єкту шляхом визначення річного паралаксу цього об’єкту, полягає в наступному. Вимірявши в кутових секундах річний паралакс (π”) відповідного об’єкту, та маючи на увазі, що базою вимірювань є одна астрономічна одиниця а = 1а.о. = 1,5∙10¹¹м, і що sinπ = πʺsin1ʺ = π”/206265, відповідну відстань визначають за формулою  ℓ = а/sinπ = (206265/π”)∙а.о. Наприклад річний паралакс найближчої до Сонячної системи зірки (Альфа Центавра) становить 0,762ʺ. А це означає, що відстань до цієї зірки дорівнює ℓ = (206265/0,762)∙а.о = 270689а.о. = 270689∙1,5·10¹¹м = 4,05·10¹⁶м.

Оскільки в астрономічній практиці відстані до зірок визначають шляхом вимірювання їх річного паралаксу, а величину цього паралаксу виражають в кутових секундах, то в астрономії часто застосовується спеціальна одиниця довжини, яка називається парсек (від паралакс та секунда). Парсек – це позасистемна одиниця вимірювання довжини, яка дорівнює такій відстані до космічного об’єкту, при якій для базисної відстані в одну астрономічну одиницю (а=1,5∙10¹¹м), кут паралактичного зміщення цього об’єкту дорівнює одній кутовій секунді (π=1″). 1пк = 1а.о./sin1ʺ = 206265а.о. = 206265∙1,5∙10¹¹ = 3,1∙10¹⁶м.

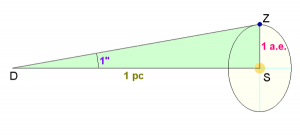
Мал.67. Парсек дорівнює такій відстані до космічного об’єкту, при якій для базової відстані в одну астрономічну одиницю, кут паралактичного зміщення цього об’єкту дорівнює одній кутовій секунді.

Втім, якщо мова йде про загально наукову практику, то в ній космічні відстані зазвичай вимірюють не в астрономічних одиницях і не в парсеках, а в світлових роках. Світловий рік – це позасистемна одиниця вимірювання довжини, яка дорівнює тій відстані яку проходить світло у вакуумі за один рік: 1св.р = с·Т = 3∙10⁸(м/с)∙365∙60∙60(с) = 9,46∙10¹⁵м. Таким чином в астрономії, в залежності від ситуації та контексту, ви можете зустріти різні одиниці вимірювання довжини, зокрема:

1а.о. = 1,5·10¹¹м;

1пк = 206265а.о.= 3,26св.р. = 3,1∙10¹⁶м;

1св.р. = 0,307пк = 63240а.о. = 9,46∙10¹⁵м.

Не важко збагнути, що на практиці максимальною базовою відстанню для паралактичних вимірювань є не 1а.о, а 2а.о. Адже якщо наприклад, кутове положення зірки буде зафіксовано спочатку 21 червня, а потім 21 грудня, тобто рівно через півроку, то базовою відстань дорівнюватиме 2а.о.= 2∙1,5∙10¹¹м. При цьому відповідний паралакс буде вдвічі більшим за той, який прийнято називати річним паралаксом. Наприклад якщо річний паралакс найяскравішої зірки нічного неба (Сіріус) дорівнює 0,308”, то подвійна величина цього паралаксу становитиме 0,616”. І це при тому, що Сіріус, це одна з найближчих до нас зірок. Якщо ж говорити про більш віддалені зірки нашої Галактики, то їх річні паралакси вимірюються сотими і тисячними частинами кутової секунди. По суті це означає, що метод річного паралаксу дозволяє вимірювати відстані лише в межах нашої Галактики. Для вимірювання міжгалактичних відстаней застосовують інші методи, зокрема фотометричний метод.

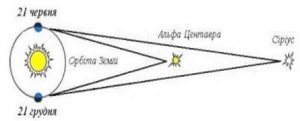
Мал.68. Максимальною базовою відстанню для річного паралаксу є 2а.о.

Фотометричний метод вимірювання відстаней базується на факті того, що видима яскравість (L) джерела світла, а по суті кількість тієї світлової енергії яка потрапляє в око спостерігача, обернено пропорційна квадрату відстані до цього джерела (закон фотометрії). Наприклад, якщо на відстані r₁ яскравість певного джерела світла (свічки, лампочки розжарювання, зірки, тощо) дорівнює L₁, а на відстані r₂, ця яскравість зменшилася у двадцять п’ять разів L₂ = L₁/25, то це означає, що відстань до джерела світла збільшилася у √25=5 разів (r₂ = 5r₁).

В реальності фотометричний метод вимірювання відстаней до космічних об’єктів працює наступним чином. На основі аналізу певної сукупності фактів, вчені складають перелік схожих за реальною світловою потужністю об’єктів, наприклад таких як надмасивні червоні гіганти, світлова потужність яких в десятки тисяч разів більша за потужність Сонця. Знаючи що в нашій Галактиці відстань до такого гіганта 25∙10³св.р. і що в сусідній галактиці яка називається Андромеда, яскравість схожого гіганта у 10000 разів менша, ми робимо висновок про те, що відстань до цього гіганта, а відповідно і Андромеди, в √10000 = 100 разів більша, а отже дорівнює 2,5∙10⁶св.р. Далі, фотометричні вимірювання показують, що світлова яскравість іншої схожої на Андромеду галактики в 100 разів менший. А це означає, що відстань до цієї галактики в √1000=31,6 разів більша аніж до Андромеди, і становить 79∙10⁶св.р.

Мал.69. При фотометричному методі, відстані до однакових за світловою потужністю об’єктів, визначають на основі аналізу їх видимої яскравості.

Ясно, що фотометричний метод вимірювання відстаней не є безумовно точним. Адже його точність визначальним чином залежить від однаковості тих джерел світла, відстані до яких вимірюються. Всі ж зірки, а тим більше галактики є індивідуальними. Тому вчені орієнтуються на певні усереднені параметри певних класів зірок і галактик. А це неминуче призводить до певних похибок вимірювань.

Втім, одним з базових принципів наукових вимірювань, є принцип перехресності вимірювань. Суть цього принципу полягає в тому, що певну величину вимірюють різними методами. При цьому, якщо результати вимірювань співпадають, то це безумовно вказує на те, що ці результати є достовірними. Якщо ж результати вимірювань суттєво відрізняються, то це вказує на відповідну похибку вимірювань. Скажімо, існує багато методів фотометричних вимірювань космічних відстаней. Ці методи відрізняються тим, що в кожному з них, в якості базового (індикаторного) джерела світла, обрано своє характерне джерело. Зокрема такими джерелами є:

– зорі головної послідовності;

– візуально подвійні зорі;

– затемнено подвійні зорі;

– змінні зорі типу RR Ліри;

– найяскравіші червоні гіганти;

– квазари;

– кулясті скупчення;

– флуктуації поверхневої яскравості;

– міжзоряні мазери;

– цефеїди;

– наднові зірки, тощо.

Зважаючи на ці обставини, відстань до тієї чи іншої галактики вимірюють різними фотометричними методами. А результати вимірювань порівнюють та роблять відповідні висновки.

Ще одним достатньо точним та перспективним методом вимірювання відстаней до далеких та наддалеких космічних об’єктів, є метод який базується на явищі червоного зміщення в спектрі далеких галактик та законі Хаббла.

Нагадаємо, в 1842 році австрійський фізик Христіан Доплер з’ясував: частотні параметри будь яких хвиль, в тому числі і світлових, певним чином залежать як від швидкості та напрямку руху джерела цих хвиль, так і від швидкості та напрямку руху того спостерігача який їх фіксує. Наприклад якщо зірка (мал.70) наближається до спостерігача, то відносно спостерігача довжина тих світлових хвиль які вона випромінює буде зменшуватись. При цьому спектральні лінії світла будуть зміщуватися в сторону фіолетового випромінювання. Якщо ж зірка віддаляється від спостерігача, то відносно спостерігача довжина тих світлових хвиль які вона випромінює збільшується, а спектральні лінії світла зміщуються в сторону червоного випромінювання. Умовно кажучи, якщо та зірка яка випромінює зелене світло віддаляється від спостерігача, то спостерігач сприйме її світло як червоне, а якщо зірка наближається до спостерігача, то для спостерігача її світло буде синім.

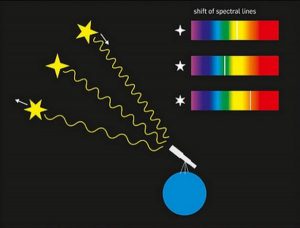
Мал.70. При віддалені джерела світла, лінії його спектру зміщуються в сторону червоного кольору, а при наближені – в сторону фіолетового кольору.

Одним з найвідоміших  проявів ефекту Доплера є так зване червоне зміщення в спектрі галактик. В 1929 році американський астроном Едвін Хаббл (1889–1953) звернув увагу на те, що в спектрі того світла яке випромінюють далекі галактики, спектральні лінії відомих атомів зміщені в сторону червоного кольору (мал.71). Це явище назвали червоним зміщенням в спектрі галактик.

Мал.71. В спектрі далеких галактик всі спектральні лінії зміщенні в сторону червоної частини спектру.

Пояснюючи даний факт, Хаббл дійшов висновку: причиною червоного зміщення в спектрі галактик є ефект Доплера. А у відповідності з цим ефектом, якщо те джерело світла що випромінює хвилі з довжиною λ₀, з швидкістю v рухається відносно спостерігача, то спостерігач сприйме це світло як таке, що має довжину хвилі λ = λ₀(1–v/c), де с=3·10⁸м/с – швидкість поширення світла. А це означає, що вимірявши відповідні довжини хвиль (λ; λ₀), швидкість руху джерела світла можна визначити за формулою v = c(λ₀ – λ)/λ₀. Наприклад якщо космічний об’єкт випромінює світло з довжиною хвилі 600нм, а земний спостерігач сприймає ці хвилі як такі, що мають довжину 602нм, то відносна швидкість цього об’єкту v = 3·10⁸(600 – 602)/600 = –1∙10⁶м/с = – 1∙10³км/с, де знак « – » вказує на те, що об’єкт віддаляється.

Подальші дослідження показали, що навколишні галактики віддаляються від нашої та одна від одної. При цьому, розрахунки та вимірювання показують: швидкість взаємного віддалення галактик (v), пропорційна відстані (ℓ) між ними і може бути визначеною за формулою  v = H₀ℓ, де H₀ = 67 (км/с)/Мпк – постійна величина, яка називається сталою Хаббла (закон Хаббла),

Таким чином, суть того методу визначення відстані до наддалеких космічних об’єктів, який базується на застосування червоного зміщення в спектрі цих об’єктів та законі Хаббла, полягає в наступному. За величиною червоного зміщення в спектрі наддалекого космічного об’єкту, визначають швидкість руху цього об’єкту: v = c(1 – λ/λ₀). А знаючи цю швидкість, за законом Хаббла визначають відстань до відповідного об’єкту: ℓ = v/H₀. Наприклад якщо певна галактика з швидкістю 1000км/с віддаляється від нашої Галактики, то відстань до цієї галактики ℓ = v/H₀ = 1000(км/с)/67(км/с)/Мпк = 14,9Мпс = 14,9·10⁶пс = 48,6·10⁶св.р.

Контрольні запитання.

1. Що вимірюють при визначенні відстані до недосяжно далекого об’єкту? За якою формулою визначають цю відстань?
2. Що називають паралактичним зміщенням (паралаксом) космічного об’єкту? В чому вимірюють це зміщення?
3. Що називають геоцентричним (добовим) паралаксом? Як вимірюють цей паралакс?
4. Як методом добового паралаксу можна виміряти відстань до Сонця?
5. Що називають кутовим розміром космічного об’єкту? Як визначається і чому дорівнює кутовий розмір Сонця?
6. Що називають геліоцентричним (річним) паралаксом? Як вимірюється цей паралакс?
7. Що називають парсеком і чому він дорівнює?
8. Чому методом річного паралаксу практично не можливо визначити відстань до тих об’єктів які знаходяться за межами нашої Галактики?
9. Поясніть суть фотометричного методу вимірювання відстаней.
10. Поясніть суть принципу перехресного вимірювання.
11. Що називають червоним зміщенням в спектрі галактик? Що означає це зміщення?
12. Поясніть суть того методу визначення відстані до наддалекого космічного об’єкту, який базується на вимірюванні червоного зміщення цього об’єкту.

Вправа 10.

1.Відомо, що середня відстань від Землі до Сонця 1,5·10¹¹м. Виразіть цю відстань в астрономічних одиницях, світлових роках та парсеках.

2. Відомо, що відстань до найяскравішої зірки нічного неба 7,75пк. Виразіть цю відстань в кілометрах, астрономічних одиницях та світлових роках.
3. Добовий паралакс Юпітера 1,7”. Яка відстань до Юпітера? Виразіть цю відстань в кілометрах, астрономічних одиницях, світлових роках та парсеках.
4. Річний паралакс Полярної зірки 0,0075”. Яка відстань до цієї зірку? Виразіть цю відстань в кілометрах, астрономічних одиницях, світлових роках та парсеках.
5. Певна галактика віддаляється від нашої з швидкістю 2000км/с. Визначте відстань до цієї галактики. Виразіть цю відстань парсеках і світлових роках.

.

§11. Спектральний аналіз – базовий метод космічних досліджень.

Не буде перебільшенням сказати, що близько 99% тієї інформації яку ми отримуємо про космічні об’єкти, надходить з тим світлом яке випромінюють ці об’єкти, а точніше кажучи – з тими електромагнітними хвилями, сукупність яких і утворює відповідне світло. Адже ті електромагнітні хвилі які випромінюють об’єкти Всесвіту, є відображенням тих подій які відбувалися і відбуваються у Всесвіті починаючи від механічних переміщень галактик, зірок, планет та їх фрагментів і закінчуючи тими подіями які відбуваються в атомах, атомних ядрах та тих частинках з яких ці ядра складаються.

А це означає, що ті електромагнітні хвилі які заповнюють Всесвіт є невичерпним джерелом об’єктивної інформації про цей Всесвіт. Основним же способом отримання цієї інформації є так званий спектральний аналіз. Власне про суть цього аналізу ми і поговоримо в даному параграфі. Зауважимо тільки, що говорячи про світло, будемо мати на увазі увесь спектр електромагнітних хвиль, починаючи від радіохвиль та інфрачервоного випромінювання і закінчуючи видимим світлом, ультрафіолетовим, рентгенівським та гамма випромінюванням.

Пропускаючи вузький пучок світла через склянну трьохгранну призму, Ньютон спостерігав фантастично дивовижну подію: перетворення чистого безбарвного світла на прекрасну райдужну картинку. Факт того, що всі ці райдужні кольори дивовижним чином виникали із звичайного безбарвного світла, став підставою для того, щоб цю райдужно кольорову картинку назвати спектром, що в змістовному перекладі означає дивовижне мариво (від лат. spektrum – мариво).

Мал.72. При проходжені через трьохгранну призму світло розкладається на його складові кольори (спектр світла).

Подальші дослідження показали, що видиме світло представляє собою потік електромагнітних хвиль довжини яких знаходяться в межах від 380нм до 760нм. При цьому кожній довжині хвилі відповідає певний колір зорових відчуттів людини. Неперервний спектр цих кольорів умовно розділяють на сім основних: червоний, оранжевий, жовтий, зелений, голубий, синій, фіолетовий. Ті ж електромагнітні хвилі довжини яких більші за 760нм називають інфрачервоними, а ті довжини яких менші за 380нм, називаються ультрафіолетовими.

Мал.73. Видиме світло, це одна з різновидностей електромагнітних хвиль, довжини яких знаходяться в межах від 380нм до 760нм.

Про те, як отримують ті кольорові картинки які називаються спектром світла, якими бувають спектри, як вони утворюються та яку інформаціє в собі містять, ви знаєте з того розділу фізики який називається «Оптика». Тому стисло повторимо раніше вивчене.

За ознакою того, випромінює речовина світло чи поглинає його, спектри поділяються на спектри випромінювання і спектри поглинання. При цьому, якщо даний спектр характеризує параметри того світла яке випромінюється тим чи іншим об’єктом, то цей спектр називають спектром випромінювання. Наприклад ті спектри які створюють нагріта спіраль лампочки розжарювання (мал.74а) та нагрітий до високої температури газ гелій (мал.74б), є спектрами випромінювання. Якщо ж спектр характеризує параметри того світла яке поглинається тим чи іншим об’єктом, то такий спектр називають спектром поглинання. Наприклад, якщо через шар холодного гелію (мал.74в) пропустити біле світло (світло повного спектрального складу), то в достатньо якісному спектроскопі, можна побачити певний набір тонких темних ліній. Сукупність цих темних ліній і є спектром поглинання гелію.

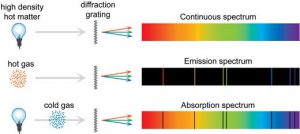
Мал.74. Спектри паділяються на спектри випромінювання і спектри поглинання.

В 1859 році, німецький фізик Густав Кірхгоф (1824–1887) з’ясував, що спектри випромінювання та поглинання будь якої речовини є взаємно оберненими. Це означає, що коли нагріта речовина випромінює певний набір електромагнітних хвиль, то в холодному стані, вона поглинає точно такий же набір хвиль. Наприклад зображений на мал.75б лінійчатий спектр, є спектром випромінювання атомів гелію, а лінійчатий спектр на мал.75в, є спектром поглинання атомів гелію. І ці спектри взаємно обернені.

За загальним виглядом спектральної картинки, спектри поділяються на суцільні, лінійчаті і смугасті. Суцільним спектром випромінювання називають такий спектр, який представляє собою суцільну спектральну картинку яка складається з усіх спектральних кольорів видимого світла (мал.74а). Дослідження показують, що всі тверді та рідкі тіла, а також гази високої густини (наприклад такої як поверхня Сонця), будучи нагрітими до достатньо високих температур, випромінюють світло суцільного спектру. При цьому, спектральний склад цього світла не залежить ні від хімічного складу речовини, ні від її агрегатного стану, ні від її сруктурного устрою.

Факт того, що розжарені тверді та рідкі тіла, а також гази високої густини, випромінюють повний набір електромагнітних хвиль, є цілком закономірним. Адже мова йде про тіла з надзвичайно великою концентрацією частинок речовини. Частинок, які в процесі інтенсивного теплового, а отже хаотичного руху, випромінюють хвилі всіх можливих довжин (частот). Іншими словами, суцільний спектр випромінювання є результатом інтенсивного хаотичного руху величезної кількості щільно упакованих заряджених частинок.

Лінійчатим спектром випромінювання називають такий спектр, який представляє собою певний набір тонких спектральних ліній. Лінійчаті спектри дають системи обособлених енергетично збуджених атомів, зокрема розріджені пари та гази атомарного складу. При цьому, кожна різновидність атомів, дає свій неповторний лінійчатий спектр. Даний факт пояснюється тим, що лінійчатий спектр є відображенням тих процесів які відбуваються в енергетично збудженому атомі. А оскільки внутрішній устрій хімічно різних атомів є різним, то відповідно різними є і їх спектральні зображення.

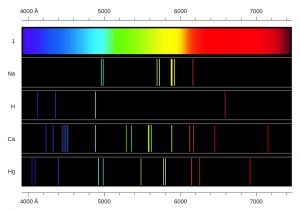
Мал.75. Кожна різновидність атомів дає свій неповторний лінійчатий спектр.

Смугастим спектром випромінювання називають такий спектр, який представляє собою певний набір відносно широких спектральних смужок, кожна з яких в свою чегу, складається з великої кількості тонких, близько розташованих спектральних ліній. Іншими словами, смугастий спектр – це складна різновидність лінійчатого спектру. Смугасті спектри дають системи обособлених, енергетично збуджених молекул, зокрема розріджені газа молекулярного складу. При цьому, кожна різновидність молекул дає свій неповторний смугастий (складний лінійчатий) спектр. Адже цей спектр є відображенням тих складних процесів які відбуваються у відповідних молекулах.

Мал.76. Кожна різновидність молекул дає свій неповторний смугастий (складний лінійчатий) спектр.

Факт того, що кожна речовина має свій неповторний спектральний відбиток, лежить в основі так званого спектрального аналізу. Спектральний аналіз, це метод визначення хімічного складу речовини та інших її параметрів, на основі аналізу лінійчатого спектру цієї речовини. (Відразу ж зауважимо: оскільки смугастий спектр є складною різновидністю лінійчатого спектру, то в подальшому ці спектри ми будемо називати лінійчатими). Суть спектрального аналізу полягає в наступному. Від об’єкту досліджень, отримують лінійчатий спектр випромінювання або поглинання. Аналізують склад, яскравість та особливості даного спектру і на основі цього аналізу роблять відповідні висновки. Зокрема, за набором характерних спектральних ліній, визначають якісний склад речовини, тобто загальну сукупність наявних в ній атомів і молекул. За яскравістю цих ліній, визначають кількісний склад речовини. За зсувом спектральних ліній, визначають швидкість та напрям руху відповідного об’єкту, тощо.

Класичною ілюстрацією можливостей спектрального аналізу є історія відкриття гелію – хімічного елементу, який в таблиці хімічних елементів займає позицію №2. Ця історія показова тим, що гелій відкрили не на Землі, а на Сонці. Як відомо, гелій відноситься до числа так званих інертних газів. Це означає, що гелій практично не проявляє себе в жодній хімічній реакції. Хімічний же аналіз базується на аналізі результатів тих реакцій які відбуваються з тими чи іншими атомами (молекулами). А якщо такі реакції не відбуваються, то для хіміків відповідні атоми просто не існують.

В 1868 році, аналізуючи отриманий в момент повного сонячного затемнення, лінійчатий спектр сонячної атмосфери (сонячної корони), вчені звернули увагу на те, що в цьому спектрі є декілька яскравих ліній, які не відповідали жодному з відомих на той час атомів. Це означало, що до складу сонячної атмосфери, а отже і до складу Сонця, входить якийсь невідомий хімічний елемент.  Цей відкритий на Сонці елемент, назвали гелієм, тобто – сонячним (від грец. helios – Сонце). Лише в 1895 році, тобто через 27 років після відкриття на Сонці, вченим вдалося відшукати гелій і на Землі. Загалом же, методами спектрального аналізу було відкрито близько 30 хімічних елементів, зокрема всі інертні гази, цезій, іридій, рубідій, талій та інші.

Тому коли наука стверджує, що фотосфера Сонця складається з водню(73,46%), гелію(24,85%), кисню (0,77%), вуглецю(0,29%), заліза(0,16%), неону(0,12%), азоту(0,09%), кремнію(0,07%), магнію(0,05%), сірки(0,04%) та незначної кількості (0,1%) інших елементів, коли наука з впевненістю говорить про хімічний склад планет, комет, зірок та недосяжних галактик, то ви маєте знати, що всі ці точні цифри і відсотки, це результат спектрального аналізу того світла яке випромінюють або поглинають відповідні об’єкти. І не вірити цим результатам, це ніби не вірити в реальність існування тих атомів які були відкриті методами спектрального аналізу.

Спектральний аналіз вигідно відрізняється від традиційних методів хімічного аналізу. До числа його безумовних переваг відносяться:

1. Надзвичайно висока чутливість і точність. Чутливість сучасного спектрального аналізу така, що дозволяє виявити речовину навіть в тому випадку коли її концентрація не перевищує 10^–11г/см³.
2. Спектральний аналіз дозволяє точно визначати хімічний склад тих об’єктів які знаходяться на недосяжно великих відстанях, наприклад таких як Сонце, зірки, галактики, космічні туманності, тощо.
3. Спектральний аналіз є гранично універсальним методом досліджень, який дозволяє визначати хімічний склад практично будь якої речовини, починаючи від простих неорганічних речовин і закінчуючи надскладними біологічними структурами.
4. Спектральний аналіз дозволяє розрізняти навіть такі атоми, які методами хімічного аналізу розрізнити практично неможливо. Ці різновидності хімічно однакових атомів називають ізотопами.
5. Спектральний аналіз дозволяє визначати не лише хімічний склад того чи іншого об’єкту, а й його температуру, параметри руху, параметри кристалічної структури, внутрішній устрій атомів, тощо.
6. Спектральний аналіз характеризується високою технологічністю, сумісністю з електронними системами обчислень, аналізу та управління, високою швидкістю проведення аналізу, відносно низькою собівартістю, надійністю та іншими чеснотами.

Те світло яке ми отримуємо від недосяжно далеких космічних об’єктів, містить інформацію про величезну кількість параметрів цих об’єктів і зокрема про температуру їх поверхні.  Наприклад температура поверхні Сонця близька до 5800К. При цій температурі, пік тієї кривої яка описує розподіл енергії в спектрі світла, припадає на ту зону в якій практично рівномірно представлені всі хвилі спектру видимого світла (мал.77б). А ці хвилі у своїй сукупності і дають те біло-жовте світло яким світить Сонце. При зменшені температури поверхні (мал.77а), пік кривої розподілу енергії зміщується в сторону червоного кольору. Якщо ж температура поверхні збільується (мал.77в), то пік кривої розподілу енергії зміщується в сторону синього кольору, що відповідно змінює і колір поверхні.

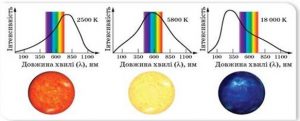
Мал.77. Загальний колір того світла що дає суцільний спектр, певним чином залежить від температури джерела світла.

А потрібно зауважити, що температура поверхні зірки, це надзвичайно важливий, та ємкий параметр відповідної зірки. Адже температура поверхні зірки, є результатом тих подій які відбуваються в її надрах. А ці події залежать від маси зірки, яка в свою чергу визначає тривалість життя зірки, її теперішнє, минуле і майбутнє. Іншими словами, загальний колір зірки, певним чином пов’язаний не лише з температурою її поверхні та надр, а й з масою зірки, тривалістю життя, а зрештою –  з минулим та майбутнім зірки.

Спектральний аналіз дозволяє визначати не лише хімічний склад та температуру відповідного космічного об’єкту, а й параметри його руху, зокрема величину та напрям швидкості руху, величину та напрям обертання, тощо. А ці параметри визначаються на основі факту того, що в залежності від величини та напрямку швидкості руху об’єкту, спектральні лінії того світла яке випромінює цей об’єкт відповідним чином зміщуються. Наприклад, якщо те джерело світла яке випромінює хвилі з довжиною λ₀, з швидкістю v рухається відносно спостерігача, то у відповідності з ефектом Доплера, спостерігач сприйме ці хвилі як такі, що мають довжину λ = λ₀(1–v/c), де с=3·10⁸м/с – швидкість поширення світла. А це означає, що вимірявши відповідні довжини хвиль (λ; λ₀), швидкість руху джерела світла можна визначити за формулою v = c(λ₀ – λ)/λ₀.

Варто зауважити, що формула λ = λ₀(1–v/c) справедлива в тих випадках, коли швидкість руху космічного об’єкту v значно менша за швидкість світла с = 3∙10⁸м/с = 300 000км/с. Якщо ж мова йде про об’єкти швидкість руху яких співрозмірна з швидкістю світла, то в цьому випадку потрібно враховувати ті ефекти про суть і величину яких говорить теорія відносності.

Зазвичай, реальна технологія спектрального визначення кінематичних параметрів далеких космічних об’єктів є наступною. Дослідження показують, що основною речовинною складовою Всесвіту є атоми водню. Дослідження показують, що атоми водню випромінюють світло строго визначених довжин хвиль (мал.78): 656,3нм; 486,1нм; 410,2нм; і т.д. Аналізуючи спектральний склад того світла яке випромінює далекий космічний об’єкт, вчені визначають довжини тих хвиль які відповідають випромінюванню атомів водню. Порівнюючи ці довжини з еталонним набором довжин хвиль атома водню, робиться висновок про величину і напрямок руху об’єкту, про відстань до нього, тощо. А потрібно сказати, що сучасні спектральні дослідження практично повністю комп’ютеризовані, і тому довжини світлових хвиль визначаються з надзвичайно великою точністю.

Мал.78. Спектральний склад того світла яке випромінюють атоми водню.

Задача. Аналізуючи спектр далекого космічного об’єкту, вчені з’ясували, що та довжина хвилі атомів водню еталонна величина якої 656,3нм, в реальності дорівнює 659,5нм. Визначте величину і напрям руху об’єкту та відстань до нього.

Дано:

λ₀ = 656,3нм

λ = 659,5нм

v = ?, ℓ = ?

Рішення. Оскільки у відповідності з ефектом Доплера λ = λ₀(1–v/c), де с=3·10⁸м/с, то відносну швидкість руху космічного об’єкту можна визначити за формулою v = c(λ₀ – λ)/λ₀ = 3·10⁸(м/с)(656,3 – 659,5)/656,3 = 3·10⁸м/с∙(–0,0048) = –1,44∙10⁶м/с = –1,44∙10³(км/с), де знак « – » вказує на те, що об’єкт віддаляється від земного спостерігача.

Оскільки у відповідності з законом Хаббла v = H₀ℓ, де H₀ = 67 (км/с)/Мпк, то ℓ = v/Н₀ = 1,44∙10³(км/с)/67 (км/с)/Мпк = 21,5Мпк = 21,5∙10⁶пк.

Відповідь: v = 1440км/с; ℓ = 21,5∙10⁶пк.

Не важко бачити, що незначним зміщенням ліній спектру, відповідають дуже великі значення швидкостей руху. І в цьому зв’язку буде не зайвим згадати одну повчально-анекдотичну історію. Одного разу відомий американський фізик Роберт Вуд, поспішаючи на роботу, проїхав на червоне світло світлофора і його зупинив поліцейський. Намагаючись виправдатись, Вуд пояснив, що світло це потік хвиль і що згідно з ефектом Доплера, довжина цих хвиль, а отже і їх колір, залежать від швидкості руху спостерігача. А тому, рухаючись назустріч світлофору він, у повній відповідності з законами природи, сприйняв червоне світло як зелене. Поліцейський непогано вчився в школі і тому знав, що для світлових хвиль ефект Доплера суттєво проявляється лише при надвисоких швидкостях. Зважаючи на ці обставини, він не став сперечатись з вченим, а просто виписав йому потрійний штраф за перевищення швидкості.

Контрольні запитання.

1. Що представляє собою видиме світло?
2. Відображенням чого є суцільний спектр випромінювання?
3. Відображенням чого є лінійчатий спектр випромінювання?
4. Чому кожна різновидність атомів і молекул дає свій неповторний простий чи складний лінійчатий спектр?
5. Що означає твердження: спектри випромінювання та поглинання будь якої речовини є взаємно оберненими?
6. Що називають спектральним аналізом?
7. Опишіть історію відкриття гелію? І чому хіміки не знали про існування цього хімічного елементу?
8. Які переваги спектрального аналізу над аналізом хімічним?
9. В чому суть ефекту Доплера?
10. Поясніть реальну технологію спектрального визначення кінематичних параметрів далеких космічних об’єктів.
11. Механічні мікрометри вимірюють довжину з точністю 0,01мм=1∙10^–5м, а точність вимірювання довжини світлової хвилі 0,1нм=1∙10^–10м. За допомогою якого приладу вимірюється ця довжина?
12. Чому поліцейський виписав штраф Роберту Вуду за перевищення швидкості?

Вправа 11.

1. Аналізуючи спектр далекого космічного об’єкту, вчені з’ясували, що та довжина хвилі атомів водню еталонна величина якої 486,1нм, в реальності дорівнює 490,5нм. Визначте величину і напрям руху об’єкту та відстань до нього.
2. Аналізуючи спектр певного космічного об’єкту, вчені з’ясували, що та довжина хвилі атомів водню еталонна величина якої 656,3нм, в реальності дорівнює 655,3нм. Визначте величину і напрям руху об’єкту.
3. Певний космічний об’єкт віддалений від Землі на 1000Мпк. З якою швидкістю рухається цей об’єкт відносно Землі? Якої довжини (за вимірюваннями земного спостерігача) будуть ті хвилі які випромінюють атоми водню космічного об’єкту, якщо еталонна довжина цих хвиль 656,3нм.
4. Річний паралакс зірки Сіріус 0,308”. Яка відстань до цієї зірку? Виразіть цю відстань в кілометрах, астрономічних одиницях, світлових роках та парсеках.

.

§12. Про прямі та непрямі вимірювання, або про те як зважують планети, зірки і галактики.

Коли наука стверджує, що маса Землі 5,98∙10²⁴кг, маса Сонці 1,98·10³⁰ кг, а маса Полярної зірки 6М_☼, що радіус Землі 6,37·10⁶м, радіус Сонця 6,95·10⁸м, а радіус Полярної зірки 30R_☼, що відстань від Землі до Сонця 1,5·10¹¹м, а від Сонця до Полярної зірки 430св.р, що температура на поверхні Сонця 5800К, а в його ядрі 13,5∙10⁶К, що фотосфера Сонця складається з водню(73,46%), гелію(24,85%), кисню (0,77%), вуглецю(0,29%), заліза(0,16%), неону(0,12%), азоту(0,09%), кремнію(0,07%), магнію(0,05%), сірки(0,04%) та незначної кількості (0,1%) інших елементів, то це означає, що числові значення всіх цих величин  отримані шляхом точних кількісних вимірювань. А якщо ви не можете уявити ті рулетки, ваги і термометри, за допомогою яких вимірюють космічні відстані, маси і температури, то це зовсім не означає, що відповідні вимірювання є недостовірними. Просто космічні відстані, маси, температури та інші величини, вимірюють не так як це прийнято в побуті.

В загальному випадку вимірювання поділяються на прямі і непрямі (опосередковані). Вимірювання, безпосереднім результатом якого є числове значення тієї величини, яку вимірюють, називають прямим вимірюванням. Наприклад, якщо довжину тіла вимірюють лінійкою, діаметр деталі – штангенциркулем, тривалість подій – секундоміром, температуру – термометром, напругу – вольтметром, силу струму – амперметром, то це пряме вимірювання відповідної величини.

Дуже часто пряме вимірювання є неефективним, або неможливим, наприклад у зв’язку з відсутністю відповідного вимірювального приладу. В такій ситуації застосовують опосередковані (непрямі) методи вимірювання. Суть цих методів полягає в тому, що фактично вимірюють не ту величину, яка нас цікавить, а іншу, з нею пов’язану величину. А потім за відповідною формулою розраховують значення потрібної величини. Скажімо, якщо ми хочемо виміряти площу круга, то вимірюємо не площу круга, а його діаметр d (або радіус r), а площу визначаємо за формулою: S=πd²/4=πr², де π=3,14. Якщо хочемо виміряти об’єм кімнати, то виміряємо її довжину (а), ширину (b) та висоту (h), а об’єм визначаємо за формулою: V = a∙b∙h. Якщо хочемо виміряти густину речовини, то виміряємо її масу m і об’єм V, а густину визначаємо за формулою: ρ=m/V.

Вимірювання при якому фактично вимірюється не та величина яку потрібно визначити, а інша, з нею пов’язана величина, і при якому значення потрібної фізичної величини визначається шляхом певних розрахунків, називають непрямим (опосередкованим) вимірюванням.

Якщо ви думаєте, що непряме вимірювання гірше, або менш точне за пряме, то спробуйте виміряти площу круга (мал.79) прямим способом, тобто шляхом підрахунку кількості квадратних сантиметрів в цьому крузі. Порівняйте отриманий результат з результатом непрямого вимірювання, тобто того вимірювання при якому ви фактично вимірюєте діаметр круга, а його площу визначаєте за формулою S=πd²/4. Як ви думаєте, який з цих результатів буде більш точним.

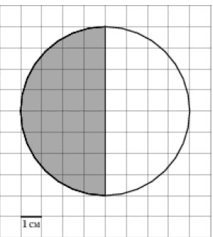
Мал.79. Як ви думаєте, який спосіб вимірювання  площі круга (прямий чи непрямий) є більш точним та ефективним?

Не важко збагнути, що основним способом вимірювання параметрів недоступно далеких космічних обєктів, є непрямі вимірювання, тобто такі вимірювання, при яких фактично вимірюють не ту величину яку потрібно виміряти, а іншу, з нею пов’язану величину. Потрібну ж величину визначають з тієї формули, яка відображає зв’язок між відповідними величинами. Наприклад визначаючи відстань до Сонця, фактично вимірюють відстань (а) між двома обсерваторіями та величину того кута (α) який називається паралаксом, а відстань до Сонця визначають за формулою ℓ=а/sinα.

Або наприклад, якщо те джерело світла яке випромінює хвилі з довжиною λ₀, з швидкістю v << c рухається відносно спостерігача, то у відповідності з ефектом Доплера, спостерігач сприйме ці хвилі як такі, що мають довжину λ = λ₀(1–v/c), де с=3·10⁸м/с – швидкість поширення світла. А це означає, що вимірявши відповідні довжини хвиль (λ; λ₀), швидкість руху джерела світла можна визначити за формулою v = c(λ₀ – λ)/λ₀. А знаючи закон Хаббла (v = H₀ℓ), де Н₀ = 67(км/с)/Мпк, не важко визначити і відстань до цього об’єкту. І не вірити достовірності такого роду непрямим вимірюванням, це все рівно ніби не вірити в достовірність визначеної за формулою S=πR² площі круга. Не вірити лише на тій підставі, що в реальності ми вимірювали не площу круга а його радіус.

Демонструючи суть та можливості непрямих методів вимірювань, розглянемо декілька конкретних задач.

Задача 1. Знаючи радіус Землі (R=6,37∙10⁶м) та прискорення вільного падіння на ній (g=9,81м/с²), визначити масу Землі.

З’ясовуючи той кількісний зв’язок що існує між масою Землі (М) та прискоренням вільного падіння на ній (g), розглянемо ту силу, з якою тіло масою m притягується до центру Землі. Цю силу, з одного боку можна назвати гравітаційною F_гр=GМm/R², а з іншого – силою тяжіння F_т=mg. Оскільки величини цих сил є практично однаковими (F_гр=F_т), то можна стверджувати: G(Мm/R²) = mg. Звідси випливає: M = gR²/G.

Розрахунки: M=gR²/G = 9,81(м/с²)(6,37∙10⁶м)²/6,67·10^–11(м²/Н·кг²) = 6,0∙10²⁴кг.

Відповідь: М = 6,0∙10²⁴кг.

Нагадаємо, в науці базовим способом перевірки достовірності тих чи інших вимірювань, є принцип перехресності вимірювань. Суть цього принципу полягає в тому, що певну величину вимірюють різними методами. При цьому, якщо результати вимірювань збігаються, то це безумовно вказує на те, що ці результати є достовірними. Якщо ж результати вимірювань суттєво відрізняються, то це вказує на відповідну похибку вимірювань. Що ж, давайте «зважимо Землю по іншому.

Задача 2. Знаючи період обертання Місяця навколо Землі (Т = 27,3доби = 2,36∙10⁶с) та відстань між центрами мас Землі і Місяця (ℓ=3,84∙10⁸м), визначити масу Землі.

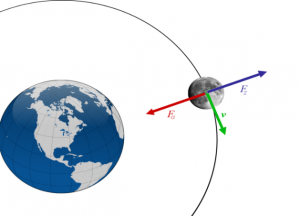
З’ясовуючи той зв’язок що існує між масою Землі (М) та періодом обертання Місяця навколо неї (Т), розглянемо ті сили що діють на Місяць та забезпечують його динамічну рівновагу. А цими силами є, сила гравітаційної взаємодії Місяця з Землею F_гр=GМm/ℓ² та обумовлена обертальним рухом Місяця сила інерції F_i = ma_д=mv²/ℓ, де v=2πℓ/T. А оскільки, діючі на Місяць гравітаційна сила та сила інерції динамічно зрівноважують одна одну (F_гр=F_і), то можна записати  GMm/ℓ² = m4πℓ/T². Звідси випливає: M=4π²ℓ³/GT².

Розрахунки: M = 4π²ℓ³/GT² = 4·3,14²(3,84∙10⁸м)³/6,67·10^–11(м²/Н·кг²)(2,36∙10⁶с)² = 6,0∙10²⁴кг.

Відповідь:  М = 6,0∙10²⁴кг.

Зверніть увагу на факт того, що масу Землі ми визначили двома абсолютно різними способами. При цьому отримані нами результати виявились практично однаковими. Що означає даний факт?

Задача 3. Знаючи швидкість обертання Землі навколо Сонця (v=29,8∙10³м/с) та відстань між центрами мас Землі і Сонця (ℓ=1,49∙10¹¹м), визначити масу Сонця (М).

Оскільки ті сили що діють на Землю в процесі її обертання навколо Сонця (F_гр=GМm/ℓ² та F_i = ma_д=mv²/ℓ) динамічно зрівноважують одна одну, то можна записати: GМm/ℓ² = mv²/ℓ. Звідси випливає: M = v²ℓ/G.

Розрахунки: M = v²ℓ/G = (29,8∙10³м/с)²·1,49∙10¹¹м/6,67·10^–11(м²/Н·кг²) = 2,0∙10³⁰кг

Відповідь: М_☼ = 2,0∙10³⁰кг.

Варто зауважити, що описаний в задачах 2 і 3 метод визначення мас, можна застосовувати не лише для системи двох окремо взятих тіл, а й для будь яких систем в яких тіло вільно обертається навколо спільного центру мас. При цьому можна довести, що визначена цим методом маса центрального тіла системи, фактично буде загальною масою всіх тих тіл які знаходяться всередині цієї системи. Наприклад наше Сонце є частиною величезної космічної Галактики в якій налічується близько 250∙10⁹ найрізноманітніших зірок. Визначаючи масу цієї Галактики зовсім не обов’язково «зважувати» кожну окрему зірку. Достатньо визначити відстань однієї з її певних  зірок до центру Галактики (ℓ) та швидкість її обертання навколо цього центру (v), а потім скористатися формулою   M=v²ℓ/G . При цьому отримана маса буде загальною масою всіх тих об’єктів які зосереджені у внутрішньому об’ємі того диску, радіус якого дорівнює відстані від центру мас Галактики до відповідної зірки.

Втім, стосовно галактик, вище описаний спосіб визначення мас не є безумовно достовірним. Про причини цієї недостовірності ми поговоримо в §21 «Загальні відомості про галактики». Однак наука стоїть на тому, що в ній достовірність результатів вимірювань перевіряється шляхом застосування різних методів вимірювань. А зважаючи на факт, що галактики практично завжди утворюють певні системи галактик, в яких вони обертаються одна навколо одної та навколо спільного центру мас, маси галактик визначаються досить точно та безумовно достовірно.

Класичним прикладом застосування непрямих методів вимірювань, а за одно й ілюстрацією тих інтелектуальних здібностей які були притаманні людям ще з прадавніх часів, є історія вимірювання радіусу Землі. А цей радіус було достатньо точно визначено ще за 240 років до нашої ери, давньогрецьким вченим Ератосфеном (275 – 194 до н.е).

Ератосфен жив в Александрії – центрі науки і мистецтв давнього світу. В одному з наукових трактатів він прочитав, що в місті Сієна (сучасне Асуан, що на півдні Єгипту), опівдні дня літнього сонцестояння, Сонце знаходиться в зеніті і предмети не залишають тіні. А потрібно сказати, що Сієна розташована приблизно на широті 24º Північної півкулі Землі, тобто на тій широті яка відповідає куту нахилу площини екліптики до площини екватора Землі. А це означає, що на цій широті, опівдні дня літнього сонцестояння, сонячні промені падають практично перпендикулярно поверхні Землі і тому предмети дійсно не залишають тіні.

Не відомо чи знав Ератосфен про нахил площини екліптики до площини екватора, але він точно знав, що в Александрії опівдні дня літнього сонцестояння, світлові промені падають під кутом 7,2º і що тому предмети створюють відповідну світлову тінь. Аналізуючи дані факти, Ератосфен дійшов висновку, що Земля кругла і що тому в один і той же день світлові промені падають на різні точки поверхні Землі під різними кутами. Знаючи що відстань між Александрією і Сієною (в сучасних одиницях вимірювань) близька до 800км, і що 7,2º – це 1/50 частина кола (360º/7,2º=50), Ератосфен визначив довжину відповідного кола ℓ=800км·50= 40000км, та йому відповідний радіус (радіус Землі) R = ℓ/2π = 40000км/6,28= 6370км.

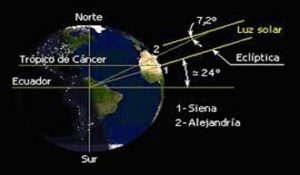
Мал.80. На основі аналізу факту того, що в один і той же день, в різних географічних широтах кут падіння променів на поверхню Землі є різним, можна визначити радіус Землі.

Звичайно, в часи Ератосфена, точність вимірювань, зокрема великих відстаней була досить приблизною. Але фактом залишається те, що два з чвертю тисячоліття тому давньогрецький вчений Ератосфен на основі аналізу факту того, що в один і той же день, в різних місцях Землі кут падіння сонячних променів є різним, з достатньо великою точністю визначив радіус Землі.

Тепер коли ви знаєте, що ще за 240 років до нашої ери, давньогрецький вчений Ератосфен, надзвичайно точно визначив радіус Землі, чи варто дивуватися тому, що через століття інший видатний давньогрецький вчений Гіппарх, з не меншою точністю визначив відстань до практично недосяжного Місяця.

Сучасні люди, а особливо ті хто не вирізняється інтелектуальними здібностями, схильні вважати, що ті люди які жили 200, 300, а тим більше 2000 років тому, були неосвіченими і грубо кажучи – дурними. Факти ж безумовно вказують на те, що люди давніх ба навіть прадавніх часів не були дурнішими за нас з вами. І якщо сьогоднішній рівень наших знань незрівнянно вищий за той, що існував в прадавні часи, то це тільки тому, що попередні покоління багатьох видатних вчених отримали та систематизували ці знання. Загалом же, ви маєте знати, що людина не народжується розумною. Вона народжується лише такою, що здатна стати розумною.

Контрольні запитання.

1. Які вимірювання називають прямими, а які – непрямими?
2. На прикладі вимірювання площі круга, поясніть чим відрізняються прямі та непрямі вимірювання? Який з цих методів є більш точним.
3. Наведіть п’ять прикладів прямих вимірювань і п’ять прикладів вимірювань непрямих.
4. Чому на Землі прискорення вільного падіння тіл 9,8м/с², а на Місяці 1,6м/с²?
5.  Масу Сонця визначили на основі аналізу параметрів руху Землі і Нептуна. При цьому отримали дещо різні результати. Який з цих результатів є більш точним? Чому?

6. Як в науці перевіряють достовірність результатів вимірювань?
7. Чому в місті Сієна опівдні дня літнього сонцестояння предмети не залишать сонячної тіні?
8. Чому Ератосфен обгрунтовано стверджував, що Земля кругла і що довжина її кругового периметру в 50 разів більша за відстань від Александрії до Сієни?

Вправа 12.

1. Відомо, що радіус Марса 3400км, а прискорення вільного падіння на ньому 3,7м/с². Визначити масу Марса.
2. Відомо, що період обертання супутника Фобос навколо планети Марс становить 7 год 40 хв. Визначити масу Марса, якщо відстань від супутника до планети 9400 км.
3. Знаючи прискорення вільного падіння (g=1,6м/с²) та радіус (R=1,74∙10⁶м) Місяця, визначити масу Місяця та його середню густину.
4.  Одна з периферійних зірок нашої Галактики віддалена від її центру на відстань 5∙10²⁰м, обертається з швидкістю 2,8∙10⁵м/с. Яка загальна маса Галактики? У скільки разів ця маса перевищує масу Сонця?
5. Відомо, що за рік, Місяць здійснює 13 обертів навколо Землі і що відстань від Землі до Сонця в 390 разів більша за відстань від Землі до Місяця. У скільки разів маса Сонця більша за масу Землі?

.

§13. Сучасні наземні та орбітальні телескопи.

З часів Галілея, одним з символів астрономії є телескоп. Телескоп (від грец. tele – далеко, skopeo – дивитись), це прилад призначений для спостереження за далекими космічними об’єктами: планетами, кометами, зірками, галактиками, тощо.

Пояснюючи загальний устрій та принцип дії телескопа будь-якої конструкції, можна сказати наступне. Оскільки космічні об’єкти знаходяться на неймовірно великих відстанях від Землі, то кількість тієї світлової (інформаційної) енергії яка від цих об’єктів потрапляє на Землю, є мізерно малою. Ця мізерність стає ще більш очевидною, якщо зважити на факт того, що людина фактично бачить та аналізує лише ту світлову інформацію яка потрапляє в той маленький отвір, що називається зіницею ока. Тому завдання будь якого телескопу, по суті полягає в тому, щоб зібрати максимально велику кількість світлової інформації про певний космічний об’єкт, сконцентрувати цю інформацію у відповідне зображення та направити це інформаційне зображення в око спостерігача або інший світлочутливий прилад (спектроскоп, спектрограф, аналітична система комп’ютера, фотопластина, фотометр, тощо).

Найбільш звичною різновидністю телескопів є телескопи оптичні, тобто такі, що збирають і фокусують електромагнітне випромінювання оптичного діапазону, а простіше кажучи – видиме світло. Втім, в загальному випадку, до оптичного діапазону електромагнітних хвиль відносять не лише видиме світло, а й світло інфрачервоне та ультрафіолетове.

Сучасне різноманіття оптичних телескопів можна розділити на три групи: лінзові або рефракторні (лат. refractus – заломлення), дзеркальні або рефракторні (лат. reflectio – відбивання) та дзеркально – лінзові або катадіоптричні. В лінзових телескопах (мал.81а) об’єктивом є збиральна лінза, яка  шляхом заломлення світлових променів фокусує (збирає) ці промені у відповідне зображення та направляє це зображення в окуляр телескопа. В дзеркальних телескопах (мал.82б) аналогічні функції виконує вгнуте (збиральне) дзеркало, а в телескопах дзеркально-лінзових (мал.83в) – система збирального дзеркала і спеціальної лінзово-дзеркальної фокусуючої системи.

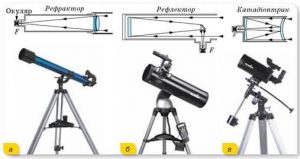
Мал.81. Оптичні телескопи поділяються на лінзові, дзеркальні і дзеркально-лінзові.

Перші оптичні телескопи (зорові труби) з’явились на початку 17-го століття. При цьому, майже одночасно було створено дві різновидності подібних приладів: телескоп Галілея (1609 р.) і телескоп Кеплера (1611 р.). Ці телескопи були лінзовими, тобто такими об’єктивом яких є збиральна лінза. Тривалий час лінзові телескопи були панівною різновидністю телескопів. Однак лінзові об’єктиви, у порівнянні з об’єктивами дзеркальними,  мають ряд суттєвих недоліків, зокрема:

1. Ці об’єктиви мають відносно велику питому масу. Адже лінза – це об’ємне тіло з двома робочими (оптично рівними, дзеркальними) поверхнями. Натомість дзеркало – це викривлена площина з однією робочою поверхнею. Крім цього, реальний лінзовий об’єктив складається з системи декількох лінз, що автоматично помножує його загальну масу.
2. Для лінз притаманна хроматична аберація, тобто таке спотворення зображення, яке обумовлено фактом того, що хвилі різних довжин (різних кольорів) заломлюються суттєво по різному. А це означає, що створюване такою лінзою зображення буде спотворене характерним спектральним обрамленням. Дзеркальні ж об’єктиви таких проблем не мають.
3. Для лінз притаманна геометрична аберація, тобто таке спотворення зображення, яке обумовлено фактом того, що лінза збирає широкий світловий потік не в певну світлову точку, а в певну світлову пляму. А це означає, що створюване такою лінзою зображення буде розмитим. Параболоїдні ж дзеркальні об’єктиви дозволяють отримувати гранично чіткі зображення об’єктів спостереження.
4. Лінзові об’єктиви мають певні обмеження щодо прозорості того матеріалу з якого вони виготовлені. Скажімо звичайне скло, практично непрозоре для ультрафіолетового світла і тому відповідні лінзові об’єктиви не можуть застосовуватись для досліджень в діапазоні ультрафіолетового випромінювання. Дзеркальні ж об’єктиви подібних обмежень не мають.
5. Лінзові об’єктиви мають відносно високу вартість. І не тільки тому, що вартість лінзи суттєво більша за вартість аналогічного за розмірами та функціями дзеркала. А ще й тому, що для боротьби з хроматичною та геометричною абераціями, реальні лінзові об’єктиви представляють собою певні системи об’ємних, масивних лінз, кожна з яких має дві робочі поверхні.

Зважаючи на ці обставини, переважна більшість сучасних оптичних телескопів є дзеркальними. Ілюструючи порівняльні характеристики та можливості сучасних лінзових і дзеркальних оптичних телескопів, достатньо сказати, що діаметр об’єктива найбільшого лінзового телескопа 1,02м, а діаметр об’єктива найбільшого дзеркального телескопа 39м.

Мал.82. В високогірній пустелі Атакама (Чилі) завершується будівництво найбільшого дзеркального оптичного телескопа, діаметр об’єктива якого 39м.

Тривалий час телескопи дозволяли спостерігати лише за тими  об’єктами, які випромінюють звичне для нашого візуального сприйняття видиме світло. Однак видиме світло, це лише маленький фрагмент того неперервного спектру електромагнітних хвиль які випромінюються космічними об’єктами і складовими якого є радіохвилі, інфрачервоне, видиме, ультрафіолетове, рентгенівське та гама випромінювання. Тому в сучасній астрономії застосовують широке різноманіття телескопів, які дозволяють проводити дослідження практично у всьому діапазоні електромагнітних хвиль. Різноманіття цих телескопів прийнято розділяти на чотири групи:

1) радіотелескопи – працюють в діапазоні радіохвиль, тобто тих електромагнітних хвиль, довжини яких більші за 1∙10^–3м;

2) оптичні телескопи – працюють в діапазоні інфрачервоного, видимого та ультрафіолетового випромінювання, тобто тих електромагнітних хвиль, довжини яких знаходяться в межах від 1∙10^–3м до 1∙10^–8м;

3) рентгенівські телескопи – працюють в діапазоні рентгенівського випромінювання, тобто тих електромагнітних хвиль, довжини яких знаходяться в межах від 1∙10^–8м до 1∙10^–11м;

4) гама-телескопи – працюють в діапазоні гама-випромінювання, тобто тих електромагнітних хвиль, довжини яких є меншими за 1∙10^–11м.

Застосовуючи сучасні телескопи, можна розгледіти деталі багатьох космічних об’єктів, зокрема Сонця, Місяця, комет та планет Сонячної системи. Однак телескопи не дозволяють побачити деталі тих зірок і планет які знаходяться за межами Сонячної системи. Не дозволяють тому, що відстані до таких об’єктів є фантастично великими. Великими настільки, що навіть в найпотужніших телескопах далекі зірки виглядають як певні світлові точки.

Втім, це зовсім не означає, що телескопи не дозволяють отримувати нову інформацію про зірки та інші наддалекі космічні об’єкти. Адже телескоп в сотні, тисячі і мільйони разів підсилює видиму яскравість зірок. Підсилює тому, що через телескоп в наше око потрапляє у стільки разів більше світлової енергії, у скільки разів площа його об’єктиву більша за площу зіниці ока. А це означає, що в телескопі ми можемо побачити не лише ті зірки які видно неозброєним оком, а й ті, які зазвичай є невидимими. Крім цього, телескоп в десятки і сотні разів збільшує видимі відстані між окремими космічними об’єктами. При цьому з’ясовується, що велика кількість тих об’єктів які виглядають як певні світлові точки, насправді представляють собою скупчення величезної кількості окремих зірок.

Сучасні оптичні телескопи дозволяють «бачити» не лише видиме світло, а й світло інфрачервоне та ультрафіолетове. Якщо ж мова йде про ті електромагнітні хвилі довжини яких вимірюються міліметрами, сантиметрами, дециметрами, метрами і десятками метрів, то їх фіксують та досліджують за допомогою сучасних радіотелескопів. Базовими елементами типового радіотелескопа є антена і приймач радіосигналу. Зазвичай, антеною радіотелескопа є параболічна відбивна поверхня, подібна до дзеркал оптичних рефлекторів. При цьому принцип дії радіотелескопа полягає в наступному. Радіохвилі, відбиваючись від поверхні антени, фокусуються в околицях певної точки, де і встановлюється приймач радіосигналу. Зафіксований радіоприймачем сигнал, після підсилення та виділення інформаційної складової, передається в комп’ютерну систему яка аналізує отриману інформацію та видає результати цього аналізу.

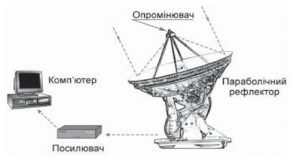
Мал.83. Схема загального устрою радіотелескопа.

Потрібно зауважити, що відбивним поверхням параболічних антен радіотелескопів не обов’язково бути такими ж дзеркально рівними як в оптичних рефлекторах. Адже для того щоб відбивна поверхня не спотворювала зображення, її нерівності (δ) не повинні перевищувати 1/8 від тієї довжини хвилі (λ), яку приймає відповідна антена (δ ≤ λ/8). Тому якщо наприклад, радіотелескоп сприймає хвилі з довжиною 8 см, то нерівності його робочої поверхні мають бути не більшими за 1 см (δ ≤ 1см). А це майже в мільйон разів більше за ті мікро нерівності які допустимі для оптичних телескопів (δ ≤ 0,5·10^–7м). Крім цього, робочі поверхні антен радіотелескопів можуть бути не суцільними, а такими що представляють собою певну металеву сітку натягнуту на параболічний каркас.

Радіотелескопи можуть мати надзвичайно великі розміри. Скажімо, якщо діаметр об’єктиву найбільшого лінзового телескопу становить 1,02 метра, найбільшого дзеркального телескопу – 39 метра, то діаметр параболічної антени найбільшого радіотелескопу – 500 метрів. Цей гігантський радіотелескоп збудовано в 2016 році в одному з високогірних районів Китаю і спеціалізується на виявленні та дослідженні так званих пульсарів – нейтронних зірок які утворюються після вибуху надмасивних червоних гігантів.

Мал.84. Загальний вигляд найбільшого в світі радіотелескопа.

Гігантські розміри 500 метрового радіотелескопа безумовно вражають. Однак не менш вражаючою є та унікальна телескопічна система, яка з 1980 року працює в США і яку прийнято називати ДВМ – Дуже Великий Масив. Ця система складається з 27 окремих телескопічних антен, кожна з яких має тарілку діаметром 25м і вагу 209 тон. Антени розподілені між трьома рукавами залізничних колій, які розташовані у формі літери Y і мають довжину 27км кожний. По суті наявна сукупність антен, утворює єдиний гігантський радіотелескоп, діаметр та параметри якого можна певним чиним змінювати.

ДВМ є багатоцільовим інструментом призначеним для дослідження багатьох астрономічних об’єктів, у тому числі радіогалактик, квазарів, пульсарів, залишків наднових, гамма-спалахів, радіо-випромінюючих зір, астрофізичних мазерів, чорних дір і звісно ж Сонця та різноманітних об’єктів Сонячної системи.

Мал.85. На південному заході США, система 27 окремих 25 метрових телескопічних антен утворює єдиний гігантський радіотелескоп.

Дослідження показують, що атмосфера Землі в тій чи іншій мірі послаблює та спотворює те інформаційне електромагнітне випромінювання яке надсилається космічними об’єктами. Більше того, земна атмосфера є практично непрозорою для тих електромагнітних хвиль які прийнято називати інфрачервоним, ультрафіолетовим, рентгенівським та гама випромінюванням. Величезна ж кількість тієї інформації яку випромінюють космічні об’єкти, випромінюється саме в діапазоні ультрафіолетових, рентгенівських та гамма хвиль. Ясно, що в такій ситуації важливу роль в дослідженні космосу відіграють ті телескопічні системи, які виводяться за межі атмосфери Землі. Прикладом такої системи є космічний телескоп «Хаббл» (мал.86).

Телескоп «Хаббл» – це унікальна, багатофункціональна орбітальна обсерваторія, яка була виведена на орбіту Землі в квітні 1990 року і буде перебувати на цій орбіті щонайменше до 2030 року. Базовим приладом цієї обсерваторії є дзеркальний телескоп з діаметром дзеркала 2,4 метра. Цей телескоп здатний фіксувати та аналізувати електромагнітні хвилі в діапазоні від 120нм до 1мм. За час роботи на навколоземній орбіті, за допомогою телескопу «Хаббл» досліджено понад 22 тисячі небесних об’єктів: зірок, туманностей, галактик, планет, тощо. Потік тієї наукової інформації яку щоденно генерує ця космічна обсерваторія, становить близько 15 гігабайт. Щорічно у списку 200 найбільш цитованих наукових статей, не менше 10% базуються на тих даних які отримані від телескопу «Хаббл».

Мал.86. Загальний вигляд орбітального телескопу «Хаббл».

Телескоп «Хаббл», це не просто телескоп, а ціла система наукових приладів, до складу якої, окрім самого телескопа входять спектрограф високої роздільної здатності, камера зйомки тьмяних об’єктів, спектрограф тьмяних об’єктів, високошвидкісний фотометр, датчики точного наведення, планетарна та ширококутна камери з системою світофільтрів і звичайно, потужна комп’ютерна система. А ще, невід’ємною та надважливою складовою цієї системи, є ті науковці які управляють всією сукупністю цих приладів, аналізують отриману інформацію та роблять відповідні узагальнюючі  висновки.

Втім, подібне можна сказати не лише про телескоп «Хаббл», а й про будь який інший сучасний науковий телескоп, який по суті представляє собою цілу наукову установу, яку прийнято називати обсерваторією (від лат. jbservo – спостерігаю, уважно стежу).

Контрольні запитання.

1. Який загальний принцип дії будь якого телескопа?
2. Чим дзеркальні телескопи відрізняються від лінзових?
3. Які переваги дзеркальних об’єктивів у порівнянні з об’єктивами лінзовими?
4. Чому переважна більшість сучасних оптичних телескопів є дзеркальними?
5. Навіть в найпотужніші телескопи зірки виглядають як світлові точки. Чи означає цей факт, що телескопи не дають нової інформації про зірки?
6. Які діапазони спостережень оптичних, рентгенівських, гама та радіотелескопів?
7. Який загальний устрій радіотелескопа?
8. Які вимоги до допустимих мікронерівностей робочої поверхні телескопа?
9. Чому робоча поверхня антени радіотелескопа може бути не суцільно дзеркальною, а такою що виготовлена з металевої сітки?
10. В чому перевага телескопів космічного базування?
11. Дайте загальну характеристику телескопа «Хаббл».