Сайт викладача фізики

Тема 3.2. Основи електродинаміки постійних струмів.

§18. Загальні відомості про електричний струм та його прояви.

§19. Сила струму. Основні елементи електричного кола. Електрична напруга.

§20. Закон Ома. Електричний опір.

§21. Резистор. Послідовне з’єднання резисторів.

§22. Паралельне з’єднання резисторів. Закони Кірхгофа.

§23. Змішане з’єднання резисторів. Метод еквівалентних схем.

§24. Робота та потужність електричного струму.

§25. Закон Джоуля-Лєнца. Шляхи зменшення втрат в лініях електропередач.

§26. Розв’язування задач. Тема: Закон збереження енергії в електричних, механічних та теплових процесах.

§27. Електричний струм в металах.

Тема 3.2. Основи електродинаміки постійних струмів.

§18. Загальні відомості про електричний струм та його прояви.

 

Вивчаючи електростатику ми познайомилися з загальними властивостями, параметрами та закономірностями поведінки відносно нерухомих електричних зарядів. Тепер же мова піде про загальні властивості, параметри, прояви та закономірності того, що прийнято називати електричним струмом.

Зазвичай електричним струмом  називають процес упорядкованого руху заряджених частинок, який відбувається в певному струмопровідному середовищі (провіднику), а бо у вакуумі. При цьому, в межах даної теми ми будемо говорити про той струм, величина і напрям якого з плином часу залишаються незмінними і який називається постійним струмом.

Матеріали які проводять електричний струм називаються провідниками (провідниками електричного струму). Характерною особливістю цих матеріалів є наявність достатньо великої кількості вільних заряджених частинок, які прийнято називати носіями струму. Наприклад в металах носіями струму є електрони.

Матеріали які не проводять електричний струм називаються діелектриками. Як і провідники, діелектрики складаються з позитивно та негативно заряджених частинок. Однак в них, всі заряджені частинки міцно з’єднані між собою і тому не можуть вільно переміщуватись в межах діелектрика (а якщо і можуть, як наприклад в газах, то лише разом з протилежно зарядженою частинкою).

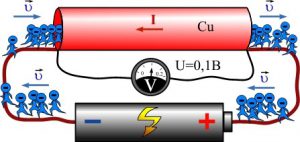
Прийнято вважати, що електричний струм «тече» від точки з позитивним потенціалом до точки з негативним потенціалом, а простіше кажучи – від (+) до (–). Те що струм тече від плюса до мінуса, власне як і назви електричний струм, електрична ємність, сила струму, тощо  є відлунням тих далеких часів, коли електрику уявляли як певну рідину. При цьому заряд (+) означав, що у відповідному тілі є певний надлишок електричної рідини, а заряд (–) відповідно означав, що в тілі є певна недостача електричної рідини. Ясно, що в такій ситуації при контакті позитивно та негативно заряджених тіл, електрична рідина перетікала від тіла з її надлишком, до тіла з її недостачею, тобто від плюса до мінуса.

Мал.70. Прийнято вважати, що електричний струм тече від (+) до (–).

Потрібно зауважити, що загально прийнята домовленість щодо напрямку електричного струму, іноді викликає певні непорозуміння. Скажімо в металах, носіями струму є електрони, тобто негативно заряджені частинки. А це означає, що в металах носії струму рухаються (течуть) не від плюса до мінуса, а навпаки – від мінуса до плюса (мал.70б). Втім, подібні непорозуміння мають сугубо психологічний характер. Адже загальні властивості електричного струму визначаються не напрямком струму, а самим фактом упорядкованого руху заряджених частинок. Тому будемо вважати, що електричний струм тече від «плюса» до «мінуса» і що в електричному сенсі немає значення які заряди (позитивні чи негативні) фактично рухаються.

Дослідження показують, що проходження струму через провідник супроводжується тими чи іншими ефектами (явищами, подіями, процесами, проявами). Найочевиднішим та найвідомішим серед подібних ефектів є теплова дія електричного струму. Загально відомими прикладами очевидної теплової дії струму є різноманіття сучасних електронагрівальних приладів починаючи від електроплит, електричних камінів, прасок та чайників, і закінчуючи фенами, тостерами та електричними запобіжниками. Втім, в процесі проходження струму, теплота виділяється не лише в спеціально створених приладах, а й в дротах ліній електропередач, обмотках електродвигунів і трансформаторів, в деталях телевізорів, комп’ютерів та смартфонів, і загалом практично у всіх тих елементах якими проходить електричний струм.

Мал.71. При проходженні струму, майже завжди виділяється певна кількість теплоти.

Факт того, що процес проходження струму супроводжується виділенням теплоти, є абсолютно закономірним. Адже в процесі проходження струму, носії струму постійно наштовхуються на атоми (молекули, іони) провідника та змушують їх рухатись інтенсивніше. При цьому, певна частина енергії упорядкованого руху носіїв струму перетворюється на відповідну кількість енергії хаотичного руху частинок провідника, тобто в теплоту.

Теплова дія струму, важливий але не єдиний його прояв. Наприклад проходження струму через сучасні світлодіодні лампи та лампи денного світла супроводжується випромінюванням світла (світлова дія струму). Проходження струму через розчини солей, лугів та кислот, супроводжується певними хімічними перетвореннями (хімічна дія струму). А проходження струму через організм людини чи тварини, викликає певну нервову реакцію цих організмів (біологічна дія струму).

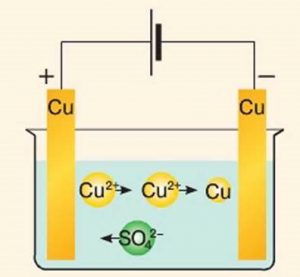
Мал.72. Електричний струм може спричиняти не лише теплову, а й світлову, хімічну та біологічну дію.

Таким чином, електричний струм може спричиняти певну теплову, світлову, хімічну та біологічну дію. При цьому ні хімічну, ні біологічну, ні світлову дію електричного струму не можна вважати його універсально характерною рисою. Адже біологічну дію, струм спричиняє лише на живі організми. Хімічна дія струму також характерна лише для певних ситуацій. І звичайно, можна навести безліч прикладів того, де проходження струму не супроводжується певними світловими явищами.

Якщо ж говорити про теплову дію струму, то її також навряд чи можна вважати універсальною. Неможна по перше тому, що один і той же струм, різні матеріали нагріває по різному. Скажімо, в спіралі електричної лампочки і в тому дроті який з’єднує цю лампочку з джерелом струму, тече один і той же струм. При цьому вольфрамова нитка лампочки розжарюється до білого накалу, тоді як мідний дріт, якщо і нагрівається то в незначній мірі.

Мал.73. В спіралі лампочки і в тому провіднику який з’єднує лампочку з джерелом струму, тече струм однакової величини. Але теплова дія цього струму є різною. Висновок: теплова дія струму не є його об’єктивною характеристикою.

По друге, за певних наднизьких температур, деякі струмопровідні матеріали, переходять до так званого надпровідного стану, тобто такого стану при якому проходження струму не супроводжуються виділенням теплоти. А це означає, що по тепловій дії практично не можливо визначити, тече  по даному надпровіднику струм чи ні. Цього не можна зробити і за іншими проявами струму, зокрема за його хімічною та світловою дією.

Втім, електричний струм все ж має певну визначально-універсальну властивість, яка проявляється за будь яких обставин і величина якої строго пропорційна величині відповідного струму. Цією універсальною властивістю струму є його магнітна дія. Коли ми говоримо про магнітну дію струму, то маємо на увазі факт того, що провідник з струмом діє на магнітну стрілку компасу, аналогічно тому як це робить постійний магніт.

 

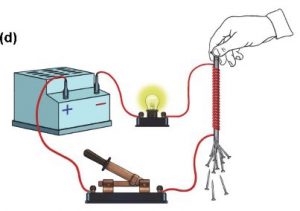
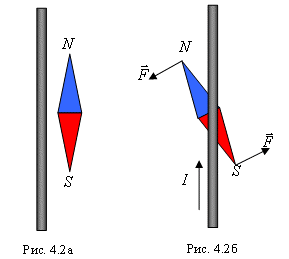
Мал.74. Будь який електричний струм має певні магнітні властивості, одним з проявів яких є силова дія струму на магнітну стрілку.

Зазвичай магнітні властивості струму є малопомітними. Однак за певних умов саме ці властивості змушують працювати електродвигуни, генератори, трансформатори, електровимірювальні прилади та безліч інших електромагнітних приладів. Приладів, без яких не можливо уявити сучасне цивілізоване життя.

Вивченню загальних магнітних властивостей електричного струму буде присвячена наступна тема даного розділу. Тому сьогодні ми просто констатуємо той факт, що універсальною властивістю електричного струму є його здатність створювати певну магнітну дію. І що величина цієї дії, завжди пропорційна величині відповідного струму.

Таким чином, з певною мірою обґрунтованості, про наявність електричного струму в провіднику можна говорити за його тепловою, світловою, хімічною, біологічною чи можливо іншими діями. Але універсальною ознакою будь якого струму є його магнітна дія. Це означає що за магнітною дією можна не лише гарантовано точно визначити наявність електричного струму в будь яких його проявах, а й об’єктивно оцінити величину цього струму.

Контрольні запитання.

1. Що називають електричним струмом? Який струм називають постійним?
2. Які матеріали називають провідниками? Чим вони відрізняються від непровідників (діелектриків)?
3. Чому прийнято вважати, що електричний струм тече від (+) до (–)?
4. Чи залежать загальні властивості струму від вибору того як тече струм: від (+) до (–) чи навпаки?
5. Чи можна тепловий рух електронів в провіднику називати електричним струмом?
6. Назвіть відомі вам приклади: а) теплової дії струму; б) світлової дії струму; в) хімічної дії струму; г) біологічної дії струму; д) магнітної дії струму.
7. Чому світлову, хімічну та біологічну дію струму, не можна вважати його визначальною ознакою?
8. Чому теплова дія струму не є визначальною та об’єктивною ознакою електричного струму?
9. Поясніть суть магнітної дії струму. Чому цю дію вважають об’єктивною, універсальною властивістю струму?

.

§19. Сила струму. Основні елементи електричного кола. Електрична напруга.

Кількісною мірою інтенсивності електричного струму є фізична величина, яка називається силою струму. А варто зауважити, що в словосполученні «сила струму», слово «сила» застосовується не в значенні міри взаємодії фізичних об’єктів, а в сенсі міри інтенсивності руху: як сильно, тобто як інтенсивно тече електричний струм.

Сила струму – це фізична величина, яка характеризує інтенсивність електричного струму і яка дорівнює відношенню величини того електричного заряду (q) що проходить через поперечний переріз провідника за час t, до величини цього проміжку часу.

Позначається: I

Визначальне рівняння: I = q/t

Одиниця вимірювання: [I] = A,   ампер.

Загальне зауваження. В фізиці, визначення однієї і тієї ж фізичної величини, як власне і будь якого терміну, можна зробити різними словами. Головне щоб ці слова правильно та максимально точно відображали фізичну суть відповідного терміну. Наприклад, можна сказати: сила струму дорівнює відношенню величини того електричного заряду (q) що проходить через поперечний переріз провідника час t до величини цього проміжку часу. А можна сказати: сила струму показує, яка кількість електричного заряду проходить через поперечний переріз провідника за одиницю часу, що також означає I = q/t.

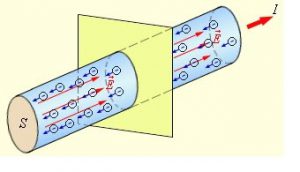
Мал.75. Сила струму показує, яка кількість електричного заряду проходить через поперечний переріз провідника за одиницю часу:  I = q/t.

В СІ, одиниця вимірювання сили струму (ампер) є базовою і такою, що визначається за магнітною дією струму. Про кількісні закономірності взаємодії електричних струмів, ви дізнаєтесь при більш детальному вивчення електродинаміки магнітних явищ (а це відбудеться лише в десятому класі). Власне тоді і буде сформульовано офіційне визначення одиниці вимірювання сили струму (ампер). Наразі ж будемо вважати, що силі струму в один ампер відповідає такий постійний струм, при якому за одну секунду через поперечний переріз провідника проходить заряд в один кулон, тобто проходить 6,25∙10¹⁸ елементарних зарядів (електронів).

Силу електричного струму вимірюють спеціальним приладом, який називається амперметром. Про будову та принцип дії амперметра ми поговоримо в наступній темі даного розділу. На разі ж зауважимо, що в електричне коло, амперметр включається послідовно з тим приладом в якому вимірюється сила струму (мал.76). Зауважимо також, що електричний опір амперметра має бути гранично малим. Адже лише в цьому випадку вплив амперметра на параметри того кола в якому він вимірює силу струму, буде мінімальним.

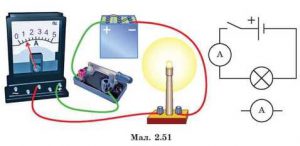
Мал.76. Загальний вигляд, умовне позначення та схема включення амперметра

Електричний струм, це результат тих процесів які відбуваються у замкнутому електричному колі. Електричним колом називають взаємопов’язану сукупність електричних приладів та  з’єднувальних струмопровідних дротів. Основними елементами електричного кола є джерело струму, споживачі струму, електровимірювальні прилади, елементи управління струмом.

Джерело струму, це прилад, який перетворює той чи інший вид неелектричної енергії в енергію електричного струму. Наприклад гальванічні елементи (батарейки) та акумулятори, перетворюють енергію хімічних взаємодій в енергію електричного струму (Е_хім → Е_ел), індукційні генератори, в енергію струму перетворюють механічну роботу (А_мех → Е_ел), а сонячні батареї –  енергію сонячного світла (Е_св → Е_ел). З загальним устроєм та принципом дії більшості різновидностей джерел струму, ви познайомитеся в процесі подальшого вивчення фізики.

Споживач струму, це прилад, в якому енергія електричного струму перетворюється в той чи інший вид неелектричної енергії. Наприклад лампочки розжарювання енергію електричного струму перетворюють в енергію світла і теплоту; електронагрівальні прилади, енергію струму перетворюють в теплоту, електродвигуни – в механічну роботу, телевізори – в зображення і звук, тощо. Втім, в загальному сенсі споживачами струму є будь які прилади які так чи інакше споживають електричну енергіє. Зокрема певними споживачами струму є дроти ліній електропередач, трансформатори, вимірювальні прилади, тощо.

Електровимірювальний прилад, це прилад, за допомогою якого вимірюють параметри електричного струму та з ним пов’язаних величин (електрична напруга, електричний опір, електрична потужність, тощо). Амперметри, вольтметри, омметри, ватметри – очевидні приклади електровимірювальних приладів.

Елемент управління струмом, це прилад який в потрібний момент вмикає та вимикає електричний струм, або регулює силу струму в електричному колі. Найпростішими елементами управління електричним струмом є вимикач (ключ, рубильник) та реостат (резистор). Вимикач вмикає та вимикає електричний струм, а реостат дозволяє регулювати величину сили струму в колі. Наприклад в зображеному на мал.76 електричному колі, джерелом струму є акумулятор, споживачем струму – лампочка розжарювання, електровимірювальним приладом – амперметр, а елементом управління – ключ.

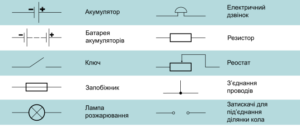
Складові частини електричного кола прийнято зображати у вигляді певних умовних символів (знаків, позначок), а саме коло представляти у вигляді йому відповідної схеми. Наприклад на тому ж мал.76 представлене як просте електричне коло так і  йому відповідна електрична схема. Умовні позначення найбільш поширених елементів електричного кола можна представити у вигляді наступної таблиці.

Загалом, електричне коло можна порівняти з замкнутою гідравлічною системою (мал.77). Системою в якій заповненими вільними електронами провідниками, є  заповнені водою труби. Джерелом струму є не батарейка (акумулятор, генератор, тощо) а водяний насос (помпа). Елементом управління струмом є не сукупність вимикача та резистора, а гідравлічний кран. Споживачем струму є не лампочка розжарювання, а батарея опалювання. Вимірювальним приладом є не амперметр, а водяний лічильник.

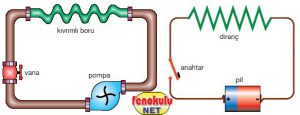
Мал.77. Порівняйте загальний устрій електричного та гідравлічного кола.

Подібно до того як у заповненій водою трубі, упорядкований рух (струм) води не виникає сам по собі, в заповненому електронами провіднику, рух електронів сам по собі не стає упорядкованим. Для того щоб в трубі виник струм води, між її входом та виходом має існувати певний перепад тиску, який прийнято називати гідравлічним напором, і джерелом якого є водяний насос. Для виникнення електричного струму в провіднику, між його входом та виходом також має існувати певний перепад електричного тиску, який називають електричною напругою і джерелом якого є джерело струму.

Електрична напруга – це фізична величина, яка є енергетичною характеристикою певної ділянки електричного кола і яка дорівнює відношенню тієї роботи яку виконують електричні сили на відповідній ділянці кола, до величини перенесеного при цьому електричного заряду.

Позначається: U

Визначальне рівняння: U = А_ел/q

Одиниця вимірювання: U = Дж/Кл = В,     вольт.

Із визначального рівняння електричної напруги (U = A_ел/q) випливає, що одиниця її вимірювання напруги [U] = Дж/Кл = В, дорівнює такій напрузі, при якій переміщення заряду в один кулон (переміщення 6,25∙10¹⁸ електронів) супроводжується виконанням роботи в один джоуль.

Тому якщо наприклад, на певній ділянці електричного кола існує напруга 220В, то це означає, що при переміщенні по цій ділянці 6,25∙10¹⁸ електронів буде виконана робота 220Дж. Якщо ж ця напруга становитиме 5В, то при переміщенні тієї ж кількості електронів, виконаної роботи буде лише 5Дж.

Ви можете запитати: «А як це виходить, що переміщення однієї і тієї ж кількості електронів, призводить до виконання різної кількості роботи?». Відповідаючи на це запитання, розглянемо наступну ситуацію. Припустимо, що є дві бригади робітників, в одній з яких зібралися умовно кажучи «трудяги», а в іншій – «ледарі». Переносячи цеглу  з точки А в точку В, кожен «трудяга» бере п’ять цеглин, а кожен «ледар» – одну. Запитується, чи однаковою буде виконана робота, якщо з точки А в точку В пройшло 10 «трудяг» і 10 «ледарів»? Відповідь очевидна: робота виконана бригадою «трудяг» буде у п’ять разів більшою за ту роботу яку виконала бригада «ледарів». Електрони, як і робітники, в одних ситуаціях рухаються з великим навантаженням (напруженням), в інших – з малим. При цьому, виконана ними робота є відповідно різною.

Мал.78. Електрична напруга показує, яку роботу виконують електричні сили на даній ділянці електричного кола, при переміщені по ній заряду в один кулон (при переміщенні 6,25·10¹⁸ електронів).

Електричну напругу вимірюють приладом, який називається вольтметром. Вольтметр відрізняється від амперметра тим, що має гранично великий опір та включається в коло відповідного споживача не послідовно як амперметр, а паралельно

   

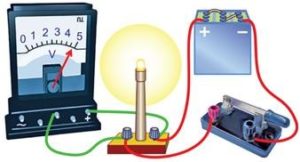
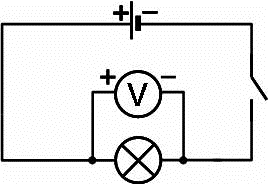
Мал.79. Загальний вигляд, умовне позначення та схема включення вольтметра.

Задача 1. Струм в електричному паяльнику 500мА. Яка кількість електричного заряду проходить через паяльник за 2хв?

Дано:

I = 500мА = 0,5A

t = 2хв = 120c

q =?

Рішення. Оскільки за визначенням І = q/t, то q = I·t.

Розрахунки:  q = 0,5А·120с = 60Кл.

Відповідь: q = 60Кл.

Задача 2. Сила струму в лампочці розжарювання 0,5А. Скільки електронів проходить через поперечний переріз спіралі лампочки за 10хв її роботи?

Дано:

I = 0,5A

t = 10хв = 600с

N = ?

Рішення. Оскільки за визначенням І=q/t, та враховуючи, що q = Ne, де е = 1,6·10^–19Кл, можна записати І = Ne/t, звідси випливає   N = І∙t/e.

Розрахунки: N = 0,5(Кл/с)∙600с/1,6·10^–19Кл = 187,5·10¹⁹ електронів.

Відповідь: N = 187,5·10¹⁹ електронів.

Задача 3. Яку роботу виконує струм силою 3А за 10хв при напрузі в колі 15В?

Дано:

I = 3A

t = 10хв = 600с

U = 15В

А_ел = ?

Рішення. Оскільки за визначенням U = A_ел/q, то A_ел = Uq.

Оскільки за визначенням I = q/t, то q = It

Таким чином А_ел = U∙q = U∙I∙t.

Розрахунки: А_ел = 15(Дж/А·с)∙3А∙600с = 27000Дж = 27кДж.

Відповідь: А_ел = 27кДж.

Задача 4. Електричне поле переміщуючи ділянкою кола заряд 40Кл, виконує таку ж роботу як і сила тяжіння при переміщенні тіла масою 2кг з висоти 10м. Чому дорівнює напруга на відповідній ділянці кола?

Дано:

А_ел = А_мех

q = 40Кл

m = 2кг

h = 10м

U = ?

Рішення. За визначенням U = A_ел/q, враховуючи що А_ел = А_мех, де А_мех = F·h = mgh, можна записати U = mgh/q, де g = 10м/с².

Розрахунки: U = 2кг·10м/с²·10м / 40Кл = 5 (Дж/Кл=В).

Відповідь: U = 5В.

Контрольні запитання.

1. Що характеризує та що показує сила струму?
2. Яка кількість електронів проходить через провідник за секунду при силі струму один ампер?
3. Що називають електричним колом? Назвіть основні елементи електричного кола.
4. Що називають джерелом струму? Які джерела струму вам відомі?
5. На основі малюнку 77 порівняйте базові елементи електричного кола та кола гідравлічного.
6. Визначте показання кожного амперметра.

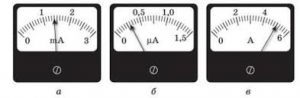
7. Що є необхідною умовою появи електричного струму в провіднику?

8. Що характеризує і чому дорівнює електрична напруга?

9. Чим вольтметр відрізняється від амперметра?

10. Ви значте показання кожного вольтметра.

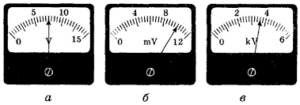
11. Напруга на лампочці електричного ліхтарика 3,5В. Що це означає?
12. Що є первинним електрична напруга чи електричний струм?

Вправа 19.

1. Визначте силу струму в провіднику, через який за 1хв проходить заряд 90Кл.
2. При електрозварюванні сила струму досягає 200А. Який електричний заряд проходить через поперечний переріз електрода за 1хв?
3. Через поперечний переріз провідника за 5хв проходить 6·10²⁰ електронів. Визначте силу струму в провіднику.

4. Через електроприлад проходить струм 8мА. Яка кількість електронів пройде через цей прилад за 30хв?
5. Напруга на затискачах електродвигуна 220В. Яка електрична робота буде виконана в двигуні при проходженні заряду 10Кл.
6. Чому дорівнює напруга на ділянці кола, в якій при силі струму 2А за 20с була здійснена робота 800Дж?
7. Яка сила струму в лампочці електричного ліхтарика, якщо при напрузі 4В в ній за 1с витрачається 0,8Дж електроенергії?
8. Яку роботу здійснить струм силою 0,5А за 10хв при напрузі в колі 220В?
9. Електричне поле переміщуючи ділянкою кола заряд 20Кл, виконує таку ж роботу як і сила тяжіння при переміщенні тіла масою 0,5кг з висоти 5м. Чому дорівнює напруга на відповідній ділянці кола?

.

§20. Закон Ома. Електричний опір.

Основний закон електродинаміки постійних струмів, був сформульований в 1826 році німецьким фізиком Георгом Омом (1787–1854). В цьому законі (законі Ома) стверджується: сила струму І на ділянці електричного кола, прямо пропорційна величині тієї електричної напруги U що існує на краях цієї ділянки і обернено пропорційна її електричному опору R. Іншими словами: I = U/R.

Фізична суть закону Ома очевидно проста: та напруга, що існує між входом та виходом даної ділянки кола, створює на цій ділянці електричний струм, величина якого прямо пропорційна наявній напрузі і обернено пропорційна електричному опору відповідної ділянки, тобто: U → I = U/R.

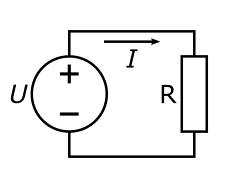
Мал.80. Електрична напруга створює електричний струм, величина якого прямо пропорційна напрузі і обернено пропорційна опору провідника: U → I = U/R.

Не важко бачити, що в законі Ома, окрім раніше визначених фізичних величин (U = A_ел/q, I = q/t), фігурує ще одна величина, яку називають електричним опором.

Електричний опір – це фізична величина, яка характеризує здатність провідника чинити опір проходженню струму по ньому і яка дорівнює відношенню тієї напруги що існує на краях провідника до сили струму в ньому

Позначається: R

Визначальне рівняння: R = U/I

Одиниця вимірювання: [R] = В/А = Ом,     ом.

Варто зауважити, що електричний опір провідника, тобто та величина яка визначається за формулою R = U/I, фактично не залежить ні від U, ні від I. Електричний опір провідника залежить від параметрів самого провідника, зокрема його довжини ℓ, площі поперечного перерізу S та електропровідних властивостей матеріалу провідника. Ці властивості характеризує величина, яка називається питомим опором провідника ρ. При цьому залежність опору провідника R від його довжини ℓ, площі поперечного перерізу S та питомого опору ρ, можна записати у вигляді R = ρℓ/S.

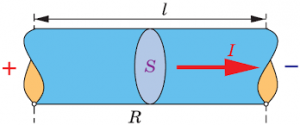
Мал.81. Електричний опір провідника R залежить від його довжини ℓ, площі поперечного перерізу S та питомого опору провідника ρ: R = ρℓ/S.

Питомий опір провідника – це фізична величина, яка характеризує струмопровідні властивості матеріалу провідника і яка чисельно дорівнює тому електричному опору який має виготовлений з даного матеріалу провідник, за умови його одиничної довжини та одиничної площі поперечного перерізу.

Позначається: ρ

Визначальне рівняння: ρ = RS/ℓ

Одиниця вимірювання: [ρ] = Ом∙м,   ом-метр.

Питомий опір провідника визначається експериментально і записується у відповідну таблицю. Наприклад для алюмінію ρ(Аl) = 2,7·10^–8(Ом·м). Це означає, що алюмінієвий провідник довжиною ℓ = 1м і площею поперечного перерізу S = 1м², має електричний опір R = 2,7·10^–8Ом = 0,000000027(Ом). Ясно, що в реальності алюмінієвих, мідних, вольфрамових, срібних чи золотих дротів площею поперечного перерізу 1м² не існує. В реальності площі поперечного перерізу подібних дротів вимірюють не в м², а в мм². Тому на практиці питомий опір провідників зазвичай вимірюють в [ρ] = Ом∙мм²/м, (ом на міліметр квадратний-метр.

Не важко довести, що між питомим опором виміряним в Ом·м²/м = Ом·м та питомим опором виміряним в Ом·мм²/м існує співвідношення: Ом·м²/м = Ом(10³мм)²/м = 10⁶Ом·мм²/м. Тому наприклад, ρ(Аl) = 2,7·10^–8(Ом·м) = 0,027(Ом·мм²/м). При цьому запис ρ(Аl)=0,027(Ом·мм²/м) означає, що алюмінієвий провідник довжиною 1м і площею поперечного перерізу 1мм², має електричний опір 0,027(Ом).

Питомий опір деяких металів та сплавів (при t=20ºС)

Речовина	ρ (Ом∙мм2/м)	Речовина	ρ (Ом∙мм2/м)
Алюміній	0,027	Хром	0,19
Вольфрам	0,053	Константан	0,50
Залізо	0,099	Манганін	0,48
Золото	0,022	Нікелін	0,42
Мідь	0,017	Ніхром	1,10
Нікель	0,073	Фехраль	1,20
Платина	0,098	Сталь	0,10 – 0,14
Срібло	0,016	Чавун	0,50 – 0,80

Що ж стосується визначального рівняння R = U/I, то воно є похідним від закону Ома (оскільки згідно з законом Ома I = U/R, то R = U/I) і вказує лише на те, що величину електричного опору будь якого провідника (чи будь якого приладу) можна визначити шляхом вимірювання тієї напруги яка існує між краями провідника та тієї сили струму що протікає при відповідній напрузі.

Наприклад якщо ви хочете визначити електричний опір обмотки трансформатора, генератора чи електродвигуна, загальний електричний опір лампочки розжарювання, телевізора чи іншого електротехнічного приладу, то для цього зовсім не обов’язково руйнувати відповідний прилад та визначати геометричні і електропровідні параметри його елементів. Достатньо на відповідний прилад подати відому наругу U і виміряти ту силу струму І яка протікає через прилад. При цьому електричний опір дорівнюватиме R = U/I. Скажімо якщо при напрузі 1,5В в обмотці (котушці) трансформатора протікає струм 0,5А, то опір цієї обмотки 3,0(Ом):  R = U/I = 1,5В/1,5А = 3,0(Ом).

Електричний опір провідника чи приладу можна виміряти як певним поєднанням джерела струму, амперметра і вольтметра, так і спеціальним приладом який називається омметром. По суті омметр відрізняється від амперметра тим, що в його коло ввімкнуто певне джерело струму (батарейка), яке створює напругу відомої величини.

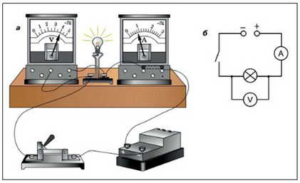
Мал.82. Електричний опір провідника (приладу) можна виміряти як певним поєднанням амперметра та вольтметра, так і спеціальним приладом – омметром.

Задача 1. У вольтметрі, який показує 120В, сила струму дорівнює 15мА. Визначте опір вольтметра.

Дано:

U = 120B

I = 15мА = 0,015А

R = ?

Рішення. У відповідності з законом Ома I = U/R, звідси I = U/R, то R = U/I U/I = 120В / 0,015А = 8000(Ом) = 8кОм.

Відповідь: R = 8кОм.

Задача 2. Сила струму в спіралі електрокип’ятильника 4А. Кип’ятильник включено в мережу з напругою 220В. Яка довжина того ніхромового дроту  з якого виготовлена спіраль кип’ятильника, якщо його переріз 0,1мм²?

Дано:

ніхром

I = 4A

U = 220В

S = 1,1мм²

ℓ = ?

Рішення. Оскільки R = ρℓ/S, то ℓ = RS/ρ, де ρ=1,1(Ом·мм²/м) – таблична величина. А зважаючи на те, що R = U/I, можна записати ℓ = US/Iρ.

Розрахунки: ℓ=220В·1,1мм²/4А·1,1(Ом·мм²/м)=55м.

Відповідь: ℓ = 55м.

Задача 3. За заданими графіками залежності сили струму від напруги, визначити електричні опори відповідних провідників.

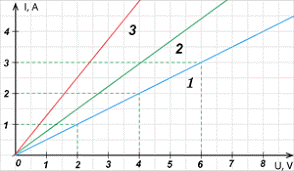
Рішення. Оскільки за визначенням R = U/I, то зручним чином обираючи величину U та йому відповідне значення І, визначаємо:

R₁ = U₁/I₁ = 2В/1А = 2,0(Ом);

R₂ = U₂/I₂ = 2В/1,5А = 1,3(Ом);

R₃ = U₃/I₃ = 2В/2,5А = 0,8(Ом).

Завершуючи розмову про закон Ома, буде не зайвим наголосити на тому, що математично правильним відображенням закону Ома є формула I = U/R, а не U = IR чи R = U/I. Бо закон (фізичний закон), це не просто математична формула, яка відображає певні зв’язки між фізичними величинами. Закон, це відображення того причинно-наслідкового зв’язку, який існує між певними проявами Природи. А це означає, що в законі та йому відповідній математичній формулі, потрібно вказувати на те, що в даному зв’язку є причиною (незалежною, первинною величиною), а що наслідком (залежною, вторинною, похідною величиною).

Наприклад закон Ома відображає факт того, що причиною появи струму є електрична напруга, і що сила струму залежить від напруги, а не навпаки. Іншими словами U → I = U/R. Звичайно, формули U = IR та R = U/I є безумовно правильними. Однак вони не є математичними відображеннями закону Ома. Ці формули є прямими наслідками закону Ома і як ці наслідки можуть застосовуватись як при розв’язуванні задач так і в якості визначальних рівнянь відповідних фізичних величин.

Контрольні запитання.

1. Що стверджується в законі Ома?
2. Яка з формул I=U/R; U=IR; R=U/I є математично правильним відображенням закону Ома? Чому?
3. Що характеризує і чому дорівнює електричний опір?
4. Визначальне рівняння електричного опору має вигляд R = U/I. Чи означає це, що опір провідника дійсно залежить від U та I? Що означає це рівняння?
5. Від чого залежить опір провідника?
6. Питомий опір міді 0,017(Ом·мм²/м). Що це означає?
7. На основі аналізу таблиці питомих опорів, назвіть п’ять найкращих провідників.
8. Як визначити довжину ізольованого мідного дроту, намотаного у великий моток, не розмотуючи його?

Вправа 20.

1. За заданими графіками залежності сили струму від напруги, визначити електричні опори відповідних провідників.

а)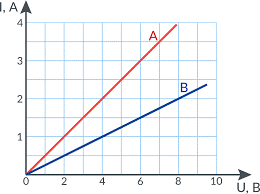  б)

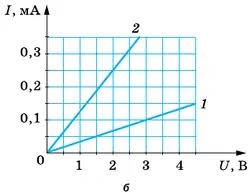
2. У вольтметрі, який показує 120В, сила струму дорівнює 12мА. Визначте опір вольтметра.
3. Яку напругу слід прикласти до опору 1000(Ом), щоб одержати при цьому струм 8мА?
4. У провіднику, до кінців якого прикладено напругу 12В, за 5хв пройшов заряд 60Кл. Визначте опір провідника.
5. Визначте силу струму, який проходить алюмінієвим дротом довжиною 1000м і перерізом 2мм², при напрузі 10В.
6. По мідному провіднику з поперечним перерізом 2мм² і довжиною 50м, тече струм 2А. Визначте напругу на кінцях цього провідника.
7. Сила струму в нагрівальному елементі електричного чайника дорівнює 4А при напрузі 120В. Визначити питомий опір того матеріалу з якого виготовлено нагрівальний елемент, якщо на його виготовлення пішло 18м дроту перерізом 0,24мм².
8. Скільки метрів нікелінового дроту перерізом 0,1мм² потрібно для виготовлення реостата з опором 180(ом)?

.

§21. Резистори. Послідовне з’єднання резисторів.

Базовим приладом електродинаміки постійних струмів є резистор (від лат. resisto – опір). Резистор – це прилад, який представляє собою провідник з певним, наперед визначеним опором, величина якого може бути як постійною так і змінною. Резистори дозволяють регулювати силу струму на ділянках електричного кола та розподіляти ці струми розгалуженнями кола. Основною характеристикою резистора є його електричний опір R. Принцип дії резистора очевидно простий: оскільки згідно з законом Ома, сила струму на ділянці електричного кола залежить від електричного опору ділянки (I = U/R), то змінюючи цей опір, відповідним чином змінюють і силу струму.

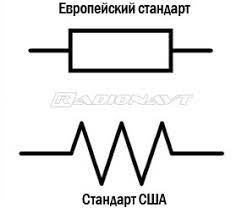
Мал.84. Загальний вигляд та умовне позначення резисторів.

Резистори поділяються на резистори постійного (сталого) опору та резистори змінного опору (реостати і потенціометри). Класичним прикладом резистора змінного опору є повзунковий реостат (мал.85). Цей прилад представляє собою керамічний циліндр на тіло якого щільно намотана металева проволока з великим питомим опором (нікелін, константан, ніхром, тощо). Над циліндром знаходиться металевий стержень по якому переміщується повзунок струмопровідні контакти якого притиснуті до циліндра. Переміщуючи повзунок від точки Б до точки А, ми збільшуємо довжину тієї проволоки по якій протікає струм (ℓ↑), а відповідно збільшуємо і опір проходженню цього струму (R = ρℓ/S). Коли ж повзунок переміщується від точки А до точки Б, то електричний опір реостата відповідно зменшується. Таким чином змінюючи положення повзунка ми можемо змінювати опір реостата від 0 (Ом) до певної максимальної величини R_max, яка є паспортною характеристикою відповідного реостата.

 

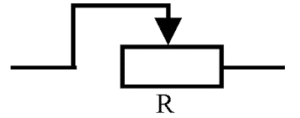
Мал.85. Загальний вигляд та умовне позначення реостата.

З теоретичної точки зору, резистори важливі не лише як окремі прилади, а і як певні ідеалізовані моделі інших електричних приладів. Адже будь який струмопровідний прилад, будь то простий провідник, лампочка розжарювання чи телевізор, має певний електричний опір і тому може бути представленим у вигляді відповідного резистора. А це означає, що ті закономірності які притаманні для тих кіл що складаються з резисторів, цілком обгрунтовано можна застосовувати і в тих випадках де складовими частинами кола є інші, більш складні електричних приладів.

В загальному випадку, резистори можна з’єднувати по різному. При цьому, все різноманіття подібних з’єднань так чи інакше зводяться до двох простих різновидностей: послідовне та паралельне з’єднання. Розглянемо кожне з цих базових з’єднань і на основі відомих законів та визначальних рівнянь, сформулюємо ті закономірності що є характерними для них.

Послідовне з’єднання резисторів (споживачів струму).

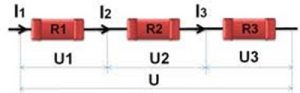
Аналізуючи послідовне з’єднання довільно взятих резисторів можна довести:

1. Сила струму на кожній ділянці послідовно з’єднаних резисторів (І₁; І₂; І₃; …) та загальна сила струму у відповідному колі (І_заг) є однаковими: I_заг = I₁ = I₂ = … = I_n.

Дане твердження є прямим наслідком закону збереження заряду, застосованому до системи послідовно з’єднаних резисторів.

2. Напруга (падіння напруги) на кожній послідовній ділянці кола може бути різною. При цьому загальна напруга кола дорівнює сумі падінь напруг на всіх його послідовних ділянках: U_заг = U₁ + U₂ + … + U_n.

Дане твердження є прямим наслідком закону збереження енергії (роботи), застосованому до системи послідовно з’єднаних резисторів (адже U = A/q).

3. Електричний опір на кожній послідовній ділянці кола може бути різним. При цьому загальний опір кола дорівнює сумі електричних опорів на всіх його послідовних ділянках: R_заг = R₁ + R₂ + … + R_n.

Дане твердження є прямим наслідком двох попередніх тверджень. Дійсно Оскільки для послідовно з’єднаних резисторів виконується співвідношення  U_заг = U₁ + U₂ + U₃, та враховуючи що U = IR, можна записати І_загR_заг = I₁R₁ + I₂R₂ + I₃R₃. А оскільки при послідовному з’єднанні І_заг = І₁ = І₂ = І₃, то R_заг = R₁ + R₂ + R₃.

Таким чином, для системи n послідовно з’єднаних резисторів (споживачів струму) виконуються співвідношення:

I_заг = I₁ = I₂ = … = I_n.

U_заг = U₁ + U₂ + … + U_n.

R_заг = R₁ + R₂ + … + R_n.

Основний недолік системи послідовно з’єднаних резисторів (споживачів струму) полягає в тому, що при такому з’єднанні, вихід з ладу або відключення бодай одного споживача, автоматично призводить до відключення всіх інших елементів системи. Крім цього, при послідовному з’єднанні, падіння напруги на кожному споживачі є таким, що залежить як від параметрів конкретного приладу, так і від кількості включених в коло приладів. Тому в побутовій практиці, послідовне з’єднання застосовують лише в тих випадках, коли мова йде певну сукупність однакових приладів, наприклад лампочок новорічних гірлянд.

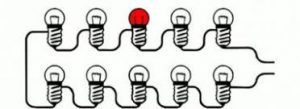
Мал.86. При послідовному з’єднанні, вихід з ладу бодай одного елемента схеми, автоматично призводить до відключення всіх інших елементів системи.

Оскільки нема кращого способу засвоєння теоретичного матеріалу, ніж той який передбачає розв’язування відповідних цьому матеріалу задач, то власне розв’язуванням задач і займемося. Але перед цим, зробимо декілька важливих зауважень які стосуються тих вимірювальних приладів, які можуть бути включеними в електричне коло.

Даючи загальну характеристику тих вимірювальних приладів які називаються амперметрами і вольтметрами, ми наголошували на тому, що електричний опір амперметра є гранично малим (R_A→0), а електричний опір вольтметра навпаки – гранично великим (R_V→∞). Наголошували і на тому, що амперметр включається в електричне коло послідовно з споживачами струму, а вольтметр – паралельно з ними (мал.87).

По суті це означає, що правильне включення амперметрів і вольтметрів в електричне коло, практично не змінює параметрів цього кола. Тому визначаючи параметри того чи іншого електричного кола, відповідні розрахунки виконують виходячи з того, що наявність амперметрів і вольтметрів, не впливає на загальні параметри кола (не впливає на величину сили струму в колі та на його окремих ділянках, не впливає на величину напруги як на всьому колі, так і на його окремих ділянках, не впливає на величину як загального опору кола, так і опору його окремих ділянок).

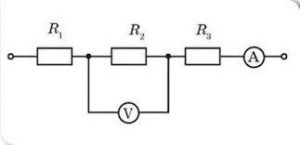
Мал.87. Наявність в електричному колі правильно ввімкнутих амперметрів і вольтметрів, практично не впливає на параметри відповідного кола.

Задача 1. В зображеному на малюнку електричному колі протікає струм 0,5А. Визначити падіння напруги на кожній ділянці кола та на всьому колі.

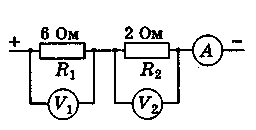
Рішення. Оскільки при послідовному з’єднанні І_заг = І₁ = І₂, то можна записати U₁ = I₁R₁ = 0,5А·6(Ом) = 3В; U₂ = I₂R₂ = 0,5А·2(Ом) = 1В.

Оскільки при послідовному з’єднанні R_заг= R₁ + R₂ = 6(Ом) + 2(Ом) = 8(Ом), то можна записати U_заг = I_загR_заг = 0,5А·8(Ом) = 4В.

Перевірка: U_заг = U₁ + U₂ = 3В + 1В = 4В.

Відповідь: U_заг = 4В; U₁ = 3В; U₂ = 1В.

Задача 2. На основі аналізу заданої електричної схеми, визначити силу струму в електричному колі та падіння напруги на кожній його ділянці.

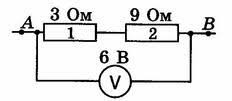
Рішення. Оскільки при послідовному з’єднанні R_заг = R₁ + R₂ = 3(Ом) + 9(Ом) = 12(Ом), то І_заг = U_заг/R_заг = 6В/12(Ом) = 0,5А.

Оскільки при послідовному з’єднанні  І_заг = І₁ = І₂ = 0,5А, то U₁ = I₁R₁ = 0,5А·3(Ом) = 1,5В; U₂ = I₂R₂ = 0,5А·9(Ом) = 4,5В.

Перевірка: U_заг = U₁ + U₂ = 1,5В + 4,5В = 6В.

Задача 3. Обчисліть опір кола, яке складається з електричної лампочки опором 9,5(Ом), реостата опором 12,0(Ом) і мідних провідників довжиною 5м і перерізом 0,4мм², з’єднаних послідовно.

Дано:

R₁ = 9,5(Ом)

R₂ = 12,0(Ом)

мідь

ℓ = 5м

S = 0,3мм²

R_заг= ?

Рішення. Оскільки всі три складові електричного кола з’єднані послідовно, то R_заг = R₁ + R₂ + R₃, де  R₃ = ρℓ/S, ρ(міді) = 0,017(Ом·мм²/м).

R₃ = 0,017(Ом·мм²/м)·5м/0,3мм² = 0,3(Ом).

R_заг= 9,5 + 12,0 + 0,3 = 21,8(Ом).

Відповідь: R_заг= 21,8(Ом).

Задача 4. У коло послідовно включені три провідники опором 5(Ом), 6(Ом) і 12(Ом) відповідно. Яка сила струму в колі і яка напруга прикладена до кінців кола, якщо напруга на другому провіднику 1,2В.

Дано:

R₁ = 5(Oм)

R₂ = 6(Oм)

R₃ = 12(Oм)

U₂ = 1,2В

I_заг=?

U_заг=?

Рішення. 1) Оскільки при послідовному з’єднані, сила струму на всіх ділянках є однаковою, то можна стверджувати І_заг = І₂, де I₂ = U₂/R₂ = 1,2В/6(Ом) = 0,2А.

2) Оскільки І_заг = U_заг/R_заг, то U_заг=I_загR_заг, де  R_заг = R₁ + R₂ + R₃ = 5(Ом) + 6(Ом) + 12(Ом) = 23(Ом).

Таким чином, І_заг = І₂ = 0,2А; U_заг = I_загR_заг = 0,2(А)·23(Ом) = 4,6(В)

Відповідь; І_заг = 0,2(А); U_заг = 4,6(В).

Задача 5. Визначити опори кожного резистора, якщо І₂=0,5А.

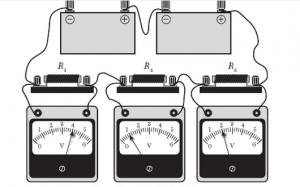
Рішення. Оскільки при послідовному з’єднанні резисторів І₁ = І₂ = І₃ = 0,5А. Та зважаючи на те, що за показаннями вольтметрів U₁ = 4В, U₂ = 1В, U₁ = 2В. Можна записати: R₁ = U₁/I₁ = 4В/0,5А = 8(Ом);

R₂ = U₂/I₂ = 1В/0,5А = 2(Ом);

R₃ = U₃/I₃ = 2В/0,5А = 4(Ом).

Зверніть увагу на факт того, що при послідовному з’єднанні резисторів, падіння напруги (напруга U) на кожному резисторі є різним. І це закономірно. Адже напруга характеризує ту роботу яку виконують електричні сили по переміщенню заряду відповідною ділянкою кола U = A/q. Величина ж цієї роботи залежить як від величини перенесеного за одиницю часу заряду, а фактично від величини сили струму І = q/t в провіднику, так і від величини електричного опору провідника (чим більший опір, тим більша величина роботи). А оскільки при послідовному з’єднанні резисторів, сила струму в кожному з них є однаковою, то величина виконаної на резисторі роботи, а отже і величина падіння напруги на ньому, є пропорційними електричному опору резистора: чим більший опір (R), тим більше падіння напруги (U). Що і підтверджує експеримент.

Контрольні запитання.

1. Що представляє собою резистор, та який його принцип дії?
2. Поясніть загальний устрій та принцип дії повзункового реостату.
3. Що можна сказати про величину сили струму на кожній послідовній ділянці кола?
4. Що можна сказати про величину електричної напруги на кожній послідовній ділянці кола?
5. Що можна сказати про величину електричного опору на кожній послідовній ділянці кола?
6. Які недоліки послідовного з’єднання споживачів струму?
7. Як змінюватимуться показання амперметра та інтенсивність випромінювання лампочки розжарювання, якщо повзунок реостата переміщувати вправо, вліво? Відповідь обґрунтуйте.

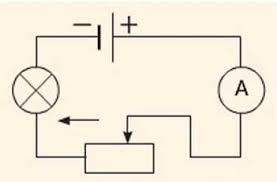
8. Чи можна використати дві однакові лампочки, розраховані на 110В, в мережі з напругою 220В? Якщо можна, то як це зробити?

9. За яких умов показання тих вольтметрів які зображені на малюнку до задачі 5, будуть однаковими?

Вправа 21.

1. В зображеному на малюнку електричному колі протікає струм 0,5А. Визначити падіння напруги на кожній ділянці кола та на всьому колі.

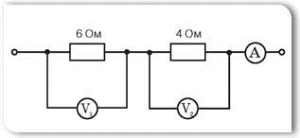
2.  На основі аналізу заданої електричної схеми, визначити силу струму в електричному колі та падіння напруги на ділянці 2.

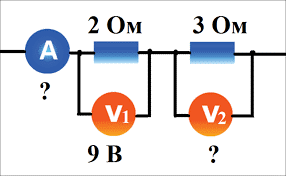
3. На основі аналізу тих даних які представлені на малюнку, визначити силу струму в кожному з резисторів, та падіння напруги на кожному з них.

4. Загальний опір п’яти однакових, з’єднаних послідовно споживачів електроенергії 250(Ом). Який опір кожного споживача?

5. Резистори опори яких 30(Ом) і 60(Ом), з’єднані послідовно і підключені до батарейки. Напруга на першому резисторі 3В. Яка напруга на другому резисторі?

6. На основі аналізу малюнку визначте напругу на кожному резисторі.

7. Скільки електричних лампочок треба взяти для виготовлення ялинкової гірлянди, щоб її можна було вмикати в мережу з напругою 220В, якщо кожна лампочка має опір 20(Ом) і розрахована на силу струму 0,25А?
8. В електричну мережу з напругою 120В ввімкнені послідовно три резистори, опори яких 12(Ом), 9(Ом) і 3(Ом). Визначте силу струму в колі і напругу на кожному резисторі.
9. В мережу з напругою 220В потрібно увімкнути 10 послідовно з’єднаних ламп кожна з яких розрахована на 12В та має опір 24(Ом). Який додатковий опір потрібно включити в систему, за для її нормальної роботи.

.

§22. Паралельне з’єднання резисторів. Закони Кірхгофа.

Характерною ознакою паралельного з’єднання є наявність двох вузлових точок, в одній з яких загальний струм розгалужується на певну кількість гілок (шляхів), а в другій – ці розгалужені струми знову збираються в єдине ціле.

Паралельне з’єднання резисторів (споживачів струму).

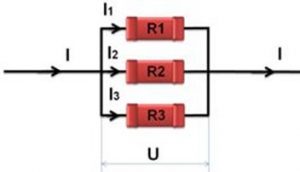
Аналізуючи паралельне з’єднання довільно взятих резисторів можна довести:

1. Сила струму на кожній паралельній ділянці кола може бути різною. При цьому загальна сила струму в колі дорівнює сумі струмів на всіх паралельних ділянках цього кола: I_заг = I₁ + I₂ + … + I_n.

Дане твердження є прямим наслідком закону збереження заряду, застосованому до системи паралельно з’єднаних резисторів.

2. Напруга на кожній паралельній ділянці кола та загальна напруга кола є однаковими: U_заг = U₁ = U₂ = … = U_n.

Дане твердження є прямим наслідком закону збереження енергії (роботи), застосованому до системи паралельно з’єднаних резисторів.

3. Електричний опір на кожній паралельній ділянці кола може бути різним. При цьому загальний електричний опір кола та опори його паралельних ділянок, зв’язані співвідношенням 1/R_заг = 1/R₁ + 1/R₂ + … + 1/R_n.

Даний висновок є прямим наслідком двох попередніх висновків. Дійсно. Виходячи з того, що при паралельному з’єднані І_заг  = І₁ + І₂ + І₃, та враховуючи, що I = U/R, можна записати U_заг/R_заг = U₁/R₁ + U₂/R₂ + U₃/R₃. А оскільки при паралельному з’єднані U = U₁ = U₂ = U₃, то 1/R_заг  = 1/R₁ + 1/R₂ + 1/R₃.

Таким чином, для системи n паралельно з’єднаних резисторів (споживачів струму) виконуються співвідношення:

I_заг  = I₁ + I₂ + … + I_n;

U_заг = U₁ = U₂ = … = U_n;

1/R_заг = 1/R₁ + 1/R₂ + … + 1/R_n.

Задача 1. Визначити загальний опір системи двох резисторів R₁ = 6(Ом); R₂ = 4(Ом) при їх послідовному та паралельному з’єднанні.

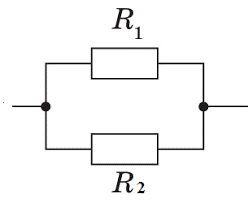
Рішення. При послідовному з’єднанні: R₁₂ = R₁ + R₂ = 6 + 4 = 10(Ом);

При паралельному з’єднанні: 1/R₁₂ = 1/R₁ + 1/R₂ = (R₂+R₁)/R₁·R₂.

Оскільки 1/R₁₂=(R₂+R₁)/R₁·R₂, то R₁₂=R₁R₂/(R₁+R₂).

Таким чином, при паралельному з’єднанні R₁₂ = 4·6/(4+6) = 2,4(Ом)

Загальні зауваження. Застосовуючи формулу 1/R_заг=1/R₁+1/R₂+…+1/R_n, потрібно пам’ятати, що за цією формулою визначається не величина загального опору (R_заг) системи, а величина обернена до цього опору (1/R_заг), і що тому, отриманий результат 1/R_заг = a/b (1/Ом) потрібно привести до вигляду R_заг = b/a (Ом).

Запам’ятай. На практиці, для системи двох паралельно з’єднаних резисторів R₁; R₂, зазвичай застосовують не формулу 1/R₁₂ = 1/R₁+1/R₂, а похідну від неї формулу  R₁₂=R₁∙R₂/(R₁+R₂). Перевага цієї формули в тому, що вона дозволяє визначати опір паралельно з’єднаних резисторів, без додаткових математичних маніпуляцій.

На перший погляд може здатися дивним, що загальний опір системи паралельно з’єднаних резисторів R₁₂ = 2,4(Ом) є меншим за опір кожного окремого елемента цієї системи R₁ = 6(Ом), R₂ = 4(Ом). Насправді ж, нічого дивного в такому стані речей нема. Адже опір провідника фактично залежить від його довжини (ℓ) та площі поперечного перерізу (S):  R=ρℓ/S. І не важко збагнути, що при послідовному з’єднані провідників фактично збільшується їх загальна довжина (ℓ_заг = ℓ₁ + ℓ₂ + … + ℓ_n), а при паралельному з’єднані – збільшується загальна площа поперечного перерізу (S_заг = S₁ + S₂ + … + S_n). А це означає, що при послідовному з’єднанні провідників, їх загальний опір збільшується, а при паралельному з’єднанні – зменшується (буде меншим за найменший з опорів системи).

Говорячи про послідовне та паралельне з’єднання провідників, доречно зауважити, що саме паралельне з’єднання є основним методом з’єднання споживачів електроенергії в побутовій та виробничій практиці (основним методом включення споживачів в систему ліній електропередач). Переваги паралельного з’єднання є очевидними. Адже при такому з’єднані, кожен споживач вмикається в електричну мережу в незалежності від того включені в цю мережу інші прилади чи ні. При цьому кожен споживач може мати свою індивідуальну потужність та стандартизовані параметри базової напруги.

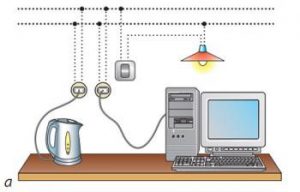
Мал.87. В побутовій та виробничій практиці, основним методом включення електричних приладів в систему ліній електропередач є паралельне з’єднання.

Коли ми стверджували та доводили, що при паралельному з’єднанні резисторів I_заг = I₁ + I₂ + … + I_n, а при їх послідовному з’єднані U_заг = U₁ + U₂ + … + U_n, то по суті застосовували закони, які були сформульовані в 1847 році німецьким фізиком Густавом Кірхгофом (1824–1887). Ці закони називаються законами Кірхгофа.

Перший закон Кірхгофа (правило вузлів) – це закон, в якому стверджується: сума струмів які входять в електричний вузол, дорівнює сумі струмів які виходять з цього вузла. Іншими словами: ∑I_вх = ∑I_вих .

Другий закон Кірхгофа – це закон, в якому стверджується: сума падінь напруг на всіх послідовних ділянках кола, дорівнює тій загальній напрузі що існує між входом та виходом цього кола: ∑U_i = U_заг.

По суті, перший та другий закони Кірхгофа є прямими наслідками відповідно: закону збереження заряду та закону збереження енергії.

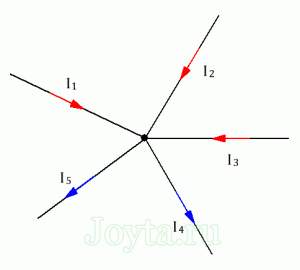
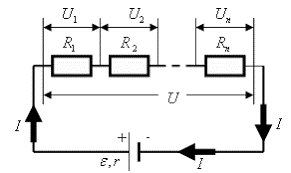
I₁ + I₂ + I₃ = I₄ + I₅                         U₁ + U₂ + … + U_n = U_заг

Мал.88. Приклади які ілюструють закони Кірхгофа.

Задача 1. Визначте загальний опір системи трьох резисторів R₁ = 4(Oм), R₂ = 6(Oм), R₃ =12(Oм), при їх послідовному та паралельному з’єднані.

   

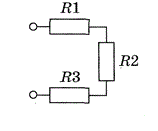
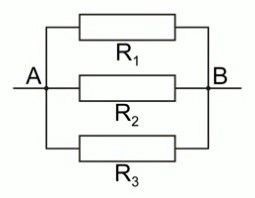
Дано:

R₁=4(Oм)

R₂=6(Oм)

R₃=12(Oм)

R_посл = ?    R_пар = ?

Рішення. Послідовне з’єднання: R_посл = R₁ + R₂ + R₃ = 4 + 6 + 12 = 22(Ом)

Паралельне з’єднані 1/R_пар = 1/R₁ + 1/R₂ + 1/R₃ = 1/4 + 1/6 + 1/12 = 3/12 + 2/12 + 1/12 = 6/12 (1/Ом). Оскільки 1/R_пар = 6/12(1/Oм), то R_пар = 12/6 = 2(Ом).

Відповідь: R_посл = 22(Ом),  R_пар = 2(Ом).

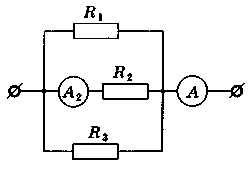
Задача 2. Амперметр (А) показує силу струму 1,6А, а вольтметр (V) показує напругу 120В. Опір резистора R₁ = 100(Ом). Визначити опір резистора R₂ і показання амперметрів (А₁) і (А₂).

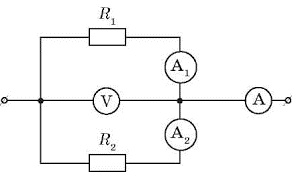
Дано:

І_заг= 1,6А

U_заг= 120В

R₁ = 100(Ом)

R₂ = ?   І₁=?    І₂=?

Рішення.  Оскільки U_заг = U₁ = U₂ = 120В, то І₁= U₁/R₁ = 120В/100(Ом) = 1,2А.

Оскільки І₁ + І₂ = І_заг, то І₂ = І_заг – І₁ = 1,6А – 1,2А = 0,4А. Отже

R₂ = U₂/I₂ = 120В/0,4А = 300(Ом).

Відповідь: І₁ = 1,2А; І₂ = 0,4А; R₂ = 300(Ом).

Задача 3. За наведеними на електричній схемі даними, визначити І₁ = ?, І₂ = ?, І₃ = ?, R₃ = ?

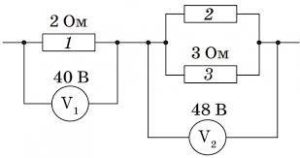
Рішення. На основі аналізу тих даних які представлені на схемі, можна записати. І₁ = U₁/R₁ = 40В/2(Ом) = 20А. Оскільки U₂ = U₃ = 48В, то І₃ = U₃/R₃ = 48В/3(Ом) = 16А.

Оскільки І₂ + І₃ = І₁, то І₂ = І₁ – І₃ = 20А – 16А = 4А, отже R₂ = U₂/I₂ = 48В/4А = 12(Ом).

Відповідь: І₁ = 20А, І₂ = 4А, І₃ = 16А, R₂ = 12(Ом).

Задача 4. Два резистори R₁ = 4(Oм), R₂ = 6(Oм), з’єднані паралельно. Визначити силу струму на кожній ділянці електричного кола, якщо напруга на краях кола 4,8В.

 

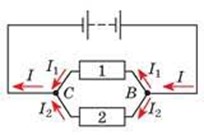
Дано:

R₁ = 4(Oм)

R₂ = 6(Oм)

U_заг = 4,8В

І_заг = ?   І₁=?   І₂=?

Рішення. У відповідності з законом Ома І_заг=U_заг/R_заг;  І₁=U₁/R₁;  І₂=U₂/R₂.

Для паралельного з’єднання двох резисторів R_заг = R₁₂ = R₁·R₂/(R₁+R₂) = 4·6/(4+6) = 2,4(Ом). Тому І_заг = U_заг/R_заг = 4,8В/2,4(Ом) = 2,0А.

Оскільки при паралельному з’єднанні U₁ = U₂ = U_заг= 4,8В, то І₁ = 4,8В/4(Ом) = 1,2А; І₂ = 4,8В/6(Ом) = 0,8А.

Перевірка: І_заг = І₁ + І₂ = 1,2А + 0,8А = 2,0А

Відповідь: І_заг=2А; І₁=1,2А; І₂=0,8А.

Контрольні запитання.

1. Яка характерна ознака паралельного з’єднання резисторів?
2. Що можна сказати про величину сили струму в паралельних ділянках кола?
3. Що можна сказати про величину напруги в паралельних ділянках кола?
4. Чому формула R₁₂ = R₁∙R₂/(R₁+R₂), зручніша за формулу 1/R₁₂ = 1/R₁ + 1/R₂?
5. Доведіть, що загальний опір системи n однакових паралельно з’єднаних опорів (R) можна визначити за формулою: R_заг=R/n.
6. Поясніть, чому при послідовному з’єднанні провідників їх загальний опір збільшується, а при паралельному з’єднанні – зменшується?
7. Чому в побутовій та виробничій практиці, основним методом включення споживачів в мережу ліній електропередач є паралельне включення, а не послідовне?
8. Що стверджується в першому та другому законах Кірхгофа?
9. Наслідками яких базових законів є перший і другий закони Кірхгофа?

Вправа 22.

1. Визначте загальний опір системи двох резисторів R₁ = 15(Oм), R₂ = 20(Oм), при їх послідовному та паралельному з’єднані.
2. Визначте загальний опір системи трьох резисторів R₁ = 10(Oм), R₂ = 15(Oм), R₃ =30(Oм), при їх послідовному та паралельному з’єднані.
3. Два резистори, опори яких 5(Ом) і 10(Ом), підключені паралельно до батарейки. Визначте загальній опір з’єднання. Сила струму в якому з резисторів буде більшою?
4. Два резистори, опори яких 20(Ом) і 30(Ом), підключені до батарейки. Сила струму в першому резисторі 0,2А. Який струм протікає у другому резисторі?
5. В зображеній на малюнку схемі R₁ = 20(Ом), R₂ = 10(Ом), R₃ = 5(Ом). При цьому амперметр (А₂) показує силу струму 0,5А, а амперметр (А) показує 1,75А. Визначити силу струму в резисторах R₁ і R₃.

6. Який резистор треба з’єднати паралельно з резистором у 300(Ом), щоб одержати опір 120(Ом) ?

7. Провідники опором 4(Ом) і 12(Ом) з’єднані паралельно і підключені в коло з напругою 3В. Визначити силу струму у кожному провіднику.

8. Три провідники опором 2(Ом), 3(Ом) і 6(Ом) з’єднані паралельно. Визначте силу струму в кожному провіднику, якщо загальна сила струму в колі 6А.

9. Визначте величину опору R₃, якщо R₁=6(Ом), R₂=4(Ом), І₂=3А, І=9А.

.

§23. Змішане з’єднання резисторів. Метод еквівалентних схем.

Послідовне та паралельне з’єднання, це базові способи з’єднання резисторів (провідників, конденсаторів, котушок індуктивності і загалом споживачів струму). Однак якщо мова йде про реальні електротехнічні прилади, то вони представляють собою певні сукупності відносно простих деталей з’єднаних змішаним способом, тобто таким способом, який представляє собою певні комбінації послідовних та паралельних з’єднань. Наприклад в зображеній на мал.89 ситуації, електричні лампочки з’єднані змішаним способом.

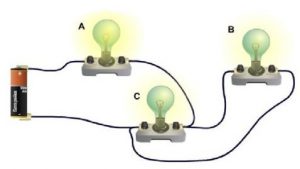
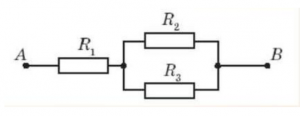
Мал.89. Приклад простого змішаного з’єднання.

Визначаючи електричні опори та параметри струмів і напруг системи змішано з’єднаних резисторів, зазвичай застосовують так званий метод еквівалентних схем. Суть цього методу полягає в тому, що складне електричне коло, послідовно розбивають на прості ділянки, де резистори з’єднані або послідовно або паралельно. При цьому кожну таку ділянку замінюють одним еквівалентним опором та отримують відповідну більш просту еквівалентну схему.

Наприклад  в зображеній на малюнку схемі, послідовно з’єднані опори R₁ і R₂, замінюють еквівалентним опором  R₁₂ = R₁+R₂, a паралельно з’єднані R₃ і R₄ замінюють R₃₄ = R₃R₄/(R₃+R₄). На наступному етапі спрощення, послідовно з’єднані R₁₂, R₃₄ та R₅, замінюють результуючим еквівалентним опором R_рез= R₁₂ + R₃₄ + R₅.

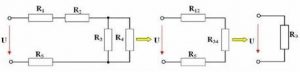
Застосовуючи метод еквівалентних схем, потрібно мати на увазі, що певні еквівалентні заміни можна робити лише в межах двох сусідніх вузлів. Скажімо, не можна вважати, що резистори R₁, R₂, R₃ та R₅ з’єднані послідовно (вважати лише на тій підставі, що ми можемо провести певну неперервну лінію, яка послідовно з’єднує ці резистори). Не можна тому, що в електричному колі, струми розподіляються не так як нам зручно і не по тим лініям які ми можемо намалювати, а у відповідності з певними законами електродинаміки.

Загальні зауваження. Аналізуючи електричні схеми, потрібно мати на увазі, що одна і та ж схема може мати суттєво різний вигляд. Наприклад, на мал.90. представлена одна і та ж електрична схема, загальний опір якої R_заг = R₁ + R₂₃, де R₂₃ = R₂R₃/(R₂+R₃).

Мал.90. Одна і та ж електрична схема, може виглядати по різному.

Задача 1. Виходячи з того, що в системі зображених на малюнку резисторів, їх електричні опори однакові і дорівнюють 8(Ом) кожний, визначити загальний опір системи.

     

Рішення. Застосовуючи метод еквівалентних схем, можна записати:

R₄, R₆ і R₅ з’єднані послідовно і тому R₄₅₆ = R₄ + R₅ + R₆ = 8 + 8 + 8 = 24(Ом);

R₃ і R₄₅₆ з’єднані паралельно і тому R₃₄₅₆ = R₃∙R₄₅₆/(R₃ + R₄₅₆) = 8∙24/(8+24) = 6(Ом),

R₁, R₃₄₅₆ і R₂ з’єднані послідовно і тому R_заг = R₁ + R₃₄₅₆ + R₂ = 8 + 6 + 8 = 22(Ом).

Відповідь: R_заг = 22(Ом).

Задача 2. Виходячи з того, що в системі зображених на малюнку резисторів, їх електричні опори однакові і дорівнюють 6(Ом) кожний, визначити загальний опір системи.

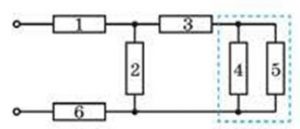
Рішення. Застосовуючи метод еквівалентних схем, можна записати:

R₄ і R₅ з’єднані паралельно і тому R₄₅ = R₄∙R₅/(R₄+R₅) = 6∙6/(6+6) = 3(Ом),

R₃ і R₄₅ з’єднані послідовно і тому R₃₄₅ = R₃ + R₄₅ = 3 + 6 = 9(Ом),

R₂ і R₃₄₅ з’єднані паралельно і тому R₂₃₄₅ = R₂∙R₃₄₅/(R₂+R₃₄₅) = 6∙9/(6+9) = 3,6(Ом),

R₁, R₂₃₄₅ і R₆ з’єднані послідовно і тому R_заг = R₁+R₂₃₄₅+R₆ = 6+3,6+6 = 15,6(Ом).

Відповідь: R_заг = 15,6(Ом).

Задача 3. На основі аналізу заданої схеми визначте показання амперметра, якщо вольтметр показує 5В.

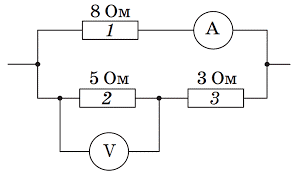
Рішення. Оскільки R₂ = 5(Ом), U₂ = 5В, то I₂ = U₂/R₂ = 5В/5(Ом)=1А.

Оскільки резистори R₂ і R₃ з’єднані послідовно, то І₂ = І₃ = 1А, тому

U₃ = I₃R₃ = 1А·3(Ом) = 3В.

Оскільки при послідовному з’єднанні U₂₃ = U₂ + U₃, то U₂₃ = 5В + 3В = 8В.

Оскільки при паралельному з’єднанні  U₁ = U₂₃ = 8В, то І₁ = U₁/R₁ = 8В/8(Ом) = 1А.

Відповідь: І₁ = 1А.

Задача 4. На основі аналізу заданої схеми визначте показання вольтметра і загальну напругу на заданій ділянці кола.

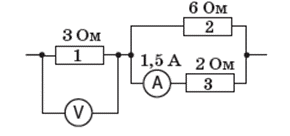
Рішення. Оскільки R₃ = 2(Ом), I₃ = 1,5A, то U₃ = I₃·R₃ = 1,5А·2(Ом) = 3В.

Оскільки при паралельному з’єднанні U₂ = U₃ = 3В, то I₂ = U₂/R₂ = 3В/6(Ом) = 0,5А.

Оскільки І₁ = І_заг = І₂ + І₃ = 1,5А+0,5А = 2,0А, то U₁ = I₁·R₁ = 2,0А·3(Ом) = 6В.

Оскільки при послідовному з’єднанні U_заг = U₁ + U₂₃, то U_заг = 6В + 3В = 9В.

Відповідь: U₁ = 6В; U_заг = 9В.

Задача 5. Визначити силу струму на кожній ділянці електричного кола, якщо R₁ = 3(Ом), R₂ = 4(Ом), R₃ = 6(Ом), R₄ = 4,6(Ом). Напруга між точками А і В 10В.

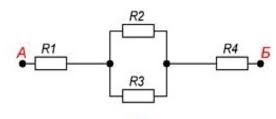
Дано:

R₁=3(Ом)

R₃=4(Ом)

R₂=6(Ом)

R₄=4,6(Ом)

U_заг =10(В)

I₁, I₂, I₃, I₄ – ?

Рішення. Подібні задачі розв’язуються у два етапи: 1) визначається загальна сила струму в колі; 2) визначається сила струму на кожній ділянці кола.

1). Згідно з законом Ома  I_заг=U_заг/R_заг, де R_заг=? Застосовуючи метод еквівалентних схем, можна записати: R₂₃ = R₂∙R₃/(R₂+R₃) = 4∙6/(4+6) = 2,4(Ом). Отже R_заг = R₁ + R₂₃ + R₄ = 3 + 2,4 + 4,6 = 10(Ом).

Таким чином I_заг = U_заг/R_заг = 10(В)/10(Ом) = 1,0(А).

2). Визначаємо силу струму на кожній ділянці електричного кола. Оскільки для тих ділянок кола де відсутні його розгалуження, величини відповідних струмів дорівнюють І_заг, то можна стверджувати: І₁ = І₄ = І_заг = 1,0(А).

Якщо ж мова йде про ділянки розгалуження, то для них сили струмів (І₂, І₃) визначаються із наступних міркувань. Оскільки для паралельного з’єднання  U₂ = U₃ = U₂₃, та враховуючи, що U₂₃ = I₂₃∙R₂₃ = I_заг∙R₁₂₃ = 1,0(А)∙2,4(Ом) = 2,4(В), можна записати: І₂ = 2,4(В)/4(Ом) = 0,6(А), І₃ = 2,4(В)/6(Ом) = 0,4(А).

Перевірка: І₂ + І₃ = 0,6(А) + 0,4(А) = 1,0(А).

Відповідь: І₁ = 1,0(А), І₂ = 0,6(А), І₃ = 0,4(А), І₄ = 1,0(А).

Задача 6. Визначити силу струму на кожній ділянці електричного кола, якщо: R₁ = R₂ = R₃ = R₄ = 6(Ом), U_заг = 10В.

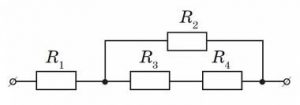
Дано:

R₁ = R₂ = R₃ = R₄ = 6(Ом)

U_заг = 10В

I₁, I₂, I₃, I₄ – ?

Рішення. 1)  I_заг=U_заг/R_заг, де R_заг=?

Застосовуючи метод еквівалентних схем, можна записати:

R₃₄ = R₃ + R₄ = 6 + 6 =12(Ом)

R₂₃₄ = R₂R₃₄/(R₂+R₃₄) = 6·12/(6+12) = 4(Ом)

R_заг = R₁ + R₂₃₄ = 4 + 6 = 10(Ом)

І_заг=10В/10(Ом)=1А

2) І₁ = І_заг = 1А;  I₂ =? I₃ = ? I₄ = ?

Зважаючи на те, що І₃ = І₄ = І₃₄ = U₃₄/R₃₄,

а також на факт того, що при паралельному з’єднанні

U₂ = U₃₄ = U₂₃₄ = I₂₃₄R₂₃₄ = I_загR₂₃₄ = 1А∙4(Ом) = 4В,

можна записати:

І₂ = 4В/6(Ом) = (2/3)А

І₃ = І₄ = 4В/12(Ом) = (1/3)А

Відповідь: І₁ = 1А; І₂ = (2/3)А; І₃ = (1/3)А; І₄ = (1/3)А.

Вправа 23.

1. Визначити загальний опір кола, якщо опір кожного резистора 6(Ом).

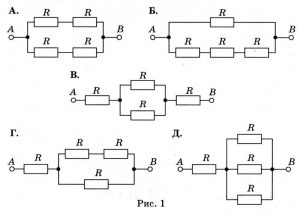
2. Визначити загальний опір електричного кола, якщо R₁=6(Ом), R₂=4(Ом), R₃=3,6(Ом), R₄=5(Ом), R₅=10(Ом).

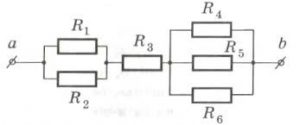
3. Визначити загальний опір кола, якщо R = 10(Ом).

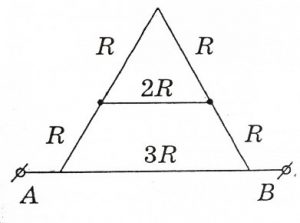
4. На основі аналізу заданої схеми визначте показання вольтметра, якщо амперметр показує 0,5А.

5. На основі аналізу заданої схеми визначте опір резистора R₃ та струми в резисторах R₁ i R₂.

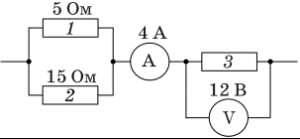
6. Визначте загальну силу струму в колі та на кожній ділянці цього кола, якщо: U_заг = 10(В), R₁ = 7,9(Ом), R₂ = 3(Ом), R₃ = 7(Ом).

7. Визначити силу струму на кожній ділянці електричного кола, якщо R₁ = R₂ = R₃ = R₄ = 4(Ом), U_заг = 8(В)

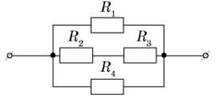
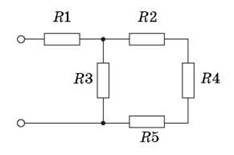
8. Визначити силу струму на кожній ділянці електричного кола, якщо R₁ = 5(Ом), R₂ = 3(Ом), R₃ = 6(Ом), R₄ = 5(Ом), R₅ = 4(Ом), R₆ = 3(Ом) U_заг = 12В.

.

§24. Робота та потужність електричного струму.

Нагадаємо.  Робота – це фізична величина, яка характеризує затрати енергії на виконання роботи і яка дорівнює цим затратам.

Позначається:  А

Визначальне рівняння:  А = ΔЕ

Одиниця вимірювання:  [А] = Дж,    джоуль.

Формула А = ∆Е є базовим, визначальним рівнянням роботи. При цьому за різних обставин, це базове рівняння може набувати різного вигляду. Скажімо якщо мова йде про механічну роботу, тобто ту роботу яку виконує сила F по переміщенню тіла на відстань s, то її зазвичай визначають за формулою A_мех = F∙s.

Якщо ж говорити про роботу електричного струму А_ел, то формула для її визначення з усією очевидністю випливає з визначальних рівнянь напруги U = А_ел/q та сили струму I = q/t. Дійсно, оскільки U = А_ел/q, то А_ел = U∙q. А враховуючи, що q = I∙t, можна записати А_ел=U∙I∙t.

Мал.91. Механічну та електричну роботи визначають за суттєво різними формулами: A_мех = F∙s,  А_ел=U∙I∙t.

Таким чином, роботу електричних сил (роботу електричного струму), можна визначити за формулою А_ел = U∙I∙t, де

U – напруга (падіння напруги) на заданій ділянці електричного кола,

I – сила струму в колі,

t – час проходження струму.

Наприклад, якщо в лампочці розжарювання при напрузі 220В протікає струм 0,5А, то загальна кількість виконаної в ній електричної роботи (витраченої електроенергії) за 10хв (за 600с) становить А_ел = 220В·0,5А·600с = 66000Дж.

Інша справа, що лише 4-5% цієї електричної роботи піде на виконання роботи корисної, тобто на утворення видимого світла. Але то ж не проблема електрики, а проблема її неефективного використання. Бо як би там не було, а лічильник нарахує 66000Дж виконаної електрикою роботи.

До речі, у побутовій та виробничій практиці, кількість виконаної електричної роботи, вимірює прилад який прийнято називати лічильником електроенергії. При цьому кількість цієї роботи зазвичай вимірюють не в джоулях, а в кіловат-годинах. Кіловат-година, це позасистемна одиниця вимірювання роботи (енергії), яка дорівнює тій загальній роботі яку виконує прилад потужністю один кіловат, за годину своєї роботи: 1кВт∙год = 10³Вт∙3,6∙10³с = 3,6∙10⁶Дж.

Говорячи про роботу загалом та про механічну і електричну роботу зокрема, не важко бачити, що ті формули за якими визначають та вимірюють одну і ту ж величину в механіці і електродинаміці є суттєво різними:

.                A_мех = F∙s,           [А] = Н∙м = Дж,

А = ∆Е

.                А_ел = U∙I∙t,          [А] = В∙А∙с = Дж.

Втім, ніяких протиріч в тому, що роботу в одному випадку визначають за формулою A = F∙s, а в іншому – за формулою А = U∙I∙t, нема. Рівно як нема протиріч і в тому, що в одному випадку Дж = Н∙м, а в іншому – Дж = В∙А∙с. Просто потрібно пам’ятати, що за визначенням U = А_ел/q = А_ел/І∙t, і тому U∙I∙t = (А_ел/І∙t)∙І∙t = А_ел;  В∙А∙с = (Дж/А∙с)∙А∙с = Дж.

Задача 1. Яка сила струму в лампочці ліхтарика, якщо при напрузі 4В, вона за 1хв споживає 48Дж електроенергії?

Дано:

U = 4B

t = 1хв = 60с

A_ел = 48Дж

І = ?

Рішення. Оскільки А_ел = U∙I∙t, то І = А_ел / U∙t = 48Дж / (4В∙60с) = 0,2А.

Відповідь: І = 0,2А.

Задача 2. В електроприладі за 45хв струмом 5А виконана робота 162кДж. Визначити електричний опір приладу.

Дано:

t = 45хв = 2,7∙10³с

I = 5A

A = 162кДж = 162∙10³Дж

R = ?

Рішення. Оскільки А_ел = U∙I∙t, та враховуючи, що І = U/R, а отже U = I∙R, можна записати A_ел = I∙R∙I∙t = I²∙R∙t, звідси  R = A_ел/I²t.

Розрахунки.  R = A_ел/I²t = 162∙10³Дж / (5А)²∙2,7∙10³с = 162(В∙А∙с) / 25А²∙2,7с = 2,4(В/А=Ом).

Відповідь: R = 2,4(Ом).

Оскільки величина тієї роботи яку виконує прилад, залежить не лише від енергетичних параметрів самого приладу, а й від тривалості виконання роботи, то на практиці основною енергетичною характеристикою будь якого приладу є його потужність. Нагадаємо.

Потужність – це фізична величина, яка характеризує роботу виконану за одиницю часу і яка дорівнює відношенню виконаної роботи до того проміжку часу за який ця робота виконана.

Позначається: N

Визначальне рівняння: N = А/t

Одиниця вимірювання: [N] = Дж/с = Вт.

Оскільки за визначенням N = А/t, та враховуючи, що А_ел = U∙I∙t, можна записати N_ел = А_ел/t = U∙I∙t/t = U·I. При цьому [N_ел] = В∙А = Вт.

Із аналізу рівняння N_ел = U·I ясно, що потужність електричного приладу можна виміряти за допомогою системи двох приладів: амперметра і вольтметра. Наприклад, в зображеній на мал.92 ситуації, напруга між входом та виходом електричної лампочки 4В, а сила струму в ній 0,8А. А це означає, що електрична потужність лампочки N_ел = U·I = 4В·0,8А = 3,2Вт. Втім, електричну потужність можна виміряти не лише сукупністю вольтметра і амперметра, а й спеціальним приладом який називається ватметром. На електричних схемах ватметр позначають символом –W–.

Мал.92. Потужність електричного приладу можна виміряти як поєднанням амперметра і вольтметра, так і спеціальним приладом – ватметром.

Виходячи з того, що N = А/t та враховуючи що A_мех = F∙s і що s/t = v, можна записати N_мех = А_мех/t = F∙s/t = F∙v. При цьому [N_мех] = Н∙м/с = Вт.

Таким чином, механічні та електричні потужності визначають за візуально різними формулами (N_мех = F∙v; N_ел = U∙I) і вимірюють візуально різними одиницями (Вт = Н·м/с; Вт = В·А).

.                  N_мех= F∙v,         [N]=Н·м/с=Вт,

N=А/t

.                  N_ел=U∙I,            [N]=В∙А=Вт.

Втім, ніяких суперечностей між цими формулами та одиницями вимірювання нема. Просто треба пам’ятати, що за визначенням U = А_ел/q = А_ел/І∙t, і тому U∙I = (А_ел/І∙t)∙I = А_ел/t = N_ел;  В·А = (Дж/А∙с)∙А = Дж/с = Вт.

На завершення зауважимо, що електричну потужність часто позначають літерою Р (Р = N_ел = A_ел/t).

Задача 3. На цоколі лампочки розжарювання написано 220В; 75Вт. На яку силу струму розрахована ця лампочка і який її робочий електричний опір?

Дано:

U = 220В

N_ел = 75Вт

I = ?  R = ?

Рішення. Оскільки N_ел=U∙I, то І = N_ел/U = 75Вт/220В = 0,34А.

Оскільки R = U/I, то R = 220В/0,34А = 647(Ом).

Відповідь: І = 0,34А, R = 647(Ом).

Задача 4. Лампа розжарювання розрахована на напругу 127В і потужність 50Вт. Який додатковий опір треба приєднати до лампи, щоб увімкнути її в мережу з напругою 220В?

 

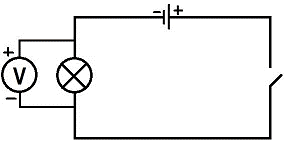
Дано:

U₁ = 127В

N₁ = 50Вт

U₂= 220В

R_д = ?

Рішення. Ясно, якщо лампу розраховану на напругу 127В безпосередньо увімкнути в мережу з напругою 220В, то вона згорить. А для того щоб цього не сталося, в коло лампи послідовно з нею треба увімкнути додатковий опір, падіння напруги на якому має становити U_д = U₂ – U₁ = 220В – 127В= 93В.

Величину цього додаткового опору (R_д = U_д/I_д), можна визначити із наступних міркувань. Оскільки при послідовному з’єднані, струм у лампі та в додатковому опорі має бути однаковим (І_д = І₁), та враховуючи, що N₁ = U₁I₁, можна записати I₁ = N₁/U₁ = 50Вт/220В = 0,227А. Таким чином R_д = U_д/І_д = 93В/0,227А = 410(Ом).

Відповідь: R_д = 410(Ом).

Задача 5. Підчас ремонту, спіраль електричної плитки вкоротили на 10%. Як і у скільки разів змінилась потужність плитки?

Дано:

ℓ₂ = 0,9ℓ₁

N₂/N₁ = ?

Рішення. Оскільки за визначенням N = N_ел = U∙I, та враховуючи що I = U/R, R = ρ∙ℓ/S, можна записати N_ел = U∙I = U²/R = U²∙S/ρ∙ℓ. Ясно, що в умовах нашої задачі U₁ = U₂, S₁ = S₂, ρ₁ = ρ₁, тому можна записати  N₂/N₁ = ℓ₁/ℓ₂ = ℓ₁/0,9ℓ₁ = 1/0,9 = 1,1. Або N₂ = 1,1N₁

Відповідь: N₂ = 1,1N₁ (потужність збільшиться в 1,1 рази).

Контрольні запитання.

1. Що характеризує і чому дорівнює робота?
2. Доведіть, що А_ел = U∙I∙t.
3. Доведіть, що В·А·с = Дж.
4. Що характеризує і чому дорівнює потужність?
5. Доведіть, що N_ел = U∙I
6. Доведіть, що В·А = Вт.
7. Як можна виміряти електричну потужність?
8. Що вимірюють в кіловат-годинах і чому дорівнює 1кВт∙год?
9. За якими формулами визначають механічну роботу та потужність?
10. Гусеничний трактор набагато сильніший за легковий автомобіль. При цьому їх потужності є однаковими. Як це можна пояснити?

Вправа 24.

1. Яку роботу здійснить струм силою 2А за 10хв при напрузі у колі 30В?
2. По провіднику, до кінців якого прикладена напруга 6В пройшов заряд 200Кл. Визначити роботу струму.
3. Електрична плитка за 30хв споживає 1080кДж енергії. Визначте опір плитки, якщо сила струму в ній 2А.
4. При напрузі 220В, електропраска за одну хвилину споживає 108кДж енергії. Яка сила струму в електропрасці та яка її потужність?
5. На цоколі лампочки написано 220В, 100Вт. На яку силу струму розрахована ця лампочка? Який її електричний опір?
6. Електродвигун при напрузі 220В має потужність 2кВт. Яка робоча сила струму в електродвигуні. Який його електричний опір? Яку кількість електроенергії споживає двигун за 8 годин неперервної роботи? Яка вартість цієї енергії, якщо 1кВт∙год вартує 5 гривень?
7. З якого матеріалу виготовлена спіраль електронагрівального елемента потужністю 480Вт, якщо його довжина 16м, переріз 0,24мм², а напруга в мережі 120В?
8. Підчас ремонту, спіраль електричної плитки замінили на аналогічну, але на 10% довшу спіраль. Як і у скільки разів змінилась потужність плитки?
9. Трамвай розвиває швидкість 20м/с при силі тяги електродвигуна 1,2кН. Напруга в контактній мережі 600В, сила струму в двигуні 50А. Визначте ККД електродвигуна трамвая.

.

§25. Закон Джоуля-Лєнца. Шляхи зменшення втрат в лініях електропередач.

 

В процесі проходження електричного струму, певна частина енергії цього струму практично неминуче перетворюється на теплоту, тобто в енергію хаотичного руху молекул (атомів) провідника.

В 1841 році, англійський фізик Джоуль, а в 1842 році російський фізик Лєнц, незалежно один від одного, експериментально довели: при проходженні електричного струму виділяється теплота, кількість якої (Q)пропорційна квадрату сили струму в провіднику (I²), опору провідника (R) та часу проходження струму(t), іншими словами  Q = I²∙R∙t. Дане твердження прийнято називати законом Джоуля–Лєнца.

Схема загального устрою того приладу за допомогою якого можна перевірити достовірність закону Джоуля–Лєнца представлена на мал.93. Цей прилад представляє собою калориметр в тіло якого занурено досліджуваний провідник. При проходженні електричного струму провідник нагрівається, а відповідно нагріває і ту рідину яка знаходиться в калориметрі. Вимірюючи електричні, часові та теплові параметри експерименту, неважко переконатися в тому, що в процесі проходження електричного струму дійсно виділяється теплова енергія (Q_н = с∙m∙Δt), і що кількість цієї теплоти дійсно пропорційна квадрату сили струму в провіднику (I²), опору провідника (R) та часу проходження струму (t). Іншими словами Q = I²·R·t.

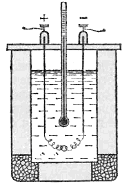
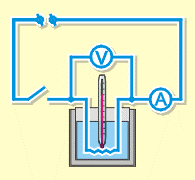
Мал.93. Загальний устрій приладу для дослідження теплової дії струму.

Те, що в процесі проходження струму виділяється теплота є очевидно закономірним явищем. Адже при упорядкованому русі заряджених частинок (при проходженні струму), ці частинки неминуче наштовхуються на атоми та молекули струмопровідного середовища (провідника). В процесі ж зіткнень, частина енергії упорядкованого руху носіїв струму перетворюється на енергіє хаотичного (теплового) руху частинок середовища. І не важко збагнути, що кількість тієї енергії яка при взаємодії носіїв струму з частинками провідника перетворюється на енергію теплового руху цих частинок залежить:

1. Від електричного опору провідника Q ~ R: адже чим більший опір провідника, тим частіше носії струму наштовхуються на частинки провідника та відповідно більшу кількість енергії віддають цим частинкам;
2. Від часу проходження струму Q ~ t: адже абсолютно очевидно, що за однакових умов, кількість зіткнень носіїв струму з частинками провідника за дві секунди буде у два рази більшою ніж за одну секунду;
3. Від сили струму в провіднику Q ~ І: адже чим більша сила струму в провіднику, тим більша швидкості руху носіїв струму (І ~ v), а отже і більша кількість зіткнень з частинками провідника. А оскільки в теплоту перетворюється не швидкість носіїв струму, а їх кінетична енергія (Е_к = m₀v²/2), то можна передбачити, що кількість тієї теплоти яка виділяється при проходженні струму, залежить не просто від сили струму в провіднику, а від квадрату сили струму Q ~ Е_к ~ v² ~ I². Власне експериментальним підтвердженням цього передбачення і є закон Джоуля – Лєнца: Q = I²·R·t.

Таким чином, в процесі проходження електричного струму, носії струму постійно наштовхуючись на частинки струмопровідного середовища, віддають цим частинкам певну кількість енергії свого упорядкованого руху. При цьому певна частина енергії електричного струму перетворюється на відповідну кількість енергії теплового руху частинок середовища, тобто на теплоту. І кількість цієї теплоти визначається законом Джоуля – Лєнца: Q = I²·R·t.

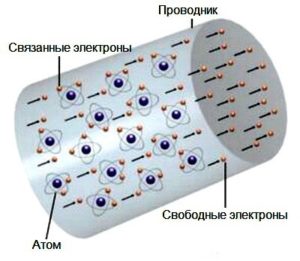
Мал.94. В процесі проходження струму, носії струму постійно наштовхуючись на частинки струмопровідного середовища, віддають їм певну кількість своєї енергії.

Та теплота яка виділяється в процесі проходження електричного струму, може бути як корисною так і шкідливою. Наприклад, якщо мова йде про електронагрівальні прилади, то та теплота що в них виділяється є корисною. Корисною в тому сенсі, що відповідні прилади створюють саме для того, щоб енергію електричного струму перетворювати на теплоту. Якщо ж ви маєте справу з телевізором, електродвигуном, трансформатором, комп’ютером чи пилососом, то та теплота яка неминуче виділяється в цих приладах є шкідливою. Шкідливою не в сенсі загрози здоров’ю, а в сенсі того, що та електрична енергія яка витрачається на створення цього тепла, витрачається не за призначенням.

Мал.95. В яких з наявних електроприладів виділення теплової енергії є корисним, а в яких шкідливим?

Ясно, що проектуючи ті прилади в яких виділення тепла є корисним, прагнуть до того щоб цієї теплоти виділялось як найбільше. В тих же випадках, де виділення теплоти є шкідливим, навпаки – прагнуть до максимального зменшення теплових втрат.

Ілюструючи практику застосування закону Джоуля–Лєнца, а за одно і суть науково–проектної роботи, розглянемо конкретну ситуацію. Припустимо, що перед вами стоїть завдання: розробити ефективну систему ліній електропередач, тобто таку систему яка забезпечує ефективну передачу великої кількості електроенергії від виробника (електростанції) до споживача.

Оскільки лінії електропередач створюють не для нагрівання атмосфери, а для передачі енергії електричного струму, то ясно, що та теплота яка неминуче виділяється в цих лініях є шкідливою. А це означає, що проектуючи систему ліній електропередач, потрібно робити все можливе задля того, щоб мінімізувати теплові втрати в них.

На перший погляд, задача мінімізації теплових втрат є гранично простою. Дійсно. Згідно з законом Джоуля–Лєнца Q = I²∙R∙t, а враховуючи що R = ρℓ/S, можна записати Q  = I²∙(ρℓ/S)∙t. Звідси, з усією очевидністю випливає, що для мінімізації теплових втрат (Q = min) необхідно: I = min, ρ = min, ℓ = min, S = max, t = min. Іншими словами: гранично зменшуй силу струму в дротах ліній електропередач, виготовляй ці дроти з найкращих струмопровідних матеріалів, гранично зменшуй довжину дротів та збільшуй площу їх поперечного перерізу – і матимеш мінімальні теплові втрати.

Втім, реалізуючи ці вимоги на практиці, ви неминуче стикаєтесь з цілою низкою проблем та обмежень. Скажімо, теплові втрати в лініях електропередач пропорційні довжині цих ліній. А це означає, що для мінімізації теплових втрат, електростанцію потрібно ставити в центрі мегаполісу. Однак вартість землі в цьому центрі, інтереси екологічної, пожежної, ядерної та інших безпек, вимагають абсолютно протилежного рішення. Крім цього, електростанцію потрібно ставити в тому місці де є відповідні умови: наявність необхідних водних ресурсів, наявність запасів вугілля, наявність відповідних вітрових потоків, наявність потрібного рельєфу місцевості, сейсмічна безпечність місцевості, тощо.

Або наприклад, інтереси мінімізації теплових втрат вимагають того, щоб струмопровідні дроти мали максимально велику площу поперечного перерізу (S = max). А це автоматично призводить до збільшення маси дротів, їх вартості, до збільшення кількості опор ліній електропередач, тощо.

Або скажімо, вимога що до мінімальності питомого опору матеріалу провідника (ρ = min) означає, що дроти ліній електропередач мають бути мідними, срібними чи золотими. В реальності ж ми обираємо не найкращий матеріал – алюміній. За своїми електропровідними властивостями алюміній в 1,6 рази гірший за мідь, натомість більш як у 3 рази дешевший і більш як у 3 рази легший.

Довжина дротів ліній електропередач, їх матеріал та площа поперечного перерізу, безумовно впливають на величину теплових втрат у відповідних лініях. Але жоден з цих факторів не може кардинально вирішити наявну проблему. Аналіз же закону Джоуля–Лєнца безумовно вказує на те, що найефективнішим методом боротьби з тепловими втратами в лініях електропередач є шлях зменшення сили струму в них (І=min). Адже згідно з цим законом, теплові втрати пропорційні квадрату сили струму (Q ~ I²). А це означає, що зменшивши силу струму в дротах ліній електропередач у 10 разів, теплові втрати в цих дротах зменшаться в 100 разів. Якщо ж силу струму зменшити у 100 разів, то теплові втрати зменшаться в 10 000 разів.

З іншого боку, прагнучи зменшити силу струму в дротах ліній електропередач, ми не повинні зменшувати потужність того енергетичного потоку який цими дротами передається (N = A/t = U∙I =const). Адже як би там не було, а за кожну секунду від виробника до споживача має передаватись певна, визначена кількість енергії. Бо лінії електропередач ми власне і створюються для того, щоб ця енергія передавалась.

Вище сказане означає, що прагнучи гранично зменшити теплові втрати в лініях електропередач, ми маємо забезпечити виконання двох умов: I = min, N = U∙I = const. І не важко збагнути, що задані вимоги (I = min, N = U∙I = const), можна реалізувати лише в тому випадку, якщо максимально збільшити напругу в лініях електропередач (U = max). Втім і напругу не можна підвищувати до безкінечності. Не можна бодай тому, що надвисока напруга є джерелом смертельної небезпеки для людини та певних технічних небезпек для самої системи ліній електропередач. Крім цього, будь яка зміна (трансформація) напруги, потребує певних економічних та енергетичних затрат.

Таким чином, проектуючи ефективну систему ліній електропередач, потрібно враховувати величезну кількість науково-технічних, технологічних, економічних, екологічних, безпекових, соціальних, політичних та інших обставин. Ці обставини так чи інакше впливають на параметри кожного конкретно взятого проекту. Але якщо говорити про загально прийняту схему ефективного транспортування електроенергії, то вона полягає в наступному.

Електростанції будують в економічно, екологічно та безпеково доцільних місцях. Генерована ними електроенергія подається на потужні трансформаторні підстанції, де її напруга підвищується до сотень тисяч, а іноді й до мільйона вольт. При цій надвисокій напрузі електроенергія потрапляє в потужні магістральні лінії електропередач, які йдуть в напрямку основних споживачів (великі міста, комплекси енергоємних промислових виробництв, тощо). Від магістральних ліній електропередач поступово розгалужується мережа менш потужних та менш високовольтних ліній, які в свою чергу діляться на ще більш дрібні лінії. У підсумку, напруга в мережі знижується до відносно безпечної величини (220В) і розподіляється між будинками, квартирами та кімнатами.

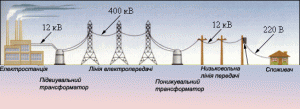
Мал.96. Загальна схема системи ліній електропередач.

Ми розглянули один конкретний приклад того, як вирішується певна науково-практична задача. Приклад, який є наочною ілюстрацією суті будь якої науково-практичної діяльності. А ця суть полягає в наступному. Мистецтво проектувальника, конструктора, інженера, технолога, архітектора, програміста та інших подібних спеціалістів, полягає в тому, щоб на основі аналізу всього комплексу суттєвих обставин, знайти та реалізувати у відповідному проекті, найбільш оптимальне рішення поставленої задачі. Результатом же реалізації цих рішень є нові автомобілі, нові літаки, нові космічні кораблі, нові комп’ютерні системи, нові технології, тощо.

Задача 1. Два провідники опори яких 20(Ом) і 40(Ом) включені в мережу з напругою 60В. Яка кількість теплоти виділиться в кожному з цих провідників за одну хвилину при їх а) послідовному з’єднанні; б) паралельному з’єднанні? Визначте загальну кількість виділеної теплоти в кожному випадку.

Дано:

R₁ = 20(Ом)

R₂ = 40(Ом)

U = 60В

t = 1хв =60с

Q_посл= ?  Q_пар= ?  Q_заг = ?

Рішення. Згідно з законом Джоуля–Лєнца Q = I²·R·t. Для послідовного з’єднання  R₁₂ = R₁+R₂ = 20+40= 60(Ом); І₁₂ = І₁ = І₂ = U/R₁₂ = 60В/60(Ом) = 1А. При цьому:

Q_посл1 = I₁²·R₁·t = (1А)²·20(Ом)·60с = 1200Дж = 1,2кДж;

Q_посл2 = I₂²·R₂·t = (1А)²·40(Ом)·60с = 2400Дж = 2,4кДж;

Q_заг = 1,2кДж + 2,4кДж = 3,6кДж.

Для паралельного з’єднання U₁₂ = U₁ = U₂ = 60В, тому І₁ = U₁/R₁ = 60В/20(Ом) = 3А; І₂ = U₂/R₂ = 60В/40(Ом) = 1,5А. При цьому:

Q_пар1 = I₁²·R₁·t = (3А)²·20(Ом)·60с = 10800Дж = 10,8кДж;

Q_пар2 = I₂²·R₂·t = (1,5А)²·40(Ом)·60с = 5400Дж = 5,4кДж;

Q_заг = 10,8кДж + 5,4кДж = 16,2кДж.

Задача 2. З ніхромового дроту площею поперечного перерізу 1мм², потрібно виготовити розрахований на напругу 220В нагрівальний елемент, потужністю 1,2кВт. Якої довжини має бути дріт?

Дано:

ніхром

S = 1мм²

N = 1,2кВт = 1200Вт

U = 220В

ℓ = ?

Рішення. Оскільки в нагрівальному елементі, та електрична енергія (робота) мірою якої є потужність, йде на виділення теплоти, то N = A_ел/t = Q/t. Враховуючи, що згідно з законом Джоуля-Лєнца Q = I²·R·t, можна записати N = Q/t = I²·R. А оскільки I = U/R, R = ρℓ/S, то N = I²·R = (U/R)²∙R = U²∙R = U²∙S/ρℓ = N. Звідси ℓ = U²∙S/ρN. Таким чином довжину ніхромового дроту можна визначити за формулою ℓ = U²∙S/ρN, де ρ = 1,1(Ом∙мм²/м) – таблична величина.

Розрахунки. ℓ = U²∙S/ρN = (220В)²∙1мм² / 1,1(Ом∙мм²/м)∙1200(В∙А) = 36,7м

Відповідь: ℓ = 36,7м.

Контрольні запитання.

1. Що стверджується в законі Джоуля-Лєнца?
2. Поясніть, чому в процесі проходження струму виділяється теплота?
3. В яких випадках створювана струмом теплота є корисною, а в яких – шкідливою? Наведіть приклади.
4. Коли ми стверджуємо, що та теплота яка виділяється в лініях електропередач з шкідливою, то що це означає?
5. Із аналізу закону Джоуля-Лєнца випливає, що для мінімізації теплових втрат необхідно: ρ=min, ℓ=min, S=max, t=min. Чому на практиці можливості мінімізації цих параметрів є дуже обмеженими?
6. Доведіть, що для мінімізації теплових втрат в ЛЕП, напруга в цих лініях має бути максимально великою.
7. Опишіть загальну схему устрою системи ліній електропередач.
8. Спіраль електричного каміну виготовляють з ніхрому (матеріалу з великим питомим опором), а спіраль лампочки розжарювання виготовляють з вольфраму – матеріалу з малим питомим опором. Чому?

Вправа 25.

1. Скільки теплоти виділиться в електричному нагрівачі протягом 4хв, якщо його опір 20(Ом), а сила струму в колі 5А.
2. Електрична піч для плавлення металу споживає струм 800А при напрузі 60В. Скільки теплоти виділяється в печі за 1хв? Яка потужність печі?
3. За 5хв в реостаті при силі струму 2А виділилося 60кДж теплоти. Який електричний опір реостата?
4. Два провідники опори яких 20(Ом) і 30(Ом) включені в мережу з напругою 100В. Яка кількість теплоти виділиться в кожному з цих провідників за 10с при їх послідовному з’єднанні.
5. Два провідники опори яких 20(Ом) і 30(Ом) включені в мережу з напругою 100В. Яка кількість теплоти виділиться в кожному з цих провідників за 10с при їх паралельному з’єднанні?
6. Скільки теплоти виділиться за 30хв в тих мідних дротах які підводять струм до електроплитки якщо їх переріз 1мм², а довжиною 10м. Сила струму в спіралі плитки 5А?
7. Скільки часу триватиме нагрівання 2кг води від 20ºС до закипання, в електричному чайнику потужністю 800Вт, якщо ККД процесу 80%?
8. З нікелінового дроту площею поперечного перерізу 1мм² потрібно виготовити нагрівальний елемент розрахований на напругу 220В і потужність якого 800Вт. Якої довжини має бути дріт?

.

§26. Розв’язування задач. Тема: закон збереження енергії в електричних механічних та теплових процесах.

В умовах даної теми (закон збереження енергії в електричних механічних та теплових процесах), тими базовими формулами спираючись на які ви маєте розв’язувати задачі є:

1) загально енергетичні процеси: ∑Е_до = ∑Е_після,   η = А_кор/А_заг;

2) електричні процеси: А_ел = U∙I∙t, N_ел = U∙I, Q = I²·R·t;

3) механічні процеси: А_мех = F∙s, Е_к = mv²/2, Е_п = mgh, N_мех = A_мех/t;

4) теплові процеси: Q_н = с∙m∙∆t; Q_пл = λ∙m; Q_пар = r∙m; Q_гор = q∙m, де c, λ, r, q – табличні величини.

Звісно, за необхідності при розв’язуванні задач застосовуються й інші формули, наприклад I = U/R,  R = ρ∙ℓ/S, v = s/t, тощо.

Задача 1. В електричному бойлері потужністю 2кВт міститься 80кг води. На скільки нагріється ця вода за годину роботи бойлера? ККД процесу 95%.

Дано:

N = 2кВт

m = 80кг

t = 1год = 3600с

η = 95% = 0,95

Δt = ?

Рішення. За визначенням η = А_кор/А_заг. В умовах нашої задачі корисною є та енергія яка йде на нагрівання води, тобто А_кор = Q_н = cm∆t, де с = 4200(Дж/кг·ºС), ∆t = ?.

Загальною (А_заг = Q_заг) є та енергія яка виділяється електронагрівальним елементом бойлера (водонагрівача), потужність якого (N = A_заг/t) є відомою, і тому А_заг = N∙t.

Таким чином, η = А_кор/А_заг = cm∆t / N∙t, звідси Δt = N∙t∙η/c∙m.

Розрахунки. Δt = N∙t∙η/c∙m = 2000(Дж/с)∙3600с∙0,95 / 4200(Дж/кг°С)∙80кг = 20,4°С.

Відповідь: Δt = 20,4°С.

Задача 2. Визначте на яку напругу розрахований електрокип’ятильник, який за 4хв, нагріває 0,4кг води від 20°С до кипіння, за умови що в його обмотці протікає струм 2,5А. Втратами енергії знехтувати.

Дано:

t = 4хв = 240с

m = 0,4кг

t₀ = 20°С

t_k = 100°С

I = 2,5A

U = ?

Рішення. В умовах даної задачі, та теплота яка виділяється в електронагрівальному приладі Q = I²·R·t,  повністю йде на нагрівання води Q_н = с∙m∙∆t, де Δt = 100 – 20 = 80°C, с = 4200(Дж∙кг/°С) – таблична величина. Іншими словами, I²·R·t = с∙m∙∆t. Оскільки R = U/I, то I²·R·t = I²∙(U/I)∙t = I∙U∙t.

Таким чином, I∙U∙t = с∙m∙∆t, звідси U = с∙m∙∆t / I∙t.

Розрахунки. U = с∙m∙∆t / I∙t = 4200(Дж∙кг/°С)∙0,4кг∙80°C / 2,5А∙240с = 224В.

[U] = Дж∙кг/°С)∙кг∙°C / А∙с = Дж/А∙с = В.

Відповідь: U = 224В.

Задача 3. В алюмінієвому калориметрі маса якого 120г, міститься 0,5кг води. В калориметрі знаходиться електронагрівальний прилад. На скільки нагріється вода в калориметрі за 1хв, якщо струм в приладі 2А, а його опір 100(Ом)?

Дано:

m₁ = 120г = 0,12кг

m₂ = 0,5кг

t = 1хв = 60с

I = 2A

R = 100(Ом)

Δt = ?

Рішення. В умовах даної задачі, та теплота яка виділяється в електронагрівальному приладі Q = I²·R·t,  повністю йде на нагрівання тіла калориметра Q_н1 = с₁∙m₁∙∆t₁, та води в ньому Q_н2 = с₂∙m₂∙∆t₂, де Δt₁ = Δt₂ = Δt = ? с₁ = 880(Дж∙кг/°С),  с₂ = 4200(Дж∙кг/°С) – табличні величини.

Таким чином  I²·R·t = (с₁∙m₁ + с₂∙m₂)∙Δt, звідси Δt = I²·R·t / (с₁∙m₁ + с₂∙m₂).

Розрахунки. Δt = I²·R·t / (с₁∙m₁ + с₂∙m₂) = (2А)²∙100(Ом)∙60с / (880∙0,12 + 4200∙0,5)(Дж/°С) = 12000(А²(В/А)с = В∙А∙с = Дж) / 2200(Дж/°С) = 5,5°С.

Відповідь: Δt = 5,5°С.

Задача 4. Електрокип’ятильник опір якого 70(Ом) занурили у посудину яка містить 1кг води при 20ºС і увімкнули в мережу з напругою 220В. Через який час вода закипить, якщо ККД процесу 81%?

Дано:

R = 70(Ом)

m = 1кг

t₁ = 20ºC

t₂ = 100ºC

U = 220В

η = 81% = 0,81

t = ?

Рішення. За визначенням η = А_кор/А_заг. В умовах нашої задачі корисною є та енергія яка йде на нагрівання води, тобто А_кор = Q_н = cm∆t, де с = 4200(Дж/кг·ºС), ∆t = 100ºC – 20ºC = 80ºC.

Загальною ж (затраченою) є та теплота яка виділяється при проходженні струму, тобто А_заг = Q_ел = I²·R·t, а оскільки I = U/R, то А_заг = Q_ел = U²∙t/R.

Таким чином, η = cm∆t·R / U²t, звідси   t = cm∆t·R/U²η.

Розрахунки: t = 4200·1·80·70 / 220²·0,81 = 600с = 10хв

[t] = (Дж/кг·ºС)∙кг∙°С∙Ом / В² = Дж∙Ом /В² = (В∙А∙с)∙(В/А) / В² = с.

Відповідь: t = 10хв.

Задача 5. Підйомний кран підняв вантаж масою 6т на 12м за 2хв. Визначити ККД підйомного крану, якщо в колі його електродвигуна при напрузі 400В протікає струм 18А.

Дано:

m = 6т = 6000кг

h = 12м

t = 2хв = 120с

U = 400В

I = 18A

η = ?

Рішення. За визначенням η = А_кор/А_заг. В умовах нашої задачі корисною є та робота яка йде на піднімання вантажу, і яку можна визначити за формулою А_кор = mgh. Загальною ж є та робота яку виконують електричні сили в електричному двигуні, і величину якої можна визначити за формулою А_кор = U∙I∙t. Таким чином η = А_кор/А_заг = m∙g∙h / U∙I∙t.

Розрахунки. η = 6000кг∙9,8(м/с²)∙12м / 400В∙18А∙120с = 0,82(Дж/Дж) = 82%

Відповідь: η = 82%.

Задача 6. Тролейбус рухається рівномірно зі швидкістю 10м/с. Визначте силу тяги двигуна тролейбуса, якщо при ККД 80% і напрузі 550В в обмотках його електродвигуна тече струм 50А.

Дано:

v = 10м/с

η = 80% = 0,8

U = 550В

I = 50A

F_тяги=?

Рішення. За визначенням η = А_кор/А_заг. В умовах нашої задачі А_кор = А_мех = F_тяги∙s; А_заг = А_ел = U∙I∙t, а враховуючи що s/t=v, можна записати η = F_тягиs/UIt = F_тягиv/UI. Звідси випливає F_тяги = U∙I∙η/v

Розрахунки: F_тяги = 550·50·0,8/10·100 = 2200Н.

[F]=В·А/(м/с) = Вт/(м/с) = Дж/с(м/с) = Н·м/м=Н.

Відповідь: F_тяги = 2200Н = 2,2кН.

Задача 7. Електродвигун потужністю 1,1кВт, працює при напрузі 220В. Скільки теплоти виділиться в обмотках електродвигуна за 10хв його роботи, якщо електричний опір цих обмоток 10(Ом)?

Дано:

N = 1,1кВт = 1100Вт

U = 220В

t = 10хв = 600с

R = 10(Ом)

Q = ?

Рішення 1 (неправильне). Оскільки згідно з законом Джоуля-Лєнца Q = I²·R·t, та враховуючи, що у відповідності з законом Ома I = U/R, можна записати Q = (U/R)²·R·t = U²·t/R. Таким чином, кількість тієї теплоти яка виділяється в електродвигуні можна визначити за формулою Q = U²·t/R.

Розрахунки. Q = U²·t/R = (220В)²∙600с / 10(Ом) = 2904000(В²∙с/(В/А) = В∙А∙с = Дж) = 2900кДж.

Відповідь: Q = 2900кДж.

На перший погляд рішення задачі є правильним. Однак вас мають насторожити дві обставини:

1) В рішенні задачі не задіяна одна з заданих величин – потужність двигуна N.

2) Отриманий результат Q = 2900кДж, є занадто великим. Адже за такої кількості теплоти, усереднено залізний двигун (с ≈ 500Дж/кг°С), маючи масу 20кг, мав би нагрітися на Δt = Q/cm = 2900000Дж /500(Дж/кг°С)∙20кг = 290°С.

І дане рішення задачі, дійсно є неправильним. Пояснюючи причини цієї неправильності можна сказати наступне.

Виходячи з того, що згідно з законом Ома I = U/R, формулу Q = I²·R·t можна записати у вигляді Q = (U/R)²·R·t = U²·t/R, або Q = I²·(U/I)·t = I·U·t. З формально математичної точки зору, формули Q = I²·R·t, Q = U²·t/R, Q = I·U·t є тотожними. Однак в реальності ці формули тотожні лише в тому випадку, якщо у відповідному приладі вся надана йому електрична енергія (робота А_ел), повністю перетворюється на теплоту.

Дійсно, коли ми стверджуємо, що у відповідності з законом Ома I = U/R, то маємо на увазі, що у відповідному приладі (на відповідній ділянці електричного кола), вся надана приладу електрична напруга, а фактично електрична робота (U = A_ел/q) повністю перетворюється в енергію електричного струму. Наприклад в нашому електродвигуні, електричний опір якого R = 10(Ом), мав би протікати струм I = U/R = 220В/10(Ом) = 22А. При цьому в двигуні виділялось би Q = I²·R·t = (22А)²∙10(Ом)∙600с = 2900кДж теплоти

В реальності ж, при напрузі U = 220В в електродвигуні з потужністю N = U∙I = 1100Вт протікає струм I = N/U = 1100Вт/220В = 5А. При цьому виділяється Q = I²·R·t = (5А)²∙10(Ом)∙600с = 150кДж теплоти. А це  майже у 20 разів менше за 2900кДж.

І це закономірно. Адже в електродвигуні, більша частина наданої йому електричної енергії йде не на нагрівання електродвигуна (Q), а на виконання ним механічної роботи (А_мех), при цьому А_ел = А_мех + Q.

Таким чином, при визначенні кількості тієї теплоти яка виділяється в процесі проходження струму, формула Q = I²·R·t (закон Джоуля-Лєнца) дає гарантовано правильний результат. Натомість той результат який дають формули Q = I·U·t, Q = U²·t/R,  буде правильними лише в тому випадку, коли у відповідному приладі, енергія струму не виконує іншої роботи окрім теплової.

Наприклад в задачах 2, 3, 4, виділену кількість теплоти з однаковим результатом можна визначити як за законом Джоуля-Лєнца Q = I²·R·t, та і за похідними від нього формулами Q = I·U·t, чи Q = U²·t/R. В задачі ж 7, правильний результат можна отримати лише на основі закону Джоуля-Лєнца, та факту відомої потужності електродвигуна (N = U∙I).

Рішення 2 (правильне). Згідно з законом Джоуля-Лєнца Q = I²·R·t, де І = ? Оскільки N = U∙I, то І = N/U = 1100Вт / 220В = 5А.

Розрахунки. Q = I²·R·t = (5А)²∙10(Ом)∙600с = 150кДж.

Відповідь: Q = 150кДж.

Вправа 26.

1. Скільки теплоти виділяється в електро нагрівальному приладі за 10хв роботи, якщо його потужність 1,5кВт.
2. В електричному бойлері потужністю 1,8кВт міститься 50кг води. На скільки нагріється ця вода за годину роботи бойлера?
3. На яку силу струму розрахований електрокип’ятильник, який при напрузі 220В за 5хв, нагріває 0,5кг води від 20°С до кипіння. Втратами енергії знехтувати.
4. В алюмінієвому калориметрі маса якого 120г, міститься 0,5кг води. В калориметрі знаходиться електронагрівальний прилад. Яка потужність цього приладу, якщо він за 1хв нагріває воду на 30°С?
5. На скільки нагріється мідне тіло при падінні з висоти 38м, якщо ККД процесу 60%?
6. На яку висоту можна було б підняти тіло масою 1т, якби вдалося повністю використати ту енергію яка виділяється при конденсації 1кг водяного пару, температура якого 200°С?
7. Скільки бензину витрачає тепловий двигун за годину неперервної роботи, якщо його потужність 70кВт, а ККД 30%?
8. Потяг масою 2000т рухається з швидкістю 72км/год. Скільки теплоти виділяється в процесі зупинки потягу?
9. Електродвигун потужністю 1,1кВт, працює при напрузі 220В. Яку механічну роботу виконує цей двигун за 10хв роботи, якщо електричний опір його обмоток 10(Ом)?

.

§27. Електричний струм в металах.

 

         Коли ми говоримо про струмопровідні матеріали (провідники), то перш за все маємо на увазі метали. І це закономірно. Адже саме метали є найкращими провідниками струму та основними струмопровідними елементами електричних кіл. Секрет високих струмопровідних властивостей металів обумовлений особливостями їх внутрішнього устрою. А ці особливості полягають в тому, що атоми металів постійно обмінюються валентними електронами. При цьому кожен атом почергово обмінюється електронами з усією сукупністю сусідніх атомів. Власне за рахунок цього інтенсивного обміну електронами, атоми металів і об’єднуються в ті матеріали які ми називаємо металами.

Факт того, що кожен атом металу обмінюється валентними електронами з усією сукупністю сусідніх атомів, по суті означає, що валентні електрони металу є колективізованими, тобто такими, які належать всій сукупності атомів відповідного металу (мал.97а). В такій ситуації, за відсутності зовнішнього електричного поля (зовнішньої електричної напруги), рух колективізованих електронів є усереднено хаотичним. За наявності ж електричного поля, цей хаотичний рух стає хаотично-упорядкованим. Власне упорядковану складову цього хаотично-упорядкованого руху електронів і називають електричним струмом в металах.

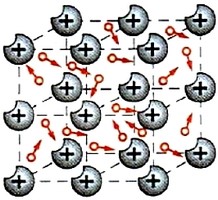
Мал.97. Електричний струм в металах, представляє собою упорядкований рух електронів.

Потрібно зауважити, що швидкість того упорядкованого руху електронів, який називається електричним струмом, є надзвичайно малою і зазвичай не перевищує 1мм/с. При цьому швидкість хаотичного руху електронів в мільярди разів більша і близька до 1000км/с. Ясно, що в такій ситуації електричний струм не правильно уявляти як строго упорядкований рух електронів уздовж провідника. Адже в реальності під дією електричного поля, електрони рухаються хаотично-упорядковано. При цьому хаотична складова цього складного руху, в мільярди разів більша за упорядковану складову. По суті, в процесі проходження струму, електрони рухаючись хаотично та забезпечуючи зв’язки між атомами металу, лише поступово зміщуються (дрейфують) у певному напрямку.

Факт того, що в процесі проходження електричного струму швидкість упорядкованого руху електронів є мізерно малою, зовсім не означає, що відповідно малою є і та швидкість з якою електричний струм поширюється від джерела струму до споживача. Адже колективізовані електрони заповнюють всі струмопровідні елементи електричного кола. А це означає, що за наявності електричної напруги лампочка загорається практично з моменту замикання відповідного кола навіть в тому випадку, коли вона знаходиться у Києві, а джерело струму і вимикач – у Львові. Якщо ж говорити про ті електрони які із Львова рухатимуться в напрямку Києва, то в кращому випадку вони досягнуть останнього років через сто.

Власне дещо схоже відбувається і в процесі руху газів та рідин відповідними трубопроводами. Скажімо, коли ви відкриваєте кран системи водопостачання, то з нього практично миттєво починає витікати вода. І це при тому, що джерело цієї води може знаходитись за десятки кілометрів від вас, і що та вода яка потрапляє в систему від джерела, досягає вашої квартири через тижні, місяці чи роки.

Втім, потрібно мати на увазі, що швидкість поширення електричних сигналів не є безкінечно великою. Адже ця швидкість дорівнює швидкості поширення електричного поля і становить 3·10⁸м/с = 300 000км/с. А це означає, що відстань від Львова до Києва (≈500км) електричні сигнали долають за 0,0017 секунди.

В §20 ми говорили про те, що опір провідника і зокрема провідника металевого, залежить від його довжини (ℓ), площі поперечного перерізу (S) та питомого опору провідника (ρ), і що цю залежність можна записати у вигляді R = ρℓ/S. При цьому ми не вказали на факт того, що питомий опір провідника (ρ), а відповідно і його електричний опір (R = ρℓ/S), залежать не лише від електропровідних властивостей відповідного матеріалу, а й від температури провідника: з підвищенням температури питомий опір металу збільшується і навпаки. Іншими словами: якщо t↑, то ρ↑, а відповідно R↑; якщо t↓, то ρ↓, а відповідно R↓.

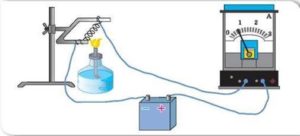
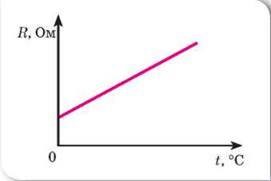
Мал.98. При збільшенні температури електричний опір металу збільшується, а при зменшенні температури – зменшується.

Гранично стисло та спрощено пояснюючи суть залежності опору провідника від його температури, можна сказати наступне. В процесі свого упорядкованого руху, носії струму постійно наштовхуються на атоми (молекули) речовини, що відповідно гальмує цей упорядкований рух. Оскільки в процесі нагрівання інтенсивність хаотичного руху атомів речовини збільшується, то відповідно збільшується і число зіткнень цих атомів з носіями струму, а отже і електричний опір провідника.

Залежність електричного опору провідника від його температури, характеризує величина яка називається температурним коефіцієнтом опору. Температурний коефіцієнт опору – це фізична величина, яка характеризує залежність опору провідника від його температури і яка визначається за формулою α = (R_t–R₀)/R₀∆t, де

R₀ – опір провідника при температурі t₀;

R_t – опір провідника при температурі t;

∆t = t – t₀ – різниця температур провідника.

Одиниця вимірювання: [α] = 1/ºС.

Температурний коефіцієнт опору провідника визначається експериментально і записується у відповідну таблицю, наприклад таку.

Температурний коефіцієнт опору деяких металів і сплавів.

Речовина	α (1/ºС)	Речовина	α (1/ºС)
Алюміній	0,0042	Срібло	0,0040
Вольфрам	0,0046	Константан	0,00002
Мідь	0,0042	Манганін	0,00003
Платина	0,0038	Нікелін	0,0001
Свинець	0,0042	Ніхром	0,0002

Не важко бачити, що для більшості хімічно чистих металів величина температурного коефіцієнту опору близька до 0,004(1/ºС) = 1/250(1/ºС). Це означає, що при збільшенні температури металу від 0ºС до 250ºС його електричний опір збільшиться від R₀ до R = 2R₀. Якщо ж говорити про сплави з відносно великим питомим опором, то їх температурні коефіцієнти опору зазвичай в десятки разів менші ніж у чистих металів.

Із визначального рівняння α = (R_t–R₀)/R₀∆t випливає, що залежність опору провідника від його температури, можна представити у вигляді R_t = R₀ + αR₀∆t. Наприклад якщо при температурі 20ºС опір вольфрамового провідника дорівнює 12,0(Ом), то при температурі 1020ºС, цей опір становитиме R_t = 12,0(Ом) + 0,0046(1/ºС)·12(Ом)·(1020–20)ºС = 12,0(Ом) + 4,6·12(Ом) = 67,2(Ом).

Залежність опору провідника від його температури, потрібно враховувати при проектуванні та експлуатації тих електротехнічних приладів які працюють в умовах значних температурних коливань. Наприклад, якщо в процесі експлуатації приладу, перепад температур становить 60ºС, то коливання електричного опору його металевих провідників може становити 25%. Ясно, що в багатьох випадках, подібні коливання є недопустимо великими. В таких ситуаціях передбачається певний комплекс запобіжних заходів. Скажімо, регламентують певні температурні умови експлуатації приладу.

Факт того, що електричний опір металів певним чином залежить від їх температури, корисно застосовується в приладах які називаються термометрами опору. В цих приладах, термочутливим елементом є металевий, зазвичай платиновий провідник. Платинові термометри опору є надзвичайно точними та надійними приладами. Достатньо сказати, що в інтервалі температур від –260ºС до +630ºС ці термометри вимірюють температуру з точністю 0,0001ºС. Тому не випадково, що в цьому інтервалі температур саме платинові термометри опору є еталонними.

Говорячи про електротехнічні застосування металів можна сказати наступне. Метали, це найкращі провідники струму. І тому їх головне електротехнічне застосування – бути струмопровідними елементами найрізноманітніших приладів та їх систем. При цьому, в залежності від тих завдань які вирішує той чи інший прилад, застосовують і відповідні метали.

Наприклад, якщо в лініях електропередач, електричну енергію потрібно передавати з мінімальними тепловими втратами, то в якості струмопровідних елементів цих ліній застосовують метали з мінімальним питомим опором (мідь, алюміній). Якщо електронагрівальні прилади створюються для перетворення енергії струму в теплоту, то в якості струмопровідних елементів цих приладів застосовують метали з максимально високим питомим опором (ніхром, фехраль). Якщо спіраль лампочки розжарювання має витримувати надвисокі температури, то цю спіраль виготовляють з тугоплавкого вольфраму. Якщо струмопровідний елемент знаходиться в хімічно агресивному середовищі, то його виготовляють з стійкого до цього середовища металу. І т.д.

Задача 1. За представленими на малюнку результатами лабораторної роботи, визначити температурний коефіцієнт опору провідника.

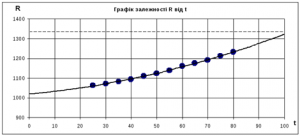
Рішення. За визначенням α = (R_t – R₀)/R₀∆t, аналізуючи наявний графік, обираємо найбільш зручні точки. Наприклад для t₁ = 40°C, R₁ = 1100(Oм), a для  t₂ = 70°C, R₂ = 1200(Ом). При цьому α = (R₂– R₁)/R₁∆t = (1200 – 1100) / 1100∙30°С = 0,003(1/°С).

Відповідь: α = 0,003(1/°С).

Задача 2. При температурі 20ºС опір вольфрамової нитки лампочки розжарювання становить 20(Ом). Визначте опір тієї ж нитки при температурі 2100ºС.

Дано:

вольфрам

t₀ = 20ºС

R₀ = 20(Ом)

t = 2100ºС

R_t = ?

Рішення. Оскільки за визначенням α = (R_t–R₀)/R₀∆t, то R_t – R₀ = R₀∆tα, звідси R_t = R₀∆tα + R₀ = R₀(∆tα + 1), де α = 0,0046(1/ºС); ∆ t= 2100ºC – 20ºC = 2080ºC.

Розрахунки: R_t = 20(Ом)·(2080ºС·0,0046(1/ºС) + 1) = 211(Ом).

Відповідь: R_t = 211(Ом).

Задача 3. На лампочці розжарювання кишенькового ліхтарика написано 3,5В; 0,28А. Яка робоча температура вольфрамової нитки розжарювання цієї лампочки, якщо при температурі 20ºС її опір 4(Ом)?

Дано:

вольфрам

U = 3,5В

I = 0,28А

t₀ = 20ºС

R₀ = 4(Ом)

t = ?

Рішення. Параметри U = 3,5В, I = 0,28А вказують на ту напругу і той струм, які відповідають ситуації коли лампочка світить. А це означає, що опір нитки розжарювання лампочки при температурі t дорівнює R = U/I = 3,5В/0,28А = 12,5(Ом).

Оскільки за визначенням α = (R_t – R₀)/R₀∆t, то ∆t=(R_t–R₀)/R₀α, а враховуючи, що ∆t = t – t₀, можна записати t = (R_t – R₀)/R₀α – t₀, де α = 0,0046(1/ºС).

Розрахунки: t = (12,5–4)Ом/4(Ом)·0,0046(1/ºС) – 20ºС == 462ºС – 20ºС = 442ºС.

Відповідь: t = 442ºC.

Контрольні запитання.

1. Які частинки є носіями струму в металах? Який механізм появи цих частинок?
2. За рахунок чого атоми металів об’єднуються у відповідні тверді тіла?
3. Що означає твердження: в металі при проходженні струму електрони провідності рухаються упорядковано-хаотично?
4. Яка приблизна швидкість упорядкованого руху електронів при проходженні електричного струму? Від чого залежить ця швидкість?
5. Яка швидкість поширення струму в лініях електропередач?
6. Як і чому електричний опір металів залежить від їх температури?
7. Який параметр характеризує залежність опору провідника від температури? Як визначається цей параметр?
8. 8. В яких приладах застосовують залежність опору провідника від температури?
9. Як ви думаєте, чому вільні електрони не вилітають за межі металу?

Вправа 27.

1. При температурі 20ºС опір вольфрамової нитки лампочки розжарювання становить 20(Ом). Опір тієї ж нитки в робочому стані 188(Ом). Визначте температуру накалу нитки.
2. Вольфрамова нитка лампочки накалювання при температурі 2100°С має опір 484(Ом). Визначте опір цієї нитки при 20°С.
3. При проходженні електричного струму через залізний провідник, його температура збільшилась на 170°С, а опір збільшився вдвічі. Визначити температурний коефіцієнт опору заліза.
4. Опір реостата при 20ºС дорівнює 15(Ом). Наскільки збільшиться цей опір при нагріванні ніхромового дроту реостата до 100ºС?
5. При 0°С електричний опір нитки лампи розжарювання в десять разів більший ніж при 1900°С. Визначте температурний коефіцієнт опору матеріалу нитки.
6. На цоколі лампочки розжарювання написано 220В; 75Вт. Визначте температуру вольфрамової нитки цієї лампочки в робочому стані, якщо при 20ºС її опір (Ом).
7. При зростанні температури графітового стержня від 50ºС до 500ºС, його опір зменшився від 5,0(Ом) до 4,5(Ом). Визначте температурний коефіцієнт опору графіту.

.