МЕХАНІКА РІДИН ТА ГАЗІВ

Тема 1.5. Механіка рідин та газів.
§53. Тиск. Закон Паскаля. Закон Архімеда.
§54. Розв’язування задач. Тема: Механіка рідин та газів.
§55. Загальні відомості про гідродинаміку.
§56. Закон Бернуллі – основний закон механіки рідин та газів.
§57. Практичне застосування закону Бернуллі. Піднімальна сила крила. Ефект Магнуса.
§58. Механічна картина світу.
Тема 1.5. Механіка рідин та газів.
Механіка рідин та газів – це розділ механіки, в якому вивчають механічні властивості рідин і газів, параметри, закономірності та причини їх механічного руху, а також закономірності їх механічної взаємодії з твердими тілами. З загальними основами механіки рідин та газів ви ознайомились в процесі вивчення фізики за сьомий клас. Тому в межах даної теми, ми стисло повторимо раніше вивчене, та доповнимо його новими знаннями.
.
§51. Тиск. Закон Паскаля. Закон Архімеда.
Однією з основних фізичних величин механіки рідин та газів є тиск.
Тиск – це фізична величина, яка характеризує усереднену силове дію що припадає на одиницю площі поверхні і яка дорівнює відношенню діючої на дану поверхню сили F до площі цієї поверхні S.
Позначається: р
Визначальне рівняння: р = F/S
Одиниця вимірювання: [р] = Н/м2 = Па, паскаль.
Паскаль – це одиниця вимірювання тиску, що дорівнює такому тиску який чинить сила в 1Н, будучи рівномірно розподіленою по поверхні площею 1м2. Наприклад, якщо 102г води (Fт = mg = 0,102кг∙9,8м/с2 = 1Н), рівномірно розподілити по поверхні площею 1м2, то тиск води на цю поверхню становитиме один паскаль. Ясно, що такий тиск є відносно незначним.
На поверхні тиснуть не лише тверді тіла та рідини, а й гази. Скажімо, над кожним об’єктом земної поверхні знаходиться шар атмосферного повітря який створює певний атмосферний тиск. Дослідження показують, що на рівні моря усереднена величина цього тиску 101∙103Па (точніше 101325Па). А це еквівалентно тому тиску який чинить на горизонтальну поверхню площею 1м2 вантаж масою 10,3 тон!!!
Ви можете запитати, а чому знаходячись під постійною дією такого величезного тиску, ми практично не відчуваємо його? До речі, однією з причин того, чому люди довгий час відмовлялися визнавати факт існування атмосферного тиску, була та, що вони не могли зрозуміти, чому за наявності такого шалено великого тиску, ми не відчуваємо його силової дії. А й дійсно, чому? Перш ніж відповісти на це запитання, візьміть аркуш паперу і тримаючи його в горизонтальному положенні запитайте себе, чому під дією атмосферного тиску, тонкий папір навіть не прогинається? Правильно! Це пояснюється тим, що атмосферне повітря рівномірно тисне з усіх сторін, зокрема як зверху так і знизу. А це означає, що результуюча силова дія цього тиску є нулевою.
Подібна ситуація характерна не лише для аркушів паперу, а й для таких надскладних об’єктів як живі організми. Адже ці організми складаються з клітин, які представляють собою тонку оболонку наповнену водою та певною кількістю надскладних органічних молекул. При цьому, тиск внутріклітинної рідини практично не відрізняється від зовнішнього атмосферного тиску. А це означає, що результуюча силова дія цих тисків є практично нулевою. Більше того, живий організм, це певна саморегульована система, в якій зміна зовнішнього тиску автоматично призводить до відповідної зміни внутріклітинного тиску. Про можливості такого саморегулювання говорить той факт, що треновані аквалангісти здатні пірнати на стометрову глибину. А це означає, що їх організм витримує десятикратне тискове перевантаження.
В 1651–1654 роках, розмірковуючи над тим, чому атмосферний тиск в кімнаті та за її межами однаковий, чому аркуш паперу і людський організм не відчувають силової дії атмосферного тиску, чому занурені в рідину тіла виштовхуються з неї, а також проводячи відповідні експериментальні дослідження, французький фізик Блез Паскаль (1623 – 1662) з’ясував: той зовнішній тиск що діє на поверхню механічно зрівноваженої рідини (газу) без змін передається у всі точки цієї рідини і діє у всіх можливих напрямках. (закон Паскаля). Наприклад, якщо поршень (мал.162) створює певний тиск на усталену рідину або газ, то цей тиск без змін передається у всі точки відповідної рідини або газу.
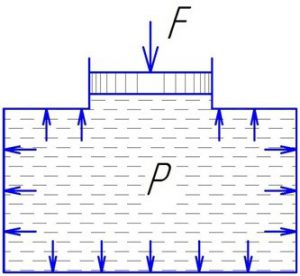
Мал.166. Той зовнішній тиск що діє на поверхню механічно зрівноваженої рідини без змін передається у всі точки цієї рідини і діє у всіх можливих напрямках.
Застосовуючи закон Паскаля потрібно мати на увазі, що окрім діючого на рідину (газ) зовнішнього тиску, в ній неминуче існує певний додатковий тиск, поява якого обумовлена дією на рідину сили тяжіння, тобто вагою самої рідини. Цей тиск прийнято називати ваговим.
Ваговий тиск – це той тиск, який створює певний шар рідини (газу) за рахунок того що на неї діє сила тяжіння, тобто за рахунок своєї ваги.
Позначається: рв
Визначальне рівняння: рв = ρgh, де
ρ – густина рідини (газу),
g – прискорення вільного тяжіння,
h – висота рідини над заданим рівнем.
Одиниця вимірювання: [рв] = Па.
Потрібно зазначити, що величина того вагового тиску який створює рідина на дно посудини, не залежить ні від площі цього дна, ні від форми посудини, ні від кількості рідини в ній. Величина цього тиску залежить лише від густини рідини (ρ), прискорення діючої на рідину сили тяжіння (g) та висоти рідини над заданим рівнем (h). Скажімо, маса (а відповідно і вага) тієї рідини що міститься в зображених на мал.167 посудинах, є різною. При цьому тиск рідини на дно кожної посудини є однаковим. Не відповідність між тиском рідини на дно посудини та кількістю налитої в цю посудину рідини, часто називають гідростатичним парадоксом або парадоксом Паскаля.
Втім, невідповідність між тиском рідини на дно посудини та кількістю рідини в ній, є не більш парадоксальною аніж невідповідність між мізерністю тієї кількості повітря що знаходиться у вашій квартирі, та величиною того тиску з яким це повітря тисне на підлогу квартири. Бо цей тиск фактично створюється не тим повітрям яке знаходиться в квартирі, а всією сукупністю атмосферного повітря. Адже повітря вашої квартири є невід’ємною складовою земної атмосфери. При цьому, у відповідності з законом Паскаля, загально атмосферний тиск передається у всіх можливих напрямках, в тому числі і в напрямку вашої квартири. І величина цього атмосферного тиску залежить не від висоти вашої квартири, не від кількості повітря в ній, чи площі її підлоги, а від загальної висоти атмосфери. Власне за тієї ж причини, величина того вагового тиску який створює рідина на будь яку поверхню посудини, залежить не від площі цієї поверхні, не від кількості рідини в посудині, а від загальної висоти рідини над рівнем відповідної поверхні.
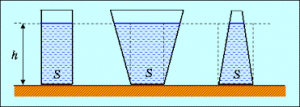
Мал.167. Тиск рідини на дно посудини не залежить від кількості налитої в посудину рідини.
Застосовуючи закон Паскаля можна пояснити будову та принцип дії багатьох приладів, зокрема гідравлічних пресів, домкратів, гальмівних систем, тощо. Пояснити чому в сполучених посудинах рівень рідини однаковий, чому на занурені в рідину (газ) тіла діє виштовхувальна сила (сила Архімеда), тощо. Що ж давайте зробимо вище згадані пояснення. І почнемо з гідравлічних систем, зокрема гідравлічних пресів.
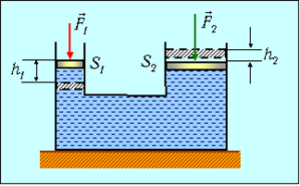
На мал.168 зображена система двох сполучених циліндрів, які заповнені рідиною і закриті відповідними поршнями. Не важко довести, що коли на поршень площею S1 діє сила F1, то діюча на поршень S2 сила F2, визначатиметься за формулою F2 = F1(S2/S1). Дійсно. Діюча на поршень S1 сила F1 створює тиск р1 = F1/S1. Цей тиск, згідно з законом Паскаля без змін передається у всі точки рідини, в тому числі і ті що знаходяться під поршнем S2. При цьому діючий на поршень S2 тиск р2 = р1, створюватиме відповідне силове зусилля: F2 = p2S2 = (F1/S1)S2 = F1(S2/S1).

Мал.168 Схема гідравлічної системи, що дозволяє збільшувати силове зусилля.
Таким чином, зображена на мал.168 система, дозволяє в n = S2/S1 разів збільшувати силове зусилля. Однак, говорячи про те, що певна гідравлічна система в певну кількість разів збільшує силову дію, не слід забувати про закон збереження енергії. А згідно з цим законом, та робота яку виконує сила F2 і яка дорівнює A2 = F2h2, не може перевищувати ту роботу яку виконує сила F1: A1 = F1h1. А це означає, що виграючи в силі (F2 = nF1) ми неминуче програєм в пройденому шляху (h2 = h1/n) – золоте правило механіки.
Зважаючи на вище сказане не важко пояснити будову та принцип дії зображеного на мал.169 гідравлічного преса. А ця будова та цей принцип дії полягають в наступному.
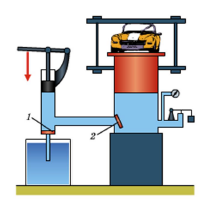
1, 2 – малий та великий поршні; 3, 4 – вхідний та вихідний клапани; 5 – нерухома платформа; 6 – резервуар з рідиною.
Мал.169. Загальний устрій та принципова схема гідравлічного пресу.
Коли під дією зовнішньої сили F1, малий поршень площею S1 опускається на висоту Δh1, то відповідна кількість рідини через клапан 2 заштовхується у великий циліндр. При цьому, у відповідності з законом Паскаля, на поршень великого циліндра площею S2, діє тиск p2 = p1 = F1/S1. А це означає, що силове навантаження на поршень великого циліндра буду в n=S2/S1 разів більшим аніж на поршень малого циліндра: F2=nF1. З іншого боку, поршень великого циліндра підніметься на відносно меншу висоту: Δh2=Δh1/n. Для збільшення цієї висоти, в об’єм великого циліндра потрібно заштовхати відповідно велику кількість рідини. А це заштовхування забезпечується багаторазовістю повторювальних рухів (вверх-вниз) поршня малого циліндра, та наявністю в системі додаткового резервуара з рідиною і двох автоматично працюючих клапанів.
Дійсно, в процесі піднімання поршня малого циліндра, клапан 2 автоматично закривається, а клапан 1 автоматично відкриваються (поясніть чому). При цьому, певна порція рідини із додаткового резервуара засмоктуються в малий циліндр. При опусканні поршня малого циліндра, клапан 1 автоматично закривається, натомість клапан 2 – відкривається і додаткова порція рідини заштовхується в об’єм великого циліндра, забезпечуючи тим самим відповідне додаткове піднімання його поршня.
Таким чином, в процесі багаторазових повторювальних рухів поршня малого циліндра, в об’єм великого циліндра заштовхується все більша і більша кількість рідини, яка з одного боку забезпечує відповідно велике силове навантаження на поршень (F2 = nF1), а з іншого – необхідно велике піднімання цього поршня (h2 = NΔh1, де N – кількість тих циклів (качань) які здійснює поршень малого циліндра).
Застосовуючи закон Паскаля не важко пояснити факт того, що в сполучених посудинах, рівень однорідної рідини є однаковим. Дійсно, припустимо що висота рідини над точками довільно взятого горизонтального рівня АВ є різною і дорівнює h1 і h2 (мал.170). У відповідності з законом Паскаля, в точках однакового горизонтального рівня однорідної рідини, тиск цієї рідини має бути однаковим: рА = рВ. З іншого боку, тиск над рівнем АВ складається із діючого на поверхню рідини зовнішнього (атмосферного) тиску р0 та відповідного цьому рівню вагового тиску ρgh і тому pА = p0+ρgh1, pВ = p0+ρgh2. Таким чином, у відповідності з законом Паскаля та наявною ситуацією можна записати p0+ρgh1 = p0+ρgh2. А це можливо лише в тому випадку якщо h1 = h2, адже густина рідини (ρ) в обох колінах є однаковою, атмосферний тиск (р0) – однаковий, прискорення сили тяжіння (g) – однакове. Висновок. У відповідності з законом Паскаля, в сполучених посудинах рівень однорідної рідини має бути однаковим.
а)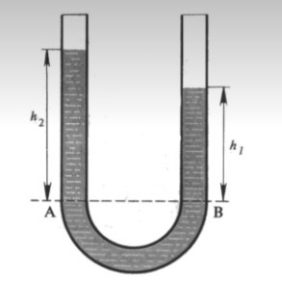 б)
б)
Мал.170. Якщо в сполучених посудинах міститься однорідна рідина, то її рівень в цих посудинах однаковий.
Звичайно, якщо в сполучених посудинах містяться рідини різної густини, то рівень цих рідин може бути різним. Однак і в цьому випадку все відбувається у відповідності з законом Паскаля. Адже якщо ρ1 ≠ ρ2, то із формули ρ1gh1 = ρ2gh2 випливає, що h2 ≠ h1; (h2 = h1ρ1/ρ2) .
Знаючи та застосовуючи закон Паскаля можна довести, що на будь яке занурене в рідину (газ) тіло, діє виштовхувальна сила, величина якої дорівнює вазі виштовхнутої тілом рідини (закон Архімеда). Дійсно. Розглянемо силову дію рідини на занурене в неї тіло. Для простоти розрахунків та пояснень, в якості такого тіла візьмемо прямокутний паралепіпед висотою h і площею основи S (мал.171). Оскільки сили тиску рідини на бічні грані паралепіпеда попарно симетричні і попарно протилежні, то їх результуюча дія дорівнює нулю. З іншого боку, згідно з законом Паскаля, сили тиску рідини на верхню F1 і нижню F2 основи паралепіпеда суттєво різні:
F1 = p1S = (p0 + ρgh1)S,
F2 = p2S = (p0 + ρgh2)S.
Рівнодіюча цих сил і є виштовхувальною силою Архімеда:
FА = F2 – F1 = (p0 + ρgh2 – p0 – ρgh1)S = ρghS.
А враховуючи що Sh =V – об’єм тіла; ρV = m – маса тієї рідини яку виштовхує тіло; mg=Pр – вага тієї рідини, яку виштовхнуло тіло, можна записати: FА=ρgV=mg=Pp. Що і потрібно було довести.
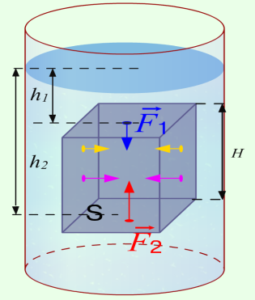
Мал.171. На будь яке занурене в рідину тіло, діє виштовхувальна сила, яка дорівнює вазі виштовхнутої тілом рідини.
Задача 1. Площа меншого поршня гідравлічного преса 10см2. Під дією сили 200Н цей поршень опускається на 40см. Яка сила діє на великий поршень преса і на скільки він піднімається під дією цієї сили, якщо площа великого поршня 200см2. Вагою поршнів і тертям знехтувати.
Дано:
S1 = 10см2
F1 = 200Н
h1 = 40см
S2 = 200см2
F2 = ? h2 = ?
Рішення. Оскільки згідно з законом Паскаля, величина того гідравлічного тиску, що діє на великий та малий поршні преса є однаковою (р1 = р2), та враховуючи що р1 = F1/S1, р2 = F2/S2, можна записати F1/S1 = F2/S2, звідси F2 = F1S2/S1 = 200Н200см2/10см2 = 4000Н.
Оскільки згідно з законом збереження енергії, величина тієї роботи яку виконує сила F1 (A1 = F1h1), має дорівнювати величині тієї роботи яку виконує сила F2 (A2 = F2h2), то можна записати: F1h1 = F2h2, звідси h2 = h1F1/F2 = 40см200Н/4000Н = 2см.
Відповідь: F2 = 4000Н; h2 = 2см.
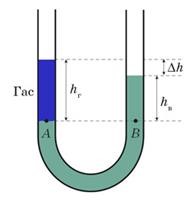
Задача 2. В одне з колін U-подібної трубки, в якій міститься певна кількість води, налили шар гасу висотою 12,5см. Визначте різницю рівнів води і гасу в правому і лівому колінах трубки. Гас і вода не змішуються.
Дано:
hг = 12,5см
вода
гас
Δh = ?
Рішення. Виконуємо малюнок, який наочно відображає фізичну суть задачі. В якості нульового горизонтального рівня обираємо рівень АВ. Рівень, нижче якого знаходиться лише однорідна рідина (вода). Оскільки нижче горизонтального рівня АВ в трубці міститься лише однорідна рідина, то згідно з законом Паскаля, той тиск який існує над цим рівнем в обох колінах трубки має бути однаковим. А враховуючи, що для точок А і В величина цього тиску становить: рА = р0+ρгghг; рВ = р0+ρвghв, можна записати р0+ρгghг = р0+ρвghв, або ρгghг = ρвghв, або ρгhг = ρвhв. Звідси випливає, що hв = hгρг/ρв, де ρв, ρг – визначаються з відповідної таблиці (або запам’ятовуються): ρв =1000кг/м3, ρг = 800кг/м3. Зважаючи на те, що Δh = hг–hв, виконуємо відповідні розрахунки.
Розрахунки: hв = 12,5(см)800(кг/м3)/1000(кг/м3) = 10см;
Δh = 12,5(см) – 10(см) = 2,5см.
Відповідь: Δh = 2,5см.
Контрольні запитання.
- Поясніть, чому ми не відчуваємо того величезного тиску з яким атмосфера Землі діє на її поверхню?
- Поясніть, чому той шар повітря який знаходиться в кімнаті і висота якого менша 3м, створює такий же тиск, як і те повітря яке знаходиться за вікном кімнати і висота якого десятки кілометрів?
- Який тиск називають ваговим? Від чого залежить цей тиск?
- Виходячи з загального визначального рівняння тиску р = F/S, доведіть, що ваговий тиск рідини можна визначити за формулою р = ρgh.
- 5. На основі аналізу мал.167 скажіть: а) чи з однаковим тиском діє рідина на дно кожної посудини? б) чи з однаковим тиском кожна посудина діє на поверхню стола?
- Чому в зображеній на мал.168 системі, сили F1 і F2 є різними? Як в цій системі проявляється золоте правило механіки.
- Поясніть будову та принцип дії зображеного на мал.169 гідравлічного пресу.
- Чому в момент піднімання малого поршня (мал.169) клапан 1 відчиняється, а клапан 2 зачиняється, а при його опусканні – навпаки?
- Що стверджується в законі Архімеда?
Вправа 51.
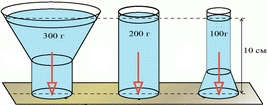
- Який тиск створює шар води висотою 10м; 100м? Відповідь дайте в паскалях та в атмосферах.
- За даними представленими на малюнку, визначте тиск рідини (води) на дно кожної посудини, та тиск кожної посудини на поверхню стола. Площа дна кожної
- В підводній частині корабля, на глибині 3м від рівня води, утворилась пробоїна загальною площею 20см2. Яке мінімальне зусилля знадобиться для того, щоб втримати латку з внутрішньої частини корабля?
- Якщо на малий поршень гідравлічного преса діє сила 90Н, то на більший поршень площею 2700см2 діє сила 36кН. Яка площа меншого поршня?
- Ширина шлюзу 10м. Шлюз заповнений водою, надлишковий рівень якої 7м. З якою силою вода тисне на ворота шлюзу?
- В циліндричну посудину налита ртуть і вода в рівних за масою кількостях. Загальна висота двох шарів рідин становить 29,2см. Визначити тиск рідини на дно посудини. Густина ртуті 13,6∙103кг/м3.
- В сполучених посудинах міститься ртуть, коли в праве коліно посудини налили шар гасу, то рівень ртуті в лівому коліні піднявся на 2см. Визначте висоту налитого в посудину гасу.
- Крижина площею 60м2 і товщиною 40см плаває у воді. Тіло якої максимальної маси може втримати на плаву ця крижина? Густина льоду 900кг/м3.
- Знаючи радіус землі (R = 6,4∙106м) і величину атмосферного тиску (р0 = 1∙105Па) визначте масу земної атмосфери.
.
§52. Розв’язування задач. Тема: механіка рідин та газів
Задача 1. Визначити густину однорідного тіла, якщо відомо, що його вага у повітрі 28,5Н, а у воді 16,9Н. Втратами ваги у повітрі знехтувати.

Дано:
Рп = 28,5Н
Рв = 16,9Н
ρт = ?
Рішення. Оскільки за визначенням ρ = m/V, то рішення задачі зводиться до того, щоб визначити масу та об’єм тіла. Оскільки втратами ваги в повітрі можна знехтувати, то Рп=mg, звідси випливає: m = Pп/g = 28,5Н/9,81м/с2 = 2,9кг.
Величину об’єму тіла (V) визначаємо із наступних міркувань. Оскільки вага тіла у воді (Pв) дорівнює різниці між діючою на тіло силою тяжіння (Fт = mg) і діючою на нього силою Архімеда (FA = ρвVg), та зважаючи на те, що в умовах нашої задачі діюча на тіло сила тяжіння і його вага у повітрі є чисельно рівними (Pп = Fт), можна записати: Pв = mg – ρвVg = Pп – ρвVg. Звідси випливає: ρвVg = Pп – Pв. Звідси V = (Pп – Pв/ρвg) = (28,5Н – 16,9Н)/1·103(кг/м3)9,81(м/с2) = 1,18·10–3м3.
Таким чином, в умовах даної задачі густина тіла дорівнює:
ρт = m/V = 2,9кг/1,18·10–3м3 = 2,45·103кг/м3.
Відповідь: ρт = 2,45·103кг/м3.
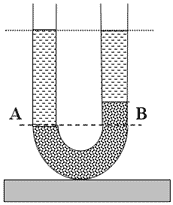
Задача 2. У U-подібній трубці знаходиться певна кількість ртуті. В праве коліно трубки долили 25,2см гасу. Скільки води треба долити в ліве коліно трубки, щоб вільні поверхні води і гасу були на одному рівні?
Дано:
hг = 25,2см
ρг = 800кг/м3
ρв = 1000кг/м3
ρр = 13600кг/м3
hв = ?
Рішення. Виконуємо малюнок, який відображає фізичний зміст задачі. Оскільки густина води більша за густину гасу, то в заданій системі, вільні поверхні води і гасу будуть на одному рівні лише в тому випадку коли висота води над поверхнею ртуті, буде дещо більшою за відповідну висоту гасу (hв > hг). Зважаючи на ці обставини, в якості нульового горизонтального рівня обираємо рівень АВ. Рівень, нижче якого знаходиться лише однорідна рідина (ртуть). Враховуючи, що над точкою А знаходиться лише шар води (hв), а над точкою В – шар гасу (hг) та певний шар ртуті (hр), та без урахування зовнішнього атмосферного тиску, який для обох колін трубки є однаковим, можна записати: рА = ρвghв; рВ = ρгghг+ρрghр.
Оскільки згідно з законом Паскаля, тиск над точками горизонтального рівня АВ має бути однаковим: рА = рВ, то ρвghв = ρгghг+ρрghр, або ρвhв = ρгhг+ρрhр.
На перший погляд рівняння ρвhв = ρгhг+ρрhр не має однозначного рішення, адже містить дві невідомі величини (hв = ? hр = ?). Однак, якщо врахувати факт того, що загальна висота шарів гасу і ртуті (hг+hр), має дорівнювати висоті води hг+hр = hв, то ми отримаємо систему двох незалежних рівнянь з двома невідомими:
(1) ρвhв = ρгhг+ρрhр;
(2) hв = hг+hр.
Розв’яжемо дану систему рівнянь та визначимо невідому величину:
Із (1) → hв = (ρгhг+ρрhр)/ρв;
Із (2) → hв = hг+hр.
Оскільки hв = hв, то (ρгhг+ρрhр)/ρв = hг+hр, де hр = ?
Загальні зауваження. Розв’язуючи задачі фізики, важливо не забувати про принцип доцільності. Скажімо в умовах даної задачі нам потрібно розв’язати рівняння з великою кількістю схожих величин ускладнених неменшою кількістю індексів: (ρгhг+ρрhр)/ρв = hг+hр. При цьому існує ймовірність того, що в процесі загального розв’язку рівняння, ми можемо переплутати ці величини та індекси і отримати неправильний результат. Зважаючи на ці обставини, доцільно розв’язувати дане рівняння не у загальному вигляді, а у вигляді рівняння з конкретними числовими значеннями. А ці значення є наступні:
(800·25,2 + 13600· hр)/1000 = 25,2 + hр, або 0,8·25,2 + 13,6· hр = 25,2 + hр, звідси
13,6· hр – hр = 25,2 – 25,2·0,8 = 25,2·0,2 звідси hр = 25,2·0,2/12,6 = 0,4см.
Таким чином: hв = hг+hр = 25,2 + 0,4 = 25,6см.
Відповідь: hв = 25,6см.
Задача 3. В посудині з водою плаває шматок льоду до якого примерзла коркова пробка. Як зміниться рівень води в посудині після того як лід розтане? Розглянути два варіанти: в початковий момент часу примерзла пробка знаходиться 1) над водою; 2) під водою.
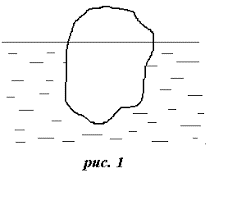
Загальні зауваження. На перший погляд, дана задача представляється такою, що не має кількісно обгрунтованого рішення. Насправді ж, таке рішення є. Однак, воно буде реалізовано лише в тому випадку, якщо аналізуючи умову задачі, ви звернете увагу на факт того, що в процесі плавлення льоду, тиск рідини на дно посудини залишається незмінним.
Рішення. В незалежності від того плаває щось в рідині чи не плаває, її тиск на дно посудини визначається за формулою р = ρgh, де h – висота рідини над рівнем дна посудини. Оскільки загальна маса тих речовин що знаходяться в посудині як до, так і після плавлення льоду залишається незмінною, та зважаючи на те, що в обох випадках на дно посудини тисне лише вода, можна стверджувати, що тиск води на дно посудини як в процесі так і після плавлення льоду залишається незмінним. При цьому, величина цього тиску не буде залежати від того де початково знаходилась коркова пробка – над водою, під водою чи де інде.
Таким чином, з одного боку тиск води на дно посудини до (р1) і після (р2) танення льоду має визначатись за формулами р1 = ρgh1; р2 = ρgh2. З іншого ж боку: р1 = р2. А це означає, що ρgh1 = ρgh2 і тому h1 = h2.
Відповідь: в обох випадках рівень води в посудині залишається незмінним і рівним його початковій величині.
Зауваження. Якби частиною шматка льоду було не пробкове тіло, а тіло яке тоне у воді, то після танення льоду, це тіло опинилось би на дні посудини. При цьому тиск рідини на дно посудини дещо зменшився б. Зменшився б на ту величину яку спричиняло те додаткове занурення льоду, джерелом якого була сила ΔF = Fт–FА, де Fт, FА – діючі на тіло, відповідно сила тяжіння та сила Архімеда. А це означає що рівень рідини у відповідній посудині дещо зменшився б. Втім, загальний тиск рідини та тіла на дно посудини залишився б незмінним.
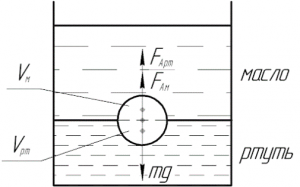
Задача 4. Куля плаває таким чином, що одна її половина занурена у ртуть (ρ = 13,6∙103кг/м3), а друга – в машинне масло (ρ = 0,9∙103кг/м3). Визначити густину кулі.
Дано:
ρ1 = 13,6∙103кг/м3
ρ2 = 0,9∙103кг/м3
V1 = V2 = V/2
ρ3 = ?
Рішення. Виконуємо малюнок який відображає фізичний зміст задачі. Розглянемо діючі на кулю сили і виходячи з умови її рівноваги (∑F=0), визначимо невідому величину.
На дану нерухому кулю діють три сили: сила тяжіння Fт, сила Архімеда збоку ртуті F1 та сила Архімеда збоку машинного масла F2. При цьому:
Fт = mg = ρ3gV
F1 = ρ1gV1 = ρ1gV/2
F2 = ρ2gV2 = ρ2gV/2.
Оскільки, згідно з умовою рівноваги кулі:
Fт = F1 + F2, то
ρ3gV = ρ1gV/2 + ρ2gV, або ρ3gV = gV(ρ1+ρ2)/2.
Звідси ρ3 = (ρ1 + ρ2)/2.
Розрахунки: ρ3 = (13,6·103 + 0,9·103)/2 = 7,25∙103кг/м3 .
Відповідь: ρ3 = 7,25∙103кг/м3.
Задача 5. Циліндри гідравлічного підйомника площею перерізу 1м2 і 25см2, в якості робочої рідини використовують технічну оливу густина якої 800кг/м3. Нехтуючи вагою поршнів і тертям, визначте на яку висоту підніметься малий поршень, якщо на платформу великого поршня покласти вантаж масою 200кг.

Дано:
S1 = 1м2
S2 = 25см2 = 25·10–4м2
m = 200кг
ρ = 800кг/м3
h2 = ?
Рішення. Виконуємо малюнок який відображає фізичний зміст задачі. Оскільки згідно з законом Паскаля тиск рідини на горизонтальному рівні О1О2 в обох циліндрах має бути однаковим р1 = р2, та враховуючи, що р1 = mg/S1, a p2 = ρg(h1+h2), можна записати mg/S1 = ρg(h1+h2).
З іншого боку, той об’єм рідини який виштовхується великим циліндром V1 = S1h1, має дорівнювати тому об’єму рідини який піднімається в малому циліндрі V2 = S2h2, тобто S1h1 = S2h2.
Таким чином, ми маємо два рівняння з двома невідомими:
1) mg/S1 = ρg(h1+h2);
2) S1h1 = S2h2.
Розв’язуємо систему цих рівнянь, та визначаємо невідому величину (h2).
Із (1) випливає h1 = [(mg/S1)–ρgh2]/ρg;
Із (2) випливає h1 = S2h2/S1.
Оскільки Із (1) випливає h1 = h1, то [(mg/S1)–ρgh2]/ρg = S2h2/S1, звідси
[(mg/S1ρg) –h2] = h2S2/S1, звідси h2[(S2/S1) – 1] = m/S1ρ,
h2 = m/S1ρ[(S2/S1) – 1] = 200/[1·800(25·10–4/1)+1] = 200/800 = 0,25м = 25см.
Відповідь: h2 = 25см.
Вправа 52.
- 1. Під дією сили 80Н малий поршень гідравлічного преса площею 8см2 опускається на 20см. При цьому великий поршень преса піднімається на 5мм. З якою силою рідина тисне на великий поршень преса? Яка площа цього поршня?
- В одне з колін U-подібної трубки, в якій міститься певна кількість води, налили шар гасу висотою 20см. Визначте різницю рівнів води і гасу в правому і лівому колінах трубки. Гас і вода не змішуються.
- На одній чаші вагів лежить шматок срібла масою 105г, а на іншій – шматок скла масою 130г. Яка чаша переважить при зануренні вагів у воду? Густина срібла 10,5∙103кг/м3, скла 2,6∙103кг/м3.
- Шматок заліза у воді важить 40,0Н. Визначити його об’єм. Густина заліза 7,8∙103кг/м3.
- Тіло кубічної форми плаває у ртуті так, що в ртуть занурено 0,25 його об’єму. Яка частина об’єму тіла буде занурена в ртуть після того як зверху неї налити шар води, який повністю вкриє тіло?
- В двох циліндричних, сполучених посудинах, площі поперечних перерізів яких однакові і становлять по 11,5см2, знаходиться ртуть. В одну з посудин поверх ртуті налили 2л води і опустили плавати в воду тіло масою 150г. На яку висоту підніметься рівень ртуті в другій посудині?
- В сполучених посудинах знаходиться ртуть. Діаметр вузької посудини в 2 рази менший за діаметр широкої. В широку посудину налили шар води висотою 50см. На скільки підніметься ртуть у вузькій посудині і наскільки опуститься в широкій?
.
§53. Загальні відомості про гідродинаміку.
До тепер ми вивчали загальні механічні властивості відносно нерухомих рідин (газів) та їх механічну дію на нерухомі тверді тіла. Іншими словами, ми вивчали основи гідростатики (гідрогазостатики). На разі ж мова піде про основи гідродинаміки, тобто того розділу гідромеханіки в якому вивчають загальні механічні властивості рухомих рідин та їх механічну дію на тверді тіла. Відразу ж зауважимо, що все, що в подальшому буде сказано про динамічні параметри рідини, з певними поправками стосується не лише рідин, а й газів.
До числа основних понять (базових термінів) гідродинаміки відносяться: усталений (стаціонарний) та неусталений (нестаціонарний) потік рідини, в’язкість рідини та ідеальна рідина.
Усталеним (стаціонарним) називають такий рух рідини (газу) при якому її швидкість в заданій точці потоку з плином часу залишається незмінною. При цьому, в інших точках потоку ця швидкість може бути іншою. Якщо ж в заданій точці потоку, швидкість рідини змінюється, то такий рух називають неусталеним або нестаціонарним. В реальних умовах ідеально усталений рух рідини (газу) зустрічається надзвичайно рідко. Тому на практиці усталеним прийнято вважати такий рух, в процесі якого через заданий переріз потоку, наприклад через поперечний переріз труби, за однакові проміжки часу протікає однакова кількість рідини. В подальшому ми будемо говорити лише про усталені рухи рідини.
Однією з основних властивостей будь якої рідини є її в’язкість. Напевно, кожен з вас інтуїтивно розуміє яку властивість рідини характеризує термін в’язкість. Скажімо, якби вас запитали, чому із отвору в посудині мед витікає повільніше за воду, то скоріш за все ви б сказали, що мед має велику в’язкість і що тому він погано тече. І це правильно. Правильно по-перше тому, що в’язкість це дійсно щось протилежне текучості (плинності). А по-друге, величину в’язкості дійсно оцінюють по тому як швидко рідина витікає через стаціонарний отвір, або як швидко падає в ній стандартна металева кулька. Втім, в’язкість є тією складною та неоднозначною властивістю середовища, яка за різних обставин визначається та оцінюється по різному. Зазвичай в’язкістю (внутрішнім тертям) називають ту властивість середовища (рідини або газу), яка проявляється в здатності цього середовища чинити опір переміщенню однієї його частини відносно іншої.
На практиці, в’язкість рідини кількісно оцінюють на основі ряду експериментально отриманих співвідношень, які в тій чи іншій мірі відображають залежність в’язкості від різних обставин: сорту рідини, характеру її руху, температури, тиску, тощо. При цьому існує щонайменше шість методів визначення в’язкості: метод падаючої кульки, капілярний метод, ротаційний метод, ультразвуковий метод, вібраційний метод, бульбочковий метод.
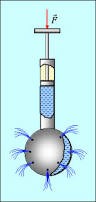
Найбільш простими та очевидними методами визначення в’язкості (коефіцієнту в’язкості) рідини є метод падаючої кульки та капілярний метод. В методі падаючої кульки (мал.172а) в’язкість рідини визначають шляхом вимірювання часу падіння стандартизованої кульки, між двома позначками в трубці заповненій досліджуваною рідиною. В капілярному методі (мал.172б), в’язкість рідини оцінюють за часом протікання заданого об’єму рідини через вузьку трубку (капіляр) при заданій різниці тисків.
а) 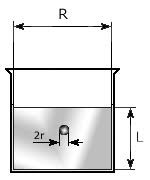 б)
б) 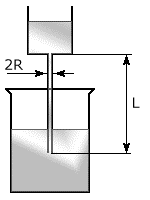
Мал.172. Найбільш очевидно простими методами визначення коефіцієнту в’язкості рідини, є метод падаючої кульки (а) та капілярний метод (б).
Загально прийнятою кількісною мірою в’язкості є величина, яка називається коефіцієнтом в’язкості. Ця величина має складне визначення. Тому просто зауважимо, що коефіцієнт в’язкості позначається η і вимірюється η = Па∙с (паскаль-секунда). Числове значення коефіцієнту в’язкості (або просто в’язкості) визначається експериментально і записується у відповідну таблицю. Прилад за допомогою якого визначають коефіцієнт в’язкості речовини називається віскозиметром (від лат. viscosus – в’язкий).
В механіці рідин та газів, при теоретичних поясненнях та наближених розрахунках, реальну рідину зазвичай замінюють її спрощеною (ідеалізованою) моделлю яка називається ідеальною рідиною. Ідеальна рідина – це спрощена (ідеалізована) модель реального середовища (рідини або газу), яка представляє собою таке умовне середовище яке не стискається та має нульову в’язкість.
Потрібно зауважити, що реальні рідини і реальні гази певною мірою схожі і певною мірою несхожі на ідеальну рідину. При цьому рідини схожі тим що практично не стискаються, а несхожі тим що мають відносно велику в’язкість. Гази ж, навпаки – схожі тим, що мають малу в’язкість і несхожі тим, що сильно стискаються. Тим не менше, в багатьох практично важливих ситуаціях ті закони які можна отримати на основі теоретичного аналізу поведінки ідеальної рідини, достатньо точно описують механічну поведінку як реальних рідин так і реальних газів. Звичайно за умови, що в’язкість цих рідин не надто велика, а швидкість газів не перевищує 100м/с (при таких швидкостях стисненням газу в процесі його руху можна знехтувати).
Як уже зазначалось, однією з основних фізичних величин механіки рідин та газів загалом і гідродинаміки зокрема є тиск. При цьому в гідродинаміці розрізняють три різновидності тиску: ваговий, статичний та динамічний.
Ваговий тиск – це той тиск, який створює певний шар рідини (газу) за рахунок своєї ваги.
Позначається: рв
Визначальне рівняння: рв = ρgh
Одиниця вимірювання: [рв] = Па.
Наприклад на бокові поверхні та на дно тієї посудини в якій знаходиться рідина, діє певний ваговий тиск, величина якого залежить від висоти рідини над відповідною точкою поверхні (мал.173). Або наприклад, в незалежності від того рухається рідина чи не рухається, тиск на нижню поверхню труби більший за тиск на її верхню поверхню, більший на величину вагового тиску відповідної рідини.
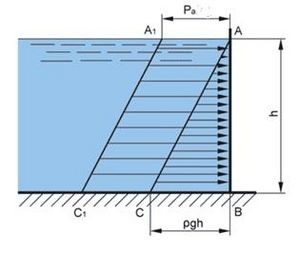
Мал.133. На дно та бічні поверхні тієї посудини в якій знаходиться рідина, діє певний ваговий тиск цієї рідини (рв=ρgh).
Статичний тиск (або просто, тиск) – це той фактичний тиск, з яким нерухома рідина (газ) тисне на її обмежуючу поверхню, або з яким потік рідини (газу) тисне на ту поверхню що є паралельною до цього потоку.
Позначається: р
Визначальне рівняння: р = F/S
Одиниця вимірювання: [р] = Па.
Наприклад, той тиск з яким та рідина що знаходиться під поршнем циліндра тисне на поршень (р0), на дно циліндра (р = р0+ρgh) та на його бічні поверхні, є статичним тиском. Або якщо наприклад, в трубі тече рідина, то той тиск з яким ця рідина тисне на паралельні до потоку поверхні труби, є статичним тиском рідини.
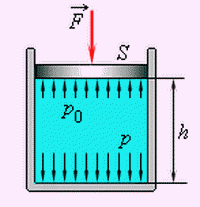
Мал.174. Статичний тиск, це той тиск, з яким нерухома рідина тисне на її обмежуючу поверхню, або з яким потік рідини тисне на ту поверхню що є паралельною до цього потоку.
Динамічний тиск – це той додатковий тиск, який створює потік рідини (газу) за рахунок енергії свого руху і який діє на ту поверхню, що є перпендикулярною до цього потоку.
Позначається: рд
Визначальне рівняння: рд = ρv2/2,
де ρ – густина рідини; v – швидкість її руху.
Одиниця вимірювання: [рд]=Па.
Наприклад, якщо рідина з швидкістю v тече горизонтальним прямолінійним відрізком труби діаметром d, то той тиск з яким рідина тисне на верхню, нижню чи будь яку іншу паралельну потоку поверхню труби є статичним тиском. Той додатковий тиск між верхньою та нижньою поверхнями труби, який створює рідина за рахунок своєї ваги і який дорівнює рв = ρgd, є ваговим тиском. А той додатковий тиск який створює рідина за рахунок енергії свого руху, який дорівнює рд = ρv2/2 і який діє лише на ті поверхні що розташовані перпендикулярно (поперек) потоку, є динамічним тиском.
а)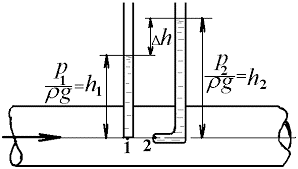 б)
б)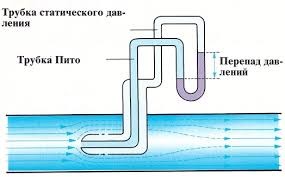
Мал.175. Динамічний тиск – це той тиск, який створює потік рідини на ту поверхню, що є перпендикулярною до цього потоку.
Динамічний тиск рідин та газів вимірюють за допомогою так званої трубки Піто (названа ім’ям винахідника, французького інженера Анрі Піто).Трубка Піто (мал.175б) представляє собою Г-подібну трубку, центральний отвір якої сприймає повний тиск рідини (динамічний + статичний), а бічний отвір – лише статичний. Різниця цих тисків і є тим динамічним тиском, що існує у відповідній точці потоку.
Задача. У пожежному шлангу вода тече з швидкістю 9м/с, при цьому на виході пожежного брандспойта швидкість водяного потоку 36м/с. Який динамічний тиск води у шлангу та на виході брандспойта?
Дано:
v1 = 9м/с
v2 = 36м/с
ρ = 1·103кг/м3
pд = ?
Рішення. У відповідності з визначальним рівнянням
рд1 = ρv12/2 = 1·103(кг/м3)(9м/с)2/2 = 40,5·103Па = 0,4атм.
рд2 = ρv22/2 = 1·103(кг/м3)(36м/с)2/2 = 648·103Па = 6,4атм.
Відповідь: рд1 = 40,5·103Па = 0,4атм; рд2 = 648·103Па = 6,4атм.
Контрольні запитання.
- Який рух рідини називають усталеним (стаціонарним)?
- Що називають в’язкістю (внутрішнім тертям) рідини?
- Який зв’язок між в’язкістю та текучістю (плинністю) рідини?
- Що називають ідеальною рідиною?
- Чим реальні рідини і реальні гази схожі на ідеальну рідину і чим відрізняються від неї?
- Який тиск називають ваговим?
- Який тиск називають статичним?
- Який тиск називають динамічним?
- Поясніть загальний устрій та принцип дії трубки Піто.
.
§54. Закон Бернуллі – основний закон механіки рідин та газів.
В 1738 році швейцарський фізик Даніель Бернуллі (1700–1782) сформулював базовий закон сучасної механіки рідин та газів (закон Бернуллі). З’ясовуючи фізичну суть цього закону, розглянемо енергетичні параметри ідеальної рідини, що усталено (стаціонарно) рухається в гравітаційному полі Землі по трубі довільного поперечного перерізу.

Якщо виходити з того що: 1) рідина ідеальна, тобто така, що не стискається і в якій відсутні енергетичні втрати на внутрішнє тертя (нулева в’язкість); 2) в процесі руху, відсутній теплообмін рідини з навколишнім середовищем; 3) гравітаційне поле Землі є потенціальним, тобто таким в якому будь яке зменшення потенціальної енергії тіла, призводить до еквівалентного збільшення його кінетичної енергії і навпаки (а гравітаційне поле, дійсно потенціальне), то можна стверджувати, що повна механічна енергія довільно вибраної маси Δm ідеальної рідини, в процесі руху має залишатись незмінною, тобто зберігатись (закон збереження енергії). А це означає, що коли в точці 1 певна елементарна маса Δm ідеальної рідини має певний запас енергії Е1, то опинившись в точці 2, ця ж маса повинна мати той же запас енергії: Е2 = Е1 .
Оскільки довільно вибраний фрагмент рідини масою Δm, по-перше рухається, по-друге взаємодіє з Землею, по-третє знаходиться під дією певного зовнішнього тиску, то його повна механічна енергія складається з трьох частин:
- Тієї кінетичної енергії Ек яку має рідина масою Δm за рахунок її руху: Ек = Δmv2/2;
- Тієї потенціальної енергії Еп, яку має рідина масою Δm за рахунок її взаємодії з Землею: Еп = Δmgh;
- Тієї внутрішньої механічної енергії Евн (а по суті потенціальної енергії сили пружності), яку має рідина масою Δm за рахунок її всебічного стиснення і яка визначається як добуток внутрішнього тиску рідини р на її об’єм ΔV: Евн=рΔV.
Таким чином, в довільній точці потоку, наприклад в точці 1, повна механічна енергія Е1 елементарної маси Δm рідини, визначається за формулою: Е1 = p1ΔV + Δmgh1 + Δmv12/2; або, враховуючи що Δm=ρΔV:
E1 = p1ΔV + ρΔVgh1 + ρΔVv12/2. А оскільки, згідно з законом збереження енергії Е1 = Е2, то p1ΔV + ρΔVgh1 + ρΔVv12/2 = p2ΔV + ρΔVgh2 + ρΔVv22/2.
Розділивши на ΔV, отримаємо: p1 + ρgh1 + ρv12/2 = p2 + ρgh2 + ρv22/2,
або p + ρgh + ρv2/2 = const.
Висновок: При усталеному (стаціонарному) русі ідеальної рідини, сума її статичного, вагового і динамічного тисків в будь якому поперечному перерізі труби залишається незмінною, тобто зберігається. Іншими словами: p + ρgh + ρv2/2 = const.
Даний висновок був математично доведений, експериментально перевірений та сформульований швейцарським фізиком Даніелем Бернуллі і тому по праву називається законом Бернуллі.
В механіці рідин і газів, закон Бернуллі відіграє надзвичайно важливу роль. Достатньо сказати, що закон Паскаля, закон сполучених посудин та закон Архімеда, є прямими наслідками закону Бернуллі. Дійсно. Якщо рух рідини в трубі відсутній (v = 0), то формула p + ρgh + ρv2/2 = const, набуває вигляду p + ρgh = const, тобто того вигляду, який можна вважати математичним формулюванням як закону Паскаля так і закону сполучених посудин.
Однак, найбільш важливі та цікаві наслідки закону Бернуллі стосується саме динаміки рідин і газів. При цьому, деякі з цих наслідків здаються такими, що суперечать нашому «здоровому глузду», тобто тим не системним поглядам на навколишній світ, які підсвідомо формуються на основі нашого повсякденного досвіду. Скажімо, якби вас запитали: «В якому місці труби – вузькому чи широкому – тиск рухомої води на стінки труби буде більшим?», то скоріш за все, ви б сказали, що у вузькому. І це абсолютно прогнозована відповідь. Адже загально відомо, що коли воду, повітря чи що завгодно, з великого об’єму заштовхувати в малий, то в процесі цього заштовхування тиск відповідного середовища зростає. Керуючись цим повсякденним досвідом «здоровий глузд» твердо заявляє: «у вузькому місці труби, тиск водяного потоку на стінки труби має бути більшим!». Та от парадокс. Якщо ви дійсно в різних місцях труби виміряєте той тиск що діє на її поверхню, то неминуче з’ясуєте, що в найвужчому місці труби, цей тиск буде найменшим.
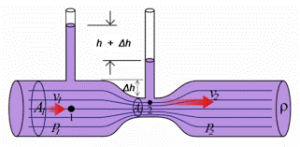
Мал.176. Всупереч передбаченням «здорового глузду», у вузькому місці труби, тиск водяного потоку на стінки цієї труби є меншим аніж в широкому.
Наявний результат здається дивним. Втім, не будемо поспішати з висновками. Не будемо бодай тому, що передбачення нашого «здорового глузду» грунтуються на аналізі тих ситуацій в яких, при заштовхуванні речовини в меншу посудину, об’єм цієї речовини зменшується. В нашому ж випадку, ніякого зменшення об’єму рідини не відбувається. Просто в процесі руху, ця рідина в одних місцях тече повільніше, а в інших – швидше. При цьому, згідно з законом Бернуллі, а по суті згідно з законом збереження енергії, в тих місцях труби де швидкість рідини збільшується, тиск цієї рідини на стінки труби зменшується і навпаки.
Дійсно. Для поперечних перерізів труби 1-1 і 2-2 (мал.176б) можна записати p1 + ρgh1 + ρv12/2 = p2 + ρgh2 + ρv22/2. Оскільки в будь якому поперечному перерізі труби, величина того вагового тиску що діє на її верхню поверхню є нулевою, то для цієї поверхні, закон Бернуллі набуває вигляду p1 + ρv12/2 = p2 + ρv22/2. З факту ж усталеного руху рідини, а отже і факту того, що v2>v1, з усією очевидністю випливає, що р2 < р1.
Таким чином: при усталеному русі ідеальної рідини, збільшення швидкості її руху призводить до відповідного зменшення її статичного тиску і навпаки, тобто: якщо v↑ то р↓; якщо v↓ то р↑.
Якщо у вашій фізичній лабораторії знайдеться труба змінного поперечного перерізу, яка до того ж буде обладнана відповідними індикаторами тиску, то ви легко переконаєтесь в тому, що у вузькому місці труби тиск водяного потоку на її стінки є найменшою. Ви навіть з’ясуєте, що за достатньо малої площі поперечного перерізу труби і відповідно великої швидкості потоку в ній, тиск на поверхню цієї труби стає меншим атмосферного. А це означає, що коли в такій трубі зробити отвір, то з нього не те що не вдарить фонтан рідини, а скоріш навпаки – атмосферне повітря буде засмоктуватись всередину труби.
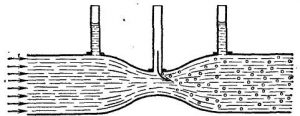
Мал.177. При достатньо великій швидкості водяного потоку, його тиск на поверхню труби може стати меншим атмосферного.
Однак, як бути в тому випадку, коли у вас нема спеціального обладнання? Чи можна в такій ситуації перевірити справедливість закону Бернуллі? Виявляється, можна. І для цього не потрібні надскладні прилади. Достатньо вашої кмітливості та вміння логічно мислити. Скажімо, якщо ви візьмете аркуш папера і покладете його на дві паралельно розташовані книги так, щоб утворилась імпровізована труба (мал.178а), а потім, за допомогою своїх легень змусите повітря рухатись в цій «трубі», то неодмінно з’ясуєте, що у повній відповідності з законом Бернуллі, статичний тиск всередині цієї “труби” зменшиться і зовнішній атмосферний тиск відповідним чином деформує паперову стінку «труби». При цьому, повітряний потік не підніматиме цю стінку, як того вимагає логіка “здорового глузду”, а навпаки – притисне її до поверхні стола.
Або наприклад, якщо над аркушем паперу що зігнувся під дією сили тяжіння, тим же легеневим “насосом” створите повітряний потік, то всупереч дії сили тяжіння цей аркуш почне випрямлятись. І це відбуватиметься тому, що згідно з законом Бернуллі, повітряний потік зменшить тиск над паперовим аркушем.
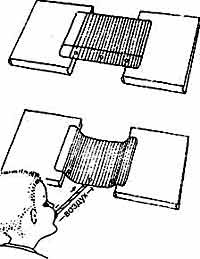


Мал.178. Деякі прості прояви закону Бернуллі.
Або коли наприклад, в потоці вітру вашу парасольку піднімає догори і вивертає навиворіт, то це не що інше як один з проявів закону Бернуллі. Адже обтікаючи округлу поверхню парасольки, повітряний потік створює над нею область зниженого тиску, що і спричиняє вивертання парасольки.
А от ще один простий експеримент. В склянку з водою опускають трубку невеликого діаметру, наприклад трубчасту основу звичайної ручки. Опускають так, щоб вода не доходила до верхнього краю трубки на 2-3см. Створивши над цим краєм повітряний потік, ви побачите що вода піднімається вгору і потрапляючи в повітряний потік відповідним чином розбризкується. Не важко збагнути, що і в цьому досліді, закон Бернуллі відіграє визначальну роль: повітряний потік створює над трубкою область зниженого тиску і тому вода, під дією зовнішнього атмосферного тиску піднімається вгору.
Багато цікавих експериментів можна провести використовуючи в якості джерела повітряного потоку звичайний фен. Наприклад, якщо в створений феном повітряний струмінь помістити тенісну кульку (мал.179), то з’ясується, що в цьому струмені кулька перебуватиме в стані стійкої рівноваги. На перший погляд, така поведінка кульки здається дивною та неприродньою. Однак нічого неприроднього в цій поведінці нема. Просто і в даному випадку ми маємо справу з проявами закону Бернуллі. Дійсно. Згідно з цим законом, повітряний потік сильніше зменшує тиск з тієї сторони кульки, де його інтенсивність більша. Тому, коли кулька відхиляється, наприклад вправо, то більша частина потоку обтікає її зліва. При цьому тиск повітря з цієї сторони зменшується і кулька повертається в попереднє положення.
Мал.179. Повітряний потік зменшує тиск з тієї сторони де його інтенсивність більша.
Звичайно, подібні експерименти не є такими що кількісно доводять справедливість співвідношення p + ρgh + ρv2/2 = const. Однак в даному випадку нас більше цікавить сам факт того, що збільшення швидкості потоку рідини або газу, призводить до зменшення його тиску на відповідну поверхню. Власне, не будемо забувати і про те, що співвідношення p + ρgh + ρv2/2 = const в точності справедливо лише для усталеного потоку ідеальної рідини і лише за умови відсутності теплообміну з навколишнім середовищем. А це означає, що в реальних ситуаціях користуючись формулою p + ρgh + ρv2/2 = const, потрібно робити певні поправки:
1) на наявність в’язкості в реальних рідинах і газах;
2) на факт стискання цих рідин, а особливо газів;
3) на наявність теплообміну з навколишнім середовищем;
4) на характер руху (ламінарний чи турбулентний) рідини або газу.
Та як би там не було, а закон Бернуллі є тією теоретичною основою, на базі якої можна розв’язати велику кількість практично важливих задач. Втім, про практичне застосування закону Бернуллі, ми поговоримо в наступному параграфі.
Задача. Швидкість течії води в широкій частині труби 3м/с. Визначте величину динамічного тиску води в широкій та вузькій частині труби, якщо площа поперечного перерізу вузької частини труби в 4 рази менша за площу її широкої частини. Визначте різницю статичного тиску води в її широкій та вузькій частинах.
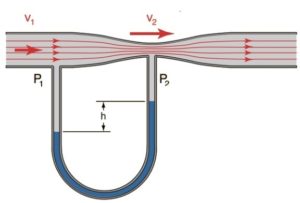
Дано:
v1 = 3м/с
S1/S2 = 4
рдин1 = ? рдин2 =? Δрст = ?
Рішення. Оскільки за визначенням рдин = ρv2/2, то рдин1 = ρv12/2 = 1·103(кг/м3)∙(3м/с)2/2 = 9·103Па.
Оскільки при усталеному русі рідини, маса тієї рідини яка за певний проміжок часу проходить через будь який поперечний переріз труби залишається незмінною (Δm1/t=Δm2/t=), та зважаючи на те, що Δm/t = ρΔV/t = ρSΔℓ/t = ρSv, можна записати ρS1v1 = ρS2v2, звідси v2 = v1S2/S1 = 3(м/с)4 = 12м/с.
Тому рдин2 = ρv22/2 = 1·103(кг/м3)(12м/с)2/2 = 144·103Па.
Оскільки згідно з законом Бернуллі p1 + ρgh1 + ρv12/2 = p2 + ρgh2 + ρv22/2, та враховуючи що для труби величина вагового тиску є мізерно малою (а для верхніх поверхонь труби – завжди нулевою), можна записати p1 + ρv12/2 = p2+ ρv22/2, звідси Δрст = р2–р1 = ρv22/2 – ρv12/2 = 144·103 – 9·103 = 135·103Па.
Відповідь: рдин1 = 9·103Па, рдин2 = 144·103Па, Δрст = 135·103Па.
Контрольні запитання.
- Сформулюйте закон збереження енергії.
- Який зв’язок між законом Бернуллі та законом збереження енергії?
- Який зв’язок між законом Паскаля, законом сполучених посудин, законом Архімеда та законом Бернуллі?
- За яких умов закон Бернуллі виконується у повному кількісному обсязі? Чи виконуються ці умови на практиці?
- Чому ми звикли вважати що в вузькому місці труби, тиск потоку рідини на стінки труби має бути більшим аніж в широкому?
- Поясніть прояви закону Бернуллі в зображених на мал.174 ситуаціях.
- Придумайте, реалізуйте на практиці та поясніть експеримент в якому наочно проявляється дія закону Бернуллі.
Вправа 54.
- Швидкість течії води в широкій частині труби 2м/с. Яка швидкість цієї води у вузькій частині труби, якщо її площа в 3 рази менший за площу широкої частини.
- Швидкість течії води в широкій частині труби 2м/с. Яка швидкість цієї води в вузькій частині труби, якщо її діаметр в 3 рази менший за діаметр широкої частини.
- Площа поперечного перерізу русла річки 150м2, швидкість течії в цьому місці 0,3м/с. Яка швидкість течії у вузькому місці річки площа перерізу якого 45м2?
- Швидкість течії води в широкій частині труби 4м/с. Визначте величину динамічного тиску води в широкій та вузькій частині труби, якщо площа поперечного перерізу вузької частини труби у 3 рази менша за площу її широкої частини. Визначте різницю статичного тиску води в її широкій та вузькій частинах.
- Виходячи з того, що при усталеному русі рідини через будь який поперечний переріз труби, за однакові проміжки часу проходить однакова кількість рідини (Δm1/Δt = Δm2/Δt), доведіть що для будь якого поперечного перерізу труби, добуток площі цього перерізу на швидкість рідини в ньому є величиною постійною: v1S1 = v2S2 = const.
- Підводний човен знаходиться на глибині 100м. З якою швидкістю через отвір в корпусі човна вривається струмінь води? Скільки води проникне в човен за одну годину, якщо діаметр отвору 6см2? Тиск повітря в човні дорівнює атмосферному.
- У водопровідній трубі утворився отвір перерізом 4мм2 з якого б’є струмінь води висотою 80см. З якою швидкістю вода витікає з труби?
.
§55. Практичне застосування закону Бернуллі. Піднімальна сила крила. Ефект Магнуса.
Закон Бернуллі та зокрема той факт, що збільшення швидкості потоку рідини або газу супроводжується зменшенням їх статичного тиску, широко застосовується в сучасній техніці. Розглянемо деякі з цих застосувань.
Загально відомим прикладом практичного застосування закону Бернуллі є різноманітні пульвізатори-розпилювачі. В цих приладах (мал.180а) повітряний потік створює над зануреною в рідину трубкою певне зниження тиску. В такій ситуації, під дією зовнішнього атмосферного тиску, рідина по трубці піднімається вгору і потрапляючи у повітряний потік розпилюється. В побуті і промисловості пульвізатори-розпилювачі застосовуються для нанесення фарб. В сільському господарстві – для розпилювання хімікатів. В медицині – для розпилювання лікарських речовин.
а)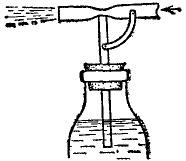 б)
б)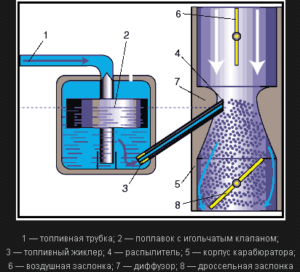
Мал.180. Схема принципового устрою пульвізатора-розпилювача (а) та карбюратора (б).
По суті певною різновидністю пульвізатора-розпилювача є такий важливий елемент автомобільного двигуна як карбюратор. Карбюратор – це прилад, який готує бензиново-повітряну суміш для карбюраторних (бензинових) двигунів внутрішнього згорання. Основним технологічним елементом карбюратора (мал.180б) є коротка трубка, звужена частина якої з’єднана з бензиновим резервуаром. Принцип дії карбюратора полягає в наступному. Коли поршень двигуна рухаючись вниз створює в циліндрі відповідне розрідження і атмосферне повітря починає втягуватись в циліндр, то проходячи через звужену частину трубки карбюратора, воно створює в ній область зниженого тиску. При цьому бензин засмоктується повітряним потоком і розпилюється в ньому. Ця повітряно-бензинова суміш потрапляє в циліндр двигуна і в процесі подальшого згорання, виконує корисну роботу.
Важливим прикладом практичного застосування закону Бернуллі є струменеві насоси. Такий насос (мал.181) представляє собою пустотілий корпус, через який проходить система двох трубок – вхідної та вихідної. У звуженій частині вхідної трубки, водяний потік розганяється до такої швидкості при якій його статичний тиск значно менший атмосферного. В такій ситуації, через отвір який з’єднує струменевий насос з сторонньою рідиною, газом, сипучим матеріалом, тощо, ця стороння речовина всмоктується в корпус насоса і разом з водяним потоком виноситься за його межі. Певними різновидностями струменевих насосів є ежектори (від лат. ejecter – викидати) – застосовуються для всмоктування рідин і газів, та інжектори (від лат. injecter – викидати) – застосовуються для нагнітання рідин і газів. Очевидними перевагами струменевих насосів є простота конструкції, відсутність рухомих механічних деталей, надійність, довговічність та простота в обслуговуванні. Недоліком струменевих насосів є відносно низький коефіцієнт корисної дії (до 30%).


Мал.181. Принциповий устрій та загальний вигляд струменевого насосу.
Напевно одним з найвидатніших винаходів людства є літак. Та чи задумувались ви над тим, які сили змушують багатотонну металеву конструкцію прогнозовано літати у повітряному просторі. А між іншим, відповідь на це запитання має безпосереднє відношення до закону Бернуллі.
Головний секрет літака полягає в тому, що його крило має таку форму і таку орієнтацію (мал.182) при яких набігаючий повітряний потік, над крилом рухається швидше аніж під крилом. При цьому, згідно з законом Бернуллі, між верхньою і нижньою поверхнями крила, виникає певний перепад тиску Δр, який і створює відповідну піднімальну силу Fпс = ΔрS, де S – площа нижньої поверхні крила.
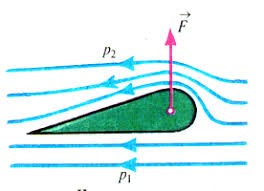
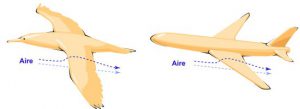
Мал.182. Профіль крила має таку форму при якій набігаючий повітряний потік над крилом рухається швидше аніж під ним (v2>v1 і тому p2<p1).
Звичайно, вище наведене пояснення є гранично спрощеним. Адже в реальності ми маємо справу з турбулентним (вихровим) рухом повітря при аналізі якого потрібно враховувати складні вихрові процеси. Але якби там не було, а кінцевим підсумком цих процесів є факт того, що швидкість повітряного потоку над крилом (v2) є більшою за його швидкість під крилом (v2 > v1). При цьому, згідно з законом Бернуллі, статичний тиск повітря на нижню поверхню крила (p1) дещо перевищує відповідний тиск на його верхню поверхню (p1 > p2). Результатом такого перепаду тисків і є відповідно піднімальна сила крила: Fпс = ΔрS.
Потрібно зауважити, що окрім тієї піднімальної сили поява якої обумовлена різницею статичних тисків над крилом та під ним і яку називають статичною, існує ще одна різновидність піднімальної сили, поява якої обумовлена дією на крило певного динамічного тиску і яка називається динамічною. Дійсно. Якщо крило під певним кутом (цей кут називають кутом атаки, позначається α) розташоване відносно набігаючого повітряного потоку (мал. 183), то на його нижню поверхню діє певний динамічний тиск (р = ρv2/2), вертикальна складова якого і створює відповідну піднімальну силу: Fпс = ρv2Ssinα/2.

Мал.183. Якщо крило розташоване до напрямку набігаючого потоку під кутом α, то на нього діє відповідний динамічний тиск, який створює відповідну додаткову піднімальну силу.
Зважаючи на вище сказане, можна дати наступне визначення. Піднімальна сила крила – це та вертикальна сила яка діє на крило в набігаючому потоці рідини або газу і яка обумовлена дією двох силових чинників: 1) різницею статичного тиску над крилом та під ним; 2) наявністю динамічного тиску на нижню поверхню крила з боку набігаючого потоку.
Позначається: Fпс
Визначальне рівняння: Fпс= ΔpS + ρv2Ssinα/2
Одиниця вимірювання: [Fпс] = H.
Відразу ж зауважимо, що вище наведене визначальне рівняння відображає лише загальну фізичну суть піднімальної сили крила. Фактична ж величина цієї сили за різних обставин може визначатись за суттєво уточненими формулами. Тим не менше, формула Fпс= ΔpS + ρv2Ssinα/2 є загально прийнятим визначальним рівнянням піднімальної сили крила. Дослідження показують, що результуюча піднімальна сила крила (Fпс= ΔpS + ρv2Ssinα/2) досягає максимальних та безпечних для польотів величин при кутах атаки близьких до 16°.
Прояви закону Бернуллі можуть бути не лише корисними а й шкідливими. Наприклад, 20 вересня 1911 року стався наступний прикрий випадок. Англійський військовий крейсер «Хаук», рухаючись паралельним курсом наздоганяв величезний пасажирський лайнер «Олімпік» (до речі, «Олімпік» – це брат близнюк сумно відомого «Титаніка»). Порівнявшись з лайнером, крейсер несподівано втратив керованість і змінивши курс протаранив його.

Мал.184. Аварія обумовлена дією закону Бернуллі.
Проведені дослідження показали, що причиною даного інциденту став один з проявів закону Бернуллі. Дійсно. Коли великі кораблі, на відносно невеликій відстані рухаються паралельними курсами, то в проміжку між їх корпусами потік води набуває великої швидкості. При цьому, згідно з законом Бернуллі статичний тиск цього потоку зменшується. А це означає, що на кожен з кораблів починає діяти певна, обумовлена перепадом тисків сила, яка прагне зблизити ці кораблі. А оскільки крейсер рухався швидше і був значно легшим, то наявний перепад тисків визначально змінив саме його курс, і всупереч намаганням екіпажу перешкодити аварії, спричинив її. На щастя, даний інцидент не призвів до трагічних наслідків. Натомість тепер моряки знають про підступні прояви закону Бернуллі і у відповідних випадках враховують це.
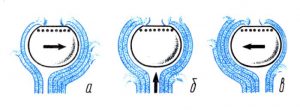
Існує ще одне явище, яке тісно пов’язане з законом Бернуллі. З’ясовуючи суть цього явища розглянемо циліндр, який примусово обертається в набігаючому повітряному потоці (мал.185а). Оскільки в процесі свого обертального руху, циліндр неминуче змушує при поверхневий шар повітря обертатись за ним, то в тих місцях де напрямки поступального і обертального рухів співпадають, швидкість повітря збільшується, а в тих, де ці напрямки протилежні – зменшується. А це означає що даний циліндр обтікають фактично різношвидкісні потоки. При цьому, згідно з законом Бернуллі виникає певний перепад тисків, результатом якого є відповідна, поперечна до потоку сила. Ця сила, по суті має ту ж природу що і піднімальна сила крила, а точніше та її складова, яку ми назвали статичною піднімальною силою.
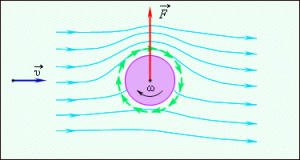

Мал.185. На тіло, що обертається в набігаючому потоці газу або рідини, діє певна поперечна до потоку сила (ефект Магнуса).
Явище, суть якого полягає в тому, що на тіло яке обертається в набігаючому потоці рідини або газу, діє певна поперечна до потоку сила, поява якої обумовлена дією закону Бернуллі, називається ефектом Магнуса. Цей ефект був відкритий та досліджений в 1852 році німецьким фізиком Генріхом Магнусом (1802–1870). Криволінійні траєкторії руху «підкручених» футбольних, волейбольних, тенісних та інших м’ячів, при їх поступально-обертальному русі, є один з проявів ефекту Магнуса.
Екзотичним прикладом застосування ефекту Магнуса є кораблі в яких замість традиційних вітрил застосовують систему обертальних циліндричних башт (мал.186). В потоці вітру на ці башти, у відповідності з законом Бернуллі, діє певна перпендикулярна до напрямку вітрового потоку сила, яка і надає кораблю відповідного поступального руху. Регулюючи швидкість та напрям обертання башт можна регулювати швидкість та напрям руху корабля. Втім, вітрові двигуни мають низький коефіцієнт корисної дії, який великою мірою залежить від примх погоди. Тому відповідні кораблі не отримали широкого застосування.
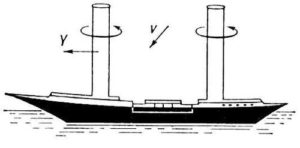
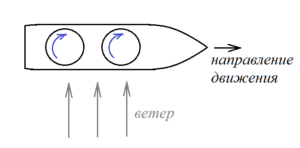
Мал.186. Корабель з обертальними вітрильними баштами, як приклад застосування ефекту Магнуса.
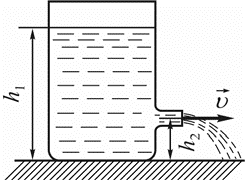
Задача. Бак заввишки 1,5м заповнений до краю водою. На відстані 1м від верхнього краю бака утворився невеликий отвір. На якій відстані від бака падає на підлогу струмінь тієї води що витікає з отвору? Опором повітря знехтувати.
Дано:
h1 = 1,5м
h2 = 0,5м
ℓ =?
Рішення. Для визначення дальності польоту води потрібно визначити швидкість її вильоту з отвору баку. А цю швидкість можна визначити із аналізу закону Бернуллі. Дійсно, згідно з законом Бернуллі, для будь якого поперечного перерізу усталеного потоку рідини має виконуватись співвідношення
p1 + ρgh1 + ρv12/2 = p2 + ρgh2 + ρv22/2. В якості базових поперечний перерізів потоку води обираємо її поверхневий шар та переріз того отвору через який витікає вода. Оскільки як для поверхневого шару води так і для її вихідного отвору статичний тиск дорівнює атмосферному (р1 = ратм, р2 = ратм) та враховуючи, що швидкість потоку води в баку є практично нулевою, а отже ρv12/2 = 0, а також, що для отвору h = h1–h2 =1,0м, можна записати pатм = pатм + ρgh + ρv2/2. Звідси ρgh = ρv2/2, звідси v=√(2gh) = √(2·10·1) = 4,5м/с.
Визначаючи дальність польоту води, запишемо рівняння її руху, тобто формулу яка має вигляд х=х0+v0t+(a/2)t2. А оскільки рух води є криволінійним, то його описують два рівняння:
по горизонталі: ℓ = vt;
по вертикалі: h = h2 + (g/2)t2.
Оскільки в момент падіння вода (t=tпад) h=0, то (g/2)t2 = h2, звідси t=√2h2/g = √2·0,5/10 = √0,1 = 0,33с.
Таким чином ℓ = vt = 4,5(м/с)0,33с = 1,5м.
Відповідь: ℓ = 1,5м.
Контрольні запитання.
- Поясніть загальний устрій та принцип дії пульвізатора-розпилювача (мал.180а).
- Поясніть принцип дії карбюратора (мал.180б).
- Поясніть загальний устрій та принцип дії струменевого насосу (мал.181).
- Поясніть загальний устрій та принцип дії крила літака (мал.182).
- Що є причиною появи статичної складової піднімальної сили крила?
- Що є причиною появи динамічної складової піднімальної сили крила?
- Що називають кутом атаки крила? За якої величини цього кута політ літака є безпечним?
- Яка небезпека може спіткати великі кораблі, які на невеликій відстані рухаються паралельними курсами?
- Поясніть суть ефекту Магнуса.
- Поясніть загальний устрій та принцип дії корабля з обертальними вітрильними баштами (мал.186).
Вправа 55.
- Швидкість води в широкій частині труби 3м/с. Яка швидкість цієї води у вузькій частині труби, якщо її діаметр в 3 рази менший за діаметр широкої частини.
- Доведіть, що швидкість витікання ідеальної рідини з великої посудини через маленький отвір в ній, визначається за формулою v=√(2gh), де h – висота рідини над відповідним отвором.
- В підводній частині корабля на глибині 3м виникла пробоїна площею 20см2. З якою швидкістю через цю пробоїну вривається струмінь води? Скільки води проникне в корабель за одну годину?
- У водопровідній трубі утворився отвір перерізом 3мм2 з якого б’є струмінь води висотою 60см. Скільки води витече з цієї труби за добу?
- Бак заввишки 3м до краю заповнений водою. В його дні утворився маленький отвір. З якою швидкістю вода витікатиме з отвору. Скільки води витече за годину, якщо площа отвору 2мм2
- Одну з двох однакових посудин заповнили ртуттю, а другу – водою. З якої посудини швидше витече рідина, якщо пробиті в дні отвори однакові? Рідини вважати ідеальними.
.
§56. Механічна картина Всесвіту.
З незапам’ятних часів, люди розмірковували над тим, як влаштований навколишній світ (Всесвіт). Створення першої науково подібної систему знань про навколишній світ, нерозривно пов’язано з видатним давньогрецьким філософом-енциклопедистом Арістотелем (384–322 до н.е). Саме Арістотель зібрав, систематизував та критично узагальнив всю сукупність знань античного світу. Результати цих узагальнень він представив у вигляді системи літературно філософських творів, які прийнято називати трактатами. Арістотелівські трактати стосувались не лише тих питань що є предметом вивчення сучасних природничих наук, а й питань загально філософських, морально-етичних, психологічних, релігійних, медичних, літературних, політичних та інших.
Свої погляди на загальний устрій навколишнього світу Арістотель виклав в таких трактатах як «Фізика», «Механіка», «Метереологіка», «Про небо», «Про походження і знищення» та деяких інших. Згідно з Арістотелем, в центрі Всесвіту знаходиться нерухома Земля, навколо якої певним чином обертаються Сонце, Місяць, п’ять відомих на той час планет (Меркурій, Венера, Марс, Юпітер, Сатурн) та небесна зоряна сфера.

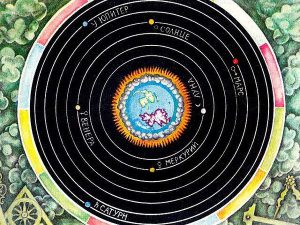
Мал.187. Згідно з Арістотелем, в центрі Всесвіту знаходиться нерухома Земля, навколо якої певним чином обертаються всі інші космічні об’єкти.
Звичайно сьогодні, в епоху телебачення, інтернету та суцільної комп’ютеризації, навіть діти знають, що не Сонце обертається навколо Землі, а Земля обертається навколо Сонця та власної осі. Виходячи з цього, ми схильні вважати, що прадавні уявлення про будову Всесвіту, а точніше Сонячної системи, є примітивними та абсолютно хибними. Подібні твердження не є ані коректними, ані безумовно правильними. Не є бодай тому, що відносність руху в тому й полягає, що різні спостерігачі, спостерігаючи за одними і тими ж об’єктами, можуть бачити суттєво різні рухи, а відповідно по різному і описувати їх. Скажімо, той спостерігач, який знаходиться так би мовити над Сонячною системою («сторонній спостерігач») бачить: в центрі системи знаходиться Сонце, навколо якого на фоні зоряного неба обертаються планети, в тому числі і Земля. Той же спостерігач, який знаходиться на Землі («земний спостерігач») дивлячись на ті ж об’єкти, бачить: навколо відносно нерухомої Землі, обертаються Сонце, Місяць, планети та зірки. Будучи земними спостерігачами, та не відчуваючи руху самої Землі, стародавні вчені цілком обгрунтовано вважали, що Земля знаходиться в центрі Всесвіту і що всі інші космічні об’єкти так чи інакше обертаються навколо цього центру.
Якщо ж говорити про загальний устрій земних об’єктів (об’єктів підмісячного світу), то згідно з Арістотелем вони складаються з двох пар взаємно протилежних якостей: тепле – холодне, сухе – вологе. Ці якості в певних комбінаціях та пропорціях утворюють основні елементи (стихії) підмісячного (земного) світу, зокрема: поєднання сухого і холодного утворюють тверді тіла (земля); поєднання холодного і вологого утворюють рідини (вода); поєднання вологого і теплого утворюють газоподібне (повітря), а поєднання теплого з сухим утворюють те, що прийнято називати плазмою (вогонь). При цьому ті пропорції в яких поєднуються базові якості, визначають різноманіття наявних на Землі твердих, рідких, газоподібних та плазмових речовин.
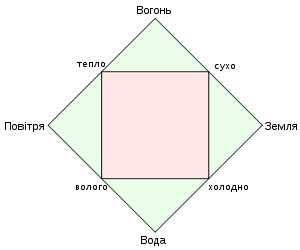
Мал.188. У відповідності з Арістотелем, все різноманіття матеріальних об’єктів неживої природи, є результатом поєднання двох пар взаємно протилежних якостей: тепле – холодне, сухе – вологе.
Арістотель безумовно був видатним вченим. Він не лише зібрав, систематизував та творчо опрацював величезну кількість знань, а й запровадив в наукову практику інструмент, який дозволяв отримувати ці знання. Сьогодні цей інструмент називають дедуктивним методом досліджень. Дедуктивний метод досліджень – це такий метод отримання теоретичних знань, при якому на базі певних припущень та на основі логічно очевидних міркувань, робляться певні узагальнюючі висновки. Класичним прикладом успішного застосування дедуктивного методу є та геометрія, основи якої заклав давньогрецький математик Евклід (325–270 до н.е). Евклід на базі невеликої кількості очевидно правильних тверджень (аксіом) та дедуктивного методу досліджень, створив цілісну систему знань яка пояснювала широке різноманіття властивостей геометричних фігур.
Сам по собі дедуктивний метод отримання теоретичних знань, був видатним відкриттям. Але він мав і має один недолік: зроблені на основі цього методу висновки, будуть правильними лише в тому випадку, якщо базові припущення є правильними. А ось тут-то і була «ахілесова п’ята» в системі знань Арістотеля. Скажімо, виходячи з того, що все різноманіття об’єктів неживої природи, це результат поєднання певних якостей (тепла, холоду, сухості та вологості), логічно передбачити, що змішуючи ці якості в певних пропорціях можна отримати будь який матеріал, в тому числі дорогоцінні метали, коштовне каміння, еліксир молодості, філософський камінь, тощо.
Власне те, що прийнято називати алхімією і що представляє собою певне поєднання наукових та антинаукових практик (хімії, фізики, металургії, астрології, містицизму, спіритизму, тощо), є прямим наслідком ідеї про те, що будь яку матеріальну субстанцію можна отримати шляхом механічного змішування певних базових елементів. Алхіміки вважали, що варто вдало підібрати базові матеріали, в потрібних пропорціях їх змішати, прочитати магічне заклинання і, о диво: свинець, пісок чи що завгодно, перетворюються на золото. Протягом багатьох століть, вони придумували все нові і нові рецепти, випробовували все нові і нові співвідношення, шептали, стогнали та викрикували все нові і нові заклинання. Однак, диво не відбулося. Вони працювали не покладаючи рук. Сподівались… Вірили… Чекали… Вони відчували, ось-ось…, вже зовсім поряд…, вже майже те що треба… Але диво не відбувалось. І не могло відбутися. Адже базові твердження алхімії були хибними.
Протягом вісімнадцяти століть арістотелівський підхід до вирішення наукових проблем був панівним на теренах всього цивілізованого світу. А невтішним результатом цього панування є факт того, що за цей шалено великий історичний період, тогочасною наукою не було створено жодної достовірної теорії і не було зроблено жодного більш менш суттєвого наукового відкриття.
Не відомо скільки б ще тривав цей інтелектуальний застій, якби не видатний італійський вчений Галілео Галілей (1564–1642). Галілей першим зрозумів, що арістотелівський шлях розвитку науки та його метод здобуття наукових знань є хибним. Він зрозумів, що в науці критерієм істини має бути не суб’єктивна логіка наших думок, а об’єктивні експериментальні докази.
Геніальність Галілея полягала не лише в тому, що він першим почав експериментально перевіряти сумнівні теорії, а й в тому, що саме він запропонував та почав застосовувати на практиці такий метод дослідження Природи, який прийнято називати фізичним методом досліджень. Фізичний метод досліджень – це такий метод отримання достовірних знань, при якому вибір правильних теорій здійснюється на основі експериментальної перевірки тих передбачень, які випливають з цих теорій. Це означає, що для перевірки правильності тієї чи іншої теорії (а точніше гіпотези), необхідно на основі цієї теорії та дедуктивного методу досліджень, зробити логічно обгрунтовані передбачення і перевірити їх на практиці. При цьому, якщо передбачення справджуються, значить теорія правильна, а якщо не справджуються – не правильна.
Сьогодні кожен вчений знає, якщо результати експериментів не співпадають з передбаченнями теорії, значить теорія хибна. При цьому немає значення, хто автор теорії. Наскільки він відомий, розумний чи авторитетний. Немає значення, подобається нам теорія, чи не подобається, розуміємо її, чи не розуміємо. Якщо результати експериментів не співпадають з передбаченнями теорії, значить теорія не правильна. От і все.
Звичайно, експерименти мають бути достовірними і такими, що враховують всі суттєві обставини. Адже якщо наприклад, на основі факту того, що важкий камінь падає швидше за легку пір’їну, ви почнете заперечувати те, що всі тіла падають однаково швидко, то у своїх запереченнях будете спиратись на результати неправильно поставленого експерименту. Неправильного в тому сенсі, що при його проведенні ви не врахували суттєво важливу обставину – гальмуючу дію навколишнього повітря.


Мал.189. Галілей – правильність теорії визначається експериментальною достовірністю її передбачень.
Запровадивши новий підхід до вирішення наукових проблем, Галілей заклав основи сучасної науки. Науки, яка за неповні чотириста років не лише кардинально змінила наші уявлення про навколишній світ, а й саме цивілізоване життя. Ефективність запровадженого Галілеєм методу наукового пізнання навколишнього світу, з усією очевидністю була продемонстрована геніальним англійським фізиком Ісааком Ньютоном (1643–1727). Аналізуючи широкий спектр експериментальних фактів, Ньютон сформулював базові закони сучасної класичної механіки: три закони Ньютона та закон всесвітнього тяжіння. Спираючись на ці закони та сформульований Галілеєм принцип відносності, Ньютон створив першу, дійсно наукову теорію Всесвіту. Тобто таку цілісну систему достовірних знань, яка не лише описувала загальний устрій Всесвіту та Сонячної системи, а й пояснювала, яким чином ця система працює.
Згідно з Ньютоном, наша Сонячна система є мізерним фрагментом безкінечного, вічного, ізотропного та стаціонарного Всесвіту. Це означає, що ньютонівський Всесвіт є безмежним в просторі та вічним в часі. Що в ньому міститься безкінечно велика кількість зірок та зіркових систем. Що ці зірки усереднено рівномірно (ізотропно) розкидані в безмежних просторах Всесвіту. Що ті події, які відбуваються у Всесвіті, не змінюють ані усереднено рівномірного розподілу матерії в ньому, ані параметрів його простору, ані монотонності плину часу.

Мал.190. Ньютон – перша безумовно наукова теорія Сонячної системи та Всесвіту загалом.
З механічної точки зору, ньютонівський Всесвіт нагадував бездоганний годинниковий механізм, об’єкти якого у повній відповідності з законами механіки утворюють дивовижно гармонійну та саморегульовану систему. В цьому механізмі не було місця для гіпотетичних сфер, напівсфер, важелів, канатів, тощо. Він не потребував ремінних, зубчатих чи будь яких інших механічних передач. Його основними дійовими особами та виконавцями були закони механіки, сили гравітаційної взаємодії та сили інерції. При цьому, гравітаційні взаємодії не потребували будь яких посередників. Адже у відповідності з поглядами тогочасної науки, ці взаємодії здійснювались безпосередньо через пустоту.
Створена Ньютоном система світу була дивовижно гармонійною, точною та передбачуваною. Вона не лише з математичною точністю описувала поведінку всіх відомих космічних об’єктів, а й дозволяла робити нові відкриття. Наприклад, існування планети Нептун було спочатку теоретично передбаченим, а лише потім експериментально підтвердженим. При цьому відповідна планета виявилась саме в тому місці Сонячної системи на яку вказувала теорія Ньютона.
Звичайно, ньютонівська теорія Всесвіту не була такою що відповідала на всі наявні запитання. Зокрема, вона не пояснювала яким чином та за рахунок чого Сонце і зірки постійно випромінюють величезну кількість енергії. Не пояснювала відомі магнітні та електричні явища. Не пояснювала різноманіття хімічних та механічних властивостей речовин. Не пояснювала як виник Всесвіт і чому він саме такий.
І це закономірно. Адже реальний Всесвіт набагато складніший та багатогранніший за ту механістичну картину яка була «намальована» великим Ньютоном понад три століття тому. Достатньо сказати, що в ньютонівській теорії Всесвіту поведінка та властивості всього різноманіття матеріальних об’єктів Природи, по суті описуються лише однією фундаментальною взаємодією – гравітаційно-інерційною. Насправді ж ці властивості та ця поведінка визначаються чотирма фундаментальними взаємодіями – гравітаційно-інерційною, електромагнітною, сильною ядерною та слабкою ядерною.
Зважаючи на вище сказане, не будемо забувати, що та система знань яку прийнято називати ньютонівською механікою, була лише першим вагомим кроком сучасної науки на шляху пізнання навколишнього світу. Про наступні ж кроки науки на цьому складному, тернистому та дивовижно цікавому шляху, ви дізнаєтесь в процесі подальшого вивчення фізики – науки про Природу.
.