Рідини та їх властивості. Тверді тіла та їх властивості.


Тема 2.3 Рідини та їх властивості.
§17. Поверхневий натяг рідини.
§18. Явища на межі рідина – тверде тіло. Капілярні явища.
§19. Гідросфера Землі.
Тема 2.4. Тверді тіла та їх властивості.
§20. Кристалічні тіла та їх властивості.
§21. Види кристалічних структур.
§22. Аморфні тіла та їх властивості.
§23. Фази речовини. Фазові переходи.
§24. Фазові перетворення, як один з проявів закону
переходу кількісних змін в якісні.
§25. Рідкі кристали.
§26. Полімери та їх властивості.
Тема 2.3 Рідини та їх властивості.
Рідинами – називають такі речовинні об’єкти, які мають певний сталий об’єм, але не мають певної сталої форми і в яких середня потенціальна енергія молекул, мінімально більша за їх середню кінетичну енергію, тобто: V=const; Ф≠const; Еп ≥ Ек.
Факт того, що в рідинах потенціальна енергія молекул мінімально більша за їх кінетичну енергію (Еп ≥ Ек), безумовно вказує на те, що пояснюючи фізичні властивості тієї чи іншої рідини, потрібно враховувати величину потенціальної енергії її молекул. А як відомо, теоретично визначати цю величину ми не вміємо (Еп=?). По суті це означає, що стрункої теорії рідин, подібної до теорії газів, не існує. Це звичайно не означає, що сучасна наука не може пояснити властивості тієї чи іншої конкретної рідини. Мова йде лише про те, що фізичні властивості різних рідин є суттєво різними і що різноманіття цих властивостей не можливо описати простою теоретичною схемою, подібною до тієї яка представлена на мал.33.
Про загальні механічні властивості рідин та про ті закони що описують ці властивості, ми говорили в процесі вивчення теми «механіка рідин та газів». Тому наразі коротко зупинимся лише на деяких загально фізичних особливостях рідин та пояснимо їх. Пояснимо виходячи з того, що всі речовини складаються з молекул, які рухаються та взаємодіють між собою.
§17. Поверхневий натяг рідини.
Напевно, ви звертали увагу на те, що поверхневий шар рідини має певні пружні властивості, тобто веде себе так, ніби ця рідина вкрита надтонкою пружною плівкою. Якщо ні, то уважно придивіться до процесу формування краплі води (мал.52). Не важко бачити, що ця вода знаходиться у своєрідному еластичному мішечку, який до певної межі збільшується в розмірах, а потім відривається і у вигляді круглої краплі падає вниз. Ясно, що насправді, ніякого окремого від води мішечка не існує. Адже в краплі води, нічого окрім молекул води нема. Просто сам поверхневий шар рідини має певні властивості пружної плівки.


Мал.52. Процес формування краплі є наочним прикладом того, що поверхневий шар рідини має певні пружні властивості.
Чому ж поверхневий шар рідини веде себе як пружна плівка? Відповідаючи на це не просте запитання, розглянемо дві довільно вибрані молекули (мал.53), одна з яких (1) знаходиться всередині рідини, а інша (2) – в її поверхневому шарі. Не важко бачити, що молекула 1, з усіх сторін щільно і практично рівномірно оточена сусідніми молекулами, кожна з яких притягує її. Ясно, що в такій ситуації, та усереднена результуюча сила з якою сусідні молекули діють на молекулу 1, дорівнює нулю.
Молекула ж поверхневого шару рідини (молекула 2), оточена близькими сусідами лише з одного боку – з боку рідини. І не важко збагнути, що та результуюча сила з якою сусідні молекули притягують молекулу поверхневого шару не дорівнює нулю і є такою що направлена всередину рідини. А це означає, що на кожну молекулу поверхневого шару рідини діє певна результуюча сила, яка намагається втягнути цю молекулу всередину рідини. Цю силу називають силою поверхневого тиску (Fp).
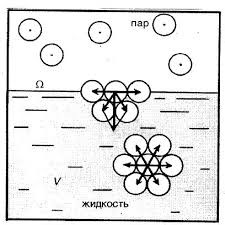
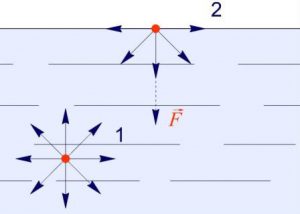
Мал.53. На кожну молекулу поверхневого шару рідини діє певна результуюча сила, яка прагне втягнути цю молекулу всередину рідини.
Прямим наслідком дії сил поверхневого тиску є факт того, що за відсутності зовнішніх силових впливів, будь яка рідина прагне набути форму кулі. І це закономірно. Адже якщо кожна молекула поверхневого шару рідини прагне потрапити всередину рідини, то це означає що рідина прагне набути такої форми, при якій кількість молекул на її поверхні є мінімально можливою. А такою формою є куля. Бо саме куля є тією геометричною фігурою, яка при мінімальній площі поверхні (а отже, при мінімальній кількості молекул на цій поверхні) має максимально можливий об’єм.
Інша справа, що ті сили які прагнуть надати рідині кулястої форми є досить слабкими. Тому, за наявності суттєвих зовнішніх силових впливів, зокрема сили тяжіння, рідина приймає форму тієї посудини в якій вона знаходиться. Однак, навіть в цьому випадку, вільна поверхня рідини прагне бути рівною, тобто такою на якій міститься мінімально можлива кількість молекул.
Сила поверхневого тиску має ту особливість, що її практично не можливо виміряти. Не можливо головним чином тому, що намагаючись максимально ущільнити молекули поверхневого шару рідини, сила поверхневого тиску створює такі умови, при яких між цими молекулами виникають відповідні сили відштовхування. А це означає, що на той прилад за допомогою якого ви будете вимірювати силу поверхневого тиску, неминуче діятимуть дві рівні за величиною і протилежно направлені сили, результуюча яких дорівнює нулю.
Практично важливим наслідком силової дії поверхневого тиску є так званий поверхневий натяг. Поверхневий натяг рідини – це явище, суть якого полягає в тому, що поверхневий шар рідини веде себе як пружна плівка яка прагне до максимального скорочення. Міцнісні властивості поверхневого шару рідини характеризує сила поверхневого натягу. Фізичну суть та механізм дії цієї сили надзвичайно важко пояснити шляхом певних механічних аналогій. Тому просто зауважимо, що сила поверхневого натягу є результуючою всієї сукупності тих міжмолекулярних взаємодій що відбуваються в приповерхневому шарі рідини і яка протидіє збільшенню площі цього приповерхневого шару. Сила поверхневого натягу вигідно відрізняється від сили поверхневого тиску тим, що її можна безпосередньо виміряти.
Сила поверхневого натягу – це направлена вздовж поверхні рідини сила, яка є результуючою всієї сукупності тих міжмолекулярних взаємодій, що відбуваються в приповерхневому шарі рідини і яка протидіє збільшенню площі цього приповерхневого шару.
Позначається: Fпн
Визначальне рівняння: Fпн=σℓ, де σ – коефіцієнт поверхневого натягу; ℓ – довжина тієї лінії поверхні, на якій діє відповідна сила поверхневого натягу.
Одиниця вимірювання: [Fпн] = Н.
Коефіцієнт поверхневого натягу рідини – це фізична величина, яка є силовою характеристикою поверхневого шару рідини і яка дорівнює відношенню сили поверхневого натягу, до довжини тієї лінії поверхні на якій ця сила діє.
Позначається: σ
Визначальне рівняння: σ= Fпн/ℓ
Одиниця вимірювання: [σ] = Н/м.
Величина коефіцієнту поверхневого натягу рідини визначається експериментально і записується у відповідну таблицю.
Таблиця. Коефіцієнт поверхневого натягу деяких рідин (для t = 20ºC)
| Речовина | σ (Н/м) | Речовина | σ (Н/м) |
| Ацетон | 0,024 | Мильний розчин | 0,040 |
| Бензин | 0,029 | Ртуть | 0,465 |
| Вода | 0,073 | Спирт етиловий | 0,023 |
| Гліцерин | 0,059 | Ефір етиловий | 0,017 |
| Гас | 0,024 |
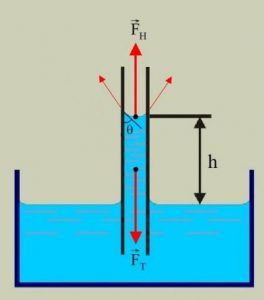
Потрібно зауважити, що пружні властивості поверхневого шару рідини, суттєво відрізняються від властивостей звичайної пружної плівки. З’ясовуючи суть цих відмінностей, звернемось до наступного експерименту (мал.54). П-подібну дротяну рамку опустимо в мильний розчин і за допомогою чутливого динамометра будемо повільна піднімати її (або повільно опускати посудину з рідиною). Спостереження показують, що допоки рамка знаходиться в рідині показання динамометра чисельно дорівнюють вазі рамки (звичайно з врахуванням діючої на неї сили Архімеда). Коли ж горизонтальна частина рамки стикається з поверхневим шаром рідини і починає виходити за його межі, показання динамометра суттєво збільшуються. Збільшуються на величину тієї сили поверхневого натягу, що діє на горизонтальну частину рамки. І от що цікаво, в процесі подальшого піднімання рамки, збільшення площі тієї плівки що тягнеться за нею, не супроводжується збільшенням діючої на рамку сили поверхневого натягу.
Такий стан речей здається дивним. Адже згідно з законом Гука, в процесі пружної деформації плівки, величина деформуючої сили (а відповідно і сили пружності) має збільшуватись. Однак в тому то й справа, що пружні властивості поверхневого шару рідини і пружні властивості звичайної плівки, це абсолютно різні властивості, які мають абсолютно різне походження. Адже коли розтягується гумова плівка, то її пружні властивості є результатом того, що відстані між молекулами гуми збільшуються і відповідно збільшуються сили міжмолекулярної взаємодії. Коли ж розтягується поверхневий шар рідини, то відстані між його молекулами залишаються незмінними, а змінюється лише кількість тих молекул що утворюють відповідний поверхневий шар. При цьому та сила під дією якої збільшується площа поверхневого шару рідини, залишається практично незмінною.
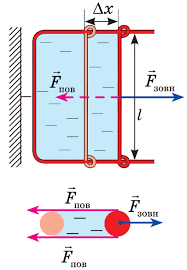
Мал.54. В процесі «розтягування» поверхневого шару рідини, величина деформуючої сили залишається незмінною.
Крім всього іншого, представлений на мал.54 експеримент, відображає суть одного з найбільш ефективних методів визначення коефіцієнту поверхневого натягу – методу відриву тіла від поверхні рідини. А ця суть полягає в наступному. Експериментально вимірявши величину тієї додаткової сили що йде на відрив тіла від поверхні рідини (сили поверхневого натягу Fпн) та довжину тієї лінії на якій ця сила діє (ℓ), визначають відповідне значення коефіцієнту поверхневого натягу (σ). При цьому, потрібно зважити на факт того, що та плівка яка тягнеться за рамкою вимірювального приладу, має дві вільні поверхні. Тому, в умовах даного експерименту σ = Fпн/2ℓ.
В процесі вивчення фізики, ми неодноразово наголошували на тому, що одне і те ж явище може мати декілька наукових пояснень. І в цьому сенсі, явище поверхневого натягу не є винятком. Адже це явище можна пояснити не лише на основі аналізу тих сил що діють на молекули речовини в тій чи іншій ситуації (силовий метод досліджень), а й на основі аналізу енергетичних параметрів цих молекул (енергетичний метод досліджень).
Дійсно. Для того щоб молекула внутрішнього шару рідини (молекула 1, мал.53) перемістилась в поверхневий шар цієї рідини, потрібні певні енергетичні затрати. А це означає, що в поверхневому шарі рідини неминуче зосереджена певна кількість надлишкової енергії. В одному ж з базових законів Природи, який прийнято називати принципом мінімуму стверджується: будь яка система, прагне прийти до такого стану, при якому кількість зосередженої в ній надлишкової енергії буде мінімально можливою. В нашій ситуації, очевидним способом зменшення кількості тієї надлишкової енергії що міститься в поверхневому шарі рідини є граничне зменшення площі цього шару.
Таким чином, у відповідності з базовими законами Природи, поверхневий шар рідини, маючи певну кількість надлишкової енергії, завжди прагне до того щоб гранично зменшити величину цієї надлишкової енергії. Реалізацією цих енергетичних прагнень, є факт того, що поверхневий шар рідини веде себе як пружна плівка яка прагне до максимального скорочення.
На завершення додамо, що застосовуючи енергетичний метод пояснення того явища яке називають поверхневим натягом, замість тієї величини яку прийнято називати силою поверхневого натягу, застосовують величину яку називають енергією поверхневого натягу або поверхневою енергією.
Енергія поверхневого натягу (поверхнева енергія) – це та надлишкова енергія, яку має поверхневий шар рідини (порівняно з її внутрішніми шарами) і яка завжди протидіє збільшенню площі відповідного поверхневого шару.
Позначається: Епн
Визначальне рівняння: Епн= σS, де σ – коефіцієнт поверхневого натягу рідини; S – площа відповідного поверхневого шару рідини.
Одиниця вимірювання: [Епн] = Дж.
Ясно, що при енергетичному методі пояснення поверхневого натягу, та величина яку називають коефіцієнтом поверхневого натягу, набуває нового фізичного змісту.
Коефіцієнт поверхневого натягу – це фізична величина, яка є енергетичною характеристикою поверхневого шару рідини і яка дорівнює відношенню тієї енергії (∆Епн) що йде на збільшення площі вільної поверхні рідини, до величини цієї площі (∆S).
Позначається: σ
Визначальне рівняння: σ = ∆Епн/∆S
Одиниця вимірювання: [σ] = Дж/м2.
І потрібно зауважити, що жодних протиріч між визначальними рівняннями σ=Fпн/ℓ та σ=∆Епн/∆S нема. Дійсно. В умовах представленого на мал.54 експерименту ∆Епн=Fпн∆x; ∆S=ℓ∆x. Тому: σ = ∆E/∆S = Fпн∆х/ℓ∆х = Fпн/ℓ = σ.
Поверхневий натяг рідини суттєво залежить від наявності домішок в ній. При цьому, деякі домішки посилюють поверхневий натяг рідини, а деякі – послаблюють його. Наприклад сіль і цукор дещо збільшують поверхневий натяг води, а спирти та ефіри – зменшують цей натяг. Домішки які суттєво послаблюють поверхневий натяг рідини називають поверхнево активними речовинами. Загально відомим прикладом поверхнево активної речовини є мило.
Наочною демонстрацією дії поверхнево активної речовини є наступний простий експеримент. Наберіть в чисту посудину, наприклад тарілку, чистої води. Більш менш рівномірним шаром посипте поверхню цієї води меленим коріандром, перцем, тальком чи чимсь подібним. Змочіть олівець чи власний палець миючим засобом і торкніться цим олівцем (пальцем) поверхні води (мал.55). При цьому ви побачите, як наявні на поверхні частинки швидко розбігаються від місця дотику. Розбігаються тому, що з тієї сторони де з’являються молекули поверхнево активної речовини, діяча на тверді частинки сила поверхневого натягу зменшується і тому ці частинки рухаються в той бік де ця сили залишилась попередньо великою.
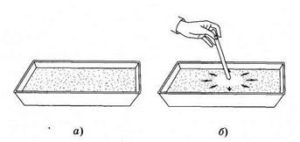
Мал.55. Ілюстрація впливу поверхнево активної речовини на силу поверхневого натягу рідини.
У побуті, поверхнево активні речовини широко застосовуються як миючі засоби (мило, шампуні, пральні порошки). В промисловості, поверхнево активні речовини використовуються при виробництві фарб, клеїв, дезінфікуючих засобів, для очищення поверхонь від пилу жирів та мастил, для покращення умов фарбування, адгезії (прилипання, зчеплення), тощо. В сільському господарстві – для покращення змочуваності поверхонь рослин засобами живлення рослин, боротьби з хворобами та шкідниками. В організмі людини, поверхнево активні речовини приймають участь в процесі дихання та роботі травної системи. Втім, поверхнево активні речовини можуть бути не лише корисними, а й шкідливими. Деякі з них викликають зниження імунітету, алергічні реакції, ураження печінки, нирок, тощо.
Задача 1. Яку роботу треба виконати, щоб видути мильну бульбашку діаметром 12см?
Дано: Рішення:
d = 12см = 0,12м Виходячи з того, що за визначенням А=ΔЕ, де ΔЕ –
А = ? затрати енергії на виконання роботи, та враховуючи,
що в умовах нашої задачі ΔЕ=σΔS, де σ=0,04Н/м=0,04Дж/м2, ΔS – зміна площі поверхні бульбашки в процесі її видування. А оскільки у бульбашки дві поверхні, то ΔS=2·Sсфери =2πd2. Таким чином А= ΔЕ=σΔS=σ2πd2.
Розрахунки: А=2σπd2 = 2·0,04(Дж/м2)3,14(0,12м)2 = 3,6·10–3Дж.
Відповідь: А=3,6·10–3Дж.
Задача 2. Яку масу має крапля води при витіканні з скляної трубки діаметром 3мм, якщо вважати, що діаметр шийки краплі дорівнює діаметру трубки.
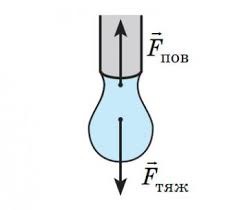
Дано: Рішення:
d = 3мм = 3·10–3м Виконуємо малюнок який відображає
m = ? фізичний зміст задачі. Будемо виходити з
того, що в момент утворення шийки краплі, її маса є максимально можливою, і що діючі на краплю сили (сила тяжіння Fт=mg та сила поверхневого натягу Fпн=σℓ) зрівноважують одна одну: mg=σℓ, де ℓ=πd – довжина тієї лінії поверхні на якій діє сила поверхневого натягу. Таким чином m=σπd/g.
Розрахунки: m=σπd/g = 0,073(Н/м)·3,14·3·10–3м/9,8(м/с2) = 7·10–5кг.
Відповідь: m = 7·10–5кг.
Контрольні запитання.
1. Чим відрізняються ті ситуації в яких знаходяться молекули поверхневого шару рідини та її внутрішніх шарів?
2. Яку силу називають силою поверхневого тиску?
3. Яку силу називають силою поверхневого натягу? Чим сила поверхневого натягу вигідно відрізняється від сили поверхневого тиску?
4. Поясніть суть та причини тих відмінностей які існують між пружними властивостями поверхневого шару рідини та звичайної пружної плівки.
5. Що називають енергією поверхневого натягу?
6. Дайте силове визначення коефіцієнту поверхневого натягу.
7. Дайте енергетичне визначення коефіцієнту поверхневого натягу.
8. Поясніть явище поверхневого натягу на основі енергетичного методу досліджень.
9. Які речовини називають поверхнево активними?
Вправа 17.
1. З якою силою діє мильна плівка на дротину АВ, якщо довжина дротини 3см? Яку роботу потрібно виконати, щоб перемістити дротину на 2см?
2. Яку масу має крапля води що витікає з скляної трубки діаметром 4мм, якщо діаметр шийки краплі дорівнює діаметру трубки?
3. Яке зусилля необхідне для того щоб відірвати тонке кільце масою 4г від поверхні води? Діаметр кільця 8см.
4. Яку роботу потрібно виконати, щоб видути мильну бульбашку діаметром 10см?
5. Однакові маси холодної і гарячої води витікають через однакові крапельниці. При цьому, холодної води витекло 40 крапель, а гарячої – 48 крапель. Порівняйте коефіцієнти поверхневого натягу холодної і гарячої води.
6. Вода з інтервалом 1с, крапля за краплею витікає з бюретки через отвір діаметром 2мм. За який час з бюретки витече 25см3 води.
7. Скільки енергії потрібно витратити на те, щоб краплю ртуті радіусом 1см розділити на дві однакові краплі?
8. Мильна кулька має радіус 2см. Визначити різницю тисків всередині та назовні кульки. Вважати що коефіцієнт поверхневого натягу мильного розчину 0,07Н/м.
§18. Явища на межі рідина – тверде тіло. Капілярні явища.
Дослідження показують, що крапля однієї і тієї ж рідини на одних твердих поверхнях розтікається, а на інших – не розтікається, тобто залишається у вигляді приплюснутої силою тяжіння краплі. Наприклад, крапля води розтікається поверхнею скла (мал.56б) і не розтікається на поверхні парафіну (мал.56а). При цьому говорять, що вода змочує скло і не змочує парафін.
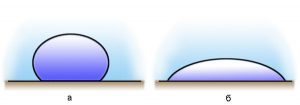

Мал.56. Крапля рідини на одних твердих поверхнях розтікається (змочує поверхню), а на інших – не розтікається (не змочує поверхню).
Пояснюючи факт змочування рідиною твердої поверхні чи не змочування її, можна сказати наступне. Поведінка краплі рідини на тій чи іншій твердій поверхні, визначальним чином залежить від того, які сили більші: сили взаємодії між молекулами самої рідини (fр), чи сили взаємодії між молекулами рідини та молекулами твердого тіла (fт). При цьому ясно, якщо сили взаємодії між молекулами самої рідини більші за сили взаємодії між молекулами рідини та твердого тіла (fр ˃ fт), то рідина не змочує тверду поверхню. А якщо сили взаємодії між молекулами рідини менші за сили їх взаємодії з молекулами твердої поверхні (fр ˂ fт), то рідина відповідну поверхню змочує.
На практиці, факт змочування чи не змочування даної твердої поверхні, визначають наступним чином. На відповідну поверхню кладуть краплю рідини. Змінюючи кут нахилу поверхні, змушують цю краплю переміщуватись. При цьому, якщо в процесі переміщення на поверхні залишається суцільний слід рідини, то це означає що рідина змочує поверхню. Якщо ж крапля рідини скочується поверхнею не залишаючи суцільного сліду, то ця рідина дану поверхню не змочує. Потрібно зауважити, що змочуваність тієї чи іншої поверхні суттєво залежить від того наскільки чистою є ця поверхня. Адже якщо наприклад, скло покрито непомітним шаром бруду чи жиру, то його змочуваність суттєво погіршується.
Зазвичай, ступінь змочуваності тіла рідиною, оцінюють параметром, який називається кутом змочування або краєвим кутом. Кут змочування (краєвий кут) – це величина, яка характеризує ступінь змочуваності твердої поверхні рідиною і яка дорівнює куту між цією твердою поверхнею та дотичною до поверхні рідини проведеною в точці дотику рідини і твердої поверхні та виміряному з боку рідини. Позначається θ. Прийнято вважати, що коли кут змочування менший за 90º (θ < 90º), то відповідна рідина в тій чи іншій мірі змочує тверду поверхню. А якщо цей кут більший за 90º (θ > 90º) – не змочує її.
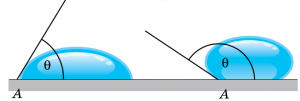
Мал.57. Ступінь змочуваності твердої поверхні рідиною, оцінюють кутом змочування (θ) .
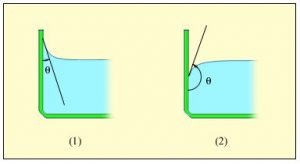
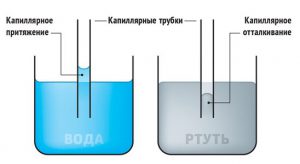
Ступінь змочуваності тіла рідиною, можна оцінити не лише за формою відповідної краплі, а й за параметрами меніску рідини. Меніском (від грец. meniskos – півмісяць) називають те викривлення вільної поверхні рідини, яке відбувається в місці контакту рідини з поверхнею твердого тіла. Наприклад, якщо в скляну посудину налити воду (мал.57в), то можна помітити, що в місці її контакту з поверхнею скла, вода дещо піднята вгору з утворенням відповідного викривлення її поверхні. Факт того, що в місці контакту з скляною поверхнею вода «тягнеться» за склом, є закономірним результатом того, що сили взаємодії між молекулами скла та молекулами води, значно потужніші за сили взаємодії між молекулами самої води.
Якщо ж воду налити в парафінову посудину (або занурити в неї парафінову свічку), то неодмінно з’ясується, що в місці контакту з парафіном, поверхня води закруглюється таким чином, ніби вода відштовхується від парафіну (мал.57г). По суті, ніякого відштовхування води від парафіну не відбувається. Просто молекули води взаємодіють між собою значно сильніше ніж з молекулами парафіну. В такій ситуації, сили їх взаємодії (сили поверхневого натягу), прагнучи надати поверхні води енергетично доцільної круглої форми, створюють ефект відштовхування рідини від тієї поверхні яку вона не змочує.
З тими процесами які відбуваються на межі контакту рідини з твердою поверхнею, тісно пов’язані так звані капілярні явища. Напевно ви добре знаєте про те, що в системі сполучених посудин, рівень наявної в ній однорідної рідини є однаковим (мал.58а). Однак, можливо ви не знаєте, що цей закон (його називають законом сполучених посудин) виконується не завжди. В цьому не важко переконатись за допомогою простого приладу, який представляє собою систему сполучених скляних трубок різних та достатньо малих діаметрів (мал.58б). Наливши в цю систему певну кількість води, ви неодмінно з’ясуєте, що рівень рідини в цих сполучених посудинах є суттєво різним.
а)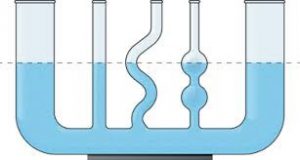 б)
б)
Мал.58. В сполучених посудинах, рівень налитої в них однорідної рідини може бути різним.
Тепер, коли ви знаєте, що вода змочує скло і що це відбувається завдяки сильному взаємному притягуванню між молекулами води і скла, не важко зрозуміти, чому в вузьких скляних трубках вода піднімається на певну надлишкову висоту. Правильно, скло сильно взаємодіючи з при поверхневою водою, піднімає її на певну додаткову висоту. Власне, скло завжди піднімає певну кількість приповерхневої води. Однак, якщо ця піднята приповерхнева вода знаходиться в посудині відносно великих розмірів, наприклад склянці води, то її кількість здається несуттєво малою. Якщо ж аналогічна кількість піднімається в трубці малого діаметру, то висота цього піднімання стає відповідно великою.
Тонкі трубки, судини, пори, щілини, тощо, прийнято називати капілярами (від лат. capillaris – волосина). Сукупність же тих явищ, які пов’язані з перебуванням та рухом рідин в капілярах, називають капілярними явищами.
З’ясовуючи закономірності поведінки рідини в капілярі, розглянемо ті сили що діють на підняту в капілярній трубці рідину (мал.59). Відразу ж зауважимо, що фактичною причиною піднімання рідини в капілярі є результуюча тих взаємодій, які відбуваються між молекулами рідини і молекулами стінок капіляру. Однак, ця результуюча сила не може підняти рідини більше за ту її кількість, яку спроможні втримати сили поверхневого натягу. Виходячи з цього, прийнято вважати, що тією силою яка утримує підняту в капілярі рідину, є сила поверхневого натягу: Fпн = σℓ, де ℓ – довжина тієї лінії по якій поверхня рідини, взаємодіє з поверхнею капіляру.
Мал.59. Якщо рідина змочує стінки капіляру, то вона піднімається на певну додаткову висоту, а якщо не змочує – то на відповідну висоту опускається.
Таким чином, на підняту в капілярі рідину діють дві сили: сила тяжіння Fт=mg (де m – маса піднятої в капілярі рідини) та сила поверхневого натягу Fпн=σℓ. При цьому, зважаючи на стан механічної рівноваги рідини, можна записати: Fт= Fпн , або mg=σℓ, де ℓ=πd; m=ρV=ρSh=ρπd2h/4.
Звідси: h = 4σ/ρgd.
Висновок. Та висота на яку піднімається рідина в капілярі, прямо пропорційна величині коефіцієнту поверхневого натягу рідини і обернено пропорційна густині рідини та діаметру капіляру.
Не важко збагнути, що знаючи густину рідини (ρ), та вимірявши діаметр капіляру (d) і ту висоту (h) на яку рідина піднімається в капілярі, можна визначити коефіцієнт поверхневого натягу відповідної рідини: σ = ρgdh/4. Порівняно з іншими методами експериментального визначення коефіцієнту поверхневого натягу, капілярний метод має ряд суттєвих переваг. По перше, він не потребує складного та коштовного обладнання, а отже є дешевим та простим. По друге, ті величини які фігурують в формулі σ = ρgdh/4 є такими що легко і достатньо точно вимірюються. По третє, цей метод є статичним, тобто таким в якому аналізується та ситуація при якій рідина знаходиться в стані механічного спокою.
В капілярній трубці, рідина може не лише підніматись, а й навпаки – опускатись. Це відбувається в тому випадку, коли матеріал капілярної трубки не змочується рідиною. Наприклад, якщо скляний капіляр занурювати у ртуть, то рівень ртуті в капілярі виявиться нижчим за її загальний рівень. Або якщо наприклад, капілярна трубка виготовлена з парафіну, то при її зануренні у воду, рівень води в капілярі буде нижчим за її загальний рівень. При цьому можна довести, що та висота на яку опускається рідина в незмочуваному капілярі, також визначається за формулою h = 4σ/ρgd.
Капілярні явища відіграють надзвичайно важливу роль як в живій так і в неживій природі. Скажімо ґрунт представляє собою певну капілярну систему по якій вода та розчинені в ній речовини піднімаються вгору та живлять коріння рослин. В рослинах, капілярна система забезпечує підйом вологи від дрібних корінців до найвіддаленішого листя. Саме в капілярах відбуваються основні процеси, пов’язані з диханням і живленням організмів. Достатньо сказати, що в капілярній системі організму людини налічується понад 160 мільярдів капілярів, загальна довжина яких майже 80 000 кілометрів.
Капілярні явища застосовуються і в побуті. Скажімо, завдяки наявності капілярів рушники, серветки, марлі та промокальні папери, швидко вбирають наявну вологу. Капілярні явища можуть бути не лише корисними, а й шкідливими. Наприклад будівельна цегла представляє собою певну капіляру систему яка активно поглинає вологу. Тому, за наявності контакту цегли з ґрунтовими водами, цей контакт переривають за допомогою гідроізоляційних матеріалів – бітум, руберойд, тощо.
Задача. Ртутний барометр має внутрішній діаметр трубки 3мм. Яку поправку в показання барометра потрібно внести, щоб врахувати капілярне опускання ртуті?
Дано: Рішення:
d = 3мм = 3·10–3м Будемо виходити з того, що трубка діаметром 3мм
Δh = ? є капіляром, що ртуть не змочує скло і тому її рівень
в капілярі буде нижчим за рівень без урахування капілярності на висоту Δh. Величину цієї висоти можна визначити із наступних міркувань. В умовах ртутного барометра, сила зовнішнього атмосферного тиску прагне підняти ртуть на висоту відповідну цьому тиску. І якщо ця висота на величину Δh виявляється меншою за очікувану, то це тільки тому, що відповідному підніманню протидіє сила поверхневого натягу ртуті Fпн=σℓ=σπd. І величина цієї протидії дорівнює вазі тієї маси ртуті, що відповідає висоті Δh, тобто силі F=mg=ρVg=ρSΔhg=ρ(πd2/4)Δhg. Іншими словами σπd= ρ(πd2/4)Δhg, звідси Δh = 4σ/ρgd, де σ=0,47Н/м коефіцієнт поверхневого натягу ртуті, ρ=13,6·103кг/м3 густина ртуті.
Розрахунки: Δh = 4σ/ρgd = 4·0,47/13,6·103·9,8·3·10–3 = 0,0046м = 4,6мм.
Відповідь: Δh = 4,6мм.
Контрольні запитання.
1. Що означає твердження: а) рідина змочує тверду поверхню; б) рідина не змочує тверду поверхню?
2. Як перевіряють на практиці змочує чи не змочує дана рідина ту чи іншу тверду поверхню?
3. Як пояснюється факт того, що крапля води на поверхні скла розтікається, а на поверхні парафіну – не розтікається?
4. Чому вода піднімається в скляному капілярі?
5. Від чого залежить висота піднімання (опускання) рідини в капілярі?
6. Чи залежить висота підняття рідини в капілярі від температури? Чому?
7. Що стверджується в законі сполучених посудин? Чому цей закон в системі сполучених капілярів різного діаметру не виконується?
8. Поясніть суть капілярного методу визначення коефіцієнту поверхневого натягу? Які переваги цього методу над методом відриву краплі?
Вправа 8.
1. В капілярній трубці діаметром 1мм, бензин піднявся на висоту 17мм. Визначити коефіцієнт поверхневого натягу бензину і його кількість в капілярі. Густина бензину 700кг/м3.
2. Яким має бути діаметр капілярної трубки, щоб вода в ній піднялась на 10см?
3. Визначте масу піднятої в капілярі води, якщо діаметр капіляру: а) 1мм; б) 0,5мм; в) 0,1мм.
4. Дві однакові капілярні трубки, діаметром 0,5мм опустили в воду і бензин. На скільки відрізняються висоти рідин в цих капілярах?
5. Водяний манометр має внутрішній діаметр трубки 3мм. Яку поправку в показання манометра потрібно внести, щоб врахувати капілярне піднімання води?
6. Скляний капіляр діаметром 0,1мм опустили в воду при температурі 20ºС. При нагріванні води до 70ºС висота рідини в капілярі зменшилась на 3,2см. Визначте коефіцієнт поверхневого натягу води при 70ºС. Розширенням води і скла при нагріванні знехтувати.
7. Решето діаметром 20см утворюють паралельні та перпендикулярні тонкі нитки, відстані між якими 1мм. Скільки води можна винести в такому решеті?
§19. Гідросфера Землі.
Гідросферою Землі називають всю сукупність тієї твердої, рідкої та газоподібної води, що міститься на Землі. Складовими цієї сукупності є океани, моря, льодовики, річки, озера, болота, сніги, ґрунтові та підземні води, атмосферна волога і навіть та вода що входить до складу живих організмів. Загальна маса гідросфери Землі близька до 1,46·1021кг. Це в 275 разів більше за масу атмосфери Землі і приблизно 0,025% від загальної маси всієї планети. Левова частина гідросфери Землі (приблизно 96,5%) зосереджена в водах Світового океану, складовими якого є океани та моря, а також океанські та морські затоки. Ще приблизно 3,5% гідросфери Землі відносять до вод суходолу, складовими яких є річки, озера, болота, штучні водойми, льодовики, підземні та грунтові води. При цьому, левова частина вод суходолу зосереджена в льодовиках та підземних водах. Відносно незначна частина гідросфери (приблизно 0,001%) постійно зосереджено в атмосфері Землі.
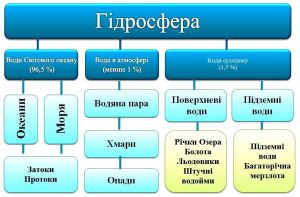
Мал.60. Загальна структура гідросфери Землі.
Роль гідросфери в кругообігу тих подій що відбуваються на Землі важко переоцінити. Ілюструючи значимість цієї ролі, розглянемо лише декілька аспектів того гігантського кругообігу енергії та речовини що постійно відбувається на Землі.
Дослідження показують, що на Землі щорічно випаровується 4,5·105км3 води. Це трохи менше аніж її міститься в такому достатньо великому та глибокому морі як Чорне і в 1750 разів більше аніж її міститься в такому невеликому і неглибокому морі як Азовське.
450000км3 перетвореної на пар води. Щоб уявити енергетичні масштаби цієї величини можна сказати, що для випаровування 450000км3 води знадобиться щонайменше 1·1024Дж енергії. Ви не розумієте скільки це 1·1024Дж енергії? Тоді можливо вам стане зрозумілішим, якщо сказати, що для отримання такої кількості енергії, потрібно спалити 5·1016кг вугілля. Ви не уявляєте скільки це 5·1016кг вугілля? Тоді давайте розв’яжемо простеньку задачу. Відомо, що стандартний вантажний вагон довжиною 13,5м, будучи вщерть заповненим вміщує 60т вугілля. Скільки таких вагонів знадобиться для того щоб перевезти 5·1016кг вугілля. Якої довжини буде відповідний потяг? Порівняйте цю довжину з відстанню до Сонця (L=1,49·1011м).
Розрахунки:
N = m/m0 = 5·1016кг/6·104кг = 83,3·1010 вагонів;
ℓ = Nℓ0 = 83,3·1010·13,3м = 112,5·1011м;
n = ℓ/L = 112,5·1011м/1,49·1011м = 82,2 рази.
Ну що, уявляєте вщерть заповнений вугіллям потяг, довжина якого в понад 82 рази більша за відстань до Сонця, в 30000 разів більша за відстань до Місяця і в 280000 разів більша за довжину периметру Землі виміряного вздовж екватора? Не уявляєте? І тим не менше, щорічно на Землі на випаровування води витрачається така колосальна кількість енергії (Це приблизно 18% від тієї енергії, яка щорічно надходить на Землю з сонячним світлом). Саме за рахунок цієї енергії, утворюються і течуть всі струмки і потужні ріки, йдуть всі дощі, випадають всі сніги, роси, тумани, тощо.
При цьому, ви маєте розуміти, що та енергія яка поглинається в процесі випаровування, в процесі конденсації виділяється. І виділяється її рівно стільки ж, скільки витрачається на процес випаровування. А це означає, що та енергія яка, наприклад, вдень витрачається на випаровування, вночі виділяється в процесі конденсації. Або, наприклад, вода випаровується в тому місці де жарко, а конденсується і відповідно віддає свою енергію в тому місці де холодно.
Додайте до цього той факт, що гідросфера Землі приймає активну участь не лише в процесі випаровування – конденсації, а й в інших теплових процесах, зокрема процесі нагрівання – охолодження. При цьому, та вода яка нагрівається вдень, охолоджується а відповідно і віддає акумульовану енергію вночі. Та вода, яка нагрівається в жарких, екваторіальних областях планети, у вигляді надпотужних океанських течій, рухається в напрямку полярних областей і робить ці області більш теплими. Натомість, холодна вода приполярних областей, рухаючись в зворотньому напрямку, робить жаркий екваторіальний клімат більш прохолодним.
Вище сказане по суті означає, що гідросфера Землі, це надзвичайно потужний та ефективний енерго акумулюючий та енерго регулюючий пристрій, який робить клімат Землі помірно м’яким. І якби цей пристрій не працював, то ми б мали ситуацію при якій денна частина Землі нагрівалась би до майже 120ºС плюс, а нічна – охолоджувалась би до майже 100ºС мінус.
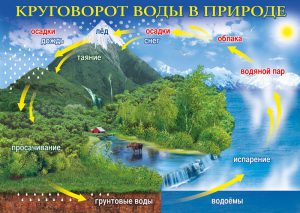
Мал.61. Кругообіг води в природі – одна з основ життя на Землі.
Але гідросфера, це не лише кліматоутворюючий фактор і не лише «кухня» погоди. Гідросфера, це і «колиска» життя на Землі. Адже, якщо на Землі виникло та успішно процвітає життя, то це головним чином завдяки двом визначальним факторам: наявності прийнятного для життя джерела енергії – Сонця, та наявності достатньо великої кількості води. При цьому, вода це не лише необхідна умова існування життя, а і його основна складова частина. Скажімо, тіло людини на 70% складається з води, а тіло огірка є водою на 98%.
Гідросфера Землі перебуває в постійній взаємодії з її атмосферою, літосферою (земною корою) та біосферою. Власне всі ці «сфери» утворюють єдиний цілісний організм. В цьому організмі, атмосфера насичує гідросферу повітряними газами, а гідросфера – насичує атмосферу водяними парами. В цьому організмі, повітряні та водяні маси значною мірою формують ландшафт земної поверхні, а підземні річки та озера є не менш чисельними та повноводними за наземні. В цьому організмі, атмосфера, літосфера та гідросфера у своїй сукупності створюють сприятливі умови для процвітання життя, а те в свою чергу суттєво впливає на ті процеси що відбуваються в повітрі, воді та під землею.
Тема 2.4. Тверді тіла та їх властивості.