Сайт викладача фізики

Розділ 6. Основи теорії відносності.

.

Лекційне заняття №26. Тема: Принцип відносності – базовий закон сучасної науки. З історії теорії відносності. Про відносне та абсолютне.

Лекційне заняття №27. Тема: Про відносність часу, парадокс близунюків та подорож у майбутнє.

Лекційне заняття №28. Тема: Про відносність простору. Про відносність маси та про зв’язок маси з енергією.

Лекційне заняття №29. Тема: Релятивістський закон додавання швидкостей. Парадокси теорії відносності.

Лекційне заняття №30. Тема: Основи загальної теорії відносності. Про геометричну суть тяжіння.

.

Загальні зауваження.

Одним з найвидатніших досягнень науки 20-го століття, стало створення теорії відносності. Теорії, яка кардинально змінила наші уявлення про Всесвіт та визначально вплинула на хід історії людства. Втім, теорія відносності, це не просто видатна наукова теорія, а й неймовірно цікавий та дивовижний світ. Світ, в якому сорокарічний батько може зустрітися зі своїм вісімдесятирічним сином. В якому крива може виявитись коротшою за пряму, атом – важчим за камінь, а секунда – тривалішою за століття. А якщо ви чули, що теорія відносності це надто складно, надто не зрозуміло та надто суперечливо – не вірте. Не вірте, бо це повна маячня. Теорія відносності це цікаво, пізнавально і зовсім не складно.

Якщо ж в теорії відносності і є певні складнощі, то вони не математичні, а сугубо психологічні. Бо теорія відносності якщо і виглядає складною, незрозумілою та парадоксальною, то головним чином тому, що багато з її тверджень здаються такими, що суперечать нашому «здоровому глузду». Зважаючи на ці обставини, буде не зайвим бодай в декількох словах сказати про «здоровий глузд». В словнику філософських термінів зазначено: здоровий глузд – це сукупність поглядів, навичок та форм мислення пересічних людей, яка стихійно формується в процесі їх повсякденного життя та є основою для їх практичної діяльності.

Про роль «здорового глузду» в процесі наукового пізнання Природи, ми говорили нераз. При цьому, неодноразово переконувались, що багато з того, що з точки зору «здорового глузду» здається очевидно правильним, насправді виявляється хибним. Скажімо, нам здається очевидним, що Сонце обертається навколо Землі, а не навпаки. Що Земля є нерухомою, а не такою, що з швидкістю 30 км/с обертається навколо Сонця і з швидкістю 250км/с – навколо центру Галактики. Що у вузькому місті труби, тиск потоку рідини на стінки цієї труби має бути більшим .ніж в широкому. Що маса атомного ядра, повинна дорівнювати загальній масі тих частинок з яких це ядро складається. Що гранітну брилу не можливо перетворити на піщинку аналогічної маси. І тим не менше, в кожному з цих випадків наш «здоровий глузд» дає абсолютно неправильні відповіді.

Ясно, що в процесі еволюційного розвитку науки та під її впливом, еволюційно змінюється і наш «здоровий глузд». Скажімо сьогодні, кожен знає, що Земля кругла, а не плоска, як думали раніше. Що вона обертається навколо Сонця, а не навпаки. Що тіла складаються з атомів і молекул, а не з сухості, вологості, тепла і холоду, як стверджував Аристотель. Що тепло це не особлива рідина, а наше сприйняття енергії хаотичного руху молекул… Однак навіть сьогодні, розв’язуючи ті чи інші наукові проблеми не варто забувати, що підказки «здорового глузду» можуть виявитись хибними. Тому, вивчаючи будь яку наукову теорію, а особливо теорію відносності, ви повинні керуватись не підказками  «здорового глузду», а реальними фактами. При цьому не поспішайте заперечувати ці факти лише на підставі того, що вони здаються безглуздими.

Зважаючи на вище сказане, ласкаво просимо в дивовижний світ теорії відносності.

.

Лекційне заняття №26.

Тема: Принцип відносності – базовий закон сучасної науки. З історії теорії відносності. Про відносне та абсолютне.

В 1630 році, в своїх знаменитих «Діалогах про дві системи світу – Птоломеєву та Коперникову» видатний італійський вчений Галілео Галілей (1564–1642) сформулював закон, який лежить в основі сучасної науки і який прийнято називати принципом відносності або принципом Галілея.

Як відомо, заперечуючи факт обертання Землі навколо Сонця, прибічники середньовічної церкви стверджували: «Якби Земля дійсно рухалась, то ми б фізично відчували цей рух. Відчували б подібно до того, як відчуваємо рух карети, човна чи будь чого іншого». Відповідаючи на подібні аргументи, Галілей стверджував: Дійсно, сидячи в кареті, ми безумовно відчуваємо, рухається вона чи не рухається. Відчуваємо тому, що карета їде не по ідеально рівній дорозі, її колеса не ідеально круглі, тягові зусилля коней постійно змінюються, дорога вкрита дрібними камінчиками, ямками, тріщинками, піщинками, соломинками, тощо. А це означає, що сидячи в кареті, ми постійно відчуваємо певні поштовхи, тобто різкі, короткотривалі зміни швидкості, які власне і вказують на те, що карета рухається. А от якби мене, вас чи кого завгодно посадити в закриту, ізольовану карету, яка б дійсно рухалась рівномірно, тобто без будь яких змін швидкості, то ні ви, ні я, ні хто завгодно, не змогли б визначити, рухається карета чи стоїть.

Ніякими експериментами, які проводяться всередині закритої ізольованої кабіни, не можливо встановити стоїть ця кабіна чи рівномірно рухається. Не можливо тому, що всі фізичні процеси, які відбуваються в кабіні що стоїть (v=0) і в кабіні що рівномірно рухається (v=const), відбуваються абсолютно однаково. (Принцип відносності).

Якщо вам потрібні докази того, що принцип відносності безумовно правильний, безумовно достовірний, то ось один з них. Кожен з нас знаходиться в кабіні, яка називається планета Земля. Ця кабіна з швидкістю 30км/с=108000км/год обертається навколо Сонця. При цьому, жоден з нас не відчуває факту того, що Земля мчить з такою шаленою швидкістю. Швидкістю, яка в 60 разів перевищує швидкість кулі. І даний факт, це не результат певних особливостей людського організму, а реальний факт який стосується всіх подій що відбуваються на Землі. Адже в незалежності від наших відчуттів, всі фізичні процеси на Землі відбуваються так, ніби вона знаходиться в стані механічного спокою.

Мал.165. Земля з швидкістю 30км/с обертається навколо Сонця. Чи відчуваєте ви факт цього надшвидкого руху?

Щоправда, Земля рухається не зовсім рівномірно. Адже в процесі обертання навколо Сонця та своєї осі, напрям руху Землі, а отже і тіл на її поверхні, повільно але неухильно змінюється. А це означає, що факт обертального руху Землі можна експериментально довести, наприклад за допомогою спеціальних маятників. А от якби Земля дійсно рухалась прямолінійно і рівномірно, то з якою б швидкістю вона не рухалась, ви б не змогли встановити, рухається вона чи не рухається.

Іноді думають, що в законі, який називається принципом відносності, стверджується, що все в цьому світі відносне. Це не правда. Не правда по-перше тому, що не все у Всесвіті відносне. Наприклад абсолютно незмінною є швидкість світлових фотонів. Абсолютно незмінною є загальна кількість зосередженого у Всесвіті електричного заряду, мас-енергії, спіну, тощо. По-друге, в законі який називається принципом відносності стверджується те що стверджується, а саме: Ніякими експериментами, які проводяться всередині закритої ізольованої кабіни, не можливо встановити стоїть ця кабіна чи рівномірно рухається. Не можливо тому, що всі фізичні процеси, які відбуваються в кабіні що стоїть (v=0) і в кабіні що рівномірно рухається (v=const), відбуваються абсолютно однаково.

Інша справа, що в сучасній науці принцип відносності формулюють дещо по іншому. І це сучасне формулювання є наступним: У всіх інерціальних системах відліку, тобто таких системах де виконується закон інерції (перший закон Ньютона) всі фізичні процеси відбуваються абсолютно однаково. А це означає, що в тих системах відліку де виконується закон інерції, діють ті ж закони, що й в інших подібних системах.

Нагадаємо, в тому законі  який називається законом інерції і який є складовою частиною першого закону Ньютона, стверджується: причиною зміни швидкості руху тіла (причиною прискореного руху тіла) є дія на це тіло зовнішньої сили. Іншими словами, у відповідності з законом інерції, безпричинних змін швидкості руху тіл не буває, а цією причиною є дія на тіло певної зовнішньої сили. При цьому мається на увазі, що те прискорення яке отримує тіло під дією зовнішньої сили, направлене в ту ж сторону що і сила.

Отже, сучасна наука стоїть на тому, що у всіх інерціальних системах відліку, всі фізичні процеси відбуваються абсолютно однаково. Однак в природі,  існує безліч систем відліку які не є інерціальними. Власне кожна система відліку яка жорстко зв’язана з прискорено рухомим тілом є неінерціальною. Наприклад Місяць з певним доцентровим прискоренням обертається навколо Землі. При цьому зв’язана з Місяцем система відліку є неінерціальною, тобто такою в якій закон інерції очевидно не виконується.

Дійсно, в системі Земля – Місяць, на Місяць діє лише одна зовнішня сила – сила гравітаційного притягування до Землі (F_гр= GMm/ℓ²). А у відповідності з першим законом Ньютона, під дією направленої до центру Землі сили тяжіння, Місяць мав би рухатися в напрямку Землі та неминуче падати на неї. І тим не менше фактом є те, що Місяць не падає на Землю, а обертається навколо неї.

Звісно, це не означає, що в неінерціальних системах відліку діють закони які передбачають безпричинний обертальний рух Місяця навколо Землі, Землі навколо Сонця, Сонця навколо центру Галактики. Це навіть не означає, що в цих системах закон інерції дійсно не виконується. Просто в неінерціальних системах відліку, цей закон набуває дещо іншого вигляду. А цей інший вигляд обумовлений тим, що в неінерціальних системах відліку окрім тих сил які є зовнішніми і які прийнято називати силами взаємодії (сила тяжіння, сила тертя, сили пружності, сила поверхневого натягу, сила Ампера, сила Лоренца, сила Архімеда, тощо), неминуче діє сила інерції (F_і = – mа). Сила, поява якої обумовлена не взаємодією прискорено рухомого тіла з іншими тілами системи, а самим фактом прискореного руху тіла, а фактично – фактом його взаємодії з тим фізичним об’єктом який називається простором Всесвіту.

Таким чином, будь яка неінерціальна система відліку відрізняється від інерціальної лише тим, що в ній, описуючи поведінку того чи іншого фізичного об’єкту, потрібно враховувати ту силу інерції, поява якої обумовлена прискореним рухом самої системи відліку. Наприклад описуючи рух Місяця навколо Землі, тобто той рух який відбувається з певним доцентровим прискоренням (a=v²/ℓ), потрібно враховувати факт того, що цей рух відбувається не лише під дією певної гравітаційної сили (F_гр=GMm/ℓ²), а і під дією їй відповідної сили інерції (F_і=mv²/ℓ). Результатом же дії цих двох рівних за величиною і протилежних за напрямком сил є динамічна рівновага тіла. Рівновага, яка передбачає рух тіла не з постійною швидкістю, а з постійним прискоренням.

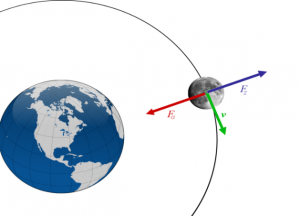
Мал.166. Місяць не падає на Землю не тому, що існують певні системи відліку, а тому, що на нього діють дві рівні за величиною і протилежні за напрямком сили.

Потрібно особливо наголосити на тому, що ті об’єкти які існують у Всесвіті і ті події які відбуваються в ньому, існують та відбуваються не тому, що є певні системи відліку, а тому, що у Всесвіті діють певні об’єктивні закони Природи. А всі ці інерціальні та неінерціальні системи відліку, то лише спосіб описання тих об’єктів та тих подій які існують та відбуваються у Всесвіті. Бо Місяць не падає на Землю не тому, що існують якісь системи відліку, а тому, що на нього окрім тієї сили яка називається силою гравітаційної взаємодії (F=GMm/ℓ²), діє не менш реальна сила інерції (F=mv²/ℓ). А якщо описуючи ті події які відбуваються у Всесвіті, ми зазвичай будемо говорити про інерціальні системи відліку, то це тільки тому, що в цих системах наукове пояснення відповідних подій є найпростішим.

Твердження про те, що в інерціальних та неінерціальних системах відліку діють одні і ті ж закони Природи, це не лише експериментальний факт, а й суть того базового закону сучасної науки який називається загальним принципом відносності. В цьому законі стверджується: в інерціальних та неінерціальних системах відліку всі, фізичні процеси відбуваються абсолютно однаково.

Ви можете запитати: «Ну добре, в рівномірно рухомих і нерухомих системах відліку всі події відбуваються однаково. Це зрозуміло, це факт який можна довести на прикладі того, що ми не відчуваємо руху Землі навколо своєї осі, навколо Сонця та центру Галактики. З інерціальними та неінерціальними системами відліку, менш зрозуміло, але приймемо на віру, що в таких системах, всі події дійсно відбуваються однаково. Але чому вчені стверджують, що саме принцип відносності є тим базовим, тим найголовнішим, найважливішим законом, який лежить в основі всієї сучасної науки? І що це за закон, який навіть певного математичного вираження не має? А якщо не має, то яка користь від такого закону?»

Відповідаючи на ці слушні запитання, можна сказати наступне. Чи задумувались ви над тим, чому вчені з такою впевненістю говорять про ті події, які відбуваються в практично недосяжних частинах Всесвіту? Чому вони впевнені в тому, що ті закони які відкривались на тій піщинці Всесвіту яка називається планета Земля, діють і в інших куточках Всесвіту. А можливо там, в інших галактиках, все відбувається по іншому? Можливо там, діють інші закони, існують інші атоми, інші молекули, інші біологічні структури? Хто був в тих далеких світах та перевіряв це?

Відповіді на ці та їм подібні запитання дає принцип відносності. Адже згідно з цим принципом для з’ясування того, діють чи не діють відкриті на Землі закони природи в інших місцях Всесвіту зовсім не обов’язково вирушати в далеку космічну подорож. Достатньо з’ясувати, виконується чи не виконується у відповідному місці закон інерції. І якщо цей закон виконується, то це автоматично означає, що у відповідному куточку Всесвіту діють ті ж закони що і на Землі.

І от ми вдивляємось в безмежні простори Всесвіту, аналізуємо ті події які відбуваються в ньому і бачимо, що у всіх його найвіддаленіших куточках, всі об’єкти рухаються у повній відповідності з законом інерції. А це означає, що у всіх куточках Всесвіту діють одні і ті ж закони. І що ці закони співпадають з тими що діють на Землі. Не вірити цьому факту, це все рівно ніби заперечувати факт того, що Земля обертається навколо Сонця та своєї осі. Заперечувати лише на тій підставі, що ми не відчуваємо відповідного руху. Звичайно, можна скільки завгодно заперечувати і скільки завгодно не вірити, але від того, факт обертання Землі навколо Сонця та своєї осі не перестане бути фактом, а принцип відносності не перестане бути достовірним.

Мал.167. Бачимо: у Всесвіті безпричинних змін швидкості не буває. Висновок: у всіх куточках Всесвіту діють одні і ті ж закони Природи.

Коли ми говоримо, що сформульований Галілеєм принцип відносності є базовим законом сучасної науки, то під цією наукою перш за все маємо на увазі теорію Ньютона (ньютонівську механіку). Теорію, яка практично бездоганно пояснює ті механічні події що відбуваються як на Землі так і у Всесвіті. А потрібно зауважити, що у своєму еволюційному розвитку, ньютонівська механіка пережила декілька еволюційних трансформацій. Результатом однієї з цих трансформацій є теорія відносності, яка по суті є уточненим варіантом теорії Ньютона. Власне про цю трансформацію ми і поговоримо.

         Наприкінці 19-го століття, в фізиці виникла серйозна кризова ситуація. Суть кризи полягала в тому, що певні передбачення двох базових наукових теорій, теорії Ньютона (ньютонівської механіки) та теорії Максвела (максвелівської електродинаміки), явно суперечили одне одному. А як відомо, наука стоїть на тому, що в ній для спростування будь якого закону, будь якого принципу чи будь якої теорії, достатньо надати лише один експериментальний факт, який суперечить відповідному закону, принципу чи теорії. А якщо на одне і те ж питання, дві наукові теорії дають дві різні відповіді, то це явно означає, що бодай одна з них є не правильною. У всякому разі – неточною. Оскільки ж мова йшла про базові теорії тогочасної науки, то і відповідна кризова ситуація була надзвичайно серйозною.

Дійсно. В теорії Ньютона стверджувалось, що швидкість руху будь якого фізичного об’єкту є відносною, тобто такою яка залежить від вибору системи відліку. Математичним відображенням цього твердження є ньютонівський закон додавання швидкостей. В цьому законі стверджується: якщо в рухомій системі відліку швидкість тіла u’, а ця система з швидкістю v рухається відносно нерухомої системи (мал.168а), то швидкість даного тіла в нерухомій системі відліку u визначається за формулою u = u’+ v. Наприклад якщо у вагоні швидкість якого 50км/год, пасажир з швидкістю 3км/год рухається в напрямку руху вагона, то його швидкість відносно землі 50км/год + 3км/год = 53км/год. Якщо ж пасажир рухається в протилежному напрямку, то ця швидкість становить 50км/год – 3км/год = 47км/год.

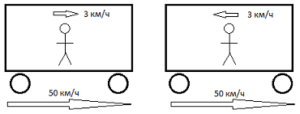
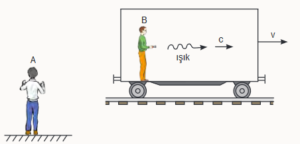
Мал.168.  Згідно з ньютонівським законом додавання швидкостей  u = u‘ + v і тому : c +v > 3·10⁸м/с;  c – v < 3·10⁸м/с.

Із ньютонівського закону додавання швидкостей випливає, що коли з платформи яка рухається з швидкістю v випромінюється світловий фотон швидкість якого с=3·10⁸м/с, то в залежності від напрямку руху платформи (чи спостерігача), швидкість світлового фотона може бути як більшою за 3·10⁸м/с так і меншою за цю величину:

.               c + v > 3·10⁸м/с;

.                c – v < 3·10⁸м/с.

Іншими словами, в теорії Ньютона стверджувалось, що швидкість світлових фотонів  (швидкість світла у вакуумі) є відносною, і що тому вона може бути як більшою так і меншою за 3·10⁸м/с.

В теорії ж Максвела стверджувалося, що швидкість світлових фотонів визначається за формулою  v=1/√(ε₀μ₀),  де  ε₀, μ₀ – постійні величини, значення яких  визначається експериментально і які відповідно дорівнюють   ε₀=8,854·10^–12 Ф/м;  μ₀=12,566·10^–7 Гн/м. А це означає, що згідно з теорією Максвела, швидкість світлових фотонів (а отже і швидкість світла у вакуумі) є абсолютно незмінною і чисельно рівною 3·10⁸ м/с: v =1/√(ε₀μ₀) =3·10⁸ м/с=const=c. Виходячи з цього, по відношенню до представленої на мал.168б ситуації, відповідь теорії Максвела була наступною:

.                   c + v = 3·10⁸м/с

.                    c – v = 3·10⁸м/с.

Таким чином, відповідаючи на одне і те ж запитання, а саме на запитання про швидкість руху світлових фотонів (швидкість світла у вакуумі), теорія Ньютона і теорія Максвела давали кардинально різні відповіді. Теорія Ньютона стверджувала, що швидкість світлових фотонів  є відносною, і що тому c + v > 3·10⁸м/с; c – v < 3·10⁸м/с. Теорія ж Максвела, наполягала на тому, що швидкість світлових фотонів є абсолютною, і що тому: c + v =3·10⁸м/с; c – v =3·10⁸м/с.

Не важко збагнути, що передбачення теорії Максвела (c + v =3·10⁸м/с; c – v = 3·10⁸м/с) явно суперечили «здоровому глузду» і тому переважна більшість вчених були схильними вважати, що певні недоліки потрібно шукати не в ньютонівській механіці, а в максвелівській електродинаміці. Не будемо забувати і проте, що наприкінці 19-го століття теорія Максвела була зовсім молодою науковою теорією. Власне науковою теорією вона стала лише після того, як в 1888 році німецький фізик Генріх Герц експериментально довів, що ті передбачення які випливають з рівнянь Максвела дійсно справджуються.

Ясно, що в такій ситуації, ті вчені які намагались вирішити наявні суперечності між теорією Ньютона та теорією Максвела, шукали певні недоліки в максвелівській електродинаміці. Шукали – і не знаходили. Більше того, експериментальні факти безумовно доводили, що теорія Максвела є правильною і що швидкість світла дійсно абсолютно незмінна. Вирішальний внесок у справу з’ясування цього факту, зробив американський фізик Альберт Майкельсон (1853–1931). Застосовуючи створений ним інтерферометр (про загальний устрій та принцип дії інтерферометра Майкельсона ми говорили на лекційному заняття №12), він безумовно довів, що швидкість світла не залежить а ні від швидкості руху джерела світла, а ні від швидкості руху спостерігача.

Не вдаючись в технічні деталі експериментів Майкельсона, розглянемо лише їх фізичну суть. А ця суть полягає в наступному. Відомо, що Земля обертається навколо Сонця з швидкістю 30 км/с. Припустимо, що в червні Земля рухається назустріч тому світлу яке випромінюється певною далекою зіркою (мал.169). Через пів року, тобто в грудні, наша планета рухатиметься в протилежному напрямку і «тікатиме» від відповідного світла. Ясно, що згідно з ньютонівським законом додавання швидкостей, відносна швидкість тих фотонів, які фіксуються в червні, має становити 300 030 км/с, а тих, які фіксуються у грудні – 299 970 км/с. Однак, найточніші вимірювання показують, що ця швидкість в червні, грудні чи коли завгодно є незмінною і чисельно рівною 300 000км/с=3∙10⁸м/с.

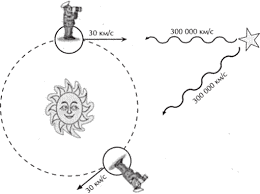
Мал.169. Швидкість світла у вакуумі є абсолютною, тобто такою, яка не залежить а ні від швидкості руху джерела світла, а ні від швидкості руху спостерігача (експериментальний факт).

Таким чином, експериментальні факти безумовно доводили, що передбачення теорії Максвела є достовірними і що швидкість світла у вакуумі  дійсно є абсолютно незмінною. В такому випадку виходило, що неправильною є теорія Ньютона. Однак сумніватись в достовірності віками перевіреної ньютонівської механіки, означало сумніватись в тому, що Земля кругла і що саме вона обертається навколо Сонця а не навпаки.

Вихід з даної кризової ситуації запропонував молодий німецький фізик Альберт Ейнштейн (1879–1955). Ейнштейн не став піддавати сумніву факт того, що швидкість світла у вакуумі є абсолютною. Він цілком слушно вирішив: оскільки факт постійності швидкості світла є надійно експериментально доведеним, то нема підстав сумніватися в його достовірності. З іншого боку, нема жодних підстав сумніватися і в достовірності теорії Ньютона та того принципу який лежить в основі цієї теорії і який називається принципом відносності.

Більше того, Ейнштейн зрозумів – якщо виходити з цих двох базових принципів то можна не лише розв’язати ті протиріччя що існують між ньютонівською механікою та максвелівською електродинамікою, а й об’єднати ці на перший погляд абсолютно різні науки в єдине ціле. Реалізуючи цю ідею Ейнштейн в 1905році створює свою знамениту теорію відносності. Відразу ж зауважимо, що в 1905 році фактично була створена перша частина теорії відносності, яку прийнято називати частковою або спеціальною теорією відносності. В основі цієї теорії лежать два твердження:

1. Принцип відносності: у всіх інерціальних системах відліку, тобто таких системах де виконується закон інерції (перший закон Ньютона), всі фізичні процеси відбуваються абсолютно однаково.
2. Принцип постійності швидкості світла: у всіх інерціальних системах відліку, швидкість світла у вакуумі залишається незмінною і чисельно рівною 3·10⁸м/с. При цьому ця швидкість є гранично великою. (Це означає, що в інерціальних системах відліку жодні фізичні об’єкти і жодні інформаційні сигнали не можуть рухатися з швидкістю більшою за 3·10⁸м/с).

Виходячи з цих базових тверджень, Ейнштейн довів, що наші уявлення про час та простір, про теперішнє, минула та майбутнє, про одночасність та неодночасність подій, про масу та енергію, про закон додавання швидкостей та про багато інших фундаментальних речей, не зовсім відповідають дійсності. Втім, про суть та про кількісні параметри цих невідповідностей, поговоримо на наступних лекційних заняттях. Наразі ж в декількох словах скажемо про те, що з точки зору теорії відносності є відносним, а що абсолютним.

Загально відомо, що величезна кількість тих понять і величин які використовуються у повсякденному житті та науковій практиці, є очевидно відносними. Велика чи мала більярдна куля? Звісно, порівняно з атомом, більярдна куля надзвичайно велика, а порівняно з Землею – надзвичайно мала. Великою чи малою є тривалість в одну секунду? Якщо цю тривалість порівнювати з тривалістю життя  π⁰ мезона (10^–16с) то вона є надзвичайно великою, а порівняно з віком Землі (4,5·10⁹років) – мізерно малою. Великою чи малою є густина заліза (7,8г/см³)? Порівняно з густиною того розрідженого газу який прийнято називати вакуумом (10^–8г/см³), густина заліза є безумовно великою, а порівняно з густиною нейтронної зірки (10¹⁴г/см³) – безмежно малою.

   

Мал.170. Цікаво, чи все в цьому світі відносне?

Теорія відносності значно розширює перелік тих понять які є відносними. Наприклад в ній стверджується, що відносні не лише параметри руху та простору (швидко – повільно, великий – маленький, вверх – вниз, вправо – вліво, тощо), а й такі на перший погляд безвідносні часові поняття як одночасно – неодночасно, раніше – пізніше, минуле – майбутнє.

Дійсно. Виходячи з того, що жоден об’єкт і жоден інформаційний сигнал не можуть рухатись з швидкістю більшою за швидкість світла у вакуумі, давайте розглянемо наступну ситуацію. Припустимо що зірки А і В (мал.171) знаходяться на відстані відповідно 3 і 5 світлових років від Землі. (Світловий рік – це та відстань,  на яку поширюється світло у вакуумі за один рік: 1с.р= 300000км/с×365×24×60×60с= 9,46·10¹²км). Спостерігаючи за цими зірками всі жителі Землі бачать: 1.09.2005року о 10⁰⁰ за київським часом, зірки А і В одночасно вибухнули.  Чи означає даний факт, що відповідні події дійсно відбулися одночасно і дійсно 1.09.2005? Звісно, не означає! Адже фактично зірка А вибухнула за 3 роки, а зірка В за 5 років до тієї дати яку зафіксували жителі Землі.

.                                                                   © А

.                                              3 с.р.                                                    © В

.                                                                  5 с.р.

⊕

Мал.171.   Ми бачимо, що зірки А і В вибухнули сьогодні і одночасно. Чи означає цей факт, що відповідні події дійсно відбулись сьогодні та одночасно?

Вище сказане означає, що поняття «в даний момент часу», «одночасно», «раніше», «пізніше», тощо – є відносними. Звичайно, в умовах повсякденного земного життя, відчути або виміряти цю відносність практично не можливо. Адже відстані навіть між дуже далекими земними об’єктами, світло долає за тисячні і мільйонні долі секунди. Однак, якщо говорити про космічні масштаби, то для них відносність часових понять стає безумовно очевидною. Скажімо сьогодні, за допомогою сучасних телескопів можна спостерігати за об’єктами віддалених від Землі на 10 і більше мільярдів світлових років. А це означає, що сьогодні ми бачимо ці об’єкти такими, якими вони були 10 мільярдів років тому. Тобто тоді, коли ще не було не те що Сонця, а й умовно кажучи його матері.

Тепер, давайте поговоримо про минуле, теперішнє та майбутнє. Історію Всесвіту можна представити як певну послідовність подій, які вже відбулися (минуле), які відбуваються в даний момент часу (теперішнє) і які ще мають відбутися (майбутнє). І нам важко уявити, що минуле, теперішнє та майбутнє, можуть бути відносними. Втім, не будемо поспішати з висновками.

В науковій та повсякденній практиці, минулим називають такі події, про які можна говорити як про факт що вже відбувся і на хід яких не можливо вплинути навіть гіпотетично (навіть в принципі). Майбутнім, називають такі події про які ще рано говорити як про факт що вже відбувся і на хід яких так чи інакше, бодай гіпотетично, можна вплинути. Теперішнім, називають ті події які відбуваються в даний момент часу і які відділяють минуле від майбутнього. Виходячи з такого розуміння минулого, теперішнього та майбутнього, давайте проведемо ряд гіпотетичних експериментів.

Припустимо, що зірка А, відстань до якої 3 світлових роки вибухнула два роки тому. Запитується: для нас – жителів Землі, ця подія (вибух зірки А) минула, теперішня чи майбутня? З одного боку, подія вже відбулася і тому її потрібно вважати минулою. Однак з іншого боку, про те що дана подія вже відбулася, нам нічого не відомо і не може бути відомо в принципі. Ми ще продовжуємо жити так, ніби зірка А «жива і здорова».

Навіть якщо якийсь астроном стверджує, що за його розрахунками, зірка А мала б вибухнути два роки тому, ми в праві і навіть зобов’язані розглядати це твердження лише як гіпотезу вченого, яка потребує експериментального підтвердження. І це підтвердження ми не можемо отримати раніше, ніж через рік (через три роки після вибуху зірки А).  Іншими словами, для нас вибух зірки А ще не відбувся і відбудеться лише через рік. Подія яка вже відбулася, але інформація про яку ще не дійшла до спостерігача, не дійшла тому, що швидкість поширення інформаційних сигналів та наслідків подій є обмеженою, називається неконтрольованим минулим.

Не важко збагнути, що у вище наведеному прикладі, одна і таж, фактично минула подія, в різних місцях Всесвіту може бути минулою, теперішньою чи майбутньою. Скажімо, подія яка відбулася три роки тому, для об’єктів розташованих на відстані меншій за три світлових роки є подією безумовно минулою. Для об’єктів віддалених більш як на три світлових роки, ця ж подія фактично буде майбутньою (неконтрольованим минулим). А для тих об’єктів відстань до яких в даний момент в точності дорівнює трьом світловим рокам, відповідна подія буде теперішньою.

Розглянемо ще один характерний приклад. Припустимо, що космічний корабель знаходиться в околицях зірки А, тобто на відстані трьох світлових років від Землі. Припустимо, що через рік на цьому кораблі має відбутися певний, заздалегідь запланований експеримент. Припустимо, що за час космічної подорожі, на Землі виконали уточнені розрахунки і з’ясували: експеримент проводити не можна, бо експеримент призведе до катастрофи.

Запитується, чи можемо ми попередити астронавтів про небезпеку, тобто бодай якось вплинути на хід подій? Ясно, що такої можливості у нас нема. Намагатись щось зробити вже пізно. Адже найшвидший з можливих сигналів долетить до космічного корабля лише через три роки. Подія ж відбудеться через рік. Подія, яка фактично ще не відбулася, але вплинути на хід якої принципово не можливо (не можливо, в силу обмеженості швидкості поширення інформаційних сигналів), називається неконтрольованим майбутнім. Із вище сказаного ясно, що одна і таж фактично майбутня подія, в різних місцях Всесвіту може бути як майбутньою так і неконтрольовано майбутньою, а по суті минулою подією.

Таким чином, із факту того, що швидкість поширення сигналів та  наслідків подій принципово обмежена (v ≤ 3·10⁸м/с), неминуче випливає, що такі часові поняття як «одночасно», «в даний момент часу», «раніше», «пізніше», «минуле», «теперішнє», «майбутнє» – є відносними. Більше того, в теорії відносності стверджується, що відносними є не лише параметри подій, а й параметри фізичних об’єктів.

Наприклад, ми переконані в тому, що довжина тіла та його маса не залежать від того, рухається це тіло чи не рухається. І тим більше, не залежать від того, хто дивиться на це тіло – рухомий чи нерухомий спостерігач. А от і ні. Виявляється, що наш  «здоровий глузд» в котре обманює нас. Виявляється, що маса тіла, його довжина, а відповідно й інші з ними пов’язані величини, залежать від того, рухається це тіло чи не рухається, рухається спостерігач чи залишається на місці. Виявляється, що тривалість однієї і тієї ж події, довжина та маса одного і того ж тіла, певним чином залежать від того хто вимірює цю тривалість, цю довжину, цю масу, та з якою швидкістю він рухається. Втім, про відносність часу, маси та довжини, ми поговоримо на наступних лекційних заняттях. Наразі ж, зробимо ще одне важливе зауваження, яке безпосередньо стосується абсолютного та відносного.

 

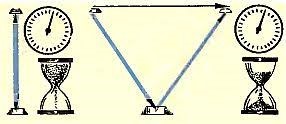
Мал.172. В теорії відносності стверджується, що тривалості подій, розміри та маси тіл, залежать від того, в якій системі відліку ці тривалості, розміри і маси вимірюються.

Ви можете подумати, що в теорії відносності стверджується, ніби все в цьому світі відносне. Ця думка абсолютно хибна. Дійсно, в теорії відносності стверджується, що багато з тих речей які ми схильні вважати абсолютними, насправді є відносними. Однак, це зовсім не означає, що в Природі нема абсолютно незмінних речей. В теорії відносності не тільки не стверджується, що все відносне. Навпаки, теорія відносності стоїть на тому, що в Природі існують абсолютно незмінні речі, наприклад такі, як швидкість світла у вакуумі.

В класичній фізиці, швидкість світла була відносною. Відносною в тому сенсі, що вона змінювалась в залежності від напрямку та швидкості руху спостерігача. В теорії ж відносності швидкість світла є абсолютною. Не важливо рухається чи не рухається джерело світла, не важливо рухається чи не рухається спостерігач, важливо лише те, що швидкість світла як відносно його джерела так і відносно спостерігача є незмінною і чисельно рівною 3∙10⁸м/с. У всіх інерціальних системах відліку швидкість світла залишається незмінною і чисельно рівною 3·10⁸м/с.

Тому, якщо в теорії відносності  потрібно щось довести, то завжди виходять не з того, що здається правильним, розумним чи очевидним, а з того, що у всіх інерціальних системах відліку швидкість світла є абсолютно незмінною величиною.

Контрольні запитання.

1. Що стверджували ті, хто заперечував факт обертання Землі навколо Сонця?
2. Чому, сидячи в реальній закритій кабіні (кареті, автомобілі, потязі, тощо) ми практично завжди можемо визначити рухається ця кабіна чи не рухається?
3. Чи відчуваєте ви факт того, що Земля рухається? Чому?
4. Що стверджується в принципі відносності (два формулювання)?
5. Чим інерціальні системи відліку відрізняються від неінерціальних?
6. Як формулюється закон додавання швидкостей в ньютонівській механіці?
7. Що стверджується в максвелівській електродинаміці стосовно швидкості світла у вакуумі? Чому це твердження суперечило ньютонівській механіці?
8. Чому більшість вчених були схильні вважати, що при вирішенні тих проблем які виникли між теорією Ньютона та теорією Максвела, певні недоліки потрібно шукати в теорії Максвела?
9. Поясніть суть та результати експериментальних досліджень Майкельсона. Що доводили ці результати?
10. Сформулюйте базові твердження теорії відносності.
11. Поясніть, чому поняття «в даний момент часу» та «одночасно» є відносними?
12. Чи є теорія відносності такою яка стверджує, що в нашому Всесвіті все відносне?

.

Лекційне заняття №27.

Тема: Про відносність часу, парадокс близнюків та подорож у майбутнє.

На попередньому лекційному занятті ми говорили про те, що з факту принципової обмеженості швидкості поширення інформаційних сигналів, неминуче випливає, що такі часові поняття як в даний момент часу, одночасно і неодночасно, раніше і пізніше, минуле, теперішнє і майбутнє, є відносними. По суті це означає, що час відносний. Такий висновок здається абсурдним. Хіба плин часу від чого небуть залежить? Невже час не існує сам по собі?  Невже час не існував і не буде існувати завжди? Невже плин часу не однаковий у всіх куточках Всесвіту? Невже геніальний Ньютон помилявся коли стверджував: «Абсолютний, істинний, математичний час, сам по собі та по своїй природі тече однаково і безвідносно до будь чого зовнішнього».

Що ж, давайте поговоримо про відносність часу та про те, що це означає. Зазвичай, ми уявляємо час як щось вічне, безперервне, яке існує само пособі і плин якого не залежить ні від чого іншого,  як тільки від самого себе. Однак, напевно ви погодитесь з тим, що поняття «час» нерозривно пов’язане з тими чи іншими подіями. Адже коли ми говоримо про час, то маємо на увазі тривалість певних подій, тривалість тих проміжків які відділяють одні події від інших, тривалість тих проміжків які характеризують послідовність подій тощо. Зважаючи на ці обставини, маємо визнати, що без подій, без тих чи інших процесів, поняття «час» немає сенсу. Бо без тих подій які відбуваються у Всесвіті загалом і в кожному його коточку зокрема, слово «час», нічого не означає.

Неупереджений аналіз показує, що не існує часу самого по собі, а є події які мають певну тривалість та певну послідовність. Позначаючи цю тривалість та послідовність, ми і говоримо про час. Іншими словами: Час – це таке базове поняття, суть якого полягає в констатації факту того, що всі природні події мають певну тривалість та послідовність, або, як прийнято говорити, відбуваються у часі. Не будемо забувати і про те, що час – це фізична величина, яка характеризує тривалість подій і яка дорівнює цій тривалості.

Наші уявлення про безвідносність часу, по суті ґрунтуються на підсвідомій впевненості в тому, що тривалість будь якої події не залежить від того, хто і яким чином вимірює цю тривалість. На підсвідомій впевненості в тому, що коли подія одна і таж, то хто б не вимірював її тривалість, результат має бути однаковим. Звичайно за умови, що відповідні вимірювальні прилади є абсолютно однаковими.

Дійсно. Припустимо, що пасажир потягу який рухається з постійною швидкістю, підкидає яблуко і ловить його (мал.173). Припустимо, що тривалість цієї події фіксують два спостерігачі: пасажир цього ж потягу і людина яка стоїть на пероні вокзалу. Наш «здоровий глузд», який як відомо спирається на повсякденний досвід, стверджує: оскільки подія одна і таж (яблуко вилітає з руки пасажира і через певний проміжок часу знову опиняється в цій же руці), то в незалежності від того хто фіксуватиме тривалість  цієї події, ця тривалість має бути однаковою. Іншими словами, наш повсякденний досвід, а відповідно і «здоровий глузд» стверджують: тривалість однієї і тієї ж події в рухомій (t) та нерухомій (t₀) системах відліку, є однаковою t=t₀.

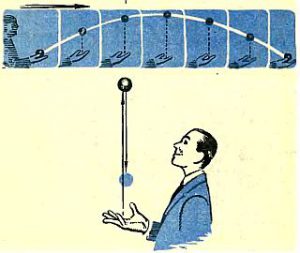
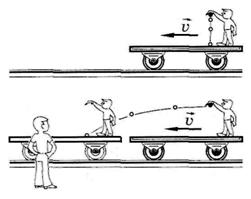
Мал.173. Різні спостерігачі, одну і туж подію бачать по різному.

А що коли і на цей раз «здоровий глузд» обманює нас? Адже абсолютно очевидно, що наші спостерігачі бачать суттєво різні події. Той з них що знаходиться у вагоні потягу бачить: яблуко вилітає з руки експериментатора, вертикальною прямою піднімається вгору, а потім тією ж прямою опускається в руку експериментатора. Той же спостерігач, що стоїть на пероні вокзалу бачить: яблуко, вилітаючи з руки експериментатора піднімається вгору і рухається вперед, потім продовжуючи рухатись вперед, опускається і знову потрапляє в руку експериментатора. Чи не означає даний факт, що тривалість цих суттєво різних подій має бути різною?

Що ж давайте проаналізуємо дану ситуацію. Тільки тепер будемо розглядати не рух яблука, а рух світлового фотона. Адже в теорії відносності, пояснюючи ті чи інші події, можна піддавати сумніву все що завгодно, окрім факту того, що в усіх інерціальних системах відліку, швидкість світла (швидкість світлових фотонів) є абсолютно незмінною величиною: с =3·10⁸м/с = const.

Припустимо, що у вагоні який рухається з постійною швидкістю v, встановлено джерело світлових фотонів (прожектор) над яким знаходиться плоске, горизонтально розташоване дзеркало. Система відрегульована таким чином, що фотон вилітає з прожектора, відбивається від дзеркала і повертається назад в прожектор. Припустимо, що за рухом фотона спостерігають два спостерігачі: перший знаходиться у вагоні, другий – на пероні вокзалу. Не важко збагнути, що той спостерігач який сидить у вагоні, зафіксує що фотон рухається ломаною вверх–вниз (мал.174а). Натомість той спостерігач який стоїть на пероні, бачитиме що фотон рухається вздовж ломаної вверх вперед – вниз вперед (мал.174б)

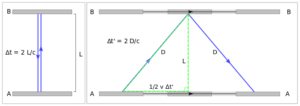
Мал.174. В різних системах відліку траєкторія руху одного і того ж фотона є різною.

Виходячи з того, що швидкість вагона (v), швидкість світла (c) та відстань між прожектором і дзеркалом (L) є відомими величинами, визначимо час польоту фотона від прожектора до дзеркала у відносно нерухомій (t₀) та відносно рухомій (t) системах відліку. Відразу ж зауважимо, що при теоретичний поясненнях нерухомою вважають ту систему відліку, в якій відбувається відповідна подія. Наприклад в нашому випадку, подія відбувається у вагоні потягу і тому та система відліку яка жорстко зв’язана з цим вагоном є нерухомою.

Оскільки в нерухомій системі відліку, фотон пролітає відстань L, то час його польоту від прожектора до дзеркала можна визначити за формулою t₀ = L/c. В відносно рухомій системі відліку, той же фотон пролітає відстань D і тому в цій системі, тривалість польоту фотона має визначатись за формулою t = D/c. А оскільки в рухомій системі відліку, за час польоту фотона від прожектора до дзеркала, вагон а відповідно і дзеркало переміщуються на відстань ℓ=v·t, то у відповідності з теоремою Піфагора D² = (v·t)² + L². А враховуючи що D = t·c; L = t₀·c, можна записати: (t·c)² = (t·v)² + (t₀·c)², звідси t²(c²–v²) = t₀²c²,  звідси  t² = t₀²(c²/(c²–v²)), звідси t = t₀√(с²/(c²–v²)) = t₀(1/√(1–v²/c²), або t = t₀k, де  k=1/√(1–v²/c²).

Таким чином, неупереджений математичний  аналіз доводить: тривалість однієї і тієї ж події, в рухомій (t) та нерухомій (t₀) системах відліку є різною. При цьому, ці тривалості зв’язані співвідношенням  t = k·t₀, де k=1/√(1–v²/c²) – коефіцієнт відносності, або релятивістський коефіцієнт (від лат. relativus – відносний).

Висновок 1. Тривалість однієї і тієї ж події (або абсолютно аналогічних подій) в рухомій та нерухомій системах відліку є різною. При цьому виконується співвідношення: t = k∙t₀,

де t₀ – тривалість події в нерухомій системі відліку;

t – тривалість тієї ж події в рухомій системі відліку;

k = 1/(1–v²/c²)^1/2– коефіцієнт відносності (релятивістський коефіцієнт).

Не важко довести, що величина коефіцієнту відносності знаходиться в межах 1 ≤  k < ∞. Дійсно:

Якщо v = 0,  то k = 1/√(1–0/с²) = 1/1 = 1.

Якщо v = с,  то k = 1/√(1–с²/с²)  = 1/0 = ∞.

До речі. Коли математики стверджують, що на нуль ділити не можна, то чомусь забувають пояснити, а що ж це означає. Чому на 0,1  ділити можна (1:0,1=10), на 0,01 – можна (1:0,01=100), на 0,001 – можна (1:0,001=1000), а на нуль – не можна? А не можна в тому сенсі, що не існує того конкретного числа, яке б було точним результатом ділення на нуль. Це число називається «безкінечність»: а/о = ∞.

Мал.175. В рухомій та нерухомій системах відліку, одна і та ж подія виглядає по різному, і тривалість цієї події в цих системах є різною.

Таким чином, в теорії відносності стверджується. Якщо за однією і тією ж подією спостерігають рухомий та нерухомий спостерігачі, то за їх абсолютно однаковими та абсолютно точними годинниками, тривалість цієї події виявиться різною. При цьому нерухомий спостерігач буде стверджувати, що в рухомій системі відліку час тече повільніше. Адже якщо наприклад, рухома система відліку рухається з швидкістю для якої k=10 і в цій системі відбувається подія тривалість якої t₀=2с, то той спостерігач який знаходиться в рухомій системі відліку зафіксує, що тривалість цієї події t = k∙t₀ = 10·2с = 20с. При цьому спостерігач з нерухомій системі відліку буде стверджувати, що в рухомій системі час тече повільніше.

Ви можете запитати: а чому в повсякденному житті ми не помічаємо тих ефектів про існування яких говорить теорія відносності? Відповідь проста: у повсякденному житті ми маємо справу з такими швидкостями, для яких релятивістський коефіцієнт практично не відрізняється від одиниці. Наприклад для літака що рухається з швидкістю 0,3км/с =1080км/год  k=1,000 000 000 0005. А це означає, що для того, щоб показання бортового годинника даного літака відрізнялися від показань аналогічного земного годинника всього на одну секунду, необхідно щоб політ тривав 63400 років.

Ясно, що в такій ситуації помітити факт відставання тих годинників які встановлені на сучасних автомобілях, потягах, літаках чи навіть ракетах, практично не можливо. А отже не можливо й помітити факт сповільнення відповідних подій. Однак, якщо мова йде про ситуації в яких швидкість об’єктів близька до швидкості світла, то в цих випадках, часові ефекти теорії відносності стають не лише суттєвими, а й визначальними. Наприклад, якщо об’єкт рухається з швидкістю 150000км/с (тобто v=0,5с), то для нього k=1,15. Якщо v=0,75с, то k=1,5. Якщо v=0,87с, то k=2. Якщо v=0,98с, то k=5. Якщо v=0,995с, то k=10. Якщо v=0,9999с, то k=70 і т.д. Сучасні прискорювачі елементарних частинок, розганяють ці частинки до таких швидкостей, для яких k > 40000.

Загалом же, залежність релятивістського коефіцієнту від швидкості руху об’єкту (системи відліку), можна представити у вигляді наступного графіку.

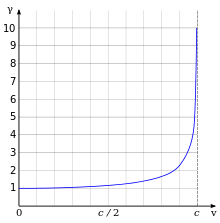
Мал.176. Графік залежності коефіцієнту відносності від швидкості руху системи відліку.

В процесі пояснення тих чи інших ефектів теорії відносності, завжди постає питання: яка система відліку в тій чи іншій ситуації є рухомою, а яка нерухомою? Скажімо на ракеті яка летить зі швидкістю k=10 відбувається певна подія: астронавт, вітаючи землянина піднімає та опускає руку і за годинником астронавта ця подія триває 2с. Натомість землянин, відповідаючи на привітання також піднімає руку і також фіксує, що його привітання триває 2с.

Оскільки ракета рухається з постійною швидкістю, то у відповідності з принципом відносності, в ракеті всі фізичні процеси відбуваються так ніби вона не рухається. Тому астронавт обгрунтовано стверджує, що його система відліку є нерухомою, і що рухається землянин. При цьому він фіксує факт того, що на Землі усі події відбуваються дуже повільно, і що привітання землянина триває цілих 20с. Землянин же з неменшим обгрунтуванням бачить і відчуває, що саме його система відліку є нерухомою, що рухається ракета, що на ракеті всі події відбуваються повільно і що привітання астронавта триває цілих 20с.

І от питання: а хто в цій ситуації правий і яка система відліку є рухомою, а яка нерухомою? Адже астронавт явно бачить, відчуває і фіксує всіма можливими приладами, що його система відліку є нерухомою, і що рухається саме Земля. Натомість землянин бачить, відчуває і фіксує, що саме його система відліку є нерухомою, і що рухається ракета.

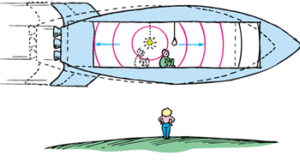
Мал.177. Землянин бачить: в ракеті події відбуваються повільніше ніж на Землі. Астронавт бачить: на Землі події відбуваються повільніше ніж на ракеті. Хто правий?

Геніальний Ейнштейн не тільки створив теорію відносності, а й пояснив всі ті уявні (надумані) парадокси які ніби то випливають з цієї теорії. Зокрема пояснив як відрізнити рухому систему відліку від нерухомої. Суть цього пояснення наступна.

Допоки ракета рухається з постійною швидкістю, можна скільки завгодно сперечатись з приводу того, що рухається – ракета чи Земля. При цьому жоден експеримент не зможе довести пасажирам ракети, що рухаються саме вони. Але для того щоб перевірити той чи інший ефект теорії відносності, в даному випадку – звірити показання годинників, потрібно зустрітися. А означає, що комусь треба повернутися (ракеті повернутися на Землю, чи Землі повернутися на ракету). При цьому неодмінно з’ясується, що тому спостерігачу який змушений буде повертатися, Природа неодмінно скаже, що саме його системи відліку є рухомою. Адже для того щоб повернутися, спочатку потрібно зупинитися, потім розвернутися, розігнатися і знову зупинитися. І на кожній з цих ділянок відповідний спостерігач буде рухатися з певним прискоренням. А це означає, що на нього неминуче діятиме певна сила інерції яка безумовно вказуватиме на те, що саме його система відліку є рухомою, і що тому, ефекти теорії відносності він має оцінювати з позицій рухомої системи відліку.

Таким чином, пояснюючи той чи інший ефект теорії відносності і відповідаючи на питання, яка система відліку є рухомою, а яка нерухомою, потрібно відповісти на інше питання: а кому прийдеться повертатися для перевірки відповідного ефекту. При цьому той хто буде повертатися неодмінно відчує, що саме його система відліку є рухомою, і що тому ефекти теорії відносності він має оцінювати з позицій рухомої системи відліку.

Напевно найвідомішим ефектом теорії відносності є так званий парадокс близнюків. З’ясовуючи суть цього парадоксу розглянемо наступну ситуацію. Припустимо, що ми створили таку міжзоряну ракету, швидкість руху якої 298500км/с=0,995с. За такої швидкості, величина коефіцієнту відносності становить k=10. Припустимо, що дана ракета здійснює космічну подорож за маршрутом Земля – зірка Альдебаран – Земля. Оскільки відстань до даної зірки приблизно дорівнює 50 світлових років, то космічна подорож триватиме 100 земних років. Припустимо, що одним з пасажирів космічного корабля є молодий 25-річний юнак, в якого на Землі залишається дружина, новонароджений син, брат–близнюк, знайомі, родичі, дерева, будинки тощо.

Оскільки швидкість ракети відповідає значенню k=10, то згідно з законами теорії відносності, ті процеси що відбуваються на ракеті, будуть  відбуватися у 10 разів повільніше ніж на Землі. А це означає, що за ракетним годинником, дана космічна подорож триватиме не 100, а лише 10 років. Причому, це буде не просто обманне враження людей та приладів. Відповідна тривалість польоту буде підтверджена всім комплексом об’єктивних фактів: показаннями годинників, витратами харчів, відчуттями людей, розпадом радіоактивних речовин, старінням організмів і т.д. і т.п.

Відразу ж зауважимо, що на рухомій ракеті, факт сповільнення часу не буде зафіксований а ні найточнішими приладами, а ні будь якими відчуттями людини. Для цих приладів та відчуттів, все що відбуватиметься в рухомій ракеті, буде відбуватися аналогічно тому ніби це відбувається на Землі. Звичайно з врахуванням відсутності гравітаційного поля. Втім, якщо в процесі польоту космічний корабель з певною кутовою швидкістю обертатиметься навколо власної осі, то створювана цим обертанням сила інерції може бути певним аналогом сили тяжіння.

Таким чином, якщо ракета буде летіти з швидкістю k=10 і якщо космічна подорож триватиме 100 земних років, то на самій ракеті пройде лише 10 років. Тому наш мандрівник повернеться на Землю постарілим лише на 10 років. І якою б дивною не виглядала зустріч 35-річного мандрівника з його 75-річним внуком та з 50-річним правнуком, але нічого неймовірного та над природнього в такій зустрічі нема.

Мал.178. У відповідності з теорією відносності, зустріч 40 річного астронавта з його 90 річним братом-близнюком є цілком можливою.

Ясно, що в даній ситуації наш мандрівник зробить висновок про те, що він потрапив у майбутнє. Теорія відносності не лише допускає можливість такої подорожі, а й вказує на шлях її здійснення. І нам залишається лише збудувати ракету, яка б рухалась з швидкістю k=5, k=10 чи, скажімо k=100. На жаль, а можливо на щастя, подібних ракет ми ще не вміємо будувати. Все на що ми на тепер здатні, так це на створення ракет, для яких k=1,0000002.

Говорячи про вище описану подорож в майбутнє, доречно наголосити на деяких особливостях цієї подорожі. А ці особливості є наступними. По-перше, ви маєте розуміти, що потрапити в майбутнє можна лише в тому випадку, якщо ви залишите Землю на певному етапі її розвитку і повернувшись назад з’ясуєте, що земні об’єкти постаріли більше ніж ви. Адже якщо ви опинитесь на якійсь іншій планеті, скажімо такій де рівень цивілізації значно вищий земного, то це зовсім не означатиме, що ви потрапили в майбутнє. Просто ви опинились на іншій планеті, цивілізаційний розвиток якої вищий земного. Аналогічно, ви не зможете вважати минулим ту ситуацію, коли потрапивши на іншу планету з’ясуєте, що її мешканці живуть в «кам’яному віці». Адже їх «кам’яний вік» не має жодного відношення до «кам’яного віку» нашої  Землі та до нашого минулого. Іншими словами, подорож в майбутнє має сенс лише в тому випадку, коли ви з «земного теперішнього» потрапляєте в «земне майбутнє».

По-друге. Ви маєте розуміти, що повернутися з «земного майбутнього» в «земне теперішнє» принципово не можливо. Адже таке повернення є аналогічним поверненню в минуле. А подорож в минуле є принципово не можливою. Не можливою тому, що за визначенням і за суттю, минулим називають ті події які вже відбулися і на хід яких не можливо вплинути навіть в принципі, навіть гіпотетично. А якщо ми допускаємо подорож в минуле, то відповідно допускаємо і ситуацію, коли син, опинившись в минулому стає причиною смерті маленької дівчинки, яка в майбутньому мала б стати його матір’ю. А така ситуація є принципово неможливою.

По-третє. Ви маєте розуміти, що коли астронавт фактично постарівший на 10 років повертається на Землю і з’ясовує, що вона постаріла на 100 років, то це зовсім не означає що за ці 10 років астронавт прожив 100. Скажімо, якщо на надгробному каменю нашого астронавта, буде написано 2000–2165р.р., то це зовсім не означатиме, що в дійсності він прожив більше ніж його брат–близнюк, на надгробку якого написано 2000-2085р.р. Адже фактично, астронавт прожив не 165 років, а лише 75 (поясніть чому?).

Втім, давайте поговоримо про те, що власне називають парадоксом близнюків. Адже цей парадокс полягає не в тому, що з точки зору «здорового глузду», зустріч 35-річного мандрівника з його 50-річним правнуком здається абсурдною. Парадокс близнюків полягає в іншому. А саме.

В теорії відносності стверджується: у всіх інерціальних системах відліку, всі фізичні процеси відбуваються абсолютно однаково. А це означає, що коли ракета рухається з постійною швидкістю (v=const), то ні пасажири ракети, ні будь які прилади на ній встановлені, не будуть відчувати та фіксувати факту руху ракети. Більше того,  спостерігаючи за тими подіями які відбуваються на Землі, пасажири ракети та наявні прилади будуть бачити і фіксувати, що на Землі всі події відбуваються у 10 разів повільніше ніж на ракеті. Виходячи з цього, вони зроблять висновок про те, що коли за їх бортовим годинником пройде 10 років, то на Землі має пройти лише 1 рік.

Не важко бачити, що ми маємо справу з явно парадоксальною ситуацією: земляни бачать, що події на ракеті відбуваються повільніше і що тому астронавти повільніше старіють. Астронавти ж бачать, що повільнішими є  події на Землі і що тому, повільніше старіють саме земляни. Власне це протиріччя і називають парадоксом близнюків.

Пояснюючи даний парадокс, можна сказати наступне. Головним джерелом тих непорозумінь та парадоксів які виникають в теорії відносності, в тому числі і парадоксу близнюків, є питання про те, яка система відліку є рухомою, а яка – нерухомою. Втім, про те як теорія відносності відповідає на це питання ви вже знаєте. Правильно! Відповідаючи на питання про рухому та нерухому системи відліку, завжди потрібно запитувати: а кому прийдеться повертатися для того, щоб перевірити ефекти теорії відносності. В даному випадку перевірити те, хто за час космічної подорожі постаріє менше, астронавти чи земляни?

Коли ми говорили про подорож в майбутнє, то наголошували на тому, що в це майбутнє можна потрапити лише в тому випадку, якщо космічна подорож починається і закінчується на Землі. І це має принципове значення. Адже до поки ракета рухається з постійною швидкістю, можна скільки завгодно сперечатись з приводу того, хто менше постаріє – земляни чи пасажири ракети. Однак для того щоб це перевірити комусь прийдеться повернутися. І цьому «комусь» Природа обов’язково скаже, що рухомою є саме його система відліку, і що тому у відповідності з теорією відносності та законами Природи, за час космічної подорожі саме цей «комусь» постаріє менше.

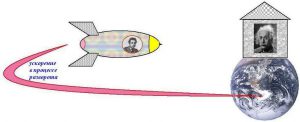
Мал.179.  Перевіряючи передбачення теорії відносності та визначаючись з тим яка система відліку є рухомою, завжди задаються питанням: а кому прийдеться повертатися для перевірки цих передбачень.

Дійсно. Для того щоб ракета здійснила подорож в майбутнє, вона має стартувати з Землі і повернутись на Землю. При цьому, стартуючи з Землі, ракета повинна набрати певну надвисоку  швидкість, тобто певний час рухатись з прискоренням. Наприклад, для того щоб рухаючись з прискоренням 9,8м/с² ракета досягла швидкості 298500км/с, необхідно щоб цей прискорений рух тривав цілий рік. І протягом цього року пасажири ракети будуть відчувати дію сили інерції, яка буде вказувати на те, що рухаються саме вони, а не Земля.

Потім, коли ракета буде рухатись з постійною швидкістю, можна скільки завгодно сперечатися хто рухається а хто не рухається, хто постаріє більше а хто менше. Однак для того щоб це перевірити, комусь прийдеться повернутися. І як ви розумієте цим «кимось» буде не Земля а ракета. А це означає, що принаймі ще на трьох ділянках траєкторії руху ракети, сила інерції буде вказувати астронавтам, що рухаються саме вони і що тому саме вони постаріють менше. Повернувшись на Землю, астронавти неодмінно переконаються в тому, що за час космічної подорожі вони дійсно постаріли менше, і що теорія відносності дійсно права.

І потрібно зауважити, що ніякими хитромудрими штучками, на кшталт руху ракети по колу великого радіусу, та руху з над малими прискореннями, Природу не обдурити. А якщо ви не помітили чи не захотіли помічати факту того, що саме ваша система відліку є рухомою, так то ж ваша особиста проблема, яка жодним чином не впливає на реальний хід подій. А ця реальність полягає в тому, що у відповідності з теорією відносності та законами Природи, плин часу в рухомій та нерухомій системах відліку є суттєво різним, і що цю різність відображає співвідношення: t = k∙t₀, де k=1/√(1–v²/c²).

Узагальнюючи вище сказане можна констатувати факт того, що з об’єктивно – математичної точки зору, теорія відносності (у всякому разі та її частина, яку ми вивчаємо і яку зазвичай називають частковою або спеціальною теорією відносності) є гранично простою. Адже логічно та математично обгрунтовуючи те, що в рухомій і нерухомій системах відліку тривалість однієї і тієї ж події є різною, ми застосовували гранично прості математичні міркування найскладнішим з яких, є відома ще з незапам’ятних часів теорема Піфагора (в прямокутному трикутнику, сума квадратів катетів дорівнює квадрату гіпотенузи).

Якщо ж говорити про складність теорії відносності, то вона не об’єктивно – математична, а суб’єктивно – психологічна. І ця складність полягає в наступному. По-перше, переважна більшість висновків (передбачень) теорії відносності є такими, що явно суперечать нашому повсякденному досвіду, а отже і «здоровому глузду». Суперечать тому, що наш повсякденний досвід є обмеженим та неповним. По-друге, в теорії відносності, передбачаючи результати тих чи інших подій, зазвичай важко визначити, яка система відліку є рухомою, а яка нерухомою. Втім, застосовуючи ейнштейнівський підхід до вирішення цієї проблеми ви завжди знайдете правильне рішення. По-третє, в теорії відносності існує багато надумано суперечливих ситуацій (підкреслюю – надумано суперечливих), які прийнято називати парадоксами теорії відносності. Про один з таких парадоксів (парадокс близнюків) ви вже знаєте, а про інші, поговоримо дещо пізніше

Контрольні запитання.

1. На чому грунтуються наші уявлення про безвідносність часу?
2. Чому ми впевнені в тому, що тривалість будь якої події не залежить від того, в рухомій чи нерухомій системі відліку ця подія відбувається?
3. Чому часові ефекти теорії відносності не спостерігаються у повсякденному житті?
4. Що означає твердження: на нуль ділити не можна?
5. Космічний корабель пролітає повз Землю з швидкістю k=5. Опишіть те, що бачать та фіксують астронавти цього корабля, спостерігаючи за подіями на Землі?
6. Поясніть як визначають, яка система відліку є рухомою, а яка нерухомою?
7. Поясніть, чому пасажири тієї ракети яка з швидкістю k=10 подорожувала 100 земних років, постаріли лише на 10 років?
8. Поясніть суть парадоксу близнюків.
9. Чому, пасажири тієї ракети що рухається з постійною швидкістю, спостерігаючи за тими подіями які відбуваються на Землі, роблять висновок про те, що рухається саме Земля?
10. Поясніть, яким чином Природа, нагадуватиме мандрівнику в майбутнє, що саме він знаходиться в рухомій системі відліку?

                   Вправа 27.

1. Доведіть, що числове значення коефіцієнту відносності знаходиться в межах 1 ≤ k ˂ ∞
2. У скільки разів сповільниться плин часу в ракеті яка рухається з швидкістю 0,6с; 0,9с; 2,9·10⁸м/с ?
3. В ракеті яка рухається з швидкістю 0,96с зафіксовано час польоту 20 років. Скільки років за цей час пройшло на Землі?
4. Скільки часу пройде на зорельоті, який рухається відносно Землі з швидкістю 0,4с, за 25 земних років?
5. З якою швидкістю повинен рухатися космічний корабель відносно Землі, щоб годинник на ньому йшов у 4 рази повільніше ніж на Землі?
6. Скільки часу для жителів Землі і для космонавтів займе подорож до зірки в ракеті, яка летить зі швидкістю 0,9с, якщо відстань до зірки 40 світлових років?
7. В атмосфері Землі мю-мезон при швидкості руху 0,995с встигає пролетіти 6км. Яка тривалість життя мю-мезона за «земним» та «власним» годинником?

.

Лекційне заняття №28.

Тема: Про відносність простору. Про відносність маси та зв’язок маси з енергією.

         Зазвичай ми уявляємо простір як певну незмінну, безкінечну, безструктурну та вічну пустоту, в якій знаходяться різні тіла та відбуваються різноманітні події. Ми схильні вважати, що ця вічна та незмінна пустота існує сама по собі, і що її параметри не залежать від тих об’єктів які в ній знаходяться, та тих подій які в ній відбуваються.

Однак, якщо ви неупереджено проаналізуєте відомі факти, то напевно погодитесь з тим, що простір нерозривно пов’язаний з тими фізичними об’єктами які в цьому просторі знаходяться, і що в Природі не існує тієї пустоти яка б не була наповнена певними фізичними об’єктами ы певними подыями. Адже навіть там, де нема жодного атома і жодної елементарної частинки, простір неминуче наповнений безліччю матеріальних об’єктів, які називаються полями. По суті це означає, що поняття «простір», без тих об’єктів які в ньому знаходяться та тих подій які в ньому відбуваються, не має сенсу. Не має бодай тому, що в Природі простору в чистому вигляді, тобто простору без матеріальних об’єктів та подій, просто не існує. Зважаючи на вище сказане можна дати наступне визначення.

Простір – це базове поняття, яке констатує той факт, що всі матеріальні об’єкти Природи мають певні геометричні параметри, певне місцезнаходження, певним чином розташовані один відносно одного, або як прийнято говорити, існують у просторі.

         Загальновідомо, що такі просторові поняття як великий – маленький, вправо – вліво, вверх – вниз, вперед – назад, тощо є відносними. Однак ми схильні вважати, що ця відносність жодним чином не вказує на відносність самого простору. По суті наша впевненість в незмінності та безвідносності простору, грунтується  на підсвідомій впевненості в тому, що лінійні розміри будь якого об’єкту не залежать від того, рухається цей об’єкт чи не рухається і хто та яким чином ці розміри вимірює. Іншими словами, наш повсякденний досвід, а відповідно і «здоровий глузд» стверджують, що довжина тіла в рухомій (ℓ) та нерухомій (ℓ₀) системах відліку є однаковою. Що ж давайте перевіримо і це, на перший погляд очевидно правильне твердження.

Припустимо, що ви хочете  виміряти довжину вагона в відносно рухомій та відносно нерухомій системах відліку. Ясно, якщо це вимірювання здійснювати традиційним способом, тобто за допомогою еталонного метра, то встановити будь які зміни цієї довжини ви не зможете. Адже якщо ці зміни відбудуться, то неминуче зміняться не лише лінійні розміри самого вагона, а й відповідні розміри всіх його об’єктів, в тому числі і еталонного метра.

В такій ситуації єдиним об’єктивним вимірювальним інструментом може бути лише світло, про яке достовірно відомо, що його швидкість за будь яких обставин залишається незмінною і чисельно рівною 3∙10⁸м/с. Зважаючи на ці обставини, довжину вагона ми будемо вимірювати наступним чином.

В одному кінці вагона встановимо джерело світлових фотонів (прожектор), а в іншому – плоске дзеркало (мал.180). Налаштуємо систему таким чином, щоб світловий фотон, вилітаючи з прожектора і відбиваючись від дзеркала, знову потрапляв у прожектор. Визначивши час польоту фотона від прожектора до дзеркала (t), та знаючи величину його швидкості (с=3∙10⁸м/с), відповідну довжину вагона (ℓ) можна визначити за формулою:  ℓ=c∙t .

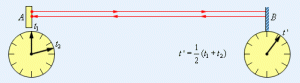
Мал.180. В теорії відносності довжину вагона (l) визначають шляхом вимірювання часу польоту світлового фотона (t): ℓ=c·t.

Припустимо, що вагон з постійною швидкістю (v) рухається відносно перону і що його довжину, шляхом вимірювання часу польоту фотона, визначають два спостерігачі, один з яких знаходиться у вагоні, другий – на пероні вокзалу. Визначаючи довжину вагона потрібно зробити два суттєвих зауваження.

Зауваження перше. Оскільки те обладнання за допомогою якого вимірюється довжина (прожектор і дзеркало) встановлено у вагоні, то відносно довжини нерухомою системою відліку є «вагон», а рухомою – «перон». Тому виміряну в системі «вагон» довжину позначаємо ℓ₀, а довжину виміряну в системі «перон» позначаємо ℓ.

Зауваження друге. Оскільки вагон з швидкістю v рухається відносно перону, то застосовуючи формулу t=k∙t₀ нерухомою системою відліку потрібно вважати «перон», а рухомою – «вагон». Тому визначений в системі «вагон» час позначаємо t, а час визначений в системі «перон» позначаємо t₀.

Зважаючи на вище сказане можна стверджувати. Визначаючи довжину вагона шляхом вимірювання часу польоту фотона від прожектора до дзеркала, спостерігач з системи відліку «вагон» з’ясує, що в цій системі, довжина вагона (ℓ₀) становить: ℓ₀=c·t,  де t – час польоту фотона від прожектора до дзеркала, виміряний в системі відліку «вагон». Той же спостерігач, який знаходиться в системі відліку «перон», з’ясує що в його системі, довжина вагону (ℓ) становить: ℓ=c·t₀,  де  t₀ – час польоту фотона від прожектора до дзеркала виміряний в системі відліку «перон». Оскільки між тривалістю подій в системі відліку «вагон» (t) та системі відліку «перон» (t₀) існує співвідношення t=k·t₀, або t₀=t/k то можна записати: ℓ=c·t₀=c·t/k=ℓ₀/k. Таким чином, довжина вагону в рухомій (ℓ) та нерухомій (ℓ₀) системах відліку є різною, при цьому виконується співвідношення ℓ=ℓ₀/k.

Висновок 2. Довжина одного і того ж об’єкту (або абсолютно аналогічних об’єктів) в рухомій (ℓ) та нерухомій (ℓ₀) системах відліку є різною. При цьому виконується співвідношення ℓ=ℓ₀/k, де k=1/√(1–v²/c²) – коефіцієнт відносності (релятивістський коефіцієнт).

Ілюструючи ті ефекти які пов’язані з відносністю просторових параметрів тіл, розглянемо наступну ситуацію. Припустимо, що у нас є два абсолютно однакових еталонних метра. Припустимо, що один з цих метрів ми залишаємо на Землі (нерухома система відліку), а інший – розміщуємо в ракеті, яка з швидкістю k=3 рухається відносно Землі (рухома система відліку). Спостерігаючи за тими об’єктами які знаходяться в ракеті, ми побачимо, що рухомий метр у 3 рази коротший за наш земний, еталонний метр. І взагалі, в рухомій ракеті, абсолютно всі об’єкти починаючи від самої ракети та астронавтів і закінчуючи тими атомами, протонами, нейтронами та електронами з яких вони складаються, будуть у 3 рази коротшими за відповідні земні аналоги.

Мал.181.  В рухомій ракеті, лінійні розміри всіх фізичних об’єктів певним чином зменшуються.

Але от парадокс. Оскільки ракета рухається з сталою швидкістю, то її астронавти не відчуваючи будь яких ознак руху, цілком обгрунтовано вважають, що їхня система відліку є нерухомою. При цьому вони бачать, що повз ракету з швидкістю k=3 пролітає планета Земля і що на ній всі об’єкти починаючи від самої планети та еталонного метра і закінчуючи тими протонами, нейтронами та електронами з яких вона складається у 3 рази зменшені. І до поки ракета рухається з постійною швидкістю, можна скільки завгодно сперечатися відносно того хто рухається а хто не рухається і у кого еталонний метр правильний, а у кого – неправильний. Цей спір можна вирішити лише у випадку персональної зустрічі тих хто сперечається. А щоб така зустріч відбулася, комусь треба зупинитися, розвернутися, розігнатися і знову зупинитися. І на всіх цих етапах руху, цьому «комусь» Природа обов’язково скаже, що саме він знаходиться в рухомій системі відліку і що тому всі ефекти теорії відносності він має сприймати з точки зору цієї системи.

Пояснюючи те як це може бути, щоб факт зменшення розмірів однаково бачили як ті хто рухається так і ті хто не рухається, можна сказати наступне. Уявіть собі, що учні класів А і Б знаходяться в сусідніх навчальних кімнатах і що стіна між цими кімнатами представляє собою прозору (невидиму) розсіювальну лінзу. Учні класу А, спостерігаючи за класом Б, неминуче бачать, що в класі Б всі об’єкти зменшені. На цій підставі вони стверджують, що у їх класі учні «нормальні», а в класі Б – «зменшені». Натомість учні класу Б, з неменшою неминучістю бачать, що зменшеними є всі об’єкти класу А. На цій підставі вони стверджують, що у їх класі учні «нормальні», а в класі А – «зменшені». І до поки учні класів А і Б перебувають у своїх кімнатах (у своїх системах відліку), можна скільки завгодно сперечатися відносно того, хто «нормальний» а хто «зменшений». Цей спір можна вирішити лише одним способом – учні класів А і Б мають зустрітися. При цьому неминуче з’ясується, що в обох класах учні «нормальні» і що факт ними побаченого у своїх системах відліку – то оптична ілюзія обумовлена тим, що розсіювальна лінза певним чином заломлює світло і тому відповідним чином викривляє дійсність.

В певному сенсі, ситуація з тим, що об’єктивно бачать спостерігачі в рухомій та нерухомій системах відліку, є аналогічною ситуації з класами А і Б. Адже те, що бачать рухомі астронавти спостерігаючи за нерухомими землянами, а нерухомі земляни бачать спостерігаючи за рухомими астронавтами, по суті є певною ілюзією. Але ця ілюзія створюється не скляною лінзою, а тим викривленням простору–часу яке відбувається в процесі відносного руху фізичних об’єктів (систем відліку). А треба сказати, що ілюзія – то не продукт чиєїсь багатої уяви, а цілком об’єктивне відображення реальності. Але відображення певним чином викривлене.

Мал.182. Зменшення розмірів об’єктів, як результат викривлення параметрів простору–часу та як результат оптичної ілюзії.

Говорячи про ті зменшення розмірів які обумовлені відносним рухом систем відліку, потрібно зауважити, що у відповідності з законами теорії відносності, зменшення довжини рухомого об’єкту відбувається лише в напрямку його руху. Дійсно. Припустимо, що за допомогою годинника та світлових фотонів ми будемо вимірювати висоту ракети, яка з швидкістю v пролітає повз планету (мал.183). Виконуючи такі вимірювання, спостерігач з системи відліку «ракета» зафіксує, що висота ракети L_p=c·t₀. Натомість, той спостерігач який знаходиться в системі  відліку «планета» зафіксує, що від прожектора до дзеркала, фотон проходить відстань (сt)²=L_п²+(vt)², звідси L_п=t√(c²–v²). А оскільки   t = kt₀ = t₀/√(1–v²/c²) =  t₀c/√(c²–v²), то   L_п = t√(c²–v²) = t₀c√(c²–v²)/√(c²–v²) = с·t₀. Таким чином, як в рухомій так і в нерухомій системах відліку, висота ракети  залишається незмінною: L_p=c·t₀;   L_п=c·t₀.

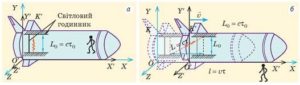
Мал.183. В рухомій та нерухомій системах відліку висота ракети є однаковою.

Із вище сказаного випливає, що згідно з законами теорії відносності в рухомій системі відліку зменшуються лише поздовжні розміри об’єктів, тоді як їх поперечні розміри залишаються незмінними (поздовжні і поперечні відносно напрямку руху системи). Наприклад, якщо ракета з швидкістю k=2 рухається відносно нерухомого спостерігача, то спостерігач побачить, що ті астронавти тіло яких орієнтовано вздовж напрямку руху, мають нормальну товщину але виглядають у двічі коротшими (мал.184). Натомість ті астронавти тіло яких орієнтовано перпендикулярно до напрямку руху, мають нормальну висоту, але виглядають у двічі тоншими.

Звісно, самі астронавти ні про які зміни своїх розмірів навіть не здогадуються. Навпаки, вони бачать, що зменшуються не їх розміри, а розміри тих об’єктів які знаходяться на Землі. Втім, про те, як і чому це відбувається, ви вже знаєте. Звичайно в межах розуміння факту того, що простір–час, це надзвичайно складний фізичний об’єкт, багатогранні властивості та прояви якого практично не можливо пояснити звичними словами і категоріями.

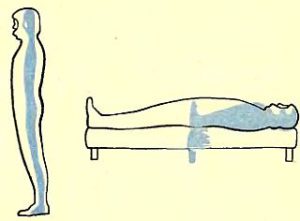
Мал.184. У відносно рухомій системі відліку зменшуються лише ті розміри тіла, напрям яких збігається з напрямком руху системи.

На ряду з простором і часом, надважливим параметром Всесвіту загалом і його окремих елементів зокрема, є маса. В ньютонівській механіці стверджується, що маса тіла не залежить від того де це тіло знаходиться, на Землі, Місяці чи Юпітері. Вона не залежить від того, рухається тіло чи не рухається, тверде воно чи рідке, холодне чи гаряче. Іншими словами, в ньютонівській механіці, маса тіла є абсолютною, тобто такою, яка не залежить ні від чого іншого як тільки від кількості речовини у відповідному тілі. Що ж, давайте перевіримо і це, на перший погляд очевидно правильне твердження. З цією метою виміряємо масу одного і того ж тіла в рухомій та нерухомій системах відліку.

Відразу ж зауважимо, що існує два методи вимірювання маси: гравітаційний та інерційний. Суть гравітаційного методу полягає в тому, що маса тіла визначається шляхом вимірювання тієї гравітаційної сили, а фактично сили тяжіння(F_т=mg), з якою тіло притягується до Землі або до іншого космічного об’єкту. А оскільки ця сила залежить від маси тіла, то цю масу визначають із співвідношення m=F_т/g, де g – силова характеристика відповідного гравітаційного поля, яку в умовах Землі ми називаємо прискоренням вільного падіння. В побутовій практиці, гравітаційний метод є основним методом вимірювання маси. Адже коли масу тіла визначають шляхом його зважування, то в незалежності від того на які ваги (пружинні, електронні, важільні чи інші) кладуть це тіло, по суті застосовують гравітаційний метод вимірювання маси.

Мал.185. Існує два методи вимірювання маси: а) гравітаційний; б) інерційний.

Гравітаційний метод визначення маси, має той недолік, що він працює лише там, де є достатньо потужне гравітаційне поле, параметри якого відомі. Тому в науковій практиці, а особливо в тих випадках коли мова йде про теоретичні пояснення, основним способом вимірювання маси є інерційний метод. Суть інерційного методу визначення маси полягає у визначенні того прискорення (a) яке отримує тіло під дією певної наперед визначеної сили (F). Скажімо, якщо під дією сили 10Н тіло отримує прискорення 5м/с², то маса тіла 2кг:  m=F/a=2кг.

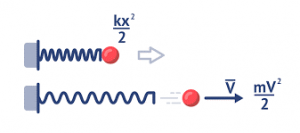
Ясно, що те гравітаційне поле яке створює та ракета, в якій ми збираємося визначати масу тіла, є мізерно малим. Тому цю масу ми будемо визначати не гравітаційним, а інерційним методом. З цією метою застосуємо простий прилад, який представляє собою стиснуту пружину, яка у потрібний момент розправляється і штовхає еталонне тіло. Принцип дії цієї системи полягає в наступному. Початково деформована пружина, в процесі свого випрямлення надає еталонному тілу певного прискорення. Визначивши величину цього прискорення, та знаючи величину діючої на тіло сили, визначають масу тіла.

Звичайно, в умовах даного приладу, задача ускладнюється фактом того, що величина діючої на тіло сили пружності є змінною. Однак, не будемо вдаватися в деталі даного експерименту, а розглянемо лише його фізичну суть. А ця суть полягає в тому, що в процесі випрямлення пружини, еталонне тіло отримує певне прискорення, величина якого залежить від маси цього тіла.

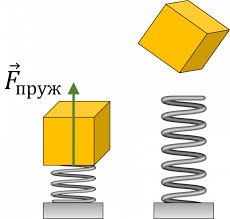
Мал.186. В процесі випрямлення пружини, тіло отримує певне прискорення, величина якого залежить від маси тіла.

Припустимо, що у нашому розпорядженні є два абсолютно однакових еталонних тіла масою 1кг кожне, та два абсолютно однакових еталонних прилади які інерційним методом вимірюють масу. Припустимо, що одне з цих тіл і один з цих приладів знаходяться на ракеті, яка з швидкістю k=2 пролітає  повз нашу планету. Враховуючи факт того, що в рухомій системі відліку поздовжня довжина всіх об’єктів зменшується, а поперечна залишається незмінною, вимірювальний прилад встановлюємо таким чином, щоб вісь пружини та напрям руху тіла були перпендикулярними до напрямку руху ракети.

Спостерігаючи за тими подіями які відбуваються в процесі вимірювання маси, земний спостерігач неодмінно зафіксує, що на ракеті еталонний прилад надає еталонному тілу вдвічі меншого прискорення. А це означає, що на ракеті яка рухається з швидкістю k=2, тіло масою 1кг веде себе так, ніби його маса 2кг. І така поведінка тіла повністю підтверджує третє базове передбачення теорії відносності: маси тіла в рухомій (m) та нерухомій (m₀) системах відліку зв’язані співвідношенням m = km₀, де  k = 1/√(1–v²/c²) – коефіцієнт відносності. Теоретично доводити достовірність співвідношення  m=km₀, ми не будемо. Однак знаючи про факт того, що в рухомій системі відліку плин часу сповільнюється, ви напевно погодитеся з тим, що на ракеті під дією заданої еталонної сили, тіло заданої еталонної маси буде рухатись повільніше, а отже з меншим прискоренням, а отже так, ніби його маса стала більшою.

Висновок 3. Маса одного і того ж фізичного об’єкту (або абсолютно аналогічних об’єктів) в рухомій (m) та нерухомій (m₀) системах відліку є різною. При цьому виконується співвідношення m = km₀, де k = 1/√(1–v²/c²) – коефіцієнт відносності.

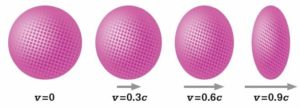
Мал.187. При збільшені швидкості руху тіла, його довжина зменшується, а маса – збільшується.

Факт того, що в процесі наближення швидкості руху тіла до швидкості світла, його маса неухильно збільшується, з усією очевидністю пояснює, чому жоден з тих об’єктів які мають масу спокою (m₀≠0) не можуть не те що перевищити швидкість світла, а навіть досягти її.

Дійсно. Згідно з теорією відносності, по мірі наближення швидкості тіла до швидкості світла (v→c), зв’язаний з цим тілом коефіцієнт відносності стрімко зростає до безкінечно великих значень (k→∞). При цьому маса відповідного тіла з аналогічною стрімкістю зростає до безкінечних величин (m→∞). А це означає, що для бодай мізерного збільшення швидкості тіла, знадобиться безкінечно велика сила. І якщо навіть це мізерне збільшення швидкості відбудеться, то воно автоматично призведе до нового неспіврозмірно великого витка збільшення маси, а відповідно і тієї сили яка потрібна для наступного мізерного збільшення швидкості. Ясно, що в такій ситуації можна як завгодно близько наближатись до швидкості світла, але ніколи її не досягти. Фактично з швидкістю світла можуть рухатись лише ті об’єкти, які не мають маси спокою, зокрема фотони та гравітони.

         Таким чином, в теорії відносності стверджується, що відносними є не лише довжина тіла та часові параметри тих подій які з ним пов’язані, а й та величина яка називається масою. Звичайно, в масштабах звичних для нас швидкостей, ефект збільшення маси рухомого тіла є мізерно малим. Однак, коли мова заходить про швидкості співрозмірні з швидкістю світла, то в цьому випадку, релятивістські ефекти стають не лише суттєвими а й визначальними. Скажімо, в сучасних прискорювачах елементарних частинок, ці частинки розганяються до швидкості 0,99999999с. За такої швидкості, маса частинки збільшується майже в 40 000 разів. Зважаючи на ці обставини в сучасній науці розрізняють масу спокою (m₀) та масу руху (m=km₀) частинки (тіла).

         Вивчаючи фізику ми неодноразово говорили про те, що всі ті об’єкти кількісною мірою яких є маса, нерозривно пов’язані з певними процесами (рухами), а отже і з кількісною мірою цих процесів – енергією. Наприклад, вивчаючи речовини ми стверджували, що вони складаються з молекул, молекули – з атомів, атоми – з ядер та електронів, атомні ядра – з протонів та нейтронів. При цьому ми підкреслювали, що всі ці частинки постійно рухаються і взаємодіють між собою, а отже є носіями певної кількості кінетичної та потенціальної енергії. Вивчаючи ті матеріальні об’єкти які називаються елементарними частинками, ми стверджували, що ці частинки фактично є певними згустками подій, а отже і відповідними згустками енергії.

Констатуючи нерозривний зв’язок матерії та руху, філософи стверджують, що матерія є невід’ємною від руху і що рух є способом існування матерії. Теорія відносності не лише підтверджує даний філософський висновок, а й визначає той кількісний зв’язок який існує між тим що прийнято називати матерією і мірою чого є маса, та тим що прийнято називати рухом і мірою чого є енергія. Цей зв’язок визначається знаменитою формулою Ейнштейна: E=mc², де m – маса тіла (фізичного об’єкту),  Е – загальна кількість зосередженої в цьому тілі енергії, с=3·10⁸м/с – швидкість світла в вакуумі.

Висновок 4. Будь яке тіло масою m, представляє собою згусток енергії загальна кількість якої визначається за формулою Е=mc², де с=3·10⁸м/с=const.

Формула Е=mс²  фактично вказує на те, що маса та енергія, це не просто взаємопов’язані величини, а різні назви однієї і тієї ж величини – масенергії. Звичайно, ці різні назви виникли не випадково. Вони по суті відображають той факт, що за звичайних умов, масенергія може знаходитись в двох суттєво різних станах: пасивному та активному. Активною масенергією називають ту частину масенергії яка представляє собою енергію руху та енергію взаємодії частинок речовини або макротіл, яка здатна до виконання тієї чи іншої роботи і яка за звичайних умов не перетворюється на пасивну масенергію. Різновидностями активної масенергії є теплова енергія, хімічна енергія, біологічна енергія, електрична енергія, електромагнітна енергія, механічна енергія, тощо. Зазвичай, активну масенергію ми називаємо просто енергією і вимірюємо в джоулях.

Пасивною масенергією називають ту частину масенергії яка сконденсована в частинках речовини та макротілах, яка за звичайних умов не перетворюється в активну масенергію і не спричиняє виконання тієї чи іншої роботи. Пасивну масенергію ми називаємо масою і вимірюємо в кілограмах. Визначаючи енергію як міру здатності тіла, частинки або поля виконати роботу, ми цілком обгрунтовано не сприймаємо пасивну масенергію (масу) як енергію. Сконденсовану в тілі пасивну масенергію ми сприймаємо як щось незмінно ціле, яке має певні інерційні та гравітаційні властивості і мірою чого є маса.

         Поділ масенергії на активну та пасивну є досить умовним. Умовним бодай тому, що на рівні елементарних частинок, відмінності між активною і пасивною масенергією зникають. При цьому пасивна масенергія може перетворюватись на активну і навпаки. Наприклад, при анігіляції електрон-позитронних пар, та масенергія яка сконденсована в електроні та позитроні і яка є пасивною, перетворюється на відповідну кількість масенергії фотонів, яка є активною: e₊₁+e_–1 →2γ .

Крім всього іншого формула Ейнштейна Е=mс² вказує ще й на те, що коли в результаті того чи іншого процесу, енергія тіла збільшується (зменшується), то відповідно збільшується (зменшується) і маса цього тіла. Наприклад, якщо в процесі нагрівання енергія тіла збільшилась на ΔЕ=900Дж, то і маса цього тіла збільшилась на Δm =ΔЕ/с² = 1·10^–14кг. І навпаки, якщо в процесі охолодження, тіло втратило 900Дж енергії, то воно втратило і 1·10^–14кг своєї маси. Ясно, що зафіксувати такі мізерні зміни маси тіла, практично не можливо. Однак, як кажуть, справа принципу.

Завершуючи розмову про масу, а точніше мас-енергію, буде не зайвим нагадати, що в сучасній науці нема більш ємкої та більш складної фізичної величини ніж маса. Дійсно. Вивчаючи механіку ми стверджували: маса є мірою інерціальних властивостей тіла, тобто мірою здатності тіла (частинки) протидіяти зміні його швидкості. Вивчаючи гравітаційні явища ми стверджували: маса є мірою гравітаційних властивостей тіла, тобто мірою його здатності створювати гравітаційні поля (гравітаційну дію). Вивчаючи молекулярну фізику, тобто загальні властивості твердих, рідких та газоподібних речовин, ми стверджували: маса є мірою кількості речовини в тілі, виміряної в кілограмах. І від тепер ви знаєте, що маса є мірою загальної кількості зосередженої в тілі енергії, а по суті – загальною мірою руху матерії.  Кожне з вище згаданих тверджень є правильним і в той же час неповним. Адже маса, це і міра інерції, і міра гравітації, і міра кількості речовини в тілі, і міра загальної кількості зосередженої в цьому тілі енергії.

                   Контрольні запитання.

1. Зазвичай простір уявляють як певну незмінну, безкінечну, безструктурну та вічну пустоту. Поясніть значення кожного виділеного терміну.
2. Чи існує в Природі така пустота яку можна було б назвати чистим простором? Чи можна створити таку пустоту? Чи можна її уявити?
3. Як змінюються розміри об’єктів в рухомій системі відліку?
4. Поясніть чим схожі ті оптичні ілюзії які створює розсіювальна лінза та факт надшвидкого руху системи відліку?
5. В чому суть гравітаційного методу вимірювання маси? Які переваги та недоліки цього методу?
6. В чому суть інерційного методу вимірювання маси? Які переваги та недоліки цього методу?
7. Чи може електрон рухатись з швидкістю світла? Чому?
8. Наведіть приклади активної масенергії. В чому її вимірюють?
9. Як називають пасивну масенергію і в чому її вимірюють?
10. Наведіть приклади того, як пасивна масенергія перетворюється на активну і навпаки.
11. Чи змінюється маса тіла при його нагріванні; плавленні; намагнічуванні?

Вправа 28.

1. Власна довжина стержня 1,0(м). Визначте його довжину для спостерігача який рухається з швидкістю 0,6с; 0,9с; 0,99с.
2. Тіло, маса спокою якого 1,00кг рухається з швидкістю 2,5·10⁵км/с. Визначити масу цього тіла відносно нерухомої системи відліку.
3. Тіло з швидкістю v рухається відносно нерухомого спостерігача. Як зміняться відносно цього спостерігача розміри тіла; його маса; густина речовини?
4. Який імпульс та яку кінетичну енергію матиме електрон, при швидкості руху 0,9с? Маса спокою електрона 9,1·10^–31кг.
5. Маса спокою потягу 2000т. На скільки збільшиться ця маса при швидкості руху потягу 90км/год?
6. На скільки збільшується маса пружини жорсткість якої 10кН/м, при її розтягуванні на 5см?
7. Прискорювач розганяє протон до кінетичної енергії 70·10⁹ еВ. З якою швидкістю рухається протон? У скільки разів збільшується його маса?
8. Відомо, що на кожний квадратний метр навколоземного простору потрапляє 1,37·10³Дж сонячної енергії. Визначте величину тієї маси яку щосекундно втрачає Сонце. Відстань від Землі до Сонця 1,5·10¹¹м.
9. При якій швидкості, кінетична енергія частинки, дорівнює енергії спокою цієї частинки?

.

Лекційне заняття №29.

Тема: Релятивістський закон додавання швидкостей. Парадокси теорії відносності.

Як відомо, поштовхом до створення теорії відносності стала та суперечність, що виникли між ньютонівською механікою і максвелівською електродинамікою. А ця суперечність стосувалася ньютонівського закону додавання швидкостей та твердження максвелівської електродинаміки про незмінність швидкості світла.

Нагадаємо. В ньютонівському законі додавання швидкостей стверджується: якщо в рухомій системі відліку швидкість тіла u’, а ця система з швидкістю v рухається відносно нерухомої системи відліку, то швидкість тіла в нерухомій системі відліку u визначається за формулою   u=u’+v. Із даного формулювання закону випливає, що коли з ракети яка рухається зі швидкістю v випромінюється світловий фотон швидкість якого u’=c=3·10⁸м/c, то в залежності від напрямку руху ракети, швидкість світлового фотона відносно землі (нерухомої системи відліку) може бути як більшою так і меншою за 3·10⁸м/с. Іншими словами, в теорії Ньютона стверджувалося, що швидкість світла є відносною і що тому, вона може бути як більшою так і меншою за 3·10⁸м/с.

Мал.188.  Згідно з ньютонівським законом додавання швидкостей  u = u‘ + v і тому : c +v > 3·10⁸м/с;  c – v < 3·10⁸м/с.

В теорії ж Максвела стверджувалося, що швидкість світла у вакуумі визначається за формулою v = 1/ε₀μ₀, де ε₀ = 8,854·10^–12Ф/м = const; μ₀ = 12,566·10^–7Гн/м = const, і що тому, ця швидкість є абсолютно незмінною і чисельно рівною 3·10⁸м/с.

Намагаючись розв’язати дане протиріччя, Ейнштейн власне і створив свою знамениту теорію відносності. Ця теорія не лише кардинально змінила наші погляди на навколишній світ, а й довела, що для швидкостей співрозмірних з швидкістю світла, ньютонівський закон додавання швидкостей (u=u’+v) потребує суттєвого уточнення. Дійсно. Стверджуючи що u=u‘+v, Ньютон виходив з того, що в рухомій та нерухомій системах відліку, одна і таж подія має однакову часову тривалість (t=t₀) і що лінійні розміри будь якого об’єкту при переході від однієї системи відліку до іншої не змінюються (ℓ=ℓ₀).

В теорії ж відносності доводиться, що такі уявлення про час та простір є досить приблизними і що при великих швидкостях ці уявлення потребують суттєвих уточнень. В ній доводиться, що в рухомій та нерухомій системах відліку, тривалості подій та розміри об’єктів можуть суттєво відрізнятись, і що ці відмінності характеризуються співвідношеннями:  t = kt₀;  ℓ = ℓ₀/k,  де  k = 1/√(1–v²/c²)  – коефіцієнт відносності. Враховуючи ці співвідношення, Ейнштейн довів, що закон додавання швидкостей потрібно записувати не у вигляді u=u’+v, а у вигляді: u=(u’+v)/(1+u’v/c²). Дане формулювання закону прийнято називати релятивістським законом додавання швидкостей.

Висновок 5. Якщо в рухомій системі відліку швидкість тіла u’, а ця система з швидкістю v рухається відносно нерухомої системи, то швидкість даного тіла в нерухомій системі відліку u визначається за формулою u = (u’+v)/(1+u’v/c²).

Не важко довести, що для відносно невеликих швидкостей (v<<c ; u'<<c) закон u = (u’+v)/(1+u’v/c²) набуває вигляду u = u‘+v, тобто того вигляду в якому його прийнято формулювати в ньютонівській механіці. Дійсно, якщо v<<c; u'<<c, то u’v/c²≈0 і тому u = (u’+v)/(1+u’v/c²) = (u’+v)/(1+0) = u’+v. А оскільки швидкості земних макротіл в тисячі і мільйони разів менші за швидкість світла, то зрозуміло чому ми, абсолютно обгрунтовано не зважаємо на ті мікро неточності, що притаманні ньютонівському закону додавання швидкостей.

Однак, якщо мова йде про швидкості співрозмірні з швидкістю світла, то в цьому випадку, ньютонівський закон додавання швидкостей стає неприйнятно неточним. Скажімо, якщо встановлене на рухомій платформі джерело світла, випромінює фотони в напрямку руху платформи (u’=c), то застосовуючи формулу (u=u’+v), ви отримаєте принципово неправильний результат: u=u’+v=c+v>c. Натомість відповідь релятивістського закону додавання швидкостей буде такою, що співпадає як з передбаченнями теорії Максвела, так і з експериментальними фактами: u = (u’+v)/(1+u’v/c²) = (c+v)/(1+cv/c²) = (c+v)/(c+v)/c = c.

Ця відповідь буде вірною і в тому випадку, коли світлові фотони будуть летіти в протилежному (протилежному до напрямку руху платформи) напрямку: u = (u’–v)/(1–u’v/c²) = (c–v)/(1–cv/c²) = (c–v)/(c–v)/c = c. Вона буде вірною і в тому випадку якщо два фотони, швидкість кожного з яких  с=3·10⁸м/с  летітимуть назустріч один одному: u = (c+c)/(1+c∙c/c²) = 2c/2 =c. І в тому випадку коли фотони летять в протилежні сторони: u = (c–с)/(1–cс/c²) = (c–с)/(c–с)/c = c. І в тих незліченних випадках коли вектори u‘ та v направлені під будь яким кутом один до одного.

Задача 1. Дві ракети рухаються на зустріч одна одній з швидкістю 0,8с кожна. З якою швидкістю зближуються ракети?

Дано:

v₁ = v₂ = 0,8c

v_відн = ?

Загальні зауваження. Говорячи про те, що ракета (чи будь який інший фізичний об’єкт), рухається з швидкістю 0,8с, мають на увазі швидкість ракети відносно нерухомої системи відліку, а по суті – відносно нерухомого простору Всесвіту. Якщо ж мова йде про швидкість зближення ракет, то мається на увазі та швидкість з якою ракети в реальності наближаються одна до одної, яка фіксується приладами кожної з ракет, і яка визначається за формулою v_відн = (v₁+v₂)/(1+v₁∙v₂/c²).

Рішення. У відповідності з релятивістським законом додавання швидкостей v_відн = (v₁+v₂)/(1+v₁∙v₂/c²) = (0,8с + 0,8с) / (1 + 0,8с∙0,8с/с²) =  1,6с /(1 + 0,64) = 0,9756∙с.

Відповідь: v_відн = 0,9756∙с.

Ознайомившись з основами теорії відносності, а точніше тієї її частини яка називається спеціальною або частковою теорією відносності, ви не могли не помітити, що математична складова цієї теорії не надто складна. А якщо теорія відносності і виглядає складною та парадоксальною, то тільки тому, що з точки зору нашого повсякденного досвіду виразником якого є так званий «здоровий глузд», базові висновки (передбачення) цієї теорії виглядають дивними.

Дійсно, наш повсякденний досвід стверджує, що в рухомій і нерухомій системах відліку тривалість однієї і тієї ж події є однаковою (t=t₀), що довжина одного і того ж тіла є однаковою (ℓ=ℓ₀), що маса одного і того ж тіла є однаковою (m=m₀). Наш повсякденний досвід стверджує, що маса і енергія це різні речі і що маса тіла не залежить від того рухається це тіло чи не рухається. Наш повсякденний досвід стверджує, що швидкість будь якого фізичного об’єкту є відносною і що тому той хто рухається назустріч світлу, зустрінеться з цим світлом раніше, аніж той хто тікає від світла. Натомість теорія відносності доводить:

Висновок 1. Тривалість однієї і тієї ж події (або абсолютно аналогічних подій) в рухомій (t) та нерухомій (t₀) системах відліку є різною. При цьому виконується співвідношення: t = k∙t₀, де k = 1/√(1–v²/c²) – коефіцієнт відносності.

Висновок 2. Довжина одного і того ж об’єкту (або абсолютно аналогічних об’єктів) в рухомій (ℓ) та нерухомій (ℓ₀) системах відліку є різною. При цьому виконується співвідношення ℓ = ℓ₀/k, де k = 1/√(1–v²/c²).

Висновок 3. Маса одного і того ж фізичного об’єкту (або абсолютно аналогічних об’єктів) в рухомій (m) та нерухомій (m₀) системах відліку є різною. При цьому виконується співвідношення m = km₀, де k = 1/√(1–v²/c²).

Висновок 4. Будь яке тіло масою m, представляє собою згусток енергії загальна кількість якої визначається за формулою Е = mc², де с = 3·10⁸м/с = const.

Висновок 5. Якщо в рухомій системі відліку швидкість тіла u’, а ця система з швидкістю v рухається відносно нерухомої системи, то швидкість даного тіла в нерухомій системі відліку u визначається за формулою u = (u’+v)/(1+u’v/c²).

Чесно кажучи претензії «здорового глузду» до теорії відносності, м’яко кажучи необґрунтовані. І не тільки тому, що всі висновки (передбачення) цієї теорії отримали безумовне експериментальне підтвердження. Ці претензії необґрунтовані ще й тому, що жодне з тверджень теорії відносності не суперечить нашому повсякденному досвіду. Адже для тих швидкостей з якими ми зустрічаємся у повсякденному житті (v<<300 000км/с), рівняння теорії відносності набувають звичного для нас вигляду. Адже якщо v<<c, то

t = k∙t₀ набуває вигляду t = t₀;

ℓ = ℓ₀/k набуває вигляду ℓ = ℓ₀;

m = km₀ набуває вигляду m = m₀;

u = (u’+v)/(1+u’v/c²) набуває вигляду u = (u’+v).

А якщо комусь висновки теорії відносності здаються дивними та парадоксальними, то це сугубо психологічне враження. Бо теорія відносності жодним чином не суперечить ні нашому повсякденному досвіду ні теорії Ньютона яка є науковим виразником цього досвіду. Теорія відносності лише уточнює цей досвід та розширює наші знання про навколишній світ. Теорія відносності жодним чином не суперечить ньютонівській механіці, а тим більше не заперечує її. Теорія відносності, лише певним чином уточнює цю механіку, та розширює межі її достовірності.

Історія з теорією відносності є класичною ілюстрацією еволюційності розвитку науки. Адже наука влаштована таким чином, що в ній будь яка нова наукова теорія не заперечує попередню теорію, а є певним діалектичним продовженням та розвитком цієї теорії.  (Звичайно за умови, що ця попередня теорія – дійсно наукова). І це не випадково. Адже будь яка наукова теорія базується на певній сукупності експериментальних фактів і підтверджується відповідною сукупністю цих фактів. А це означає, що заперечувати наукову теорію, це все рівно ніби заперечувати ті факти на яких ця теорія базується і якими підтверджується. Як вдало зауважив відомий французький математик, фізик та філософ Анрі Пуанкаре: “Розвиток науки, потрібно порівнювати не з перебудовою міста, де старі будинки безжально руйнуються і на їх місці з’являються нові, а з еволюційним розвитком зоологічних видів.”

         Говорячи про теорію відносності ми неодноразово наголошували на тому, що ця теорія представляється складною, незрозумілою та парадоксальною лише тому, що багато з її тверджень суперечать так званому «здоровому глузду». Зважаючи на ці обставини, завжди знаходяться люди, які вважають за необхідне відшукати в теорії відносності певні суперечності (протиріччя) і тим самим, спростувати цю «безглузду» теорію.

Звісно, жодна з подібних спроб не закінчилась і не могла закінчитись чимось путнім. Адже теорія відносності, це не просто кимось придумана науковоподібна байка, а наукова теорія, тобто цілісна система достовірних знань, яка базується на непохитному фундаменті експериментальних фактів. І ці факти не може спростувати жодна примха «здорового глузду». А тим більше в ситуації, коли при уважному, неупередженому аналізі, ті протиріччя які віднаходить «здоровий глузд» в теорії відносності, завжди виявляються надуманими, ілюзорними та маніпулятивними. Зазвичай ці надумані протиріччя теорії відносності називають парадоксами (від лат. paradoxos – дивний, неочікуваний).

Різноманіття тих парадоксів які вбачає «здоровий глузд» в теорії відносності, можна розділити на дві групи: 1) парадокси, які намагаються спростувати принцип відносності; 2) парадокси, які намагаються спростувати принцип постійності швидкості світла.

Нагадаємо. Принцип відносності – це базовий закон, в якому стверджується: у всіх інерціальних системах відліку, тобто таких системах, де виконується закон інерції, всі фізичні процеси відбуваються абсолютно однаково. Принцип постійності швидкості світла – це базовий закон, в якому стверджується: у всіх інерціальних системах відліку швидкість світла є незмінною і чисельно рівною 3·10⁸м/с, при цьому жодний фізичний об’єкт і жодний інформаційний сигнал не може рухатись з більшою швидкістю.

Левову частину парадоксів теорії відносності складають ті, які «спростовують» принцип постійності швидкості світла. Суть цих парадоксів зводиться до того, що в них наводяться «очевидні» приклади того, коли швидкість певних об’єктів перевищує швидкість світла. На основі цих прикладів, робиться висновок про те, що принцип постійності швидкості світла є хибним, а відповідно хибна і та теорія яка базується но цьому принципі. Що ж, давайте поговоримо про ті об’єкти які рухаються з надсвітловими швидкостями і про те, що це означає.

Перш за все зауважимо, що твердження: в інерціальних системах відліку жоден фізичний об’єкт не може рухатись з надсвітловою швидкістю, зовсім  не означає, що сторонній спостерігач не може бачити, як певні реальні об’єкти рухаються з надсвітловими швидкостями. Скажімо, дивлячись на зоряне небо, ви скоріш за все не підозрюєте, що та кругова швидкість з якою зірки видимо обертаються навколо Землі, у тисячі і мільйони разів перевищує швидкість світла.

Дійсно. Відомо, що найближча до Сонячної системи зірка (її називають Альфа Центавра) знаходиться на відстані 4,4 світлових років (4,2·10¹⁶м). Спостерігаючи за цією зіркою, жителі Землі бачать, що вона, робить один оберт навколо Землі за одну добу. Виходячи з цього, можна зробити висновок: швидкість обертального руху Альфа Центаври навколо Землі, становить  v = 2πR/T = 3·10¹²м/с , а це у 10 000 разів перевищує швидкість світла.

Ясно, що в даному випадку мова йде про певну ілюзорну швидкість, яка обумовлена не рухом самої зірки, а фактом обертання Землі навколо своєї осі. І тим не менше таку надсвітлову швидкість руху зірки можна спостерігати і певним чином фіксувати. Однак це зовсім не означає, що відповідна зірка дійсно рухається з надсвітловою швидкістю і що тому, принцип постійності швидкості світла, а відповідно і теорія відносності є хибними.

Втім, можна навести безліч прикладів, коли швидкість певних фізичних об’єктів (зазвичай об’єктів умовних) дійсно перевищує 300 000км/с. Розглянемо один з таких прикладів. Припустимо, що в центрі величезної сфери знаходиться прожектор, тонкий промінь якого утворює на внутрішній поверхні сфери світлову пляму – «зайчик» (мал.188). Ясно, що за один оберт прожектора «зайчик» опише коло довжиною 2πR. При цьому швидкість руху «зайчика» становитиме v=2πR/T. А оскільки радіус сфери може бути необмежено великим, то відповідно необмежено великою може бути і та швидкість, з якою «зайчик» рухається поверхнею сфери. Скажімо, якщо один повний оберт прожектора відбувається за одну секунду (Т=1с), а радіус сфери дорівнює 100000км, то швидкість руху «зайчика» становитиме v=2πR/T=628 000км/с, що більш як вдвічі перевищує швидкість світла у вакуумі. І це буде не якась ілюзія, а реальне переміщення світлової плями поверхнею реальної сфери з швидкістю більшою за швидкість світла.

Мал.189. Швидкість руху світлового «зайчика» може бути більшою за швидкість світла.

Вище описана ситуація є цілком можливою. Однак, чи суперечить даний факт принципу відносності? Нагадаємо, в цьому принципі стверджується: в інерціальних системах відліку, жоден фізичний об’єкт і жоден інформаційний сигнал, не можуть рухатись з швидкістю більшою за 300 000км/с. Не будемо сперечатись відносно того, наскільки інерціальною є та система відліку в якій обертальним чином рухається світловий «зайчик». Зупинимся лише на аналізі того, чи є цей рух, рухом певного фізичного об’єкту і чи можна вважати рух світлового «зайчика» таким, що здатний забезпечити передачу інформаційного сигналу з надсвітловою швидкістю.

В певному сенсі, ту світлову пляму яку прийнято називати світловим «зайчиком», можна назвати певним фізичним об’єктом. Однак ви маєте розуміти, що рух цього об’єкту поверхнею сфери, не є результатом переміщення того матеріалу з якого виготовлено цей об’єкт. Дійсно. Світлову пляму утворюють ті світлові фотони, джерелом яких є прожектор. І якщо ми бачимо, що ця пляма перемістилась з точки 1 в точку 2, то це зовсім не означає, що відповідно перемістились і ті фотони які утворили пляму в точці 1. Адже пляма в точці 1 і пляма в точці 2, утворені абсолютно різними фотонами. Таким чином, неупереджений аналіз показує, що рух світлового «зайчика» не пов’язаний з переміщенням того матеріалу (тих світлових фотонів), з якого цей «зайчик» виготовлено. А це означає, що відповідний рух не є рухом реального фізичного об’єкту.

Ви можете запитати: «А чи не можна використати світловий «зайчик» в якості того інформаційного сигналу, який поширюється з надсвітловою швидкістю?». Ні неможна! Не можна тому, що той «зайчик» який знаходиться в точці 1 і той, який знаходиться в точці 2, це два абсолютно різні «зайчики». І яку б інформацію ви не написали на тому «зайчику» який знаходиться в точці 1, вона з надсвітловою швидкістю не потрапить в точку 2. Не потрапить навіть тоді, якщо ви придумаєте якийсь неймовірно хитрий спосіб кодування. Наприклад кодування шляхом зміни кольору «зайчика», його яскравості, форми, швидкості та напрямку руху, тощо. Адже реалізація всіх цих кодувань  може відбутися лише в тому місці, де знаходиться прожектор. А в це місце жоден «зайчик» не може потрапити швидше за світло.

Таким чином, факт того що світловий «зайчик» може переміщуватись з надсвітловою швидкістю, абсолютно не суперечить принципу постійності швидкості світла. Не суперечить по-перше тому, що рух світлового «зайчика» не є рухом реального фізичного об’єкту. А по-друге тому, що цей рух не може забезпечити передачу інформаційного сигналу з надсвітловою швидкістю.

«Здоровий глузд» може придумати безліч інших прикладів того коли, як йому здається, порушується принцип постійності швидкості світла. Одним з таких прикладів є так званий парадокс ножиць. Уявіть собі гігантські ножиці, маленькі кільця та вісь обертання яких знаходяться на Землі, а кінці лез сягають крайньої планети Сонячної системи (планети Нептун). І от ви, легким поштовхом руки зближуєте малі кільця ножиць і бачите як кінці їх лез зближуються з швидкістю, що перевищує швидкість світла.

Мал.190. Чи можуть маніпуляції з кільцями ножиць, передаватися до віддалених країв цих ножиць з швидкістю більшою за швидкість світла?

Залишимо у спокої питання про те, наскільки реальною є перспектива створення вище описаної абракадабри. Припустимо, що така абракадабра існує. І от ви туди – сюди рухаєте маленькі кільця ножиць, і в режимі азбуки Морзе передаєте інформаційні сигнали з швидкістю більшою за швидкість світла. А що, стверджують прихильники дикунських теорій (здоровим глуздом, тут звісно й не пахне), – в принципі можливо.

Та ні, дорогенькі – не можливо. Бо якими б фантастичними не були ваші ножиці, а вони неминуче складаються з певних частинок (атомів, молекул, іонів, нейтронів чи чого завгодно). І не можуть ваші маніпуляції з маленькими кільцями передаватися до країв фантастичних ножиць з швидкістю більшою за швидкість світла. А всі ці розмови про абсолютно тверді та абсолютно жорсткі тіла, не відміняють факту того, що всі ці тіла складаються з певних частинок, швидкість взаємодії між якими не може бути більшою за швидкість світла.

До речі, якби такі ідеально тверді та ідеально жорсткі тіла існували, то не треба було б вигадувати абракадабру з ножицями. Достатньо було б взяти відповідну палицю та в режимі азбуки Морзе штурхати нею Нептуна. При цьому корисна інформація для інопланетян передавалась би не те що з швидкістю світла, а практично миттєво.

Ясно, що немає сенсу розглядати та аналізувати все різноманіття подібних до парадоксу ножиць абракадабр. Просто зауважимо, що нема жодного реального доказу того, що принцип постійності швидкості світла не виконується. Натомість є мільйони доказів його достовірності.

Другу групу парадоксів теорії відносності складають ті, в яких «спростовується» принцип відносності. Про один з таких парадоксів, – парадокс близнюків, ви вже знаєте. Нагадаємо, суть цього парадоксу полягає в наступному. Той спостерігач який знаходиться на Землі бачить, що в рухомій ракеті (v=const) всі події відбуваються повільніше, що всі її об’єкти певним чином сплющені, що маси цих об’єктів в певне число разів збільшені, тощо. Виходячи з цього і не відчуваючи руху самої Землі, цей спостерігач цілком обгрунтовано стверджує, що рухомою є ракета. Той же спостерігач який знаходиться в ракеті бачить, що на Землі всі події відбуваються повільніше, що на Землі всі об’єкти сплющені і що їх маси в певне число разів збільшені. Виходячи з цього і не відчуваючи руху самої ракети цей спостерігач з не меншим обгрунтуванням стверджує, що рухомою є не ракета а Земля.

Таким чином, у повній відповідності з принципом відносності, ми отримали очевидно парадоксальну ситуацію. Ситуацію, в якій два спостерігачі, на основі аналізу об’єктивних фактів, роблять два діаметрально протилежні передбачення. Виходячи з цього можна зробити висновок про те, що принцип відносності є внутрішньо суперечливим, а отже хибним.

Втім, відповідь теорії відносності на подібні аргументи загально відома. Дійсно. Допоки ракета рухається з постійною швидкістю, можна скільки завгодно сперечатись з приводу того хто рухається, Земля чи ракета. Однак для того щоб перевірити чия точка зору є правильною, потрібно зустрітися. А це означає, що комусь прийдеться повертатися. І цьому «комусь», Природа неодмінно скаже, що саме він знаходиться в рухомій системі відліку і що тому всі події він має оцінювати з позицій такої системи. І якщо цей рухомий спостерігач «проспить» ті моменти коли Природа вказуватиме на факт його руху, то це не є проблемою Природи і не є проблемою принципу відносності. Бо повернувшись на Землю він неодмінно з’ясує, що всупереч тому що він бачив, і що фіксували його прилади, земляни прожили більше часу ніж прожив він і відповідно більше постаріли.

Варто зауважити, що в ряду тих надуманих тверджень, які називаються парадоксами теорії відносності, парадокс близнюків займає особливе місце. І це особливе місце обумовлено тим, що в парадоксі близнюків, факт залежності плину часу від швидкості руху системи відліку, маніпулятивно пов’язують з такими психологічно чутливими поняттями як процес старіння чи не старіння, подорож в минуле та майбутнє, взаємозв’язки між батьками та дітьми, тощо.

І от вже ми починаємо розмірковувати над тим, а як це може бути, щоб в рухомій системі відліку старіння відбувалось повільніше. А якщо згідно з принципом відносності в рухомій та нерухомій системах відліку всі фізичні процеси відбуваються абсолютно однаково, то чому в рухомій ракеті час тече повільніше? А на якому етапі руху ракети люди старіють менше, на етапі її розгону, зупинки, повороту чи рівномірного руху? А чи постаріють менше ті астронавти які не будуть повертатися на Землю? І таких психологічно чутливих питань можна поставити безліч.

І от вже ми забуваємо про суть теорії відносності, про об’єктивність законів Природи, про експериментальні факти та докази, і починаємо демагогічно наполягати на тому, що теорія відносності якась незрозуміло суперечлива, а отже неправильна. Втім, критично мислячі люди вже давно зрозуміли, що в Природі загалом і в науці зокрема, критерієм істини є не те, що нам подобається чи не подобається і не те, що нам зрозуміло чи не зрозуміло, а його величність експеримент. Експериментальні ж факти безумовно доводять, що теорія відносності загалом та її твердження про відносність часу зокрема, є безумовно правильними.

А що стосується факту того, що в теорії відносності деякі речі здаються незрозумілими і парадоксальними, то в цьому нічого дивного нема. Бо вкотре нагадую, Природа влаштована таким дивним чином, що її найпростіші об’єкти є найскладнішими. Найскладнішими в тому сенсі, що надзвичайно складно а то й неможливо пояснити як вони влаштовані і на що це схоже. А одним з таких елементарно простих і в той же час надскладних фізичних об’єктів є те, що у фізиці називають простір–час. Власне про властивості цього самого простору–часу та про його нерозривний зв’язок з тими об’єктами та тими подіями які в ньому знаходяться та відбуваються і розповідає теорія відносності. Розповідає переконливо, аргументовано та доказово.

       До числа парадоксів теорії відносності можна віднести не лише ті, що стосуються її базових принципів, а й ті які пов’язані з законом збереження енергії. Дійсно. В теорії відносності стверджується, що в незалежності від того наближається спостерігач до джерела світлових фотонів чи віддаляється від нього, швидкість цих фотонів відносно спостерігача, має бути незмінною – 3·10⁸м/с. З іншого ж боку, згідно з законом збереження енергії, той спостерігач який рухається назустріч світловому фотону, при цій зустрічі має отримати більший енергетичний імпульс, аніж той, який «тікає» від фотона.

  

Мал.191. При зустрічі з фотоном, спостерігач А має отримати більший енергетичний імпульс. (Закон збереження енергії).

Таким чином, ми отримали парадоксальну ситуацію. З одного боку, назустріч спостерігачам летять два абсолютно однакових фотони (фотони з однаковою довжиною хвилі λ₀, з однаковою частотою ν₀ та однаковою енергією E₀=hc/λ₀=hν₀ ). З іншого боку, у відповідності з законом збереження енергії, величина того енергетичного імпульсу, який при зустрічі з фотоном повинен отримати кожний спостерігач, має бути різною (Е_А>Е_В).

Втім, даний парадокс має своє пояснення, яке безумовно доводить, що ніякого протиріччя між теорією відносності та законом збереження енергії, нема. Це пояснення називається ефектом Доплера. Нагадаємо, в 1842 році австрійський фізик Христіан Доплер з’ясував: частотні параметри будь яких хвиль, в тому числі і світлових (електромагнітних), певним чином залежать як від швидкості та напрямку руху джерела цих хвиль, так і від швидкості та напрямку руху того спостерігача який їх фіксує. По суті це означає, що в умовах представленої на мал.191 ситуації, той спостерігач який рухається назустріч світловому фотону (спостерігач з ракети А), побачить цей фотон як такий, що має більшу частоту, а отже – і більшу енергію. Натомість, той спостерігач який «тікає» від фотона (спостерігач з ракети В), сприйме цей фотон як такий, що має меншу частоту, а отже і відповідно меншу енергію. Умовно кажучи, якщо базовий фотон є «зеленим», то перший спостерігач побачить його «синім», а другий – «червоним».

Ми розглянули лише декілька показових прикладів, якими прихильники «здорового глузду», а по суті сучасні алхіміки намагаються спростувати теорію відносності. І таких потуг можна навести велику множину. Але от парадокс, всі потуги сучасних алхіміків представити теорію відносності як таку, що суперечить «здоровому глузду» та реальним фактам, закінчуються одним – пшиком. А ті парадокси які з точки зору «здорового глузду» здаються такими, що спростовують теорію відносності, насправді виявляються надуманими, ілюзорними та маніпулятивними. А якщо в тій чи іншій ситуації ми не можемо визначити яка з систем відліку є рухомою, а яка нерухомою, яка інерціальною, а яка неінерціальною, то це ж не проблеми Природи та теорії відносності, а проблеми нашого «здорового глузду» та браку знань.

Контрольні запитання.

1. В чому суть тих протирічь, які виникли між ньютонівською механікою та максвелівською електродинамікою?
2. Чи є релятивістський закон додавання швидкостей таким, що відміняє ньютонівський закон додавання швидкостей?
3. Чому ми стверджуємо, що теорія відносності не відміняє ньютонівську механіку, а лише уточнює її?
4. Чому нові наукові теорії не відміняють попередні наукові теорії?
5. Наведіть приклади тих ситуацій в яких ми бачимо об’єкти, що рухаються з надсвітловими швидкостями. Чи спростовують ці ситуації теорію відносності?
6. Чому рух світлового «зайчика» не можна вважати рухом реального фізичного об’єкту?
7. Чи може той світловий «зайчик» який переміщується з надсвітловою швидкістю, з такою ж швидкістю передавати інформаційні сигнали? Чому?
8. Поясніть суть «парадоксу ножиць». Чи можуть такі ножиці передавати інформаційні сигнали з надсвітловою швидкістю? Чому?
9. Поясніть суть «парадоксу близнюків». Чи доводить цей парадокс що принцип відносності є хибним?

                   Вправа 29.

1. Відносно нерухомого спостерігача, дві ракети рухаються назустріч одна одній з швидкостями 0,9с кожна. Яку швидкість руху ракети зафіксує той спостерігач який знаходиться в одній із них?
2. Відносно нерухомого спостерігача, дві ракети рухаються назустріч одна одній з швидкостями 2,0·10⁸м/с кожна. На скільки відрізняються швидкості їх відносного руху визначені за ньютонівською та релятивістською формулами додавання швидкостей?
3. Два електрони рухаються вздовж однієї прямої з швидкостями 0,9с і 0,8с відносно нерухомого спостерігача. Яка відносна швидкість електронів при їх русі: в одному напрямку; в протилежних напрямках?
4. Відомо, що відносна швидкість двох електронів що летять назустріч один одному 0,9с. при цьому швидкість одного з них 0,7с . Яка швидкість другого електрона?
5. Жителі Землі бачать, що зірка А, відстань до якої 30св.років за добу робить повний оберт навколо Землі. Визначте видиму швидкість обертання зірки. Як пояснити даний факт.
6. Земляни бачать, що зірка Х відстань до якої 500 св. років, за добу робить повний оберт навколо Землі. Яка видима швидкість руху цієї зірки? Чи означає цей факт, що зірка Х дійсно рухається з такою швидкістю?

 .

Лекційне заняття №30.

Тема: Основи загальної теорії відносності. Про геометричну суть тяжіння.

         Відповідаючи на чисельні привітання з нагоди присудження Нобелівської премії, Ейнштейн якось зауважив: «Навіщо стільки слів. Я просто не відступав у своїй роботі. От і все.» Здатність Ейнштейна доводити до повної ясності рішення будь якої наукової проблеми, була дивовижною. Поставивши за мету усунути наявні протиріччя між ньютонівською механікою та максвелівською електродинамікою, і послідовно дотримуючись надійно підтверджених принципів, Ейнштейн в 1905 році створив нову теорію, яку сьогодні називають спеціальною теорією відносності, або частковою теорією відносності, або просто – теорією відносності. Ця теорія не лише гармонізувала відносини між ньютонівською механікою та максвелівською електродинамікою, а й об’єднала ці на перший погляд абсолютно різні теорії в єдине гармонічне ціле. Лише цього було б достатньо, щоб поставити Ейнштейна в ряд найвидатніших вчених всіх часів і народів.

Та Ейнштейн не був би Ейнштейном, якби зупинявся на півдорозі. Розуміючи значимість створеної ним теорії, Ейнштейн як ніхто інший бачив і її недоліки, точніше – межі достовірності. Ці межі обумовлені двома обставинами. По-перше, часткова теорія відносності в точності справедлива лише для так званих інерціальних систем відліку. В Природі ж існує безліч систем відліку які не є інерціальними. Скажімо звична для нас «земна» система відліку, строго кажучи неінерціальна. Неінерціальна тому, що обертаючись навколо Сонця та своєї осі, Земля, а разом з нею і всі її об’єкти, рухаються з певним прискоренням.

По-друге, часткова теорія відносності не була органічно пов’язаною з ньютонівською теорією тяжіння. Більше того, ці теорії певним чином суперечать одна одній. Суперечать бодай тому, що в ньютонівській теорії тяжіння, гравітаційні взаємодії передаються миттєво. Теорія ж відносності стоїть на тому, що жодні сигнали та жодні взаємодії не можуть поширюватися швидше за 3·10⁸м/с.

Розуміючи обмеженість часткової теорії відносності, Ейнштейн ставить нову задачу – створити більш загальну теорію. Теорію, яка б була  справедливою для будь якої системи відліку і яка б кількісно пояснювала не лише механічні та електромагнітні явища, а й явища гравітаційні. Вирішуючи дану задачу, Ейнштейн звертає увагу на факт того, що маса одночасно є як мірою гравітації так і мірою інерції. Він розуміє, що цей факт безумовно вказує на те, що між гравітацією, тобто здатністю тіла створювати поля тяжіння, та інерцією, тобто здатністю тіла зберігати стан свого рівномірного руху, існує певний зв’язок.

Потрібно зауважити, що в ньютонівській механіці терміном маса (m) позначають фактично дві різні фізичні величини: інерційна маса (m_i) та гравітаційна маса (m_гр). Дійсно. В другому законі Ньютона стверджується: чим більша маса тіла, тим важче змінити його швидкість. По суті це означає, що в другому законі Ньютона маса є мірою інерціальних властивостей тіла (m=m_i). З іншого боку, в законі всесвітнього тяжіння стверджується: сила гравітаційної взаємодії пропорційна добутку взаємодіючих мас. А це означає, що в цьому законі маса є мірою гравітаційних властивостей тіла (m=m_гр).

Вважаючи інерцію і гравітацію абсолютно різними явищами, Ньютон вводить в наукову практику дві фактично різні величини – інерційну масу (m_i) та гравітаційну масу (m_гр). Однак, дивовижним чином з’ясовується, що ці різні величини є еквівалентними. Це означає, що при узгодженому виборі одиниць вимірювання, маса тіла виміряна на основі другого закону Ньютона, в точності дорівнює тій масі яка виміряна на основі закону всесвітнього тяжіння (m_i=m_гр). Вперше, факт еквівалентності інерційної та гравітаційної мас був експериментально встановлений самим Ньютоном. Аналізуючи параметри руху різних маятникових систем, Ньютон з’ясував: інерційна та гравітаційна маси з точністю 0,01% еквівалентні. Подальші дослідження довели, що гравітаційна та інерційна маси еквівалентні при будь якій практично досяжній точності вимірювань (на сьогоднішній день, ця точність становить 1·10^–12%).

Факт еквівалентності інерційної та гравітаційної мас оцінювався Ньютоном та наступними поколіннями вчених як певний випадковий збіг. І лише геніальний Ейнштейн побачив за цим на перший погляд випадковим збігом, глибинну фізичну суть. Він зрозумів, що гравітація та інерція, це не просто взаємопов’язані явища, а два різні слова якими позначають різні прояви одного і того ж природнього явища. Пояснюючи суть цього парадоксального твердження, проведемо наступний уявний експеримент.

Уявіть собі закриту ізольовану кабіну яка стоїть на поверхні планети, наприклад Землі (мал.192). Перебуваючи в кабіні і випускаючи з рук яблука та інші тіла, спостерігач неодмінно з’ясує, що вони падають з певним прискоренням –прискоренням вільного падіння g. Вважаючи свою систему відліку інерціальною, тобто такою в якій прискорений рух тіла відбувається лише під дією певної зовнішньої сили, спостерігач зробить висновок: тіла падають тому, що на них діє гравітаційна сила (сила тяжіння) яку створює та планета що знаходиться під кабіною.

Тепер уявіть, що одного разу, коли спостерігач спав, планета миттєво зникла, а натомість, під дією певної зовнішньої сили, кабіна почала підніматись з прискоренням а, величина якого в точності дорівнює прискоренню вільного падіння а=g. Прокинувшись, спостерігач бачить, що яблука та інші тіла, як і раніше падають з прискоренням g. Не помітивши жодних змін у поведінці тіл, він буде наполягати на тому, що його система відліку як і раніше є інерціальною, і що як і раніше кабіна знаходиться в гравітаційному полі планети. І це при тому, що насправді ситуація кардинально змінилась. Адже тепер, під кабіною ніякої планети нема, а зв’язана з кабіною система відліку стала неінерціальною.

З огляду на вище сказане, запитується: чи може той спостерігач який знаходиться в закритій ізольованій кабіні визначити, чому падають тіла: тому, що на них діє сила тяжіння F_т=mg, яка створюється гравітаційним полем планети; чи тому, що на них діє сила інерції  F_i=mg, яку створює прискорений рух самої кабіни?

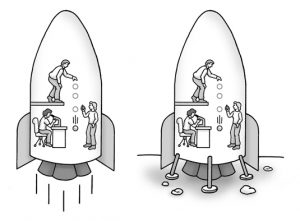
Мал.192. Перебуваючи в закритій ізольованій кабіні не можливо визначити, що є причиною падіння тіл: гравітаційне поле планети (сила тяжіння), чи прискорений рух самої кабіни (сила інерції).

Аналізуючи дану та їй подібні ситуації, Ейнштейн приходить до висновку: ніякими експериментами які проводяться в закритій ізольованій кабіні не можливо встановити, що є причиною падіння тіл – гравітаційне поле планети (сила тяжіння) чи інерційне поле самої прискорено рухомої кабіни (сила інерції). Не можливо тому, що силові прояви сили тяжіння та сили інерції є еквівалентними. А зважаючи на цю еквівалентність, можна стверджувати: в інерціальних та неінерціальних системах відліку всі фізичні процеси відбуваються абсолютно однаково.

Таким чином, аналізуючи експериментальні факти, зокрема факт еквівалентності інерційної і гравітаційної мас, та спираючись на результати багатьох реальних та уявних експериментів, Ейнштейн з притаманною йому чіткістю формулює три базові принципи:

1. Загальний принцип відносності: в інерціальних та неінерціальних системах відліку всі, фізичні процеси відбуваються абсолютно однаково.
2. Загальний принцип постійності швидкості світла: в інерціальних та неінерціальних системах відліку, ніякі взаємодії і ніякі інформаційні сигнали, в тому числі і гравітаційні, не можуть поширюватися з швидкістю більшою за швидкість світла у вакуумі.
3. Принцип еквівалентності: силові прояви гравітації та інерції є еквівалентними.

Спираючись на ці базові принципи, Ейнштейн в 1916 році створює загальну теорію відносності. Теорію, яка кількісно пояснила все різноманіття механічних, електромагнітних та гравітаційно-інерційних явищ, і яка була достовірною для будь якої системи відліку.

Потрібно зауважити, що в загальній теорії відносності Ейнштейн не просто постулював факт того, що силові прояви гравітації та інерції є еквівалентними, а й зумів пояснити ті очевидні відмінності які існують між цими проявами. Ілюструючи суть цих відмінностей проведемо наступний уявний експеримент.

Уявіть собі ізольовану кабіну, яка в одному випадку знаходиться в гравітаційному полі планети, а в іншому – рухається з прискоренням вільного падіння відповідної планети (a=g). Перебуваючи в цих кабінах експериментатори випускають з рук по два яблука і спостерігають за траєкторією їх руху (мал.193). При цьому вони з’ясують, що ті яблука які падають в гравітаційному полі планети, в процесі падіння наближаються одне до одного. Натомість траєкторії руху тих яблук які падають в прискорено рухомій кабіні є строго паралельними.

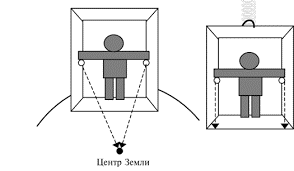
Мал.193. В гравітаційному полі планети та в інерційному полі рухомої кабіни, тіла падають суттєво по різному.

Ясно, що факт зближення вільно падаючих яблук, буде суттєвим лише в тому випадку, коли розміри кабіни та масштаб руху яблук будуть співрозмірними з розмірами тієї планети яка створює відповідне гравітаційне поле. І як ви розумієте, створити таку експериментальну кабіну надзвичайно складно. Однак, якщо мати на увазі принциповий бік питання, то потрібно визнати, що певні відмінності між геометричною структурою істинно–гравітаційного та інерційно–гравітаційного поля все ж існують.

Факт певних відмінностей між істинно–гравітаційними та інерційно–гравітаційними полями здається мізерно несуттєвим. Однак Ейнштейн не був би Ейнштейном якби не звертав увагу на здавалося б незначущі факти. Будучи переконаним в тому, що силові прояви гравітації і інерції є еквівалентними, та намагаючись пояснити ті відмінності які існують між геометричною структурою гравітаційного поля планети та інерційного поля прискорено рухомої кабіни, Ейнштейн приходить до висновку: гравітація нерозривно пов’язана з певним викривленням навколишнього простору, а точніше того, що прийнято називати чотири вимірним простором-часом. Власне ідея про те, що гравітація певним чином впливає на параметри простору та часу і є тією ключовою ідеєю  яка блискуче реалізована в загальній теорії відносності.

Адже в цій теорії по суті стверджується, що гравітацію можна представити як результат геометричного викривлення простору. На перший погляд, обгрунтованість такого твердження є сумнівною. Однак, з’ясувавши суть проблеми, починаєш розуміти, що ейнштейнівське тлумачення фізичної суті того, що прийнято називати гравітаційним полем є цілком закономірним та логічно обгрунтованим. Адже коли ми стверджуємо, що масивне тіло створює гравітаційне поле, то по суті це означає, що відповідне тіло певним чином збурює навколишній простір. І якщо параметри цього простору прийнято характеризувати довжиною, площею, об’ємом та кривизною поверхні, то чому нас дивує те, що збурений простір виглядає як простір викривлений?

Та як би там не було, а фактом залишається те, що згідно з загальною теорією відносності, в зображеній на мал.193 ситуації, встановити причину падіння тіл в кабіні, ви не зможете. Не зможете тому, що в результаті викривлення того простору яке створюється масивною планетою і яке ми називаємо гравітаційним полем планети, ті прямі які на мал.193а зображені непаралельними, за показаннями будь яких об’єктивних приладів будуть паралельними. А це означає, що які б експерименти не проводились в закритій ізольованій кабіні, вони не зможуть встановити, чому в цій кабіні падають тіла: тому, що під нею знаходиться певна масивна планета, чи то тому, що сама кабіна з певним прискоренням рухається. І потрібно зауважити, що це не домисли теорії, а експериментально встановлений факт.

Таким чином, та ситуація яка представлена на мал.193, і яка на думку «здорового глузду» є беззаперечним доказом нееквівалентність силових проявів гравітації та інерції, а отже і доказом не достовірності загальної теорії відносності, в реальності є черговим парадоксом, який суперечить експериментальним фактам.

Що правда, даний парадокс настільки правдоподібний, що важко повірити в його хибність. І тим не менше, експериментальні факти безумовно доводять, що силові прояви інерції та гравітації дійсно еквівалентні, і що ніякими експериментами які проводяться в закритій ізольованій кабіні не можливо встановити, чому падають тіла: тому що на них діє сила тяжіння, чи тому що на них діє сила інерції.

Крім всього іншого, в загальній теорії відносності стверджується, що параметри простору–часу певним чином залежать не лише від швидкості руху фізичного об’єкту, а й від потужності того гравітаційного поля в якому ці параметри вимірюються: чим потужніше гравітаційне поле, тим повільніший плин часу та менші розміри простору.

Звісно, в умовах відносно слабкого гравітаційного поля Землі, ефекти залежності просторово–часових параметрів об’єктів та подій від параметрів цього поля є малопомітними. Однак навіть ці малопомітні ефекти можна виміряти. Достатньо сказати, що сучасні системи GPS враховують поправки на гравітаційне сповільнення часу. Якщо ж мова йде про такі надпотужні джерела гравітаційного поля як нейтронні зірки та чорні діри, то в їх околицях гравітаційний вплив на параметри простору–часу стає визначально великим. Скажімо в надрах чорних дір плин часу практично припиняється, а простір ущільнюється до розмірів геометричної точки.

Оскільки два із трьох базових тверджень загальної теорії відносності, є розширеними формулюваннями базових тверджень спеціальної (часткової) теорії відносності, то ясно, що спеціальна теорія відносності є органічною частиною загальної теорії відносності. А це означає, що всі висновки, передбачення та ефекти спеціальної теорії відносності, одночасно є і висновками, передбаченнями та ефектами загальної теорії відносності.

Говорять, що одного разу на запитання сина: «Татку, а чому ти такий знаменитий?», Ейнштейн відповів: «Розумієш, коли сліпий жук повзе поверхнею великої кулі, то не помічає що пройдений ним шлях викривлений. Мені ж пощастило це помітити».

Знаєте, в історії науки є такі поворотні моменти, які кардинально змінюють хід цієї історії. При цьому невідомо, яким би чином склалася ця історія, якби не ті видатні особистості які помічають те, чого не помічають інші. Скажімо в 17-му столітті Галілео Галілей (1564–1642) помітив, що та дорога наукового пізнання яку вказав людству великий Аристотель (384–322 р.р. до н.е.), і якою людство безуспішно крокувало два тисячоліття, є дорогою в нікуди. Бо критерієм істини є не логічність обгрунтувань (як вважав Аристотель), а його величність експеримент. В 19-му столітті Майкл Фарадей (1791–1867) помітив, що в Природі окрім тих об’єктів які називаються речовинами, існують невидимі, невідчутні і тим не менше матеріальні об’єкти які називаються полями. І от нарешті в 20-му столітті Альберт Ейнштейн помітив, що час, простір, матерія та рух, то частини єдиного цілого і що гравітація та інерція, а по суті матерія та рух, є певними викривленнями того, що ми називаємо простором – часом.

Спираючись на факт еквівалентності інерційної і гравітаційної мас, та прагнучи пояснити ті на перший погляд очевидні відмінності між геометричною структурою гравітаційного поля планети та інерційного поля прискорено рухомої кабіни (мал.192), Ейнштейн дійшов висновку, що гравітаційне поле створює певне геометричне викривлення простору–часу. Математичною реалізацією цього висновку і стала загальна теорія відносності.

Наочні уявлення про геометричну суть тяжіння, можна отримати на основі наступного експерименту. Уявіть собі горизонтальну поверхню виготовлену із тонкого шару пружно–еластичної гуми. Цю поверхню ми будемо розглядати як певну модель двовимірного (плоского) простору. При цьому, якщо дана горизонтальна поверхня є геометрично рівною (не викривленою), то її можна вважати певним аналогом гравітаційно не збуреного простору, тобто простору в якому нема гравітаційного поля.

Нагадаємо. Коли ми стверджуємо, що в даній точці простору нема гравітаційного поля, то це означає, що при внесенні в цю точку пробної маси, на неї не буде діяти гравітаційна сила і що тому, ця маса нерухомо залишиться у відповідній точці. Якщо ж пробна маса відчує дію гравітаційної сили, то вона почне відповідним чином переміщуватися, вказуючи тим самим на наявність та параметри гравітаційного поля.

Поклавши пробну кульку на геометрично не викривлену гумову поверхню та з’ясувавши що кулька залишається на місці, ми робимо висновок: в геометрично не викривленому «гумовому просторі» гравітаційного поля нема. Тепер внесемо в наш «гумовий простір» масивне тіло (мал.194). Під його вагою, гума прогнеться і відповідний простір стане викривленим. Досліджуючи цей викривлений простір, ви неодмінно з’ясуєте,  що в ньому пробна кулька прискорено скочується до джерела викривлення. А це означає, що в геометрично викривленому просторі, силове поле є.

Мал.194. В геометрично не викривленому «гумовому просторі» силового поля нема, а в геометрично викривленому – є.

Подібні експерименти наводять на думку, а чи не можна реальне гравітаційне поле представити як результат викривлення реального простору. Власне така ідея і була блискучу реалізована в загальній теорії відносності. Звичайно, наочно представити викривлення тривимірного простору практично не можливо. Не можливо тому, що ми ніколи і ніде не бачили тривимірної поверхні. А зважаючи на те, що в теорії відносності говориться про викривлення чотиривимірного  простору–часу, наочне представлення такого викривлення стає ще менш можливим. Однак, те що не під силу нашій уяві, можна представити у вигляді математичних моделей та формул.

Виходячи з базових принципів загальної теорії відносності та застосовуючи сучасний математичний аналіз, Ейнштейн записав систему рівнянь, які відображають той кількісний зв’язок що існує між мас–енергією (джерелом гравітаційного поля) та параметрами простору–часу. Ці рівняння не лише кількісно пояснили все різноманіття відомих гравітаційних явищ, а й зробили сучасну теорію тяжіння невід’ємною складовою цілісної системи знань.

Математична та фізична суть ейнштейнівських рівнянь досить складна. Тому,  ми не будемо ані записувати, ані аналізувати ці рівняння. Зауважимо тільки, що рівняння загальної теорії відносності певним чином відображають залежність параметрів простору і часу від тієї кількості мас–енергії, яка створює те, що називають гравітаційним полем. Зауважимо також, що в широкому діапазоні відносно невеликих напруженостей гравітаційного поля, рівняння Ейнштейна набувають вигляду звичного для нас закону всесвітнього тяжіння: F=Gm₁m₂/r². Даний факт, безумовно вказує на те, що загальна теорія відносності є правильною. Адже, якщо закон всесвітнього тяжіння є наслідком загальної теорії відносності, то це означає, що всі ті експериментальні факти які підтверджують достовірність цього закону, автоматично підтверджують і відповідну теорію.

Втім, факту того, що експериментально підтверджений закон всесвітнього тяжіння є прямим наслідком загальної теорії відносності, явно не достатньо для того, щоб цю теорію вважати безумовно правильною. Адже для безумовного підтвердження будь якої теорії, потрібні такі експериментальні факти, які можна пояснити лише цією теорією. Отримати ж такі факти для загальної теорії відносності, надзвичайно складно. Складно головним чином тому, що специфічні ефекти загальної теорії відносності (тобто такі ефекти, які не можливо пояснити на основі ньютонівської теорії тяжіння), відчутно проявляються лише в надзвичайно потужних гравітаційних полях. Штучно ж створити такі поля практично не можливо. Та й в природніх умовах вони зустрічаються досить рідко і на надзвичайно великих відстанях від Землі. Звідси ясно з якими труднощами стикаються вчені, намагаючись експериментально перевірити передбачення загальної теорії відносності. Тим не менше, існує достатньо велика кількість експериментальних доказів того, що загальна теорія відносності є безумовно правильною. Розглянемо деякі з цих доказів.

Ще з ньютонівських часів було відомо, що еліптична орбіта планети Меркурій з певною кутовою швидкістю дрейфує навколо Сонця (мал.195). Цей обертальний дрейф еліптичної орбіти планети, прийнято називати прецесійним. Вимірювання показують, що швидкість прецесійного обертання Меркурія становить 543″ (кутових секунд) за століття. Пояснюючи даний факт, ньютонівська теорія тяжіння цілком обгрунтовано стверджувала, що в процесі обертання навколо Сонця, будь яка планета відчуває гравітаційну дію інших планет. А ця дія і спричиняє прецесійний дрейф планети. Однак розрахунки показували, що згідно з ньютонівською теорією тяжіння швидкість прецесійного дрейфу Меркурія має становити 500″, що на 43″ менше фактичної величини.

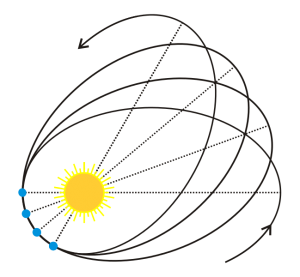
Мал.195. Схема прецесійного обертання орбіти Меркурія.

Аномальну прецесію орбіти Меркурія, намагалися пояснити впливом певної невідомої планети. Для неї навіть придумала назву – Вулкан. Однак, всі спроби відшукати цю планету виявились марними. Адже такої планети просто не існувало. Лише в 1916 році, Ейнштейн на основі аналізу рівнянь загальної теорії відносності довів, що згідно з цією теорією, обертальний рух планети має супроводжуватись певним круговим дрейфом її орбіти. При цьому для Меркурія, кутова швидкість цього дрейфу має становити 43″ за століття. Дане передбачення та його точне співпадіння з реальним фактом, стало першим відчутним успіхом загальної теорії відносності.

Наступним кроком на шляху визнання загальної теорії відносності, стало експериментальне підтвердження того, що гравітаційні поля певним чином впливають на траєкторію руху світлових фотонів. За звичайних умов цей вплив є мізерно малим. Його можна помітити лише в тому випадку, коли фотони пролітають повз надмасивні космічні об’єкти, наприклад такі як Сонце. Однак Сонце, є надпотужним джерелом власних фотонів. І в потоці цих сонячних фотонів, помітити сторонні фотони, практично не можливо. Це можна зробити лише в тому випадку, коли ці сторонні фотони пролітатимуть повз Сонце  в момент його повного затемнення. Зважаючи на ці обставини, в 1919 році було проведено наступний експеримент.

В момент повного сонячного затемнення, вчені зафіксували (сфотографували) візуальне положення тієї зірки світлові промені якої проходили максимально близько від сонячного диску (мал.196, положення Sꞌ). Потім, вони зафіксували положення тієї ж зірки за відсутності впливу гравітаційного поля Сонця (мал.196, положення S). Співставивши відповідні положення, вчені з’ясували, що вони не співпадають і що причиною цього неспівпадіння є дія гравітаційного поля Сонця. Дійсно. В момент сонячного затемнення, дана зірка фактично перебувала в положенні S. Однак, в результаті того, що її світлові промені, проходячи повз сонячний диск змінювали напрям свого розповсюдження, земляни бачили цю зірку не в положенні S, а в положенні Sꞌ.

    

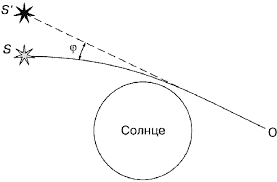
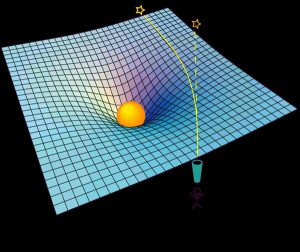
Мал.196. В гравітаційному полі Сонця, світлові промені суттєво змінюють напрям свого розповсюдження.

Ви можете зауважити. Оскільки фотони мають певну енергію (E=hν), а отже і певну масу (m=E/c²), то факт їх притягування до Сонця є закономірним результатом дії ньютонівського закону всесвітнього тяжіння. Дійсно. Певне відхилення світлових променів в гравітаційному полі Сонця, передбачає не лише ейнштейнівська а й ньютонівська теорія тяжіння. Різниця лише в тому, що згідно з теорією Ньютона, це відхилення має бути набагато меншим аніж згідно з теорією Ейнштейна. Тому коли в 1919 році були проведені відповідні експерименти і коли з’ясувалося, що їх результати практично в точності співпадають з передбаченнями загальної теорії відносності, то це стало вагомим підтвердженням правильності цієї теорії.

Далі. В загальній теорії відносності стверджується, що ті фотони які випромінює зірка, долаючи її гравітаційне поле, втрачають частину своєї енергії. А втрачаючи енергію, вони мають змінювати свої частотні параметри, а отже і свій колір. По суті це означає, що лінійчаті спектри випромінювання тих атомів які знаходяться на Сонці, мають дещо відрізнятись від аналогічних спектрів «земних атомів». (Спектр «сонячних атомів» має бути зміщеним в сторону червоного кольору). Експериментальні факти повністю підтверджують дане передбачення теорії.

Далі. В загальній теорії відносності стверджується, що по мірі наближення до джерела потужного гравітаційного поля, плин часу сповільнюється. Це означає, що в потужних гравітаційних полях, всі фізичні процеси відбуваються повільніше, порівняно з тими місцями де гравітаційне поле відсутнє або слабке. Сучасні експериментальні дослідження повністю підтверджують це передбачення теорії.

Далі. В загальній теорії відносності стверджується, що за певних умов, певні космічні об’єкти, перетворюються на так звані чорні діри, тобто такі надзвичайно маленькі за розміром і величезні за масою об’єкти (зірки), гравітаційне поле яких таке потужне, що навіть світлові фотоне не можуть подолати його. Експериментальні дослідження підтверджують і це передбачення теорії.

Далі. В загальній теорії відносності стверджується, що в процесі прискореного руху будь яке масивне тіло створює певну гравітаційну хвилю. За звичайних умов енергетична потужність таких хвиль мізерно мала. Тому довгий час вченим не вдавалося експериментально підтвердити факт існування таких хвиль. Лише у вересні 2015 року, американські вчені зафіксували та дослідили достатньо потужні гравітаційні хвилі які утворилися в процесі злиття (колапсу) двох чорних дір масою 36 і 29 сонячних мас. Це злиття відбулося на відстані 1,3 мільярдів світлових років від Землі, а отже 1,3 мільярди років тому. При цьому параметри цих гравітаційних хвиль в точності підтвердили передбачення загальної теорії відносності.

Вище згадані та багато інших фактів, безумовно доводять, що загальна теорія відносності є правильною.

                   Контрольні  запитання.

1. В чому полягає обмеженість часткової теорії відносності?
2. В чому ньютонівська теорія тяжіння суперечила частковій теорії відносності?
3. Чому в ньютонівській механіці маса з одного боку є мірою інерційних властивостей тіла, а з іншого – мірою гравітаційних властивостей тіла.
4. Сформулюйте базові твердження загальної теорії відносності та порівняйте їх з базовими твердженнями спеціальної теорії відносності.
5. Як ви розумієте твердження: інерційна та гравітаційна маси є еквівалентними?
6. На основі зображеної на мал.192 ситуації, поясніть суть твердження: силові прояви гравітації та інерції є еквівалентними.
7. На основі зображеної на мал.193 ситуації, поясніть чим на думку «здорового глузду» відрізняється силова дія гравітаційного поля, від силової дії інерційного поля? Чи є ця думка правильною? Чому?
8. Як залежать параметри простору–часу від потужності того гравітаційного поля де ці параметри вимірюються?
9. Чому спеціальна теорія відносності є частиною загальної теорії відносності?
10. На основі мал.194, поясніть геометричну суть гравітації.
11. Як впливають потужні гравітаційні поля на плин часу? На лінійні розміри об’єктів?

.