ЕЛЕКТРОСТАТИКА

Тема 4.1. Електростатика.
§38. Загальні відомості про електричні явища. Електричний заряд. Закон збереження електричного заряду.
§39. Закон Кулона.
§40. Загальні відомості про поля.
§41. Електричне поле. Напруженість електричного поля. Принцип суперпозиції.
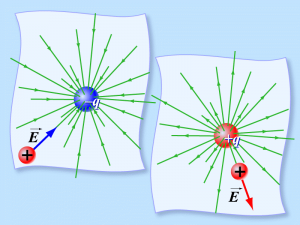
§42. Графічне зображення електричних полів.
§43. Провідники та діелектрики в електричному полі. Сегнетоелектрики. П’єзоефект.
§44. Робота та потенціал електричного поля. Електрична напруга.
§45. Електрична ємність. Конденсатори.
§46. Електростатика. Узагальнююче повторення.
.
Тема 4.1 Електростатика.
Електростатика, це розділ електродинаміки в якому вивчають параметри, властивості та закономірності взаємодії відносно нерухомих електричних зарядів і тих електричних полів які ці заряди створюють.
.
§38. Загальні відомості про електричні явища. Електричний заряд. Закон збереження заряду.
З античних часів було відомо, що в процесі натирання, бурштин набуває здатності притягувати дрібні предмети, як то шматочки сухого листя, шкіри, хутра, тканини, тощо. Бурштинову смолу давні греки називали «електрон». Тому, ті тіла властивості яких були схожими на властивості натертого бурштину («електрону») стали називати наелектризованими, а відповідні явища – електричними.


Мал.115. Сукупність явищ подібних до тих які проявляв натертий хутром бурштин («електрон»), стародавні греки стали називати електричними.
На протязі багатьох століть, знання людства про електрику обмежувались констатацією факту того, що в процесі натирання деякі матеріали набувають здатності притягувати дрібні предмети. Щоправда, з незапам’ятних часів люди знали про ще одне електричне явище – грозову блискавку. Однак нікому не спадало на думку, що між грізною блискавкою та ледь помітними силовими властивостями натертого бурштину, існує певний зв’язок і що ці абсолютно несхожі явища мають спільне походження.
Лише з середини 17-го століття, електричні явища почали досліджувати більш менш системно та цілеспрямовано. А перші успіхи на шляху цих досліджень були зроблені французьким фізиком Шарлем Дюфе (1698–1739). В 1733 році Дюфе звернув увагу на те, що деякі наелектризовані тіла по різному діють на інші, попередньо наелектризовані предмети. По різному в тому сенсі, що коли одні з них притягують наелектризоване тіло, то інші, це ж тіло навпаки – відштовхують. Зокрема Дюфе з’ясував, що коли наелектризований гірський кришталь (скло) притягує пробне наелектризоване тіло, то наелектризований бурштин (смола) – відштовхує його. І навпаки.
Аналізуючи подібні факти, вчений дійшов висновку: «В природі існує два види електрики – «смоляна» та «скляна», які відрізняються тим, що тіла наділені електрикою одного і того ж виду, взаємно відштовхуються, а тіла наділені електрикою різних видів – взаємно притягуються». В перекладі на мову сучасної науки, це означає: «В Природі існує два види електричних зарядів, які відрізняються тим, що однойменні заряди відштовхуються, а різнойменні – притягуються».

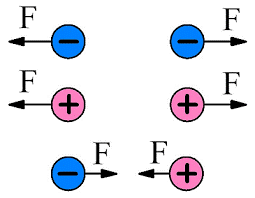
Мал.116. В 1733 році було встановлено, що існує два види електричних зарядів і що різнойменні заряди притягуються, а однойменні – відштовхуються.
В 1749 році, американський фізик та громадський діяч Бенджамін Франклін (1706-1790) (той самий Франклін, портрет якого красується на банкноті номіналом 100$), намагаючись пояснити фізичну суть електрики, висунув гіпотезу про те, що електрика представляє собою особливу електричну рідину (флюїд), яка в тій чи іншій мірі міститься в кожному тілі. При цьому, якщо кількість цієї рідини є збалансованою, то відповідне тіло не проявляє електричних властивостей. Якщо ж за певних обставин тіло втрачає електричну рідину, то воно заряджається негативно (–), а якщо отримує її – позитивно (+).
Невідомо чому, але Франклін вирішив, що в процесі натирання, бурштинова смола втрачає електричну рідину і що тому вона заряджається негативно (–). Натомість, гірський кришталь (скло), в процесі натирання отримує певну надлишкову кількість електричної рідини і тому заряджається позитивно (+). Іншими словами, «смоляну» електрику Франклін назвав негативною (–), а «скляну» – позитивною (+).
Лише в кінці 19-го століття з’ясувалося, що насправді ніякої електричної рідини не існує, і що носієм електрики є не якась гіпотетична рідина, а складові частинки атома, зокрема електрони. При цьому дослідження показали, що за тією класифікаційною схемою яку запропонував Франклін, заряд електрона виявився негативним (–), а заряд атомного ядра, а відповідно і протона – позитивним (+). Ясно, що якби Франклін «смоляну» електрику назвав позитивною, а «скляну» – негативною, то заряд електрона виявився б позитивним, а заряд протона – негативним. Не менш очевидно і те, що від подібної заміни назв, атоми не стали б іншими і світ не перевернуся б.
Потрібно зауважити, що фізична суть того, що називають електрикою є надзвичайно складною. Складною настільки, що навіть сьогодні ми не можемо чітко та однозначно пояснити цю суть. Тому ідея Франкліна представити електрику у вигляді особливої рідини (флюїду) виявилась надзвичайно плідною та корисною. Адже вона дозволяла вченим, не заглиблюючись в подробиці фізичної суті терміну «електрика», усвідомлено досліджувати властивості цієї самої електрики. А в широкому спектрі явищ, пояснення цих властивостей практично не залежать від того, як представляти електрику – у вигляді певної електричної рідини, чи у вигляді певної сукупності заряджених електронів. Скажімо, факт того що при контакті різнойменно заряджених тіл, вони обмінюються не якоюсь гіпотетичною зарядженою рідиною, а зарядженими електронами, практично не впливає на характер та результати цього обміну.
Та як би там не було, а на сьогоднішній день ми точно знаємо, що ніякої спеціальної електричної рідини не існує, і що носіями електрики (електричного заряду) є певні елементарні частинки, зокрема протони (+) та електрони (–). Якщо ж говорити про сучасне розуміння фізичної суті електрики, а точніше того що прийнято називати електричним зарядом, то вона полягає в наступному.
Електрика (електричний заряд), це та матеріальна сутність, яка нерозривно пов’язана з деякими елементарними частинками, зокрема протонами та електронами і яка є джерелом електромагнітних взаємодій (джерелом електромагнітного поля). При цьому, потрібно мати на увазі, що електрика (електричний заряд), не є певною речовинною субстанцією, яка існує сама по собі і яку тим чи іншим способом можна відділити від тих елементарних частинок що є носіями цієї електрики. По суті електрикою (електричним зарядом) називають не приналежну частинці певну речовинну субстанцію, а здатність цієї частинки певним чином взаємодіяти з іншими, подібними частинками.
Дослідження показують, що електричні заряди будь якого знаку є дискретними і що величина найменшої, неподільної (елементарної) порції електричного заряду становить 1,6∙10–19Кл (кулон). При цьому електрон є носієм елементарного негативного заряду, а протон – носієм елементарного позитивного заряду.
Кількісною мірою тієї сутності яка називається електричним зарядом (електрикою) є фізична величина яка також називається електричним зарядом. Електричний заряд, це фізична величина, яка характеризує здатність тіла або частинки до електромагнітних взаємодій і яка дорівнює добутку величини елементарного електричного заряду (е=1,6∙10–19Кл) на загальну кількість (N) тих нескомпенсованих елементарних зарядів що містяться в даному тілі.
Позначається: q
Визначальне рівняння: q = ±Ne
Одиниця вимірювання: [q] = Кл, кулон.
По суті електричний заряд показує скільки нескомпенсованих (незрівноважених) елементарних зарядів того чи іншого знаку міститься в даному тілі. А оскільки на практиці тими зарядженими частинками які переходять від тіла до тіла, від атома до атома, від молекули до молекули, є електрони, то можна стверджувати, що електричний заряд показує, скільки нескомпенсованих електронів міститься у відповідному зарядженому тілі. При цьому, якщо тіло має заряд (+) то це означає що воно втратило певну кількість електронів. А якщо заряд тіла (–), то це означає що відповідне тіло має певний надлишок електронів.
Задача. Скільки електронів має втратити тіло, щоб набути заряд 1Кл?
Дано:
q = 1Кл
N = ?
Рішення. Оскільки за визначенням q = Ne, де e = 1,6∙1–19Кл, то N = q/e = 1/1,6∙10–19Кл = 6,25∙1018електронів.
Відповідь: для того щоб тіло набуло заряд в 1Кл, воно має втратити 6,25∙1018електронів.
6,25∙1018 електронів – це багато чи мало? З одного боку, це безумовно багато. Однак, якщо говорити про масштаб тих чисел в яких вимірюються кількості молекул та електронів в речовині, то число 6,25∙1018електронів не є надто великим. Дійсно. В 18г води (один моль води) міститься 6,02∙1023 молекул Н2О, а отже 10∙6,25∙1018електронів. А це означає, що число 6,25∙1018 майже в мільйон разів менше за кількість тих електронів що містяться в 18г води.
Визначаючи ту фізичну величину яка називається електричним зарядом, доречно бодай декілька слів сказати про одиницю вимірювання цієї величини – кулон (Кл). По суті, кулон є тією базовою одиницею вимірювання, яка наряду з метром, секундою та кілограмом має входити до числа основних одиниць СІ. Однак з практичної точки зору, набагато зручніше вимірювати не величину електричного заряду (q=Ne), а величину сили електричного струму (I=q/t). Зважаючи на ці обставини, в якості базової одиниці вимірювання електродинамічних величин обрано не одиницю електричного заряду, а одиницю сили електричного струму – ампер ([I]=Кл/с=А). А оскільки величину ампера ми ще не визначали, то будемо вважати, що кулон це одиниця вимірювання електричного заряду, яка дорівнює загальному заряду 6,25∙1018 електронів.
В 1849 році, видатний англійський фізик Майкл Фарадей (1791–1869) на основі аналізу багатьох експериментальних фактів, сформулював один з базових законів електродинаміки – закон збереження електричного заряду. В цьому законі стверджується: при будь яких процесах, що відбуваються в замкнутій (електроізольованій) системі, загальна кількість електричного заряду цієї системи залишається незмінною, тобто зберігається. Іншими словами: ∑qдо = ∑qпісля (сума зарядів до події дорівнює сумі зарядів після події), або ∑q = const.
Закон збереження заряду, входить до числа фундаментальних законів Природи. А це означає, що цей закон вточності виконується у всіх відомих явищах. Наприклад, якщо в процесі натирання хутром, ебоніт заряджається негативно, то це означає що частина електронів перейшла від хутра до ебоніту. При цьому, якщо ебоніт набув певного негативного заряду, то хутро неминуче набуло аналогічного позитивного заряду. І навіть якщо ви не зможете зафіксувати факту того, що заряд хутра став позитивним, або зафіксуєте що цей заряд виявився меншим від очікуваного, то не поспішайте стверджувати, що у відповідному експерименті, закон збереження заряду не виконується. Просто, скоріш за все, система ебоніт – хутро не є замкнутою. Адже ці тіла неминуче контактують з навколишнім повітрям та тілом експериментатора, а через них і з всією земною кулею. А зважаючи на те, що над рухливі електрони можуть надзвичайно швидко переходити від одного тіла до іншого і навпаки, ви можете просто не помітити факту того, що ті електрони які ще мить тому були частиною хутра, можуть виявитись зовсім в іншому місці. Однак, якщо ви дійсно врахуєте всі обставини, то неодмінно з’ясуєте, що в замкнутій системі алгебраїчна сума зарядів, дійсно залишається незмінною, тобто зберігається.

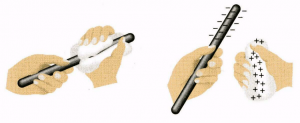
Мал.117. При будь яких процесах що відбуваються в замкнутій системі, загальна кількість заряду цієї системи залишається незмінною.
Потрібно особливо наголосити на тому, що в законі збереження заряду, говориться не про збереження загальної кількості заряджених частинок, а саме про збереження загальної (сумарної) кількості електричного заряду системи. І це не випадково. Справа в тому, що в Природі існує безліч процесів, при яких заряджені частинки як з’являються так і зникають. Але вони завжди зникають і з’являються лише попарно (плюс і мінус одночасно). А це означає, що за будь яких обставин, загальна кількість електричного заряду замкнутої системи залишається незмінною. При цьому кількість заряджених частинок в системі може змінюватись.
Наприклад, вивчаючи ядерну фізику, ви дізнаєтесь про те, що за межами атомного ядра, та незаряджена частинка яка називається нейтроном (1n0) неминуче розпадається на дві заряджені частинки: протон (1p+1) та електрон (0e–1): 1n0 → 1p+1 + 0e–1. А це означає, що в тому місці де знаходіться вільні нейтрони і де нема жодної зарядженої частинки (∑qдо=0), через певний час ці частинки неминуче з’являться. Однак якщо ви порахуєте кількість цих заряджених частинок, то неодмінно з’ясується, що число позитивних і негативних зарядів вточності однакове і що тому, загальна кількість заряду системи залишається незмінною і чисельно рівною нулю (∑qпісля=0).
Взаємне перетворення заряджених та незаряджених частинок, відбувається не лише на рівні так званих елементарних частинок, а й на рівні атомів і молекул. Скажімо, в процесі розпаду молекул та руйнації кристалічних структур, певні електронейтральні групи атомів, розпадаються на відповідні позитивні та негативні іони: NaCℓ → Na+ + Cℓ–. В процесі іонізації газів, їх електронейтральні молекули перетворюються на відповідні позитивні іони та електрони: О2 → О2+ + е–. А в процесі рекомбінації, позитивні іони та електрони, знову стають електронейтральними молекулами: О2+ + е–→ О2.
Вивчаючи фізику ви ще не раз переконаєтесь в тому, що кількість заряджених частинок в замкнутій системі може змінюватись. Однак при будь яких змінах, загальна кількість електричного заряду цієї системи залишається незмінною.
Контрольні запитання.
1. Чим наелектризоване тіло відрізняється від тіла не наелектризованого?
2. Що відбувається, коли при контакті двох тіл одне набуває позитивного заряду, а інше – негативного?
3. Чому втрачаючи електрони, тіло набуває заряд (+)?
4. Чому в міжнародній системі одиниць (СІ), в якості основної одиниці обрано не одиницю електричного заряду, а одиницю електричного струму?
5. Чи була гіпотеза про існування електричної рідини (флюїду) правильною? Чому?
6. Чи була гіпотеза про існування електричної рідини корисною? Чому?
7. Чому в законі збереження заряду говориться про збереження загальної кількості заряду, а не про збереження загальної кількості заряджених частинок?
8. Чому через певний час наелектризовані тіла неминуче стають електро нейтральними?
9. Наведіть приклади процесів при яких заряджені частинки: а) з’являються; б) зникають.
Вправа 38.
1. З електронейтральної краплі рідини вилетів електрон. Потім крапля поглинула протон. Визначте заряд краплі після цих перетворень.
2. Електричні заряди тіл становлять q1 = +5,0∙10–11Кл; q2 = –4,0∙10–12Кл; q3=6,0∙10–14Кл. Яку кількість електронів втратили чи отримали відповідні тіла?
3. Металева кулька має 5,0∙105 надлишкових електронів. Який заряд цієї кульки? Скільки нескомпенсованих електронів залишиться на кульці після її контакту з іншою такою ж кулькою, якщо заряд цієї кульки +3,2∙10–14Кл?
4. Металеву кульку, що має заряд –4,8∙10–11Кл привели в контакт з такою ж незарядженою кулькою. Скільки надлишкових електронів залишиться на цій кульці?
5. Якого б заряду набула суцільна алюмінієва кулька радіусом 1см, якби кожен її атом втратив по одному електрону?
6. Кожен атом свинцевої та мідної кульок діаметром по 1см кожна, втрачає по одному електрону. Порівняйте величини зарядів цих кульок.
.
§39. Закон Кулона.
В 1733 році французький фізик Шарль Дюфе експериментально встановив, що існує дві різновидності електричних зарядів, і що однойменні заряди відштовхуються, а різнойменні – притягуються. Якщо ж говорити про той закон, який кількісно описує взаємодію електричних зарядів, то він був експериментально встановлений та сформульований в 1785 році іншим французьким фізиком Шарлем Кулоном (1736–1806).
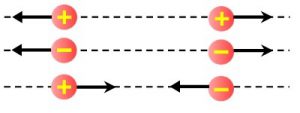
В законі Кулона стверджується: два точкові електричні заряди q1 і q2 взаємодіють між собою (однойменні заряди відштовхуються, різнойменні – притягуються) з силою, величина якої прямо пропорційна добутку взаємодіючих зарядів (q1∙q2) і обернено пропорційна квадрату відстані між ними (r2). Іншими словами: Fел = kq1q2/r2, де k – коефіцієнт пропорційності, величина якого залежить від електричних властивостей того середовища яке оточує взаємодіючі заряди, та від вибору одиниць вимірювання сили, відстані та електричного заряду. Наприклад, якщо сила вимірюється в ньютонах (Н), відстань – в метрах (м), а електричний заряд – в кулонах (Кл), то для вакууму k=k0=9∙109Н∙м2/Кл2. Це означає, що два точкових електричних заряди по одному кулону кожний (q1=q2=1Кл) будучи розташованими на відстані один метр один від одного (r=1м), у вакуумі, взаємодіють з силою F0 = 9∙109H = 9 000 000 000Н. Аналізуючи фізичну суть та числове значення коефіцієнту k0=9∙109 Н∙м2/Кл2, можна зробити два висновки:
1. Заряд в один кулон – це надзвичайно великий заряд.
2. Електричні сили – це сили надзвичайно потужні.
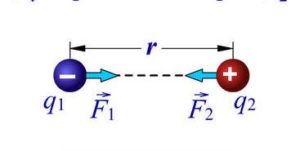
Мал.118. Два точкові електричні заряди q1 і q2 взаємодіють між собою з силою, величина якої визначається за формулою Fел = kq1q2/r2,
Залежність коефіцієнту пропорційності k, а відповідно і сили електростатичної взаємодії Fел=kq1q2/r2 від електричних, а точніше діелектричних властивостей того середовища яке оточує взаємодіючі заряди, можна представити у вигляді k=k0/ε, де ε – діелектрична проникливість середовища.
Діелектрична проникливість середовища, це фізична величина, яка характеризує діелектричні властивості даного середовища і яка показує у скільки разів сила електростатичної взаємодії зарядів в даному середовищі (F), менша за силу взаємодії тих же зарядів у вакуумі (F0).
Позначається: ε
Визначальне рівняння: ε = F0/F
Одиниця вимірювання: [ε] = Н/Н = – , (рази).
Діелектрична проникливість середовища визначається експериментально і записується у відповідну таблицю. Таблиця 1.
Діелектрична проникливість деяких середовищ (при t=20ºС)
| Речовина | ε | Речовина | ε |
| алмаз | 5,7 | лід (при –18ºС) | 3,2 |
| бензин | 2,3 | масло трансформаторне | 2,3 |
| бурштин | 2,8 | повітря | 1,0006 |
| вакуум | 1,0000000 | спирт | 26 |
| вода | 81 | слюда | 6 – 9 |
| вода (при 0ºС) | 88 | скло | 5 – 10 |
| гас | 2,0 | титанат барію | 1500 |
| гліцерин | 39 | сульфід сурми | 2200 |
Потрібно зауважити, що говорити про силову взаємодію електричних зарядів можна лише в тому випадку, якщо ці заряди знаходяться у вакуумі або в діелектричному середовищі, тобто такому середовищі де практично відсутні вільні заряджені частинки. Якщо ж мова йде про струмопровідні середовища, то в них електростатичні взаємодії заряджених тіл є практично неможливими. Неможливими тому, що в струмопровідному середовищі є практично необмежена кількість вільних заряджених частинок. А це означає, що навіть в тому випадку якщо заряджені тіла електроізольованій і не можуть втратити свій заряд за рахунок контакту з струмопровідним середовищем, в силовому полі взаємодіючих зарядів, вільні заряджені частинки середовища неминуче перерозподіляються таким чином, що практично повністю нейтралізують взаємодіючі заряди (будь-яке заряджене тіло неминуче оточує себе зарядами протилежного знаку і фактично стає не зарядженим).
Пояснюючи факт того, що всі діелектричні середовища в тій чи іншій мірі зменшують силу електричної взаємодії зарядів, можна сказати наступне. Дослідження показують, що практично всі електронейтральні атоми і молекули, представляють собою певні дипольні системи. Це означає, що в тілі молекули електричні заряди розподілені нерівномірно і що тому одна її частина має переважно позитивний заряд, а інша – переважно негативний (мал.119а). За відсутності зовнішніх електричних впливів, просторова орієнтація молекул-диполів є усереднено хаотичною, тобто такою, при якій кількість диполів орієнтованих в одному напрямку і кількість диполів орієнтованих в протилежному напрямку є практично однаковою. Якщо ж в дипольному середовищі з’являється сторонній електричний заряд, то під дією цього заряду, молекули-диполі переорієнтовуються таким чином, що електричні властивості заряду частково нейтралізуються (мал.119).
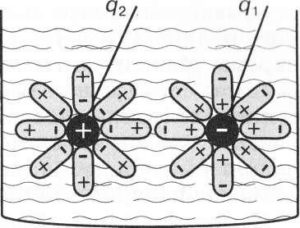
Мал.119. Під дією електричних зарядів молекули-диполі орієнтуються таким чином, що зменшують силу взаємодії цих зарядів.
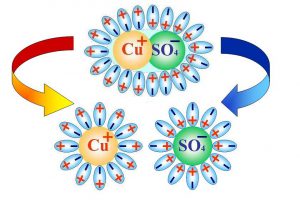
До речі, факт того, що молекули води мають яскраво виражені дипольні властивості, а сама вода – відповідно велику діелектричну проникливість (ε=81), є основною причиною того, що вода є добрим розчинником для солей та основ (лугів), тобто тих матеріалів які мають яскраво виражену іонну структуру.
З точки зору зручності вивчення і практичного застосування закону Кулона, було б доцільним та логічно обгрунтованим, постійну величину k0=9∙109Н∙м2/Кл2, на ряду з гравітаційною сталою G=6,67∙10–11Нм2/кг2, віднести до числа фундаментальних фізичних сталих. При цьому, було б не менш доцільним та обґрунтованим, представляти залежність сили електричної взаємодії зарядів від властивостей того середовища яке ці заряди оточує, у вигляді k = k0/ε. Однак, те що представляється доцільним з точки зору окремо взятого закону електростатики, не завжди співпадає з тією доцільністю яку диктує вся сукупність законів електродинаміки. А ця загально електродинамічна доцільність вимагає того, щоб залежність сили електричної взаємодії зарядів від властивостей того середовища яке ці заряди оточує, записували не у вигляді k = k0/ε, а у вигляді k = 1/4πε0ε, де ε0 = 1/4πk0 = 8,85∙10–12 Кл2/Нм2, постійна величина яку прийнято називати електричною сталою. Саме цю величину ви і знайдете в таблиці базових фізичних сталих.
Та як би там не було, а ви маєте знати, що сила електричної взаємодії зарядів, певним чином залежить від діелектричних властивостей того середовища яке ці заряди оточує. І що цю залежність можна представити у вигляді: k=k0/ε, де k0=9∙109 Н∙м2/Кл2=const; або k=1/4πε0ε, де ε0 = 8,85∙10–12 Кл2/Нм2 = const.
Говорячи про закон Кулона та формулу Fел=kq1q2/r2, важливо зауважити, що мова йде про взаємодію точкових зарядів, тобто таких зарядів, лінійні розміри яких набагато менші за відстань між ними. Пояснюючи важливість даного зауваження розглянемо наступну ситуацію. Припустимо, що відстані між геометричними центрами двох маленьких і двох великих струмопровідних куль є однаковими і рівними r. Припустимо, що електричні заряди цих куль також попарно однакові і дорівнюють q1 та q2. Запитується, чи однаковими будуть сили електричної взаємодії кожної пари куль?
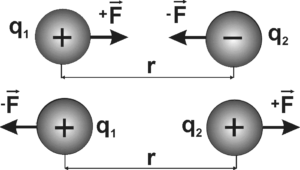
Мал.120. Заряди тіл однакові, відстані між їх геометричними центрами однакові, а сили електричної взаємодії різні. Чому?
З формальної точки зору, тобто у відповідності з бездумним застосуванням формули Fел=kq1q2/r2, ці взаємодії будуть однаковими. В реальності ж, вони будуть різними. Різними тому, що електричні заряди і зокрема електрони, це надзвичайно рухливі структури, які легко переміщуються в межах струмопровідного тіла. А це означає, що при взаємодії однойменних зарядів, ці заряди зосереджуються на гранично віддалених частинах тіл, а при взаємодії різнойменних зарядів – на гранично наближених частинах. Ясно, що в такій ситуації, однойменно заряджені тіла будуть взаємодіяти з меншою силою, а різнойменні – з більшою.
Звичайно, це зовсім не означає, що формула Fел=kq1q2/r2 є неправильною. Просто застосовуючи цю формулу потрібно мати на увазі, що в ній відстань r, це не відстань між геометричними центрами взаємодіючих тіл, а відстань між взаємодіючими зарядами, і що лише для точкових зарядів ці відстані однакові.
Той факт, що всі тіла складаються з рухливих заряджених частинок, є основною причиною того, що електростатичні взаємодії можуть відбуватись не лише між зарядженими тілами, а й між тілами зарядженими та тілами формально незарядженими. Наприклад, якщо біля зарядженого тіла опиняється тіло незаряджене, то під дією електричних сил (під дією зовнішнього електричного поля), заряджені частинки незарядженого тіла, певним чином перерозподіляються. Перерозподіляються так, що формально незаряджене тіло притягується до зарядженого (мал.121).

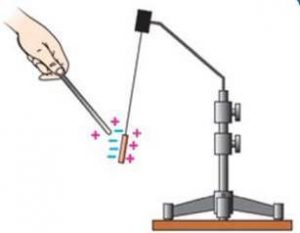
Мал.121. Під дією зовнішніх силових впливів (зовнішнього електричного поля) заряджені частинки формально незарядженого тіла перерозподіляються таким чином, що це тіло набуває певних електричних властивостей.
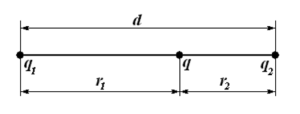
Задача 1. Два точкові однойменні заряди 9q і q знаходяться на відстані 1м один від одного. В якій точці тієї лінії що з’єднує заряди треба розмістити протилежний за знаком заряд q0, щоб діючі на нього сили зрівноважували одна одну.
Дано:
q1 = 9q
q2 = q
q0
d = 1м
r = ?
Рішення: Оскільки в точці рівноваги діючі на заряд q0 сили F1=k9qq0/r2 та F2=kqq0/(d–r)2
зрівноважують одна одну, то можна записати k9qq0/r2 = kqq0/(d–r)2, звідси 9/r2=1/(d–r)2, звідси 9(d–r)2=r2, звідси 9d2 – 18dr + 9r2 = r2, звідси 8r2 – 18dr + 9d = 0, а враховуючи що d=1,
8r2–18r+9=0.
Таким чином, ми маємо квадратне рівняння, яке має два рішення:
r1,2=(18±√(182 – 4·8·9))/2·8 = (18±6)/16, звідси r = r1 = 0,75м; r = r2 = 1,5м.
Відповідь: r = r1 = 0,75м; r = r2 = 1,5м.
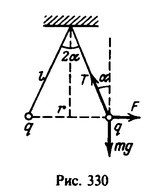
Задача 2. Дві невеличкі кульки масою 1г кожна, висять на двох закріплених в одній точці нитках довжиною 20см кожна. Після того як кулькам надали одинакові заряди вони відхилилися так, що кут між нитками становить 60°. Визначити величину наданого кожній кульці заряду.
Дано:
m1=m2=1г=1·10–3кг
q1=q2=q
ℓ=20см=0,2м
2α=60°
q = ?
Рішення: Виконуємо малюнок на якому вказуємо всі діючі на заряд сили: сила тяжіння Fт=mg; сила електричної взаємодії зарядів F=kq2/(2r)2; сила натягу нитки Т. Задаємо систему координат: вісь 0х – горизонтальна, вісь 0у – вертикальна. Записуємо умову механічної рівноваги заряду:
∑Fx = F – Tsinα = kq2/(2r)2 – Tsinα = 0, звідси Т = kq2/sinα(2r)2
∑Fy = Tcosα – Fт = Tcosα – mg = 0, звідси T = mg/cosα.
Оскільки Т=Т, то kq2/sinα(2r)2 = mg/cosα, звідси q = √(mg·tgα(2r)2/k) = 2r√(mg·tgα/k). Таким чином: q = 2r√(mg·tgα/k), де k=9·109(Н·м2/Кл2), α=30°, r=ℓsinα= 0,2·0,5=0,1м, tg30°=0,57.
Розрахунки: q = 2r√(mg·tgα/k) = 2·0,1√(1·10–3·10·0,57/9·109) = 16·10–6Кл.
Відповідь: q = 16·10–6Кл.
Контрольні запитання.
1. Поясніть фізичну суть коефіцієнту k0=9∙109Н∙м2/Кл2.
2. Чому ми стверджуємо, що заряд в один кулон, це надзвичайно великий заряд?
3. Чому ми стверджуємо, що електричні сили, це надзвичайно потужні сили?
4. Що означає твердження: діелектрична проникливість води 81?
5. Чому діелектрична проникливість вакууму в точності дорівнює одиниці?
6. Які речовини називають діелектриками?
7. Чому діелектрики зменшують силу електричної взаємодії?
8. Чому солі і луги добре розчиняються у воді?
Вправа 39.
1. З якою силою взаємодіють два однойменні заряди 6,6∙10–6Кл і 1,1∙10–5Кл у воді на відстані 3,3см? На якій відстані потрібно розмістити ці заряди, щоб сила їх взаємодії залишалась попередньою?
2. Два точкові, рівні за величиною від’ємні заряди, в повітрі відштовхуються з силою 0,9Н. Визначити число надлишкових електронів в кожному заряді, якщо відстань між ними 8см?
3. На шовковій нитці в повітрі висить нерухома заряджена кулька масою 2г і зарядом 3∙10–8Кл. визначити силу натягу нитки, якщо під кулькою на відстані 10см розташована інша кулька з протилежним за знаком зарядом 2,4∙10–7Кл.
4. В вершинах квадрату розташовані чотири однакові заряди q. Який заряд Q потрібно розмістити в центрі квадрату, щоб система знаходилась в рівновазі? Чи буде ця рівновага стійкою?
5. Порівняйте силу електростатичної та гравітаційної взаємодій між протоном та електроном в атомі водню, якщо відомо: mp=1,67∙10–27кг, me=9,1∙10–31кг. Зробіть відповідні висновки.
6. Однойменні заряди 9,0∙10–8Кл і 1,0∙10–8Кл розташовані на відстані 40см один від одного. Де потрібно розташувати третій заряд, щоб він перебував в стані рівноваги?
7. Два точкові заряди q1 і q2 розташовані на відстані r один від одного. Після того як відстань між зарядами зменшилась на Δr=5,0см сила взаємодії зарядів збільшилась у двічі. Визначити відстань r.
8. Дві невеличкі кульки масою по 0,2г кожна, висять на двох закріплених в одній точці нитках довжиною 25см кожна. Після того як кулькам надали однакові заряди вони розійшлись на відстань 5см. Визначити заряди кульок.
.
§40. Загальні відомості про поля.
Про те, що тіла притягуються до Землі знають всі. Знають і про те, що між об’єктами Сонячної системи діють сили всесвітнього тяжіння, або, як прийнято говорити, гравітаційні сили (від лат. gravitas – тяжіння). Але далеко не всі ясно усвідомлюють, яким чином фантастично потужна силова дія передається від Землі до Місяця, від Сонця до Землі і навпаки. Адже між цими об’єктами нічого окрім пустого простору нема. І тим не менше, саме через цей пустий простір надпотужна силова дія передається від Сонця до Землі, від Землі до Місяця і т. д.
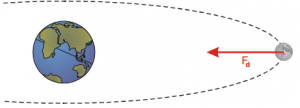
Мал.122. Місяць з силою 2∙1020Н притягується до Землі. Яким чином ця фантастично велика сила передається від Землі до Місяця і навпаки?
Пояснюючи механізм гравітаційних взаємодій наука стверджує. Будь який масивний об’єкт (об’єкт який має масу), створює навколо себе певне силове збурення навколишнього простору яке називається гравітаційним полем. Якщо в це поле потрапляє інший масивний об’єкт, то поле діє на нього з певною гравітаційною силою. Іншими словами, гравітаційне поле є тим матеріальним посередником який забезпечує гравітаційні взаємодії тіл.
Що ж таке – поле? На що воно схоже? З чого складається? Які властивості має? Відповідаючи на ці та їм подібні запитання, перш за все зауважимо, що все різноманіття матеріальних об’єктів Природи, тобто тих об’єктів які реально існують і так чи інакше проявляють себе, умовно розділяють на дві групи: речовини та поля. Пояснити що таке речовина не складно. Речовинами називають такі матеріальні об’єкти, які складаються з тих чи інших частинок і мають масу спокою. Власне все те що ми бачимо, чуємо та відчуваємо, що сприймаємо на смак, нюх та дотик, є тими чи іншими проявами речовини. Речовини можуть бути твердими, рідкими та газоподібними. Вони можуть бути хімічно простими та хімічно складними, живими та неживими, великими та маленькими, зеленими, червоними та безбарвними, крихкими, пластичними і взагалі – різними. Вони можуть складатись з атомів, молекул, іонів, нейтронів чи чогось іншого. Але в будь якому випадку, речовина – це те що складається з частинок і має масу спокою.
Будь який речовинний об’єкт має величезну кількість властивостей, кожна з яких характеризується відповідною фізичною величиною. Довжина, маса, об’єм, густина, тиск, температура, внутрішня енергія, теплоємність, твердість, міцність, механічна напруга, поверхневий натяг, питомий опір, питома теплота плавлення – ці та їм подібні величини характеризують певні властивості речовин.
Але різноманіття матеріальних об’єктів Природи не вичерпується різноманіттям речовин. В Природі є ще одна група матеріальних об’єктів які називаються полями. Поля не викликають у нас певних відчуттів. Вони не мають кольору, смаку чи запаху. Не мають об’єму, густини, твердості, міцності і взагалі тих звичних якостей які притаманні речовинам і які ми маємо на увазі, коли говоримо про матеріальність навколишнього світу. І тим не менше, поля матеріальні, тобто такі які реально існують і певним чином проявляють себе.
На відміну від речовин, кожна з яких має сотні а то й тисячі властивостей, поле має лише одну властивість – здатність певним чином діяти на певні об’єкти. Наприклад гравітаційні поля, діють на маси, тобто на ті об’єкти що мають масу. Електричні поля, діють на електричні заряди. Магнітні поля, діють на заряди що рухаються. По суті це означає, що існує лише один спосіб з’ясування факту того, є в даній точці простору певне поле чи нема. І цей спосіб полягає в тому, що у відповідну точку потрібно внести певний пробний об’єкт (пробну масу, пробний заряд чи заряд який рухається) і подивитись на його поведінку. При цьому, якщо на пробний об’єкт не діятиме гравітаційна, електрична чи магнітна сила, то це означатиме, що у відповідній точці простору відповідного поля нема. А якщо така сила діятиме – значить поле є.
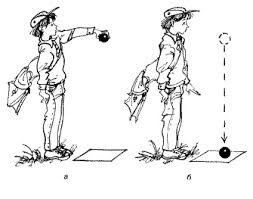

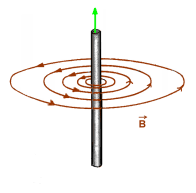
Мал.123. Поле має лише одну властивість – здатність певним чином діяти на певні матеріальні об’єкти.
Наприклад, з’ясовуючи наявність чи відсутність гравітаційного поля, у відповідну точку простору вносять пробне тіло (пробну масу) і аналізують його поведінку. При цьому: якщо на пробне тіло не діє гравітаційна сила (сила тяжіння), то це означає що в даній точці простору гравітаційного поля нема; а якщо така сила діє – значить поле є.
Звичайно, проводячи подібні експерименти, потрібно враховувати те, що в реальних обставинах на пробне тіло, окрім сили тяжіння можуть діяти й інші силові фактори. Скажімо, якщо в навколоземний простір внести заповнену гелієм надлегку кульку і відпустити її, то скоріш за все вона почне підніматись вгору. Однак це зовсім не означатиме, що у відповідному місці гравітаційного поля нема, або що джерело цього поля знаходиться десь вгорі. Просто в даному випадку, на поведінку легкої кульки визначальним чином впливає сила Архімеда, яка і змушує кульку, всупереч дії сили тяжіння, рухатися вгору.
За своїми фізичними властивостями поле схоже на простір (пустоту, вакуум). Як і простір, воно не має кольору, запаху, смаку, твердості, м’якості, поверхневого натягу, електропровідності, тощо. Власне поле, це і є простір. Тільки простір збурений, або якщо хочете – викривлений простір. Намагаючись наочно пояснити суть того, що прийнято називати полем, проведемо наступний експеримент. Еластичну гумову плівку розтягнемо таким чином, щоб її поверхня була рівною і горизонтальною (мал.124). Ця рівна горизонтальна поверхня буде механічною моделлю незбуреного (невикривленого) простору. З’ясовуючи наявність чи відсутність силового поля в тій чи іншій точці нашого модельного простору, візьмемо маленьку пробну кульку і будемо вносити її у відповідні точки цього незбуреного простору. Виконавши серію експериментів ви неодмінно з’ясуєте, що в даному незбуреному (невикривленому) просторі, силового поля нема. Нема тому, що пробна кулька будучи внесеною в будь яку точку простору, залишається в цій точці.


Мал.124. Механічна модель не викривленого (а) та викривленого (б) простору. В невикривленому просторі поля нема, у викривленому – є.
Тепер, в наш модельний простір внесемо велику масивну кулю. При цьому поверхня гуми відповідним чином викривиться (мал.124б). Вносячи пробну кульку в різні точки цього викривленого модельного простору, ви неодмінно з’ясуєте, що вона скочується до джерела викривлення. А це означає, що масивне тіло створює навколо себе силове поле. Зауважте, модельний простір (гумова поверхня) не став іншим. В ньому не з’явились додаткові атоми, молекули чи інші частинки. Просто у викривленому (збуреному) стані, властивості простору стали іншими.
Вивчаючи фізику, ви не раз переконаєтесь в тому, що Природа влаштована таким дивним чином, що її найпростіші об’єкти є надзвичайно складними. Ну здавалося б, що може бути простішим за пустий простір? Адже простір, це просто та безструктурна пустота, в якій нема нічого окрім самої пустоти. І тим не менше, простір – це надзвичайно складний фізичний об’єкт, властивості якого визначальним чином залежать від тих об’єктів що в ньому знаходяться та тих подій що в ньому відбуваються. Наприклад, якщо в просторі знаходиться масивне тіло, то своєю присутністю воно надає цьому простору тих властивостей, характеризуючи які ми говоримо про наявність гравітаційного поля. Якщо ж в просторі знаходиться заряджене тіло, то цей простір набуває властивостей електричного поля. А коли це заряджене тіло починає рухатись, то і властивості простору відповідним чином змінюються та стають такими, що притаманні не лише електричному полю, а й полю магнітному.
Узагальнюючи вище сказане, можна дати наступні визначення. Полями називають такі матеріальні об’єкти, які не складаються з тих чи інших частинок, не мають маси спокою і представляють собою певне силове збурення простору, основною властивістю якого є здатність певним чином діяти на певні матеріальні об’єкти. В залежності від того, що є джерелом поля і на які об’єкти воно діє, поля поділяються на гравітаційні, електричні та магнітні. При цьому: гравітаційним називають таке поле, яке створюється масами і діє на маси; електричним називають таке поле, яке створюється електричними зарядами і діє на електричні заряди; магнітним називають таке поле, яке створюється зарядами що рухаються і діє на заряди які рухаються.
Таким чином, загальну структуру матеріальних об’єктів Природи, можна представити
у вигляді наступної схеми.
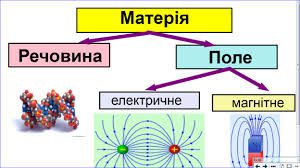
Мал.125. Структура та загальні властивості матеріальних об’єктів Природи.
Відразу ж зауважимо, що вище наведені визначення гравітаційних, електричних та магнітних полів не є бездоганними та безумовно вичерпними. Не є бодай тому, що джерелом електричних та магнітних полів можуть бути не лише рухомі та нерухомі заряди, а й змінні магнітні та електричні поля. Тому будемо вважати, що вище сформульовані визначення, це лише перший крок на шляху пізнання суті та властивостей того що називають гравітаційними, електричними та магнітними полями.
Зауважимо також, що поділ матеріальних об’єктів на речовини та поля є досить умовним. Адже в Природі не існує тієї чіткої межі, яка відділяє речовинні об’єкти від об’єктів полевих. Наприклад стіл – це об’єкт безумовно речовинний, структура якого загально відома. Стіл складається з молекул, молекули складаються з атомів, атоми – з ядра та електронів, ядра – з протонів та нейтронів. А от електрони, протони та нейтрони, це об’єкти речовинні чи полеві? З одного боку, ці елементарні частинки мають явні ознаки речовини, зокрема масу спокою. З іншого – вони не є тими дискретними частинками, які мають певну форму, певні розміри, певну траєкторію руху, тощо. Фактично, елементарні частинки представляють собою певні згустки мас–енергії, які мають як ознаки речовини так і ознаки сконденсованого поля. Або наприклад, світло – це речовина чи поле? З одного боку, світло представляє собою певне збурення електромагнітного поля, яке розповсюджується у вигляді електромагнітної хвилі. З іншого ж боку, світло має властивості потоку частинок, тобто властивості речовинного об’єкту.
Умовним, є не лише поділ матеріальних об’єктів на речовини та поля, а й поділ полів на гравітаційні, електричні та магнітні. Скажімо електрон – яке поле він створює? З одного боку електрон має масу і тому створює відповідне гравітаційне поле. З іншого – електрон є частинкою зарядженою, а отже такою що створює певне електричне поле. В третіх, електрон перебуває в постійному русі і тому є джерелом певного магнітного поля. На кінець, електрон, це цілісна частинка і тому ті поля які ним створюються нерозривно пов’язані між собою.
Розмова про поля буде не повною, якщо не згадати того видатного вченого який збагатив сучасну науку уявленнями про ці специфічні невидимі об’єкти. А цим вченим є геніальний англійський фізик Майкл Фарадей (1791-1867). Розмірковуючи над механізмом гравітаційних, електричних та магнітних взаємодій, Фарадей дійшов висновку: в Природі, окрім тих об’єктів які прийнято називати речовинами, має існувати ще одна різновидність матеріальних об’єктів які і забезпечують гравітаційні, електричні та магнітні взаємодії. Ці об’єкти Фарадей назвав полями і достатньо точно описав їх властивостей. Певний час ідеї Фарадея не визнавались науковою спільнотою. І лише після того як в 1864 році, ще один видатний англійський фізик Д. Максвел (1831–1879) реалізуючи ідеї Фарадея створив теорію електромагнітного поля, а німецький фізик Г. Герц (1857–1894) в 1888 році експериментально підтвердив її достовірність, реальність існування полів стала експериментально доведеним фактом.
Не буде перебільшенням сказати, що ідея Фарадея щодо факту існування полів, стала одним з найвизначніших відкриттів сучасної науки. По суті, це відкриття кардинально вплинуло не лише на розвиток науки, а й на увесь еволюційний розвиток людства. Втім, про те який зв’язок між ідеєю поля і епохою радіо, телебачення та інтернету, ми поговоримо дещо пізніше. Наразі ж зауважимо, що до Фарадея простір вважали тією пасивною, безструктурною ємністю, яка здатна лише на те, щоб в ній знаходились ті чи інші речовинні об’єкти і відбувались ті чи інші події. Після Фарадея, простір став об’єктом наукових досліджень. Активним, багатофункціональним співучасником подій та явищ.
Контрольні запитання.
1. Поясніть яким чином гравітаційна дія передається від Землі до Місяця і навпаки?
2. Як довести факт того, що в даній точці простору існує: а) гравітаційне поле; б) електричне поле?
3. На який фізичний об’єкт схоже поле? В чому ця схожість?
4. Поясніть суть уявлень про поле як про викривлений простір.
5. Якщо поле, це збурена пустота, то чому цю пустоту ми називаємо матеріальною?
6. Наведіть докази того, що поділ матеріальних об’єктів на речовини та поля є умовним.
7. Наведіть докази того, що поділ полів на гравітаційні, електричні та магнітні є умовним.
Вправа 40.
1. Відомо: маса Землі 6,0∙1024кг, маса Місяця 7,3∙1022кг, відстань між центрами Землі та Місяця 3,84∙108м. Визначити силу гравітаційної взаємодії між Землею та Місяцем.
2. Якої площі поперечного перерізу і якої маси має бути сталевий трос, щоб витримати ту силу з якою Земля притягує Місяць? Допустима механічна напруга для сталі 2∙108Па. Порівняйте масу цього троса з масою Місяця; з масою Землі. (Густина сталі 7,8∙103кг/м3).
3. Відомо, що маса Землі 6,0∙1024кг, маса Сонця 2,0∙1030кг, а відстань між ними 1,5∙1011м. Визначте силу гравітаційної взаємодії між Землею та Сонцем. Порівняйте цю силу з силою взаємодії між Землею та Місяцем.
.
§41. Електричне поле. Напруженість електричного поля. Принцип суперпозиції.
Дослідження показують, що будь який електричний заряд створює в навколишньому просторі певне силове збурення цього простору яке прийнято називати електричним полем. Електричне поле, це таке поле, тобто таке силове збурення простору, яке створюється електричними зарядами і діє на електричні заряди.
Потрібно зауважити, що в науковій практиці термін «електричне поле» є синонімом терміну «електростатичне поле». Однак ви маєте знати, що існує дві різновидності електричного поля: електростатичне поле та індукційне електродинамічне поле. Вони відрізняються тим, перше створюються електричними зарядами, а друге – змінними магнітними полями. Втім, про індукційні електродинамічні поля та про те чим вони відрізняються від електростатичних полів, ми поговоримо ще не скоро. Тому в подальшому, електричними полями ми будемо називати саме поля електростатичні, тобто такі, які створюються електричними зарядами.
Ілюструючи ті відмінності що існують між речовинами та полями, проведемо гранично стислий порівняльний аналіз базових властивостей тих фізичних об’єктів які називаються електричними полями та речовинами.
| Властивості електричних полів | Властивості речовинних об’єктів |
| . 1. Електричні поля і речовинні об’єкти так чи
. інакше проявляють себе і тому є матеріальними. . 2. Електричні поля та речовинні об’єкти є . взаємопов’язаними чистинами єдиного цілого – Природи. |
|
| 3. Електричні поля не мають певного внутрішнього устрою, тобто не складаються з тих чи інших більш простих елементів. | Речовинні об’єкти мають певний внутрішній устрій, тобто є такими які складаються з певних більш простих структурних одиниць: молекул, атомів, іонів, тощо. |
| 4. Електричні поля характеризуються неперервністю. Це означає, що вони не складаються з тих чи інших дискретних (обособлених) частинок і що їх властивості якщо і змінюються то плавно неперервним чином. | Речовинні об’єкти характеризуються дискретністю. Це означає, що вони складаються з певних обособлених частинок, кожна з яких є згустком певних властивостей. |
| 5. Електричні поля не обмежені в просторі. Це означає, що створене зарядом поле, в тій чи іншій мірі проявляється в усіх точках навколишнього середовища і що тому поля не мають певного об’єму, форми, розмірів, тощо. | Речовинні об’єкти обмежені в просторі. Це означає, що характеризуючи той чи інший речовинний об’єкт, можна говорити про його об’єм, форму, розміри, площу поперечного перерізу, тощо. |
| 6. Електричні поля взаємно проникливі і такі що діють незалежно одне від одного. Це означає, що в одній і тій же точці простору, одночасно може знаходитись безліч полів, які діють незалежно одне від одного і не заважаючи одне одному. | Речовинні об’єкти взаємно не проникливі і такі що заважають один одному. Це означає, що дві дискретні частинки речовини не можуть одночасно знаходитись в одній і тій же точці простору і що в цьому сенсі речовини впливають одна на одну і одна одній заважають. |
За визначенням, єдиним зовнішнім проявом електричного поля є його здатність певним чином діяти на електричні заряди. Це означає, що для з’ясування факту того є в даній точці простору електричне поле чи нема, у відповідну точку потрібно внести певний пробний заряд і подивитись на його поведінку. При цьому: якщо на пробний заряд подіє електрична сила, то це означатиме, що у відповідній точці електричне поле є; а якщо така сила не подіє – значить поля нема. От і все. Оскільки електричні заряди бувають позитивними та негативними, то за домовленістю в якості пробного заряду (qп) завжди обирають відносно невеликий, позитивний, точковий заряд. Іншими словами, за домовленістю, пробний заряд є позитивним (qп = +).
Зважаючи на факт того, що визначальною властивістю електричного поля є його здатність до певної силової дії, логічно передбачити, що саме та сила з якою поле діє на пробний заряд і є основною силовою характеристикою електричного поля. Однак, дане передбачення навряд чи можна вважати обгрунтованим. Адже вносячи в одну і ту ж точку поля різні пробні заряди, ми отримаємо різні значення діючих на ці заряди сил. Дійсно, згідно з законом Кулона: Fел = kqqп/r2 = ƒ(qп). А це означає, що діючу на пробний заряд силу не можна вважати об’єктивною силовою характеристикою електричного поля. Цією характеристикою є величина яка називається напруженістю електричного поля.
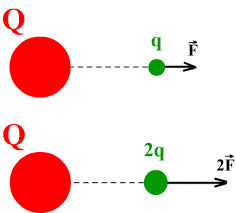
Мал.126. Електричне поле, одне і те ж, а діючі на пробні заряди сили – різні. Висновок: сила не є об’єктивною характеристикою поля.
Напруженість електричного поля, це фізична величина, яка є силовою характеристикою електричного поля і яка дорівнює відношенню тієї електричної сили що діє на пробний заряд в даній точці поля, до величини цього пробного заряду.
Позначається: Е
Визначальне рівняння: Е = Fел/qп
Одиниця вимірювання: [Е] = Н/Кл , (ньютон на кулон).
Напруженість електричного поля – величина векторна. При цьому, із визначального рівняння Е = Fел/qп ясно, що напрям вектора напруженості співпадає з напрямком тієї сили що діє на пробний (позитивний) заряд у відповідній точці поля.
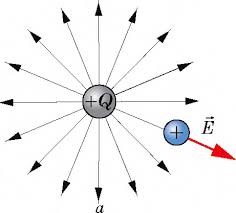
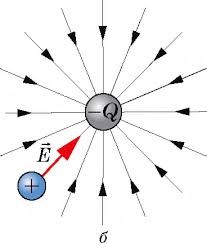
Мал.127. Напрям вектора напруженості електричного поля співпадає з напрямком тієї сили що діє на пробний (позитивний) заряд у відповідній точці поля.
Не важко довести, що величина напруженості того електричного поля яке створюється точковим зарядом q, в будь якій точці цього поля визначається за формулою Е = kq/r2 або E = q/4πεε0r2, де r – відстань від заряду до даної точки. Дійсно. Згідно з законом Кулона, два точкових заряди q та qп взаємодіють між собою з силою Fел = kqqп/r2 де k = 1/4πεε0. А оскільки за визначенням Е = Fел/qп то Е = kq/r2 або E = q/4πεε0r2 .
В загальному випадку, кожна точка простору характеризується своїм індивідуальним значенням вектора напруженості. Але існують поля, параметри яких в усіх токах однакові. Ці поля називаються однорідними. Прикладом однорідного електричного поля є те поле, що існує між двома протилежно зарядженими, близько розташованими, паралельними пластинами, лінійні розміри яких набагато більші за відстань між ними.
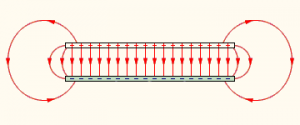
Мал.128. Поле, вектор напруженості якого в усіх точках однаковий називається однорідним.
Ясно, що кількісно описати ті процеси, що відбуваються в однорідному полі набагато простіше аніж в полі неоднорідному. Тому з’ясовуючи характерні властивості полів, ми зазвичай будимо говорити про поля однорідні. А потім, на основі отриманих результатів, робити певні узагальнюючі висновки. Вміти кількісно оцінювати властивості та прояви однорідних полів важливо ще й тому, що будь яке надскладне поле, завжди можна представити як певну сукупність однорідних фрагментів.
Однією з визначальних відмінностей між речовинами та полями є факт того, що речовини характеризуються взаємною непроникливістю, а поля – взаємною проникливістю. Коли ми говоримо, що речовини взаємно непроникливі, то маємо на увазі факт того, що дві різні частинки речовини (два різні атоми, дві різні молекули, дві різні піщинки, два різних твердих тіла) не можуть одночасно знаходитись в одній і тій же точці простору. І в цьому сенсі речовини є такими що заважають одна одній. Натомість поля є взаємно проникливими і такими що не заважають одне одному. Це означає, що в один і той же момент часу, в одній і тій же точці простору, може знаходитись безліч полів, які діють незалежно одне від одного і одне одному не заважають.
Закон, який констатує факт того, що поля діють незалежно одне від одного і не заважаючи одне одному називається принципом накладання полів, або принципом суперпозиції полів. Цей закон справедливий для будь яких полів. Але оскільки ми вивчаємо поля електричні, то відповідно для них і сформулюємо цей закон. Принцип суперпозиції електричних полів, це закон, в якому стверджується: електричні поля діють незалежно одне від одного (не заважаючи одне одному) при цьому, напруженість результуючого електричного поля, дорівнює векторній сумі напруженостей кожного окремого поля системи. Іншими словами: Ерез= Е1+Е2+ …+ЕN , або Ерез=∑ Еі.
У відповідності з принципом суперпозиції можливі ситуації, в яких за наявності великої кількості електричних зарядів, наявність цих зарядів може бути не зафіксованою. Наприклад, якщо пробний заряд знаходиться в центрі рівномірно зарядженої сфери, то кожний заряд цієї сфери буде діяти на пробний заряд (мал.129). А оскільки заряди сфери є рівновіддаленими від пробного заряду, то величини діючих на нього сил будуть однаковими і результуюча цих сил дорівнюватиме нулю. А це означає, що при внесенні пробного заряду в центр рівномірно зарядженої сфери, ви неодмінно з’ясуєте, що на цей заряд електричні сили не діють, і що тому у відповідній тоці простору електричного поля нема. Більше того, можна довести, що в будь якій точці оточеного струмопровідною поверхнею простору, електричне поле відсутнє. Напруженість електричного поля всередині будь якої струмопровідної поверхні завжди дорівнює нулю. По суті це означає, що всередині того простору який оточений струмопровідною поверхнею електричне поле відсутнє.
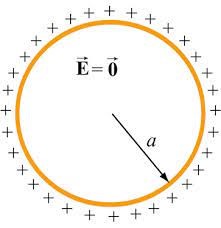
Мал.129. Зарядів багато, а електричного поля нема.
Оскільки визначення результуючого вектора напруженості електричного поля нерозривно пов’язано з додаванням векторів, то буде не зайвим нагадати. Розрізняють два методи додавання векторних величин: геометричний (графічний) та алгебраїчний (аналітичний). При геометричному методі, результат додавання векторів отримують шляхом відповідних геометричних побудов. Ці побудови здійснюють так званим методом багатокутника. Суть цього методу гранично проста. Якщо на точку К (мал.130) діє система N векторів, то величину і напрям результуючого вектора (R = F1+F2+ … +FN) визначають наступним чином. З точки К відкладають вектор F1, з кінця вектора F1 відкладають вектор F2, з кінця вектора F2 – вектор F3 і так до останнього вектора FN. Вектор, який з’єднує точку К з кінцем останнього вектора і буде результуючим вектором R = F1+F2+ … +FN.
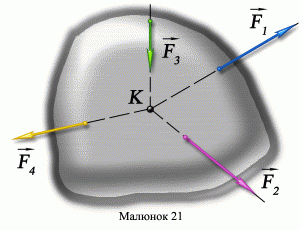
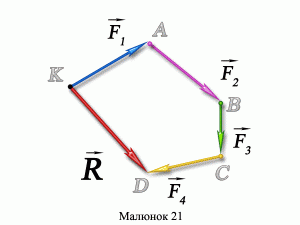
Мал.130. Величину та напрям результуючого вектору визначають методом багатокутника (геометричне додавання векторів).
Геометричний метод додавання векторів виглядає досить простим та наочним. Однак, він має ряд суттєвих недоліків. Перший полягає в тому, що точність його результатів залежить від масштабу та точності геометричних побудов. При цьому, будь яка точність цих побудов, не гарантує безумовно точного результату. Другим суттєвим недоліком геометричного методу додавання векторів полягає в тому, що таке додавання погано поєднується з тими теоріями, в яких закони представляють у вигляді певних математичних формул. А переважна більшість фізичних теорій є саме такими. Тому зазвичай вектори додаються алгебраїчним методом. Суть цього методу полягає в наступному. Якщо на точку К діє система N векторів, то величину і напрям результуючого вектора Fр = F1 + F2 + … + FN визначають наступним чином:
1.Кожний вектор системи розкладають на його проекції.
2. Визначають суму проекцій всіх векторів на кожну з осей системи координат:
Fxр= Fx1 + Fx2 + … +Fxn;
Fyр= Fy1 + Fy2 + … + Fyn.
3. Визначають величину Fр та напрям α результуючого вектора:
Fр=√(Fxр2 + Fyр2);
α = arctg(Fyр/Fxр).
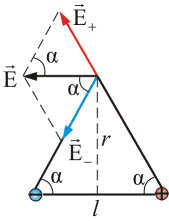
Задача. В двох вершинах рівностороннього трикутника знаходяться два різнойменні заряди по 18нКл кожний. Визначити напруженість електричного поля в третій вершині трикутника, якщо довжина його сторони 1м.
Дано:
q1=q2=q=10нКл
ℓ = 1м
Eрез = ?
Рішення: Виконуємо малюнок на якому вказуємо вектори напруженостей поля в третій вершині трикутника. Задаємо систему координат: вісь 0х – горизонтальна, вісь 0у – вертикальна. Згідно з принципом суперпозиції Ерез = Е+ + Е–. Або, в проекціях на осі прямокутної системи координат:
(Ерез)х = (Е+)х + (Е–)х = Еcosα + Ecosα = 2Ecosα;
(Ерез)у = (Е+)у + (Е–)у = Esinα – Esinα = 0
В умовах нашої задачі: E+ = E– = E = kq/r2 = 9·109·10·10–9/12 = 90Н/Кл, оскільки трикутник рівносторонній, то α=60°
Таким чином: Ерез = 2Ecosα = 2·90·0,87 = 157Н/Кл
Відповідь: Ерез= 157(Н/Кл).
Контрольні запитання.
1. Що означає «електричні поля характеризуються неперервністю»?
2. Що означає «електричні поля не обмежені в просторі»?
3. Що означає «електричні поля є такими що не заважають одне одному»?
4. Чому ту силу що діє на пробний заряд в даній точці поля не можна вважати об’єктивною характеристикою поля?
5. Доведіть, що величина напруженості поля точкового заряду, визначається за формулою Е = kq/r2.
6. Які поля називають однорідними? Які переваги цих полів?
7. В чому суть геометричного методу додавання векторів?
8. В чому суть алгебраїчного методу додавання векторів?
Вправа 41.
1. В певній точці поля на заряд 1∙10–7Кл діє сила 4∙10–3Н. Визначити напруженість поля в цій точці та величину того заряду який створює поле, якщо точка віддалена від заряду на 0,3м.
2. В атомі водню електрон рухається навколо ядра круговою орбітою радіус якої 5,3∙10–11м. Визначте величину тієї електричної сили з якою взаємодіють ядро атома та електрон, напруженість того поля яке створює ядро в точках траєкторії руху електрона, та швидкість руху електрона. Маса електрона 9,1∙10–31кг.
3. З яким прискоренням рухається електрон в електричному полі з напруженістю 10кН/Кл?
4. Краплина масою 1,0∙10–4г знаходиться в рівновазі в однорідному електричному полі з напруженістю 98Н/Кл. Визначити заряд крапельки.
5. В двох протилежних вершинах квадрату з стороною 30см, знаходяться точкові заряди по 2∙10–7Кл. Визначити напруженості поля в двох інших вершинах квадрату.
6. Два точкові заряди 2,0∙10–8Кл і 1,6∙10–7Кл знаходяться на відстані 5см один від одного. Визначити напруженість поля в точці віддаленій від першого заряду на 3см, а від другого на 4см.
7. В вершинах рівностороннього трикутника зі стороною 10см знаходяться заряди q1=2∙10–7Кл, q2= –2∙10–7Кл, q3 =2∙10–7Кл. Визначити напруженість поля в центрі трикутника.
.
§42. Графічне зображення електричних полів.
Поля є тими об’єктами, які не мають смаку, запаху та кольору. Не мають об’єму, форми та густини. І звичайно, поля невидимі. Тим не менше, поле можна представити у вигляді певної візуальної картинки. Звичайно, мова не йде про якесь художнє зображення того, чого ми ніколи не бачили. Мова йде про графічне відображення певних реальних властивостей того об’єкту який називається електричним полем.
Здається очевидним, що картину електричного поля потрібно «малювати» векторами його напруженості. Адже саме ці вектори об’єктивно відображають реальні силові властивості поля. Однак, намагаючись реалізувати такий підхід на практиці, ви швидко та неминуче переконаєтесь в тому, що «намальована» векторами напруженості картина поля (навіть найпростішого), представляє собою сукупність величезної кількості різнонаправлених та різновеликих векторів, які накладаючись один на одного, практично унеможливлюють будь який аналіз отриманої картини.
Проблему графічного зображення гравітаційних, електричних та магнітних полів, вирішив все той же великий Фарадей. Ідея Фарадея полягала в тому, що електричні поля потрібно зображати не за допомогою векторів напруженостей поля, а за допомогою спеціальних умовних ліній, які прийнято називати лініями напруженості електричного поля. Лінія напруженості електричного поля, це така умовна лінія, яка проводиться таким чином, що дотична до неї в будь якій точці співпадає з напрямком результуючого вектора напруженості поля в цій точці. Оскільки лінії напруженості електричного поля є дотичними не лише до векторів напруженості поля, а й до векторів діючих на пробні заряди сил, то ці лінії іноді називають силовими лініями електричного поля.
Ілюструючи технологію побудови та властивості ліній напруженості поля, розглянемо конкретний приклад. Припустимо, що в точках А і В знаходяться два однакових за величиною і протилежних за знаком заряди qА і qВ (мал.131). Розв’язуючи задачу графічного зображення того електричного поля яке створюють ці заряди, в близьких околицях заряду qА виберемо довільну точку, наприклад т.1, і застосовуючи принцип суперпозиції визначаємо результуючий вектор напруженості поля і цій точці: Е1 = Еа1 + Ев2. Проводимо невеличкий фрагмент дотичної до цього вектора. На цьому фрагменті вибираємо наступну точку т.2 і повторюємо процедуру визначення та побудови результуючого вектора напруженості: Е2=Еа2+Ев2. З врахуванням напрямку вектора Е2 продовжуємо дотичну і на ній вибираємо наступну точку. І т.д. Результатом такої послідовності побудов, буде неперервна лінія, яка і є лінією напруженості електричного поля. Обираючи все нові і нові початкові точки, ми отримаємо певний набір ліній, сукупність яких і є візуальним зображенням відповідного електричного поля.

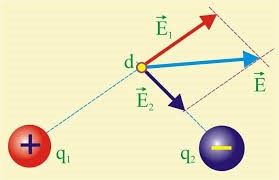
Мал.131. Картина електричного поля двох однакових різнойменних зарядів, та механізм побудови ліній напруженості цього поля.
Потрібно зауважити, що для правильної побудови картини поля, початкові точки обирають не як завгодно, а за певною процедурою. Наприклад навколо заряду qА проводять коло малого радіусу, на якому обирають певну кількість рівновіддалених точок, які і стають початковими точками відповідних геометричних побудов.
Ясно, що «намалювати» точну кількісну картину поля системи багатьох довільно розташованих зарядів надзвичайно складно. На щастя, наукова практика рідко вимагає точного кількісного зображення електричних полів. В науковій практиці важливим є не сам факт точного зображення поля, а чітке розуміння тих загальних закономірностей які цьому зображенню та відповідному полю притаманні. А ці закономірності є наступними.
1.Будь яка лінія напруженості електричного (електростатичного) поля починається на заряді «плюс» і закінчується на заряді «мінус». Дане твердження є прямим наслідком факту того, що Природа влаштована таким чином, що в ній різнойменні заряди виникають і зникають лише попарно. А це означає, що в Природі для кожного заряду «+» є відповідний йому заряд «–». Тому, якщо картина поля створеного обособленим зарядом «плюс» виглядає таким чином, ніби лінії напруженості прямують в безкінечність, знайте – десь там, в цій безкінечності ці лінії закінчуються і закінчуються на заряді «мінус».
2. Лінії напруженості електричного поля ніде не перетинаються. Це випливає з того, що будь яку точку електричного поля характеризує лише один результуючий вектор напруженості, до якого можна провести лише одну дотичну (лише одну лінію напруженості).
3. Лінії напруженості електричного поля направлені від заряду «плюс» до заряду «мінус». Дане твердження не є наслідком певних природних закономірностей. Воно є прямим результатом того, що в якості пробного заряду, ми за домовленістю обрали заряд «плюс». Тому в електричному полі, цей пробний заряд буде рухатись від «плюса» до «мінуса».
4. Густина ліній напруженості поля в околицях будь якої точки, пропорційна величині вектора напруженості в цій точці. Це випливає з того, що лінії напруженості електричного поля є неперервними і тому в процесі віддалення від заряду їх густина зменшується. При цьому можна довести, що зменшується обернено пропорційно квадрату відстані до заряду, тобто саме так як зменшується напруженість електричного поля (Е ~ 1/r2).
Загальний вигляд деяких простих електричних полів представлено на мал.132.
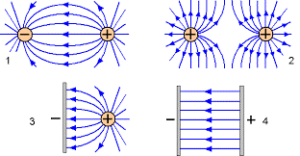
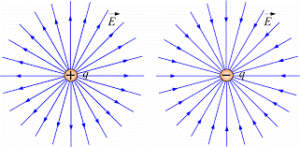
Мал.132. Картина деяких простих електричних полів.
Потрібно зауважити, що лінії напруженості електричного поля, це лінії умовні, тобто такі які в реальності не існують. Однак ці лінії цілком об’єктивно відображають реальні властивості поля. Наприклад, якщо в будь яку точку електричного поля внести надлегкий заряд, то він полетить до заряду протилежного знаку не по прямій і не як попало, а вздовж відповідної лінії напруженості поля. Тому, якщо наприклад, в околицях заряду «мінус» рівномірно посипати електронами, то вони полетять до заряду «плюс» таким чином, що намалюють картину відповідного електричного поля.
Напевно ви розумієте, що здійснити вище описаний експеримент в умовах шкільного кабінету фізики практично не можливо. Але навіть в цих умовах, певні наглядні уявлення про геометричну структуру електричних полів можна отримати. З цією метою візьмемо скляне блюдце і наллємо в нього невелику кількість прозорої діелектричної олії, наприклад касторової. В цю олію додамо невелику кількість дрібно нарізаного волосся і доб’ємось того, щоб отримана суміш була однорідною. Опускаючи в посудину електроди різної форми, та підключаючи їх до джерела постійної напруги (наприклад електрофорної машини) ми будемо створювати поля різної конфігурації. При цьому, поляризовані шматочки волосся будуть орієнтуватись вздовж ліній напруженості поля і «малювати» це поле (мал.133).
Увага! Подібні експерименти не можна проводити в домашніх умовах. Адже побутова електрика смертельно небезпечною. Крім цього, побутова напруга, це напруга змінна. Ми ж говоримо про напругу постійну.

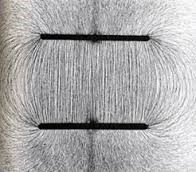
Мал.133. В електричному полі дрібні фрагменти волосся орієнтуються певним чином і «малюють» картину відповідного поля.
Пояснюючи суть того що називається полем, ми говорили про те, що поле можна представити як певне викривлення простору яке на певні матеріальні об’єкти спричиняє певну силову дію. І в цьому сенсі електричне поле не є винятком (мал.134). Однак на відміну від гравітаційного поля, поле електричне є більш складним. Більш складним в тому сенсі, що в залежності від знаку пробного заряду, може спричиняти як його притягування (рух заряду до джерела поля) так і відштовхування (рух заряду від джерела поля). Ситуація нагадує таку, ніби різнойменні пробні заряди знаходяться по різні боки викривленого простору і тому те, що для одного заряду є пагорбом, для іншого – є западиною і навпаки.
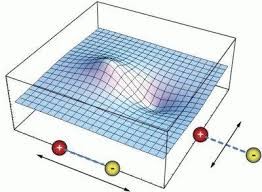
Мал.134. Електричне поле можна представити як певне викривлення простору.
Задача. Три однакових за величиною, негативних точкових заряди, знаходяться в вершинах рівностороннього трикутника. Визначте напруженість електричного поля в центральній точці трикутника (в точці перетину бісектрис).
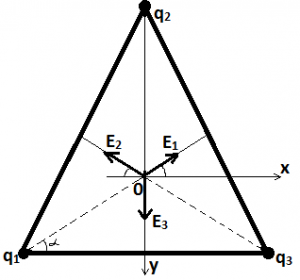
Дано:
q1=q2=q3
Ерез=?
.Рішення: Виконуємо малюнок на якому вказуємо всі вектори напруженостей поля в заданій точці, задаємо систему координат та вказуємо відповідні кутові величини.
Геометричне рішення. Згідно з принципом суперпозиції, напруженість результуючого поля системи N зарядів, дорівнює векторній сумі напруженостей кожного окремого поля цієї системи. В умовах нашої задачі Ерез = Е1 + Е2 + Е3 .
Застосовуючи правила додавання векторів та зважаючи на те, що Е1=Е2=Е3, виконуємо відповідні геометричні побудови. (Оскільки, в умовах даної задачі числові значення векторів Е1, Е2, Е3 не задані, то ці значення ми задаємо умовно, наприклад у вигляді трьох відповідно направлених відрізків довжиною по 4см).
Із аналізу отриманого геометричного рішення ясно, що в точці А напруженість результуючого поля дорівнює нулю Ерез = Е1 + Е2 + Е3 = 0 (Н/Кл)
Відповідь: Ерез=0Н/Кл.
Алгебраїчне рішення. У вибраній системі координат, позначаємо всі задані векторні та кутові величини.
Згідно з принципом суперпозиції Ерез = Е1 + Е2 + Е3.
Або, в проекціях на осі прямокутної системи координат:
(Ерез)х = (Е1)х + (Е2)х + (Е3)х ;
(Ерез)у = (Е1)у + (Е2)у+ (Е3)у .
В умовах нашої задачі (дивись малюнок)
(Ерез)х = –Е2cos30º + E1cos30º = –Еcos30º + Ecos30º = 0 (Н/Кл)
(Ерез)у = E3 – E2sin30º –E1sin30º = E – 2Esin30º = E – 2E∙0,5 = 0 (Н/Кл).
Ерез = √(02 + 02) = 0 (Н/Кл).
Відповідь: Ерез= 0 (Н/Кл).
Контрольні запитання.
1. Чому електричні поля не «малюють» векторами напруженості поля?
2. Яка технологія побудови ліній напруженості електричного поля?
3. Яка причина того, що лінії напруженості електричного поля починаються на заряді «плюс» і закінчуються на заряді «мінус»?
4. Чому лінії напруженості електричного поля ніде не перетинаються?
5. Чому густина ліній напруженості поля в околицях будь якої точки, пропорційна величині вектора напруженості в цій точці.
6. Чому в електричному полі двох різнойменних зарядів, електрони летять до заряду плюс не по прямій, а вздовж ліній напруженості поля?
7. Що можна сказати про величину позитивного і негативного заряду зображеного на малюнку поля? Відповідь обґрунтуйте.
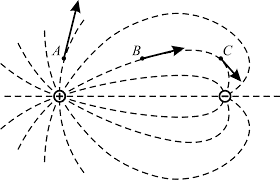
Вправа 42.
1. В певній точці поля на заряд 6нКл діє сила 5мН. Визначити напруженість поля в цій точці та величину того заряду який створює поле, якщо відстань до нього 20см.
2. В однорідному електричному полі електрон рухається з прискоренням 3,2·1013м/с2. Визначити напруженість поля, якщо маса електрона 9,1·10–31кг.
3. В вершинах рівностороннього трикутника з стороною а знаходяться заряди +q, +q, –q. Визначити напруженість поля в центрі трикутника.
4. Два різнойменні заряди один з яких у 4 рази більший за другий, розташовані на відстані а один від одного. В якій точці простору напруженість поля дорівнює нулю?
5. В однорідному електричному полі з напруженістю 3·106Н/м, силові лінії якого утворюють з вертикаллю кут 30°, висить на нитці кулька масою 2г та зарядом 3,3нКл. Визначити силу натягу нитки.
6. Три однакових позитивних заряди розташовані в вершинах рівностороннього трикутника зі стороною а. Визначити величину напруженості поля в точці, яка знаходиться на відстані а від кожного з зарядів.
.
§43. Провідники та діелектрики в електричному полі. Сегнетоелектрики. П’єзоефект.
Нагадаємо. Провідниками називають такі матеріали, які проводять електричний струм. Проводять тому, що в них є достатньо велика кількість вільних заряджених частинок (носіїв струму), тобто таких заряджених частинок які можуть вільно переміщуватись в межах даного матеріалу. Наприклад в металах, цими вільними зарядженими частинками є електрони. Діелектриками називають такі матеріали, які не проводять електричний струм. Не проводять тому, що в них нема вільних заряджених частинок. В цих матеріалах всі заряджені частинки міцно зв’язані між собою і тому не можуть переміщуватись відповідним матеріалом. Провідники та діелектрики суттєво по різному ведуть себе в зовнішніх електричних полях. З’ясуванню загальних закономірностей цієї поведінки і присвячено даний параграф.
Коли провідник потрапляє в зовнішнє електричне поле (мал.135), то під дією сил цього поля, вільні заряджені частинки провідника починають певним чином перерозподілятись. Цей індукційний (тобто спричинений дією зовнішнього електричного поля) перерозподіл продовжується до тих пір, поки ті сили що діють на заряди збоку зовнішнього електричного поля (Fзовн) не зрівноважаться тими силами які діють на ті ж заряди збоку створеного цим перерозподілом внутрішнього електричного поля (Fвн): Fзовн = –Fвн. Тобто до тих пір поки Fрез = Fзовн + Fвн = 0. А це означає, що зовнішнє електричне поле, спричиняє такий індукційний перерозподіл вільних зарядів в тілі провідника, при якому напруженість результуючого поля всередині провідника дорівнює нулю: Ерез = Езовн + Евн = 0.
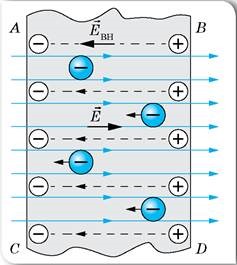
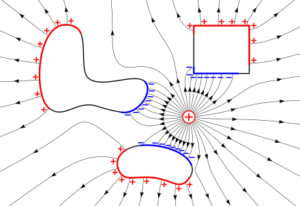
Мал.135. Напруженість результуючого електричного поля всередині провідника завжди дорівнює нулю.
Те явище, суть якого полягає в тому, що під дією зовнішніх електричних полів заряджені частинки фактично незарядженого тіла перерозподіляються таким чином, що одна частина тіла набуває певного позитивного заряду, а інша – відповідного негативного заряду, називають електростатичною індукцією. Зазвичай, говорячи про електростатичну індукцію, мають на увазі той індукційний перерозподіл зарядів який відбувається в провідниках.
Дослідження показують, що індукційний перерозподіл зарядів відбувається не лише в суцільних провідниках, а й на будь яких струмопровідних поверхнях. При цьому, результат такого перерозподілу завжди один і той же: в оточеному струмопровідною поверхнею об’ємі, напруженість результуючого електричного поля завжди дорівнює нулю: Ерез = Езовн + Евн = 0.
Факт того, що в оточеному струмопровідною поверхнею об’ємі, силові прояви електричного поля відсутні, корисно застосовується для захисту (екранування) приладів від зовнішніх електричних впливів. Суть цього захисту очевидно проста. Відповідний прилад, розміщують в металевому корпусі, або оточують металевою сіткою. В такій ситуації, прилад буде повністю захищеним від будь яких зовнішніх електричних впливів. Важливою властивістю такого простого та ефективного захисту є його природня автоматизованість. Адже будь яка зміна параметрів зовнішнього електричного поля, автоматично призводить до такого індукційного перерозподілу зарядів при якому напруженість поля всередині оточеного провідником об’єму незмінно дорівнює нулю.
На відміну від провідників, діелектрики не мають вільних заряджених частинок. Втім, це зовсім не означає, що вони не мають певних електричних властивостей. А ці властивості полягають в тому, що потрапляючи в зовнішнє електричне поле, діелектрики поляризуються. Поляризація діелектрика (індукційна поляризація), це явище, суть якого полягає в тому, що під дією зовнішнього електричного поля, молекули діелектрика по перше набувають певних дипольних властивостей (або підсилюють ці властивості), а по друге, орієнтуються таким чином, що одні ділянки поверхні діелектрика набувають позитивного заряду, а інші – негативного.
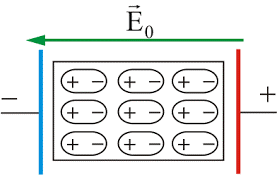
Мал.136. В процесі поляризації одні ділянки поверхні діелектрика набувають позитивного заряду, а інші – негативного.
Спрощено пояснюючи ті процеси що відбуваються при індукційній поляризації діелектрика, можна сказати наступне. Все різноманіття електронейтральних молекул (атомів) можна розділити на дві групи: молекули які мають постійні дипольні властивості, та молекули які таких властивостей не мають. В молекулах першої групи, електричні заряди розподілені не симетрично і тому в них завжди можна виділити два електричних полюси. Такі постійно поляризовані молекули називаються диполями («ди» – два, «поль» – полюс). В молекулах другої групи, електричні заряди розподілені симетрично і тому вони не мають постійних дипольних властивостей. Наприклад, молекула води (Н2О) має постійні яскраво виражені дипольні властивості, а молекула вуглекислого газу (СО2) – таких властивостей не має.
Електричні властивості дипольних та недипольних молекул суттєво різні. Однак, загальна електрична поведінка відповідних діелектриків є схожою. Схожою тим, що за відсутності зовнішнього електричного поля, ці діелектрики є неполяризованими, а за наявності такого поля – стають поляризованими. І це при тому, що механізм цієї поляризації суттєво різний. Скажімо, за відсутності зовнішнього електричного поля, просторова орієнтація молекул–диполей усереднено безладна і тому відповідний діелектрик є неполяризованим (мал.137а). Коли ж цей діелектрик потрапляє в зовнішнє електричне поле, то його молекули–диполі орієнтуються вздовж ліній напруженості поля (мал.137б). При цьому відбувається так звана орієнтаційна поляризація діелектрика.
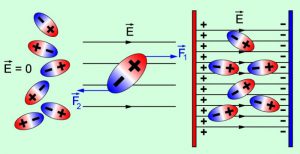
Мал.137. а) За відсутності зовнішнього електричного поля молекули-диполі орієнтовані усереднено хаотично; б) за наявності такого поля, ця орієнтація стає усереднено упорядкованою.
Якщо ж діелектрик складається з молекул які не мають постійних дипольних властивостей, то за відсутності зовнішнього електричного поля, ані самі молекули, ані діелектрик в цілому не є поляризованими. Однак, як тільки такий діелектрик опиняється в електричному полі, його молекули набувають певних дипольних властивостей, а сам діелектрик поляризується. Такий хід подій є очевидно закономірним. Адже в електричному полі на позитивно заряджені ядра та негативно заряджені електрони, діють протилежно направлені сили, які неминуче деформують молекулу і надають їй відповідних дипольних властивостей (мал.138). При цьому говорять про деформаційну поляризацію діелектрика.
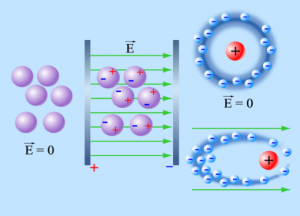
Мал.138. За наявності зовнішнього електричного поля, початково неполяризовані молекули деформуються і набувають дипольних властивостей. При цьому діелектрик поляризується.
Таким чином, потрапляючи в зовнішнє електричне поле будь який діелектрик поляризується. Неминучим та закономірним результатом цієї поляризації є певне зменшення напруженості того результуючого електричного поля що пронизує діелектрик. Дійсно. Припустимо, що у вакуумі між двома зарядженими пластинками існує однорідне електричне поле з напруженістю Е0. Якщо простір між цими пластинками заповнити діелектричним середовищем, то воно поляризується. При цьому поляризоване середовище створить своє поле напруженість якого (Е‘) буде протилежно направленою до напруженості зовнішнього поля. А це означає, що в діелектричному середовищі напруженість результуючого поля (Е) завжди менша за напруженість того поля що існує у вакуумі: Е = Е0 – Е’.
На практиці поляризаційні можливості діелектрика характеризує величина яка називається діелектричною проникливістю середовища. Діелектрична проникливість середовища, це фізична величина, яка характеризує поляризаційні властивості діелектричного середовища і яка показує, у скільки разів напруженість електричного поля в даному середовищі (Е) менша за напруженість того ж поля у вакуумі (Е0).
Позначається: ε
Визначальне рівняння: ε = Е0/Е
Одиниця вимірювання: [ε] = – , (рази).
Нагадаємо. В §42 діелектричну проникливість середовища ми визначали як величину яка дорівнює відношенню сили взаємодії електричних зарядів у вакуумі (F0) до сили їх взаємодії в даному середовищі (F): ε = F0/F. Що ж, діелектрична проникливість середовища відноситься до числа тих фізичних величин, які в різних контекстах визначаються по різному. При цьому кожне з цих визначень є безумовно правильним. І не важко довести, що співвідношення ε = F0/F і ε = Е0/Е є тотожними. Дійсно. За визначенням E=F/qп. Тому F0/F = E0qп/Еqп = Е0/Е.
Серед різноманіття кристалічних діелектриків, можна виділити особливу групу речовин які називаються сегнетоелектриками. Ця назва походить від назви тієї речовини в якій вперше виявили відповідні властивості. А цією речовиною є сегнетова сіль (NaKC4H4O6∙4H2O). Сегнетоелектриками називають такі діелектричні речовини, які мають надзвичайно високу діелектричну проникливість (ε > 200), величина якої складним чином залежить від багатьох зовнішніх обставин, зокрема напруженості електричного поля, температури, зовнішнього механічного тиску, тощо.
Особливі властивості сегнетоелектриків пояснюються тим, що їх молекули–диполі, утворюють певні цілісні групи які називаються електричними доменами. В межах одного домену, всі молекули–диполі орієнтовані однаково і тому їх дипольні властивості суттєво підсилюються. За відсутності зовнішнього електричного поля, різні домени орієнтовані усереднено хаотично. Тому відповідний сегнетоелектрик є неполяризованим. За наявності ж електричного поля, електричні домени орієнтуються таким чином, що відповідне середовище поляризується. Результатом такої інтенсивної поляризації є надзвичайно велика діелектрична проникливість сегнетоелектриків. Наприклад для титанату барію (ВаТіО3) ε=1500, для сульфід сурми (SbSI) ε=2200.

Мал.139. Поляризація сегнетоелектриків відбувається в результаті індукційної переорієнтації електричних доменів.
Поляризація діелектриків, зокрема сегнетоелектриків може відбуватись не лише під дією зовнішнього електричного поля (індукційна поляризація), а й під дією інших енергетичних впливів, наприклад в процесі механічного деформування. Таку поляризацію називають п’єзоелектричним ефектом або просто п’єзоефектом (від грец. piezo – натискаю, тисну).
П’єзоефект, це явище, суть якого полягає в тому, що в процесі механічної деформації (в процесі натискання) деякі кристалічні діелектрики, зокрема сегнетоелектрики поляризуються. Це означає, що в процесі механічного деформування п’єзоелектрика, між відповідними поверхнями виникає певна електрична напруга, величина якої залежить як від властивостей самого п’єзоелектрика, так і від ступеню та напрямку його деформації.
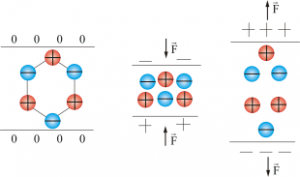
Мал.140. При деформації п’єзоелектрики поляризуються, а при поляризації – деформуються.
Важливою властивістю п’єзоефекту є його зворотність. Ця зворотність проявляється в тому, що ті матеріали які в процесі примусової механічної деформації поляризуються, при зворотньому процесі, тобто в процесі примусової електричної поляризації – деформуються. Іншими словами, якщо п’єзоелектрика деформувати, то між його відповідними поверхнями виникає певна електрична напруга. А якщо між цими поверхнями створити певну електричну напругу, то п’єзоелектрика відповідним чином деформуються.
Прямий та зворотній п’єзоефект широко застосовується в сучасній науці та техніці. Зокрема це явище застосовують для точного вимірювання змін тиску, довжини та об’єму; для перетворення звукових та ультразвукових коливань у відповідні коливання електричної напруги і струму; для перетворення енергії змінної електричної напруги у відповідні механічні коливання, тощо. П’єзоефект застосовується в радіоелектроніці, дефектоскопії, гідроакустиці, медицині та багатьох інших сферах науки, техніки та побуту.
Контрольні запитання.
1.Що називають електростатичною індукцією?
2. Поясніть, чому за будь яких зовнішніх обставин, в оточеному струмопровідною поверхнею об’ємі, електричне поле відсутнє?
3. Поясніть яким чином прилади захищають від впливу електричних полів.
4. Поясніть, чому в зовнішніх електричних полях неполяризовані молекули поляризуються?
5. Чому діелектричне середовище послаблює зовнішні електричні поля?
6. Доведіть тотожність співвідношень ε = F0/F і ε = Е0/Е.
7. Що називають електричними доменами?
8. Чому сегнетоелектрики мають високу діелектричну проникливість?
9. В чому суть прямого та зворотнього п’єзоефекту?
Вправа 43.
1.Електричне поле в гліцерині утворене точковим зарядом 7,0·10–8Кл. Яка напруженість поля в точці віддаленій від заряду на 7,0см?
2. Електрон в атомі водню рухається навколо ядра круговою орбітою радіус якої 5,3·10–11м. Визначіть напруженість поля створеного зарядом ядра на відстані, що дорівнює радіусу орбіти електрона та швидкість руху електрона по цій орбіті.
3. В двох протилежних вершинах квадрату сторона якого 30см знаходяться однойменні заряди по 40мкКл. Визначити напруженість поля в двох інших вершинах. Якою буде ця напруженість якщо заряди стануть різнойменними?
4. Крапля масою 5мг знаходиться в рівновазі в однорідному електричному полі напруженість якого 50Н/Кл. Визначити заряд краплі.
5. Електрон з швидкістю 1,8·103км/с рухається в напрямку ліній напруженості електричного поля, напруженість якого 90Н/Кл. З яким прискоренням рухається електрон?
6. Мідна куля радіус якої 0,5см занурена в машинну оливу густина якої 0,8·103кг/м3. Який заряд кулі, якщо в однорідному електричному полі з напруженістю 3,3кН/м вона знаходиться в стані механічної рівноваги.
.
§44. Робота та потенціал електричного поля. Електричну напругу.
Задача. Позитивний точковий заряд q переміщується в однорідному електричному полі напруженістю Е з точка А в точку В. Визначити роботу сил електричного поля при різних траєкторіях руху заряду (мал.141).
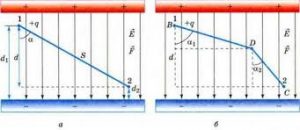
Мал.141. Траєкторії руху різні – виконана робота однакова: A = qEd.
Рішення. Розв’язуючи поставлену задачу, спочатку розглянемо ситуацію при якій заряд q переміщується з точки А в точку В по прямій (мал.141а). Виходячи з того, що А=Fℓcosα, та враховуючи що в однорідному полі на заряд діє постійна електрична сила F=qE, можна записати А=qEℓcosα. Оскільки ℓcosα=d, де d – проекція відрізка АВ на напрям ліній напруженості електричного поля, то A=qEd.
Тепер припустимо, що заряд q переміщується з точки А в точку В ломаною АСВ (мал.141б). В цьому випадку, виконану роботу можна розділити на дві складові А=ААС+АСВ. При цьому: A = qEℓ1cosα1 + qEℓ2cosα2 = qE(d1+d2) = qEd, тобто A = qEd.
Виберемо ще більш складну траєкторію АСДВ (мал.141в). В цьому випадку: А=ААС–АСД+АДВ= qEℓ1cosα1 – qEℓ2cosα2 + qEℓ3cosα3 = qE(d1–d2+d3) = qEd, тобто A = qEd. Зауважимо, що на ділянці СД електричне поле протидіє рухові заряду і тому виконує від’ємну роботу.
Висновок: робота електричного поля по переміщенню заряду в ньому, не залежить від траєкторії руху цього заряду і визначається лише параметрами початкової та кінцевої точок цієї траєкторії.
Можна довести, що даний висновок є справедливим не лише для однорідних полів, а й для й для будь яких електростатичних полів. Не важко довести і те, що на замкнутій траєкторії руху заряду, робота будь якого електростатичного поля дорівнює нулю. Дорівнює нулю тому, що на одних ділянках, поле виконує додатню роботу (сприяє переміщенню заряду), а на інших – від’ємну (протидіє такому переміщенню). Поле, робота сил якого на замкнутій траєкторії дорівнює нулю називається потенціальним (робота сил потенціального поля не залежить від траєкторії руху того об’єкту який переміщує поле і визначається лише параметрами початкової та кінцевої точок цієї траєкторії). Потенціальними є не лише електростатичні поля, а й поля гравітаційні. Адже коли тіло рухається вниз, то гравітаційне поле виконує додатню роботу, а коли вверх – від’ємну, при цьому на замкнутій траєкторії руху, загальна робота сил гравітаційного поля дорівнює нулю.
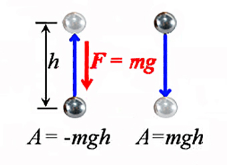
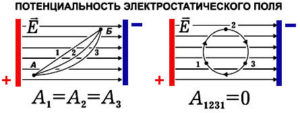
Мал.142. Гравітаційні та електричні поля – поля потенціальні, тобто такі робота сил яких не залежить від траєкторії руху того об’єкту який переміщує поле і визначається лише параметрами початкової та кінцевої точок цієї траєкторії.
Факт того, що електричне поле здатне виконувати певну роботу, безумовно вказує на те, що воно має певні енергетичні властивості. І не важко збагнути, що робота не є об’єктивною мірою цих властивостей. Адже величина виконаної електричним полем роботи A=qEd, залежить не лише від параметрів самого поля (напруженості поля Е), а й від величини перенесеного полем заряду (q) та координати (d) тієї точки в яку цей заряд перенесено. Зважаючи на ці обставини, в якості об’єктивної енергетичної характеристики електричного поля обрано величину яка називається потенціалом електричного поля.
Потенціал електричного поля – це фізична величина, яка є енергетичною характеристикою електричного поля і яка дорівнює відношенню тієї роботи що виконує поле переміщуючи пробний заряд з даної точки поля в безкінечність (тобто туди де прояви поля практично відсутні), до величини цього пробного заряду.
Позначається: φ
Визначальне рівняння: φ = А1→∞/qп
Одиниця вимірювання: [φ] = Дж/Кл = В, (вольт)
Потенціал – величина скалярна, тобто така що характеризується величиною (числовим значенням) та знаком. При цьому, поле створене зарядом «плюс», має додатній потенціал (+φ). А поле, створене зарядом «мінус», має від’ємний потенціал (–φ). Це означає, що те поле яке створене зарядом «плюс», саме переміщує пробний заряд з даної точки в безкінечність і тому виконує додатню роботу. Те ж поле яке створює заряд «мінус», протидіє переміщенню пробного заряду в безкінечність і тому виконує від’ємну роботу.

Мал.143. Заряд «+» створює поле з додатним потенціалом (+φ), заряд «–» створює поле з від’ємним потенціалом (–φ).
Можна довести, що потенціал поля створеного точковим зарядом q, в будь якій точці цього поля визначається за формулою φ = Еr або φ = q/4πεε0r, де r – відстань від заряду q до відповідної точки поля; Е – напруженість поля в цій точці. Можна довести і те, що на поверхні рівномірно зарядженої кулі та за зовнішніми межами цієї поверхні (тобто для r ≥ R, де R – радіус кулі), потенціал поля також визначається за формулою φ = Еr або φ = q/4πεε0r.
Задача 2. Заряд ядра атому цинку дорівнює 4,8·10–18Кл. Визначити потенціал створеного цим ядром електричного поля, на відстані 10нм.
Дано:
q = 4,8·10–18Кл
r = 10нм = 1·10–8м
φ = ?
Рішення: Для точкового заряду φ = q/4πεε0r, де ε=1, ε0=8,8510–12Кл2/Нм2. Отже φ = q/4πεε0r = 4,8·10–18Кл/(4·3,14·1·8,8510–12Кл2/Н·м2) = 4,3В.
Відповідь: φ = 4,3В.
Задача 3. N однакових кулястих крапель ртуті однойменно заряджених до одного і того ж потенціалу φ. Яким буде потенціал тієї великої краплі яка утвориться після злиття малих крапель?
Дано:
N
φ
φN = ?
Рішення: Будемо виходити з того, що в результаті злиття малих крапель радіусом r утвориться велика куляста крапля радіусом R. Потенціал точок поверхні цієї великої краплі можна визначається за формулою φN = qN/4πεε0R, де qN=Nq. Оскільки для малої краплі φ=q/4πεε0r, то r=q/4πεε0φ. Співвідношення між радіусами великої R та малої r крапель, визначаємо із наступних міркувань. Оскільки маси великої М та малої m крапель зв’язані співвідношенням М=Nm, та враховуючи, що М = ρV = ρ(4/3)πR3, m = ρv = ρ(4/3)πr3, можна записати ρ(4/3)πR3 = Nρ(4/3)πr3, звідси R3 = Nr3, звідси R = rN1/3.
Таким чином φN = qN/4πεε0R = Nq/4πεε0rN1/3 = Nφ/N1/3 = φN2/3.
Відповідь: φN = φN2/3.
Оскільки на практиці, електричні заряди із даної точки (т.1) переміщують не в якусь невизначену «безкінечність», а в іншу цілком конкретну точку (т.2), то практичне значення має не сам потенціал поля в тій чи іншій точці, а різниця потенціалів між двома конкретними точками (∆φ=φ1-φ2). Цю різницю потенціалів називають електричною напругою.
Електрична напруга (різниця потенціалів), це фізична величина, яка характеризує різницю потенціалів між двома точками електричного поля і яка дорівнює відношенню тієї роботи що виконує електричне поле переміщуючи пробний заряд між цими точками, до величини пробного заряду.
Позначається: U
Визначальне рівняння: U = A1→2/qп
Одиниця вимірювання: [U] = Дж/Кл = В, вольт.
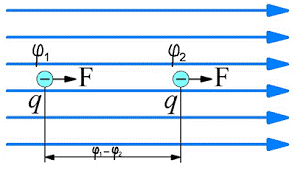
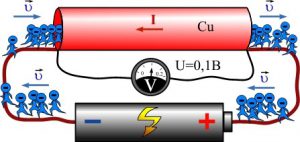
Мал.144. Практичне значення має не потенціал поля в тій чи іншій точці, а різниця потенціалів між двома конкретними точками.
Оскільки в побутовій та електротехнічній практиці електричні заряди переміщуються не в збуреній пустоті яку прийнято називати електричним полем, а струмопровідними ділянками електричного кола, то в умовах цих практик електричну напругу визначають наступним чином. Електрична напруга, це фізична величина, яка характеризує різницю потенціалів між двома точками електричного кола і яка дорівнює відношенню тієї роботи що виконують електричні сили на даній ділянці кола до величини перенесеного ними заряду.
Позначається: U
Визначальне рівняння: U = Aел/q
Одиниця вимірювання: [U] = Дж/Кл = В, вольт
По суті, вище наведені визначення електричної напруги є правильними та рівнозначними. Нюанси цих визначень вказують лише на сферу їх переважного застосування. При цьому, характеризуючи параметри електричного поля застосовують перше формулювання, а характеризуючи параметри електричного кола – друге.
Задача 4. Маленьку кульку масою 1г та зарядом 0,15мкКл, кинули здалеку зі швидкістю 1м/с в сферу заряд якої 0,3мкКл. При якому мінімальному значенні радіусу сфери, кулька досягне її поверхні?
Дано:
m=1г=1·10–3кг
q1=0,15мкКл=15·10–8Кл
v = 1м/с
q2=0,30мкКл=30·10–8Кл
R = ?
Рішення: Будемо виходити з того, що та кінетична енергія (Ек=mv2/2) яку має маленька кулька піде на подолання сил електричного відштовхування однойменних зарядів великої та малої кульок, тобто на виконання роботи Аел = φq1. А зважаючи на те, що потенціал точок поверхні кулі φ = q2/4πεε0R, можна записати mv2/2 = q1q2/4πεε0R, звідси R = 2q1q2/4πεε0mv2.
Розрахунки: R = 2q1q2/4πεε0mv2= 2·15·10–8·30·10–8/4·3,14·1·8,85·10–12·1·10–3·12 = 0,81м.
Відповідь: R=81см.
Контрольні запитання.
1.Чому робота електричного поля на замкнутій траєкторії дорівнює нулю?
2. Чому робота сил тертя на замкнутій траєкторії не дорівнює нулю?
3. Чому гравітаційне поле є потенціальним?
4. Роботи однорідного гравітаційного та електричного полів визначаються за формулами Агр=mgh та Аел=qEd. Порівняйте ці формули.
5. Чому роботу не можна вважати об’єктивною мірою енергетичних властивостей електричного поля?
6. Чому практичне значення має не потенціал поля в тій чи іншій точці, а різниця потенціалів між цими точками?
7. Доведіть що формули φ = Еr і φ = q/4πεε0r є тотожними.
Вправа 44.
1. Заряд ядра атома ртуті становить 12,8∙10–18Кл. Визначте потенціал створеного цим ядром електричного поля на відстані 10нм.
2. Якої додаткової швидкості може надати електрону поле з різницею потенціалів 1000В? Маса електрона 9,1∙10–31кг.
3. Із ядра атома радію зі швидкістю 2·107м/с вилітає α-частинка масою 6,67·10–27кг. Визначити енергію частинки та ту різницю потенціалів яка надала часинці таку енергію. Заряд α-частинки 3,2·10–19Кл.
4. Маленьку кульку масою 1г та зарядом 1∙10–7Кл, здалеку кинули з швидкістю 1м/с в напрямку сфери загальний заряд якої 2∙10–7Кл. При якому мінімальному значенні радіусу сфери, кулька досягне її поверхні?
5. Два точкових заряди 2∙10–8Кл і 3∙10–9Кл знаходяться на відстані 0,5м. Яку роботу треба виконати, щоб наблизити ці заряди на відстань 25см?
6. Два точкових заряди 4∙10–6Кл і 8∙10–6Кл знаходяться на відстані 0,8м. На скільки зміниться енергія взаємодії цих зарядів при зменшені відстані між ними вдвічі?
7. В вершинах квадрату сторона якого 4см знаходяться точкові заряди q1=4,8∙10–7Кл, q2=q3=1,6∙10–7Кл, q4=–1,6∙10–7Кл. Визначити потенціал результуючого електричного поля в центрі квадрату.
8. Між двома плоскими горизонтальними пластинками в завислому стані знаходиться пилинка масою 1∙10–7г. Визначити електричний заряд пилинки, якщо відстань між пластинками 5см, а електрична напруга між ними 500В.
.
§45. Електрична ємність. Конденсатори.
Термін «електрична ємність» є відлунням тих часів коли електрику уявляли як певну рідину, яку можна накопичувати і зберігати в спеціальних ємностях, на кшталт скляних пляшок, банок, тощо. Сьогодні ми знаємо, що ніякої електричної рідини не існує і що електрику в пляшках та банках не зберігають. І тим не менше, електрика дійсно веде себе як певна субстанція, яку можна певним чином отримувати, накопичувати та зберігати. І в цьому сенсі термін «електрична ємність» достатньо точно відображає суть того що характеризує. А ця суть полягає в тому, що електрична ємність є мірою здатності провідника або приладу накопичувати та зберігати електричні заряди.
Ясно, що самі собою заряди на провіднику не накопичуються і що для їх накопичення потрібно виконати певну роботу. А як відомо, кількісною мірою тієї роботи яку виконують електричні сили по переміщенню зарядів, є електрична напруга: U=Aел/q. Зважаючи на ці обставини, можна дати наступне визначення.
Електрична ємність – це фізична величина, яка характеризує здатність провідника, або спеціального приладу, накопичувати електричні заряди (енергію електричного поля) і яка дорівнює відношенню величини того заряду, який накопичується на провіднику до величини тієї електричної напруги що призвела до цього накопичення.
Позначається: С
Визначальне рівняння: С = q/U
Одиниця вимірювання: С = Кл/В =Ф, (фарада).
Потрібно зауважити, що електрична ємність провідника, тобто величина яка визначається за формулою С=q/U, фактично не залежить ні від q ні від U. Електрична ємність провідника залежить від параметрів самого провідника. Наприклад, якщо цим провідником є струмопровідна куля, то її електрична ємність залежить від радіусу кулі (R) та діелектричних властивостей (εε0) того середовища в якому ця куля знаходиться. Дійсно. Відомо, що потенціал незарядженої кулі дорівнює нулю (φ0=0), а потенціал зарядженої кулі, визначається за формулою φ = q/4πεε0R. Враховуючи що за визначенням U=∆φ=φ – φ0=q/4πεε0R, можна записати: Скулі=q/U=4πεε0R, де R – радіус кулі, ε0=8,8510–12Ф/м – електрична стала, ε – діелектрична проникливість того середовища яке оточує кулю.
Задача. Якого радіусу має бути струмопровідна куля, щоб її електрична ємність у вакуумі (ε=1) дорівнювала одній фараді?
Дано:
С = 1Ф
ε = 1
R = ?
Рішення: Оскільки для кулі С = 4πεε0R, де ε0 = 8,85∙10–12Ф/м то R = C/4πεε0.
Розрахунки: R = 1Ф/4∙3,14∙8,85∙10–12(Ф/м) = 9∙109м.
Щоб мати уявлення про розміри тієї кулі електрична ємність якої одна фарада, достатньо сказати, що радіус Сонця 7∙108м, а радіус Землі 6,37∙106м. А це означає, що в об’ємі кулі радіусом 9∙109м, може поміститися близько 2000 Сонць і понад 2,8 мільярдів Земель.
Із аналізу вище сказаного можна зробити два очевидних висновки.
Висновок 1. Електрична ємність в одну фараду, це надзвичайно велика ємність. Тому на практиці електроємність вимірюють не в фарадах, а в значно дрібніших одиницях, зазвичай в мікрофарадах (мкФ=10–6Ф) або пікофарадах (пкФ=10–12Ф).
Висновок 2. Обособлені кулі і загалом обособлені струмопровідні тіла, мають надзвичайно малу електроємність. Тому на практиці електричні заряди накопичують та зберігають не на кулях, кубах чи пірамідах, а в спеціальних приладах, які називаються конденсаторами.
Конденсатор, це прилад, який дозволяє накопичувати, зберігати та корисно застосовувати енергію електричних зарядів (енергію електричного поля). На електричних схемах конденсатор позначається символом . Цей символ певним чином відображає внутрішній устрій конденсатора, який представляє собою систему двох струмопровідних поверхонь, розділених тонким шаром діелектрика.
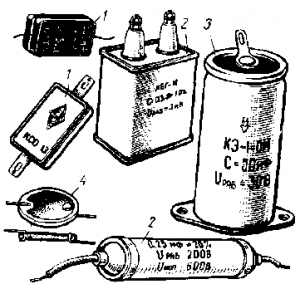
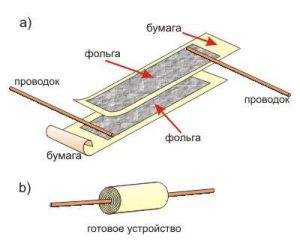
Мал.145. Загальний вигляд (а), внутрішній устрій (б) та ілюстрація принципу дії (в) конденсатора.
Принцип дії конденсатора очевидно простий: при підключенні до зовнішнього джерела напруги, на обкладинках конденсатора накопичуються різнойменні заряди, а оскільки ці заряди взаємно притягуються, то вони залишаються на цих обкладинках і після відключення приладу від зовнішнього джерела напруги.
Основною характеристикою будь якого конденсатора є його електрична ємність. Експериментальні та теоретичні дослідження показують, що ємність конденсатора залежить від: площі взаємного перекриття обкладинок конденсатора (S); відстані між обкладинками (d); діелектричних властивостей того середовища що знаходиться між обкладинками (εε0). Цю залежність можна записати у вигляді С = εε0S/d.
Другою важливою характеристикою будь якого конденсатора є та оптимальна (номінальна) і в той же час максимально допустима напруга, яка гарантує нормальний режим роботи приладу. Необхідність введення такої характеристики є очевидною. Адже при певній напрузі, сили електростатичної взаємодії зарядів стають такими великими, що відбувається так званий пробій діелектрика. Це означає, що при певній напрузі індукційна поляризація атомів діелектрика стає такою великою, що валентні електрони відриваються від своїх атомів і непровідник стає провідником. При цьому між обкладинками конденсатора проскакує потужний електричний імпульсний струм, який супроводжується виділенням великої кількості теплоти і тепловою руйнацією системи.
Накопичуючи електричні заряди, конденсатор накопичує і певну кількість електричної енергії, тобто здатності виконати роботу. Дійсно. Якщо те електричне коло в яке включено заряджений конденсатор замкнути, то в процесі розрядки конденсатора буде виконана певна робота: нагріються з’єднувальні дроти, блимне лампочка розжарювання, промайне іскровий розряд, виникне електромагнітна хвиля, тощо.
Оцінити величину тієї електричної роботи (Аел) яку здатен виконати заряджений конденсатор, а отже і величину накопиченої в ньому електричної енергії (Wел=Аел), можна з наступних міркувань. Із визначального рівняння напруги (U=Aел/q) випливає, що та робота яку виконують електричні сили в процесі переміщення заряду q з однієї обкладинки конденсатора на іншу, визначається за формулою Аел=Uq. А оскільки в процесі розрядження конденсатора, та напруга що існує між його обкладинками лінійним чином змінюється від певної максимальної величини (U=Uм) до нуля (U=0), то застосовуючи формулу Аел=Uq, потрібно мати на увазі що в даному випадку U=(Uм–0)/2. Тому Аел=(qUм)/2. Якщо ж величину накопиченого в конденсаторі заряду (q) виразити через його електричну ємність (q=CUм), то можна записати Аел=(СUм2)/2.
Таким чином, заряджений до напруги Uм конденсатор ємністю С, є джерелом електричної енергії, кількість якої визначається за формулою Wел=(CUм2)/2. Потрібно зауважити, що коли ми говоримо про величину накопиченого в конденсаторі заряду q, то маємо на увазі величину того заряду який накопичується на одній з обкладинок конденсатора. Адже загальний заряд зарядженого конденсатора завжди дорівнює нулю.
За необхідності конденсатори з’єднують в батарею конденсаторів. При цьому розрізняють два базові способи такого з’єднання: 1) паралельне з’єднання; 2) послідовне з’єднання.
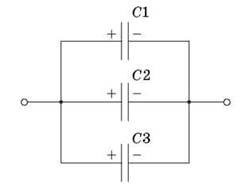
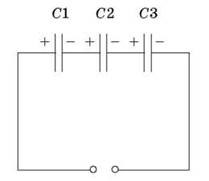
Мал.146. Паралельне (а) та послідовне (б) з’єднання конденсаторів.
Можна довести, що:
При паралельному з’єднанні конденсаторів:
1.Напруга на кожному окремому конденсаторі системи є однаковою і чисельно рівною величині тієї загальної напруги що існує між входом та виходом системи:
Uзаг = U1 = U2 = … = Un
2. Загальна кількість заряду накопиченого системою конденсаторів, дорівнює сумі зарядів накопичених в кожному окремому конденсаторі системи:
qзаг = q1 + q2 + … + qn
3. Загальна електрична ємність системи конденсаторів, дорівнює сумі електроємностей кожного окремого конденсатора системи:
Сзаг = С1 + С2 + … + Сn .
При послідовному з’єднанні конденсаторів:
1.Загальна напруга що існує між входом та виходом системи конденсаторів, дорівнює сумі напруг на кожному окремому конденсаторі системи:
Uзаг = U1 + U2 + … + Un
2. Загальна кількість заряду накопиченого системою конденсаторів, і кількість заряду накопиченого в кожному окремому конденсаторі системи є однаковою:
qзаг = q1 = q2 = … = qn
3. Загальна електрична ємність системи і електроємності її окремих конденсаторів, зв’язані співвідношеннями:
1/Сзаг = 1/С1 + 1/С2 + … + 1/Сn
Не важко довести, що при паралельному з’єднані конденсаторів, загальна ємність системи збільшується, а при послідовному з’єднанні – зменшується. Дійсно. Якщо С1=4мкФ, С2=6мкФ, то:
– при паралельному з’єднанні: С12= С1 + С2 = 4+6 = 10мкФ;
– при послідовному з’єднані: 1/С12=1/С1+1/С2=(С2+С1)/С1С2, звідси
С12 = С1С2/(С1+С2) = 4∙6/(4+6) = 2,4мкФ.
Факт того, що при паралельному з’єднані конденсаторів їх загальна ємність збільшується, а при послідовному – зменшується, є абсолютно закономірним. Дійсно. При паралельному з’єднані конденсаторів, електричні заряди накопичуються на всіх обкладинках системи. При цьому загальна площа робочої поверхні системи збільшується (Sзаг=S1+S2+…+Sn), а відповідно збільшується і її загальна електрична ємність: С = εε0S/d.
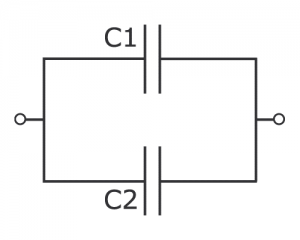
При послідовному з’єднані конденсаторів, електричні заряди фактично накопичуються на зовнішніх обкладинках крайніх конденсаторів. Адже внутрішні обкладинки послідовно з’єднані між собою і тому їх загальний заряд дорівнює нулю. В такій ситуації, ми по суті отримуємо конденсатор, площа робочої поверхні якого фактично дорівнює площі найменшого за ємністю конденсатора (Sзаг=Smin), а відстань між його обкладинками, дорівнює загальній відстані між обкладинками кожного окремого конденсатора системи (dзаг=d1+d2+…+dn). А це означає, що загальна ємність системи буде меншою за ємність найменшого з її елементів.
Існуюче різноманіття конденсаторів можна класифікувати за різними ознаками. Наприклад, за особливостями конструкції та за типом того діелектричного середовища, яке застосовується в даному приладі, конденсатори поділяються на вакуумні, повітряні, керамічні, паперові, слюдяні, електролітичні, напівпровідникові, тощо. Окрему групу конденсаторів складають конденсатори змінної ємності (позначаються ). Вони поділяються на конденсатори з механічним та електричним регулюванням ємності. В перших, електрична ємність регулюється шляхом механічної зміни площі перекриття обкладинок конденсатора (рідше, шляхом зміни відстані між обкладинками, або кількості того діелектрика що знаходиться між ними). В конденсаторах з електричним регулюванням ємності, використовують той факт, що діелектрична проникливість деяких матеріалів, зокрема сегнетоелектриків, певним чином залежить від напруженості зовнішнього електричного поля. А це означає, що змінюючи цю напруженість, відповідним чином змінюють і ємність конденсатора.
Конденсатори мають достатньо широке практичне застосування. При цьому, зазвичай вони застосовуються не як самостійні прилади, а як складові елементи більш складних електротехнічних систем. Зокрема радіопередавальних та радіоприймальних приладів, систем перетворення змінного струму в постійний і навпаки, різноманітних електровимірювальних приладах, системах оперативної пам’яті, тощо.
Задача 2. Незаряджений конденсатор ємністю 100мкФ з’єднали паралельно з конденсатором ємністю 50мкФ, зарядженим до напруги 300В. Якою буде напруга в системі конденсаторів? Як розподілиться заряд між ними?
Дано:
С1=100мкФ=100·10–6Ф
U1 = 0В
С2=50мкФ=50·10–6Ф
U2 = 300В
U12′ = ? q1′ = ? q1′ = ?
Рішення: За визначенням С2=q2/U2, звідси q2=C2U2=50·10–6Ф·300В=15·10–3Кл. Згідно з законом збереження електричного заряду q12′=q1+q2=0+15·10–3=15·10–3Кл. При паралельному з’єднанні конденсаторів С12=С1+С2=100·10–6Ф+50·10–6Ф=150·10–6Ф.
При паралельному з’єднанні конденсаторів U1′= U2′= U12′= q12′/C12=15·10–3Кл/150·10–6Ф = 100В.
q1′ = C1U1′ = 100·10–6Ф·100В = 10·10–3Кл =0,01Кл;
q2′ = C2U2′ = 50·10–6Ф·100В = 5·10–3Кл =0,005Кл.
Відповідь: U12′ = 100В; q1′ = 0,01Кл; q2′ = 0,005Кл.
Задача 3. Плоский повітряний конденсатор ємністю 20нФ заряджений до різниці потенціалів 100В. Яку роботу потрібно виконати, щоб у двічі збільшити відстань між обкладинками конденсатора.
Дано:
С1 =20нФ=20·10–9Ф
U1 = 100В
d2 = 2d1
A = ?
Рішення: В процесі віддалення обкладинки конденсатора величина її заряду залишається незмінною: q2=q1=C1U1=20·10–9Ф·100В=2·10–6Кл. При цьому ємність конденсатора (С=εε0S/d), а відповідно інапруга між його обкладинками (U=Cq) зменшуються: C2= εε0S/2d1=C1/2, а отже U2=U1/2=50В. Таким чином, в процесі віддалення обкладинок конденсатора, електрична напруга між цими обкладинками зменшується на ΔU=U1–U2=50В. Власне на зменшення цієї напруги і йде та робота яку потрібно визначити. І величина цієї роботи: А=ΔUq=50В·2·10–6Кл=100·10–6Дж=0,1мДж.
Відповідь: А=0,1мДж.
Узагальнюючу інформацію про основні поняття, величини, закони та прилади електростатики можна представити у вигляді наступної таблиці.
| Основні поняття | Основні величини | Основні закони | Основні прилади |
| Електричний заряд
Електричне поле, Лінії напруженості ел.поля |
Ел. заряд
q = ±Ne (Кл) Напруженість ел. поля Е = Fел/qп (Н/Кл) Потенціал ел. поля φ = А1→∞/qп (В) Ел. напруга U = A1→2/qп (В) Ел. ємність С = q/U (Ф) |
Закон збереження заряду
∑qдо = ∑qпісля Закон Кулона Fел = kq1q2/r2, де k=1/4πεε0 або Fел = Eq Принцип суперпозиції Ерез=∑Еі |
Конденсатор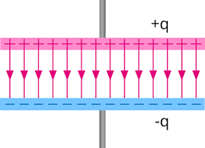
С=q/U C=εε0S/d Wел=CU2/2 |
Контрольні запитання.
1.Що характеризує і чому дорівнює електрична ємність провідника?
2. Чому кулі не застосовують в якості накопичувачів електричних зарядів?
3. Чому ми стверджуємо, що ємність в одну фараду, це надзвичайно велика ємність?
4. Чому ми стверджуємо, що в об’ємі кулі радіусом 9∙109м поміститься близько 2000 Сонць, тоді як радіус Сонця менший за радіус цієї кулі лише в 13 разів?
5. Від чого залежить електрична ємність: а) струмопровідної кулі; б) конденсатора?
6. Поясніть будову та принцип дії конденсатора.
7. Поясніть будову та принцип дії конденсатора змінної ємності.
8. Поясніть, чому при паралельному з’єднані конденсаторів їх загальна ємність збільшується, а при послідовному – зменшується.
Вправа 45.
1.При наданні струмопровідній кулі заряду 3∙10–8Кл її потенціал збільшився на 6кВ. Визначте електричну ємність кулі та її радіус.
2. Три конденсатори ємністю 12мкФ, 6мкФ, 4мкФ з’єднали спочатку паралельно а потім послідовно. Визначити загальну ємність конденсаторів в обох випадках.
3. Конденсатори ємністю 2мкФ і 4мкФ заряджені до різниці потенціалів 40В і 100В. Визначити різницю потенціалів після паралельного з’єднання конденсаторів. Визначити величину накопиченого на конденсаторах заряду та електричної енергії до та після з’єднання.
4. Конденсатори С1=4,0мкФ, С2= С3=8,0мкФ С4=4,0мкФ з’єднані так як показано на малюнку і підключені до джерела напруги 120В. Визначити загальну ємність системи конденсаторів та напругу на кожному з них.
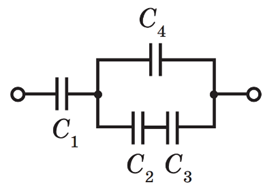
5. Конденсатори однакової ємності С1=С2=С3=С4=С5=2мкФ з’єднані так як показано на мал. а); б). Визначити загальну ємність системи конденсаторів.
а)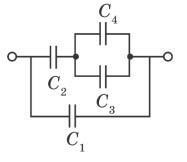 б)
б) 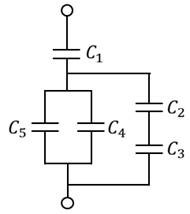
6. Два послідовно з’єднані конденсатори ємністю 4мкФ та 8мкФ приєднані до джерела постійної напруги 220В. Визначити напругу на кожному конденсаторі. Визначити величину накопиченого на кожному конденсаторі заряду та електричної енергії.
7. З якою силою F взаємно притягуються обкладинки конденсатора ємністю С, якщо різниця потенціалів між ними Δφ, а відстань d?
.