КІНЕМАТИКА

§3. Кінематика. Основні поняття кінематики.

§4. Основні фізичні величини кінематики поступального руху.

§5. Загальні відомості щодо методики розв’язування задач фізики. Розв’язування задач. Тема: Визначення середньої швидкості руху тіла.

§6. Рівняння руху – основний закон кінематики.

§7. Графічний метод розв’язування задач кінематики.

§8. Вільне падіння тіл. Рух тіла кинутого вертикально.

§9. Рух тіла кинутого горизонтально та під кутом до горизонту.

§10. Рух матеріальної точки по колу. Доцентрове прискорення.

§11. Основні поняття, величини та закони кінематики обертального руху.

§12. Рівняння обертального руху. Про співвідношення між лінійними та кутовими параметрами обертального руху.

§13. Розв’язування задач. Тема: Кінематика обертального руху.

.

Тема 1.1.   Кінематика.

.

§3. Кінематика. Основні поняття кінематики.

Кінематика (від грецького «kinematos» – рух) – це розділ механіки, в якому вивчають параметри і закономірності механічного руху тіл, без врахування їх мас та діючих на них сил. Іншими словами, в кінематиці вивчають параметри та закономірності механічного руху і не вивчають причини цього руху, а також не враховують фізичні властивості рухомого тіла.

До числа основних понять кінематики, тобто тих загальних слів (термінів) які є термінологічною основою кінематики і суть яких треба знати, відносяться: механічний рух, поступальний рух, обертальний рух, матеріальна точка, абсолютно тверде тіло, система відліку, траєкторія, відносність руху.

         Механічний рух – це такий рух (процес), при якому тіло як єдине ціле, або певні цілісні фрагменти цього тіла, переміщується відносно інших тіл. Розрізняють дві прості різновидності механічного руху: рух поступальний та рух обертальний.

Поступальний рух – це такий механічний рух, при якому будь-яка приналежна тілу пряма залишається паралельною сама собі. Наприклад, якщо книга рухається поверхнею стола таким чином, що будь яка з її бічних сторін залишається паралельними самі собі, то рух книги є поступальним. Він буде поступальним навіть тоді, коли книга не змінюючи своєї кутової орієнтації, рухатиметься по колу, або будь-якій іншій складній кривій. Якщо в процесі руху будь-яка приналежна тілу пряма залишається паралельною сама собі, то це тіло рухається поступально.

    

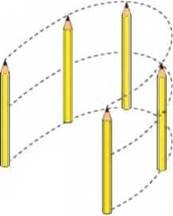
Мал.5. В процесі поступального руху тіла, будь-яка приналежна тілу пряма залишається паралельною сама собі.

Характерною та практично важливою особливістю поступального руху тіла є факт того, що при такому русі, всі точки тіла рухаються однаково. Однаково в тому сенсі, що мають однакові траєкторії руху, за однакові проміжки часу проходять однакові відстані, мають однакові миттєві і середні швидкості, однакові прискорення, тощо. А це означає, що описуючи поступальний рух тіла, нема потреби описувати рух кожної його окремої точки. Достатньо охарактеризувати рух будь-якої з цих точок, наприклад, центру маси тіла. Зважаючи на ці обставини, описуючи поступальний рух тіла, це тіло зазвичай замінюють його спрощеною (ідеалізованою) моделлю, яку прийняти називати матеріальною точкою.

Матеріальна точка, це така умовна точка, якою теоретично замінюють певне реальне тіло, в ситуаціях коли розмірами, формою та внутрішнім устроєм цього тіла можна знехтувати. Матеріальна точка зберігає лише одну механічну характеристику реального тіла – його масу. При цьому положення матеріальної точки практично завжди співпадає з положенням центру мас відповідного тіла.

Представляючи реальне тіло у вигляді матеріальної точки, ми абстрагуємося від несуттєвих в умовах даної задачі характеристик тіла і зосереджуємо свою увагу на його суттєво важливих характеристиках. В кінематиці поступального руху (кінематиці матеріальної точки) такими характеристиками є час руху, траєкторія руху, швидкість руху, прискорення, пройдений шлях, тощо.

Потрібно підкреслити, що визначаючись з тим, можна чи не можна дане тіло вважати матеріальною точкою, в першу чергу враховують не реальні розміри тіла, а характер його руху та характер тих запитань які поставлені в даній задачі. Наприклад, якщо книга поступально рухається поверхнею стола і ми говоримо про швидкість її руху, її прискорення, пройдений шлях, то цю книгу можна вважати матеріальною точкою. Адже в процесі поступального руху, всі точки книги проходять однаковий шлях, рухаються з однаковими швидкостями та з однаковими прискореннями. Якщо ж описуючи положення книги, ми говоримо про її координати, то скоріш за все цю книгу не можна вважати матеріальною точкою. Адже в масштабах стола, різні точки мають суттєво різні координати. Та як би там не було, а зазвичай в кінематиці поступального руху, тіла представляють у вигляді відповідних матеріальних точок.

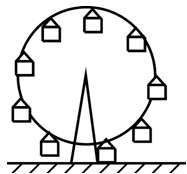
Обертальний рух – це такий механічний рух, при якому всі точки тіла описують кола, центри яких знаходяться на одній прямій, яка називається віссю обертання. Наприклад, обертально рухаються стрілка годинника, колесо автомобіля, двері класної кімнати, тощо. Звичайно за умови, що годинник «іде», колесо крутиться, двері відчиняються.

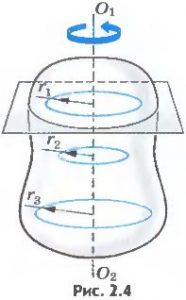
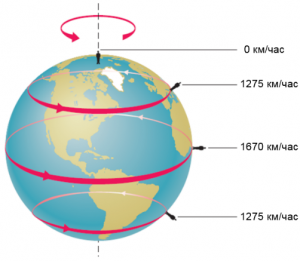
Мал.6. В процесі обертального руху тіла, всі його точки описують кола, центри яких знаходяться на одній прямій (осі обертання).

При обертальному русі різновіддалені від осі обертання точки тіла, рухаються суттєво по-різному: мають різні траєкторії руху, різні пройдені шляхи, різні лінійні швидкості, різні прискорення, тощо. А це означає, що описуючи обертальний рух навіть мізерно малого тіла, це тіло не можна замінювати матеріальною точкою. Не можна тому, що різні точки тіла мають суттєво різні параметри руху.

Описуючи обертальний рух тіла, це тіло зазвичай представляють не у вигляді матеріальної точки, а у вигляді так званого абсолютно твердого тіла. Абсолютно тверде тіло, це таке умовне тіло, яким теоретично замінюють певне реальне тіло, в ситуаціях коли його механічними деформаціями можна знехтувати.

В загальному випадку механічний рух тіла представляє собою певну комбінацію поступального і обертального рухів. Наприклад, коли ви кидаєте камінь, або б’єте футбольного м’яча, то скоріш за все рухи цих тіл будуть поступально-обертальними. Або наприклад, якщо автомобіль їде прямолінійною дорогою, то його корпус рухається поступально, колеса – поступально-обертально, а рух поршнів двигуна є певною комбінацією двох поступальних рухів. Якщо ж рельєф дороги складний, то всі ці руху стають набагато складнішими. Але яким би складним не був механічний рух тіла, його завжди можна представити як певну комбінацію двох простих рухів: поступального і обертального. А це означає, що вивчивши параметри та закономірності поступального і обертального руху можна описати та спрогнозувати будь-який найскладніший механічний рух.

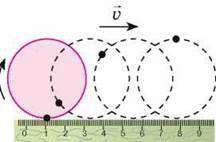
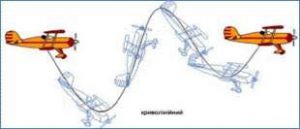
Мал.7. В загальному випадку рух тіла є поступально-обертальним.

Зважаючи на ці обставини та реалізуючи базовий методологічний принцип науки – від простого до складного, від часткового до загального, механіку загалом і кінематику зокрема, розділяють на дві частини  механіка поступального руху (механіка матеріальної точки) та механіка обертального руху. І потрібно зауважити, що у відповідності з програмою загальноосвітньої школи, левову частину навчальних годин відведено вивченню механіки матеріальної точки, тобто механіки поступального руху.

Напевно ви чули про те, що будь-який механічний рух є відносним. Факт цієї відносності закарбовано в самому визначені механічного руху. Механічний рух, це такий рух при якому тіло переміщується відносно інших тіл. Автомобіль рухається відносно дороги. Поршень автомобільного двигуна рухається як відносно двигуна так і відносно тієї дороги якою їде автомобіль. Дорога разом з Землею рухається відносно Сонця, разом з Сонячною системою – відносно центру Галактики і т.д. При цьому рух поршня відносно двигуна автомобіля, суттєво відрізняється від руху того ж поршня відносно дороги.

По суті, твердження про те, що механічний рух є відносним означає, що різні спостерігачі, спостерігаючи за рухом одного і того ж тіла можуть бачити суттєво різні рухи. Дійсно. Уявіть собі велосипед, який з певною постійною швидкістю рухається прямолінійною дорогою. Уявіть, що за певним елементом цього велосипеда, наприклад, за штуцером колеса (мал.8) спостерігають три спостерігачі. При цьому перший сидить на рамі велосипеда, другий – на землі, а третій – на самому колесі.

Кожен із спостерігачів дивиться на один і той же об’єкт (штуцер колеса) та описує його поведінку. Аналізуючи побачене, перший буде стверджувати, що штуцер рухається по колу. Другий, буде запевняти, що штуцер рухається певною кривою, яку прийнято називати циклоїдою. Третій же буде наполягати на тому, що штуцер не рухається. Не рухається тому, що розташування (положення) штуцера відносно елементів колеса велосипеда, а отже і відносно третього спостерігача, з плином часу залишається незмінним. І як це не дивно, але кожен з спостерігачів абсолютно правий. Адже відносно рами велосипеда штуцер дійсно рухається по колу, відносно дороги – по циклоїді, а відносно елементів колеса – не рухається взагалі.

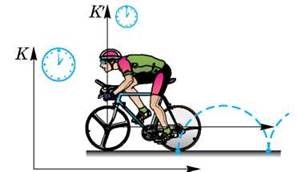
Мал.8. Різні спостерігачі, спостерігаючи за рухом одного і того ж об’єкту можуть бачити суттєво різні рухи.

Із вище сказаного ясно, що описуючи механічний рух тіла, необхідно чітко вказати, в якій системі відліку описується цей рух. Адже в різних системах відліку один і той же рух може виглядати по різному. Скажімо, якщо не вказати ту систему відліку в якій описується рух штуцера, то можна як завгодно довго та як завгодно запекло сперечатись стосовно того, як рухається штуцер – по колу, по циклоїді чи якось інакше. І кінця краю цій суперечці не буде.

Звичайно, якщо в тому чи іншому контексті, або в умові тієї чи іншої задачі не вказана система відліку, то скоріш за все, це означає що цією системою є та, що жорстко з’єднана з умовно нерухомою землею. Наприклад, коли ми говоримо, що будинок не рухається, то маємо на увазі що він не рухається відносно землі. Або, якщо наприклад ми стверджуємо, що автомобіль рухається з швидкістю 90 км/год, то скоріш за все маємо на увазі його швидкість відносно дороги. При цьому відносно іншого автомобіля ця швидкість може бути іншою.

Говорячи про систему відліку мають на увазі взаємопов’язану сукупність (систему) трьох складових: точки відліку, системи координат та вимірювача часу (годинник, секундомір, тощо). Ця сукупність дозволяє однозначно описати просторово-часові параметри руху тіла. Це означає, що система відліку не лише визначає «адресу» (координати) рухомої точки, а й вказує на те в який момент часу ця «адреса»  зафіксована.

Система відліку – це взаємопов’язана сукупність точки відліку, системи координат та вимірювача часу, яка застосовується для того, щоб кількісно описати механічний рух матеріальної точки (тіла) в цій системі. Система координат – це взаємопов’язана сукупність осей системи координат з вказаним на цих осях масштабом вимірювань. Точка відліку – це та умовно нерухома точка, яка є центром (нулевою точкою) відповідної системи координат. Задати систему координат означає: 1) вказати точку відліку даної системи; 2) задати просторову орієнтацію осей системи координат; 3) на кожній осі координат вказати масштаб вимірювань.

Мал.9. Система відліку – це взаємопов’язана сукупність точки відліку, системи координат та вимірювача часу, яка застосовується для кількісної характеристики механічного руху матеріальної точки (тіла) в цій системі.

Розташування (місцезнаходження) матеріальної точки в заданій системі координат, однозначно визначається її координатами. При цьому, якщо мова йде про одновимірну (лінійну) систему координат (мал.10а), то в ній місцезнаходження матеріальної точки характеризується однією координатою М(х). В двовимірній (плоскій) системі координат (мал.10б), розташування точки характеризується двома координатами М(х;y), а в тривимірній (об’ємній, мал.10в) – трьома М(х;y;z).

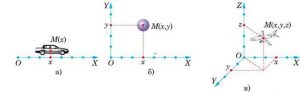
Мал.10. Розташування (місцезнаходження) матеріальної точки в заданій системі координат, однозначно визначається її координатами.

Лінію яку описує матеріальна точка в процесі свого руху в вибраній системі відліку називають траєкторією. В різних системах відліку траєкторія руху однієї і тієї ж матеріальної точки може бути суттєво різною. Наприклад, в системі відліку пов’язаною з землею, траєкторією руху велосипедного штуцера (мал.8) є сукупність послідовних циклоїд. В системі ж відліку пов’язаною з рамою велосипеда, цієї траєкторією буде сукупність співпадаючих кіл. А в системі відліку пов’язаній з колесом велосипеда – нерухома точка.

За формою траєкторії, механічні рухи поділяються на прямолінійні та криволінійні. Прямолінійним називають такий поступальний рух матеріальної точки, траєкторія якого представляє собою пряму лінію. Криволінійним називають такий поступальний рух матеріальної точки, траєкторія якого представляє собою криву лінію. Наприклад рух вертикально падаючого тіла (мал.11б) є прямолінійним, а рух тіла кинутого горизонтально (мал.11г) – криволінійним. Криволінійним є і рух тіла кинутого вертикально вгору (мал.11в). Його криволінійність полягає в тому, що відповідна траєкторія представляє собою ламану яка складається з двох прямолінійних відрізків.

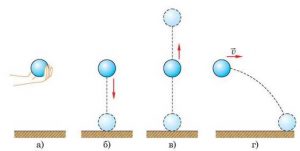
Мал.11. За формою траєкторії, поступальні рухи поділяються на прямолінійні та криволінійні.

Та якою б криволінійною не була траєкторія руху тіла, її завжди можна представити як певну сукупність послідовних прямолінійних відрізків. А це означає, що вивчивши параметри та закономірності прямолінійного руху матеріальної точки, можна описати будь-який криволінійний рух. Виходячи з цього, вивченню параметрів та закономірностей прямолінійного руху ми будемо приділяти особливу увагу.

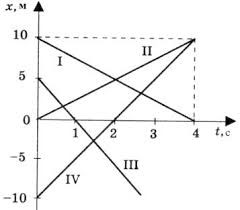
Задача 1. За заданими графіками руху тіл 1 і 2, визначити їх координати в момент часу 0с; 1с; 2с; 4с. Визначити де і коли ці тіла зустрінуться?

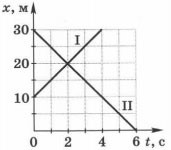
Рішення. На основі аналізу заданих графіків, можна стверджувати:

х₁(0) = 10м;   х₂(0) = 30м;

х₁(1) = 15м;   х₂(1) = 25м;

х₁(2) = 20м;   х₂(2) = 20м;

х₁(4) = 30м;   х₂(4) = 10м.

На основі аналізу заданих графіків, можна стверджувати, що задані тіла зустрінуться через 2с в точці з координатою 20м.

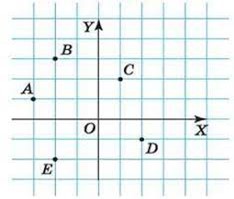
Задача 2. В заданій системі координат, визначити координати точок А, B, C, D, K, M.

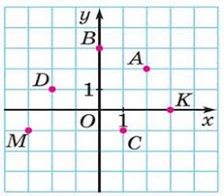
Рішення. На основі аналізу заданої системи координат та розтушування заданих точок в ній, можна записати: А(2; 2), B(0; 3), C(1; –1), D(1; –2), K(3; 0), M(–3; –1).

Задача 3. Задайте плоску прямокутну систему координат і побудуйте в ній точки з координатами А(–60; 20), В(–40; 60), С(20; 40), D(40; –20), Е(–40; –40).

Рішення. Задаємо плоску прямокутну систему координат. (Нагадаємо, задати систему координат означає: 1) вказати точку відліку даної системи; 2) задати просторову орієнтацію осей системи координат; 3) на кожній осі координат вказати масштаб вимірювань). При цьому масштаб вимірювань вибираємо таким чином, щоб він відповідав умові конкретної задачі. Наприклад в умовах нашої задачі, довжині однієї клітинки малюнку відповідає 20 одиниць (на малюнку цифри масштабу не позначено). В заданій системі координат позначаємо відповідні точки.

Контрольні запитання.

1. Який рух називають поступальним? Яка особливість цього руху?
2. За яких умов рух тіла по колу буде поступальним. Чи є рух Землі навколо Сонця поступальним? Чому?
3. Який рух називають обертальним? Чи можна описуючи обертальний рух тіла, представляти це тіло у вигляді матеріальної точки? Чому?
4. Що називають матеріальною точкою? Які критерії є визначальними при з’ясуванні того, можна чи не можна дане тіло вважати матеріальною точкою?
5. Що означає твердження: механічний рух є відносним? Наведіть приклади.
6. Які частини велосипеда підчас рівномірного руху описують прямолінійні, а які криволінійні траєкторії відносно дороги?
7. Що означає задати систему координат?
8. Чим система відліку відрізняється від системи координат? Яка з цих систем є більш загальною
9. Що називають траєкторією і чи є траєкторія руху матеріальної точки відносною? Наведіть приклади.
10. Траєкторії руху двох тіл перетинаються. Чи означає це що тіла зіштовхуються? Поясніть.

Вправа №3.

1. Задайте плоску прямокутну систему координат і побудуйте в ній точки з координатами А(20;20); В(–20;40); С(20;0); Д(10;–30); К(0;20); М(–10;–20); N(0;0); Р(30;–20).
2. Задайте лінійну систему координат і побудуйте в ній точки з координатами: А(200); В(–150); С(50);  Д(250);  К(–50);  М(0);  N(100).
3. За заданими графіками руху тіл 1, 2 і 3, визначити їх координати в момент часу 0; 5с; 10с; 20с. Визначити де і коли тіла 2 і 3 зустрінуться?

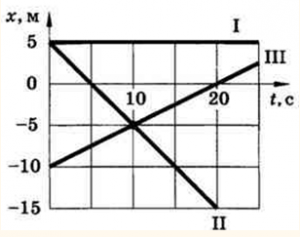
4. За заданими графіками руху тіл 1 і 2, визначити їх координати в момент часу 0с; 20с; 40с; 60с. Визначити де і коли ці тіла зустрінуться?

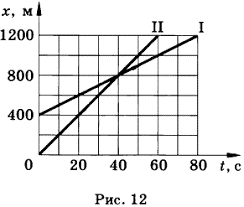
5. Хлопчик випустив з рук м’яч на висоті 1,5м, а коли м’яч відскочив від підлоги, спіймав його на висоті 1м. Який шлях пройшов м’яч? На якій відстані від вихідної точки було спіймано м’яч?

6. Три тіла рухаються з швидкостями v₁ = 36см/год, v₂ = 0,01м/с, v₃ = 10мм/с. Порівняйте ці швидкості.

7. За 5год 30хв велосипедист проїхав шлях 99км. З якою середньою швидкістю рухався велосипедист?

8. Один велосипедист протягом 12с рухався зі швидкістю 6м/с, а другий велосипедист проїхав ту саму ділянку за 9с. Яка середня швидкість другого велосипедиста на цій ділянці шляху?

9. У змаганнях з бігу беруть участь 4 учні, які можуть бігти зі швидкостями 6м/с, 20км/год, 360м/хв, 0,35км/хв. Хто переможе і хто прибіжить останнім?

10. Відстань від Землі до Сонця 150млн. км. Скільки часу потрібно світлу, щоб подолати цю відстань? Швидкість світла 300 000км/с.

.

§4. Основні фізичні величини кінематики поступального руху.

 

До числа основних фізичних величин кінематики поступального руху відносяться: час (t), координата (x), пройдений шлях (s) швидкість (v), прискорення (a).

Оскільки загальні основи механіки поступального руху (механіки матеріальної точки) вивчалися у сьомому класі, і ті фізичні величини які називаються час, координата, пройдений шлях, швидкість та прискорення вам відомі, то про ці величини ми будемо говорити в режимі узагальнюючого повторення. А в цьому режимі про час (t), координату (x), пройдений шлях (s) швидкість (v) та прискорення (a), можна сказати наступне.

              Час – це фізична величина, яка характеризує тривалість подій (явищ, процесів, рухів, тощо) і яка дорівнює цій тривалості.

Позначається:  t

Визначальне рівняння:  нема

Одиниця вимірювання:  [t] = с,  (секунда).

Твердження про те, що час немає визначального рівняння означає, що час належить до числа тих базових фізичних величин, одиниці вимірювання яких за домовленістю прийнято вважати основними. В механіці такими базовими величинами є час (t), довжина (ℓ) і маса (m).

Координата – це фізична величина, яка характеризує положення (місцезнаходження) матеріальної точки в заданій системі координат і яка дорівнює відстані від точки відліку цієї системи до проекції даної точки на відповідну вісь координат.

Позначається: х

Визначальне рівняння: х = ℓ_х

Одиниця вимірювання: [х] = м,   (метр)

Наприклад, в зображеній на мал.12а лінійній системі координат, автобус має координату (300), а вантажний автомобіль (–100). Це означає, що відносно точки відліку системи координат, автобус знаходиться на відстані 300м в додатному напрямку осі Х, а автомобіль – на відстані 100м у від’ємному напрямку цієї осі. Або наприклад, в зображеній на мал.12б плоскій системі координат, трактор має координати А(300;100). Це означає, що для потрапляння в точку розташування трактора потрібно пройти 300м вздовж додатного напрямку осі 0Х, а потім пройти 100м вздовж додатного напрямку осі 0У.

а)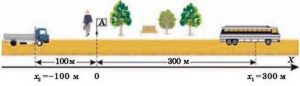

б)

Мал.12. Координата точки дорівнює відстані від точки відліку системи координат до даної точки, виміряній вздовж відповідної осі системи координат.

Пройдений шлях – це фізична величина, яка характеризує пройдений матеріальною точкою (тілом) шлях і яка дорівнює довжині тієї траєкторії яку описує ця точка в процесі відповідного руху.

Позначається: s

Визначальне рівняння: s = ℓ_тр, для прямолінійного руху s = Δх

Одиниця вимірювання: [s] = м,   (метр).

Нагадаємо. В науці загалом і в фізиці зокрема, символом ∆ – дельта (∆х, ∆t, ∆v, ….) позначають різницю між кінцевим та початковим значенням відповідних величин:

∆х = х_к – х_п, або  ∆х = х – х₀,

∆t = t_к – t_п,   або  ∆t = t – t₀,

∆v = v_к – v_п, або  ∆v = v – v₀,   і т.д.

Ілюструючи можливості та межі застосуванні формули s = ∆х, розглянемо декілька простих ситуацій. Припустимо, що в заданій системі відліку точки А і В мають координати А(300); В(–100). Виходячи з цього, визначимо пройдений тілом шлях при його переміщенні: a) з точки А в точку В; б) з точки В в точку А; в) з точки А в точку В, а потім знову в точку А.

Із аналізу малюнка ясно, що при переміщенні    А → В пройдений тілом шлях становить s₁ = 400м, при переміщенні В → А: s₂ = 400м, при переміщенні А → В → А: s₃ = 400 + 400 = 800м.

Тепер, застосуємо формулу s = ∆х та отримаємо відповідні результати так би мовити теоретичним шляхом:

якщо А → В, то s₁ = ∆x = х_к – х_п = (–100) – (300) = –400м, де знак « – » вказує на те, що в заданій системі координат, переміщення за маршрутом А → В відбувалося у від’ємному напрямку;

якщо В → А, то s₂ = ∆x= х_к – х_п = (300) – (–100) = 400м;

якщо А → В → А, то s₃ = ∆x = х_к – х_п = (300) – (300) = 0м.

Не важко бачити, що останній результат явно суперечить реальному стану речей. Це пояснюється тим, що за визначенням, формула s = ∆x справедливою лише для прямолінійних ділянок руху. Рух же тіла за маршрутом А→В→А є криволінійним. І тому пройдений тілом шлях потрібно визначати не за формулою s = ∆х, а за формулою s = ℓ_тр = |s₁| + |s₂|  + …  + |s_N| ,  де  N – кількість тих послідовних прямолінійних відрізків які утворюють відповідну криволінійну траєкторію. Наприклад, в умовах нашої задачі s = |s₁| + |s₂|  = |–400| + |400| = 800м. (Запис |–400| означає модуль, тобто абсолютну величину відповідного числа, а модуль числа завжди додатний |–400| = 400).

Таким чином, застосовуючи визначальне рівняння s = ∆х потрібно пам’ятати, що воно є справедливим лише для прямолінійної ділянки руху. Втім, зважаючи на те, що будь який криволінійний рух можна представити як певну сукупність прямолінійних відрізків, саме прямолінійний рух є тією базовою різновидністю поступального руху, на основі якої описуються інші рухи. Тому в переважній більшості випадків, говорячи про визначальне рівняння пройденого шляху, мають на увазі формулу s = ∆х.

Швидкість – це фізична величина, яка характеризує швидкість поступального руху тіла (матеріальної точки), і яка дорівнює відношенню вектора того переміщення Δх яке здійснило тіло за гранично малий проміжок часу Δt, до величини цього проміжку часу.

Позначається: v

Визначальне рівняння: v = ∆x/∆t

Одиниця вимірювання: [v] = м/с,  (метр на секунду).

Нагадаємо, фізичні величини поділяються на векторні і скалярні. Наприклад сила (F), швидкість (v) та прискорення (a) – величини векторні, тобто такі які характеризуються як числовим значенням (величиною) так і напрямком. Натомість час (t), маса (m), густина (ρ) та пройдений шлях (s) – величини скалярні, тобто такі, що характеризуються лише числовим значенням (величиною). Векторні величини позначають відповідною жирною буквою (F,  v, a), або нежирною буквою та стрілочкою над нею. Скалярні ж величини позначають нежирною буквою без стрілочки (t, m, ρ, s). При цьому, в тих випадках коли мова йде лише про числове значення векторної величини, цю величину позначають відповідною нежирною буквою без стрілочки (F, v, a).

Формула v = ∆x/∆t, є базовим визначальним рівнянням швидкості, яке справедливе для будь яких ситуацій, і яке за різних обставин може набувати різного вигляду. Наприклад, якщо мова йде про прямолінійний рух, тобто такий рух в процесі якого напрям швидкості не змінюється, то рівняння v = ∆x/∆t, набуває вигляду v = ∆x/∆t. Різниця між цими рівняннями в тому, що перше (v = ∆x/∆t) дозволяє визначати як величину так і напрям швидкості, а друге (v = ∆x/∆t) – лише величину швидкості. Втім, для прямолінійного руху, напрям швидкості є визначеним і таким, що співпадає з напрямком руху тіла.

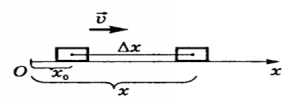
Мал.13. Якщо за час Δt тіло (матеріальна точка) переміщується на відстань Δх, то швидкість цього тіла v = Δx/Δt.

Якщо ж мова йде про прямолінійний рівномірний рух, тобто такий рух, швидкість якого не змінюється ні за величиною ні за напрямком (v = const), то в цьому випадку обмежень що до мінімальності величин ∆t = t – t₀ і Δх = х – х₀ = s нема. При цьому за умови t₀ = 0, а отже Δt = t – t₀ = t, рівняння  v = ∆x/∆t набуває вигляду v = s/t.

Таким чином:

– в загальному випадку v = ∆x/∆t;

– для прямолінійного руху v = ∆x/∆t;

– для прямолінійного рівномірного руху v = s/t.

Формула v = s/t характеризує не лише швидкість тіла при його прямолінійно рівномірному русі, а й так звану середню шляхову швидкість тіла, яку зазвичай називають середньою швидкістю

         Середня швидкість (середня шляхова швидкість) – це та усереднена швидкість з якою тіло долає певну ділянку шляху і яка дорівнює відношенню пройденого тілом загального шляху s, до того загального проміжку часу t, за який цей шлях пройдено.

Позначається: v_с

Визначальне рівняння: v_с = s/t

Одиниця вимірювання: [v_с] = м/с,  метр за секунду.

На відміну від швидкості тіла в даний момент часу (миттєвої швидкості), середня шляхова швидкість є величиною скалярною, тобто такою яка характеризується лише числовим значенням.

Задача 1. За представленим на малюнку графіком руху птаха, визначити його швидкість на кожній ділянці шляху, та середню швидкість на всьому шляху.

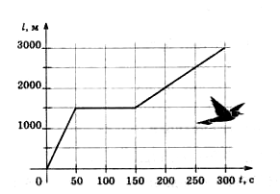
Рішення. На основі аналізу малюнку можна стверджувати, що рух птаха складається з трьох ділянок. При цьому:

Ділянка 1: t₁ = Δt₁ = 50c – 0c =50c; s₁ = Δx₁ = 1500м – 0м = 1500м;

v₁ = s₁/t₁ = 1500м/50с = 30м/с.

Ділянка 2: t₂ = Δt₂ = 150c – 50c =100c; s₂ = Δx₂ = 1500м – 1500м = 0м;

v₁ = s₂/t₂ = 0м/100с = 0м/с.

Ділянка 3: t₃ = Δt₃ = 300c – 150c =150c; s₃ = Δx₃ = 3000м – 1500м = 1500м;

v₃ = s₃/t₃ = 1500м/150с = 10м/с.

Середня швидкість: v_c = (s₁+s₂+s₃) / (t₁+t₂+t₃) = 3000м/300с = 10м/с.

         Якщо швидкість тіла так чи інакше змінюється, то говорять що воно рухається з прискоренням. Прискорення – це фізична величина, яка характеризує зміну швидкості руху тіла, і яка дорівнює відношенню тієї зміни швидкості Δv, що відбулася за проміжок часу Δt, до величини цього проміжку часу.

Позначається: а

Визначальне рівняння: а = ∆v/∆t,

Одиниця вимірювання: [a] = м/с²,   (метр на секунду в квадраті).

Оскільки швидкість, величина векторна, то вона може змінюватись як за величиною, так і за напрямком. Тому розрізняють дві різновидності прискорення: 1) прискорення, яке характеризує зміну швидкості за величиною (лінійне прискорення); 2) прискорення, яке характеризує зміну швидкості за напрямком (доцентрове прискорення).

Про доцентрове прискорення ми поговоримо вивчаючи тему «Рух матеріальної точки по колу». На разі ж, терміном «прискорення» ми будемо позначати те прискорення, яке характеризує зміну швидкості за величиною, і яке називається лінійним прискоренням, а частіше – просто прискоренням.

Лінійне прискорення (прискорення) – це таке прискорення, яке характеризує зміну швидкості руху тіла за величиною і яке дорівнює відношенню величини зміни швидкості Δv, до величини того проміжку часу Δt, за який ця зміна відбулася.

Позначається: а_л   або  а

Визначальне рівняння: а = ∆v/∆t

Одиниця вимірювання: [а] = м/с²

Лінійне прискорення завжди направлено вздовж лінії швидкості руху тіла. При цьому, якщо величина швидкості зростає (v↑), то вектори швидкості та прискорення співнаправлені, а якщо швидкість зменшується (v↓) – то ці напрямки протинаправлені. Наприклад, коли автомобіль рушає з місця (мал.14а), то його швидкість збільшується  (v↑) і тому напрям того прискорення з яким рухається автомобіль, співпадає з напрямком його руху (з напрямком швидкості). Якщо ж автомобіль гальмує (мал.14б), то його швидкість зменшується (v↓) і тому напрям того прискорення з яким рухається автомобіль, протилежний до напрямку його руху (протилежний до напрямку швидкості руху автомобіля).

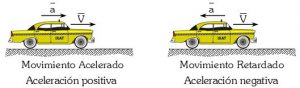
Мал.14. Якщо швидкість автомобіля збільшується (мал.а), то вектори a і v співнаправлені, а якщо зменшується (мал.б) – то протинаправлені.

Із визначального рівняння прискорення а = (v – v₀)/t, з усією очевидністю випливає, що при рівноприскореному русі (а = соnst) швидкість тіла можна визначити за формулою v_к = v₀ + at або v = v₀+at, де v₀ – початкова швидкість тіла. Дійсно, оскільки а = (v_к – v₀)/t, то розкривши дужки отримаємо а = v_к/t – v₀/t. Звідси випливає v_к/t = v₀/t + а, або v_к = v₀ + at. Зазвичай формулу v = v₀ + at (точніше v = v₀ ± at) називають рівнянням швидкості.

Варто зауважити, що коли рухаючись з постійним прискоренням (а = соnst), тіло збільшує свою швидкість (v↑), то відповідний рух називають рівноприскореним. При цьому говорять, що тіло має додатне прискорення (а > 0). Якщо ж швидкість тіла зменшується (v↓), то відповідний рух називають рівносповільненим, а відповідне прискорення – від’ємним (а < 0).

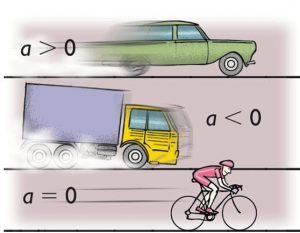
Мал.15. При рівноприскореному русі тіло має додатне прискорення (а > 0), а при рівносповільненому русі – від’ємне (а < 0).

Задача 2. Автомобіль що рухається зі швидкістю 108км/год, в процесі гальмування зупинився через 10с. З яким прискоренням рухався автомобіль?

Загальні зауваження. Дехто вважає, що задачі фізики є складними. Звичайно, якщо ви не знаєте, що час позначається t, швидкість – v, прискорення – а, якщо не знаєте, що визначальне рівняння прискорення а = (v_к–v₀)/t, якщо не розумієте, що твердження «автомобіль в процесі гальмування зупиняється» – означає, що кінцева швидкість автомобіля дорівнює нулю (v_к = 0м/с), то задачі фізики дійсно складні. Однак якщо ви знаєте суть тих слів (термінів) які є азбукою фізики, якщо уважно читаєте умову задачі та бачите за цією умовою реальну ситуацію, то неминуче погодитесь з тим, що фізика, це зовсім нескладно, натомість цікаво, повчально і потрібно. Бо фізика, то ж не формули, а вміння творчо та логічно мислити.

Дано:

v₀ = 108 км/год = 30м/с

v_к = 0 м/с

t  = 10 с

а = ?

Рішення. За визначенням а = (v_к – v₀)/t. В умовах нашої задачі а = (0м/с – 30м/с)/10с = –3м/с², де знак «–» вказує на те, що рух автомобіля є рівносповільненим (швидкість зменшується).

Відповідь: а = –3м/с².

Задача 3. За який час автомобіль рухаючись зі стану спокою з прискоренням 0,6м/с² набуде швидкості 90км/год?

Дано:

v₀ = 0м/с

v_к = 90км/год = 25м/с

a = 0,6м/с²

t = ?

Рішення. Оскільки за визначенням а = (v_к – v₀)/t, то t = (v_к – v₀)/а = (25м/с – 0м/с)/0,6(м/с²) = 41,7с

Відповідь: t = 41,7с.

Задача 4. За заданим графіком швидкості руху тіла, визначити його прискорення на кожній ділянці шляху.

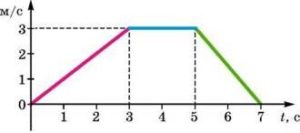
Рішення. На основі аналізу заданого графіку швидкості можна стверджувати, що даний рух складається з трьох ділянок. При цьому:

Ділянка 1: Δt₁ = 3c – 0c = 3c; Δv₁ = 3м/с – 0м/с = 3м/с;

а₁ = Δv₁/Δt₁ = 3(м/с)/3с = 1м/с².

Ділянка 2: Δt₂ = 5c – 3c = 2c; Δv₂ = 3м/с – 3м/с = 0м/с;

а₂ = Δv₂/Δt₂ = 0(м/с)/2с = 0м/с².

Ділянка 3: Δt₃ = 7c – 5c = 2c; Δv₃ = 0м/с – 3м/с = –3м/с;

а₃ = Δv₃/Δt₃ = –3(м/с)/2с = –1,5м/с², де знак «–» вказує на те, що рух тіла є рівносповільненим (швидкість руху зменшується).

Контрольні запитання.

1. Чому час, довжина і маса не мають визначальних рівнянь?
2. В яких випадках пройдений шлях визначають за формулою s = ℓ_тр, а в яких s = Δх?
3. Чи відрізняються записи v = const і v = const? Якщо відрізняються то чим?
4. За якої умови Δt = t?
5. За яких умов, формула v = ∆x/∆t набуває вигляду v = s/t?
6. Відстань від Києва до Черкас автомобіль проїхав зі швидкістю 60км/год. Про яку швидкість іде мова? Поясніть.
7. Чому розрізняють дві різновидності прискорення?
8. В якому випадку вектори швидкості і прискорення є співнаправленими, а в якому протинаправленими?
9. Прискорення тіла дорівнює –2м/с². Що це означає?
10. Потяг відходить від станції. Як направлене його прискорення?
11. Потяг починає гальмувати. Як направлене його прискорення?

Вправа №4.

1. Антилопа розвиває швидкість 25м/с, лев – 80км/год, а зебра – 1км/хв. У кого з них швидкість найбільша.
2. Турист пройшов 5км за 1,5год, а потім ще 2км за 0,5год. Яка середня швидкість туриста на всьому шляху?
3. Один велосипедист протягом 12с рухався зі швидкістю 6м/с, а другий велосипедист проїхав ту саму ділянку шляху за 9с. Якою була швидкість другого велосипедиста?
4. Коло радіусом 50м велосипедист долає за 40с. Визначати швидкість його руху.
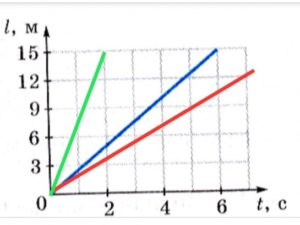
5. За заданими графіками руху (червона, синя, зелена прямі), визначити відповідні швидкості руху.

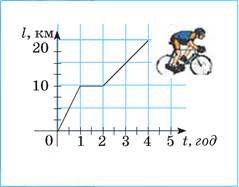
6. За представленим на малюнку графіком руху велосипедиста, визначити швидкість руху на кожній ділянці шляху, та середню швидкість на всьому шляху.

7. Через 20 с після початку руху спідометр автомобіля показував 72 км/год. З яким середнім прискоренням рухався автомобіль

8. За який час автомобіль, рухаючись з прискореннями 0,2 м/с² збільшить свою швидкість від 10м/с до 20м/с ?

9. Автобус рухаючись з прискоренням 2м/с², зупинився через 3с. Визначити швидкість автобуса на початку гальмування.

10. Автомобіль рухається під ухил з прискоренням 0,4м/с². Яку швидкість матиме автомобіль через 10с, якщо його початкова швидкість 36км/год?

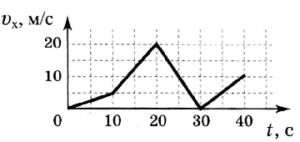
11. За заданим графіком швидкості руху тіла, визначити його прискорення на кожній ділянці шляху.

.

§5. Загальні відомості щодо методики розв’язування задач фізики. Розв’язування задач. Тема: Визначення середньої швидкості руху тіла.

Задачі фізики суттєво відрізняються від тих задач, з якими ви маєте справу наприклад в математиці. Скажімо коли в математиці вам говорять, що рівняння виду ах² + bx + c = 0 називається квадратним рівнянням, і що в загальному випадку воно має два рішення: x_1,2 = [– b ± √(b² – 4ac)]/2a, то вчителю достатньо розв’язати два, три подібних рівнянь, щоб в подальшому ви змогли самостійно розв’язувати будь-яку їх кількість.

З задачами фізики ситуація значно складніша. Наприклад, ви розв’язуєте задачі на визначення середньої швидкості, тобто на застосування формули v_с = s/t.  Не важко бачити, що ця формула надзвичайно проста. У всякому разі, значно простіша за x_1,2 = [– b ± √(b² – 4ac)]/2a. Та от парадокс. Ви скільки завгодно можете знати цю формулу і не вміти розв’язувати задачі на визначення середньої швидкості. Навіть після того, як вчитель розв’яже вам п’ять,  десять ба навіть сто подібних задач, нема гарантії того, що задана вам сто перша задача буде розв’язана. І справа не в тому що ви забули формулу v_с = s/t. Справа в іншому:  в фізиці, головне не формули, а вміння логічно мислити. Ви можете скільки завгодно «зазубрювати» правильні формули і навіть зазубрити їх, але якщо за цими формулами ви не будете бачити реальних об’єктів і подій, то всі ваші зусилля будуть марними – ви не будете знати, розуміти і любити фізику.

Різноманіття фізичних задач таке величезне, що практично не можливо сформулювати такі універсальні рекомендації, реалізація яких гарантовано забезпечує правильне рішення будь-якої задачі.  І тим не менше існує певний загально прийнятий порядок (алгоритм) розв’язку задач, який є тією методологічною основою, на базі якої можна розв’язувати переважну більшість задач фізики. Цей алгоритм полягає в наступному.

1. Уважно (бажано декілька разів) прочитати умову задачі і з’ясувати її (задачі) фізичну суть. Не буде перебільшенням сказати, що успішне рішення задачі на 50% залежить від того, настільки уважно ви прочитали її умову, настільки точно зрозумієте фізичну суть цієї умови, настільки правильно зрозумієте суть поставлених в задачі запитань.
2. Зробити стислий запис умови задачі, зазначивши в ньому всі суттєві моменти цієї умови.
3. Проаналізувати розмірності заданих фізичних величин і при необхідності привести ці розмірності до загальноприйнятої системи одиниць (СІ).
4. Виконати малюнок, який графічно відображає умову задачі і допомагає представити її фізичну суть. Для очевидно простих задач, виконання цього пункту не є обов’язковим. Але в будь-якому випадку, графічне представлення умов конкретної задачі є надзвичайно корисним. Якщо ж рішення задачі передбачає додавання векторних величин, то в цьому випадку, малюнок є обов’язковим. Адже без такого малюнку це рішення не має сенсу.
5. Провести теоретичний аналіз задачі. Суть цього аналізу полягає в тому, що на основі відомих базових формул (зазвичай базовими формулами є визначальні рівняння фізичних величин та математичні формулювання фізичних законів) та на основі логічного аналізу умов конкретної задачі, отримують відповідне розрахункове рівняння.

Розрахункове рівняння, це отримана в процесі рішення задачі формула, в якій з одного боку знаходиться величина, значення якої потрібно визначити, а з іншого –  відомі величини. Варто підкреслити: розрахункове рівняння це та формула, яку ви повинні не списати, наприклад з аналогічної задачі, а теоретично вивести на основі аналізу умов даної задачі  та відомих базових формул.

Звичайно, в простих задачах, розрахункове рівняння може співпадати з базовою формулою. Наприклад. Задача. З якою середньою швидкістю рухався пішохід, якщо за 60с він пройшов шлях 150м? Рішення: оскільки за визначенням v_с = s/t, то v_с = 150м/60с = 2,5м/с. Відповідь:  v_с=2м/с. Однак, якщо ви будете орієнтуватись на розв’язування лише таких гранично простих задач, то користі від такого навчання буде не багато.

6. Методом аналізу розмірностей, перевірити правильність розрахункового рівняння. Необхідність такої перевірки обумовлена тим, що в процесі теоретичного аналізу, ви можете зробити певні помилки і отримати відповідно неправильне розрахункове рівняння. Наприклад, якщо ваше розрахункове рівняння має вигляд v_с = (v₁+v₂)/v₁v₂, то це рівняння принципово неправильне. Неправильне тому, що в ньому, розмірність тієї величини яка зліва [v_c] = м/с не співпадає з розмірністю тієї величини яка справа [(v₁+v₂)/v₁v₂] = (м/с)/(м/с)² = 1/(м/с) = с/м. Висновок: формула v_c = (v₁+v₂)/v₁v₂ принципово неправильна. А це означає, що в процесі виведення цієї формули (розрахункового рівняння)  ви припустились певних помилок.  Якщо ж ваше розрахункове рівняння має вигляд v_c = v₁v₂/(v₁+v₂), то таке рівняння принципово правильне, адже [v₁v₂/(v₁+v₂)] = м/с = [v_c]

Звичайно, метод аналізу розмірностей не дає сто відсоткової гарантії того, що отримане вами розрахункове рівняння є безумовно правильним. Наприклад, цей метод не дозволяє відрізнити формулу v_c = v₁v₂/(v₁+v₂), від формули v_c = 2v₁v₂/(3v₁+v₂). Однак як правило, практичне застосування методу аналізу розмірностей є надзвичайно ефективним і корисним.

7. Виконати математичні розрахунки, тобто підставити числові значення відомих величин в розрахункове рівняння і, виконавши відповідні розрахунки, отримати числове значення невідомої величини. На практиці етап перевірки правильності розрахункового рівняння часто поєднують з етапом математичних розрахунків. Для цього в процесі розрахунків виконують відповідні дії не лише над числовими значеннями величин, а й над одиницями їх вимірювання. Але якщо визначальне рівняння складне, або складається з багатьох різновимірних одиниць, то перевірку правильності цього рівняння доцільно виконувати окремо.
8. Проаналізувати правильність отриманої відповіді. Це означає, що отриману відповідь потрібно проаналізувати на предмет її відповідності очікуваному результату. Справа в тому, що вже на першому етапі розв’язку задачі, тобто на етапі «Уважно прочитати умову задачі», ви повинні мати певне уявлення про очікуваний результат її розв’язку. Наприклад, якщо за умовою задачі на першій ділянці шляху, тіло  рухалось з швидкістю 10м/с, а на другій – з швидкістю 20 м/с, то абсолютно очевидно, що середня швидкість тіла на всьому шляху не може бути меншою за 10м/с, і більшою за 20м/с. Тому якщо в результаті рішення задачі ви отримали v_с = 8м/с,  або  v_с = 23м/с, то ясно, що така відповідь є неправильною. А це означає, що на певному етапі розв’язку задачі ви зробили помилку.

До речі, та формула яку ми аналізували  v_с = v₁v₂/(v₁+v₂) і яка успішно пройшла перевірку методом аналізу розмірностей, не є і не може бути правильною. Адже для v₁ = 10м/с;  v₂ = 20м/с,  вона дає результат v_с = 6,67м/с.

Якщо на тому чи іншому етапі розв’язку задачі з’ясується, що отриманий результат є неправильним, то ви повинні ще раз уважно проаналізувати попередні етапи та з’ясувати на якому з них зроблена помилка і виправити її.

9.Записати відповідь.

Таким чином, алгоритм розв’язку задачі коротко можна представити у вигляді наступної послідовності дій:

1. Уважно прочитати умову задачі.
2. Зробити стислий запис цієї умови.
3. Проаналізувати розмірності заданих фізичних величин.
4. Виконати малюнок, який відображає фізичну суть задачі.
5. На основі теоретичного аналізу умови задачі та базових формул (певних законів і визначальних рівнянь фізичних величин), вивести розрахункове рівняння.
6. Методом аналізу розмірностей перевірити правильність розрахункового рівняння.
7. Виконати розрахунки.
8. Проаналізувати правильність отриманої відповіді.
9. Записати відповідь.

Звісно, далеко не кожну задачу можна і потрібно розв’язувати строго дотримуючись вище заданого алгоритму.  Однак в загальних рисах, цей алгоритм є достатньо універсальним та ефективним. І якщо розв’язуючи конкретні задачі ви будете його дотримуватись, то рано чи пізно переконаєтесь в цьому.

В фізиці нема іншого способу навчитися розв’язувати задачі як той, що передбачає їх практичне розв’язування. Тому цим і займемося.

Задача 1. Рух автомобіля тривав 6 годин. З них 1 годину автомобіль рухався з швидкістю 110км/год, а решту часу – з швидкістю 50км/год. Визначити середню швидкість автомобіля на всьому шляху.

Дано:

t = t₁+t₂ = 6год

t₁ = 1год

t₂ = 5год

v₁ = 110км/год

v₂ = 50км/год

v_c = ?

Рішення. За визначенням  v_c = s/t = (s₁+s₂)/(t₁+t₂) = (s₁+s₂)/t, де s₁ = ? s₂ = ?.

Оскільки при рівномірному русі v = s/t, то:

v₁ = s₁/t₁, звідси s₁ = v₁∙t₁ = 110(км/год)∙1год = 110км;

v₂ = s₂/t₂, звідси s₂ = v₂∙t₂ = 50(км/год)∙5год = 250км.

Таким чином, v_c = (s₁+s₂)/t = (110км + 250км)/6год = 60км/год.

Відповідь: v_c = 60км/год.

Задача 2. Перші 10км потяг проходить з швидкістю 80км/год, другі 10км – з швидкістю 40км/год, а треті 10км – з швидкістю 60км/год. Яка середня швидкість потягу на всьому шляху?

Дано:

s₁ = s₂ = s₃ = 10км

v₁ = 80км/год

v₂ = 40км/год

v₃ = 60км/год

v_c = ?

Рішення. За визначенням  v_c = s/t = (s₁+s₂+s₃)/(t₁+t₂+t₃) = s/(t₁+t₂+t₃), де s = s₁+s₂+s₃ = 30км, t₁ = ? t₂ = ? t₃ = ?

Оскільки при рівномірному русі v = s/t, то:

v₁ = s₁/t₁, звідси t₁ = s₁/v₁ = 10км/80км/год = (1/8)год;

v₂ = s₂/t₂, звідси t₂ = s₂/v₂ = 10км/40км/год = (1/4)год;

v₃ = s₃/t₃, звідси t₃ = s₃/v₃ = 10км/60км/год = (1/6)год.

При цьому, t₁+t₂+t₃ = 1/8 + 1/4 + 1/6 = (6+12+8)/48 = (26/48)год.

Таким чином, v_c = s/(t₁+t₂+t₃) = 30км/(26/48)год = 55,4км/год.

Відповідь: v_c = 55,4км/год.

Задача 3. Велосипедист півтори години їхав зі швидкістю 20км/год. Потім велосипед зламався і останній кілометр велосипедист пройшов пішки за 30хв. Визначити середню швидкість велосипедиста на всьому шляху.

Дано:

v₁ = 20км/год

t₁ = 1,5год

t₂ = 30хв = 0,5год

s₂ = 1км

v_c = ?

Рішення. Оскільки за визначенням v_c = s/t, та враховуючи, що в умовах нашої задачі s = s₁+s₂, t = t₁+t₂, можна записати v_c = (s₁+s₂)/(t₁+t₂), де s₁=?

Оскільки v₁ = s₁/t₁, то s₁ = v₁·t₁ = 20(км/год)1,5год = 30км.

Таким чином v_c = (s₁+s₂)/(t₁+t₂) = (30км+1км)/(1,5год+0,5год) = 15,5км/год.

Відповідь: v_c = 15,5км/год.

Задача 4. За представленим на малюнку графіком руху, визначити швидкість руху на кожній ділянці шляху, та середню швидкість на всьому шляху.

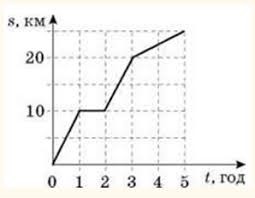
Рішення. Оскільки на кожній ділянці графік руху представляє певну пряму, то відповідні рухи є рівномірними (v = const). А це означає, що швидкість такого руху визначається за формулою v = s/t. Тому, на основі кількісного аналізу графіку можна записати:

1) ділянка 1: t₁ = 1год, s₁ = 10км, v₁ = s₁/t₁ = 10км/1год = 10км/год;

2) ділянка 2: t₂ = 1год, s₂ = 0км, v₂ = s₂/t₂ = 0км/1год = 0км/год;

3) ділянка 3: t₃ = 1год, s₃ = 10км, v₃ = s₃/t₃ = 10км/1год = 10км/год;

4) ділянка 4: t₄ = 2год, s₁ = 5км, v₄ = s₄/t₄ = 5км/2год = 2,5км/год;

v_c = s/t = (s₁+s₂+s₃+s₄)/(t₁+t₂+t₃+t₄) = (10+0+10+5)км/(1+1+1+2)год = 5км/год.

Відповідь: v₁ = 10км/год, v₂ = 0км/год, v₃ = 10км/год, v₄ = 2,5км/год, v_с = 5км/год.

Задача 5. Першу половину шляху автомобіль проїхав з швидкістю 10м/с, а другу – з швидкістю 20м/с. Визначити середню швидкість автомобіля на  всьому шляху.

Загальні зауваження.  Дана задача є класичним прикладом того, як  на перший  погляд очевидно проста задача, в реальності виявляється не такою вже й простою. Дійсно. На перший погляд здається, що в даній задачі середню швидкість автомобіля потрібно визначати за формулою:  v_c = (v₁+v₂)/2 = 15м/с. Насправді ж, таке рішення є неправильним.

Неправильним  по-перше тому, що в якості розрахункового рівняння, ми абсолютно не обґрунтовано вибрали сумнівну формулу, яка не входить до числа базових формул кінематики і яка лише на перший погляд здається очевидно правильною. В принципі формула v_c = (v₁+v₂)/2  має право на існування. Але це зовсім не означає, що в умовах даної задачі, середню швидкість потрібно визначати саме за цією формулою.

По-друге, навіть  якби формула v_c = (v₁+v₂)/2  виявилась правильною і такою що підходить для розв’язування даної задачі, її необґрунтоване застосування в якості розрахункового рівняння, потрібно визнати неправомірним. Адже розрахункове рівняння треба не вигадувати і не списувати, а теоретично доводити на основі відомих базових формул та аналізу умов конкретної задачі.

Враховуючи вище сказане,  розв’яжемо задачу так, як це потрібно, тобто дотримуючись загально прийнятого порядку розв’язування задач.

Дано:

s₁ = s₂ = s/2

v₁ = 10м/с

v₂ =20м/с

v_c=?

Рішення. За визначенням  v_c = s/t ,  де s =?  t =?

Загальні зауваження. На перший погляд здається, що в умовах даної задачі, визначити середню швидкість автомобіля за формулою v_c = s/t неможливо. Адже ми маємо одне рівняння з двома невідомими: v_с = s/t,  де s = ? t  = ? А це означає, що таке рівняння не має гарантовано однозначного рішення. І якби ми дійсно спробували визначити числові значення s і t з тим, щоб підставивши їх у формулу v_с = s/t, отримати правильний результат, то такого результату ми б не отримали. І тим не менше дана задача має гарантовано однозначне рішення. Це рішення є можливим тому, що в процесі математичних перетворень, одна з невідомих величин (в даному випадку s) скорочується. Тому, коли ви будете мати справу з подібними ситуаціями, то не поспішайте опускати руки, а шукайте можливості того, щоб в процесі математичних перетворень, одна з невідомих величин скоротилась. А як правило, такі можливості існують. Адже вам задають такі задачі, які мають певне рішення.

Зважаючи на вище сказане, уважно проаналізуємо умову задачі і виразити невідомі величини (s; t) через відомі (v₁; v₂).

Отже, за умовою задачі:

s = s₁ + s₂,  де    s₁ = s/2;      s₂ = s/2

t = t₁ + t₂,   де      t₁ = ?         t₂ =?

По суті це означає, що в умовах нашої задачі, величини t₁ і t₂ потрібно виразити через v та s. А оскільки, для рівномірного руху  v = s/t,  то

v₁ = s₁/t₁ = s/2t₁,  звідси   t₁ = s/2v₁;

v₂ = s₂/t₂ = s/2t₂, звідси   t₂ = s/2v₂.

При цьому, t₁ + t₂ = s/2v₁ + s/2v₂ = (sv₂ + sv₁)/2v₁v₂ = s(v₂ + v₁)/2v₁v₂.

Таким чином: v_c = s/t = s/(t₁+t₂) = s / s(v₂ + v₁) / 2v₁v₂ = 2v₁v₂/(v₁+v₂).

Розрахунки: v_c = 2v₁v₂/(v₁+v₂) = 2∙10(м/с)∙20(м/с) / (10(м/с) + 20(м/с)) = 400(м/с)²/30(м/с) = 13,3м/с.

Відповідь: v_c=13,3м/с.

Задача 6. Третину шляху автомобіль проїхав з швидкістю 10м/с, а решту шляху – з швидкістю 20м/с. Визначити середню швидкість автомобіля на  всьому шляху.

Дано:

s₁ =  s/3

s₂ = 2s/3

v₁ = 10м/с

v₂ = 20м/с

v_с = ?

Рішення. За визначенням: v_с = s/t,  де  s = ?,   t = ?

За умовою задачі:

s = s₁ + s₂,   де  s₁  = s/3, s₂ = 2s/3

t = t₁ + t_2,    де   t₁ =   t₂  =  ?

Оскільки для рівномірного руху v = s/t , то

v₁ = s/3t₁   звідси    t₁ = s/3v₁;

v₂=2s/3t₂  звідси    t₂ = 2s/3v₂;

при цьому: t₁ + t₂ = s/3v₁ + 2s/3v₂ = (sv₂ + 2v₁)/3v₁v₂ = s(v₂ + 2v₁)/3v₁v₂.

Враховуючи вище сказане можна записати:

v_c = s/t = s/(t₁+t₂)=s / s(v₂ + 2v₁) / 3v₁v₂ = 3v₁v₂/(v₂+2v₁).

Таким чином: v_c = 3v₁v₂/(v₂+2v₁).

Розрахунки: v_c = 3v₁v₂/(v₂+2v₁) = 3∙10(м/с)∙20(м/с) / (20(м/с) + 2∙10(м/с)) = 600(м/с)²/40(м/с) = 15м/с.

Відповідь: v_c = 15м/с.

Задача 7. Першу половину часу автомобіль рухався з швидкістю 10м/с, а другу половину часу – з швидкістю 20м/с.  Визначити середню швидкість автомобіля за увесь час руху.

Дано:

t₁ = t₂ = t/2

v₁ = 10 м/с

v₂ = 20м/с

v_c=?

Рішення. За визначенням v_c = s/t,  де  s =?    t =?

За умовою задачі

s = s₁+s₂, де   s₁ = ?    s₂ = ?

t = t₁ + t₂, де   t₁ = t/2; t₂ = t/2.

Оскільки для рівномірного руху  v = s/t, то

v₁ = s₁/t₁ = s₁/(t/2) = 2s₁/t, звідси    s₁ = v₁t/2;

v₂ = s₂/t₂ = s₂/(t/2) = 2s₂/t, звідси    s₂ = v₂t/2;

при цьому, s = s₁+s₂ = v₁t/2 + v₂t/2 = t(v₁+v₂)/2.

Враховуючи вище сказане можна записати

v_c = s/t = (s₁+s₂)/(t₁+t₂) = t(v₁+v₂)/2t = (v₁+v₂)/2.

Таким чином:  v_c = (v₁+v₂)/2.

Розрахунки: v_c = (v₁+v₂)/2 = (10(м/с) + 20(м/с))/2 = 15м/с.

Відповідь:  v_c=15м/с.

Контрольні запитання.

1. 1. Які формули при проведенні теоретичного аналізу задачі є базовими?
2. Що називають розрахунковим рівнянням?
3. Що означає: розрахункове рівняння має вигляд ? = ƒ (Дано)
4. В чому суть методу аналізу розмірностей?
5. Чи можна методом аналізу розмірностей гарантовано точно встановити, що дана формула правильна? Наведіть приклад.
6. В чому полягає аналіз правильності, отриманої в результаті розв’язування задачі, відповіді?
7. Чи може розрахункове рівняння мати вигляд v_с =(v₁+v₂)/v₁v₂ ? Поясніть.
8. Чи може розрахункове рівняння мати вигляд v_c=v₁v₂/(v₁+v₂) ? Чи правильне це рівняння для: v₁=10м/с; v₂=15м/с? Поясніть.

Вправа 3.

1. Турист за 25 хв пройшов 2 км, потім пів години відпочивав, а потім пробіг ще 800 м за 5 хв. Визначити середню швидкість туриста на всьому шляху.
2. Велосипедист проїхав 40 км зі швидкістю 20 км/год, а потім ще 30 км проїхав за 3 год. Яка середня швидкість велосипедиста на всьому шляху?
3. Рухаючись по шосе, велосипедист проїхав 900 м зі швидкістю 10 м/с, а потім ґрунтовою дорогою 400 м зі швидкістю 5 м/с. З якою середньою швидкістю він проїхав увесь шлях?
4. Автобус перші 4км шляху проїхав за 12хв, а наступні 12км – за 18хв. Визначити середню швидкість автобуса на всьому шляху.
5. За представленим на малюнку графіком руху, визначити швидкість руху на кожній ділянці шляху, та середню швидкість на всьому шляху.

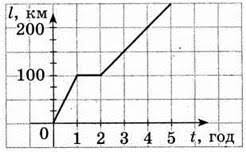
6. На основі аналізу малюнку описати рух велосипедиста та визначити його середню швидкість на всьому шляху.

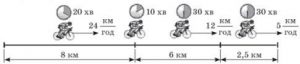
7. Мандрівник піднімався на гору зі швидкістю 3 км/год, а потім спускався назад зі швидкістю 6 км/год. Яка середня швидкість мандрівника на всьому шляху?

8. Третину шляху велосипедист проїхав зі швидкістю 30км/год, а решту шляху – зі швидкістю 10км/год. Визначити середню швидкість велосипедиста на всьому шляху.

9. Швидкість потягу на підйомі 30 км/год, а на спуску 90 км/год. Визначити середню швидкість потягу на всьому шляху, якщо спуск в два рази довший за підйом .

10. Пішохід частину шляху пройшов зі швидкістю 3 км/год затративши на це 3/4 часу свого руху. За час що залишився він пройшов решту шляху зі швидкістю 6 км/год. Яка середня швидкість пішохода на всьому шляху?

.

§6. Рівняння руху – основний закон кінематики.

 

         Нагадаємо, до числа основних фізичних величин кінематики поступального руху відносяться: час (t), координата (х = ℓ_х), пройдений шлях (s = ∆x), швидкість (v = ∆x/∆t) та прискорення (а = ∆v/∆t). Якщо ж говорити про основний закон кінематики поступального руху, то він називається рівнянням руху.

Рівняння руху – це закон, в якому стверджується: в загальному випадку, прямолінійний рух матеріальної точки можна описати рівнянням:

х = х₀ + v₀t + (а/2)t², де

х – координата матеріальної точки в момент часу t,

х₀  – початкова координата точки, тобто її координата в момент часу t = 0,

v₀ – початкова швидкість матеріальної точки,

а – прискорення матеріальної точки.

Потрібно зауважити, що в рівнянні х = х₀ + v₀t + (а/2)t² арифметичний знак (плюс чи мінус) кожного доданку визначається із умов конкретної задачі. А це означає, що в загальному випадку рівняння руху має вигляд х = ±х₀  ± v₀t ± (а/2)t².

Не буде перебільшенням сказати, що знаючи рівняння руху х = х₀ + v₀t + (a/2)t² та визначальні рівняння базових фізичних величин кінематики (s = ∆x, v = ∆x/∆t, а = ∆v/∆t), можна розв’язати практично будь-яку задачу кінематики. У всякому разі ті задачі, складність яких не виходить за межі програми загальноосвітньої школи.

Втім, в фізиці не достатньо знати формули. В фізиці набагато важливіше бачити за цими формулами реальні події та їх параметри. Наприклад, в математиці рівняння х = 200 – 10t + 0,2t² це просто квадратне рівняння, яке в загальному випадку має два рішення і яке графічно можна представити у вигляді відповідної параболи. В фізиці, все те що вивчалося в математиці ви маєте знати та вміти застосовувати на практиці. Однак цього зовсім не достатньо для розв’язування задач фізики. Адже в фізиці за кожним рівнянням, за кожною цифрою, за кожною буквою та за кожним знаком, ви маєте бачити реальні події та їм відповідні характеристики.

Скажімо, просто поглянувши на рівняння х = 200 – 10t + 0,2t², та розуміючи що це рівняння руху, тобто рівняння вигляду х = х₀ + v₀t + (а/2)t², ви відразу ж уявляєте наступну ситуацію. В момент часу t = 0с, дане тіло знаходиться в точці з координатою х₀ = 200м і рухається у від’ємному напрямку з швидкістю v₀ = –10м/с. При цьому величина цієї швидкості зменшується (зменшується тому, що знаки (напрямки) швидкості та прискорення є протилежними), а числове значення прискорення становить 0,4м/с², (а/2 = 0,2 і тому а = 0,2·2 = 0,4).

Таким чином, на основі порівняльного аналізу рівнянь

х = х₀ + v₀t + (а/2)t²,

х = 200 – 10t + 0,2t²,

можна стверджувати:

х₀ = 200м;   v₀ = –10м/с;   а = 0,4м/с²;   v↓

Загальні зауваження. Якщо в поясненнях до рівняння руху не вказані одиниці вимірювання відповідних величин, то потрібно вважати що цими одиницями є основні одиниці міжнародної системи (СІ): [t] =c; [x] = м; [v] = м/с; [a]=м/с².

Задача 1. За заданим рівнянням руху x = 100 – 18t – 0,3t², дати загальну характеристику цього руху

Рішення. На основі порівняльного аналізу загального рівняння руху та заданого конкретного рівняння руху

х = х₀ + v₀t + (а/2)t²,

x = 100 – 18t – 0,3t², можна записати:

х₀ = 100м;    v₀ = –18м/с;   а = –0,6м/с²;  v↑ (швидкість зростає тому, що знаки (напрямки) швидкості та прискорення є однаковими).

Задача 3. За заданим рівнянням руху x = 200 – 0,5t², дати загальну характеристику цього руху

Рішення. На основі порівняльного аналізу загального рівняння руху та заданого конкретного рівняння руху

х = х₀ + v₀t + (а/2)t²,

x = 200 – 0,5t², можна записати:

х₀ = 200м;    v₀ = 0м/с;   а = –1м/с²;   v↑.

Задача 3. За заданим рівнянням руху дати загальну характеристику цього руху.

x₁ = –200 + 15t – 0,4t²:    х₀ = –200м;  v₀ = 15м/с;  а = –0,8м/с²;  v↓

x₂ = 100 – 8t – 0,1t²:        х₀ = 100м;    v₀ = –8м/с;   а = –0,2м/с²;  v↑

х₃ = 50 + 4t :                     х₀ = 5м;        v₀ = 4м/с;   а = 0м/с²;  v = const

x₄ = –5t:                            х₀ = 0м;        v₀ = –5м/с;   а = 0м/с²;  v = const

x₄ = 200 – 0,5t²:                х₀ = 200м;    v₀ = 0м/с;   а = –1м/с²;   v↑

x₅ = –100:                          х₀ = –100м;  v₀ = 0м/с;  а = 0м/с²;  не рухається

Зверніть увагу, ми просто дивимося на рівняння руху і отримуємо з нього достатньо велику кількість інформації. Тепер уявіть, скільки інформації можна отримати на основі математичного та логічного аналізу цього рівняння. Ілюструючи лише малу частину цих інформаційних можливостей, розглянемо конкретну задачу.

Задача 4. За заданим рівнянням руху  х = 100 + 12t – 0,4t²:

1) дати загальну характеристику руху тіла;

2) визначити пройдений тілом шлях за десять секунд;

3) визначити пройдений тілом шлях за десяту секунду

4) записати  рівняння швидкості руху тіла та визначити цю швидкість через 10с;

5) визначити де і коли тіло зупиниться;

6) визначити пройдений тілом шлях до його зупинки;

7) визначити в який момент часу тіло буде в точці з координатою 150м;

8) визначити в який момент часу тіло буде в точці з координатою 200м.

Відповідаючи на кожне з поставлених запитань можна сказати наступне.

1. Дати загальну характеристику руху тіла: х₀ =? v₀=? а =?

Із порівняльного аналізу рівнянь

х = х₀ + v₀t + (а/2)t² та

х = 100 +12t – 0,4t²,  ясно:

х₀ =100м; v₀ = 12м/с; а = –0,8м/с²;  v↓.

2. Визначити пройдений тілом шлях за десять секунд: s(10) = ?

Оскільки за визначенням s = ∆х = х_к –х_п та враховуючи що в умовах даної задачі х_п = х₀ = 100м, х_к = х(10) = 100 + 12∙10 – 0,4∙10² = 180м, можна записати

s(10) = х(10) – х₀ = 180 – 100 = 60м.

3. Визначити пройдений тілом шлях за десяту секунду: s(10_ту) = ?

Не важко збагнути, що в даному випадку потрібно визначити той шлях, який пройде тіло за одну, а саме за десяту секунду. При цьому десятою секундою є та, що між дев’ятою і десятою, тобто s(10_ту) = х(10) – х(9).

Оскільки х(10) = 180м, а х(9) = 100 + 12∙9 – 0,4∙9² = 100+108–32,4 = 175,6м, то

s(10_ту)= х(10) – х(9) = 180 – 175,6 = 4,4м

4. 4. Записати рівняння швидкості руху тіла та визначити цю швидкість через 10с

Оскільки при рівноприскореному русі v = v₀ + at, то в умовах нашої задачі (v₀ = 12м/с, а = –0,8м/с²) можна записати v = 12 – 0,8t.

При цьому, якщо t = 10c, то  v(10) = 12 – 0,8∙10 = 4м/с.

5. Визначити, де і коли тіло зупиниться: х_зуп =? t_зуп=?

Оскільки в момент зупинки швидкість тіла дорівнює нулю (v = 0), то можна записати: якщо t = t_зуп, то  v = 12 – 0,8t_зуп = 0, звідси   t_зуп = 12/0,8 = 15c

А це означає, що  х_зуп = х(15) = 100 + 12∙15 – 0,4∙15²  = 100+180–90 = 190м.

6. Визначити пройдений тілом шлях до його зупинки: s_зуп = ?

s_зуп = х_зуп – х₀ = 190м – 100м = 90м.

7. Визначити в який момент часу тіло буде в точці з координатою 150м: х = 150м, t = ?

Для х = 150м задане рівняння руху набуває вигляду

150 = 100 +12t – 0,4t²,  або –50 +12t – 0,4t² = 0,  або –0,4t² + 12t – 50 = 0.

Таким чином, ми маємо стандартне квадратне рівняння, тобто рівняння вигляду аt² + вt + с = 0. В загальному випадку таке рівняння має два рішення: t_1,2 = [–b ± √(b² – 4ac)]/2a.

В умовах нашої задачі (а = –0,4; в = 12; с = –50):

t_1,2 = [–12 ± √(12² – 4∙(–0,4)∙(–50))]/2(–0,4) = –12 ± √(144–80)/(–0,8) =

= (–12 ± √64)/(–0,8) = (–12 ± 8)/(–0,8)

Звідси   t₁ = (–12 + 8)/(–0,8) = 5с;    t₂ = (–12 – 8)/(–0,8) = 25 с.

Отриманий результат означає, що в точці з координатою х = 150м дане тіло буде двічі: в моменти часу t₁ = 5с, та t₂ = 25с. І це закономірно. Адже через 15с від моменту початку відліку часу, наше тіло в точці з координатою х = 190м запинилось і з того моменту почало рухатись у зворотному напрямку.

8. Визначити в який момент часу тіло буде в точці з координатою 200м: х = 200м, t = ?

Із попереднього рішення задачі відомо, що в точці з координатою х = 200м, наше тіло ніколи не було і не буде. Що ж, подивимся що з його приводу скаже рівняння руху. А для х = 200м, це рівняння набуває вигляду:

200 = 100 +12t – 0,4t²,  або –100 +12t – 0,4t² = 0,  або –0,4t² + 12t – 100 = 0, тому

t_1,2 = [–12 ± √(12² – 4∙(–0,4)∙(–100))]/2(–0,4) = –12 ± √(144–160)/(–0,8) =

= (–12 ± √(–16)/(–0,8);

Оскільки квадратного кореня з від’ємного числа (√–16) не існує, то не існує і такого моменту часу в який дане тіло знаходилося б в точці з координатою х = 200м.

Загальні зауваження. Нагадаємо, рівняння вигляду ах² + bx + c = 0, називається квадратним рівнянням. Цьому рівнянню відповідає певна крива, яка називається параболою. В загальному випадку рішення квадратного рівняння визначаються за універсальною формулою: х_1,2 = [– b ± √(b²– 4ac)]/2a. При цьому, якщо під коренем квадратним буде від’ємне число, то відповідне рівняння не має рішення. Це означає, що відповідна парабола не перетинає числову вісь х, а в реаліях механічного руху – вісь часу (t).

Потрібно зауважити, що рівняння руху дає формально-математичні відповіді на всі запитання які стосуються цього рівняння. При цьому ви маєте розуміти, що в реальності, у відповідності з певним рівнянням, тіло рухається певний обмежений проміжок часу. Скажімо в процесі руху, автомобіль на певних ділянках набирає швидкість, на певних пригальмовує, на певних їде з постійною швидкістю, а на певних робить ті чи інші маневри. При цьому кожна ділянка описується своїм рівнянням руху і має свої часові обмеження. Та якби там не було, а не важко бачити, що на основі аналізу рівняння руху, можна розв’язувати величезну кількість кінематичних задач. І відтепер ви розумієте, чому це рівняння називають основним законом кінематики.

Задача 5. За заданим малюнком записати рівняння руху автомобіля і автобуса. Визначити де і коли вони зустрінуться.

Загальні зауваження. Рівняння руху х = х₀ + v₀t + (а/2)t² є справедливим і в тому випадку коли одиниці вимірювання відповідних величин не є основними одиницями СІ. Важливо лише те, щоб всі одиниці вимірювань були відповідними. Наприклад в умовах нашої задачі всі задані одиниці вимірювань є відповідними: [t] = год; [x] = км; [v] = км/год.

Рішення. На основі аналізу малюнку можна записати:

автомобіль: х₁ = 0 + 80t;

автобус:  х₂ = 360 – 40t.

Оскільки в момент зустрічі х₁ = х₂, то можна записати 80t = 360 – 40t, звідси 80t + 40t = 360, звідси 120t = 360, звідси t = 3год = t_зустр.

х_зустр = х₁(3) = 80(км/год)∙3год = 240км,

х_зустр = х₂(3) = 360км – 40(км/год)∙3год = 360км – 120км = 240км,

Відповідь: t_зустр = 3год, х_зустр = 240км.

Задача 6. За заданим графіком руху, записати рівняння руху на кожній ділянці шляху (вважати, що вісь 0ℓ є віссю координати, тобто віссю 0х).

Загальні зауваження. Якщо графіком руху є пряма (відрізок прямої), то відповідний рух є рівномірним (v = const), тобто рухом з нульовим прискоренням (а = 0). А це означає, що рівняння такого руху має вигляд х = х₀ + vt.

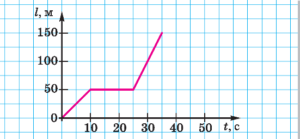
Рішення. На основі аналізу заданого графіку руху можна стверджувати, що даний рух складається з трьох ділянок. При цьому:

Ділянка 1: х₀ = 0м, х_к = 50м, Δх = 50м, Δt = 10c, v = Δx/Δt = 50м/10c = 5м/с,

рівняння руху х₁ = 5t.

Ділянка 2: х₀ = 50м, х_к = 50м, Δх = 0м, Δt = 15c, v = Δx/Δt = 0м/15c = 0м/с,

рівняння руху х₂ = 50.

Ділянка 3: х₀ = 50м, х_к = 150м, Δх = 100м, Δt =10c, v = Δx/Δt =100м/10c =10м/с,

рівняння руху х₃ = 50 + 10t.

Задача 7. Відходячи від станції, потяг протягом однієї хвилини рухається з прискоренням 0,4м/с². Визначте той шлях який проїхав потяг за цей час, і швидкість вкінці цього шляху.

Дано:

v₀ = 0м/с

t = 1хв = 60с

a = 0,4м/с²

s = ?  v_к = ?

Рішення. Для пройденого шляху (s = х–х₀) рівняння руху (х = х₀ + v₀t + (а/2)t²) набуває вигляду s = v₀t + (a/2)t². А зважаючи що в умовах нашої задачі v₀ = 0, можна записати s = (a/2)t² = [(0,4м/с²)/2](60c)² = 0,2(м/с²)3600с² = 720м.

Оскільки при рівноприскореному русі v_к = v₀ + at, то v_к = 0(м/с) + 0,4(м/с²)60с = 24м/с.

Відповідь: s = 720м; v_к = 24м/с.

Задача 8. Рушаючи з місця, автомобіль рухається з прискоренням 2м/с² і набуває швидкості 20м/с. Визначити пройдений автомобілем шлях.

Дано:

а = 2м/с²

v₀ = 0м/с

v_к = 20м/с

s = ?

Рішення. В умовах нашої задачі (v₀ = 0м/с), рівняння пройденого шляху s = v₀t + (а/2)t², набуває вигляду s = (а/2)t², де t = ? Оскільки швидкість автомобіля змінюється за законом v = v₀ + at, та зважаючи на те, що v₀ = 0м/с, можна записати v = at, звідси t = v/a. Таким чином s = (а/2)t² = (а/2)(v/a)² = v²/2a.

Розрахунки: s = v_к²/2a = (20м/с)²/2∙2м/с² = 100м

Відповідь: s = 100м.

Загальні зауваження. На основі аналізу рівняння руху можна довести, що при рівноприскореному русі, пройдений тілом шлях s, можна визначити за формулою s = (v_к² – v₀²)/2a, де а –  прискорення тіла, v₀ і v_к – відповідно початкова і кінцева швидкості тіла. Дане співвідношення не є а ні визначальним рівнянням певної фізичної величини, а ні базовим законом кінематики. Однак зазвичай, при розв’язуванні задач формулу s = (v_к² – v₀²)/2a, використовують як базову. Тому запам’ятайте, що величину пройденого шляху можна визначити не лише за рівнянням пройденого шляху s = v₀t + (а/2)t², а й за формулою s = (v_к² – v₀²)/2a.

Задача 9. Куля яка летить з швидкістю 500м/с потрапляє в земляний вал і проникає в нього на глибину 50см. З яким прискоренням рухалась куля в земляному валу?

Дано:

v₀ = 500м/с

v_к = 0м/с

s = 50см = 0,5м

a = ?

Рішення. Будемо виходити з того, що рух кулі в земляному валу відбувається з постійним прискоренням (а = const), і що для такого руху виконується співвідношення s = (v_к² – v₀²)/2a. Звідси а = (v_к² – v₀²)/2s, а враховуючи, що v_к = 0, а = – v₀²/2s = –(500м/с)²/2∙0,5м = –25∙10⁴м/с². Знак « – » вказує на те, що рух кулі є рівносповільненим (v↓).

Відповідь: а = –25∙10⁴м/с².

Контрольні запитання.

1. Як змінюється швидкість руху тіла (збільшується чи зменшується), якщо в рівнянні руху:

а) прискорення і швидкість мають знак «+»;

б) прискорення і швидкість мають знак «–»;

в) прискорення має знак «+», а швидкість – знак «–»;

г) прискорення має знак «–», а швидкість – знак «+»?

2. Якого вигляду набуває рівняння руху для рівномірного руху (а=0)?
3. Якого вигляду набуває рівняння руху в ситуації коли х₀=0?
4. Якого вигляду набуває рівняння руху в ситуації коли v₀=0 ?
5. Якого вигляду набуває рівняння руху в ситуації коли х₀=0; v₀=0 ?
6. Виходячи з того що s = ∆х = х – х₀, запишіть рівняння пройденого шляху.

Вправа 6.

1. За заданим рівнянням руху дати загальну характеристику відповідного руху:

х₁  = 100 + 10t + 0,5t²

х₂  = –100 + 5t – 0,2t²

х₃  = –10t – 0,3t²

х₄  = 150 – 0,25t²

х₅  = t² .

2. За заданим рівнянням руху х = 100 –15t + 0,5t²:

1) дати загальну характеристику руху тіла;

2) визначити координати тіла через 10 і 20 секунд;

3) визначити швидкість тіла через 10 і 20 секунд;

4) визначити де і коли тіло зупиниться;

5) визначити пройдений тілом шлях за десять секунд;

6) визначити пройдений тілом шлях за десяту секунду;

7) в який момент часу тіло буде в точці з координатою 0м; –200м?

3. В заданій системі відліку рівняння руху тіл мають вигляд х₁ =15t, х₂= 200 +10t. Де і коли зустрінуться ці тіла?
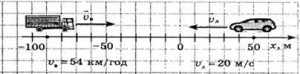
4. На основі аналізу малюнку, записати рівняння руху вантажного і легкового автомобілів, визначити де і коли вони зустрінуться.

5.  Велосипедист що рухається зі швидкістю 3м/с почав спускатися з гори з прискоренням 0,8м/с². Визначити довжину гори, якщо спуск тривав 6с.

6. Із станції вийшов товарний потяг зі швидкістю 36км/год. Через 0,5год, в тому ж напрямку вийшов пасажирський потяг, швидкість якого 72км/год. Через який час і на якій відстані від станції пасажирський потяг наздожене товарний.

7. З яким прискоренням рухається куля в стволі гвинтівки, якщо на виході ствола її швидкість 700м/с? Довжина ствола 70см.

8. За заданими на малюнку графіками запишіть відповідні рівняння руху.

.

§7. Графічний метод розв’язування задач кінематики.

В фізиці є два базові методи розв’язування задач: алгебраїчний (аналітичний) та графічний (геометричний). Ілюструючи сильні та слабкі сторони цих методів, розв’яжемо конкретну задачу.

Задача 1. За заданими рівняннями руху х₁ = 140 – 14t; х₂ = 4t, визначити де і коли тіла зустрінуться. Задачу розв’язати алгебраїчним та графічним методом.

Алгебраїчне рішення. Суть алгебраїчного рішення полягає в тому, що виходячи з умов конкретної задачі та відомих базових формул, шляхом логічних міркувань (аналізу) та відповідних математичних перетворень і розрахунків, отримують алгебраїчне рішення задачі. В умовах нашої задачі алгебраїчне рішення є наступним.

Оскільки в момент зустрічі х₁ = х₂, то 140 – 14t = 4t. Звідси 18t = 140, звідси t = 140/18 = 7,78с = t_зустр. А це означає, що х_зустр= х₂(7,78) = 4∙7,78 = 31,1м;

х_зустр= х₁(7,78) = 140 – 14∙7,78 = 140 – 108,9 = 31,1м.

Відповідь: t_зустр = 7,78с;  х_зустр= 31,1м.

Графічне рішення. Суть графічного (геометричного) рішення полягає в тому, що на основі максимально точних геометричних побудов, з дотриманням вибраного масштабу та з застосуванням відповідних геометричних приладів (лінійка, транспортир, циркуль, тощо), отримують графічну відповідь на поставлене в задачі запитання. В умовах нашої задачі графічне рішення є наступним.

На основі аналізу заданих рівнянь руху, та факту того, що ці рівняння є лінійними, тобто рівняннями прямих, визначаємо координати довільно вибраних базових точок:

х₁ = 140 – 14t:      якщо t = 0с   то  х = 140м,   А₁(0; 140)

якщо t = 10с  то  х = 0м,      А₂(10; 0).

х₂= 4t:                   якщо t = 0с   то   х = 0м,      В₁(0; 0)

якщо t = 10с  то  х = 40м,    В₂(10; 40).

Задаємо систему координат і виконуємо необхідні геометричні побудови.

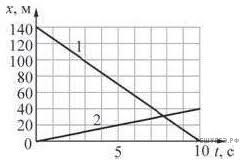
Координати (х, t) точки перетину побудованих прямих і є параметрами часу та місця зустрічі відповідних тіл: t_зустр ≈ 7,8с;  х_зустр≈ 31м.

Відповідь: t_зустр ≈ 7,8с;  х_зустр≈ 31м.

Варто зауважити, що побудувавши графіки заданих рухів та аналізуючи ці графіки, можна відповісти на безліч кінематичних запитань. Наприклад, визначити час та місце зустрічі тіл: зустрінуться приблизно через 7,8с в точці з координатою приблизно 30м. Можна встановити координати рухомих тіл в будь який момент часу. Скажімо, в момент часу t = 5с: х₁ ≈ 50м; х₂ ≈ 20м. Для будь якого моменту часу, визначити відстань між рухомими об’єктами. Наприклад: для t = 5с, ℓ ≈ 50м; для t =10с, ℓ ≈ 40м. Визначити швидкість тіла (v = ∆x/∆t), його прискорення (a = ∆v/∆t), напрям руху, тощо. Іншими словами, геометричний аналіз графіків руху, дозволяє відповісти на той же спектр запитань що і математичний аналіз відповідних рівнянь руху.

Головною перевагою графічного методу є його візуальна наочність. А основним недоліком – факт того, що точність графічного рішення залежить від точності геометричних побудов. Крім цього, графічне рішення задачі є ефективним лише в тому випадку, якщо відповідні графіки є лінійними функціями, тобто можуть бути представленими у вигляді певних прямих. Адже якщо наприклад, рівняння руху має вигляд х = 40t – 5t², то графіком цього руху буде зображена на малюнку парабола для побудови якої потрібно визначити координати максимально великої кількості точок.

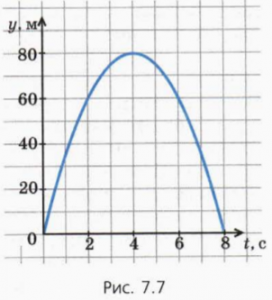
Мал.16. Графічний метод розв’язування задач є ефективним лише в тому випадку, коли відповідні графіки є лінійними.

Задача 2. За заданим графіком руху матеріальної точки визначити її швидкість на кожній ділянці шляху та записати відповідне рівняння руху.

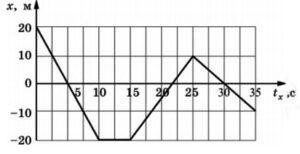
Рішення. Оскільки на кожній ділянці графік руху представляє собою певну пряму, то відповідні рухи є рівномірними (а = 0). А це означає, що швидкість такого руху визначається за формулою v = Δх/Δt, і що рівняння руху має вигляд х = х₀ + vt.

Кількісно аналізуючи графіки руху на кожній ділянці  можна записати:

Ділянка 1: Δt = 10c, х₀ = 20м, Δx = –40м, v₁ = Δx/Δt = –20м/10с = –4м/с,

x₁ =20 – 4t;

Ділянка 2: Δt = 5c, х₀ = –20м, Δx = 0м, v₂ = Δx/Δt = 0м/5с = 0м/с;

x₂ = – 20;

Ділянка 3: Δt = 10c, х₀ = – 20м, Δx = 30м, v₃ = Δx/Δt = 30м/10с = 3м/с,

x₃ = –20 + 4t;

Ділянка 4: Δt = 10c, х₀ = 10м, Δx = –20м, v₄ = Δx/Δt = –20м/10с = –2м/с,

x₄ = 10 –2t;

Задача 3. За заданим графіком швидкості, описати рух тіла на кожній ділянці шляху. Визначити пройдений тілом шлях на кожній ділянці руху та величину загального пройденого тілом шляху.

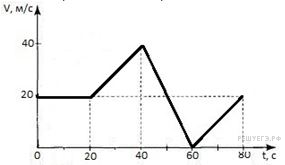
Рішення. Оскільки задані графіки швидкостей представляють собою певні прямі, то можна стверджувати, що відповідні рухи є рівноприскореними (а = соnst), а отже такими, які описуються формулами:

а = ∆v/∆t;

s = v₀t + at²/2;

s_заг = |s₁| + |s₂| + …

Кількісно аналізуючи графік швидкості на кожній ділянці, можна сказати наступне:

Ділянка 1: ∆t = 20c; v₀ = 20м/c;  Δv = 20 – 20 = 0м/с;  a = 0/20 = 0м/с²;

s₁ = v₀Δt = 20∙20 = 400м.

Ділянка 2: ∆t = 20c; v₀ = 20м/c; Δv = 40 – 20 = 20м/с; a = 20/20 = 1м/с²;

s₂ = v₀Δt + aΔt²/2 = 20∙20 + 1∙20²/2 = 600м.

Ділянка 3: ∆t = 20c; v₀ = 40м/c; Δv = 0 – 40 = –40м/с; a = –40/20 = –2м/с²;

s₃ = v₀Δt + aΔt²/2 = 40∙20 –2∙20²/2 = 400м.

Ділянка 4: ∆t = 20c; v₀ = 0м/c; Δv = 20 – 0 = 20м/с; a = 20/20 = 1м/с²;

s₄ = v₀Δt + aΔt²/2 = 0∙20 + 1∙20²/2 = 200м.

s_заг = |s₁| + |s₂| + … = 400 + 600 + 400 + 200 = 1600м

Відповідь: s₁ = 400м, s₂ = 600м, s₃ = 400м, s₄ = 200м, s_заг = 1600м.

Загальні зауваження. Аналіз графіку швидкості руху тіла дозволяє визначати пройдений тілом шлях не лише алгебраїчним, а й геометричним способом. А цей спосіб полягає в тому, що величина пройденого тілом шляху дорівнює площі тієї фігури, яка з одного боку обмежена графіком швидкості та віссю 0–t, а з іншого – тими вертикальними лініями, які відповідають тому проміжку часу в межах якого визначається пройдений шлях. Наприклад в умовах нашої задачі:

s₁ = 20∙20 = 400м;

s₂ = 20∙20 + 20∙20/2 = 600м;

s₃ = 20∙40/2 = 400м;

s₄ = 20∙20/2 = 200м;

Задача 5. За заданим графіком руху, визначити швидкість руху тіла на кожній ділянці. Побудувати відповідний графік швидкості руху тіла.

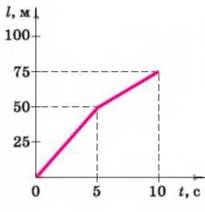
Рішення. Оскільки на кожній ділянці графік руху представляє певну пряму, то відповідні рухи є рівномірними (v = const). А це означає, що швидкість такого руху визначається за формулою v = Δℓ/Δt. Тому, на основі кількісного аналізу графіку можна записати

v₁ = Δℓ₁/Δt₁ = 50м/5с = 10м/с;

v₂ = Δℓ₂/Δt₂ = 25м/5с = 5м/с.

Отримані результати представляємо у вигляді відповідного графіка швидкості.

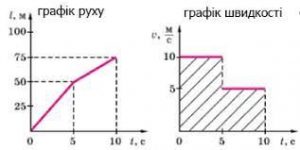
Задача 6. На основі аналізу заданого графіку руху тіл 1 і 2, скласти відповідну задачу, та розв’язати її алгебраїчним способом.

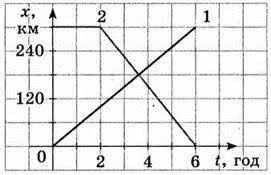
Загальні зауваження. Не втомлююся наголошувати на тому, що в фізиці недостатньо знати правильні формули. В фізиці на багато важливіше бачити за цими формулами їм відповідні фізичні об’єкти та події. Вміти представляти формули у вигляді відповідних графіків, і навпаки – за заданими графіками, записувати їм відповідні формули. Вміти описувати задані графіки і формули їм відповідними словами, і навпаки – заданий текст представляти у вигляді відповідних формул і графіків. Наприклад на основі аналізу заданих графіків руху тіл, скажімо автомобілів 1 і 2, можна сформулювати наступну задачу.

Задача. З пункту А в напрямку пункту Б виїхав вантажний автомобіль (1) швидкість якого v₁ = 300км/6год = 50км/год. Через 2 години з пункту Б в напрямку пункту А виїхав легковий автомобіль (2) швидкість якого v₂ = 300км/4год = 75км/год. Де і коли зустрінуться ці транспортні засоби, якщо відстань між пунктами А і Б 300км?

Дано:

ℓ = 300км

v₁ = 50км/год

v₂ = 75км/год

t₂ = t₁ – 2

x_зустр=? t_зустр=?

Рішення. Записуємо рівняння руху  кожного автомобіля:

х₁ = 50t₁;   х₂ = 300 – 75(t₁ – 2).

Оскільки в момент зустрічі х₁ = х₂, то 50t₁ = 30 – 75(t₁ – 2), або

50t₁ = 300 – 75t₁ + 2∙75, або  50t₁ + 75t₁ = 300 + 150, або 125t₁ = 450, або t₁ = 450/125 = 3,6год. Це означає, що автомобілі зустрінуться через 3,6 години, від моменту виїзду першого автомобіля. При цьому зустрінуться в точці з координатою

х_зустр = х₁ = 50t_зуст = 50∙3,6 = 180км,

х_зустр = х₂ = 300 – 75(t_зустр – 2) = 300 – 75∙(3,6 – 2) = 300 – 120 = 180км.

І не важко бачити, що алгебраїчне рішення задачі в точності відповідає її геометричному рішенню.

Відповідь: t_зустр = 3,6год, х_зустр = 180км.

Задача 7. За заданим графіком швидкості, описати рух тіла та визначити пройдений ним шлях за 6с.

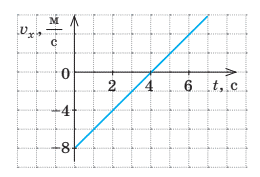
Рішення. На перший погляд, рішення задачі є елементарно простим: ∆t = 6c;

v₀ = –8м/c; a = ∆v/∆t = (12м/с)/6с = 2м/с²; s = v₀Δt + aΔt²/2 = –8∙6 + 2∙6²/2 = –12м.

В реальності ж таке рішення є хибним.

Помилковість вище наведеного рішення задачі полягає в наступному. Визначаючи пройдений шлях за формулою s = v₀Δt + aΔt²/2 = –12м, ми виходили з того, що на всьому проміжку часу Δt = 6с рух тіла є прямолінійним. В реальності ж, цей рух є криволінійним і таким, що складається з двох прямолінійних відрізків. Адже ми маємо ситуацію, коли до моменту часу t = 4с тіло з певним прискоренням рухається в одному напрямку (при цьому швидкість тіла зменшується), а після цього моменту тіло з таким же прискоренням рухається в протилежному напрямку (при цьому швидкість тіла збільшується).

Прикладом такого руху є рівносповільнений рух тіла похилою площиною: до моменту зупинки, тіло рухається в одному напрямку (вгору), а після зупинки – в протилежному (вниз). При цьому, як до зупинки так і після зупинки, тіло рухається з одним і тим же прискоренням (одним і тим же як за величиною, так і за напрямком).

Оскільки на ділянці Δt = 6с, рух тіла є криволінійним (складається з двох частин: s₁ – до зупинки, s₂ – після зупинки), то на цій ділянці загальна величина пройденого шляху має визначатись за формулою s = |s₁| + |s₂|. При цьому, як алгебраїчне так і геометричне рішення дають однаковий результат.

Алгебраїчне рішення: s₁ = v₀₁Δt₁ + aΔt₁²/2 = –8∙4 + 2∙4²/2 = 16м; s₂ = v₀₂Δt₂ + aΔt₂²/2 = 0∙2 + 2∙2²/2 = 4м; s_заг = s₁ + s₂ = 16м + 4м = 20м.

Геометричне рішення: s₁ = 8∙4/2 = 16м; s₂ = 4∙2/2 = 4м; s_заг = 16м + 4м = 20м.

Відповідь: s_заг = 20м.

Вправа №7.

1. Рух тіл вздовж осі ох задано рівняннями х₁ = 5t, х₂ = 150 – 10t. Визначити час та місце їх зустрічі. Задачу розв’язати алгебраїчно і графічно.
2. За заданими графіками руху записати відповідні рівняння руху. Визначити час та місце зустрічі тіл. Задачу розв’язати алгебраїчно і графічно.

3. За заданим графікам швидкості визначити прискорення тіла на кожній ділянці шляху, записати відповідні рівняння пройденого шляху та визначити величину цього шляху на кожній ділянці руху (алгебраїчним та геометричним методом).

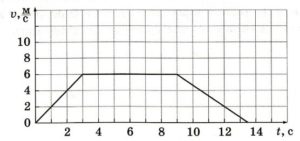
4. За заданим графіком руху, визначити швидкість руху тіла на кожній ділянці. Побудувати відповідний графік швидкості руху тіла. Графічним методом визначити пройдений тілом шлях на кожній ділянці руху.

5. За заданими графіками швидкості руху матеріальної точки визначити її прискорення на кожній ділянці шляху та записати відповідні рівняння пройденого шляху. Побудувати відповідний графік  прискорення тіла.

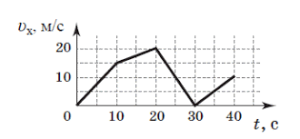
6. За заданим графіком визначити пройдені тілом шляхи на кожній ділянці руху та на всьому шляху. Задачу розв’язати геометричним та алгебраїчним методом.

7. За заданим малюнком скласти відповідну задачу та розв’язати її алгебраїчним і графічним способом.

8. На основі аналізу заданих графіків руху тіл 1 і 2, скласти відповідну задачу, та розв’язати її алгебраїчним способом.

9. На основі аналізу заданих графіків руху тіл 1 і 2, скласти відповідну задачу, та розв’язати її алгебраїчним способом.

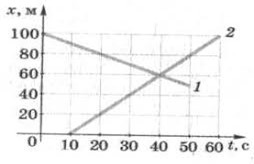
10. На основі аналізу заданих графіків руху тіл, скласти відповідну задачу, та розв’язати її алгебраїчним способом.

.

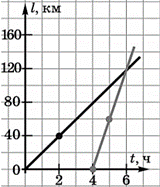
§8. Вільне падіння тіл. Рух тіла кинутого вертикально.

 

         Вільним падінням називають такий рух тіла, який відбувається під дією сили тяжіння та за відсутності суттєвого впливу інших зовнішніх сил, зокрема сили опору повітря. В загальному випадку вільно падаючими вважають не лише ті тіла падіння яких починається з нулевою швидкістю, а й ті які з певною швидкістю кинули вертикально вниз, вертикально вгору, горизонтально або під кутом до горизонту (мал.17). Адже в кожному з цих випадків, тіло після отримання певного початкового поштовху, рухається під дією лише однієї зовнішньої сили – сили тяжіння (звичайно за умови, що сила опору повітря є не суттєвою).

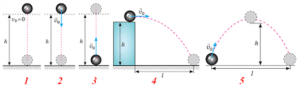
Мал.17. Рух тіла що відбувається під дією сили тяжіння та за відносності дії інших зовнішніх сил (зокрема суттєвого впливу опору повітря), називають вільним падінням тіла.

Вільне падіння тіла відбувається з певним прискоренням яке називається прискоренням вільного падіння або прискоренням сили тяжіння. Підкреслюючи важливість та значимість прискорення вільного падіння (прискорення сили тяжіння), його позначають окремою літерою g (від лат. gravitas – тяжіння). Для Землі, усереднена величина цього прискорення становить g = 9,8067м/с².

Зазвичай числове значення прискорення вільного падіння приймають рівним g = 9,8м/с². Однак зважаючи на те, що числове рішення переважної більшості задач на вільне падіння тіл є досить приблизним (приблизним бодай тому, що не враховує силу опору повітря), при наближених розрахунках величину прискорення вільного падіння часто округлюють до g =10м/с².

На перший погляд факт того, що важкі і легкі тіла падають з однаковим прискоренням, здається дивним. Адже та сила тяжіння з якою важкий камінь притягується до Землі в сотні разів перевищує ту силу тяжіння, з якою до Землі притягується легкий камінчик. І тим не менше, важкий камінь і легкий камінчик падають однаково швидко. Сьогодні ми не будемо говорити про те, чому важкі і легкі тіла падають однаково швидко. Сьогодні ми просто констатуємо той експериментальний факт, що під дією сили тяжіння, та за відсутності суттєвого впливу опору повітря, всі тіла падають з однаковим прискоренням, яке називається прискоренням вільного падіння.

Мал.18. Під дією сили тяжіння та за відсутності суттєвого впливу опору повітря, всі тіла падають з однаковим прискоренням – прискоренням вільного падіння (експериментальний факт).

Прискорення вільного падіння визначальним чином залежить від маси та розмірів того космічного об’єкту який створює відповідну силу тяжіння. Наприклад, для Місяця g = 1,6 м/с², для Марса g = 3,8 м/с², для Венери g = 8,8 м/с², для Юпітера g = 23,5 м/с², а для Сонця g = 274,0 м/с².

Потрібно зауважити, що величина та напрям прискорення вільного падіння не залежать від того в якому напрямку рухається тіло і з якою початковою швидкістю воно рухається. Наприклад, в незалежності від того чи вільно відпустили піднятий над землею камінь (мал19), чи з певною швидкістю кинули його вертикально вниз, вгору чи під кутом до горизонту, цей камінь рухається з прискоренням g = 9,8м/с², і це прискорення завжди направлено вертикально вниз. Навіть в точці максимального підйому тіла, де його швидкість дорівнює нулю, тіло має прискорення g = 9,8м/с². Іншими словами, на всій траєкторії вільного польоту, тіло рухається з прискоренням вільного падіння.

 

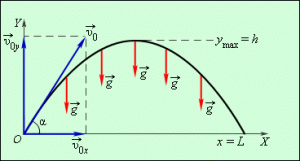
Мал.19. У всіх точках траєкторії вільного польоту, тіло рухається з прискоренням вільного падіння (g = 9,8м/с²)

Як і будь-який рівноприскорений рух, вільне падіння тіла можна описати рівнянням виду х = х₀ + v₀t + (a/2)t². Відмінність лише в тому, що говорячи про вільне падіння матеріальної точки, її вертикальну координату (висоту) зазвичай позначають літерою h, а прискорення – літерою g. Іншими словами, рух вільно падаючого тіла можна описати формулою h = h₀ + v₀t + (g/2)t².

Ілюструючи закономірності того руху який називається вільним падінням тіла, а заодно ілюструючи практичну значимість того закону який називається рівнянням руху, розв’яжемо ряд конкретних задач.

Задача 1. Визначити глибину колодязя, якщо відомо, що випущений із руки камінь досягає води за 2с.

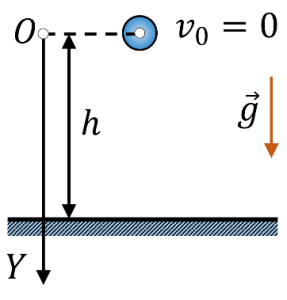
Дано :

v₀ = 0 м/с

 t = 2 с

h = ?

Рішення. Виконуємо малюнок, задаємо систему координат та записуємо рівняння руху тіла в цій системі, тобто формулу яка має вигляд h = h₀ + v₀t + (g/2)t². В умовах даної задачі та заданої системи координат (h₀ = 0м; v₀ = 0м/с), це рівняння набуває вигляду: h = (g/2)t², де g=10м/с². Враховуючи, що t = 2c, виконуємо відповідні розрахунки.

Розрахунки:  h = (10(м/с²)(2с)²/2 = 20м;

Відповідь: h=20м.

Загальні зауваження. Конкретний вигляд рівняння руху залежить не лише від самого руху, а й від вибору системи координат. Наприклад, якщо в умовах даної задачі за початок відліку обрати точку на дні колодязя, а вісь 0h направити вертикально вгору, то рівняння руху каменю матиме вигляд не h = (g/2)t², а h = h₀ – (g/2)t², де h₀ – висота каменю над поверхнею дна колодязі, а отже – глибина колодязі. Втім, результат розв’язку задачі буде одним і тим же. Дійсно, для рівняння h = h₀ – (g/2)t², в момент падіння камінь буде на рівні h = 0 і тому h₀ – (g/2)t² = 0. Звідси h₀ = (g/2)t² = (10(м/с²)(2с)²/2 = 20м.

Задача 2. Тіло вільно падає з висоти 45м. Визначте час падіння тіла.

Дано:

h = 45м

t_пад= ?

Рішення.    Виконуємо малюнок, задаємо систему координат та записуємо відповідне рівняння руху тіла, тобто формулу яка має вигляд h = h₀ + v₀t + (g/2)t². В умовах даної задачі та заданої системи координат (h₀=0м; v₀=0м/с), це рівняння набуває вигляду: h = (g/2)t². Звідси випливає t² = 2h/g, звідси t = √(2h/g).

Розрахунки: t = √(2·45м/10(м/с²)) = √(9с²) = 3с

Відповідь: t_пад= 3с.

Задача 3. На яку максимальну висоту підніметься тіло. Якщо його кинули вертикально вгору з швидкістю 20м/с?

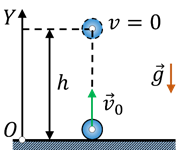
Дано :

v₀ = 20 м/с

h_max = ?

Рішення. Виконуємо малюнок, задаємо систему координат та записуємо відповідне рівняння руху тіла, тобто формулу яка має вигляд h = h₀ + v₀t + (g/2)t². А оскільки в умовах даної задачі h₀ = 0м; g = 10м/с², то рівняння руху набуває вигляду: h = v₀t – (g/2)t², або h = 20t – 5t². Із аналізу рівняння руху ясно, що для визначення максимальної висоти підйому тіла (h = h_max) необхідно визначити час цього підйому t = t_max.

Оскільки на максимальній висоті, тобто в момент часу t = t_max, швидкість тіла дорівнює нулю, та зважаючи на те, що величина цієї швидкості визначається за формулою v = v₀–gt,  можна записати: v₀ – gt_max = 0. Звідси,  t_max = v₀/g = 20(м/с)/10(м/с²) = 2с.

Таким чином: h_max = 20t_max – 5t_max² = 20(м/с)∙2с – 5(м/с²)∙(2с)² = 40м – 20м = 20м.

Відповідь:  h_max = 20м.

Задача 4. З якою швидкістю тіло кинули вертикально вгору, якщо воно повернулося через дві секунди?

Дано :

t_пол = 2с

v₀ = ?

Рішення. Виконуємо малюнок, задаємо систему координат та записуємо відповідне рівняння руху тіла, тобто формулу яка має вигляд h = h₀ + v₀t + (g/2)t².

А оскільки в умовах даної задачі h₀ = 0м; g = 10м/с², то рівняння руху набуває вигляду: h = v₀t – (g/2)t². Виходячи з того, що 2с, це час польоту тіла, тобто той час за який тіло вилетівши з рівня h = 0 знову повертається на рівень h = 0, можна записати v₀t – (g/2)t² = 0, звідси v₀t = (g/2)t², звідси v₀ = gt/2.

Розрахунки: v₀ = gt/2 = 10(м/с²)2с/2 = 10м/с.

Відповідь: v₀ = 10м/с.

Задача 5. Дві кульки кинули вертикально вгору з інтервалом 1с. Початкова швидкість кожної кульки 10м/с. На якій висоті зустрінуться ці кульки?

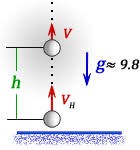
Дано:

∆t = 1c

v₀₁ = v₀₂ = 10м/c

h_зустр = ?

Рішення. Виконуємо малюнок та задаємо систему координат (на малюнку: h = h₀₁; v_н = v₀₂; v = v₁). Враховуючи, що через час Δt, тіло 1 буде на висоті h₀₁ та матиме швидкість v₁, записуємо рівняння руху кожного тіла:

1)  h₁ = h₀₁ + v₁t – (g/2)t²;

2)  h₂ = v₀₂t – (g/2)t².

Числові значення h₀₁ та v₁ визначаємо із наступних міркувань:

h₀₁ = v₀₁∆t – (g/2)∆t² = 10(м/с)1с – 5(м/с²)(1с)² = 5м

v₁ = v₀₁ – g∆t = 10(м/с) – 10(м/с²)1с = 0м/с.

При цьому рівняння руху даних тіл набувають наступного конкретного вигляді:

1) h₁ = 5 – 5t²;

2) h₂ = 10t – 5t².

Оскільки в момент зустрічі куль h₁ = h₂,  то:

5 – 5t² = 10t – 5t², звідси 5 = 10t, звідси t = 5/10 = 0,5с = t_зустр.

Таким чином, кулі зустрінуться через 0,5с після вильоту другої кулі. Зустрінуться в точці з координатою

h_зустр = h₁(0,5) = 5м – 5(м/с²)(0,5с)² = 5м – 1,25м = 3,75м.

Відповідь: h_зустр= 3,75м

Контрольні запитання.

1. Що називають вільним падінням тіла?
2. Чи можна стверджувати, що кинуте в горизонтальному напрямку тіло, знаходиться в стані вільного падіння? Чому?
3. Чи залежить величина і напрям прискорення вільного падіння тіла від напрямку руху цього тіла?
4. Чи залежить прискорення вільного падіння від маси падаючого тіла?
5. Чи залежить прискорення вільного падіння від маси Землі?
6. Одне тіло випустили з руки, а друге кинули вертикально вниз. Яке з цих тіл матиме більше прискорення вільного падіння?
7. Тіло кинули вертикально вгору. Чому ми стверджуємо, що те прискорення з яким рухається тіло направлене вертикально вниз?
8. Чи може тіло, маючи нульову швидкість, мати певне прискорення? Наведіть приклад.

                   Вправа 8.

1. Визначити глибину ущелини, якщо камінь, падаючи без початкової швидкості досягне її дна за 5с.
2. Тіло без початкової швидкості падає з висоти 30м. Визначити його швидкість в момент падіння.
3. Камінь кинули вертикально вниз з початковою швидкістю 7м/с. З якої висоти кинули камінь, якщо він падав 1,5с?
4. Тіло вільно падає з висоти 60м. Визначте пройдений тілом шлях за останню секунду його падіння.
5. Стрілу випустили з лука вертикально вгору. При цьому, вона впала на землю через 6с. Яка початкова швидкість стріли і максимальна висота її підйому?
6. З висоти 10м без початкової швидкості падає тіло. Одночасно з висоти 2м, вертикально вгору кинули друге тіло з початковою швидкістю 10м/с. На якій висоті зустрінуться ці тіла кинули це тіло?
7. Кулька падає на підлогу з висоти 1,5м і відбиваючись від неї втрачає 25% своєї швидкості. Через який час після відбивання, кулька знову вдариться об підлогу?
8. З башти висотою 20м одночасно кинули дві кульки: одну – вгору з швидкістю 15м/с, другу – униз з швидкістю 5м/с. Який проміжок часу відділяє моменти падіння куль на землю?

.

§9. Рух тіла кинутого горизонтально, або під кутом до горизонту.

Нагадаємо, вільним падінням називають такий рух тіла, який відбувається під дією сили тяжіння та за відсутності суттєвого впливу інших зовнішніх сил, зокрема сили опору повітря. На всій траєкторії вільного падіння, в незалежності від швидкості та напрямку руху тіла, воно рухається з постійним, направленим вертикально вниз прискоренням, яке називається прискоренням вільного падіння (прискоренням сили тяжіння), яке позначається літерою g і величина якого 9,8м/с² (при наближених розрахунках g = 10м/с²). В загальному випадку, для того поступального руху який називається вільним падінням, рівняння руху х = х₀ + v₀t + (a/2)t² набуває вигляду h = h₀ + v₀t + (g/2)t².

Рух тіла кинутого горизонтально, або під кутом до горизонту є криволінійним, причому таким, який завжди можна розкласти на дві складові: рівномірний (v = const) горизонтальний та рівноприскорений (a = g =const) вертикальний. А це означає, що описуючи такий криволінійний рух, можна записати два незалежних рівняння, аналіз яких дозволяє розв’язати відповідну задачу. Ілюструючи вище сказаного розв’яжемо ряд конкретних задач.

Задача 1. Тіло, що знаходиться на висоті 10м кинули горизонтально з швидкістю 20 м/с. Визначити горизонтальну дальність польоту тіла.

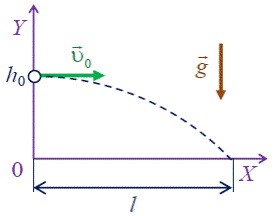
Дано:

h₀ = 10 м

v₀ = 20 м/с

ℓ = ?

Рішення. Виконуємо малюнок який відображає наявну ситуацію та задаємо відповідну систему координат.

Криволінійний рух даного тіла по суті є результатом двох незалежних рухів: рівномірного горизонтального та рівноприскореного вертикального. Зважаючи на ці обставини, записуємо рівняння кожного окремого руху, тобто формулу яка має вигляд х = х₀ + v₀t + (a/2)t².

– горизонтальний рух: оскільки х = ℓ; х₀ = ℓ₀ = 0; a = 0, отже  ℓ=v₀t;

– вертикальний рух: х = h; х₀ = h₀; v₀ = 0; a =g, отже  h = h₀ – gt²/2.

Таким чином даний рух описують два рівняння:

1) ℓ = v₀t, або ℓ = 20t;

2) h = h₀ – gt²/2, або h = 10 – 5t².

Із аналізу рівнянь ясно, що для того щоб визначити дальність польоту тіла (ℓ = 20t), необхідно визначити тривалість цього польоту (t = t_пол). А оскільки в момент падіння тіла, h = 0, то 10 – 5(t_пол)² = 0, звідси (t_пол)² = (10/5) = 2с², звідси t_пол = √2 = 1,4с.

Розрахунки: ℓ = 20t_пол = 20(м/с)∙1,4с = 28м.

Відповідь: ℓ = 28м.

Задача 2. Тіло, що знаходиться на висоті 10м кинули горизонтально з швидкістю 20 м/с. Визначити горизонтальну дальність польоту тіла та його швидкість в момент падіння на землю.

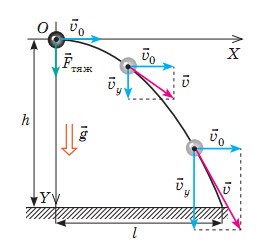
Дано:

h = 10 м

v₀ = 20 м/с

ℓ = ? v = ?

Рішення. Виконуємо малюнок який відображає наявну ситуацію та задаємо відповідну систему координат. Записуємо рівняння горизонтальної та вертикальної складової даного руху (тобто формулу яка має вигляд х = х₀ + v₀t + (a/2)t²).

– горизонтальний рух: х = ℓ; х₀ = ℓ₀ = 0; a = 0, отже ℓ = v₀t

– вертикальний рух: х = h; х₀ = h₀ = 0; v₀ = 0; a = g, отже h = gt²/2.

Таким чином даний рух описують два рівняння:

1) ℓ = v₀t, або ℓ = 20t;

2) h = gt²/2, або h = 5t².

Оскільки в момент падінні тіла (t = t_пол), h = 10м, то 5(t_пол)² = 10, звідси (t_пол)² = (10/5) = 2с², звідси t_пол = √2 = 1,4с.

Розрахунки: ℓ = 20t_пол= 20(м/с)1,4с = 28м.

Визначаючи величину швидкості тіла в момент його падіння, потрібно зважити на те, що ця швидкість має дві складові:

– горизонтальну v_x, значення якої залишається незмінною: v_x = v₀ = 20м/с

– вертикальну v_y, величина якої змінюється за законом v_y = gt.

Оскільки час польоту тіла відомий t_пол=√2=1,4с, то для моменту падіння v_y = gt_пол =14м/с.

Таким чином, результуючий вектор швидкості має дві складові: v_x = 20м/с; v_y = 14м/с. Знаючи правила додавання векторів та теорему Піфагора не важко визначити величину (v) результуючої швидкості: v = v_x + v_y

v = √(v_x² +v_y²) = √(20² + 14²) = √596 = 26,4м/с

Відповідь: ℓ=28м, v = 26,4м/с.

Загальні зауваження. Зверніть увагу на факт того, що рівняння одного і того ж руху, визначально залежить від заданої системи координат. Наприклад в задачі (1), вертикальний рух тіла описує рівняння h = h₀ – gt²/2 = 10 – 5t², а в задачі (2), той же рух описується рівнянням h = gt²/2 = 5t². При цьому результати розв’язку задач в обох випадках є однаковими.

Задача 3. З якою горизонтальною швидкістю потрібно кинути тіло, щоб дальність його польоту дорівнювала тій висоті з якої кинули це тіло?

Дано:

h₀

ℓ = h₀

v₀ = ?

Рішення. Виконуємо малюнок який відображає наявну ситуацію та задаємо відповідну систему координат. Записуємо рівняння горизонтальної та вертикальної складової даного руху (тобто формулу яка має вигляд х = х₀ + v₀t + (a/2)t²).

– горизонтальний рух: х = ℓ; х₀ = ℓ₀ = 0; a = 0, отже ℓ = v₀t

– вертикальний рух: х = h; х₀ = h₀; v₀ = 0; a = g, отже  h = h₀ – gt²/2.

Таким чином даний рух описують два рівняння:

1) ℓ = v₀t;

2) h = h₀ – gt²/2.

Оскільки в момент падіння тіла (t = t_x), h = 0м, то h₀ – gt_x²/2 = 0, звідси t_x = √(2h₀/g).

Таким чином, дальність польоту тіла визначається за формулою

ℓ = v₀√(2h₀/g), звідси v₀ = ℓ/√(2h₀/g) = ℓ√(g/2h₀).

Оскільки за умовою задачі ℓ = h₀  то  v₀ = h₀√(g/2h₀) = √(h₀g/2).

Відповідь: v₀ = √(h₀g/2).

Тепер, коли ви ознайомилися з закономірностями руху тіла кинутого горизонтально, можна розглянути і більш загальний рух – рух тіла кинутого під кутом до горизонту.

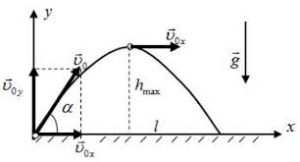
Мал.19. Кінематика руху тіла кинутого під кутом до горизонту.

На перший погляд, такий рух здається значно складнішим за рух тіла кинутого горизонтально. Насправді ж відмінності між цими рухами не такі вже й суттєві. Дійсно. Якщо вектор початкової швидкості (v₀) розкласти на дві складові:

– горизонтальну  v_x = v₀cosα

– вертикальну      v_y = v₀sinα,

то даний криволінійний рух можна представити як результуючу двох лінійних рухів: рівномірного горизонтального та рівноприскореного вертикального. При цьому, кожен з цих рухів можна описати відповідним рівнянням. Наприклад, представлений на мал.19 рух, можна описати системою двох рівнянь:

ℓ = (v₀cosα)t;

h = (v₀sinα)t – gt²/2.

Доречно зауважити, що в процесі руху тіла кинутого під кутом до горизонту, горизонтальна складова його швидкості (v_x = v₀cosα) залишається незмінною (звичайно за умови не суттєвості опору повітря), а вертикальна складова цієї швидкості, змінюється за законом v_y = v₀sinα – gt (спочатку зменшується до нуля, а потім збільшується).

Загальні зауваження. Сподіваюсь ви бодай щось чули про синус та косинус кута. А якщо не чули, то на даному етапі просто запам’ятайте:

кут  α	0°	30°	45°	60°	90°
sinα	0,00	0,50	0,71	0,87	1,00
cosα	1,00	0,87	0,71	0,50	0,00

Задача 4. Снаряд вилетів з дула гармати під кутом 30° до горизонту, з швидкістю 800м/с. Визначити дальність польоту снаряду та максимальну висоту його підйому.

Дано:

v₀ = 800м/с

α = 30°

ℓ = ?   h_м = ?

Рішення. Виконуємо малюнок який відображає наявну ситуацію та задаємо відповідну систему координат. Розкладаємо вектор початкової швидкості (v₀) на дві складові:

v_x = v₀cosα = v₀cos30° =  800(м/с)·0,87 = 696м/с;

v_y = v₀sinα = v₀sin30° = 800(м/с)·0,5 = 400м/с.

Записуємо рівняння горизонтальної та вертикальної складової руху снаряду:

ℓ = (v₀cosα)t = 696t;

h = (v₀sinα)t – gt²/2 = 400t – 5t².

Виходячи з того, що в момент падіння h = 0м, визначаємо час польоту снаряду:

якщо t = t_пол то  h = 400t – 5t² = 0, або t(400 – 5t) = 0, звідси

1) t = 0с

2) 400 – 5t = 0, або  5t = 400, або  t = 400/5 = 80c.

Отримані результати говорять про те, що на нульовій висоті (h = 0) снаряд був двічі: в момент вильоту з дула гармати (t = 0c); в момент падіння на землю (t = 80с). При цьому ясно, що  t_пол = 80с.

Знаючи час польоту снаряду, не важко визначити дальність його польоту:

ℓ = 696∙t_пол = 696(м/с)80с = 55680м = 55,68км.

Оскільки траєкторія руху снаряду є симетричною, то ясно, що на максимальній висоті снаряд буде в момент часу t_м = t_пол/2 = 80с/2 = 40с. При цьому h_м = 400∙t_м – 5∙t_м² = 400∙40 – 5∙40² = 8000м = 8км.

Відповідь: ℓ = 55,68км; h_м = 8км.

Варто зауважити, що для тих швидкостей з якими рухаються снаряди, опір атмосферного повітря є дуже великим. Тому реальні параметри траєкторії руху снаряду, суттєво відрізняються від тих, які отримані без врахування опору повітря.

Задача 5. З балкону який знаходиться на висоті 10м, кинули камінь під кутом 45° до лінії горизонту. На якій відстані від підніжжя балкону впаде камінь, якщо його початкова швидкість 15м/с?

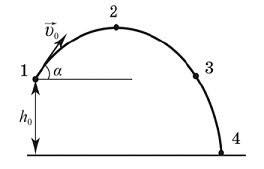
Дано:

h₀ = 10м

v₀ = 10м/с

α = 45°

ℓ_пол= ?

Рішення. Виконуємо малюнок який відображає наявну ситуацію та задаємо відповідну систему координат. Розкладаємо вектор початкової швидкості на горизонтальну та вертикальну складові:

v_x= v₀cos45° =  10(м/с)·0,71 = 7,1м/с;

v_y= v₀sin45° = 10(м/с)·0,71 = 7,1м/с.

Записуємо рівняння горизонтальної та вертикальної складової руху тіла:

ℓ = (v₀cosα)t = 7,1t;

h = h₀ + (v₀sinα)t – gt²/2 = 10 + 7,1t – 5t².

Виходячи з того, що в момент падіння тіла h = 0м, визначаємо час його польоту: якщо t = t_пол, то  h = 10 + 7,1t – 5t² = 0.

Пам’ятаючи, що рішення квадратного рівняння має вигляд t_1,2 =[–b ± √(b² – 4ac)]/2a, та розуміючи, що в умовах нашого рівняння а = –5; b = 7,1; с = 10,  можна записати t_1,2 =[–7,1 ± √(7,1² – 4(–5)10)]/2(–5) = [–7,1 ± √250]/(–10) = (–7,1 ± 15,8)/(–10). Звідси t₁ = 2,3c  t₂ = –0,8c.

Відповідь t₂ = –0,8c означає, що відповідна подія (тіло знаходилось на висоті 0м) відбулась в минулому. В минулому, в тому сенсі, що якби дане тіло за даним законом рухалось до початку відліку часу, тобто до того моменту коли воно було на висоті 10м, то на висоті 0м, воно було б за 0,8с до цього.

Таким чином, t_пол= 2,3с; ℓ_пол = 7,1t_пол = 7,1(м/с)2,3с = 16,3м.

Відповідь: ℓ_пол= 16,3м.

Контрольні запитання.

1. По якій траєкторії рухається тіло, кинуте горизонтально?
2. З яким прискоренням рухається тіло, кинуте горизонтально?
3. Чи залежить час польоту тіла, кинутого горизонтально, від величини його початкової швидкості?
4. Від чого залежить час польоту тіла кинутого горизонтально?
5. Від чого залежить дальність польоту тіла кинутого горизонтально?
6. Тіло кинули горизонтально. Як змінюється в процесі польоту швидкість тіла?
7. По якій траєкторії рухається тіло кинуте під кутом до горизонту?
8. Від чого залежить дальність польоту тіла кинутого під кутом до горизонту?
9. Як змінюється в процесі польоту швидкість тіла кинутого під кутом до горизонту?

Вправа 9.

1. Тіло, що знаходиться на висоті 15м кинули горизонтально з швидкістю 15м/с. Визначити горизонтальну дальність польоту тіла.
2. Тіло, що знаходиться на висоті 20м кинули горизонтально з швидкістю 20м/с. Визначити горизонтальну дальність польоту тіла, та його швидкість в момент падіння.
3. Тіло, що знаходиться на висоті 15м кинули горизонтально з швидкістю 20 м/с. Визначите координати цього тіла через 1с польоту.
4. З вікна в горизонтальному напрямку кинули м’яч з швидкістю 10м/с. При цьому м’яч упав на землю через 2с. З якої висоти було кинуто м’яч і на якій відстані від будинку він упав?
5. У скільки разів зміниться час польоту тіла кинутого горизонтально з певної висоти, якщо цю висоту збільшити в 2 рази?
6. Тіло кинули під кутом 60° до горизонту, з швидкістю 20м/с. Визначити дальність польоту та максимальну висоту підйому тіла.
7. Тіло кинули з висоти 20м під кутом 30° до лінії горизонту. Визначте горизонтальну дальність польоту тіла, якщо його початкова швидкість 10м/с?
8. Камінь кинуто під кутом 45º до горизонту з швидкістю 10м/с. Через який час камінь буде на висоті 1м?
9. Тіло кинуто під кутом 60º до горизонту з початковою швидкістю 20м/с. Через який час воно рухатиметься під кутом 45º до горизонту?

.

§10. Рух матеріальної точки по колу. Доцентрове прискорення.

До тепер ми говорили про прямолінійний рух матеріальної точки. Навіть в тому випадку коли мова йшла про криволінійний рух, наприклад вільний політ тіла кинутого під кутом до горизонту, ми представляли цей криволінійний рух як такий, що описується системою рівнянь фактично прямолінійного руху.

В загальному ж випадку поступальний рух матеріальної точки (тіла) може бути певною сукупністю прямолінійних та криволінійних ділянок. Наприклад траєкторія руху автомобіля дорогами міста, є складною сукупністю прямолінійних та криволінійних ділянок (мал.20а). При цьому будь яку криволінійну траєкторію можна представити як певну сукупність фрагментів кіл (мал.20б). А це означає, що знаючи закономірності руху матеріальної точки по колу, можна описати будь який криволінійний рух.

 

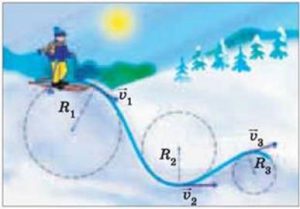
Мал.20. Довільний рух матеріальної точки, представляє собою певну сукупність прямолінійних та криволінійних ділянок. При цьому, будь який криволінійний рух, можна представити як певну сукупність фрагментів кіл.

Характерною особливістю руху матеріальної точки по колу є те, що в незалежності від швидкості руху, ця точка завжди рухається з певним прискоренням, яке характеризує зміну швидкості за напрямком.

Дійсно, припустимо що матеріальна точка з певною незмінною за величиною (модулем) швидкістю (|v₁| = |v₂| = … = const), рухається по колу радіусу R (мал.21а). Не важко бачити, що в процесі такого руху, напрям швидкості постійно змінюється(v₁ ≠ v₂ ≠… ≠ const). А це означає, що відповідна точка рухається з певним прискоренням, яке характеризує зміну швидкості за напрямком. Це прискорення називають доцентровим (позн. а_д). Така назва обумовлена фактом того, що в будь якій точці траєкторії, доцентрове прискорення направлено до центру того кола яке описує відповідна точка (мал.21б).

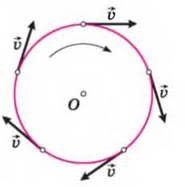
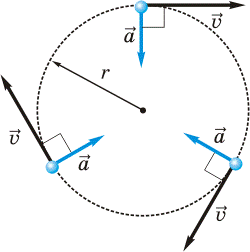
v₁ = v₂  = const      v₁ ≠ v₂  ≠ const

Мал.21. В процесі руху матеріальної точки по колу, напрям її швидкості постійно змінюється і тому вона рухається з відповідним прискоренням.

Виходячи з визначального рівняння прискорення (а = ∆v/∆t), можна довести, що величина доцентрового прискорення визначається за формулою а_д = v²/R, де v – швидкість тіла в даній точці траєкторії; R – радіус кривизни цієї траєкторії.

Доцентрове прискорення – це таке прискорення, яке характеризує зміну швидкості за напрямком і яке дорівнює відношенню квадрату швидкості руху тіла (матеріальної точки) до радіусу кривизни його траєкторії у відповідній точці.

Позначається: а_д

Визначальне рівняння: а_д = v²/R

Одиниця вимірювання: [а_д] = м/с²,  метр за секунду в квадраті.

Таким чином, якщо тіло рухається по колу, то в незалежності від того змінюється модуль його швидкості, чи не змінюється, це тіло має певне доцентрове прискорення, величина якого визначається за формулою  а_д = v²/R, і яке завжди направлено до центру відповідного кола.

Не важко збагнути, що на прямолінійних ділянках траєкторії, доцентрове прискорення неминуче дорівнює нулю. І це природньо. Адже на таких ділянках, напрям швидкості залишається незмінним і тому прискорення, яке характеризує зміну швидкості за напрямком має бути нульовим. Те, що на прямолінійних ділянках траєкторії, доцентрове прискорення дорівнює нулю, випливає не лише з визначення цього прискорення, а й з його визначального рівняння. Дійсно. Будь-яку прямолінійну ділянку траєкторії, можна вважати частиною кола з безкінечно великим радіусом (R = ∞). А це означає, що для таких ділянок a_д = v²/R = v²/∞ = 0.

Задача 1. Літак виконує так звану «мертву петлю», яка представляє собою вертикальну колову траєкторію. З яким доцентровим прискоренням рухається літак, якщо швидкість літака 360км/год, а радіус петлі 400м?

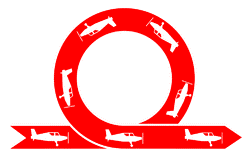
Дано:

v = 360км/год = 100м/с

R = 400м

а_д = ?

Рішення: За визначенням a_д = v²/R = (100м/с)²/400м = 25м/с².

Відповідь: а_д = 25м/с².

Якщо швидкість тіла змінюється як за величиною так і за напрямком, то воно має як звичайне (лінійне) прискорення (а_л = (v_к–v_п)/t) так і доцентрове прискорення (a_д = v²/R). При цьому загальне (повне) прискорення тіла (а) дорівнює векторній сумі лінійного (а_л) та доцентрового (а_д) прискорень.    Повне прискорення – це таке прискорення, яке дорівнює векторній сумі лінійного і доцентрового прискорень тіла.

Позначається: а

Визначальне рівняння : а = а_л + а_д

Одиниця вимірювання: [а]= м/с²,  метр за секунду в квадраті

Оскільки вектори а_л і а_д взаємно перпендикулярні, то величину повного прискорення можна визначити за формулою  а = √(а_л²+а_д²)

         

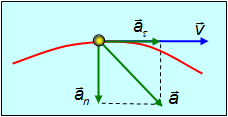
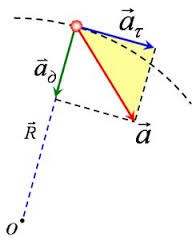
Мал.22. Якщо швидкість тіла змінюється як за  величиною так і за напрямком,  то його повне прискорення визначається як векторна сума лінійного і доцентрового прискорень.

Варто зауважити, що лінійне прискорення, тобто те прискорення яке характеризує зміну швидкості за величиною і напрям якого співпадає з лінією швидкості тіла в даній точці, часто називають тангенціальним прискоренням і позначають а_τ. Доцентрове ж прискорення, часто називають нормальним прискоренням і позначають а_n. Така назва обумовлена тим, що в науковій практиці термін «нормаль» є синонімом терміну «перпендикуляр». А оскільки доцентрове прискорення перпендикулярне (нормальне) до напрямку швидкості руху тіла, то воно має і відповідну назву.

Задача 2. Рухаючись заокругленням дороги радіус якого 50м, автомобіль пригальмовує і в даній точці має лінійне (тангенціальне) прискорення 2м/с². Визначте величину повного прискорення автомобіля, якщо його швидкість у відповідній точці траєкторії 36км/год. Задачу розв’язати алгебраїчним та графічним методом.

Дано:

R = 50м

a_л = 2м/с²

v = 36км/год = 10м/с

a = ?

Алгебраїчне рішення. Оскільки автомобіль рухається по колу, то окрім наявного лінійного прискорення a_л = 2м/с², він має певне доцентрове прискорення a_д = v²/R = (10м/с)²/50м = 2м/с². При цьому величина загального прискорення автомобіля дорівнює а = √(а_л²+а_д²) = √(2² + 2²) = √8 = 2,83м/с².

Відповідь: а = 2,83м/с².

Графічне рішення. Виходячи з того, що лінійне (тангенціальне) а_τ = 2м/с² і доцентрове a_д = v²/R = (10м/с)²/50м = 2м/с² прискорення є взаємно перпендикулярними, та враховуючи напрямки цих прискорень, у вибраному масштабі виконуємо відповідні геометричні побудови (додаємо вектори а_τ і a_д). Вимірюємо довжину результуючого вектора а = а_τ + а_д та враховуючи масштаб побудов, отримуємо величину повного прискорення а ≈ 2,8м/с².

Відповідь: а ≈ 2,8м/с².

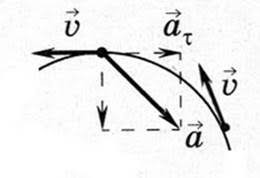
Рух по колу є надзвичайно поширеним як в природі загалом так і в штучно створеній техніці зокрема. По колу рухаються елементи коліс, шківів, валів та шестерень машин і механізмів. По колу рухаються точки секундних, хвилинних та годинникових стрілок годинників, лопатей вентиляторів, вітряків, турбін та корабельних двигунів. Практично по колу Місяць обертається навколо Землі, Земля – навколо Сонця, Сонце – навколо центру Галактики, а Галактика – навколо центру Метагалактики. Певною комбінації кіл рухаємся ми з вами в процесі обертання Землі навколо своєї осі, навколо Сонця, навколо центра Галактики та центру Метагалактики.

 

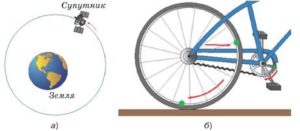
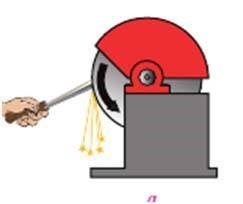
Мал. 23. Деякі приклади руху тіл та елементів тіл по колу.

Якщо в процесі руху по колу, модуль швидкості матеріальної точки залишається незмінним (v = const), то відповідний рух називають рівномірним рухом матеріальної точки по колу. Рівномірний рух матеріальної точки по колу характеризується не лише певною швидкістю (v) та певним доцентровим прискоренням (а_д), а й певною повторюваністю (періодичністю). Цю повторюваність характеризують двома величинами: періодом обертання (Т) та частотою обертання (ν). Наприклад, період обертання секундної стрілки годинника становить 60с, період обертання Землі навколо своєї осі – одна доба (Т = доба = 86400с); період обертання Місяця навколо Землі – 27,3доби (Т = 27,3доби = 2,36·10⁶с); період обертання Землі навколо Сонця – один рік (Т = рік = 3,2·10⁷с), а період обертання Сонячної системи навколо центру Галактики – 240 мільйонів земних років.

 

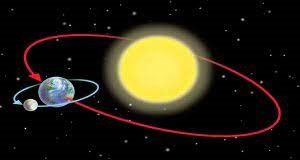
Мал.24. Рівномірний рух по колу, характеризується не лише певною швидкістю (v) та певним доцентровим прискоренням (а_д), а й певною повторюваністю (періодичністю).

Період обертання (період) – це фізична величина, яка характеризує часову періодичність (повторюваність) обертального процесу і яка дорівнює тому проміжку часу за який система здійснює один повний оберт.

Позначається: Т

Визначальне рівняння: Т = t/n, де n – кількість обертів системи здійснених за час t;

Одиниця вимірювання: [Т] = с,  секунда.

Наприклад, якщо матеріальна точка в процесі рівномірного руху по колу за 5с здійснила 10 обертів, то період її обертання  Т = t/n = 5с/10 = 0,5с.

Частота обертання (частота) – це фізична величина, яка характеризує частотну періодичність обертального процесу і яка дорівнює тій кількості обертів системи, яку вона здійснює за одиницю часу.

Позначається: ν (ню)

Визначальне рівняння: ν = n/t

Одиниця вимірювання: [ν] = 1/c = Гц,  герц.

Наприклад, якщо матеріальна точка в процесі рівномірного руху по колу за 5с здійснила 10 обертів, то період її обертання  ν = n/t = 10/5c = 2Гц.

Із визначальних рівнянь періоду і частоти (T = t/n; ν = n/t) з усією очевидністю випливає, що ці фізичні величини взаємопов’язані, і що цю взаємопов’язаність відображають співвідношення: T = 1/ν; ν = 1/T. Тому якщо наприклад, в умові задачі задано період обертання системи Т = 4с, то ви завжди можете визначити частоту цього обертання ν = 1/Т = 1/4с = 0,25Гц. І навпаки, якщо ν = 50Гц, то Т = 1/50Гц = 0,02с.

Задача 3. За 10с колесо автомобіля зовнішній радіус якого 25см, здійснює 100 обертів. Визначте період та частоту обертання колеса. Визначте  швидкість руху автомобіля.

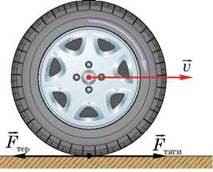
Дано:

t = 10с

n = 100

R = 25см = 0,25м

T=?; ν=?  v_авт = ?

Рішення. Оскільки за визначенням T = t/n; ν = n/t, то Т = 10с/100 = 0,1с; ν = 100/10с = 10Гц. Оскільки v = s/t, та зважаючи на те, що за один оберт колеса (t = Т), автомобіль переміщується на довжину кола виміряну по зовнішній поверхні колеса s = 2πR, можна записати v_авт = s/t = 2πR/T = 2·3,14·0,25м/0,1с = 15,7м/c.

Відповідь: Т = 0,1с; ν = 10Гц; v_авт = 15,7м/с.

Задача 4. Відомо, що радіус Землі 6370км, а період її обертання навколо власної осі 1 доба. Визначити швидкість обертання тих тіл які знаходяться на екваторі Землі та величину їх доцентрового прискорення.

Дано:

R = 6400км = 6,4·10⁶м

T = 1доба = 8,64·10⁴с

v = ?  а_д = ?

Рішення. Оскільки за визначенням v = s/t, та враховуючи, що за один повний оберт Землі (t = T), ті тіла які знаходяться на її екваторі проходять шлях s = 2πR, можна записати v = s/t = 2πR/T.

Розрахунки: v = 2πR/T = 2·3,14·6,4·10⁶м/8,64·10⁴с = 465м/с = 1670км/год.

Оскільки за визначенням a_д = v²/R, то a_д = v²/R = (465(м/с))²/6,4·10⁶м = 0,216·10⁶/6,4·10⁶ = 0,034м/с².

Відповідь: v = 1670км/год; а_д = 0,034м/с².

Контрольні запитання.

1. Чому матеріальна точка, яка з постійною за модулем швидкістю рухається по колу, рухається з прискоренням? Як називається це прискорення? Чому воно має таку назву?
2. Доведіть, що на прямолінійних ділянках траєкторії, доцентрове прискорення завжди дорівнює нулю.
3. Чи може тіло, яке рухається прямолінійно, рухатись з доцентровим прискореннями? з лінійним прискоренням?
4. Чи може тіло, яке рухається по колу, рухатись без доцентрового прискорення? без лінійного прискорення?
5. Чи може повне прискорення тіла дорівнювати його лінійному прискоренню? його доцентровому прискоренню? нулю?
6. Які величини характеризують повторюваність обертального руху? Як пов’язані ці величини?
7. Доведіть, що між періодом обертання Т, радіусом кола R та тією лінійною швидкістю v з якою матеріальна точка рухається по колу, існує співвідношення v = 2πR/T.
8. Чому в процесі добового обертання Землі, лінійні швидкості різних за широтою точок її поверхні є різними? В яких місцях ця швидкість є найбільшою, а в яких – найменшою?

Вправа №10.

1. Автомобіль рухається заокругленням дороги радіус якого 100м, зі швидкістю 36км/год. Чому дорівнює доцентрове прискорення автомобіля?
2. Якого радіусу має бути заокруглення дороги, щоб при швидкості 72км/год доцентрове прискорення автомобіля становило 1м/с²?
3. Рухаючись заокругленням дороги радіус якого 100м, автомобіль набирає швидкість і в даній точці має лінійне (тангенціальне) прискорення 2м/с². Визначте величину повного прискорення автомобіля, якщо його швидкість у відповідній точці траєкторії 54км/год. Задачу розв’язати алгебраїчним та графічним методом.
4. За 20 секунд колесо автомобіля здійснює 40 обертів. Визначити період та частоту обертання колеса.
5. Визначити період і частоту обертання секундної, хвилинної та годинникової стрілок годинника.
6. Вал діаметром 20см при обертанні робить один оберт за 0,4с. Визначте лінійну швидкість точок на поверхні вала.
7. Частота обертання коліс автомобіля 15Гц. З якою швидкістю рухається автомобіль, якщо зовнішній радіус його коліс 30см?
8. З якою лінійною швидкістю Земля обертається навколо Сонця, якщо радіус земної орбіти 1,5∙10⁸км? Порівняйте цю швидкість зі швидкістю кулі 0,5км/с. Зробіть висновки.

.

§11. Основні поняття та базові фізичні величини кінематики обертального руху.

До тепер ми вивчали так звану кінематику матеріальної точки, а по суті – кінематику поступального руху. Навіть говорячи про рух тіла по колу, ми мали на увазі, що цей рух є поступальним, тобто таким в процесі якого будь яка приналежна тілу пряма залишається паралельною сама собі (мал.25). Вивчаючи кінематику поступального руху ми з’ясували, що основними характеристиками цього руху є час (t), координата (x = ℓ_x), пройдений шлях (s = Δx), швидкість (v = Δx/Δt) та прискорення (a = Δv/Δt), а основним законом – рівняння поступального руху x = x₀ + v₀t + (a/2)t².

Мал.25. Рух кабіни оглядового колеса є поступальним, тобто таким в процесі якого будь яка приналежна кабіні пряма залишається паралельною сама собі.

Наразі ж прийшов час поговорити про параметри та закономірності ще однієї базової різновидності механічного руху, яку називають обертальним рухом тіла. Обертальний рух тіла – це такий механічний рух, при якому всі точки тіла описують кола, центри яких знаходяться на одній прямій, яка називається віссю обертання. Наприклад, обертально рухаються стрілка годинника, колесо автомобіля, двері класної кімнати, тощо. Звичайно за умови, що годинник «іде», колесо крутиться, двері відчиняються.

Мал.26. В процесі обертального руху тіла, всі його точки описують кола, центри яких знаходяться на одній прямій (осі обертання).

При обертальному русі різновіддалені від осі обертання точки тіла, рухаються суттєво по-різному: мають різні траєкторії руху, різні пройдені шляхи, різні лінійні швидкості, різні прискорення, тощо. А це означає, що описуючи обертальний рух тіла, це тіло не можна замінювати матеріальною точкою. Не можна тому, що різні точки тіла мають суттєво різні параметри руху.

Описуючи обертальний рух тіла, це тіло зазвичай представляють не у вигляді матеріальної точки, а у вигляді так званого абсолютно твердого тіла. Абсолютно тверде тіло, це таке умовне тіло, яким теоретично замінюють певне реальне тіло, в ситуаціях коли його механічними деформаціями можна знехтувати.

До числа основних фізичних величин кінематики обертального руху відносяться: час (t), кутова координата (φ), кут повороту (Δφ), кутова швидкість (ω) та кутове прискорення (ε). Визначаючи ці величини і перш за все ту, яка називається кутовою координатою (φ), або просто кутом, можна сказати наступне.

В кінематиці поступального руху, місцезнаходження тіла (матеріальної точки) визначається його координатою (х). При цьому, в процесі поступального руху тіла, відповідно змінюється і його координата. Якщо ж говорити про обертальний рух тіла, то в процесі цього руху, координата тіла по суті залишається незмінною. При обертальному русі, змінюється не координатне положення тіла, а його кутова орієнтація (мал.27). Цю орієнтацію характеризують величиною, яка називається кутом, а точніше – кутовою координатою.

 

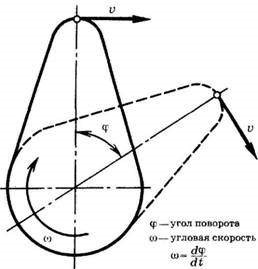
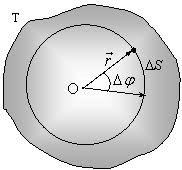
Мал.27. В процесі обертального руху тіла змінюється його кутова орієнтація.

Кутова координата (кут) – це фізична величина, яка характеризує просторову (кутову) орієнтацію тіла в заданій системі координат і яка дорівнює відношенню довжини (ℓ) тієї дуги що обмежує даний центральний кут, до радіусу (R) цієї дуги.

Позначається: φ

Визначальне рівняння: φ = ℓ/R

Одиниця вимірювання: [φ] = рад,   радіан.

Радіан – це одиниця вимірювання кутових величин, яка дорівнює такому центральному куту, довжина обмежуючої дуги якого дорівнює радіусу цієї дуги. Іншими словами, якщо довжина тієї дуги що обмежує центральний кут φ дорівнює радіусу цієї дуги (ℓ = R), то відповідний кут дорівнює одному радіану (від слова «радіус»).

По суті та величина яка називається кутом, є безрозмірною  величиною [φ] = [ℓ/R] = м/м = рад. Однак, щоб підкреслити, факт того, що ця безрозмірна величина характеризує саме кутову орієнтацію тіла, вона має спеціальну назву – радіан.

Вимірювання показують, що у повному колі міститься приблизно 6,28 радіан, а точніше 2π радіан, де π = 3,141592653…≈ 3,14. Відображенням даного факту є та формула за якою визначають довжину кола: ℓ = 2πR.

 

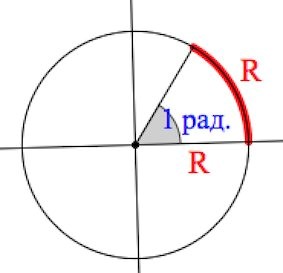
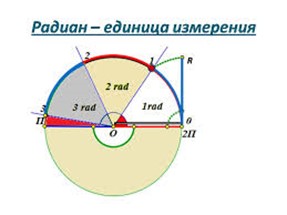
Мал.28. Радіан – такий центральний кут, довжина обмежуючої дуги якого дорівнює радіусу цієї дуги.

Напевно ви знаєте, що в математиці, геометрії та повсякденному житті, кутові величини зазвичай вимірюють не в радіанах, а в градусах. Градус – це одиниця вимірювання кутових величин, яка дорівнює такому центральному куту, що становить триста шістдесяту (1/360) частину повного кола. Іншими словами, якщо коло поділити на 360 рівних частин, то кутовий сектор в одну таку частину і є градусом.

Мал.29. Градус – це такий центральний кут, який дорівнює 1/360 частині кола.

Як ви думаєте, чому визначаючи одиницю кутових величин, люди з незапам’ятних часів, поділили коло на 360 частин? Не на 10, не на 100, чи скажімо на 250, а саме на 360? Правильно! З незапам’ятних часів, люди звернули увагу на факт того, що приблизно через 360 днів, все в цьому світі повторюється. Виходячи з цієї повторюваності, коло життя, а за ним і геометричне коло, поділили на 360 частин.

З практичної точки зору, градус є надзвичайно зручною одиницею. Тому в сфері геометричних побудов та повсякденного життя, кутові величини зазвичай вимірюють в градусах. Але, ця одиниця має один суттєвий недолік – вона жодним чином не пов’язана з параметрами того кола яке ми поділили на певну кількість кутових сегментів. А це означає, що градус не є органічною частиною цілісної системи взаємопов’язаних одиниць, а отже і цілісної системи знань про навколишній світ.

Для того щоб одиниця вимірювання кутових величин стала органічною частиною цілісної системи знань, коло потрібно поділити не так як нам подобається, чи здається зручним, а так щоб цей поділ відображав той реальний зв’язок який існує між кутовими та лінійними величинами. А цей зв’язок полягає в тому, що для будь якого кутового сегменту (φ) відношення його обмежуючої дуги (ℓ) до радіусу цієї дуги (R) є постійною величиною. Власне це відношення і є тим кутом, величина якого виміряна в радіанах.

Оскільки у повному колі, з одного боку міститься 360 градусів, а з іншого – 2π радіан, то між відповідними одиницями існує співвідношення 2π(рад) = 360º. Звідси випливає, що 1рад = 360º/2π ≈ 57º.

З побутово-практичної точки зору, вимірювати кутові величини в радіанах (1рад ≈ 57º) досить незручно. Тому в побутовій практиці та при геометричних побудовах, кутові величини вимірюють в градусах. Однак якщо мова йде про фізику та сучасну науку загалом, то в ній основною одиницею вимірювання кутових величин є не градус, а радіан. Адже виміряний в радіанах кут є не лише мірою кутових величин, а й певним відображенням тих зв’язків, які об’єктивно існують між кутовими та лінійними величинами.

Тепер, коли ви знаєте що просторову орієнтацію тіла характеризують певним кутом і що величина цього кута вимірюється в радіанах, можна визначити й інші характеристики обертального руху тіла, зокрема його кут повороту, кутову швидкість та кутове прискорення.

Кут повороту – це фізична величина, яка характеризує зміну кутової орієнтації тіла і яка дорівнює тому куту на який повернулось тіло в процесі його обертального руху.

Позначається: ∆φ

Визначальне рівняння: ∆φ = φ_к – φ₀

Одиниця вимірювання: [∆φ] = рад,  радіан.

Кутова швидкість – це фізична величина, яка характеризує кутову швидкість тіла (швидкість обертального руху тіла) і яка показує на який кут повертається тіло за одиницю часу.

Позначається: ω

Визначальне рівняння: ω = ∆φ/∆t

Одиниця вимірювання: [ω] = рад/с,  радіан за секунду.

Кутове прискорення – це фізична величина, яка характеризує кутове прискорення тіла і яка показує на скільки змінюється кутова швидкість тіла за одиницю часу.

Позначається: ε

Визначальне рівняння: ε = ∆ω/∆t

Одиниця вимірювання: [ε] = рад/с²,  радіан за секунду в квадраті.

По суті, кутова швидкість (ω) та кутове прискорення (ε) – величини векторні. Однак, зважаючи на факт того, що в межах програми загальноосвітньої школи, вивчають лише загальні основи механіки обертального руху, ми не будемо формулювати ті правила які визначають напрям цих векторів. Натомість будемо вважати, що кутова швидкість того тіла яке обертається за годинниковою стрілкою має знак «+», а проти годинникової стрілки – знак «–». При цьому, якщо в процесі обертання, кутова швидкість збільшується, то знаки кутової швидкості та кутового прискорення є однаковими. А якщо ця швидкість зменшується, то відповідні знаки є протилежними.

Задача 1. Виходячи з того, що період обертання Землі навколо своєї осі становить 24год, визначити кутову швидкість обертального руху Землі.

Дано:

Т = 24год = 86400с

ω = ?

Рішення. Оскільки за час ∆t = Т Земля здійснює один повний оберт навколо своєї осі, тобто повертається на кут Δφ = 2π радіан, то ω = ∆φ/∆t = 2π/Т = 2∙3,14рад/86400с = 12,7∙10^–6рад/с.

Відповідь: ω = 12,7∙10^–6рад/с.

Задача 2. В процесі руху, колесо велосипеда за 12 секунд здійснює 30 обертів. Визначити кутову швидкість обертального руху колеса, лінійну швидкість точок на його поверхні та швидкість руху велосипеда. Радіус колеса 35см.

Дано:

t = 12с

n = 30

R = 35см = 0,35м

ω = ? v = ?  v_вел = ?

Рішення. Оскільки за час одного повного оберту ∆t = t/n = 12с/30 = 0,4с колесо повертається  на кут Δφ = 2π радіан, то ω = ∆φ/∆t  = 2∙3,14рад/0,4с = 15,7рад/с.

Оскільки за час одного повного оберту ∆t = 0,4с, точки зовнішньої поверхні колеса описують повне коло довжина якого s = 2πR, то лінійна швидкість цих точок v = s/Δt = 2πR/Δt = 2·3,14·0,35м/0,4с = 5,5м/c.

Якщо виходити з того, що колесо велосипеда не пробуксовує відносно поверхні дороги, то можна стверджувати, що за час одного повного оберту колеса ∆t = 0,4с, велосипед переміститься на відстань, яка дорівнює довжині кола виміряної по зовнішній поверхні колеса s = 2πR. А це означає, що швидкість поступального руху велосипеда v_вел = s/t = 2πR/Δt = 2·3,14·0,35м/0,4с = 5,5м/c.

Відповідь: ω = 15,7рад/с; v = 5,5м/с;  v_вел = 5,5м/с.

Задача 3. Тіло обертається з кутовою швидкістю 10рад/с. Визначити лінійні швидкості тих точок тіла які знаходяться на відстані 5см, 10см, 15см від осі його обертання. Визначте доцентрові прискорення цих точок.

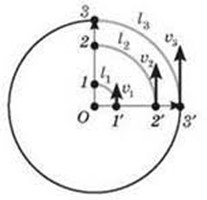
Дано:

ω = 10рад/с

r₁ = 5см = 0,05м

r₂ = 10см = 0,10м

r₃ = 15см = 0,15м

v₁ = ?  v₂ = ?  v₃ = ?

а_д1 = ? а_д2 = ? а_д3 = ?

Рішення. Оскільки за час одного повного оберту тіла (за час Δt), тіло повертається на кут Δφ = 2π, а кожна його точка долає шлях s = 2πr, де r – відстань від цієї точки до осі обертання тіла, то можна записати ω = Δφ/Δt = 2π/Δt; v = s/Δt = 2πr/Δt. Звідси випливає, що між кутовою швидкістю тіла ω та лінійними швидкостями v його точок, існує співвідношення v = ω∙r.

Дійсно, оскільки ω = 2π/Δt, то Δt = 2π/ω; оскільки v = 2πr/Δt, то Δt = 2πr/v. А враховуючи що в обох випадках тривалість обертального та лінійного рухів є однаковою (Δt = Δt), можна записати 2π/ω = 2πr/v, звідси v = ω∙r.

Таким чином:

v₁ = ω∙r₁ = 10(рад/с)∙0,05м = 0,5м/с;

v₂ = ω∙r₂ = 10(рад/с)∙0,10м = 1,0м/с;

v₃ = ω∙r₃ = 10(рад/с)∙0,15м = 1,5м/с.

Оскільки доцентрове прискорення матеріальної точки визначається за формулою а_д = v²/r, то:

а_д1 = v₁²/r₁ = (0,5м/с)²/0,05м = 5м/с²;

а_д2 = v₂²/r₂ = (1,0м/с)²/0,10м = 10м/с²;

а_д3 = v₃²/r₃ = (1,5м/с)²/0,15м = 15м/с².

Відповідь: v₁ = 0,5м/с, v₂ = 1,0м/с, v₃ = 1,5м/с.

.                  а_д1 = 5м/с²,  а_д2 = 10м/с², а_д3 = 15м/с²,

Контрольні  запитання.

1. Чому, описуючи обертальний рух тіла, це тіло не можна представляти у вигляді матеріальної точки?
2. Чому визначаючи кутовий градус, коло поділили на 360 частин?
3. Чому, в науковій практиці основною одиницею вимірювання кутових величин є не градус а радіан?
4. Якщо в будь якому повному колі міститься 2π радіан, то чому дорівнює довжина кола?
5. Які величини характеризують обертальний рух тіла?
6. Чи однаковою є кутова швидкість різних точок тіла при його обертальному русі?
7. Чи однаковою є лінійна швидкість різних точок тіла при його обертальному русі?
8. Чи однаковим є кутове прискорення різних точок тіла при його обертальному русі?
9. Чи однаковим є доцентрове прискорення різних точок тіла при його обертальному русі?

Вправа 11.

1. Чому дорівнює кут повороту хвилинної стрілки годинника за 15хв; за 30хв; за 2 години? Відповідь дайте в градусах та в радіанах.
2. Визначте кутову швидкість секундної, хвилинної та годинної стрілок годинника.
3. Колесо обертається з кутовою швидкістю 12рад/с. Визначити лінійні швидкості точок віддалених від осі обертання на: а) 10см; б) 20см; в) 30см.
4. Вал діаметром 20см обертається з частотою 20Гц. Визначити лінійну швидкість поверхневих точок валу та їх доцентрове прискорення.
5. Колесо велосипеда має діаметр 70см. З якою швидкістю їде велосипед, якщо колесо робить 180об/хв? Який період обертання колеса?
6. Колесо діаметром 60см, рухаючись рівномірно проходить відстань 4м за 4с. Яка кутова швидкість обертання колеса? Який період його обертання?
7. 7. Щоб шліфувальний камінь діаметром 30см не зруйнувався, лінійна швидкість точок його поверхневого шару не повинна перевищувати 100м/с. Визначте максимально допустиму частоту обертання цього каменю. Визначте доцентрове прискорення його поверхневих точок.
8. Визначити радіус обертового колеса, якщо відомо, що лінійна швидкість точки, яка лежить на його ободі, у 2,5 рази більша за лінійну швидкість точки, яка лежить на 6см ближче до осі колеса.

.

§12. Рівняння обертального руху. Про співвідношення між лінійними та кутовими параметрами обертального руху.

Подібно до того як поступальний рух матеріальної точки описується рівнянням х = х₀ + v₀t + (a/2)/t², обертальний рух тіла описується аналогічним рівнянням φ = φ₀ + ω₀t + (ε/2)t². Це рівняння називають рівнянням обертального руху. По суті рівняння обертального руху є основним законом кінематики обертального руху тіла.

Рівняння обертального руху – це закон в якому стверджується: в загальному випадку обертальний рух тіла можна описати рівнянням  φ = φ₀ + ω₀t + (ε/2)t², де

φ – кутова координата тіла в момент часу t;

φ₀ – початкова кутова координата тіла;

ω₀ – початкова кутова швидкість тіла;

ε – кутове прискорення тіла.

В кінематиці обертального руху, рівняння φ = φ₀ + ω₀t + (ε/2)t² відіграє ту ж роль, що і рівняння х = х₀ + v₀t + (a/2)/t² в кінематиці поступального руху. А це означає, що на основі аналізу рівняння обертального руху тіла, можна розв’язати безліч задач які стосуються цього руху. Ілюструючи лише незначну частину інформаційних можливостей рівняння обертального руху, розв’яжемо ряд конкретних задач.

Задача 1. За заданим рівнянням обертального руху φ = π/2 + 10t – 0,1t² дати загальну характеристику цього руху.

Рішення. Із порівняльного аналізу рівнянь

φ = φ₀ + ω₀t + (ε/2)t²,

φ = π/2 + 10t –  0,1t², ясно:

φ₀ = π/2 рад;  ω₀ = 10 рад/с;  ε = –0,2 рад/с²;  ω↓.

Це означає, що в заданій системі координат, початкова кутова координата тіла відповідає куту π/2 рад. При цьому тіло обертається в додатному напрямку (за годинниковою стрілкою) з початковою кутовою швидкістю 10 рад/с. Величина цієї швидкості зменшується, а числове значення кутового прискорення становить 0,2 рад/с².

Задача 2. За заданим рівнянням обертального руху φ = π – 12t + 0,2t²

1) дати загальну характеристику руху;

2) визначити кут повороту тіла за 10с;

3) визначте кутову швидкість тіла через 10с;

4) через який час тіло зупиниться?

Рішення.

1) Дати загальну характеристику руху.

Із порівняльного аналізу рівнянь

φ = φ₀ + ω₀t + (ε/2)t²,

φ = π – 12t + 0,2t², ясно:

φ₀ = π рад;  ω₀ = –12 рад/с;  ε = 0,4 рад/с²;  ω↓.

Це означає, що в заданій системі координат, початкова кутова координата тіла відповідає куту π рад. При цьому тіло обертається у від’ємному напрямку (проти годинникової стрілки) з початковою кутовою швидкістю 12 рад/с. Величина цієї швидкості зменшується, а числове значення кутового прискорення становить 0,4 рад/с².

2) Визначити кут повороту тіла за 10с: Δφ(10) = ?

Оскільки за визначенням Δφ = φ_к – φ_п = φ(10) – φ₀, та враховуючи, що

φ(10) = π – 12(10) + 0,2(10)² = π – 120 + 20 = π – 100, можна записати

Δφ(10) = π – 100 – π = –100рад.

Це означає, що за 10с тіло повернеться у від’ємному напрямку (проти годинникової стрілки) на кут величиною 100 рад.

3) Визначте кутову швидкість тіла через 10с:  ω(10) = ?

Подібно до того як при рівноприскореному (а = cons) поступальному русі v = v₀ + at, при рівноприскореному (ε = const) обертальному русі ω = ω₀+εt. В умовах нашої задачі ω = –12 + 0,4t. При цьому ω(10) = –12 + 0,4(10) = –8 рад/с.

4) Через який час тіло зупиниться? t_зуп= ?

Оскільки в момент зупинки ω = 0, то –12 + 0,4t_зуп = 0, звідси t_зуп=12/0,4=30с.

         Поділ механічних рухів на поступальні та обертальні, значною мірою умовний. Наприклад кабіна «оглядового колеса», з одного боку рухається поступально (в процесі руху будь яка приналежна тілу пряма залишається паралельною сама собі), а з іншого – обертально (в процесі руху, всі точки кабіни описують практично концентричні кола). Загалом, рух будь якої матеріальної точки по колу, з одного боку можна вважати обертальним, а з іншого – поступальним. А це означає, що описуючи такий рух, з одного боку говорять про кутову швидкість (ω), кутове прискорення (ε) і кут повороту (∆φ), а з іншого – про лінійну швидкість (v), лінійне прискорення (a) та пройдений шлях (s).

  

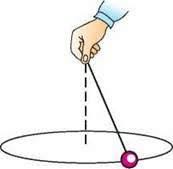
Мал.30. Рух кабіни «оглядового колеса» та рух матеріальної точки по колу, одночасно є як поступальним так і обертальним.

Оскільки у вище наведених прикладах мова йде про один і той же поступально-обертальний рух, то між параметрами його поступальної та обертальної складових, існують певні кількісні співвідношення. Власне, ці співвідношення випливають із визначальних рівнянь відповідних фізичних величин.

Дійсно. Якщо в процесі обертального руху матеріальна точка здійснює поворот на кут ∆φ = s/R, то її лінійне переміщення (пройдений шлях) становитиме s = ∆φ∙R. Якщо кутова швидкість матеріальної точки ω = ∆φ/∆t, то її лінійна швидкість v = s/∆t = ∆φR/∆t = ω∙R. Якщо кутове прискорення матеріальної точки ε = ∆ω/∆t , то її лінійне прискорення а = ∆v/∆t = ∆ω∙R/∆t = ε∙R.

Таким чином між лінійними та кутовими параметрами обертального руху існують прості співвідношення: s = ∆φ∙R,    v = ω∙R, а = ε∙R. І навпаки: ∆φ = s/R, ω = v/R, ε = a/R.

Задача 3. Колесо радіус якого 30см обертається з кутовою швидкістю 10рад/с. Визначити лінійні швидкості та доцентрові прискорення точок колеса віддалених від осі обертання на: а) 0см; б) 10см; в) 20см; г) 30см.

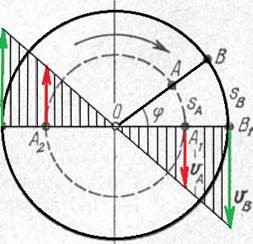
Дано:

ω = 10 рад/с

r₁ = 0см = 0м

r₂ = 10см = 0,1м

r₃ = 20см = 0,2м

r₄ = 30см = 0,3м

v₁, v₂, v₃, v₄ – ?

а_д1, а_д2, а_д3, а_д4 – ?

Рішення. Оскільки між кутовою (ω) та лінійною (v) швидкостями того тіла що обертається існує співвідношення v = ω∙R, то:

v₁ = ω∙r₁ = 10(рад/с)·0м = 0м/с;

v₂ = ω∙r₂ = 10(рад/с)·0,1м = 1м/с;

v₃ = ω∙r₃ = 10(рад/с)·0,2м = 2м/с;

v₄ = ω∙r₄ = 10(рад/с)·0,3м = 3м/с.

Оскільки за визначенням а_д = v²/R, та враховуючи що v = ω∙R, можна записати а_д = (ω∙R)²/R = ω²∙R. Тому:

а_д1 = ω²∙r₁ = (10рад/с)²∙0м = 0м/с²;

а_д2 = ω²∙r₂ = (10рад/с)²∙0,1м = 10м/с²:

а_д3 = ω²∙r₃ = (10рад/с)²∙0,2м = 20м/с²;

а_д4 = ω²∙r₄ = (10рад/с)²∙0,3м = 30м/с².

Аналізуючи параметри та закони поступального і обертального рухів, не важко бачити, що між цими параметрами і законами є певні очевидні аналогії. Ці аналогії можна представити у вигляді наступної узагальнюючої таблиці.

Параметри та закони поступального руху	Параметри та закони обертального руху	Взаємозв’язок між  параметрами
час                         t	час                     t	t = t
координата            x = ℓ	кутова координата φ = ℓ/R	.                     ℓ = φ∙R
пройдений шлях  s = ∆x	кут повороту ∆φ = s/R	.                       s = ∆φ∙R
швидкість         v = ∆x/∆t	кутова швидкість ω = ∆φ/∆t	.                       v = ω∙R
прискорення    a = ∆v/∆t	кутове прискорення ε = ∆ω/∆t	.                        a = ε∙R
р – ня поступального руху  x = x0 + v0t + (a/2)t2	рівняння обертального руху  φ = φ0 + ω0t +(ε/2)t2

Той обертальний рух який відбувається з сталою кутовою швидкістю (ω = const), крім всього іншого є ще й певним періодичним процесом. А це означає, що цей рух можна охарактеризувати не лише певною кутовою швидкістю ω = Δφ/t, а й певним періодом Т = t/n, та частотою ν = n/t. А оскільки мова йде про один і той же рух, то між його кутовою швидкістю та параметрами періодичності існують певні співвідношення.

Дійсно. Оскільки за один повний оберт (n=1) тіло повертається на кут  Δφ = 2π радіан, то довільному числу n таких обертів відповідає кут Δφ = 2π∙n. При цьому ω = Δφ/t = 2π∙n/t =2π∙ν. А враховуючи, що ν = 1/Т, можна записати ω =2π/Т. Таким чином, якщо тіло обертається з постійною кутовою швидкістю (ω = const), то між величиною цієї швидкості ω, кількістю обертів тіла n за час t, періодом Т і частотою ν обертання тіла, існує співвідношення  ω = 2π∙n/t = 2π∙ν = 2π/Т.

Задача 4. В режимі віджимання, частота обертання барабану пральної машини 800 об/хв. Який період обертання барабану та його кутова швидкість? З якою лінійною швидкістю обертаються точки поверхні барабану, якщо його радіус 25см?

Дано:

ν = 800(1/хв) = 13,33(1/с=Гц)

R = 25см = 0,25м

Т = ? ω = ? v = ?

Рішення.

Т = 1/ν = 1/13,33(1/с) = 0,075с;

ω = 2π∙ν = 2∙3,14(рад)∙13,33(1/с) = 83,7(рад/с);

v = ω∙R = 83,7(рад/с)∙0,25м = 21м/с.

Відповідь: Т = 0,075с; ω = 83,7рад/с; v = 21м/с.

Задача 5. Заведена дзиґа вільно падає з висоти 45см. Скільки обертів зробить дзиґа до удару об землю, якщо частота її обертання 5Гц?

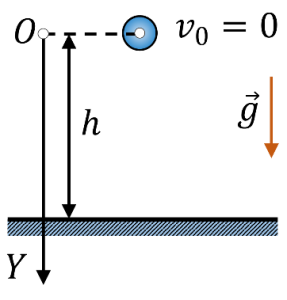
Дано:

h = 45см = 0,45м

ν = 5Гц

g = 10м/с²

n = ?

Рішення. Оскільки за визначенням ν = n/t, то n = ν∙t, де t – час падіння дзиги. Визначаючи цей час запишемо рівняння руху (падіння) дзиги: h = g∙t²/2. Звідси t = √2h/g = √(2∙0,45м/10(м/с²)) = √(0,09с²) = 0,3с.

Таким чином, n = ν∙t = 5(1/с)∙0,3с = 1,5 обертів.

Відповідь: n = 1,5 обертів.

Контрольні запитання.

1. Запишіть загальні рівняння поступального та обертального рухів тіла. Вкажіть на ті аналогії які притаманні цим рівнянням.
2. Наведіть приклади механічних рухів які одночасно є як поступальними так і обертальними.
3. Які величини характеризують поступальний рух тіла?
4. Які величини характеризують обертальний рух тіла?
5. Який зв’язок між кутовою швидкістю тіла та лінійною швидкістю його точок?
6. Який зв’язок між кутовою швидкістю тіла та доцентровим прискоренням його точок?
7. Які величини характеризують періодичність обертального руху?
8. За якої умови обертальний рух тіла є періодичним?
9. Який зв’язок між кутовою швидкістю, частотою та періодом обертання тіла?
10. Обертальний рух тіла описує рівняння φ = π/2 + 10t – 0,2t². Чи є цей рух періодичним?

Вправа 12.

1. За заданим рівнянням обертального руху, дати загальну характеристику цього руху:

а)  φ = π/3 + 10t – 0,3t²;

б)  φ = –π + 10t;

в)  φ = π/2 – 0,2t²;

г)  φ = –5t + 0,2t².

2. За заданим рівнянням обертального руху φ = π/2 + 10t – 0,1t²

1) дати загальну характеристику руху;

2) визначити кут повороту тіла за 10с;

3) визначте кутову швидкість тіла через 10с;

4) через який час тіло зупиниться?

3. Колесо діаметр якого 50см має частоту обертання 5Гц. Визначити лінійні швидкості та доцентрові прискорення точок колеса віддалених від осі обертання на: а) 0см; б) 10см; в) 20см.
4. У скільки разів швидкість кінця секундної стрілки годинника, більша за швидкість кінця хвилинної стрілки, якщо довжини цих стрілок однакові?
5. У скільки разів швидкість кінця секундної стрілки годинника, більша за швидкість кінця хвилинної стрілки, якщо секундна стрілка у 2 рази довша за хвилинну?
6. Дзиґа обертаючись з кутовою швидкістю 62,8рад/с, вільно падає з висоти 5м. Скільки обертів зробить дзиґа за час падіння?
7. Точки на ободі колеса велосипеда мають доцентрове прискорення 100м/с². Яка кутова швидкість, частота і період обертання колеса, якщо його радіус 40см? Яка швидкість велосипеда?

.

§13. Розв’язування задач. Тема: Кінематика обертального руху.

Задача 1. Хлопчик і дівчинка рухаються по колах, радіуси яких знаходяться у співвідношенні r₂/r₁ = 1,5. У якому співвідношенні мають бути швидкості руху хлопчика (v₂) і дівчинки (v₁), щоб в процесі руху вони постійно знаходилися на одному радіусі?

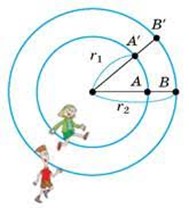
Дано:

r₂/r₁ = 1,5

v₂/v₁ = ?

Рішення. За визначенням v₁ = s₁/t₁, v₂ = s₂/t₂, тому v₂/v₁ = s₂∙t₁/s₁∙t₂. Оскілки в процесі руху хлопчик і дівчинка постійно перебувають на лінії радіусу кола, то той час за який вони здійснюють один оберт, а отже проходять шлях відповідно s₂ = 2π∙r₂ і s₁ = 2π∙r₁, має бути однаковим t₂ = t₁ = t. Зважаючи на це, можна записати: v₂/v₁ = s₂∙t₁/s₁∙t₂ = 2π∙r₂∙t/2π∙r₁∙t = r₂/r₁ = 1,5.

Таким чином, v₂/v₁ =  1,5 або v₂ = 1,5v₁.

Відповідь: v₂/v₁ =  1,5.

Задача 2. Колесо радіусом R з постійною кутовою швидкістю ω котиться горизонтальною поверхнею. Визначити лінійні швидкості верхньої (Р), нижньої (О) та центральної (С) точок колеса.

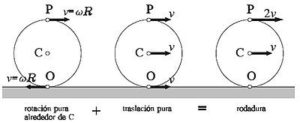
Дано:

R

ω

v_Р=?  v_О=? v_С=?

Рішення. Для того щоб визначити лінійні швидкості точок Р, О, С, потрібно усвідомити факт того, що точка О, тобто та точка в якій колесо в даний момент часу жорстко контактує з нерухомою поверхнею, має нульову швидкість: v_О = 0.

На перший погляд таке твердження здається суперечливим. Адже точка О є не від’ємною частиною колеса що обертається і тому, як будь яка інша частина цього колеса, повинна мати лінійну обертальну швидкість v_об = ωR (мал.а). І це дійсно так.

Однак з іншого боку, потрібно врахувати факт того, що наше колесо не просто обертається, а ще й поступально рухається, причому рухається з швидкістю v_пост = ωR (мал.б). Дійсно. Оскільки за один оберт колеса, тобто за той проміжок часу який називається періодом обертання (t = T), колесо проходить відстань ℓ = 2πR, то v_пост= ℓ/t = 2πR/T = 2πνR = ωR.

Таким чином, всі точки кола приймають участь в двох одночасних рухах: поступальному та обертальному. А це означає, що кожна точка колеса має дві складові лінійної швидкості: обертальну v_об та поступальну v_пост. При цьому величина поступальної складової швидкості для всіх точок колеса є однаковою і чисельно рівною v_пост = ωR. А величина обертальної складової – для різних точок є різною (різною як за величиною так і за напрямком) і такою що змінюється від 0 до ωR. Результатом векторного додавання цих двох швидкостей є певна результуюча швидкість, яка власне і є швидкістю поступального руху відповідної точки колеса (мал.в). І не важко бачити, що для точок О, С, Р величина результуючої швидкості дорівнює:

точка О: v_О = ωR – ωR = 0;

точка C: v_С = ωR + 0 = ωR;

точка P: v_Р = ωR + ωR = 2ωR.

Відповідь: v_О = 0; v_С = ωR; v_Р = 2ωR.

Можна довести, що в ситуації коли колесо (куля, циліндр, тощо) з постійною кутовою швидкістю (ω = const), без ковзання котиться певною поверхнею (мал.31), то лінійна швидкість точки контакту колеса з поверхнею дорівнює нулю. При цьому лінійні швидкості інших точок колеса, чисельно дорівнюють добутку швидкості його обертання ω на довжину того відрізку r, що з’єднує відповідну точку з точкою контакту v = ω∙r, а напрям цієї швидкості є перпендикулярним до відповідного відрізку.

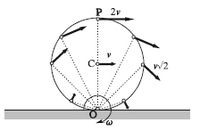
Мал.31. Характер розподілу лінійних швидкостей точок того колеса, яке без ковзання котиться певною поверхнею.

Варто наголосити на тому, що в тих випадках коли мова йде про винятково обертальний рух тіла, то визначаючи лінійні швидкості його точок, застосовується ситуація зображена на мал.32а. Якщо ж мова йде про той обертально-поступальний рух, який є результатом двох рухів – обертального руху тіла навколо свого центру та його поступального руху відносно нерухомої поверхні, то в цьому випадку, то визначаючи лінійні швидкості його точок, застосовується ситуація зображена на мал.32б.

а)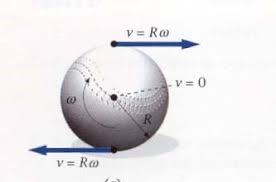б)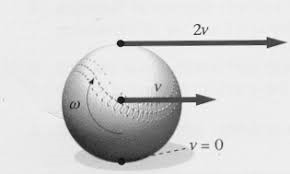

Мал.32. Розподіл лінійних швидкостей тіла: а) при його обертальному русі; б) при його обертально-поступальному русі.

Задача 3. Колесо радіус якого 20см без ковзання котиться горизонтальною поверхнею. При цьому лінійна швидкість центру колеса дорівнює 1м/с. Визначити лінійні швидкості приналежних ободу колеса точок А, Б, В, Г і Д. Кут α = 30°.

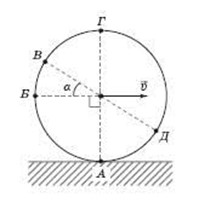
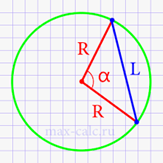
Дано:

R = 20

v = 1

α = 30°

v_A, v_Б, v_В, v_Г, v_Д – ?

Рішення. Якщо колесо, маючи обертальну (кутову) швидкість ω, без ковзання котиться певною поверхнею, то лінійна швидкість v будь якої його точки є перпендикулярною до того відрізку ℓ який з’єднує дану точку з точкою опори колеса (в нашому випадку ℓ_АА, ℓ_АБ, ℓ_АВ, ℓ_АГ, ℓ_АД), а величина цієї швидкості v = ω∙ℓ. Оскільки лінійна швидкість центру колеса відома v = ω∙R = 1м/с, то ω = v/R = 1(м/с)/0,2м = 5рад/с.

Із очевидних міркувань ясно, що ℓ_АА = 0м, ℓ_АБ = 2R = 0,4м. Що ж стосується відрізків ℓ_АБ, ℓ_АВ, ℓ_АД, то їх довжина визначається за відомою з геометрії формулою хорди L = 2R∙sin(α/2). В умовах нашої задачі:

ℓ_АБ = 2R∙sin(90°/2) = 2R∙sin45° = 2∙0,2м∙0,71 = 0,28м;

ℓ_АВ = 2R∙sin(120°/2) = 2R∙sin60° = 2∙0,2м∙0,87 = 0,35м;

ℓ_АД = 2R∙sin(60°/2) = 2R∙sin30° = 2∙0,2м∙0,50 = 0,20м.

Таким чином:

v_АА = ω∙ℓ_АА = 5(рад/с)∙0,00м = 0,00м/с;

v_АБ = ω∙ℓ_АБ = 5(рад/с)∙0,28м = 1,40м/с;

v_АВ = ω∙ℓ_АВ = 5(рад/с)∙0,35м = 1,35м/с;

v_АГ = ω∙ℓ_АГ = 5(рад/с)∙0,40м = 2,00м/с;

v_АД = ω∙ℓ_АД = 5(рад/с)∙0,20м = 1,00м/с.

Задача 4.  Обертальний рух від шківа 1 до шківа 2 передається за допомогою паскової передачі. Визначити частоту обертання шківа 2, якщо шків 1 робить 1200об/хв, а радіуси шківів становлять R₁ = 4см, R₂ = 16см.

 

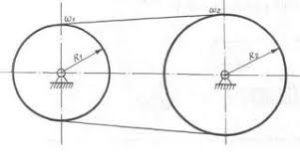
Дано:

ν₁=1200об/хв

R₁ = 4см

R₂ = 16см

ν₂ = ?

Рішення. Оскільки шківи 1 і 2 жорстко (без ковзання) з’єднані пасковою передачею, то лінійні швидкості точок їх поверхонь v₁ і v₂ є однаковими: v₁ = v₂. А враховуючи що v₁ = ω₁R₁ = 2πν₁R₁, v₂ = ω₂R₂ = 2πν₂R₂, можна записати 2πν₂R₂ = 2πν₁R₁.Звідси ν₂ = ν₁R₁/R₂.

Розрахунки: ν₂ = ν₁R₁/R₂ = 1200(об/хв)8см/32см = 300об/хв.

Відповідь: ν₂ = 300об/хв.

Задача 5. Ланцюгова передача передає обертання педалей велосипеда на зубчате коліща колеса. З якою швидкістю їде велосипед якщо частота обертання педалей 1Гц? Радіуси зубчатих коліс педалей і колеса відповідно 10см і 4см. Радіус колеса 40см.

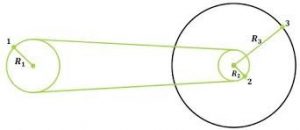
Дано:

ν₁ = 1Гц

R₁ = 10см

R₂ = 4см

R₃ = 40см

v = ?

Рішення. Оскільки рух велосипеда обумовлений фактом обертання його колеса відносно нерухомої дороги, то величину цієї швидкості можна визначити за формулою v = ω₃R₃, де ω₃ = ?

Величину ω₃ визначаємо із наступних міркувань. Оскільки частота обертання зубчатого колеса педалей є відомою ν₁ = 1Гц, то ω₁ = 2πν₁ = 6,28(рад/с).  Оскільки зубчаті колеса 1 і 2 жорстко (без ковзання) з’єднані ланцюговою передачею, то лінійні швидкості точок їх поверхонь v₁ і v₂ є однаковими: v₁ = v₂. А враховуючи що v₁ = ω₁R₁, v₂ = ω₂R₂, можна записати ω₁R₁ = ω₂R₂, звідси ω₂ = ω₁R₁/R₂ = 6,28(рад/с)∙10см/4см = 15,7(рад/с). Оскільки зубчате колесо 2 жорстко з’єднане з колесом 3, то їх кутові швидкості є однаковими ω₃ = ω₂ = 15,7(рад/с).

Таким чином, v = ω₃R₃ = 15,7(рад/с)∙0,4м = 6,28м/с = 22,6км/год.

Відповідь: v = 6,28м/с = 22,6км/год.

Задача 6. Дві паралельні рейки рухаються з швидкостями v₁ = v і v₂ = 2v назустріч одна одній. Між рейками затиснутий циліндр радіусом R, що котиться по рейках без проковзування. З якою швидкістю u рухається циліндр та яка кутова швидкість ω його обертання?

 

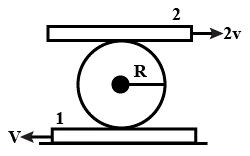
Дано:

v₁ = v

v₂ = 2v

R

u = ?  ω = ?

Рішення. Циліндр приймає участь у двох рухах. З одного боку він з певною кутовою швидкістю ω обертається навколо свого центру. А з іншого – з певною лінійною швидкістю u поступально рухається в напрямку руху більш швидкої рейки. При цьому величина швидкості u має бути такою, щоб виконувалися співвідношення:

v₂ = u + ωR,

v₁ = ωR – u.

А з цих співвідношень випливає:

1) ωR = v₂ – u,

2) ωR = v₁ + u.

Звідси v₂ – u = v₁ + u, звідси 2u = v₂ – v₁, звідси u = (v₂ – v₁)/2.

Підставивши значення  в (1) або (2)  рівняння, отримаємо:

ωR = v₂ – u = v₂ – (v₂ – v₁)/2 = 2v₂ – v₂ + v₁)/2 = (v₂ + v₁)/2, звідси ω = (v₂ + v₁)/2R

Таким чином:

u = (v₂ – v₁)/2 = (2v – v)/2 = v/2;

ω = (v₂ + v₁)/2R = (2v + v)/2R = 3v/2R.

Відповідь: u = v/2; ω = 3v/2R.

Вправа 13.

1. Колесо діаметром 50см, рухаючись рівномірно проходить відстань 20м за 4с. Яка кутова швидкість обертання колеса?
2. З якою швидкістю їде велосипед, якщо частота обертання його коліс 4Гц, а їх діаметр 70см?
3. Колесо радіусом 20см з постійною кутовою швидкістю 10рад/с котиться горизонтальною поверхнею. Визначити лінійні швидкості верхньої, нижньої та центральної точок колеса. Якими будуть ці швидкості, якщо колесо буде обертатися з тією ж кутовою швидкістю, але не торкатиметься поверхні?
4. Колесо радіусом 20см котиться горизонтальною поверхнею з швидкістю 1м/с. Визначте кутову швидкість обертання колеса. Визначити лінійні швидкості точок А, В, С, Д. Якими будуть ці швидкості, якщо колесо буде обертатися з тією ж кутовою швидкістю, але не торкатиметься поверхні?

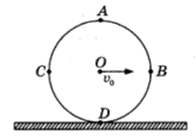
5. В процесі обертання колеса, лінійна швидкість точок його поверхні у 2 рази більша за лінійну швидкість тих точок які на 5см ближчі до осі обертання колеса. Визначте радіус колеса.

6. Яку поступальну швидкість мають верхні точки ободу велосипедного колеса, якщо велосипед їде зі швидкістю 20км/год?

7. Обертальний рух від шківа радіусом 12см за допомогою паскової передачі передається шківу радіусом 3см. Визначити частоту обертання меншого шківа, якщо більший шків робить 300об/хв. Яка швидкість поступального руху паску передачі?

8. Діаметр педальної шестерні велосипеда 32см. Вона з’єднана ланцюговою передачею з малою шестернею діаметром 8см, яка в свою чергу, жорстко з’єднана з колесом велосипеда діаметр якого 72см. Частота обертання педальної шестерні 1,5Гц. Визначте швидкість руху велосипеда.

9. З якою швидкістю рухається дошка що притиснута до циліндричного катка, якщо каток без ковзання рухається горизонтальною поверхнею з швидкістю 10см/с?

.