
Тема 1.4. Механіка рідин та газів.
§45. Основи механіки рідин та газів. Тиск. Атмосферний тиск.
§46. Закон Паскаля.
§47. Сполучені посудини.
§48. Закон Архімеда. Сила Архімеда. Умова плавання тіла.
§49. Що важче, кілограм заліза чи кілограм вати?
.
Тема. 1.4. Основи механіки рідин та газів.
Тема 1.4. Основи механіки рідин та газів.
Механіка рідин та газів – це розділ механіки, в якому вивчають механічні властивості рідин і газів, параметри, закономірності та причини їх механічного руху, а також закономірності їх механічної взаємодії з твердими тілами.
.
§45. Тиск. Атмосферний тиск.
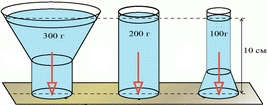
Коли спираючись на обидві ноги ви стоїте на підлозі, то чините на неї певну силову дію. Піднявши одну ногу, ви не зміните загальну силову дію на підлогу. І тим не менше, дещо зміниться. Характеризуючи цю зміну говорять, що ваш тиск на підлогу збільшився вдвічі. Збільшився тому, що площа на яку діє вага вашого тіла стала вдвічі меншою. Або наприклад в зображених на мал.107 ситуаціях, тиск одного і того ж тіла на опору є різним. Різним тому, що та площа на яку спирається тіло є різною, а тиск (р), це відношення діючої на поверхню сили (F) до площі (S) цієї поверхня (р = F/S).


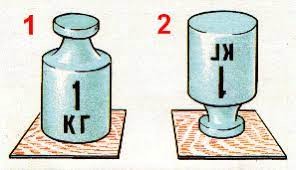
Мал.107. Діючі на опору сили є однаковими, а відповідні тиски – різними.
Тиск – це фізична величина, яка характеризує усереднену силове дію, що припадає на одиницю площі поверхні і яка дорівнює відношенню діючої на дану поверхню сили F до площі цієї поверхні S.
Позначається: р
Визначальне рівняння: р = F/S
Одиниця вимірювання: [р] = Н/м2 = Па, паскаль.
Паскаль – це одиниця вимірювання тиску, яка дорівнює такому тиску який чинить сила в 1Н, будучи рівномірно розподіленою поверхнею площа якої 1м2. Наприклад, якщо 102г води (Fт = mg = 0,102кг∙9,8м/с2 = 1Н), рівномірно розподілити поверхнею площа якої 1м2, то тиск води на цю поверхню становитиме один паскаль. Ясно, що такий тиск є відносно незначним. Наприклад людина масою 70кг спираючись на дві ступні загальною площею 0,05м2, чинить тиск на підлогу величиною р = Fт/S = mg/S = 70кг9,8(м/с2)/0,05м2 = 13 700Па.
Певний тиск створюють не лише тверді тіла та рідини, а й гази. Скажімо, над кожним об’єктом земної поверхні знаходиться шар атмосферного повітря який створює відповідний атмосферний тиск. Першим хто виміряв величину цього тиску, був італійський вчений Еванджеліста Торрічеллі (1608–1647).
Дослідження Торрічеллі були пов’язані з вирішенням однієї нагальної технічної проблеми. Суть проблеми полягала в тому, що тогочасні водяні насоси «відмовлялись» піднімати воду на висоту більшу за десять метрів. При цьому виникало закономірне запитання – чому? Відповідаючи на це запитання проведемо та проаналізуємо наступний експеримент (мал.108). Опустивши вхідний отвір медичного шприцу у воду, та піднімаючи його поршень, ви неодмінно з’ясуєте, що простір під поршнем заповнюється водою. Заповнюється тому, що поверхня води знаходиться під постійною дією зовнішнього атмосферного тиску. Тому коли в процесі піднімання поршня, над певною ділянкою води утворюється безповітряний простір, то зовнішній атмосферний тиск змушує воду заповнювати цей простір.
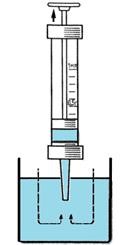
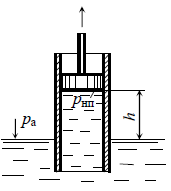
Мал.108. В процесі піднімання поршня, вода під дією зовнішнього атмосферного тиску, заповнює безповітряний простір.
Розуміючи факт того, що причиною піднімання води за поршнем є дія атмосферного тиску, Торрічеллі розмірковував приблизно так. Якщо атмосферний тиск здатний піднімати воду на приблизно десятиметрову висоту, то напевно у 13,6 разів важчу ртуть він підніме на висоту яка буде в 13,6 разів меншою, тобто на висоту меншу за 1м.
Виходячи з таких міркувань, Торрічеллі взяв запаяну з одного краю скляну трубку довжина якої була близькою до одного метра і заповнив її ртуттю. Потім, він закрив вільний кінець трубки, перевернув її та вертикально опустивши в чашку з ртуттю, відкрив попередньо закритий отвір (мал.109). При цьому, частина ртуті вилилась в чашку, а висота тієї ртуті що залишилась в трубці становила приблизно 76см. Це означало, що тиск атмосферного повітря, еквівалентний тому тиску який створює шар ртуті висотою 76см
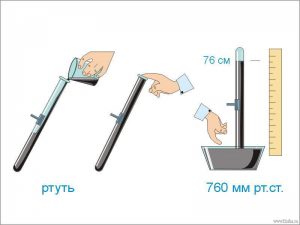
Мал.109. В 1643р. Торрічеллі експериментально виміряв величину атмосферного тиску.
Сучасні вимірювання показують, що на рівні моря (світового океану), усереднена величина атмосферного тиску дорівнює 760мм.рт.ст. Цей тиск прийнято називати нормальним атмосферним тиском. Ясно, що по мірі збільшення висоти, шар того атмосферного повітря яке знаходиться над цією висотою зменшується, а відповідно зменшується і величина атмосферного тиску. Вимірювання показують, що в нижніх шарах атмосфери на кожні 100м підйому, тиск атмосферного повітря зменшується на 10мм.рт.ст.
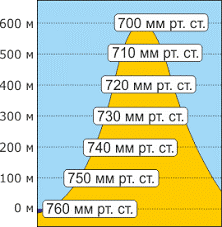
Мал.110. В нижніх шарах атмосфери на кожні 100м підйому, тиск атмосферного повітря зменшується на 10мм.рт.ст.
Знаючи величину атмосферного тиску виміряну в міліметрах ртутного стовпчика, не важко визначити цю величину в паскалях. Дійсно.
Задача 1. Знаючи густину ртуті (ρ = 13,6∙103кг/м3), виразити тиск 760мм.рт.ст. в паскалях. Знайти співвідношення між 1мм.рт.ст. і Па.
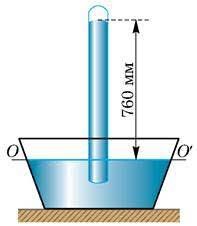
Дано:
ра = 760мм.рт.ст.
ρ = 13,6∙103кг/м3
h = 760мм = 0,76м
ра = ? (Па)
1мм.рт.ст = ? (Па)
Рішення. Виходячи з того, що p = F/S; ρ = m/V; V = S·h, та враховуючи, що в умовах нашої задачі F = Fт = mg = ρVg = ρShg, можна записати p = F/S = ρShg/S = ρhg. Тобто ра = ρgh
Розрахунки: ра = ρgh = 13,6∙103(кг/м3)·9,8(м/с2)·0,76м = 101,3·103 (Н/м2 = Па).
Таким чином, тиску ра = 760мм.рт.ст. відповідає тиск ра = 101,3·103Па = 101,3кПа. А це означає, що тиску 1мм.рт.ст. відповідає тиск 101300Па/760 = 133,3Па.
Відповідь: ра=760мм.рт.ст.= 101,3·103Па= 101,3кПа; 1мм.рт.ст.=133,3Па.
Отже, вимірювання і розрахунки показують, що на рівні світового океану, тиск атмосферного повітря становить 101,3кПа (точніше 101 325Па). А це еквівалентно тому якби на горизонтальну поверхню площею 1м2 поставили вантаж масою 10,3 тон!!!
Ви можете запитати, а чому знаходячись під постійною дією такого величезного тиску, ми практично не відчуваємо його? До речі, однією з причин того, чому люди довгий час відмовлялися визнавати факт існування атмосферного тиску, була та, що вони не могли зрозуміти, чому за наявності такого величезного тиску, ми не відчуваємо його силової дії. А й дійсно, чому?
Перш ніж відповісти на це запитання, візьміть аркуш паперу і тримаючи його в горизонтальному положенні, запитайте себе: чому під дією величезного атмосферного тиску, тонкий папір навіть не прогинається? (А якщо і прогинається, то не під дією атмосферного тиску, а під дією сили тяжіння). Правильно! Це пояснюється тим, що атмосферне повітря однаково тисне з усіх сторін, зокрема як зверху так і знизу. А це означає, що результуюча силова дія цього тиску є нулевою. Аналогічне можна сказати і про тонку поверхню мильної бульбашки чи повітряної кульки, яка «не відчуває» результуючої дії зовнішнього і внутрішнього тиску.


Мал.111. Якщо зовнішній і внутрішній тиск на поверхню зрівноважують один одного, то відповідна поверхня «не відчуває» ці тиски.
Подібна ситуація характерна не лише для аркушу паперу, чи поверхні мильної бульбашки, а й для таких надскладних об’єктів як живі організми. Адже ці організми складаються з клітин, які представляють собою тонку оболонку наповнену водою та певною кількістю надскладних органічних структур. При цьому, тиск внутріклітинної рідини практично не відрізняється від зовнішнього атмосферного тиску. А це означає, що результуюча силова дія цих тисків є практично нулевою. Більше того, живий організм, це певна саморегульована система, в якій зміна зовнішнього тиску автоматично призводить до відповідної зміни внутріклітинного тиску. Про можливості такого саморегулювання говорить той факт, що треновані аквалангісти здатні пірнати на стометрову глибину. А це означає, що їх організм витримує десятикратне тискове перевантаження.
Якщо ж говорити про ті зміни атмосферного тиску які відбуваються в самій атмосфері, то вони відносно не значні і зазвичай повільні. Тому здорові люди практично не відчувають коливань атмосферного тиску. Однак іноді, особливо у людей похилого віку, організм не встигає за відносно швидкими змінами атмосферного тиску, що призводить до певних больових відчуттів. І ви напевно чули, як іноді люди бідкаються, що на зміну погоди у них болить голова, «крутять» ноги, тощо.
Прилади, які безпосередньо вимірюють атмосферний тиск називаються барометрами ( від грец. barus – важкий, metros – міряти). Першим барометром був той прилад яким Торрічеллі виміряв атмосферний тиск. Подібні барометри називаються ртутними. Сучасні ртутні барометри є еталонними вимірювачами атмосферного тиску, тобто тими базовими приладами за якими налаштовують та перевіряють всі інші барометри.

Мал.112. Ртутний барометр є еталонним вимірювачем атмосферного тиску,
Однак з практичної точки зору ртутні барометри мають ряд суттєвих недоліків. По-перше, вони досить громіздкі та масивні. По-друге, ці прилади потребують обережного поводження з ними (їх не можна нахиляти, перевертати, піддавати значним ударним навантаженням, тощо). По-третє, ртуть – це отруйна та шкідлива речовина, заборонена для вільного використання. Тому в науковій, а тим більше в побуті практиці, атмосферний тиск вимірюють механічними барометрами які часто називають барометрами–анероїдами тобто безрідинними барометрами. Основним вимірювальним елементом такого приладу (мал.113) є герметична коробка (К) внутрішній тиск якої незмінний і значно менший атмосферного. Однією з сторін цієї коробки є гофрована пружна мембрана (М), рівновага якої підтримується пружиною (П). При зміні зовнішнього тиску, мембрана деформується, що призводить до відповідного відхилення стрілки приладу.
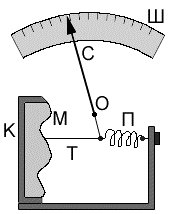
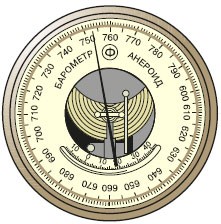
Мал.113. Механічний барометр: а) принципова схема; б) загальний вигляд.
Оскільки атмосферний тиск певним чином залежить від висоти, то барометром можна вимірювати не лише атмосферний тиск, а й висоту над рівнем моря, наприклад висоту польоту літака, гелікоптера, тощо. Барометр за шкалою якого визначають висоту над рівнем моря називають барометричним альтиметром (від лат. altus – високо).
Коли ми говоримо про тиск повітря в футбольному м’ячі, тиск в шинах автомобіля, тиск газу в газопроводі чи води у водопроводі, то маємо на увазі не тиск так би мовити «взагалі», а те наскільки даний тиск перевищує атмосферний. Навіть в тому випадку, коли ми стверджуємо, що шар води створює на дно відкритої посудини певний тиск, то фактично мова йде про певний надатмосферний тиск. Адже сама вода знаходиться під тиском в одну атмосферу. Із вище сказаного ясно, що на практиці нас майже зазвичай цікавить той надатмосферний тиск який існує в тій чи іншій ситуації. Прилади які вимірюють не атмосферний тиск, а те на скільки наявний тиск рідини або газу відрізняється від атмосферного, називаються манометрами (від грец. manos – не густий).
Існує багато різновидностей манометрів. При цьому, в технічній практиці найбільш поширеними є так звані деформаційні манометри і зокрема ті з них, в яких чутливим елементом є спеціальна манометрична трубка (мал.114а). Ця трубка представляє собою з одного краю запаяну, суттєво сплющену металеву трубку зігнуту у вигляді напівкільця.
Принцип дії такого манометра полягає в наступному. Коли в манометричну трубку надходить зовнішній тиск (тиск який вимірюють), то вона деформується і відповідним чином відхиляє стрілку приладу. Деформація кільцеподібної трубки відбувається тому, що при одному і тому ж внутрішньому тиску, на поверхню більшого радіусу, а отже і більшої площі, діє більша сила.
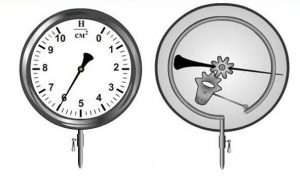
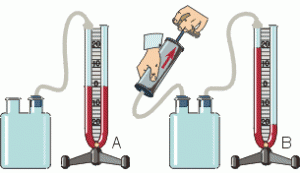
Мал.114. Деформаційний манометр (а); рідинний манометр (б).
В лабораторній практиці часто застосовують рідинні манометри (мал.114б). Вони представляють собою відкриту U-подібну скляну трубку частково заповнену рідиною. Коли в одне з колін цієї трубки надходить той тиск який потрібно виміряти, то рівень рідини відповідним чином змінюється. За цією зміною і визначають величину тиску.
Задача 2. При вході в метро барометр показує 101кПа. Якими будуть показання барометра на платформі, що перебуває на глибині 35м?
Дано:
р1 = 101,0 кПа
h = 40м
р2 = ?
Рішення. Оскільки при зміні висоти (глибини) на 10м показання барометра змінюються на 1мм.рт.ст. та зважаючи на те, що 1мм.рт.ст. = 133,3Па, можна записати р2 = р1 + ∆р, де ∆р = (h/10)·1мм.рт.ст. = (40м/10м)·1мм.рт.ст .= 4мм.рт.ст.= 4·133,3Па= 533,2Па.
Таким чином р2 = р1+∆р = 101,0кПа + 0,5кПа = 101,5кПа.
Відповідь: р2 = 101,5кПа.
Задача 3. Встановлений на батискафі манометр показує 9,8МПа. На якій глибині перебуває батискаф.
Дано:
р = 9,8МПа = 9,8·106Па
h = ?
Рішення. Оскільки манометр фіксує той ваговий тиск який створює шар води висотою h, та виходячи з того, що густина води ρ = 1·103кг/м3, можна записати p = F/S = mg/S = ρVg/S = ρShg/S = ρgh, звідси h = p/ρg.
Розрахунки: h = p/ρg = 9,8·106 / 1·103·9,8 = 1·103м.
[h] = Па / (кг/м3)∙(м/с2) = (кг(м/с2)/м2) / (кг/м3)∙(м/с2) = м.
Відповідь: h = 1·103м= 1000м.
Контрольні запитання.
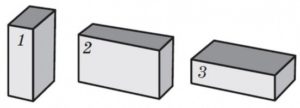
- На основі аналізу малюнку скажіть, чи однаковий тиск цеглини на поверхню стола в ситуаціях 1, 2, 3? Чому?
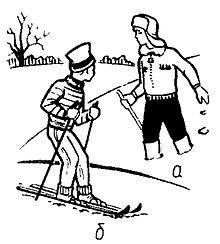
- На основі аналізу малюнку поясніть, чому результат силового впливу людини на поверхню снігу в ситуаціях (а) і (б) є різним?
- Людина стоїть на підлозі. Як зміниться тиск на підлогу після того як людина підніме одну ногу?
- Відомо, що атмосферний тиск становить 760мм.рт.ст. Яким є цей тиск виміряний в паскалях та в метрах водяного стовпчика?
- Чому ми практично не відчуваємо дію атмосферного тиску?
- Чому в рідинних барометрах використовують ртуть а не воду?
- Чому в побуті застосовують не ртутні, а механічні барометри?
- Поясніть загальний устрій та принцип дії механічного барометра (мал.106)
- Яким приладом, барометром чи манометром, вимірюють тиск в шинах автомобіля? Чому?
Вправа №45.
- Штормовий вітер створює тиск 100Па. З якою силою тисне цей вітер на стіну будинку площею 25м2?
- На опору якої площі потрібно поставити вантаж масою 20кг, щоб створюваний ним тиск становив 1∙105Па?
- Визначте величину того тиску який чинить на арену цирку слон, що стоїть на одній нозі, якщо маса слона 3,9т, а площа підошви його ноги 750см2.
- Площа дна каструлі 20дм2. На скільки збільшиться тиск каструлі на стіл, якщо в неї налити воду об’ємом 4л.
- Площа різального краю лопати становить 70мм2. Який тиск створює лопата на ґрунт, якщо людина діє на лопату з силою 210Н?
- Порівняйте тиски які чинять на поверхню снігу турист і лижник, якщо маса кожного з них 80кг. При цьому площа підошв туриста 500см2, а площа лиж 3200см2.
- Дослідження показують, що жало оси створює тиск 3·1010Па. Порівняйте цей тиск з тим тиском який створює слон на поверхню ґрунту, якщо маса слона 6т, а загальна площа його підошв 3000см2.
- Атмосферний тиск на Венері 9,3·106Па. Яким є цей тиск: а) в земних атмосферах; б) в міліметрах ртутного стовпчика?
- Відома, що радіус Землі 6,4·106м, а її атмосферний тиск 1·105Па. Визначити загальну масу атмосфери Землі.
.
§46. Закон Паскаля.
В 1651–1654 роках, розмірковуючи над тим, чому атмосферний тиск в кімнаті та за її межами однаковий, чому аркуш паперу і людський організм не відчувають силової дії атмосферного тиску, чому занурені в рідину тіла виштовхуються з неї, а також проводячи відповідні експериментальні дослідження, французький фізик Блез Паскаль (1623–1662) з’ясував: той зовнішній тиск що діє на поверхню механічно зрівноваженої рідини (газу) без змін передається у всі точки цієї рідини і діє у всіх можливих напрямках. (закон Паскаля). Наприклад, якщо поршень (мал.115) створює певний тиск на усталену рідину або газ, то цей тиск без змін передається у всі точки відповідної рідини або газу.
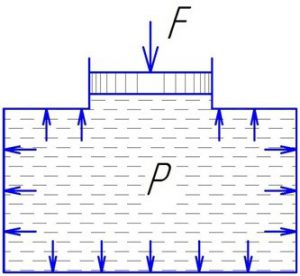
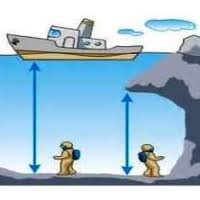
мал.115. Тиск (р) який створює вантаж, передається у всі точки рідини (газу) і діє в кожній з цих точок у всіх можливих напрямках.
Застосовуючи закон Паскаля потрібно мати на увазі, що окрім діючого на рідину (газ) зовнішнього тиску, в ній неминуче існує певний додатковий тиск, поява якого обумовлена вагою самої рідини. Цей тиск прийнято називати ваговим або гідростатичним.
Ваговий (гідростатичний) тиск – це той тиск, який створює певний шар рідини (газу) за рахунок того що на неї діє сила тяжіння, тобто за рахунок своєї ваги.
Позначається: рв
Визначальне рівняння: рв = ρgh, де
ρ – густина рідини (газу),
g – прискорення сили тяжіння (вільного падіння),
h – висота рідини над заданим рівнем.
Одиниця вимірювання: [рв] = Па, паскаль
Аналізуючи рівняння рв = ρgh не важко бачити, що по мірі занурення в рідину, величина її вагового тиску лінійним чином зростає. Звичайно, якщо мова йде про гази, то в багатьох випадках величиною їх вагового тиску можна знехтувати. Адже густина газів відносно мала. Однак, якщо мова йде про великі перепади висот, то ваговий тиск газу може бути суттєвим. До речі, той тиск який ми називаємо атмосферним фактично є ваговим тиском того шару повітря, що знаходиться над рівнем даної точки.
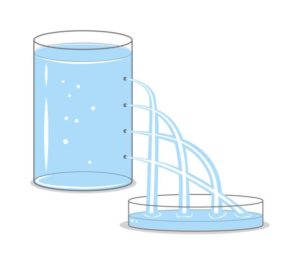
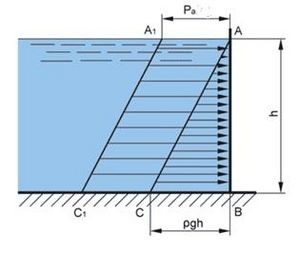
Мал.116. По мірі занурення в рідину, величина її вагового тиску лінійним чином збільшується.
Потрібно зазначити, що величина того вагового тиску який створює рідина на дно посудини, не залежить ні від площі цього дна, ні від форми посудини, ні від кількості рідини в ній. Величина цього тиску залежить лише від густини рідини (ρ), прискорення діючої на рідину сили тяжіння (g) та висоти рідини над заданим рівнем (h). Скажімо, маса (а відповідно і вага) тієї рідини яка міститься в зображених на мал.117а посудинах, є різною. При цьому тиск рідини на дно кожної посудини є однаковим. Невідповідність між тиском рідини на дно посудини та кількістю налитої в цю посудину рідини, часто називають гідростатичним парадоксом або парадоксом Паскаля.
Втім, невідповідність між тиском рідини на дно посудини та кількістю рідини в цій посудині, є не більш парадоксальною ніж невідповідність між мізерністю тієї кількості повітря що знаходиться у вашій квартирі, та величиною того тиску з яким це повітря тисне на підлогу квартири. Бо цей тиск фактично створюється не тим повітрям яке знаходиться в квартирі, а всією сукупністю атмосферного повітря. Адже повітря вашої квартири є невід’ємною складовою земної атмосфери. При цьому, у відповідності з законом Паскаля, загально атмосферний тиск передається у всіх можливих напрямках, в тому числі і в напрямку вашої квартири. І величина цього атмосферного тиску залежить не від висоти вашої квартири чи площі її підлоги, а від загальної висоти атмосфери. Власне за тієї ж причини, величина того вагового тиску який створює рідина на будь яку поверхню посудини, у відповідності з законом Паскаля, не залежить ні від площі цієї поверхні, ні від кількості рідини в посудині. Ця величина визначається лише висотою рідини над рівнем відповідної поверхні.
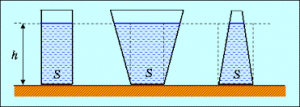

Мал.117. Тиск рідини на дно посудини не залежить від кількості налитої в посудину рідини.
Демонструючи факт того, що тиск рідини на дно та бічні поверхні посудини не залежить від кількості рідини в цій посудині, Паскаль в 1648 році провів наступний показовий експеримент (мал.117б). В невеличкий отвір наповненої водою герметичної діжки, він вставив відповідну за діаметром довгу трубку. Піднявшись на балкон другого поверху, Паскаль влив в цю трубку кухоль води. Яким же було здивування присутніх, коли під силовою дією цієї відносно мізерної кількості води, міцна винна діжка лопнула.
Застосовуючи закон Паскаля можна пояснити будову та принцип дії багатьох приладів, зокрема гідравлічних пресів, домкратів, гальмівних систем, тощо. Що ж давайте зробимо ці пояснення.
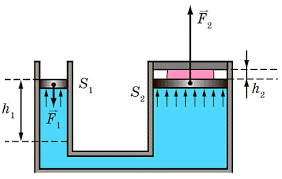
На мал.118а зображена система двох сполучених циліндрів, які заповнені рідиною і закриті відповідними поршнями. Не важко довести, що коли на поршень площею S1 діє сила F1, то діюча на поршень S2 сила F2, визначатиметься за формулою F2=F1(S2/S1) .
Дійсно. Діюча на поршень S1 сила F1 створює тиск р1 = F1/S1. Цей тиск, згідно з законом Паскаля без змін передається у всі точки рідини, в тому числі і ті, що знаходяться під поршнем S2. При цьому діючий на поршень S2 тиск р2 = р1, створюватиме відповідне силове зусилля: F2 = p2S2 = (F1/S1)S2 = F1(S2/S1).

Мал.118. Схема гідравлічної системи, що дозволяє збільшувати силове зусилля.
Таким чином, зображена на мал.118 система, дозволяє в n = S2/S1 разів збільшувати силове зусилля. Однак, говорячи про те, що певна гідравлічна система в певну кількість разів збільшує силову дію, не слід забувати про закон збереження енергії. А згідно з цим законом, та робота яку виконує сила F2 і яка дорівнює A2 = F2h2, не може перевищувати ту роботу яку виконує сила F1: A1 = F1h1. А це означає, що виграючи в силі (F2 = nF1) ми неминуче програєм в пройденому шляху (h2 = h1/n) – золоте правило механіки.
Зважаючи на вище сказане не важко пояснити будову та принцип дії зображеного на мал.119 гідравлічного преса. А ця будова та цей принцип дії полягають в наступному.
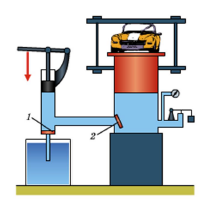
1, 2 – малий та великий поршні,
3, 4 – вхідний та вихідний клапани,
5 – нерухома платформа,
6 – резервуар з рідиною.
Мал.119. Загальний устрій та принципова схема гідравлічного пресу.
Коли під дією зовнішньої сили F1, малий поршень площею S1 опускається на висоту Δh1, то відповідна кількість рідини через клапан 2 заштовхується у великий циліндр. При цьому, у відповідності з законом Паскаля, на поршень великого циліндра площею S2, діє тиск p2 = p1 = F1/S1. А це означає, що силове навантаження на поршень великого циліндра буду в n = S2/S1 разів більшим аніж на поршень малого циліндра: F2 = nF1.
З іншого боку, поршень великого циліндра підніметься на відповідно меншу висоту: Δh2 = Δh1/n. Для збільшення цієї висоти, в об’єм великого циліндра потрібно заштовхати відповідно велику кількість рідини. А це заштовхування забезпечується багаторазовістю повторювальних рухів (вверх-вниз) поршня малого циліндра, та наявністю в системі додаткового резервуара з рідиною і двох автоматично працюючих клапанів.
Дійсно, в процесі піднімання поршня малого циліндра, клапан 2 автоматично закривається, а клапан 1 автоматично відкриваються (поясніть чому). При цьому, певна порція рідини із додаткового резервуара засмоктуються в малий циліндр. При опусканні поршня малого циліндра, клапан 1 автоматично закривається, натомість клапан 2 – відкривається і додаткова порція рідини заштовхується в об’єм великого циліндра, забезпечуючи тим самим відповідне додаткове піднімання його поршня.
Таким чином, в процесі багаторазових повторювальних рухів поршня малого циліндра, в об’єм великого циліндра заштовхується все більша і більша кількість рідини, яка з одного боку забезпечує відповідно велике силове навантаження на поршень (F2 = nF1), а з іншого – необхідно велике піднімання цього поршня (h2 = NΔh1, де N – кількість тих циклів (качань) які здійснює поршень малого циліндра).
Задача 1. У підводному човні, на глибині 300м утворилась пробоїна загальною площею 10см2. Яке мінімальне зусилля знадобиться для того, щоб втримати латку з внутрішньої частини човна?
Дано:
h = 300м
S = 10см2 = 10·10–4м2
F = ?
Рішення. Виходячи з того, що шар води висотою h створює на корпус човна ваговий тиск p = ρgh, де ρ =1·103кг/м3, g = 9,8м/с2, та враховуючи, що за визначенням p = F/S, можна записати F = р·S = ρghS.
Розрахунки: [F] = (кг/м3)(м/с2)м·м2 = кг(м/с2) = Н;
F = 1·103·9,8·300·10·10–4 = 2940Н.
Відповідь: F = 2940Н.
Задача 2. Діаметр дна каструлі 20см. На скільки збільшиться тиск каструлі на поверхню стола, якщо у неї налити 3л води?
Дано:
d = 20см = 0,2м
V =3л = 3дм3 = 3·10–3м3
ρ = 1·103кг/м3
∆р = ?
Рішення. Виходячи з того, що ∆р=∆F/S, та враховуючи, що в умовах нашої задачі ∆F = mg = ρVg, S = πd2/4, можна записати
∆р = ∆F/S = 4ρVg/πd2.
Розрахунки: [∆р] = (кг/м3)(м3)(м/с2)/м2=Н/м2 = Па;
∆р=4·1·103·3·10–3·9,8/3,14·(0,2)2 = 936 Па.
Відповідь: ∆р = 936 Па.
Задача 3. Під дією сили 300Н малий поршень гідравлічного пресу опустився на 10см, а великий – піднявся на 0,5см. Визначте силу, що діє на великий поршень.
Дано:
F1 = 300Н
h1 = 10см
h2 = 0,5см
F2 = ?
Рішення. Оскільки у відповідності з законом Паскаля р1 = р2, то F1/S1 = F2/S2, звідси F2 = F1(S2/S1). Оскільки об’єм тієї рідини яку виштовхує малий поршень V1 = S1h1, дорівнює тому об’єму який заповнює великий поршень V2 = S2h2, то S2h2 = S1h1, звідси S2/S1 = h1/h2. Таким чином F2 = F1(S2/S1) = F1(h1/h2) = 300Н(10см/0,5см) = 6000Н.
Відповідь: F2 = 6000Н.
Контрольні запитання.
- Що стверджується в законі Паскаля?
- Наведіть приклади, які підтверджують достовірність закону Паскаля.
- Виходячи з загального визначального рівняння тиску р = F/S, доведіть, що ваговий тиск рідини можна визначити за формулою р = ρgh.
- Чому в зображеній на мал.118 системі, сили F1 і F2 є різними? Як в цій системі проявляється золоте правило механіки.
- Поясніть будову та принцип дії зображеного на мал.119 гідравлічного пресу.
- Чому в момент піднімання малого поршня (мал.119) клапан 1 відкривається, а клапан 2 закривається. А при його опусканні – навпаки?
- В зображених на малюнку посудинах, площа дна однакова. Чи з однаковою силою тисне рідина на дно кожної посудини? Чи з однаковою силою тиснуть ці посудини на поверхню стола?
Вправа №46.
- За тими даними які представлені на попередньому малюнку, визначити величину вагового тиску води на дно кожної посудини та величини тих тисків, які створюють ці посудини на поверхню стола. Площа дна кожної посудини 10см2. Масою посудин знехтувати.
- В підводній частині корабля, на глибині 3м від рівня води, утворилась пробоїна загальною площею 12дм2. Яке мінімальне зусилля знадобиться для того, щоб втримати латку з внутрішньої частини корабля?
- В підводному човні, на глибині 200м утворилась пробоїна загальною площею 20см2. Яке мінімальне зусилля знадобиться для того, щоб втримати латку з внутрішньої частини човна?
- Визначити тиск людини на лід, якщо її маса 70кг і вона стоїть на ковзанах довжина лез яких 25см, а їх товщина 4мм.
- Визначити глибину занурення батискафа, якщо на його ілюмінатор площею 20см2 діє сила тиску 1,2МН.
- Площа малого поршня гідравлічного пресу 10см2, а великого – 3дм2. Яке силове зусилля створюватиме цей прес, якщо на малий поршень діє сила 250Н?
- Під дією сили 200Н малий поршень гідравлічного пресу опустився на 15см, а великий – піднявся на 0,5см. Визначте силу, що діє на великий поршень.
- Ширина шлюзу 10м. Шлюз заповнений водою, надлишковий рівень якої 6м. З якою силою вода тисне на ворота шлюзу?
.
§47. Сполучені посудини.
Посудини (ємності), які з’єднані таким чином, що рідина може перетікати з однієї в іншу і навпаки, називаються сполученими. Досліджуючи поведінку рідини в сполучених посудинах проведемо наступний експеримент. В одне з колін U–подібної трубки будемо наливати воду. При цьому неодмінно з’ясується, що вода буде перетікати в друге коліно і перетікатиме до тих пір, поки горизонтальний рівень рідини в обох колінах не стане рівним. Таким чином експериментальні дослідження показують, що у відкритих сполучених посудинах, вільні поверхні однорідної нерухомої рідини встановлюється на одному горизонтальному рівні. Причому цей рівень буде однаковим в незалежності від кількості з’єднаних посудин, від їх форми та орієнтації у просторі.
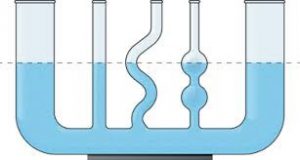
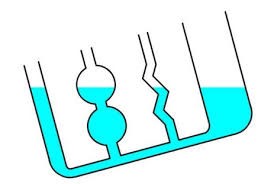
Мал.120. У відкритих сполучених посудинах горизонтальний рівень нерухомої, однорідної рідини є однаковим.
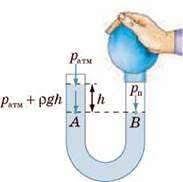
Факт того, що у відкритих сполучених посудинах горизонтальний рівень нерухомої, однорідної рідини однаковий, є прямим наслідком закону Паскаля. Дійсно, припустимо що висота рідини над точками довільно взятого горизонтального рівня АВ є різною і дорівнює h1 і h2 (мал.121). У відповідності з законом Паскаля, в точках однакового горизонтального рівня однорідної рідини, тиск цієї рідини має бути однаковим: рА = рВ. З іншого боку, тиск над рівнем АВ складається із діючого на поверхню рідини зовнішнього (атмосферного) тиску р0 та відповідного цьому рівню вагового тиску ρgh і тому pА = p0 + ρgh1, pВ = p0 + ρgh2. Таким чином, у відповідності з законом Паскаля та наявною ситуацією можна записати p0 + ρgh1 = p0 + ρgh2. А це можливо лише в тому випадку якщо h1 = h2, адже густина рідини (ρ) в обох колінах є однаковою, атмосферний тиск (р0) – однаковий, прискорення сили тяжіння (g) – однакове. Висновок. У відповідності з законом Паскаля, в сполучених посудинах рівень однорідної рідини має бути однаковим.
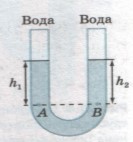
Мал.121. Якщо над рівнем АВ рідини однакової густини, то у відповідності з законом Паскаля (рА = рВ), висоти h2 і h1 мають бути однаковими (h2 = h1).
Звичайно, якщо в сполучених посудинах містяться рідини різної густини, то рівень цих рідин може бути різним. Однак і в цьому випадку все відбувається у відповідності з законом Паскаля. Адже якщо ρ1 ≠ ρ2, то із формули р0 + ρ1gh1 = р0 + ρ2gh2 випливає, що h2 ≠ h1.
Рівень рідини буде не однаковим і в тому випадку, якщо той зовнішній тиск який існує над її різними вільними поверхнями є різним. Наприклад, якщо за допомогою того чи іншого пристрою над вільною поверхнею одного з колін U–подібної сполученої посудини створити певний додатковий тиск (мал.122б), то рівень вільних поверхонь цієї рідини буде різним. Втім і в цьому випадку, все відбувається у відповідності з законом Паскаля. Адже якщо р01 ≠ р02, то із факту того, що для рівня АВ має виконуватись співвідношення p01 + ρgh1 = p0 + ρgh2 випливає, що h1 ≠ h2.
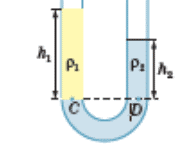
Мал.122. Якщо в сполучених посудинах містяться різні рідини (а), або величина зовнішнього тиску над вільними поверхнями є різною (б), то рівень рідини в цих сполучених посудинах може бути різним.
Сполучені посудини широко застосовуються у побуті і техніці. Скажімо відомі кожному з вас чайники і лійки є певними сполученими посудинами, принцип дії яких грунтується на факті того, що рівень рідини в сполучених посудинах є однаковим.
Або наприклад в тих приладах які так чи інакше зв’язані з каналізаційними системами (мийки, пральні машини, унітази, тощо), практично неминуче наявні так звані гідро затвори (мал.123б), які запобігають потраплянню каналізаційних газів у побутові приміщення. Прикладом застосування закону сполучених посудин на виробництві є так званий гідравлічний рівень (мал.123в) за допомогою якого визначають горизонтальність розташування віддалених точок.
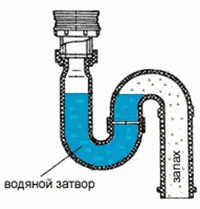
Мал.123. Деякі приклади застосування сполучених посудин.
Важливим прикладом застосування закону сполучених посудин є гідротехнічні споруди які називаються шлюзами. Шлюзи забезпечують перехід водного транспорту через ті ділянки шляху, які характеризуються різким перепадом рівня води. Наприклад на Дніпрі існує каскад великих водосховищ. Ці водосховища утворюються за рахунок потужних дамб, які стримуючи потік річкової води, піднімають її на певну висоту. При цьому по різні боки дамби існує великий перепад рівня води. Власне для подолання транспортними засобами цього перепаду і призначені шлюзи.
Найпростіший (одно каскадний) шлюз (мал.124) представляє собою перехідну камеру обмежену потужними вхідними і вихідними воротами та обладнану клапанами для перетікання води. Принцип дії цієї системи наступний. При закритих вихідних воротах, вхідні ворота відчиняються і судно заходить в перехідну камеру. Вхідні ворота зачиняються. Відкривається перепускний клапан. При цьому вода з більш високого рівня перетікає в перехідну камеру і заповнюючи її піднімає судно на відповідну висоту. (При зворотному переході, вода із перехідної камери витікає і судно відповідно опускається). Нарешті вихідні ворота відчиняються і судно виходить на простори більш високого рівня води.
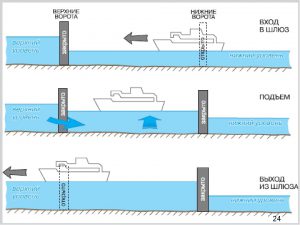
Мал.124. Схема загального устрою та принципу дії шлюзу.
Ще одним прикладом практично важливого застосування закону сполучених посудин є система водопостачання за допомогою водонапірних башт (мал.125). Принцип дії цієї системи очевидно простий. За допомогою електро насосу, вода періодично закачується у водонапірну башту, що височіє над навколишніми споживачами води. А оскільки ця башта за допомогою водопровідної мережі з’єднана з цими споживачами, то у відповідності з законом сполучених посудин, вода піднімається до кожного з них.
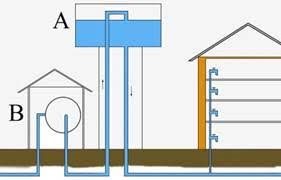
Мал.125. Схема загального устрою та принципу дій системи водопостачання за допомогою водонапірних башт.
Задача 1. Який тиск у колбі В якщо тиск в колбі А 100кПа? В колінах манометра вода.
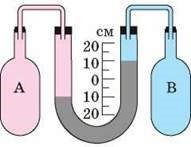
Рішення. Із аналізу малюнку ясно, що тиск у колбі А більший за тиск у колбі В на ∆h = 20см = 0,2м водного стовпчика, тобто на ∆р = ρg∆h = 1·103(кг/м3)·9,8(м/с2)·0,2м = 2·103Па = 2кПа. Таким чином, рВ = рА – ∆р = 100кПа – 2кПа = 98кПа.
Відповідь: рВ = 98кПа.
Задача 2. В сполучених посудинах міститься ртуть, коли в праве коліно посудини налили шар води, то рівень ртуті в лівому коліні піднявся на 2см. Визначте висоту налитого в посудину води. Густина ртуті 13,6·103кг/м3.
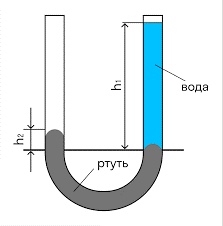
Дано:
ρ1 = 1·103кг/м3
ρ2 = 13,6·103кг/м3
h2 = 2,0см
h1 = ?
Рішення. Виконуємо малюнок який відображає фізичний зміст задачі. В якості нульового горизонтального рівня обираємо рівень АВ. Рівень, нижче якого знаходиться лише однорідна рідина (ртуть). Оскільки нижче рівня АВ в трубці міститься лише однорідна рідина, то згідно з законом Паскаля, той тиск який існує над цим рівнем в обох колінах трубки має бути однаковим. А враховуючи, що для точок А і В величина цього тиску становить: рА = р0 + ρ2gh2; рВ = р0 + ρ1gh1, можна записати р0 + ρ2gh2 = р0 + ρ1gh1, або ρ2gh2 = ρ1gh1, або ρ2h2 = ρ1h1. Звідси випливає, що h1 = h2ρ2/ρ1.
Розрахунки: h1 = h2ρ2/ρ1 = 2см·13,6·103(кг/м3)/1·103(кг/м3)= 27,2см.
Задача 3. В одне з колін U-подібної трубки, в якій міститься певна кількість води, налили шар гасу висотою 12,5см. Визначте різницю рівнів води і гасу в правому і лівому колінах трубки. Гас і вода не змішуються. Густина гасу 800кг/м3.
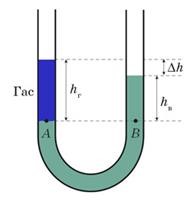
Дано:
hг = 12,5см
ρг = 800 кг/м3
ρв = 1000 кг/м3
Δh = ?
Рішення. Виконуємо малюнок, який відображає фізичний зміст задачі. В якості нульового горизонтального рівня обираємо рівень АВ. Оскільки нижче горизонтального рівня АВ в трубці міститься лише однорідна рідина, то згідно з законом Паскаля, той тиск який існує над цим рівнем в обох колінах трубки має бути однаковим. А враховуючи, що для точок А і В величина цього тиску становить: рА = р0 + ρгghг; рВ = р0 + ρвghв, можна записати р0 + ρгghг = р0 + ρвghв, або ρгghг = ρвghв, або ρгhг = ρвhв. Звідси випливає, що hв = hгρг/ρв. Зважаючи на те, що Δh = hг–hв, виконуємо відповідні розрахунки.
Розрахунки: hв = 12,5(см)800(кг/м3)/1000(кг/м3) = 10см; Δh = 12,5(см) – 10(см) = 2,5см.
Відповідь: Δh = 2,5см.
Контрольні запитання.
1.За яких умов, рівень рідини в сполучених посудинах буде однаковим?
- Чи впливає на рівень рідини в сполучених посудинах атмосферний тиск?
- Чи впливає густина рідини на положення рівня рідини в сполучених посудинах?
- Чому в зображених на малюнку ситуаціях рівень рідини в сполучених посудинах є різним?


- На основі аналізу мал.124 поясніть загальний устрій та принцип дії шлюзу.
- Поясніть загальний устрій та принцип дії зображеної на мал.125 системи водопостачання.
- В деяких храмах Стародавньої Греції демонструвалось диво під назвою «невичерпна чаша». Поясніть принцип дії даного «дива».
Вправа №47.
- У рідинному манометрі (мал.а) міститься вода. Ліве коліно манометра відкрите. Який тиск у балоні, якщо атмосферний тиск 100кПа?
- У рідинному манометрі (мал.б) міститься ртуть. Ліве коліно манометра відкрите. Який тиск у балоні, якщо атмосферний тиск 100кПа?
- Який тиск в колбі В (мал.в) якщо тиск в колбі А 100кПа? В колінах манометра ртуть.
а)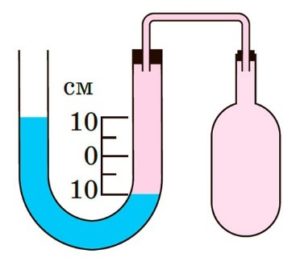 б)
б)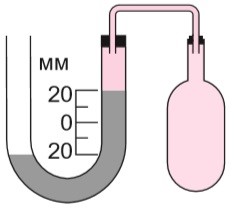 в)
в) 
- В одне з колін U-подібної трубки, в якій міститься певна кількість води, налили шар гасу висотою 20см. Якою відносно нижнього рівня гасу буде висота стовпця води в іншому коліні?
- В одне з колін U-подібної трубки, в якій міститься певна кількість ртуті, налили шар води висотою 68см. Якою відносно нижнього рівня води буде висота стовпця ртуті в іншому коліні?
- Нижню частину сполучених посудин заповнили ртуттю. У ліве коліно налили гас, а в праве воду, висота стовпчика якої 48см. Якої висоти має бути стовпчик гасу, щоб рівень ртуті був однаковим?
- В сполучених посудинах міститься ртуть, коли в праве коліно посудини налили шар гасу, то рівень ртуті в лівому коліні піднявся на 1,5см. Визначте висоту налитого в посудину гасу.
- В сполучених посудинах міститься ртуть. В праве коліно посудини налили шар води висотою 20см. На яку висоту піднялась ртуть в лівому коліні.
.
§48. Закон Архімеда. Сила Архімеда. Умова плавання тіла.
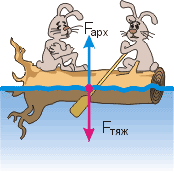
Понад дві тисячі років тому, видатний давньогрецький вчений Архімед (287–212р.р. до н.е.) відкрив закон, який прийнято називати законом Архімеда. В цьому законі стверджується: на будь яке занурене в рідину (або газ) тіло, діє виштовхувальна сила, величина якої дорівнює вазі виштовхнутої тілом рідини.
Наочно переконатися в достовірності закону Архімеда дозволяє проста система, складовими якої є (мал.126): штатив, пружинний динамометр (1), маленьке відерце (2), досліджуване тіло (3), відливний стакан (4), стакан для відлитої води (5).
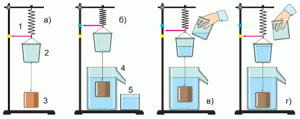
Мал.126. На занурене в рідину тіло діє виштовхувальна сила, величина якої дорівнює вазі виштовхнутої тілом рідини (закон Архімеда).
Принцип дії даної системи очевидно простий. Під вагою досліджуваного тіла, пружина динамометра видовжується (мал.126а) і це видовження фіксує стрілка приладу, вказуючи на жовту точку відповідної шкали. Коли досліджуване тіло опиняється у воді вщерть заповненого відливного стакана (мал.126б), то: по-перше, діюче на пружину динамометра навантаження зменшиться на величину тієї виштовхувальної сили яка діє на тіло; по-друге, певна кількість води вилляється з відливного стакана і ця кількість дорівнюватиме об’єму зануреного у воду тіла. Якщо ж взяти виштовхнуту тілом воду і вилити у відерце системи (мал.126в), то неодмінно з’ясується, що вага цієї води в точності дорівнює величині діючої на тіло сили Архімеда (стрілка динамометра знову вказує на жовту точку).
Не важко довести, що величина тієї виштовхувальної сили, яка називається силою Архімеда (FA) і яка дорівнює вазі виштовхнутої тілом рідини (FA = Pр), залежить від густини рідини (ρр), об’єму зануреної в рідину частини тіла (V) та прискорення сили тяжіння (g), і що цю залежність можна записати у вигляді FA = ρрVg. Дійсно. Оскільки в нерухомій системі, вага витісненої тілом рідини визначається за формулою Рр = mрg, та враховуючи, що маса витісненої тілом рідини дорівнює добутку густини рідини ρр на її об’єм (mр = ρрV), можна записати: FA = Pр = mрg = ρрVg. Зважаючи на вище сказане, можна дати наступне визначення:
Сила Архімеда – це та сила, з якою тіла виштовхуються з рідин та газів і яка дорівнює вазі виштовхнутої тілом рідини або газу.
Позначається: FА
Визначальне рівняння: FА = ρрVтg, де ρр – густина рідини (газу); Vт – об’єм зануреної в рідину (газ) частини тіла; g – прискорення сили тяжіння;
Одиниця вимірювання: [FА] = H, ньютон.
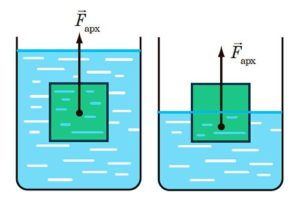
Мал.127. На будь яке занурене в рідину або газ тіло діє виштовхувальна сила Архімеда, величина якої визначається за формулою FА = ρрVтg.
Характерною особливістю сили Архімеда є факт того, що її величина залежить не від загального об’єму тіла, а від об’єму тієї частини тіла яка занурена в рідину. А це означає, що по мірі занурення тіла в рідину, величина діючої на нього сили Архімеда збільшується. Збільшується до тих пір поки тіло повністю не зануриться в рідину. При цьому в процесі подальшого занурення, величина діючої на тіло сили Архімеда залишається сталою.
Загально відомо, що деякі тіла плавають у воді, а деякі – тонуть в ній. Тепер, коли ви знаєте про силу Архімеда та її основні властивості не важко пояснити все різноманіття тих явищ, які пов’язані з плаванням чи не плаванням тіл. Дійсно. Якщо діюча на тіло сила тяжіння зрівноважується виштовхувальною силою Архімеда (Fт = FA), то відповідне тіло не тоне в рідині. А якщо сила тяжіння більша за силу Архімеда (Fт > FA), то відповідне тіло тоне в рідині.

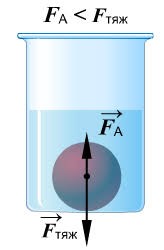
Мал.128. Якщо діюча на тіло сила тяжіння зрівноважується силою Архімеда (Fт = FA), то відповідне тіло не тоне, а якщо сила тяжіння більша за силу Архімеда (Fт > FA), то тіло тоне в рідині.
Говорячи про те, що дане тіло не тоне в рідині, потрібно мати на увазі, що ступінь отого «не тоне» може бути різною. Скажімо у воді, пінопласт (ρ ≈ 20кг/м3) занурюється лише на 2% свого об’єму, пробкове дерево (ρ = 240кг/м3) – на 24%, суха сосна (ρ = 500кг/м3) – на 50%, а сухий дуб (ρ = 800кг/м3) – на 80%. Якщо ж густина тіла дорівнює густині води (ρ = 1000кг/м3), то в цьому випадку тіло буде повністю зануреним у воду і у стані вільного плавання може знаходитися на будь якій глибині.
Потрібно зауважити, що говорячи про усереднену густину тіла (ρт), мають на увазі не густину того матеріалу з якого виготовлено тіло, а саме усереднену густину всього тіла. Скажімо, якщо ви візьмете суцільний шматок сталі (ρ = 7800кг/м3) і опустите його у воду (ρ = 1000кг/м3), то він неодмінно потоне. Потоне тому, що густина сталі більша за густину води. Але якщо з цієї сталі ви виготовите пустотілий корпус човна, то він залишатиметься на плаву. Адже усереднена густина корпусу човна буде значно меншою за густину води. Меншою тому, що об’єм корпусу човна складається не лише з об’єму тієї сталі з якої він виготовлений, а й з об’єму того простору який знаходиться всередині корпусу та є недоступним для потрапляння води.
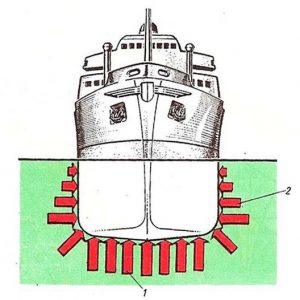
Мал.129. Усереднена густина човна, менша за густину води.
В певному сенсі, всі плаваючі тіла починаючи від деревяних колод і закінучуючи океанськими лайнерами, представляють собою певні саморегульовані системи. Саморегульовані в тому сенсі, що збільшення навантаження на плаваюче тіло, автоматично призводить до відповідного додаткового занурення цього тіла, яке в свою чергу призводить до автоматичного збільшення виштовхувальної сили Архімеда.
Ясно, що така саморегуляція може відбуватися лише до тих пір поки об’єм зануреної в рідину частини тіла не зрівняється з загальним об’ємом цього тіла. Втім, якщо мова йде про плаваючі транспортні засоби, то для них зазвичай передбачена певна обмежувальна межа, яка гарантує безпечну експлуатацію відповідного транспортного засобу. Цю межу називають ватерлінією.
Цікавим прикладом застосування сили Архімеда є підводні човни. Підводний човен (мал.130) може знаходитись над водою, під водою або лежати на дні водойми. Він може занурюватись на глибину та виринати з цієї глибини. Реалізацію всіх цих можливостей забезпечує наявна на підводному човні система баластових відсіків (мал.130б). В залежності від потреб, ці відсіки заповнюються навколишньою водою, або звільняються від неї. При цьому реальний об’єм човна (Vт), тобто той об’єм який недоступний для потрапляння навколишньої води, змінюється, а відповідно змінюється і усереднена густина човна (ρт = mт/Vт).
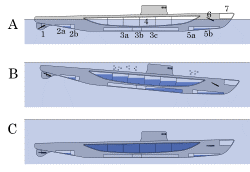
Мал.130. Загальний вигляд підводного човна та схема його занурення у воду.
В живій природі, подібний до застосованого в підводних човнах способу регуляції плавучості тіла, можна спостерігати у риб. Адже всередині будь якої риби є так званий плавальний міхур. В процесі плавання та в залежності від потреб, риба шляхом мязових зусиль, змінює об’єм свого плавального міхура, а відповідно і загальний об’єм свого тіла. А це в свою чергу дозволяє здійснювати маневри стосовно зміни глибини плавання.
Коли ми стверджуємо, що на занурене в рідину тіло діє певна виштовхувальна сила Архімеда, то повинні мати на увазі, що за певних умов ця сила може і не діяти. Це буває в тому випадку, коли тіло лежить на дні і щільно до нього прилягає. В цьому випадку вода не потрапляє під нижню поверхню тіла і не створює на цю поверхню відповідний виштовхувальний тиск. Натомість тіло притискається до дна не тільки силою тяжіння, а й силою того гідравлічного та атмосферного тиску який діє на верхню поверхню тіла.
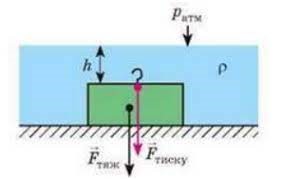
Мал.131. На тіло яке щільно прилягає до дна водойми, сила Архімеда практично не діє. Натомість діє сила яка додатково притискає тіло до дна.
Завершуючи розмову про силу Архімеда зауважимо, що все вище сказане стосується не лише рідин, а й газів. Суттєва різниця лише в тому, що в газах і зокрема у повітрі, прояви сили Архімеда є менш помітними. І це закономірно. Адже густина повітря (ρ = 1,29кг/м3) в 775 разів менша за густину води. А це означає, що у повітрі, діюча на тіло сила Архімеда в 775 разів менша аніж у воді. В газах прояви сили Архімеда стають очевидними лише в тому випадку, коли усереднена густина тіла є співрозмірною або меншою за густину відповідного газу. Наочними прикладами дії сили Архімеда у повітрі є заповнені гелієм або теплим повітрям гумові кульки, величезні повітряні кулі, дирижаблі, тощо.


Мал.132.Наочні приклади дії сили Архімеда у повітрі.
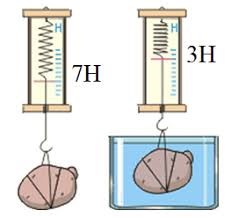
Задача 1. На основі аналізу малюнку визначте об’єм зануреного у воду тіла.

Рішення. Із аналізу малюнку ясно, що на занурене у воду тіло діє виштовхувальна сила Архімеда величина якої 7Н – 3Н = 4Н. А оскільки за визначенням FА = ρрVтg, то Vт = FA/ρрg= 4Н / 1·103(кг/м3)∙10(м/с2) = 0,4·10–3м3 = 0,4дм3 = 0,4л.
Відповідь: Vт = 0,4дм3.
Задача 2. На скільки зменшиться вага залізної болванки об’єм якої 5дм3 при її повному зануренні у воду?

Дано:
V = 5дм3 = 5·10–3м3
∆Р = ?
Рішення. Виконуємо малюнок який відображає фізичну суть задачі. Виходячи з того, що за визначенням вага (Р), це та сила з якою тіло діє на опору і яка чисельно дорівнює реакції цієї опори (Р = N, на малюнку N = Fпр), розглянемо ті сили які діють на тіло у повітрі (Fт = mg, N1) та у воді (Fт = mg, N2 , FА = ρVg).
У відповідності з умовою механічної рівноваги тіла, можна записати: N1 = mg; N2 = Fт – FА = mg – ρVg.
Таким чином: ∆Р = ∆N = N1– N2 = mg – (mg – ρVg) = mg – mg + ρVg = ρVg.
Розрахунки. ∆Р = ρVg = 1·103(кг/м3)·5·10–3м3·9,8(м/с2) = 49Н.
Відповідь: ∆Р = 49Н.
Задача 3. Повітряна куля має об’єм 300м3. Визначте діючу на кулю силу Архімеда. Вантаж якої максимальної маси може підняти ця куля, якщо її власна маса 180кг? Густина повітря 1,29кг/м3
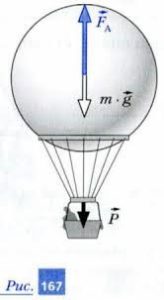
Дано:
Vк = 300м3
m1 = 180кг
ρп = 1,29кг/м3
m2 = ?
Рішення. Розглянемо ті сили, що діють на кулю в умовах її механічної рівноваги. А цими силами є: 1) сила Архімеда FA = ρпVкg, 2) діюча на тіло сила тяжіння Fт1 = m1g; 3) вага вантажу Р = Fт2 = m2g. У відповідності з умовою механічної рівноваги кулі, можна записати:
FA = Fт1 + P, або ρпVкg = m1g + m2g, або ρпVк = m1 + m2, звідси m2 = ρпVк – m1.
Розрахунки. m2 = ρпVк – m1 = 1,29(кг/м3)∙300м3 – 180кг = 207кг.
Відповідь: m2 = 207кг.
Контрольні запитання.
- Що стверджується в законі Архімеда?
- Від чого залежить діюча на тіло виштовхувальна сила Архімеда?
- На основі аналізу малюнку, порівняйте густини плаваючих в рідині тіл.
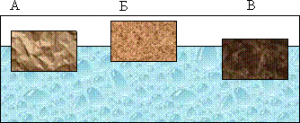
- На основі аналізу малюнку порівняйте густини тих рідин в яких знаходяться однакові тіла.
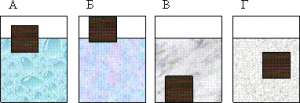
- Залізне і дерев’яне тіла однакових розмірів знаходяться у воді. При цьому, залізне тіло лежіть на дні посудини, а дерев’яне плаває. На яке тіло діє більша сила Архімеда? Чому?
- Що мають на увазі коли говорять про усереднену густину плаваючого тіла?
- В чому полягає саморегульованість плаваючого тіла? Які межі цієї саморегульованості?
- Яким чином підводні човни досягають того, що можуть плавати як над водою так і підводою?
Вправа №48.
- З якою силою камінь об’ємом 0,5м3 виштовхується із води?
- На основі аналізу малюнку визначте об’єм зануреного у воду тіла.
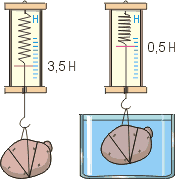
3. На гачку пружинного динамометра висить гиря, об’ємом 130см3 і масою 1кг. Що покаже динамометр, якщо гирю занурити у воду?
4. Визначте показання динамометра якщо тіла об’ємом 100см3 з алюмінію, заліза, міді і свинцю зважувати у воді.
5. Повітряна куля має об’єм 350м3. Визначте діючу на кулю силу Архімеда. Вантаж якої максимальної маси може підняти ця куля, якщо її власна маса 190кг?
6. На тіло яке перебуває у воді діє виштовхувальна сила 270Н. З якою силою це тіло виштовхується гасом? Густина гасу 800кг/м3.
7. Крижина площею 40м2 і товщиною 40см плаває у воді. Тіло якої максимальної маси може втримати на плаву ця крижина? Густина льоду 900кг/м3.
8. Якого мінімального об’єму має бути надувний човен масою 8кг, щоб утримувати на воді рибалку масою 80кг?
.
§49. Що важче, кілограм заліза чи кілограм вати?
В параграфі 29 ми з’ясували, що вага одного і того ж тіла за різних обставин може бути різною, і що вона залежить як від силових параметрів того гравітаційного поля в якому знаходиться тіло (від діючої на тіло сили тяжіння), так і від величини та напрямку того прискорення з яким рухається тіло (від діючої на тіло сили інерції).
Однак вага тіла залежить не лише від діючої на нього сили тяжіння та сили інерції, а й від інших силових факторів, зокрема сили Архімеда. Дійсно. Загально відомо, що у воді камінь суттєво легший ніж на суходолі (мал.133). І це закономірно. Адже у воді на камінь діє значна виштовхувальна сила Архімеда, яка і зменшує його вагу.

Мал.133. У воді камінь легший аніж у повітрі, і це пов’язано з виштовхувальною дією сили Архімеда.
Звичайно, коли тіло знаходиться в рідині, то завжди можна сказати, що рідина є певною не жорсткою опорою, і що тому певна частина ваги тіла зрівноважується цією не жорсткою опорою. З одного боку це правда, рідину дійсно можна вважати певною не жорсткою об’ємною опорою для того тіла яке знаходиться в цій рідині. Скажімо, коли тіло вільно плаває у воді і не тисне на тверду опору, то це зовсім не означає, що воно знаходиться в стані невагомості. Просто діюча на тіло сила тяжіння зрівноважується відповідною силою Архімеда, яка для цього тіла фактично є не жорсткою, об’ємною реакцією опори.
З іншого ж боку, щоб ми не говорили, а будь яка жорстка опора на якій висить, лежить чи стоїть тіло, неодмінно зафіксує, що вага тіла у воді значно менша ніж у повітрі. Тому, якщо вага, це та сила з якою тіло діє на опору, а опора, це те що жорстко обмежує рух тіла, то потрібно визнати, що вага залежить не тільки від сили тяжіння та сили інерції, а й від діючої на тіло сили Архімеда.
Іноді можна почути, як старші школярі провокативно запитують своїх молодших колег: «що важче, кілограм заліза чи кілограм вати?» І коли ті відповідають що залізо важче – дружно сміються, хизуючись своєю кмітливістю. І потрібно сказати, сміються абсолютно безпідставно. Адже кілограм заліза дійсно важчий за кілограм вати. Звичайно за умови, що мова йде саме про кілограм, тобто про масу в 1000,00г.
Обґрунтовуючи тезу про те, що кілограм заліза важчий за кілограм пір’я, вати, пінопласту чи дерева, розв’яжемо наступну задачу.
Задача. Визначити на скільки кілограм заліза (ρ1 = 7800кг/м3) важчий за кілограм пінопласту (ρ2 = 20кг/м3). Густина повітря ρ = 1,3кг/м3.
Дано:
m1 = m2 = 1,000кг
ρ1 = 7800кг/м3
ρ2 = 20кг/м3
ρ = 1,3кг/м3
g = 9,81м/с2
ΔP = P1 – P2 = ?
Рішення. Оскільки за визначенням, вага тіла чисельно дорівнює реакції відповідної опори (Р1 = N1; Р2 = N2), то рішення задачі полягає у визначенні цих реакцій Виходячи з цього, розглянемо ті сили що діють на залізне (1) та пінопластове (2) тіло і визначимо відповідні реакції опор. Із умов рівноваги тіл випливає:
N1 = Fт – FА1 = m1g – ρV1g, де V1 = m1/ρ1 = 1кг/7800(кг/м3) = 0,000128м3;
N2 = Fт – FА2 = m2g – ρV2g, де V2 = m2/ρ2 = 1кг/20(кг/м3) = 0,05м3.
Розрахунки.
P1 = N1 = m1g – ρV1g = 1кг∙9,81(м/с2) – 1,3(кг/м3)∙ 0,000128м3∙9,81м/с2 = 9,81Н – 0,0016Н = 9,81Н;
P2 = N2 = m2g – ρV2g = 1кг∙9,81(м/с2) – 1,3(кг/м3)∙ 0,05м3∙9,81м/с2 = 9,81Н – 0,64Н = 9,17Н;
ΔP = P1 – P2 = 9,81Н – 9,17Н = 0,64H
Відповідь: кілограм заліза на 0,64Н важчий за кілограм пінопласту, що відповідає додатковій масі Δm = 0,065кг = 65г. Іншими словами, кілограм пінопласту на 6,5% легший за кілограм заліза (за умови, що визначення ваги відбувається у повітряному середовищі).
Таким чином, теорія стверджує що кілограм пінопласту на 6,5% легший за кілограм заліза. Причина появи цієї різниці очевидна – на більш об’ємний пінопласт діє більша сила Архімеда і тому його вага, тобто та сила з якою пінопласт тисне на опору (на ваги) виявляється дещо меншою.
Чому ж ми вважаємо, що кілограм заліза і кілограм пінопласту мають однакову вагу? Більше того, якщо ми дійсно порівняємо вагу реального кілограму заліза і реального кілограму пінопласту, то скоріш за все ця вага виявиться однаковою. І справа не втому, що точність вимірювальних приладів не дозволяє зафіксувати наявну різницю ваги. Справа в іншому – цієї різниці просто не існує.
Не існує тому, що зазвичай масу тіла ми визначаємо шляхом зважування. І як ви розумієте, це зважування відбувається не у вакуумі, а у повітряному середовищі. А це означає, що в реальному кілограмі пінопласту, фактично не 1,000кг а 1,065кг. Поява цієї різниці знову ж таки обумовлена дією сили Архімеда. Адже для того, щоб пінопластове тіло зрівноважило залізу гирю масою 1,000кг, маса цього тіла має бути на 65г більшою за масу гирі. Більшою на ту величину яка дозволяє компенсувати надлишкову силу Архімеда.
Таким чином, якщо кілограм вати і кілограм заліза мають однакову вагу, то це тільки тому, що фактична маса вати дещо більша за кілограм. Якщо ж ми дійсно візьмемо кілограм заліза і кілограм вати, то вага заліза буде більшою за вагу вати. Звичайно за умови, що процес зважування відбувається у повітряному середовищі.
До речі. Не відомо, чи знають продавці пінопласту, вати, пір’я та інших їм подібних легких матеріалів, що в кілограмі їх товару більше речовини ніж в тій кілограмовій гирі за допомогою якої цей товар зважують. Але фактом залишається те, що подібні легкі матеріали кілограмами ніхто не міряє. А якщо і міряє, то собі у збиток.
Задача. Визначити вагу каменю масою 50кг в повітрі та у воді (густина каменю 3,2·103кг/м3).

Дано:
m = 50кг
ρ = 3,2·103кг/м3
Р1 = ? Р2 = ?
Рішення. Виходячи з того, що вага тіла (Р) чисельно дорівнює діючій на тіло реакції опори (N), виконуємо малюнок на якому вказуємо діючі на тіло сили в двох ситуаціях. Виходячи з умови рівноваги тіла, визначаємо діючу на тіло реакцію опори (N), а отже і їй відповідну вагу тіла (Р = N). У повітрі, дією сили Архімеда нехтуємо і тому вважаємо, що на тіло діють сила тяжіння (Fт = mg) та реакція опори (N1). При цьому N1 = Fт = mg = 50кг·9,8м/с2 = 490Н.
У воді на тіло діють сила тяжіння (Fт = mg), реакція опори (N2) та сила Архімеда (FA = ρрVтg). При цьому N2 = Fт – FA. Визначаємо величину діючої на тіло сили Архімеда: FA = ρрVтg, де ρр=1·103кг/м3 – густина води; Vт = m/ρ = 50кг/3,2·103кг/м3 = 15,6·10–3м3 – об’єм тіла. FA = ρрVтg = 1·103(кг/м3)·15,6·10–3м3·9,8м/с2 = 153Н. Таким чином N2 = Fт – FA = 490Н – 153Н = 337Н.
Відповідь: Р1 = 490Н, Р2 = 337Н.
Контрольні запитання.
- Що називають вагою тіла?
- Що називають опорою?
- Чому у воді камінь легший аніж у повітрі?
- Чому звичайним способом виміряний кілограм заліза і кілограм пінопласту мають однакову вагу?
- Чи означає факт того, що той пінопласт який на шальках терезів зрівноважив гирю масою 1,000кг, також має масу 1,000кг? Чому?
- На основі аналізу малюнку, порівняйте густину кожного тіла з густиною рідини.
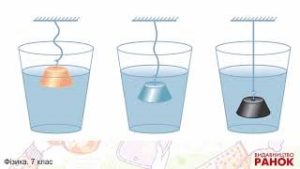
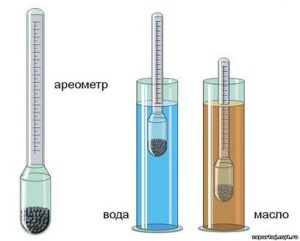
7. На основі аналізу малюнку (б), поясніть принцип дії аерометра – приладу для вимірювання густини рідини.
- Чому на практиці кількість речовини в надлегких товарах не вимірюють в кілограмах?
Вправа №49.
- Визначити вагу алюмінієвої деталі масою 8кг в повітрі та у воді.
- Визначити вагу залізного тіла масою 40кг в повітрі та у воді.
- У 1990 році, в США була синтезована тверда речовина з найменшою густиною – кремнієвий аерозоль. Густина цієї речовини всього 5кг/м3. Яку реальну масу цієї речовини треба покласти на точні терези, щоб урівноважити сталеву гирю масою 1,000кг?
- З якою силою виштовхується з води тіло об’ємом 125см3, якщо воно виготовлено з алюмінію, скла, свинцю, корка?
- Яку максимальну піднімальну силу має пліт, який складається з 10 колод об’ємом по 0,6м3 кожна, якщо густина дерева 500кг/м3?
- Кулю-зонд, об’єм якої 8м3, перед запуском у верхні шари атмосфери наповнили гелієм. Яка піднімальна сила кулі-зонда? Густина гелію 0,18кг/м3. Який вантаж може підняти ця куля, якщо маса її оболонки 3кг?
- Оболонка повітряної кулі масою 60кг вміщує 300м3 газу густина якого 0,5кг/м3. Який вантаж може підняти ця куля?
- На одній чаші ваг лежить шматок срібла масою 105г, а на іншій – шматок скла масою 130г. Яка чаша переважить при зануренні ваг у воду? Густина срібла 10,5·103кг/м3, скла 2,6·103кг/м3.
.