Сайт викладача фізики

Розділ 4. Основи геометричної оптики.

§32. Загальні відомості про світло. Світлові промені. Джерела світла.

§33. Закон прямолінійного поширення світла.

§34. Закон відбивання світла. Дзеркальне та розсіюване відбивання світла.

§35. Загальні відомості про дзеркала.

§36. Заломлення світла. Закон заломлення світла.

§37. Повне внутрішнє відбивання світла. Загальні відомості про оптичні призми та оптичні волокна.

§38. Загальні відомості про лінзи та параметри тих зображень які вони формують.

§39. Графічне та алгебраїчне визначення параметрів тих параметрів які формують лінзи. Формула лінзи.

§40. Оптичні прилади.

§41. Око як природний оптичний прилад. Дефекти зору.

          Розділ 4. Основи геометричної оптики.

§32. Загальні відомості про світло, світлові промені та джерела світла.

Оптика (від грец. optos – видимий), це розділ фізики в якому вивчається все різноманіття тих явищ які пов’язані з випромінюванням, поширенням та різноманітними проявами світла. Іншими словами, оптика – це наука про світло.

Що ж таке «світло»? Відповідаючи на це запитання можна сказати наступне. Природа влаштована таким дивним чином, що в ній найпростіші об’єкти є найскладнішими. Найскладнішими в тому сенсі, що надзвичайно важко, а то і не можливо пояснити як вони влаштовані. Скажімо в Природі нема нічого простішого за світло. Адже світло, в мільярди разів прості за те скло через яке воно потрапляє у вашу кімнату. І тим не менше, на питання «що таке світло?» відповідають чотири великі розділи «Оптики», а по суті – чотири науки. При цьому: Геометрична оптика обгрунтовано стверджує, що світло – це потік світлових променів. Хвильова оптика, не менш обгрунтовано наполягає на тому, що світло – це потік світлових (електромагнітних) хвиль. Квантова оптика, обгрунтовано доводить, що світло – це потік світлових частинок (фотонів). А фотометрія наполягає на тому, що світло – це потік світлової енергії. Іншими словами:

.                                         потік світлових променів

.                  світло            потік світлових хвиль

.                                         потік світлових частинок

.                                         потік світлової енергії

Ви все життя будете вивчати властивості світла, знатимете про світло все, що тільки можна знати, і в той же час не матимете певного уявлення про те, як воно влаштовано і на що схоже. Бо промінь – це щось пряме, а хвиля – це щось хвилясте. Бо хвиля – це щось неперервне і певним чином розподілене у просторі, а частинка – це щось дискретне і зосереджене у певному місці. І уявити те, що є частинкою-хвилею-променем одночасно, практично не можливо. Бо нічого подібного в тому макросвіті який ми бачимо, відчуваємо та аналізуємо, просто не існує.

І тим не менше, світло реально існує і має той набір властивостей який має. Бо в одних обставинах веде себе як потік променів, в інших – як потік хвиль, в третіх – як потік частинок, а в четвертих – як потік енергії. І можна скільки завгодно розказувати, що вам це не подобається, що такого не може бути, що це суперечить здоровому глузду. Однак від цього реальність не стане іншою, а властивості світла не стануть такими, що вам подобаються та не суперечать вашому «здоровому глузду».

Вивченню цього парадоксального, надважливого та надцікавого об’єкту і присвячено той розділ фізики який називається оптикою – наукою про світло. Оптика, це дуже великий розділ фізики, складовими частинами якого є геометрична оптика, хвильова оптика, квантова оптика та фотометрія. Крім цього, окремим розділом оптики є фізіологічна оптика, яка вивчає і пояснює зорові відчуття живих істот з об’єднавчих позицій фізики, фізіології та психології. Якщо ж говорити про навчальну програму для 8-го класу, то у відповідності з цією програмою ми будемо вивчати лише той розділ оптики, який називається геометричною оптикою.

І варто зауважити, що геометричну оптику ми будемо вивчати на тому мінімально необхідному рівні, який не передбачає її додаткового вивчення на другому етапі вивчення фізики. Це означає, що на другому, поглибленому етапі вивчення фізики, в розділі «Оптика» ми будемо вивчати загальні основи хвильової та квантової оптики, тоді як про геометричну оптику згадаємо лише побіжно.

         Геометрична оптика – це розділ оптики, в якому світло представляють як потік світлових променів і в якому вивчають ті явища, які пояснюється виходячи з того, що світло це потік променів.

 

Мал.120. В геометричній оптиці світло представляють як потік світлових променів.

Світловий промінь (промінь) – це умовна лінія, яка вказує на напрям поширення (розповсюдження) світла в тій чи іншій конкретній ситуації. Наочні уявлення про світлові промені та їх властивості дають тонкі пучки світла, які можна отримати за допомогою дрібних отворів, що знаходяться в потужному світловому потоці або спеціальних приладів, наприклад тих, що називаються лазерами. Однак навіть найтонші світлові пучки, є лише грубими моделями світлового променя. Бо промінь, це та умовна лінія яка вказує на напрям поширення світла.

По суті світловий промінь є тією гранично спрощеною (ідеалізованою) фізичною моделлю світла, застосування якої дозволяє пояснити широке різноманіття оптичних явищ, починаючи від відбивання та заломлення світла і закінчуючи фактом того, що ми бачимо об’єкти навколишнього світу такими, якими вони є в реальності.

Потрібно зауважити, що в науці пояснюючи ті чи інші явища, реальні об’єкти практично завжди замінюють їх спрощеними (ідеалізованими) фізичними моделями. Матеріальна точка, абсолютно тверде тіло, абсолютно пружний удар, ідеальна рідина, ідеальний газ, кристалічна решітка – ось лише деякі приклади вам відомих фізичних моделей. Фізична модель, абстрагуючись від несуттєвих в умовах вирішення даної задачі властивостей реального об’єкту, зосереджує увагу на його суттєвих властивостях. Скажімо представляючи світло як потік неперервних променів, ми абстрагуємося від факту того, що реальне світло має як певні хвильові так і певні корпускулярні (від лат. «corpusculum» – дрібненька частинка) властивості. Абстрагуємося тому, що для пояснення тих явищ які є предметом вивчення геометричної оптики ці властивості є несуттєвими. Однак це зовсім не означає, що за інших обставин, ці «несуттєві» властивості не стануть визначальними.

Уявлення про світлові промені, виникли на базі двох обставин. Перша полягає в тому, що у повсякденному житті, ми часто стикаємося з ситуаціями, коли суцільний потік сонячного чи іншого світла, проходячи через хмари, листя дерев, вії очей, тощо, розсікається на окремі світлові пучки, які сприймаються нами як відповідні світлові промені.

Друга важлива обставина полягає в тому, що в потоці світла, непрозорі тіла залишають чітку тінь. При цьому параметри тіні є такими, ніби вона отримана шляхом геометричної проекції здійсненої за допомогою прямолінійних променів, джерелом яких є відповідне джерело світла. Навіть в тих випадках, коли тінь предмету представляє собою певну комбінацію тіні та півтіні, нема підстав стверджувати, що світло не є потоком світлових променів. Просто в цих випадках, ми маємо справу з сукупністю декількох точкових джерел світла, або з джерелом яке не можна вважати точковим.

  

Мал.121. Наочні приклади того, що світло – це потік променів.

Виходячи з того, що світло це потік світлових променів, геометрична оптика пояснює загальний устрій та принцип дії великого різноманіття приладів починаючи від різноманіття дзеркал, лінз та оптичних призм, і закінчуючи різномкніттям фото об’єктивів, телескопів, мікроскопів та систем волоконної оптики.

Важливим поняттям оптики загалом і геометричної оптики зокрема є джерело світла. Зазвичай, джерелом світла прийнято вважати будь який природний або штучний об’єкт в якому той чи інший вид енергії перетворюється на енергію видимого світла. Звідси ясно, що Сонце, зірки, блискавка, багаття, полумя свічки, спіраль лампочки розжарювання, монітор комп’ютера, тіло світлячка є джерелами світла. А планети, дерева, столи, будинки, книги, люди – джерелами світла не являються.

Однак, в багатьох галузях науки, в тому числі і в геометричній оптиці, джерелами світла вважають всі тіла що випромінюють світло. А це означає, що джерелами світла є не лише ті об’єкти які дійсно генерують світлову енергію, а й всі видимі тіла. Наприклад, пояснюючи яким чином ми бачимо в дзеркалі своє відображення та відображення оточуючих предметів, виходять з того, що будь яке видиме тіло загалом і кожна його точка зокрема є певними джерелами світла, яке відбиваючись від поверхні дзеркала утворює те зображення яке ми бачимо.

Зважаючи на вище сказане, в геометричній оптиці прийнято вважати, що джерелом світла є будь який об’єкт що  випромінює ним генероване або ним відбите світло. А це означає, що будь який видимий об’єкт та будь яка точка цього об’єкту, в геометричній оптиці вважається певним джерелом світла.

Мал.122. В геометричній оптиці, пояснюючи принцип дії дзеркал, лінз та інших приладів, виходять з того, що кожна точка видимого тіла є джерелом світла.

В геометричній оптиці часто говорять про так звані точкові джерела світла, тобто такі джерела, розміри яких гранично малі порівняно з тією відстанню на якій оцінюють їх світлову дію. Важливість точкових джерел світла полягає в тому, що результат поведінки світлових променів в тих чи інших обставинах, легко передбачаються лише в тому випадку коли ці промені виходять з однієї точки. Зважаючи на ці обставини, в геометричній оптиці будь яке джерело світла представляють як сукупність окремих світлових точок (точкових джерел світла).

Наприклад, пояснюючи факт того, що в потоці світла від об’ємного джерела, непрозора перешкода залишає певну комбінацію тіні та напівтіні, в геометричній оптиці виходять з того, що кожна точка цього джерела є точковим джерелом світлових променів. При цьому знаючи хід тих променів які виходять з переферійних точок об’ємного джерела світла, геометрична оптика точно визначає параметри тіні та півтіні в кожній конкретній ситуації.

Мал.123. В геометричній оптиці, пояснюючи ті чи інші явища, виходять з того, що кожна точка об’ємного джерела світла є точковим джерелом світлових променів.

Контрольні запитання.

1. Як представляють світло в: а) геометричній оптиці, б) хвильовій оптиці, в) квантовій оптиці, г) фотометрії?
2. Що називають світловим променем?
3. Що означає: світловий промінь – це фізична модель світла?
4. Що називають фізичною моделлю певного обєкту? Які фізичні моделі вам відомі?
5. На базі яких фактів виникли уявлення про те, що світло це потік променів?
6. Чому в геометричній оптиці джерелами світла вважають не лише ті обʼєкти які генерують світлову енергію, а й ті, які її відбивають?
7. Чому в геометричній оптиці такими важливими є саме точкові джерела світла?
8. За яких обставин за напрозорим тілом утворюється певна комбінація тіні та напівтіні?

.

§33. Закон прямолінійного поширення світла.

В основі геометричної оптики лежать три твердження, які називаються законами геометричної оптики:

1) закон прямолінійного поширення світла;

2) закон відбивання світла;

3) закон заломлення світла.

Закон прямолінійного поширення світла – це закон, в якому стверджується: в оптично прозорих, однорідних середовищах, світлові промені поширюються прямолінійно. Ілюструючи достовірність даного закону можна провести наступний простий експеримент. На шляху до екрану виставте ряд непрозорих перешкод з невеликими отворами в них (мал.124). Перешкоди виставте таким чином щоб їх отвори були на одній прямій. Застосовуючи в якості джерела направленого світлового пучка (моделі світлового променя) лазенну указку, переконайтеся в тому, що світлові промені дійсно поширюються прямолінійно.

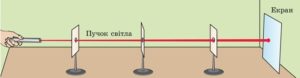
Мал.124. Експеримент який підтверджує факт прямолінійності поширення світла.

Говорячи про закон прямолінійного поширення світла, варто зауважити, що у відповідності з цим законом, світлові промені поширюються прямолінійно не завжди, а лише в тих середовищах які є оптично однорідними, тобто такими, оптичні властивості яких в усіх точках  однакові. Якщо ж середовище оптично неоднорідне, то відповідно не прямолінійним буде і хід світлових променів.

Наприклад атмосфера Землі має певну шаристу структуру, різні шари якої суттєво відрізняються температурою, густиною, хімічним складом, а відповідно і оптичними властивостями. Результатом цих відмінностей є факт того, що те світло яке потрапляє на земну поверхню від Сонця, Місяця, зірок та інших космічних об’єктів, в процесі проходження черуз атмосферу Земілі, суттєво відхиляється від прямолінійної траєкторії руху. Це явище називають атмосферною рефракцією світла.

Одним з результатів атмосферної рефракції світла, є факт того, що Сонце видимо з’являється над лінією горизонту на декілька хвилин раніше, а заходить на декілька хвилин пізніше, порівняно з тим, якби Земля не мала атмосфери. А це означає, що завдяки атмосферній рефракції світла, тривалість дня на Землі дещо більша за ту, якою б вона була за відсутності земної атмосфери.

Мал.125. Атмосфера Землі не є оптично однорідною і тому в ній, світлові промені певним чином відхиляються від прямолінійної траєкторії.

Ще однією загально відомою, але в реальності не надто поширеною групою оптичних явищ, які обумовлені викривленням світлових променів в атмосферному повітрі, є міражі. Міражі виникають в тих ситуаціях, коли сусідні шари атмосферного повітря, мають достатньо різкі перепади температур.

Наприклад якщо приповерхневий шар повітря є гарячим, а повітря над ним відносно холодним, то можна спостерігати так званий нижній міраж (мал.126а). Прикладом нижнього міражу є ілюзія того, що в спекотний день на горизонті автостради, спостерігаються неіснуючі калюжі води, які фактично є відображенням фрагментів неба. Це відображення обумовлене тим викривленням світлових променів, яке відбувається на межі гарячого приповерхневого повітря та того відносно прохолодного повітря що знаходиться над ним.

Якщо ж нижній шар повітря є холодним, а верхній значно теплішим, то за певних додаткових умов, можна спостерігати так званий верхній міраж, який є відображенням тих об’єктів які знаходяться за лінією горизонту (мал.126б). Втім, верхні міражі, це досить рідкісне явище.

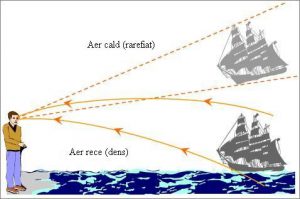
Мал.126. Міражі є результатом того заломлення світлових променів яке відбувається на межі різно нагрітих шарів атмосферного повітря.

Потрібно звернути увагу і на те, що про поширення світлових променів можна говорити лише в тому випадку, якщо відповідне середовище є оптично прозорим. Оптично прозорим називають таке середовище, в якому процес поширення світла не супроводжується значним перетворенням світлової енергії в енергію теплового руху частинок середовища. Оптично прозорими є повітря, скло, вода, лід, алмаз, переважна більшість газів та значну кількість рідин. Ідеально ж оптично прозорим «середовищем» є вакуум. Оптично непрозорим називають таке середовище, яке поглинає ту світлову енергію що потрапляє в це середовище, або відбиває цю енергію. Скажімо темна тканина непрозора тому, що поглинає світло, а дзеркало непрозоре тому, що світло відбиває.

Поділ середовищ на оптично прозорі та оптично непрозорі є досить умовним. Наприклад метали, цілком обгрунтовано вважаються оптично непрозорими. Однак, якщо мова йде про надтонкі металеві плівки, то їх з не меншим обгрунтуванням можна вважати оптично прозорими. Або наприклад, вода є оптично прозорою. Однак, якщо мова йде про великі товщі води, то вони можуть бути оптично непрозорими. Скажімо шар води товщиною 100м поглинає 99% світлової енергії. Та як би там не було, а в геометричній оптиці ми будемо розглядати ситуації в яких світло поширюється в оптично прозорих та оптично однорідних середовищах.

Застосовуючи закон прямолінійного поширення світла, можна пояснити широке коло явищ і зокрема ті, які пов’язані з утворенням тіні, півтіні та певних комбінацій тіней і півтіней. Загальний підхід до пояснення подібних явищ полягає в тому, що будь яке джерело світла представляють як певну сукупність точкових джерел. При цьому, виходячи з того, що ті світлові промені які випромінюються точковим джерелом поширюються прямолінійно, шляхом простих геометричних побудов, або їм відповідних геометричних розрахунків, визначають параметри тієї тіні яку утворює непрозоре тіло в потоці світла відповідного джерела.

Наприклад досвід показує, якщо в потоці світла точкового (далекого об’ємного) джерела, знаходиться непрозоре тіло, то на екрані спостерігається чітка тінь відповідного тіла. Якщо ж це тіло знаходиться в потоці того світла яке випромінює відносно близьке об’ємне джерело, то на екрані буде певна комбінація тіні та півтіні.

а)б)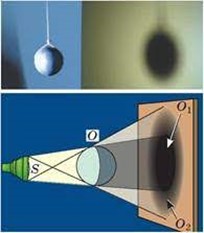

Мал.127. В потоці точкового джерела світла, непрозоре тіло залишає на екрані чітку тінь, а в потоці світла об’ємного джерела – певну комбінацію тіні та півтіні.

Пояснюючи дані факти можна сказати наступне. Ті промені які виходять з точкового джерела світла і потрапляють на непрозоре тіло, не потрапляють на екран і тому на екрані спостерігається чітка тінь відповідного тіла. Якщо ж джерело світла є об’ємним, то те світло яке випромінює кожна його точка, також залишає чітку тінь перешкоди. А оскільки цих точок багато і вони не збігаються одна з одною, то і відповібні тіні одна з одною не збігаються. В такій ситуації, в певну частину екрану світло не потрапляє взагалі (цю частину називають повною тінню), а в певні частини, від одних точковиж джерел світло потрапляє, а від інших – не потрапляє (цю частину називають півтінню).

Параметри тієї тіні та півтіні які утворюються при освітленні непрозорого тіла об’ємним джерелом світла, визначаються наступним чином. З переферійних точок об’ємного джерела (на плоскому малюнку таких точок дві S₁ i S₂) проводять промені які проходять через крайні точки непрозорого тіла. Обмежена цими променями частина екрану буде областю тіні тіла від відповідної точки джерела світла. При цьому спільна для обох джерел тінь, буде областю повної тіні даного тіла, а та частина екрану на яку падає тінь лише від однієї точки, буде областю півтіні.

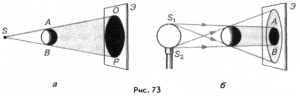
Мал.128. В потоці світла, непрозоре тіло залишає певну тінь, або певну комбінацію тіні та півтіні, параметри яких можна визначити виходячи з того, що світло – це потік променів.

Варто зауважити, що за певного розташування тіла, точкових джерел світла та екрану, на екрані можна спостерігати певну комбінацію півтіней і не спостерігати повної тіні. Наприклад на мал.129 між двома фрагментами півтіней кулі, буде область повного освітлення екрану, тобто та частина екрану в яку світло безперешкодно потрапляє як від джерела А₁ так і від джерела А₂.

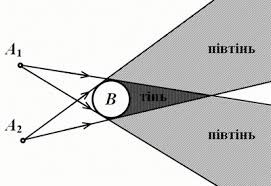
Мал.129. За певного розташування тіла, точкових джерел світла і екрану, на екрані буде лише певна комбінація півтіней і не буде повної тіні.

Важливо сказати і про те, що за різних обставин, одне і те ж джерело світла може бути як точковим, так і об’ємним. Наприклад якщо ми говоримо про ту тінь яку в потоці сонячного світла створює непрозоре тіло на екрані (поверхні землі, стіні будинку, тощо) то в цьому випадку Сонце є точковим джерелом практично паралельних світлових променів. Ця точковість визначається тим, що в масштабі відстані від тіла до екрану, відстань до Сонця є фантастично великою. Якщо ж мова йде про ті явища які називаються сонячним та місячним затемненням (мал.129), то в цьому випадку, Сонце є певним об’ємним ждерелом світла. Ця об’ємність визначається тим, що в масштабі відстані від Землі до Місяця, відстань до Сонця є співрозмірно великою.

Мал.130. Точковість чи неточковість джерела світла визначається не реальними розмірами джерела, а співвідношенням розмірів джерела і тіла та відстаней між джерелом світла, тілом і екраном.

Застосовуючи закон прямолінійного поширення світла, та загальні правила визначення області тіні від точкового джерела світла, розглянемо ряд конкретних задач.

Задача 1. На малюнку (а) зображено два точкових джерела світла S₁, S₂ та непрозорий предмет А. Визначити в якій області (тіні, півтіні чи освітленій) знаходиться точка В.

а)    б)

Рішення. З кожного точкового джерела світла, через крайні відносно цього джерела точки непрозорого тіла проводимо два промені. Ці промені визначають область тієї тіні яку залишає тіло в потоці світла відповідного джерела (мал. б). При цьому, спільна для обох точкових джерел тінь і буде тією повною тінню, яку залишає тіло в потоці світла двох джерел. Аналізуючи отриману картину та розташування точки В на ній, робимо відповідний висновок. В нашому випадку: точка В знаходиться в області повної тіні.

Задача 2. Око спостерігача розташовано перед щілиною в точці А. Яку частину дерева бачить спостерігач. В якій точці має знаходитися око, щоб спостерігач бачив все дерево?

Рішення. З точки А, через крайні точки щілини проводимо дві прямі. Простір між цими прямими і є тією частиною простору яка з точки А видима спостерігачу через задану щілину.

Визначаючи ту точку з якої через задану щілину спостерігач бачитиме все дерево, з верхньої і нижньої точок дерева, через відповідні крайні точки щілини, проводимо дві прямі. Точка перетину цих прямих і буде тією точкою А′ з якої спостерігач бачитиме все дерево.

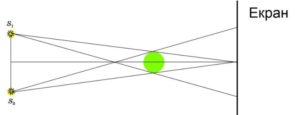
Задача 3. Два вертикально розташовані точкові джерела світла S₁ i S₂, відстань між якими 25см, знаходяться на відстані 100см від вертикально розташованого екрану. На середній лінії між джерелами світла і екраном знаходиться непрозорий м’яч діаметром 10см. На якій найменшій відстані від екрану потрібно розташувати м’яч щоб він не створював повної тіні?

Дано:

D = 25см

L = 100см

d = 10см

ℓ = ?

Рішення. М’яч не створюватиме на екрані повної тіні в тому випадку, якщо ті промені які виходять з верхньої S₁  і нижньої S₂ точок, та проходять через відповідно верхню і нижню точки м’яча, будуть перетинатися в центрі екрану.

Аналізуючи отриманий малюнок, можна стверджувати. Оскільки відрізки D і d є паралельними і знаходяться між одним і тим же центральним кутом, то відношення довжин цих відрізків D/d, дорівнює відношенню їх відстаней до екрану L/ℓ, тобто D/d = L/ℓ. Звідси ℓ = L∙d/D = 100см∙10см/25см = 40см.

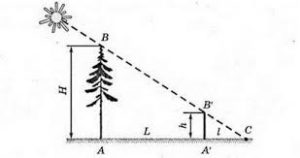
Задача 4. Довжина тієї тіні яку залишає дерево в потоці сонячного світла, дорівнює 5м. При цьому довжина тіні вертикально встановленої метрової палиці дорівнює 0,5м. Визначити висоту дерева.

Дано:

L = 5м

h = 1м

ℓ = 0,5м

H = ?

Рішення. Виконуємо малюнок, на якому вказуємо всі важливі деталі умови задачі. На основі аналізу малюнку можна стверджувати, що трикутники АВС і АꞌВꞌС є подібними.  А це означає, що H/L = h/ℓ, звідси

H = L∙h/ℓ = 5м·1м/0,5м = 10м.

Відповідь: H = 10м.

Загальні зауваження. Задачі геометричної оптики можна розв’язувати двома базовими способами: геометричним та алгебраїчним. Наприклад вище наведене рішення, є алгебраїчним рішенням задачі. Суть же геометричного рішення полягає в тому, що на основі максимально точних геометричних побудов, з дотриманням відповідного масштабу та з застосуванням відповідних приладів (лінійка, транспортир, циркуль, тощо), отримують геометричну відповідь, яку вимірюють або візуально аналізують. Наприклад в умовах даної задачі, розуміючи факт того, що два вертикальних відрізки H і h, висота одного з яких відома (h = 1м), будучи розташованим на відомих відстанях від спільного центру (ℓ = 0,5м; L = 5м), який є центром того кута що проходить через вершини обох відрізків, виконують відповідні геометричні побудови та вимірюють невідому величину: висоту Н. Основна перевага геометричного рішення – візуальна очевидність та загальна простота. Основний недолік – залежність результату від точності геометричних побудов та відсутність гарантії точності відповіді.

Якщо ж говорити про алгебраїчне рішення задачі, то воно не передбачає точності геометричних побудов і дає гарантовано точний результат (звичайно за умови, що рішення є правильним). Тому говорячи про рішення задачі, зазвичай мають на увазі її алгебраїчне рішення. Однак ви маєте знати, що приблизне рішення цієї ж задачі можна отримати і геометричним способом.

Контрольні запитання.

1. Що стверджується в законі прямолінійного поширення світла?
2. За яких умов виконується цей закон?
3. Які середовища називаються оптично прозорими, а які – оптично непрозорими?
4. Чи може одне і те ж середовище за різних обставин бути як оптично прозорим так і оптично непрозорим?
5. Поясніть суть атмосферної рефракції світла.
6. За яких умов можуть спостерігатися міражі?
7. За яких умов Сонце є точковим джерелом світла, а за яких – об’ємним джерелом?
8. Поясніть суть геометричного рішення задачі.
9. Які переваги і які недоліки геометричного рішення задачі?

Вправа 33.

1. Скопіюйте малюнок у зошит і вкажіть на ньому тіні та півтіні від мяча який освітлюється двома точковими джерелами світла S₁ i S₂.

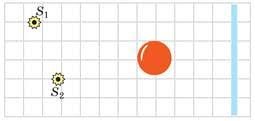
2. Скопіюйте малюнок у зошит і вкажіть на ньому тіні та півтіні від мяча який освітлюється обємним джерелом світла.

3. На малюнку зображено два точкових джерела світла S₁, S₂ та непрозорий предмет А. Визначити в якій області (тіні, півтіні чи освітленій) знаходиться точка В.

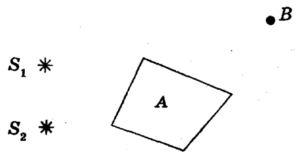
4. Перед непрозорим педметом знаходиться об’ємне джерело світла S. Які точки простору знаходяться в області повної тіні тіла.

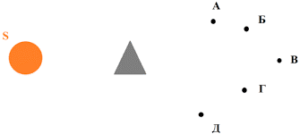
5. Око спостерігача може знаходитись в точках А, В, С. Визначте яку частину дерева бачитиме спостерігач з відповідних точок.

6. Точкове джерело світла S освітлює непрозору кульку діаметром 5см. Який діаметр тіні на стіні?

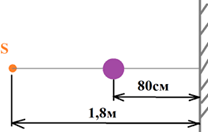
7. У сонячний день висота тіні від прямовисно поставленої метрової лінійки дорівнює 30см, а від дерева – 6м. Яка висота дерева.

8. Джерелом світла є куля діаметром 4см, а непрозорим тілом – куля діаметром 2см. Ці кулі розташовані на лінії яка перпендикулярна до екрану. При цьому відстань від джерела світла до екрану 10см, а від непрозорого тіла до екрану 5см. Шляхом геометричних побудов та відповідних вимірювань визначте діаметри тіні та півтіні.

9. Джерелом світла є куля діаметром 2см, а непрозорим тілом – куля діаметром 4см. Ці кулі розташовані на лінії яка перпендикулярна до екрану. При цьому відстань від джерела світла до екрану 10см, а від непрозорого тіла до екрану 5см. Шляхом геометричних побудов та відповідних вимірювань визначте діаметри тіні та півтіні.

.

§34. Закон відбивання світла. Дзеркальне та розсіяне відбивання світла.

Напевно ви зустрічались з ситуаціями, коли предмети навколишнього світу відображаються у тихих водах річок, озер, ставків чи калюж. В такому випадку ви спостерігали явище, яке називається відбиванням світла. Відбивання світла – це явище, суть якого полягає в тому, що на межі двох оптично різних середовищ, частина світлового потоку відбивається від цієї межі і змінюючи напрям свого розповсюдження повертається в попереднє середовище.

Мал.131. Природній прояв явища відбивання світла.

Дасліджуючи явище відбивання світла звернемось до експерименту. З цією метою застосуємо прилад, який називається оптична шайба (мал.132). Цей прилад педставляє собою поєднання рухомого джерела направленого пучка світла та круглого планшету з шкалою, за якою можна визначати ті кути під якими падає та відбивається світло.

Закріпивши в центрі планшета смужку плоскої дзеркальної поверхні та направляючи на цю поверхню пучок світла, не важко бачити, що будь яка зміна кута падіння світла, автоматично призводить до відповідної зміни кута його відбивання. При цьому, кут відбивання світла (β) завжди дорівнює куту його падіння (α). А потрібно зауважити, що кутом падіння променя (α) називають кут між падаючим променем та перпендикуляром до відбивної поверхні, проведеним в точці падіння променя. Кутом відбивання променя (β) називають кут між відбитим променем та перпендикуляром до відбивної поверхні, проведеним в точці падіння променя.

 

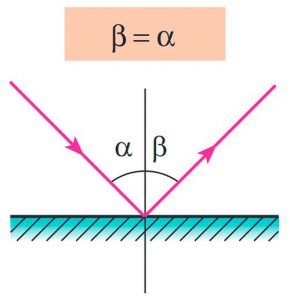
Мал.132. Кут відбивання світла (β) завжди дорівнює куту його падіння (α)

Дослідження показують, що відбивання світла відбувається таким чином, що падаючий та відбитий промені завжди знаходяться в площині, яка перепендикулярна до відбивної поверхні. Скажімо, якщо в умовах нашого експерименту, відбитий промінь залишає світловий слід на поверхні планшету, то це тільки тому, що дзеркальна відбивна поверхня є перепендикулярною до площини поверхні планшету. Якщо ж дзеркальну поверхню дещо відхилити від цієї площини, то відбитий промінь відповідно відхилиться і не залишатиме сліду на поверхні планшету.

Результати проведених експериментів можна узагальнити у вигляді закону, який називають законом відбивання світла. В цьому законі стверджується: на межі двох оптично різних середовищ світлові промені відбиваються, при цьому: 1) проміннь падаючий, промінь відбитий і перпендикуляр до поверхні в точці падіння променя, лежать в одній площині; 2) кут відбивання променя (β) дорівнює куту його подіння (α): β = α. Прийнято вважати, що закон відбивання світла, був сформульований давньогрецьким вченим Евклідом ще в 3 ст. до н.е.

Варто зауважити, що закон відбивання світла іноді формулюють наступним чином: на межі двох оптично різних середовищ світлові промені відбиваються, при цьому, кут падіння променя дорівнює куту його відбивання: α = β. Таке формулювання закону є неправильним. Неправильним по перше тому, що з точки падіння променя можна провести безліч променів для яких виконується співвідношення β = α. Насправді ж реально відбитим буде лише один з цих променів. І цей єдино правильний промінь буде знаходитися в тій площині що є перпендикулярною відбивній поверхні. Власне цей факт і констатує перша частина закону відбивання світла: промінь падаючий, промінь відбитий і перпендикуляр до поверхні в точці падіння променя, лежать в одній площині.

Ще однією суттєвою помилкою вище наведеного неправильного формулювання закону є те, що в ньому стверджується: «при відбиванні світла, кут падіння променя дорівнює куту його відбивання: α  = β». В контексті того що називають законом, це означає: кут падіння променя залежить від кута його відбивання: α = ƒ(β). Насправді ж кут падіння променя залежить не від кута відбивання, а від взаємного розташування джерела світла, відбивної поверхні та точки падіння променя (мал.133). А от кут відбивання променя, дійсно залежить від куту його падіння. І цю залежність відображає формулювання: кут відбивання променя дорівнює куту його падіння: β = α.

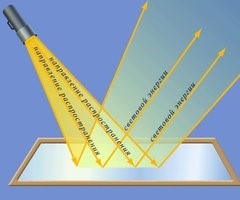
Мал.133. Кут падіння променя (α) залежить не від кута його відбивання (β), а від взаємного розташування джерела світла, відбивної поверхні та точки падіння променя.

Говорячи про закон відбивання світла, буде не зайвим сказати, що у відповідності з цим законом, та у відповідності з експериментальними фактами, промінь падаючий та промінь відбитий є взаємно оборотними. Це означає, що коли падаючий промінь направити шляхом відбитого променя, то відповідний відбитий промінь піде шляхом падаючого.

Явище відбивання світла демонструють і досліджують на прикладі так званих дзеркальних поверхонь. Однак світло відбивається не лише від дзеркальних, а й від будь яких інших поверхонь. Адже всі ті предмети які ми бачимо і які не є самостійними джерелами світла, видимі тільки тому, що відбивають падаюче на них світло. Чим же відрізняється дзеркальне відбивання від недзеркального, дзеркальні поверхні від недзеркальних?

Напевно ви погодитесь з тим, що дзеркальні поверхні є гладенькими, а недзеркальні – шорсткими. Можливо погодитесь і з тим, що шляхом шліфування та полірування однорідну тверду, шорстку поверхню можна перетворити на поверхню дзеркальну. Власне дзеркальна поверхня тим і відрізняється від недзеркальної, що величина її мікронерівностей є гранично малою. Саме величина наявних на поверхні мікронерівностей і є тим критерієм який дозволяє відрізнити дзеркальну (оптично рівну) поверхню від недзеркальної (оптично нерівної).

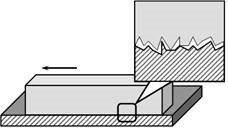
Мал.134. Дзеркальність чи недзеркальність поверхні визначається величиною її мікронерівностей.

Загально прийнятими є наступні визначення. Дзеркальною (оптично ріною) називають таку поверхню, розміри мікронерівностей якої не перевищують довжини світлової хвилі (δ ≤ 7,6·10^–7м, на практиці δ ≤ 1·10^–6м = 0,001мм). Недзеркальною (оптично нерівною) називають таку поверхню, розміри мікронерівностей якої суттєво більші за довжину світлової хвилі.

Дослідження показують, що дзеркальні (оптично рівні) та недзеркальні (оптично нерівні) поверхні, відбивають світло суттєво по різному. По різному в тому сенсі, що початково паралельні промені відбиваючись дзеркальною поверхнею залишаються паралельними (мал.135а), а відбиваючись недзеркальною поверхнею – стають безладно розсіяними (мал.135б). Зазвичай, відбивання світла від дзеркальної поверхні називають дзеркальним, а відбивання від недзеркалної поверхні – дифузним або розсіяним.

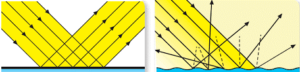
Мал.135. Дзеркальні (а) та недзеркальні (б) поверхні відбивають світло суттєво по різному.

Факт того, що кожен фрагмент недзеркальної (розсіювальної, матової) поверхні відбиває світло у всіх можливих напрямках, по суті означає, що розсіяно відбите світло несе інформацію не про джерело первинного світла, а про той предмет від якого це світло відбивається. Тому дивлячись на шорстку поверхню, ми бачимо саму поверхню, а не відбите в ній джерело світла. Якщо ж мова йде про дзеркальну поверхню, то відбите нею світло фактично несе інформацію не про саму поверхню, а про джерело первинного світла. Власне тому, дивлячись в дзеркало ми бачимо не його поверхню, а зображення тих предметів, світло яких відбивається в ньому.

Факт того, що поведінка тих світлових променів які падають на дзеркальну (оптично рівну) поверхню є прогнозованою (строго визначеною), корисно застосовується в найрізноманітніших оптичних приладах, зокрема дзеркалах, оптичних призмах, лінзах та їх комбінаціях (мікроскопи, телескопи, біноклі, фотообʼєктиви, тощо).

   

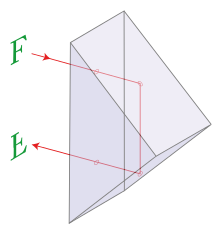
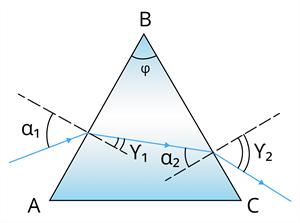
Мал.136. Робочі поверхні оптичних приладів є оптично рівними і тому поведінка світлових променів в цих приладах є прогнозованою.

Потрібно зауважити, що термін «дзеркальна поверхня» є частковим випадком більш загального терміну «оптично рівна поверхня». Адже коли говорять про дзеркальну поверхню, то зазвичай мають на увазі оптично рівну відбивну поверхню, прикладом якої є відбивна поверхня дзеркала. Оптично ж рівні поверхні можуть бути не лише відбивними, а й прозорими або темними. При цьому перші практично безперешкодно пропускають світло, а другі – практично повністю поглинають його.

Загалом же, коли світло з одного середовища потрапляє на поверхню іншого середовища, то можливі три ідеалізовані варіанти його поведінки. 1). Світло відбивається від поверхні та не втрачаючи енергії повертається в перше середовище; 2). Світло проникає в друге середовище та не втрачаючи енергії поширюється в ньому; 3) Світло проникає в друге середовище та поглинається ним, при цьому енергія світла перетворюється в енергію руху частинок відповідного середовищи.

І потрібно сказати, що в переважній більшості випадків, поведінка світла є певною комбінацією всіх трьох варіантів. Просто в одних випадках 98-99% світлової енергії поглинається середовищем, при цьому говорять, що відповідне середовище непрозоре і чорне. В інших випадках 98-99% світлової енергії безперешкодно проходить через середовище, при цьому говорять, що відповідне середовище є оптично прозорим. В третьому випадку 98-99% світлової енергії відбивається середовищем, при цьому говорять, що відповідне середовище є дзеркально непрозорим. В четвертому, п’ятому і тисячному випадках, можлива будь яка комбінація вище описаних варіантів. При цьому співвідношення цих варіантів залежатиме не лише від властивостей першого та другого середовиш, а й від параметрів самого світла, величини кута падіння, а також від того в якому напрямку рухається світло – від першого середовища в друге, чи навпаки. Що ж, не забувайте, світло – це надзвичайно складний об’єкт, логіку поведінки якого складно пояснити і ще складніше, зрозуміти.

На завершення додамо, що терміни «оптично рівна поверхня» та «геометрично рівна поверхня» є суттєво різними. Скажімо, поверхня стіни геометрично рівна, а оптично не рівна. Натомість поверхня опуклої лінзи – геометрично не рівна, а оптично рівна.

Задача 1. На малюнку зображені падаючий і відбитий від дзеркала промені. Визначте кут між падаючим променем і дзеркалом.

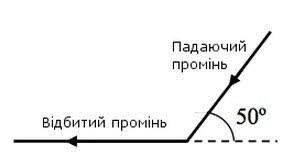
Рішення. Із аналізу малюнку ясно, що загальний кут між падаючим та відбитим променями α + β = 180° – 50° = 130°. А враховуючи, що β = α, можна стверджувати, що α = 130°/2 = 65°.

З іншого боку, кут α (кут падіння променя), це кут між падаючим променем та перпендикуляром до поверхні дзеркала. А це означає, що між падаючим променем і самою поверхнею дзеркала буде кут 90° – 65° = 25°.

Відповідь: кут між падаючим променем і дзеркалом 25°.

Задача 2. Вранці сонячні промені падають під кутом 10° до горизонту. Як треба розмістити плоске дзеркало, щоб відбиті промені освітлювали дно глибокого колодязя?

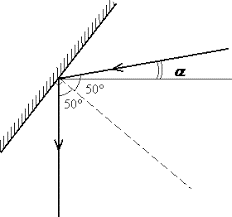
Дано:

α = 10°

β = ?

Рішення. Оскільки відбитий промінь має бути вертикальним, а отже перпендикулярним до лінії горизонту, то модна стверджувати, що загальний кут між падаючим на відбитим променями, має дорівнювати 90° + α = 100°. А оскільки кут падіння променя дорівнює куту його відбивання, то можна стверджувати, що між перпендикуляром до поверхні дзеркала та вертикально відбитим променем має бути кут (кут відбивання) 100°/2 = 50°. А це означає, що площина дзеркала має бути нахиленою до вертикалі під кутом 90° – 50° = 40°.

Відповідь: дзеркало має бути нахиленим до лінії вертикалі під кутом 40°, а відповідно до лінії горизонту – під кутом 60°

Контрольні запитання.

1.Який кут називають кутом падіння променя; кутом відбивання променя?

2. Чи є правильним наступне формулювання закону? «На межі двох оптично різних середовищ, світлові промені відбиваються. При цьому, кут падіння променя дорівнює куту його відбивання: α = β». Чому?

3. Від чого залежить кут падіння променя?

4. Чим відрізняється дзеркальна (оптично рівна) поверхня від недзеркальної (оптично нерівної) поверхні?

5. Чим відрізняється дзеркальне відбивання світла від недзеркального (дифузного, розсіяного) відбивання?

6. Що бачить спостерігач дивлячись на шорстку (недзеркальну) поверхню?

7. Що бачить спостерігач дивлячись на дзеркальну поверхню?

8. Чим схожі і чим відрізняються терміни «дзеркальна поверхня» та «оптично рівна поверхня»?

9. Яке середовище називають оптично прозорим?

10. Чим схожі і чим відрізняються чорна поверхня та дзеркальна поверхня?

Вправа 34.

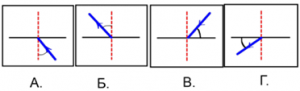
1. На якому з малюнків правильно позначено кут падіння променя?

2. При якому куті падіння кут між падаючим та відбитим променями дорівнює 60°?

3. Накресліть у зошиті кожний малюнок та доповніть його відповідним відбитим чи падаючим променем.

4. Накресліть у зошиті заданий малюнок і добудуйте падаючі та відбиті промені (промені відбиваються від усіх трьох дзеркал).

5. Промінь світла падає на плоске дзеркало під кутом 35° до його поверхні. Чому дорівнює кут між падаючим променем і відбитим?

6. Кут між падаючим променем і плоским дзеркалом дорівнює куту між падаючим променем і відбитим. Чому дорівнює кут падіння променя?

7. Промінь світла падає на дзеркало перепендикулярно. На який кут відхилиться відбитий промінь від падаючого, якщо дзеркало повернути на 20°?

8. Сонячне світло падає під кутом 50° до земної поверхні. Як треба розташувати плоске дзеркало, щоб відбите від нього сонячне світло освітлювало дно колодязя?

9. Промені, що йдуть від Сонця утворюють з горизонтом кут 30°. Як за допомогою плоского дзеркала направити їх паралельно лінії горизонту?

.

§35. Загальні відомості про дзеркала.

Захоплюючись тими дивовижними речами які демонструють професійні ілюзіоністи, ми зазвичай не звертаємо увагу на ті не менш дивовижні речі, які оточують нас у повсякденному житті. Дійсно. Підійдіть до звичайного дзеркала і ви неодмінно побачите себе там де вас нема і бути неможе. Чи це не диво?

Говорячи про будову та принцип дії дзеркала можна сказати наступне. Дзеркало – це оптичний прилад, який представляє собою оптично рівну, відбивну (дзеркальну) поверхню, що має певну, геометрично правильну форму. Цією геометрично правильною формою може бути фрагмент площини, сфери, циліндра, тора, еліпсоїда, параболоїда, тощо. Принцип дії будь якого дзеркала базується на застосуванні закону відбивання світла. Це означає, що застосовуючи закон відбивання світла, можна передбачити параметри того зображення яке створює відповідне дзеркало в тій чи іншій ситуації.

Найпростішою та найбільш поширеною різновидністю дзеркал є дзеркала плоскі, тобто такі, робочою поверхнею яких є фрагмент площини. Пояснюючи принцип дії плоского дзеркала, розглянемо конкретну ситуацію. Припустимо, що відрізок МN – це поске дзеркало, а точка S – точкове джерело світла (мал.137). Візьмемо ряд довільних променів що виходять з точки S та застосовуючи закон відбивання світла, побудуємо відповідні відбиті промені.

Не важко бачити, що дзеркально відбиті промені певним чином розходяться. Але розходяться так, що їх уявні задзеркальні продовження перетинаються в одній і тій же точці – точці Sʹ. По суті це означає, що будь який спостерігач, дивлячись в дзеркало, візуально зафіксує, що всі промені виходять з точки Sʹ і що тому точка Sʹ є точковим джерелом світла.

Зауважимо, що фактично всі світлові промені виходять з точки S. Однак, дивлячись в дзеркало, спостерігач побачить цю точку не там де вона є в реальності, а в іншому місці – у відповідній точці задзеркалля. При цьому, те що побачить спостерігач, буде певною ілюзією, тобто оптичним обманом (від лат. illusio – обман). Можна довести, що реальна точка S та її дзеркальне відображення Sʹ є симетричними відносно площини дзеркала. Це означає, що точки S та Sʹ є рівновіддаленими від площини дзеркала і лежать на прямій яка перпендикулярна цій площині.

 

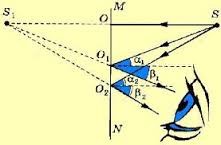
Мал.137. Дивлячись в дзеркало, спостерігач бачить точку S не там де вона є в реальності.

Знаючи закономірності побудови дзеркальних зображень окремих світлових точок, не важко визначити параметри зображення цілого тіла. Адже будь яке тіло завжди можна представити як певну сукупність окремих точок.

Характеризуючи те зображення яке створює плоске дзеркало, говорять що воно пряме, геометрично рівне, уявне та дзеркально симетричне. Коли говорять що зображення пряме, то це означає що воно не перевернуте, і що в зображені як і в оригіналі верх є верхом, а низ – низом. Коли говорять що зображення є геометрично рівним, то це означає, що воно не більше і не менше за оригінал, а в точності дорівнює цьому оригіналу. Коли говорять що зображення уявне, то мають на увазі те, що відповідне зображення отримано в результаті уявного перетинання відбитих або заломлених променів, і що в реальності ці промені у відповідних точках зображення не перетинаються. Коли говорять, що зображення є дзеркально симетричним, то мають на увазі не лише те, що відповідні точки тіла та його зображення симетричні відносно площини дзеркала, а й факт того що дзеркальне зображення є оберненим. Оберненим в тому сенсі, що предмет та його зображення «дивляться» в протилежні сторони, і що ті елементи зображення які для оригіналу є правими, для дзеркального зображення є лівими і навпаки.

 

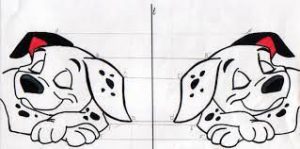
Мал.138. Відображення в дзеркалі є дзеркально симетричним, тобто таким в якому предмет та його зображення дивляться в протилежні сторони, а їх праві та ліві сторони міняються місцями.

Переконатися в тому, що те зображення яке можна побачити в плоскому дзеркалі є прямим, геометрично рівним, уявним та дзеркально симетричним, зовсім не складно. Для цього достатньо підійти до наявного у вашій кімнаті плоского дзеркала і подивитись на своє відображення в ньому. При цьому ви неминуче з’ясуєте, що відповідне зображення є не перевернутим, а прямим. Що воно не збільшене, не зменшене, а в точності рівне оригіналу. Переконаєтесь і в тому, що ваше зображення є уявним, адже за дзеркалом вас нема і бути не може. Ну і звичайно ви не будите заперечувати проти того, що ви та ваше зображення дивитесь в різні сторони: ви – на зображення, а зображення – на вас. Якщо ж ви візьмете в праву руку гребінець, то зображення «візьме» свій гребінець у свою ліву руку.

В різноманітних оптичних системах, наряду з плоскими дзеркалами часто застосовують і дзеркала криві, тобто такі,  відбивна поверхня яких є частиною тієї чи іншої викривленої поверхні, зокрема сфери, циліндра, тора, еліпсоїда, параболоїда, тощо. Найпростішою та найбільш поширеною різноводністю кривих дзеркал є дзеркала сферичні. Відбивною поверхнею таких дзеркал є певна частина сфери.

В загальному випадку криві дзеркала поділяються на опуклі або розсіювальні та увігнуті або збиральні. Опуклі (розсіювальні) дзеркала характеризуються тим, що їх робоча поверхня є опуклою, і що вони розсіюють падаючі на них паралельні промені, причому розсіюють так, що уявні продовження відбитих променів перетинаються в околицях певної точки яку називають фокусом опуклого дзеркала (мал.139а). Увігнуті (збиральні) дзеркала характеризуються тим, що їх робоча поверхня є увігнуті, і що вони збирають падаючі на них паралельні промені, причому збирають так, що ці промені перетинаються в околицях певної точки яку називають фокусом увігнутого дзеркала (мал.139б). І не важко бачити, що фокус опуклого дзеркала є уявним, а фокус увігнутого дзеркала – дійсним.

 

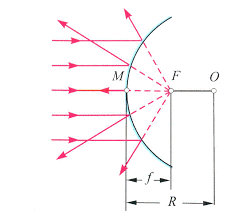
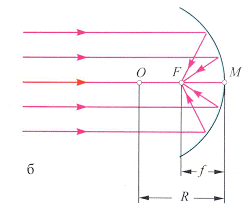
Мал.139. Криві дзеркала поділяються на опуклі (розсіювальні) і увігнуті (збиральні).

Збиральні властивості увігнутих та розсіювальні властивості опуклих дзеркал, є закономірним результатом їх геометричної форми та дії закону відбивання світла. Сьогодні ми не будемо заглиблюватись в деталі того, як на основі закону відбивання світла пояснюється принцип дії та функціональні можливості опуклих і увігнутих дзеркал. Зауважимо тільки, що подібні дзеркала мають достатньо широке практичне застосування.

Наприклад в кожному джерелі направленого світлового потоку, будь то кишеньковий ліхтарик, фари автомобіля чи прожектор маяка, направленість цього потоку створюється за допомогою відповідного увігнутого (збирального) дзеркала. Принцип дії такого дзеркала очевидно простий. Адже якщо паралельний потік світлових променів після відбивання від поверхні увігнутого дзеркала збинається у фокусі цього дзеркала (мал139б), то розмістивши в цьому фокусі джерело світла, ми отримаємо ситуацію при якій відбиті від поверхні дзеркала промені будуть паралельними і направленими в певному напрямку (мал.140а).

Увігнуті (збиральні) дзеркала дозволяють не лише створювати направлені світлові потоки, а й збирати велику кількість світлової енергії в одній точці (фокусі дзеркала) та сприяють перетворенню цієї енергії в енергію електричну, теплову чи скажімо ту інформаційну енергію, яка за допомогою дзеркальних телескопів перетвоюється в нові знання про Всесвіт.

Або наприклад в тому ж автомобілі можна побачити невеликі опуклі дзеркала які дозволяють на відносно малій площі дзеркала побачити відображення тих подій які відбуваються у великих об’ємах навколишнього простору.

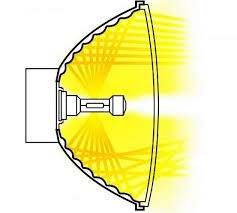
Мал.140. Деякі приклади практичного застосування сферичних дзеркал.

Задача 1. Побудувати дзеркальне відображення вектора АВ.

а) б)

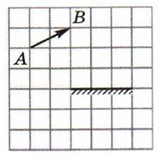
Рішення. Оскільки дзеркальне відображення будь якої точки, є симетричним відносно площини дзеркала, то для побудови цього зображення достатньо з відповідної точки провести перпендикуляр до площини дзеркала і на його задзеркальному продовженні відкласта відстань аналогічну відстані від точки до площини дзеркала.

Навіть в тому випадку, якщо відповідна точка, відрізок чи тіло знаходиться так би мовити за межами прямої видимості у дзеркалі (мал.б), побудова зображення здійснююється таким чином, ніби дзеркало є безкінечно довгим.

Різниця між ситуаціями (а) і (б) лише в тому, що в ситуації (а), перебуваючи в точці А ми бачимо її відображення в дзеркалі, а в ситуації (б) – не бачимо його. Втім, це зовсім не означає, що в ситуації (б), дзеркальне відображення точки А не бачать інші спостерігачі. Просто для цього потрібно знаходитися в області бачення точки А.

Задача 2. Перекресліть малюнок у зошит. Визначте область бачення точки S в дзеркалі та відстань від цієї точки до її зображення в дзеркалі.

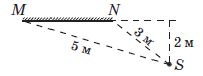
Загальні зауваження. Для того щоб визначити область бачення певної точки в дзеркалі обмежених розмірів, із цієї точки до країв дзеркала проводять два падаючі промені та застосовуючи закон відбивання світла будують їм відповідні відбиті промені. Область між цими відбитими променями і є областю бачення даної точки в даному дзеркалі.

На практиці, напрямки відбитих променів визначають не шляхом вимірювання кутів падіння та відкладання їм відповідних кутів відбивання, а шляхом проведення променя від точки дзеркального зображення (S’) до точки падіння відповідного променя (K, L). Точка ж дзеркального відображення заданої точки визначається дуже просто: через задану точку S проводиться перпендикуляр до лінії дзеркала (або до продовження цієї лінії), а точку зображення (S’) будують як таку, що знаходиться на такій же відстані від лінії дзеркала як і точка S. Наприклад:

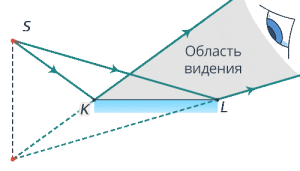
Рішення. Оскільки дзеркальне відображення будь якої точки, є симетричним відносно площини дзеркала, то відстань між точкою S та її зображенням S′,становитиме 2м + 2м = 4м.

Визначаючи область бачиння точки S в дзеркалі  MN, з цієї точки до крайніх точок дзеркала (точки M і N), проводимо падаючі промені, і у відповідності з законом відбивання світла, будуємо промені відбиті. Проміжок між цими відбитими променями і є областю бачення точки S в дзеркалі MN.

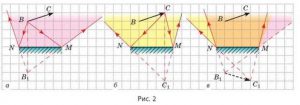
Задача 3. На малюнку схематично зображено предмет ВС і дзеркало NM. Визначте графічно ділянку, з якої зображення ВС видно повністю.

Рішення: Зображення відрізку ВС в дзеркалі NM буде видно в тій області простору, яка є спільною між областями бачення точок В і С. Тому, вище описаним способом графічно визначаємо області бачення точок В і С. При цьому, перетин цих областей і буде тією областю простору з якої відрізок ВС в дзеркалі NM видно повністю.

Задача 4. В кімнаті вертикально висить дзеркало, верхній край якого знаходиться на рівні маківки голови людини, ріст якої 180см. Якої мінімальної довжини має бути дзеркало, щоб людина бачила себе у повний ріст?

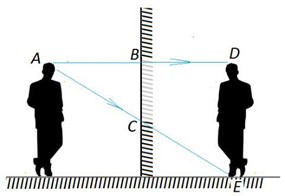
Рішення. Оскільки зображення людини в дзеркалі, знаходиться на тій же відстані як і сама людина, то трикутники ABC і ADE є подібними. При цьому коефіцієнт подібності дорівнює 1/2. А це означає, що довжина відрізка ВС, а відповідно і довжина дзеркала є вдвічі меншою за довжину відрізка DE (за ріст людини). Таким чином, мінімальна довжина дзеркала має становити 180см/2 = 90см.

Контрольні запитання.

1. Що називають дзеркалом?
2. На основі аналізу мал.137 поясніть принцип дії плоского дзеркала.
3. Що означає твердження: дзеркальне відображення є уявним?
4. Що означає твердження: відображення в плоскому дзеркалі є дзеркально симетричним?
5. Що треба зробити, щоб переконатися, що зображення предмету в плоскому дзеркалі є прямим, рівним, уявним та дзеркально симетричним? Зробіть це.
6. Чому опуклі дзеркала називають розсіювальними, а увігнуті – збиральними?
7. Що означає твердження: фокус опуклого дзеркала уявний, а фокус увігнутого дзеркала дійсний?
8. Поясніть принцип дії тих дзеркал які застосовуються в фарах автомобіля.

Вправа 35.

1. Людина стоїть перед дзеркалом. Як зміниться відстань між людиною та її зображенням, якщо вона відійде від дзеркала на 2м?
2. Людана йде в напрямку плоского дзеркала зі швидкістю 1,5м/с. З якою швидкістю вона наближається до свого зображення?
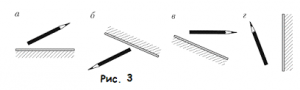
3. Перекресліть кожний малюнок у зошит та побудуйте зображення олівця у відповідному дзеркалі.

4. Перекресліть малюнок у зошит та обудуйте дзеркальне відображення трикутника АВС.

5. Перекресліть малюнок у зошит. Визначте область бачення точки S в дзеркалі та відстань від цієї точки до її зображення в дзеркалі.

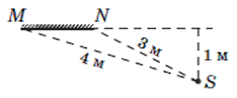
6. На якому з малюнків дзеркальне відображення букви Р є правильним.

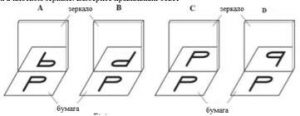
7. В кімнаті вертикально висить дзеркало, верхній край якого знаходиться на рівні маківки голови людини, ріст якої 180см. Якої довжини має бути дзеркало, щоб людина бачила себе до пояса?

8. Промінь відбивається від поверхні 1 і падає на поверхню 2. Яким буде кут падіння променя на поверхню 2.

9. На розташоване під кутом 50° до горизонту дзеркало, падає спрямований вертикально вниз промінь світла і відбивається. Який кут утворює відбитий промінь з горизонтом?

.

§36. Заломлення світла. Закон заломлення світла.

Дослідження показують, що на межі двох оптично різних, прозорих середовищ, наприклад повітря – скло, повітря – вода, вода – скло, скло – повітря, тощо, світлові промені частково відбиваються, а частково заломлюються, тобто проникаючи в нове середовище змінюють напрям свого поширення. Заломлення світла – це явище, суть якого полягає в тому, що на межі двох оптично різних, прозорих середовищ, частина світлового потоку проникає в нове середовище і змінюючи напрям свого руху (заломлюючись) продовжує поширюватись в цьому новому середовищі.

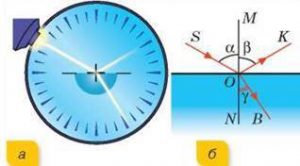
Мал.141. На межі двох опитично різних, прозорих середовищ, світло частково відбивається, а частково проникає в нове середовище, змінюючи при цьому напрям свого поширення.

З’ясовуючи закономірності заломлення світла звернемось до експерименту. А цей експеримент проведемо за допомогою все тієї ж оптичної шайби (мал.141, 142). Єдине що замінимо, так це дзеркальну смужку на прозору напівциліндричну пластину. Направивши пучок світла на плоску поверхню пластини, не важко бачити, що частина світла відбивається від цієї поверхні, а частина, змінюючи напрям свого поширення, проникає в нове середовище. При цьому те світло яке проникає в нове оптично прозоре середовище називають заломленим, а йому відповідні промені – заломленими. Якщо ж говорити про кутову орієнтацію заломленого променя, то вона характеризується відповідним кутом заломлення. Кутом заломлення променя (γ – гама) називають кут між заломленим променем та перпендикуляром до відбивної поверхні, проведеним в точці падіння променя.

Змінюючи кут падіння світлового променя, не важко бачити, що автоматично змінюється і кут його заломлення. Але на відміну від того простого співвідношення яке існує між кутом падіння (α) та кутом відбивання (β) променя і яке визначається формулою β = α, співвідношення між кутом падіння (α) та кутом заломлення (γ) променя, є значно складнішим. Це співвідношення було експериментально встановлено в 1621 році голанським вчерим В.Снеліусом (1580–1626). Снеліус з’ясував, що при будь якій зміні кута падіння променя, відношення синусу кута падіння променя (sinα) до синусу кута його заломлення (sinγ) є постійною величиною, значення якої залежить від оптичних властивостей відповідних середовищ. Іншими словами: sinα/sinγ = n = const.

 

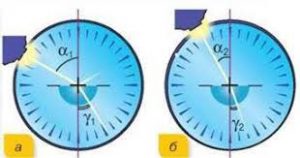
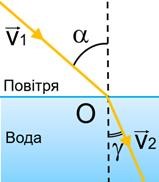
Мал.142. Дослідження показують, що між кутом падіння променя (α) та кутом його заломлення (γ) існує співвідношення sinα/sinγ = n₁₂ = const.

Змінюючи нахил відбивної (заломлюючої) поверхні до площини планшету, можна переконатися в тому, що промінь падаючий і промінь заломлений лежать в тій площині яка перпендикулярна до відбивної (заломлюючої) поверхні. Тобто переконатися в тому, що промінь падаючий, промінь заломлений та перпендикуляр до поверхні в точці падіння променя, лежать в одній площині.

Узагальнюючи вище сказане, можна сформулювати закон, який називається законом заломлення світла. В цьому законі стверджується: на межі двох оптично різних та оптично прозорих середовищ, світлові промені заломлюються, тобто проникаючи в нове середовище змінюють напрям свого розповсюдження. При цьому: 1) промінь падаючий, промінь заломлений та перпиндикуляр до поверхні в точці падіння променя, лежать в одній площині; 2) відношення синуса кута падіння променя (sinα) до синусу кута його заломлення (sinγ) для даної пари середовищ є постійною величиною, яка називається показником заломлення світла. Іншими словами: sinα/sinγ = n₁₂ = const, де n₁₂ – показник заломлення світла першого середовища відносно другого.

Показник заломлення світла певним чином характеризує оптичні властивості даного оптично прозорого середовища по відношенню до іншого оптично прозорого середовища. І якщо цим іншим середовищем є вакуум, то відповідний показник заломлення називають абсолютним.

Абсолютний показник заломлення світла, це фізична величина, яка характеризує оптичні властивості даного оптично прозорого середовища і яка з одного боку дорівнює відношенню синусу кута падіння променя до синусу кута його заломлення (sinα/sinγ), за умови переходу світла з вакууму в дане середовище, а з іншого – показує у скільки разів швидкість світла в даному середовищі (v) менша за швидкість світла у вакуумі (с=3·10⁸м/с).

Позначається: n

Визначальне рівняння: n = sinα/sinγ = c/v

Одиниця вимірювання: [n] = –,  безрозмірна величина (рази).

Абсолютний показник заломлення світла визначається експериментально і записується у відповідну таблицю, наприклад таку:

Речовина	n	Речовина	n
Повітря	1,0003	Скло віконне	1,52
Вода	1,33	Камяна сіль	1,54
Гліцерін	1,47	Цукор	1,56
Олія кедрова	1,52	Спирт етиловий	1,36
Олія сонячникова	1,47	Сапфір, рубін	1,77
Лід	1,31	Алмаз	2,42

Оскільки абсолютні показники заломлення світла повітря (n = 1,0003) та вакууму (n = 1,000000) є практично однаковими, то на практиці абсолютний показник заломлення даного середовища і його показник заломлення відносно повітря, прийнято вважати чисельно рівними.

Говорячи про закон заломлення світла, буде не зайвим сказати і про те, що у відповідності з цим законом, та у відповідності з експериментальними фактами, промінь падаючий та промінь заломлений є взаємно оборотними. Це означає, що коли падаючий промінь направити шляхом заломленого променя, то відповідний заломлений промінь піде шляхом падаючого.

     

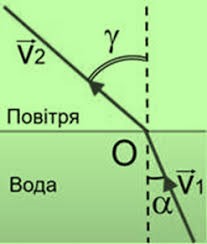
Мал.143. Промінь падаючий  промінь заломлений – взаємно оборотні.

Дослідження показують, що причиною заломлення світла є факт того, що в різних середовищах швидкість поширення світла є різною. При цьому, показник заломлення світла фактично показує, у скільки разів швидкість світла в першому середовищі (v₁) більша за швидкість світла в другому середовищі (v₂), тобто n₁₂ = v₁/v₂. Наприклад, якщо для пари повітря–вода n₁₂=1,33, то це означає, що швидкість світла у повітрі в 1,33 рази більша за швидкість світла у воді.

Потрібно зауважити, що швидкість світла є надзвичайно великою. Наприклад у вакуумі, ця швидкість дорівнюю 3·10⁸м/с = 300 000км/с, для порівняння, швидкість звуку у повітрі 0,34км/с. Швидкість світла у вакуумі є не лише фантастично великою, а й надзвичайно важливою величиною. Справа в тому, що Природа влаштована таким чином, що в ній швидкість світла у вакуумі (3·10⁸м/с) є гранично великою та абсолютною величиною. Це означає, що в Природі жоден фізичний обʼєкт не може рухатись з швидкістю більшою за швидкість світла у вакуумі (3·10⁸м/с), і що величина цієї швидкості не залежить ні від швидкості руху джерела світла, ні від швидкості руху спостерігача. Підкреслюючи факт абсолютності (незмінності) швидкості світла у вакуумі, цю швидкість позначають окремою літерою с=3·10⁸м/с, від лат. constans – постійний.

Порівнюючи оптичні властивості двох прозорих середовищ говорять, що те з них яке має більше значення абсолютного показника заломлення є оптично більш густим, а те яке має менше значення абсолютного показника заломлення – оптично менш густим. Наприклад алмаз (n = 2,42) оптично густіший за скло (n = 1,52), скло оптично густіше за воду (n = 1,33), а вода оптично густіша за повітря (n=1,0003).

Побутовими проявами заломлення світла є факти того, що частково занурені у воду предмети здаються зламаними, видима глибина водойм здається меншою за реальну, видиме розташування предметів у воді не співпадає з їх реальним розташуванням, тощо.

  

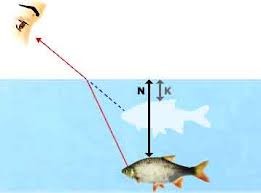
Мал.144. Побутові прояви заломлення світла.

Напевно ви ще не знайомі з тими математичними функціями які називаються синусом (sinα) і косинусом (cosα) кута. А якщо і знайомі, то скоріш за все, маєте хибне уявлення про фізичну суть цих важливих функцій. Бо та математика, яка існує за ради математики, дає саме таке, хибне уявлення про фізичну та загально наукову суть функцій sinα і cosα. І це при тому, що ця суть є досить простою.

З’ясовуючи суть того, що називають синусом (sinα) і косинусом (cosα) кута, проведемо прості побудови і не менш прості вимірювання. А для цих побудов та вимірювань потрібні циркуль, транспортир і лінійка.

Отже. Задаємо прямокутну систему координат, в якій горизонтальну вісь 0х називаємо віссю cosα, а вертикальну вісь 0у називаємо віссю sinα. В заданій системі координат, за допомогою циркуля, радіусом 10см, описуємо чверть кола і приймаємо заданий радіус за безрозмірну одиницю (10см = 1). Від осі cosα (від осі 0х) відкладаємо кути 0°, 30°, 45°, 60°, 90°. Із отриманих на колі точок опускаємо перпендикуляри на вісь cosα і sinα. Наприклад куту α = 30°, на колі відповідає точка А. При цьому проекцією цієї точки на вісь cosα буде точка В, а на вісь sinα – точа М (на малюнку не позначена). Виміряна в заданому масштабі (10см = 1) довжина відрізку 0В буде косинусом кута 30°, а довжина відрізку 0М буде синусом кута 30°. Вимірювання ж показують, що cos30° = 0,87; sin30° = 0,50.

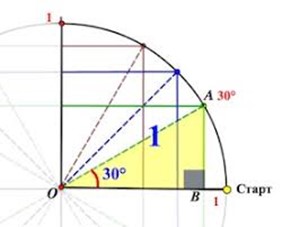
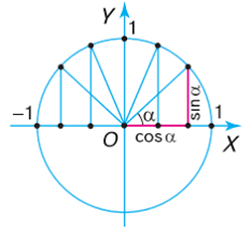
Загальні результати вимірювань записуємо в таблицю:

α	0°	30°	45°	60°	90°
cosα	1,00	0,87	0,71	0,50	0,00
sinα	0,00	0,50	0,71	0,87	1,00

Звісно, наші вимірювання є приблизними і стосуються лише певних, найбільш вживаних кутів. Втім, навіть цих побудов і вимірювань достатньо, щоб з’ясувати суть тих функцій які називаються синусом і косинусом кута, та помітити ті загальні закономірності, що є характерними для них. Якщо ж говорити про точні значення функцій cosα; sinα, то вони містяться у відповідних тригонометрични таблицях, та можуть бути визначеними через пошукову систему Google.

Задача 1. Промінь світла падає на межу двох прозорих середовищ. При цьому кут падіння промення дорівнює 40º, а кут між відбитим променем і заломленим 110º. Чому дорівнює кут заломлення променя.

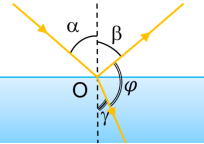
Дано:

α = 40º

φ = 110º

γ = ?

Рішення. Виконуємо малюнок який відображає описану в умові задачі ситуацію. На основі аналізу цього малюнка можна стверджувати: Оскільки згідно з законом відбивання світла β = α = 40º, та зважаючи на те, що β + φ + γ = 180º, можна записати γ = 180º – β – φ = 180º – 40º – 110º =  30º.

Відповідь: γ = 30º.

Задача 2. Промінь світла падає під кутом 60° з повітря на поверхню деякого прозорого середовища. При цьому, заломлений промінь зміщується на 15° від свого початкового напрямку. Визначте швидкість світла в другому середовищі, якщо у повітрі вона становить 3·10⁸м/с.

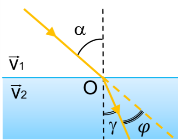
Дано:

α = 60°

φ = 15°

v₁ = 310⁸м/с

v₂ = ?

Рішення. Виконуємо малюнок на якому відображаємо наявну ситуацію. У відповідності з законом заломлення світла sinα/sinγ = v₁/v₂, звідси випливає v₂ = v₁sinγ/sinα. Із аналізу малюнку ясно, що γ + φ = α і тому γ = α – φ = 60°– 15°= 45°. Таким чином v₂ = v₁sinγ/sinα = v₁sin45φ/sin60°.

Розрахунки: v₂=3·10⁸(м/с)0,71/0,87 = 2,45·10⁸м/с.

Відповідь: v₂ = 2,45·10⁸м/с.

Контрольні запитання.

1. Що називають заломленням світла?
2. Що називають кутом заломлення променя?
3. Що стверджується в законі заломлення світла?
4. Чому на межі двох оптично різних середовищ світло заломлюється?
5. Що характеризує і чому дорівнює абсолютний показник заломлення світла?
6. Абсолютний показник заломлення води 1,33. Що це означає?
7. Абсолютний показник заломлення води 1,33, а льоду 1,31. Яке з цих середовищ оптично більш густе?
8. Що означає твердження: промінь падаючий та промінь заломлений взаємно оборотні?
9. Чи може світловий промінь переходити з повітря у скло, не змінюючи свого напрямку?

Вправа 36.

1. Промінь падає на межу повітря-скло. Який з малюнків є правильний?

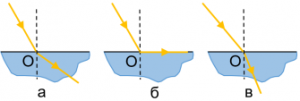
2. На якому з малюнків правильно показані промені та кути?

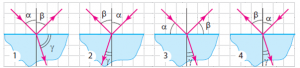
3. Шляхом геометричних побудов визначте синуси і косинуси кутів 15°, 25°, 50°, 75°. Порівняйте отримані результати з табличними значеннями відповідних величин.

4. Світловий промінь переходить з повітря в прозору рідину, при цьому кут падіння променя 45º, а кут його заломлення 30º. На який кут відхилився промінь від початкового напрямку?

5. Кут падіння променя 40º, а кут між падаючим і зпломленим променем променем 170º. Визначити кут заломлення променя.

6. Кут падіння променя на поверхню рідини дорівнює 60°, а кут заломлення 45°. Визначте показник заломлення рідини.

7. Світловий промінь переходить з повітря в прозору рідину, при цьому кут падіння променя 45º, а кут його заломлення 30º. Визначте показник заломлення рідини та швидкість світла в ній.

8. Швидкість світла в рідині 240000км/с. З повітря на поверхню цієї рідини падають світлові промені під кутом 30º. Визначити кут заломлення променів.

9. Світло падає на поверхню води під кутом 50º. Під яким кутом має падати світло на поверхню скла, щоб кут його заломлення в обох випадках був однаковим?

.

§37. Повне внутрішнє відбивання світла. Загальні відомості про оптичні призми та оптичні волокна.

Уважно спостерігаючи за тими експериментами які ми проводили при дослідженні закономірностей заломлення світла, можна помітити цікаву закономірність. По мірі збільшення кута падіння променів, кількість того світла яке відбивається від поверхні стає все більшою і більшою, а кількість світла яке проникає в нове середовище стає відповідно меншою. Якщо ж кут падіння світла дорівнює нулю (α = 0°), то світло практично не відбиваючись проникає в нове середовище.

Мал.145. При збільшенні кута падіння, кількість відбитого світла поступово збільшується, а кількість заломленого – відповідно зменшується.

Ще однією характерною закономірністю переходу світла із повітря (n = 1,0) в скло (n = 1,52), тобто з оптично менш густого середовища в оптично більш густе, є те, що при будь яких кутах падіння, кут заломлення променя менший за кут падіння (γ ˂ α).

А що буде, при зворотному переході, тобто при переході світла із скла в повітря. Або в загальному випадку – при переході з оптично більш густого середовища в оптично менш густе? Відповідаючи на це запитання звернемося до експерименту.

Цей експеримент допоможе зробити все та ж оптична шайба. А єдине що ми змінимо у порівнянні з попередніми експериментами, так це просторову орієнтацію напівциліндричної пластини. Змінимо таким чином, щоб падаючий промінь падав не на плоску поверхню цієї пластини (мал.146а), а на її циліндричну (круглу) поверхню (мал.146б). В такій ситуації падаючий промінь, за умови його направленості в геометричний центр пластини, завжди буде перпендикулярним до поверхні скла. А це означає, що цей промінь практично без енергетичних втрат і без зміни напрямку свого поширення потраплятиме у скло, а відповідно і на ту рівну поверхню яка відділяє скло від повітря.

  

Мал.146. При переході світла з оптично менш густого срередовища в оптично більш густе, кут заломлення променя менший за кут його падіння (γ ˂ α), а при зворотному переході – навпаки (γ ˃ α).

Не важко бачити, що при переході світла із скла у повітря, тобто з оптично більш густого середовища в оптично менш густе, кут заломлення світла γ більший за кут його падіння: γ ˃ α.  Ясно, що в такій ситуації при певному граничному куті падіння (α = α_гр) кут заломлення світлових променів становитеме 90º, і що при більших кутах падіння, величина кута заломлення має бути більшою за 90º. По суті це означає шо при певних кутах падіння (α ≥ α_гр) увесь світловий потік, повністю відбиватиметься від межі двох оптично прозорих середовищ. Таке відбивання називають повним внутрішнім відбиванням світла.

Повне внутрішнє відбивання світла, це явище, суть якого полягає в тому, що при певних кутах падіння (α ≥ α_гр) те світло яке поширюється в оптично більш густому середовищі, повністю відбивається від межі з оптично менш густим середовищем.

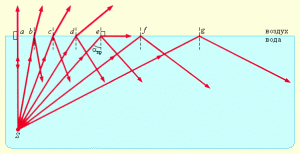
Мал.147.  При певних кутах падіння (α ≥ α_гр) те світло яке поширюється в оптично більш густому середовищі, повністю відбивається від межі з оптично менш густим середовищам.

Той найменший кут падіння при якоку відбувається повне внутрішнє відбивання світла, називають граничним кутом повного відбивання (позначається α_гр). Вимірювання показують, що відносно повітря, кут повного відбивання світла становить:

– для води (n = 1,33)  α_гр = 49º;

– для скла (n = 1,52)   α_гр = 41º;

– для алмазу (n = 2,42)  α_гр = 24º.

Повне відбивання світла, корисно застосовують в багатьох приладах, зокрема в оптичних призмах. Оптична призма, це прилад, який представляє собою оптично прозоре тіло, робочі поверхні якого геометрично та оптично рівні. Геометрична форма оптичної призми може бути різною. При цьому, в залежності від цієї форми та відносної просторової орієнтації, призма може виконувати певний набір функцій.

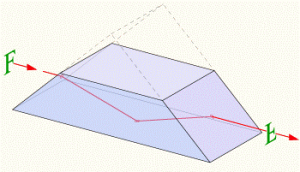
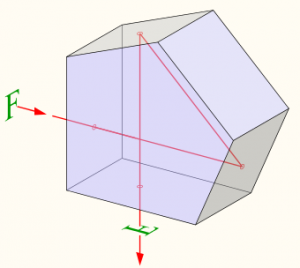
Мал.148. Геометрична форма та функціональні можливості оптичних призм можуть бути різними.

Принцип дії та функціональні можливості оптичної призми розглянемо на прикладі рівнобедреної прямокутно–трикутної призми (мал.149). В залежності від просторової орієнтації, ця призма може виконувати ряд оптичних функцій. Наприклад. Якщо призма розташована так як показано на мал.149а, то вона виконує функцію певним чином розташованого плоского дзеркала. Дійсно. За такого розташування призми, паралельні промені 1 і 2 падають на вертикальну поверхню під кутом 0º. При цьому, практично не відбиваючись і не заломлюючись, прормені проникають в скляне тіло призми. Розповсюджуючись в склі, промені під кутом 45º падають на похилу поверхню. А оскільки кут падіння променів більший за граничний кут повного відбивання скла (45º > 41º), то ці промені дзеркально відбиваються і під кутом 0º падають на горизонтальну поверхню. Практично не відбиваючись і не заломлюючись цією поверхнею, промені виходять з скляного тіла призми. Виходять, зберігаючи свою паралельність. А це означає, що за заданого розташування, призма не змінюючи параметрів зображення, змінює хід променів на 90º. Іншими словами, призма виконує роль плоского дзеркала яке розташоване під кутом 45º до напрямку розповсюдження світлових променів.

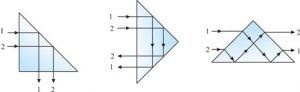
Мал.149. В залежності від просторової орієнтації, одна і та ж призма може виконуватии рід фупнкцій.

Аналогічним чином можна довести, що в ситуації 149б, дана призма виконує функції двох плоских дзеркал, які змінюють хід променів на 360º і перевертають вхідне зображення. Не важко довести і те, що в ситуації 149в, призма виконує функції двох заломлюючих поверхонь і одного плоского дзеркала та дозволяє, не змінюючи загального ходу променів, перевернати вхідне зображення.

Таким чином, в залежності від просторової орієнтації, одна і та ж рівнобедрена прямокутно–трикутна призма, може виконувати ряд функцій, зокрема: функцію певним чином розташованого плоского дзеркала, або функцію системи двох плоских дзеркал, або функцію дзеркала та двох заломлюючих поверхонь. При цьому, практично важливою особливістю призматичних дзеркал є факт того, що вони не мають спеціального шару відбивного матеріалу. А отже не потребують нанесення та захисту цього матеріалу, не бояться корозійного впливу навколишнього середовища, тощо. Крім цього, в залежності від просторової орієнтації, робоча поверхня оптичної призми може бути дзеркальною, напівдзеркальною чи оптичнор прозорою.

Із вище сказаного ясно, що оптична призма, це важливий багатофункціональний оптичний прилад. Прилад, який широко застосовується в багатьох більш складнох оптичних системах, зокрема біноклях, перескопах, мікроскопах, кутовимірювальних візирах, тощо.

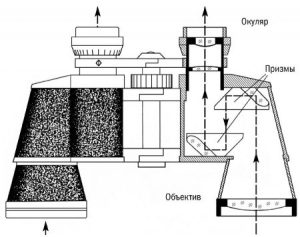
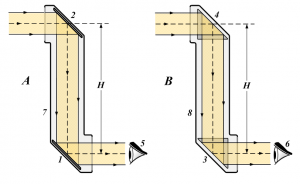
Мал.150. Призми є складовими елементами більш складних оптичних систем, зокрема: а)біноклів, б) пирескопів.

Однією з важливих та надзвичайно перспективних  сфер застосування повного відбивання світла є так звана волоконна оптика. Оптичними волокнами називають тонкі оптично прозорі волокна, які дозволяють передавати світлові потоки та світлову інформацію криволінійними траєкторіями. Принцип дії оптичного волокна полягає в наступному. Те світло, яке на вході потрапляє всередину оптично прозорого волокна, багаторазово відбиваючись від його поверхневого шару (шару який контактує з оптично менш густим середовищем) досягає вихідного зрізу цього волокна.

Мал.151. В оптичному волокні повне відбивання світла забезпечує рух світла за заданою траєкторією.

Зазвичай в волоконно–оптичних приладах застосовують не окремі оптичні волокна, а їх певну сукупність яку прийнято називати оптоволоконними кабелями. Оптоволоконний кабель (мал.151б), це прилад, який забезпечує криволінійний рух світлових потоків та світлової інформації і який представляє собою сукупність великої кількості щільно упакованих оптичних волокон.

Оптико–волоконні прилади мають широке застосування в багатьх галузях сучасної науки та техніки. В медицині, за допомогою гнучких світловодів досліджують стан внутрішніх органів людини та лікують ці органи. В промисловості, за допомогою світловодів досліджують технічний стан важкодоступних частин складних технічних систем. В системах комп’ютерних мереж та системах радіозвʼязку, за допомогою оптико–волоконних кабелів здійснюють передачу інформації. В військовій справі, світловоди застосовують для кодування інформації. За допомогою оптичних волокон вимірюють температуру, електричну напругу, тиск, тощо. Оптичні волокна застосовують в сейсмічних та гідролокаційних приладах, в лазерних гіроскопах та лазерних мікрофонах. Оптико-волоконне освітлення все частіше використовують в комерційній рекламі, мистецтві та побутовій техніці.

Задача. Шляхом геометричних побудов покажіть хід променя через скляну плоско паралельну пластину товщиною 20мм, якщо відомо, що кут падіння променя 50º, а кут його заломлення 30º. Визначте величину паралельного зміщення променя на виході з пластини.

Загальні зауваження. Алгебраїчне рішення подібних задач є достатньо складним і виходить за межі навчальної програми для 8-го класу. Однак якщо говорити про геометричне (графічне) рішення даної задачі, то воно є досить простим, і може слугувати наочним прикладом переваг та недоліків графічного рішення задач.

Рішення.

Дано:

d = 20мм

α = 50º

γ = 30º

ℓ = ?

Рішення. З застосуванням лінійки і транспортира та з дотриманням масштабу і правил геометричних побудов, виконуємо малюнок на якому d=20мм; α=50º; γ=30º. А оскільки у відповідності з законами геометричної оптики, падаючий

і заломлений промені взаємно оборотні, то можна стверджувати, що на виході з плоско паралельної пластини кут виходу променя буде дорівнювати куту його входу. А це означає, що вихідний промінь буде паралельним вхідному, але зміщеним відносно нього на певну відстань ℓ. Величину цієї відстані визначаємо експериментально, тобто шляхом вимірювання. А це вимірювання показує, що ℓ≈8мм. (Потрібно зауважити, що з метою отримання більш точних результатів, масштаб побудов можна збільшити, наприклад товщину пластинки взяти не 20мм а 40мм.

Відповідь: ℓ ≈ 8мм.

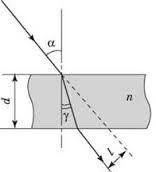
Таким чином, закони геометричної оптики стверджують, а експериментальні факти це підтверджують, що при проходженні через прозорі плоско паралельні пластини, світлові промені не змінюючи напрямку свого розповсюдження зміщуються на певну відстань, величина якої залежить від товщини пластини, показника її заломлення та кута падіння променів.

Контрольні запитання.

1. Від чого залежить співвідношенні між кількістю відбитого та заломленого світла? Якою є ця залежність?
2. Яке середовище називають оптично більш густим, а яке – оптично менш густим?
3. Що називають повним внутрішнім відбиванням світла?
4. Чому при переході з повітря в скло повного відбивання світла не відбувається а пи переході з скла в повітря – відбувається.
5. Для скла граничний кут повного відбивання дорівнює 41°. Що це означає?
6. Поясніть поведінку світлових променів в ситуаціях зображених на мал.161
7. Які переваги призматичного дзеркала над звичайним?
8. Які функції виконує рівнобедрена прямокутно-трикутна призма в а) біноклі; б) перископі (мал.162)
9. Поясніть принцип дії оптичного волокна.

Вправа 37.

1. На якому з малюнків зображено промінь який переходить з оптично більш густого середовища в оптично менш густе.

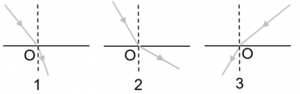
2. Перекресліть кожний малюнок у зошит та вкажіть хід променів в кожному з скляних тіл.

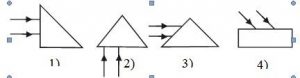
3. Перекресліть кожний малюнок у зошит. Вважаючи що середовище 1 має більшу оптичну густину, для кожного випадку побудуйте відсутній на малюнку падаючий або заломлений промінь. Позначте кут падіння та кут заломлення.

4. Для кожної представленої на малюнку ситуації, вкажіть напрямки відбитих та заломлених променів (верхнє середовище повітря, нижнє – вода).

5. На якому малюнку правильно показано хід променів крізь скляну призму?

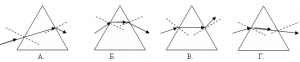
6. Шляхом геометричних побудов покажіть хід променя через скляну плоско паралельну пластину товщиною 20мм, якщо відомо, що кут падіння променя 70º, а кут його заломлення 38º. Визначте величину паралельного зміщення променя на виході з пластини.

7. Шляхом геометричних побудов покажіть хід променя через скляну плоско паралельну пластину товщиною 20мм, якщо відомо, що кут падіння променя 40º, а кут його заломлення 25º. Визначте величину паралельного зміщення променя на виході з пластини.

.

§38. Загальні відомості про лінзи та параметри тих зображень які вони формують.

Лінза (оптична лінза), це прилад, який представляє собою оптично прозоре тіло обмежене двома оптично рівними криволінійними або криволінійною та плоскою, поверхнями і який визначеним чином формує відповідне оптичне зображеня. В залежності від форми обмежуючих поверхонь, лінзи поділяються на сферичні, циліндричні, тороїдальні та інші. При цьому, найбільш поширеною різновидністю лінз є лінзи сферичні. Власне, про такі лінзи ми і будемо говорити в подальшому.

Характерною властивістю будь якої лінзи є її здатність заломлювати світлові промені та формувати відповідне оптичне зображення. За зовнішніми ознаками та характером поведінки заломлених променів, лінзи поділяються на збиральні або опуклі та розсіювальні або вгнуті.

Збиральними (опуклими) називають такі лінзи, які будучи розташованими в оптично менш густому середовищі, збирають початково паралельні промені в околицях певної точки, яку називають фокусом лінзи. Характерною зовнішньою ознакою збиральних лінз є їх опуклість, тобто факт того, що центральна частина лінзи, товща за краєву. В залежності від особливостей геометричної форми, збиральні лінзи поділяються на: подвійноопуклі, плоскоопуклі та вгнутоопуклі.

         Розсіювальними (увігнутими) називають такі лінзи, які будучи розташованими в оптично менш густому середовищі, розсіюють початково паралельні промені, причому розсіюють таким чином, що їх уявні продовження перетинаються в околицях певної точки, яку називають фокусом розсіювальної лінзи. Характерною зовнішньою ознакою розсіювальних лінз є їх увігнутість, яка проявляється в тому, що центральна частина розсіювальної лінзи тонща за краєву. В залежності від особливостей геометричної форми, розсіювальні лінзи поділяються на: подвійноувігнуті, плоскоувігнуті та опуклоувігнуті.

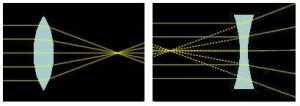
Мал.152. За зовнішніми ознаками та характером поведінки заломлених променів, лінзи поділяються на збиральні (опуклі) та розсіювальні (увігнуті).

До числа основних геометричних характеристик оптичної лінзи відносяться: оптичний центр лінзи (т.O), головна оптична вісь лінзи (пряма, що проходить через оптичний центр лінзи та є перпендикулярною до площини лінзи), фокус лінзи (т.F) фокусна відстань (ƒ) та оптична сила лінзи (D = 1/ƒ).

Фокусом (головним фокусом) лінзи, називають ту точку, в якій дійсно або уявно перетинаються ті заломлені лінзою промені, які до проходження через лінзу були паралельними її головній оптичній осі. При цьому, якщо у відповідній точці заломлені промені дійсно перетинаються, то фокус є дійсним, а якщо заломлені промені у відповідній точці перетинаються уявно, то фокус є уявним. Наприклад в збиральних лінзах фокус є дійсним, а в розсіювальних – уявним. Відстань від фокусу лінзи до її оптичного центру називають фокусною відстанню лінзи (позн.ƒ).

а)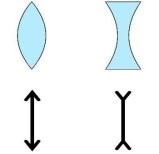 б)

Мал.153.  Умовне позначення та основні геометричні характеристики лінзи.

На практиці, заломлювальні властивості оптичної лінзи характеризують величиною яка називається оптичною силою лінзи. Оптична сила лінзи, це фізична величина, яка характеризує заломлювальні властивості опричної лінзи і яка обернена до її фокусної відстані.

Позначається:  D

Визначальне рівняння:  D = 1/ƒ

Одиниця вимірювання:  [D] = 1/м = дп,   діоптрія.

Прийнято вважати, що оптична сила збиральної лінзи є дадатною (D > 0), а оптична сила розсіювальної лінзи – від’ємною (D < 0). Наприклад, Якщо D = +2дп, то це означає: збиральна лінза має фокусну відстань 0,5м (ƒ = 1/D = 1/2дп = 0,5м). Якщо D = –0,5дп, то це означає: розсіювальна лінза має фокусну відстань 2м (ƒ = 1/D = 1/0,5дп = 2м).

Заломлювальні властивості лінзи, а відповідно і її фокусна відстань (ƒ) та оптична сила (D = 1/ƒ), визначально залежать від ступеню опуклості (увігнутості) лінзи. При цьому чим більш опуклою (чим більш увігнутою) є лінза, тим менша її фокусна відстань і навпаки.

Мал.154. Чим більш опукла лінза, тим менша її фокусна відстань і навпаки.

В залежності від того з якого боку світло падає на лінзу, її фокус може бути як з однієї так і з протилежної сторони. При цьому часто говорять, що лінза має два фокуси. А оскільки ці фокуси є симетричними відносно оптичного центру лінзи, та враховуючи, що «правильні» фокуси збиральних і розсіювальних лінз знаходяться по різні боки цих лінз, «правильні» і «неправильні» фокуси часто плутають між собою. Тому запам’ятайте, при побудовах, розрахунках та поясненнях, «правильним» фокусом лінзи є той, в якому після заломлення, дійсно (для збиральних лінз) чи уявно (для розсіювальних лінз) перетинаються ті промені які падають на лінзу. Наприклад зображені на малюнку 153б фокуси, є «правильними». І давайте домовимося «правильний» фокус лінзи називати просто «фокус» лінзи. Якщо ж мова йтиме про симетричного близнюка «правильного» фокусу, то його будемо називати допоміжним фокусом.

Застосовуючи закон заломлення світла, можна визначити хід будь якого променя в будь якій лінзі. Однак, практичне застосування цього закону є надзвичайно складним. Адже для того щоб передбачити поведінку лише одного заломленого лінзою променя, потрібно виконати цілу низку точних побудов, вимірювань та розрахунків. Зважаючи на ці обставини, параметри того зображення яке створює лінза, визначають на основі певного набору базових променів, поведінка яких є загальновідомою. Хід цих базових променів представлений на мал.155 і є наступним:

1 – якщо падаючий промінь проходить через оптичний центр лінзи, то промінь заломлений є прямим продовженням падаючого променя;

2 – якщо падаючий промінь паралельний головній оптичній осі лінзи, то промінь заломлений дійсно (для збиральних) або уявно (для розсіювальних) проходить через фокус лінзи;

3 – якщо падаючий промінь дійсно або уявно проходить через допоміжний фокус лінзи, то заломлений промінь є паралельним головній оптичній осі відповідної лінзи.

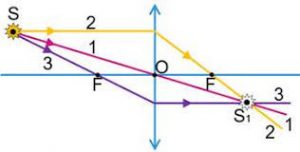
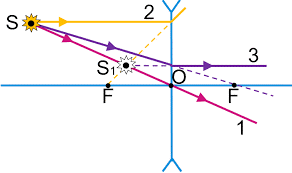
Мал.155.  Виконуючи геометричні побудови тих зображень які утворюють збиральні (а) та розсіювальні (б) лінзи, застосовують певний набір базових променів.

Втім на практиці, для отримання того зображення яке дає лінза, достатньо застосувати два базові промені. Зазвичай цими базовими променями є (1) і (2). При цьому третій базовий промінь якщо і застосовується, то лише з метою перевірки достовірності отриманого результату.

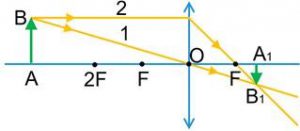
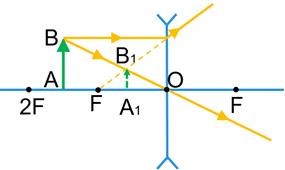
Мал.156. На практиці побудову того зображення яке дає лінза виконують за допомогою двох базових променів.

Варто зауважити, що при практичній реалізації графічного методу визначення параметрів зображень, часто зустрічаються ситуації коли лінійні розміри предмету більші за лінійні розміри тієї лінзи яка формує зображення цього предмету (мал.157). Подібні ситуації не повинні змінювати логіку ваших геометричних побудов. Адже параметри того зображення яке формує лінза, не залежать від того потрапляє чи не потрапляє на неї той паралельний промінь який виходить з крайньої точки тіла і який після заломлення має пройти через фокус лінзи. Бо це зображення формує не один і не два промені, а вся незліченна сукупність тих променів які виходять з усіх точок тіла. І вся ця сукупність сформує зображення предмету там, де воно і має бути у відповідності з законами геометричної оптики. А це означає, що визначаючи параметри зображення, ви можете використовувати будь які зручні для вас промені, в тому числі і ті, які в реальності не проходять крізь лінзу. Головне щоб хід цих променів був визначений у відповідності з законами геометричної оптики.

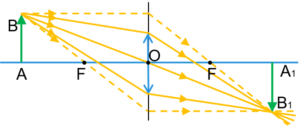
Мал.157. Визначаючи параметри зображення, ви можете використовувати будь які зручні для вас промені, в тому числі і ті, які в реальності не проходять крізь лінзу.

Очевидною перевагою геометричного методу визначення параметрів тих зображень які створюють лінзи, є його простота та очевидність результату. Скажімо одного погляду достатньо, щоб дати загальну характеристику того зображення яке створюють представлені на мал.156 збиральна і розсіювальна лінзи. Адже ці характеристики є очевидними: те зображення яке створює збиральна лінза (мал.156а) є перевернутим, зменшеним і дійсним; а те зображення яке створює розсіювальна лінза (мал.156б) є прямим, зменшеним і уявним.

Ілюструючи можливості графічного методу визначення параметрів тих зображень які створюють збиральні і розсіювальні лінзи, а заодно і досліджуючи властивості самих лінз, розглянемо конкретні ситуації.

1. Предмет розташований за подвійним фокусом збиральної лінзи.

 

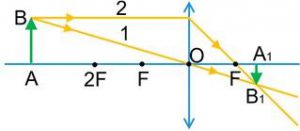
Результат побудов: зображення предмету є дійсним, перевернутим, зменшеним. Подібна ситуація реалізується наприклад, в оптичній системі ока людини, яка фокусує зображення віддалених предметів на сітківці ока.

2. Предмет розташований на подвійній фокусній відстані від збиральної лінзи.

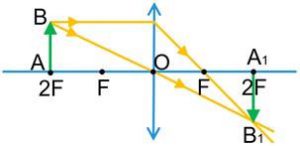
Результат побудов: зображення предмету є дійсним, перевернутим, рівним. Подібна ситуація не має практичного застосування. Адже зазвичай лінзи застосовуються для отримання збільшених або зменшених зображень.

3. Предмет розташований між фокусом і подвійним фокусом збиральної лінзи.

 

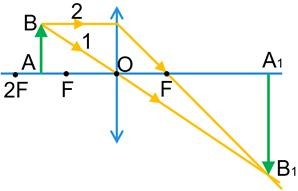
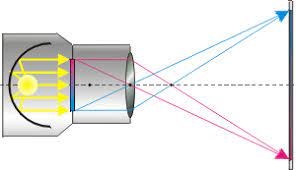
Результат побудов: зображення предмету є дійсним, перевернутим, збільшеним. Такі зображення створюють на екранах різноманітні проекційні апарати.

4. Предмет розташований на фокусній відстані від збиральної лінзи.

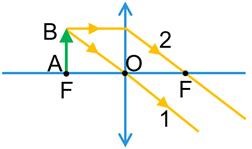
Результат побудов: за такого розташування, заломлені лінзою промені будуть паралельними, а отже такими, які ніде не перетинаються. А це означає, що у цьому випадку ані дійсного, ані уявного зображення лінза не створює.

5. Предмет розташований між фокусом і збиральною лінзою.

  

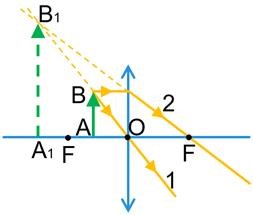
Результат побудов: зображення предмету є уявним, прямим, збільшеним. Подібна ситуація реалізується в тих практично важливих випадках коли збиральну лінзу ми використовуємо в якості так званого збільшувального скла (лупи).

Не важко бачити, що в залежності від розташування тіла, його зображення в збиральній лінзі може бути як дійсним так і уявним, як збільшеним так і зменшеним, як прямим так і перевернутим. Крім цього, якщо тіло знаходиться в фокальній площині збиральної лінзи, то воно не має певного зображення, а точніше, це зображення розчиняється в безкінечності.

Зверніть увагу на динаміку зміни того зображення яке дає збиральна лінза в процесі наближення предметів до неї. А ця динаміка є наступною. По мірі наближення безкінечно віддалегого предмету до збиральної лінзи, його дійсне, перевернуте, зменшене зображення, поступово збільшується. При цьому на фокусній відстані від лінзи, це зображення стає безкінечно великим і таким що розчиняється в безкінечності. Коли ж відстань стає меншою за фокусну, зображення ніби виринає з безкінечності і стає прямим, уявним та збільшеним.

Якщо ж говорити про ті зображення які дає розсіювальна лінза, то в незалежності від відстані від предмету до лінзи, створюване лінзою зобрадення буде уявним, зменшеним і прямим.

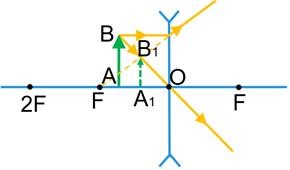
6. Результат побудов: в незалежності від відстані від предмету до розсіювальної лінзи, створюване лінзою зобрадення цього предмету буде уявним, зменшеним і прямим.

Варто зауважити, що ті дійсні зображення які створюють збиральні лінзи, ми бачимо лише у вигляді їх відображення на сторонньому екрані. Якщо ж говорити про ті зображення які називаються уявними, то спостерігач чітко бачить ці зображення в незалежності від того що створює уявне зображення, плоске дзеркало, опукле дзеркало, збиральна лінза чи лінза розсіювальна, і в незалежності від того на якій відстані від цього зображення знаходиться спостерігач.

Мал.158. Уявні зображення ми бачимо в незалежності від того, який оптичний прилад ці зображення створює.

Завершуючи розмову про оптичні лінзи, зробимо ще одне важливе зауваження. Коли ми стверджуємо, що опуклі лінзи є збиральними, а увігнуті – розсіювальними, то маємо на увазі, що оптична густина того матеріалу з якого виготовлена лінза (зазвичай скло n=1,52) більша за оптичну густину того середовища в якому знаходиться лінза (зазвичай повітря n=1,0003). Однак закони геометричної оптики стверджують, а експериментальні факти це підтверджують, що при зворотній ситуації, властивості лінз будуть зворотніми. Наприклад, якщо розташованій у воді повітряній бульбашці надати форму опуклої лінзи, то ця лінза буде розсіювальною, а відповідна вгнута лінза – збиральною. Втім, враховуючи факт того, що в реальних ситуаціях лінзи практично завжди оточені менш густим середовищем, прийнято вважати, що опуклі лінзи є збиральними, а вгнуті – розсіювальними.

Мал.159. В оптично більш густому середовищі, збиральна лінза стає розсіювальною, а розсіювальна – збиральною.

Контрольні запитання.

1. Які лінзи називають збаральними? Чому їх друга назва – опуклі?
2. Які лінзи називають розсіювальними? Чому їх друга назва – увігнуті?
3. Що називають фокусом лінзи? Фокусною відстанню лінзи? Чому фокус збиральної лінзи дійсний, а розсіювальної – уявний?
4. Що характеризує і чому дорівнює оптична сила лінзи?
5. Від чого залежить оптична сила лінзи?
6. Опишіть хід тих базових променів за допомогою яких визначають параметри тих зображень які формують збиральні і розсіювальні лінзи.
7. Опишіть динаміку змін того зображення, яке дає збиральна лінза в процесі наближення предмету до неї.
8. Опишіть динаміку змін того зображення, яке дає розсіювальна лінза в процесі наближення предмету до неї.
9. Опишіть принцип дії приладу який називається лупа.
10. За яких умов опукла лінза стає розсіювальною, а увігнута – збиральною?

Вправа 38.

1. Які із зображених лінз є збиральними:

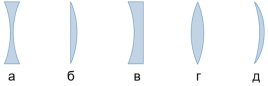
2. Яка з лінз має більшу оптичну силу?

3. Оптична сила лінзи дорівнює: а) +4дп; б) +0,4дп; в) –3дп; г) –0,25дп. Які це лінзи і яка їх фокусна відстань.

4. Фокусна відстань збиральної лінзи 25см, а розсіювальної 1,5м. Визначте оптичні сили цих лінз.

5. Шляхом геометричних побудов, визначити параметри зображення вертикильного відрізку висотою h=1,5см, яке дає збиральна лінза фокусна відстань якої ƒ=3см. Відстань від предмету до оптичного центру лінзи: а) ℓ₁=8см; б) ℓ₂=6см; в) ℓ₃=4см; г) ℓ₄=3см; д) ℓ₅=2см. Параметри зображення: це 1) загальна характеристика зображення; 2) висота зображення hꞌ=?; 2) відстань від лінзи до зображення ℓꞌ=?

6. Шляхом геометричних побудов, визначити параметри зображення вертикильного відрізку висотою 1,5см, яке дає розсіювальна лінза фокусна відстань якої 4см. Відстань від предмету до оптичного центру лінзи: а) 10см; б) 8см; в) 6см; г) 4см; д) 2см.

.

§39. Графічне та алгебраїчне визначення параметрів тих зображень які формують лінзи. Формула лінзи.

В попередньому параграфі ми навели велику кількість доказів того, що параметри тих зображень які формують збиральні і розсіювальні лінзи, можна визначити графічно, оперуючи при цьому лише двома базовими променями. Наразі ж ми не лише помножимо кількість цих доказів, а й покажемо як подібні задачі розв’язуються алгебраїчно.  Але спочатку зробимо одне важливе зауваження.

Це зауваження стосується факту того, що вище описаний графічний метод визначення параметрів тих зображень які формують лінзи, є задовільно точним лише для так званих тонких лінз, тобто таких лінз товщина яких є відносно малою. Обгрунтованість такої вимоги випливає бодай з того, що твердження «якщо падаючий промінь проходить через оптичний центр лінзи, то промінь заломлений є прямим продовженням падаючого», не зовсім відповідає дійсності. Адже при проходженні променя через плоско паралельну пластину (а центральна частина як збиральних так і розсіювальних лінз, фактично і є такою пластиною), відбувається певне паралельне зміщення променя, величина якого залежить від товщини пластини. А це означає, що та точка зображення якої ми визначаємо виходячи з того, що заломлений промінь є прямим продовженням падаючого, незовсім співпадає з її реальною координатою. І величина цього неспівпадіння залежить від товщини лінзи.

В попередніх задачах, ми розглядали ситуації, в яких одна з точок заданого тіла знаходиться на головній оптичній осі, а саме тіло є перпендикулярним до цієї осі. Але ті загальні правила які ми застосовували при розв’язуванні цих простих задач, дозволяють розв’язувати і значно складніші задачі. Просто в складніших задачах потрібно визначати параметри не однієї точки, а більшої їх кількості. Ілюструючи вище сказане розглянемо ряд конкретних ситуацій.

Задача 1. Шляхом геометричних побудов визначити параметри зображення тіла.

Загальні зауваження. Одна з переваг графічного рішення задачі полягає в тому, що воно є наочним і зазвичай таким, що не потребує додаткових пояснень. Наприклад рішення всіх нище наведених задач полягає в тому, що із крайніх точок наявного тіла проводять два базові промені, які після їх заломлення перетинаються в певній точці яка і є точкою відповідного зображення.

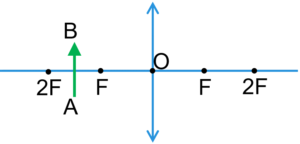
1) Зображення предмету: дійсне, збільшене, перевернуте.

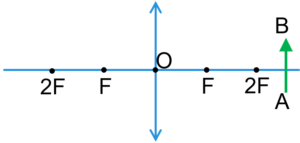
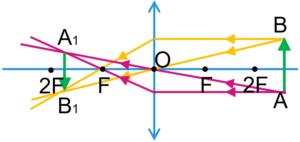
2) Зображення предмету є дійсним, зменшеним, перевернутим.

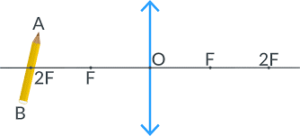
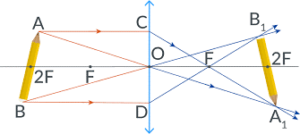
3) Зображення предмету є дійсним, рівним, перевернутим.

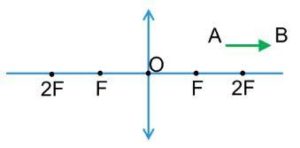
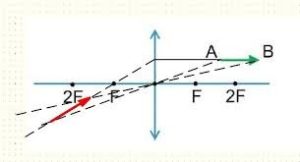
4) Зображення предмету є дійсним (кутова орієнтація та розміри зображення визначаються індивідуально).

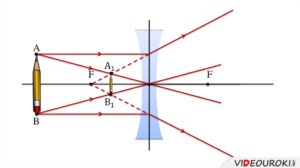
5) Зображення предмету є уявним, прямим, зменшеним).

Задача 2. На малюнку показано головну оптичну вісь лінзи (KN), світлову току S та її зображення S₁. Визначити розташування оптичного центру та фокусу лінзи, тип лінзи і тип зображення.

Рішення. 1. Оскільки світлова точка та її зображення знаходяться на тій прямій, яка проходить через оптичний центр лінзи, то провівши пряму SS₁ та визначивши точку її перетину з головною оптичною віссю лінзи (точка О), ми фактично визначаємо оптичний центр лінзи.

2. Оскільки оптична площина лінзи перпендикулярна до її головної оптичної осі, то провівши через точку О пряму (площину) яка перпендикулярна до цієї осі, ми визначаємо положення оптичної осі (площини) лінзи, тобто тієї умовної лінії на якій відбувається зміна напрямку поширення променя.

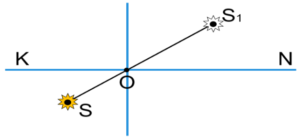
3. Із аналізу малюнку видно, що точки S і S₁ знаходяться по різні боки лінзи, а це можливо лише в тому випадку якщо відповідна лінза збиральна.

4. Оскільки той промінь який виходить з точки S і є паралельним головній оптичній осі лізи, після заломлення проходить як через фокус цієї лінзи, так і через зображення точки S, тобто через точку S₁, то виконавши відповідну побудову, ми визначаємо місцезнаходження фокусу лінзи (точка F).

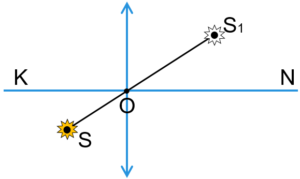
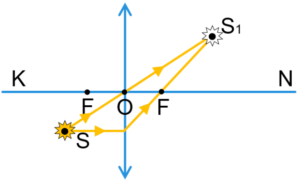
5. Оскільки ті базові промені які виходять з точки S, дійсно перетинаються в точці S₁, то відповідне зображення є дійсним.

Можна довести, що між відстанню від предмету до лінзи ℓ, відстанню від лінзи до зображення предмету ℓꞌ та фокусною відстанню лінзи ƒ, існує співвідношенням 1/ℓ + 1/ℓꞌ = 1/ƒ. Це співвідношення називають формулою лінзи.

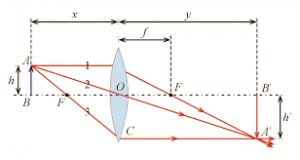
Мал.160. Відстань від предмету до лінзи ℓ, від лінзи до зображення предмету ℓꞌ та фокусна відстань лінзи ƒ, зв’язані співвідношенням 1/ℓ + 1/ℓꞌ = 1/ƒ, (на малюнку ℓ = х, ℓ′= у).

Аналізуючи формулу 1/ℓ + 1/ℓꞌ = 1/ƒ, та те очевидне    співвідношення яке випливає із подібності трикутників АВО і ОВꞌАꞌ (мал.160) і в якому стверджується, що h/hꞌ = ℓ/ℓꞌ, не важко вивести ті кількісні співвідношення які існують між фокусною відстанню лінзи (ƒ), координатами заданої точки (ℓ, h) та координатами її зображення (ℓʹ, hʹ).

Дійсно. Із рівняння 1/ℓ + 1/ℓꞌ = 1/ƒ, випливає 1/ℓ′ = 1/ƒ – 1/ℓ = (ℓ – ƒ) / ƒ∙ℓ, звідси ℓ′ = ƒ∙ℓ / (ℓ – ƒ). Оскільки h/hꞌ = ℓ/ℓꞌ, то hꞌ = h∙ℓ′/ℓ = h∙ƒ∙ℓ / ℓ∙(ℓ – ƒ) = h∙ƒ / (ℓ – ƒ) = h′. Таким чином, координати зображення заданої точки, можна визначити за формулами   ℓ′ = ƒ∙ℓ/(ℓ – ƒ), hꞌ = h∙ƒ/(ℓ – ƒ).

Вище сказане означає, що параметри того зображення яке формує тонка збиральна чи розсіювальна лінза, можна визначити не лише шляхом геометричних побудов, а й шляхом алгебраїчних розрахунків. Ці розрахунки здійснюються за формулами ℓʹ = ℓƒ/(ℓ–ƒ); hʹ = hƒ/(ℓ–ƒ), де

ƒ – фокусна відстань лінзи;

ℓ – відстань від тіла до лінзи;

h – висота тіла;

ℓꞌ – відстань від лінзи до зображення тіла;

hꞌ – висота зображення.

Застосовуючи дані формули та аналізуючи отримані результати, керуються наступними правилами знаків:

1. Фокусна відстань збиральної лінзи є додатньою (ƒ > 0), а фокусна відстань розсіювальної лінзи – від’ємною (ƒ ˂ 0).
2. Якщо ℓʹ > 0, то зображення дійсне, а якщо ℓʹ ˂ 0 – уявне.
3. Якщо h i hʹ мають однакові знаки, то зображення перевернуте, а якщо ці знаки є різними – то пряме.

Ілюструючи можливості формул ℓʹ = ℓƒ/(ℓ–ƒ); hʹ = hƒ/(ℓ–ƒ), розв’яжемо задачі 5 і 6 з вправи 41, алгебраїчним способом. А оскільки графічним способом ці задачі ви вже розв’язували, то матимете можливість порівняти результати графічного і алгебраїчного рішень та зробити відповідні висновки.

Задача 3. Шляхом алгебраїчних розрахунків, визначити параметри зображення вертикильного відрізку висотою h = 1,5см, яке дає збиральна лінза фокусна відстань якої ƒ = 3см. Відстань від предмету до оптичного центру лінзи: а) ℓ₁ = 8см; б) ℓ₂ = 6см; в) ℓ₃ = 4см; г) ℓ₄ = 3см; д) ℓ₅ = 2см.

На малюнку х = ℓ, у = ℓ′.

Дано:

ƒ = 3см;

h = 1,5см;

ℓ₁ = 8см;

ℓ₂ = 6см;

ℓ₃ = 4см;

ℓ₄ = 3см;

ℓ₅ = 2см.

Визначити та охарактеризувати параметри зображення.

Рішення. Застосовуючи формули ℓʹ = ℓƒ/(ℓ–ƒ); hʹ = hƒ/(ℓ–ƒ), визначаємо координати (ℓ′, h′) зображення вершини заданого відрізку в кожній з заданих ситуацій, і на основі вище сформульованих правил знаків, характеризуємо відповідне зображення.

1) ℓ₁ʹ = 8·3/(8–3) = 4,8см;  h₁ʹ = 1,5·3/(8–3) = 0,9см.

Зображення: дійсне (ℓʹ > 0), зменшене (h′ < h), перевернуте (h i hʹ мають однакові знаки).

2) ℓ₂ʹ = 6·3/(6–3) = 6,0см;  h₂ʹ = 1,5·3/(6–3) = 1,5см.

Зображення: дійсне (ℓʹ > 0), рівне (h′ = h), перевернуте (h i hʹ мають однакові знаки).

3) ℓ₃ʹ = 4·3/(4–3) = 12,0см;  h₃ʹ = 1,5·3/(4–3) = 4,5см.

Зображення: дійсне (ℓʹ > 0), збільшене (h′ > h), перевернуте (h i hʹ мають однакові знаки).

4) ℓ₄ʹ = 3·3/(3–3) = ∞см;  h₄ʹ = 1,5·3/(3–3) = ∞см.

Предмет не має зображення (зображення розчиняється в безкінечності).

5) ℓ₅ʹ = 2·3/(2–3) = –6,0см;  h₅ʹ = 1,5·3/(2–3) = –4,5см.

Зображення: уявне (ℓʹ < 0), збільшене (h′ > h), пряме (h i hʹ мають різні знаки).

Задача 4. Шляхом алгебраїчних розрахунків, визначити параметри зображення вертикильного відрізку висотою 1,5см, яке дає розсіювальна лінза фокусна відстань якої 4см. Відстань від предмету до оптичного центру лінзи: а) 10см; б) 8см; в) 6см; г) 4см; д) 2см.

На малюнку АО = ℓ, А₁О = ℓ′, FO = ƒ.

Дано:

ƒ = –4см;

h = 1,5см;

ℓ₁ = 10см;

ℓ₂ = 8см;

ℓ₃ = 6см;

ℓ₄ = 4см;

ℓ₅ = 2см.

Визначити та охарактеризувати параметри зображення.

Рішення. Застосовуючи формули ℓʹ = ℓƒ/(ℓ–ƒ); hʹ = hƒ/(ℓ–ƒ), визначаємо координати (ℓ′, h′) зображення вершини заданого відрізку в кожній з заданих ситуацій, і на основі вище сформульованих правил знаків, характеризуємо відповідне зображення.

1) ℓ₁ʹ = 10(–4)/(10+4) = –2,86см;  h₁ʹ = 1,5(–4)/(10+4) = –0,43см.

Зображення: уявне (ℓʹ < 0), зменшене (h′ < h), пряме (h i hʹ мають різні знаки).

2) ℓ₂ʹ = 8(–4)/(8+4) = –2,67см;  h₂ʹ = 1,5(–4)/(8+4) = –0,50см.

Зображення: уявне (ℓʹ < 0), зменшене (h′ < h), пряме (h i hʹ мають різні знаки).

3) ℓ₃ʹ = 6(–4)/(6+4) = –2,40см;  h₃ʹ = 1,5(–4)/(6+4) = –0,60см.

Зображення: уявне (ℓʹ < 0), зменшене (h′ < h), пряме (h i hʹ мають різні знаки).

4) ℓ₄ʹ = 4(–4)/(4+4) = –2,00см;  h₄ʹ = 1,5(–4)/(4+4) = –0,75см.

Зображення: уявне (ℓʹ < 0), зменшене (h′ < h), пряме (h i hʹ мають різні знаки).

5) ℓ₅ʹ = 2(–4)/(2+4) = –1,33см;  h₅ʹ = 1,5(–4)/(2+4) = –1,00см.

Зображення: уявне (ℓʹ < 0), зменшене (h′ < h), пряме (h i hʹ мають різні знаки).

Не важко бачити, що ті результати які ми отримали шляхом алгебраїчних розрахунків як кількісно так і якісно співпадають з тими результатами які були отримані шляхом геометричних побудов. Однак, не варто забувати, що точність геометричного рішення задачі, значною мірою залежить від масштабу та точності геометричних побудов. І в цьому сенсі, результати алгебраїчного рішення є гарантовано точнішими.

Контрольні запитання.

1. Чи є загально прийнята поведінка базових променів такою, що в точності відображає їх реальну поведінку? Наведіть докази.
2. Чи можна застосовувати базові промені в тих випадках, коли вони фактично не проходять через лінзу?
3. Яке розташування відносно головної оптичної осі лінзи мають: оптичний центр лінзи; фокус лінзи; оптична площина лінзи?
4. Що стверджується в формулі лінзи?
5. Якого вигляду набуває формула лінзи, при заміні в ній фокусної відстані на оптичну силу лінзи?
6. За якими формулами алгебраїчно визначають параметри того зображення яке формує лінза?
7. Сформулюйте правила знаків, які застосовують при алгебраїчному методі визначення параметрів того зображення що створює лінза.
8. Назвіть переваги та недоліки геометричного і алгебраїчного методів розв’язування задач геометричної оптики.

Вправа 39.

1. Перекресліть малюнок у зошит і для кожного випадку побудуйте зображення предмету у відповідній лінзі. Охарактеризуйте це зображення.

а)    

б)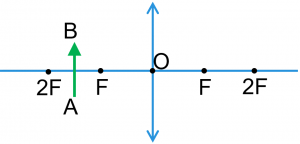   

в)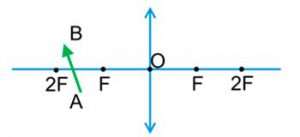   

г)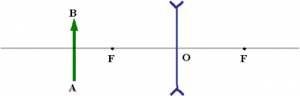    

д)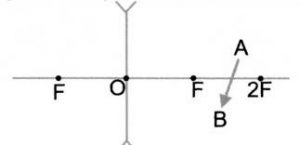   

2. Визначити параметри зображення вертикального відрізка висотою 2см в збиральній лінзі, фокусна відстань якої 2см. Відстань від підніжжя відрізку до оптичного центру лінзи: а) 6см; б) 4см; в) 3см; г) 2см д) 1см. Задачу розв’яжіть геометричним та алгебраїчним способом.
3. Визначити параметри зображення вертикального відрізки висотою 3см в розсіювальній лінзі, фокусна відстань якої 5см. Відстань від підніжжя відрізку до оптичного центру лінзи: а) 10см; б) 5см; в) 3см; г) 1см. Задачу розв’яжіть геометричним та алгебраїчним способом.
4. На малюнку показано головну оптичну вісь лінзи (KN), світну точку S та її зображення S₁. Перекресліть малюнок та визначте розташування оптичного центру і фокусів лінзи.

.

§40. Оптичні прилади.

 

Дзеркала, лінзи та призми є тими базовими оптичними приладами, на основі яких створюються більш складні оптичні системи: телескопи, мікроскопи, біноклі, відеокамери, фотоапарати, перископи, проєктори, фотооб’єктиви, тощо. На разі ми розглянемо загальний устрій та принцип дії деяких з подібних систем.

Перископ (від грец. peri – навколо та skopеo – дивитись), це прилад який дозволяє спостерігати за навколишніми обʼєктами із укриття (підводних човнів, окопів, бронетехніки, тощо). Перископи можуть бути як простими (мал.161а) так і складними (мал.161б). Однак, якщо мова йде про принциповий устрій перископа то він досить простий. Перископ представляє собою трубу з двома нахиленими під кутом 45° до її осі дзеркальними поверхнями (верхньою та нижньою), які розташовані таким чином, що вхідні промені світла відбиваючись від верхньої дзеркальної поверхні потраплять на нижню, а від неї в око спостерігача.

Принцип дії перископа полягає в наступному. Світлова інформація через вхідний (верхній) отвір перископа (обʼєктив) потрапляє на систему певним чином розташованих дзеркальних поверхонь, та відбиваючись від цих поверхонь виходить через вихідний (нижній) отвір перископа (окуляр).

 

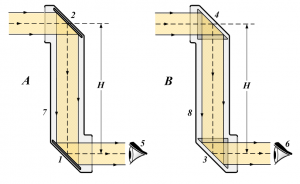
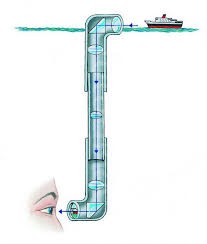
Мал.161. Схема загального устрою та принципу дії перископа.

Фотоапарат (фотокамера, від грец. fotos – світло) – прилад для фіксації зображень нерухомих обʼєктів шляхом фокусування світла на світлочутливий носій (фотоплівка, світлочутливі напівпровідники, електронні карти памʼяті, тощо).

Фотоапарати можуть бути різними та надзвичайно складними. Але загальний (принциповий) устрій будь якого фотоапарату досить простій. Основними елементами цього устрою є фотообʼєктив та чутливий до світла фотоелемент. Принцип дії фотоапарата полягає в наступному. Світлова інформація проходячи через фотообʼєктив, фокусується на світлочутливому елементі, який перетворює цю інформацію у відповідне зображення. (Способи такого перетворення вивчаються та пояснюються в інших розділах фізики).

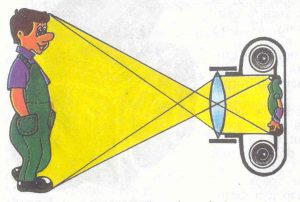
Мал.162. В фотоапараті світло від обʼєкту фотографування, проходячи через фотообʼєктив, у повній відповідності з законами геометричної оптики, фокусується на світлочутливому елементі.

Проєктор, це прилад, який дозволяє за допомогою джерела світла проєктувати зображення предметів на розташовану за межами приладу поверхню – екран. Існує велике різноманіття проєкторів: кінопроєктори, діапроєктори, фотозбільшувачі, кодоскопи, епіскопи, епідіоскопи, мультимедійні проєктори, лазерні проєктори, тощо. Втім, не дивлячись на таке різноманіття, принциповий устрій всіх проєкторів схожий. І цей устрій полягає в наступному. В проєкторі, достатньо потужний світловий потік, проходячи через обʼєкт проєктування, або відбиваючись від цього обʼєкту, у відповідності з законами геометричної оптики проєктується на екран.

Мал.163. В проєкторі світловий потік, проходячи через обʼєкт проєктування, або відбиваючись від цього обʼєкту, проєктується на екран.

Телескоп (від грец. tele – далеко, skopeo – дивитись), це прилад, призначений для візуального спостереження за далекими космічними об’єктами: планетами, кометами, зірками, галактиками, тощо. Пояснюючи загальний устрій та принцип дії телескопа будь-якої конструкції, можна сказати наступне.

Оскільки космічні об’єкти знаходяться на неймовірно великих відстанях від Землі, то кількість тієї світлової (інформаційної) енергії яка від цих об’єктів потрапляє на Землю, є мізерно малою. Ця мізерність стає ще більш очевидною, якщо зважити на факт того, що людина бачить та аналізує лише ту світлову інформацію яка потрапляє в той маленький отвір, що називається зіницею ока. Тому завдання будь якого телескопу, по суті полягає в тому, щоб зібрати максимально велику кількість світлової інформації про певний космічний об’єкт, сконцентрувати цю інформацію у відповідне зображення та направити це інформаційне зображення в око спостерігача або інший світлочутливий прилад.

Сучасне різноманіття оптичних телескопів можна розділити на три групи: лінзові або рефракторні (лат. refractus – заломлення), дзеркальні або рефлекторні (лат. reflectio – відбивання) та дзеркально – лінзові або катадіоптричні. В лінзових телескопах (мал.164а) об’єктивом є збиральна лінза, яка  шляхом заломлення світлових променів фокусує (збирає) ці промені у відповідне зображення та направляє це зображення в окуляр телескопа. В дзеркальних телескопах (мал.164б) аналогічні функції виконує вгнуте (збиральне) дзеркало, а в телескопах дзеркально-лінзових (мал.164в) – система збирального дзеркала і спеціальної лінзово-дзеркальної фокусуючої системи.

Варто зауважити, що переважна більшість сучасних телескопів є дзеркальними, або дзеркально-лінзовими. Ілюструючи порівняльні характеристики та можливості сучасних лінзових і дзеркальних телескопів, достатньо сказати, що діаметр об’єктива найбільшого лінзового телескопа 1,02м, а діаметр об’єктива найбільшого дзеркального телескопа 39м.

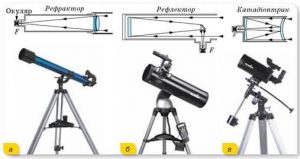
Мал.164. Оптичні телескопи поділяються на лінзові, дзеркальні і дзеркально-лінзові.

Перші телескопи (зорові труби) з’явились на початку 17-го століття. При цьому, майже одночасно було створено дві різновидності подібних приладів: телескоп Галілея (1609) та телескоп Кеплера (1611).

Телескоп Кеплера складається з двох, певним чином розташованих збиральних лінз. При цьому велика (довгофокусна) лінза розташована з боку досліджуваного об’єкту і виконує роль об’єктива (від лат. objectus – предмет, об’єкт), а мала (короткофокусна) лінза, розташована з боку спостерігача і виконує роль окуляра (від лат. oculus – око). Принцип дії цієї системи полягає в наступному. Об’єктив телескопа збирає максимально велику кількість світлової інформації та створює відповідне дійсне зображення. При цьому, це зображення розташоване між окуляром та його фокусом. А це означає, що спостерігач через окуляр бачить відповідне зображення уявним, збільшеним та перевернутим.

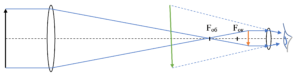
Мал.165. Схема принципового устрою телескопа Кеплера.

На відміну від телескопа Кеплера, в телескопі Галілея окуляром є не збиральна лінза, а лінза розсіювальна. Ця лінза розташована таким чином, що створюване об’єктивом дійсне зображення знаходиться за розсіювальною лінзою окуляру. А це означає, що спостерігач через окуляр бачить відповідне зображення уявним, збільшеним та прямим.

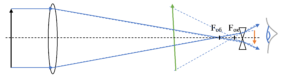
Мал.166. Схема принципового устрою телескопа Галілея.

Застосовуючи сучасні телескопи, можна розгледіти деталі багатьох космічних об’єктів, зокрема Сонця, Місяця, комет, планет Сонячної системи, тощо. Однак телескопи не дозволяють побачити деталі тих зірок та планет які знаходяться за межами Сонячної системи. Не дозволяють тому, що відстані до таких об’єктів є фантастично великими. Великими настільки, що навіть в найпотужніших телескопах далекі зірки виглядають як певні світлові точки.

Втім, це зовсім не означає, що телескопи не дозволяють отримувати нову інформацію про зірки та інші наддалекі космічні об’єкти. Адже телескоп в сотні, тисячі і мільйони разів посилює видиму яскравість зірок. Посилює тому, що через телескоп в наше око потрапляє у стільки разів більше світлової енергії, у скільки разів площа його об’єктиву більша за площу зіниці ока. А це означає, що в телескопі ми можемо побачити не лише ті зірки які видно неозброєним оком, а й ті, які зазвичай є невидимими. Крім цього, телескоп в десятки і сотні разів збільшує видимі відстані між окремими космічними об’єктами. При цьому з’ясовується, що велика кількість тих об’єктів які виглядають як цілісні світлові точки, насправді представляють собою скупчення величезної кількості окремих зірок.

Ще одним важливим та загально відомим оптичним приладом є бінокль (від лат. bini – два, oculus – око). Бінокль, це прилад який складається з двох паралельно з’єднаних зорових труб та призначений для візуального спостереження за віддаленими земними об’єктами.

Біноклі поділяються на театральні і польові (або призмові). Театральний бінокль (мал.167а) по суті представляє собою систему двох невеликих, паралельно з’єднаних зорових труб Галілея. Такі біноклі мають просту будову, малі габарити, малі втрати світлового потоку та великий кут огляду. Однак кутове збільшення театральних біноклів є відносно малим і зазвичай становить від 2 до 4 одиниць.

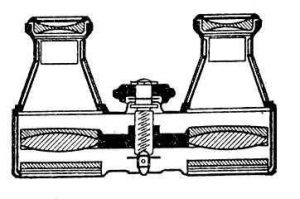
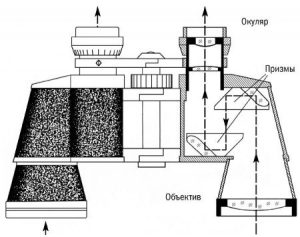
Мал.167. Загальний устрій театрального (а) та польового (б) біноклів.

Значно більше кутове збільшення (до 22 одиниць), забезпечують так звані польові або призмові біноклі (мал.167б). Такі біноклі по суті представляють собою систему двох, паралельно з’єднаних зорових труб Кеплера. Зорова труба Кеплера має той недолік, що створюване нею зображення є перевернутим. Звичайно, коли мова йде про далекі космічні об’єкти, то факт перевернутості їх зображень не має суттєвого значення. Однак для земних об’єктів, цей факт є суттєво негативним. Зважаючи на ці обставини, в польовому біноклі застосовують певну систему скляних призм, яка не лише забезпечує формування прямого зображення, а й практично вдвічі зменшує довжину бінокля.

Потрібно зауважити, що візуальне сприйняття величини предмету, залежить не від його реальних розмірів, а від величини його зображення на сітківці ока. А це зображення залежить від величини того кута зору під яким спостерігач бачить відповідний предмет. Зважаючи на ці обставини, мірою збільшуваних властивостей оптичних приладів, є величина яку називають кутовим збільшенням оптичної системи.

Мал.168. Видимі розміри предмету, залежать від величини того кута зору під яким цей предмет (або його зображення) видно.

До числа загально відомих оптичних приладів відносяться мікроскопи. Мікроскоп (від грец.  mikros – маленький, skopeo – дивитись), це прилад, призначений для візуального спостереження за мікрооб’єктами, тобто тими об’єктами що є невидимими для «неозброєного» ока людини. По суті, мікроскоп представляє собою систему двох збиральних лінз, одна з яких називається об’єктивом, інша окуляром Ці лінзи розташовані таким чином, що коли дрібний предмет (об’єкт досліджень) знаходиться перед фокусом об’єктива, то його збільшене дійсне зображення, знаходиться за фокусом окуляра. А це означає, що спостерігач буде бачити уявне, подвійно збільшене зображення предмету. Іншими словами, система двох, певним чином розташованих збиральних лінз, дозволяє подвійно збільшувати зображення дрібних предметів. При цьому, якщо об’єктив  збільшує видимі розміри предмету у 20 разів, а окуляр – в 10 разів, то загальне збільшення мікрооб’єкту становитиме 20·10 = 200 разів. Загалом же, сучасні оптичні мікроскопи забезпечують збільшення досліджуваних об’єктів до 2500 разів.

   

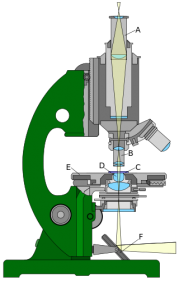
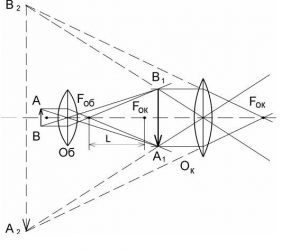
Мал.169.  Загальний устрій та принципова схема оптичного мікроскопа.

Говорячи про принциповий устрій того чи іншого оптичного приладу, потрібно мати на увазі, що ті його елементи, які на принциповій схемі позначаються однією лінзою, в реальності можуть виявитися досить складними оптичними системами. Наприклад в гранично простому випадку об’єктивом фотоапарату є збиральна лінза яка фокусує зображення об’єкту фотографування на фотоплівці чи іншому світлочутливому елементі.

В реальності ж, навіть найпростіший фотооб’єктив представляє собою достатньо складну оптичну систему (мал.169б,в). Систему, до якої висувається ціла низка вимог. По перше, те зображення яке створює фотооб’єктив не повинно мати суттєвих оптичних спотворень (аберацій). По друге, те зображення яке створює фотооб’єктив, має бути максимально чітким та сфокусованим. По третє, фотооб’єктив за певний короткий проміжок часу повинен пропускати певну, визначену кількість світлового потоку. Нарешті, фотооб’єктив має бути достатньо універсальним, тобто таким, що якісно виконує свої функції за різних умов: за різної відстані до об’єкту фотографування; за різної освітленості цього об’єкту; за різної чутливості фотоплівки, тощо. Ясно, що оптична система яка забезпечує виконання всього спектру подібних вимог не може бути надто простою.

Мал.170. Схема принципу дії (а) та реальний устрій (б, в) фотооб’єктиву.

Різноманіття оптичних приладів не вичерпується різноманіттям мікроскопів, телескопів, біноклів та фотооб’єктивів. Окуляри, лупи, фото- діа- кіно-проектори, спектроскопи, оптиметри, профілографи, сферометри, теодоліти, військові приціли – ось далеко не повний перелік тих приладів, які з повним правом називають оптичними. Крім цього, оптичні прилади та їх елементи є складовими частинами безлічі інших приладів, які не вважаються оптичними. Ми не будемо розглядати будову та принцип дії кожного відомого оптичного приладу. Зауважимо тільки, що базовими елементами практично всіх оптичних приладів є лінзи, дзеркала та призми. І що принцип дії переважної більшості оптичних приладів базується на застосуванні законів геометричної оптики.

Контрольні запитання.

1. Поясніть загальний устрій та принцип дії перископа.
2. Де і для чого застосовують перископи?
3. Поясніть загальний устрій та принцип дії фотоапарата.
4. Поясніть загальний устрій та принцип дії проектора.
5. Поясніть загальний устрій та принцип дії телескопа Кеплера.
6. Поясніть загальний устрій та принцип дії телескопа Галілея.
7. Якщо навіть у найпотужнішому телескопі далекі зірки виглядають як світлові точки, то чому ми стверджуємо, що телескопи дозволяють отримувати багато нової інформації про ці зірки?
8. Поясніть загальний устрій та принцип дії мікроскопа.

.

§41. Око як природний оптичний прилад. Дефекти зору.

Важливість наших зорових відчуттів важко переоцінити. Достатньо сказати, що близько 90% інформації про навколишній світ, ми отримуємо через зорові відчуття, а отже через ту систему яка ці відчуття створює. В загальних рисах принцип дії цієї системи полягає в наступному. Світлова інформація, через оптичну систему ока фокусується на його сітківці, яка представляє собою складну систему світлочутливих рецепторів (колбочок і  паличок), з’єднаних з клітинами (нейронами) центральної нервової системи. В світлочутливих рецепторах сітківки, енергія світлових імпульсів трансформується у відповідні біоелектричні сигнали, які через клітини центральної нервової системи передаються у відповідні відділи кори головного мозку, де аналізуються та перетворюються у відповідні зорові образи.

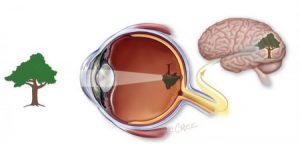
Мал.171. Схема загального устрою та принципу дії системи зорових відчуттів людини.

Ясно, що в межах даної теми, ми не будемо заглиблюватись в деталі тих надскладних нейрофізіологічних та психологічних процесів, результатом яких є наші зорові відчуття. Ми просто опишемо гранично загальний устрій та принцип дії тієї складової зорової системи, яка називається оком.

Око людини, це надзвичайно складна система елементами якої є склера, рогівка, судинна оболонка, райдужна оболонка, передня камера, зіниця ока, кришталик, зв’язки кришталика, скловидне тіло, сітківка ока, зоровий нерв, тощо. І кожен з цих елементів має свою складну структуру, своє важливе призначення, і так чи інакше впливає на наші зорові відчуття.

Однак якщо говорити про гранично спрощений, загальний устрій ока, то його базовими елементами є кришталик, рогівка та сітківка ока. При цьому загальний принцип дії цієї системи полягає в наступному. Світлова інформація від об’єкту спостережень, через отвір який називається зіницею ока і площа якого регулюється райдужною оболонкою, потрапляє на кришталик, який виконує функції збиральної лінзи, та фокусує зображення предмету на сітківці ока.

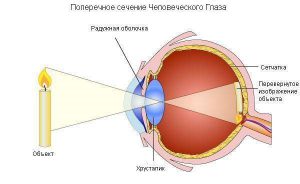
Мал.172.  Схема загального устрою та принципу дії ока людини.

В певному сенсі око можна порівняти з фотоапаратом. Як і фотоапарат, око сприймає світлову інформацію, певним чином дозує цю інформацію та фокусує її на фото чутливий елемент системи, яким в фотоапараті є фотоплівка, а в оці – сітківка (мал.173). Втім, оптична система ока значно досконаліша за будь який фотоапарат. І ця досконалість забезпечується не кількістю лінз, призм та дзеркал, а універсальністю та саморегульованістю тих небагатьох елементів системи, які забезпечують ефективне виконання поставлених завдань.

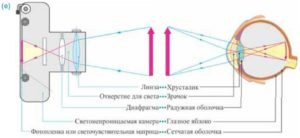
Мал.173. В певному сенсі око можна порівняти з фотоапаратом.

Ілюструючи універсальність та саморегульованість оптичної системи ока, розглянемо декілька показових прикладів. Найочевидніший з них полягає в тому, що в залежності від інтенсивності зовнішнього освітлення, автоматично змінюється діаметр зіниці ока, а отже і кількість того світла, що проникає всередину очного яблука. Це означає, що в залежності від інтенсивності зовнішнього освітлення, райдужна оболонка ока рефлекторно скорочується або розширюється і відповідно регулює величину того світлового потоку, що потрапляє в око людини. Іншими словами, автоматично працююча райдужна оболонка, виконує функції діафрагми фотоапарату.

Мал.174. Райдужна оболонка ока виконує функції діафрагми фотоапарату.

Крім цього, подібно до того як в залежності від інтенсивності освітлення, досвідчений фотограф може застосовувати фотоплівки різної чутливості, в оці людини також застосовуються різночутливі «фотоплівки». Одна з них складається з світлочутливих рецепторів які називаються паличками, інша – з світлочутливих рецепторів які називаються колбочками. Палички є фоторецепторами присмеркового зору. Вони пристосовані для сприйняття слабкого світла, однак не дозволяють розрізняти кольори та формувати чітке зображення. Колбочки, це фоторецептори денного зору. Вони пристосовані для сприйняття яскравого денного світла, сприйняття різних кольорів та формування чіткого зображення.

Ще одним прикладом універсальності оптичної системи ока, є її здатність автоматично (рефлекторно) фокусуватися на різновіддалених предметах. Необхідність такого регулювання є очевидною. Адже у відповідності з законами геометричної оптики, по мірі наближення тіла до збиральної лінзи (кришталика ока), зображення цього тіла поступово віддаляється від лінзи. А це означає, що по мірі наближення об’єкту спостереження до ока спостерігача, те зображення яке проектується на сітківку ока, має все більше і більше віддалятися від цієї сітківки, а отже бути все більш і біль розмитим та нечітким.

.           

.                 

Мал.175. У відповідності з законами геометричної оптики, по мірі наближення тіла до збиральної лінзи, зображення цього тіла віддаляється від лінзи.

В фотоапараті дана ситуація вирішується шляхом механічного переміщення лінз фотооб’єктиву відносно фотоплівки: механічно переміщуючи фотооб’єктив, фотограф досягає того, щоб зображення предмету було сфокусованим на фотоплівці. В оці, подібне фокусування здійснюється не шляхом збільшення чи зменшення відстані між кришталиком та сітківкою, а шляхом деформації самого кришталика. Механізм такого фокусування полягає в наступному.

Око влаштоване таким чином, що коли ви дивитесь на суттєво віддалені предмети, то його кришталик знаходиться в недеформованому стані. При цьому, зображення віддаленого предмету є чітко сфокусованим на сітківці ока. Якби оптичні властивості кришталика залишались незмінними, то при наближенні предмету, його зображення поступово віддалялось би від сітківки ока. А це означає, що візуальне сприйняття того предмету який наближається до спостерігача, ставало б все більш і більш розмитим (не чітким).

Однак в дійсності нічого подібного не відбувається. Не відбувається тому, що оптичні властивості кришталика можуть певним чином змінюватись. Механізм цих змін полягає в тому, що по мірі наближення предмету до спостерігача, ті м’язи які утримують кришталик скорочуються і певним чином деформують його. При цьому кришталик стає все більш і більш опуклим, а зображення предмету виявляється постійно сфокусованим на сітківці ока. Здатність ока пристосовуватися до сфокусованого сприйняття різновіддалених предметів називають акомодацією ока (від лат. accommodation – пристосовуватись).

Мал.176. В процесі наближення предмету, кришталик деформується. При цьому зображення предмету виявляється постійно сфокусованим на сітківці ока.

Потрібно зауважити, що оптична система ока складається не лише з райдужної оболонки та кришталика. Складовими елементами цієї системи є рогівка, передня камера ока, райдужна оболонка ока, кришталик та скловидне тіло. Кожен з цих елементів так чи інакше заломлює світлові промені та приймає участь в їх фокусуванні на сітківку ока. Кожен з цих елементів в тій чи іншій мірі універсальний та багатофункціональний оптичний прилад. При цьому лише взаємопов’язана сукупність цих приладів і утворюють той досконалий та універсальний фотоапарат, який називається оптичною системою ока.

Та якою б досконалою не була оптична система ока, але і вона може мати певні дефекти. Найпоширенішими та найвідомішими з цих дефектів є далекозорість та короткозорість. Пояснюючи суть цих дефектів зору можна сказати наступне.  Дослідження показують, що в людини з нормальним зором, недеформований кришталик забезпечує чітке фокусування віддалених предметів на сітківку ока (мал.177а). Однак, якщо ті чи інші елементи оптичної системи ока мають певні вади, то недеформований кришталик не забезпечує чіткого фокусування зображень віддалених об’єктів. При цьому, якщо  зображення фокусується за сітківкою (мал.177б), то око називають далекозорим, а якщо перед сітківкою (мал.177в) – короткозорим.

.                  а)                                     б)                                  в)

Мал.177. У своєму ненапруженому стані, нормальне око (а) фокусує зображення віддалених предметів на сітківці;  далекозоре (б) – за сітківкою; короткозоре (в) – перед сітківкою.

Ясно, що як при короткозорості так і при далекозорості, зображення віддалених предметів будуть не чіткими (не сфокусованими). При цьому, якщо далекозорість не надто велика, то завдяки механізму акомодації, тобто механізму рефлекторно-примусового деформування кришталика, око здатне рефлекторно компенсувати шкідливі прояви далекозорості. А це означає, що віддалені предмети далекозора людина бачить практично так же добре як і людина з нормальним зором. Однак, акомодаційні можливості ока не безмежні. Тому, починаючи з певної відстані, акомодаційний механізм не може компенсувати шкідливі прояви далекозорості. А це означає, що починаючи з певної відстані, далекозора людина не може чітко бачити близько розташовані об’єкти.

При короткозорості, зображення віддаленого предмету також на сфокусоване на сітківці ока. Але в цьому випадку, воно знаходиться не за сітківкою, а перед нею. В такій ситуації, механізм акомодації не може компенсувати даний дефект зору. Єдина природня можливість короткозорої людини чітко побачити віддалений предмет, полягає в тому, щоб наблизитись до цього предмету. Адже при такому наближенні, зображення предмету природнім шляхом зміщується вбік сітківки і за певної, відстані опиняється на ній. По суті це означає, що короткозора людина здатна чітко бачити лише ті предмети, які знаходяться ближче за певну відстань.

Потрібно зауважити, що далекозорість є практично неминучим наслідком тих чи інших вікових змін. Адже з віком пружно-еластичні властивості як кришталика так і тих м’язів які його деформують, погіршуються. А це означає, що відповідно погіршуються акомодаційні властивості ока. Тому зображення близько розташованих предметів буде сфокусованим не на сітківці ока, а за нею.

Якщо ж говорити про короткозорість, то в більшості випадків цей дефект зору є набутим. Не буде перебільшенням сказати, що короткозорість – це хвороба цивілізованої людини. Людини, яка постійно знаходиться в приміщенні, постійно бачить близькі предмети, годинами дивиться телевізор, сидить за комп’ютером, читає, пише, тощо. В таких умовах, погляд людини постійно зосереджений на близько розташованих предметах. А це означає, що оптична система ока знаходиться в постійному напруженні. Поступово це напруження трансформується в незворотні, залишкові деформації кришталика та інших елементів оптичної системи ока. Результатом цих незворотних деформацій і є короткозорість. Зважаючи на ці малоприємні обставини, ви маєте розуміти, що відпочиваючи на свіжому повітрі, ви не лише дихаєте цим повітрям, не лише насолоджуєтесь мальовничими краєвидами, а й даєте відпочинок своїм постійно напруженим очам та запобігаєте ймовірній короткозорості.

Цивілізація не лише створила умови для появи певних дефектів зору, а й винайшла ефективні методи боротьби з ними. Найпоширенішим з цих методів є застосування окулярів та контактних лінз. Принцип дії окулярів, а відповідно і контактних лінз очевидно простий. Для того щоб компенсувати короткозорість, перед оком розташовують відповідну розсіювальну лінзу (мал.178а). Ця лінза заломлює промені таким чином, щоб потрапляючи в оптичну систему ока, вони фокусувались на його сітківці. Для запобігання далекозорості, перед оком ставлять відповідну збиральну лінзу (мал.178б), яка заломлює промені таким чином, щоб потрапляючи в оптичну систему ока, вони фокусувались на його сітківці.

Мал.178. Короткозорість (а) та далекозорість (б) можна виправити шляхом застосування відповідних лінз (окулярів).

На завершення зауважимо, що короткозорість і далекозорість, це не хвороби зору, а його дефекти. Або, якщо хочете, малоприємні індивідуальні особливості системи зору конкретної людини. При цьому, ці особливості можуть бути як вродженими так і набутими.

Контрольні запитання.

1. Які функції виконує око?
2. Яке призначення та принцип дії райдужної оболонки?
3. Яке призначення та принцип дії кришталика?
4. Поясніть загальну схему формування зорових відчуттів.
5. Поясніть фізичну суть акомодації ока.
6. Поясніть фізичну суть далекозорості.
7. Поясніть фізичну суть короткозорості.
8. Чому короткозорість називають хворобою цивілізованих людей?
9. Яким чином виправляють а) короткозорість ока; б) далекозорість ока?

 .