Сайт викладача фізики

РОЗДІЛ 1. Механіка. частина 2.

Лекційне заняття №15. Тема: Пара сил. Момент сили. Важелі. Рівновага тіла, що має вісь обертання.

Лекційне заняття №16. Тема: Рівновага тіла під дією довільної системи сил. Розв’язування задач.

Тема 1.3. Динаміка.

Лекційне заняття №17. Тема: Динаміка. Основні поняття, величини та закони динаміки. Принцип відносності. Закони Ньютона.

Лекційне заняття №18. Тема: Енергія. Механічна енергія. Закон збереження енергії. Розв’язування задач.

Лекційне заняття №19. Тема: Робота. Потужність. Коефіцієнт корисної дії. Розв’язування задач.

Лекційне заняття №20. Тема: Імпульс. Закон збереження імпульсу. Розв’язування задач.

Лекційне заняття №21. (Практичне заняття) Тема: Імпульсно-енергетичний метод розв’язування задач.

Лекційне заняття №22. Тема: Загальні відомості про коливання. Період та частота коливань. Фізичний, математичний та пружинний маятники.

Лекційне заняття №23. Тема: Механічна картина світу. Механіка, узагальнююче повторення.

.

Лекційне заняття №15.

Тема: Пара сил. Момент сили. Важелі. Механічні блоки. Рівновага тіла, що має вісь обертання.

До сих пір, говорячи про механічну та динамічну рівновагу тіла, ми мали на увазі, що це тіло знаходиться під дією так званої збіжної системи сил, тобто такої сукупності одночасно діючих сил, лінії дії яких перетинаються в одній точці. По суті це означає, що до сих пір ми вивчали статику матеріальної точки, тобто ту частину статики в якій тіло можна вважати матеріальною точкою, а діючу на це тіло систему сил, можна замінити однією рівнодіючою силою. Силою, яка надає тілу поступального руху.

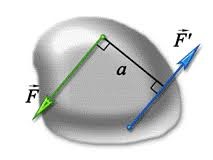
Однак, далеко не всяка діюча на тіло система сил є збіжною і далеко не всяку систему сил можна замінити рівнодіючою. Наприклад, якщо на тіло діють дві рівні за величиною і протилежні за напрямком сили F і Fꞌ які не лежать на одній прямій (мал.60), то замінити цю систему сил відповідною рівнодіючою, не можливо. Дійсно. Формально визначивши результуючу сил F і Fꞌ ми отримаємо нульову величину: F+Fꞌ=0. Та чи означає це, що загальна механічна дія сил F і Fꞌ є нульовою? Очевидно що ні. Адже дана система сил надає або намагається надати тілу певного обертального руху.

   

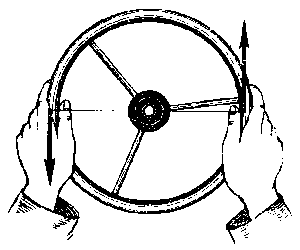
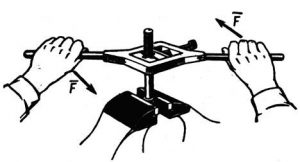
Мал.65.  Пару сил не можливо замінити  рівнодіючою силою.

Систему двох рівних за величиною і протилежних за напрямком сил, які не лежать на одній прямій і спільно діють на одне і те ж тіло, називають парою сил (або парою). Пара сил надає (або намагається надати) тілу обертального руху. Пару сил не можливо замінити або зрівноважити однією силою. Пару сил можна замінити чи зрівноважити лише іншою парою сил.

Ви можете заперечити в тому сенсі, що в певних випадках тіло може обертатись під дією лише однієї сили. Наприклад, відчиняючи двері, ми прикладаємо лише одну силу яка і надає їм обертального руху. Дійсно. На перший погляд здається, що двері обертаються під дією лише однієї сили. Насправді ж, одна сила не може змусити тіло обертатись. Це може зробити лише пара сил. І якщо двері обертаються, то це тільки тому, що на них діють дві сили які і утворюють відповідну пару. При цьому не важко збагнути, що другою силою пари є та реакція опори, яка виникає в петлях дверей. Петлях, які утворюють нерухому вісь обертання тіла.

 

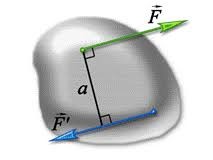
Мал.66.  Пара сил надає тілу, або прагне надати, обертального руху.

Основною характеристикою пари сил, або тієї сили що діє на тіло з нерухомою віссю обертання, є фізична величина яка називається моментом сили або моментом пари сил. Момент сили – це фізична величина, яка характеризує обертальну дію сили (пари сил) і яка дорівнює добутку цієї сили F на плече її дії d, тобто на найкоротшу відстань між лінією дії сили та віссю обертання тіла.

Позначається: М

Визначальне рівняння: М=F·d

Одиниця вимірювання:  [М] = Н∙м,   (ньютон-метр).

По суті, момент сили – величина векторна. Однак, зважаючи на те, що в межах програми загальноосвітньої школи вивчають лише плоскі системи сил, момент сили можна вважати величиною скалярною, тобто такою яка характеризується абсолютною величиною та знаком. При цьому, знак моменту сили зазвичай визначають за правилом: якщо сила повертає (або намагається повернути) тіло за годинниковою стрілкою, то момент сили додатній, а якщо проти годинникової стрілки – від’ємний.

   

 

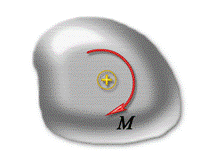
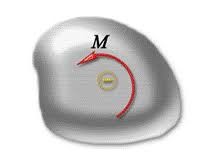
Мал.67. Якщо пара сил повертає тіло за годинниковою стрілкою, то момент сили додатній, а якщо проти годинникової стрілки – від’ємний.

Коли ми стверджували, що тіло буде знаходитись в стані механічної рівноваги тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил дорівнює нулю (∑F=0), то мали на увазі, що система діючих на тіло сил є збіжною, тобто такою, яка надає тілу поступального руху. В загальному ж випадку, система діючих на тіло сил може бути довільною. І ця довільна система сил може надавати тілу не лише поступального руху, а й руху обертального. В такій ситуації основний закон статики  (загальна умова рівноваги тіла) набуває вигляду: тіло буде знаходитись в стані загальної механічної рівноваги (v=0; ω=0) тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил та моментів цих сил дорівнюють нулю. Іншими словами: якщо {∑F=0; ∑M=0} то {v=0; ω=0} і навпаки. (ω – кутова швидкість)

Оскільки те тіло яке має нерухому вісь обертання, поступально не рухається і рухатись не може, то векторна сума діючих на нього зовнішніх сил гарантовано дорівнює нулю. А це означає, що для тіла з нерухомою віссю обертання, умова рівноваги набуває вигляду: якщо ∑М=0, то ω=0 або ω=const і навпаки. Іншими словами, для тіла що має нерухому вісь обертання, умова механічної (обертальної) рівноваги набуває вигляду: тіло що має нерухому вісь обертання буде знаходитись в стані обертальної рівноваги (ω=0 або ω=const) тоді і тільки тоді, коли сума діючих на нього моментів сил дорівнює нулю (∑М=0).

Простий механізм принцип дії якого базується на застосуванні умови рівноваги тіла що має нерухому вісь обертання, називається важелем. Важіль – це прилад, який представляє собою довге тверде тіло, що може обертатись навколо відносно нерухомої точки, яку називають точкою опори. Так чи інакше важелі застосовувались з незапам’ятних часів. Скажімо, коли використовуючи підручну палицю, прадавня людина зрушувала з місця важкий камінь, то вона  фактично застосовувала важіль. Якщо ж говорити про історично зафіксовані факти системного застосування важелів, то вони відносяться до періоду будівництва великих єгипетських пірамід (приблизно 4600 років тому).

Мал.68. Люди використовували важелі з прадавніх часів.

Зазвичай важіль застосовується для підсилення силової дії. Таке підсилення відбувається за рахунок того, що плече дії «вхідної» сили, тобто тієї сили яку ми прикладаємо до важеля і яка потребує підсилення, значно більше за плече дії сили «вихідної». Дійсно. Якщо сила F₁ має плече d₁ (мал.69), а сила F₂ – плече d₂, то у відповідності з умовою рівноваги даного тіла (важеля) F₁d₁=F₂d₂. А це означає, що коли плече дії сили F₁ буде більшим за плече дії сили F₂ (d₁˃d₂) то у відповідну кількість разів сила F₂ буде більшою за силу F₁:   F₂=F₁(d₁/d₂).

З іншого боку було б дивним та неприроднім, якби за допомогою важеля ми отримували виграш в силі, що називається «безкоштовно», тобто не програючи в чомусь іншому. І очевидно, що цим «іншим» є програш в тому переміщенні яке спричиняє підсилена сила. Дійсно. З геометричних міркувань (мал.64) випливає, що виграючи в силі (F₂=nF₁ де n=d₁/d₂=h₁/h₂) ми в таку ж кількість разів програємо в тому переміщенні яке здійснює ця сила (h₂=h₁/n).

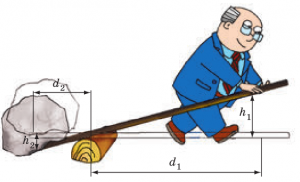
Мал.69.   Важіль – механізм який підсилює силову дію. При цьому, виграючи в силі (F₂>F₁), ми неминуче програємо у відстані (h₂<h₁).

Про те, що «безкоштовних» виграшів у силі не буває, вчені знали ще з стародавніх часів. Досліджуючи властивості важеля, Архімед сформулював правило, яке стосувалось всіх простих механізмів і в якому стверджувалось: у скільки разів виграєш в силі, у стільки ж разів програєш у відстані. Це правило прийнято називати золотим правилом механіки. По суті, золоте правило механіки є одним з перших формулювань базового закону сучасної науки – закону збереження енергії.

Важільні системи можна побачити в найрізноманітніших сучасних приладах, починаючи від дитячих гойдалок, весел, шлагбаумів та ножиць і закінчуючи елементами піднімально-транспортних механізмів, автомобілів, кораблів, літаків, тощо. Деякі приклади простих важільних систем представлені на мал.70.

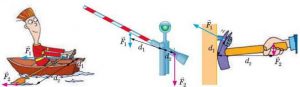
Мал.70. Деякі приклади простих важільних систем.

Певні важільні системи можна помітити не лише в штучно створених приладах, а й в організмах живих істот, зокрема в організмі людини. Наприклад ліктьова кістка руки, ліктьовий суглоб та той м’яз який називають біцепсом (мал.71а) утворюють важільну систему, яка забезпечує рухливість ліктьової частини руки. Аналогічне можна сказати і про ступню ноги (мал.71в), рухливість якої забезпечує важільна система елементами якої є кістки стопи, великогомілкова кістка та ахілесове сухожилля. Або наприклад череп людини (мал.71б), у поєднанні з кістками шийного відділу хребта та ремінним м’язом, утворюють важільну систему яка забезпечує рухливість голови.

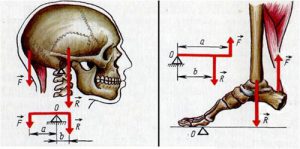
Мал.71. Приклади важільних систем людського тіла.

Задача 1. В точці 1 (дивись мал.) прикріплено вантаж масою 2кг. Якої маси вантаж треба закріпити в точці 2, щоб важіль був у рівновазі. Маса важеля 4кг.

Дано:

m₁ = 2кг

m₃ = 4кг

d₁ = 9 од.

d₂ = 1 од.

d₃ = 4 од.

m₂ = ?

Рішення: Виконуємо малюнок на якому вказуємо діючі на важіль сили (F₁=m₁g=2кг·10м/с²=20Н, F₂=m₂g, F₃=m₃g=4кг·10м/с²=40Н), та їх відстані до осі обертання важеля. Ці відстані визначаємо на основі аналізу малюнку та факту того, що точкою прикладання сили тяжіння важеля (F₃) є геометричний центр цього важеля. Записуємо умову рівноваги важеля відносно осі його обертання:

∑M_O = –F₁d₁ – F₃d₃ + F₂d₂ = 0, звідси F₂d₂ = F₁d₁ + F₃d₃, звідси F₂ = (F₁d₁ + F₃d₃)/d₂ = (20·9 + 40·4)/1 = 340 Н. А оскільки F₂=m₂g, то m₂=F₂/g=340Н/10м/с²)=34кг.

Відповідь: m₂ = 34кг.

Задача 2. До кінців важеля довжиною 1,2м  підвішені вантажі масою 12кг і 6кг. Де потрібно встановити опору, щоб вантажі перебували у рівновазі?

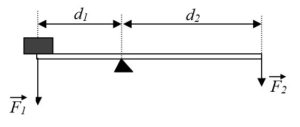
Дано:

ℓ=1,2м

F₁=m₁g=120Н

F₂=m₂g=60Н

d₁ = ?

d₂ = ?

Рішення: Виконуємо малюнок на якому вказуємо діючі на важіль сили та відстані до них. Зважаючи на те, що d₂=ℓ–d₁ записуємо умову рівноваги важіля відносно осі його обертання.

∑M_O = –F₁d₁ + F₂(ℓ–d₁) = 0, або  –F₁d₁ + F₂ℓ– F₂d₁ = 0, звідси d₁(F₁ +F₂) = F₂ℓ, звідси d₁= F₂ℓ/(F₁ +F₂).

Розрахунки: d₁= F₂ℓ/(F₁ +F₂) = 60Н·1,2м/(120Н+60Н)= 0,4м;

d₂=ℓ–d₁= 1,2м – 0,4м= 0,8м.

Відповідь: d₁=0,4м; d₂=0,8м.

Окрім важелів до числа найбільш поширених простих механізмів відносяться різноманітні блоки. Блок – це прилад (механізм), який представляє собою круглий шків що має вісь обертання і по жолобу якого проходить елемент гнучкого зв’язку (канат, мотузка, трос, ланцюг, тощо). Якщо в процесі руху вантажу вісь блоку залишається нерухомою (мал.72а), то блок називається нерухомим. А якщо в процесі руху вантажу вісь блоку рухається разом з вантажем (мал.72б), то відповідний блок називають рухомим.

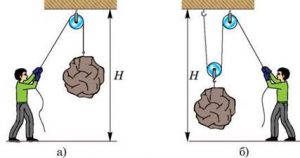
Мал.72.  Загальний устрій та найпростіші застосування блоку.

Оскільки шків блоку вільно обертається, то силовий натяг перекинутого через нього канату на вході та на виході шківа має бути однаковим. Власне ця однаковість випливає з умови обертальної рівноваги шківа. Дійсно. Під дією двох різнонаправлених сил F₁ і F₂ (мал.73), шків буде знаходитись в стані обертальної рівноваги за умови, що момент тієї сили яка обертає  шків за годинниковою стрілкою (M₂=F₂R) дорівнює моменту тієї сили яка обертає його проти годинникової стрілки (M₁=F₁R), тобто за умови F₂R=F₁R, де R – радіус шківа. А це можливо лише тоді, якщо  F₂=F₁.

І потрібно зауважити, що натяг перекинутого через шків канату, не залежить від того, в якому напрямку цей канат натягують (мал.68б). А це означає, що нерухомий блок, не даючи виграшу в силі, дозволяє змінювати напрям цієї сили. Вже цей факт, робить подібні механізми потрібними та загальновживаними.

а)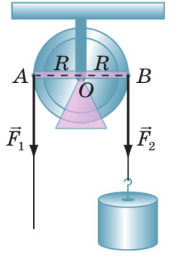  б)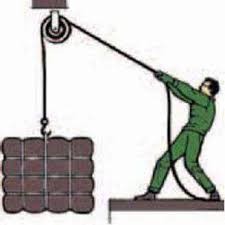

Мал.73. За відсутності сил тертя, натяг перекинутого через шків канату в усіх його точках є однаковим.

Але можливості блоків не вичерпуються лише зміною напрямку дії сили. В цьому не важко переконатись на прикладі системи яка складається з рухомого та нерухомого блоків (мал.74а). Не важко бачити, що в такій системі на рухомий блок, а отже і на те тіло яке він піднімає, діють дві рівні за величиною співнаправлені сили. А це означає, що натягуючи канат з силою F, на осі рухомого блоку ми отримаємо вдвічі більше тягове зусилля. Якщо ж в системі буде два рухомих блоки (мал.74б), то та загальна вага яку підніматиме ця система, буде у 4 рази більшою за величину тієї сили з якою натягують канат. Загалом же, загальну вантажопід’ємність (F_заг) системи рухомих та нерухомих блоків можна визначити за формулою F_заг=2nF, n – кількість рухомих блоків в системі  F – сила натягу канату.

а)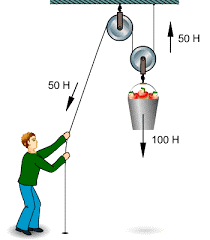 б)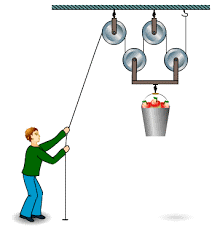

Мал.74. Кожний рухомий блок, збільшує вантажопід’ємність системи на 2F, де F – сила натягу канату.

Втім, потрібно мати на увазі, що загальна вантажопід’ємність системи рухомих та нерухомих блоків залежить не лише від числа рухомих блоків, а й від місця закріплення нерухомого кінця канату. При цьому, якщо цей кінець кріпиться до нерухомої опори (75а), то загальна вантажопід’ємність системи n рухомих блоків дорівнює 2nF. Якщо ж нерухомий кінець канату кріпиться до рухомої опори, тобто тієї опори яка рухається разом з рухомими блоками (мал.75б,в), то в цьому випадку загальна вантажопід’ємність системи n блоків дорівнює (2n+1)F. Дійсно. Оскільки сила натягу канату в усіх його точках однакова, то в зображеній на мал.70б системі, на рухому опору діють три рівні за величиною співнаправлені сили, кожна з яких дорівнює силі натягу канату. При цьому величина результуючої сили становить (2n+1)F.

 

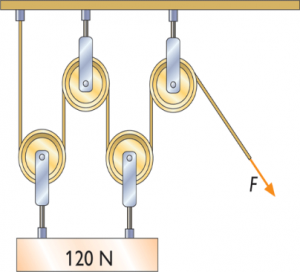
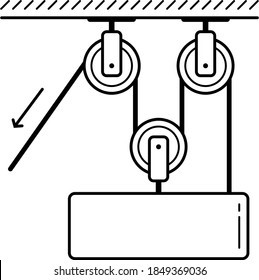
Мал.75. Загальна вантажопід’ємність системи блоків, залежить не лише від числа рухомих блоків в ній, а й від місця закріплення нерухомого кінця канату.

Ясно, що у вище наведених ситуаціях, отриманий виграш в силі не може бути «безкоштовним». Платою за цей виграш є неминучий програш в пройденому шляху. Дійсно. Для того, щоб за допомогою представленого на мал.74а рухомого блоку, підняти вантаж на ℓ метрів, потрібно на ℓ метрів зменшити довжину як правої так і лівої частин того канату який піднімає блок. А це означає, що той робітник який тягне канат з силою F, повинен прикладаючи цю силу протягнути 2ℓ метрів канату. Якщо ж система блоків дозволяє збільшити піднімальну силу в 4 рази (мал.74б), то відповідно в 4 рази зменшується та висота на яку піднімається вантаж (порівняно з довжиною переміщеного канату).

Таким чином, виграючи в тій силі яка піднімає вантаж, ми неминуче та у відповідну кількість разів програємо у тій висоті на яку піднімається цей вантаж. Що ж, Природу не можливо обманути: у скільки разів виграєш в силі, у стільки ж разів програєш в пройденому шляху (золоте правило механіки).

Задача 3. Який виграш у силі дає зображена на малюнку система блоків? Чому дорівнює сила натягу мотузки b, якщо маса вантажу 40кг?

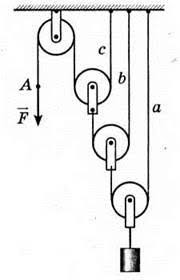
Рішення. Будемо виходити з того, що натяг суцільної мотузки в усіх її точках однаковий. Зважаючи на це, можна стверджувати:

1) Оскільки натяг мотузки с дорівнює силі F, то на рухомий блок с діє сила 2F.

2) Оскільки натяг мотузки b дорівнює силі 2F, то на рухомий блок b діє силa 2(2F)=4F.

3) Оскільки натяг мотузки a дорівнює силі 4F, то на рухомий блок a діє силa 2(4F)=8F.

Таким чином, дана система блоків забезпечує 8 разовий виграш в силі. А це означає, що ту силу тяжіння яка діє на вантаж масою 40кг і яка дорівнює 400Н, зрівноважить сила F=400H/8=50H. При цьому, враховуючи що напяг мотузки b дорівнює 2F, можна стверджувати що величина цього натягу 100Н.

Задача 4. За допомогою рухомого блока піднімають вантаж прикладаючи силу 100Н. Визначте силу тертя, якщо вага блоку 20Н, а вага вантажу 165Н.

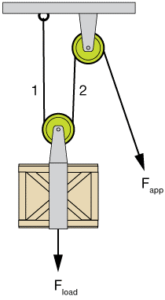
Зауваження. В системах реальних блоків неминуче проявляють себе певні сили тертя які протидіють обертанню шківів. Результатом наявності цих сил є факт того, що натяг кануту на виході шківа дещо менший аніж на його вході. Крім цього потрібно мати на увазі, що реальні шківа та їх блоки мають певну масу і тому оцінюючи вантажопідємність системи потрібно враховувати вагу рухомих блоків.

Рішення. За відсутності сил тертя рухомий блок мавби піднімати вантаж величина якого вдвічі більша за величину прикладеної до канату сили, тобто вантаж величиною 2·100Н = 200Н. В реальності ж цей блок піднімає вантаж величиною 165Н + 20Н = 185Н. А це означає, що загальна величина виникаючих в системі сил тертя дорівнює 200Н – 185Н = 15Н.

Відповідь: F_тер= 15Н.

Задача 5. Через нерухомий блок перекинуто нитку до кінців якої прив’язано вантажі масою 1,5кг та 1,0кг. З яким прискоренням будуть рухатись тягарці?

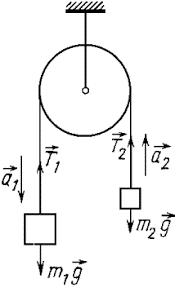
Дано:

m₁ = 1,5кг

m₂ = 1,0кг

а =?

Рішення: Виконуємо малюнок на якому вказуємо всі діючі на кожне тіло сили. А цими силами є: сила тяжіння F_т1=m₁g, F_т1=m₁g; сила натягу нитки Т₁ = Т₂; сила інерції F_i1=m₁a, F_i2=m₂a; (на малюнку

силу інерції не позначено). Із аналізу малюнку, а по суті з умови динамічної рівноваги тіл, випливає:

Т₁ = m₁g – m₁a;

Т₂ = m₂g + m₂a.

А оскільки  Т₁=Т₂, то m₁g – m₁a =  m₂g + m₂a, звідси m₂а + m₁a = m₁g – m₂g, звідси

а = g(m₁–m₂)/(m₁+m₂) = 10(1,5–1,0)/(1,5+1,0) = 2,0(м/с²)

Відповідь:  а = 2,0м/с².

Контрольні запитання.

1. Яку систему сил називають збіжною? Чи може така система надати тілу обертального руху?
2. Чому пару сил не можна замінити рівнодіючою силою?
3. Що називають моментом сили та плечем дії сили?
4. Чому загальна умова рівноваги тіла (∑F=0; ∑M=0), для тіла що знаходиться під дією збіжної системи сил набуває вигляду ∑F=0, а для тіла що має нерухому вісь обертання ∑М=0.
5. Чому дверні ручки розташовують на краю дверей, а не на їх середині?
6. Чи означає факт підсилення важелем силової дії, що це підсилення є «безкоштовним»?
7. Що стверджується в золотому правелі механіки?
8. Чи дає виграш в силі зображений на малюнку (а) блок? Який сенс застосування такого блоку?
9. За рахунок чого зображена на малюнку (б) система нерухомого та рухомого блоків, забезпечує подвійний виграш в силі? Як працює золоте правило мехатіки в цій системі?

а)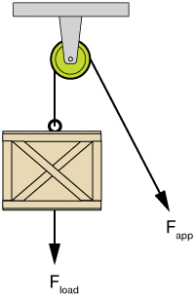  б)

10. Чи може подвійний виграш в силі забезпечити лише один рухомий блок?
11. Чи може система яка складається з двох рухомих та двох нерухомиж блоків забезпечити пятикратний виграш у силі. Якщо може, то як?

Вправа 15.

Загальні зауваження. При розв’язуванні задач, діючу на тіло силу тяжіння прикладають в центрі мас цього тіла. В однорідних тілах (ρ=const) постійної площі поперечного перерізу (стержні, труби, балки, тощо), центр мас тіла співпадає з його геометричним центром.

1.В точці 1 прикріплено вантаж масою 20кг. Яку силу треба прикласти в точці 2, щоб важіль був у рівновазі. Маса важеля 4кг.

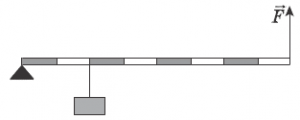
2. На землі лежить балка масою 80кг. Яку силу потрібно прикласти, щоб підняти один кінець цієї балки.

3. До кінців важеля довжиною 1м підвішені вантажі масою 6кг і 14кг. Де потрібно встановити опору, щоб вантажі перебували у рівновазі?

4. Відомо що маса слона 5т, а маса мухи 0,1г. Якої довжини має бути довше плече важіля, щоб муха зрівноважила слона. Довдина того плеча на якому стоїть слон 2м. Масу важеля не враховувати. На скільки має опуститися муха, щоб слон піднявся на 10см?

5. Стержень довжиною 1м горизонтально висить на двох динамометрах. При цьому перший знаходиться на відстані 10см від лівого кінця стержня і показує 30Н, а другий – знаходиться на відстані 30см від правого кінця. Яка маса стержня і що показує другий динамометр?

6. Який виграш у силі забезпечують зображені на малюнку системи блоків?

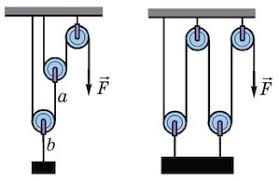
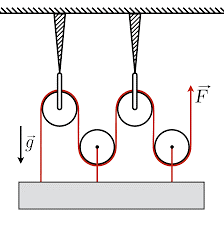
7. Який виграш у силі забезпечують зображені на малюнку системи блоків?

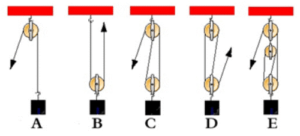
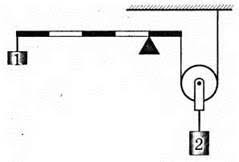
8. На основі аналізу малюнку визначте масу вантажу 2, якщо маса вантажу 1 дорівнює 20кг, а система перебуває в рівновазі.

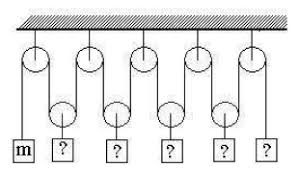
9. Яка маса кожного вантажу зображеної на малюнку системи, якщо m=12кг?

10. На одному кінці нитки перекинутої через нерухомий блок, підвішено вантаж масою 1кг, а на другому– 2кг. З яким прискоренням рухатиметься дана система тіл?

.

Лекційне заняття №16. (Практичне заняття)

Тема: Рівновага тіла під дією довільної системи сил.  Розв’язування задач.

         В загальному випадку умову рівноваги тіла що знаходиться під дією плоскої системи довільних сил, можна записати у вигляді:

∑ F_x = 0

∑ F_y = 0

∑ M = 0

Виходячи з цієї умови та дотримуючись загально прийнятого порядку розв’язку задач статики, розв’яжемо декілька з них. А загально прийнятий порядок розв’язку задач на рівновагу тіла під дією довільної системи сил, є наступним:

1.На основі аналізу умови задачі виконати малюнок (обов’язково), на якому чітко вказати всі діючі на задане тіло сили, їх кутові орієнтації, відстані між ними, та діючі на тіло обертальні моменти.

2.Оптимальним чином задати систему координат.

3. Записати умову рівноваги даного тіла, тобто систему рівнянь:

∑ F_x = 0

∑ F_y = 0

∑ M = 0

4. Розв’язавши цю систему, визначити невідомі величини.

Загальні зауваження. До числа тих базових опор, які широко застосовуються в інженерно-технічній практиці, відносяться:

1) Шарнірно рухома опора (мал.76в). Реакція опори (R) направлена перпендикулярно до напрямку можливого руху опори.

2) Шарнірно нерухомі опори (мал.76б). Реакція опори має дві складові: вертикальну R_y (або Y) та горизонтальну R_x (або Х).

3) Жорстко закріплений стержень (мал.76а). Реакція опори має три складові: вертикальну R_y горизонтальну R_x та протидіючий момент сили М.

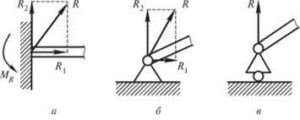
Мал.76. Базові опори інженерно-технічної практики.

Задача 1. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: Р₁=200H, Р₂=300Н, α=30º. Вагою балки знехтувати.

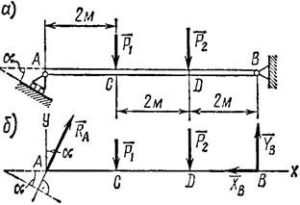
Рішення.

1.Виконуємо малюнок на якому вказуємо всі діючі на балку сили та відстані між ними. Задаємо систему координат.

2. Записуємо систему рівнянь які відповідають умові рівноваги даної балки.

1) ∑F_x = R_Asinα – X_B = 0;

2) ∑F_y = R_Acosα – P₁ – P₂ – Y_B = 0;

3) ∑M_A = P₁·2 + P₂·4 – Y_B·6 = 0.

Сили R_A та Х_В обертальних моментів відносно точки А не створюють. Не створюють тому, що лінії дії цих сил проходять через т.А і тому плече дії цих сил дорівнює нулю.

3. Розв’язавши систему рівнянь, визначаємо невідомі величини:

Із (3) → Y_B = (P₁·2 + P₂·4)/6 = (200·2+300·4)/6 = 267Н;

Із (2) → R_A = (P₁ + P₂ + Y_B)/cos30° = (200 + 300 + 267)/0,87 = 882Н;

Із (1) → Х_В = R_Asin30° = 882·0,5 = 441Н.

Відповідь: R_A = 882Н, X_B = 441Н, Y_B = 267Н.

Задача 2. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: q=100H/м, F=300H, α=60º, M=400Н∙м. Вагою балки знехтувати.

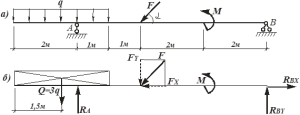
Рішення.

1.Виконуємо малюнок на якому вказуємо всі діючі на балку сили та відстані між ними. Задаємо систему координат. (Розподілене навантаження q=100H/м, замінюємо рівнодіючою силою Q=q∙ℓ=100Н/м∙3м=300Н).

2. Записуємо систему рівнянь які відповідають умові рівноваги даної балки.

∑ F_х = Fcosα – R_Bx = 0                                   (1)

∑ F_у = –Q + R_A – Fsinα + R_By = 0                  (2)

∑ M_B = –Q∙6,5 + R_A∙6 – Fsinα∙4 – M = 0       (3)

Зауваження.  1). Визначаючи момент сили F відносно точки B, доцільно розкладати цю силу на дві складові:  F_x = Fcosα;  F_y = Fsinα.  При цьому:  M(F_x) = 0,  (d=0);   M(F_y) = (Fsinα)4,  (d=4м). 2). Ту точку відносно якої визначаються моменти сил, обирається довільно. При цьому зазвичай її обирають таким чином, щоб максимальне число невідомих сил створювали нульові моменти.

3. Розв’язавши систему рівнянь, визначаємо невідомі величини:

Із (1) → R_Bx = Fcos60° = 300∙0,5=150H

Із (3) → R_A = [Q∙6,5 + Fsin60º∙4 + M]/6 = … = 406H

Із (2) → R_By = Q – R_A + Fsinα = … = 155H.

Відповідь: R_Bx=150H; R_By=155H; R_A= 406H.

Задача 3. Під дією зображеної на малюнку системи сил жорстко закріплена балка знаходиться в стані механічної рівноваги. Визначити наявні в точці закріплення реакції опори. Вагою балки знехтувати.

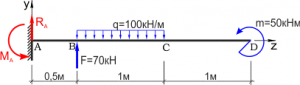
Зауваження. В загальному випадку реакція жорстко закріпленої опори має три складові: горизонтальну R_x, вертикальну R_у, та протидіючий момент сили М. Однак в умовах нашої задачі, горизонтально діючі сили відсутні і тому горизонтальна складова реакції опори дорівнює нулю.

Рішення.

1.Виконуємо малюнок на якому вказуємо всі діючі на балку сили та відстані між ними. Задаємо систему координат.

2. Записуємо систему рівнянь які відповідають умові рівноваги даної балки.

∑ F_у = R_A + F – Q = 0                            (1)

∑ M_A = –M_A – F∙0,5 + Q∙1 – M = 0       (2)

де Q = q∙1 = 100кH.

3. Розв’язавши систему рівнянь, визначаємо невідомі величини:

Із (1) → R_A = –F + Q = –70+100 =30кH

Із (2) → M_A = – F∙0,5 + Q∙1 – M = … = 15кH∙м

Відповідь: R_A=30кН ; M=15кН∙м.

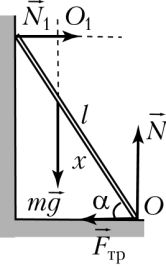
Задача 4. Труба масою 30кг і довжиною 4м приставлена до стіни під кутом 30° до поверхні стіни. З якою, прикладеною до центру труби горизонтальною силою F потрібно тягнути трубу, щоб відірвати її від стіни? Нижній кінець труби не ковзає.

Дано:

m = 30кг

ℓ = 4м

α = 30°

F = ?

Рішення: Виконуємо малюнок, на якому вказуємо діючі на трубу сили і задаємо систему координат: вісь 0х направлена вздовж труби, діюча на центр маси тіла горизонтальна сила F, на малюнку не позначена. Враховуємо, що в момент відриву труби від вертикальної стіни, труба і стіна перестають взаємодіяти, і тому N₁=0. В таких умовах на трубу діють чотири сили: F_т=mg, F, N, F_тер, при цьому три з них є невідомими. Визначаючи ці сили ми могли б записати три рівняння рівноваги і розв’язавши їх, визначити F, N, F_тер. Однак, за умовою задачі, нас цікавить лише одна величина – сила F. Тому ми запишемо і розв’яжемо лише одне рівняння ∑M_O=0. В цьому випадку моменти сил N і F_тер дорівнюють нулю.

∑ M_O = F∙d₁ – F_т∙d₂ = F(ℓ/2)cos30º – F_т(ℓ/2)sin30º = 0.   Звідси F = [F_т(ℓ/2)sin30º]/[(ℓ/2)cos30º] = F_тtg30º = mgtg30º.

Розрахунки: F = mgtg30º = 30кг∙10м/с²∙0,577= 173H .

Відповідь: F = 173H.

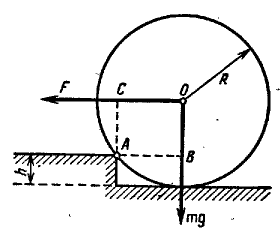
Задача 5. Колесо радіусом R і масою m стоїть перед сходинкою висотою h. Яку горизонтальну силу F потрібно прикласти до осі колеса, щоб воно викотилось (піднялось) на сходинку?

Рішення.

Виконуємо малюнок на якому вказуємо всі діючі на колесо сили. При цьому враховуємо, що в момент відриву колеса від горизонтальної поверхні, його взаємодія з цією поверхнею буде нулевою. А це означає, що в момент відриву колеса від горизонтальної поверхні, на колесо діють три сили: сила тяжіння F_т=mg; діюча в точці А реакція опори N_A яка направлена до центру колеса; горизонтально направлена сила F. При цьому для визначення невідомої сили F достатньо записати лише одне рівняння ∑M_A=0. Адже відносно точки А силові моменти створюють лише сила тяжіння (F_т) і та зовнішня горизонтальна сила (F) яка і піднімає колесо на сходинку.

Плечі сил F та F_т відносно точки А  (відповідно АС і АВ) визначаємо із геометричних міркувань (див. мал.): 1) АС = R – h;  2) (АВ)² + (АС)² = R², або (АС)² + (R – h)² = R². Звідси  (АВ)² = R² – (R – h)² = 2Rh – h², або АВ = √(2Rh – h²).

Враховуючи вище сказане, можна записати

∑ М_А= F(R – h) – F_т√(2Rh – h²) = 0.

Звідси  F = [F_т√(2Rh – h²)]/(R – h) = [mg√(2Rh – h²)]/(R – h).

Відповідь: F = [mg√(2Rh – h²)]/(R – h).

Вправа 16.

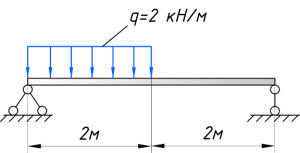
1.Балка масою 100кг під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опори.

2. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: q=100H/м, F=300H, α=60º. Вагою балки знехтувати.

3. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: q=75H/м, Р=300H, G=200H, M=400H∙м. Вагою балки знехтувати.

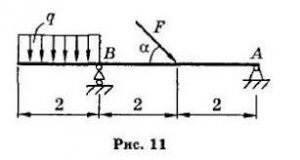
4. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: q=75H/м, Р=300H, G=200H, M=400H∙м. Вагою балки знехтувати.

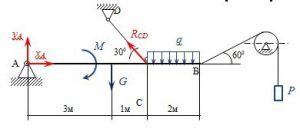
5. Під дією зображеної на малюнку системи сил жорстко закріплена балка знаходиться в стані механічної рівноваги. Визначити наявні в точці закріплення реакції опори. Вагою балки знехтувати.

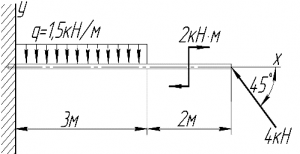
6. Однорідна балка лежить на платформі так, що одна четверта її довжини звисає з платформи. До звисаючого краю балки прикладають силу, направлену вертикально вниз. Коли ця сила досягає 2000Н протилежний край балки починає підніматись. Визначити масу балки.

7. До кінців стержня масою 10кг і довжиною 80см підвішено вантажі масами 40кг і 10кг. Де треба розмістити опору, щоб стержень перебував у рівновазі?

8. Драбина довжиною 4м приставлена до гладенької стіни під кутом 30º. Коефіцієнт тертя між драбиною та підлогою 0,3. На яку відстань виміряну вздовж драбини може піднятись людина, перш ніж драбина почне зсковзувати підлогою.

9. Однорідна куля підвішена на нитці, кінець якої закріплено на вертикальній стіні. Яким повинен бути коефіцієнт тертя μ між кулею і стіною, щоб точка кріплення нитки до кулі і центр кулі могли знаходитися на одній вертикалі? Радіус кулі R, довжина нитки ℓ.

.

Лекційне заняття №17.

Тема: Динаміка. Основні поняття, величини та закони динаміки. Принцип відносності. Закони Ньютона.

Динаміка – це узагальнюючий розділ механіки, в якому вивчаються силові та імпульсно-енергетичні параметри механічного руху тіл в усіх його проявах. В динаміці, ті знання які були отримані при вивченні кінематики та статики, доповнюються новими знаннями і узагальнюються. До числа основних фізичних величин динаміки, а точніше динаміки матеріальної точки, відносяться: маса (m), енергія (Е), робота (А), потужність (N), коефіцієнт корисної дії (η) та імпульс (р). До числа основних законів динаміки і механіки загалом, відносяться: перший, другий і третій закони Ньютона, закон збереження енергії та закон збереження імпульсу, закон всесвітнього тяжіння. При цьому базовим законом всієї механіки і фізики загалом є принцип відносності.

В 1630 році, в своїх знаменитих «Діалогах про дві системи світу – Птоломеєву та Копернікову» видатний італійський вчений Галілео Галілей (1564–1642) сформулював закон, який лежить в основі сучасної науки і який прийнято називати принципом відносності або принципом Галілея.

Як відомо, заперечуючи факт обертання Землі навколо Сонця, прибічники середньовічної церкви стверджували: «Якби Земля дійсно рухалась, то ми б фізично відчували цей рух. Відчували б подібно до того, як відчуваємо рух карети, човна чи будь чого іншого». Відповідаючи на подібні аргументи, Галілей стверджував: Дійсно, сидячи в кареті, ми безумовно відчуваємо, рухається вона чи не рухається. Відчуваємо тому, що карета їде не по ідеально рівній дорозі, її колеса не ідеально круглі, тягові зусилля коней постійно змінюються, дорога вкрита дрібними камінчиками, ямками, тріщинками, піщинками, тощо. А це означає, що сидячи в кареті, ми постійно відчуваємо певні поштовхи, тобто різкі, короткотривалі зміни швидкості, які власне і вказують на те, що карета рухається. А от якби мене, вас чи кого завгодно посадити в закриту, ізольовану карету, яка б дійсно рухалась рівномірно, тобто без будь яких змін швидкості, то ні ви, ні я, ні хто завгодно, не змогли б визначити, рухається карета чи стоїть.

Ніякими експериментами, які проводяться в середині закритої ізольованої кабіни, не можливо встановити стоїть ця кабіна чи рівномірно рухається. Не можливо тому, що всі фізичні процеси, які відбуваються в кабіні що стоїть (v=0) і в кабіні що рівномірно рухається (v=const), відбуваються абсолютно однаково/

Звичайно, в умовах повсякденного життя, ми практично ніколи не опиняємося в ситуаціях коли не можемо визначити рухається та «кабіна» в якій ми знаходимось, чи не рухається. Не опиняємося по перше тому, що реальні «кабіни» (автомобілі, літаки, човни, велосипеди, тощо), практично ніколи не рухаються ідеально рівномірно (без жодних поштовхів та вібрацій). А по друге, реальні кабіни не є ідеально ізольованими від навколишнього світу та тих процесів, що спричиняють їх рух. Тому в процесі цього руху, ми так чи інакше бачимо, чуємо та відчуваємо певні ознаки того, що наша «кабіна» рухається.

Втім, якщо вам потрібні докази того, що принцип відносності безумовно правильний, безумовно достовірний, то ось один з них. Кожен з нас знаходиться в кабіні, яка називається планета Земля. Ця кабіна з швидкістю 30км/с=108000км/год обертається навколо Сонця. При цьому, жоден з нас не відчуває факту того, що Земля мчить з такою шаленою швидкістю. Швидкістю, яка в 60 разів перевищує швидкість кулі. І даний факт не є результатом певних особливостей людського організму. Адже в незалежності від наших відчуттів, всі фізичні процеси на Землі відбуваються так, ніби вона знаходиться в стані механічного спокою.

Мал.77. Земля з швидкістю 30км/с обертається навколо Сонця. Чи відчуваєте ви факт цього надшвидкого руху?

Щоправда, Земля рухається не зовсім рівномірно. Адже в процесі обертання навколо Сонця та своєї осі, напрям руху Землі, а отже і тіл на її поверхні, повільно але неухильно змінюється. А це означає, що факт обертального руху Землі можна експериментально довести, наприклад за допомогою спеціальних маятників. А от якби Земля дійсно рухалась прямолінійно та рівномірно, то з якою б швидкістю вона не рухалась, ви б не змогли встановити, рухається вона чи не рухається.

Іноді думають, що в законі, який називається принципом відносності, стверджується, що все в цьому світі відносне. Це не правда. Не правда по-перше тому, що не все у Всесвіті відносне. Скажімо, наскільки нам відомо,  абсолютно незмінними є ті співвідношення які називаються законами Природи і які відображають ті зв’язки що існують між об’єктами та явищами Всесвіту. Абсолютно незмінною є швидкість світлових фотонів. Абсолютно незмінною є загальна кількість зосередженого у Всесвіті електричного заряду, мас-енергії, спіну, тощо. По-друге, в законі який називається принципом відносності стверджується те що стверджується, а саме: Ніякими експериментами, які проводяться в середині закритої ізольованої кабіни, не можливо встановити стоїть ця кабіна чи рівномірно рухається. Не можливо тому, що всі фізичні процеси, які відбуваються в кабіні що стоїть (v=0) і в кабіні що рівномірно рухається (v=const), відбуваються абсолютно однаково.

Інша справа, що в сучасній науці принцип відносності формулюють дещо по іншому. І це сучасне формулювання є наступним: У всіх інерціальних системах відліку, тобто таких системах де виконується закон інерції (перший закон Ньютона) всі фізичні процеси відбуваються абсолютно однаково. Іншими словами, в тих системах відліку де виконується закон інерції, діють ті ж закони, що і в інших подібних (інерціальних) системах. Наприклад наша земна система відліку є інерціальною, тобто такою в якій виконується закон інерції. А в цьому законі стверджується: якщо швидкість того чи іншого фізичного об’єкту змінюється, то це означає, що на нього діє певна зовнішня сила, яка і спричиняє цю зміну.        Ви можете запитати: «Ну добре, в рівномірно рухомих і нерухомих системах відліку всі події відбуваються однаково. Це зрозуміло, це факт, який можна довести. З інерціальними системами відліку, менш зрозуміло, але приймемо на віру, що в них як і в системах рухомих та нерухомих, всі події відбуваються однаково. Але чому вчені стверджують, що саме принцип відносності є тим базовим, тобто найголовнішим, найважливішим законом, який лежить в основі всієї сучасної науки? І що це за закон, який навіть певного математичного вираження не має? А якщо не має, то яка користь від такого закону?»

Відповідаючи на ці слушні запитання, можна сказати наступне. Чи задумувались ви над тим, чому вчені з такою впевненістю говорять про ті події, які відбуваються в практично недосяжних частинах Всесвіту? Чому вони впевнені в тому, що ті закони які відкривались на тій піщинці Всесвіту яка називається планета Земля, діють і в інших куточках Всесвіту. А можливо там, в інших галактиках, все відбувається по іншому? Можливо там, діють інші закони, існують інші атоми, інші молекули, інші біологічні структури? Хто був в тих далеких світах та перевіряв це?

Відповіді на ці та їм подібні запитання дає принцип відносності. Адже згідно з цим принципом для з’ясування того, діють чи не діють відкриті на Землі закони природи в інших місцях Всесвіту зовсім не обов’язково вирушати в далеку космічну подорож. Достатньо з’ясувати, виконується чи не виконується у відповідному місці закон інерції. І якщо цей закон виконується, то це автоматично означає, що відповідна система є інерціальною, і що тому у відповідному куточку Всесвіту діють ті ж закони що і на Землі.

І от ми вдивляємось в безмежні простори Всесвіту, аналізуємо ті події які відбуваються в ньому і бачимо, що у всіх його куточках, всі об’єкти рухаються у повній відповідності з законом інерції. А це означає, що у всіх частинах Всесвіту діють одні і ті ж закони. І що ці закони співпадають з тими що діють на Землі. Не вірити цьому факту, це все рівно ніби заперечувати факт того, що Земля обертається навколо Сонця та своєї осі. Заперечувати лише на тій підставі, що ми не відчуваємо відповідного руху.

Мал.78. Бачимо: у Всесвіті безпричинних змін швидкості не буває. Висновок: у всіх куточках Всесвіту діють одні і ті ж закони Природи.

Принцип відносності є теоретичною основою механіки і всієї сучасної науки загалом. Однак сам по собі цей принцип ще не є тим законом який пояснює широке коло явищ та дозволяє розв’язувати відповідно широке коло конкретних задач. Цю функцію виконує наукова теорія, тобто цілісна система достовірних знань про певну групу споріднених явищ.

В 1687 році видатний англійський фізик Ісаак Ньютон (1643–1727) опублікував свої знамениті «Математичні начала натуральної філософії», в яких виклав основи першої наукової теорії сучасного зразку. Теорії, яку прийнято називати механікою або ньютонівською механікою. В основі цієї теорії лежать три твердження, які називаються законами Ньютона. Сформулюємо ці твердження та проаналізуємо їх.

         Перший закон Ньютона, це закон, в якому стверджується: Будь-яке тіло буде знаходитись в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v=const), до тих пір поки на нього не подіє зовнішня сила, яка і змусить тіло змінити цей стан.

На перший погляд, даний закон не має суттєвого практичного значення. Його навіть важко записати у вигляді відповідної формули. Однак насправді, мова йде про надзвичайно важливий, по суті базовий закон не лише механіки, а й всієї сучасної науки. Адже в рамках першого закону Ньютона по суті стисло сформульовано два базові закони: принцип відносності та закон інерції.

         Дійсно. В першому законі Ньютона стверджується: будь-яке тіло буде знаходитись в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v=const), до тих пір поки на нього не подіє зовнішня сила, яка і змусить тіло змінити цей стан. По суті це означає, що з фізичної точки зору, стан спокою (v=0) і стан прямолінійного рівномірного руху (v=const), це один і той же механічний стан (цей стан). Один і той же в тому сенсі, що всі фізичні процеси які відбуваються в кабіні що стоїть і  в кабіні що рівномірно рухається, відбуваються абсолютно однаково (принцип відносності). Іншими словами: v=0  « = »  v=const, де знак « = » вказує на те, що ті фізичні процеси які відбуваються в кабіні яка стоїть і в кабіні яка рівномірно рухається, відбуваються «однаково».

         З іншого боку, в тому ж першому законі Ньютона  стверджується, що причиною зміни стану спокою, або стану прямолінійного рівномірного руху, тобто причиною зміни швидкості руху тіла, є дія на це тіло певної зовнішньої сили. Іншими словами, в першому законі Ньютона стверджується, що безпричинних змін швидкості руху тіла не буває, і що цією причиною є дія зовнішньої сили (закон інерції). А зважаючи на те, що зміну швидкості руху тіла характеризує величина яка називається прискоренням, закон інерції можна сформулювати у вигляді: причиною прискореного руху тіла, є дія на це тіло певної зовнішньої сили: F → a.

Наприклад, якщо Місяць обертається навколо Землі, Земля обертається навколо Сонця, а Сонце обертається навколо центру Галактики, то напрям їх швидкості постійно змінюється. А у відповідності з тією частиною першого закону Ньютона, яка називається законом інерції, така зміна не може бути безпричинною, і що має існувати та зовнішня сила яка змушує Місяць, Землю та Сонце змінювати напрям свого руху (рухатись з доцентровим прискоренням). І в кожному з цих та в мільярдах подібних випадків, така сила дійсно існує і називається силою гравітаційної взаємодії. Силою, яка у повній відповідності з законом всесвітнього тяжіння об’єднує планети і зірки в планетарні системи, зірки – в галактики, галактики – в метагалактики, а все разом – у Всесвіт.

Мал.79. Безпричинних змін швидкості руху тіл не буває, а цією причиною є дія певної зовнішньої сили (закон інерції).

Таким чином, в першому законі Ньютона, опосередковано сформульовано два твердження: принцип відносності та закон інерції.

а) v=0  « = »  v=const (принцип відносності)

б)  F → a  (закон інерції)

Другий закон Ньютона, це закон, в якому стверджується: Під дією зовнішньої сили F, тіло масою m отримує прискорення   а   величина якого прямо пропорційна діючій на тіло силі і обернено пропорційна його масі. Іншими словами:   F  →   a = F/m.

Не важко бачити, що другий закон Ньютона, є логічним продовженням першого. Адже в тій частині першому законі Ньютона яка називається законом інерції, по суті стверджується, що причиною зміни швидкості руху тіла, а отже причиною його прискореного руху, є дія зовнішньої сили, тобто стверджується, що сила породжує прискорення: F → a. В другому ж законі Ньютона, це твердження формулюється в явному вигляді та конкретизується:  F →  a = F/m.

Мал.80. Сила – є причиною прискореного руху тіла, при цьому величина прискорення прямо пропорційна діючій на тіло силі і обернено пропорційна масі тіла:  F  →   a = F/m.

Звичайно, говорячи про те, що сила, а точніше зовнішня сила, є причиною прискореного руху тіла, мається на увазі, що на відповідне тіло діє лише дана сила. Адже якщо наприклад, під дією певної сили тіло рухається з постійною швидкістю, або не рухається взагалі, то це означає лише те, що на відповідне тіло, окрім даної сили діють й інші сили, які зрівноважують її дію.

Третій закон Ньютона, це закон, в якому стверджується: Діюча на тіло сила F, завжди породжує рівну їй за величиною і протилежну за напрямком протидіючу силу F′. Іншими словами: F → F′ = –F

Наприклад, якщо тіло з певною силою діє на опору, то опора з такою ж силою діє на тіло. Якщо нога футболіста діє на м’яч, то м’яч з такою ж силою діє на ногу футболіста. Якщо Місяць притягується до Землі, то Земля з такою ж силою притягується до Місяця.

 

Мал.81. Діюча F та протидіюча Fꞌ сили, завжди рівні за величиною, протилежні за напрямком і прикладені до різних тіл.

Говорячи про діючу та протидіючу сили, потрібно зауважити, що ці сили завжди чисельно рівні, однак результат їх дії може бути абсолютно різним. Наприклад, підняте над Землею тіло з певною силою F притягується до Землі, а Земля з такою ж силою F′ притягується до тіла. Однак, якщо для відносно легкого тіла сила F є значною, то для надмасивної Землі, така ж сила F′ є мізерно малою. Тому в системі Земля – тіло, тіло падає на Землю, а не Земля «підстрибує» до тіла.

Потрібно наголосити й на тому, що діюча та протидіюча сили, завжди прикладені до різних тіл. А це означає, що ці сили не можуть забезпечити механічну рівновагу системи діюче-протидіюче тіло. М’яч, в результаті взаємодії з ногою футболіста з певним прискоренням відлітає від ноги. Тіло, в результаті взаємодії з Землею з певним прискоренням падає на підлогу. Земля в результаті взаємодії з Сонцем з певним доцентровим прискоренням обертається навколо Сонця, і т.д. І якщо книга що лежить на столі, знаходиться в стані механічної рівноваги, то це не тому що діюча і протидіюча сили зрівноважують одна одну. Бо в системі опора-книга, книга діє на опору з силою яка називається вагою книги (Р), а опора діє на книгу з протидіючою силою яка називається реакцією опори (N). При цьому на книгу фактично діє лише одна з цих сил – реакція опори. Рівновага ж книги забезпечується не зрівноваженням діючої та протидіючої сил, а фактом того, що на книгу окрім реакції опори діє ще одна зовнішня сила – сила тяжіння.

Аналізуючи закони Ньютона, не важко бачити, що це не просто набір правильних тверджень, а струнка система взаємопов’язаних та взаємодоповнюючих законів. Законів, які у своїй сукупності дозволяють пояснити величезне різноманіття механічних явищ. Законів, в яких при ґрунтовному аналізі можна відшукати не лише формулювання принципу відносності та закону інерції, а й приховані формулювання інших законів, зокрема закону збереження механічної енергії та закону збереження імпульсу. Взаємопов’язаність та взаємодоповнюваність законів Ньютона з усією очевидністю випливає з їх наступних математичних формулювань:

1. а) v=0  « = »  v=const

б)  F → a

2. F → a = F/m
3. F → Fꞌ = – F

Контрольні запитання.

1. Що стверджує принцип відносності (перше формулювання)?
2. Чому, сидячи в реальній закритій кабіні (кареті, автомобілі, потязі, тощо) ми практично завжди можемо визначити рухається ця кабіна чи не рухається?
3. Чи є правильним твердження: у Всесвіті все відносне? Наведіть приклади тих речей які є абсолютно незмінними.
4. Що стверджує принцип відносності (друге формулювання)?
5. Які системи відліку називають інерціальними? Що стверджується в законі інерції?
6. Як з’ясовують те, діють чи не діють відкриті на Землі закони природи в інших куточках Всесвіту?
7. Якими словами в першому законі Ньютона сформульовано принцип відносності?
8. Що стверджується в законі інерції і якими словами це відображено в першому законі Ньютона?
9. Чому ми говоримо, що другий закон Ньютона є логічним продовженням першого?
10. Чому діюча та протидіюча сили не можуть забезпечити механічну рівновагу тіла?
11. Тіло висить на мотузці. Які сили діють на тіло? Чи є ці сили діючою і протидіючою? Чому?

Вправа 17.

1. З яким прискоренням рухається під час розгону реактивний літак масою 60т, якщо сила тяги двигунів 90кН?
2. Сила 40Н надає тілу прискорення 0,8м/с². Яка сила надасть цьому ж тілу прискорення 2,0м/с² ?
3. Снаряд масою 5кг при пострілі набуває швидкості 800м/с. Визначити середню силу тиску порохових зарядів, якщо довжина дула гармати 2м. Рух снаряду вважати рівноприскореним.
4. М’яч масою 400г в процесі удару який триває 0,02с набуває швидкості 15м/с. Яка середня сила удару?
5. Під дією сили 5Н, швидкість матеріальної точки змінюється за законом v=6 – 0,3t. Яка маса матеріальної точки?
6. Тіло масою 4кг рухаючись прямолінійно та маючи деяку початкову швидкість, за 5с під дією сили 6Н набуло швидкості 10м/с. Визначити початкову швидкість тіла.
7. На яку висоту підніметься тіло масою 6кг за 2с під дією вертикальної сили 100Н? Рух тіла є рівноприскореним.
8. Кулька масою 500г скочується з похилої площини довжиною 2м, маючи початкову швидкість 2м/с. Яку швидкість матиме кулька в кінці похилої площини, якщо рівнодійна діючих на неї сил дорівнює 4Н?

.

Лекційне заняття №18.

Тема: Енергія. Механічна енергія. Закон збереження енергії. Розв’язування задач.

         Уявити сучасну науку без величини яка називається енергією (від грец. energeia – дія, діяльність) практично не можливо. Адже саме енергія є тією стержневою фізичною величиною яка об’єднує найрізноманітніші явища Природи в цілісну наукову картину. Сучасне розуміння суті того, що називають енергією, це результат тривалого еволюційного розвитку науки, вінцем якого є теорія відносності. Лише після створення цієї теорії, стало зрозумілим, що енергія є загальною мірою всіх видів рухів та взаємодій, і що будь який фізичний об’єкт масою m, представляє собою згусток енергії загальна кількість якої визначається за формулою Е=mс², де с=3∙10⁸м/с=соnst. Це означає, що повністю перетворивши все те з чого складається дане тіло, а отже всі його молекули, атоми, атомні ядра, протони, нейтрони, електрони та всі ті процеси які відбуваються з ними, в те що називається чистою енергією, а по суті в світло, ви отримаєте цієї енергії в кількості Е=mс². Наприклад в будь якому тілі масою 1кг міститься Е=1кг(3·10⁸м/с)²=9·10¹⁶Дж енергії. Щоб мати уявлення про величину цієї енергії, достатньо сказати, що аналогічну кількість енергії можна отримати при повному згоранні 4 500 000 тон кам’яного вугілля. Для перевезення такої кількості вугілля потрібно більше 75000 вщерть заповнених залізничних вагонів, загальна довжина яких майже 1000км.

Твердження про те, що енергія це загальна міра всіх видів рухів і взаємодій, є загально прийнятою та вичерпною характеристикою того, що називають енергією. Однак воно має той суттєвий недолік, що не дозволяє визначати величину конкретного виду енергії в тій чи іншій конкретній ситуації. А потрібно зауважити, що на практиці говорячи про енергію тіла, мають на увазі не ту загальну енергію яка зосереджена в даному тілі і кількість якої визначається за формулою Е=mс², а певну, зазвичай мізерну частину цієї енергії яка пов’язана з тим чи іншим конкретним явищем. При цьому твердження про те, що той чи інший об’єкт має певну енергію, по суті означає, що за певних умов відповідний об’єкт може виконати певну роботу, тобто певну енерго затратну дію.

Наприклад, коли ми стверджуємо, що підняте над підлогою тіло (мал.82а) має енергію, то це означає, що за певних умов (за умови падіння тіла) буде виконана певна робота: в процесі удару об підлогу, тіло деформується і деформує підлогу; в процесі падіння та удару, тіло, підлога та повітря нагріються; в процесі удару, тіло заб’є гвіздок, створить звукову хвилю, тощо. Коли ми стверджуємо, що тіло масою m, рухаючись з швидкістю v, має енергію (мал.82б), то це означає, що за певних умов (за умови зустрічі тіла з перешкодою) буде виконана певна робота. Коли ми стверджуємо, що деформована пружина (мал.82в) має енергію, то це означає, що за певних умов (за умови випрямлення пружини), буде виконана певна робота. Коли ми стверджуємо, що шматок вугілля має енергію, то це означає, що за певних умов вугілля буде горіти і що в процесі горіння буде виконана певна робота.

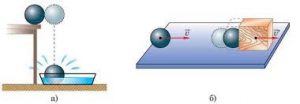
Мал.82.  Коли ми стверджуємо, що певний фізичний об’єкт має певну енергію, то це означає, що цей об’єкт здатний виконати певну роботу (певну енергозатратну дію).

Зважаючи на вище сказане, можна дати наступне визначення: Енергія – це фізична величина, яка є загальною мірою всіх видів рухів та взаємодій і яка характеризує здатність тіла, частинки або поля виконати роботу.

Позначається: Е

Визначальне рівняння:

1) для загальної кількості енергії:  Е=mс²;

2) для конкретних видів енергії:  різні.

Одиниця вимірювання: [E] = Дж = Н∙м = кг∙м²/с²,   джоуль.

Джоуль – це одиниця вимірювання енергії та роботи, яка дорівнює тій роботі (тим затратам енергії) яку виконує сила в один ньютон при переміщенні тіла (матеріальної точки) на один метр в напрямку дії сили: Дж=Н∙м=кг∙м²/с². Щоб мати уявлення про величину роботи в один джоуль, візьміть тіло масою 102г та підніміть його на висоту один метр. При цьому виконана вами робота, а відповідно і затрачена вами енергія, дорівнюватимуть одному джоулю. Або якщо наприклад, яблуко масою 102гр впаде з висоти 1м, то виконана силою тяжіння робота дорівнюватиме 1Дж.

Мал.83. Піднімаючи тіло масою 102г з висоту 1м, ви виконуєте роботу 1Дж.

Вивчаючи фізику ви неминуче переконаєтесь в тому, що енергія невичерпно різноманітна в своїх проявах. Різноманітна в тій же мірі як і самі явища Природи. Наприклад говорять про енергію гравітаційних, електричних, електромагнітних та інших полів. Про енергію механічну, теплову, звукову, світлову, хімічну, біологічну, електричну, магнітну, електромагнітну, ядерну, внутрішню. Про енергію піднятого тіла та енергію пружно деформованого тіла, про енергію нагрітого тіла та енергію тіла що горить, про енергію хімічних реакцій та енергію термоядерного синтезу. І навіть те що не називають енергією, як то температура, кількість теплоти, робота чи маса, фактично характеризує ті чи інші прояви енергії.

Вивчаючи механіку, ми будемо говорити про ту частину енергії, яка характеризує тіло як єдине ціле і яка пов’язана з його механічним рухом, пружними деформаціями та гравітаційними взаємодіями. Цю енергію називають механічною. Механічна енергія, це така енергія, яку має тіло як єдине ціле і яка пов’язана з його механічним рухом, пружними деформаціями та гравітаційними взаємодіями. Енергію загалом і механічну енергію зокрема, можна представити як певну комбінаціє двох базових різновидностей: енергії руху (кінетична енергія) та енергії взаємодії (потенціальна енергія).

Кінетична енергія (енергія руху) – це та енергія, яку має фізичний об’єкт за рахунок того що він рухається і яка дорівнює половині добутку маси об’єкту на квадрат його швидкості.

Позначається: Е_к

Визначальне рівняння: Е_к=mv²/2

Одиниця вимірювання: [Е_к] = кг∙м²/с²=Дж.

Якщо той чи інший фізичний об’єкт, будь то камінь, планета, атом чи фотон світла, рухається, то він має певну кінетичну енергію величина якої визначається за формулою Е_к=mv²/2. Наприклад, якщо велосипедист маса якого 70кг рухається з швидкістю 36км/год=10м/с, то величина його кінетичної енергії Е_к= 70кг(10м/с)²/2 = 3500Дж.

Мал.84. Кінетична енергія – це та енергія, яку має фізичний об’єкт за рахунок того, що він рухається.

Кінетична енергія є явною, очевидною, активною формою енергії, наявність і величину якої легко встановити: якщо тіло, частинка чи що завгодно, маючи масу m рухається з швидкістю v, то воно має кінетичну енергію величина якої визначається за формулою Е_к = mv²/2.  Але окрім цією активної енергії, практично з кожним тілом нерозривно пов’язана певна кількість пасивної, прихованої енергії, яку прийнято називати потенціальною

Потенціальна енергія (енергія взаємодії) – це та енергія яку має фізичний об’єкт за рахунок того, що він так чи інакше взаємодіяє з іншими об’єктами, або за рахунок тих взаємодій які відбуваються в середині цього об’єкту.

Позначається: Е_п

Визначальне рівняння: Е_п=?, це означає, що єдиної, універсальної формули для визначення потенціальної енергії не існує.

Одиниця вимірювання: [Е_п] = Дж.

Потенціальна енергія, це дуже складний вид прихованої енергії, величину якої в загальному випадку ми не вміємо визначати. Не вміємо в тому сенсі, що на сьогоднішній день нема тієї універсальної формули, яка б дозволяла визначати потенціальну енергію системи в усьому різноманітті проявів цієї енергії. Втім, це зовсім не означає, що ми не вміємо визначати величину потенціальної енергії в тих чи інших конкретних випадках. Наприклад, в механіці вивчають дві різновидності потенціальної енергії: потенціальна енергія сили тяжіння та потенціальна енергія сили пружності.

Потенціальна енергія сили тяжіння (піднятого тіла) –  це така енергія яку має тіло за рахунок його взаємодії з Землею і яка дорівнює добутку маси тіла (m), прискорення сили тяжіння (g) та тієї висоти (h) на яку піднято тіло.

Позначається: Е_п

Визначальне рівняння: Е_п =mgh,

Одиниця вимірювання: [Е_п] = Н, ньютон.

Наприклад, якщо тіло масою 2кг піднято над підлогою на висоту 1,5м, то величина її потенціальної енергії відносно підлоги становить Е_п=2кг·9,81м/с²·1,5м=29,4Дж.

Мал.85. Потенціальна енергія сили тяжіння – це та енергія яку має тіло за рахунок його взаємодії з Землею

Потенціальна енергія сили пружності (пружно деформованого тіла) – це та енергія яку має пружно деформоване тіло за рахунок тих внутрішніх взаємодій які відбуваються в ньому і яка дорівнює половині добутку жорсткості тіла (k) на величину його абсолютної деформації (Δℓ).

Позначається: Е_п

Визначальне рівняння: Е_п=kΔℓ²/2,

Одиниця вимірювання: [Е_п] = Н, ньютон.

Наприклад, якщо пружину жорсткістю 400Н/м деформували на 0,1м, то величина їх потенціальної енергії Е_п=400(Н/м)(0,1м)²/2=2Дж.

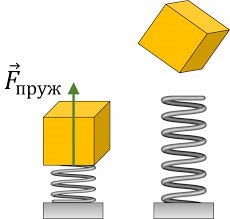
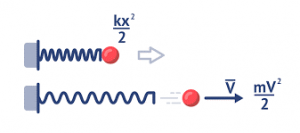
Мал.86. Потенціальна енергія сили пружності – це та енергія яку має тіло за рахунок тих взаємодій що відбуваються всередині пружно деформованого тіла.

Задача. Маса піщинки 0,1мг. Яка загальна кількість енергії зосереджена в цій піщинці? Якої маси має бути тіло, щоб рухаючись з швидкістю 108км/год мати аналогічну кількість кінетичної енергії?

Дано:                       СІ

m₁ = 0,1мг          1·10^–7кг

v₂ = 108км/год     30м/с

Е_заг1 = Е_к2

Е_заг1 = ?;  m₂ = ?

Рішення: Загальна кількість тієї енергії яка зосереджена в тілі масою m₁ визначається за формулою Е_заг1 =m₁с², де с=3·10⁸м/с=const. В нашому випадку: Е_заг1= 1·10^–7кг(3·10⁸м/с)²= 1·10^–7·9·10¹⁶Дж=9·10⁹Дж. Оскільки за умовою задачі Е_к2 = Е_заг1, та враховуючи, що  Е_к2 = m₂v²/2, можна записати m₂v²/2 = Е_заг1 , звідси m₂ = 2·Е_заг1/v².

Розрахунки: m₂ = 2·Е_заг1/v² = 2·9·10⁹Дж/(30м/с)² = 18·10⁹/9·10² = 2·10⁷кг = 20000т

Відповідь: Е_заг1 = 9·10⁹Дж; m₂ = 20 000т.

Напевно енергія не мала б такого фундаментального загальнонаукового значення, якби не той закон який називається законом збереження енергії. В цьому законі стверджується: при будь яких процесах, що відбуваються в замкнутій (енергоізольованій) системі, загальна кількість енергії цієї системи залишається незмінною, тобто зберігається. Іншими словами:∑Е_до = ∑Е_після  або  ∑Е = соnst.

Ілюструючи дію закону збереження енергії в механічних процесах, розглянемо конкретну ситуацію. Припустимо що тіло масою 1кг знаходиться на висоті 5м. Ясно, що в процесі вільного падіння тіла, величина його потенціальної енергії (E_п=mgh) буде зменшуватись (оскільки h↓ то Е_п↓). З іншого боку, в процесі того ж падіння, кінетична енергія тіла (Е_к=mv²/2) буде збільшуватись (оскільки v↑ то Е_к↑). І не важко довести, що на всьому шляху вільного польоту тіла, загальна кількість його механічної енергії (Е=Е_п+Е_к) залишається незмінною. Дійсно. Виходячи з того, що в процесі вільного падіння, висота тіла над поверхнею землі зменшується за законом h=h₀–gt²/2, а його швидкість – збільшується за законом v=v₀+gt, визначимо параметри падаючого тіла (h, v, Е_п, Е_к, Е=Е_п+Е_к) через кожні 0,2с польоту. Результати обчислень запишемо у відповідну таблицю.

t (c)	h (м)	v (м/с)	Ек (Дж)	Еп (Дж)	Е=Ек+Еп(Дж)
0,0	5,0	0,0	0,0	50,0	50,0
0,2	4,8	2,0	2,0	48,0	50,0
0,4	4,2	4,0	8,0	42,0	50,0
0,6	3,2	6,0	18,0	32,0	50,0
0,8	1,8	8,0	32,0	18,0	50,0
1,0	0,0	10,0	50,0	0,0	50,0

Не важко бачити, що в процесі вільного падіння тіла, загальна кількість його механічної енергії залишається незмінною, тобто зберігається.

   

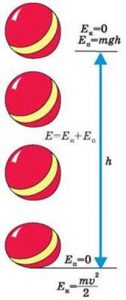
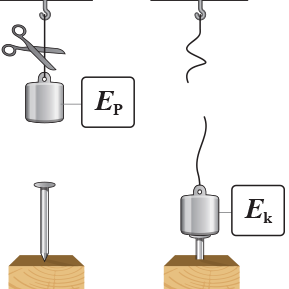
Мал.87. При будь яких процесах що відбуваються в замкнутій системі, загальна кількість енергії цієї системи залишається незмінною.

Ви можете заперечити в тому сенсі, що коли тіло впаде, то його кінетична і потенціальна енергії матимуть нульову величину. Чи не означатиме це, що енергія зникла і що закон збереження енергії не виконується? Ні, не означатиме! Просто в процесі взаємодії з землею (підлогою, поверхнею стола, тощо), та механічна енергія яка спочатку була потенціальною, а потім кінетичною, перетворилась у відповідну кількість внутрішньої енергії, тобто в кінетичну та потенціальну енергію молекул взаємодіючих тіл. Простіше кажучи, механічна енергія перетворилась в енергію теплову.

А якщо ви не помітили цього перетворення, то це тільки тому, що енергоємність тіл є надзвичайно великою. Скажімо, для того щоб один літр води нагріти всього на 1°С потрібно витратити 4200Дж енергії. Це означає, що смертельна для людини пістолетна куля масою 6г яка летить зі швидкістю 200м/с, і енергія якої 120Дж зможе нагріти 1 літр води всього на 0,03°С. Якщо ж мова йде про енергію 50Дж то вона спромоглась би нагріти літр води всього на 0,012°С. Тому не дивно, що спостерігаючи за тими подіями які відбуваються в процесі падіння даного тіла, ви не помітили факту того, що навколишнє повітря, земля і саме тіло дещо нагрілись. Однак, якщо ви дійсно виконаєте необхідні вимірювання, то неодмінно з’ясуєте, що в процесі падіння тіла і в процесі його взаємодії з поверхнею землі, загальна кількість внутрішньої енергії взаємодіючих тіл дійсно збільшилась, і збільшилась рівно на 50Дж.

До речі, якщо в момент падіння тіла, його кінетична енергія становитиме не 50Дж, а скажімо 47Дж, то не поспішайте стверджувати, що закон збереження енергії не працює. Просто в процесі падіння тіла та в результаті його тертя об повітря, частина механічної енергії тіла (а саме 3Дж) перетворилась на відповідну кількість внутрішньої енергії тіла і повітря.

Таким чином незліченна кількість експериментальних досліджень та фактів доводять. Енергія не виникає безпричинно і не зникає безслідно. Вона лише перетворюється з одного виду в інший та переходить від одних фізичних об’єктів до інших. При цьому, за будь яких перетворень та будь яких переходів загальна кількість енергії залишається незмінною, тобто зберігається.

Ілюструючи практичну значимість закону збереження енергії та ефективність його застосування при розв’язування задач, розглянемо конкретний приклад.

Задача 1. З якою початковою швидкістю v₀ потрібно кинути вниз м’яч з висоти h, щоб він підскочив на вдвічі більшу висоту H=2h? Удар об землю вважати абсолютно пружним.

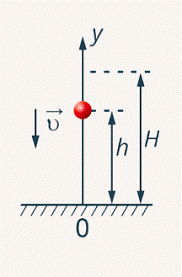
Як і багато інших задач, дану задачу можна розв’язати по різному. Дійсно. З одного боку, цю задачу можна вважати задачею кінематики і розв’язати відповідним кінематичним методом. З іншого боку, цю ж задачу можна, ба навіть потрібно розв’язувати енергетичним методом. Щоб переконатись в цьому «потрібно», давайте розв’яжемо задачу обома способами. А висновки ви зробите самі.

Кінематичне рішення.

Дано:

h

H=2h

v₀=?

Рішення: Будемо виходити з того, що та швидкість v₀ з якою потрібно кинути м’яч, є результатом вільного падіння тіла з певної додаткової висоти, величина якої H – h = h. Іншими словами, будемо виходити з того, що м’яч вільно падає з висоти H=2h. Намагаючись встановити залежність v₀=ƒ(h) опишемо рух тіла на різних його ділянках, зокрема:

1) на ділянці 2h→0:  2h=gt₁²/2, де t₁ – тривалість руху на ділянці 2h→0;

2) на ділянці h→0:   h=v₀t₂ + gt₂²/2, де t₂ – тривалість руху на ділянці h→0.

Оскільки ми маємо систему двох рівнянь з трьома невідомими (t₁=?, t₂=?, v₀=?) то така система не має однозначного рішення. Однак, аналізуючи дану ситуацію можна записати ще два незалежних рівняння:

3) на ділянці 2h→h:  v₀= 0 +gt₃;    4) t₂ + t₃ = t₁.

Таким чином, аналізуючи дану кінематичну ситуацію ми можемо записати систему чотирьох незалежних рівнянь з чотирма невідомими:

1) 2h=gt₁²/2;

2) h=v₀t₂ + gt₂²/2;

3) v₀= gt₃;

4) t₂ + t₃ = t₁.

Розв’язуючи систему цих рівнянь можна визначити залежність v₀=ƒ(h). Дійсно:

Із  (1)→ t₁=2(h/g)^1/2;

з  (3)→ t₃=v₀/g;

з  (4)→  t₂=t₁–t₃.

Підставляючи ці дані в (2) отримаємо:

h = v₀(t₁–t₃) + (g/2)(t₁–t₃)² = v₀[2(h/g)^1/2 – v₀/g)] + (g/2)[2(h/g)^1/2 – v₀/g]² =

= 2v₀(h/g)^1/2 – v₀²/g + g/2(4h/g – 2(h/g)^1/2(v₀/g) + v₀²/g²) =

= 2v₀(h/g)^1/2 – v₀/g + 2h – 2v₀(h/g)^1/2 +v₀²/2g = 2h – v₀²/g + v₀²/2g = 2h – v₀²/2g = h.

Звідси  h = v₀²/2g,  або    v₀ = (2gh)^1/2.

Відповідь: v₀ = (2gh)^1/2= √(2gh).

Енергетичне рішення.

Оскільки абсолютно пружний удар не супроводжується втратами механічної енергії, то можна стверджувати, то згідно з законом збереження енергії, загальна кількість механічної енергії в момент вильоту м’яча Е = mgh + mv₀²/2, та в момент його максимального підйому (v₁=0м/с) Е = mgН + 0 = 2mgh; має бути однаковою. Тобто mgh + mv₀²/2 = 2mgh. Звідси v₀ = √(2gh).

Відповідь: v₀ = √(2gh).

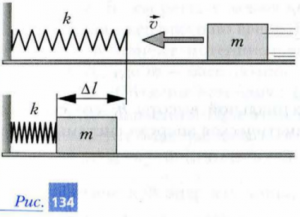
Задача 2. Тіло масою 500г, що рухається з швидкістю 15м/с, при взаємодії з горизонтально розташованою пружиною деформує її на 10см. Визначити жорсткість пружини.

Дано:           СІ

m=500г       0,5кг

v = 15м/с       –

Δℓ=10см     0,1м

k = ?

Рішення: На основі аналізу умови задачі виконуємо малюнок, на якому вказуємо енергетичні параметри системи до та після взаємодії. Оскільки в процесі взаємодії тіла з пружиною, його кінетична енергія Е_к=mv²/2 повністю перетворюється на потенціальну енергію деформованої пружини Е_п=kΔℓ²/2, то у відповідності з законом збереження енергії mv²/2= kΔℓ²/2. Звідси випливає k=mv²/Δℓ².

Розрахунки: k=0,5кг(15м/с)²/(0,1м)²=112,5Н/0,01м=11250Н/м.

Відповідь: k=11250Н/м.

Контрольні запитання.

1. Що означає твердження: будь яке тіло масою m, представляє собою згусток енергії загальна кількість якої визначається за формулою Е=mс²?
2. Як ви розумієте твердження: енергія є мірою здатності фізичного об’єкту виконати роботу?
3. Дайте визначення терміну «джоуль». Джоуль, це багато чи мало?
4. В загальному випадку визначальне рівняння потенціальної енергії можна записати у вигляді Е_п=? Що це означає?
5. Результатом яких взаємодій є потенціальна енергія сили тяжіння?
6. Результатом яких взаємодій є потенціальна енергія сили пружності?
7. Камінь кинули вертикально вгору. Які перетворення енергії відбуваються в процесі його польоту? Чи буде кінетична енергія каменя в момент його вильоту та момент падіння абсолютно однаковою? Чому?
8. Теплові втрати тіла масою 1кг при його падінні з висоти 5м становлять 1Дж. Чому ці втрати є практично непомітними?
9. Які перетворення енергії відбуваються в зображених на малюнку ситуаціях?

   

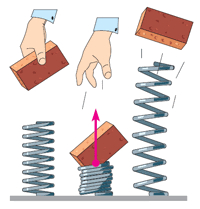
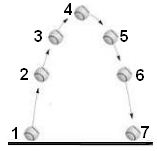
Вправа №18.

1. Автомобіль масою 5т рухається з швидкістю 90км/год. Визначте кінетичну енергію автомобіля.
2. Земля з швидкістю 30км/с обертається навколо Сонця. Яка кінетична енергія Землі, якщо її маса 6·10²⁴кг?
3. Літак Ан-22 загальною масою 200т летить на висоті 12км. Визначте величину його потенціальної енергії.
4. Пружину жорсткістю 400Н/м стиснули на 10см. Визначте потенціальну енергію деформованої пружини.
5. Під дією вантажу 200кг пружина деформувалась на 5см. Визначте енергію деформованої пружини.
6. Тіло масою 200г кинули вертикально вгору зі швидкістю 15м/с. Якою буде кінетична і потенціальна енергія цього тіла на висоті 5м?
7. На яку максимальну висоту підніметься тіло, якщо його кинули вертикально вгору з швидкістю 10м/с?
8. Тіло кинули вертикально вгору з швидкістю 20м/с. На якій висоті, його кінетична енергія дорівнюватиме потенціальній?
9. На якій висоті кінетична енергія вільно падаючого тіла дорівнює його потенціальній енергії, якщо на висоті 10м швидкість цього тіла 8м/с?
10. Горизонтально розташована пружина жорсткістю 5кН/м стиснута на10см. Якої швидкості в процесі свого випрямлення надасть ця пружина тілу масою 100г?

 .

Лекційне заняття №19.

Тема: Робота. Потужність. Коефіцієнт корисної дії. Розв’язування задач.

В науковій практиці термін «робота» має два значення: робота, як певна енергозатратна подія і робота, як певна фізична величина. Наприклад, коли ми стверджуємо, що піднімаючи стілець учень виконує роботу, то маємо на увазі певну подію. А коли говоримо, що піднімаючи стілець учень виконав роботу величиною 40Дж, то маємо на увазі фізичну величину яка певним чином характеризує виконану роботу.

Загалом, виконання роботи нерозривно пов’язано по-перше з передачею енергії від одного тіла до іншого, а по-друге, з перетворенням енергії з одного виду в інший. Наприклад, в процесі вільного падіння тіла (мал.88а), гравітаційна енергія Землі передається тілу, при цьому потенціальна енергія тіла перетворюється на його кінетичну енергію. В процесі взаємодії того тіла що рухається з тілом яке не рухається (мал.88б), енергія від рухомого тіла передається до нерухомого, при цьому кінетична енергія рухомого тіла спочатку перетворюється на потенціальну енергію пружної взаємодії тіл, а потім в кінетичну енергію нерухомого тіла. В процесі стиснення пружини (мал.88в), м’язова енергія руки передається пружині та перетворюється на її потенціальну енергію. Коли ж пружина випрямляється і штовхає тіло, то її потенціальна енергія передається тілу та перетворюється на його кінетичну енергію.

 

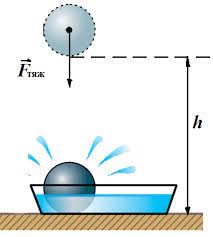
Мал.88. Виконання роботи нерозривно пов’язане з переходом енергії від одного тіла до іншого та з перетворенням одного виду енергії в інший.

В подальшому, терміном «робота» ми будемо позначати відповідну фізичну величину. Виходячи з цього дамо лише одне визначення терміну «робота».

Робота – це фізична величина, яка характеризує затрати енергії на виконання роботи, тобто певної енергозатратної дії і яка дорівнює цим затратам.

Позначається: А

Визначальне рівняння: А=ΔЕ

Одиниця вимірювання: А=Дж,   джоуль.

Формула А = ΔЕ = Е_кінц – Е_поч є базовим, визначальним рівнянням роботи. Однак, якщо мова йде про механічну роботу, то її часто визначають за формулою А=Fscosα, де F – усереднена величина тієї сили що виконує роботу, s – величина того переміщення яке відбувається під дією даної сили, α – кут між напрямком вектора сили (F) та напрямком вектора переміщення (s). Зверніть увагу, в формулі A=Fscosα символом F позначають середнє значення діючої на тіло сили (середнє на ділянці переміщення s). Тому, якщо наприклад, на ділянці виконання роботи, величина діючої на тіло сили лінійним чином змінюється від F₁ до F₂, то визначаючи виконану роботу, в якості діючої на тіло сили потрібно обирати F=(F₁+F₂)/2.

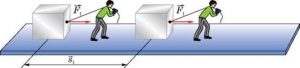
Мал.89. Якщо під дією сили F тіло перемістилось на відстань s то виконана цією силою робота дорівнює А=Fscosα.

Аналіз формули А=Fscosα вказує на те, що механічна робота виконується за умови виконання трьох вимог: 1) наявність діючої на тіло сили (F); 2) наявність переміщення тіла (s); 3) кут між напрямком дії сили та напрямком переміщення не повинен дорівнювати 90° (для α=90°, соsα=0 і тому А=Fscos90°=0). Наприклад, якщо ви штовхаєте важке тіло, а воно залишається на місці (мал.90а), то роботу по механічному переміщенню тіла ви не виконуєте. Не виконуєте тому, що переміщення тіла дорівнює нулю (s=0), а отже А=Fscosα=0. Можливо ви виконуєте якусь іншу роботу, скажімо роботу по деформації поверхні тіла, або роботу по розігріву своїх м’язів, але роботу по механічному переміщенню тіла ви не виконуєте.

Механічна робота не виконується і в тому випадку, коли тіло не зустрічаючи жодного опору з боку зовнішніх сил рухається за інерцією (мал.90б). Адже в цьому випадку рух тіла фактично відбувається без дії зовнішньої сили (F=0) і тому А=Fscosα=0. Звичайно, таке тіло має певний запас кінетичної енергії. Однак в процесі рівномірного руху ця енергія не змінюється і не передається іншим тілам, а отже і не призводить до виконання певної роботи.

Механічна робота не виконується і в тому випадку, коли діюча на тіло сила є перпендикулярною до напрямку переміщення тіла. Наприклад, в процесі обертання штучного супутника навколо Землі (мал.90в), діюча на нього гравітаційна сила не виконує механічної роботи. Не виконує тому, що кут між напрямком дії цієї сили і напрямком руху супутника становить 90°, а сos90°=0, і тому А=Fscosα=0

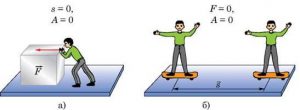
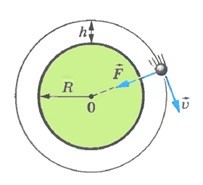
Мал.90. Ситуації в яких механічна робота не виконується.

Механічна робота може бути як додатною так і від’ємною. При цьому, якщо напрям діючої на тіло сили співпадає з напрямком переміщення тіла, то робота відповідної сили є додатною (сила сприяє переміщенню тіла). Якщо ж напрям діючої на тіло сили протилежний до напрямку його переміщення, то робота відповідної сили є від’ємною (сила протидіє переміщенню тіла). Наприклад робота сили тертя завжди від’ємна.

Потрібно зауважити, що робота однієї і тієї ж сили може бути як додатною, так і від’ємною. Наприклад, коли ви відпускаєте яблуко і воно під дією сили тяжіння падає на землю, то сила тяжіння виконує додатню роботу (сприяє переміщенню яблука). Якщо ж ви піднімаєте яблуко, то сила тяжіння протидіє переміщенню яблука і тому виконує від’ємну роботу. Власне аналогічні результати випливають не лише з логічних міркувань, а й з формули А=Fscosα. Дійсно, якщо під дією сили тяжіння яблуко падає вниз, то α=0°, cos0°=1 і тому A=mghcos0°=+mgh. Якщо ж всупереч дії сили тяжіння яблуко піднімається вгору, то кут між напрямком дії сили тяжіння та напрямком руху тіла дорівнює 180° і тому: α=180°, cos180°= –1 а отже A=mghcos180°= –mgh.

 

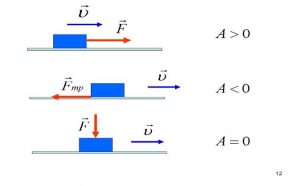
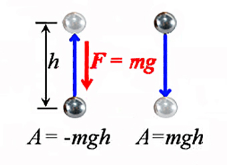
Мал.91. Механічна робота може бути як додатною так і від’ємною.

На перший погляд, формули А=ΔЕ і А=Fscosα є абсолютно різними. Насправді ж мова йде про споріднені і в певному сенсі тотожні формули. Різниця між ними лише в тому, що перша (А=ΔЕ) дозволяє визначати роботу енергетичним методом, а друга (А=Fscosα) – силовим. Ілюструючи та перевіряючи фізичну тотожність формул А=ΔЕ і А=Fscosα, а заодно і порівнюючи силовий та енергетичний методи розв’язування задач, розглянемо декілька конкретних прикладів.

         Задача 1. Під дією сили тяжіння тіло масою m падає з висоти h на землю. Визначити величину виконаної при цьому роботи.

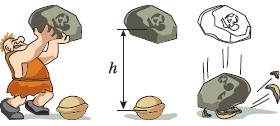
Дано:

m

h

g

А=?

Рішення: Виконуємо малюнок який відображає: а) для енергетичного рішення: енергетичні параметри системи; б) для силового рішення: силові параметри системи.

Енергетичне рішення.

Оскільки в процесі виконання роботи (в процесі падіння тіла) величина потенціальної енергії тіла змінилась від Е_п=mgh  до Е_п=0, то А=ΔЕ=0 – mgh = –mgh, де знак  « – » вказує на те, що в процесі виконання роботи потенціальна енергія тіла зменшилась.

Відповідь: А=mgh.

Силове рішення.

Виходячи з того що дану роботу виконує постійна за величиною сила тяжіння F=mg, та враховуючи що напрям цієї сили співпадає з напрямком переміщення тіла (α=0°; соs0°=1) можна записати: А=Fscosα=mgh.

Відповідь: A=mgh.

Задача 2. Горизонтально розташована та деформована на величину Δℓ пружина жорсткістю k, штовхає тіло. Визначити величину виконаної при цьому роботи.

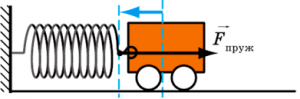
Дано:

Δℓ

k

А=?

Рішення: Виконуємо малюнок який відображає: а) для енергетичного рішення: енергетичні параметри системи; б) для силового рішення: силові параметри системи.

Енергетичне рішення.

Оскільки в процесі виконання роботи, величина потенціальної енергії пружини змінюється від Е_п=kΔℓ²/2  до  Е_п=0,  то А=ΔЕ=0 –  kΔℓ²/2= – kΔℓ²/2, де знак « – » вказує на те, що в процесі виконання роботи, величина потенціальної енергії пружини зменшилась.

Відповідь:  А= kΔℓ²/2 .

Силове рішення.

Оскільки в процесі виконання роботи величина діючої на тіло сили пружності лінійним чином змінюється від максимального значення (F=kΔℓ) до нуля (F=0), то усереднена величина цієї сили становитиме F_c=kΔℓ/2. А враховуючи що напрям сили пружності співпадає з напрямком переміщення (α=0°; соs0°=1), можна записати: A=F_cscosα=(kΔℓ/2)Δℓ=kΔℓ²/2.

Відповідь:   A=kΔℓ²/2.

Задача 3.  Тіло масою m, рухається з горизонтальною швидкістю v . При взаємодії з горизонтально розташованою пружиною, тіло деформує її і зупиняється. Визначити величину виконаної при цьому механічної роботи.

Дано:

m

v

А=?

Рішення: Виконуємо малюнок який відображає: а) для енергетичного рішення: енергетичні параметри системи; б) для силового рішення: силові параметри системи.

Енергетичне рішення.

Оскільки в процесі виконання роботи величина кінетичної енергії тіла змінюється від Е_к=mv²/2  до Е_к=0, то А=ΔЕ=0 – mv²/2 = – mv²/2,

де знак « – » вказує на те, що в процесі виконання роботи, величина кінетичної енергії тіла зменшилась.

Відповідь:  А=mv²/2.

Силове рішення.

По суті, тією силою яка виконує роботу по деформації пружини є сила інерції, тобто та сила поява якої обумовлена прискореним рухом тіла і величина якої визначається за формулою F_i=ma. Величину того прискорення з яким рухається тіло в процесі деформації пружини, можна визначити із кінематичних міркувань:

Δℓ=(v_k² – v₀²)/2a = – v₀²/2a=v²/2a;  звідси  a = – v²/2Δℓ, де знак « – » вказує на те, що рух тіла є рівносповільненим.

Враховуючи, що напрям тієї сили яка виконує роботу (сили інерції) співпадає з напрямком деформації пружини, тобто що α=0°; соs0°=1, можна записати:  A=Fℓcosα=m(v²/2Δℓ)Δℓ=mv²/2 .

Відповідь:  A=mv²/2.

Висновок. Таким чином, визначаючи величину виконаної механічної роботи, практично з однаковим успіхом можна застосовувати як формулу А=ΔЕ так і формулу А=Fscosα. Однак потрібно мати на увазі, що в формулі А=Fscosα  знак результату вказує на те яку роботу (додатню чи від’ємну) виконує відповідна сила. В формулі ж А=ΔЕ, знак результату говорить про те, як змінюється (збільшується чи зменшується) відповідна енергія в процесі виконання роботи.

         До числа основних характеристик будь якого приладу відносяться потужність та коефіцієнт корисної дії (к.к.д.).

Потужність – це фізична величина, яка характеризує швидкість виконання роботи і яка дорівнює відношенню виконаної роботи (А) до того проміжку часу (t) за який ця робота була виконана.

Позначається: N (або Р)

Визначальне рівняння: N=А/t

Одиниця вимірювання: [N]=Дж/с=Вт,  ват.

Ват – це одиниця вимірювання потужності, яка дорівнює такій потужності при якій за одну секунду виконується робота в один джоуль. Скажімо, якщо ви візьмете в руку вантаж масою 102г то відчуєте силу в один ньютон. Якщо цей вантаж ви піднімете на один метр – то виконаєте роботу в один джоуль. А якщо цю роботу ви виконаєте за одну секунду – то розвинута вами середня потужність становитиме один ват.

Задача 4. Гиря годинника має масу 0,8 кг і за добу опускається на 110см. Яка потужність годинникового механізму?

Дано:              СІ

m=0,8кг          –

t = 1доба    86400с

h = 110см     1,1м

N = ?

Рішення: За визначенням N=A/t. Будемо виходити з того, що джерелом тієї роботи яку виконує годинниковий механізм є та енергія яку отримує цей механізм в процесі опускання гирі і яка дорівнює А=F_тh=mgh. А це означає, що N=А/t=mgh/t.

Розрахунки: N=0,8кг·10(м/с²)1,1м/86400с=0,0001Вт.

Відповідь N= 0,0001Вт.

Формула N=А/t є базовим визначальним рівнянням потужності. Однак, якщо мова йде про потужність тих приладів які виконують механічну роботу (А=Fℓcosα), то для них формула потужності набуває вигляду: N=А/t=(Fℓcosα)/t=Fvcosα.  Тобто N=Fvcosα, де F – усереднене значення тієї сили що виконує роботу; v – швидкість того тіла що рухається під дією сили F; α – кут між напрямком дії сили та напрямком руху тіла. Зазвичай α=0° і тому N=Fv.

Таким чином, механічна потужність приладу, наприклад автомобіля, визначається добутком тієї тягової сили що змушує прилад рухатись на швидкість його руху. Знаючи даний факт, не важко збагнути, як це так виходить, що сильний трактор і значно слабший легковий автомобіль мають однакову потужність. Правильно, трактор – сильний але повільний, натомість легковик – слабкий але швидкий. Втім, той же трактор чи той же автомобіль, маючи один і той же двигун, на різних передачах можуть мати дуже різну величину як сили так і швидкості. Скажімо перша передача, забезпечує максимальну силову тягу при мінімальній швидкості руху. Четверта ж передача навпаки, забезпечує максимальну швидкість руху при мінімальній тяговій силі.

В процесі виконання роботи, в будь якому механічному, електричному, тепловому чи іншому приладі, частина наданої йому енергії неминуче і безповоротно втрачається. Характеризуючи ці втрати, або якщо хочете, характеризуючи ефективність використання енергії в приладі, говорять про його коефіцієнт корисної дії (к.к.д.).

Коефіцієнт корисної дії (к.к.д) – це фізична величина, яка характеризує ефективність використання енергії в тому чи іншому приладі і яка дорівнює відношенню тієї енергії що йде на виконання корисної роботи (Е_кор=А_кор), до загальної кількості наданої приладу енергії (Е_заг=А_заг).

Позначається: η

Визначальне рівняння: η=(Е_кор/Е_заг)100%,  або   η=(А_кор/А_заг)100%

Одиниця вимірювання: [η] = %,  відсотки.

Потрібно зауважити, що певний коефіцієнт корисної дії мають не лише двигуни, генератори, автомобілі та інші складні прилади які власне і виконують роботу, а й прості механізми, які самі по собі роботу не виконують, а являються лише певними посередниками при її виконанні (важелі, блоки, похилі площини, тощо).

Напевно найпростішим простим механізмом є похила площина. Принцип дії цього механізму розглянемо на конкретному прикладі. Припустимо, що вантаж масою 80кг вам потрібно підняти на кузов автомобіля висотою 1,2м (мал.92). Звичайно, якщо габарити вантажу та ваші силові можливості дозволяють, що називається запросто підняти вантаж масою 80кг на висоту 1,2м, то ви з легкістю виконаєте дану роботу і ваші енергетичні затрати становитимуть А=F_тh=mgh=960Дж. Однак на практиці далеко не кожен з нас важкоатлет, та й вантаж не є зручною гирею з руків’ям. Тому, будучи людиною розумною, ви застосовуєте…, правильно – похилу площину. Адже в цьому випадку для піднімання вантажу вам знадобиться значно менше силове зусилля. Реалізуючи свій задум, ви неминуче з’ясуєте, що  вантаж потрібно переміщувати на значно більшу довжину, скажімо не на 1,2м а на 2,4м. І тут нічого не вдієш – виграєш в силі, програєш у пройденому шляху.

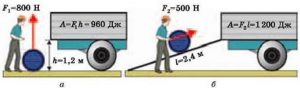
Мал.92. Виграєш в силі, програєш у пройденому шляху.

Звичайно, якби вантаж переміщувався похилою площиною без жодних проявів сили тертя, то для його переміщення було б достатньо сили 400Н (у відстані програли вдвічі, у силі вдвічі виграли). Однак, як ви розумієте, сила тертя між поверхнею вантажу та поверхнею похилої площини неминуче присутня, і тому для підйому вантажу вам знадобиться сила не 400Н, а скажімо 500Н. При цьому ваші енергетичні затрати становитимуть А=F₂ℓ=500Н·2,4м= 1200Дж.

Таким чином, застосування похилої площини, дозволило прикладаючи менше зусилля виконати важку роботу. Платою ж за виконання цієї роботи став факт того, що замість мінімально необхідних енергетичних затрат величиною 960Дж, ми витратили 1200Дж енергії. При цьому к.к.д. похилої площини становить η=А_кор/А_заг=mgh/F₂ℓ=960Дж/1200Дж=0,8=80%.

Оскільки на практиці робота будь якого простого механізму чи складного приладу неминуче пов’язана з певними енергетичними втратами, то задачі в яких фігурує коефіцієнт корисної дії є надзвичайно поширеними. Приємною особливістю цих задач є те, що їх рішення практично завжди починається з визначального рівняння к.к.д тобто з формули η=(А_кор/А_заг)100%. При цьому в подальшому дотримуються наступної послідовності дій.

1.На основі аналізу умов конкретної задачі визначаються з тим, яка робота в цих умовах є корисною (А_кор), а яка затраченою, загальною (А_заг).

2. На основі аналізу умов задачі, виражають А_кор та А_заг через відомі величини та ту величину яку треба зайти:

А_кор = ….

А_заг = ….

3. Підставляють отримані результати в базову формулу: η=(А_кор/А_заг)100% = …

4. Із отриманої формули визначають невідому величину.

Ілюструючи дієвість вище описаного алгоритму, розв’яжемо ряд конкретних задач.

Задача 5.  Електровоз рухаючись з швидкістю 54км/год споживає потужність 600кВт. Визначити силу тяги електровоза, якщо його к.к.д 75%.

Дано:                    СІ

v=54км/год       15м/с

N=600кВт       6∙10⁵Вт

η=75%                  –

F_тяг=?

Рішення: За визначенням   η = (А_кор/А_заг)100% . Із аналізу умови задачі ясно, що корисною роботою є та механічна робота яку виконує сила тяги електровозу і яку можна визначити за формулою А_кор=F_тягs. Оскільки, величина тієї загальної потужності яку споживає електровоз визначається за формулою N=А_заг/t, то А_заг= Nt. Таким чином η = (А_кор/А_заг)100% =(F_тягs100%)/Nt. А враховуючи, що при рівномірному русі електровоза s/t=v, можна записати η=(F_тягv100%)/N,  звідси   F_тяг=ηN/v100%.

Розрахунки: [F] = (%Вт)/(%м/с) = Н(м/с)/(м/с) = Н

F_тяг = 6·10⁵·75/15·100 =15∙10³Н=15кН.

Відповідь: F_тяг = 15кН .

Задача 6. Підйомний кран піднімає вантаж 3т на висоту 8м зі сталою швидкістю. За який час піднімається цей вантаж, якщо потужність двигуна 12кВт, а к.к.д. крана 80%?

Дано:             СІ

m = 3т         3·10³кг

h = 8м

N = 12кВт  12·10³Вт

η = 80%

t = ?

Рішення: За визначенням   η = (А_кор/А_заг)100% . Із аналізу умови задачі ясно, що корисною роботою є та, що йде на піднімання вантажу, тобто А_кор=mgh. Загальною ж роботою є та робота яку виконує двигун потужністю N. А оскільки N=A_заг/t, то A_заг= Nt. Таким чином  η = mgh100%/Nt. Звідси t = mgh100%/Nη.

Розрахунки: [t] = (кг(м/с²)м%)/(Вт%) = Дж/Дж/с = с

t = mgh100%/Nη = (3·10³кг·10(м/с²)·8м·100%)/12·10³Вт·80% = 25с

Відповідь: t = 25с

Задача 7.  Ящик з цвяхами, маса якого 54кг піднімають за допомогою рухомого блока, діючи на мотузку з силою 360Н. Визначити к.к.д установки.

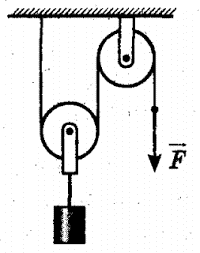
Дано:

m=54кг

F=360Н

η=?

Розрахунки: За визначенням η = (А_кор/А_заг)100%. Із аналізу умови задачі ясно, що корисною є та робота яка йде на піднімання вантажу. Цю роботу можна визначити за формулою А_кор=mgh. Оскільки загальну роботу виконує прикладена до мотузки сила F, та зважаючи на те, що для переміщення рухомого блоку на висоту h переміщення мотузки має становити ℓ=2h, можна записати: A = Fℓ = F2h. Таким чином  η = (А_кор/А_заг)100% =(mgh100%)/2Fh. Звідси  η = (mg100%)/2F .

Розрахунки:  η = 54кг9,8(м/с²)100%/2·360Н = 73,5% .

Відповідь:  η = 73,5%.

Контрольні запитання.

1. Які енергетичні перетворення відбуваються в процесі: а) вільного падіння тіла; б) стиснення пружини; в) непружного удару; г) пружного удару?
2. Наведіть приклади того коли процес переміщення тіла не супроводжується виконанням механічної роботи.
3. Наведіть приклади того, коли діюча на тіло сила не призводить до виконання механічної роботи.
4. В якому випадку робота сили є додатною, а в якому від’ємною? Робота якої сили завжди від’ємна?
5. Тіло підкинули вертикально вгору і піймали в тій же точці. Яку загальну роботу виконала при цьому сила тяжіння.
6. Що характеризує величина яка називається потужність?
7. Тягове зусилля гусеничного трактора майже в 10 разів більше за тягове зусилля легкового автомобіля. При цьому потужності їх двигунів практично однакові. Як це пояснити?
8. Що характеризує к.к.д. приладу? Що означає, к.к.д. приладу 75%?
9. Чому к.к.д. будь якого приладу завжди менший за 100%?
10. Поясніть загальний устрій та принцип дії похилої площини.

Вправа №19.

1. Автокран, піднімаючи вантаж масою 1,5т виконав роботу 22,5кДж. На яку висоту піднято при цьому вантаж?
2. Пружину жорсткістю 600Н/м деформували на 10см. Визначити величину виконаної при цьому роботи.
3. Вантаж масою 50кг вільно падає протягом 3с. Яку роботу виконує при цьому сила тяжіння?
4. Визначити роботу сил тертя, якщо автомобіль масою 2т переміщується горизонтальною дорогою на 500м. Коефіцієнт тертя 0,02
5. Тіло масою 2кг падає з висоти 10м, при цьому в момент падіння на землю його швидкість становить 11м/с. Визначити роботу сили опору повітря.
6. Насос, двигун якого розвиває потужність 2кВт, за 8хв піднімає певну масу води на висоту 6м. Визначте цю масу, якщо к.к.д установки 80%.
7. Підйомний кран піднімає вантаж 4т на висоту 10м зі сталою швидкістю. За який час піднімається цей вантаж, якщо потужність двигуна 15кВт, а к.к.д. крана 75%?
8. Вантаж масою 150кг за допомогою важеля піднімають на висоту 0,2м. При цьому, до довшого плеча важеля прикладають силу 600Н, під дією якої кінець цього плеча опускається на 0,6м. Визначте к.к.д важеля.
9. Визначте к.к.д похилої площини довжиною 2м і висотою 0,5м, якщо коефіцієнт тертя 0,2.

.

Лекційне заняття №20.

Тема: Імпульс. Закон збереження імпульсу. Реактивний рух. Розв’язування задач.

         В ньютонівській механіці, величина яка називається кількістю руху, або за сучасною термінологією – імпульсом (від лат. impulsus – удар, поштовх), є однією з найважливіших. Достатньо сказати, що в «Математичних началах натуральної філософії» першою визначеною величиною є кількість матерії (маса), а другою – кількість руху (імпульс).

         Імпульс (кількість руху) – це фізична величина, яка є мірою кількості механічного руху тіла (матеріальної точки) і яка дорівнює добутку маси тіла m на вектор його швидкості v.

Позначається: р

Визначальне рівняння: p=mv

Одиниця вимірювання: [p]=кг∙м/с,  кілограм-метр на секунду.

Із визначального рівняння р=mv ясно, що імпульс – величина векторна і що напрям вектора імпульсу співпадає з напрямком швидкості руху тіла.

На основі математичного аналізу законів Ньютона можна довести ряд тверджень, значимість яких виходить за межі ньютонівської механіки. Одним з таких тверджень є закон збереження імпульсу, закон в якому стверджується: При будь яких процесах що відбуваються в замкнутій системі, загальна кількість імпульсу цієї системи залишається незмінною тобто зберігається. Іншими словами:  ∑р_до=∑р_після,   або    ∑р = соnst.

Зазвичай закон збереження імпульсу (∑р_до = ∑р_після) застосовують в тих випадках коли мова йде про короткотривалі взаємодії (удари, поштовхи, вибухи, тощо). Дане обмеження пояснюється фактом того, що в процесі відносно тривалих механічних взаємодій, значна частина механічного імпульсу взаємодіючих тіл, передається їх атомам та перетворюється на енергію хаотичного руху цих атомів (теплоту).

Розрізняють дві ідеалізовані різновидності короткотривалих взаємодій: абсолютно пружні та абсолютно непружні удари. Абсолютно пружним ударом називають таку ідеалізовану, короткотривалу механічну взаємодію тіл, яка не супроводжується перетворенням механічної енергії в теплоту і після якої взаємодіючі тіла повністю відновлюючи свою попередню форму відокремлюються одне від одного. Абсолютно непружним ударом називають таку короткотривалу механічну взаємодію тіл, яка супроводжується перетворенням механічної енергії в теплоту і після якої взаємодіючі тіла не відновлюючи свою попередню форму рухаються як єдине ціле.

а)

б)

Мал.93. Закон збереження імпульсу виконується як при пружних (а) так і при непружних (б) ударах.

Задачі на застосування закону збереження імпульсу, зазвичай розв’язують дотримуючись наступного порядку дій:

1.Виконують малюнок на якому вказують маси та напрямки швидкостей всіх тіл системи, до та після їх взаємодії. Задають систему координат.

2. На базі векторної картини імпульсів, записують рівняння вигляду ∑р_до=∑р_після. При цьому, якщо векторна картина імпульсів не лінійна, то вектори імпульсів розкладають на відповідні проекції і записують систему двох рівнянь:

∑(р_до)_х = ∑(р_після)_х

∑(р_до)_у = ∑(р_після)_у

3. Математично розв’язуючи дані рівняння, визначають невідомі величини.

Зважаючи на вище сказане, розв’яжемо декілька конкретних задач.

Задача 1. Вагонетка масою 100кг рухаючись зі швидкістю 5м/с, непружним чином зіштовхується з аналогічною за масою нерухомою вагонеткою. Визначити швидкість вагонеток після їх непружної взаємодії (зчеплення).

Дано:

m₁ = 100кг

v₁ = 5м/с

m₂ = m₁

v₂ = 0м/с

u₁₂= ?

Рішення: Виконуємо малюнок на якому вказуємо маси і швидкості вагонеток до та після їх непружної взаємодії. Задаємо систему координат. Відповідно малюнку та заданій системі координат, записуємо рівняння закону збереження імпульсу, тобто рівняння виду ∑р_до=∑р_після. В умовах нашої задачі, це рівняння набуває вигляду: m₁v₁ + 0 = (m₁+m₂)u₁₂  звідси  u₁₂=m₁v₁/(m₁+m₂).

Розрахунки: u₁₂=m₁v₁/(m₁+m₂) = (100кг5м/с)/(100кг+100кг) = 2,5м/с.

Відповідь: u₁₂= 2,5м/с.

Загальні зауваження. Застосовуючи закон збереження імпульсу, швидкості елементів системи після їх взаємодії зазвичай позначають символом «u» або «vʹ».

Задача 2. З корми початково не рухомого човна масою 100кг, на берег зістрибує підліток масою 50кг. Якої швидкості при цьому набуває човен, якщо горизонтальна складова швидкості стрибка підлітка 5м/с? Опором води знехтувати.

Дано:

m₁=100кг

m₂=50кг

v₁=v₂=0м/с

u₂=5м/с

u₁= ?

Рішення:  Виконуємо малюнок на якому вказуємо маси і швидкості всіх тіл системи до та після їх взаємодії. Задаємо систему координат. Відповідно малюнку та заданій системі координат, записуємо рівняння виду ∑р_до=∑р_після. В умовах нашої задачі це рівняння набуває вигляду: (m₁+m₂)0= –m₁u₁+m₂u₂  звідси m₁u₁=m₂u₂  звідси  u₁=m₂u₂/m₁.

Розрахунки: u₁=m₂u₂/m₁ = (50кг5м/с)/100кг = 2,5м/с.

Відповідь: u₁= 2,5м/с.

Із аналізу задачі ясно, що коли з початково нерухомого човна в певному напрямку викидати камінці, весла чи що завгодно, то згідно з законом збереження імпульсу, човен з відповідною швидкістю буде рухатись в протилежному напрямку. Подібний рух тіл прийнято називати реактивним рухом. Реактивний рух – це такий механічний рух тіла, поява якого обумовлена відокремленням від цього тіла частини його маси (відштовхуванням цієї частини від базового тіла). Наприклад, рух гармати (мал.94а) обумовлений вильотом снаряду з неї, є реактивним. Рух гумової повітряної кульки (мал94б), обумовлений витіканням з неї струменю повітря, є реактивним. Рух ракети (мал.94в), обумовлений вильотом з неї продуктів згорання її двигуна, є реактивним.

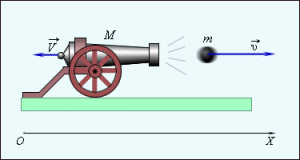
Мал.94. Якщо рух тіла обумовлений тим, що певна частина його маси відокремлюється (відштовхується) від базового тіла, то цей рух є реактивним.

Найбільш відомими та практично значимими проявами реактивного руху є рух різноманітних реактивних снарядів, реактивних літаків та космічних ракет. Принципова суть цих рухів дуже проста: продукти згорання палива, через спеціальний отвір, який називається соплом, з максимально великою швидкістю та максимально досяжною направленістю, вилітають за межі базового тіла (снаряду, літака, ракети, тощо). При цьому, згідно з законом збереження імпульсу, відповідне тіло отримує певну кількість поступального руху.

Потрібно зауважити, що роль тієї частини реактивного двигуна яка називається соплом (мал.95б) і яка представляє собою характерне поєднання звуження та розширення, полягає в тому, щоб надати енергійним частинкам продуктів згорання двигуна, максимально направленого вигляду. Адже якби ці частинки вилітали через звичайний отвір, то напрям їх руху був би різним. Якщо ж перед вильотом з двигуна частинки продуктів згорання проходять через плавне звуження, а потім через характерне розширення, то у відповідності з законами гадової динаміки, їх рух стає максимально направленим.

а) б)

Мал.95. Реактивний рух – прямий наслідок закону збереження імпульсу.

Характерною та надзвичайно важливою особливістю реактивного руху є його автономність, яка полягає в тому, що цей рух не потребує силового контакту з навколишнім середовищем. Наприклад, людина рухається тому, що відштовхується від землі. Човен пливе тому, що так чи інакше відштовхується від води. Гвинтокрил (гелікоптер) летить тому, що певним чином відштовхується від повітряного середовища. Якщо ж говорити про реактивний рух, то він не є результатом того, що тіло так чи інакше відштовхується від інших зовнішніх тіл чи навколишнього середовища. Реактивний рух відбувається за рахунок відштовхування однієї частини початково єдиного тіла, від іншої його частини. А це означає, що реактивний рух може відбуватись не лише в тому чи іншому середовищі, а й в пустоті (вакуумі).

Задача 3. В платформу з піском що рухається зі швидкістю 2,0м/с влучає та застряє в піску снаряд який рухався назустріч платформі з швидкістю 400м/с. Визначте швидкість платформи після влучання снаряду. Маса платформи 10тон, а маса снаряду 10кг.

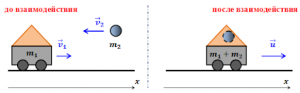
Дано:               СІ

m₁ = 10т       10000кг

m₂ = 10кг          –

v₁ = 2,0м/с         –

v₂ = 400м/с        –

u₁₂ = ?

Рішення: Виконуємо малюнок на якому вказуємо маси і швидкості всіх тіл системи до та після їх взаємодії. Задаємо систему координат. У відповідності з малюнком та заданою системою координат, записуємо рівняння закону збереження імпульсу (∑р_до=∑р_після): m₁v₁ – m₂v₂ = (m₁+m₂)u₁₂. Звідси u₁₂ = (m₁v₁ – m₂v₂)/(m₁+m₂).

Розрахунки: u₁₂ = … = 1,6м/с

Відповідь: u₁₂ = 1,6м/с.

Задача 4. В платформу з піском що рухається зі швидкістю 5,0м/с влучає та застряє у піску снаряд який рухався в напрямку руху платформі з швидкістю 500м/с. Визначте швидкість платформи після влучання снаряду, якщо маса платформи 10т, маса снаряду 10кг, а напрям швидкості снаряду 30° до горизонту.

Дано:               СІ

m₁ = 10т       10000кг

m₂ = 10кг          –

v₁ = 5,0м/с         –

v₂ = 500м/с        –

α = 30°

u₁₂ = ?

Рішення: Виконуємо малюнок на якому вказуємо маси і швидкості всіх тіл системи до та після їх взаємодії. Задаємо систему координат. У відповідності з малюнком і заданою системою координат, та з урахуванням того, що рух платформи як до так і після влучання снаряду відбувається вздовж осі 0х, записуємо рівняння закону збереження імпульсу (∑р_до=∑р_після) в проекції на вісь 0х. (При цьому враховуємо те, що в момент влучання снаряду в платформу, його швидкість вздовж осі 0х становить v_2x = v₂cos30° = (500м/с)0,87 = 435м/с). m₁v₁ + m₂v₂cos30° = (m₁+m₂)u₁₂, звідси u₁₂ =(m₁v₁ + m₂v₂cos30°)/(m₁+m₂).

Розрахунки: u₁₂ = (10000кг5м/с + 10кг435м/с)/(10000кг+10кг) = 5,43м/с.

Відповідь: u₁₂ = 5,43с/м.

Задача 5. Коли вагонетка масою 100кг проїжджала під містком, на неї опустили вантаж масою 50кг. Якою стала швидкість вагонетки після цієї події, якщо її початкова швидкість дорівнювала 6м/с?

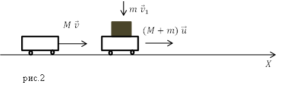
Дано:

М = 100кг

m = 50кг

v = 6м/с

u₁₂ = ?

Рішення: Виконуємо малюнок на якому вказуємо маси і швидкості всіх тіл системи до та після їх взаємодії. Задаємо систему координат. У відповідності з малюнком і заданою системою координат та з урахуванням того, що рух вагонетки як до так і після взаємодії відбувається вздовж осі 0х,  записуємо рівняння закону збереження імпульсу (∑р_до=∑р_після) в проекції на вісь 0х: Мv = (M+m)u₁₂,  звідси  u₁₂ = Mv/(M+m)

Розрахунки: u₁₂ = Mv/(M+m) = (100кг6м/с)/(100кг+50кг) = 4м/с

Відповідь: u₁₂ = 4м/с.

         Задача 6. На краю стола висотою 0,8м лежить тіло масою 1кг. В це тіло влучає та застряє в ньому куля масою 7г, що летить з горизонтальною швидкістю 400м/с. На якій відстані від підніжжя стола впаде тіло?

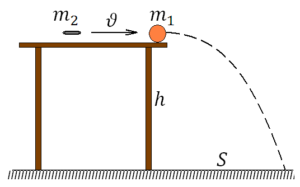
Дано:

h = 0,8м

m₁ = 1,0кг

m₂ = 0,007кг

v₂ = 400м/с

s = ?

Рішення: Виконуємо малюнок який відображає наявну ситуацію. Оскільки після взаємодії з кулею тіло отримує певну горизонтальну швидкість u₁₂, яка в процесі падіння тіла залишається незмінною, то можна записати s = u₁₂t_пад, де t_пад – час падіння тіла, величину якого можна визначити із рівняння руху тіла по вертикалі: h=(g/2)t_пад², звідси t = √(2h/g) = √(2·0,8м/10м/с²) = 0,4с. Величину тієї горизонтальної швидкості яку отримує тіло після взаємодії з кулею, визначаємо із закону збереження імпульсу (∑р_до=∑р_після): m₁·0 + m₂v₂ = (m₁+m₂)u₁₂. Звідси u₁₂ = m₂v₂/(m₁+m₂) = (0,007кг400м/с)/1,007кг = 2,8м/с.

Розрахунки: s = u₁₂t_пад = (2,8м/с)·0,4с = 1,12м

Відповідь: s = 1,12м.

Контрольні запитання.

1. Тіло рівномірно рухається по колу. Чи змінюється при цьому його імпульс?
2. Чим схожі і чим відрізняються кінетична енергія та імпульс тіла?
3. Що стверджується в законі збереження імпульсу?
4. Який удар називають абсолютно пружним?; абсолютно непружним?
5. Поясніть зображені на малюнку 88 події та результати цих подій.
6. Який зв’язок між законом збереження імпульсу та реактивним рухом?
7. Яка роль тієї частини реактивного двигуна яка називається соплом?
8. В чому полягає автономність реактивного руху?
9. Наведіть приклади корисних та шкідливих проявів реактивного руху.
10. Який алгоритм розв’язку задач на застосування закону збереження імпульсу?

Вправа 20.

1. З якою швидкістю має летіти хокейна шайба масою 160г, щоб її імпульс дорівнював імпульсу кулі масою 6г при її польоті з швидкістю 300м/с?
2. Снаряд масою 20кг, що летить з горизонтальною швидкістю 500м/с влучає в платформу з піском загальною масою 10т і застряє в піску. З якою швидкістю почне рухатись платформа?
3. У човен масою 150кг, який пропливає під містком, опускають вантаж масою 50кг. Якою стане після цього швидкість човна, якщо його початкова швидкість 4м/с?
4. Кулька масою 300г падає вертикально вниз, вдаряється об підлогу зі швидкістю 5м/с і підстрибує на висоту 46см. На скільки змінюється імпульс кульки в процесі удару?
5. З нерухомого човна загальна маса якого 155кг кидають на берег весло масою 5кг з горизонтальною швидкістю 10м/с. Якої швидкості при цьому набуває човен?
6. Якої швидкості набуває ракета масою 600г, якщо гази масою 25г вилітають з неї зі швидкістю 600м/с?
7. Ядро, що летіло горизонтально зі швидкістю 50м/с, розірвалось на два осколки масами 5кг і 10кг. При цьому, менший осколок з швидкістю 200м/с продовжував летіти в попередньому напрямку. Визначити напрям та швидкість руху більшого осколку.
8. Два тіла масою 5кг і 4кг рухаються назустріч одне одному з швидкостями відповідно 5м/с і 8м/с. Визначити швидкості цих тіл після їх непружного зіткнення.
9. Мисливець стріляє з рушниці з рухомого човна у напрямку його руху. Яку швидкість мав човен, якщо він зупинився після трьох пострілів? Маса човна разом з мисливцем 150кг, маса заряду 20г, швидкість вильоту заряду 500м/с.
10. Снаряд вилітає з гармати під кутом 60º до горизонту з початковою швидкістю 800м/с. Визначити початкову швидкість відкату гармати, якщо маса снаряду 10кг, а маса гармати 500кг.

.

Лекційне заняття №21. (Практичне заняття)

Тема: Імпульсно-енергетичний метод розв’язування задач.

Чітко класифікувати задачі динаміки практично не можливо. Тим не менше, можна виділити два базових методи їх розв’язку: силовий та імпульсно-енергетичний. Суть силового методу полягає в тому, що невідомі величини визначають на основі векторного аналізу діючих на тіло сил та на базі умови його динамічної рівноваги (∑F+F_i=0). При імпульсно-енергетичному методі, невідомі величини визначають на основі аналізу імпульсно-енергетичних параметрів тіл (імпульс, енергія, робота, потужність, к.к.д) та їм відповідних визначальних рівнянь і на базі законів збереження енергії та імпульсу.

Звичайно, подібна класифікація є досить умовною. Умовною по-перше тому, що в багатьох випадках одну і ту ж задачу можна розв’язати як силовим так і імпульсно-енергетичним методом. А по-друге, рішення багатьох задач передбачає застосування певної комбінації обох методів. Втім, нема кращого способу розібратися в різноманітті динамічних задач та методах їх рішення, як практичне розв’язування максимально великої їх кількості.

Задача 1. Визначити швидкість вильоту кульки масою m з дула пружинного пістолета при горизонтальному пострілі, якщо жорсткість пружини k, а її деформація Δℓ.

Дано:

m

k

Δℓ

v= ?

Рішення: Виконуємо малюнок на якому вказуємо енергетичні параметри системи пружина-кулька до та після пострілу. Будемо виходити з того, що в процесі пострілу, потенціальна енергія пружно деформованої пружини Е^пр=kΔℓ²/2 йде на збільшення кінетичної енергії кульки Е_к=mv²/2. При цьому, згідно з законом збереження енергії можна записати: kΔℓ²/2 = mv²/2, звідси v = √(kΔℓ²/m) = Δℓ√k/m.

Відповідь: v = Δℓ√k/m.

Задача 2. Визначити швидкість вильоту кульки масою m з дула пружинного пістолета при вертикальному пострілі, якщо жорсткість пружини k, а її деформація Δℓ.

Дано:

m

k

Δℓ

v= ?

Рішення: Виконуємо малюнок на якому вказуємо енергетичні параметри системи пружина-кулька до та після пострілу. Будемо виходити з того, що в процесі пострілу, потенціальна енергія пружно деформованого тіла Е^пр=kΔℓ²/2 йде не лише на збільшення кінетичної енергії кульки Е_к=mv²/2, а й на збільшення її потенціальної енергії Е_п=mgΔℓ. При цьому, згідно з законом збереження енергії можна записати: kΔℓ²/2 = mv²/2 + mgΔℓ,  або  mv²/2 = kΔℓ²/2  – mgΔℓ, звідси v = √(kΔℓ²/m – 2gΔℓ).

Відповідь: v = √(kΔℓ²/m – 2gΔℓ).

Задача 3. Тіло без тертя зісковзує з похилої площини, яка переходить у так звану «мертву петлю». З якої мінімальної висоти Н має зісковзувати тіло, щоб бути здатним описати «мертву петлю» радіусом R.

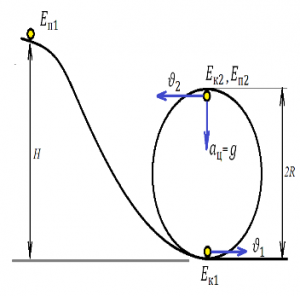
Рішення:  Оскільки за умовою задачі, в процесі руху тіла втратами енергії можна знехтувати, то та потенціальна енергія яку має тіло на висоті Н (Е_п1=mgH), в нижній точці спуску перетвориться на відповідну кількість кінетичної енергії Е_к1=Е_п1. При цьому, цієї енергії має вистачити на те, щоб по перше підняти тіло на висоту h=2R, тобто щоб надати тілу потенціальної енергії Е_п2=mg2R. А по друге, забезпечити таку швидкість руху тіла в верхній точці петлі, при якій діюча на нього сила тяжіння (F_т=mg), буде зрівноваженою відповідною силою інерції (F_i=ma_д=mv₂²/R). А це означає, що у верхній точці петлі, тіло повинно мати певний запас кінетичної енергії Е_к2=mv₂²/2, де v₂² визначається із співвідношення mv₂²/R = mg. Звідси v₂²=gR. При цьому Е_к2=mgR/2.

Таким чином, для тієї мінімальної висоти Н, яка за відсутності енергетичних втрат забезпечує виконанням тілом «мертвої петлі», має виконуватись співвідношення mgH = 2mgR + mgR/2. Звідси H = 2R+R/2=2,5R.

Відповідь: H = 2,5R.

Задача 4. Куля масою 7г летить в горизонтальному напрямку зі швидкістю 500м/с і влучає в центр дерев’яного бруска масою 2,0кг який висить на нитках, та застряє в ньому. На яку висоту підніметься брусок після удару кулі? Визначте величину тієї енергії, яка в процесі взаємодії кулі з бруском перетворилась в енергію теплову.

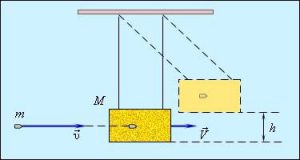
Загальні зауваження. Розв’язуючи подібні задачі (особливо в тих випадках, де не згадується про перетворення механічної енергії в теплову) можна подумати, що у відповідності з законом збереження енергії, та кінетична енергія яку мала куля до взаємодії з бруском Е_к=mv₁²/2, у підсумку перетворюється на потенціальну енергію системи брусок-куля Е_п=(М+m)gh, і що тому h=mv₁²/2(M+m)g=44м. Втім, отриманий результат явно суперечить як здоровому глузду так і експериментальним фактам. І це закономірно, адже застосовуючи закон збереження енергії, ми не врахували того, що в процесі гальмування кулі, левова частина її кінетичної енергії перетворилась на теплоту, тобто енергію хаотичного руху молекул системи куля-тіло. В подібних ситуаціях рішення задачі базується на комбінованому застосуванні законів збереження енергії та імпульсу. Адже закон збереження імпульсу (∑р_до = ∑р_після) виконується навіть в тих випадках коли короткотривала подія (поштовх) відбувається з перетворенням механічної енергії в теплоту.

Дано:               СІ

m=7г            7∙10^–3кг

v₁=500м/с       –

М=2,0кг         –

v₂=0м/с           –

h = ?;   Q =?

Рішення: Виконуємо малюнок який відображає фізичну суть задачі. Керуючись законом збереження імпульсу визначаємо швидкість бруска (v₁₂) після взаємодії з кулею: mv₁+Мv₂ = (m+М)v₁₂. Враховуючи що v₂=0, можна записати v₁₂ = mv₁/(m+М) = (7·10^–3кг500м/с)/2,007кг = 1,75м/с.

Виходячи з того, що після взаємодії з кулею, брусок отримав певну кількість кінетичної енергії  Е_к=(m+М)v₁₂²/2 = 3Дж, і що в процесі підйому бруска, ця енергія повністю перетворилась на відповідну кількість потенціальної енергії Е_п=(m+М)gh  можна записати:  (m+М)gh = (m+М)v₁₂²/2, звідси h=v₁₂²/2g = (1,75м/с)²/2·9,8м/с² = 0,156м = 15,6см

Кількість тієї енергії яка в процесі взаємодії кулі з бруском перетворилась на теплоту (Q), можна визначити як різницю між кінетичною енергією кулі до взаємодії (Е_к= mv₁²/2 = 875Дж) та кінетичною енергією системи брусок-куля після взаємодії (Е_к=(m+М)v₁₂²/2 = 3Дж), тобто: Q = 875Дж – 3Дж = 872Дж. А це означає, що в процесі гальмування кулі 99,65% її механічної кінетичної енергії перетворилось на енергію теплового (хаотичного) руху молекул системи куля- брусок.

Відповідь:   h = 15,6см;  Q = 872Дж;  Q/E_k1 = 99,65%.

Задача 5. Дві кулі маси яких 4кг і 1кг рухаються назустріч одна одній з швидкістю 10м/с кожне. Визначити швидкість куль після їх лобового абсолютно непружного зіткнення.

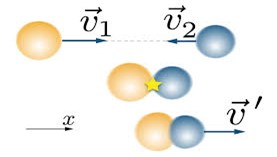
Дано:

m₁ = 4кг

m₂ = 1кг

v₁= v₂=10м/с

v₁₂ʹ =?

Рішення: Виконуємо малюнок який відображає фізичну суть задачі. Задаємо систему координат (вісь 0х). На основі аналізу імпульсно-енергетичної ситуації, та зважаючи на факт того, що після абсолютно непружного удару кулі об’єднаються і будуть рухатись як єдина цілісна система, записуємо рівняння закону збереження імпульсу, тобто рівняння виду ∑р_до=∑р_після. В умовах нашої задачі, це рівняння набуває вигляду: m₁v₁ – m₂v₂ = (m₁ + m₂)v₁₂ʹ. Звідси v₁₂ʹ= (m₁v₁ – m₂v₂)/(m₁ + m₂).

Розрахунки: v₁₂ʹ= (4кг·10(м/с) – 1кг·10(м/с))/(4кг + 1кг) = 6(м/с).

Відповідь: v₁₂ʹ= 6(м/с).

Задача 6. Дві кулі маси яких 4кг і 1кг рухаються назустріч одна одній з швидкістю 10м/с кожне. Визначити швидкість куль після їх лобового абсолютно пружного зіткнення.

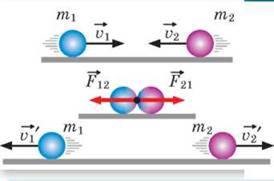
Дано:                                      Рішення:

m₁ = 4кг                  Виконуємо малюнок який відображає фізичну суть

m₂ = 1кг                  задачі. Задаємо систему координат (вісь 0х).

v₁= v₂=10м/с           Оскільки після абсолютно пружного удару кулі з

v₁ʹ =?; v₂ʹ =?

Рішення: Виконуємо малюнок який відображає фізичну суть задачі. Задаємо систему координат (вісь 0х). Оскільки після абсолютно пружного удару кулі з швидкостями v₁ʹ і v₂ʹ взаємно віддаляються, то ми маємо дві невідомі величини. А це означає, що для рішення задачі потрібно записати два незалежних рівняння. Одним з цих рівнянь є рівняння закону збереження імпульсу ∑р_до=∑р_після. А зважаючи на факт того, що абсолютно пружні удари відбуваються без перетворення механічної енергії в теплоту, другим незалежним рівнянням, буде рівняння закону збереження енергії ∑Е_до = ∑Е_після. Таким чином, розв’язуючи дану задачу, ми можемо записати два незалежних рівняння: рівняння закону збереження імпульсу ∑р_до=∑р_після  та рівняння закону збереження енергії ∑Е_до = ∑Е_після. При цьому в умовах нашої задачі ці рівняння набувають вигляду:

1) m₁v₁ – m₂v₂ = –m₁v₁ʹ+m₂v₂ʹ, а оскільки v₁=v₂, то v₁(m₁ – m₂) = –m₁v₁ʹ+m₂v₂ʹ

2) m₁v₁²/2+m₂v₂²/2 = m₁v₁ʹ²/2+m₂v₂ʹ²/2,  або (v₁²/2)(m₁+m₂) = m₁v₁ʹ²/2+m₂v₂ʹ²/2.

Таким чином, ми маємо систему двох рівнянь з двома невідомими (v₁ʹ=?; v₂ʹ=?):

1) v₁(m₁ – m₂) = –m₁v₁ʹ+m₂v₂ʹ

2) (v₁²/2)(m₁+m₂) = m₁v₁ʹ²/2+m₂v₂ʹ²/2.

Загальне математичне рішення подібних систем є досить складним. Тому розв’яжемо цю систему з врахуванням числових значень відомих величин. При цьому для зручності запису позначимо v₁ʹ=х; v₂ʹ=у. Зважаючи на вище сказане можна записати:

у відповідності з рівнянням (1): 10(4–1) = –4х+1у, звідси у=4х+30;

у відповідності з рівнянням (2): (10²/2)(4+1) = 4х²/2+1у²/2, звідси 250=2х²+0,5у².

Таким чином ми маємо систему двох рівнянь з двома невідомими.

1) у=4х+30;

2) 2х²+0,5у²=250.

Розв’язуючи цю систему значення у=4х+30 підставляємо в рівняння (2) і отримуємо рівняння з одним невідомим.

2х²+0,5(4х+30)²=250, або 2х²+0,5((4х)² +2·4х·30+(30)²)=250, або

2х²+0,5(16х²+240х+900)=250, або 2х²+8х²+120х+450=250, або 10х²+120х+200=0, або х²+12х+20=0.

Стандартним чином розв’язуємо відповідне квадратне рівняння:

х_1,2 = (–12 ± √[12² – (4∙1∙20)])/2∙1 = (–12 ± 8)/2, звідси

х₁ = (–12 + 8)/2 = –2м/с; у₁=4х₁+30 = 4·(–2) + 30 = 22м/с;

х₂ = (–12 – 8)/2 = –10м/с; у₂=4х₂+30 = 4·(–10) + 30 = –10м/с;

Таким чином, ми отримали два рішення:

1) v₁ʹ = –2м/с; v₂ʹ = 22м/с.

2) v₁ʹ = –10м/с; v₂ʹ = –10м/с.

Пояснюючи отримані результати, можна сказати наступне. Згідно з умовою задачі, тіла рухаються назустріч одне одному. Однак, записана нами система рівнянь, дає відповіді як на пряму задачу (тіла рухаються назустріч одне одному) так і на зворотню задачу (тіла рухаються в одному напрямку). А це означає, що перша відповідь (v₁ʹ = –2м/с; v₂ʹ = 22м/с), стосується ситуації коли тіла рухаються назустріч одне одному. При цьому знак « – » вказує на те, що після взаємодії тіло з масою 4кг буде рухатись в напрямку протилежному від того який вказано на малюнку. І це закономірно, адже абсолютно очевидно, що при пружній взаємодії тіл з масами 4кг і 1кг, перше тіло дещо зменшить свою швидкість, але не змінить напрямку свого руху. Власне про це і говорить отриманий нами результат.

Що ж стосується другої відповіді (v₁ʹ = –10м/с; v₂ʹ = –10м/с), то вона вказує на те, що після гіпотетичної взаємодії тіл які з однаковими швидкостями (v₁= v₂=10м/с) рухаються в одному напрямку (від’ємному напрямку), величини їх швидкостей та напрямки руху залишаються незмінними. І це закономірно, адже рухаючись в одному напрямку та маючи однакові швидкості тіла ніколи не зіштовхнуться, а відповідно ніколи не змінять ні напрям, ні величину своєї швидкості.

Відповідь: v₁ʹ = –2м/с; v₂ʹ = 22м/с.

Задача 6. Людина масою 60кг переходить з носової частини на кормову частину початково нерухомого човна, проходячи при цьому відстань 3м. На яку відстань переміститься човен, якщо його маса 120кг. Опором води знехтувати.

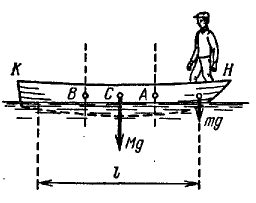
Дано:

m₁=60кг

m₂=120кг

v₁₂=0м/с

ℓ=3м

Δℓ= ?

Рішення: Виконуємо малюнок який відображає наявну ситуацію. У вибраній системі координат розглянемо імпульсні характеристики тіл системи човен-людина до та після початку руху.

Загальні зауваження. В черговий раз наголошуємо, що рішення практично будь якої задачі, в тій чи іншій мірі ідеалізоване. Адже якщо, наприклад, в умовах даної задачі ми почнемо врахувати всі ті обставини які так чи інакше впливають на рух реального човна в процесі реального переходу людини з носової частини човна на його кормову частину, то практично гарантовано не зможемо отримати будь яке рішення. Напевно найголовнішим вмінням якому ви маєте навчитися в процесі розв’язування задач, є вміння виділяти в наявній ситуації головне, суттєве, визначальне і абстрагуватись від неголовного, несуттєвого, невизначального. Скажімо, в умовах даної задачі, потрібно абстрагуватись від нюансів того, яким чином людина переміщувалась з одного краю човна до іншого, скільки кроків вона зробила, з якою швидкістю рухалась, які перешкоди долала в процесі свого руху, тощо. Абстрагувавшись від цих обставин, ви по суті маєте уявити ситуацію при якій людина з певною швидкістю відштовхуючись від одного краю човна, «приземляється» на його протилежному краю. При цьому, в момент відштовхування, людина надає човну певної реактивної швидкості, а в момент «приземлення» – гасить цю швидкість до нуля. За час же умовного польоту людини (за час переходу людини від носової частини до кормової), човен встигає пропливти певну відстань, яку і потрібно визначити.

Рішення (продовження). Будемо виходити з того, що в момент початку руху, людина відштовхуючись від човна і набуваючи швидкості v₁, надає човну реактивної швидкості v₂. Потім, певний час Δt, людина з постійною швидкістю v₁ рухається вздовж човна і проходить відстань ℓ=v₁Δt. При цьому човен, рухаючись з швидкістю v₂ проходить відстань Δℓ=v₂Δt. Після того як людина проходить відстань ℓ=3м, вона зупиняється, тобто імпульсно взаємодіючи з човном, зменшує свою швидкість до нуля. При цьому, згідно з законом збереження імпульсу, швидкість човна також стає нулевою. Із аналізу вище сказаного ясно, що за час Δt=ℓ/v₁ човен проходить відстань Δℓ=v₂Δt=v₂ℓ/v₁=ℓ(v₂/v₁).

Таким чином, рішення задачі зводиться до того, щоб визначити величину співвідношення v₂/v₁. З цією метою запишемо рівняння закону збереження імпульсу системи човен-людина для моментів до та після початку руху людини: (m₁+m₂)∙0 = –m₁v₁ + (m₁+m₂)v₂,  або   m₁v₁ = (m₂+m₁)v₂; звідси  v₂/v₁ = m₁/(m₂+m₁). Таким чином: Δℓ = ℓ(v₂/v₁) = ℓm₁/(m₁+m₂).

Розрахунки:  Δℓ= 3м∙60кг/(60кг+120кг) = 1м.

Відповідь:  Δℓ=1м.

Рішення багатьох задач динаміки передбачає поєднання як імпульсно-енергетичного так і силового методів. Розглянемо один з прикладів такої задачі.

Задача 7. Тіло нитяного маятника масою 5кг відхилено на 60° від вертикалі. Яка сила натягу нитки при проходженні маятником положення рівноваги?

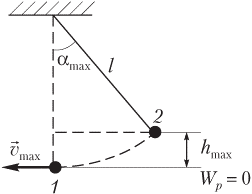
Дано:                                         Рішення:

m = 5кг        Виконуємо малюнок який відображає фізичну суть задачі.

α = 60º         Розглянемо ті сили які діють на тіло маятника а момент

Т = ?

Рішення: Виконуємо малюнок який відображає фізичну суть задачі.  Розглянемо ті сили які діють на тіло маятника а момент проходження ним положення рівноваги. А цими силами є: сила тяжіння F_т=mg, сила натягу нитки Т та сила інерції F_і=ma=mv²/ℓ. При цьому в момент проходження тілом точки рівноваги Т = F_т+ F_і = mg + mv²/ℓ = m(g+v²/ℓ), де v²=? ℓ=? Величину швидкості тіла (а точніше v²) визначаємо із енергетичних міркувань. А ці міркування є наступними. В точці 2 тіло мало потенціальну енергію mgh, яка в точці 1 перетворилась на відповідну кількість кінетичної енергії mv²/2=mgh, при цьому v²=2gh.

Співвідношення між кутом відхилення маятника (α), його довжиною (ℓ) та висотою (h), визначаємо із геометричних міркувань. А ці міркування є наступними. Із аналізу малюнку ясно, що h = ℓ – y, де y=ℓcosα (на малюнку у не позначено). Звідси випливає h = ℓ – ℓcosα = ℓ(1 – cosα). А це означає, що v²=2gh=2gℓ(1 – cosα).

Таким чином Т = m(g+v²/ℓ) = m(g+2gℓ(1–cosα)/ℓ = mg(1+2(1–cosα) = mg(1+2–2cosα) = mg(3 – 2cosα). У підсумку Т= mg(3 – 2cosα), де cosα= cos60º=0,5.

Розрахунки: Т = 5кг·10(м/с²)·(3 – 2·0,5) = 100Н.

Відповідь: Т = 100Н.

Вправа 21.

1. В пружинному пістолеті жорсткість пружини 400Н/м. З якою швидкістю вилітатиме з нього кулька масою 5г, якщо пружина стиснута на 10см?
2. Тіло масою 500г, кинуте вертикально вгору зі швидкістю 20м/с, впало на землю зі швидкістю 16м/с. Визначити величину енергетичних втрат в процесі польоту тіла.
3. Тіло масою кинули вертикально вгору зі швидкістю 12м/с. На якій висоті швидкість руху тіла зменшиться вдвічі?
4. Куля масою 10г, що летить зі швидкістю 800м/с, пробила дошку завтовшки 8см. Після цього швидкість кулі зменшилась до 400м/с. Визначте середню силу опору, з якою дошка діє на кулю.
5. Тіло масою 1кг рівномірно обертаючись на нитці у вертикальній площині описує коло радіусом 1м. На скільки сила натягу нитки в нижній точці траєкторії більша аніж у верхній?
6. Кулька підвішена на невагомій нерозтяжній нитці довжиною 0,5м. Яку мінімальну швидкість потрібно надати кульці, щоб вона описала коло у вертикальній площині? Опором повітря знехтувати.
7. На якій висоті кінетична енергія вільно падаючого тіла дорівнює його потенціальній енергії, якщо на висоті 20м швидкість тіла дорівнює 4м/с?
8. Кулька масою 10г вилітає з горизонтально розташованого пружинного пістолети і влучає в центр підвішеного на нитці пластилінового бруска масою 30г. На яку висоту підніметься брусок, якщо перед пострілом пружина була стиснута на 4см, а її жорсткість 256Н/м?
9. Людина масою 70кг переходить з носової частини на кормову частину початково нерухомого човна, проходячи при цьому відстань 5м. На яку відстань переміститься човен, якщо його маса 120кг. Опором води знехтувати.

.

Лекційне заняття №22.

Тема: Загальні відомості про коливання. Період і частота коливань. Фізичний, математичний та пружинний маятники.

В фізиці, процеси які так чи інакше повторюються називаються коливаннями. Коливається наприклад збурена поверхня води. В поривах вітру коливаються гілки дерев та листя на них. Під дією потягів та машин що рухаються, коливаються мости і дороги. Вібрують струни музичних інструментів та мембрани динаміків. Коливальним чином рухаються маятники, стрілки та шестерні механічних годинників, поршні, клапани і колінчасті вали автомобільних двигунів. Періодично змінюються дні і ночі, пори року та їм відповідні життєві цикли рослин і тварин. Ритмічно б’ється серце і працюють легені вашого організму. Певним чином коливаються атоми, молекули і ті частинки з яких вони складаються. Звук який ви чуєте і світло яке бачите, це також результат певних коливальних процесів. Не буде перебільшенням сказати, що майже все що відбувається в Природі, так чи інакше пов’язано з тими чи іншими коливальними процесами.

За різними класифікаційними ознаками коливання поділяються на:

– періодичні та неперіодичні;

– вільні та вимушені;

– згасаючі та незгасаючі;

– гармонічні та негармонічні;

– механічні та електромагнітні.

Стисло характеризуючи вище згадані класифікаційних груп, можна сказати наступне.

1. За точністю і ритмічністю повторювань, коливання поділяються на періодичні та неперіодичні. Періодичними називають такі коливання, які через певні, однакові проміжки часу вточності повторюються. Наприклад, періодично коливається маятник годинника, його рухомі шестерні, секундна, хвилинна та годинникова стрілки. Періодично обертаються елементи колеса при його рівномірно-обертальному русі. За умови рівномірної роботи, періодично коливаються деталі двигуна внутрішнього згорання (поршень, колінвал, шатун, клапани, …). Періодичним є рух Землі навколо своєї осі та навколо Сонця.

Неперіодичними називають такі коливання, які повторюються через різні проміжки часу, або повторюються частково. Неперіодично наприклад, коливаються елементи колеса що обертається зі змінною кутовою швидкістю. Неперіодичними є коливання листя і гілок дерев, вібрації автомобіля що їде бруківкою. Неперіодично відбуваються землетрусами, виверження вулканів, зміни атмосферного тиску, буревії, цунамі, тощо.

2. За ступенем автономності коливальної системи, коливання поділяються на вільні та вимушені. Вільними називають такі коливання, які починаються після виведення коливальної системи з стану рівноваги і продовжуються самостійно, а точніше, під дією певної комбінації внутрішньо системних сил. Наприклад, підвішене на нитці тіло в сукупності з гравітаційним полем Землі, утворюють коливальну систему, яка називається нитяним маятником (мал.96). Якщо цю систему вивести з рівноваги, то в подальшому вона буде здійснювати вільні коливання. Ці коливання не є безпричинними. Вони обумовлені дією на тіло певної системи постійно діючих сил: сили тяжіння F_т, реакції опори N, та тієї сили інерції F_i що виникає в процесі прискореного руху тіла. При цьому, ці сили є результатом природної взаємодії тих елементів які утворюють дану коливальну систему: тіло, нитка, Земля.

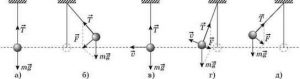
Мал.96. Вільні коливання не є безпричинними.

Вимушеними називають такі коливання, які відбуваються під дією певної змінної зовнішньої сили, сили, джерелом якої не є коливальна система. При цьому мається на увазі, що після припинення дії цієї сили, коливання припиняються. Скажімо, якщо ваша рука змушує книгу здійснювати певні коливальні рухи, то коливання книги є вимушеними. Вимушено наприклад, коливаються всі елементи двигуна внутрішнього згорання, шестерні та стрілки механічного годинника, елементи працюючої швацької машинки, крила птаха що летить, тощо.

а)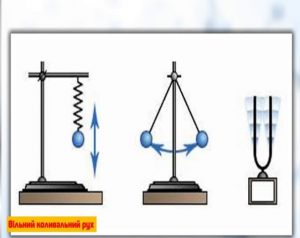  б)

Мал.97. Приклади вільних (а) та вимушених (б) коливань.

3. За ступенем енергетичних втрат в коливальній системі, коливання поділяються на згасаючі та незгасаючі. Згасаючими називають такі коливання, амплітуда яких з плином часу зменшується. Зменшується тому, що в процесі коливань, певна кількість енергії упорядкованого руху елементів коливальної системи, незворотнім чином перетворюється в теплоту, тобто в енергію хаотичного руху молекул речовини. Незгасаючими називають такі коливання, амплітуда яких з плином часу залишається незмінною. Залишається незмінною тому, що ті енергетичні втрати які неминуче відбуваються в процесі коливань є несуттєвими, або тому, що ці втрати компенсуються зовнішнім джерелом енергії.

Наприклад, коливання простого фізичного маятника (мал.98а) є згасаючими. Вони згасають тому, що в процесі коливань, частина енергії коливальної системи неминуче витрачається на теплові втрати, джерелом яких є ті чи інші сили тертя. Якщо ж аналогічний маятник є частиною годинникового механізму (мал.98б), то його коливання є незгасаючими. Вони не згасають тому, що в годинниковому механізмі є спеціальна автоматизована система, яка постійно поповнює енергетичні втрати маятника.

                          

 

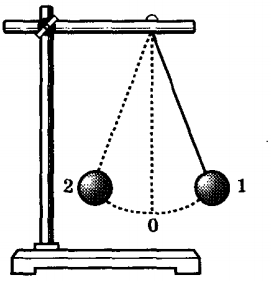
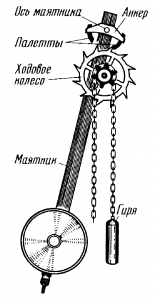
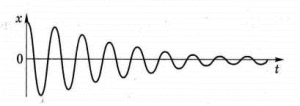
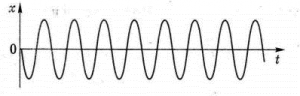
Мал.98.  Згасаючі (а) та незгасаючі (б) коливання.

4. За характером зміни параметрів коливальної системи, коливання поділяються на гармонічні та негармонічні. Гармонічними називають такі коливання які відбуваються за гармонічним законом. Це означає, що будь яке гармонічне коливання можна описати формулою x = х_мsinφ, або x = х_мcosφ, де

х – миттєве значення змінної величини;

х_м – амплітудне значення змінної величини;

φ – фаза коливань.

Наприклад коливання того фізичного маятника, що є частиною годинникового механізму (мал.98б) є гармонічними. Якщо ж говорити про вільні коливання нитяного маятника (мал.98а), то вони наближено гармонічні. Наближено гармонічні тому, що є згасаючими, а отже такими амплітуда коливань яких поступово зменшується. Загалом, практично всі вільні природні коливань є гармонічними, наближено гармонічними або комбіновано гармонічними. Зважаючи на цей факт, вивченню гармонічних коливань ми будемо приділяти особливу увагу.

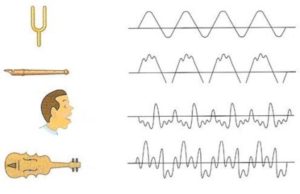
Мал.99. Звук камертона є гармонічним, а голос людини – комбіновано гармонічним, тобто таким, що складається з певної сукупності гармонічних коливань.

Негармонічними називають такі коливання які не є гармонічними, наближено гармонічними чи комбіновано гармонічними. Це означає, що негармонічні коливання не можна представити у вигляді певної сукупності гармонічних коливань. Зазвичай негармонічними є спеціально створені (штучні) вимушені коливання. Наприклад, негармонічно коливаються елементи клапанного механізму двигуна внутрішнього згорання (мал.100а), елементи так званого храпового механізму (мал.100б), тощо.

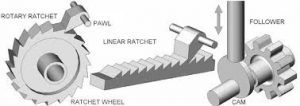
Мал.100. Приклади коливальних систем, елементи яких здійснюють вимушені негармонічні коливання.

5. За фізичною суттю тих процесів які відбуваються в коливальній системі, коливання поділяються на механічні та електромагнітні. Механічними називають такі коливання, які пов’язані з механічними переміщеннями тіл та їх частин, або частин пружного середовища. Механічними є коливання рухомих деталей двигуна внутрішнього згорання, пульсації нашого серця, коливання гілок та листя на цих гілках, обертальні рухи коліс, тощо. Механічними є і ті коливання середовища, які ми називаємо звуком, поверхневими хвилями, сейсмічними хвилями, тощо.

Електромагнітними називають такі коливання, які пов’язані з коливаннями електричних зарядів та електромагнітних полів. Електромагнітними є ті коливання які називаються змінним електричним струмом, радіохвилями, інфрачервоним випромінюванням, видимим світлом, ультрафіолетовим, рентгенівським та гама випромінюванням.

Практично всі природні коливання є гармонічним, наближено гармонічними (згасаюче гармонічними), або такими, що є певною комбінацією гармонічних чи наближено гармонічних коливань. Гармонічно або наближено гармонічно коливаються різноманітні маятникові системи, частинки збуреної поверхні рідини, струни та робочі поверхні музикальних інструментів, точки тіла що обертаються і тіла що рухаються по колу. Результатом певних гармонічних коливань є звук, світло і те що називають радіохвилями, інфрачервоним, ультрафіолетовим та рентгенівським випромінюванням. Гармонічні коливання відбуваються в лініях електропередач, трансформаторах, електродвигунах, тощо.

До числа тих фізичних величин які характеризують коливання загалом і гармонічні зокрема, відносяться: період та частота коливань, амплітуда коливань, фаза коливань.

Період коливань (період) – це фізична величина, яка характеризує часову періодичність (повторюваність) коливального процесу і яка дорівнює тому проміжку часу за який система здійснює одне повне коливання.

Позначається: Т

Визначальне рівняння: Т=t/n, де n – кількість коливань системи здійснених за час t;

Одиниця вимірювання: [Т] = с,  секунда.

Наприклад, якщо нитяний маятник за 20 секунд здійснює 16 повних коливань, то період цих коливань 1,25с:  Т= t/n = 20с/16 = 1,25с.

Частота коливань (частота) – це фізична величина, яка характеризує частотну періодичність коливального процесу і яка дорівнює тій кількості коливань системи, яку здійснює ця система за одиницю часу.

Позначається: ν

Визначальне рівняння: ν = n/t

Одиниця вимірювання: [ν] = 1/c = Гц,  герц.

Наприклад, якщо за 20 секунд нитяний маятник здійснює 16 коливань, то частота цих коливань 0,8Гц:  ν = n/t = 16/20c = 0,8Гц.

Із визначальних рівнянь періоду і частоти (T=t/n; ν=n/t) з усією очевидністю випливає, що ці фізичні величини взаємопов’язані, і що цю взаємопов’язаність відображають співвідношення: T=1/ν; ν=1/T. Тому якщо наприклад, за умовою задачі задано період коливань системи Т=2с, то ви завжди можете визначити частоту цих коливань ν=1/Т=1/2с=0,5Гц і навпаки.

Амплітуда коливань (амплітуда) – це фізична величина, яка характеризує максимальне за величиною (амплітудне) значення змінної величини і яка дорівнює цьому значенню. Позначається символом відповідної змінної величини з індексом «м»: х_м, v_м, І_м, U_м, тощо. Визначається як параметр конкретного коливального процесу. Вимірюється в одиницях відповідної фізичної величини: [x_м]=м; [v_м]=м/с; [I_м]=А; [U_м]=В і т.д.

Фаза коливань (фаза) це фізична величина яка характеризує стан коливальної системи в заданий момент часу і яка однозначно визначає параметри системи в цей момент.

Позначається: φ

Визначальне рівняння: фазу коливань можна визначити по різному, зокрема:

– через кут повороту системи: φ=α,

– через кількість коливань системи: φ=2πn,

– через частоту коливань системи: φ=2πνt,

– через період коливань системи: φ=2πt/T,

іншими словами: φ=α=2πn=2πνt=2πt/T. Зазвичай: φ = 2πνt.

Одиниця вимірювання: [φ] = рад,   радіан.

Співвідношення α=2πn=2πνt=2πt/T випливають із визначальних рівнянь періоду (T=t/n) і частоти (ν=n/t), та розуміння того, що між кутом повороту тіла α та кількістю здійснених ним обертів n існує співвідношення α=2πn. Дійсно, якщо тіло зробило один оберт (n=1), то кут його повороту дорівнює α=1·2π=2πрад; якщо n=2, то α=2·2π=4πрад; якщо n=0,5, то α=0,5·2π=πрад і т.д.

Будь яке гармонічне коливання можна представити у вигляді математичної формули, яка називається рівнянням гармонічного коливання. В загальному випадку це рівняння має вигляд: х=х_мsinφ, де  х – миттєве значення змінної величини, х_м – амплітудне (максимальне) значення змінної величини, φ – фаза коливань. Оскільки фазу коливань можна визначити по різному (φ=α=2πn=2πνt=2πt/T), то зустрічаються і відповідно різні записи рівняння гармонічного коливання. Зазвичай, це рівняння записують у вигляді: х=х_мsin2πνt.

Коли ми стверджуємо, що гармонічне коливання описується рівнянням х=х_мsin2πνt, то це означає, що в процесі коливань величина певного параметру коливальної системи змінюється за законом х=х_мsin2πνt та описується відповідною плавною кривою яка називається синусоїдою. Наприклад, описуючи коливання нитяного маятника (мал.101а), пружинного маятника (мал.101б) та тієї матеріальної точки, що рівномірно обертається навколо нерухомого центру (мал.101в), можна говорити про те, що з плином часу координата (х) відповідних матеріальних точок змінюється за законом х=х_мsin2πνt.

 

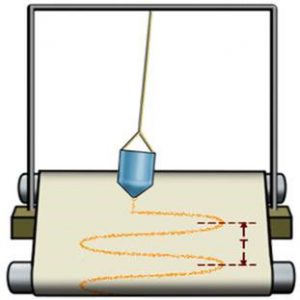
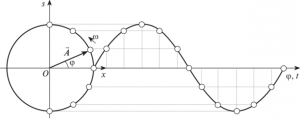
Мал.101. В процесі гармонічних коливань, певні параметри коливальної системи змінюються за законом х=х_мsin2πνt.

Потрібно зауважити, що синусоїда і косинусоїда, це по суті дві різні назви однієї і тієї ж кривої. Наприклад, зображений на мал.102а графік коливань матеріальної точки є синусоїдою, а рівняння відповідного гармонічного коливання має вигляд х=х_мsin2πνt. Графіком же тих коливань які представлені на мал.102б є косинусоїда, а рівняння відповідного гармонічного коливання має вигляд х=х_мcos2πνt. При цьому це рівняння можна записати у вигляді х =х_мsin(2πνt+π/2). Іншими словами, косинусоїда, це таж сама синусоїда, тільки зсунута в додатному напрямку на чверть періоду (на π/2рад). І навпаки, синусоїда, це таж сама косинусоїда тільки зсунута у від’ємному напрямку на чверть періоду.

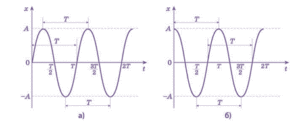
Мал.102. Синусоїда і косинусоїда, це дві аналогічні криві зсунуті одна відносно одної на чверть періоду.

Рівняння гармонічного коливання містить велику кількість інформації про відповідний коливальний процес. Воно дозволяє не лише визначити числове значення змінної величини в будь який момент часу, а й максимально повно описати інші параметри цього процесу. Ілюструючи лише незначну частину можливостей цього рівняння, розглянемо конкретну задачу.

Задача 1. Тіло нитяного маятника здійснює гармонічні коливання за законом х = 0,1sinπt. Визначити: 1) амплітуду, період та частоту коливань; 2) координату тіла в момент часу 0,5с; 10с; 3) кількість коливань маятника здійснених за 0,5с; за 10с.

Дано:

х = 0,1sinπt

1) х_м, Т, ν – ?

2) х(0,5)-? х(10)-?

3) n(0,5)-?  n(10)-?

Рішення: 1).  Із порівняльного аналізу заданого рівняння  х = 0,1sinπt  та загального вигляду цього рівняння х = х_мsin2πνt,   ясно що: х_м = 0,1м; ν = 0,5Гц;   (оскільки  2πνt = πt, то ν=0,5Гц). А оскільки Т=1/ν, то   Т =1/0,5= 2с .

2). Розв’язуючи рівняння х=0,1sinπt  для заданих значень часу (t=0,5с; t=2с) визначаємо відповідні значення координати тіла маятника:

х(0,5) =  0,1sinπ·0,5 = 0,1·1 = 0,1м;

х(10) = 0,1sinπ·10 = 0,1·0 = 0,0м.

3). Кількість коливань системи (n) за час t можна визначити із співвідношень: n = t/T = νt   Тому:

n(0,5) = 0,5c/2c = 0,25 (коливань).

n(10) = 10c/2c = 5,0 (коливань).

Задача 2. За заданим графіком визначити амплітуду, період та частоту коливань. Записати рівняння відповідного коливання.

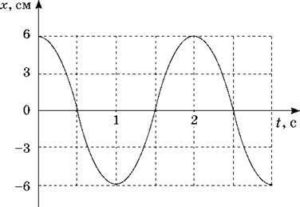
Рішення. Із аналізу заданого графіку випливає: 1) амплітуда коливань х_м=6см=0,06м; 2) період коливань Т=2с; 3) частота коливань ν=1/Т=1/2с=0,5Гц; 4) рівняння коливань х = 0,06cos2π·0,5t = 0,06cosπt.

         Однією з найпростіших коливальних систем є так званий фізичний маятник. Фізичний маятник, це механічна коливальна система, яка представляє собою тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо осі, що не проходить через центр маси тіла. Наприклад, якщо ви візьмете будь яке тверде тіло, скажімо лінійку, виделку, ножиці чи молоток і закріпите його так щоб воно могло вільно обертатись навколо осі яка не проходить через центр маси тіла, то отримаєте відповідний фізичний маятник. Однією з різновидностей фізичного маятника є так званий нитяний маятник, який представляє собою масивне тіло що висить на тонкій нитці (мотузці, дротині, тощо).

 

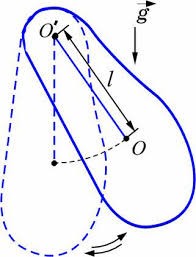
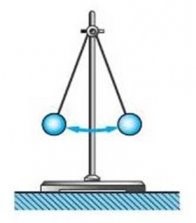
Мал.103. Приклади фізичних маятників.

Оскільки коливання фізичного маятника є згасаючими, то при теоретичних дослідженнях, реальний фізичний маятник замінюють відповідною ідеалізованою моделлю яка називається математичним маятником. Математичний маятник, це ідеалізована модель фізичного маятника, яка представляє собою масивну матеріальну точку що висить на надтонкій, невагомій та нерозтяжній нитці і в процесі коливань якої відсутні будь які втрати енергії. Якщо нитка реального нитяного маятника достатньо тонка, міцна та легка, а прикріплене до неї тіло достатньо масивне і таке що виготовлено з щільного матеріалу (залізо, мідь, свинець, тощо), то фізичні властивості цього реального маятника майже не відрізнятимуться від властивостей відповідного за довжиною математичного маятника.

Можна довести, що період коливань математичного маятника визначається за формулою Т=2π√(ℓ/g), де ℓ – довжина маятника (відстань від точки закріплення нитки маятника до центру мас його тіла), g – прискорення сили тяжіння. Формула Т=2π√(ℓ/g) в достатній мірі точності справедлива не лише для ідеалізованого математичного маятника, а й для реальних фізичних маятників. При цьому для фізичних маятників довжина маятника ℓ дорівнює відстані від осі обертання тіла до центру його маси. По суті, основна відмінність фізичного маятника від відповідного математичного маятника полягає в тому, що вільні коливання реального фізичного маятника в тій чи іншій мірі згасаючі, а коливання математичного маятника – незгасаючі. І потрібно зауважити, що факт згасання коливань в реальному фізичному маятнику практично не впливає на періодичність цих коливань.

                        

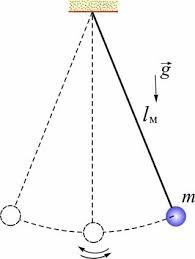
Мал.104. Вільні коливання реального фізичного маятника в тій чи іншій мірі згасаючі, а коливання математичного маятника – незгасаючі.

Із аналізу формули Т=2π√(ℓ/g) видно, що період коливань математичного маятника не залежить ні від маси тіла ні від кута його відхилення. Цей період визначальним чином залежить лише від довжини маятника ℓ та прискорення сили тяжіння g. Наприклад на Землі (g=9,8м/с²), період коливань математичного маятника довжиною 1м дорівнює Т=2π√(ℓ/g) = 2·3,14√1/9,8 = 2с, а період коливань такого ж маятника на Місяці (g=1,6м/с²): Т=2π√(ℓ/g) = 2·3,14√1/1,6 = 5с.

Ще однією простою коливальною системою є так званий пружинний маятник. Пружинний маятник – це така механічна коливальна система, яка складається з легкої пружини та масивного тіла і в якій це тіло здійснює поступальні коливання вздовж осі пружини. Потрібно зауважити, що в науковій практиці реальні та ідеалізовані (ідеальні) пружинні маятники, позначають одним і тим же терміном – пружинний маятник.

      

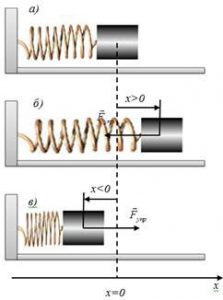
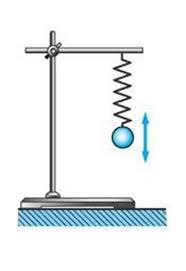
Мал.105.  Загальний вигляд пружинного маятника.

Можна довести, що період коливань ідеального пружинного маятника визначається за формулою Т=2π√(m/k), m – маса тіла маятника, k – жорсткість пружини маятника. В достатній мірі точності, формула Т=2π√(m/k) справедлива не лише для ідеальних, а й для реальних пружинних маятників.

Не важко бачити, що ті формули за якими визначаються періоди коливань фізичних та пружинних маятників (Т=2π√(ℓ/g); Т=2π√(m/k)) характеризуються певним набором споріднених рис, головною з яких є наявність коефіцієнту 2π, який по суті є ознакою періодичності (повторюваності) будь якого процесу. Адже результатом повороту тіла на 2π радіан є повернення цього тіла до початкового положення.

Задача 3. Коливання математичного маятника відбуваються за законом х = 0,2sinπt. Визначити: 1) амплітуду (х_м), період (Т) та частоту (ν) коливань; 2) довжину маятника (ℓ); 3) максимальне значення висоти тіла над рівнем точки рівноваги (h_м); 4) кут максимального відхилення маятника (α_м); 5) максимальне значення швидкості руху тіла маятника (v_м).

     .

Рішення.

1).  Із порівняльного аналізу заданого рівняння х = 0,2sinπt  та загального вигляду цього рівняння х = х_мsin2πνt, ясно що: х_м = 0,2м; ν = 0,5Гц; (оскільки  2πνt = πt, то ν=0,5Гц). А оскільки Т=1/ν, то   Т =1/0,5= 2с.

2).  Оскільки період коливань математичного маятника визначається за формулою Т=2π√(ℓ/g), де =9,8м/с², то можна записати Т²=[2π√(ℓ/g)]² звідси Т²=4π²ℓ/g звідси ℓ=Т²g/4π² = (2с)²9,8(м/с²)/4(3,14)² = 1,0м.

3). Максимальне значення висоти тіла (h_м) над рівнем точки рівноваги визначаєм із геометричних міркувань: h_м=ℓ – |0-2ʹ|.  Оскільки в прямокутному трикутнику 0-2-2Ꞌ відрізок 0-2=ℓ= 1,0м=100см, а відрізок 2-2Ꞌ = х_м = 0,2м = 20см, то у відповідності з теоремою Піфагора можна записати 0-2Ꞌ = √(ℓ² – х²) = √(100² – 20²) = 98см. Тому h_м=100см – 98см = 2см.

4). Оскільки cosα_м = |0-2ʹ|/ℓ = 98/100 = 0,98, то α_м = arccos(0,98) = 11,5º.

5). Оскільки в точці максимального відхилення маятника (т.2) величина його потенціальної енергії дорівнює mgh_м, та зважаючи на те, що у відповідності з законом збереження енергії, в нижній точці траєкторії руху тіла маятника (т.1) ця енергія повністю перетворюється на енергію кінетичну mv_м²/2, можна записати mv_м²/2 = mgh_м, звідси  v_м = √2gh_м = √2·9,8·0,02 = 0,62м/с.

Контрольні запитання.

1. Які коливання називаються а) вільними; б) вимушеними? Наведіть приклади.
2. Чи є вільні коливання безпричинними? Які силові причини коливань нитяного маятника?
3. Які коливання називаються а) гармонічними; б) негармонічними? Наведіть приклади.
4. Чому коливання простого маятника згасаючі, а коливання того маятника який є частиною годинникового механізму – незгасаючі?
5. Які перетворення механічної енергії відбуваються при вільних коливаннях нитяного маятника?
6. М’яч вільно падає з певної висоти і зробивши декілька стрибків зупиняється. Які перетворення енергії відбуваються при цьому? Дайте класифікаційну характеристику коливального руху м’яча. Чому ці коливання є згасаючими?
7. Який зв’язок між періодом та частотою коливань? Звідки випливає цей зв’язок?
8. Що називають фазою коливань? Через які величини вона визначається? Запишіть ці визначення.
9. Чим схожі та чим відрізняються синусоїда і косинусоїда?

Вправа 22.

1. Визначте період та частоту обертання: а) секундної стрілки годинника; б) хвилинної стрілки годинника; в) Землі навколо своєї осі та навколо Сонця.
2. Напишіть рівняння гармонічного коливання, якщо частота коливань 0,5Гц, а її амплітуда 50см.
3. Тіло нитяного маятника здійснює гармонічні коливання за законом х = 0,3sinπt/2. Визначити: 1) амплітуду, період та частоту коливань; 2) координату тіла в момент часу 0,5с; 10с; 3) кількість коливань маятника здійснених за 0,5с; за 10с.
4. Матеріальна точка здійснює гармонічні коливання за законом х=0,2cos2πt. Визначити амплітуду, період та частоту цих коливань. Визначте кількість коливань за 5с.
5. За заданими графіками визначте амплітуду, період та частоту коливань. Запишіть рівняння відповідних коливань.

а)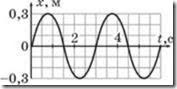  б)

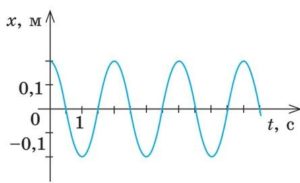
6. Довжина математичного маятника 0,5м. Визначте період та частоту коливань цього маятника.
7. Виконуючи лабораторну роботу по визначенню прискорення сили тяжіння, учень встановив, що маятник довжиною 80см, за 1хв здійснює 34 коливань. Який результат отримав учень?
8. Вантаж масою 4кг коливаючись на легкій пружині робить 5 коливань за 4 секунди. Визначте жорсткість пружини.
9. Рівняння коливань математичного маятника має вигляд х = 0,4sin0,5πt. Визначити: амплітуду, період та частоту коливань; довжину маятника; максимальне значення висоти тіла над рівнем точки рівноваги; максимальне значення швидкості руху тіла маятника.
10. Вантаж масою 300г є частиною пружинного маятника і здійснює коливання за законом х=0,06sinπt. Визначте період і частоту коливань, жорсткість пружини та максимальну швидкість тіла.

.

Лекційне заняття №23.

Тема: Механічна картина світу. Механіка, узагальнююче повторення.

         З незапам’ятних часів, люди розмірковували над тим, як влаштований навколишній світ (Всесвіт). Створення першої науково подібної систему знань про навколишній світ, нерозривно пов’язано з видатним давньогрецьким філософом-енциклопедистом Арістотелем (384–322 до н.е). Саме Арістотель зібрав, систематизував та критично узагальнив всю сукупність знань античного світу. Результати цих узагальнень він представив у вигляді системи літературно філософських творів, які прийнято називати трактатами. Арістотелівські трактати стосувались не лише тих питань що є предметом вивчення сучасних природничих наук, а й питань загально філософських, морально-етичних, психологічних, релігійних, медичних, літературних, політичних та інших.

Свої погляди на загальний  устрій навколишнього світу Арістотель виклав в таких трактатах як «Фізика», «Механіка», «Метереологіка», «Про небо», «Про походження і знищення» та деяких інших. Згідно з Арістотелем, в центрі Всесвіту знаходиться нерухома Земля, навколо якої певним чином обертаються Сонце, Місяць, п’ять відомих на той час планет (Меркурій, Венера, Марс, Юпітер, Сатурн) та небесна зоряна сфера.

  

Мал.106. Згідно з Арістотелем, в центрі Всесвіту знаходиться нерухома Земля, навколо якої певним чином обертаються всі інші космічні об’єкти.

Звичайно сьогодні, в епоху телебачення, інтернету та суцільної комп’ютеризації, навіть діти знають, що не Сонце обертається навколо Землі, а Земля обертається навколо Сонця та власної осі. Виходячи з цього, ми схильні вважати, що прадавні уявлення про будову Всесвіту, а точніше Сонячної системи, є примітивними та абсолютно хибними. Подібні твердження не є ані коректними, ані безумовно правильними. Не є бодай тому, що відносність руху в тому й полягає, що різні спостерігачі, спостерігаючи за одними і тими ж об’єктами, можуть бачити суттєво різні рухи, а відповідно по різному і описувати їх. Скажімо, той спостерігач, який знаходиться так би мовити над Сонячною системою («сторонній спостерігач») бачить: в центрі системи знаходиться Сонце, навколо якого на фоні зоряного неба обертаються планети, в тому числі і Земля. Той же спостерігач, який знаходиться на Землі («земний спостерігач») дивлячись на ті ж об’єкти, бачить: навколо відносно нерухомої Землі, обертаються Сонце, Місяць, планети та зірки. Будучи земними спостерігачами, та не відчуваючи руху самої Землі, стародавні вчені цілком обгрунтовано вважали, що Земля знаходиться в центрі Всесвіту і що всі інші космічні об’єкти так чи інакше обертаються навколо цього центру.

Якщо ж говорити про загальний устрій земних об’єктів (об’єктів підмісячного світу), то згідно з Арістотелем вони складаються з двох пар взаємно протилежних якостей: тепле – холодне, сухе – вологе. Ці якості в певних комбінаціях та пропорціях утворюють основні елементи (стихії) підмісячного (земного) світу, зокрема: поєднання сухого і холодного утворюють тверді тіла (земля); поєднання холодного і вологого утворюють рідини (вода); поєднання вологого і теплого утворюють газоподібне (повітря), а поєднання теплого з сухим утворюють те, що прийнято називати плазмою (вогонь). При цьому ті пропорції в яких поєднуються базові якості, визначають різноманіття наявних на Землі твердих, рідких, газоподібних та плазмових речовин.

Мал.107.  У відповідності з Арістотелем, все різноманіття матеріальних об’єктів неживої природи, є результатом поєднання двох пар взаємно протилежних якостей: тепле – холодне, сухе – вологе.

Арістотель безумовно був видатним вченим. Він не лише зібрав, систематизував та творчо опрацював величезну кількість знань, а й запровадив в наукову практику інструмент, який дозволяв отримувати ці знання. Сьогодні цей інструмент називають дедуктивним методом досліджень. Дедуктивний метод досліджень – це такий метод отримання теоретичних знань, при якому на базі певних припущень та на основі логічно очевидних міркувань, робляться певні узагальнюючі висновки. Класичним прикладом успішного застосування дедуктивного методу є та геометрія, основи якої заклав давньогрецький математик Евклід (325–270 до н.е). Евклід на базі невеликої кількості очевидно правильних тверджень (аксіом) та дедуктивного методу досліджень, створив цілісну систему знань яка пояснювала широке різноманіття властивостей геометричних фігур.

Сам по собі дедуктивний метод отримання теоретичних знань, був видатним відкриттям. Але він мав і має один недолік: зроблені на основі цього методу висновки, будуть правильними лише в тому випадку, якщо базові припущення є правильними. А ось тут-то і була «ахілесова п’ята» в системі знань Арістотеля. Скажімо виходячи з того, що все різноманіття об’єктів неживої природи, це результат поєднання певних якостей (тепла, холоду, сухості та вологості), логічно передбачити, що змішуючи ці якості в певних пропорціях можна отримати будь який матеріал, в тому числі дорогоцінні метали, коштовне каміння, еліксир молодості, філософський камінь, тощо.

Власне те, що прийнято називати алхімією і що представляє собою певне поєднання наукових та антинаукових практик (хімії, фізики, металургії, астрології, містицизму, спіритизму, тощо), є прямим наслідком ідеї про те, що будь яку матеріальну субстанцію можна отримати шляхом механічного змішування певних базових елементів. Алхіміки вважали, що варто вдало підібрати базові матеріали, в потрібних пропорціях їх змішати, прочитати магічне заклинання і, о диво: свинець, пісок чи що завгодно, перетворюються на золото. Протягом багатьох століть, вони придумували все нові і нові рецепти, випробовували все нові і нові співвідношення, шептали, стогнали та  викрикували все нові і нові заклинання. Однак, диво   не відбулося. Вони працювали не покладаючи рук. Сподівались… Вірили… Чекали… Вони відчували, ось-ось…, вже зовсім поряд…, вже майже  те що треба… Але диво не відбувалось. І не могло відбутися. Адже базові твердження алхімії  були хибними.

Протягом вісімнадцяти століть арістотелівський підхід до вирішення наукових проблем був панівним на теренах всього цивілізованого світу. А невтішним результатом цього панування є факт того, що за цей шалено великий історичний період, тогочасною наукою не було створено жодної достовірної теорії і не було зроблено жодного більш менш суттєвого наукового відкриття.

Не відомо скільки б ще тривав цей інтелектуальний застій, якби не видатний італійський вчений Галілео Галілей (1564–1642). Галілей першим зрозумів, що арістотелівський шлях розвитку науки та його метод здобуття наукових знань є хибним. Він зрозумів, що в науці критерієм істини має бути не суб’єктивна логіка наших думок, а об’єктивні експериментальні докази.

Геніальність Галілея полягала не лише в тому, що він першим почав експериментально перевіряти сумнівні теорії, а й в тому, що саме він запропонував та почав застосовувати на практиці такий метод дослідження Природи, який прийнято називати фізичним методом досліджень. Фізичний метод досліджень – це такий метод отримання достовірних знань, при якому вибір правильних теорій здійснюється на основі експериментальної перевірки тих передбачень, які випливають з цих теорій. Це означає, що для перевірки правильності тієї чи іншої теорії (а точніше гіпотези), необхідно на основі цієї теорії та дедуктивного методу досліджень, зробити логічно обгрунтовані передбачення і перевірити їх на практиці. При цьому, якщо передбачення справджуються, значить теорія правильна, а якщо не справджуються – не правильна.

Сьогодні кожен вчений знає, якщо результати експериментів не співпадають з передбаченнями теорії, значить теорія хибна. При цьому немає значення, хто автор теорії. Наскільки він відомий, розумний чи авторитетний. Немає значення, подобається нам теорія, чи не подобається, розуміємо її, чи не розуміємо. Якщо результати експериментів не співпадають з передбаченнями теорії, значить теорія не правильна. От і все.

Звичайно, експерименти мають бути достовірними і такими, що враховують всі суттєві обставини. Адже якщо наприклад, на основі факту того, що важкий камінь падає швидше за легку пір’їну, ви почнете заперечувати те, що всі тіла падають однаково швидко, то у своїх запереченнях будете спиратись на результати неправильно поставленого експерименту. Неправильного в тому сенсі, що при його проведенні ви не врахували суттєво важливу обставину – гальмуючу дію навколишнього повітря.

   

Мал.108. Галілей – правильність теорії визначається експериментальною достовірністю її передбачень.

Запровадивши новий підхід до вирішення наукових проблем, Галілей заклав основи сучасної науки. Науки, яка за неповні чотириста років не лише кардинально змінила наші уявлення про навколишній світ, а й саме цивілізоване життя. Ефективність запровадженого Галілеєм методу наукового пізнання навколишнього світу, з усією очевидністю була продемонстрована геніальним англійським фізиком Ісааком Ньютоном (1643–1727). Аналізуючи широкий спектр експериментальних фактів, Ньютон сформулював базові закони сучасної класичної механіки: три закони Ньютона та закон всесвітнього тяжіння. Спираючись на ці закони та сформульований Галілеєм принцип відносності, Ньютон створив першу, дійсно наукову теорію Всесвіту. Тобто таку цілісну систему достовірних знань, яка не лише описувала загальний устрій Всесвіту та Сонячної системи, а й пояснювала, яким чином ця система працює.

Згідно з Ньютоном, наша Сонячна система є мізерним фрагментом безкінечного, вічного, ізотропного та стаціонарного Всесвіту. Це означає, що ньютонівський Всесвіт є безмежним в просторі та вічним в часі. Що в ньому міститься безкінечно велика кількість зірок та зіркових систем. Що ці зірки усереднено рівномірно (ізотропно) розкидані в безмежних просторах Всесвіту. Що ті події, які відбуваються у Всесвіті, не змінюють ані усереднено рівномірного розподілу матерії в ньому, ані параметрів його простору, ані монотонності плину часу.

 

Мал.109. Ньютон – перша безумовно наукова теорія Сонячної системи та

Всесвіту загалом.

З механічної точки зору, ньютонівський Всесвіт нагадував бездоганний годинниковий механізм, об’єкти якого у повній відповідності з законами механіки утворюють дивовижно гармонійну та саморегульовану систему. В цьому механізмі не було місця для гіпотетичних сфер, напівсфер, важелів, канатів, тощо. Він не потребував ремінних, зубчатих чи будь яких інших механічних передач. Його основними дійовими особами та виконавцями були закони механіки, сили гравітаційної взаємодії та сили інерції. При цьому, гравітаційні взаємодії не потребували будь яких посередників. Адже у відповідності з поглядами тогочасної науки, ці взаємодії здійснювались безпосередньо через пустоту.

Створена Ньютоном система світу була дивовижно гармонійною, точною та передбачуваною. Вона не лише з математичною точністю описувала поведінку всіх відомих космічних об’єктів, а й дозволяла робити нові відкриття. Наприклад, існування планети Нептун було спочатку теоретично передбаченим, а лише потім експериментально підтвердженим. При цьому відповідна планета виявилась саме в тому місці Сонячної системи на яку вказувала теорія Ньютона.

Звичайно, ньютонівська теорія Всесвіту не була такою що відповідала на всі наявні запитання. Зокрема, вона не пояснювала яким чином та за рахунок чого Сонце і зірки постійно випромінюють величезну кількість енергії. Не пояснювала відомі магнітні та електричні явища. Не пояснювала різноманіття хімічних та механічних властивостей речовин. Не пояснювала як виник Всесвіт і чому він саме такий.

І це закономірно. Адже реальний Всесвіт набагато складніший та багатогранніший за ту механістичну картину яка була «намальована» великим Ньютоном понад три століття тому. Достатньо сказати, що в ньютонівській теорії Всесвіту поведінка та властивості всього різноманіття матеріальних об’єктів Природи, по суті описуються лише однією фундаментальною взаємодією – гравітаційно-інерційною. Насправді ж ці властивості та ця поведінка визначаються чотирма фундаментальними взаємодіями – гравітаційно-інерційною, електромагнітною, сильною ядерною та слабкою ядерною.

Зважаючи на вище сказане, не будемо забувати, що та система знань яку прийнято називати ньютонівською механікою, була лише першим вагомим кроком сучасної науки на шляху пізнання навколишнього світу. Про наступні ж кроки науки на цьому складному, тернистому та дивовижно цікавому шляху, ви дізнаєтесь в процесі подальшого вивчення фізики – науки про Природу.

.

Завершуючи вивчення основ ньютонівської механіки матеріальної точки, представимо ці основи у вигляді гранично стислої узагальнюючої таблиці.

Основи ньютонівської механіки матеріальної точки (узагальнююче повторення)

Основні поняття	Основні величини	Основні закони
Кінематика
механічний рух поступальний рух обертальний рух матеріальна точка система відліку траєкторія	час                       t              (c) координата          x=lx         (м) пройдений шлях s=Δx        (м) швидкість            v=Δx/Δt  (м/с) прискорення       a=Δv/Δt (м/с2)	рівняння руху: x = x0 + v0t + (a/2)t2
Статика
механічна рівновага рівнодіюча сила	сила                     Fi = ma     (Н) основні сили механіки: сила інерції         Fi = -ma сила тяжіння       Fт = mg сила гравітаційної взаємодії             Fгр= Gm1m2/ℓ2 реакція опори     N вага                      P = –N сила пружності   Fпр = k(Δℓ) сила тертя            Fтер = µN сила Архімеда     FA= ρVg	умова механічної рівноваги тіла: якщо v=const, то ∑F=0
Динаміка
інерція гравітація інерціальна система відліку динамічна рівновага	маса               m                (кг) імпульс          р = mv       (кг∙м/с) енергія           E                 (Дж) робота        А = ΔЕ             (Дж) потужність N=A/t               (Вт) к.к.д.           η = (Акор/Азаг)100%	принцип відносності 1 закон Ньютона 2 закон Ньютона 3 закон Ньютона закон всесвітнього тяжін. закон збереження енергії закон збереж. імпульсу умова динамічної рівноваги тіла: якщо v≠const, то ∑F+Fi=0

.