Сайт викладача фізики

 

РОЗДІЛ 1. Механіка. частина 1.

 

Лекційне заняття №1. Тема: Фізика – наука про Природу

Лекційне заняття №2. Тема: Загальні відомості про механіку.

Кінематика, основні поняття кінематики.

Лекційне заняття №3. Тема: Основні фізичні величини кінематики:

час, координата, пройдений шлях, швидкість, прискорення.

Лекційне заняття №4. Тема: Рівняння руху – основний закон

кінематики. Практичне застосування рівняння руху.

Лекційне заняття №5. Тема: Вільне падіння тіл. Рух тіла кинутого

вертикально, горизонтально та під кутом до горизонту.

Лекційне заняття №6. Тема. Алгебраїчний та графічний

методи розв’язування задач.

Лекційне заняття №7. Тема: Основні поняття, величини та

закони кінематики обертального руху.

Лекційне заняття №8. Тема: Статика. Основні поняття, величини

та закони статики. Про силу звичайну та силу інерції.

Лекційне заняття №9. Тема: Закон всесвітнього тяжіння. Про

силу гравітаційну та силу тяжіння. Механіка Сонячної системи.

Лекційне заняття №10. Тема: Про вагу, невагомість та силу

Архімеда. Або про те, що важче кілограм заліза чи кілограм вати?

Лекційне заняття №11. Тема: Механічні деформації. Сила

пружності. Механічна напруга. Закон Гука.

Лекційне заняття №12. Тема: Чи завжди 2+2=4? Або, про

додавання векторних величин.

Лекційне заняття №13. Тема: Розв′язування задач статики.

Лекційне заняття №14. Тема: Силовий метод розв′язування

задач динаміки.

 

 

Лекційне заняття №1.

Тема: Фізика – наука про Природу.

         Слово “фізика” в перекладі з грецької означає “природа”. Фізика – наука про Природу. Більш вичерпного та більш ємного визначення для тієї сфери людської діяльності, яку прийнято називати фізикою, годі й шукати. Що ж означає слово “Природа”?

Відразу ж зауважимо, що в науці загалом і в фізиці зокрема, звичні для нас слова, часто означають не зовсім те, а іноді і зовсім не те, що ми про них думаємо у повсякденному житті. Зауважимо також, що знати фізику, на половину означає знати і розуміти ті слова, які в ній застосовуються, бачити за цими словами реальні об’єкти і події. Тому вивченню мови фізичної науки, ми будемо приділяти надзвичайно серйозну та повсякденну увагу. І почнемо це вивчення з найголовнішого та найбільш ємного слова – “Природа”.

В науці, Природа – це не тільки дерева, звірі та чисте повітря. Не тільки навколишні пейзажі і зоряне небо. Природа – це щось значно більше, аніж просто навколишній світ. Значно більше за те, що ми здатні бачити і відчувати. Це навіть більше, аніж просто Всесвіт. Природа, це і далекі, неосяжно великі галактики і неймовірно малі атоми. Це наша душа, наші думки і наші почуття. Це наше минуле, теперішнє і майбутнє. Природа, це все що існувало, існує і буде існувати взагалі.

Дати точне та вичерпне визначення терміну “Природа” практично неможливо. Адже не можливо осягнути неосяжне. Напевно найбільш вдалим та гранично вичерпним є наступне визначення. Природа – це безкінечний у своєму різноманітті та проявах Всесвіт, який представляє собою діалектичне поєднання матерії, руху, часу та простору, матеріального та духовного, минулого, теперішнього та майбутнього.

          Сучасна наука виходить з того, що Природа, це єдиний цілісний організм, в якому все взаємопов’язано і взаємообумовлено. Що цей організм працює за певними правилами, які називаються законами природи. Що ці закони не можливо змінити, але їх можна пізнати, а пізнавши – застосувати на практиці. При цьому людина, будучи частиною Природи, на основі аналізу тих подій, які в ній (Природі) відбуваються, на основі аналізу спеціальних експериментів, вимірювань та досліджень, створила науку, яка називається  фізикою – наукою про Природу. Іншими словами:

Фізика – це наука, яка представляє собою об’єктивне і точне відображення Природи в свідомості людини, викладене у вигляді певної системи достовірних знань, які описують, пояснюють і прогнозують природні об’єкти та події.

Не буде перебільшенням сказати, що в системі наукових знань про Природу не було, нема і не буде більш важливої, значимої та всеосяжної навчальної дисципліни аніж фізика. Бо фізика, це і про Всесвіт, і про галактики, і про зірки, і про планети, і про життя, і про людину, і про клітину, і про молекули, і про атоми, і про елементарні частинки та  поля, і про все різноманіття існуючих та ще не існуючих машин, механізмів та приладів, і про теперішнє, минуле та майбутнє, і взагалі про все що було, є і буде. Бо вивчаючи фізику, ви по суті вивчаєте і хімію, і біологію, і географію, і астрономію, і технічну механіку, і електротехніку, і взагалі все різноманіття тих наук, які називаються природничими. І навпаки – вивчаючи все різноманіття природничих наук, ви фактично, вивчаєте певні фрагменти головної науки про Природу – фізики. При цьому лише в фізиці, всі ці фрагменти стають єдиним цілим і отримують своє узагальнено філософське пояснення.

Ясно, що все різноманіття того, що вивчає та пояснює сучасна фізика, не можливо вивчити інакше як у вигляді певної системи знань. А основою цих знань є певний набір взаємопов’язаних та взаємодоповнюючих наукових теорій. Наукова (фізична) теорія – це система достовірних знань, яка на основі певних базових тверджень, кількісно описує і пояснює певну групу споріднених явищ, та дозволяє робити точні кількісні передбачення. Аналізуючи дане  визначення можна сказати наступне.

1.Теорія – це система знань, яка на основі певних базових, експериментально доведених та безумовно достовірних тверджень, пояснює певну групу споріднених явищ. Наприклад ньютонівська механіка, на основі тих базових тверджень які називаються законами Ньютона пояснює широке різноманіття механічних явищ. Молекулярно-кінетичної теорія, на основі твердження про те, що всі речовини складаються з певних частинок (молекул), які безперервно рухаються та певним чином взаємодіють між собою, пояснює широке різноманіття властивостей твердих, рідких і газоподібних речовин та ті теплові процеси які з цими речовинами відбуваються.

Не буде перебільшенням сказати, що процес вивчення фізики є свідомим та ефективним лише тому, що основою цього процесу є певна система знань, яку прийнято називати теорією. Без теорії фізична наука неминуче перетворилась би на купу обособлених експериментальних фактів, розібратися в різноманітті яких було б практично не можливо. І не тому, що ці факти є надто складними, а тому, що їх надто багато. Виходячи з цього, ми будемо вивчати фізику не як певну сукупність окремих фактів, а як науку, в якій теорія займає провідне місце.

2.Теорія – це система достовірних знань. Говорячи про достовірність наукової теорії, мають на увазі виконання наступної сукупності вимог:

1) ті базові твердження які лежать в основі теорії є такими, що надійно та безумовно, експериментально підтвердженні;

2) нема жодного, підкреслюю жодного, експериментально підтвердженого факту який би суперечив даній теорії;

3) значна кількість передбачень даної теорії мають достовірне експериментальне підтвердження.

3.Теорія – це така система знань, яка не лише пояснює відомі явища та минулі події, а й дозволяє кількісно передбачити хід майбутніх подій та існування нових, до появи теорії невідомих, явищ та об’єктів. Скажімо, ньютонівська механіка не лише пояснює рух планет Сонячної системи, а й гарантовано точно передбачає їх майбутню механічну поведінку. Або наприклад, до появи теорії електромагнітного поля (теорії Максвелла) ніхто не здогадувався про те, що в Природі існують електромагнітні хвилі, що однією з різновидностей цих хвиль є видиме світло, що відомі закони геометричної оптики тісно пов’язані з законами електромагнетизму, тощо.

4.Теорія – це система знань, яка пояснює певну групу споріднених явищ. Це означає, що будь-яка із до сих пір відомих наукових теорій пояснює не все різноманіття відомих фізичних явищ, а лише певну їх частину. Наприклад ньютонівська механіка, пояснює механічну поведінку макротіл в ситуаціях, коли швидкість руху цих тіл значно менша за швидкість світла. Молекулярна фізика – пояснює загальні властивості твердих рідких і газоподібних речовин та ті теплові процеси які відбуваються з ними. Електродинаміка – пояснює все різноманіття електричних, магнітних та електромагнітних явищ.

Загалом же в сучасній фізиці є дві базові теорії на основі яких можна пояснити практично все різноманіття відомих фізичних явищ. Цими теоріями є квантова механіка і теорія відносності. Але фізична і математична суть цих теорій стає зрозумілою лише після того, як пройдено певний еволюційний шлях інтелектуального розвитку і з’ясована суть тих, менш загальних теорій, які були історичними попередниками теорії відносності і квантової механіки. А це означає, що в межах загальноосвітньої школи, фізику вивчають і, напевно завжди будуть вивчати, як сукупність окремих розділів, в кожному з яких  пояснюється певна група споріднених явищ. До числа таких розділів відносяться:

1.ньютонівська механіка;

2.молекулярна фізика;

3.термодинаміка;

4.електродинаміка;   5.оптика;

6.фізика атома і атомного ядра;

7.квантова механіка;

8.теорія відносності;

9.космологія.

Зважаючи на вище сказане, загальну структуру Природи, загальну структуру науки про Природу та ту роль, яку відіграє при цьому людина, можна представити у вигляді наступної схеми

 

·   ПРИРОДА                                                     ФІЗИКА                             

                                                                           наука про Природу                

 

Всесвіт                                                               Механіка

 

Галактика                                                        Молекулярна фізика

·                                         спостерігає

Зірка                                 аналізує                 Термодинаміка

·                                         досліджує

Планета                                                           Електродинаміка

 

Людина                         Людина                         Оптика

 

Клітина                                                            Фізика  атома  і

·                                      на основі                   атомного ядра

Молекула                     аналізу та

·                                       досліджень             Квантова механіка

Атом                                створює

·                                                                         Теорія відносності

Елементарні

частинки і поля                                                Космологія

 

Мал.1 Фізика – це об’єктивне і точне відображення Природи, викладене у вигляді певної системи знань.

Якщо ж говорити про набір тих конкретних речей які вивчає і пояснює сучасна фізика, та про ті конкретні задачі які вона вирішує, то можна сказати наступне. Фізика вивчає  загальні властивості фізичних об’єктів і фізичних явищ, закони які визначають ці властивості та ті теорії які ці властивості пояснюють. Іншими словами, предметом вивчення фізики є фізичні об’єкти і фізичні явища.

         Фізичним об’єктом називають будь-який реально існуючий об’єкт, який є предметом спостережень, досліджень та експериментів. Подивіться навколо себе і ви побачите величезне різноманіття великих і малих, твердих і рідких, живих і неживих одним словом різноманітних об’єктів, кожен з яких може стати предметом ваших спостережень, а отже є фізичним об’єктом. Більше того, навіть те, що ви ніколи не бачили і напевно ніколи не побачите, як-то атоми, елементарні частинки, поля, електромагнітні хвилі, або скажімо Всесвіт у всій його цілісності – все це фізичні об’єкти, тобто конкретні предмети вивчення фізики.

         Фізичним явищем називають будь-яку подію, що відбувається з фізичним об’єктом, будь-то механічне переміщення тіла, зміна його кольору, форми, температури, твердості, пружності, електропровідності, чи чогось іншого. Наприклад камінь, це певний фізичний об’єкт. А камінь падає, світиться, нагрівається, плавиться – це певні фізичні явища.

         Потрібно зауважити, що поділ єдиного цілісного організму який називається Природою на те, що прийнято називати фізичними об’єктами і фізичними явищами, є досить умовним. Скажімо, блискавка – це фізичний об’єкт чи фізичне явище? З одного боку, блискавка – це певний фізичний об’єкт, який може стати предметом спостережень, досліджень та експериментів. З іншого ж боку, блискавка – це певне фізичне явище, яке обумовлене низкою подій пов’язаних з рухом заряджених частинок.

Загалом ви маєте знати, що будь який фізичний об’єкт представляє собою певний згусток фізичних процесів (явищ). От наприклад камінь – це фізичний об’єкт чи фізичне явище? Безумовно, фізичний об’єм – скажете ви. І будите абсолютно праві. Камінь – це фізичний об’єкт. Однак з іншого боку, камінь складається з атомів, атоми – з атомних ядер і електронів, атомні ядра – з протонів та нейтронів. І всі ці атоми, атомні ядра, протони, нейтрони та електрони, знаходяться в постійному русі і в постійних взаємодіях. Більше того, всі ці протони, нейтрони та електрони, представляють собою певні згустки рухів і взаємодій.

Говорю це для того, щоб ви постійно пам’ятали: Природа – це єдиний цілісний організм, і тому будь який класифікаційний поділ цього організму на певні класифікаційні групи є досить умовним.

Та як би там не було, а різноманіття того що вивчається в фізиці, ми будемо розділяти на дві групи: фізичні об’єкти та фізичні явища. При цьому терміни «фізичні об’єкти» і «фізичні явища» ми будемо застосовувати як в найширшому розумінні. Наголошую на цьому тому, що дуже часто фізичними називають лише ті явища, які не супроводжуються перетвореннями однієї речовини в іншу. А виходячи з цього, хімічні та біологічні явища розглядають як такі, що не пов’язані з явищами фізичними.

Такий класифікаційний підхід є безпідставним і хибним. Безпідставним та хибним по перше тому, що всі хімічні і всі біологічні явища відбуваються у повній відповідності з законами фізики і по суті є проявами певної сукупності фізичних явищ. А по друге, поділ природних явищ на фізичні, хімічні та біологічні є досить умовним.

От наприклад, електроліз – це явище фізичне чи хімічне? З одного боку, електроліз нерозривно пов’язаний з проходженням електричного струму через електроліт і тому є явищем фізичним. З іншого ж боку, це явище пов’язане з певними хімічними перетвореннями і тому є хімічним. Або скажімо, фотосинтез. З одного боку фотосинтез нерозривно пов’язаний з властивостями світла і тому є явищем фізичним. З іншого боку, фотосинтез пов’язаний з певними хімічними перетвореннями і тому є явищем хімічним. З третього ж боку, фотосинтез відбувається в клітинах ростин та ціанобактерій і тому є явищем біологічним.

Звичайно, вивчаючи фізику ми не будемо заглиблюватись в деталі хімічних та біологічних процесів. Однак це зовсім не означає, що різноманіття фізичних явищ можна і потрібно вивчати у відриві від тих явищ які прийнято називати хімічними, біологічними чи якимись іншими. Рівно як і не означає, що різноманіття фізичних об’єктів можна і потрібно обмежувати різноманіттям хімічно простих тіл неживої природи.

Якщо ж говорити про ті задачі які має вирішувати фізика як навчальний предмет, то вони полягають в тому, щоб кількісно описати та пояснити властивості всього різноманіття існуючих фізичних об’єктів, описати та пояснити все різноманіття фізичних явищ, розкрити існуючі між ними взаємозв’язки, і на основі цих знань побудувати узагальнюючу картину Природи.

Словник фізичних термінів.

         Природа – це безкінечний у своєму різноманітті та проявах Всесвіт, який представляє собою діалектичне поєднання матерії, руху, часу та простору, матеріального та духовного, минулого, теперішнього та майбутнього.

         Фізика – це наука про Природу, яка представляє собою об’єктивне та точне відображення Природи в свідомості людини, викладене у вигляді системи достовірних знань, які описують, пояснюють і прогнозують природні об’єкти та події (явища). Фізика вивчає загальні властивості неживої Природи та закони, які визначають ці властивості. Предметом її досліджень є фізичні об’єкти і фізичні явища.

Наукова (фізична) теорія – це система достовірних знань, яка на основі певних базових тверджень, кількісно описує і пояснює певну групу споріднених явищ, та дозволяє робити точні кількісні передбачення.

Задача фізики полягає в тому, щоб кількісно описати та пояснити властивості всього різноманіття існуючих фізичних об’єктів, описати та пояснити все різноманіття фізичних явищ, розкрити існуючі між ними взаємозв’язки, і на основі цих знань побудувати узагальнюючу картину Природи.

Фізичний об’єкт – це реально існуючий об’єкт, який є предметом наукових спостережень, досліджень та експериментів.

         Фізичне явище – це та подія, що відбувається з фізичним об’єктом.

Контрольні запитанні.

1.Чому в фізиці слово Природа пишуть з великої літери?

2.Який взаємозв’язок між Природою, людиною та фізикою?

3.Як ви розумієте твердження: “фізика представляє собою об’єктивне і точне відображення Природи в свідомості людини, викладене у вигляді системи достовірних знань?”

4.Що означає твердження: «теорія – це певна система знань»?

5.Що означає твердження: «теорія – це система достовірних знань»?

6.Наведіть десять прикладів фізичних об’єктів.

7.Наведіть десять прикладів фізичних явищ.

 

 

Лекційне заняття № 2.

Тема. Загальні відомості про механіку. Кінематика. Основні поняття кінематики.

Механіка – це розділ фізики, в якому вивчають параметри, закономірності та причини механічного руху тіл в усіх його проявах. Іншими словами, механіка – це наука  про механічний рух.

Коли ми говоримо про механічний рух, то маємо на увазі такий процес (рух) при якому тіло, як єдине ціле, або певні цілісні фрагменти цього тіла, переміщуються відносно інших тіл. Човен  пливе, автомобіль іде, вода тече, Земля обертається, колесо крутиться, газ розширюється, яблуко падає, собака біжить, дерево хитається, м’яч стрибає, стержень деформується – все це конкретні приклади механічного руху тих чи інших фізичних об’єктів (тіл). Потрібно зауважити, що однією з різновидностей механічного руху є такий рух, швидкість якого дорівнює нулю (v=0). Цю різновидність руху називають механічним спокоєм. Крім цього, різновидністю механічного руху тіла є його механічна деформація, тобто та чи інша зміна форми (розмірів) тіла, що відбувається під дією певної сили. А це означає, що в механіці вивчають не лише параметри, закономірності та причини власне самого механічного руху (спокою) тіла, а й параметри, закономірності та причини всіх видів його механічної деформації.

Коли ми говоримо про тіла, то маємо на увазі такі фізичні об’єкти, механічна поведінка яких практично не залежить від руху молекул навколишнього середовища. Дрібна пісчинка і масивний камінь, вода в склянці і сама склянка, і стіл на якому вона стоїть і будинок, в якому вони знаходяться, і планета, на якій ми всі живемо, все це приклади конкретних фізичних тіл.

Як правило, в механіці не вивчається глибинна суть тих процесів, результатом яких є механічний рух тіла. Наприклад, вивчаючи механіку, ми не будемо цікавитись тим, чому деформована пружина штовхає тіло? Чому повітряно-бензинова суміш в процесі згорання штовхає поршень двигуна? В чому причина появи сили тертя, сили опору повітря, сили пружності, сили тяги автомобіля, м’язової сили людини, тощо. В механіці просто констатується той факт, що причиною зміни швидкості руху тіла і причиною його пружної деформації є певна механічна дія на це тіло іншого фізичного об’єкту, і що мірою цієї дії є фізична величина, яка називається силою.

Теоретичну основу механіки складають принцип відносності, три закони Ньютона та закон всесвітнього тяжіння. Це означає, що на базі цих законів, можна кількісно пояснити практично все різноманіття механічних явищ. Але це не означає, що в механіці не діють і не мають широкого застосування інші закони. Просто ці закони, як-то закон збереження механічної енергії, закон збереження імпульсу, умова рівноваги тіла, рівняння руху, закон Бернуллі, тощо, – так чи інакше випливають із законів Ньютона та визначальних рівнянь відповідних фізичних величин. Щоправда, в механіці є і такі закони, які не є прямими наслідками законів Ньютона. Скажімо, закон Гука не є похідним ані від законів Ньютона, ані від закону всесвітнього тяжіння.

Сучасна Ньютонівська механіка дозволяє пояснити надзвичайно широкий спектр явищ і не лише механічних. Наприклад, на її основі можна пояснити теплові і звукові явища, різноманітні властивості твердих, рідких і газоподібних тіл. Ця механіка дозволяє точно передбачити механічну поведінку як простих тіл, так і їх складних систем, починаючи від дрібної пісчинка і закінчуючи гігантськими зірковими системами, від простого футбольного м’яча до складного автомобіля, від підводного човна до космічного корабля.

Але ньютонівська механіка не є тією теорією, яка дозволяє пояснити все. Наприклад, вона не може пояснити електричні, магнітні, оптичні та ядерні явища. Пояснити хімічні властивості речовин, будову атомів і молекул, властивості елементарних частинок, тощо. Іншими словами, ньютонівська механіка має певні межі свого застосування і певні межі своєї достовірності. При цьому, ці межі визначаються не лише рамками визначення “ механіка – це наука про механічний рух тіл”, а й тим, що параметри цього руху, параметри простору, часу та самих тіл, певним чином залежать від багатьох факторів, зокрема – від швидкості руху тієї системи відліку в якій описується відповідний рух. Тому, наприклад, при швидкостях близьких до швидкості світла (300 000 км/с), закони ньютонівської механіки, а разом з ними і наші уявлення про навколишній світ, потребують певного суттєвого уточнення.

Та як би там не було, а ньютонівська механіка була і залишається однією з основ сучасної науки. І якщо сьогодні ми говоримо про існування нових, більш точних наукових теорій, зокрема квантової механіки і теорії відносності, то ви маєте знати, що ці нові теорії не “відміняють” ньютонівську механіку, а лише доповнюють та уточнюють її, розширюючи тим самим її можливості.

Намагаючись певним чином систематизувати процес вивчення механіки ми умовно розділимо її на три базові теми:

1.Кінематика

2.Статика

3.Динаміка

При цьому ви маєте знати, що в рамках цих тем ми будемо вивчати лише основи механіки. Адже насправді, сучасна механіка це надзвичайно ємка та багатогранна наука, складовими частинами якої, окрім кінематики, статики і динаміки є механіка періодичних процесів, механіка рідин і газів, механіка тіл змінної маси, теорія пружності і теорія пластичності, теорія коливань і теорія стійкості, теорія гіроскопів, теорія ударів, тощо. Крім цього, прикладними розділами механіки є безліч технічних дисциплін: технічна механіка, деталі машин та механізмів, опір матеріалів (сопромат), підіймально-транспортні механізми, тощо.

Кінематика. Основні поняття кінематики.

Слово “ кінематика” в перекладі з грецької означає “рух” (від грецького “kinematos” – рух). Кінематика – це розділ механіки, в якому вивчають параметри та закономірності механічного руху тіл, без врахування їх мас та діючих на них сил. Іншими словами, в кінематиці вивчають параметри та закономірності механічного руху і не вивчають причини цього руху, а також не враховують фізичні властивості рухомого тіла.

До числа основних понять кінематики, тобто тих загальних термінів суть яких потрібно знати, відносяться: механічний рух, поступальний рух, обертальний рух, матеріальна точка, абсолютно тверде тіло, відносність руху, система відліку, траєкторія.

         Механічний рух – це такий рух (процес), при якому тіло як єдине ціле, або певні цілісні фрагменти цього тіла, переміщується відносно інших тіл. Розрізняють дві прості різновидності механічного руху: поступальний та обертальний. Поступальний рух – це такий механічний рух, при якому будь-яка приналежна тілу пряма залишається паралельною сама собі. Наприклад, якщо книга рухається поверхнею стола таким чином, що будь яка з її бічних сторін залишається паралельними самі собі, то рух книги є поступальним (мал.7). Він буде поступальним навіть тоді, коли книга рухається по колу, або будь-якій іншій складній кривій. Якщо в процесі руху будь-яка приналежна тілу пряма залишається паралельною сама собі, то це тіло рухається поступально.

    

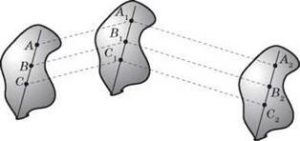
Мал.2. При поступальному русі, будь-яка приналежна тілу пряма залишається паралельною сама собі..

Характерною та практично важливою особливістю поступального руху тіла є факт того, що при такому русі, всі точки тіла рухаються однаково. Однаково в тому сенсі, що мають однакові траєкторії руху, за однакові проміжки часу проходять однакові відстані, мають однакові миттєві і середні швидкості, однакові прискорення, тощо. А це означає, що описуючи поступальний рух тіла, нема потреби описувати рух кожної його окремої точки. Достатньо охарактеризувати рух будь-якої з цих точок, наприклад, центру маси тіла. Зважаючи на ці обставини, описуючи поступальний рух тіла, це тіло зазвичай замінюють його спрощеною (ідеалізованою) моделлю, яку прийняти називати матеріальною точкою.

Матеріальна точка, це така умовна точка, якою теоретично замінюють певне реальне тіло, в ситуаціях коли розмірами, формою та внутрішнім устроєм цього тіла можна знехтувати. Матеріальна точка зберігає лише одну механічну характеристику реального тіла – його масу. При цьому положення матеріальної точки практично завжди співпадає з положенням центру мас відповідного тіла. Представляючи реальне тіло у вигляді матеріальної точки, ми абстрагуємося від несуттєвих в умовах даної задачі характеристик тіла і зосереджуємо свою увагу на його суттєво важливих характеристиках. В кінематиці такими характеристиками є час руху, траєкторія руху, швидкість руху, прискорення, пройдений шлях, тощо.

Потрібно підкреслити, що визначаючись з тим, можна чи не можна дане тіло вважати матеріальною точкою, в першу чергу враховують не реальні розміри тіла, а характер його руху та характер тих запитань які поставлені в даній задачі. Наприклад, якщо книга поступально рухається поверхнею стола і ми говоримо про швидкість її руху, її прискорення, пройдений шлях, то цю книгу можна вважати матеріальною точкою. Адже при поступальному русі всі точки книги проходять однаковий шлях, рухаються з однаковими швидкостями та з однаковими прискореннями. Якщо ж описуючи положення книги, ми говоримо про її координати, то скоріш за все цю книгу не можна вважати матеріальною точкою. Адже в масштабах стола, різні точки мають суттєво різні координати. Та як би там не було, а зазвичай в кінематиці поступального руху, тіла представляють у вигляді відповідних матеріальних точок.

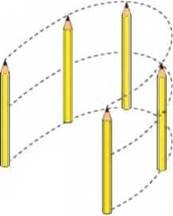
Обертальний рух – це такий механічний рух, при якому всі точки тіла описують кола, центри яких знаходяться на одній прямій, яка називається віссю обертання. Наприклад, обертально рухаються стрілка годинника, колесо автомобіля, двері класної кімнати, – звичайно за умови, що годинник “іде”, колесо крутиться, двері відчиняються.

 

Мал.3. При обертальному русі, всі точки тіла описують кола, центри яких знаходяться на одній прямій (осі обертання).

При обертальному русі різновіддалені від осі обертання точки тіла, рухаються суттєво по-різному: мають різні траєкторії руху, різні пройдені шляхи, різні лінійні швидкості, різні прискорення, тощо. А це означає, що обертальний рух тіла не можна описати, охарактеризувавши рух його однієї точки. Описуючи обертальний рух тіла, це тіло зазвичай представляти у вигляді так званого абсолютно твердого тіла. Абсолютно тверде тіло, це таке умовне тіло, яким теоретично замінюють певне реальне тіло, в ситуаціях коли його механічними деформаціями можна знехтувати.

В загальному випадку механічний рух тіла представляє собою певну комбінацію поступального і обертального рухів. Наприклад, коли ви кидаєте камінь, або б’єте футбольного м’яча, то скоріш за все рухи цих тіл будуть поступально-обертальними. Або, наприклад, якщо автомобіль їде прямолінійною дорогою, то його корпус рухається поступально, колеса – поступально-обертально, а рух поршнів двигуна є певною комбінацією двох поступальних рухів. Якщо ж рельєф дороги складний, то всі ці руху стають набагато складнішими. Але яким би складним не був механічний рух тіла, його завжди можна представити як певну комбінацію двох простих рухів: поступального і обертального. А це означає, що вивчивши параметри та закономірності поступального і обертального руху можна описати та спрогнозувати будь-який найскладніший механічний рух.

 

Мал.4. В загальному випадку рух тіла є поступально-обертальним.

Зважаючи на ці обставини та реалізуючи базовий методологічний принцип науки – від простого до складного, від часткового до загального, кінематику розділяють на дві частини  кінематика поступального та кінематика обертального руху. І потрібно зауважити, що у відповідності з програмою загальноосвітньої школи, левову частину уваги та часу ми приділимо вивченню кінематики поступального руху тіла.

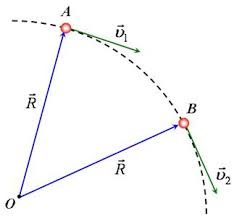
Напевно ви чули про те, що будь-який механічний рух є відносним. Факт цієї відносності закарбовано в самому визначені механічного руху. Механічний рух, це такий рух при якому тіло переміщується відносно інших тіл. Автомобіль рухається відносно дороги. Поршень автомобільного двигуна рухається як відносно двигуна так і відносно тієї дороги якою їде автомобіль. Дорога разом з Землею рухається відносно Сонця, разом з Сонячною системою – відносно центру Галактики і т.д. При цьому рух поршня відносно двигуна автомобіля, суттєво відрізняється від руху того ж поршня відносно дороги.

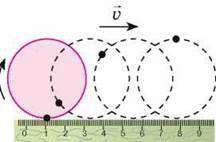
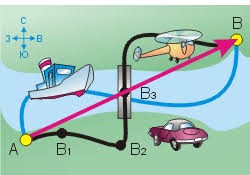
По суті, твердження про те, що механічний рух є відносним означає, що різні спостерігачі, спостерігаючи за рухом одного і того ж об’єкту можуть бачити суттєво різні рухи. Дійсно. Уявіть собі велосипед, який з певною постійною швидкістю рухається прямолінійною дорогою. Уявіть також, що за певним елементом цього велосипеда, наприклад, за штуцером колеса (мал.5) спостерігають три спостерігачі. При цьому перший сидить на рамі велосипеда, другий – на землі, а третій – на самому колесі.

Кожен із спостерігачів дивиться на один і той же об’єкт (штуцер колеса) та описує його поведінку. Аналізуючи побачене, перший буде стверджувати, що штуцер рухається по колу. Другий, буде запевняти, що штуцер рухається певною кривою, яку прийнято називати циклоїдою. Третій же буде наполягати на тому, що штуцер не рухається. І як це не дивно, але кожен з спостерігачів абсолютно правий. Адже відносно рами велосипеда штуцер дійсно рухається по колу, відносно дороги – по циклоїді, а відносно елементів колеса – не рухається взагалі.

 

Мал.5. Різні спостерігачі, спостерігаючи за рухом одного і того ж об’єкту бачать суттєво різні рухи.

Із вище сказаного ясно, що описуючи механічний рух тіла, необхідно чітко вказати, в якій системі відліку описується цей рух. Адже в різних системах відліку один і той же рух може виглядати по різному. Тому, наприклад, якщо не вказати ту систему відліку в якій описується рух штуцера, то можна як завгодно довго та як завгодно запекло сперечатись відносно того, як рухається штуцер – по колу, по циклоїді чи якось інакше. І кінця краю цій суперечці не буде.

Звичайно, якщо в тому чи іншому контексті, або в умові тієї чи іншої задачі не вказана система відліку, то скоріш за все, це означає що цією системою є та, що жорстко з’єднана з умовно нерухомою землею. Наприклад, коли ми говоримо, що будинок не рухається, то маємо на увазі що він не рухається відносно землі. Або, якщо ми стверджуємо, що автомобіль рухається з швидкістю 90 км/год, то скоріш за все маємо на увазі його швидкість відносно дороги. При цьому відносно іншого автомобіля ця швидкість може бути іншою.

Говорячи про систему відліку мають на увазі взаємопов’язану сукупність (систему) двох складових: системи координат та вимірювача часу (годинник, секундомір, тощо). Ця сукупність дозволяє однозначно описати просторово-часові параметри руху тіла. Це означає, що система відліку не лише визначає “адресу” (координати) рухомої точки, а й вказує на те в який момент часу ця “адреса”  зафіксована.

Система відліку – це взаємопов’язана сукупність системи координат та вимірювача часу, яка застосовується для того, щоб кількісно описати механічний рух матеріальної точки (тіла) в цій системі.

Система координат – це взаємопов’язана сукупність точки відліку та осей системи координат, яка застосовується для того щоб кількісно описати положення (розташування, місцезнаходження) матеріальної точки в цій системі.

Точка відліку – це така умовно нерухома точка, яка є центром (нулевою точкою) відповідної системи координат.

Задати систему координат означає: 1) вказати точку відліку даної системи; 2) задати просторову орієнтацію осей координат системи; 3) на кожній осі координат вказати масштаб вимірювань.

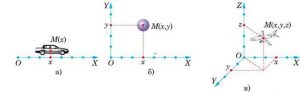
Мал.6. Системи відліку, це сукупність системи координат та вимірювача часу.

Розташування (місцезнаходження) матеріальної точки в заданій системі координат, однозначно визначається її координатами. При цьому, якщо мова йде про одновимірну (лінійну) систему координат (мал.6а), то в ній місцезнаходження матеріальної точки характеризується однією координатою М(х). В двовимірній (плоскій) системі координат (мал.6б), розташування точки характеризується двома координатами М(х;y), а в тривимірній (об’ємній, мал. 6в) – трьома М(х;y;z).

Потрібно зауважити, що координата, це не просто число яке визначає положення матеріальної точки в вибраній системі координат. Координата, це величина яка дорівнює відстані від точки відліку заданої системи координат до проекції даної точки на відповідну вісь координат. Наприклад, в зображеній на мал.7а лінійній системі координат, автобус має координату (300), а вантажний автомобіль (-100). Це означає, що відносно точки відліку системи координат, автобус знаходиться на відстані 300м в додатному напрямку, а автомобіль – на відстані -100м в від’ємному напрямку. Або наприклад, в зображеній на мал.7б плоскій системі координат, точка А має координати А(5;3). Це означає, що для потрапляння в точку А потрібно пройти 5м вздовж додатного напрямку осі х, а потім пройти 3м вздовж додатного напрямку осі y

  

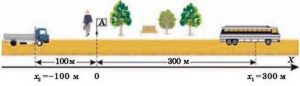
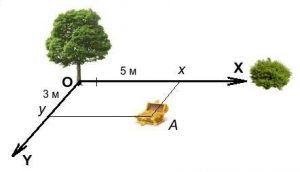
Мал.7. Координата точки дорівнює відстані від точки відліку системи координат до даної точки, виміряній вздовж відповідної осі системи координат.

Лінію яку описує матеріальна точка в процесі свого руху в вибраній системі відліку називають траєкторією. В різних системах відліку траєкторія руху однієї і тієї ж матеріальної точки може бути суттєво різною. Наприклад, в системі відліку пов’язаною з землею, траєкторією руху велосипедного штуцера (мал.8) є сукупність послідовних циклоїд. В системі ж відліку пов’язаною з рамою велосипеда, цієї траєкторією буде сукупність співпадаючих кіл. А в системі відліку пов’язаній з колесом велосипеда – нерухома точка.

За формою траєкторії, механічні рухи поділяються на прямолінійні та криволінійні. Прямолінійним називають такий поступальний рух матеріальної точки, траєкторія якого представляє собою пряму лінію. Криволінійним називають такий поступальний рух матеріальної точки, траєкторія якого представляє собою криву лінію. Наприклад рух вертикально падаючого тіла (мал.8б) є прямолінійним, а рух тіла кинутого під кутом до горизонту (мал.8г) – криволінійним. Криволінійним є і рух тіла кинутого вертикально вгору (мал.8в). Його криволінійність полягає в тому, що відповідна траєкторія представляє собою ламану яка складається з двох прямолінійних відрізків.

     

Мал.8. За формою траєкторії, поступальні рухи поділяються на прямолінійні (б) та криволінійні (в; г)

Та якою б криволінійною не була траєкторія руху тіла, її завжди можна представити як певну сукупність послідовних прямолінійних відрізків. А це означає, що вивчивши параметри та закономірності прямолінійного руху матеріальної точки, можна описати будь-який криволінійний рух. Виходячи з цього, вивченню параметрів та закономірностей прямолінійного руху ми будемо приділяти особливу увагу.

На завершення додамо, що кінематика, це один з найскладніших розділів не лише механіки, а й фізики загалом. Він складний по-перше тому, що саме в кінематиці ви зробите перші серйозні кроки як на шляху вивчення теоретичного матеріалу, так і на шляху застосування цього матеріалу на практиці, якою по суті є розв’язування задач. А як відомо, перші кроки завжди найважчі.

По-друге, кінематика це дійсно складна наука. Достатньо сказати, що вивчаючи наприклад статику, ви будете мати справу лише з двома фізичними величинами – сила і момент сили. В кінематиці ж таких величин щонайменше дев’ять: час, координата, пройдений шлях, швидкість, прискорення, кут, кут повороту, кутова швидкість, кутове прискорення. Тому, починаючи вивчення кінематики ви маєте налаштуватись на серйозну клопітку роботу, яка можливо не відразу принесе бажані результати. Але, якщо ви будете наполегливими, то ці результати обов’язково прийдуть.

Словник фізичних термінів.

         Механіка (ньютонівська механіка) – це розділ фізики, в якому вивчають параметри,  закономірності та причини механічного  руху тіл в усіх його проявах, за умови, що швидкість цього руху значно менша за швидкість світла в вакуумі (300 000 км/с). Теоретичною основою механіки є принцип відносності, три закони Ньютона та закон всесвітнього тяжіння.

Кінематика – це розділ механіки, в якому вивчають параметри та закономірності механічного руху тіл, без врахування їх мас і діючих на них сил.

Механічний рух – це такий рух (процес), при якому тіло як єдине ціле, або певні цілісні фрагменти цього тіла, переміщується відносно інших тіл.

Поступальний рух – це такий механічний рух, при якому будь-яка приналежна тілу пряма залишається паралельною сама собі.

Обертальний рух – це такий механічний рух, при якому всі точки тіла описують кола, центри яких знаходяться на одній прямій, яка називається віссю обертання.

Матеріальна точка – це така умовна точка, якою теоретично замінюють певне реальне тіло, в ситуаціях коли розмірами, формою та внутрішнім устроєм цього тіла можна знехтувати. Матеріальна точка зберігає лише одну динамічну характеристику реального тіла – його масу.

Відносність руху полягає в тому, що різні спостерігачі спостерігаючи за рухом одного і того ж об’єкту  можуть бачити суттєво різні рухи.

Система відліку – це взаємопов’язана сукупність системи координат та вимірювача часу, яка застосовується для того щоб кількісно описати механічний рух матеріальної точки (тіла) в цій системі.

Система координат – це взаємопов’язана сукупність точки відліку та осей системи координат, яка застосовується для того щоб кількісно описати положення (розташування, місцезнаходження) матеріальної точки в цій системі.

Траєкторія – це умовна лінія яку описує матеріальна точка в процесі свого руху в вибраній системі координат.

Контрольні запитання.

1.Що називають механічним рухом?

2.Чи є механічна деформація тіла, механічним рухом цього тіла?

3.Який рух називають поступальним? Яка характерна особливість цього руху?

4.Які критерії є визначальними при з’ясуванні того, можна чи не можна вважати дане тіло матеріальною точкою?

5.Що означає твердження: “механічний рух є відносним”?

6.Чим система відліку відрізняється від системи координат? Яка з цих систем є більш загальною?

6Траєкторії руху двох тіл перетинаються. Чи означає це що тіла зіштовхуються? Поясніть.

Вправа 1.

1.Задайте плоску прямокутну систему координат і побудуйте в ній точки з координатами А(20;20); В(-20;40); С(20;0); Д(10;-30); К(0;20); М(-10;-20); N(0;0); Р(30;-25).

2.Задайте лінійну систему координат і побудуйте в ній точки з координатами: А(200); В(-150); С(50);  Д(250);  К(-50);  М(0);  N(100).

3.Човен пливе перпендикулярно лінії берегів річки. Намалюйте приблизний вигляд траєкторії руху човна відносно: а) берегів річки; б) плоту, що пливе за течією; в) іншого човна, що пливе поруч

4.Пасажир потягу, що рухається з постійною швидкістю, підкидає вертикально вгору яблуко і ловить його. Намалюйте траєкторію руху яблука відносно: а) пасажира який сидить поруч; б) людини, яка стоїть на пероні вокзалу.

 

Лекційне заняття № 3.

Тема. Основні фізичні величини кінематики.

До числа основних фізичних величин кінематики поступального руху відносяться: час (t), координата (x), пройдений шлях (s), швидкість (v), прискорення (a). Час – це фізична величина, яка характеризує тривалість подій (явищ, процесів, рухів, тощо) і яка дорівнює цій тривалості.

Позначається:  t

Визначальне рівняння:  нема

Одиниця вимірювання:  [t] = с, (секунда)

Твердження про те, що час немає визначального рівняння по суті означає, що час відноситься до числа тих базових фізичних величин одиниці вимірювання яких за домовленістю прийнято вважати основними. В механіці такими базовими величинами є час (t), довжина (ℓ) і маса (m).

Зважаючи на те, що координати та пройдений шлях, а за одно і переміщення, висота, ширина, товщина, діаметр, радіус, периметр, діагональ, тощо, є різновидностями тієї фізичної величини яка називається довжина, визначимо цю величину.

Довжина – це фізична величина, яка характеризує відстань між двома точками, виміряну вздовж певної лінії і яка дорівнює цій відстані.

Позначається: ℓ

Визначальне рівняння: нема

Одиниця вимірювання: [ℓ] = м.

Координата – це фізична величина, яка характеризує положення (місцезнаходження) матеріальної точки в заданій системі координат і яка дорівнює відстані від точки відліку цієї системи до проекції даної точки на відповідну вісь координат.

Позначається: х

Визначальне рівняння: х =ℓ_х

Одиниця вимірювання: [х] = м, (метр)

Пройдений шлях – це фізична величина, яка характеризує пройдений матеріальною точкою (тілом) шлях і яка дорівнює довжині тієї траєкторії яку описує ця точка в процесі відповідного руху.

Позначається: s

Визначальне рівняння: s = ℓ_тр

Одиниця вимірювання: [s]  = м

Реалізуючи базовий методологічний принцип науки – від простого до складного, від часткового до загального, та зважаючи на факт того, що будь який криволінійний рух можна представити як певну сукупність прямолінійних рухів, ми перш за все будемо вивчати кінематику прямолінійного руху. А в цій кінематиці, рівняння s = ℓ_тр набуває вигляду s = ∆х,  де ∆х = х_к– х_п.

 Зауваження. В науці загалом і в фізиці зокрема, символом ∆ – дельта (∆х, ∆t, ∆v, ∆m і т.д.) позначають різницю між кінцевим та початковим значенням відповідних величин:

∆х = х_к – х_п

∆t = t_к – t_п

∆v = v_к – v_п

∆m = m_к – m_п  і т.д.

Ілюструючи можливості та межі застосуванні формули s=∆х, розглянемо декілька простих ситуацій. Припустимо, що в заданій системі відліку точки А і В мають координати А(-300); В(200). Виходячи з цього, визначимо пройдений тілом шлях при його переміщенні: a) з точки А в точку В; б) з точки В в точку А; в) з точки А в точку В, а потім знову в точку А.

·                        А                                                                       В                               х(м)

·       ————–•———-•————•———-•———-•———–•———-•—————–→

·                     -300     -200        -100           0         100         200       300

Із аналізу малюнка ясно, що при переміщенні    А → В пройдений тілом шлях становить s₁ = 500м, при переміщенні В → А: s₂ = 500м, при переміщенні А → В → А: s₃ = 500 + 500= 1000м.

Тепер, застосуємо формулу s = ∆х та отримаємо відповідні результати так би мовити теоретичним шляхом:

s₁ = ∆x= х_к– х_п = (200) – (-300) = 500 м

s₂ = ∆x= х_к– х_п = (-300) – (-200) = -500 м

s₃ = ∆x= х_к– х_п = (-300) – (-300) = 0 м

Не важко бачити, що останній результат явно суперечить реальному стану речей. Це пояснюється тим, що формула s = ∆x є справедливою лише для прямолінійних ділянок руху тіла. Рух же тіла за маршрутом А→В→А є криволінійним. І тому пройдений тілом шлях потрібно визначати не за формулою s=∆х, а за формулою s = ℓ_тр = |s₁| + |s₂|  + …  + |s_N| ,  де  N – кількість тих послідовних прямолінійних відрізків які утворюють відповідну криволінійну траєкторію. Наприклад, в умовах нашої задачі s = |s₁| + |s₂|  = |500| + |-500| = 1000 м 

Таким чином, застосовуючи визначальне рівняння s=∆х потрібно пам’ятати, що воно є справедливим лише для прямолінійної ділянки руху і лише за умови, що цей рух описується в лінійній системі координат. Втім, в котре наголошуємо, що будь-який криволінійний рух, завжди можна представити як певну сукупність прямолінійних відрізків, кожен з яких можна описати в певній лінійній системі координат.

Потрібно зауважити, що рівняння s=∆х не лише визначає величину пройденого тілом прямолінійного шляху, а й вказує на той напрямок в якому цей шлях пройдено. Наприклад, при переміщенні з точки А в точку В тіло рухається в додатному напрямку і тому s₁= +500м. Коли ж тіло переміщується з точки В в точку А, то воно рухається у від’ємному напрямку і тому s₂ = -500м.

В механіці наряду з пройденим шляхом, часто застосовують величину яка називається переміщення. Прагнучи максимально спростити процес вивчення кінематики, ми не будемо визначати цю величину. Просто зауважимо, що на відміну від пройденого шляху, переміщення є величиною векторною, і що воно дорівнює тому вектору, який з’єднує початкову та кінцеву координати точки. Наприклад, в вище розглянутій ситуації (в), пройдений тілом шлях дорівнює 1000м, а його переміщення 0м.

Важливими характеристиками поступального руху тіла є його швидкість та прискорення.

Швидкість – це фізична величина, яка характеризує швидкість поступального руху тіла (матеріальної точки), і яка показує на скільки переміщується це тіло в заданій системі відліку, за одиницю часу.

Позначається: v

Визначальне рівняння: v =∆x/∆t, де ∆х = х_к – х_п – переміщення тіла за час ∆t, за умови, що величина цього часу достатньо мала (наближається до нуля ∆t→0)

Одиниця вимірювання: [v] = м/с,  (метр за секунду).

Відразу ж зауважимо, що вище наведене визначальне рівняння швидкості є рівнянням так званої миттєвої швидкості, тобто тієї швидкості яку має матеріальна точка в даний момент часу. При цьому, мається на увазі що величина того проміжку часу ∆t за який відбувається переміщення ∆х є гранично малою, тобто такою що наближається до нуля (∆t→0). Після того як на уроках математики ви ознайомитесь з тим що називають “похідною” і що характеризує швидкість зміни функції, стане ясно, що швидкість є похідною від координат і що вона визначається за формулою v = dx/dt.

Швидкість – величина векторна, тобто така, що характеризується як певною величиною, так і певним напрямком. Напрям вектора швидкості завжди співпадає з напрямком руху тіла (матеріальної точки) у відповідній точці траєкторії. А це означає, що вектор швидкості завжди направлений по дотичній до траєкторії руху тіла.

  

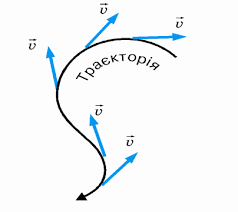
Мал.9. Напрям вектора швидкості завжди співпадає з напрямком руху тіла в заданій точці траєкторії, тобто направлений по дотичній до цієї траєкторії.

Зазвичай, терміном швидкість позначають швидкість тіла в даний момент часу, тобто його миттєву швидкість. Але окрім миттєвої швидкості, існує багато різновидностей певним чином усереднених швидкостей: середня шляхова швидкість, середня швидкість переміщення, середня арифметична швидкість, середня квадратична швидкість, тощо. В кінематиці поступального руху ми будемо говорити лише про одну різновидність усередненої швидкості – середню шляхову швидкість, яку будемо називати просто: середня швидкість.

         Середня швидкість (середня шляхова швидкість) – це та усереднена швидкість з якою тіло долає певну ділянку шляху і яка дорівнює відношенню пройденого тілом шляху s, до того проміжку часу t, за який цей шлях пройдено.

Позначається: v_с

Визначальне рівняння: v_с= s/t

Одиниця вимірювання: [v_с] = м/с,  метр за секунду.

Найпростішою різновидністю прямолінійного руху є так званий прямолінійно-рівномірний рух. Тобто такий рух при якому величина і напрям швидкості залишаються незмінними (v=const). Для прямолінійного рівномірного руху визначальне рівняння v =∆x/∆t набуває вигляду v = s/t. А це означає, що для такого руху (v=const) відмінності між середньою та миттєвою швидкостями практично зникають.

Якщо ж рух матеріальної точки є прямолінійно-рівнозмінним (v≠ const, а=const), то в цьому випадку рівняння v =∆x/∆t набуває вигляду v=v₀+a·t,

де   v – швидкість матеріальної точки в момент часу t;

v₀ – початкова швидкість точки, тобто її швидкість в момент часу t=0;

а – прискорення точки.

Зазвичай формулу v=v₀ + a·t називають рівнянням швидкості.

         Таким чином, на практиці швидкість прямолінійного руху тіла визначають за формулами:

1.для v = const:    v = s/t;

2.для v ≠ const:    v=v₀ + a·t.

         Якщо швидкість тіла так чи інакше змінюється, то говорять що воно рухається з прискоренням. Прискорення – це фізична величина, яка характеризує зміну швидкості руху тіла, і яка показує на скільки змінюється ця швидкість за одиницю часу.

Позначається: а

Визначальне рівняння: а=∆v/∆t,

Одиниця вимірювання: [a] = м/с²,  метр за секунду в квадраті

Оскільки швидкість, величина векторна, то вона може змінюватись як за величиною (модулем) так і за напрямком. Виходячи з цього розрізнюють дві різновидності прискорення:

1.Прискорення яке характеризує зміну швидкості за величиною (його називають тангенціальним прискоренням, або просто прискоренням);

2.Прискорення, яке характеризує зміну швидкості за напрямком (його називають доцентровим прискоренням).

Тангенціальне (дотичне) прискорення (прискорення) – це таке прискорення, яке характеризує зміну швидкості за величиною

Позначається: а_τ     або   а

Визначальне рівняння: а_τ=∆v/∆t

Одиниця вимірювання: [а_τ]= м/с²

Зазвичай, тангенціальне прискорення називають просто “прискоренням”. Наприклад, коли ми говоримо, що той автомобіль який починає рух, рухається з прискоренням, що автомобіль, який зупиняється має певне прискорення, що вільно падаюче тіло падає з прискоренням, то маємо на увазі тангенціальне прискорення, тобто те прискорення, яке характеризує зміну швидкості за величиною. Тангенціальне (дотичне) прискорення завжди направлено вздовж лінії швидкості, тобто по дотичній до траєкторії руху тіла (власне тому це прискорення і називають тангенціальним, що в перекладі з латинської означає «дотичним»). При цьому, якщо величина швидкості зростає(v↑), то вектори швидкості та тангенціального прискорення співнаправлені, а якщо швидкість зменшується (v↓) – то ці напрямки взаємно протинаправлені. На мал.10 зображено декілька ситуацій, які наглядно демонструють вище сказане.

 

 

Мал.10. Якщо швидкість зростає (v↑), то напрям вектора a_л співпадає з напрямком швидкості. А якщо швидкість зменшується (v↓), то ці напрямки взаємно протилежні.

Таким чином, якщо модуль швидкості змінюється (збільшується, або зменшується), то це тіло рухається з певним тангенціальним прискоренням. Величина цього прискорення визначається за формулою а_τ=∆v/∆t,а його напрям, або співпадає з напрямком швидкості (якщо v↑), або протилежний йому (якщо v↓). Якщо ж модуль швидкості залишається незмінним( v₁ = v₂ = … = const), то тангенціальне прискорення дорівнює нулю. Дійсно: якщо v₁=v₂, то а_τ=∆v/∆t=(v₂-v₁)/∆t=0/∆t=0.

Однак бувають ситуації, в яких величина швидкості залишається незмінною (v₁ = v₂ = … = const), а тіло рухається з певним прискоренням. Наприклад, якщо автомобіль з незмінною за модулем швидкістю рухається по колу (мал.11) то він неминуче рухається з певним прискоренням. Це прискорення називають доцентровим (позначається а_д). Його поява обумовлена не тим, що швидкість змінюється не за величиною (адже v=const), а тим, що вона змінюється за напрямком.

  

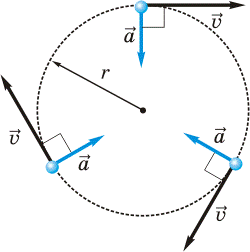
v₁ = v₂ = const

v₁ ≠ v₂ ≠ const

Мал.11. Тіло, що рухається криволінійною траєкторією, неминуче рухається з доцентровим прискоренням.

Виходячи з визначального рівняння прискорення (а=∆v/∆t), можна довести, що величина доцентрового прискорення визначається за формулою а_д =v²/R, де v – швидкість тіла в даній точці траєкторії; R – радіус кривизни в цій точці траєкторії.

Коли ми говоримо про радіус кривизни в даній точці траєкторії, то маємо на увазі, що невеликі фрагменти будь-якої кривої лінії можна вважати частинами кола певного радіусу. При цьому для довільної кривої, цей радіус від точки до точки може змінюватись. І лише найпростіша крива, – коло, в усіх точках має один і той же радіус кривизни.

Доцентрове прискорення – це таке прискорення, яке характеризує зміну швидкості за напрямком.

Позначається: а_д

Визначальне рівняння: а_д=v²/R

Одиниця вимірювання: [а_д]= м/с²,  метр за секунду в квадраті.

Доцентрове прискорення завжди направлено до центру кривизни в даній точці траєкторії, тобто по перпендикуляру (нормалі) до напрямку швидкості в цій точці. Зважаючи на ці обставини доцентрове прискорення іноді називають нормальним тобто перпендикулярним.

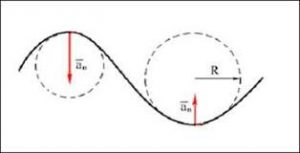
Таким чином, якщо тіло рухається криволінійною траєкторією, то в незалежності від того змінюється модуль його швидкості, чи не змінюється, це тіло має певне доцентрове прискорення, величина якого визначається за формулою  а_д=v²/R, і яке завжди направлено до центру кривизни в даній точці траєкторії.

Не важко збагнути, що на прямолінійних ділянках траєкторії, доцентрове прискорення неминуче дорівнює нулю. І це природньо. Адже на таких ділянках, напрям швидкості залишається незмінним і тому прискорення, яке характеризує зміну швидкості за напрямком має бути нулевим. Те, що на прямолінійних ділянках траєкторії доцентрове прискорення дорівнює нулю, випливає не лише з визначення цього прискорення, а й з його визначального рівняння. Дійсно. Будь-яку прямолінійну ділянку траєкторії, можна вважати частиною кола з безкінечно великим радіусом (R = ∞) А це означає, що для таких ділянок a_д=v²/R=v²/∞= 0.

Словник фізичних термінів.

Час – це фізична величина, яка характеризує тривалість подій (явищ, процесів, рухів, тощо) і яка дорівнює цій тривалості.

Позначається: t

Визначальне рівняння: нема

Одиниця вимірювання: [t] = с,  секунда

Довжина – це фізична величина, яка характеризує відстань між двома точками виміряну вздовж певної лінії і яка дорівнює цій відстані.

Позначається: ℓ

Визначальне рівняння: нема

Одиниця вимірювання: [ℓ] = м,  метр

Координата – це фізична величина, яка характеризує положення (місцезнаходження) матеріальної точки в заданій системі координат і яка дорівнює відстані від точки відліку цієї системи до проекції даної точки на відповідну вісь координат.

Позначається: х

Визначальне рівняння: х =ℓ_х

Одиниця вимірювання: [х] = м,  метр

Пройдений шлях – це фізична величина, яка характеризує пройдений матеріальною точкою (тілом) шлях і яка дорівнює довжині тієї траєкторії яку описує ця точка в процесі відповідного руху.

Позначається: s

Визначальне рівняння: s = ℓ_тр   або   s =∆х

Одиниця вимірювання: [s]  = м

Швидкість – це фізична величина, яка характеризує швидкість поступального руху тіла (матеріальної точки) в заданій системі відліку і яка показує на скільки переміщується тіло в цій системі, за одиницю часу.

Позначається: v

Визначальне рівняння: v =∆x/∆t,  де  ∆t → 0

Одиниця вимірювання:[v] = м/с,  метр за секунду

Середня швидкість (середня шляхова швидкість) – це та усереднена швидкість з якою тіло долає певну ділянку шляху і яка дорівнює відношенню пройденого тілом шляху s, до того проміжку часу t, за який цей шлях пройдено.

Позначається: v_с

Визначальне рівняння: v_с= s/t

Одиниця вимірювання: [v_с] = м/с,  метр за секунду

Прискорення – це  фізична величина, яка характеризує  зміну швидкості

руху тіла, і яка показує на скільки змінюється ця швидкість за одиницю часу.

Позначається: а

Визначальне рівняння: а =∆v/∆t

Одиниця вимірювання: [a] = м/с²,  метр за секунду в квадраті.

Тангенціальне (дотичне) прискорення (прискорення) – це таке прискорення, яке характеризує зміну швидкості за величиною.

Позначається: а_τ     або    а

Визначальне рівняння: а_τ=∆v/∆t

Одиниця вимірювання: [а_τ]=м/с²

Доцентрове прискорення – це таке прискорення, яке характеризує зміну     швидкості за напрямком.

Позначається: а_д

Визначальне рівняння: а_д=v²/R

Одиниця вимірювання: [а_д]=м/с²

Контрольні запитання.

1.Чому довжина та час не мають визначальних рівнянь?

2.Які різновидності довжини ви знаєте?

3.За яким рівнянням визначають швидкість: а) при прямолінійно-рівномірному русі; б) при прямолінійно-рівнозмінному русі.

4.Якщо тіло рухається прямолінійно і рівномірно, то чи відрізняються числові значення його миттєвої і середньої швидкостей?

5.Чи може тіло, яке рухається прямолінійно, рухатись з доцентровим прискореннями? з тангенціальним прискоренням?

6.Чи може тіло, яке рухається по колу, рухатись без доцентрового прискорення? без тангенціального прискорення?

Вправа 2.

1.Яка швидкість більша 6м/с чи 18км/год?

2.Під час рівномірного прямолінійного руху, координата тіла за 5с змінилась від значення 10м до значення -10м. Яка швидкість і напрям руху тіла?

3.Велосипедист їде прямолінійною дорогою зі швидкістю 20км/год. Через пів години, він повертає назад і рухається з тією ж швидкістю ще 45 хв. Визначити пройдений велосипедистом шлях та модуль його переміщення за повний час руху. Визначити координату велосипедиста через 30 хв від початку руху і в кінці руху.

4.За 20с перший автомобіль проїхав такий же шлях як і другий за 15с. Визначте швидкість першого автомобіля, якщо швидкість другого 72км/год.

5.Через 20 с після початку руху спідометр автомобіля показував 72 км/год. З яким середнім прискоренням рухався автомобіль

 

 

Лекційне заняття № 4.

Тема. Рівняння руху – основний закон кінематики.

         Нагадаємо, до числа основних фізичних величин кінематики поступального руху відносяться: час (t), координата (х=ℓ_х), пройдений шлях (s=∆x), швидкість (v=∆x/∆t) та прискорення (а=∆v/∆t). Якщо ж говорити про основний закон кінематики поступального руху, то він називається рівнянням руху. Рівняння руху – це закон, в якому стверджується: в загальному випадку, прямолінійний рух матеріальної точки можна описати рівнянням:

х = х₀ + v₀t + (а/2)t²

де     х – координата матеріальної точки в момент часу t,

х₀  – початкова координата точки, тобто її координата в момент часу t = 0

v₀ – початкова швидкість матеріальної точки

а – прискорення матеріальної точки.

Відразу ж зауважимо, що в загальному випадку поступальний рух матеріальної точки може мати неймовірно складну траєкторію. Але якою б складною не була ця траєкторія, її завжди можна розкласти на прямолінійні відрізки. А це означає, що вивчивши параметри та закономірності прямолінійного руху матеріальної точки, можна пояснити будь-який її рух. Скажімо рівняння х=х₀+v₀t+(а/2)t² фактично є рівнянням прямолінійного руху матеріальної точки і воно не може описати її довільний криволінійний рух. Однак, з’ясувавши фізичну суть цього рівняння та навчившись застосовувати його на практиці, ви не матимете проблем з тим щоб описати будь-який плоско- чи об’ємно- криволінійний рух. Адже такий рух описує система двох або трьох  аналогічних рівнянь.

Не буде перебільшенням сказати, що знаючи рівняння руху х=х₀+v₀t+(a/2)t² та визначальні рівняння базових фізичних величин кінематики, можна розв’язати практично будь-яку задачу кінематики. У всякому разі ті задачі, складність яких не виходить за межі програми загальноосвітньої школи.

Втім, в фізиці не достатньо знати формули. В фізиці набагато важливіше бачити за цими формулами реальні події та їх параметри. Наприклад, в математиці рівняння х = 200 –10t + 0,2t² це просто квадратне рівняння, яке в загальному випадку має два рішення і яке графічно можна представити у вигляді відповідної параболи. В фізиці, все те що вивчалося в математиці ви маєте знати та вміти застосовувати на практиці. Однак цього зовсім не достатньо для того щоб розв’язувати фізичні задачі. Адже в фізиці за кожним рівнянням, за кожною цифрою за кожною буквою та за кожним знаком, ви маєте бачити реальні події та їх характеристики. Скажімо, просто поглянувши на рівняння х= 200 –10t + 0,2t², та розуміючи що це рівняння руху, тобто рівняння вигляду х = х₀ +v₀t +(а/2)t², ви відразу ж уявляєте наступну ситуацію. В момент часу t=0, дане тіло знаходиться в точці з координатою 200м і рухається в від’ємному напрямку з швидкістю 10м/с. При цьому величина цієї швидкості зменшується, а числове значення прискорення становить 0,4м/с². (Сподіваюсь, ви розумієте, що з факту а/2=0,2 випливає а=0,4). Іншими словами, із аналізу заданого рівняння руху ясно: х_о= 200м;   v_o= -10м/с;   а = 0,4м/с²  ;   v↓

Потрібно зауважити, якщо в поясненнях до рівняння руху не вказані одиниці вимірювання відповідних величин, то потрібно вважати що цими одиницями є основні одиниці міжнародної  системи (СІ):  [x]=м;  [v]=м/с;  [a]=м/с².

Таким чином, вже першого погляду на рівняння руху, має бути достатньо для того, щоб дати загальну характеристику цього руху. Наприклад:

x₁ = -200 +15t – 0,4t²:    х_о = -200м;  v_o = 15м/с;  а = -0,8м/с² ;  v↓

x₂ = 100 – 8t – 0,1t²:       х_о = 100м;   v_o = -8м/с;   а =  -0,2м/с² ; v↑

x₃ = -5t:                            х_о = 0м;       v_o = -5м/с;   а =   0м/с² ;  v = const

x₄ = 200 – t²:                   х_о = 200м;   v_o = -0м/с;   а =  -2м/с² ;   v↑

x₅ = -100:                        х_о = -100м;  v_o =  0м/с;   а = 0м/с²;  не рухається

Зверніть увагу, ми просто дивимося на рівняння руху і отримуємо з нього достатньо велику кількість інформації. Тепер же уявіть скільки інформації можна отримати на основі математичного та логічного аналізу цього рівняння. Ілюструючи лише частину цих інформаційних можливостей, розглянемо конкретну задачу.

         Задача 1. За заданим рівнянням руху х = 100 + 10t – 0,4t²:

1) дати загальну характеристику руху тіла;

2) визначити координату тіла через десять секунд;

3) визначити пройдений тілом шлях за десять секунд;

4) визначити пройдений тілом шлях за десяту секунду;

5) записати рівняння швидкості руху тіла;

6) визначити де і коли тіло зупиниться.

7) визначити в який момент часу, тіло буде в точці з координатою 50м?

Відповідаючи на кожне з поставлених запитань можна сказати наступне.

1.Дати загальну характеристику руху тіла: х_о =? v_o = ? а = ? малюнок

Відповідь:  Із аналізу рівняння х=100+10t –0,4t² ясно:

х_о =100м; v_o = 10м/с; а = – 0,8м/с²;  v↓. Малюнок.

2.Визначити координату тіла через 10с: х(10)=?

Відповідь: Із аналізу рівняння руху ясно:

якщо  t = 10c, то  х(10) = 100 + 10(10)- 0,4(10)² = 160м

3.Визначити пройдений тілом шлях за десять секунд: s(10)=?

Відповідь:  Оскільки за визначенням s=∆х= х_к – х_п, то в умовах нашої задачі

s(10)= х(10) – х_о = 160 – 100 = 60м

4.Визначити пройдений тілом шлях за десяту секунду: s(10_ту)=?

Зауваження. Сподіваюсь ви розумієте, що в даному випадку потрібно визначити той шлях, який пройде тіло за одну, а саме за десяту секунду. При цьому не важко збагнути, що десятою секундою є та, що між дев’ятою і десятою.

Відповідь:  Оскільки х_к=х(10)=160м,   х_п=х(9)=100+10(9)–0,4(9)² =157,6м,

то: s(10_ту) = х(10)–х(9) = 160 -157,6=2,4м

5.Записати рівняння швидкості руху даного тіла.

Відповідь:  Оскільки при рівноприскореному русі v=v₀+at, то в умовах нашої задачі (v_o=10м/с, а= – 0,8м/с²) рівняння швидкості набуває вигляду v=10-0,8t

6.Визначити, де і коли тіло зупиниться: х_зуп =? t_зуп=?

Відповідь:  Оскільки в момент зупинки швидкість тіла дорівнює нулю (v=0), то можна записати: якщо t=t_зуп, то  v=10 – 0,8t_зуп = 0, звідси   t_зуп=10/0,8=12,5c

А це означає, що х_зуп =х(12,5)=100+10(12,5) – 0,4(12,5)²=162,5м

7.Визначити в який момент часу тіло буде в точці з координатою 50м?: х=50м; t=?

Відповідь:  Для х=50м, задане рівняння руху набуває вигляду: 100 + 10t – 0,4t²=50, або

50 + 10t – 0,4t²=0.

А зважаючи на те, що розв’язки (корені) рівняння аt²+вt+с=0 визначаються

за формулою t_1,2=[- b ± (b² – 4ac)^1/2]/2a, можна записати

t_1,2=[- b ± (b² – 4ac)^1/2]/2a=[-10 ± (10² – 4∙(-0,4)∙50)^1/2 ]/2(-0,4) =

= -10 ± (100+80)^1/2/(-0,8) = (-10 ± 13,4)/(-0,8).

Звідси   t₁= – 4,25с;    t₂= 29,25с.

Отриманий результат означає наступне: в точці з координатою х=50м дане тіло побуває двічі:  1) t₁= –4,25с, тобто за 4,24 секунди до початку відліку часу. Знак “-“ вказує на те що подія відбулась в минулому;  2) t₂=29,25с, тобто через 29,25 секунди після початку відліку часу.

Потрібно зауважити, що рівняння руху дає формально-математичні відповіді на всі запитання які стосуються цього рівняння. При цьому ви маєте розуміти, що в реальності, у відповідності з певним рівнянням, тіло рухається певний обмежений проміжок часу. Скажімо в процесі руху, автомобіль на певних ділянках набирає швидкість, на певних пригальмовує, на певних їде з постійною швидкістю, а на певних робить ті чи інші маневри. При цьому кожна ділянка описується своїм рівнянням руху і має свої часові обмеження. А це означає, що в реальності, тіло яке на даний момент рухається за законом х=100+10t –0,4t², в точці з координатою 50м можливо ніколи не було і не буде. Однак якщо в часовому інтервалі від 5с до початку відліку часу, до 30с після цього початку, тіло дійсно рухалось у відповідності з рівнянням х=100+10t –0,4t², то в точці з координатою 50м, воно дійсно побувало двічі: за 4,25с до початку відліку часу, та за 29,25с після цього початку.

Та якби там не було, а не важко бачити, що на основі аналізу рівняння руху, можна розв’язувати величезну кількість кінематичних задач. І відтепер ви розумієте, чому це рівняння називають основним законом кінематики.

На завершення додамо, що в умовах переважної більшості задач, кінематична ситуація задається не певними рівняннями руху, а описується відповідними словами. Тому ви повинні не лише вміти за заданими рівняннями руху уявляти відповідну ситуацію, а й навпаки – за заданою ситуацією записувати відповідні рівняння руху. А це вміння формується в процесі розв’язування конкретних задач.

         Задача 2. Із пункту А в пункт В відстань між якими 1км, виїхав автомобіль зі швидкістю 25м/с. Одночасно на зустріч йому із пункту В виїхав другий автомобіль зі швидкістю 15м/с. Де і коли ці автомобілі зустрінуться?

         Зауваження. Якщо в умові задачі фізичний зміст того чи іншого параметру чітко не визначений то завжди обирають таке значення цього параметру яке є найпростішим та дозволяє розв’язати дану задачу. Наприклад, в умові даної задачі чітко не сказано якою (прямолінійною чи криволінійною) є та дорога що з’єднує пункти А і В. В подібних ситуаціях завжди обирають найбільш простий варіант. А цим варіантом є прямолінійна дорога. Крім цього, в умові даної задачі не визначена початкова координата жодного з автомобілів. Тому будемо вважати, що в початковий момент часу один з автомобілів знаходиться в нульовій точці нашої системи координат.

Дано :             СІ                       Аналіз.

v₁ = 25м/с          –              ♦—→ v₁                                                        v₂  ←—♦

v₂ = 15м/с          –           —•——————————-•———————————•—→x(м)

ℓ = 1км          1∙10³м        0                                   500                                   1000

 

t = ?

х = ?           Представивши рух автомобілів у відповідній системі координат запишемо рівняння руху кожного з них: х₁=25t;  х₂=1000 – 15t;

Оскільки в момент зустрічі автомобілів      х₁= х₂,  то

25t=1000 – 15t,   звідси  25t + 15t=1000,  звідси    t=25с

Для    t=25с;   х₁(25)=25(25)=625м;     х₂(25) = 1000-15(25)=625м

Відповідь: автомобілі зустрінуться через 25 секунд в точці з координатою 625м, тобто на відстані 625м від пункту А.

Звичайно, дану задачу можна розв’язати й по-іншому, наприклад так. Оскільки автомобілі їдуть назустріч один одному з швидкостями v₁ і v₂ то швидкість їх взаємного наближення становить v=v₁+v₂. Оскільки до моменту зустрічі автомобілі мають проїхати шлях s = 1000 м, та зважаючи на те, що при рівномірному русі s=vt, можна записати: t=s/v=s/(v₁+v₂)=25с. Таким чином автомобілі зустрінуться через 25 секунд. При цьому за ці 25с перший автомобіль проїде відстань s₁=v₁∙t =625м. А це означає, що автомобілі зустрінуться через 25с в точці віддаленій від пункту А на 625м.

Вище наведене рішення має право на існування. І напевно в 7-му класі дану задачу ви б розв’язали саме так. Однак подібний розв’язок має ряд суттєвих недоліків. По-перше, його практично не можливо зробити органічною частиною більш-менш універсальної системи розв’язку задач. По-друге. Такий спосіб дозволяє розв’язувати лише очевидно прості задачі. Тому, якщо ви хочете кваліфіковано та системно розв’язувати задачі кінематики то повинні максимально широко застосовувати рівняння руху.

Словник фізичних термінів.

         Рівняння руху –  це закон в якому стверджується: в загальному випадку,

прямолінійний рух матеріальної точки можна описати рівнянням

х = х₀ +v₀t +(а/2)t²

де    х – координата матеріальної точки в момент часу t,

х₀ – початкова координата точки, тобто її координата в момент часу t= 0

v₀ – початкова швидкість матеріальної точки

а – прискорення матеріальної точки.

Контрольні запитання.

1.Чи можна стверджувати, що рівняння х=х₀+v₀t+(a/2)t² описує не лише рівноприскорений (а=const), а й рівномірний рух (v=const) ?

2.Якого вигляду набуває рівняння руху для рівномірного руху?

3.Чи може рівняння руху описати ті події які відбувались в минулому?

4.Виходячи з того що s=∆х= х – х₀, запишіть рівняння пройденого шляху.

5.Якого вигляду набуває рівняння пройденого шляху за умови v₀=0м/с?

Вправа 3.

1.За рівнянням руху дати загальну характеристику відповідного руху:

х₁  = 100 + 10t + 0,5t²

х₂  = – 100 + 5t – 0,2t²

х₃  = – 10t – 0,3t²

х₄  = 150 –  0,25t²

х₅  = t²

2.За заданими рівняннями руху 1)х =100 – 15t + 0,5t²; 2) х= -50 – 10t +0,3t²:

1) дати загальну характеристику руху тіла;

2) визначити пройдений тілом шлях за 10 секунд;

3) записати рівняння швидкості руху тіла;

4) визначити де і коли тіло зупиниться;

3.В заданій системі відліку рівняння руху тіл мають вигляд х₁=15t, х₂= 200 +10t. Де і коли зустрінуться ці тіла?

4.Велосипедист що рухається зі швидкістю 3м/с почав спускатися з гори з прискоренням 0,8м/с². Визначити довжину гори, якщо спуск тривав 6с.

5.Який шлях проїде тіло за 5с, якщо його прискорення 2м/с²?

 

Лекційне заняття №5.

Тема. Вільне падіння тіл. Рух тіла кинутого вертикально, горизонтально та під кутом до горизонту.

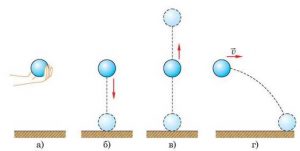
         Вільним падінням називають такий рух тіла, який відбувається під дією сили тяжіння та за відсутності суттєвого впливу інших зовнішніх сил, зокрема сили опору повітря. В загальному випадку вільно падаючими вважають не лише ті тіла падіння яких починається з нулевої швидкості (мал.12а), а й ті які з певною швидкістю кинули вертикально вниз, вертикально вгору, або під кутом до горизонту (мал.12б,в,г,д). Адже в кожному з цих випадків, тіло після отримання певного початкового поштовху, рухається під дією лише однієї зовнішньої сили – сили тяжіння (звичайно за умови, що сила опору повітря є не суттєвою).

 

Мал.12. Рух тіла що відбувається під дією сили тяжіння та за відносності  дії інших зовнішніх сил (зокрема суттєвого впливу опору повітря), називають вільним падінням тіла.

Характерною особливістю того руху який називається вільним падінням, є те що це падіння відбувається з певним постійним прискоренням, величина якого не залежить від маси тіла, а отже і від діючої на нього сили тяжіння.  На перший погляд, така поведінка важкого і легкого тіл здається дивною. Адже та сила з якою важкий камінь притягується до Землі в сотні разів перевищує ту, з якою до Землі притягується легкий камінчик. І тим не менше, легкий камінчик і важкий камінь падають однаково швидко. Сьогодні ми не будемо говорити про те, чому важкі і легкі тіла падають однаково швидко. Сьогодні ми просто констатуємо той факт, що під дією сили тяжіння, та за відсутності суттєвого впливу опору повітря, всі тіла падають з однаковим прискоренням яке називається прискоренням сили тяжіння або прискоренням вільного падіння. Підкреслюючи важливість та значимість прискорення вільного падіння, його позначають окремою літерою g (від лат. gravitas – тяжіння). Напрям прискорення вільного падіння співпадає з напрямком діючої на тіло сили тяжіння, тобто є направленим вертикально вниз. Для Землі, усереднена величина прискорення вільного падіння становить g = 9,8067 м/с².

По суті, прискорення вільного падіння є силовою характеристикою того, що прийнято називати гравітаційним полем планети. При цьому кожна планета має своє гравітаційне поле (поле тяжіння), яке характеризується своїм прискоренням вільного падіння. Наприклад, для Землі g = 9,8 м/с², для Місяця g = 1,6 м/с², для Марса g = 3,8 м/с², для Венери g = 8,8 м/с², для Юпітера g = 23,5 м/с², а для Сонця g = 274,0 м/с².

Коли ми стверджуємо, що на Землі прискорення вільного падіння становить g = 9,8067 м/с² то маємо на увазі певне усереднене значення цієї величини. Насправді ж, в різних місцях земної поверхні, прискорення вільного падіння може бути суттєво різним. Наприклад, на екваторі g = 9,78 м/с², а на полюсі g = 9,83 м/с². Ця різниця обумовлена фактом обертання Землі навколо своєї осі. А також фактом певної деформованості земної кулі.

Крім цього, числове значення прискорення вільного падіння певним чином залежить від тієї висоти на якій це прискорення вимірюється. Наприклад на Землі, для:

h = 0 км               g = 9,8067 м/с²

h = 1 км               g = 9,8036 м/с²

h = 10 км             g = 9,7736 м/с²

h = 50 км             g = 9,6542 м/с²

h = 500 км           g = 8,505 м/с²

h = 5000 км         g = 3,08 м/с²

При розв’язуванні задач, числове значення прискорення вільного падіння зазвичай приймають рівним g=9,8м/с². При наближених розрахунках допускається g=10м/с².

Потрібно зауважити, що величина та напрям прискорення вільного падіння не залежать від того в якому напрямку рухається тіло і з якою початковою швидкістю воно рухається. Наприклад, в незалежності від того вільно відпустили піднятий над землею камінь (мал13а), чи з певною швидкістю кинули вертикально вниз (мал.13б), вгору (мал.13в) чи під кутом до горизонту (мал.13г), цей камінь буде падати з прискоренням g=9,8м/с². В незалежності від того рухається камінь вгору чи падає вниз, він рухається з прискоренням g=9,8м/с² і це прискорення завжди направлено вертикально вниз. Навіть в точці максимального підйому тіла, де його швидкість дорівнює нулю, тіло має прискорення g=9,8м/с². Іншими словами, на всій траєкторії вільного польоту тіла, це тіло рухається з прискоренням вільного падіння.

 

Мал.13. У всіх точках траєкторії вільного польоту, тіло рухається з прискоренням вільного падіння (g=9,8м/с²)

Щоправда, коли ми говоримо про вільне падіння тіла та про прискорення вільного падіння (g=9,8м/с²), то маємо на увазі ситуацію, коли опір повітря є несуттєвим. Насправді ж цей опір існує і певним чином впливає на величину того реального прискорення з яким падають тіла. Тому коли ми стверджуємо, що вільно падаюче тіло рухається з постійним прискоренням, величина якого 9,8м/с², то не враховуємо той факт, що цей рух відбувається в повітряному середовищі яке певним чином гальмує рух тіла. Втім, питання про вплив опору повітря на величину прискорення вільного падіння тіла, виходить за межі програми загально освітньої школи. Тому в подальшому будемо вважати, що на всьому шляху вільного польоту, тіло рухається з прискоренням яке називається прискоренням вільного падіння і величина якого 9,8м/с².

Як і будь-який рівноприскорений рух, вільне падіння тіла можна описати рівнянням виду х=х_о+v₀t+(a/2)t². Відмінність лише в тому, що говорячи про вільне падіння матеріальної точки, її вертикальну координату (висоту) позначають літерою h, а прискорення – літерою g. Іншими словами, рух вільно падаючого тіла можна описати формулою h=h_о+v₀t+(g/2)t².

Ілюструючи закономірності того руху який називається вільним падінням тіла, а заодно ілюструючи практичну значимість того закону який називається рівнянням руху, розв’яжемо ряд конкретних задач.

Задача 1. Визначити глибину колодязя, якщо відомо, що випущений із руки камінь досягає води за 2с. Яку швидкість має камінь в момент падіння на воду?

1) Задача 1;                                                   2) Задача 2.

Дано :                                    Аналіз.

v₀ = 0 м/с

 t = 2 с                                 Малюнок

h = ?

v = ?

Задаємо систему координат і записуємо рівняння руху (h=h_о+v₀t+(g/2)t²) та рівняння швидкості (v=v₀+gt) даного тіла.

Оскільки: h₀ = 0(м), v₀ = 0м/с, то  h=(g/2)t²; v=gt.

Враховуючи, що t=2c, виконуємо відповідні розрахунки.

Розрахунки.    h=…=20 м;

v=…=20 м/с.

Відповідь: h=20 м;  v=20 м/с.

         Задача 2. На яку максимальну висоту підніметься тіло. Якщо його кинули вертикально вгору з швидкістю 20м/с ?

 

Дано :                                 Аналіз.

v₀ = 20 м/с

Малюнок

h_max = ?

 

Задаємо систему координат та записуємо рівняння руху тіла в ній (h_о=0м): h=v₀t – (g/2)t². Із аналізу рівняння руху ясно, що для визначення максимальної висоти підйому тіла (h=h_max) необхідно визначити час цього підйому t=t₁.

Оскільки на максимальній висоті, тобто в момент часу t=t₁, швидкість тіла дорівнює нулю, та зважаючи на те, що величина цієї швидкості визначається за формулою  v=v_o–gt,   можна записати: v_o–gt₁=0. Звідси,  t₁=v₀/g=20(м/с)/10(м/с²)=2с

Таким чином: h_max = v₀t₁ – (g/2)t₁² = … =20м

Відповідь:  h_max =20 м .

Задача 3. Тіло, що знаходиться на висоті 5м кинули горизонтально з швидкістю 20 м/с. Визначити горизонтальну дальність польоту тіла.

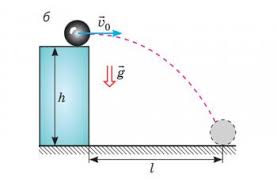
Дано:                                    Аналіз.

h₀ = 5 м

v₀= 20 м/с                            Малюнок

ℓ = ?

Загальні зауваження. Рух тіла кинутого горизонтально, або під кутом до горизонту є криволінійним, причому таким, який завжди можна розкласти на дві складові: рівномірний (v=const) горизонтальний та рівноприскорений (a=const) вертикальний. А це означає, що описуючи такий криволінійний рух, можна записати два незалежних рівняння, аналіз яких дозволяє відповісти на практично будь які запитання кінематики.

Зважаючи на вище сказане, задаємо систему координат і записуємо рівняння двох складових даного криволінійного руху.

– горизонтальний рух: (ℓ₀=0м; a=0м/с²);          ℓ=v₀t

– вертикальний рух: (v₀=0м/с; a=g=10м/с²);    h=h₀ – gt²/2.

Із аналізу рівнянь ясно, що для того щоб визначити дальність польоту тіла (ℓ=v₀t), необхідно визначити тривалість цього польоту (t=t_x). А оскільки в момент падіння тіла, h=0, то: h₀ – gt_x²/2 = 0, звідси t_х=(2h₀/g)^1/2.

Тому: ℓ = v₀(2h₀/g)^1/2 = …= 20м.

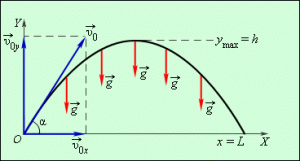
Тепер, коли ви ознайомились з закономірностями руху тіла кинутого горизонтально, можна розглянути і більш загальний рух, – рух тіла кинутого під кутом до горизонту.

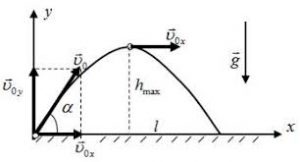
Мал.14. Кінематика руху тіла кинутого під кутом до горизонту.

На перший погляд, такий рух здається значно складнішим за рух тіла кинутого горизонтально. Насправді ж відмінності між цими рухами не такі вже й суттєві. Дійсно. Якщо вектор початкової швидкості (v₀) розкласти на дві складові:

– горизонтальну  v_x= v₀cosα

– вертикальну      v_y= v₀sinα,

то даний криволінійний рух можна представити як результуючу двох лінійних рухів: рівномірного горизонтального та рівноприскореного вертикального. При цьому, кожен з цих рухів можна описати відповідним рівнянням. Наприклад, представлений на мал.19 рух, можна описати системою двох рівнянь:

ℓ = (v₀cosα)t;

h = (v₀sinα)t – gt²/2.

Доречно зауважити, що в процесі руху тіла кинутого під кутом до горизонту, горизонтальна складова його швидкості (v_x=v₀cosα) залишається незмінною (звичайно за умови не суттєвості опору повітря), а вертикальна складова цієї швидкості, змінюється за законом v_y = v₀ sinα – gt (спочатку зменшується до нуля, а потім збільшується, мал.19б).

Задача 4. Снаряд вилетів з дула гармати під кутом 30° до горизонту, з швидкістю 800м/с. Визначити дальність польоту снаряду та максимальну висоту його підйому.

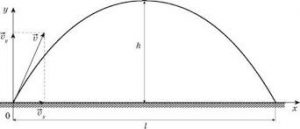
Дано:                                              Аналіз.

v₀ = 800м/с

α = 30°                                            Малюнок

ℓ = ?

h_м = ?

В вибраній системі координат, вектор початкової швидкості розкладаємо на дві складові (v_x=v₀cosα, v_y=v₀sinα) та записуємо рівняння горизонтального і вертикального руху снаряду:

ℓ = (v₀cosα)t;

h = (v₀sinα)t – gt²/2.

Виходячи з того, що в момент падіння h=0м, визначаємо час польоту снаряду (t=t_пол): (v₀sinα)t – gt²/2=0, або t(v₀sinα – gt/2)=0, звідси:

1) t=0

2) v₀sinα – gt/2=0;  gt/2=v₀sinα;  t= v₀sinα/g=2∙800∙0,5/10=80с

Отримані результати говорять про те, що на нулевій висоті (h=0) снаряд побував двічі: 1) в момент вильоту з дула гармати (t=0c); 2) в момент падіння на землю (t=80с).

Оскільки, тривалість польоту снаряду визначається як проміжок часу між моментом його вильоту та моментом падіння, то ясно, що t_пол =80с.

Знаючи час польоту снаряду, не важко визначити дальність його польоту:

ℓ = (v₀cosα)t_пол = (800∙0,87)80=55000м=55км

Для того щоб визначити максимальну висоту підйому снаряду (h_м), потрібно знати час цього підйому(t_м). А оскільки рух снаряду є симетричним (тривалість підйому снаряду дорівнює тривалості його падіння), то можна стверджувати:  t_м= t_пол/2 = 40с. Звідси h_м = (v₀sinα)t_м – gt_м²/2= (800∙0,5)40 – 10∙40²/2 = 8000м = 8км

Відповідь: ℓ = 55км;  h_м = 8км.

Звичайно, якби тривалість польоту снаряду була невідомою, то значення того моменту часу який відповідає максимальній висоті підйому снаряду (t_м), ми б визначали з інших міркувань. А ці міркування є наступними. В точці максимального підйому снаряду, вертикальна складова його швидкості (v_в) дорівнює нулю. А оскільки ця складова змінюється за законом v_в=v₀sinα-gt, то для v_в=0, t=v₀sinα/g = 800∙0,5/10=40с.

Словник фізичних термінів.

Вільним падінням називають такий рух тіла, який відбувається під дією сили тяжіння та за відсутності суттєвого впливу інших зовнішніх сил, зокрема сили опору повітря.

Прискорення вільного падіння –  це те прискорення, яке  надає тілу сила тяжіння. Для Землі, усереднена величина прискорення вільного падіння становить g=9,8м/с².

Контрольні запитання.

1.Чи можна стверджувати, що кинуте в горизонтальному напрямку тіло, знаходиться в стані вільного падіння? Чому?

2.Чи залежить прискорення вільного падіння від маси падаючого тіла?

3.Чи залежить прискорення вільного падіння від маси Землі?

4.Одне тіло випустили з руки, а друге кинули вертикально вниз. Яке з цих тіл матиме більше прискорення вільного падіння?

5.Від чого залежить прискорення вільного падіння?

6.Як змінюється величина того реального прискорення з яким падає тіло в атмосферному повітрі?

                   Вправа 4.

1.Визначити глибину ущелини, якщо камінь, падаючи без початкової швидкості досягне її дна за 5с.

2.Тіло без початкової швидкості падає з висоти 30м. Визначити його швидкість в момент падіння.

3.Камінь кинули вертикально вниз з початковою швидкістю 7м/с. З якої висоти кинули камінь, якщо він падав 1,5с?

4.З балкону, в горизонтальному напрямку кинули камінь з швидкістю 15м/с. При цьому камінь упав на землю через 2с. З якої висоти кинули камінь і на якій відстані від підніжжя балкону він упав?

5.Визначити максимальну висоту підйому каменя кинутого з швидкістю 20м/с під кутом 45º до горизонту.

 

Лекційне заняття №6.

Тема. Алгебраїчний та графічний методи розв’язування задач.

В фізиці існує два базових методи розв’язування задач: алгебраїчний (аналітичний) та графічний (геометричний). До сих пір, задачі кінематики ми розв’язували алгебраїчним методом. Суть цього методу полягає в тому, що виходячи з умов конкретної задачі та відомих базових формул, шляхом логічних міркувань (аналізу) та відповідних математичних перетворень, отримують алгебраїчне рішення задачі, тобто те розрахункове рівняння яке і дозволяє визначити невідому величину.

Задача.1. За заданими рівняннями руху х₁=100 – 5t; х₂= -50 + 5t, визначити де і коли тіла зустрінуться.

Рішення. Оскільки в момент зустрічі х₁=х₂, то можна записати 100 – 5t = -50 + 5t. Звідси 10t =150, звідси t=15c=t_зустр. А це означає, що х_зустр= х(15)=100 – 5(15)=25м.

Відповідь: тіла зустрінуться через 15с, в точці з координатою 25м.

Алгебраїчний метод є основним методом розв’язування задач фізики. Однак, фізика влаштована таким чином, що в ній одну і ту ж задачу можна розв’язати по різному, скажімо не шляхом математичного аналізу, а шляхом відповідних геометричних побудов. При цьому, геометричне (графічне) рішення задачі часто є більш простим та ефективним за відповідне алгебраїчне рішення.

Суть графічного (геометричного) методу розв’язування задач полягає в тому, що на основі максимально точних геометричних побудов, з дотриманням вибраного масштабу та з застосуванням відповідних геометричних приладів (лінійка, транспортир, циркуль, тощо), отримують графічну відповідь на поставлене в задачі запитання. Головною перевагою графічного методу є його візуальна наочність. А основним недоліком – факт того, що точність графічного рішення залежить від точності геометричних побудов. Крім цього, графічне рішення задачі може бути ефективним лише в тому випадку, коли досліджувані величини описуються лінійними функціями, тобто можуть бути представленими у вигляді певних прямих.

Ілюструючи можливості, переваги та недоліки графічного методу розв’язування задач кінематики, розглянемо декілька конкретних прикладів.

Задача 2. За рівняннями руху х₁ =100 – 5t; х₂ = -50 +5t   побудувати відповідні графіки та виконати їх кінематичний аналіз.

Загальні зауваження. З курсу математики відомо, що рівняння виду

y = ax + b, це лінійне рівняння, графіком якого є пряма. Для побудови цієї прямої достатньо знати координати двох її довільних точок. Обираючи ці точки керуються наступними правилами: 1) вибрані точки мають бути зручними для математичних розрахунків та геометричних побудов; 2) вибрані точки мають бути максимально віддаленими одна від одної (це забезпечує максимальну точність геометричних побудов).

Дано:                            Рішення

х₁ = 100 – 5t                     На основі аналізу заданих рівнянь руху визначаємо

х₂ = -50 + 5t                      координати базових точок:

побудувати                  х₁ = 100 – 5t:  якщо t = 0с   то  х = 100м,   А₁(0;100)

графіки x=ƒ(t)                                     якщо t = 20с  то  х = 0м,     А₂(20;0)  .

х₂ = -50 + 5:   якщо t = 0с   то   х = -50м,  В₁(0;-50)

якщо t = 20с  то  х = 50м,   В₂(20;50) .

Задаємо систему координат і виконуємо необхідні геометричні побудови.

x(м)

100

80

60

40

20

0      •———-•————•————•————•————•—————→ t(c)

-20  0            5             10            15           20            25

-40

-60

Побудувавши графіки заданих рухів та аналізуючи ці графіки, можна відповісти на безліч кінематичних запитань. Наприклад, можна встановити координати рухомих тіл (матеріальних точок) в будь який момент часу. Скажімо, в момент часу t=6с: х₁=70м;  х₂= -20м. Для будь якого моменту часу, визначити відстань між рухомими об’єктами.  Наприклад: для   t=10с , ℓ=50м; для t= 6с, ℓ= 90м. Визначити час та місце зустрічі тіл: зустрінуться через 15с в точці з координатою 25м. Визначити швидкість тіла (v=∆x/∆t), його прискорення (a=∆v/∆t), напрям руху, тощо. Іншими словами, геометричний аналіз графіків руху, дозволяє відповісти на той же спектр запитань що і математичний аналіз відповідних рівнянь руху.

Зазвичай, графічний метод розв’язування задач є ефективним лише в тих випадках, коли досліджувана величина (координата, пройдений шлях, швидкість, тощо) змінюється лінійним чином. Адже якщо, наприклад, рух матеріальної точки описується рівнянням х = 100 – 10t + 0,2t², то графіком цього руху буде відповідна парабола, тобто певна крива. А як відомо, для побудови такої кривої потрібно визначити координати максимально великої кількості точок. В такій ситуації графічний метод розв’язування задач стає занадто громіздким, занадто не точним та занадто не ефективним.

Задача 3. За заданими графіками руху матеріальної точки, записати відповідні рівняння руху.

Оскільки задані графіки руху представляють собою певні прямі, то можна стверджувати, що відповідні рухи є такими що відбуваються з постійною швидкістю, тобто такими які описуються формулою x=x₀+vt . При цьому, із кількісного аналізу заданих графіків можна записати:

1) x₀=10м; v=∆x/∆t=(0-10)/(4-0)= -2,5м/c;  тому x₁=10 – 2,5t;

2) x₀=0м; v=∆x/∆t=(10-0)/(4-0)= 2,5м/c;  тому x₁=0 + 2,5t;

3) x₀=5м; v=∆x/∆t=(0-5)/(1-0)= -5м/c;  тому x₁=5 – 5t;

4) x₀=-10м; v=∆x/∆t=(0-(-10))/(2-0)= 5м/c;  тому x₁=-10 + 5t;

Не важко збагнути, що визначаючи швидкість руху матеріальної точки v=∆x/∆t, значення величин ∆x, ∆t  вибирають виходячи з міркувань практичної доцільності.

Задача 4. За заданими графіками швидкостей матеріальних точок, записати відповідні рівняння швидкостей та рівняння пройденого шляху.

На основі кількісного аналізу заданих графіків можна записати:

1).v₀=2м/c; a=∆v/∆t=(5-2)/(2-0)= 1,5м/c, тому  v=2+1,5t;  s=2t+0,75t²;

2).v₀= -3м/c; a=∆v/∆t=(0-(-3))/(3-0)= 1м/c, тому  v=-3+1t;  s=-3t+0,5t²;

3).v₀= 1м/c; a=∆v/∆t=(1-1)/(2-0)= 0м/c, тому  v=1м/с=const;  s=1t;

4).v₀= 5м/c; a=∆v/∆t=(0-5)/(2,5-0)= -2м/c, тому  v=5- t;  s=2t – t².

Крім всього іншого, аналіз графіку швидкості руху тіла дозволяє графічним способом визначати величину пройденого шляху як на певній ділянці руху так і на будь якій сукупності цих ділянок. А величина цього шляху дорівнює площі тієї фігури, яка з одного боку обмежена графіком швидкості та віссю 0-t, а з іншого – тими вертикальними лініями, які відповідають тому проміжку часу в межах якого визначається пройдений шлях (мал.15).

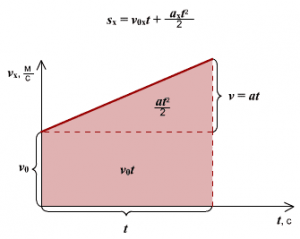
Мал.15. Пройдений тілом шлях дорівнює площі тієї фігури, яка обмежена відповідним графіком швидкості та межами відповідного часового інтервалу.

Задача 5. За заданим графіком швидкості, описати рух тіла на кожній ділянці шляху. Визначити пройдений тілом шлях на кожній ділянці. Побудувати відповідний графік прискорення.

Оскільки задані рівняння швидкостей представляють собою певні прямі, то можна стверджувати, що відповідні рухи є рівноприскореними (а=соnst), тобто такими, які описуються формулами:

v = v₀ + at – рівняння швидкості;

s = v₀t + at²/2 – рівняння пройденого шляху;

для криволінійного руху: s = |s₁| + |s₂| + …

Кількісно аналізуючи графік швидкості на кожній ділянці, можна сказати наступне:

1.Ділянка №1: ∆t=20c; v=20м/c=const; a=0; s=15Δt=20∙20=400м

2.Ділянка №2: ∆t=20c; v≠const; v↑; v₀=20м/c; a=∆v/∆t=(20м/с)/20с=1м/с²;

s = v₀Δt + aΔt²/2 = 20∙20 + 0,5∙20² = 600м.

3.Ділянка №3: ∆t=20c; v≠const; v↓; v₀=40м/c; a=∆v/∆t=(-40м/с)/20с= -2м/с²;

s = v₀Δt + aΔt²/2 = 40∙20 – 1∙20² = 400м.

4.Ділянка №4: ∆t=20c; v≠const; v↑; v₀=0м/c; a=∆v/∆t=(20м/с)/20с=1м/с²;

s = v₀Δt + aΔt²/2 = 0∙20 + 0,5∙20² = 200м.

Для кожної ділянки графіку швидкості будуємо відповідний графік прискорень.

1  a(м/с²)

 

0             20          40          60          80                t(c)

– 1

 

– 2

Задача 6. За заданим графіком швидкості, описати рух тіла та визначити пройдений ним шлях за 6с.

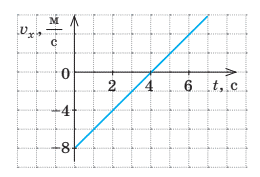
На перший погляд, рішення задачі є елементарно простим: ∆t=6c;

v₀= – 8м/c; a=∆v/∆t=(12м/с)/6с=2м/с²; s=v₀Δt + aΔt²/2 = -8∙6+1∙6²= – 12м. Втім, останній результат явно насторожує. І не тільки своїм знаком (знак « – » може вказувати на той напрямок в якому рухається тіло), а й величиною (s=12м). Адже як з графічних, так і з аналітичних міркувань ясно, що величина пройденого тілом шляху є значно більшою за 12м. До речі, якщо ви думаєте, що в умовах даної задачі величина пройденого шляху дорівнює площі трикутника А(0;-8), В(0;4), С(6;4), яка становить (12∙6)/2=36м, то помиляєтесь.

А справа втому, що в даному випадку рух тіла не є прямолінійним. Адже факт того, що на заданій ділянці, знак швидкості змінюється на протилежний, по суті означає, що на цій ділянці, до певного моменту (до моменту v=0) тіло рухається в одному напрямку, а після цього моменту – в протилежному напрямку. Прикладом такого руху є рівносповільнений рух тіла похилою площиною: до моменту зупинки, тіло рухається в одному напрямку (вгору), а після зупинки – в протилежному (вниз). При цьому, як до зупинки так і після неї, тіло рухається з одним і тим же прискоренням (одним і тим же як за величиною, так і за напрямком).

Оскільки на заданій ділянці, рух тіла фактично є криволінійним (складається з двох частин: s₁ – до зупинки, s₂ – після зупинки), то на цій ділянці загальна величина пройденого шляху має визначатись за формулою s = |s₁| + |s₂|. При цьому: s₁= -8Δt₁ + 1∙Δt₁² = -8∙4 + 1∙4² = 16;  s₂= 0∙Δt₂ + 1∙Δt₂²= 0 + 2²=4м. Таким чином, загальна величина пройденого тілом шляху становить 20м.

Вправа 5.

1.За заданими графіками руху матеріальної точки, дайте загальну характеристику її руху та запишіть відповідне рівняння руху.

    

2.За заданими графіками руху, записати відповідні рівняння руху. Визначити час і місце зустрічі тіл 1 і 2. Задачу розв’язати алгебраїчно та графічно.

3.За заданими графіками швидкості, записати відповідні рівняння швидкості та пройденого шляху. Визначити пройдені тілами шляхи на кожній ділянці руху.

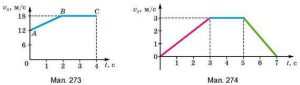
4.Рух тіл вздовж осі ох задано рівняннями х₁=5t, х₂=150 -10t. Визначити час та місце їх зустрічі. Задачу розв’язати алгебраїчно і графічно.

5.З пунктів А і В, відстань між якими 160м одночасно і в одному напрямку почали рухатись два тіла з швидкостями 10м/с і 6м/с відповідно. Де і коли зустрінуться ці тіла? Задачу розв’язати алгебраїчно та графічно.

 

Лекційне заняття №7.

Тема: Основні поняття, величини та закони кінематики

 обертального руху.

Нагадаємо. Обертальний рух – це такий механічний рух, при якому всі точки тіла описують кола, центри яких знаходяться на одній прямій, яка називається віссю обертання. Оскільки при обертальному русі, різні точки тіла мають суттєво різні кінематичні характеристики (рухаються з різними швидкостями та прискореннями, описують різні траєкторії, проходять різні шляхи, тощо), то ясно, що описуючи такий рух, представляти тіло у вигляді матеріальної точки не припустимо. Як правило, в кінематиці обертального руху, реальне тіло представляють не у вигляді матеріальної точки, а у вигляді так званого абсолютно твердого тіла. Абсолютно тверде тіло – це таке умовне (ідеалізоване) тіло, яке в процесі механічних рухів та взаємодій не деформується.

До числа основних фізичних величин кінематики обертального руху відносяться: час (t), кутова координата (φ), кут повороту (Δφ), кутова швидкість (ω), кутове прискорення (ε).

Визначаючи базові величини кінематики обертального руху і перш за все ту, яка називається кутовою координатою (φ), або просто кутом, можна сказати наступне. В кінематиці поступального руху, розташування (місцезнаходження) матеріальної точки визначають її координатою (х). При цьому, в процесі поступального руху матеріальної точки, відповідно змінюється і її координата. Якщо ж говорити про обертальний рух тіла, то в процесі цього руху, координата тіла (тіла як матеріальної точки) по суті залишається незмінною. При обертальному русі, змінюється не координатне положення тіла, а його кутова орієнтація (мал.14). Цю орієнтацію характеризують величиною, яка називається кутом, а точніше – кутовою координатою.

мал.14  В процесі обертального руху тіла змінюється його кутова орієнтація.

Кутова координата (кут) – це фізична величина, яка характеризує просторову (кутову) орієнтацію тіла в вибраній системі координат і яка дорівнює відношенню довжини тієї дуги що обмежує даний центральний кут, до радіусу цієї дуги.

Позначається:  φ

Визначальне рівняння:  φ=ℓ/R

Одиниця вимірювання:  [φ]=рад ,   радіан.

Із визначального рівняння φ=ℓ/R  ясно, що виміряти кут в радіанах, означає поділити довжину тієї дуги (ℓ) що обмежує даний кут, на радіус цієї дуги (R). При цьому, якщо довжина обмежуючої дуги дорівнює її радіусу (ℓ=R), то відповідний кут дорівнює одному радіану (від слова “радіус”).

Радіан – це одиниця вимірювання кутових величин, яка дорівнює такому центральному куту, довжина обмежуючої дуги якого дорівнює радіусу цієї дуги. По суті, радіан – величина безрозмірна [φ]=м/м=рад. Однак, щоб підкреслити, факт того, що ця безрозмірна величина характеризує саме кутову орієнтацію тіла, вона має спеціальну назву – радіан.

Вимірювання показують, що в повному колі міститься приблизно 6,28 радіан, а точніше 2π радіан, де  π=3,141592653…≈ 3,14 . Відображенням даного факту є та формула за якою визначають довжину кола: ℓ=2πR .

Напевно ви знаєте, що в математиці, геометрії та повсякденному житті, кутові величини зазвичай вимірюють не в радіанах, а в градусах. Градус – це одиниця вимірювання кутових величин, яка дорівнює такому центральному куту, що становить триста шістдесяту (1/360) частину повного кола. Іншими словами, якщо коло поділити на 360 рівних частин, то кутовий сектор в одну таку частину і є градусом.

Як ви думаєте, чому визначаючи одиницю кутових величин, люди з незапам’ятних часів, поділили коло на 360 частин? Не  на 10, не на 100, чи скажімо на 250, а саме на 360? Правильно! З незапам’ятних часів, люди звернули увагу на те, що приблизно через 360 днів, все в цьому світі повторюється. Виходячи з цієї повторюваності, коло життя, а за ним і геометричне коло, поділили на 360 частин.

З практичної точки зору, градус є надзвичайно зручною одиницею. Тому в сфері геометричних побудов та повсякденного життя, кутові величини зазвичай вимірюють в градусах. Але, ця одиниця має один суттєвий недолік –  вона жодним чином не пов’язана з параметрами того кола яке ми поділили на певну кількість кутових сегментів. А це означає, що градус не є органічною частиною цілісної системи взаємопов’язаних одиниць, а отже і цілісної системи знань про навколишній світ.

Для того щоб одиниця вимірювання кутових величин стала органічною частиною цілісної системи знань, коло потрібно поділити не так як нам подобається, чи здається зручним, а так щоб цей поділ відображав той реальний зв’язок який існує між кутовими та лінійними величинами. А цей зв’язок полягає в тому, що для будь якого кутового сегменту (φ) відношення його обмежуючої дуги (ℓ) до радіусу цієї дуги (R) є постійною величиною (мал.15). Власне це відношення і є тим кутом величина якого виміряна в радіанах.

    

мал.15.  Для будь якого кута φ відношення його обмежуючої дуги ℓ до радіусу R цієї дуги є постійною величиною.

Оскільки у повному колі, з одного боку міститься 360 градусів, а з іншого – 2π радіан, то між відповідними одиницями існує співвідношення 2π(рад)=360º. Звідси випливає, що 1рад=360º/2π ≈ 57º. З побутово-практичної точки зору, вимірювати кутові величини в радіанах (1рад ≈ 57º) досить незручно. Тому в побутовій практиці та при геометричних побудовах, кутові величини зазвичай вимірюють в градусах. Однак якщо мова йде про фізику та сучасну науку загалом, то в ній основною одиницею вимірювання кутових величин є не градус, а радіан. Адже виміряний в радіанах кут є не лише мірою кутових величин, а й певним відображенням тих зв’язків, які об’єктивно існують між кутовими та лінійними величинами.

Тепер, коли ви знаєте що просторову орієнтацію тіла характеризують певним кутом і що величина цього кута вимірюється в радіанах, можна визначити й інші характеристики обертального руху тіла, зокрема його кут повороту, кутову швидкість та кутове прискорення.

Кут повороту – це фізична величина, яка характеризує кут повороту тіла і яка дорівнює цьому куту (тобто тому куту, на який повернулось тіло в процесі свого обертального руху).

Позначається:  ∆φ

Визначальне рівняння: ∆φ=φ_к – φ₀ ,  або  ∆φ=s/R

де s – довжина того шляху який пройшла певна точка тіла, рухаючись по колу радіусу R, при повороті тіла на кут ∆φ.

Одиниця вимірювання:  [∆φ]=рад,  радіан.

Кутова швидкість – це фізична величина, яка характеризує кутову швидкість тіла (швидкість обертального руху тіла) і яка показує на який кут повертається тіло за одиницю часу.

Позначається: ω

Визначальне рівняння: ω=∆φ/∆t

Одиниця вимірювання:  ω=рад/с,  радіан за секунду.

Кутове прискорення – це фізична величина, яка характеризує кутове прискорення тіла і яка показує на скільки змінюється кутова швидкість тіла за одиницю часу.

Позначається: ε

Визначальне рівняння: ε=∆ω/∆t

Одиниця вимірювання:  ε=рад/с², радіан за секунду в квадраті.

По суті, кутова швидкість (ω) та кутове прискорення (ε) – величини векторні. Однак, зважаючи на факт того, що в межах програми загальноосвітньої школи, вивчають лише загальні основи механіки обертального руху, ми не будемо формулювати ті правила які визначають напрям цих векторів. Натомість будемо просто вважати, що кутова швидкість того тіла яке обертається за годинниковою стрілкою має знак “+” , а проти годинникової стрілки – знак “-“ . При цьому, якщо в процесі обертання, кутова швидкість збільшується, то знаки кутової швидкості та кутового прискорення є однаковими. А якщо ця швидкість зменшується, то відповідні знаки є різними.

Основний закон кінематики обертального руху називається рівнянням обертального руху.  В цьому законі стверджується: в загальному випадку  обертальний рух тіла можна описати рівнянням    φ = φ₀ + ω₀t + (ε/2)t²

де  φ – кутова координата тіла в момент часу t;

φ₀ – початкова кутова координата тіла;

ω₀ – початкова кутова швидкість тіла;

ε – кутове прискорення тіла.

В кінематиці обертального руху, рівняння  φ=φ₀ + ω₀t + (ε/2)t²  відіграє ту ж роль, що і рівняння  х=х₀ + v₀t + (a/2)/t²  в кінематиці поступального руху. А це означає, що на основі аналізу рівняння обертального руху тіла, можна розв’язати безліч задач які стосуються цього руху. Втім, програма загальноосвітньої школи не передбачає розв’язування подібних задач. Зважаючи на ці обставини, обмежимся лише тією загальною характеристикою обертального руху, яка з усією очевидністю випливає з аналізу рівняння цього руху.

Задача. За заданим рівнянням обертального руху φ=π/2+10t – 01t² дати загальну характеристику цього руху.

Із порівняльного аналізу рівнянь

φ=φ₀ + ω₀t + (ε/2)t²

φ=π/2 + 10t – 01t²

ясно:  φ₀ = π/2 рад;    ω₀ = 10 рад/с;  ε = 0,2 рад/с²;  ω↓  .

Це означає, що в заданій системі координат, початкова кутова координата тіла відповідає куту π/2 рад. При цьому тіло обертається в додатному напрямку (за годинниковою стрілкою) з початковою кутовою швидкістю 10 рад/с. Величина цієї швидкості зменшується, а числове значення кутового прискорення становить 0,2 рад/с² .

         Поділ механічних рухів на поступальні та обертальні, в значній мірі є умовним. Наприклад кабіна “оглядового колеса” (мал.16а), з одного боку, рухається поступально (в процесі руху будь яка приналежна тілу пряма залишається паралельною сама собі), а з іншого – обертально (в процесі руху, всі точки кабіни описують практично концентричні кола). Загалом, рух будь якої матеріальної точки по колу, з одного боку можна вважати обертальним, а з іншого – поступальним. А це означає, що описуючи такий рух, з одного боку говорять про кутову швидкість (ω), кутове прискорення (ε) і кут повороту (∆φ), а з іншого – про лінійну швидкість (v), лінійне прискорення (a) та пройдений шлях (s).

    

Мал.16  Рух кабіни “оглядового колеса” (а) та рух матеріальної точки по колу (б), одночасно є як поступальним так і обертальним.

Оскільки в вище наведених прикладах мова йде про один і той же поступально-обертальний рух, то між параметрами його поступальної та обертальної складових, існують певні кількісні співвідношення. Власне, ці співвідношення випливають із визначальних рівнянь відповідних фізичних величин. Дійсно. Якщо в процесі обертального руху матеріальна точка здійснює поворот на кут ∆φ=s/R, то її лінійне переміщення (пройдений шлях) становитиме s=∆φR. Якщо кутова швидкість матеріальної точки ω, то її лінійна швидкість v=ωR  (за визначенням ω=∆φ/∆t=s/R∆t=v/R, звідси  v=ωR ). Якщо кутове прискорення матеріальної точки ε, то її лінійне прискорення  а=εR  (за визначенням ε=∆ω/∆t=∆v/R∆t=a/R, звідси а=εR).

Таким чином, якщо матеріальна точка рухається по колу радіусу R, то між параметрами її поступального (лінійного) та обертального руху існують

співвідношення:    s=∆φR;     v=ωR;    a=εR,  або

·                                 ∆φ=s/R;    ω=v/R;    ε=a/R.

Характерною особливістю руху матеріальної точки по колу є те, що в незалежності від швидкості цього руху, ця точка завжди рухається з певним доцентровим прискоренням, яке характеризує зміну швидкості за напрямком і яке визначається за формулою а=v²/R. А зважаючи на те, що v=ωR, цю формулу можна записати у вигляді  а_д=ω²R.

Аналізуючи параметри та закономірності поступального і обертального рухів, не важко бачити, що між цими параметрами та закономірностями є певні очевидні аналогії. Ці аналогії та взаємопов’язаність поступального і обертального рухів, можна представити у вигляді наступної узагальнюючої

таблиці.

Параметри та законипоступального руху	Параметри та закониобертального руху	Взаємопов’язаністьцих параметрів
час                         t	час                         t	t=t
координата           x=ℓ	кутова                   φ=ℓ/Rкоордината	ℓ=φR
пройдений            s=∆xшлях	кут                        ∆φ=s/Rповороту	s=∆φR
швидкість         v=∆x/∆t	кутова                   ω=∆φ/∆tшвидкість	v=ωR
прискорення     a=∆v/∆t	кутове                  ε=∆ω/∆tприскорення	a=εR
доцентрове       aд =v2/Rприскорення	_	ад =ω2R
рівняння поступальногоруху x = x0 + v0t + (a/2)t2	рівняння обертальногоруху  φ = φ0 + ω0t +(ε/2)t2

Словник фізичних термінів.

Кутова координата (кут) – це фізична величина, яка характеризує просторову (кутову) орієнтацію тіла в вибраній системі координат і яка дорівнює відношенню довжини тієї  дуги що обмежує даний центральний кут до радіусу цієї дуги.

Позначається:  φ

Визначальне рівняння:  φ=ℓ/R

Одиниця вимірювання:  [φ]=рад,   радіан.

Радіан – це одиниця вимірювання кутових величин, яка дорівнює такому центральному куту, довжина обмежуючої дуги якого дорівнює радіусу цієї дуги.

Кут повороту – це фізична величина, яка характеризує кут повороту тіла і яка дорівнює цьому куту

Позначається:  ∆φ

Визначальне рівняння: ∆φ=φ_к – φ₀, або  ∆φ=s/R

Одиниця вимірювання:  [∆φ]=рад,  радіан.

Кутова швидкість – це фізична величина, яка характеризує кутову швидкість тіла (швидкість обертального руху тіла) і яка показує на який кут повертається тіло за одиницю часу.

Позначається: ω

Визначальне рівняння: ω=∆φ/∆t

Одиниця вимірювання:  ω=рад/с,  радіан за секунду.

Кутове прискорення – це фізична величина, яка характеризує кутове прискорення тіла і яка показує на скільки змінюється кутова швидкість тіла за одиницю часу.

Позначається: ε

Визначальне рівняння: ε=∆ω/∆t

Одиниця вимірювання:  ε=рад/с²,  радіан за секунду в квадраті.

Рівняння обертального руху – це закон, в якому стверджується: в загальному випадку, обертальний рух тіла описується рівнянням

φ = φ₀ + ω₀t + (ε/2)t²

Контрольні  запитання.

1.Чому, описуючи обертальний рух тіла, це тіло не можна представляти у вигляді матеріальної точки?

2.Чому, визначаючи кутовий градус, коло поділили на 360 частин?

3.Чому, в науковій практиці основною одиницею вимірювання кутових величин є не градус а радіан?

4.Якщо в будь якому повному колі міститься 2π радіан, то чому дорівнює довжина кола?

5.Чому дорівнює кут повороту хвилинної стрілки годинника за 15хв; за 30хв; за 2 години?

6.Визначте кутову швидкість секундної, хвилинної та годинної стрілок годинника.

7.За заданим рівнянням обертального руху, дати загальну характеристику цього руху а)  φ= -2π/3 +8t -0,1t² ; б)  φ= π – 10t – 0,2t²; в)  φ= -5t + 0,2t² .

 

Лекційне заняття №8.

Тема: Статика. Основні поняття, величини та закони статики. Про силу звичайну та силу інерції. 

         Статика (від грецького  statike – рівновага) – це розділ механіки в якому вивчають параметри, закономірності та причини стану механічної рівноваги тіл. Механічною рівновагою тіла (матеріальної точки) називають такий механічний стан тіла, при якому воно знаходиться в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v=const). Зазвичай в статиці розглядають ті ситуації коли тіло знаходиться в стані механічного спокою. Однак ви маєте знати, що з фізичної точки зору, між станом механічного  спокою тіла (v=0) та станом його прямолінійного рівномірного руху (v=const) нема суттєвої різниці. Втім, про те що це означає, ми поговоримо дещо пізніше. Наразі ж, будемо вважати, що ті силові закономірності що є справедливими для стану механічного спокою тіла, будуть справедливими і в тому випадку, коли це тіло перебуватиме в стані прямолінійного рівномірного руху.

Основною фізичною величиною статики є сила. Сила – це фізична величина, яка характеризує силову дію одного тіла на інше (є мірою взаємодії фізичних об’єктів) і яка дорівнює добутку маси тіла на величину того прискорення яке воно отримує під дією даної сили.

Позначається:  F

Визначальне рівняння:  F=ma

Одиниця вимірювання:  [F]=H,   ньютон.

Ньютон – це одиниця вимірювання сили, що дорівнює такій силі яка тілу масою 1кг надає прискорення 1м/с² :  1Н=1кг∙1м/с². Іншими словами, якщо тіло масою 1кг рухається з прискоренням 1м/с², то це означає, що на нього діє сила 1Н. (Звичайно, мається на увазі, що тіло масою 1кг знаходиться під дією лише однієї зовнішньої сили, або, що ця сила є результуючою всіх діючих на тіло зовнішніх сил.)

Відразу ж зауважимо, що величину сили в один ньютон не можливо оцінити візуально, як це, наприклад, можна зробити з одиницею довжини,- метром. Ньютон, це одиниця вимірювання сили, тобто тієї величини яка характеризує силову дію одного фізичного об’єкту на інший. Тому величину ньютона можна оцінити лише за його силовою дією. Скажімо, загально відомо, що всі тіла притягуються до землі з силою яку прийнято називати силою тяжіння. Відомо й про те, що під дією сили тяжіння всі тіла, в тому числі і ті маса яких 1кг, падають з прискоренням 9,8м/с². А це означає, що на тіло масою 1кг діє сила тяжіння 9,8Н:   F =1кг∙9,8м/с²=9,8Н.

Таким чином, якщо ви візьмете в руку тіло масою 1кг, то відчуєте силу 9,8Н. Запитується: тіло якої маси потрібно взяти в руку, щоб вона відчула силу в один ньютон? Правильно, маса цього тіла має становити 102г :

m=F/a=1Н/9,8(м/с²)=0,102кг=102г.

Мал.17. Один Ньютон дорівнює тій силі, з якою тіло масою 102 грами притягується до Землі.

От тільки не потрібно стверджувати, що в одному ньютоні міститься 102 грами. Бо це все рівно ніби наполягати на тому, що в одному метрі міститься сто секунд, або, що кілограм більший за секунду. Адже кілограм не більший і не менший за секунду. Бо кілограм – це кілограм, метр – це метр, секунда – це секунда, а ньютон – це ньютон. І порівнювати ці абсолютно різні одиниці не можна. Метр можна порівнювати з міліметром, кілометром чи, скажімо, з дюймом, тобто з іншими одиницями довжини. Але метр не можна порівнювати з секундою, кілограмом, ньютоном чи, наприклад, з метром квадратним. Тому, коли ми говоримо, що силі в один ньютон відповідає вага тіла масою 102 грами, то маємо на увазі лише те, що силу в один ньютон можна відчути тримаючи в руці тіло масою 102 грами.

Аналізуючи визначальне рівняння сили F=ma, потрібно зауважити, що це рівняння не потрібно сприймати як таке, що вказує на факт залежності сили від маси тіла та його прискорення. Адже в загальному випадку, діюча на тіло сила не залежить від маси цього тіла та того прискорення яке воно може отримати. Скажімо, сила ваших м’язів не залежить від маси того тіла що лежить на столі і того прискорення яке отримає це тіло під дією вашої сили.

Формула F=ma по суті вказує лише на універсальний спосіб визначення (вимірювання) величини та напрямку дії будь якої сили. А цей спосіб полягає в тому, що для визначення величини будь якої сили, наприклад, м’язової сили вашої руки, цю силу потрібно прикласти до тіла відомої маси (m) і подивитесь на те прискорення (a) яке отримає це тіло під дією даної сили. При цьому, величина та напрям сили визначаться за формулою  F=ma .

Крім цього, визначальне рівняння F=ma, вказує ще й на факт того, що сила є причиною прискореного руху тіл: сила F надає тілу масою m прискорення а.

В фізиці, так чи інакше розрізняють багато різновидностей сили. Лише в механіці ми будемо вивчати що найменше дев’ять таких різновидностей:

– сила інерції                    F_i

– сила тяжіння                 F_т

– гравітаційна сила        F_гр

– реакція опори               N

– вага                                  P

– сила пружності             F_пр

– сила тертя                      F_тер

– підйомна сила крила   F_п.с

– сила Архімеда               F_a .

Втім, кожна з цих різновидностей, по суті є мірою одного і того ж – мірою взаємодії фізичних об’єктів. До речі. Твердження про те, що сила є мірою взаємодії фізичних об’єктів, вказує на той факт, що будь яка силова дія одного фізичного об’єкту на інший, неминуче породжує рівну їй за величиною і протилежну за напрямком силову протидію з боку цього “іншого” об’єкту. Власе це і означає, що фізичні об’єкти взаємодіють.

Сукупність тих сил що діють на дане тіло в даний момент часу називають системою сил. Систему сил, лінії дії яких лежать в одній площині називають плоскою системою сил. В межах програми загальноосвітньої школи ми, ми будемо вивчати лише плоскі системи сил. Систему сил, лінії дії яких перетинаються в одній точці, називають збіжною системою сил. Якщо абсолютно тверде тіло знаходиться під дією збіжної системи сил, то: по-перше, це тіло можна вважати матеріальною точкою, а по-друге, систему таких сил можна замінити однією рівнодіючою силою (мал.17).

Рівнодіючою силою, називають таку силу, яка чинить на тіло (матеріальну точку) таку ж силову дію як і вся система реально діючих на нього сил (позначається F_р). Рівнодіюча сила дорівнює векторній сумі всіх діючих на тіло зовнішніх сил:  F_р=F₁+F₂+ … +F_N=∑F_i  (тут і в подальшому запис ∑F_i є спрощеним варіантом запису  ) .

  

Мал.17.  Систему діючих на абсолютно тверде тіло збіжних сил, можна замінити  їх рівнодіючою.

Основний закон статики називають умовою рівноваги тіла. В цьому законі стверджується: тіло (матеріальна точка) буде знаходитись в стані механічної рівноваги (v=0 або v=const ) тоді і тільки тоді, якщо векторна сума діючих на нього зовнішніх сил дорівнює нулю. Іншими словами:

якщо ∑F_i=0 то v=0 , або v=const  і навпаки: якщо v=0 або v=const  то ∑F_i=0 .

Зважаючи на те, що в загальному випадку, будь яку довільну силу F можна розкласти на три складові – проекції цієї сили на осі системи координат (F_x,F_y,F_z), умову рівноваги матеріальної точки ∑F_i=0, можна записати у вигляді системи трьох рівнянь:

·                                                        ∑F_x=0

·                                                         ∑F_y=0

·                                                         ∑F_z=0 .

А оскільки в межах шкільної програми розглядають лише плоскі системи сил, то для таких систем, умова рівноваги набуває вигляду:

·                                                         ∑F_x=0

·                                                         ∑F_y=0 .

Ми нераз говорили про те, що механіку загалом та її складові частини зокрема, умовно розділяють на механіку поступального руху (механіку матеріальної точки) та механіку обертального руху. І в цьому сенсі статика не є винятком. Адже коли ми стверджуємо, що основною фізичною величиною статики є сила (F), а основним законом – умова рівноваги тіла (∑F=0), то по суті маємо на увазі ту частину статики де тіло можна представити у вигляді матеріальної точки. Тобто ту частину статики в якій на тіло діє збіжна система сил.  Система яка може надати тілу лише поступального руху. В загальному ж  випадку, тіло може знаходитись під дією довільної системи сил. А така система може надавати тілу як поступального так і обертального руху. Описуючи поведінку такого тіла, говорять не лише про діючі на нього сили, а й про діючі моменти сил. Втім, про те, що таке момент сили та про загальну умову рівноваги тіла, ми поговоримо дещо пізніше.

Наразі ж додамо, що в межах даної теми (статики) ми будемо вивчити не лише ті ситуації в яких тіло під дією певної системи сил знаходиться в стані механічної рівноваги (v=0 або v=const), а й ті, коли ця рівновага є динамічною, тобто такою при якій тіло рухається з постійним прискоренням (a=const). По суті такі ситуації є предметом вивчення динаміки. Однак, з методичної точки зору, їх доцільніше вивчати в тому розділі, де основною фізичною величиною є сила, а основним законом – умова рівноваги тіла. А цим розділом є статика.

На протязі тисячоліть люди вважали, що сила – це те що змушує тіла рухатись. Вони думали, хіба плуг, карета чи віз рухаються не тому що на них діє певна сила? І хіба після припинення дії цієї сили, вони не зупиняться. Хіба камінь не буде лежати на землі допоки на нього не подіє сила? Хіба камінь падає не тому, що на нього діє певна сила ?

Подібні міркування наводили на думку, що сила – це те що змушує тіла рухатись. Однак більш глибокий аналіз вказує на явні недоліки цієї думки. Дійсно. Футбольний м’яч починає рухатись тому, що на нього діє сила удару футболіста. Але ж м’яч продовжує рухатись і після припинення дії цієї сили. Кинутий камінь продовжує рухатись і після того як відривається від руки. Куля продовжує рухатись і після припинення дії тиску порохових газів. При цьому говорять що м’яч, камінь та куля рухаються за інерцією. Виходячи з того, що будь-яке тіло має інерцію тобто здатність зберігати стан спокою або стан прямолінійного рівномірного руху, Галілей а за ним і Ньютон дійшли висновку: Сила – це не те що змушує тіла рухатись, а те що змушує їх змінювати швидкість свого руху.

Оскільки на практиці причиною зміни швидкості руху тіла, а отже джерелом сили, є дія на це тіло іншого фізичного об’єкту, то можна стверджувати, що сила є кількісною мірою цієї дії. Виходячи з цього можна дати наступне визначення сили:

Сила – це фізична величина яка є мірою взаємодії тіл (фізичних об’єктів) і яка дорівнює добутку маси тіла на величину того прискорення яке воно отримує під дією даної сили.

Позначається:  F

Визначальне рівняння:  F = ma

Одиниця вимірювання:  [F] = кг·м/с² = Н ,   (ньютон)

Твердження про те, що сила це міра взаємодії фізичних об’єктів є загальновизнаним та загальноприйнятим. Однак це зовсім не означає що воно є бездоганно правильним. Дійсно. З нього випливає, що будь-яка сила, це результат взаємодії тих чи інших фізичних об’єктів. Наприклад, сила тяжіння – результат взаємодії даного тіла з Землею; сила пружності – результат взаємодії атомів і молекул деформованого тіла; сила тертя – результат взаємодії контактуючих поверхонь; електрична сила – результат взаємодії  електричних зарядів; магнітна сила – результат взаємодії електричних струмів і т.д.,

Однак в Природі існує одна сила, яка явно не вписується в рамки загальноприйнятого визначення. Цю силу називають силою інерції. Коли в момент різкої зупинки автомобіля вас щось штовхає вперед, знайте – це сила інерції. Коли на крутому повороті вас щось притискає до бокових дверей автомобіля, знайте – це сила інерції. Коли на атракціоні “американські гірки” ваш дух перехоплює від постійних перевантажень та станів невагомості , знайте, це прояви сили інерції.

Мал.18. Деякі прояви сили інерції.

З’ясовуючи фізичну суть сили інерції, звернемося до експерименту. Припустимо що до пружинного динамометра (мал.19) прикріплено вантаж масою 0,1кг. Коли система динамометр-вантаж знаходиться в стані механічної рівноваги (v =0  або  v = const) то деформована пружина вказує на те, що вантаж притягується до Землі з силою 1Н (приблизно)F_т =mg≈1кг·1м/с²=1Н. Але, як тільки система почне прискорено рухатись вгору, пружина динамометра додатково розтягнеться, вказуючи на те що на тіло діє певна додаткова сила, напрям якої протилежний до напрямку прискорення. Ця сила і є силою інерції.

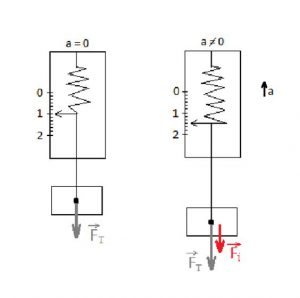
Мал.19 Прискорений рух тіла завжди породжує силу інерції, яка протидіє появі та зростанню цього прискорення.

Тепер давайте з’ясуємо дія якого фізичного об’єкту призвела до появи сили інерції? Ви можете як завгодно довго шукати цей об’єкт і скоріш за все не знайдете його. Не знайдете тому, що його просто не існує. Силу інерції породжує не взаємодія даного тіла з тим чи іншим фізичним об’єктом, а сам факт прискореного руху тіла.*

*)  Чесно кажучи поява сили інерції обумовлена взаємодією даного тіла з тим фізичним об’єктом який називається простір. Однак, про властивості цього об’єкту та про його зв’язок з силою інерції ми поговоримо лише в тому розділі фізики який називається теорією відносності.

 

В певному сенсі, сила інерції не вписується в рамки загальноприйнятого визначення: “Сила – це міра взаємодії фізичних об’єктів”. На цій підставі часто можна почути, що сила інерції, це якась неіснуюча, придумана, віртуальна сили. Подібні твердження – абсолютно безпідставні. Вся “нереальність” сили інерції лише в тому, що наше спрощене пояснення природи цієї сили, не вписується в рамки того визначення яке ми придумали для поняття “сила”.

Сьогодні ми не будемо обговорювати питання про походження сили інерції. Відповідь на це питання дає загальна теорія відносності. Сьогодні, ми просто констатуємо той факт, що при прискореному русі будь-якого фізичного об’єкту на нього діє сила інерції, величина якої дорівнює добутку маси об’єкту на його прискорення і напрям якої протилежний напрямку цього прискорення.

Сила інерції – це та сила, поява якої обумовлена прискореним рухом тіла і яка завжди протидіє появі та зростанню цього прискорення.

Позначається: F_і

Визначальне рівняння: F_і = – ma

Одиниця вимірювання: [F_і] = Н

 

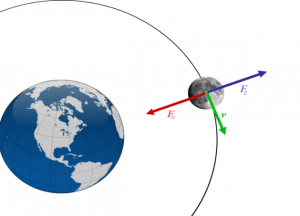
Мал.20.  Якщо тіло рухається з прискоренням, то на нього неминуче діє певна сила інерції.

Потрібно зауважити, що сила інерції це саме та сила яка, як за своєю природою так і за своєю величиною, дійсно залежить від маси тіла та його прискорення.

Сила інерції, це надзвичайно важлива сила, без розуміння суті якої не можливо логічно пояснити величезний пласт явищ. Наприклад, не можливо пояснити чому різні тіла падають з однаковим прискореннями?; чому тіла рухаються за інерцією?; чому Земля розтягнута в екваторіальній площині?; чому Місяць не падає на Землю, а Земля не падає на Сонце, тощо.

Дійсно. Чи задумувались ви над тим, чому тіла різної маси падають однаково швидко? Адже на більш масивне тіло діє більша сила тяжіння, яка очевидно мала б надавати йому більшої швидкості падіння. І тим не менше, важкий камінь і легка пісчинка падають однаково швидко, а точніше – з однаковим прискоренням.

Пояснюючи даний факт можна сказати наступне. На будь-яке тіло діє певна сила тяжіння (мал.21). При цьому, на важке тіло, діє велика сила тяжіння (F_т = Mg), а на легке – відповідно мала (F_т = mg). Коли під дією сили тяжіння тіло починає прискорено рухатись (a=g) то автоматично з’являється (індуцирується) відповідна протидіюча сила – сила інерції. При цьому, на важке тіло діятиме велика сина інерції (F_т = – Mg), а на легке – мала сила інерції (F_т = -mg). Під дією цих рівних за величиною і протилежних за напрямком  сил (сили тяжіння та сили інерції) будь-яке вільно падаюче тіло і рухається з певним постійним прискоренням – прискоренням вільного падіння.

 

Мал. 21. Важкі і легкі тіла падають з однаковим прискоренням тому, що в процесі вільного падіння, діючі на них сили тяжіння динамічно зрівноважуються відповідними силами інерції.

Ви можете запитати: “А як бути з умовою рівноваги тіла, тобто з законом в якому говориться про те, що коли діючі та тіло зовнішні сили зрівноважують одна одну, то тіло знаходиться в стані спокою (v=0), або прямолінійного рівномірного руху (v =const)?” Відповідаючи на це слушне запитання, можна сказати наступне. Дійсно. В умові рівноваги тіла стверджується: якщо векторна сума діючих на тіло зовнішніх сил дорівнює нулю, то тіло буде знаходитись в стані механічної рівноваги. Іншими словами: якщо Σ F = 0, то v=0 або v=const. Аналізуючи дане твердження зверніть увагу на те, що в ньому говориться про векторну суму зовнішніх сил, тобто звичайних сил взаємодії: сила тяжіння, сила тертя, сила пружності, сила Архімеда, реакція опори, сила тяги, тощо. В нашому ж випадку, ми маємо справу з силою інерції, тобто силою яка не є зовнішньою. З силою, поява якої обумовлена не взаємодією тіла з тими чи іншими об’єктами, а самим фактом прискореного руху тіла. Тому, коли ми стверджуємо що в процесі вільного падіння тіла, встановлюється рівновага між силою тяжіння і силою інерції, то маємо на увазі так звану динамічну рівновагу, яка передбачає рух тіла не з постійною швидкістю (v=const), а з постійним прискоренням (а= const).

Динамічною рівновагою називають такий механічний стан тіла, при якому воно, під дією зовнішніх сил та сили інерції, знаходиться в стані рівноприскореного руху (а =const).

Потрібно зауважити, що ті задачі, в яких тіло під дією певної системи сил рухається з постійним прискоренням є задачами динаміки. Однак, алгоритм рішення цих динамічних задач практично не відрізняється від алгоритму рішення задач статики. В основі цього рішення лежить твердження (закон) яке називається умовою динамічної рівноваги тіла. Тіло (матеріальна точка) буде знаходитись в стані динамічної рівноваги (а =const) тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил та сили інерції дорівнює нулю. Іншими словами :

якщо    Σ F + F_i = 0     то     а=const,  або

якщо    а=const            то     Σ F + F_i = 0.

Знаючи властивості сили інерції можна відповісти на ще одне важливе запитання: “ Чому тіло після припинення дії зовнішньої сили рухається за інерцією?” На перший погляд такий рух здається безпричинним, тобто таким який не підтримується жодною зовнішню силою. І це правда, – жодна зовнішня сила не є причиною руху тіла за інерцією. Та все ж інерційний рух має свою силову причину. Ця причина – сила інерції, тобто та внутрішня сила, яка протидіє будь-якій зміні швидкості руху тіла. Дійсно, як тільки тіло прагне зменшити свою швидкість, автоматично з’являється сила інерції, яка протидіє цим намаганням i так би мовити “підштовхує” тіло. І якщо тіло, всупереч дії сили інерції все ж зупиняється, то це тільки тому, що на нього діють певні зовнішні гальмуючі сили, зокрема різноманітні сили тертя. Якщо ж дія цих сил відсутня, або мізерно мала, то тіло може зберігати стан рівномірного руху як завгодно довго. Наприклад, Земля вже на протязі 4,5 мільярдів років обертається навколо Сонця з практично незмінною швидкістю.

Словник фізичних термінів.

Статика– це розділ механіки в якому вивчають параметри, закономірності та причини стану механічної рівноваги тіл.

Механічною рівновагою тіла (матеріальної точки) називають такий механічний стан тіла, при якому воно знаходиться в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v=const).            

Сила – це фізична величина, яка характеризує силову дію одного тіла на інше (є мірою взаємодії фізичних об’єктів) і яка дорівнює добутку маси тіла на величину того прискорення яке воно отримує під дією даної сили.

Позначається:  F

Визначальне рівняння:  F=ma

Одиниця вимірювання:  [F]=H ,   ньютон.

Ньютон – це одиниця вимірювання сили, що дорівнює такій силі яка тілу масою 1кг надає прискорення 1м/с².

Рівнодіючою силою, називають таку силу, яка чинить на тіло (матеріальну точку) таку ж силову дію як і вся система реально діючих на нього сил (позначається F_р).

Умова рівноваги тіла (матеріальної точки) – це закон, в якому стверджується: тіло (матеріальна точка) буде знаходитись в стані механічної рівноваги (v=0 або v=const ) тоді і тільки тоді, якщо векторна сума діючих на нього зовнішніх сил дорівнює нулю. Іншими словами:

якщо ∑F_i=0 то v=0 , або v=const  і навпаки: якщо v=0 або v=const  то ∑F_i=0 .

Сила інерції – це та сила, поява якої обумовлена прискореним рухом тіла і яка завжди протидіє появі та зростанню цього прискорення.

Позначається: F_і

Визначальне рівняння: F_і = – ma

Одиниця вимірювання: [F_і] = Н

Динамічною рівновагою називають такий механічний стан тіла, при якому воно, під дією зовнішніх сил та сили інерції, знаходиться в стані рівноприскореного руху (а=const).

Умова динамічної рівноваги тіла – це закон в якому стверджується: тіло (матеріальна точка) буде знаходитись в стані динамічної рівноваги

(а=const), тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил та сили інерції дорівнює нулю. Іншими словами:

якщо    Σ F+F_i = 0     то     а=const,  або

якщо    а=const          то     Σ F+F_i = 0.

Контрольні запитання.

1.Поясніть, що потрібно зробити, щоб відчути силу в один ньютон?

2.Один ньютон – це багато чи мало?

3.Чи означає визначальне рівняння F=ma, що будь яка сила залежить від маси та прискорення? Про що говорить це рівняння?

4.Наведіть приклади ситуацій, в яких проявляється сила інерції.

5.Поясніть, чому важкі і легкі тіла падають з однаковим прискоренням?

6.Поясніть, чому Земля дещо “розтягнута” в екваторіальній площині ?

7.Чим динамічна рівновага тіла відрізняється від його механічної рівноваги?

 

Лекційне заняття №9.

Тема: Сила тяжіння. Реакція опори. Сила тертя.

До числа тих сил які найчастіше зустрічаються в задачах статики відносяться, сила тяжіння, реакція опори та сила тертя.

         Сила тяжіння – це та сила,  з якою тіла притягуються до Землі.

Позначається:  F_т

Визначальне рівняння:  F_т=ma  де  m – маса тіла;   g=9,8м/c² – прискорення вільного падіння (прискорення сили тяжіння).

Одиниця вимірювання:  [F_т]=H .

Мал.22.  На будь яке земне тіло діє певна сила тяжіння.

По суті, сила тяжіння є тією силою, елементарні фрагменти якої діють на всі точки тіла. Однак прийнято вважати, що ця сила прикладена до центру мас відповідного тіла. При цьому, прийнято вважати, що сила тяжіння направлена точно до центру мас Землі. Останнє твердження не є безумовно правильним. Не є тому, що сила тяжіння – це результуюча двох постійно діючих на земні тіла сил: сили гравітаційної взаємодії даного тіла з Землею (F_гр) та діючої на це ж тіло сили інерції (F_i), поява якої обумовлена добовим обертанням Землі навколо своєї осі (F_т=F_гр+F_i). А в загальному випадку, ця результуюча не направлена точно до центру мас Землі. Однак відхилення від цього центру  є не суттєвим. І тому будемо вважати, що сила тяжіння направлена до центру мас Землі.

Сила тяжіння прагне перемістити будь яке тіло в центр Землі. А оскільки земні тіла не опиняються в цьому центрі, то ясно, що на своєму шляху вони неминуче зустрічають певні протидіючі фактори. Цими факторами часто є ті об’єкти які прийнято називати опорами. Ту ж силу з якою опора діє на тіло називають реакцією опори.

Реакція опори – це та сила, з якою опора діє на тіло.

Позначається:  N

Визначальне рівняння:  величина і напрям реакції опори визначається з умов конкретної задачі.

Одиниця вимірювання:  [N]=H .

Опорою називають будь яку механічну перешкоду, яка так чи інакше жорстко обмежує рух тіла. Наприклад, та підлога на якій ви стоїте, обмежує ваш рух в напрямку центру Землі. Гнучка опора (канат, ланцюг, дріт, тощо), обмежує рух тіла в напрямку розтягування цієї опори. Шарнірно закріплений жорсткий стержень, обмежує рух тіла як в напрямку його розтягування так і в напрямку його стиснення. Жорстко закріплений стержень, обмежує рух тіла в усіх можливих напрямках. На мал.23 представлені найбільш поширені варіанти простих механічних опор та їх реакцій.

 

Мал.23.  Деякі різновидності механічних опор та реакції цих опор.

Потрібно зауважити, що сила тяжіння і реакція опори є тими зовнішніми силами, які діють на відповідне тіло, а не на опору чи щось інше. Що правда, точки прикладання цих сил є суттєво різними: сила тяжіння прикладена до центру мас тіла, а реакція опори діє в точках контакту тіла з відповідною опорою (мал.24а). Втім, в більшості задач механіки матеріальної точки, прийнято вважати що і сила тяжіння і реакція опори, прикладені до центру мас тіла (мал.24б).

  

Мал.24. Сила тяжіння і реакція опори, діють на тіло, а не на опору чи щось інше.

В механіці, сили які так чи інакше протидіють взаємному переміщенню контактуючих поверхонь, називають силами тертя. По суті, сила тертя є усередненою результуючою багатьох силових факторів, різноманіття яких не можливо врахувати. Про складність того, що прийнято називати тертям, говорить бодай той факт, що на сьогоднішній день точної кількісної теорії тертя не існує. А це означає що по-перше, не існує тієї єдиної універсальної формули, яка б дозволяла визначати силу тертя в будь якій можливій ситуації. По-друге, ті формули за якими натепер визначають силу тертя в тому чи іншому конкретному випадку, є в тій чи іншій мірі наближеними. По-третє,  в наявних визначальних рівняннях сил тертя, завжди присутні величини (коефіцієнти) значення яких визначається експериментально і є індивідуальним для кожного конкретного випадку.

Розрізняють дві основні різновидності тертя: сухе і в’язке. Сухим називають таке тертя, яке виникає при взаємодії твердих поверхонь і яке протидіє їх взаємному переміщенню. В’язким називають таке тертя, яке виникає при взаємодії твердих поверхонь з рідинами або газами, а також між внутрішніми шарами цих середовищ, і яке протидіє їх взаємному переміщенню. Наприклад автомобіль, рухаючись автострадою, відчуває гальмуючу дію двох сил тертя: 1) сили того в’язкого тертя, поява якого обумовлена взаємодією поверхні автомобіля з атмосферним повітрям (цю силу зазвичай називають силою опору середовища); 2) силою того сухого тертя, поява якого обумовлена взаємодією коліс автомобіля з поверхнею автостради.

В свою чергу, сухе тертя прийнято розділяти на тертя ковзання і тертя кочення. Наприклад, якщо в процесі аварійного гальмування, задні колеса автомобіля не обертаються, а передні продовжують вільно обертатись, то на перші діє сила тертя ковзання, а на другі – сила тертя кочення. Крім цього, тертя ковзання, поділяють на тертя спокою і тертя руху. Наприклад, якщо брусок нерухомо лежить на похилій площині, то діюча на нього сила тертя є силою тертя спокою. Якщо ж, той таки брусок рухається похилою площиною, то діюча на нього сила тертя є силою тертя руху.

Мал.25.  Види тертя та загальний устрій приладу для дослідження сили тертя.

Досліджуючи загальні властивості сили тертя, зокрема тертя ковзання, можна провести ряд простих експериментів. Суть цих експериментів представлена на мал.25б. Зображена на малюнку експериментальна установка дозволяє легко і прогнозовано змінювати умови експерименту. Наприклад, змінюючи масу тягарців у ваговій чашці, ми відповідним чином змінюємо діючу на тіло силу тяги. Навантажуючи тими ж тягарцями саме тіло, ми прогнозованим чином змінюємо ту силу з якою тіло тисне на поверхню стола і яка дорівнює відповідній реакції опори. Змінюючи одне дослідне тіло на інше, можна змінювати матеріали взаємодіючих поверхонь, якість їх механічної обробки, площу їх взаємодії, тощо.

Дослідження показують:

1.Сила тертя ковзання, практично не залежить від площі взаємодіючих поверхонь.

2.Сила тертя ковзання пропорційна тій силі з якою взаємодіючі поверхні притискаються одна до одної і яка чисельно дорівнює відповідній реакції опори(N).

3.Максимальна величина сили тертя спокою, дещо більша за величину відповідної сили тертя руху (мал.26)

4.Сила тертя, складним чином залежить від механічних та хімічних властивостей взаємодіючих поверхонь, якості їх механічної обробки, їх температури, швидкості відносного руху, тощо.

Мал.26.  Максимальна сила тертя спокою дещо більша за силу тертя руху.

Узагальнюючи результати подібних досліджень, можна дати наступне визначення. Сила тертя (сила тертя ковзання) – це та сила, з якою поверхні взаємодіючих твердих тіл протидіють їх взаємному поступальному (ковзальному) переміщенню, або можливості такого переміщення.

Позначається:  F_тер

Визначальне рівняння: F_тер =µN, де N – реакція опори (сила, з якою взаємодіючі поверхні притискаються одна до одної);  µ – коефіцієнт тертя ковзання.

Одиниця вимірювання: [F_тер] = Н.

Коефіцієнт тертя ковзання – це величина, яка складним чином залежить від багатьох обставин і значення якої визначається експериментально (µ=F_тер/N). Результати деяких з цих експериментальних досліджень представлені в таблиці 1.                                                            Таблиця 1.   Коефіцієнти тертя ковзання

Контактуючі   поверхні       Коефіцієнт тертя  (µ) метал по металу                 0,15 – 0,22 метал по металу за наявності мастила                  0,02 – 0,08 дерево по дереву                  0,25 – 0,50 сталь по льоду (ковзани)                        0, 02 шини по сухому асфальту                   0,50 – 0,70 шини по мокрому асфальту                    0,40 – 0,50 мідь по чавуну                         0,27

Специфіка сили тертя полягає в тому, що вона виникає як певна реакція на дію тих сил які намагаються зсунути одну поверхню відносно іншої. І якщо таких сил нема, то відповідно нема і певної сили тертя. Наприклад, якщо тіло знаходиться на горизонтальній площині (мал.27а), то на нього сила тертя не діє. Не діє тому, що нема того силового фактору який намагався б зсунути тіло відносно площини (F_т+N=0). Однак як тільки площина стане похилою (мал.27б), автоматично з’явиться і відповідна сила тертя. З’явиться тому, що результуюча постійно діючих на тіло сил (сила тяжіння F_т та реакція опори N) вже не буде дорівнювати нулю (F_т+N≠0) і намагатиметься зсунути тіло відносно площини. І якщо це тіло знаходиться в стані спокою, то це тільки тому, що цей спокій забезпечує певна сила тертя. При цьому, по мірі зростання кута нахилу площини, автоматично зростатиме і відповідна сила тертя. Зростатиме до тих пір, поки не досягне певної критичної величини, за межами якої, тертя спокою перетворюється на тертя руху.

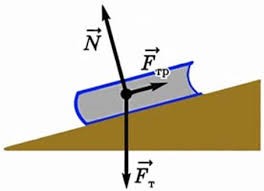
Мал.27. Сила тертя виникає лише за наявності тієї сили яка прагне зсунути тіло відносно поверхні.

Якщо на площині знаходиться кругле (сферичне, циліндричне, тороїдне) тіло, яке може вільно обертатись (котитись), то в цьому випадку говорять про тертя кочення.

Сила тертя кочення – це та сила, з якою поверхні взаємодіючих тіл протидіють обертальному переміщенню (коченню) одного тіла відносно іншого, або можливості такого переміщення.

Позначається:  F_тер

Визначальне рівняння:  F_тер = kN/R ,  де  R – радіус того тіла що котиться, k – коефіцієнт тертя кочення (визначається експериментально k=F_терR/N) .

Одиниця вимірювання:  [F_тер] = Н .

Зазвичай, сила тертя кочення в десятки разів менша за силу тертя ковзання. Тому, в тих випадках де потрібно мінімізувати тертя, ковзання замінюють на кочення, наприклад шляхом застосування відповідних підшипників. Іншим ефективним способом зменшення сили тертя є заміна сухого тертя на в’язке. Така заміна здійснюється шляхом застосування відповідних мастил, що дозволяє зменшити силу тертя в 5-8 разів.

Мал.28.  Зазвичай, сила тертя кочення в десятки разів менша за відповідну силу тертя ковзання.

Як правило, терміном “сила тертя” позначають силу тертя ковзання. Тому, якщо в умовах конкретної задачі, не вказана різновидність сили тертя, то вважайте що цією силою є сила тертя ковзання, тобто та сила, величина якої визначається за формулою  F_тер =µN.

Завершуючи розмову про сили тертя, доречно сказати, що ці сили можуть бути як корисними так і шкідливими. Наприклад, ті сили сухого тертя що діють на автомобіль в процесі його руху, з одного боку є корисними, тобто такими що сприяють поступальному руху автомобіля, а з іншого – шкідливими, тобто такими що протидіють цьому руху. Дійсно. Поступальний рух автомобіля, є результатом взаємодії його коліс з поверхнею дороги. При цьому, виникаюча між ними сила тертя ковзання, по суті є тією тяговою силою яка і надає автомобілю поступального руху, і без якої цей рух є не можливим (мал.29). З іншого боку, при своєму обертальному русі, колеса автомобіля неминуче відчувають гальмуючу дію сили тертя кочення, яка протидіє поступальному руху автомобіля. І якщо автомобіль під дією цих протилежно направлених сил все таки рухається, то це тільки тому, що сила тертя кочення в десятки разів менша за силу тертя ковзання .

Мал.29.  Поступальний рух автомобіля є результатом того, що між його ведучими (тяговими) колесами і поверхнею дороги виникає певна сила тертя ковзання.

На перший погляд здається, що та сила тертя завдяки якій люди, автомобілі та інші об’єкти переміщуються відносно відповідних поверхонь, не вписується в рамки загально прийнятого визначення: “сила тертя, це та сила з якою взаємодіючі поверхні протидіють їх взаємному переміщенню”. Однак, неупереджений аналіз вказує на безпідставність подібних звинувачень. Адже та сила тертя ковзання, що виникає між колесами автомобіля і дорогою, дійсно протидіє їх взаємному переміщенню, тобто протидіє ковзанню коліс відносно поверхні дороги. При цьому ця сила не протидіє поступальному руху автомобіля. Більше того, без цієї сили такий рух стає просто неможливим. Адже лише завдяки силі тертя ковзання, обертальний рух ведучих коліс автомобіля перетворюється на його поступальний рух.

Словник фізичних термінів.

Сила тяжіння – це та сила,  з якою тіла притягуються до Землі.

Позначається:  F_т

Визначальне рівняння:  F_т= ma

Одиниця вимірювання:  [F_т]= H.

Реакція опори – це та сила, з якою опора діє на тіло.

Позначається:  N

Визначальне рівняння:  визначається з умов конкретної задачі.

Одиниця вимірювання:  [N]=H .

Опорою називають будь яку механічну перешкоду, яка так чи інакше жорстко обмежує рух тіла.

Сила тертя (сила тертя ковзання) – це та сила, з якою поверхні взаємодіючих твердих тіл протидіють їх взаємному поступальному (ковзальному) переміщенню, або можливості такого переміщення.

Позначається:  F_тер

Визначальне рівняння:  F_тер =µN,

Одиниця вимірювання: [F_тер] = Н.

Сила тертя кочення – це та сила, з якою поверхні взаємодіючих тіл протидіють обертальному переміщенню (коченню) одного тіла відносно іншого, або можливості такого переміщення.

Позначається:  F_тер

Визначальне рівняння:  F_тер = kN/R

Одиниця вимірювання:  [F_тер] = Н.

Сухим тертям називають таке тертя, яке виникає при взаємодії твердих поверхонь і яке протидіє їх взаємному переміщенню.

В’язким тертям називають таке тертя, яке виникає при взаємодії твердих поверхонь з рідинами або газами, а також між внутрішніми шарами цих середовищ, і яке протидіє їх взаємному переміщенню.

Контрольні запитання.

1.Що означає твердження: “на сьогоднішній день кількісної теорії тертя не існує”?

2.В процесі аварійного гальмування, задні колеса автомобіля не обертаються, а передні вільно обертаються. Які сили тертя діють на ці колеса? Яка з цих сил є більшою?

3.Чому на те тіло яке лежить на горизонтальній поверхні стола, сила тертя не діє, а на те що лежить на похилій площині – діє?

4.Назвіть основні способи суттєвого зменшення сили тертя.

5.Автомобіль піднімається похилою дорогою. Які сили тертя діють на цей автомобіль? Як вони направлені?

6.Іноді визначальне рівняння сили тертя записують у вигляді F_тер = µN або  F_тер = -µN . Чи є такий запис правильним? Чому?

 

Лекційне заняття №10.

Тема: Про вагу, невагомість та силу Архімеда. Або про те, що важче кілограм заліза чи кілограм пір’я?  

Однією з найбільш суперечливих фізичних величин механіки є вага. В науковій літературі її часто плутають з силою тяжіння, а в побуті – з масою. Насправді ж:   Вага – це та сила з якою тіло діє на опору.

Позначається: Р

Визначальне рівняння: Р = – N, де N – реакція опори

Одиниця вимірювання: [P] = H ,          (ньютон).

Більшість людей схильні вважати, що вага тіла вимірюється в кілограмах. Ця, глибоко вкорінена помилкова думка, має своє логічне пояснення. І це пояснення полягає в наступному. Коли ви приходите в крамницю за цукром, картоплею чи м’ясом, то приходите за певною речовиною, мірою якої є маса, тобто та величина яка вимірюється в кілограмах. А як вимірюють цю саму кількість речовини? Правильно – шляхом зважування. І це зважування полягає в тому, що відповідну речовину кладуть на спеціальну опору (ваги), ця опора відчуває відповідну силу (вагу тіла) і відповідним чином реагує на цю силу. Результатом цієї реакції є відповідне відхилення стрілки приладу або показання на електронному табло. А оскільки ви прийшли не за силою (не за ньютонами), а за певною речовиною, тобто за тим що вимірюється в кілограмах, то результат зважування вам видають в цих самих кілограмах.

Ясно, що така повсякденно повторювана практика, формує в вашій свідомості впевненість в тому, що вага – це те що вимірюється в кілограмах. Насправді ж, вага – це сила яку відчуває та опора на якій знаходиться дане тіло. І як будь яка сила, вага вимірюється в ньютонах.

Ще однією загально розповсюдженою помилкою є думка про те, що вага тіла дорівнює тій силі з якою тіло притягується до Землі і що тому вага визначається за формулою P = mg. Насправді ж, вага – це та сила з якою тіло діє на опору. А це означає, що у повній відповідності з третім законом Ньютона, вага чисельно рівна і протилежно направлена тій силі з якою опора діє на тіло. А цією силою є реакція опори. Нагадаємо, реакція опори – це та сила з якою опора діє на тіло. Власне констатацією даних фактів і є визначальне рівняння P = – N.

Загалом, на відміну від маси тіла, яка за будь яких обставин залишається незмінною (звичайно, якщо не враховувати ті практично не помітні ефекти про які ви дізнаєтесь вивчаючи теорію відносності), вага цього тіла в різних обставинах може бути абсолютно різною. Скажімо, на Землі (g=9,81м/с²) вага тіла масою 10кг становитиме 98,1Н. На Місяці (g=1,6м/с²) ця вага буде рівною 16Н; на Марсі (g=3,7м/с²) – 37Н; на Юпітері (g=25,9м/с²) – 259Н; а на Сонці (g=274,1м/с²) – 2741Н.

Більше того, вага тіла залежить не лише від параметрів того гравітаційного поля яке створює відповідна планета, а й від багатьох інших обставин. Зокрема від того, з яким прискоренням і в якому напрямку рухається система опора–тіло.  Ілюструючи цю залежність розглянемо конкретну задачу.

Задача. Тіло масою 70кг знаходиться в ліфті. Визначити вагу цього тіла в наступних ситуаціях: а) ліфт знаходиться в стані механічної рівноваги (v=0 або v=const , тобто а=0м/с²);  б) ліфт рухається з прискоренням а=5м/с² і це прискорення направлене вгору;  в) ліфт рухається з прискоренням а=5м/с² і це прискорення направлене вниз;  г) ліфт знаходиться в стані вільного падіння тобто падає з прискоренням а=g=10м/с².

Дано:                                      Аналіз:

m = 70кг                 Будемо виходити з того, що вага тіла – це та сила з якою

а₁ = 0м/с²                тіло діє на опору, в нашому випадку – на підлогу ліфта,

а₂ = 5м/с²↑               і що величина цієї сили дорівнює відповідній реакції

а₃ = 5м/с²↓               опори (Р=N). А це означає, що рішення задачі зводиться

а₄ =g=10м/с²↓          до того, щоб визначити величину реакції опори в

кожній з чотирьох ситуацій. Розв’язуючи цю задачу,

Р₁=?,  Р₂=?,              виконуємо відповідні малюнки на яких вказуємо ті сили

Р₃=?,  Р₄=?               що діють на дане тіло в системі опора-тіло. Аналізуємо

кожну з чотирьох ситуацій і визначаємо вагу тіла в

кожній з них.

а=0м/с²                     а=5м/с²↑                   а=5м/с²↓          а=g=10м/с²↓

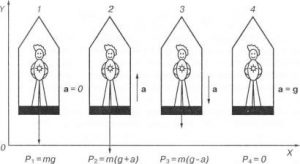
P₁ = N₁ = F_т               P₂ = N₂ = F_т + F_i         P₃ = N₃ = F_т – F_i        P₄ = N₄ = F_т – F_i

P₁ = mg                       P₂ = m(g+a)              P₃ = m(g-a)              P₄ = mg-mg=0

P₁ =700H                     P₂ =1050H                P₃ =350H                 P₄ =0H (невагомість)

Не важко бачити, що вага тіла, тобто та сила з якою тіло тисне на опору, не є постійною величиною. При цьому, лише в тому випадку коли система опора – тіло знаходиться в стані механічної рівноваги (v=0 або v=const), вага тіла чисельно дорівнює діючій на нього силі тяжіння: Р₁=mg . В інших випадках, вага тіла може бути як більшою так і меншою за цю силу: Р₂=m(g+a); Р₃=m(g-a). Якщо ж система опора – тіло знаходиться в стані вільного падіння (а=g), то тіло не тисне на опору і тому його вага дорівнює нулю: Р₄=mg-mg=0. Характеризуючи дану ситуацію говорять про те, що тіло знаходиться в стані невагомості.

Зверніть увагу, тіло знаходиться в стані невагомості (має нульову вагу) не тому що на нього не діє сила тяжіння, а тому, що дія цієї сили зрівноважується відповідною силою інерції. Наприклад загальновідомо, що на борту штучного супутника Землі, тіла знаходяться в стані невагомості. При цьому люди часто думають, що ця невагомість пояснюється відсутністю сили тяжіння. Насправді ж, на тих висотах де зазвичай літають наші пілотовані космічні кораблі (200км – 400км), сила тяжіння майже така ж як і на поверхні землі. А невагомість в космічному кораблі (штучному супутнику Землі) пояснюється не відсутністю сили тяжіння, а фактом того, що ця сила зрівноважується відповідною силою інерції.

Невагомість – це такий стан системи опора – тіло, при якому тіло та його окремі елементи не мають ваги, тобто не тиснуть на опору і одне на одне. Не мають ваги тому, що діюча на них сила тяжіння зрівноважується відповідною силою інерції.

 

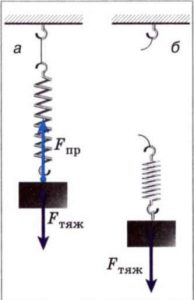
Мал.29а.  Невагомість, це не тому що на тіло не діє сила тяжіння, а тому що діюча на тіло сила тяжіння зрівноважується силою інерції.

Вага тіла залежить не лише від діючої на нього сили тяжіння та сили інерції, а й від інших силових факторів, зокрема сили Архімеда.  Дійсно. Загально відомо, що у воді камінь суттєво легший аніж на суходолі (мал.30). І це закономірно. Адже у воді на камінь діє значна виштовхувальна сила Архімеда, яка і зменшує його вагу.

 

Мал.30. У воді камінь легший аніж в повітрі, і це пов’язано з виштовхувальною дією сили Архімеда.

Нагадаємо. Сила Архімеда – це та сила, з якою тіла виштовхуються з рідин та газів і яка дорівнює вазі виштовхнутої тілом рідини або газу.

Позначається: F_a

Визначальне рівняння: F_a=ρVg, де ρ – густина рідини (газу); V- об’єм зануреної в рідину (газ) частини тіла;  g-прискорення вільного падіння;

Одиниця вимірювання: [F_a] = H.

Звичайно, коли тіло знаходиться в рідині, то завжди можна сказати, що рідина є певною не жорсткою опорою для тіла. З одного боку це правда, – рідину дійсно можна вважати певною не жорсткою об’ємною опорою для тіла. Скажімо, коли тіло вільно плаває в рідині і не тисне на тверду опору, то це зовсім не означає, що воно знаходиться в стані невагомості. Просто діюча на тіло сила тяжіння зрівноважується відповідною силою Архімеда, яка для цього тіла фактично є не жорсткою, об’ємною реакцією опори.

Однак з іншого боку, щоб ми не говорили, а будь яка жорстка опора на якій висить, лежить чи стоїть тіло, неодмінно зафіксує, що вага тіла у воді значно менша аніж у повітрі. Тому, якщо вага, це та сила з якою тіло діє на  опору, а опора, це те що жорстко обмежує рух тіла, то потрібно визнати, що вага залежить не тільки від сили тяжіння та сили інерції, а й від діючої на тіло сили Архімеда.

Іноді можна почути, як старші школярі провокативно запитують своїх молодших колег: “що важче, кілограм заліза чи кілограм пір’я?” І коли ті відповідають що залізо важче, – дружно сміються, хизуючись своєю кмітливістю. І потрібно сказати, сміються абсолютно безпідставно. Адже кілограм заліза дійсно важчий за кілограм пір’я. Звичайно за умови, що мова йде саме про кілограм, тобто про масу в 1000,00г.

Обґрунтовуючи тезу про те, що кілограм заліза важчий за кілограм пір’я, вати, пінопласту чи дерева, розв’яжемо наступну задачу.

Задача.  Визначити на скільки тона заліза (ρ=7800кг/м³) важча за тону дерева (ρ=500кг/м³). Густина повітря ρ=1,3кг/м³.

Дано:                                   Аналіз:

m₁=m₂=1000,00кг     Оскільки за визначенням, вага тіла

ρ₁=7800кг/м³        чисельно дорівнює реакції відповідної

ρ₂=500кг/м³        опори (Р₁=N₁; Р₂=N₂), то рішення задачі

ρ = 1,3кг/м³            полягає у визначенні цих реакцій.

Виходячи з цього, розглянемо ті сили

ΔP = P₁ – P₂ = ?      що діють на залізне (1) та дерев’яне (2)

тіло і визначимо відповідні реакції опор.

Із умов рівноваги тіл випливає:

N₁= F_т – F_a1 = m₁g – ρV₁g = m₁g – ρm₁g/ρ₁ = m₁g(1 – ρ/ρ₁) ;

N₂ = F_т – F_a2 = m₂g – ρV₂g = m₂g – ρm₂g/ρ₂ = m₂g(1 – ρ/ρ₂) .

Таким чином:   N₁ = m₁g(1 – ρ/ρ₁) ;   N₂ = m₂g(1 – ρ/ρ₂) .

Розрахунки:  P₁ = N₁ = … = 9798,4H;

P₂ = N₂ = … = 9774,5H.

ΔP = P₁ – P₂ = 23,9H

Відповідь:  тона заліза на 23,9Н важча за тону дерева (за умови, що визначення ваги відбувається в повітряному середовищі).

Таким чином, теорія стверджує що тона заліза на 23,9Н важча за тону дерева. Причина появи цієї різниці очевидна – на більш об’ємне дерево діє більша сила Архімеда і тому його вага виявляється дещо меншою (В умовах нашої задачі F_a1 = 1,6H;  F_a2 = 25,5H;  ΔF_a = 23,9H).

Чому ж ми вважаємо, що тона заліза і тона дерева мають однакову вагу? Більше того, якщо ми дійсно зважимо реальну тону заліза і реальну тону дерева, то скоріш за все ця вага виявиться однаковою. І справа не втому, що точність вимірювальних приладів не дозволяє зафіксувати наявну різницю ваги. Справа в іншому – цієї різниці просто не існує. Не існує тому, що зазвичай масу тіла ми визначаємо шляхом зважування. І як ви розумієте, це зважування відбувається в повітряному середовищі. А це означає, що в реальній тоні дерева фактично не 1000,0кг а приблизно 1002,4кг. поява цієї різниці знову ж таки обумовлена дією сили Архімеда.  Адже для того, щоб залізне і дерев’яне тіло зрівноважили одне одне, маса дерев’яного тіла має бути дещо більшою за масу залізного. Більшою на ту величину яка дозволяє компенсувати надлишкову силу Архімеда (в умовах нашої задачі Δm=2,4кг).

Таким чином, якщо кілограм пір’я і кілограм заліза мають однакову вагу, то це тільки тому, що фактична маса пір’я дещо більша за кілограм. Якщо ж ми дійсно візьмемо кілограм заліза і кілограм пір’я, то вага заліза буде більшою за вагу пір’я. Звичайно за умови, що процес зважування відбувається в повітряному середовищі.

На завершення скажемо декілька узагальнюючих слів про чотири сили, які часто плутають одна з одною та застосовують не за призначенням. Ситуація ускладнюється ще й тим, що в багатьох випадках числові значення цих сил є однаковими. Тому, фактично не правильно застосувавши сили, ви можете отримати формально правильну відповідь і заслужено не задовільну оцінку.

Мова йде про силу тяжіння (F_т), вагу (P), реакцію опори (N) та силу пружності (F_пр). Нагадаємо. Сила тяжіння (F_т) – це та сила з якою тіло притягується до Землі. Вага (P) – це та сила з якою тіло діє на опору. Реакція опори (N) – це та сила з якою опора діє на тіло. Сила пружності (F_пр) – це та сила яка виникає в пружно деформованому тілі і яку протидіє цій деформації.

Із визначень ясно, що коли ми говоримо про ті сили які діють на тіло (мал.29) то ними є сила тяжіння (F_т) та реакція опори (N). Якщо ж мова йде про ті сили які діють на опору,  то ними є вага тіла (P) та виникаюча в опорі сила пружності (F_пр).

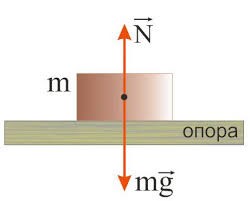
Мал.31. На тіло діє сила тяжіння та  реакція опори. На опору діє вага тіла та сила пружності.

Словник фізичних термінів.

Вага – це та сила з якою тіло діє на опору.

Позначається: Р

Визначальне рівняння: Р = – N  , де N – реакція опори

Одиниця вимірювання: [P] = H ,          (ньютон).

Невагомість – це такий стан системи опора – тіло, при якому тіло та його окремі елементи не мають ваги, тобто не тиснуть на опору і одне на одне. Не мають ваги тому, що діюча на них сила тяжіння зрівноважується відповідною силою інерції.

Сила Архімеда – це та сила, з якою тіла виштовхуються з рідин та газів і яка дорівнює вазі виштовхнутої тілом рідини або газу.

Позначається: F_a

Визначальне рівняння: F_a=ρVg, де  ρ- густина рідини (газу); V- об’єм зануреної в рідину (газ) частини тіла;  g-прискорення вільного падіння;

Одиниця вимірювання: [F_a] = H.

Контрольні запитання.

1.Чому вагу тіла та відповідну їй реакцію опори вважають діючою та протидіючою силами?

2.Чому рівняння Р=mg не можна вважати визначальним рівнянням ваги?

3.Чи правильні твердження: а) на тіло діє його вага; б) на опору діє сила тяжіння тіла; в) на тіло діє сила пружності опори? Сформулюйте ці твердження правильно.

4.Залізне і дерев’яне тіла однакових розмірів знаходяться у воді. При цьому, залізне тіло лежіть на дні посудини, а дерев’яне плаває. Чи однакові сили Архімеда діють на ці тіла? Поясніть.

5.Тіло кинули вертикально вгору. Коли тіло перебуває в стані невагомості: а) тільки в верхній точці польоту; б) тільки підчас руху вниз; в) тільки підчас руху вгору; г) протягом всього вільного польоту?

6.Чому на Землі тіло в процесі вільного падіння, перебуває не в стані абсолютної а лише наближеної невагомості?

Вправа 5.

1.Прямокутна баржа довжиною 10м і шириною 4м після завантаження осіла на 50см. Визначити масу взятого на борт вантажу.

2.Ліфт рівноприскорено розганяється до швидкості 7м/с за 5с. За такий же час він і зупиняється. Визначити вагу людини масою 80кг на ділянках розгону та зупинки ліфта.

3.Яка вага тіла масою 40кг в точках А і В якщо R₁=20м, v₁=10м/с, R₂=10м, v₂=5м/с. малюнок.

4.Тіло плаває у воді занурюючись при цьому на 3/4 свого об’єму. Яка густина речовини тіла?

 

 

Лекційне заняття №11.

Тема: Механічні деформації. Сила пружності. Механічна напруга. Закон Гука. 

         Будь яку зміну форми або розмірів тіла, що відбувається під дією зовнішніх чи внутрішніх механічних сил, називають механічною деформацією тіла (від лат. deformatio – викривлення). Наприклад, якщо ви згинаєте, скручуєте чи розтягуєте лінійку, то відповідна деформація є механічною. Механічною, вважають і ту деформацію яка виникає в процесі обертального руху тіла і поява якої обумовлена дією сили інерції. Наприклад, та деформованість Земної кулі яка обумовлена фактом її обертання навколо своєї осі, є механічною.

За реакцією тіла на припинення дії деформуючої сили, механічні деформації поділяються на пружні та пластичні. Пружною називають таку механічну деформацію, яка повністю зникає після припинення дії деформуючої сили. Пластичною називають таку механічну деформацію, яка після припинення дії деформуючої сили зберігається (залишається). Іншими словами, якщо після припинення дії деформуючої сили, тіло повністю відновлює свою попередню форму, то його деформація була пружною. Якщо ж, після припинення дії деформуючої сили, тіло зберігає надану йому форму, то його деформація є пластичною. На практиці часто зустрічаються ситуації в яких, після припинення дії деформуючої сили, тіло відновлює попередню форму (розміри) лише частково. В цьому випадку говорять про пружно-пластичну деформацію тіла.

За характером діючих на тіло деформуючих сил та за характером тих геометричних змін що відбуваються в деформованому тілі, все різноманіття пружних механічних деформацій прийнято розділяти на чотири різновидності:

– деформація розтягнення-стиснення (мал.32а,б) ;

– деформація згинання (мал.32д) ;

– деформація кручення (мал.32г) ;

– деформація зсуву (мал.32в)

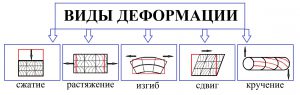
Мал.32.  Геометрична суть основних видів пружних механічних деформацій.

В межах програми загальноосвітньої школи, вивчають параметри та закономірності лише однієї різновидності механічної деформації тіл – пружну деформацію розтягнення-стиснення. Однак ви маєте знати, що з певними термінологічними поправками, ці параметри і закономірності притаманні будь якій різновидності пружної деформації та для будь якої комбінації цих різновидностей.

Характеризуючи геометричні та силові параметри не деформованого та пружно деформованого тіла, говорять про наступні величини (мал.33):

– початкова довжина тіла                      ℓ₀                (м);

– площа поперечного перерізу тіла    S                (м²) ;

– абсолютна деформація тіла               ∆ℓ= ℓ – ℓ₀   (м);

– відносна деформація тіла                   ε = ∆ℓ/ℓ₀     (-);

– деформуюча сила                                 F                  (Н);

– сила пружності                                      F_пр = -k∆ℓ    (Н);

– жорсткість тіла                                      k = F/∆ℓ       (Н/м);

– модуль пружності                                 E = σ/ε          (Па);

– механічна напруга                               σ = F_пр/S        (Н/м²=Па).

Мал.33.    Пружно деформоване тіло та його характеристики.

Абсолютна деформація – це фізична величина, яка характеризує абсолютну деформацію тіла і яка дорівнює цій деформації, тобто тому  видовженню (вкороченню) тіла, яке воно отримує під дією деформуючої сили.

Позначається:  ∆ℓ

Визначальне рівняння:  ∆ℓ=ℓ-ℓ₀

Одиниця вимірювання:  [∆ℓ] = м .

Відносна деформація – це фізична величина, яка характеризує відносну (порівняльну) деформацію тіла і яка дорівнює відношенню абсолютної деформації тіла до його початкової довжини .

Позначається:  ε

Визначальне рівняння:  ε=∆ℓ/ℓ₀

Одиниця вимірювання:  [ε]= м/м= – , (рази)

Деформуюча сила – це та зовнішня сила, дія якої призводить до пружної деформації тіла.

Позначається:  F

Визначальне рівняння: визначається умовою конкретної задачі

Одиниця вимірювання: [F]=H

Сила пружності – це та внутрішня сила, яка виникає в пружно деформованому тілі і яка завжди протидіє появі та зростанню цієї деформації.

Позначається:  F_пр

Визначальне рівняння:  F_пр = -k∆ℓ

Одиниця вимірювання:  [F_пр] =H

   

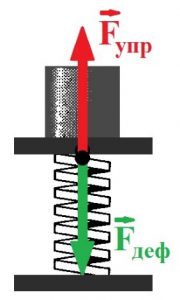
Мал.34. Сила пружності завжди протидіє деформуючій силі.

Жорсткість тіла – це фізична величина, яка характеризує пружні властивості даного конкретного тіла і яка дорівнює відношенню тієї сили що деформує тіло до величини отриманої  при цьому абсолютної деформації.

Позначається:  k

Визначальне рівняння:  k=F/∆ℓ

Одиниця вимірювання:  [k]=H/м.

Потрібно зауважити, що жорсткість тіла, тобто та величина яка визначається за формулою k=F/∆ℓ, фактично не залежить ні від величини деформуючої сили F, ні від величини отриманої при цьому абсолютної деформації ∆ℓ . Жорсткість тіла, залежить від параметрів самого тіла, зокрема від:1) пружних властивостей того матеріалу, з якого виготовлено тіло (ці властивості характеризує величина яка називається модулем пружності,  позначається Е. Значення цієї величини визначається експериментально і записується у відповідну таблицю);  2)  площі поперечного перерізу тіла S ; 3) початкової довжини тіла ℓ₀. Цю залежність можна записати у вигляді  k=ES/ℓ₀.

Механічна напруга – це фізична величина, яка характеризує внутрішній механічний стан пружно деформованого тіла і яка дорівнює відношенню виникаючої в тілі сили пружності до величини його площі поперечного перерізу.

Позначається: σ

Визначальне рівняння: σ=F_пр/S

Одиниця вимірювання:  [σ]=H/м²=Па, (паскаль).

Основний закон механіки пружно деформованого тіла був експериментально встановлений в 1660 році англійським фізиком Робертом Гуком (1635-1703). В цьому законі (законі Гука) стверджується: при пружних деформаціях тіла, величина його абсолютної деформації (∆ℓ), пропорційна діючій на нього деформуючій силі F. Іншими словами: ∆ℓ=F/k , де  k – жорсткість тіла, величина якої визначається експериментально, або за формулою k=ES/ℓ₀ .

Мал.35.  Абсолютна деформація тіла (ΔƖ), прямо пропорційна деформуючій силі (F) – закон Гука .

Вище наведене формулювання закону Гука є безумовно правильним, очевидно простим та історично автентичним. Однак в сучасній науці цей закон прийнято формулювати по іншому: при пружних деформаціях тіла, величина виникаючої в ньому механічної напруги σ, пропорційна його відносній деформації ε. Іншими словами: σ=Еε , де Е – модуль пружності (модуль Юнга), постійна для даного матеріалу величина, значення якої визначається експериментально і записується у відповідну таблицю.

На перший погляд, формули ∆ℓ=F/k  і  σ=Еε  є абсолютно різними. Насправді ж, ці формули математично тотожні. Дійсно. Враховуючи що

k=ES/ℓ₀;  ε=∆ℓ/ℓ₀;  σ=F_пр/S;  F_пр=F, можна записати:

∆ℓ= F/k = F_пр/(ES/ℓ₀) = F_прℓ₀/ES = σℓ₀/E.  Звідси   σ = E∆ℓ/ℓ₀ = Eε .

Ви можете запитати: “А чому в сучасній науці, закон Гука прийнято записувати не у вигляді ∆ℓ=F/k, а у вигляді σ=Eε ?”. Пояснюючи такий стан речей, розглянемо декілька простих ситуацій. Припустимо, що у вашому розпорядженні є два гумових (E₁=E₂) стержні, однакової площі поперечного перерізу (S₁=S₂), але різної довжини, скажімо ℓ₁=10см, ℓ₂=100см (мал.36). Припустимо, що кожен з цих стержнів ви розтягнули (деформували) на одну і ту ж абсолютну величину, наприклад на 10см (∆ℓ₁ = ∆ℓ₂ = 10см ). Запитується, чи однаковою є ступінь деформованості цих стержнів? Відповідь очевидна – ні не однаковою. Адже для першого стержня (ℓ₁ = 10см) абсолютна деформація величиною в 10см є відносно великою, тоді як для другого стержня та ж деформація є відносно малою. Висновок: абсолютна деформація (∆ℓ) не є тією величиною яку об’єктивно і повно характеризує деформованість тіла. В цьому сенсі, більш об’єктивною величиною є відносна деформація (ε=∆ℓ/ℓ₀), яка чітко вказує, що ступінь деформованості першого тіла (ε₁=1) в десять разів більша за ступінь деформованості другого тіла (ε₂=0,1).

 

 

Мал.36.  Абсолютні деформації тіл однакові (∆ℓ₁=∆ℓ₂), а ступені їх                              деформованості – різні.

Тепер уявіть, що два гумових (E₁=E₂) стержні, однакової довжини(ℓ₁=ℓ₂) але різної площі поперечного перерізу (скажімо S₁=1см², S₂=10см²), навантажені однаковими силами (F₁=F₂), наприклад по 100Н кожна (мал.37). Запитується, чи можна за величиною тієї сили пружності що виникає в тілі (за величиною деформуючої сили) об’єктивно оцінити внутрішній механічний стан пружно деформованого тіла? Відповідь очевидна – ні не можна. Адже для першого стержня (S₁=1см²), сила в 100Н є відносно великою, тоді як для другого стержня (S₂=10см²) – відносно малою. Висновок: виникаюча в тілі сила пружності не є тією величиною, яка в повній мірі об’єктивності, характеризує внутрішній механічний стан пружно деформованого тіла. В цьому сенсі більш об’єктивною величиною є механічна напруга (σ=F_пр/S). Адже механічна напруга чітко вказує на те, що внутрішній механічний стен першого тіла (σ₁=100Н/см²) в десять разів більш напружений аніж другого (σ₂=10Н/см²).

 

 

Мал.37.   Сили пружності однакові, а внутрішні механічні стани деформованих тіл – різні.

Не важко бачити, що ті величини які фігурують в першому формулюванні закону Гука (∆ℓ=F/k), є такими, що не в повній мірі об’єктивності характеризують як ступінь деформованості тіла, так і його внутрішній механічний стан. Натомість, ті величини які фігурують в другому формулюванні цього закону (σ=Еε) характеризують ті ж параметри пружно деформованого тіла більш об’єктивно та повно. Додайте сюди факт того, для визначення жорсткості (k=ES/ℓ₀) кожного тіла, потрібні певні індивідуальні експериментальні або теоретичні дослідження, тоді як модуль пружності (E), це певна таблична величина – і ви зрозумієте чому в сучасній науці та інженерній практиці, закон Гука записують не у вигляді ∆ℓ=F/k, а у вигляді  σ=Еε. До речі, той розділ прикладної механіки в основі якого лежить практичне застосування закону Гука (σ=Еε) називають опором матеріалів (сопроматом)

Словник фізичних термінів.

Механічною деформацією тіла – називають будь яку зміну форми або розмірів тіла, що відбувається під дією зовнішніх чи внутрішніх механічних сил.

Пружна деформація – це така механічна деформація тіла, яка повністю зникає після припинення дії деформуючої сили.

Пластична деформація – це така механічна деформація тіла, яка після припинення дії деформуючої сили зберігається.

Відносна деформація – це фізична величина, яка характеризує відносну (порівняльну) деформацію тіла і яка дорівнює відношенню абсолютної деформації тіла до його початкової довжини .

Позначається:  ε

Визначальне рівняння:  ε=∆ℓ/ℓ₀

Одиниця вимірювання:  [ε]= м/м= – , (рази)

Сила пружності – це та внутрішня сила, яка виникає в пружно деформованому тілі і яка завжди протидіє появі та зростанню цієї деформації.

Позначається:  F_пр

Визначальне рівняння:  F_пр = -k∆ℓ

Одиниця вимірювання:  [F_пр] =H

Механічна напруга – це фізична величина, яка характеризує внутрішній механічний стан пружно деформованого тіла і яка дорівнює відношенню виникаючої в тілі сили пружності до величини його площі поперечного перерізу.

Позначається: σ

Визначальне рівняння: σ=F_пр/S

Одиниця вимірювання:  [σ]=H/м²=Па , (паскаль).

Закон Гука (перше формулювання) – це закон, в якому стверджується: при пружних деформаціях тіла, величина його абсолютної деформації (∆ℓ) пропорційна величині діючої на нього деформуючої сили (F): ∆ℓ=F/k .

Закон Гука (друге формулювання) – це закон, в якому стверджується: при пружних деформаціях тіла, величина виникаючої в ньому механічної напруги (σ) пропорційна його відносній деформації (ε):  σ=Еε .

Контрольні запитання.

1.Які деформації виникають в: а) в ніжках стола, б) перекинутій через канаву дошці, в) в папері який розрізають ножицями?

2.Чим схожі і чим відрізняються деформуюча сила та сила пружності?

3.Яку деформацію називають пружно-пластичною?

4.Від чого залежить жорсткість тіла?

5.Чому в сучасній науці закон Гука прийнято записувати не у вигляді ∆ℓ=F/k, а у вигляді σ=Еε?

6.Чому табличною величиною є не жорсткість тіла , а модуль пружності?

                   Вправа 6.

1.Під дією сили 1кН стержень діаметром 1см подовжився на 1мм. Яка жорсткість цього стержня та виникаюча в ньому механічна напруга?

2.До закріпленої одним кінцем дротини діаметром 2мм підвісили вантаж масою 10кг. Визначити виникаючу в дротині силу пружності та механічну напругу.

3.Жорсткість дротини k. Чому дорівнюватиме жорсткість половини цієї дротини?

4.Яка максимальна механічна напруга виникає в вертикально висячому мідному стержні під дією власної ваги? Як залежить ця напруга від а) діаметру стержня; б) маси стержня; в) довжини стержня?

5.На дротині довжиною ℓ висить вантаж масою m. Дротину склали вдвічі і підвісили той же вантаж. Порівняйте абсолютні та відносні деформації дротин в цих двох випадках. Порівняйте їх жорсткості.

 

Лекційне заняття №12.

Тема: Чи завжди 2 + 2 = 4? Або, про додавання векторних величин.

         Фізичні величини поділяються на скалярні та векторні. Наприклад, час (t), маса (m), площа (S), об’єм (V), густина (ρ), температура (T), енергія (E), робота (A), потужність (P) – величини скалярні. Натомість, сила (F), швидкість (v), прискорення (a), переміщення (s), імпульс (p) – величини векторні.

Скалярними називають такі фізичні величини, які характеризуються лише числовим значенням, тобто лише своєю абсолютною величиною.

Векторними називають такі фізичні величини, які характеризуються як величиною так і напрямком в просторі (в вибраній системі координат).

Наприклад, маса тіла (m) характеризується лише числовим значенням (величиною) і тому є величиною скалярною. А та сила (F) що діє на тіло, характеризується як числовим значенням (модулем), так і напрямком дії і тому є величиною векторною.

Векторна величина позначається відповідною буквою з стрілочкою над нею, або буквою написаною жирним шрифтом (F,v,a,s,p). При цьому, якщо в тій чи іншій ситуації, векторна величина позначається буквою без стрілочки або буквою написаною не жирним шрифтом (F,v,a,s,p), то це означає, що мова йде лише про числове значення відповідної величини.

Наприклад, визначальне рівняння сили пружності буде записано у вигляді F_пр= – k(∆ℓ) . Це означає, що дане рівняння відповідає на два питання: 1) яка величина сили пружності: F_пр=k(∆ℓ) ; 2) куди направлена ця сила: сила пружності направлена в сторону протилежну від напрямку вектора ∆ℓ. Натомість, визначальне рівняння сили тертя буде записано в вигляді F_тер=µN. Це означає що дане рівняння відповідає лише на одне питання: яка величина сили тертя (F_тер=µN). На питання ж про те, куди направлена ця сила, має відповідати певна додаткова інформація. Наприклад така: сила тертя протидіє взаємному переміщенню контактуючих поверхонь.

Векторні та скалярні величини суттєво відрізняються в багатьох відношеннях і перш за все тим, що арифметичні дії над ними виконуються по різному. Наприклад, якщо до тіла масою 3кг (m₁=3кг) додати тіло масою 2кг (m₂=2кг), то в результаті ми отримаємо тіло загальною масою 5кг, тобто: m₁+m₂=3кг+2кг=5кг . Якщо ж на тіло (мал.38) діють дві сили F₁=3H i F₂=2H  , то результат їх загальної дії (F₁+F₂) буде залежати від того, як направлені ці сили. При цьому, в загальному випадку F₁+F₂ не дорівнює F₁+F₂ :

F₁+F₂ ≠  F₁+F₂ .

 

 

Мал.38.  Результат додавання векторів залежить не лише від їх величин, а й від їх відносної орієнтації. При цьому, в загальному випадку F₁+F₂≠F₁+F₂.

Розрізняють два методи додавання векторних величин: геометричний (графічний) та алгебраїчний (аналітичний). При геометричному методі, результат додавання векторів отримують шляхом відповідних геометричних побудов. Ці побудови здійснюють так званим методом багатокутника. Суть цього методу гранично проста. Якщо на точку А (мал.39) діє система N векторів, то величину і напрям результуючого вектора (F_р = F₁+F₂+ … +F_N) визначають наступним чином. З точки А відкладають вектор F₁ , з кінця вектора F₁ відкладають вектор F₂ , з кінця вектора F₂ – вектор F₃ і так до останнього вектора F_N . Вектор, який з’єднує точку А з кінцем останнього вектора і буде результуючим вектором  F_р = F₁+F₂+ … +F_N .

 

Мал.39. Величину та напрям результуючого вектору визначають методом багатокутника ( геометричне додавання векторів).

Геометричний метод додавання векторів виглядає досить простим та наочним. Однак, він має ряд суттєвих недоліків. Перший полягає в тому, що точність його результатів залежить від масштабу та точності геометричних побудов. При цьому, будь яка точність цих побудов, не гарантує безумовно точного результату. Другим суттєвим недоліком геометричного методу додавання векторів є факт того, що таке додавання погано поєднується з тими теоріями, в яких закони представляються у вигляді певних математичних формул. А переважна більшість фізичних теорій є саме такими.

Ці недоліки відсутні в алгебраїчному методі додавання векторів, тобто такому методі при якому результат додавання визначають не шляхом геометричних побудов, а шляхом алгебраїчних розрахунків. Реалізуючи цю ідею, вектор F розкладають на дві складові: проекції цього вектора на осі системи координат F_x та F_y. Наприклад, вектор F₁ (мал.40) розкладають на F_x1=4Н і F_y1=2Н ; вектор F₂ розкладають на F_x2= -4Н і F_y2=1Н ; вектор F₃ – на  F_x3=0Н , F_y3= -3Н .

 

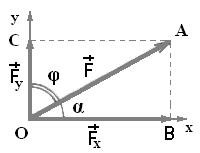
Мал.40.   Будь який вектор можна геометрично розкласти на дві складові – його проекції на осі системи координат.

По суті, проекції вектора на осі системи координат також є векторами. Однак, враховуючи факт того, що направлені вздовж однієї прямої вектори, додаються як скалярні величини, можна стверджувати: проекції вектора на осі системи координат, мають властивості скалярних величин. Тому в подальшому, ці проекції ми будемо вважати скалярними величинами, тобто такими які характеризуються лише величиною і знаком (“+” якщо напрям проекції співпадає з додатним напрямком відповідної осі; “ – “ якщо ці напрямки протилежні).

Проекції вектора на осі прямокутної системи координат можна визначити не лише шляхом геометричних побудов, а й шляхом алгебраїчних розрахунків. Ці розрахунки полягають в наступному.  Якщо в заданій прямокутній системі координат (мал.41) вектор F має числову величину F та кутову орієнтацію α , то проекції цього вектора на осі системи координат визначаються за формулами : F_x=Fcosα ; F_y=Fsinα . З іншого боку, за відомими проекціями вектора F_x і F_y , можна визначати як величину F так і кутову орієнтацію α відповідного вектора F . При цьому:

F=(F_x² + F_y²)^1/2 ;  tgα=F_y/F_x  ;   α=arctg(F_y/F_x)

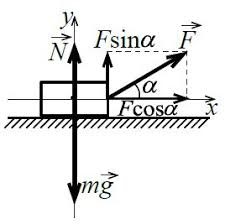
Мал.41.  Будь який вектор F(F,α) можна представити у вигляді двох по суті скалярних величин: F_x=Fcosα ;  F_y=Fsinα .

Таким чином, будь який вектор F з параметрами F,α , можна представити у вигляді двох по суті скалярних величин – проекцій даного вектора на осі відповідної системи координат:  F_x=Fcosα,  F_y=Fsinα . І навпаки: за цими величинами (F_x , F_y), алгебраїчно визначити параметри базового вектора: F=(F_x² + F_y²)^1/2;  α=arctg(F_y/F_x). Власне ці обставини і лежать в основі алгебраїчного методу додавання векторів. А суть цього методу полягає в наступному. Якщо на точку А діє система N векторів, то величину і напрям результуючого вектора

F_р = F₁ + F₂ + … + F_N  визначають наступним чином:

1.Кожний вектор системи розкладають на його проекції.

2.Визначають суму проекцій всіх векторів на кожну з осей системи координат:

F_xр= F_x1 + F_x2 + … +F_xn ;

F_yр= F_y1 + F_y2 + … + F_yn  .

3.Визначають величину F_р та напрям α результуючого вектора:

F_р=(F_xр² + F_yр²)^1/2,

α = arctg(F_yр/F_xр) .

Практична реалізація алгебраїчного методу додавання векторів не може бути успішною без розуміння фізичної суті того, що називають синусом і косинусом кута. В математиці ці функції зазвичай визначають наступним чином. Синусом гострого кута α прямокутного трикутника називають відношення протилежного катета а до гіпотенузи с: sinα=a/c. Косинусом гострого кута α прямокутного трикутника називають відношення прилеглого катета b до гіпотенузи с : cosα=b/c.

 

       

·                   cosα=b/c                                                     cosα=F_x/F

·                    sinα=a/c                                                     sinα=F_y/F

мал.42.  Синус та косинус кута можна визначити як: а) певні співвідношення між сторонами прямокутного трикутника; б) певні співвідношення між вектором та його проекціями на осі системи координат.

З формальної точки зору, вище сформульовані визначення (cosα=b/c ; sinα=a/c) є правильними. Однак вони мають ряд суттєвих недоліків. По-перше, дозволяють визначати синуси та косинуси лише гострих кутів, тоді як ці функції мають певні значення для будь яких кутів, будь-то 30°; 60°; 135° чи 5784°. По-друге, не пояснюють факту того, чому значення косинусів та синусів можуть бути як додатними так і від’ємними. По-третє, не пояснюють факту того, чому дані функції є періодичними. І головне, вище наведені визначення не розкривають фізичного змісту тих функцій які називаються синусом та косинусом кута. А цей зміст полягає в тому, що дані функції дозволяють переходити від векторних обчислень до скалярних і навпаки.

Дійсно. Для того щоб перейти від геометричного додавання векторів до відповідного алгебраїчного додавання, кожен з цих векторів розкладають на дві фактично скалярні величини: проекції даного вектора на осі прямокутної системи координат:   F_x=Fcosα; F_y=Fsinα .  При цьому функції  cosα та sinα  по суті визначаються як відношення відповідних проекцій вектора до його загальної довжини:  cosα=F_x/F; sinα=F_y/F .

З формально математичної точки зору, визначальні рівняння сosα=b/c; sinα=a/c  (мал.42а) та сosα=F_x/F; sinα=F_y/F  (мал.42б), є тотожними. Однак з фізичної точки зору, векторний спосіб визначення даних тригонометричних функцій є очевидно більш загальним. Більш загальним по-перше тому, що є справедливим не лише для гострих кутів, а й для кутів будь якої величини (в тому числі для α=5784°). По-друге, чітко визначає в яких випадках значення тригонометричних функцій є додатним, а в яких від’ємним. По-третє, чітко пояснює факт періодичності тригонометричних функцій. В четвертих, визначає функції cosα та sinα як такі, що забезпечують перехід від векторних обчислень до скалярних і навпаки.

Крім цього, якщо виходити з того, що базовий радіус-вектор має одиничну довжину, а та вісь прямокутної системи координат від якої вимірюють кут α є віссю косинусів, а їй перпендикулярна вісь – віссю синусів, то можна дати наступі визначення. Косинус кута α – це безрозмірна величина, яка дорівнює проекції відповідного цьому куту одиничного радіус-вектора на вісь косинусів. Синус кута α – це безрозмірна величина, яка дорівнює проекції відповідного цьому куту одиничного радіус-вектора на вісь синусів.

         Дані визначення мають ту очевидну перевагу, що дозволяють визначати величини та знаки відповідних тригонометричних функцій шляхом прямого вимірювання довжини. При цьому стають очевидними не лише динаміка залежності значень тригонометричних функцій від величини відповідного кута, а й ті загальні співвідношення що існують між самими функціями.

Ілюструючи механізм практичного застосування вище сформульованих визначень, розв’яжемо конкретну задачу.

Задача. Шляхом прямих вимірювань, визначити синуси та косинуси наступних кутів: 0°;30°;45°;60°;90°;120°;135°;150°;180°.

Загальне зауваження. Визначаючи синус та косинус кута α, потрібно мати на увазі, що та вісь від якої вимірюють (відкладають) цей кут є віссю косинусів, а їй перпендикулярна вісь – віссю синусів.

Рішення.  В вибраній системі координат, циркулем проводимо напівколо максимально великого радіусу і приймаємо величину цього радіусу за одиницю. З застосуванням транспортира та лінійки, почергово відкладаємо потрібні кути та проводимо відповідні одиничні радіус-вектори. З кінців цих векторів опускаємо перпендикуляри на осі системи координат і враховуючи масштаб побудов, вимірюємо довжини відповідних проекцій. Величини та знаки цих довжин і є значеннями відповідних функцій. Результати вимірювань записуємо в таблицю. Порівнюємо ці результати з відповідними табличними (точними) значеннями. (Ясно, що точність отриманих вами результатів визначальним чином залежатиме від точності та масштабу геометричних побудов і вимірювань).

Мал. 43 Синус та косинус довільного кута можна визначити як проекції відповідного цьому куту одиничного радіус-вектора на осі прямокутної системи координат.

 

α	0°	30°	45°	60°	90°	120°	135°	150°	180°
cosα	1,00	0,87	0,71	0,50	0,00	– 0,50	– 0,71	– 0,87	– 1,00
sinα	0,00	0,50	0,71	0,87	1,00	0,87	0,71	0,50	0,00

З фізичної точки зору, векторно-проекційний спосіб визначення тих тригонометричних функцій які називаються синусом та косинусом кута, є очевидно більш загальним. Більш загальним по-перше тому, що є справедливим не лише для гострих кутів, а й для кутів будь якої величини (в тому числі для α=5784°). По-друге, чітко визначає в яких випадках значення тригонометричних функцій є додатним, а в яких від’ємним. По-третє, пояснює факт періодичності тригонометричних функцій. В четвертих, визначає функції cosα та sinα як такі, що забезпечують перехід від векторних обчислень до скалярних і навпаки. В п’ятих, дозволяє визначати величини та знаки відповідних тригонометричних функцій шляхом прямого вимірювання довжини. В шостих, робить очевидними ті співвідношення, які в математиці називаються формулами приведення і які зазвичай є предметом банального зазубрювання: cos(90º-α) = sinα;      sin(90º-α) = cosα

cos(90º+α) = – sinα;   sin(90º+α) = cosα

cos(180º-α) = – cosα;  sin(180º-α) = sinα  і т.д.

Потрібно зауважити, коли ми стверджуємо: проекції вектора F на осі прямокутної системи координат визначаються за формулами: F_x=Fcosα; F_y=Fsinα, то маємо на увазі, що кут α відкладено від осі 0х. Адже якщо наприклад, положення цього вектора охарактеризувати не кутом α, а кутом φ=90º-α (мал.34а), то в цьому випадку відповідні проекції потрібно визначати за формулами F_x=Fsinφ;  F_y=Fcosφ. І не важко довести, що загальний результат в обох випадках буде однаковим: F_x=Fsinφ=Fsin(90-α)=Fcosα; F_y=Fcosφ= Fcos(90-α)=Fsinα.

Доречно зауважити і те, що на практиці кутову орієнтацію вектора в заданій системі координат, задають кутом меншим за 90º. Наприклад в зображеній на мал.34д ситуації, положення вектора F характеризують не кутом α>90º, а йому відповідним кутом β=180º-α < 90º. Крім цього, проекції тих векторів, що є паралельними або перпендикулярними осям системи координат (мал.34.в,г), визначають із міркувань очевидності: наприклад, в ситуації мал.34в: F_x=F; F_y=0; мал.34г: F_x=0; F_y=−F.

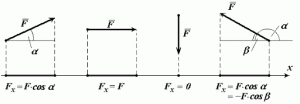
Мал.44. Визначаючи параметри проекцій вектора, потрібно враховувати від якої осі і в якому напрямку виміряно той кут, що характеризує положення відповідного вектора.

Словник фізичних термінів.

          Скалярними називають такі фізичні величини, які характеризуються лише числовим значенням, тобто лише своєю абсолютною величиною.

         Векторними називають такі фізичні величини, які характеризуються як величиною так і напрямком в просторі (в вибраній системі координат).

         Косинус кута α – це безрозмірна величина, яка дорівнює проекції відповідного цьому куту одиничного радіус-вектора на вісь косинусів, тобто ту вісь від якої виміряно кут α.

Синус кута α – це безрозмірна величина, яка дорівнює проекції відповідного цьому куту одиничного радіус-вектора на вісь синусів, тобто ту вісь що є перпендикулярною до осі косинусів.

Вправа 7.

1.Визначте проекції векторів на осі системи координат. Числові значення векторів однакові: F₁=F₂=F₃=5H. Задачу розв’язати геометричним та алгебраїчним методом. Отримані результате порівняйте. (мал. а, б, в, г )

 

2.За заданими проекціями векторів F_x i F_y, визначте їх числове значення та кутову орієнтацію. Задачу розв’язати геометричним та алгебраїчним методом

а)   F_x = 3,5H ;    F_y = 3,5H .                  б)   F_x = -5,0H ;   F_y = 0,0H

в)    F_x = -2,5H ; F_y = -4,3H .                 г)    F_x = 3,0H ;   F_y = -5,2H .

д)     F_x = 0,0H ; F_y = -4,0H .                ж)    F_x =2,8H ;    F_y = -2,8H .

3.Методом геометричних побудов, визначте синуси та косинуси кутів від 0° до 180°, з інтервалом 15°. Отримані результати порівняйте з відповідними табличними значеннями.

 

Лекційне заняття №13.

Тема: Розв’язування задач статики.

Задачі статики мають ту перевагу, що зазвичай, порядок (алгоритм) їх розв’язку є досить чітко визначеним. І цей порядок полягає в наступному.

1. На основі аналізу умови задачі виконати малюнок (обов’язково), на якому чітко вказати всі діючі на задане тіло (матеріальну точку) сили та напрямки цих сил (ці напрямки визначаються відповідними кутами).

2.Оптимальним чином задати систему координат.

3.Записати умову рівноваги даної матеріальної точки, тобто систему рівнянь:

.                            ∑F_x=0;

.                            ∑F_y=0.

4.Розв’язавши цю систему, визначити невідомі величини.

Загальні зауваження. При розв’язуванні задач: 1) Діючу на абсолютно тверде тіло силу, можна переносити вздовж лінії її дії. 2) Силу можна переносити вздовж гнучкого зв’язку (канат, ланцюг, дріт, тощо).

Дотримуючись вище наведеного алгоритму розв’язку та враховуючи вище зазначені зауваження, розв’яжемо декілька конкретних задач.

Задача 1. Тіло масою 20кг на дротах підвішено так, як показано на малюнку (α=30º). Визначити зусилля в дротах 2 і 3.

 

Дано:                               Аналіз

m = 20кг

α = 30º                         Малюнок

N₂=?

N₃=?

Виконуємо малюнок, на якому вказуємо діючі на точку рівноваги сили та задаємо систему координат. Записуємо умову рівноваги системи.

∑F_x = -N₂ + N₃sin30º= 0

∑F_y = -F_T + N₃cos30º= 0.

Розв’язавши систему рівнянь, визначаємо невідомі величини:

із (2) → N₃cos30º = F_T = mg; → N₃ = mg/cos30º = 20∙10/0,87= 230H;

із (1) → N₂ = N₃sin30º = 230∙0,5= 115H.

Відповідь: N₂ = 115H; N₃ = 230H.

         Задача. До кронштейну АВС в т.В підвішено вантаж масою m=60кг, так як це показано на малюнку (α=30º). Визначити зусилля в стержнях АВ і СВ.

Загальні зауваження. В задачах статики, часто зустрічаються ситуації коли точний напрямок реакції опори не відомий або сумнівний. Наприклад, в нашій задачі стержень СВ явно “працює” на стиснення і тому його реакція N_C   має бути направленою вздовж лінії СВ в напрямку від точки С. Стержень же АВ, явно “працює” на розтягнення і тому його реакція N_A має бути направленою вздовж лінії АВ в напрямку до точки А. Однак припустимо, що ви сумніваєтесь стосовно того в яку сторону направлена та чи інша реакція. В цьому випадку сміливо направляйте сумнівну реакцію в будь яку можливу сторону (вздовж лінії стержня) і розв’язуйте задачу. При цьому, якщо в результаті рішення задачі, невідома реакція матиме знак “+”, то це означатиме, що вибраний вами напрямок є правильним. Якщо ж ця реакція виявиться зі знаком “ ̶ “ то це означатиме, що насправді відповідна реакція має протилежний (протилежний від вибраного) напрямок. Перевіряючи вище сказане направимо реакцію N_c в гарантовано неправильному напрямку.

Дано:                         Аналіз:

m=60кг

α=30°                       Малюнок

N_А= ?

N_С= ?

Виконуємо малюнок на якому: вказуємо діючі на т.В сили; задаємо систему координат; вказуємо кутову орієнтацію сил. Оскільки кут α=30º безпосередньо не прилеглий до т.В, то із геометричних міркувань визначаємо йому відповідний та прилеглий до т.В кут. Наприклад із факту того, що в прямокутному трикутнику АВС сума кутів дорівнює 180º, випливає, що прилеглий до т.В кут β=60º

Записуємо умову рівноваги точки В і, розв’язавши систему відповідних рівнянь, визначаємо невідомі величини.

∑ F_x = N_A + N_C cos60º = 0              (1)

∑ F_y = N_C sin60º + mg = 0               (2)

із (2)→ N_C = – mg/sin60º = – (60∙10/0,87)= -690 Н

із (1)→ N_A = -N_Ccos60º = – (-690)0,5 = 345 Н

Знак “-“ вказує на те, що реакція N_C фактично направлена в протилежну (протилежну від зображеної на малюнку) сторону.

         Задача 3. Тіло масою 10кг під дією сили тяжіння знаходиться в стані механічного спокою на похилій площині. Визначити величини діючих на тіло сил, якщо кут нахилу площини до лінії горизонту 30°.

Зауваження. Рішення будь якої задачі механіки, в тій чи іншій мірі ідеалізоване. Наприклад в умовах нашої задачі, ті сили які ми називаємо реакцією опори та силою тертя, виникають в місті контакту тіла з відповідною поверхнею і є розподіленими по цій поверхні. Ми ж зображаємо ці сили такими, що сконцентровано прикладені до центру мас тіла. До речі, те ж стосується і сили тяжіння, дія якої фактично розподілена по всьому об’єму тіла і яку ми зображаємо такою, що діє в центрі мас цього тіла.

Дано:                     Аналіз:

m = 10кг

α =30°                    Малюнок

N = ?

F_тер = ?

Виконуємо малюнок на якому: вказуємо діючі на тіло (на центр мас тіла) сили; задаємо систему координат; вказуємо кутову орієнтацію сил. Записуємо умову рівноваги тіла і, розв’язавши систему відповідних рівнянь, визначаємо невідомі величини. ( F_т = mg = … =100H )

∑ F_x = – F_тер + F_т sinα = 0       (1)

∑ F_y = N – F_т cosα = 0            (2).

Із (1) → F_тер = F_т sinα .

Із (2) → N = F_т cosα .

Розрахунки:     F_тер = 100∙0,5 = 50Н

N = 100∙0,87 = 87H

Відповідь: N = 87H;  F_тер = 50H.

Ілюструючи важливість ефективного вибору системи координат, розв’яжемо ту ж задачу в ситуації, коли система координат задана так би мовити звичним чином: вісь 0х – горизонтальна, вісь 0y – вертикальна.

На основі аналізу малюнку записуємо умову рівноваги тіла і, розв’язавши систему відповідних рівнянь, визначаємо невідомі величини.

∑ F_x = – F_терcosα + Nsinα = 0              (1)

∑ F_y = Ncosα + F_тер sinα – F_т  = 0         (2).

Із (1) → Nsinα = F_терcosα, звідси N = F_терcosα/sinα.

Отриманий результат підставляємо в рівняння (2):

(F_терcosα/sinα)cosα + F_терsinα – F_т = 0, або

F_тер(cosα²/sinα + sinα) = F_т = mg, звідси

F_тер = mg/(cosα²/sinα + sinα).

Розрахунки:

F_тер = 10∙10/((0,87²/0,5)+0,5) = 100/2 = 50Н;

N = 50∙0,87/0,5 = 87Н.

Відповідь: N = 87H;  F_тер = 50H.

Задача 4. Куля масою 20кг розташована між двома площинами так, як зображено на малюнку. Визначити діючі на кулю реакції опори.

 

 

Дано:                                       Аналіз

m=20кг

Малюнок

N_А=?

N_В=?

Загальні зауваження. Зазвичай, оптимальність введення системи координат полягає в тому, що бодай одна з осей цієї системи, має співпадати з напрямком невідомої сили.(В цьому випадку бодай одне з рівнянь умови рівноваги тіла, міститиме лише одну невідому величину, що значно полегшує математичне рішення системи рівнянь). Однак в багатьох випадках, проблеми з визначенням кутів між силами та «оптимально» введеними осями координат, значно більші за ті проблеми які пов’язані з математичним рішенням системи рівнянь. Прикладом такого випадку є дана задача.

Зважаючи на вище сказане, а також на те, що реакція опори між кулею та площиною проходить через центр кулі, виконуємо малюнок на якому: вказуємо діючі на центр мас кулі сили; задаємо систему координат; вказуємо кутову орієнтацію сил та записуємо рівняння умови рівноваги тіла.

∑F_x= -N_Bsin30º + N_Asin30º=0;

∑F_y= N_Bcos30º + N_Acos30º – F_T=0.

із (1) → N_Asin30º = N_Bsin30º → N_A = N_B;

із (2) → 2N_Acos30º = F_T = mg; → N_A=mg/2cos30º = 20∙10/2∙0,87=115H

Відповідь: N_A=N_B=115H.

Вправа 8.

1.В зображених на мал. а, б, в ситуаціях, визначити реакції опор. а) m=20кг, α=30º, β=60º; б) m=40кг, α=30º; в) m=30кг, β=45º;

2.Куля масою 30кг знаходиться між двома взаємно перпендикулярними площинами (дивись мал.). Визначити діючі на кулю реакції опори.

3.На двох тросах однакової довжини висить вантаж масою 50кг. При цьому кут між тросами 60º. Визначити сили натягу тросів.

4.Канат загальною довжиною ℓ закріплено в двох горизонтально розташованих точках. До середини канату підвісили вантаж масою m. На яку висоту Δh опуститься при цьому точка підвісу вантажу, якщо виникаюча в канаті сила натягу дорівнює Т.

5. Однорідна куля масою m і радіусом R підвішена на нитці довжиною ℓ до гладенької вертикальної стіни. Визначити силу натягу нитки та силу тиску кулі на стіну (тертям між кулею та стіною знехтувати).

 

Лекційне заняття №14.

Тема: силовий метод розв’язування задач динаміки.

 

Загальні зауваження. Фізика загалом і механіка зокрема, це єдиний цілісний організм всі частини якого, взаємопов’язані та взаємопереплетені. Тому, коли ми ділимо механіку на кінематику, статику та динаміку, то робимо це досить умовно. Скажімо, на даний момент ми вивчаємо тему, яка називається “статика”. Тобто ту тему в якій вивчають параметри, закономірності та причини стану механічної рівноваги тіл (v=0 або v=const). В цій темі основною фізичною величиною є сила, а основним законом – умова механічної рівноваги тіла.

З іншого боку, однією з найважливіших сил механіки є сила інерції, тобто та сила, поява якої обумовлена прискореним рухом тіла.  Формально, ті задачі в яких тіло під дією певної системи сил рухається з прискоренням, є задачами динаміки. Однак ці силові задачі динаміки є органічним продовженням та доповненням задач статики. По суті, мова йде про пласт фактично одних і тих же задач. І розв’язувати ці задачі в відриві одна від одної є не доцільним та методологічно не правильним. Тому ті ситуації, в яких тіло під дією певної системи сил рухається з прискоренням, ми будемо розглядати не лише в динаміці, а й в статиці.

За великим рахунком є два базові методи розв’язування задач динаміки: силовий та імпульсно-енергетичний. Про суть та можливості імпульсно-енергетичного методу ми поговоримо в найближчому майбутньому. Наразі ж, мова піде про силовий метод розв’язування задач динаміки. Суть цього методу дуже проста: на основі аналізу діючих на тіло сил (втому числі і сили інерції), та на базі умови його динамічної рівноваги (якщо а=const, то ∑F+F_i=0) визначаються невідомі величини.

Задача 1. З яким прискоренням рухається брусок похилою площиною кут нахилу якої 30°, якщо коефіцієнт тертя 0,2?

.                      

Дано:                     Аналіз:

α=30°

µ=0,2                  Малюнок

а=?

Виконуємо малюнок на якому: вказуємо всі діючі на тіло сили (сила тяжіння, реакція опори, сила тертя, сила інерції); задаємо систему координат; вказуємо кутову орієнтацію сил.

Записуємо умову динамічної рівноваги тіла і, розв’язавши систему відповідних рівнянь, визначаємо невідому величину.

∑F_х = − F_тер − F_і + F_т sinα = 0        (1)

∑F_у = N – F_т cosα = 0                     (2)

Враховуючи, що: F_тер =µN,  F_і = ma,  F_т = mg,  можна записати

− µN − ma + mgsinα = 0,  звідси ma = mgsinα − µN .

Враховуючи, що згідно з рівнянням (2)

N = F_т cosα = mgcosα,  отримаємо

ma = mgsinα − µmgcosα,  звідси

a = g(sinα − µcosα).

Розрахунки:   а = … = 3,2м/с².

Відповідь:  а = 3,2м/с².

Задача 2. Пілот літака виконує так звану «петлю Нестерова», яка представляє собою вертикальну колову траєкторію (мал.60). З якою силою пілот тисне на сидіння літака (на опору) у верхній та нижній точках «петлі Нестерова», якщо швидкість літака 360км/год, а радіус петлі 200м? Маса пілота 80кг.

.       

Дано:                   СІ                      Аналіз

m = 80кг               –

v = 360км/год    100м/с              Малюнок

R = 200м               –

P₁ = ?

P₂ = ?

В процесі руху по колу на пілота діють три сили:

1) Сила тяжіння F_т = mg.

2) Реакція опори N тобто та сила з якою опора діє на пілота і яка чисельно дорівнює тій силі Р з якою пілот діє на опору: N = Р.

3) Сила інерції поява якої обумовлена фактом того, що рухаючись по колу, тіло рухається з певним доцентровим прискоренням а = v²/R, якому відповідає певна сила інерції: F_i = mv²/R.

При цьому, у верхній та нижній точках траєкторії, вище згадані сили діють вздовж вертикалі 0у. Зважаючи на це, запишемо умову рівноваги тіла (пілота) для верхньої (1) і нижньої (2) точок траєкторії та визначимо з цієї умови невідому величину Р₁ = N₁; P₂ = N₂.

1) ∑F_y = F_i – F_т – N₁= 0, звідси випливає:

N₁ = F_i – F_т = mv²/R – mg = 80(100²/200 – 10) =3200Н

2) ∑F_y = − F_i – F_т + N₂= 0, звідси випливає:

N₂ = F_i + F_т = mv²/R + mg = 80(100²/200 + 10) =4800Н

Відповідь: Р₁ = 3200Н; Р₂ = 4800Н.

Потрібно зауважити, що ту силу Р з якою тіло діє на опору, називають вагою тіла. Про суть та особливості цієї сили ми поговоримо в §27. Наразі ж зауважимо, що за звичайних умов, вагу тіла прийнято визначати за формулою Р = mg. Скажімо за звичайних умов вага тіла масою 80кг становить 800Н. А це означає, що в умовах попередньої задачі, вага того пілоту який виконує «петлю Нестерова» у верхній точці петлі збільшується у 3200/800=4 рази, а в нижній точці, збільшується в 4800/800=6 разів.

Задача 3. З якою максимальною швидкістю може їхати мотоцикліст горизонтальною дорогою, описуючи дугу радіусом 90м, якщо коефіцієнт тертя коліс об дорогу 0,4? Під яким кутом відносно вертикалі має нахилятися мотоцикліст, забезпечуючи відповідну швидкість руху?

.                            

Загальні зауваження. Оскільки мотоцикліст з швидкістю v рухається по колу радіусу R, то він рухається з доцентровим прискоренням а=v²/R. А це означає, що на мотоцикліста (точніше, на систему мотоцикліст-мотоцикл) окрім трьох зовнішніх сил (сила тяжіння F_т=mg, реакція опори N та сила тертя F_тер) діє прикладена до центру мас системи сила інерції F_i= -ma.

Рухаючись по колу та прагнучи забезпечити механічну рівновагу системи, мотоцикліст має нахилятися на такий кут ? при якому рівнодійна реакції опори та сили тертя Q = N + F_тер проходить через центр мас системи мотоцикліст-мотоцикл. Інакше, діючі на систему сили будуть створювати певний обертальний момент сил, наявність якого призведе до падіння мотоцикліста.

Факт того, що рівнодійна реакції опори та сили тертя проходить через центр мас системи мотоцикліст-мотоцикл, по суті означає, що динамічна рівновага цієї системи забезпечується трьома діючими на центр мас системи силами: сила тяжіння F_т=mg, сила інерції F_i=mv²/R та рівнодійна реакції опори і сили тертя Q = N + F_тер.

Зважаючи на вище сказане, розв’яжемо нашу задачу.

Дано:                      Аналіз

R = 90м

μ = 0,4                   Малюнок

v_м = ?

α_м = ?            Максимальну швидкість руху мотоцикла (v_м) заокругленням горизонтальної дороги та їй відповідний кут нахилу мотоцикла (α_м), можна визначити із наступних міркувань.

1) Діюча на систему мотоцикліст-мотоцикл сила інерції F_i=mv²/R має бути не більшою за ту максимальну силу тертя, що виникає між дорогою та колесами мотоцикла. Іншими словами: F_i ≤ F_т, або mv²/R ≤ μmg. А це означає, що та швидкість з якою може рухатись мотоцикліст заокругленням горизонтальної дороги, має задовільняти умові v² ≤ μgR або v ≤ (μgR)^1/2. При цьому максимальне значення цієї швидкості становить: v_м = (μgR)^1/2. В умовах нашої задачі: v_м = (0,4·9,8·90)^1/2=18,8м/с.

2) Оскільки для забезпечення динамічної рівноваги системи, рівнодіюча реакції опори (N) та сили тертя (F_тер) Q = N + F_тер має проходити через центр мас системи мотоцикл-мотоцикліст, то кут нахилу цієї системи відносно вертикалі, має дорівнювати куту між векторами N i Q. Виходячи з цього можна записати:

N = Qcosα;

F_тер = Qsinα.

Звідси випливає, що Qsinα/Qcosα = F_тер/N, або tgα = F_тер/N.

Таким чином, величину кута нахилу системи мотоцикл-мотоцикліст до вертикалі, можна визначити за формулою α = arctg(F_тер/N). При цьому, якщо мова йде про максимальне значення цього кута, тобто те значення при якому величина сили тертя є гранично великою (F_тер= μN), то в цьому випадку, α_м = arctg(F_тер/N) = arctg(μN/N) = arctgμ. В умовах нашої задачі α_м = arctg0,4=22°

Відповідь: v_м =18,8м/с; α_м =22°.

На завершення зауважимо, що заокруглені ділянки сучасних доріг мають певний нахил, який сприяє максимально безпечному руху транспорту на цих ділянках.

Задача 4. Через нерухомий блок перекинуто нитку до кінців якої прив’язано вантажі масою М=0,24кг кожний. На один з вантажів поклали тягарець масою m=10г. На якій вертикальній відстані один від одного будуть вантажі через 2с, якщо на початку руху вони перебували на одній висоті?

.                                  

Зауваження.  Нерухомий блок представляє собою легкий шків, що вільно обертається навколо нерухомої осі. Вважається, що рухомий шків не змінює натяг перекинутої через нього нитки (мотузки, канату, тощо). А це означає, що на ті тіла які знаходяться по обидва боки шківа діють однакові реакції опори (Т₁=Т₂) Зазвичай ту силу з якою нитка діє на тіло називають силою натягу нитки і позначають Т). За відсутності додаткової інформації, прийнято вважати, що маса рухомого шківа є нулевою, а тертя в його осі відсутнє.

Дано:         СІ                        Аналіз:

М=0,24кг        –

m =10г      0,01кг               Малюнок

t=2с                –

s =?

Під дією тієї додаткової сили тяжіння що діє на тіло масою m₁=M+m, це тіло буде опускатись з певним прискоренням а. При цьому тіло масою m₂=M з таким же прискоренням буде підніматись. А це означає, що дані тіла будуть віддалятись одне від одного з прискоренням 2а, і тому рівняння їх відносного руху можна записати у вигляді s=2at²/2=at².

Таким чином, задача зводиться до того, щоб визначити величину того прискорення з яким рухаються тіла. Вирішуючи цю задачу, виконуємо малюнок на якому вказуємо всі діючі на кожне тіло сили в тому числі і сили інерції. З аналізу малюнку, а по суті з умови динамічної рівноваги тіла,

випливає:  Т₁ = m₁g – m₁a = (M+m)g – (M+m)a,

Т₂ = m₂g + m₂a = Mg + Ma.

А оскільки  Т₁=Т₂ , то  Mg + Ma = (M+m)g – (M+m)a, або

Ma + (M+m)a = (M+m)g – Ma, або  a(2M+m) = mg.

Звідси  a = mg/(2M+m) .

Враховуючи що  s = at², можна записати s = [mg/(2M+m)]t².

Розрахунки:  s = … = 0,8м

Відповідь:  s = 0,8м

Задача5. На горизонтальному диску який обертається з кутовою швидкістю 4рад/с встановлено вертикальний стержень, до вершини якого прикріплена нитка з кулькою. На якій відстані від центру диску треба встановити стержень, щоб в процесі обертання диску, відхилення системи кулька-нитка становило 30° від вертикалі?

 

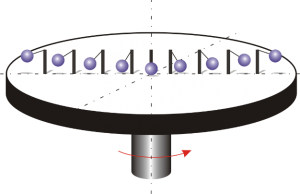
Дано:                              Аналіз

ω = 4рад/с

α = 30°                           Малюнок

l = ?

Розглянемо ті сили, що діють на кульку в процесі обертання диску. А цими силами є:

1) сила тяжіння F_т = mg (на малюнку Р);

2) сила натягу нитки Т;

3) виникаюча в процесі обертання системи сила інерції F_i=ma=mv²/?.

Оскільки лінійна швидкість (v) тіла що обертається, зв’язана з кутовою швидкістю його обертання (ω) співвідношенням v=ωl, то можна записати F_i=mv²/l=m(ωl)²/l=mω²l, звідси l= F_i/mω².

Визначаючи величину діючої на кульку сили інерції, запишемо рівняння умови динамічної рівноваги кульки в проекціях на осі системи координат.

∑F_x = F_i – Tsinα = 0;

∑F_y = Tcosα – F_т = 0.

Із (2) → Т = F_т/cosα = mg/cosα.

Із (1) → F_i = Tsinα = mgsinα/cosα = mgtgα.

Таким чином: l= F_i/mω² = mgtgα/mω² = gtgα/ω².

Розрахунки. l = gtg30°/4² = 10(м/с²)0,577/(4рад/с)² = 0,36м = 36см.

Відповідь: l = 36см.

Вправа 16.

1.При якому прискоренні розірветься трос міцність якого 10кН, якщо ним піднімають вантаж масою 500кг?

2. З якою швидкістю має рухатись автомобіль опуклою ділянкою дороги радіус кривизни якої 40м, щоб в верхній точці опуклості, тиск на дорогу дорівнював нулю?

3. Літак виконує “мертву петлю” радіусом 480м і рухається по ній з швидкістю 432км/год. З якою силою льотчик масою 85кг буде тиснути на сидіння літака: а) у верхній точці петлі, б) в нижній точці петлі?

4. На одному кінці нитки перекинутої через нерухомий блок, прив’язано вантаж масою m, а на другому – в двічі легший вантаж. З яким прискоренням рухаються вантажі?

5. Вантажі m₁ m₂ з’єднані ниткою перекинутою через блок (мал.). Маса вантажу m₁=2кг, кути α=30°, β=60°. Якою має бути маса m₂, щоб вантажі рухались з прискоренням 4м/с²? Тертям знехтувати.

6. Два вантажі масою 200г і 400г з’єднані ниткою перекинутою через блок, підвішений на пружинних терезах. Визначити прискорення вантажів, показання пружинних терезів та силу натягу нитки. Масою блока знехтувати.

7. З вершини похилої площини довжиною 10м і кутом нахилу 30° починає зісковзувати тіло. Визначити швидкість тіла вкінці спуску та тривалість спуску. Коефіцієнт тертя тіла об площину 0,1.