Сайт викладача фізики

Електродинаміка. частина 2.

РОЗДІЛ 3. ЕЛЕКТРОДИНАМІКА. частина 2.

         Тема 3.4. Електродинаміка магнітних явищ.

Лекційне заняття №35. Тема: Загальні відомості про магнітні явища. Теорія Ампера. Закон Ампера.

Лекційне заняття №36. Тема: Магнітне поле. Індукція магнітного поля.

Лекційне заняття №37. Тема: Сила Ампера та її застосування.

Лекційне заняття №38. Тема: Сила Лоренца та її застосування.

Лекційне заняття №39. Тема: Магнітний потік. Індуктивність. Котушка індуктивності. Узагальнююче повторення теми.

Лекційне заняття №40. Тема: Основи сучасної теорії магнітних властивостей речовини.

Семестр 3

Тема 3.5. Електромагнітні явища.

Лекційне заняття №1. Тема: З історії електромагнітної індукції. Закон електромагнітної індукції.

Лекційне заняття №2. Тема: Індукційний струм та його застосування. Індукційний генератор, трансформатор, електродвигун.

Лекційне заняття №3. Тема: Електродвигун змінного струму. Струми Фуко. Електричний скін-ефект.

Лекційне заняття №4. Тема: Змінний струм та його характеристики. Трифазна система струму.

Лекційне заняття №5. Тема: Резистори, конденсатори та котушки індуктивності в колі постійного та змінного струмів. Коливальний контур. Генератор високочастотних коливань.

Тема 3.6. Основи теорії електромагнітного поля.

Лекційне заняття №6. Тема: З історії теорії електромагнітного поля. Основи теорії Максвела.

Лекційне заняття №7. Тема: Основні передбачення теорії Максвела.

Лекційне заняття №8. Тема: Система радіозв’язку.

Лекційне заняття №9. Тема: Електродинаміка, узагальнююче повторення. Розв’язування задач.

.

Лекційне заняття №35.

Тема: Загальні відомості про магнітні явища. Теорія Ампера. Закон Ампера.

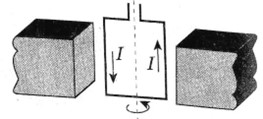
З незапам’ятних часів люди знали про те, що в природі зустрічаються дивні сріблясто чорні камінці, які певним чином взаємодіють між собою та притягують залізо. Ці природні мінерали у великій кількості зустрічались в околицях стародавнього міста Магнезія, що на території сучасної Туреччини. Тому ще за 600 років до нашої ери, один з засновників давньогрецької науки Фалес Мілетський назвав ці привезені з Магнезії камінці Magnitys litos – камінь з Магнезії. Згодом ця назва трансформувалась до звичного нам магніти. До речі, сьогодні  Magnitys litos ми називаємо магнетитом або магнітним залізняком (F₃O₄).

Магніти мали ще одну характерну особливість: маючи можливість вільно обертатись, вони завжди орієнтувались у певному напрямку, і цей напрямок практично співпадав з віссю південь – північ (мал.200). Цей факт було покладено в основу надзвичайно важливого навігаційного приладу – компасу. Хто автор цього видатного винаходу, достовірно невідомо. Відомо лише те, що про компас європейці дізнались від арабів.

   

Мал.200. Магнетит – природний магніт. Маючи можливість вільно обертатись магніт (магнітна стрілка) завжди орієнтується в певному напрямку.

Та якби там не було, а починаючи з 12-го століття, компас отримав широке застосування в навігаційній практиці. При цьому люди по суті не розуміли принцип дії компасу. Не розуміли суті магнітних явищ. Не розуміли, чому магніти діють на залізо і практично не діють на золото, срібло, мідь, деревину та інші матеріали. Лише в 1788 році, французький фізик Шарль Кулон зробив першу, більш-менш вдалу спробу створити теорію магнетизму. В основі теорії Кулона лежало твердження про те, що в магнетизмі як і в електриці існує два види магнітних зарядів і що полюси магнітів є зосередженням цих зарядів.

Теорія Кулона виглядала цілком логічною. Адже в електриці теорія різнойменних зарядів успішно пояснювала все різноманіття відомих електричних явищ. Тому було цілком логічним припустити, що і в схожих магнітних явищах, теорія різнойменних магнітних зарядів мала би працювати.

Та от біда. Те, що спрацьовувало в електриці не спрацьовувало в магнетизмі. Дійсно. Якщо різнойменні магнітні заряди існують, а північний і південний полюси магніту є місцями їх накопичення, то логічно передбачити, що при поділі магніту на дві рівні частини, на одній з них мав би бути певний надлишок «південних» зарядів, а на іншій – «північних». Здійснивши відповідний експеримент, ви неодмінно з’ясуєте, що дві половини магніту є новими магнітами, в кожному з яких є свої північний і південний полюси.

Ви можете скільки завгодно ділити магніт, вигадувати які завгодно технології цього поділу, але результат виявиться одним і тим же: будь які, навіть найдрібніші частинки магніту неминуче мають два полюси, розділити які не можливо. Цей експериментальний факт, явно суперечив теорії магнітних зарядів і безумовно вказував на те, що ця теорія хибна.

Мал.201. Розділити магнітні полюси не можливо – експериментальний факт.

Потрібно зауважити, що в часи Кулона вчені вважали, що електрика і магнетизм – це абсолютно різні, непов’язані явища. Лише в 1820 році сталася подія, яка кардинально змінила історію магнетизму. В цьому році данський фізик Ганс Крістіан Ерстед (1777–1851) експериментально встановив, що магнітна стрілка реагує не лише на присутність постійного магніту, а й на присутність електричного струму (мал.202). Це означало, що між електричними і магнітними явищами існує певний зв’язок, і що магнітну дію створюють не лише постійні магніти, а й електричні струми.

 

Мал.202.  Магнітна стрілка реагує не лише на присутність постійного магніту, а й на присутність провідника з струмом.

Існує студентська байка про те, що своїм відкриттям Ерстед має завдячувати одному уважному студенту. Згідно з цією байкою, професор Ерстед на одній з лекцій пояснював студентам загально прийняту на той час гіпотезу про те, що електрика і магнетизм, це абсолютно різні явища між якими нема жодного зв՚язку. А щоб його пояснення були більш переконливими, професор супроводжував їх наступними демонстраціями.

Ілюструючи суть магнетизму, Ерстед наближав постійний магніт до магнітної стрілки і та відповідним чином реагувала на це наближення. Потім говорячи про факт непов՚язаності магнітних та електричних явищ, Ерстед наголошував на тому, що магнітна стрілка на магніт реагує, а от на електричний струм – не реагує. І от коли професор включив електричний струм, магнітна стрілка ледь помітно відхилилась. При цьому говорять, що сам Ерстед даний факт не помітив. А от один з студентів звернув увагу професора на факт відхилення стрілки. Коли ж експеримент повторили, то з՚ясувалося що магнітна стрілка дійсно реагує на присутність електричного струму. А це означало що між електричними та магнітними явищами існує певний зв’язок.

Та як би там не було, а фактом залишається те, що в червні 1820 році данський фізик Ерстед опублікував невеличку статтю, в якій оприлюднив факт того, що магнітна стрілка реагує не лише на присутність постійних магнітів, а й на присутність електричних струмів. І що тому між електричними та магнітними явищами існує певний зв’язок.

Таким чином, на середину 1820 року наукові знання в сфері магнетизму представляли собою сукупність наступних експериментальних фактів:

1. Пепеважна більшість речовин, суттєвих магнітних властивостей не проявляють.
2. Потужні магнітні властивості мають лише так звані феромагнетики, до числа яких відносяться залізо, кобальт, нікель та деякі їх сполуки і сплави.
3. Магнітні властивості феромагнетиків можуть бути як активними (постійні магніти) так і пасивними (ненамагнічене залізо).
4. Постійні магніти мають два полюси (південний і північний), які взаємодіють між собою: однойменні полюси відштовхуються, різнойменні – притягуються.
5. Розділити магнітні полюси не можливо.
6. Магнітну дію створюють не лише постійні магніти, а й електричні струми.

Аналізуючи дані факти, французький фізик Анре Ампер (1775–1836) в кінці 1820 року створив першу, науково обгрунтовану теорію магнетизму. В основі теорії Ампера лежать два твердження: 1. Джерелом магнетизму (джерелом магнітного поля) є електричний струм. 2. В кожному тілі існують внутрішні «молекулярні» струми, які і надають цьому тілу відповідних магнітних властивостей.

Згідно з теорією Ампера, кожний «молекулярний струм» створює певну елементарну магнітну дію. При цьому, в залежності від просторової орієнтації цих елементарних дій (елементарних магнітів), тіло набуває відповідних магнітних властивостей. Скажімо, якщо елементарні магніти орієнтовані хаотично (мал.4а), то їх магнітні дії нівелюють одна одну і відповідне тіло магнітних властивостей не проявляє. Якщо ж елементарні магніти співнаправлені (мал.4б), то їх магнітні дії підсилюються і тіло має відповідні магнітні властивості.

Мал.203. В залежності від просторової орієнтації елементарних «молекулярних струмів», відповідне тіло має магнітні власчтивості (б), або не має їх (а).

Теорія Ампера дозволила аргументовано пояснити велике різноманіття відомих на той час магнітних явищ, в тому числі і факт неможливості розділення магнітних полюсів. Адже згідно з цією теорією, магнітні властивості створюють не зосереджені на полюсах різнойменні магнітні заряди, а ті процеси які відбуваються в кожній молекулі тіла і та просторова орієнтація яка цим процесам притаманна. І якщо в кожному фрагменті великого магніту, всі елементарні магніти (елементарні «молекулярні струми») орієнтовані в одному напрямку, то скільки б ми не ділили цей магніт, кожен його фрагмент буде відповідним магнітом.

Сьогодні, коли ви знаєте про будову атома і про те, що в атомі електрони обертаються навколо ядра, не важко збагнути, що тими «молекулярними» струмами про які говорив Ампер є ті мікро струми які створюють електрони в процесі їх обертання навколо ядра (мал.5). Ампер не знав і не міг знати про будову атома та про існування електронів. Його наукове передбачення, це результат аналізу експериментальних фактів та інтуіції видатного вченого.

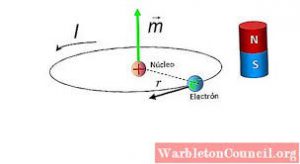
Мал.204. Процес обертання електрона навколо ядра атома еквівалентний певному мікроструму, який і надає атому відповідних магнітних властивостей.

Звичайно теорія Ампера ще не була тією теорією, яка дозволяла кількісно та безумовно доказово пояснити все різноманіття відомих магнітних явищ. Наприклад вона не могла пояснити, чому серед всього різноманіття речовин, потужні магнітні властивості мають лише так звані феромагнетики? Чому магнітні властивості феромагнетиків можуть бути як активними (постійні магніти) так і пасивними (ненамагнічене залізо)? Чому магнітні властивості феромагнетиків зберігаються лише до певної визначеної температури? Відповіді на ці та їм подібні запитання стали можнивими лише після створення сучасної квантової механіки.

Однак якщо говорити про загальну картину наукового пояснення причинно наслідкової суті магнітних явищ, то в цьому сенсі теорія Ампера була безумовно достовірною науковою теорією. Теорією яка з плином часу поступово вдосконалювалась та уточнювалась.

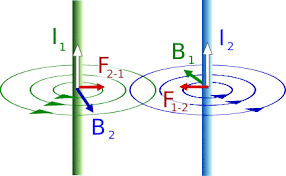
Ампер не лише пояснив фізичну суть магнітних взаємодій, а й зробив великий внесок в експериментальне дослідження цих взаємодій. Зокрема він експериментально встановив, що взаємодіють не лише полюси магнітів (однойменні полюси відштовхуються, різнойменні притягуються), а й електричні струми. При цьому, співнаправлені струми притягуються, а протинаправлені – відштовхуються.

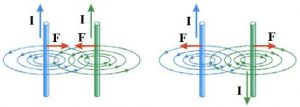
Мал.205. Співнаправлені струми притягуються, протинаправлені – відштовхуються.

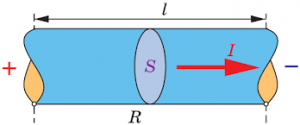
Подальші експериментальні дослідження Ампера показали, що сила магнітної взаємодії струмів залежить від величини цих струмів, відстані між ними, їх просторової орієнтації та довжини ділянки взаємодії. У підсумку Ампер сформулював закон, який прийнято називати законом Ампера. В цьому законі стверджується:

Електричні струми взаємодіють між собою: співнаправлені струми притягуються, протинаправлені – відштовхуються. При цьому, з боку безкінечно довгого, прямолінійного провідника з стумом І₁ на достатньо малий фрагмент струму І₂ діє магнітна сила F_м, величина якої визначається за формулою F_м=kI₁I₂∆ℓsinα/r, де

І₁, І₂ – величини взаємодіючих струмів;

∆ℓ – довжина ділянки взаємодії струмів;

r – відстань між струми;

α – кут який характкризує взаємну орієнтацію струмів;

k – коефіцієнт пропорційності, величина якого залежить від властивостей того середовища в якому знаходяться взаємодіючі струми.

.

α = 90º                               α = 30º                           α = 0º

sinα=1                               sinα=0,71                      sinα=0

F_м=max                            F_м=0,71max                   F_м= 0

Мал.206. З боку струму І₁ на будь який достатньо малий фрагмент струму І₂∆ℓsinα діє магнітна сила, величина якої визначається за формулою F_м=kI₁I₂∆ℓsinα/r.

Відразу ж зауважимо, що загально прийняте визначення кута α буде сформульовано дещо пізніше. Наразі ж порсто констатуємо те, що для паралельних струмів sinα=1, при цьому F_м=kI₁I₂∆/r=max, якщо ж струми І₁, І₂ перпендикулярні, то sinα=0, при цьому F_м=0.

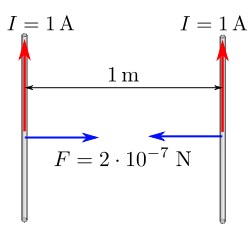
Експерементально встановлено, що для вакууму, величина коефіцієнту пропорційності в законі Ампера становить k=k₀=2∙10^–7Н/А². Це означає, що у вакуумі два паралельних (sinα=1) провідники з струмом по одному амперу кожний (І₁=І₂=1А), розташованих на відстані 1м (r=1м), на ділянці взаємодії 1м (Δℓ=1м), взаємодіють з силою F_м=2∙10^–7Н. Іншими словами: якщо І₁=І₂=1А; r=1м; Δℓ=1м; sinα=1, то у вакуумі F_м=2∙10^–7Н=0,0000002Н

Залежність коефіцієнту k від магнітних властивостей того середовища в якому знаходяться взаємодіючі струми, можна передставити у вигляді k=μk₀, де μ – магнітна проникливість середовища.

Магнітна проникливість середовища, це фізична величина, яка характеризує магнітні властивості даного середовища і яка показує, у скільки разів сила магнітної взаємодії стумів в даному середовищі (F) більша за силу їх взаємодії у вакуумі (F₀).

Позначається: μ

Визначальне рівняння: μ = F/F₀

Одиниця вимірювання: [μ]=H/H= – ,  (рази).

Для переважної більшості матеріалів μ≈1. Це означає, що магнітні властивості цих матеріалів майже не відрізняються від магнітних властивостей вакууму. Лише для так званих феромагнетиків, до числа яких відносяться залізо (Fe), кобальт (Co), нікель (Ni) та деякі їх сплави, магнітна проникливість середовища вимірюється сотнями, тисячами та десятками тисяч одиниць. Наприклад для кобальту μ=175, для нікелю μ=1100, для заліза μ=8000, а для сплаву який називається пермалой-68 (68%Ni + 32%Fe) μ=250000.

Факт того, що феромагнетики в тисячі разів підсилють магнітну дію струмів, має надзвичайно важливе практичне значення. Адже по суті, магнітні сили не є надто потужними (k₀=2∙10^–7Н/А²). І якщо ці малопутужні сили мають широке практичне застосування, то це тільки тому, що в природі є матеріали які потужно підсилюють магнітну дію струмів. І нам надзвичайно пощастило, що такі матеріали існують, і що на Землі цих матеріалів (зокрема заліза та нікеля) достатньо багато.

З точки зору зручності вивчення закону Ампера, було б доцільним та логічно обгрунтованим, постійну величину k₀=2∙10^–7Н/А², на ряду з гравітаційною сталою G=6,67∙10^–11Н·м²/кг², віднести до числа фундаментальних фізичних сталих. При цьому, було б не менш доцільним та обґрунтованим, представляти залежність сили магнітної взаємодії струмів від властивостей того середовища яке ці струми оточує, у вигляді k=μk₀.

Однак, те що виглядає доцільним з точки зору окремо взятого закону, не завжди співпадає з тією доцільністю яку диктує вся сукупність законів електродинаміки. А ця загально електродинамічна доцільність вимагає, щоб залежність сили магнітної взаємодії струмів від властивостей того середовища яке ці струми оточує, записували не у вигляді k=μk₀, де k₀=2∙10^–7Н/А², а у вигляді k=μμ₀/2π, де μ₀=2πk₀=12,56∙10^–7Н/А² – постійна величина яка називається магнітною сталою.

Та як би там не було, а ви маєте знати, що сила магнітної взаємодії струмів, певним чином залежить від магнітних властивостей того середовища яке ці струми оточує. І що цю залежність можна записати у вигляді: k=μk₀, де k₀=2∙10^–7Н/А², або k=μμ₀/2π, де μ₀=2πk₀=12,56∙10^–7Н/А².

Закон Ампера на ряду з законом Кулона та закону всесвітнього тяжіння, відноситься до тих базових законів Природи які описують відповідно магнітні, електричні та гравітаційні взаємодії. Загальну порівняльну інформацію про ці закони можна представити у вигляді:

 

F_гр=Gm₁m₂/r²                      F_ел=kq₁q₂/r²                       F_м=kI₁I₂∆ℓsinα/r

G₀=6,67∙10^–11Н∙м²/кг²        k₀=9∙10⁹Н∙м²/Кл²              k₀=2∙10^–7Н/А²

G = G₀                                     k=k₀/ε=1/4πεε₀                 k=μk₀=μμ₀/2π

Оскільки ті коефіцієнти які фігурують в законі всесвітнього тяжіння (G₀=6,67∙10^–11Нм²/кг²), законі Кулона (k₀=9∙10⁹Нм²/Кл²) та законі Ампера (k₀=2∙10^–7Н/А²), по суті характеризують питому величину відповідної сили, то можна стверджувати, що в масштабі загально прийнятої системи одиниць (кілограм – метр – секунда – ампер) магнітні сили є набагато слабшими за електричні але значно потужнішими за гравітаційні: F_гр < F_м << F_ел .

Не важко бачити, що формула F_м=kI₁I₂∆ℓsinα/r є значно складнішою за математичні формулювання законів Кулона та всесвітнього тяжіння. Пояснюючи даний факт можна сказати наступне. В законі Кулона та законі всесвітнього тяжіння, мова йде про взаємодії точкових зарядів і точкових мас. А для таких взаємодій, ні розміри, ні просторова орієнтація взаємодіючих об’єктів не мають значення. В законі ж Ампера, мова йде про взаємодію електричних струмів, тобто об’єктів які не можуть бути точковими. А це означає, що описуючи відповідні взаємодії, потрібно враховувати як лінійні розміри взаємодіючих струмів, так і їх просторову орієнтацію. Тому в законі Ампера і фігурують відповідні характеристики струмів: ∆ℓ – довжина ділянки взаємадії, α – кут який характеризує взаємну орієнтацію струмів.

На завершення додамо, що вище наведене формулювання закону Ампера F_м=kI₁I₂∆ℓsinα/r є дещо спрощеним. Спрощеним в тому сенсі, що в ньому розглядається не загальний випадок взаємодії струмів, а ситуація в якій безкінечно довгий прямолінійний провідник з струмом І₁, взаємодіє з безкінечно коротким фрагментом струму І₂. Втім, формула F_м=kI₁I₂∆ℓsinα/r дозволяє визначати не лише величину тієї сили що діє на окремий фрагмент провідника, а й на увесь провідник вцілому. Для цього провідник розбивають на певну кількість (N) достатньо малих ділянок. За формулою F_м=kI₁I₂∆ℓsinα/r визначають величину тієї магнітної сили що діє на кожну з цих ділянок. А результуючу силу визначають як векторну суму відповідних елементарних сил: F_м=∑(∆F)_i.

Безумовним доказом достовірності закону Ампера та формули F_м=kI₁I₂∆ℓsinα/r є факт того, що саме на основі цього закону та цієї формули сформульовано сучасне офіційне визначення тієї базової одиниці електродинамічних величин, яка називається ампером. Ось це офіційне визначення. Ампер – це одиниця вимірювання сили струму, яка дорівнює величині такого постійного струму, який при проходженні через два паралельні прямолінійні провідники безкінечної довжини і гранично малої площі круглого поперечного перерізу, розташованих у вакуумі на відстані 1м, створюють на кожній ділянці провідника довжиною 1м силу взаємодії 2∙10^–7Н.

Контрольні запитання.

1. В чому суть теорії Кулона і який факт явно суперечив цій теорії?
2. Що було відомо про магнітні явища на середину 1820 року?
3. Що стверджується в теорії Ампера?
4. Як теорія Ампера пояснювала факт того що деякі матеріали мають магнітні властивості, а інші – таких властивостей не мають?
5. Чи є факт взаємодії магнітних полюсів та електричних струмів, результатом дії кулонівських сил? Чому?
6. Від чого залежить сила магнітної взаємодії струмів?
7. На основі аналізу закону всесвітнього тяжіння F_гр=Gm₁m₂/r², поясніть фізичний зміст коефіцієнту G₀=6,67∙10^–11Н∙м²/кг².
8. На основі аналізу закону Кулона F_ел=kq₁q₂/r² поясніть фізичний зміст коефіцієнту k₀=9∙10⁹Нм²/Кл².
9. На основі аналізу закону Ампера F_м=kI₁I₂∆ℓsinα/r поясніть фізичний зміст коефіцієнту k₀=2∙10^–7Н/А².
10. Чому математичне формулювання закону Ампера є складнішим за аналогічне формулювання законів Кулона та всесвітнього тяжіння?
11. Поясніть, чому відносно слабкі магнітні сили, мають широке практичне застосування?

.

Лекційне заняття №36.

Тема: Магнітне поле та його характеристики.

Дослідження показують, що подібно до електричних та гравітаційних взаємодій, магнітні взаємодії здійснюються через особливий матеріальний посередник який називається магнітним полем, і що механізм цих взаємодій полягає в наступному. Будь який електричний струм створює в навколишньому просторі певне силове збурення цього простору, яке називається магнітним полем і яке є тим матеріальним посередником який передає силову дію від одного струму до іншого і навпаки.

Магнітне поле має одну визначальну властивість – здатність певним чином діяти на електричні струми (на заряди що рухаються). Це означає, що для з’ясування факту того, є в даній точці простору магнітне поле чи нема, в цю точку потрібно внести певний пробний струм (пробну магнітну стрілку) і подивитись на його реакцію (поведінку). При цьому, якщо на пробний струм не подіє магнітна сила, то це означатиме, що у відповідній точці простору поля нема. А якщо така сила подіє – значить поле є.

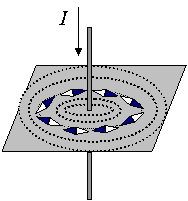
Мал.207. Для визначення факту того, є в даній точці простору магнітне поле чи нема, у відповідну точку потрібно внести пробний струм (пробну магнітну стрілку) і подивитись на його поведінку.

Таким чином, магнітне поле – це таке поле, тобто таке силове збурення простору, яке створюється електричними струмами (зарядами що рухаються) і діє на електричні струми. Коли ми стверджуємо – магнітні поля створюються електричними струмами і діють на електричні струми, то маємо на увазі, що цими струмами можуть бути не лише провідники з струмом, а й ті внутрішні струми які існують в феромагнітних та інших тілах, а також ті струми які характеризують рух окремо взятої зарядженої частинки.

Варто зауважити, що з практичної точки зору, в якості того індикатора який реагує на наявність магнітного поля, зручно брати не маленький фрагмент провідника з струмом, а маленьку магнітну стрілку. Однак з точки зору теоретичних пояснень, такий індикатор не є вдалим. Адже зазвичай, ми не знаємо кількісних параметрів тих внутрішніх струмів які надають стрілці відповідних магнітних властивостей. Тому кількісно описуючи магнітні поля, в якості чутливого до них індикатора зазвичай обирають певний пробний струм, який характеризується певною величиною (І_п), певною довжиною (∆ℓ) та певною орієнтацією в просторі (α).

Мал.208. Описуючи параметри магнітного поля в якості індикатора поля беруть маленький пробного струму, який характеризується певною величиною (І_п), довжиною (Δℓ) та просторовою орієнтацією (α)

Згідно з законом Ампера, величина тієї магнітної сили (F_м), що діє на пробний струм в даній точці поля, залежить не лише від параметрів цього поля, а й від параметрів самого пробного струму: F_м=kII_п∆ℓsinα/r =ƒ(І_п∆ℓsinα). А це означає, що за наявністю діючої на пробний струм сили, можна стверджувати лише те, що у відповідній точці простору поле є. Але за величиною цієї сили не можливо сказати, яке це поле – «сильне» чи «слабке». Адже вносячи в одну і ту ж точку поля пробні струми різної величини, різної довжини та різної просторової орієнтації, ви отримуватимете різні значення діючих на ці струми сил. Зважаючи на ці обставини, магнітні поля характеризують не тією силою що діє на пробний струм в тій чи іншій точці поля, а величиною яка називається магнітною індукцією.

Магнітна індукція – це фізична величина, яка є силовою характеристикою магнітного поля і яка дорівнює скалярному відношенню тієї магнітної сили (F_м) що діє на пробний струм в даній точці поля, до добутку тих величин, які цей струм характеризують (І_п∆ℓsinα).

Позначається: В

Визначальне рівняння: В=F_м/І_п∆ℓsinα

Одиниця вимірювання: [B]=H/A∙м=Тл,  (тесла)*

*) Названо на честь сербського фізика Миколи Тесла (1856–1943).

Малоприємною особливістю теми «Електродинаміка магнітних явищ» є факт того, що визначення тих величин які характеризують магнітні поля, набагато складніші за ті їх аналоги які характеризують поля електричні. Наприклад напруженість електричного поля Е та індукція магнітного поля В, є векторними силовими характеристиками відповідно електричного та магнітного полів. Але якщо визначальне рівняння напруженості електричного поля Е = F_ел/q_п, однозначно визначає як величину так і напрям цієї напруженості, то визначальне рівняння індукції магнітного поля В=F_м/І_п∆ℓsinα, мало того що є значно складнішим, та ще й визначає лише величину цієї індукції. Напрям же вектора магнітної індукції визначається системою двох додаткових правил.

Наприклад ви хочете визначити напрям вектора В того поля яке в певній точці простору створює струм І (мал.209). З цією метою у відповідну точку ви вносите пробний струм І_п. При цьому на пробний струм діятиме певна магнітна сила F_м, яка є перпендикулярною до напрямку базового струму І. Що ж стосується напрямку вектора В, то він не співпадатиме ні з напрямком вектора F_м, ні з напрямком вектора І. Напрям вектора  В визначається за сукупністю двох правил:

1.Вектор магнітної індукції В перпендикулярний як до того струму І який створює магнітне поле, так і до тієї магнітної сили F_м, що діє на пробний струм у відповідній точці поля: В ┴ (І ┴ F_м). Це означає, що вектор В є перпендикулярним до тієї площини в якій знаходяться вектори І та F_м. При цьому можливі два варіанти такого напрямку (умовно кажучи: за годинниковою стрілкою чи проти годинникової стрілки). Цей напрямок однозначно визначає так зване правило зігнутої кісті правої руки.

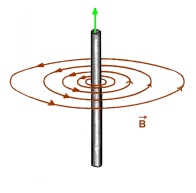
2. Правило зігнутої кісті правої руки: якщо зігнуту в кулак кість правої руки розташувати так, щоб її відігнутий на 90° великий палець вказував напрям струму в провіднику (струму який створює магнітне поле), то чотири зігнутих пельці руки, вкажуть напрям вектора магнітної індукції (напрям ліній магнітної індукції).

    

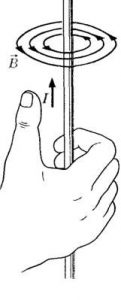
Мал.209.  Напрям вектора магнітної індукції та ліній магнітної індукції  визначають правилом зігнутої кісті правої руки (правилом буравчика).

Потрібно зауважити, що в науковій літературі, те правило яке дозволяє визначати напрям вектора магнітної індукції, напрям ліній магнітної індукції, напрям «молекулярних струмів» та полярність котушки індуктивності, часто називають правилом буравчика або правилом правого гвинта. Це правило стверджує: якщо буравчик (правий гвинт) подумки вкручувати таким чином, щоб його поступальний рух співпадав з напрямком струму в провіднику, то напрям обертального руху рукоятки буравчика вкаже напрям вектора В (напрям ліній магнітної індукції).

Правило буравчика і правило зігнутої кісті правої руки є тотожними. Проблема з правилом буравчика полягає в тому, що далеко не кожна людина має чіткі уявлення про те, що таке буравчик (правий гвинт) і чим він відрізняється від гвинта лівого. Далеко не всі розуміють, яким чином напрям поступального руху буравчика залежить від напрямку обертання його рукоятки і навпаки. І в цьому сенсі, правило зігнутої кісті правої руки має очевидні переваги.

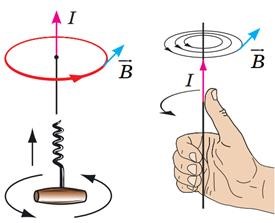
Мал.210. Правило буравчика і правило зігнутої правої руки є тотожними. При цьому з практичної точки зору, правило зігнутої кісті правої руки є значно зручнішим.

Подібно до того як електричні поля зображають за допомогою ліній напруженості електричного поля, магнітні поля зображають за допомогою ліній індукції магнітного поля.

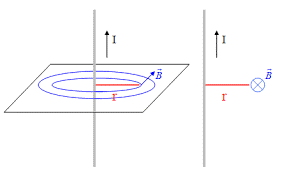
Лінії магнітної індукції, це такі умовні лінії, за допомогою яких зображають магнітні поля і які проводиться таким чином, що дотична до цієї лінії в будь якій точці поля, співпадає з напрямком результуючого вектора магнітної індукції в цій точці. Технологія правильного графічного зображення магнітних полів є досить складною. І тому, ми не будемо заглиблюватись в деталі цієї технології. Натомість, просто сформулюємо ті загальні властивості, що притаманні лініям магнітної індукції. А ці властивості є наступними.

1. Лінії магнітної індукції ніде не перетинаються. Це випливає з того, що будь яку точку магнітного поля характеризує лише один результуючий вектор магнітної індукції, до якого можна провести лише одну дотичну.
2. Лінії магнітної індукції завжди замкнуті (вихрові). Це випливає з того, що в Природі не існує обособлених різнойменних магнітних зарядів. Тобто нема тих об’єктів на яких лінії магнітної індукції могли б починатися та закінчуватися.
3. Напрям тих ліній магнітної індукції які описують поле обособленого провідника з струмом, визначають за правилом зігнутої кісті правої руки (правилом буравчики). Це випливає з самого визначення терміну «лінія магнітно індукції» та способу визначення напрямку вектора В.
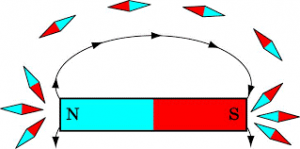
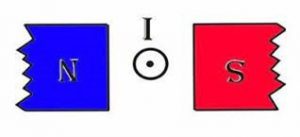
4. Ті лінії магнітної індукції які описують поле постійного магніту (за межами цього магніту) направлені від північного магнітного полюса (N) до південного (S). Це випливає як з результатів експериментів так і з застосування правила зігнутої кісті правої руки до відповідних ситуації.
5. Густина ліній магнітної індукції в околицях будь якої точки поля, пропорційна величині вектора В в цій точці. Це випливає з технології графічного зображення магнітних полів. А ця технологія така, що забезпечує певну відповідність між властивостями поля та тією картинкою яка ці властивості описує.

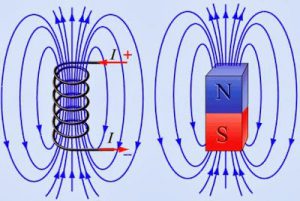
Мал.211. Загальна картина того магнітних полів яке створює прямолінійний провідник з струмом, котушка з струмом та постійний магніт.

Потрібно зауважити, що правильно «намальована» наукова картина магнітного поля, це не певна фантазія художника, а об’єктивне відображення реальних властивостей відповідного магнітного поля. Адже, якщо в це поле внести достатньо велику кількість дрібних магнітних стрілок, то вони розташуються таким чином, що «намалюють» картинку дуже схожу на ту яка намальована лініями магнітної індукції.

   

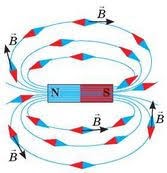
Мал.212. Якщо в магнітне поле внести достатньо велику кількість дрібних магнітних стрілок, то вони розташуються таким чином, що «намалюють» картину відповідного поля.

Як і поля електричні, магнітні поля підпорядковані дії закону, який називається принципом суперпозиції полів. Відносно магнітних полів цей закон стверджує: магнітні поля діють незалежно одне від одного (не заважаючи одне одному), і тому при їх накладанні магнітна індукція результуючого поля дорівнює векторній сумі індукцій кожного окремого поля системи, іншими словами В_рез=∑В_і.

Зважаючи на факт того, що у величезній кількості практично важливих приладів так чи інакше застосовується магнітна дія як електричних струмів так і постійних магнітів, практично важливим є вміння визначати параметри магнітного поля. А це вміння формується в процесі розв’язування конкретних задач.

Задача 1. За заданим напрямком струму в провіднику (мал. а), вказати напрям ліній магнітної індукції та напрямки вектора магнітної індукції у вказаних точках.

а)  б)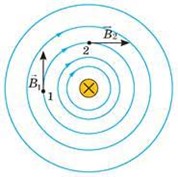

Загальні зауваження. Оскільки вектори I, B, F не знаходяться в одній площині, то на плоских малюнках, той вектор який є перпендикулярним до площини малюнку зображають або точкою (якщо вектор направлений до спостерігача), або хрестиком (якщо вектор направлений від спостерігача). Наприклад в умовах нашої задачі, струм І є перпендикулярним до площини малюнку і направленим в сторону від спостерігача.

Рішення. Визначаючи напрям ліній магнітної індукції та вектора магнітної індукції застосовуємо правило зігнутої кісті правої руки: якщо зігнуту кість правої руки розташувати так, щоб відігнутий великий палець вказував напрям струму в провіднику, то чотири зігнуті пальці руки вкажуть напрям ліній індукції магнітного поля. В умовах нашої задачі ці лінії направлені за годинниковою стрілкою. При цьому вектор індукції магнітного поля в будь якій точці буде дотичним до лінії індукції у відповідній точці і направленим в напрямку цієї лінії.

Задача 2. За заданим напрямком ліній магнітної індукції, вказати напрям струму в провіднику.

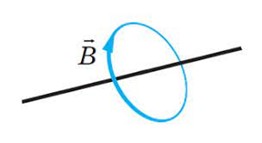
Рішення. Застосовуючи правило зігнутої кісті правої руки, цю кість розташовуємо таким чином, щоб її чотири зігнуті пальці вказували напрям заданої лінії індукції магнітного поля. при цьому відігнутий великий палиць вкаже напрям струму в провіднику. А цей напрям вліво-вниз.

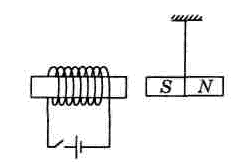
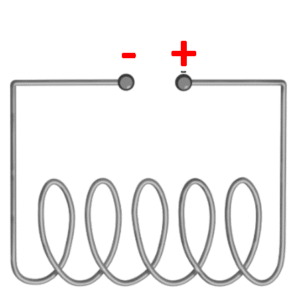
Задача 3. Магнітна стрілка повернута до котушки індуктивності так, як показано на мал.(а). Визначте на якій клемі котушки знак плюс, а на якій мінус.

а)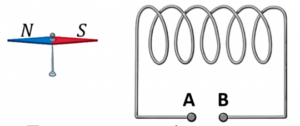б)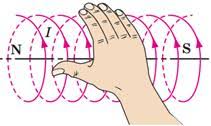

Рішення. Оскільки різнойменні магнітні полюси притягуються, а однойменні відштовхуються, то із аналізу малюнку ясно, що збоку південного полюса (S) магнітної стрілки, має знаходитись північний (N) полюс котушки індуктивності. А для котушки з струмом розташування цих полюсів визначається за правилом зігнутої кісті правої руки. Для даного ж випадку це правило стверджує. Якщо зігнуту кість правої руки (дивись мал.б) розташувати так, щоб чотири зігнутих пальці вказували напрям струму в котушці, то відігнутий на 90° великий палець руки вкаже напрям на північний полюс котушки.

Зважаючи на вище сказане, та враховуючи що місцезнаходження північного полюса котушки є відомим (північний полюс котушки там де південний полюс магнітної стрілки), визначаємо напрям струму в провіднику: струм тече від точки В (+) до точки А (–).

Відповідь: в точці В (+), в точці А (–).

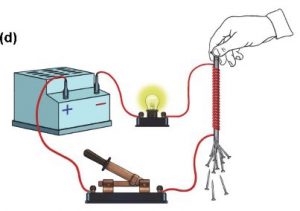
Задача 4. В якому напрямку рухатиметься зображений на малюнку магніт, при замиканні відповідного електричного кола?

Рішення. Оскільки напрям струму відомий: від + (довший відрізок) до – (короткий відрізок), то застосовуючи правило зігнутої кісті правої руки, можна визначити полярність котушки індуктивності – північний полюс (N) справа. А це означає, що магніт буде притягуватися до котушки (різнойменні полюси N – S притягуються).

Задача 5. Визначити напрям тих внутрішніх «молекулярних» струмів, які створюють поле зображеного на мал.а постійного магніту.

а)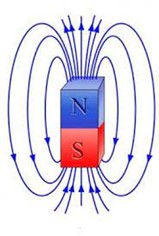  б)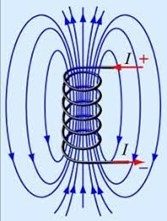

Рішення. Оскільки полярність магніту відома, то розташовуємо зігнуту кість правої руки так, щоб її відігнутий великий палець був направлений в сторону північного () полюса магніту. При цьому інші пальці руки вкажуть напрям тих внутрішніх «молекулярних» струмів які і створюють відповідне магнітне поле. А цей напрямок співпадає з тим, що зображено на мал.б.

Задача 6. Два паралельні стуми І₁, І₂ направлені так як показано на мал.а. Визначити напрям вектора індукції результуючого поля в рівновіддаленій від струмів точці А, якщо І₁ > І₂.

а)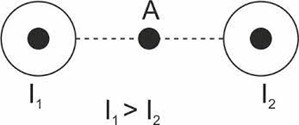  б)

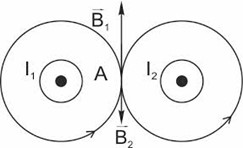
Рішення. Застосовуючи правило зігнутої кісті правої руки визначаємо напрямки векторів В₁ і В₂ для заданої точки А. А в цій точці вектор В₁ буде направленим вертикально вгору, а вектор В₂ – вертикально вниз (мал.б). Оскільки І₁ > І₂, та враховуючи що відстань від струмів до точки А однакова, можна стверджувати, що В₁ > В₂. А це означає, що результуючий вектор В_рез = В₁ + В₂ буде направленим вертикально вгору і чисельно дорівнюватиме алгебраїчній різниці між модулями векторів В_рез = В₁ – В₂.

Контрольні запитання.

1. Поясніть, яким чином силова дія передається від одного струму до іншого?
2. Чому ту магнітну силу що діє на пробний струм в даній точці поля не можна вважати об’єктивною силовою характеристикою цього поля?
3. Поясніть чим схожі і чим відрізняються напруженість електричного поля та індукція магнітного поля?
4. Поясніть чому визначальне рівняння тієї векторної величини яка називається індукцією магнітного поля В, записують в скалярному вигляді В=F_м/І_п∆ℓsinα?
5. Як визначають напрям вектора магнітної індукції?
6. Поясніть чому лінії магнітної індукції завжди вихрові, тобто такі які ніде не починаються і ніде не закінчуються?
7. Чому лінії магнітної індукції ніде не перетинаються?
8. Сформулюйте принцип суперпозиції для магнітних полів.

Вправа 36.

1. За заданим напрямком струму в провіднику визначте напрям ліній магнітної індукції.

1. За заданим напрямком ліній магнітної індукції, визначте напрям струму в провіднику.

а) б)

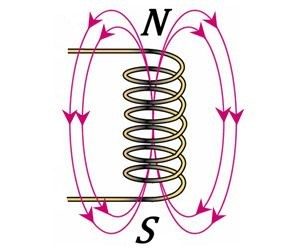
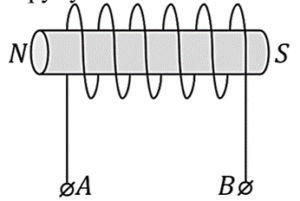
3. Визначте магнітні полюси зображених на малюнку котушки індуктивності.

4. За заданим положенням мангітних полюсів електромангіту, визначити полюси джерела струму.

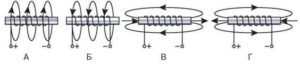
5. На якому з малюнків правильно вказано напрям ліній індукції того магнітного поля яке створює котушка з струмом?

6. У якому напрямку рухатимуться зображені на малюнку постійні магніти, при замиканні відповідного електричного кола?

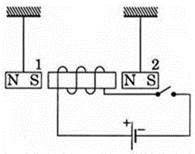
7. На основі аналізу малюнка визначте поведінку магнітної стрілки при появі електричного струму.

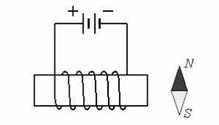
8. На основі аналізу малюнку визначте напрям струму в котушці.

.

Лекційне заняття №37.

Тема: Сила Ампера та її застосування. 

Враховуючи факт існування магнітного поля параметри якого характеризує вектор магнітної індукції (В=F_м/І_п∆ℓsinα), закон Ампера можна сформулювати наступним чином: На будь який фрагмент струму І∆ℓsinα, що знаходиться в магнітному полі з індукцією В, діє магнітна сила F_м, величина якої визначається за формулою  F_м=ВІ∆ℓsinα, де α – кут між напрямком вектора магнітної індукції (В) та напрямком струму в провіднику (І): α= < (В та І) .

На практиці ту магнітну силу з якою магнітне поле діє на провідник з струмом, або на певний фрагмент цього провідника називають силою Ампера.

Сила Ампера, це сила з якою магнітне поле діє на провідник з струмом, або на певний фрагмент цього провідника і яка дорівнює скалярному добутку магнітної індукції поля (В) на параметри того струму, що знаходиться в полі (ІΔℓsinα).

Позначається: F_А

Визначальне рівняння: F_А=ВІ∆ℓsinα, де

В – індукція магнітного поля;

І – сила струму в провіднику;

∆ℓ – довжина провідника;

α – кут між напрямком вектора В та напрямком струму в провіднику І.

Одиниця вимірювання: [F_А] = H.

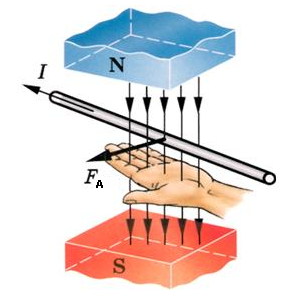
Визначальне рівняння сили Ампера F_А=ВІ∆ℓsinα не визначає напрям дії цієї сили. Не визначає тому, що напрям жодної з тих величин які фігурують в цьому рівнянні (В, І, Δℓ), не співпадає з напрямком дії сили Ампера і не є протилежним цьому напрямку. Напрям сили Ампера визначають за спеціальним правилом, яке називається правилом лівої руки. Це правило стверджує: якщо розкриту долоню лівої руки розташувати так, щоб лінії магнітної індукції (лінії вектора В) входили в долоню, а чотири пальці вказували напрям струму в провіднику, то відігнутий великий палець руки вкаже напрям сили Ампера.

Мал.213. В магнітному полі на провідник з струмом діє сила Ампера, напрям якої визначається правилом лівої руки.

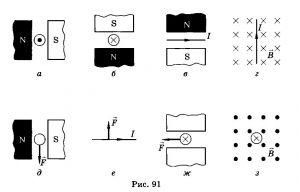
Задача 1. На основі аналізу малюнку визначити напрям сили Ампера.

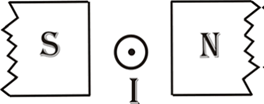
Рішення. Зважаючи на те, що лінії магнітної індукції направлені від північного () полюса магніту до його південного полюса (), застосовуємо правило лівої руки та визначаємо напрям сили Ампера.

Відповідь: сила Ампера направлена вертикально вниз.

Задача 2. На основі аналізу малюнків визначити: малюнки а, б – напрям сили Ампера; малюнок в – напрям струму в провіднику; малюнок г – напрям ліній магнітної індукції; малюнок д – напрям сили Ампера.

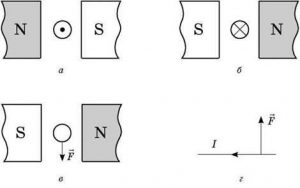  д)

Рішення.

1. Малюнки (а), (б). Застосовуємо правило лівої руки і визначаємо, що як для мал.(а) так і для мал.(б) сила Ампера направлена вертикально вгору.
2. Малюнок (в). В зображеній на малюнку (в) ситуації потрібно визначити напрям струму в провіднику. А для такої ситуації правило лівої руки набуває вигляду: якщо розкриту долоню лівої руки розташувати так, щоб лінії індукції магнітного поля входили в долоню, а відігнутий великий палець вказував напрям діючої на провідник сили Ампера, то чотири пальці долоні вкажуть напрям струму в провіднику. І не важко бачити, що у відповідності з цим правилом, в зображеній на мал.(в) ситуації струм направлений на спостерігача (в центрі кружечка треба поставити точку).
3. Малюнок (г). В зображеній на малюнку (г) ситуації потрібно визначити напрям ліній магнітної індукції. А для такої ситуації правило лівої руки набуває вигляду: якщо розкриту долоню лівої руки розташувати так, щоб відігнутий великий палець вказував напрям сили Ампера, а чотири пальці вказували напрям струму в провіднику, то лінії індукції поля входитимуть в долоню. І не важко бачити, що у відповідності з цим правилом, в зображеній на мал.(г) ситуації, лінії індукції магнітного поля будуть перпендикулярними до площини малюнку і направленими на спостерігача (відповідне поле зображується системою точок).
4. Малюнок (д). В даному випадку ми маємо ситуацію коли правило лівої руки не працює. Адже в зображеній на малюнку (д) ситуації струм направлений вздовж ліній магнітної індукції. При цьому розкриту долоню руки не можливо розташувати так, щоб лінії індукції магнітного поля входили в долоню, а чотири пальці вказували на напрям струму в провіднику. Не можливо тому, що розкрита ж долоня є певною площиною яка не може одночасно бути як перпендикулярною до певного напрямку так і паралельною до нього.

Пояснюючи дану ситуацію можна сказати наступне. Як відомо, сала Ампера визначається за формулою F_А=ВІ∆ℓsinα, де α – кут між напрямком вектора В та напрямком струму в провіднику І. В зображених на малюнках а, б, в, г ситуаціях α=90° (або 270°). А це означає, що sinα = 1 = max, і тому F_А = max. В ситуації ж (д) α=0° (або 180°). При цьому sinα = 0, і тому F_А = 0. Таким чином, в зображеній на малюнку (д) ситуації, правило лівої руки не дозволяє визначити напрям сили Ампера тому, що ця сила відсутня (F_А = 0).

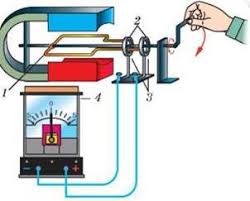
Сила Ампера має широке практичне застосування. Класичним прикладом такого застосування є електровимірювальні прилади загалом і амперметри зокрема. Основними елементами таких приладів (мал.214б) є: постійний магніт (М), циліндричне феромагнітне осердя (1), легка струмопровідна рамка (2), механічна пружина (3) та стрілка приладу (4). Принцип дії цієї системи полягає в наступному. Постійний магніт у поєднанні з феромагнітним осердям, створює (індуцирує) однорідне магнітне поле (В=const). В цьому полі знаходиться легка струмопровідна рамка, яка за допомогою механічної пружини утримується в певному нульовому положенні і до якої жорстко прикріплена стрілка приладу. При появі в рамці електричного струму, на її бічні сторони починають діяти дві рівні за величиною і протилежні за напрямком сили Ампера. Під дією цих сил рамка, а відповідно і стрілка приладу, повертаються на певний кут. Кут, величина якого залежить від сили струму в рамці та жорсткості тієї пружини яка протидіє її обертанню.

       

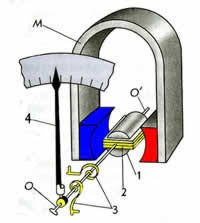
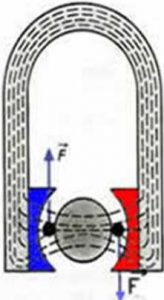
Мал.214. Схема загального устрою та принципу дії демонстраційного амперметра.

Не важко довести, що величина тієї сили Ампера яка повертає рамку, а отже і того кута на який вона повертається, є прямо пропорційною силі струму в рамці. Дійсно. За визначенням  F_А=ВІℓsinα. Оскільки в умовах даного приладу В=const, ℓ=const, α=90º=const (в процесі обертання рамки її бічні сторони залишаються перпендикулярними до ліній магнітної індукції), то  F_А=kІ, де k=const.

Вище описані електровимірювальні прилади мають високу точність, чутливість та надійність. Їх вимірювальна шкала є рівномірною. Недоліком цих приладів є те, що вони безпосередньо вимірюють лише постійні струми. Втім, цей недолік легко долається шляхом включення в коло вимірювального приладу певного випрямного елементу.

Важливим прикладом застосування сили Ампера є електродвигун постійного струму – прилад, який перетворює енергію постійного струму в механічну роботу. У своєму принциповому устрої електродвигун постійного струму схожий на амперметр. Власне амперметр і є певною спрощеною моделлю електродвигуна. Адже за наявності струму, струмопровідна рамка амперметра повертається, перетворюючи тим самим енергію струму в механічну роботу. Інша справа, що навіть за відсутності опору пружини, та за відсутності прикріпленої до рамки стрілки приладу, рамка амперметра може повернутися лише до тієї межі поки її площина не стане перпендикулярною до напрямку ліній індукції магнітного поля. Адже в цьому випадку діючі на рамку сили Ампера будуть не повертати рамку, а розтягувати її.

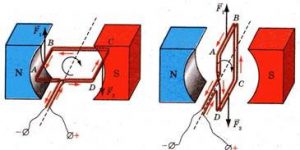
Мал.215. В магнітному полі рамка з струмом повертається лише до тих пір, поки її площина не стане перпендикулярною до ліній магнітної індукції поля.

Що ж треба зробити за для забезпечення безперервного обертання системи? Очевидне рішення полягає в тому, щоб замість однієї рамки застосувати систему багатьох рамок. При цьому процес потрібно організувати таким чином, щоб в момент максимальної обертальної дії сил Ампера, струм через відповідну рамку проходив, а в момент малої обертальної дії цих сил – не проходив. Цю задачу вирішує простий пристрій, який називається колектором.

Колектор представляє собою циліндричну конструкцію яка складається з електроізольованих струмопровідних пластин, діаметрально протилежні пари яких є входом та виходом відповідної струмопровідної рамки електродвигуна. По суті колектор у поєднанні з рухомими контактами джерела струму, є тим механічним перемикачем який в потрібні моменти вмикає та вимикає струм в рамках електродвигуна, та забезпечує безперервне обертання цих рамок. А потрібно зауважити, що на відміну від амперметра в якому струмопровідна рамка та феромагнітне осердя не з’єднані між собою, в електродвигуні, ці елементи утворюють цілісну систему, яка називається якорем. Така система  по перше підсилює силову дію магнітного поля, а по друге надає системі осердя–рамка тих інерційних властивостей, які забезпечують рівномірність її обертання.

Зважаючи на вище сказане, неважко пояснити загальний устрій та принцип дії електродвигуна постійного струму. Дійсно. Основними вузлами електродвигуна постійного струму є (мал.216):

1 – постійний або електричний магніт, який прийнято називати індуктором;

2 – система струмопровідних рамок жорстко з’єднаних з феромагнітним осердям (цю систему називають якорем);

3 – спеціальний пластинчастий циліндр, який називається колектором і який знаходиться в рухомому контакті з графітовими пластинками (щітками) системи подачі електричного струму.

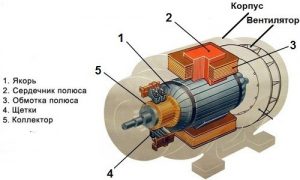
Мал.216. Загальний устрій електродвигуна постійного струму.

Принцип дії електродвигуна постійного струму полягає в наступному. Індуктор, разом з феромагнітним осердям якоря, створюють (індуцирують) однорідне магнітне поле в якому знаходяться струмопровідні рамки якоря. Електричний струм, через колектор подається на ту рамку якоря, яка розташована в площині ліній індукції магнітного поля. При проходженні струму, на бічні сторони цієї рамки діють дві рівні за величиною і протилежні за напрямком сили Ампера, які надають рамці, а разом з нею і тілу якоря, певного обертального руху. В процесі обертання, ті пластинки колектора які є входом та виходом даної рамки, виходять із механічного контакту з системою подачі електричного струму. Натомість в контакт з цією системою входить нова пара сусідніх пластин. При цьому якір отримує новий обертальний імпульс. Ясно, що в такій ситуації, сила Ампера буде постійно підтримувати обертальний рух якоря.

Електродвигуни постійного струму мають ту перевагу, що їх тягове зусилля та частоту обертання ротора можна плавно змінювати (регулювати). До числа недоліків цих електродвигунів можна віднести їх відносно велику складність та високу вартість. Не будемо забувати і про те, що в наявних лініях електропередач тече змінний струм. А це означає, що в систему електродвигуна постійного струму потрібно включати відповідний випрямний пристрій. Електродвигуни постійного струму широко застосовуються в електропобутовій техніці. Вони є основними силовими двигунами на всіх видах електротранспорту (трамваї, тролейбуси, електровози, електромобілі, тощо).

Малопотужні електродвигуни постійного струму можуть бути і значно простішими (216а). Вони складаються з постійного магніту та однієї струмопровідної котушки яка у поєднанні з феромагнітним осердям виконує роль електромагніту змінної полярності. Принцип дії такого електродвигуна полягає в наступному. Через колектор який складається з двох півкілець, постійна напруга подається так, що половину періоду в котушці струм тече в одному напрямку, а іншу половину – в протилежному. А оскільки котушка намотана таким чином, що у поєднанні з феромагнітним осердям утворює електромагніт, то при зміні напрямку струму, полярність цього магніту змінюється. Змінюється так, що однойменні полюси постійного магніту (індуктора) та електромагніту (якоря), постійно відштовхуються і змушують якір постійно обертатися. Головний недолік таких електродвигунів  – низький ККД, який не перевищує 50%.

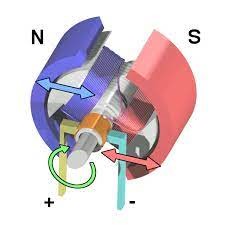
Мал.216а. Загальний устрій електродвигуна постійного струму з електромагнітом змінної полярності.

Ще одним важливим прикладом застосування сили Ампера є електродинамічний гучномовець (динамік) – прилад, який перетворює енергію того змінного електричного струму в якому міститься звукова інформація, в енергію відповідних механічних коливань пружного середовища, тобто в енергію звуку. Основними складовими гучномовця є (мал.217): постійний циліндричний магніт, легка струмопровідна котушка та дифузор.

 

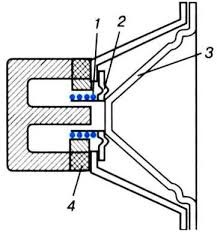
Мал.217. Схема принципового устрою електродинамічного гучномовця.

Принцип дії гучномовця полягає в наступному. Постійний циліндричний магніт, створюють однорідне магнітне поле. В цьому полі знаходиться легка струмопровідна котушка жорстко з’єднана з циліндричною частиною дифузора. В процесі проходження змінного струму (струму в якому міститься звукова інформація), на котушку діє відповідна змінна сила Ампера. Під дією цієї сили, котушка, а разом з нею і тіло дифузора, здійснюють відповідні поступально-коливальні рухи. При цьому, механічні коливання тіла дифузора породжують відповідні коливання повітря, які розповсюджуються у вигляді звукової хвилі.

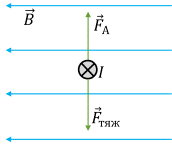
Задача 3. Сила струму в горизонтально розташованому провіднику 5А, його довжина 20см, а маса 10г. В полі з якою магнітною індукцією має знаходитись провідник, щоб діюча на нього сила Ампера зрівноважувала силу тяжіння?

Загальні зауваження. Складність подібних задач полягає в тому, щоб максимально ефективно виконати той малюнок який відповідає суті задачі. Наприклад в умовах даної задачі, потрібно врахувати, що сила Ампера зрівноважує силу тяжіння і тому направлена вертикально вгору. Враховуючи цей напрямок та факт того, що провідник з струмом горизонтальний, застосовуємо правило лівої руки і визначаємо та вказуємо на малюнку напрям ліній магнітної індукції.

Дано:

І = 5А

ℓ = 20см = 0,2м

m = 10г = 0,01кг

F_A = F_Т

В = ?

Рішення. Виконуємо малюнок на якому вказуємо діючі на провідник сили. А цими силами є: сила тяжіння F_T = mg та сила Ампера F_A = BIℓsinα, де α=90° і тому sinα=1. Оскільки за умовою задачі F_A = F_Т, то BIℓ = mg, звідси В = mg/Іℓ.

Розрахунки. В = mg/Іℓ = 0,01кг∙9,8(м/с²) / 5А∙0,2м = 0,98 (Н/А∙м = Тл).

Відповідь: В = 0,98Тл.

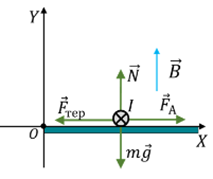
Задача 4. У вертикальному однорідному магнітному полі з індукцією 1,5Тл знаходяться горизонтальні рейки відстань між якими 40см. На рейках, перпендикулярно до них лежить струмопровідний стержень масою 500г. Яка сила струму протікає в стержні при його рівномірному русі вздовж рейок. Коефіцієнт тертя стержня об рейки 0,2.

Дано:

В = 1,5Тл

ℓ = 40см = 0,4м

m = 500г = 0,5кг

μ = 0,2

І = ?

Рішення. Виконуємо малюнок на якому вказуємо всі діючі на стержень сили. А цими силами є: сила тяжіння F_T = mg; реакція опори N; сила тертя F_тер = μN; сила Ампера F_A = BIℓsinα, де α=90° і тому sinα=1. Задаємо систему координат та враховуючи, що рух стержня є рівномірним (v=const), записуємо умову механічної рівноваги стержня.

∑F_x = F_A – F_тер = BIℓ –  μN = 0,

∑F_y = N – F_T = N – mg = 0.

Із (1) випливає BIℓ =  μN, звідси І = μN/Вℓ. А враховуючи, що у відповідності з рівнянням (2) N = mg, можна записати І = μmg /Вℓ.

Розрахунки: І = μmg /Вℓ = 0,2∙0,5кг∙9,8(м/с²) / 1,5Тл∙0,4м = 1,6А

Відповідь: І = 1,6А.

Контрольні запитання.

1. Що називають силою Ампера, яке визначальне рівняння цієї сили і звідки випливає це рівняння?
2. За яким правилом визначають напрям сили Ампера? Сформулюйте це правило.
3. На основі аналізу мал.214 поясніть загальний устрій та принцип дії амперметра.
4. На основі аналізу мал.215, поясніть чому одинарна рамка з струмом не може обертатись в однорідному магнітному полі?
5. На основі аналізу мал.216 поясніть загальний устрій та принцип дії електродвигуна постійного струму.
6. Яку функцію в зображеному на мал.216 електродвигуні виконує колектор?
7. Що називають якорем електродвигуна?
8. Що називають індуктором електродвигуна?
9. На основі аналізу мал.216а поясніть загальний устрій та принцип дії електродвигуна з електромагнітом змінної полярності.
10. Поясніть загальний устрій та принцип дії електродинамічного гучномовця.

Вправа 37.

1. На основі аналізу малюнків визначте напрям сили Ампера.

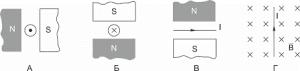
2. На основі аналізу малюнків визначити: 1) напрям сили Ампера (а,б,в,г,з) 2) напрям сили струму в провіднику (д); 3) напрям вектора магнітної індукції (е, ж).

3. На основі аналізу малюнку визначте полярність магніту.

4. Прямолінійний провідник довжиною 50см, знаходиться в однорідному магнітному полі з індукцією 0,02Тл та орієнтований перпендикулярно лініям цього поля. Визначити силу струму в провіднику, якщо діюча на нього сила Ампера 0,15Н.

5. На прямолінійний провідник з струмом 15А в однорідному магнітному полі з індукцією 0,3Тл діє сила 1,5Н. Визначити довжину провідника, якщо він розташований під кутом 30º до ліній магнітної індукції.

6. В однорідному магнітному полі з індукцією 0,8Тл на провідник з струмом 3А, довжина активної частини якого 10см, діє сила 0,15Н. Під яким кутом до вектора індукції поля орієнтовано провідник?

7. Прямолінійний провідник довжиною 45см і масою 50г, розташований однорідному магнітному полі з індукцією 1Тл так, як показано на малюнку і знаходиться в стані механічної рівноваги. Визначити силу струму в провіднику.

8. Прямолінійний, горизонтально розташований провідник з струмом висить на двох тонких нитках в однорідному магнітному полі. При цьому діюча на провідник сила Ампера направлена вертикально вниз. Який струм треба пропустити через провідник, щоб нитки обірвалися, якщо довжина провідника 0,5м, його маса 50г, індукція магнітного поля 2Тл, а кожна нитка розривається під дією сили 1,0Н?

9. У вертикальному однорідному магнітному полі з індукцією 0,5Тл на двох тонких нитках горизонтально підвісили провідник довжина якого 20см, а маса 20г. На який кут від вертикалі відхиляться нитки, якщо сила струму в провіднику 2А?

.

Лекційне заняття №38.

Тема: Сила Лоренца та її застосування. 

В науковій практиці розрізняють дві різновидності магнітної сили: сила Ампера та сила Лоренца. Нагадаємо. Сила Ампера, це сила з якою магнітне поле діє на провідник з струмом, або на певний фрагмент цього провідника і яка дорівнює скалярному добутку магнітної індукції поля (В) на параметри того струму, що знаходиться в полі (ІΔℓsinα).

Позначається: F_А

Визначальне рівняння: F_А=ВІ∆ℓsinα

Одиниця вимірювання: [F_А]=H.

         Сила Лоренца,*⁾ це сила з якою магнітне поле діє на окрему заряджену частинку що рухається в цьому полі і яка дорівнює скалярному добутку магнітної індукції поля (В) на електро–кінематичні параметри цієї частинки (q₀vsinα).

Позначається: F_Л

Визначальне рівняння: F_Л=Bq₀vsinα

де  В – індукція магнітного поля,

q₀ – заряд частинки,

v – швидкість руху частинки,

α – кут між напрямком вектора магнітної індукції та напрямком того струму що характеризує рух зарядженої частинки: α= < (В та І).

*) Названо на честь нідерландського фізика Гендріка Лоренца (1853–1923).

Напрям сили Лоренца, як і напрям сили Ампера, визначається за правилом лівої руки. І потрібно підкреслити, що згідно з цим правилом, чотири пальці розкритої долоні лівої руки мають вказувати не на напрям руху зарядженої частинки, а на напрям того електричного струму, що характеризує цей рух. А це означає, що в тому випадку, коли в магнітному полі рухається негативно заряджена частинка, наприклад електрон, то чотири пальці мають вказувати не на напрям руху електрона, а на протилежний до цього руху напрямок.

   

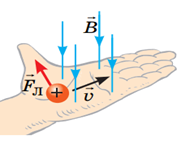
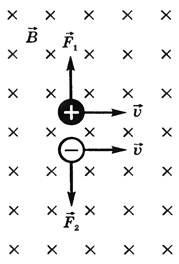
Мал.218. Напрям сили Лоренца визначається за правилом лівої руки.

Задача 1. На основі аналізу малюнка визначити напрям діючої на заряджену частинку сили Лоренца.

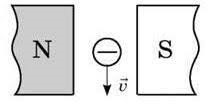
Рішення. Застосовуючи правило лівої руки, та враховуючи факт того, що в магнітному полі рухається від’ємна заряджена частинка (чотири пальці руки мають вказувати напрям протилежний від напрямку швидкості руху частинки), визначаємо напрям сили Лоренца. І цей напрям – перпендикулярний до площини малюнку і направлений в сторону від спостерігача.

Задача 2. На основі аналізу малюнку визначити знак електричного заряду тієї частинки, що рухається в магнітному полі.

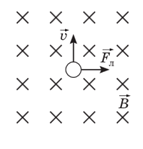
Рішення. Визначаючи знак заряду частинки, застосовуємо правило лівої руки. При цьому, для даної ситуації це правило набуває вигляду. Якщо розкриту долоню лівої руки розташувати так, щоб лінії індукції магнітного поля входили в долоню, а відігнутий на 90° великий палець вказував напрям сили Лоренца, то чотири інші пальці вкажуть напрям відповідного струму. В нашому випадку напрям цього струму – вертикально вниз. А оскільки частинка рухається вертикально вгору, тобто в сторону протилежну від напрямку струму, то це означає, що заряд цієї частинки «мінус».

Не важко довести, що діюча на провідник з струмом сила Ампера, є результуючою тих сил Лоренца, які діють на окремо взяті заряджені частинки цього провідника. Дійсно. Оскільки  I=q/t;  q=Nq₀;  v=∆ℓ/t;  то F_А = BI∆ℓsinα = B(q/t)∆ℓsinα = BNq₀(∆ℓ/t)sinα = NBq₀vsinα = NF_Л.  А по суті   F_А = ∑(F_Л)_і .

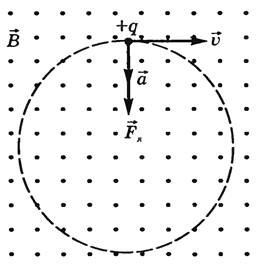
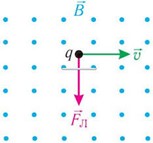
З’ясовуючи загальні закономірності поведінки заряджених частинок в магнітному полі, а заодно і певні особливості самих полів, розглянемо конкретну ситуацію. Припустимо, що заряджена частинка, наприклад електрон(q₀=e), рухаючись з швидкістю v влітає в однорідне магнітне поле з індукцією В під кутом 90º до ліній магнітної індукції поля (мал.219). Рухаючись в магнітному полі, ця частинка буде знаходитись під дією постійної за величиною сили Лоренца (F_Л=Bq₀vsinα, де sinα = sin90° = 1).  Сили, напрям якої завжди перпендикулярний до напрямку траєкторії руху частинки. А це означає, що під дією доцентрової сили Лоренца (F_Л=Bq₀v) напрям руху частинки буде змінюватися і вона буде рухатися з доцентровим прискоренням а = v²/R. В такій ситуації на частинку неминуче діятиме відцентрова сила інерції F_i = m₀a = m₀v²/R. Результатом сукупної дії сили Ампера та сили інерції, буде факт того, що відповідна частинка рухатиметься по колу. І не важко довести, що радіус цього кола має визначатися за формулою  R = m₀v/Bq₀, де  m₀ – маса частинки, q₀ – заряд частинки, В – індукція магнітного поля.

 

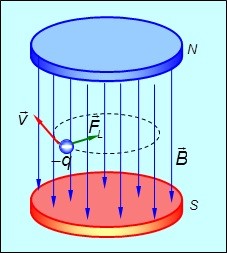
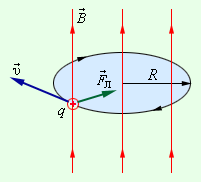
Мал.219. Якщо заряджена частинка влітає в однорідне магнітне поле під кутом 90º до його ліній індукції, то під дією сила Лоренца та сили інерції, ця частинка буде рухатися по колу.

Задача 3. α-частинка (m₀ = 4а.о.м.; q₀ = +2е) з швидкістю 10⁶м/с влітає в однорідне магнітне поле, під кутом 90° до ліній його індукції. Визначити радіус того кола яку описуватиме частинка в процесі свого руху, якщо індукція магнітного поля 0,2Тл.

Дано:

m₀ = 4а.о.м. = 4∙1,66∙10^{– 27}кг

q₀ = +2e = +2∙1,6∙10^{– 19}Кл

v = 10⁶м/с

α = 90°

B = 0,2Тл

R = ?

Рішення. Виконуємо малюнок на якому вказуємо діючі на α-частинку сили. А цими силами є: 1) доцентрова сила Лоренца F_Л=Bq₀vsinα, де sinα = sin90° = 1; 2) відцентрова сила інерції F_i = m₀a = m₀v²/R (на малюнку не показана). У відповідності з умовою динамічної рівноваги частинки  F_i = F_Л, а отже m₀v²/R = Bq₀v, звідси R = m₀v²/Bq₀v = m₀v/Bq₀.

Розрахунки. R = m₀v/Bq₀ = 4∙1,66∙10^{– 27}кг∙10⁶(м/с) / 0,2Тл∙2∙1,6∙10^{– 19}Кл = 10∙10^–2м = 10см.

Відповідь: R = 10см.

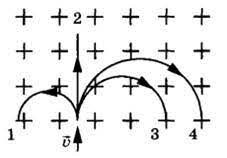
Задача 4. На малюнку представлені траєкторії руху двох частинок заряди яких однакові. Частинки влітають в однорідне магнітне поле з однаковими швидкостями. При цьому радіус траєкторії руху однієї частинки у 2 рази більший ніж у іншої. Визначити знак заряду частинок. Порівняти їх маси.

Дано:

В = const

q₁ = q₂

v₁ = v₂

R₁/R₂ = 2

m₁/m₂ = ?

знак заряду = ?

Рішення. Знаючи напрям вектора В та напрям діючої на частинку сили Лоренца (ця сила направлена до центру кола і зокрема в точці А, цей напрям вправо), застосовуємо правило лівої руки і визначаємо напрям того струму який відповідає руху частинки. Для точки А напрям цього струму вертикально вгору і співпадає з напрямком руху частинки. А це означає, що заряд частинок «плюс».

Оскільки в умовах нашої задачі частинки рухаються по колу радіус якого можна визначити за формулою R = m₀v/Bq₀, то можна записати R₁/R₂ = m₁v₁∙Bq₂ / m₂v₂∙Bq₁, а враховуючи що q₁ = q₂, v₁ = v₂, отримаємо R₁/R₂ = m₁/m₂ = 2.

Відповідь: Знак зарядів «плюс», m₁/m₂ = 2 (частинка радіус траєкторії якої більший має більшу масу).

Можна довести, що коли заряджена частинка влітає в однорідне магнітне поле під кутом α до ліній його магнітної індукції (мал.220), то під дією сили Лоренца та сили інерції, траєкторією руху цієї частинки буде гвинтова лінія, радіус (R) та шаг (h) якої визначаються за формулами: R = m₀vsinα/Bq₀;  h= 2πRctgα. Якщо α=90° (sin90°=1, ctg90°=0), то вище згадані формули набувають вигляду R = m₀v/Bq₀; h=0.

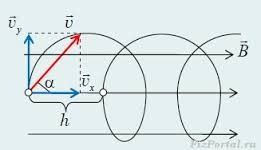
Мал.220. Якщо заряджена частинка влітає в однорідне магнітне поле під кутом α≠90º до його ліній індукції, то траєкторією руху цієї частинки буде певна спіраль.

Факт того, що магнітні поля певним чином діють на заряди що рухаються, корисно застосовується в багатьох важливих та цікавих приладах. Не маючи можливості розглянути все різноманіття подібних приладів, коротко зупинимся лише на деяких з них.

Вивчаючи електронно вакуумні прилади і зокрема кінескопи, ми говорили про те, що силова дія магнітного поля застосовується для управління електронним променем кінескопа телевізора. Принципова суть цього управління досить проста (мал.221). Той змінний електричний струм в якому міститься інформація про зображення, проходячи через витки спеціальної котушки управління, створює відповідне магнітне поле. Направлений потік електронів (електронний промінь), пролітаючи через це поле, відповідним чином відхиляється і «малює» на екрані відповідне зображення.

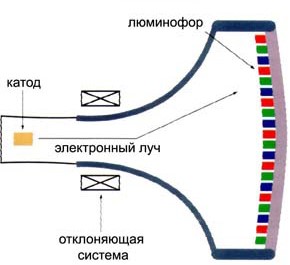
Мал.221.  В кінескопі телевізора, сила Лоренца управляє електронним променем.

В кінескопі телевізора магнітне поле не лише змушує електронний промінь «малювати» зображення, а й значною мірою формує сам промінь. Справа в тому, що електрони, як частинки однойменно заряджені, неминуче відштовхуються. Тому той вузький потік електронів який вилітає з електронної гармати поступово розширюється. Результатом потрапляння на екран такого «набряклого» променя, буде не чітка світлова точка, а розмита світлова пляма, а отже і відповідно розмите зображення.

Ясно, що в такій ситуації необхідно передбачити певний механізм фокусування електронного променя. В оптиці подібну задачу вирішують просто: на шляху світла ставлять збиральну лінзу, яка і фокусує (збирає) світловий потік в потрібній точці (мал.222а). Виявляється, електрони також можна сфокусувати за допомогою лінзи. Але лінзи не оптичної а магнітної. Цією магнітною лінзою є спеціальна котушка індуктивності, яка створює таке магнітне поле, лінії індукції якого сфокусовані в потрібній точці (мал.222б). Потрапляючи в поле такої магнітної лінзи, електрони рухаючись по сфокусованій спіралі, потрапляють в чітко визначену точку.

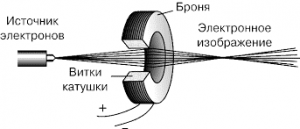
Мал.222. Лінзи можуть бути не лише оптичними, а й магнітними.

Магнітні лінзи застосовуються не лише в кінескопах телевізорів, а й в надзвичайно потужних збільшувальних системах, які називаються електронними мікроскопами. За своїм принциповим устроєм, електронні мікроскопи мало чим відрізняються від мікроскопів оптичних. Просто в них замість світла застосовують потік електронів, а замість оптичних лінз – лінзи магнітні. Недолік оптичних мікроскопів полягає в тому, що вони дозволяють бачити лише ті об’єкти, лінійні розміри яких не перевищують довжини світлової хвилі (~0,5·10^–6м=0,5мкм). А це означає, що навіть в найпотужніші оптичні мікроскопи, побачити молекули і атоми принципово не можливо. Адже розміри цих об’єктів мають порядок 10^–10м. Якщо ж говорити про електронні мікроскопи, то їх роздільна здатність в десятки тисяч разів перевищує роздільну здатність оптичних мікроскопів, і дозволяє досліджувати об’єкти атомарних розмірів.

Силова дія магнітного поля на заряди що рухаються, корисно застосовується в ще одному важливому та цікавому приладі, який називається мас-спектрометром. Цей прилад дозволяє розділяти заряджені частинки (зазвичай позитивні іони) за їх масами. Принцип дії мас-спектрометра базується на факті того, що в однорідному магнітному полі, радіус траєкторії руху зарядженої частинки певним чином залежить від її маси: r = m₀ (v/Bq₀).

Мас-спектрометр (мал.223) представляє собою вакуумну камеру (1) в якій знаходиться джерело позитивних іонів (2), дві сортувальні камери (3 і 4) та приймальний пристрій (5). Принцип дії цієї системи полягає в наступному. Від джерела іонізованих частинок потік швидких іонів потрапляє в першу сортувальну камеру, де опиняється під перехресною дією електричного та магнітного полів. В цій камері на кожен іон діють дві протилежно направлені сили: магнітна сила Лоренца  F_Л=B₁q₀v  та електрична сила Кулона F_ел =E₁q₀. При цьому, не важко збагнути, що рух частинки буде прямолінійним лише в тому випадку, коли діюча на неї електрична та магнітна сили будуть чисельно рівними, тобто за умови: B₁q₀v=E₁q₀. А це означає, що в розташований на виході першої сортувальної камери центральний отвір, потраплять лише ті іони, які рухаються з швидкістю v=E₁/B₁, де Е₁ – напруженість електричного поля в першій сортувальній камері; В₁ – індукція магнітного поля в цій камері.

Потрапляючи в другу сортувальну камеру, іони опиняються під дією ще одного магнітного поля з індукцією В₂. Це поле змушує кожну заряджену частинку рухатись по колу, радіус якого пропорційний масі відповідної частинки. При цьому іони різних мас потрапляють в різні відділи приймального пристрою.

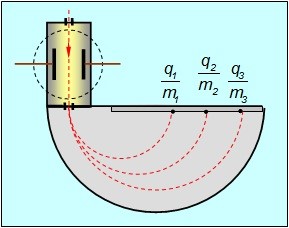
Мал.223. Схема устрою та принципу дії мас-спектрометра.

За допомогою мас-спектрометра були точно визначені маси багатьох елементарних частинок та практично всіх відомих атомів. При цьому було з’ясовано, що хімічно однакові атоми можуть мати суттєво різні маси. Такі різновидності хімічно однакових атомів називають ізотопами (від. грец. isos – однаковий, та topos – місце). Дана назва вказує на те, що відповідні різні за масою атоми, займають одне і те ж місце в періодичній системі хімічних елементів, а отже мають однакову назву та практично однакові хімічні властивості.

Ще одним прикладом практичного застосування сили Лоренца є МГД  (магнітогідродинамічний) генератор – прилад, в якому енергія інтенсивного теплового (хаотичного) руху заряджених частинок, перетворюється в енергію електричного струму. МГД генератор дуже схожий на реактивний двигун (мал.224). Різниця лише в тому, що в МГД генераторі внутрішня енергія палива перетворюється не в механічну роботу, а в енергію електричного струму. Якщо ж говорити про конструктивні особливості МГД генератора, то головна з них полягає в тому, що в сопловій частині генератора знаходиться потужний електромагніт. Крім цього, в генераторі певні фрагменти внутрішньої поверхні сопла є вихідними електродами системи.

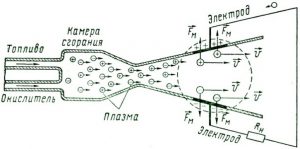
Мал.224. Схема устрою та принципу дії МГД генератора.

Принцип дії МГД генератора полягає в наступному. При згоранні палива, в камері згорання генератора утворюється високотемпературна (~2500ºС) електронно-іонна плазма. В сопловій частині генератора, плазмовий потік прискорюється і стає максимально упорядкованим. Потрапляючи в потужне постійне магнітне поле, заряджені частинки плазми під дією сили Лоренца певним чином відхиляються. При цьому, негативно заряджені електрони потрапляють на один електрод, а позитивно заряджені іони – на протилежно розташований електрод. Виникаюча між цими електродами різниця потенціалів (напруга) реалізується у вигляді відповідного електричного струму.

Переваги МГД генератора стануть очевидними, якщо згадати, що традиційні способи перетворення внутрішньої енергії палива в енергію електричного струму є двоступеневими: тепловий двигун перетворює внутрішню енергію палива в механічну роботу, а індукційний генератор, перетворює механічну роботу в енергію електричного струму. В МГД ж генераторі, проміжний цикл перетворень відсутній. А отже, відсутні і відповідні економічні та енергетичні затрати.

Втім, не будемо забувати, що МГД генератор перетворює енергію хаотичного руху частинок речовини (теплоту) в енергію їх упорядкованого руху (електричний струм). А як відомо, таке перетворення відбувається з великими енергетичними втратами. Тому коефіцієнт корисної дії МГД генераторів є не надто високим (≈30%), а відповідно обмеженим є і їх практичне застосування. Якщо ж зважити на те, що МГД генератор не менш гучний за реактивний двигун, то перспективи його широкого практичного застосування виглядають ще більш примарними.                Контрольні запитання.

1. Чим схожі і чим відрізняються сила Ампера та сила Лоренца?
2. Що потрібно пам’ятати, визначаючи напрям тієї сили Лоренца яка діє на негативно заряджену частинку?
3. Рухаючись перпендикулярно лініям індукції магнітного поля, заряджена частинка описує коло певного радіусу. Які сили змушують частинку рухатись по колу?
4. Електрон влітає в газове середовище перпендикулярно до ліній індукції однорідного магнітного поля. Чи буде цей електрон рухатись по колу?
5. Поясніть загальний устрій та принцип дії кінескопа.
6. Поясніть загальний устрій та принцип дії мас-спектрометра.
7. Поясніть загальний устрій та принцип дії МГД генератора.

Вправа 38.

1. На основі аналізу малюнків визначити напрям сили Лоренца

2. На основі аналізу малюнків визначте напрямки: а), б) сили Лоренца, в) швидкості частинки, г) індукції магнітного поля.

3. На основі аналізу малюнку визначити знак електричного заряду тієї частинки, що рухається в магнітному полі.

4. На малюнку показано траєкторії руху чотирьох частинок які з однаковими швидкостями влітають в однорідне магнітне поле. Визначте знаки зарядів частинок. Яка з заряджених частинок має найбільшу масу, а яка найменшу?

5. Електрон з швидкістю 5·10⁷м/с влітає в однорідне магнітне поле з індукцією 0,04Тл і рухається перпендикулярно лініям цієї індукції. Визначити радіус того кола яке опише електрон в магнітному полі (m_е=9,1∙10^–31кг).
6. Протон в однорідному магнітному полі з індукцією 0,02Тл описує коло радіусом 5см. Визначити швидкість руху протона (m_р=1,67∙10^–27кг).
7. Електрон швидкість якого 4·10⁶м/с в магнітному полі рухається по колу радіусом 5мм. Визначте індукцію цього поля.
8. Електрон і протон рухаючись з однаковими швидкостями потрапляють в однорідне магнітне поле. Порівняйте радіуси кривизни траєкторій руху цих частинок.
9. Однорідне електричне поле з напруженістю 1∙10⁴Н/Кл є перпендикулярним до однорідного магнітного поля з індукцією 0,02Тл. В це поле, перпендикулярно векторам Е і В влітають а) електрон, б) протон, в) α – частинка. За яких швидкостей, рух цих частинок буде прямолінійним?

.

Лекційне заняття №39.

Тема: Магнітний потік. Індуктивність. Котушка індуктивності. Узагальнююче повторення теми.

Однією з базових фізичних величин електродинаміки магнітних та електромагнітних явищ, наряду з магнітною індукцією (В) є магнітний потік.

Магнітний потік, це фізична величина, яка характеризує загальний потік індукції магнітного поля через задану поверхню площею S і яка дорівнює добутку індукції магнітного поля В на площу тієї поверхні яку пронизує ця індукція.

Позначається: Ф

Визначальне рівняння: Ф=ВScosβ, де S – площа тієї поверхні яку пронизує постійна за величиною та напрямком магнітна індукція В; β – кут між напрямком вектора В та перпендикуляром (нормаллю n_s) до поверхні S:

β =< (B, n_s)

Одиниця вимірювання: [Ф] = Тл∙м² = Вб,  вебер*⁾.

*) Названо на честь німецького фізика Вільгельма Вебера (1804–1891).

Потрібно зауважити, що формула Ф=ВScosβ безумовно достовірна лише для однорідних магнітних полів (В=const). Якщо ж мова йде про поля неоднорідні, то в цьому випадку визначальне рівняння магнітного потоку записується у вигляді  Ф=∑В_i∆S_icosβ_i.

Задача 1. На основі аналізу малюнку, визначте величину того магнітного потоку, що пронизує струмопровідну рамку, та зміну цього потоку при переході рамки з положення 1  в положення 2. Площа рамки 200см², індукція створюваного магнітом постійного поля 1,5Тл.

Дано:

S = 200см² = 0,02м²

В = 1,5Тл

Ф₁ = ?, Ф₂ = ?, ΔФ = ?

Рішення. За визначенням Ф=ВScosβ, де β – кут між напрямком вектора В та перпендикуляром (нормаллю n_s) до площини S. Із аналізу малюнку ясно, що у першому випадку кут між магнітної індукції поля та перпендикуляром до площини рамки становить 90° або 270°. А оскільки cos90° = cos270° = 0, то Ф₁ = ВScosβ = ВS∙0 = 0Вб. В другому випадку β = 0° або 180°. А оскільки cos0° = |cos180°| = 1 = max, то Ф₂ = ВScosβ = 1,5Тл∙0,02м²∙1 = 0,03Вб. При цьому ΔФ = Ф₂ – Ф₁ = 0,03Вб – 0,00Вб = 0,03Вб.

Відповідь: Ф₁ = 0,00Вб, Ф₂ = 0,03Вб, ΔФ = 0,03Вб.

В певному сенсі, магнітний потік є енергетичною характеристикою того фрагменту магнітного поля, що пронизує замкнутий контур площею S. Про зв’язок магнітного потоку з енергією (роботою), говорить бодай той факт, що одиниці вимірювання цих величин (вебер та джоуль), є взаємопов’язаними величинами: Вб= Тл∙м²= (Н/А∙м)м²= (Н∙м)А= Дж/А.

З’ясовуючи суть того зв’язку що існує між магнітним потоком та енергією (роботою), а заодно і вирішуючи практично важливе питання про визначення тієї роботи яку виконує магнітна сила (сила Ампера) по переміщенню провідника з струмом, розглянемо конкретну задачу.

Задача 2. В однорядному магнітному полі з індукцією В, в площині перпендикулярній до вектора цієї індукції, прокладені металеві рейки на яких встановлена рухома металева вісь. Через контур, який складається з рейок та рухомої осі, проходить електричний струм І. Визначити величину тієї роботи яку виконує сила Ампера, переміщуючи вісь на відстань ∆х. Відстань між рейками b.

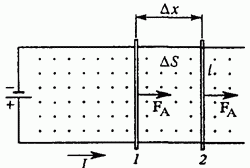
Дано:

В=const

І

b

Δx

α=90°

A = ?

Рішення. Якщо під дією сили Ампера F_A=IBbsinα (де sinα=1), рухома вісь переміщується на відстань Δх, то це означає, що сила Ампера виконує роботу A = F_A∆x = IBb∆x = IB∆S = I∆Ф, де ∆Ф – величина тієї зміни магнітного потоку (потоку через контур обмежений струмом І), яка відбулася в процесі виконання роботи.

Відповідь: А = I∆Ф.

Таким чином, величина тієї роботи яку виконує магнітне поле по переміщенню провідника з струмом, визначається за формулою А = І∆Ф. І можна довести, що дана формула є справедливою не лише для вище розглянутої конкретної ситуації, а й для будь якої ситуації при якій відбувається  зміна того магнітного потоку який пронизує замкнутий контур.

Потрібно підкреслити, що робота виконується не за наявності магнітного потоку (Ф), а в процесі зміни цього потоку (∆Ф). Зауважимо також, що визначаючи величину тієї роботи яку виконують магнітні сили, не потрібно визначати величину цих сил. Достатньо визначити ту зміну магнітного потоку яку ці сили спричиняють: А = І∆Ф.

Нагадаємо, робота – це фізична величина, яка характеризує затрати енергії на виконання роботи, тобто певної енергозатратної дії. Визначальне рівняння А=ΔЕ. Формула А=ΔЕ, є базовим, визначальним рівнянням роботи. Однак, якщо мова йде про певні різновидності роботи, то в цьому випадку зазвичай застосовують похідні від базового рівняння формули, зокрема:

– для механічної роботи    А_мех = F∙ℓ∙cosα,  [A] = Дж = Н∙м;

– для електричної роботи   А_ел = U∙I∙t,         [A] = Дж = В∙А∙с = (Дж/А∙с)∙А∙с = Дж;

– для магнітної роботи       А_магн = І∙ΔФ,       [A] = Дж = А∙Вб = А∙(Дж/А) = Дж.

І ніяких протиріч між цими на перший погляд різними формулами та одиницями вимірювання нема.

Задача 3. Струмопровідна рамка яка складається з 20 витків розташована вздовж ліній магнітного поля з індукцією 2Тл. Що відбудеться з рамкою при включенні струму 2А? Яка робота буде виконана при цьому? Площа рамки 40см².

Дано:

N = 20

B = 2Тл

I = 2А

S=40см²=40·10^–4м²

A = ?

Рішення. Якщо рамка з струмом розташована вздовж ліній індукції магнітного поля, то на її бічні сторони будуть діяти дві рівні за величиною і протилежні за напрямком сили Ампера, які повернуть рамку на 90°. При цьому буде виконана робота величину якої можна визначити за формулою А = І∙ΔФ. А враховуючи, що рамка складається з N витків, то А = N·І∙ΔФ. Оскільки за визначенням Ф=ВScosβ, де β =< (B,n_s), та враховуючи що в процесі обертання рамки, величина кута β змінюється від β=90° (сos90°=0), до β=0° (сos0°=1), можна записати ΔФ=BS(1–0)=BS. Таким чином А = N·І∙ΔФ = N·I·B·S = 20·2А·2Тл·40·10^–4м² = 0,32Дж.

Відповідь: А = 0,32Дж.

Здатність струмопровідного контура (замкнутого електричного кола) створювати магнітні потоки, характеризує величина, яка називається індуктивністю. Індуктивність, це фізична величина, яка характеризує здатність струмопровідного контура створювати магнітні потоки і яка дорівнює відношенню того магнітного потоку який створює даний контур, до величини того струму що призвів до появи цього потоку.

Позначається: L

Визначальне рівняння:  L=Ф/І

Одиниця вимірювання: [L]=Вб/А=Гн,   генрі *⁾

*)  Названо на честь американського фізика Джозефа Генрі (1797–1878).

Певну індуктивність має будь який провідник з струмом. Однак суттєвою ця величина є лише для спеціальних приладів – котушок індуктивності. Тому в подальшому, ми будемо говорити про індуктивність лише таких приладів.

Котушка індуктивності – це прилад, який дозволяє створювати зосереджені в певному, відносно невеликому фрагменті простору відносно потужні магнітні потоки. Котушка індуктивності представляє собою суцільний струмопровідний, електро ізольований дріт, скручений в щільну спіралеподібну котушку. На електричних схемах котушка індуктивності позначається символом       . Циліндричні котушки індуктивності зазвичай називають соленоїдами, що в перекладі з грецької означає «трубкоподібні». Якщо в середині котушки індуктивності знаходиться феромагнітне осердя, то таку котушку часто називають дроселем.

  

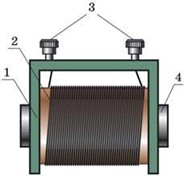
Мал.225.  Загальний вигляд, схема принципу дії та умовне позначення котушки індуктивності.

Котушки індуктивності можуть бути як самостійними приладами, так і складовими частинами більш складних приладів, зокрема електровимірювальних приладів, електромагнітів, електромагнітних реле, електродвигунів, індукційних генераторів, трансформаторів, гучномовців, кінескопів, тощо.

Принцип дії котушки індуктивності полягає в наступному. Будь який провідник з струмом, створює в навколишньому просторі певне магнітне поле. По суті, загальна кількість того магнітного поля яке створює довгий прямолінійний провідник з струмом, і такий же за довжиною але скручений в котушку провідник, є однаковою. Різниця лише в тому, що поле прямолінійного провідника «розмазане» по великій ділянці простору, кожен фрагмент якого характеризується малим магнітним потоком. Поле ж котушки індуктивності сконцентровано (сконденсовано) у певній невеликій ділянці простору і характеризується відповідно великими магнітними потоками.

Крім цього, те магнітне поле яке створюється котушкою індуктивності легко підсилюється та регулюється. Для цього достатньо в отвір котушки внести феромагнітне осердя. Під дією поля котушки, осердя намагнічується і збільшує параметри результуючого магнітного потоку в сотні і тисячі разів. Якщо ж положення осердя змінювати (вводити осердя в котушку, або витягувати з неї), то параметри відповідного магнітного потоку будуть змінюватись.

Мал.226. Феромагнітне осердя підсилює магнітну дію котушки з струмом.

Потрібно зауважити, що твердження «феромагнітне осердя підсилює магнітну дію котушки», означає лише те, що при одному і тому ж струмі, магнітна дія котушки з осердям буде більшою за магнітну дію тієї ж котушки без осердя. Однак це зовсім не означає, що ця додаткова магнітна дія виникає з нічого. Згодом ви дізнаєтесь, що електричний опір котушки з феромагнітним осердям, набагато більший за опір тієї ж котушки без осердя. А це означає, що для створення того електричного струму який тече в котушці з осердям, потрібні набагато більші енергетичні затрати, ніж для створення такого ж струму в котушці без осердя. Тому поява додаткової магнітної дії в котушці з феромагнітним осердям не є безпричинною і такою, що суперечить закону збереження енергії.

Основною характеристикою котушки індуктивності є її індуктивність, тобто величина, яка визначається за формулою L=Ф/І. При цьому індуктивність котушки фактично не залежить ні від Ф ні від І. Формула  L=Ф/І, вказує лише на те, що для будь якої котушки індуктивності, відношення того магнітного потоку який створює струм в цій котушці, до величини цього струму, за будь яких обставин залишається незмінним, і що це відношення певним чином характеризує магнітні властивості відповідної котушки.

Насправді ж індуктивність котушки залежить від параметрів самої котушки, зокрема її розмірів, форми, числа витків в ній та магнітних властивостей осердя. Наприклад, якщо довжина котушки суттєво більша за її внутрішній діаметр, то індуктивність цієї котушки визначається за формулою L=μμ₀N²S/ℓ, де  μμ₀ – параметри того феромагнітного осердя що знаходиться в котушці; N – число витків в котушці; S – площа поперечного перерізу котушки; ℓ – довжина (висота) котушки.

Котушка індуктивності дозволяє не лише створювати потужні магнітні потоки, а й накопичувати певну кількість магнітної енергії (звичайно за наявності в котушці електричного струму). Можна довести, що величина тієї енергії яка зосереджена в магнітному полі котушки з струмом, визначається за формулою  W_маг=LI²/2, де L – індуктивність котушки, І – сила струму в ній.

Дійсно. Те магнітне поле яке створює котушка індуктивності, створюється в момент включення електричного струму, тобто в момент коли: 1) сила струму в котушці змінюється від нуля до певної максимальної величини І_м; 2) магнітний потік в котушці змінюється від нуля до певної максимальної величини Ф_м. Оскільки в процесі зміни магнітного потоку виконується робота А=І∆Ф і ця робота йде на створення енергії магнітного поля, то можна записати W_маг=І∆Ф. А враховуючи, що в умовах даної задачі І = І_сер= (І_м–0)/2 = І_м/2;  ∆Ф=Ф_м–0=Ф_м, а також факт того, що за визначенням L=Ф_м/І_м, а отже Ф_м=LІ_м, можна записати W_маг = І∆Ф = (І_м/2)Ф_м = LІ_м²/2, або W_маг=LІ²/2.

Задача 4. Котушка з залізним осердям довжиною 40см і площею поперечного перерізу 20см², містить 1200 витків. Визначити енергію магнітного поля котушки, якщо в ній протікає струм 1А. Магнітна проникливість заліза 8000.

Дано:

ℓ = 40см = 0,4м

S = 20 = 20∙10^–4м²

N = 1200

I = 1A

μ = 8000

W_маг = ?

Рішення. Виходячи з того, що W_маг=LI²/2, та враховуючи що для котушки L=μμ₀N²S/ℓ, можна записати W_маг=LI²/2 = μμ₀N²SІ²/2ℓ, де μ₀=12,56∙10^{– 7}Гн/м.

Розрахунки. W_маг = μμ₀N²SІ²/2ℓ = 8000∙12,56∙10^–7Гн/м∙1200²∙20∙10^–4м²∙(1А)² / 2∙0,4м = (8∙12,56∙1,2²∙20 / 0,8)∙10^{3– 7+6–4} = 3600∙10^–2(Гн∙А² = Дж) = 36Дж

Відповідь: W_маг = 36Дж.

Задача 5. Дві довгі котушки намотані на одне осердя. Індуктивність котушок 1,6Гн і 0,1Гн. У скільки разів число витків першої котушки більша ніж у другій?

Дано:

L₁ = 1,6Гн

L₂ = 0,1Гн

N₁/N₂ = ?

Рішення. Оскільки для довгої котушки L=μμ₀N²S/ℓ, та враховуючи що в умовах даної задачі μ₁ = μ₂, S₁ = S₂, ℓ₁ = ℓ₂, можна записати L₁/L₂ = N₁²/N₂² = (N₁/N₂)² = 1,6/0,1 = 16. А це означає, що N₁/N₂ = √16 = 4.

Відповідь: N₁/N₂ = 4.

Індуктивність (L), знаходиться в тому ж ряду фізичних величин що і електрична ємність (С) та електричний опір (R). Кожна з цих величин характеризує певні параметри електричного приладу (котушки індуктивності, конденсатора, резистора). При цьому кожна величина характеризується не лише визначальним рівнянням, а й формулою яка відображає її зв’язок з параметрами відповідного приладу. Кожен же з цих приладів виконує певні енергетичні функції: резистор R – перетворює певну кількість електричної енергії у відповідну кількість теплоти Q = I²Rt; конденсатор С – накопичує певну кількість електричної енергії W_ел=CU²/2; котушка індуктивності L – накопичує певну кількість магнітної енергії W_маг=LІ²/2.

Узагальнені порівняльні відомості про базові прилади електродинаміки та про їх основні характеристики, можна представити у вигляді наступної таблиці.

Прилад	Основна характеристика		Енергетичні перетворення
	Визначальне р-ня	Від чого залежить
Резистор	R = U/I     (Ом)	R = ρℓ/S	Q = I2Rt
Конденсатор	C = q/U     (Ф)	C = εε0S/d	Wел=CU2/2
Котушка	L = Ф/І      (Гн)	L = μμ0N2S/ℓ	Wмаг=LІ2/2

Вивчення теми «Електродинаміка магнітних явищ» завершимо традиційною узагальнюючою таблицею, яка містить базову інформацію про основні поняття, величини, закони та прилади електродинаміки магнітних явищ .

Основні поняття	Основні величини	Основні закони	Основні прилади
Електричний струм Магнітне поле; Лінії індукції магнітного поля	Сила струму I = q/t    (A) Магнітна індукція В = Fм/І∆ℓsinα (Тл) Магнітний потік Ф = ВScosβ  (Вб) Індуктивність L = Ф/І    (Гн)	Закон Ампера Fм=kI1I2∆ℓsinα/r де k=μμ0/2π або Fм=ВІ∆ℓsinα Принцип суперпозиції Врез=∑Ві	Котушка індуктивності L = Ф/І L = μμ0N2S/ℓ Wмаг= LI2/2

Фізика така всеосяжна наука та навчальна дисципліна, що її практично не можливо вивчити інакше, як тільки у вигляді певної системи знань. А ця системність передбачає певний, строго визначений порядок вивчення розділів і тем. Певну системність формулювань та пояснення фізичної суті всього різноманіття фізичних термінів. І звичайно системність знань передбачає постійне застосування певних узагальнень та порівнянь.

А ще, надважливою складовою системності знань, є розуміння факту того, що Природа – це єдиний, цілісний організм в якому все взаємопов’язано і взаємообумовлено. Відображенням же цього факту є подібність тих законів і величин які описують та пояснюють на перший погляд різні явища. Наприклад дана тема завершує вивчення тієї частини електродинаміки в якій електричні і магнітні взаємодії розглядаються як певні окремі, обособлені явища. При цьому прагнучи до систематизації знань, надзвичайно важливо провести певний порівняльний аналіз гравітаційних, електричних та магнітних взаємодій. Аналіз який можна представити у вигляді певної порівняльної таблиці, наприклад такої.

 

Гравітаційні взаємодії	Електричні взаємодії	Магнітні взаємодії
Закон тяжіння Fгр=G∙m∙mп/r2	Закон Кулона Fел=k∙q∙qп/r2	Закон Ампера Fм=k∙I∙Iп∙∆ℓ∙sinα/r
G = G0 = const G0=6,67∙10–11Н∙м2/кг2	k = k0/ε, де  ε=F0/F k0=9∙109Н∙м2/Кл2	k=μk0, де  μ = F/F0 k0=2∙10–7Н/А2
в сучасній науці
–	k = 1/4πεε0	k = μμ0/2π
G0=6,67∙10–11Н∙м2/кг2 гравітаційна стала	ε0 = 8,85∙10–12 Ф/м електрична стала	μ0 = 12,56∙10–7 Гн/м магнітна стала
головна характеристика поля
g = Fгр/mп напруженість гравітаційного поля	E = Fел/qп напруженість електричного поля	В=Fм/Іп∆ℓsinα індукція магнітного поля
закони записані на мові параметрів полів
Закон тяжіння Fгр = g∙m	Закон Кулона Fел = E∙q	Закон Ампера Fм = В∙І∙∆ℓ∙sinα

Контрольні запитання.

1. Що характеризує і чому дорівнює кут β в формулі Ф=ВScosβ?
2. За якою формулою визначають: а) механічну роботу; б) електричну роботу; в) магнітну роботу.
3. Доведіть що Н∙м = В∙А∙с = Вб∙А
4. Поясніть принцип дії котушки індуктивності.
5. Як регулюють індуктивність в котушці індуктивності?
6. Що означає твердження: «феромагнітне осердя підсилює магнітну дію котушки»? Чи означає це, що відповідне підсилення відбувається без певних енергетичних затрат?
7. Що характеризує і чому дорівнює індуктивність провідника (котушки)?
8. Індуктивність визначається за формулою L=Ф/І. Чи означає це, що індуктивність котушки залужить від сили струму в цій котушці?
9. Від чого залежить індуктивність котушки індуктивності?
10. Які енергетичні функції резистора, конденсатора та котушки індуктивності?

Вправа 39.

1. Установіть відповідність між назвою (1 – 4) та визначальним рівнянням (А – Д) фізичної величини.

1). магнітна індукція            А.  Ф=ВScosβ

2) індуктивність                   Б.   F=ma

3)сила                                  В.   І=q/t

4) магнітний потік               Г.   L=Ф/I

5)                                          Д.   B=F/I∆ℓsinα

2. Установіть відповідність між назвою одиниці фізичної величини (1 – 4) та її вираженням в основних одиницях СІ (А – Д)

1)тесла                             А.   кг·м/с²

2) генрі                            Б.   кг/с²·А

3) ньютон                         В.   кг·м²/с²·А

4) вебер                            Г.   кг·м²/с²

5)                                       Д.   кг·м²/с²·А²

3. Установіть відповідність між назвою одиниці вимірювання фізичної величини (1 – 5), її визначенням за визначальним рівнянням (а – е) та вираженням в основних одиницях СІ (А – Е)

1) тесла          а.   Вб/А                          А.   кг·м/с²

2) вольт          б.   А·с                             Б.   кг·м²/с²·А²

3) вебер         в.   Н/А·м                        В.   кг·м²/с²

4) джоуль        г.   Тл·м²                         Г.   кг·м²/с²·А

5) генрі           д.   Дж/Кл                       Д.   кг·м²/с³·А

6)                     е.   Н·м                            Е.   кг/с²·А

4. Струмопровідна рамка діаметром 10см знаходиться в однорідному магнітному полі з індукцією 2Тл. На скільки зміниться той магнітний потік що пронизує рамку за один її оберт?
5. В котушці, індуктивність якої 0,6Гн тече струм 10А. Яку енергію має магнітне поле цієї котушки?
6. Визначте енергію магнітного поля соленоїду в якому при силі струму 10А виникає магнітний потік 0,5Вб.
7. При зміні сили струму в котушці, індуктивність якої 0,5Гн в два рази, енергія її магнітного поля збільшилась на 3Дж. Визначити початкові значення енергії та сили струму в котушці.
8. Яку індуктивність матиме соленоїд виготовлений з дроту довжиною 20м і діаметром 0,5мм, якщо його висота 10см, а середній діаметр 3см: а) за відсутності осердя; б) за наявності осердя (μ=5000)?
9. Кільце радіусом 20см по якому тече струм 5А розташовано перпендикулярно лініям поля з індукцією 0,3Тл. Скільки енергії потрібно витратити на те, щоб розвернути кільце вздовж ліній магнітного поля?
10. Котушка електромагніту має індуктивність 0,6Гн, опір 10(Ом) і перебуває під постійною напругою. За який час в цій котушці виділяється стільки ж теплоти, скільки енергії магнітного поля зосередженого в котушці?

.

Лекційне заняття №40.

Тема: Основи сучасної теорії магнітних властивостей речовини. 

Вивчення теми «Електродинаміка магнітних явищ», ми почали з констатації факту того, що на кінець 1820 року про магнітні явища було відомо наступне:

1. Пепеважна більшість матеріалів, суттєвих магнітних властивостей не проявляють.
2. Суттєві магнітні властивості мають лише так звані феромагнетики, до числа яких відносяться залізо, кобальт, нікель та деякі їх сплави.
3. Магнітні властивості феромагнетиків можуть бути як активними (постійні магніти) так і пасивними (ненамагнічене залізо).
4. Постійні магніти мають два полюси (південний і північний), які взаємодіють між собою: однойменні полюси відштовхуються, різнойменні – притягуються.
5. Розділити магнітні полюси не можливо.
6. Магнітну дію створюють не лише постійні магніти, а й електричні струми.

Говорячи про магнітні властивості речовин, до вище сказаного доречно додати, що за цими властивостями речовини поділяються на парамагнетики, діамагнетики та феромагнетики.

Парамагнетиками називають такі речовини, магнітна проникливість яких мінімально більша за одиницю (μ≈1,0005). В потужних магнітних полях парамагнетики намагнічуються таким чином, що слабо притягуються до джерела поля. До числа парамагнетиків відносяться марганець, хром, платина, алюміній, вольфрам, лужні та лужноземельні метали, тощо.

Діамагнетиками називають такі речовини, магнітна проникливість яких мінімально менша за одиницю (μ≈0,9995). В потужних магнітних полях, діамагнетики намагнічуються таким чином, що слабо відштовхуються від джерела поля. До числа діамагнетиків відносяться вода, вісмут, цинк, свинець, мідь, срібло, золото, більшість газів, більшість органічних сполук, тощо.

Феромагнетиками називають такі речовини, магнітна проникливість яких набагато більша за одиницю (μ ˃˃ 1). Феромагнетики поділяються на магнітно м’які та магнітно тверді. Магнітно м’які феромагнетики легко намагнічуються і швидко розмагнічуються. В магнітних полях вони намагнічуються таким чином що сильно притягуються до джерела поля. Магнітно тверді феромагнетики важко намагнічуються і повільно розмагнічуються. Після намагнічування ці феромагнетики стають самостійними джерелами магнітного поля. До числа феромагнетиків відносяться залізо, кобальт, нікель та велика група  сплавів, основою яких можуть бути не лише залізо, кобальт, нікель, а й марганець та хром.

Мал.227. Базовими феромагнітними матеріалами є: залізо (μ≈8000), кобальт (μ≈200) та нікель (μ≈300).

Як відомо, перший крок на шляху пояснення магнітних властивостей речовин зробив французький фізик Ампер. В основі теорії Ампера лежать два твердження: 1. Джерелом магнетизму (джерелом магнітного поля) є електричний струм. 2. В кожному тілі існують внутрішні «молекулярні» струми, які і надають тілу відповідних магнітних властивостей.

Згідно з теорією Ампера, кожний «молекулярний струм» створює певну елементарну магнітну дію. При цьому, в залежності від просторової орієнтації цих елементарних дій (елементарних магнітів), тіло набуває відповідних магнітних властивостей. Скажімо, якщо «молекулярні струми» орієнтовані хаотично, то їх магнітні дії нівелюють одна одну і відповідне тіло магнітних властивостей не проявляє. Якщо ж «молекулярні струми» співнаправлені, то їх магнітні дії підсилюються і тіло має відповідні магнітні властивості. Або якщо наприклад магнітно мякий феромагетик не проявляє активних магнітних властивостей, то це означає, що його «молекулярні струми» орієнтовані усереднено хаотично. Якщо ж цей феромагнетик потрапляє в зовнішню магнітне поле, то її «молекулярні струми» орієнтуються таким чином, що підсилюють магнітну дію зовнішнього поля.

Мал.228. За відсутності зовнішнього магнітного поля магнітно м’які феромагнетики є ненамагніченими, а за наявності поля стають намагніченими.

Сьогодні, коли достовірно відомо про будову атома, абсолютно очевидно, що ті «молекулярні струми» про які говорив Ампер, це результат обертання електронів навколо атомного ядра. Втім, світ атомів і елементарних частинок так сильно відрізняється від звичного для нас світу макротіл, що будь які наші порівняння та аналогії є гранично умовними. Та як би там не було, а ситуація виглядає таким чином, ніби надзвичайно дрібненька негативно заряджена частинка (електрон) обертається навколо позитивно зарядженого ядра атома і фактом свого обертання створює певну магнітну дію.

Крім цього, подібно до того як Земля обертається не лише навколо Сонця, а і навколо власної осі, електрон також веде себе так ніби він обертається як навколо ядра так і навколо власної осі. Зверніть увагу на оте «ніби» і не намагайтеся представити справу таким чином ніби електрони дійсно обертаються навколо своєї осі, подібно до того як це робить розкручена дзиґа, чи планета Земля. Не намагайтеся тому, що електрон абсолютно не схожий а ні на дзиґу, а ні на Землю, а ні на маленьку кульку, а ні на будь які інші відомі вам тіла.

 

Мал.229. Електрон веде себе таким чином ніби він обертається як навколо ядра атома, так і навколо власної осі.

Характеризуючи ті властивості електрона які певним чином схожі на властивості тіла що обертається навколо власної осі, говорять про те, що електрон має спін (від англ. spin – крутитись). По суті, спін – це внутрішня, невід’ємна властивість елементарної частинки, така ж як її маса та електричний заряд. Електрон не може втратити свій спін, як не може втратити свою масу чи електричний заряд. Спін, це сугубо квантове поняття і тому сьогодні ми не будемо говорити про його фізичний зміст. Ми просто констатуємо факт того, що електрон має певний спін, який характеризує певні магнітні властивості самого електрона, який за будь яких обставин залишається незмінним і який може бути або додатнім або від’ємним.

Дослідження показують, що ті магнітні властивості які створює електрон в атомі, визначаються двома обставинами: орбітальним рухом електрона навколо ядра та його внутрішньою властивістю яку характеризує величина під назвою спін. При цьому саме спін визначає полярність того умовного магніту який створює рух даного електрона. Умовно кажучи, знак спіну визначає в якому напрямку буде обертатись електрон: справа наліво чи зліва направо.

Варто зауважити, що магнітні властивості електрона в атомі і атома загалом, характеризує величина яка називається магнітним моментом. Магнітний момент (позначається р_м іноді μ або m) – це векторна величина, яка характеризує магнітні властивості замкнутого електричного струму. По суті магнітний момент характеризує величину та полярність того магнітного яке створює електрон в атомі і атом загалом.

Мал.230. Циркуляція електрона в атомі створює певний магнітний момент.

Максимально стисло та гранично спрощено пояснюючи суть сучасної теорії магнітних властивостей речовини, можна сказати наступне. В будь якому атомі, електрони розташовані в певному порядку який визначається законами квантової фізики. Ми не будемо формулювати ці закони. Ми просто представимо результати їх застосування у вигляді загально прийнятих умовних схем, які певним чином відображають розташування електронів в тому чи іншому атомі, а відповідно і його загальні магнітні властивості. Власне з цими схемами ви знайомі з курсу хімії, де пояснюючи будову атома, а відповідно і його хімічні властивості, ви малювали певний набір клітинок які заповнювали певним набором стрілок (мал.231). Ці клітинки і стрілки певним чином характеризують не лише хімічні властивості атома, а і його магнітні властивості.

Мал.231. Схема розподілу електронів в деяких атомах.

Оскільки ми говоримо про магнітні властивості речовин, то буде доречним пояснити лише магнітний зміст зображених на мал.231 схем. Перш за все зауважимо, що кожній зображеній на схемі стрілці відповідає один електрон. При цьому напрям стрілки вказує на знак його спіну, а відповідно і його магнітного моменту. Наприклад в атомі гелію міститься два електрони, один з яких має додатній спін, а інший – від’ємний. Умовно кажучи, в атомі гелію один електрон обертається зліва направо, а інший – справа наліво. І не важко збагнути, що загальний магнітний момент атома гелію буде нульовим (р_м=0). В атомі водню міститься лише один електрон, спін якого може бути або додатнім, або від’ємним. При цьому ясно, що атом водню має певний магнітний момент (р_м=1), а отже і відповідні магнітні властивості.

Не важко бачити, що у переважній більшості атомів, кількість електронів з додатними і від’ємними спінами є незбалансованою. А це означає, що відповідні атоми мають певні магнітні властивості. З іншого боку загально відомо, що переважна більшість речовин суттєвих магнітних властивостей не проявляє. Тому виникає закономірне питання: якщо атоми мають магнітні властивості, то чому ж ті речовини які складаються з цих атомів таких властивостей не мають?

Дійсно. Якщо атом азоту (N) має великі магнітні властивості (р_м=3), то чому ж ті речовини які складаються з цих атомів (N₂, NH₃, NO₂, HNO₃, тощо) таких властивостей не мають? Відповідь на це запитання полягає в наступному. Коли атоми азоту об’єднуються в ті чи інші молекули або кристали, то вони завжди паруються таким чином, що їх магнітні моменти взаємно компенсуються. Скажімо, в молекулі азоту (N₂) ніколи не буває двох однакових атомів. В цій молекулі один атом має додатний магнітний момент, а інший – від’ємний. І як ви розумієте, загальні магнітні властивості такої молекули є практично нульовими.

Подібним чином ведуть себе майже всі атоми. Вони або за своєю природою не мають суттєвих магнітних властивостей (Не, Ве, Ne, Mg, Ar, …), або маючи такі властивості при об’єднанні з іншими атомами, ці властивості втрачають. Втрачають тому, що об’єднуються так, що їх магнітні моменти взаємно компенсуються. Наприклад атоми хрому (Сr) мають надзвичайно потужні магнітні властивості (р_м=6). При цьому кристалічний хром суттєвих магнітних властивостей не має. Не має тому, що в кристалічному хромі атоми орієнтовані таким чином, що їх магнітні моменти взаємно компенсуються (мал.232а)

На щастя, існує група атомів, які ведуть себе на так як всі. Об’єднуючись в кристалічні структури, ці атоми орієнтуються таким чином, що їх магнітні моменти взаємно підсилюються. Цими унікальними атомами є атоми заліза (Fe), кобальту (Со) та нікелю (Ni). Магнітні властивості обособлених атомів заліза (р_м=4) значно скромніші за відповідні властивості обособлених атомів хрому (р_м=6). Але на відміну від хрому, в кристалічному залізі атоми орієнтуються так, що їх магнітні моменти не компенсуються, а підсилюються (мал.232б).

Сr   

Fe  

Мал.232. В кристалі хрому магнітні моменти сусідніх атомів взаємно компенсуються, а в кристалі заліза – взаємно підсилюються.

На разі ми не будемо говорити про те, чому атоми заліза, кобальту і нікелю ведуть себе не так як всі. Зауважимо тільки, що їх поведінка не є якоюсь аномальною, і що вона повністю відповідає законам квантової фізики.

Ви можете запитати: «А чому одні феромагнітні тіла є постійно намагніченими (постійні магніти), тоді як інші, стають намагніченими лише в присутності стороннього магніту чи струму, а за їх відсутності, набуті магнітні властивості швидко втрачають?». Відповідаючи на це слушне запитання можна сказати наступне. Дослідження показують, що в феромагнітних тілах, атоми завжди об’єднуються в певні групи, які називаються магнітними доменами (від. франц. domain – певна область, володіння). В межах домену магнітні моменти всіх атомів орієнтовані в одному напрямку. І тому кожний домен представляє собою маленький магніт, момент якого дорівнює сумі магнітних моментів всіх його атомів. При цьому, якщо домени орієнтовані безладно, то відповідне феромагнітне тіло активних магнітних властивостей не проявляє. А якщо домени орієнтовані в одному напрямку, то їх магнітні моменти додаються і відповідне тіло проявляє активні магнітні властивості.

Мал.233. При хаотичній орієнтації доменів (а), феромагнітне тіло не проявляє активних магнітних властивостей. А при упорядкованій орієнтації (б) – проявляє їх.

В залежності від рухливості доменів, тобто від їх здатності швидко чи повільно змінювати свою просторову орієнтацію, феромагнітні речовини поділяються на магнітно м’які та магнітно тверді. В магнітно м’яких феромагнетиках, домени надзвичайно рухливі і тому відповідні речовини легко намагнічуються і легко розмагнічуються. З магнітно м’яких феромагнетиків виготовляють осердя трансформаторів, електродвигунів, генераторів, тощо. В магнітно твердих феромагнетиках, домени неповороткі і тому відповідні речовини з великими потугами намагнічуються, і з не меншими потугами розмагнічуються. З магнітно твердих феромагнетиків виготовляють постійні магніти.

Факт того що феромагнітні тіла неминуче діляться на окремі магнітні домени, є прямим наслідком одного з базових законів Природи – принципу мінімуму. В цьому законі стверджується: будь яка відкрита система, прагне прийти до такого стану, при якому кількість зосередженої в ній надлишкової енергії буде мінімально можливою. Скажімо, в намагніченому шматку заліза енергії більше аніж в аналогічному ненамагніченому шматку. А це означає, що згідно з принципом мінімуму, намагнічене залізо прагне розмагнітитись. За певних умов (t ≥ 770ºС) це розмагнічування відбудеться практично миттєво. А за інших умов, може тривати мільярди років. Однак в будь якому випадку система прагне до того щоб кількість зосередженої в ній надлишкової енергії була мінімально можливою.

Власне одним з шляхів реалізації принципу мінімуму, є факт поділу феромагнітних речовин на такі обособлені магнітні фрагменти (домени) які прагнуть до такої орієнтації при якій загальна кількість енергії в системі буде мінімально можливою. Адже якщо згідно з одним законом, атоми заліза мають вишиковуватись у певному порядку який передбачає збільшення загальної кількості енергії в системі, а згідно з іншим законом, цієї енергії має бути як найменше, то Природа неминуче знайде певне компромісне рішення. Цим компромісним рішенням і є формування обособлених феромагнітних груп, які називаються доменами.

Дослідження показують, що феромагнітні властивості речовини зберігаються лише до певної температури. Наприклад, нагріваючи залізо ви неодмінно з’ясуєте, що при температурі 770ºС воно різко (стрибкоподібно) втрачає свої феромагнітні властивості. І навпаки, якщо сильно нагріте залізо охолоджувати, то в момент досягнення температури 770ºС, воно стрибкоподібно набуває феромагнітних властивостей. Аналогічним чином ведуть себе й інші феромагнетики. Зокрема кобальт, втрачає свої феромагнітні властивості при температурі 1130ºС, а нікель – при 358ºС. Температура при якій феромагнетик втрачає свої феромагнітні властивості, або навпаки, називається точкою Кюрі.

Намагаючись пояснити причини того, що при певній температурі, феромагнетики різко втрачають свої унікальні властивості, ми вкотре вимушені послатись на закони квантової фізики. Втім, навіть вони не можуть вичерпно пояснити дане явище. Тому, якщо вам коли небуть спаде на думку взятись за вирішення ще не розв’язаної наукової проблеми, знайте, така проблема існує і чекає на свого Ейнштейна.

Потрібно зауважити, що в природі не існує атомів, молекул чи макротіл, які б в тій чи іншій мірі не проявляли магнітних властивостей. Тому говорячи про те, що даний атом, дана молекула чи дана речовина не мають магнітних властивостей, мають на увазі лише те, що ці властивості є надзвичайно слабкими. Різноманіття ж тих речовин магнітні властивості яких є малопомітними, прийнято розділяти на дві групи: парамагнетики та діамагнетики. Основна зовнішня відмінність між пара- та діа- магнетиками полягає в тому, що перші ледь помітно притягуються до джерела сильного магнітного поля, а другі, навпаки – ледь помітно відштовхуються від такого джерела.

Стисло пояснюючи механізм діамагнетизму, можна сказати наступне. В атомах (молекулах) діамагнетиків (μ≈0,9995), спінові та орбітальні магнітні моменти збалансовані таким чином, що їх результуюча величина є практично нульовою. Можна передбачити, що подібні атоми не повинні проявляти магнітних властивостей. Втім, дане передбачення не підтверджується. Не підтверджується тому, що під дією зовнішнього магнітного поля, траєкторія руху електронів дещо змінюється. Ця зміна еквівалентна появі певного додаткового струму який прийнято називати індукційним. Згодом ви дізнаєтесь, що індукційні струми завжди направлені таким чином, що протидіють причині їх появи. А оскільки в даному випадку причиною появи індукційних струмів є дія зовнішнього магнітного поля, то протидіючи цій причині, індукційні струми спричиняють відштовхування відповідних атомів від джерела зовнішнього поля.

В тій чи іншій мірі діамагнетизм притаманний всім речовинам. Але величина діамагнітного ефекту настільки мала, що має суттєве значення лише для тих речовин, атоми (молекули) яких практично не мають власного магнітного моменту.

На відміну від діамагнетиків, атоми парамагнетиків (μ≈1,0005) мають достатньо потужні магнітні моменти. Об’єднуючись в молекули та кристалічні структури, ці атоми орієнтуються таким чином, що їх магнітні моменти взаємно компенсуються, але компенсуються не повністю, утворюючи так звані магнітні диполі. За відсутності зовнішнього магнітного поля, магнітні диполі орієнтовані хаотично і тому парамагнітна речовина не проявляє магнітних властивостей. Якщо ж ця речовина потрапляє в зовнішнє магнітне поле, то її магнітні диполі орієнтуються так, що парамагнетик притягуються до джерела поля та підсилює це поле. Однак магнітні моменти диполів дужу малі і тому підсилення зовнішнього поля є незначним.

Контрольні запитання.

1. Від чого залежать магнітні властивості обособленого атома?
2. Чи має суттєві магнітні властивості: а) атом гелію; б) атом водню; в) молекула водню? Чому?
3. Відомо, що магнітні властивості атомів марганцю (р_м=5) потужніші за магнітні властивості атомів заліза (р_м=4). Чому ж марганець не є феромагнетиком?
4. Як пояснити факт того, що магнітні властивості феромагнетиків можуть бути як пасивними (ненамагнічене залізо) так і активними (намагнічене залізо)?
5. Які матеріали називають: магнітно м’якими? магнітно твердими?
6. Що називають точкою Кюрі?
7. З яких матеріалів і яким чином виготовляють постійні магніти?
8. Чи можна змінити полярність постійного магніту? Якщо можна, то як?

.

Семестр 3.

.

Лекційне заняття №1.

Тема: З історії електромагнітної індукції. Закон електромагнітної індукції. 

Практична значимість того явища яке було відкрите і досліджене видатним англійським фізиком Майклом Фарадеєм, і яке прийнято називати електромагнітною індукцією, така величезна, що це явище, той закон який його описує, та ті прилади принцип дії яких базується на його застосуванні, потребують особливої уваги та окремого розгляду.

Одна з визначальних рис геніальності вченого полягає в здатності бачити глибину суть явищ. Яскравим прикладом такого вченого є Майкл Фарадей. Той самий Фарадей, офіційна освіта якого чотири класи початкової школи, і який на ряду з Галілеєм, Ньютоном, Максвелом та Ейнштейном входить в п’ятірку найвидатніших вчених всіх часів і народів.

Не будучи видатним математиком, Фарадей вирізнявся розумінням глибинної суті природних явищ. Розумінням того, що Природа, це єдиний, цілісний організм, в якому все гармонічно взаємопов’язано та взаємообумовлено. Що одним з проявів гармонічності Природи є симетричність тих процесів які в ній відбуваються: нагрівання – охолодження, плавлення – кристалізація, пароутворення – конденсація, сублімація – десублімація, тощо. Тому коли 1821 році Фарадей ознайомився з основами теорії Ампера, теорії в якій стверджувалося, що електричні струми створюють магнетизм, то відразу ж зрозумів: якщо електричний струм створює магнетизм, то має існувати і зворотній процес, процес при якому магнетизм створює електричний струм. Виходячи з цього,  великий вчений занотував: «перетворити магнетизм в електрику». А занотувавши, поклав до кишені маленький магніт, який мав нагадувати про те, що за допомогою подібного магніту треба отримати електричний струм.

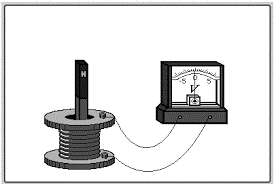
Мал.1. Ампер – електричний струм створює магнетизм. Фарадей – якщо струм створює магнетизм, то і магнетизм має створювати струм.

Сьогодні, коли в нашому розпорядженні є потужні та надійні джерела постійного і змінного струмів, коли в будь якому кабінеті фізики є чутливі електровимірювальні прилади, потужні постійні магніти, феромагнітні осердя та різноманітні котушки індуктивності, «відкрити» та дослідити те явище яке відкрив Фарадей не складно. Ілюструючи цю нескладність проведемо наступний експеримент.

Зберемо електричне коло яке складається з гальванометра (міліамперметра) і котушки індуктивності в отворі якої знаходиться постійний магніт. Допоки магніт нерухомо перебуває в котушці, стрілка гальванометра не фіксує наявності струму. Але як тільки магніт починає рухатися, стрілка відхиляється фіксуючи тим самим появу струму. При цьому не важко бачити, що напрям відхилення стрілки приладу, а отже і напрям струму, залежать як від орієнтації полюсів магніту, так і від напрямку його руху. Скажімо, якщо при введенні магніту, стрілка приладу відхиляється вправо, то при його виведені – вліво і навпаки.

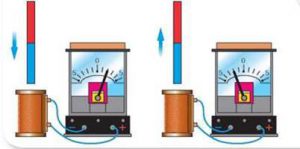
Мал.2.В процесі поступального руху магніту, в котушці з’являється індукційний струм.

Аналізуючи результати експерименту, можна зробити висновок про те, що причиною появи струму в котушці індуктивності, є зміна того магнітного потоку який пронизує котушку. Власне цей висновок і є суттю того явища яке відкрив Фарадей і яке прийнято називати електромагнітною індукцією. Варто зауважити, що ті струми які створюються (наводяться) змінними магнітними потоками, називають індукційними струмами (від лат. induction – створювати, наводити).

Таким чином, електромагнітна індукція, це явище, суть якого полягає в тому, що  при будь якій зміні того магнітного потоку, що пронизує замкнутий струмопровідний контур, в цьому контурі виникає індукційний струм, параметри якого залежать від швидкості зміни магнітного потоку.

Нагадаємо, Магнітний потік, це фізична величина, яка характеризує загальний потік індукції магнітного поля через задану поверхню площею S і яка дорівнює добутку вектора індукції магнітного поля В на площу тієї поверхні яку пронизує ця індукція.

Позначається: Ф

Визначальне рівняння: Ф=ВScosβ, де  β – кут між напрямком вектора В та перпендикуляром (нормаллю) до поверхні S: β =< B та n_s

Одиниця вимірювання:  [Ф] = Тл∙м² = Дж/А = Вб,  вебер.

Оскільки індукційні струми створюються не просто магнітними потоками, а потоками які змінюються, то досліджуючи явище електромагнітної індукції, в якості джерела змінного магнітного поля доречно застосовувати змінний електричний струм. Зважаючи на ці обставини, в якості джерела змінного магнітного поля візьмемо потужну котушку індуктивності з стержнеподібним феромагнітним осердям, яку зазвичай називають котушкою Томсона (мал.3). Якщо через котушку Томсона пропустити змінний електричний струм, то він в сукупності з феромагнітним осердям створить відповідне змінне магнітне поле. Вносячи в це поле ті чи інші струмопровідні об’єкти, не важко з’ясувати загальні властивості індукційних струмів.

Наприклад якщо в поле змінного струму вносити струмопровідну котушку, то неодмінно з’ясується, що при наближенні котушки до джерела поля, величина виникаючої в ній індукційної напруги, а відповідно й індукційного струму, будуть збільшуватися, а при віддаленні від джерела поля – зменшуватися. Якщо в змінне магнітне поле котушки Томсона вносити вторинні котушки з різним числом витків, то не важко переконатися в тому, що величина виникаючої в них індукційної напруги, а відповідно й індукційного струму, буде пропорційною числу витків в цих котушках: чим більше число витків, тим більша індукційна напруга.

Мал.3. Величина індукційного струму, залежать від швидкості зміни того магнітного потоку що пронизує котушку та від числа витків в ній.

Якщо в змінне магнітне поле котушки Томсона внести алюмінієве кільце, то неодмінно з’ясується, що всупереч дії сили тяжіння, кільце буде «висіти» в магнітному полі. А це означає, що на кільце діє певна сила, яка прагне виштовхнути його з магнітного поля. А оскільки співнаправлені струми притягуються, а протинаправлені – відштовхуються, то з факту виштовхування кільця з магнітного поля, можна зробити висновок про те, що напрямки струмів в котушці Томсона (первинний струм) та індукційного струму кільця (вторинний струм) є взаємно протилежними. Фактично це означає, що індукційний струм має такий напрямок, при якому магнітна дія цього струму протидіє причині його появи, а цією причиною є зміна магнітного потоку.

Факт протидії індукційного струму причині його появи, особливо ефектно проявляється в наступному експерименті. Алюмінієве кільце надіте на феромагнітне осердя відключеної від джерела струму котушки Томсона. В момент вмикання струму, кільце в буквальному сенсі «вистрибує» з наростаючого магнітного потоку, демонструючи тим самим протидію індукційного струму причині його появи.

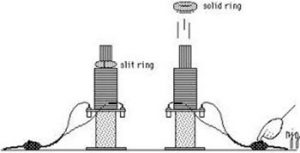
Мал.3а. Напрямки струмів в котушці Томсона (первинний струм) та індукційного струму кільця є взаємно протилежними.

Узагальнюючи результати вище наведених експериментальних фактів, можна сформулювати закон, який прийнято називати законом електромагнітної індукції і який по праву мав би називатись законом Фарадея. Та перш ніж сформулювати цей надважливий закон, буде доречним визначити послідовність тих подій, кінцевим результатом яких є електричний струм. А ця послідовність є наступною. Те, що називається ЕРС (електро рушійна сила) джерела струму (ℰ = А_ст/q), створює між полюсами цього джерела відповідну електричну напругу (U = A_ел/q), яка в свою чергу, створює відповідний електричний струм (I = U/R). Іншими словами: ℰ→U→I. Зважаючи на ці обставини, в законі електромагнітної індукції говориться не про індукційний струм, а про першопричину цього струму – ЕРС індукції.

Закон електромагнітної індукції (закон Фарадея) – це закон, в якому стверджується: при будь якій зміні того магнітного потоку що пронизує струмопровідний контур, в цьому контурі виникає ЕРС індукції (ЕРС→ напруга→ струм), величина якої пропорційна числу витків в контурі (N) та швидкості зміни магнітного потоку (ΔФ/Δt). Іншими словами:

якщо Ф=ВScosβ=ƒ(t) то індуцирується ℰ_ін = –N(ΔФ/Δt) → U_ін = ℰ_ін → І_ін = U_ін/R.

Потрібно зауважити: коли ми стверджуємо, що ЕРС індукції створює рівну їй за величиною індукційну напругу (U_ін = ℰ_ін), то під цією напругою маємо на увазі її максимально можливе значення. При цьому, визначаючи силу струму за формулою  І_ін = U_ін/R, символом R позначаємо загальний опір кола, тобто той опір який складається з опору зовнішньої та внутрішньої ділянок відповідного кола. Саме в такому контексті в потрібно сприймати систему формул: ℰ_ін = –N(ΔФ/Δt) → U_ін = ℰ_ін → І_ін = U_ін/R.

В законі електромагнітної індукції знак «–» вказує на те, що індукційний струм має такий напрямок, при якому своєю магнітною дією, протидіє причині появи цього струму, тобто протидіє зміні магнітного потоку (правило Лєнца).

По суті, правило Лєнца, та наявний в законі електромагнітної індукції знак «–», вказують на те, що при будь яких індукційних перетвореннях, виконується закон збереження енергії, і що тому індукційний струм не можливо отримати без відповідних енергетичних затрат. Скажімо, якщо в постійному магнітному полі обертати замкнуту струмопровідну рамку, той магнітний потік що пронизує цю рамку буде змінюватися і в ній неминуче виникне певний індукційний струм. Однак, якщо ви думаєте, що одного разу штовхнувши рамку та змусивши її обертатись за інерцією, ви отримаєте джерело «дармової» електроенергії, то знайте – так не буває. Власне про це і нагадує знак «–». Адже він фактично вказує на те, що як тільки в рамці з’явиться індукційний струм, так відразу ж з’являться і ті сили які протидіятимуть її обертанню. І чим більшою буде величина струму, тим більшими будуть протидіючі сили.

Перевіряючи факт того, що індукційний струм, завжди протидіє причині появи цього струму, проведемо ще один показовий експеримент. На мал.4 зображено простий пристрій, який складається з двох легких алюмінієвих кілець, одне з яких суцільне, а інше – має розріз. Наближуючи магніт до кільця з розрізом, ви не помітите певної взаємодії між ними. І це природньо. Адже розрізане кільце по суті є розімкнутим електричним колом і тому в ньому індукційний струм не виникає, а отже не виникає й індукційна протидія переміщенню магніту.

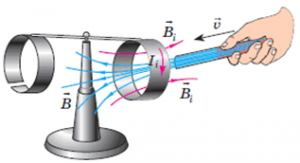
Мал.4. Своєю магнітною дією індукційний струм завжди протидіє причині появи цього струму (протидіє зміні магнітного потоку).

Тепер, будемо наближати магніт до суцільного кільця. Не важко бачити, що в процесі цього наближення, кільце відштовхується від магніту. Відштовхується тому, що при наближенні магніту, величина того потоку що пронизує кільце збільшується. При цьому в кільці виникає певний індукційний струм, який своєю магнітною дією протидіє причині появи цього струму. А цією причиною є зростання того магнітного потоку що  викликає з наближенням магніту. Якщо ж внесений в суцільне кільце магніт витягувати з кільця, то кільце буде рухатися за магнітом. Це відбувається тому, що при віддалені магніту, величина того магнітного потоку що пронизує кільце зменшується. При цьому в кільці виникає відповідний індукційний струм, який протидіє причині появи цього струму, тобто протидіє зменшенню того магнітного потоку яке спричинене віддаленням магніту.

Задача 1. В зображеній на малюнку а) ситуації, магніт віддаляють від котушки індуктивності. Визначити напрям того індукційного струму, що виникає в котушці. Яким буде цей напрямок при наближенні магніту?

а)  б)

Рішення. Згідно з правилом Лєнца, індукційний струм завжди протидіє причині появи цього струму. В нашому випадку цією причиною є віддалення магніту, а фактом протидії цьому віддаленню, має бути такий індукційний струм, магнітне поле якого протидіє віддаленню магніту. По суті це означає, що збоку північного (N) полюсу магніту, має бути південний полюс (S) котушки індуктивності.

Визначаючи напрям того струму який створює індукційний магніт відомої полярності, застосовуємо правило зігнутої кісті правої руки: якщо зігнуту кість правої руки розташувати так, щоб її чотири пальці вказували напрям струму в котушці, то відігнутий великий палець вкаже на напрям північного (N) полюса цієї котушки. А у відповідності з цим правилом, напрям струму в котушці має відповідати напрямку проти годинникової стрілки.

Ясно, що при наближенні магніту, напрям індукційного струму буде протилежним і відповідатиме напрямку за годинниковою стрілкою.

Задача 2. Котушки А і Б надіті на спільне феромагнітне осердя. Визначити напрям індукційного струму в котушці А, якщо в колі котушки Б: 1) замкнути коло; 2) розімкнути коло; 3) перемістити повзунок реостату ліворуч; 4) перемістити повзунок реостату праворуч.

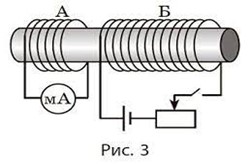
Рішення. 1). В момент вмикання кола котушки Б, сила струму в котушці зростає, а відповідно зростає і створюваний нею магнітний потік. При цьому в котушці А виникає індукційний струм, який у відповідності з правилом Лєнца, має протидіяти зростанню магнітного потоку. А це означає, що котушка А має відштовхуватися від котушки Б, і що тому напрямки струму в котушках мають бути протилежними. А оскільки напрям струму в котушці Б за годинниковою стрілкою, то в котушці А цей напрям проти годинникової стрілки.

2). В момент розмикання кола, електричний струм, а відповідно і магнітний потік котушки Б зменшується. При цьому, індукційний струм котушки А, протидіючи зменшенню магнітного потоку, має притягуватися до струму котушки Б, а отже бути направленим в ту ж сторону що і струм Б, тобто за годинниковою стрілкою.

3). При переміщенні повзунка реостата ліворуч, електричний опір реостата зменшується, а сила струму і магнітний потік в котушці Б збільшуються. При цьому індукційний струм котушки А, протидіючи збільшенню магнітного потоку, має відштовхуватися від струму котушки Б, а отже бути направленим в протилежну сторону, тобто проти годинникової стрілки.

4). При переміщенні повзунка реостата праворуч, опір реостата збільшується, а сила струму і магнітний потік в котушці Б зменшується. При цьому індукційний струм котушки А, протидіючи зменшенню магнітного потоку, має притягуватися до струму котушки Б, а отже бути направленим в ту ж сторону, тобто за годинниковою стрілкою.

Задача 3. В котушці індуктивності з числом витків 100, за 0,2с магнітний потік змінився на 0,06Вб. Яка швидкість зміни магнітного потоку? Яка ЕРС індукції в контурі? За якої умови ЕРС індукції в контурі буде постійною.

Дано:

N = 100

Δt = 0,2c

ΔФ = 0,06Вб

ΔФ/Δt = ?

Ɛ = ?

Рішення. Оскільки швидкість зміни магнітного потоку визначається як ΔФ/Δt , то в умовах нашої задачі ΔФ/Δt = 0,06Вб/0,2с = 0,3Вб/с.

Згідно з законом електромагнітної індукції ℰ_ін= N(ΔФ/Δt) = 100∙0,3Вб/с = 30В.

[ℰ_ін] = Вб/с = Тл∙м²/с = (Н/А∙м)∙м²/с = Н∙м/А∙с = Дж/А∙с = Дж/Кл = В.

В заданому контурі (котушці) ЕРС індукції буде постійним за умови незмінності швидкості зміни магнітного потоку, тобто за умови ΔФ/Δt = const.

Загальні зауваження. В тих випадках, коли визначаючи величину ΔФ/Δt, ми фактично не визначаємо і не враховуємо знак величини ΔФ=Ф_к–Ф_п, застосовуючи формулу ℰ_ін= –N(ΔФ/Δt), знак «–» не враховують.

Задача 4. Струмопровідна рамка площею 100см², будучи розташованою в магнітному полі з індукцією 1,5Тл так, що площина рамки паралельна до ліній індукції цього поля. Яка ЕРС індукції виникає в рамці при її повороті на 90° за 0,025с?

Дано:

S = 100см² = 0,01м²

B=1,5Тл

β₀ = 90°

β_к = 90° + 90° = 180°

Δt = 0,025c

ℰ_ін = ?

Рішення. Згідно з законом електромагнітної індукції  ℰ_ін= –N(ΔФ/Δt). В умовах даної задачі N = 1, ΔФ = Ф_к – Ф₀ = ВScos180° – BScos90° = BS(–1) – BS∙0 = – ВS Таким чином ℰ_ін= –(ΔФ/Δt) =и –(– ВS)/Δt = ВS/Δt

Розрахунки: ℰ_ін= BS/Δt = 1,5Тл·0,01м²/0,025с = 0,6В.

Відповідь: ℰ_ін= 0,6В.

Закон електромагнітної індукції є не лише експериментально встановленим фактом, а й твердженням, достовірність якого можна довести теоретично. Дійсно. Припустимо, що під дією зовнішньої механічної сили, провідник з швидкістю v рухається перпендикулярно лініям індукції однорідного магнітного поля (мал.5). Оскільки разом з провідником в магнітному полі упорядковано рухаються і носії струму (електрони) то на кожен з них діє певна сила Лоренца:  F_Л = Bq₀vsinα, де B – індукція магнітного поля, q₀ – заряд носія струму, v – швидкість руху провідника, α – кут між векторами B та v, в даному випадку α=90º, sinα=1.

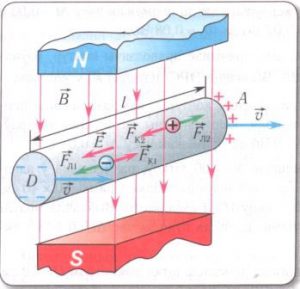
Мал.5. В провіднику що рухається в магнітному полі, відбувається такий індукційний перерозподіл зарядів, який створює між краями цього провідника відповідну електричну напругу.

Під дією сили Лоренца, носії струму зміщуються в напрямку який визначається правилом лівої руки. Це зміщення триватиме до тих пір, поки діюча на носії струму сила Лоренца не зрівноважиться силою електростатичної взаємодії зарядів. (F_ел=q₀E), тобто допоки  Bq₀vsinα = q₀E, де Е – напруженість того електричного поля яке утворюється в провіднику, в результаті індукційного перерозподілу зарядів.

Таким чином, в процесі поступального руху провідника в однорідному магнітному полі, його носії струму під дією сили Лоренца, певним чином перерозподіляються і створюють між краями цього провідника відповідну індукційну напругу. Величину цієї напруги, а точніше величину тієї ЕРС індукції яка призводить до її появи, можна визначити із наступних міркувань.

Оскільки в умовах даної задачі тими сторонніми силами які виконують роботу по переміщенню зарядів на внутрішній ділянці електричного кола (на ділянці провідника що рухається в магнітному полі) є магнітна сила Лоренца (А_ст=А_магн), та враховуючи що А_магн=І∆Ф, де І=q/∆t, можна записати: ℰ_ін =А_магн/q =I∆Ф/q =q∆Ф/q∆t =∆Ф/∆t. А оскільки індукційний струм завжди протидії зміні магнітного потоку (протидіє переміщенню провідника), то ℰ_ін= –ΔФ/Δt. Якщо ж в магнітному полі рухається не один провідник, а N паралельно з’єднаних  провідників, то величина загальної ЕРС такої системи становитиме: ℰ_ін= –N(ΔФ/Δt).

Задача 5. Провідник довжиною 20см, зі швидкістю 10м/с рухається перпендикулярно до ліній індукції однорідного магнітного поля з індукцією 1Тл. Визначити величину індукційної напруги між краями провідника.

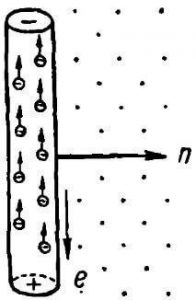
Дано:

ℓ =20см = 0,2м

v = 10м/с

B = 1Тл

U_ін = ?

Рішення. Оскільки в умовах даної задачі виникаючої в провіднику індукційної напруги, чисельно дорівнює величині тієї ЕРС індукції яка створює цю напругу, то можна стверджувати, що у відповідності з законом електромагнітної індукції U_ін =  ℰ_ін = N(ΔФ/Δt) = NΔ(ВScosβ)/Δt. В умовах даної задачі N=1, В=const, cosβ = cos0° = 1 = const, S = ℓΔx, де Δх – та відстань на яку переміщається провідник за час Δt. А зважаючи на те, що Δx/Δt = v, можна записати U_ін = BℓΔx/Δt = Bℓv.

Розрахунки: U_ін = Bℓv = 1Тл·0,2м·10(м/с) = 2В.

Відповідь: U_ін = 2В.

Контрольні запитання.

1. Чому Фарадей дійшов висновку: магнетизм має створювати електричний струм?
2. Чи правильне твердження: магнітний потік створює індукційний струм?
3. Що називають електромагнітною індукцією?
4. Що стверджується в законі електромагнітної індукції?
5. Чому в законі електромагнітної індукції, говориться не про індукційний струм, а про ЕРС індукції?
6. Який зв’язок між правилом Лєнца та законом збереження енергії?
7. Поясніть, чому між краями прямолінійного провіднику який рухається в магнітному полі, виникає певна електрична напруга?
8. Чи може прямолінійний провідник рухатись в магнітному полі таким чином, щоб напруга між його краями дорівнювала нулю?
9. Струмопровідне кільце з розрізом знаходиться в змінному магнітному полі. Чи існуватиме між краями кільця індукційна напруга? Чи виникне в цьому кільці індукційний струм?
10. Крізь горизонтальне струмопровідне кільце падають з однакової висоти мідний брусок і магніт. Який предмет упаде першим?

Вправа 1.

1. Дві нерухомі котушки розташовані так, як показано на малюнку. За яких умов міліамперметр зафіксує наявність струму в зовнішній котушці?

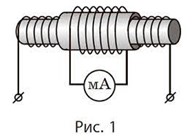
2. Визначте напрямок індукційного струму в зображених на малюнках ситуаціях.

3. На основі аналізу малюнків а) і б) визначте напрямки індукційних струмів в котушці А.

а) б)

4. Визначте швидкість зміни магнітного потоку в струмопровідній котушці яка має 2000 витків при збудженні в ній ЕРС індукції 120В.
5. Струмопровідне кільце радіусом 5см, будучи розташованим в магнітному полі з індукцією 0,2Тл так, що площина кільця перпендикулярна до ліній індукції цього поля. Яка ЕРС індукції виникає в кільці при його повороті на 90° за 0,025с?
6. Струмопровідна рамка що складається з 25 витків знаходиться в магнітному полі. Яка ЕРС індукції виникає в рамці при зміні магнітного потоку в ній з 0,098Вб до 0,013Вб за 0,16с?
7. Скільки витків повинна мати котушка, щоб при зміні магнітного потоку від 0,024 до 0,056Вб за 0,32с, в ній виникла ЕРС індукції 10В?
8. З якою швидкістю треба переміщувати провідник довжиною 1м в однорідному магнітному полі з індукцією 0,2Тл, щоб у провіднику виникала ЕРС індукції 1В? Провідник рухається в площині, яка перпендикулярна до ліній індукції поля.

.

Лекційне заняття №2.

Тема: Індукційний струм та його застосування. Індукційні генератори. Трансформатори. 

На одній з наукових конференцій, де Фарадей доповідав про результати своїх досліджень в області електромагнітної індукції, хтось запитав: «А яка користь від вашого відкриття?». На що Фарадей відповів: «А яка користь від немовляти?».

Пройшли роки і безпомічне немовля, перетворилось на диво богатиря, який невпізнанно змінив життя людства. Уявити сучасне цивілізоване життя без тих приладів, робота яких базується на застосуванні явища електромагнітної індукції, неможливо. Достатньо сказати, що близько 95% тієї електроенергії яку споживає людство, отримують за допомогою індукційних генераторів – приладів, в яких явище електромагнітної індукції застосовується для перетворення механічної роботи в енергію електричного струму.

В принциповому вигляді індукційний генератор представляє собою сукупність трьох базових елементів (мал.6): постійного магніту (1), струмопровідної рамка (2), та механізму обертання рамки (3). Принцип дії цієї системи полягає в наступному. Постійний магніт (індуктор), створює постійне магнітне поле, в якому знаходиться струмопровідна рамка. В процесі примусового обертання рамки, той магнітний потік що пронизує рамку, постійно змінюється. При цьому в рамці, згідно з законом електромагнітної індукції, виникає індукційна ЕРС, яка створює на краях рамки відповідну електричну напругу, яка в свою чергу (за умови замкнутості зовнішнього електричного кола) створює відповідний електричний струм. Іншими словами, в індукційному генераторі реалізується ситуація: В =const, S=const, β=ƒ(t). При цьому  Ф=ВScosβ=ƒ(t) і тому в рамці генератора індуцирується  ℰ_ін = –N(ΔФ/Δt) → U_ін = ℰ_ін → І_ін = U_ін/R.

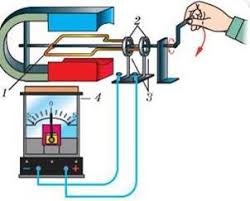
Мал.6. Схема принципового устрою індукційного генератора.

Не важко довести, що ті індукційні ЕРС, напруга та струм які виникають в процесі рівномірного обертання рамки в однорідному магнітному полі, є такими що змінюються за гармонічним синусоїдальним законом. Дійсно. Якщо струмопровідна рамка постійної площі (S=const) з постійною кутовою швидкістю (ω=β/t=const), обертається в однорідному магнітному полі (В=const), то згідно з законом електромагнітної індукції, в ній виникає ЕРС індукції, величина якої визначається за формулою  ℰ_ін = –N(ΔФ/Δt) = –N(dФ/dt) = –NФ′= –N(BScosβ)′. Враховуючи, що В та S – величини постійні, тобто такі які можна винести за знак похідної, а також факт того, що (cosβ)′= –sinβ, можна записати: ℰ_ін= –N(BScosβ)′ = –NBS(cosβ)′= +NBSsinβ. А оскільки β=ωt=2πν, та враховуючи що добуток NBS фактично дорівнює тій максимальній ЕРС що генерується даним приладом (NBS=ℰ_м), можна записати: ℰ_ін = ℰ_мsinβ = ℰ_мsinωt = ℰ_мsin2πνt, де ν – частота обертання рамки.

Таким чином, при рівномірному обертанні струмопровідної рамки в однорідному магнітному полі, в ній генерується індукційна ЕРС, величина якої змінюється за законом   е = ℰ_мsin2πνt, де е – миттєве значення ЕРС. А зважаючи на те, що змінна ЕРС створює відповідну їй змінну напругу, яка в свою чергу створює відповідний змінний електричний струм, можна записати:

е = ℰ_мsin2πνt,

u = U_мsin2πνt,

i = I_мsin2πνt.

де  е, u, i – миттєві значення відповідно ЕРС, напруги та сили струму;

ℇ_м, U_м, І_м – амплітудні значення відповідно ЕРС, напруги та сили струму;

ν – частота коливань ЕРС, напруги та сили струму.

Про параметри, закономірності та прояви змінного струму, ми поговоримо в процесі вивчення теми «Електродинаміка змінних струмів». Наразі ж зупинимся на конструктивних особливостях реальних генераторів змінного струму. А ці особливості є наступними. По перше, в більшості реальних генераторів, джерелом магнітного поля (індуктором) є не постійні магніти, а електромагніти. По друге, для підсилення того магнітного поля яке пронизує струмопровідну рамку генератора, цю рамку вмонтовують в феромагнітне осердя. При цьому, сукупність струмопровідної рамки та феромагнітного осердя, зазвичай називають якорем генератора. По третє, в генераторах середньої та великої потужності, рухомою частиною (ротором) зазвичай є електромагніт (індуктор), а нерухомою частиною (статором) – струмопровідна рамка з осердям (якір). Це пов’язано з тим, що ті потужні струми які генеруються в рамці якоря, доцільніше передавати через нерухомі (стаціонарні) контакти. Натомість ті невеликі струми які живлять електромагніт індуктора, передаються через рухомі контакти.

Четвертою конструктивною особливістю більшості реальних генераторів змінного струму полягає в тому, що в них замість однієї струмопровідної рамки застосовують певну сукупність таких рамок. Такі системи дозволяють генерувати струми потрібної частоти, при відносно невеликих швидкостях обертання ротора. Адже для того щоб в генераторі з однією рамкою створити струм з частотою 50Гц, необхідно щоб швидкість обертання ротора становила 50 обертів за секунду (3000об/хв). Ясно, що для масивних деталей потужних генераторів така швидкість є неприйнятно високою. Зменшити цю швидкість можна шляхом збільшення кількості рамок. Наприклад, якщо таких рамок буде 50, то для генерації змінного струму з частотою 50Гц, ротор генератора має обертатись з частотою 0,5об/с=30об/хв.

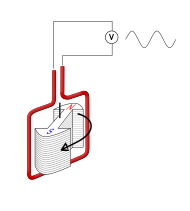
Мал.7. Схема принципового та загального устрою генератора змінного струму.

Індукційні генератори можуть генерувати не лише змінний, а й постійний струм. По суті, з будовою генератора постійного струму ви вже знайомі. Адже той прилад, який при вивчені теми «Сила Ампера та її застосування», ми називали електродвигуном постійного струму і той, який зараз називаємо генератором постійного струму – це фактично один і той же прилад.

Дійсно. В зображеному на мал.8 електродвигуні постійного струму, постійна напруга, через графітові контакти і пластини колектора, подається в ту рамку якоря яка знаходяться в площині ліній індукції магнітного поля індуктора і створює в ній відповідний постійний струм.  При цьому на бічні сторони рамки діють дві рівні за величиною і протилежні за напрямком сили Ампера які надають якорю обертального руху.

Тепер уявіть, що на колектор приладу ми не подаємо постійної напруги, а замість цього примусово обертаємо тіло якоря в магнітному полі індуктора. В такій ситуації, на краях кожної рамки якоря, згідно з законом електромагнітної індукції, виникає змінна напруга. А оскільки ті пластини колектора які контактують з графітовими щітками з’єднані саме з тією рамкою між краями якої на даний момент існує максимально велика напруга, то саме цю напругу ми отримуємо на виході приладу, який тепер буде називатися генератором постійного струму.

Мал.8. Принциповий устрій двигуна постійного струму та генератора постійного струму є аналогічним.

Звісно, якщо певний прилад створюють для того, щоб він був ефективним електродвигуном, то нема сенсу ускладнювати цей прилад тими деталями які можуть зробити з нього не ефективний генератор. І навпаки. Тому між реальними електродвигунами постійного струму і реальними генераторами постійного струму є суттєві конструктивні відмінності. Однак ці відмінності не заперечують факту принципової схожості відповідних приладів.

Як і практично всі індукційні прилади, індукційні генератори є приладами саморегульованими. Саморегульованими в тому сенсі, що ті енергетичні затрати які забезпечують роботу генератора, автоматично залежать від величини спожитої в зовнішньому колі енергії. Адже згідно з законом електромагнітної індукції та правилом Лєнца, величина індукційної протидії обертанню ротора генератора, пропорційна величині тієї електричної енергії яка спожита в зовнішньому електричному колі. А це означає, що будь яке збільшення або зменшення зовнішнього енергетичного навантаження, автоматично призводить до відповідного збільшення або зменшення кількості тієї енергії яка забезпечує роботу генератора.

Індукційні генератори є надзвичайно ефективними приладами. Їх ККД 95–98%. Для порівняння, коефіцієнт корисної дії сучасних теплових двигунів не перевищує 45%, сучасних МГД генераторів не перевищує 30%, а сонячних батарей – 40%. Втім, ви маєте розуміти, що мова йде про ККД самого індукційного генератора, тобто приладу, який перетворює механічну роботу в енергію електричного струму. Адже якщо, наприклад, такий генератор є частиною теплової чи атомної електростанції, то загальний ККД цієї станції навряд чи перевищуватиме 40%. І це закономірно. Закономірно тому, що на подібних електростанціях електрична енергія є результатом двох етапів енергетичних перетворень. На першому етапі, та теплова енергія яку отримують в результаті хімічного чи ядерного горіння, перетворюється на механічну роботу. На другому – механічна робота перетворюється на енергію електричного струму. І не важко збагнути, що перше перетворенні робить відповідний тепловий двигун, ККД якого не перевищує 45%.

Завершуючи розмову про електрогенератори та електродвигуни, варто звернути увагу на ті терміни, в застосуванні яких навіть спеціалісти часто плутаються. Мова йде про те, що називають індуктором, якорем, статором і ротором. А ці терміни такі, що не допускають вільного тлумачення і не є взаємозамінними. Загально ж прийнятий зміст цих термінів наступний.

Пара індуктор – якір, характеризує функціональне призначення базових елементів електродвигунів і генераторів. При цьому. Індуктор, це та базова частина приладу яка створює (індуцирує) постійне чи змінне магнітне поле. Індуктором може як постійний магніт так і електромагніт. Якір, це та базова частина приладу яка знаходиться в магнітному полі індуктора, і яка представляє собою сукупність феромагнітного осердя та струмопровідних рамок.

Пара статор – ротор, характеризує конструктивне призначення базових елементів електродвигунів і генераторів. При цьому статор, це та базова частина приладу яка є нерухомою, а ротор – та базова частина приладу яка є рухомою. Наприклад, в зображеному на мал.7 генераторі, статором є якір (система струмопровідних рамок та феромагнітного осердя), а ротором – індуктор (електромагніт). В зображеному ж на мал.8 електродвигуні навпаки, статором є індуктор, а ротором – якір.

Трансформатори.

В багатьох практично важливих ситуаціях, електричний струм однієї напруги потрібно перетворювати (трансформувати) на струм іншої напруги. Наприклад в магістральних лініях електропередач республіканського значення, величина напруги 500 000В, в лініях електропередач обласного значення величина напруги 150 000В, районного значення – 20 000В, в побутових мереж – 220В, а та напруга яка подається на вхід вашого смартфона має становити 5В. І всі ці зміни напруги забезпечують прості прилади які називаються трансформаторами (від лат. transformо – перетворювати, змінювати). А потрібно зауважити, що здійснити ефективну трансформацію напруги постійного струму надзвичайно складно. Натомість напруга змінного струму трансформується легко та ефективно. Тому говорячи про трансформатори, мають на увазі ті прилади які трансформують напругу в колі змінного струму.

Трансформатор – це прилад, який трансформує, тобто змінює, напругу в колі змінного струму. В загальному випадку, трансформатор представляє собою сукупність трьох взаємоповязаних деталей: двох електроізольованих котушок індуктивності (обмоток трансформатора) об’єднаних замкнутим феромагнітним осердям (магнітопроводом). При цьому, ту обмотку трансформатора яку підключають до джерела вхідної (первинної) напруги називають первинною, а ту в якій отримують трансформовану напругу – вторинною.

Мал.9. Принципова схема трансформатора.

В загальних рисах принцип дії трансформатора полягає в наступному. Наявна змінна первинна напруга u₁, створює в первинній котушці трансформатора відповідний змінний струм і₁, який в свою чергу в сукупності з феромагнітним осердям створює відповідний змінний магнітний потік Ф₁. Цей потік пронизує витки вторинної котушки і згідно з законом електромагнітної індукції створює в них вторинну напругу u₂, величина якої залежить від числа витків у вторинній котушці (N₂): u₂ = –N₂(dФ₁/dt). А це означає, що змінюючи число витків у вторинній котушці трансформатора, можна отримувати практично будь яку напругу.

Включений в мережу первинної напруги трансформатор, може працювати в двох режимах: режим холостого ходу та робочий режим. В режимі холостого ходу, коло вторинної обмотки трансформатора не замкнуте, а отже таке в якому електричний струм відсутній (і₂ = 0). В робочому режимі, коло вторинної обмотки трансформатора є замкнутим, а отже таким в якому протікає певний змінний струм (і₂ ≠ 0).

Однією з основних характеристик трансформатора є величина, яка називається коефіцієнтом трансформації. Коефіцієнт трансформації, це фізична величина, яка показує у скільки разів ефективне значення вихідної напруги трансформатора (U₂) більше за ефективне значення його вхідної напруги (U₁), за умови, що величини цих напруг виміряні в режимі холостого ходу.

Позначається: k

Визначальне рівняння: k=U₂/U₁

Одиниця вимірювання: [k]= –,   рази.

Потрібно зауважити, що величина і напрям змінної напруги та змінного струму, постійно змінюються. Тому, коли ми говоримо про певне значення змінної напруги чи змінного струму, то маємо на увазі так зване ефективне (діюче) значення відповідної величини. Наприклад, коли ми стверджуємо, що в мережі ліній електропередач існує змінна напруга величиною 220В, то маєм на увазі ефективне значення цієї напруги. Про те, що таке ефективне значення змінного струму (напруги) ми поговоримо в процесі вивчення теми «Електродинаміка змінних струмів».

Зазвичай, ті трансформатори коефіцієнт трансформації яких більший за одиницю (U₂ > U₁) називають підвищувальними (підвищуючими). А ті, для яких k < 1, (U₂ < U₁) – понижувальними (понижуючими). Можна довести, що коефіцієнт трансформації приблизно дорівнює відношенню числа витків у вторинній обмотці трансформатора (N₂), до їх числа в первинній обмотці (N₁), тобто що k ≈ N₂/N₁.

Коли ми стверджуємо, що одні трансформатори збільшують напругу (U₂ > U₁), а інші – зменшують її (U₂ < U₁), то це зовсім не означає, що в першому випадку додаткову напругу ми отримуємо «безкоштовно», а в другому випадку певну кількість напруги безслідно втрачаємо. Зважаючи на те, що ККД трансформатора близький до 98%, можна стверджувати, що згідно з законом збереження енергії, ті електричні роботи які виконуються в первинній та вторинній обмотках трансформатора, є практично однаковими, і що тому  U₁I₁t₁ ≈ U₂I₂t₂ . Оскільки тривалість роботи первинної і вторинної обмоток трансформатора є однаковою (t₁=t₂), то можна записати  U₁I₁ ≈ U₂I₂. А це означає, що той трансформатор який знижує напругу (U₂ < U₁), автоматично і в таку ж кількість разів підвищує силу струму (I₂ > I₁). І навпаки.

Як і всі індукційні прилади, трансформатор представляє собою певну саморегульовану систему. Ця саморегульованість проявляється в тому, що ті струми які протікають в первинній та вторинній обмотках трансформатора пов’язані таким чином, що будь які зміни сили струму у вторинній обмотці, автоматично призводять до відповідних змін в обмотці первинній. Пояснюючи суть цього взаємозв’язку, можна сказати наступне.

Якщо коло вторинної обмотки трансформатора не замкнуте (режим холостого ходу), то виникаюча в ній індукційна напруга u₂ не призводить до появи відповідного електричного струму (і₂=0). При цьому, той магнітний потік який створює первинна обмотка, практично в незмінному вигляді знову потрапляє в цю ж обмотку. А це означає, що в режимі холостого ходу, в первинній обмотці трансформатора, згідно з законом електромагнітної індукції, виникає індукційна напруга u₁′ знак якої протилежний до знаку первинної напруги u₁. Величина цієї вторинної напруги (u₁′) якщо і відрізняється від первинної напруги u₁, то лише на відсоток тих теплових втрат які неминуче відбуваються в трансформаторі і які зазвичай становлять 1–2%.

Таким чином, в режимі холостого ходу на вільні електрони первинної обмотки трансформатора, з одного боку діє зовнішня напруга u₁, а з іншого – практично така ж за величиною але протилежна за напрямком індукційна напруга u₁′. В такій ситуації в колі первинної обмотки протікає незначний електричний струм, який називають струмом холостого ходу. В першому наближенні величину струму холостого ходу можна вважати нульовою.

Якщо ж трансформатор знаходиться в робочому режимі, то в колі його вторинної обмотки протікає певний змінний струм і₂. Цей струм створює відповідний змінний магнітний потік, напрям якого протилежний до напрямку того потоку який створює струм і₁. А це означає, що в робочому режимі, той результуючий магнітний потік який пронизує витки первинної обмотки трансформатора, зменшується. А відповідно зменшується і величина тієї індукційної напруги (u₁′) яка протидіє зовнішній напрузі u₁. В такій ситуації, сила струму в колі первинної обмотки трансформатора автоматично збільшується на величину пропорційну силі струму в його вторинній обмотці. Таким чином, будь які зміни сили струму у вторинній обмотці трансформатора автоматично призводять до відповідних змін струму в його первинній обмотці.

Сучасні трансформатори не лише ефективно змінюють параметри напруг та струмів, а й об’єднують різні частини складних електротехнічних систем і єдині цілісні організми; розширюють можливості вимірювальних приладів; забезпечують електрозварювання металів; роботу індукційних плавильних печей; перетворення синусоїдальних струмів у відповідні імпульсні струми, тощо.

Задача 1. Скільки витків повинна мати вторинна обмотка трансформатора для підвищення напруги від 220В до 11000В, якщо в первинній обмотці 40 витків.

Дано:

U₁ = 220B

U₂ = 11000B

N₁ = 40

N₂ = ?

Рішення. Виходячи з того, що коефіцієнт трансформації k = U₂/U₁ практично дорівнює співвідношенню k = N₂/N₁, можна записати N₂/N₁ = U₂/U₁, звідси N₂ = N₁∙U₂/U₁ = 40∙11000В/220В = 2000 витків.

Відповідь: N₂ = 2000 витків.

Задача 2. Первинна обмотка знижувального трансформатора включена в мережу змінного струму з напругою 220В. Напруга на затискачах вторинної обмотки 20В, її опір 1(Ом), сила струму в ній 2А. Визначити коефіцієнт трансформації та ККД трансформатора.

Дано:

U₁=220В

U₂′=20В

R₂=1(Ом)

I₂ = 2А

k = ?  η = ?

Рішення. За визначенням k=U₂/U₁, де U₂ напруга виміряна в режимі холостого ходу трансформатора. А оскільки в умовах нашої задачі U₂′ виміряно в умовах робочого ходу трансформатора, то U₂=U₂′+ΔU, де ΔU – втрата напруги в колі вторинної обмотки трансформатора. ΔU = I₂R₂ 2А∙1(Ом) = 2В. Таким чином U₂ = 20B + 2B = 22B, k = U₂/U₁ = 22B/220B = 0,1.

За визначенням η=(А_кор/А_заг)100%.

В умовах трансформатора корисною є та електрична робота яка виконується у його вторинній обмотці і яка дорівнює А_кор=А₂=U₂′I₂t. Загальною є та робота яка виконується в первинній обмотці трансформатора і яка дорівнює А_заг=U₁I₁t. Враховуючи, що І₁=kІ₂=0,1·2А=0,2А, можна записати: η=(А_кор/А_заг)100% = U₂′I₂t·100%/ U₁I₁t = U₂′I₂·100%/ U₁I₁ =20В·2А·100%/220В·0,2А= 91%

Відповідь: k = 0,1; η = 91%.

Контрольні запитання.

1. Поясніть загальний устрій та принцип дії генератора змінного струму.
2. Поясніть, чому в потужних генераторах змінного струму рухомою частиною є електромагніт (індуктор)?
3. Яку частину генератора називають індуктором, а яку – якорем?
4. Яку частину генератора називають статором, а яку – ротором?
5. Поясніть, що означає твердження: індукційні генератори є приладами саморегульованими?
6. Поясніть загальний устрій та принцип дії трансформатора.
7. Чи може трансформатор працювати в колі постійного струму? Чому?
8. Поясніть, чому в режимі холостого ходу, сила струму в первинній обмотці трансформатора є практично нульовою?
9. Поясніть, чому в понижувальному трансформаторі дріт вторинної обмотки має більшу площу поперечного перерізу (порівняно з дротом первинної обмотці).
10. На основі аналізу малюнку поясніть загальний устрій та принцип дії електрозварювального трансформатора.

Вправа 2.

1.Рівняння змінного струму має вигляд і = 4sin100πt. Визначте амплітудне значення сили струму, період та частоту його коливань. Побудуйте графік цих коливань.

2. У первинній обмотці трансформатора 100 витків, а у вторинній обмотці – 20. Вкажіть усі правильні твердження.

А. Трансформатор є знижувальним.

Б. Коефіцієнт трансформації дорівнює 0,2.

В. Коефіцієнт трансформації дорівнює 5.

3. Сила струму в первинній обмотці трансформатора 2А, напруга на ній 120В. Напруга на вторинній обмотці 30В. Вкажіть усі правильні твердження.

А. Сила струму у вторинній обмотці 0,5А.

Б. Сила струму у вторинній обмотці 8А.

В. Коефіцієнт трансформації 4.

4. Первинна обмотка трансформатора включена в мережу з напругою 220В. Якою буде напруга на його вторинній обмотці, якщо коефіцієнт трансформації 5.

5. Трансформатор підвищує напругу з 220В до 11кВ і має 200 витків в первинній обмотці. Скільки витків у вторинній обмотці?

6. Під якою напругою перебуває первинна обмотка трансформатора, яка має 100 витків, якщо у вторинній обмотці 3500 витків і напруга 105В? Який коефіцієнт трансформації?

7. Сила струму в первинній обмотці трансформатора 0,6А а напруга на її кінцях 220В. При цьому аналогічні параметри вторинної обмотки: 10,5А та 12В. Визначити ККД трансформатора.

8. Знижувальний трансформатор з коефіцієнтом трансформації 0,1 включено в мережу з напругою 220В. Визначте напругу у вторинній обмотці трансформатора, якщо її опір 0,4(Ом), а сила струму в ній 5А.

9. Сила струму в первинній обмотці трансформатора 0,5А, напруга на її кінцях 220В. Сила струму у вторинній обмотці трансформатора 11А, а напруга на її кінцях 9,5В. Визначити ККД трансформатора.

10. Первинна обмотка трансформатора включена в мережу змінного струму з напругою 220В. Відомо, що при силі струму у вторинній обмотці 6А, напруга на її краях 19В. Визначте коефіцієнт трансформації та ККД трансформатора, якщо опір вторинної обмотки 0,5(Ом).

.

Лекційне заняття №3.

Тема: Електродвигун змінного струму та інші індукційні прилади. Струми Фуко. Електричний скін-ефект.     

До числа тих безумовно важливих приладів, принцип дії яких базується на застосуванні закону електромагнітної індукції, відносяться електродвигуни змінного струму. Електродвигун змінного струму – це прилад, який перетворює енергію змінного струму в механічну роботу. Пояснюючи загальний устрій та принцип дії двигуна змінного струму проведемо наступний експеримент. Перед полюсами підковоподібного магніту поставимо легкий алюмінієвий диск, який може вільно обертатись навколо своєї осі (мал.10). Надаючи магніту обертального руху, ви неодмінно з’ясуєте, що диск також починає обертатись, причому обертатись в напрямку обертання магнітного поля.

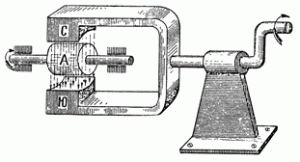
Мал.10. Експеримент який пояснює принцип дії електродвигуна змінного струму.

Пояснюючи результати даного експерименту, можна сказати наступне. Оскільки обертальне магнітне поле створює відносно нерухомого струмопровідного диску певний змінний (обертальний) магнітний потік, то в тілі диску, згідно з законом електромагнітної індукції, неминуче виникає певний індукційний струм. При цьому, згідно з тим же законом, цей струм своєю магнітною дією має протидіяти причині його появи, тобто протидіяти обертанню магнітного поля. Не важко збагнути, що легкий диск не спроможний зупинити обертання магнітного поля. Адже це обертання створює відносно потужна зовнішня сила. В такій ситуації диск, намагаючись зменшити швидкість зміни магнітного потоку, змушений обертатись в напрямку обертання цього потоку. Саме це обертання ми і спостерігаємо у відповідному експерименті.

По суті, принцип дії електродвигуна змінного струму нічим не відрізняється від принципу дії тих установок що зображені на мал.10. Різниця лише в тому, що в електродвигуні, обертальне магнітне поле створюється не шляхом механічного обертання постійного магніту, а шляхом проходження змінного струму через відповідні обмотки електродвигуна.

В загальному випадку електродвигун змінного струму складається з двох базових частин: індуктора та якоря (мал.11). При цьому індуктор, представляє собою сукупність пустотілого циліндричного феромагнітного осердя та системи струмопровідних обмоток. Якорем двигуна змінного струму в найпростішому випадку може бути суцільний залізний циліндр, який має вісь обертання і знаходиться в середині індуктору. Втім, будова якоря може бути і більш складною. Зокрема, для покращення струмопровідних властивостей приповерхневого шару якоря, в його феромагнітне тіло часто вкладають мідні стержні, які в своїй сукупності утворюють так зване «біляче колесо».

Мал.11. Загальний устрій електродвигуна змінного струму.

Ми не будемо заглиблюватись в деталі того, яким чином змінний струм, протікаючи обмотками нерухомого індуктора, створює обертальне магнітне поле. Проста констатуємо той факт, що електричний двигун змінного струму влаштований таким чино, що при проходженні змінного струму через обмотки його індуктора, в середині цього індуктора створюється обертальне магнітне поле. Зважаючи на цей факт, про принцип дії двигуна змінного струму можна сказати наступне. Змінний електричний струм, протікаючи обмотками індуктора, створює в середині цього індуктора обертальне магнітне поле. При цьому, в тілі якоря, згідно з законом електромагнітної індукції, виникає індукційний струм, який своєю магнітною дією змушує якір обертатись в напрямку обертання магнітного поля.

Електродвигуни змінного струму, можуть бути однофазними та трифазними. При цьому більш поширеними та більш ефективними (з більшим ККД) є трифазні двигуни, тобто такі двигуни що працюють від системи трифазного змінного струму. Про суть та особливості цієї системи ми поговоримо дещо пізніше. Наразі ж зауважимо, що порівняно з двигунами постійного струму, трифазні двигуни змінного струму є простішими за конструкцією, технологічнішими та дешевшими у виробництві, дешевшими в експлуатації, надійнішими та економнішими в роботі. До числа недоліків таких двигунів можна віднести факт того, що вони не дозволяють безпосередньо регулювати швидкість обертання ротора. Крім цього, такі двигуни потребують системи трифазного струму, яка в побутовій практиці майже не застосовується. Трифазні двигуни широко застосовуються в різних сферах промислового виробництва. В побутовій практиці, зазвичай застосовуються двигуни постійного струму або однофазні двигуни змінного струму.

Індукційні генератори, трансформатори та електродвигуни, це ті базові прилади які фактично складають основу сучасної електричної цивілізації. Але закон електромагнітної індукції застосовується не лише в цих надважливих приладах, а й у величезній кількості менш важливих та не менш цікавих і потрібних приладів. Ми не будемо розглядати все різноманіття подібних приладів. Зупинимся лише на деяких з них, зокрема на індукційних спідометрах (тахометрах), електродинамічних мікрофонах та індукційних лічильниках електроенергії.

Спідометр (від англ. speed – швидкість) – це прилад, який вимірює швидкість поступального руху машин та механізмів. Тахометр (від грец. tachos – швидкість) – це прилад, який вимірює швидкість обертального руху валів машин та механізмів. За своїм принциповим устроєм індукційні спідометри та тахометри практично не відрізняються. Їх основними елементами є (мал.12). Постійний магніт (1) який за допомогою тросового ланцюга з’єднаний з об’єктом вимірювання (вал коліс автомобіля, вихідний вал двигуна, тощо). Цей магніт знаходиться в середині легкого алюмінієвого напівциліндра (2) вісь якого жорстко з’єднана з пружинним механізмом (3) та вказівною стрілкою приладу (4).

Мал.12. Загальний устрій індукційного спідометра.

Принцип дії цієї системи полягає в наступному. При обертальному русі магніту, той магнітний потік що пронизує напівциліндр обертальним чином змінюється. При цьому, згідно з законом електромагнітної індукції, в тілі напівциліндра виникає певний індукційний струм, який своєю магнітною дією змушує напівциліндр обертатися. А оскільки вісь напівциліндра жорстко з’єднана з пружинним механізмом, то напівциліндр, а разом з ним і стрілка приладу повертаються на певний кут, величина якого залежить від швидкості обертання магніту, а отже і від швидкості обертання тієї деталі з яким цей магніт з’єднаний.

Ще одним прикладом застосування закону електромагнітної індукції є електродинамічний мікрофон. Мікрофон – це прилад, який перетворює енергію звукових коливань у відповідні коливання тієї чи іншої електричної величини, а у підсумку – в коливання електричного струму. За своїм загальним устроєм та принципом дії, мікрофони бувають різними: порошковими, конденсаторними, п’єзоелектричними, електродинамічними та іншими. Сьогодні ми розглянемо загальний устрій та принцип дії мікрофона електродинамічного. Тобто того мікрофона принцип дії якого базується на застосуванні закону електромагнітної індукції.

По суті, електродинамічний мікрофон (мал.13) мало відрізняється від електродинамічного гучномовця. Основним складовими елементами такого мікрофона є: 1 – постійний циліндричний магніт з феромагнітним осердям, 2 – легка струмопровідна котушка індуктивності, 3 – чутлива до звукових коливань мембрана (діафрагма).

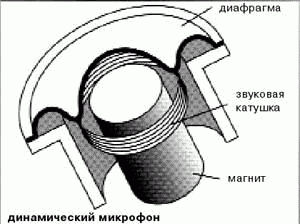
Мал.13. Загальний устрій електродинамічного мікрофона.

Принцип дії електродинамічного мікрофона полягає в наступному. Постійний циліндричний магніт створює однорідне магнітне поле. В цьому полі знаходиться легка струмопровідна котушка яка жорстко з’єднана з чутливою до звукових коливань мембраною. В потоці звукових хвиль, мембрана, а разом з нею і струмопровідна котушка, здійснюють відповідні механічні коливання. При цьому, той магнітний потік що пронизує котушку змінюється. А це означає, що згідно з законом електромагнітної індукції, на виході котушки генерується змінна напруга, частотні та амплітудні  параметри якої в точності повторюють параметри відповідної звукової хвилі.

Цікавим та повчальним прикладом застосування закону електромагнітної індукції є індукційні лічильники електроенергії. Лічильник електроенергії – це прилад, який вимірює загальну кількість тієї електричної енергії яка була використана у відповідному електричному колі. Основними елементами індукційного лічильника є (мал.14):

1 – феромагнітне осерді спеціальної форми з двома струмопровідними обмотками: обмотка напруги (а) та обмотка струму (б);

2 – алюмінієвий диск що має вісь обертання;

3 – лічильний механізм;

4 – гальмуючий постійний магніт.

Мал.14. Схема устрою індукційного лічильника електроенергії.

Не заглиблюючись в деталі тих процесів що відбуваються в індукційному лічильнику, про принцип дії цього приладу можна сказати наступне. При проходженні змінного струму, в проміжку між напруговою та струмовою обмотками лічильника, створюється відповідне обертальне (вихрове) магнітне поле. Це поле, згідно з законом електромагнітної індукції, створює в тілі диску індукційний струм, який своєю магнітною дією змушує диск обертатись. При цьому обертатись з швидкістю, величина якої залежить як від сили струму в колі, так і від падіння напруги в ньому, тобто від величини тієї роботи яку виконують електричні сили за одиницю часу (А/t=U∙I). Лічильний механізм, фіксує кількість обертів диску і виражає цю кількість в цифровому еквіваленті спожитої електроенергії.

Якщо ж говорити про ту роль яку в індукційному лічильнику відіграє постійний магніт, то вона полягає в наступному. Для того щоб показання лічильника в точності відповідали величині фактично спожитої електроенергії, необхідно передбачити певну протидію самовільному обертанню диска. Адже, якщо такої протидії не буде, то розкручений в процесі проходження струму диск, за інерцією буде продовжувати обертатись і після відключення струму. Власне таку протидію і створює постійний магніт.

Дійсно. Якщо струмопровідний диск знаходиться в полі постійного магніту, то в процесі обертання диску, той магнітний потік що його пронизує буде змінюватися. При цьому, згідно з законом електромагнітної індукції, в тілі диску неминуче виникає індукційний струм, який протидіє зміні магнітного потоку, тобто протидіє обертанню диску.

Індукційні генератори, трансформатори, електродвигуни, спідометри, тахометри, мікрофони та лічильники електроенергії – це далеко не повний перелік тих приладів, принцип дії яких базується на застосуванні закону електромагнітної індукції. Але вже цього переліку достатньо, щоб з усією очевидністю зрозуміти, наскільки значимим є даний закон для всього устрою сучасної цивілізації.

Індукційні струми виникають не лише в спеціально створених приладах, а і в будь яких ситуаціях де струмопровідні тіла знаходяться в змінних магнітних полях. Адже по суті, будь яке струмопровідне тіло представляє собою певну сукупність замкнутих струмопровідних контурів. І якщо ці контури знаходіться в змінному магнітному полі, то згідно з законом електромагнітної індукції, в них неминуче виникають індукційні струми. Ці струми називають вихровими індукційними струмами, або струмами Фуко. (Названо на честь французького фізика Жана Фуко (1819–1868)).

Струми Фуко (вихрові індукційні струми) – це замкнуті (вихрові) індукційні струми, які виникають в суцільних струмопровідних тілах, що знаходяться в змінних магнітних полях. Різноманіття тих ситуацій в яких виникають струми Фуко можна звести до двох простих випадків: 1) нерухоме струмопровідне тіло знаходиться в змінному магнітному полі (мал.15а); 2) струмопровідне тіло рухається відносно нерухомого магнітного поля (мал.15б).

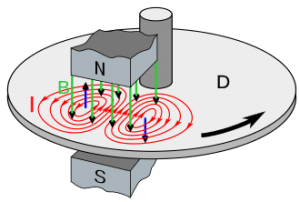
Мал.15. При будь якій зміні того магнітного потоку що пронизує струмопровідне тіло, в цьому тілі виникають струми Фуко.

З’ясовуючи властивості та прояви струмів Фуко, звернемось до експерименту. На мал.16 зображено прилад, який представляє собою електромагніт, між полюсами якого може рухатись алюмінієва (мідна) пластина що є частиною маятникового механізму. За відсутності магнітного поля (за відсутності струму в котушці електромагніту), виведена з рівноваги пластина здійснює механічні коливання, які повільно згасають (згасають завдяки дії сил механічного тертя). Однак, як тільки між полюсами електромагніту з’являється магнітне поле, рух пластини в цьому полі стає таким, ніби воно потрапляє в надзвичайно в’язке середовище. І це «середовище» швидко зупиняє пластину. Така поведінка струмопровідного тіла в магнітному полі є цілком закономірною. Адже в процесі руху через магнітне поле, той магнітний потік що пронизує тіло пластини змінюється. При цьому в пластині, згідно з законом електромагнітної індукції, з’являється індукційний струм, який своєю магнітною дією протидіє причині появи цього струму, тобто протидіє руху пластини в магнітному полі.

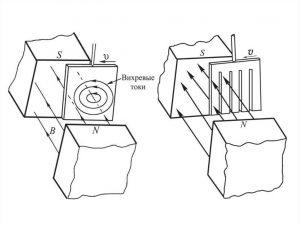
Мал.16. Величина виникаючих в тілі індукційних струмів, певним чином залежить від лінійних розмірів цього тіла.

Дослідження показують, що величина індукованих в тілі вихрових струмів, а отже і величина діючої на тіло гальмуючої сили, залежить не лише від параметрів магнітного поля та швидкості руху тіла, а й від лінійних розмірів цього тіла. З’ясовуючи цю залежність, в умовах попереднього експерименту, суцільну пластину замінимо на пластину яка має ряд розрізів. Повторивши експеримент, ви неодмінно з’ясуєте, що пластина з розрізами гальмується в магнітному полі набагато слабше за аналогічну суцільну пластину. Це означає, що за однакових умов, ті індукційні струми які виникають в пластині з розрізами є суттєво меншими за ті струми які виникають в пластині без розрізів.

Пояснюючи даний факт можна сказати наступне. Відомо, що сила струму в провіднику залежить від величини тієї напруги що призводить до появи цього струму, та від електричного опору провідника: І=U/R. В умовах нашого експерименту, тією напругою яка створює струми Фуко є та ЕРС індукції що виникає в процесі зміни магнітного потоку. А оскільки умови експерименту в обох дослідах є однаковими, то відповідно однаковими є і ті ЕРС індукції які спричиняють появу струмів Фуко. В такій ситуації, величина цих струмів залежить лише від опору провідника. А як відомо, цей опір обернено пропорційний площі того поперечного перерізу через який протікає відповідний електричний струм (R=ρℓ/S). Звідси ясно, що розрізаючи пластину на окремі ділянки, ми фактично зменшуємо площу тієї поверхні на якій виникають індукційні струми, а отже збільшуємо величину того електричного опору який протидіє появі цих струмів.

Факт залежності величини струмів Фуко від геометричних розмірів тих тіл в яких ці струми виникають, широко застосовується в тих випадках коли поява індукційних струмів є небажаною (шкідливою). Наприклад, невід’ємними складовими трансформаторів, генераторів та електродвигунів є масивні феромагнітні (залізні) деталі, розміри яких визначаються потужністю відповідного приладу і не можуть бути меншими за ті, які відповідають цій потужності. При цьому, ці струмопровідні деталі неминуче знаходяться в змінних магнітних полях. А це означає, що в них неминуче виникають шкідливі для приладу струми Фуко. І не існує іншого способу боротьби з цими струмами, як тільки шлях зменшення площі тієї поверхні в якій ці струми циркулюють.

Таким чином, перед нами стоїть дилема. З одного боку площа поперечного перерізу струмопровідної деталі має бути незмінно великою. А з іншого – ця площа має бути гранично малою. Рішення даної дилеми полягає в тому, що відповідну деталь виготовляють не суцільною, а такою що складається з великої кількості тонких, електроізольованих пластин. Таке  конструктивне рішення, з одного боку забезпечує необхідно велику феромагнітну потужність деталі, а з іншого – ефективно протидіє появі в цій деталі значних вихрових струмів.

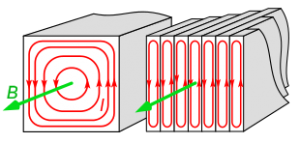
Мал.17. Основний метод боротьби з струмами Фуко полягає в тому, що відповідні деталі виготовляють не суцільними а пластинчастими.

Перспективним методом боротьби з струмами Фуко є застосування спеціальних матеріалів, які називаються магнітодіелектриками. В певному сенсі структура магнітодіелектрика схожа на структуру чавуну – матеріалу, в якому кристали заліза відділені один від одного тонким шаром вуглецю. Але на відміну від чавуну, в магнітодіелектриках, дрібні зерна феромагнетика розділені не струмопровідним вуглецем, а тонким шаром діелектрика (полістирол, бакеліт, гума, тощо). Недоліком подібних матеріалів є відносно висока вартість та велика крихкість. А зважаючи на факт того, що деталі генераторів, трансформаторів та електродвигунів неминуче перебувають під впливом потужних вібраційних навантажень, крихкість деталі є надзвичайно вагомим недоліком.

Струми Фуко можуть бути не лише шкідливими, а й корисними. Наприклад теплова дія цих струмів застосовується в різноманітних індукційних плавильних печах. Така піч, представляє собою потужну котушку індуктивності, в середині якої знаходиться теплоізольована плавильна ємність. Принцип дії цієї системи гранично простий. Змінний струм протікаючи через котушку індуктивності, створює в плавильній ємності потужне змінне магнітне поле, яке в свою чергу створює в металевій сировині потужні струми Фуко. При цьому, згідно з законом Джоуля-Лєнца (Q=I²Rt) виділяється велика кількість теплоти, яка і призводить до плавлення металу.

Вихрові індукційні струми виникають не лише в тих струмопровідних тілах, що знаходяться в зовнішніх змінних магнітних полях, а й в тих випадках коли у відповідному тілі протікає змінний електричний струм. І це закономірно. Адже змінний струм, створює в навколо провідника змінне магнітне поле, яке в свою чергу, згідно з законом електромагнітної індукції, створює в тому ж провіднику відповідний індукційний струм – струм самоіндукції.

Струм самоіндукції, це такий вихровий індукційний струм, який створюється основним змінним струмом і який протікає в тому ж провіднику що і основний струм. По суті це означає, що в провіднику фактично протікає певний результуючий струм (і_рез), який можна представити як суму двох струмів: основного струму (і_осн) та струму самоіндукції (і_s).

Можна довести, що вихрові струми самоіндукції, завжди направлені таким чином що на поверхні провідника їх напрям співпадає з напрямком основного струму, а в центрі провідника – ці напрямки взаємно протилежні (мал.18). Це означає, що в тому провіднику в якому протікає змінний електричний струм, в результаті індукційних процесів (в результаті явища самоіндукції), відбувається певний перерозподіл струмового потоку. Результатом цього перерозподілу є факт того, що сила струму в поверхневих шарах провідника збільшується, а в його внутрішніх шарах – відповідно зменшується.

   

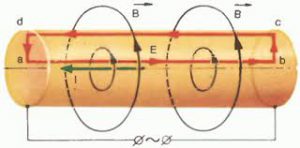
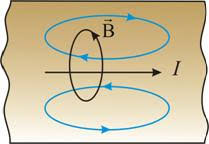
Мал.18. В провіднику зі змінним струмом, в результаті індукційних процесів відбувається певний перерозподіл цього струму.

Таким чином, в результаті індукційних процесів, в провіднику зі змінним струмом, відбувається такий перерозподіл цього струму, наслідком якого є певне збільшення сили струму в  приповерхневих шарах провідника та відповідне зменшення цього струму в центральних шарах. Це явище прийнято називати скін-ефектом (від англ. skin – шкіра, поверхневий шар).

Варто зауважити, що загальна кількість того струму який протікає через провідник, в результаті скін-ефекту не стає ні більшою, ні меншою. При скін-ефекті, наявний струм лише певним чином перерозподіляється по площі поперечного перерізу провідника.

Оскільки, згідно з законом електромагнітної індукції, величина індукційного струму (струму самоіндукції) пропорційна швидкості зміни магнітного потоку, а по суті – частоті основного струму в провіднику, то ясно, що при збільшенні цієї частоти, інтенсивність скін-ефекту збільшується. Дослідження показують, що для струмів промислової частоти (ν=50–60Гц) і дротів відносно невеликих діаметрів (d≤5мм), прояви скін-ефекту є не суттєвими. Але, по мірі зростання частоти струму та поперечних розмірів провідника, ці прояви стають все більш і більш суттєвими. Якщо ж мова йде про високочастотні струми (ν>1000Гц), то навіть в дротах звичайних діаметрів (d>1мм), ці струми фактично протікають тонким приповерхневим шаром відповідних дротів.

Не важко збагнути, що в мережах ліній електропередач, а особливо в тих випадках коли мова йде про високочастотні струми, прояви скін-ефекту є шкідливими. Адже в результаті цього явища, частина площі поперечного перерізу провідника, фактично не приймає участі в передачі струму. Ця шкідливість поглиблюється фактом того, що теплові втрати в провіднику, пропорційні як квадрату сили струму в ньому, так і опору провідника (Q=I²Rt). І якщо в результаті скін-ефекту, наявний струм протікає лише поверхневим шаром провідника, то теплові втрати зростають як за рахунок збільшення сили струму в приповерхневому шарі (I↑) так і за рахунок збільшення його електричного опору (оскільки S↓ то R↑).

Основний методом боротьби з шкідливими проявами скін-ефекту, полягає в тому, що високочастотні струми, передають не суцільними а багатожильними дротами. В такій ситуації, високочастотні струми протікають не по загальній поверхні провідника, а по кожній його електроізольованій жилі.

Контрольні запитання.

1. Поясніть принцип дії того приладу який зображений на мал.10.
2. Поясніть будову та принцип дії електродвигуна змінного струму.
3. Які переваги двигуна змінного струму порівняно з двигуном постійного струму?
4. Поясніть будову та принцип дії індукційного спідометра.
5. Поясніть будову та принцип дії електродинамічного мікрофону.
6. Чим схожі і чим відрізняються електродинамічний мікрофон та електродинамічний гучномовець?
7. Які функції того постійного магніту, що є складовою частиною лічильника електроенергії? Як реалізуються ці функції?
8. Поясніть, чому осердя трансформаторів пластинчасті?
9. Поясніть принцип дії індукційної плавильної печі.
10. Поясніть, чому в провіднику зі змінним струмом виникає скін-ефект?
11. Поясніть, як борються з шкідливими проявами скін-ефекту?

.

Лекційне заняття №4.

Тема: Змінний струм та його характеристики. Трифазна система струму. 

         Вивчаючи попередню тему ми з’ясували, що при рівномірному обертанні струмопровідної рамки в однорідному магнітному полі, в ній згідно з законом електромагнітної індукції генерується змінна ЕРС індукції (е), яка створює відповідну змінну напругу (u), яка в свою чергу (за умови замкнутості зовнішнього електричного кола) створює відповідний змінний електричний струм (і). При цьому, параметри цих ЕРС, напруги та струму змінюються за законом:

е = ℇ_мsin2πνt,

u = U_мsin2πνt,

i = I_мsin2πνt.

де  е, u, i – миттєві значення відповідно ЕРС, напруги та сили струму;

ℇ_м, U_м, І_м – амплітудні значення відповідно ЕРС, напруги та сили струму;

ν – частота коливань ЕРС, напруги та сили струму.

Мал.19. Величина і напрям змінного струму змінюється за законом i = I_мsin2πνt.

Змінним струмом називають такий електричний струм, величина і напрям якого змінюються за гармонічним законом, тобто за законом i = I_мsin2πνt. Потрібно зауважити, що формула i = I_мsin2πνt є спрощеним варіантом більш загальної формули i = I_мsin(2πνt±φ₀), де φ₀ – початкова фаза коливань струму.

Як і будь який періодичний процес, змінний струм (змінна напруга) характеризується його миттєвим (і) та амплітудним (І_м) значенням, періодом (Т), частотою (ν) та фазою (φ) коливань. Нагадаємо.

Період коливань (період) – це фізична величина, яка характеризує часову періодичність (повторюваність) коливального процесу і яка дорівнює тому проміжку часу за який система здійснює одне повне коливання.

Позначається: Т

Визначальне рівняння: Т = t/n

Одиниця вимірювання: [Т] = с  (секунда).

Частота коливань (частота) – це фізична величина, яка характеризує частотну періодичність коливального процесу і яка дорівнює тій кількості коливань системи, яку здійснює ця система за одиницю часу.

Позначається: ν

Визначальне рівняння: ν = n/t

Одиниця вимірювання: [ν] = 1/c = Гц   (герц).

Амплітуда коливань (амплітуда) – це фізична величина, яка характеризує максимальне за величиною (амплітудне) значення змінної величини і яка дорівнює цьому значенню.

Позначається: х_м, v_м, І_м, U_м, тощо,

Визначається як параметр конкретного коливального процесу,

Одиниця вимірювання: [x_м]=м; [v_м]=м/с; [I_м]=А; [U_м]=В і т.д.

Фаза коливань (фаза) це фізична величина яка характеризує стан коливальної системи в заданий момент часу і яка однозначно визначає параметри цієї системи в цей момент часу.

Позначається: φ

Визначальне рівняння: φ=α , або φ=2πn=2πνt=2πt/T,  зазвичай: φ = 2πνt.

Одиниця вимірювання: [φ] = рад   (радіан).

Рівняння змінного струму (напруги, ЕРС) можна записати не лише у вигляді i= I_мsin2πνt, чи i = I_мsin(2πνt±φ₀), а й у вигляді i = I_мcos2πνt, чи i = I_мcos(2πνt±φ₀). Адже синус і косинус, синусоїда і косинусоїда, це дві взаємопов’язані функції, значення яких з певною періодичністю повторюються.

Мал.20. Синусоїда та косинусоїда, це дві аналогічні криві зсунуті одна відносно одної на чверть періоду.

Задача 1. Рівняння змінної напруги має вигляд u=308cos100πt. Визначте амплітудне значення напруги, період та частоту її коливань. Побудуйте графік цих коливань.

Рішення. На основі порівняльного аналізу заданого рівняння u=308cos100πt з загальною формою запису аналогічного рівняння u = U_мcos2πνt, можна стверджувати: U_м=308В, оскільки 2πνt = 100πt, то 2ν = 100, отже ν = 50Гц, оскільки Т=1/ν, то Т=1/50=0,02с. Зважаючи на отримані результати будуємо графік рівняння u=308cos100πt.

Задача 2. За заданим графіком визначити параметри змінного струму, та записати рівняння цього струму.

Рішення. На основі аналізу заданого графіку можна стверджувати. І_м = 3А; Т = 6мс = 0,006с; ν = 1/Т = 1/0,006с = 166,(6)Гц, i = I_мsin2πνt = 3sin333,(3)πt.

Коли ми стверджуємо, що в мережі ліній електропередач існує змінна напруга величиною 220В і що в лампочці розжарювання протікає змінний струм величиною 0,5А, то виникає абсолютно закономірне питання: а про яку власне напругу, та про яку силу струму йде мова. Адже ми говоримо про ту напругу і той струм величини яких постійно змінюються. При цьому, характеризуючи ці змінні величини, ми називаємо певне постійне число. Намагаючись пояснити суть цього числа, стисло проаналізуємо можливі варіанти пояснень.

Ясно, коли ми стверджуємо, що в колі змінного струму тече струм величиною 0,5А, то цією величиною не може бути миттєве значення змінного струму. Адже це значення постійно змінюється від нуля (і=0), до певної максимальної величини (і=І_м) і навпаки. Можливо ми говоримо про середнє значення змінного струму? Але ж змінний струм тому і змінний, що половину періоду протікає в одному напрямку, а другу половину – в протилежному. А це означає, що середнє значення змінного струму завжди дорівнює нулю (І_сер=0). Можливо, говорячи про певну величину змінного струму, ми маємо на увазі його амплітудне (максимальне) значення? Але ж амплітудне значення, це лише одне з миттєвих. Умовно кажучи, той прилад який би реагував на амплітудне значення струму, мав би фіксувати певні струмові імпульси. При чому імпульси протилежно направлені, а отже такі, сумарна дія яких дорівнює нулю. Той же амперметр який вимірює змінний струм, показує певну постійну величину і ця величина 0,5А.

Таким чиним, коли ми стверджуємо що в колі змінного струму існує напруга 220В і тече струм 0,5А, то маємо на увазі не миттєве (u, i), не середнє (U_c, I_c) і не амплітудне (U_м, І_м) значення відповідно напруги та струму. Тоді яке?

Обираючи критерій оцінювання сили змінного струму, необхідно подбати про те, щоб у відповідності з цим критерієм, дія одного амперу змінного струму і дія одного амперу постійного струму, були еквівалентними, тобто однаковими. Адже змінний струм величиною 0,5А має бодай чимось бути схожим  на постійний струм величиною 0,5А. В іншому випадку нема жодних підстав і жодного сенсу позначати абсолютно різні струми однаковою величиною.

За домовленістю, в якості того критерію за яким порівнюють постійні і змінні струми, обрано теплову дію струму. Обгрунтованість такого вибору є цілком очевидною. Адже згідно з законом Джоуля-Лєнца, в процесі проходження змінного струму виділяється теплота, кількість якої визначається за формулою Q = I²Rt. При цьому, факт того, що ця кількість теплоти пропорційна квадрату сили струму (Q~I²), безумовно вказує на те, що теплота виділяється за будь якого (додатного чи від’ємного) напрямку струму: (+I)²Rt=+Q; (–I)²Rt=+Q. Іншими словами, в незалежності від того який (постійний чи змінний) струм протікає через провідник і в незалежності від напрямку протікання цього струму, у відповідному провіднику виділяється певна кількість теплоти. А це означає, що величини постійного і змінного струмів можна порівняти за їх тепловою дією. При цьому напрошується обгрунтовано розумна домовленість: якщо теплові дії постійного та змінного струмів однакові, то величини відповідних струмів також є однаковими. Власне ця домовленість і була реалізована на практиці. Величину ж тієї сили змінного струму яка визначається за вище сформульованим критерієм називають ефективним (або діючим) значенням змінного струму (позначається І_еф).

Ефективним (діючим) значенням змінного струму називають таку умовну силу змінного струму, величина якої визначається за наступним критерієм: якщо теплова дія постійного і змінного струмів є однаковою, то величина постійного струму І та ефективне значення змінного струму І_еф є однаковими. Наприклад, якщо дві однакові лампочки розжарювання в колі постійного і змінного струмів світять однаково, то сила постійного струму (І) та ефективне значення змінного струму (І_еф) є однаковими.

Мал.20. Якщо теплова дія постійного і змінного струмів однакова (Q_±=Q_~), то величина постійного струму (І) та ефективне значення змінного струму (І_еф) є однаковими.

Таким чином:

.                                   і – ні                                                 u – ні

.     ~ І = 0,5А             І_ср – ні                  ~ U 220В             U_ср – ні

.                                  І_м – ні                                                U_м – ні

.                                 І_еф – так                                             U_еф – так

Ефективним значенням оцінюють не лише силу змінного струму, а і відповідну електричну напругу. Наприклад, коли ми стверджуємо, що в мережі ліній електропередач існує змінна напруга величиною 220В, то маємо на увазі ефективне значення цієї напруги (U_еф=220В). І це значення вказує на те, що теплова дія даної змінної напруги (U_еф=220В) є еквівалентною тепловій дії постійної напруги величиною 220В. По суті це означає, що лампочка розжарювання в колі змінної напруги ефективне значення якої 220В, буде горіти так само як і в колі постійної напруги величиною 220В.

Потрібно підкреслити, що постійна напруга U=220В і змінна напруга U_еф=220В є гарантовано тотожними лише за їх тепловою дією. Інші ж дії цих напруг, а відповідно і струмів, можуть бути абсолютно різними. Скажімо, електродвигун змінного струму, в колі змінного струму буде працювати, а в колі постійного струму, працювати не буде. Електродвигун постійного струму, навпаки – в колі постійного струму працює, а в колі змінного струму не працює. Трансформатор – в колі постійного струму не працює, а в колі змінного струму працює. І т.д. Іншими словами, факт того, що теплова дія постійного і змінного струмів є однаковою, зовсім не означає що відповідно однаковими будуть й інші дії цих струмів. Втім, про те як ведуть себе різні прилади в колі постійного та змінного струмів, ми поговоримо в наступному параграфі.

Можна довести, що ефективні та амплітудні значення змінних струмів і напруг зв’язані співвідношеннями:

І_еф = І_м/√2 = 0,71І_м       або   І_м = І_еф√2 = 1,41І_еф

U_еф = U_м/√2 = 0,71U_м  або  U_м = U_еф√2 = 1,41U_еф.

Наприклад якщо U_еф = 220В то U_м = U_еф√2 = 310В

Задача 3. Для фази π/4, миттєве значення сили змінного струму частотою 50Гц дорівнює 2А. Яке амплітудне та ефективне значення сили струму? Запишіть загальне рівняння даного змінного струму. Визначте миттєве значення сили струму через 0,015с від початку періоду.

Дано:

φ = π/4

ν = 50Гц

і = 2А

t₁ = 0,015c

І_м = ?  І_еф = ?  і₁ = ?

Загальні зауваження. В незалежності від того як записано рівняння гармонічного коливання i = I_мsin2πνt, i = I_мsin(2πνt±φ₀), i = I_мcos2πνt, i = I_мcos(2πνt±φ₀), чи якось інакше, фазою коливань φ називають той вираз, а фактично кут, що заходиться під знаком sin або cos.

Рішення. Для φ = π/4, і = 2А, рівняння змінного струму (i = I_мsin2πνt) набуває вигляд 2 = І_мsinπ/4. Звідси І_м = 2/sinπ/4 = 2/(√2/2) = 2∙2/√2 = 4/√2 ≈ 2,8А.

І_еф = І_м/√2 = 4/(√2∙√2) = 4/2 = 2А.

Загальне рівняння має вигляд i = (4/√2)sin2π∙50t = (4/√2)sin100π∙t.

Для t₁ = 0,015c, i₁ = (4/√2)sin100π∙0,015 = (4/√2)sin1,5π = (4/√2)∙0 = 0А.

Як відомо, переважна більшість тієї електроенергії яка генерується сучасними електростанціями, є енергією змінного струму. При цьому, ця енергія генерується, передається та застосовується у вигляді так званої трифазної системи струму. Трифазною системою змінного струму називають таку систему трьох взаємоповязаних електричних кіл, коливання напруги в яких зсунуті одне відносно одного на третину періоду, тобто на 120º (на 2π/3 радіан).

Суть та принцип дії трифазної системи полягає в наступному. В процесі примусового обертання постійного магніту (індуктора), в трьох незалежних обмотках індукційного генератора, згідно з законом електромагнітної індукції генерується змінна електрична напруга (мал.21). А оскільки обмотки трифазного генератора повернуті одна відносно одної на кут 120º=2π/3радіан, то і зсув фаз між відповідними напругами також становить 120º (φ₀=120º=2π/3). Це означає, що в трьох електричних колах, генеруються три взаємопов’язані напруги, коливання яких описуються рівняннями:  u₁=U_мsin2πνt ;

.                    u₂=U_мsin(2πνt –2π/3);

.                     u₃=U_мsin(2πνt –4π/3).

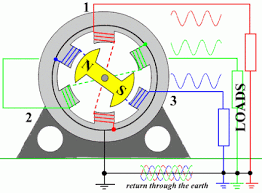
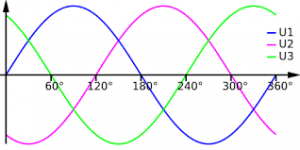
Мал.21. Схема принципового устрою генератора трифазного струму.

По суті, кожну обмотку трифазного генератора, можна розглядати як самостійне джерело змінного струму. При цьому, на базі кожної з цих трьох обмоток можна створити три незалежні електричні кола. Ясно, що забезпечуючи нормальне функціонування цих кіл, потрібно задіяти три пари дротів. На перший погляд, зменшити кількість цих дротів не можливо. Адже ми маємо три незалежні лінії електропередач, кожна з яких має бути замкнутою, а отже такою, яка складається з системи двох дротів: один дріт йде від генератора до споживача, другий – від споживача до генератора.

Однак виявляється, що нормальну роботу трифазної системи струму можна забезпечити не шістьма, а лише чотирма, а за певних умов навіть трьома дротами. Це означає, що при певному способі з’єднання обмоток трифазного генератора, можна практично вдвічі зменшити кількість тих дротів які забезпечують передачу однієї і тієї ж кількості електроенергії. При цьому, ми практично вдвічі зменшимо не лише кількість дротів в системі ліній електропередач, а отже їх вартість, навантаження на систему опор, тощо, а й кількість тих енергетичних втрат які неминуче відбуваються в цих дротах.

Організовуючи таку економічно та енергетично доцільну систему передачі електроенергії, застосовують два способи з’єднання обмоток трифазного генератора: з’єднання зіркою та з’єднання трикутником. При з’єднанні зіркою (мал.22), вхідні кінці всіх трьох обмоток генератора, об’єднують в одну точку, яку називають нульовою точкою або нейтраллю. В цій ситуації, функціонування системи забезпечується чотирма дротами: трьома лінійними (фазовими) та одним нульовим. В такій чотирьох дротовій системі, напруга між лінійним та нульовим дротами називають фазовою (U_ф), а напругу між двома лінійними дротами – лінійною (U_л). Можна довести, що між ефективними значеннями фазових та лінійних напруг існує співвідношення: U_л=U_ф√3≈1,73U_ф. Наприклад, якщо фазова напруга становить 220В, то лінійна напруга дорівнює 380В.

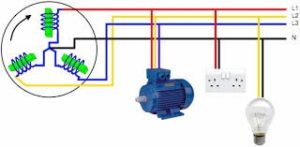
Мал.22. Загальна схема трифазної системи ліній електропередач при з’єднанні обмоток генератора зіркою.

Можна довести, що в тому випадку, коли енергетичне навантаження на кожну фазу є однаковим, тобто таким коли в кожному лінійному (фазовому) дроті протікає практично однаковий струм, сила струму в нульовому дроті дорівнюватиме нулю. Дійсно, якщо в трифазній системі ліній електропередач організованій за схемою «зірка», в кожному лінійному (фазовому) дроті протікають змінні струми однакової величини, то в нульовому дроті має протікати струм, який є результатом додавання трьох складових: i₁=I_мsin2πνt; i₂=I_мsin(2πνt–2π/3); i₃=I_мsin(2πνt–4π/3). При цьому згідно з першим законом Кірхгофа, ефективні значення змінних струмів додаються як певні векторні величини: І_заг = І₁+І₂+І₃. А оскільки числові значення складових векторів є однаковими (І₁=І₂=І₃), а зсув фаз між ними дорівнює 120º, то результатом додавання цих векторів, буде вектор нульової величини (мал.23). Аналогічний результат можна отримати і в тому випадку, якщо додавати миттєві значення трьох рівних за амплітудою та частотою коливань струмів, зсув фаз між якими становить 120º.

 

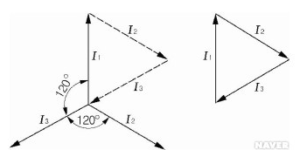
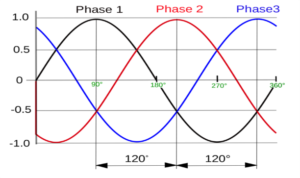
Мал.23. Результатом додавання трьох струмів однакової періодичності та амплітуди, які відрізняються зсувом фаз 120º є струм нульової величини.

По суті вище сказане означає, що в ситуації, коли енергетичне навантаження на кожну фазу трифазної системи ліній електропередач є однаковим, від нульового дроту можна відмовитись. Втім, досягти ідеальної збалансованості системи, достатньо складно. Тому в більшості випадків, трифазні лінії електропередач є чотирьох дротовими. При цьому площа поперечного перерізу нульового дроту завжди набагато менша за відповідну площу фазових дротів. Адже створюючи трифазну систему ліній електропередач, завжди прагнуть до того, щоб енергетичне навантаження на кожну фазу було приблизно однаковим. А це означає, що в нульовому дроті якщо і протікає певний струм, то відносно малий.

З’єднання зіркою є основним способом з’єднання обмоток трифазового генератора та організації систем ліній електропередач. Однак, якщо мова йде про системи з гарантовано збалансованим навантаженням фаз (наприклад в трифазних двигунах змінного струму), то в цьому випадку зазвичай застосовують з’єднання трикутником. За такого з’єднання, вихідний край однієї обмотки з’єднують з вхідним краєм сусідньої обмотки. При цьому, система трьох обмоток утворює замкнутий трикутник .

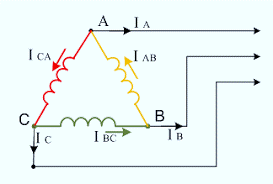
Мал.24. Схема трифазної системи змінного струму, при з’єднані трикутником.

Завершуючи розмову про трифазну систему змінного струму, перелічимо ті основні переваги які має ця система порівняно з системою однофазного струму.

1. Практично в двічі зменшує кількість дротів в системі ліній електропередач.
2. Практично в двічі зменшує теплові втрати в лініях електропередач.
3. Практично в двічі зменшує навантаження на опори ліній електропередач.
4. Практично в двічі зменшує витрати на трансформацію електроенергії в силових лініях електропередач.
5. Забезпечує ефективне перетворення енергії змінного струму в механічну роботу.
6. Дозволяє застосовувати два види напруги: фазову (220В) та лінійну (380В).

Контрольні запитання.

1. Коли ми стверджуємо, що в колі змінного струму протікає струм 0,5А, то чому цим струмом не може бути: а) миттєве; б) середнє; в) амплітудне значення цього струму?
2. Поясніть, чому обираючи критерій порівняльної оцінки постійних та змінних струмів, вчені обрали теплову дію цих струмів?
3. Поясніть, що означає твердження: в мережі ліній електропередач існує змінна напруга 220В?
4. Спрогнозуйте поведінку: а) лампочки розжарювання; б) резистора; в) конденсатора; г)котушки індуктивності; д) діода; в колі постійного та змінного струму.
5. Поясніть будову та принцип дії трифазного генератора змінного струму. Чим цей генератор відрізняється від однофазного?
6. В одній з обмоток трифазного генератора ЕРС змінюється за законом е=ℰ₀sin314t. Запишіть рівняння ЕРС для двох інших обмоток?
7. Як з’єднують обмотки трифазного генератора (електродвигуна): при з’єднанні зіркою; при з’єднанні трикутником?
8. Яку напругу називають фазовою, а яку лінійною? Яке співвідношення між цими напругами?
9. Трифазна система ліній електропередач може бути чотирьох дротовою та трьох дротовою. Яка з цих систем є більш вживаною і чому?
10. Сформулюйте та поясніть ті переваги які має трифазна система змінного струму порівняно з однофазною системою.

Вправа 4.

1. Електричний струм змінюється за законом і=1,5sin100πt. Визначте період і частоту цього струму. Визначте амплітудне та ефективне значення струму.
2. Електрична напруга змінюється за законом u=120cos40πt. Визначте період, частоту, амплітудне та ефективне значення цієї напруги. Побудуйте графік цієї напруги.
3. За заданими графіками записати рівняння а) змінного струму, б) змінної напруги.

а) б)

4. Відомо, що в мережі ліній електропередач існує змінна напруга величиною 220В і частотою 50Гц. Запишіть рівняння гармонічних коливань цієї напруги.
5. Миттєве значення змінного струму частотою 50Гц для фази π/3 дорівнює 1А. Визначте амплітудне та діюче значення сили струму. Запишіть рівняння цього струму.
6. Миттєве значення змінної напруги для фази 60° дорівнює 120В. Яке амплітудне значення цієї напруги? Яким буде миттєве значення цієї напруги через 0,25с, рахуючи від початку періоду?

.

Лекційне заняття №5.

Тема: Резистори, конденсатори і котушки індуктивності в колі постійного та змінного струмів. Коливальний контур. Генератор високочастотних коливань. 

До числа найпростіших і в той же час найважливіших електротехнічних приладів відносяться резистори, конденсатори і котушки індуктивності. Про призначення будову, принцип дії та застосування цих приладів ми детально говорили в процесі вивчення попередніх тем. Тому наразі просто дослідимо поведінку кожного з цих приладів в колі постійного та змінного струмів і на основі цих досліджень зробимо відповідні висновки.

Резистор. Оскільки резистор представляє собою звичайний провідник (а по суті шматок струмопровідного дроту) з певним наперед визначеним опором, то можна передбачити, що в колі постійного і змінного струмів, електрична поведінка резистора буде однаковою: резистор проводитиме електричний струм. При цьому, згідно з законом Ома, величина відповідного струму буде обернено пропорційною опору резистора, який в свою чергу залежатиме від питомого опору матеріалу провідника (ρ), його довжини (ℓ) та площі поперечного перерізу (S): I=U/R,  де  R=ρℓ/S.

Для перевірки наших теоретичних передбачень, збираємо просте електричне коло (мал.25) яке складається з універсального джерела струму (джерела в якому є як постійна так і змінна напруга), та послідовно з’єднаних демонстраційного резистора (реостата) і лампочки розжарювання (ця лампочка виконуватиме роль індикатора струму). Включаючи зв’язку резистор – лампочка в коло постійного, а потім змінного струмів, ви неодмінно з’ясуєте, що в обох випадках поведінка резистора є практично однаковою: резистор проводить електричний струм. При цьому, опір резистора як в колі постійного так і в колі змінного струмів є однаковим, і таким що залежить від питомого опору матеріалу провідника, довжини провідника та площі його поперечного перерізу. Цей опір прийнято називати активним. (Ясно, що умови нашого експерименту дозволяють дослідити лише факт залежності опору провідника (резистора) від його довжини).

  

Мал.25. В колі постійного і змінного струмів електрична поведінка резистора є однаковою.

Висновок 1. Резистор, в колі постійного і змінного струмів веде себе однаково: проводить електричний струм. При цьому, резистор має певний електричний опір, величина якого залежить від питомого опору матеріалу провідника, його довжини та площі поперечного перерізу. Цей опір називають активним.

Активний опір – це такий електричний опір, який має провідник як в колі постійного так і в колі змінного струмів, і величина якого залежить від питомого опору провідника (ρ), його довжини (ℓ) та площі поперечного перерізу (S).

Позначається: R_A

Визначальне рівняння: R_A=ρℓ/S

Одиниця вимірювання: [R_A]=Ом.

Конденсатор. Оскільки конденсатор представляє собою систему двох струмопровідних поверхонь, розділених шаром діелектрика, тобто матеріалу який не проводить електричний струм, то можна передбачити, що при включенні цієї системи в коло постійної напруги, у відповідному колі, струму не буде. (Поясніть, чому?). Не буде, за винятком моменту вмикання електричного кола. Адже в цей момент, конденсатор буде заряджатись і тому у відповідному колі протікатиме короткотривалий струм. Якщо ж говорити про коло змінного струму, то в ньому конденсатор буде постійно перезаряджатися. А це означає, що у відповідному колі постійно протікатиме змінний електричний струм.

Таким чином, наше передбачення полягає в тому, що електрична поведінка конденсатора в колі постійного та змінного струмів буде різною. В колі постійного струму, конденсатор не проводитиме струм, а в колі змінного струму – проводитиме його.

Перевіряючи ці теоретичні передбачення збираємо електричне коло яке складається з універсального джерела струму, батареї конденсаторів (системи конденсаторів ємність якої можна змінювати) і лампочки розжарювання (мал.26). Включаючи систему конденсатор – лампочка в коло постійної напруги, ви з’ясуєте, що за будь якої доступної величини цієї напруги та за будь якої ємності конденсатора, електричного струму у відповідному колі не буде. По суті це означає, що в колі постійного струму, конденсатор має безкінечно великий опір і тому не проводить струм. (Увага. В момент включення того кола яке містить конденсатор, цей конденсатор буде швидко заряджатись і тому в колі може виникнути достатньо потужний імпульс струму. Зважаючи на ці обставини, відповідне коло потрібно вмикати при мінімальній напрузі, а потім цю напругу збільшувати до необхідно великих величин).

 

Мал.26. В колі постійного і змінного струмів електрична поведінка конденсатора є різною.

Якщо ж систему конденсатор-лампочка включити в коло змінної напруги, то у відповідному колі протікатиме певний електричний струм. При цьому, величина того опору який матиме конденсатор залежатиме від його електричної ємності: при зменшенні ємності – опір збільшується (лампочка тухне), а при збільшенні ємності – опір зменшується (лампочка розгорається). Крім цього, якби ми мали можливість змінювати частоту струму, то неодмінно  з’ясували б, що електричний опір конденсатора залежить не лише від його ємності, а й від частоти змінного струму, і що ця залежність є обернено пропорційною.

Таким чином, експериментальні та теоретичні дослідження показують, що в колі змінного струму конденсатор проводить струм і що величина його електричного опору обернено пропорційна ємності конденсатора та частоті струму. Цей опір прийняти називати ємкісним.

Висновок 2.  Конденсатор, в колі постійного і змінного струмів веде себе по різному. В колі постійного струму, конденсатор має безкінечна великий опір і тому не проводить електричний струм. В колі змінного струму, конденсатор має певний електричний опір, величина якого залежить від ємності конденсатора та частоти змінного струму. Цей опір називають ємкісним. При цьому конденсатор проводить відповідний електричний струм.

Ємнісний опір – це такий електричний опір, який має провідник (конденсатор) в колі змінного струму і величина якого обернено пропорційна електричній ємності провідника (С) та частоті змінного струму (ν).

Позначається: R_C

Визначальне рівняння: R_C=1/2πνC

Одиниця вимірювання: [R_C]=Ом.

Котушка індуктивності. Оскільки котушка індуктивності представляє собою скручений в котушку суцільний струмопровідний дріт, то ясно, що цей дріт має проводити як постійний так і змінний струм. Втім, якщо в котушці протікає змінний струм, то він створює відповідний змінний магнітний потік. А це означає, що згідно з законом електромагнітної індукції, в цій котушці неминуче виникає певна протидія зміні магнітного потоку, а отже і тому змінному струму який створює цей потік. Цю протидію можна називати по різному: ЕРС самоіндукції, напруга самоіндукції, струм самоіндукції, тощо. Однак електричний результат цієї протидії по суті полягає в тому, що в колі змінного струму, в котушці індуктивності з’являється певний додатковий електричний опір, величина якого прямо пропорційна індуктивності котушки та частоті змінного струму. Цей опір прийнято називати індуктивним.

Таким чином, наше теоретичне передбачення полягає в тому, що електрична поведінка котушки індуктивності в колі постійного і змінного струмів має бути суттєво різною. В колі постійного струму, котушка матиме звичайний активний опір і проводитиме відповідний електричний струм (I=U/R_А). В колі змінного струму, в котушці, окрім звичайного активного опору, має виникати певний додатковий індуктивний опір (R_L) і тому сила струму у відповідному електричному колі має зменшуватися (I=U/(R_А+R_L).

Крім цього, можна передбачити, що в момент включення постійного струму, цей струм досягатиме своєї номінальної величини (I=U/R_А) не відразу, а з певною затримкою (лампочка загорається з певним запізненням). Дійсно, в момент включення постійного струму, той магнітний потік що виникає в котушці буде змінюватись (зростати). При цьому в котушці, згідно з законом електромагнітної індукції, неминуче виникає певна протидія зростанню магнітного потоку, а отже і швидкому зростанню струму.

Перевіряючи ці теоретичні передбачення, збираємо електричне коло, яке складається з універсального джерела струму, котушки індуктивності (котушки з рухомим феромагнітним осердям) та лампочки розжарювання. Включаючи зв’язку котушка-лампочка в коло постійного струму, ви неодмінно з’ясуєте, що у відповідному колі протікає певний електричний струм і що величина цього струму не залежить від індуктивності котушки (цю індуктивність змінюють шляхом виймання осердя з отвору котушки, або навпаки – його опускання в отвір). А це означає, що в колі постійного струму, котушка веде себе як звичайний провідник, опір якого практично не залежить від того скручено цей провідник у вигляді котушки, чи розтягнуто у вигляді  прямолінійного дроту. Не важко перевірити і факт того, що в момент включення постійної напруги, лампочка загорається з певним запізненням. Що в точності співпадає з передбаченнями теорії.

Якщо ж зв’язку котушка-лампочка включити в коло змінного струму, то ви неодмінно з’ясуєте, що в цьому колі загальний опір котушки збільшується, і що величина цього збільшення буде пропорційною індуктивності котушки: при вийманні осердя з котушки (при зменшенні індуктивності) – опір зменшується і лампочка розгорається; при опусканні осердя в котушку (при збільшенні індуктивності) – опір збільшується і лампочка гасне. А це означає, що наші теоретичні прогнози стосовно електричної поведінки котушки індуктивності, в точності підтверджуються.

        

Мал.27.  В колі постійного та змінного струмів, електрична поведінка котушки індуктивності є різною.

Висновок 3.  Котушка індуктивності в колі постійного і змінного струмів веде себе по різному. В колі постійного струму, котушка має певний активний опір і проводить відповідний електричний струм. В колі змінного струму, в котушці виникає певний додатковий індуктивний опір, величина якого залежить від індуктивності котушки та частоти змінного струму. При цьому сила струму в колі відповідно зменшується.

Індуктивний опір, це такий електричний опір, який має провідник (котушка індуктивності) в колі змінного струму і величина якого прямо пропорційна індуктивності провідника (L) та частоті змінного струму (ν).

Позначається: R_L

Визначальне рівняння: R_L=2πνL

Одиниця вимірювання: [R_L]=Ом.  

         Таким чином, теоретичні та експериментальні дослідження показують, що існує три різновидності електричного опору: активний, індуктивний та ємнісний.

.                                             R_A=ρℓ/S

.                        R=U/I           R_L=2πνL

.                                             R_C=1/2πνC

Всі ці опори вимірюються в омах і є різновидностями однієї і тієї ж фізичної величини – електричного опору. Однак між ними існують і суттєві відмінності. А ці відмінності полягають в тому, що активні, індуктивні та ємкісні опори додаються як певні векторні величини. Втім, розгляд питання про причини такого стану речей виходить за межі програми загальноосвітньої школи.

На завершення зауважимо, що формули R_L=2πνL та R_C=1/2πνC, дають правильні результати навіть в тому випадку, коли їх застосовують для кіл постійного струму. Дійсно. Постійний струм, можна вважати такою різновидністю змінного струму, період коливань якого є безкінечно великим (Т=∞), а отже частота коливань якого дорівнює нулю (ν=1/Т=1/∞=0). А це означає, що для постійного струму R_C=1/2πС∙0=1/0=∞(Ом); R_L=2πL∙0=0(Ом). Що в точності співпадає з результатами наших експериментів.

Індукційні генератори, перетворюючи енергію механічного обертання в енергію змінного електричного струму, створюють струми відносно низьких частот (50 – 60 Гц). Сучасна ж система радіозв’язку (радіо, телебачення, мобільний зв’язок, системи дистанційного управління, тощо) базуються на застосуванні струмів високої частоти (ν > 100.000Гц). Створити такий струм за допомогою індукційного генератора, тобто приладу який перетворює механічну енергію в енергію електричного струму, практично не можливо. Адже практично не можливо створити таку механічну систему, масивні деталі якої обертались би з частотою понад 100.000Гц. До того ж, важко уявити мобільний телефон, чи скажімо кишеньковий пульт дистанційного управління телевізором, складовою частиною якого є громіздка електромеханічна система.

На практиці високочастотні струми (високочастотні електромагнітні коливання) створюють генератори високочастотних електромагнітних коливань, а простіше кажучи – генератори високої частоти (ГВЧ). Основним елементом таких генераторів є просте електричне коло яке називається коливальним контуром і яке складається з послідовно з’єднаних конденсатора та котушки індуктивності.

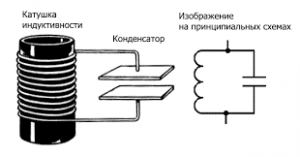
Мал.28. Схема принципового устрою коливального контура.

Коливальний контур представляє собою певну коливальну систему, яка дозволяє отримувати вільні, високочастотні, згасаючі електромагнітні коливання. В певному сенсі ті процеси які відбуваються в коливальному контурі аналогічні тому, що відбувається в будь якій коливальній системі, наприклад в фізичному (математичному) чи  пружинному маятнику. Нагадаємо, вивчаючи механіку ми говорили про те, що вільні коливання будь якої механічної системи, супроводжуються періодичними перетвореннями тієї чи іншої різновидності потенціальної енергії в енергію кінетичну і навпаки. Зокрема:

– в математичному маятнику: Е_п=mg∆h ↔ Е_к=mv²/2;

– в пружинному маятнику:      Е_п=k∆ℓ²/2 ↔ Е_к=mv²/2.

Дещо подібне відбувається і в коливальному контурі. Різниця лише в тому, що в коливальному контурі, певною різновидністю потенціальної енергії є та електрична енергія яка зосереджується в зарядженому конденсаторі (W_ел=CU²/2), а певною різновидністю кінетичної енергії, є та магнітна енергія яка зосереджується в індукційній котушці зі струмом (W_маг=LI²/2).

 

W_ел ↔ W_маг ↔ W_ел                               Е_п ↔ Е_к ↔ Е_п

Мал.29. В певному сенсі ті процеси які відбуваються в коливальному контурі є аналогічними тому що відбувається в процесі коливань механічних маятників.

Зважаючи на вище сказане, розглянемо ті процеси що відбуваються в коливальному контурі після виведення його з стану електромагнітної рівноваги.  Описуючи ці процеси будемо аналізувати зміни чотирьох величин: напруги між обкладинками конденсатора (U), накопиченої в конденсаторі електричної енергії (W_ел=CU²/2), сили струму в колі (І) та накопиченої в котушці з струмом магнітної енергії (W_маг=LI²/2).

Припустимо, що коливальний контур виведено з стану електромагнітної  рівноваги шляхом зарядження конденсатора. Замкнемо електричне коло коливального контура та стисло опишемо ті процеси що відбуваються в ньому. А ці процеси будуть наступними (мал.30).

Мал.30. Графічна ілюстрація тих процесів що відбуваються в коливальному контурі та графіки коливань струму і напруги в ньому.

1. Конденсатор заряджений (t=0). При цьому: напруга між обкладинками конденсатора та кількість накопиченої в ньому електричної енергії є гранично великими, а сила струму в колі та кількість накопиченої в котушці магнітної енергії дорівнюють нулю: U=max, W_ел=max, I=0, W_маг=0.
2. Конденсатор розряджається (t: 0→t₁). При цьому: U↓, W_ел↓, I↑, W_маг↑. І потрібно зауважити, що у відповідності з законом електромагнітної індукції, зростання струму в котушці індуктивності, а відповідно і зміна інших параметрів системи, відбувається не різко, а плавно-гармонічно.
3. Конденсатор розрядився (t=t₁). При цьому: U=0, W_ел=0, I=max, W_маг=max.
4. Конденсатор перезаряджається (t: t₁→t₂). При цьому: –U↑, –W_ел↑, I↓, W_маг↓. І потрібно зауважити, що та магнітна енергія яка була накопичена в котушці індуктивності, в процесі перезарядки конденсатора, у відповідності з законом електромагнітної індукції, протидіє швидкому зменшенню сили струму в колі, та робить це зменшення плавно-гармонічним.
5. Конденсатор перезарядився (t=t₂). При цьому: –U=max, –W_ел=max, I=0, W_маг=0.

6, 7, 8, 9 – процес повторюється, при цьому напрям струму змінюється на протилежний.

Таким чином, після виведення коливального контуру з стану електромагнітної рівноваги, в ньому відбуваються певні вільні електромагнітні коливання, одним з проявів яких є відповідний високочастотний струм. І можна довести, що період тих коливань які виникають в коливальному контурі визначається за формулою  T=2π√(LC), де L, C – індуктивність та електрична ємність відповідних елементів контура.

Не важко бачити, що формула T=2π√(LC) явно подібна до тих формул, за якими визначають періодичність інших коливальних систем, зокрема:

– математичного маятника: T = 2π√(ℓ/g);

– пружинного маятника:      T = 2π√(m/k).

Ясно, що ті вільні електромагнітні коливання які за певних умов виникають в коливальному контурі є згасаючими, тобто такими амплітуда та енергетичні параметри яких з плином часу зменшуються. Незгасаючі високочастотні електромагнітні коливання (високочастотні струми) створюють за допомогою генераторів високої частоти (ГВЧ).

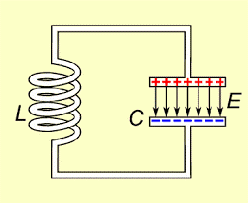
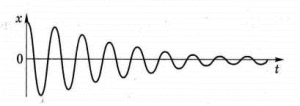
Мал.31. Після виведення системи із електромагнітної рівноваги, коливальний контур стає джерелом згасаючих високочастотних коливань (струмів).

Генератор високої частоти (генератор високочастотних електромагнітних коливань) – це прилад, який представляє собою певну автоколивальну систему, в якій енергія постійного джерела струму перетворюється на енергію високочастотних незгасаючих електромагнітних коливань (високочастотних струмів).

Основними елементами генератора високої частоти є коливальний контур, транзистор, джерело постійного струму та котушка зворотнього зв’язку (мал.31). Принцип дії цієї системи полягає в наступному. В момент включення генератора, певна кількість електричного заряду проходить через транзистор та заряджає конденсатор коливального контура. При цьому коливальний контур виводиться з стану електромагнітної рівноваги і в ньому починаються високочастотні електромагнітні коливання, періодичність яких визначається параметрами коливального контура Т=2π√(LC). В процесі цих коливань, в ті моменти коли в котушці коливального контура протікає електричний струм, в іншій з нею індуктивно зв’язаній котушці (котушці зворотнього зв’язку), генерується протилежно направлений індукційний струм. При цьому, в залежності від напрямку індукційного струму, потенціал бази транзистора стає то додатнім то від’ємним. А це означає, що в певні моменти через транзистор проходить певний електричний імпульс який компенсує втрати енергії в коливальному контурі.

 

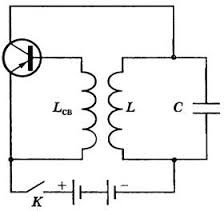
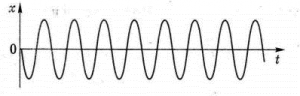
Мал.32. Генератора високої частоти (ГВЧ) є джерелом незгасаючих високочастотних струмів.

Генератор високої частоти є класичним прикладом так званої автоколивальної системи. Автоколивальна система, це така автоматизована коливальна система, яка є джерелом умовно вільних незгасаючих коливань і в якій енергетичні втрати базової коливальної системи автоматично компенсуються за рахунок додаткового джерела енергії. Будь яка автоколивальна система представляє собою сукупність чотирьох елементів, взаємопов’язаність яких можна представити у вигляді наступної принципової схеми.

І не важко збагнути, що в тій автоколивальній системі яка називається генератором високої частоти (ГВЧ), джерелом енергії є джерело постійного струму, коливальною системою – коливальний контур, пристроєм що керує надходженням енергії – транзистор, а системою зворотнього зв’язку – сукупність індуктивно зв’язаних котушки коливального контура та котушки зворотнього зв’язку.

На завершення додамо, що ГВЧ є базовими елементами практично всіх радіопередавальних приладів починаючи від мобільних телефонів та пультів дистанційного управління побутовою технікою і закінчуючи потужними радіостанціями, телевізійними центрами, радарними системами, тощо.

Задача. У коливальному контурі залежність сили струму від часу описується рівнянням і=0,06sin10⁶πt. Визначити частоту коливань в контурі, ємність включеного в контур конденсатора, максимальну енергію магнітного поля та максимальну напругу на конденсаторі, якщо індуктивність включеної в контур котушки 0,1Гн.

Дано:

і=0,06sin10⁶πt

L = 0,1Гн

ν=?; C=?; W_маг=?; U_м=?.

Рішення. Із порівняльного аналізу рівнянь i = I_мsin2πνt та і=0,06sin10⁶πt випливає, що І_м=0,06А; 2πνt=10⁶πt, звідси ν=0,5·10⁶Гц.

Оскільки частота коливань в коливальному контурі визначається за формулою ν=1/Т=1/√(СL), то ν²=1/СL, C=1/ν²L=1/0,1·(5·10⁵)²= 0,4·10^–10Ф= 40·10^–12Ф= 40пкФ.

Оскільки максимальна величина накопиченої в котушці індуктивності магнітної енергії визначається за формулою W_маг=LI_м²/2, то W_маг = 0,1Гн·0,06A = 0,006Дж = 6мДж.

Оскільки в процесі тих коливань які відбуваються в коливальному контурі, електрична енергія конденсатора перетворюється в магнітну енергію котушки і навпаки, то у відповідності з законом збереження енергії W_маг=W_ел=CU_м²/2, звідси U_м=√(2W_маг/C)= √(2·6·10^–3/40·10^–12) = √0,3·10⁹= 1,75·10⁴В= 17,5кВ.

Відповідь: ν=0,5·10⁶Гц; С=40пкФ; W_маг=6мДж; U_м= 17,3кВ

Контрольні запитання.

1. Поясніть, чому конденсатор в колі постійного струму не проводить струм, а в колі змінного – проводить?
2. Поясніть, чому в системі котушка-лампочка, при одній і тій же напрузі, в колі постійного струму тече великий струм, а в колі змінного струму – малий?
3. Поясніть, чому в колі змінного струму, при витягуванні з котушки феромагнітного осердя лампочка розгорається, а при його опусканні – гасне?
4. Наведіть докази того, що однакові за величиною постійні та змінні напруги, це напруги суттєво різні.
5. Доведіть що одиницями вимірювання ємнісного та індуктивного опорів є Ом.
6. Опишіть ті процеси, що відбуваються в математичному (нитяному) маятнику після виведення його з стану механічної рівноваги?
7. Опишіть ті процеси що відбуваються в коливальному контурі після виведення його з стану електромагнітної рівноваги.
8. Чому ті коливання які відбуваються в коливальному контурі є згасаючими? Від чого залежить інтенсивність цього згасання?
9. Поясніть будову та принцип дії генератора високої частоти.
10. Які функції в ГВЧ виконує: а) транзистор; б) котушка зворотнього зв’язку?

Вправа 5.

1. В колі змінного струму з частотою 50Гц, ємкісний опір конденсатора 1кОм. Визначити електричну ємність конденсатора.
2. В колі змінного струму з частотою 50Гц, індуктивний опір котушки 1(Ом). Визначити індуктивність котушки.
3. Яка ємність конденсатора якщо при його включенні в коло з наругою 220В та частотою 50Гц, протікає струм 1,5А?
4. Котушку індуктивності з гранично малим активним опором ввімкнули в коло з напругою 220В та частотою 50Гц. При цьому сила струму в колі котушки 2,0А. Яка індуктивність котушки?
5. Індуктивність котушки коливального контура 6·10^–4Гн. Якою має бути ємність конденсатора, щоб частота коливань в ньому становила 0,5МГц?
6. Струм в коливальному контурі змінюється за законом і=0,01cos10³πt. Визначіть період і частоту коливань в цьому контурі. Визначте індуктивність контура, якщо ємність наявного в контурі конденсатора 20мкФ.
7. Струм в коливальному контурі змінюється за законом і=0,02sin500πt. Індуктивність контура 0,1Гн. Визначити частоту коливань в контурі, ємність включеного в контур конденсатора, максимальну енергію магнітного поля і максимальну напругу на конденсаторі.
8.  Струм в колі змінюється за законом і=0,2sin314t (A). На яку напругу має бути розрахований включений в це коло конденсатор ємністю 2,0∙10^–6Ф?

.

Лекційне заняття №6.

Тема: Про електростатичні та електродинамічні поля. З історії теорії електромагнітного поля. 

Аналіз явища електромагнітної індукції неминуче вказує на те, що в Природі існує дві суттєво відмінні різновидності електричного поля: поле електростатичне та поле електродинамічне. Говорячи про суть того спільного та того відмінного, що є між електростатичними та електродинамічними полями, можна сказати наступне.

         До тепер ми виходили з того, що електричне поле – це таке силове збурення простору, яке створюється електричними зарядами і діє на електричні заряди. Але, чесно кажучи, дане визначення не є безумовно правильним. Адже по суті є визначенням тієї різновидності електричного поля яке називається електростатичним. Вивчаючи електростатику, ми фактично вивчали параметри, закономірності та прояви електростатичних полів, тобто тих електричних полів які створюються електричними зарядами і певним чином діють на електричні заряди. При цьому ми з’ясували:

1. Електростатичні поля створюються електричними зарядами.
2. Електростатичні поля певним чином діють на електричні заряди.
3. Основною характеристикою електростатичного поля є фізична величина яка називається напруженістю електричного поля: Е=F_ел/q_п.
4. Електростатичні поля діють незалежно одне від одного, при цьому напруженість результуючого поля системи багатьох зарядів, дорівнює векторній сумі напруженостей кожного окремого поля системи (принцип суперпозиції): Е_рез=∑Е_і
5. Електростатичні поля зображуються умовними лініями, які називаються лініями напруженості електричного поля.
6. Кожна лінія напруженості електростатичного поля починається на заряді «плюс» і закінчуються на заряді «мінус».
7. Електростатичні поля, це поля стаціонарні, тобто такі, параметри яких в будь якій точці поля з плином часу не змінюються (звичайно за умови, що не змінюються параметри тих зарядів які створюють відповідне поле).
8. Електростатичні поля, це поля потенціальні, тобто такі, робота яких на замкнутій траєкторії дорівнює нулю: А_O=0.

Мал.33. Електростатичне поле стаціонарне і потенціальне.

Аналізуючи явище електромагнітної індукції, можна дійти висновку, що в Природі окрім електростатичного поля існує ще одна, суттєво від нього відмінна різновидність електричного поля. Дійсно. Досліджуючи явище електромагнітної індукції, ми з’ясували, що при будь якій зміні того магнітного потоку, що пронизує струмопровідний контур, в цьому контурі виникає певний електричний струм. Це означає, що змінне магнітне поле якимось чином змушує початково нерухомі заряди упорядковано рухатись. Але ж за визначенням, магнітне поле не діє на нерухомі заряди і тому не може безпосередньо створити електричний струм. І тим не менше, такий струм виникає. Аналізуючи дану ситуацію, логічно передбачити що  змінне магнітне поле створює (індуцирує) в навколишньому просторі певне електричне поле, яке і створює відповідний електричний струм.

Мал.34. Оскільки в змінному магнітному полі включена в коло котушки лампочка постійно горить, то це означає, що змінне магнітне поле створює (індуцирує) певне електричне поле, яке і створює відповідний струм.

Таким чином, експериментальні факти безумовно вказують на те, що електричні поля створюються не лише електричними зарядами, а й змінними магнітними полями. Досліджуючи властивості цієї нової різновидності електричного поля, яку ми будемо називати електродинамічним полем, проведемо та проаналізуємо наступний простий експеримент. Котушку індуктивності з довгим феромагнітним осердям (котушку Томсона), включимо в коло змінного струму і в створене нею змінне магнітне поле внесемо іншу струмопровідну котушку в коло якої включена лампочка розжарювання (мал.35). Не важко бачити, що в колі вторинної котушки, згідно з законом електромагнітної індукції, виникає індукційний струм, наявність якого фіксує лампочка розжарювання.

Аналізуючи результати даного експерименту можна сказати наступне. Оскільки те електричне коло що знаходиться в змінному магнітному полі котушки Томсона є замкнутим, то факт наявності струму в цьому колі, безумовно вказує на те, що індукційне електродинамічне поле, змушує носії струму рухаються замкнутими траєкторіями. При цьому, факт того, що в процесі цього руху, включена в коло лампочка розжарювання постійно горить, безумовно вказує на те, що робота сил електродинамічного поля на замкнутій траєкторії не дорівнює нулю. А це означає, що електродинамічне поле є непотенціальним.

 

Мал.35. Змінне магнітне поле, створює в навколишньому просторі вихрове, непотенціальне електричне поле.

Далі. Факт того, що електродинамічне поле змушує заряди рухатись замкнутим колом, безумовно вказує на те, що лінії напруженості електродинамічного поля є вихровими, тобто такими які ніде не починаються і ніде не закінчуються. Власне даний факт є прямим наслідком того, що джерелом електродинамічного поля є не позитивні та негативні заряди, а певні вихрові магнітні процеси, які створюють в навколишньому просторі відповідні вихрові електричні процеси.

Далі. Оскільки той індукційний струм який виникає у вторинній котушці нашої системи є змінним, то відповідно змінним є і те електродинамічне поле яке цей струм створює. А це означає, що електродинамічне поле є нестаціонарним, тобто таким параметри якого в будь якій точці поля постійно змінюються.

Втім, дане твердження не є безумовно правильним. Адже за певних обставин і в певному обмеженому інтервалі часу, електродинамічне поле може бути стаціонарним. Наприклад, якщо в обмотці електромагніту, сила струму з постійною швидкістю збільшується, то між його полюсами виникає постійно зростаюче магнітне поле, яке в свою чергу створює стаціонарне електродинамічне поле. Ясно, що таке поле не може існувати безкінечно довго. Адже в будь якій системі, сила струму не може постійно та безкінечно довго зростати.

Та як би там не було, а зазвичай змінні магнітні поля створюються гармонічно змінними електричними струмами, і тому відповідні електродинамічні поля є гармонічно нестаціонарними.

Таким чином, говорячи про загальні властивості електродинамічних полів та способи наукового відображення цих властивостей, можна сказати наступне.

1. Електродинамічні поля створюються змінними магнітними полями.
2. Електродинамічні поля певним чином діють на електричні заряди.
3. Основною характеристикою електродинамічного поля є фізична величина яка називається напруженістю електричного поля: Е=F_ел/q_п.
4. Електродинамічні поля діють незалежно одне від одного, при цьому напруженість результуючого поля системи багатьох джерел, дорівнює векторній сумі напруженостей кожного окремого поля системи (принцип суперпозиції): Е_рез=∑Е_і .
5. Електродинамічні поля зображають за допомогою умовних ліній, які називаються лініями напруженості електричного поля.
6. Лінії напруженості електродинамічного поля є вихровими, тобто такими які ніде не починаються і ніде не закінчуються.
7. Електродинамічні поля, це поля нестаціонарні. Однак, за певних умов та в коротких часових інтервалах, вони можуть бути стаціонарними.
8. Електродинамічні поля, це поля непотенціальні, тобто такі, робота яких на замкнутій траєкторії не дорівнює нулю: А_О≠0.

Не важко бачити, що між електростатичними та електродинамічними полями існують суттєві відмінності. І тим не менше, ці суттєво різні поля є полями електричними. Вони електричні по перше тому, що кожному з них притаманна основна риса електричного поля – здатність певним чином діяти на нерухомі та рухомі  електричні заряди. По друге тому, що величина цієї силової дії визначається за одним і тим же законом: F=Eq. По третє тому, що загальні властивості обох різновидностей електричного поля, описуються одними і тими ж фізичними величинами та зображуються одними і тими ж умовними лініями (лініями напруженості електричного поля). Нарешті, згідно з принципом суперпозиції, електростатичні та електродинамічні поля, накладаючись одне на одне утворюють єдине результуюче електричне поле, напруженість якого визначається як векторна сума кожного окремого поля системи.

Узагальнюючи вище сказане, можна дати наступні визначення. Електричне поле – це таке поле, тобто таке силове збурення простору, яке створюється електричними зарядами та змінними магнітними полями і яке певним чином діє на електричні заряди. Розрізняють дві різновидності електричного поля: поле електростатичне та поле електродинамічне.  Електростатичне поле, це таке потенціальне електричне поле, яке створюється електричними зарядами і певним чином діє на електричні заряди. Електродинамічне поле (вихрове електричне поле), це таке непотенціальне електричне поле, яке створюється змінними магнітними полями і певним чином діє на електричні заряди.

Говорячи про потенціальність електростатичних та непотенціальність електродинамічних полів, буде не зайвим нагадати, що гравітаційне поле, це поле потенціальне. Якщо ж говорити про магнітне поле, то його не можна назвати ні потенціальними, ні непотенціальними. Не можна тому, що магнітне поле фактично не виконує певну роботу по переміщенню електричних зарядів. Магнітне поле лише змінює напрям руху цих зарядів. А якщо ми і говоримо про певну енергію магнітного поля, то лише тому, що це поле нерозривно пов’язане з полем електричним, і що при певній зміні магнітного поля неминуче індуцирується відповідне електродинамічне поле, яке і виконує певну роботу.

На завершення додамо, що подібно до того як електричні поля створюються не лише електричними зарядами, а й змінними магнітними полями, поля магнітні також створюються не лише електричними струмами, а й змінними електричними полями. Однак, якщо між електростатичними та електродинамічними полями є суттєві відмінності, то між тими магнітними полями які створюються електричними струмами та тими які створюються змінними електричними полями, суттєвих відмінностей нема. Вони однаково діють на електричні струми та заряди що рухаються. Кожне з цих полів є вихровим, кожне з них не є ані потенціальним, ані непотенціальним, кожне з них характеризується певною магнітною індукцією та зображується аналогічним набором ліній магнітної індукції.

Починаючи вивчення електродинаміки, ми говорили про те, що в основі цієї величної науки лежать чотири твердження, які сформульовані видатним англійським вченим Джеймсом Максвелом (1831–1879) і які називаються рівняннями Максвела. Говорили і про те, що бодай елементарне розуміння суті цих базових тверджень, не можливе без попереднього вивчення багатьох явищ, фізичних величин, законів та експериментальних фактів. І що тому, формулювання основних тверджень теорії Максвела ми будемо розглядати як певну кінцеву мету. Як завершальний етап вивчення електродинаміки.

І от настав той час, коли ми практично готові підкорити одну з найнеприступніших вершин сучасної науки, яка називається динамічною теорією електромагнітного поля або теорією Максвела. Втім, в даному випадку, слово «готові» навряд чи відображає реальний стан речей. Адже максвелівська електродинаміка представляє собою органічне поєднання фізики та вищої математики. Математики, вивчення якої виходить за межі програми не лише загально освітньої школи, а й більшості вищих навчальних закладів. Зважаючи на ці обставини, теорія Максвела у своєму повному обсязі вивчається лише в невеликій кількості спеціалізованих вузів. Однак, якщо говорити про фізичну суть цієї теорії, то вона може і має бути предметом вивчення загальноосвітнього курсу фізики. Власне з’ясуванню цієї суті і присвячена дана тема.

Говорячи про теорію Максвела, доречно згадати ті історичні події які передували появі цієї теорії. Це важливо бодай тому, що без розуміння історичних коренів теорії, важко розраховувати на глибоке розуміння тих визначальних ідей які лежать в основі відповідної теорії, в даному випадку – теорії Максвела. А ці ідеї формувались в процесі наступних подій.

Приблизно з середини 17-го століття, в науці набула загального поширення так звана концепція далекодії. Прихильники цієї концепції стверджували, що гравітаційні, електричні та магнітні взаємодії, відбуваються без будь якого матеріального посередника. Наприклад, гравітаційна дія від Землі до Місяця, від Сонця до Землі і навпаки, передається через пустий простір. При цьому мається на увазі, що в цьому просторі нема нічого такого що забезпечує передачу гравітаційної сили від одного тіла до іншого. Іншими словами, згідно з концепцією далекодії, гравітаційна дія миттєво передається в усі точки простору і ця передача відбувається без будь якого матеріального посередника.

Становленню та поширенню концепції далекодії сприяло те, що відкритий Ньютоном закон всесвітнього тяжіння, кількісно описував характер гравітаційних взаємодій і нічого не говорив про механізм передачі цих взаємодій.  При цьому не було жодних видимих ознак наявності такого механізму. Ситуація виглядала таким чином ніби гравітаційні взаємодії миттєво передаються через пустоту.

Факт того, що відкриття закону всесвітнього тяжіння сприяло поширенню концепції далекодії, часто тлумачать таким чином, ніби Ньютон був автором та пропагандистом цієї концепції. Подібні твердження є абсолютно безпідставними. Ми можемо лише здогадуватись, скільки інтелектуальних зусиль витратив великий Ньютон, намагаючись зрозуміти та пояснити механізм гравітаційних взаємодій. Адже навряд чи можна назвати випадковим той факт, що своє найвидатніше відкриття – закон всесвітнього тяжіння, Ньютон не публікував майже двадцять років.

Розуміючи всю глибину та складність проблеми наукового пояснення механізму гравітаційних взаємодій, і керуючись своїм знаменитим принципом «гіпотез не вигадую», геніальний Ньютон свідомо уникав публічних дискусій на предмет обговорення концепції далекодії. Лише деякі факти з усією очевидністю вказують на те, що Ньютон не був безумовним прихильником цієї концепції. Ось один з цих фактів. У своєму листі до Річарда Бентлі  від 25.02.1693 року, Ньютон писав: «Як на мене, стверджувати що тяжіння може передаватись від одного тіла до іншого без певного посередника – це абсурд. Передачу тяжіння має забезпечувати певний, постійно діючий агент, який діє за певними законами».

Та як би там не було, а починаючи з середини 17-го століття, число прихильників теорії далекодії неухильно зростало. І на початок 19-го століття в науці майже не залишилося тих хото б сумнівався в достовірності цієї «теорії». Втім, знайшовся один сміливець, який не просто висловлював сумніви щодо наукової обгрунтованості концепції далекодії, а був її свідомим та затятим противником. Цим сміливцем був видатний англійський фізик Майкл Фарадей (1791–1867).

Сьогодні важко повірити, що людина, офіційна освіта якої передбачала початкові навички читання, письма та арифметики, людина, яка з дванадцятирічного віку була змушеною заробляти на шматок хліба, зуміла піднятись до вершин сучасної науки і стати одним з найвидатніших вчених всіх часів і народів. І тим не менше, факт залишається фактом – Майкл Фарадей, син простого коваля і прибиральниці, офіційна освіта якого не виходила за межі початкової школи, став тим видатним вченим, який кардинально змінив хід історії науки.

Цілком ймовірно, що якби Фарадей отримав повноцінну середню та вищу освіту, то разом з нею засвоїв би й те, що гравітаційні, електричні і магнітні взаємодії не можливо пояснити інакше, як тільки на основі концепції далекодії. Однак Фарадей мав свій, особливий шлях в науці. І цей шлях базувався на абсолютній, непохитній вірі в те, що Природа, це єдиний цілісний організм в якому все гармонійно взаємопов’язано та взаємообумовлено. Тому, не будучи обтяженим загально прийнятими догмами, великий Фарадей був абсолютно переконаним в тому, що між взаємодіючими на відстані тілами, має бути певний матеріальний посередник. Іншими словами, Фарадей був палким та переконаним прихильником концепції близькодії, тобто тих поглядів, згідно з якими між взаємодіючими на відстані тілами, має бути певний посередник, який і передає цю взаємодію.

 

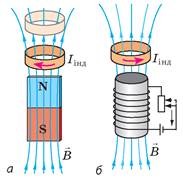
Мал.36. Фарадей – гравітаційні, електричні і магнітні взаємодії передаються через особливий матеріальний посередник – фізичне поле.

Аналізуючи електричні та магнітні взаємодії, Фарадей все більше і більше переконувався в тому, що ці взаємодії можуть і мають бути поясненими на основі концепції близькодії. Реалізуючи це переконання, він вводить в наукову практику поняття силового поля, під яким розуміє певне силове збурення простору, яке створюється взаємодіючими тілами і яке має певні ознаки реально існуючого матеріального об’єкту. Не маючи можливості описати цей об’єкт мовою математичних формул (давався в знаки брак математичної освіти), Фарадей створює і вводить в наукову практику мову графічних пояснень. Пояснень, які базуються на застосуванні спеціальних умовних ліній, які сьогодні прийнято називати лініями напруженості електричного поля та лініями індукції магнітного поля.

Сучасники без особливого ентузіазму сприйняли фарадеєвську ідею поля. Скоріш навпаки, зустріч виявилась якщо не ворожою, то іронічно поблажливою. Навіть після того, як спираючись на ідею поля та його силових ліній, Фарадей відкрив, дослідив та пояснив явище електромагнітної індукції, прихильники концепції далекодії вперто не бажали серйозно сприймати його наукові погляди на польовий механізм гравітаційних, електричних і магнітних взаємодій. Ось що писав про той період розвитку фарадеєвських ідей лауреат Нобелевської премії,  американський фізик Роберт Міллікен (1868–1953):  «Навіть після того як Фарадей підтвердив свої геніальні ідеї не менш геніальними відкриттями, ці ідеї не отримали бодай мінімального визнання. Формалісти школи Ампера – Вебера, з прихованим, а то і явним презирством дивились на грубі матеріальні силові лінії, що були породжені плебейською фантазією лабораторного сторожа Фарадея».

Однак, геніальні ідеї Фарадея не відійшли та й не могли відійти у вічність. Вони просто чекали свого часу. Чекали на людину, яка б перетворила їх на математично струнку та логічно бездоганну наукову теорію. І через понад три десятиліття така людина з’явилась. Це був видатний англійський фізик і математик Джеймс Клерк Максвел.

На відміну від Фарадея, представник знатного та заможного шотландського роду Максвел, отримав блискучу освіту. Ще будучи студентом, він зацікавився вивченням електричних і магнітних явищ. При цьому, із всіх робіт на цю тему юного Максвела найбільш вразила книга «Експериментальні дослідження з електрики». Автором цієї книги був Фарадей. Пізніше Максвел писав: «Я твердо вирішив не читати жодної роботи з цієї тематики допоки досконало не вивчу фарадеєвські «Експериментальні дослідження з електрики».

Ознайомившись з роботами Фарадея, юний Максвел стає палким та переконаним послідовником його ідей. Прагнучи реалізувати ці ідеї, він ставить перед собою задачу неймовірної складності. Задача, яку напевно не зміг би розв’язати жоден з його сучасників. Максвел вирішує розкрити механізм електричних та магнітних взаємодій і довести, що в цьому механізмі роль посередника між взаємодіючими тілами виконує особливий матеріальний об’єкт який називається електромагнітним полем.

Вирішуючи це завдання, Максвел вводить в наукову практику цілу низку фізичних величин які певним чином характеризують електричні та магнітні поля. Записує відомі на той час закони електромагнетизму на мові цих фізичних величин. З’ясовує та усуває наявні в цих законах неточності та протиріччя. Доповнює систему відомих знань новими знаннями. І у підсумку, створює цілісну, математично та фізично бездоганну теорію електромагнітного поля. Теорію, яка і на сьогоднішній день є взірцем практично ідеальної наукової теорії. Теорію, яка фантастично розширила обрії сучасної науки і стала основою сучасної електронно-інформаційної цивілізації.

Мал.37. Максвел – на основі ідей Фарадея про існування електричних і магнітних полів, створив струнку наукову теорію – теорію електромагнітного поля.

Контрольні запитання.

1. Чому закон всесвітнього тяжіння сприяв поширенню концепції далекодії?
2. Як ви думаєте, чому Ньютон уникав публічних дискусій стосовно концепції далекодії?
3. Які поля називаються: а) стаціонарними? б) нестаціонарними?
4. Які поля називаються: а) потенціальними? б) непотенціальними?
5. При внесенні струмопровідної котушки в змінне магнітне поле, в цій котушці виникає певний електричний струм. Чому цей експериментальний факт вказує на: а) змінне магнітне поле створює певне електричне поле; б) що це електричне поле є непотенціальним; в) що лінії напруженості цього поля є вихровими (замкнутими)?
6. Назвіть спільні риси електростатичних та електродинамічних полів.
7. Назвіть відмінні риси електростатичних та електродинамічних полів.
8. Чому гравітаційні поля є полями потенціальними?
9. Чому магнітні поля не є ані потенціальними, ані непотенціальними?
10. Якщо магнітне поле не виконує роботу по переміщенню зарядів, то чому ми стверджуємо, що воно має певну енергію, тобто те, що характеризує здатність виконати роботу?

.

Лекційне заняття №7.

Тема: Загальні основи теорії Максвела. Основні передбачення теорії Максвела. 

На середину 19-го століття, сукупність знань про електричні, магнітні та електромагнітні явища, фактично зводилась до п’яти відносно незалежних, експериментально встановлених тверджень (законів):

1. При будь яких процесах що відбуваються в замкнутій системі, загальна кількість електричного заряду цієї системи залишається незмінною, тобто зберігається: ∑q_i=const (закон збереження заряду).
2. Два точкових заряди q₁ і q₂ взаємодіють між собою (однойменні заряди відштовхуються, різнойменні – притягуються) з силою, величина якої визначається за формулою F=kq₁q₂/r² (закон Кулона).
3. Електричні струми (заряди що рухаються) взаємодіють між собою (співнаправлені струми притягуються, протинаправлені – відштовхуються) з силою, величина якої визначається за формулою F=kI₁I₂∆ℓsinα/r (закон Ампера).
4. В Природі не існує обособлених магнітних зарядів.
5. При будь якій зміні того магнітного потоку що пронизує замкнутий струмопровідний контур, в цьому контурі виникає ЕРС індукції, величина якої залежить від швидкості зміни магнітного потоку: ℰ= –N(dФ/dt) (закон електромагнітної індукції).

До створення теорії Максвела, ці твердження розглядались як певні не пов’язані експериментальні факти, кожен з яких описує певну групу явищ. Іншими словами, ці твердження не утворювали цілісну систему знань. Напевно першим хто усвідомив глибинний зв’язок між вище сформульованими законами був Джеймс Максвел. Максвел зрозумів, що на базі цих законів та фарадеєвські ідеї про силові поля, можна не лише пояснити механізм електромагнітних взаємодій, а й створити цілісну наукову теорію, яка з єдиних позицій пояснить все різноманіття електричних, магнітних та електромагнітних явищ. Створюючи таку теорію, Максвел в 1860–1863 роках виконує наступний обсяг науково-теоретичних робіт:

1. Вводить в наукову практику систему фізичних величин, які певним чином характеризують електричні та магнітні поля.
2. Записує вище сформульовані закони електромагнетизму на мові введених ним фізичних величин.
3. На базі теоретичного аналізу нових формулювань законів електромагнетизму з’ясовує, що деякі положення цих законів є такими, що дублюють одне одного, а деякі – такими, що суперечать одне одному (такі суперечності були між тогочасним формулюванням закону Ампера та законом збереження заряду).
4. Гармонізує систему базових тверджень, та записує їх у вигляді системи рівнянь які прийнято називати рівняннями Максвела.
5. На основі аналізу рівнянь Максвела, пояснює механізм електромагнітних взаємодій та формулює велику кількість точних наукових передбачень.

Потрібно зауважити, що математична складова базових тверджень теорії Максвела досить складна. Тому ми лише стисло сформулюємо та проаналізуємо фізичну суть цих тверджень, а математичні формули запишемо в гранично спрощеному вигляді.

Основні твердження теорії Максвела.

1. Електричні заряди створюють внавколишньому просторі потенціальніелектричні (електростатичні) поля, параметри яких залежать від величини  того заряду що створює поле: q → E=ƒ(q)
2. Заряди що рухаються (електричні струми) створюють в навколишньомупросторі вихрові магнітні поля, параметрияких залежать як від величини відповідного заряду так і від швидкості його руху: (q,v) → B=ƒ(q,v).
3. Змінні магнітні поля створюють в навколишньому просторі вихрові,непотенціальні електричні (електродинамічні) поля, параметри якихзалежать від швидкості зміни первинного магнітного поля: B=ƒ(t) → E=ƒ(dB/dt).
4. Змінні електричні поля створюють в навколишньому просторі вихрові магнітні поля, параметри яких залежать відшвидкості зміни первинного електричногополя: E=ƒ(t) → B=ƒ(dE/dt).

      Е = ƒ(q)               B = ƒ(q,v)                B = ƒ(dE/dt)                 E = ƒ(dB/dt)

Мал.38. Фізична суть базових тверджень теорії Максвела.

Не важко бачити, що вище сформульовані закони, представляють собою систему взаємопов’язаних та взаємодоповнюючих тверджень, які утворюють цілісну систему знань. Виходячи з цих тверджень, Максвел не лише пояснив все різноманіття відомих електричних, магнітних та електромагнітних явищ, а й зробив велику кількість наукових передбачень. Про основні з яких ми поговоримо дещо пізніше. Наразі ж, зробимо декілька зауважень стосовно самих базових тверджень теорії Максвела.

Перш за все наголосимо, що ці твердження не є в точності еквівалентними тим математичним формулам, які називаються рівняннями Максвела. Ці твердження лише відображають загальну фізичну суть системи цих рівнянь. Втім, це зовсім не означає, що вище сформульовані твердження та їм відповідні спрощені рівняння є неправильними чи вульгарно примітивними. Мова йде лише про те, що вище наведені гранично спрощені формули не дозволяють розв’язувати конкретні задачі.

Зауважимо також, що перші три із вище сформульованих базових тверджень, по суті є певними формулюваннями відомих до Максвела базових законів: закону Кулона, закону Ампера та закону електромагнітної індукції (закону Фарадея). Просто Максвел сформулював та записав ці закони по новому, точніше – на мові параметрів електричних та магнітних полів. А потрібно зауважити, що один і той же закон можна сформулювати і записати по різному. Наприклад закон Кулона можна сформулювати так: сила взаємодії двох точкових, відносно нерухомих електричних зарядів q₁ і q₂, прямо пропорційна добутку цих зарядів і обернено пропорційна квадрату відстані між ними: F_ел = kq₁q₂/r². А можна так: на будь який заряд q, що знаходиться в електричному полі з напруженістю Е, діє сила, величина і напрям якої визначаються за формулою  F_ел = Eq. А можна і так: потік напруженості електричного поля через будь яку замкнуту поверхню, пропорційний величині того заряду який зосереджений в середині цієї поверхні і визначається за формулою:  Ф_Е=q/εε₀. Власне формулювання подібні до останнього (це формулювання називається теоремою Гауса) і є тими твердженнями та тими формулами які називаються рівняннями Максвела.

До Максвела, закон Кулона, закон Ампера та закон електромагнітної індукції, розглядалися як окремі не пов’язані один з одним закони, кожен з яких описує певну групу явищ. Коли ж ці закони Максвел записав на мові параметрів електричних і магнітних полів, то з’ясувалося, що ті твердження (закони) які раніше вважалися абсолютно автономними і не пов’язаними одне з одним, фактично є взаємопов’язаними та взаємодоповнюючими.

Більше того з’ясувалося, що система наявних базових тверджень (законів) є логічно незавершеною. Дійсно. Якщо у відповідності з законом електромагнітної індукції, змінні магнітні поля створюють в навколишньому просторі відповідні електричні поля, то логічно передбачити, що в Природі має існувати і зворотній процес. Процес, при якому змінні електричні поля створюють відповідні магнітні поля. Обгрунтованість такого твердження випливала не лише з логіки взаємопов’язаності природних явищ, а й з математичного аналізу закону Ампера та факту того, що в Природі не існує обособлених магнітних зарядів (полюсів).

Зважаючи на ці обставини, Максвел доповнив систему раніше відомих законів (закону Кулона, закону Ампера та закону електромагнітної індукції), твердженням про те, що змінні електричні поля створюють в навколишньому просторі вихрові магнітні поля, параметри яких залежать від швидкості зміни первинного електричного поля. Це твердження можна було б назвати законом Максвела. Однак, така назва не є офіційно прийнятою.

Таким чином, записавши відомі базові закони електромагнетизму на мові параметрів електричних та магнітних полів, і доповнивши ці закони науково обгрунтованим твердженням про те, що змінні електричні поля створюють відповідні магнітні поля, Максвел отримав систему взаємопов’язаних та взаємодоповнюючих тверджень, які і складають теоретичну основу динамічної теорії електромагнітного поля, а простіше кажучи – теорії Максвела.

На завершення додамо, що в деяких наукових джерелах, систему вище сформульованих базових тверджень, доповнюють ще одним: при будь яких процесах, що відбуваються в замкнутій системі, загальна кількість електричного заряду цієї системи залишається незмінною, тобто зберігається: ∑q_i = const (закон збереження електричного заряду). Загалом, таке доповнення має право на існуванні, і в багатьох випадках є незайвим. Однак, можна довести, що в системі рівнянь Максвела, закон збереження заряду є похідним, тобто таким, який випливає з чотирьох попередніх тверджень. А це означає, що в системі базових тверджень теорії Максвела, закон збереження заряду, строго кажучи є зайвим, а отже таким, окреме формулювання якого є недоречним.

Нагадаємо, теорія (наукова теорія) – це система достовірних знань, яка на основі певних базових тверджень, кількісно описує і пояснює певну групу споріднених явищ, та дозволяє робити точні кількісні передбачення. Із визначення ясно, що наукова теорія має не лише системно пояснювати відомі явища та минулі події, а й робити точні кількісні передбачення.

Важливість передбачувальних здібностей теорії важко переоцінити. Ці передбачення не лише розширюють наші уявлення про навколишній світ, а й фактично є єдиним способом з’ясування факту того, правильна дана теорія чи не правильна. Адже достовірність теорії визначається не авторитетністю її автора і навіть не тим, наскільки якісно вона пояснює відомі явища та минулі події. Достовірність чи недостовірність теорії, визначається лише фактом того, збуваються її передбачення чи не збуваються. А це означає, що та теорія яка не вміє робити точних кількісних передбачень, не має жодного шансу стати тим, що називають науковою теорією. І в цьому сенсі, максвелівська електродинаміка є неперевершеним взірцем блискучої наукової теорії. Теорії, передбачення якої кардинально змінили обличчя сучасної науки та життя цивілізованого людства.

На разі ми розглянемо лише ті передбачення теорії Максвела вивчення яких не виходять за межі програми загальноосвітньої школи і які є визначальними з точки зору розширення наших знань про навколишній світ. Перше з таких передбачень можна сформулювати наступним чином. В Природі не існує окремих електричних і окремих магнітних полів. В Природі існує єдине електромагнітне поле.

Дійсно. Вже факт того, що будь який рухомий заряд, з одного боку є джерелом електричного поля, а з іншого – джерелом магнітного поля, безумовно вказує на те, що електричні та магнітні поля є нерозривно пов’язаними. Або наприклад, постійний магніт. Яке поле він створює. З одного боку, відносно нерухомий спостерігач скаже, що магніт створює магнітне поле і не створює електричне. Не створює тому, що магніт є тілом електрично не зарядженим. З іншого ж боку, будь який рухомий спостерігач неодмінно з’ясує, що навколо магніту існує не лише магнітне поле, а й поле електричне (мал.39). Адже відносно рухомого спостерігача, те магнітне поле яке створюється постійним магнітом, є таким що змінюється. А це означає, що згідно з базовими твердженнями теорії Максвела, змінне магнітне поле створює відповідне електричне поле, що і зафіксує будь який рухомий спостерігач.

 

Мал.39. Магніт створює не лише магнітне поле, а й поле електричне. Електричний заряд створює не лише електричне поле, а й поле магнітне.

Таким чином, коли ми стверджуємо, що постійний магніт створює магнітне поле і не створює електричне, то маємо на увазі лише факт того, що будучи нерухомими відносно магніту, ми просто не помічаємо електричної складової того електромагнітного поля яке створює цей магніт. Адже будь який інший рухомий відносно магніту спостерігач, неминуче зафіксує що магніт створює не лише магнітне а й електричне поле. Аналогічне можна сказати і про ті поля які створюють електричні заряди, електричні струми, тощо.

На перший погляд, твердження про те, що електричні і магнітні поля, це різні прояви одного й того ж електромагнітного поля, не має суттєвого практичного значення. Однак, з точки зору розуміння суті тих подій що відбуваються в Природі, дане твердження є надзвичайно важливим. Адже воно фактично вказує на те, що все різноманіття відомих електричних, магнітних та електромагнітних явищ, це різні прояви одного і того ж багатогранного явища, яке відбувається у відповідності з одними і тими ж законами та пояснюється однією і тією ж науковою теорією.

Наступним важливим передбаченням теорії Максвела є твердження про те, що будь які коливання (будь які зміни швидкості руху) електричних зарядів, струмів чи магнітів, створюють певне енергетичне збурення електромагнітного поля, яке поширюється в просторі у вигляді відповідної електромагнітної хвилі. Дійсно. Згідно з теорією Максвела, будь яке коливання електричного заряду (електричного струму, магніту, тощо) неминуче спричиняє відповідне коливання електричної складової наявного електромагнітного поля, яке в свою чергу спричиняє коливання магнітної складової цього поля, а те – спричиняє коливання електричної складової поля і т.д. А це означає, що будь яка зміна швидкості руху електричного заряду магніту чи електричного струму, неминуче породжує певне збурення електромагнітного поля, яке з певною швидкістю поширюються простором у вигляді хвильового процесу, який прийнято називати електромагнітною хвилею.

Нагадаємо, хвилею називають процес поширення збурення матеріального середовища (речовини або поля), який супроводжується переносом енергії, але не супроводжується переносом самого середовища (частинки середовища або параметри поля, лише здійснюють певні гармонічні коливання).

Представити електромагнітну хвилю у вигляді відповідної наочної моделі практично не можливо. По суті, коли говорять про електромагнітну хвилю, то мають на увазі наступне. Електромагнітне поле, це особливий стан збуреного простору, який характеризується здатністю цього поля певним чином діяти на рухомі і нерухомі електричні заряди. Характеризуючи цю здатність говорять про дві взаємно перпендикулярні векторні величини: вектор напруженості електричного поля Е та вектор індукції магнітного поля В. Ці вектори взаємопов’язані таким чином, що будь яка зміна вектора Е автоматично призводить до відповідної зміни вектора В і навпаки. В такій  ситуації, будь яке збурення електромагнітного поля, спричиняє взаємопов’язані коливання векторів Е і В, які поширюються у вигляді певного хвильового процесу.

Електромагнітна хвиля, це таке енергетичне збурення електромагнітного поля, яке з певною швидкістю поширюється цим полем і яке характеризується періодичними коливаннями взаємопов’язаних векторів електричної напруженості Е та магнітної індукції В цього поля. Зазвичай, електромагнітну хвилю представляють у вигляді системи двох взаємно перпендикулярних синусоїд, одна з яких описує зміну вектора Е, а інша – зміну вектора В.

Мал.40. Умовне зображення електромагнітної хвилі.

Наступне надважливе передбачення теорії, яке випливало із рівнянь Максвела стверджувало: швидкість поширення електромагнітних хвиль визначається за формулою  v=1/√(εε₀μμ₀), де ε, μ – відповідно, електрична та магнітна проникливості того середовища в якому поширюється електромагнітна хвиля; ε₀, μ₀ – відповідно електрична та магнітна сталі  (ε₀ = 8,85·10^–12Кл²/Н·м²;  μ₀ = 12,56·10^–7Н/А²).

Із аналізу рівняння v=1/√(εε₀μμ₀) з усією очевидністю випливає ще один надважливий висновок: у вакуумі, електромагнітні хвилі поширюються з швидкістю 3·10⁸м/с і величина цієї швидкості за будь яких обставин залишається незмінною. Дійсно, для вакууму ε=1; μ=1, тому v=1/√(ε₀μ₀)=3·10⁸м/с=const=c.

Твердження про те, що у відповідності з теорією Максвела швидкість поширення електромагнітних хвиль є абсолютною, тобто такою яка не залежить ні від швидкості руху джерела хвиль, ні від швидкості руху спостерігача, перевернуло наші уявлення про навколишній світ і призвело до створення теорії відносності. Втім, про теорію відносності та її зв’язок з твердженням про абсолютність швидкості електромагнітних хвиль, ми поговоримо дещо пізніше. Наразі ж сформулюємо ще декілька важливих передбачень теорії Максвела.

На межі двох різних середовищ, електромагнітні хвилі можуть як відбиватись так і заломлюватись. При цьому, якщо напрям поширення електромагнітної хвилі охарактеризувати відповідним променем, то можна стверджувати.

Закон відбивання електромагнітних хвиль: на межі двох різних середовищ електромагнітні хвилі відбиваються, при цьому: 1) проміннь падаючий, промінь відбитий і перпендикуляр до поверхні в точці падіння променя, лежать в одній площині; 2) кут відбивання променя (β) дорівнює куту його подіння (α): ˂β = ˂α.

Закон заломлення електромагнітних хвиль: на межі двох різних середовищ, електромагнітні хвилі заломлюються, тобто проникаючи в нове середовище змінюють напрям свого розповсюдження. При цьому: 1) промінь падаючий, промінь заломлений та перпиндикуляр до поверхні в точці падіння променя, лежать в одній площині; 2) відношення синуса кута падіння променя (sinα) до синусу кута його заломлення (sinγ) для даної пари середовищ є постійною величиною, значення якої визначається відношенням швидкостей хвиль у відповідних середовищах:  sinα/sinγ = v₁/v₂.

     

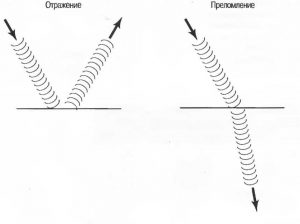
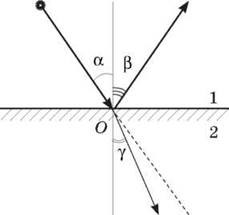
Мал.41. На межі двох різних середовищ електромагнітні хвилі можуть як відбиватись так і заломлюватись.

Теорія Максвела передбачала і те, що електромагнітні хвилі створюють певний силовий тиск на перешкоди. Дійсно. Електромагнітна хвиля представляє собою взаємопов’язані коливання векторів напруженості електричного Е та індукції магнітного В полів (мал.42). В такій ситуації, збоку електричної складової хвилі, на кожну заряджену частинку перешкоди діє певна електрична сила (F_ел=q₀E) яка змушує цю частинку рухатись вздовж напрямку вектора Е. При цьому, вже на рухому частинку, збоку магнітної складової хвилі діятиме магнітна сила Лоренца (F_л=Bq₀vsinα) напрям якої співпадає з напрямком поширення хвилі. А це означає, що при взаємодії з перешкодою, електромагнітна хвиля створює певний силовий тиск на цю перешкоду.

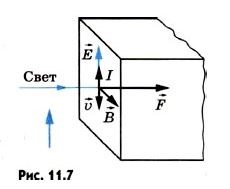
Мал.42.  Електромагнітна хвиля створює певний тиск на перешкоду.

Розуміючи суть того що називають електромагнітною хвилею, не важко зробити ще одне передбачення: електромагнітні хвилі, це хвилі поперечні. Дійсно. Електромагнітна хвиля представляє собою коливання взаємопов’язаних векторів Е і В. При цьому, ці вектори розташовані в площині яка перпендикулярна (поперечна) напрямку поширення хвилі. А це і означає, що електромагнітна хвиля є поперечною.

Важливим передбаченням теорії Максвела було твердження про те, що світло є однією з різновидностей електромагнітних хвиль. Дійсно, факти того, що швидкості поширення світлових та електромагнітних хвиль є однаковими, що закони відбивання та заломлення світлових і електромагнітних хвиль є тотожними, що світлові та електромагнітні хвилі є хвилями поперечними і що ці хвилі спричиняють аналогічні тиски на перешкоди, безумовно вказували на те, що світло є однією з різновидностей електромагнітних хвиль. А це означає, що після створення теорії Максвела, оптика – наука про світло, фактично стала частиною електродинаміки – науки про електричні та магнітні явища.

Варто зауважимо, що до створення теорії Максвела, ніхто навіть не підозрював, що світло має бодай якесь відношення до електрики чи магнетизму. Коли ж теорія була створена, то з’ясувалося, що світло є результатом тих електромагнітних процесів які відбуваються на Сонці, в спіралі лампочки розжарювання, в полум’ї свічки, тощо.

Вище згадані передбачення, це далеко не повний перелік тих відкриттів які зробила і продовжує робити теорія Максвела. Говорячи про передбачувальні здібності цієї теорії, німецький фізик Генріх Герц (1857–1894) писав: «Вивчаючи цю дивовижну теорію, з часом починаєш розуміти, що її математичні формули наділені власним розумом та живуть власним життям. Здається, що ці формули розумніші за нас з вами, розумніші навіть за самого автора. Здається ніби ці формули дають нам більше, а ніж в свій час було в них закладено».

І потрібно сказати, що в словах Герца нема жодного перебільшення. Починаючи роботу над створенням своєї теорії, Максвел навіть не здогадувався, що вона стане основою всієї сучасної науки, починаючи від механіки та молекулярної фізики і закінчуючи оптикою та теорією відносності. Адже все до чого прагнув великий Максвел, так це пояснити механізм електричних і магнітних взаємодій. Однак, після того як визначальні ідеї теорії поля були записані у формі відповідних математичних рівнянь, з’ясувалося що аналіз цих рівнянь дозволяє пояснити не лише відомі та невідомі електромагнітні явища, а й широкий спектр оптичних, теплових, хімічних, механічних та інших явищ, які до того ніколи не вважались електромагнітними.

До речі, саме Генріх Герц в 1888 році експериментально довів, що електромагнітні хвилі дійсно існують, і що їх властивості саме такі, як передбачала теорія Максвела. А це означає, що в 1888 році, тобто через 25 років після створення теорії Максвела, ця теорія набула статусу експериментально доведеної наукової теорії. Власне  з цього ж року починається й історія практичного застосування штучно створених електромагнітних хвиль. Адже по суті Генріх Герц створив перший радіопередавач (іскровий генератор Герца) і перший радіоприймач (резонатор Герца) та застосував цю систему для передачі інформації за допомогою електромагнітних хвиль. Інша справа, що дану систему Герц застосував не для передачі побутової інформації, а для наукових досліджень.

Контрольні запитання.

1. Сформулюйте ті базові закони які були відомі до створення теорії Максвела?
2. Чому ці твердження не утворювали цілісну систему знань?
3. Яке з базових тверджень теорії Максвела є похідним від закону електромагнітної індукції?
4. Як ви думаєте, яке з математичних формулювань закону Кулона F_ел = kq₁q₂/r² чи F_ел = Eq є більш інформативним? Чому?
5. Чому Максвел вирішив, що система відомих до нього базових законів електромагнетизму є неповною.
6. Чому в системі базових тверджень теорії Максвела відсутнє формулювання закону збереження заряду?
7. Чому здатність робити точні кількісні передбачення, є визначальною ознакою будь якої наукової теорії?
8. Чому ми стверджуємо, що навколо постійного магніту існує не лише магнітне, а й електричне поле?
9. Поясніть, яким чином переміщення магніту створює електромагнітну хвилю?
10. Доведіть, що швидкість поширення електромагнітних хвиль у вакуумі становить 3·10⁸м/с.
11. Які факти вказують на те, що світло є однією з різновидностей електромагнітних хвиль?
12. Поясніть яким чином електромагнітна хвиля тисне на перешкоду.
13. Чому електромагнітні хвилі є поперечними, а звукові – поздовжніми?

.

Лекційне заняття №8.

Тема: Система радіозв’язку. 

Системою радіозв’язку називають сукупність взаємопов’язаних радіопередавальних та радіоприймальних приладів, які забезпечують передачу інформації за допомогою електромагнітних хвиль. Існує багато різновидностей сучасних систем радіозв’язку. Такі системи забезпечують не лише радіо, телевізійний, мобільний та інтернет зв’язок, а й різноманітні види  радіолокації, радіонавігації, радіоуправління, тощо. Різні системи радіозв’язку мають певні особливості. Однак загальна структура, та загальний принцип дії будь якої з цих систем є однаковими. Цю структуру та цей принцип дії ми розглянемо на прикладі тієї системи радіозв’язку, яка забезпечує передачу звукової інформації. Головними складовими такої системи є радіопередавач та радіоприймач.

Радіопередавач, це прилад, який генерує певний високочастотний струм, зашифровує в цьому струмі корисну інформацію та перетворює його в потік відповідних електромагнітних хвиль. Основними елементами радіопередавача є генератор високочастотних коливань (ГВЧ), модулятор, радіопередавальна антена та підсилювачі сигналів.

Радіопередавач виконує три базові функції: 1 – створює струм певної високої частоти (цю функцію виконує генератор високочастотних коливань); 2 – «зашифровує» в цьому струмі корисну інформацію (цю функцію виконує модулятор); 3 – перетворює зашифрований високочастотний струм у відповідні електромагнітні хвилі (цю функцію виконує радіопередавальна антена). Структурна схема радіопередавача представлена на мал.43.

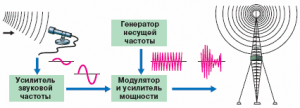
Мал.43. Структурна схема радіопередавача.

Ви можете запитати: а чому радіопередавач не генерує такі електромагнітні хвилі які напряму несуть звукову інформацію, тобто хвилі частотні параметри яких знаходяться в межах від 20Гц до 20кГц? Відповідаючи на це запитання можна сказати наступне. По перше, якби радіопередавач генерував хвилі аналогічні звуковим і те ж саме робили інші радіопередавачі, то кожен радіоприймач сприймав би та відтворював ту суміш звуків які одночасно генеруються всією сукупністю радіопередавачів. По друге, радіоприймачу для сприйняття тих електромагнітних хвиль які відповідають частотним параметрам усередненого голосу людини (ν≈250Гц) знадобилась би антена довжиною понад 300км. По третє, енергія електромагнітної хвилі пропорційна частоті її коливань. При цьому дальність поширення тих хвиль, частотні параметри яких відповідають частоті людського голосу, навряд чи перевищує декілька кілометрів.

Зважаючи на вище сказане, в реальних системах радіозв’язку використовують хвилі високої частоти (ν>200 000Гц). Такі хвилі створюють відповідні високочастотні струми, джерелом яких є генератори високочастотних електромагнітних коливань (ГВЧ). Про будову та принцип дії генератора високочастотних електромагнітних коливань (ГВЧ), ви вже знаєте. Тому просто зауважимо, що кожний радіопередавач працює на своїй наперед визначеній частоті і що тому, його ГВЧ генерує струм певної частоти та певної незмінної амплітуди коливань.

Сам по собі такий струм ще не несе корисної інформації. Але таку інформацію в цьому струмі можна зашифрувати. Найпростіший спосіб шифрування полягає в тому, що за допомогою механічного вимикача (ключа) неперервний високочастотний струм, перетворюють в певний набір коротких («крапка») та довгих («тире») сигналів. Власне такий спосіб шифрування і був реалізований в перших системах радіозв’язку.

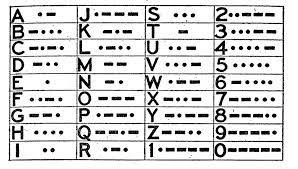
Мал.44. В перших системах радіозв’язку, передача інформації здійснювалася за допомогою умовних знаків: «крапка», «тире».

Ясно, що подібне шифрування не дозволяє передавати живу мову, музику, візуальне зображення, тощо. Тому в сучасній радіотехніці застосовують більш досконалі методи шифрування, зокрема так званий метод амплітудної модуляції. Суть цього методу полягає в тому, що амплітуда коливань високочастотного струму змінюється у відповідності з параметрами корисної інформації (параметрами звуку, зображення, тощо)

Зазвичай, ту частину радіопередавача яка забезпечує «шифрування» корисної інформації називають модулятором. Основним елементом звукового модулятора є мікрофон – прилад, який перетворює механічні звукові коливання повітря або іншого середовища у відповідні коливання того чи іншого електричного параметру (електричного опору, сили струму, напруги, електричної ємності, тощо). Мікрофони бувають різними: порошковими, електродинамічними, конденсаторними, п’єзоелектричними та іншими. Вони можуть мати різну будову та різні принципи дії. Однак загальне призначення будь якого мікрофона залишається незмінним і полягає в тому, щоб перетворити звукові коливання середовища у відповідні коливання певного електричного параметру.

Будучи включеним в систему радіопередавача, мікрофон сприяє тому, що коливання амплітуди високочастотного струму в точності повторюють коливання тієї звукової хвилі яку сприймає мікрофон.

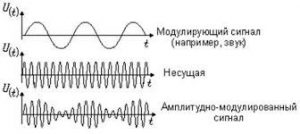
Мал.45. При амплітудній модуляції, амплітуда високочастотних коливань змінюється у відповідності з параметрами корисної інформації.

Зважаючи на вище сказане, принцип дії радіопередавача можна представити у вигляді наступної послідовності подій. Генератор високочастотних електромагнітних коливань (ГВЧ), створює високочастотний струм постійної амплітуди коливань. В модуляторі, амплітуда коливань цього струму стає такою, що в точності повторює ті звукові коливання які надходять в мікрофон модулятора. Цей модульований високочастотний струм надходить в антену радіопередавача де перетворюється на відповідні електромагнітні хвилі (тілом антени тече високочастотний модульований струм, який створює відповідні електромагнітні хвилі). Іншими словами, принциповий устрій радіопередавача можна представити у вигляді наступної структурної схеми.

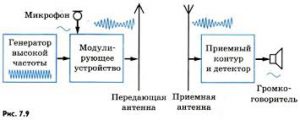
Мал.46. Загальна схема системи радіозв’язку.

Радіоприймач – це прилад, який із всього різноманіття електромагнітних хвиль, обирає хвилі потрібної частоти (потрібної радіостанції), перетворює енергію цих хвиль у відповідний високочастотний струм, виділяє зашифровану в цьому струмі інформаційну складову та перетворює її у відповідну інформацію. Реалізацію зазначених у визначенні функцій, забезпечує наступна принципова схема радіоприймача.

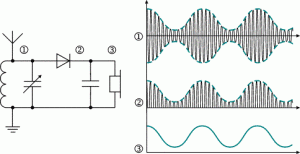
Мал.47.  Принципова схема радіоприймача.

Пояснюючи будову та принцип дії радіо приймального приладу можна сказати наступне. Антена радіоприймача сприймає хвилі багатьох одночасно працюючих радіостанцій. Для того щоб із всього різноманіття цих хвиль вибрати хвилі потрібної радіостанції (потрібної частоти) в коло антени включають коливальний контур, частотні параметри якого ν=1/2π√(LC) можна змінювати. Змінюючи електричну ємність (С) або індуктивність (L) цього контура, досягають того, що частота системи антена-коливальний контур ν_кк співпадає з частотою хвиль потрібної радіостанції ν_рс. При цьому, в результаті електромагнітного резонансу, хвилі потрібної радіостанції індуцирують в антені відповідний модульований високочастотний струм. Струм, в якому міститься звукова інформації.

Нагадаємо, Резонанс це явище, суть якого полягає в тому, що при співпадінні частоти коливань зовнішніх силових (енергетичних) впливів (ν_зовн), з власною частотою (ν_вл) тієї коливальної системи на яку ці впливи спрямовані, відбувається розгойдування коливальної системи, тобто відносно швидке збільшення амплітуди її коливань. Іншими словами: якщо ν_зовн=ν_вл, то резонанс (розгойдування системи, підсилення коливань).

Оскільки модульований високочастотний струм є симетричним (мал.47.1), а отже таким результуюча інформаційна дія якого є нульовою, то в першу чергу потрібно позбутися симетричної складової цього струму. З цією метою, на шляху високочастотного модульованого струму ставлять напівпровідниковий діод (детектор), який маючи односторонню провідність, відтинає поперечно симетричну частину струму (мал.47.2).

В подальшому, радіоприймач має відділити високочастотну складову струму від його інформаційної, низькочастотної складової та перетворити останню у відповідний звуковий сигнал. Це завдання вирішується наступним чином. За детектором знаходиться електричне розгалуження, в одній частині якого міститься так званий фільтруючий конденсатор, в іншій – котушка індуктивності, яка є струмопровідною частиною динаміка (динамічного гучномовця).

Принцип дії такого розгалуження очевидно простий. Конденсатор має певний ємнісний опір, величина якого обернено пропорційна частоті струму: R_C=1/2πνC. А це означає, що для високочастотної складової струму, опір конденсатора є гранично малим, а для низькочастотної – гранично великим. Опір же котушки індуктивності, навпаки – прямо пропорційний частоті струму (R_L=2πνL) і тому для високочастотної складової струму, цей опір є гранично великим, а для його низькочастотної складової – гранично малим. Ясно, що в такій ситуації, високочастотна складова струму буде проходити через коло конденсатора, а низькочастотна, інформаційна складова (мал.47.3) – через коло динаміка, де і перетворюється на відповідний звуковий сигнал.

Не важко бачити, що у вище описаному радіоприймальному приладі відсутнє джерело енергії. А це означає що ті процеси які відбуваються в цьому приладі, відбуваються лише за рахунок енергії тієї радіохвилі яку сприймає його антена. А оскільки величина цієї енергії є мізерно малою (адже антена радіоприймача сприймає лише ту мізерну частину генерованої передавачем енергії яка припадає на площу поверхні цієї антени), то ясно, що відповідний прилад не може забезпечити якісного та достатньо гучного мовлення. Тому будова реального радіоприймача є суттєво складнішою. Складнішою головним чином за рахунок того, що до його складу входять підсилювачі високої та низької частоти. До речі, подібна ситуація є характерною і для радіо передавального пристрою в реальній схемі якого присутні підсилювачі як низької так і високої частот.

Мал.48. Структурна схема реального радіоприймача.

Модульовані радіохвилі дозволяють передавати не лише звукову інформацію, а й інформацію візуальну. Таку інформацію передають за допомогою тієї різновидності радіозв’язку яку називають телевізійним зв’язком. В загальних рисах механізм телевізійного зв’язку мало чим відрізняється від механізму того радіозв’язку який забезпечує передачу звукової інформації. Щоправда, технічна та технологічна складові системи телевізійного зв’язку значно складніші за відповідні складові звукового радіозв’язку.

Ми не будемо заглиблюватись в деталі того, яким чином візуальне зображення перетворюється на відповідний набір електромагнітних сигналів і навпаки. Зауважимо тільки, що передачу та відтворення кольорового зображення здійснюють шляхом накладання трьох взаємопов’язаних кольорових картинок: червоної, зеленої та синьої. А це означає, що для передачі кольорового зображення потрібна система трьох взаємопов’язаних модульованих електромагнітних хвиль. Крім цього, телевізійна картинка супроводжується відповідним звуковим сигналом, для передачі якого потрібна ще одна модульована електромагнітна хвиля. Додайте до цього факт того, що телевізійний сигнал є таким, в якому за кожну секунду передається інформація про 25 нерухомих взаємопов’язаних світлин (кадрів) і ви зрозумієте наскільки технічно та технологічно складною є система телевізійного зв’язку. Однак, якщо говорити про принциповий устрій цієї системи, то він практично не відрізняється від устрою звукового радіозв’язку:

1. Телевізійний передавач, генерує високочастотний струм, зашифровує в ньому відео інформацію та перетворює цей модульований високочастотний струм у відповідні електромагнітні хвилі.
2. Телевізійний радіоприймач (телевізор), сприймає ці хвилі, перетворює їх у відповідний високочастотний струм, виділяє з цього струму інформаційну складову та перетворює її на відповідне зображення.

Різноманіття систем радіозв’язку не обмежується тими системами які забезпечують передачу звукової та візуальної інформації (радіозв’язок, телевізійний зв’язок, мобільний зв’язок, інтернет зв’язок, тощо). Важливими різновидностями систем радіозв’язку є ті системи які забезпечують дистанційне управління різноманітними технічними приладами та технологічними процесами. Скажімо, коли за допомогою дистанційного пульту управління ви вмикаєте і вимикаєте телевізор, обираєте потрібний телевізійний канал, регулюєте звук, тощо – то застосовуєте відповідну систему радіозв’язку.

До числа систем радіозв’язку, цілком обгрунтовано можна віднести і ті системи які на основі випромінювання та реєстрації певних імпульсів електромагнітних хвиль дозволяють отримувати певну інформацію про навколишній світ. Прикладом таких інформаційних радіосистем є різноманітні радіолокаційні та радіонавігаційні системи.

Системою радіолокації (від лат. radio – випромінювати та location – розташування) називають сукупність радіотехнічних засобів, які дозволяють визначати розташування та параметри руху стороннього, віддаленого об’єкту, шляхом його опромінювання імпульсами високочастотних електромагнітних хвиль. Принцип дії радіолокаційної системи (радіолокатори, радари, тощо) полягає в наступному. Радіопередавальна частина радіолокатора з певною періодичністю випромінює короткотривалі імпульси високочастотних електромагнітних хвиль. Ці хвильові імпульси відбиваються від об’єкту спостережень та повертаються до антени радіолокатора. Аналізуючи ті проміжки часу які відділяють момент випромінювання електромагнітного імпульсу та момент його повернення, визначають відстань до об’єкту спостережень, його швидкість, напрям руху, тощо.

Мал.49. Загальний устрій системи радіолокації.

Системою радіонавігації (від лат radio – випромінювати та  navigation –  керувати човном) називають сукупність радіотехнічних засобів, які дозволяють визначати координати та параметри руху даного тіла (приладу) на основі обміну електромагнітними імпульсами з іншими тілами. Принцип дії сучасної радіонавігаційної системи (системи глобального позиціювання GPS), полягає в наступному. Певна, достатньо велика кількість (зазвичай 24) штучних супутників Землі, з певною періодичністю та певними орбітами обертаються навколо Землі. При цьому кожний супутник, постійно випромінює імпульси високочастотних електромагнітних хвиль, які містять інформацію про номер супутника, про його координати та час надсилання імпульсу. Ці інформаційні імпульси фіксує спеціальний радіоприймач (GPS – навігатор) який на основі аналізу отриманої інформації визначає координати тіла, параметри його руху тощо.

Мал.50. Загальний устрій сучасної системи радіонавігації.

Говорячи про сучасні системи радіозв’язку, потрібно мати на увазі, що ці системи динамічно розвиваються і що тому їх окремі конструктивні та технологічні деталі можуть так чи інакше змінюватись. Скажімо, в сучасних системах радіозв’язку на ряду з амплітудною модуляцією сигналів, широко застосовують й інші методи кодування сигналів, зокрема метод частотної модуляції, імпульсної модуляції, фазової модуляції, кутової модуляції, тощо.

Загалом же розрізняють два базові види модуляції: аналогова та цифрова. При аналоговій модуляції, інформаційний сигнал накладається на високочастотні (несучі) коливання таким чином, що певні параметри цих коливань (амплітуда, фаза, частота, тощо) змінюються у повній відповідності (аналогічно) з інформаційним сигналом. Наприклад, представлена на мал.45 амплітудна модуляція є аналоговою.

При цифровій модуляції, інформаційний сигнал представляється у вигляді певного набору двох цифр 0 і 1. При цьому, в процесі модуляції параметри високочастотних коливань (їх амплітуда, частота, фаза, тощо), через певні однакові проміжки часу, дискретно змінюються у відповідності з інформаційним набором цифр 0; 1. Наприклад, на мал.51 представлені три різновидності цифрової модуляції: амплітудна, частотна та фазова.

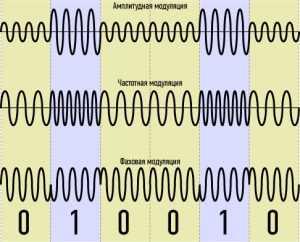
Мал.51. Приклади цифрової модуляції інформаційного сигналу.

Аналогова модуляція має той недолік, що в процесі поширення електромагнітна хвиля неминуче зазнає певних сторонніх впливів і тому до радіоприймача доходить в тій чи іншій мірі спотвореною. А це означає, що аналогова система модуляції не може гарантувати високу якість радіозв’язку. І в цьому сенсі цифрова модуляція має безумовні переваги. Адже спотворити сигнал «0» настільки, щоб він став «1» чи навпаки, практично не можливо.

Та як би там не було і які б технологічні новації не запроваджувалися, а принциповий устрій систем радіозв’язку залишається незмінним:

– радіопередавач, генерує високочастотний струм, зашифровує в ньому корисну інформацію та перетворює цей зашифрований високочастотний струм у відповідні електромагнітні хвилі;

–  радіоприймач, сприймає ці хвилі, перетворює їх на відповідний високочастотний струм, виділяє з цього струму інформаційну складову та перетворює її на відповідну інформацію.

Контрольні запитання.

1. Назвіть основні складові будь якої системи радіозв’язку.
2. Які базові функції виконує радіопередавач?
3. Поясніть суть методу амплітудної модуляції.
4. Які базові функції виконує радіоприймач?
5. Поясніть, яким чином із всього різноманіття електромагнітних хвиль, радіоприймач обирає хвилі потрібної радіостанції.
6. Поясніть суть того, що називають резонансом.
7. Поясніть, яким чином в радіоприймачі високочастотну складову струму відділяють від низькочастотної, інформаційної складової.
8. Поясніть принцип дії системи радіолокації.
9. Поясніть принцип дії GPS навігації.
10. Поясніть суть методу цифрової модуляції.
11. Які переваги цифрової модуляції над аналоговою модуляцією.

.

Лекційне заняття №9.

Тема: Електродинаміка, узагальнююче повторення. Розв’язування задач.

Не втомлюємося наголошувати на тому, що фізика така всеосяжна наука і навчальна дисципліна, яку практично не можливо вивчити інакше, як тільки у вигляді цілісної системи знань. А одним з основних елементів цієї системи знань є узагальнюючі повторення. Власне якщо фізику вивчати не як набір певних обособлених фактів, формул, законів, явищ та приладів, а як цілісну систему знань, то неминуче з’ясовується, що не така вже й складна ця сама фізика. Що навіть той її найбільший і можливо найскладніший розділ який називається «Електродинаміка» в реальності не такий вже й складний, не такий вже й незрозумілий і не таки й вже нецікавий.

Електростатика.

Основні поняття	Основні величини	Основні закони	Основні прилади
Електричний заряд Електричне поле, Лінії напруженості ел.поля	Ел. заряд q = ±Ne   (Кл) Напруженість ел. поля Е = Fел/qп   (Н/Кл) Потенціал ел. поля φ = А1→∞/qп    (В) Ел. напруга U = Aел/q        (В) Ел.  ємність С = q/U           (Ф)	Закон збереження заряду ∑qдо = ∑qпісля Закон Кулона Fел = kq1q2/r2, де k=1/4πεε0 або Fел = Eq Принцип суперпозиції Ерез=∑Еі	Конденсатор С=q/U C=εε0S/d Wел=CU2/2

Задача 1. Скільки електронів має втратити тіло, щоб набути заряд 1Кл?

Дано:

q = 1Кл

N = ?

Рішення.     Оскільки за визначенням q = Ne, де e = 1,6∙1^–19Кл, то

N = q/e = 1/1,6∙10^–19Кл = 6,25∙10¹⁸електронів.

Відповідь: для того щоб тіло набуло заряд в 1Кл, воно має втратити 6,25∙10¹⁸ електронів.

Задача 2. У повітрі на шовковій нитці висить нерухома заряджена кулька масою 5г і зарядом 5∙10^–7Кл. Визначити силу натягу нитки, якщо під кулькою на відстані 10см розташована інша кулька з таким же за знаком зарядом 4∙10^–8Кл.

Дано:

m = 5г = 5·10^–3кг

q₁ = 5·10^–7Kл

r =10см = 0,1м

q₂ = 4·10^–8Kл

T = ?

Рішення. Виконуємо малюнок на якому вказуємо всі діючі на дане тіло сили. А цими силами є: 1) сила тяжіння F_т=mg= 5·10^–3кг·9,8м/с² = 49·10^–3Н;

2) направлена вертикально вгору сила електричної взаємодії однойменних зарядів F_ел=kq₁q₂/r² = 9·10⁹·5·10^–7·4·10^–8/(0,1)² = 180·10^–4 = 18·10^–3Н;

3) сила натягу нитки Т = ?

Із умови рівноваги тіла ∑F_y = T + F_ел – F_т = 0, випливає

T = F_т – F_ел = 49·10^–3Н – 18·10^–3Н = 31·10^–3Н = 0,031 Н

Відповідь: Т = 0,031 Н = 31мН.

Задача 3. Якого радіусу має бути струмопровідна куля, щоб її електрична ємність у вакуумі (ε=1) дорівнювала одній фараді?

Дано:

С = 1Ф

ε = 1

R = ?

Рішення. Оскільки для кулі С=4πεε₀R, де ε₀=8,85∙10^–12Ф/м, то R=C/4πεε₀.

Розрахунки: R = 1Ф/4∙3,14∙8,85∙10^–12(Ф/м) = 9∙10⁹м.

Електродинаміка постійних струмів.

Основні поняття	Основні величини	Основні закони	Основні прилади
Електричний струм Провідник Електричне коло	Сила струму I=q/t          (A) Електрична напруга U=Aел/q      (В) Електричний опір R=U/q      (Ом) ЕРС джерела струму ℰ =Аст/q     (В) Робота струму Аел=U∙I∙t    (Дж) Потужність струму Рел=U∙I      (Вт)	Закон Ома: а) для ділянки кола    I=U/R, б) для повного кола   I=Ɛ/(R+r). Перший закон Кірхгофа: ∑Iвх=∑Iвих Другий закон Кірхгофа: ℰ=∑Ui Закон Джоуля- Лєнца: Q=I2Rt	Резистор R=U/I R=ρℓ/S Послідовне: R12=R1+R2 Паралельне: R12=R1∙R2/(R1+R2) Джерело струму ℰ=Aст/q ℰ=Umax

Задача 4. Сила струму в лампочці розжарювання 0,5А. Який заряд і скільки електронів проходить через поперечний переріз спіралі лампочки за 10хв її роботи?

Дано:

I = 0,5A

t = 10хв = 600с

q = ?  N = ?

Рішення. Оскільки І = q/t, то q = It = 0,5А∙600с = 300Кл. Оскільки q = Ne, де е = 1,6·10^–19Кл, то N = q/e = 300Кл/1,6·10^–19Кл = 187,5·10¹⁹ електронів.

Відповідь: N = 187,5·10¹⁹ електронів.

Задача 5. Виходячи з того, що в системі зображених на малюнку резисторів, їх електричні опори однакові і дорівнюють 6(Ом), визначити загальний опір системи.

Рішення. Застосовуючи метод еквівалентних схем, можна записати:

R₄ і R₅ з’єднані паралельно і тому R₄₅ = R₄∙R₅/(R₄+R₅) = 6∙6/(6+6) = 3(Ом),

R₃ і R₄₅ з’єднані послідовно і тому R₃₄₅ = R₃+R₄₅ = 3+6 = 9(Ом),

R₂ і R₃₄₅ з’єднані паралельно і тому R₂₃₄₅ = R₂∙R₃₄₅/(R₂+R₃₄₅) = 6∙9/(6+9) = 3,6(Ом),

R₁, R₂₃₄₅ і R₆ з’єднані послідовно і тому R_заг = R₁+R₂₃₄₅+R₆ = 6+3,6+6 = 15,6(Ом).

Відповідь: R_заг = 15,6(Ом).

Задача 6. Визначити силу струму на кожній ділянці електричного кола, якщо R₁=3(Ом), R₂=4(Ом), R₃=6(Ом), R₄=4,6(Ом). Напруга між точками А і В U_заг=10В.

Дано:

R₁=3(Ом)

R₃=4(Ом)

R₂=6(Ом)

R₄=4,6(Ом)

U_заг =10(В)

I₁, I₂, I₃, I₄ – ?

Рішення. Подібні задачі розв’язуються в два етапи:

1) Визначається загальна сила струму в колі. Згідно з законом Ома  I_заг=U_заг/R_заг, де R_заг=?  Застосовуючи метод еквівалентних схем, можна записати: R₂₃ = R₂∙R₃/(R₂+R₃) = 4∙6/(4+6) = 2,4(Ом), R_заг = R₁+R₂₃+R₄ = 3+2,4+4,6 = 10(Ом). Таким чином I_заг=U_заг/R_заг = 10(В)/10(Ом) = 1,0(А).

2) Визначається сила струму на кожній ділянці кола I₁, I₂, I₃, I₄ – ?

Оскільки для тих ділянок кола де відсутні його розгалуження, величини відповідних струмів дорівнюють І_заг, то можна стверджувати: І₁ = І₄ = І_заг = 1,0(А).

І₂ = U₂/R₂   де  U₂ = ?

І₃ = U₃/R₃ , де  U₃ = ?

Знаю: U₂ = U₃ = U₂₃ , де U₂₃ = I₂₃∙R₂₃ = I_заг∙R₂₃ = 1,0(А)∙2,4(Ом) = 2,4(В),

І₂ = U₂/R₂ =  2,4(В)/4(Ом)= 0,6(А),

І₃ = U₃/R₃ = 2,4(В)/6(Ом) = 0,4(А).

Перевірка: І₂ + І₃ = 0,6(А) + 0,4(А) = 1,0(А).

Відповідь: І₁ = 1,0(А), І₂ = 0,6(А), І₃ = 0,4(А), І₄ = 1,0(А).

Задача 7.  Скільки часу триватиме нагрівання 1,5л води від 20ºС до закипання, в електричному чайнику потужністю 900Вт, якщо ККД процесу 80%?

Дано:

V = 1,5л

t_п = 20ºС

t_к = 100ºС

N = 900Вт

η = 80%

t =?

Рішення. За визначенням η=(А_кор/А_заг)100%. В умовах нашої задачі А_кор= Q_н = cm∆t, де с=4200(Дж/кг·ºС); m=ρV=1,5кг: ∆t=100ºC–20ºC=80ºC. А_заг=А_ел. Оскільки N=А_ел/t, то A_ел=Nt. Таким чином η=cm∆t100%/Nt, звідси t=cm∆t100%/Nη.

Розрахунки: t=cm∆t100%/Nη = 4200·1,5·80·100/900·80 = 4200·1,5/9 = 700с = 11,7хв.

Відповідь: t = 700с =11,7хв.

Електродинаміка магнітних явищ.

Основні поняття	Основні величини	Основні закони	Основні прилади
Електричний струм Магнітне поле; Лінії індукції магнітного поля	Сила струму I = q/t    (A) Магнітна індукція В = Fм/І∆ℓsinα (Тл) Магнітний потік Ф = ВScosβ  (Вб) Індуктивність L = Ф/І    (Гн)	Закон Ампера Fм=kI1I2∆ℓsinα/r де k=μμ0/2π або Fм=ВІ∆ℓsinα Принцип суперпозиції Врез=∑Ві	Котушка індуктивності L = Ф/І L = μμ0N2S/ℓ Wмаг= LI2/2

Задача 8.  Магнітна стрілка повернута до котушки індуктивності так, як показано на мал.(а). Визначте на якій клемі котушки знак плюс, а на якій мінус.

а)б)

Рішення. Оскільки різнойменні магнітні полюси притягуються, а однойменні відштовхуються, то із аналізу малюнку ясно, що збоку південного полюса (S) магнітної стрілки, має знаходитись північний (N) полюс котушки індуктивності. А для котушки з струмом розташування цих полюсів визначається за правилом зігнутої кісті правої руки. Для даного ж випадку це правило стверджує. Якщо зігнуту кість правої руки (дивись мал.б) розташувати так, щоб чотири зігнутих пальці вказували напрям струму в котушці, то відігнутий на 90° великий палець руки вкаже напрям на північний полюс котушки.

Зважаючи на вище сказане, та враховуючи що місцезнаходження північного полюса котушки є відомим (північний полюс котушки там де південний полюс магнітної стрілки), визначаємо напрям струму в провіднику: струм тече від точки В (+) до точки А (–).

Відповідь: в точці В (+), в точці А (–).

Задача 9. Сила струму в горизонтально розташованому провіднику 5А, його довжина 20см, а маса 10г. В полі з якою магнітною індукцією має знаходитись провідник, щоб діюча на нього сила Ампера зрівноважувала силу тяжіння?

Дано:

І = 5А

ℓ = 20см = 0,2м

m = 10г = 0,01кг

F_A = F_Т

В = ?

Рішення. Виконуємо малюнок на якому вказуємо діючі на провідник сили. А цими силами є: сила тяжіння F_T = mg та сила Ампера F_A = BIℓsinα, де α=90° і тому sinα=1. Оскільки за умовою задачі F_A = F_Т, то BIℓ = mg, звідси В = mg/Іℓ.

Розрахунки. В = mg/Іℓ = 0,01кг∙9,8(м/с²) / 5А∙0,2м = 0,98 (Н/А∙м = Тл).

Відповідь: В = 0,98Тл.

Задача 10. α-частинка (m₀ = 4а.о.м.; q₀ = +2е) з швидкістю 10⁶м/с влітає в однорідне магнітне поле, під кутом 90° до ліній його індукції. Визначити радіус того кола яку описуватиме частинка в процесі свого руху, якщо індукція магнітного поля 0,2Тл.

Дано:

m₀ = 4а.о.м. = 4∙1,66∙10^{– 27}кг

q₀ = +2e = +2∙1,6∙10^{– 19}Кл

v = 10⁶м/с

α = 90°

B = 0,2Тл

R = ?

Рішення. Виконуємо малюнок на якому вказуємо діючі на α-частинку сили. А цими силами є: 1) доцентрова сила Лоренца F_Л=Bq₀vsinα, де sinα = sin90° = 1; 2) відцентрова сила інерції F_i = m₀a = m₀v²/R (на малюнку не показана). У відповідності з умовою динамічної рівноваги частинки  F_i = F_Л, а отже m₀v²/R = Bq₀v, звідси R = m₀v²/Bq₀v = m₀v/Bq₀.

Розрахунки. R = m₀v/Bq₀ = 4∙1,66∙10^{– 27}кг∙10⁶(м/с) / 0,2Тл∙2∙1,6∙10^{– 19}Кл = 10∙10^–2м = 10см.

Відповідь: R = 10см.

Тема: Електромагнітні явища. Теорія Максвела.

Основні поняття	Основні величини	Основні закони	Основні прилади
Електромагнітне поле Електромагнітна хвиля	Напруженість електричного поля Е = Fел/q Індукція магнітного поля В = Fм/І∆ℓsinα Магнітний потік Ф = ВScosβ	Закон електро- магнітної індукції Ф=ƒ(t) → Ɛін = –N(ΔФ/Δt) Рівняння змінного струму i = Iмsin2πνt Рівняння Максвела q → E = ƒ(q) q,v → B = ƒ(q,v) B=ƒ(t)→E=ƒ(ΔB/Δt) E=ƒ(t)→B=ƒ(ΔE/Δt)	Коливальний контур CU2/2 ↔  LI2/2 Т=2π√(LC)

Задача 11. Рівняння змінної напруги має вигляд u=308cos100πt. Визначте амплітудне значення напруги, період та частоту її коливань. Побудуйте графік цих коливань.

Рішення. На основі порівняльного аналізу заданого рівняння u=308cos100πt з загальною формою запису аналогічного рівняння u = U_мcos2πνt, можна стверджувати: U_м=308В, оскільки 2πνt = 100πt, то 2ν = 100, отже ν = 50Гц, оскільки Т=1/ν, то Т=1/50=0,02с. Зважаючи на отримані результати будуємо графік рівняння u=308cos100πt.

Задача 12. У коливальному контурі залежність сили струму від часу описується рівнянням і=0,06sin10⁶πt. Визначити частоту коливань в контурі, ємність включеного в контур конденсатора, максимальну енергію магнітного поля та максимальну напругу на конденсаторі, якщо індуктивність включеної в контур котушки 0,1Гн.

Дано:

і=0,06sin10⁶πt

L = 0,1Гн

ν=?; C=?; W_маг=?; U_м=?.

Рішення. Із порівняльного аналізу рівнянь i = I_мsin2πνt та і=0,06sin10⁶πt випливає, що І_м=0,06А; 2πνt=10⁶πt, звідси ν=0,5·10⁶Гц.

Оскільки частота коливань в коливальному контурі визначається за формулою ν=1/Т=1/√(СL), то ν²=1/СL, C=1/ν²L=1/0,1·(5·10⁵)²= 0,4·10^–10Ф= 40·10^–12Ф= 40пкФ.

Оскільки максимальна величина накопиченої в котушці індуктивності магнітної енергії визначається за формулою W_маг=LI_м²/2, то W_маг = 0,1Гн·0,06A = 0,006Дж = 6мДж.

Оскільки в процесі тих коливань які відбуваються в коливальному контурі, електрична енергія конденсатора перетворюється в магнітну енергію котушки і навпаки, то у відповідності з законом збереження енергії W_маг=W_ел=CU_м²/2, звідси U_м=√(2W_маг/C)= √(2·6·10^–3/40·10^–12) = √0,3·10⁹= 1,75·10⁴В= 17,5кВ.

Відповідь: ν=0,5·10⁶Гц; С=40пкФ; W_маг=6мДж; U_м= 17,3кВ

Вправа 9.

1. Електричні заряди тіл становлять q₁ = +5,0∙10^–11Кл; q₂ = –4,0∙10^–12Кл; q₃=6,0∙10^–14Кл. Яку кількість електронів втратили чи отримали відповідні тіла?
2.  Дві кулі масою по одному кілограму кожна, мають електричні заряди по одному кулону кожна. Порівняйте сили електричної та гравітаційної взаємодій цих куль, якщо відстань між ними 1м. Зробіть висновок.
3.  Конденсатори ємності кожного з яких 4мкФ з’єднані так, як показано на малюнках. Визначити загальну ємність системи конденсаторів.

4. За заданими графіками залежності сили струму від напруги, визначити електричні опори відповідних провідників.

5. Визначити ККД джерела струму, якщо його ЕРС 1,6В, внутрішній опір 0,4(Ом), а сила струму в колі 1,0А.

6. Визначити силу струму на кожній ділянці електричного кола: R₁=5(Ом), R₂=3(Ом), R₃=6(Ом), R₄=5(Ом), R₅=4(Ом), R₆=3(Ом) U_заг=12В.

7. Два провідники опори яких 20(Ом) і 30(Ом) включені в мережу з напругою 100В. яка кількість теплоти виділиться в кожному з цих провідників за 10с при їх а) послідовному з’єднанні; б) паралельному з’єднанні?

8. На основі аналізу малюнків визначте напрям сили Ампера.

9. Електрон з швидкістю 610⁷м/с влітає в однорідне магнітне поле з індукцією 0,05Тл і рухається перпендикулярно лініям цієї індукції. Визначити радіус того кола яке опише електрон в магнітному полі (m_е=9,1∙10^–31кг).

10. За заданим графіком записати рівняння: а) змінного струму, б) змінної напруги.

а)  б)

.