Сайт викладача фізики

Тема 1.3. Основи динаміки.

§33. Принцип відносності – базовий закон сучасної науки.

§34. Закони Ньютона – теоретична основа механіки.

§35. Загальні відомості про енергію. Кінетична енергія.

§36. Потенціальна енергія сили тяжіння та сили пружності. Закон збереження енергії.

§37. Розв’язування задач. Тема: Енергетичний метод розв’язування задач.

§38. Робота. Механічна робота.

§39. Енергетичний та силовий методи визначення роботи.

§40. Потужність.

§41. Коефіцієнт корисної дії. ККД простих механізмів.

§42. Розв’язування задач. Тема: Коефіцієнт корисної дії.

§43. Закон всесвітнього тяжіння. Загальний устрій Сонячної системи.

§44. Динаміка. Узагальнююче повторення.

Тема 1.3. Основи динаміки.

Динаміка – це узагальнюючий розділ механіки, в якому вивчаються силові та імпульсно-енергетичні параметри механічного руху тіл в усіх його проявах. В динаміці, ті знання які були отримані при вивченні кінематики та статики, доповнюються новими знаннями і узагальнюються. Теоретичною основою механіки загалом і динаміки зокрема є три закони Ньютона. Ці закони представляють собою систему взаємопов’язаних та взаємодоповнюючих тверджень, в яких опосередковано сформульовані й інші базові твердження, зокрема принцип відносності, закон інерції, закон збереження механічної енергії та закон збереження механічного імпульсу.

.

§33. Принцип відносності – базовий закон сучасної науки.

В 1630 році, в своїх знаменитих «Діалогах про дві системи світу – Птоломеєву та Коперникову» видатний італійський вчений Галілео Галілей (1564–1642) сформулював закон, який лежить в основі сучасної науки і який прийнято називати принципом відносності або принципом Галілея.

Як відомо, заперечуючи факт обертання Землі навколо Сонця, прибічники середньовічної церкви стверджували: «Якби Земля дійсно рухалась, то ми б фізично відчували цей рух. Відчували б подібно до того, як відчуваємо рух карети, човна чи будь чого іншого».

Відповідаючи на подібні аргументи, Галілей стверджував: Дійсно, сидячи в кареті, ми безумовно відчуваємо, рухається вона чи не рухається. Відчуваємо тому, що карета їде не по ідеально рівній дорозі, її колеса не ідеально круглі, тягові зусилля коней постійно змінюються, дорога вкрита дрібними камінчиками, ямками, тріщинками, піщинками, тощо. А це означає, що сидячи в кареті, ми постійно відчуваємо певні поштовхи, тобто різкі, короткотривалі зміни швидкості, які власне і вказують на те, що карета рухається. А от якби мене, вас чи кого завгодно посадити в закриту, ізольовану карету, яка б дійсно рухалась рівномірно, тобто без будь яких змін швидкості, то ні ви, ні я, ні хто завгодно, не змогли б визначити, рухається карета чи стоїть.

Ніякими експериментами, які проводяться в середині закритої ізольованої кабіни, не можливо встановити стоїть ця кабіна чи рівномірно рухається. Не можливо тому, що всі фізичні процеси, які відбуваються в кабіні що стоїть (v=0) і в кабіні що рівномірно рухається (v=const), відбуваються абсолютно однаково.

Якщо вам потрібні докази того, що принцип відносності безумовно правильний, безумовно достовірний, то ось один з них. Кожен з нас знаходиться в кабіні, яка називається планета Земля. Ця кабіна з швидкістю 30км/с = 108000км/год обертається навколо Сонця. При цьому, жоден з нас не відчуває факту того, що Земля мчить з такою шаленою швидкістю. Швидкістю, яка в 60 разів перевищує швидкість кулі. І даний факт не є результатом певних особливостей людського організму. Адже в незалежності від наших відчуттів, всі фізичні процеси на Землі відбуваються так, ніби вона знаходиться в стані механічного спокою.

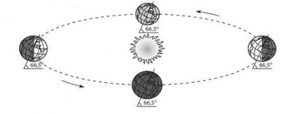
Мал.84. Земля з швидкістю 30км/с обертається навколо Сонця. Чи відчуваєте ви факт цього надшвидкого руху?

Щоправда, Земля рухається не зовсім рівномірно. Адже рівномірність руху передбачає незмінність швидкості руху як за величиною так і за напрямком (v=const). В процесі ж обертання навколо Сонця та своєї осі, напрям руху Землі, а отже і тіл на її поверхні, повільно але неухильно змінюється. А це означає, що факт обертального руху Землі можна експериментально довести, наприклад за допомогою спеціальних маятників. А от якби Земля дійсно рухалась прямолінійно та рівномірно, то з якою б швидкістю вона не рухалась, ви б не змогли встановити, рухається вона чи не рухається.

Іноді думають, що в законі, який називається принципом відносності, стверджується, що все в цьому світі відносне. Це не правда. Не правда по-перше тому, що не все у Всесвіті відносне. Скажімо, абсолютно незмінною є та швидкість з якою рухаються світлових фотонів. Абсолютно незмінною є загальна кількість зосередженого у Всесвіті електричного заряду, мас-енергії, спіну, тощо.

По-друге, в законі який називається принципом відносності стверджується те що стверджується, а саме: Ніякими експериментами, які проводяться в середині закритої ізольованої кабіни, не можливо встановити стоїть ця кабіна чи рівномірно рухається. Не можливо тому, що всі фізичні процеси, які відбуваються в кабіні що стоїть (v = 0) і в кабіні що рівномірно рухається (v = const), відбуваються абсолютно однаково.

Інша справа, що в сучасній науці принцип відносності формулюють дещо по іншому. І це сучасне формулювання є наступним: У всіх інерціальних системах відліку, тобто таких системах де виконується закон інерції (перший закон Ньютона) всі фізичні процеси відбуваються абсолютно однаково. Іншими словами, в тих системах відліку де виконується закон інерції, діють ті ж закони, що і в інших подібних (інерціальних) системах. В законі ж інерції стверджується, що безпричинних змін швидкості руху тіл не буває, і що цією причиною є дія на тіло певної зовнішньої сили.

Ви можете запитати: «Ну добре, в рівномірно рухомих і нерухомих системах відліку всі події відбуваються однаково. Це зрозуміло, це факт, який можна довести. З інерціальними системами відліку, менш зрозуміло, але приймемо на віру, що в них як і в системах рухомих та нерухомих, всі події відбуваються однаково. Але чому вчені стверджують, що саме принцип відносності є тим базовим, тобто найголовнішим, найважливішим законом, який лежить в основі всієї сучасної науки? І що це за закон, який навіть певного математичного вираження не має? А якщо не має, то яка користь від такого закону?»

Відповідаючи на ці слушні запитання, можна сказати наступне. Чи задумувались ви над тим, чому вчені з такою впевненістю говорять про ті події, які відбуваються в практично недосяжних частинах Всесвіту? Чому вони впевнені в тому, що ті закони які відкривались на тій піщинці Всесвіту яка називається планета Земля, діють і в інших куточках Всесвіту. А можливо там, в інших галактиках, все відбувається по іншому? Можливо там, діють інші закони, існують інші атоми, інші молекули, інші біологічні структури? Хто був в тих далеких світах та перевіряв це?

Відповіді на ці та їм подібні запитання дає принцип відносності. Адже згідно з цим принципом для з’ясування того, діють чи не діють відкриті на Землі закони природи в інших місцях Всесвіту зовсім не обов’язково вирушати в далеку космічну подорож. Достатньо з’ясувати, виконується чи не виконується у відповідному місці закон інерції. І якщо цей закон виконується, то це автоматично означає, що відповідна система є інерціальною, і що тому у відповідному куточку Всесвіту діють ті ж закони що і на Землі.

І от ми вдивляємось в безмежні простори Всесвіту, аналізуємо ті події які відбуваються в ньому і бачимо, що у всіх куточках Всесвіту безпричинних змін швидкості руху фізичних об’єктів не буває, і що причиною цих змін є дія на відповідний об’єкт певної зовнішньої сили. А це означає, що у всіх частинах Всесвіту діють одні і ті ж закони. І що ці закони співпадають з тими що діють на Землі.

Не вірити цьому факту, це все рівно ніби заперечувати факт того, що Земля обертається навколо Сонця та своєї осі. Заперечувати лише на тій підставі, що ми не відчуваємо відповідного руху. Звичайно, можна скільки завгодно заперечувати і скільки завгодно не вірити, але від того, факт обертання Землі навколо Сонця та своєї осі не перестане бути фактом, а принцип відносності не перестане бути достовірним.

Мал.85. Бачимо: у Всесвіті безпричинних змін швидкості не буває. Висновок: у всіх куточках Всесвіту діють одні і ті ж закони Природи.

Принцип відносності не лише обгрунтовано доводить, що відкриті на Землі закони Природи діють і в інших частинах Всесвіту, а й дозволяє представити наші знання про навколишній світ у вигляді стислої, цілісної системи знань. Адже якби в кожній рухомій системі відліку, події відбувались по різному, то описуючи ці події, ми були б змушені досліджувати кожну конкретну ситуацію. І кожну конкретну ситуацію описувати своєю системою законів. При цьому, для кожної системи відліку ми б мали своє рівняння руху, свою умову рівноваги, свої закони Ньютона, свій закон всесвітнього тяжіння, свій закон Гука, свій закон Ома, свій закон електромагнітної індукції і т.д.

Ясно, що в такій ситуації, наука про Природу була б сукупністю безкінечно великої кількості експериментальних фактів. Фактів, які б описувались в мільйонах книг і які було б не можливо представити у вигляді стислої, цілісної системи знань. І якщо така система знань існує, то це тільки тому, що в нерухомій (v = 0) та в будь якій рівномірно рухомій (v = const) системах відліку всі фізичні процеси відбуваються абсолютно однаково (принцип відносності).

Таким чином, коли ми стверджуємо, що принцип відносності є базовим законом сучасної науки, то маємо на увазі факт того, що застосування цього принципу дозволяє по-перше, обгрунтовано довести, що відкриті на Землі закони Природи діють і в інших частинах Всесвіту, а по-друге, представити відому інформацію про Природу у вигляді стислої, цілісної системи знань.

Контрольні запитання.

1. Що стверджували ті, хто заперечував факт обертання Землі навколо Сонця?
2. Чому, сидячи в реальній закритій кабіні (кареті, автомобілі, потязі, тощо) ми практично завжди можемо визначити рухається ця кабіна чи не рухається?
3. Чи відчуваєте ви, що Земля рухається? Чому?
4. Чи є правильним твердження: у Всесвіті все відносне?
5. Наведіть приклади тих речей які є абсолютно незмінними.
6. Що стверджується в принципі відносності (два формулювання)?
7. Що стверджується в законі інерції?
8. Як з’ясовують те, діють чи не діють відкриті на Землі закони природи в інших куточках Всесвіту?
9. Яка роль принципу відносності в створенні цілісної системи знань про Природу?

.

§34. Закони Ньютона – теоретична основа механіки.

 

В попередньому параграфі ми говорили про те, що теоретичним фундаментом механіки і всієї сучасної науки загалом є принцип відносності. Однак сам по собі цей принцип ще не є тим законом який пояснює широке коло явищ та дозволяє розв’язувати відповідно широке коло конкретних задач. Цю функцію виконує наукова теорія, тобто цілісна система достовірних знань про певну групу споріднених явищ.

В 1687 році видатний англійський фізик Ісаак Ньютон (1643–1727) опублікував свої знамениті «Математичні начала натуральної філософії», в яких виклав основи першої наукової теорії сучасного зразку. Теорії, яку прийнято називати механікою або ньютонівською механікою. В основі цієї теорії лежать три твердження, які називаються законами Ньютона. Сформулюємо ці твердження та проаналізуємо їх.

         Перший закон Ньютона – це закон, в якому стверджується: Будь-яке тіло буде знаходитись в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v=const), до тих пір поки на нього не подіє зовнішня сила, яка і змусить тіло змінити цей стан.

На перший погляд, даний закон не має суттєвого практичного значення. Його навіть важко записати у вигляді відповідної формули. Однак, насправді, мова йде про надзвичайно важливий, по суті базовий закон не лише механіки, а й всієї сучасної науки. Адже в рамках першого закону Ньютона по суті стисло сформульовано два базові закони: принцип відносності та закон інерції.

         Дійсно. В першому законі Ньютона стверджується: будь-яке тіло буде знаходитись в стані механічного спокою (v = 0), або в стані прямолінійного рівномірного руху (v = const), до тих пір поки на нього не подіє зовнішня сила, яка і змусить тіло змінити цей стан. По суті це означає, що з фізичної точки зору, стан спокою (v = 0) і стан прямолінійного рівномірного руху (v = const), це один і той же механічний стан (цей стан). Один і той же в тому сенсі, що всі фізичні процеси які відбуваються в кабіні що стоїть і  в кабіні що рівномірно рухається, відбуваються абсолютно однаково (принцип відносності). Іншими словами: v = 0  « = »  v = const, де знак « = » вказує на те, що ті фізичні процеси які відбуваються в кабіні яка стоїть і в кабіні яка рівномірно рухається, відбуваються «однаково».

         З іншого боку, в тому ж першому законі Ньютона  стверджується, що причиною зміни стану спокою, або стану прямолінійного рівномірного руху, тобто причиною зміни швидкості руху тіла, є дія на це тіло певної зовнішньої сили. Іншими словами, в першому законі Ньютона стверджується, що безпричинних змін швидкості руху тіла не буває, і що цією причиною є дія зовнішньої сили (закон інерції). А зважаючи на те, що зміну швидкості руху тіла характеризує величина яка називається прискоренням, закон інерції можна сформулювати у вигляді: причиною прискореного руху тіла, є дія на це тіло певної зовнішньої сили: F → a.

Наприклад, якщо Місяць обертається навколо Землі, Земля обертається навколо Сонця, а Сонце обертається навколо центру Галактики, то напрям їх швидкості постійно змінюється. А у відповідності з тією частиною першого закону Ньютона, яка називається законом інерції, така зміна не може бути безпричинною, і що має існувати та зовнішня сила яка змушує Місяць, Землю та Сонце змінювати напрям свого руху (рухатись з доцентровим прискоренням). І в кожному з цих та в мільярдах подібних випадків, така сила дійсно існує і називається силою гравітаційної взаємодії. Силою, яка у повній відповідності з законом всесвітнього тяжіння об’єднує планети і зірки в планетарні системи, зірки – в галактики, галактики – в метагалактики, а все разом – у Всесвіт.

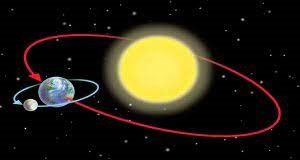
Мал.86. Безпричинних змін швидкості руху тіл не буває, і цією причиною є дія певної зовнішньої сили (закон інерції).

Таким чином, в першому законі Ньютона, опосередковано сформульовано два твердження: принцип відносності та закон інерції.

а) v = 0  « = »  v = const (принцип відносності)

б)  F → a  (закон інерції)

Другий закон Ньютона – це закон, в якому стверджується: Під дією зовнішньої сили F, тіло масою m отримує прискорення   а   величина якого прямо пропорційна діючій на тіло силі і обернено пропорційна його масі. Іншими словами:   F  →   a = F/m

Не важко бачити, що другий закон Ньютона, є логічним продовженням першого. Адже в тій частині першому законі Ньютона яка називається законом інерції, по суті стверджується, що причиною зміни швидкості руху тіла, а отже причиною його прискореного руху, є дія зовнішньої сили, тобто стверджується, що сила породжує прискорення: F → a. В другому ж законі Ньютона, це твердження формулюється в явному вигляді та конкретизується:  F →  a = F/m.

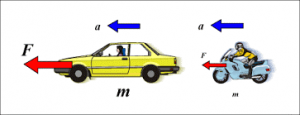
Мал.87. Сила – є причиною прискореного руху тіла, при цьому величина прискорення прямо пропорційна діючій на тіло силі і обернено пропорційна масі тіла:  F  →   a = F/m.

Звичайно, говорячи про те, що сила, а точніше зовнішня сила, є причиною прискореного руху тіла, мається на увазі, що на відповідне тіло діє лише дана сила. Адже якщо наприклад, під дією певної сили тіло рухається з постійною швидкістю, або не рухається взагалі, то це означає лише те, що на відповідне тіло, окрім даної сили діють й інші сили, які зрівноважують її ді

Малоприємним фактом є те, що другий закон Ньютона часто формулюють наступним чином: сила що діє на тіло, дорівнює добутку маси тіла на його прискорення, тобто F = ma. Таке формулювання і така формула не є правильним формулюванням другого закону Ньютона. Бо закон (фізичний закон), це не просто математична формула, яка відображає певні зв’язки між фізичними величинами. Закон, це відображення того причинно-наслідкового зв’язку, який існує між певними проявами Природи. А це означає, що в законі та йому відповідній математичній формулі, потрібно вказувати на те, що в даному зв’язку є причиною (незалежною величиною), а що наслідком (залежною величиною).

Наприклад другий закон Ньютона відображає той факт, що причиною прискореного руху тіла є діюча на нього зовнішня сила, і що саме прискорення тіла залежить від сили, а не навпаки. Відображенням же цієї залежності є формула a = F/m, а не F = ma чи m = F/a.

Звісно, формули F = ma та m=F/a є безумовно правильними. Однак вони не є математичними відображеннями другого закону Ньютона. Ці формули є прямими наслідками другого закону Ньютона. І як ці наслідки можуть застосовуватись як при розв’язуванні задач так і в якості визначальних рівнянь відповідних фізичних величин. Наприклад визначальним рівнянням сили є саме формула F = ma.

Третій закон Ньютона – це закон, в якому стверджується: Діюча на тіло сила F, завжди породжує рівну їй за величиною і протилежну за напрямком протидіючу силу F′. Іншими словами:

F → F′ = –F

Наприклад, якщо тіло з певною силою діє на опору, то опора з такою ж силою діє на тіло. Якщо нога футболіста діє на м’яч, то м’яч з такою ж силою діє на ногу футболіста. Якщо Місяць притягується до Землі, то Земля з такою ж силою притягується до Місяця.

 

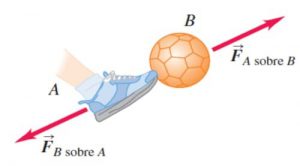
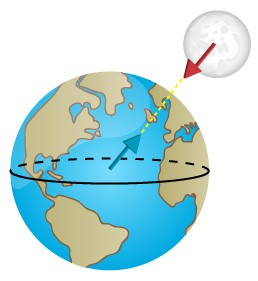
Мал.88. Діюча F та протидіюча Fꞌ сили, завжди рівні за величиною, протилежні за напрямком і прикладені до різних тіл.

Говорячи про діючу та протидіючу сили, потрібно зауважити, що ці сили завжди чисельно рівні, однак результат їх дії може бути абсолютно різним. Наприклад, підняте над Землею тіло з певною силою F притягується до Землі, а Земля з такою ж силою F′ притягується до тіла. Однак, якщо для відносно легкого тіла сила F є значною, то для надмасивної Землі, така ж сила F′ є мізерно малою. Тому в системі Земля – тіло, тіло падає на Землю, а не Земля «підстрибує» до тіла.

Потрібно наголосити й на тому, що діюча та протидіюча сили, завжди прикладені до різних тіл. А це означає, що ці сили не можуть забезпечити механічну рівновагу системи діюче-протидіюче тіло. М’яч, в результаті взаємодії з ногою футболіста з певним прискоренням відлітає від ноги. Тіло, в результаті взаємодії з Землею з певним прискоренням падає на підлогу. Земля в результаті взаємодії з Сонцем з певним доцентровим прискоренням обертається навколо Сонця, і т.д.

І якщо та книга що лежить на столі, знаходиться в стані механічної рівноваги, то це не тому що діюча і протидіюча сили зрівноважують одна одну. Бо в системі опора-книга, книга діє на опору з силою яка називається вагою книги (Р), а опора діє на книгу з протидіючою силою яка називається реакцією опори (N). При цьому на книгу фактично діє лише одна з цих сил – реакція опори. Рівновага ж книги забезпечується не зрівноваженням діючої та протидіючої сил, а фактом того, що на книгу окрім реакції опори діє ще одна зовнішня сила – сила тяжіння.

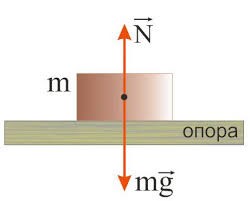
Мал.89. Книга знаходиться в стані механічної рівноваги не тому що діюча і протидіюча сили зрівноважують одна одну. Бо діюча і протидіюча сили діють на різні тіла.

Аналізуючи закони Ньютона, не важко бачити, що це не просто набір правильних тверджень, а струнка система взаємопов’язаних та взаємодоповнюючих законів. Законів, які у своїй сукупності дозволяють пояснити величезне різноманіття механічних явищ. Законів, в яких при ґрунтовному аналізі можна відшукати не лише формулювання принципу відносності та закону інерції, а й приховані формулювання інших законів, зокрема закону збереження механічної енергії та закону збереження імпульсу.

Взаємопов’язаність та взаємодоповнюваність законів Ньютона з усією очевидністю випливає з їх наступних математичних формулювань:

1. а) v=0  « = »  v=const

б)  F → a

2. F → a = F/m
3. F → Fꞌ = – F

Задача 1. Тіло масою 5кг рухається з прискоренням 4м/с²? Визначте величину діючої на тіло сили.

Дано:

m = 5кг

а = 4м/с²

F = ?

Рішення. У відповідності з другим законом Ньютона а = F/m, тому F = ma = 5кг∙4м/с² = 20Н.

Відповідь: F = 20Н.

Задача 2. Хокейна шайба масою 160г, після удару ключкою який триває 0,02с набуває швидкості 25м/с. Визначте усереднену силу удару.

Дано:

m = 160г = 0,16кг

v₀ = 0м/с

v_k = 25м/с

∆t = 0,02c

F = ?

Рішення. У відповідності з другим законом Ньютона а = F/m, тому F = ma, де а = ? Оскільки за визначенням а = (v_к – v₀)/∆t, та враховуючи, що v₀ = 0м/с, можна записати F = ma = m∙v_к/∆t = 0,16кг∙25(м/с)/0,02с = 200Н.

Відповідь: F = 200Н.

Контрольні запитання.

1. Які два базові закони опосередковано сформульовані в першому законі Ньютона?
2. Якими словами в першому законі Ньютона стисло сформульовано принцип відносності?
3. Що стверджується в законі інерції і якими словами це відображено в першому законі Ньютона?
4. Чому ми говоримо, що другий закон Ньютона є логічним продовженням першого?
5. Чому формула F = ma не є правильним математичним формулюванням другого закону Ньютона?
6. Чому діюча та протидіюча сили не можуть забезпечити механічну рівновагу тіла?
7. Тіло висить на мотузці. Які сили діють на тіло? Чи є ці сили діючою і протидіючою? Чому?

Вправа 34.

1. Визначте силу, під дією якої тіло масою 80г рухається з прискоренням 8м/с²?
2. З яким прискоренням рухається під час розгону реактивний літак масою 60т, якщо сила тяги двигунів 90кН?
3. Визначте масу футбольного м’яча, якщо після удару він набув прискорення 500м/с², а сила удару дорівнює 420Н
4. Сила 40Н надає тілу прискорення 0,8м/с². Яка сила надасть цьому ж тілу прискорення 2,0м/с²?
5. Два хлопчики розтягують динамометр, при цьому кожен прикладає силу 90Н. Що покаже динамометр?
6. На тіло масою 800г діють дві сили направлені в протилежні сторони: 12Н і 8Н. Визначте модуль та напрям прискорення тіла.
7. Снаряд масою 5кг при пострілі набуває швидкості 800м/с за 0,005с. Визначити середню силу тиску порохових заряду. Рух снаряду вважати рівноприскореним.
8. М’яч масою 400г в процесі удару який триває 0,02с набуває швидкості 15м/с. Яка середня сила удару?

.

§35. Загальні відомості про енергію. Кінетична енергія.

         Уявити сучасну науку без величини яка називається енергією (від грец. energeia – дія, діяльність) практично не можливо. Адже саме енергія є тією стержневою фізичною величиною яка об’єднує найрізноманітніші явища Природи в цілісну наукову картину.

Сучасне розуміння суті того, що називають енергією, це результат тривалого еволюційного розвитку науки, вінцем якого є теорія відносності. Лише після створення цієї теорії, стало зрозумілим, що енергія є загальною мірою всіх видів рухів та взаємодій, і що будь який фізичний об’єкт масою m, представляє собою згусток енергії загальна кількість якої визначається за формулою Е = mс², де с = 3∙10⁸м/с = соnst. Це означає, що повністю перетворивши все те з чого складається дане тіло, а отже всі його молекули, атоми, атомні ядра, протони, нейтрони, електрони та всі ті процеси які відбуваються з ними, в те що називається чистою енергією, а по суті в світло, ви отримаєте цієї енергії в кількості Е = mс².

Наприклад в будь якому тілі масою 1кг міститься Е = 1кг(3·10⁸м/с)² = 9·10¹⁶Дж енергії. Щоб мати уявлення про величину цієї енергії, достатньо сказати, що аналогічну кількість енергії можна отримати при повному згоранні 4 500 000 тон кам’яного вугілля. Для перевезення такої кількості вугілля потрібно більше 75000 вщерть заповнених залізничних вагонів, загальна довжина яких становитиме майже 1000км.

Твердження про те, що енергія це загальна міра всіх видів рухів і взаємодій, є загально прийнятою та вичерпною характеристикою того, що називають енергією. Однак воно має той суттєвий недолік, що не дозволяє визначати величину конкретного виду енергії в тій чи іншій конкретній ситуації. А потрібно зауважити, що на практиці говорячи про енергію тіла, мають на увазі не ту загальну енергію яка зосереджена в даному тілі і кількість якої визначається за формулою Е = mс², а певну, зазвичай мізерну частину цієї енергії яка пов’язана з тим чи іншим конкретним явищем.

Наприклад коли ми стверджуємо, що рухоме тіло має певну енергію, то маємо на увазі не повну енергію цього тіла (Е = mс²), а ту її мізерну частину яка обумовлена фактом механічного руху тіла. Коли ми стверджуємо, що підняте над підлогою тіло має певну енергію, то маємо на увазі не повну енергію цього тіла (Е = mс²), а ту її мізерну частину яка обумовлена взаємодією даного тіла з Землею. Коли ми стверджуємо, що деформована пружина має певну енергію, то маємо на увазі не повну енергію цієї пружини (Е = mс²), а ту її мізерну частину яка обумовлена взаємодією атомів та молекул пружно деформованого тіла.

З практичної точки зору твердження про те, що той чи інший об’єкт має певну енергію, по суті означає, що за певних умов відповідний об’єкт може виконати певну роботу, тобто певну енерго затратну дію. Власне енергія і є мірою здатності фізичного об’єкту виконати роботу. Наприклад, коли ми стверджуємо, що підняте над підлогою тіло (мал.90а) має енергію, то це означає, що за певних умов (за умови падіння тіла) буде виконана певна робота: в процесі удару об підлогу, тіло деформується і деформує підлогу; в процесі падіння та удару, тіло, підлога та повітря нагріються; в процесі удару, тіло заб’є гвіздок, створить звукову хвилю, тощо.

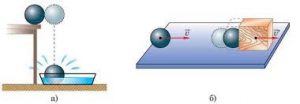
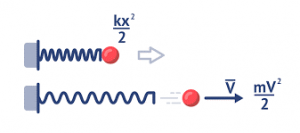
Мал.90.  Коли ми стверджуємо, що певний фізичний об’єкт має певну енергію, то це означає, що цей об’єкт здатний виконати певну роботу (певну енергозатратну дію).

Коли ми стверджуємо, що тіло масою m, рухаючись з швидкістю v, має енергію (мал.90б), то це означає, що за певних умов (за умови зустрічі тіла з перешкодою) буде виконана певна робота. Коли ми стверджуємо, що деформована пружина (мал.90в) має енергію, то це означає, що за певних умов (за умови випрямлення пружини), буде виконана певна робота. Коли ми стверджуємо, що шматок вугілля має енергію, то це означає, що за певних умов вугілля буде горіти і що в процесі горіння буде виконана певна робота.

Зважаючи на вище сказане, можна дати наступне визначення: Енергія – це фізична величина, яка є загальною мірою всіх видів рухів та взаємодій і яка характеризує здатність тіла, частинки або поля виконати роботу.

Позначається: Е

Визначальне рівняння:

1) для загальної кількості енергії:   Е=mс², де с=3∙10⁸м/с = const

2) для конкретних видів енергії:   різні.

Одиниця вимірювання: [E] = кг∙м²/с² = Н∙м = Дж,   джоуль.

Джоуль – це одиниця вимірювання енергії та роботи, яка дорівнює тій роботі (тим затратам енергії) яку виконує сила в один ньютон при переміщенні тіла (матеріальної точки) на один метр в напрямку дії сили: Дж = Н∙м = кг∙м²/с².

Щоб мати уявлення про величину роботи в один джоуль, візьміть тіло масою 102г і підніміть його на висоту один метр. При цьому виконана вами робота, а відповідно і затрачена вами енергія, дорівнюватимуть одному джоулю. Або якщо наприклад, яблуко масою 102гр впаде з висоти 1м, то виконана силою тяжіння робота дорівнюватиме 1Дж.

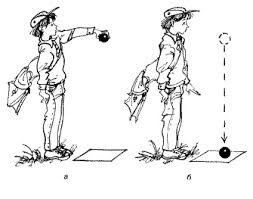
Мал.91. Піднімаючи тіло масою 102г з висоту 1м, ви виконуєте роботу 1Дж.

Вивчаючи фізику ви неминуче переконаєтесь в тому, що енергія невичерпно різноманітна в своїх проявах. Різноманітна в тій же мірі як і самі явища Природи. Наприклад говорять про енергію гравітаційних, електричних, електромагнітних та інших полів. Про енергію механічну, теплову, звукову, світлову, хімічну, біологічну, електричну, магнітну, електромагнітну, ядерну, внутрішню. Про енергію піднятого тіла та енергію пружно деформованого тіла, про енергію нагрітого тіла та енергію тіла що горить, про енергію хімічних реакцій та енергію термоядерного синтезу. І навіть те що не називають енергією, як то температура, кількість теплоти, робота чи маса, фактично характеризує ті чи інші прояви енергії.

Вивчаючи механіку, ми будемо говорити про ту частину енергії, яка характеризує тіло як єдине ціле і яка пов’язана з його механічним рухом, пружними деформаціями та гравітаційними взаємодіями. Цю енергію називають механічною. Механічна енергія, це така енергія, яку має тіло як єдине ціле і яка пов’язана з його механічним рухом, пружними деформаціями та гравітаційними взаємодіями.

Енергію загалом і механічну енергію зокрема, можна представити як певну комбінаціє двох базових різновидностей: енергії руху (кінетична енергія) та енергії взаємодії (потенціальна енергія).

Кінетична енергія (енергія руху) – це та енергія, яку має фізичний об’єкт за рахунок того що він рухається і яка дорівнює половині добутку маси об’єкту на квадрат його швидкості.

Позначається: Е_к

Визначальне рівняння: Е_к = mv²/2

Одиниця вимірювання: [Е_к] = кг∙м²/с² = Дж,   джоуль.

Якщо той чи інший фізичний об’єкт, будь то камінь, планета, атом чи фотон світла, рухається, то він має певну кінетичну енергію величина якої визначається за формулою Е_к = mv²/2. Наприклад, якщо велосипедист маса якого 70кг рухається з швидкістю 36км/год = 10м/с, то величина його кінетичної енергії Е_к = 70кг(10м/с)²/2 = 3500Дж. Щоб мати уявлення про можливий вплив кінетичної енергії тіла на організм людини, достатньо сказати, що кінетична енергія потенційно смертельної для людини кулі, приблизно дорівнює 100Дж.

Мал.92. Кінетична енергія – це та енергія, яку має фізичний об’єкт за рахунок того, що він рухається.

Кінетична енергія є явною, очевидною, активною формою енергії, наявність і величину якої легко встановити: якщо тіло, частинка чи що завгодно, маючи масу m рухається з швидкістю v, то воно має кінетичну енергію величина якої визначається за формулою Е_к = mv²/2.  Але окрім цією активної енергії, практично з кожним тілом нерозривно пов’язана певна кількість пасивної, прихованої енергії, яку прийнято називати потенціальною. Про цю енергію та про той базовий закон Природи який називається законом збереження енергії, ми поговоримо в наступному параграфі.

Задача 1. Для того щоб нагріти 1кг води на 1°С потрібно 4200Дж енергії. Порівняйте цю енергію з кінетичною енергією тієї кулі яка вилітає з дула пістолету, якщо маса цієї кулі 5г, а її швидкість 300м/с.

Дано:

Е_нагр= 4200Дж

m = 5г = 0,005кг

v = 300м/с

Е_нагр/Е_к = ?

Рішення. За визначенням Е_к = mv²/2 = 0,005кг∙(300м/с)²/2 = 225Дж.

Отже Е_нагр/Е_к = 4200Дж/225Дж = 18,7 рази.

Відповідь: Е_нагр/Е_к = 18,7 рази.

Висновок. Та кінетична енергія (225Дж), яка є смертельною для людини, майже в 20 разів менша за ту непомітну енергію, яку потрібно витратити на те, щоб один літр води нагріти на 1°С.

Задача 2. Тіло масою 1кг падає з висоти 20м. Визначити кінетичну енергію тіла в момент падіння.

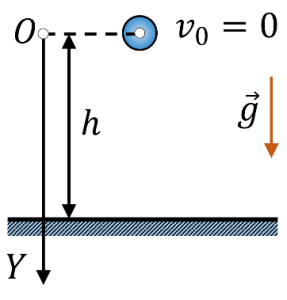
Дано:

m = 1кг

h = 20м

Е_к = ?

Рішення. За визначенням Е_к = mv²/2, де v = ?

При рівноприскореному русі v = v₀ + gt, в умовах нашої задачі v₀ = 0, тому v =  gt,  де t = t_пад = ?

Визначаючи час падіння тіла запишемо рівняння руху цього тіла, тобто формулу яка має вигляд h = h₀ + v₀t + (g/2)t². Оскільки в умовах даної задачі h₀ = 0м; v₀ = 0м/с, то h = (g/2)t², звідси t² = 2h/g, звідси

t = √2h/g = √(2∙20(м/с)/10(м/с²)) = √4с² = 2с.

Таким чином, v = gt = 10(м/с²)∙2с = 20м/с,

Е_к = mv²/2 = 1кг∙(20м/с)²/2 = 200Дж.

Відповідь: Е_к = 200Дж.

Контрольні запитання.

1. Що означає слово «енергія»?
2. Що означає твердження: будь яке тіло масою m, представляє собою згусток енергії загальна кількість якої визначається за формулою Е=mс² ?
3. Який недолік визначення: «Енергія – це загальна міра всіх видів рухів та взаємодій»?
4. Коли ми стверджуємо, що той чи інший об’єкт має певну енергію, то маємо на увазі …?
5. Дайте загально прийняте визначення терміну «енергія».
6. Дайте визначення терміну «джоуль». Джоуль, це багато чи мало?
7. Яку енергію називають механічною?
8. Яку енергію називають кінетичною? Чому вона дорівнює?

Вправа №35.

1. Хокейна шайба масою 160г летить зі швидкістю 20м/с. Визначити кінетичну енергію шайби.
2. Автомобіль масою 5т рухається з швидкістю 90км/год. Визначте кінетичну енергію автомобіля.
3. При швидкості 36км/год кінетична енергія тіла 100Дж. Яка маса цього тіла?
4. З якою швидкістю має летіли куля масою 3г, щоб її кінетична енергія дорівнювала 100Дж?
5. Земля з швидкістю 30км/с обертається навколо Сонця. Яка кінетична енергія Землі, якщо її маса 6·10²⁴кг?
6. Маса піщинки 0,1мг. Яка загальна кількість енергії зосереджена в цій піщинці? Якої маси має бути тіло, щоб рухаючись з швидкістю 108км/год мати аналогічну кількість кінетичної енергії?
7. Цеглина масою 4,5кг падає з висоти 10м. Визначити кінетичну енергію цеглини в момент падіння на землю.

.

§36. Потенціальна енергія. Закон збереження енергії.

 

Не дивлячись на все різноманіття видів енергії, практично будь яку її різновидність можна представити як певну комбінацію двох складових: енергії руху (кінетична енергія) та енергії взаємодії (потенціальна енергія). Про кінетичне енергію ми говорили в попередньому параграфі. На разі ж гранично стисло охарактеризуємо ту багатолику різновидність прихованої енергії яку називають потенціальною енергією.

Потенціальна енергія (енергія взаємодії) – це та енергія, яку має фізичний об’єкт за рахунок того, що він так чи інакше взаємодіяє з іншими об’єктами, або за рахунок тих взаємодій які відбуваються в середині цього об’єкту.

Позначається: Е_п

Визначальне рівняння: Е_п = ?, це означає, що єдиної універсальної формули для визначення потенціальної енергії нема.

Одиниця вимірювання: [Е_п] = Дж,  джоуль.

Потенціальна енергія, це дуже складний вид прихованої енергії, величину якої в загальному випадку ми не вміємо визначати. Не вміємо в тому сенсі, що на сьогоднішній день нема тієї універсальної формули, яка б дозволяла визначати потенціальну енергію фізичного об’єкту в усьому різноманітті проявів цієї енергії. Однак це зовсім не означає, що ми не вміємо визначати величину потенціальної енергії в тих чи інших конкретних випадках. Наприклад, в механіці вивчають дві різновидності потенціальної енергії: потенціальна енергія сили тяжіння та потенціальна енергія сили пружності.

Потенціальна енергія сили тяжіння (піднятого тіла) –  це та енергія яку має тіло за рахунок його взаємодії з Землею і яка дорівнює добутку маси тіла (m), прискорення сили тяжіння (g) та тієї висоти (h) на яку піднято тіло.

Позначається: Е_п

Визначальне рівняння: Е_п = mgh,

Одиниця вимірювання: [Е_п] = Дж,   джоуль.

Наприклад, якщо тіло масою 2кг піднято над підлогою на висоту 1,5м, то величина його потенціальної енергії відносно підлоги становить Е_п = 2кг·9,8м/с²·1,5м = 29,4Дж.

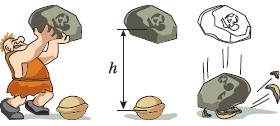
Мал.93. Потенціальна енергія сили тяжіння – це та енергія яку має тіло за рахунок його взаємодії з Землею

Потенціальна енергія сили пружності (пружно деформованого тіла) – це та енергія яку має пружно деформоване тіло за рахунок тих внутрішніх взаємодій які відбуваються в ньому і яка дорівнює половині добутку жорсткості тіла (k) на величину його абсолютної деформації (Δℓ).

Позначається: Е_п

Визначальне рівняння: Е_п = kΔℓ²/2,

Одиниця вимірювання: [Е_п] = Дж,     джоуль.

Наприклад, якщо пружину жорсткістю 400Н/м деформували на 0,1м, то величина їх потенціальної енергії Е_п = 400(Н/м)(0,1м)²/2 = 2Дж.

 

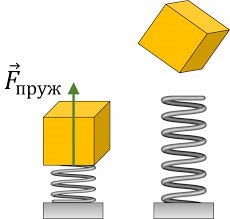
Мал.94. Потенціальна енергія сили пружності – це та енергія яку має тіло за рахунок тих взаємодій що відбуваються всередині пружно деформованого тіла.

Напевно, енергія не мала б такого фундаментального, загальнонаукового значення, якби не той закон який називається законом збереження енергії. В цьому законі стверджується: при будь яких процесах, що відбуваються в замкнутій (енергоізольованій) системі, загальна кількість енергії цієї системи залишається незмінною, тобто зберігається. Іншими словами:∑Е_до = ∑Е_після  або  ∑Е = соnst.

Ілюструючи дію закону збереження енергії в механічних процесах, розглянемо конкретну ситуацію. Припустимо що тіло масою 1кг знаходиться на висоті 5м. Ясно, що в процесі вільного падіння тіла, величина його потенціальної енергії (E_п = mgh) буде зменшуватись (оскільки h↓ то Е_п↓). З іншого боку, в процесі того ж падіння, кінетична енергія тіла (Е_к = mv²/2) буде збільшуватись (оскільки v↑ то Е_к↑). І не важко довести, що на всьому шляху вільного польоту тіла, загальна кількість його механічної енергії (Е = Е_п + Е_к) залишається незмінною.

Дійсно. Виходячи з того, що в процесі вільного падіння, висота тіла над поверхнею землі зменшується за законом h = h₀ – gt²/2, а його швидкість – збільшується за законом v = v₀ + gt, визначимо параметри падаючого тіла (h, v, Е_п, Е_к, Е = Е_п + Е_к) через кожні 0,2с польоту. Результати обчислень запишемо у відповідну таблицю.

t (c)	h (м)	v (м/с)	Ек (Дж)	Еп (Дж)	Е=Ек+Еп(Дж)
0,0	5,0	0,0	0,0	50,0	50,0
0,2	4,8	2,0	2,0	48,0	50,0
0,4	4,2	4,0	8,0	42,0	50,0
0,6	3,2	6,0	18,0	32,0	50,0
0,8	1,8	8,0	32,0	18,0	50,0
1,0	0,0	10,0	50,0	0,0	50,0

Не важко бачити, що в процесі вільного падіння тіла, загальна кількість його механічної енергії залишається незмінною, тобто зберігається.

         

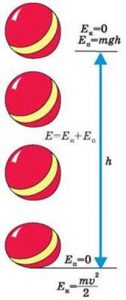
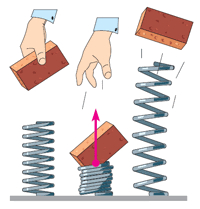
Мал.95. При будь яких процесах що відбуваються в замкнутій системі, загальна кількість енергії цієї системи залишається незмінною.

Ви можете заперечити в тому сенсі, що коли тіло впаде, то його кінетична і потенціальна енергії матимуть нульову величину. Чи не означатиме це, що енергія зникла і що закон збереження енергії не виконується? Ні, не означатиме! Просто в процесі взаємодії тіла з землею (підлогою, поверхнею стола, тощо), та механічна енергія яка спочатку була потенціальною, а потім кінетичною, перетворилась у відповідну кількість внутрішньої енергії, тобто в кінетичну та потенціальну енергію молекул взаємодіючих тіл. Простіше кажучи, механічна енергія перетворилась в енергію теплову.

А якщо ви не помітили цього перетворення, то це тільки тому, що енергоємність тіл є надзвичайно великою. Скажімо, для того щоб один літр води нагріти всього на 1°С потрібно витратити 4200Дж енергії. А це означає, що кінетична енергія величиною 50Дж (енергія яку набуває сталева куля масою 102г при її падінні з висоти 50м, і яка за певних обставин може бути смертельною для людини), здатна нагріти літр води всього на 0,012°С.

Тому не дивно, що спостерігаючи за тими подіями які відбуваються в процесі падіння даного тіла, ви не помітили факту того, що навколишнє повітря, земля і саме тіло дещо нагрілись. Однак, якщо ви дійсно виконаєте необхідні вимірювання, то неодмінно з’ясуєте, що в процесі падіння тіла і в процесі його взаємодії з поверхнею землі, загальна кількість внутрішньої енергії взаємодіючих тіл дійсно збільшилась, і збільшилась рівно на 50Дж.

До речі, якщо в момент падіння тіла, його кінетична енергія становитиме не 50Дж, а скажімо 47Дж, то не поспішайте стверджувати, що закон збереження енергії не працює. Просто в процесі падіння тіла та в результаті його тертя об повітря, частина механічної енергії тіла (а саме 3Дж) перетворилась на відповідну кількість внутрішньої енергії тіла та повітря.

Незліченна кількість експериментальних досліджень та фактів доводять. Енергія не виникає безпричинно і не зникає безслідно. Вона лише перетворюється з одного виду в інший та переходить від одних фізичних об’єктів  до інших. При цьому, за будь яких перетворень та будь яких переходів загальна кількість енергії залишається незмінною, тобто зберігається.

Задача 1. Тіло масою 1кг падає з висоти 20м. Визначити кінетичну енергію тіла в момент падіння.

Дано:

m = 1кг

h = 20м

Е_к = ?

Рішення. На основі аналізу умови задачі виконуємо відповідний малюнок, на якому вказуємо енергетичні параметри системи на висоті h = h_мах та h = 0.

на висоті h = h_мах :  Е_п = mgh,   Е_к = 0;

на висоті  h = 0 :     Е_п = 0,         Е_к = mv²/2.

У відповідності з законом збереження (∑Е_до = ∑Е_після), можна записати:

mgh + 0 = 0 + Е_к, звідси Е_к = mgh = 1кг∙10(м/с²)∙20м = 200Дж

Відповідь: Е_к = 200Дж.

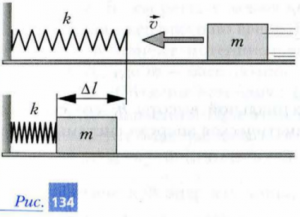
Задача 2. Тіло масою 500г, що рухається з швидкістю 15м/с, при взаємодії з горизонтально розташованою пружиною деформує її на 10см. Визначити жорсткість пружини.

Дано:

m = 500г = 0,5кг

v = 15м/с

Δℓ=10см = 0,1м

k = ?

Рішення. На основі аналізу умови задачі виконуємо відповідний малюнок, на якому вказуємо енергетичні параметри системи до та після взаємодії.

до взаємодії:       Е_к = mv²/2,   Е_п = 0;

після взаємодії:  Е_к = 0,           Е_п = kΔℓ²/2.

У відповідності з законом збереження (∑Е_до = ∑Е_після), можна записати:

mv²/2 + 0 = 0 + kΔℓ²/2, звідси mv² = kΔℓ², звідси  k = mv²/Δℓ².

Розрахунки: k = mv²/Δℓ² = 0,5кг(15м/с)²/(0,1м)²=112,5Н/0,01м=11250Н/м.

Відповідь: k=11250Н/м.

Задача 3. Визначити швидкість вильоту кульки масою m з дула пружинного пістолета при горизонтальному пострілі, якщо жорсткість пружини k, а її деформація Δℓ.

Дано:

m

k

Δℓ

v= ?

Рішення. Виконуємо малюнок на якому вказуємо енергетичні параметри системи пружина-кулька до та після пострілу.

до пострілу:       Е_к = 0,               Е_п = kΔℓ²/2;

після пострілу:  Е_к = mv²/2,        Е_п = 0.

У відповідності з законом збереження (∑Е_до = ∑Е_після), можна записати:

0 + kΔℓ²/2 = mv²/2 + 0, звідси kΔℓ² = mv², звідси v = √(kΔℓ²/m) = Δℓ√k/m

Відповідь: v = Δℓ√k/m.

Контрольні запитання.

1. Яку енергію називають потенціальною?
2. В загальному випадку визначальне рівняння потенціальної енергії можна записати у вигляді Е_п=? Що це означає?
3. Які різновидності потенціальної енергії вивчають в механіці? Які визначальні рівняння цих енергій?
4. Результатом яких взаємодій є потенціальна енергія сили тяжіння?
5. Результатом яких взаємодій є потенціальна енергія сили пружності?
6. Камінь кинули вертикально вгору. Які перетворення енергії відбуваються в процесі його польоту? Чи буде кінетична енергія каменя в момент його вильоту та момент падіння абсолютно однаковою? Чому?
7. Коли ми стверджуємо, що шматок вугілля має певну енергію, то що це означає? Якою (кінетичною чи потенціальною) є ця енергія?
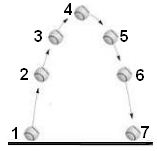
8. Які перетворення енергії відбуваються в зображених на малюнку ситуаціях?

 

Вправа №36.

1. Визначте потенціальну енергію молота масою 200кг піднятого на висоту 3м.
2. Літак Ан-22 загальною масою 200т летить на висоті 12км. Визначте величину його потенціальної енергії.
3. Пружину жорсткістю 400Н/м стиснули на 10см. Визначте потенціальну енергію деформованої пружини.
4. Під дією вантажу 200кг пружина деформувалась на 5см. Визначте енергію деформованої пружини.
5. Тіло масою 200г кинули вертикально вгору зі швидкістю 15м/с. Якою буде кінетична і потенціальна енергія цього тіла на висоті 5м?
6. На яку максимальну висоту підніметься тіло, якщо його кинули вертикально вгору з швидкістю 10м/с?
7. Визначте потенціальну і кінетичну енергію тіла масою 4кг, що вільно падає з висоти 6м, на відстані 2м від поверхні землі.

.

§37. Розв’язування задач. Тема: Енергетичний метод розв’язування задач.

Однозначно класифікувати різноманіття тих задач які вирішуються в механіці, надзвичайно складно. І тим не менше можна виділити три базові методи розв’язування цих задач: кінематичний, силовий та енергетичний (точніше імпульсно-енергетичний).

Суть кінематичного методу розв’язування задач полягає в тому, що невідомі величини визначають на основі аналізу кінематичних параметрів руху тіла (час, координата, пройдений шлях, швидкість, прискорення) та їм відповідних визначальних рівнянь, і на базі того закону, який називається рівнянням руху. Закону в якому стверджується: в загальному випадку прямолінійний рух тіла (матеріальної точки) описується рівняння x = x₀ + v₀t + (a/2)t².

Суть силового методу розв’язування задач полягає в тому, що невідомі величини визначають на основі аналізу діючих на тіло сил та визначальних рівнянь цих сил, і на базі тих законів які називаються:

умова механічної рівноваги тіла: якщо а = 0, то ∑F = 0;

умова динамічної рівноваги тіла: якщо а ≠ 0, то ∑F + F_i = 0.

Суть енергетичного методу розв’язування задач полягає в тому, що невідомі величини визначають на основі аналізу енергетичних параметрів руху тіла (енергія, робота, потужність, ККД) і їм відповідних визначальних рівнянь, та на базі того закону який називається законом збереження енергії. Закону в якому стверджується: при будь-яких процесах що відбуваються в замкнутій системі, загальна кількість енергії цієї системи залишається незмінною: ∑Е_до = ∑Е_після, (загальна кількість енергії системи до події, має дорівнювати загальній кількості енергії цієї системи після події)

З основами кінематичного та силового методів розв’язування задач ви вже знайомі. На разі ж поговоримо про ті задачі, які розв’язуються енергетичним методом. А оскільки нема кращого способу навчитися розв’язувати задачі, як практично розв’язувати їх, то власне цим і займемося.

Загальні зауваження. В реальних процесах завжди присутні ті чи інші енергетичні втрати. Наприклад в процесі падіння тіла, частина його кінетичної енергії неминуче йде на подолання сил опору повітря (перетворюється на теплоту). Однак в переважній більшості задач розглядаються ідеалізовані (спрощені) ситуації. Ситуації в яких енергетичні втрати не враховуються. Тому якщо в умові задачі нема прямої вимоги враховувати енергію енергетичних втрат, то прийнято вважати, що ці втрати є нульовими.

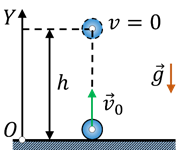
Задача 1. На яку максимальну висоту підніметься тіло, якщо його кинули вертикально вгору з швидкістю 10м/с?

Дано :

v₀ = 10 м/с

h_max = ?

Рішення. На основі аналізу умови задачі виконуємо малюнок на якому вказуємо енергетичні параметри тіла в початковий та кінцевий моменти часу: на висоті h = 0:       E_k = mv₀²/2;    E_п = 0;

на висоті h = h_max:   E_k = 0;             E_п = mgh_max.

У відповідності з законом збереження (∑Е_до = ∑Е_після), можна записати:

mv₀²/2 + 0 = 0 + mgh_max, звідси  v₀²/2 = gh_max, звідси h_max = v₀²/2g.

Розрахунки: h_max = v₀²/2g = (10м/с)²/2·10(м/с²) = 5м

Відповідь:  h_max=5м.

Задача 2. Тіло що знаходиться на висоті 10м, кинули вертикально вниз з швидкістю 10м/с. Визначити швидкість тіла в момент його падіння на землю.

Дано:

h = 10м

v₀ = 10м/с

v = ?

Рішення. На основі аналізу умови задачі виконуємо малюнок на якому вказуємо енергетичні параметри тіла в початковий та кінцевий моменти часу: на висоті h:        E_k = mv₀²/2;     E_п = mgh ;

на висоті h = 0:  E_k = mv²/2;      E_п = 0.

У відповідності з законом збереження (∑Е_до = ∑Е_після), можна записати:

mv₀²/2 + mgh = mv²/2, звідси v₀²/2 + gh = v²/2, звідси v² = 2(v₀²/2 + gh), звідси v = √2(v₀²/2 + gh).

Розрахунки: v = √2(v₀²/2 + gh) = √2[(10м/с)²/2 + 10(м/с²)∙10м] = √(300м²/с²) = 17,3м/с.

Відповідь: v = 17,3м/с.

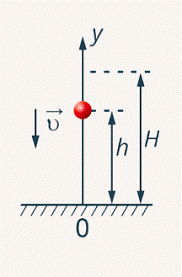
Задача 3. З якою початковою швидкістю v₀ потрібно кинути вниз м’яч з висоти h, щоб він підстрибнув на вдвічі більшу висоту H=2h? Удар об землю вважати абсолютно пружним.

Дано:

h

   H=2h

v₀=?

Рішення. На основі аналізу умови задачі виконуємо малюнок на якому вказуємо енергетичні параметри тіла в початковий та кінцевий моменти часу: на висоті h:        E_k = mv₀²/2;     E_п = mgh;

на висоті 2h:      E_k = 0;               E_п = 2mgh.

Оскільки абсолютно пружний удар не супроводжується втратами механічної енергії, то у відповідності з законом збереження (∑Е_до = ∑Е_після), можна записати:  mv₀²/2 + mgh = 2mgh, звідси mv₀²/2 = mgh, звідси v₀² = 2gh, звідси v₀ = √(2gh).

Відповідь: v₀ = √(2gh).

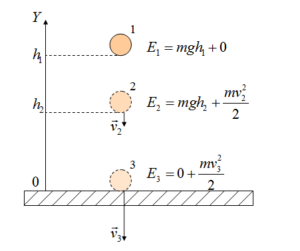
Задача 4. Тіло масою 1кг починає падати на поверхню землі з висоти 20м. На якій висоті кінетична енергія тіла дорівнюватиме 50Дж?

Дано:

m = 1кг

h₁=20м

v₁=0м/с

E_к2=50Дж

h₂ = ?

Рішення. На основі аналізу умови задачі виконуємо малюнок на якому вказуємо енергетичні параметри тіла на висоті h₁ і h₂ .

на висоті h₁:    E_к = 0;         E_п = mgh₁,

на висоті h₂:    E_к2 = 50Дж;  E_п = mgh₂.

У відповідності з законом збереження (∑Е_до = ∑Е_після), можна записати:

mgh₁ = E_к2 + mgh₂, звідси mgh₂ = mgh₁ – E_к2,

звідси h₂ = (mgh₁ – E_к)/mg = h₁ – E_к/mg.

Розрахунки: h₂ = 20м – 50Дж/1кг10м/с² = 20м – 5м = 15м.

Відповідь: h₂ = 15м.

Задача 5. Тіло кинули вертикально вгору зі швидкістю 20м/с. На якій висоті його кінетична енергія дорівнюватиме потенціальній?

Дано:

v₀=20м/с

E_k = E_п

h = ?

Рішення. На основі аналізу умови задачі виконуємо малюнок на якому вказуємо енергетичні параметри тіла в початковий та кінцевий моменти часу: на висоті h = 0:   E_к = mv₀²/2;    E_п = 0;

на висоті h:         E_к = mv²/2      E_п = mgh, а оскільки на висоті h, mv²/2 = mgh, то можна записати, що на цій висоті mv²/2 + mgh = 2mgh.

Таким чином, у відповідності з законом збереження (∑Е_до = ∑Е_після), можна записати:  mv₀²/2 + 0 = 2mgh, звідси h = v₀²/4g.

Розрахунки h = v₀²/4g = (20м/с)²/4·10м/с² = 10м.

Відповідь: h = 10м.

Варто зауважити, що одну і ту ж задачу динаміки можна розв’язати різними методами, наприклад енергетичним або кінематичним, чи енергетичним або силовим. При цьому зазвичай енергетичний метод розв’язування задач є найбільш ефективним. Цю ефективність проілюструємо на конкретному прикладі.

Задача 6. Тіло масою 1кг падає з висоти 20м. Визначити кінетичну енергію тіла в момент падіння.

Дано:

m = 1кг

h = 20м

Е_к = ?

Кінематичне рішення. За визначенням Е_к = mv²/2, де v = ?

При рівноприскореному русі v = v₀ + gt, в умовах нашої задачі v₀ = 0, тому v =  gt,  де t = t_пад = ?

Визначаючи час падіння тіла запишемо рівняння руху цього тіла, тобто формулу яка має вигляд h = h₀ + v₀t + (g/2)t². Оскільки в умовах даної задачі h₀ = 0м; v₀ = 0м/с, то h = (g/2)t², звідси t² = 2h/g, звідси

t = √2h/g = √(2∙20(м/с)/10(м/с²)) = √4с² = 2с.

Таким чином, v = gt = 10(м/с²)∙2с = 20м/с,

Е_к = mv²/2 = 1кг∙(20м/с)²/2 = 200Дж.

Відповідь: Е_к = 200Дж.

Енергетичне рішення. На основі аналізу умови задачі виконуємо відповідний малюнок, на якому вказуємо енергетичні параметри системи на висоті h = h_мах та h = 0.

на висоті h = h_мах :  Е_п = mgh,   Е_к = 0;

на висоті  h = 0 :     Е_п = 0,         Е_к = mv²/2.

У відповідності з законом збереження (∑Е_до = ∑Е_після), можна записати:

mgh + 0 = 0 + Е_к, звідси Е_к = mgh = 1кг∙10(м/с²)∙20м = 200Дж

Відповідь: Е_к = 200Дж.

Вправа №37.

1. Тіло масою 400г кинули вертикально вгору зі швидкістю 20м/с. Визначте кінетичну і потенціальну енергію тіла на висоті 10м.
2. З якою вертикальною швидкістю потрібно кинути тіло, щоб воно піднялось на висоту 10м?
3. В пружинному пістолеті жорсткість пружини 100Н/м. З якою швидкістю вилітатиме з нього кулька масою 3г, якщо пружина стиснута на 10см? Розташування пістолета горизонтальне.
4. Тіло масою 500г, кинуте вертикально вгору зі швидкістю 20м/с, впало на землю зі швидкістю 16м/с. Визначити величину енергетичних втрат в процесі польоту тіла.
5. Тіло масою 200г рухаючись з швидкістю 20м/с стикається з пружиною жорсткість якої 100Н/м. На скільки деформується пружина після взаємодії з цим тілом?
6. З якою початковою швидкістю потрібно кинути вниз м’яч з висоти 5м, щоб він відбившись від пружної поверхні, підскочив на вдвічі більшу висоту?
7. Тіло масою кинули вертикально вгору зі швидкістю 12м/с. На якій висоті швидкість руху тіла зменшиться вдвічі?

.

§38. Робота. Механічна робота.

 

В науковій практиці термін «робота» має два значення: робота, як певна енергозатратна подія і робота, як певна фізична величина. Наприклад, коли ми стверджуємо, що піднімаючи стілець учень виконує роботу, то маємо на увазі певну подію. А коли говоримо, що піднімаючи стілець учень виконав роботу величиною 40Дж, то маємо на увазі фізичну величину яка певним чином характеризує виконану роботу.

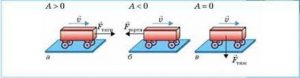
Загалом, виконання роботи нерозривно пов’язано по-перше з передачею енергії від одного тіла до іншого, а по-друге, з перетворенням енергії з одного виду в інший. Наприклад, в процесі вільного падіння тіла (мал.96а), енергія сили тяжіння Землі передається тілу, при цьому потенціальна енергія тіла перетворюється на його кінетичну енергію. В процесі взаємодії того тіла що рухається з тілом яке не рухається (мал.96б), енергія від рухомого тіла передається до нерухомого, при цьому кінетична енергія рухомого тіла спочатку перетворюється на потенціальну енергію пружної взаємодії тіл, а потім в кінетичну енергію нерухомого тіла. В процесі стиснення пружини (мал.98в), м’язова енергія руки передається пружині та перетворюється на її потенціальну енергію. Коли ж пружина випрямляється і штовхає тіло, то її потенціальна енергія передається тілу та перетворюється на його кінетичну енергію.

Мал.96. Виконання роботи нерозривно пов’язане з переходом енергії від одного тіла до іншого та з перетворенням одного виду енергії в інший.

В подальшому, терміном «робота» ми будемо позначати відповідну фізичну величину. Виходячи з цього дамо лише одне визначення терміну «робота».

Робота – це фізична величина, яка характеризує затрати енергії на виконання роботи, тобто певної енергозатратної дії і яка дорівнює цим затратам.

Позначається: А

Визначальне рівняння: А = ΔЕ

Одиниця вимірювання: [А] = Дж,   джоуль.

Формула А = ΔЕ = Е_кінц – Е_поч, по-перше вказує на універсальний спосіб визначення (вимірювання) роботи, а по-друге, на факт того, що процес виконання будь якої роботи нерозривно пов’язаний з затратами енергії.

Із аналізу визначень, енергія – характеризує здатність виконати роботу; робота – характеризує затрати енергії на виконання роботи, з усією очевидністю випливає, що ці величини є дуже схожими та взаємопов’язаними. Якщо ж говорити про ті відмінності які існують між роботою та енергією, то вони полягають в наступному.

По перше робота характеризує певну конкретну подію, а енергія є загальною характеристикою всіх подій, і в цьому сенсі, енергія є більш загальною величиною. По друге, робота характеризує лише ту частину енергії яка йде на виконання певної конкретної дії (певної роботи). Енергія ж характеризує загальну здатність фізичного об’єкту до виконання енергозатратної дії, не вказуючи при цьому яким чином ця здатність буде реалізована. Крім цього, робота характеризує дію яка вже виконана або буде виконана. Енергія ж характеризує саму здатність виконати роботу, не вказуючи де, коли і як ця здатність буде реалізована.

Формула А = ΔЕ є базовим, визначальним рівнянням роботи. Однак, якщо мова йде про механічну роботу, то її часто визначають за формулою А = F∙s∙cosα, де F – усереднена величина тієї сили що виконує роботу, s – величина того переміщення яке відбувається під дією даної сили, α – кут між напрямком вектора сили (F) та напрямком вектора переміщення (s).

Загальні зауваження. Якщо ви не знаєте, що називають косинусом кута α (cosα = ?), то просто запам’ятайте: cos0° = 1, cos90° = 0, cos180° = –1.

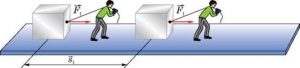
Мал.96. Якщо під дією сили F тіло перемістилось на відстань s то виконана цією силою робота дорівнює А = F∙s∙cosα.

Аналіз формули А = F∙s∙cosα вказує на те, що механічна робота виконується за умови виконання трьох вимог: 1) наявність діючої на тіло сили (F); 2) наявність переміщення тіла (s); 3) кут між напрямком дії сили та напрямком переміщення не повинен дорівнювати 90° (для α = 90°, соsα = 0 і тому А = F∙s∙cos90° = 0).

Наприклад, якщо ви штовхаєте важке тіло, а воно залишається на місці (мал.97а), то роботу по механічному переміщенню тіла ви не виконуєте. Не виконуєте тому, що переміщення тіла дорівнює нулю (s = 0), а отже А = F∙s∙cosα = 0. Можливо ви виконуєте якусь іншу роботу, скажімо роботу по деформації поверхні тіла, або роботу по розігріву своїх м’язів, але роботу по механічному переміщенню тіла ви не виконуєте.

Механічна робота не виконується і в тому випадку, коли тіло не зустрічаючи жодного опору з боку зовнішніх сил рухається за інерцією (мал.97б). Адже в цьому випадку рух тіла фактично відбувається без дії зовнішньої сили (F = 0) і тому А = F∙s∙cosα = 0. Звичайно, таке тіло має певний запас кінетичної енергії. Однак в процесі рівномірного руху ця енергія не змінюється і не передається іншим тілам, а отже і не призводить до виконання певної роботи. Лише в тому випадку коли рухоме тіло відчує протидію зовнішніх сил, наприклад сили тертя чи сили пружності зустрічної перешкоди, воно виконуватиме певну роботу.

Механічна робота не виконується і в тому випадку, коли діюча на тіло сила є перпендикулярною до напрямку переміщення тіла. Наприклад, в процесі обертання штучного супутника навколо Землі (мал.97в), діюча на супутник гравітаційна сила не виконує механічної роботи. Не виконує тому, що кут між напрямком дії цієї сили і напрямком руху супутника становить 90°, а сos90° = 0, і тому А = F∙s∙cosα = 0

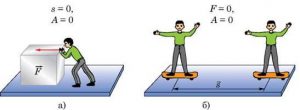
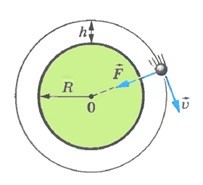
s = 0                                 F = 0                                   cosα = 0

Мал.97. Ситуації в яких механічна робота не виконується.

Механічна робота може бути як додатною так і від’ємною. При цьому, якщо напрям діючої на тіло сили співпадає з напрямком переміщення тіла, то робота відповідної сили є додатною (α = 0°, соs0° = 1, А = F∙s∙cos∙1 = +; сила сприяє переміщенню тіла).  Якщо ж напрям діючої на тіло сили протилежний до напрямку його переміщення, то робота відповідної сили є від’ємною (α = 180°, соs180° = –1, А = F∙s∙cos∙(–1) = –;  сила протидіє переміщенню тіла). Наприклад робота сили тертя завжди від’ємна.

Варто зауважити, що робота однієї і тієї ж сили може бути як додатною, так і від’ємною. Наприклад, коли ви відпускаєте яблуко і воно під дією сили тяжіння падає на землю, то сила тяжіння виконує додатну роботу (сприяє переміщенню яблука). Якщо ж ви піднімаєте яблуко, то сила тяжіння протидіє переміщенню яблука і тому виконує від’ємну роботу.

Власне аналогічні результати випливають не лише з логічних міркувань, а й з формули А = F∙s∙cosα. Дійсно, якщо під дією сили тяжіння яблуко падає вниз, то α = 0°, cos0° = 1 і тому A = mg∙h∙cos0° = mgh. Якщо ж всупереч дії сили тяжіння яблуко піднімається вгору, то кут між напрямком дії сили тяжіння та напрямком руху тіла дорівнює 180° і тому: α = 180°, cos180° = –1 а отже A = mghcos180° = –mgh.

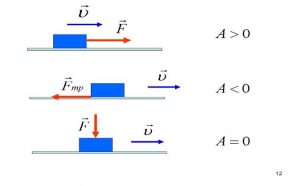
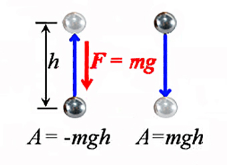
Мал.98. Механічна робота може бути як додатною так і від’ємною.

На завершення зауважимо, що в формулі A = Fscosα символом F позначають середнє значення діючої на тіло сили (середнє на ділянці переміщення s). Тому, якщо наприклад, на ділянці виконання роботи, величина діючої на тіло сили лінійним чином змінюється від F₁ до F₂, то визначаючи виконану роботу, в якості діючої на тіло сили потрібно обирати F = (F₁+F₂)/2.

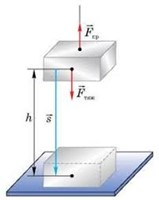
Задача 1. Підйомний кран з постійною швидкістю піднімає вантаж масою 3т на висоту 10м. Яку роботу виконує сила тяги крана? Яку роботу виконує сила тяжіння?

Дано:

m = 3т = 3000кг

h = 10м

v = const

А_кр = ?

А_т = ?

Рішення. Роботу механічної сили можна визначити за формулою A = F∙s∙cosα. Оскільки рух вантажу є рівномірним, то діючі на нього  сила тяжіння F_т = mg і сила тяги крану F_кр, є рівними за величиною і протилежними за напрямком (F_кр = F_т = mg).

Оскільки рух вантажу відбувається в напрямку дії сили тяги, то для цієї сили α = 0°, cos0° = 1 і тому A_кр = mg∙h∙1 = 3000кг∙10(м/с²)∙10м = 300000Н = 300кДж. Для сили тяжіння α = 180°, cos180° = –1 і тому A_т = mg∙h∙(–1) = – 3000кг∙10(м/с²)∙10м = –300000Дж = –300кДж.

Відповідь: А_кр = 300кДж,  А_т = –300кДж.

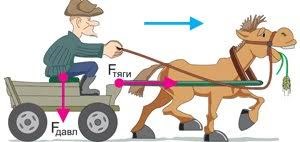
Задача 2. Кінь рівномірно везе віз зі швидкістю 0,8м/с, прикладаючи зусилля 400Н. Яка робота виконується при цьому за 1год?

Загальні зауваження. Якщо в умові задачі чітко не вказаний напрям тієї сили яка виконує роботу, то вважається, що цей напрям співпадає з напрямком переміщення тіла (α = 0°, cos0° = 1).

Дано:

v = 0,8м/с

F_тяги = 400Н

t = 1год = 3600с

А_тяги = ?

Рішення. Роботу механічної сили можна визначити за формулою A = F∙s∙cosα. В умовах нашої задачі F = F_тяги, s = v∙t, cosα = 1. Тому А_тяги = F_тяги∙ v∙t∙1 = 400Н∙0,8(м/с)∙3600с = 1152000Дж = 1152кДж.

Відповідь: А_тяги = 1152кДж.

Задача 3. Швидкість вільно падаючого тіла масою 2кг, на певній ділянці шляху збільшилась з 2м/с до 10м/с. Визначте роботу сили тяжіння на цьому шляху.

Дано:

m = 2кг

v_п = 2м/с

v_к = 10м/с

A = ?

Рішення. Оскільки за визначенням А = ΔЕ та враховуючи, що в процесі падіння тіла його кінетична енергія збільшилася від Е_кп = mv_п²/2, до Е_кк = mv_к²/2, можна записати А = ΔЕ = mv_к²/2 – mv_п²/2 = m(v_к² – v_п²)/2 = 2кг(10² – 2²)(м²/с²)/2 = 96Дж.

Відповідь: А = 96Дж

Контрольні запитання.

1. Які значення має термін «робота» у фізиці?
2. Якими процесами супроводжується виконання роботи?
3. Які енергетичні перетворення відбуваються в процесі: а) вільного падіння тіла; б) стиснення пружини.
4. Який термін «робота» чи «енергія» є більш загальним? Чому?
5. Наведіть приклади того, коли діюча на тіло сила не призводить до виконання механічної роботи.
6. В якому випадку робота сили є додатною, а в якому від’ємною?
7. Робота якої сили завжди від’ємна?
8. Тіло підкинули вертикально вгору і піймали в тій же точці. Яку загальну роботу виконала при цьому сила тяжіння?

Вправа №38.

1. Яка робота виконується при підніманні тіла масою 4кг на висоту 150см?
2. Автокран, піднімаючи вантаж масою 1,5т виконав роботу 22,5кДж. На яку висоту піднято при цьому вантаж?
3. Яку роботу виконує сила тяжіння в процесі падіння дощової краплі масою 20мг з висоти 2км?
4. З греблі щохвилини падає 18000м³ води з висоти 20м. Яка при цьому виконується робота?
5. Пружину жорсткістю 600Н/м деформували на 10см. Визначити величину виконаної при цьому роботи.
6. Яку роботу треба виконати, щоб змусити автомобіль масою 2т збільшити свою швидкість від 0 до 36км/год? Опором рухові знехтувати?
7. Вантаж масою 3кг вільно падає зі стану спокою протягом 2с. Яку роботу виконує при цьому сила тяжіння?

.

§39. Енергетичний та силовий методи визначення роботи.

На перший погляд, формули А = ΔЕ і А = F∙s∙cosα є абсолютно різними. Насправді ж мова йде про споріднені і в певному сенсі тотожні формули. Різниця між ними лише в тому, що перша (А = ΔЕ) дозволяє визначати роботу енергетичним методом, а друга (А = F∙s∙cosα) – силовим. Ілюструючи та перевіряючи фізичну тотожність формул А = ΔЕ і А = F∙s∙cosα, а заодно і порівнюючи силовий та енергетичний методи розв’язування задач, розглянемо декілька конкретних прикладів.

Задача 1. Під дією сили тяжіння тіло масою m падає з висоти h на землю. Визначити величину виконаної при цьому роботи.

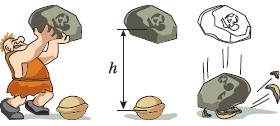
Дано:

m

h

g

А=?

Енергетичне рішення. Оскільки в процесі виконання роботи (в процесі падіння тіла) величина потенціальної енергії тіла змінилась від Е_п = mgh  до Е_п = 0, то А = ΔЕ = 0 – mgh = –mgh, де знак  “ – “ вказує на те, що в процесі виконання роботи потенціальна енергія тіла зменшилася.

Відповідь: А = mgh.

Силове рішення. Виходячи з того що дану роботу виконує постійна за величиною сила тяжіння F = mg, та враховуючи що напрям цієї сили співпадає з напрямком переміщення тіла (α = 0°; соs0° = 1) можна записати: А = F∙s∙cosα =  mg∙h∙1 = mgh.

Відповідь: A = mgh.

Задача 2. Горизонтально розташована та деформована на величину Δℓ пружина жорсткістю k, штовхає тіло. Визначити величину виконаної при цьому роботи.

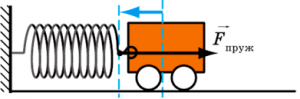
Дано:

Δℓ

k

А=?

Енергетичне рішення. Оскільки в процесі виконання роботи, величина потенціальної енергії пружини змінилась від Е_п = kΔℓ²/2  до  Е_п = 0,  то А = ΔЕ = 0 –  kΔℓ²/2 = – kΔℓ²/2, де знак “ – “ вказує на те, що в процесі виконання роботи, величина потенціальної енергії пружини зменшилася.

Відповідь:  А = kΔℓ²/2 .

Силове рішення. Оскільки в процесі виконання роботи величина діючої на тіло сили пружності лінійним чином змінюється від максимальної величини (F = kΔℓ) до нуля (F = 0), то усереднена величина цієї сили становитиме F_c = kΔℓ/2. А враховуючи що напрям сили пружності співпадає з напрямком переміщення (α = 0°; соs0° = 1), можна записати: A = F_c ∙s∙cosα = (kΔℓ/2)∙Δℓ∙1 = kΔℓ²/2.

Відповідь:   A = kΔℓ²/2.

Таким чином, в багатьох ситуаціях величину виконаної механічної роботи з практично однаковим успіхом можна визначити як за формулою А = ΔЕ, так і за формулою А = F∙s∙cosα. Однак потрібно мати на увазі, що в формулі А = F∙s∙cosα  знак результату вказує на те, яку роботу (додатну чи від’ємну) виконує відповідна сила. В формулі ж А = ΔЕ, знак результату говорить про те, як змінюється (збільшується чи зменшується) відповідна енергія в процесі виконання роботи.

На питання ж про те, а який метод розв’язування задач динаміки є більш ефективним, може відповісти лише практика розв’язуванні відповідних задач. Бо в одних випадках більш ефективним, а то і єдино можливим є енергетичне рішення задачі, а в інших – навпаки.

Задача 3. Тіло масою 2кг падає з висоти 10м, при цьому в момент падіння на землю його швидкість становить 13м/с. Визначити роботу сили опору повітря.

Дано:

m = 2кг

h = 10м

v_к = 13м/с

А_оп = ?

Рішення. Виходячи з того, що в початковий момент часу Е_к = 0, Е_п = mgh, а в кінцевий момент Е_к= mv_к²/2, Е_п = 0,  визначаємо числові значення відповідних енергій:

Е_поч = mgh = 2кг∙9,8(м/с²)∙10м = 196Дж;

Е_кінц = mv_к²/2 = 2кг∙(13м/с)²/2 = 169Дж.

Оскільки величина початкової енергії тіла (Е_поч = 196Дж) більша за величину його кінцевої енергії (Е_кінц = 169Дж), то це означає, що в процесі падіння, частина енергії тіла пішла на подолання сил опору повітря, і що робота цих сил має дорівнювати різниці між початковим і кінцевим значенням енергії тіла, тобто А_оп = 196Дж – 169Дж = 27Дж.

Відповідь: А_оп = 27Дж.

Задача 4. Автомобіль сила тяги якого 2кН, їде горизонтальною ділянкою дорогою з швидкістю 72км/год. Яку роботу за 10хв руху виконують: сила тяги автомобіля, сила тертя (сила опору руху автомобіля), сила тяжіння?

Дано:

F_тяги = 2кН = 2000Н

v = 72км/год = 20м/с

t = 10хв = 600с

А_тяги = ?  А_тер = ?   А_тяж = ?

Рішення. Роботу механічної сили можна визначити за формулою A = F∙s∙cosα, де α – кут між напрямком відповідної сили та напрямком руху тіла. В умовах нашої задачі: 1) s = v∙t = 20(м/с)∙600с = 12000м; 2) Для F_тяги, α = 0°, соs0° = 1; для F_тер, α = 180°, соs180° = –1; для F_тяж, α = 90°, соs90° = 0; 3) Оскільки автомобіль рухається з постійною швидкістю, то можна стверджувати, що F_тер = F_тяги = 2000Н. Таким чином:

A_тяги = F_тяги∙s∙cos0° = 2∙10³Н∙12∙10³(м)∙1 = 24∙10⁶Дж;

A_тер = F_тер∙s∙cos180° = 2∙10³Н∙12∙10³(м)∙(–1) = – 24∙10⁶Дж;

A_тяж = F_тяж∙s∙cos90° = F_тяж∙s∙0 = 0Дж.

Відповідь: A_тяги = 24∙10⁶Дж;  A_тер = – 24∙10⁶Дж;  A_тяж = 0Дж.

Задача 5. Яку роботу треба виконати, щоб підняти вантаж масою 20кг на висоту 5м з прискоренням 1м/с²?

Дано:

m = 20кг

h = 5м

а = 1м/с²

А = ?

Рішення. На перший погляд здається, що оскільки в процесі підйому тіла, величина його потенціальної енергії збільшилась від 0 до mgh, то величину виконаної роботи можна визначити за формулою А = ∆Е = mgh – 0 = mgh. Таке рішення є неправильним. Адже в умовах даної задачі, та сила яка виконувала роботу долала опір не лише сили тяжіння F_т = mg, а й сили інерції F_і = ma.

В подібних ситуаціях, силовий метод визначення роботи є більш надійним. А у відповідності з цим методом А = F∙s∙cosα, де F – та сила яка виконує роботу і яка чисельно дорівнює сумі сили тяжіння та сили інерції F = F_т + F_і = mg + ma = m(g+a).  s = h, α=0°, cos0° = 1, тому: A = F∙s∙cosα = m(g+a)h.

Розрахунки: A = m(g+a)h = 20кг∙(10м/с²+1м/с²)∙5м = 1100Дж.

Відповідь: А = 1100Дж.

Задача 6. Пружину жорсткістю 400Н/м деформували на 15см. Визначити величину виконаної при цьому роботи.

Дано:

k = 400Н/м

Δℓ = 15см = 0,15м

A = ?

Рішення. Оскільки за визначенням А = ΔЕ та враховуючи, що в процесі стиснення  пружини величина її потенціальної енергії змінилась від Е_пп = 0Дж до Е_пк = kΔℓ²/2 = 400(Н/м)∙(0,15м)²/2 = 4,5Дж, можна записати А = ΔЕ = Е_пк – Е_пп = 4,5Дж – 0Дж = 4,5Дж.

Відповідь: А = 4,5Дж.

Задача 7. Під дією сили 20Н тіло рухається за законом х = 10 + 2t + 0,5t². Яку роботу виконує ця сила за 10с руху тіла?

Дано:

F = 20

х = 10 + 2t + 0,5t²

t = 10c

A = ?

Рішення. Із аналізу рівняння руху ясно, що рух тіла є рівноприскореним (), і що тому діюча на тіло сила направлена в напрямку руху тіла (α = 0°, соs0° = 1). Оскільки A = F∙s∙cosα, та враховуючи, що s = x – x₀ = 10 + 2t + 0,5t² – 10 = 2t + 0,5t², можна записати s(10) = 2∙10 + 0,5∙10² = 20 + 50 = 70м.

Таким чином, A = F∙s∙cosα = 20Н∙70м∙1 = 1400Дж.

Відповідь: А = 1400Дж.

Вправа №39.

1. Яку роботу виконує сила тяжіння в процесі падіння тіла масою 2кг з висоти 3м?
2. Яку роботу виконує сила пружності при розтягуванні пружини жорсткістю 1000Н/м на 6см?5
3. Під дією якої сили виконується робота 200кДж на шляху 0,8км?
4. Автокран, піднімаючи вантаж масою 1,5т виконав роботу 60кДж. На яку висоту піднято при цьому вантаж?
5. М’яч масою 0,5кг падає з висоти 10м, при цьому в момент падіння на землю його швидкість становить 10м/с. Визначити роботу сили опору повітря.
6. Яку роботу треба виконати, щоб підняти вантаж масою 3кг на висоту 2м з прискоренням 4м/с²?
7. Вантаж масою 2кг вільно падає протягом 2с. Яку роботу виконує при цьому сила тяжіння?
8. Під дією сили 20Н тіло рухається за законом х = 100 – 5t – 0,5t². Яку роботу виконує ця сила за 10с руху тіла?

.

§40. Потужність.

 

         Напевно ви погодитесь з тим, що одну і ту ж роботу можна виконувати з різною швидкістю. Скажімо екскаватор риє траншею набагато швидше за робітника з лопатою, трактор оре землю значно швидше ніж плуг запряжений конем, а той в свою чергу швидше за селянина який тягне соху. Характеризуючи швидкість виконання роботи, тобто кількість роботи виконану за одиницю часу, говорять про потужність.

Мал.99. Одну і ту ж роботу можна виконувати з різною швидкістю.

Потужність – це фізична величина, яка характеризує швидкість виконання роботи і яка дорівнює відношенню виконаної роботи (А) до того проміжку часу (t) за який ця робота була виконана.

Позначається: N (або Р)

Визначальне рівняння: N = А/t

Одиниця вимірювання: [N] = Дж/с = Вт,    ват.

Ват – це одиниця вимірювання потужності, яка дорівнює такій потужності при якій за одну секунду виконується робота в один джоуль. Скажімо, якщо ви візьмете в руку вантаж масою 102г то відчуєте силу в один ньютон. Якщо цей вантаж ви піднімете на один метр – то виконаєте роботу в один джоуль. А якщо цю роботу ви виконаєте за одну секунду – то розвинута вами середня потужність становитиме один ват.

Одиниця потужності (ват) названа на честь англійського винахідника Джеймса Ватта  (1736-1819), який в 1776 році створив перший автоматизований тепловий двигун (парову машину). До речі, саме Ватт в якості одиниці вимірювання потужності запропонував кінську силу. Кінська сила – це позасистемна одиниця вимірювання потужності, яка дорівнює такій потужності при якій тіло масою 75кг піднімається на висоту 1м за 1с:  1к.с. = 735,5Вт.

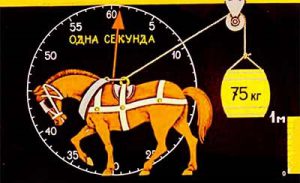
Мал.100. Кінська сила – позасистемна одиниця вимірювання потужності.

Формула N = А/t є базовим визначальним рівнянням потужності. Однак якщо мова йде про потужність тих приладів які виконують механічну роботу (А = F∙s∙cosα), то для них формула потужності набуває вигляду:

N = А/t = F∙s∙cosα/t = F∙v∙cosα.  Тобто N = F∙v∙cosα ,

де F – усереднене значення тієї сили що виконує роботу;

v – швидкість того тіла що рухається під дією сили F;

α – кут між напрямком дії сили та напрямком руху тіла.

Зазвичай α = 0° і тому N=F∙v.

Таким чином, механічна потужність приладу, наприклад автомобіля, визначається добутком тієї тягової сили що змушує прилад рухатись на швидкість його руху. Знаючи даний факт, не важко збагнути, як це так виходить, що великий трактор і легковий автомобіль мають однакову потужність. Правильно, трактор – сильний але повільний, натомість легковик – слабкий але швидкий. Втім, той же трактор чи той же автомобіль, маючи один і той же двигун, на різних передачах можуть мати дуже різну величину як сили так і швидкості. Скажімо перша передача, забезпечує максимальну силову тягу при мінімальній швидкості руху. Четверта ж передача навпаки, забезпечує максимальну швидкість руху при мінімальній тяговій силі.

Прийнято вважати, що потужність середньо статистичної людини при її спокійній ходьбі близька до 75Вт. Звісно, ця величина є досить умовною. Адже якщо наприклад важкоатлет за 1,5с піднімає штангу масою 150кг на висоту 2м, то він розвиває потужність  N = mg∙s/t = 150кг∙10(м/с²)∙2м/1,5с = 2000Вт.   Загалом же потужність живих організмів є надзвичайно різноманітною. Скажімо, потужність хатньої мухи близька до 1мкВт = 1∙10^{– 6}Вт, а потужність слона приблизно дорівнює 200кВт = 2∙10⁵Вт.

Потужність рукотворних приладів більш прогнозована і може становити від декількох нановат (нВт = 10^–9Вт) до сотень гігават (ГВт = 10⁹Вт). Наприклад, потужність пружинного механізму наручного годинника близька до 1∙10^–7Вт, а загальна потужність двигунів ракетоносія «Енергія» – 125∙10⁹Вт.

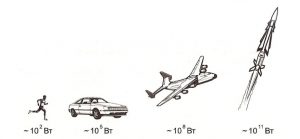
Мал.101. Масштаб потужностей деяких приладів.

Задача 1. Гиря маятникового годинника має масу 0,8 кг і за добу опускається на 110см. Яка потужність годинникового механізму?

Дано:

m = 0,8кг

t = 1доба = 86400с

h = 110см = 1,1м

N = ?

Рішення. За визначенням N = A/t. Будемо виходити з того, що джерелом тієї роботи яку виконує годинниковий механізм є та енергія яку отримує цей механізм в процесі опускання гирі і яка дорівнює А = F_т∙h = mgh. Таким чином N = mgh/t.

Розрахунки: N = mgh/t = 0,8·10∙1,1/86400 = 0,0001Вт.

[N] = кг∙(м/с²)∙м/с = кг∙м²/с³ = Вт.

Відповідь N = 0,0001Вт.

Загальні зауваження. Нагадаємо: [N] = Вт = Дж/с = Н∙м/с = кг∙(м/с²)∙м/с = кг∙м²/с³.

Задача 2. Вантаж масою 3т, кран піднімає з постійною швидкістю 30м/хв. Яка потужність відповідного двигуна?

Дано:

m = 3т = 3·10³кг

v = 30м/хв = 0,5м/с

N = ?

Рішення. За визначенням N = A/t. А оскільки в умовах даної задачі А = mgh, та враховуючи, що h/t = v, можна записати N = A/t = mgh/t = mgv = 3·10³кг·10(м/с²)·0,5м/с = 15·10³Вт = 15кВт.

Відповідь: N = 15кВт.

Задача 3. Скільки часу повинен працювати насос потужністю 50кВт, щоб із шахти глибиною 150м відкачати воду об’ємом 200м³?

Дано:

N = 50кВт = 50∙10³Вт

h = 150м

V = 200м³

t = ?

Рішення. За визначенням N = A/t. В умовах нашої задачі насос виконує роботу по підніманню води на висоту h. Величина ж цієї роботи А = mgh. Оскільки m = ρ∙V, де ρ = 1∙10³кг/м³ – густина води (таблична величина),  то можна записати N = A/t = mgh/t = ρVgh/t, звідси t = ρVgh/N

Розрахунки: t = ρVgh/N = 1∙10³∙200∙10∙150/50∙10³ = 200∙10∙150/50 = 6000с = 100хв = 1год 40хв.

[t] = (кг/м³)∙м³∙(м/с²)∙м/Вт = кг∙ м²/с²/Вт = (Вт∙с)/Вт = с

Відповідь: t = 6000с = 100хв = 1год 40хв.

Контрольні запитання.

1. Що характеризує величина яка називається потужність?
2. Великою чи малою є потужність в один ват?
3. З якою середньою потужністю людина виконує довготривалу роботу?
4. Відро води з колодязя людина рівномірно піднімає, одного разу за 20с, а іншого – за 30с. Чи однакову роботу виконувала людина в цих випадка? Чи однаковою була її потужність?
5. Два хлопці різної ваги наввипередки бігли сходами і одночасно піднялися на третій поверх будинку. Чи однакову потужність розвинули вони?
6. Тягове зусилля гусеничного трактора майже в 10 разів більше за тягове зусилля легкового автомобіля. При цьому потужності їх двигунів практично однакові. Як це пояснити?
7. Чи однакову потужність розвиває двигун автобуса, коли він рухається з однаковою швидкістю без пасажирів і з пасажирами?
8. Що більше 1Вт чи 100Дж?

Вправа №40.

1. Кран рівномірно піднімає вантаж масою 5т на висоту 10м за 20с. Яку потужність розвиває кран?
2. Яку середню потужність розвиває людина піднімаючи відро води масою 12кг з криниці глибиною 15м за 15с?
3. Яка потужність насосу який щохвилини 1200л води подає на висоту 20м?
4. Вантаж масою 4т, кран піднімає з постійною швидкістю 0,4м/с. Яка потужність відповідного двигуна?
5. Тепловоз потужністю 3000кВт тягне потяг, прикладаючи силу 150кН. Який час потрібний для проходження потягом шляху 48км?
6. Трактор зі сталою потужністю 100кВт розвиває тягове зусилля 50кН, 25кН та 10кН. Як при цьому змінюється швидкість трактора?
7. Підйомний кран з двигуном потужністю 50кВт рівномірно піднімає вантаж зі швидкістю 0,1м/с. Яка маса вантажу?

.

§41. Коефіцієнт корисної дії.

В процесі виконання роботи, в будь якому механічному, електричному, тепловому чи іншому приладі, частина наданої йому енергії неминуче і безповоротно втрачається, наприклад завдяки наявності сил тертя. Характеризуючи ці втрати, або якщо хочете, характеризуючи ефективність використання енергії в приладі, говорять про його коефіцієнт корисної дії (ККД).

Коефіцієнт корисної дії (ККД) – це фізична величина, яка характеризує ефективність використання енергії в тому чи іншому приладі і яка дорівнює відношенню тієї енергії, що йде на виконання корисної роботи (Е_кор = А_кор), до загальної кількості наданої приладу енергії (Е_заг = А_заг).

Позначається: η   (ета)

Визначальне рівняння: η = (А_кор/А_заг)100% , або    η = А_кор/А_заг

Одиниця вимірювання: [η] = %,     відсотки.

Варто зауважити, що відсоток або процент (від лат. pro centum – сота частина) – це безрозмірна величина, яка є сотою частиною від одиниці: 1% = 0,01. Тому записи 75% і 0,75 є тотожними (75% = 0,75), а ККД часто виражають не у відсотках, а відповідним безрозмірним числом. При цьому визначальне рівняння ККД набуває вигляду η = А_кор/А_заг. Зважаючи на вище сказане, та прагнучи спростити розрахункову частину рішення задачі, в якості визначального рівняння ККД, будемо застосовувати формулу η = А_кор/А_заг, а отриманий результат, будемо переводити у відсотки.

Коефіцієнти корисної дії різних приладів можуть бути різними. Наприклад ККД лампочки розжарювання 5%, а лампочки світлодіодної 75%. Це означає, що в лампочці розжарювання, тобто приладі який перетворює енергію електричного струму в енергію світла, власне у світло перетворюється лише 5Дж із спожитих 100Дж. Натомість в світлодіодній лампочці цей показник непорівнянно більший: 75Дж із спожитих 100Дж.

Або наприклад, якщо мова йде про електродвигуни (прилади які перетворюють енергію електричного струму в механічну роботу Е_ел → А_мех), то їх ККД близький до 95%. Натомість ККД теплових двигунів (приладів які перетворюють теплову енергію палива в механічну роботу Е_тепл → А_мех), то їх ККД близький до 33%. Це означає, що електричні двигуни більш ефективно використовують надану їм енергію. Адже в них із кожних 100Дж наданої електричної енергії, в корисну (механічну) роботу перетворюється 95Дж, тоді як в теплових двигунах – лише 33Дж.

До речі, факт того, що ККД сучасних теплових двигунів (тобто тих двигунів які стоять на сучасних автомобілях, літаках, ракетах, кораблях, мотоциклах, тощо) є відносно низьким (≈33%), зовсім не означає, що ці двигуни є поганими чи недосконалими. Просто теплова енергія (енергія хаотичного руху молекул речовини) погано та неохоче перетворюється в механічну роботу. Втім, про причини такого стану речей, ви дізнаєтесь вивчаючи закон який називається другим началом термодинаміки. Наразі ж зауважимо, що в будь якому приладі неминуче присутні певні енергетичні втрати і тому його ККД не може бути не те що більшим за 100%, а навіть дорівнювати цим 100%. Іншими словами, ККД будь якого приладу завжди менший за 100%.

Певний час люди намагалися, а деякі намагаються і до тепер, обдурити Природу та створити так званий «вічний двигун», тобто прилад ККД якого більший за 100%. І яких тільки проектів, яких тільки механізмів, яких тільки схем вони не вигадували. От тільки результат всіх цих вигадок був один – пшик. Нарешті в 1775 році, Паризька академія наук прийняла історичне рішення – не приймати до розгляду будь які проекти, автори яких стверджують, що винайшли «вічний двигун». Бо вже тоді, думаючі люди зрозуміли – обдурити закони Природи не можливо. А згідно з цими законами виконаної приладом роботи не може бути більше за ту кількість енергії яку споживає цей прилад.

Застосовуючи формулу η = А_кор/А_заг, з значеннями тих величин які називаються корисною та загальною (затраченою) роботою, визначаються на основі аналізу умови конкретної задачі та розуміння того, яке призначення того чи іншого приладу або процесу. Наприклад якщо мова йде про ККД лампочки розжарювання, тобто приладу який перетворює енергію (роботу) електричного струму А_ел, в енергію світла Е_св, то для цього приладу корисною є світлова енергія А_кор = Е_св, а загальною енергією – робота електричного струму А_заг = А_ел. Якщо мова йде про ККД електродвигуна, тобто приладу який перетворює роботу електричного струму А_ел, в роботу механічну А_мех, то для нього корисною є механічна робота А_кор = А_мех, а загальною – робота електрична А_заг = А_ел

Якщо підйомний кран, маючи потужність N, піднімає вантаж масою m на висоту h, то в цьому випадку корисною є та робота яка йде на піднімання вантажу (А_кор = mgh), а загальною – та робота яку характеризує потужність крану N = A/t і яку можна визначити за цією потужністю А_заг = N∙t. Якщо електровоз потужністю N, створює тягове зусилля F_тяги, то корисною є та робота яку виконує сила тяги А_кор = F_тяги∙s. Адже електровоз для того й існує, щоб тягнути потяг. Загальною ж роботою є та, яку характеризує загальна потужність електровоза N =A/t і яку можна визначити за цією потужністю А_заг = N∙t.

Одним словом – параметри А_кор, А_заг, визначаються на основі аналізу умов конкретної задачі, знань про призначення того чи іншого приладу, розуміння суті тих подій, відображенням яких є відповідна задача.

Певний коефіцієнт корисної дії мають не лише двигуни, генератори, автомобілі та інші складні прилади які власне і виконують роботу, а й прості механізми, які самі по собі роботу не виконують, а лише є певними посередниками при її виконанні (важелі, блоки, похилі площини, тощо).

Напевно найпростішим простим механізмом є похила площина. Принцип дії цього механізму розглянемо на конкретному прикладі. Припустимо, що вантаж який представляє собою діжку масою 80кг, вам потрібно підняти на кузов автомобіля висота якого 1,2м (мал.102). Звісно, якщо габарити вантажу та ваші силові можливості дозволяють, що називається запросто підняти вантаж масою 80кг на висоту 1,2м, то ви з легкістю виконаєте дану роботу і ваші енергетичні затрати становитимуть А = F_тh = mgh = 960Дж.

Однак на практиці далеко не кожен з нас важкоатлет, та й діжка не є зручною гирею з руків’ям. Тому, будучи людиною розумною, ви застосовуєте…, правильно – похилу площину. Адже в цьому випадку для піднімання вантажу вам знадобиться значно менше силове зусилля.

Реалізуючи свій задум, ви неминуче з’ясуєте, що  вантаж потрібно переміщувати не на 1,2м, а на значно більшу довжину, скажімо на 2,4м. І тут нічого не вдієш – виграєш в силі, програєш у пройденому шляху.

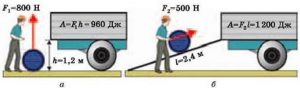
Мал.102. Виграєш в силі, програєш у пройденому шляху.

Звичайно, якби вантаж переміщувався похилою площиною без жодних проявів сили тертя, то для його переміщення на відстане не 1,2м, а 2,4м, було б достатньо сили 400Н (у відстані програли вдвічі, у силі вдвічі виграли). Однак, як ви розумієте, сила тертя між поверхнею вантажу та поверхнею похилої площини неминуче присутня, і тому для підйому вантажу вам знадобиться сила не 400Н, а скажімо 500Н. При цьому ваші енергетичні затрати становитимуть А = F₂ℓ = 500Н·2,4м = 1200Дж.

Таким чином, застосування похилої площини, дозволяє меншими силовими зусиллями виконати потрібну (корисну) роботу. Платою ж за виконання цієї роботи є факт того, що замість мінімально необхідних енергетичних затрат величиною 960Дж, ми витрачаємо 1200Дж енергії. При цьому ККД похилої площини становить η = А_кор/А_заг = mgh/F₂ℓ = 960Дж/1200Дж = 0,8 = 80%.

Про те, що «безкоштовних» виграшів у силі не буває, вчені знали ще з стародавніх часів. Досліджуючи властивості важелів, Архімед сформулював правило, яке стосувалось всіх простих механізмів. Це правило (закон) прийнято називати золотим правилом механіки. В ньому стверджується: в простих механізмах, у скільки разів виграєш в силі, у стільки ж разів програєш у відстані. По суті, золоте правило механіки є одним з перших формулювань базового закону сучасної науки – закону збереження енергії.

Задача 1. Висота похилої площини 1,2м а її довжина 10,8м. Під дією якої сили підніматиметься вантаж, якщо ККД похилої площини 80%?

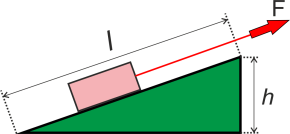
Дано:

h = 1,2м

ℓ = 10,8м

m = 180кг

η = 80% = 0,8

F = ?

Рішення. За визначенням η = А_кор/А_заг. В умовах даної задачі, корисною є та робота яка йде на піднімання тіла на висоту h. А це означає, що А_кор = mgh. Загальною є та робота яку виконує сила F при переміщенні тіла на відстань ℓ, тобто А_заг=F·ℓ. Таким чином: η = mgh / F·ℓ, звідси F = mgh / η·ℓ

Розрахунки: F = mgh / η·ℓ = 180·10·1,2 / 10,8·0,8 = 250Н.

[F] = кг∙(м/с²)·м/м = кг∙(м/с²) = Н

Відповідь: F = 250Н.

Задача 2. Кран піднімає вантаж масою 3т з постійною швидкістю 30м/хв. Яка потужність відповідного двигуна, якщо ККД процесу 75%

Дано:

m = 3т = 3·10³кг

v =30м/хв = 0,5м/с

η = 75% = 0,75

N = ?

Рішення. За визначенням η = А_кор/А_заг. В умовах даної задачі А_кор= mgh. А оскільки N = A_заг/t, то A_заг= Nt, та враховуючи, що h/t = v, можна записати η = mgh / Nt = mgv / N.  Звідси N = mgv / η.

Розрахунки: N = mgv/η = 3·10³∙10∙0,5/0,75 = 20·10³Вт = 20кВт.

[N] = кг∙(м/с²)∙ (м/с) = кг∙м²/с³ = Вт

Відповідь: N = 20кВт.

Контрольні запитання.

1. Що характеризує ККД приладу?
2. Чому ККД будь якого приладу завжди менший за 100%?
3. Що означає, ККД приладу 75%?
4. Чому дешеві лампочки розжарювання, замінюють на більш дорогі світлодіодні лампочки?
5. Яке рішення прийняла у 1775 році Паризька академія наук? Чому було прийнято таке рішення?
6. Як визначаються з тим, яка робота є корисною, а яка загальною?
7. Поясніть загальний устрій та принцип дії похилої площини.
8. Що стверджується у золотому правилі механіки і як це стосується похилої площини.

Вправа №41.

1. В колодязі відро з водою загальною масою 12кг піднімають прикладаючи зусилля 140Н. Визначити ККД процесу.
2. Висота похилої площини 2м а її довжина 10м. Для рівномірного підйому по цій площині вантажу масою 150кг знадобилась сила 400Н. Визначити ККД похилої площини.
3. Висота похилої площини 1,5м а її довжина 10м. Під дією якої сили підніматиметься вантаж, якщо ККД похилої площини 80%?
4. Кран рівномірно піднімає вантаж масою 5т на висоту 10м за 30с. Яку потужність розвиває кран, якщо ККД процесу 80%?
5. Яку середню потужність розвиває людина піднімаючи відро води масою 12кг з криниці глибиною 15м за 15с, якщо ККД процесу 60%?
6. Електровоз при русі зі швидкістю 54км/год споживає потужність 500кВт. Визначте силу тяги електровоза, якщо його ККД 80%.

.

§42. Розв’язування задач. Тема: Коефіцієнт корисної дії.

 

         Загальні зауваження. Рішення тих задач в яких так чи інакше фігурує коефіцієнт корисної дії, практично завжди починається з визначального рівняння ККД, тобто з формули η = А_кор/А_заг. При цьому в подальшому дотримуються наступної послідовності дій.

1. На основі аналізу умов конкретної задачі визначаються з тим, яка робота в цих умовах є корисною (А_кор), а яка загальною (затраченою) (А_заг).
2. На основі аналізу умов задачі, виражають А_кор та А_заг через відомі величини та ту величину яку треба зайти:

А_кор = ….

А_заг = ….

3. Підставляють отримані результати в базову формулу: η = А_кор/А_заг = …
4. Із отриманої формули визначають невідому величину.

Доповнюючи вище сказане, варто вкотре наголосити на тому, що розв’язуючи задачі фізики, потрібно зосереджувати свою увагу на основному та максимально абстрагуватись від другорядного. Скажімо, вас не має обходити те, що не розумієте як працює той насос який піднімає воду на певну висоту, не розумієте як працює той електровоз що створює певну тягову силу, як працює той електродвигун що виконує певну роботу і т.д. Ви просто маєте розуміти, що є певний прилад, який виконує певну роботу, і що величину цієї роботи потрібно визначити із умов конкретної задачі.

Задача 1. Прикладаючи зусилля 750Н, бочку масою 200кг викочують на висоту 1,5м за допомогою похилої площини довжиною 5м. Визначити ККД похилої площини.

Дано:

F = 750Н

m = 200кг

h = 1,5м

ℓ = 5м

η = ?

Рішення. За визначенням η = А_кор/А_заг. В умовах нашої задачі, корисною є та робота яка йде на піднімання вантажу на висоту h, і яка дорівнює А_кор = mgh. Загальною ж (затраченою) є та робота яку виконує сила F на ділянці шляху ℓ і величина якої визначається за формулою А_заг= F∙ℓ. Таким чином, η = А_кор/А_заг = mgh / Fℓ.

Розрахунки:  η = mgh / Fℓ = 200∙10∙1,5 / 750∙5 = 0,8 = 80%

[η] = кг∙(м/с²)∙м / (кг∙м/с²)∙м = – = %

Відповідь: η = 80%.

Задача 2. Насос, двигун якого розвиває потужність 2кВт, за 8хв піднімає певну масу води на висоту 6м. Визначте цю масу, якщо ККД установки 80%.

Дано:

N = 2кВт = 2∙10³Вт

t = 8хв = 480с

h = 6м

η = 80% = 0,8

m = ?

Рішення. За визначенням η = А_кор/А_заг. Із аналізу умови задачі ясно, що корисною є та робота яка йде на піднімання води масою m на висоту h. Величину цієї роботи, можна визначити за формулою А_кор = mgh. Оскільки корисну роботу виконує двигун насосу потужність якого N = А_заг/t, то величину загальної роботи, можна визначити за формулою А_заг = Nt. Таким чином η= А_кор/А_заг = mgh / Nt. Звідси m = ηNt / gh.

Розрахунки: m = ηNt / gh = 0,8·2·10³·480/9,8·6·100 = 13·10³кг = 13т.

[m] = (Вт·с)/(м·м/с²) = Дж/(м²/с²) = кг(м²/с²)/(м²/с²) = кг

Відповідь:  m = 13т.

Задача 3. Електровоз рухаючись з швидкістю 54км/год споживає потужність 600кВт. Визначити силу тяги електровоза, якщо його ККД 75%.

Дано:

v = 54км/год = 15м/с

N = 600кВт = 6∙10⁵Вт

η = 75% = 0,75

F_тяг=?

Рішення. За визначенням   η = А_кор/А_заг. Із аналізу умови задачі ясно, що корисною роботою є та механічна робота яку виконує сила тяги електровозу і яку можна визначити за формулою  А_кор = F_тяг∙s. Оскільки, величина тієї загальної потужності яку споживає електровоз визначається за формулою N = А_заг/t,  то А_заг = Nt. Таким чином  η = А_кор/А_заг = F_тяг∙s/Nt. А враховуючи, що при рівномірному русі електровоза s/t = v, можна записати η = F_тяг∙v/N,  звідси   F_тяг = ηN/v.

Розрахунки: F_тяг = 6·10⁵·0,75/15 = 15∙10³Н = 15кН.

[F] = Вт/(м/с) = Н∙м/с / (м/с) = Н

Відповідь: F_тяг = 15кН .

Задача 4. Підйомний кран піднімає вантаж 3т на висоту 8м зі сталою швидкістю. За який час піднімається цей вантаж, якщо потужність двигуна 12кВт, а ККД крана 80%?

Дано:

m = 3т = 3·10³кг

h = 8м

N = 12кВт = 12·10³Вт

η = 80% = 0,8

t = ?

Рішення. За визначенням   η = А_кор/А_заг. Із аналізу умови задачі ясно, що корисною роботою є та, що йде на піднімання вантажу, тобто А_кор = mgh. Загальною роботою є та робота яку виконує двигун потужністю N. А оскільки N = A_заг/t, то A_заг = Nt.

Таким чином  η = mgh/Nt. Звідси t = mgh/Nη.

Розрахунки: t = mgh/Nη = 3·10³·10·8м/12·10³·0,8 = 25с

[t] = кг(м/с²)м/Вт = Дж/Дж/с = с

Відповідь: t = 25с

Вправа №42.

1 Висота похилої площини 1,5м а її довжина 6м. Для рівномірного підйому по цій площині вантажу масою 80кг знадобилась сила 200Н. Визначити ККД похилої площини.

2. Підйомний кран піднімає вантаж 4т на висоту 10м зі сталою швидкістю. За який час піднімається цей вантаж, якщо потужність двигуна 15кВт, а ККД крана 75%?
3. Насос, двигун якого розвиває потужність 800Вт, за 10хв піднімає певну масу води на висоту 6м. Визначте цю масу, якщо ККД установки 70%.
4. Автомобіль потужність двигуна якого 70кВт рухається з швидкістю 90км/год. Визначити силу тяги автомобіля, якщо ККД процесу 75%
5. Який опір долає трактор при розрівнювання ґрунту, якщо він рухається зі швидкістю 3,6км/год і розвиває потужність 100кВт. При цьому ККД двигуна трактора 60%
6. Двигун насосу, розвиваючи певну потужність піднімає 20т води на висоту 10м за 5хв. ККД двигуна 70%. Визначте потужність двигуна.

.

§43. Закон всесвітнього тяжіння. Загальний устрій Сонячної системи.

 

         В 1667 році аналізуючи поведінку Місяця та планет Сонячної системи видатний англійський фізик Ісаак Ньютон дійшов висновку: масивні тіла взаємно притягуються з силою, величина якої прямо пропорційна добутку взаємодіючих мас і обернено пропорційна квадрату відстані між ними. Однак, лише через двадцять років, цей висновок був офіційно опублікований у вигляді закону всесвітнього тяжіння.

В цьому законі стверджується: два тіла масою m₁ і m₂ взаємно притягуються з гравітаційною силою (F_гр), величина якої прямо пропорційна добутку взаємодіючих мас (m₁∙m₂) і обернено пропорційна квадрату відстані між ними (r²). Іншими словами: F_гр = Gm₁m₂/r², де G = 6,67∙10^–11 (Н∙м²/кг²) – гравітаційна стала, постійна величина значення якої визначається експериментально. (Термін «гравітація» походять від латинського gravitas – тяжіння).

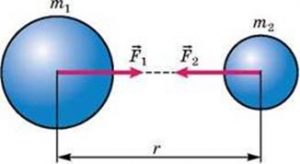
Мал.103. Два тіла масою m₁ і m₂ взаємно притягуються з силою, величина якої визначається за формулою F_гр = Gm₁m₂/r² (закон всесвітнього тяжіння).

Гравітаційна стала (G = 6,67∙10^–11Н∙м²/кг²) – це постійна величина, яка чисельно дорівнює тій гравітаційній силі з якою взаємодіють два тіла масою по 1кг кожне, будучи розташованими на відстані 1м одне від одної. Іншими словами: якщо m₁ = m₂ = 1кг; r = 1м то F_гр = 6,67∙10^–11Н = 0,0000000000667Н.

Із вище сказаного ясно, що за питомою (одиничною) величиною, сили гравітаційної взаємодії є надзвичайно слабкими. Тому ми абсолютно не помічаємо факту того, що з певною гравітаційною силою притягуємся до навколишніх предметів. Однак, коли мова заходить про тіла космічних масштабів, то для них питомо слабкі гравітаційні сили, набувають фантастично великих значень. Скажімо Місяць притягується до Землі (а відповідно і Земля до Місяця) з силою 2∙10²⁰Н.

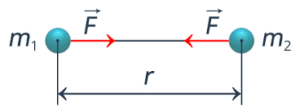
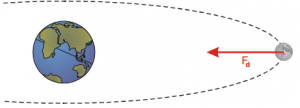
.      1кг       1м        1кг         Земля                                      Місяць

F_гр=0,0000000000667Н       F_гр=200 000 000 000 000 000 000Н

Мал.104. В масштабах земних тіл, сили гравітаційної взаємодії є гранично малими, а в масштабах космічних об’єктів  – фантастично великими.

Задача 1. З якою гравітаційною силою людина масою 70кг притягується до дев’ятиповерхової будівлі загальна маса якої 10 000т, якщо відстань між їх центрами мас 10м (людина знаходиться впритул до будинку)?

Дано:

m₁ = 70 кг

m₂ = 10 000т = 1∙10⁷кг

r = 10м

F_гр = ?

Рішення. Згідно з законом всесвітнього тяжіння

F_гр = Gm₁m₂/r², де G=6,67∙10^–11 (Н∙м²/кг²)

Розрахунки. F_гр = Gm₁m₂/r² = 6,67∙10^–11∙70∙1∙10⁷ / 10² = 47∙10^–5Н.

Відповідь: F_гр = 47∙10^–5Н.

Задача 2. Визначте силу гравітаційної взаємодії між Землею та Місяцем, якщо відомо що відстань між ними 3,8∙10⁸м, а їх маси відповідно 6,0∙10²⁴кг і 7,3∙10²²кг.

Дано:

М = 6,0∙10²⁴кг

m = 7,3∙10²²кг

r = 3,8∙10⁸м

F_гр = ?

Рішення. Згідно з законом всесвітнього тяжіння

F_гр = GMm/r², де G=6,67∙10^–11 (Н∙м²/кг²).

Розрахунки. F_гр = GMm/r² = 6,67∙10^–11∙6,0∙10²⁴∙7,3∙10²²/(3,8∙10⁸)² =

(6,67∙6,0∙7,3/3,8²)∙10^{(–11+24+22–16)} = 20∙10¹⁹Н = 2,0∙10²⁰Н.

Відповідь: F_гр = 2,0∙10²⁰Н.

Оцінюючи значимість гравітаційних сил достатньо сказати, що саме ці сили об’єднують зірки, їх планети, супутники планет, астероїди та купу дрібніших об’єктів, у відповідні планетарні системи. Саме сили гравітаційної взаємодії об’єднують зірки в галактики, галактики – в метагалактики, метагалактики – у Всесвіт. Саме гравітаційні сили стискають та розігрівають надра зірок до таких тисків і температур при яких відбуваються ті термоядерні реакції які є джерелом світла, енергії та життя не тільки на Землі, а і у всьому Всесвіті.

Однак якщо говорити про роль гравітаційних сил в тих взаємодіях які відбуваються між тілами земних масштабів, то вона є мізерно малою. Звісно, за винятком того, що всі земні тіла потужно притягуються до того масивного космічного об’єкту який називається планета Земля.

Ілюструючи роль гравітаційних взаємодій, в загальному устрої Всесвіту, пояснимо загальний устрій тієї частини Всесвіту, яка називається Сонячною системою. Сонячна система, це складний, злагоджений саморегульований механізм, всі елементи якого рухаються і взаємодіють у строгій відповідності з законом всесвітнього тяжіння.  Якщо ж говорити про загальний устрій та принцип дії цього механізму, то він досить простий і полягає в наступному.

Кожен елемент системи, під дією сили гравітаційної взаємодії та сили інерції, обертається навколо центрального тіла. При цьому, швидкість обертання є такою, що забезпечує динамічну рівновагу між силою гравітаційної взаємодії та силою інерції. Наприклад Місяць обертається навколо Землі з такою швидкістю при якій діюча на нього гравітаційна сила (F_гр = GMm/ℓ²) динамічно зрівноважується відповідною силою інерції (F_i = mv²/ℓ). Дійсно.

Задача 3. Відомо що маса Землі 6,0∙10²⁴кг, а відстань між Землею і Місяцем 3,8∙10⁸м. Визначити з якою швидкістю Місяць має обертатися навколо Землі, щоб не віддалятися і не падати на неї.

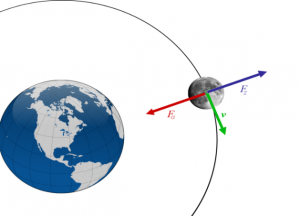
Дано:

М = 6,0∙10²⁴кг

r = 3,8∙10⁸м

v = ?

Рішення. Оскільки в процесі обертання навколо Землі, Місяць не падає на Землю і не віддаляється від неї, то можна стверджувати, що діючі на Місяць сили (гравітаційна сила F_гр = GMm/r² та сила інерції F_i = mv²/r), динамічно зрівноважують одна одну (F_гр = F_і), і що тому GMm/r² = mv²/r. Звідси v² = GM/r, звідси v=√(GM/r).

Розрахунки: v = √[6,67·10^–11·6·10²⁴/3,8·10⁸] = √[(6,67·6/3,8)·10^–11+24–8] = √(10∙10⁵) = √(100∙10⁴) =   10·10²м/с = 1,0·10³м/с = 1,0км/с.

Відповідь: v = 1,0км/с.

Переконатись в тому, що Місяць дійсно обертається з швидкістю 1км/с не важко. Дійсно. Оскільки за один оберт навколо Землі, який як відомо, триває t = Т = 27,3діб = 27,3∙24∙60∙60с = 2,36∙10⁶с, Місяць проходить відстань L = 2πr = 2∙3,14∙ 3,8∙10⁸м = 23,8∙10⁸м, то його швидкість становить  v = L/T = 23,8·10⁸м/2,36·10⁶с = 10·10²м/с = 1,0·10³м/с = 1,0км/с.

Мал.105. Схема загального устрою Сонячної системи.

Створена Ньютоном картина Всесвіту загалом і Сонячної системи зокрема, була Дивовижно простою, гармонічною та передбачуваною. Вона не лише з математичною точністю описувала поведінку всіх відомих космічних об’єктів, а й дозволяла робити нові відкриття. Наприклад, існування планети Нептун було спочатку теоретично передбаченим, а лише потім експериментально підтвердженим. При цьому відповідна планета виявилась саме в тому місці Сонячної системи на яку вказувала теорія Ньютона.

Звичайно, ньютонівська теорія Всесвіту не була такою що відповідала на всі наявні запитання. Зокрема, вона не пояснювала яким чином та за рахунок чого Сонце і зірки постійно випромінюють величезну кількість енергії. Не пояснювала відомі магнітні та електричні явища. Не пояснювала різноманіття хімічних та механічних властивостей речовин. Не пояснювала як виник Всесвіт і чому він саме такий.

По суті та система знань яку прийнято називати ньютонівською механікою, була лише першим вагомим кроком сучасної науки на шляху пізнання навколишнього світу. Про наступні ж кроки науки на цьому складному, тернистому та дивовижно цікавому шляху, ви дізнаєтесь в процесі подальшого вивчення фізики – науки про Природу.

Говорячи про силу гравітаційної взаємодії, не можна не згадати і про ту силу, яку називають силою тяжіння. Часто думають, що діюча на земні тіла сила тяжіння (F_т = mg) та сила гравітаційної взаємодії цих тіл з Землею (F_гр = GMm/R²), це дві назви однієї і тієї ж сили. Така думка не є безумовно правильною. Сила тяжіння і сила гравітаційної взаємодії дійсно дуже схожі і майже однакові як за величиною так і за напрямком. І тим не менше, мова йде хоч і про дуже схожі, але все таки суттєво різні сили. Про те, чим відрізняється сила тяжіння від сили гравітаційної взаємодії, ми поговоримо при більш детальному вивчення механіки. На разі ж будемо вважати, що в першому наближені діюча на земні тіла сила тяжіння (F_т = mg) та сила гравітаційної взаємодії цих тіл з Землею (F_гр = GMm/R²), це дві рівні як за величиною так і за напрямком сили (F_т = F_гр).

Задача 4. Виходячи з того, що маса Землі 6,0∙10²⁴кг, а її радіус 6,37∙10⁶м,  доведіть, що діюча на земні тіла сила тяжіння F_т = mg, де g = 9,8м/с² та діюча на ті ж тіла сила гравітаційної взаємодії з Землею  F_гр = mGM/R², де G = 6,67∙10^–11Н∙м²/кг², є чисельно рівними.

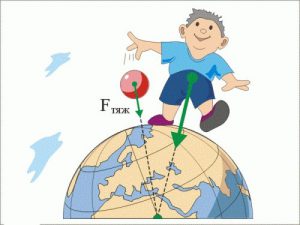
Рішення. Оскільки те тіло що знаходиться на поверхні Землі, віддалене від її центру мас на відстань R = 6,37∙10⁶м, то у відповідності з законом всесвітнього тяжіння на нього діє гравітаційна сила

F_гр = mGM/R² = m∙[6,67∙10^–11∙6,0∙10²⁴ / (6,37∙10⁶)²] = m∙(0,98∙10^{–11+24 – 12}) = m∙9,8м/с² = m∙g = F_т.

[GM/R²] = (Н∙м²/кг²)∙кг /м² = Н/кг = (кг∙м/с²) / кг = м/с² = [g].

Відповідь: F_т = F_гр

Контрольні запитання.

1. Що стверджується в законі всесвітнього тяжіння.
2. Поясніть фізичний зміст гравітаційної сталої.
3. Чому в космічних масштабах гравітаційні сили є фантастично потужними, тоді як в умовах земного життя, практично не проявляють себе?
4. Чи могла б існувати планетарна Сонячна система, якби її об’єкти не рухались? Чому?
5. Які сили забезпечують динамічну рівновагу кожного об’єкту Сонячної системи?
6. Який загальний принцип дії того механізму який називається Сонячною системою?

Вправа 43.

1. Дві кулі масою по 100кг кожна, знаходяться на відстані 1м одна від одної. З якою силою притягуються ці кулі? Чи можна відчути таку силу?
2. Космічний корабель масою 8т наблизився до орбітальної космічної станцій масою 20т на відстань 100м. Визначте силу їх взаємного притягування.
3. Визначте силу гравітаційної взаємодії між Землею та Сонцем, якщо відомо, що відстань між ними 1,5∙10¹¹м, а їх маси відповідно 6∙10²⁴кг і 2∙10³⁰кг.
4. Знаючи прискорення вільного падіння (g=9,8м/с²) та радіус Землі (R=6,4∙10⁶м), визначити масу Землі.

.

§44. Динаміка. Узагальнююче повторення.

 

Динаміка – це узагальнюючий розділ механіки, в якому вивчаються силові та імпульсно-енергетичні параметри механічного руху тіл в усіх його проявах. В динаміці, ті знання які були отримані при вивченні кінематики та статики, доповнюються новими знаннями і узагальнюються. Теоретичною основою механіки загалом і динаміки зокрема є три закони Ньютона. Ці закони представляють собою систему взаємопов’язаних та взаємодоповнюючих тверджень, в яких опосередковано сформульовані й інші базові твердження, зокрема принцип відносності, закон інерції, закон збереження механічної енергії та закон збереження механічного імпульсу.

Принцип відносності (перше формулювання) – це закон, в якому стверджується: Ніякими експериментами, які проводяться в середині закритої ізольованої кабіни, не можливо встановити стоїть ця кабіна чи рівномірно рухається. Не можливо тому, що всі фізичні процеси, які відбуваються в кабіні що стоїть (v=0) і в кабіні що рівномірно рухається (v=const), відбуваються абсолютно однаково.

Принцип відносності (друге формулювання) – це закон, в якому стверджується: У всіх інерціальних системах відліку, тобто таких системах де виконується закон інерції (перший закон Ньютона) всі фізичні процеси відбуваються абсолютно однаково.

Неоціненна значимість принципу відносності полягає в тому, що застосування цього принципу дозволяє по-перше, обгрунтовано довести, що відкриті на Землі закони Природи діють і в інших частинах Всесвіту, а по-друге, представити відому інформацію про Природу у вигляді стислої та цілісної системи знань.

Перший закон Ньютона – це закон, в якому стверджується: Будь-яке тіло буде знаходитись в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v=const), до тих пір поки на нього не подіє зовнішня сила, яка і змусить тіло змінити цей стан. Іншими словами:

а) v=0  « = »  v=const (принцип відносності);

б) F  →   a  (закон інерції).

Другий закон Ньютона – це закон, в якому стверджується: Під дією зовнішньої сили F, тіло масою m отримує прискорення а величина якого прямо пропорційна діючій на тіло силі і обернено пропорційна його масі. Іншими словами:  

F  →   a = F/m.

Третій закон Ньютона – це закон, в якому стверджується: Діюча на тіло сила F, завжди породжує рівну їй за величиною і протилежну за напрямком протидіючу силу F′. Іншими словами:

F → F′ = – F.

До числа основних понять динаміки відносяться: динамічна рівновага тіла, інерція та гравітація.  Динамічна рівновага тіла – це такий механічний стан тіла, при якому воно, під дією зовнішніх сил та сили інерції, знаходиться в стані рівноприскореного руху (а ≠ 0).

Інерція, це універсальна властивість тіла, яка полягає в тому, що відповідне тіло протидіє будь якій зміні його швидкості. Кількісною мірою інерційних властивостей тіла є його маса.

Гравітація, це універсальна властивість тіла, яка полягає в його здатності притягуватись до Землі, або в більш загальному сенсі – в здатності тіла до гравітаційних взаємодій. Кількісною мірою гравітаційних властивостей тіла є його маса.

До числа основних фізичних величин динаміки, а точніше динаміки матеріальної точки, відносяться: маса (m), енергія (Е), робота (А), потужність (N) та коефіцієнт корисної дії (η).

         Маса – це фізична величина яка є мірою :

1) інерціальних властивостей тіла;

2) гравітаційних властивостей тіла;

3) енергетичних властивостей тіла;

4) кількості речовини в тілі, виміряну в кілограмах.

Позначається:  m

Визначальне рівняння:  нема

Одиниця вимірювання:  [m]= кг,  кілограм.

Енергія – це фізична величина, яка є загальною мірою всіх видів рухів та взаємодій і яка характеризує здатність тіла, частинки або поля виконувати роботу.

Позначається: Е

Визначальне рівняння:

1) для загальної кількості енергії:   Е=mс²;

2) для конкретних видів енергії:   різні.

Одиниця вимірювання: [E] = Дж = Н∙м = кг∙м²/с²,   джоуль.

Джоуль – це одиниця вимірювання енергії та роботи, яка дорівнює тій роботі (тим затратам енергії) яку виконує сила в один ньютон при переміщенні тіла (матеріальної точки) на один метр в напрямку дії сили: Дж=Н∙м=кг∙м²/с².

Енергію загалом і механічну енергію зокрема, можна представити як певну комбінаціє двох базових різновидностей: енергії руху (кінетична енергія) та енергії взаємодії (потенціальна енергія).

Кінетична енергія (енергія руху) – це та енергія, яку має тіло (фізичний об’єкт) за рахунок того, що воно рухається і яка дорівнює половині добутку маси тіла на квадрат його швидкості.

Позначається: Е_к

Визначальне рівняння: Е_к = mv²/2

Одиниця вимірювання: [Е_к] = кг∙м²/с² = Дж.

Потенціальна енергія (енергія взаємодії) – це та енергія, яку має фізичний об’єкт за рахунок того, що він так чи інакше взаємодіяє з іншими об’єктами, або за рахунок тих взаємодій які відбуваються в середині цього об’єкту.

Позначається: Е_п

Визначальне рівняння: Е_п=?, єдиної універсальної формули для визначення потенціальної енергії нема.

Одиниця вимірювання: [Е_п] = Дж.

В механіці вивчають дві різновидності потенціальної енергії: потенціальна енергія сили тяжіння та потенціальна енергія сили пружності.

Потенціальна енергія сили тяжіння (піднятого тіла) –  це така енергія яку має тіло за рахунок його взаємодії з Землею і яка дорівнює добутку маси тіла (m), прискорення сили тяжіння (g) та тієї висоти (h) на яку піднято тіло.

Позначається: Е_п

Визначальне рівняння: Е_п = mgh,

Одиниця вимірювання: [Е_п] = Дж,  джоуль.

Потенціальна енергія сили пружності (пружно деформованого тіла) – це та енергія яку має пружно деформоване тіло за рахунок тих внутрішніх взаємодій які відбуваються в ньому і яка дорівнює половині добутку жорсткості тіла (k) на величину його абсолютної деформації (Δℓ).

Позначається: Е_п

Визначальне рівняння: Е_п = kΔℓ²/2,

Одиниця вимірювання: [Е_п] = Дж,  джоуль.

Робота – це фізична величина, яка характеризує затрати енергії на виконання роботи, тобто певної енергозатратної дії і яка дорівнює цим затратам.

Позначається: А

Визначальне рівняння: А = ΔЕ

Одиниця вимірювання: [А] = Дж,   джоуль.

Формула А=ΔЕ є базовим, визначальним рівнянням роботи. Однак, якщо мова йде про механічну роботу, то її часто визначають за формулою А = F∙s∙cosα, де F – усереднена величина тієї сили що виконує роботу, s – величина того переміщення яке відбувається під дією даної сили, α – кут між напрямком вектора сили (F) та напрямком вектора переміщення (s).

Потужність – це фізична величина, яка характеризує роботу виконану за одиницю часу і яка дорівнює відношенню виконаної роботи (А) до того проміжку часу (t) за який ця робота була виконана.

Позначається: N

Визначальне рівняння: N = А/t

Одиниця вимірювання: [N] = Дж/с = Вт,  ват.

Коефіцієнт корисної дії (ККД) – це фізична величина, яка характеризує ефективність використання енергії в тому чи іншому приладі і яка дорівнює відношенню тієї енергії що йде на виконання корисної роботи (Е_кор = А_кор), до загальної кількості витраченої енергії (Е_заг = А_заг).

Позначається: η

Визначальне рівняння:  η = (А_кор/А_заг)100%,  або η = А_кор/А_заг

Одиниця вимірювання:  [η] = %,    відсотки.

Розрізняють два базові методи розв’язування задач динаміки: силовий та енергетичний. Суть силового методу полягає в тому, що невідомі величини визначають на основі аналізу діючих на тіло сил та визначальних рівнянь цих сил, і на базі того закону який називається умовою динамічної рівноваги тіла.

Умова динамічної рівноваги тіла, це закон в якому стверджується: Тіло (матеріальна точка) буде знаходитись в стані динамічної рівноваги (а ≠ 0) тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил та сили інерції дорівнює нулю. Іншими словами: якщо а ≠ 0, то ∑F + F_i = 0 і навпаки.

Задача 1. Автомобіль масою 900кг, маючи тягову силу 2кН, рухається з прискоренням 1м/с². Визначити загальну силу опору руху автомобіля (загальну силу тертя).

Загальні зауваження. Як не прикро констатувати, але історично склалося так, що всупереч реальним фактам, всупереч сучасній науці, у вітчизняняй освіті, факт реальності сили інерції зазвичай заперечується. Тому малюнків на яких була б вказана сила інерції надзвичайно мало. Зважаючи на ці мало приємні обставини, присутність сили інерції в тій чи іншій ситуації вам прийдеться «домальовувати». А зробити це неважко – сила інерції направлена в протилежну сторону від прискорення.

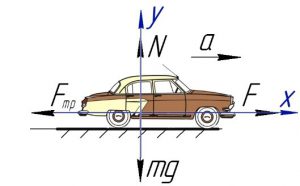
Дано:

m = 1,5т = 1500кг

F_тяги = 3кН = 3000Н

a = 1м/с²

F_тер = ?

μ = ?

Рішення. Виконуємо малюнок на якому вказуємо всі діючі на автомобіль сили. А цими силами є: сила тяжіння F_т = mg, реакція опори N, сила тяги F_тяги = F, сила тертя F_тер та направлена в протилежну сторону від прискорення сила інерції F_і = ma (на малюнку не позначена). Задаємо відповідну систему координат.  Записуємо умову рівноваги тіла

∑F_x = F_тяги – F_тер – F_i = 0.

∑F_y = N – mg = 0.

Із (1) рівняння виплмває:

F_тер = F_тяги – F_i = F_тяги – mа = 3000Н – 1500кг∙1м/с² = 1500Н.

Оскілки μ = F_тер/N, та враховуючи, що у відповідності з другим рівнянням N = mg = 1500кг∙10м/с² = 15000Н, можна записати

μ = F_тер/N = 1500Н / 15000Н = 0,1.

Відповідь: F_тер = 1500Н, μ = 0,1.

Суть енергетичного методу розв’язування задач полягає в тому, що невідомі величини визначають на основі аналізу енергетичних параметрів руху тіла (енергія, робота, потужність, ККД) та їм відповідних визначальних рівнянь і на базі того закону який називається законом збереження енергії.

Закон збереження енергії, це закон, в якому стверджується: при будь яких процесах, що відбуваються в замкнутій (енергоізольованій) системі, загальна кількість енергії цієї системи залишається незмінною, тобто зберігається. Іншими словами:∑Е_до = ∑Е_після.

Задача 5. Тіло кинули вертикально вгору зі швидкістю 10м/с. На якій висоті його кінетична енергія дорівнюватиме потенціальній?

Дано:

v₀=10м/с

E_k = E_п

h = ?

Рішення. На основі аналізу умови задачі виконуємо малюнок на якому вказуємо енергетичні параметри тіла в початковий та кінцевий моменти часу: на висоті h = 0:   E_к = mv₀²/2;    E_п = 0;

на висоті h:         E_к = mv²/2      E_п = mgh, а оскільки на висоті h,

mv²/2 = mgh, то можна записати, що на цій висоті mv²/2 + mgh = 2mgh.

Таким чином, у відповідності з законом збереження (∑Е_до = ∑Е_після):

mv₀²/2 + 0 = 2mgh, звідси h = v₀²/4g.

Розрахунки h = v₀²/4g = (10м/с)²/4·10м/с² = 2,5м.

Відповідь: h = 2,5м.

По суті частковим випадком енергетичного методу розв’язування задач, є задачі в яких так чи інакше фігурує коефіцієнт корисної дії (ККД). Рішення таких задач практично завжди починається з визначального рівняння ККД (η = А_кор/А_заг), кількісний аналіз якого і дозволяє визначити невідому величину.

Задача 3. Автомобіль потужність двигуна якого 70кВт рухається з швидкістю 25м/с. Визначити силу тяги автомобіля, якщо ККД процесу 75%.

Дано:

N = 70кВт = 70000Вт

v = 25м/с

η = 75% = 0,75

F_тяги = ?

Рішення. За визначенням η = А_кор/А_заг. В умовах нашої задачі корисною є та робота яку виконує сила тяги автомобіля: А_кор = F_тяги∙s. Загальною є та робота яку генерує двигун потужністю N. А оскільки за визначенням N = A/t, то A_заг = Nt. Зважаючи на те, що s/t = v, можна записати: η = А_кор/А_заг = F_тяги∙s / Nt = F_тяги∙v/N.  Звідси  F_тяги= Nη / v.

Розрахунки: F_тяги= Nη/v = 70000·0,75 / 25 = 2100Н.

[F] = Вт/(м/с) = (Н∙м/с)/(м/с) = Н.

Відповідь: F_тяги = 2100Н.

Вправа 44.

1. На тіло масою 0,6кг діють дві направлені в протилежні сторони сили: 8Н і 14Н. Визначте модуль та напрям прискорення тіла.
2. Місяць з швидкістю 1км/с обертається навколо Землі. Яка кінетична енергія Місяця, якщо його маса 7,33·10²²кг?
3. Яку роботу виконує сила тяжіння в процесі падіння тіла масою 4кг з висоти 5м?
4. Яку роботу виконує сила пружності при розтягуванні пружини жорсткістю 500Н/м на 10см?
5. Визначити швидкість вильоту кульки масою 10г з дула пружинного пістолета при горизонтальному пострілі, якщо жорсткість пружини 400Н/м, а її деформація 10см.
6. Висота похилої площини 2м а її довжина 8м. Для рівномірного підйому по цій площині вантажу масою 120кг знадобилась сила 400Н. Визначити ККД похилої площини.
7. Електровоз при швидкості руху 72км/год споживає потужність 500кВт. Визначте силу тяги електровоза, якщо його ККД 80%.
8. З якою початковою швидкістю потрібно кинути вниз м’яч з висоти 5м, щоб він відбившись від пружної поверхні, підскочив на висоту 12м? Опором повітря та втратами енергії в момент удару знехтувати.

.

.