ОСНОВИ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ

Тема 2.1. Основи молекулярно-кінетичної теорії.
§2. Основні положення молекулярно-кінетичної теорії.
§3. Про силу міжмолекулярної взаємодії.
§4. Про маси та розміри молекул.
§5. Про кількість речовини в тілі, та про ті величини
які цю кількість характеризують
§6. Маса, як міра кількості речовини
§6. Температура, як міра нагрітості тіла. Шкала температур.
§7. Температура, як міра середньої кінетичної енергії
молекул тіла.
§8. Загальні відомості про тверді, рідкі та газоподібні речовини.
Плазма, як особливий стан речовини.
Тема 2.1 Основи молекулярно – кінетичної теорії.
§2. Основні положення молекулярно − кінетичної теорії.
Теоретичну основу молекулярної фізики складають три базові твердження, які називаються основними положеннями молекулярно – кінетичної теорії (м. к. т.). Ось ці твердження.
1. Всі речовини складаються з молекул (молекул, атомів, іонів).
2. Молекули в речовині безперервно та безладно (хаотично) рухаються.
3. На невеликих відстанях (~10–9м) молекули взаємодіють між собою – в залежності від відстані, притягуються або відштовхуються.
Виходячи з цих базових тверджень та застосовуючи статистичний метод досліджень, можна пояснити практично все, що є предметом вивчення молекулярної фізики. Тобто пояснити загальні властивості твердих, рідких та газоподібних речовин та ті теплові процеси які відбуваються з цими речовинами.
Однак, чому ми вирішили що речовини складаються з надзвичайно дрібненьких частинок, які рухаються і певним чином взаємодіють між собою? Адже ніхто з нас цих частинок ніколи не бачив і напевно не побачить. А якщо ви чули, що ті прилади які називаються електронними мікроскопами дозволяють побачити молекули (атоми), то маєте знати, що ці молекули представляють собою певні розмиті згустки матерії які не мають певних, чітко визначених розмірів, не мають певної чітко визначеної форми, певної густини, певної твердості і взагалі тих властивостей, що притаманні звичним для нас тілам.
І тим не менше, ще за сотні років до нашої ери, думаючі люди обгрунтовано стверджували, що всі тіла складаються з надзвичайно дрібненьких частинок (атомів), які безперервно рухаються і певним чином взаємодіють між собою. Ось що з цього приводу писав один з засновників атомістичного (молекулярного) вчення, давньогрецький філософ Демокрит (приблизно 460–370 р.р. до н.е.). «Не існує нічого окрім атомів та чистого простору. Атоми є неподільні і не мають внутрішнього устрою. Атоми безкінечні за своєю кількістю і безкінечно різноманітні за своєю формою. Відмінності між речами, визначаються відмінностями між тими атомами з яких вони складаються. Атоми діють один на одного шляхом тиску та удару.»
*) Потрібно зауважити, що оригінали книг Демокрита не збереглися. І тому, про суть його філософських поглядів ми знаємо з книг більш пізніх авторів, зокрема Епікура (341–270 р.р. до н.е.) та Лукреція (99–55 р.р. до н.е.)
Ви можете запитати: «А як це може бути, щоб ті люди які не мали бодай елементарного наукового обладнання, з такою впевненістю говорили про ті речі, факт існування яких був науково доведений лише в 1908 році?» Відповідаючи на це запитання можна сказати наступне. По суті люди кардинально відрізняються від інших істот лише одним – здатністю логічно мислити. Власне ця здатність і дозволяє людям «бачити» те, чого вони ніколи не бачили і чого наочно побачити взагалі не можливо.
Скажімо, ми говоримо про те існують молекули чи не існують. Відповідаючи на це запитання зовсім не обов’язково мати надскладне обладнання та проводити надскладні експерименти. Цілком достатньо придивитись до навколишнього світу і проаналізувати ті події що в ньому відбуваються. Наприклад, ви берете склянку води і кладете у воду шматочок цукру. При цьому цукор швидко зникає (розчиняється). Ви можете скільки завгодно роздивлятись воду під мікроскопом в надії відшукати видимі частинки цукру і не знайдете їх. І тим не менше цукор нікуди не зник. Адже збереглась його визначальна смакова властивість відома кожному з вас. Чи не говорить даний експериментальний факт про те, що цукор складається з надзвичайно дрібненьких частинок? Частинок, які настільки дрібні, що їх не видно навіть в найпотужніший оптичний мікроскоп і про факт існування яких говорить те, що після розчинення та візуального зникнення цукру, зберігається його визначальна смакова, а по суті хімічна властивість. І чи не говорить факт рівномірного розподілу цукру в наявному об’ємі води про те, що наддрібні частинки цукру рухаються?
Або, скажімо, ви наливаєте в склянку певну кількість води і помічаєте, що з плином часу цієї води стає все менше і менше. Ви можете скільки завгодно придивлятись до того що ж відбувається і не помітите нічого, окрім факту того, що води стає все менше і менше. Чи не говорить цей експериментальний факт про те, що вода складається з надзвичайно дрібненьких частинок, які непомітно вилітають (випаровуються) зменшуючи тим самим загальну кількість води?
Або, наприклад, той факт що крапля пахучої рідини поступово зникає, а натомість ви відчуваєте відповідний запах у всіх куточках кімнати. Чи не говорить цей факт про те, що відповідна рідина складається з надзвичайно дрібненьких частинок які є носіями певних властивостей цієї рідини і що ці частинки рухаються?
Або, скажімо, факт того, що в процесі охолодження повітря, в ньому та на тих предметах що в цьому повітрі знаходяться, з’являються (конденсуються) крапельки води. Чи не говорить цей факт про те, що відповідна вода й до того знаходилась у повітрі і що ми її не помічали тільки тому, що відповідні мікрочастинки води є неймовірно маленькими?
А хімічні реакції? А процес горіння? А електроліз? А факт того, що атмосфера Землі представляє собою однорідну суміш різних газів? Чи не вказують ці та їм подібні явища і факти на те, що речовини складаються з дрібненьких частинок які постійно рухаються? А той факт, що загальний об’єм суміші двох різних речовин, наприклад води і солі, або води і спирту, виявляється суттєво меншим за суму об’ємів окремих складових цієї суміші. Чи не вказує він на те, що речовини складаються з дрібних частинок, між якими є проміжки пустоти?
Мал.2 Деякі факти, які вказують на молекулярну структуру речовини.
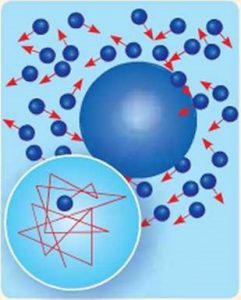
Звичайно, вище наведені факти не є такими, що безумовно доводять факт існування молекул. Однак вони безумовно вказують на те, що гіпотеза про молекулярну будову речовини є науково обгрунтованою. Якщо ж говорити про ті експериментальні дослідження які науково доводять факт існування молекул, то вони тісно пов’язані з явищем, яке було відкрите та описане англійським ботаніком Робертом Броуном (1773–1858). В 1827 році, намагаючись за допомогою мікроскопа розгледіти будову квіткового пилку, Броун звернув увагу на те, що у водному розчині окремі пилинки постійно рухаються. Він розумів, що пилинки не є тими об’єктами які можуть самостійно рухатись. І тим не менше вони рухались. Дослідивши цей рух Броун з’ясував, що рух пилинок є безперервним та безладним і що його інтенсивність залежить від розмірів пилинок: чим дрібніші пилинки, тим інтенсивніше вони рухаються. Однак Броун так і не зумів пояснити причини відкритого ним явища.
Певний час причини броунівського руху були не зрозумілими. Цей рух намагались пояснити тремтінням того стола на якому стоїть мікроскоп; впливом того світла яким опромінюють ті об’єкти що знаходяться під мікроскопом; конвекційними потоками тієї рідини в якій плавають броунівські частинки, тощо. Однак, експериментальні факти вказували на те, що ці та їм подібні обставини практично не впливають на поведінку броунівських частинок. На цю поведінку суттєво впливали лише розміри частинок та температура того середовища яке їх оточує.
Поступово вчені прийшли но того висновку, що єдиним обгрунтованим поясненням броунівського руху є хаотичний рух молекул того середовища яке оточує броунівські частинки: невидимі молекули середовища, барабанять дрібні частинки речовини, а ті, реагуючи на ці хаотичні удари, відповідним чином рухаються. Броунівський рух – це безладний рух дрібних, видимих частинок речовини, причиною якого є хаотичний (тепловий) рух молекул навколишнього середовища. Потрібно зауважити, що хаотичний рух молекул речовини називають тепловим рухом. Така назва пояснюється тим, що хаотичний (тепловий) рух молекул речовими ми сприймаємо у вигляді відповідних теплових відчуттів – чим інтенсивніший хаотичний рух молекул речовини, тим теплішим (гарячішим) за нашими відчуттями є відповідне тіло.
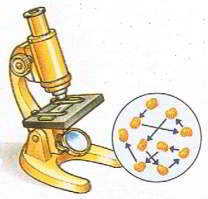

Мал.3 Хаотичний рух видимих мікрочастинок речовини (броунівський рух), є прямим наслідком хаотичного руху молекул навколишнього середовища.
Броунівський рух не лише вказує на те, що молекули речовини рухаються, а й несе в собі певну кількісну інформацію про цей рух. А це означає, що знаючи геометричні та вагові параметри броунівських частинок і кількісно аналізуючи їх поведінку, можна визначити параметри руху невидимих молекул. Наукову теорію броунівського руху розробив в 1905 році видатний німецький фізик Альберт Ейнштейн (1879–1955). Виходячи з того, що рух броунівських частинок є результатом хаотичного руху тих молекул які їх оточують, Ейнштейн теоретично описав закономірності руху цих частинок.
Ейнштейнівська теорія броунівського руху була експериментально перевірена і підтверджена в 1908 році французьким фізиком Жаном Переном (1870–1942). Власне лише після експериментів Перена, реальність існування молекул стала науково доведеним фактом.
До числа тих явищ які вказують на факт хаотичного руху молекул, відносяться дифузія та осмос. Розповсюдження запахів у повітрі, перемішування молекул тієї речовини що розчиняється, з молекулами розчинника, і взагалі все що пов’язано з перемішуванням різнорідних молекул, причиною якого є хаотичний рух цих молекул, прийнято називати дифузією (від лат. diffusion – розповсюдження). Дифузія – це явище, суть якого полягає в тому, що в процесі хаотичного руху, молекули однієї речовини перемішуються з молекулами іншої речовини. При цьому, кожна різновидність молекул прагне до того, щоб їх концентрація в усьому доступному об’ємі була однаковою. Наприклад якщо в стакан води капнути краплю барвника, чи скажімо вкинути кристалик марганцівки, то через певний час забарвлення води стане однаковим у всьому її об’ємі. І не важко збагнути, що даний факт пояснюється тим, що в процесі хаотичного руху, різнорідні молекули перемішуються.
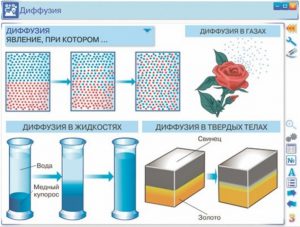
Мал.4. Дифузія, це процес перемішування різнорідних молекул, причиною якого є хаотичний рух цих молекул.
Дифузія відбувається не лише в рідинах та газах, а й в твердих тілах. Щоправда, в твердих тілах дифузійні процеси відбуваються надзвичайно повільно. Наприклад в одному з експериментів, дзеркально відполіровані пластини золота і свинцю поклали одна на одну і навантажили зовнішньою силою. Коли через п’ять років дані пластини спробували роз’єднати, то з’ясувалось, що вони в буквальному сенсі зрослись. При цьому, на межі контакту двох речовин утворився міліметровий шар суміші їх молекул.
Потрібно зауважити, що в твердженні: «кожна різновидність молекул прагне до того, щоб їх концентрація в усьому доступному об’ємі була однаковою», – термін «прагне», зовсім не означає, що молекули мають певні прагнення та бажання. Просто у відповідності з законами Природи, одним з результатів хаотичного руху частинок, є факт їх перемішування. І тому, якщо в одному місці певних молекул багато, а в іншому – подібних молекул мало, то через певний час, концентрація цих молекул в усьому їм доступному об’ємі виявиться однаковою. І причиною цього вирівнювання концентрації, є не якесь міфічне прагнення молекул, а їх хаотичний рух.
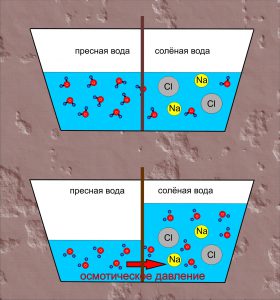
Однією з важливих різновидностей дифузії є осмос (від грец. osmos – тиск). Осмос – це явище, суть якого полягає в тому, що в процесі хаотичного руху молекул, одні з них проникають через напівпроникну перешкоду, а інші – не проникають через неї. При цьому, проникаючі через перешкоду молекули, прагнучи до вирівнювання їх концентрації по обидві сторони перешкоди, створюють певний додатковий тиск який називається осмотичним тиском.
Ілюструючи фізичну суть осмосу проведемо наступний експеримент. В наповнену водою посудину, опустимо конструкцію що складається з заповненої концентрованим розчином цукру пробірки, яка виготовлена з напівпроникного матеріалу і в яку вставлена скляна трубка (мал.5). Говорячи про напівпроникну стінку, ми маємо на увазі таку перешкоду через яку молекули води проникають, а більш об’ємні молекули цукру – не проникають. Подібними стінками є оболонки (мембрани) клітин. Тому відносно тонкі шари більшості органічних речовин є напівпроникними. По суті це означає, що в якості напівпроникної пробірки можна використати певну рослину, наприклад моркву, в тілі якої зроблено відповідне заглиблення.
Припустимо, що на початку експерименту рівень рідин в посудині та пробірці є однаковим. Спостерігаючи за рівнем рідини в пробірці, ви неодмінно з’ясуєте, що з плином часу цей рівень поступово зростатиме. Зростатиме до тих пір поки не досягне певної надлишкової висоти Δh, якій відповідає певний гідростатичний тиск Δр=ρgΔh.
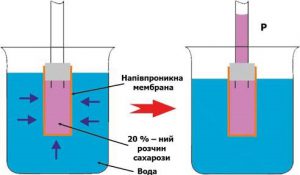
Мал.5. Проникаючі через напівпроникну перешкоду молекули, прагнучи до вирівнювання їх концентрації по обидві сторони перешкоди, створюють певний додатковий тиск який називається осмотичним тиском.
Пояснюючи результати експерименту можна сказати наступне. Різні молекули мають суттєво різні розміри та різні фізико-хімічні властивості. Тому один і той же матеріал для одних молекул може бути «прозорим», а для інших – «непрозорим». Наприклад, той матеріал з якого виготовлена морква, відносно легко пропускає дрібні молекули води (Н2О) і майже не пропускає значно об’ємніші молекули цукру (С6Н12О6). А оскільки концентрація молекул води в розчині цукру значно менша за їх концентрацію у чистій воді, то кількість молекул Н2О які проникають в розчин, значно більша за ту їх кількість яка покидає його. А це означає, що в процесі осмосу, кількість води в цукровому розчині буде збільшуватись. При цьому, надлишкова вода створює відповідний надлишковий тиск, який прийнято називати осмотичним.
Дифузія і осмос відіграють надзвичайно важливу роль в багатьох життєво важливих процесах. Наприклад, завдяки осмосу поживні і мінеральні речовини із навколишнього середовища потрапляють в тіла рослин, грибів та бактерій. Завдяки осмосу здійснюється обмін речовинами на міжклітинному і внутріклітинному рівнях всіх складних організмів. Завдяки дифузії, атмосфера Землі є тим чим вона є – однорідною сумішшю різних газів. Завдяки дифузії, розчини різних речовин є однорідними, тощо.
Контрольні запитання.
1. Сформулюйте основні положення молекулярно-кінетичної теорії.
2. Поясніть, на підставі чого думаючі люди, ще з прадавніх часів стверджували, що всі тіла складаються з надзвичайно дрібненьких частинок, які постійно рухаються та певним чином взаємодіють між собою?
3. Наведіть приклади тих явищ та фактів які вказують на те, що тіла складаються з молекул і що ці молекули рухаються.
4. Що називають броунівським рухом? Від чого залежить інтенсивність цього руху?
5. Чому хаотичний рух молекул речовини називають тепловим рухом?
6. Чим схожі і чим відрізняються броунівський та тепловий рухи?
7. Що називають дифузією? Наведіть відомі вам прояви дифузії.
8. Що називають осмосом? Наведіть відомі вам прояви осмосу.
9. Як ви думаєте, чому в твердих тілах дифузійні процеси відбуваються набагато повільніше аніж в рідинах?
§3. Про силу міжмолекулярної взаємодії.
В попередньому параграфі ми навели вагомі докази того, що всі речовини складаються з молекул (молекул, атомів, іонів), і що ці молекули безперервно та безладно рухаються. Однак, чому ми вирішили що молекули взаємодіють між собою, та ще й таким дивним чином, що в залежності від міжмолекулярної відстані, притягуються або відштовхуються? Втім, переконатися в факті того, що молекули дійсно взаємодіють і взаємодіють саме таким чином, зовсім не складно. Достатньо взяти в руки будь яке тверде тіло, будь то лінійка, олівець, ручка чи гвіздок і запитати себе: «Якщо це тіло складається з молекул які рухаються, то чому ці молекули не розлітаються, а утворюють єдине ціле?».
Більше того, якщо ви спробуєте розтягнути тіло, тобто збільшити відстань між його молекулами, то неминуче відчуєте, силу протидії, яка означає що молекули притягуються. Якщо ж ви спробуєте стиснути тіло, тобто зменшити відстань між його молекулами, то з не меншою неминучістю відчуєте, що молекули відштовхуються. Висновок очевидний: молекули прагнуть розташуватися на певній відстані одна від одної, при цьому, якщо ця відстань збільшується, то молекули починають притягуватись, а якщо зменшується – відштовхуватись. І не важко переконатися в тому, що сили міжмолекулярної взаємодії суттєво проявляють себе лише на дуже маленьких відстанях. Адже якщо ви розіб’єте чашку, або зламаєте брусочок крейди, а потім спробуєте об’єднати фрагменти раніше цілого тіла, то нічого путнього з цього не вийде. Не вийде тому, що для молекул, навіть візуально мікроскопічна тріщинка між наявними фрагментами є нездоланною прірвою.
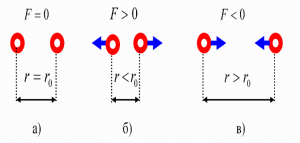
Мал.6. Механічні властивості твердих тіл безумовно вказують на те, що молекули взаємодіють між собою: в залежності від відстані – притягуються, або відштовхуються.
Пояснюючи вище наведені експериментальні факти можна сказати наступне. Та сила яку прийнято називати силою міжмолекулярної взаємодії представляє собою результуючу багатьох сил які так чи інакше впливають на поведінку молекул. Сьогодні ми не будемо говорити про природу та механізм дії цих сил. Сьогодні, ми просто констатуємо той факт, що сила міжмолекулярної взаємодії представляє собою результуючу складної комбінації електромагнітних та квантово-механічних сил, з властивостями та проявами яких ми поговоримо у відповідних розділах фізики.
Та навіть не маючи уявлення про походження і механізм дії тих сил які визначають поведінку молекул, ми все ж спробуємо стисло пояснити, як це виходить, що ця поведінка таким складним чином залежить від міжмолекулярної відстані. Відразу ж зауважимо, що наші пояснення будуть гранично спрощеними, однак такими, що максимально точно відображають суть міжмолекулярних взаємодій.
Уявіть собі ситуацію, коли до відносно нерухомої молекули повільно наближається інша молекула. При цьому, ця рухома молекула обладнана двома датчиками, один з яких фіксує силу міжмолекулярного притягування (Fпр), інший – силу міжмолекулярного відштовхування (Fвід). Ми спостерігаємо за поведінкою молекул, фіксуємо показання приладів та аналізуємо їх. І ось що ми бачимо. Допоки молекули знаходяться на відносно великій відстані (r > 1∙10–9м), прилади показують, що сили міжмолекулярного притягування і сили міжмолекулярного відштовхування практично не проявляють себе (Fпр=0; Fвід=0). Та коли міжмолекулярна відстань зменшиться до величини r ≈1∙10–9м, прилад який реагує на силу міжмолекулярного притягування, зафіксує що така сила з’являється, і що по мірі наближення молекул вона зростає. Аналізуючи характер цього зростання, ми приходимо до висновку, що воно відбувається за законом: Fпр=а/r7, де а – коефіцієнт пропорційності, величина якого залежить від сорту взаємодіючих молекул. Даний закон говорить про те, що коли в області дії сил міжмолекулярного притягування, відстань між молекулами зменшиться в 2 рази, то сила їх притягування збільшиться в 27=128 разів.
Ясно, що якби між молекулами діяли лише сили притягування, та ще й такі що так швидко зростають, то ці сили із всіх молекул тіла зробили б одну надмасивну молекулу. Тому не важко передбачити, що на певному етапі зближення молекул, мають з’явитися достатньо потужні сили міжмолекулярного відштовхування. І такі сили дійсно з’являються. Приблизно на відстані r≈0,5∙10–9м, прилад який реагує на сили міжмолекулярного відштовхування фіксує, що відповідні сили з’являються і що по мірі наближення молекул вони зростають. Аналізуючи характер цього зростання, ми приходимо до висновку, що воно відбувається за законом Fвід=b/r13, де b – коефіцієнт пропорційності величина якого залежить від сорту взаємодіючих молекул. Даний закон вказує на те, що коли в області дії сил міжмолекулярного відштовхування, відстань між молекулами зменшується в 2 рази, то сила їх відштовхування збільшиться в 213=8192 разів.
Таким чином, на відстані міжмолекулярної взаємодії, на молекулу одночасно діють дві незалежні сили – сила міжмолекулярного притягування (Fпр) та сила міжмолекулярного відштовхування (Fвід). При цьому, сила притягування починає діяти раніше, але зростає відносно повільно. Сила ж відштовхування з’являється пізніше, але зростає відносно швидко. Ясно, що в такій ситуації поведінка молекули визначатиметься результуючою цих сил: F=Fпр+Fвід. А знаючи характер залежності сил притягування та відштовхування від відстані між молекулами, не важко побудувати графік відповідної результуючої сили (мал.7). І цей графік представляє собою характерну яму, сторони якої мають різну кривизну.
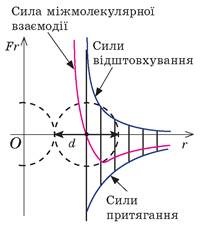
Мал.7. Поведінка молекули визначається результуючою двох сил – сили міжмолекулярного притягування та сили міжмолекулярного відштовхування.
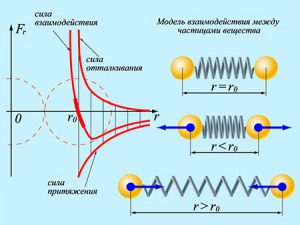
Із аналізу графіку результуючої сили міжмолекулярної взаємодії ясно, що під дією цієї сили, молекули прагнуть розташуватись на тій відстані для якої Fпр = Fвід, тобто на відстані r = r0. Адже, якщо r > r0, то молекули взаємно притягуються і прагнуть наблизитись одна до одної. А якщо r < r0, то молекули взаємно відштовхуються і прагнуть віддалитися одна від одної. Ситуація нагадує таку, в якій дві кульки з’єднані пружиною: при наближені кульок, пружина стискається і кульки взаємно відштовхуються, а при віддалені – пружина розтягується і кульки взаємно притягуються (мал.7б). Втім, аналогія з пружно зв’язаними кульками є наочною, але надто грубою та надто неточною моделлю міжмолекулярних взаємодій. Більш вдалою та більш адекватною моделлю цих взаємодій є так звана модель потенціальної ями. Потенціальною ямою називають графічне відображення тієї області міжмолекулярного простору, в якій потенціальна енергія молекули менша аніж за межами цієї області.
Пояснюючи суть того, що прийнято називати потенціальною ямою, можна сказати наступне. Взаємодію молекул характеризує не лише результуюча сила міжмолекулярної взаємодії, а й енергія цієї взаємодії, тобто потенціальна енергія молекул. А оскільки енергія (Е) і сила (F), це взаємопов’язані величини (ΔЕ=FΔℓ), то та крива яка описує залежність потенціальної енергії взаємодіючих молекул від відстані між цими молекулами, буде певним відображенням тієї кривої яка характеризує результуючу силу міжмолекулярної взаємодії (мал.8). Найбільш суттєва відмінність між цими кривими полягає в тому, що в тій кривій яка характеризує потенціальну енергію взаємодіючих молекул і яка називається потенціальною ямою, найнижча точка цієї ями, тобто та точка для якої потенціальна енергія молекули є мінімальною, відповідає тій відстані (r0) для якої результуюча сила міжмолекулярної взаємодії дорівнює нулю (якщо r=r0 то F=0; Eп=min).
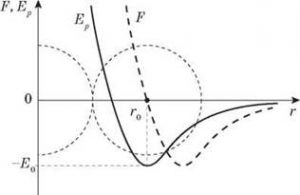
Мал.8. Та крива що описує залежність потенціальної енергії взаємодіючих молекул від відстані між ними, називається потенціальною ямою.
А тепер уявіть собі яму з ідеально гладенькою поверхнею, профіль якої аналогічний профілю потенціальної ями (мал.8). Якщо в такій ямі опиниться пружна кулька, то її поведінка значною мірою буде схожою на поведінку взаємодіючих молекул. Дійсно, маючи певний запас кінетичної енергії та прагнучи опинитись в нижній точці потенціальної ями, молекула буде здійснювати певні коливання відносно цієї точки. А це еквівалентно тому, що при зменшені відстані між молекулами, вони автоматично починають відштовхуватись, а при збільшенні цієї відстані – притягуватись.
Потрібно зауважити, що модель потенціальної ями не просто пояснює загальний характер взаємодії молекул, а є точним, кількісним відображенням цієї взаємодії. По суті та крива яку ми називаємо потенціальною ямою, є графічним відображенням тих складних процесів які відбуваються при взаємодії молекул речовини і які визначають загальні фізичні властивості цієї речовини. Важливою кількісною характеристикою енергії взаємодії молекул, а відповідно і потенціальної ями, є величина яка називається енергією зв’язку молекул. Енергією зв’язку молекул (глибиною потенціальної ями Еп0), називають ту мінімальну кількість енергії яку потрібно витратити на те, щоб молекула з мінімальною кількістю потенціальної енергії (молекула що перебуває на відстані r0) безповоротно вийшла за межі ділянки взаємодії молекул (за межі потенціальної ями). Іншими словами, енергією зв’язку молекули називають ту мінімальну кількість енергії яку необхідно витратити на те, щоб молекулу з дна потенціальної ями, перемістити за межі цієї ями.
Аналізуючи модель потенціальної ями, можна пояснити багато властивостей речовини. Зокрема пояснити чому в процесі нагрівання тверді тіла та рідини розширюються, чому при наближенні до температури плавлення, коефіцієнт теплового розширення твердих тіл збільшується, чому в процесі нагрівання певним чином змінюються механічні властивості твердих тіл та рідин, і від чого визначально залежать ці властивості, чому в процесі нагрівання речовини переходять з одного агрегатного стану в інший і від чого залежить цей агрегатний стан, тощо.
Наприклад пояснюючи факт того, що в процесі нагрівання речовини переходять з одного агрегатного стану в інший (тверді → рідкі → газоподібні), можна сказати наступне. Дослідження показують, що та величина яку ми називаємо температурою, нерозривно пов’язана з середньою кінетичною енергією молекул речовини, і що в процесі нагрівання, кінетична енергія молекул збільшується, а в процесі охолодження – зменшується. По суті це означає, що в процесі нагрівання речовини, амплітуда коливань її молекул збільшується, а в процесі охолодження – зменшується. А оскільки температура характеризує середню кінетичну енергію молекул, то факт хаотичності руху цих молекул вказує на те, що при одній і тій же температурі в будь якій речовині неминуче присутні як більш так і менш енергійні молекули.
Зважаючи на вище сказане, можна стверджувати. 1) Якщо середня кінетична енергія молекул речовини значно менша за величину їх потенціальну енергію (за глибину потенціальної ями: Ек < Еп0), то молекули в процесі їх коливань не будуть виходити за межі потенціальної ями. А це означає, що у відповідному температурному інтервалі, молекули речовини будуть нерозривно пов’язані одна з одною, забезпечуючи тим самим визначальну властивість твердого тіла – наявність певної незмінної форми. Іншими словами, якщо Ек < Еп0, то відповідна речовина знаходиться в твердому стані. 2) Якщо середня кінетична енергія молекул речовини значно більша за їх потенціальну енергію (за глибину потенціальної ями: Ек > Еп0), то здійснивши певне коливання, молекули будуть виходити за межі потенціальної ями та безповоротно віддалятись одна від одної. А це еквівалентно тому, як молекули газу, після їх взаємодії безповоротно розлітаються та заповнюють увесь їм доступний об’єм. Іншими словами, якщо Ек > Еп0, то відповідна речовина знаходиться в газоподібному стані. 3) Якщо середня кінетична енергія молекул речовини співрозмірна з потенціальною енергією цих молекул (Ек ≈ Еп0), то в процесі коливань, молекули час від часу викочуються за межі потенціальної ями, даючи можливість речовині змінювати свою форму. Іншими словами, якщо Ек ≈ Еп0, то відповідна речовина знаходиться в рідкому стані.
Таким чином, аналізуючи модель потенціальної ями, можна зробити обґрунтований висновок про те, що агрегатний стан речовини визначальним чином залежить від співвідношення між середньою кінетичною та потенціальною енергіями її молекул. При цьому:
для газів Ек > Еп0;
для рідин Ек ≈ Еп0;
для твердих тіл Ек < Еп0.
На завершення додамо, що кожна речовина має свої індивідуальні властивості і що тому, загальний вигляд та глибина її потенціальної ями є відповідно індивідуальними.
Контрольні запитання.
1. Наведіть докази того, що молекули взаємодіють між собою і що в залежності від міжмолекулярної відстані вони можуть як притягуватись так і відштовхуватись.
2. Наведіть докази того що молекули взаємодіють на надзвичайно малих відстанях.
3. Чому частинки зламаного твердого тіла не об’єднуються в єдине ціле? Що можна зробити для того щоб з’єднати ці частинки?
4. Поясніть, яким чином виходить так що на одних відстанях молекули притягуються, а на інших – відштовхуються?
5. Наведіть приклади механічних моделей які певним чином пояснюють поведінку взаємодіючих молекул.
6. Що називають потенціальною ямою?
7. Що називають глибиною потенціальної ями?
8. Чим відрізняється та крива яка називається потенціальною ямою, від тієї кривої яка характеризує силу міжмолекулярної взаємодії?
9. Поясніть яким чином агрегатний стан речовини залежить від співвідношення між потенціальною та кінетичною енергіями їх молекул.
§4. Про маси та розміри молекул.
В молекулярній фізиці ми не будемо вивчати подробиці будови атомів і молекул. Не будемо вивчати їх електричні, хімічні та біологічні властивості. Однак загальні відомості про атоми та молекули і перш за все про їх маси та розміри, ви все ж маєте знати.
Як зважити атом? Наївно думати, що існують такі надточні терези, на одну шальку яких можна покласти атом, а на іншу – гирьку відповідної маси. Ясно, що таких терезів не існує. Натомість існують опосередковані (непрямі) методи вимірювань, застосування яких дозволяє визначити масу атома з надзвичайно високою точністю. Сьогодні ми не будемо заглиблюватись в деталі того, як вчені вимірюють маси атомів та молекул. Зауважимо тільки, що не довіряти цим вимірюванням, це все рівно ніби не довіряти тим вимірюванням які визначають площу круга за формулою S=πR2. Не довіряти лише на тій підставі, що визначаючи площу, ми фактично вимірюємо не площу круга а його радіус. Зважаючи на вище сказане, ми зупинимся лише на тих аспектах вимірювання мас атомів, які пов’язані з фактом того, що різні атоми вступають в хімічні взаємодії в певних, строго визначених пропорціях.
На основі аналізу величезної кількості хімічних реакцій, було з’ясовано, що атомні маси всіх хімічних елементів знаходяться в певних співвідношеннях. При цьому вимірювання показували, що найлегшим атомом є атом водню (гідрогену Н). Виходячи з цього, в якості одиниці вимірювання атомних мас була обрана воднева одиниця маси. В такій системі вимірювань, маса атома водню приймалась за одиницю (m0(Н)=1,0000), а маси інших атомів визначались на основі того, в яких співвідношеннях ці атоми реагують з воднем. Так, наприклад, маса атому кисню (оксигену О) становила 15,874 водневих одиниць маси, а маса атому вуглецю (карбону С) – 11,917 цих одиниць і т.д.
Вимірювати атомні маса в водневих одиницях маси, тобто в масах найлегшого з атомів, представлялось абсолютно логічним та доцільним. Однак, в хімічній практиці маси переважної більшості елементів, визначались на основі того в яких пропорціях вони взаємодіють не з воднем, а з киснем. І це закономірно. Адже кисень, це один з найактивніших хімічних елементів. Тому хіміки наполягли на тому, щоб атомну масу кисню вважати рівною 16,0000, а маси інших елементів вимірювати не у водневих, а в кисневих одиницях маси. При цьому за таку потрібно було вважати 1/16 маси атома кисню.
Якщо ви думаєте, що на цьому епопея з вибором одиниці вимірювання атомних мас закінчилась, то помиляєтесь. Через певний час, фізики з’ясували, що навіть хімічно найчистіший кисень, представляє собою певну суміш дуже схожих але все таки суттєво різних атомів кисню. Ці схожі атоми називають ізотопами. Ізотопи мають практично однакові хімічні властивості але суттєво різні маси.
Оскільки хімічними методами розділити ізотопи практично не можливо, то хіміки за кисневу одиницю маси вважали 1/16 маси усередненого атома кисню. Фізики ж вміли розділяти ізотопи і тому за кисневу одиницю маси вважали 1/16 маси кисню ізотопу-16. Це означало що в хімії і фізиці атомні маси вимірювались фактично різними одиницями, які до того ж мали одну і ту ж назву. Так тривало до 1961 року. В цьому році було прийнято компромісне рішення – маси атомів, молекул, іонів та елементарних частинок вимірювати в атомних одиницях маси.
Атомна одиниця маси (а.о.м.) – це позасистемна одиниця вимірювання маси, яка дорівнює 1/12 маси атома вуглецю-12: а.о.м. = m0(С612)/12. На основі точних експериментальних досліджень встановлено: а.о.м. = 1,6605655∙10–27кг.
Загальні відомості про атоми, в тому числі і про їх маси, можна знайти в таблиці яка називається періодичною системою хімічних елементів (мал.9). В цій таблиці, кожен атом характеризується двома числами: порядковим номером атома (Z) та його масовим числом (Мr). Наприклад: Н11,0079; Не24,0026; С612,011; О815,999; СƖ1735,453; Рb82207,20.
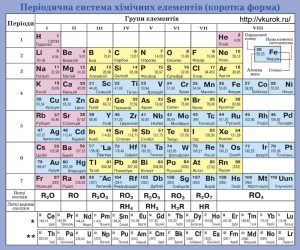
Мал.9. Періодична система хімічних елементів.
Масове число (відносна атомна маса) – це безрозмірна величина, яка показує у скільки разів маса усередненого атома даного хімічного елементу (m0) більша за одну атомну одиницю маси. Позначається Мr (“r” – від англ. relative – відносний). Відносна атомна маса даного хімічного елементу визначається на основі аналізу відповідних хімічних реакцій і записується у відповідну клітинку періодичної системи хімічних елементів.
Коли ми говоримо про усереднену масу атома (m0) даного хімічного елементу, то маємо на увазі той факт, що практично будь яка хімічно проста речовина, представляє собою певну суміш хімічно однакових але різних за масою ізотопів. Ізотопами – називають різновидності хімічно однакових атомів, в ядрах яких міститься однакова кількість протонів але різна кількість нейтронів. Це означає, що ізотопи мають практично однакові хімічні властивості, але суттєво різні атомні маси.
Наприклад, хімічно чистий природний хлор приблизно на 75% складається з ізотопу хлор-35, атомна маса якого 35а.о.м. і на 25% з ізотопу хлор-37, атомна маса якого 37а.о.м. А це означає, що визначаючи відносну атомну масу природної суміші цих ізотопів, завжди отримують Мr(Сℓ)=35,45. Тому, коли масу атома хлору визначають на основі записаного в таблиці хімічних елементів масового числа (Мr=35,45), то фактично визначають не масу конкретного атома, а усереднену масу атомів даного хімічного елементу: m0(CƖ) = 35,45(а.о.м.) = 35,45∙1,66∙10–27кг.
До речі, те що масові числа більшості хімічних елементів суттєво відрізняються від цілих чисел, це прямий наслідок того, що відповідні елементи представляють собою певну суміш різних ізотопів. Наприклад:
С612,011 = 98,89% С612 + 1,11% С613 ;
Сu2963,546 = 69,1% Cu2963 + 30,9% Cu2965 ;
Зважаючи на вище сказане, усереднену масу атома певного хімічного елемента (цю масу зазвичай називають масою відповідного атома) ми будемо визначати за формулою m0 = Mr (а.о.м.) = Mr∙1,66∙10–27кг, де Мr – масове число, значення якого визначається з таблиці хімічних елементів. Якщо ж мова йтиме про масу однієї молекули, то вона визначатиметься як сума мас тих атомів з яких ця молекула складається. Наприклад:
m0(H2O) = (2∙1+16)а.о.м. = 18∙1,66∙10–27кг ;
m0(H2SO4) = (2∙1+32+4∙16)а.о.м. = 98∙1,66∙10–27кг ;
m0(NaCl) = (23+35,5)а.о.м. = 58,5∙1,66∙10–27кг .
Зауважимо. Маса атома (m0) виражена в а.о.м. та його відносна атомна маси (Mr) – чисельно рівні величини. Однак це не означає, що поняття «маса атома» і «відносна атомна маса» є тотожними. Тому потрібно говорити і писати: m0(H2O) = 18а.о.м.; Mr = 18, а не Mr = 18а.о.м.
Закінчуючи розмову про маси атомів і молекул, наведемо простий приклад, який наочно демонструє масштаби цих мас: маса середнього яблука (≈100гр) у скільки разів більша за масу атома водню, у скільки разів маса Землі більша за масу цього яблука. Іншими словами:
Говорячи про розміри молекул (атомів) ви маєте розуміти, що молекули зовсім не схожі на все те що ви звикли бачити. Що вони не мають а ні чітких обрисів, а ні чітких меж. Молекули взагалі не мають того що прийнято називати розмірами, формою, об’ємом, густиною, тощо. Тому, коли ми говоримо про певні геометричні параметри молекули, то маємо на увазі параметри тієї умовної пружної кульки яка є гранично спрощеною моделлю відповідної молекули і яка лише віддалено схожа на неї.
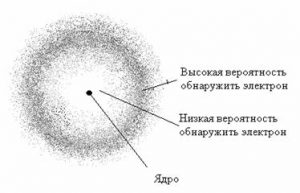

Мал.10. Атом, а тим більше молекулу, лише досить умовно можна представити у вигляді певної пружної кульки.
Наближено оцінити умовні розміри молекул можна на основі наступних міркувань. Відомо, що в 18г води (1моль води) міститься 6,02∙1023 її молекул. Відомо, що 18г води займають об’єм 18см3 =18∙10–6м3. А це означає, що на одну молекулу води припадає об’єм 3∙10–29м3: V0 = V/N = 18∙10–6м3/6∙1023 = 3∙10–29м3, і що діаметр цієї гіпотетичної молекули становить 0,38∙10–9м: оскільки Vкулі =πd3/6, то d = (6V0/π)1/3 = 0,38∙10–9м. Ясно, що реальні розміри молекули води дещо менші. Менші по перше тому, що кулі не можливо ущільнити настільки щоб між ними не було проміжків пустоти. А по друге, нам достеменно відомо що молекули рухаються і що тому вони знаходяться на певній відстані одна від одної.
В науковій практиці умовні розміри молекули (атома) характеризують величиною яка називається ефективним діаметром молекули (атома). Дослідження показують, що ефективні діаметри атомів та хімічно простих молекул знаходяться в межах (0,2÷0,4)нм = (0,2÷0,4)10–9м. Наприклад: d(H2O) = 0,26нм = 0,26∙10–9м; d(H2) = 0,23нм; d(O2) = 0,29нм; d(N2) = 0,31нм; d(He) = 0,19нм; d(CO2) = 0,32нм. Ілюструючи мізерність цього числа достатньо сказати, що молекула води у стільки разів менша за середнє яблуко, у скільки разів це яблуко менше за Землю. Іншими словами:
Задача 1. Скільки молекул міститься в 98г Н2SО4?
Дано:
m(H2SO4) = 98г = 98·10–3кг
N = ?
Рішення. Будемо виходити з того, що кількість молекул в заданій масі (m) речовини, визначається за формулою N=m/m0, де m0 – маса однієї молекули відповідної речовини. Оскільки маса молекули визначається за формулою m0 = Mr (a.o.м.) = Mr·1,6610–27(кг), де Mr – масове число величина якого визначається з таблиці хімічних елементів (Mr(H)=1; Mr(S)=32; Mr(O)=16), то можна записати m0(Н2SO4) = 2·1(a.o.м.) + 32(а.о.м.) + 4·16(а.о.м) = 98(а.о.м) = 98·1,6610–27(кг).
Таким чином: N=m/m0 = 98·10–3кг/98·1,6610–27(кг) = 6,02·1023молекул.
Відповідь: в 98г H2SO4 міститься 6,02·1023молекул H2SO4.
Задача 2. Крапля машинної оливи масою 2,2·10–8кг утворила на поверхні води пляму площею 5,68·10–2м2. Виходячи з того, що пляма утворена одним шаром молекул, визначте діаметр цих молекул. Густина машинної оливи 900кг/м3.
Дано:
m = 2,2·10–8кг
S = 5,68·10–2м2
ρ = 900кг/м3
d = ?
Рішення. Будемо виходити з того, що діаметр молекули (d) дорівнює товщині плями оливи. А оскільки за визначенням ρ=m/V, та враховуючи що V=Sd, можна записати ρ=m/Sd, звідси d=m/Sρ.
Розрахунки: d=m/Sρ = 2,2·10–8кг/5,68·10–2(м2)900кг/м3 = 0,043·10–8м = 0,43·10–9м.
Відповідь: d = 0,43·10–9м = 0,43нм.
Загальні зауваження. Ясно, рішення даної задачі є значною мірою спрощеним (ідеалізованим). Адже ми по суті виходили з того, що молекули машинної оливи мають форму куба сторона якого дорівнює діаметру вписаної в нього кулі, і що ці куби щільно прилягають одна до одної утворюючи тим самим суцільну плівку. Втім, таке спрощення є цілком виправданим. Виправданим по-перше тому, що реальна форма молекул оливи нам невідома. По-друге, представляючи молекулу у формі куба, а отже дещо зменшуючи їх діаметр порівняно з діаметром аналогічної за масою кулі, ми фактично компенсуємо ті проміжки простору які безумовно існують між молекулами та забезпечують їх коливальні рухи. По-третє, дане спрощення дозволяє розв’язати задачу. Адже якби наприклад ми спробували представити молекули у вигляді куль, то в процесі розв’язування задачі, неминуче стикнулися б з необхідністю визначити масу однієї молекули. А за даної умови задачі, це неможливо, а отже неможливим стає і загальне рішення задачі.
Загалом, одним з тих корисних вмінь які ви маєте розвивати шляхом розв’язування задач, полягає в тому, щоб на основі аналізу умови задачі, виділяти основне та нехтувати другорядним.
Контрольні запитання.
1. На основі чого було встановлено, що маси хімічних елементів знаходяться в певних співвідношеннях?
2. Чому хімікам не сподобалась абсолютно логічна та обгрунтована ідея визначати маси атомів та молекул в водневих одиницях маси?
3. Еволюцію одиниці вимірювання мас атомів та молекул відображає схема: воднева одиниця маси → киснева одиниця маси → атомна одиниця маси. Опишіть історію цієї еволюції.
4. Що називають атомною одиницею маси?
5. Якщо а.о.м. це 1/12 маси атома вуглецю-12, то чому в таблиці хімічних елементів відносна атомна маса вуглецю не 12,000 а 12,011?
6. Що називають ізотопами?
7. Що називають масовим числом (відносною атомною масою) хімічного елемента?
8. Чи правильне твердження: масове число оксигену – 16а.о.м.?
9. В яких межах знаходяться розміри (діаметри) атомів та хімічно простих молекул?
Вправа 4.
1. Визначити масу одного атома в а.о.м, та в кг: Не; Na; Cℓ; Cu; Ag; Au (масові числа округляти до цілого числа).
2. Визначити масу однієї молекули (в а.о.м. та кг): О2; СО2; АgNO3; CuSO4; Ca(OH)2; C12H22O11.
3. Скільки атомів в 12 грамах вуглецю (С612)?
4. Скільки молекул (атомів) міститься в: а) 18г Н2О; б) 27г АƖ; в) 207г Рb? На основі отриманих результатів, зробіть узагальнюючий висновок.
5. За 5 діб випарувалось 50г води. Скільки молекул води вилітало за 1с?
6. Де більше атомів: у склянці води чи в склянці ртуті? (густина ртуті 13,6·103кг/м3)
§5. Про кількість речовини в тілі, та про ті величини які цю кількість характеризують.
Нагадаємо, речовина – це вид матерії який складається з тих чи інших частинок і має масу (масу спокою). Оскільки речовина, це те що складається з певних частинок (структурних одиниць) та має масу, то ясно, що кількість речовини в тілі (фізичному об’єкті) можна оцінити як масою цього тіла (чим більша маса – тим більше речовини) так і кількістю структурних одиниць в ньому (чим більше структурних одиниць – тим більше речовини). Крім цього, дане тіло можна розділити на певні порції та полічити їх. При цьому, чим більшою виявиться кількість порцій в тілі, тим відповідно більшою буде і кількість речовини в ньому. Виходячи з цього, в науковій практиці застосовують три фізичні величини, які по суті характеризують одне і те ж – кількість речовини в тілі. Цими величинами є: маса (m), кількість структурних одиниць (N) та кількість речовини (ν).
Маса (в молекулярній фізиці) – це фізична величина, яка є загальною мірою кількості речовини в тілі, виміряну в кілограмах.
Позначається: m
Визначальне рівняння: нема
Одиниця вимірювання: [m] = кг .
Кількість структурних одиниць – це фізична величина, яка характеризує кількість речовини в тілі, виміряну числом структурних одиницях цієї речовини.
Позначається: N
Визначальне рівняння: N=m/m0, де m – загальна маса речовини; m0 – маса однієї структурної одиниці даної речовини;
Одиниця вимірювання: [N] = ст.од. (атоми, молекули, іони).
Кількість речовини – це фізична величина, яка характеризує кількість речовини в тілі, виміряну в молях, тобто в певним чином вибраних порціях (кучках) цієї речовини.
Позначається: ν
Визначальне рівняння: ν= m/M, де m – загальна маса речовини; M – молярна маса даної речовини (маса тієї порції речовини яка називається молем).
Одиниця вимірювання: [ν] = моль.
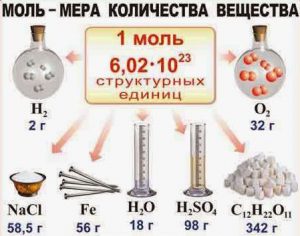
Моль (від лат. moles – маса) – це одиниця вимірювання кількості хімічно простої та хімічно однорідної речовини, яка дорівнює такій порції цієї речовини, в якій міститься стільки її структурних одиниць, скільки атомів міститься в 12 грамах вуглецю-12.
Задача. Скільки атомів міститься в 12 грамах вуглецю-12?
Дано:
m(C612)=12г = 12∙10–3кг
N=?
Рішення. За визначенням N=m/m0, де m0(C612) = 12а.о.м. = 12∙1,66∙10–27кг.
Розрахунки: N = (12∙10–3кг)/(12∙1,66∙10–27кг) = 6,022∙1023атомів.
Відповідь: в 12г вуглецю-12 міститься 6,022∙1023 його атомів.
Висновок: В одному молі будь якої речовини міститься 6,022∙1023 її структурних одиниць.
Таким чином, молем називають таку порцію хімічно простої та хімічно однорідної речовини, в якій міститься 6,022∙1023 її структурних одиниць. Постійна величина, яка дорівнює числу структурних одиниць в одному молі речовини, називають сталою Авогадро* (позн. NA): NA = 6,022∙1023 (1/моль).
*) Названо на честь одного з засновників сучасної молекулярної фізики, італійського вченого Амадео Авогадро (1776–1856).
Молярна маса речовини – це фізична величина, яка характеризує молярну масу даної хімічно простої речовини і яка дорівнює цій масі, тобто масі тієї порції речовини яка називається молем.
Позначається: M
Визначальне рівняння: M=m0NA
Одиниця вимірювання: [M] =кг/моль .
На практиці, молярну масу речовини зазвичай визначають не за визначальним рівнянням М=m0NA, а за формулою М=Мr (г/моль), де Мr – відносна атомна (молекулярна) маса відповідної речовини. І не важко довести, що формула М=Мr(г/моль) є похідною від визначального рівняння М=m0NA. Дійсно:
M=m0NA =Mr∙1,66∙10–27(кг)∙6,022∙1023(1/моль) =Мr∙10–3(кг/моль) =Мr(г/моль).
Практичні переваги формули М=Мr(г/моль) над визначальним рівнянням М=m0NA є очевидними. Адже застосовуючи формулу М=Мr(г/моль), ми оминаючи низку проміжних розрахунків, відразу ж отримуємо правильний результат. Наприклад: М(Н2О) = 18г/моль; М(Н2SО4) = 98г/моль; М(АƖ) = 27г/моль; М(Рb) = 207г/моль; М(С12Н22О11) = 342г/моль.
Ще одне практично важливе спрощення полягає в тому, що кількість молекул в речовині зазвичай визначають не за визначальним рівнянням N=m/m0, a за формулою N=νNA. Достовірність цієї формули є очевидною. Адже якщо в одному малі речовини міститься NА її молекул, то в ν молях, цих молекул буде в ν разів більше, тобто N=νNA.
Потрібно зауважити, коли ми стверджуємо, що в 18г води (Н2О), 98г сірчаної кислоти (Н2SО4), 27г алюмінію (АƖ), 207г свинцю (Рb) та 342г цукру (С12Н22О11), міститься однакова кількість речовини (один моль речовини), то це означає лише те, що в кожній з цих різних за масою порціях різних речовини, міститься однакова кількість (а саме 6,022∙1023) молекул (структурних одиниць) відповідної речовини. Факт того, що в різних за масою порціях різних речовин міститься однакова кількість молекул, є прямим наслідком факту того, що маси різних молекул є різними. Скажімо, якщо маса одного атома Pb (m0=207а.о.м.) в 7,67 раз більша за масу одного атома Al (m0=27а.о.м.), то відповідно більшою буде і маса одного моля Pb порівняно з масою одного моля Al.
Мал.12. Кількість речовин різна, а кількість молей і кількість структурних одиниць в них – однакова. Чому?
З точки зору хімічної практики, вимірювати кількість речовини в молях надзвичайно зручно. Зручно головним чином тому, що хімічні взаємодії речовин відбуваються в певних вагових співвідношеннях, які пропорційні їх молярним масам. Тому в хімії кількість тієї чи іншої речовини зазвичай вимірюють в молях. Додайте до цього той малоприємний факт, що та фізична величина яка характеризує кількість речовини виміряну в молях називається «кількістю речовини» і ви зрозумієте чому, дехто вважає, що кількість речовини можна охарактеризувати лише величиною яка так і називається «кількість речовини».
Таке твердження є абсолютно хибним. Хибним по перше тому, що виміряти кількість речовини в молях, можна лише в тому випадку, якщо мова йде про хімічно просту та хімічно однорідну речовину. Тобто таку речовину яка складається з певних однакових структурних одиниць які можна представити у вигляді відповідної хімічної формули. По друге, визначити кількість речовини в молях не можливо без вимірювання маси відповідної речовини (ν= m/M). По третє, стверджувати що в одному молі алюмінію (27г) і в одному молі свинцю (207г) міститься однакова кількість речовини, можна лише в сенсі однаковості числа атомів в цих фактично різних кількостях речовини. Бо якщо виходити з суті загально прийнятого визначення терміну речовина, то стверджувати що в 27г алюмінію стільки ж речовини як і в 207г свинцю, це все рівно ніби наполягати на тому, що в 1кг вишень стільки ж речовини як і в 500кг кавунів (кількість же структурних одиниць в обох кучках однакова).
Мал.13 Чи можна, на основі того, що в кожній кучці міститься однакова кількість структурних одиниць, стверджувати що кількість речовини в кожній кучці однакова?
Та якби там не було, а в науковій практиці, в залежності від ситуації та поставлених задач, кількість речовини в тому чи іншому фізичному об’єкті вимірюють в кілограмах, структурних одиницях або молях. Іншими словами, в науковій практиці, кількість речовини в тілі характеризують трьома фізичними величинами: масою (m), кількістю структурних одиниць (N=m/m0) та кількістю речовини (ν=m/M). При цьому головною, загальною, універсальною та найбільш об’єктивною мірою кількості речовини є маса. Вона є такою по перше тому, що масою можна виміряти кількість будь якої речовини. А по друге, не визначивши маси речовини не можливо визначити а ні кількість її структурних одиниць, а ні кількість молей в ній.
Таким чином:
. характеризують вимірюють
кількість m кг
речовини N=m/m0 ст.од.
. ν=m/M моль
Говорячи про кількість речовини в тілі та про ті фізичні величини які цю кількість характеризують, доречно звернути увагу на ще один факт. Факт, який ілюструє багатогранність фізики – науки про Природу. Адже ми стикнулись з ситуацією, коли один і той же параметр фізичного об’єкту, а саме кількість речовини в ньому, характеризують три різні фізичні величини: маса (m), кількість структурних одиниць (N) та кількість речовини (ν). І ця ситуація в певному сенсі протилежна тому, коли одна і та ж фізична величина, а саме маса, характеризує чотири різні параметри фізичного об’єкту: його інерціальні властивості, гравітаційні властивості, енергетичні властивості та кількість речовини в цьому об’єкті. Нагадаємо:
Маса – це фізична величина, яка є:
– мірою інерціальних властивостей тіла;
– мірою гравітаційних властивостей тіла;
– мірою енергетичних властивостей тіла;
– міра кількості речовини в тілі, виміряної в кілограмах.
Позначається: m
Визначальне рівняння: нема
Одиниця вимірювання: [m] = кг .
Завершуючи розмову про ті фізичні величини які характеризують кількість речовини в тілі, визначимо і ті з них, які певним чином характеризують кількість речовини в одиниці об’єму. До числа таких величин відносяться: густина (ρ); концентрація молекул (n0); молярна концентрація (с).
Густина – це фізична величина, яка характеризує кількість речовини в одиниці об’єму і яка показує скільки кілограм даної однорідної речовини міститься в одиниці її об’єму.
Позначається: ρ
Визначальне рівняння: ρ = m/V
Одиниця вимірювання: [ρ] = кг/м3 .
Концентрація молекул – це фізична величина, яка характеризує кількість речовини в одиниці об’єму і яка показує скільки молекул (структурних одиниць) даної однорідної речовини міститься в одиниці її об’єму.
Позначається: n0
Визначальне рівняння: n0 = N/V
Одиниця вимірювання: [n0] = 1/м3 .
Молярна концентрація – це фізична величина, яка характеризує кількість речовини в одиниці об’єму і яка показує скільки молей даної однорідної речовини міститься в одиниці її об’єму.
Позначається: с
Визначальне рівняння: с = ν/V
Одиниця вимірювання: [с] = моль/м3.
Задача 1. Визначити масу однієї молекули, молярну масу, кількість молей та кількість молекул в 200г AgNO3.
Дано:
m(AgNO3) = 200г
m0=?; M=?; ν=?; N=?
Рішення.
m0(AgNO3) = Мr·1,66·10–27кг = (108+14+3·16)а.о.м. = 170·1,66·10–27кг;
М(AgNO3) = Мr(г/моль) = (108+14+3·16)г/моль = 170г/моль;
ν(AgNO3) = m/M = 200г/170(г/моль) = 1,17моль;
N(AgNO3) = νNA = 1,17моль·6,02·1023(1/моль) = 7,0·1023молекул AgNO3.
Задача 2. Знаючи число Авогадро визначити об’єм і діаметр атома золота.
Дано:
Au
NA=6,02·10231/моль
V0=?; d=?
Рішення. За заданим матеріалом можна визначити багато табличних характеристик цього матеріалу і зокрема його густину: ρ(Au)=19,3·103кг/м3. За визначенням ρ=m/V. Оскільки за умовою задачі, відомою величиною є стала Авогадро, тобто кількість атомів Аu в одному молі золота, то будемо виходити з того, що маса золота дорівнює його молярній масі, тобто m=М=197·10–3кг/моль. А в такій ситуації V=V0NA. Таким чином, ρ=m/V = М/V0NA, звідси V0=M/ρNA.
Виходячи з того, що атом Au представляє собою кулю діаметром d, та враховуючи, що об’єм кулі визначається за формулою V0=πd3/6, можна записати d=(6V0/π)1/3.
Розрахунки:
V0=M/ρNA = 197·10–3 (кг/моль)/19,3·103(кг/м3)6,02·1023(1/моль) = 17·10–30м3.
d=(6V0/π)1/3 = 6·17·10–30м3/3,14)1/3 = 10–10(32)1/3 = 3,2·10–10 = 0,32·10–9м.
Відповідь: V0(Au)= 17·10–30м3; d(Au)=0,32·10–9м.
Контрольні запитання.
1. Які фізичні величини характеризують кількість речовини в тілі?
2. Яка з тих фізичних величин які характеризують кількість речовини в тілі є основною (базовою)? Чому?
3. В яких одиницях можна виміряти кількість речовини в тілі?
4. Дайте визначення терміну «моль».
5. Чи можна визначити кількість паперу: а) в структурних одиницях; б) в молях; в) в кілограмах? Про що це говорить?
6. Що мають на увазі хіміки, коли стверджують, що в 18г води, 98г сірчаної кислоти і в 342г цукру, міститься однакова кількість речовини?
7. Чому різні речовини в кількості один моль мають різні маси?
8. Доведіть що формули М = m0NA і M = Mr (г/моль) є тотожними.
9. Чим схожі і чим відрізняються ті величини які називаються густина, концентрація молекул та молярна концентрація.
Вправа 5.
1. Визначити масу однієї молекули, молярну масу, кількість молей і кількість молекул в 200г: а) Н2О; б) CuSO4; в) NaCℓ; г) Ca(OH)2 .
2. Відомо, що за нормальних умов, один моль будь якого газу займає об’єм 22,4 літра (закон Авогадро). Визначити концентрацію молекул за цих умов.
3. За 5 діб випарувалось 60г води. Скільки молекул вилітало при цьому за одну секунду.
4. Який об’єм одного моля алюмінію (густина алюмінію 2,7·103кг/м3)?
5. Де більше атомів, в 100г кухонної солі чи в 100г цукру (C12H22O11)?
6. Знаючи число Авогадро визначте приблизний об’єм та діаметр атома міді (густина міді 8,9г/м3).
7. Кухонна сіль має кубічну кристалічну структуру в вузлах якої розташовані іони натрію та хлору. Знаючи густину солі (2200кг/м3) визначте відстані між центрами найближчих іонів.
.
§6. Температура, як міра нагрітості тіла, та як міра середньої кінетичної енергії його молекул.
Слово «температура» в перекладі з латинської означає «суміш». Така назва обумовлена фактом того, що колись вчені вважали, що температура тіла залежить від того, в яких пропорціях в цьому тілі змішані відповідна речовина та особлива теплова матерія яку називали теплородом. Згодом з’ясувалося, що ніякого теплороду не існує і від ідеї суміші теплороду з речовиною відмовились. А от слово «температура» залишилось, і сьогодні, як і сотні років тому характеризує ступінь нагрітості тіла. Втім, температура, це та фізична величина, яка має що найменше чотири різні, загально прийняті наукові визначення. При цьому вчені так і не дійшли згоди відносно того, а яке ж з цих визначень є найбільш правильним.
Вивчаючи фізику, ми стикались з ситуацією коли одним і тим же терміном, зокрема словом «маса», позначали чотири фактично різні фізичні величини: маса – міра інерції; маса – міра гравітації; маса – міра енергії; маса – міра кількості речовини. Стикались з ситуацією, коли навпаки, один і той же параметр фізичного об’єкту, а саме кількість речовини в тілі, характеризують трьома фактично різними фізичними величинами – масою (m), кількістю структурних одиниць (N) та кількістю речовини (ν). Наразі ж мова йде про те, що одна і та ж фізична величина, яка позначається одним і тим же словом, і яка характеризує одну і ту ж властивість фізичного об’єкту, в різних обставинах та в різних розділах фізики, визначається по різному. І цією величиною є температура.
З точки зору повсякденної практики безумовно найзручнішим є наступне наукове визначення температури. Температура – це фізична величина, яка характеризує ступінь нагрітості тіла, виміряну термометром за температурною шкалою Цельсія.
Позначається: t
Визначальне рівняння: нема, (нема тому, що у відповідності з даним визначенням, температура є абсолютно автономною (незалежною від інших) величиною)
Одиниця вимірювання: [t] = °C, градус Цельсія.
Градус Цельсія (°С) – це одиниця вимірювання температури, яка дорівнює сотій частині інтервалу температур між точкою плавлення та точкою кипіння чистої води, визначеними при нормальному атмосферному тиску.
Аналізуючи визначення терміну температура, доречно зауважити, що температуру тіла визначають не за суб’єктивними відчуттями людини, а за показаннями спеціального приладу який називається термометром. Термометри бувають різними: рідинні, газові, біметалічні, електричні, електронні, оптичні, тощо. Основним вимірювальним елементом будь якого термометра є чутливе до зміни температури термометричне тіло. При цьому принцип дії термометра грунтується на тому, що певний параметр термометричного тіла, певним визначеним чином залежить від температури. Наприклад, в процесі зміни температури, можуть змінюватись лінійні розміри термометричного тіла, його об’єм, форма, пружність, електропровідність, тощо. Власне за величиною цих змін і визначають відповідну температуру.
Важливою складовою процесу вимірювання температури є температурна шкала, тобто та система відліку в якій задано початок відліку температури (нулева точка), одиниця її вимірювання та еталонний метод цього вимірювання. З побутової точки зору найбільш зручною та розповсюдженою температурною шкалою є шкала Цельсія. Цю шкалу запровадив в 1742 році шведський вчений Андерс Цельсій (1701–1744). В температурній шкалі Цельсія за початок відліку температур прийнято температуру плавлення води (льоду); за одиницю вимірювання – градус Цельсія; за еталонний метод вимірювання – вимірювання температури ртутним термометром.
Будова сучасного побутового термометра загально відома. Його основною деталлю є висока скляна колба, частково заповнена певною рідиною (зазвичай ртуттю або забарвленим спиртом). Напевно ви здогадуєтесь і про те, яким чином градуюють термометр?! Правильно. Його спочатку опускають в суміш води і льоду, і відповідний рівень термометричної рідини позначають 0°С (мал.14а). Потім термометр опускають в окріп і наявний рівень термометричної рідини позначають 100°С (мал.14б). Після цього, відстань між отриманими точками ділять на сто рівних чистин і термометр готовий до застосування.
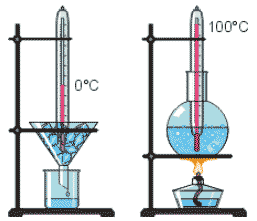
Мал.14. При градуюванні термометра, відстань між його показаннями при температурі плавлення льоду (а) і температурі кипіння води (б), ділять на сто рівних частин.
Якщо виходити з того, що теплове розширення термометричного тіла є рівномірним (лінійним), то вище описаний спосіб градуювання термометра не викликає жодних заперечень. Однак, чи можемо ми бути впевненими в тому, що теплове розширення ртуті, спирту та інших матеріалів дійсно рівномірне? Виявляється, не можемо. Дослідження показують, що теплове розширення переважної більшості тіл, складним чином залежить від температури, і що в загальному випадку ця залежність є не лінійною. Тому якщо наприклад, на основі ртуті, заліза, міді, скла та повітря виготовити п’ять однакових термометра і стандартним чином проградуювати їх, то неодмінно з’ясується, що за одних і тих же температурних умов, показання різних термометрів будуть суттєво різними. Скажімо, якщо повітряний термометр буде показувати 300°С то ртутний зафіксує 314°С, залізний 373°С, мідний 329°С, а скляний 353°С.
В такій ситуації неминуче виникає запитання: «А який з цих термометрів показує правильну температуру? І чи є серед цих показань бодай одне безумовно правильне?» Відповісти на це запитання можна лише втому випадку, якщо створити такий термометр, в якому певний параметр термометричного тіла гарантовано лінійно залежатиме від температури. І такий еталонний термометр дійсно існує. Його називають газовим термометром.
В 1802 році французький фізик Гей-Люсак (1778–1850) експериментально встановив, що при постійному тиску певної маси газу (m=const; p=const), всі гази розширюються однаково, і що при цьому виконується співвідношення Vt = V0(1+βt),
де Vt – об’єм газу при температурі t°C;
V0 – об’єм газу при температурі 0°С ;
β =1/273 – температурний коефіцієнт об’ємного розширення газу.
По суті це означало, що при постійному тиску певної маси газу, його об’єм лінійним чином залежить від температури (мал.15) і що тому термометр в якому термометричним тілом є газ, можна вважати еталонним? Крім цього, закон Гей-Люсака вказував на те, що в Природі існує нижня межа температур і що числове значення цієї межі –273°С. Детальні дослідження та точні вимірювання показали, що гранично низька температура дійсно існує, і що її величина дійсно дорівнює –273°С (точніше –273,15°С). Цю гранично низьку температуру прийнято називати абсолютним нулем.
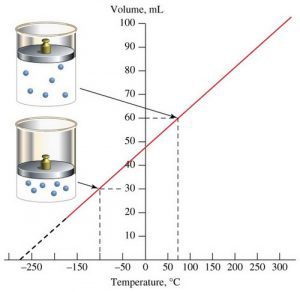
Мал.15. В процесі ізобаричного (m=const; p=const) нагрівання (охолодження) газу, його об’єм лінійним чином збільшується (зменшується).
Дослідження, проведені з застосуванням еталонних газових термометрів показали, що в більш-менш широких температурних інтервалах, переважна більшість твердих та рідких матеріалів, розширюються не рівномірно (не лінійно). Однак, якщо мова йде про побутово важливий інтервал температур (від –30°С до +150°С), то в цьому інтервалі ртуть розширюється майже лінійно. Тому в температурному інтервалі від –30°С до +150°С ртутні термометри вважаються одними з найкращих.
Обираючи в якості точки відліку температур, температуру плавлення льоду, ми керувались міркуваннями практичної доцільності та зручності. Але, чесно кажучи, за такого підходу в якості нулевої точки можна вибрати будь яку іншу сталу температуру, наприклад температуру плавлення свинцю, золота, міді чи скажімо суміші води, солі та нашатирю. Тепер же, коли з’ясувалось що в Природі існує певна, гранично низька температура (–273°С), чи не буде розумним саме цю температуру обрати за об’єктивну точку відліку температур? Таке цілком логічне рішення було прийнято. При цьому відповідну температурну шкалу назвали абсолютною шкалою температур або шкалою Кельвіна (на честь англійського фізика Уільяма Томсона (лорда Кельвіна) який в 1848 році і запропонував абсолютну шкалу температур).
В абсолютній шкалі температур, за початок відліку прийнято температуру абсолютного нуля, за одиницю вимірювання – кельвін, а за еталонний метод вимірювання – вимірювання за допомогою еталонного газового термометра. При цьому, визначення температури набуває вигляду:
Температура – це фізична величина, яка характеризує ступінь нагрітості тіла виміряну еталонним газовим термометром за абсолютною шкалою температур.
Позначається: Т
Визначальне рівняння: нема
Одиниця вимірювання: [Т] = К, кельвін.
Кельвін (К) – це одиниця вимірювання температури, яка дорівнює 1/273,16 частині інтервалу температур між температурою абсолютного нуля (–273,15°С) та температурою потрійної точки води (0,01°С).
На перший погляд, офіційні визначення тих температурних одиниць які називаються кельвіном та градусом Цельсія є різними. Однак суть цих різних визначень полягає в тому, що у відповідності з ними, кельвін (К) та градус Цельсія (°С) є чисельно рівними одиницями: К=°С. Дійсно:
К=[0,01ºС–(–273,15ºС)]/273,16=273,16ºС/273,16=ºС. Якщо ж говорити про ту різницю яка безумовно існує між температурою виміряною в градусах Цельсія (t) та температурою виміряною в кельвінах (Т), то вона полягає в тому, що в першому випадку за початок відліку температур (за 0°С) прийнято температуру плавлення льоду, а в другому (за 0К) – температуру абсолютного нуля, тобто ту гранично низьку температуру, нижче якої в Природі просто не існує.
Оскільки величини градуса Цельсія та кельвіна є однаковими (ºС=К), то між температурою виміряної в кельвінах (Т) і температурою виміряною в градусах Цельсія (t) існує просте співвідношення: Т = t + 273; t = T – 273. Наприклад, якщо t=20ºС, то Т=293К; якщо t=100ºС, то Т=373ºС; якщо t= –20ºС, то Т=253К; якщо Т=100К то t = –173ºС і т.д. При цьому, потрібно зауважити: якщо мова йде про різницю температур, то ця різниця визначена в градусах Цельсія (Δt) і в кельвінах (ΔТ) є чисельно рівною: Δt=ΔT.
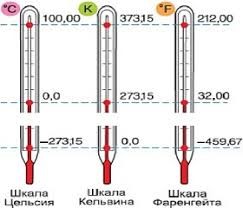
Мал.16. Чим схожі і чим відрізняються температури виміряні за шкалою Цельсія та за шкалою Кельвіна?
В науковій практиці бузовою шкалою вимірювання температур є шкала Кельвіна (абсолютна шкала температур). В побутовій же практиці, температуру зазвичай вимірюють за шкалою Цельсія. Втім, в деяких країнах, зокрема США, температуру часто вимірюють за шкалою Фаренгейта. Ця шкала була запроваджена в 1724 році німецьким вченим Габріелем Фаренгейтом (1686–1736). Шкала Фаренгейта побудована на трьох базових точках:
0°F – температура суміші льоду, солі та нашатирю (–17,8°С)
32°F – температура плавлення льоду (0°С)
98°F – температура людського тіла (36,6°С).
Визначення, температура – це фізична величина, яка характеризує ступінь нагрітості тіла виміряну термометром, має два суттєві недоліки. По перше, воно не пояснює ні фізичної суті того що називають нагрітістю тіла, ні фізичної суті того що називається температурою. Це визначення лише констатує факт того, що певні параметри термометричного тіла, певним чином залежать від ступеню нагрітості цього тіла (від його температури) і на цій підставі, визначає спосіб вимірювання цієї нагрітості.
По друге, дане визначення вводить температуру як абсолютно автономну величину, яка жодним чином не пов’язана з іншими величинами. Сучасна ж наука стоїть на тому, що Природа – це єдиний цілісний організм, в якому все взаємопов’язано та взаємообумовлено. І якщо ми прагнемо об’єктивно відобразити устрій цього цілісного організму, то маємо спиратись на відповідну систему взаємопов’язаних фізичних величин.
Крім цього, починаючи вивчення молекулярної фізики, ми домовились, що загальні властивості речовин та ті теплові процеси які відбуваються з ними, будемо пояснювати виходячи з трьох базових тверджень:
1) всі речовини складаються з молекул;
2) молекули в речовині безперервно та безладно рухаються;
3) на невеликих відстанях, молекули взаємодіють між собою.
А це означає, що в молекулярній фізиці, визначення тієї величини яка називається температурою, потрібно пов’язати з фактом того, що речовини складаються з молекул які рухаються та взаємодіють між собою. І не важко збагнути, що температура (нагрітість тіла) певним чином пов’язана з інтенсивністю хаотичного руху молекул. На цей зв’язок з усією очевидністю вказує той факт, що в процесі збільшення температури, інтенсивність дифузії, осмосу, броунівського руху та інших подібних явищ, збільшується і навпаки.
Аналізуючи величезну сукупність явищ та експериментальних фактів, вчені дійшли висновку: температура, це не просто міра нагрітості тіла, а величина, яка характеризує середню кінетичну енергію теплового (хаотичного) руху молекул. При цьому, теоретичні та експериментальні дослідження довели, що між температурою речовини виміряну в кельвінах (Т) та середньою кінетичною енергією молекул цієї речовини (Ек) виміряну в джоулях, існує співвідношення: Т=Ек/(3/2)k, де Eк=m0vc2/2 – середня кінетична енергія поступального руху однієї молекули речовини; vc – середня квадратична швидкість молекули: vc=√[(v12+v22+…+vn2)/n]; k = 1,38∙10–23 Дж/К – постійна величина, яка називається сталою Больцмана (названа на честь одного з творців сучасної молекулярно кінетичної теорії, австрійського фізика Людвіга Больцмана (1844–1906)).
Таким чином, в молекулярній фізиці прийнято наступне визначення температури. Температура – це фізична величина, яка характеризує середню кінетичну енергію поступального руху молекул речовини, виміряну не в джоулях а в кельвінах.
Позначається: Т
Визначальне рівняння: Т = Ек/(3/2)k
Одиниця вимірювання: [Т] = К, кельвін.
Прийняте в молекулярній фізиці визначення температури, має ряд безумовних переваг. По перше, воно розкриває фізичну суть температури, а ця суть полягає в тому, що температура є мірою середньої кінетичної енергії молекул речовини, виміряну не в джоулях, а в значно дрібніших одиницях – кельвінах. По друге, розкриває фізичну суть абсолютного нуля: абсолютний нуль – це температура при якій припиняється поступальний рух молекул речовини. По третє, визначає температуру не як певну автономну величину, а як величину яка тісно пов’язана з іншими, раніше введеними величинами. В четвертих, дозволяє визначати середню кінетичну енергію поступального руху молекул не шляхом вимірювання їх мас (m0) та середньої квадратичної швидкості (vc), а шляхом вимірювання температури речовини (Т): Ек = (3/2)kT.
На завершення зауважимо, що температура характеризує середню кінетичну енергію хаотичного руху молекул. Адже сам факт хаотичного руху молекул безумовно вказує на те, що при одній і тій же температурі, в будь якій речовині містяться молекули з різними кінетичними енергіями. Умовно кажучи, в будь якій речовині, при одній і тій же температурі наявні як «холодні» так і «гарячі» молекули.
Крім цього, потрібно зауважити, що формула Ек=(3/2)kT визначає середню кінетичну енергію поступального руху однієї молекули речовини. В загальному ж випадку молекули рухаються не лише поступально, а й обертально. А це означає, що їх загальна кінетична енергія складається з кінетичної енергії поступального руху та кінетичної енергії обертального руху. При цьому можна довести, що величина загальної кінетичної енергії молекули залежить від кількості атомів в ній і визначається за формулами:
для одноатомних молекул Ек=(3/2)kT=1,5kT;
для двохатомних молекул Ек=(5/2)kT=2,5kT;
для трьох і більше атомних молекул Ек=(6/2)kT=3,0kT.
Задача. Визначити середню кінетичну енергію поступального руху та середню квадратичну швидкість молекул кисню і водню при температурі 27°С. Порівняти отримані результати.
Дано: СІ:
t=27°C 300К
Ек(О2)=? Ек(Н2)=?
vс(О2)=? vс(Н2)=?
Рішення. Оскільки за визначенням Т=Ек/(3/2)k, де k = 1,38∙10–23Дж/К, то Ек = (3/2)kT. Із аналізу даної формули ясно, що величина середньої кінетичної енергії молекул речовини, не залежить а ні від маси, а ні від інших параметрів цих молекул. Тому: Ек(О2)= Ек(Н2)= (3/2)kT = 1,5·1,38∙10–23Дж/К·300К =621·10–23Дж.
Оскільки за визначенням Eк=m0vc2/2, то vc=√(2Ek/m0). Враховуючи, що m0(Н2) = 2·1,66·10–27кг; m0(О2) = 32·1,66·10–27кг, можна записати:
vc(Н2)=√(2Ek/m0) = √(2·621·10–23Дж/2·1,66·10–27кг = √(374·104(м2/с2)) = 1934м/с;
vc(О2)=√(2Ek/m0) = √(2·621·10–23Дж/32·1,66·10–27кг = √(374·104(м2/с2)) = 483м/с.
vc(Н2)/vc(О2) = 1934/483 = 4(рази).
Контрольні запитання.
1. Слово “температура” в перекладі з латинської означає “суміш”. Чому величина яка характеризує ступінь нагрітості тіла, отримала таку назву?
2. Чому сталева ложка, температура якої 20°С на дотик здається холодною, тоді як аналогічний за температурою пінопласт – теплим? Що означає даний факт?
3. Чим схожі і чим відрізняються шкала Цельсія та шкала Кельвіна?
4. Чому t ≠ Т, а Δt = ΔТ ?
5. Які недоліки визначення: температура – міра нагрітості тіла?
6. Які переваги визначення: температура – міра середньої кінетичної енергії молекул речовини?
7. На основі молекулярно кінетичної теорії поясніть, чому температура речовини не може бути меншою за абсолютний нуль.
8. Про що говорить твердження: температура є мірою середньої кінетичної енергії молекул речовини?
9. Про що говорить твердження: температура є мірою середньої кінетичної енергії поступального руху молекул речовини?
Вправа 6.
1. Воду нагріли від 20°С до 48°С. На скільки змінилась температура води в процесі нагрівання? Відповідь дати в градусах Цельсія і в кельвінах.
2. Визначте середню кінетичну енергію молекул Н2 та О2 при температурах 20°С і 200°С.
3. Визначте кінетичну енергію поступального руху та загальну кінетичну енергію молекули гелію, кисню і води при температурі 27°С.
4. Знаючи, що маса молекули кисню в 16 разі в більша за масу молекули водню, порівняйте середні квадратичні швидкості цих молекул при однакових температурах відповідних речовин.
5. Визначте середню квадратичну швидкість молекул водню (Н2), азоту (N2) вуглекислого газу (СО2) при температурі 20°С. Порівняйте цю швидкість з швидкістю кулі (500м/с).
6. При якій температурі середня квадратична швидкість молекул кисню становитиме 500м/с?
7. Яку температуру повинен мати водень, щоб середня квадратична швидкість його молекул дорівнювала середній квадратичній швидкості молекул кисню при температурі 27°С?
8. Визначте загальну кінетичну енергію одного моля гелію при температурі 27°С.
.
§7. Закон розподілу молекул за швидкостями. Про докази того, що молекулярно-кінетична теорія є правильною.
Факт того, що молекули рухаються хаотично, по суті означає, що в будь який момент часу різні молекули речовини мають різні швидкості і що значення цих швидкостей можуть суттєво відрізнятись від середніх величин. При цьому виникає питання: «Чи існує певна закономірність розподілу молекул за їх швидкостями? І чи можна сказати, скільки молекул в тій чи іншій ситуації рухається з певною швидкістю?»
В 1859 році видатний англійський фізик Джеймс Максвел (1831-1879) теоретично довів, що при будь якій температурі, молекули газу можуть мати різні швидкості, при цьому характер розподілу цих швидкостей можна представити у вигляді певної кривої, яку прийнято називати кривою нормального розподілу молекул за швидкостями або кривою Максвела. Загальний вигляд цієї кривої представлено на мал.17. Відразу ж зауважимо, що крива Максвела є похідною від відповідної математичної формули. Ця формула досить складна і тому немає сенсу ані записувати, ані аналізувати її. Ви просто маєте знати, що є певна математична формула (закон Максвела), яка дозволяє для будь якої конкретної ситуації, побудувати відповідну криву нормального розподілу молекул за швидкостями.
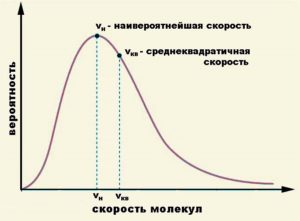
Мал.17. Загальний вигляд кривої нормального розподілу молекул за швидкостями (кривої Максвела).
Фізичний зміст кривої Максвела полягає в наступному. Якщо в заданому масштабі, площа тієї фігури що обмежена кривою Максвела і віссю швидкостей, дорівнює загальній кількості молекул наявного газу (N), то площа тієї фігури яка обмежена вертикальною смугою Δv та відповідним фрагментом кривої Максвела, дорівнює числу тих молекул (ΔN), швидкості яких знаходиться в інтервалі Δv.
Теоретичні дослідження Максвела вказували на те, що серед всього різноманіття швидкостей, можна виділити дві характерні швидкості:
1) найбільш імовірна швидкість молекул (vi), тобто та швидкість яку має найбільша кількість молекул і яка відповідає піку кривої Максвела;
2) середня квадратична швидкість молекул: vкв=[(v12+v22+…+vn2)/n]1/2.
При цьому за розрахунками Максвела, ці швидкості мають визначатись за формулами: vi = √(2kT/m0); vкв = √(3kT/m0), де Т – абсолютна температура речовини, m0 – маса однієї молекули речовини, k = 1,38∙10–23 Дж/К – стала Больцмана.
Важливість середньої квадратичної швидкості та тієї формули яка відображає її зв’язок з абсолютною температурою речовини vкв = √(3kT/m0), полягає в тому, що саме на основі цієї формули було визначено кількісний зв’язок між температурою речовини (Т) та середньою кінетичною енергією її молекул (Ек=m0vкв2/2). Дійсно, оскільки vкв = √(3kT/m0), то vкв2 = 3kT/m0, звідси m0vкв2 = 3kT, або m0vкв2/2 = (3/2)kT. Іншими словами Ек = (3/2)kT.
Не важко бачити, що параметри кривої Максвела та тих конкретних швидкостей які характеризують цю криву, визначальним чином залежать від двох величин: абсолютної температури речовини (Т) та маси (m0) тих молекул з яких ця речовина складається. Ілюструючи цю залежність, на мал.18 представлено три криві, які характеризують нормальний розподіл молекул однієї і тієї ж речовини за їх швидкостями для трьох різних температур.
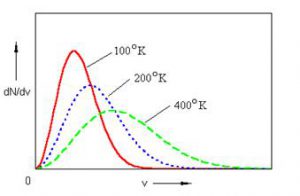
Мал.18. Криві розподілу молекул за їх швидкостями для різних температур.
Аналізуючи представлені на мал.18 криві, можна зробити декілька узагальнень. 1. Якщо кількість наявних в системі молекул є незмінною, то для будь яких значень температур, площі тих фігур які обмежені кривою Максвела та віссю швидкостей, є однаковими. 2. По мірі збільшення температури, числове значення найбільш ймовірної швидкості молекул (vi) – збільшується, а кількість тих молекул (ΔN) швидкість яких близька до найбільш ймовірної (vi) – зменшується. 3. По мірі збільшення температури, інтервал між найбільшими та найменшими швидкостями молекул збільшується.
Максвелівський закон розподілу молекул за їх швидкостями і та крива яка описує цей розподіл, є надзвичайно важливою складовою не лише фізики, а й всієї сучасної науки. Адже цей закон та йому відповідна крива, вточності справедливі не лише для газів, а й для речовин в будь якому агрегатному стані та будь якого хімічного складу. Більше того, практично в будь якій природній багаточисельній системі, відносно випадкові події описуються статистичною кривою подібною до кривої Максвела. Це звичайно не означає, що розподіл темпераменту, зросту, тривалості життя чи, скажімо, кольору очей серед людей, описується законом Максвела. Подібний розподіл взагалі не можливо представити у вигляді певної, достовірної математичної формули. Адже якщо навіть розподіл швидкостей між молекулами описується надскладною формулою, то що можна сказати про закон розподілу тривалості життя, якщо ця тривалість залежить не від двох, а від мільярдів обставин? Але от що дивовижно. Якщо ми дійсно дослідимо розподіл тривалості життя серед багатьох мільйонів людей і результати цих досліджень представимо у вигляді відповідної узагальнюючої статистичної кривої, то неодмінно з’ясується, що ця крива буде схожою на криву Максвела.
Напевно, найважливішою властивістю будь якої наукової теорії є її здатність робити точні, кількісні передбачення. Власне, наукова теорія стає теорією лише після того, коли її теоретичні передбачення отримують належне експериментальне підтвердження. Які ж точні кількісні передбачення можна зробити на основі гіпотези про те, що всі тіла складаються з молекул які хаотично рухаються та певним чином взаємодіють між собою? І яким чином ці точні, кількісні передбачення можна перевірити на практиці? Про деякі з цих передбачень та про їх експериментальне підтвердження ми вже згадували.
В 1905 році, тоді ще нікому невідомий молодий німецький фізик Альберт Ейнштейн створив теорію броунівського руху, тобто теорію яка кількісно пояснювала закономірності поведінки броунівських частинок. Пояснювала виходячи з того, що рух цих видимих частинок, це результат хаотичного руху невидимих молекул навколишнього середовища.
Ейнштейнівська теорія броунівського руху була прямим наслідком молекулярно-кінетичної теорії і мала одну, але надзвичайно важливу перевагу – її передбачення можна було відносно легко перевірити. Адже на відміну від молекул, броунівські частинки видимі і тому їх поведінку можна відносно легко проконтролювати. Тому не випадково, що вже в 1908 році французький фізик Жан Перен експериментально перевірив теорію броунівського руху і довів, що ця теорія правильна. А це означало, що молекули дійсно існують, що вони дійсно хаотично рухаються та певним чином взаємодіють між собою.
Сьогодні ми не будемо детально говорити про теорію броунівського руху, про ті передбачення які дає ця теорія та про ті експерименти що підтверджують ці передбачення. Не будемо, головним чином тому, що у нас нема а ні часу, а ні вагомої потреби, детально вивчати теорію одного конкретного явища. Ми просто констатуємо той факт, що експериментальне підтвердження ейнштейнівської теорії броунівського руху, стало вирішальним та безумовним доказом того, що молекули дійсно існують і що молекулярно-кінетична теорія правильна (достовірна).
Сьогодні ми зосередимо свою увагу на тих перших експериментальних дослідженнях, які безумовно підтвердили ті передбачення які випливали з максвелівського закону розподілу молекул за швидкостями. А ці передбачення є наступними:
1. Розподіл молекул за швидкостями описує крива Максвела, параметри якої певним визначеним чином залежать від абсолютної температури (Т) та маси (m0) відповідних молекул.
2. Величини найімовірнішої (vi) та середньої квадратичної (vкв) швидкостей молекул, визначаються за формулами vi=√(2kT/m0); vкв=√(3kT/m0). Наприклад, для срібла з температурою 1200ºС (1473К): vi=476м/с, vкв=583м/с.
3. Середня кінетична енергія молекул речовини (Ек=m0vкв2/2) та її абсолютна температура (Т) зв’язані співвідношенням Ек = (3/2)kT.
4. При одній і тій же температурі (Т1=Т2) більш легкі молекули (m01 ˂ m02) мають відповідно більшу середню квадратичну швидкість (v1˃v2), при цьому виконується співвідношення v1/v2=√(m02/m01). Наприклад у повітрі, середня квадратична швидкість молекул водню (m0=2а.о.м.) за будь якої температури має бути в 4 рази більшою за середню квадратичну швидкість молекул кисню (m0=32а.о.м.): v(H2)/v(O2)=√[m0(O2)/m0(H2)]=√(32/2)=4. (Співвідношення v1/v2=√(m02/m01) справедливе не лише для середніх квадратичних швидкостей, а й для швидкостей найбільш імовірних).
5. Інші передбачення.
В 1920 році німецький фізик Отто Штерн (1888–1969) здійснив перші вдалі експериментальні дослідження, результати яких вточності співпадали з передбаченнями максвелівського закону розподілу молекул за швидкостями. А це означало, що цей закон, а відповідно і вся молекулярно-кінетична теорія є безумовно правильними (достовірними).
Експериментальна установка Штерна (мал.19) представляла собою систему двох жорстко з’єднаних циліндрів (зовнішнього В та внутрішнього А) які мають спільну вісь обертання і в середині яких створено глибокий вакуум. При цьому внутрішній циліндр (А) має вузьку вертикальну щілину, а вздовж осі обертання установки, натягнута дротина виготовлена з тугоплавкого металу покритого тонким шаром відносно легкоплавкого срібла (tпл=960ºС)
Мал.19. Загальна схема дослідів Штерна. ( коли система не обертається, атоми срібла потрапляють в точку В, а коли обертається – в точку Вꞌ.
Принцип дії приладу полягає в наступному. Через тугоплавку металеву дротину пропускають електричний струм, під дією якого вона нагрівається до 1200ºС. При цій температурі атоми срібла інтенсивно випаровуються і розлітаються у всіх напрямках. Переважна більшість цих атомів осідає на внутрішній поверхні циліндру А. Однак ті з них які потрапляють в щілину цього циліндру долітають до циліндру В і осідають на ньому.
Дослід Штерна проводиться в два етапи. На першому (мал.19а) – установка не обертається. При цьому, атоми срібла, пролітаючи через щілину потрапляють в точку В і осідають в ній. На другому етапі (мал.19б), установка обертається з певною частотою (з певною кутовою швидкістю ω=2πν) і тому ті атоми які пролітають через щілину, потрапляють не в точку В, а в точку Вʹ. Це відбувається тому, що за той час поки атоми срібла летять від внутрішнього циліндру до зовнішнього, система повертається на певний кут. Знаючи радіуси циліндрів (R, r), частоту обертання системи (ν) та вимірявши відстань між точками В і Вꞌ (s), можна визначити швидкість польоту атомів. Дійсно.
Задача. В досліді Штерна, відстань між точками В і Вꞌ становить s=1,6см. З якою швидкістю рухаються атоми срібла, якщо відомо, що система обертається з частотою 40об/с, а радіуси внутрішнього (r) та зовнішнього (R) циліндрів відповідно дорівнюють 5см і 20см? Визначте відносну похибку досліду, якщо відомо, що середня кінетична енергія атомів срібла відповідає температурі 1200ºС.
Дано: СІ:
s = 1,6см 0,016м
ν = 40Гц –
r = 5см 0,05м
R = 20см 0,20м
t = 1200ºC 1473К
v =? δ =?
Рішення. Виконуємо малюнок який відображає фізичну суть та результати дослідів Штерна (мал.19) Оскільки атоми срібла рухаються у вакуумі, то на всій ділянці руху їх швидкість залишається незмінною. Величину цієї швидкості можна визначити за формулою v = (R – r)/t, де t – той час за який атоми пролітають відстань R – r . Цей час можна визначити із наступних міркувань. Оскільки за той час поки атоми пролітають відстань R – r, точка В проходить шлях s , то швидкість цієї точки можна визначити за формулою vВ=s/t. З іншого боку, точка В обертається з лінійною швидкістю vВ=ωR=2πνR. Тому 2πνR=s/t, звідси t=s/2πνR.
Таким чином, можна записати: v=(R – r)/t = (R – r)2πνR/∆s.
Розрахунки: v = (R – r)2πνR/s = (0,20 – 0,05)2·3,14·40·0,2/0,016 = 471м/с.
Якщо виходити з того, що точка Вꞌ це точка в яку потрапляють ті атоми срібла швидкість яких дорівнює найбільш імовірній швидкості (vi) і якщо теоретичне значення цієї найімовірнішої швидкості прийняти за точне значення швидкості атомів срібла, то відносну похибку досліду можна визначити за формулою δ = (vi –v)100%/vi, де vі для срібла при Т=1473К, vi=√(2kT/m0) = 476м/с.
Отже: δ=(476 – 471)100%/476=1%
Висновок. Результати дослідів Штерна, в межах допустимої похибки, співпадають з передбаченнями молекулярно-кінетичної теорії. А це означає, що відповідна теорія є правильною.
Потрібно зауважити, що в тій частині дослідів Штерна де система оберталась, атоми срібла потрапляли не тільки в точку Вꞌ, а й в певні околиці цієї точки. При цьому атоми розподілялись таким чином, що їх концентрація в тій чи іншій точці відповідала максвелівському розподілу молекул за їх швидкостями. А це означало, що при одній і тій же температурі різні атоми мають різні швидкості і що характер розподілу цих швидкостей, співпадає з передбаченнями теорії.
В подальшому, передбачення молекулярно-кінетичної теорії, і не лише ті які згадувались в даному параграфі, неодноразово провірялись та перепровірялись. При цьому кожного разу експериментальні факти доводили, що молекулярно-кінетична теорія є безумовно правильною.
Контрольні запитання.
1. Поясніть фізичний зміст зображеної на мал.14 кривої Максвела.
2. Яка швидкість молекул є більшою, найбільш імовірна чи середньо квадратична? У скільки разів?
3. На мал.18 зображено чотири криві Максвела для однієї і тієї ж маси газу. Який параметр цих кривих залишається незмінним?
4. За виконання якої умови, наукова гіпотеза стає відповідною теорією?
5. Чим теорія броунівського руху вигідно відрізнялась від молекулярно-кінетичної теорії?
6. Чому експериментальне підтвердження теорії броунівського руху, автоматично стало підтвердженням молекулярно-кінетичної теорії?
7. Яку будову має експериментальна установка Штерна?
8. Який принцип дії цієї установки?
9. Які передбачення молекулярно-кінетичної теорії підтвердили досліди Штерна?
Вправа 7.
1. Визначте величину найімовірнішої та середньо квадратичної швидкості молекул водню при температурі 27°С.
2. У скільки разів середня квадратична швидкість молекул більша за їх найімовірнішу швидкість? Чи залежить це співвідношення від температури речовини? Від молекулярного складу речовини?
3. Визначте температуру речовини, якщо середня кінетична енергія її молекул 5,6·10–21Дж
4. При якій температурі знаходиться речовина, якщо середня кінетична енергія її молекул на 20% більша ніж при температурі 0°С?
5. При якій температурі середня квадратична швидкість молекул азоту становитиме 500м/с?
6. Яку температуру повинен мати кисень, щоб середня квадратична швидкість його молекул дорівнювала середній квадратичній швидкості молекул водню при температурі 27°С?
7. Визначте загальну кінетичну енергію одного моля кисню при температурі 27°С.
§8. Загальні відомості про тверді, рідкі та газоподібні речовини. Плазма, як особливий стан речовини.
Нагадаємо. Речовинами називають такі матеріальні об’єкти, які складаються з тих чи інших частинок і мають масу спокою. Все різноманіття хімічно простих речовин умовно розділяють на тверді, рідкі та газоподібні.
Коли ми стверджуємо, що лід, залізо та пінопласт – тверді, вода, ртуть та олія – рідкі, а водяний пар, повітря та вуглекислий газ – газоподібні, то це означає, що існують певні класифікаційні ознаки, керуючись якими можна чітко визначити, до якої класифікаційної групи відноситься той чи інший об’єкт. І не важко збагнути, що цими ознаками є не густина, не електропровідність, не хімічний склад, не колір, не смак і навіть не твердість чи м’якість, а об’єм (V) та форма (Ф).
Дійсно. Коли ми стверджуємо, що лід, залізо і пінопласт тверді, то маємо на увазі факт того, що ці абсолютно різні за твердістю, густиною, електропровідністю та іншими ознаками тіла, мають певну сталу форму (Ф=const) і певний сталий об’єм (V=const). Коли ми стверджуємо, що вода, ртуть та олія рідкі, то маємо на увазі, що ці абсолютно різні речовини мають певний сталий об’єм (V=const) але не мають певної сталої форми (Ф≠const). Якщо ж мова йде про газоподібні речовини, то їх визначальною ознакою є те, що вони не мають ні певного сталого об’єму, ні певної сталої форми (V≠const; Ф≠const). Не мають в тому сенсі, що займають увесь наданий їм об’єм і приймають форму тієї посудини в якій вони знаходяться.
. V=const V=const V≠const
. Ф=const Ф≠const Ф≠const
Мал.20. Форма і об’єм є тими зовнішніми класифікаційними ознаками за якими різноманіття речовин розділяють на тверді, рідкі та газоподібні.
Класифікаційний поділ хімічно простих речовин за ознаками форма–об’єм, по суті відображає зовнішні відмінності між твердими, рідкими та газоподібними речовинами. Молекулярна ж фізика стоїть на тому, що в ній, загальні властивості твердих, рідких та газоподібних речовин, в тому числі і ті, які визначаються наявністю чи відсутністю певної форми та об’єму, пояснюються виходячи з трьох базових тверджень:
1) речовини складаються з молекул;
2) молекули рухаються;
3) молекули взаємодіють.
І такі пояснення безумовно існують. Дійсно. Оскільки молекули рухаються, то вони мають певну енергію руху, яку прийнято називати кінетичною Ек. Оскільки молекули взаємодіють, то вони мають певну енергію взаємодії, яку прийнято називати потенціальною Еп. Не важко збагнути, що енергія взаємодії молекул прагне об’єднати молекули в єдине ціле. Натомість енергія руху, навпаки – прагне розірвати зв’язки між молекулами і розкидати їх. Ясно, що в такій ситуації агрегатний стан речовини та її загальні фізичні властивості, визначальним чином залежать від того, який енергетичний, а відповідно і силовий, фактор є сильнішим.
Скажімо, якщо тверді тіла мають певну сталу форму і певний сталий об’єм, то напевно це пояснюється тим, що потенціальна енергія молекул твердого тіла (глибина потенціальної ями) значно більша за їх середню кінетичну енергію (Еп ˃ Ек). Факт же того, що газоподібні речовини займають увесь наданий їм об’єм, очевидно означає, що після взаємодії, молекули неминуче розлітаються і тому їх кінетична енергія значно більша за енергію потенціальну (Еп ˂ Ек). Якщо ж мова йде про рідини, то їх молекули, з одного боку тримаються купи (V=const), а з іншого – ця купа є надзвичайно хиткою (Ф≠const). І не важко збагнути, що таку ситуацію можна пояснити лише тим, що в рідинах, енергія взаємодії молекул якщо і перевищує енергію їх руху, то лише мінімально (Еп ≥ Ек).
Таким чином, визначаючи ті речовинні об’єкти які називаються твердими, рідкими та газоподібними, можна сказати наступне.
Твердими називають такі речовинні об’єкти, які мають певну сталу форму та певний сталий об’єм, і в яких потенціальна енергія молекул значно більша за їх середню кінетичну енергію. Іншими словами, для твердих речовин: Ф=const; V=const; Еп ˃ Ек.
Рідинами називають такі речовинні об’єкти, які мають певний сталий об’єм але не мають певної сталої форми, і в яких потенціальна енергія молекул мінімально більша за їх середню кінетичну енергію. Іншими словами, для рідин: Ф≠const; V=const; Еп ≥ Ек.
Газоподібними називають такі речовинні об’єкти, які не мають а ні певної сталої форми, а ні певного сталого об’єму, і в яких потенціальна енергія молекул значно менша за їх середню кінетичну енергію. Іншими словами, для газоподібних речовин: Ф≠const; V≠const; Еп ˂ Ек.
Потрібно зауважити, що коли ми говоримо про потенціальну, а особливо про кінетичну енергію молекул, то маємо розуміти, що фактично мова йде про певні усереднені значення цих енергій. При цьому величину середньої кінетичної енергії поступального руху молекул речовини (точніше, однієї молекули речовини) визначають за універсальною формулою Ек=(3/2)kT, де Т – абсолютна температура речовини, k=1,38·10–23 Дж/К – стала Больцмана. Якщо ж мова йде про потенціальну енергію молекул, то в загальному випадку визначати величину цієї енергію ми не вміємо: Еп=? Не вміємо в тому сенсі, що певної універсальної формули за якою можна визначити величину потенціальної енергії молекул у всьому різноманітті можливих ситуацій не існує.
Загалом, говорячи про потенціальну енергію молекул, потрібно розуміти, що мова йде про надзвичайно складний вид прихованої енергії, яку не лише важко кількісно визначити, а й навіть пояснити звідки вона береться і на що перетворюється в тій чи іншій конкретній ситуації. Наприклад при температурі 0°С вода може бути твердою, рідкою та газоподібною. Запитується, в якому агрегатному стані, потенціальна енергія молекул Н2О є найбільшою? Керуючись визначеннями, для твердих тіл Еп ˃ Ек, для рідин Еп ≈ Ек, для газів Еп < Ек, ви скоріш за все скажете, що потенціальна енергія молекул льоду є найбільшою. А от і ні! Адже для того щоб при температурі 0°С, 1кг льоду перетворити на 1кг води, потрібно витратити 3,35·105Дж енергії. Якщо ж ви захочите отримати 1кг пару з температурою 0°, то вам знадобиться ще 2,26·106Дж енергії. І вся ця енергія піде на збільшення потенціальної енергії молекул. А це означає, що в системі лід – вода – пар, загальна потенціальна енергія молекул пару є найбільшою. (Адже при 0°С кінетична енергія молекул льоду, води та пару залишається незмінною).
Ви можете запитати: а як бути з співвідношеннями: для твердих тіл Еп ˃ Ек, для рідин Еп ≈ Ек, для газів Еп < Ек? Відповідаючи на це непросте запитання, можна сказати наступне. Говорячи про потенціальну енергію загалом і потенціальну енергію молекул зокрема, потрібно мати на увазі, що мова йде про відносну величину. Наприклад, якщо перебуваючи в кімнаті третього поверху, ви піднімаєте над столом тіло і стверджуєте, що воно має потенціальну енергію величина якої Еп=mgh, де h – висота тіла над рівнем стола, то маєте на увазі не потенціальну енергію тіла «взагалі», а ту її різновидність яка називається потенціальною енергією сили тяжіння і ту частину цієї енергії, яка визначена відносно рівня поверхні стола. Адже відносно інших рівнів, скажімо рівнів полу першого, другого і третього поверхів, ця енергія буде іншою.
Аналогічне можна сказати і про величину тієї потенціальної енергії яка характеризує взаємодію молекул речовини на рівні різних агрегатних станів цієї речовини. Наприклад в процесі плавлення, надана твердому тілу теплова енергія йде на збільшення потенціальної енергії його молекул, точніше – на збільшення внутрішньо молекулярних взаємодій. При цьому молекули переходять з більш низького енергетичного рівня (рівень «тверде тіло») на більш високий енергетичний рівень (рівень «рідина»). В процесі ж кристалізації, тобто в процесі переходу речовини з рідкого стану в твердий, відбувається зворотнє енергетичне перетворення: молекули рідини переходять з більш високого енергетичного рівня (рівень «рідина») на більш низький енергетичний рівень (рівень «тверде тіло»), при цьому раніше накопичена потенціальна енергія молекул перетворюється на відповідну кількість теплоти.
Таким чином, коли ми стверджуємо, що потенціальна енергія молекул газу набагато менша за їх середню кінетичну енергію (Еп < Ек), то маємо на увазі не загальну величину потенціальної енергії молекул газу, а ту її незначну частину яка проявляє себе на енергетичному рівні «газ». А ця енергія дійсно набагато менша за кінетичну енергію молекул газу. Однак це зовсім не означає, що за певних умов, зокрема в процесі переходу речовини з газоподібного стану в рідкий (в процесі конденсації), та прихована потенціальна енергія яка на енергетичному рівня «газ» практично не проявляла себе, виявиться джерелом величезної кількості теплоти, а по суті, кінетичної енергії молекул.
Вище сказане означає, що оцінюючи величину та прояви потенціальної енергії молекул, потрібно обережно ставитись до категоричних оцінок і завжди пам’ятати, що мова йде про дуже складний вид прихованої енергії, яка за одних обставин може практично не проявляти себе, а за інших – бути джерелом величезної кількості явної (кінетичної) енергії.
Напевно ви погодитесь з тим, що за певних умов, одна і таж речовина, може бути твердою, рідкою або газоподібною. Погодитесь тому, що одна загально відома, та загально розповсюджена речовина, навіть за звичних для нас умов зустрічається у всіх трьох агрегатних станах. І напевно ви здогадались, що цією речовиною є вода. Адже твердий лід, рідка вода і газоподібний водяний пар, це різні стани однієї і тієї ж речовини – води (Н2О).
Звичайно, далеко не всі речовини можуть знаходитись у всіх трьох агрегатних станах. Наприклад, карбонат кальцію (СаСО3), а простіше кажучи – звичайна крейда, не буває а ні рідкою, а ні газоподібною. Не буває тому, що в процесі нагрівання, цей матеріал, не досягнувши температури плавлення, розкладається на більш прості речовини: СаО та СО2. Подібне можна сказати і про переважну більшість хімічно складних речовин, як то біологічні матеріали, органічні сполуки, полімери, тощо. Однак, якщо говорити про хімічно прості речовини, то більшість з них за певних умов можуть бути і твердими, і рідкими, і газоподібними.
Якби вас запитали: «від чого залежить агрегатний стан тієї чи іншої речовини?», то скоріш за все ви б сказали, від температури. А подумавши, добавили б – і від тиску. Відповівши таким чином, ви будете абсолютно праві. Адже стан речовини дійсно визначальним чином залежить від її температури і зовнішнього тиску.
Досліджуючи характер цієї залежності, звернемось до експерименту. Припустимо, що у вас є шматок льоду, температура якого –20ºС. Нагріваючи лід, ви неодмінно зясуєте, що більшість його фізичних властивостей поступово змінюються. Але вцілому, ці зміни можна вважати не суттєвими. Адже і при –20ºС, і при –10ºС, і при –0,1ºС, лід залишається льодом, тоб то твердою речовиною з відповідним набором фізичних властивостей. Коли ж температура льоду досягне 0ºС, то неодмінно з’ясується, що подальше її зростання неможливе без кардинальної, якісної зміни властивостей льоду. Адже при цій температурі лід плавиться і в процесі цього плавлення впрачає ознаки твердого тіла (наявність певної форми, наявність твердості, міцності, крихкості, тощо) і набуває ознак рідини (відсутність певної форми, наявність в’язкості, поверхневого натягу, тощо). Крім цього, в процесі плавлення, стрибкоподібно змінюються й інші властивості льоду, зокрема його питома теплоємність, густини, діелектрична проникливість, показник заломлення світла, тощо.
Ще однією визначальною ознакою плавлення, є факт того, що цей процес відбувається з поглинанням певної кількості енергії. При цьому, ця енергія йде не на збільшення кінетичної енергії молекул (адже температура речовини залишається незмінною), а на збільшення їх потенціальної енергії.
Після того як лід повністю перетвориться на рідину, та теплова енергія яка продовжує надходити до речовини, призведе до нового витка підвищення температури. Але, як тільки ця температура досягне позначки 100ºС, неодмінно з’ясується, що подальше її підвищення пов’язано з новим сприбком змін властивостей, тільки тепер вже рідкої води. Це означає, що ви не зможете нагріти воду, скажімо до 101ºС без того, щоб не змінити її агрегатного стану. При цьому, це нове агрегатне перетворення води, також відбуватиметься при певній постійній температурі і супроводжуватиметься збільшенням потенціальної енергії молекул. Сподіваюсь, ви розумієте, що в даному випадку, ми розглядаємо ситуацію, при якій зовнішній тиск залишається незмінним і чисельно рівним нормальному атмосферному тиску. Адже змінюючи зовнішній тиск, можна досягти того, що вода закипить при 20ºС, або не закипить при 200ºС
Факт того, що зміна агрегатного стану речовини супроводжується різкою, стрибкоподібною зміною багатьох фізичних властивостей цієї речовини та стрибкоподібною зміною потенціальної енергії її молекул, лежить в основі наукового визначення терміну «агрегатний стан речовини».
Агрегатний стан речовини це такий фізичний стан даної речовини, який характеризується певним набором визначальних властивостей (зокрема наявністю або відсутністю форми та об’єму) і перехід до якого супроводжується стрибкоподібною зміною багатьох, в тому числі і визначальних властивостей цієї речовини, а також стрибкоподібною зміною потенціальної енергії її молекул. Розрізняють три агрегатні стани речовини: твердий, рідкий та газоподібний.
Говорячи про можливі стани речовини, варто згадати про ще один. Цей стан рідко зустрічається на Землі і надзвичайно часто у Всесвіті. Його називають плазмою. Пояснюючи суть того що називають плазмою, давайте розглянемо ті події які відбуваються в процесі нагрівання певної речовини, скажімо тієї ж води. Ось вона тверда, потім – рідка і на нарешті – газоподібна. Але що буде з газоподібною водою в процесі її подальшого нагрівання? А буде наступне. При певному рівні температур, молекули води почнуть розпадатись на атоми та групи атомів. А ті в свою чергу, втрачаючи валентні електрони, почнуть перетворюватись на відповідні іони. У підсумку, та речовина яка була водою, тобто такою що складалась з молекул Н2О, перетворюється на певну суміш окремих атомів, позитивних і негативних іонів та вільних електронів. Саме цю суміш і називають плазмою.
Плазмою називають частково або повністю іонізований газ, в якому концентрація вільних позитивно та негативно заряджених частинок є усереднено однаковою. Процес переходу речовини з газоподібного стану в стан плазми, прийнято називати іонізацією газу. Зворотній процес, тобто перехід речовини з стану плазми до стану газу, зазвичай називають рекомбінацією плазми.
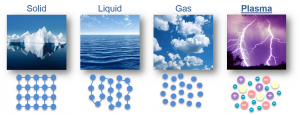
Мал.21. Плазма – це частково або повністю іонізований газ.
Фізичні властивості плазми суттєво відрізняються від властивостей газу. Головна причина цих відмінностей полягає в тому, що гази складаються з електронейтральних (незаряджених) частинок, а плазма – з певної суміші заряджених та не заряджених частинок (або лише з заряджених частинок). А це означає, що плазма проводить електричний струм. Що на її поведінку визначальним чином впливають зовнішні електричні та магнітні поля. Що її частинки взаємодіють не лише в момент безпосереднього контакту, а й на великих відстанях.
Сукупність цих відмінностей, дозволяє стверджувати, що плазма – це особливий, четвертий стан речовини. Однак, з формальної точки зору, цей стан навряд чи правомірно називати четвертим агрегатним станом речовини. По перше тому, що в стані плазми, будь яка речовина не є тією речовиною, якою вона була в твердому, рідкому та газоподібному стані. Адже складовими частинками плазми є не ті молекули з яких складалась базова речовина, а певна суміш окремих атомів, іонів та електронів. По друге, перехід речовини від її газоподібного стану до стану плазми відбувається поступово та без певних стрибкоподібних змін властивостей цієї речовини. А це означає, що формальних підстав вважати плазму четвертим агрегатним станом речовини нема.
Та як би там не було, а при достатньо високих температурах, будь яка речовина набуває якісно нових властивостей, сукупність яких дозволяє стверджувати, що ця речовина перебуває в особливому стані. І цей стан прийнято називати плазмою. Прийнято вважати, що тією умовною температурною межею, за якою газоподібна речовина починає набувати суттєвих ознак плазмового стану є 1000ºС. Якщо ж говорити про ту температуру при якій будь який газ набуває безумовних ознак плазми, то вона близька до 4000ºС. Плазму, температура якої менша за 1·106(ºС) прийнято вважати низькотемпературною. А та плазма температура якої більша за мільйон градусі Цельсія (кельвінів), вважається високотемпературною плазмою.
Дослідження показують, що близько 99% наявної у Всесвіті речовини, знаходиться в стані плазми. В стані плазми знаходяться зірки та їх атмосфери, галактичні туманності та міжзоряне середовище. Плазмаю є та частина атмосфери Землі яку називають іоносферою. Плазмою є той розжарений газ який називають блискавкою, електричною дугою, полум’ям, тощо. Але не потрібно думати, що плазмою можуть бути лише високотемпературні гази. Скажімо, температура того розрідженого газу що світиться в лампі денного світла не є надто високою. І тим не менше, цей газ є плазмою. Або, наприклад, температура того газу що забезпечує кольорове зображення так званих плазмових екранів, мало відрізняється від кімнатної. І тим не менше, відповідний газ є плазмою.
Контрольні запитання.
1. Чому густина, електропровідність та температура не є тими класифікаційними ознаками які дозволяють розділити речовини на тверді, рідкі та газоподібні?
2. Виходячи з яких міркувань ми стверджуємо, що для твердих тіл Еп ˃ Ек, для рідин Еп ≈ Ек, для газів Еп < Ек?
3. Що означає твердження: в загальному випадку визначати величину потенціальної енергії молекул речовини ми не вміємо (Еп=?)?
4. Потенціальна енергія яких молекул, льоду чи води є більшою? Чому?
5. Як змінюється кінетична і потенціальна енергія молекул в процесі а) плавлення; б) кристалізації; в) пароутворення; г) конденсації.
6. Які визначальні ознаки переходу речовини з одного агрегатного стану в інший?
7. Опишіть ті процеси які відбуваються при нагріванні твердої речовини.
8. Чим плазма відрізняється від звичайного газу? Які основні властивості плазми?
9. Чи є формальні підстави вважати плазму четвертим агрегатним станом речовини? Чому?