МЕХАНІКА КОЛИВАНЬ ТА ХВИЛЬ


Тема 1.4. Механіка коливань та хвиль.
§46. Загальні відомості про коливання.
§47. Гармонічні коливання та їх характеристики.
Рівняння гармонічного коливання.
§48. Фізичний, математичний та пружинний маятники.
§49. Розв’язування задач. Тема: механічні коливання.
§50. Автоколивання.
§51. Вимушені коливання. Резонанс.
§52. Загальні відомості про хвилі.
§53. Звукові хвилі. Інфразвукові та ультразвукові хвилі.
§54. Ефект Доплера.
Тема 1.4 Механіка коливань та хвиль.
§45. Загальні відомості про коливання.
В фізиці, процеси які так чи інакше повторюються називаються коливаннями. Коливається наприклад, збурена поверхня води. В поривах вітру коливаються гілки дерев та листя на них. Під дією потягів та машин що рухаються, коливаються мости і дороги. Вібрують струни музичних інструментів та мембрани динаміків. Коливальним чином рухаються маятники, стрілки та шестерні механічних годинників, поршні, клапани і колінчасті вали автомобільних двигунів. Періодично змінюються дні і ночі, пори року та їм відповідні життєві цикли рослин і тварин. Ритмічно б’ється серце і працюють легені вашого організму. Певним чином коливаються атоми, молекули і ті частинки з яких вони складаються. Звук який ви чуєте і світло яке бачите, це також результат певних коливальних процесів. Не буде перебільшенням сказати, що майже все що відбувається в Природі, так чи інакше пов’язано з тими чи іншими коливальними процесами.
За різними класифікаційними ознаками коливання поділяються на:
– періодичні та неперіодичні;
– вільні та вимушені;
– згасаючі та незгасаючі;
– гармонічні та негармонічні;
– механічні та електромагнітні.
Стисло пояснюючи ознаки та властивості вище згаданих класифікаційних груп, можна сказати наступне.
1. За точністю і ритмічністю повторювань, коливання поділяються на періодичні та неперіодичні. Періодичними називають такі коливання, які через певні, однакові проміжки часу вточності повторюються. Наприклад, періодично коливається маятник годинника, його рухомі шестерні, секундна, хвилинна та годинникова стрілки. Періодично обертаються елементи колеса при його рівномірно-обертальному русі (ω=const). За умови рівномірної роботи, періодично коливаються деталі двигуна внутрішнього згорання (поршень, колінвал, шатун, клапани, …). Періодичним є рух Землі навколо своєї осі та навколо Сонця.
Потрібно зауважити, що в науково-технічній практиці, періодичними прийнято вважати такі коливання які повторюються через однакові проміжки часу. При цьому повторюваність самих коливань може бути неповною. Наприклад коливання нитяного маятника є згасаючими і тому повторюються не у повному обсязі. Однак зважаючи на те, що ці коливання дійсно повторюються через певні однакові проміжки часу (періоди), подібні згасаючі коливання вважаються періодичними.
Неперіодичними називають такі коливання, які повторюються через різні проміжки часу, або повторюються частково. Неперіодично наприклад, коливаються елементи колеса що обертається зі змінною кутовою швидкістю (ω ≠ const). Неперіодичними є коливання листя і гілок дерев, вібрації автомобіля що їде бруківкою. Неперіодично відбуваються землетрусами, виверження вулканів, зміни атмосферного тиску, буревії, цунамі, тощо.
2. За ступенем автономності коливальної системи, коливання поділяються на вільні та вимушені. Вільними називають такі коливання, які починаються після виведення коливальної системи з стану рівноваги і продовжуються самостійно, а точніше, під дією певної комбінації внутрішньо системних сил. Наприклад, підвішене на нитці тіло в сукупності з гравітаційним полем Землі, утворюють коливальну систему, яка називається нитяним маятником (мал.127). Якщо цю систему вивести з рівноваги, то в подальшому вона буде здійснювати вільні коливання. Ці коливання не є безпричинними. Вони обумовлені дією на тіло певної системи сил: сили тяжіння Fт, реакції опори N, та тієї сили інерції Fi що виникає в процесі прискореного руху тіла. При цьому, ці сили є результатом природної взаємодії тих елементів які утворюють дану коливальну систему: тіло, нитка, Земля.
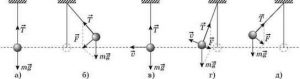
Мал.127. Вільні коливання не є безпричинними.
Вільно коливаються наприклад, елементи виведеного з рівноваги пружинного маятника, виведена з рівноваги падінням каменя поверхня води, вібруючий камертон, елементи колеса що вільно обертається навколо своєї осі, м’яч який вільно підстрибує після падіння, тощо.
Вимушеними називають такі коливання, які відбуваються під дією певної змінної зовнішньої сили, сили, джерелом якої не є коливальна система. При цьому мається на увазі, що після припинення дії цієї сили, коливання припиняються. Скажімо, якщо ви змушуєте книгу здійснювати певні коливальні рухи, то коливання книги є вимушеними. Вимушено наприклад, коливаються всі елементи двигуна внутрішнього згорання, шестерні та стрілки механічного годинника, елементи працюючої швацької машинки, крила птаха що летить, тощо.
а)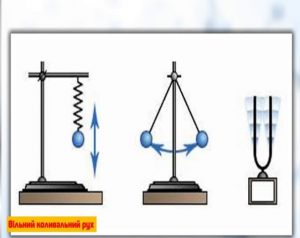 б)
б)

Мал.128 Приклади вільних (а) та вимушених (б) коливань.
3. За ступенем енергетичних втрат в коливальній системі, коливання поділяються на згасаючі та незгасаючі. Згасаючими називають такі коливання, амплітуда яких з плином часу зменшується. Зменшується тому, що в процесі коливань, певна кількість енергії упорядкованого руху елементів коливальної системи, незворотнім чином перетворюється в теплоту, тобто в енергію хаотичного руху молекул речовини. Незгасаючими називають такі коливання, амплітуда яких з плином часу залишається незмінною. Залишається незмінною тому, що ті енергетичні втрати які неминуче відбуваються в процесі коливань є несуттєвими, або тому, що ці втрати компенсуються зовнішнім джерелом енергії.
Наприклад, коливання простого фізичного маятника (мал.129а) є згасаючими. Вони згасають тому, що в процесі коливань, частина енергії коливальної системи неминуче витрачається на теплові втрати, джерелом яких є ті чи інші сили тертя. Якщо ж аналогічний маятник є частиною годинникового механізму (мал.129б), то його коливання стають незгасаючими. Вони не згасають тому, що в годинниковому механізмі є спеціальна автоматизована система, яка постійно поповнює енергетичні втрати маятника.
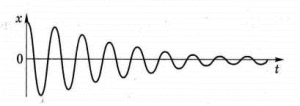
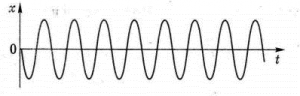
Мал.129. Згасаючі (а) та незгасаючі (б) коливання.
4. За характером зміни параметрів коливальної системи, коливання поділяються на гармонічні та негармонічні. Гармонічними називають такі коливання які відбуваються за гармонічним законом. Це означає, що будь яке гармонічне коливання можна описати формулою x = хмsinφ, або x = хмcosφ, де
х – миттєве значення змінної величини;
хм – амплітудне значення змінної величини;
φ – фаза коливань.
Наприклад, коливання того фізичного маятника що є частиною годинникового механізму (мал.129б) є гармонічними. Якщо ж говорити про вільні коливання нитяного маятника (мал.129а), то вони наближено гармонічні. Наближено гармонічні тому, що є згасаючими, а отже такими амплітуда коливань яких поступово зменшується. Наближено гармонічними є коливання нитяного маятника, коливання виведеної з рівноваги поверхні води, вібрації камертона, тощо. Складними, комбінаціями наближено гармонічних коливань є коливання гілок дерев та листя на цих гілках. Комбіновано гармонічними є ті звукові коливання які створюють музикальні інструменти, наші голоси, тощо. Загалом, практично всі вільні природні коливань є гармонічними, наближено гармонічними або комбіновано гармонічними. Зважаючи на цей факт, вивченню гармонічних коливань ми будемо приділяти особливу увагу.
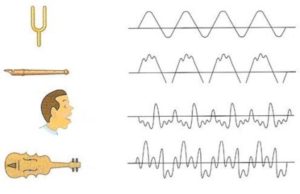
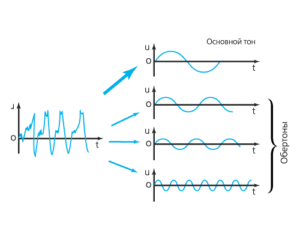
Мал.130. Звук камертона є гармонічним, а голос людини – комбіновано гармонічним, тобто таким, що складається з певної сукупності гармонічних коливань.
Негармонічними називають такі коливання які не є гармонічними, наближено гармонічними чи комбіновано гармонічними. Це означає, що негармонічні коливання не можна представити у вигляді певної сукупності гармонічних коливань. Зазвичай негармонічними є спеціально створені, штучні коливання. Наприклад, негармонічно коливаються елементи клапанного механізму двигуна внутрішнього згорання (мал.131а), елементи так званого храпового механізму (мал.131б), тощо.
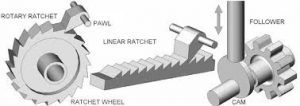
Мал.131. Приклади коливальних систем, елементи яких здійснюють вимушені негармонічні коливання.
5. За фізичною суттю тих процесів які відбуваються в коливальній системі, коливання поділяються на механічні та електромагнітні. Механічними називають такі коливання, які пов’язані з механічними переміщеннями тіл та їх частин, або частин пружного середовища. Механічними є коливання рухомих деталей двигуна внутрішнього згорання, пульсації нашого серця, коливання гілок та листя на цих гілках, обертальні рухи коліс, тощо. Механічними є і ті коливання середовища, які ми називаємо звуком, поверхневими хвилями, сейсмічними хвилями, тощо.
Електромагнітними, називають такі коливання, які пов’язані з коливаннями електричних зарядів та електромагнітних полів. Електромагнітними є ті коливання які називаються змінним електричним струмом, радіохвилями, інфрачервоним випромінюванням, видимим світлом, ультрафіолетовим, рентгенівським та гама випромінюванням.
Таким чином, керуючись різними класифікаційними критеріями, будь яке коливання можна описати певним набором характеристик. Наприклад, характеризуючи коливання нитяного маятника, можна сказати що вони є механічними, вільними, періодичними, згасаючими та гармонічними (наближено гармонічними). Втім, різноманіття коливань таке величезне, що його практично не можливо втиснути в рамки певної класифікаційної схеми. Це завдання ускладнюється ще й тим, що в різних навчально-методичних джерелах, один і той же термін часто-густо визначають суттєво по різному.
На завершення нагадаємо, що загально прийнятий науковий підхід до вирішення складних проблем полягає в тому, що по суті складний об’єкт досліджень замінюють його ідеалізованою (спрощеною) моделлю. А ця ідеалізація передбачає врахування визначально важливих обставин і свідоме нехтування тих обставин, які в умовах даної задачі є другорядними. Тому, описуючи коливальні процеси ми фактично будемо описувати певні ідеалізовані системи та відповідно ідеалізовані коливання. Однак це зовсім не означає, що отримані нами результати будуть суттєво відрізнятись від реального стану справ. Адже факт того, що описуючи рух Землі навколо Сонця та своєї осі, ми не враховуємо рухи слонів, пацюків та комарів, зовсім не означає що теорія руху Землі є неправильною та неточною.
Контрольні запитання.
1. Які процеси називаються коливаннями? Наведіть приклади?
2. Які коливання називаються а) вільними; б) вимушеними? Наведіть приклади.
3. Чи є вільні коливання безпричинними? Які силові причини коливань нитяного маятника?
4. Які коливання називаються а) гармонічними; б) негармонічними? Наведіть приклади.
5. Які коливання називаються а) згасаючими; б) незгасаючими? Наведіть приклади.
6. Чому коливання простого маятника є згасаючими, а маятника як частини годинникового механізму – незгасаючими?
7. Які перетворення механічної енергії відбуваються при вільних коливаннях нитяного маятника?
8. М’яч вільно падає з певної висоти і зробивши декілька стрибків зупиняється. Які перетворення енергії відбуваються при цьому? Дайте класифікаційну характеристику коливального руху м’яча. Чому ці коливання є згасаючими?
§46. Періодичні коливання та їх характеристики. Рівняння гармонічного коливання.
В межах програми загальноосвітньої школи вивчають лише так звані періодичні коливання, тобто такі коливання, які через певні однакові проміжки часу вточності повторюються. Основними характеристиками таких коливань є період, частота, амплітуда та фаза коливань.
Період коливань (період) – це фізична величина, яка характеризує часову періодичність (повторюваність) коливального процесу і яка дорівнює тому проміжку часу за який система здійснює одне повне коливання.
Позначається: Т
Визначальне рівняння: Т=t/n, де n – кількість коливань системи здійснених за час t;
Одиниця вимірювання: [Т] = с, секунда.
Наприклад, якщо нитяний маятник за 20 секунд здійснює 16 повних коливань, то період цих коливань 1,25с: Т= t/n = 20с/16 = 1,25с.
Частота коливань (частота) – це фізична величина, яка характеризує частотну періодичність коливального процесу і яка дорівнює тій кількості коливань системи, яку здійснює ця система за одиницю часу.
Позначається: ν
Визначальне рівняння: ν = n/t
Одиниця вимірювання: [ν] = 1/c = Гц, герц.
Наприклад, якщо за 20 секунд нитяний маятник здійснює 16 коливань, то частота цих коливань 0,8Гц: ν = n/t = 16/20c = 0,8Гц.
Із визначальних рівнянь періоду і частоти (T=t/n; ν=n/t) з усією очевидністю випливає, що ці фізичні величини взаємопов’язані, і що цю взаємопов’язаність відображають співвідношення: T=1/ν; ν=1/T. Тому якщо наприклад, за умовою задачі задано період коливань системи Т=2с, то ви завжди можете визначити частоту цих коливань ν=1/Т=1/2с=0,5Гц і навпаки.
Амплітуда коливань (амплітуда) – це фізична величина, яка характеризує максимальне за величиною (амплітудне) значення змінної величини і яка дорівнює цьому значенню. Позначається символом відповідної змінної величини з індексом «м»: хм, vм, Ім, Uм, тощо. Визначається як параметр конкретного коливального процесу. Вимірюється в одиницях відповідної фізичної величини: [xм]=м; [vм]=м/с; [Iм]=А; [Uм]=В і т.д.
Фаза коливань (фаза) це фізична величина яка характеризує стан коливальної системи в заданий момент часу і яка однозначно визначає параметри цієї системи в цей момент часу.
Позначається: φ
Визначальне рівняння: фазу коливань можна визначити по різному, зокрема:
– через кут повороту системи: φ=α,
– через кількість коливань системи: φ=2πn,
– через частоту коливань системи: φ=2πνt,
– через період коливань системи: φ=2πt/T,
іншими словами: φ=α=2πn=2πνt=2πt/T. Зазвичай: φ = 2πνt.
Одиниця вимірювання: [φ] = рад, радіан.
Співвідношення α=2πn=2πνt=2πt/T випливають із визначальних рівнянь періоду (T=t/n) і частоти (ν=n/t), та розуміння того, що між кутом повороту тіла α та кількістю здійснених ним обертів n існує співвідношення α=2πn. Дійсно, якщо тіло зробило один оберт (n=1), то кут його повороту становить α=1·2π=2πрад; якщо n=2, то α=2·2π=4πрад; якщо n=0,5, то α=0,5·2π=πрад і т.д.
Найбільш поширеною різновидністю періодичних коливань є так звані гармонічні коливання. Гармонічно або наближено гармонічно коливаються різноманітні маятникові системи, частинки збуреної поверхні рідини, струни та робочі поверхні музикальних інструментів, точки тіла що обертаються і тіла що рухаються по колу. Результатом певних гармонічних коливань є звук, світло і те що називають радіохвилями, інфрачервоним, ультрафіолетовим та рентгенівським випромінюванням. Гармонічні коливання відбуваються в лініях електропередач, трансформаторах, електродвигунах, тощо. Власне, практично всі природні вільні коливання є гармонічними або наближено гармонічними.
Будь яке гармонічне коливання можна представити у вигляді математичної формули, яка називається рівнянням гармонічного коливання. В загальному випадку це рівняння має вигляд: х=хмsinφ, де х – миттєве значення змінної величини, хм – амплітудне (максимальне) значення змінної величини, φ – фаза коливань. Оскільки фазу коливань можна визначити по різному (φ=α=2πn=2πνt=2πt/T), то зустрічаються і відповідно різні записи рівняння гармонічного коливання. Зазвичай, це рівняння записують у вигляді: х=хмsin2πνt.
Коли ми стверджуємо, що обертальний рух колеса (мал.132) є певним гармонічним коливанням, і що цей процес описується формулою x = хмsinφ, то це означає, що в процесі рівномірного обертання колеса (ω=const), координата будь якої точки цього колеса буде змінюватись за законом x = хмsinφ. При цьому графіком зміни цієї координати в системі відліку координата-час, буде відповідна синусоїда.
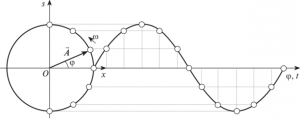
Мал.132. В процесі рівномірного обертання колеса, координата х точки 1, змінюється за законом x = хмsinφ.
Якщо в початковий момент часу (t0=0c) коливальна система знаходиться в певному не нульовому положенні, то це положення характеризують відповідною початковою фазою φ0. При цьому рівняння гармонічного коливання набуває вигляду х=хмsin(2πνt+φ0). Наприклад на мал.133а зображено графік гармонічного коливання початкова фаза якого φ0=0, а відповідне рівняння х=хмsin2πνt. На мал.133б зображено графік гармонічного коливання початкова фаза якого φ0= –π/2 і рівняння якого х=хмsin(2πνt–π/2). На мал.133в зображено графік гармонічного коливання початкова фаза якого φ0=+π/2 і рівняння якого х=хмsin(2πνt+π/2). Величина і знак початкової фази φ0 по суті вказують, наскільки і в якому напрямку потрібно зсунути даний графік, щоб отримати графік вигляду х=хмsin2πνt.
а) б)
б)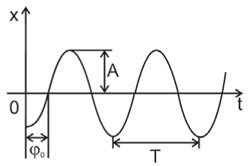 в)
в)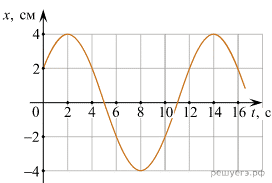
Мал.133. Якщо в початковий момент часу (t0=0c) коливальна система знаходиться в певному не нульовому положенні, то це положення характеризують відповідною початковою фазою φ0.
В подальшому ми будемо виходити з того, що початкова фаза коливань є нульовою (φ0=0), і що тому рівняння гармонічного коливання має вигляд х=хмsin2πνt.
Потрібно зауважити, що синусоїда і косинусоїда, це по суті дві різні назви однієї і тієї ж кривої. Наприклад, зображений на мал.134а графік коливань матеріальної точки є синусоїдою, а рівняння відповідного гармонічного коливання має вигляд х=хмsin2πνt. Графіком же тих коливань які представлені на мал.134б є косинусоїда, а рівняння відповідного гармонічного коливання має вигляд х=хмcos2πνt. При цьому це рівняння можна записати у вигляді х =хмsin(2πνt+π/2). Іншими словами, косинусоїда, це таж сама синусоїда, тільки зсунута в додатному напрямку на чверть періоду (на π/2рад). І навпаки, синусоїда, це таж сама косинусоїда тільки зсунута у від’ємному напрямку на чверть періоду.
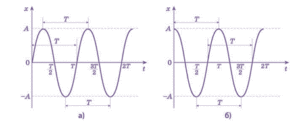
Мал.134. Синусоїда та косинусоїда, це дві аналогічні криві зсунуті одна відносно одної на чверть періоду.
Коли ми стверджуємо, що гармонічне коливання описується рівнянням х=хмsin2πνt, то це означає, що в процесі коливань величина певного параметру коливальної системи змінюється за законом х=хмsin2πνt. Наприклад, описуючи коливання нитяного маятника (мал.135а), пружинного маятника (мал.135б) та тієї матеріальної точки, що рівномірно обертається навколо нерухомого центру (мал.135в), можна говорити про те, що з плином часу координата (х) відповідних матеріальних точок змінюється за законом х=хмsin2πνt.
Втім, описуючи коливання нитяного та пружинного маятників, можна говорити не лише про гармонічні коливання координати тіла, а й про гармонічні коливання швидкості його руху v=vмsin2πνt; сили пружності F=Fмsin2πνt; потенціальної та кінетичної енергій Е= Емsin2πνt, тощо. Якщо ж говорити про гармонічні коливання точок того колеса що вільно обертається навколо своєї осі, то вони вирізняються тим, що не супроводжуються перетвореннями одного виду енергії в інший. І тому ці коливання не характеризуються певними коливаннями швидкості, енергії, тощо.
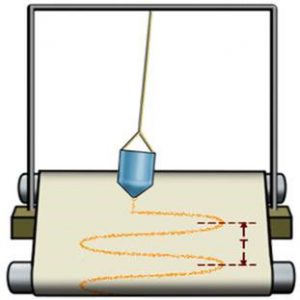
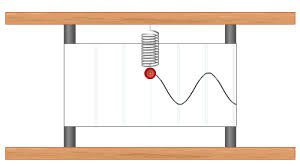
Мал.135. В процесі гармонічних коливань, певні параметри коливальної системи змінюються за законом х=хмsin2πνt.
Рівняння гармонічного коливання містить велику кількість інформації про відповідний коливальний процес. Воно дозволяє не лише визначити числове значення змінної величини в будь який момент часу, а й максимально повно описати інші параметри цього процесу. Ілюструючи лише незначну частину можливостей цього рівняння, розглянемо конкретну задачу.
Задача 1. Тіло нитяного маятника здійснює гармонічні коливання за законом х = 0,1sinπt. Визначити: 1) амплітуду, період та частоту коливань; 2) координату тіла в момент часу 0,5с; 10с; 3) кількість коливань маятника здійснених за 0,5с; за 10с.
Дано: Рішення.
х = 0,1sinπt
1) хм, Т, ν – ? 1). Із порівняльного аналізу заданого рівняння
2) х(0,5)-? х(10)-? х = 0,1sinπt та загального вигляду цього рівняння
3) n(0,5)-? n(10)-? х = хмsin2πνt, ясно що: хм = 0,1м;
. ν = 0,5Гц; (оскільки 2πνt = πt, то ν=0,5Гц).
. А оскільки Т=1/ν, то Т =1/0,5= 2с
2). Розв’язуючи рівняння х = 0,1sinπt для заданих значень часу (t=0,5с; t=2с) визначаємо відповідні значення координати тіла маятника:
х(0,5) = 0,1sinπ·0,5 = 0,1·1 = 0,1м;
х(10) = 0,1sinπ·10 = 0,1·0 = 0,0м.
3). Кількість коливань системи (n) за час t можна визначити із співвідношень: n = t/T = νt Тому:
n(0,5) = 0,5c/2c = 0,25 (коливань).
n(10) = 10c/2c = 5,0 (коливань).
Аналізуючи рівняння х=0,1sinπt можна відповісти на значно більшу кількість запитань. Наприклад, можна представити даний коливальний процес у вигляді відповідного графіка, визначити довжину відповідного маятника, величину максимального кута його відхилення, швидкість тіла в момент проходження ним положення рівноваги та в будь який інший момент часу, пройдений тілом шлях за певний проміжок часу, тощо. Знаючи рівняння гармонічного коливання тіла та масу цього тіла, можна не лише вичерпно описати кінематику коливального руху, а й динаміку цього руху. Втім, оцінити реальні можливості та значимість рівняння гармонічного коливання, ви зможете лише в процесі розв’язування задач та вивчення наступних параграфів даної теми.
Задача 2. За заданим графіком визначити амплітуду, період та частоту коливань. Записати рівняння відповідного коливання.
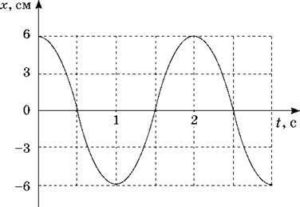
Рішення. Із аналізу заданого графіку випливає: 1) амплітуда коливань хм = 6см = 0,06м; 2) період коливань Т=2с; 3) частота коливань ν=1/Т=1/2с=0,5Гц; 4) рівняння коливань х = 0,06cos2π·0,5t = 0,06cosπt.
Потрібно зауважити: за відсутності додаткової інформації, в рівнянні гармонічних коливань, одиниці вимірювання всіх фізичних величин мають відповідати Міжнародній системі одиниць (СІ). Наприклад, у відповідності з заданим графіком хм = 6см, в рівнянні ж гармонічного коливання записують хм = 0,06м
Контрольні запитання.
1. Який зв’язок між періодом та частотою коливань? Звідки випливає цей зв’язок?
2. Дайте визначення терміну «герц».
3. Що називають амплітудою коливань? В чому вона вимірюється?
4. Які коливання називаються гармонічними? Наведіть приклади таких коливань.
5. Що називають фазою коливань? Через які величини вона визначається? Запишіть ці визначення.
6. На що вказують величина і знак початкової фази коливань φ0?
7. Чим схожі та чим відрізняються синусоїда та косинусоїда?
Вправа 46.
1. .Визначте період та частоту коливань тіла, що здійснює 50 повних коливань за 20с.
2. Визначте період та частоту обертання: а) секундної стрілки годинника; б) хвилинної стрілки годинника; в) Землі навколо своєї осі та навколо Сонця.
3. Напишіть рівняння гармонічного коливання, якщо частота коливань 0,5Гц, а її амплітуда 50см.
4. Частота коливань крил комара 600Гц, а період коливань крил бджоли 5мс. Яка з камах і наскільки більше зробить помахів крил за 1хв польоту?
5. Тіло нитяного маятника здійснює гармонічні коливання за законом х = 0,3sinπt/2. Визначити: 1) амплітуду, період та частоту коливань; 2) координату тіла в момент часу 0,5с; 10с; 3) кількість коливань маятника здійснених за 0,5с; за 10с.
6. Матеріальна точка здійснює гармонічні коливання за законом х=0,2cos2πt. Визначити амплітуду, період та частоту цих коливань. Визначте кількість коливань за 5с.
7. Амплітуда коливань точки струни становить 1мм, а частота цих коливань 1кГц. Який шлях пройде ця точка за 0,2с? запишіть рівняння відповідного гармонічного коливання.
8. За заданими графіками визначте амплітуду, період та частоту коливань. Запишіть рівняння відповідних коливань.
а)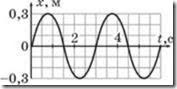 б)
б)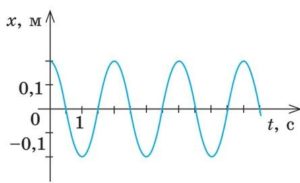
§47. Фізичний, математичний та пружинний маятники.
Однією з найпростіших коливальних систем є так званий фізичний маятник. Фізичний маятник, це механічна коливальна система, яка представляє собою тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо осі, що не проходить через центр маси тіла. Наприклад, якщо ви візьмете будь яке тверде тіло, скажімо лінійку, виделку, ножиці чи молоток і закріпите його так щоб воно могло вільно обертатись навколо осі яка не проходить через центр маси тіла, то отримаєте відповідний фізичний маятник. Однією з різновидностей фізичного маятника є так званий нитяний маятник, який представляє собою масивне тіло що висить на тонкій нитці (мотузці, дротині, тощо).


Мал.135 Приклади фізичних маятників.
Параметри коливального руху реального фізичного маятника, складним чином залежать від багатьох обставин: геометричних і вагових характеристик тіла, величини сили опору повітря, величини виникаючих в осі обертання тіла сил тертя, деформаційних енергетичних втрат, тощо. Тому, при теоретичних дослідженнях, реальний фізичний маятник замінюють відповідною ідеалізованою моделлю яка називається математичним маятником.
Математичний маятник, це ідеалізована модель фізичного маятника, яка представляє собою масивну матеріальну точку що висить на надтонкій, невагомій та нерозтяжній нитці і в процесі коливань якої відсутні будь які втрати енергії. Якщо нитка реального нитяного маятника достатньо тонка, міцна та легка, а прикріплене до неї тіло достатньо масивне і таке що виготовлено з щільного матеріалу (залізо, мідь, свинець, тощо), то фізичні властивості цього реального маятника майже не відрізнятимуться від властивостей відповідного за довжиною математичного маятника.
Можна довести, що період коливань математичного маятника визначається за формулою Т=2π√(ℓ/g), де ℓ – довжина маятника (відстань від точки закріплення нитки маятника до центру мас його тіла), g – прискорення сили тяжіння. Формула Т=2π√(ℓ/g) в достатній мірі точності справедлива не лише для ідеалізованого математичного маятника, а й для реальних фізичних маятників. При цьому для фізичних маятників довжина маятника ℓ дорівнює відстані від осі обертання тіла до центру його маси. По суті, основна відмінність фізичного маятника від відповідного математичного маятника полягає в тому, що вільні коливання реального фізичного маятника в тій чи іншій мірі згасаючі, а коливання математичного маятника – незгасаючі. І потрібно зауважити, що факт згасання коливань в реальному фізичному маятнику практично не впливає на періодичність цих коливань.
. 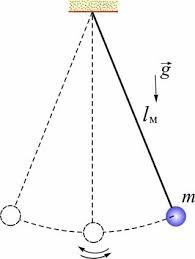



Мал.136. Вільні коливання реального фізичного маятника в тій чи іншій мірі згасаючі, а коливання математичного маятника – незгасаючі.
Із аналізу формули Т=2π√(ℓ/g) видно, що період коливань математичного маятника не залежить ні від маси тіла ні від кута його відхилення. Цей період визначальним чином залежить лише від довжини маятника ℓ та прискорення сили тяжіння g. Наприклад на Землі (g=9,8м/с2), період коливань математичного маятника довжиною 1м дорівнює Т=2π√(ℓ/g) = 2·3,14√1/9,8 = 2с, а період коливань такого ж маятника на Місяці (g=1,6м/с2): Т=2π√(ℓ/g) = 2·3,14√1/1,6 = 5с.
Строго кажучи, формула Т = 2π√(ℓ/g) в точності справедлива лише для малих кутів відхилення маятника (α ≤ 10º). Для більших кутів, ця формула потребує певних уточнень. Втім, величина цих уточнень є незначною.
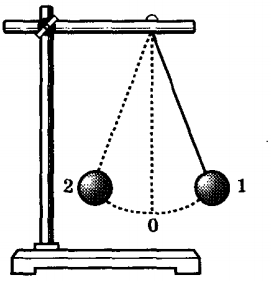
Аналізуючи вільні коливання математичного маятника не важко бачити, що вони нерозривно пов’язані з певними періодичними перетвореннями одного виду механічної енергії в інший її вид. Дійсно. Коли маятник знаходиться в положенні максимального відхилення (мал.137б) його матеріальна точка є піднятою на певну максимальну висоту (відносно того рівня де положення цієї точки є найнижчим). При цьому маятник має певний максимальний запас надлишкової потенціальної енергії та нулеву величину енергії кінетичної (Еп=mg∆h=max, Ek=mv2/2=0). В процесі руху маятника в напрямку центру його рівноваги, потенціальна енергія маятника зменшується, а кінетична – відповідно збільшується (Еп↓, Ек↑). В момент проходження положення механічної рівноваги маятника (мал.137в), величина його потенціальної енергії стає нулевою, натомість кінетична енергія – досягає максимальної величини (Еп=0, Ек=max). Продовжуючи рухатись за інерцією (мал.137г) кінетична енергія тіла маятника поступово зменшується, а потенціальна – відповідно збільшується (Ек↓, Еп↑). В протилежно крайньому положенні (мал.137д), величина потенціальної енергії маятника знову досягає своєї максимальної величини, а величина кінетичної енергії – знову стає нулевою (Еп=max, Ек=0). Ясно, що в подальшому процес повториться. При цьому напрям руху матеріальної точки зміниться на протилежний.

Мал.137. Коливання математичного (фізичного) маятника супроводжуються перетвореннями потенціальної енергії сили тяжіння в кінетичну енергію і навпаки: mg∆h ↔ mv2/2.
Таким чином, коливання математичного, а відповідно і фізичного маятників, супроводжуються не лише певними коливаннями координати тіла маятника, а й відповідними коливаннями інших параметрів системи, зокрема:
– коливаннями висоти ∆h центру мас системи над нулевим рівнем;
– коливаннями швидкості руху v центру мас системи;
– коливаннями величини потенціальної енергії системи Еп;
– коливаннями величини кінетичної енергії системи Ек;
– коливаннями кута відхилення маятника α, тощо.
Ще однією простою коливальною системою є так званий пружинний маятник. Пружинний маятник – це така механічна коливальна система, яка складається з легкої пружини та масивного тіла і в якій це тіло здійснює поступальні коливання вздовж осі пружини.
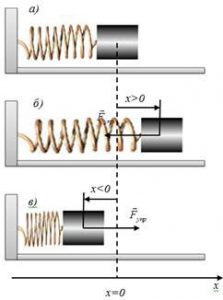
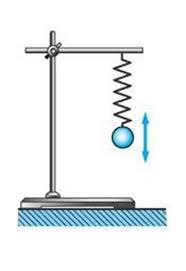
Мал.138. Загальний вигляд пружинного маятника.
Потрібно зауважити, що в науковій практиці реальні та ідеалізовані (ідеальні) пружинні маятники, позначають одним і тим же терміном – пружинний маятник. Параметри коливального руху реального пружинного маятника, складним чином залежать від багатьох обставин: геометричних та вагових характеристик пружини і тіла маятника; тих енергетичних втрат які неминучі при періодичних деформаціях пружини; втрат на механічне тертя, тощо. Тому при теоретичних дослідженнях, реальні пружинні маятники замінюють на їм відповідні ідеальні пружинні маятники, які відрізняються від реальних тим, що маса їхньої пружини є нульовою, а в процесі коливань відсутні будь-які енергетичні втрати. І не важко збагнути, що коливання реальних пружинних маятників є згасаючими, а ідеальних – незгасаючими.
Якщо пружинний маятник вивести з стану механічної рівноваги, то він буде здійснювати вільні коливання. Джерелом цих коливань є взаємопов’язана дія двох силових факторів: тієї сили пружності (Fпр= –k∆ℓ) що виникає в процесі деформації пружини, та тієї сили інерції (Fi= –ma) що виникає в процесі прискореного руху тіла. При цьому можна довести, що період коливань ідеального пружинного маятника визначається за формулою Т=2π√(m/k), m – маса тіла маятника, k – жорсткість пружини маятника. В достатній мірі точності, формула Т=2π√(m/k) справедлива не лише для ідеальних, а й для реальних пружинних маятників.
Не важко бачити, що період коливань пружинного маятника практично не залежить від прискорення сили тяжіння (g), а отже і від самої сили тяжіння. На перший погляд, такий стан речей здається дивним. Адже здається очевидним, що при вертикальному розташуванні маятника, активну роль в коливальному процесі має відігравати сила тяжіння. Насправді ж, результуючий вплив цієї сили є практично нулевим. Адже сила тяжіння, це постійна за величиною та напрямком сила, яка в рівній мірі як сприяє так і протидіє коливальному процесу. Єдиним суттєвим результатом дії сили тяжіння є те, що при вертикальному розташуванні маятника, точка його рівноваги зсувається на величину ∆ℓ=mg/k. При цьому, якщо тіло знаходиться під пружиною, то відстань до точки рівноваги збільшується (ℓ=ℓ0 + Δℓ), а якщо тіло знаходиться над пружиною – зменшується (ℓ=ℓ0 – Δℓ).
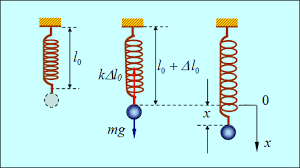
мал.139. Положення точки рівноваги пружинного маятника суттєво залежить від маси тіла маятника.
Механічні коливання пружинного маятника нерозривно пов’язані з періодичними перетвореннями одного виду механічної енергії в інший її вид. Дійсно. Коли пружина маятника знаходиться в положенні максимального розтягнення (мал.140), кількість зосередженої в ній потенціальної енергії буде максимальною, а кількість кінетичної енергії тіла – нулевою (Еп= k∆ℓ2/2=max; Ek=mv2/2=0). В процесі руху тіла в напрямку положення рівноваги, потенціальна енергія пружини буде зменшуватись, а кінетична енергія тіла – відповідно збільшуватись (Еп↓; Ек↑). При цьому, в положенні рівноваги потенціальна енергія пружини стає нулевою, а кінетична енергія тіла досягає максимальної величини (Еп=0; Ек=max). Рухаючись за інерцією в напрямку стиснення пружини, кінетична енергія тіла зменшується, а потенціальна енергія пружини збільшується (Еп↑; Ек↓). В положенні максимального стиснення пружини, її потенціальна енергія знову стає максимальною, а кінетична енергія тіла – нулевою (Еп=max; Ек=0). В подальшому, процес повторюється. При цьому, напрям руху тіла змінюється на протилежний.
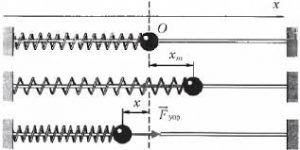
Мал.140. Коливання пружинного маятника супроводжуються періодичними перетворюваннями потенціальної енергії сили пружності в кінетичну енергію і навпаки: k∆ℓ2/2 ↔ mv2/2.
Таким чином, механічні коливання пружинного маятника супроводжуються певними коливаннями багатьох параметрів цієї системи, зокрема:
– коливаннями абсолютної деформації пружини;
– коливаннями виникаючої в пружині сили пружності;
– коливаннями швидкості руху тіла;
– коливаннями діючої на тіло сили інерції;
– коливаннями потенціальної енергії деформованої пружини;
– коливаннями кінетичної енергії тіла, тощо.
Не важко бачити, що ті формули за якими визначаються періоди коливань фізичних та пружинних маятників (Т=2π√(ℓ/g); Т=2π√(m/k)) характеризуються певним набором споріднених рис, головною з яких є наявність коефіцієнту 2π, який по суті є ознакою періодичності (повторюваності) будь якого процесу. Адже результатом повороту тіла на 2π радіан є повернення цього тіла до початкового положення.
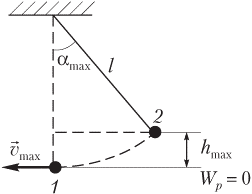
Задача 1. Коливання математичного маятника відбуваються за законом х = 0,1sin2πt. Визначити: 1) амплітуду, період та частоту коливань; 2) довжину маятника; 3) максимальне значення висоти тіла над рівнем точки рівноваги; 4) максимальне значення швидкості руху тіла маятника.
. 
Рішення.
1). Із порівняльного аналізу заданого рівняння х = 0,2sin2πt та загального вигляду цього рівняння х = хмsin2πνt, ясно що: хм = 0,1м; ν = 1Гц; (оскільки 2πνt = 2πt, то ν=1Гц). А оскільки Т=1/ν, то Т =1/1= 1с.
2). Оскільки період коливань математичного маятника визначається за формулою Т=2π√(ℓ/g), де =9,8м/с2, то можна записати Т2=[2π√(ℓ/g)]2 звідси Т2=4π2ℓ/g звідси ℓ=Т2g/4π2 = (1с)29,8(м/с2)/4(3,14)2 = 0,25м.
3). Максимальне значення висоти тіла (hmax) над рівнем точки рівноваги визначаєм із геометричних міркувань. Оскільки в прямокутному трикутнику 0-2-2Ꞌ відрізок 0-2 = ℓ = 0,25м = 25см, а відрізок 2-2Ꞌ = хм = 0,1м = 10см, то у відповідності з теоремою Піфагора можна записати 0-2Ꞌ = √(ℓ2 – х2) = √(252 – 102) = 23см. Із аналізу малюнку ясно, що hmax=ℓ – 23см = 2см.
4). Оскільки в точці максимального відхилення маятника (т.2) величина його потенціальної енергії дорівнює mghmax. Та зважаючи на те, що у відповідності з законом збереження енергії, в нижній точці траєкторії руху тіла маятника (т.1) ця енергія повністю перетворюється на енергію кінетичну mvmax2/2, можна записати mvmax2/2 = mghmax. vmax = √2ghmax = √2·9,8·0,02 = 0,62м/с.
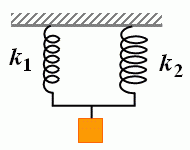
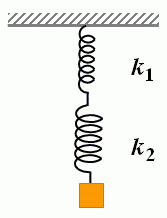
Задача 2. Визначити період коливань пружинного маятника який складається з тіла масою 1кг та системи двох пружин жорсткості яких 30Н/м і 70Н/м. При цьому, у першому випадку пружини з’єднані паралельно, а в другому – послідовно.
Дано: Рішення:
m = 1кг Виконуємо малюнок який відображає фізичний зміст задачі.
k1 = 30Н/м Період коливань пружинного маятника визначається за
k2 = 70Н/м формулою Т=2π√(m/k), де k – загальна жорсткість
Т1 = ? пружини маятника.
Т2 = ? Оскільки при паралельному з’єднані пружин k=k1+k2=100Н/м,
то Т1=2π√(m/k) = 2·3,14√(1/100) = 0,628с.
Оскільки при послідовному з’єднані пружин k=k1·k2/(k1+k2) = 30·70/(30+70) =21Н/м, то Т2=2π√(m/k) = 2·3,14√(1/21) = 1,38с.
Контрольні запитання.
1. Результатом дії яких сил є коливання математичного маятника?
2. Чому коливання фізичного маятника є згасаючими, а коливання математичного маятника – незгасаючими?
3. Чи залежить період коливань математичного маятника від амплітуди цих коливань? Від маси матеріальної точки?
4. Чи змінюється в процесі згасання коливань нитяного маятника, період цих коливань?
5. Які сили визначають механічну поведінку пружинного маятника?
6. Які енергетичні перетворення відбуваються в процесі коливань пружинного маятника та чим вони відрізняються від аналогічних перетворень в фізичному маятнику?
7. Чому сила тяжіння не впиває на період коливань пружинного маятника.
8. Порівняйте формули періодів коливань математичного та пружинного маятників. На що вказує в цих формулах коефіцієнт 2π?
Вправа 47.
1. Довжина математичного маятника 0,5м. Визначте період та частоту коливань цього маятника.
2. Виконуючи лабораторну роботу по визначенню прискорення сили тяжіння, учень встановив, що маятник довжиною 80см, за 1хв здійснює 34 коливань. Який результат отримав учень?
3. Вантаж масою 4кг коливаючись на легкій пружині робить 5 коливань за 4 секунди. Визначте жорсткість пружини.
4. Під дією сили 2Н пружина розтягується на 1см. До цієї пружини прикріпили вантаж масою 2кг. Визначте період коливань даного пружинного маятника.
5. Визначити період коливань пружинного маятника який складається з тіла масою 1кг та системи двох пружин жорсткість кожної з яких 40Н/м. При цьому, у першому випадку пружини з’єднані паралельно, а в другому – послідовно.
6. Рівняння коливань математичного маятника має вигляд х = 0,1sin2πt. Визначте період і частоту коливань маятника. Визначте довжину маятника.
7. Вантаж масою 300г є частиною пружинного маятника і здійснює коливання за законом х=0,06sinπt. Визначте період і частоту коливань, жорсткість пружини та максимальну швидкість тіла.
8. Коливання математичного маятника масою 0,2кг відбуваються за законом х = 0,2sinπt. Визначити: амплітуду, період та частоту коливань; довжину маятника; максимальне значення висоти тіла над рівнем точки рівноваги; максимальне значення швидкості руху тіла маятника.
§48*. Крутильний маятник. Маятник Максвела.
В межах програми загальноосвітньої школи, зазвичай вивчають дві механічні коливальні системи: фізичний маятник та пружинний маятник. Однак в науці і техніці широко застосовують й інші механічні коливальні системи, зокрема крутильний маятник та маятник Максвела.
Крутильний маятник – це така механічна коливальна система, яка представляє собою закріплене на жорсткій підвісці масивне тверде тіло, яке під дією тих сил пружності що виникають при деформації кручення підвіски (або спеціальної плоскої пружини), може здійснювати крутильно-обертальні коливання.
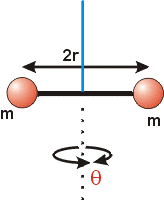
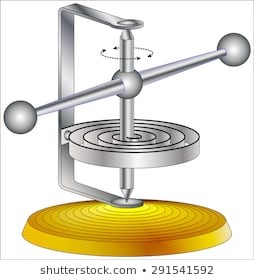
Мал.141. Загальний устрій крутильного маятника.
Пояснюючи принцип дії крутильного маятника, можна сказати наступне. В момент максимального закручення спіральної пружини (підвіски) маятника, в ній накопичується певна, максимальна кількість потенціальної енергії сили пружності, величина якої визначається за формулою Еп = DΔφ2/2, де Δφ – виміряний в радіанах кут закручення пружини, D – крутильна жорсткість пружини (певний аналог жорсткості пружини при її розтягненні-стисненні). При цьому кінетична енергія обертального руху тіла маятника (Ек=Jω2/2), дорівнює нулю: (Еп = max; Ек = 0).
В процесі розкручування пружини (підвіски) маятника, кількість зосередженої в ній потенціальної енергії зменшується. Натомість, кількість кінетичної енергії обертального руху тіла маятника – відповідно збільшується (Еп↓; Ек↑). В момент проходження маятником положення крутильної рівноваги, потенціальна енергія спіральної пружини стає нулевою, а кінетична енергія тіла – максимально великою (Еп=0; Ек=max).
Продовжуючи обертатись за інерцією, тіло маятника знову закручує пружину, але вже в протилежну сторону. При цьому, потенціальна енергія пружини зростає, а кінетична енергія тіла відповідно зменшується (Еп↑; Ек↓). В момент максимального закручення пружини, тіло маятника зупиняється. При цьому, його кінетична енергія стає нулевою, а потенціальна енергія спіральної пружини – максимально великою (Еп=max; Ек=0). Ясно, що в подальшому, процес повторюється. При цьому напрям обертального руху маятника змінюється на протилежний.
Таким чином, вільні механічні коливання крутильного маятника, супроводжуються періодичними перетворюваннями потенціальної енергії деформованої спіральної пружини (закрученої нитки, мотузки, троса, тощо), в кінетичну енергію обертального руху тіла і навпаки: Еп ↔ Ек.
Можна довести, що період коливань ідеального крутильного маятника (маятника в якому відсутні будь які теплові втрати енергії і масою спіральної пружини якого можна знехтувати), визначається за формулою Т=2π√(J/D), де J – момент інерції тіла маятника; D – крутильна жорсткість пружини (визначається експериментально). Втім, формула Т=2π√(J/D) в достатній мірі точності справедлива і для реальних крутильних маятників.
Крутильні маятники широко застосовуються в годинникових механізмах. Наприклад, якщо мова йде про наручний годинник, то застосувати в ньому звичайний фізичний маятник практично не можливо. Базовим елементом наручних та переважної більшості побутових механічних годинників є крутильний маятник. Цей маятник (мал.142а) представляє собою відносно масивне колесо («балансир») до осі якого прикріплена легка спіральна пружина (“волосок”). В годинниковому маятнику балансир періодично повертається то в одну то в іншу сторону. При цьому, періодичні коливання балансиру і є мірою відліку однакових проміжків часу та основою точної роботи годинника.
а)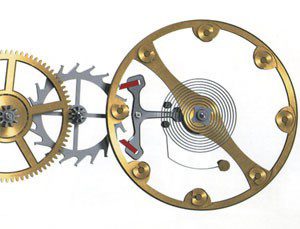 б)
б)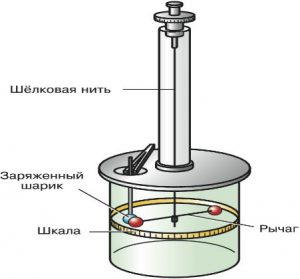
Мал.142. Приклади застосування крутильного маятника.
Ще одним прикладом практичного застосування крутильної маятникової системи, є так звані крутильні ваги (терези). Крутильні ваги (мал.142б) представляють собою вимірювальну систему, яка складається з важеля, який збалансовано відносно свого центру мас висить на тонкій пружній нитці. Принцип дії цієї системи полягає в наступному. Під дією вимірюваної сили, тіло важеля повертається на кут, величина якого пропорційна діючій силі. Вимірявши цей кут та знаючи параметри важеля і пружної нитки, визначають величину вимірюваної сили.
Крутильні ваги є надзвичайно чутливими до силової дії. А це означає, що ці ваги дозволяють вимірювати сили мізерної величини. Достатньо сказати, що саме за допомогою крутильних вагів, англійський фізик Генрі Кавендіш, ще в 1798 році виміряв величину гравітаційної сталої (G=6,67∙10-11Н·м2/кг2).
Перші крутильні ваги виготовив в 1784 році французький фізик Шарль Кулон. Саме за допомогою цих вагів, Кулон відкрив закон взаємодії електричних зарядів (закон Кулона).
Цікавою різновидністю простих коливальних систем є маятник Максвела (мал.143). Цей маятник представляє собою масивний диск, горизонтальна вісь якого утримується двома вертикально закріпленими паралельними нитками які намотані на цю вісь.


Мал.143. Загальний устрій маятника Максвела.
Пояснюючи загальний устрій та принцип дії маятника Максвела можна сказати наступне. Коли тіло маятника знаходиться в гранично верхньому положенні, кількість зосередженої в ньому потенціальної енергії сили тяжіння є максимальною, а кількість його кінетичної енергії – нулевою (Еп=mgΔh=max; Ек=0). В процесі опускання тіла маятника, його потенціальна енергія зменшується, а кінетична – відповідно збільшується (Еп↓; Ек↑). При цьому потрібно зауважити, що кінетична енергія тіла маятника Максвела складається з кінетичної енергії його поступального руху (Ек=mv2/2) та кінетичної енергії його обертального руху (Ек=Jω2/2, де J – момент інерції тіла маятника, ω – кутова швидкість цього тіла). Коли тіло маятника опиняється в гранично нижньому положенні, кількість зосередженої в ньому потенціальної енергії (відносно цього положення) буде нулевою, а кількість кінетичної енергії обертального руху тіла – гранично великою (Еп=0; Ек= Jω2/2=max).
Продовжуючи обертатись за інерцією, тіло маятника намотує вертикальні нитки на вісь свого обертання і за рахунок цього піднімається вгору. При цьому потенціальна енергія тіла збільшується, а його загальна кінетична енергія – зменшується (Еп↑; Ек↓). В точці гранично верхнього положення, маятник знову зупиняється. При цьому, кількість зосередженої в ньому потенціальної енергії знову стає максимальною, а кількість кінетичної енергії – нулевою (Еп=max; Ек=0). В подальшому процес повторюється і тіло маятника здійснює відповідні періодичні коливання.
Маятник Максвела не є певною різновидністю крутильного маятника. За фізичною суттю тих процесів які відбуваються в маятнику Максвела, він скоріше схожий на фізичний маятник. Різниця лише в тому, що в фізичному маятнику, потенціальна енергія сили тяжіння тіла маятника, перетворюється в кінетичну енергію його поступального руху і навпаки: mgΔh↔mv2/2. В маятнику ж Максвела, потенціальна енергія піднятого тіла також перетворюється в кінетичну енергію, але кінетичну енергію обертального руху тіла маятника: mgΔh ↔ Jω2/2.
Можна довести, що період коливань ідеального маятнику Максвела визначається за формулою Т = 2π√(2h/g(1+J1/J2), де h – амплітуда коливань маятника; g – прискорення сили тяжіння; J1 – момент інерції тіла маятника: J2 – момент інерції тієї осі на яку накручуються нитки маятника.
Маятники Максвела не мають серйозного практичного застосування. Однак як демонстраційні прилади, вони є неперевершеними ілюстраторами взаємопов’язаності механіки поступального та обертального рухів, закону збереження енергії в механіці, тощо. Крім цього, маятник Максвела та похідні від нього коливальні системи є основою багатьох цікавих навчально-пізнавальних приладів та іграшок.
На завершення розмови про механічні коливальні системи, представимо головні параметри цих систем у вигляді наступної порівняльної таблиці.
| Маятник | Енергетичні перетворення | Період коливань |
| Фізичний | mgΔh ↔ mv2/2 | T = 2π√(ℓ/g) |
| Пружинний | kΔℓ2/2 ↔ mv2/2 | T = 2π√(m/k) |
| Крутильний | DΔφ2/2 ↔ Jω2/2 | Т = 2π√(J/D) |
| Максвела | mg∆h ↔ Jω2/2 | Т = 2π√(2h/g(1+J1/J2) |
Контрольні запитання.
1. Поясніть будову і принцип дії крутильного маятника.
2. Чим схожі і чим відрізняються пружинні та крутильні маятники?
3. Чим схожі і чим відрізняються формули періодів коливань пружинного та крутильного маятників?
4. Чому в наручних годинниках застосовують не фізичні а пружинні маятники?
5. Які перетворення енергії відбуваються в процесі коливань маятника Максвела?
6. Чим схожий та чим відрізняється маятник Максвела від: а) фізичного маятника; б) крутильного маятника?
7. В формулах періодів коливань маятників присутній коефіцієнт 2π. На що вказує цей коефіцієнт?
§49. Розв’язування задач. Тема: Механічні коливання.
Задача 1. Вантаж висить на пружині і коливається з періодом 0,5с. На скільки вкоротиться пружина, якщо зняти з неї вантаж?

Дано: Рішення:
Т = 0,5с Виконуємо малюнок який відображає фізичну суть задачі.
Δℓ0 = ? Виходячи з того, що в стані механічної рівноваги на те тіло
яке висить на пружині діють дві рівні за величиною і протилежні за напрямком сили (сила тяжіння Fт= mg та реакція опори яка дорівнює силі пружності N=Fпр= kΔℓ0), можна записати mg = kΔℓ0, звідси Δℓ0 = mg/k.
На перший погляд, в умовах даної задачі визначити величину Δℓ0 за формулою Δℓ0 = mg/k, не можливо. Адже ми маємо рівняння з трьома невідомими: Δℓ0, m, k. Втім, не будемо поспішати. Адже в рівнянні Δℓ0 = mg/k, нас цікавить не m і k, а їх відношення (m/k). А саме це відношення і міститься в формулі періоду коливань пружинного маятника Т = 2π√(m/k), звідси Т2=4π2(m/k), звідси m/k=T2/4π2.
Таким чином, Δℓ0 = mg/k = gT2/4π2 = 9,8(0,5)2/4·3,142 = 0,06м = 6см.
Відповідь: Δℓ0 = 6см.
Задача 2. Математичний маятник здійснює коливання за законом х=0,1sin(πt+π/2). Визначити: 1) початкову фазу, амплітуду, період та частоту коливань; 2) довжину нитки маятника; 3) величину максимального кута відхилення маятника; 4) максимальну швидкість руху тіла маятника; 5) пройдений тілом маятника шлях за одне його повне коливання.
. 
Дано: Рішення:
х=0,1sin(πt+π/2)
1) φ0, хм, Т, ν – ? 2) ℓ = ?
3) αм = ? 4) vм = ? 5) s = ?
1) Із порівняльного аналізу заданого рівняння х=0,1sin(πt+π/2) та загального вигляду рівняння гармонічного коливання х = хмsin(2πνt+φ0), ясно:
хм = 0,1м;
φ0 = π/2 рад;
ν = 0,5Гц (оскільки 2πνt = πt то ν = 0,5Гц);
Т = 2с (оскільки Т = 1/ν)
2) Оскільки період коливань математичного маятника визначається за формулою Т = 2π√(ℓ/g), та зважаючи на те що Т=2с, можна записати Т2=4π2(ℓ/g). Звідси ℓ = Т2g/4π2 = 0,994м = 99,4см.
3) Із геометричних міркувань (дивись мал.) ясно, що хм = ℓsinαм , тому sinαм = хм/ℓ, звідси: αм = arcsin(xм/ℓ) = arcsin0,1 ≈ 6º.
4) Максимальну швидкість матеріальної точки, тобто її швидкість в момент проходження маятником положення рівноваги, можна визначити на основі закону збереження енергії. А згідно з цим законом: mgΔh = mvм2/2. Звідси vм = √(2gΔhм). Величину Δhм визначаєм із геометричних міркувань (див. мал.) Δhм = ℓ – ℓcosαм = ℓ(1 – cos6°) = 0,994(1 – 0,96) = 0,04м. Отже vм = √(2gΔhм) = √(2·9,8·0,04)= 0,89м/с.
5) Оскільки для повного кола, тобто для α=360º, s=2πℓ, то для тієї частини цього кола якій відповідає кут α, s = 2πℓ(α/360º). Зважаючи на те, що за одне повне коливання системи, маятник 4 рази проходить кут αм, можна записати α = 4αм = 24º. Звідси s = 2πℓ(24º/360º) = 0,416м = 41,6м.
Задача 3. Вантаж масою 200г є частиною пружинного маятника і здійснює коливання за законом х=0,08sin10πt. Визначте період, частоту та амплітуду коливань, жорсткість пружини та максимальну швидкість тіла.

Дано: Рішення:
х=0,08sin10πt
m = 200г = 0,2кг
1) хм, Т, ν – ?
2) k = ? 3) vм = ?
1) Із порівняльного аналізу заданого рівняння х=0,08sin10πt та загального вигляду рівняння гармонічного коливання х = хмsin2πνt, ясно:
хм = 0,08м = 8см;
оскільки 2πνt = 10πt то ν = 5Гц;
Т = 0,2с (оскільки Т = 1/ν)
2) Оскільки період коливань пружинного маятника визначається за формулою Т = 2π√(m/k), та зважаючи на те що Т=0,2с, можна записати Т2=4π2(m/k). Звідси k = 4π2m/T2 = 4·3,142·0,2кг/(0,2с)2 = 197(кг/с2=Н/м).
3) Оскільки в процесі коливань пружинного маятника, потенціальна енергія сили пружності перетворюється в кінетичну енергію рухомого тіла і навпаки (kΔℓ2/2 ↔ mv2/2), то у відповідності з законом збереження енергії, для максимальних значень цих енергій можна записати kхм2/2 = mvм2/2, звідси vм =xм√(k/m) = 0,08√(197/0,2) = 2,5м/с.
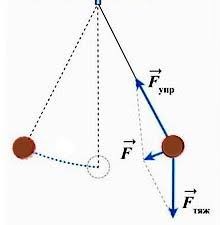
Задача 4. Визначити період коливань математичного маятника довжиною ℓ який з прискоренням а рухається: а) вертикально вгору; б) вертикально вниз.
а) а↑ б) а↓

Дано: Рішення:
ℓ Виконуємо малюнок який відображає фізичну суть задачі.
g ↓ Формула Т = 2π√(ℓ/g) по суті відображає факт того,
a1 ↑ що тією зовнішньою силою яка визначає період коливань
a2 ↓ математичного маятника є сила тяжіння Fт = mg.
T1, Т2, Т3=? При цьому, мається на увазі, що та система відліку в якій
знаходиться маятник є інерціальною (а=0). Якщо ж ця система неінерціальна, тобто така що рухається з певним прискоренням (а≠0), то на матеріальну точку, окрім сили тяжіння активно діє сила інерції Fi = –ma. А це означає, що періодичність коливань математичного маятника буде визначатися результуючою двох сил: R = Fт + Fi. А зважаючи на те, що сила інерції направлена в сторону протилежну від напрямку прискорення тіла, можна записати R = mg – ma = m(g – a).
Таким чином, в тих випадках коли математичний маятник рухається з прискоренням а, формула Т = 2π√(ℓ/g) набуває вигляду Т = 2π√(ℓ/(g –а)). В умовах нашої задачі:
а) Т1 = 2π√(ℓ/(g+а)), оскільки прискорення а направлено в протилежну сторону від прискорення g, то g – a = g +a;
б) Т2 = 2π√(ℓ/(g –а));
Задача 5. На рівні моря маятниковий годинник іде абсолютно точно. Чи буде цей годинник таким же точним на висоті 4км? Якою буде похибка його показань за добу? Радіус Землі 6,37∙103 км.
Дано: Рішення:
h = 4км 4·103м
R = 6,37∙103км 6,67·106м
t0 = 24год 86400с
∆t = ? Оскільки період коливань математичного (фізичного) маятника залежить від прискорення сили тяжіння Т = 2π√(ℓ/g), а величина цього прискорення в процесі віддалення від центру Землі зменшується (g = GM/(R+h)2), то можна стверджувати, що на висоті h, період коливань математичного маятника стане більшим: оскільки g↓ то Т↑. А це означає, що на висоті h маятник зробить менше коливань і тому відповідна стрілка годинника повернеться на менший кут. Іншими словами, на висоті h маятниковий годинник буде відставати.
Визначаючи величину цього відставання, будемо виходити з того, що час який фіксує маятниковий годинник, пропорційний кількості коливань його маятника і що тому t0/t1 = n0/n1, де t0, t1 – час, який фіксує годинник за добу відповідно: на рівні моря і на висоті h; n0, n1 – кількість коливань які здійснює маятник годинника за добу, відповідно: на рівні моря і на висоті h.
Зважаючи на те, що кількість тих коливань які здійснює маятник за час t визначається за формулою n=t/T, де Т – період коливань маятника, можна записати: n0/n1= tT1/T0t =T1/T0 , звідси t0/t1 = T1/T0.
Враховуючи, що:
T0 = 2π√(ℓ/g0) = 2π√[ℓR2/GM];
T1 = 2π√(ℓ/g1) = 2π√[ℓ(R+h)2/GM],
можна записати: t0/t1 = T1/T0 = = (R+h)/R.
Звідси: t1 = t0R/(R+h); ∆t = t0 – t1
Розрахунки: t1 = t0R/(R+h) = 8640·6,67·106/(6,67·106+0,004·106)= 86348c;
∆t = 86400 – 86348 = 52c
Відповідь: ∆t = 52c.
Вправа 49.
1. Яка довжина математичного маятника, якщо період його коливань 2с?
2. Визначити масу вантажу, який на пружині жорсткістю 250Н/м робить 20 коливань за 16 секунд.
3. На Землі математичний маятник робить 20 коливань за хвилину. Скільки коливань за хвилину зробить такий же маятник на Місяці (g=1,6м/с2)?
4. Математичний маятник здійснює коливання за законом х = 0,2cosπt. Визначити: а) початкову фазу, амплітуду, період та частоту коливань; б) довжину маятника; в) максимальну швидкість тіла маятника; г) пройдений тілом маятника шлях за 10с.
5. Вантаж масою 300г є частиною пружинного маятника і здійснює коливання за законом х=0,06sin20πt . Визначте період і частоту коливань, жорсткість пружини та максимальну швидкість тіла.
6. В ракеті, що вертикально стартує з поверхні землі, період коливань математичного маятника зменшився вдвічі. З яким прискоренням рухається ракета?
7. Як і настільки за добу будуть відрізнятись показання абсолютно однакових маятникових годинників один з яких знаходиться на полюсі (g=9,83м/с2), а другий – на екваторі (g=9,78м/с2).
8. На Місяці математичний маятник довжиною 1м за 1хв робить 12 коливань. Визначте масу Місяця, якщо відомо, що його радіус 1740км.
9. Математичний маятник довжиною 0,5м відхилили на 30º. Яку швидкість матиме кулька маятника в нижній точці траєкторії. Запишіть рівняння коливань маятника.
§50. Автоколивання.
Вільні коливання будь якої коливальної системи характеризуються певною наперед заданою періодичністю. Наприклад, період коливань фізичного маятника визначається за формулою Т=2π√(ℓ/g) і практично не залежить ні від способу виведення системи з рівноваги, ні від амплітуди її коливань, ні від величини наданої системі енергії. Змінити цю власну періодичність коливальної системи, можна лише шляхом зміни параметрів самої системи, наприклад шляхом зміни довжини маятника.
Основним недоліком будь яких вільних механічних коливань є те, що вони в тій чи іншій мірі згасаючі. Вони згасають тому, що будь який механічний процес, неминуче супроводжується тими чи іншими енергетичними втратами: втратами на тертя, опір повітря, деформаційне нагрівання, тощо. Для того щоб вільні механічні коливання стали незгасаючими, необхідно так чи інакше постійно компенсувати енергетичні втрати коливальної системи. Скажімо, енергетичні втрати фізичного маятника можна поповнювати шляхом періодичних підштовхувань тіла маятника. Однак ясно, що ручний спосіб поповнення енергетичних втрат системи є незручним, неефективним і мало прогнозованим. Тому на практиці дозовану та вчасну компенсацію енергетичних втрат коливальної системи здійснюють автоматизовано і за рахунок певного, наперед визначеного джерела енергії. При цьому коливальна система стає автоколивальною, а її вільні коливання стають автоколиваннями.
Автоколивальна система, це така автоматизована коливальна система, яка є джерелом незгасаючих, умовно вільних коливань, енергетичні втрати якої автоматично компенсуються за рахунок додаткового джерела енергії. При цьому, ті умовно вільні коливання які створює автоколивальна система називають автоколиваннями.
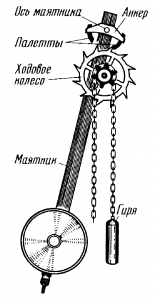
Класичним прикладом механічної автоколивальної системи є маятниковий механізм годинника (мал.144). Основними елементами цього механізму є маятник, ходове колесо, спеціальний зубчастий важіль (анкер) та джерело додаткової енергії – піднята гиря або скручена пружина. Принцип дії такої автоколивальної системи полягає в наступному. Ходове колесо знаходиться під постійним силовим навантаженням піднятої гирі і через спеціальний зубчастий важіль (анкер) перебуває в рухомому контакті з маятником годинника. Конструкція анкера та ходового колеса така, що за одне напівколивання маятника, колесо повертається на один зубець. При цьому, в момент переходу від одного зубця до іншого, анкер, а разом з ним і маятник, отримують певний додатковий енергетичний імпульс (поштовх), джерелом якого є піднята гиря. А це означає що за одне повне коливання, маятник в певні наперед визначені моменти часу, двічі отримує додаткові енергетичні імпульси, які повністю компенсують всі енергетичні втрати системи. При цьому коливання системи будуть строго періодичними та незгасаючими.


Мал.144. Загальний устрій автоколивальної системи маятникового механізму годинника.
В будь якій автоколивальній системі можна виділити три основні елементи: 1) коливальна система; 2) джерело енергії; 3) регулюючий пристрій, тобто пристрій який забезпечує передачу дозованих порцій енергії від її джерела до коливальної системи. Наприклад, в зображеному на мал.144 маятниковому механізмі, коливальною системою є фізичний маятник, джерелом енергії – піднята гиря, а регулюючим пристроєм – система, що складається з ходового колеса та анкера.
Однак, сам по собі факт наявності вище названих базових елементів, ще не гарантує того, що в своїй сукупності ці елементи утворюють автоколивальну систему. Адже ті енергетичні імпульси які компенсують втрати енергії в коливальній системі, потрібно надавати в строго визначені моменти часу і ці моменти визначаються положенням самої коливальної системи. Тому невід’ємною складовою будь якої автоколивальної системи є наявність в ній так званого зворотного зв’язку. Цей зв’язок полягає в тому, що коливальна система певним, автоматично визначеним чином впливає на роботу регулюючого пристрою, а регулюючий пристрій певним чином впливає на енергетичні параметри коливальної системи. Наприклад в нашому випадку, система зворотного зв’язку обумовлена тим, що анкер, будучи жорстко з’єднаним з тілом маятника, в певні визначені моменти контактує то з одним, то з іншим зубцем ходового колеса. А оскільки це колесо знаходиться під постійним силовим навантаженням, яке забезпечує джерело енергії, то у відповідні моменти, певні енергетичні імпульси передаються коливальній системі, забезпечуючи тим самим сталість її коливань.
Таким чином, принцип дії будь якої автоколивальної системи полягає в наступному. Коливальна система (в нашому випадку фізичний маятник), створює певні періодичні коливання. Регулюючий пристрій (в нашому випадку анкер) отримує енергію від відповідного постійного джерела (піднятої гирі) і керуючись командами коливальної системи, імпульсно компенсує енергетичні втрати цієї системи. Загальний устрій та принцип дії автоколивальної системи можна представити у вигляді наступної принципової схеми.
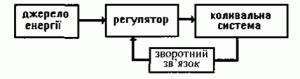
Мал.145. Принципова схема автоколивальної системи.
Автоколивання можна назвати як умовно вільними так і умовно вимушеними. Від вимушених автоколивання відрізняються тим, що їх періодичність визначається не періодичністю зовнішньої змінної сили, а параметрами самої коливальної системи. При цьому, вплив сторонніх сил полягає лише в тому, щоб підтримувати по суті вільні коливання системи на енергетично незмінному рівні. Від вільних коливань, автоколивання відрізняються тим, що підтримуються імпульсами певної сторонньої сили і тому є незгасаючими.
Контрольні запитання.
1. Чи можна період коливань нитяного маятника змінити шляхом зміни: а) маси тіла; б) амплітуди коливань; в) довжини нитки маятника?
2. Який основний недолік вільних механічних коливань і яким чином усувається цей недолік?
3. Що називають автоколивальною системою?
4. Назвіть основні елементи автоколивальної системи годинника.
5. Поясніть принцип дії автоколивальної системи годинника.
6. Які деталі механічного годинника є джерелом енергії; регулятором; коливальною системою?
7. В чому суть зворотнього зв’язку автоколивальної системи? Як цей зв’язок реалізується в маятниковому механізмі годинника?
8. Чим схожі і чим відрізняються автоколивання від а) вимушених коливань; б) вільних коливань?
§51. Вимушені коливання. Резонанс.
До тепер ми говорили про так звані вільні коливання, тобто такі коливання які починаються після виведення системи з стану рівноваги і продовжуються самостійно, а точніше – під дією певної комбінації внутрішньо системних сил. При цьому ми з’ясували, що періодичність вільних коливань визначається параметрами самої коливальної системи, що амплітуда цих коливань залежить від величини наданої системі енергії, і що з плином часу, амплітуда вільних коливань зменшується.
Однак в науковій, побутовій та природничій практиці, окрім вільних часто зустрічаються і різноманітні вимушені коливання. Такі коливання відбуваються під дією певної зовнішньої змінної сили і після припинення дії цієї сили – припиняються. Наприклад, якщо ви змушуєте книгу здійснювати певні коливальні рухи, то коливання книги є вимушеними. Частотні та амплітудні параметри вимушених коливань можуть бути найрізноманітнішими. Скажімо, коливання мембрани (дифузора) того гучномовця з якого лине музика чи голосовий текст, є вимушеними. При цьому, параметри цих вимушених коливань підпорядковані не певним строго визначеним закономірностям, а відображають параметри того змінного струму в якому записана певна звукова інформація, і який власне й створює відповідні механічні коливання. Вимушено коливаються рухомі деталі двигуна внутрішнього згорання та механічної моделі цього двигуна. Вимушено коливаються рухомі деталі електричних та механічних швейних машинок. Вимушені коливання здійснюють м’язи нашого серця. Вимушено коливаються легені нашого організму, деталі машин та механізмів, тощо.



Мал.146. Деякі приклади джерел вимушених коливань.
Ясно, що описати все різноманіття можливих варіантів вимушених коливань практично неможливо. Тому стисло зупинимся лише на одній, але надзвичайно важливій різновидності вимушених коливань. А саме, на тих коливаннях в яких зовнішня змінна сила діє на об’єкт який сам по собі є коливальною системою. Досліджуючи поведінку такого об’єкту звернемось до експерименту. Суть цього експерименту полягає в наступному. Пружинний маятник (мал.147а) через нитку та кільце з’єднаний з кривошипним вигином горизонтальної осі, яку можна обертати з контрольованою швидкістю. В процесі рівномірного обертання цієї осі, на маятник буде діяти змінна за величиною та напрямком сила, період коливань якої дорівнює періоду обертання осі (кривошипного вигину).
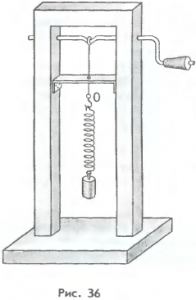
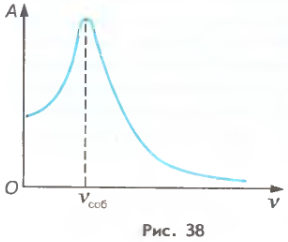
Мал.147. Прилад для дослідження залежності амплітуди коливань коливальної системи, від частотних параметрів діючої на цю систему зовнішньої сили та графік цієї залежності.
Дослідження показують, що при рівномірному обертанні осі приладу (бажано щоб таке обертання здійснювалось електродвигуном, частотні параметри якого можна контрольовано змінювати), масивне тіло маятника починає здійснювати певні коливальні рухи. Спочатку ці рухи є досить складними. Але вже через декілька обертів осі, коливання вантажу стають гармонічними та незгасаючими. При цьому, частота цих коливань співпадає з частотою коливань діючої на маятник зовнішньої сили. Таким чином, якщо коливальна система знаходиться під дією зовнішньої періодичної сили, то через деякий час ця система починає здійснювати вимушені, незгасаючі коливання, частота яких дорівнює частоті коливань зовнішньої сили.
Досліджуючи вимушені коливання вантажу, звернемо увагу на залежність амплітуди цих коливань від швидкості обертання осі, тобто від періодичності (частоти) дії зовнішньої сили. Припустимо, що жорсткість пружини маятника дорівнює 40Н/м, а маса його вантажу 0,1кг. Не важко визначити, що за таких умов, період власних коливань маятника становить 0,314с, а їх частота 3,18Гц: Т=2π√(m/k)= 0,314с; ν=1/Т=3,18Гц.
Дослідження показують, що коли частота коливань зовнішньої сили значно менша за частоту власних коливань маятника, то амплітуда коливань вантажу практично не відрізняється від амплітуди коливань точки О. Але по мірі того як частота коливань зовнішньої сили наближається до частоти власних коливань маятника, амплітуда коливань вантажу неухильно зростає і досягає своєї максимальної величини при співпадінні цих частот. При подальшому збільшенні швидкості обертання осі приладу (при збільшенні частоти зовнішніх коливань), амплітуда коливань вантажу швидко зменшується і при відносно великих частотах обертання, стає практично нулевою. Характер залежності амплітуди коливань вантажу від частоти коливань зовнішньої сили, представлено на мал.147б.
Таким чином, експериментальні дослідження показують, що при співпадінні частоти зовнішніх силових впливів з власною частотою коливальної системи, спостерігається різке збільшення амплітуди коливань цієї системи. Це явище прийнято називати резонансом. Резонанс це явище, суть якого полягає в тому, що при співпадінні частоти коливань зовнішніх силових (енергетичних) впливів (νзовн), з власною частотою (νвл) тієї коливальної системи на яку ці впливи спрямовані, відбувається розгойдування коливальної системи, тобто відносно швидке збільшення амплітуди її коливань. Іншими словами: якщо νзовн=νвл, то резонанс (розгойдування системи, підсилення коливань).
Явище резонансу наочно ілюструє наступний простий експеримент. До натягнутого між двома нерухомими точками горизонтального шпагату (міцної нитки, проволоки, тощо) прив’язано два однакових за довжиною (с і f) і декілька різних нитяних маятників (мал.148). Це означає, що серед наявного різноманіття маятників, лише маятники с і f мають однакові періоди, а відповідно і частоти коливань. Змусивши вільно коливатись маятник f, ви неодмінно з’ясуєте, що тільки маятник с відреагує на ці коливання і почне розгойдуватись. При цьому, по мірі зростання амплітуди коливань маятника с, амплітуда коливань маятника f буде зменшуватись. Поступово маятник f майже зупиниться, натомість амплітуда коливань маятника с досягне максимальної величини. В подальшому процес повториться у зворотньому напрямку: амплітуда коливань маятника f збільшується, а маятника с – зменшується.
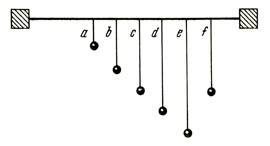
Мал.148. Прилад який дозволяє наочно продемонструвати прояви того явища яке називається резонансом.
Пояснюючи дані експериментальні факти, можна сказати наступне. Вільні коливання маятника f спричиняють відповідні вимушені коливання того горизонтального шпагату на якому висять інші маятники. А оскільки серед цих маятників, лише маятник с має таку ж частоту власних коливань як і маятник f (νc=νf), то в результаті явища резонансу, саме маятник с почне розгойдуватись. З іншого боку таке розгойдування потребує певних енергетичних затрат. А це означає, що у відповідності з законом збереження енергії, по мірі збільшення амплітуди коливань маятника с, амплітуда коливань маятника f має зменшуватись і навпаки, що власне і відбувається в реальності.
Загально відомим прикладом дії явища резонансу є різноманітні гойдалки (мал.149). Адже всі з дитинства знають, що для розгойдування гойдалки, певні силові поштовхи (імпульси) потрібно здійснювати не коли попало, а з певною строго визначеною періодичністю. Періодичністю, яка узгоджена з власним періодом коливань системи гойдалка-людина.


Мал.149. При співпадінні частоти зовнішніх силових поштовхів з власною частотою коливань системи, відбувається розгойдування цієї системи.
Потрібно зауважити, що власну частоту коливань мають не лише прості коливальні системи як то математичний, фізичний чи пружинний маятники, а й практично всі пружні тіла, починаючи від струн музичних інструментів і закінчуючи складними будівельними спорудами, мостами, літаками, підводними човнами, танкерами, тощо. А це означає, що проектуючи та експлуатуючи подібні об’єкти, необхідно враховувати те, що вони можуть перебувати під дією певних періодичних сил, наприклад під дією періодичних поривів вітру, періодичних ударів коліс потягу на стиках рейок, періодичних ударів хвиль, тощо. При цьому, потрібно робити все можливе за для того, щоб частота зовнішніх силових впливів не співпадала з власною частотою коливальної системи. Адже при такому співпадінні, навіть відносно незначні силові впливи можуть призвести до руйнації відповідного об’єкту.
Наприклад, в 1831 році невеликий загін солдат (60 осіб) що парадним кроком («в ногу») марширував по одному з мостів Манчестера (Англія), зруйнував цей міст. Зруйнував тому, що частота тих узгоджених поштовхів які спричиняли синхронні кроки солдат, виявилась близькою до власної частоти коливань тієї коливальної системи якою є міст. Подібні руйнації мостів відбувались в 1850 році у Франції, в 1868 році в Англії, в 1906 році в Росії. І навіть відносно недавно, а саме в 1940 році, в результаті спричинених поривами вітру резонансних коливань, був зруйнований суперсучасний підвісний міст в Сполучених Штатах.
Існує два основних методи запобігання резонансу. 1) Забезпечення такого режиму роботи системи при якому частота зовнішніх силових впливів істотно відрізняється від власної частоти коливань системи. Наприклад режими роботи поршневих та турбінних двигунів обирають таким чином, щоб частотні параметри створюваних ними коливань значно відрізнялись від частотних параметрів деталей цих двигунів. Або скажімо на мостах великим групам людей забороняється марширувати що називається «в ногу». 2) Збільшення швидкості згасання коливань системи. Наприклад ті ємності в яких транспортують рідини, обладнують спеціальними лопатями (демпферами) які сприяють зменшенню розмаху (амплітуди) коливань рідини.
Явище резонансу може бути не лише шкідливим, а й корисним. Наприклад в акустиці, резонанс застосовують для підсилення звуку. В радіотехніці – для налаштування радіо- та телевізійних приймачів на потрібну станцію. В ядерній фізиці – для прискорення елементарних частинок.
Явище резонансу має важливе значення і в нашому повсякденному біологічному житті. Адже здатність людини говорити і чути безпосередньо пов’язані з цим явищем. Пояснюючи суть того зв’язку що існує між явищем резонансу та нашою здатністю говорити і чути, можна сказати наступне. Джерелом голосу людини є складна акустична система, основними елементами якої є легені, голосові зв’язки, гортань та ротова порожнина. Загальний принцип дії цієї системи полягає в наступному. Легені створюють достатньо потужний потік повітря. Цей повітряний потік, проходячи через голосові зв’язки організму, примушує їх вібрувати і створювати відповідні звукові хвилі. Проходячи через гортань і ротову порожнину, ці хвилі резонансно підсилюються та перетворюються на той звук який ми чуємо.
Якщо ж говорити про наші слухові відчуття, то вони ще в більшій мірі залежать від явища акустичного резонансу. І ця залежність полягає в наступному. Основним звуко чутливим елементом слухової системи людини є так звана слухова мембрана. Ця мембрана представляє собою сукупність величезної кількості (близько 4500) тонких пружних волокон, кожне з яких має свою довжину, а відповідно і свою власну частоту коливань. Звукові хвилі, проходячи через слухову мембрану, примушують резонансно коливатись ті її волокна, власна частота яких співпадає з частотою даної хвилі. При цьому, відповідні елементи нервової системи фіксують ці вібрації, та передають отриману інформацію в мозок людини, який і формує відповідне слухове відчуття.
Задача. Тіло масою m одночасно є частиною вертикального нитяного маятника довжиною 1м та горизонтально розташованого пружинного маятника, жорсткість кожної пружини якого 20Н/м (дивись мал.). Якою має бути маса цього тіла, щоб обидві коливальні системи здійснювали резонансні коливання?
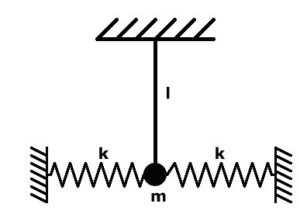
Дано: Рішення:
ℓ = 1м Оскільки обидві коливальні системи знаходяться в
k1=k2=20 резонансі, то частоти, а отже і періоди їх коливань
m = ? є однаковими, тобто ν1=ν2, або Т1=Т2.
Враховуючи, що для нитяного маятника Т1=2π√(ℓ/g), а для пружинного маятника Т2=2π√(m/k), де в умовах нашої задачі k=k1+k2=40Н/м, можна записати
2π√(ℓ/g) = 2π√(m/k), звідси ℓ/g = m/k, звідси m =ℓk/g = 1м40(Н/м)/10(м/с2) = 4кг.
Відповідь: m = 4кг.
Контрольні запитання.
1. Які коливання називаються: а) вільними; б) вимушеними?
2. Поясніть загальний устрій та принцип дії зображеного на мал.147а приладу.
3. Що в зображеному на мал.147а приладі, є коливальною системою, а що джерелом зовнішньої змінної сили?
4. Що називають резонансом?
5. Чому в зображеному на мал.148 коливання маятника f спричиняють коливання маятника с і не спричиняють коливань інших маятників?
6. Чому при збільшенні амплітуди резонансних коливань маятника с (мал.148) амплітуда коливань маятника f зменшується?
7. Яку цистерну безпечніше транспортувати, повну чи напівповну? Чому?
8. Чому військовим підрозділам забороняється проходити мостами стройовим кроком?
9. Поясніть механізм формування слухових відчуттів людини.
Вправа 51.
1. Якою має бути довжина нитяного маятника, щоб його резонансна частота становила 0,5Гц?
2. Якою має бути маса тіла пружинного маятника, щоб його резонансна частота становила 4Гц? Жорсткість пружини маятника 40Н/м.
3. Визначити резонансну частоту пружинного маятника який складається з двох однакових пружин жорсткістю по 20Н/м, при їх паралельному та послідовному з’єднанні. Маса тіла маятника 0,2кг.
4. Якою має бути довжина нитяного маятника, щоб на Місяці його резонансна частота дорівнювала 5Гц?
5. Тіло масою m одночасно є частиною вертикального нитяного маятника довжиною 0,7м та горизонтально розташованого пружинного маятника, жорсткість якого 20Н/м (дивись мал.). Якою має бути маса цього тіла, щоб обидві коливальні системи здійснювали резонансні коливання?
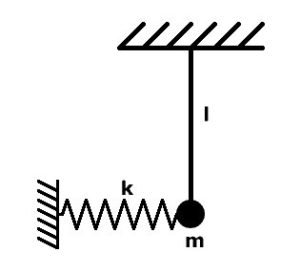
6. У вагоні потягу висить нитяний маятник довжиною 40см. З якою швидкістю має їхати потяг, щоб від тих поштовхів які створюють колеса потягу на стиках рейок, відбувались резонансні коливання маятника. Довжина рейок 25м.
7. Потяг їде зі швидкістю 54км/год. Під дією тих поштовхів які створюють колеса потягу на стиках рейок, пружинний маятник маса тіла якого 0,2кг здійснює резонансні коливання. Яка жорсткість пружини маятника? Довжина рейок 25м.
§52. Загальні відомості про хвилі.
Дрібні хвилі на поверхні води та потужні океанські цунамі, звук і руйнівні ударні хвилі вибухів, світло і сейсмічні коливання земної кори, радіохвилі і рентгенівське випромінювання – все це приклади тих чи інших хвильових процесів, а простіше кажучи, хвиль.
Наочно зобразити процес утворення та розповсюдження хвилі, надзвичайно складно. Однак фізична суть цього процесу не надто складна. І вона полягає в тому, що молекули речовини певним чином взаємопов’язані (мал.150) і тому коливання однієї молекули спричиняє аналогічні коливання сусідніх молекул, які в свою чергу спричиняють коливання інших сусідніх молекул і т.д. А оскільки передача силової інформації від однієї молекули до іншої потребує певного часу, то коливання кожної наступної молекули дещо відстає від коливань попередньої молекули. Результатом цього відставання і є та характерна синусоїдальна форма, яку ми називаємо хвилею.
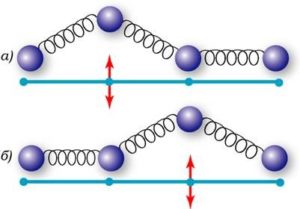
Мал.150. В системі взаємоповязаних кульок, коливання однієї з них, породжує аналогічні коливання сусідніх. Результатом цих взаємоповязаних коливань і є відповідна хвиля.
Визначальною рисою будь якої хвилі, є факт того, що процес її розповсюдження супроводжується переносом енергії збуреного матеріального середовища (речовини або поля) але не супроводжується переносом самого середовища. Наприклад, коли камінь падає на поверхню води, то в процесі удару він енергетично збурює цю поверхню та породжує відповідну поверхневу хвилю. В процесі розповсюдження, ця хвиля переносить надану воді енергію. При цьому сама вода по суті залишається на місці. Адже в процесі розповсюдження хвилі, частинки води лише здійснюють певні коливальні рухи. Або, наприклад, коли вчитель говорить, то він енергетично збурює навколишнє повітря та створює відповідну звукову хвилю. Оскільки ви чуєте вчителя, то це означає що в процесі розповсюдження, звукова хвиля переносить енергію. З іншого ж боку, цей процес не супроводжується переносом самого повітря. Адже за великим рахунком, повітря залишається на місці і лише здійснює коливальні вібрації.
Таким чином, визначаючи термін «хвиля» можна сказати наступне. Хвилею називають процес розповсюдження збурення матеріального середовища (речовини або поля), який супроводжується переносом енергії, але не супроводжується переносом самого середовища (частинки середовища або параметри поля, лише здійснюють певні гармонічні коливання).
Зазвичай хвилі поділяються на механічні та електромагнітні, а також на поздовжні, поперечні та поздовжньо-поперечні. Механічними (або пружними) називають такі хвилі, які розповсюджуються в пружному середовищі і які представляють собою взаємопов’язані коливання частинок цього середовища. До числа механічних відносяться звукові хвилі, поверхневі хвилі (хвилі на поверхні рідини), сейсмічні хвилі, ударні хвилі вибухів і взагалі будь які пружні хвилі що розповсюджуються в твердих, рідких та газоподібних середовищах.
Електромагнітними називають такі хвилі, які розповсюджуються в електромагнітному полі і які представляють собою взаємопов’язані коливання параметрів цього поля. Про те, що таке електромагнітне поле, які параметри його характеризують і яким чином коливання цих параметрів породжують відповідну електромагнітну хвилю, ми поговоримо ще не скоро. Наразі ж просто зауважимо, що радіохвилі, світло, інфрачервоне, ультрафіолетове, рентгенівське та гамма випромінювання – це різновидності електромагнітних хвиль.
В залежності від того як коливання частинок середовища (або параметрів поля), орієнтовані відносно напрямку розповсюдження хвилі, хвилі поділяються на поздовжні, поперечні та поздовжньо-поперечні. Поздовжніми називають такі хвилі, в яких коливання частинок середовища відбуваються вздовж напрямку розповсюдження хвилі. Наприклад звукові хвилі є поздовжніми. Адже в них коливання частинок повітря відбувається вздовж напрямку розповсюдження звуку.
Поперечними називають такі хвилі, в яких коливання частинок середовища (параметрів поля) відбуваються в площині що є перпендикулярною (поперечною) до напрямку розповсюдження хвилі. Прикладом строго поперечних хвиль є хвилі електромагнітні. В них коливання параметрів електричного і магнітного поля відбуваються в площині яка перпендикулярна до напрямку розповсюдження хвилі.
Поздовжньо-поперечними називають такі хвилі, в яких коливання частинок середовища мають як поздовжню так і поперечну складову. Наприклад в поверхневій хвилі, частинки поверхневого шару рідини рухаються не строго вверх-вниз, чи вперед-назад, а описують певні кола, тобто мають як поздовжню так і поперечну складову руху. В цьому не важко переконатись, уважно спостерігаючи за поведінкою дерев’яної трісочки що знаходиться в потоці поверхневих хвиль. (Звичайно за умови, що вода не тече і вітер не жене трісочку за хвилею).

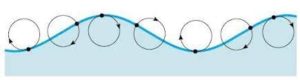
Мал.151. За характером коливань частинок середовища (параметрів поля) відносно напрямку розповсюдження хвилі, хвилі поділяються на поперечні, поздовжні та поздовжньо-поперечні.
На відміну від коливань, хвилі характеризуються подвійною періодичністю. Дійсно. З одного боку, кожна частинка хвилі здійснює певні гармонічні коливання, параметри яких можна охарактеризувати відповідним набором фізичних величин: період коливань (Т), частота коливань (ν), амплітуда коливань (хм), фаза коливань (φ). З іншого боку, взаємопов’язані частинки хвилі, мають певне просторове розташування, яке періодично повторюється. Характеризуючи цю просторову повторюваність говорять про довжину хвилі.
Довжина хвилі – це фізична величина, яка характеризує просторову періодичність (повторюваність) хвильового процесу і яка дорівнює тій відстані на яку розповсюджується хвильове збурення за той проміжок часу що дорівнює періоду коливань частинок даної хвилі.
Позначається: λ
Визначальне рівняння: λ = vT, де v – швидкість хвилі, Т – період коливань частинок хвилі.
Одиниця вимірювання: [λ] = м (метр).
По суті, довжина хвилі дорівнює відстані між двома її сусідніми гребнями, або двома сусідніми западинами, або взагалі – між будь якими двома сусідніми точками хвилі, фази коливань яких однакові.
Будь яка хвиля, це певний динамічний процес, який практично не можливо представити у вигляді відповідної статичної картинки. Зазвичай хвилю зображають у вигляді певної послідовності згущень та розріджень середовища, або у вигляді певної синусоїди, відстань між сусідніми гребнями якої дорівнює довжині відповідної хвилі.
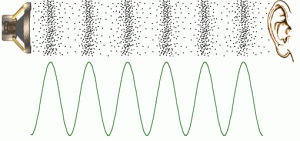
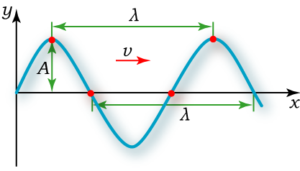
Мал.152. Звукову хвилю можна представити як у вигляді певного набору згущень та розріджень середовища, так і у вигляді відповідної синусоїди.
Хвилю можна не лише намалювати чи описати певним набором слів, а й представити у вигляді певної математичної формули. Цю формулу прийнято називати рівнянням хвилі. Рівняння хвилі – це рівняння, яке описує поведінку тих частинок середовища (параметрів поля) взаємопов’язані коливання яких утворюють дану хвилю і яке дозволяє визначати параметри будь якої з цих частинок в будь який момент часу. В загальному випадку рівняння хвилі має вигляд х = хмsin2π(νt – ℓ/λ), де х – миттєве значення змінної величини в момент часу t; хм – амплітудне значення змінної величини; ν – частота коливань частинок хвилі; λ – довжина хвилі; ℓ – відстань від джерела хвильового збурення до даної точки.
За визначенням, хвиля – це процес розповсюдження хвильового збурення матеріального середовища, який супроводжується переносом енергії але не супроводжується переносом самого середовища. А це означає, що розповсюдження хвиль нерозривно пов’язане з переносом енергії. При цьому, та енергія яку ми називаємо енергією хвилі має дві характерні особливості. По перше, в будь якій точці хвильового збурення, кількість зосередженої в ній хвильової енергії постійно змінюється. По друге, носієм хвильової енергії є не якась окремо взята частинка, а певний фрагмент хвилі. Тому, говорячи про енергію хвилі мають на увазі усереднене значення тієї енергії, носієм якої є певний фрагмент хвилі.
Задача. Катер рухається озером зі швидкістю 36км/год. Відстань між гребнями хвиль 5м, а період їх коливань 1с. З якою періодичністю битимуться хвилі об корпус катера якщо він рухається: а) назустріч хвилям; б) в напрямку руху хвиль?
Дано: Рішення:
vк=36км/год=10м/с Будемо виходити з того, що удари хвилі об катер
λ = 5м визначаються моментами зустрічі катера з гребнями
T = 1с хвилі відстань між якими λ=5м.
Δt1 = ? Оскільки як хвиля так і катер рухаються, то відстань
Δt2 = ? λ буде пройдена за час Δt=λ/vв, де vв – швидкість катера
відносно хвилі. При цьому: якщо катер рухається назустріч хвилі, то vв=vк+vхв, а якщо катер рухається в напрямку руху хвилі, то vв=vк–vхв. Швидкість хвилі визначаємо із визначального рівняння довжини хвилі: λ=vхвT, звідси vхв =λ/T=5м/1c = 5м/с.
Таким чином: Δt1 = λ/(vк+vхв) = 5м/15м/с = (1/3)с;
. Δt2 = λ/(vк–vхв) = 5м/5м/с = 1с.
Відповідь: Δt1 = (1/3)с; Δt2 =1с.
Контрольні запитання.
1. Яка визначальна риса всіх хвиль?
2. Опишіть процес поширення хвиль.
3. Чи можна гармонічні коливання однієї частинки речовини вважати хвилею?
4. Які хвилі називаються механічними. Наведіть приклади таких хвиль.
5. Поздовжніми чи поперечними є хвилі на поверхні води? Чому?
6. Чому ми стверджуємо, що хвиля має подвійну періодичність?
7. Які величини характеризують періодичність коливань а) окремих частинок хвилі; б) всієї хвилі?
8. Які особливості тієї енергії яку називають енергією хвилі?
Вправа 52.
1. Визначте довжину звукової хвилі, якщо швидкість її розповсюдження 340м/с, а частота коливань 200Гц.
2. Рибалка помітив, що за 10с поплавок зробив на хвилях 5 коливань, а відстань між сусідніми гребнями хвиль 4м. Яка швидкість поширення хвиль?
3. В океані довжина хвилі сягає 270м, а період її коливань 13,5с. Яка швидкість поширення такої хвилі?
4. Відстань між найближчими гребнями хвиль у морі 10м. Яка частота ударів хвиль об корпус човна, якщо швидкість хвиль 3м/с?
5. Спостерігач, що знаходиться на відстані 2,1км від джерела звуку, зафіксував цей звук при його розповсюджені у воді на 4,8с раніше аніж при його розповсюджені у повітрі. Визначити швидкість звуку у воді, якщо у повітрі вона дорівнює 340м/с.
6. Довжина звукової хвилі у повітрі 17см (при швидкості 340м/с). Визначте швидкість поширення звуку в середовищі, де при тій же частоті коливань, довжина хвилі дорівнює 102см.
7. Джерело хвиль створює коливання, рівняння яких х=3sin20πt. Запишіть рівняння хвилі для точки яка віддалена від джерела на 10м, якщо довжина хвилі 4м. Визначте швидкість розповсюдження та амплітуду коливань цих хвиль.
§53. Звукові хвилі.
Звуковими хвилями (звуком, чутними звуками) називають такі пружні, об’ємні хвилі, які розповсюджуються в суцільному пружному середовищі та викликають у людини слухові відчуття. Прийнято вважати, що звуковими є такі механічні коливання середовища, частотні параметри яких знаходяться в межах від 16Гц до 20кГц.
Джерелом звукових хвиль може бути будь яке тіло що знаходиться в пружному середовищі і коливається з відповідною частотою. Наприклад, в струнних інструментах джерелом звуку є коливання струн; в духових інструментах – коливання певного об’єму повітря; в гучномовцях – коливання пружної мембрани; в організмі людини – коливання елементів надскладної системи, частинами якої є легені, голосові зв’язки, гортань та ротова порожнина; а джерелом тих звуків які створюють комарі, мухи та джмелі є коливальні рухи їх крил.
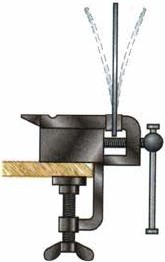
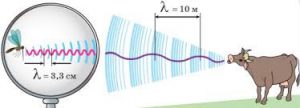
Мал.153. Практично всі вібруючі тіла, створюють відповідні звукові хвилі.
Звукові хвилі можуть поширюватись в будь якому пружному середовищі. При цьому, в рідинах і газах звукові хвилі можуть бути лише поздовжніми, а в твердих тілах – як поздовжніми так і поперечними. Швидкість поширення звукових хвиль (швидкість звуку) практично не залежить від частотних та енергетичних параметрів цих хвиль. Ця швидкість визначальним чином залежить від властивостей того середовища в якому розповсюджуються хвилі, зокрема від його модуля пружності, густини та температури. Втім, говорячи про швидкість розповсюдження звукових хвиль, потрібно мати на увазі, що мова йде про надзвичайно складний динамічний процес, який лише приблизно можна описати певними фізичними моделями та певними математичними формулами. Скажімо, в твердих тілах, звукова хвиля має як поздовжню так і поперечну складову. При цьому поздовжня складова звукової хвилі розповсюджується майже вдвічі швидше за її поперечну складову. Зазвичай, говорячи про швидкість звуку в твердому середовищі, мають на увазі швидкість поширення поздовжніх хвиль. Дані про швидкість розповсюдження звуку в деяких середовищах, представлені в наступній таблиці.
Швидкість звуку в деяких середовищах (при температурі 20ºС).
| Речовина | v (м/с) | Речовина | v (м/с) |
| Алюміній | 6260 | Скло: флінт | 4450 |
| Мідь | 4700 | Скло: крон | 5220 |
| Свинець | 2160 | Лід ( t = –4ºC) | 3980 |
| Сталь | 5500 | Вода | 1480 |
| Чавун | 3850 | Повітря | 343 |
Потрібно зауважити, що при переході звукових хвиль (і хвиль загалом) з одного середовища в інше середовище, частота (ν) та період (Т) коливань цих хвиль залишаються незмінними. Натомість довжина хвилі (λ=vТ=v/ν) змінюється: при збільшені швидкості, довжина хвилі відповідно збільшується, а при зменшені швидкості – зменшується. Наприклад, якщо звукова хвиля з частотою 500Гц у повітрі має довжину λ=v/ν=340/500=0,68м, то у воді ця ж хвиля матиме довжину λ=v/ν=1480/500=2,96м.
Як і будь яка біжуча хвиля, звук переносить енергію, параметри якої можна оцінити різними величинами, зокрема:
– енергія звуку: ∆Е (Дж);
– густина енергії звуку: w = ∆E/∆V (Дж/м3);
– потужність звуку: Р = ∆Е/∆t (Вт).
Однак, зважаючи на факт того, що людина сприймає лише ту частину звукової енергії яка за одиницю часу потрапляє на поверхню певної площі (потрапляє у вухо слухача), основною енергетичною характеристикою звуку є його інтенсивність або сила звуку.
Інтенсивність звуку (сила звуку) – це фізична величина, яка характеризує кількість тієї звукової енергії що проходить за одиницю часу через одиницю площі поверхні і яка дорівнює цій кількості.
Позначається: J
Визначальне рівняння: J = ∆E/S∆t
Одиниця вимірювання: [J] = Дж/м2с = Вт/м2.
По суті інтенсивність звуку (сила звуку), визначальним чином залежить від амплітуди звукових коливань: чим більша амплітуда коливань, тим більша інтенсивність звуку і навпаки.
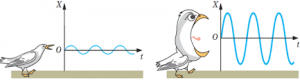
Мал.154. Інтенсивність звуку (сила звуку) пропорційна амплітуді звукових коливань.
Органи слуху людини мають надзвичайно високу чутливість. Вони здатні відчувати звукові коливання повітря інтенсивність яких становить всього 10-12Вт/м2. Однак, потрібно мати на увазі, що величина цієї чутливості сильно залежить від частотних параметрів звуку. Наприклад, чутливість нашого слуху до звуків середньої частоти (ν~103Гц) в десятки тисяч разів більша за його чутливість до звуків низької (ν < 100Гц) і високої (ν > 10кГц) частоти.
Ту мінімальну інтенсивність звуку, що забезпечує певний мінімальний рівень слухових відчуттів людини, називають порогом чутності. А ту його максимальну інтенсивність при якій звукові хвилі починають викликати больові відчуття, називають порогом больових відчуттів.
Оскільки звуки однієї і тієї ж енергетичної інтенсивності але різної частоти, викликають у людини суттєво різні відчуття (сприймаються як звуки суттєво різної інтенсивності), то на практиці енергетичні параметри звуку часто оцінюють не інтенсивністю звуку, а його гучністю. Гучність звуку – це фізична величина яка характеризує енергетичну інтенсивність звуку, виміряну за суб’єктивними слуховими відчуттями людини з усереднено нормальним слухом. Гучність звуку складним чином залежить від інтенсивності звуку (амплітуди звукових коливань), його частотних параметрів та багатьох інших обставин. Цю залежність практично не можливо представити у вигляді простої математичної формули. Адже вона відображає суб’єктивні особливості тієї надскладної системи яка називається організмом людини.
Гучність звуку визначається експериментально і регламентується певними медичними нормами. Зазвичай гучність звуку вимірюють в позасистемних одиницях гучності, які називаються децибелами (дБ). При цьому порогу чутності відповідає гучність в 0дБ, а порогу больових відчуттів відповідає гучність 130дБ (визначених для ν=103Гц). Певні уявлення про джерела звуку та про рівні тієї гучності які вони створюють, можна почерпнути з мал.155.
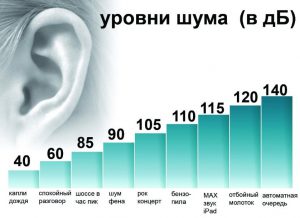
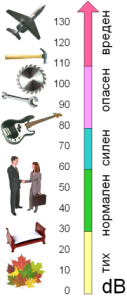
Мал.155. Джерела звуку та їм відповідні гучності.
Ще однією суб’єктивною характеристикою звуку, є його висота. Висота звуку – це фізична величина, яка характеризує частотні параметри звуку визначені за суб’єктивними слуховими відчуттями людини з усереднено нормальним слухом. Висота звуку практично напряму залежить від частоти його коливань: чим більша частота звукових коливань, тим більша висота звуку.
Ви можете запитати: «якщо висота звуку пропорційна його частоті, то навіщо взагалі вводити цю величину, та ще й визначати її не за показаннями об’єктивного вимірювального приладу, а за суб’єктивними відчуттями людини?». Відповідаючи на це слушне запитання, можна сказати наступне. Справа в тому, що переважна більшість реальних звуків, це складна сукупність великої кількості коливань, кожне з яких має свої частотні параметри. А це означає, що в реальній звуковій хвилі, міститься цілий спектр звукових частот, усереднену величину яких і характеризує висота звуку. Скажімо, на мал.156 зображено дві синусоїди і та крива, що є результатом їх накладання. Реальний же звук може бути, і як правило є, результатом накладання десятків, сотень, а іноді й тисяч подібних синусоїд.
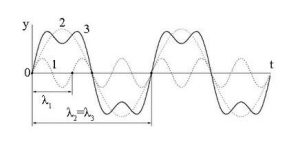

Мал.156. Реальний звук є результатом накладання багатьох гармонічних коливань.
До числа найпростіших звуків відносяться так звані тональні або музичні звуки. Коли ми говоримо про простоту музичних звуків, то маємо на увазі те, що їх частотні параметри знаходяться в певних простих співвідношеннях. Наприклад, натягнута струна довжиною ℓ може створювати звукові хвилі довжини яких визначаються за формулою λ=ℓ/n, де n – ціле число (n=1; 2; 3; 4; …). Це означає, що ті звукові хвилі які створює певна струна можуть мати лише певний набір частот: ν=v/λ=vn/ℓ. Кожну з цих частот називають тоном звуку. При цьому той найнижчий тон (ν0=v/ℓ) який здатна створити дана струна, називають її основним тоном, а решту тонів (2ν0; 3ν0; 4ν0; …) називають обертонами.
Музикальні звуки відрізняються не лише своїм основним тоном та обертонами, а й певним звуковим забарвленням, яке називається тембром звуку. Тембр звуку визначається кількістю та частотними параметрами обертонів, їх амплітудами та розподілом цих амплітуд.
Голос людини складніший за будь який музикальний звук. Складніший в тому сенсі, що ті прості тони які є складовими голосу, не зв’язані між собою певними простими співвідношеннями. Крім цього, тембральне забарвлення голосу набагато складніше за тембр музикального звуку. За частотним діапазоном, чоловічі та жіночі голоси прийнято поділяти наступним чином.

Мал.157. Класифікація чоловічих та жіночих голосів за їх частотними діапазонами.
До числа математично найскладніших звуків відносяться шуми. Шуми представляють собою складні суміші величезної кількості звукових коливань, частотні та амплітудні параметри яких, практично не пов’язані між собою.
Важливість та значимість звукових хвиль є очевидною. Достатньо сказати, що звукові хвилі, це основний засіб спілкування між людьми, одне з основних джерел інформації про навколишній світ та невичерпне джерело естетичних задоволень будь то від музики, співу, щебету пташок чи просто шуму дощу.
Звуки які ми чуємо (чутні звуки), це лише частина того різноманіття пружних, об’ємних хвиль що оточують нас. Це різноманіття можна розділити на три групи: інфразвуки, чутні звуки та ультразвуки.
Інфразвуком (інфразвуковими хвилями), називають ті пружні об’ємні хвилі, які розповсюджуються в суцільному пружному середовищі і частота коливань яких менша за нижню межу чутних хвиль, тобто менша за 16Гц (на практиці менша за 20Гц). Джерелами інфразвуків є землетруси і виверження вулканів, грозові розряди і вітрові потоки, коливання дерев та поверхневі хвилі річок, морів і океанів. Власне будь які механічні коливання які відбуваються з відносно малими частотами (ν<16Гц) створюють відповідні інфразвукові хвилі.
Інфразвукові хвилі не викликають у людини слухових відчуттів. Однак певну дію на людський організм вони все ж можуть мати. Ця дія обумовлена тим, що складові частини нашого організму як то печінка, серце, нирки, тощо, представляють собою певні коливальні системи, які характеризуються певною власною частотою коливань. І як правило, ця частота знаходиться в межах від 6 до 9 герц. А це означає, що в потоці відповідних інфразвукових хвиль, в організмі людини можуть відбуватись певні резонансні явища, які можуть викликати певні відчуття та негативні емоції. Втім, вагомих доказів того що інфразвукові хвилі є шкідливими для організму людини на сьогоднішній день не існує.
Ультразвуком (ультразвуковими хвилями) називають ті пружні об’ємні хвилі, які розповсюджуються в суцільному пружному середовищі і частота коливань яких більша за верхню межу частоти чутних хвиль, тобто більша за 20кГц (В сучасній науці ультразвуки надвисокої частоти (ν>109Гц) називають гіперзвуками).
Ультразвуки мають надзвичайно широке практичне застосування. Наприклад, за допомогою імпульсних ультразвукових ехолотів, визначають глибини річок, морів та океанів, визначають рельєф їх дна, наявність і параметри підводних та надводних човнів, айсбергів, косяків риб, тощо. В промисловості, за допомогою ультразвукових дефектоскопів, здійснюють неруйнівний контроль за якістю деталей машин і механізмів. На транспорті, за допомогою ультразвукових радарів, здійснюють контроль за швидкістю руху автомобілів. В медицині, за допомогою ультразвукових діагностичних апаратів, досліджують стан внутрішні органів людини. Якщо ж мова йде про деяких представників тваринного світу, наприклад таких як кажани, то для них роль ультразвуку не менша аніж роль світла для людини. Адже саме за допомогою ультразвуків ці тварини спілкуються між собою та орієнтуються в просторі.
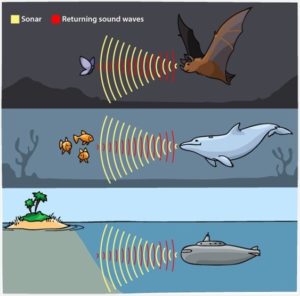
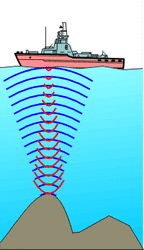
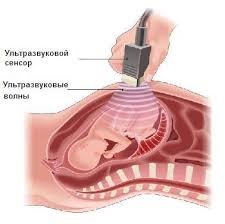
Мал.158. Приклади деяких застосувань ультразвукових хвиль.
Основним джерелом того ультразвуку який використовується в науці і техніці є електромеханічні випромінювачі, різноманіття яких можна розділити на три групи: електродинамічні, п’єзоелектричні та магнітострикційні. Загальний принцип дії цих приладів однаковий і полягає в тому, що в них енергія високочастотного електричного струму, перетворюється у відповідні механічні коливання робочої поверхні приладу. Однак механізм такого перетворення в різних приладах є суттєво різним. Втім, про різноманіття електричних, магнітних та електромагнітних явищ, в тому числі і тих які використовуються для створення ультразвукових хвиль, ми поговоримо в тому розділі фізики який називається електродинамікою.
Контрольні запитання.
1. Що називають звуком (чутними звуками)?
2. Від чого залежить швидкість поширення звуку?
3. Що називають інтенсивністю звуку (силою звуку)? Чим інтенсивність звуку відрізняється від потужності звуку?
4. Що називають: порогом чутності? порогом больових відчуттів?
5. Що називають гучністю звуку? Чим гучність звуку відрізняється від інтенсивності звуку (сили звуку)?
6. Що називають висотою звуку? Чим висота звуку відрізняється від частоти звуку?
7. На які групи поділяються людські голоси за їх частотними параметрами?
8. Поясніть принцип дії ультразвукового ехолота (мал.100б).
9. Що спільного між кажаном та ультразвуковим радаром?
Вправа 53.
1. Спостерігач що знаходиться на відстані 4км від гармати почув звук від пострілу через 12с після того як побачив спалах від нього. Визначити швидкість звуку в повітрі.
2. Людина сприймає звуки з частотного інтервалу від 20Гц до 20кГц. Визначити інтервал довжин відповідних хвиль. Швидкість звуку в повітрі 340м/с.
3. Визначте довжину звукової хвилі частотою 800Гц у повітрі; воді; сталі.
4. Залежність швидкості звуку в повітрі від температури має вигляд v=20√(t+273). Визначте швидкість звуку при –20ºС та 20ºС. На скільки збільшується швидкість звуку при даному перепаді температур? Відповідь дайте в м/с і км/год.
5. З першого корабля на другий одночасно посилають два звукових сигнали, один повітрям, другий – водою. При цьому на другому кораблі повітряний сигнал отримали через 2с після сигналу «водного». Визначте відстань між кораблями.
6. У людини слухові відчуття зберігаються приблизно 0,1с. На якій відстані від перешкоди має знаходитись людина, щоб роздільно чути основний і відбитий перешкодою звуки?
7. В океані на невеличкій глибині зроблено вибух. Гідроакустики корабля, що знаходиться на відстані 2,25км від місця вибуху, зафіксували два звукових сигнали, другий через 1с після першого. Яка глибина океану в цьому районі?
§54. Ефект Доплера.
Можливо ви звертали увагу на факт того, що частотні параметри тих звукових сигналів які надходять від рухомого транспорту, суттєво залежать від того наближається цей транспорт чи навпаки віддаляється. Скажімо частота тих звукових імпульсів які ви чуєте при наближені потягу та при його віддаленні, є суттєво різною. І це при тому, що швидкість потягу є незмінною і тому, частотні параметри тих звукових імпульсів які створюють колеса потягу натикаючись на стики рейок, є однаковими. Даний експериментальний факт є суттю так званого ефекту Доплера. Ефекту названому на честь австрійського фізика Крістіана Доплера (1803-1853), який в 1842 році дослідив та пояснив це явище.
Ефект Доплера, це явище, суть якого полягає в тому, що частотні параметри звукових, електромагнітних та інших хвиль, певним чином залежать від швидкості та напрямку руху як джерела цих хвиль, так і того спостерігача який їх фіксує.
Мал.159. Частотні параметри тих звукових хвиль які фіксує спостерігач, певним чином залежать від швидкості та напрямку руху як джерела хвиль, так і самого спостерігача.
Ефект Доплера пояснюється тим, що швидкість звуку по відношенню до того середовища в якому цей звук розповсюджується є абсолютною, тобто такою яка не залежить ні від швидкості руху джерела звукових хвиль, ні від швидкості руху спостерігача. Ясно, що в такій ситуації той спостерігач який рухається назустріч звуковій хвилі, за одиницю часу зустрінеться з більшою кількістю звукових коливань. А той спостерігач який «тікає» від звукової хвилі, за той же проміжок часу сприйме меншу кількість аналогічних коливань. А це означає, що перший спостерігач сприйме відповідну звукову хвилю як таку, що має більшу частоту (меншу довжину хвилі), а другий – як таку що має меншу частоту (більшу довжину хвилі).
Можна довести, що в незалежності від того хто наближається, спостерігач до нерухомого джерела хвиль чи навпаки, спостерігач сприйме ці хвилі як такі, що мають меншу довжину (більшу частоту). В незалежності від того хто віддаляється, спостерігач від нерухомого джерела хвиль чи навпаки, спостерігач сприйме ці хвилі як такі, що мають більшу довжину (меншу частоту). При цьому будуть виконуватись співвідношення:
1) при наближенні: λн=λ0(1–v/vзв); νн=ν0/(1–v/vзв);
2) при віддалені: λв=λ0/(1–v/vзв); νв=ν0(1–v/vзв),
де v – швидкість руху спостерігача відносно хвиль (чи навпаки),
λ0, ν0 – параметри тих хвиль які створює нерухоме джерело звуку,
λ, ν – параметри тих же хвиль по відношенню до рухомого спостерігача.
Мал.160. Частотні параметри тих звукових хвиль які фіксує спостерігач, певним чином залежать від швидкості та напрямку руху як джерела хвиль, так і самого спостерігача.
Задача 1. Джерело звуку генерує хвилі з частотою 500Гц. З якою частотою будуть сприймати цей звук два спостерігачі, один з яких з швидкістю v наближається до джерела звуку, а інший – з такою ж швидкістю, віддаляється від нього. Розглянути ситуації: а) v1=30м/с; б) v2=vзв/2; в) v3=vзв.
Дано: vзв = 340м/с; ν0 = 500Гц; v1=30м/с; v2=vзв/2; v3=vзв.
Визначити: νн=? νв=?
Рішення:
а) νн = ν0/(1–v1/vзв) = 500/(1 – 30/340) = 500/0,912 = 548Гц;
νв = ν0(1–v1/vзв) = 500(1 – 30/340) = 500·0,912 = 456Гц.
б) νн = ν0/(1–v2/vзв) = ν0/(1–vзв/2vзв) = ν0/0,5 = 2ν0 = 1000Гц;
νв = ν0(1–v2/vзв) = ν0(1–vзв/2vзв) = ν0·0,5 = 250Гц.
в) νн = ν0/(1–v3/vзв) = ν0/(1–vзв/vзв) = ν0/0 = ∞Гц;
νв = ν0(1–v3/vзв) = ν0(1–vзв/vзв) = ν0·0 = 0Гц.
Таким чином, у відповідності з ефектом Доплера, в залежності від того в якому напрямку і з якою швидкістю спостерігач рухається відносно джерела хвиль (чи джерело хвиль відносно спостерігача, чи спостерігач і джерело хвиль відносно один одного), частотні параметри зафіксованих спостерігачем хвиль можуть бути як більшими так і меншими за базову величину цих параметрів. При цьому, якщо швидкість руху спостерігача дорівнюватиме швидкості поширення хвиль (v=vзв), то в залежності від напрямку руху спостерігача (джерела), частота сприйнятих ним хвиль може бути як безкінечно великою частотою (ν=∞Гц), так і нулевою (ν=0Гц).
Дійсно, якщо джерело хвиль з швидкістю звуку (v=vзв) рухається в напрямку розповсюдження цієї хвилі, то в цьому напрямку хвиля «сплющується» до розмірів хвильового фронту, тобто стає хвилею безкінечно великої частоти і відповідно нулевої довжини: νн=ν0/(1–vзв/vзв)=ν0/0=∞Гц; λн=λ0(1–vзв/vзв)=λ0∙0=0(м).
Якщо ж джерело хвиль з швидкістю звуку (v=vзв) рухається в напрямку протилежному до напрямку розповсюдження звуку («тікає» від звуку), то в цьому напрямку звукова хвиля безкінечно розтягується і перетворюється на хвилю з безкінечно великою довжиною, а отже нулевою частотою коливань:
νв=ν0(1–vзв/vзв)=ν0∙0=0(Гц); λв=λ0/(1–vзв/vзв)=λ0/0=∞(м);
Вище сказане по суті означає, що коли джерело звукових хвиль з звуковою чи надзвуковою швидкістю (v≥vзв) наближається до спостерігача (або спостерігач рухається назустріч звуковому сигналу), то той звуковий сигнал який генерується джерелом, «сплющується» в певне ущільнення середовища яке називається ударною хвилею. Ця хвиля розповсюджується з швидкістю звуку і сприймається спостерігачем як різкий звуковий удар (грім, тріск, тощо). Дію ударної звукової хвилі ви могли чути в тих випадках, коли над вами пролітав надзвуковий літак.
а) б)
б)
Мал.161. Рухаючись з надзвуковою швидкістю, тіло створює певну ударну хвилю.
У своєму об’ємному вигляді, те що називають ударною хвилею, утворює конусоподібну поверхню яку називають конусом Маха (названо на честь австрійського фізика Ернста Маха (1838 – 1916)). Конус Маха характеризують кутом Маха (α), величина якого залежить від швидкості руху (v) тіла: sinα=1/M, де M=v/vзв – число Маха. Наприклад, якщо v=vзв, то M=v/vзв=1; sinα=1/M=1; α=90°. Якщо v=1,4vзв, то M=v/vзв=1,4; sinα=1/M=1/1,4=0,71; α=45°. Якщо v=2vзв, то M=v/vзв=2; sinα=1/M=1/2=0,5; α=30°.
Вище описані прояви та закономірності ефекту Доплера притаманні не лише звуковим, а й всім іншим хвилям, зокрема поверхневим та електромагнітним (радіохвилі, інфрачервоне випромінювання, видиме світло, тощо).
Ефект Доплера широко застосовується в сучасних методах визначення швидкості та напрямку руху найрізноманітніших об’єктів, починаючи від автомобілів та літаків і закінчуючи елементарними частинками та галактиками. Прикладом такого застосування є радіолокаційні станції (РЛС) або радари. Існує велике різноманіття сучасних радіолокаційних станцій (радарів), які розрізняються за призначенням, за сферою застосування, за мобільністю, за параметрами хвиль, за методом та типом дії, тощо. Однак принцип дії всіх радарних систем є практично однаковим. І цей принцип дії полягає в тому, що радар випромінює певні електромагнітні чи інфразвукові хвилі, які відбиваючись від об’єкту спостережень, повертаються в радарну систему, аналізуються та перетворюються на відповідну корисну інформацію. Ілюструючи принцип дії радара та його зв’язок з ефектом Доплера, розглянемо конкретну ситуацію.
Задача 2. Радар випромінює ультразвукові хвилі з частотою 30кГц. При цьому, частота відбитих від автомобіля хвиль становить 32кГц. Яка швидкість автомобіля якщо швидкість ультразвуку 340м/с?
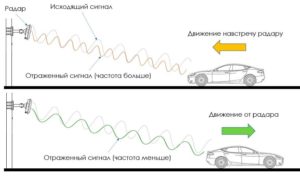
Дано: Рішення:
ν0 = 30кГц=30·103Гц Виконуємо малюнок який відображає
νн = 32кГц=32·103Гц фізичний зміст задачі.
vзв = 340м/с Оскільки частота відбитих більша за частоту
v = ? базових хвиль, то це означає, що автомобіль
рухається назустріч джерелу хвиль (радару). А у відповідності з ефектом Доплера, для такої ситуації νн=ν0/(1–v/vзв), звідси 1–v/vзв = ν0/ν, звідси v/vзв = 1 – ν0/ν, звідси v=vзв(1 – ν0/ν).
Розрахунки: v=vзв(1 – ν0/ν) = 340(1 – 30/32) = 21,25м/с = 76,5км/год.
Відповідь: v = 21,25м/с = 76,5км/год.
На завершення додамо, що у нас ще буде нагода поговорити, про ту важливу роль яку відіграв і продовжує відігравати ефект Доплера в пізнанні навколишнього світу.
Контрольні запитання.
1. Чому при наближені потягу стукіт його коліс частіший аніж при віддалені?
2. Як змінюється частота звукових хвиль (по відношенню до спостерігача) якщо: а) джерело хвиль рухається від спостерігача; б) джерело хвиль рухається назустріч спостерігачу.
3. Чи залежить швидкість поширення звуку відносно середовища від швидкості та напрямку руху: а) джерела звуку; б) спостерігача?
4. Джерело звуку з швидкістю v>vзв рухається в напрямку спостерігача. Як сприйме його звуковий сигнал спостерігач?
5. Джерело звуку з швидкістю v>vзв віддаляється від спостерігача. Як сприйме його звуковий сигнал спостерігач?
6. З якою швидкістю поширюється та ударна хвиля яку створює тіло, що рухається з надзвуковою швидкістю?
7. Що називають числом Маха?
8. Поясніть загальний устрій та принцип дії радара.
Вправа54.
1. Джерело звуку генерує хвилі з частотою коливань 500Гц. Яку частоту та довжину хвилі зафіксує спостерігач якщо: а) джерело з швидкістю 72км/год рухається назустріч спостерігачу; б) джерело з швидкістю 72км/год віддаляється від нерухомого спостерігача; в) джерело та спостерігач рухаються назустріч один одному з швидкістю 72км/год кожний?
2. Два автомобілі їдуть назустріч один одному з швидкостями відповідно 20м/с і 30м/с. Перший з них подає сигнал з частотою 600Гц. Яку частоту матиме цей сигнал за відчуттями водія другого автомобіля: а) до зустрічі автомобілів; б) після зустрічі?
3. Радар випромінює ультразвукові хвилі з частотою 30кГц. При цьому, частота відбитих від автомобіля хвиль становить 27кГц. Яка швидкість автомобіля якщо швидкість ультразвуку 340м/с?
4. Сирена автомобіля що рухається з швидкістю 108км/год генерує звук з частотою 1000Гц. На скільки зміниться ця частота при переході від руху в напрямку спостерігача до руху від спостерігача?
5. Джерело звуку, що рухається з швидкістю 30м/с дає сигнал тривалістю 4с. Якою буде ця тривалість якщо джерело: а) наближається до спостерігача; б) віддаляється від спостерігача?
6. Проїжджаючи повз залізничну платформу потяг посилає звуковий сигнал. При цьому, спостерігач при наближені потягу чує звук з частотою 900Гц, а при віддалені потягу 700Гц. Яка швидкість потягу, та частота звуку його джерела.
7. Літак рухається з швидкістю 2000км/год. Визначити число Маха та кут Маха для цієї швидкості.