СТАТИКА

Тема 1.2. Статика.
§14. Статика. Основні поняття, величини та закони статики.
§15. Про додавання векторних величин, або про те, чи завжди 2 + 2 = 4?
§16. Сила тяжіння. Реакція опори. Загальні відомості щодо розв’язування задач статики.
§17. Сила тертя.
§18. Розв’язування задач. Тема: Силовий метод розв’язування задач статики.
§19. Сила інерції.
§20. Розв’язування задач. Тема: Силовий метод розв’язування задач динаміки.
§21. Про вагу та невагомість.
§22. Про силу Архімеда, або про те, що важче кілограм заліза чи кілограм пір’я?
§23. Закон всесвітнього тяжіння. Про силу гравітаційну та силу тяжіння.
§24. Розв’язування задач. Тема: Закон всесвітнього тяжіння.
§25. Механічні деформації. Сила пружності. Механічна напруга. Закон Гука.
§26. Пара сил. Момент сили. Важелі.
§27. Механічні блоки та їх системи.
§28. Розв’язування задач. Тема: Рівновага тіла під дією довільної системи сил.
§29. Центр тяжіння та центр мас тіла. Розв’язування задач.
§30. Про види механічної рівноваги тіла та про ступінь механічної стійкості тіл.
Тема 1.2 Статика.
§14. Статика. Основні поняття, величини та закони статики.
Статика (від грецького statike – рівновага) – це розділ механіки в якому вивчають параметри, закономірності та причини стану механічної рівноваги тіла. Механічною рівновагою тіла (матеріальної точки) називають такий механічний стан тіла, при якому воно знаходиться в стані механічного спокою (v = 0), або в стані прямолінійного рівномірного руху (v = const).
Зазвичай в статиці розглядають ті ситуації коли тіло знаходиться в стані механічного спокою. Однак ви маєте знати, що з фізичної точки зору, між станом механічного спокою тіла (v = 0) та станом його прямолінійного рівномірного руху (v = const) нема суттєвої різниці. А якщо вам потрібні докази цьому на перший погляд парадоксальному факту, то запитайте себе чи відчуваєте факт того, що Земля з швидкістю 30км/с обертається навколо Сонця, а з швидкістю 250км/с – навколо центру нашої Галактики?
Втім, про те, що означає твердження «з фізичної точки зору, між станом механічного спокою тіла (v = 0) та станом його прямолінійного рівномірного руху (v = const) нема суттєвої різниці», ми поговоримо дещо пізніше, а точніше – коли буде з’ясовано фізичну суть того базового закону який називається принципом відносності. Наразі ж, будемо вважати, що ті силові закономірності які справедливі для стану механічного спокою тіла, є справедливими і в тому випадку, коли це тіло перебуватиме в стані прямолінійного рівномірного руху.
Основною фізичною величиною статики є сила. Сила – це фізична величина, яка характеризує силову дію одного тіла (фізичного об’єкту) на інше тіло (є мірою взаємодії фізичних об’єктів) і яка дорівнює добутку маси тіла на величину того прискорення, яке воно отримує під дією даної сили.
Позначається: F
Визначальне рівняння: F = ma
Одиниця вимірювання: [F] = кг∙м/с2 = H, ньютон.
Ньютон – це одиниця вимірювання сили, що дорівнює такій силі, яка тілу масою 1кг надає прискорення 1м/с2: 1Н = 1кг∙1м/с2. Іншими словами, якщо тіло масою 1кг рухається з прискоренням 1м/с2, то це означає, що на нього діє сила 1Н. Звичайно, мається на увазі, що тіло масою 1кг знаходиться під дією лише однієї зовнішньої сили. Адже якщо наприклад, дерев’яний брусок масою 1кг прибити, прикрутити чи приклеїти до підлоги, а потім прикласти до нього силу 1Н, то брусок не отримає очікуваного прискорення. Не отримає тому, що в місці з’єднання бруска з підлогою неминуче виникне ще одна сила, яка протидіятиме переміщенню бруска.
Відразу ж зауважимо, що величину сили в один ньютон не можливо оцінити візуально, як це наприклад можна зробити з одиницею довжини метром. Ньютон, це одиниця вимірювання сили, тобто тієї величини яка характеризує силову дію одного фізичного об’єкту на інший. Тому величину ньютона можна оцінити лише за його силовою дією. Скажімо, загально відомо, що всі тіла притягуються до землі з силою, яку прийнято називати силою тяжіння. Відомо й те, що під дією сили тяжіння всі тіла, в тому числі і ті маса яких 1кг, падають з прискоренням 9,8м/с2. А це означає, що на тіло масою 1кг діє сила тяжіння 9,8Н: F =1кг∙9,8м/с2 = 9,8Н.
Таким чином, якщо ви візьмете в руку тіло масою 1кг, то відчуєте силу 9,8Н. Запитується: тіло якої маси потрібно взяти в руку, щоб вона відчула силу в один ньютон? Правильно, маса цього тіла має становити 102г :
m = F/a = 1Н/9,8(м/с2) = 0,102кг =102г.

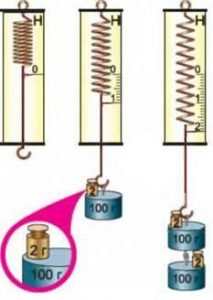
Мал.33. Один Ньютон дорівнює тій силі, з якою тіло масою 102 грами притягується до Землі.
От тільки не потрібно стверджувати, що в одному ньютоні міститься 102 грами. Бо це все рівно ніби наполягати на тому, що в одному метрі міститься сто секунд, або, що кілограм більший за секунду. Адже кілограм не більший і не менший за секунду. Бо кілограм – це кілограм, метр – це метр, секунда – це секунда, а ньютон – це ньютон. І порівнювати ці абсолютно різні одиниці не можна. Метр можна порівнювати з міліметром, кілометром чи, скажімо, з дюймом, тобто з іншими одиницями довжини. Але метр не можна порівнювати з секундою, кілограмом, ньютоном чи наприклад, з метром квадратним. Тому, коли ми говоримо, що силі в один ньютон відповідає вага тіла масою 102 грами, то маємо на увазі лише те, що на Землі силу в один ньютон можна відчути тримаючи в руці тіло масою 102 грами.
Аналізуючи визначальне рівняння сили F = m∙a, потрібно зауважити, що це рівняння не треба сприймати як таке, що вказує на факт залежності сили від маси тіла та його прискорення. Адже в загальному випадку, діюча на тіло сила не залежить від маси цього тіла та того прискорення яке воно може отримати. Скажімо, сила ваших м’язів не залежить від маси того тіла що лежить на столі та того прискорення яке може отримати це тіло під дією вашої сили. Ваша м’язова сила залежить від незліченної кількості обставин пов’язаних з вами особисто, починаючи від вашого віку, маси вашого тіла, вашої тренованості і закінчуючи вашим настроєм та вологістю того повітря яким ви дихаєте. І представити цю залежність у вигляді певної формули практично не можливо.
Ось тут то на допомогу і приходить визначальне рівняння сили. Адже формула F = m∙a по суті вказує на універсальний спосіб визначення (вимірювання) величини та напрямку дії будь якої сили. І цей спосіб полягає в тому, що для визначення величини тієї чи іншої сили, наприклад м’язової сили вашої руки, цю силу потрібно прикласти до тіла відомої маси (m) і подивитесь на те прискорення (a) яке отримає це тіло під дією даної сили. При цьому, величина та напрям сили визначаться за формулою F = m∙a. Наприклад якщо під дією певної сили, тіло масою 0,5кг отримає прискоренням 15м/с2, то це означатиме, що величина діючої на тіло сили F = ma = 0,5кг·15м/с2 = 7,5Н.
Втім на практиці, величину сили визначають не за ознакою того, якого прискорення надає ця сила тілу визначеної маси, а за тим, як вона деформує пружне тіло, наприклад пружину. Прилади які працюють за даним принципом називаються динамометрами (від грец. dynamis – сила та metreo – вимірювати). Динамометр, це прилад який дозволяє вимірювати величину діючої на нього сили. Основним елементом динамометра (мал.34) є певне пружне тіло (пружина), яке під дією зовнішньої сили певним чином деформується. Власне за величиною цієї деформації і визначають величину деформуючої сили.
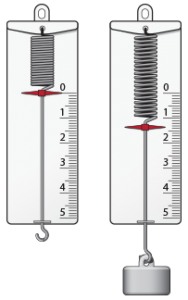
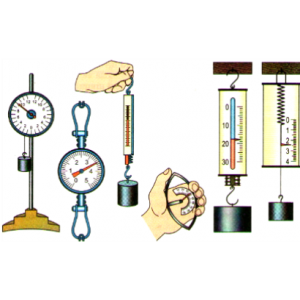
Мал.34. Загальний вигляд деяких різновидностей динамометрів.
Сила – величина векторна, тобто така, яка характеризується не лише величиною (модулем) а й напрямком дії. І це закономірно, адже результат дії сили залежить не лише від її величини, а й від того напрямку в якому ця сила діє. Скажімо якщо сила F штовхає тіло вправо, то тіло буде рухатись вправо (або деформуватися в напрямку дії сили). Якщо ж сила штовхатиме тіло вліво, то воно буде рухатись вліво.
Буде не зайвим зауважити, що визначальне рівняння F = m∙a є похідним від того базового закону механіки, який називається другим законом Ньютона. Закону в якому стверджується: під дією зовнішньої сили F, тіло масою m отримує прискорення а, величина якого прямо пропорційна діючій на тіло силі і обернено пропорційна масі тіла. Іншими словами F → a = F/m. Наприклад якщо на яблуко масою m = 0,1кг діє сила 1Н, то під дією цієї сили яблуко отримає прискорення a = F/m = 1Н/0,1кг = 10м/с2. Якщо ж сила в 1Н діятиме на кавун масою m = 6кг, то кавун отримає прискорення a = F/m = 1Н/6кг = 0,17м/с2.
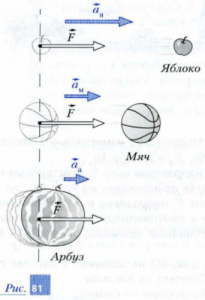
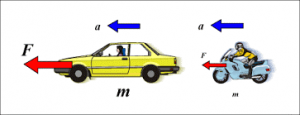
Мал.35. У відповідності з другим законом Ньютона, сила – є причиною прискореного руху тіла.
Задача 1. Снаряд масою 15кг при пострілі набуває швидкість 600м/с. Визначте усереднену величину тієї сили, з якою порохові гази тиснуть на снаряд, якщо довжина ствола гармати 1,8м. Рух в стволі гармати вважати рівноприскореним
Дано:
m = 15кг
v0 = 0м/с
vк = 600м/с
s = 1,8м
F = ?
Рішення. За визначенням F = m∙a, де а = ? Величину прискорення снаряду визначаємо за відомим кінематичним співвідношенням s = (vк2 – v02)/2a, звідси а = (vк2 – v02)/2s = (600м/с)2/2∙1,8м = 1∙105м/с2.
Таким чином, F = m∙a = 15кг∙1∙105м/с2 = 15∙105Н =1,5∙106Н.
Відповідь: F =1,5∙106Н.
Загальні зауваження. Нагадаємо. Рішення задачі полягає не в тому, щоб із безкінечного різноманіття правильних формул, вибрати розрахункове рівняння, тобто ту формулу, підставивши в яку задані величини, отримують правильну відповідь. Рішення задачі полягає в тому, щоб на основі обмеженого числа базових формул, шляхом логічних міркувань та математичних перетворень, вивести розрахункове рівняння. Базовими ж формулами зазвичай є визначальні рівняння фізичних величин та математичні формулювання відомих законів. Формула s = (vк2 – v02)/2a не є ані визначальним рівнянням пройденого шляху, ані математичним формулюванням певного закону. Ця формула є похідною від базового закону кінематики – рівняння руху. Однак, зважаючи на значимість цієї формули, її зазвичай використовують в якості базової.
З іншого боку, і визначальне рівняння сили F = m∙a, і математичне формулювання другого закону Ньютона a = F/m, є базовими формулами фізики. Тому при розв’язуванні задач, з практично однаковим обгрунтуванням, можна застосовувати будь яку з цих формул. Наприклад визначаючи величину прискорення, можна стверджувати: 1) у відповідності з другим законом Ньютона a = F/m; 2) оскільки за визначенням F = m∙a, то a = F/m.
Задача 2. Під дією сили 8Н, тіло масою 400г набуває швидкості 36км/год. Визначте величину пройденого тілом шляху.
Дано:
F = 8Н
m = 400г = 0,4кг
v0 = 0м/с
vк = 36км/год = 10м/с
s = ?
Рішення. Оскільки s = (vк2 – v02)/2a, та враховуючи, що у відповідності з другим законом Ньютона a = F/m = 8Н/0,4кг = 20м/с2, можна записати s = (vк2 – v02)/2a = (10м/с)2/2∙20(м/с2) = 2,5м
Відповідь: s = 2,5м.
Зазвичай на тіло діє не одна сила, а їх певна сукупність. Сукупність тих сил що діють на дане тіло в даний момент часу називають системою сил. Систему сил, лінії дії яких перетинаються в одній точці, називають збіжною системою сил. Наприклад зображена на мал.36 система сил є збіжною. Адже лінії дії всіх чотирьох сил перетинаються в одній точці – точці К.
Якщо тверде тіло знаходиться під дією збіжної системи сил, то це тіло по перше можна вважати матеріальною точкою, а по друге, систему таких сил можна замінити однією рівнодійною силою. Рівнодійною силою (позначається Fр або R), називають таку силу, яка чинить на тіло (матеріальну точку) таку ж силову дію як і вся система реально діючих сил і яка дорівнює векторній сумі тих сил що реально діють на дане тіло, тобто Fр = F1+F2+ … +FN. Це означає, що заміна системи реально діючих на тіло сил, відповідною рівнодійною силою, не змінить механічну поведінку тіла.
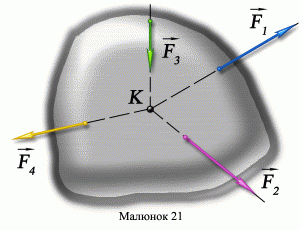
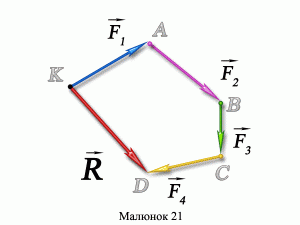
Мал.36. Систему діючих на тіло збіжних сил, можна замінити їх рівнодійною силою.
Графічний (геометричний) метод додавання векторів загалом і сил зокрема принципово простий і полягає в наступному. Від точки прикладання сил (точка К), з дотриманням обраного масштабу та відповідних напрямків, відкладають вектор F1, з кінця вектора F1 відкладають вектор F2, з кінця F2 відкладають F3 і т.д. Вектор який з’єднує початок першого вектора (F1) і кінець останнього (FN) і є відповідною рівнодійною силою Fр. При цьому величина рівнодійної сили пропорційна довжині вектора Fр, а її напрям – збігається з напрямком вектора Fр.
Задача 3. Графічним методом визначити рівнодійну зображених на малюнку сил.
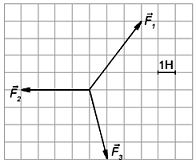
Рішення. В умовах даної задачі, наявність масштабної сітки значно спрощує її графічне рішення. А це рішення полягає в наступному. З кінця вектора F1 відкладаємо вектор F2 (чотири горизонтальні клітинки вліво). З кінця вектора F2 відкладаємо вектор F3 (чотири клітинки вниз і одна клітинка вправо). Оскільки в даній ситуації початок першого вектора (F1) співпадає з кінцем останнього (F3), то це означає, що величина результуючого вектора дорівнює нулю.
Відповідь: F1+ F2+ F3 = 0.
Основний закон статики називається умовою механічної рівноваги тіла. В цьому законі стверджується: тіло (матеріальна точка) буде знаходитись в стані механічної рівноваги (v = 0, або v = const ), тоді і тільки тоді, якщо векторна сума діючих на нього зовнішніх сил дорівнює нулю. Іншими словами: якщо ∑F = 0 то v = 0, або v = const і навпаки.
Зауваження. В науці загалом і в фізиці зокрема знак Σ (сигма) є знаком суми. Наприклад запис ∑F = 0 означає: векторна сума всіх діючих на тіло сил, дорівнює нулю: ∑F = F1+F2+ … +FN = 0.
Ми не раз говорили про те, що механіку загалом та її складові частини зокрема, умовно розділяють на механіку поступального руху (механіку матеріальної точки) та механіку обертального руху. І в цьому сенсі статика не є винятком. Адже коли ми стверджуємо, що основною фізичною величиною статики є сила (F), а основним законом – умова рівноваги тіла (∑F = 0), то по суті маємо на увазі ту частину статики де тіло можна представити у вигляді матеріальної точки. Тобто ту частину статики в якій на тіло діє збіжна система сил. А ця система надає тілу винятково поступального руху. В загальному ж випадку, тіло може знаходитись під дією довільної системи сил. А така система може надавати тілу як поступального так і обертального руху. Описуючи поведінку такого тіла, говорять не лише про діючі на нього сили, а й про діючі моменти сил (М = F∙d). Втім, про те, що таке момент сили та про загальну умову рівноваги тіла, ми поговоримо дещо пізніше.
Контрольні запитання.
- Поясніть, що потрібно зробити, щоб відчути силу в один ньютон?
- Чи правильне твердження 1Н = 102г?
- Чи означає визначальне рівняння F = m∙a, що діюча на тіло сила залежить від маси тіла та його прискорення? Від чого залежить ця сила?
- На що вказує визначальне рівняння сили: F = m∙a?
- Що стверджується в другому законі Ньютона?
- Яку систему сил називають збіжною?
- Як визначають величину та напрямок рівнодійної сили?
- Що стверджується в законі, який називається умовою механічної рівноваги тіла?
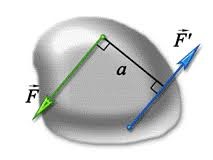
- На зображене на малюнку тіло діють дві рівні за величиною і протилежні за напрямком сили. Чи означає це, що рівнодійна даних сил дорівнює нулю? Поясніть чому?
Вправа №14.
- З яким прискоренням рухається під час розгону реактивний літак масою 60т, якщо сила тяги його двигунів 90кН?
- Визначити масу футбольного м’яча, якщо в процесі удару він набув прискорення 500м/с2, а сила удару дорівнює 420Н.
- Сила 60Н надає тілу прискорення 0,8м/с2. Яка сила надасть цьому тілу прискорення 2м/с2?
- М’яч масою 0,5кг після удару що триває 0,02с набуває швидкості 10м/с. Визначити силу удару.
- На тіло масою 5кг вздовж однієї прямої діють дві сили: 12Н і 8Н. Визначити прискорення цього тіла, якщо: а) сили співнаправлені; б) сили протинаправлені.
- Графічним методом визначте величину і напрям рівнодійної сили. Масштаб сил в обох ситуаціях однаковий: одна клітинка → 5Н.
а)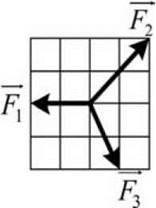 б)
б)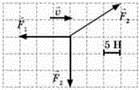
- Під дією сили 100Н тіло рухається за законом х = 100 + 5t + 1,5t2. Яка маса тіла? Який напрямок сили?
- Рух тіла описує рівняння х = 50 – 10t + 0,5t2. Під дією якої сили відбувається цей рух, якщо маса тіла 0,5кг? Як направлена ця сила?
- Літак масою 30т торкається посадкової смуги при швидкості 144км/год. Якою є сила опору руху, якщо літак до зупинки пробігає по смузі 800м?
.
§15. Про додавання векторних величин, або про те, чи завжди 2 + 2 = 4?
Фізичні величини поділяються на скалярні та векторні. Наприклад, час (t), маса (m), площа (S), об’єм (V), густина (ρ), температура (T), енергія (E), робота (A), потужність (N) – величини скалярні. Натомість, сила (F), швидкість (v), прискорення (a), імпульс (p) – величини векторні.
Скалярними називають такі фізичні величини, які характеризуються лише числовим значенням, тобто лише своєю абсолютною величиною. Векторними називають такі фізичні величини, які характеризуються як величиною так і напрямком у просторі (кутовою орієнтацією у вибраній системі координат).
Векторна величина позначається відповідною буквою з стрілкою над нею, або буквою написаною жирним шрифтом (F, v, a, p). При цьому, якщо в тій чи іншій ситуації, векторна величина позначається буквою без стрілки, або буквою написаною не жирним шрифтом (F, v, a, p), то це означає, що мова йде лише про числове значення відповідної величини.
Векторні та скалярні величини суттєво відрізняються в багатьох відношеннях і перш за все тим, що арифметичні дії над ними виконуються по різному. Наприклад, якщо до тіла масою 3кг (m1 = 3кг) додати тіло масою 2кг (m2 = 2кг), то в результаті ми отримаємо тіло загальною масою 5кг, тобто: m1+m2 = 3кг+2кг = 5кг. Якщо ж на тіло діють дві сили F1 = 3H i F2 = 2H (мал.37), то результат їх загальної дії (F1 + F2) буде залежати від того, як направлені ці сили. При цьому, якщо сили співнаправлені, то F1 + F2 = 5Н, якщо сили протилежно направлені, то F1 + F2 = 1Н, а якщо сили перпендикулярно направлені, то F1 + F2 = 3,5Н.
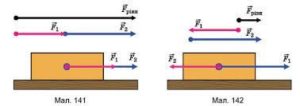
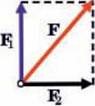
Мал.37. Результат додавання векторів залежить не лише від їх величин, а й від їх відносної орієнтації. При цьому, в загальному випадку F1 + F2 ≠ F1 + F2.
Розрізняють два способи додавання векторних величин: геометричний (графічний) та алгебраїчний (аналітичний). При геометричному способі, результат додавання векторів отримують шляхом відповідних геометричних побудов. Ці побудови здійснюють так званим методом багатокутника. Суть цього методу гранично проста. Якщо на точку К (мал.38) діє система N векторів, то величину і напрям результуючого (рівнодійного) вектора (Fр = F1 + F2 + … + FN) визначають наступним чином. З точки К відкладають вектор F1, з кінця вектора F1 відкладають вектор F2, з кінця вектора F2 – вектор F3 і так до останнього вектора FN. Вектор, який з’єднує точку К з кінцем останнього вектора і буде результуючим вектором Fр = F1 + F2 + … + FN.


Мал.38. При геометричному додаванні векторів величину та напрям результуючого (рівнодійного) вектору визначають методом багатокутника.
Геометричний метод додавання векторів виглядає досить простим і наочним. Однак, він має ряд суттєвих недоліків. Перший полягає в тому, що точність його результатів залежить від масштабу та точності геометричних побудов. При цьому, будь яка точність побудов, не гарантує безумовно точного результату. Другим суттєвим недоліком геометричного методу додавання векторів є те, що таке додавання погано поєднується з тими теоріями, в яких закони записують у вигляді певних математичних формул. А переважна більшість фізичних теорій є саме такими.
Ці недоліки відсутні в алгебраїчному методі додавання векторів, тобто такому методі при якому результат додавання визначають не шляхом геометричних побудов, а шляхом алгебраїчних розрахунків. Реалізуючи цю ідею, вектор F розкладають на дві складові: проекції вектора на осі системи координат Fx та Fy. При цьому, якщо той кут α який характеризує кутову орієнтацію вектора F виміряно від осі 0х, то Fx=Fcosα; Fy=Fsinα.
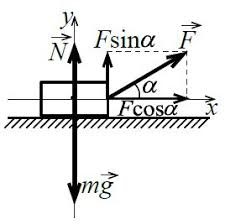
Мал.39. Будь який вектор F(F,α) можна представити у вигляді двох по суті скалярних величин – проекцій цього вектора на осі системи координат Fx=Fcosα; Fy=Fsinα.
По суті, проекції вектора на осі системи координат також є векторами. Однак враховуючи факт того, що направлені вздовж однієї прямої вектори, додаються як скалярні величини, можна стверджувати, що проекції вектора на осі системи координат, мають властивості скалярних величин. Тому в подальшому, ці проекції ми будемо вважати скалярними величинами, тобто такими які характеризуються лише величиною і знаком: «+» якщо напрям проекції співпадає з додатним напрямком відповідної осі; «–» якщо ці напрямки протилежні.
В загальних рисах, суть алгебраїчного методу додавання сил (векторів) є наступною.
- Кожний вектор діючих на тіло сил, розкладають на його проекції Fx, Fy.
- 2. Визначають суму проекцій на вісь 0х (∑Fx) та вісь 0у (∑Fу).
- Визначають величину результуючого вектора Fр = √[(∑Fx)2+∑Fу)2] – теорема Піфагора.
Практична реалізація алгебраїчного методу додавання векторів, а відповідно і розв’язування задач статики, не можуть бути успішними без розуміння фізичної суті того, що називають синусом і косинусом кута.
Нажаль в тій математиці яка існує за ради самої математики, синус і косинус кута визначають не як надважливі загально наукові функції, а як певні містечкові співвідношення між сторонами прямокутного трикутника: Синусом кута α прямокутного трикутника, називають відношення протилежного катета a до гіпотенузи с: sinα = a/c. Косинусом кута α прямокутного трикутника називають відношення прилеглого катета b до гіпотенузи с: cosα = b/c.
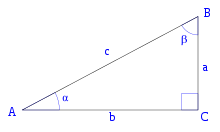
мал.40. В математиці синус та косинус кута визначають як певні співвідношення між сторонами прямокутного трикутника: sinα = a/c, cosα = b/c
З формальної точки зору, вище сформульовані визначення (sinα = a/c, cosα = b/c) є правильними. Однак ця правильність стосується лише мільйонної частини того, чим в реальності є синус і косинус кута.
Достатньо сказати, що ці «правильні» визначення дозволяють визначати синуси та косинуси лише гострих кутів, тоді як ці функції мають певні значення для будь яких кутів, будь то 30°; 60°; 135° чи 1470°. Ці «правильні» визначення не пояснюють факту того, чому значення косинусів та синусів можуть бути як додатними так і від’ємними. Не пояснюють факту періодичності даних функцій. Не пояснюють купу тих співвідношень які в математиці називаються формулами приведення і які зазвичай є предметом банального зазубрювання. Не пояснюють того, що синус і косинус, то ж не просто певні співвідношення між сторонами прямокутного трикутника, а метод описання періодичних процесів та спосіб переходу від векторних обчислень до скалярних і навпаки. А всі ці пояснення не потребують знання вищої математики. Бо вони з усією очевидністю випливають з наступних, загально наукових визначень:
Косинус кута α (cosα) – це безрозмірна величина, яка дорівнює проекції відповідного цьому куту одиничного радіус-вектора на ту вісь від якої виміряно кут α.
Синус кута α (sinα) – це безрозмірна величина, яка дорівнює проекції відповідного цьому куту одиничного радіус-вектора на ту вісь, що є перпендикулярною до осі від якої виміряно кут α.
Ілюструючи суть даних визначень, розв’яжемо конкретну задачу.
Задача 1. Шляхом прямих вимірювань, визначити синуси і косинуси наступних кутів: 0°; 30°; 45°; 60°; 90°; 120°; 135°; 150°; 180°.
Рішення. Задаємо прямокутну систему координат, в якій горизонтальна вісь 0х буде віссю cosα (тобто тією віссю від якої відраховується кут α), а вісь 0у – віссю sinα. В заданій системі координат, за допомогою циркуля проводимо півколо максимально великого радіусу (наприклад R = 10см) і приймаємо величину цього радіусу за безрозмірну одиницю (10см = 1). З застосуванням транспортира, від осі cosα (від осі 0х) відкладаємо кути 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°. Із отриманих на колі точок опускаємо перпендикуляри на вісь cosα і sinα та виконуємо відповідні вимірювання.
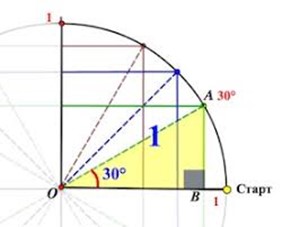
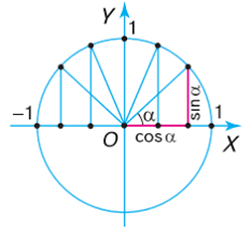
Наприклад куту α = 30°, на колі відповідає точка А. При цьому проекцією цієї точки на вісь cosα буде точка В, а на вісь sinα – точка М (на малюнку не позначена). Виміряна в заданому масштабі (10см = 1) довжина відрізку 0В буде косинусом кута 30°, а довжина відрізку 0М буде синусом кута 30°. Вимірювання ж показують, що cos30° = 0,87; sin30° = 0,50.
Результати вимірювань записуємо в таблицю.
| α | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
| сosα | 1,00 | 0,87 | 0,71 | 0,50 | 0,00 | –0,50 | –0,71 | –0,87 | –1,00 |
| sinα | 0,00 | 0,50 | 0,71 | 0,87 | 1,00 | 0,87 | 0,71 | 0,50 | 0,00 |
Звісно, вище наведене геометричне (графічне) рішення задачі, як власне і будь яке геометричне рішення, дає приблизні результати. Результати, точність яких залежить від масштабу і точності геометричних побудов, точності вимірювань, кваліфікації того хто виконує ці побудови і вимірювання, тощо. Скажімо, при алгебраїчному рішенні цієї ж задачі ми б отримали cos30° = √3/2 ≈ 0,87; cos45° = √2/2 ≈ 0,71.
Втім, графічний метод розв’язування задачі має ту перевагу, що з усією очевидністю пояснює фізичну та загально наукову суть того, що називають синусом і косинусом кута. Пояснює, чому значення косинусів та синусів можуть бути як додатними так і від’ємними. Пояснює факт періодичності даних функцій. Пояснює, що cos1470° = cos(4∙360 + 30)° = cos30° = 0,87. Що cos(–α) = cosα, а sin(–α) = –sinα, що sin(90–α) = cosα, а cos(90–α) = sin(α), що cos(180+α) = cosα, а sin(180+α) = –sinα. Пояснює десятки, якщо не сотні інших тригонометричних співвідношень, які в математиці невідомо для чого, банально зазубрюються.
Варто зауважити, що коли ми стверджуємо: проекції вектора F на осі прямокутної системи координат визначаються за формулами: Fx = Fcosα; Fy = Fsinα, то маємо на увазі, що кут α виміряно від осі 0х. Якщо ж орієнтацію вектора R (мал.41) охарактеризувати кутом φ який веде свій відлік від осі 0у, то в цьому випадку Rx = Rsinφ; Ry = Rcosφ. Адже за визначенням, віссю косинусів є та вісь від якої веде відлік відповідний кут.
Втім, жодних суперечностей між даними формулами немає. Дійсно. Якщо кутова орієнтація вектора R характеризується виміряним від осі 0у кутом φ = 30°, то Ry = Rcos30° = R∙0,87; Rx = Rsin30° = R∙0,50. Якщо ж цю орієнтацію задати кутом виміряним від осі 0х, то цей кут становитиме не 30°, а 60°. При цьому Ry = Rsin60° = R∙0,87; Rx = Rcos60° = R∙0,50.
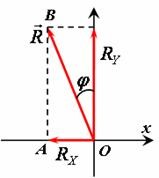
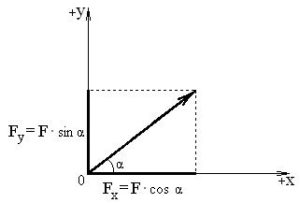
Rx = Rsinφ, Ry = Rcosφ; Fx = Fcosα, Fy = Fsinα
Мал.41. За визначенням віссю cosφ є та вісь від якої виміряно кут φ.
Зауважимо також, що на практиці проекції тих векторів, що є паралельними або перпендикулярними осям системи координат, визначають із міркувань очевидності: наприклад, в ситуації мал.42б Fх = F, а в ситуації мал.42в Fx = 0. Крім цього, оскільки орієнтацію вектора F зазвичай характеризують кутом меншим за 90°, то знак проекції визначають із міркувань очевидності. Наприклад в ситуації мал.42г, проекція вектора F на вісь 0х має знак «–».
Втім, в кожній з цих ситуацій можна скористатися універсальною формулою Fx = Fcosα, пам’ятаючи при цьому, що в даному випадку, кут α це кут виміряний від додатного напрямку осі х. Дійсно: а) Fx = Fcosα; б) Fx = Fcosα = Fcos0° = F∙1 = F; в) Fx = Fcosα = Fcos270° = F∙0 = 0; г) Fx = Fcosα = – Fcosβ, де β = 180° – α.
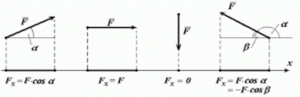
Мал.42. Проекції тих векторів, що є паралельними або перпендикулярними осям системи координат, визначають із міркувань очевидності.
Задача 1. За заданим малюнком визначити проекції векторів F1, F2, F3, F4 на осі системи координат.
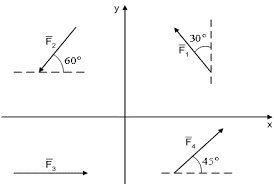
Рішення. На основі аналізу малюнку та числових значень відповідних величин, можна записати:
Fx1 = – F1sin30°, Fу1 = F1cos30°;
Fx2 = – F2cos60°, Fy2 = – F2sin60°;
Fx3 = F3, Fy3 = 0;
Fx4 = F4cos45°, Fy4 = F4sin45°.
Задача 2. За заданим малюнком визначити величину рівнодійної тих сил, що діють та точку О (F1=15кН, F2=10кН, F3=6кН, F4=9кН).

Рішення. Визначаємо проекції сил на осі заданої системи координат:
∑Fx = 0 + F2cos45° + F3cos45° – F4 = 0 + 10∙0,71 + 6∙0,71 – 9 = 2,36кН;
∑Fу = F1 + F2sin45° – F3sin45° + 0 = 15 + 10∙0,71 – 6∙0,71 = 17,84кН.
Визначаємо величину рівнодійного (результуючого) вектора:
Fр = √[(∑Fx)2+∑Fу)2] = √(2,362 + 17,842) = √324 = 18кН.
Відповідь: Fр = 18кН.
Контрольні запитання.
- Чим відрізняються векторні величини від скалярних?
- В чому суть геометричного методу додавання векторів?
- Які основні недоліки геометричного методу додавання векторів?
- Чому проекції вектора на осі системи координат, можна вважати скалярними величинами?
- В чому суть алгебраїчного методу додавання векторів?
- Що стверджується в теоремі Піфагора?
- Які недоліки прийнятих в математиці визначень: sinα = a/c, cosα = b/c?
- В чому суть векторно-проекційного визначення функцій sinα і cosα?
- Які переваги векторно-проекційного визначення функцій sinα і cosα?
- З якої теореми випливає, що cos2α + sin2α = 1?
Вправа 15.
- Шляхом геометричних побудов визначте косинуси і синуси кутів 20°, 50°, 70°. Порівняйте отримані результати з відповідними табличними значеннями.
- За заданим малюнком визначити проекції векторів F1, F2, F3 на осі системи координат.
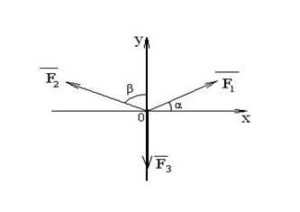
3. За заданим малюнком визначити проекції векторів F1, F2, F3, F4 на осі системи координат (сили позначте самостійно).
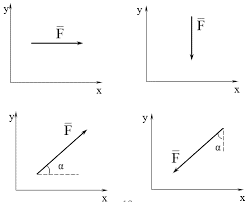
4. Вектор сили F=5H орієнтований відносно осі 0х під кутом: а) 0º; б) 30º; в) 90º; г) 135º; д) 210º; е) 270º; є) 300º. Визначте проекції даних векторів на осі прямокутної системи координат.
5. За заданим малюнком визначити величину рівнодійної тих сил, що діють та точку О: F1 = F2 = F3 = F4 = 10Н. Задачу розв’язати графічним та алгебраїчним методом.
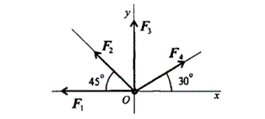
6. Визначте суму векторів: а) F1(5H;0º), F2(5H;90º), F3(5H;45º). Задачу розв’язати графічним та алгебраїчним методом.
7. За заданим малюнком визначити величину рівнодійної тих сил, що діють та точку О. Задачу розв’язати графічним та алгебраїчним методом.
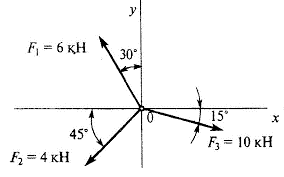
8. За заданими проекціями векторів Fx i Fy, визначте їх числову величину. Задачу розв’язати геометричним та алгебраїчним методом
а) Fx = 3,5H, Fy = 3,5H; б) Fx = –5,0H, Fy = 0,0H; в) Fx = –2,5H, Fy = –4,0H.
.
§16. Сила тяжіння. Реакція опори. Загальні відомості щодо розв’язування задач статики.
В фізиці розрізняють багато різновидностей сили. Лише в механіці ми будемо вивчати що найменше вісім таких різновидностей:
– сила тяжіння Fт
– реакція опори N
– сила тертя Fтер
– сила інерції Fi
– вага P
– сила пружності Fпр
– гравітаційна сила Fгр
– сила Архімеда Fa .
Втім, кожна з цих сил є різновидністю однієї і тієї ж фізичної величини – сили, яка є мірою взаємодії фізичних об’єктів і яка вимірюється в ньютонах. Якщо ж говорити про ті сили які найчастіше зустрічаються в задачах статики, то ними є сила тяжіння та реакція опори.
Факт того, що на Землі тіла падають з певним прискоренням, безумовно вказує на те, що на них в напрямку прискореного руху діє певна сила. І як будь яку силу, її можна визначити за формулою F = ma. А оскільки величина того прискорення з яким падають земні тіла, становить a = g = 9,8м/с2, то діюча на них сила має визначатись за формую F = mg. Цю силу називають силою тяжіння.
Мал.43. На всі земні тіла діє певна сила тяжіння, величина та напрям якої визначаються за формулою F=mg.
Сила тяжіння – це та сила, з якою тіло притягується до Землі і яка дорівнює добутку маси тіла на прискорення його вільного падіння.
Позначається: Fт
Визначальне рівняння: Fт = mg, де g = 9,8м/с2
Одиниця вимірювання: [Fт] = кг·м/с2 = H, ньютон
По суті, сила тяжіння є тією силою, елементарні фрагменти якої діють на всі точки тіла. Однак можна довести, що результуюча тих елементарних сил тяжіння які діють на фрагменти даного тіла, прикладена до центру мас цього тіла. Тому вважається, що сила тяжіння діє на центр маси тіла.
Сила тяжіння прагне перемістити будь яке тіло в центр Землі. А оскільки земні тіла не опиняються в цьому центрі, то ясно, що на своєму шляху вони неминуче зустрічають певні перешкоди. Цими перешкодами часто є ті об’єкти які прийнято називати опорами. Ту ж силу з якою опора діє на тіло називають реакцією опори.
Опорою називають будь яку механічну перешкоду, яка так чи інакше жорстко обмежує рух тіла. Наприклад та підлога на якій ви стоїте, обмежує ваш рух в напрямку до центру Землі. Гнучка опора (канат, ланцюг, дріт, тощо), обмежує рух тіла в напрямку розтягування цієї опори. Шарнірно закріплений стержень, обмежує рух тіла як в напрямку розтягування стержня так і в напрямку його стискання.
Реакція опори – це та сила, з якою опора діє на тіло та жорстко протидіє переміщенню цього тіла.
Позначається: N
Визначальне рівняння: величина і напрям реакції опори визначається з умов конкретної задачі.
Одиниця вимірювання: [N] = H, ньютон.

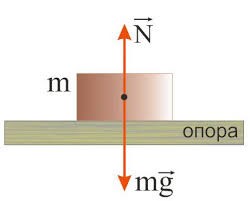
Мал.44. Опора – це та перешкода яка жорстко обмежує рух тіла. Реакція опори – це та сила з якою опора діє на тіло.
Найпростішими і в той же час найпоширенішими опорами є плоска опора, гнучка опора та шарнірно закріплений стержень. Плоскою опорою називають тверду рівну поверхню, яка протидіє переміщенню тіла в напрямку перпендикулярному до площини цієї поверхні. Реакція плоскої опори перпендикулярна до площини опори (мал.45а). Гнучкою опорою називають тверде гнучке тіло (трос, канат, нитка, мотузка, тощо), яке протидіє переміщенню іншого тіла в напрямку розтягування цієї опори. Реакція гнучкої опори направлена вздовж опори в напрямку точки її закріплення (мал.45б). Реакцію гнучкої опори часто позначають буквою Т і називають силою натягу нитки, канату, троса, тощо.
а)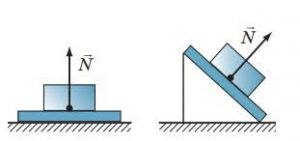 б)
б)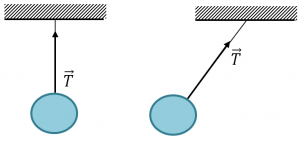
Мал.45. Напрямки реакцій опор: а) плоска опора, б) гнучка опора.
Шарнірно закріпленим стержнем називають такий стержень, який шарнірно (обертально рухомо) з’єднаний з відносно нерухомою поверхнею і який протидіє переміщенню тіла як в напрямку стискання стержня, так і в напрямку його розтягування. Реакція шарнірно закріпленого стержня направлена вздовж стержня. При цьому: якщо стержень розтягується, то реакція опори направлена до точки закріплення стержня, а якщо стержень стискається – то від точки закріплення. Наприклад в зображеній на мал.46 ситуації, стержень АС розтягується, а стержень ВС – стискається. При цьому діючі на точку С реакції опори FАС і FВС, мають відповідні напрямки.

Мал.46. Шарнірно закріплений стержень, може «працювати» як на розтягнення (стержень АС), так і на стиснення (стержень ВС).
Потрібно зауважити, що сила тяжіння і реакція опори є тими зовнішніми силами, які діють на відповідне тіло, а не на опору чи щось інше. Що правда, точки прикладання цих сил є суттєво різними: сила тяжіння прикладена до центру мас тіла, а реакція опори діє в точках контакту тіла з відповідною опорою (мал.47а). Втім, в більшості задач механіки матеріальної точки, прийнято вважати що і сила тяжіння і реакція опори, прикладені до центру мас тіла (мал.47б).
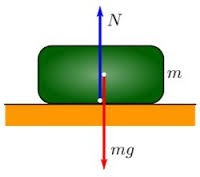

Мал.47. Сила тяжіння і реакція опори, діють на тіло, а не на опору чи щось інше.
Задачі статики мають ту перевагу, що порядок (алгоритм) їх розв’язку є досить строго визначеним. І цей порядок є наступним:
- На основі аналізу умови задачі виконують малюнок (обов’язково), на якому чітко вказують всі діючі на дане тіло (точку рівноваги) сили .
- Задають систему координат та вказують кутову орієнтацію сил в ній.
- Записують умову рівноваги тіла, тобто систему рівнянь: ∑Fx = 0; ∑Fy = 0.
- Розв’язавши цю систему, визначають невідомі величини.
Дотримуючись вище наведеного алгоритму, розв’яжемо декілька конкретних задач.
Задача 1. На гнучких опорах, тіло масою 20кг підвішено так, як показано на малюнку (α=30º). Визначити реакції опор (зусилля в дротах 2 і 3).
Загальні зауваження. При розв’язуванні задач статики, діючу на абсолютно тверде тіло (в тому числі і гнучку опору) силу, можна переносити вздовж лінії дії цієї сили. Наприклад в умовах нашої задачі, діюча на тіло сила тяжіння, через гнучку опору 1, переноситься в точку дії трьох сил: Fт, N2, N3. Зазвичай, діючі на точку рівноваги сили, зображають на тому малюнку який відповідає умові задачі. На тому ж малюнку вказується і система координат. В нашому ж випадку, ці сили та система координат зображені окремо.
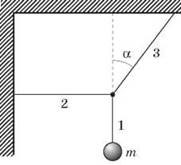
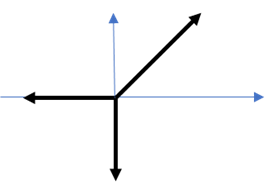
Дано:
m = 20кг
α = 30º
N2=? N3=?
Рішення. Виконуємо малюнок, на якому вказуємо діючі на точку рівноваги сили та задаємо систему координат. Записуємо умову рівноваги системи.
∑Fx = –N2 + N3sin30º= 0
∑Fy = –FT + N3cos30º= 0.
Розв’язавши систему рівнянь, визначаємо невідомі величини:
із (2) → N3cos30º = Fт = mg; → N3 = mg/cos30º = 20∙10/0,87= 230H;
із (1) → N2 = N3sin30º = 230∙0,5= 115H.
Відповідь: N2 = 115H; N3 = 230H.
Задача 2. До кронштейну АВС в т.В підвішено вантаж масою 60кг, так як це показано на малюнку (α = 30º). Визначити зусилля в стержнях АВ і СВ.
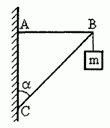
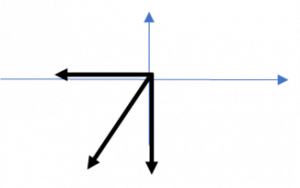
Загальні зауваження. В задачах статики, часто зустрічаються ситуації коли точний напрямок реакції опори невідомий або сумнівний. Наприклад, в нашій задачі стержень СВ явно «працює» на стиснення і тому його реакція NC має бути направленою вздовж лінії СВ в напрямку від точки С. Однак припустимо, що ви сумніваєтесь стосовно того в яку сторону направлена ця реакція. В такому випадку сміливо направляйте сумнівну реакцію в будь яку можливу сторону (вздовж лінії стержня) і розв’язуйте задачу. При цьому, якщо в результаті рішення задачі, невідома реакція матиме знак «+», то це означатиме, що вибраний вами напрямок є правильним. Якщо ж ця реакція виявиться зі знаком «–» то це означатиме, що в реальності відповідна реакція має протилежний (протилежний від вибраного) напрямок. Перевіряючи вище сказане направимо реакцію NС в гарантовано неправильному напрямку.
Дано:
m = 60кг
NА= ? NС= ?
Рішення. Виконуємо малюнок на якому: вказуємо діючі на т. В сили; задаємо систему координат; вказуємо кутову орієнтацію сил. Оскільки кут α=30º безпосередньо не прилеглий до т. В то із геометричних міркувань визначаємо йому відповідний та прилеглий до т. В кут. Записуємо умову рівноваги точки В і, розв’язавши систему відповідних рівнянь, визначаємо невідомі величини.
∑ Fx = –NA – NC sin30º = 0 (1)
∑ Fy = –NC cos30º – mg = 0 (2)
із (2)→ NC = –mg/cos30º = –(60∙10/0,87)= –690 Н
із (1)→ NA = –NCsin30º = – (–690)0,5 = 345 Н
Знак «–» вказує на те, що реакція NC фактично направлена в протилежну (протилежну від зображеної на малюнку) сторону.
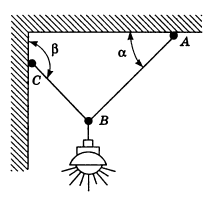
Задача 3. Визначити реакції опори в зображеній на малюнку ситуації, якщо маса вантажу 20кг, а кут між стіною та стержнем ВС 30°.
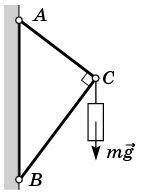
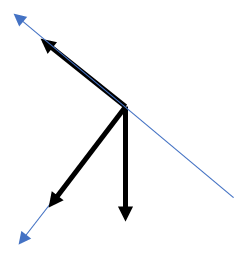
Загальні зауваження. Математична складова рішення задач статики визначальним чином залежить від того як задана система координат. Зазвичай, оптимальність введення системи координат полягає в тому, що бодай одна з осей цієї системи, має співпадати з напрямком невідомої сили. (В цьому випадку бодай одне з рівнянь умови рівноваги тіла, міститиме лише одну невідому величину, що значно полегшує математичне рішення системи рівнянь).
Дано:
m = 20кг
β = 30º
NА= ? NС= ?
Рішення. Виконуємо малюнок на якому: вказуємо діючі на т.С сили; задаємо систему координат; вказуємо кутову орієнтацію сил. Записуємо умову рівноваги точки С. Розв’язавши систему відповідних рівнянь, визначаємо невідомі величини.
∑ Fx = NA – mgsin30º = 0 (1)
∑ Fy = NB + mgcos30º = 0 (2)
із (1)→ NA = mgsin30º = 20∙10·0,50= 100 Н;
із (2)→ NB = – mgcos30º = = –20·10·0,87= –174 Н, де знак «–» вказує на те, що реакція NВ фактично направлена в протилежну (протилежну від зображеної на малюнку) сторону.
Контрольні запитання.
- На що вказує факт того, що земні тіла падають з певним прискоренням?
- Що називають опорою?
- В якому напрямку протидіє переміщенню тіла: а) плоска опора; б) гнучку опора; в) шарнірно закріплений стержень?
- Що називають реакцією опори? В чому вимірюється реакція опори?
- Що стверджується в умові механічної рівноваги тіла?
- Який алгоритм (порядок) розв’язування задач статики?
- В результаті правильного рішення задачі, реакція опори отримала знак «–». Що це означає?
- Що означає твердження: оптимальним чином вводимо систему координат?
Вправа 16.
- Яка сила тяжіння діє на зайця, вовка, ведмедя, носорога та слона, якщо їх маси відповідно дорівнюють 6кг; 40кг; 400кг; 2т; 4т?
- Тіло масою 8кг лежить на горизонтальній поверхні. Визначте діючі на тіло сили.
- Визначте реакції опори в зображеній на малюнку ситуації (F = 100Н).

- Визначте реакції опори в зображених на малюнках а) і б) ситуаціях. Маса вантажу в обох випадках 3кг.
а)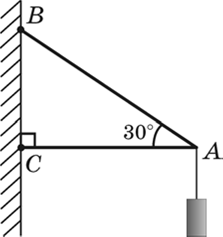 б)
б) 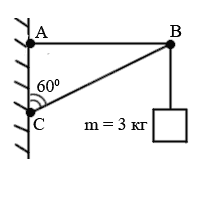
- Визначити реакції опори в зображеній на малюнку ситуації, якщо маса вантажу 5кг, α=60º, β=120°.
- На двох тросах однакової довжини висить вантаж масою 50кг. При цьому кут між тросами 60º. Визначити сили натягу тросів.
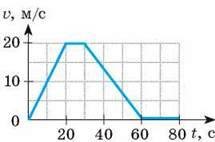
- На малюнку зображено графік швидкості руху тіла масою 2кг. Визначити величину діючої на тіло сили, на кожній ділянці шляху.
.
§17. Сила тертя.
В механіці, сили які так чи інакше протидіють взаємному переміщенню контактуючих поверхонь, називають силами тертя. По суті, сила тертя є результуючою багатьох силових факторів, різноманіття яких не можливо врахувати. Про складність того, що прийнято називати тертям, говорить бодай той факт, що на сьогоднішній день точної кількісної теорії тертя не існує. А це означає що по-перше, не існує тієї єдиної універсальної формули, яка б дозволяла визначати силу тертя в будь якій можливій ситуації. По-друге, ті формули за якими натепер визначають силу тертя в тому чи іншому конкретному випадку, є в тій чи іншій мірі наближеними. По-третє, в наявних визначальних рівняннях сил тертя, завжди присутні величини значення яких визначається експериментально (коефіцієнти тертя) і які є індивідуальним для кожного конкретного випадку.
Розрізняють дві основні різновидності тертя: сухе і в’язке. Сухим називають таке тертя, яке виникає при взаємодії твердих поверхонь і яке протидіє їх взаємному переміщенню. В’язким називають таке тертя, яке виникає при взаємодії твердих поверхонь з рідинами або газами, а також між внутрішніми шарами рідин та газів, і яке протидіє їх взаємному переміщенню. Наприклад те тертя яке протидіє взаємному переміщенню двох твердих сухих поверхонь, є сухим. Якщо ж між цими поверхнями знаходиться шар мастила (рідини), то відповідне тертя буде в’язким. А оскільки ви знаєте, що для зменшення тертя застосовують певні рідини які називають мастилами, то напевно погодитесь з тим, що за однакових умов, в’язке тертя значно менше за сухе.
В свою чергу, сухе тертя прийнято розділяти на тертя ковзання та тертя кочення. Наприклад, якщо важкий предмет ви намагаєтесь зсунути відносно підлоги, то вам протидіє сила тертя ковзання (мал.48а). А якщо той же предмет стоятиме на платформі з коліщатами (мал.48б), то переміщенню цієї системи протидіятиме сила тертя кочення. І напевно ви знаєте, що за схожих умов, тертя кочення значно менше за тертя ковзання.
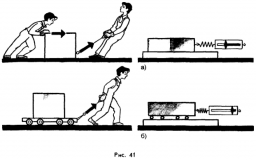
Мал.48. Тертя яке виникає між твердими поверхнями прийнято розділяти на тертя ковзання (а) та тертя кочення (б).
В межах програми загальноосвітньої школи, говорячи про силу тертя, зазвичай мають на увазі силу тертя ковзання. Досліджуючи загальні властивості цієї сили, можна провести ряд простих експериментів. Суть цих експериментів представлена на малюнку 49. І ця суть полягає в наступному. За допомогою пружинного динамометра певне тіло з постійною швидкістю протягують певною горизонтальною поверхнею і фіксують показання динамометра, які фактично дорівнюють величині сили тертя.
Змінюючи умови експерименту, наприклад шляхом збільшення або зменшення тієї сили з якою тіло тисне на поверхню, шляхом зміни матеріалу взаємодіючих поверхонь, якості їх механічної обробки, площі взаємодії, тощо, можна дослідити загальні властивості сили тертя ковзання. А ці властивості є наступними.
- Сила тертя ковзання, практично не залежить від площі взаємодіючих поверхонь. 2. Сила тертя ковзання пропорційна тій силі з якою взаємодіючі поверхні притискаються одна до одної і яка чисельно дорівнює відповідній реакції опори (N). 3. Максимальна величина сили тертя спокою, дещо більша за величину відповідної сили тертя руху. 4. Сила тертя, складним чином залежить від механічних та хімічних властивостей взаємодіючих поверхонь, якості їх механічної обробки, їх температури, швидкості відносного руху, тощо.
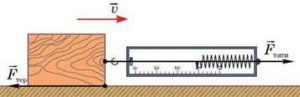
Мал.49. Загальний вигляд приладу для дослідження тертя ковзання.
Узагальнюючи результати подібних досліджень, можна дати наступне визначення. Сила тертя (сила тертя ковзання) – це та сила, з якою поверхні взаємодіючих твердих тіл протидіють їх взаємному поступальному (ковзальному) переміщенню, або можливості такого переміщення і яка дорівнює добутку коефіцієнту тертя ковзання (μ) та тієї сили з якою взаємодіючі поверхні тиснуть одна на одну (реакції опори N)
Позначається: Fтер
Визначальне рівняння: Fтер = µN
Одиниця вимірювання: [Fтер] = Н, ньютон.
Коефіцієнт тертя ковзання – це фізична величина, яка характеризує здатність певної пари твердих поверхонь протидіяти їх відносному ковзальному переміщенню і яка дорівнює відношенню виникаючої між цими поверхнями сили тертя, до величини тієї сили з якою поверхні притискаються одна до одної.
Позначається: μ
Визначальне рівняння: μ = Fтер/N
Одиниця вимірювання: [μ] = Н/Н = – , безрозмірна величина.
Коефіцієнт тертя складним чином залежить від багатьох обставин і визначається експериментально. Результати деяких з цих експериментальних досліджень представлені в наступній таблиці.
|
Сила тертя завжди направлена в сторону протилежну від напрямку руху тіла, або напрямку його можливого руху. Наприклад, якщо тіло рухається вправо, то сила тертя направлена вліво, а якщо тіло рухається вліво, то сила тертя направлена вправо. Якщо певна зовнішня сила F прагне зсунути тіло в одному напрямку, а тіло залишається в стані спокою (v = 0), то це тільки тому, що на дане тіло в протилежному напрямку діє відповідна сила тертя Fтер. Наприклад, якщо в супереч дії тих сил які прагнуть зсунути тіло похилою поверхнею, тіло залишається в стані спокою, то це тільки тому, що в напрямку протилежному до напрямку можливого руху на тіла діє відповідна сила тертя, яка і протидіє цьому можливому руху.
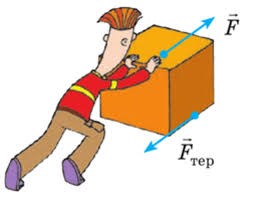
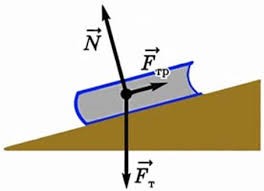
Мал.50. Сила тертя завжди направлена в сторону протилежну від напрямку руху тіла, або напрямку його можливого руху.
Специфіка сили тертя полягає в тому, що вона виникає як певна реакція на дію тих сил які намагаються зсунути одну поверхню відносно іншої. І якщо такі сили відсутні, то відповідно відсутня і певна сили тертя. Наприклад, якщо тіло знаходиться на горизонтальній поверхні (мал.51а), то на нього сила тертя не діє. Не діє тому, що нема того силового фактору який намагається зсунути тіло відносно поверхні (Fт + N = 0). Однак як тільки поверхня стане похилою (мал.51б), автоматично з’явиться і відповідна сила тертя. З’явиться тому, що результуюча постійно діючих на тіло сил (сила тяжіння Fт та реакція опори N) вже не буде дорівнювати нулю (Fт + N ≠ 0) і намагатиметься зсунути тіло вниз. І якщо тіло знаходиться в стані спокою, то це тільки тому, що цей спокій забезпечує певна сила тертя. При цьому, по мірі зростання кута нахилу площини, автоматично зростатиме і відповідна сила тертя. Зростатиме до тих пір, поки не досягне певної критичної величини, за межами якої, тертя спокою перетворюється на тертя руху.
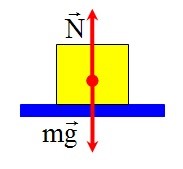
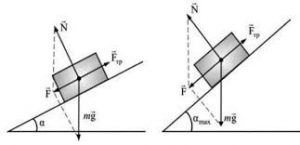
Мал.51. Сила тертя виникає лише за наявності тієї сили яка прагне зсунути тіло відносно поверхні.
По суті, сила тертя є результуючою всієї сукупності тих складних процесів, які відбуваються в місці контакту поверхонь. При цьому, якщо мова йде про тертя ковзання, то основними складовими відповідної сили тертя, є: 1) наявність сил взаємодії між молекулами контактуючих поверхонь; 2) наявність певних мікро нерівностей (шороховатостей) поверхонь.

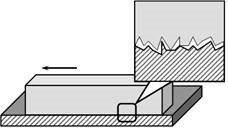
Мал.52. Основними причинами тертя ковзання є: взаємодія між молекулами контактуючих поверхонь та наявність мікро нерівностей на цих поверхнями.
Якщо на площині знаходиться кругле (циліндричне) тіло, яке може вільно обертатись (котитись), то в цьому випадку говорять про тертя кочення. Порівнюючи величини сил тертя ковзання та кочення, проведіть наступний простий експеримент. На горизонтальну поверхню покладіть циліндр та йому відповідний за масою брусок. Нахиляючи поверхню, ви неодмінно з’ясуєте, що циліндр покотиться при гранично малому куті нахилу поверхні, тоді як рух бруска починається при в десятки разів більших кутах нахилу. Висновок очевидний: за однакових умов, сила тертя кочення набагато менша за силу тертя ковзання. Зважаючи на даний факт, в тих випадках де потрібно мінімізувати тертя, ковзання замінюють на кочення, наприклад шляхом застосування відповідних підшипників. Іншим ефективним способом зменшення сили тертя є застосування відповідних мастил.

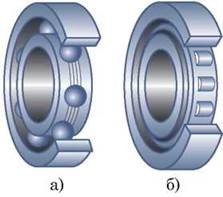
Мал.53. За аналогічних умов, сила тертя кочення значно менша за силу тертя ковзання.
Варто зауважити, що визначальне рівняння тертя кочення суттєво відрізняється від визначального рівняння тертя ковзання, тобто від формули Fтер = µN. Однак в гранично спрощеному варіанті прийнято вважати, що всі види тертя визначаються за формулою Fтер = µN. При цьому відмінності між різними видами тертя регламентуються різною величиною коефіцієнту тертя. Наприклад якщо коефіцієнт тертя ковзання автомобільних коліс об асфальт близький до 0,6, то їх коефіцієнт кочення співрозмірний з 0,06.
На перший погляд, та сила тертя завдяки якій люди, велосипеди та автомобілі переміщуються відносно відповідних поверхонь, не вписується в рамки загально прийнятого визначення: «сила тертя, це та сила з якою взаємодіючі поверхні протидіють їх взаємному переміщенню». Однак, неупереджений аналіз вказує на безпідставність подібних звинувачень. Адже та сила тертя ковзання, що виникає між дорогою і ведучими колесами велосипедів та автомобілів (тобто тими колесами обертання яких спричиняє поступальний рух відповідного транспортного засобу), дійсно протидіє їх взаємному переміщенню, тобто протидіє ковзанню коліс та підошви, відносно поверхні дороги. При цьому ця сила не протидіє поступальному руху відповідних тіл. Більше того, без цієї сили такий рух стає просто неможливим. Адже лише завдяки силі тертя ковзання, обертальний рух ведучого колеса велосипеда та м’язові зусилля пішохода перетворюється на поступальний рух відповідних тіл.

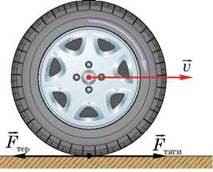
Мал.54. Наявність сили тертя, є необхідною умовою поступального руху тіл.
Якщо ж говорити про ту силу тертя яка протидіє руху автомобіля (велосипеда, тощо), то цією силою є сила тертя кочення (а також загальний опір повітря). І якщо під дією тієї рушійної сили джерелом якої є двигун автомобіля і яку прийнято називати силою тяги, автомобіль рухається вперед, то це тільки тому, що тертя кочення набагато менше за тертя ковзання.
Задача 1. Для того щоб зрушити з місця тіло масою 40кг потрібно прикласти горизонтальну силу 200Н. Визначити коефіцієнт тертя.
Дано:
m = 40кг
F = 200Н
μ = ?
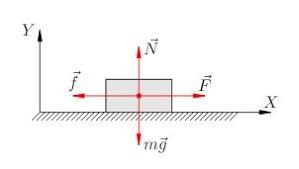
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили та задаємо відповідну систему координат. (на малюнку Fтер позначено ƒ). Записуємо умову механічної рівноваги даного тіла:
1) ∑Fx = F – Fтер = F – μN = 0;
2) ∑Fy = N – Fт = N – mg.
Із (2) випливає N = mg.= 40кг·10м/с2 = 400Н.
Із (1) випливає F = μN, звідси μ = F/N = 200Н/400Н = 0,5.
Відповідь: μ = 0,5.
Задача 2. Тіло масою 10кг знаходиться в стані механічного спокою на похилій площині. Визначити величину діючої на тіло сили тертя та коефіцієнт тертя, якщо кут нахилу площини до лінії горизонту 30°.
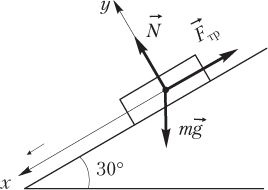
Зауваження. Рішення будь якої задачі механіки, в тій чи іншій мірі ідеалізоване. Наприклад в умовах нашої задачі, ті сили які ми називаємо реакцією опори та силою тертя, виникають в місті контакту тіла з відповідною поверхнею і є розподіленими по цій поверхні. Ми ж зображаємо ці сили такими, що сконцентровано прикладені до центру мас тіла. До речі, те ж стосується і сили тяжіння, дія якої фактично розподілена по всьому об’єму тіла і яку ми зображаємо такою, що діє в центрі мас цього тіла.
Дано:
m = 10кг
α = 30°
Fтер = ? μ = ?
Рішення. Виконуємо малюнок на якому: вказуємо діючі на тіло (на центр мас тіла) сили; задаємо систему координат; вказуємо кутову орієнтацію сил (кут між напрямком сили тяжіння та віссю 0у, визначаємо із геометричних міркувань, а згідно з цими міркуваннями, цей кут дорівнює куту нахилу площини α=30°). Записуємо умову рівноваги тіла і, розв’язавши систему відповідних рівнянь, визначаємо невідомі величини. (Fт = mg = 10кг·10м/с2 =100H).
∑ Fx = –Fтер + Fт sinα = 0 (1)
∑ Fy = N – Fт cosα = 0 (2).
Із (1) → Fтер = Fт sinα .
Із (2) → N = Fт cosα .
Розрахунки: Fтер = 100∙0,5 = 50Н
. N = 100∙0,87 = 87H
Оскільки за визначенням μ = Fтер/N, то μ =50Н/87Н = 0,57
Відповідь: N = 87H; Fтер = 50H; μ = 0,57.
Контрольні запитання.
- Яке тертя називають сухим, а яке в’язким? Яке з них є більшим?
- Що називають силою тертя (тертя ковзання)? Від чого залежить сила тертя ковзання? Як направлена сила тертя ковзання?
- Що називають коефіцієнтом тертя? Від чого залежить коефіцієнт тертя і як він визначається?
- Чому на те тіло яке лежить на горизонтальній поверхні стола, сила тертя не діє, а на те що лежить на похилій площині – діє?
- В процесі аварійного гальмування, задні колеса автомобіля не обертаються, а передні вільно обертаються. Які сили тертя діють на ці колеса? Яка з цих сил є більшою?
- Назвіть основні способи суттєвого зменшення сили тертя.
- Які сили тертя діють на автомобіль в процесі його руху? Які з цих сил протидіють руху автомобіля, а які сприяють цьому руху?
- Іноді визначальне рівняння сили тертя записують у вигляді Fтер = µN або Fтер = –µN. Чи є такий запис правильним? Чому?
Вправа 17.
- Для того щоб зрушити з місця тіло масою 40кг потрібно прикласти горизонтальну силу 200Н. Визначити коефіцієнт тертя.
- Під дією сили 1Н брусок рівномірно рухається горизонтальною поверхнею стола. Яка маса бруска, якщо коефіцієнт тертя між бруском і столом 0,3?
- Автомобіль масою 2т рівномірно рухається горизонтальною дорогою. Яка сила тяги автомобіля, якщо коефіцієнт тертя сил опору 0,1?
- Тіло масою 5кг знаходиться в стані механічного спокою на похилій площині. Визначити величину діючої на тіло сили тертя та коефіцієнт тертя, якщо кут нахилу площини до лінії горизонту 30°.
- Яку силу треба прикласти до тіла масою 5кг, щоб воно рівномірно рухалося вгору похилою поверхнею, кут нахилу якої до лінії горизонту 30°? Коефіцієнт тертя між тілом та поверхнею 0,4.
- З якою силою потрібно притиснути книгу масою 0,5кг до вертикальної стіни, щоб книга не зісковзувала вниз? Коефіцієнт тертя між книгою та стіною 0,45.
- Брусок тягнуть горизонтальною поверхнею прикладаючи горизонтальну силу 2Н. Яка маса бруска, якщо він рухається рівномірно, а коефіцієнт тертя між бруском і поверхнею 0,25.
- На столі лежить стоса із 10 однакових книг. Що легше: зсунути шість верхніх книг, чи витягнути з стоси третю книгу притримуючи решту?
.
§18. Розв’язування задач. Тема: Силовий метод розв’язування задач.
Суть силового методу розв’язування задач полягає в тому, що невідомі величини визначають на основі векторного аналізу діючих на тіло сил та на базі умови його механічної рівноваги: якщо v = 0 або v = const то ∑F = 0, або в проекціях на осі системи координат ΣFx = 0; ΣFy = 0. По суті це означає, що силовий розв’язку задач має чітко визначений порядок дій. І цей порядок є наступним:
- На основі аналізу умови задачі виконують малюнок (обов’язково), на якому чітко вказують всі діючі на дане тіло (точку рівноваги) сили .
- Задають систему координат та вказують кутову орієнтацію сил в ній.
- Записують умову рівноваги тіла, тобто систему рівнянь: ∑Fx = 0; ∑Fy = 0.
- Розв’язавши цю систему, визначають невідомі величини.
Втім, не будемо забувати, що фізика, це цілісна система взаємопов’язаних та взаємодоповнюючих знань. І тому в фізиці, як і в житті, часто доводиться розв’язувати задачі, які передбачають застосування різних методів розв’язку зокрема кінематичного, силового та імпульсно-енергетичного.
Загальні зауваження. В механіці матеріальної точки, а саме таку механіку ми і вивчаємо, прийнято вважати, що всі діючі на тіло сили, діють на його центр мас. Тому, якщо в умові задачі нема конкретних вказівок щодо точки прикладання конкретної сили, вважається що ця сила діє на цент мас відповідного тіла.
Дотримуючись вище наведеного алгоритму та зважаючи на зроблене зауваження, розв’яжемо декілька конкретних задач.
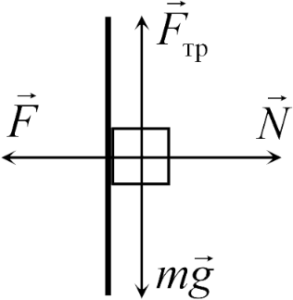
Задача 1. З якою мінімальною силою потрібно притиснути книгу масою 0,8кг до вертикальної стіни, щоб книга не зісковзувала вниз? Коефіцієнт тертя між книгою та стіною 0,4.
Дано:
m=0,8кг
μ = 0,4
F = ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили та задаємо відповідну систему координат. Записуємо умову рівноваги даного тіла:
ΣFx = N – F = 0;
ΣFy = Fтер – Fт = μN – mg = 0.
Із рівняння (1) випливає F = N, де N=?
Із рівняння (2) випливає μN = mg, звідси N = mg/μ.
Таким чином F = N = mg/μ = 0,8кг·9,8(м/с2)/0,4 = 19,8Н
Відповідь: F = 19,8Н.
Задача 2. Визначити силу тяги, яку розвиває тепловоз при рівномірному русі на горизонтальній ділянці шляху, якщо коефіцієнт тертя 0,03, а сила тиску на рейки 25∙106Н?
Загальні зауваження. При розв’язуванні задач фізики, надзвичайно важливим вмінням, є вміння виділяти суттєве (важливе) і не звертати особливу увагу на несуттєве (другорядне, неважливе). Наприклад в умовах даної задачі неважливо чи знаєте ви як влаштований тепловоз і як він створює ту силу яка називається силою тяги. Неважливо скільки коліс в цьому тепловозі і яким чином вони взаємодіють з рейками залізниці. Важливим є те, що на певній горизонтальній поверхні (опорі), є певне тіло, яке під дією певної горизонтальної сили (сили тяги Fтяги) з певною вертикальною силою (силою тиску Fт, а по суті силою тяжіння) діє на опору (рейки залізниці). Важливим є те, що руху тіла протидіє певна узагальнена сила тертя (сила протидії руху тепловоза), основною характеристикою якої є відповідний коефіцієнт тертя. Важливим є те, що тепловоз рухається з певною постійною швидкістю (v = const), бо це означає, що дана задача є задачею статики і що тому мають виконуватись співвідношення: ∑Fx = 0; ∑Fy = 0. Власне таке розуміння суті задачі і дозволяє отримати відповідне рішення.

Дано:
μ = 0,03
Fт = 25·106Н
Fтяги= ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили та задаємо відповідну систему координат. (на малюнку Fтяги позн. F; Fт позн. mg; Fтер позн. ƒ) Записуємо умову рівноваги даного тіла:
ΣFx = Fтяги – Fтер = Fтяги – μN = 0;
ΣFy = N – Fт = 0.
Із рівняння (1) випливає Fтяги = μN, де N=?
Із рівняння (2) випливає N = Fт = 25·106Н .
Таким чином Fтяги = μN = 0,03·25·106Н = 0,75·106Н = 750кН
Відповідь: F = 750кН.
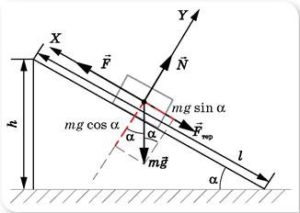
Задача 3. Тіло масою 15кг знаходиться на похилій площині, кут нахилу якої до горизонту 30°. Яку направлену вздовж площини силу треба прикласти до тіла, щоб воно піднімалось вгору з постійною швидкістю? Коефіцієнт тертя 0,35.
Дано:
m = 15кг
α = 30°
v = const
μ = 0,35
F = ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили; задаємо систему координат; вказуємо кутову орієнтацію сил (кут між силою тяжіння та віссю 0у (α=30°) визначаємо із геометричних міркувань). Записуємо умову механічної рівноваги тіла. Розв’язавши систему відповідних рівнянь, визначаємо невідому величину.
∑Fx = F – Fтsinα – Fтер = F – mgsin30° – μN = 0;
∑Fy = N – Fтcosα = N – mgcos30° = 0.
Із рівняння (2) випливає N = mgcos30° = 15кг10(м/с2)0,87 = 130Н,
Із рівняння (1) випливає F = mgsin30° + μN = 15кг·10(м/с2)0,5 + 0,35·130Н = 120Н.
Відповідь: F = 120Н.
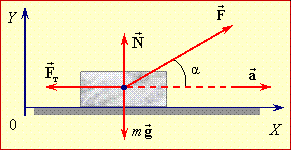
Задача 4. Тіло масою 50кг за допомогою мотузки яка утворює кут 30° з горизонтом, рівномірно тягнуть горизонтальною поверхнею. Яку силу прикладають при цьому, якщо коефіцієнт тертя 0,25?
Дано:
m = 50кг
α = 30°
v = const
μ = 0,25
F = ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили; задаємо систему координат; вказуємо кутову орієнтацію сил. Записуємо умову механічної рівноваги тіла. Розв’язавши систему відповідних рівнянь, визначаємо невідому величину.
∑Fx = Fcosα – Fтер = Fcos30° – μN = 0;
∑Fy = N + Fsinα – Fт = N + Fsin30° – mg = 0.
Таким чином, ми маємо систему двох рівнянь з двома невідомими (F, N). Порядок розв’язку таких систем загально відомий. Одну з невідомих визначають з одного рівняння і отриманий результат підставляють у друге рівняння. При цьому отримують рівняння з одним невідомим. Наприклад в умовах нашої задачі, із рівняння (1) визначаємо реакцію опори (N), а отриманий результат підставляємо в рівняння (2).
Із рівняння (1) випливає N = Fcos30°/μ.
Отриманий результат підставляємо в рівняння (2), при цьому:
Fcos30°/μ + Fsin30° – mg = F(cos30°/μ + sin30°) – mg = 0, звідси
F = mg/(cos30°/μ + sin30°).
Розрахунки: F = mg/(cos30°/μ + sin30°) = 50кг10(м/с2)/(0,87/0,25 + 0,5) = 125Н.
Відповідь: F = 125Н.
Задача 5. На столі лежать один на одному чотири однакові бруски. При цьому нижній брусок жорстко прикріплений до столу. В якому випадку треба прикласти більшу силу: щоб зрушити три верхні бруски разом, чи щоб витягти другий брусок зверху, притримуючи решту?
Рішення. Як в першому так і в другому випадку переміщенню брусків протидіє сила тертя, величина якої визначається за формулою F=μN. Оскільки бруски однакові, то в обох випадках коефіцієнт тертя (μ) є однаковим. Якщо ж говорити про реакцію опори (N), а по суті про ту силу з якою контактуючі поверхні притискаються одна до одної, то в першому випадку (переміщують три бруски) N1 = 3mg, де m – маса одного бруска. В другому ж випадку N2 = mg + 2mg = 3mg. Адже на верхню поверхню другого бруска тисне сила mg, а його нижня поверхня притискається до поверхні третього бруска з силою 2mg. Таким чином F1 = μ3mg, F2 = μ3mg.
Відповідь: Зусилля в обох випадках будуть однаковими.
Задача 6. Куля масою 2кг розташована між двома площинами так, як зображено на малюнку. Визначити діючі на кулю реакції опори.
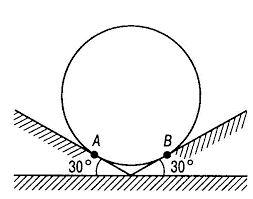

Загальні зауваження. 1) Із геометрії відомо, що дотична до кола є перпендикулярною до його радіусу, тобто до лінії яка проходить через центр кола. А оскільки плоска опора є дотичною до кола (кулі), то реакція опори завжди проходить через центр кола (сфери). 2) Зазвичай, оптимальність введення системи координат полягає в тому, що бодай одна з осей цієї системи, має співпадати з напрямком невідомої сили. Однак в деяких випадках, проблеми з визначенням кутів між силами та «оптимально» введеними осями координат, значно більші за ті проблеми які пов’язані з математичним рішенням системи рівнянь. Прикладом такого випадку є дана задача.
Дано:
m=20кг
NА=?
NВ=?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на кулю сили: Fт, NA, NB. А оскільки лінії дії цих сил перетинаються в центрі кулі, то саме цей центр буде як точкою прикладання всіх сил, так центром системи координат. Записуємо умову рівноваги кулі.
∑Fx= –NBsin30º + NAsin30º=0;
∑Fy= NBcos30º + NAcos30º – FT=0.
із (1) → NAsin30º = NBsin30º → NA = NB;
із (2) → 2NAcos30º = FT = mg; → NA=mg/2cos30º = 2∙10/2∙0,87=11,5H
Відповідь: NA=NB=11,5H.
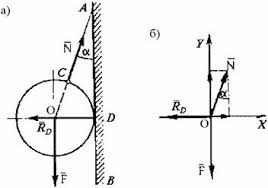
Задача 7. Куля масою m і радіусом R підвішена на нитці довжиною ℓ до гладенької вертикальної стіни. Визначити силу натягу нитки та силу тиску кулі на стіну (тертям між кулею та стіною знехтувати).
Дано:
m
R
ℓ
N = ? RD = ?
Рішення. За відсутності сили тертя між поверхнею кулі та поверхнею стіни, куля неминуче розвернеться таким чином, що напрям лінії нитки буде проходити через центр мас кулі. Зважаючи на ці обставини, зображаємо діючі на центр мас сили (Fт=mg, N, RD), задаємо систему координат та записуємо умову рівноваги кулі.
(1) ∑Fx = – RD + Nsinα = 0;
(2) ∑Fy = – mg + Ncosα = 0.
Із (2) → N = mg/cosα,
підставивши в рівняння (1) отримаємо
– RD + mgsinα/cosα = – RD + mgtgα = 0, звідси
RD = mg∙tgα, де tgα = ?
З геометричного аналізу прямокутного трикутника АDO випливає: tgα = ОD/AD = R/AD. У відповідності з теоремою Піфагора OD2 + AD2 = OA2, або R2 + AD2 = (R+ℓ)2, звідси AD2 = (R+ℓ)2 – R2, звідси AD = √[(R+ℓ)2 – R2] = √(2Rℓ+ℓ2)
Таким чином: tgα = R/√(2Rℓ+ℓ2); cosα = AD/OA = (R+ℓ)/√(2Rℓ+ℓ2);
RD = mg∙ R/√(2Rℓ+ℓ2);
N = mg/cosα = mg∙√(2Rℓ+ℓ2)/(R+ℓ).
Відповідь: RD = mg∙ R/√(2Rℓ+ℓ2);
. N = mg∙√(2Rℓ+ℓ2)/(R+ℓ).
Вправа №18.
- Тіло під дією горизонтальної сили 6Н рухається з постійною швидкістю. Яка маса тіла, якщо коефіцієнт тертя між тілом і поверхнею 0,4?
- Учень за допомогою динамометра рівномірно переміщує дерев’яний брусок масою 200г горизонтальною поверхнею. Який коефіцієнт тертя, якщо динамометр показує 0,6?
- Коефіцієнт тертя ящика масою 100кг об підлогу 0,3. Ящик тягнуть за мотузку, що утворює кут 45º з горизонтом. Яку силу треба прикласти, щоб ящик рухався рівномірно?
- Тіло масою 12кг знаходиться на похилій площині, кут нахилу якої до горизонту 30°. Яку направлену вздовж площини силу треба прикласти до тіла, щоб воно піднімалось вгору з постійною швидкістю? Коефіцієнт тертя 0,3.
- На двох тросах однакової довжини висить вантаж масою 10кг. При цьому кут між тросами 90º. Визначити сили натягу тросів.
- Вантаж масою 5кг притискають до вертикальної стіни силою 12Н. Яка потрібна сила, щоб тягнути вантаж вгору, якщо коефіцієнт тертя 0,3?
- На прикріпленій до вертикальної стіни нитці висить куля масою 2кг. Визначити силу натягу нитки та силу тиску кулі на стіну, якщо кут між ниткою та стіною 30°. Тертям між кулею та стіною знехтувати.
- 8. Зображена на малюнку куля масою 10кг, знаходиться між двома взаємно перпендикулярними площинами. Визначити діючі на кулю реакції опори.
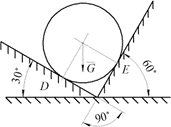
- Визначити реакції опори в зображеній на малюнку ситуації, якщо маса вантажу 10кг, α = 30°.

.
§19. Сила інерції.
28 квітня 1686 року, Лондонському королівському товариству з розвитку знань про природу, було представлено перший том ньютонівських «Математичних начал натуральної філософії». В цій фундаментальній праці геніальний Ісаак Ньютон не лише чітко визначив базові фізичні величини класичної механіки та сформулював її основні закони, а й з максимально можливою точністю описав властивості та прояви тієї «вродженої сили», яку прийнято називати силою інерції.
Позначаючи силу інерції терміном «вроджена сила», Ньютон підкреслював факт того, що поява цієї сили обумовлена не взаємодією даного тіла з іншими тілами, а його вродженою, природною здатністю протидіяти будь якій зміні швидкості руху самого тіла. Описуючи ж властивості «вродженої сили», Ньютон наголошував на тому, що ця сила виникає в процесі прискореного руху тіла, дорівнює добутку маси тіла на його прискорення і направлена в сторону протилежну від прискорення.
По суті поява сили інерції обумовлена взаємодією прискорено рухомого тіла з тим фізичним об’єктом який називається простором-часом Всесвіту. Бо простір-час, то ж не просто безкінечна, безструктурна, вічна пустота, а надзвичайно складний, багатогранний, багатофункціональний фізичний об’єкт, параметри та властивості якого, певним чином залежать від тих речовинних об’єктів які знаходяться в цьому просторі-часі, та тих подій (рухів) які відбуваються в ньому. Проявами ж цих властивостей є гравітаційні, електричні та магнітні поля, електромагнітні та гравітаційні хвилі, видиме світло, інфрачервоне, ультрафіолетове, рентгенівське та гама випромінювання, тощо. Якщо ж говорити про фізичну суть того зв’язку який існує між простором-часом та силою інерції, то ця суть є предметом пояснень загальної теорії відносності.
Зважаючи на вище сказане, ми не будемо вдаватися в деталі механізму взаємодії прискорено рухомого тіла з простором-часом Всесвіту. Ми просто констатуємо факт того, що на будь яке прискорено рухоме тіло, неминуче діє сила інерції, величина якої пропорційна добутку маси тіла на його прискорення і яка направлена в сторону протилежну від прискорення.
Сила інерції – це така сила, поява якої обумовлена прискореним рухом тіла, яка дорівнює добутку маси тіла на його прискорення, і яка завжди протидіє появі та зростанню цього прискорення.
Позначається: Fі
Визначальне рівняння: Fі = –ma
Одиниця вимірювання: [Fі] = Н, ньютон
Подібно до того як сила тертя протидіє переміщенню контактуючих поверхонь, як сила пружності протидіє пружній деформації тіла, сила інерції протидіє прискореному руху тіла. А це означає, що як тільки тіло починає рухатись з певним прискоренням, автоматично з’являється сила інерції напрям якої протилежний до напрямку прискорення.
Наприклад якщо в момент розгону, прискорення ракети направлено вгору, то діюча на ракету сила інерції направлена вниз. Якщо в процесі гальмування, прискорення автомобіля направлено назад (в сторону протилежну від напрямку руху), то діюча на автомобіль сила інерції направлена вперед. Якщо в процесі обертання навколо Землі, Місяць рухається з доцентровим прискоренням, то діюча на нього сила інерції є відцентровою. Якщо прискорення тіла направлено вправо, то діюча на тіло сила інерції направлена вліво. Якщо прискорення вліво – сила інерції вправо, прискорення вперед – сила інерції назад і т.д.
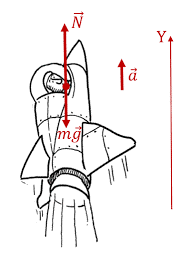

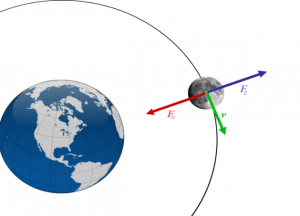
Мал.55. Якщо тіло рухається з прискоренням, то на нього неминуче діє певна сила інерції, направлена в сторону протилежну від напрямку прискорення.
Вивчаючи фізику ви неминуче переконаєтесь в тому, наскільки незамінно важливою є та сила, яку прийнято називати силою інерції. Сила, без розуміння суті якої не можливо логічно пояснити величезний пласт явищ. Не можливо пояснити чому різні тіла падають з однаковим прискореннями; чому тіла рухаються за інерцією; чому Земля розтягнута в екваторіальній площині; чому Місяць не падає на Землю, а Земля не падає на Сонце; чому в процесі вертикально прискореного руху системи опора-тіло, вага тіла в залежності від напрямку та величини прискорення може бути різною; чому в кабіні штучного супутника Землі, тіла перебувають в станів невагомості і що представляє собою цей стан; чим сила тяжіння (Fт = mg) відрізняється від сили гравітаційної взаємодії (Fгр = GMm/R2) і чому в загальному випадку сила тяжіння не проходить через центр маси Землі. І таких «чому?» незліченна кількість.
До речі, той факт, що в процесі вільного падіння, важкі і легкі тіла падають з однаковим прискоренням (g = 9,8м/с2), є прямим наслідок того, що на ці тіла, окрім направленої вертикально вниз сили тяжіння (Fт = mg), неминуче діє рівна їй за величиною і протилежно направленої сила інерції (Fі = –mg). Власне під дією цих двох рівних за величиною і протилежних за напрямком сил, тіло і рухається з певним прискоренням. І величина цього прискорення не залежить ні від маси тіла, ні від величини діючої на нього сили тяжіння. Адже на важке тіло діє не лише велика сила тяжіння, а й відповідно велика сила інерції. Натомість на легке тіло діє мала сила тяжіння і відповідно мала сила інерції.
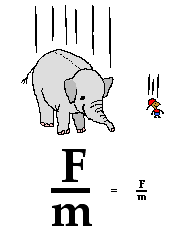
Мал.56. На вільно падаюче тіло діють дві рівні за величиною і протилежні за напрямком сили: сили тяжіння (Fт = mg) та сила інерції (Fі = –mg).
Ви можете запитати: «А як бути з умовою механічної рівноваги тіла, тобто з законом в якому говориться про те, що коли діючі та тіло зовнішні сили зрівноважують одна одну, то тіло знаходиться в стані спокою (v = 0), або прямолінійного рівномірного руху (v = const)?» Відповідаючи на це слушне запитання, можна сказати наступне.
Дійсно. В умові механічної рівноваги стверджується: якщо векторна сума діючих на тіло зовнішніх сил дорівнює нулю, то тіло знаходиться в стані механічної рівноваги. Іншими словами: якщо ∑F = 0, то а = 0. Аналізуючи дане твердження зверніть увагу на те, що в ньому говориться про векторну суму зовнішніх сил, тобто звичайних сил взаємодії: сила тяжіння, сила тертя, сила пружності, сила Архімеда, реакція опори, сила тяги, тощо. В нашому ж випадку, ми маємо справу з силою інерції, тобто силою яка не є зовнішньою. З силою, поява якої обумовлена самим фактом прискореного руху тіла. Тому, коли ми стверджуємо що в процесі вільного падіння тіла, існує рівновага між силою тяжіння і силою інерції, то маємо на увазі так звану динамічну рівновагу. Рівновагу, яка передбачає рух тіла не з постійною швидкістю (а = 0), а з постійним прискоренням (а ≠ 0).
Динамічна рівновага тіла (матеріальної точки) – це такий механічний стан тіла, при якому воно, під дією зовнішніх сил та сили інерції, знаходиться в стані рівноприскореного руху (а = const ≠ 0).
Знаючи властивості сили інерції можна відповісти на ще одне важливе запитання: «Чому після припинення дії зовнішньої сили, тіло рухається за інерцією?» На перший погляд такий рух здається безпричинним, тобто таким який не підтримується жодною зовнішню силою. І це правда, жодна зовнішня сила не є причиною руху тіла за інерцією. Та все ж інерційний рух має свою силову причину. І ця причина – сила інерції, тобто та внутрішня сила, яка протидіє будь-якій зміні швидкості руху тіла.
Дійсно, як тільки рухоме тіло прагне зменшити свою швидкість, автоматично з’являється сила інерції, яка протидіє цим намаганням i так би мовити «підштовхує» тіло. І якщо тіло, всупереч дії сили інерції все ж зупиняється, то це тільки тому, що на нього діють певні зовнішні гальмуючі сили, зокрема різноманітні сили тертя. Якщо ж дія цих сил відсутня, або мізерно мала, то тіло може зберігати стан рівномірного руху як завгодно довго. Наприклад, Земля вже протягом 4,5 мільярдів років обертається навколо Сонця з практично незмінною швидкістю. А якщо напрям цієї швидкості змінюється, то це тому, що цю зміну спричиняє сила гравітаційної взаємодії Землі з Сонцем.
Варто зауважити, що ті задачі, в яких тіло під дією певної системи сил рухається з постійним прискоренням є задачами динаміки. Однак, алгоритм силового рішення цих динамічних задач практично не відрізняється від алгоритму рішення задач статики. В основі цього рішення лежить твердження (закон) яке називається умовою динамічної рівноваги тіла.
Умова динамічної рівноваги тіла – це закон, в якому стверджується:
Тіло (матеріальна точка) буде знаходитись в стані динамічної рівноваги (а = const ≠ 0) тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил та сили інерції дорівнює нулю. Іншими словами:
якщо ∑F + Fi = 0, то а = const ≠ 0 і навпаки: якщо а = const ≠ 0, то ∑F + Fi = 0.
Як і задачі статики (а = 0), задачі динаміки (а ≠ 0) розв’язуються у повній відповідності з строго визначеним алгоритмом:
- Виконуємо малюнок, на якому вказуємо всі діючі на тіло сили, в тому числі і силу інерції.
- Задаємо систему координат та вказуємо кутові орієнтації сил.
- Записуємо відповідну малюнку систему рівнянь, які відповідають умові динамічної рівноваги тіла (∑F+Fi=0): ∑Fx = 0; ∑Fy = 0.
- Розв’язавши наявну систему рівнянь, визначаємо невідомі величини.
Ілюструючи суть та можливості вище описаного силового методу розв’язування задач динаміки, розглянемо декілька конкретних прикладів. (Відразу ж зауважимо, що графічних ілюстрацій з позначеною на них силою інерції надзвичайно мало. Тому в графічних поясненнях до задач, зображення сили інерції зазвичай відсутнє. А це означає, що відповідну силу ви маєте позначати самостійно.
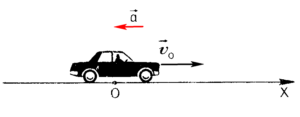
Задача 1. При аварійному гальмуванні, автомобіль масою 3т рухається з прискоренням 3м/с2. Яка сила інерції діє на цей автомобіль. Як направлена ця сила відносно напрямку руху автомобіля?

Дано:
m = 3т = 3000кг
a = 3м/с2
Fі = ?
Рішення. За визначенням Fі = –ma. Це означає, що величина сили інерції визначається за формулою Fі = ma = 3000кг·3м/с2 = 9000Н, а напрям цієї сили є протилежним до напрямку прискорення тіла. А оскільки в процесі гальмування (зменшення швидкості), прискорення тіла направлено в сторону протилежну від напрямку швидкості, то сила інерції буде направлена в ту ж сторону що і швидкість, тобто в сторону руху автомобіля.
Відповідь: Fі = 9000Н. При гальмуванні, сила інерції направлена в напрямку руху автомобіля.
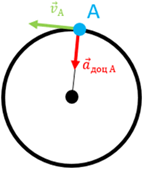
Задача 2. Автомобіль масою 3т зі швидкістю 54км/год рухається заокругленням дороги радіус якого 300м. Визначити величину діючої на автомобіль сили інерції.

Дано:
m = 3т = 3000кг
v = 54км/год =15м/с
R = 300м
Fi = ?
Рішення. Рухаючись заокругленням дороги, автомобіль рухається з певним доцентровим прискоренням (ад = v2/R) і тому на нього неминуче діє відповідна і направлена в протилежну сторону від прискорення (тобто відцентрова) сила інерції Fi = maд = mv2/R (на малюнку ця сила не показана).
Розрахунки Fi = 3000кг∙(15м/с)2/300м = 2250Н.
Відповідь: Fi = 2250Н.
Задача 3. Автомобіль масою 1,2т, маючи тягову силу 3кН, рухається з прискоренням 1,5м/с2. Визначити загальну силу опору руху автомобіля (загальну силу тертя).
Дано:
m = 1,2т = 1200кг
Fтяги = 3кН = 3000Н
a = 1,5м/с2
Fтер = ?
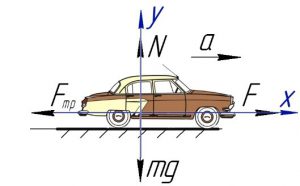
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на автомобіль сили. А цими силами є: сила тяжіння Fт = mg, реакція опори N, сила тяги Fтяги =F, сила тертя Fтер та направлена в протилежну сторону від прискорення сила інерції Fі = ma. (на малюнку не позначена) Задаємо відповідну систему координат. Записуємо умову рівноваги тіла вздовж осі 0х:
ΣFx = Fтяги – Fтер – Fi = Fтяги – Fтер – mа = 0. Звідси випливає
Fтер = Fтяги – mа.
Розрахунки: Fтер = 3000Н – 1200кг∙1,5м/с2 = 3000Н – 1800Н = 1200Н
Відповідь: Fтер = 1200Н = 1,2кН.
Задача 4. З яким прискоренням рухається брусок похилою площиною кут нахилу якої 30°, якщо коефіцієнт тертя 0,2?
Дано:
α = 30°
µ = 0,2
а = ?
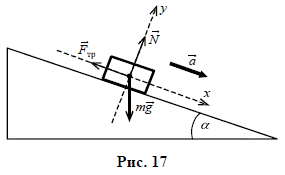
Рішення. Виконуємо малюнок на якому: вказуємо всі діючі на тіло сили (сила тяжіння, реакція опори, сила тертя, сила інерції); задаємо систему координат; вказуємо кутову орієнтацію сил (на малюнку сила інерції не вказана). Записуємо умову динамічної рівноваги тіла і, розв’язавши систему відповідних рівнянь, визначаємо невідому величину.
∑ Fх = –Fтер –Fі + Fтsinα = – µN – ma + mgsinα = 0 (1)
∑ Fу = N – Fтcosα = N – mgcosα = 0 (2)
Із (1) → ma = mgsinα – µN, де N = ?
Із (2) → N = mgcosα.
Таким чином, ma = mgsinα – µmgcosα, звідси a = g(sinα – µcosα).
Розрахунки: a = g(sin30° – µcos30°) = 9,8(м/с)2(0,50 – 0,2·0,87) = 3,2м/с2.
Відповідь: а = 3,2м/с2.
Контрольні запитання.
- Ньютон називав силу інерції «вродженою силою». Що підкреслював геніальний вчений такою назвою?
- Взаємодією з яким фізичним об’єктом обумовлена поява сили інерції?
- Від чого залежить і як направлена сила інерції?
- Чи діє на тіло сила інерції при його рівномірному прямолінійному русі?; при рівномірному русі тіла по колу?
- Поясніть, чому важкі і легкі тіла падають з однаковим прискоренням?
- Що називають динамічною рівновагою тіла?
- Що стверджується в умові динамічної рівноваги тіла?
- Чим динамічна рівновага тіла відрізняється від його механічної рівноваги?
- Чи є рух тіла за інерцією безпричинним, тобто таким, що не підтримується жодною з відомих сил?
- Який напрям сили інерції в зображених на малюнку ситуаціях? Як змінюється при цьому швидкість тіла?
Вправа №19.
- При аварійному гальмуванні, автомобіль масою 2,5т рухається з прискоренням 5м/с2. Яка сила інерції діє на цей автомобіль. Як направлена ця сила відносно напрямку руху автомобіля?
- Гоночний автомобіль розганяється до швидкості 108км/год за 5с. Яка сила інерції діє при розгоні на водія автомобіля, якщо маса водія 80кг?
- Автомобіль з швидкістю 72км/год рухається заокругленням дороги радіус якого 400м. Яка сила інерції діє при цьому на водія автомобіля, якщо маса водія 80кг? Який напрям цієї сили?
- З якою силою тіло масою 50кг тисне на опору в ситуаціях:
а) система опора-тіло знаходиться в стані механічного спокою;
б) система опора-тіло рухається з направленим вгору прискоренням 5м/с2;
в) система опора-тіло рухається з направленим вниз прискоренням 5м/с2?
- В процесі аварійного гальмування, автомобіль масою 1,5т рухається з прискоренням 4м/с2. Визначити діючу на автомобіль силу тертя та коефіцієнт тертя
- 6. З яким прискоренням рухатиметься брусок похилою площиною, якщо кут нахилу площини 30°, а коефіцієнт тертя 0,15?
- Автомобіль масою 2т рушаючи з місця досягає швидкості 30м/с за 20с. Визначити силу тяги автомобіля, якщо коефіцієнт опору руху становить 0,05.
- З якою силою буде тиснути автомобіль масою 2т на середину опуклого моста, якщо радіус моста 100м, а швидкість автомобіля 36км/год?
.
§20. Розв’язування задач. Тема: Силовий метод розв’язування задач динаміки.
Фізика загалом і механіка зокрема, це єдиний цілісний організм всі частини якого взаємопов’язані та взаємо переплетені. Тому, коли ми ділимо механіку на кінематику, статику та динаміку, то робимо це досить умовно. Скажімо, на даний момент ми вивчаємо тему, яка називається «статика», тобто ту тему в якій вивчають параметри, закономірності та причини стану механічної рівноваги тіл (v = 0 або v = const). В цій темі основною фізичною величиною є сила, а основним законом – умова механічної рівноваги тіла.
З іншого боку, однією з найважливіших сил механіки є сила інерції, тобто та сила, поява якої обумовлена прискореним рухом тіла. Формально ті задачі в яких тіло під дією певної системи сил рухається з прискоренням, є задачами динаміки. Однак, якщо мова йде про силове рішення цих задач, то воно практично не відрізняється від рішення задач статики. А це означає, що як з логічної, так і з методологічної точок зору, ту силу яка називається силою інерції і ті задачі рішення яких базується на застосування умови динамічної рівноваги тіла, доцільно вивчати і розв’язувати в межах того розділу механіки, який називається статикою.
Варто зауважити, що є два базові методи розв’язування задач динаміки: силовий та імпульсно-енергетичний. Про суть та можливості імпульсно-енергетичного методу ми поговоримо в найближчому майбутньому. Наразі ж, мова піде про силовий метод розв’язування задач динаміки. Суть цього методу дуже проста: на основі аналізу діючих на тіло сил (в тому числі і сили інерції), та на базі умови його динамічної рівноваги (якщо а = const, то ∑F+Fi = 0) визначаються невідомі величини. За такого підходу задачі динаміки (а ≠ 0), стають абсолютними аналогами задач статики (а = 0). А це означає, що ці задачі розв’язуються за універсальним, чітко визначеним алгоритмом:
- Виконуємо малюнок, на якому вказуємо всі діючі на тіло сили, в тому числі і силу інерції.
- Задаємо систему координат та вказуємо кутові орієнтації сил.
- Записуємо відповідну малюнку систему рівнянь, які відповідають умові динамічної рівноваги тіла (∑F + Fi = 0): ∑Fx = 0; ∑Fy = 0.
- Розв’язавши наявну систему рівнянь, визначаємо невідомі величини.
Ілюструючи суть та можливості вище описаного силового методу розв’язування задач динаміки, розглянемо ряд конкретних прикладів.
Задача 1. Тіло масою 15кг знаходиться на похилій площині, кут нахилу якої до горизонту 30°. Яку направлену вздовж площини силу треба прикласти до тіла, щоб воно піднімалося вгору з прискоренням 1м/с2? Коефіцієнт тертя 0,35.
Дано:
m = 15кг
α = 30°
а = 1м/с2
μ = 0,35
F = ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили (сила інерції не позначена). Задаємо систему координат; вказуємо кутову орієнтацію сил. Записуємо умову механічної рівноваги тіла. Розв’язавши систему відповідних рівнянь, визначаємо невідому величину.
∑Fx = F – Fтsinα – Fтер – Fi = F – mgsin30° – μN – ma = 0;
∑Fy = N – Fтcosα = N – mgcos30° = 0.
Із рівняння (2) випливає N = mgcos30° = 15кг10(м/с2)0,87 = 130Н,
Із рівняння (1) випливає F = mgsin30° + μN + ma = 15кг·10(м/с2)0,5 + 0,35·130Н + 15кг∙1(м/с2) = 135Н.
Відповідь: F = 135Н.
Задача 2. Через який час після початку аварійного гальмування зупиниться автомобіль, що рухається зі швидкістю 16м/с, якщо коефіцієнт тертя 0,4? Яким буде гальмівний шлях автомобіля?
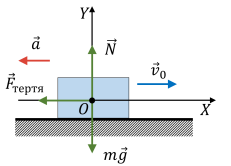
Дано:
v0 = 16м/с
vкv = 0м/с
μ = 0,4
t = ? s = ?
Рішення. Оскільки за визначенням а = (vк – v0)/t, то t = (vк – v0)/a, де а = ?
Пройдений автомобілем шлях можна визначити як за рівнянням пройденого шляху s = v0t + (a/2)t2, так і за формулою s = (vк2–v02)/2a, де а = ?
Таким чином, в будь якому випадку рішення задачі зводиться до визначення прискорення. А оскільки це прискорення міститься у визначальному рівнянні сили інерції Fi = ma, то величину прискорення визначаємо на основі аналізу тих сил які діють на автомобіль в процесі його гальмування. З цією метою виконуємо малюнок на якому вказуємо всі діючі на автомобіль сили (сила інерції як завжди не позначена). Задаємо відповідну систему координат. Записуємо умову рівноваги тіла.
∑Fx = Fi – Fтер = ma – μN = 0;
∑Fy = N – mg, звідси N = mg
Із (1) → a = μN/m, а враховуючи що N = mg, a = μmg/m = μg = 0,4∙10м/с2 = 4м/с2. Оскільки рух автомобіля є сповільненим (v↓), то його прискорення має знак « – », тобто а = – 4м/с2. Враховуючи даний факт, можна записати:
t = (vк – v0)/a = (0м/с – 16м/с)/(– 4м/с2) = 4с
s = v0t + (a/2)t2 = 16(м/с)∙4с + (– 4м/с2)∙(4с)2/2 = 64м – 32м = 32м;
s = (vк2–v02)/2a = [(0м/с)2 – (16м/с)2]/2∙(– 4м/с2) = 32м.
Відповідь: t = 4с; s = 32м.
Задача 3. Автомобіль масою 2т проходить по опуклому мосту з радіусом кривизни 40м зі швидкістю 36км/год. З якою силою автомобіль тисне на середину моста?
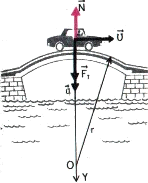
Дано:
m = 2т = 2·103кг
R = 40м
v = 36км/год = 10м/с
N = ?
Рішення. Оскільки та сила з якою автомобіль тисне на опору (міст), чисельно дорівнює тій силі з якою опора тисне на автомобіль (реакція опори N), то рішення задачі зводиться до визначення діючої на автомобіль реакції опори. Визначаючи цю реакцію, виконуємо малюнок на якому вказуємо ті сили які діють на автомобіль у верхній точці моста. А враховуючи факт того, що автомобіль з швидкістю v рухається по колу, а отже рухається з доцентровим прискоренням a = v2/R, можна стверджувати, що вздовж вертикальної осі на автомобіль окрім сили тяжіння та реакції опори діє сила інерції Fi = ma = mv2/R, і що у верхній точці моста вона направлена вертикально вгору.
Записуємо умову динамічної рівноваги даного тіла в напрямку вертикальної осі (оскільки на малюнку ця вісь направлена вниз, то і знаки сил є відповідними):
∑Fx = Fт – Fi – N = mg – mv2/R – N = 0. Звідси випливає:
N = mg – mv2/R = m(g – v2/R)
Розрахунки: N = 2·103кг(10м/с2 – (10м/с)2/40м) = 2·103кг7,5м/с2 = 15·103Н.
Відповідь: N = 15кН.
Задача 4. Літак виконує так звану «мертву петлю», яка представляє собою вертикальну колову траєкторію. З якою силою пілот тисне на сидіння літака (на опору) у верхній та нижній точках «мертвої петлі», якщо швидкість літака 360км/год, а радіус петлі 400м? Маса пілота 80кг.
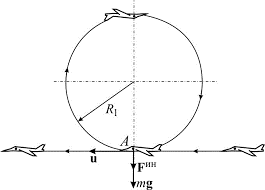
Дано:
m = 80кг –
v = 360км/год = 100м/с
R = 400м
N1 = ? N2 = ?
Рішення: Виконуємо малюнок на якому вказуємо всі діючі на пілота літака сили у верхній та нижній точках «мертвої петлі». А цими силами є: 1) Сила тяжіння Fт = mg. 2) Реакція опори N. 3) Сила інерції, тобто та сила поява якої обумовлена тим, що рухаючись по колу, тіло рухається з певним доцентровим прискоренням а=v2/R, якому відповідає певна сила інерції: Fi = mv2/R.
При цьому, у верхній та нижній точках траєкторії, вище згадані сили діють вздовж вертикалі 0у, направленої вгору. Зважаючи на це, запишемо умову рівноваги тіла (пілота) для нижньої (1) і верхньої точки траєкторії. При цьому будемо вважати, що в обох точках, реакція опори направлена вгору.
1) ∑Fy = –Fi – Fт + N1= 0, звідси випливає:
N1 = Fi + Fт = mv2/R + mg = 80(1002/400 + 10) = 2800Н
2) ∑Fy = Fi – Fт + N2= 0, звідси випливає:
N2 = Fт – Fі = mg – mv2/R = 80(10 – 1002/400) = 80(10 – 25) = –1200 Н, знак «–» вказує на те, що в реальності реакція опори N2 направлена вниз. А це означає, що пілот з силою 1200Н тисне на опору (сидіння) і ця сила направлена вгору.
Відповідь: N1 = 2800Н; N2 = 1200Н.
Варто зауважити, що ту силу з якою тіло діє на опору, називають вагою тіла. Про суть та особливості цієї сили ми поговоримо в наступному параграфі. Наразі ж зауважимо, що за звичайних умов, вагу тіла дорівнює діючій на тіло силі тяжіння. Скажімо за звичайних умов вага тіла масою 80кг становить 800Н. А це означає, що в умовах попередньої задачі, вага того пілоту який виконує «мертву петлю» у верхній точці петлі збільшується у 1200/800 = 1,5 рази, а в нижній точці, збільшується в 2800/800 = 3,5 рази. При цьому пілот відчуває відповідні перевантаження.
Задача 5. Через нерухомий блок перекинуто нитку до кінців якої прив’язано вантажі масою 2,0кг і 2,2кг. З яким прискоренням рухатимуться ці тягарці?
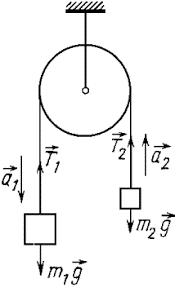
Зауваження. Нерухомий блок представляє собою легкий шків, що вільно обертається навколо нерухомої осі. Вважається, що рухомий шків не змінює натяг перекинутої через нього нитки (мотузки, канату, тощо). А це означає, що на ті тіла які знаходяться по обидва боки шківа діють однакові реакції опори Т1 = Т2 = Т. (Зазвичай ту силу з якою нитка діє на тіло називають силою натягу нитки і позначають Т). За відсутності додаткової інформації, прийнято вважати, що маса рухомого шківа є нулевою, а тертя в його осі відсутнє.
Дано:
М = 2,2кг
m = 2,0кг
а =?
Рішення. Ясно, що в заданій системі вантаж М з певним прискоренням а буде опускатися, в вантаж m, з аналогічним прискоренням підніматися. Зважаючи на вище сказане, виконуємо малюнок на якому вказуємо всі діючі на кожне тіло сили в тому числі і сили інерції. З аналізу малюнку, а по суті з умови динамічної рівноваги тіла, випливає:
Т1 = Т = Мg – Мa;
Т2 = Т = mg + ma.
Оскільки Т1 = Т2 , то Mg – Ma = mg + ma, або Mg – mg = Ma + ma, або g(M – m) = a(M + m), звідси а = g(M – m)/(M + m).
Розрахунки: а = g(M – m)/(M + m) = 10(2,2 – 2,0)/(2,2 + 2,0) = 0,48м/с2
Відповідь: а = 0,48м/с2.
Задача 6. Визначити прискорення вантажів зв’язаних ниткою перекинутою через невагомий блок як помазано на малюнку, якщо маса лівого вантажу 0,6кг, а правого 0,3кг. Коефіцієнт тертя між лівим вантажем та похилою поверхнею 0,1. Кут нахилу поверхні 45°.
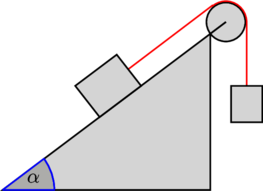
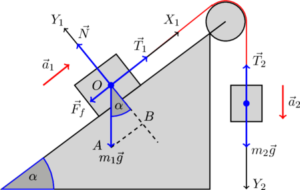
Загальні зауваження. В умовах даної задачі не зовсім ясно, в якому напрямку будуть рухатись вантажі, а відповідно як направлені їх прискорення, а отже і сили інерції. Звичайно, можна провести певний аналіз ситуації і точно визначити напрямки руху тіл. Однак ми вже говорили про те, що в подібних ситуаціях із двох можливих варіантів напрямку сумнівної сили, можна обирати як перший так і другий. При цьому, якщо в результаті розв’язування задачі, числове значення відповідної сили (в нашому випадку сили інерції, а отже і прискорення) виявиться зі знаком «–», то це означатиме, що в реальності ця сила направлена в протилежну сторону від нами вибраної. Зважаючи на вище сказане будемо вважати, що вертикально висяче тіло з прискоренням а опускається вниз, і що тому діюча на це тіло сила інерції направлена вертикально вгору. При цьому тіло на площині з аналогічним прискоренням рухатиметься вгору, а сила інерції буде направленою вниз (вздовж площини).
Дано:
m1 = 0,6кг
m2 = 0,3кг
μ = 0,1
α = 45°
a = ?
Рішення. Виходячи з того, що невідома величина (прискорення а) є складовою сили інерції (Fi = ma), виконуємо малюнок на якому вказуємо діючі на кожне тіло сили (сила інерції на малюнку не позначена). Задаємо систему координат та записуємо умову динамічної рівноваги кожного тіла. При цьому зважимо на те, що натяг нитки у всіх її точках є однаковим (Т1 = Т2). А це означає, що визначивши із умови рівноваги кожного тіла сили Т1 і Т2 та прирівнявши праві частини відповідних рівнянь, ми отримаємо рівняння з одним невідомим. Керуючись цією логікою можна записати. Перше тіло:
∑Fx = T1 – Fт1sinα – Fтер – Fi1 = T1 – m1gsin45° – μN – m1a = 0;
∑Fy = N – Fт1cosα = N – m1gcos45° = 0, звідси N = m1gcos45°.
Отриманий результат (N = m1gcos45°) підставляємо в перше рівняння:
T1 – m1gsin45° – μm1gcos45° – m1a = 0, звідси
T1 = m1gsin45° + μm1gcos45° + m1a.
Друге тіло:
∑Fy = Fт2 – T2 – Fi2 = m2g – T2 – m2а = 0, звідси
Т2 = m2g – m2а.
Оскільки Т1 = Т2, то m1gsin45° + μm1gcos45° + m1a = m2g – m2а, звідси
m1a + m2a = m2g – m1gsin45° – μm1gcos45°, звідси
a = (m2g – m1gsin45° – μm1gcos45°)/(m1 + m2).
Розрахунки:
а = (0,3·10 – 0,6·10·0,71 – 0,1·0,6·10·0,71)/(0,6 + 0,3) = –1,87м/с2,
де знак «–» вказує на те, що в реальності рух даної системи тіл відбувається в напрямку протилежному від нами обраного та зображеного на малюнку.
Відповідь: а = 1,87м/с2.
Вправа 20.
- Тіло масою 500г знаходиться на похилій площині, кут нахилу якої до горизонту 30°. Яку направлену вздовж площини силу треба прикласти до тіла, щоб воно піднімалося вгору з прискоренням 1,5м/с2? Коефіцієнт тертя 0,3.
- При якому прискоренні розірветься трос міцність якого 10кН, якщо ним піднімають вантаж масою 500кг?
- З якою швидкістю має рухатись автомобіль опуклою ділянкою дороги радіус кривизни якої 40м, щоб в верхній точці опуклості, тиск на дорогу дорівнював нулю?
- З яким максимальним прискоренням може рухатися автомобіль, якщо коефіцієнт тертя між шинами коліс і дорогою 0,5?
- Літак виконує «мертву петлю» радіусом 480м і рухається по ній з швидкістю 432км/год. З якою силою льотчик масою 85кг буде тиснути на сидіння літака: а) у верхній точці петлі, б) в нижній точці петлі?
- На одному кінці нитки перекинутої через нерухомий блок, прив’язано вантаж масою m, а на другому – в двічі легший вантаж. З яким прискоренням рухаються вантажі?
- Вантажі m1 m2 з’єднані ниткою перекинутою через блок (мал.). Маса вантажу m1=2кг, кути α=30º, β=60º. Якою має бути маса m2, щоб вантажі рухались з прискоренням 4м/с2? Тертям знехтувати.
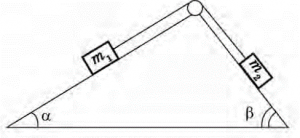
8. Два вантажі масою 200г і 400г з’єднані ниткою перекинутою через блок, підвішений на пружинних терезах. Визначити прискорення вантажів, показання пружинних терезів та силу натягу нитки. Масою блока знехтувати.
9. З вершини похилої площини довжиною 10м і кутом нахилу 30° починає зісковзувати тіло. Визначити швидкість тіла вкінці спуску та тривалість спуску. Коефіцієнт тертя тіла об площину 0,1.
10. На обмерзлій ділянці шосе коефіцієнт тертя між колесами і дорогою у дев’ять разів менший, ніж на необмерзлій. У скільки разів потрібно зменшити швидкість автомобіля, щоб гальмівний шлях на обмерзлій ділянці шосе залишався колишнім?
.
§21. Про вагу та невагомість.
Однією з найбільш суперечливих фізичних величин механіки є вага. В науковій літературі її часто плутають з силою тяжіння, а у побуті – з масою. Насправді ж вага, це та сила з якою тіло діє на опору. Скажімо та сила з якою ви тиснете на підлогу є вашою вагою. Виходячи з того, що за визначенням вага (Р) – це та сила з якою тіло діє на опору, а реакція опори (N) – це та сила з якою опора діє на тіло, та враховуючи що ці сили є діючою і протидіючою силами, а отже рівними за величиною і протилежними за напрямком, можна дати наступне визначення.
Вага – це та сила з якою тіло діє на опору і яка чисельно дорівнює реакції цієї опори.
Позначається: Р
Визначальне рівняння: Р = – N, де N – реакція опори
Одиниця вимірювання: [P] = H, ньютон.
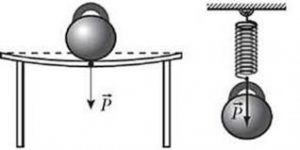
Мал.57. Вага – це та сила з якою тіло діє на опору.
Більшість людей схильні вважати, що вага тіла вимірюється в кілограмах. Ця, глибоко вкорінена помилкова думка, має своє логічне пояснення. І це пояснення полягає в наступному. Коли ви приходите в крамницю за цукром, картоплею чи м’ясом, то приходите за певною кількістю речовини. А універсальною мірою кількості речовини в тілі є його маса, тобто та величина яка вимірюється в кілограмах. А як на практиці вимірюють масу тіла? Правильно – шляхом зважування. І це зважування полягає в тому, що відповідне тіло кладуть на спеціальну опору (ваги), ця опора відчуває вагу тіла і відповідним чином реагує на цю вагу (силу). Результатом же цієї реакції є відповідне відхилення стрілки приладу. А оскільки ви прийшли не за силою (не за ньютонами), а за певною речовиною, тобто за тим що вимірюється в кілограмах, то результат зважування вам видають в цих самих кілограмах. Ясно, що така повсякденна практика, формує впевненість в тому, що вага – це те що вимірюється в кілограмах. Насправді ж, вага – це сила яку відчуває та опора на якій знаходиться дане тіло. І як будь яка сила, вага вимірюється в ньютонах.


Мал.58. Оскільки на практиці масу тіла, тобто те що вимірюється в кілограмах визначають шляхом зважування, то в свідомості пересічної людини, термін зважування а отже «вага» асоціюється з тим, що вимірюється в кілограмах.
Ще однією загально поширеною помилкою є думка про те, що вага тіла дорівнює тій силі з якою тіло притягується до Землі і що тому вага визначається за формулою P = mg. Насправді ж, вага – це та сила з якою тіло діє на опору і яка чисельно дорівнює тій силі з якою опора діє на тіло P = N, а з урахуванням напрямку цих сил P = –N. Інша справа, що в тих ситуаціях, коли система опора-тіло перебуває в стані механічної рівноваги (v=0, або v=const), вага тіла дійсно дорівнює діючій на це тіло силі тяжіння P = mg. Але навіть в цьому випадку, ототожнювати вагу тіла з діючою на нього силою тяжіння не можна. Не можна бодай тому, що сила тяжіння діє на тіло, а вага тіла діє на опору.
Загалом, на відміну від маси тіла, яка за будь яких обставин залишається незмінною (звичайно, якщо не враховувати ті практично не помітні ефекти про які ви дізнаєтесь вивчаючи теорію відносності), вага тіла в різних обставинах може бути абсолютно різною. Скажімо, на Землі (g=9,81м/с2) вага тіла масою 10кг становить 98,1Н. На Місяці (g=1,6м/с2) ця вага дорівнюватиме 16Н; на Марсі (g=3,7м/с2) – 37Н; на Юпітері (g=25,9м/с2) – 259Н; а на Сонці (g=274,1м/с2) – 2741Н. Тому наприклад на Місяця, тіло масою 600кг, важитиме стільки ж як на Землі тіло масою 98кг.

Мал.59. На Місяці вага тіла у шість разів менша ніж на Землі.
Більше того, вага тіла залежить не лише від параметрів того гравітаційного поля яке створює відповідна планета, а й від багатьох інших обставин. Зокрема від того, з яким прискоренням і в якому напрямку рухається система опора-тіло. Ілюструючи цю залежність розглянемо конкретну задачу.
Задача 1. Тіло масою 70кг знаходиться в ліфті. Визначити вагу цього тіла в наступних ситуаціях: а) ліфт знаходиться в стані механічної рівноваги (v=0 або v=const, тобто а=0м/с2); б) ліфт рухається з прискоренням а=5м/с2 і це прискорення направлене вгору; в) ліфт рухається з прискоренням а=5м/с2 і це прискорення направлене вниз; г) ліфт знаходиться в стані вільного падіння тобто падає з прискоренням а=g=10м/с2.
Дано:
m = 70кг
а1 = 0м/с2
а2 = 5м/с2↑
а3 = 5м/с2↓
а4 =g=10м/с2↓
Р1=?, Р2=?,
Р3=?, Р4=?
Рішення. Будемо виходити з того, що вага тіла – це та сила з якою тіло діє на опору, в нашому випадку – на підлогу ліфта, і що величина цієї сили дорівнює відповідній реакції опори (Р=N). А це означає, що рішення задачі зводиться до того, щоб визначити величину реакції опори в кожній з чотирьох ситуацій.
Розв’язуючи цю задачу, виконуємо відповідні малюнки на яких вказуємо ті сили що діють на дане тіло. А цими силами є: сила тяжіння Fт = mg, реакція опори N та, за наявності прискорення, сила інерції Fi = –ma. Зважаючи на вище сказане, проаналізуємо кожну з чотирьох ситуацій і визначаємо вагу тіла в кожній з них. (На жаль на малюнку позначена лише та сила яка є результуючою діючих на тіло сили тяжіння та сили інерції. При цьому ця результуюча сила, ще й позначена як вага тіла. Нагадаємо, вага – це та сила яка діє на опору, а не на тіло).
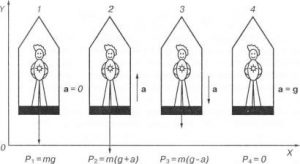
. а=0м/с2 а=5м/с2↑ а=5м/с2↓ а=g=10м/с2↓
P1 = N1 = Fт = mg = 700Н
P2 = N2 = Fт + Fi = mg + ma = 1050Н
P3 = N3 = Fт – Fi = mg – ma = 350Н
P4 = N4 = Fт – Fi = mg – mg = 0Н
Висновок: Маса тіла одна і таж, а вага – різна.
Достовірність описаних в задачі ефектів може підтвердити кожен, хто бодай раз користувався ліфтом. Адже коли ліфт починає рухатися вгору (а↑), навантаження на підлогу збільшується. Збільшується тому, що вага вашого тіла стала більшою. Коли ж ліфт, рухаючись вгору зупиняється (а↓), навантаження на підлогу зменшується, зменшується тому що вага тіла стала меншою. Якщо ж ліфт рухається вниз, то все відбувається навпаки: на початку руху (а↓) вага зменшується, а вкінці руху (а↑) – збільшується.
Не важко бачити, що вага тіла, тобто та сила з якою тіло тисне на опору, не є постійною величиною. При цьому, лише в тому випадку коли система опора-тіло знаходиться в стані вертикальної механічної рівноваги (v = 0 або v = const), вага тіла чисельно дорівнює діючій на нього силі тяжіння: Р1 = mg. В інших випадках, вага тіла може бути як більшою Р2 = m(g+a) так і меншою Р3 = m(g–a) за цю силу. Якщо ж система опора – тіло знаходиться в стані вільного падіння (а = g), то тіло не тисне на опору і тому його вага дорівнює нулю: Р4 = mg – mg = 0. Характеризуючи дану ситуацію говорять про те, що тіло знаходиться в стані невагомості.
Зверніть увагу, тіло знаходиться в стані невагомості (має нульову вагу) не тому що на нього не діє сила тяжіння, а тому, що дія цієї сили зрівноважується відповідною силою інерції. Невагомість – це такий стан системи опора-тіло, при якому тіло та його окремі елементи не мають ваги, тобто не тиснуть на опору і одне на одне. Не мають ваги тому, що діюча на них сила тяжіння зрівноважується відповідною силою інерції.
Факт того, що стан невагомості обумовлений не відсутністю сили тяжіння, а її зрівноваженням силою інерції, з усією очевидністю підтверджує спосіб знайомства майбутніх космонавтів з станом невагомості. А цей спосіб полягає в наступному. Спеціальний літак, внутрішній простір якого позбавлений зайвих предметів, піднімається на максимально велику висоту, а потім певний час вільно падає з цієї висоти. В процесі ж вільного падіння літака, його пасажири перебувають в стані невагомості.
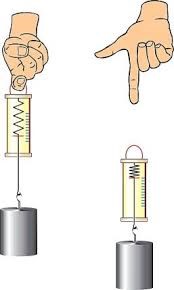

Мал.60. Невагомість, це не тому що на тіло не діє сила тяжіння, а тому що діюча на тіло сила тяжіння зрівноважується силою інерції.
Загально відомим прикладом невагомості є невагомість на борту штучних супутників Землі. При цьому часто думають, що ця невагомість пояснюється відсутністю сили тяжіння. Насправді ж, на тих висотах де зазвичай літають наші пілотовані космічні кораблі (200км – 400км), сила тяжіння майже така ж як і на поверхні Землі. А невагомість в космічному кораблі (штучному супутнику Землі) пояснюється не відсутністю сили тяжіння (Fт = mg), а фактом того, що ця сила зрівноважується відповідною силою інерції (Fi = –ma). Силою, поява якої обумовлена обертанням супутника навколо Землі, а отже його рухом з певним доцентровим прискоренням ад = v2/R. І це прискорення та йому відповідна швидкість мають бути такими, які забезпечують динамічну рівновагу між силою тяжіння (Fт = mg) та силою інерції (Fі = maд = mv2/R).
Що ж давайте визначимо ту швидкість, з якою тіло має обертатися навколо Землі і не падати на неї. Цю швидкість прийнято називати першою космічною швидкістю.
Задача 2. Відомо, що радіус Землі 6,37·106м, а прискорення вільного падіння на ній 9,8м/с2. Визначити ту швидкість з якою тіло (штучний супутник) має обертатись навколо Землі і не падати на неї.
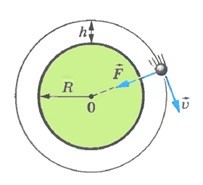
Дано:
R = 6,37·106м
g = 9,8м/с2
Fі = Fт
v = ?
Рішення. Виконуємо малюнок на якому вказуємо наявну ситуацію та ті сили, що діють на супутник в процесі його обертання навколо Землі. А цими силами є: сила тяжіння Fт = mg та сила інерції Fі = mад = mv2/R (як завжди, сила інерції на малюнку не позначена). Оскільки супутник не падає на Землю і не віддаляється від неї, то це означає, що діючі на нього сила тяжіння та сила інерції урівноважують одна одну (Fі = Fт) і тому mv2/R = mg. Звідси v2 = mgR/m, звідси v2 = gR, звідси v = √gR.
Розрахунки: v = √gR = √(9,8м/с2 6,37·106м) = √(62,4·106м2/с2) = 7,9·103м/с.
Відповідь:v = 7,9·103м/с = 7,9км/с.
Ясно, що біля поверхні Землі змусити тіло тривалий час рухатися з швидкістю 7,9км/с практично не можливо. Не можливо по перше тому, що щільна атмосфера Землі шалено протидіє швидкому руху тіл і гальмує цей рух. А по друге, в процесі надшвидкого руху в атмосфері Землі, тіла надзвичайно швидко нагріваються і по суті згорають. Власне тому, штучні супутники потрібно виводити за межі щільних шарів атмосфери Землі, а це що найменше 100км над її поверхнею.
Можна довести, що траєкторія руху штучного супутника Землі, певним чином залежить від величини наданої йому швидкості. Наприклад, при швидкості 7,9км/с, цією траєкторією буде коло. А при швидкостях більших за 7,9км/с але менших за 11,2км/с – еліпс, витягнутість якого пропорційна швидкості супутника (мал.61). Якщо ж швидкість супутника дорівнює, або перевищує 11,2км/с, то траєкторія його руху стає параболічною. А це означає, що земне тяжіння не зможе перешкодити супутнику відірватись від Землі і, стати супутником Сонця. Величину тієї мінімальної швидкості при якій тіло, здолавши гравітаційне поле планети зможе назавжди відірватись від неї, називають другою космічною швидкістю. Можна довести, що перша (v1) та друга (v2) космічні швидкості планети, зв’язані співвідношенням v2 = v1√2 =1,41v1.
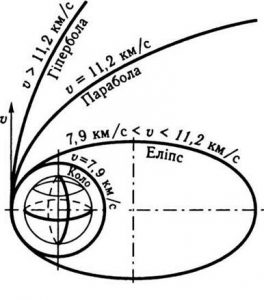
Мал.61. Траєкторія руху штучного супутника Землі, визначається величиною його швидкості.
Якщо ж земному тілу надати швидкість яка дорівнює або перевищує 16,6км/с, то воно зможе не лише назавжди відірватись від Землі, а й від всієї Сонячної системи. Цю швидкість називають третьою космічною швидкістю.
Якщо ж ви захочите здійснити міжгалактичну подорож, тобто вилетіти за межі нашої Галактики, то маєте надати своїй ракеті швидкість не меншу за 550км/с. Цю швидкість називають четвертою космічною швидкістю.
Можливо ви подумали, що за певної швидкості зможете вилетіти не лише за межі нашої Галактики, а й за межі нашого Всесвіту? Облиште ці сподівання. Бо це принципово не можливо. Втім, про те як влаштований наш Всесвіт і чому не можливо зазирнути за його межі, ми поговоримо в тому розділі фізики який так і називається космологія – наукою про Всесвіт.
Контрольні запитання.
- Що називають вагою тіла?
- Чому люди часто вважають, що вага тіла вимірюється в кілограмах?
- В яких випадках формула Р = mg є правильною, а в яких не правильною?
- Чи є вага тіла безумовно постійною величиною? Від чого залежить вага тіла?
- Що називають невагомістю?
- В кабіні штучного супутника Землі тіло знаходиться в стані невагомості. Чи означає цей факт, що на нього не діє сила тяжіння?
- Коли ліфт рухаючись вгору набирає швидкість, пружини під його підлогою дещо просідають, а коли зупиняється – дещо випрямляються. Чому це відбувається?
- Чи може вага тіла бути направленою вертикально вгору?
- Чи правильне твердження: на тіло діє вага тіла та реакція опори?
- Яку швидкість називають першою космічною?
Вправа №21.
- Визначте вагу тіла масою 70кг на Землі; на Місяці, на Марсі; на Юпітері.
- Ракета піднімається вертикально вгору з прискоренням а = 3g. Якою буде в цій ракеті вага тіла масою 50кг?
- З якою силою людина масою 80кг тисне на підлогу ліфта, що рухається з прискоренням 2м/с2, направленим а) вгору; б) вниз?
- Ліфт рівноприскорено розганяється до швидкості 7м/с за 5с. За такий же час він і зупиняється. Визначити вагу людини масою 80кг на ділянках розгону та зупинки ліфта.
- З якою швидкістю має рухатись автомобіль по опуклому мосту, радіус кривизни якого 90м, щоб у верхній точці моста, тиск автомобіля на поверхню моста дорівнював нулю?
- Відомо, що радіус Місяця 1,74·106м, а прискорення вільного падіння на ньому 1,6м/с2. Визначити ту швидкість з якою тіло (штучний супутник) має обертатись навколо Місяця і не падати на нього.
- Визначити першу космічну швидкість для Марса якщо його радіус 3,4·106м, а прискорення вільного падіння на ньому 3,7м/с2.
- Парашутист, досягши в затяжному стрибку швидкості 55м/с, розкриває парашут, після чого за 2с його швидкість зменшується до 5м/с. Визначте вагу парашутиста під час гальмування, якщо його маса 80кг.
- Якої тривалості має бути доба на Землі, щоб тіла на її екваторі були невагомі?
.
§22. Про силу Архімеда та про те, що важче кілограм заліза чи кілограм пір’я?
Понад дві тисячі років тому, видатний давньогрецький вчений Архімед (287–212р.р. до н.е.) відкрив закон, який прийнято називати законом Архімеда. В цьому законі стверджується: на будь яке занурене в рідину (або газ) тіло, діє виштовхувальна сила, величина якої дорівнює вазі виштовхнутої тілом рідини.
Наочно переконатися в достовірності закону Архімеда дозволяє проста система, складовими якої є (мал.62): штатив, пружинний динамометр (1), маленьке відерце (2), досліджуване тіло (3), відливний стакан (4), стакан для виштовхнутої тілом води (5).
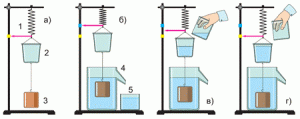
Мал.62. На занурене в рідину тіло діє виштовхувальна сила, величина якої дорівнює вазі виштовхнутої тілом рідини (закон Архімеда).
Принцип дії даної системи очевидно простий. Під вагою досліджуваного тіла, пружина динамометра видовжується і це видовження фіксує стрілка приладу, вказуючи на жовту точку відповідної шкали. Коли досліджуване тіло опиняється у воді вщерть заповненого відливного стакана, то: по-перше, діюче на пружину динамометра навантаження зменшиться на величину тієї виштовхувальної сили яка діє на тіло (стрілка динамометра вказує на синю позначку шкали); по-друге, певна кількість води вилляється з відливного стакана і ця кількість дорівнюватиме об’єму зануреного у воду тіла. Якщо ж виштовхнуту тілом воду вилити у відерце системи, то неодмінно з’ясується, що вага цієї води в точності дорівнює величині діючої на тіло сили Архімеда (стрілка динамометра знову вказує на жовту точку).
Не важко довести, що величина тієї виштовхувальної сили, яка називається силою Архімеда (FA) і яка дорівнює вазі виштовхнутої тілом рідини (FA = Pр), залежить від густини рідини (ρр), об’єму зануреної в рідину частини тіла (V) та прискорення сили тяжіння (g), і що цю залежність можна записати у вигляді FA = ρрVg. Дійсно. Оскільки в нерухомій системі, вага витісненої тілом рідини визначається за формулою Рр = mрg, та враховуючи, що маса витісненої тілом рідини дорівнює добутку густини рідини ρр на її об’єм (mр = ρрV), можна записати: FA = Pр = mрg = ρрVg. Зважаючи на вище сказане, можна дати наступне визначення:
Сила Архімеда – це та сила, з якою тіла виштовхуються з рідин та газів і яка дорівнює вазі виштовхнутої тілом рідини або газу.
Позначається: FА
Визначальне рівняння: FА = ρрVтg
Одиниця вимірювання: [FА] = H, ньютон.
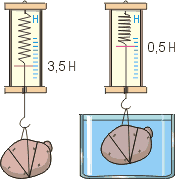
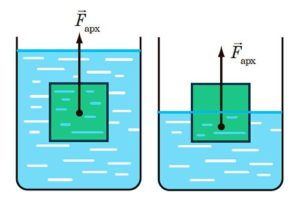
Мал.63. На будь яке занурене в рідину або газ тіло діє виштовхувальна сила Архімеда, величина якої визначається за формулою FА = ρрVтg.
Характерною особливістю сили Архімеда є факт того, що її величина залежить від об’єму тієї частини тіла яка занурена в рідину. А це означає, що по мірі занурення тіла в рідину, величина діючої на нього сили Архімеда збільшується. Збільшується до тих пір поки тіло повністю не зануриться в рідину. При цьому в процесі подальшого занурення, величина діючої на тіло сили Архімеда залишається незмінною.
Загально відомо, що деякі тіла плавають у воді, а деякі – тонуть в ній. Тепер, коли ви знаєте про силу Архімеда та її основні властивості не важко пояснити все різноманіття тих явищ, які пов’язані з плаванням чи не плаванням тіл. Дійсно. Якщо діюча на тіло сила тяжіння зрівноважується виштовхувальною силою Архімеда (Fт = FA), то відповідне тіло не тоне в рідині, а якщо сила тяжіння більша за силу Архімеда (Fт > FA) – тоне в ній.

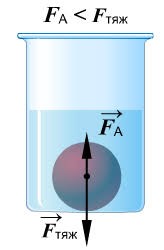
Мал.64. Якщо діюча на тіло сила тяжіння зрівноважується силою Архімеда (Fт = FA), то відповідне тіло не тоне, а якщо сила тяжіння більша за силу Архімеда (Fт > FA), то тіло тоне в рідині.
Говорячи про те, що дане тіло не тоне в рідині, потрібно мати на увазі, що ступінь отого «не тоне» може бути різною. Скажімо у воді, пінопласт (ρ ≈ 20кг/м3) занурюється лише на 2% свого об’єму, пробкове дерево (ρ = 240кг/м3) – на 24%, суха сосна (ρ = 500кг/м3) – на 50%, а сухий дуб (ρ = 700кг/м3) – на 70%. Якщо ж густина тіла дорівнює густині води (ρ = 1000кг/м3), то в цьому випадку тіло буде повністю зануреним у воду і у стані вільного плавання може знаходитися на будь якій глибині.
Варто зауважити, що говорячи про усереднену густину тіла (ρт), мають на увазі не густину того матеріалу з якого виготовлено тіло, а саме усереднену густину всього тіла. Скажімо, якщо ви візьмете суцільний шматок сталі (ρ = 7800кг/м3) і опустите його у воду (ρ = 1000кг/м3), то він неодмінно потоне. Потоне тому, що густина сталі більша за густину води. Але якщо з цієї сталі ви виготовите пустотілий корпус човна, то він залишатиметься на плаву. Адже усереднена густина корпусу човна буде значно меншою за густину води. Меншою тому, що об’єм корпусу човна складається не лише з об’єму тієї сталі з якої він виготовлений, а й з об’єму того простору який знаходиться всередині корпусу та є недоступним для потрапляння води.
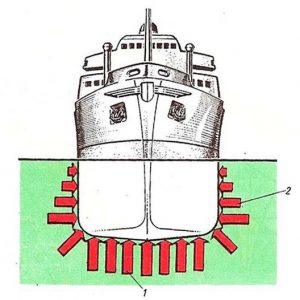
Мал.65. Усереднена густина човна, менша за густину води.
В певному сенсі, всі плаваючі тіла починаючи від деревяних колод і закінучуючи океанськими лайнерами, представляють собою певні саморегульовані системи. Саморегульовані в тому сенсі, що збільшення навантаження на плаваюче тіло, автоматично призводить до відповідного додаткового занурення цього тіла, яке в свою чергу призводить до автоматичного збільшення виштовхувальної сили Архімеда.
Ясно, що така саморегуляція може відбуватися лише до тих пір поки об’єм зануреної в рідину частини тіла не зрівняється з загальним об’ємом цього тіла. Втім, якщо мова йде про плаваючі транспортні засоби, то для них зазвичай передбачена певна обмежувальна межа, яка гарантує безпечну експлуатацію відповідного транспортного засобу. Цю межу називають ватерлінією.
Цікавим прикладом застосування сили Архімеда є підводні човни. Підводний човен (мал.66) може знаходитись над водою, під водою або лежати на дні водойми. Він може занурюватись на глибину та виринати з цієї глибини. Реалізацію всіх цих можливостей забезпечує наявна на підводному човні система баластових відсіків. В залежності від потреб, ці відсіки заповнюються навколишньою водою, або звільняються від неї. При цьому реальний об’єм човна (Vт), тобто той об’єм який недоступний для потрапляння навколишньої води, змінюється, а відповідно змінюється і усереднена густина човна (ρт = mт/Vт).
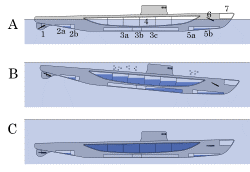
Мал.66. Загальний вигляд підводного човна та схема його занурення у воду.
Сила Архімеда проявляє себе не лише в рідинах, а й в газах. Різниця лише в тому, що в газах і зокрема у повітрі, прояви сили Архімеда є менш помітними. І це закономірно. Адже густина повітря (ρ = 1,29кг/м3) в 775 разів менша за густину води. А це означає, що у повітрі, діюча на тіло сила Архімеда в 775 разів менша ніж у воді. В газах прояви сили Архімеда стають очевидними лише в тому випадку, коли усереднена густина тіла є співрозмірною або меншою за густину відповідного газу. Наочними прикладами дії сили Архімеда у повітрі є заповнені гелієм або теплим повітрям гумові кульки, величезні повітряні кулі, дирижаблі, тощо.


Мал.67.Наочні приклади дії сили Архімеда у повітрі.
Задача 1. Визначити вагу каменю масою 50кг в повітрі та у воді (густина каменю 3,2·103кг/м3).
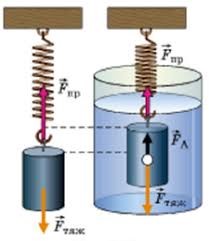
Дано:
m = 50кг
ρ = 3,2·103кг/м3
Р1 = ? Р2 = ?
Рішення. Виходячи з того, що вага тіла (Р) чисельно дорівнює діючій на тіло реакції опори (N), виконуємо малюнок на якому вказуємо діючі на тіло сили в двох ситуаціях. Виходячи з умови рівноваги тіла, визначаємо діючу на тіло реакцію опори (N), а отже і їй відповідну вагу тіла (Р = N). У повітрі, дією сили Архімеда нехтуємо і тому вважаємо, що на тіло діють сила тяжіння (Fт = mg) та реакція опори (N1). При цьому N1 = Fт = mg = 50кг·9,8м/с2 = 490Н.
У воді на тіло діють сила тяжіння (Fт = mg), реакція опори (N2) та сила Архімеда (FA = ρрVтg). При цьому N2 = Fт – FA. Визначаємо величину діючої на тіло сили Архімеда: FA = ρрVтg, де ρр = 1·103кг/м3 – густина води; Vт = m/ρ = 50кг/3,2·103кг/м3 = 15,6·10–3м3 – об’єм тіла. FA = ρрVтg = 1·103(кг/м3)·15,6·10–3м3·9,8м/с2 = 153Н. Таким чином N2 = Fт – FA = 490Н – 153Н = 337Н.
Відповідь: Р1 = 490Н, Р2 = 337Н.
Іноді можна почути, як старші школярі провокативно запитують своїх молодших колег: «що важче, кілограм заліза чи кілограм вати?» І коли ті відповідають що залізо важче – дружно сміються, хизуючись своєю кмітливістю. І потрібно сказати, сміються абсолютно безпідставно. Адже кілограм заліза дійсно важчий за кілограм вати. Звичайно за умови, що мова йде саме про кілограм, тобто про масу в 1,0000кг.
Обґрунтовуючи тезу про те, що кілограм заліза важчий за кілограм пір’я, вати, пінопласту чи деревини, розв’яжемо наступну задачу.
Задача 2. Що важче, кілограм заліза (ρ1 = 7800кг/м3) чи кілограм пінопласту (ρ2 = 20кг/м3). Густина повітря ρ = 1,3кг/м3.
.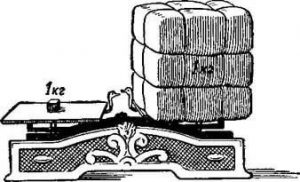
Дано:
m1=m2=1,00кг
ρ1 = 7800кг/м3
ρ2 = 20кг/м3
ρ = 1,3кг/м3
g =9,81м/с2
ΔP = P1 – P2 = ?
Рішення. Оскільки за визначенням, вага тіла чисельно дорівнює реакції відповідної опори (Р1 = N1; Р2 = N2), то рішення задачі полягає у визначенні цих реакцій. Виходячи з цього, розглянемо ті сили що діють на залізне (1) та пінопластове (2) тіло. А цими силами є: сила тяжіння Fт = mg, реакція опори яка і дорівнює вазі тіла (Р1 = N1; Р2 = N2), та сила Архімеда FA= ρVg.
Із аналізу діючих на тіло сил (із умови рівноваги тіл) випливає:
N1= Fт – FА1 = m1g – ρV1g = m1g – ρm1g/ρ1 = 1∙9,81 – 1,3∙1∙9,81/7800 = 9,81 – 0,0016 = 9,81Н
N2 = Fт – FА2 = m2g – ρV2g = m2g – ρm2g/ρ2 = 1∙9,81 – 1,3∙1∙9,81/20 = 9,81 – 0,64 = 9,17Н.
Таким чином:
P1 = N1 = 9,81H;
P2 = N2 = 9,17H.
ΔP = P1 – P2 = 0,64H
Відповідь: кілограм заліза важчий за кілограм пінопласту на 0,64Н, що відповідає додатковій масі Δm = 102г∙0,64 = 65г. Іншими словами, кілограм пінопласту на 6,5% легший за кілограм заліза (за умови, що визначення ваги відбувається у повітряному середовищі).
Таким чином, теорія стверджує що кілограм пінопласту на 6,5% легший за кілограм заліза. Причина появи цієї різниці очевидна – на більш об’ємний пінопласт діє більша сила Архімеда і тому його вага, тобто та сила з якою пінопласт тисне на опору (на ваги) виявляється дещо меншою.
Чому ж ми вважаємо, що кілограм заліза і кілограм пінопласту мають однакову вагу? Більше того, якщо ми дійсно порівняємо вагу реального кілограму заліза і реального кілограму пінопласту, то скоріш за все ця вага виявиться однаковою. І справа не втому, що точність вимірювальних приладів не дозволяє зафіксувати наявну різницю ваги. Справа в іншому – цієї різниці просто не існує.
Не існує тому, що зазвичай масу тіла ми визначаємо шляхом зважування. І як ви розумієте, це зважування відбувається не у вакуумі, а у повітряному середовищі. А це означає, що в реальному кілограмі пінопласту, фактично не 1,000кг а 1,065кг. Поява цієї різниці знову ж таки обумовлена дією сили Архімеда. Адже для того, щоб пінопластове тіло зрівноважило залізу гирю масою 1,000кг, маса цього тіла має бути на 65г більшою за масу гирі. Більшою на ту величину яка дозволяє компенсувати надлишкову силу Архімеда.
Таким чином, якщо кілограм вати і кілограм заліза мають однакову вагу, то це тільки тому, що фактична маса вати дещо більша за кілограм. Якщо ж ми дійсно візьмемо кілограм заліза і кілограм вати, то вага заліза буде більшою за вагу вати. Звичайно за умови, що процес зважування відбувається у повітряному середовищі.
Задача 3. Повітряна куля має об’єм 300м3. Визначте діючу на кулю силу Архімеда. Вантаж якої максимальної маси може підняти ця куля, якщо її власна маса 180кг? Густина повітря 1,29кг/м3
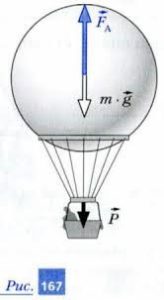
Дано:
Vк = 300м3
m1 = 180кг
ρп = 1,29кг/м3
m2 = ?
Рішення. Розглянемо ті сили, що діють на кулю в умовах її механічної рівноваги. А цими силами є: 1) сила Архімеда FA = ρпVкg, 2) діюча на тіло сила тяжіння Fт1 = m1g; 3) вага вантажу Р = Fт2 = m2g. У відповідності з умовою механічної рівноваги кулі, можна записати:
FA = Fт1 + P, або ρпVкg = m1g + m2g, або ρпVк = m1 + m2, звідси m2 = ρпVк – m1.
Розрахунки. m2 = ρпVк – m1 = 1,29(кг/м3)∙300м3 – 180кг = 207кг.
Відповідь: m2 = 207кг.
Контрольні запитання.
- Що стверджується в законі Архімеда?
- Від чого залежить діюча на тіло виштовхувальна сила Архімеда?
- На основі аналізу малюнку порівняйте густини тих рідин в яких знаходяться однакові тіла.
- Залізне і дерев’яне тіла однакових розмірів знаходяться у воді. При цьому, залізне тіло лежіть на дні посудини, а дерев’яне плаває. На яке тіло діє більша сила Архімеда? Чому?
- Що мають на увазі коли говорять про усереднену густину плаваючого тіла?
- В чому полягає саморегульованість плаваючого тіла? Які межі цієї саморегульованості?
- Яким чином підводні човни досягають того, що можуть плавати як над водою так і підводою?
- Чи однакова вага каменю у повітрі і воді? Чому?
- Чи означає факт того, що той пінопласт який на шальках терезів зрівноважив гирю масою 1,000кг, також має масу 1,000кг? Чому?
- На основі аналізу малюнку, поясніть принцип дії аерометра – приладу для вимірювання густини рідини.
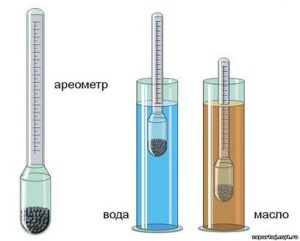
Вправа №22.
- З якою силою камінь об’ємом 0,5м3 виштовхується із води?
- На скільки зменшиться вага залізної болванки об’єм якої 5дм3 при її повному зануренні у воду?
- На основі аналізу малюнку визначте об’єм зануреного у воду тіла.
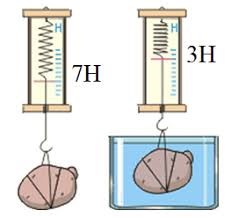
4. Повітряна куля має об’єм 350м3. Визначте діючу на кулю силу Архімеда. Вантаж якої максимальної маси може підняти ця куля, якщо її власна маса 190кг?
5. На тіло яке перебуває у воді діє виштовхувальна сила 270Н. З якою силою це тіло виштовхується гасом? Густина гасу 800кг/м3.
6. Крижина площею 40м2 і товщиною 40см плаває у воді. Тіло якої максимальної маси може втримати на плаву ця крижина? Густина льоду 900кг/м3.
7. У 1990 році, в США була синтезована тверда речовина з найменшою густиною – кремнієвий аерозоль. Густина цієї речовини всього 5кг/м3. Яку реальну масу цієї речовини треба покласти на точні терези, щоб урівноважити сталеву гирю масою 1,000кг?
8. З якою силою виштовхується з води тіло об’ємом 125см3, якщо воно виготовлено з алюмінію, свинцю, корка?
9. Оболонка повітряної кулі масою 60кг вміщує 300м3 газу густина якого 0,5кг/м3. Який вантаж може підняти ця куля?
10. На одній чаші ваг лежить шматок срібла масою 105г, а на іншій – шматок скла масою 130г. Яка чаша переважить при зануренні ваг у воду? Густина срібла 10,5·103кг/м3, скла 2,6·103кг/м3.
.
§23. Закон всесвітнього тяжіння. Про силу гравітаційну та силу тяжіння.
В 1667 році аналізуючи поведінку Місяця та планет Сонячної системи видатний англійський фізик Ісаак Ньютон сформулював закон, який прийнято називати законом всесвітнього тяжіння. В цьому законі стверджується: дві матеріальні точки масою m1 і m2 взаємно притягуються з силою (Fгр), величина якої прямо пропорційна добутку взаємодіючих мас (m1∙m2) і обернено пропорційна квадрату відстані між ними (r2). Іншими словами: Fгр= G∙m1∙m2/r2, де G = 6,6720∙10–11 (Н∙м2/кг2) – постійна величина, значення якої визначається експериментально і яка називається гравітаційною сталою (від латинського gravitas – тяжіння).
Гравітаційна стала (G = 6,6720∙10–11Н∙м2/кг2) – це постійна величина, яка чисельно дорівнює тій гравітаційній силі з якою взаємодіють дві матеріальні точки масою по 1кг кожна, будучи розташованими на відстані 1м одна від одної. Іншими словами: якщо m1 = m2 = 1кг; r = 1м то Fгр = 6,67∙10–11Н = 0,0000000000667Н.
Із вище сказаного ясно, що за питомою (одиничною) величиною, сили гравітаційної взаємодії є надзвичайно слабкими. Тому ми абсолютно не помічаємо факту того, що з певною гравітаційною силою притягуємося до навколишніх предметів. Єдиний земний об’єкт, гравітаційну дію якого ми явно відчуваємо і спостерігаємо, це той, який називається планета Земля. І це закономірно, адже маса Землі така величезна (М = 6,0∙1024кг), що створювана нею гравітаційна дія є відчутною навіть для тих дрібних об’єктів, маси яких вимірюються грамами і міліграмами.
Коли ж мова заходить про тіла космічних масштабів, то для них питомо слабкі гравітаційні сили, набувають фантастично великих значень. Скажімо Місяць притягується до Землі (а відповідно Земля до Місяця) з силою 2∙1020Н. Ілюструючи масштаб цієї сили, достатньо сказати, що для її передачі від Землі до Місяця знадобився б сталевий трос діаметром 5000км і масою, яка дорівнює масі Землі.
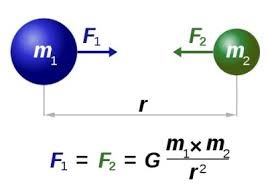
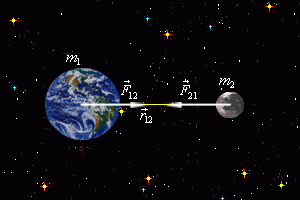
. 1кг 1м 1кг Земля Місяць
Fгр=0,0000000000667Н Fгр=200 000 000 000 000 000 000Н
Мал.68. В масштабах земних тіл, сили гравітаційної взаємодії є гранично малими, а в масштабах космічних об’єктів – фантастично великими.
Оцінюючи значимість гравітаційних сил достатньо сказати, що саме ці сили об’єднують зірки, їх планети, супутники планет, астероїди та купу дрібніших об’єктів, у відповідні планетарні системи. Саме сили гравітаційної взаємодії об’єднують зірки в галактики, галактики – в метагалактики, метагалактики – у Всесвіт. Саме гравітаційні сили стискають та розігрівають надра зірок до таких тисків і температур при яких відбуваються ті термоядерні реакції, енергія яких наповнює світлом і життям увесь Всесвіт.
Можна довести, що формула Fгр = G∙m1∙m2/r2 справедлива не лише для матеріальних точок, а й для тіл довільних розмірів. При цьому, має виконуватись лише одна умова: речовина у відповідному тілі має бути симетрично розподіленою відносно його центру мас. Наприклад, при взаємодії Землі з тілом що лежить на її поверхні, нашу планету навряд чи можна назвати матеріальною точкою. Але оскільки Земля, це куля з практично ідеально симетричним розподілом речовини в ній, то при розрахунках цілком обгрунтовано застосовують формулу Fгр = G∙M∙m/R2, де m – маса тіла, М – маса Землі (М = 6,0∙1024кг), R – радіус Землі (R = 6,37∙106м).
Говорячи про силу гравітаційної взаємодії, не можна не згадати і про ту силу, яку називають силою тяжіння. Часто думають, що діюча на земні тіла сила тяжіння (Fт = m∙g) та сила гравітаційної взаємодії цих тіл з Землею (Fгр = G∙M∙m/R2), це дві назви однієї і тієї ж сили. Така думка не є безумовно правильною. Адже мова йде хоч і про дуже схожі, але все таки суттєво різні сили. Пояснюючи суть тих відмінностей які існують між силою тяжіння та силою гравітаційної взаємодії, можна сказати наступне.
Коли говорять про силу гравітаційної взаємодії, то мають на увазі ту силу з якою взаємодіють тіла, у відповідності з законом всесвітнього тяжіння. Іншими словами: Сила гравітаційної взаємодії (гравітаційна сила) – це та сила, з якою тіла взаємодіють згідно з законом всесвітнього тяжіння.
Позначається: Fгр
Визначальне рівняння: Fгр = G∙m1∙m2/r2, де G = 6,67∙10–11 (Н∙м2/кг2)
Одиниця вимірювання: [Fгр] = H.
Для тих тіл, що знаходяться на поверхні Землі та в близьких околицях цієї поверхні (r = R), визначальне рівняння сили гравітаційної взаємодії між Землею та відповідним тілом набуває вигляду Fгр = G∙M∙m/R2.
Якби Земля не оберталась навколо своєї осі, то та сила яку ми називаємо силою тяжіння (Fт = m∙g) в точності дорівнювала б тій силі яку прийнято називати гравітаційною (Fгр = G∙M∙m/R2). Однак як відомо, Земля обертається і тому, всі тіла на її поверхні рухаються відповідними круговими траєкторіями, а отже рухаються з певним доцентровим прискоренням: aд = v2/r = ω2∙r, де ω – кутова швидкість добового обертання Землі, r – відстань від даного тіла до осі обертання Землі (для полюсів r = 0; для екватора r = R). А це означає, що на кожне тіло земної поверхні діє певна сила інерції Fi = m∙aд = m∙ω2∙r, яка направлена в протилежну сторону від доцентрового прискорення. При цьому на полюсах величина цієї сили дорівнює нулю, а на екваторі – є максимально великою.
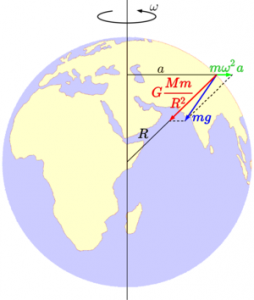
Мал.69. Оскільки Земля обертається, то на кожне тіло її поверхні окрім гравітаційної сили неминуче діє і певна сила інерції.
Таким чином, на кожний земний об’єкт масою m постійно та одночасно діють дві сили: сила гравітаційної взаємодії тіла з Землею Fгр = m(G∙M/R2), та обумовлена добовим обертанням Землі сила інерції Fі = m∙ад = m∙v2/r = m∙ω2∙r. В загальній же теорії відносності стверджується, що силові прояви інерції та гравітації є тотожними (еквівалентними), і що ніякими експериментами і ніякими приладами не можливо відрізнити силу інерції від сили гравітації. А це означає, що та сила яку ми називаємо силою тяжіння, фактично є результуючою двох сил: сили гравітаційної взаємодії тіла з Землею, та діючої на це ж тіло сили інерції, поява якої обумовлена обертанням Землі навколо своєї осі. Іншими словами:
Сила тяжіння – це та сила, з якою тіла притягуються до Землі і яка дорівнює векторній сумі сили гравітаційної взаємодії тіла з Землею та обумовленої добовим обертанням Землі сили інерції.
Позначається: Fт
Визначальне рівняння: Fт = Fгр + Fі
Одиниця вимірювання: [Fт] = H
Зазвичай силу тяжіння визначають дещо простіше: Сила тяжіння – це та сила з якою тіла притягуються до Землі і яка визначається за формулою Fт = m∙g, де g – прискорення сили тяжіння (прискорення вільного падіння).
По суті, визначальні рівняння Fт = Fгр + Fі та Fт = m∙g є тотожними. При цьому ясно, що з практичної точки зору, рівняння Fт = m∙g є більш зручним і тому більш вживаним.
Можна довести, що інерційна складова сили тяжіння, набагато менша за її гравітаційну складову. Навіть на екваторі, ця складова в 300 разів менша за гравітаційну складову. Тому прийнято вважати, що визначена за формулою Fт = m∙g сила тяжіння, і визначена за формулою Fгр = m(G∙M/R2) сила гравітаційної взаємодії тіла з Землею, є практично тотожними. Дійсно, зважаючи на те, що G = 6,67∙10–11 (Н∙м2/кг2), М = 6,0∙1024кг, R = 6,37∙106м, можна записати: Fгр = m(GM/R2) = m(6,67∙10–11∙6,0∙1024 / (6,37∙106)2 = m∙9,8м/с2 = m∙g = Fт.
Та як би там не було, а ви маєте знати, на земні об’єкти, окрім гравітаційної сили, постійно діє певна сила інерції, і що сила тяжіння є результуючою цих двох сил.
До речі. Саме факт обертання Землі навколо своєї осі, а відповідно і факт дії на всі її об’єкти певної сили інерції, є причиною того, що наша планета не є безумовно круглою (кулястою). Адже якби Земля не оберталась навколо власної осі, то під дією об’ємна-центральних сил гравітації, вона б набула практично ідеальної кулястої форми. (Звичайно, за винятком тих поверхневих нерівностей, які є результатом певних геологічних процесів і які називаються горами, нагір’ями, впадинами, каньйонами, тощо).
Однак в реальності Земля обертається і тому на всі її об’єкти неминуче діють плоско-відцентрові сили інерції, які відповідним чином деформують Землю та надають їй форму еліпсоїда. Щоправда, різниця між екваторіальним та полярним радіусом Землі є незначною і становить всього 21,4км. Тим не менше, ця різниця існує і її поява обумовлена фактом добового обертання Землі та реальності існування сили інерції.
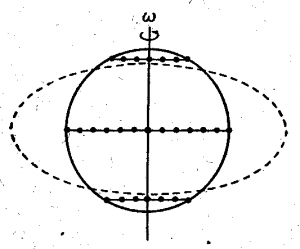
Мал.70. Оскільки Земля обертається навколо своєї осі, то під дією сил інерції вона набуває відповідної еліпсоїдної форми.
Закон всесвітнього тяжіння кількісно описує гравітаційні взаємодії, але нічого не говорить про механізм передачі цих взаємодій. Дійсно, яким чином фантастично потужна силова дія передається від Землі до Місяця, від Сонця до Землі і навпаки. Адже між цими об’єктами нема нічого окрім пустого простору. І тим не менше, саме через цей пустий простір надпотужна силова дія передається від Сонця до Землі, від Землі до Місяця і т. д.
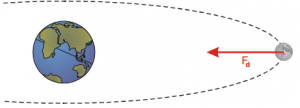
Мал.71. Місяць з силою 2∙1020Н притягується до Землі. Яким чином ця фантастично велика сила передається від Землі до Місяця і навпаки?
Пояснюючи механізм гравітаційних взаємодій сучасна наука стверджує. Будь який масивний об’єкт (об’єкт який має масу), створює навколо себе певне силове збурення навколишнього простору яке називається гравітаційним полем. Якщо в це поле потрапляє інший масивний об’єкт, то поле діє на нього з певною гравітаційною силою. Іншими словами, гравітаційне поле є тим матеріальним посередником який забезпечує гравітаційні взаємодії тіл.
На відміну від речовин, кожна з яких має сотні властивостей, поле має лише одну властивість – здатність певним чином діяти на певні об’єкти. Наприклад гравітаційні поля, діють на маси, тобто на ті об’єкти що мають масу. Це означає, що існує лише один спосіб з’ясування факту того, є в даній точці простору гравітаційне поле чи нема. І цей спосіб полягає в тому, що у відповідну точку потрібно внести пробну масу і подивитись на її поведінку. При цьому, якщо на пробну масу гравітаційна сила подіє, то це означатиме, що у відповідній точці поле є. А якщо така сила не діятиме – значить поля нема.
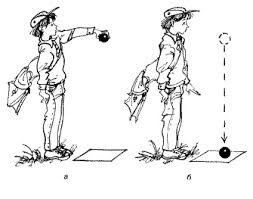
Мал.72. Поле має лише одну властивість – здатність певним чином діяти на певні матеріальні об’єкти.
Звісно, проводячи подібні експерименти, потрібно враховувати те, що в реальних обставинах на пробне тіло, окрім гравітаційної сили (сили тяжіння) можуть діяти й інші силові фактори. Скажімо, якщо в навколоземний простір внести заповнену гелієм надлегку кульку і відпустити її, то скоріш за все вона почне підніматись вгору. Однак це зовсім не означатиме, що у відповідному місці гравітаційного поля нема, або що джерело цього поля знаходиться десь вгорі. Просто в даному випадку, на поведінку легкої кульки визначальним чином впливає сила Архімеда, яка і змушує кульку, всупереч дії сили тяжіння, рухатися вгору.
Оскільки сила F = m∙a, це те що надає тілу масою m прискорення а = F/m, то саме за величиною прискорення вільного падіння тіл g, оцінюють силові параметри відповідного гравітаційного поля. Наприклад, якщо в близьких околицях Землі g = 9,8м/с2, а в близьких околицях Місяця g = 1,6м/с2, то це означає, що гравітаційне поле Землі у 9,8/1,6 = 6,125 разів потужніше за гравітаційне поле Місяця.
Прискорення вільного падіння g по суті є силовою характеристикою гравітаційного поля, яку в теорії поля називають напруженістю гравітаційного поля, і яку визначають як відношення тієї гравітаційної сили, що діє на пробну масу в даній точці поля Fгр = G∙М∙mп/r2, до величини цієї пробної маси mп: g = Fгр/mп, або g = G∙М∙mп/mп∙r2 = G∙М/r2, [g] = Н/кг = м/с2.
Наприклад для близьких околиць Землі (М = 6,0∙1024кг, r = R = 6,37∙106м), g0 = G∙M/R2 = 9,8м/с2. Якщо ж мова йде про ті висоти на яких зазвичай літають наші пілотовані космічні кораблі (h ≈ 200км = 0,2∙106м), то для них g = G∙M/(R+h)2 = 6,67∙10–11∙6,0∙1024/(6,37+0,2)106 = 9,2м/с2. Загалом же, якщо r = 2R, то g = G∙M/(2R)2 = g0/4; якщо r = 3R, то g = G∙M/(3R)2 = g0/9, і т.д.
Варто зауважити, що формула g = G∙M/R2, або в більш загальному випадку g = G∙M/(R+h)2, де h – висота тіла над поверхнею Землі, справедлива лише в тих випадках, коли мова йде про ті точки гравітаційного поля які знаходяться на поверхні Землі, або за її зовнішніми межами. Адже всередині земної кулі, оцінюючи параметри гравітаційного поля, а відповідно і гравітаційної сили, потрібно враховувати всю сукупність тих мас які оточують відповідну точку. І можна довести, що по мірі наближення до центру земної кулі, та результуюча гравітаційна сила що діє на тіло яке знаходиться всередині цієї кулі, поступово наближається до нуля.
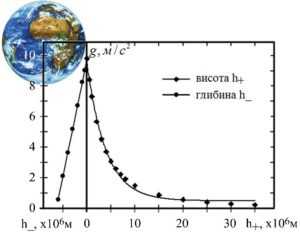
Мал.73. По мірі наближення до центру Землі, величина діючої на тіло гравітаційної сили зменшується і в центрі Землі стає нулевою.
Завершуючи ознайомчу розмову про ті матеріальні об’єкти які називаються полями, буде не зайвим сказати, що за своїми фізичними властивостями поле схоже на простір (пустоту, вакуум). Як і простір, воно не має кольору, запаху, смаку, твердості, м’якості, поверхневого натягу, електропровідності, тощо. Як і простір, поле не складається з певних частинок, не має певного внутрішнього устрою, не має певних розмірів, певної форми, певної маси спокою, тощо. Власне поле, це і є простір. Тільки простір збурений, або якщо хочете – викривлений простір.
Вивчаючи фізику, ви не раз переконаєтесь в тому, що Природа влаштована таким дивним чином, що її найпростіші об’єкти є надзвичайно складними. Ну здавалося б, що може бути простішим за пустий простір? Адже простір, це просто та безструктурна пустота, в якій нема нічого окрім самої пустоти. І тим не менше, простір – це надзвичайно складний фізичний об’єкт, властивості якого визначальним чином залежать від тих об’єктів що в ньому знаходяться та тих подій які в ньому відбуваються.
Контрольні запитання.
- Поясніть фізичний зміст гравітаційної сталої.
- Чому в космічних масштабах гравітаційні сили є фантастично потужними, тоді як в умовах земного життя, практично не проявляють себе?
- Чому на земні тіла, окрім гравітаційної сили діє сила інерції?
- Чому Земля дещо розтягнута в екваторіальній площині і дещо приплюснута на полюсах?
- Чим схожі і чим відрізняються діючі на земні тіла сила тяжіння та гравітаційна сила?
- Чи проходить лінія дії сили тяжіння через центр мас Землі? Якщо проходить то де і чому?
- Як теорія поля пояснює механізм гравітаційних взаємодій?
- Як визначити, є в даній точці простору гравітаційне поле, чи нема?
- Від чого залежить прискорення вільного падіння на поверхні тієї чи іншої планети?
- З якого географічного місця (полюса, екватора чи середніх широт) енергетично доцільніше запускати космічні кораблі?
Вправа 23.
- З якою силою притягуються дві кулі масою по 100кг кожна, якщо відстань між їхніми центрами мас 1м?
- Визначте силу гравітаційної взаємодії між Землею та Сонцем, якщо відомо що відстань між ними 1,5∙1011м, а їх маси відповідно 6∙1024кг і 2∙1030кг.
- Космонавт масою 75кг знаходиться на висоті 300км над поверхнею Землі. З якою силою він притягується до Землі? Порівняйте цю силу з тією яка діяла б на нього на поверхні Землі. Радіус Землі 6400км.
- З якою максимальною гравітаційною силою можуть притягуватись дві однакові бетонні кулі масою по 1т кожна? Густина бетону 2,4∙103кг/м3.
- На якій відстані від поверхні Землі сила притягування космічного корабля до Землі буде у 100 разів меншою ніж на її поверхні?
- Знаючи період обертання Місяця навколо Землі (27,3 доби) та відстань між центрами Землі і Місяця (3,84·108м), визначте масу Землі.
- При якій тривалості доби вага тіла на екваторі Землі буде у два рази менше ніж на полюсі?
- Тіло масою 1т знаходиться на екваторі Землі. На скільки діюча на нього гравітаційна сила більша за відповідну їй силу тяжіння?
.
§24. Розв’язування задач. Тема: Закон всесвітнього тяжіння.
Знаючи закон всесвітнього тяжіння та розуміючи фізичну суть сили інерції, можна розв’язати величезну кількість практично та теоретично важливих задач, наприклад пояснити загальний устрій та «принцип дії» Сонячної системи, «зважити» Землю, Сонце чи галактику, визначити параметри гравітаційного поля того чи іншого космічного об’єкту чи системи таких об’єктів, тощо.
В свій час, ми поговоримо про те як і коли виникла Сонячної системи. Сьогодні ж, просто констатуємо факт того, що сучасна Сонячна система, це злагоджений цілісний механізм, який сформувався приблизно 4,5 мільярдів років тому і який з тих пір бездоганно працює. Центральним об’єктом цього механізму є зірка середніх розмірів, яку ми називаємо Сонцем і навколо якої обертаються її великі та малі природні супутники: планети, астероїди, комети та інші тіла При цьому, більшість планет мають свої супутники. Наприклад Земля має один, але відносно великий природний супутник – Місяць. Марс, має два супутники, Юпітер – 95, а Сатурн – 146.
Принцип дії ж цієї надскладної космічної системи гранично простий і полягає в наступному. Кожен елемент системи, під дією сили гравітаційної взаємодії та сили інерції, обертається навколо центрального тіла, при цьому швидкість обертання є такою, що забезпечує динамічну рівновагу між силою гравітаційної взаємодії та силою інерції. Достовірність вище сказаного проілюструємо на прикладі системи Земля – Місяць.

Мал.74. Схема загального устрою Сонячної системи.
Задача 1. З якою швидкістю Місяць має обертатися навколо Землі, щоб не наближатися до Землі і не віддалятися від неї? Якою в реальності є ця швидкість, якщо період обертанні Місяця навколо Землі 27,3доби? Маса Землі 6,0∙1024кг, відстань між центрами мас Землі та Місяця 3,84∙108м.

Дано:
М = 6,0∙1024кг
ℓ = 3,84∙108м
Т = 27,3доби = 23,6∙105с
v = ?
Рішення. Для того щоб Місяць не наближався до Землі і не віддалявся від неї, необхідно щоб він рухався з такою швидкістю v, яка забезпечує динамічну рівновагу між доцентровою силою гравітаційної взаємодії з Землею Fгр = GMm/ℓ2, та відцентровою силою інерції Fі = m∙ад = mv2/ℓ. Іншими словами, у відповідності з умовою динамічної рівноваги Місяця Fгр = Fi , тому GMm/ℓ2 = mv2/ℓ, звідси v = √(GM/ℓ), де G = 6,67·10–11м3/кг·с2.
Розрахунки: v = √(GM/ℓ) = √(6,67·10–11∙6·1024/3,84·108) = 1,02·103м/с = 1,02км/с. Таким чином, теорія стверджує, що Місяць має обертатися навколо Землі з швидкістю 1,02км/с. Якою ж в реальності є ця швидкість?
А в реальності ми маємо факт того, що за один оберт навколо Землі, який триває Т = 27,3доби = 23,6∙105с, Місяць проходить відстань L = 2πℓ = 24,1∙108м. А це означає, що його швидкість: v = L/T = 24,1·108м/23,6·105с = 1,02·103м/с =1,02км/с.
Відповідь: Реальна швидкість обертання Місяця навколо Землі (v = 1,02км/с), в точності дорівнює тій швидкості яка забезпечує динамічну рівновагу між діючими на Місяць гравітаційною силою та силою інерції.
Задача 2. Знаючи прискорення вільного падіння (g = 9,81м/с2) та радіус Землі (R = 6,4∙106м), визначити масу Землі.

Дано:
g = 9,81м/с2
R = 6,4·106м
М = ?
Рішення. Виходячи з того, що ту силу з якою тіло масою m притягується до Землі, з одного боку можна визначити як силу тяжіння Fт = mg, а з іншого – як силу гравітаційної взаємодії Fгр = GMm/R2, і що ці сили є практично рівними (Fт = Fгр), можна записати: mg = GMm/R2, звідси M = gR2/G = 9,81(м/с2)(6,4·106м)2/6,67·10–11(м3/кг·с2) = 60·1023кг = 6,0·1024кг.
Відповідь: М = 6,0·1024кг.
Задача 3. Знаючи швидкість обертання Місяця навколо Землі (v = 1,02км/с) та відстань між центрами мас Землі і Місяця (ℓ = 3,84∙108м), визначити масу Землі.

Дано:
v = 1,02км/с = 1,02·103м/с
ℓ = 3,84∙108м
М = ?
Рішення. Оскільки діючі на Місяць гравітаційна сила Fгр = GМm/ℓ2 та сила інерції Fi = mv2/ℓ, зрівноважують одна одну (Fгр = Fі), можна записати GMm/ℓ2 = mv2/ℓ, звідси M = v2∙ℓ/G, де G = 6,67·10–11м3/кг·с2.
Розрахунки: M = v2∙ℓ/G = (1,02·103)2∙3,84∙108/6,67·10–11 = 6,0∙1024кг.
Відповідь: М = 6,0∙1024кг.
Загальні зауваження. Зверніть увагу, в задачах 2 і 3 масу Землі, ми визначили (виміряли) двома абсолютно різними способами. При цьому отримані результати виявились практично однаковими. Як ви думаєте: що це означає? Правильно, це означає, що отриманий нами результат є гарантовано достовірним. Власне в науці, достовірність вимірювань визначається саме таким підходом: одну і ту ж величину вимірюють декількома різними методами. При цьому, якщо результати різних вимірювань співпадають, то це є гарантією достовірності відповідних вимірювань.
Задача 4. Знаючи період обертання Землі навколо Сонця (365 днів) та відстань між їх центрами (1,49∙1011м) визначити масу Сонця та швидкість обертання Землі навколо Сонця.

Дано:
Т = 365 днів = 31,54∙106с
ℓ = 1,49∙1011м
v = ? М☼ = ?
Рішення. У відповідності з умовою динамічної рівноваги Землі Fгр = Fi , тому
GM☼m/ℓ2 = mv2/ℓ, звідси M☼ = v2∙ℓ/G, де G = 6,67·10–11м3/кг·с2; v – швидкість обертання Землі навколо Сонця.
Величину тієї швидкості з якою Земля обертається навколо Сонця, можна визначити із наступних міркувань. Оскільки за рік (Т = 365 днів = 31,54∙106с) Земля проходить відстань L=2πℓ, то швидкість її руху v = 2πℓ/T.
Розрахунки:
v = 2πℓ/T = 2·3,14·1,49·1011м/31,54·106с = 3∙104м/с = 30км/с
М☼ = v2ℓ/G = 3·104м/с)21,49·1011м/6,67·10–11(м3/кг·с2) = 2,0∙1030кг.
Відповідь: v = 30км/с; M☼ =2,0·1030кг.
Вище описаний метод визначення мас, можна застосовувати не лише для системи двох окремо взятих тіл, а й для будь яких систем в яких тіло вільно обертається навколо спільного центру мас. Скажімо наше Сонце є частиною величезної зіркової системи (галактики), яку називають Чумацький Шлях, і в якій налічується близько 200∙109 зірок. Визначаючи масу цієї галактики зовсім не обов’язково «зважувати» кожну окрему зірку. Достатньо визначити відстань певної зірки від центру галактики (ℓ) та швидкість її обертання навколо цього центру (v), а потім скористатися формулою M = v2ℓ/G. При цьому отримана маса буде загальною масою всіх тих об’єктів які зосереджені у внутрішньому об’ємі того диску, радіус якого дорівнює відстані від центру мас галактики до відповідної зірки.
Втім, стосовно галактик, вище описаний спосіб визначення мас потребує певних уточнень. Про причини цих уточнень ми поговоримо в процесі вивчення космології. Наразі ж зауважимо, що галактики практично завжди утворюють певні системи галактик, в яких вони обертаються одна навколо одної та навколо спільного центру мас. А це означає, що маси галактик досить точно та безумовно достовірно визначаються на основі аналізу їх міжгалактичних обертань.
Те як «зважують» планети, зірки і галактики, є класичним прикладом непрямих вимірювань, тобто таких вимірювань при яких фактично вимірюють не ту величину яку потрібно виміряти, а інші з нею пов’язані величини. При цьому значення потрібної величини визначається за відповідною формулою.
Наприклад визначаючи площу круга, ми фактично вимірюємо його радіус (R) або діаметр (d), а площу визначаємо за тією формулою яка відображає зв’язок між площею круга та його радіусом (діаметром): S = πR2 = πd2/4. Або наприклад визначаючи масу Землі (M), вчені фактично вимірюють не її масу, а залежне від цієї маси прискорення вільного падіння. При цьому масу Землі визначають за тією формулою яка відображає зв’язок між масою планети та прискоренням вільного падінні на ній.
І не вірити результатам подібних вимірювань, це все рівно ніби не вірити тому, що визначена за формулою S = πR2 площа круга, є достовірною. Не вірити лише на підставі того, що ми вимірювали не площу круга, а його радіус. А якщо ви думаєте, що непряме вимірювання гірше, чи менш точне за пряме, то спробуйте виміряти площу круга (мал.75) прямим способом, тобто шляхом підрахунку кількості квадратних сантиметрів в цьому крузі. Порівняйте отриманий результат з результатом вимірювання за формулою S = πR2 і зробіть відповідні висновки.
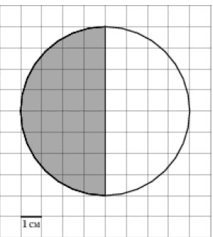
Мал.75. Виміряйте площу круга шляхом підрахунку кількості квадратних сантиметрів в ньому (пряме вимірювання) та за формулою S = πR2 (непряме вимірювання) і зробіть відповідні висновки.
Задача 5. На якій відстані від поверхні Землі, величина прискорення вільного падіння буде у два рази менша ніж на поверхні Землі? Радіус Землі 6,4·106м.

Дано:
R = 6,4·106м
g0/g = 2
h = ?
Рішення. Виходячи з того, що на поверхні Землі g0 = G∙M/(R)2, а на висоті h над цією поверхнею g = G∙M/(R+h)2, можна записати g0/g = [G∙M/(R)2] : [G∙M/(R+h)2] = (R+h)2/R2 = (R2+2Rh+h2)/R2 = 2, звідси R2+2Rh+h2 = 2R2, звідси R2 + 2Rh + h2 – 2R2 = 0, звідси h2 + 2Rh – R2 = 0, де h = ?
Таким чином, ми отримали рівняння вигляду ах2 + вх + с = 0, яке прийнято називати квадратним рівнянням, і яке в загальному випадку має два рішення: х12 = (–в ± √(в2 – 4ас)/2а. В умовах нашого рівняння (h2 + 2Rh – R2 = 0), а = 1; в = 2R; c = – R2. Враховуючи з цього можна записати.
h12 = [– 2R ± √((– 2R)2 – 4∙1∙(– R2)] / 2∙1 = [– 2R ± √(4R2 + 4R2)] / 2 = [– 2R ± √8R2] / 2 = [– 2R ± 2R√2] / 2 = –R ± R√2 = R(±√2 – 1).
Таким чином ми маємо два рішення:
h1 = R(√2 – 1) = R(1,41 – 1) = 0,41R = 2,6·106м = 2600км
h2 = R(–√2 – 1) = R(–1,41 – 1) = – 2,41R.
Відповідь h2 = – 2,41R здається дещо дивною. Однак в реальності ця відповідь є абсолютно правильною. Адже співвідношення g0/g = 2 виконується не лише для тієї точки яка знаходиться на висоті h1 = 0,41R = 2600км над поверхнею землі, а й на відстані h2 = 2,41R, виміряній у протилежному напрямку, тобто на висоті 0,41R але з протилежного боку Землі.
Відповідь: h1 = 0,41R; h2 = – 2,41R.
Задача 6. З якою максимальною гравітаційною силою можуть притягуватися дві однакові алюмінієві кулі масою по 1кг кожна? Густина алюмінію 2,7∙103кг/м3.
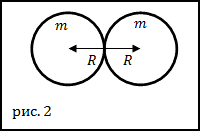
Дано:
m1 = m2 = m = 1кг
ρ = 2,7∙103кг/м3
Fгр = ?
Рішення. Виходячи з того, що відстань між центрами мас куль не може бути меншою за r = 2R, можна записати: Fгр = G∙m1∙m2/r2 = Gm2/(2R)2, де G = 6,67∙10–11(Н∙м2/кг2), де R = ?
Оскільки ρ = m/V, то V = m/ρ = 1кг/2,7∙103кг/м3 = 0,37∙10–3м3. З іншого боку, об’єм кулі V = 4πR3/3, звідси R3 = 3V/4π, R = 3√(3V/4π) = 3√(3∙0,37∙10–3/4∙3,14) = 3√(0,08∙10–3) = 3√(80∙10–6) = 4,3∙10–2м.
Розрахунки. Fгр = Gm2/(2R)2 = 6,67∙10–11∙12/(2∙4,3∙10–2)2 = 0,09∙10–7Н = 9∙10–9Н.
Відповідь: Fгр = 9∙10–9Н.
Контрольні запитання.
- Чи могла б існувати планетарна Сонячна система, якби її об’єкти з певними швидкостями не оберталися навколо Сонця? Чому?
- Які сили забезпечують динамічну рівновагу кожного об’єкту Сонячної системи?
- Що б було, якби Місяць обертався навколо Землі з швидкістю: більшою за наявну; меншою за наявну?
- Який загальний принцип дії того механізму який називається Сонячною системою?
- В чому суть непрямих вимірювань? Наведіть приклади.
- Чи є непрямі вимірювання гіршими чи менш точними за прямі вимірювання? Відповідь аргументуйте.
- Як вчені переконуються в тому, що їх вимірювання є достовірними?
Вправа 24.
- Визначте силу гравітаційної взаємодії між Землею та Сонцем, якщо відомо що відстань між ними 1,5∙1011м, а їх маси відповідно 6∙1024кг і 2∙1030кг.
- Знаючи прискорення вільного падіння (g=1,6м/с2) та радіус Місяця (R=1,74∙106м), визначити масу Місяця.
- Космонавт масою 80кг знаходиться на висоті 300км над поверхнею Землі. З якою силою він притягується до Землі? Порівняйте цю силу з тією яка діяла б на нього на поверхні Землі. Радіус Землі 6400км.
- З якою максимальною гравітаційною силою можуть притягуватись дві однакові сталеві кулі масою по 1кг кожна? Густина сталі 7,9∙103кг/м3.
- Визначте масу Юпітера, якщо відомо, що один з його супутників (Ганімед), будучи на відстані 1,1∙106км, має період обертання навколо Юпітера 7,15 земних діб. Порівняйте масу Юпітера з масою Землі.
- Визначити першу космічну швидкість для Марса, якщо маса Марса 6,4∙1023кг, а його радіус 3,4∙104км.
- На якій відстані від поверхні Землі сила притягування космічного корабля до Землі буде у 100 разів меншою ніж на її поверхні?
- Визначте прискорення вільного падіння на Місяці, якщо його маса 7,3∙1022кг, а радіус 1700км.
- При якій тривалості доби вага тіла на екваторі Землі буде у два рази меншою ніж на полюсі?
.
§25. Механічні деформації. Сила пружності. Механічна напруга. Закон Гука.
Нагадаємо, механіка, це розділ фізики в якому вивчають параметри, закономірності та причини механічного руху тіл в усіх його проявах. А одним з проявів механічного руху є механічна деформація тіла, тобто будь яка зміна форми або розмірів тіла, що відбувається під дією зовнішніх сил (від лат. deformatio – викривлення). З загальними основами тієї частини механіки яка вивчає параметри, закономірності та причини механічних деформацій тіла ми стисло ознайомимся в цьому параграфі.
За реакцією тіла на припинення дії деформуючої сили, механічні деформації поділяються на пружні та пластичні. Пружною називають таку механічну деформацію, яка повністю зникає після припинення дії деформуючої сили. Пластичною називають таку механічну деформацію, яка після припинення дії деформуючої сили зберігається (залишається). Іншими словами, якщо після припинення дії деформуючої сили, тіло повністю відновлює свою попередню форму, то його деформація є пружною. Якщо ж, після припинення дії деформуючої сили, тіло зберігає надану йому форму, то його деформація є пластичною.
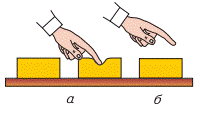
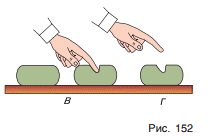
Мал.76. Приклади пружної та пластичної деформації.
Оскільки деталі машин і механізмів зазвичай виготовляють з пружних матеріалів, то властивості саме таких матеріалів та їм відповідних тіл і вивчаються в механіці.
За характером діючих на тіло деформуючих сил та за характером тих геометричних змін які відбуваються в деформованому тілі, все різноманіття пружних механічних деформацій прийнято розділяти на чотири різновидності:
- деформація розтягнення-стиснення (мал.77а,б);
- деформація згинання (мал. 77д);
- деформація кручення (мал. 77г);
- деформація зсуву (мал. 77в).
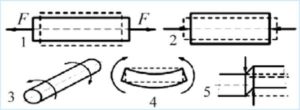
Мал.77. Геометрична суть основних видів механічних деформацій.
В межах програми загальноосвітньої школи, стисло вивчають параметри та закономірності лише однієї різновидності пружної деформації – деформації розтягнення-стиснення. Однак ви маєте знати, що з певними термінологічними поправками, ці параметри і закономірності притаманні будь якій різновидності пружної деформації та для будь якої комбінації цих різновидностей.
Характеризуючи геометричні та силові параметри не деформованого та пружно деформованого тіла, говорять про наступні величини:
– початкова довжина тіла ℓ0 (м);
– абсолютна деформація тіла ∆ℓ= ℓ – ℓ0 (м);
– відносна деформація тіла ε = ∆ℓ/ℓ0 (–);
– деформуюча сила F (Н);
– сила пружності Fпр = –k∆ℓ (Н);
– жорсткість тіла k = F/∆ℓ (Н/м);
– механічна напруга σ = Fпр/S (Н/м2 = Па);
– модуль пружності E = σ/ε (Па);
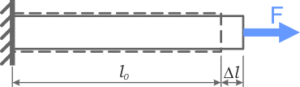
Мал. 78. Пружно деформоване тіло та його характеристики.
Абсолютна деформація – це фізична величина, яка характеризує абсолютну деформацію тіла і яка дорівнює різниці між довжиною тіла після деформації (ℓ) та його довжиною до деформації (ℓ0).
Позначається: ∆ℓ
Визначальне рівняння: ∆ℓ = ℓ – ℓ0
Одиниця вимірювання: [∆ℓ] = м.
Відносна деформація – це фізична величина, яка характеризує відносну (порівняльну) деформацію тіла і яка дорівнює відношенню абсолютної деформації тіла Δℓ до його початкової довжиниℓ0.
Позначається: ε
Визначальне рівняння: ε = ∆ℓ/ℓ0
Одиниця вимірювання: [ε]= м/м = – , (рази)
Наприклад якщо під дією деформуючої сили, довжина стержня збільшилась від ℓ0 = 20см до ℓ = 21см, то його абсолютна деформація ∆ℓ = ℓ – ℓ0 = 21см – 20см = 1см, а відносна деформація ε = ∆ℓ/ℓ0 = 1см/20см = 0,05.
Ту зовнішню силу F, дія якої спричиняє пружну деформацію тіла, називають деформуючою силою. Діюча на тіло деформуюча сила (F), породжує рівну їй за величиною і протилежну за напрямком протидіючу силу, яку називають силою пружності (Fпр).
Сила пружності – це та внутрішня сила, яка виникає в пружно деформованому тілі і яка завжди протидіє появі та зростанню цієї деформації.
Позначається: Fпр
Визначальне рівняння: Fпр = –k∆ℓ, де k – жорсткість тіла; Δℓ – абсолютна деформація тіла; знак «–» вказує на те, що напрям сили пружності протилежний до напрямку деформації Δℓ;
Одиниця вимірювання: [Fпр] = H, ньютон.
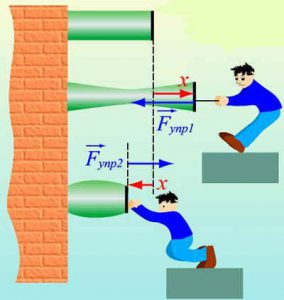
Мал.79. Сила пружності завжди протидіє деформуючій силі.
Сила пружності є результуючою тих складних процесів, які відбуваються всередині пружно деформованого тіла. Суть цих процесів полягає в наступному. У відповідності з законами Природи, атоми (молекули) речовини прагнуть до того, щоб бути розташованими на певних, енергетично доцільних відстанях один від одного. Коли ж під дією зовнішніх сил відстані між атомами змінюються (збільшуються або зменшуються), автоматично виникають сили, які прагнуть повернути атоми до попереднього, енергетично доцільного положення. Результуючою цих сил і є сила пружності.
Сила пружності залежить не лише від величини абсолютної деформації тіла (Δℓ), а й від його пружних властивостей. А ці властивості характеризує величина, яка називається жорсткістю тіла (k).
Жорсткість тіла – це фізична величина, яка характеризує здатність тіла протидіяти його пружній деформації і яка дорівнює відношенню тієї сили що деформує тіло, до величини отриманої при цьому абсолютної деформації.
Позначається: k
Визначальне рівняння: k = F/∆ℓ
Одиниця вимірювання: [k] = H/м, ньютон на метр.
Потрібно зауважити, що жорсткість тіла, тобто та величина яка визначається за формулою k = F/∆ℓ, фактично не залежить ні від величини деформуючої сили F, ні від величини отриманої при цьому абсолютної деформації ∆ℓ. Жорсткість тіла, залежить від параметрів самого тіла. Зокрема, якщо мова йде про тіла простої геометричної форми (стержні, балки, дроти, тощо), то їх жорсткість залежить від: 1) площі поперечного перерізу тіла S (чим більша площа – тим більша жорсткість); 2) початкової довжини тіла ℓ0 (чим більша довжина – тим менша жорсткість); 3) пружних властивостей того матеріалу, з якого виготовлено тіло. Цю залежність, можна записати у вигляді k = ES/ℓ0, де Е – модуль пружності, величина яка характеризує пружні властивості того матеріалу з якого виготовлено тіло, і значення якої визначається експериментально та записується у відповідну таблицю.
За необхідності пружні тіла і зокрема пружини об’єднують в певні пружні системи. При цьому розрізняють два базові способи таких об’єднань: паралельне з’єднання (мал.80а); послідовне з’єднання (мал.80б).
а)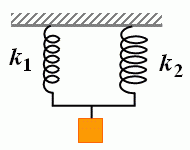 б)
б) 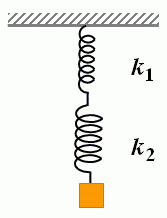
. k = k1+k2 k = k1·k2/(k1+k2)
Мал.80. Розрізняють два базові способи з’єднання пружин (пружних тіл): а) паралельне з’єднання; б) послідовне з’єднання.
Можна довести, що у випадку паралельного з’єднання пружин жорсткістю k1 і k2, їх загальна жорсткість k дорівнюватиме k = k1+k2. Якщо ж аналогічні пружини з’єднані послідовно, то їх загальна жорсткість становитиме k = k1·k2/(k1+k2). Наприклад якщо k1 = 40Н/м, а k2 = 60Н/м, то загальна жорсткість системи цих пружин при їх паралельному з’єднанні дорівнює k = k1+k2 = 40 + 60 = 100Н/м, а при послідовному з’їданні k = k1·k2/(k1+k2) = 40·60/(40+60) = 24Н/м. І не важко бачити, що при паралельному з’єднанні пружин їх загальна жорсткість збільшується, а при паралельному з’єднанні – зменшується.
Важливою характеристикою пружно деформованого тіла, є величина яка називається механічною напругою. Механічна напруга – це фізична величина, яка характеризує внутрішній механічний стан пружно деформованого тіла і яка дорівнює відношенню виникаючої в тілі сили пружності до величини його площі поперечного перерізу.
Позначається: σ
Визначальне рівняння: σ = Fпр/S
Одиниця вимірювання: [σ] = H/м2 = Па, (паскаль).
Основний закон механіки пружно деформованого тіла був експериментально встановлений в 1660 році англійським фізиком Робертом Гуком (1635–1703). В цьому законі (законі Гука) стверджується: при пружних деформаціях тіла, величина його абсолютної деформації (∆ℓ), прямо пропорційна деформуючій силі F і обернено пропорційна жорсткості тіла k. Іншими словами: ∆ℓ = F/k.
а)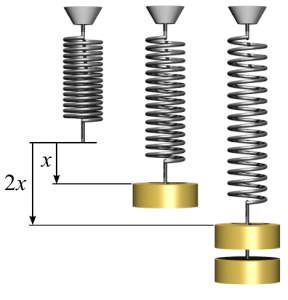 б)
б) 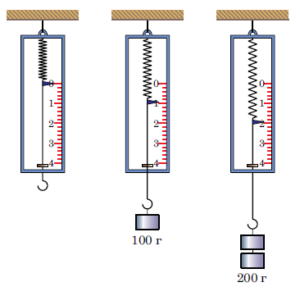
Мал.81. Абсолютна деформація тіла (ΔƖ), прямо пропорційна деформуючій силі (F): ∆ℓ = F/k – закон Гука.
Факт того, що абсолютна деформація тіла пропорційна деформуючій силі, корисно застосовується в приладах які називаються динамометрами (від грец. dynamis – сила та metreo – вимірювати). Динамометр, це прилад який дозволяє вимірювати величину діючої на нього сили. Основним елементом динамометра (мал.81б) є певне пружне тіло (пружина), яке під дією зовнішньої сили певним чином деформується. Власне за величиною цієї деформації і визначають величину деформуючої сили.
До речі, аналізуючи роботу динамометра неважко довести, що жорсткість його пружини (k = F/∆ℓ) не залежить ні від величини деформуючої сили (F), ні від величини отриманої при цьому деформації (∆ℓ). Дійсно, якщо під дією сили 1Н пружина видовжується на 2,5см, під сили 2Н – видовжується на 5,0см, а під дією сили 3Н – на 7,5см, то жорсткість пружини в кожному з випадків дорівнює:
k1 = F1/∆ℓ1 = 1Н/2,5см = 0,4Н/см;
k2 = F2/∆ℓ2 = 2Н/5,0см = 0,4Н/см;
k3 = F3/∆ℓ3 = 3Н/7,5см = 0,4Н/см.
Вище наведене формулювання закону Гука є безумовно правильним, очевидно простим та історично автентичним. Однак в сучасній науці цей закон прийнято формулювати по іншому: при пружних деформаціях тіла, величина виникаючої в ньому механічної напруги σ, пропорційна відносній деформації ε тіла. Іншими словами: σ = Еε, де Е – модуль пружності (модуль Юнга), постійна для даного матеріалу величина, значення якої визначається експериментально і записується у відповідну таблицю.
На перший погляд, формули ∆ℓ = F/k і σ = Еε абсолютно різні. Насправді ж, ці формули математично тотожні. Дійсно. Враховуючи що k = ES/ℓ0; ε = ∆ℓ/ℓ0; σ = Fпр/S; Fпр = F, можна записати: ∆ℓ = F/k = Fпр/(ES/ℓ0) = Fпрℓ0/ES = σℓ0/E. Звідси σ = E∆ℓ/ℓ0 = Eε .
Ви можете запитати: «А чому в сучасній науці, закон Гука прийнято записувати не у вигляді ∆ℓ = F/k, а у вигляді σ = Eε?» Пояснюючи такий стан речей, розглянемо декілька простих ситуацій.
Припустимо, що у вашому розпорядженні є два гумових (E1 = E2) стержні, однакової площі поперечного перерізу (S1 = S2), але різної довжини, скажімо ℓ1 = 10см, ℓ2 = 100см. Припустимо, що кожен з цих стержнів ви розтягнули (деформували) на одну і ту ж абсолютну величину, наприклад на 10см (∆ℓ1 = ∆ℓ2 = 10см). Запитується, чи однаковою є ступінь деформованості цих стержнів? Відповідь очевидна – ні не однаковою. Адже для першого стержня (ℓ1 = 10см) абсолютна деформація величиною в 10см є відносно великою, тоді як для другого стержня (ℓ2 = 100см) та ж деформація є відносно малою. Висновок: абсолютна деформація (∆ℓ) не є тією величиною яка у повній мірі об’єктивності характеризує деформованість тіла. В цьому сенсі, більш об’єктивною величиною є відносна деформація (ε = ∆ℓ/ℓ0), яка чітко вказує, що ступінь деформованості першого тіла (ε1 = 1) в десять разів більша за ступінь деформованості другого тіла (ε2 = 0,1).
Тепер уявіть, що два гумових (E1 = E2) стержні, однакової довжини(ℓ1 = ℓ2) але різної площі поперечного перерізу (скажімо S1 = 1см2, S2 = 10см2), навантажені однаковими силами (F1 = F2), наприклад по 100Н кожна. Запитується, чи є однаковим внутрішній механічний стан пружно деформованих тіла? Відповідь очевидна – ні не є. Адже для першого стержня (S1 = 1см2), сила в 100Н є відносно великою, тоді як для другого стержня (S2 = 10см2) – відносно малою. Висновок: виникаюча в тілі сила пружності не є тією величиною, яка у повній мірі об’єктивності, характеризує внутрішній механічний стан пружно деформованого тіла. В цьому сенсі більш об’єктивною величиною є механічна напруга (σ = Fпр/S). Адже механічна напруга чітко вказує на те, що внутрішній механічний стан першого тіла (σ1 = 100Н/см2) у десять разів більш напружений ніж другого (σ2 = 10Н/см2).
Не важко бачити, що ті величини які фігурують в першому формулюванні закону Гука (∆ℓ = F/k), є такими, що не у повній мірі об’єктивності характеризують як ступінь деформованості тіла, так і його внутрішній механічний стан. Натомість, ті величини які фігурують в другому формулюванні цього закону (σ = Еε) характеризують ті ж параметри пружно деформованого тіла більш об’єктивно та повно.
Додайте до цього факт того, що жорсткість кожного тіла (k = ES/ℓ0) є індивідуальною і такою, що потребує певних експериментальних або теоретичних досліджень, тоді як модуль пружності (E), це певна таблична величина, яка є однаковою для всіх виготовлених із даного матеріалу тіл – і ви зрозумієте чому в сучасній науці та інженерній практиці, закон Гука записують не у вигляді ∆ℓ = F/k, а у вигляді σ = Еε. До речі, той розділ прикладної механіки в основі якого лежить практичне застосування закону Гука (σ = Еε) називають опором матеріалів (сопроматом).
Завершуючи розмову про силу пружності та сили загалом, буде не зайвим сказати декілька слів про чотири сили, які часто плутають одна з одною та застосовують не за призначенням. Ситуація ускладнюється тим, що в багатьох випадках числові значення цих сил є однаковими. Тому, фактично неправильно застосувавши сили, ви можете отримати формально правильну відповідь і заслужено незадовільну оцінку.
Мова йде про силу тяжіння (Fт), вагу (P), реакцію опори (N) та силу пружності (Fпр). Нагадаємо. Сила тяжіння (Fт) – це та сила з якою тіло притягується до Землі. Вага (P) – це та сила з якою тіло діє на опору. Реакція опори (N) – це та сила з якою опора діє на тіло. Сила пружності (Fпр) – це та сила яка виникає в пружно деформованому тілі і яка протидіє його деформації. Із визначень ясно, що коли ми говоримо про ті сили які діють на тіло, то ними є сила тяжіння (Fт) та реакція опори (N). Якщо ж мова йде про ті сили які діють на поверхню опори, то ними є вага тіла (P) та виникаюча в опорі сила пружності (Fпр).

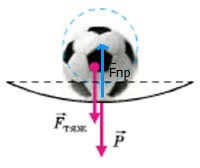
Мал.82. На тіло діє сила тяжіння та реакція опори. На поверхню опори діє вага тіла та виникаюча в опорі сила пружності.
Зважаючи на вище сказане та дотримуючись загально прийнятих визначень, неправильно говорити і писати, що на те тіло яке лежить чи висить на опорі діє вага тіла та виникаюча в опорі сила пружності. Бо на тіло діє сила тяжіння та реакція опори. Неправильно говорити і писати, що на поверхню опори діє сила тяжіння тіла та реакція опори. Бо на поверхню опору діє вага тіла та виникаюча в опорі сила пружності. Неправильно говорити і писати, що тіло падає під дією своєї ваги. Бо тіло падає під дією сили тяжіння.
Контрольні запитання.
- Яку силу називають деформуючою силою? Чи залежить величина деформуючої сили від властивостей того тіла яке вона деформує?
- Яку силу називають силою пружності? Від чого залежить ця сила?
- Чи означає визначальне рівняння k = F/∆ℓ, що жорсткість тіла залежить від величини тієї сили яка деформує тіло та його абсолютної деформації? Від чого залежить жорсткість тіла?
- Що стверджує автентичне формулюванні закону Гука?
- Поясніть загальний устрій та принцип дії динамометра.
- Як прийнято формулювати закон Гука в сучасній науці?
- Чому в сучасній науці закон Гука прийнято записувати не у вигляді ∆ℓ = F/k, а у вигляді σ = Еε?
- Доведіть що формули ∆ℓ = F/k та σ = Еε є тотожними.
- 9. На поверхні стола лежить тіло масою m. Які сили діють на тіло? Які сили діють на поверхню стола? Чому дорівнює кожна з цих сил?
Вправа №25.
- Відносна деформація дроту 0,001. Визначити абсолютну деформацію цього дроту, якщо його початкова довжина 80см.
- Якої довжини має бути сталевий дріт, щоб при відносній деформації 0,0005 його абсолютна деформація дорівнювала 1см?
- Жорсткість кожної з двох пружин 50Н/м. Визначте загальну жорсткість системи цих пружин при їх паралельному та послідовному з’єднанні. Зробіть висновки.
- Під дією сили 1кН стержень діаметром 1см подовжився на 1мм. Яка жорсткість цього стержня та виникаюча в ньому механічна напруга?
- До закріпленої одним кінцем дротини діаметром 2мм підвісили вантаж масою 10кг. Визначити виникаючу в дротині силу пружності та механічну напругу.
- Жорсткість дротини k. Чому дорівнюватиме жорсткість половини цієї дротини?
- Яка максимальна механічна напруга виникає в вертикально висячому мідному стержні під дією власної ваги? Як залежить ця напруга від а) діаметру стержня; б) маси стержня; в) довжини стержня?
- На дротині довжиною ℓ висить вантаж масою m. Дротину склали вдвічі і підвісили той же вантаж. Порівняйте абсолютні та відносні деформації дротин в цих двох випадках. Порівняйте їх жорсткості.
- Два однакові вантажі масою 0,2кг кожний з’єднані пружиною, жорсткість якої 100Н/м. На скільки розтягнеться пружина, якщо за один вантаж тягнути всю систему вгору силою 6,0Н? Масою пружини знехтувати.
.
§26. Пара сил. Момент сили. Важелі.
До сих пір, говорячи про механічну та динамічну рівновагу тіла, ми мали на увазі, що це тіло знаходиться під дією так званої збіжної системи сил, тобто такої сукупності одночасно діючих сил, лінії дії яких перетинаються в одній точці. По суті це означає, що до сих пір ми вивчали статику матеріальної точки, тобто ту частину статики в якій тіло можна вважати матеріальною точкою, а діючу на це тіло систему сил, можна замінити однією рівнодійною силою. Силою, яка надає тілу поступального руху.
Однак, далеко не всяка діюча на тіло система сил є збіжною і далеко не всяку систему сил можна замінити рівнодійною силою. Наприклад, якщо на тіло діють дві рівні за величиною і протилежні за напрямком сили F і Fꞌ які не лежать на одній прямій (мал.83), то замінити цю систему сил відповідною рівнодійною, не можливо. Дійсно. Формально визначивши рівнодійну сил F і Fꞌ ми отримаємо нульову величину: F + Fꞌ = 0. Та чи означає це, що загальна механічна дія сил F1 і Fꞌ є нульовою? Очевидно що ні. Адже дана система сил надає або намагається надати тілу певного обертального руху.
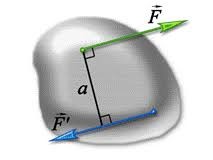
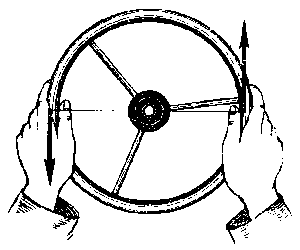
Мал.83. Пару сил не можливо замінити рівнодіючою силою.
Систему двох рівних за величиною і протилежних за напрямком сил, які не лежать на одній прямій і спільно діють на одне і те ж тіло, називають парою сил (або парою). Пара сил надає (або намагається надати) тілу обертального руху. Пару сил не можливо замінити або зрівноважити однією силою. Пару сил можна замінити чи зрівноважити лише іншою парою сил.
Ви можете заперечити в тому сенсі, що в певних випадках тіло може обертатись під дією лише однієї сили. Наприклад, відчиняючи двері, ми прикладаємо лише одну силу яка і надає їм обертального руху. Дійсно. На перший погляд здається, що двері обертаються під дією лише однієї сили. Насправді ж, одна сила не може змусити тіло обертатися. Це може зробити лише пара сил. І якщо двері обертаються, то це тільки тому, що в реальності на них діють дві сили які і утворюють відповідну пару. При цьому не важко збагнути, що другою силою пари є та реакція опори, яка виникає в петлях дверей. Петлях, які утворюють нерухому вісь обертання тіла.
Загалом, тіло яке має нерухому вісь обертання може рухатись лише обертально. І це обертання створює відповідна пара сил. Інша справа, що однією з цих сил може бути та реакція опори яка виникає в нерухомій осі обертання.
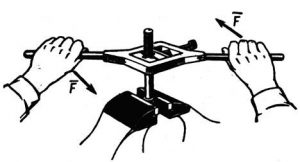

Мал.84. Пара сил надає тілу, або прагне надати, обертального руху.
Основною характеристикою пари сил, або тієї сили що діє на тіло з нерухомою віссю обертання, є фізична величина яка називається моментом сили або моментом пари сил. Момент сили – це фізична величина, яка характеризує обертальну дію сили (пари сил) і яка дорівнює добутку цієї сили F на плече її дії d, тобто на найкоротшу відстань між лінією дії сили та віссю обертання тіла.
Позначається: М
Визначальне рівняння: М=Fd
Одиниця вимірювання: [М] = Н∙м, ньютон-метр.
По суті, момент сили – величина векторна. Однак, зважаючи на те, що в межах програми загальноосвітньої школи вивчають лише плоскі системи сил, момент сили можна вважати величиною скалярною, тобто такою яка характеризується абсолютною величиною та знаком. При цьому, знак моменту сили зазвичай визначають за правилом: якщо сила повертає (або намагається повернути) тіло за годинниковою стрілкою, то момент сили додатній, а якщо проти годинникової стрілки – від’ємний.

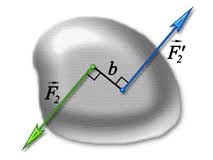
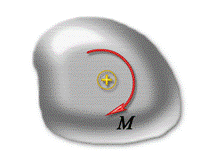
Мал.85. Якщо пара сил повертає тіло за годинниковою стрілкою, то момент сили додатній, а якщо проти годинникової стрілки – від’ємний.
Коли ми стверджували, що тіло буде знаходитись в стані механічної рівноваги тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил дорівнює нулю (∑F = 0), то мали на увазі, що система діючих на тіло сил є збіжною, тобто такою, яка надає тілу поступального руху. В загальному ж випадку, система діючих на тіло сил може бути довільною. І ця довільна система сил може надавати тілу не лише поступального руху, а й руху обертального. В такій ситуації основний закон статики (загальна умова рівноваги тіла) набуває вигляду: тіло буде знаходитись в стані загальної механічної рівноваги (v = 0; ω = 0) тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил та моментів цих сил дорівнюють нулю. Іншими словами: якщо {∑F = 0 і ∑M = 0} то {v = 0; ω = 0} і навпаки.
З’ясовуючи закономірності так би мовити обертальної рівноваги тіла, розглянемо ситуацію в якій тіло має нерухому вісь обертання. Оскільки те тіло яке має нерухому вісь обертання, поступально не рухається і рухатися не може, то векторна сума діючих на нього зовнішніх сил гарантовано дорівнює нулю. А це означає, що для тіла з нерухомою віссю обертання, умова рівноваги набуває вигляду: якщо ∑М = 0, то ω = 0 або ω = cons і навпаки. Зауважте, подібно до того, як за виконання умови ∑F = 0, тіло може знаходитись як в стані поступального спокою (v = 0) так і в стані прямолінійного рівномірного руху (v = const), виконання умови ∑M = 0, передбачає як можливість обертального спокою тіла (ω = 0), так і можливість його рівномірного обертального руху (ω = const).
Одним з практично важливих прикладів тіла, що має нерухому вісь обертання є простий механізм який називається важелем. Важіль – це прилад, який представляє собою довге тверде тіло, що може обертатись навколо відносно нерухомої точки, яку називають точкою опори.
Так чи інакше важелі застосовувались з незапам’ятних часів. Скажімо, коли використовуючи підручну палицю, прадавня людина зрушувала з місця важкий камінь, то вона фактично застосовувала важіль. Якщо ж говорити про історично зафіксовані факти системного застосування важелів, то вони відносяться до періоду будівництва великих єгипетських пірамід (приблизно 4600 років тому).

Мал.86. Люди використовували важелі з прадавніх часів.
Напевно першим хто дослідив важіль як науковець, хто пояснив його принцип дії та основні властивості, був видатний давньогрецький вчений Архімед (287–212 р.р. до н.е.). Саме Архімеду належить крилатий вираз: «Дайте мені точку опори і я підніму Землю».
Зазвичай важіль застосовується для підсилення силової дії. Таке підсилення відбувається за рахунок того, що плече дії тієї сили яку ми прикладаємо до важеля і яка потребує підсилення, значно більше за плече дії сили «вихідної». Дійсно. Якщо сила F1 (мал.87) має плече d1, а сила F2 – плече d2, то у відповідності з умовою рівноваги даного тіла (важеля) F1d1 = F2d2. А це означає, що коли плече дії сили F1 буде більшим за плече дії сили F2 (d1˃d2) то у відповідну кількість разів сила F2 буде більшою за силу F1: F2 = F1(d1/d2).
З іншого боку було б дивним та неприроднім, якби за допомогою важеля ми отримували виграш в силі, що називається «безкоштовно», тобто не програючи в чомусь іншому. І очевидно, що цим «іншим» є програш в тому переміщенні яке спричиняє підсилена сила. Дійсно. З геометричних міркувань (дивись мал.79) випливає, що виграючи в силі (F2 = nF1 де n = d1/d2 = h1/h2) ми в таку ж кількість разів програємо в тому переміщенні яке здійснює ця сила (h2 = h1/n).
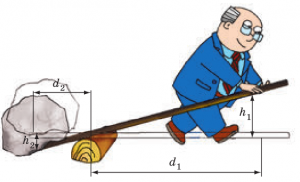
Мал.87. Важіль – механізм який підсилює силову дію. При цьому, виграючи в силі (F2 > F1), ми неминуче програємо у відстані (h2 < h1).
Про те, що «безкоштовних» виграшів у силі не буває, вчені знали ще з стародавніх часів. Досліджуючи властивості важеля, Архімед сформулював правило, яке стосувалось всіх простих механізмів і в якому стверджувалось: у скільки разів виграєш в силі, у стільки ж разів програєш у відстані. Це правило прийнято називати золотим правилом механіки. По суті, золоте правило механіки є одним з перших формулювань базового закону сучасної науки – закону збереження енергії.
Певні важільні системи можна побачити в найрізноманітніших сучасних приладах, починаючи від дитячих гойдалок, весел, шлагбаумів та ножиць і закінчуючи елементами піднімально-транспортних механізмів, автомобілів, кораблів, літаків, тощо. Деякі приклади простих важільних систем представлені на мал.88.
Мал.88. Деякі приклади простих важільних систем.
Певні важільні системи можна побачити не лише в штучно створених приладах, а й в організмах живих істот, зокрема в організмі людини. Наприклад ліктьова кістка руки, ліктьовий суглоб та той м’яз який називають біцепсом (мал.89а) утворюють важільну систему, яка забезпечує рухливість ліктьової частини руки. Аналогічне можна сказати і про ступню ноги (мал.89в), рухливість якої забезпечує важільна система елементами якої є кістки стопи, великогомілкова кістка та ахілесове сухожилля. Або наприклад череп людини (мал.89б), у поєднанні з кістками шийного відділу хребта та ремінним м’язом, утворюють важільну систему яка забезпечує рухливість голови.
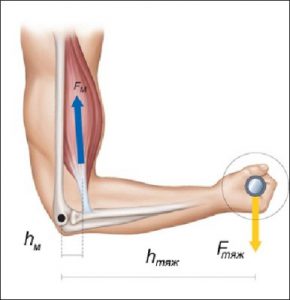
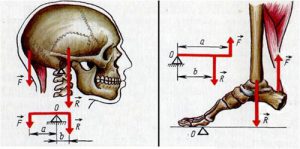
Мал.89. Приклади важільних систем людського тіла.
Задача 1. В точці 1 (дивись мал.) прикріплено вантаж масою 2кг. Якої маси вантаж треба закріпити в точці 2, щоб важіль був у рівновазі. Маса важеля 4кг.
Дано:
m1 = 2кг
m3 = 4кг
d1 = 9 од.
d2 = 1 од.
d3 = 4 од.
m2 = ?
Рішення. Виконуємо малюнок на якому вказуємо діючі на важіль сили (F1 = m1g =2кг·10м/с2 = 20Н, F2 = m2g, F3 = m3g = 4кг·10м/с2 = 40Н), та їх відстані до осі обертання важеля. Ці відстані визначаємо на основі аналізу малюнку та факту того, що точкою прикладання сили тяжіння важеля (F3) є геометричний центр цього важеля. Записуємо умову рівноваги важеля відносно осі його обертання:
∑MO = –F1d1 – F3d3 + F2d2 = 0, звідси F2d2 = F1d1 + F3d3, звідси F2 = (F1d1 + F3d3)/d2 = (20·9 + 40·4)/1 = 340 Н. А оскільки F2=m2g, то m2 = F2/g = 340Н/10м/с2 = 34кг.
Відповідь: m2 = 34кг.
Задача 2. До кінців важеля довжиною 1,2м підвішені вантажі масою 12кг і 6кг. Де потрібно встановити опору, щоб вантажі перебували у рівновазі?
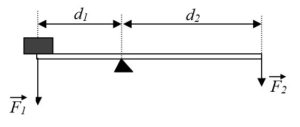
Дано:
ℓ=1,2м
F1=m1g=120Н
F2=m2g=60Н
d1 = ? d2 = ?
Рішення. Виконуємо малюнок на якому вказуємо діючі на важіль сили та відстані до них. Зважаючи на те, що d2 = ℓ – d1 записуємо умову рівноваги важіля відносно осі його обертання. ∑MO = –F1d1 + F2(ℓ–d1) = 0, або –F1d1 + F2ℓ– F2d1 = 0, звідси d1(F1 +F2) = F2ℓ, звідси d1 = F2ℓ/(F1 +F2).
Розрахунки: d1= F2ℓ/(F1 +F2) = 120Н∙1,2м/(120Н+60Н) = 0,8м;
d2 = ℓ – d1 = 1,2м – 0,8м = 0,4м.
Відповідь: d1 = 0,8м; d2 = 0,4м.
Завершуючи розмову про важелі, розглянемо питання про те, наскільки реальним є вислів Архімеда: «Дайте мені точку опори і я підніму Землю»? Ясно, що мова йде про певну гіпотетичну задачу, гіпотетичне рішення якої базується на властивостях того простого механізму який називається важелем.
Припустимо, що у Всесвіті є така точка спираючись на яку Архімед мігби підняти Землю. Припустимо, що знайшовся такий надзвичайно довгий, надміцний, невагомий стержень, за допомогою якого Архімед міг би підняти Землю. Припустимо, що Земля має такі маленькі розміри, які дозволять розмістити її на короткій частині важеля, плече якої d = 1м. Запитується, плече якої довжини (D) повинен мати важіль, щоб Архімед прикладаючи силу еквівалентну масі m = 60кг, міг би підняти Землю маса якої M = 60·1023кг? На яку відстань (H) має переміститися той кінець стержня на який буде тиснути Архімед, щоб Земля піднялася на h = 1см? Скільки часу знадобиться Архімеду, щоб постійно рухаючись з швидкістю 1м/с подолати цю відстань?

Мал.90. Дайте мені точку опори і я підніму Землю.
Рішення. Оскільки маса Землі 60·1023кг, то для того щоб сила еквімалентна масі 60кг, зрушила Землю, знадобиться важіль плечі якого знаходяться у співвідношенні: D/d = M/m = 60·1023кг/60кг = 1·1023разів. Таким чином, якщо довжина короткого плеча важеля становитиме 1м, то довжина його довгого плеча має дорівнювати D = d·1023 = 1·1023м. Для порівняння, відстань від Землі до Сонця 1,49·1011м, тобто в 670 000 000 000 разів менша.
Тепер давайте визначимо ту відстань (H) на яку Архімед, постійно тиснучи на свій край важеля з силою 600Н повинен перемістити цей край, щоб Земля піднялась на h = 1см. А цю відстань можна визначити із співвідношення: Н/h = D/d. Звідси H = hD/d = 1см1·1023 = 1·1021м. А це «всього» у 6 700 000 000 разів більше за відстань від Землі до Сонця.
Скільки ж часу знадобиться Архімеду, щоб постійно рухаючись з швидкістю 1м/с подолати цей шлях? А цей час визначити не складно: t = H/v =1·1021м/1(м/с) = 1·1021с = 1·1021/365·24·60·60 = 31,7·1012років. А це «всього» у 2300 разів більше за вік нашого Всесвіту.
Висновки зробіть самі.
Контрольні запитання.
- Яку систему сил називають збіжною? Чи може така система надати тілу обертального руху?
- Чому пару сил не можна замінити рівнодійною силою?
- Що називають моментом сили та плечем дії сили?
- Чому загальна умова рівноваги тіла (∑F = 0; ∑M = 0), для тіла що знаходиться під дією збіжної системи сил набуває вигляду ∑F = 0, а для тіла що має нерухому вісь обертання ∑М = 0.
- Чому дверні ручки розташовують на краю дверей, а не на їх середині?
- Поясніть принцип дії важеля.
- Чи означає факт підсилення важелем силової дії, що це підсилення є «безкоштовним»?
- Що стверджується в золотому правелі механіки?
Вправа 26.
Загальні зауваження. При розв’язуванні задач, діючу на тіло силу тяжіння прикладають в центрі мас цього тіла. В однорідних тілах (ρ = const) постійної площі поперечного перерізу (стержні, труби, балки, тощо), центр мас тіла співпадає з його геометричним центром.
- В точці 1 (мал.а) прикріплено вантаж масою 20кг. Яку силу треба прикласти в точці 2, щоб важіль був у рівновазі. Маса важеля 4кг.
- На основі аналізу малюнку (б) визначте величину тієї сили яка діє на біцепс руки що утримує гирю масою 2кг.
а) б)
б)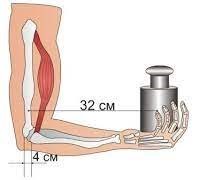
- Відомо що маса слона 5т, а маса мухи 0,1г. Якої довжини має бути довше плече важіля, щоб муха зрівноважила слона. Довдина того плеча на якому стоїть слон 2м. Масу важеля не враховувати. На скільки має опуститися муха, щоб слон піднявся на 10см?
- На землі лежить балка масою 80кг. Яку силу потрібно прикласти, щоб підняти один кінець цієї балки.
- Щоб підняти один кінець труби що лежить на землі, потрібно прикласти силу 400Н. Яка маса труби
- До кінців важеля довжиною 1м підвішені вантажі масою 6кг і 14кг. Де потрібно встановити опору, щоб вантажі перебували у рівновазі?
- До кінців стержня масою 20кг і довжиною 1м підвішено вантажі масою 10кг і 40кг. Де потрібно встановити опору щоб стержень був в горизонтальному положенні.
- Стержень довжиною 1м горизонтально висить на двох динамометрах. При цьому перший знаходиться на відстані 10см від лівого кінця стержня і показує 30Н, а другий – знаходиться на відстані 30см від правого кінця. Яка маса стержня і що показує другий динамометр?
.
§27. Механічні блоки та їх системи.
Окрім важелів до числа найбільш поширених простих механізмів, відносяться різноманітні блоки. Блок – це прилад (механізм), який представляє собою круглий шків що має вісь обертання і по жолобу якого проходить елемент гнучкого зв’язку (канат, мотузка, трос, ланцюг, тощо). Якщо в процесі руху вантажу вісь блоку залишається нерухомою (мал.91а), то блок називається нерухомим. А якщо в процесі руху вантажу вісь блоку рухається разом з вантажем (мал.91б), то відповідний блок називають рухомим.

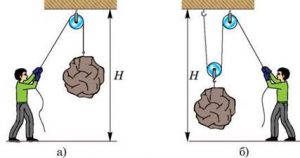
Мал.91. Загальний устрій та найпростіші застосування блоку.
Оскільки шків блоку вільно обертається, то силовий натяг перекинутого через нього канату на вході та на виході шківа має бути однаковим. Власне ця однаковість випливає з умови обертальної рівноваги шківа. Дійсно. Під дією двох різнонаправлених сил F1 і F2 (мал.92а), шків буде знаходитись в стані обертальної рівноваги за умови, що момент тієї сили яка обертає шків за годинниковою стрілкою (M2 = F2R) дорівнює моменту тієї сили яка обертає його проти годинникової стрілки (M1 = F1R), тобто за умови F2R = F1R, де R – радіус шківа. А це можливо лише тоді, якщо F2 = F1.
І потрібно зауважити, що натяг перекинутого через шків канату, не залежить від того, в якому напрямку цей канат натягують. А це означає, що нерухомий блок, не даючи виграшу в силі, дозволяє змінювати напрям цієї сили. Вже цей факт, робить подібні механізми потрібними та загальновживаними.
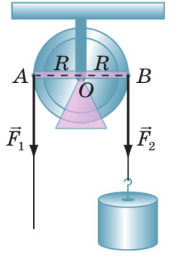
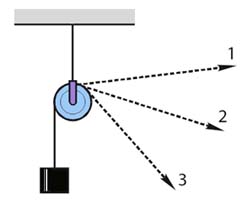
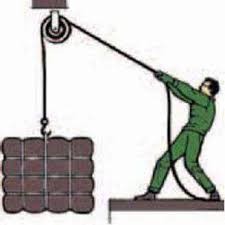
Мал.92. Нерухомий блок, не даючи виграшу в силі, дозволяє змінювати напрям цієї сили.
Але можливості блоків не вичерпуються лише зміною напрямку дії сили. В цьому не важко переконатись на прикладі системи яка складається з рухомого та нерухомого блоків (мал.93а). Не важко бачити, що в такій системі на рухомий блок, а отже і на те тіло яке він піднімає, діють дві рівні за величиною співнаправлені сили. А це означає, що натягуючи канат з силою F, на осі рухомого блоку ми отримаємо вдвічі більше тягове зусилля. Якщо ж в системі буде два рухомих блоки (мал.93б), то та загальна вага яку підніматиме ця система, буде у 4 рази більшою за величину тієї сили з якою натягують канат. Загалом же, загальну вантажопід’ємність (Fзаг) системи рухомих та нерухомих блоків можна визначити за формулою Fзаг=2nF, n – кількість рухомих блоків в системі F – сила натягу канату.
а)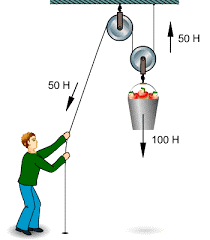 б)
б)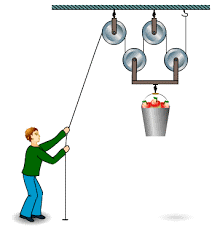
Мал.93. Кожний рухомий блок, збільшує вантажопід’ємність системи на 2F, де F – сила натягу канату.
Втім, потрібно мати на увазі, що загальна вантажопід’ємність системи рухомих та нерухомих блоків залежить не лише від числа рухомих блоків, а й від місця закріплення нерухомого кінця канату. При цьому, якщо цей кінець кріпиться до нерухомої опори (94а), то загальна вантажопід’ємність системи n рухомих блоків дорівнює 2nF. Якщо ж нерухомий кінець канату кріпиться до рухомої опори, тобто тієї опори яка рухається разом з рухомими блоками (мал.94б,в), то в цьому випадку загальна вантажопід’ємність системи n блоків дорівнює (2n+1)F. Дійсно. Оскільки сила натягу канату в усіх його точках однакова, то в зображеній на мал.94б системі, на рухому опору діють три рівні за величиною співнаправлені сили, кожна з яких дорівнює силі натягу канату. При цьому величина результуючої сили становить (2n+1)F.
а)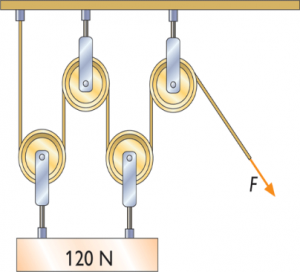 б)
б) 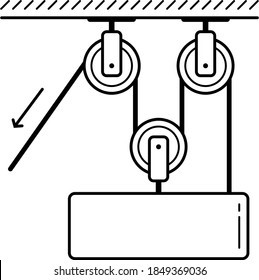 в)
в) 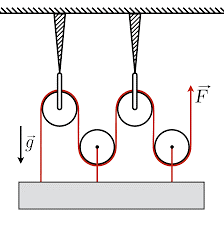
Мал.94. Загальна вантажопід’ємність системи блоків, залежить не лише від числа рухомих блоків в ній, а й від місця закріплення нерухомого кінця канату.
Ясно, що у вище наведених ситуаціях, отриманий виграш в силі не може бути «безкоштовним». Платою за цей виграш є неминучий програш в пройденому шляху. Дійсно. Для того, щоб за допомогою представленого на мал.93а рухомого блоку, підняти вантаж на ℓ метрів, потрібно на ℓ метрів зменшити довжину як правої так і лівої частин того канату який піднімає блок. А це означає, що той робітник який тягне канат з силою F, повинен прикладаючи цю силу протягнути 2ℓ метрів канату. Якщо ж система блоків дозволяє збільшити піднімальну силу в 4 рази (мал.93б), то відповідно в 4 рази зменшується та висота на яку піднімається вантаж (порівняно з довжиною переміщеного канату).
Таким чином, виграючи в тій силі яка піднімає вантаж, ми неминуче та у відповідну кількість разів програємо у тій висоті на яку піднімається вантаж. Що ж, Природу не можливо обманути: у скільки разів виграєш в силі, у стільки ж разів програєш в пройденому шляху (золоте правило механіки).
На практиці часто застосовують системи блоків, які називаються поліспастами. Поліспаст (мал.95) представляє собою систему двох блоків, кожен з яких складається з n шківів які мають спільний корпус та спільну вісь обертання. При цьому, один блок є нерухомою частиною поліспасти, а інший – його рухомою частиною. Принцип дії цієї системи полягає в наступному. Якщо до вільного кінця канату, який почергово огинає шківи рухомого та нерухомого блоків, прикласти силу F, то натяг всіх частин цього канату буде однаковим і чисельно рівним силі F. А це означає, що на рухомий блок системи діятимуть 2n однакових співнаправлених сил F, які можуть зрівноважити (підняти) результуючу силу Fрез = 2nF, де n – кількість шківів в рухомій частині поліспасти. Втім, формула Fрез= 2nF є справедливою лише в тому випадку, якщо нерухомий кінець канату кріпиться до нерухомої частини поліспасти (мал.95а). Якщо ж нерухомий кінець канату кріпиться до рухомої частини поліспасти (95б), то в цьому випадку Fрез= (2n+1)F.
а) 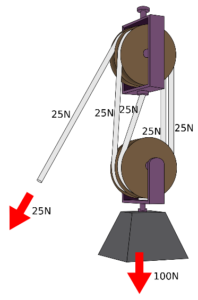 б)
б) 
Мал.95. Загальний устрій поліспаст.
Поліспасти є важливими частинами механізмів підйому та зміни вильоту стріли різноманітних підйомно-транспортних засобів. Вони використовуються для підйому та опускання вантажів в автомайстернях, на будівництві, на річковому та морському транспорті. В альпінізмі поліспасти застосовують для натягування канатів, для підйому вантажів, постраждалих людей, тощо.
На завершення зауважимо, що визначаючи вантажопідйомність блоків та їх систем, треба враховувати не лише кількість рухомох блоків та місце закріплення нерухомого кінця канату, а й загальну вагу рухомих блоків. Крім цього, в реальних умовах між шківом та віссю його обертання діють певні сили тертя, які протидіють обертанню шківа, а отже певним чином зменшують вихідний натяг канату. Та якби там не було, а якщо в умовах задачі не наголошується на необхідності врахування ваги блоків та наявних сил тертя, то це означає, що враховувати цю вагу і ці сили не потрібно.
Задача 1. Який виграш у силі дає зображена на малюнку система блоків? Чому дорівнює сила натягу мотузки b, якщо маса вантажу 40кг?
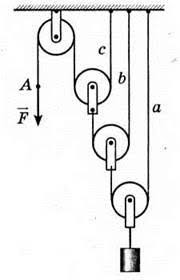
Рішення. Будемо виходити з того, що натяг суцільної мотузки в усіх її точках однаковий. Зважаючи на це, можна стверджувати:
1) Оскільки натяг мотузки с дорівнює силі F, то на рухомий блок с діє сила 2F.
2) Оскільки натяг мотузки b дорівнює силі 2F, то на рухомий блок b діє силa 2(2F) = 4F.
3) Оскільки натяг мотузки a дорівнює силі 4F, то на рухомий блок a діє силa 2(4F) = 8F.
Таким чином, дана система блоків забезпечує 8 разовий виграш в силі. А це означає, що ту силу тяжіння яка діє на вантаж масою 40кг і яка дорівнює 400Н, зрівноважить сила F=400H/8=50H. При цьому, враховуючи що напяг мотузки b дорівнює 2F, можна стверджувати що величина цього натягу 100Н.
Задача 2. Визначити прискорення системи зображених на малюнку тіл, якщо m1 = 0,2кг, m2 = 0,1кг, коефіцієнт тертя 0,3.
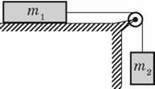
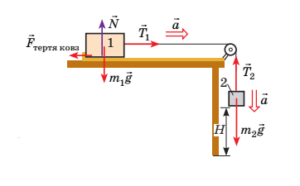
Дано:
m1 = 0,2кг
m2 = 0,1кг
μ = 0,1
а = ?
Рішення. Виходячи з того, що невідома величина (прискорення а) є складовою сили інерції (Fi=ma), виконуємо малюнок на якому вказуємо діючі на кожне тіло сили (як завжди, сила інерції на малюнку не позначена). Задаємо систему координат та записуємо умову динамічної рівноваги кожного тіла. При цьому, логіка рішення задачі полягає в тому, щоб використати той факт, що натяг нитки у всіх її точках є однаковим (Т1 = Т2). А це означає, що визначивши із умови рівноваги кожного тіла сили Т1 і Т2 та прирівнявши праві частини відповідних рівнянь, ми отримаємо рівняння з одним невідомим. Керуючись цією логікою можна записати.
Перше тіло:
∑Fx = T1 – Fтер1 – Fi1 = T1 – μN – m1a = 0;
∑Fy = N – Fт1 = N – m1g = 0, звідси N = m1g.
Отриманий результат (N = m1g) підставляємо в перше рівняння:
T1 – μm1g – m1a = 0, звідси
T1 = μm1g + m1a.
Друге тіло: (вісь 0у направлена вертикально вниз)
∑Fy = Fт2 – T2 – Fi2 = m2g – T2 – m2а = 0, звідси
Т2 = m2g – m2а.
Оскільки Т1 = Т2, то μm1g + m1a = m2g – m2а, звідси
m1a + m2a = m2g – μm1g, звідси
a = (m2g – μm1g)/(m1 + m2).
Розрахунки:
а = (0,1·10 – 0,3·0,2·10)/(0,2 + 0,1) = 1,33м/с2,
Відповідь: а = 1,33м/с2.
Контрольні запитання.
- З яких деталей складається механічний блок?
- Який блок називають нерухомим, а який – рухомим?
- Чи дає виграш в силі зображений на малюнку (а) блок? Який сенс застосування такого блоку?
- За рахунок чого зображена на малюнку (б) система нерухомого та рухомого блоків, забезпечує подвійний виграш в силі?
а) 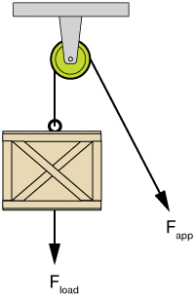 б)
б) 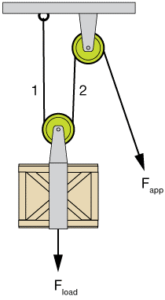 в)
в) 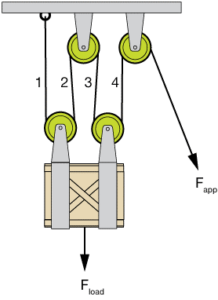
- Як працює золоте правило мехатіки, в зображених на малюнках (б) і (в) системах блоків?
- Чи може подвійний виграш в силі забезпечити лише один рухомий блок?
- Чи може система яка складається з двох рухомих та двох нерухомиж блоків забезпечити пятикратний виграш у силі. Якщо може, то як?
- Що називають поліспастом? Наведіть приклади застосування поліспастів.
Вправа №27.
- Який виграш у силі забезпечують зображені на малюнку системи блоків?
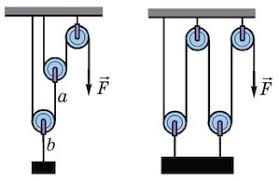

- Який виграш у силі забезпечують зображені на малюнку системи блоків?
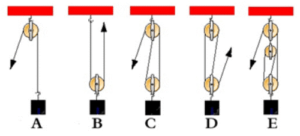
- На основі аналізу малюнку визначте масу вантажу 2, якщо маса вантажу 1 дорівнює 20кг, а система перебуває в рівновазі.
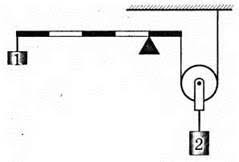
4. Яка маса кожного вантажу зображеної на малюнку системи, якщо m=12кг?
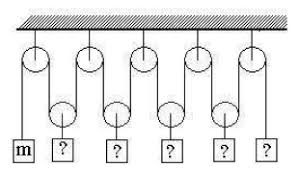
- За допомогою рухомого блока піднімають вантаж прикладаючи силу 100Н. Визначте силу тертя, якщо вага блоку 20Н, а вага вантажу 165Н.
- На одному кінці нитки перекинутої через нерухомий блок, підвішено вантаж масою 1кг, а на другому– 2кг. З яким прискоренням рухатиметься дана система тіл?
- В зображеній на малюнку системі тіл, визначити діючу на тіло m1=400г силу тертя, якщо вантаж m2=100г, рухаючись зі стану спокою, за 2с опустився на 80см.

.
§28. Розв’язування задач. Тема: Рівновага тіла під дією довільної системи сил.
В загальному випадку умову рівноваги тіла що знаходиться під дією плоскої системи довільних сил, можна записати у вигляді:
. ∑ Fx = 0
. ∑ Fy = 0
. ∑ M = 0
Виходячи з цієї умови та дотримуючись загально прийнятого порядку розв’язку задач статики, розв’яжемо декілька з них. А загально прийнятий порядок розв’язку задач на рівновагу тіла під дією довільної системи сил, є наступним:
- На основі аналізу умови задачі виконати малюнок (обов’язково), на якому чітко вказати всі діючі на задане тіло сили, їх кутові орієнтації, відстані між ними, та діючі на тіло обертальні моменти.
- Оптимальним чином задати систему координат.
- Записати умову рівноваги даного тіла, тобто систему рівнянь:
. ∑ Fx = 0
. ∑ Fy = 0
. ∑ M = 0
- Розв’язавши цю систему, визначити невідомі величини.
Загальні зауваження. До числа тих базових опор, які широко застосовуються в інженерно-технічній практиці, відносяться:
1) Шарнірно рухома опора (мал.96в). Реакція опори (R) направлена перпендикулярно до напрямку можливого руху опори.
2) Шарнірно нерухомі опори (мал.96б). Реакція опори має дві складові: вертикальну Ry (або Y) та горизонтальну Rx (або Х).
3) Жорстко закріплений стержень (мал.96а). Реакція опори має три складові: вертикальну Ry горизонтальну Rx та протидіючий момент сили М.
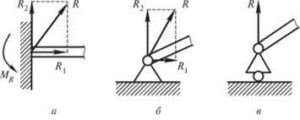
Мал.96. Базові опори інженерно-технічної практики.
Задача 1. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: Р1=200H, Р2=300Н, α=30º. Вагою балки знехтувати.
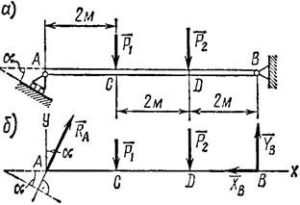
Рішення.
- Виконуємо малюнок на якому вказуємо всі діючі на балку сили та відстані між ними. Задаємо систему координат.
- Записуємо систему рівнянь які відповідають умові рівноваги даної балки.
1) ∑Fx = RAsinα – XB = 0;
2) ∑Fy = RAcosα – P1 – P2 – YB = 0;
3) ∑MA = P1·2 + P2·4 – YB·6 = 0.
Сили RA та ХВ обертальних моментів відносно точки А не створюють. Не створюють тому, що лінії дії цих сил проходять через т.А і тому плече дії цих сил дорівнює нулю.
- Розв’язавши систему рівнянь, визначаємо невідомі величини:
Із (3) → YB = (P1·2 + P2·4)/6 = (200·2+300·4)/6 = 267Н;
Із (2) → RA = (P1 + P2 + YB)/cos30° = (200 + 300 + 267)/0,87 = 882Н;
Із (1) → ХВ = RAsin30° = 882·0,5 = 441Н.
Відповідь: RA = 882Н, XB = 441Н, YB = 267Н.
Задача 2. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: q=100H/м, F=300H, α=60º, M=400Н∙м. Вагою балки знехтувати.
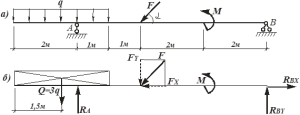
Рішення.
- Виконуємо малюнок на якому вказуємо всі діючі на балку сили та відстані між ними. Задаємо систему координат. (Розподілене навантаження q=100H/м, замінюємо рівнодіючою силою Q=q∙ℓ=100Н/м∙3м=300Н).
- Записуємо систему рівнянь які відповідають умові рівноваги даної балки.
∑ Fх = Fcosα – RBx = 0 (1)
∑ Fу = –Q + RA – Fsinα + RBy = 0 (2)
∑ MB = –Q∙6,5 + RA∙6 – Fsinα∙4 – M = 0 (3)
Зауваження. 1). Визначаючи момент сили F відносно точки B, доцільно розкладати цю силу на дві складові: Fx = Fcosα; Fy = Fsinα. При цьому: M(Fx) = 0, (d=0); M(Fy) = (Fsinα)4, (d=4м). 2). Ту точку відносно якої визначаються моменти сил, обирається довільно. При цьому зазвичай її обирають таким чином, щоб максимальне число невідомих сил створювали нульові моменти.
- Розв’язавши систему рівнянь, визначаємо невідомі величини:
Із (1) → RBx = Fcos60° = 300∙0,5=150H
Із (3) → RA = [Q∙6,5 + Fsin60º∙4 + M]/6 = … = 406H
Із (2) → RBy = Q – RA + Fsinα = … = 155H.
Відповідь: RBx=150H; RBy=155H; RA= 406H.
Задача 3. Під дією зображеної на малюнку системи сил жорстко закріплена балка знаходиться в стані механічної рівноваги. Визначити наявні в точці закріплення реакції опори. Вагою балки знехтувати.
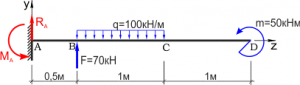
Зауваження. В загальному випадку реакція жорстко закріпленої опори має три складові: горизонтальну Rx, вертикальну Rу, та протидіючий момент сили М. Однак в умовах нашої задачі, горизонтально діючі сили відсутні і тому горизонтальна складова реакції опори дорівнює нулю.
Рішення.
- Виконуємо малюнок на якому вказуємо всі діючі на балку сили та відстані між ними. Задаємо систему координат.
- Записуємо систему рівнянь які відповідають умові рівноваги даної балки.
∑ Fу = RA + F – Q = 0 (1)
∑ MA = –MA – F∙0,5 + Q∙1 – M = 0 (2)
де Q = q∙1 = 100кH.
- Розв’язавши систему рівнянь, визначаємо невідомі величини:
Із (1) → RA = –F + Q = –70+100 =30кH
Із (2) → MA = – F∙0,5 + Q∙1 – M = … = 15кH∙м
Відповідь: RA=30кН ; M=15кН∙м.
Задача 4. Труба масою 30кг і довжиною 4м приставлена до стіни під кутом 30° до поверхні стіни. З якою, прикладеною до центру труби горизонтальною силою F потрібно тягнути трубу, щоб відірвати її від стіни? Нижній кінець труби не ковзає.
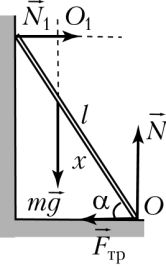
Дано:
m = 30кг
ℓ = 4м
α = 30°
F = ?
Рішення. Виконуємо малюнок, на якому вказуємо діючі на трубу сили і задаємо систему координат: вісь 0х направлена вздовж труби, діюча на центр маси тіла горизонтальна сила F, на малюнку не позначена.
Враховуємо, що в момент відриву труби від вертикальної стіни, труба і стіна перестають взаємодіяти, і тому N1=0. В таких умовах на трубу діють чотири сили: Fт=mg, F, N, Fтер, при цьому три з них є невідомими. Визначаючи ці сили ми могли б записати три рівняння рівноваги і розв’язавши їх, визначити F, N, Fтер. Однак, за умовою задачі, нас цікавить лише одна величина – сила F. Тому ми запишемо і розв’яжемо лише одне рівняння ∑MO=0. В цьому випадку моменти сил N і Fтер дорівнюють нулю.
∑ MO = F∙d1 – Fт∙d2 = F(ℓ/2)cos30º – Fт(ℓ/2)sin30º = 0. Звідси
F = [Fт(ℓ/2)sin30º]/[(ℓ/2)cos30º] = Fтtg30º = mgtg30º.
Розрахунки: F = mgtg30º = 30кг∙10м/с2∙0,577= 173H .
Відповідь: F = 173H.
Задача 5. Колесо радіусом R і масою m стоїть перед сходинкою висотою h. Яку горизонтальну силу F потрібно прикласти до осі колеса, щоб воно викотилось (піднялось) на сходинку?
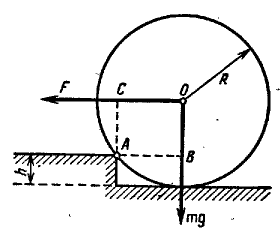
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на колесо сили. При цьому враховуємо, що в момент відриву колеса від горизонтальної поверхні, його взаємодія з цією поверхнею буде нулевою. А це означає, що в момент відриву колеса від горизонтальної поверхні, на колесо діють три сили: сила тяжіння Fт=mg; діюча в точці А реакція опори NA яка направлена до центру колеса; горизонтально направлена сила F. При цьому для визначення невідомої сили F достатньо записати лише одне рівняння ∑MA=0. Адже відносно точки А силові моменти створюють лише сила тяжіння (Fт) і та зовнішня горизонтальна сила (F) яка і піднімає колесо на сходинку.
Плечі сил F та Fт відносно точки А (відповідно АС і АВ) визначаємо із геометричних міркувань (див. мал.): 1) АС = R – h; 2) (АВ)2 + (АС)2 = R2, або (АС)2 + (R – h)2 = R2. Звідси (АВ)2 = R2 – (R – h)2 = 2Rh – h2, або АВ = (2Rh – h2)1/2.
Враховуючи вище сказане, можна записати
∑ МА= F(R – h) – Fт(2Rh – h2)1/2 = 0 .
Звідси F = [F (2Rh – h2)1/2]/(R – h) = [mg(2Rh – h2)1/2]/(R – h).
Відповідь: F = [mg(2Rh – h2)1/2]/(R – h).
Вправа 28.
- Балка масою 100кг під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опори.
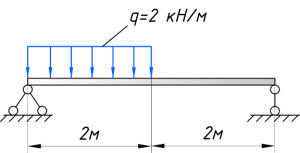
2. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: q=100H/м, F=300H, α=60º. Вагою балки знехтувати.
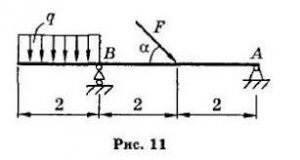
3. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: q=75H/м, Р=300H, G=200H, M=400H∙м. Вагою балки знехтувати.
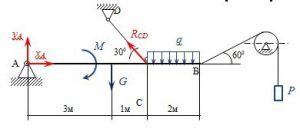
- Під дією зображеної на малюнку системи сил жорстко закріплена балка знаходиться в стані механічної рівноваги. Визначити наявні в точці закріплення реакції опори. Вагою балки знехтувати.
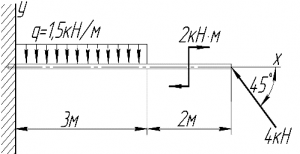
- Однорідна балка лежить на платформі так, що одна четверта її довжини звисає з платформи. До звисаючого краю балки прикладають силу, направлену вертикально вниз. Коли ця сила досягає 2000Н протилежний край балки починає підніматись. Визначити масу балки.
- До кінців стержня масою 10кг і довжиною 80см підвішено вантажі масами 40кг і 10кг. Де треба розмістити опору, щоб стержень перебував у рівновазі?
- Драбина довжиною 4м приставлена до гладенької стіни під кутом 30º. Коефіцієнт тертя між драбиною та підлогою 0,3. На яку відстань виміряну вздовж драбини може піднятись людина, перш ніж драбина почне зсковзувати підлогою.
- Колесо радіусом 20см і масою 2кг стоїть перед сходинкою висотою 5см. Яку горизонтальну силу F потрібно прикласти до осі колеса, щоб воно викотилось (піднялось) на сходинку?
- Однорідна куля підвішена на нитці, кінець якої закріплено на вертикальній стіні. Яким повинен бути коефіцієнт тертя μ між кулею і стіною, щоб точка кріплення нитки до кулі і центр кулі могли знаходитися на одній вертикалі? Радіус кулі R, довжина нитки ℓ.
.
§29. Центр тяжіння та центр мас тіла. Розв’язування задач.
Коли ми говоримо, що на тіло діє певна сила тяжіння, то маємо на увазі ту результуючу силу, що є рівнодійною величезної кількості співнаправлених елементарних сил, з якими окремі дрібні фрагменти тіла притягуються до Землі. Точку прикладання цієї результуючої сили, називають центром тяжіння тіла. Центром тяжіння тіла – називають ту пов’язану з цим тілом умовну геометричну точку, яка є точкою прикладання результуючої сили тяжіння і яка визначається як точка перетину ліній дій цієї результуючої сили, визначених при різних орієнтаціях тіла у просторі.
В науковій та побутовій практиці на ряду з поняттям центр тяжіння тіла застосовують більш загальне поняття – центр мас тіла. Центром мас (центром інерції) тіла – називають ту пов’язану з цим тілом умовну геометричну точку, яка характеризує розподіл мас в тілі і яка визначається як точка перетину ліній дій результуючої тих сил, які надають тілу поступального руху при різних орієнтаціях тіла у просторі. На відміну від центру тяжіння, який має сенс лише за наявності діючої на тіло сили тяжіння, центр мас тіла має сенс навіть за відсутності будь якого силового впливу на тіло.
Не заглиблюючись в деталі тих відмінностей які існують між центром тяжіння та центром мас тіла зауважимо, що за винятком певних, дуже специфічних умов, ці центри практично в точності співпадають. Тому на практиці терміни «центр тяжіння тіла» та «центр мас тіла» є тотожними. А зважаючи на більшу загальність терміну «центр мас тіла», саме цей термін є більш вживаним.
На практиці центр тяжіння (центр мас) будь якого (зазвичай плоского) тіла можна визначити наступним чином. Відповідне тіло, за допомогою нитки (мотузки, ланцюга чи іншої гнучкої опори) вільно підвішують за довільно обрану периферійну точку (мал.97а). При цьому, діючі на тіло сили, сила тяжіння F та реакція опори N, зрівноважують одна одну. А це означає, що центр тяжіння даного тіла лежить на тій прямій яка є продовженням напрямку нитки. Уявно чи реально помічаємо цей напрям. Закріпивши нитку в іншій точці тіла, повторюємо експеримент і проводимо ще одну пряму (мал.97б). Точка перетину цих двох прямих і є центром тяжіння (центром мас) даного тіла. Закріплюючи нитку в різних місцях та багаторазово повторюючи експеримент, ви неодмінно переконаєтесь в тому, що за будь якого положення тіла, лінії дії результуючої сили тяжіння дійсно перетинаються в одній і тій же точці, яка і є центром тяжіння тіла.
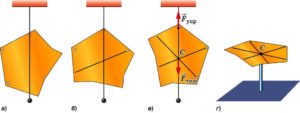
Мал.97. Ілюстрація способів експериментального визначення центру тяжіння тіла.
Якщо ви думаєте, що центр тяжіння (центр мас) тіла, це реальна приналежна тілу точка, до якої прикладена реальна сила тяжіння, то помиляєтесь. Помиляєтесь по-перше тому, що центр тяжіння часто знаходиться за межами відповідного тіла. Скажімо, якщо ви визначите центри тяжіння кільця, чайника, каструлі чи будь якого іншого пустотілого предмету, то неодмінно переконаєтесь в тому, що ці центри знаходяться за межами відповідних тіл. По-друге, центр тяжіння, це лише певна умовна точка до якої прикладена умовна результуюча сила тяжіння. Втім, якщо реальне тіло дійсно зосередити в тій точці яка називається центром тяжіння, і якщо до цієї точки дійсно прикласти ту силу яка називається силою тяжіння, то механічна поведінка цієї точки і відповідного реального тіла будуть однаковими.
Можна довести: якщо однорідне тіло має вісь симетрії, то центр тяжіння цього тіла знаходиться на цій осі. Керуючись цим твердженням не важко визначити центри тяжіння тих однорідних тіл які мають дві і більше осей симетрії (прямокутники, паралелограми, куби, циліндри, стержні, кулі, тощо).
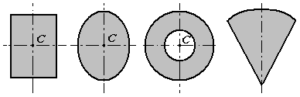
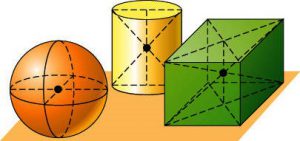
Мал.98. Якщо однорідне тіло має вісь (площину) симетрії, то центр тяжіння (центр мас) цього тіла знаходиться на цій осі (в цій площині).
Якщо ж мова йде про геометрично складні фігури, то їх завжди можна представити у вигляді певної сукупності геометрично простих фігур. Фігур, центри тяжінь яких легко визначаються. При цьому можна довести, що координати результуючого центру тяжіння складного тіла визначаються за формулами: xc=∑mixi/∑mi; yc=∑miyi/∑mi; zc=∑mizi/∑mi (1)
де mi – маса і-того тіла системи; xi, yi, zi – координати центру тяжіння і-того тіла системи.
Для однорідних плоских тіл (тіл постійної товщини) формули (1) набувають вигляду: хс = ∑Sixi/∑Si; yc = ∑Siyi/∑Si , (2)
де Si – площа і-того тіла системи. Власне за системою формул (2) ми і будемо визначати центрів тяжіння складних геометричних фігур.
Задача 1. Визначити центр тяжіння плоского однорідного тіла, геометричні параметри якого представлені на малюнку.
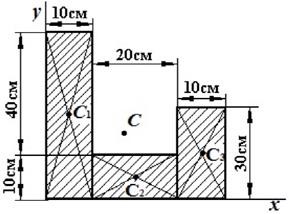
Рішення.
- Задаємо систему координат і максимально зручним чином розбиваємо складну фігуру на геометрично прості.
- Визначаємо площі і координати центрів тяжіння кожної окремої фігури.
1) S1 = 50∙10 = 500см2; x1 = 5см; y1 = 25см
2) S2 = 20∙10 = 200см2; x2 = 20см; y2 = 5см
3) S3 = 10∙30 = 300см2; x3 = 35см; y3 =15см .
- Визначаємо координати центру тяжіння всієї фігури.
хс =(500∙5 + 200∙20 + 300∙35)/(500+200+300) = 17см
ус =(500∙25 + 200∙5 + 300∙15)/(500+200+300) = 18см .
Відповідь: хс = 17см; ус = 18см .
Потрібно зауважити, що числові значення координат центру тяжіння тіла залежать від вибору системи координат. При цьому, за будь якого вибору цієї системи, фактичне розташування центру тяжіння тіла залишається незмінним
Задача 2. Визначити центр тяжіння плоского однорідного тіла, геометричні параметри якого представлені на малюнку (розміри в мм).
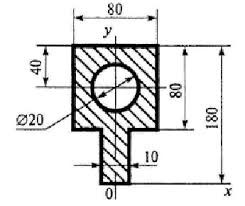
Загальне зауваження: якщо в однорідному тілі є отвори (пустоти), то визначаючи центр тяжіння цього тіла, в формулах (1) і (2), відповідно маси та площі отворів беруть зі знаком « – ».
Рішення.
- Задаємо систему координат і максимально зручним чином розбиваємо складну фігуру на геометрично прості.
Оскільки дане тіло є однорідним та симетричним відносно осі 0у, то центр тяжіння цього тіла знаходиться на осі 0у. А це означає, що у вибраній системі координат, координата хс є відомою (хс = 0мм), і тому залишається визначити лише координату ус.
- Визначаємо площу і координату (у) кожної окремої фігури.
1) S1 = 100∙10 = 1000мм2; y1 = 50мм
2) S2 = 80∙80 =6400мм2; y2 = 140мм
3) S3 = –πr2 = –3,14∙102 = –314мм2; y3 =140мм .
- Визначаємо координати центру тяжіння всієї фігури.
ус =(1000∙50 + 6400∙140 – 314∙140)/(1000+6400–314) = 127,3мм.
Відповідь: хс = 0,0мм; ус = 127,3мм.
Задача 3. Визначити центр тяжіння представленої на малюнку плоскої однорідної фігури.
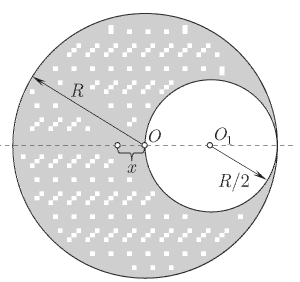
Рішення.
- Задаємо систему координат (центр системи т.О, вісь ОХ горизонтальна, вісь ОУ вертикальна)
Оскільки дане тіло є однорідним та симетричним відносно осі ОХ, то центр тяжіння цього тіла знаходиться на осі ОХ. А це означає, що у вибраній системі координат, координата хс є відомою (ус = 0), і тому залишається визначити лише координату хс.
- Визначаємо площу і координату (х) кожної окремої фігури.
1) S1 = πR2, x1 = 0
2) S2 = – π(R/2)2 = – πR2/4, x2 = – R/2;
- Визначаємо координати центру тяжіння всієї фігури.
xс = [πR2∙0 + (– πR2/4)∙(– R/2)] / (πR2 – πR2/4) = (πR3/8) /(πR2/3) = 3R/8.
Відповідь: xс = 3R/8, ус = 0.
Задача 4. Дві кулі маси яких 3кг і 5кг з’єднані стержнем, маса якого 2кг. Визначити положення центру мас системи, якщо радіус першої кулі 5см, радіус другої кулі 7см, а довжина стержня 30см.
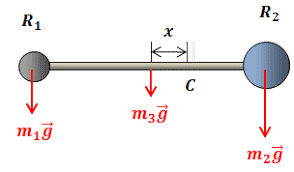
Рішення.
- Задаємо систему координат: точкою відліку системи обираємо центр мас стержня; вісь 0х направляємо вздовж стержня.
- В заданій системі координат визначаємо координати центру мас кожної деталі системи: х1 = –(15+2,5) = –17,5см; х3 = 0см; х2 = 15+3,5см = 18,5см.
- Оскільки дана система тіл симетрична відносно лосі 0х, її центр мас знаходиться на цій осі. При цьому, координату цього центру вздовж осі 0х визначаємо за формулою xc=∑mixi/∑mi :
хс = 3·(–17,5) + 2·0 + 5·18,5 = 4см.
Задача 5. Довести, що центр тяжіння трикутника знаходиться в точці перетину його медіан.
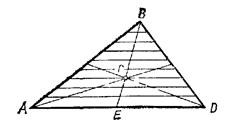
Рішення. Визначаючи центр тяжіння трикутника, розіб’ємо його на велику кількість максимально тонких смужок, кожна з яких паралельна одній з сторін трикутника, наприклад стороні АD. Оскільки кожну з цих смужок можна вважати тонким прямокутником, а центр тяжіння прямокутника знаходиться на перетині тих ліній які ділять цей прямокутник навпіл, то ясно, що центр тяжіння всього трикутника має знаходитись на лінії яка проходить через центри цих смужок. Цю лінію називають медіаною. (Медіана – лінія проведена з вершини трикутника до середини протилежної сторони). Аналогічним чином можна довести, що центр тяжіння трикутника має належати кожній з трьох його медіан. А це означає, що точка перетину цих медіан і є центром тяжіння трикутника.
Відповідь: центр тяжіння трикутника знаходиться в точці перетину його медіан.
Важливими складовими багатьох плоских тіл є прямокутні трикутники та півсфери. І можна довести, що координати центрів тяжіння (центрів мас) цих геометричних фігур визначаються за представленими на малюнку формулами.
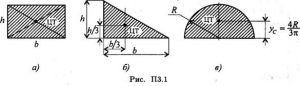
Контрольні запитання.
- Чи є сила тяжіння тією силою, що дійсно діє на центр тяжіння тіла?
- Чи є центр тяжіння тіла тією реальною точкою на яку діє результуюча сила тяжіння?
- Чи може центр тяжіння тіла знаходитись за межами цього тіла?
- Як експериментально визначити центр тяжіння тіла?
- Чи залежать визначені за формулами хс = ∑Sixi/∑Si; yc = ∑Siyi/∑Si, координати центру тяжіння тіла, від вибору системи координат?
- Чи впливає вибір системи координат на реальне розташування центру тяжіння тіла?
- Яке із понять «центр тяжіння» чи «центр мас» є більш загальним? Чому?
- Зі шматка картону виріжте тіло довільної форми і визначте його центр тяжіння.
Вправа 29.
- В заданій системі координат визначити координати центру тяжіння представлених на малюнку геометричних фігур (розміри в см).
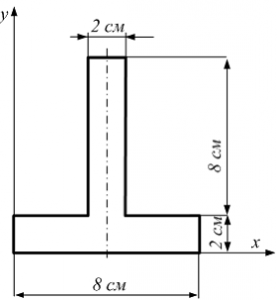
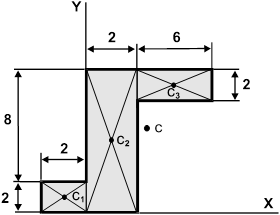
- В заданій системі координат визначити координати центру тяжіння представленої на малюнку геометричної фігури (а = 10см).
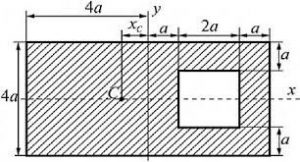
3. Визначити координати центру тяжіння представленої на малюнку геометричної фігури (а = 10см).
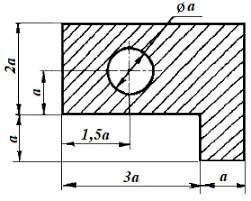
- Дві однорідні кулі маси яких m1=10кг і m2=12кг та радіусами R1=4см і R2=6см з’єднані стержнем масою 4кг і довжиною 8см. Центри куль лежать на осі стержня. Визначити центр тяжіння цієї системи.
- Визначити положення центру тяжіння квадратної пластинки зі стороною d, в якій вирізали круглий отвір радіусом d/4 так, що утворене коло торкається середини однієї з сторін квадрата.
- Визначите координати центру тяжіння представленої на малюнку геометричної фігури. R=10см.
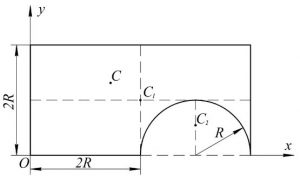
- Визначте центри тяжіння плоских тіл, геометричні параметри яких представлені на малюнку, а=10см.
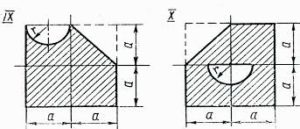
.
§30. Про види механічної рівноваги та про ступінь механічної стійкості тіл.
Зазвичай механічною рівновагою називають такий стан тіла, при якому воно під дією зовнішніх сил знаходиться в стані механічного спокою (v = 0; ω = 0). Однак, сама по собі механічна рівновага тіла може бути суттєво різною. Наприклад, в зображених на мал.99 ситуаціях, під дією зовнішніх сил (сили тяжіння Fт та реакції опори N) куля знаходиться в стані механічної рівноваги. І не важко бачити, що кожна з цих рівноваг є суттєво різною. Ця відмінність рівноваг з усією очевидністю відображена у відповідних назвах:
(3) – стійка рівновага,
(2) – нестійка рівновага,
(1) – байдужа рівновага.
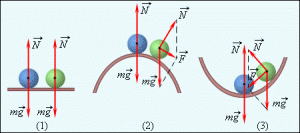
Мал.99. За характером поведінки тіла після виведення його із стану рівноваги, ця рівновага буває: стійкою (3), нестійкою (2) та байдужою (1).
Пояснюючи поведінку кулі при стійкій, нестійкій та байдужій рівновазі, розглянемо ситуацію в якій куля під дією випадкових зовнішніх чинників отримує незначне відхилення від положення рівноваги (мал.99). Не важко бачити, що в незалежності від виду рівноваги, на кулю постійно діють дві зовнішні сили: сила тяжіння Fт і реакція опори N. Однак результат дії цих сил в кожному випадку буде суттєво різним.
Дійсно. При стійкій рівновазі (мал.99;3), результуюча сили тяжіння і реакції опори повертає кулю в початкове положення. При нестійкій рівновазі (мал.99;2), результуюча сили тяжіння та реакції опори віддаляє кулю від початкового положення. При байдужій рівновазі (мал.99;1), результуюча сили тяжіння та реакції опори дорівнює нулю, а отже є такою що не повертає і не віддаляє кулю від початкового положення.
Таким чиним, за характером поведінки тіла після відхилення його від заданого положення рівноваги, розрізняють три різновидності цієї рівноваги: стійка, нестійка та байдужа. При цьому:
- Якщо після незначного відхилення тіла від положення рівноваги, система діючих на нього зовнішніх сил повертає тіло до попереднього положення, то таку рівновагу називають стійкою.
- Якщо після незначного відхилення тіла від положення рівноваги, система діючих на нього зовнішніх сил, віддаляє тіло від попереднього положення, то таку рівновагу називають нестійкою.
- Якщо після незначного відхилення тіла від положення рівноваги, система діючих на нього зовнішніх сил, не повертає тіло до попереднього положення, але й не віддаляють від нього, то таку рівновагу називають байдужою.
Важливим прикладом стійкої, нестійкої та байдужої рівноваги, є рівновага тіла що має вісь обертання. Аналізуючи таку рівновагу (мал.100) не важко бачити, що її характер визначається розташуванням центру тяжіння тіла відносно його осі обертання. При цьому, якщо центр тяжіння знаходиться нижче цієї осі, то рівновага є стійкою, якщо вище – нестійкою, а якщо на осі – байдужою.
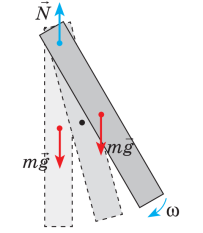
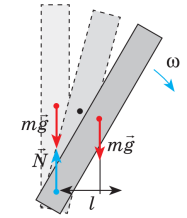
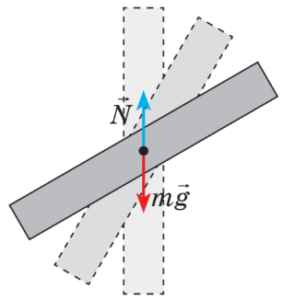
Мал.100. Характер рівноваги тіла що має вісь обертання залежить від розташування його центру тяжіння відносно осі обертання.
Вище розглянуті ситуації, наочно демонструють і пояснюють суть стійкої, нестійкої та байдужої рівноваги того тіла що має одну точку опори. Однак у повсякденному житті, ми зазвичай маємо справу з стійкістю тіл які спираються не на одну, а на велику кількість точок опори. Столи і стільці, телевізори і холодильники, книги і чайники, будинки і автомобілі, всі вони певним чином спираються на велику кількість точок опор і мають певну механічну стійкість. Однак ступінь цієї стійкості може бути різною. При цьому, ми майже завжди зацікавлені в тому, щоб ступінь стійкості тіла була максимально великою.
З’ясовуючи ті фактори які так чи інакше впливають на ступінь стійкості тіла, розглянемо ряд простих ситуацій. Припустимо, що тіло у формі прямокутного паралепіпеда лежить на горизонтальній поверхні так, як це показано на мал.101. Не важко збагнути, що рівновага цього тіла в ситуації (б) є більш стійкою. Більш стійкою тому, що в цій ситуації центр тяжіння тіла знаходиться нижче, а площа його опори більша. Висновок очевидний: чим більша площа опори тіла і чим нижче центр його тяжіння, тим більша механічна стійкість тіла.
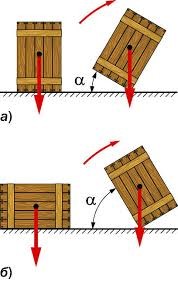
Мал.101. Чим нижче центр тяжіння тіла і чим більша площа його опори, тим стійкіша рівновага. Чим більший кут стійкості (α) тіла тим більша його механічна стійкість.
Важливим кількісним критерієм механічної стійкості тіла є так званий кут стійкості (α). Тобто той гранично великий кут, на який потрібно нахилити тіло до положення його нестійкої рівноваги. Наприклад в зображеній на мал.101 ситуаціях, механічна стійкість тіл є різною, бо відповідно різними є їх кути стійкості. При цьому, потрібно мати на увазі, що кут стійкості тіла, а відповідно і його механічна стійкість, залежать не лише від площі та форми його опори, а й від того, в якому напрямку діють ті сили які спонукають тіло до втрати механічної стійкості. Наприклад механічна стійкість цеглини залежить не лише від того яка її сторона є опорною, а й від того, в якому напрямку нахиляють цеглину.
Варто зауважити, що коли ми говоримо про площу опори того тіла яке спирається на декілька точок, то маємо на увазі не ту фактичну площу на яку спираються наприклад ніжки стола, а ту площу яка знаходиться в середині того чотирикутника, вершинами якого є ці ніжки.
Ступінь механічної стійкості тіла визначається не лише величиною його площі опори та висотою центру тяжіння над цією площею. Ця ступінь певним чином залежить і від того, як центр тяжіння тіла розташований відносно геометричного центру його опори. Дійсно. В зображених на мал.102 ситуаціях, тіла а, б, в, мають однакові площі опори, а їх центри тяжіння знаходяться на одній і тій же висоті. І тим не менше, ступінь стійкості цих тіл є очевидно різною. Різною тому, що центр тяжіння тіла по різному розташований відносно геометричного центру його опори.
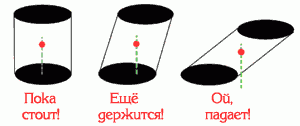

Мал.102. Ступінь стійкості тіла, певним чином залежить від розташування вертикальної проекції його центру тяжіння відносно площі опори.
Загально відомим прикладом будівлі вісь симетрії якої суттєво нахилена до вертикалі, є Пізанська вежа. Ця вежа має форму циліндра висотою 55м і радіусом опори 7м. При цьому вершина вежі відхилена від вертикалі на 4,5м. По суті це означає, що кут відхилення вежі від вертикалі становить α = arcsin(4,5/55) ≈ 5º. Граничний же кут стійкості для подібної геометричної фігури, близький до 15º. Так що Пізанській вежі ще далеко до втрати механічної стійкості.
Втім, ми говоримо про певну ідеалізовану ситуацію, в якій суцільне абсолютно тверде тіло стоїть на абсолютно твердій та дещо нахиленій поверхні. Реальні ж будівлі та їх опори не є суцільними та абсолютно твердими. Крім цього, вони знаходяться під постійним впливом величезної кількості силових навантажень, починаючи від вітрів, дощів та створюваних транспортом і людьми вібрацій, і закінчуючи ураганами, землетрусами, виверженнями вулканів, тощо.
Цікавим і практично важливим прикладом стійкої рівноваги є загально відомі ляльки на кшталт «ванька-встанька». Секрет подібних люльок в тому, що нижня частина їх сферичної поверхні заповнена важким матеріалом і тому центр тяжіння системи значно нижчий за геометричний центр відповідної сфери.
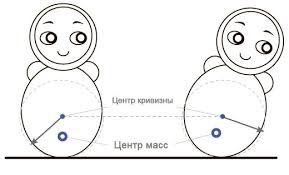


Мал.103. Ляльки які демонструють стійку рівновагу певних систем.
Пояснюючи загальний устрій та принцип дії ляльки «ванька-встанька» можна сказати наступне. Якщо центр мас кулі (сфери) співпадає з її геометричним центром, то на твердій горизонтальній поверхні ця куля перебуває в стані байдужої рівноваги. І це закономірно. Адже за будь якого положення кулі, діючі на неї сила тяжіння (F = mg) та реакція опори (N) знаходяться на одній вертикальній прямій та зрівноважують одна одну (мал.103а).
Тепер уявіть, що куля неоднорідна, наприклад така, половина якої є свинцевою, а інша – пустотілою сферою. Простіше кажучи, уявіть однорідну півкулю (мал.103б). В півкулі центр тяжіння С знаходиться нижче її геометричного центру О (геометричного центру тієї кулі масивною частиною якої є відповідна півкуля). В такій ситуації відхилення півкулі в будь яку сторону призводить до того, що діючі на неї сила тяжіння та реакція опори, створюють такий обертальний момент який повертає півкулю до початкового положення. Іншими словами, на горизонтальній опорі, півкуля (куля зі зміщеним центром тяжіння) знаходиться в стані стійкої рівноваги.
а)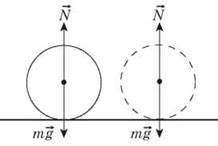 б)
б)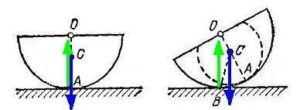
Мал.104. Куля (півкуля) центр тяжіння якої нижчий за її геометричний центр, знаходиться в стані стійкої рівноваги.
Принцип «ванька-встанька», це не лише основа для створення забавних ляльок, а й той базовий принцип, реалізація якого забезпечує стійку рівновагу практично всіх надводних транспортних засобів, починаючи від човнів та байдарок і закінчуючи круїзними лайнерами, танкерами та авіаносцями. Схема яка забезпечує таку рівновагу передбачає наявність трьох базових точок (мал.105):
1) С – точка прикладання тієї результуючої сил Архімеда які діють на занурену у воду частину корабля (ця точка є певним аналогом точки дотику кулі з горизонтальною поверхнею, а відповідно і прикладання тієї сили, яка називається реакцією опори);
2) G – центр тяжіння корабля (точка прикладання результуючої сил тяжіння);
3) МС – метацентр корабля, точка в напрямку якої діє результуюча сил Архімеда (ця точка є певним аналогом геометричного центру кулі).
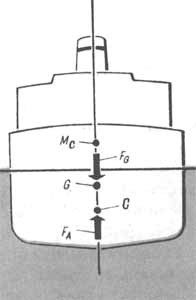
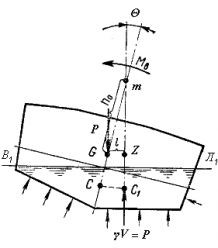
Мал.105. Схема яка забезпечує стійку рівновагу корабля.
Принцип дії тієї системи яка забезпечує стійку рівновагу корабля полягає в наступному. При нахилі корабля в будь яку сторону, точка прикладання результуючої сили Архімеда відповідним чином зміщується (С → С1). При цьому діюча в точці G сила тяжіння і діюча в точці С1 сила Архімеда, створюють такий обертальний момент який забезпечує повернення корабля до того положення при якому точки МС, G, C знаходяться на одній вертикальній прямій.
Контрольні запитання.
- Яку рівновагу називають стійкою; нестійкою; байдужою?
- Наведіть приклади стійкої, нестійкої та байдужої рівноваг.
- Від чого залежить вид рівноваги тіла що має нерухому вісь обертання?
- Від чого залежить механічна стійкість того тіла яке має велику кількість точок опори?
- Які заходи сприяють збільшенню механічної стійкості тіла?
- Вантажний автомобіль перевозить вантажі однакової маси: в одному випадку – залізобетонні блоки, в іншому – дрова. В якому випадку автомобіль буде стійкішим?
- В якій рівновазі буде перебувати куля на горизонтальній площині, якщо одна половина кулі дерев’яна, а інша – свинцева?
- Які сили забезпечують стійку рівновагу кулі зі зміщеним центром мас? Як направлені ці сили?
- Які сили забезпечують стійку рівновагу корабля? Які точки прикладання та напрямки дії цих сил?
.