
Тема 1.2. Основи статики.
§22. Загальні відомості про масу.
§23 Загальні відомості про густину.
§23. Розв’язування задач. Тема: Густина.
§25. Загальні відомості про силу та основні сили механіки.
§26. Система сил. Умова механічної рівноваги тіла.
§27. Сила тяжіння. Реакція опори.
§28. Сила тертя.
§29. Розв’язування задач. Тема: Силовий метод розв’язування задач.
§30. Сила інерції.
§31. Розв’язування задач. Тема: Силовий метод розв’язування
задач динаміки.
§32. Вага. Невагомість.
§33. Сила пружності. Жорсткість тіла. Закон Гука.
§34. Статака. Узагальнююче повторення.
Тема 1.2. Основи статики.
Статика (від грецького statike – рівновага) – це розділ механіки в якому вивчають параметри, закономірності та причини стану механічної рівноваги тіла. Механічною рівновагою тіла (матеріальної точки) називають такий механічний стан тіла, при якому воно знаходиться в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v=const). Зазвичай в статиці розглядають ті ситуації коли тіло знаходиться в стані механічного спокою. Однак ви маєте знати, що з фізичної точки зору, між станом механічного спокою тіла (v=0) та станом його прямолінійного рівномірного руху (v=const) нема суттєвої різниці. А якщо вам потрібні докази цьому на перший погляд парадоксальному факту, то запитайте себе чи відчуваєте факт того, що Земля з швидкістю 30км/с обертається навколо Сонця, а навколо центру нашої Галактики – з швидкістю 250км/с? Втім, про те що означає твердження «з фізичної точки зору, між станом механічного спокою тіла (v=0) та станом його прямолінійного рівномірного руху (v=const) нема суттєвої різниці», ми поговоримо дещо пізніше, а точніше – коли буде з’ясовано фізичну суть того базового закону який називається принципом відносності. Наразі ж, будемо вважати, що ті силові закономірності які справедливі для стану механічного спокою тіла, будуть справедливими і в тому випадку, коли це тіло перебуватиме в стані прямолінійного рівномірного руху.
§22. Загальні відомості про масу.
В фізиці нема більш ємкої, більш складної та більш суперечливої величини як та, яку називають «маса». На перший погляд, пояснити що характеризує маса тіла, не важко. Якщо ви візьмете кулю великої і малої маси, то неодмінно з’ясуєте, що більш масивна куля сильніше притягується до Землі. Пояснюючи даний факт ви напевно скажете, що велика куля має більшу масу, і що тому вона сильніше притягується до Землі. Відповівши таким чином, ви будете праві. Адже маса дійсно характеризує здатність тіла притягуватись до Землі, або в більш загальному сенсі – здатність тіла до гравітаційних взаємодій.
Гравітація (від лат. gravitas – тяжіння), це універсальна властивість тіла, яка полягає в його здатності притягуватись до Землі, або в більш загальному сенсі – здатність тіла до гравітаційних взаємодій. Кількісною мірою гравітаційних властивостей тіла є його маса.
Висновок 1. Маса є мірою гравітаційних властивостей тіла.
Мал.44. Маса – міра гравітаційних властивостей тіла.
Тепер розглянемо ті ж кулі в інших обставинах. Припустимо, що кулі великої і малої маси рухаються з однаковими швидкостями. Якщо вас запитають: «Яку кулю зупинити важче?», то напевно ви скажете що більш важку, і що це пов’язано з величиною її маси. Відповівши таким чином ви будете абсолютно праві. Адже здатність тіла протидіяти будь якій зміні його швидкості, дійсно залежить від маси цього тіла.
Якщо тіло важко зупинити, важко зрушити з місця і взагалі, важко примусити змінювати свою швидкість, то про таке тіло говорять, що воно має велику інерцію (інертність). При цьому мають на увазі, що тіло важко зрушити з місця не тому що воно занурене в пісок чи прибите гвіздками до підлоги, а тому що воно саме по собі має певну інерцію, кількісною мірою якої є маса тіла.
Інерція (віл. лат. inertia – бездіяльність, спокій), це універсальна властивість тіла, яка полягає в тому, що відповідне тіло протидіє будь якій зміні його швидкості. Кількісною мірою інерційних властивостей тіла є його маса.
Висновок 2. Маса є мірою інерційних властивостей тіла.
Мал.45. Маса – міра інерційних властивостей тіла.
Коли Альберт Ейнштейн створив теорію відносності, то одним з її найважливіших висновків було твердження про те, що будь яке тіло масою m представляє собою згусток енергії, кількість якої визначається за формулою Е=mс2, де с=3∙108м/с – постійна величина яка дорівнює швидкості світла в вакуумі. По суті це означало, що масу можна вважати мірою кількості енергії і що цю кількість можна вимірювати не лише в одиницях енергії (джоулях) а й в кілограмах.
Зроблений Ейнштейном висновок отримав своє експериментальне підтвердження і сьогодні його справедливість не викликає жодних сумнівів. Енергія Сонця і зірок, енергія ядерних та термоядерних вибухів, енергія атомних електростанцій, – це прямий результат перетворення певної кількості маси у відповідну кількість енергії. І це перетворення відбувається у повній відповідності з формулою Ейнштейна Е=mс2.
Висновок 3. Маса є мірою енергетичних властивостей тіла.

Мал.46. Маса – міра енергетичних властивостей тіла.
Про те, що маса є кількісною мірою інерційних, гравітаційних та енергетичних властивостей фізичних об’єктів , написано практично в кожному довіднику з фізики. Однак, щоб вам не говорили про масу, а кожен знає, маса – це міра кількості речовини в тілі. Адже коли в крамниці ви цікавитесь масою (в побутовій практиці – вагою) товару, то вам нема діла до його інерційних, гравітаційних чи загально енергетичних властивостей. Вас цікавить кількість певної речовини у відповідному товарі, і ви знаєте, чим більша маса товару, тим більше в ньому відповідної речовини.
Маса є мірою кількості речовини не лише в побуті, а й в науці. Втім, питання про масу, як міру кількості речовини, настільки важливе та складне, що потребує окремої розмови. Наразі ж, ми просто констатуємо той факт, що маса є універсальною мірою кількості речовини в тілі, і що це випливає з самого визначення терміну «речовина». Речовина – це вид матерії, який складається з тих чи інших частинок і має масу спокою.
Висновок 4. Маса є загальною мірою кількості речовини в тілі, виміряну в кілограмах.

Мал.47. Маса – міра кількості речовини в тілі.
Таким чином: Маса – це фізична величина яка є мірою :
1) інерційних властивостей тіла;
2) гравітаційних властивостей тіла;
3) енергетичних властивостей тіла;
4) кількості речовини в тілі, виміряну в кілограмах.
Позначається: m
Визначальне рівняння: нема
Одиниця вимірювання: [m]= кг, кілограм.
Кілограм – це одиниця вимірювання маси, яка в точності дорівнює масі Міжнародного еталону кілограма. Один кілограм приблизно дорівнює масі одного літра (1дм3) дистильованої води, взятої при температурі 15°С.
Потрібно зауважити, що в різних розділах фізики термін «маса» має різні значення. Наприклад, в механіці, маса – міра інерційних та гравітаційних властивостей тіла, в молекулярній фізиці – міра кількості речовини в тілі, а в фізиці елементарних частинок – міра енергетичних властивостей цих частинок. Зважаючи на ці обставини дамо те визначення маси, яке є загально прийнятим в механіці.
Маса (в механіці) – це фізична величина, яка є мірою інерційних та гравітаційних властивостей тіла.
Позначається: m
Визначальне рівняння: нема
Одиниця вимірювання: [m]=кг.
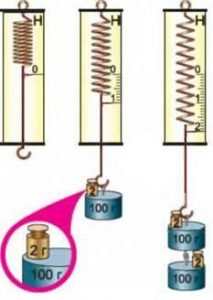
На практиці масу тіла визначають шляхом зважування. Це означає, що відповідне тіло кладуть на певну опору, яка є частиною відповідного вимірювального приладу (терезів). При цьому на опору діє певна сила (вага тіла) величина якої залежить від маси тіла. Власне під дією цієї сили (ваги тіла) і спрацьовує відповідний (пружинний, важільний, електронний чи інший) механізм, який і фіксує відповідне значення маси тіла.

Мал.48. Прилади за допомогою яких вимірюють масу тіла.
Найпростішою різновидністю терезів є так звані аптечні терези. Вони представляють собою збалансований відносно осі обертання стержень, до країв якого кріпляться шальки терезів. Принцип дії цієї системи очевидно простий. На одну шальку терезів кладуть тіло масу якого потрібно визначити, а на іншу – тягарці (гирьки) відомих мас. Досягнувши рівноваги системи, визначають загальну масу тягарців яка і відповідає масі зважуваного тіла. Наприклад маса того тіла яке представлено на мал.49а становить 25,2г. А маса того тіла яке представлено на мал.49б – 113,0г.
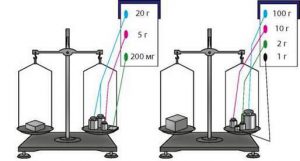
. а) б)
Мал.49. Загальний вигляд аптечних терезів.
Контрольні запитання.
- Що означає твердження: маса – міра інерційних властивостей тіла?
- Що означає твердження: маса – міра гравітаційних властивостей тіла?
- Що означає твердження: маса – міра енергетичних властивостей тіла?
- Що означає твердження: маса – міра кількості речовини в тілі?
- Мірою чого є маса: а) в механіці; б) в побуті?
- Чи залежала величина еталонного кілограма від величини еталонного метра?
- Як визначають масу на практиці? В чому суть технології зважування?
- Поясніть загальний устрій та принцип дії аптечних терезів.
.
§23. Загальні відомості про густину.
Якщо ви візьмете виготовлені з різних матеріалів тіла однакових об’ємів (V1=V2=V3), то практично неминуче з’ясуєте, що маси цих тіл будуть різними (m1 ≠ m2 ≠ m3). Наприклад алюмінієвий циліндр (мал.50) виявиться значно легшим за залізний, а залізний – легшим за циліндр свинцевий. Пояснюючи даний факт говорять про те, що різні матеріали (різні речовини) мають різну густину.
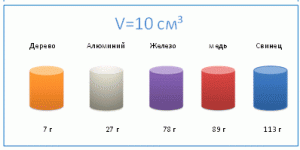
Мал.50. Тіла однакових об’ємів але різних матеріалів, мають суттєво різні маси.
Густина – це фізична величина, яка характеризує кількість однорідної речовини в одиниці її об’єму і яка дорівнює відношенню маси (m) відповідної однорідної речовини, до величини того об’єму (V) в якому ця речовина знаходиться.
Позначається: ρ, (ро)
Визначальне рівняння: ρ = m/V
Одиниця вимірювання: [ρ] = кг/м3, кілограм на метр кубічний.
На практиці густину речовини часто вимірюють не в кг/м3, а в г/см3. І не важко довести, що кг/м3 = (1000г)/(100см)3 = (103г)/(102см)3 = (103г)/(106см3) = 10–3г/см3. Тому: ρ(Al) = 2,7·103кг/м3 = 2,7г/см3; ρ(Fe) = 7,8·103кг/м3 = 7,8г/см3 і т.д.
Густина речовини визначається експериментально і записується у відповідну таблицю. Наприклад таку:
| Речовина | ρ, кг/м3 | ρ, г/см3 | Речовина | ρ, кг/м3 | ρ, г/см3 |
| Алюміній | 2700 | 2,7 | Скло | 2500 | 2,5 |
| Залізо (сталь) | 7800 | 7,8 | Сосна суха | 400 | 0,4 |
| Золото | 19300 | 19,3 | Срібло | 10500 | 10,5 |
| Лід | 900 | 0,9 | Вода | 1000 | 1,0 |
| Мідь | 8900 | 8,9 | Ртуть | 13000 | 13,0 |
| Свинець | 11300 | 11,3 | Повітря | 1,29 | 0,00129 |
Потрібно зауважити, що говорити про певну густину речовини (тіла) доречно тільки тоді, коли відповідна речовина є однорідною. Адже якщо, наприклад, в середині свинцевого циліндра є пустоти (повітряні бульбашки), то густина такого неоднорідного свинцю може виявитись меншою за густину міді, чи скажімо заліза.
Густина речовини певним чиним залежить від її температури. І це закономірно, адже в процесі нагрівання переважна більшість речовин розширюється. А це означає, що в процесі нагрівання густина відповідної речовини зменшується. Дійсно: якщо V збільшується, то ρ = m/V зменшується. Втім, для твердих тіл та рідин, залежність густини від температури є незначною. Якщо ж мова йде про гази, то їх густина дуже сильно залежить від зовнішніх умов і в першу чергу, від тиску та температури. Тому, говорячи про певну густину газу неодмінно вказують ті умови за яких ця густина визначається. Зазвичай це так звані нормальні умови: тиск – одна атмосфера, температура – 0ºС.
В різних агрегатних станах густина однієї і тієї ж речовини є різною. Наприклад в твердому стані густина води (льоду) 900кг/м3, в рідкому стані густина води 1000кг/м3, а в стані газоподібному при температурі 100ºС та тиску одна атмосфера, густина води (водяного пару) всього 0,59кг/м3.

Мал.51. В різних агрегатних станах, густина хімічно однієї і тієї ж речовини є різною.
Із аналізу визначального рівняння ρ=m/V ясно, що для визначення густини тіла потрібно виміряти його масу (m) та об’єм (V). Про те як вимірюється маса тіла ви вже знаєте. Якщо ж говорити про об’єм тіла, то він може визначатись по різному. Наприклад, якщо тіло має форму паралепіпеда (мал.52а), то вимірявши довжину (а), ширину (b) та висоту (h) цього паралепіпеда, його об’єм визначають за формулою V=a∙b∙h. Якщо тіло має форму циліндра (мал.52б), то вимірявши його висоту (h) і радіус (R), та знаючи, що площа круга визначається за формулою S=πR2, об’єм циліндра визначають за формулою V=Sh=πR2h.
Якщо ж форма тіла геометрично складна, то його об’єм можна визначити за допомогою мірної колби, мірного стакана чи інших подібних приладів (мал.52в). Принцип дії таких приладів очевидно простий. В мірній посудині знаходиться певний початковий об’єм води (Vп), величина якого фіксується. Вимірюване тіло занурюють у воду мірної посудини і воно виштовхує такий об’єм води, який дорівнює об’єму тіла (Vт). При цьому об’єм води в посудині збільшується до позначки Vк. Різниця між кінцевим та початковим показаннями приладу і є вимірюваним об’ємом тіла: Vт=Vк–Vп. Наприклад в зображеній на мал.52в ситуації, об’єм тіла становить Vт=Vк–Vп = 40см3 – 20см3 = 20см3.
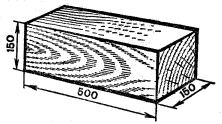
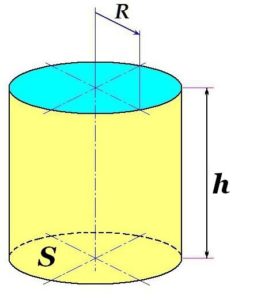
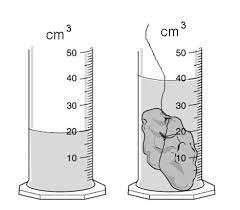
Мал.52. Способи визначення об’єму тіла.
Густину рідини часто вимірюють за допомогою приладу, який називається ареометром (від грец. araios – рідкий та metreo – міряти). Ареометр (мал.53) представляє собою герметичну скляну колбу на дні якої міститься певна кількість важкого матеріалу, зазвичай свинцю. Принцип дії ареометра полягає в наступному. Відомо, що на занурене в рідину тіло, діє певна виштовхувальна сила, яку прийнято називати силою Архімеда. А оскільки величина цієї сили залежить від густини рідини, то і ступінь занурення тіла ареометра в рідину також залежить від густини цієї рідини: чим більша густина рідини, тим менша ступінь занурення ареометра, і навпаки.
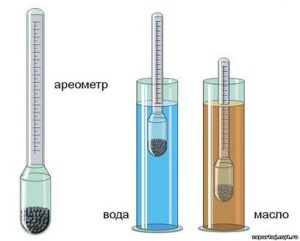
Мал.53. Ареометр – прилад, який дозволяє визначати густину рідини.
Задача 1. Виходячи з того, що 1л = 1дм3, виразити об’єми 1л, 5л і 5мл в см3.
Рішення. 1л = 1дм3 = 1∙(10см)3 = 1∙1000см3 = 1000см3.
5л = 5дм3 = 5∙(10см)3 = 5∙1000см3 = 5000см3.
Оскільки 1мл = 0,001л = 0,001∙1000см3 = 1см3, то 5мл = 5см3.
Відповідь: 1л = 1000см3; 5л = 5000см3; 5мл = 5см3
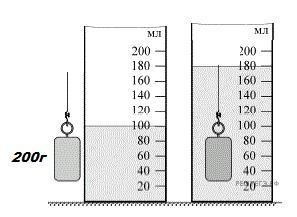
Задача 2. За тими даними які представлені на малюнку, визначте масу тіла, якщо матеріалом тіла є залізо.
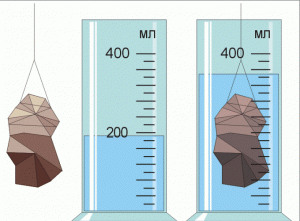
Дано:
залізо
Vп=200мл = 200см3
Vк=350мл = 350см3
m = ?
Рішення. Оскільки за визначенням ρ=m/V, то m=ρV. Оскільки за умовою задачі матеріал речовини задано (залізо), то густину цієї речовини визначаємо за відповідною таблицею: ρ = 7,8г/см3. Об’єм вимірюваного тіла визначаємо за тими даними які представлені на малюнку Vт = Vк–Vп = 350см3 – 200см3 = 150см3.
Таким чином, m=ρV = 7,8(г/см3)∙150см3 = 1170г.
Відповідь: m = 1170г = 1,17кг
Контрольні запитання.
- Що характеризує густина речовини?
- Чому так важливо підкреслювати, що густина характеризує кількість однорідної речовини в одиниці її об’єму?
- Яка з тих твердих речовин, що представлених в таблиці густин, має найбільшу густину?; найменшу густину?.
- Чому характеризуючи густину газу, вказують відповідну температуру та тиск?
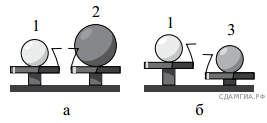
- За тими даними які представлені на малюнку, порівняйте густини 1 і 2; 1 і 3 тіл.
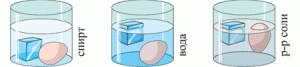
6. За тими даними які представлені на малюнку, порівняйте густини спирту, води та розчину солі.
- Поясніть загальну суть представленого на малюнку способу визначення об’єму тіла.
Вправа №23.
1.Виразіть об’єми 4дм3, 8л, 25мл, 500мм3 в см3.
2.Виразіть об’єми 400дм3, 200л, 500см3 в м3.
3.За тими даними які наведені на малюнку (а), порівняйте маси та густини тіл, (об’єми тіл однакові).
4.Визначте масу соснового бруска розміри якого (в мм) наведені на малюнку (б), якщо густина сосни 0,51г/см3.
а) б)
б)
- Визначте масу соснової дошки товщиною 25мм, шириною 20см і довжиною 4м, якщо густина сосни 0,51г/см3.
- Визначте масу колоди довжина якої 4м, а діаметр 30см.
- Яка маса 2-х літрів меду, якщо його густина 1,35г/дм3.
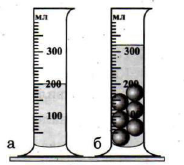
- За тими даними які наведені на малюнку, визначте масу однієї свинцевої кульки.
- За тими даними які наведені на малюнку, визначте густину матеріалу тіла.
до задачі 6 до задачі 7
.
§ 24. Розв’язування задач. Тема: Густина.
Нема іншого способу навчитися розв’язувати задачі фізики, як той, що передбачає їх практичне розв’язування. А потрібно сказати, що задачі фізики суттєво відрізняються від тих задач, з якими ви маєте справу наприклад в математиці. Скажімо, коли в математиці вам говорять, що рівняння виду ах2+bx+c=0 називається квадратним рівнянням, і що в загальному випадку воно має два рішення: x1,2= [–b±√(b2–4ac)]/2a, то вчителю достатньо розв’язати два, три подібних рівнянь, щоб в подальшому ви змогли самостійно розв’язувати будь-яку їх кількість.
З задачами фізики ситуація значно складніша. Наприклад, ви розв’язуєте задачі на тему «густина», тобто на застосування формули ρ=m/V. Не важко бачити, що ця формула надзвичайно проста. У всякому разі, значно простіша за x1,2 = [–b ±√(b2–4ac)]/2a. Та от парадокс. Ви скільки завгодно можете знати цю формулу і не вміти розв’язувати задачі на застосування формули ρ=m/V. Навіть після того, як вчитель розв’яже вам п’ять, десять ба навіть сто подібних задач, нема гарантії того, що задана вам сто перша задача буде розв’язана. І справа не в тому що ви забули формулу ρ=m/V. Справа в іншому: в фізиці, головне не формули, а вміння логічно мислити. Ви можете скільки завгодно «зазубрювати» правильні формули і навіть зазубрити їх, але якщо за цими формулами ви не будете бачити реальних об’єктів і подій, то всі ваші зусилля будуть марними – ви не будете знати, розуміти і любити фізику.
Якщо ж ви дійсно хочете навчитися розв’язувати задачі фізики, а по суті навчитися логічно мислити, то маєте усвідомити: це не можливо зробити просто спостерігаючи за тим як розв’язує задачі вчитель. Скажімо, ви хочете навчитися грати в хокей. Для цього ви наймаєте тренера і він пояснює вам всі нюанси цієї гри. Пояснює день, два,…., місяць,….рік. Ви схвально киваєте головою і вам все зрозуміло. Але якщо ви думаєте, що через рік такого навчання, ви станете класним хокеїстом, то неминуче помиляєтесь. Навчитися грати в хокей, просто спостерігаючи за тим як це роблять інші – неможливо. Для того, щоб стати хокеїстом, потрібно взувати ковзани, брати в руки ключку, виходити на лід і …. падати, вставати, знову падати і знову вставати, тобто вчитися грати в хокей. І якщо поруч буде фаховий тренер, то процес навчання буде успішним та ефективним.
Вчитель, це той же тренер. Без його допомоги навчитися розв’язувати задачі надзвичайно важко, але можливо. А от що дійсно неможливо, так це навчитися розв’язувати задачі не розв’язуючи їх самостійно. І якщо на шляху опанування мистецтвом розв’язування задач, вас будуть переслідувати труднощі і помилки, знайте, ще нікому не вдавалось пройти цей шлях без труднощів і помилок. Але якщо ви будете наполегливими і кмітливими, то вас неминуче очікує успіх. І ви не лише будете знати фізику, а й безумовно полюбите цю найвеличнішу і найпрекраснішу з наук. Отже, до справи.
Задача 1. Суцільний куб ребро якого 3см має масу 73г. З якої речовини виготовлено куб?
Дано:
а = 3см
m = 73г
речовина – ?
Рішення. Оскільки кожній речовині відповідає певне значення густини і ці значення містяться у відповідній таблиці, то визначивши густину, можна визначити їй відповідну речовину. Тому, враховуючи що для куба V=a3, можна записати ρ = m/V = m/a3 = 73г/(3см)3 = 73г/27см3 = 2,7г/см3. З таблиці густин дізнаємося, що густину 2,7г/см3 має алюміній.
Відповідь: куб виготовлено із алюмінію.
Задача 2. Маса залізної деталі 1,5кг. Який об’єм цієї деталі?
Дано:
залізо
m = 1,5кг
V = ?
Рішення. Оскільки за визначенням ρ = m/V, то V= m/ρ. А оскільки матеріал деталі відомий, то його густину визначаємо за відповідною таблицею: ρ(Fe) = 7,8г/см3. А враховуючи, що 1,5кг = 1500г, можна записати V = m/ρ = 1500г/7,8г/см3 = 192см3.
Відповідь: V = 192см3.
Загальні зауваження. Розв’язуючи задачі фізики, потрібно керуватись логікою практичної доцільності. Скажімо, з формальної точки зору, об’єми речовин потрібно виражати в м3, а їх густину – в кг/м3. Але в такому випадку розрахункова частина задачі була б набагато складнішою. Тому в умовах нашої задачі густину доцільно виражати в г/см3, а масу в грамах. Єдина за чим потрібно уважно слідкувати, так це за тим, щоб відповідні величини були співрозмірними. Адже якщо наприклад, густину виразити в г/см3, а масу залишити в кг, то рішення задачі буде не правильним.
Задача 3. Паливний бак автомобіля має об’єм 90л. Скільки кілограм бензину можна залити в цей бак? Густина бензину 0,71(г/см3)
Дано:
ρ = 0,71(г/см3)
V = 90л = 90дм = 90 000см3
m = ?
Рішення. Оскільки за визначенням ρ=m/V, то m= ρV.
Розрахунки: m = ρV = 0,71(г/см3)∙90000см3 = 63900г = 63,9кг.
Відповідь: m = 63,9кг.
Задача 4. На скільки маса одного літра води більша за масу одного літра бензину? Густина бензину 0,71(г/см3).
Дано:
ρб = 0,71(г/см3)
ρв = 1,00(г/см3)
Vв = Vб = V = 1л = 1000см3
Δm = mв – mб=?
Рішення. Оскільки ρ=m/V, m=ρV, то Δm=mв – mб= ρвVв – ρбVб = (ρв – ρб)V.
Розрахунки: Δm = (ρв – ρб)V = (1,00г/см3– 0,71г/см3)1000см3 = 290г=0,29кг.
Відповідь: Δm=0,29кг.
Задача 5. Свинцеве тіло об’ємом 55см3 має масу 565г. Чи має це тіло порожнини? Якщо має, то який їх об’єм?
Дано:
свинець
Vт = 55см3
mсв = 565г
ρсв=11,3г/см3
Vпор = ?
Рішення. Якщо свинцеве тіло масою 565г є суцільним, то його об’єм повинен дорівнювати Vсв = mсв/ρсв = 565г/11,3(г/см3) = 50см3. А оскільки реальний об’єм тіла 55см3, то це означає, що в цьому тілі є порожнини і що загальний об’єм цих порожнин Vпор = 55см3 – 50см3 = 5см3.
Відповідь: Vпор= 5см3.
Вправа №24.
- Маса алюмінієвої деталі 2кг. Який об’єм цієї деталі?
- Шматок металу масою 544г має об’єм 64см3. Який це метал?
- Яка густина рідини, 125л якої мають масу 100кг?
- На скільки маса золота об’ємом 1см3 більша від маси міді такого ж об’єму?
- У скільки разів маса золота більша за масу міді аналогічного об’єму?
- Застосовуючи формулу ρ=m/V, визначте невідому фізичну величину (m, V або ρ).
а) m = 18кг, V =0,02м3;
б) m = 140г, ρ = 700кг/м3;
в) V = 10м3, ρ = 2,5г/см3.
Зверніть увагу на одиниці вимірювання фізичних величин.
- У скільки разів той об’єм який займає ртуть, менший за об’єм нафти такої ж маси?
- Золото можна розплющити до товщини 0,1мкм. Яку площу можна покрити золотом масою 10г?
.
§ 25. Загальні відомості про силу.
Основною фізичною величиною статики є сила. Сила – це фізична величина, яка характеризує силову дію одного тіла на інше (є мірою взаємодії фізичних об’єктів) і яка дорівнює добутку маси тіла на величину того прискорення яке воно отримує під дією даної сили.
Позначається: F
Визначальне рівняння: F=ma
Одиниця вимірювання: [F]= кг∙м/с2= H, ньютон.
Ньютон – це одиниця вимірювання сили, що дорівнює такій силі, яка тілу масою 1кг надає прискорення 1м/с2: 1Н=1кг∙1м/с2. Іншими словами, якщо тіло масою 1кг рухається з прискоренням 1м/с2, то це означає, що на нього діє сила 1Н. Звичайно, мається на увазі, що тіло масою 1кг знаходиться під дією лише однієї зовнішньої сили. Адже якщо наприклад, дерев’яний брусок масою 1кг прибити, прикрутити чи приклеїти до підлоги, а потім прикласти до нього силу 1Н, то брусок не отримає очікуваного прискорення (залишиться на місці). Не отримає тому, що в місці з’єднання бруска з підлогою неминуче виникне ще одна сила, яка протидіятиме переміщенню бруска.
Відразу ж зауважимо, що величину сили в один ньютон не можливо оцінити візуально, як це наприклад, можна зробити з одиницею довжини метром. Ньютон, це одиниця вимірювання сили, тобто тієї величини яка характеризує силову дію одного фізичного об’єкту на інший. Тому величину ньютона можна оцінити лише за його силовою дією. Скажімо загально відомо, що всі тіла притягуються до землі з силою, яку прийнято називати силою тяжіння. Відомо й те, що під дією сили тяжіння всі тіла, в тому числі і ті маса яких 1кг, падають з прискоренням 9,8м/с2. А це означає, що на тіло масою 1кг діє сила тяжіння 9,8Н: F =1кг∙9,8м/с2=9,8Н.
Таким чином, якщо ви візьмете в руку тіло масою 1кг, то відчуєте силу 9,8Н. Запитується: тіло якої маси потрібно взяти в руку, щоб вона відчула силу в один ньютон? Правильно, маса цього тіла має становити 102г :
m=F/a=1Н/9,8(м/с2)=0,102кг=102г.

Мал.54. Один Ньютон дорівнює тій силі, з якою тіло масою 102 грами притягується до Землі.
От тільки не потрібно стверджувати, що в одному ньютоні міститься 102 грами. Бо це все рівно ніби наполягати на тому, що в одному метрі міститься сто секунд, або що кілограм більший за секунду. Адже кілограм не більший і не менший за секунду. Бо кілограм – це кілограм, метр – це метр, секунда – це секунда, а ньютон – це ньютон. І порівнювати ці абсолютно різні одиниці не можна. Метр можна порівнювати з міліметром, кілометром чи, скажімо, з дюймом, тобто з іншими одиницями довжини. Але метр не можна порівнювати з секундою, кілограмом, ньютоном чи, наприклад, з метром квадратним. Тому коли ми говоримо, що силі в один ньютон відповідає вага тіла масою 102 грами, то маємо на увазі лише те, що на Землі силу в один ньютон можна відчути тримаючи в руці тіло масою 102 грами.
Аналізуючи визначальне рівняння сили F=ma, потрібно зауважити, що це рівняння не треба сприймати як таке, що вказує на факт залежності сили від маси тіла та його прискорення. Адже в загальному випадку, діюча на тіло сила не залежить від маси цього тіла та того прискорення яке воно може отримати. Скажімо, сила ваших м’язів не залежить від маси того тіла що лежить на столі та того прискорення яке може отримати це тіло під дією вашої сили. Ваша м’язова сила залежить від незліченної кількості обставин пов’язаних з вами особисто, починаючи від вашого віку, маси вашого тіла, вашої тренованості і закінчуючи вашим настроєм та вологістю того повітря яким ви дихаєте. І представити цю залежність у вигляді певної формули практично не можливо.
Ось тут то на допомогу і приходить визначальне рівняння сили. Адже формула F=ma по суті вказує на універсальний спосіб визначення (вимірювання) величини та напрямку дії будь якої сили. І цей спосіб полягає в тому, що для визначення величини тієї чи іншої сили, наприклад, м’язової сили вашої руки, цю силу потрібно прикласти до тіла відомої маси (m) і подивитесь на те прискорення (a) яке отримає це тіло під дією даної сили. При цьому, величина та напрям сили визначаться за формулою F=ma. Наприклад якщо під дією певної сили, тіло масою 0,5кг отримає прискоренням 15м/с2, то це означатиме, що величина діючої на тіло сили F=ma=0,5кг·15м/с2=7,5Н.
Втім на практиці, величину сили зазвичай визначають не за тим якого прискорення надає ця сила тілу визначеної маси, а за тим як вона деформує пружне тіло, наприклад пружину. Прилади які працюють за даним принципом називаються динамометрами (від грец. dynamis – сила та metreo – вимірювати). Динамометр, це прилад який дозволяє вимірювати величину діючої на нього сили. Основним елементом динамометра (мал.55) є певне пружне тіло (пружина), яке під дією зовнішньої сили певним чином деформується. Власне за величиною цієї деформації і визначають величину деформуючої сили.
Мал.55. Загальний вигляд деяких різновидностей динамометрів.
Буде не зайвим зауважити, що визначальне рівняння F=ma є похідним від того базового закону механіки, який називається другим законом Ньютона. Закону в якому стверджується: під дією зовнішньої сили F, тіло масою m отримує прискорення а, величина якого прямо пропорційна діючій на тіло силі і обернено пропорційна масі тіла. Іншими словами F → a=F/m. Наприклад якщо на яблуко масою m=0,1кг діє сила 1Н, то під дією цієї сили яблуко отримає прискорення a=F/m=1Н/0,1кг=10м/с2. Якщо ж сила в 1Н діятиме на кавун масою m=6кг, то кавун отримає прискорення a=F/m=1Н/6кг=0,17м/с2.
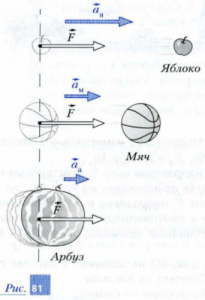
Мал. 56. Сила – є причиною прискореного руху тіла.
В фізиці, так чи інакше розрізняють багато різновидностей сили. Лише в механіці ми будемо вивчати що найменше вісім таких різновидностей:
– сила тяжіння Fт
– реакція опори N
– сила тертя Fтер
– сила інерції Fi
– вага P
– сила пружності Fпр
– гравітаційна сила Fгр
– сила Архімеда Fa .
Втім, кожна з цих сил є різновидністю однієї і тієї ж фізичної величини, яка називається силою, яка є мірою взаємодії фізичних об’єктів і яка вимірюється в ньютонах.
Задача 1. Під дією сили 8Н тіло отримує прискорення 10м/с2. Яка маса тіла?
Дано:
F = 5Н
a = 10м/с2
m = ?
Рішення. Оскільки за визначенням F=ma, то m=F/a.
Розрахунки: m=8(кг·м/с2)/10(м/с2)=0,8кг.
Відповідь: m=0,8кг.
Задача 2. Хокейна шайба масою 250г, після удару ключкою який тривав 0,02с набула швидкості 30м/с. Визначте середню силу удару.
Дано:
m = 250г = 0,25кг
Δt = 0,02с
v0 = 0м/с
vk = 30м/с
F = ?
Рішення. За визначенням F=ma, де а = Δv/Δt = (vk–v0)/Δt = (30м/с – 0м/с)/0,02с = 1500м/с2. Таким чином F=0,25кг1500м/с2=375Н.
Відповідь: F = 375Н.
Задача 3. Тіло масою 2кг рухається за законом х=200–12t+0,8t2. Під дією якої сили відбувається цей рух?
Дано:
х=200–12t+0,8t2
m = 2кг
F = ?
Рішення. За визначенням F = ma, де a=? Із порівняльного аналізу рівнянь х = х0 + v0t + (a/2)t2 та х = 200 – 12t + 0,8t2, випливає, що дане тіло рухається з прискоренням а=1,6м/с2 (оскільки а/2=0,8м/с2, то а = 2∙0,8м/с2 = 1,6м/с2). А оскільки в рівнянні х = 200 – 12t + 0,8t2, знаки швидкості і прискорення є протилежними, то це означає, що рух відповідного тіла є рівносповільненим. При цьому величина гальмівної сили дорівнює F=ma=2кг∙1,6м/с2=3,2Н.
Відповідь: F = 3,2Н.
Контрольні запитання.
- Дайте визначення терміну «сила».
- Дайте визначення терміну «ньютон».
- Що треба зробити щоб відчути силу в один ньютон?
- Чи правильне твердження 1Н = 102г?
- Чи означає визначальне рівняння F=ma, що діюча на тіло сила залежить від маси тіла та його прискорення? Від чого залежить ця сила?
- На що вказує визначальне рівняння сили: F=ma ?
- Що стверджується в другому законі Ньютона?
Вправа №25.
- Під дією якої сили тіло масою 400г отримає прискорення 3м/с2?
- З яким прискоренням рухається під час розгону реактивний літак масою 60т, якщо сила тяги його двигунів 90кН?
- Визначити масу футбольного м’яча, якщо в процесі удару він набув прискорення 500м/с2, а сила удару дорівнює 420Н.
- Сила 60Н надає тілу прискорення 0,8м/с2. Яка сила надасть цьому тілу прискорення 2м/с2?
- М’яч масою 0,5кг після удару що триває 0,02с набуває швидкості 10м/с. Визначити силу удару.
- На тіло масою 5кг вздовж однієї прямої діють дві сили: 12Н і 8Н. Визначити прискорення цього тіла, якщо: а) сили співнаправлені; б) сили протинаправлені.
- Прямолінійний рух тіла описує рівняння х=50+10t – 0,5t2. Під дією якої сили відбувається цей рух, якщо маса тіла 0,5кг?
- Лижник масою 60кг, маючи в кінці спуску з гори швидкість 10м/с, зупинився через 30с. Визначити силу опору руху.
.
§ 26. Система сил. Умова механічної рівноваги тіла.
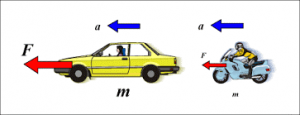
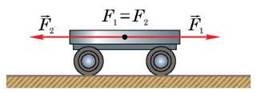
Сила – величина векторна, тобто така, яка характеризується не лише величиною (модулем) а й напрямком дії. І це закономірно, адже результат дії сили залежить не лише від її величини, а й від того напрямку в якому ця сила діє. Скажімо якщо сила F штовхає автомобіль вправо (мал.57), то автомобіль буде рухатись вправо. Якщо ж аналогічна сила штовхатиме автомобіль вліво, то він буде рухатись вліво.

Мал.57. Результат дії сили залежить не лише від її величини, а й напрямку дії.
Зазвичай на тіло діє не одна сила, а їх певна сукупність. Сукупність тих сил що діють на дане тіло в даний момент часу називають системою сил. Наприклад, на представлене на мал.58 тіло, діє системи чотирьох сил: F1; F2; F3; F4. Систему сил, лінії дії яких перетинаються в одній точці, називають збіжною системою сил. Скажімо, зображена на мал.58 система сил є збіжною. Адже лінії дії всіх чотирьох сил перетинаються в одній точці – точці К.
Якщо тверде тіло знаходиться під дією збіжної системи сил, то: по-перше, це тіло можна вважати матеріальною точкою, а по-друге, систему таких сил можна замінити однією рівнодійною силою. Рівнодійною силою (позначається R або Fр), називають таку силу, яка чинить на тіло (матеріальну точку) таку ж силову дію як і вся система реально діючих сил і яка дорівнює векторній сумі тих сил що реально діють на дане тіло, тобто R=F1+F2+ … +FN. Це означає, що заміна системи реально діючих на тіло сил, відповідною рівнодійною силою, не змінить механічну поведінку тіла. Потрібно підкреслити, що рівнодійною силою можна замінити лише систему збіжних сил, тобто таких сил лінії дії яких перетинаються в одній точці.
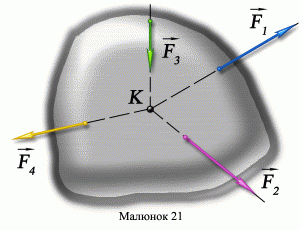
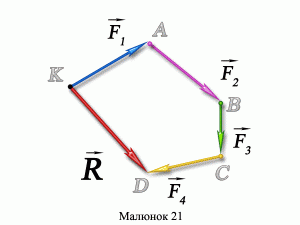
Мал.58. Систему діючих на тіло збіжних сил, можна замінити їх рівнодійною силою.
Механізм додавання векторів загалом і сил зокрема принципово простий і полягає в наступному. Від точки прикладання сил (точка К), з дотриманням обраного масштабу та відповідних напрямків, відкладають вектор F1, з кінця вектора F1 відкладають вектор F2, з кінця F2 відкладають F3 і т.д. Вектор який з’єднує початок першого вектора (F1) і кінець останнього (FN) і є відповідною рівнодійною силою R. При цьому величина рівнодійної сили пропорційна довжині вектора R, а її напрямок – збігається з напрямком вектора R.
Задача 1. Графічним методом визначити рівнодійну зображених на малюнку сил.
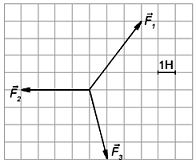
Нагадаємо. Суть графічного (геометричного) методу розв’язування задач полягає в тому, що на основі максимально точних геометричних побудов, з дотриманням вибраного масштабу та з застосуванням відповідних геометричних приладів (лінійка, транспортир, циркуль, тощо), отримують графічну відповідь на поставлені в задачі запитання. Головна перевага графічного методу, його наочність та загальна простота. Основний недолік – залежність точності отриманого результату від точності геометричних побудов. Втім, в умовах даної конкретної задачі, наявність масштабної сітки значно спрощує графічне рішення задачі.
Рішення. З кінця вектора F1 відкладаємо вектор F2 (чотири горизонтальні клітинки вліво), а з отриманого при цьому кінця вектора F2 відкладаємо вектор F3 (чотири клітинки вниз і одна клітинка вправо). Оскільки в даній ситуації початок першого вектора (F1) співпадає з кінцем останнього вектора (F3), то це означає, що величина результуючого вектора дорівнює нулю.
Відповідь: F1+ F2+ F3=0, рівнодійна сила дорівнює нулю.
Якщо мова йде про ті прості ситуації в яких діючі на тіло сили співнаправлені або протинаправлені, то в цьому випадку вектори додаються як звичайні числа які характеризуються певною величиною та знаком (плюс або мінус). Наприклад, в зображеній на мал.59а ситуації, на тіло діють дві співнаправлені сили: F1=5Н, F2=3Н. При цьому рівнодійна цих сил дорівнює арифметичній сумі сил F1 і F2: R = F1 + F2 = 5Н + 3Н = 8Н. Якщо ж діючі на тіло сили є протинаправленими (мал.59б), то рівнодійна сила дорівнює арифметичній різниці діючих сил і направлена в сторону більшої сили: R = F1 – F2 = 5Н – 3Н = 2Н.
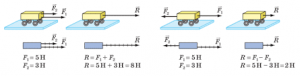
Мал.59. Якщо діючі на тіло сили співнаправлені або протинаправлені, то вони додаються як відповідні числові величини.
Не важко збагнути, що тіло буде знаходитись в стані механічної рівноваги (механічного спокою) лише в тому випадку, якщо діючі на нього сили урівноважують одна одну. Адже якщо наприклад, автомобіль штовхають дві рівні за величиною і протилежні за напрямком сили (мал.60а), то автомобіль залишатиметься на місці (звичайно за умови, що до цього він не рухався). Або якщо наприклад, два хлопці з однаковими силами тягнуть канат в різні сторони (мал60б), то канат залишатиметься на місці.
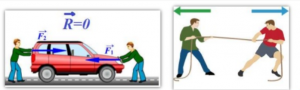
Мал.60. Якщо діючі на тіло сили урівноважують одна одну, то тіло знаходитись в стані механічної рівноваги.
Науковою констатацією вище описаних фактів є закон, який називають умовою механічної рівноваги тіла. В цьому законі стверджується: тіло (матеріальна точка) буде знаходитись в стані механічної рівноваги тоді і тільки тоді, якщо векторна сума діючих на нього зовнішніх сил дорівнює нулю. Іншими словами: якщо v=0, або v=const то ∑Fi=0 і навпаки.
Нагадаємо. Механічною рівновагою тіла (матеріальної точки) називають такий механічний стан тіла, при якому воно знаходиться в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v=const). Тому, в незалежності від того стоїть тіло (v=0) чи рівномірно прямолінійно рухається (v=const), векторна сума діючих на нього сил дорівнює нулю: ∑Fi=0.
Зауваження. В науці загалом і в фізиці зокрема знак ∑ (сигма) є знаком суми. Наприклад запис ∑Fі=0 означає: векторна сума всіх діючих на тіло сил, від першої до останньої дорівнює нулю: ∑Fі = F1+F2+ … +FN =0
В проекціях на осі системи координат, умову механічної рівноваги тіла, зазвичай записують так: якщо v=0, або v=const то ∑Fx = 0; ∑Fy = 0. Наприклад, в зображеній на малюнку (а) ситуації, на тіло діє система чотирьох сил. При цьому, якщо тіло знаходиться в стані механічної рівноваги v=0, або v=const, то:
∑Fx = F – ƒ = 0;
∑Fy = N – mg = 0.
а)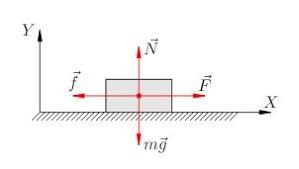 б)
б)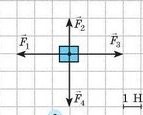
Натомість в зображеній на малюнку (б) ситуації
∑Fx = F3 – F1 = 3Н – 3Н = 0Н;
∑Fу = F2 – F4 = 2Н – 3Н = – 1Н.
Це означає, що вздовж осі 0х умова рівноваги виконується (∑Fx = 0) і тому руху тіла в напрямку осі 0х не буде. А от стосовно осі 0у, умова рівноваги не виконується (∑Fу = – 1Н) і тому тіло з певним прискоренням буде рухатись у від’ємному напрямку осі 0у.
Задача 2. На тіло масою 0,5кг діє зображена на малюнку система сил. З яким прискоренням та в якому напрямку рухається тіло? (масштаб зображених на малюнку сил: одна клітинка → 1Н).
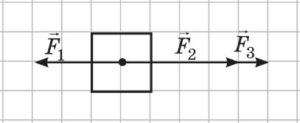
Рішення. Із аналізу малюнку ясно, що на дане тіло вздовж горизонтальної осі (0х), діє система трьох сил. При цьому сили F2=4Н і F3=1Н діють в додатному на осі 0х, а сила F1=3Н – в від’ємному напрямку цієї осі. В такій ситуації результуюча діючих на тіло сил не дорівнює нулю:
ΣFx = F2 + F3 – F1 = 4Н + 1Н – 3Н = 2Н.
Це означає, що тіло буде рухатись в додатному напрямку осі 0х з прискоренням а=F/m=2Н/0,5кг=4м/с2.
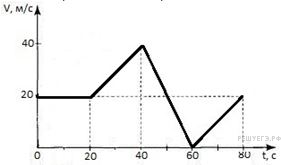
Задача 3. За заданим графіком швидкості руху тіла, визначити величину діючої на нього рівнодійної сили на кожній ділянці руху. Маса тіла 5кг.
Рішення. За визначенням F=ma. На основі кількісного аналізу графіку швидкості, визначаємо величину того прискорення з яким тіло рухається на кожній ділянці шляху, а відповідно і величину діючої на нього сили.
ділянка 1: а1 = ∆v/∆t = (3м/с – 0м/с)/3с = 1м/с2, отже F1 = ma1 = 5кг∙1м/с2 = 5Н;
ділянка 2: а2 = ∆v/∆t = (3м/с – 3м/с)/3с = 0м/с2, отже F1 = ma1 = 5кг∙0м/с2 = 0Н;
ділянка 3: а3 = ∆v/∆t = (0м/с – 3м/с)/3с = –1м/с2, отже F1 = ma1 = 5кг∙(–1м/с2) = – 5Н, де знак «–» вказує на те, що на ділянці 3 діюча на тіло сила, гальмує рух тіла.
Контрольні запитання.
- Від чого залежить результат дії сили на дане тіло?
- Яку систему сил називають збіжною?
- Яку силу називають рівнодійною?
- Як визначають величину та напрямок рівнодійної сили?
- Що називають механічною рівновагою?
- Що стверджується в законі, який називається умовою механічної рівноваги тіла.
Вправа №26.
- Кожній з представлених на малюнку ситуації (1, 2, 3, 4, 5) поставте у відповідність правильну відповідь (А, Б, В, Г, Д).
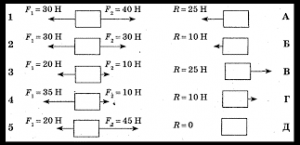
- На основі аналізу малюнку визначте величину та напрямок рівнодійної сили.
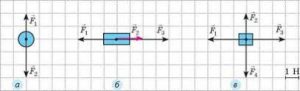
- Графічним методом визначте величину і напрям рівнодійної сили. Масштаб сил в обох ситуаціях однаковий: одна клітинка → 5Н.
а)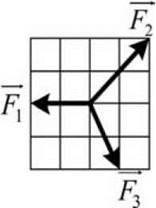 б)
б)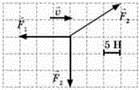
- На тіло масою 1кг діє зображена на малюнку система сил. З яким прискоренням рухається тіло?
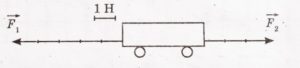
- На тіло масою 5кг діє зображена на малюнку система сил. З яким прискоренням рухається тіло?
6. Під дією сили 150Н тіло рухається за законом х=100+5t+0,5t2. Яка маса тіла?
7. Під дією якої сили тіло масою 20кг рухається за законом х=10t–0,4t2? Як направлена ця сила?
8. За заданим графіком швидкості руху тіла, визначити величину діючої на нього рівнодійної сили на кожній ділянці руху. Маса тіла 2кг.
.
§ 27. Сила тяжіння. Реакція опори.
Факт того, що на Землі тіла падають з певним прискоренням, безумовно вказує на те, що на них в напрямку прискореного руху діє певна сила. І як будь яку силу, її можна визначити за формулою F=ma. А оскільки величина того прискорення з яким падають земні тіла становить a=g=9,8м/с2, то діюча на них сила має визначатись за формую F=mg. Цю силу називають силою тяжіння. Таким чином, на всі земні тіла діє певна сила тяжіння, величина та напрям якої визначаються за формулою F=mg, де g=9,8м/с2 – прискорення сили тяжіння (прискорення вільного падіння).
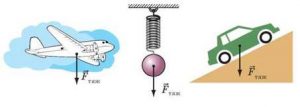
Мал.61. На всі земні тіла діє певна сила тяжіння, величина та напрям якої визначаються за формулою F=mg.
Сила тяжіння – це та сила, з якою тіло притягується до Землі і яка дорівнює добутку маси тіла на прискорення його вільного падіння.
Позначається: Fт
Визначальне рівняння: Fт = mg, де g=9,8м/с2
Одиниця вимірювання: [Fт] = кг·м/с2 = H, ньютон
По суті, сила тяжіння є тією силою, елементарні фрагменти якої діють на всі точки тіла. Однак можна довести, що результуюча тих елементарних сил тяжіння які діють на фрагменти даного тіла, прикладена до центру мас цього тіла. Тому вважається, що сила тяжіння діє на центр маси тіла.
Потрібно зауважити, що на різних космічних об’єктах, прискорення сили тяжіння (g), а відповідно і сила тяжіння (Fт = mg), є різними. Наприклад на Місяці g = 1,6м/с2, на Марсі g = 3,7м/с2, а на Юпітері g = 25,9м/с2. Даний факт пояснюється тим, що різні космічні об’єкти мають різні маси та різні розміри, і тому з різною силою притягують ті тіла які знаходяться в околицях їх поверхні. Більше того, в різних місцях Землі, величина прискорення сили тяжіння є суттєво різною. Наприклад на полюсах g = 9,82м/с2, в середніх широтах g = 9,81м/с2, а на екваторі g = 9,78м/с2. Про причини такого стану речей ви дізнаєтесь після того, як познайомитесь з тією надважливою силою, яка називається силою інерції, та тим законом який називається законом всесвітнього тяжіння. На разі ж будемо вважати, що на Землі g = 9,81м/с2.
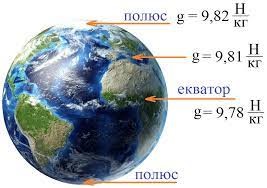
Мал.62. В різних місцях Землі величина прискорення сили тяжінні(g), а відповідно і величина діючої на тіла сили тяжіння (Fт = mg), може бути дещо різною.
Сила тяжіння прагне перемістити будь яке тіло в центр Землі. А оскільки земні тіла не опиняються в цьому центрі, то ясно, що на своєму шляху вони неминуче зустрічають певні протидіючі фактори. Цими факторами часто є ті об’єкти які прийнято називати опорами. Ту ж силу з якою опора діє на тіло називають реакцією опори.
Опорою називають будь яку механічну перешкоду, яка так чи інакше жорстко обмежує рух тіла. Наприклад, та підлога на якій ви стоїте, обмежує ваш рух в напрямку до центру Землі. Гнучка опора (канат, ланцюг, дріт, тощо), обмежує рух тіла в напрямку розтягування цієї опори.
Реакція опори – це та сила, з якою опора діє на тіло та жорстко протидіє переміщенню цього тіла.
Позначається: N
Визначальне рівняння: величина і напрям реакції опори визначається з умов конкретної задачі.
Одиниця вимірювання: [N] = H, ньютон

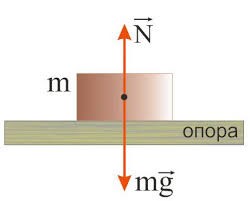
Мал.63. Опора – це та перешкода яка жорстко обмежує рух тіла. Реакція опори – це та сила з якою опора діє на тіло.
В межах навчальної програми для 7-го класу по суті розглядають лише дві найпростіші різновидності опор: 1) Плоска опора – тверда рівна поверхня, яка протидіє переміщенню тіла в напрямку перпендикулярному до площини цієї поверхні. Реакція плоскої опори (мал.64а) перпендикулярна до площини опори. 2) Гнучка опора – тонка гнучка опора (трос, канат, нитка, мотузка, тощо), яка протидіє переміщенню тіла вздовж цієї опори, в напрямку від точки її закріплення. Реакція гнучкої опори (мал.64б) направлена вздовж опори в напрямку точки її закріплення. Реакцію гнучкої опори часто позначають буквою Т і називають силою натягу нитки, канату, троса, тощо.
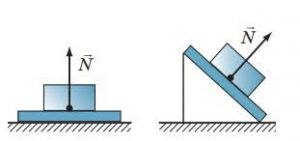
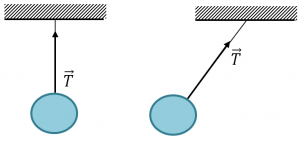
Мал.64. Напрямки плоских (а) та гнучких (б) опор.
Потрібно зауважити, що сила тяжіння і реакція опори є тими зовнішніми силами, які діють на відповідне тіло, а не на опору чи щось інше. Що правда, точки прикладання цих сил є суттєво різними: сила тяжіння прикладена до центру мас тіла, а реакція опори діє в точках контакту тіла з відповідною опорою (мал.65а). Втім, в більшості задач механіки матеріальної точки, прийнято вважати що і сила тяжіння і реакція опори, прикладені до центру мас тіла (мал.65б).
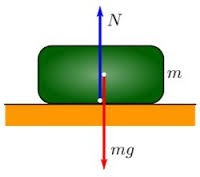
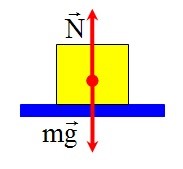
Мал.65. Сила тяжіння і реакція опори, діють на тіло, а не на опору чи щось інше.
Задача 1. На горизонтальній поверхні лежить тіло масою 20кг. Визначити діючі на це тіло сили.

Дано:
m= 20кг
Fт=? N=?
Рішення. 1. Виконуємо малюнок на якому вказуємо діючі на тіло сили. А цими силами є: направлена вертикально вниз сила тяжіння Fт=mg, та направлена вертикально вгору реакція опори N. За визначенням Fт=mg=20кг·9,8м/с2=196Н. Оскільки тіло знаходиться в стані механічної рівноваги, а сила тяжіння і реакція опори направлені вздовж однієї осі, то можна стверджувати, що ці сили рівні за величиною і протилежні за напрямком, тобто: N = Fт= mg = 196Н.
Відповідь: Fт=196Н; N=196Н.
Задача 2. З якою силою мідна куля об’єм якої 10см3 притягується до Землі?
Дано:
мідь
V = 10см3
Fт = ?
Рішення. За визначенням Fт=mg, де g=9,8м/с2 m=? Оскільки матеріал кулі відомий, то відповідно відома і її густина ρ(міді)=8,9г/см3. А враховуючи що ρ=m/V, можна записати m=ρV. Таким чином Fт = mg = ρVg.
Розрахунки: Fт = ρVg = 8,9(г/см3)·10см3·9,8м/с2 = 870г·м/с2 = 0,87кг·м/с2 = 0,87Н.
Відповідь: Fт = 0,87Н.
Контрольні запитання.
- На що вказує факт того, що земні тіла падають з певним прискоренням?
- Наведіть приклади явищ, які спостерігаються на Землі і пояснюються дією сили тяжіння.
- Який напрямок має сила тяжіння і на який об’єкт вона діє?
- Що називають опорою?
- В якому напрямку протидіє переміщенню тіла: а) плоска опора; б) гнучку опора?
- Що називають реакцією опори? В чому вимірюється реакція опори?
- Як направлена реакція опори і на який об’єкт вона діє.
Вправа №27.
- Яка сила тяжіння діє на людину масою 70кг?
- Яка маса тіла, на яке діє сила тяжіння 2кН?
- Яка сила тяжіння діє на зайця, вовка, ведмедя, носорога та слона, якщо їх маси відповідно дорівнюють 6кг; 40кг; 400кг; 2т; 4т?
- Маса людини 80кг. Визначте величину діючої на неї сили тяжіння на: а) Землі, б) Місяці, в) Марсі, г) Юпітері.
- Тіло масою 8кг лежить на горизонтальній поверхні. Визначте діючі на тіло сили.
- На нитці висить тіло масою 700г. Визначити діючі на тіло сили.
- З якою силою залізне тіло об’єм якої 0,1м3 притягується до Землі?
- Яка сила тяжіння діє на мідний брусок розміром 10×8×5см?
.
§ 28. Сила тертя.
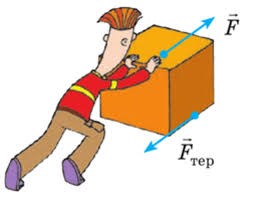
В механіці ті сили які так чи інакше протидіють взаємному переміщенню контактуючих поверхонь, називають силами тертя. Існує багато різновидностей сили тертя. Однак зазвичай, говорячи про силу тертя мають на увазі ту силу яка виникає між контактуючими твердими поверхнями та протидіє їх взаємному переміщенню. Тертя яке виникає між твердими поверхнями (сухе тертя) прийнято розділяти на тертя ковзання та тертя кочення. Наприклад, якщо важкий предмет ви намагаєтесь зсунути відносно підлоги, то вам протидіє сила тертя ковзання (мал.66а). А якщо той же предмет стоятиме на платформі з коліщатами (мал.66б), то переміщенню цієї системи протидіятиме сила тертя кочення. І напевно ви знаєте, що за схожих умов, тертя кочення значно менше за тертя ковзання.
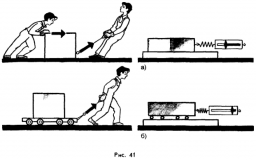
Мал.66. Тертя яке виникає між твердими поверхнями прийнято розділяти на тертя ковзання (а) та тертя кочення (б).
В межах програми загальноосвітньої школи, говорячи про силу тертя, зазвичай мають на увазі силу тертя ковзання. Досліджуючи загальні властивості цієї сили, можна провести ряд простих експериментів. Суть цих експериментів представлена на мал.67. І ця суть полягає в наступному. За допомогою пружинного динамометра певне тіло з постійною швидкістю протягують певною горизонтальною поверхнею і фіксують показання динамометра, які фактично дорівнюють величині сили тертя.
Змінюючи умови експерименту, наприклад шляхом збільшення або зменшення тієї сили з якою тіло тисне на поверхню, шляхом зміни матеріалу взаємодіючих поверхонь, якості їх механічної обробки, площі взаємодії, тощо, можна дослідити загальні властивості сили тертя ковзання. А ці властивості є наступними. 1. Сила тертя ковзання, практично не залежить від площі взаємодіючих поверхонь. 2. Сила тертя ковзання пропорційна тій силі з якою взаємодіючі поверхні притискаються одна до одної і яка чисельно дорівнює відповідній реакції опори (N). 3. Максимальна величина сили тертя спокою, дещо більша за величину відповідної сили тертя руху. 4. Сила тертя, складним чином залежить від механічних та хімічних властивостей взаємодіючих поверхонь, якості їх механічної обробки, їх температури, швидкості відносного руху, тощо.
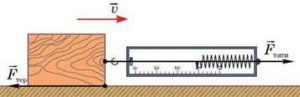
Мал.67. Загальний вигляд приладу для дослідження тертя ковзання.
Узагальнюючи результати подібних досліджень, можна дати наступне визначення. Сила тертя (сила тертя ковзання) – це та сила, з якою поверхні взаємодіючих твердих тіл протидіють їх взаємному поступальному (ковзальному) переміщенню, або можливості такого переміщення і яка дорівнює добутку коефіцієнту тертя ковзання (μ) та тієї сили з якою взаємодіючі поверхні тиснуть одна на одну (реакції опори N)
Позначається: Fтер
Визначальне рівняння: Fтер =µN
Одиниця вимірювання: [Fтер] = Н.
Зверніть увагу на факт того, що сила тертя, як власне і будь яка сила, є векторною величиною (Fтер), а визначальне рівняння цієї величини записано у скалярному вигляді (Fтер =µN). І це не випадково. Адже якби це рівняння було записано у вигляді Fтер =µN, або Fтер = –µN, то це б означало, що в першому випадку сила тертя направлена в ту ж сторону що й реакція опори, а в другому випадку – в сторону протилежну від напрямку реакції опори. В реальності ж сила тертя направлена не в напрямку реакції опори і не в протилежному напрямку, а в напрямку перпендикулярному до реакції опори. Тому формула Fтер =µN визначає лише величину сили тертя, при цьому напрям цієї сили визначається із умов конкретної задачі (сила тертя протидіє взаємному переміщенню контактуючих поверхонь, або можливості такого переміщення).
Коефіцієнт тертя ковзання – це фізична величина, яка характеризує здатність певної пари твердих поверхонь протидіяти їх відносному ковзальному переміщенню і яка дорівнює відношенню виникаючої між цими поверхнями сили тертя, до величини тієї сили з якою поверхні притискаються одна до одної.
Позначається: μ
Визначальне рівняння: μ = Fтер/N
Одиниця вимірювання: [μ] = Н/Н = ̶ , безрозмірна величина.
Коефіцієнт тертя складним чином залежить від багатьох обставин і визначається експериментально. Результати деяких з цих експериментальних досліджень представлені в наступній таблиці.
|
Сила тертя завжди направлена в сторону протилежну від напрямку руху тіла, або напрямку його можливого руху. Наприклад, якщо тіло рухається вправо, то сила тертя направлена вліво, а якщо тіло рухається вліво, то сила тертя направлена вправо. Якщо певна зовнішня сила F прагне зсунути тіло в одному напрямку (мал.68а), а тіло залишається в стані спокою (v=0), то це тільки тому, що на дане тіло в протилежному напрямку діє відповідна сила тертя Fтер. Якщо в супереч дії тих сил які прагнуть зсунути тіло похилою поверхнею (мал.68б), тіло залишається в стані спокою, то це тільки тому, що в напрямку протилежному до напрямку можливого руху на тіла діє відповідна сила тертя, яка і протидіє цьому можливому руху.
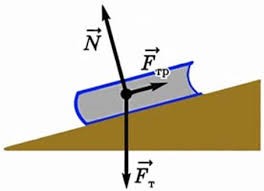
Мал.68. Сила тертя завжди направлена в сторону протилежну від напрямку руху тіла, або напрямку його можливого руху.
Специфіка сили тертя полягає в тому, що вона виникає як певна реакція на дію тих сил які намагаються зсунути одну поверхню відносно іншої. І якщо такі сили відсутні, то відповідно відсутня і певна сили тертя. Наприклад, якщо тіло знаходиться на горизонтальній поверхні (мал.69а), то на нього сила тертя не діє. Не діє тому, що нема того силового фактору який намагається зсунути тіло відносно поверхні (Fт+N=0). Однак як тільки поверхня стане похилою (мал.69б), автоматично з’явиться і відповідна сила тертя. З’явиться тому, що результуюча постійно діючих на тіло сил (сила тяжіння Fт та реакція опори N) вже не буде дорівнювати нулю (Fт+N≠0) і намагатиметься зсунути тіло вниз. І якщо тіло знаходиться в стані спокою, то це тільки тому, що цей спокій забезпечує певна сила тертя. При цьому, по мірі зростання кута нахилу площини, автоматично зростатиме і відповідна сила тертя. Зростатиме до тих пір, поки не досягне певної критичної величини, за межами якої, тертя спокою перетворюється на тертя руху.

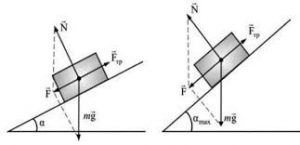
Мал.69. Сила тертя виникає лише за наявності тієї сили яка прагне зсунути тіло відносно поверхні.
По суті, сила тертя є результуючою всієї сукупності тих складних процесів, які відбуваються в місці контакту поверхонь. При цьому, якщо мова йде про тертя ковзання, то основними складовими відповідної сили тертя, є: 1) наявність сил взаємодії між молекулами контактуючих поверхонь; 2) наявність певних мікро нерівностей (шороховатостей) поверхонь.

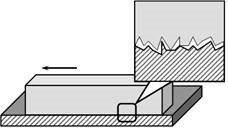
Мал.70. Основними причинами тертя ковзання є: взаємодія між молекулами контактуючих поверхонь та наявність мікро нерівностей на цих поверхнями.
Якщо на площині знаходиться кругле (циліндричне) тіло, яке може вільно обертатись (котитись), то в цьому випадку говорять про тертя кочення. Порівнюючи величини сил тертя ковзання та кочення, проведіть наступний простий експеримент. На горизонтальну поверхню покладіть циліндр та йому відповідний за масою брусок. Нахиляючи поверхню, ви неодмінно з’ясуєте, що циліндр покотиться при гранично малому куті нахилу поверхні, тоді як рух бруска починається при в десятки разів більших кутах нахилу. Висновок очевидний: за однакових умов, сила тертя кочення набагато менша за силу тертя ковзання. Зважаючи на даний факт, в тих випадках де потрібно мінімізувати тертя, ковзання замінюють на кочення, наприклад шляхом застосування відповідних підшипників. Іншим ефективним способом зменшення сили тертя є застосування відповідних мастил.

Мал.71. За аналогічних умов, сила тертя кочення значно менша за силу тертя ковзання.
На перший погляд, та сила тертя завдяки якій люди, велосипеди та автомобілі переміщуються відносно відповідних поверхонь, не вписується в рамки загально прийнятого визначення: «сила тертя, це та сила з якою взаємодіючі поверхні протидіють їх взаємному переміщенню». Однак, неупереджений аналіз вказує на безпідставність подібних звинувачень. Адже та сила тертя ковзання, що виникає між колесами велосипеда і дорогою, або між дорогою і підошвами взуття, дійсно протидіє їх взаємному переміщенню, тобто протидіє ковзанню коліс та підошви, відносно поверхні дороги. При цьому ця сила не протидіє поступальному руху відповідних тіл. Більше того, без цієї сили такий рух стає просто неможливим. Адже лише завдяки силі тертя ковзання, обертальний рух ведучого колеса велосипеда та м’язові зусилля пішохода перетворюється на поступальний рух відповідних тіл.

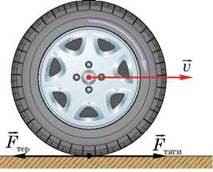
Мал.72. Наявність сили тертя, є необхідною умовою поступального руху тіл.
Контрольні запитання.
- Що називають силою тертя (тертя ковзання)?
- Від чого залежить сила тертя ковзання?
- Як направлена сила тертя ковзання?
- Що називають коефіцієнтом тертя?
- Від чого залежить коефіцієнт тертя і як він визначається?
- Чому на те тіло яке лежить на горизонтальній поверхні стола, сила тертя не діє, а на те що лежить на похилій площині – діє?
- Назвіть основні способи суттєвого зменшення сили тертя.
- Наведіть приклади шкідливих та корисних проявів сили тертя.
Вправа №28.
- Чому коефіцієнт тертя – безрозмірна величина.
- Тіло лежить на горизонтальній поверхні. Які сили діють на це тіло?
- Тіло нерухомо лежить на похилій площині. Які сили діють на це тіло?
- Чи може сила тертя, що діє на тіло яке лежить на похилій площині, бути направленою вниз вздовж цієї площини. Якщо може, то в якому випадку?
- Чи може сила тертя бути причиною руху тіла?
- Тіло масою 1,5кг під дією сили 3Н з постійною швидкістю рухається горизонтальною поверхнею. Визначити коефіцієнт тертя між тілом та поверхнею.
- Тіло масою 8кг з постійною швидкістю рухається горизонтальною поверхнею. Під дією якої сили рухається тіло, якщо коефіцієнт тертя між тілом і поверхнею 0,3?
- Тіло під дією горизонтальної сили 6Н рухається з постійною швидкістю. Яка маса тіла, якщо коефіцієнт тертя між тілом і поверхнею 0,4?
.
§ 29. Розв’язування задач. Тема: Силовий метод розв’язування задач.
Нагадаємо, в основному законі статики, який називається умовою механічної рівноваги тіла, стверджується: тіло (матеріальна точка) буде знаходитись в стані механічної рівноваги (v=0, або v=const) тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил дорівнює нулю. Іншими словами: якщо v=0, або v=const то ∑Fх = 0, ∑Fу = 0.
Перевага задач статики полягає в тому, що порядок (алгоритм) їх розв’язку є чітко визначеним. І цей порядок наступний:
- Уважно прочитати умову задачі та зробити стислий запис цієї умови.
- Обов’язково виконати малюнок, на якому чітко вказати всі діючі на задане тіло (матеріальну точку) сили та напрямки цих сил.
- Задати систему координат.
- Записати умову рівноваги даної матеріальної точки, тобто систему рівнянь: ∑Fx=0; ∑Fy=0.
- Розв’язавши цю систему, визначити невідомі величини.
Загальні зауваження. В механіці матеріальної точки, а саме таку механіку ми і вивчаємо, прийнято вважати, що всі діючі на тіло сили, діють на його центр мас. Тому, якщо в умові задачі нема конкретних вказівок щодо точки прикладання конкретної сили, вважається що ця сила діє на цент мас відповідного тіла.
Дотримуючись вище наведеного алгоритму та зважаючи на зроблене зауваження, розв’яжемо декілька конкретних задач.
Задача 1. Тіло масою 15кг знаходиться на горизонтальній поверхні. Яку горизонтальну силу треба прикласти до тіла щоб зрушити його змісця, якщо коефіцієнт тертя 0,4?

Дано:
m=15кг
μ = 0,4
F = ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили та задаємо відповідну систему координат (на малюнку Fтер позначено ƒ). Записуємо умову рівноваги даного тіла:
ΣFx = F – Fтер = F – μN = 0;
ΣFy = N – Fт = N – mg = 0.
Із рівняння (1) випливає F = μN, де N=?
Із рівняння (2) випливає N = mg = 15кг·10м/с2 = 150Н.
Таким чином F = μN = 0,4·150Н =60Н.
Відповідь: F = 60Н.
Задача 2. Брусок тягнуть горизонтальною поверхнею стола прикладаючи силу 4Н. Яка маса бруска, якщо він рухається рівномірно, а коефіцієнт тертя між бруском і столом 0,2?

Дано:
F = 4H
μ = 0,2
m = ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили та задаємо відповідну систему координат.
Записуємо умову рівноваги даного тіла:
ΣFx = F – Fтер = F – μN = 0;
ΣFy = N – Fт = N – mg = 0.
Таким чином, ми маємо систему двох рівнянь з двома невідомими: m=?; N=?
Розвязуємо цю систему та визначаємо невідомі величини.
Із рівняння (2) випливає N = mg. Підставляємо цей результат в рівняння (1):
F – μmg = 0, звідси μmg = F, звідси m = F/μg.
Розрахунки: m = 4Н/0,2·10(м/с2) = 2кг.
Відповідь: m = 2кг.
Задача 3. Визначити силу тяги, яку розвиває тепловоз при рівномірному русі на горизонтальній ділянці шляху, якщо коефіцієнт тертя 0,03, а сила тиску на рейки 25∙106Н?
Загальні зауваження. При розв’язуванні задач фізики, надзвичайно важливим вмінням, є вміння виділяти суттєве (важливе) і не звертати особливу увагу на несуттєве (другорядне, неважливе). Наприклад в умовах нашої задачі неважливо чи знаєте ви як влаштований тепловоз і як він створює ту силу яка називається силою тяги. Неважливо скільки коліс в цьому тепловозі і яким чином вони взаємодіють з рейками залізниці. Важливим є те, що на певній горизонтальній поверхні (опорі), є певне тіло, яке під дією певної горизонтальної сили (сили тяги Fтяги) з певною вертикальною силою (силою тиску Fт, а по суті силою тяжіння) діє на опору (рейки залізниці). Важливим є те, що руху тіла протидіє певна узагальнена сила тертя (сила протидії руху тепловоза), основною характеристикою якої є відповідний коефіцієнт тертя. Важливим є те, що тепловоз рухається з певною постійною швидкістю (v=const), бо це означає, що дана задача є задачею статики і що тому мають виконуватись співвідношення: ∑Fx=0; ∑Fy=0. Власне таке розуміння суті задачі і дозволяє отримати відповідне рішення.

Дано:
μ = 0,03
Fт = 25·106Н
Fтяги= ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили та задаємо відповідну систему координат. (на малюнку Fтяги позн. F; Fт позн. mg; Fтер позн. ƒ)
Записуємо умову рівноваги даного тіла:
ΣFx = Fтяги – Fтер = Fтяги – μN = 0;
ΣFy = N – Fт = 0.
Із рівняння (1) випливає Fтяги = μN, де N=?
Із рівняння (2) випливає N = Fт = 25·106Н .
Таким чином Fтяги = μN = 0,03·25·106Н = 0,75·106Н = 750кН
Відповідь: F = 750кН.
Задача 4. З якою мінімальною силою потрібно притиснути книгу масою 0,8кг до вертикальної стіни, щоб книга не зісковзувала вниз? Коефіцієнт тертя між книгою та стіною 0,4.
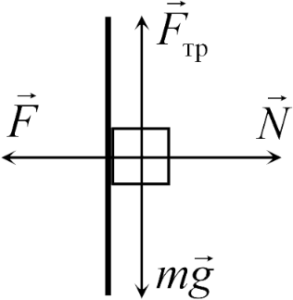
Дано:
m=0,8кг
μ = 0,4
F = ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили та задаємо відповідну систему координат. Записуємо умову рівноваги даного тіла:
ΣFx = N – F = 0;
ΣFy = Fтер – Fт = μN – mg = 0.
Із рівняння (1) випливає F = N, де N=?
Із рівняння (2) випливає μN = mg, звідси N = mg/μ.
Таким чином F = N = mg/μ = 0,8кг·9,8(м/с2)/0,4 = 19,8Н
Відповідь: F = 19,8Н.
Вправа №29.
- За допомогою динамометра учень з постійною швидкістю переміщує залізний брусок масою 300г по горизонтальній поверхні стола. При цьому динамометр показує 0,6Н. Який коефіцієнт тертя між бруском та поверхне стола?
- Тіло масою 8кг з постійною швидкістю рухається горизонтальною поверхнею. Під дією якої сили рухається тіло, якщо коефіцієнт тертя між тілом і поверхнею 0,3?
- Тіло під дією горизонтальної сили 6Н рухається з постійною швидкістю. Яка маса тіла, якщо коефіцієнт тертя між тілом і поверхнею 0,4?
- З якою мінімальною силою потрібно притиснути тіло масою 5кг до вертикальної стіни, щоб воно не зісковзувала вниз? Коефіцієнт тертя між тілом та стіною 0,3.
- На підлозі лежить дерев’яний брус об’ємом 0,2м3. Яку мінімальну силу треба прикласти щоб зрушити брус з місця, якщо коефіцієнт тертя 0,3? Густина деревини 500кг/м3.
- На горизонтальній поверхні стола лежить залізний брусок об’ємом 1дм3. Під дією якої горизонтальної сили брусок зрушиться з місця, якщо коефіцієнт тертя 0,3?
- На горизонтальній поверхні лежать три покладені одна на одну однакові книги, маса кожної з яких 1кг. Яку мінімальну силу потрібно прикласти щоб витягнути середню книгу? (Верхню і нижню книги вважати нерухомими). Коефіцієнт тертя між поверхнями книг 0,3.
.
§ 30. Сила інерції.
В процесі вивчення фізики ви неминуче переконаєтесь в тому, наскільки незамінно важливою є та сила, яку прийнято називати силою інерції. Наразі ж
відбудеться лише перше знайомство з цією цікавою та надважливою силою.
З’ясовуючи фізичну суть сили інерції, звернемося до експерименту. Припустимо що до пружинного динамометра (мал.67) прикріплено вантаж масою 0,102кг. Коли система динамометр-вантаж знаходиться в стані механічної рівноваги (v=0 або v=const) то деформована пружина вказує на те, що вантаж притягується до Землі з силою 1Н: Fт=mg=0,102кг·9,8м/с2=1Н. Але, як тільки система почне прискорено рухатись вгору, пружина динамометра додатково розтягнеться, вказуючи на те що на тіло діє певна додаткова сила, напрям якої протилежний до напрямку прискорення. Ця сила і є силою інерції .
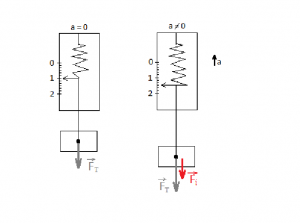
Мал.73. Прискорений рух тіла завжди породжує силу, яка протидіє появі та зростанню цього прискорення і яка називається силою інерції
Сила інерції – це така сила, поява якої обумовлена прискореним рухом тіла і яка завжди протидіє появі та зростанню цього прискорення.
Позначається: Fі
Визначальне рівняння: Fі = –ma
Одиниця вимірювання: [Fі] = Н, ньютон
Із визначального рівняння сили інерції (Fі = –ma) випливає, що до тих пір поки тіло знаходиться в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v=const), ніяка сила інерції на нього не діє. Але як тільки тіло починає рухатись з прискоренням, на нього автоматично починає діяти певна сила інерції (Fі = –ma), величина якої залежить від маси тіла та його прискорення і напрям якої протилежний до напрямку прискорення. Наприклад якщо в момент розгону, прискорення ракети направлено вгору, то діюча на ракету сила інерції направлена вниз. Якщо в процесі вільного падіння прискорення тіла направлено вниз, то діюча на тіло сила інерції направлена вгору. Якщо в процесі обертання навколо Землі, Місяць рухається з доцентровим прискоренням, то діюча на нього сила інерції є відцентровою. Якщо прискорення тіла направлено вправо, то діюча на тіло сила інерції направлена вліво. Якщо прискорення вліво – сила інерції вправо, прискорення вперед – сила інерції назад і т.д.
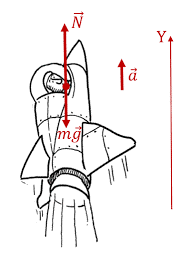
Мал.74. Якщо тіло рухається з прискоренням, то на нього неминуче діє певна сила інерції, направлена в сторону протилежну від напрямку прискорення.
До речі, факт того, що в процесі вільного падіння, важкі і легкі тіла падають з однаковим прискоренням (g=9,8м/с2), пояснюється тим, що на кожне з цих тіл, окрім направленої вертикально вниз сили тяжіння (Fт=mg), неминуче діє рівна їй за величиною і направлена вертикально вгору сила інерції (Fі=–mg). Власне під дією цих двох рівних за величиною і протилежних за напрямком сил, тіло і рухається з певним прискоренням. При цьому величина цього прискорення не залежить від маси тіла, а відповідно і від величини діючої на нього сили тяжіння. Адже на важке тіло діє не лише велика сила тяжіння, а й відповідно велика сила інерції. Натомість на легке тіло діє мала сила тяжіння і відповідно мала сила інерції.
Ви можете запитати: «А як бути з умовою механічної рівноваги тіла, тобто з законом в якому говориться про те, що коли діючі та тіло зовнішні сили зрівноважують одна одну, то тіло знаходиться в стані спокою (v=0), або прямолінійного рівномірного руху (v=const)?» Відповідаючи на це слушне запитання, можна сказати наступне.
Дійсно. В умові механічної рівноваги стверджується: якщо векторна сума діючих на тіло зовнішніх сил дорівнює нулю, то тіло буде знаходитись в стані механічної рівноваги. Іншими словами: якщо ΣF=0, то v=0 або v=const. Аналізуючи дане твердження зверніть увагу на те, що в ньому говориться про векторну суму зовнішніх сил, тобто звичайних сил взаємодії: сила тяжіння, сила тертя, сила пружності, сила Архімеда, реакція опори, сила тяги, тощо. В нашому ж випадку, ми маємо справу з силою інерції, тобто силою яка не є зовнішньою. З силою, поява якої обумовлена самим фактом прискореного руху тіла. Тому, коли ми стверджуємо що в процесі вільного падіння тіла, встановлюється рівновага між силою тяжіння і силою інерції, то маємо на увазі так звану динамічну рівновагу. Рівновагу, яка передбачає рух тіла не з постійною швидкістю (v=const), а з постійним прискоренням (а=const).
Динамічною рівновагою називають такий механічний стан тіла, при якому воно, під дією зовнішніх сил та сили інерції, знаходиться в стані рівноприскореного руху (а=const).
Сьогодні ми не будемо говорити про походження сили інерції. Зауважимо тільки, що поява сили інерції обумовлена взаємодією даного тіла з тим фізичним об’єктом який називається «простір». Фізичні властивості простору надзвичайно багатогранні та складні. Певними проявами цих властивостей є гравітаційні, електричні та магнітні поля, а також те, що ми називаємо світлом. Якщо ж говорити про фізичну суть того зв’язку який існує між простором та силою інерції, то ця суть є предметом пояснень загальної теорії відносності.
Зважаючи на вище сказане, просто констатуємо факт того, що при прискореному русі будь-якого тіла, на нього неминуче діє сила інерції, величина якої дорівнює добутку маси тіла на його прискорення, і напрям якої протилежний напрямку цього прискорення. Наприклад коли в момент різкої зупинки автомобіля якась невидима сила штовхає вас уперед, знайте – це сила інерції. Коли на крутому повороті якась незрозуміла бічна сила притискає вас до бокових дверей автомобіля, знайте – це сила інерції. Коли на атракціоні «американські гірки» ваш подих перехоплює від постійних перевантажень та станів невагомості, знайте, це прояви сили інерції.


Мал.75. Деякі прояви сили інерції.
Потрібно зауважити, що ті задачі, в яких тіло під дією певної системи сил рухається з постійним прискоренням є задачами динаміки. Однак, алгоритм рішення цих динамічних задач практично не відрізняється від алгоритму рішення задач статики. В основі цього рішення лежить закон який називається умовою динамічної рівноваги тіла. В цьому законі стверджується: Тіло (матеріальна точка) буде знаходитись в стані динамічної рівноваги (а =const) тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил та сили інерції дорівнює нулю. Іншими словами:
якщо а=const, то Σ F + Fi = 0 і навпаки
Задача 1. При аварійному гальмуванні, автомобіль масою 3т рухається з прискоренням 3м/с2. Яка сила інерції діє на цей автомобіль. Як направлена ця сила відносно напрямку руху (напрямку швидкості) автомобіля?

Дано:
m = 3т = 3000кг
a = 3м/с2
Fі = ?
Рішення. За визначенням Fі = –ma. Це означає, що величина сили інерції визначається за формулою Fі = ma = 3000кг·3м/с2 = 9000Н, а напрям цієї сили є протилежним до напрямку прискорення тіла. А оскільки в процесі гальмування (зменшення швидкості), прискорення тіла направлено в сторону протилежну від напрямку швидкості, то сила інерції буде направлена в ту ж сторону що і швидкість, тобто в сторону руху автомобіля.
Відповідь: Fі = 9000Н. При гальмуванні, сила інерції направлена в напрямку руху автомобіля.
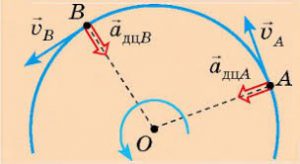
Задача 2. Автомобіль масою 3т зі швидкістю 54км/год рухається заокругленням дороги радіус якого 300м. Визначити величину діючої на автомобіль сили інерції.

Дано:
m = 3т = 3000кг
v = 54км/год = 15м/с
R = 300м
Fi = ?
Рішення. Рухаючись заокругленням дороги, автомобіль рухається з певним доцентровим прискоренням (ад=v2/R) і тому на нього неминуче діє відповідна, направлена в протилежну сторону від прискорення (тобто відцентрова) сила інерції Fi=maд=mv2/R (на малюнку ця сила не показана).
Розрахунки Fi=3000кг(15м/с)2/300м=2250Н.
Відповідь: Fi = 2250Н.
Контрольні запитання.
- Яку силу називають силою інерції?
- Чи діє на тіло сила інерції при його рівномірному прямолінійному русі?
- Чи діє сила інерції при рівномірному русі тіла по колу?
- В момент аварійного гальмування автобуса, якась сила штовхає пасажирів вперед. Що це за сила і чому вона з’являється?
- В момент різкого повороту автомобіля якась сила штовхає пасажирів вбік. Що це за сила і чому вона з’являється?
- Що називають динамічною рівновагою тіла?
- Що стверджується в умові динамічної рівноваги тіла?
- Який напрям сили інерції в зображених на малюнку ситуаціях? Як змінюється при цьому швидкість тіла?
Вправа №30.
- При розгоні автомобіль масою 2т рухається з прискоренням 4м/с2. Яка сила інерції діє на автомобіль? Як направлена ця сила відносно напрямку руху автомобіля?
- При аварійному гальмуванні, автомобіль масою 2,5т рухається з прискоренням 4м/с2. Яка сила інерції діє на цей автомобіль. Як направлена ця сила відносно напрямку руху (напрямку швидкості) автомобіля?
- Гоночний автомобіль розганяється до швидкості 108км/год за 5с. Яка сила інерції діє при розгоні на водія автомобіля, якщо маса водія 80кг?
- При аварійному гальмуванні, автомобіль який рухався з швидкістю 90км/год зупинився через 5с. Яка сила інерції діяла на водія автомобіля в процесі гальмування, якщо маса водія 80кг?
- Автомобіль масою 4т зі швидкістю 36км/год рухається заокругленням дороги радіус якого 200м. Визначити величину діючої на автомобіль сили інерції. Як направлена ця сила?
- Автомобіль з швидкістю 72км/год рухається заокругленням дороги радіус якого 400м. Яка сила інерції діє при цьому на водія автомобіля? Який напрям цієї сили?
- З якою силою буде тиснути автомобіль масою 2т на середину опуклого моста, якщо радіус моста 100м, а швидкість автомобіля 36км/год?
.
§ 31. Розв’язування задач. Тема: Силовий метод розв’язування задач динаміки.
Зазвичай силовий метод розв’язування задач, застосовують в тих випадках коли мова йде про задачі статики, тобто ті задачі в яких тіло під дією певної системи сил не рухаються (v=0), або рухаються з постійною швидкістю (v=const). Однак, з не меншою ефективністю цей метод працює і в тих випадках коли мова йде про задачі динаміки, тобто ті задачі в яких тіло рухаються з певним прискоренням (а=const≠0). Різниця розв’язку лише в тому, що в задачах динаміки, потрібно враховувати факт того, що на тіло окрім звичайних сил взаємодії (сила тяжіння, реакція опори, сила тертя, сила Архімеда, тощо), діє певна сила інерції Fi= –ma і що при цьому умова рівноваги тіла набуває вигляду: якщо а=const≠0, то ΣF+Fi=0.
А це означає, що алгоритм силового рішення задач динаміки в точності аналогічний алгоритму рішення задач статики:
- Уважно прочитати умову задачі та зробити стислий запис цієї умови.
- Обов’язково виконати малюнок, на якому чітко вказати всі діючі на задане тіло сили, в тому числі і силу інерції та вказати напрямки цих сил.
- Задати систему координат.
- Записати умову рівноваги даного, тобто систему рівнянь: ∑Fx=0; ∑Fy=0.
- Розв’язавши цю систему, визначити невідомі величини.
Що ж дотримуючись даного алгоритму розв’яжемо ряд показових задач.
Задача 1. Автомобіль масою 900кг, маючи тягову силу 2кН, рухається з прискоренням 1м/с2. Визначити загальну силу опору руху автомобіля (загальну силу тертя).
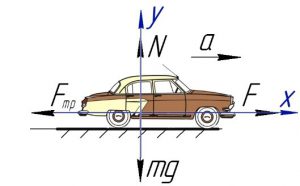
Дано:
m = 900кг
Fтяги = 2кН = 2000Н
a = 1м/с2
Fтер = ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на автомобіль сили. А цими силами є: сила тяжіння Fт=mg, реакція опори N, сила тяги Fтяги =F, сила тертя Fтер та направлена в протилежну сторону від прискорення сила інерції Fі=ma. (На жаль, малюнків на яких була б вказана сила інерції знайти практично не можливо. Тому наявність цієї сили просто уявіть) Задаємо відповідну систему координат. Записуємо умову рівноваги тіла вздовж осі 0х:
ΣFx = Fтяги – Fтер – Fi = Fтяги – Fтер – mа = 0. Звідси випливає
Fтер = Fтяги – mа.
Розрахунки: Fтер = 2000Н – 900кг1м/с2 = 2000Н – 900Н = 1100Н
Відповідь: Fтер = 1100Н.
Задача 2. З якою силою тіло масою 5кг тисне на опору в ситуаціях:
а) система опора-тіло знаходиться в стані механічного спокою;
б) система опора-тіло рухається з направленим вгору прискоренням 5м/с2;
в) система опора-тіло рухається з направленим вниз прискоренням 5м/с2?
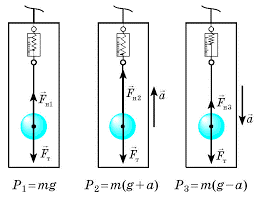
Дано:
m = 5кг
a1 =0м/с2
a2 = 5м/с2↑
a3 = 5м/с2↓
N1=? N2=? N3=?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили, а цими силами є: сила тяжіння Fт=mg, реакція опори N, сила інерції Fi= –ma (на малюнку сила інерції не вказана, а реакції опори позначені F1, F2, F3). Задаємо відповідну систему координат: вісь 0х направлена вертикально вгору. Записуємо умову рівноваги тіла для кожної ситуації та визначаємо відповідну реакцію опори:
1) ∑Fx = N1 – Fт = N1 – mg = 0, звідси N1 = mg = 5кг·10м/с2 = 50Н;
2) ∑Fx = N2 – Fт – Fi = N2 – mg – ma = 0, звідси N2 = mg + ma = 5кг·10м/с2 + 5кг·10м/с2 = 75Н;
3) ∑Fx = N3 – Fт + Fi = N3 – mg + ma = 0, звідси N3 = mg – ma = 5кг·10м/с2 – 5кг·10м/с2 = 25Н.
Відповідь: N1 = 50Н; N2 = 75Н; N3 = 25Н.
Задача 3. В процесі аварійного гальмування, автомобіль масою 900кг рухається з прискоренням 4м/с2. Визначити діючу на автомобіль силу тертя та коефіцієнт тертя.
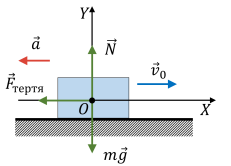
Дано:
m = 900кг
а = 4м/с2
Fтер=?
μ = ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили та задаємо відповідну систему координат (як завжди, сила інерції на малюнку не показана).
Записуємо умову рівноваги даного тіла:
ΣFx = Fі – Fтер = ma – Fтер = 0;
ΣFy = N – mg = 0.
Із рівняння (1) випливає Fтер = ma = 900кг·4м/с2 = 3600Н.
Оскільки за визначенням F = μN, та зважаючи на те, що з рівняння (2) випливає N = mg = 900кг·10м/с2=9000Н, можна записати
μ = Fтер/N = 3600H/9000Н = 0,4
Відповідь: Fтер = 3600Н; μ = 0,4.
Задача 4. З якою силою буде тиснути автомобіль масою 800кг на середину опуклого моста, якщо радіус моста 50м, а швидкість автомобіля 36км/год?
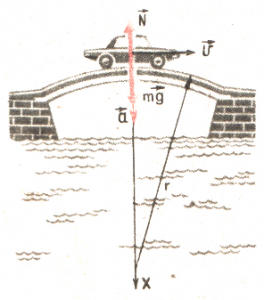
Потрібно зауважити, що ту силу з якою тіло діє на опору прийнято називати вагою тіла (позначається Р). А оскільки та сила з якою тіло діє на опору (вага тіла Р), чисельно дорівнює тій силі з якою опора діє на тіло (реакція опори N), то рішення задачі по суті зводиться до визначення діючої на тіло (автомобіль) реакції опори: P = N = ?
Дано:
m = 800кг
R = 50м
v = 36км/год =10м/с
P = N = ?
Рішення. Виконуємо малюнок на якому вказуємо ті сили які діють на автомобіль у верхній точці моста. А враховуючи факт того, що автомобіль з швидкістю v рухається по колу, а отже рухається з доцентровим прискоренням (a=v2/R), можна стверджувати, що на автомобіль окрім сили тяжіння та реакції опори діє сила інерції Fi = ma = mv2/R, і що у верхній точці моста вона направлена вертикально вгору.
Записуємо умову рівноваги даного тіла в напрямку вертикальної осі (оскільки на малюнку ця вісь направлена вниз, то і знаки сил є відповідними):
ΣFx = Fт – Fi – N = mg – mv2/R – N = 0. Звідси випливає:
N = mg – mv2/R = m(g – v2/R)
Розрахунки: N = 800кг(10м/с2 – (10м/с)2/50м) = 800кг·8м/с2 = 6400Н.
Відповідь: Р = 6400Н.
Вправа №31.
- Автомобіль масою 1,5т, маючи тягову силу 3кН, рухається з прискоренням 1м/с2. Визначити загальну силу опору руху автомобіля (загальну силу тертя).
- В процесі аварійного гальмування автомобіль масою 4т рухається з прискоренням 2м/с2. Визначити діючу на автомобіль силу тертя та коефіцієнт тертя.
- З якою силою тіло масою 50кг тисне на горизонтальну опору в ситуаціях:
а) система опора-тіло знаходиться в стані механічного спокою;
б) система опора-тіло з прискоренням 4м/с2 рухається вертикально вгору;
в) система опора-тіло з прискоренням 6м/с2 рухається вертикально вниз?
г) в) система опора-тіло з прискоренням 10м/с2 рухається вертикально вниз?
- З якою силою тисне автомобіль масою 2т на середину опуклого моста, якщо радіус моста 100м, а швидкість автомобіля 54км/год?
- Тіло масою 50кг з швидкістю 10м/с рухається по колу радіусом 100м. З яким прискоренням рухається тіло. Яка сила інерції діє на тіло?
- Під дією якої сили, тіло масою 5кг рухається горизонтальною поверхнею маючи прискорення 2м/с2, якщо коефіцієнт тертя між тілом та поверхнею 0,2?
- Хлопчик масою 40кг гойдається на гойдалці із довжиною підвісу 3м. З якою силою він тисне на сидіння при проходженні середнього положення зі швидкістю 3м/с?
.
§ 32. Вага тіла. Невагомість.
Однією з найбільш суперечливих фізичних величин механіки є вага. В науковій літературі її часто плутають з силою тяжіння, а у побуті – з масою. Насправді ж вага, це та сила з якою тіло діє на опору. Скажімо та сила з якою ви тиснете на підлогу є вашою вагою. Виходячи з того, що вага (Р) – це та сила з якою тіло діє на опору, а реакція опори (N) – це та сила з якою опора діє на тіло, та враховуючи що ці сили є діючою і протидіючою силами, о отже рівними за величиною і протилежними за напрямком, можна дати наступне визначення.
Вага – це та сила з якою тіло діє на опору і яка чисельно дорівнює реакції цієї опори.
Позначається: Р
Визначальне рівняння: Р = – N, де N – реакція опори
Одиниця вимірювання: [P] = H, ньютон.
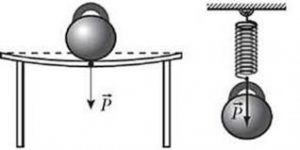
Мал.76. Вага – це та сила з якою тіло діє на опору.
Більшість людей схильні вважати, що вага тіла вимірюється в кілограмах. Ця, глибоко вкорінена помилкова думка, має своє логічне пояснення. І це пояснення полягає в наступному. Коли ви приходите в крамницю за цукром, картоплею чи м’ясом, то приходите за певною кількістю речовини. А універсальною мірою кількості речовини в тілі є його маса, тобто та величина яка вимірюється в кілограмах. А як на практиці вимірюють масу тіла? Правильно – шляхом зважування. І це зважування полягає в тому, що відповідне тіло кладуть на спеціальну опору (ваги), ця опора відчуває вагу тіла і відповідним чином реагує на цю вагу (силу). Результатом же цієї реакції є відповідне відхилення стрілки приладу. А оскільки ви прийшли не за силою (не за ньютонами), а за певною речовиною, тобто за тим що вимірюється в кілограмах, то результат зважування вам видають в цих самих кілограмах. Ясно, що така повсякденна практика, формує впевненість в тому, що вага – це те що вимірюється в кілограмах. Насправді ж, вага – це сила яку відчуває та опора на якій знаходиться дане тіло. І як будь яка сила, вага вимірюється в ньютонах.

Мал.77. Оскільки на практиці масу тіла, тобто те що вимірюється в кілограмах визначають шляхом зважування, то в свідомості пересічної людини, термін зважування а отже «вага» асоціюється з тим, що вимірюється в кілограмах.
Ще однією загально розповсюдженою помилкою є думка про те, що вага тіла дорівнює тій силі з якою тіло притягується до Землі і що тому вага визначається за формулою P = mg. Насправді ж, вага – це та сила з якою тіло діє на опору і яка чисельно дорівнює тій силі з якою опора діє на тіло P = N, а з урахуванням напрямку цих сил P = –N. Інша справа, що в тих ситуаціях, коли система опора-тіло перебуває в стані механічної рівноваги (v=0, або v=const), вага тіла дійсно дорівнює діючій на це тіло силі тяжіння P = mg. Але навіть в цьому випадку, ототожнювати вагу тіла з діючою на нього силою тяжіння не можна. Не можна бодай тому, що сила тяжіння діє на тіло, а вага тіла діє на опору.
Загалом, на відміну від маси тіла, яка за будь яких обставин залишається незмінною (звичайно, якщо не враховувати ті практично не помітні ефекти про які ви дізнаєтесь вивчаючи теорію відносності), вага тіла в різних обставинах може бути абсолютно різною. Скажімо, на Землі (g=9,81м/с2) вага тіла масою 10кг становитиме 98,1Н. На Місяці (g=1,6м/с2) ця вага дорівнюватиме 16Н; на Марсі (g=3,7м/с2) – 37Н; на Юпітері (g=25,9м/с2) – 259Н; а на Сонці (g=274,1м/с2) – 2741Н. Тому наприклад на Місяця, тіло масою 600кг, важитиме стільки ж як на Землі тіло масою 98кг.

Мал.78. На Місяці вага тіла у шість разів менша ніж на Землі.
Більше того, вага тіла залежить не лише від параметрів того гравітаційного поля яке створює відповідна планета, а й від багатьох інших обставин. Зокрема від того, з яким прискоренням і в якому напрямку рухається система опора-тіло. Ілюструючи цю залежність розглянемо конкретну задачу.
Задача 1. Тіло масою 70кг знаходиться в ліфті. Визначити вагу цього тіла в наступних ситуаціях: а) ліфт знаходиться в стані механічної рівноваги (v=0 або v=const, тобто а=0м/с2); б) ліфт рухається з прискоренням а=5м/с2 і це прискорення направлене вгору; в) ліфт рухається з прискоренням а=5м/с2 і це прискорення направлене вниз; г) ліфт знаходиться в стані вільного падіння тобто падає з прискоренням а=g=10м/с2.
Дано:
m = 70кг
а1 = 0м/с2
а2 = 5м/с2↑
а3 = 5м/с2↓
а4 =g=10м/с2↓
Р1=?, Р2=?,
Р3=?, Р4=?
Рішення. Будемо виходити з того, що вага тіла – це та сила з якою тіло діє на опору, в нашому випадку – на підлогу ліфта, і що величина цієї сили дорівнює відповідній реакції опори (Р=N). А це означає, що рішення задачі зводиться до того, щоб визначити величину реакції опори в кожній з чотирьох ситуацій.
Розв’язуючи цю задачу, виконуємо відповідні малюнки на яких вказуємо ті сили що діють на дане тіло. А цими силами є: сила тяжіння Fт = mg, реакція опори N та, за наявності прискорення, сила інерції Fi = –ma. (На жаль, на малюнку позначена лише та сила яка називається вагою). Зважаючи на вище сказане, проаналізуємо кожну з чотирьох ситуацій і визначимо вагу тіла в кожній з них.
. а=0м/с2 а=5м/с2↑ а=5м/с2↓ а=g=10м/с2↓
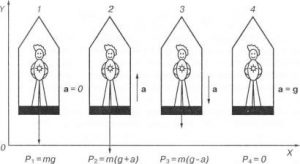
P1 = N1 = Fт = mg = 700Н
P2 = N2 = Fт + Fi = mg + ma = 1050Н
P3 = N3 = Fт – Fi = mg – ma = 350Н
P4 = N4 = Fт – Fi = mg – mg = 0Н
Висновок: Маса тіла одна і таж, а вага – різна.
Достовірність описаних в задачі ефектів може підтвердити кожен, хто бодай раз користувався ліфтом. Адже коли ліфт починає рухатися вгору (а↑), навантаження на колінні суглоби ваших ніг, які є опорою для вашого тулуба, відчутно збільшується. Збільшується тому, що вага тулуба стала більшою. Коли ж ліфт, рухаючись вгору зупиняється (а↓), навантаження на суглоби зменшується, зменшується тому що вага тулуба стала меншою. Якщо ж ліфт рухається вниз, то все відбувається навпаки: на початку руху (а↓) вага зменшується, а вкінці руху (а↑) – збільшується.
Не важко бачити, що вага тіла, тобто та сила з якою тіло тисне на опору, не є постійною величиною. При цьому, лише в тому випадку коли система опора-тіло знаходиться в стані механічної рівноваги (v=0 або v=const), вага тіла чисельно дорівнює діючій на нього силі тяжіння: Р1=mg. В інших випадках, вага тіла може бути як більшою так і меншою за цю силу: Р2=m(g+a); Р3=m(g–a). Якщо ж система опора – тіло знаходиться в стані вільного падіння (а=g), то тіло не тисне на опору і тому його вага дорівнює нулю: Р4=mg–mg=0. Характеризуючи дану ситуацію говорять про те, що тіло знаходиться в стані невагомості.
Зверніть увагу, тіло знаходиться в стані невагомості (має нульову вагу) не тому що на нього не діє сила тяжіння, а тому, що дія цієї сили зрівноважується відповідною силою інерції. Невагомість – це такий стан системи опора-тіло, при якому тіло та його окремі елементи не мають ваги, тобто не тиснуть на опору і одне на одне. Не мають ваги тому, що діюча на них сила тяжіння зрівноважується відповідною силою інерції.
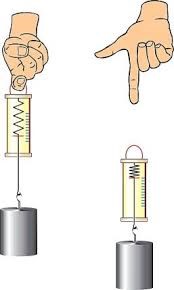

Мал.79. Невагомість, це не тому що на тіло не діє сила тяжіння, а тому що діюча на тіло сила тяжіння зрівноважується силою інерції.
Наприклад один з способів підготовки космонавтів, та їх знайомства з станом невагомості, полягає в наступному. Спеціально обладнаний літак (літак внутрішній простір якого позбавлений зайвих предметів), піднімається на гранично велику висоту, а потім певний час вільно падає з цієї висоти. Власне в цей час ті люди які знаходяться всередині літака і перебувають в стані невагомості.
Загально відомим прикладом невагомості є невагомість на борту штучних супутників Землі. При цьому люди часто думають, що ця невагомість пояснюється відсутністю сили тяжіння. Насправді ж, на тих висотах де зазвичай літають наші пілотовані космічні кораблі (200км – 400км), сила тяжіння майже така ж як і на поверхні землі. А невагомість в космічному кораблі (штучному супутнику Землі) пояснюється не відсутністю сили тяжіння, а фактом того, що ця сила зрівноважується відповідною силою інерції. Силою, поява якої обумовлена обертанням супутника навколо Землі, а отже його рухом з певним доцентровим прискоренням ад=v2/R. І це прискорення та йому відповідна швидкість мають бути такими, які забезпечують динамічну рівновагу між силою Тяжіння (Fт = mg) та силою інерції (Fі = maд = mv2/R).
Контрольні запитання.
- Що називають вагою тіла?
- Чому люди часто вважають, що вага тіла вимірюється в кілограмах?
- В яких випадках формула Р=mg є правильною, а в яких не правильною?
- Чи є вага тіла безумовно постійною величиною? Від чого залежить вага тіла?
- Що називають невагомістю?
- В кабіні штучного супутника Землі тіло знаходиться в стані невагомості. Чи означає цей факт, що на нього не діє сила тяжіння?
- Коли ліфт рухаючись вгору набирає швидкість, пружини під його підлогою дещо просідають, а коли зупиняється – дещо випрямляються. Чому це відбувається?
Вправа №32.
- Визначте вагу тіла масою 70кг на Землі; на Місяці, на Марсі; на Юпітері.
- Ракета при старті з поверхні Землі рухається вертикально з прискоренням 20м/с2. Яка вага космонавта в кабіні ракети, якщо його маса 90кг?
- Ракета піднімається вертикально вгору з прискоренням а=3g. Якою буде в цій ракеті вага тіла масою 50кг?
- З якою силою тисне людина масою 80кг на підлогу ліфта, що рухається з прискоренням 2м/с2, направленим а) вгору; б) вниз?
- Ліфт рівноприскорено розганяється до швидкості 7м/с за 5с. За такий же час він і зупиняється. Визначити вагу людини масою 80кг на ділянках розгону та зупинки ліфта.
- З якою швидкістю має рухатись автомобіль по опуклому мосту, радіус кривизни якого 90м, щоб у верхній точці моста, тиск автомобіля на поверхню моста дорівнював нулю?
- Відомо, що радіус Землі 6,37·106м, а прискорення вільного падіння на ній 9,8м/с2. Визначити ту швидкість з якою тіло (штучний супутник) має обертатись навколо Землі і не падати на неї.
.
§ 33. Сила пружності. Жорсткість тіла. Закон Гука.
Нагадаємо, механіка, це розділ фізики в якому вивчають параметри, закономірності та причини механічного руху тіл в усіх його проявах. При цьому механічним рухом вважають не лише механічне переміщення тіла, а і його механічну деформацію, тобто будь яку зміну форми або розмірів тіла, що відбувається під дією зовнішніх сил (від лат. deformatio – викривлення).
За реакцією тіла на припинення дії деформуючої сили, механічні деформації поділяються на пружні та пластичні. Пружною називають таку механічну деформацію, яка повністю зникає після припинення дії деформуючої сили. Пластичною називають таку механічну деформацію, яка після припинення дії деформуючої сили зберігається (залишається). Іншими словами, якщо після припинення дії деформуючої сили, тіло повністю відновлює свою попередню форму, то його деформація є пружною. Якщо ж, після припинення дії деформуючої сили, тіло зберігає надану йому форму, то його деформація є пластичною. Наприклад, деформація пластиліну є пластичною, а деформація гуми – пружною.
Мал.84. Приклади пружної (а, б) та пластичної (в, г) деформації.
Зазвичай, ті матеріали які під дією зовнішніх сил отримують пластичні деформації, не застосовуються в якості конструктивних матеріалів деталей машин та механізмів. Тому в механіці по суті вивчають властивості лише пружних матеріалів та відповідних тіл. При цьому в межах програми загальноосвітньої школи по суті вивчають параметри і закономірності тієї пружної деформації яку називають розтягненням – стисненням.
До певної межі, практично всі тверді матеріали деформуються пружним чином. Інша справа, що для більшості твердих матеріалів як то граніт, бетон, сталь, скло, тощо величина їх деформованості є мало помітною. Тому досліджуючи закономірності пружних деформацій, ми будемо орієнтуватися на ті матеріали (гума) і ті прилади (пружина), деформованості яких є очевидними.
Ту зовнішню силу, дія якої спричиняє пружну деформацію тіла, називають деформуючою силою. Наприклад та сила з якою тіло тисне на пружину і деформує її, є деформуючою силою. Та сила з якою палець деформує шматок поролону, є деформуючою силою. Та м’язова сила з якою хуліган розтягує гумові джгути рогатки, є деформуючою силою.
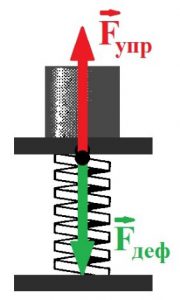

Мал.85. Деформуюча сила, це та сила яка спричиняє пружну деформацію тіла.
Величину тієї деформації яку отримує пружне тіло під дією деформуючої сили F, зазвичай характеризують параметром який називається абсолютна деформація.
Абсолютна деформація – це фізична величина, яка характеризує абсолютну деформацію тіла і яка дорівнює різниці між довжиною тіла після деформації (ℓ) та його довжиною до деформації (ℓ0).
Позначається: ∆ℓ (іноді ∆х, або х)
Визначальне рівняння: ∆ℓ=ℓ – ℓ0
Одиниця вимірювання: [∆ℓ] = м.
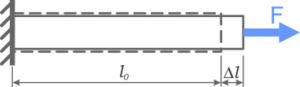
Мал.86. Під дією деформуючої сили F, тіло отримує абсолютну деформацію ∆ℓ.
Діюча на тіло деформуюча сила (F), породжує рівну їй за величиною і протилежну за напрямком протидіючу силу, яку називають силою пружності (Fпр). Наприклад та сила яка виникає в деформованій пружині і протидіє її деформації, є силою пружності. Та сила, яка виникає в деформованому поролоні і протидіє його деформації, є силою пружності. Та сила яка виникає в деформованих гумових джгутах, є силою пружності. Та сила яка виникає в стержні під дією деформуючої сили F і яка протидіє цій деформуючій силі, є силою пружності Fпр.
Сила пружності – це та внутрішня сила, яка виникає в пружно деформованому тілі і яка завжди протидіє появі та зростанню цієї деформації.
Позначається: Fпр
Визначальне рівняння: Fпр = –k∆ℓ, де k – жорсткість тіла; Δℓ – абсолютна деформація тіла; знак «–» вказує на те, що напрям сили пружності протилежний до напрямку деформації Δℓ;
Одиниця вимірювання: [Fпр] =H, ньютон.
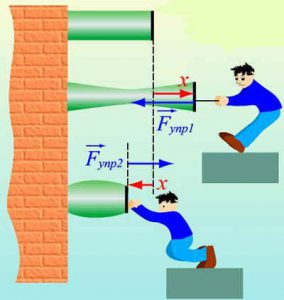
Мал.87. Сила пружності завжди протидіє деформуючій силі.
Жорсткість тіла – це фізична величина, яка характеризує здатність тіла протидіяти його пружній деформації і яка дорівнює відношенню тієї сили що деформує тіло, до величини отриманої при цьому абсолютної деформації.
Позначається: k
Визначальне рівняння: k=F/∆ℓ
Одиниця вимірювання: [k]=H/м, ньютон на метр.
В загальному випадку, жорсткість тіла визначається експериментально. Наприклад, якщо під дією вантажу масою 1кг, а відповідно сили F=10Н (мал.82) перша пружина деформувалась (видовжилась) на 10см, друга – на 5см, а третя – на 2см (Δℓ1=10см; Δℓ2=5см; Δℓ3=2см), то жорсткості цих пружин відповідно дорівнюють
k1=F1/Δℓ1=10Н/10см=1Н/см;
k2=F2/Δℓ2=10Н/5см=2Н/см;
k3=F3/Δℓ3=10Н/2см=5Н/см.
Мал.88. Жорсткість тіла дорівнює відношенню тієї сили що деформує тіло, до величини отриманої при цьому абсолютної деформації.
Сила пружності є результуючою тих складних процесів, які відбуваються всередині пружно деформованого тіла. Гранично спрощена суть цих процесів є наступною. У відповідності з законами Природи, атоми (молекули) речовини прагнуть до того, щоб бути розташованими на певних, енергетично доцільних відстанях один від одного. Коли ж під дією зовнішніх сил відстані між атомами змінюються (збільшуються або зменшуються), автоматично виникають сили, які прагнуть повернути атоми до попереднього, енергетично доцільного положення. Результуючою цих сил і є сила пружності.
Основний закон механіки пружно деформованого тіла був експериментально встановлений в 1660 році англійським фізиком Робертом Гуком (1635–1703). В цьому законі (законі Гука) стверджується: при пружних деформаціях, величина абсолютної деформації (∆ℓ) тіла, прямо пропорційна діючій на нього деформуючій силі F. Іншими словами: ∆ℓ=F/k, де k – жорсткість тіла.
Мал.89. Абсолютна деформація тіла (ΔƖ), прямо пропорційна деформуючій силі (F) – закон Гука.
Факт того, що абсолютна деформація тіла пропорційна деформуючій силі, корисно застосовується в приладах які називаються динамометрами (від грец. dynamis – сила та metreo – вимірювати). Динамометр, це прилад який дозволяє вимірювати величину діючої на нього сили. Основним елементом динамометра (мал.84б) є певне пружне тіло (пружина), яке під дією зовнішньої сили певним чином деформується. Власне за величиною цієї деформації і визначають величину деформуючої сили.
До речі, аналізуючи роботу динамометра неважко довести, що жорсткість його пружини (k=F/∆ℓ) не залежить ні від величини деформуючої сили (F), ні від величини отриманої при цьому деформації (∆ℓ). Дійсно, якщо під дією сили 1Н пружина видовжується на 2,5см, під сили 2Н – видовжується на 5,0см, а під дією сили 3Н – на 7,5см, то жорсткість пружини в кожному з випадків дорівнює:
k1 = F1/∆ℓ1 = 1Н/2,5см = 0,4Н/см;
k2 = F2/∆ℓ2 = 2Н/5,0см = 0,4Н/см;
k3 = F3/∆ℓ3 = 3Н/7,5см = 0,4Н/см.
Завершуючи розмову про силу пружності та сили загалом, буде не зайвим сказати декілька слів про чотири сили, які часто плутають одна з одною та застосовують не за призначенням. Ситуація ускладнюється тим, що в багатьох випадках числові значення цих сил є однаковими. Тому, фактично неправильно застосувавши сили, ви можете отримати формально правильну відповідь і заслужено незадовільну оцінку.
Мова йде про силу тяжіння (Fт), вагу (P), реакцію опори (N) та силу пружності (Fпр). Нагадаємо. Сила тяжіння (Fт) – це та сила з якою тіло притягується до Землі. Вага (P) – це та сила з якою тіло діє на опору. Реакція опори (N) – це та сила з якою опора діє на тіло. Сила пружності (Fпр) – це та сила яка виникає в пружно деформованому тілі і яка протидіє його деформації. Із визначень ясно, що коли ми говоримо про ті сили які діють на тіло, то ними є сила тяжіння (Fт) та реакція опори (N). Якщо ж мова йде про ті сили які діють на поверхню опори, то ними є вага тіла (P) та виникаюча в опорі сила пружності (Fпр).

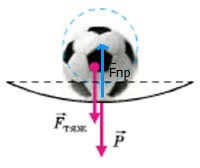
Мал.90. На тіло діє сила тяжіння та реакція опори. На поверхню опори діє вага тіла та виникаюча в опорі сила пружності.
Зважаючи на вище сказане та дотримуючись загально прийнятих визначень, неправильно говорити і писати, що на те тіло яке лежить чи висить на опорі діє вага тіла та виникаюча в опорі сила пружності. Бо на тіло діє сила тяжіння та реакція опори. Неправильно говорити і писати, що на поверхню опори діє сила тяжіння тіла та реакція опори. Бо на поверхню опору діє вага тіла та виникаюча в опорі сила пружності. Неправильно говорити і писати, що тіло падає під дією своєї ваги. Бо тіло падає під дією сили тяжіння.
Задача 1. На основі аналізу заданих графіків залежності виникаючої в тілі сили пружності Fпр від величини його абсолютної деформації Δℓ, визначити жорсткості відповідних тіл.
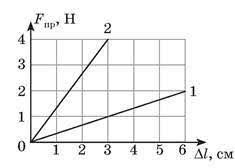
Рішення. Оскільки за визначенням k=F/Δℓ, або k=Fпр/Δℓ, то на основі аналізу заданих графіків можна записати:
k1 = 2Н/6см = 0,33Н/см;
k2 = 4Н/3см = 1,33Н/см.
Задача 2. Під дією сили 320Н пружина амортизатора стиснулась на 9мм. На скільки міліметрів стиснеться пружина якщо навантаження становитиме 1,60кН?
Дано:
F1 = 320H
∆ℓ1 = 9мм
F2=1,6кН=1600Н
∆ℓ2 = ?
Рішення. Оскільки пружина одна і таж, то її жорсткість (k=F/Δℓ) є постійною величиною і тому можна записати: F1/Δℓ1 = F2/Δℓ2. Звідси ∆ℓ2 = F2Δℓ1/F1.
Розрахунки: ∆ℓ2 = 1600Н·9мм/320Н = 45мм.
Відповідь: ∆ℓ2 = 45мм.
Контрольні запитання.
- Яку силу називають деформуючою силою? Чи залежить величина деформуючої сили від властивостей того тіла яке вона деформує?
- Яку силу називають силою пружності? Від чого залежить ця сила?
- Що характеризує жорсткість: властивості тіла чи того матеріалу з якого воно виготовлене?
- Чи означає визначальне рівняння k=F/∆ℓ, що жорсткість тіла залежить від величини тієї сили яка деформує тіло та його абсолютної деформації? Від чого залежить жорсткість тіла?
- Що стверджується в законі Гука?
- Поясніть загальний устрій та принцип дії динамометра.
- На поверхні стола лежить тіло масою m. Які сили діють на тіло? Які сили діють на поверхню стола? Чому дорівнює кожна з цих сил?
- На малюнку зображено три сили. Які правильні назви кожної з них?
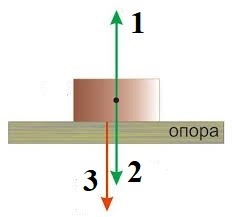
Вправа №33.
- На скільки деформується пружина жорсткістю 500Н/м під дією сили 20Н?
- Під дією якої сили, пружина жорсткістю 100Н/м розтягується на 4см?
- Яка жорсткість стержня, якщо під дією сили 1кН він подовжується на 1мм?
- За заданими графіками визначити жорсткість тіла.
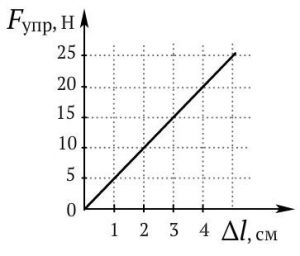
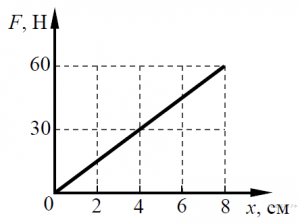
- На основі аналізу заданих малюнків, визначити жорсткість пружини, якщо маса тягарця 1кг.
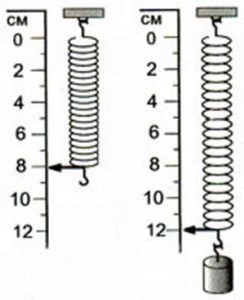
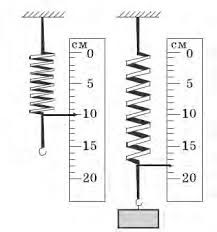
- Пружина жорсткістю 100Н/м під дією певної сили подовжилася на 5см. Яка жорсткість іншої пружини, якщо під дією тієї ж сили вона подовжилась на 1см?
- На скільки подовжиться рибальська волосінь жорсткістю 0,5кН/м, при рівномірному підніманні вертикально вгору риби масою400г?
- Яке подовження горизонтальної пружини жорсткістю 50Н/с, якщо пружина надає візку масою 500г прискорення 2м/с2? Тертям знехтувати.
.
§ 34. Статика. Узагальнююче повторення.
Статика – це розділ механіки в якому вивчають параметри, закономірності та причини стану механічної рівноваги тіл. Основним поняттям статики є механічна рівновага. Механічна рівновага – це такий механічний стан тіла, при якому воно під дією системи зовнішніх сил знаходиться в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v=const). Основною фізичною величиною статики є сила.
Сила – це фізична величина, яка характеризує силову дію одного тіла на інше (є мірою взаємодії фізичних об’єктів) і яка дорівнює добутку маси тіла на величину того прискорення яке воно отримує під дією даної сили.
Позначається: F
Визначальне рівняння: F = ma
Одиниця вимірювання: [F]= кг·м/с2 = H, ньютон.
Ньютон – це одиниця вимірювання сили, що дорівнює такій силі, яка тілу масою 1кг надає прискорення 1м/с2: 1Н=1кг∙1м/с2.
До числа основних сил статики і механіки загалом, відносяться:
сила тяжіння Fт = mg
реакція опори N
сила тертя Fтер = µN
сила інерції Fi = –ma
вага P = –N
гравітаційна сила Fгр=Gm1m2/r2, де G=6,67∙10–11 (Н∙м2/кг2)
сила пружності Fпр = –k(Δℓ)
Сила тяжіння – це та сила, з якою тіло притягується до Землі і яка дорівнює добутку маси тіла на прискорення його вільного падіння.
Позначається: Fт
Визначальне рівняння: Fт = mg, де g=9,8м/с2
Одиниця вимірювання: [Fт] = кг·м/с2 = H, ньютон.
Реакція опори – це та сила, з якою опора діє на тіло та жорстко протидіє переміщенню цього тіла.
Позначається: N
Визначальне рівняння: величина і напрям реакції опори визначається з умов конкретної задачі.
Одиниця вимірювання: [N] = H, ньютон.
Сила тертя (тертя ковзання) – це та сила, з якою поверхні взаємодіючих твердих тіл протидіють їх взаємному поступальному (ковзальному) переміщенню, або можливості такого переміщення і яка дорівнює добутку коефіцієнту тертя ковзання (μ) та тієї сили з якою взаємодіючі поверхні тиснуть одна на одну (реакції опори N)
Позначається: Fтер
Визначальне рівняння: Fтер =µN
Одиниця вимірювання: [Fтер] = Н.
Коефіцієнт тертя ковзання – це фізична величина, яка характеризує здатність певної пари твердих поверхонь протидіяти їх відносному ковзальному переміщенню і яка дорівнює відношенню виникаючої між цими поверхнями сили тертя, до величини тієї сили з якою поверхні притискаються одна до одної.
Позначається: μ
Визначальне рівняння: μ = Fтер/N
Одиниця вимірювання: [μ] = Н/Н = ̶ , безрозмірна величина.
Сила інерції – це така сила, поява якої обумовлена прискореним рухом тіла і яка завжди протидіє появі та зростанню цього прискорення.
Позначається: Fі
Визначальне рівняння: Fі = –ma
Одиниця вимірювання: [Fі] = Н, ньютон
На відміну від всіх інших сил механіки, які прийнято називати зовнішніми силами і поява яких обумовлена взаємодією даного тіла з тими чи іншими зовнішніми речовинними об’єктами (сила тяжіння, реакція опори, вага, сила тертя, сила Архімеда), або тими взаємодіями які відбуваються всередині даного тіла (сила пружності), сила інерції не є зовнішньою силою. Поява сили інерції обумовлена не взаємодією даного тіла з певими речовинними об’єктами, а самим фактом прискореного руху тіла. По суті, поява сили інерції обумовлена взаємодією даного тіла з тим фізичним об’єктом який називається «простір».
Вага – це та сила з якою тіло діє на опору і яка чисельно дорівнює реакції цієї опори.
Позначається: Р
Визначальне рівняння: Р = – N, де N – реакція опори
Одиниця вимірювання: [P] = H, ньютон.
На відміну від маси тіла, яка за будь яких обставин залишається незмінною, вага тіла в різних обставинах може бути різною. Скажімо, на Землі (g=9,81м/с2) вага тіла масою 10кг становитиме 98,1Н. На Місяці (g=1,6м/с2) ця вага дорівнюватиме 16Н; на Марсі (g=3,7м/с2) – 37Н; на Юпітері (g=25,9м/с2) – 259Н; а на Сонці (g=274,1м/с2) – 2741Н. Більше того, вага тіла залежить не лише від параметрів того гравітаційного поля яке створює відповідна планета, а й від багатьох інших обставин. Зокрема від того, з яким прискоренням і в якому напрямку рухається система опора-тіло. Одним з проявів цієї залежності є те, що називають невагомістю. Невагомість – це такий стан системи опора-тіло, при якому тіло та його окремі елементи не мають ваги, тобто не тиснуть на опору і одне на одне. Не мають ваги тому, що діюча на них сила тяжіння зрівноважується відповідною силою інерції.
Закон всесвітнього тяжіння – це закон, в якому стверджується: два тіла масою m1 і m2 взаємно притягуються з гравітаційною силою (Fгр), величина якої прямо пропорційна добутку взаємодіючих мас (m1∙m2) і обернено пропорційна квадрату відстані між ними (r2). Іншими словами: Fгр=Gm1m2/r2, де G=6,67∙10–11 (Н∙м2/кг2) – гравітаційна стала, постійна величина значення якої визначається експериментально.
Сила гравітаційної взаємодії (гравітаційна сила) – це та сила, з якою тіла взаємодіють згідно з законом всесвітнього тяжіння.
Позначається: Fгр
Визначальне рівняння: Fгр =Gm1m2/r2
Одиниця вимірювання: [Fгр]=H.
Закон Гука – це закон, в якому стверджується: при пружних деформаціях, величина абсолютної деформації (∆ℓ) тіла, прямо пропорційна діючій на нього деформуючій силі F. Іншими словами: ∆ℓ=F/k, де k – жорсткість тіла.
Сила пружності – це та сила, яка виникає в пружно деформованому тілі і яка завжди протидіє появі та зростанню цієї деформації.
Позначається: Fпр
Визначальне рівняння: Fпр = –k∆ℓ, де k – жорсткість тіла; Δℓ – абсолютна деформація тіла;
Одиниця вимірювання: [Fпр] =H, ньютон.
Жорсткість тіла – це фізична величина, яка характеризує здатність тіла протидіяти його пружній деформації і яка дорівнює відношенню тієї сили що деформує тіло, до величини отриманої при цьому абсолютної деформації.
Позначається: k
Визначальне рівняння: k=F/∆ℓ
Одиниця вимірювання: [k]=H/м, ньютон на метр.
Основний закон статики називається умовою механічної рівноваги тіла.
Умова механічної рівноваги тіла (матеріальної точки) – це закон, в якому стверджується: тіло буде знаходитись в стані механічної рівноваги (v=0; або v=const) тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил дорівнює нулю. Іншими словами: якщо ∑F=0 то v=0, або v=const і навпаки.
Задачі статики мають ту перевагу, що алгоритм (порядок) розв’язку цих задач, чітко визначений. І цей алгоритм є наступним.
- Уважно прочитати умову задачі та зробити стислий запис цієї умови.
- Обов’язково виконати малюнок, на якому чітко вказати всі діючі на дане тіло (матеріальну точку) сили та напрямки цих сил.
- Задати систему координат.
- Записати умову рівноваги даної матеріальної точки, тобто систему рівнянь: ∑Fx=0; ∑Fy=0 .
- Розв’язавши цю систему, визначити невідомі величини.
Задача 1. Тіло масою 12кг знаходиться на горизонтальній поверхні. Яку горизонтальну силу треба прикласти до тіла щоб зрушити його змісця, якщо коефіцієнт тертя 0,35?

Дано:
m=12кг
μ = 0,35
F = ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на тіло сили та задаємо відповідну систему координат (на малюнку Fтер позначено ƒ). Записуємо умову рівноваги даного тіла:
ΣFx = F – Fтер = F – μN = 0;
ΣFy = N – Fт = N – mg = 0.
Із рівняння (1) випливає F = μN, де N=?
Із рівняння (2) випливає N = mg = 12кг·10м/с2 = 120Н.
Таким чином F = μN = 0,35·120Н =42Н.
Відповідь: F = 42Н.
Силовий метод розв’язування задач, зазвичай застосовують в тих випадках коли мова йде про задачі статики, тобто ті задачі в яких тіло під дією певної системи сил не рухаються (v=0), або рухаються з постійною швидкістю (v=const). Однак, з не меншою ефективністю цей метод працює і в тих випадках коли мова йде про задачі динаміки, тобто ті задачі в яких тіло рухаються з певним прискоренням (а=const≠0). Різниця розв’язку лише в тому, що в задачах динаміки, потрібно враховувати факт того, що на тіло окрім звичайних сил взаємодії (сила тяжіння, реакція опори, сила тертя, сила Архімеда, тощо), діє певна сила інерції Fi= –ma і що при цьому умова рівноваги тіла набуває вигляду: якщо а=const≠0, то ΣF+Fi=0.
Задача 2. Автомобіль масою 1,5т, маючи тягову силу 3кН, рухається з прискоренням 1м/с2. Визначити загальну силу опору руху автомобіля (загальну силу тертя).

Дано:
m = 1,5т =1500кг
Fтяги = 3кН = 3000Н
a = 1м/с2
Fтер = ?
Рішення. Виконуємо малюнок на якому вказуємо всі діючі на автомобіль сили. А цими силами є: сила тяжіння Fт=mg, реакція опори N, сила тяги Fтяги = F, сила тертя Fтер та направлена в протилежну сторону від прискорення сила інерції Fі=ma. (на малюнку не позначена). Задаємо відповідну систему координат.
Записуємо умову рівноваги тіла вздовж осі 0х:
ΣFx = Fтяги – Fтер – Fi = Fтяги – Fтер – mа = 0. Звідси випливає Fтер = Fтяги – mа.
Розрахунки: Fтер = 3000Н – 1500кг1м/с2 = 3000Н – 1500Н = 1500Н
Відповідь: Fтер = 1500Н.
Вправа 34.
- Тіло масою 5кг рухається за законом х=10t – 0,5t2. Під дією якої сили відбувається цей рух? Як направлена ця сила?
- На горизонтальній поверхні лежить тіло масою 15кг. Визначити діючі на це тіло сили.
- Для того щоб зрушити з місця тіло масою 50кг потрібно прикласти горизонтальну силу 150Н. Визначити коефіцієнт тертя.
- Автомобіль з швидкістю 54км/год рухається заокругленням дороги радіус якого 300м. Яка сила інерції діє при цьому на водія автомобіля? Який напрям цієї сили?
- З якою силою тисне людина масою 70кг на підлогу ліфта, що рухається з прискоренням 3м/с2, направленим а) вгору; б) вниз?
- Відомо, що радіус Марса 3,38·106м, а прискорення вільного падіння на ньому 3,7м/с2. Визначити ту швидкість з якою тіло (штучний супутник) має обертатись навколо Марса і не падати на нього.
- Дерев’яний брусок масою 2кг, за допомогою пружини жорсткістю 100Н/м рівномірно тягнуть горизонтальною поверхнею. Яким буде видовження пружини, якщо коефіцієнт тертя між бруском та поверхнею 0,3?
- З якою швидкістю має рухатись автомобіль по опуклому мосту, радіус кривизни якого 40м, щоб у верхній точці моста, тиск автомобіля на поверхню моста дорівнював нулю?
.