Молекулярна фізика. Термодинаміка.

Семестр №2
РОЗДІЛ 2. Молекулярна фізика і термодинаміка.
Тема 2.1. Основи молекулярно – кінетичної теорії.
Лекційне заняття №1. Тема: Загальні відомості про молекулярну фізику. Основні положення молекулярно-кінетичної теорії.
Лекційне заняття №2. Тема: про масу та розміри молекул. Про кількість речовини та ті фізичні величини які цю кількість характеризують.
Лекційне заняття №3. Тема: Температура, як міра нагрітості тіла та як міра середньої кінетичної енергії теплового руху молекул.
Лекційне заняття №4. (Практичне заняття) Тема: Розв’язування задач молекулярної фізики.
Лекційне заняття №5. Тема: Загальні відомості про тверді рідкі та газоподібні речовини.
Тема 2.2. Загальні властивості речовин.
Лекційне заняття №6. Тема: Гази та їх властивості. Газові закони, як узагальнення експериментальних фактів, та як прямі наслідки молекулярно-кінетичної теорії.
Лекційне заняття №7. (Практичне заняття) Тема: Розв’язування задач на застосування газових законів.
Лекційне заняття №8. Тема: Пари та їх властивості. Пароутворення. Критичний стан речовини.
Лекційне заняття №9. Тема: Вологість повітря. Методи вимірювання вологості.
Лекційне заняття №10. Тема: Рідини та їх властивості. Поверхневий натяг. Капілярні явища.
Лекційне заняття №11. Тема: Тверді тіла та їх властивості. Кристалічні і аморфні тіла.
Лекційне заняття №12. Тема: Види кристалічних структур.
Тема 2.3. Теплові процеси.
Лекційне заняття № 13. Тема: Про внутрішню енергію та кількість теплоти. Рівняння теплового балансу. Нагрівання – охолодження.
Лекційне заняття № 14. Тема: Загальні відомості про енергетичні параметри плавлення, пароутворення та горіння.
Лекційне заняття № 15. (Практичне заняття) Тема: Теплові процеси. Розв’язування задач.
Лекційне заняття № 16. Тема: Про сили міжмолекулярної взаємодії. Теплове розширення тіл. Особливості теплового розширення води.
Лекційне заняття № 17. Тема: Загальні відомості про термодинаміку. Про динамічний, статистичний та термодинамічний методи досліджень. Перше і друге начала термодинаміки.
Лекційне заняття №18. (Практичне заняття) Тема: Розв’язування задач термодинаміки.
Лекційне заняття № 19. Тема: Теплові двигуни.
.
Лекційне заняття №1.
Тема: Загальні відомості про молекулярну фізику. Основні положення молекулярно-кінетичної теорії.
Якщо ви думаєте, що молекулярна фізика, це наука про будову та властивості молекул, то помиляєтесь. Молекулярна фізика не вивчає молекули. Молекулярна фізика – це розділ фізики, в якому вивчаються загальні властивості твердих, рідких і газоподібних речовин та ті теплові процеси які відбуваються з ними. Іншими словами, предметом вивчення молекулярної фізики є речовини та різноманіття тих теплових процесів які відбуваються з ними.
Ви можете запитати: «А чому наука про загальні властивості речовин, називається молекулярною фізикою?» Відповідь на це слушне запитання очевидно проста. В молекулярній фізиці, властивості твердих, рідких і газоподібних речовин та ті теплові процеси які відбуваються з ними, пояснюють виходячи з того, що ці речовини складаються з надзвичайно дрібних частинок, які прийнято називати молекулами. Звичайно, хімічно прості речовини можуть складатись не лише з молекул, а й з атомів, іонів або певної суміші цих частинок. Наприклад вода складається з молекул води (Н2О), залізо складається з атомів заліза (феруму Fe), а кухонна сіль – з іонів натрію (Na+) та хлору (Cℓ–). Однак, в межах молекулярної фізики, ми без нагальної потреби не будемо заглиблюватись в деталі внутрішнього устрою тих структурних одиниць з яких складається та чи інша конкретна речовина. Ми будемо виходити з того, що всі речовини складаються з надзвичайно дрібних, невидимих частинок. І давайте домовимося, називати ці частинки молекулами.

Мал.1 Молекулярна фізика вивчає загальні властивості речовин та ті теплові процеси які відбуваються з ними.
Із визначення ясно, що предметом вивчення та основним поняттям молекулярної фізики є те, що прийнято називати речовиною. Загалом, все різноманіття матеріальних об’єктів Природи, тобто тих об’єктів які реально існують і так чи інакше проявляють себе, розділяють на дві групи: речовини і поля. Про властивості та прояви полів ми поговоримо в розділі «Електродинаміка». Наразі ж зауважимо, що речовина – це вид матерії який складається з тих чи інших частинок і має масу (масу спокою). Іншими словами, речовина це те, що складається з тих чи інших частинок і має масу, а отже має певну кількість інерціальних, гравітаційних та енергетичних властивостей.
В загальному сенсі речовинами є не лише хімічно прості об’єкти, як то залізо, вода, сіль, вапно чи нітрат амонію і не лише хімічно складні полімери, а й об’єкти органічного походження як то деревина, шкіра, бавовна, а з рештою і самі живі структури. Втім, в фізиці ми будемо вивчати загальні властивості лише тих хімічно простих речовин які складаються з атомів, молекул та іонів або їх сумішей.
Про те, що тіла складаються з дрібних, невидимих частинок, люди здогадувались дуже давно. Ще за 400 років до нашої ери, давньогрецький філософ Демокрит стверджував, що всі тіла складаються з надзвичайно дрібненьких, неподільних частинок (атомів, від грец. atomos – неподільний), які безперервно рухаються та певним чином взаємодіють між собою. Однак, гіпотезі про молекулярну (атомарну) будову речовини, доля приготувала складний та тернистий шлях. Шлях довжиною в понад два тисячоліття. Лише в 1908 році ця гіпотеза стала безумовно доведеною науковою теорією. Та як би там не було, а сьогодні ми точно знаємо, що всі тіла складаються з надзвичайно дрібненьких частинок (молекул, атомів, іонів), які безперервно рухаються і певним чином взаємодіють між собою. Власне ці знання і лежать в основі тієї науки яка називається молекулярною фізикою.
Ви можете запитати: «А як це може бути, щоб ті люди які не мали бодай елементарного наукового обладнання, ще за 400 років до нашої ери з такою впевненістю говорили про ті речі, факт існування яких був науково доведений лише в 1908 році?» Відповідаючи на це запитання можна сказати наступне. По суті люди кардинально відрізняються від інших істот лише одним – здатністю логічно мислити. Саме ця здатність і дозволяє людям «бачити» те, чого вони ніколи не бачили і чого наочно побачити взагалі не можливо.
Скажімо ми говоримо про те існують молекули чи не існують. Відповідаючи на це запитання зовсім не обов’язково мати надскладне обладнання та проводити надскладні експерименти. Цілком достатньо придивитись до навколишнього світу і проаналізувати ті події що в ньому відбуваються. Наприклад, ви берете склянку води і кладете у воду шматочок цукру. При цьому цукор швидко зникає (розчиняється). Ви можете скільки завгодно роздивлятись воду під мікроскопом в надії відшукати видимі частинки цукру і не знайдете їх. І тим не менше цукор нікуди не зник. Адже збереглась його визначальна смакова властивість відома кожному з вас. Чи не говорить даний експериментальний факт про те, що цукор складається з надзвичайно дрібненьких частинок? Частинок, які настільки дрібні, що їх не видно навіть в найпотужніший оптичний мікроскоп і про факт існування яких говорить те, що після розчинення та візуального зникнення цукру, зберігається його визначальна смакова, а по суті хімічна властивість. І чи не говорить факт рівномірного розподілу цукру в наявному об’ємі води про те, що наддрібні частинки цукру рухаються?
Або наприклад, ви наливаєте у склянку певну кількість води і помічаєте, що з плином часу цієї води стає все менше і менше. Ви можете скільки завгодно придивлятись до того що ж відбувається і не помітите нічого, окрім факту того, що води стає все менше і менше. Чи не говорить цей експериментальний факт про те, що вода складається з надзвичайно дрібненьких частинок, які непомітно вилітають (випаровуються) зменшуючи тим самим загальну кількість води?
А факт того, що крапля пахучої рідини поступово зникаючи наповнює відповідним запахом навколишній простір, чи не вказує те, що відповідна рідина складається з надзвичайно дрібненьких частинок які є носіями певних властивостей цієї рідини і що ці частинки рухаються? А той факт, що в процесі охолодження повітря, в ньому та на навколишніх предметах з’являються (конденсуються) крапельки води, чи не вказує на те, що відповідна вода й до того знаходилась у повітрі і що ми її не помічали тільки тому, що відповідні мікрочастинки води є неймовірно маленькими?
А хімічні реакції? А процес горіння? А електроліз? А факт того, що атмосфера Землі представляє собою однорідну суміш різних газів? Чи не вказують ці та їм подібні явища і факти на те, що речовини складаються з дрібненьких частинок які постійно рухаються? А той факт, що загальний об’єм суміші двох різних речовин, наприклад води і солі, або води і спирту, суттєво менший за суму об’ємів окремих складових цієї суміші, чи не вказує на те, що речовини складаються з дрібних частинок, між якими є проміжки пустоти?
розчинність випаровування
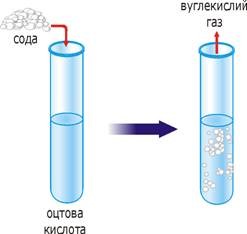
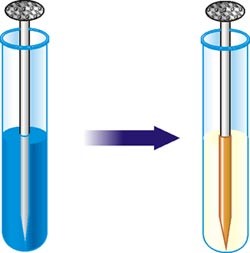
хімічні реакції електроліз
Мал.2 Деякі факти, які вказують на молекулярну структуру речовини.
Звичайно, вище наведені факти не є такими, що безумовно доводять факт існування молекул. Однак вони безумовно вказують на те, що гіпотеза про молекулярну будову речовини є науково обґрунтованою. Якщо ж говорити про ті експериментальні дослідження які науково доводять факт існування молекул, то вони тісно пов’язані з явищем, яке було відкрите та описане англійським ботаніком Робертом Броуном (1773–1858). В 1827 році, намагаючись за допомогою мікроскопа розгледіти будову квіткового пилку, Броун звернув увагу на те, що у водному розчині окремі пилинки постійно рухаються. Він розумів, що пилинки не є тими об’єктами які можуть самостійно рухатись. І тим не менше вони рухались. Дослідивши цей рух Броун з’ясував, що рух пилинок є безперервним та безладним і що його інтенсивність залежить від розмірів пилинок: чим дрібніші пилинки, тим інтенсивніше вони рухаються. Однак Броун так і не зумів пояснити причини відкритого ним явища.
Певний час причини броунівського руху були не зрозумілими. Цей рух намагались пояснити тремтінням того стола на якому стоїть мікроскоп; впливом того світла яким опромінюють ті об’єкти що знаходяться під мікроскопом; конвекційними потоками тієї рідини в якій плавають броунівські частинки, тощо. Однак експериментальні факти вказували на те, що ці та їм подібні обставини практично не впливають на поведінку броунівських частинок. На цю поведінку суттєво впливали лише розміри частинок та температура того середовища яке їх оточує.
Поступово вчені дійшли висновку, що єдиним обгрунтованим поясненням броунівського руху є хаотичний рух молекул того середовища яке оточує броунівські частинки: невидимі молекули середовища, барабанять дрібні частинки речовини, а ті, реагуючи на ці хаотичні удари, відповідним чином рухаються. Броунівський рух – це безладний рух дрібних, видимих частинок речовини, причиною якого є хаотичний (тепловий) рух молекул навколишнього середовища. Потрібно зауважити, що хаотичний рух молекул речовини називають тепловим рухом. Така назва пояснюється тим, що хаотичний (тепловий) рух молекул речовими ми сприймаємо у вигляді відповідних теплових відчуттів – чим інтенсивніший хаотичний рух молекул речовини, тим теплішим (гарячішим) за нашими відчуттями є відповідне тіло.
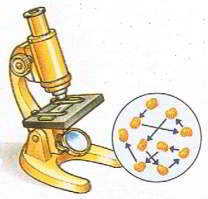
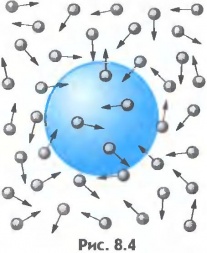
Мал.3 Хаотичний рух видимих мікрочастинок речовини (броунівський рух), є прямим наслідком хаотичного руху молекул навколишнього середовища.
Броунівський рух не лише вказує на те, що молекули речовини рухаються, а і є носієм певної кількісної інформації про цей рух. А це означає, що знаючи геометричні та вагові параметри броунівських частинок і кількісно аналізуючи їх поведінку, можна визначити параметри руху невидимих молекул. Наукову теорію броунівського руху розробив в 1905 році видатний німецький фізик Альберт Ейнштейн (1879–1955). Виходячи з того, що рух броунівських частинок є результатом хаотичного руху тих молекул які їх оточують, Ейнштейн теоретично описав закономірності руху цих частинок.
Важливість ейнштейнівської теорії броунівського руху полягала в тому, що цю теорію можна було експериментально перевірити. Адже на відміну від руху невидимих молекул, кінематичні параметри видимих броунівських частинок можна кількісно виміряти і порівняти з теоретичними передбаченнями. Така перевірка була здійснена в 1908 році французьким фізиком Жаном Переном (1870–1942). При цьому Перен експериментально довів, що кінематична поведінка броунівських частинок в точності співпадає з передбаченнями ейнштейнівської теорії. А це означало, що відповідна теорія є правильною, а отже правильні і ті базові твердження які лежать в основі теорії. Цими ж базовими твердженнями є основні положення молекулярно кінетичної теорії. Власне лише після експериментів Перена, реальність існування молекул стала науково доведеним фактом.
До числа тих явищ які вказують на факт хаотичного руху молекул, відносяться дифузія та осмос. Розповсюдження запахів у повітрі, перемішування молекул тієї речовини що розчиняється, з молекулами розчинника, і взагалі все що пов’язано з перемішуванням різнорідних молекул, причиною якого є хаотичний рух цих молекул, прийнято називати дифузією (від лат. diffusion – розповсюдження). Дифузія – це явище, суть якого полягає в тому, що в процесі хаотичного руху, молекули однієї речовини перемішуються з молекулами іншої речовини. При цьому, кожна різновидність молекул прагне до того, щоб їх концентрація в усьому доступному об’ємі була однаковою.
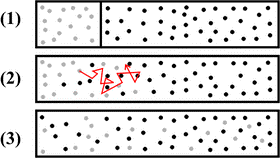
Мал.4. Дифузія, це процес перемішування різнорідних молекул, причиною якого є хаотичний рух цих молекул.
Наприклад якщо в стакан води капнути краплю барвника, чи скажімо вкинути кристалик марганцівки, то через певний час забарвлення води стане однаковим у всьому її об’ємі. І не важко збагнути, що даний факт пояснюється тим, що в процесі хаотичного руху, різнорідні молекули перемішуються. Дифузія відбувається не лише в рідинах та газах, а й в твердих тілах. Щоправда, в твердих тілах дифузійні процеси відбуваються надзвичайно повільно. Наприклад в одному з експериментів, дзеркально відполіровані пластини золота і свинцю поклали одна на одну і навантажили зовнішньою силою. Коли ж через п’ять років дані пластини спробували роз’єднати, то з’ясувалось, що вони в буквальному сенсі зрослися. При цьому, на межі контакту двох речовин утворився міліметровий шар суміші їх молекул.
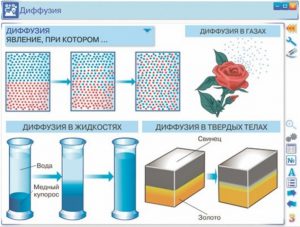
Мал.5. Деякі приклади дифузії в газах, рідинах та твердих тілах.
Потрібно зауважити, що в твердженні: «кожна різновидність молекул прагне до того, щоб їх концентрація в усьому доступному об’ємі була однаковою», – термін «прагне», зовсім не означає, що молекули мають певні прагнення та бажання. Просто у відповідності з законами Природи, одним з результатів хаотичного руху частинок, є факт їх перемішування. І тому, якщо в одному місці певних молекул багато, а в іншому – подібних молекул мало, то через певний час, концентрація цих молекул в усьому їм доступному об’ємі виявиться однаковою. І причиною цього вирівнювання концентрації, є не якесь міфічне прагнення молекул, а їх хаотичний рух.
Однією з важливих різновидностей дифузії є осмос (від грец. osmos – тиск). Осмос – це явище, суть якого полягає в тому, що в процесі хаотичного руху молекул, одні з них проникають через напівпроникну перешкоду, а інші – не проникають через неї. При цьому, проникаючі через перешкоду молекули, прагнучи до вирівнювання їх концентрації по обидві сторони перешкоди, створюють певний додатковий тиск який називається осмотичним тиском.
Ілюструючи фізичну суть осмосу проведемо наступний експеримент. У наповнену водою посудину, опустимо заповнену концентрованим розчином цукру пробірку, яка виготовлена з напівпроникного матеріалу і в яку вставлена скляна трубка (мал.6). Говорячи про напівпроникну стінку, ми маємо на увазі таку перешкоду через яку молекули води проникають, а більш об’ємні молекули цукру – не проникають. Подібними стінками є оболонки (мембрани) клітин. Тому відносно тонкі шари більшості органічних речовин є напівпроникними. По суті це означає, що в якості напівпроникної пробірки можна використати певну рослину, наприклад моркву, в тілі якої зроблено відповідне заглиблення.
Припустимо, що на початку експерименту рівень рідин в посудині і пробірці є однаковим. Спостерігаючи за рівнем рідини в пробірці, ви неодмінно з’ясуєте, що з плином часу цей рівень поступово зростатиме. Зростатиме до тих пір поки не досягне певної надлишкової висоти Δh, якій відповідає певний гідростатичний тиск Δр=ρgΔh.
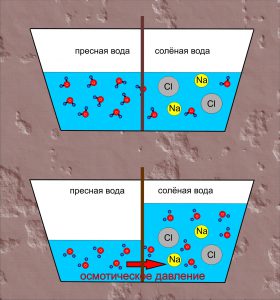
Мал.6. Проникаючі через напівпроникну перешкоду молекули, прагнучи до вирівнювання їх концентрації по обидві сторони перешкоди, створюють певний додатковий тиск який називається осмотичним тиском.
Пояснюючи результати експерименту можна сказати наступне. Різні молекули мають суттєво різні розміри та різні фізико-хімічні властивості. Тому один і той же матеріал для одних молекул може бути «прозорим», а для інших – «непрозорим». Наприклад той матеріал з якого виготовлена морква, відносно легко пропускає дрібні молекули води (Н2О) і майже не пропускає значно об’ємніші молекули цукру (С6Н12О6). А оскільки концентрація молекул води в розчині цукру значно менша за їх концентрацію у чистій воді, то кількість молекул Н2О які проникають в розчин, значно більша за ту їх кількість яка покидає його. А це означає, що в процесі осмосу, кількість води в цукровому розчині буде збільшуватись. При цьому, надлишкова вода створює відповідний надлишковий тиск, який прийнято називати осмотичним.
Дифузія і осмос відіграють важливу роль в багатьох життєво важливих процесах. Наприклад завдяки осмосу поживні і мінеральні речовини із навколишнього середовища потрапляють в тіла рослин, грибів та бактерій. Завдяки осмосу здійснюється обмін речовинами на міжклітинному і внутріклітинному рівнях всіх складних організмів. Завдяки дифузії, атмосфера Землі є тим чим вона є – однорідною сумішшю різних газів. Завдяки дифузії, розчини різних речовин є однорідними, тощо.
Броунівський рух, дифузія, осмос, випаровування, горіння, розчинність та безліч інших фактів безумовно вказують на те, що речовини складаються з надзвичайно дрібненьких невидимих частинок (молекул), які безперервно та безладно рухаються. Однак, чому ми вирішили що молекули взаємодіють між собою, та ще й таким дивним чином, що в залежності від міжмолекулярної відстані, притягуються або відштовхуються? Втім, переконатися в факті того, що молекули дійсно взаємодіють і взаємодіють саме таким чином, зовсім не складно. Достатньо взяти в руки будь яке тверде тіло, будь то лінійка, олівець, ручка чи гвіздок і запитати себе: «Якщо це тіло складається з молекул які рухаються, то чому ці молекули не розлітаються, а утворюють єдине ціле?».
Більше того, якщо ви спробуєте розтягнути тіло, тобто збільшити відстань між його молекулами, то неминуче відчуєте силову протидії, яка означає що молекули притягуються. Якщо ж ви спробуєте стиснути тіло, тобто зменшити відстань між його молекулами, то з не меншою неминучістю відчуєте, що молекули відштовхуються. Висновок очевидний: молекули прагнуть розташуватися на певній відстані одна від одної, при цьому, якщо ця відстань збільшується, то молекули починають притягуватись, а якщо зменшується – відштовхуватись. І не важко переконатися в тому, що сили міжмолекулярної взаємодії суттєво проявляють себе лише на дуже маленьких відстанях (~10–9м). Адже якщо ви розіб’єте чашку, або зламаєте брусочок крейди, а потім спробуєте об’єднати фрагменти раніше цілого тіла, то нічого путнього з цього не вийде. Не вийде тому, що для молекул, навіть візуально мікроскопічна тріщинка між наявними фрагментами є нездоланною прірвою.
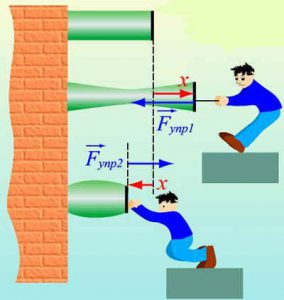
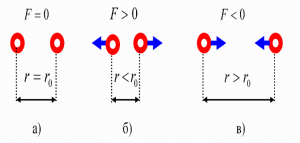
Мал.7. Механічні властивості твердих тіл безумовно вказують на те, що молекули взаємодіють між собою, і що в залежності від відстані вони притягуються, або відштовхуються.
Пояснюючи вище наведені експериментальні факти можна сказати наступне. Та сила яку прийнято називати силою міжмолекулярної взаємодії представляє собою результуючу багатьох сил які так чи інакше впливають на поведінку молекул. Сьогодні ми не будемо говорити про природу та механізм дії цих сил. Сьогодні, ми просто констатуємо той факт, що сила міжмолекулярної взаємодії представляє собою результуючу складної комбінації електромагнітних та квантово-механічних сил, з властивостями та проявами яких ми поговоримо у відповідних розділах фізики.
Таким чином, молекулярна фізика – це розділ фізики, в якому вивчаються загальні властивості твердих, рідких і газоподібних речовин та ті теплові процеси які відбуваються з ними. Теоретичною основою молекулярної фізики є три базові твердження, які називаються основними положеннями молекулярно – кінетичної теорії (м. к. т.). І ці твердження є наступними:
- Всі речовини складаються з молекул (молекул, атомів, іонів).
- Молекули в речовині безперервно та безладно (хаотично) рухаються.
- На невеликих відстанях (~10–9м) молекули взаємодіють між собою – в залежності від відстані, притягуються або відштовхуються.
Виходячи з цих базових тверджень та застосовуючи статистичний метод досліджень (про суть цього методу ми поговоримо дещо пізніше), можна пояснити практично все, що є предметом вивчення молекулярної фізики. Це означає, що пояснюючи загальні (зокрема механічні та теплові) властивості твердих, рідких і газоподібних речовин, пояснюючи все різноманіття теплових явищ, визначаючи широке коло фізичних величин, пояснюючи велике різноманіття явищ і законів, ми будемо виходити з того, що всі речовини складаються з молекул які хаотично рухаються і певним чином взаємодіють між собою.
Контрольні запитання.
- Поясніть, на підставі чого думаючі люди, ще з прадавніх часів стверджували, що всі тіла складаються з надзвичайно дрібненьких частинок, які постійно рухаються та певним чином взаємодіють між собою?
- Наведіть приклади тих явищ та фактів які вказують на те, що тіла складаються з молекул і що ці молекули рухаються.
- Що називають броунівським рухом? Від чого залежить інтенсивність цього руху?
- Чому хаотичний рух молекул речовини називають тепловим рухом?
- Чим схожі і чим відрізняються броунівський та тепловий рухи?
- Що називають дифузією? Наведіть відомі вам прояви дифузії.
- Що називають осмосом? Наведіть відомі вам прояви осмосу.
- Як ви думаєте, чому в твердих тілах дифузійні процеси відбуваються набагато повільніше ніж в рідинах?
- Наведіть докази того, що молекули взаємодіють між собою і що в залежності від міжмолекулярної відстані вони можуть як притягуватись так і відштовхуватись.
- Наведіть докази того що молекули взаємодіють на надзвичайно малих відстанях.
.
Лекційне заняття №2.
Тема: Про масу та розміри молекул. Про кількість речовини та ті фізичні величини які цю кількість характеризують.
В молекулярній фізиці ми не будемо вивчати внутрішній устрій атомів і молекул. Не будемо вивчати їх електричні, хімічні та біологічні властивості. Однак загальні відомості про атоми та молекули, і перш за все про їх маси та розміри, ви все ж маєте знати.
Як зважити атом? Наївно думати, що існують такі надточні терези, на одну шальку яких можна покласти атом, а на іншу – гирьку відповідної маси. Ясно, що таких терезів не існує. Натомість існують опосередковані (непрямі) методи вимірювань, застосування яких дозволяє визначити масу атома з надзвичайно високою точністю. Сьогодні ми не будемо заглиблюватись в деталі того, як вчені вимірюють маси атомів і молекул. Зауважимо тільки, що не довіряти цим вимірюванням, це все рівно ніби не довіряти тим вимірюванням які визначають площу круга за формулою S=πR2. Не довіряти лише на тій підставі, що визначаючи площу, ми фактично вимірюємо не площу круга а його радіус. Зважаючи на вище сказане, ми зупинимося лише на тих аспектах вимірювання мас атомів, які пов’язані з фактом того, що різні атоми вступають в хімічні взаємодії в певних, строго визначених пропорціях.
На основі аналізу величезної кількості хімічних реакцій, було з’ясовано, що атомні маси всіх хімічних елементів знаходяться в певних співвідношеннях. При цьому вимірювання показували, що найлегшим атомом є атом водню (гідрогену Н). Виходячи з цього, в якості одиниці вимірювання атомних мас була обрана воднева одиниця маси. В такій системі вимірювань, маса атома водню приймалась за одиницю (m0(Н)=1,0000), а маси інших атомів визначались на основі того, в яких співвідношеннях ці атоми реагують з воднем. Так наприклад, маса атому кисню (оксигену О) становила 15,874 водневих одиниць маси, маса атому вуглецю (карбону С) – 11,917 цих одиниць і т.д.
Вимірювати атомні маса в водневих одиницях маси, тобто в масах найлегшого з атомів, було абсолютно логічним та доцільним. Однак в хімічній практиці маси переважної більшості атомів, визначались на основі того в яких пропорціях вони взаємодіють не з воднем, а з киснем. І це закономірно. Адже кисень, це один з найактивніших хімічних елементів. Тому хіміки наполягли на тому, щоб атомну масу кисню вважати рівною 16,0000, а маси інших хімічних елементів вимірювати не у водневих, а в кисневих одиницях маси. При цьому за таку потрібно було вважати 1/16 маси атома кисню.
Якщо ви думаєте, що на цьому епопея з вибором одиниці вимірювання атомних мас закінчилась, то помиляєтесь. Через певний час фізики з’ясували, що навіть хімічно найчистіший кисень, представляє собою певну суміш дуже схожих але все таки суттєво різних атомів кисню. Ці схожі атоми називають ізотопами. Слово «ізотоп» походить від грецьких слів «isos» – однаковий і «topos» – місце, а це підкреслює факт того, що відповідні атоми знаходяться в одній і тій же клітинці (в одному і тому ж місці) періодичної системи. Ізотопи мають практично однакові хімічні властивості але суттєво різні маси.
Оскільки хімічними методами розділити ізотопи практично не можливо, то хіміки за кисневу одиницю маси вважали 1/16 маси усередненого атома кисню (оксигену). Фізики ж вміли розділяти ізотопи і тому за кисневу одиницю маси вважали 1/16 маси кисню ізотопу-16. Це означало що в хімії і фізиці атомні маси вимірювались фактично різними одиницями, які до того ж мали одну і ту ж назву. Так тривало до 1961 року. В цьому році було прийнято компромісне рішення – маси атомів, молекул, іонів та елементарних частинок вимірювати в атомних одиницях маси.
Атомна одиниця маси (а.о.м.) – це позасистемна одиниця вимірювання маси, яка дорівнює 1/12 маси атома карбону-12: а.о.м.=m0(С612)/12. На основі точних експериментальних досліджень встановлено: а.о.м. = 1,6605655∙10–27кг.
Мал.8. Атомна одиниця маси (а.о.м.) дорівнює 1/12 маси атома карбону-12.
Загальні відомості про атоми, в тому числі і про їх маси, можна знайти в таблиці яка називається періодичною системою хімічних елементів. В цій таблиці, кожен атом характеризується двома числами: порядковим номером атома (Z) та його масовим числом (Мr). Наприклад: Н11,0079; Не24,0026; С612,011; О815,999; СƖ1735,453; Рb82207,20.
Масове число (відносна атомна маса) – це безрозмірна величина, яка показує у скільки разів маса усередненого атома даного хімічного елементу (m0) більша за одну атомну одиницю маси. Позначається Мr (« r » – від англ. relative – відносний). Відносна атомна маса даного хімічного елементу визначається на основі аналізу відповідних хімічних реакцій і записується у відповідну клітинку періодичної системи хімічних елементів.
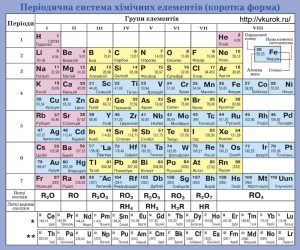
Мал.9. Періодична система хімічних елементів.
Коли ми говоримо про усереднену масу атома (m0) даного хімічного елементу, то маємо на увазі факт того, що практично будь яка хімічно проста речовина, представляє собою певну суміш хімічно однакових але різних за масою ізотопів. Наприклад, хімічно чистий природний хлор приблизно на 75% складається з ізотопу хлор-35, маса якого 35а.о.м. і на 25% з ізотопу хлор-37, маса якого 37а.о.м. А це означає, що визначаючи відносну атомну масу природної суміші цих ізотопів, завжди отримують Мr(Сℓ)=35,45. Тому, коли масу атома хлору визначають на основі записаного в таблиці хімічних елементів масового числа (Мr=35,45), то фактично визначають не масу конкретного атома, а усереднену масу атомів даного хімічного елементу: m0(CƖ) = 35,45(а.о.м.) = 35,45∙1,66∙10–27кг.
До речі, те що масові числа більшості хімічних елементів суттєво відрізняються від цілих чисел, це прямий наслідок того, що відповідні елементи представляють собою певну суміш різних ізотопів. Наприклад:
С612,011 = 98,89% С612 + 1,11% С613;
Сu2963,546 = 69,1% Cu2963 + 30,9% Cu2965;
Зважаючи на вище сказане, усереднену масу атома певного хімічного елемента (цю масу зазвичай називають масою відповідного атома) ми будемо визначати за формулою m0 = Mr·(а.о.м.) = Mr∙1,66∙10–27кг, де Мr – масове число, значення якого визначається з таблиці хімічних елементів. Якщо ж мова йтиме про масу однієї молекули, то вона визначатиметься як сума мас тих атомів з яких ця молекула складається. Наприклад:
m0(H2O) = (2∙1+16)а.о.м. = 18∙1,66∙10–27кг;
m0(H2SO4) = (2∙1+32+4∙16)а.о.м. = 98∙1,66∙10–27кг;
m0(NaCl) = (23+35,5)а.о.м. = 58,5∙1,66∙10–27кг.
Потрібно зауважити, що в хімії масове число Мr зазвичай позначають Аr і називають відносною атомною масою, тобто масою атома виміряною в а.о.м. Тому нагадуємо: за визначенням, масове число (Мr) – це безрозмірна величина, яка показує у скільки разів маса усередненого атома даного хімічного елементу (m0) більша за одну атомну одиницю маси. А це означає, що атомне число вимірюється не в атомних одиницях маси, а є безрозмірним числом. Якщо ж говорити про масу атома (m0), то її можна виміряти як в атомних одиницях маси (а.о.м.) так і в кілограмах (кг). При цьому m0=Mr·(а.о.м.)=Mr·1,66·10–27(кг). Наприклад:
Mr(Н2О) = 18, m0(H2O) = 18а.о.м.= 18·1,66·10–27кг;
Мr(H2SO2) = 98, m0(H2SO4) = 98а.о.м. = 98∙1,66∙10–27кг;
Mr(NaCℓ) = 58,5, m0(NaCl) = 58,5а.о.м. = 58,5∙1,66∙10–27кг.
Говорячи про розміри молекул (атомів) ви маєте розуміти, що молекули зовсім не схожі на все те що ви звикли бачити. Адже молекули не мають а ні чітких обрисів, а ні чітких меж. Молекули взагалі не мають того що прийнято називати розмірами, формою, об’ємом, густиною, тощо. Тому коли ми говоримо про певні геометричні параметри молекули, то маємо на увазі параметри тієї умовної пружної кульки яка є гранично спрощеною моделлю відповідної молекули і яка лише віддалено схожа на неї.
Мал.10. Атом, а тим більше молекулу, лише досить умовно можна представити у вигляді певної пружної кульки з відповідними розмірами.
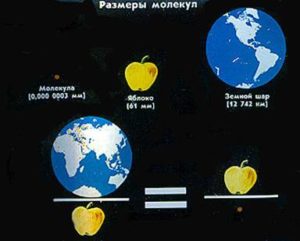
В науковій практиці умовні розміри молекули (атома) характеризують величиною яка називається ефективним діаметром молекули (атома). Дослідження показують, що ефективні діаметри атомів та хімічно простих молекул знаходяться в межах (0,2÷0,4)нм = (0,2÷0,4)10–9м. Наприклад: d(H2O) = 0,26нм = 0,26∙10–9м; d(H2) = 0,23нм; d(O2) = 0,29нм; d(N2) = 0,31нм; d(He) = 0,19нм; d(CO2) = 0,32нм. Ілюструючи мізерність цього числа достатньо сказати, що молекула води у стільки разів менша за середнє яблуко, у скільки разів це яблуко менше за Землю. Іншими словами:
Тепер коли ви дещо знаєте про масу і розміри молекул, буде доречно поговорити про ті величини які характеризують кількість речовини в тілі. Нагадаємо, речовина – це вид матерії який складається з тих чи інших частинок і має масу. Оскільки речовина, це те що складається з певних частинок (структурних одиниць: молекул, атомів, іонів) та має масу, то ясно, що кількість речовини в тілі (фізичному об’єкті) можна оцінити як масою цього тіла (чим більша маса – тим більше речовини) так і кількістю структурних одиниць в ньому (чим більше структурних одиниць – тим більше речовини). Крім цього, дане тіло можна розділити на певні порції та полічити їх. При цьому, чим більшою буде кількість порцій в тілі, тим відповідно більшою буде і кількість речовини в ньому. Виходячи з цього, в науковій практиці застосовують три фізичні величини, які по суті характеризують одне і те ж – кількість речовини в тілі. Цими величинами є: маса (m), кількість структурних одиниць (N) та кількість речовини (ν).
Таким чином, подібно до того як кількість наявних в товарному вагоні яблук, можна виміряти їх загальною масою (m), числом яблук (N), або кількістю тих ящиків (Я) які заповнені цими яблуками, кількість речовини в тілі можна виміряти її загальною масою (m), кількістю її структурних одиниць (N) та кількістю певним чином вибраних порцій цієї речовини які прийнято називати молями (ν). Визначаючи вище згадані фізичні величини можна сказати наступне.
Маса (в молекулярній фізиці) – це фізична величина, яка є загальною мірою кількості речовини в тілі, виміряну в кілограмах.
Позначається: m
Визначальне рівняння: нема
Одиниця вимірювання: [m] = кг.
Кількість структурних одиниць – це фізична величина, яка характеризує кількість речовини в тілі, виміряну числом структурних одиницях цієї речовини.
Позначається: N
Визначальне рівняння: N=m/m0, де m – загальна маса речовини; m0 – маса однієї структурної одиниці даної речовини;
Одиниця вимірювання: [N] = ст.од. (атоми, молекули, іони).
Кількість речовини – це фізична величина, яка характеризує кількість речовини в тілі, виміряну в молях, тобто в певним чином вибраних порціях (кучках) цієї речовини.
Позначається: ν
Визначальне рівняння: ν=m/M, де m – загальна маса речовини; M – молярна маса даної речовини (маса тієї порції речовини яка називається молем).
Одиниця вимірювання: [ν] = моль.
Моль (від лат. moles – маса) – це одиниця вимірювання кількості хімічно простої та хімічно однорідної речовини, яка дорівнює такій порції цієї речовини, в якій міститься стільки її структурних одиниць, скільки атомів міститься в 12 грамах вуглецю-12 (карбону-12).
Задача. Скільки атомів міститься в 12 грамах вуглецю-12?
Дано:
m(C612)=12г = 12∙10–3кг
N=?
Рішення: За визначенням N=m/m0, де m0(C612) = 12а.о.м. = 12∙1,66∙10–27кг
Розрахунки: N = (12∙10–3кг)/(12∙1,66∙10–27кг) = 6,022∙1023атомів.
Відповідь: в 12г вуглецю-12 міститься 6,022∙1023 його атомів.
Таким чином, молем називають таку порцію хімічно простої та хімічно однорідної речовини, в якій міститься 6,022∙1023 її структурних одиниць. Постійна величина, яка дорівнює числу структурних одиниць в одному молі речовини, називають сталою Авогадро* (позн. NA): NA = 6,022∙1023 (1/моль). (*) Названо на честь одного з засновників сучасної молекулярної фізики, італійського вченого Амадео Авогадро (1776–1856).

Мал.11. В одному молі будь якої речовини міститься 6,02∙1023 її структурних одиниць.
Якщо в тій порції речовини яка називається молем, міститься 6,022∙1023 її структурних одиниць (NA=6,022∙1023(1/моль)), то неважко збагнути, що масу цієї порції (М) можна визначити за формулою M=m0NA, де m0 – маса однієї структурної одиниці (однієї молекули) відповідної речовини.
Молярна маса речовини – це фізична величина, яка характеризує молярну масу даної хімічно простої речовини і яка дорівнює цій масі, тобто масі тієї порції речовини яка називається молем.
Позначається: M
Визначальне рівняння: M=m0NA
Одиниця вимірювання: [M] =кг/моль.
На практиці, молярну масу речовини зазвичай визначають не за визначальним рівнянням М=m0NA, а за формулою М=Мr (г/моль), де Мr – атомне (молекулярне) число відповідної речовини. І не важко довести, що формула М=Мr(г/моль) є похідною від визначального рівняння М=m0NA. Дійсно:
M=m0NA =Mr∙1,66∙10–27(кг)∙6,022∙1023(1/моль) =Мr∙10–3(кг/моль) =Мr(г/моль).
Практичні переваги формули М=Мr(г/моль) над визначальним рівнянням М=m0NA є очевидними. Адже застосовуючи формулу М=Мr(г/моль), ми оминаючи низку проміжних розрахунків, відразу ж отримуємо правильний результат. Наприклад: М(Н2О)= (2·1+16)г/моль= 18г/моль; М(Н2SО4)= (2·1+32+4·16)г/моль= 98г/моль; М(АƖ)=27г/моль; М(Рb)=207г/моль; М(С12Н22О11)= (12·12+22·1+11·16) г/моль= 342г/моль.
Потрібно зауважити, коли ми стверджуємо, що в 18г води (Н2О), 98г сірчаної кислоти (Н2SО4), 27г алюмінію (АƖ), 207г свинцю (Рb) та 342г цукру (С12Н22О11), міститься однакова кількість речовини (один моль речовини), то це означає лише те, що в кожній з цих різних за масою порціях різних речовини, міститься однакова кількість (а саме 6,022∙1023) молекул (структурних одиниць) відповідної речовини. Факт того, що в різних за масою порціях різних речовин міститься однакова кількість молекул, є прямим наслідком факту того, що маси різних молекул є різними. Скажімо, якщо маса одного атома Pb (m0=207а.о.м.) у 7,67 рази більша за масу одного атома Al (m0=27а.о.м.), то відповідно більшою буде і маса одного моля свинцю порівняно з масою одного моля алюмінію.
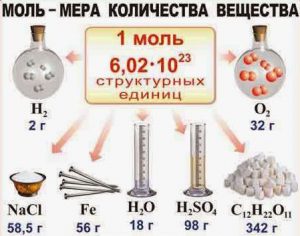
Мал.12. Кількість речовин різна, а кількість молей і кількість структурних одиниць в них – однакова. Чому?
З точки зору хімічної практики, вимірювати кількість речовини в молях надзвичайно зручно. Зручно головним чином тому, що хімічні взаємодії речовин відбуваються в певних вагових співвідношеннях, які пропорційні їх молярним масам. Тому в хімії кількість тієї чи іншої речовини зазвичай вимірюють в молях. Додайте до цього той малоприємний факт, що та фізична величина яка характеризує кількість речовини виміряну в молях називається «кількістю речовини» і ви зрозумієте чому дехто вважає, що кількість речовини можна охарактеризувати лише величиною яка так і називається «кількість речовини».
Таке твердження є абсолютно хибним. Хибним по перше тому, що виміряти кількість речовини в молях, можна лише в тому випадку, якщо мова йде про хімічно просту та хімічно однорідну речовину. Тобто таку речовину яка складається з певних однакових структурних одиниць які можна представити у вигляді відповідної хімічної формули. По друге, визначити кількість речовини в молях не можливо без вимірювання маси відповідної речовини (ν=m/M). По третє, стверджувати що в одному молі алюмінію (27г) і в одному молі свинцю (207г) міститься однакова кількість речовини, можна лише в сенсі однаковості числа атомів в цих фактично різних кількостях речовини. Бо якщо виходити з суті загально прийнятого визначення терміну речовина, то стверджувати що в 27г алюмінію стільки ж речовини як і в 207г свинцю, це все рівно ніби наполягати на тому, що в 1кг вишень стільки ж речовини як і в 500кг кавунів (кількість же структурних одиниць в обох кучках однакова).
Та якби там не було, а в науковій практиці, в залежності від ситуації та поставлених задач, кількість речовини в тому чи іншому фізичному об’єкті вимірюють кілограмами, структурними одиницями або молями. Іншими словами, в науковій практиці, кількість речовини в тілі характеризують трьома фізичними величинами: масою (m), кількістю структурних одиниць (N=m/m0) та кількістю речовини (ν=m/M). При цьому головною, загальною, універсальною та найбільш об’єктивною мірою кількості речовини є маса. Вона є такою по перше тому, що масою можна виміряти кількість будь якої речовини. А по друге, не визначивши маси речовини не можливо визначити а ні кількість її структурних одиниць, а ні кількість молей в ній.
Говорячи про кількість речовини в тілі та про ті фізичні величини які цю кількість характеризують, доречно звернути увагу на ще один факт. Факт, який ілюструє багатогранність фізики. Адже ми стикнулись з ситуацією, коли один і той же параметр фізичного об’єкту, а саме кількість речовини в ньому, характеризують три різні фізичні величини: маса (m), кількість структурних одиниць (N) та кількість речовини (ν). І ця ситуація в певному сенсі протилежна тому, коли одна і та ж фізична величина, а саме маса, характеризує чотири різні параметри фізичного об’єкту. Нагадаємо, вивчаючи механіку ми говорили про те, що маса є мірою інерціальних властивостей тіла, мірою його гравітаційних властивостей та мірою загальної кількості тієї енергії яка зосереджена в тілі. Тепер же ми з’ясували, що крім всього іншого маса є загальною мірою кількості речовини в тілі. Іншими словами:
Маса – це фізична величина, яка є:
– мірою інерціальних властивостей тіла;
– мірою гравітаційних властивостей тіла;
– мірою енергетичних властивостей тіла;
– міра кількості речовини в тілі, виміряної в кілограмах.
Позначається: m
Визначальне рівняння: нема
Одиниця вимірювання: [m] = кг .
Завершуючи розмову про ті фізичні величини які характеризують кількість речовини в тілі, визначимо і ті з них, які певним чином характеризують кількість речовини в одиниці об’єму. До числа таких величин відносяться: густина (ρ); концентрація молекул (n0); молярна концентрація (с).
Густина – це фізична величина, яка характеризує кількість речовини в одиниці об’єму і яка показує скільки кілограм даної однорідної речовини міститься в одиниці її об’єму.
Позначається: ρ
Визначальне рівняння: ρ = m/V
Одиниця вимірювання: [ρ] = кг/м3.
Концентрація молекул – це фізична величина, яка характеризує кількість речовини в одиниці об’єму і яка показує скільки молекул (структурних одиниць) даної однорідної речовини міститься в одиниці її об’єму.
Позначається: n0
Визначальне рівняння: n0 = N/V
Одиниця вимірювання: [n0] = 1/м3.
Молярна концентрація – це фізична величина, яка характеризує кількість речовини в одиниці об’єму і яка показує скільки молей даної однорідної речовини міститься в одиниці її об’єму.
Позначається: с
Визначальне рівняння: с = ν/V
Одиниця вимірювання: [с] = моль/м3.
Задача 1. Визначити масу однієї молекули, молярну масу, кількість молей та кількість молекул в 200г AgNO3.
Загальні зауваження. Кількість молекул в речовині (N) зазвичай визначають не за визначальним рівнянням N=m/m0, a за формулою N=νNA. Достовірність цієї формули є очевидною. Адже якщо в одному молі речовини міститься NА її молекул, то в ν молях, цих молекул буде в ν разів більше, тобто N=νNA.
Дано:
m(AgNO3) = 200г
m0=?; M=?; ν=?; N=?
Рішення. З таблиці хімічних елементів визначаємо масові числа потрібних нам атомів (значення цих чисел округляємо до цілого числа):
Мr(Ag)=108, Mr(N)=14, Mr(O)=16.
За базовими формулами (m0=Мr·1,66·10–27кг, М=Мr(г/моль), ν=m/M, N=νNA) визначаємо невідомі величини:
m0(AgNO3) = Мr·1,66·10–27кг = (108+14+3·16)а.о.м. = 170·1,66·10–27кг;
М(AgNO3) = Мr(г/моль) = (108+14+3·16)г/моль = 170г/моль;
ν(AgNO3) = m/M = 200г/170(г/моль) = 1,17моль;
N(AgNO3) = νNA = 1,17моль·6,02·1023(1/моль) = 7,0·1023молекул AgNO3.
Задача 2. Яку масу мають 2∙1023 молекул кисню?
Дано:
N(О2) = 2∙1023
m(О2) = ?
Рішення. Виходячи з того, що m=m0N, та враховуючи, що m0(O2) = 2∙16 (а.о.м.) = 32∙1,66∙10–27кг, можна записати m(О2) = m0N = 2∙1023∙32∙1,66∙10–27кг = 64∙10–4кг = 6,4г.
Відповідь: m(О2) = 6,4г.
Задача 3. Який об’єм п’яти молей міді (густина міді 8,9·103кг/м3)?
Дано:
Cu
ν = 5моль
ρ = 8,9·103кг/м3
V = ?
Рішення. Оскільки за визначенням ρ=m/V, то V=m/ρ. Оскільки за визначенням ν=m/M, то m=νM, де М(Cu)= 63,5(г/моль)= 63,5·10–3(кг/моль).
Таким чином, V=m/ρ= νМ/ρ.
Розрахунки. V= νМ/ρ= 5моль·63,5·10–3(кг/моль)/ 8,9·103кг/м3= 35,7·10–6м3= 35,7см3.
Відповідь: V = 35,7см3.
Задача 4. Знаючи число Авогадро визначити об’єм і діаметр атома золота.
Дано:
Au
NA=6,02·10231/моль
V0=?; d=?
Рішення. За заданим матеріалом можна визначити багато табличних характеристик цього матеріалу і зокрема його густину (ρ=m/V): ρ(Au)=19,3·103кг/м3, та відносну атомну масу Мr(Аu) = 197, а відповідно і молярну масу M = 197·10–3кг/моль. Оскільки за умовою задачі, відомою величиною є стала Авогадро, тобто кількість атомів Аu в одному молі золота, та враховуючи, що маса одного моля речовини дорівнює її молярній масі (m=М=197·10–3кг/моль), а загальний об’єм V=V0NA, можна записати ρ=m/V = М/V0NA, звідси
V0=M/ρNA = 197·10–3(кг/моль)/19,3·103(кг/м3)∙6,02·1023(1/моль) = 17·10–30м3.
Виходячи з того, що атом Au представляє собою кулю діаметром d, та враховуючи, що об’єм кулі визначається за формулою V0=πd3/6, можна записати d = 3√(6V0/π) = 3√(6·17·10–30м3/3,14)= (10–10)3√(32) = 3,2·10–10м = 0,32·10–9м.
Відповідь: V0(Au)= 17·10–30м3; d(Au)=0,32·10–9м.
Загальні зауваження. Ясно, що рішення даної задачі є дещо спрощеним (ідеалізованим). Спрощеним бодай тому, що величина того об’єму (V) який фігурує в визначальному рівнянні густини (ρ=m/V) складається не лише з загального об’єму відповідних атомів (NV0), а й з об’єму тих пустот які наявні між цими атомами (V=NV0+Vпуст). А це означає що отриманий нами результат, зокрема d(Au)=0,32·10–9м, є дещо завищеним. І результати точних вимірювань повністю підтверджують даний висновок. Адже реальний ефективний діаметр атомів золота 0,29·10–9м. Втім, вище сказане зовсім не означає, що наше рішення задачі є неправильним. Бо в умовах даної задачі, її рішення має бути саме таким. Просто ви маєте пам’ятати, що рішення переважної більшості фізичних задач в тій чи іншій мірі ідеалізовані (спрощені). А ця ідеалізація передбачає врахування тих обставин які в умовах даної задачі є важливими і нехтування тими обставинами які є несуттєвими, або такими, які не можливо визначити. Скажімо в умовах даної задачі точно визначити об’єм пустот між атомами, практично не можливо. Загалом, одним з тих корисних вмінь які ви маєте розвивати шляхом розв’язування задач, полягає в тому, щоб на основі аналізу умови задачі, виділяти основне та нехтувати другорядним.
Контрольні запитання.
- Чому хімікам не сподобалась абсолютно логічна та обгрунтована ідея визначати маси атомів та молекул у водневих одиницях маси?
- Еволюцію одиниці вимірювання мас атомів та молекул відображає схема: воднева одиниця маси → киснева одиниця маси → атомна одиниця маси. Опишіть історію цієї еволюції.
- Якщо а.о.м. це 1/12 маси атома вуглецю-12, то чому ж в таблиці хімічних елементів відносна атомна маса вуглецю не 12,000 а 12,011?
- Яка з тих фізичних величин, що характеризують кількість речовини в тілі є основною (базовою)? Чому?
- В яких одиницях можна виміряти кількість речовини в тілі?
- Чи можна визначити кількість паперу: а) в структурних одиницях; б) в молях; в) в кілограмах? Чому? Про що це свідчить?
- Що мають на увазі хіміки, коли стверджують, що в 18г води, 98г сірчаної кислоти і в 342г цукру, міститься однакова кількість речовини?
- Чому різні речовини в кількості один моль мають різні маси?
- Доведіть що формули М = m0NA і M = Mr (г/моль) є тотожними.
- Чим схожі і чим відрізняються ті величини які називаються густина, концентрація молекул та молярна концентрація.
Вправа 2.
- Визначити масу одного атома в а.о.м. і в кг: Не; Na; Cℓ; Cu; Ag; Au (масові числа округляти до одного знаку після коми).
- Визначити масу однієї молекули (в а.о.м. і в кг): О2; СО2; АgNO3; CuSO4; Ca(OH)2; C12H22O11.
- Скільки молекул в 1кг води?
- Скільки молекул (атомів) міститься в: а) 18г Н2О; б) 27г АƖ; в) 207г Рb?
- За 5 діб випарувалось 50г води. Скільки молекул води вилітало за 1с?
- Відомо, що діаметр атому гідрогену 0,23нм, а радіус Землі 6,37·106м. Скільки разів опояше Землю по екватору «нитка» яка складається з розташованих один за одним 6,02·1023 атомів гідрогену? Якою буде маса цієї «нитки»?
- Де більше атомів: у склянці води чи в склянці ртуті? (густина ртуті 13,6·103кг/м3)
- Визначити масу однієї молекули, молярну масу, кількість молей і кількість молекул в 200г: а) Н2О; б) CuSO4; в) NaCℓ; г) Ca(OH)2 .
- Відомо, що за нормальних умов, один моль будь якого газу займає об’єм 22,4 літра (закон Авогадро). Визначити концентрацію молекул за цих умов.
- Кухонна сіль має кубічну кристалічну структуру в вузлах якої розташовані іони натрію та хлору. Знаючи густину солі (2200кг/м3) визначте відстані між центрами найближчих іонів.
.
Лекційне заняття №3.
Тема: Температура як міра нагрітості тіла, та як міра середньої кінетичної енергії молекул.
Слово «температура» в перекладі з латинської означає «суміш». Така назва обумовлена фактом того, що колись вчені вважали, що температура тіла залежить від того, в яких пропорціях в цьому тілі змішані відповідна речовина та особлива теплова матерія яку називали теплецем (теплородом). Згодом з’ясувалося, що ніякого теплецю не існує і від ідеї суміші теплецю з речовиною відмовились. А от слово «температура» залишилось, і сьогодні, як і сотні років тому характеризує ступінь нагрітості тіла. Втім, температура, це та фізична величина, яка має що найменше чотири різні, загально прийняті наукові визначення. При цьому вчені так і не дійшли згоди відносно того, а яке ж з цих визначень є найбільш правильним.
Вивчаючи фізику, ми стикались з ситуацією коли одним і тим же терміном, зокрема словом «маса», позначали чотири фактично різні фізичні величини: маса – міра інерції; маса – міра гравітації; маса – міра енергії; маса – міра кількості речовини. Стикались з ситуацією, коли навпаки, один і той же параметр фізичного об’єкту, а саме кількість речовини в тілі, характеризують трьома фактично різними фізичними величинами – масою (m), кількістю структурних одиниць (N) та кількістю речовини (ν). Наразі ж мова йде про те, що одна і та ж фізична величина, яка позначається одним і тим же словом, і яка характеризує одну і ту ж властивість фізичного об’єкту, в різних обставинах та в різних розділах фізики, визначається по різному. І цією величиною є температура.
З точки зору повсякденної практики безумовно найзручнішим є наступне наукове визначення температури. Температура – це фізична величина, яка характеризує ступінь нагрітості тіла, виміряну термометром за температурною шкалою Цельсія.
Позначається: t
Визначальне рівняння: нема, (нема тому, що у відповідності з даним визначенням, температура є абсолютно автономною (незалежною від інших) величиною)
Одиниця вимірювання: [t] = °C, градус Цельсія.
Градус Цельсія (°С) – це одиниця вимірювання температури, яка дорівнює сотій частині інтервалу температур між точкою плавлення та точкою кипіння чистої води, визначеними при нормальному атмосферному тиску.
Важливою складовою процесу вимірювання температури є температурна шкала, тобто та система відліку в якій задано початок відліку температури (нулева точка), одиниця її вимірювання та еталонний метод цього вимірювання. З побутової точки зору найбільш зручною та поширеною температурною шкалою є шкала Цельсія. Цю шкалу запровадив в 1742 році шведський вчений Андерс Цельсій (1701–1744). В температурній шкалі Цельсія за початок відліку температур прийнято температуру плавлення води (льоду); за одиницю вимірювання – градус Цельсія; за еталонний метод вимірювання – вимірювання температури ртутним термометром.
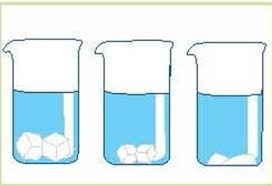
Будова сучасного побутового термометра загально відома. Його основною деталлю є висока скляна колба, частково заповнена певною рідиною (зазвичай ртуттю або забарвленим спиртом). Напевно ви здогадуєтесь і про те, яким чином градуюють термометр?! Правильно. Його спочатку опускають у суміш води і льоду, і відповідний рівень термометричної рідини позначають 0°С (мал.13а). Потім термометр опускають в окріп і наявний рівень термометричної рідини позначають 100°С (мал.13б). Після цього, відстань між отриманими точками ділять на сто рівних чистин і термометр готовий до застосування.
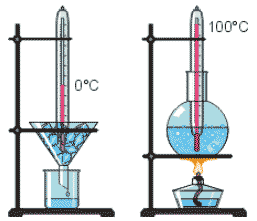
Мал.13. При градуюванні термометра, відстань між його показаннями при температурі плавлення льоду і температурі кипіння води, ділять на сто рівних частин.
Якщо виходити з того, що теплове розширення термометричного тіла є рівномірним (лінійним), то вище описаний спосіб градуювання термометра не викликає жодних заперечень. Однак, чи можемо ми бути впевненими в тому, що теплове розширення ртуті, спирту та інших матеріалів дійсно рівномірне? Виявляється, не можемо. Дослідження показують, що теплове розширення переважної більшості тіл, складним чином залежить від температури, і що в загальному випадку ця залежність є нелінійною. Тому якщо наприклад, на основі ртуті, заліза, міді, скла та повітря виготовити п’ять однакових термометра і стандартним чином проградуювати їх, то неодмінно з’ясується, що за одних і тих же температурних умов, показання різних термометрів будуть суттєво різними. Скажімо, якщо повітряний термометр буде показувати 300°С то ртутний зафіксує 314°С, залізний 373°С, мідний 329°С, а скляний 353°С.
В такій ситуації неминуче виникає запитання: «А який з цих термометрів показує правильну температуру? І чи є серед цих показань бодай одне безумовно правильне?» Відповісти на це запитання можна лише втому випадку, якщо створити такий термометр, в якому певний параметр термометричного тіла гарантовано лінійно залежатиме від температури. І такий еталонний термометр дійсно існує. Його називають газовим термометром.
В 1802 році французький фізик Гей-Люсак (1778–1850) експериментально встановив, що при постійному тиску певної маси газу (m=const; p=const), всі гази розширюються однаково, і що при цьому виконується співвідношення Vt = V0(1+βt),
де Vt – об’єм газу при температурі t°C;
V0 – об’єм газу при температурі 0°С ;
β =1/273 – температурний коефіцієнт об’ємного розширення газу.
По суті це означало, що при постійному тиску певної маси газу, його об’єм лінійним чином залежить від температури (мал.14), і що тому термометр в якому термометричним тілом є газ, можна вважати еталонним? Крім цього, закон Гей-Люсака вказував на те, що в Природі існує нижня межа температур і що числове значення цієї межі –273°С. Детальні дослідження та точні вимірювання показали, що гранично низька температура дійсно існує, і що її величина дійсно дорівнює –273°С (точніше –273,15°С). Цю гранично низьку температуру прийнято називати абсолютним нулем.
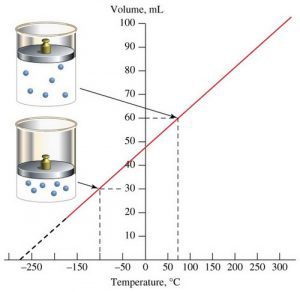
Мал.14. В процесі ізобаричного (m=const; p=const) нагрівання (охолодження) газу, його об’єм лінійним чином збільшується (зменшується).
Дослідження проведені з застосуванням еталонних газових термометрів показали, що в більш-менш широких температурних інтервалах, переважна більшість твердих та рідких матеріалів, розширюються нерівномірно (нелінійно). Однак, якщо мова йде про побутово важливий інтервал температур (від –30°С до +150°С), то в цьому інтервалі ртуть розширюється майже лінійно. Тому в температурному інтервалі від –30°С до +150°С ртутні термометри вважаються одними з найкращих.
Обираючи в якості точки відліку температур, температуру плавлення льоду, ми керувались міркуваннями практичної доцільності та зручності. Але чесно кажучи, за такого підходу в якості нулевої точки можна вибрати будь яку іншу сталу температуру, наприклад температуру плавлення свинцю, золота, міді чи скажімо суміші води, солі та нашатирю. Тепер же, коли з’ясувалось що в Природі існує певна, гранично низька температура (–273°С), чи не буде розумним саме цю температуру обрати за об’єктивну точку відліку температур? Таке цілком логічне рішення було прийнято. При цьому відповідну температурну шкалу назвали абсолютною шкалою температур або шкалою Кельвіна (на честь англійського фізика Уільяма Томсона (лорда Кельвіна) який в 1848 році і запропонував абсолютну шкалу температур).
В абсолютній шкалі температур, за початок відліку прийнято температуру абсолютного нуля, за одиницю вимірювання – кельвін, а за еталонний метод вимірювання – вимірювання за допомогою еталонного газового термометра. При цьому, визначення температури набуває вигляду:
Температура – це фізична величина, яка характеризує ступінь нагрітості тіла виміряну еталонним газовим термометром за абсолютною шкалою температур.
Позначається: Т
Визначальне рівняння: нема
Одиниця вимірювання: [Т] = К, кельвін.
Кельвін (К) – це одиниця вимірювання температури, яка дорівнює 1/273,16 частині інтервалу температур між температурою абсолютного нуля (–273,15°С) та температурою потрійної точки води (0,01°С).
На перший погляд, офіційні визначення тих температурних одиниць які називаються кельвіном та градусом Цельсія є різними. Однак суть цих різних визначень полягає в тому, що у відповідності з ними, кельвін (К) і градус Цельсія (°С) є чисельно рівними одиницями: К=°С. Дійсно: К=[0,01ºС–(–273,15ºС)]/273,16 =273,16ºС/273,16=ºС. Якщо ж говорити про ту різницю яка безумовно існує між температурою виміряною в градусах Цельсія (t) та температурою виміряною в кельвінах (Т), то вона полягає в тому, що в першому випадку за початок відліку температур (за 0°С) прийнято температуру плавлення льоду, а в другому (за 0К) – температуру абсолютного нуля, тобто ту гранично низьку температуру, нижче якої в Природі просто не існує.
Оскільки величини градуса Цельсія і кельвіна є однаковими (ºС=К), то між температурою виміряної в кельвінах (Т) і температурою виміряною в градусах Цельсія (t) існує просте співвідношення: Т = t + 273; t = T – 273. Наприклад, якщо t=20ºС, то Т=293К; якщо t=100ºС, то Т=373ºС; якщо t= –20ºС, то Т=253К; якщо Т=100К то t = –173ºС і т.д. При цьому, потрібно зауважити: якщо мова йде про різницю температур, то ця різниця визначена в градусах Цельсія (Δt) і в кельвінах (ΔТ) є чисельно рівною: Δt=ΔT.
Мал.15. Чим схожі і чим відрізняються температури виміряні за шкалою Цельсія та за шкалою Кельвіна?
В науковій практиці бузовою шкалою вимірювання температур є шкала Кельвіна (абсолютна шкала температур). В побутовій же практиці, температуру зазвичай вимірюють за шкалою Цельсія. Втім, в деяких країнах, зокрема США, температуру часто вимірюють за шкалою Фаренгейта. Ця шкала була запроваджена у 1724 році німецьким вченим Габріелем Фаренгейтом (1686–1736). Шкала Фаренгейта побудована на трьох базових точках:
0°F – температура суміші льоду, солі та нашатирю (–17,8°С)
32°F – температура плавлення льоду (0°С)
98°F – температура людського тіла (36,6°С).
Визначення, температура – це фізична величина, яка характеризує ступінь нагрітості тіла виміряну термометром, має два суттєві недоліки. По перше, воно не пояснює ні фізичної суті того що називають нагрітістю тіла, ні фізичної суті того що називається температурою. Це визначення лише констатує факт того, що певні параметри термометричного тіла, певним чином залежать від ступеню нагрітості цього тіла (від його температури), і на цій підставі визначає спосіб вимірювання цієї нагрітості.
По друге, дане визначення вводить температуру як абсолютно автономну величину, яка жодним чином не пов’язана з іншими величинами. Сучасна ж наука стоїть на тому, що Природа – це єдиний цілісний організм, в якому все взаємопов’язано та взаємообумовлено. І якщо ми прагнемо об’єктивно відобразити устрій цього цілісного організму, то маємо спиратись на відповідну систему взаємопов’язаних фізичних величин.
Крім цього, починаючи вивчення молекулярної фізики ми домовились, що загальні властивості речовин та ті теплові процеси які відбуваються з ними, будемо пояснювати виходячи з трьох базових тверджень:
1) всі речовини складаються з молекул;
2) молекули в речовині безперервно та безладно рухаються;
3) на невеликих відстанях, молекули взаємодіють між собою.
А це означає, що в молекулярній фізиці, визначення тієї величини яка називається температурою, потрібно пов’язати з фактом того, що речовини складаються з молекул які рухаються та взаємодіють між собою. І не важко збагнути, що температура (нагрітість тіла) певним чином пов’язана з інтенсивністю хаотичного руху молекул. На цей зв’язок з усією очевидністю вказує той факт, що в процесі збільшення температури, інтенсивність дифузії, осмосу, броунівського руху та інших подібних явищ, збільшується і навпаки.
Аналізуючи величезну сукупність явищ і експериментальних фактів, вчені дійшли висновку: температура, це не просто міра нагрітості тіла, а величина, яка характеризує середню кінетичну енергію теплового (хаотичного) руху молекул. При цьому, теоретичні і експериментальні дослідження довели, що між температурою речовини виміряну в кельвінах (Т) та середньою кінетичною енергією молекул цієї речовини (Ек) виміряну в джоулях, існує співвідношення: Т=Ек/(3/2)k, де Eк=m0vc2/2 – середня кінетична енергія поступального руху однієї молекули речовини; vc – середня квадратична швидкість молекули: vc=√[(v12+v22+…+vn2)/n]; k=1,38∙10–23 Дж/К – постійна величина, яка називається сталою Больцмана (названа на честь одного з творців сучасної молекулярно кінетичної теорії, австрійського фізика Людвіга Больцмана (1844–1906)).
Таким чином, в молекулярній фізиці прийнято наступне визначення температури. Температура – це фізична величина, яка характеризує середню кінетичну енергію поступального руху молекул речовини, виміряну не в джоулях а в кельвінах.
Позначається: Т
Визначальне рівняння: Т = Ек/(3/2)k, де k=1,38∙10–23 Дж/К,
Одиниця вимірювання: [Т] = К, кельвін.
Прийняте в молекулярній фізиці визначення температури, має ряд безумовних переваг. По перше, воно розкриває фізичну суть температури. А ця суть полягає в тому, що температура є мірою середньої кінетичної енергії молекул речовини, виміряну не в джоулях, а в значно дрібніших одиницях – кельвінах. По друге, розкриває фізичну суть абсолютного нуля: абсолютний нуль – це температура при якій припиняється поступальний рух молекул речовини. По третє, визначає температуру не як певну автономну величину, а як величину яка тісно пов’язана з іншими, раніше введеними величинами. В четвертих, дозволяє визначати середню кінетичну енергію поступального руху молекул не шляхом вимірювання їх мас (m0) та середньої квадратичної швидкості (vc), а шляхом вимірювання температури речовини (Т): Ек = (3/2)kT.
На завершення зауважимо, що температура характеризує середню кінетичну енергію хаотичного руху молекул. Адже сам факт хаотичного руху молекул безумовно вказує на те, що при одній і тій же температурі, в будь якій речовині містяться молекули з різними кінетичними енергіями. Умовно кажучи, в будь якій речовині, при одній і тій же температурі наявні як «холодні» так і «гарячі» молекули.
Задача. Визначити середню кінетичну енергію поступального руху та середню квадратичну швидкість молекул кисню і водню при температурі 27°С. Порівняти отримані результати.
Дано: СІ
t=27°C 300К
Ек(О2)=? Ек(Н2)=?
vс(О2)=? vс(Н2)=?
Рішення: Оскільки за визначенням Т=Ек/(3/2)k, де k = 1,38∙10–23Дж/К, то Ек = (3/2)kT. Із аналізу даної формули ясно, що величина середньої кінетичної енергії молекул речовини, не залежить ні від маси, ні від інших параметрів цих молекул. Тому: Ек(О2)= Ек(Н2)= (3/2)kT = 1,5·1,38∙10–23Дж/К·300К =621·10–23Дж.
Оскільки за визначенням Eк=m0vc2/2, то vc=√(2Ek/m0). Враховуючи, що m0(Н2) = 2·1,66·10–27кг; m0(О2) = 32·1,66·10–27кг, можна записати:
vc(Н2)=√(2Ek/m0) = √(2·621·10–23Дж/2·1,66·10–27кг = √(374·104(м2/с2)) = 1934м/с;
vc(О2)=√(2Ek/m0) = √(2·621·10–23Дж/32·1,66·10–27кг = √(374·104(м2/с2)) = 483м/с.
vc(Н2)/vc(О2) = 1934/483 = 4(рази).
Контрольні запитання.
- Слово “температура” в перекладі з латинської означає “суміш”. Чому величина яка характеризує ступінь нагрітості тіла, отримала таку назву?
- Чому сталева ложка, температура якої 20°С на дотик здається холодною, тоді як аналогічний за температурою пінопласт – теплим? Що означає даний факт?
- Чим схожі і чим відрізняються шкала Цельсія та шкала Кельвіна?
- Чому t ≠ Т, а Δt = ΔТ ?
- Які недоліки визначення: температура – міра нагрітості тіла?
- Які переваги визначення: температура – міра середньої кінетичної енергії молекул речовини?
- На основі молекулярно кінетичної теорії поясніть, чому температура речовини не може бути меншою за абсолютний нуль.
- Про що говорить твердження: температура є мірою середньої кінетичної енергії молекул речовини?
- Про що говорить твердження: температура є мірою середньої кінетичної енергії поступального руху молекул речовини?
Вправа 3.
- Температура тіла 293К, 310К, 200К, 500К, 23К. Виразіть цю температуру в градусах Цельсія. Температура тіла 10°; –23°С; 120°С; –150°С. Виразіть цю температуру в кельвінах.
- Воду нагріли від 20°С до 48°С. На скільки змінилась температура води в процесі нагрівання? Відповідь дати в градусах Цельсія і в кельвінах.
- Визначте середню кінетичну енергію молекул Н2О та СО2 при температурах 20°С і 200°С.
- Визначте кінетичну енергію поступального руху та загальну кінетичну енергію молекули гелію, кисню і води при температурі 27°С.
- Знаючи, що маса молекули кисню в 16 разі в більша за масу молекули водню, порівняйте середні квадратичні швидкості цих молекул при однакових температурах відповідних речовин.
- Визначте середню квадратичну швидкість молекул водню (Н2), азоту (N2) вуглекислого газу (СО2) при температурі 20°С. Порівняйте цю швидкість з швидкістю кулі (500м/с).
- При якій температурі середня квадратична швидкість молекул кисню становитиме 500м/с?
- Яку температуру повинен мати водень, щоб середня квадратична швидкість його молекул дорівнювала середній квадратичній швидкості молекул кисню при температурі 27°С?
- Визначте загальну кінетичну енергію одного моля гелію при температурі 27°С.
.
Лекційне заняття №4. (Практичне заняття).
Тема: Розв’язування задач молекулярної фізики.
Важливою складовою тих знань які ви маєте отримати в процесі вивчення фізики, є вміння застосовувати теорію на практиці. А це вміння формується шляхом розв’язування задач. Побутує думка ніби рішення задачі фізики полягає в тому, щоб серед незліченого різноманіття правильних формул вибрати потрібне розрахункове рівняння, тобто ту формулу підставивши в яку задані величини, можна визначити невідому величину. Така думка є абсолютно хибною. Хибною бодай тому, що в фізиці кожна задача індивідуальна. А це означає, що кожна з сотень, тисяч і мільйонів задач має своє розрахункове рівняння. І запам’ятовувати, зазубрювати чи заучувати різноманіття подібних рівнянь нема ані можливості ані сенсу. Бо рішення задачі фізики полягає не в тому, щоб із незліченного різноманіття правильних формул вибрати потрібну, а в тому щоб на основі аналізу умови конкретної задачі та певного, обмеженого набору базових формул (базових законів і визначальних рівнянь фізичних величин), шляхом логічних міркувань та математичних дій вивести потрібне розрахункове рівняння.
Звичайно якщо мова йде про прості задачі, на кшталт «визначити масу однієї молекули, молярну масу, кількість молей та кількість молекул в 100г Н2О», то в цьому випадку ви просто застосовуєте відповідні базові формули і виконуєте відповідні математичні розрахунки:
m0(Н2О) = Мr·1,66·10–27кг = (2·1 + 16)а.о.м. = 18·1,66·10–27кг;
М(Н2О) = Мr(г/моль) = (2·1 + 16)г/моль = 18г/моль;
ν(Н2О) = m/M = 100г/18(г/моль) = 5,56моль;
N(Н2О) = νNA = 5,56моль·6,02·1023(1/моль) = 33,5·1023молекул Н2О.
Але навіть в цьому випадку, рішення задачі передбачає розуміння того, що молекула Н2О складається з двох атомів гідрогену (Н) і одного атома оксигену (О), і що маса молекули є сумою мас відповідних атомів. Розуміння того, що масове число Мr, є тим параметром інформація про який міститься в таблиці хімічних елементів. Розумінні того, що молярна маса М, це маса тієї порції речовини, яка називається молем і в якій міститься 6,02·1023 молекул цієї речовини. Розуміння того, що якщо в одному молі речовини міститься NA = 6,02·1023 її молекул, то в ν молях цієї речовини цих молекул N = νNA. Про вміння виконувати математичні розрахунки, просто мовчу.
Якщо ж ви маєте справу з більш складними задачами, то їх рішення передбачає не лише знання базових формул та розуміння їх фізичної суті, а й вміння потрібним чином трансформувати ці формули. Скажімо якщо ρ=m/V, то m=ρV, а V=m/ρ ; якщо Т=Ек/(3/2)k, то Ек=(3/2)kT; якщо Ек=m0v2/2, то v2=2Ek/m0, a v=√(2Ek/m0), і т.д.
Знати базові формули, вміти ці формули потрібним чином трансформувати та вміти виконувати математичні розрахунки, це важливі складові процесу розв’язування задач фізики. Однак головною складовою цього процесу є не формули і не розрахунки, а розуміння суті того про що йде мова в даній задачі та вміння логічно мислити. Бо фізика, це не формули, а розуміння фізичної суті подій і вміння логічно мислити. Ви можете скільки завгодно «зазубрювати» правильні формули і навіть зазубрити їх, але якщо за цими формулами ви не будете бачити реальних об’єктів і подій, то всі ваші зусилля будуть марними – ви не будете знати, розуміти і любити фізику.
Якщо ж ви дійсно хочете навчитися розв’язувати задачі фізики, а по суті навчитися логічно мислити, то маєте усвідомити: це не можливо зробити просто спостерігаючи за тим як розв’язує задачі вчитель. Скажімо, ви хочете навчитися грати в хокей. Для цього наймаєте тренера і він пояснює вам всі нюанси цієї гри. Пояснює день, два,…., місяць,….рік. Ви схвально киваєте головою і вам все зрозуміло. Але якщо ви думаєте, що через рік такого навчання, станете класним хокеїстом, то неминуче помиляєтесь. Навчитися грати в хокей, просто спостерігаючи за тим як це роблять інші – неможливо. Для того щоб стати хокеїстом, потрібно взувати ковзани, брати в руки ключку, виходити на лід і …. падати…, вставати…, знову падати і знову вставати, тобто вчитися грати в хокей. І якщо поруч буде фаховий тренер, то процес навчання буде успішним та ефективним.
Вчитель, це той же тренер. Без його допомоги навчитися розв’язувати задачі надзвичайно важко, але можливо. А от що дійсно неможливо, так це навчитися розв’язувати задачі не розв’язуючи їх самостійно. І якщо на шляху опанування мистецтвом розв’язування задач, вас будуть переслідувати труднощі і помилки, знайте, ще нікому не вдавалось пройти цей шлях без труднощів і помилок. Але якщо ви будете наполегливими і кмітливими, то вас неминуче очікує успіх. І ви не лише будете знати фізику, а й безумовно полюбите цю найвеличнішу і найпрекраснішу з наук.
Отже, базові формули даної теми:
m0=Мr·1,66·10–27кг, де Мr – таблична величина;
М=Мr(г/моль); ν=m/M; N=m/m0=νNA, де NA = 6,02·1023(1/моль);
ρ=m/V; n0=N/V; Т=Ек/(3/2)k, де Ек=m0v2/2, k=1,38·10–23(Дж/К).
Задача 1. Відомо, що за нормальних умов, один моль будь якого газу займає об’єм 22,4 літра (закон Авогадро). Визначити концентрацію молекул за цих умов.
Дано:
Vмоль= 22,4л = 22,4·10–3м3
n0 = ?
Рішення. Оскільки за визначенням n0 = N/V, та враховуючи, що для одного моля N=NA=6,02·1023(1/моль), можна записати n0 = NА/Vмоль = 6,02·1023(1/моль)/ 22,4·10–3м3 = 0,27·1026(1/м3) = 27·1024(1/м3).
Відповідь: n0 = 27·1024(1/м3).
Задача 2. При якій температурі середня квадратична швидкість молекул азоту становитиме 500м/с?
Дано:
v(N2) = 500(м/с)
Т = ?
Рішення. Оскільки за визначенням Т=Ек/(3/2)k, де k=1,38·10–23(Дж/К), та враховуючи що Ек=m0v2/2, можна записати Т=Ек/(3/2)k = m0v2/2·(3/2)k = m0v2/3k. Таким чином, Т = m0v2/3k, де m0(N2) = 28·1,66·10–27кг.
[T] = кг(м/с)2/Дж/К = Дж·К/Дж = К.
Розрахунки: Т = m0v2/3k = 28·1,66·10–27·(5·102)2/3·1,38·10–23 =
(28·1,66·25/3·1,38)10–27+4+23 = 233·100 = 233К.
Відповідь: Т = 233К.
Задача 3. В п’яти кілограмах певного інертного газу міститься 1492·1023 молекул. Який це газ?
Дано:
m = 5кг
N = 1492·1023
який газ ?
Рішення. Оскільки назву хімічного елементу можна визначити за величиною його масового числа Мr, та враховуючи що m0=Мr·1,66·10–27кг, можна записати Mr = m0/1,66·10–27кг. А оскільки за умовою задачі в m = 5кг міститься N = 1492·1023 молекул, то m0=m/N. Таким чином Mr = m/N·1,66·10–27кг.
Розрахунки: Mr = 5кг/1492·1023·1,66·10–27кг = 5·104/1492·1,66 = 20,18.
За таблицею хімічних елементів визначаємо, що відповідне масове число має неон.
Відповідь: неон (Ne).
Задача 4. Який об’єм шести молей алюмінію (густина алюмінію 2,7·103кг/м3)?
Дано:
ν(Aℓ) = 6 моль
ρ(Aℓ) = 2,7·103(кг/м3)
V = ?
Рішення. За визначенням ρ=m/V, звідси V=m/ρ. Враховуючи що m=Nm0 = νNAm0, де m0(Aℓ)=27·1,66·10–27кг, NA = 6,02·1023(1/моль), можна записати V=m/ρ = νNAm0/ρ.
Розрахунки: V = νNAm0/ρ = 6·6,02·1023·27·1,66·10–27/2,7·103 = 600·10–7 = 60·10–6м3.
Відповідь: V = 60·10–6м3 = 60cм3.
Задача 5. В приміщені площею 100м2 і висотою 3,5м розлили 1г спирту. Скільки молекул спирту буде знаходитись в 1м3 повітря після того як спирт повністю випарується? Хімічна формула спирту С2Н6О.
Дано:
C2H6O
S = 100м2
h = 3,5м
m = 1г = 1·10–3кг
n0 = N/V = ?
Рішення. За визначенням n0 = N/V, де V=Sh, N=m/m0, m0(C2H6O) = (2·12+6·1+16)·1,66·10–27кг = 46·1,66·10–27кг. Таким чином n0 = N/V = m/Shm0.
Розрахунки: N/V = m/Shm0 = 1·10–3кг/100м2·3,5м·46·1,66·10–27кг = 1·1024/2,67·104м3 = 0,37·1020(1/м3) = 3,7·1019(1/м3).
Відповідь: n0 = N/V = 3,7·1019(1/м3).
Задача 6. Вважаючи що діаметр молекули води дорівнює 2,6·10–10м, визначте який відсоток від усього простору зайнятого водою, припадає на долю самих молекул.
Загальні зауваження. Розв’язуючи задачі фізики надзвичайно важливо уважно прочитати умову задачі та чітко з’ясувати, а що власне потрібно визначити в цій задачі. Скажімо в умовах даної задачі, мова йде про те, що молекули води займають лише певну частину від її загального об’єму. При цьому запитується, який відсоток від загального об’єму води Vзаг припадає на об’єм самих молекул Vмол, іншими словами запитується (Vмол/Vзаг)100%.
Дано:
d(H2O) = 2,6·10–10м
(Vмол/Vзаг)100% = ?
Рішення. Загальний об’єм води визначаємо з визначального рівняння густини ρ=m/Vзаг, звідси Vзаг=m/ρ, де ρ=1·103кг/м3. Загальний об’єм самих молекул визначаємо за формулою Vмол=NV0, де V0=πd3/6 об’єм однієї молекули, N=m/m0 кількість молекул (m0(H2O)=18·1,66·10–27кг). Зважаючи на вище сказане можна записати (Vмол/Vзаг)100% = [(m/m0)( πd3/6)100%]/( m/ρ) = ρπd3100%/6m0.
Таким чином: (Vмол/Vзаг)100% = ρπd3100%/6m0.
Розрахунки: (Vмол/Vзаг)100% = 1·103·3,14·( 2,6·10–10)3·100%/6·18·1,66·10–27 = 31%.
Відповідь: (Vмол/Vзаг)100% = 31%.
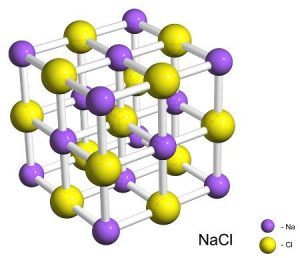
Задача 7. Кухонна сіль має кубічну кристалічну структуру в вузлах якої розташовані іони натрію і хлору. Знаючи густину солі (2200кг/м3) визначте відстані між центрами найближчих іонів.
Дано:
ρ(NaCℓ) = 2200кг/м3
а = ?
Рішення. За визначенням ρ=m/V. Враховуючи, що m=m0N, де m0(NaCℓ) = (23+34,45)·1,66·10–27кг = 95·10–27кг, N – кількість груп (NaCℓ) в масі m, а також враховуючи, що V=V0N1, де V0=a3 – об’єм одного елементарного кубика, N1 – кількість груп (NaCℓ) в цьому кубику, яка дорівнює N1=N/4, можна записати:
ρ=m/V = m0N/V0N1 = m0N/а3(N/4) = 4m0/а3, звідси а3 = 4m0/ρ, звідси а = (4m0/ρ)1/3.
Розрахунки: а = (4m0/ρ)1/3 = (4·95·10–27/2,2·103)1/3 = (172·10–30)1/3 = 1721/3·10–10 = 5,56·10–10м.
Відповідь: а = 5,56·10–10м.
Задача 8. В атмосферному повітрі на долю азоту припадає 0,76 маси, а на долю кисню 0,24 маси. Визначити молярну масу повітря.
Дано:
m1=m(N2)=0,76m
m2=m(O2)=0,24m
М = ?
Рішення. Будемо виходити з того, що тими величинами які кількісно характеризують склад суміші є маса m=m1+m2 та кількість речовини (молей) ν=ν1+ν2,
де ν1=m1/M1, ν2=m2/M2, M1=M(N2)=28г/моль, M1=M(O2)=32г/моль. Оскільки за визначенням ν=m/M, то М=m/ν = m/(ν1+ν2) = m/(m1/M1+m2/M2) = m/[(m1M2+m2M1)/(M1·M2)] = m(M1·M2)/(0,76mM2+0,24mM1) = (M1·M2)/(0,76M2+0,24M1). Таким чином, молярну масу суміші можна визначити за формулою М = (M1·M2)/(0,76M2+0,24M1).
Розрахунки: М = (28·32)/(0,76·32+0,24·28) = 29(г/моль).
Відповідь: М = 29(г/моль).
Вправа 4.
- Визначте масу однієї молекули, молярну масу, кількість молекул і кількість молей в 100г Са(ОН)2.
- В кімнаті об’ємом 50м3 випарувалась крапелька спирту маса якої 1мг. Скільки молекул спирту потрапляє в легені людини при кожному вдиху, якщо об’єм вдиху 1дм3. Хімічна формула спирту C2H6O.
- Молекула кисню рухається з швидкістю 450м/с. Визначте імпульс цієї молекули.
- Яку середню квадратичну швидкість мають молекули водню при температурі 0ºС?
- При якій температурі знаходиться газ, якщо середня кінетична енергія його молекул на 40% більша, ніж при 0ºС?
- Який об’єм 100 молей срібла (густина ртуті 13,6·103кг/м3)?
- Де більше атомів: у склянці води чи у склянці ртуті?
- Знаючи число Авогадро визначте об’єм і діаметр атома алюмінію.
- Визначте густину кристалічної речовини яка має кубічну кристалічну структуру, якщо маса кожного атома цієї речовини m0, а довжина ребра кубічної комірки ℓ.
- В суміші інертних газів на долю аргону припадає 0,65 маси, а на долю криптону 0,35 маси. Визначте молярну масу цієї суміші.
- Вважаючи що діаметр атома золота дорівнює ·10–10м, визначте який відсоток від усього простору зайнятого золотом, припадає на долю самих атомів.
.
Лекційне заняття №5.
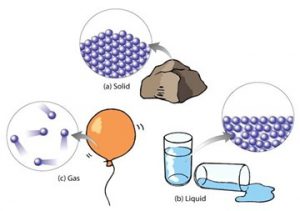
Тема: Загальні відомості про тверді, рідкі та газоподібні речовини. Агрегатні стани речовини.
Все різноманіття речовин умовно розділяють на тверді, рідкі та газоподібні. Коли ми стверджуємо, що лід, залізо і пінопласт – тверді, вода, ртуть і олія – рідкі, а водяний пар, повітря та вуглекислий газ – газоподібні, то це означає, що існують певні класифікаційні ознаки, керуючись якими можна чітко визначити, до якої класифікаційної групи відноситься той чи інший об’єкт. І не важко збагнути, що при поділі речовин на тверді, рідкі і газоподібні базовими класифікаційними ознаками є не густина, не електропровідність, не хімічний склад, не колір, не смак і навіть не твердість чи м’якість, а об’єм (V) і форма (Ф).
Дійсно. Коли ми стверджуємо, що лід, залізо і пінопласт є твердими, то маємо на увазі, що ці абсолютно різні за твердістю, густиною, електропровідністю та іншими ознаками тіла, мають певну сталу форму (Ф=const) і певний сталий об’єм (V=const). Коли ми стверджуємо, що вода, ртуть і олія рідкі, то маємо на увазі, що ці абсолютно різні речовини мають певний сталий об’єм (V=const) але не мають певної сталої форми (Ф≠const). Якщо ж мова йде про газоподібні речовини, то їх визначальною ознакою є те, що вони не мають ні певного сталого об’єму, ні певної сталої форми (V≠const; Ф≠const). Не мають в тому сенсі, що газоподібні речовини займають увесь наданий їм об’єм і приймають форму тієї посудини в якій вони знаходяться.
. V=const V=const V≠const
. Ф=const Ф≠const Ф≠const
Мал.16. Форма і об’єм є тими зовнішніми класифікаційними ознаками за якими різноманіття речовин розділяють на тверді, рідкі та газоподібні.
Класифікаційний поділ речовин за ознаками форма–об’єм, по суті відображає зовнішні відмінності між твердими, рідкими і газоподібними речовинами. Молекулярна ж фізика стоїть на тому, що в ній загальні властивості твердих, рідких та газоподібних речовин, в тому числі і ті які визначаються наявністю чи відсутністю певної форми і об’єму, пояснюються виходячи з трьох базових тверджень:
1) речовини складаються з молекул;
2) молекули рухаються;
3) молекули взаємодіють.
І такі пояснення безумовно існують. Дійсно. Оскільки молекули рухаються, то вони мають певну енергію руху, яку прийнято називати кінетичною Ек. Оскільки молекули взаємодіють, то вони мають певну енергію взаємодії, яку прийнято називати потенціальною Еп. Не важко збагнути, що енергія взаємодії молекул прагне об’єднати ці молекули в єдине ціле. Натомість енергія руху, навпаки – прагне розірвати зв’язки між молекулами і розкидати їх. Ясно, що в такій ситуації агрегатний стан речовини та її загальні фізичні властивості, визначальним чином залежать від того, який енергетичний (а відповідно й силовий) фактор є сильнішим.
Скажімо, якщо тверді тіла мають певну сталу форму і певний сталий об’єм, то напевно це пояснюється тим, що середня потенціальна енергія молекул твердого тіла значно більша за їх середню кінетичну енергію (Еп˃Ек). Факт же того, що газоподібні речовини займають увесь наданий їм об’єм, очевидно означає, що та енергія яка прагне розкидати молекули (кінетична енергія Ек), значно більша за ту енергію яка прагне об’єднати молекули (потенціальна енергія Еп). Іншими словами, для газоподібних речовин Еп < Ек. Якщо ж мова йде про рідини, то їх молекули з одного боку тримаються купи (V=const), а з іншого – ця купа є надзвичайно хиткою (Ф≠const). І не важко збагнути, що таку ситуацію можна пояснити лише тим, що в рідинах, енергія взаємодії молекул якщо і перевищує енергію їх руху, то лише мінімально (Еп ≥ Ек).
Таким чином, визначаючи ті речовинні об’єкти які називаються твердими, рідкими та газоподібними, можна сказати наступне. Твердими називають такі речовинні об’єкти, які мають певну сталу форму та певний сталий об’єм і в яких середня потенціальна енергія молекул значно більша за їх середню кінетичну енергію. Іншими словами, для твердих речовин: Ф=const; V=const; Еп ˃ Ек. Рідинами називають такі речовинні об’єкти, які мають певний сталий об’єм але не мають певної сталої форми і в яких середня потенціальна енергія молекул мінімально більша за їх середню кінетичну енергію. Іншими словами, для рідин: Ф≠const; V=const; Еп ≥ Ек. Газоподібними називають такі речовинні об’єкти, які не мають а ні певної сталої форми, а ні певного сталого об’єму і в яких середня потенціальна енергія молекул значно менша за їх середню кінетичну енергію. Іншими словами, для газоподібних речовин: Ф≠const; V≠const ; Еп ˂ Ек.

. Еп > Ек Еп ≈ Ек Еп < Ек
Мал.17. Агрегатний стан речовини залежить від співвідношення між кінетичною та потенціальною енергіями її молекул.
Відразу ж зауважимо, що коли ми стверджуємо: потенціальна енергія молекул газу набагато менша за їх середню кінетичну енергію (Еп < Ек), то маємо на увазі не загальну величину потенціальної енергії молекул газу, а ту її незначну частину яка проявляє себе на енергетичному рівні «газ». А ця енергія дійсно набагато менша за кінетичну енергію молекул газу. Однак це зовсім не означає, що за певних умов, зокрема в процесі переходу речовини з газоподібного стану в рідкий (в процесі конденсації), та прихована потенціальна енергія яка на енергетичному рівня «газ» практично не проявляла себе, виявиться джерелом величезної кількості теплоти, а по суті кінетичної енергії молекул. Тому, оцінюючи величину і прояви потенціальної енергії молекул, потрібно обережно ставитись до категоричних оцінок і завжди пам’ятати, що мова йде про дуже складний вид прихованої енергії, яка за одних обставин може практично не проявляти себе, а за інших – бути джерелом величезної кількості явної (кінетичної) енергії.
Твердження про те, що речовини бувають твердими, рідкими і газоподібними, з одного боку означає, що за одних і тих же умов одні речовини є твердими, інші – рідкими, а треті – газоподібними. Наприклад за звичайних умов дерево тверде, олія рідка, а повітря газоподібне. З іншого ж боку, за певних умов одна і таж речовина може бути твердою, рідкою або газоподібною. Наприклад вода може бути і твердою, і рідкою, і газоподібною. При цьому говорять, що вода може знаходитись в трьох агрегатних станах: твердому, рідкому чи газоподібному.
Звичайно, говорячи про те, що речовина може знаходитись в трьох агрегатних станах, мають на увазі, що мова йде про хімічно прості речовини. Адже деревина не буває ані рідкою, ані газоподібною. А якщо і буває, то не у вигляді деревини. Крім цього, далеко не всі хімічно прості речовини можуть знаходитись у всіх трьох агрегатних станах. Наприклад, карбонат кальцію (СаСО3), а простіше кажучи звичайна крейда, не буває ані рідкою, ані газоподібною. Не буває тому, що в процесі нагрівання, цей матеріал не досягнувши температури плавлення, розкладається на більш прості речовини: СаО та СО2. Подібне можна сказати і про переважну більшість хімічно складних речовин, як то біологічні матеріали, органічні сполуки, полімери, тощо. Однак якщо говорити про хімічно прості речовини, то більшість з них за певних умов можуть бути і твердими, і рідкими, і газоподібними.
Якби вас запитали: «від чого залежить агрегатний стан тієї чи іншої речовини?», то скоріш за все ви б сказали – від температури. А подумавши, можливо б добавили – і від тиску. Відповівши таким чином, ви будете абсолютно праві. Адже агрегатний стан речовини дійсно визначальним чином залежить від її температури і зовнішнього тиску. Досліджуючи характер цієї залежності, звернемось до експерименту.
Припустимо, що у вас є шматок льоду, температура якого –20ºС. Нагріваючи лід, ви неодмінно зясуєте, що більшість його фізичних властивостей поступово змінюються. Але вцілому ці зміни можна вважати не суттєвими. Адже і при –20ºС, і при –10ºС, і при –0,1ºС, лід залишається льодом, тобто твердою речовиною з відповідним набором фізичних властивостей. Коли ж температура льоду досягне 0ºС, то неодмінно з’ясується, що подальше її зростання неможливе без кардинальної, якісної зміни властивостей льоду. Адже при цій температурі лід плавиться і в процесі плавлення впрачає ознаки твердого тіла (наявність певної форми, наявність твердості, міцності, крихкості, тощо) і набуває ознак рідини (відсутність певної форми, наявність в’язкості, поверхневого натягу, тощо). Крім цього, в процесі плавлення, стрибкоподібно змінюються й інші властивості льоду, зокрема його питома теплоємність, густини, діелектрична проникливість, показник заломлення світла, тощо. Ще однією визначальною ознакою плавлення, є факт того, що цей процес відбувається з поглинанням певної кількості енергії. При цьому, ця енергія йде не на збільшення кінетичної енергії молекул (адже температура речовини залишається незмінною), а на збільшення їх потенціальної енергії.
Після того як при температурі плавлення (0ºС) лід повністю перетвориться на рідину, та теплова енергія яка продовжує надходити до речовини, призведе до нового витка підвищення температури, але вже не твердого льоду, а рідкої води. При цьому в процесі зростання температури фізичні властивості води поступово змінюватимуться. Але вцілому ці зміни можна вважати несуттєвими. Адже і при 5ºС і при 25ºС, і при 95ºС, вода залишається водою, тобто певною рідиною з відповідним набором фізичних властивостей. Але, як тільки температура води досягне позначки 100ºС, неодмінно з’ясується, що подальше підвищення цієї температури неможливе без кардинальної, якісної зміни фізичних властивостей води. Адже при цій температурі вода кипить і в процесі кипіння перетворюється на пару, тобто газоподібну воду з відповідним набором фізичних властивостей. І допоки вода не википить, температура системи вода – пар залишатиметься незмінною і чисельно рівною 100ºС.
Звичайно, коли ми стверджуємо, що температура кипіння води дорівнює 100ºС, то маємо на увазі, що це кипіння відбувається за нормального атмосферного тиску (тиску в одну атмосферу тобто 101325Па ≈ 1·105Па). Адже змінюючи зовнішній тиск, можна досягти того, що вода закипить при 20ºС, або не закипить при 200ºС.
Та як би там не було, а при температурі кипіння, поглинаючи зовнішню енергію та перетворюючи її на потенціальну енергію своїх молекул, рідина переходить до якісно нового агрегатного стану і стає газоподібною. При цьому подальше нагрівання газоподібної речовини буде супроводжуватись відповідним підвищенням її температури та відповідними поступовими змінами фізичних властивостей газоподібної речовини.
Факт того, що зміна агрегатного стану речовини супроводжується різкою, стрибкоподібною зміною багатьох фізичних властивостей цієї речовини та стрибкоподібною зміною потенціальної енергії її молекул, лежить в основі наукового визначення терміну «агрегатний стан речовини». Агрегатний стан речовини це такий фізичний стан даної речовини, який характеризується певним набором визначальних властивостей (зокрема наявністю або відсутністю форми та об’єму) і перехід до якого супроводжується стрибкоподібною зміною багатьох, в тому числі і визначальних властивостей цієї речовини, а також стрибкоподібною зміною потенціальної енергії її молекул. Розрізняють три агрегатні стани речовини: твердий, рідкий і газоподібний.
Говорячи про можливі стани речовини, варто згадати про ще один. Цей стан рідко зустрічається на Землі і надзвичайно часто у Всесвіті. Його називають плазмою. Пояснюючи суть того що називають плазмою, давайте розглянемо ті події які відбуваються в процесі нагрівання певної речовини, скажімо тієї ж води. Ось вона тверда, потім – рідка і нарешті – газоподібна. Але що буде з газоподібною водою в процесі її подальшого нагрівання? А буде наступне. При певному рівні температур, молекули води почнуть розпадатись на атоми та групи атомів. А ті в свою чергу, втрачаючи валентні електрони, почнуть перетворюватись на відповідні іони. У підсумку, та речовина яка була водою, тобто такою що складалась з молекул Н2О, перетворюється на певну суміш окремих атомів, позитивних і негативних іонів та вільних електронів. Саме цю суміш і називають плазмою.
Плазмою називають частково або повністю іонізований газ, в якому концентрація вільних позитивно і негативно заряджених частинок є усереднено однаковою. Процес переходу речовини з газоподібного стану в стан плазми, прийнято називати іонізацією газу. Зворотній процес, тобто перехід речовини з стану плазми до стану газу, зазвичай називають рекомбінацією плазми.
Мал.18. Плазма – це частково або повністю іонізований газ.
Фізичні властивості плазми суттєво відрізняються від властивостей газу. Головна причина цих відмінностей полягає в тому, що гази складаються з електронейтральних (незаряджених) частинок, а плазма – з певної суміші заряджених і незаряджених частинок, або лише з заряджених частинок. А це означає, що плазма проводить електричний струм, що на її поведінку визначальним чином впливають зовнішні електричні та магнітні поля, що її частинки взаємодіють не лише в момент безпосереднього контакту, а й на великих відстанях.
Сукупність цих відмінностей, дозволяє стверджувати, що плазма – це особливий, четвертий стан речовини. Однак з формальної точки зору, цей стан навряд чи правомірно називати четвертим агрегатним станом речовини. По перше тому, що в стані плазми, будь яка речовина не є тією речовиною, якою вона була в твердому, рідкому і газоподібному стані. Адже складовими частинками плазми є не ті атоми чи молекули з яких складалась базова речовина, а певна суміш окремих атомів, іонів та електронів. По друге, перехід речовини від її газоподібного стану до стану плазми відбувається поступово і без певних стрибкоподібних змін властивостей цієї речовини. А це означає, що формальних підстав вважати плазму четвертим агрегатним станом речовини нема.
Та як би там не було, а при достатньо високих температурах, будь яка речовина набуває якісно нових властивостей, сукупність яких дозволяє стверджувати, що ця речовина перебуває в особливому стані. І цей стан прийнято називати плазмою.
Дослідження показують, що близько 99% наявної у Всесвіті речовини, знаходиться в стані плазми. В стані плазми знаходяться зірки та їх атмосфери, галактичні туманності та міжзоряне середовище. Плазмаю є та частина атмосфери Землі яку називають іоносферою. Плазмою є той розжарений газ який називають блискавкою, електричною дугою, полум’ям, тощо. Але не потрібно думати, що плазмою можуть бути лише високотемпературні гази. Скажімо, температура того розрідженого газу що світиться в лампі денного світла не є надто високою. І тим не менше, цей газ є плазмою. Або наприклад, температура того газу що забезпечує кольорове зображення так званих плазмових екранів, мало відрізняється від кімнатної. І тим не менше, відповідний газ є плазмою.
Дослідження показують, що в межаж одного і того ж агрегатного стану, формально одна і та ж речовина може мати суттєво різні властивості. Наприклад, фізичні властивості алмазу і графіту – діаметрально протилежні. Алмаз, це міцний, крихкий, надзвичайно твердий, прозорий матеріал, який не проводить електричний струм. Натомість графіт, це неміцний, пластичний, м’який, непрозорий матеріал, який проводить електричний струм. І тим не менше, алмаз і графіт це різновидності однієї і тієї ж речовини – кристалічного вуглецю. А діаметрально протилежні властивості цих хімічно однакових речовин пояснюються тим, що в них атоми карбону (С) упорядковано розташовані суттєво по різному.
Якщо ж говорити про більш загальний приклад того, що в межах одного і того ж агрегатного стану, одна і та ж речовина може мати суттєво різні властивості, то таким прикладом є те, що газоподібні речовини (V≠const; Ф≠const; Еп ˂ Ек) поділяються на пари і гази. При цьому, одна і та ж речовина, за одних умов може бути паром, а за інших – газом. Чим же відрізняються пари від газів? Чому газоподібний кисень називають газом, а газоподібну воду – паром? За яких умов пар перетворюється на газ, а газ стає паром?
Перш за все зауважимо, що для кожної хімічно простої речовини існує певна чітко визначена температура, яку називають критичною температурою (tкр або Ткр). Наприклад для води tкр=373,2ºС, для вуглекислого газу tкр=31,0ºС, для кисню tкр= –118,4ºС, а для водню tкр= –241,0ºС. Про суть критичної температури та про умови її досягнення, ми поговоримо дещо пізніше. Наразі ж зазначимо, що критична температура є тією чітко визначеною межею яка відділяє пар даної речовини від її газу. Власне цей факт і відображають відповідні визначення.
Парами називають такі газоподібні речовини, які знаходяться при до критичних температурах (t ˂ tкр). Це означає що: 1) середня кінетична енергія молекул пару не набагато більша за їх середню потенціальну енергію (Ек > Еп); 2) пар можна перетворити на відповідну рідину шляхом його ізотермічного стиснення.
Наприклад, якщо взяти газоподібну воду, газоподібний бензин чи газоподібний ефір, і при кімнатній температурі почати зменшувати їх об’єм, то в процесі стиснення, ці газоподібні речовини почнуть конденсуватись, тобто перетворюватись на відповідну рідину. Звичайно за умови, що стискається саме пар, а не суміш пару з газом. Адже якщо наприклад, шляхом стиснення ви захочите сконденсувати ту воду, невелика кількість якої міститься в повітрі вашої квартири, то скоріш за все не зможете цього зробити. Не зможете тому, що фактично будете стискати не пари води, а суміш великої кількості того газу який називається повітрям та незначної кількості парів води.
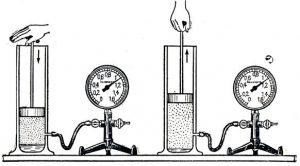
Мал.19. В процесі ізотермічного стиснення (m=const, T=const), пар перетворюється на відповідну рідину.
Газами називають такі газоподібні речовини, які знаходяться при за критичних температурах (t ˃ tкр). Це означає що: 1) середня кінетична енергія молекул газу набагато більша за їх середню потенціальну енергію (Ек >> Еп); 2) газ не можливо перетворити на відповідну рідину шляхом його ізотермічного стиснення.
Наприклад якщо взяти газоподібний кисень (О2), газоподібний водень (Н2) чи газоподібний азот (N2) і при кімнатній температурі почати зменшувати їх об’єм, то неодмінно з’ясується, що за будь якого ступеню стиснення, в посудині буде знаходитись однорідна газоподібна речовина. При цьому, навіть в тому випадку коли густина цієї речовини стане більшою за густину рідини, скажімо води, у вас не буде підстав стверджувати, що в посудині з’явилась рідина. Не буде по перше тому, що в процесі стиснення ви не зафіксуєте моменту перетворення газу на рідину. А по друге, якою б густою не була та речовина що знаходиться в посудині, вона матиме основну властивість газу – при наданні цій речовині будь якого об’єму, вона практично миттєво займе увесь цей об’єм.
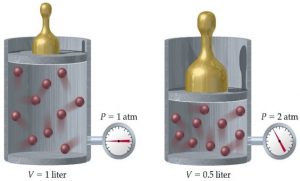
Мал.20. В процесі ізотермічного стиснення (m=const, T=const), газ не перетворюється на відповідну рідину.
Звичайно, факт того, що при кімнатній температурі газоподібний кисень, газоподібний водень і газоподібний азот не можливо перетворити на відповідну рідину, зовсім не означає, що цього не можливо зробити в принципі. Просто для того щоб газ перетворити на рідину, його спочатку треба перетворити на відповідний пар, тобто охолодити до температури меншої за критичну (t<tкр). Наприклад якщо газоподібний кисень (tкр = –118,4ºС) охолодити до –118ºС, а потім стиснути до тиску 49 атмосфер, то ви отримаєте рідкий кисень. Якщо ви захочите отримати рідкий кисень при нормальному атмосферному тиску, то маєте знизити його температуру до температури яка не перевищує температуру кипіння (для кисню tкип = –183ºС). Власне при таких наднизьких температурах відповідні речовини зазвичай і зберігаються.
Контрольні запитання.
- Чому густину не можна вважати тим критерієм, який дозволяє розділити речовинні об’єкти на тверді та рідкі?
- Виходячи з яких міркувань ми стверджуємо, що для твердих тіл Еп ˃ Ек, для рідин Еп ≈ Ек, для газів Еп < Ек?
- Як змінюється кінетична і потенціальна енергія молекул в процесі: а) плавлення; б) кристалізації; в) пароутворення; г) конденсації.
- Які визначальні ознаки переходу речовини з одного агрегатного стану в інший?
- Опишіть ті процеси які відбуваються при нагріванні хімічно простої речовини на шляху тверде – рідке – газоподібне – плазма.
- Чим плазма відрізняється від звичайного газу? Які основні властивості плазми?
- Чи є формальні підстави вважати плазму четвертим агрегатним станом речовини? Чому?
- Чому пари і гази називають газоподібними?
- Чому газоподібну воду називають пором, а газоподібний кисень – газом?
- Яке стиснення називають ізотермічним?
- Чи можна газоподібний кисень перетворити на відповідну рідину? Що для цього потрібно зробити?
.
Лекційне заняття №6.
Тема: Гази та їх властивості. Газові закони, як узагальнення експериментальних фактів, та як прямі наслідки молекулярно-кінетичної теорії.
Нагадаємо. Газами називають такі газоподібні речовини (V≠const; Ф≠const; Еп ˂ Ек), які знаходяться при за критичних температурах (t ˃ tкр). Це означає що: 1) середня кінетична енергія молекул газу набагато більша за їх середню потенціальну енергію (Ек >> Еп); 2) газ не можливо перетворити на відповідну рідину шляхом його ізотермічного стиснення.
Факт того, що середня кінетична енергія молекул газу набагато більша за їх середню потенціальну енергію (Ек >> Еп), по суті означає, що фізичні властивості хімічно різних газів є практично однаковими. Однаковими тому, що індивідуальні властивості речовини, визначальним чином залежать від енергії взаємодії її молекул. А оскільки для газів Еп << Ек, то загальна поведінка молекул газу, а отже і його загальні фізичні властивості, практично не залежать від індивідуальних особливостей тих молекул з яких цей газ складається. Те що хімічно різні гази мають практично однакові фізичні властивості, з усією очевидністю підтверджують так звані газові закони. Власне про ці закони ми і поговоримо в даному параграфі.
Фізичний стан певної маси газу (m=const) можна охарактеризувати трьома величинами: тиск (р), об’єм (V) та температура (Т). Ці величини прийнято називати основними термодинамічними параметрами газу. Процеси при яких так чи інакше змінюються термодинамічні параметри певної маси газу (m=const) називаються термодинамічними процесами. Термодинамічні процеси, при яких маса газу та один з його основних термодинамічних параметрів (р,V,Т) залишаються незмінними, називаються ізопроцесами (від грецького «ізос» – незмінний). Розрізняють три ізопроцеси:
ізотермічний: m=const, T=const;
ізобаричний: m=const, p=const;
ізохоричний: m=const, V=const;
Слова «термос», «барос», «хорема» мають грецьке походження і означають відповідно: «теплий» (температура), «важкий» (тиск), «ємність» (об’єм).
Напевно ви погодитесь з тим, що об’єм, тиск і температура певної маси газу є взаємо пов’язаними величинами. Адже кожен знає, що в процесі зменшення об’єму, тиск газу збільшується. Кожен знає, що в процесі нагрівання, гази розширюються. А якщо не розширюються, то результатом їх нагрівання є підвищення тиску. Закони, які відображають ті зв’язки що об’єктивно існують між об’ємом, тиском та температурою певної маси газу, називають газовими законами.
Важливість газових законів полягає в тому, що саме ці експериментально відкриті закони, стали тією експериментальною основою на базі якої була створена сучасна молекулярно-кінетична теорія. Достатньо сказати, що саме на основі аналізу тих співвідношень, які прийнято називати газовими законами, були визначені ті фундаментальні сталі, значимість яких виходить далеко за межі властивостей газів і які називаються абсолютним нулем (t= –273ºС), універсальною (молярною) газовою сталою (R=8,31Дж/К·моль), сталою Больцмана (k=1,38∙10–23Дж/К) та сталою Авогадро (NA= 6,02∙10231/моль). Зважаючи на ці обставини, газові закони потрібно розглядати не як певні мало значимі співвідношення між параметрами певної маси газу, а як ті експериментальні факти, які лежать в основі сучасної молекулярно-кінетичної теорії.
Газові закони.
Закон Бойля – Маріотта – це закон, в якому стверджується: при ізотермічному процесі, добуток тиску будь якого газу на його об’єм, залишається незмінним. Іншими словами: якщо m=const, T=const то pV=const.

Мал.21. Якщо m=const, T=const то pV=const. (закон Бойля–Маріотта)
Даний закон був експериментально встановлений в 1662 році англійським фізиком Робертом Бойлем (1627–1691) та незалежно від нього, французьким фізиком Едмом Маріоттом (1620–1684). Суть закону Бойля-Маріотта очевидно проста: якщо при постійній температурі, об’єм певної маси газу зменшити в n разів, то його тиск в n разів збільшиться, а якщо цей об’єм в n разів збільшити, то тиск газу в n разів зменшиться.
Закон Бойля-Маріотта можна представити у вигляді відповідного графіку, який прийнято називати ізотермою. При цьому в різних системах координат одна і та ж ізотерма виглядає по різному (мал.22)
Мал.22. Загальний вигляд ізотерми в різних системах координат.
Закон Гей-Люсака – це закон, в якому стверджується: при ізобаричному процесі, відношення об’єму будь якого газу до його абсолютної температури залишається незмінним. Іншими словами: якщо m=const, р=const то V/T = const, або V/(t+273) = const.
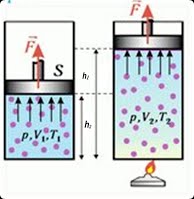
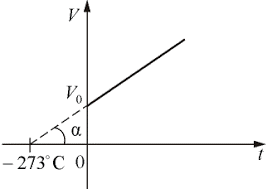
Мал.23. Якщо m=const, р=const то V/T = const. (закон Гей-Люсака)
Даний закон був експериментально встановлений в 1802 році, французьким фізиком Жозефом Луі Гей-Люсаком (1778–1850). Суть закону Гей-Люсака є наступною: якщо при постійному тиску (р=const), абсолютна температура (Т) певної маси газу збільшується в n разів, то в n разів збільшується і об’єм цього газу, а якщо температура газу зменшиться, то відповідно зменшиться і його об’єм. При цьому потрібно мати на увазі, що мова йде про абсолютну температуру газу, тобто температуру виміряну в кельвінах. Адже якщо наприклад, при постійному тиску, газ з температурою 2°С нагріти до 4°С, то його об’єм не збільшиться вдвічі. Для такого збільшення об’єму газ потрібно нагріти не до 4°С, а до 277°С, тобто від 275К (2°С) до 2·275К= 550К = 277°С.
Потрібно зауважити, що в часи Гей-Люсака температуру вимірювали не в кельвінах, а в градусах Цельсія і тому відповідний закон записувався не у вигляді V/T = const, а у вигляді V/(t+273) = const. Закон Гей-Люсака очевидно вказував на те, що в природі існує гранично низька температура, і що її величина –273ºС. Подальші дослідження показали, що таку температура дійсно існує, і що її величина дійсно дорівнює –273ºС (точніше –273,15ºС). Цю гранично низьку температуру називають абсолютним нулем.
Закон Гей-Люсака можна представити у вигляді відповідного графіку, який прийнято називати ізобарою. При цьому в різних системах координат одна і та ж ізобара виглядає по різному (мал.24)
Мал.24. Загальний вигляд ізобари в різних системах координат.
Чесно кажучи, ще за п’ятнадцять років до загально визнаної дати відкриття закону Гей-Люсака, аналогічний висновок зробив французький фізик Жак Шарль (1746–1823). Однак, результати своїх досліджень Шарль за лише йому відомих мотивів, тримав у таємниці. А це означає, що за загально прийнятими правилами, його не можна вважати автором відповідного закону. Тим не менше, в деяких наукових джерелах закон Гей-Люсака називають законом Шарля. Втім, в переважній більшості наукових джерел, законом Шарля називають ще один газовий закон, який по суті є похідним від законів Бойля – Маріотта та Гей-Люсака.
Закон Шарля – це закон, в якому стверджується: при ізохоричному процесі, відношення тиску будь якого газу до його абсолютної температури залишається незмінним. Іншими словами: якщо m=const, V=const то p/T = const, або р/(t+273) = const.

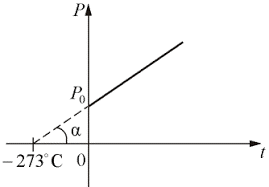
Мал.25. Якщо m=const, V=const то p/T = const. (закон Шарля)
Закон Шарля можна представити у вигляді відповідного графіку, який прийнято називати ізохорою. При цьому в різних системах координат одна і та ж ізохора виглядає по різному (мал.26)
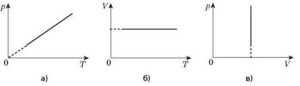
Мал.26. Загальний вигляд ізохори в різних системах координат.
Прямим наслідком законів Бойля – Маріотта, Гей-Люсака і Шарля (а фактично законів Бойля – Маріотта і Гей-Люсака), є закон який називають об’єднаним газовим законом. Об’єднаний газовий закон – це закон, в якому стверджується: для постійної маси будь якого газу, відношення добутку тиску газу на його об’єм до абсолютної температури газу, залишається незмінним. Іншими словами: якщо m=const, то pV/T=const або pV/(t+273)=const.
Дійсно. Припустимо, що певну кількість газу (m=const) з початковими параметрами р1, V1, Т1 (мал.27) спочатку ізотермічно (T=const) стискають до стану р2, Vʹ2, Т1, а потім ізобарично (p=const) нагрівають до стану р2, V2, Т2. Оскільки на першому етапі виконується закон Бойля – Маріотта: р1V1=р2Vʹ2 (1), а на другому – закон Гей-Люсака: Vʹ2/Т1=V2/Т2 (2), то можна записати: із (1) випливає Vʹ2=p1V1/p2; із (2) випливає Vʹ2=V2T1/T2. Звідси: p1V1/p2=V2T1/T2 або p1V1/T1=p2V2/T2.
Мал.27. Якщо m=const, то pV/T=const. (об’єднаний газовий закон)
В 1834 році французький фізик Бенуа Клапейрон (1799–1864) записав об’єднаний газовий закон у вигляді, який прийнято називати законом Клапейрона (рівнянням Клапейрона). Закон Клапейрона – це закон, в якому стверджується: для одного моля будь якого газу виконується співвідношення pVмоль/Т=R, де R – постійна величина, яка називається універсальною (молярною) газовою сталою. Значення цієї величини визначається експериментально і становить R=8,31Дж/К∙моль.
В 1874 році російський хімік Дмитро Менделєєв (1834–1907) записав рівняння Клапейрона pVмоль/Т=R у вигляді, який дозволяє визначати величину співвідношення рV/Т для будь якої кількості молей газу: pV/T=(m/M)R, де m – загальна маса газу, M – молярна маса цього газу. Дану форму запису об’єднаного газового закону називають законом (рівнянням) Менделєєва – Клапейрона.
Закон Менделєєва – Клапейрона – це закон, в якому стверджується: для довільної кількості молей будь якого газу, виконується співвідношення pV/T=(m/M)R, де m – загальна маса газу, M – молярна маса цього газу.
В 1811 році італійський фізик Амадео Авогадро (1776–1856), на основі аналізу багатьох експериментальних фактів, дійшов висновку: за однакових термодинамічних умов, в рівних об’ємах різних газів міститься однакова кількість молекул.
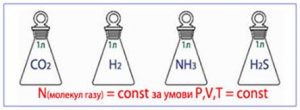
Мал.28. За однакових умов, в рівних об’ємах різних газів міститься однакова кількість молекул. (закон Авогадро)
Після того, як було сформульовано закон Клапейрона та визначено величину молярної газової сталої, закон Авогадро набув вигляду: Закон Авогадро – це закон, в якому стверджується: за нормальних умов (р=101,3кПа, Т=273К) один моль будь якого газу займає об’єм 22,4 літра (22,4∙10–3м3).
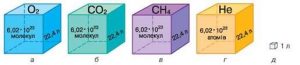
Мал.29. Якщо газу 1моль, то за нормальних умов V=22,4л. (закон Авогадро)
В 1801 році англійський вчений Джон Дальтон (1766–1844) сформулював закон, який прийнято називати законом Дальтона. В цьому законі стверджується: тиск суміші хімічно не взаємодіючих газів, дорівнює сумі тих парціальних тисків які створюють окремі складові цієї суміші, тобто р = р1 + р2 + … + рn . Наприклад, сухе повітря на 78% складається з азоту (N2) на 21% з кисню (О2) і на 1% з інших газів. При цьому, загальний тиск повітряної суміші можна представити як суму тих окремих (парціальних) тисків, які створюються складовими частинами цієї суміші.
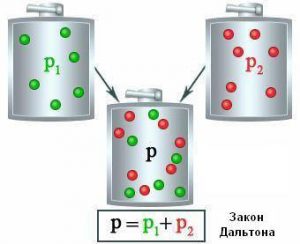
Мал.30. Тиск суміші газів, дорівнює сумі тисків окремих складових цієї суміші. (закон Дальтона)
Потрібно наголосити на тому, що кожен з вище сформульованих законів є узагальненням відповідних експериментальних досліджень. Досліджень які тривали близько двохсот років, і в яких приймали участь багато поколінь видатних вчених. Сьогодні ж, коли зусиллями цих вчених створено струнку систему знань, яка називається молекулярно-кінетичною теорією, все різноманіття газових законів можна «відкрити» буквально за 10 хвилин. Зробивши ці відкриття, ви безумовно переконаєтесь в тому, яким потужним та інформативним джерелом знань є наукова теорія.
Перш за все зауважимо, що при теоретичному описанні властивостей будь якого реального об’єкту, цей реальний об’єкт завжди замінюють певною, спрощеною (ідеалізованою) моделлю цього об’єкту. Моделлю, яка враховує всі суттєво важливі обставини і не враховує ті обставини, які в умовах даної задачі є не суттєвими. Скажімо, реальний газ, це надзвичайно складна система, яка складається з неймовірно величезної кількості молекул, кожна з яких має надзвичайно складний внутрішній устрій. При цьому кожна молекула безперервно та безладно рухається і складним чином взаємодіє з іншими молекулами. Ясно, що бездоганно точно описати поведінку цієї надскладної системи практично не можливо. Цю поведінку можна теоретично описати лише в тому випадку, якщо реальний газ замінити певним чином спрощеною (ідеалізованою) моделлю цього газу. Впроваджуючи таку модель, враховують наступні властивості реальних газів.
По перше. За нормальних умов, будь який реальний газ достатньо сильно стискається. А це означає, що відстані між молекулами газу є відносно великими і що тому, індивідуальними особливостями форми цих молекул можна знехтувати, та вважати ці молекули відповідними кульками.
По друге. Будь який реальний газ займає увесь наданий йому об’єм. А це означає, що в процесі взаємодії, молекули газу ведуть себе як пружні кульки: в процесі пружного удару, кінетична енергія кульки спочатку зменшується до нуля, а потім збільшується до початкової величини. В такій ситуації, загальна поведінка молекул газу практично не залежить від величини їх потенціальної енергії і тому цією енергією можна знехтувати, тобто вважати що для газу Еп=0.
В третіх. Тиск газу в усіх напрямках є практично однаковим. А це означає, що при хаотичному русі молекул, кожний напрям руху є однаково імовірним, і що тому, в будь який момент часу, в сторону будь якої стінки куба, рухається одна шоста частина тих молекул що знаходяться в цьому кубі.
Враховуючи вище сказане, при теоретичних дослідженнях, реальний газ можна замінити його спрощеною фізичною моделлю, яку прийнято називати ідеальним газом. Ідеальний газ – це спрощена (ідеалізована) модель реального газу, в якій: 1) молекули – ідеально круглі пружні кульки; 2) енергія взаємодії молекул дорівнює нулю (Еп=0); 3) в сторону будь якої стінки куба, в будь який момент часу рухається 1/6 частина наявних молекул.
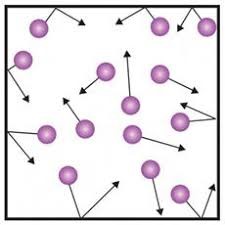
Мал.31. Ідеальний газ – це спрощена модель реального газу.
Ілюструючи суть теоретичних досліджень та узагальнюючу інформативність молекулярно-кінетичної теорії, розв’яжемо наступну задачу.
Задача. Спираючись на розуміння суті того що називають тиском, температурою, об’ємом, кількістю речовини, концентрацією молекул, тощо, «відкрити» все різноманіття газових законів, тобто тих співвідношень які існують між об’ємом (V), тиском (р) та температурою (Т) певної маси (m=const) ідеального газу.
Дано: ідеальний газ, m = const, V = SΔℓ, p = F/S, T = Eк/(3/2)k, Eк = m0v2/2, k = 1,38·10–23Дж/К, NA = 6,022·10231/моль, n0 = N/V, F = ma, a = ∆v/∆t, ν = m/M. Відкрити газові закони.
Рішення:
Аналізуючи визначальні рівняння тих фізичних величин, які є предметом наших теоретичних досліджень (V=SΔℓ; p=F/S; T = Eк/(3/2)k), не важко збагнути, що в даному переліку величин, ключовою є тиск. Адже саме в визначальному рівнянні тиску (p = F/S), опосередковано приховані як об’єм (V = SΔℓ), так і температура (тиск залежить від сили ударів молекул, яка в свою чергу пов’язана з їх кінетичною енергією, а отже – з температурою газу). Виходячи з цих міркувань, наші теоретичні дослідження почнемо з аналізу того, що називають тиском, тобто з аналізу рівняння р = F/S.
Мал.32. Тиск газу, це результат пружних ударів молекул цього газу.
З’ясовуючи ті обставини від яких залежить тиск газу, потрібно врахувати наступне. 1) Загальна силова дія газу (F) на задану поверхню, є результуючою силової дії окремих молекул цього газу, величину якої можна визначити за формулою F = NудF0, де Nуд – загальна кількість ударів молекул по заданій поверхні; F0 – сила удару однієї молекули. 2) В процесі пружного удару, швидкість молекули (v) спочатку зменшується до нуля, а потім – збільшується до початкової величини. А це означає, що за час пружного удару (∆t) швидкість молекули газу змінюється на величину ∆v=2v. 3) Оскільки в заданому напрямку рухається лише 1/6 частина молекул, то кількість тих ударів які отримує поверхня площею S за гранично малий час Δt, можна визначити за формулою Nуд = (1/6)∆N = (1/6)n0∆V = (1/6)n0S∆ℓ = (1/6)n0Sv∆t, де ΔN – кількість молекул в приповерхневому шарі газу об’ємом ΔV=SΔℓ, n0 – концентрація молекул газу.
Зважаючи на вище сказане, та враховуючи що за визначенням F0=m0a; a=∆v/∆t, можна записати: p = F/S = NудF0/S = Nудm0a/S = Nудm0∆v/S∆t = Nудm02v/S∆t = (1/6)n0S∆ℓm02v/S∆t = (1/3)n0m0vΔℓ/Δt= (1/3)n0m0v2, тобто р=(1/3)n0m0v2, або р=(2/3)n0Ек.
Таким чином, ми отримали рівняння яке кількісно відображає факт того, що тиск газу залежить від концентрації його молекул (n0) та величини їх середньої кінетичної енергії (Ек=m0v2/2). Рівняння р=(1/3)n0m0v2, або р=(2/3)n0Ек називають основним рівнянням молекулярно-кінетичної теорії газів. Така назва повністю відповідає тій винятково важливій ролі, яку відіграє дане рівняння в молекулярно-кінетичній теорії. Достатньо сказати, що на основі елементарного математичного аналізу рівняння р=(2/3)n0Ек, можна вивести (теоретично відкрити) все різноманіття відомих газових законів. Дійсно. Зважаючи на те що Ек=(3/2)kT, n0=N/V, можна записати: р=(2/3)n0Ек=(2/3)(N/V)(3/2)kT=NkT/V. Звідси: pV/T=Nk, де k=1,38·10–23Дж/К.
Із аналізу рівняння pV/T=Nk ясно, що величина співвідношення pV/T залежить від кількості молекул (N) в наявному об’ємі газу. Визначаючи цю кількість можна виділити три ситуації:
- В заданому об’ємі міститься невідома, але постійна кількість газу (m=const). В такій ситуації кількість молекул газу залишається незмінною (N=const) і тому рівняння pV/T=Nk можна записати у вигляді pV/T=const (об’єднаний газовий закон). І не важко збагнути, що прямими наслідками об’єднаного газового закону є:
– закон Бойля – Маріотта: якщо m=const, T=const то pV=const;
– закон Гей-Люсака: якщо m=const, p=const, то V/T=const;
– закон Шарля: якщо m=const, V=const, то p/T=const.
- В заданому об’ємі міститься постійна кількість газу (m=const) і величина цієї кількості 1моль. В такій ситуації: N=NA=6,022·1023 молекул. А це означає, що рівняння pV/T=Nk набуває вигляду pVмоль/T=NAk= 6,02∙1023(1/моль)·1,38∙10–23Дж/К = 8,31Дж/К·моль= R (закон Клапейрона). При цьому стає зрозумілою енергетична суть універсальної (молярної) газової сталої R=NAk. Універсальна (молярна) газова стала (R=8,31Дж/К∙моль), це постійна величина, яка показує на скільки джоулів зміниться загальна кінетична енергія одного моля ідеального газу, при зміні його температури на один кельвін.
- В заданому об’ємі міститься постійна кількість газу (m=const) і величина цієї кількості ν=m/M (моль). В такій ситуації, кількість молекул газу становить: N=νNA=(m/M)NA, де М – молярна маса газу. А це означає, що рівняння pV/T=Nk набуває вигляду pV/T=(m/M)R (закон Менделєєва-Клапейрона).
Якщо ж говорити про закони Дальтона та Авогадро, то і вони є прямими наслідками рівняння pV/T=Nk. Дійсно. Для одного моля газу, це рівняння набуває вигляду pVмоль/T= R. При цьому, за нормальних умов, тобто при температурі Тн=273К і тиску рн=1,01·105Па: Vмоль=RТн/рн=22,4∙10–3м3=22,4л. Висновок: за нормальних умов, один моль будь якого газу (ідеального газу) займає об’єм 22,4 літра (закон Авогадро).
Для суміші різних, хімічно не взаємодіючих газів, загальну кількість молекул (N) можна визначити за формулою N=N1+N2+…+Nn , де N1, N2,… Nn – кількість молекул кожної складової частини суміші. А це означає, що для суміші газів, рівняння pV/T=Nk можна записати у вигляді p = N(kT/V) = (N1+N2+…+Nn)(kT/V) = p1+p2+…+pn . Висновок: тиск суміші хімічно не взаємодіючих газів, дорівнює сумі тих парціальних тисків які створюють окремі складові цієї суміші (закон Дальтона).
Таким чином, на основі аналізу визначальних рівнянь базових фізичних величин та розуміння фізичної суті цих величин, ми теоретично «відкрили» все різноманіття відомих газових законів. Факт того, що газові закони, з одного боку є узагальнюючим результатом експериментальних фактів, а з іншого – передбаченнями молекулярно-кінетичної теорії, безумовно вказує на те, що відповідна теорія є правильною. Крім того, факт того що в широкому діапазоні тисків та температур, ті газові закони які описують властивості реальних газів, практично в точності співпадають з тими законами які описують властивості ідеального газу, безумовно вказує на те, що наша модель ідеального газу є надзвичайно вдалою.
На завершення зауважимо, що газові закони в точності виконуються лише для так званого ідеального газу. Якщо ж мова йде про реальні гази (О2, N2, H2, He, Ne, Ar), то для них, газові закони достатньо точно виконуються в області не надто високих тисків (р ˂ 20атм) і не надто низьких температур (t ˃ –100ºС).
Контрольні запитання.
- На що вказує те, що середня кінетична енергія молекул газу набагато більша за енергію їх взаємодії? Які факти це підтверджують?
- Які процеси називаються а) термодинамічними; б) ізопроцесами?
- В чому історична важливість газових законів?
- Якого вигляду набуває об’єднаний газовий закон для: а) ізобаричного процесу; б) ізохоричного процесу; в) ізотермічного процесу?
- Який газ – водень (Н2) чи гелій (Не), за однакових умов більше схожий на ідеальний? Чому?
- Яка властивість реальних газів дозволяє стверджувати, що енергія взаємодії їх молекул дорівнює нулю? Чи означає це, що відповідна енергія дійсно дорівнює нулю?
- Що називають ідеальним газом?
- Чому, теоретично з’ясовуючи ті зв’язки які існують між об’ємом, тиском та температурою, в якості ключової величини обирають тиск?
- Чим схожі і чим відрізняються стала Больцмана та універсальна газова стала?
- Наведіть приклади ситуацій, в яких тиск газу збільшується за рахунок збільшення: концентрації молекул; б) швидкості руху молекул.
- Виходячи з визначального рівняння тиску, виведіть основне рівняння молекулярно-кінетичної теорії.
- На основі аналізу основного рівняння м.к.т. визначте залежність тиску газу від його густини.
Вправа 6.
- При температурі 0ºС тиск газу в закритій посудині 101кПа. Яким буде цей тиск при температурі 40ºС?
- Об’єм газу при температурі 27°С і тиску 1,5атм становить 10л, яким буде цей об’єм за нормальних умов?
- Визначити масу вуглекислого газу в балоні ємністю 40л при температурі 17°С і тиску 50атм.
- При ізохоричному нагріванні газу, його температура зросла від 10ºС до 20ºС. У скільки разів збільшився тиск газу?
- В балоні міститься газ при температурі 17°С і тиску 1МПа. На скільки знизиться тиск газу при його охолодженні до –23°С?
- Визначити густину кисню при температурі 17°С і тиску 204кПа.
- В посудині об’ємом 5л знаходиться 10г кисню і 20г азоту. Який тиск суміші цих газів при температурі 27ºС?
- При ізобаричному нагрівання газу, його густина збільшилась вдвічі. Як і у скільки разів змінилась абсолютна температура газу?
- Густина газу при тиску 100кПа становить 1,43кг/м3. Визначте середню квадратичну швидкість молекул цього газу.
- Визначте концентрацію молекул газу при температурі 27ºС і тиску в одну атмосферу. Чи залежить ця концентрація від сорту газу?
.
Лекційне заняття №7. (Практичне заняття).
Тема: Розв’язування задач на застосування газових законів.
Газові закони можна записати як у вигляді певних формул, так і представити у вигляді відповідних графіків. Зважаючи на ці обставини, розглянемо певну сукупність алгебраїчних та графічних задач на застосування газових законів.
Газові закони в формулах.
Базові формули:
якщо m=const, то pV/T=const, pVмоль/T=R, pV/T=(m/M)R, де R=8,31Дж/К∙моль.
Задача 1. Визначити густину водню при температурі 17°С і тиску 204кПа.
Дано:
Н2
t=17°C, Т = 290К
p=204Па = 204·103Па
ρ = ?
Рішення. За визначенням ρ = m/V. Оскільки згідно з законом Менделєєва-Клапейрона pV/T = (m/M)R, то m/V = pM/TR. Таким чином, густину газу можна визначити за формулою ρ= pM/TR, де R=8,31Дж/К∙моль, М(Н2)= 2г/моль = 2·10–3кг/моль.
Розрахунки: [ρ] = (Па·кг/моль)/(Дж/К·моль)К = Па·кг/Дж = Н·кг/м2·Н·м= кг/м3;
ρ= pM/TR = (204·103·2·10–3)/(290·8,31) = 0,17кг/м3.
Відповідь: ρ = 0,17кг/м3.
Задача 2. Який об’єм повітря вийде з кімнати, при підвищенні температури в ній з 15ºС до 25ºС? Об’єм кімнати 120м3.
Дано:
tп=15°C, Т = 288К
tк=25°C, Т = 298К
V=120м3
ΔV = ?
Рішення. Будемо виходити з того, що тиск повітря в кімнаті до та після нагрівання залишається незмінним (р1=р2) і рівним атмосферному. В такій ситуації об’єднаний
газовий закон (р1V1/T1= р2V2/T2) набуває вигляду V1/T1= V2/T2. Враховуючи, що V2=V1+ΔV, можна записати. V1/T1=(V1+ΔV)/T2. Звідси V1+ΔV = V1T2/T1, звідси ΔV = V1[(T2/T1) – 1].
Розрахунки: ΔV = V1[(T2/T1) – 1] = 120м3[(298К/288К) – 1] = 4,17м3.
Відповідь: ΔV = 4,17м3.
Задача 3. Визначити середню квадратичну швидкість молекул газу, густина якого 1,8кг/м3, а тиск 1,5атм.
Дано:
ρ=1,8кг/м3
р=1,5атм=1,5105Па
v = ?
Рішення. У відповідності з основним рівнянням м.к.т. газів р=(1/3)n0m0v2. З іншого боку, за визначенням ρ=m/V=m0N/V=m0n0. А це означає, що між тиском газу (р) та його густиною (ρ) існує співвідношення р=(1/3)ρv2. Звідси випливає v=√(3p/ρ).
Розрахунки: [v]=[√(3p/ρ)] = √(Па/кг/м3) =√(кг·м3/кг·м·с2) = √(м2/с2) = м/с;
v=√(3p/ρ) = √(3·15·104/1,8) = 500м/с.
Відповідь: v = 500м/с.
Задача 4. В посудині об’ємом 1л знаходиться 2г кисню і 4г азоту. Який тиск суміші цих газів при температурі 27ºС?
Дано:
V=1л=1·10–3м3
m1= m(O2)=2г
m2= m(N2)=4г
t=27°C, Т = 300K
p = ?
Розрахунки. Згідно з законом Дальтона р = р1 + р2. Згідно з законом Менделєєва–Клапейрона pV/T=mR/M, звідси p=mRT/MV = (RT/V)(m/M) Таким чином р = p1 + p2 = RT(m1/M1 + m2/M2)/V, де M1 = M(O2) = 28(г/моль), M2 = M(N2) = 32(г/моль).
Розрахунки: р=8,31·300∙(2/32 + 4/28)/1·10–3 = 5,1·105Па.
Відповідь: р = 5,1·105Па.
Задача 5. В циліндрі під поршнем площею 100см2 знаходиться 20г азоту при температурі 0ºС. На яку висоту підніметься поршень при нагріванні газу на 100ºС? Маса поршня 100кг. Атмосферний тиск 100кПа.

Дано:
S=100см2=1·10–2м2
m(N2)=20г=20·10–3кг
t1=0°C, Т = 273К
t2=100°C, Т=373К
m=100кг
pа=100кПа=1·105Па
Δh = ?
Рішення. Виконуємо малюнок який відображає фізичний зміст задачі. Будемо виходити з того, що в обох ситуаціях газ знаходиться під тиском, що дорівнює сумі атмосферного тиску та того тиску який поршень, р1 = р2 = ра + mg/S = 1·105 + 100·10/1·10–2= 2·105Па. Оскільки згідно з законом Менделєєва–Клапейрона pV/T=mR/M, то V1=m(N2)RТ1/M(N2)р1 = 20·10–3·8,31·273/28·10–3·2·105= 8,1·10–3м3;
V2=m(N2)RТ2/M(N2)р2 = 20·10–3·8,31·373/28·10–3·2·105= 11,1·10–3м3.
Таким чиним, різниця об’ємів газу становить ΔV=V2–V1=3,0·10–3м3. А враховуючи, що ΔV=SΔh, можна записати Δh=ΔV/S= 3,0·10–3м3/1·10–2м2= 0,3м.
Відповідь: Δh = 0,3м.
Газові закони в графіках.
Загальну суть ізотермічного (m=const, T=const), ізобаричного (m=const, p=const) та ізохоричного (m=const, V=const) процесів, можна представити у вигляді відповідної ізотерми, ізобари та ізохори (мал.33). При цьому, потрібно мати на увазі, що в різних системах координат ізотерми, ізобари та ізохори виглядають по різному.
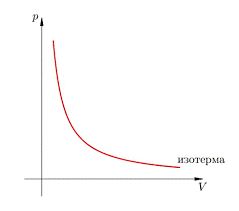

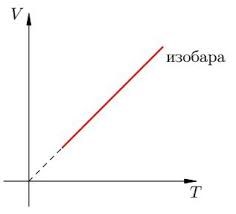

Мал.33.Загальні вигляди ізотерм, ізобар та ізохор в різних системах координат.
Рішення переважної більшості тих задач в яких термодинамічні процеси представлені у вигляді певного графіку, по суті зводиться до того, що на основі аналізу відповідного графіку та об’єднаного газового закону (якщо m=const, то pV/T=const), або похідних від нього законів Бойля – Маріотта, Гей-Люсака, Шарля, визначаються невідомі величини. А оскільки нема кращого способу навчитися розв’язувати задачі, ніж той при якому ці задачі практично розв’язуються, то власне цим способом і будемо послуговуватись.
Задача 6. На малюнку зображено дві ізобари, побудовані для однієї і тієї ж маси газу. Порівняйте тиски цих газів. Зробіть узагальнюючий висновок.
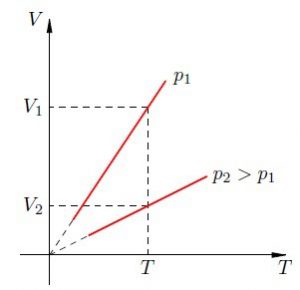
Рішення. Оскільки мова йде про одну і ту ж масу газу, то можна стверджувати, що згідно з об’єднаним газовим законом p1V1/T1=p2V2/T2. Із аналізу графіків видно, що при одній і тій же температурі (Т1=Т2) гази мають різні об’єми. При цьому, V1 ˃ V2. А це означає що р1 ˂ р2. Дійсно, якщо Т1=Т2 і V1˃V2, то із p1V1/T1=p2V2/T2 випливає, що р1 ˂ р2.
Висновок. Нахил ізобари залежить від тиску газу: чим більший тиск, тим менший нахил (відносно осі температур).
Задача 7. На малюнку зображено дві ізотерми, побудовані для однієї і тієї ж маси газу. Порівняйте температури цих газів.
Рішення. Оскільки мова йде про одну і ту ж масу газу, то можна стверджувати, що згідно з об’єднаним газовим законом p1V1/T1=p2V2/T2. Із аналізу графіків видно, що при одному і тому ж об’ємі газу (V1=V2) гази мають різні тиски. При цьому, р2˃р1. А це означає що Т2>Т1. Дійсно, якщо V1=V2 і р2˃р1, то із p1V1/T1=p2V2/T2 випливає, що Т2>Т1.
Задача 8. За представленим на малюнку графіком зміни стану ідеального газу в координатах р–V, побудувати відповідні графіки в координатах р–Т і V–T.
Рішення. Із аналізу заданого графіку ясно, що процеси які відповідають переходам 1→2 і 3→4 є ізохоричними (V=const). А це означає, що в координатах р–Т цим переходам відповідають певні ізохори, тобто прямі які проходять через точку Т=0. При цьому кут нахилу ізохори залежить від величини об’єму газу: чим більший об’єм, тим менший кут нахилу. Зважаючи на вище казане, будуємо відповідний графік в координатах р–Т. (Оскільки числові значення об’ємів, тисків та температур не задані, то відповідний графік має загальний вигляд).
Із аналізу заданого графіку ясно, що процеси які відповідають переходам 2→3 і 4→1 є ізобаричними. А це означає, що в координатах V–Т цим переходам відповідають певні ізобари, тобто прямі які проходять через точку Т=0. При цьому кут нахилу ізобари залежить від величини тиску газу: чим більший тиск, тим менший кут нахилу. Зважаючи на вище казане, будуємо відповідний графік в координатах V-Т. (Зауваження: на графіку точки 2 і 4 потрібно поміняти місцями).
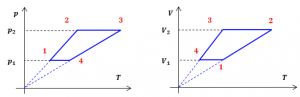
Задача 9. За заданим графіком термодинамічного процесу опишіть цей процес (ділянка 1-2 є ізотермою). Зобразіть графік цього процесу в координатах р–Т та V–T
Рішення. На основі почергового аналізу кожної ділянки заданого графіку та застосування об’єднаного газового закону (рV/T=const) можна зробити наступні висновки.
На ділянці 1-2 газ ізотермічно (Т=const) розширюється (V↑). А це означає, що на цій ділянці виконується закон Бойля-Маріотта (рV=const) і тому тиск газу зменшується р↓. Таким чином на ділянці 1-2:
– температура газу не змінюється (Т=const),
– об’єм газу збільшується (V↑),
– тиск газу зменшується (р↓),
– виконується співвідношення рV=const.
На ділянці 2-3, тиск газу залишається незмінним (р=const), а його об’єм зменшується (V↓). А це означає, що на цій ділянці виконується закон Гей-Люсака (V/T=const) і тому газ ізобарично охолоджується. При цьому:
– тиск газу не змінюється (р=const)
– об’єм газу зменшується (V↓),
– температура газу зменшується (Т↓),
– виконується співвідношення V/T=const.
На ділянці 3-1, об’єм газу залишається незмінним (V=const), а його тиск збільшується (р↑). А це означає, що на цій ділянці виконується закон Шарля (р/T=const) і тому газ ізохорично нагрівається (Т↑). При цьому:
– об’єм газу не змінюється (V=const),
– тиск газу збільшується (р↑),
– температура газу збільшується (Т↑),
– виконується співвідношення р/T=const.
На основі результатів вище проведеного аналізу зображаємо графік заданого процесу в координатах р–Т та V–T.
Задача 10. Графік термодинамічного процесу в координатах V–Т має вигляд кола. На якій ділянці цього графіку тиск газу збільшується а на якій зменшується?
Рішення. Розв’язуючи задачу 1, ми з’ясували, що кут нахилу ізобари (α) залежить від тиску газу: при зростанні тиску (р↑) цей нахил зменшується (α↓) і навпаки. А це означає, що для даного колового процесу, найбільший тиск буде в тій точці через яку пройде ізобара з найменшим нахилом, тобто в точці В. А найменший тиск буде в тій точці через яку пройде ізобара з найбільшим нахилом, тобто в точці D. Із вище сказаного ясно, що на ділянці B→C→D тиск зростає, а на ділянці D→A→B – падає.
Задача 11. За заданим графіком термодинамічного процесу, визначити характер зміни об’єму газу (маса газу незмінна).
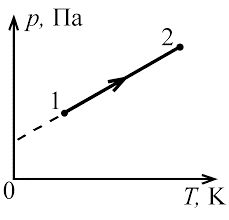
Рішення. Оскільки лінія заданого теплового процесу не проходить через точку Т=0К, то ця лінія не є ізохорою (V≠const). Для з’ясування того, як в заданому термодинамічному процесі змінюється об’єм газу, виконуємо декілька додаткових побудов. По перше, через точки 1 і 2 проводимо дві ізохори (V1=const, V2=const). По друге, проводимо довільну ізобару (р=const) яка перетинає обидві ізохори.
Із аналізу проведених побудов видно, що при р=const: Т2˃Т1. А це означає, що згідно з законом Гей-Люсака (V1/Т1=V2/Т2), об’єм газу в точці 1 має бути меншим за його об’єм в точці 2: V1 ˂ V2 . Таким чином, в заданому термодинамічному процесі об’єм газу збільшується.
Зауваження: розв’язуючи дану задачу, замість довільної ізобари можна провести довільну ізотерму, та застосовуючи закон Бойля–Маріотта, зробити аналогічний висновок.
Задача 12. За заданим графіком термодинамічного процесу, визначити температуру газу в точках 2, 3, 4, якщо відомо, що в точці 1 ця температура становить Т0. Маса газу незмінна.
Рішення. Оскільки на ділянці 1→2 об’єм газу залишається незмінним (V=const), то згідно з законом Шарля: р1/Т1=р2/Т2 або Т2=Т1р2/р1 . Враховуючи, що Т1=Т0 , р1=р0, р2=5р0 , можна записати Т2=Т0(5р0/р0)=5Т0 .
Оскільки на ділянці 2→3 тиск газу залишається незмінним (р=const), то згідно з законом Гей-Люсака: V2/T2=V3/T3 звідси T3=T2(V3/V2). Враховуючи що T2=5T0, V2=V0, V3=3V0, можна записати: T3=5T0(3V0/V0)=15T0.
Оскільки на ділянці 3→4 об’єм газу залишається незмінним (V=const), то згідно з законом Шарля: р3/Т3=р4/Т4, звідси Т4=Т3(р4/р3). Враховуючи що Т3=15Т0, р3=5р0 , р4=р0 , можна записати: Т4=15Т0(р0/5р0)=3Т0 .
Відповідь: Т1=Т0; Т2=5Т0; Т3=15Т0; Т4=3Т0.
Вправа 7.
- Об’єм газу при температурі 27°С і тиску 1,5атм становить 10л, яким буде цей об’єм за нормальних умов?
- Визначити масу вуглекислого газу в балоні ємністю 40л при температурі 17°С і тиску 50атм.
- Визначити густину кисню при температурі 17°С і тиску 204кПа.
- В посудині об’ємом 5л знаходиться 10г кисню і 20г азоту. Який тиск суміші цих газів при температурі 27ºС?
- При ізобаричному нагрівання газу, його густина збільшилась вдвічі. Як і у скільки разів змінилась абсолютна температура газу?
- В балоні міститься газ при температурі 17°С і тиску 1МПа. На скільки знизиться тиск газу при його охолодженні до –23°С?
- Густина газу при тиску 100кПа становить 1,43кг/м3. Визначте середню квадратичну швидкість молекул цього газу.
- Визначте концентрацію молекул газу при температурі 27ºС і тиску в одну атмосферу. Чи залежить ця концентрація від сорту газу?
- В лабораторних умовах при температурі 20ºС створено глибокий вакуум який відповідає тиску 1,33∙10–9Па. Скільки молекул залишатиметься при цьому в кожному см3 даного вакууму?
- На графіку зображено дві ізохори (мал.а) побудовані для однієї і тієї ж маси газу. Порівняйте об’єми цих газів. Зробіть узагальнюючий висновок.
- За заданим графіком термодинамічного процесу (мал.б) опишіть цей процес.
- За заданим графіком термодинамічного процесу (мал.в) опишіть цей процес (ділянка 3-1 є ізотермою
. а) б) в)
- За представленим на малюнку (г) графіком зміни стану ідеального газу в координатах р–V, побудувати відповідні графіки в координатах р–Т і V–T.
- Графік термодинамічного процесу в координатах р–V (мал.д) має вигляд кола. На якій ділянці цього графіку температура газу збільшується, а на якій зменшується?
- За заданим графіком термодинамічного процесу (мал.е), визначити характер зміни тиску газу (маса газу незмінна).
· г) д) е)
Лекційне заняття №8.
Тема: Пари та їх властивості. Пароутворення. Види пароутворення. Критичний стан речовини.
Загально відомо, що в герметично закритій посудині, рівень рідини з плином часу залишається незмінним. А це означає, що між рідиною і тим паром що знаходиться над нею, існує певна динамічна рівновага, тобто такий стан кругообігу їх молекул, при якому інтенсивність випаровування рідини дорівнює інтенсивності конденсації її пару. Пар, що знаходиться в стані динамічної рівноваги зі своєю рідиною називають насиченим паром.
Вивчаючи властивості різних газів, ми дійшли висновку: для постійної маси будь якого газу виконуються певні кількісні співвідношення які називаються газовими законами. При цьому виникає закономірне запитання: “А чи виконуються газові закони для тих газоподібних речовин, які називаються парами?”. Відповідаючи на це запитання звернемось до експерименту і на реальному насиченому пару, перевіримо найпростіший з газових законів – закон Бойля-Маріотта (якщо m=const, T=const, то pV=const).
Дослідження показують (мал.34), що при постійній температурі, будь які зміни об’єму насиченого пару не призводять до суттєвих змін того тиску. І це закономірно. Адже при збільшенні об’єму посудини, певна додаткова частина рідини перетворюється на пар. При зменшені ж цього об’єму, відповідна частина пару перетворюється на рідину. Це еквівалентно тому, якби перевіряючи справедливість закону Бойля – Маріотта, ми б забули закрити той кран, що відділяє досліджуваний газ від атмосферного повітря.

Мал.34. Тиск насиченого пару не можна змінити шляхом зміни його об’єму.
Дослідження показують, що тиск, а отже і густина насиченого пару визначальним чином залежать від двох обставин: індивідуальних властивостей відповідної рідини та температури системи рідина–пар. При цьому, в процесі підвищення температури, тиск насиченого пару збільшується, а при зниженні температури – зменшується. Однак, якщо в процесі ізохоричного (V=const; m=const) нагрівання газу, його тиск зростає лінійно і відносно повільно (при нагріванні від 0ºС до 273ºС тиск газу збільшується вдвічі, мал.35а), то в процесі відповідного нагрівання системи рідина–пар, тиск насиченого пару зростає параболічно швидко (мал.35б).

Мал.35. В процесі нагрівання тиск газу збільшується лінійно, а тиск пару – параболічно.
Залежність густини та тиску насиченого пару загалом і водяного пару зокрема від температури, важко представити у вигляді певного математичного співвідношення. Зазвичай цю залежність визначають експериментально і записують у відповідну таблицю, наприклад таку.
Таблиця 1. Залежність густини та тиску насиченого водяного пару від температури.
| t (°С) | pн (кПа) | ρн (г/м3) | t (°С) | pн (кПа) | ρн (г/м3) |
| 0 | 0,61 | 4,8 | 80 | 47,33 | 293 |
| 10 | 1,23 | 9,4 | 90 | 70,12 | 424 |
| 20 | 2,33 | 17,3 | 100 | 101,3 | 588 |
| 30 | 4,24 | 30,3 | 120 | 200 | 1102 |
| 40 | 7,37 | 51,2 | 140 | 361 | 1894 |
| 50 | 12,33 | 83,0 | 160 | 618 | 3092 |
| 60 | 19,92 | 130,0 | 180 | 1002 | 4792 |
| 70 | 31,18 | 198,0 | 200 | 1555 | 7121 |
Чому ж в процесі підвищення температури, тиск насичених парів зростає нелінійно і набагато швидше аніж тиск газів? Щоб відповісти на це запитання, давайте згадаємо, що таке тиск і від чого він залежить. З точки зору молекулярно кінетичної теорії, тиск газоподібної речовини, це результат ударів молекул цієї речовини по відповідній поверхні. При цьому, згідно з основним рівнянням м.к.т. газів (p=(1/3)n0m0v2=(2/3)n0Eк), величина цього тиску залежить від концентрації молекул (n0) та їх середньої кінетичної енергії (Eк). І не важко збагнути, що при ізохоричному (V=const) нагріванні газу, збільшення тиску відбувається лише за рахунок збільшення кінетичної енергії його молекул (Ек↑). Адже при такому нагріванні концентрація молекул газу (n0=N/V) залишається незмінною (n0=const). При аналогічному ж нагріванні насиченого пару, тиск збільшується як за рахунок збільшення кінетичної енергії молекул, так і за рахунок збільшення їх концентрації (Ек↑; n0↑). При цьому, в процесі зростання температури, роль другого чинника (n0↑) стає все більш і більш визначальною.
Пари можуть бути не лише насиченими, а й ненасиченими. Наприклад, якщо після повного випаровування рідини, об’єм пару збільшити, то цей пар стане ненасиченим, тобто таким густина якого менша за густину відповідного насиченого пару (ρ ˂ ρн). Іншими словами, ненасиченим паром називають такий пар, густина якого менша за густину відповідного за температурою насиченого пару.
В загальних рисах, спрогнозувати поведінку ненасиченого пару не важко. Дійсно. Якщо пар ненасичений, то будь яка зміна його об’єму не призводить до перетворення пару на рідину. Тому, коли об’єм ненасиченого пару збільшується, то його тиск (а відповідно і густина) зменшується. А коли цей об’єм зменшується, то тиск (густина) відповідно збільшується. Звичайно до тих пір поки пар не стане насиченим.
Враховуючи факт того, що в процесі зміни як об’єму так і температури, маса ненасиченого пару залишається незмінною, можна передбачити, що термодинамічна поведінка ненасиченого пару має описуватись газовими законами. Однак, дослідження показують, що дане передбачення не є безумовно правильним, і що газові закони погано відображають реальні властивості ненасичених парів. Даний факт пояснюється тим, що для парів, кінетична енергія молекул не настільки сильно перевищує енергію їх взаємодії, щоб останню можна було не враховувати. По суті це означає, що молекули пару не надто схожі на пружні кульки. Вони скоріш нагадують кульки виготовлені з липкої гуми. При взаємодії такі кульки можуть як відскакувати одна від одної (якщо їх швидкості достатньо великі), так і прилипати одна до одної (якщо їх швидкості відносно малі).
Втім, при наближених розрахунках прийнято вважати, що ненасичені пари підпорядковуються газовим законам. Виходячи з цього будемо вважати, що для ненасичених парів виконуються співвідношення pV/T = const; pV/T = (m/M)R; р = (1/3)n0m0v2, тощо.
Розрізняють дві різновидності пароутворення: випаровування та кипіння. Випаровування, це таке пароутворення, яке відбувається при будь якій температурі рідини і при якому перехід речовини з рідкого стану в газоподібний здійснюється лише з вільної поверхні рідини. Інтенсивність випаровування залежить від сорту рідини та її температури: з підвищенням температури, інтенсивність випаровування збільшується і навпаки.
Пояснюючи фізичну суть та причини випаровування можна сказати наступне. Як відомо, агрегатний стан речовини визначальним чином залежить від співвідношення між середньою кінетичною (Ек) та середньою потенціальною (Еп) енергіями її молекул. При цьому, якщо Ек ˂ Еп, то речовина знаходиться в твердому стані, якщо Ек ˃ Еп – в газоподібному, а якщо Ек ≈ Еп – в стані рідини. Відомо також, що температура характеризує середню кінетичну енергію теплового руху молекул і що при одній і тій же температурі, в будь якій речовині зустрічаються молекули, кінетична енергія яких як значно більша так і значно менша за середню величину. Ясно, що в такій ситуації, ті молекули поверхневого шару рідини, кінетична енергія яких більша за потенціальну енергію взаємодії молекул, вилітають за межі рідини і стають молекулами відповідного пару. При цьому, чим більша температура рідини, тим більшою буде інтенсивність її випаровування.
Дослідження показують, що в процесі випаровування, температура рідини знижується, а в процесі конденсації пару – підвищується. Даний експериментальний факт має своє теоретичне пояснення. Дійсно. Оскільки в процесі випаровування, рідину покидають найбільш енергійні (найбільш “гарячі”) молекули, то ясно, що загальний енергетичний рівень тих молекул які залишаються в рідині стає відповідно меншим. А отже, відповідно меншою стає і температура рідини. З іншого боку, в процесі конденсації, ті молекули пару які “падають” в рідину, в процесі падіння отримують певну кількість додаткової енергії, а отже стають відповідно більш “гарячими”. Це аналогічно тому, як підняте над землею нерухоме (“холодне”) тіло, в процесі падіння збільшує свою кінетичну енергію і падає на землю відповідно більш “гарячим”.
Потрібно зауважити, що твердження: “при випаровуванні, температура рідини зменшується, а при конденсації – збільшується”, по суті означає, що процес випаровування відбувається з поглинанням енергії, а процес конденсації – з виділенням енергії. Доречно зауважити і те, що процес випаровування, можна представити як певне розширення речовини, а процес конденсації – як її стиснення (згущення). При цьому, як і будь яке розширення, випаровування супроводжується зниженням температури відповідної речовини. Натомість, процес конденсації, як і процес будь якого стиснення, супроводжується нагріванням речовини.
Факт того, що в процесі випаровування, температура речовини знижується, а в процесі конденсації – підвищується, корисно застосовується в багатьох технічних приладах, зокрема в холодильниках (мал.36).
Мал.36. Загальний устрій та принципова схема холодильника.
Холодильна установка представляє собою замкнуту герметичну систему, заповнену речовиною яка легко переходить з газоподібного стану в рідкий і навпаки. Зазвичай, цією речовиною є фреон (фреони – технічна назва групи фторовмісних речовин, які мають відносно низьку температуру кипіння, наприклад для фреону СF2Cℓ2 ця температура становить -29ºС).
Основними технічними елементами холодильника є компресор (4), капілярна трубка (2), конденсатор-теплообмінник (1), випаровувач-морозильна камера (3). Принцип дії холодильника полягає в наступному. Компресор у поєднанні з капілярною трубкою, створює в системі теплообмінника зону підвищеного тиску (≈1,6атм), а в системі морозильної камери – зону зниженого тиску (≈0,6атм). В такій ситуації, та рідина, яка через вузьку капілярну трубку потрапляє в систему морозильної камери (випаровувач) швидко випаровується і охолоджується до температури -20ºС. Проходячи трубками морозильної камери, холодний пар охолоджує навколишній простір і за рахунок отриманої від нього енергії, нагрівається до температури -5ºС (вказані числові значення тисків та температур є усередненими). Потрапляючи через компресор в зону підвищеного тиску (в систему теплообмінника), цей пар швидко конденсується. При цьому виділяється велика кількість енергії, за рахунок якої сконденсована рідина нагрівається до температури +50ºС. Проходячи трубками теплообмінника, гаряча рідина частину своєї енергії віддає навколишньому середовищу і охолоджується до температури +20ºС. Ця охолоджена рідина, через капілярну трубку знову потрапляє в систему морозильної камери. Знову випаровується, охолоджується і т.д.
Таким чином, в процесі замкнутого кругообігу, робоче тіло холодильника, в одному місці охолоджується, а в іншому – нагрівається. При цьому холодильник, з одного боку є джерелом холоду, а з іншого – джерелом тепла. Не важко збагнути, що розмістивши морозильну камеру холодильника в одній кімнаті, а його теплообмінник в іншій, можна змусити один і той же прилад виконувати дві корисні роботи. І ці дві послуги коштуватимуть нам як одна. Втім, потенціальні можливості холодильника не завжди співпадають з нашими практичними потребами.
До числа тих приладів принцип дії яких є аналогічним принципу дії холодильника, відносяться різноманітні кондиціонери та так звані теплові насоси.
Випаровування, це відносно спокійний вид пароутворення при якому утворення пару відбувається лише з вільної поверхні рідини, тобто з тієї поверхні яка контактує з навколишнім газоподібним середовищем. Однак утворення пару може відбуватись і в усьому об’ємі рідини. Це інтенсивне пароутворення називають кипінням. Візуальною ознакою того процесу який називається кипінням є утворення в рідині заповнених її паром бульбашок. А це означає, що в процесі кипіння, утворення пару відбувається не лише з вільної поверхні рідини, а в усьому об’ємі рідини.
Кипіння – це таке інтенсивне пароутворення, яке відбувається при певній постійній температурі (температурі кипіння) і при якому утворення пару відбувається в усьому об’ємі рідини. Візуальною ознакою кипіння є утворення наповнених паром бульбашок.
Коли ми стверджуємо, що кипіння відбувається при певній постійній температурі, то маємо на увазі факт того, що величина цієї температури не залежить ні від тривалості процесу кипіння ні від його інтенсивності. Скажімо, якщо ви збільшите інтенсивність того вогню що підтримує процес кипіння, то це не призведе до підвищення температури кипіння. Просто інтенсивність процесу кипіння стане більшою.
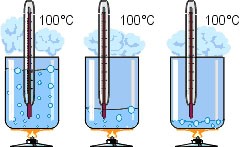
Мал.37. Температура кипіння практично не залежить ні від тривалості процесу кипіння, ні від інтенсивності цього процесу.
З іншого боку, твердження про те, що кипіння відбувається при певній постійній температурі, зовсім не означає що ця температура є абсолютно незмінною. Адже кипіння відбувається при тій температурі, при якій тиск насиченого пару рідини дорівнює зовнішньому тиску на її поверхню. А це означає, що зменшуючи зовнішній тиск, ми створюємо умови за яких кипіння відбувається при меншій температурі. І навпаки, збільшуючи зовнішній тиск, ми створюємо умови, за яких кипіння відбувається при більш високій температурі. Тому, коли ми стверджуємо, що вода кипить при температурі 100ºС, то маємо на увазі, що це кипіння відбувається за нормального атмосферного тиску. Якщо ж тиск над поверхнею води змінювати, то відповідно змінюватиметься і температура її кипіння. Наприклад, під тиском 2атм вода кипить при температурі 120ºС, під тиском 20атм – при температурі 211ºС, під тиском 0,5атм – при температурі 80ºС, а під тиском 0,01атм – при температурі 6,7ºС.
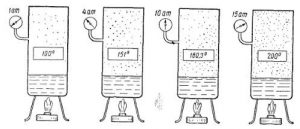
Мал.38. Температура кипіння певним чином залежить від величини зовнішнього тиску.
Температура кипіння рідини залежить не лише від зовнішнього тиску, а й від фізичних властивостей самої рідини. Скажімо, за нормального атмосферного тиску етиловий ефір кипить при температурі 35ºС, етиловий спирт – при температурі 78ºС, а рідкий кисень – при температурі -183ºС.
Факт того, що різні речовини мають різні температури кипіння, широко застосовується в багатьох технологічних процесах. Зокрема тих, які дозволяють із суміші речовин, виділити потрібну складову. Наприклад нафта, це складна суміш великої кількості хімічно різних компонентів (фракцій). При цьому, різні фракції цієї суміші мають суттєво різні температури кипіння. А це означає, що в процесі нагрівання нафти, спочатку випаровуватимуться фракції з найменшою температурою кипіння. Потім, фракції з більш високою температурою кипіння і т.д. При цьому, фізично однорідна нафта, розділяється на бензин, лігроїн, гас, газойль та мазут.
Нагадаємо. Парами називають такі газоподібні речовини, які знаходяться при докритичній температурі (t ˂ tкр). Газами називають такі газоподібні речовини, які знаходяться при закритичній температурі (t ˃ tкр). Що ж це за магічна температура яку називають критичною? Відповідаючи на це запитання можна сказати наступне.
Зазвичай густина рідини в десятки тисяч разів більша за густину її насиченого пару. Наприклад, при температурі 20ºС густина насиченого пару води становить 17,3 г/м3, що в 57800 разів менше за густину води. Візуальною ознакою наявної різниці густин, є факт того, що між рідиною та її паром існує видима межа яку називають поверхнею рідини.
Відомо, що в процесі нагрівання, рідини розширюються і що тому їх густина зменшується. Відомо і те, що густина насиченого пару залежить від температури і що з підвищенням температури ця густина збільшується. А якщо в процесі нагрівання, густина рідини зменшується, а густина її насиченого пару збільшується, то логічно передбачити, що за певних умов ці густини зрівнюються, і що при цьому різниця між рідиною та її насиченим паром зникне. Перевіряючи це теоретичне передбачення звернемось до експерименту. З цією метою, спеціальну скляну ампулу з певною кількістю етилового ефіру помістимо в невеличку металеву скриньку з скляним віконцем.
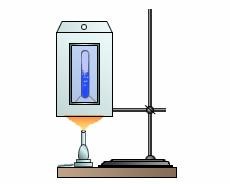
Мал.39. Прилад для ілюстрації критичного стану речовини.
Нагріваючи скриньку, а отже і ту ампулу що в ній знаходиться, ви побачите наступне. В процесі нагрівання, об’єм тієї рідини що знаходиться в ампулі буде поступово збільшуватись. При цьому, початково напівсферична вільна поверхня рідини, яку прийнято називати меніском (від грец. meniscus – напівмісяць) поступово вирівнюється. В кінцевому підсумку, при температурі 194ºС, та видима межа, що розділяє рідину і її насичений пар повністю зникає і в ампулі залишається однорідна прозора речовина. Припинивши подальше нагрівання і дочекавшись того моменту коли газоподібна речовина охолоне до температури 194ºС, ви побачите, що при цій температурі, в ампулі швидко утвориться густий туман конденсованого ефіру, і що після розсіювання цього туману, з’являються дві чітко окреслені фази речовини: рідина та її пар.
Вище описані експериментальні результати можна представити у вигляді наступного графіку.
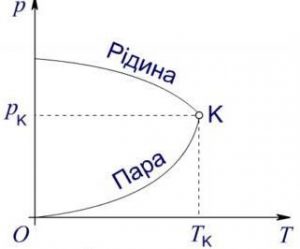
Мал.40. В процесі нагрівання, густина рідини зменшується, а густина її насиченого пару збільшується. При цьому, за певних критичних умов (tкр, ркр, ρкр), різниця між рідиною та її насиченим паром повністю зникає.
Таким чином, експериментальні дослідження показують, що при певній температурі та їй відповідному тиску, густина рідини (ρр) і густина її насиченого пару (ρн) стають чисельно рівними. При цьому, будь які відмінності між рідиною та її насиченим паром повністю зникають.
Той стан нестійкої рівноваги між рідиною та її насиченим паром, при якій густина рідини та густина пару стають чисельно рівними і при якому будь які відмінності між рідиною та її паром зникають, називають критичним станом речовини. Критичному стану речовини, відповідає певна критична температура (Ткр або tкр), певний критичний тиск (ркр) та певна критична густина (ρкр). Числові значення критичних параметрів деяких речовин представлені в таблиці.
Таблиця. Критичні параметри та температури кипіння деяких речовин.
| Речовина | Критичні параметри | Температуракипіння (ºС) | ||
| tкр (ºС) | ркр (атм) | ρкр (кг/м3) | ||
| вода | 374,2 | 218,5 | 320 | 100,0 |
| спирт етиловий | 243,1 | 63,0 | 270 | 78,4 |
| ефір етиловий | 193,8 | 35,5 | 260 | 34,6 |
| аміак | 132,4 | 111,5 | 240 | -33,3 |
| вуглекислий газ | 31,0 | 72,9 | 470 | -78,5 |
| кисень | -118,4 | 50,0 | 410 | -183,0 |
| азот | -147,0 | 33,5 | 310 | -195,8 |
| водень | -240,0 | 12,8 | 31 | -252,8 |
| гелій | -267,9 | 2,25 | 70 | -268,9 |
Оскільки ті газоподібні речовини які знаходяться при закритичній температурі (t ˃ tкр) називаються газами, а ті які знаходяться при докритичній температурі (t ˂ tкр) – парами, то ясно, чому за наявних земних умов (-50ºC ˂ t ˂ 50ºC), газоподібний кисень, газоподібний азот та газоподібний водень називають газами, а газоподібну воду, газоподібний спирт та газоподібний аміак, називають парами. До речі, якщо виходити “з букви закону”, то потрібно визнати, що в області помірних температур (до 31ºС), назва “вуглекислий газ” не є правильною. Адже вуглекислий газ фактично стає газом лише при температурах вищих за 31ºС. При нижчих температурах, цей газ фактично є паром вуглекислоти (СО2).
Тепер, коли ви знаєте про суть тих відмінностей що існують між паром та газом, не важко збагнути, що для перетворення газу на відповідну рідину, цей газ спочатку потрібно охолодити до певної докритичної температури (тобто перетворити на пар), а лише потім сконденсувати у відповідну рідину. Наприклад для того, щоб отримати рідкий кисень, його потрібно охолодити до температури нижчої за -118,4ºС. Однак, якщо ви захочите отримати таку рідину яку можна зберігати при нормальному атмосферному тиску, то її потрібно охолодити до температури нижчої за температуру кипіння відповідної рідини. Наприклад для кисню ця температура становить -183ºС. Власне при таких наднизьких температурах і зберігають рідкий кисень.
Потрібно зауважити, що критична температура є тією чіткою межею за якою будь яка речовина автоматично стає відповідним газом, тобто такою речовиною (таким станом речовини) для якої: V≠const; Ф≠const; Ек˃˃Еп. Вона стає газом навіть в тому випадку, якщо при докритичній температурі була рідиною. Наприклад вода, при закритичній температурі (t ˃ 374,2ºС) перестає бути рідиною і автоматично стає газом відповідної густини. Щоправда, нагріти воду до закритичної температури надзвичайно складно. Адже та посудина в якій ви збираєтесь це зробити має витримувати тиск в понад 218,5 атмосфер.
Доречно зауважити і те, що критичний стан речовини це такий динамічно нестійкий стан, при якому відповідна речовина одночасно є і рідиною, і паром, і газом. При цьому, при закритичній температурі, речовина автоматично стає газом, а при докритичній температурі вона, в залежності від тиску та густини може бути або рідиною, або паром, або частково рідиною а частково паром.
Задача 1. Тиск водяного пару при 15°С дорівнює 1200 Па, а його об’єм 5,7л. Яким буде тиск пару, якщо температуру підвищили до 27°С, а об’єм збільшили до 8,0л ?
Дано:
t1 = 15°С, Т = 288К
p1 = 1200 Па
V1 = 5,7л
t2 = 27°С, Т = 300К
V2 = 8,0л
р2 = ?
Рішення. Оскільки даний пар є явно ненасиченим (адже навіть при 10°С рн = 1230 Па), то будемо виходити з того, що для такого пару виконується співвідношення p1V1/T1 = p2V2/T2, p2 = p1V1T2/T1V2 = 1200Па∙5,7л∙300К/8,0л∙288К = 890 Па.
Відповідь: р2 = 890 Па.
Задача 2. В циліндрі під поршнем при температурі 30°С ізотермічно стискають 0,9г ненасиченого водяного пару. Яким буде об’єм пару в момент початку конденсації?
Дано:
m = 0,9г = 0,9∙10–3кг
t = 30°C, T = 303К
V = ?
Рішення. Оскільки пар ненасичений, то для нього виконується закон Менделєєва-Клапейрона pV/T = (m/M)R, звідси V = mТR/Мр, де R=8,31(Дж/К∙моль), М(Н2О) = 18∙10–3(кг/моль). Оскільки в момент початку конденсації р = рн(30°С) = 4240 Па, то можна записати V = mТR/Мр = 0,9∙10–3кг∙303К∙8,31(Дж/К∙моль)/18∙10–3(кг/моль)∙ 4240 Па = 30∙10–3(Дж/Па = Н∙м/Н/м2 = м3) = 30л.
Відповідь: V = 30л.
Задача 3. Визначити густину ненасиченого водяного пару при температурі 15°С, якщо величина його тиску 1200 Па.
Дано:
t = 15°C, T = 288K
р = 1200 Па
ρ = ?
Рішення. Будемо виходити з того, що для ненасиченого пару виконуються газові закони, в тому числі і закон Менделєєва-Клапейрона pV/T=(m/M)R, звідси m/V = pM/TR. Таким чином, густину ненасиченого пару можна визначити за формулою ρ= pM/TR, де R=8,31Дж/К∙моль, М(Н2О)= 18г/моль = 18·10–3 кг/моль.
Розрахунки: [ρ] = (Па·кг/моль)/(Дж/К·моль)К = Па·кг/Дж = Н·кг/м2·Н·м= кг/м3;
ρ= pM/TR = (120·103·18·10–3)/(288·8,31) = 0,90кг/м3.
Відповідь: ρ = 0,90кг/м3 = 900 г/м3.
Контрольні запитання.
- Який пар називають насиченим?
- Чому в процесі зменшення об’єму, густина насиченого пару не збільшується? Від чого залежить ця густина?
- Чому в процесі збільшення температури тиск газу збільшується лінійно, а тиск насиченого пару – параболічно?
- Чому в процесі випаровування температура рідини знижується, а в процесі конденсації – зростає?
- Поясніть загальний устрій та принцип дії холодильника (мал.36).
- Що мають на увазі коли стверджують, що кипіння відбувається при певній постійній температурі? Від чого залежить ця температура?
- Поясніть загальний устрій та принцип дії автоклава (мал.40)
- Чому по відношенню до насиченого пару газові закони не виконуються взагалі, а по відношенню до ненасиченого пару – лише частково?
- Чому залізо легко нагрівається до 1000 і більше ºС, тоді як нагріти воду до 300ºС надзвичайно складно?
- Чи можна при кімнатній температурі (20ºС) перетворити вуглекислий газ на відповідну рідину?
Вправа 8.
- За наданими в таблиці 1 даними, побудуйте графік залежності тиску насиченого пару від температури, для інтервалу температур від 0°С до 100°С.
- За наданими в таблиці 1 даними, побудуйте графік залежності густини насиченого пару від температури, для інтервалу температур від 0°С до 100°С.
- Тиск водяного пару при 27°С дорівнює 2300 Па, а його об’єм 4,5л. Яким буде тиск пару, якщо температуру знизили до 17°С, а об’єм збільшили до 7,0л ?
- Насичений водяний пар з температурою 20°С відділили від рідини і при постійному об’ємі нагріли до 30°С. Визначте тиск цього пару.
- Визначити густину ненасиченого водяного пару при температурі 35°С, якщо величина його тиску 2500 Па.
- Визначити тиск ненасиченого водяного пару при температурі 50°С, якщо його густина при цій температурі 50 г/м3.
- 276мг ненасиченого водяного пару, ізотермічно стискають. Коли об’єм пару зменшився до 12л, почалася його конденсація. При якій температурі відбувалося стиснення?
- В котел об’ємом 1м3 налили 3кг води і нагріли її до 180°С. Визначити масу, густину та тиск водяного пару.
.
Лекційне заняття №9.
Тема: Вологість повітря. Методи вимірювання вологості.
В атмосферному повітрі неминуче міститься певна кількість водяного пару. І це закономірно. Адже більша частина поверхні земної кулі вкрита водою, яка як відомо випаровується. І випаровується її надзвичайно багато. Дослідження показують, що на Землі щорічно в пар перетворюється близько 450 000км3 води (450·1012 тон). А це більше ніж її міститься в 1750 Азовських морів. При цьому абсолютно очевидно, що атмосферна волога знаходиться в постійному кругообігу. Адже паралельно з процесом випаровування неминуче відбувається і зворотній процес – процес конденсації. А це означає що ті 450 трильйонів тон води які щорічно випаровуються з поверхні Землі, неминуче повертаються на цю поверхню у вигляді дощу, снігу, роси, туману, тощо.
Кількість того водяного пару (вологи) що міститься в атмосферному повітрі, прийнято характеризувати двома величинами: абсолютна та відносна вологість повітря.
Абсолютна вологість повітря – це фізична величина, яка характеризує фактичну густину того водяного пару що міститься в повітрі і яка дорівнює цій густині.
Позначається: ρа
Визначальне рівняння: ρа = m(H2O)/V
Одиниця вимірювання: [ρа]=кг/м3, або [ρа]=г/м3.
З точки зору наших відчуттів, абсолютна вологість не є надто зручною величиною. Ця незручність полягає в тому, що при одній і тій же абсолютній вологості повітря, наші відчуття можуть бути суттєво різними. Наприклад, якщо абсолютна вологість повітря становить 6г/м3, то при температурі 5ºС це повітря ми будемо сприймати як надмірно вологе, а при температурі 25ºС – як надмірно сухе. Пояснюючи такий стан речей можна сказати наступне.
Наше сприйняття вологості є реакцією організму на результуючу двох споріднених процесів: процесу випаровування та процесу конденсації. При цьому, якщо кількість тієї вологи яку втрачає організм в процесі випаровування, значно перевищує ту кількість вологи яку він отримує в процесі конденсації, то відповідне повітря викликає у нас відчуття сухості. Якщо ж кількість випаруваної та конденсованої вологи приблизно однакова, то таке повітря ми сприймаємо як надмірно вологе.
По суті це означає, що наші відчуття визначальним чином залежать не від абсолютної вологості повітря, а від того наскільки ця вологість відрізняється від максимально можливої для даної температури вологості. Іншими словами, з точки зору наших відчуттів, більш вдалою характеристикою вологості повітря є не його абсолютна вологість, а величина яка дорівнює відношенню абсолютної вологості повітря до густини відповідного даній температурі насиченого пару. Цю величину прийнято називати відносною вологістю повітря.
Відносна вологість повітря – це фізична величина яка характеризує відносну вологість повітря і яка дорівнює відношенню фактичної густини того пару що знаходиться в повітрі (абсолютної вологості повітря), до його максимально можливої при даній температурі густини (густини насиченого пару).
Позначається: В
Визначальне рівняння: В = (ρа/ρн)100%
Одиниця вимірювання: [В] = % .
Дослідження показують, що для організму людини, максимально комфортною є ситуація при якій відносна вологість повітря знаходиться в межах від 40 до 60 відсотків. При цьому повітря, відносна вологість якого менша 40% вважається в тій чи іншій мірі сухим. А повітря, відносна вологість якого більша 60%, вважається в тій чи іншій мірі надмірно вологим.
Зважуючи на ці обставини та враховуючи факт того, що в процесі зростання температури, густина насиченого пару збільшується (дивись табл.) не важко пояснити чому, одна і та ж абсолютна вологість повітря (ρа=const) при різних температурах сприймається по різному. Дійсно. Якщо абсолютна вологість повітря 6,0г/м3, то при температурі 5ºС (для цієї температури ρн=6,8г/м3) його відносна вологість 88%, а при температурі 25ºС (для цієї температури ρн=23,0г/м3) – всього 26%.
Таблиця. Густина насиченого водяного пару при різних температурах.
| t (ºC) | ρн (г/м3) | t (ºC) | ρн (г/м3) | t (ºC) | ρн (г/м3) |
| 0 | 4,8 | 12 | 10,7 | 24 | 21,8 |
| 1 | 5,2 | 13 | 11,4 | 25 | 23,0 |
| 2 | 5,6 | 14 | 12,1 | 26 | 24,4 |
| 3 | 6,0 | 15 | 12,8 | 27 | 25,8 |
| 4 | 6,4 | 16 | 13,6 | 28 | 27,2 |
| 5 | 6,8 | 17 | 14,5 | 29 | 28,7 |
| 6 | 7,3 | 18 | 15,4 | 30 | 30,3 |
| 7 | 7,8 | 19 | 16,3 | 40 | 51,2 |
| 8 | 8,3 | 20 | 17,3 | 50 | 83,0 |
| 9 | 8,8 | 21 | 18,3 | 60 | 130,0 |
| 10 | 9,4 | 22 | 19,4 | 80 | 293 |
| 11 | 10,0 | 23 | 20,6 | 100 | 598 |
Потрібно зауважити, що відносна вологість вдало характеризує зволоженість атмосферного повітря, не лише з точки зору наших суб’єктивних відчуттів, а й з точки зору переважної більшості тих природних процесів, які так чи інакше пов’язані з випаровуванням та конденсацією води. Наприклад інтенсивність процесу висушування білизни, деревини, фруктів та інших об’єктів, визначальним чином залежить не від абсолютної вологості повітря, а від його відносної вологості. Або, наприклад, поява конденсованої атмосферної вологи (туману, роси, інею, тощо) відбувається не тоді, коли абсолютна вологість повітря є надто високою, а тоді коли його відносна вологість дещо перевищує 100%.
Дійсно. Припустимо, що в сонячний літній день, при температурі 25ºС абсолютна вологість повітря становить 16,3г/м3, що відповідає відносній вологості 71%. Припустимо також, що вночі температура повітря знизилась до 15ºС, тобто до температури при якій в одному кубічному метрі повітря може знаходитись не більше 12,8 грамів води. Ясно, що за таких умов, в кожному кубічному метрі повітря буде знаходитись 16,3–12,8=3,5г надлишкової вологи. Вологи, яка неминуче конденсується в росу, туман чи інші види опадів.
Температуру, при якій повітря в процесі охолодження стає насиченим водяними парами, прийнято називати точкою роси. Іншими словами, точка роси (позн. tр) це така температура, при якій абсолютна вологість повітря (ρа) в процесі охолодження стає рівною густині відповідного цій температурі насиченого пару (ρа = ρн(tр)). Скажімо, в умовах вище наведеного прикладу (t=25ºС; ρа=16,3г/м3), точкою роси є температура 19ºС (ρн(19ºС)=16,3г/м3).
Абсолютну і відносну вологість повітря вимірюють різними приладами, більшість з яких прийнято називати гігрометрами (від грец. hygros – волога, та metreo – вимірюю). До числа таких приладів відносяться: ваговий гігрометр, конденсаційний гігрометр, волосяний гігрометр та психрометр.
Ваговий гігрометр – це прилад, який дозволяє визначати абсолютну вологість повітря шляхом прямого вимірювання маси того пару що знаходиться в певному об’ємі повітря. Ваговий гігрометр (мал.43) представляє собою систему U-подібних трубок заповнених гігроскопічною речовиною. Принцип дії такої системи дуже простий. Через ваговий гігрометр, за допомогою насосу проганяється певна відома кількість атмосферного повітря. При цьому наявна в повітрі волога поглинається гігроскопічною речовиною і стає відповідно важчою. Визначивши масу гігроскопічного тіла до і після експерименту, а також знаючи об’єм того повітря що пройшло через гігрометр, не важко визначити відповідну абсолютну вологість повітря: ρа =∆m/V.
Мал.43. Загальний вигляд вагового гігрометра.
Конденсаційний гігрометр – це прилад, який дозволяє визначати абсолютну та відносну вологість повітря шляхом експериментального вимірювання точки роси. Принцип дії конденсаційного гігрометра базується на наступних засадах. За визначенням В = (ρа/ρн)100%. Визначити густину насиченого пару (ρн) не важко. Для цього достатньо виміряти температуру повітря і за відповідною таблицею визначити відповідну цій температурі густину насиченого пару.
Якщо ж говорити про густину того пару що фактично знаходиться в повітрі і яку називають абсолютною вологістю, то в загальному випадку ця густина є на відомою (ρа=?). Натомість відомо, що в процесі охолодження, пар рано чи пізно стає насиченим, тобто таким фактична густина якого дорівнює густині насиченого пару. А це означає, що визначивши ту температуру при якій повітря стає насиченим водяними парами (цю температуру називають точкою роси tр), ми за тією ж табл. можемо визначити абсолютну вологість повітря, яка фактично дорівнює густині насиченого пару для точки роси: ρа=ρн(tр).
Таким чином, для визначення абсолютної вологості повітря, необхідно експериментально визначити його точку роси. Власне для цього і призначений конденсаційний гігрометр. Цей прилад (мал.44) представляє собою спеціальну ємність, передня металева стінка якої відполірована до дзеркального блиску. В верхній частині цієї ємності є невеличкий отвір, через який заливається рідина з високою інтенсивністю випаровування (зазвичай – етиловий ефір) і в який вставляється відповідних розмірів термометр. Крім цього, ємність з’єднана з гумовою грушою, за допомогою якої пари рідини виштовхуються назовню.
Мал.44. Загальний вигляд (а) та внутрішній устрій (б) конденсаційного гігрометра.
Принцип дії конденсаційного гігрометра полягає в наступному. В процесі інтенсивного випаровування, рідина (ефір), а разом з нею і відполірована поверхня гігрометра охолоджуються. При цьому охолоджується і те повітря що знаходиться в безпосередньому контакті з відповідною поверхнею. Коли температура цього повітря стане дещо нижчою за точку роси, наявний в ньому пар стане перенасиченим і почне конденсуватися. При цьому відполірована поверхня запітніє. Зафіксувавши температуру при якій починається це запітніння, ми по суті визначаємо точку роси для даного повітря. А знаючи точку роси, за відповідною таблицею визначаємо і їй відповідну абсолютну вологість повітря: ρа = ρн(tр).
Таким чином, знаючи температуру повітря і визначивши його точку роси, можна визначити як абсолютну так і відносну вологість цього повітря. Наприклад, якщо температура повітря 20ºС, а його точка роси 12ºС, то ρн(20ºС)=17,3г/м3; ρа=ρн(12ºС)=10,7г/м3; В=ρн(12ºС)/ρн(20ºС)=(10,7/17,3)100% = 62%.
Визначення відносної вологості повітря за допомогою конденсаційного гігрометра є достатньо трудоємким процесом, який крім всього іншого потребує певної кваліфікації експериментатора. Адже якщо наприклад, в процесі вимірювань ви будите дихати в безпосередній близькості від дзеркальної поверхні гігрометра, то теплі і насичені вологою продукти вашого дихання, потрапляючи на цю поверхню спричинять її запотівання при суттєво більшій за точку роси температурі. І в цьому сенсі прилад який називається психрометром є значно зручнішим.
Мал.45. Загальний вигляд побутового (а) та лабораторного (б) психрометрів.
Психрометр (від грец. psicros – холодний) – це прилад, який дозволяє визначати відносну вологість повітря на основі показань сухого та зволоженого термометрів. Будова психрометра гранично проста (мал.45). Він складається з двох однакових термометрів, термочутливий елемент одного з яких обгорнутий шматком змоченої у воді тканини. Принцип дії цієї простої системи полягає в наступному. Відомо, що в процесі випаровування, температура рідини знижується, а в процесі конденсації – підвищується. При цьому, не важко збагнути, що інтенсивність процесу конденсації певним чином залежить від вологості повітря: при високій вологості, кількість конденсованих молекул буде великою, а при низькій – малою. По суті це означає, що та різниця температур (∆t) яка існує між показаннями сухого і зволоженого термометрів, певним чином залежить від температури та відносної вологості повітря. Дослідивши цю залежність вчені склали відповідну таблицю за допомогою якої і визначають відносну вологість повітря. Наприклад для зображеної на мал.45а ситуації (tc=24ºC; tв=20ºC; ∆t=4ºC) В=69%.
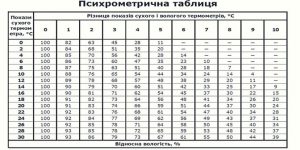
Потрібно зауважити, що зображений на мал.45(а) психрометр, має той недолік, що визначена на його основі відносна вологість, практично завжди є дещо завищеною. І це закономірно. Адже в тому місці де знаходиться зволожений термометр, вологість повітря дещо вища за її фактичну величину. Вища тому, що саме там і відбувається процес випаровування. А це означає, що зволожений термометр фактично реагує не на ту вологість яка є в кімнаті, а на ту, яка існує в місці його знаходження. Запобігаючи цьому недоліку, в сучасних лабораторних психрометрах (мал.45б) передбачено примусове перемішування повітря, яке здійснюється за допомогою спеціального механічного або електричного вентилятора.
Вагові гігрометри, конденсаційні гігрометри та лабораторні психрометри, це прилади достатньо точні, надійні та об’єктивні. Однак їх практичне застосування потребує наявності певних знань і вмінь. Крім цього, дані прилади є приладами опосередкованої (непрямої) дії. Адже визначаючи вологість повітря, ми фактично вимірюємо не вологість, а інші, з нею пов’язані величини (масу, об’єм, температуру). Сама ж вологість визначається на основі відповідних вимірювань та відомих співвідношень. Ясно, що для побутової практики, такий опосередкований спосіб вимірювань є мало прийнятним.
В побутовій практиці, відносну вологість повітря зазвичай вимірюють гігрометрами прямої дії. Принцип дії цих гігрометрів базується на тому, що певні властивості деяких об’єктів, певним чином залежать від відносної вологості повітря. Наприклад в сухому повітрі, клітини втрачають вологу і зменшуються в розмірах (всихають), а у вологому повітрі вони цю вологу накопичують і відповідно збільшуються у розмірах (набухають). А це означає, що лінійні розміри тих об’єктів які мають клітинну структуру, певним чином залежать від відносної вологості повітря. Дослідивши цю залежність можна створити відповідний прилад прямої дії. Одним з таких приладів є так званий волосяний гігрометр.
Волосяний гігрометр – це прилад, який дозволяє вимірювати відносну вологість повітря за допомогою знежиреного волосся. Основним волого чутливим елементом волосяного гігрометра є знежирена волосина (або пучок таких волосин) яка певним чином з’єднана з рухомою стрілкою приладу (мал.46). Принцип дії такої системи полягає в наступному. При зміні відносної вологості повітря, довжина волосини певним чином змінюється. При цьому, стрілка приладу відхиляється і вказує на відповідну величину відносної вологості.
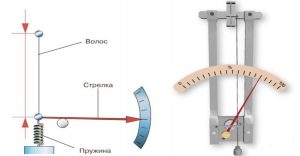
Мал.46. Принциповий устрій волосяного гігрометра.
З точки зору побутової зручності, волосяний гігрометр є надзвичайно вдалим приладом. Однак з точки зору наукової об’єктивності, він не є тим приладом, показанням якого можна безумовно довіряти. Адже в процесі експлуатації, волого чутливий елемент волосяного гігрометра практично неминуче змінює свої властивості, наприклад за рахунок того, що покривається тонким шаром жирів. А це означає, що користуючись волосяним гігрометром, потрібно періодично звіряти його показання з показаннями інших, більш надійних приладів, скажімо тих же конденсаційних гігрометрів чи психрометрів.
Задача 1. При температурі 20ºС відносна вологість повітря 70%. Скільки вологи виділиться з кожного кубічного метра повітря при його охолодженні до 11ºС?
Дано:
t1 = 20ºС
B1 = 70%
t2 = 11ºС
V=V1=V2=1м3
∆m/V = ?
Рішення. По суті рішення задачі зводиться до визначення різниці між наявною при температурі 20ºС абсолютною вологістю повітря (ρа1), та максимально можливою для температури 11ºС вологістю, яка дорівнює густині насиченого пару при температурі 11ºС, ρн(11ºС) = 10,0г/м3. Іншими словами ∆m/V = ρа1 – ρн(11ºС). Оскільки В1 = (ρа1/ρн1)100%, то ρа1 = ρн1В1/100%, а враховуючи що ρн1(20ºС) = 17,3г/м3, отримаємо ρа1 = 17,3·70/100 = 12,1г/м3. Таким чином ∆m/V = 12,1 – 10,0 = 2,1г/м3.
Відповідь: ∆m/V = 2,1г/м3.
Задача 2. У кімнаті при температурі 20ºС відносна вологість повітря 20%. Скільки води треба додатково випарувати, щоб збільшити вологість до 60%? Об’єм кімнати 60м3.
Дано:
t = 20ºC
B1 = 20%
B2 = 60%
V = 60м3
∆m = ?
Рішення. За визначенням ρ=m/V, звідси m=ρV. А оскільки в умовах нашої задачі при незмінному об’ємі кімнати (V=const) змінюється густина водяного пару в ній, то ∆m=∆ρV, де ∆ρ = ρa2 – ρa1. Оскільки за визначенням В=(ρа/ρн)100%, то ρа = ρн·В/100%, де для t=20ºC, ρн = 17,3г/м3.
Розрахунки: ρа1 = ρн·В1/100% = 17,3(г/м3)·20%/100% = 3,46(г/м3),
ρа2 = ρн·В2/100% = 17,3(г/м3)·60%/100% = 10,38(г/м3),
∆ρ = ρa2 – ρa1 = 10,38(г/м3) – 3,46(г/м3) = 6,92(г/м3),
∆m=∆ρV = 6,92(г/м3)·60м3 = 415г.
Відповідь: ∆m = 415г.
Контрольні запитання.
- Чому, з точки зору наших відчуттів, абсолютна вологість повітря не є зручною величиною.
- Чому при зниженні температури в повітрі відчувається вогкість.
- Як пояснити появу роси та туману?
- Поясніть загальний устрій та принцип дії вагового гігрометра.
- Поясніть будову та принцип дії конденсаційного гігрометра.
- Чим конденсаційний гігрометр схожий на холодильник.
- Чому температура вогкого термометра практично завжди менша за температуру сухого? За яких умов ці температури будуть однаковими?
- Поясніть будову та принцип дії психрометра.
- Поясніть будову та принцип дії волосяного гігрометра.
- Які переваги та недоліки волосяного гігрометра?
Вправа 9.
- Яка абсолютна і відносна вологість повітря, якщо його температура 18ºС, а точка роси 10ºС.
- Абсолютна вологість повітря при 28ºС становить 14г/м3, а при 2ºС – 4г/м3. В якому випадку за відчуттями, повітря буде більш вологим?
- При 25ºС відносна вологість повітря становить 70%. Скільки вологи виділиться з кожного кубічного метра повітря, при його охолоджені до 16ºС ?
- У вечері при температурі 18ºС відносна вологість повітря 75%. При якому зниженні температури вранці можна очікувати появу туману?
- При зниженні температури від 16ºС до 10ºС з кожного метра кубічного повітря виділилось 1,5г води, якою була відносна вологість повітря?
- В складському приміщенні об’ємом 1500м3 при температурі 12ºС відносна вологість повітря 75%. Що потрібно зробити для того, щоб при температурі 22ºС вологість повітря становила 60%?
- В приміщення потрібно подати 104м3 повітря з температурою 18ºС і відносною вологістю 60%. Що потрібно зробити з зовнішнім повітрям (його температура 10% , а відносна вологість 60%) щоб виконати поставлену задачу?
- Певна маса повітря при температурі 22°С та відносній з вологості 75% займає об’єм 1200л. Якою буде відносна вологість цього повітря, якщо температуру підвищити до 100°С, а об’єм зменшити до 48л?
.
Лекційне заняття №10.
Тема: Рідини та їх властивості. Поверхневий натяг. Капілярні явища.
Рідинами – називають такі речовинні об’єкти, які мають певний сталий об’єм, але не мають певної сталої форми і в яких середня потенціальна енергія молекул, мінімально більша за їх середню кінетичну енергію, тобто: V=const; Ф≠const; Еп ≥ Ек. Факт того, що в рідинах потенціальна енергія молекул мінімально більша за їх кінетичну енергію (Еп ≥ Ек), безумовно вказує на те, що пояснюючи фізичні властивості тієї чи іншої рідини, потрібно враховувати величину потенціальної енергії її молекул. А як відомо, теоретично визначати цю величину ми не вміємо (Еп=?). По суті це означає, що стрункої теорії рідин, подібної до теорії газів, не існує. Це звичайно не означає, що сучасна наука не може пояснити властивості тієї чи іншої конкретної рідини. Мова йде лише про те, що фізичні властивості різних рідин є суттєво різними і що різноманіття цих властивостей не можливо описати простою теоретичною схемою, подібної до тієї яка описує властивості ідеального газу.
Маючи на увазі факт того, що фізичні властивості різних рідин є суттєво різними, стисло зупинимся лише на деяких загально фізичних особливостях рідин та пояснимо їх. Пояснимо виходячи з того, що всі речовини складаються з молекул, які рухаються і взаємодіють між собою.
Напевно, ви звертали увагу на те, що поверхневий шар рідини має певні пружні властивості, тобто веде себе так, ніби ця рідина вкрита надтонкою пружною плівкою. Якщо ні, то уважно придивіться до процесу формування краплі води (мал.47). Не важко бачити, що ця вода знаходиться у своєрідному еластичному мішечку, який до певної межі збільшується у розмірах, а потім відривається і у вигляді круглої краплі падає вниз. Ясно, що насправді, ніякого окремого від води мішечка не існує. Адже в краплі води, нічого окрім молекул води нема. Просто сам поверхневий шар рідини має певні властивості пружної плівки.


Мал.47. Процес формування краплі є наочним прикладом того, що поверхневий шар рідини має певні пружні властивості.
Чому ж поверхневий шар рідини веде себе як пружна плівка? Відповідаючи на це не просте запитання, розглянемо дві довільно вибрані молекули, одна з яких (1) знаходиться всередині рідини, а інша (2) – в її поверхневому шарі (мал.48). Не важко бачити, що молекула 1, з усіх сторін щільно і практично рівномірно оточена сусідніми молекулами, кожна з яких притягує її. Ясно, що в такій ситуації, та усереднена результуюча сила з якою сусідні молекули діють на молекулу 1, дорівнює нулю.
Молекула ж поверхневого шару рідини (молекула 2), оточена близькими сусідами лише з одного боку – з боку рідини. І не важко збагнути, що та результуюча сила з якою сусідні молекули притягують молекулу поверхневого шару не дорівнює нулю і є такою що направлена всередину рідини. А це означає, що на кожну молекулу поверхневого шару рідини діє певна результуюча сила, яка намагається втягнути цю молекулу всередину рідини. Цю силу називають силою поверхневого тиску (Fp).
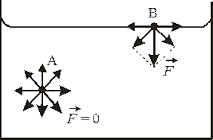
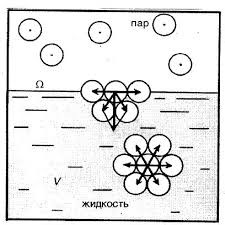
Мал.48. На кожну молекулу поверхневого шару рідини діє певна результуюча сила, яка прагне втягнути цю молекулу всередину рідини.
Прямим наслідком дії сил поверхневого тиску є факт того, що за відсутності зовнішніх силових впливів, будь яка рідина прагне набути форму кулі. І це закономірно. Адже якщо кожна молекула поверхневого шару рідини прагне потрапити всередину рідини, то це означає що рідина прагне набути такої форми, при якій кількість молекул на її поверхні є мінімально можливою. А такою формою є куля. Бо саме куля є тією геометричною фігурою, яка при мінімальній площі поверхні (а отже, при мінімальній кількості молекул на цій поверхні) має максимально можливий об’єм.
Інша справа, що ті сили які прагнуть надати рідині кулястої форми є досить слабкими. Тому, за наявності суттєвих зовнішніх силових впливів, зокрема сили тяжіння, рідина приймає форму тієї посудини в якій вона знаходиться. Однак, навіть в цьому випадку, вільна поверхня рідини прагне бути рівною, тобто такою на якій міститься мінімально можлива кількість молекул.
Сила поверхневого тиску має ту особливість, що її практично не можливо виміряти. Не можливо головним чином тому, що намагаючись максимально ущільнити молекули поверхневого шару рідини, сила поверхневого тиску створює такі умови, при яких між цими молекулами виникають відповідні сили відштовхування. А це означає, що на той прилад за допомогою якого ви будете вимірювати силу поверхневого тиску, неминуче діятимуть дві рівні за величиною і протилежно направлені сили, результуюча яких дорівнює нулю.
Практично важливим наслідком силової дії поверхневого тиску є так званий поверхневий натяг. Поверхневий натяг рідини – це явище, суть якого полягає в тому, що поверхневий шар рідини веде себе як пружна плівка яка прагне до максимального скорочення. Міцнісні властивості поверхневого шару рідини характеризує сила поверхневого натягу. Фізичну суть та механізм дії цієї сили надзвичайно важко пояснити шляхом певних механічних аналогій. Тому просто зауважимо, що сила поверхневого натягу є результуючою всієї сукупності тих міжмолекулярних взаємодій що відбуваються в приповерхневому шарі рідини і яка протидіє збільшенню площі цього приповерхневого шару. Сила поверхневого натягу вигідно відрізняється від сили поверхневого тиску тим, що її можна безпосередньо виміряти.
Сила поверхневого натягу – це направлена вздовж поверхні рідини сила, яка є результуючою всієї сукупності тих міжмолекулярних взаємодій, що відбуваються в приповерхневому шарі рідини і яка протидіє збільшенню площі цього приповерхневого шару.
Позначається: Fпн
Визначальне рівняння: Fпн=σℓ, де σ – коефіцієнт поверхневого натягу; ℓ – довжина тієї лінії поверхні, на якій діє відповідна сила поверхневого натягу.
Одиниця вимірювання: [Fпн] = Н.
Коефіцієнт поверхневого натягу рідини – це фізична величина, яка є силовою характеристикою поверхневого шару рідини і яка дорівнює відношенню сили поверхневого натягу, до довжини тієї лінії поверхні на якій ця сила діє.
Позначається: σ
Визначальне рівняння: σ= Fпн/ℓ
Одиниця вимірювання: [σ] = Н/м.
Величина коефіцієнту поверхневого натягу рідини визначається експериментально і записується у відповідну таблицю, наприклад таку:
Таблиця. Коефіцієнт поверхневого натягу деяких рідин (для t = 20ºC)
| Речовина | σ (Н/м) | Речовина | σ (Н/м) |
| Ацетон | 0,024 | Мильний розчин | 0,040 |
| Бензин | 0,029 | Ртуть | 0,465 |
| Вода | 0,073 | Спирт етиловий | 0,023 |
| Гліцерин | 0,059 | Ефір етиловий | 0,017 |
| Гас | 0,024 |
Потрібно зауважити, що пружні властивості поверхневого шару рідини, суттєво відрізняються від властивостей звичайної пружної плівки. З’ясовуючи суть цих відмінностей, звернемось до наступного експерименту (мал.49). П-подібну дротяну рамку опустимо в мильний розчин і за допомогою чутливого динамометра будемо повільна піднімати її (або повільно опускати посудину з рідиною). Спостереження показують, що допоки рамка знаходиться в рідині показання динамометра чисельно дорівнюють вазі рамки (звичайно з врахуванням діючої на неї сили Архімеда). Коли ж горизонтальна частина рамки стикається з поверхневим шаром рідини і починає виходити за його межі, показання динамометра суттєво збільшуються. Збільшуються на величину тієї сили поверхневого натягу, що діє на горизонтальну частину рамки. І от що цікаво, в процесі подальшого піднімання рамки, збільшення площі тієї плівки що тягнеться за нею, не супроводжується збільшенням діючої на рамку сили поверхневого натягу.
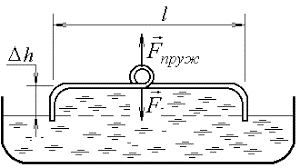
Мал.49. В процесі «розтягування» поверхневого шару рідини, величина деформуючої сили залишається незмінною.
Такий стан речей здається дивним. Адже згідно з законом Гука, в процесі пружної деформації плівки, величина деформуючої сили (а відповідно і сили пружності) має збільшуватись. Однак в тому то й справа, що пружні властивості поверхневого шару рідини і пружні властивості звичайної плівки, це абсолютно різні властивості, які мають абсолютно різне походження. Бо коли розтягується гумова плівка, то її пружні властивості є результатом того, що відстані між молекулами гуми збільшуються і відповідно збільшуються сили міжмолекулярної взаємодії. Коли ж розтягується поверхневий шар рідини, то відстані між його молекулами залишаються незмінними, а змінюється лише кількість тих молекул що утворюють відповідний поверхневий шар. При цьому та сила під дією якої збільшується площа поверхневого шару рідини, залишається практично незмінною.
Крім всього іншого, представлений на мал.49 експеримент, відображає суть одного з найбільш ефективних методів визначення коефіцієнту поверхневого натягу – методу відриву тіла від поверхні рідини. А ця суть полягає в наступному. Експериментально вимірявши величину тієї додаткової сили що йде на відрив тіла від поверхні рідини (сили поверхневого натягу Fпн) та довжину тієї лінії на якій ця сила діє (ℓ), визначають відповідне значення коефіцієнту поверхневого натягу (σ). При цьому, потрібно зважити на факт того, що та плівка яка тягнеться за рамкою вимірювального приладу, має дві вільні поверхні. Тому, в умовах даного експерименту σ = Fпн/2ℓ.
В процесі вивчення фізики, ми неодноразово наголошували на тому, що одне і те ж явище може мати декілька наукових пояснень. І в цьому сенсі, явище поверхневого натягу не є винятком. Адже це явище можна пояснити не лише на основі аналізу тих сил що діють на молекули речовини в тій чи іншій ситуації (силовий метод досліджень), а й на основі аналізу енергетичних параметрів цих молекул (енергетичний метод досліджень).
Дійсно. Для того щоб молекула внутрішнього шару рідини (молекула 1, мал.48) перемістилась в поверхневий шар цієї рідини, потрібні певні енергетичні затрати. А це означає, що в поверхневому шарі рідини неминуче зосереджена певна кількість надлишкової енергії. В одному ж з базових законів Природи, який прийнято називати принципом мінімуму стверджується: будь яка система, прагне прийти до такого стану, при якому кількість зосередженої в ній надлишкової енергії буде мінімально можливою. В нашій ситуації, очевидним способом зменшення кількості тієї надлишкової енергії що міститься в поверхневому шарі рідини є граничне зменшення площі цього шару.
Таким чином, у відповідності з базовими законами Природи, поверхневий шар рідини, маючи певну кількість надлишкової енергії, завжди прагне до того щоб гранично зменшити величину цієї надлишкової енергії. Реалізацією цих енергетичних прагнень, є факт того, що поверхневий шар рідини веде себе як пружна плівка яка прагне до максимального скорочення.
На завершення додамо, що застосовуючи енергетичний метод пояснення того явища яке називають поверхневим натягом, замість тієї величини яку прийнято називати силою поверхневого натягу, застосовують величину яку називають енергією поверхневого натягу або поверхневою енергією.
Енергія поверхневого натягу (поверхнева енергія) – це та надлишкова енергія, яку має поверхневий шар рідини порівняно з її внутрішніми шарами, і яка завжди протидіє збільшенню площі відповідного поверхневого шару.
Позначається: Епн
Визначальне рівняння: Епн= σS, де σ – коефіцієнт поверхневого натягу рідини; S – площа відповідного поверхневого шару рідини.
Одиниця вимірювання: [Епн] = Дж.
Ясно, що при енергетичному методі пояснення поверхневого натягу, та величина яку називають коефіцієнтом поверхневого натягу, набуває нового фізичного змісту.
Коефіцієнт поверхневого натягу – це фізична величина, яка є енергетичною характеристикою поверхневого шару рідини і яка дорівнює відношенню тієї енергії (∆Епн) що йде на збільшення площі вільної поверхні рідини, до величини цієї площі (∆S).
Позначається: σ
Визначальне рівняння: σ = ∆Епн/∆S
Одиниця вимірювання: [σ] = Дж/м2.
І потрібно зауважити, що жодних протиріч між визначальними рівняннями σ=Fпн/ℓ та σ=∆Епн/∆S нема. Дійсно. В умовах представленого на мал.49 експерименту ∆Епн=Fпн∆x; ∆S=ℓ∆x. Тому: σ = ∆E/∆S = Fпн∆х/ℓ∆х = Fпн/ℓ = σ.
Поверхневий натяг рідини суттєво залежить від наявності домішок в ній. При цьому, деякі домішки посилюють поверхневий натяг рідини, а деякі – послаблюють його. Наприклад сіль і цукор дещо збільшують поверхневий натяг води, а спирти та ефіри – зменшують цей натяг. Домішки які суттєво послаблюють поверхневий натяг рідини називають поверхнево активними речовинами. Загально відомим прикладом поверхнево активної речовини є мило.
Наочною демонстрацією дії поверхнево активної речовини є наступний простий експеримент. Наберіть в чисту посудину, наприклад тарілку, чистої води. Більш менш рівномірним шаром посипте поверхню цієї води меленим коріандром, перцем, тальком чи чимсь подібним. Змочіть олівець чи власний палець миючим засобом і торкніться цим олівцем (пальцем) поверхні води (мал.50). При цьому ви побачите, як наявні на поверхні частинки швидко розбігаються від місця дотику. Розбігаються тому, що з тієї сторони де з’являються молекули поверхнево активної речовини, діяча на тверді частинки сила поверхневого натягу зменшується і тому ці частинки рухаються в той бік де ця сили залишилась попередньо великою.
Мал.50. Ілюстрація впливу поверхнево активної речовини на силу поверхневого натягу рідини.
У побуті, поверхнево активні речовини широко застосовуються як миючі засоби (мило, шампуні, пральні порошки). В промисловості, поверхнево активні речовини використовуються при виробництві фарб, клеїв, дезінфікуючих засобів, для очищення поверхонь від пилу жирів та мастил, для покращення умов фарбування, адгезії (прилипання, зчеплення), тощо. В сільському господарстві – для покращення змочуваності поверхонь рослин засобами живлення рослин, боротьби з хворобами та шкідниками. В організмі людини, поверхнево активні речовини приймають участь в процесі дихання та роботі травної системи. Втім, поверхнево активні речовини можуть бути не лише корисними, а й шкідливими. Деякі з них викликають зниження імунітету, алергічні реакції, ураження печінки, нирок, тощо.
Задача 1. Яку роботу треба виконати, щоб видути мильну бульбашку діаметром 12см?
Дано:
d = 12см = 0,12м
А = ?
Рішення. Виходячи з того, що за визначенням А=ΔЕ, де ΔЕ – затрати енергії на виконання роботи, та враховуючи, що в умовах нашої задачі ΔЕ=σΔS, де σ=0,04Н/м=0,04Дж/м2, ΔS – зміна площі поверхні бульбашки в процесі її видування. А оскільки у бульбашки дві поверхні, то ΔS=2·Sсфери =2πd2. Таким чином А= ΔЕ=σΔS=σ2πd2.
Розрахунки: А=2σπd2 = 2·0,04(Дж/м2)3,14(0,12м)2 = 3,6·10–3Дж.
Відповідь: А=3,6·10–3Дж.
Задача 2. Яку масу має крапля води при витіканні з скляної трубки діаметром 3мм, якщо вважати, що діаметр шийки краплі дорівнює діаметру трубки.
Дано:
d = 3мм = 3·10–3м
m = ?
Рішення. Виконуємо малюнок який відображає фізичний зміст задачі. Будемо виходити з того, що в момент утворення шийки краплі, її маса є максимально можливою, і що діючі на краплю сили (сила тяжіння Fт=mg та сила поверхневого натягу Fпн=σℓ) зрівноважують одна одну: mg=σℓ, де ℓ=πd – довжина тієї лінії поверхні на якій діє сила поверхневого натягу. Звідси випливає m=σπd/g.
Розрахунки: m=σπd/g = 0,073(Н/м)·3,14·3·10–3м/9,8(м/с2) = 7·10–5кг.
Відповідь: m = 7·10–5кг.
Дослідження показують, що крапля однієї і тієї ж рідини на одних твердих поверхнях розтікається, а на інших – не розтікається, тобто залишається у вигляді приплюснутої силою тяжіння краплі. Наприклад, крапля води розтікається поверхнею скла (мал.51б) і не розтікається на поверхні парафіну (мал.51а). При цьому говорять, що вода змочує скло і не змочує парафін.
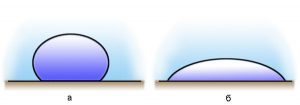
Мал.51. Крапля рідини на одних твердих поверхнях розтікається (змочує поверхню), а на інших – не розтікається (не змочує поверхню).
Пояснюючи факт змочування рідиною твердої поверхні чи не змочування її, можна сказати наступне. Поведінка краплі рідини на тій чи іншій твердій поверхні, визначальним чином залежить від того, які сили більші: сили взаємодії між молекулами самої рідини (fр), чи сили взаємодії між молекулами рідини та молекулами твердого тіла (fт). При цьому ясно, якщо сили взаємодії між молекулами самої рідини більші за сили взаємодії між молекулами рідини та твердого тіла (fр ˃ fт), то рідина не змочує тверду поверхню. А якщо сили взаємодії між молекулами рідини менші за сили їх взаємодії з молекулами твердої поверхні (fр ˂ fт), то рідина відповідну поверхню змочує.
На практиці, факт змочування чи не змочування даної твердої поверхні, визначають наступним чином. На відповідну поверхню кладуть краплю рідини. Змінюючи кут нахилу поверхні, змушують цю краплю переміщуватись. При цьому, якщо в процесі переміщення на поверхні залишається суцільний слід рідини, то це означає що рідина змочує поверхню. Якщо ж крапля рідини скочується поверхнею не залишаючи суцільного сліду, то ця рідина дану поверхню не змочує. Потрібно зауважити, що змочуваність тієї чи іншої поверхні суттєво залежить від того наскільки чистою є ця поверхня. Адже якщо наприклад, скло покрито непомітним шаром бруду чи жиру, то його змочуваність суттєво погіршується.
Зазвичай, ступінь змочуваності тіла рідиною, оцінюють параметром, який називається кутом змочування або краєвим кутом. Кут змочування (краєвий кут) – це величина, яка характеризує ступінь змочуваності твердої поверхні рідиною і яка дорівнює куту між цією твердою поверхнею та дотичною до поверхні рідини проведеною в точці дотику рідини і твердої поверхні та виміряному з боку рідини. Позначається θ. Прийнято вважати, що коли кут змочування менший за 90º (θ < 90º), то відповідна рідина в тій чи іншій мірі змочує тверду поверхню. А якщо цей кут більший за 90º (θ > 90º) – не змочує її.
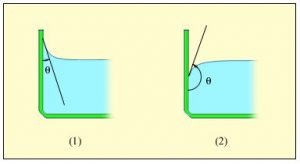
Мал.52. Ступінь змочуваності твердої поверхні рідиною, оцінюють кутом змочування (θ) .
Ступінь змочуваності тіла рідиною, можна оцінити не лише за формою відповідної краплі, а й за параметрами меніску рідини. Меніском (від грец. meniskos – півмісяць) називають те викривлення вільної поверхні рідини, яке відбувається в місці контакту рідини з поверхнею твердого тіла. Наприклад, якщо в скляну посудину налити воду (мал.52в), то можна помітити, що в місці її контакту з поверхнею скла, вода дещо піднята вгору з утворенням відповідного викривлення її поверхні. Факт того, що в місці контакту з скляною поверхнею вода «тягнеться» за склом, є закономірним результатом того, що сили взаємодії між молекулами скла та молекулами води, значно потужніші за сили взаємодії між молекулами самої води.
Якщо ж воду налити в парафінову посудину (або занурити в неї парафінову свічку), то неодмінно з’ясується, що в місці контакту з парафіном, поверхня води закруглюється таким чином, ніби вода відштовхується від парафіну (мал.52г). По суті, ніякого відштовхування води від парафіну не відбувається. Просто молекули води взаємодіють між собою значно сильніше ніж з молекулами парафіну. В такій ситуації, сили їх взаємодії (сили поверхневого натягу), прагнучи надати поверхні води енергетично доцільної круглої форми, створюють ефект відштовхування рідини від тієї поверхні яку вона не змочує.
З процесами які відбуваються на межі контакту рідини з твердою поверхнею, тісно пов’язані так звані капілярні явища. Напевно ви добре знаєте про те, що в системі сполучених посудин, рівень наявної в ній однорідної рідини є однаковим (мал.53а). Однак, можливо ви не знаєте, що цей закон (його називають законом сполучених посудин) виконується не завжди. В цьому не важко переконатись за допомогою простого приладу, який представляє собою систему сполучених скляних трубок різних та достатньо малих діаметрів (мал.53б). Наливши в цю систему певну кількість води, ви неодмінно з’ясуєте, що рівень рідини в цих сполучених посудинах є суттєво різним.

Мал.53. В сполучених посудинах, рівень налитої в них однорідної рідини може бути різним.
Тепер, коли ви знаєте, що вода змочує скло і що це відбувається завдяки сильному взаємному притягуванню між молекулами води і скла, не важко зрозуміти, чому в вузьких скляних трубках вода піднімається на певну надлишкову висоту. Правильно, скло сильно взаємодіючи з при поверхневою водою, піднімає її на певну додаткову висоту. Власне, скло завжди піднімає певну кількість приповерхневої води. Однак, якщо ця піднята приповерхнева вода знаходиться в посудині відносно великих розмірів, наприклад склянці води, то її кількість здається несуттєво малою. Якщо ж аналогічна кількість піднімається в трубці малого діаметру, то висота цього піднімання стає відповідно великою.
Тонкі трубки, судини, пори, щілини, тощо, прийнято називати капілярами (від лат. capillaris – волосина). Сукупність же тих явищ, які пов’язані з перебуванням та рухом рідин в капілярах, називають капілярними явищами.
З’ясовуючи закономірності поведінки рідини в капілярі, розглянемо ті сили що діють на підняту в капілярній трубці рідину (мал.54). Відразу ж зауважимо, що фактичною причиною піднімання рідини в капілярі є результуюча тих взаємодій, які відбуваються між молекулами рідини і молекулами стінок капіляру. Однак, ця результуюча сила не може підняти рідини більше за ту її кількість, яку спроможні втримати сили поверхневого натягу. Виходячи з цього, прийнято вважати, що тією силою яка утримує підняту в капілярі рідину, є сила поверхневого натягу: Fпн = σℓ, де ℓ – довжина тієї лінії по якій поверхня рідини, взаємодіє з поверхнею капіляру.
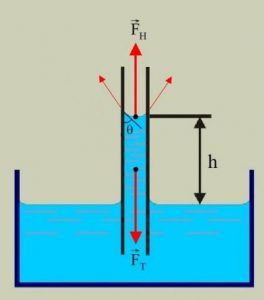
Мал.54. Якщо рідина змочує стінки капіляру, то вона піднімається на певну додаткову висоту, а якщо не змочує – то на відповідну висоту опускається.
Таким чином, на підняту в капілярі рідину діють дві сили: сила тяжіння Fт=mg (де m – маса піднятої в капілярі рідини) та сила поверхневого натягу Fпн=σℓ. При цьому, зважаючи на стан механічної рівноваги рідини, можна записати: Fт= Fпн, або mg=σℓ, де ℓ=πd; m=ρV=ρSh=ρπd2h/4.
Звідси: h = 4σ/ρgd.
Висновок. Та висота на яку піднімається рідина в капілярі, прямо пропорційна величині коефіцієнту поверхневого натягу рідини і обернено пропорційна густині рідини та діаметру капіляру.
Не важко збагнути, що знаючи густину рідини (ρ), та вимірявши діаметр капіляру (d) і ту висоту (h) на яку рідина піднімається в капілярі, можна визначити коефіцієнт поверхневого натягу відповідної рідини: σ = ρgdh/4. Порівняно з іншими методами експериментального визначення коефіцієнту поверхневого натягу, капілярний метод має ряд суттєвих переваг. По перше, він не потребує складного та коштовного обладнання, а отже є дешевим та простим. По друге, ті величини які фігурують в формулі σ = ρgdh/4 є такими що легко і достатньо точно вимірюються. По третє, цей метод є статичним, тобто таким в якому аналізується та ситуація при якій рідина знаходиться в стані механічного спокою.
В капілярній трубці, рідина може не лише підніматись, а й навпаки – опускатись. Це відбувається в тому випадку, коли матеріал капілярної трубки не змочується рідиною. Наприклад, якщо скляний капіляр занурювати у ртуть, то рівень ртуті в капілярі виявиться нижчим за її загальний рівень. Або якщо наприклад, капілярна трубка виготовлена з парафіну, то при її зануренні у воду, рівень води в капілярі буде нижчим за її загальний рівень. При цьому можна довести, що та висота на яку опускається рідина в незмочуваному капілярі, також визначається за формулою h = 4σ/ρgd.
Капілярні явища відіграють надзвичайно важливу роль як в живій так і в неживій природі. Скажімо ґрунт представляє собою певну капілярну систему по якій вода та розчинені в ній речовини піднімаються вгору та живлять коріння рослин. В рослинах, капілярна система забезпечує підйом вологи від дрібних корінців до найвіддаленішого листя. Саме в капілярах відбуваються основні процеси, пов’язані з диханням і живленням організмів. Достатньо сказати, що в капілярній системі організму людини налічується понад 160 мільярдів капілярів, загальна довжина яких майже 80 000 кілометрів.
Капілярні явища застосовуються і в побуті. Скажімо, завдяки наявності капілярів рушники, серветки, марлі та промокальні папери, швидко вбирають наявну вологу. Капілярні явища можуть бути не лише корисними, а й шкідливими. Наприклад будівельна цегла представляє собою певну капіляру систему яка активно поглинає вологу. Тому, за наявності контакту цегли з ґрунтовими водами, цей контакт переривають за допомогою гідроізоляційних матеріалів – бітум, руберойд, тощо.
Задача 3. Яким має бути діаметр капілярної трубки, щоб вода в ній піднімалась на 2см?

Дано:
h = 2cм=0,02м
d = ?
Рішення. Розглянемо ті сили, що діють на підняту в капілярі рідину: Fт=mg (де m – маса піднятої в капілярі рідини) та сила поверхневого натягу Fпн=σℓ. Оскільки Fт= Fпн, або mg=σℓ, де ℓ=πd; m=ρV=ρSh=ρπd2h/4, то ρπd2hg/4 = σπd, або ρdhg/4 = σ, звідси d = 4σ/ρgh.
Розрахунки: d = 4·0,073/1·103·10·0,02 = 0,29/200=0,00146м=1,46мм.
Задача 4. Ртутний барометр має внутрішній діаметр трубки 3мм. Яку поправку в показання барометра потрібно внести, щоб врахувати капілярне опускання ртуті?

Дано:
d = 3мм = 3·10–3м
Δh = ?
Рішення. Будемо виходити з того, що трубка діаметром 3мм є капіляром, що ртуть не змочує скло і тому її рівень в капілярі буде нижчим за рівень без урахування капілярності на висоту Δh. Величину цієї висоти можна визначити із наступних міркувань. В умовах ртутного барометра, сила зовнішнього атмосферного тиску прагне підняти ртуть на висоту відповідну цьому тиску. І якщо ця висота на величину Δh виявляється меншою за очікувану, то це тільки тому, що відповідному підніманню протидіє сила поверхневого натягу ртуті Fпн=σℓ=σπd. І величина цієї протидії дорівнює вазі тієї маси ртуті, що відповідає висоті Δh, тобто силі F=mg=ρVg=ρSΔhg=ρ(πd2/4)Δhg. Іншими словами σπd= ρ(πd2/4)Δhg, звідси Δh = 4σ/ρgd, де σ=0,47Н/м коефіцієнт поверхневого натягу ртуті, ρ=13,6·103кг/м3 густина ртуті.
Розрахунки: Δh = 4σ/ρgd = 4·0,47/13,6·103·9,8·3·10–3 = 0,0046м = 4,6мм.
Відповідь: Δh = 4,6мм.
Контрольні запитання.
- Чим відрізняються ті ситуації в яких знаходяться молекули поверхневого шару рідини та її внутрішніх шарів?
- Яку силу називають силою поверхневого натягу? Чим сила поверхневого натягу вигідно відрізняється від сили поверхневого тиску?
- Поясніть суть та причини тих відмінностей які існують між пружними властивостями поверхневого шару рідини та звичайної пружної плівки.
- Поясніть явище поверхневого натягу на основі енергетичного методу досліджень.
- Які речовини називають поверхнево активними?
- 6. Що означає твердження: а) рідина змочує тверду поверхню; б) рідина не змочує тверду поверхню?
- Як пояснюється факт того, що крапля води на поверхні скла розтікається, а на поверхні парафіну – не розтікається?
- Чому вода піднімається в скляному капілярі? Від чого залежить висота піднімання (опускання) рідини в капілярі?
- Що стверджується в законі сполучених посудин? Чому цей закон в системі сполучених капілярів різного діаметру не виконується?
- Поясніть суть капілярного методу визначення коефіцієнту поверхневого натягу? Які переваги цього методу над методом відриву краплі?
Вправа 10.
- З якою силою діє мильна плівка на дротину АВ, якщо довжина дротини 3см? Яку роботу потрібно виконати, щоб перемістити дротину на 2см?
- Яку масу має крапля води що витікає з скляної трубки діаметром 4мм, якщо діаметр шийки краплі дорівнює діаметру трубки?
- Яке зусилля необхідне для того щоб відірвати тонке кільце масою 4г від поверхні води? Діаметр кільця 8см.
- Яку роботу потрібно виконати, щоб видути мильну бульбашку діаметром 10см?
- Вода з інтервалом 1с, крапля за краплею витікає з бюретки через отвір діаметром 2мм. За який час з бюретки витече 25см3 води.
- В капілярній трубці діаметром 1мм, бензин піднявся на висоту 17мм. Визначити коефіцієнт поверхневого натягу бензину і його кількість в капілярі. Густина бензину 700кг/м3.
- Яким має бути діаметр капілярної трубки, щоб вода в ній піднялась на 10см?
- Визначте масу піднятої в капілярі води, якщо діаметр капіляру: а) 1мм; б) 0,5мм; в) 0,1мм.
- Дві однакові капілярні трубки, діаметром 0,5мм опустили в воду і бензин. На скільки відрізняються висоти рідин в цих капілярах?
- Скляний капіляр діаметром 0,1мм опустили в воду при температурі 20ºС. При нагріванні води до 70ºС висота рідини в капілярі зменшилась на 3,2см. Визначте коефіцієнт поверхневого натягу води при 70ºС. Розширенням води і скла при нагріванні знехтувати.
.
Лекційне заняття №11.
Тема: Тверді тіла та їх властивості. Кристалічні і аморфні тіла.
Твердими називають такі речовинні об’єкти (тіла), які мають певний сталий об’єм та певну сталу форму і в яких, середня потенціальна енергія молекул значно більша за їх середню кінетичну енергію, тобто: V=const; Ф=const; Еп ˃ Ек. Твердження про те, що потенціальна енергія молекул твердої речовини значно більша за їх середню кінетичну енергію, означає лише те, що на рівні тих процесів які відбуваються в твердому тілі, вплив потенціальної енергії молекул на ці процеси є визначальним.
Факт того, що в твердих тілах енергія взаємодії молекул значно більша за енергію їх руху, по суті означає: 1) фізичні властивості різних твердих речовин є різними; 2) загальної теорії твердих речовин, подібної до теорії газів, не існує.
Все різноманіття твердих тіл можна умовно розділити на три класифікаційні групи: тіла кристалічні, тіла аморфні та полімери. Однак, якщо мова йде про хімічно прості тверді речовини, то їх зазвичай поділяють на кристалічні та аморфні.
Переважна більшість хімічно простих твердих речовин є кристалічними. Кристалічні всі метали, всі солі, всі луги та майже всі ті речовини які називаються мінералами, коштовним та некоштовним камінням, тощо. Кристалічними є лід, цукор, алмаз, граніт, графіт, пісок та безліч інших вам відомих і невідомих речовин.
Кристалічними називають такі тверді речовини (тіла), атоми і молекули яких розташовані в певному періодичному порядку, який називається кристалічною структурою речовини. Переважна більшість природніх кристалічних тіл є полікристалічними, тобто такими які складаються з величезної кількості дрібненьких, міцно з’єднаних монокристалів (від грец. monos – один; polys – багато).
Зазвичай, внутрішній устрій кристалічної речовини, представляють у вигляді певним чином спрощеної (ідеалізованої) моделі, яку називають кристалічною решіткою або кристалічною граткою. Кристалічна решітка (гратка) – це спрощена (ідеалізована) модель внутрішнього устрою кристалічного тіла, в якій структурні одиниці тіла зображають у вигляді певних умовних символів (точок, кульок, тощо), а їх розташування характеризують відповідними, статистично усередненими значеннями. Дослідження показують, що практично кожен вид кристалів, має свою індивідуальну кристалічну решітку, яка характеризується певною геометричною формою та певними розмірами. Зображення деяких найпростіших кристалічних решіток представлені на мал.55.
Мал.55. Загальний вигляд характерних для металів кристалічних решіток, представлених у вигляді: а) кулестержневих моделей; б) масштабних моделей.
Упорядкована періодичність в розташуванні частинок, це визначальна ознака будь якої кристалічної речовини. Але як на практиці визначити, існує ця періодичність чи не існує? Чи нема інших, більш явних ознак кристалічності тієї чи іншої речовини? А такі ознаки дійсно існують. Одна з них полягає в тому, що кристалічні тіла мають певну температуру плавлення, тобто таку температуру при якій відбувається перехід речовини від безумовно твердого стану до безумовно рідкого, і яка в процесі цього переходу залишається незмінною. Наприклад, температура плавлення льоду (кристалічної води) 0ºС. Це означає, що при температурі меншій за 0ºС, вода знаходиться в безумовно твердому стані, а при температурі більшій за 0ºС – в безумовно рідкому. Що ж стосується стану води при температурі 0ºС, то його можна охарактеризувати як стан теплової рівноваги між твердою та рідкою фазами води. Це означає, що при цій температурі вода може бути як твердою так і рідкою, і що в залежності від того отримує вона енергію чи втрачає, вода або плавиться або кристалізується.
Плавлення – це процес переходу речовини з кристалічного стану в рідкий, який відбувається при певній постійній температурі (температурі плавлення) та супроводжується поглинанням енергії. Кристалізація – це процес переходу речовини з рідкого стану в кристалічний, який відбувається при певній постійній температурі (температурі плавлення) та супроводжується виділенням енергії.
Те, що кристалічні тіла мають певну температуру плавлення, і що в процесі плавлення ця температура залишається незмінною, є цілком закономірним результатом того внутрішнього порядку який існує в цих тілах. Дійсно. В процесі нагрівання, середня кінетична енергія молекул речовини неухильно зростає. Коли ж величина цієї енергії, стає співрозмірною з величиною потенціальної енергії молекул, зв’язки між молекулами починають руйнуватись. А оскільки в кристалі молекули розташовані в певному порядку, то і руйнація відповідної кристалічної структури відбувається упорядковано-послідовно. Спочатку в рідину перетворюється зовнішній шар кристалу, потім – наступний, наступний і т.д. Аналогічним чином відбувається і процес кристалізації: упорядковано-послідовно, шар за шаром, частинки речовини об’єднується у відповідну кристалічну структуру.
Таким чином, ті тверді речовини, які в процесі нагрівання ведуть себе як лід, тобто плавляться, є кристалічними. До речі, слово «кристал» в перекладі з грецької, означає «лід». По суті, наявність певної температури плавлення є основною зовнішньою ознакою кристалічності речовини. Однак, потрібно мати на увазі, що деякі безумовно кристалічні речовини не плавляться. Не плавляться тому, що не досягнувши температури плавлення, хімічно руйнуються (розпадаються на більш прості речовини), або сублімують (випаровуються). Наприклад при температурі близькій до 1000ºС карбонат кальцію (СаСО3), а простіше кажучи крейда, розпадається на СаО та СО2. Або, наприклад, за нормально тиску, так званий сухий лід (кристалізований вуглекислий газ) при температурі –78,5ºС інтенсивно випаровується. Таке випаровування називають сублімацією (від лат. sublimo – піднімання).
Сублімація (узгін) – це процес безпосереднього переходу речовини з кристалічного стану в газоподібний, який супроводжується поглинанням енергії і інтенсивна стадія якого відбувається при певній постійній температурі (температурі сублімації). Потрібно зауважити, що як і випаровування, сублімація може відбуватись при будь якій температурі. Однак інтенсивна фаза сублімації, як і інтенсивна фаза випаровування (кипіння), відбувається при певній постійній температурі – температурі сублімації.
Враховуючи вище сказане, будемо вважати, що основною зовнішньою ознакою кристалічності речовини є наявність певної температури плавлення (плавлення, сублімації чи хімічної руйнації). Звичайно за умови, що відповідна кристалічна речовина є хімічно однорідною, а не такою, що складається з певної сукупності різних кристалічних речовин.
Ще однією характерною ознакою кристалічності речовини є те, що її монокристали, тобто обособлені одинарні кристалики, мають певну геометричну форму. І ця форма певним чином відображає параметри кристалічної гратки відповідної речовини. Наприклад, монокристали кам’яної солі (NaCℓ) мають форму куба яка певним чином відображає той порядок, в якому іони натрію та хлору розташовані у відповідній кристалічній структурі.


Мал.56. Кубічна форма монокристалів солі, певним чином відображає той порядок, в якому іони натрію та хлору розташовані у відповідній кристалічній структурі.
Варто зауважити, що в природних умовах, ідеально правильні та достатньо великі монокристали зустрічається надзвичайно рідко. Рідко по-перше тому, що монокристали взагалі зустрічаються рідко. А по-друге тому, що в природних умовах монокристали формуються за наявності багатьох сторонніх впливів. Тому якщо наприклад, ви візьмете придбану в крамниці сіль (NaCℓ), то скоріш за все з’ясуєте, що її окремі кристалики, рідко схожі на ідеальні кубики. І це закономірно. Адже в процесі видобутку, переробки та транспортування, сіль неодноразово подрібнювалась, перемелювалась, кришилась, тощо. Але от що характерно. Якщо цю неправильну сіль розчинити у воді, а потім воду випарувати, то на дні посудини залишаться кристалики правильної кубічної форми. Форми, яка певним чином відображає той порядок, в якому іони натрію і хлору розташовані у відповідній кристалічній структурі.
Факт того, що обособлені монокристали мають певну характерну форму, є важливою ознакою кристалічності речовини. Однак, в реальних природніх умовах, достатньо великі монокристали зустрічаються надзвичайно рідко. Переважна більшість природних кристалічних тіл, є полікристалічними, тобто такими, що представляють собою сукупність величезної кількості, з’єднаних в єдине ціле дрібненьких монокристалічних фрагментів.
Певні уявлення про те, як утворюються полікристалічні тіла, можна отримати уважно спостерігаючи за початковим етапом кристалізації все того ж льоду. А цей етап полягає в тому, що поверхня води покривається тонкою, багатопроменевою льодяною кіркою. Власне фрагменти цієї кірки і є певними монокристалами льоду. Однак, в процесі кристалізації, ці окремі кристалики, поступово об’єднуються в цілісне тверде тіло. Тіло, в якому візуально визначити межі окремих кристаликів, практично не можливо. Ясно, що в такій ситуації визначити приналежність полікристалічного тіла до розряду кристалічних речовин, на підставі того, що їх монокристали мають певну форму, майже не можливо.
Щоправда, існує ще одна ознака кристалічності, яка називається анізотропією (від грец. anisos – не однаковий, tropos – напрямок), і яка полягає в тому, що в різних напрямках фізичні властивості монокристалів суттєво різні. Ілюструючи суть того, що називають анізотропією кристалів, розглянемо кристалічну структуру графіту (мал.57б).
В графіті, атоми вуглецю (карбону) розташовані певними шарами. При цьому, ті сусідні атоми які знаходяться в межах одного шару, розташовані на відносно малих відстанях (0,14нм) і тому сили взаємодії між ними є відносно великими. Ті ж атоми які знаходіться в сусідніх шарах, розташовані на відносно великих відстанях (0,34нм) і тому сили взаємодії між цими атомами є відносно слабкими. В такій ситуації, один і той же монокристал графіту, в одному напрямку твердий, а в іншому – м’який. В одному напрямку добре проводить електричний струм, а в іншому – погано. В одному напрямку має блискучу поверхню, а в іншому – матову і т.д.
Оскільки в полікристалічних тілах окремі монокристали орієнтовані хаотично, то результуючі властивості таких тіл в усіх напрямках є усереднено однаковими. А це означає, що в загальному випадку анізотропія властивостей притаманна лише монокристалам.
Узагальнюючи вище сказане, можна дати наступне визначення. Кристалічними називають такі тверді тіла, структурні одиниці яких розташовані в певному періодично повторюваному порядку. Результатом цього внутрішнього порядку є наступні властивості кристалів:
- Всі хімічно однорідні кристалічні речовини, мають певну температуру плавлення (плавлення, сублімації чи хімічної руйнації).
- Монокристали мають певну геометричну форму, яка певним чином відображає параметри відповідної кристалічної решітки.
- Монокристали анізотропні, тобто такі, фізичні властивості яких в різних напрямках суттєво різні.
Говорячи про внутрішній устрій того чи іншого кристалічного матеріалу, потрібно мати на увазі, що одні і ті ж атоми можуть бути упакованими по різному. При цьому, хімічно однакові речовини можуть мати суттєво різні, іноді діаметрально протилежні властивості. Наприклад, важко повірити, що надтвердий, міцний, крихкий, прозорий, струм непровідний та над коштовний алмаз і м’який, не міцний, не крихкий, не прозорий, струмопровідний та дешевий графіт, виготовлені із одних і тих же атомів – атомів вуглецю (карбону). І тим не менше, це дійсно так. Просто в алмазі і графіті, атоми вуглецю упаковані по різному.
Мал.57. Алмаз і графіт – класичний приклад того, як при різній упаковці одних і тих же атомів, утворюються речовини з діаметрально протилежними властивостями.
Як вже зазначалось, тверді тіла можна розділити на кристалічні та аморфні. Аморфні тіла не є такими багаточисельними як тіла кристалічні. До числа аморфних, відносять різноманітні види скла, різноманітні смоли, бурштин, каніфоль, сургуч, цукровий льодяник, різноманітні полімерні матеріали.
Слово «аморфний» в перекладі з грецької означає «той що не має певної форми». На перший погляд, така назва не є надто прийнятною для позначення тих об’єктів що є твердими, а отже такими які мають певний незмінній об’єм та певну незмінну форму. З іншого ж боку, аморфні речовини тим і відрізняються від кристалічних, що для них, дійсно нема певної характерної форми, наприклад такої як форма куба для кам’яної солі, форма октаедра для алмазу, чи форма шестигранної призми для кварцу. Умовно кажучи, якщо аморфну речовину розчинити, а потім розчинник випарувати, то на дні відповідної посудини не сконденсуються певні куби, октаедри чи шестигранні призми, а залишиться однорідний «млинець» який матиме форму дна посудини.
Аморфними називають такі умовно тверді речовини (Еп ˃ Ек; V = const; Ф = const), структурні одиниці яких розташовані без певного, періодично повторюваного порядку. Твердження про те, що частинки аморфного тіла розташовані безладно (хаотично), не є безумовно правильним. Адже насправді, частинки аморфної речовини розташовані не хаотично, а в певній послідовності. Наприклад і в кристалічному кварці (SiO2) і в аморфному кварцовому склі (SiO2) кожен атом кремнію зв’язаний з чотирма атомами кисню, а кожен атом кисню – з двома атомами кремнію. Різниця лише в тому, що в кристалічному кварці, ці атоми розташовані з певною, строго визначеною періодичністю (мал.58а), а в аморфному кварцовому склі, така періодичність відсутня (мал.58б). Тому, характеризуючи розташування частинок аморфної речовини, доречно говорити не про хаотичність цього розташування, а про відсутність певного періодичного порядку в ньому.
Мал.58. Схема розташування атомів кремнію (•) та атомів кисню (º) в структурі а) кристалічного кварцу, б) аморфного кварцового скла.
Прямим наслідком факту того, що структурні одиниці аморфного тіла розташовані без певного періодичного порядку є те, що аморфні тіла перетворюються на відповідну рідину не в процесі плавлення, а в процесі поступового розм’ягчування. І це закономірно. Адже при неупорядкованому розташуванні частинок, ті зв’язки що існують між ними не є рівноміцними. При цьому, як найміцніші так і найслабші зв’язки хаотично розкидані по всьому об’єму аморфного тіла. Ясно, що в процесі нагрівання, спочатку руйнуватимуться найбільш слабкі зв’язки, потім – менш слабкі і т.д. А це означає, що в процесі нагрівання, тверде аморфне тіло буде перетворюватись на відповідну рідину не при певній строго визначеній температурі, а в певному температурному інтервалі, межі якого є розмитими та досить умовними.
Наприклад якщо взяти звичайне скло і поступово нагрівати його, то починаючи приблизно з 400ºС скло почне поступово розм’ягчатися та перетворюватись на все менш і менш в’язку рідину. При цьому ніхто не зможе з впевненістю сказати, на якому етапі нагрівання, скло перестало бути твердим і стало рідким. Не зможе тому, що аморфні тіла не мають певної температури плавлення. Аморфні тіла не плавляться, а розм’ягчуються, не кристалізуються, а тверднуть.
Говорячи про загальні властивості аморфних тіл, потрібно сказати і те, що ці тіла ізотропні, тобто такі, фізичні властивості яких в усіх напрямках однакові. І не важко збагнути, що ізотропність аморфного тіла, є прямим наслідком того, що частинки цього тіла розташовані без певного періодичного порядку.
Узагальнюючи вище сказане, можна дати наступне визначення. Аморфними називають такі умовно тверді речовини, структурні одиниці яких, розташовані без певного періодично повторюваного порядку. Результатом відсутності цього внутрішнього порядку є наступні зовнішні ознаки аморфних тіл:
- Аморфні тіла не мають певної температури плавлення. Вони не плавляться, а розм’ягчуються, не кристалізуються, а тверднуть.
- Аморфні тіла та будь які їх фрагменти не мають певної характерної форми.
- Аморфні тіла ізотропні, тобто такі, фізичні властивості яких в усіх напрямках однакові.
Оскільки переважна більшість кристалічних тіл є полікристалічними, а отже такими які ізотропні та не мають певної характерної форми, то по суті єдиним реальним способом відрізнити полікристалічне тіло від аморфного полягає в з’ясуванні того плавиться це тіло, чи поступово розм’ягчується. Скажімо а ні за ознакою ізотропності, а ні за ознакою наявності певної форми, шматок льоду не можливо відрізнити від шматка скла. І якщо ми стверджуємо, що лід кристалічний а скло аморфне, то головним чином тому, що в процесі нагрівання лід плавиться, а скло поступово розм’ягчується.
Говорячи про те, що аморфні тіла є умовно твердими, мають на увазі, що в деяких наукових джерелах, факт схожості внутрішнього устрою аморфних та рідких речовин у поєднанні з фактом того, що перехід аморфного тіла з твердого стану в рідкий і навпаки не має чітко визначених меж, вважається достатньою підставою для того, щоб аморфні тіла віднести до розряду рідин. Що ж, ми не втомлюємся повторювати, Природа – це єдиний цілісний організм і тому, будь який класифікаційний поділ її об’єктів є досить умовним. І в цьому сенсі поділ речовин на тверді та рідкі не є винятком. Тому аморфні тіла можна вважати такими, що займають проміжне місце між тілами безумовно твердими (кристалічними) та безумовно рідкими.
Дослідження показують, що зазвичай аморфний стан хімічно простих речовин є метастабільним, тобто енергетично нестійким. Ця метастабільність пояснюється тим, що структурні одиниці аморфного тіла розташовані енергетично не оптимальним чином. А це означає, що у відповідності з законами Природи (зокрема тим, який прийнято називати принципом мінімуму), частинки аморфного тіла прагнуть вишикуватись в енергетично доцільному порядку. Результатом цих прагнень є те, що початково аморфне тіло, рано чи пізно стає кристалічним. Наприклад, в процесі достатньо швидкого охолодження високотемпературного насиченого цукрового сиропу, утворюється твердий аморфний льодяник (аморфний цукор). Якщо ж цей аморфний льодяник залишити у спокої, то через лічену кількість місяців він зацукрується, тобто перетворюється на сукупність окремих кристаликів цукру.
Подібним чином ведуть себе й інші аморфні речовини, зокрема скло. Однак тривалість кристалізації скла, вимірюється не місяцями, а тисячоліттями. Результатом подібної кристалізації є поступове перетворення склоподібних вулканічних лав, на кристалічний граніт, базальт, пісок, тощо. Власне факт того, що в природних умовах аморфні тіла зустрічаються рідко, є прямим наслідком того, що такі тіла поступово кристалізуються.
Варто зауважити, що поділ твердих речовин на аморфні і кристалічні є досить умовним. Умовним бодай тому, що велика кількість хімічно тотожних речовин, можуть бути як аморфними так і кристалічними. Якщо ж врахувати факт того, що з плином часу аморфні речовини поступово кристалізуються, то стане очевидним, що на певних етапах цієї кристалізації, однозначно визначити стан аморфно-кристалічного тіла практично не можливо.
Визначальною ознакою будь якого твердого тіла є здатність зберігати свою форму та розміри. Характеризуючи цю здатність, говорять про механічні властивості твердих тіл, зокрема їх пружність, пластичність, еластичність, крихкість, твердість та міцність.
Якщо сталеву і свинцеву лінійки в однаковій мірі зігнути, то скоріш за все, після припинення дії деформуючої сили, сталева лінійка практично повністю відновить свою попередню форту, а лінійка свинцева – залишиться деформованою. При цьому говорять, що сталь – пружний матеріал, а свинець – матеріал пластичний. Пружність – це така механічна властивість тіла (матеріалу), яка полягає в його здатності відновлювати свою форму і розміри після припинення дії деформуючої сили. Пластичність – це така механічна властивість тіла, яка полягає в його не здатності відновлювати свою форму і розміри після припинення дії деформуючої
Пружність і пластичність в тій чи іншій мірі притаманні всім твердим тілам. Просто в одних речовинах, сильніше виражені пружні властивості, а в інших – пластичні. Скажімо сталь, має яскраво виражені пружні властивості і неявно виражені пластичні. Натомість свинець, навпаки – має яскраво виражені пластичні властивості і погано виражені пружні.
Матеріали які під дією відносно невеликих навантажень зазнають великих пружних деформацій (ε=Δℓ/ℓ0 > 100%), називають еластичними. До числа таких матеріалів відносяться різноманітні сорти гуми. Еластичність – це така механічна властивість матеріалу, яка полягає в його здатності зазнавати великих пружних деформацій під дією відносно невеликих деформуючих сил.
Матеріали які руйнуються при відносно малих пружних деформаціях (ε=Δℓ/ℓ0 ˂ 3%) називаються крихкими. Наприклад чавун, скло, фарфор, граніт, алмаз, сіль – матеріали крихкі, Крихкість – це така механічна властивість тіла (матеріалу), яка полягає в тому, що воно руйнується при незначних деформаціях та без суттєвих пластичних змін.
Важливою механічною властивістю твердих речовин є їх твердість. Якби вас запитали: «який матеріал твердіший свинець чи сталь ?» – то скоріш за все, ви скажете, що сталь, і що це пов’язано з тим, що саме сталь залишає подряпини на свинцевій поверхні, а не навпаки. Відповівши таким чином, ви будете абсолютно праві. Адже з двох матеріалів більш твердим вважається той, який залишає подряпини чи вм’ятини на поверхні іншого. Твердість – це така механічна властивість матеріалу, яка полягає в його здатності протидіє появі на поверхні місцевих пластичних деформацій (подряпин, вм’ятин, надрізів, тощо).
Існує декілька методів визначення твердості. Наприклад, твердість матеріалу можна визначити за умовною десятибальною шкалою, яку запропонував ще в 1811 році німецький геолог Фрідріх Моос (1773 – 1839). Еталонами твердості за шкалою Мооса є десять мінералів (мал.56), які підібрані таким чином, що кожний наступний, залишає подряпини на попередньому. При цьому вимірювання твердості за шкалою Мооса, полягає в тому, щоб визначити місце даного матеріалу серед десяти вибраних еталонів. Наприклад, якщо досліджуваний матеріал залишає подряпини на кварці, а його в свою чергу дряпає топаз, то твердість матеріалу 7,5.

Мал. 59. Мінерали, що є еталонами твердості за шкалою Мооса.
Ясно, що вище описаний метод визначення твердості не є надто точним та безумовно об’єктивним. Тому в науковій та інженерній практиці, твердість визначають іншими, більш точними і об’єктивними методами.
Ще однією важливою механічною властивістю твердого тіла є його міцність. Міцність – це така механічна властивість тіла (матеріалу), яка полягає в його здатності витримувати максимально великі навантаження без механічної руйнації тіла. Кількісною мірою міцності тіла (матеріалу) є його межа міцності, тобто та максимально допустима механічна напруга, яку може витримати дане тіло без його руйнації (позначається σм). Наприклад, усереднена величина межі міцності при розтягуванні, для сталі σм=500МПа, для алюмінію σм= 75МПа, а для свинцю σм= 15МПа.
Контрольні запитання.
- Чи існують безумовно кристалічні речовини які не мають певної температури плавлення
- Назвіть ознаки кристалічності речовини.
- Що таке поліморфізм? Наведіть приклади.
- Поясніть, чому монокристали анізотропні, а полікристали – ізотропні?
- Чому аморфні тіла прийнято вважати умовно твердими?
- Чи є безумовно правильним твердження: частинки аморфного тіла розташовані хаотично? Чому?
- Чому аморфні тіла не плавляться, а розм’ягчуються?
- Чому в деяких наукових джерелах, аморфні тіла відносять до розряду рідин?
- Чому з плином часу, аморфні тіла поступово кристалізуються?
- Чому поділ речовин на тверді та рідкі, на кристалічні та аморфні, є умовним?
- Які з властивостей твердого тіла (пружність, пластичність, крихкість, міцність, еластичність, твердість) є взаємно протилежними?
.
Лекційне заняття №12.
Тема: Види кристалічних структур.
Питання про загальний устрій кристалів та фізичну суть тих зв’язків які об’єднують певні частинки у відповідні кристалічні структури, нерозривно пов’язане з розумінням загального устрою та базових фізико-хімічних властивостей атома. Гранично стисло і гранично спрощено про цей устрій та ці властивості можна сказати наступне. Атом представляє собою цілісну систему, яка складається з масивного позитивно зарядженого ядра та певної кількості надлегких, негативно заряджених електронів. При цьому атом є частинкою незарядженою, тобто такою в якій позитивний заряд ядра в точності дорівнює загальному негативному заряду тих електронів які обертаються навколо ядра. Атоми які втрачають електрони, перетворюються на відповідні позитивні іони. А ті атоми, які приєднують надлишкові електрони, стають відповідними негативними іонами.
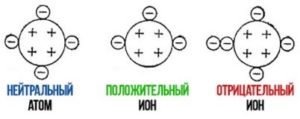
Мал. 60. Атом – частинка незаряджена. Втрачаючи електрон, атом перетворюється на позитивний іон, а приєднуючи додатковий електрон – на іон негативний.
По суті фізико-хімічні властивості атома визначально залежать від його схильності віддавати або приєднувати валентні електрони, тобто ті електрони які знаходяться на зовнішньому енергетичному рівні атома. А за цією схильністю різноманіття атомів та їм відповідних хімічно простих речовин, можна розділити на три групи: метали, неметали та інертні гази.
Металами називають такі хімічно прості речовини, атоми яких схильні легко віддавати валентні електрони та перетворюватись на відповідні позитивні іони. Наприклад, атом натрію, на зовнішньому енергетичному рівні має один валентний електрон. Цей електрон слабко утримується ядром атома і тому легко відривається від нього. При цьому атом перетворюється на відповідний позитивний іон: Na0 – e– → Na+. Близько 80% тих атомів що містяться в таблиці хімічних елементів – це атоми металів.
Неметалами називають такі хімічно прості речовини, атоми яких схильні приєднувати до себе надлишкові електрони перетворюючись при цьому на відповідні негативні іони. Наприклад, атом хлору на зовнішньому енергетичному рівні має сім валентних електронів і прагне до того, щоб цих електронів було вісім. Тому, за першої ліпшої нагоди, атом хлору приєднує до себе один додатковий електрон і стає відповідним негативним іоном: Сℓ0 + е– → Сℓ–
Яскраво виражених неметалів (окислювачів) небагато: фтор (F), кисень (О), азот (N), хлор (Сℓ), бром (Вr). Однак на базі цих атомів (головним чином кисню) можуть утворюватись стійкі цілісні групи, які мають потужні окислювальні властивості. Це означає, що такі групи атомів, за першої ліпшої нагоди, приєднують до себе певну кількість електронів і перетворюються на відповідні негативні іони:
SO40 + 2e– → SO42– ;
NO30 + e– → NO3– ;
OH0 + e– → OH– .
Інертними газами називають такі хімічно прості речовини, атоми яких не схильні а ні віддавати свої валентні електрони, а ні приєднувати до себе додаткові. Це означає, що інертні атоми (He, Ne, Ar, Kr, Xe, Rn) не приймають участі в хімічних реакціях і не утворюють жодних хімічних сполук. Зовнішні енергетичні рівні інертних атомів повністю заповнені валентними електронами, кількість яких для атома гелію дорівнює двом, а для решти атомів (Ne, Ar, Kr, Xe, Rn) – восьми.
За характером тих сил, що діють між частинками кристалу та за назвами цих частинок, розрізняють чотири види кристалічних структур:
- іонна структура,
- атомна структура,
- молекулярна структура,
- металічна структура.
Мал.61. Основні види кристалічних структур.
Стисло описуючи загальний устрій та властивості кристалічних структур можна сказати наступне.
Іонна структура – це така кристалічна структура, в вузлах якої знаходяться позитивні та негативні іони відповідної речовини, між якими діють сили іонного зв’язку. Іонний зв’язок – це такий електромагнітний зв’язок, який існує між позитивними та негативними іонами і основною складовою якого є сили електростатичної взаємодії. Іонну структуру мають ті кристалічні речовини які в хімії називаються солями (NaCℓ; CuSO4; AgNO3; …) та основами (NaOH; Cu(OH)2; AgOH; …).
Не важко бачити, що складовими частинами як солей так і основ є певні атоми металів та певні атоми або групи атомів неметалів (окислювачів). А це означає, що при взаємодії відповідних атомів, певна кількість електронів переходить від атомів металу до атомів неметалу. Наприклад при зустрічі атомів натрію (Na) та хлору (Cℓ), хлор забирає у натрію валентний електрон і перетворюється на негативний іон хлору (Cℓ–), натомість атом натрію втрачаючи електрон стає позитивним іоном натрію (Na+). А оскільки різнойменні заряди притягуються, а однойменні – відштовхуються, то кожний іон натрію (Na+) прагне оточити себе іонами хлору (Cℓ–), а кожний іон хлору прагне оточити себе іонами натрію. Реалізацією цих прагнень і є іонна кристалічна структура.
Na → e → Cℓ → Na+ Cℓ– Na → e → OH → Na+ OH–
Cu →2e→ SO4 → Cu2+ SO42– Cu → 2e → (OH)2 → Cu2+ (OH)22–
Ag → e → NO3 → Ag+ NO3– Ag → e → OH → Ag+ OH–
.
Зазвичай в іонній кристалічній структурі позитивні і негативні іони розташовуються таким чиним, що утворюють просту кубічну решітку. Наприклад, в кристалі хлориду натрію (NaCℓ), кожний позитивний іон натрію оточений шістьма рівновіддаленими негативними іонами хлору. А кожний іон хлору, оточений шістьма рівновіддаленими іонами натрію (мал.62).
Іонні кристали є крихкими, мають відносно невелику міцність та твердість. Більшість з них добре розчиняються у воді. Розчини та розплави іонних кристалів, добре проводять електричний струм. При цьому самі іонні кристали струм не проводять.

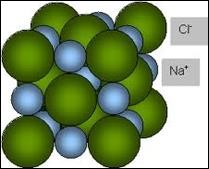
Мал.62. Кристалічна гратка хлориду натрію: а) кулестержнева модель; б) масштабна модель.
Атомна структура – це така кристалічна структура, в вузлах якої розташовані атоми відповідної речовини, між якими діють сили ковалентного зв’язку. Ковалентний зв’язок – це такий електромагнітний зв’язок, який існує між електронейтральними атомами і суть якого полягає в тому, що ці атоми інтенсивно обмінюються валентними електронами. При цьому, кожний атом обмінюється електронами лише з певною строго визначеною групою сусідніх атомів. Наприклад атом хлору на зовнішньому (валентному) енергетичному рівні має сім валентних електронів. А у відповідності з законами природи таких електронів має бути вісім. В такій ситуації два сусідніх атомів хлору постійно обмінюючись валентними електронами, утворюють міцну ковалентну сім’ю, яка називається молекулою хлору (Сℓ2). Аналогічним чином утворюються й інші молекули, зокрема: атом хлору обмінюючись валентними електронами з атомом водню утворює молекулу НСℓ; атом кисню, обмінюючись валентними електронами з двома атомами водню, утворює молекулу Н2О; атом азоту обмінюючись валентними електронами з трьома атомами водню утворює молекулу NН3 і т.д.
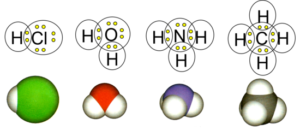
Мал.63. В молекулі, певна група атомів, постійно обмінюючись валентними електронами обособлюються та утворює відповідну ковалентну сім’ю (молекулу).
Потрібно зауважити, що вище описаний механізм ковалентного зв’язку є гранично спрощеним відображенням тієї сукупності складних електромагнітних та квантово механічних процесів які відбуваються між взаємодіючими атомами. Втім, якщо говорити про узагальнюючу фізичну суть ковалентного зв’язку, то вона дійсно полягає в тому, що взаємодіючі атоми інтенсивно обмінюються валентними електронами. Ковалентний зв’язок є тим хімічним зв’язком за рахунок якого утворюються молекули. Власне молекула, це і є обособлена група атомів об’єднаних ковалентним зв’язком.
За рахунок ковалентного зв’язку, утворюються не лише молекули, а й найміцніші кристалічні структури. Атомну структуру мають алмаз, корунд, граніт, пісок, коштовне та некоштовне каміння, тощо. На відміну від молекул в яких певна обмежена група атомів постійно обмінюючись валентними електронами утворює певну обособлену частинку, в кристалі з атомною структурою вся сукупність наявних атомів, послідовно взаємодіючи один з одним утворюють єдине ціле. Наприклад атом вуглецю має чотири валентних електрони. А за законами природи, на зовнішньому енергетичному рівні, таких електронів має бути вісім. В такій ситуації атом вуглецю розташовується таким чином, щоб постійно обмінюватись валентними електронами з чотирма сусідніми атомами. Ті ж в свою чергу, обмінюються електронами з своїми сусідами і т.д. (мал.64). При цьому, між всією сукупністю наявних атомів утворюються міцні ковалентні зв’язки, які в сукупності і формують відповідну атомну кристалічну структуру, структуру алмазу.
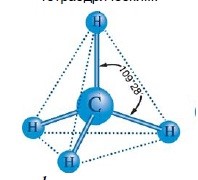

Мал. 64. В атомній кристалічній структурі, всі атоми об’єднуються міцними ковалентними зв’язками та утворюють єдине ціле – відповідний кристал.
Атомні кристали мають високу механічну міцність та надзвичайно високу твердість. Вони не розчиняються у воді, не проводять електричний струм, мають високу температуру плавлення.
Потрібно зауважити, що в атомних та іонних кристалах, поняття «молекула» втрачає сенс. Адже в цих кристалах по суті не існує тих обособлених груп атомів, які можна було б назвати молекулами. Тому ви маєте розуміти, що формули SiO2, Aℓ2O3, NaCℓ, CuSO4, AgNO3, тощо, вказують лише на те, з яких атомів (груп атомів) складається відповідна кристалічна структура і в яких співвідношеннях ці атоми зустрічаються в ній.
Металічна структура – це така кристалічна структура, в вузлах якої розташовані атоми металів, між якими діють сили металічного зв’язку. Металічний зв’язок – це такий електромагнітний зв’язок, який існує між атомами металів і суть якого полягає в тому, що ці атоми постійно обмінюються валентними електронами. При цьому, кожен атом почергово обмінюється валентними електронами з всією сукупністю сусідніх атомів. Металічну структуру мають всі метали.
За своєю фізичною природою, металічний зв’язок дуже схожий на ковалентний. Як і при ковалентному зв’язку, атоми металів постійно обмінюються валентними електронами і за рахунок цього обміну, об’єднуються у відповідну кристалічну структуру. Але, якщо при ковалентному зв’язку, певний атом взаємодіє з обмеженою кількістю чітко визначених сусідів, то при металічному зв’язку, кожен атом почергово взаємодіє (обмінюється електронами) з усіма сусідніми атомами. В такій ситуації, ті валентні електрони які забезпечують взаємодію атомів металу, постійно переміщуючись від атома до атома, можуть рухатись в будь якому напрямку. При цьому, за відсутності зовнішньої електричної напруги, рух електронів є хаотичним. За наявності ж такої напруги, цей рух стає хаотично-упорядкованим. Власне упорядковану складову цього руху і називають електричним струмом в металах.
Різноманіття металів таке велике, що серед них є як надміцні так і не надто міцні; як тверді так і не надто тверді; як тугоплавкі так і такі, що плавляться при мінусових температурах. Але от що дійсно об’єднує всі метали, так це їх висока електропровідність. Крім цього, всі метали мають високу теплопровідність та низьку теплоємність.
Мал.65. В металічній структурі, кожен атом металу обмінюється валентними електронами з усією сукупністю сусідніх атомів.
Молекулярна структура – це така кристалічна структура, в вузлах якої знаходяться молекули відповідної речовини, між якими діють сили дипольного або водневого зв’язку. Молекулярну структуру має лід, нафталін, органічні сполуки та ті хімічно прості речовини, які за звичайних умов є рідкими або газоподібними.
Дипольний зв’язок – це такий електромагнітний зв’язок, з яким молекули-диполі взаємодіють між собою як відповідні електричні системи. Пояснюючи суть дипольного зв’язку, можна сказати наступне. Дослідження показують, що в об’ємі більшості молекул, електричні заряди розподілені нерівномірно, і що тому ці молекули представляють собою певні дипольні системи. Диполь (від «два полюси») – це цілісна система двох, близько розташованих, рівних за величиною і протилежних за знаком електричних зарядів. Наприклад, в молекулі води (мал.66) атом кисню і два атоми водню розташовані не на одній прямій. При цьому кисень, будучи надзвичайно потужним окислювачем, сильно іонізує атоми водню. А це означає, що ті валентні електрони які забезпечують ковалентний зв’язок між воднем і киснем, левову частину часу перебувають біля атому кисню. (В подібних ситуаціях говорять, що ковалентний зв’язок є сильно поляризованим). Результатом такого розташування атомів та поляризованості ковалентного зв’язку, є факт того, що в молекулі води, електричні заряди розподілені нерівномірно, а вона сама представляє собою яскраво виражений диполь. В тій чи іншій мірі, дипольні властивості мають практично всі взаємодіючі молекули. Навіть ідеально симетричні молекули (Н2, О2, N2, тощо) в процесі взаємодії з іншими молекулами поляризуються і стають дипольними.
Мал.66. В електричному сенсі молекула води є диполем. Молекули-диполі взаємодіють як відповідні електричні системи.
Знаючи, що різнойменні заряди притягуються, а однойменні – відштовхуються, не важко збагнути, що молекули-диполі взаємодіють між собою і що ці взаємодії мають електричну природу. Власне ці взаємодії і називаються дипольними або силами Ван дер Ваальса (Йоханнес Ван дер Ваальс (1835-1923) голландський фізик, який дослідив і пояснив слабкі міжмолекулярні взаємодії). Дипольні взаємодії (сили Ван дер Ваальса) відносяться до слабких електромагнітних взаємодій. І тому, побудовані на їх основі молекулярні кристали є такими, що мають малу механічну міцність, низьку температуру плавлення і легко сублімують (випаровуються). За звичайних умов ті речовини молекули яких об’єднані силами дипольного зв’язку, є газоподібними або рідкими.
Серед тих кристалічних речовин які мають молекулярну структуру, особливе місце посідає лід. Чи задумувались ви над тим, чому відносно легкі молекули води (m0 = 18а.о.м.) за звичайних умов, конденсуються в рідину, а то й в достатньо міцний кристалічний лід, тоді як інші, більш масивні молекули (О2, N2, CO2, H2S, Cℓ2, тощо) за тих же умов є газоподібними? Ви можете сказати, що молекули води мають яскраво виражені дипольні властивості і що тому між ними діють відносно великі сили Ван дер Ваальса. Певною мірою це правда. Однак розрахунки показують, що якби молекули води об’єднували лише дипольні взаємодії, то вода плавилась би при температурі –90ºС, а кипіла при –80ºС.
Секрет надзвичайних властивостей води полягає в тому, що між її молекулами, окрім сил дипольного зв’язку, діють сили так званого водневого зв’язку. Водневий зв’язок – це такий електромагнітний зв’язок, з яким позитивно іонізовані атоми водню взаємодіють з негативно іонізованими атомами сусідніх молекул. Суть водневого зв’язку полягає в наступному. Атом водню відрізняється від інших тим, що при втраті валентного електрона фактично перетворюється на оголене атомне ядро. В такій ситуації іон водню (Н+) схильний глибоко проникати в електронні оболонки інших атомів та взаємодіяти з їх електронами. В молекулі води, атоми водню формально не є позитивними іонами. Однак фактично дуже схожі на них. Тому ці сильно іонізовані атоми, схильні взаємодіяти з електронами сусідніх атомів кисню та встановлювати з ними відносно міцні зв’язки (мал.67). Власне ці взаємодії та їм відповідні зв’язки і називають водневими зв’язками.
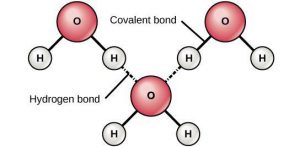
Мал.67. При водневому зв’язку, позитивно іонізовані атоми водню однієї молекули, взаємодіють з негативно іонізованими молекулами кисню іншої молекули.
За своїми силовими параметрами, водневий зв’язок в десятки разів сильніший за дипольний. І тому ті молекулярні кристали в яких суттєво проявляється цей зв’язок є відносно міцними. Наочним прикладом такої міцності є лід. До числа тих речовин в яких суттєву роль відіграють водневі зв’язки відносяться практично всі органічні сполуки: вуглеводні, спирти, прості та складні ефіри, органічні кислоти, молекули ДНК, тощо.
Завершуючи розмову про види кристалічних структур, зауважимо, що поділ цих структур на іонні, атомні, металічні та молекулярні є досить умовним. Умовним бодай тому, що в реальних кристалах часто поєднуються різні види зв’язків. Наприклад, в кристалі графіту, атом вуглецю трьома валентними електронами утворює ковалентні зв’язки, а четвертим – металічний зв’язок. Крім цього, досить умовним є сам поділ зв’язків на іонні, ковалентні, металічні, водневі та дипольні. Адже в реальних кристалах часто-густо іонний зв’язок важко відрізнити від сильно поляризованого ковалентного зв’язку, сильно поляризований ковалентний – від водневого, водневий – від іонного, іонний – від дипольного, а ковалентний – від металічного. І це закономірно. Адже всі ці зв’язки, фактично є проявами одних і тих же електромагнітних взаємодій.
Контрольні запитання.
- Поясніть чим атоми металів відрізняються від атомів неметалів?
- Як ви думаєте, чому іонні кристали не проводять електричний струм, а їх розчини і розплави – проводять?
- В чому суть ковалентного зв’язку?
- Які загальні властивості тих матеріалів які мають іонну структуру?
- Які загальні властивості тих матеріалів які мають атомну структуру?
- Чи правильне твердження: кристали оксиду кремнію складаються з молекул SiO2? Поясніть.
- Чим металічний зв’язок схожий на ковалентний і чим від нього відрізняється?
- Які загальні властивості тих матеріалів які мають металічну структуру?
- Чому легкі молекули води кристалізуються при 0°С, тоді як важкі молекули кисню – лише при –219°С?
- Чому поділ кристалічних структур на іонні, атомні, металічні та молекулярні, є умовним?
.
Лекційне заняття № 13.
Тема: Про внутрішню енергію та кількість теплоти. Рівняння теплового балансу. Нагрівання – охолодження.
Нагадаємо. Енергія – це фізична величина, яка є загальною мірою всіх видів рухів та взаємодій і яка характеризує здатність тіла, частинки або поля виконати роботу.
Позначається: Е
Визначальне рівняння: різні, в залежності від виду енергії,
Одиниця вимірювання: [Е] = Дж.
Розрізняють дві базові різновидності енергії: кінетична та потенціальна.
Кінетична енергія (енергія руху) – це та енергія, яку має фізичний об’єкт за рахунок того що він рухається і яка дорівнює половині добутку маси об’єкту на квадрат швидкості його руху.
Позначається: Ек
Визначальне рівняння: Ек = mv2/2,
Одиниця вимірювання: [Ек] = Дж.
Якщо мова йде про середню кінетичну енергію поступального руху молекул речовини, то її зазвичай визначають за формулою Ек=(3/2)kT, де k=1,38·10–23Дж/К – стала Больцмана, T – абсолютна температура речовини.
Потенціальна енергія (енергія взаємодії) – це та енергія, яку має фізичний об’єкт за рахунок того, що він так чи інакше взаємодіє з іншими фізичними об’єктами, або за рахунок тих взаємодій які відбуваються всередині самого об’єкту.
Позначається: Еп
Визначальне рівняння: Еп=? (єдиної, універсальної формули, яка б дозволяла визначати величину потенціальної енергії в будь яких її проявах, нема).
Одиниця вимірювання: [Еп] = Дж.
Наряду з силою, енергія є тією фізичною величиною яка має величезну кількість різновидностей. Енергія може бути механічною і електричною, тепловою і хімічною, магнітною і електромагнітною, звуковою і ядерною, повною і внутрішньою, потенціальною сили пружності і потенціальною сили тяжіння, кінетичною поступального руху і кінетичною обертального руху, енергією спокою, енергією зв’язку, енергією активізації, енергією іонізації і т.д. і т.п. Тому говорячи про енергію того чи іншого об’єкту або явища, потрібно визначитись з тим, про яку різновидність енергії йде мова. Це тим більш важливо, зважаючи на те, що в різних обставинах, за однією і тією ж назвою можуть приховуватись суттєво різні величини.
Наприклад сьогодні ми говоримо про внутрішню енергію тіла, тобто ту енергію яка зосереджена всередині (внутрі) даного тіла і яка чисельно дорівнює сумі кінетичних та потенціальних енергій тих частинок з яких це тіло складається. Величина цієї енергії по суті залежить від рівня деталізації внутрішнього устрою тіла. Скажімо якщо виходити з того, що тіло складається з молекул, то його внутрішня енергія має визначатись як сума кінетичних і потенціальних енергій всіх молекул цього тіла. Якщо ж врахувати, що молекули складаються з атомів, то визначаючи внутрішню енергію тіла, потрібно врахувати не лише кінетичну і потенціальну енергію його молекул, а й кінетичну та потенціальну енергію тих атомів з яких ці молекули складаються. А якщо прийняти до уваги факт того, що атоми також мають певний внутрішній устрій, то визначаючи внутрішню енергію тіла потрібно врахувати і енергію тих частинок з яких складаються його атоми.
Чесно кажучи, якщо мова йде про ту загальну кількість енергії яка зосереджена всередині (внутрі) будь якого тіла, то величину цієї енергії визначається за формулою Е=mс2, де m – маса тіла, с=3∙108м/с=соnst. Це означає, що повністю перетворивши все те з чого складається дане тіло, а отже всі його молекули, атоми, атомні ядра, протони, нейтрони, електрони та всі ті процеси які відбуваються з ними, в те що називається чистою енергією, а по суті в світло, ви отримаєте цієї енергії в кількості Е=mс2. Наприклад в будь якому тілі масою 1кг міститься Е=1кг(3·108м/с)2=9·1016Дж енергії. Щоб мати уявлення про величину цієї енергії, достатньо сказати, що аналогічну кількість енергії можна отримати при повному згоранні 4 500 000 тон кам’яного вугілля.
Однак, коли в межах молекулярної фізики, термодинаміки чи повсякденного життя ми говоримо про внутрішню енергію тіла, то маємо на увазі не ту загальну кількість енергії яка в принципі зосереджена в даному тілі і величина якої визначається за формулою Е=mс2, а ту мізерну частину цієї загальної енергії яка обумовлена рухом та взаємодією молекул відповідного тіла. Іншими словами, в молекулярній фізиці:
Внутрішня енергія – це та енергія яка зосереджена всередині даного тіла і яка чисельно дорівнює сумі кінетичних і потенціальних енергій всіх молекул цього тіла.
Позначається: U
Визначальне рівняння: U = ∑Екі + ∑Епі
Одиниця вимірювання: [U] = Дж.

Мал.68. Внутрішня енергія тіла дорівнює сумі кінетичних і потенціальних енергій всіх молекул цього тіла.
В загальному випадку, теоретично визначати внутрішню енергію довільно взятого тіла ми не вміємо. Не вміємо головним чином тому, що на сьогоднішній день не існує тієї універсальної формули, яка б дозволяла визначати потенціальну енергію молекул речовини. А оскільки Еп=? то U=∑Ек+∑Еп =?
Втім, якщо мова йде про ідеальний газ, то для нього енергією взаємодії молекул можна знехтувати, тобто вважати, що Еп=0. А це означає, що для ідеального газу U = ∑Екі = NЕк =(3/2)NkT = 1,5νNАkT = 1,5mR/T,
де m – маса газу, М – молярна маса газу, R = NAk = 8,31Дж/К·моль – універсальна газова стала, Т – абсолютна температура газу.
Теоретично обгрунтовуючи рівняння U = 1,5mR/T, ми виходили з того, що молекули газу, це пружні кульки (одноатомні). А це означає, що визначаючи кінетичну енергію цих кульок ми не враховували енергію їх обертального руху. Якщо ж врахувати цю енергію то можна довести, що в залежності від того з яких молекул складається газ, величину його внутрішньої енергії визначається за однією з наступних формул:
– для одноатомних молекул U = 1,5mRT/M;
– для двохатомних молекул U = 2,5mRT/M;
– для трьох і більше атомних молекул U = 3,0mRT/M.
Задача 1. Визначте внутрішню енергію того азоту що знаходиться в балоні ємністю 60 літрів при тиску 5атм.
Дано:
N2
V=60л=60·10–3м3
p=5атм=5·105Па
U = ?
Рішення. Оскільки молекули азоту двохатомні, то внутрішня енергія цього газу має визначатись за формулою U = 2,5mRT/M, де m = ? Оскільки згідно з законом Менделєєва-Клапейрона pV/T =mR/M, звідси m=pVM/TR. Таким чином: U = 2,5mRT/M = 2,5(pVM/TR)·( RT/M) = 2,5pV
Розрахунки: U = 2,5pV = 2,5·5·105Па·60·10–3м3 = 75000(Н·м) = 75кДж.
Відповідь: U = 75кДж.
Говорячи про потенціальну енергію молекул, потрібно мати на увазі, що ця енергія є відносною величиною. Наприклад, коли ми стверджуємо, що потенціальна енергія молекул газу дорівнює нулю, то це зовсім не означає що вона дійсно дорівнює нулю. Це навіть не означає, що ця енергія дійсно мала. Більше того, це навіть не означає, що потенціальна енергія молекул газу дійсно менша за їх кінетичну енергію. Твердження про те, що потенціальна енергія молекул газу є мізерно малою, означає лише те, що на рівні тих процесів які відбуваються в газі, вплив потенціальної енергії молекул на ці процеси є несуттєвим. Несуттєвим тому, що левова частина потенціальної енергії молекул газу прихована на рівні внутрішньо молекулярних взаємодій які на рівні міжмолекулярних взаємодій практично не проявляє себе. При цьому за інших обставин, ця прихована енергія може стати явною.
Ситуація нагадує таку, коли перебуваючи на рівні третього поверху, ви проводите експерименти з тими пружними кульками які рухаються гладенькою підлогою цього поверху. Аналізуючи кінематичну поведінку кульок, ви робите висновок, що ця поведінка не залежить від того, що відносно рівнів першого та другого поверхів, кожна кулька має певний запас потенціальної енергії. Та от в підлозі з’являється отвір, потрапляючи в який кульки опиняються на рівні підлоги другого поверху. При цьому неминуче з’ясовується, що та прихована потенціальна енергія, яка на рівні третього поверху жодним чином не проявляла себе, на рівні другого поверху, перетворюється на відповідну кількість кінетичної енергії та відповідним чином впливає на кінематичну поведінку кульок.

Мал.69. Потенціальна енергія є відносною величиною.
Зважаючи на вище сказане, не дивуйтесь тому, що в процесі конденсації виділяється величезна кількість теплової енергії. Просто в процесі конденсації молекули речовини «падають» з більш високого енергетичного рівня (поверху) на більш низький. При цьому та прихована потенціальна енергія яка на рівні поверху «газ» практично не проявляла себе, на рівні більш низького поверху «рідина» перетворюється на відповідну кількість кінетичної енергії (теплоти).
Та якби там не було, а в загальному випадку теоретично визначати внутрішню енергію тіла (U) ми не вміємо: оскільки Еп=? то U=∑Екі+∑Епі=? Однак на практиці, нас завжди цікавить не внутрішня енергія тіла, а те, на скільки вона змінюється в результаті того чи іншого теплового процесу. Іншими словами, на практиці нас цікавить не U, а ∆U. Наприклад, нас не цікавить та загальна кількість внутрішньої енергії яка зосереджена в певній кількості води, пару, заліза чи вугілля. Нас цікавить, скільки енергії ми отримаємо при згоранні певної кількості вугілля; скільки енергії потрібно для того, щоб нагріти дану кількість води на задану кількість градусів; скільки енергії ми отримаємо при перетворенні пару в рідину; скільки енергії потрібно для того, щоб розплавити певну кількість заліза; і т.д. Іншими словами, практичне значення має не внутрішня енергія тіла (U), а те на скільки вона змінюється в результаті того чи іншого теплового процесу. Цю зміну внутрішньої енергії тіла (∆U=Uк–Uп) називають кількістю теплоти.
Кількість теплоти – це фізична величина, яка показує на скільки джоулів змінюється внутрішня енергія тіла в результаті того чи іншого теплового процесу.
Позначається: Q
Визначальне рівняння: Q = ∆U
Одиниця вимірювання: [Q] = Дж.
Оскільки в загальному випадку, теоретично визначати внутрішню енергію тіла ми не вміємо, то відповідно не вміємо теоретично визначати і кількість тієї теплоти що виділяється або поглинається при тому чи іншому тепловому процесі (оскільки U=?, то Q=ΔU=?). В подібних ситуаціях, на допомогу теорії завжди приходить експеримент. Про те як експериментальні дослідження допомагають визначати ту кількість теплоти яка виділяється чи поглинається при тому чи іншому тепловому процесі, ми поговоримо дещо пізніше. Наразі ж зауважимо, що при всьому різноманітті тих процесів які відбуваються при теплообміні, виконується закон який називається рівнянням теплового балансу.
Рівняння теплового балансу – це закон, в якому стверджується: при теплообміні, загальна кількість теплоти втраченої одними тілами замкнутої (енерго ізольованої) системи, дорівнює загальній кількості теплоти отриманої іншими тілами цієї системи. Іншими словами: ∑Qвтр = ∑Qотр. Наприклад, якщо нагріте тіло опустити в посудину з холодною водою, то тіло втратить певну кількість теплової енергії, а вода і посудина аналогічну кількість енергії отримає. А якщо в результаті точних вимірювань з’ясується, що та загальна кількість тієї теплоти яку отримала вода і посудина дещо менша за ту кількість теплоти яку втратило нагріте тіло, то це означатиме лише те, що відповідна система є не замкнутою, і що в процесі вимірювань ми чогось не врахували. Наприклад того, що частина енергії нагрітого тіла пішла на випаровування рідини.
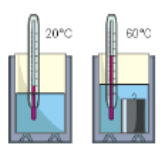
Мал.70. При теплообміні, загальна кількість теплоти втраченої одними тілами замкнутої системи, дорівнює загальній кількості теплоти отриманої іншими тілами цієї системи.
Зверніть увагу на те, що рівняння теплового балансу виконується лише в тому випадку якщо мова йде про теплообмін, тобто такий тепловий процес який відбувається без виконання механічної роботи. Адже якщо наприклад, в процесі нагрівання газ розширюється (мал.71б), то надана йому теплота буде витраченою не лише на нагрівання газу, а й на виконання ним певної механічної роботи (на розширення газу).
Мал.71. Рівняння теплового балансу в точності виконується лише при теплообміні, тобто такому тепловому процесі який відбувається без виконання механічної роботи.
Прилад за допомогою якого вимірюють кількість тієї теплоти що виділяється або поглинається в результаті того чи іншого теплового процесу називають калориметром (від лат. calor – теплота і грец. metreo – вимірюю). Сучасні калориметри мають достатньо складну будову. Однак принциповий устрій та принцип дії калориметра є досить простим і полягає в наступному. В максимально енергоізольованій посудині (мал.72) міститься відома кількість відомої рідини, наприклад води. В цю рідину опускають об’єкт теплового дослідження. При цьому, та теплова енергія яка виділяється або поглинається цим об’єктом, передається рідині. Знаючи масу рідини (m), її теплоємність (с) і те на скільки збільшилась або зменшилась температура рідини (∆t) в процесі теплообміну, визначають величину відповідної енергії (теплоти): Q=cm∆t. Ясно, що при подібних розрахунках потрібно враховувати і ту енергію яку отримують або віддають інші елементи системи, зокрема посудина калориметра, термометр, тощо.
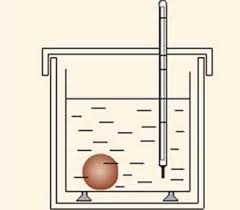
Мал.72. Схема загального устрою калориметра.
До числа найпоширеніших теплових процесів відносяться нагрівання і охолодження. Характеризуючи процес нагрівання, можна сказати наступне:
- Нагрівання відбувається з поглинанням енергії (теплоти). А це означає, що в процесі нагрівання внутрішня енергія відповідної речовини збільшується (Qн→U↑);
- 2. Нагрівання супроводжується підвищенням температури речовини. А це означає, що в процесі нагрівання відповідно збільшується середня кінетична енергія молекул речовини (якщо Т↑, то Ек↑, адже Ек=(3/2)kT);
- Нагрівання не супроводжується зміною агрегатного стану речовини. А це означає, що в процесі нагрівання, величина потенціальної енергії міжмолекулярних взаємодій залишається практично незмінною (Еп≈const). Потрібно зауважити, що в процесі нагрівання значна частина поглинутої тілом енергії йде на збільшення загальної потенціальної енергії тіла, але тієї прихованої частини цієї енергії, яка практично не впливає на міжмолекулярні взаємодії.
Узагальнюючи вище сказане можна дати наступне визначення. Нагрівання, це такий тепловий процес який відбувається з поглинанням енергії, супроводжується підвищенням температури речовини і не супроводжується зміною її агрегатного стану. При нагріванні, надана речовині теплова енергія йде на збільшення кінетичної енергії її молекул, при цьому потенціальна енергія цих молекул (енергія взаємодії молекул) залишається практично незмінною: Qн → Eк↑; Еп ≈ const.
Мал.73. Нагрівання: 1) теплота поглинається; 2) температура збільшується; 3) агрегатний стан не змінюється.
Оскільки процес охолодження відбувається з виділенням енергії, супроводжується зниженням температури речовини і не супроводжується зміною її агрегатного стану, то можна дати наступне визначення. Охолодження, це такий тепловий процес, який відбувається з виділенням енергії, супроводжується зниженням температури речовини і не супроводжується зміною її агрегатного стану. При охолодженні, виділення енергії відбувається за рахунок зменшення кінетичної енергії молекул речовини та прихованої частини їх потенціальної енергії, при цьому потенціальна енергія міжмолекулярних взаємодій залишається практично незмінною: Qох ← Eк↓; Еп ≈ const.
Очевидно, що кількість тієї теплоти яку потрібно витратити на те, щоб певне тіло нагріти на певну кількість градусів Цельсія (кельвінів), залежить від: 1) маси тіла (m); 2) різниці початкової та кінцевої температур тіла (ΔТ=Δt); 3) теплових властивостей матеріалу тіла. Цю залежність можна записати у вигляді Qн = сm∆T, або Qн = сm∆t, де с – питома теплоємність речовини.
Питома теплоємність речовини – це фізична величина, яка характеризує теплові властивості даної речовини і яка показує скільки енергії потрібно витратити на те, щоб один кілограм відповідної речовини нагріти на один кельвін (на один градус Цельсія).
Позначається: с
Визначальне рівняння: с = Qн/m∆T
Одиниця вимірювання: [с] = Дж/кг·К.
Теоретично визначити питому теплоємність довільно взятої речовини практично не можливо. Натомість її можна визначити експериментально. З цією метою, виготовлене із даного матеріалу тіло відомої маси (m) нагрівають на задану кількість кельвінів (градусів Цельсія ∆Т=Δt) і вимірюють ту кількість енергії Qн яка була витрачена на відповідне нагрівання. А потім, за формулою с=Qн/m∆T визначають числове значення питомої теплоємності відповідної речовини і записують його у відповідну таблицю.
Таблиця 1. Питомі теплоємності деяких речовин.
| Речовина | с (Дж/кгК) | Речовина | с (Дж/кгК) |
| · Тверді речовини | |||
| алюміній | 880 | платина | 125 |
| залізо, сталь | 460 | свинець | 120 |
| золото | 125 | срібло | 250 |
| лід | 2090 | скло | 840 |
| мідь | 380 | цегла | 750 |
| оливо | 250 | цинк | 400 |
| пісок | 970 | чавун | 550 |
| · Рідини | |||
| вода | 4187 | ртуть | 130 |
| гас | 2140 | спирт | 2430 |
| залізо | 830 | нафта | 2100 |
| · Гази ( р = const ) | |||
| азот | 1000 | гелій | 5200 |
| аміак | 2100 | кисень | 920 |
| водень | 14300 | повітря | 1000 |
| водяний пар | 2200 | вуглекислий газ | 830 |
Таким чином, маючи у своєму розпорядженні результати попередніх експериментальних досліджень, ту кількість теплоти яку отримує тіло в процесі нагрівання, можна визначити за формулою Qн = сm∆T, або Qн = сm∆t
Дослідження показують, що величина тієї кількості теплоти яку отримує тіло при його нагріванні (Qн), дорівнює тій кількості теплоти яку воно віддає при аналогічному охолодженні Qох=Qн=сm∆T. Втім, потрібно мати на увазі, що мова йде про взаємно протилежні процеси, які характеризуються відповідно протилежними знаками. А це означає, що для ситуації нагрівання–охолодження, рівняння Qотр=Qвтр по суті треба записувати у вигляді Qотр = –Qвтр. І тоді різниця температур в кожному випадку визначається за базовою формулою Δt=tк–tп. Якщо ж для ситуації нагрівання–охолодження рівняння теплового балансу записують у вигляді Qотр=Qвтр, то в цьому випадку Δt визначають як різницю між більшою та меншою температурами.
Не важко бачити, що серед всього різноманіття речовин, питома теплоємність води (с=4187Дж/кг°С) є практично найбільшою. Даний факт має надзвичайно важливе клімат утворююче значення. Це значення полягає в наступному. Питома теплоємність твердої поверхні Землі, приблизно в чотири рази менша за питому теплоємність води. Крім цього сонячне світло не здатне проникати в надра непрозорих поверхонь. В такій ситуації поверхневий шар континентальної землі, швидко нагрівається вдень і відповідно швидко охолоджується вночі. А це означає, що тверда поверхня Землі сприяє так званому різко континентальному клімату, який характеризується великими перепадами денних і нічних, зимових і літніх температур.
Натомість вода має велику питому теплоємність, при цьому сонячне світло глибоко проникає в товщу води, та сприяє нагріванню її величезних мас. В такій ситуації води світового океану виконують роль надпотужного теплового акумулятора, який робить клімат Землі більш м’яким та більш придатним для життя. Нагріваючись вдень, вода акумулює в собі величезну кількість теплової енергії, яку віддає вночі. Потужні океанічні течії, переносять нагріту в екваторіальних частин планети воду, в її холодні частини та роблять їх більш теплими. Натомість холодні води приполярних областей переміщуються в жаркі екваторіальні області та робить їх менш жаркими.
Задача 2. Яка маса залізної деталі, якщо на її нагрівання від 20°С до 120°С витратили 17кДж теплоти?
Загальні зауваження. В Міжнародній системі одиниць (СІ), основною одиницею вимірювання температури є кельвін (К). Однак зважаючи на те що Δt=ΔT, в тих ситуаціях коли мова йде про зміну температури, а ми маємо саме таку ситуацію (Qн=сm∆t), переведення температури з °С в К є необов’язковим.
Дано:
залізо
t1 =20°C
t2 =120°C
Qн =17кДж=17000Дж
m = ?
Рішення. Оскільки Qн = сm∆t, то m=Qн/cΔt, де с=460Дж/кг°С (таблична величина).
Розрахунки: m=17000Дж/460(Дж/кг°С)100°С=0,37кг.
Відповідь: m=0,37кг.
Задача 3. В результаті охолодження мідного паяльника до температури 20ºС виділилося 30,4кДж енергії. До якої температури було нагріто паяльник, якщо його маса 200г?
Дано:
мідь
t1 = 20ºС
Q =30,4кДж= 30400Дж
m =200г = 0,2кг
t2 = ?
Рішення. Оскільки Qох = сm∆t, то ∆t=Qн/cm, де с=380Дж/кг°С (таблична величина). ∆t = 30400Дж/380(Дж/кг·ºС)0,2кг = 400ºС. Оскільки ∆t = t2–t1, то t2 = t1+∆t = 20ºC + 400ºC = 420ºС.
Відповідь: t2 = 420ºС.
Задача 4. Ударна частина молота масою 5т вільно падає з висоти 2,5м на залізну деталь масою 50кг, скільки ударів зробив молот, якщо деталь нагрілася на 40ºС? На нагрівання деталі витрачається 30% енергії молота.
Загальні зауваження. Нагадаємо, рішення тих задач в яких фігурує параметр ККД, практично завжди починається з визначального рівняння цієї величини, тобто з формули η=(Акор/Азаг)100%. При цьому в подальшому, на основі аналізу умов конкретної задачі визначаються з тим, яка робота є корисною Акор=.., а яка загальною (затраченою) Азаг=… Результати цього аналізу записують у формулу η=(Акор/Азаг)100%, з якої і визначають потрібну величину.
Дано:
m1 = 5=5·103кг
h1 = 2,5м
m2 = 50кг
∆t2 = 40ºC
η = 30%
n = ?
Рішення. За визначенням η=(Акор/Азаг)100%. В умовах нашої задачі, корисною роботою є та енергія яка йде на нагрівання деталі, тобто Акор= Qн=с2m2∆t2, де с2 = 460Дж/кгºС. Загальною роботою є помножена на кількість ударів потенціальна енергія піднятого молота, тобто Азаг= nm1gh1, де g=10м/с2. Таким чином η = с2m2∆t2100%/nm1gh1, звідси n = с2m2∆t2100%/ηm1gh1.
Розрахунки: n = 460·50·40·100/30·5·103·10·2,5 = 46·4/3·2,5 = 25 ударів.
Відповідь: n = 25 ударів.
Задача 5. Дві однакові мідні кулі дістали однакову енергію, внаслідок чого перша куля залишаючись нерухомою нагрілась на 40ºС, натомість друга не нагріваючись набула певної швидкості. Визначити цю швидкість.
Дано:
m1 = m2
E1 = E2
v1 = 0м/с
∆t1 = 30ºC
Qн2 = 0Дж
v2 = ?
Рішення. Оскільки за умовою задачі E1 = E2 та враховуючи, що вся надана першій кулі енергія пішла на її нагрівання, тобто Е1 = с1m1∆t1, де с1= с(міді) = 380Дж/кгºС, а надана другій кулі енергія пішла на збільшення її кінетичної енергії, тобто Е2 = m2v22/2, можна записати с1m1∆t1 = m2v22/2, звідси v22 = 2с1m1∆t1/m2 = 2с1m1, звідси v2 = √2с1∆t1.
Розрахунки: v2 = √(2·380(Дж/кгºС)·30ºС = √22800(кг·м2/кг·с2) = 151м/с.
Відповідь: v2 = 151м/с.
Контрольні запитання.
- Чи є визначена за формулою Ек=(3/2)kT енергія молекули, загальною кінетичною енергією цієї молекули? Поясніть.
- Чи означає твердження: потенціальна енергія молекул газу дорівнює нулю, що ця енергія дійсно гранично мала? Поясніть.
- Чи можна за визначальним рівнянням внутрішньої енергії, визначити внутрішню енергію: а) твердого тіла; б) рідини; в) газу? Чому?
- Потенціальна енергія яких молекул більша: а) твердого тіла чи відповідної рідини; б) твердого тіла чи відповідного пару? Чому?
- В яких випадках рівняння теплового балансу виконується, а в яких – не виконується?
- Поясніть загальний устрій та принцип дії калориметра.
- Визначальне рівняння кількості теплоти має вигляд Q=∆U. Який недолік цього рівняння?
- Дайте загальну характеристику процесу: а) нагрівання; б) охолодження.
- Від чого залежить та кількість теплоти яка потрібна для нагріванні тіла?
- Чи можна теоретично визначити питому теплоємність: а) рідини; б) газу?
- Звідки береться та енергія яка виділяється в процесі охолодження тіла?
- Чому питома теплоємність газу виміряна при постійному об’ємі завжди менша за питому теплоємність того ж газу виміряній при постійному тиску?
Вправа 13.
- Щоб нагріти 110г алюмінію на 90ºС знадобилось 9,1Дж енергії. Визначити питому теплоємність алюмінію.
- Яка частина наявної в тілі енергії виділяється при його падінні з висоти 1м?
- Відомо, що питома теплоємність заліза 460Дж/кг·К. На скільки збільшується потенціальна енергія одного атому Fe при нагріванні заліза на 1ºС?
- Мідний калориметр масою 150г містить 200г води при температурі 15°С. В калориметр занурили тіло масою 220г та температурою 100°С. При цьому температура системи підвищилась до 30°С. Визначити питому теплоємність тіла.
- З якої висоти має впасти трьох кілограмова цеглина, щоб своєю кінетичною енергією нагріти літр води на 1ºС?
- На скільки джоулів зміниться внутрішні енергія одного моля ідеального газу, при його нагріванні на 1,5ºС?
- На скільки джоулів зміниться внутрішня енергія 200г азоту, при зміні його температури на 20ºС?
- Визначте внутрішню енергію того вуглекислого газу що знаходиться в балоні ємністю 50 літрів при тиску 5атм.
- Ідеальний одноатомний газ маючи тиск 0,3МПа займає об’єм 4,0л. Визначте внутрішню енергію цього газу.
- При температурі 27°С внутрішня енергія одноатомного ідеального газу 1,2кДж. Визначте число атомів в цьому газі.
.
Лекційне заняття № 14.
Тема: Загальні відомості про енергетичні параметри плавлення, пароутворення та горіння.
До числа найбільш поширених теплових процесів, окрім нагрівання та охолодження, відносяться плавлення, кристалізація, пароутворення, конденсація та горіння. З фізичною суттю більшості з цих процесів ви знайомі. Тому наразі стисло зупинимся лише на кількісній оцінці енергетичних параметрів цих процесів.
Плавлення, це такий тепловий процес який відбувається з поглинанням енергії, супроводжується переходом речовини з твердого (кристалічного) стану в рідкий і не супроводжується зміною температури речовини. При плавленні, надана речовині теплова енергія йде на збільшення потенціальної енергії її молекул, при цьому кінетична енергія цих молекул залишається незмінною: Qпл → Eп↑; Ек = const.
Зворотний до плавлення процес, тобто процес переходу речовини з рідкого стану в твердий кристалічний стан, називається кристалізацією. Кристалізація, це такий тепловий процес який відбувається з виділенням енергії, супроводжується переходом речовини з рідкого стану в твердий (кристалічний) і не супроводжується зміною температури речовини. При кристалізації виділення енергії відбувається за рахунок зменшення потенціальної енергії молекул речовини, при цьому кінетична енергія цих молекул залишається незмінною: Qкр ← Eп↓; Ек = const.
Кількість тієї теплоти яку потрібно витратити на те щоб при певній постійній температурі (температурі плавлення) розплавити певне тіло, залежить від маси тіла (m) та теплових властивостей відповідного матеріалу. Цю залежність можна записати у вигляді Qпл=λm, де λ – питома теплота плавлення.
Питома теплота плавлення – це фізична величина, яка характеризує теплові властивості даної речовини і яка показує скільки енергії потрібно витратити на те, щоб розплавити один кілограм відповідної речовини, за умови що вона вже знаходиться при температурі плавлення.
Позначається: λ, (лямбда)
Визначальне рівняння: λ = Qпл/m
Одиниця вимірювання: [λ] = Дж/кг.
Питому теплоту плавлення визначають експериментально і записують у відповідну таблицю, наприклад таку.
Таблиця 2. Температура плавлення та питома теплота плавлення деяких речовин.
| Речовина | tпл (ºC) | λ (Дж/кг) | Речовина | tпл (ºC) | λ(Дж/кг) |
| алюміній | 659 | 3,8·105 | олово | 232 | 0,58·105 |
| вода, лід | 0 | 3,35·105 | ртуть | – 39 | 0,13·105 |
| вольфрам | 3410 | 0,26·105 | свинець | 327 | 0,25·105 |
| залізо | 1530 | 2,5·105 | срібло | 960 | 0,88·105 |
| золото | 1063 | 0,66·105 | чавун білий | 1200 | 1,3·105 |
| мідь | 1083 | 1,8·105 | чавун сірий | 1150 | 0,97·105 |
Дослідження показують, що величина тієї кількості теплоти яку отримує тіло при його плавлені (Qпл), дорівнює тій кількості теплоти яку воно віддає при кристалізації Qкр=Qпл=λm.
Пароутворення, це такий тепловий процес, який відбувається з поглинанням енергії та супроводжується переходом речовини з рідкого стану в газоподібний. При пароутворенні, надана речовині теплова енергія йде на збільшення потенціальної енергії її молекул, при цьому кінетична енергія цих молекул залишається практично незмінною: Qпар → Eп↑; Ек = const.
На відміну від процесу плавлення, який відбувається при постійній температурі, пароутворення може відбуватися при будь якій температурі рідини. Інтенсивна фаза пароутворення називається кипінням. Кипіння – це таке інтенсивне пароутворення, яке відбувається при певній постійній температурі (температурі кипіння) і при якому утворення пару відбувається в усьому об’ємі рідини. Візуальною ознакою кипіння є утворення наповнених паром бульбашок.
Зворотний до пароутворення процес, тобто процес переходу речовини з газоподібного стану в рідкий, називається конденсацією. Конденсація, це такий тепловий процес, який відбувається з виділенням енергії та супроводжується переходом речовини з газоподібного стану в рідкий. При конденсації виділення енергії відбувається за рахунок зменшення потенціальної енергії молекул речовини, при цьому кінетична енергія цих молекул залишається практично: Qкр ← Eп↓; Ек = const.
На практиці, кількість тієї теплоти що поглинається в процесі пароутворення, або виділяється в процесі конденсації, визначають за формулою: Qпар= rm, де m – маса випаруваної (сконденсованої) рідини; r – питома теплота пароутворення речовини.
Питома теплота пароутворення – це фізична величина, яка характеризує теплові властивості даної речовини і яка показує, скільки енергії потрібно витратити на те, щоб при певній постійній температурі (зазвичай при температурі кипіння) випарувати один кілограм відповідної речовини.
Позначається: r
Визначальне рівняння: r = Qпар/m
Одиниця вимірювання: [r] = Дж/кг.
Питома теплота пароутворення кожної конкретної речовини визначається експериментально. А результати цих експериментів записуються у відповідну таблицю, наприклад таку:
Таблиця 3. Температура кипіння та питома теплота пароутворення деяких речовин.
| Речовина | t (ºС) | r (Дж/кг) | Речовина | t (ºС) | r (Дж/кг) |
| аміак | -33,4 | 13,7·105 | ртуть | 357 | 2,85·105 |
| ацетон | 56,2 | 5,2·105 | спирт | 78 | 8,57·105 |
| бензин | 150 | 3,0·105 | фреон -12 | -29,8 | 16,8·105 |
| вода | 100 | 22,6·105 | ефір етиловий | 35 | 3,52·105 |
| залізо | 3050 | 0,6·105 |
Нагрівання–охолодження, пароутворення–конденсація, плавлення–кристалізація, це відносно прості теплові процеси, які не супроводжуються хімічними перетвореннями речовини. Натомість горіння, це такий тепловий процес, який супроводжується певними хімічними реакціями, інтенсивним виділенням великої кількості теплової та певної кількості світлової енергії.
Зазвичай, горіння це досить складний процес, який представляє собою сукупність великої кількості екзотермічних, ланцюгових хімічних реакцій, протіканню яких сприяє низка суто фізичних явищ, як-то нагрівання, випаровування, дифузія, конвекційний теплообмін, тощо. Однак, якщо говорити про фізичну суть горіння, то вона досить проста. І ця суть полягає в тому, що в процесі горіння потенціальна енергія хімічних зв’язків і хімічно взаємодіючих речовин, перетворюється в кінетичну енергію продуктів згорання (Еп → Ек). Адже те, що ми називаємо полум’ям, по суті представляє собою сукупність величезної кількості молекул які мають надзвичайно велику кінетичну енергію та є продуктами згорання палива. Фізичну суть горіння можна представити у вигляді наступної узагальнюючої формули: С6Н12О6 + 6О2 → 6СО2 + 6Н2О + Qгор.

Мал.74. В процесі горіння потенціальна енергія хімічних зв’язків і хімічно взаємодіючих речовин, перетворюється в кінетичну енергію продуктів згорання (Еп → Ек).
На практиці кількість тієї теплоти, що виділяється в процесі горіння, визначають за формулою: Qгор = qm, де m – маса того палива, q – питома теплота згорання палива.
Питома теплота згорання – це фізична величина, яка характеризує теплові властивості даного виду палива і яка показує скільки енергії виділиться в процесі повного згорання одного кілограма цього палива.
Позначається: q
Визначальне рівняння: q = Qгор/m
Одиниця вимірювання: [q] = Дж/кг.
Питома теплота згорання кожного виду палива визначається експериментально та записується у відповідну таблицю, наприклад таку:
Таблиця 4. Питома теплота згорання деяких речовин.
| Речовина | q (Дж/кг) | Речовина | q (Дж/кг) |
| · Тверде паливо | |||
| буре вугілля | 9,3·106 | кам’яне вугілля марки АⅠ | 20·106 |
| деревне вугілля | 30·106 | кам’яне вугілля марки АⅡ | 30·106 |
| дрова сухі | 8,5·106 | торф | 15·106 |
| · Рідке паливо | |||
| бензин, нафта | 46·106 | мазут | 40·106 |
| дизельне паливо | 42·106 | спирт | 27·106 |
| гас | 43·106 | ||
| · Газоподібне паливо · (для 1м3 за нормальних умов) | |||
| коксовий газ | 16·106 | ацетилен | 48·106 |
| природний газ | 40·106 | водень | 120·106 |
Потрібно зауважити, що та кількість тієї теплоти яка виділяється в процесі горіння, практично не залежить від режиму цього горінні. Наприклад шматок деревини, в одних умовах може згоріти за дві хвилини, в інших – за десять хвилин, а в третіх (в процесі гниття) – за десять років. При цьому кількість тієї теплоти що виділяються в процесі відповідних згорань буде практично однаковою. Звичайно за умови що згорання буде повним.
На певно ви звернули увагу на те, що природні явища симетричні. Симетричні в тому сенсі, що кожному природному процесу можна поставити у відповідність певний зворотній процес. Нагрівання та охолодження, плавлення та кристалізація, пароутворення та конденсація – ось лише деякі приклади симетричності Природи. А от горіння. Чи існує процес зворотній до нього? Виявляється, існує. І цей процес називають фотосинтезом (від грец. photos – світло; synthesis – з’єднувати, створювати). Адже напевно ви чули про те, що колись всі ці нафти, вугілля, торфи та горючі гази були деревами, кущами, папоротниками, травою та іншою рослинністю. А це означає, що та енергія яка акумульована у вугіллі, нафті, природному газі та інших подібних матеріалах, по суті є законсервованою енергією фотосинтезу.
Фотосинтез, це складний багатоступеневий фотохімічний процес, суть якого полягає в тому, що в клітинах рослин та деяких бактерій, під дією енергії сонячного світла, із води та вуглекислого газу синтезуються енергоємні молекули простих вуглеводнів, зокрема глюкози. Фізичну суть фотосинтезу можна представити у вигляді наступної узагальнюючої формули: 6СО2 + 6Н2О + Е☼ → С6Н12О6 + 6О2. В процесі фотосинтезу кінетична енергія фотонів світла перетворюється на потенціальну енергію молекул палива та окислювача (Q☼=Ек → Еп). В процесі ж горіння, відбувається зворотнє перетворення. Перетворення потенціальної енергії молекул системи паливо-окислювач в кінетичну енергію продуктів згорання, тобто в ту енергію яку прийнято називати енергією горіння (Еп → Ек = Qгор).
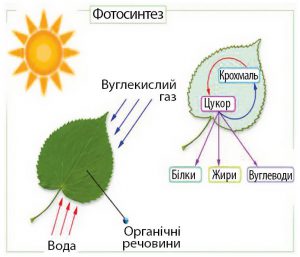
Мал.75. В процесі фотосинтезу кінетична енергія перетворюється в потенціальну енергію хімічних зв’язків (Q☼=Ек → Еп).
Узагальнюючи вище сказане можна зробити висновок: кількість тієї теплоти яка виділяється або поглинається при тому чи іншому тепловому процесі, визначається за однією з наступних формул:
Qн = Qох = cm∆t,
Qпл = Qкр = λm,
Qпар = Qконд = rm,
Qгор = qm,
де c, λ, r, q – табличні величини.
Задача 1. При повному згоранні 0,5кг палива виділяється 10МДж теплоти. Яка питома теплоємність палива? Що це за паливо?
Дано:
m = 0,5кг
Qгор= 10МДж = 10·106Дж
q = ?
Рішення. Оскільки Qгор = qm, то q = Qгор/m = 10·106Дж/0,5кг = 20·106Дж/кг. Знаючи питому теплоту згорання палива, за відповідною таблицею визначаємо сорт палива: кам’яне вугілля марки А-1.
Відповідь: q = 20·106Дж/кг; кам’яне вугілля марки А-1.
Задача 2. Скільки води можна нагріти від 10°С до кипіння, спаливши 1кг дров, якщо ККД процесу нагрівання 30%?
Дано:
вода (1), дрова (2)
tп = 10°C
tк = 100°C
m2 = 1кг
η = 30%
m1 = ?
Рішення. За визначенням η = (Акор)/Азаг)100%. Із аналізу умови задачі ясно: Акор= Qн1 = c1m1∆t1, де с1 = 4200Дж/кг·ºС, Δt1 = 100°C – 10°C = 90°C; Aзаг= Qгор2 = q2m2, де q2 = 8,5·106Дж/кг. Таким чином: η = c1m1∆t1100%/q2m2, звідси m1 = ηq2m2/c1∆t1100%.
Розрахунки. m1 = ηq2m2/c1∆t1100% = 40∙8,5·106∙1 / 4200∙90∙100 = 40∙8,5·106 / 4,2∙9∙106 = 40∙8,5 / 4,2∙9 = 9,0кг
Відповідь: m1 = 9,0кг.
Задача 3. На спиртівці нагріли 175г води від 15 до 75ºС. Початкова маса спиртівки і спирту дорівнювала 163г, а після закінчення нагрівання – 157г. Визначити ККД нагрівальної системи.
Дано:
вода (1), спирт (2)
m1 = 175г=0,175кг
∆t1 =75–15 =60º
∆m2=163–157=6г=0,006кг
η = ?
Рішення. За визначенням η = (Акор)/Азаг)100%. Із аналізу умови задачі ясно: Акор= Qн1 = c1m1∆t1, де с1 = 4200Дж/кг·ºС; Aзаг= Qгор2 = q2∆m2, де q2 = 27·106Дж/кг. Таким чином: η = c1m1∆t1100%/q2∆m2.
Розрахунки: η = 4200·0,175·60·100/27·106·6·10–3 =4200·0,175·6·103/27·6·103 = 27%
Відповідь: η=27%
Контрольні запитання.
- Дайте загальну характеристику процесу: а) плавлення; б) кристалізація.
- Питома теплота плавлення заліза 2,5·105Дж/кг. Що це означає?
- Дайте загальну характеристику процесу: а) пароутворення; в) конденсація.
- Опишіть ті теплові процеси які відбуваються на кожній ділянці представленого на малюнку графіку.
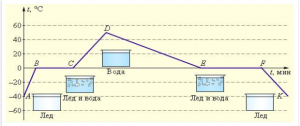
- Чим горіння відрізняється від нагрівання, пароутворення та плавлення?
- Яка фізична суть процесу горіння?
- Що представляє собою полум’я?
- Звідки береться та енергія яка виділяється в процесі згорання деревини?
- Яка фізична суть фотосинтезу?
- Який зв’язок між тією енергією яка виділяється в процесі згорання вугілля, та фотосинтезом?
Вправа 14.
- Скільки потрібно теплоти для того, щоб 1кг льоду взятого при температурі –20ºС, перетворити на воду з температурою 80ºС?
- Скільки теплоти потрібно для того, щоб 1кг води взятого при температурі 20ºС, довести до кипіння і 200г цієї води перетворити на пару?
- Порівняйте величину тієї енергії що йде на випаровування 1кг води, з кінетичною енергією смертельної для людини кулі, маса якої 5г, а швидкість 300м/с. Зробіть висновок.
- Яку максимальну кількість льоду з температурою 0ºС потрібно покласти в 1,5кг води з температурою 30ºС, щоб лід повністю розтанув?
- З якої висоти має впасти трьох кілограмова цеглина, щоб своєю кінетичною енергією а) розплавити 1кг льоду; б) випарувати 1кг води? Що можна сказати з цього приводу?
- В каструлю налили воду з температурою 10ºС і поставили на плиту. Через 10хв вода закипіла. Через який час ця вода повністю випарується?
- На спиртівці нагріли 300г води від 20°С до 80°С, витративши при цьому 8г спирту. Визначити ККД нагрівальної установки.
- Визначити ККД двигуна автомобіля, який маючи середню потужність 70кВт витрачає 17кг бензину за годину.
.
Лекційне заняття № 15. (Практичне заняття)
Тема: Теплові процеси. Розв’язування задач.
Базові формули:
Qн=сm∆t;
Qпл=λm;
Qпар=rm;
Qгор=qm,
де c, λ, r, q – табличні величини.
∑Qвтр = ∑Qотр, η=(Акор/Азаг)100%.
Задача 1. При повному згоранні 0,5кг палива виділяється 22МДж теплоти. Яка питома теплота згорання палива? Що це за паливо?
Дано:
m = 0,5кг
Qгор= 21МДж = 21·106Дж
q = ?
Рішення. Оскільки Qгор = qm, то q = Qгор/m = 21·106Дж/0,5кг = 42·106Дж/кг. Знаючи питому теплоту згорання палива, за відповідною таблицею визначаємо сорт палива: дизельне паливо.
Відповідь: q = 42·106Дж/кг; дизельне паливо.
Задача 2. Скільки води можна нагріти в алюмінієвій каструлі масою 1кг від 20°С до кипіння, спалюючи 100г гасу? ККД процесу 40%.
Дано:
вода (1), каструля (2), гас (3)
m2 = 1кг
t = 20°C
t = 100°C
m3 = 100г = 0,1кг
η = 40%
m1 = ?
Рішення. За визначенням η = (Акор)/Азаг)100%. Із аналізу умови задачі ясно: Акор= Qн1 + Qн2 = c1m1∆t1 + c2m2∆t2, де с1 = 4200Дж/кг·ºС, с2 = 880Дж/кг·ºС, Δt1 = Δt2 = 100°C – 20°C = 80°C; Aзаг= Qгор3 = q3m3, де q3 = 43·106Дж/кг. Таким чином: η = (c1m1∆t1 + c2m2∆t2)100%/q3m3, звідси c1m1∆t1 + c2m2∆t2 = ηq2m2/100%, звідси
c1m1∆t1 = ηq2m2/100% – c2m2∆t2, звідси m1 = (ηq2m2/100% – c2m2∆t2) / c1∆t1.
Розрахунки. m1 = (ηq3m3/100% – c2m2∆t2) / c1∆t1 =
= (40∙43·106∙0,1/100 – 880∙1∙80) / 4200∙80 = (4∙43·104 – 8,8∙0,8∙104) / 4,2∙8∙104 =
= (4∙43 – 8,8∙0,8) / 4,2∙8 = 4,9кг.
Відповідь: m1 = 4,9кг.
Задача 3. Скільки потрібно спалити спирту, аби 2кг льоду взятого при температурі 0°С розплавити і 1кг отриманої води перетворити на пару. ККД спиртівки 40%.
Загальні зауваження. В умовах задач фізики часто зустрічаються ситуації коли величина певного параметру вказується не явно, а опосередковано. Наприклад, в умові даної задачі опосередковано мається на увазі, що кінцевою температурою води та її пару є 100°С.
Дано:
m1 = 2кг
t1 = 0°C
t2 = 100°C
m2 = 1кг
η = 40%
m3 = ?
Рішення. За визначенням η = (Акор/Азаг)100%. В умовах нашої задачі, корисною є та робота (енергія) яка йде на плавлення льоду, нагрівання до температури кипіння отриманої води та на перетворення частини цієї води на пар з температурою 100°С, тобто Акор=Qпл+Qн+Qпар=λ1m1+c1m1Δt1+r1m2. Загальною (затраченою) є та енергія (робота) яку отримують при згоранні спирту, тобто Азаг=Q =qm3. Таким чином, в умовах нашої задачі η=(λ1m1+c1m1Δt1+r1m2)/ qm3)100%. Звідси випливає m3 = (λ1m1+c1m1Δt1+r1m2)/qη)100%, де λ1=3,35·105Дж/кг; с1=4187Дж/кг°С; r1 = 22,6·105 Дж/кг; q=27·106Дж/кг.
Розрахунки: m3 = (λ1m1+c1m1Δt1+r1m2)/qη)100% = ….= 0,35кг = 350г.
Відповідь: m3 = 0,35кг = 350г.
Задача 4. До якої температури треба нагріти алюмінієвий куб, щоб він, будучи покладений на лід, повністю в нього занурився? Температура льоду 0°С.
Дано:
алюміній (1), лід (2)
t0 = 0°С
t1 = ?
Рішення. Будемо виходити з того, що та кількість теплоти, яку нагрітий алюмінієвий куб має віддати льоду, і яка визначається за формулою Qн=c1m1(t1–t0), повністю витрачається на плавлення льоду, тобто на ту теплоту, кількість якої визначається за формулою Qпл=λ2m2. Іншими словами, будемо виходити з того, що у відповідності з рівнянням теплового балансу c1m1(t1–t0) = λ2m2. А оскільки t0=0°С, то c1m1t1 = λ2m2.
Враховуючи, що m=ρV, а також виходячи з того, що об’єм алюмінієвого куба (V1) має дорівнювати об’єму ним розплавленого льоду (V1=V2), можна записати c1ρ1V1t1 = λ2ρ2V2, або c1ρ1t1 = λ2ρ2. Звідси t1 = λ2ρ2/c1ρ1, де ρ2=0,9·103кг/м3; ρ1=2,7·103кг/м3; с1=880Дж/кг°С; λ2=3,35·105Дж/кг.
Розрахунки: t1 = 3,35·105·0,9·103/880·2,7·103 = 127°С
Відповідь: ta = 127°С.
Задача 5. У посудину з водою, взятою при температурі 0°С, впустили 1кг пари при 100°С. Через певний час у посудині встановилася температура 20°С. Скільки води було в посудині? Втратами енергії на нагрівання посудини знехтувати.
Дано:
вода (1), пар (2)
t1 = 0°C
m2 = 1кг
t2 = 100°C
tk = 20°C
m1 = ?
Рішення. В умовах нашої задачі, тим об’єктом який отримує енергію є вода масою m1. Тим же об’єктом який втрачає енергію є пар масою m2. При цьому пар втрачає енергію двічі: при конденсації та при охолодженні до температури 20°С. Зважаючи на ці обставини, рівняння теплового балансу ∑Qотр = ∑Qвтр набуває вигляду c1m1(tk – t1) = r2m2 + c2m2(t2 – tk). Звідси m1 = [r2m2 + c2m2(t2 – tk)]/ c1(tk – t1), де с1 = с2 = 4200Дж/кг°С, r2 = 22,6·105Дж/кг.
Розрахунки: m1 = (22,6·105·1 + 4200·1·80)/4200·10=62кг
Відповідь: m1 = 62кг.
Задача 6. При пострілі, куля масою 9г вилітає із дула гвинтівки з швидкістю 800м/с. Визначте масу порохового заряду, якщо ККД пострілу 24%.
Дано:
m1 = 9г = 9·10–3кг
v1 = 800м/с
порох
η = 24%
m2 = ?
Рішення. За визначенням η=(Акор/Азаг)100%. Із аналізу умови задачі ясно, що корисною є та робота яка йде на надання кулі певної кінетичної енергії, тобто Акор = m1v12/2. Загальною ж роботою є та енергія яка виділяється при згоранні пароху, тобто Азаг=qm2, де q = q(порох) = 3·106Дж/кг. Таким чином η = m1v12100%/2qm2, звідси m2 = m1v12100%/2qη.
Розрахунки: m2 = (9·10–3кг(8·102м/с)2100%)/(2· 3·106(Дж/кг)·30%) =
= (9·10–3·64·104·102Дж)/6·106·30(Дж/кг) = 4·10–3кг = 4г.
Відповідь: m2 = 4г.
Задача 7. Відомо, що для випаровування 1кг води при постійній температурі (температурі кипіння) потрібно 2,6·106Дж енергії. На скільки збільшується при цьому потенціальна енергія однієї молекули води? На скільки треба нагріти воду, щоб середня кінетична енергія поступального руху її молекул збільшилась на аналогічну величину?
Дано:
m(Н2О) = 1кг
t = const
Qпар=2,26·106Дж
∆Еп1 = ?
∆Ек1 = ∆Еп1
∆t = ?
Рішення. Оскільки в процесі випаровування температура речовини залишається незмінною, то середня кінетична енергія поступального руху молекул рідини і пару є однаковою. А це означає, що надана речовині енергія Qпар=2,6·106Дж йде на збільшення потенціальної енергії її молекул. При цьому Qпар=N·∆Еп1, де ∆Еп1 – збільшення потенціальної енергії однієї молекули речовини, N – кількість молекул в речовині: N=m/m0= 1кг/18·1,66·10–27кг = 33,5·1024молекул. Таким чином ∆Еп1= Qпар/N = 2,26·106Дж/33,5·1024 = 6,7·10–21Дж.
Виходячи з того що середня кінетична енергія поступального руху однієї молекули речовини визначається за формулою Ек1=(3/2)kT, а отже ∆Ек1=(3/2)k∆T, та враховуючи що за умовою задачі ∆Ек1 = ∆Еп1, можна записати ∆Т = ∆Еп1/(3/2)k = 6,75·10–21Дж/1,5·1,38·10–23(Дж/К) = 326К. А враховуючи, що ∆t=∆T, ∆t=326ºC.
Відповідь: ∆Еп1 = 6,7·10–21Дж; ∆t=326ºC.
Вправа 15.
- На скільки нагріється 2кг води, якщо вся теплота що виділяється при повному згоранні 8г спирту, пішла на її нагрівання?
- Скільки води взятої при температурі 15°С, можна нагріти до 60°, спаливши 40г спирту, якщо ККД процесу 50%?
- Скільки дров потрібно спалити, щоб нагріти 50л води в залізному котлі масою 10кг від 15°С до 65°С, якщо ККД процесу 60%?
- Скільки природного газу треба спалити, щоб 1кг льоду, взятого при температурі 0°С перетворити на пару з температурою 100°С? ККД процесу 50%.
- В алюмінієвій посудині масою 0,5кг міститься 2кг льоду при температурі 0°С. На скільки градусів нагріється вода, яка утвориться після танення льоду, якщо було спалено 50г гасу? ККД нагрівача 50%.
- Скільки водяного пару з температурою 100ºС потрібно ввести в мідний стакан масою 200г в якому знаходиться 150г льоду з температурою –20ºС щоб увесь лід розтанув?
- На скільки нагріється при штампуванні сталева деталь масою 1кг від удару молота масою 100кг, якщо швидкість молота в момент удару 20м/с, а на нагрівання деталі йде 40% його енергії?
- До якої температури потрібно нагріти мідний куб, щоб він будучи покладеним на лід, повністю занурився в нього? Температура льоду 0ºС.
- Відомо, що питома теплота плавлення води 3,35·105Дж/кг. На скільки збільшується потенціальна енергія однієї молекули води в процесі плавлення?
.
Лекційне заняття № 16.
Тема: Про сили міжмолекулярної взаємодії. Теплове розширення тіл. Особливості теплового розширення води.
Загально відомо, шо при нагріванні як тверді тіла так і рідини розширюються. Однак далеко не всі розуміють, чому це відбувається.
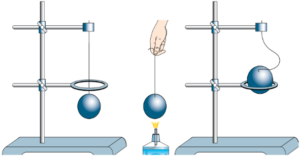
Мал.76. При нагріванні тіла розширюються.
Зазвичай, пояснюючи причини теплового розширення тіл, говорять про те, що в процесі нагрівання амплітуда коливань молекул збільшується, і що тому відповідно збільшується відстань між молекулами. З одного боку, це правильно: необхідною умовою теплового розширення твердих і рідких речовин, є збільшення амплітуди коливань їх молекул. Однак саме по собі збільшення амплітуди коливань молекул, ще не гарантує того, що відстань між молекулами буде збільшуватись. Дійсно. Якщо наприклад, в зображеній на мал.77 ситуації, амплітуду коливань кульки збільшити, то це не призведе до зміни координати центру динамічної рівноваги цієї кульки. Не призведе тому, що профіль тієї ями в якій відбуваються коливання кульки є симетричним. По суті це означає, що збільшення амплітуди коливань молекул, є необхідною, але не достатньою умовою теплового розширення тіл. Адже якби поведінка молекул була аналогічною поведінці кульки в симетричній ямі, то збільшення амплітуди коливань молекул не призводило б до збільшення відстані між центрами їх рівноваги, а отже і до розширення відповідної речовини.
Мал.77. Зміна амплітуди коливань кульки, не призводить до зміни координати її центру динамічної рівноваги.
Пояснюючи причини теплового розширення твердих тіл і рідин, потрібно більш детально поговорити про характер міжмолекулярних взаємодій. Факт того, що тверді тіла пружним чином протидіють як розтягненню так і стисненню, безумовно вказує на те, що молекули твердого тіла прагнуть до того, щоб бути розташованими на певній відстані одна від одної, і що при збільшенні цієї відстані вони автоматично притягуються, а при зменшенні – відштовхуються. Не заглиблюючись в деталі тих складних процесів які відбуваються при міжмолекулярних взаємодіях, гранично спрощено розглянемо фізичну суть цих взаємодій.
.

Мал.78. Механічні властивості твердих тіл безумовно вказують на те, що молекули взаємодіють між собою, і що в залежності від відстані вони притягуються, або відштовхуються.
Уявіть собі ситуацію, коли до відносно нерухомої молекули повільно наближається інша молекула. При цьому, ця рухома молекула обладнана двома вимірювальними приладами, один з яких фіксує силу міжмолекулярного притягування (Fпр), а інший – силу міжмолекулярного відштовхування (Fвід). Ми спостерігаємо за поведінкою молекул, фіксуємо показання приладів та аналізуємо їх. І ось що ми бачимо (мал.79). Допоки молекули знаходяться на відносно великій відстані (r > 1∙10–9м), прилади показують, що сили міжмолекулярного притягування і сили міжмолекулярного відштовхування практично не проявляють себе (Fпр=0; Fвід=0). Та коли міжмолекулярна відстань зменшиться до величини r ≈1∙10–9м, прилад який реагує на силу міжмолекулярного притягування, зафіксує що така сила з’являється, і що по мірі наближення молекул вона зростає. Аналізуючи характер цього зростання, ми приходимо до висновку, що воно відбувається за законом: Fпр=а/r7, де а – коефіцієнт пропорційності, величина якого залежить від сорту взаємодіючих молекул. Даний закон говорить про те, що коли в області дії сил міжмолекулярного притягування, відстань між молекулами зменшиться в 2 рази, то сила їх притягування збільшиться в 27=128 разів.
Ясно, що якби між молекулами діяли лише сили притягування, та ще й такі що так швидко зростають, то ці сили із всіх молекул тіла зробили б одну надмасивну молекулу. Тому не важко передбачити, що на певному етапі зближення молекул, мають з’явитися достатньо потужні сили міжмолекулярного відштовхування. І такі сили дійсно з’являються. Приблизно на відстані r≈0,5∙10–9м, прилад який реагує на сили міжмолекулярного відштовхування фіксує, що відповідні сили з’являються, і що по мірі наближення молекул вони зростають. Аналізуючи характер цього зростання, ми приходимо до висновку, що воно відбувається за законом Fвід=b/r13, де b – коефіцієнт пропорційності величина якого залежить від сорту взаємодіючих молекул. Даний закон вказує на те, що коли в області дії сил міжмолекулярного відштовхування, відстань між молекулами зменшується в 2 рази, то сила їх відштовхування збільшиться в 213=8192 разів.
Таким чином, на відстані міжмолекулярної взаємодії, на молекулу одночасно діють дві незалежні сили – сила міжмолекулярного притягування (Fпр) та сила міжмолекулярного відштовхування (Fвід). При цьому, сила притягування починає діяти раніше, але зростає відносно повільно. Сила ж відштовхування з’являється пізніше, але зростає відносно швидко. Ясно, що в такій ситуації поведінка молекули визначатиметься результуючою цих сил: F=Fпр+Fвід. А знаючи характер залежності сил притягування і відштовхування від відстані між молекулами, не важко побудувати графік відповідної результуючої сили (мал.79). І цей графік представляє собою характерну яму, сторони якої мають різну кривизну.
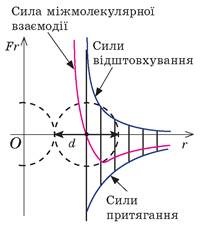
Мал.79. Поведінка молекули визначається результуючою двох сил – сили міжмолекулярного притягування та сили міжмолекулярного відштовхування.
Із аналізу графіку результуючої сили міжмолекулярної взаємодії ясно, що під дією цієї сили, молекули прагнуть розташуватись на тій відстані для якої Fпр = Fвід, тобто на відстані r = r0. Адже, якщо r > r0, то молекули взаємно притягуються і прагнуть наблизитись одна до одної. А якщо r < r0, то молекули взаємно відштовхуються і прагнуть віддалитися одна від одної. Ситуація нагадує таку, в якій дві кульки з’єднані пружиною: при наближені кульок, пружина стискається і кульки взаємно відштовхуються, а при віддалені – пружина розтягується і кульки взаємно притягуються. Втім, аналогія з пружно зв’язаними кульками є наочною, але надто грубою та надто неточною моделлю міжмолекулярних взаємодій. Більш вдалою та більш адекватною моделлю цих взаємодій є так звана потенціальна яма. В молекулярній фізиці потенціальною ямою називають ту криву яка описує залежність потенціальної енергії взаємодіючих молекул від відстані між ними,
Пояснюючи суть того, що прийнято називати потенціальною ямою, можна сказати наступне. Взаємодію молекул характеризує не лише результуюча сила міжмолекулярної взаємодії, а й енергія цієї взаємодії, тобто потенціальна енергія молекул. А оскільки енергія (Е) і сила (F), це взаємопов’язані величини (ΔЕ=FΔℓ), то та крива яка описує залежність потенціальної енергії взаємодіючих молекул від відстані між цими молекулами, буде певним відображенням тієї кривої яка характеризує результуючу силу міжмолекулярної взаємодії (мал.80). Найбільш суттєва відмінність між цими кривими полягає в тому, що в тій кривій яка характеризує потенціальну енергію взаємодіючих молекул і яка називається потенціальною ямою, найнижча точка цієї ями, тобто та точка для якої потенціальна енергія молекули є мінімальною, відповідає тій відстані (r0) для якої результуюча сила міжмолекулярної взаємодії дорівнює нулю (якщо r=r0, то F=0; Eп=min).
Мал.80. Крива яка описує залежність потенціальної енергії взаємодіючих молекул від відстані між ними, називається потенціальною ямою.
А тепер уявіть собі яму з ідеально гладенькою поверхнею, профіль якої аналогічний профілю потенціальної ями. Якщо в такій ямі опиниться пружна кулька, то її поведінка значною мірою буде схожою на поведінку взаємодіючих молекул. Дійсно, маючи певний запас кінетичної енергії та прагнучи опинитись в нижній точці потенціальної ями, молекула буде здійснювати певні коливання відносно цієї точки. А це еквівалентно тому, що при зменшені відстані між молекулами, вони автоматично починають відштовхуватись, а при збільшенні цієї відстані – притягуватись.
Аналізуючи модель потенціальної ями, можна пояснити багато властивостей речовини. Зокрема пояснити чому в процесі нагрівання тверді тіла та рідини розширюються. Дійсно, оскільки та крива яка описує поведінку молекул при їх взаємодії (потенціальна яма) є несиметричною, то при збільшенні амплітуди коливань молекул, центри їх динамічної рівноваги певним чином зміщуються, а відповідно змінюються і відстані між молекулами (мал.81).
Мал.81 При збільшенні амплітуди коливань молекули, центр її динамічної рівноваги зміщується і тому відстань між молекулами збільшується.
Таким чином, основною причиною теплового розширення рідин і твердих тіл, є факт того, що та крива яка описує поведінку молекули при її взаємодії з іншими молекулами (потенціальна яма) є несиметричною. Результатом цієї асиметрії є те, що при збільшенні температури речовини, а отже і збільшенні амплітуди коливань молекул, відстані між цими молекулами збільшуються і навпаки – при зниженні температури, ці відстані зменшуються.
Теплове розширення твердих тіл зазвичай характеризують величиною, яка називається температурним коефіцієнтом лінійного розширення. Температурний коефіцієнт лінійного розширення – це фізична величина, яка характеризує теплове лінійне розширення твердого тіла (даного матеріалу) і яка чисельно дорівнює тому лінійному видовженню (∆ℓ) яке отримує тіло довжиною 1м при його нагріванні на 1ºС.
Позначається: α
Визначальне рівняння: α=∆ℓ/ℓ0∆t, де ∆ℓ – теплове видовження тіла при його нагріванні на ∆t (ºС), ℓ0 – початкова довжина тіла;
Одиниця вимірювання: [ℓ] = 1/ºС = ºС–1.
Наприклад, якщо для міді α = 17·10–6(1/ºС), то це означає, що при нагріванні мідного стержня довжиною 1м на 1ºС, цей стержень видовжується на 17·10–6м тобто на 0,017мм. Величина температурного коефіцієнту лінійного розширення кожного матеріалу визначається експериментально і записується у відповідну таблицю, наприклад таку:
Таблиця. Температурний коефіцієнт лінійного розширення деяких матеріалів в інтервалі температур від 0ºС до 100ºС.
| Матеріал | α , 10-6 (1/ºС) | Матеріал | α , 10-6 (1/ºС) |
| алюміній | 23 | срібло | 20 |
| золото | 14 | сталь | 10 – 17 |
| залізо | 12 | чавун | 9 – 11 |
| мідь | 17 | алмаз | 1,2 |
| свинець | 29 | лід ( -20ºС – 0ºС) | 51 |
Оскільки в процесі нагрівання змінюються не лише лінійні розміри тіла, а і його об’єм, то теплове розширення характеризують не лише температурним коефіцієнтом лінійного розширення, а й температурним коефіцієнтом об’ємного розширення: β=∆V/V0∆t. Із визначального рівняння β=∆V/V0∆t випливає, що температурний коефіцієнт об’ємного розширення β чисельно дорівнює тому збільшенню об’єму ∆V, яке отримує тіло об’ємом 1м3 при його нагріванні на 1ºС: якщо V0=1м3, ∆t=1ºС, то β=∆V.
Можна довести, що для ізотропних матеріалів β≈3α. Дійсно. Розглянемо куб, довжина ребра якого 1м. Якщо цей куб нагріти на 1ºС, то кожне його ребро видовжиться на α метрів і стане рівним 1+α. З іншого боку, об’єм цього ж куба при нагріванні на 1ºС збільшиться на β метрів кубічних і стане рівним 1+ β. А це означає, що: (1+α)3 = 1+β. Враховуючи, що (1+α)3 = 1+3α+3α2+α3, де 3α2 і α3 – гранично малі величини (3α2~3(10–6)2 = 3·10–12; α3~(10–6)3= 10–18), можна записати: 1+β ≈ 1+3α, звідси β ≈ 3α.
Зазвичай температурним коефіцієнтом об’ємного розширення характеризують теплове розширення рідин. Величина цього коефіцієнту визначається експериментально і записується у відповідну таблицю, наприклад таку:
Таблиця. Температурний коефіцієнт об’ємного розширення деяких рідин, визначений для температури 20ºС.
| Рідина | β, 10-6 (1/ºС) | Рідина | β, 10-6 (1/ºС) |
| бензин | 1240 | ртуть | 181 |
| вода | 200 | сірчана кислота | 570 |
| гліцерин | 505 | етиловий спирт | 1080 |
| нафта | 1000 | етиловий ефір | 1600 |
Теплове розширення рідин відбувається з тих же причин, що і теплове розширення твердих тіл, тобто у зв’язку з несиметричністю кривої потенціальної енергії. Температурний коефіцієнт об’ємного розширення рідини, зазвичай значно більший за величину відповідного параметру твердого тіла. При цьому в процесі збільшення температури, величина коефіцієнту об’ємного розширення рідин зростає швидше аніж твердих тіл. Скажімо при температурі 20ºС коефіцієнт об’ємного розширення води 200·10–6(1/ºС), а при температурі 80ºС цей коефіцієнт вже 650·10–6(1/ºС).
Пояснення такого стану речей випливає з аналізу все тієї ж кривої потенціальної енергії. Адже факт того, що рідини не мають певного сталого об’єму, по суті означає, що амплітуди коливань їх молекул є гранично великими і відбуваються на межі розриву міжмолекулярних зв’язків. А на цій межі навіть незначні зміни температури, а відповідно і амплітуди коливань молекул, призводять до значних змін міжмолекулярних відстаней, а отже до значного розширення.
Безумовно найважливішою рідиною нашого життя є вода. Вода має велику кількість надзвичайних властивостей. І одна з них полягає в тому, що в певному температурному інтервалі, в процесі нагрівання вода не розширюється а ущільнюється (стискається). Ілюструючи достовірність даного твердження звернемося до експерименту, суть якого представлена на мал.82. Візуально зафіксувавши рівень води при температурі 0ºС і поступово нагріваючи воду, ви неодмінно з’ясуєте, що при збільшенні її температури від 0ºС до +4ºС, вода не розширюється, а навпаки – ущільнюється. І лише після того як при температурі +4ºС вода досягне максимального ущільнення, подальше її нагрівання буде супроводжуватись об’ємним розширенням.
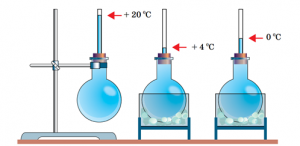
Мал.82. В процесі нагріванні від 0ºС до +4ºС вода не розширюється, а ущільнюється – експериментальний факт.
Факт того, що в процесі нагрівання від 0ºС до +4ºС вода не розширюється, а ущільнюється має своє пояснення. І це пояснення полягає в наступному. Як відомо, в кристалічній структурі льоду, молекули води розташовані у вигляді не надто щільних об’ємних шестикутників (мал.83). Результатом такого розташування є те, що густина льоду значно менша за густину води. Дослідження показують, що утворення окремих стійких, просторово упорядкованих груп молекул Н2О, починається задовго до початку явної кристалізації води (приблизно з +7ºС) і що по мірі зниження температури, кількість таких груп неухильно збільшується. Це означає, що при температурі 0ºС рідка вода представляє собою певну суміш як хаотично розташованих молекул Н2О, так і тих що об’єднані в об’ємні шестикутні групи. В процесі нагрівання води, кількість об’ємних шестикутних груп поступово зменшується, а густина рідини відповідно збільшується і досягає своєї максимальної величини при температурі +4ºС.


Мал.83. Щільність розташування молекул Н2О в рідкій воді значно більша аніж в твердому льоду.
Той факт, що густина води є максимально великою не при 0ºС, а при +4ºС, має величезне значення для багатьох природних процесів. Наприклад, якби вода не мала таких властивостей, то при тривалих мінусових температурах, ставки, річки і озера, достатньо швидко промерзали б до дна. Промерзали б тому, що та вода яка контактує з холодним повітрям, охолоджуючись опускалась би на дно водойми. При цьому, в результаті конвекційного кругообігу, температура всієї води досить швидко досягала б нулевої позначки і вся вода швидко перетворювалась би на лід. І якщо цього не відбувається, то це тільки тому, що подібним конвекційним чином, вода охолоджується лише до температури +4ºС. Подальше ж зниження температури відбувається лише за рахунок теплопровідності, яка для води є досить низькою. Крім цього, коли верхній шар води перетворюється на лід, то цей лід автоматично стає певним тепловим ізолятором, який додатково знижує інтенсивність процесу кристалізації води.
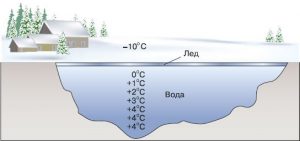
Мал.84. Характер розподілу температур в покритій кригою водоймі.
Складний характер залежності коефіцієнту об’ємного розширення води від температури, вкотре доводить, що реальні властивості реальних фізичних об’єктів, залежать від багатьох обставин. Тому, коли ми стверджуємо, що причиною теплового розширення тіл є несиметричність кривої потенціальної енергії, то маємо на увазі лише те, що ця причина є загальною та визначальною. Але це не виключає того, що за певних конкретних обставин, на теплове розширення тіла можуть суттєво впливати й інші фактори. Або наприклад, коли ми стверджуємо, що коефіцієнт об’ємного розширення рідини сильно залежить від температури, то маємо на увазі лише той факт, що для більшості рідин, така залежність має місце. Однак це зовсім не означає, що подібна залежність характерна для всіх рідин. Скажімо, коефіцієнт об’ємного розширення ртуті, в достатньо широкому інтервалі температур, залишається практично незмінним. Власне тому, саме ртуть застосовують для виготовлення точних термометрів.
Теплове розширення тіл, потрібно враховувати при спорудженні мостів, колій залізничних доріг, ліній електропередач, трубопроводів, тощо. Його обов’язково враховують при виготовлені цілісних конструкцій складовими елементами яких є різнорідні матеріали. Наприклад, при виготовлені залізобетонних конструкцій, марки сталі і бетону добирають таким чином, щоб їх температурні коефіцієнти були приблизно однаковими.

Мал.85. Деякі приклади боротьби з шкідливими проявами теплового розширення.
Про ефекти теплового розширення, потрібно пам’ятати і в тих випадках, коли тіло перебуває під дією різких перепадів температур. Наприклад, скляну банку з окропом не можна опускати в холодну воду. Пам’ятаючи про факт розширення води при її замерзанні, потрібно не допускати цього замерзання в трубах, деталях машин, відрах, тощо. Теплове розширення потрібно враховувати при виконанні вимірювальних робіт, при виготовлені вимірювальних інструментів, тощо.
Ефекти теплового розширення мають і певне корисне застосування. Наприклад, в терморегуляторах електронагрівальних приладів, в різноманітних протипожежних системах, в спеціальних термометрах, часто застосовують так звані біметалеві пластини (від лат. bini – пара, два). Ці пластини складаються з двох, жорстко з’єднаних різнорідних металів, температурні коефіцієнти яких, суттєво різні. В процесі нагрівання, складові елементи біметалевої пластини деформуються суттєво по різному. При цьому пластина відповідним чином вигинається і виконує певну корисну дію, наприклад включає чи виключає електронагрівальний прилад.
Мал.86. Загальний устрій та приклад застосування біметалевої пластини.
В процесі нагрівання розширюються не лише рідини і тверді тіла, а й гази. При цьому гази розширюються не тому, що крива потенціальної енергії є не симетричною, а за рахунок того, що в процесі нагрівання, кінетична енергія молекул збільшується, а відповідно збільшується і їх тиск на стінки посудини. В 1802 році, французький фізик Гей-Люсак експериментально встановив: при ізобаричному нагріванні, всі гази розширюються однаково, при цьому їх температурний коефіцієнт об’ємного розширення становить 1/273(1/ºС). Таким чином, на відміну від рідин та твердих тіл, характер теплового розширення яких у кожному конкретному випадку є індивідуальним, всі гази розширюються практично однаково, тобто з однаковим коефіцієнтом об’ємного розширення: β = 1/273(1/ºС) або β= 3660·10–6(1/ºС).
Потрібно зауважити, що коли ми говоримо про теплове розширення тіл, то маємо на увазі, що зовнішній тиск на ці тіла залишається незмінним. Адже якщо, наприклад, рідина знаходиться в жорсткій, міцній, герметичній посудині, то навіть при значному збільшенні температури, об’єм рідини залишиться незмінним (звичайно, якщо не враховувати розширення самої посудини).
Задача 1. При температурі 10ºС сталева ферма залізничного моста має довжину 75м. На скільки переміщується вільний кінець ферми при зміні температури від –35ºС до +40ºС?
Дано:
сталь
t0 = 10ºС
ℓ0 = 75м
t1 = –35ºС
t2 = 40ºС
∆ℓ = ?
Рішення. Із аналізу умови задачі ясно ∆ℓ = ∆ℓ1 + ∆ℓ2. Оскільки α = ∆ℓ/ℓ0∆t, то ∆ℓ = αℓ0∆t, де α(сталі) = 12·10–6(1/ºС).
Розрахунки: ∆ℓ1 = 12·10–6(1/ºС)·75м·45(ºС) = 4,1·10–2м = 4,1см; ∆ℓ2 = 12·10–6(1/ºС)·75м·30(ºС) = 2,7·10–2м = 2,7см; ∆ℓ = 4,1см + 2,7см = 6,8см.
Відповідь: ∆ℓ = 6,8см.
Задача 2. На скільки відсотків збільшиться об’єм бензину при його нагріванні від 5°С до 25°С, якщо в цьому температурному інтервалі, коефіцієнт об’ємного розширення бензину 12,0·10–4(1/°С)?
Загальні зауваження. В фізиці, на перший погляд незначні нюанси умови задачі загалом і поставленого запитання зокрема, часто мають надзвичайно велике значення. Наприклад, якби в даній задачі запитувалось: «на скільки зміниться об’єм бензину?», то це б означало, що потрібно визначити ΔV = Vк –Vп. А от запитання: «на скільки відсотків зміниться об’єм бензину?», означає що треба визначити ΔV/V0. При цьому визначити у відсотках: ΔV/V0 = (ΔV/V0)100%.
Дано:
t1 = 5°С
t2 = 25°С
β =12,0·10–4(1/°C)
(ΔV/V0)100% = ?
Рішення. Оскільки за визначенням β = ΔV/V0Δt, то ΔV/V0 = βΔt = β(t2 – t1).
Розрахунки: ΔV/V0 = 12,0·10–4(1/°C)(25°С – 5°С) = 240·10–4 = 0,0240 = 2,4%
Відповідь: ΔV/V0 = 2,4%
Висновок: влітку, восени і взимку, за одних і тих же показань лічильника, водії отримують суттєво різну кількість бензину.
Контрольні запитання.
- Наведіть докази того, що молекули взаємодіють між собою і що в залежності від міжмолекулярної відстані вони можуть як притягуватись так і відштовхуватись.
- Поясніть, яким чином виходить так що на одних відстанях молекули притягуються, а на інших – відштовхуються?
- Чим відрізняється та крива яка називається потенціальною ямою, від тієї кривої яка характеризує силу міжмолекулярної взаємодії?
- Чому збільшення амплітуди коливань молекул є необхідною але не достатньою умовою теплового розширення тіл?
- Поясніть причини теплового розширення твердих тіл і рідин.
- Температурний коефіцієнт лінійного розширення заліза 12·10–6(1/ºС). Що це означає?
- Поясніть, чому величина температурного коефіцієнту об’ємного розширення твердих та рідких речовин, при збільшені температури збільшується?
- Поясніть, чому вода при її нагріванні від 0ºС до 4ºС не розширюється а стискається?
- Поясніть, чому навіть за тривалих тріскучих морозів ставки, річки і озера не перемерзають до дна?
- Поясніть будову та принцип дії біметалевої пластини.
- Чим теплове розширення газів принципово відрізняється від теплового розширення твердих тіл та рідин?
Вправа 16.
- При температурі 20ºС відміряли 500м алюмінієвого і 500м мідного дроту. Якою буде різниця довжин цих дротів при температурі 100ºС?
- Сталеві залізничні рейки (α=14·10–61/ºС) довжиною 12м монтують при температурі 15ºС. Який зазор потрібно встановити між рейками, якщо експлуатаційні перепади температур від –30ºС до 60ºС?
- При проходженні струму через алюмінієвий дріт довжиною 6,00м, ця довжина збільшилась на 20мм. Наскільки градусів збільшилась довжина дроту?
- Густина алюмінію при 20ºС становить 2,7·103кг/м3. Визначити цю густину при 300ºС.
- В танкер при температурі 40ºС завантажили 30 000м3 нафти. На скільки меншим буде цей об’єм при розвантаженні нафти, якщо її температура становитиме 5ºС?
- На скільки відсотків зміниться об’єм води при її охолоджені від 40 до 20°С, якщо в цьому температурному інтервалі коефіцієнт об’ємного розширення води 3,0·10–4(1/°С)?
- При температурі 20ºС чавунне колесо трамваю має діаметр 1150мм, а діаметр призначеного для нього сталевого бандажу 1145мм. До якої температури потрібно нагріти бандаж, щоб зазор між ним і колесом становив 1,0мм?
.
Лекційне заняття №17.
Тема: Загальні відомості про термодинаміку. Про динамічний, статистичний та термодинамічний методи досліджень. Перше і друге начала термодинаміки.
Нагадаємо, молекулярна фізика – це розділ фізики, в якому вивчають загальні властивості твердих, рідких і газоподібних речовин, та ті теплові процеси які відбуваються з ними. Вивчають виходячи з того, що ці речовини складається з молекул які рухаються та певним чином взаємодіють між собою. Спираючись на ці прості базові твердження, ми збудували струнку наукову теорію, яка дозволяє пояснити широке коло природних явищ. І ці пояснення виявилися не лише достовірними а й гранично наглядними. Тому сьогодні нам важко уявити, що властивості твердих, рідких і газоподібних речовин, процеси нагрівання, плавлення, пароутворення, дифузії, горіння, тощо, можна пояснити не згадуючи про молекули. І тим не менше, це можливо. А доказом тому є наука, яка називається термодинамікою.
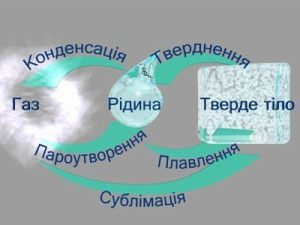

Мал.86. В молекулярній фізиці вивчають загальні властивості речовин, та ті теплові процеси які відбуваються з ними. Вивчають виходячи з того, що ці речовини складається з молекул.
Термодинаміка – це розділ фізики, в якому вивчають загальні властивості твердих, рідких і газоподібних речовин, та ті теплові процеси які відбуваються з ними. Вивчають виходячи з того, що при будь яких процесах виконується закон збереження енергії, і що теплова енергія не може переходити від холодного тіла до гарячого.

Мал.87. В термодинаміці вивчають загальні властивості речовин та ті теплові процеси які відбуваються з ними. Вивчають виходячи з того, що при будь яких процесах виконується закон збереження енергії, і що теплова енергія не може переходити від холодного тіла до гарячого.
Не важко бачити, що термодинаміка і молекулярна фізика по суті вивчають та пояснюють одне і теж. Однак вивчають і пояснюють по різному. Молекулярна фізика виходить з того, що всі речовини складаються з надзвичайно дрібненьких частинок (молекул) які безперервно рухаються і певним чином взаємодіють між собою. Термодинаміка ж, пояснюючи те саме, виходить з іншого: при будь яких процесах що відбуваються в замкнутій системі, загальна кількість енергії цієї системи залишається незмінною, при цьому теплова енергія сама по собі не може переходити від холодного тіла до гарячого.
Звичайно, твердження про те, що молекулярна фізика і термодинаміка, це дві науки про одне і теж, є певним перебільшенням. Адже мова йде про дві різні, в певному сенсі діаметрально протилежні науки, кожна з яких має свої специфічні особливості та сфери переважного застосування. Однак за великим рахунком, ці дві різні науки дійсно вивчають та пояснюють одну і туж групу споріднених явищ.
Якщо ж говорити про те, яким чином та чому виникли дві різні науки про одне і теж, то цей факт має певні історичні передумови і певні історичні пояснення. А ці передумови та пояснення полягають в наступному. Про існування молекул люди здогадувались дуже давно. Принаймі ще за 400 років до нашої ери давньогрецькі вчені обгрунтовано стверджували, що всі тіла складаються з надзвичайно дрібненьких частинок, які постійно рухаються і певним чином взаємодіють між собою. Однак факт того, що молекули дійсно існують був науково доведений лише в 1908 році. В такій ситуації, ті вчені які вірили в існування молекул, створили молекулярну фізику, тобто науку в якій загальні властивості речовин пояснювались виходячи з того, що ці речовини складаються з молекул.
З іншого боку, були вчені які намагались не приймати на віру ті твердження достовірність яких була сумнівною. Адже якби там не було, а до 1908 року, факт існування молекул не був науково доведеним. Тому ті вчені, які грубо кажучи не вірили в існування молекул, створили термодинаміку – науку, в якій загальні властивості речовин пояснювались на основі певних, на той час достовірно встановлених фактів, зокрема того, що прийнято називати законом збереження енергії.
Ви можете запитати: «якщо дві різні теорії, одні і ті ж події пояснюють по різному, то чи не означає це, що бодай одна з них є хибною?» Ні, не означає. Бо правильність чи неправильність теорії визначається не тим, подобається нам ця теорія чи не подобається. І навіть не тим, розуміємо ми її чи не розуміємо. Правильність чи неправильність теорії визначається тим, співпадають її передбачення з результатами відповідних експериментів чи не співпадають. І якщо передбачення теорії в точності співпадають з результатами експериментів, то ця теорія є науковою і правильною. А якщо не співпадають – то ми маємо справу з чим завгодно, тільки не з тим що прийнято називати науковою теорією. І в цьому сенсі як молекулярна фізика так і термодинаміка є безумовно науковими та безумовно достовірними теоріями. Адже всі передбачення кожної з них, в точності співпадають з результатами відповідних експериментів, при цьому не існує жодного експериментального факту який би суперечив цим теоріям. Звичайно в межах достовірності відповідних теорій.
Та як би там не було, а молекулярна фізика і термодинаміка, це дві абсолютно різні науки. Ці науки відрізняються не лише своїми базовими твердженнями, а й тими методами наукових досліджень які складають їх методологічну основу. Загалом, розрізняють три базових методи наукових досліджень: динамічний (або механічний), статистичний та термодинамічний. Скажімо, вивчаючи механіку ми практично завжди застосовували так званий динамічний метод досліджень. Суть цього методу полягає в тому, що знаючи початкові параметри руху тіл та ті закони за якими вони рухаються і взаємодіють, однозначно визначають параметри руху відповідних тіл в будь який момент часу. Наприклад, якщо дві пружні кульки відомих мас і відомих швидкостей, рухаються назустріч одна одній, то на основі законів ньютонівської механіки можна однозначно передбачити поведінку цих кульок як до так і після їх взаємодії.
Ясно, що застосувати динамічний метод досліджень до системи яка складається з мільярдів трильйонів молекул, практично не можливо. І не тільки тому, що цих молекул надто багато. А й тому, що самі молекули, це надзвичайно складні системи, поведінка яких описується не менш складними законами квантової механіки. Зважаючи на ці обставини, в молекулярній фізиці застосовують статистичний метод досліджень, тобто такий метод наукових досліджень при якому поведінку складної системи описують на основі відомих законів механіки та статистично усереднених параметрів окремих елементів цієї системи.
Скажімо в молекулярній фізиці ми говорили не про швидкість окремо взятої молекули, не про її кінетичну та потенціальну енергію, а про певним чим усереднену швидкість молекул, про їх середню кінетичну енергію, середню потенціальну енергію, тощо. При цьому, на основі цих усереднених характеристик молекул, та базі законів ньютонівської механіки, ми успішно пояснили широке коло тих явищ які є предметом вивчення молекулярної фізики.
Але виявляється, що поведінку складної системи можна спрогнозувати і не говорячи про її внутрішню будову. Наприклад не говорячи про те що тіла складаються з молекул. Таке прогнозування здійснюють на основі термодинамічного методу досліджень. Суть цього методу полягає в тому, що поведінку складної системи описують на основі тих параметрів які характеризують цю систему в цілому та тих законів які відображають взаємопов’язаність цих параметрів. Наприклад, охарактеризувавши стан певної маси газу (m=const) його об’ємом (V), тиском (р) та температурою (Т) і визначивши ті зв’язки що існують між цими величинами, не важко визначити відповідні параметри газу в тій чи іншій конкретній ситуації. При цьому не важливо знаєте ви про те що гази складаються з молекул, чи не знаєте. Розумієте що тиск, це усереднений результат ударів молекул чи не розумієте. Важливо лише те, що вам відомо: для постійної маси газу виконується співвідношення рV/T = const. А знаючи це співвідношення ви можете визначити параметри газу в тій чи іншій конкретній ситуації. Саме такий підхід і реалізується в термодинаміці.
В межах програми загальноосвітньої школи, переважна більшість тих явищ що є предметом вивчення термодинаміки, вивчається та пояснюється в молекулярній фізиці. Головна перевага молекулярної фізики в її наочності, а отже зрозумілості. Адже в молекулярній фізиці кожен об’єкт, кожну фізичну величину і кожне явище можна представити у вигляді певних наочних образів. Наприклад, молекули можна представити у вигляді пружних кульок; температуру – можна представити як міру середньої кінетичної енергії хаотичного руху молекул; тиск – як усереднений результат ударів молекул; пароутворення – як процес вильоту молекул з рідини і т.д.
Якщо ж говорити про термодинаміку, то ця наука є менш наочною і тому менш зрозумілою. Однак не потрібно думати, що термодинаміка чимось гірша за молекулярну фізику. Зовсім ні. Більше того. В певному сенсі, термодинаміка є більш точною і більш загальною наукою. Адже її висновки та передбачення отримують без використання спрощених моделей на кшталт ідеальний газ, ідеальна рідина, кристалічна решітка, тощо. Молекулярна ж фізика, обійтись без таких моделей не може.
Об’єктивно сильною і в той же час суб’єктивно слабкою стороною термодинаміки є те, що до вирішення поставлених задач вона підходить виключно з формально математичних позицій. В термодинаміці не важливо на скільки добре ви розумієте суть того що називаєте речовиною, теплотою, температурою, тиском, внутрішньою енергією чи ентропією. В термодинаміці важливо знати її базові аксіоми і вміти на основі цих аксіом та математичного аналізу, отримувати формальні рішення конкретних задач. Такий підхід дозволяє одержувати точні, достовірні результати, що є безумовним плюсом термодинаміки. В той же час, подібний формалізм позбавляє термодинаміку наочності і зрозумілості, що є безумовним недоліком цієї науки.
Оскільки переважна більшість того, що є предметом вивчення термодинаміки вивчається і пояснюється в молекулярній фізиці, та зважаючи на малоприємний формалізм термодинаміки, в межах програми загальноосвітньої школи нема нагальної потреби вивчати термодинаміку як окремий розділ фізики. Цілком достатньо стисло ознайомитись з базовими законами термодинаміки, які прийнято називати першим і другим началами термодинаміки і які певним чиним пов’язані з законом збереження енергії.
Закон збереження енергії, це фундаментальний закон Природи, який виконується у всіх відомих фізичних, хімічних, біологічних та інших процесах. При цьому, в різних розділах сучасної науки ви можете зустріти велике різноманіття на перший погляд різних, а по суті споріднених законів, які є прямими або опосередкованими формулюваннями закону збереження енергії. Наприклад, золоте правило механіки, закон Бернуллі, рівняння теплового балансу, другий закон Кірхгофа, перше начало термодинаміки, рівняння Ейнштейну для фотоефекту, це певні формулювання або опосередковані наслідки одного і того ж закону – закону збереження енергії. Закону в якому стверджується: При будь яких процесах, що відбуваються в замкнутій системі, загальна кількість енергії цієї системи, залишається незмінною, тобто зберігається. Іншими словами: ∑Едо = ∑Епісля (загальна кількість енергії до події, дорівнює загальній кількості енергії після події).
В термодинаміці, закон збереження енергії прийнято формулювати у вигляді першого начала (закону) термодинаміки. В цьому законі стверджується: Надана системі теплота (Q) частково йде на збільшення внутрішньої енергії системи (∆U), а частково, на виконання нею механічної роботи(А). Іншими словами: Q=∆U+A.
В науково-технічній практиці, той об’єкт який отримавши теплову енергію виконує механічну роботу, часто називають робочим тілом. Зважаючи на ці обставини, перше начало термодинаміки можна сформулювати наступним чином. Надана робочому тілу теплова енергія Q, частково йде на збільшення внутрішньої енергії робочого тіла ∆U (тобто на його нагрівання, плавлення, випаровування, тощо), а частково – на виконання ним певної механічної роботи А (на розширення робочого тіла). Наприклад, якщо газу що знаходиться під рухомим поршнем циліндру (мал.88) надати певну кількість теплоти (Q), то ця теплота частково піде на нагрівання газу, тобто на збільшення його внутрішньої енергії (∆U=Qн=cm∆t), а частково на розширення газу, тобто на виконання ним механічної роботи (А). При цьому буде виконуватись співвідношення Q=∆U+A.

Мал.88. Надане робочому тілу тепло (Q) частково йде на збільшення його внутрішньої енергії (∆U), а частково на виконання ним механічної роботи (А).
Співвідношення Q=∆U+A виконується в незалежності від того, яка речовина знаходиться в циліндрі умовної теплової машини. В незалежності від її хімічного складу, агрегатного стану чи будь яких інших властивостей. Це співвідношення виконується і в тому випадку, коли робоче тіло не отримує теплову енергію, а навпаки – втрачати її. Просто в цьому випадку, внутрішня енергія робочого тіла не збільшується, а зменшується і виконана ним механічна робота буде від’ємною, тобто такою яка виконана не робочим тілом, а над ним.
Не важко довести, що той закон який називається рівнянням теплового балансу, є похідним від більш загального закону – першого начала термодинаміки. Дійсно. В рівняння теплового балансу стверджується: при теплообміні, загальна кількість теплоти втраченої одними тілами замкнутої системи, дорівнює загальній кількості теплоти отриманої іншими тілами цієї системи, тобто ∑Qвтр = ∑Qотр. Із формулювання закону ясно, що рівняння теплового балансу виконується лише в тому випадку, якщо мова йде про теплообмін, тобто такий тепловий процес, який відбувається без виконання механічної роботи (А=0). А для такого процесу перше начало термодинаміки Q=∆U+A набуває вигляду Q=∆U. По суті це означає для теплообміну перше начало термодинаміки можна сформулювати у вигляді: при теплообміні надана робочому тілу теплова енергія Q, повністю йде на збільшення внутрішньої енергії робочого тіла ∆U (тобто на його нагрівання Qн, плавлення Qпл, випаровування Qпар, тощо), тобто Q=∆U, де ∆U=∑Qотр. Іншими словами, при теплообміні ∑Qвтр = ∑Qотр.
Оскільки в термодинаміці загалом і в першому началі термодинаміки зокрема, важливою дійовою особою є механічна робота, то буде не зайвим нагадати. Робота – це фізична величина, яка характеризує затрати енергії на виконання роботи, тобто певної енергозатратної дії і яка дорівнює цим затратам.
Позначається: А
Визначальне рівняння: А=ΔЕ
Одиниця вимірювання: А=Дж, джоуль.
Формула А=ΔЕ є базовим, визначальним рівнянням роботи. Однак, якщо мова йде про механічну роботу, то її зазвичай визначають за формулою А=Fℓcosα, де F – усереднена величина тієї сили що виконує роботу, ℓ – величина того переміщення яке відбувається при виконанні роботи, α – кут між напрямком вектора сили (F) та напрямком вектора переміщення (ℓ). Якщо напрям тієї сили що виконує роботу співпадає з напрямком переміщення тіла (α=0°; cos0°=1), то величина виконаної силою роботи визначається за спрощеною формулою А=Fℓ.
Не важко довести, що при ізобаричному розширенні газу (m=const, p=const), величина виконаної ним механічної роботи, визначається за формулою A=pΔV, де р – тиск газу, ΔV – зміна об’єму газу. Дійсно.
Задача. В процесі ізобаричного нагрівання, об’єм газу збільшився на ΔV. Визначити виконану газом механічну роботу.

Дано:
m=const
p=const
ΔV
Амех = ?
Рішення. За визначенням А= F·Δh. Оскільки в умовах нашої задачі, тією силою яка виконує роботу є сила тиску газу, та враховуючи, що р=F/S, а отже F=pS, можна записати А= F·Δh=pSΔh=pΔV.
Другим базовим законом термодинаміки є той, який прийнято називати другим началом термодинаміки. Пояснюючи суть цього надзвичайно важливого закону, можна сказати наступне.
Аналізуючи ті події які відбуваються в навколишньому світі, не важко помітити, що вони незворотні. Виведений з рівноваги маятник, рано чи пізно зупиняється. І після цього можна як завгодно довго очікувати зворотних подій, але вони не відбудуться. Не відбудуться тому, що коливання маятника є незворотними. Той газ що знаходиться в одній половині посудини, після прибирання роздільної стінки, займає увесь доступний йому об’єм. При цьому марно очікувати того, що молекули газу самі собою повернуться до попереднього об’єму. Марно тому, що даний процес є незворотним. Нагріта деталь, при занурені в холодну воду швидко охолоджується. І можна чекати скільки завгодно, але система сама собою до початкового стану не повернеться. Не повернеться тому, що процес переходу теплоти від гарячого тіла до холодного є незворотним.

Мал.89. Деякі приклади незворотних процесів.
Звичайно, для всіх вище описаних та їм подібних випадків можна придумати певний «хитрий» пристрій, який би повертав систему до початкового стану: розгойдував маятник, стискав би до попереднього об’єму газ, охолоджував воду та нагрівав деталь. Але, як ви розумієте, самі собою системи «хитрими» не стають і без певних енергетичних затрат не працюють. А тому ми констатуємо факт того, що природний хід подій є незворотний. Випускаєш з рук склянку, вона падає, розбивається і скільки не очікуй, а друзки самі собою не зберуться в єдине ціле і не стрибнуть назад в руку.
Якщо ви проаналізуєте відомі фізичні процеси та ті закони що їх описують, то неодмінно з’ясуєте, що практично всі вони симетричні. А це означає, що згідно з цими законами природні події можуть відбуватись як в прямому так і в зворотному напрямку. Але якщо закони Природи жодним чинам не протидіють зворотному ходу подій, то чому ж ці зворотні події самі собою не відбуваються? Відповідь на це та йому подібні запитання дає надзвичайно важливий закон, який називається другим началом термодинаміки.
Друге начало термодинаміки можна сформулювати по різному. Наприклад так: теплова енергія не може сама по собі переходити від холодного тіла до гарячого. Або так: неможливо здійснити такий тепловий процес при якому все надане системі тепло, повністю перетворилось би в механічну роботу. А можна і так: будь які процеси що відбуваються в замкнутій системі не можуть призвести до зменшення загальної ентропії цієї системи.
Та якими б не були формулювання другого начала термодинаміки, а його фізична суть залишається незмінною: в природних процесах, порядок легко і сам по собі перетворюється на безпорядок, а от безпорядок якщо і перетворюється на порядок то лише за наявності певної енергетичної доцільності і з певними енергетичними втратами. Ілюструючи цю фізичну суть, проведемо та проаналізуємо наступний простий експеримент.
Візьмемо дві склянки пшениці і зерна однієї з них пофарбуємо в чорний, зелений чи будь який інший колір. Акуратно висипаємо фарбоване та нефарбоване зерно в прозору скляну посудину. Висипаємо так, щоб чорне зерно було зверху а жовте знизу (або навпаки). При цьому ми отримаємо ситуацію, яка ілюструє певний порядок в розташуванні зерен: чорні – зверху, жовті – знизу.
Тепер беремо ложку, виделку, паличку чи що завгодно і починаємо перемішувати зерна. Ви робите один оберт, другий, третій, …, десятий і неодмінно бачите що чорні і жовті зерна перемішуються. Тепер давайте спробуємо повернути хід подій і зробимо ідеально такі ж оберти у зворотньому напрямку. Виконуючи ці зворотні рухи, ви неодмінно з’ясуєте, що система не повертається до попереднього стану. Ви можете як завгодно довго та як завгодно хитро перемішувати зерна в очікувані того що вони знову розташується в початковому порядку, але цього ніколи не відбудеться. І не тому, що цього не може бути взагалі, а тому що ймовірність цієї події є практично нулевою.
Оскільки ми заговорили про ймовірність тієї чи іншої випадкової події, то буде не зайвим з’ясувати суть того, що прийнято називати ймовірністю. За визначенням: ймовірність (р) певної випадкової події, це величина, яка дорівнює відношенню числа тих випадків коли очікувана подія відбувається (z), до загальної кількості можливих випадків (N), тобто: p = z/N. Наприклад, ймовірність того що в результаті неупередженого кидання грального кубика випаде цифра «5» становить р=1/6. Якщо ж ви одночасно кидаєте два кубики і очікуєте випадіння двох п’ятірок, то ця подія відбудеться з ймовірністю р=(1/6)(1/6)=1/36. Якщо ж в експерименті задіяно три кубики, то ймовірність одночасного випадіння трьох п’ятірок становить р=(1/6)(1/6)(1/6)=1/196.
Звичайно, це не означає що очікувана подія відбудеться на 196 киданні кубиків. Це навіть не означає, що в кожній серії яка складається з 196 кидань, один раз обов’язково випаде комбінація з трьох п’ятірок. Твердження: «ймовірність події становить 1/196» – означає лише те, що виконавши N експериментальних серій (де N – достатньо велике число), кожна з яких складається з 196 експериментів, ви отримаєте приблизно N очікуваних подій, тобто в середньому по одній очікуваній події на одну експериментальну серію. При цьому насправді, в деяких серіях очікувана подія може відбутися 2, 3, а то й 10 разів, а в деяких – не відбудеться жодного разу.
Зважаючи на вище сказане і виходячи з того, що в нашому експерименті з зерном приймають участь щонайменше 200 фарбованих і 200 не фарбованих зернин, не важко визначити ймовірність того, що в процесі перемішування, зерна розташуються в певному порядку, наприклад чорні – зверху, жовті – знизу. Дійсно. Ймовірність того, що певна фарбована зернина опиниться у верхній частині посудини становить р=1/2. При цьому, ймовірність того, що всі 200 фарбованих зернин одночасно опиняться у верхній частині посудини становить р=(1/2)200=1/2200≈1/1063. Ілюструючи величину цієї ймовірності можна сказати наступне. Якщо ви за одну секунду встигнете виконати операцію перемішування зерен, встигнете зупинитись і подивитись на те чи не відбулась очікувана подія, то ймовірніше за все така подія відбудеться один раз на 1063 секунд. Для порівняння зазначимо, що вік нашого Всесвіту не перевищує 14·109 років, що приблизно становить 4,4·1017 секунд.
Тепер, коли ви знаєте що в процесі тих чи інших подій, порядок легко перетворюється на безпорядок, а от безпорядок сам по собі порядком не стає, не важко пояснити чому механічна робота легко та повністю перетворюється на теплоту, а от теплота сама собою роботою не стає. Дійсно. В процесі виконання роботи, певне тіло переміщується як єдине ціле. А це означає що всі частинки цього тіла, всі його атоми, молекули та електрони, рухаються як одне ціле, а отже рухаються упорядковано. Іншими словами, механічна робота (Амех), є енергією упорядкованого руху всіх частинок даного тіла. Якщо ж говорити про теплоту (Q), то вона як за визначенням так і за своєю суттю теплова енергія є енергією хаотичного руху молекул.
Переконатись в тому, що механічна робота (порядок) легко перетворюється на теплоту (безпорядок) не складно. Для цього достатньо потерти долоні рук одна об одну. При цьому неодмінно з’ясується, що виконавши певну механічну роботу (потерши долоні одна об одну) ви отримаєте відповідну кількість теплових відчуттів. Якщо ж говорити про кількісні докази такого перетворення, то першим хто отримав ці докази був англійський експериментатор Джеймс Джоуль (1818–1889). На мал.90 представлена спрощена схема дослідів Джоуля. Суть цих дослідів очевидно проста: в процесі опускання вантажу, а отже в процесі виконання механічної роботи, занурене в рідину тіло обертається та нагріває цю рідину. Визначивши виконану вантажем механічну роботу (А=mgh) та кількість отриманої при цьому теплоти (Q=cm∆t), Джоуль встановив: механічна робота (Амех), повністю перетворюється в теплоту (Q).
Мал.90. Механічна робота легко і повністю перетворюється на теплоту, а от теплота, сама собою в механічну роботу не перетворюється.
Але, якщо в процесі обертання зануреної у воду крильчатки, енергія її механічного руху перетворюється на теплоту, то чому б молекулам води, бодай мізерну частинку своєї енергії не перетворити на механічну роботу? Адже тієї енергії яку можна отримати при охолоджені одного літра води всього на один градус, вистачить на те щоб тіло масою 1кг підняти на висоту 420м. Однак марно очікувати того, що якась мізерна частина наявної у воді теплової енергії, сама собою перетвориться на енергію механічного обертання крильчатки та піднімання бодай мізерного вантажу.
І це закономірно. Адже для того щоб крильчатка почала обертатись, рух молекул рідини має стати упорядкованим. При цьому абсолютно очевидно, що ймовірність події при якій 334·1023 хаотично рухомих молекул (а саме стільки їх міститься в одному літрі води), ні з того ні з сього почнуть рухатись в одному напрямку і що цей упорядкований рух буде тривати так довго, що крильчатка дійсно почне обертатись, практично нулева. Не менш очевидно і те, що в подібних ситуаціях терміни «малоймовірна подія» і «неможлива подія» є тотожними.
Звичайно, вище сказане не означає, що наявну у воді теплову енергію в принципі не можливо перетворити на механічну роботу. Скажімо, якщо пластинку крильчатки з одного боку нагріти, а з іншого – залишити холодною, то тиск молекул води на нагріту поверхню буде дещо більшим. При цьому за наявності достатнього перепаду температур, крильчатка почне обертатись та виконувати відповідну механічну роботу. Але як ви розумієте, самі собою поверхні крильчаток різнонагрітими не стають.
Таким чином, все різноманіття наявних фактів вказує на те, що в природі енергія порядку будь то енергія механічної роботи, енергія електричного струму, хімічних зв’язків чи біологічних процесів, легко перетворюється на енергію хаотичного руху молекул тобто теплоту. А от теплота сама собою енергією порядку не стає. Тому коли та чи інша система знаходяться в стані теплової рівноваги з навколишнім середовищем, то наявна в ній енергія теплового руху молекул сама собою не стає а ні енергією механічної роботи, а ні енергією електричного струму, а ні енергією біологічних структур.
Потрібно зауважити, що друге начало термодинаміки не суперечить ні першому началу термодинаміки, ні закону збереження енергії. В ньому лише констатується той факт, що Природа влаштована таким чином, що в ній енергія порядку легко перетворюється на енергію безпорядку, а от енергія безпорядку, якщо і перетворюється в енергію порядку то лише за наявності певних енергетичних причин.
При цьому, потрібно особливо підкреслити, що в другому началі термодинаміки не стверджується що безпорядок не може перетворюватись на порядок. В ньому говориться лише про те, що за відсутності енергетичних причин, таке перетворення є малоймовірним. Але якщо для подібного перетворення є певні енергетичні підстави, то безпорядок не лише може перетворюватись на порядок, а й практично неминуче цим порядком стає. Наприклад, в процесі кристалізації, хаотично розташовані молекули рідини, вишиковуються в певному, строго визначеному порядку. Вишиковуються тому, що такий порядок є енергетично доцільним. В процесі хімічних взаємодій, певні атоми об’єднуються в більш складні упорядковані структури – молекули. Об’єднуються тому, що таке об’єднання є енергетично доцільним. З плином часу, хаотично розташовані молекули аморфного тіла, вишиковуються в певному порядку, вишиковуються тому, що відповідний порядок є енергетично доцільним. Навіть те що ми називаємо життям і що характеризується надзвичайною складністю та упорядкованістю, є прямим наслідком факту того, що енергетично доцільна подія рано чи пізно відбувається. Втім, про енергетичні передумови виникнення та еволюційного саморозвитку життя на Землі, ми поговоримо ще не скоро.
Контрольні запитання.
- Чим схожі та чим відрізняються молекулярна фізика і термодинаміка?
- Як склалося так, що для пояснення однієї і тієї ж групи явищ, було створено дві різні науки?
- Чому в межах шкільної програми властивості речовин пояснюють головним чином на основі молекулярної фізики а не термодинаміки?
- Поясніть суть динамічного методу досліджень.
- Поясніть суть статистичного методу досліджень.
- Поясніть суть термодинамічного методу досліджень.
- Що спільного між першим началом термодинаміки та рівнянням теплового балансу? Який з цих законів є більш загальним?
- Що означає твердження: фізичні закони симетричні.
- Наведіть приклади незворотних подій. Поясніть причини цієї незворотності.
- В чому суть другого начала термодинаміки?
- Чому механічна робота легко і повністю перетворюється на теплоту, а от теплота перетворюється на роботу лише за певних умов і не повністю?
- Чому енергія електричного струму легко перетворюється на теплоту, а от теплота сама собою електричним струмом не стає?
- Наведіть приклади того, як безпорядок природним шляхом стає порядком. Чи не суперечать ці перетворення другому началу термодинаміки?
Вправа 17.
- В процесі ізобаричного розширення газу виконана робота 200Дж. При якому тиску здійснювався процес, якщо об’єм газу збільшився на 20л?
- При ізобаричному розширенні газу виконана робота 400Дж. На скільки змінився обєм газу, якщо процес відбувався при тиску 0,5 МПа?
- Яку роботу А виконує газ кількість якого ν моль, при ізобаричному нагріванні газу на ∆Т кельвінів?
- Кисень масою 200г ізобарично нагріли на 100°С. Визначте роботу розширення газу.
- При ізобаричному нагріванні 56г газу на 50°С, газом була виконана робота 831Дж. Який це газ?
- В циліндрі під поршнем знаходиться 100г повітрі. Для його ізобаричного нагрівання на 50°С витратили 5кДж теплоти. На скільки змінилась внутрішня енергія повітря? Молярна маса повітря 0,029кг/моль.
- Яка кількість теплоти потрібна для того, щоб 200г азоту ізобарично нагрівають на 200°С? Для ізобаричного процесу, питома теплоємність азоту 1000 Дж/кг∙К.
.
Лекційне заняття №18.
Тема: Розв’язування задач термодинаміки.
Нагадаємо, рішення переважної більшості задач фізики полягає в тому, щоб на основі аналізу умови задачі, та на базі певного обмеженого набору базових формул (законів, визначальних рівнянь фізичних величин, та деяких загально відомих або раніше доведених співвідношень на кшталт: якщо m=const, p=const, то A = p∆V), шляхом логічних міркувань отримати те математичне співвідношення (розрахункове рівняння) яке дозволяє відповісти на поставлене в задачі питання. Наприклад в умовах даної теми, тими базовими формулами виходячи з яких зазвичай розв’язують задачі термодинаміки є:
- Q = ∆U + A перше начало термодинаміки;
- якщо m=const, p=const, то A = p∆V;
- p∆V = νR∆T = (m/M)R∆T рівняння (закон) Менделєєва-Клапейрона;
- U1 = 1,5mRT/M; U2 = 2,5mRT/M; U3 = 3,0mRT/M формули для визначення внутрішньої енергії відповідно одноатомних, двохатомних та трьохатомних газів;
Задача 1. Азот маса якого 200г, ізобарично нагріли на 100°С. Визначте величину тієї механічної роботи яку виконує газ в процесі свого розширення.
Дано:
m(N2) = 200г = 0,2кг
p = const
∆t = 100°C, ∆T = 100K
А = ?
Рішення. Оскільки при ізобаричному розширенні газу A = p∆V, та враховуючи, що згідно з рівнянням Менделєєва-Клапейрона p∆V = (m/M)R∆T, можна записати А = p∆V = mR∆T/М, де R = 8,31(Дж/К∙моль) – молярна газова стала, М(N2) = 28(г/моль) = 0,028(кг/моль).
Розрахунки: А = mR∆T/М = 0,2кг∙8,31(Дж/К∙моль)∙100К/0,028(кг/моль) = 5900Дж.
Відповідь: А = 5900Дж = 5,9кДж.
Задача 2. Визначити питому теплоємність азоту (N2) при його ізохоричному нагріванні.

Дано:
N2
m=const
V=const
сv=?
Рішення. За визначенням с=Qн/m∆T. Оскільки в процесі ізохоричного нагрівання, газ не розширюється (V=const), а отже і не виконує механічної роботи (А=0), то ясно, що вся надана газу енергія (Qн) йде на збільшення його внутрішньої енергії Qн=∆U. А враховуючи, що для двохатомних газів U = 2,5mRT/M, а отже ∆U = 2,5mR∆T/M, можна записати cv = Qн/m∆T = ∆U/m∆T = 2,5Rm∆T/Мm∆Т = 2,5R/M. Таким чином cv = 2,5R/M, де R = 8,31Дж/К·моль; М(N2) = 28г/моль = 0,028 кг/моль.
Розрахунки: сv(N2) = 2,5R/M = 2,5·8,31(Дж/К·моль)/0,028(кг/моль)=740Дж/кг∙К.
Відповідь: сv(N2)=740Дж/кг∙К.
Задача 3. Визначити питому теплоємність азоту (N2) при його ізобаричному нагріванні.

Дано:
N2
m=const
р=const
ср=?
Рішення. За визначенням с = Qн/m∆T. Оскільки в процесі ізохоричного нагрівання, газ не лише нагрівається, а й розширюється, а отже виконує певну механічну роботу (А), то можна стверджувати, що надана газу теплота Qн частково йде на збільшення внутрішньої енергії газу ∆U (на нагрівання газу), а частково на виконання певної механічної роботи А. При цьому у відповідності з першим началом термодинаміки Qн = ∆U + A. Враховуючи, що для двохатомного газу ∆U = 2,5mR∆T/M, і що при ізохоричному процесі А = p∆V = mR∆T/М, можна записати Qн = ∆U + A = 2,5mR∆T/M + mR∆T/M = 3,5mR∆T/M. Таким чином ср = Qн/m∆T = 3,5mR∆T/Mm∆T = 3,5R/M, де R = 8,31Дж/К·моль; М(N2) = 28г/моль = 0,028 кг/моль.
Розрахунки: ср(N2) = 3,5R/M = 3,5·8,31(Дж/К·моль)/0,028(кг/моль)= 1000Дж/кг∙К.
Відповідь: ср(N2) = 1000Дж/кг∙К.
Задача 4. В процесі ізобаричного нагрівання 600 моль газу на 400К, йому надали 6МДж теплоти. На скільки збільшилась внутрішня енергія цього газу?
Дано:
р = const
ν = 600 моль
∆T = 400K
Q = 6МДж = 6∙106Дж
∆U = ?
Рішення. У відповідності з першим началом термодинаміки Q = ∆U + A, звідси ∆U = Q – A. Оскільки даний процес ізобаричний, то А = p∆V = νR∆T. Таким чином ∆U = Q – A = Q – νR∆T, де R=8,31Дж/К∙моль.
Розрахунки: ∆U = Q – νR∆T = 6∙106Дж – 600(моль)∙8,31(Дж/К∙моль)∙400К = 6∙106Дж – 2∙106Дж = 4∙106Дж.
Відповідь: ∆U = 4∙106Дж = 4МДж.
Задача 5. В процесі ізобаричного нагрівання 80г кисню з початковою температурою 27°С, його об’єм збільшився в 1,5 рази. Визначити кількість наданої кисню теплоти, зміну його внутрішньої енергії та величину виконаної газом механічної роботи.
Дано:
р = const
m(O2) = 80г = 0,08кг
V2 = 1,5V1
t = 27°C, T = 300K
Q = ? ∆U = ? A = ?
Рішення. У відповідності з першим началом термодинаміки Q = ∆U + A. Оскільки процес ізобаричний, то А = p∆V = mR∆T/M, де М(О2) = 0,032(кг/моль), ∆Т = ? Оскільки газ двохатомний, то ∆U = 2,5mR∆T/M, де ∆Т = ? Оскільки при ізобаричному процесі виконується співвідношення (закон Гей-Люссака) V1/T1 = V2/T2, то T2/T1 = V2/V1 = 1,5V1/V1 = 1,5, звідси Т2 = 1,5Т1 = 1,5∙300К = 450К, звідси ∆Т = Т2 – Т1 = 150К. Таким чином А = mR∆T/M, ∆U = 2,5mR∆T/M, Q = ∆U + A.
Розрахунки: А = mR∆T/M = 0,08кг∙8,31(Дж/К∙моль)∙150К/0,032(кг/моль) = 3100Дж; ∆U = 2,5А = 2,5∙3100Дж = 7750Дж, Q = ∆U + A = 10850Дж.
Відповідь: Q = 10850Дж; ∆U = 7750Дж; A = 3100Дж.
Задача 6. За заданою р–V діаграмою визначте яку роботу виконує газ при переході з стану 1 до стану 3?
Рішення. На ділянці 1→2, ΔV=0 і тому A12=pΔV=0Дж.
На ділянці 2→3, ΔV=1м3–3м3= –2м3 і тому A23=pΔV=30·103Па·(–2м3)= –60·103Дж, де знак «–» вказує на те, що газ виконує від’ємну роботу (на ділянці 2→3 газ ізобарично стискається і тому протидіє цьому стисненню).
Загальні зауваження. Факт того, що на ділянці 1→2 газ не виконує механічну роботу (A=0), зовсім не означає що на цій ділянці не відбуваються певні енергетичні події. Дійсно, оскільки на ділянці 1→2 відбувається ізохоричне стиснення газу (V=const, p↑), то у відповідності з об’єднаним газовим законом (pV/T=const) на цій ділянці неминуче відбувається нагрівання газу(T↑). При цьому у відповідності з першим началом термодинаміки (Q=ΔU+A) надана газу теплова енергія йде на збільшення внутрішньої енергії газу. Іншими словами, на ділянці 1→2: V=const, p↑, Т↑, ΔU↑, А=0.
Задача 7. За заданою р–V діаграмою ідеального газу, визначте яку кількість теплоти отримав або віддав цей газ при переході із стану 1 до стану 3?
Рішення. На ділянці 1→2: V=const, р↑, оскільки рV/T=const, то Т↑. Оскільки ΔV=0, то А=рΔV=0. Таким чином, оскільки на ділянці 1→2 температура газу зростає, то на цій ділянці він отримує певну кількість енергії Q12, яка повністю йде на збільшення внутрішньої енергії газу (адже А=0), тобто Q12=ΔU12.
Оскільки для ідеального, а отже одноатомного газу U=1,5νRT = 1,5pV (випливає з рівняння Менделєєва-Клапейрона νRT = pV), та зважаючи на те, що на ділянці 1→2 V=const, можна записати ΔU = 1,5VΔр. Тому Q12=ΔU12= 1,5V12(р2 – р1)= 1,5·1(30·103 – 10·103)= 30·103Дж.
На ділянці 2→3: р=const, V↑, оскільки рV/T=const, то Т↑. Оскільки ΔV=3м3 – 1м3=2м3, то А23=рΔV=30·103·2=60·103Дж=60кДж.
Оскільки на ділянці 2→3 газ по перше нагрівається (Т↑), а по друге виконує механічну роботу (А>0), то це означає, що газ отримує певну кількість енергії Q23. При цьому у відповідності з першим началом термодинаміки Q23=ΔU23+A23.
Оскільки для одноатомного газу U=1,5νRT = 1,5pV, та зважаючи на те, що на ділянці 2→3 р=const, то ΔU23 = 1,5рΔV= 1,5р23(V3 – V2)= 1,5·30·103(3 – 1)= 90·103Дж.
Q23=ΔU23+A23 = 90·103+60·103 = 150·103Дж =150кДж
У підсумку: Q = Q12 + Q23 = 30кДж + 150кДж = 180кДж.
Задача 8. Ідеальний газ із стану 1 в стан 2 може переходити трьома представленими на діаграмі р–V шляхами. Визначте при якому переході виконана газом робота буде: а) найбільшою, б) найменшою.
Рішення. Можна довести, що в системі координат p–V, величина тієї роботи яку виконує газ при його розширенні або стисненні, дорівнює площі тієї фігури яка обмеженої графіком залежності тиску від об’єму, віссю 0V та вертикальними прямими, які відповідають значенням об’єму V1 і V2. Виходячи з цього, та проаналізувавши кожний шлях переходу (мал.б,в,г), можна стверджувати, що при переході (б) виконана газом робота буде найбільшою, а при переході (г) – найменшою.
Задача 9. Ідеальний газ здійснив зображені на малюнку циклічні процеси. Визначте виконану газом роботу на кожній ділянці циклу та загальну роботу.
Рішення. Виходячи з того, що в системі координат p–V, величина тієї роботи яку виконує газ при його розширенні або стисненні, дорівнює площі тієї фігури яка обмежена графіком залежності тиску від об’єму, віссю 0V та вертикальними прямими, які відповідають значенням об’єму V1 і V2, можна стверджувати:
А1→2= 100кПа∙3м3 + (1/2)500кПа∙3м3 = 300кДж + 750кДж = 1050кДж.
А2→3= 0кДж.
А3→1= 100кПа∙(–3)м3 = –300кДж, знак «–» вказує на те, що на ділянці 3→1 (ізобаричне стиснення газу), газ протидіє його стисненню і тому виконує від’ємну роботу.
Азаг = А1→2 + А2→3 + А3→1 = 1050кДж + 0кДж – 300кДж = 750кДж, або
Азаг = (1/2)500кПа∙3м3 = 750кДж (площа трикутника 1-2-3).
Вправа 18.
- Визначити питому теплоємність вуглекислого газу (СО2) при його ізохоричному нагріванні.
- Визначити питому теплоємність вуглекислого газу (СО2) при його ізобаричному нагріванні.
- За заданими р–V діаграмами (мал. а, б), визначте яку роботу виконує газ при переході з стану 1 до стану 3?
а) б) .
б) .
- За заданими р–V діаграмами (мал. а – г), визначте яку роботу виконує газ при переході з стану 1 до стану 2?
- Ідеальний газ здійснив зображений на малюнку циклічні процеси. Визначте виконану газом роботу на кожній ділянці циклу та загальну роботу.
- За заданою р–V діаграмою ідеального одноатомного газу визначте яку кількість теплоти отримав або віддав цей газ при переході із стану 1 до стану 3?

- Яку роботу виконає газ масою m та молярною масою М при його ізобаричному нагріванні на ΔТ кельвінів?
- За нормального атмосферного тиску, температура повітря 0°С, а його об’єм 20м3. Яку роботу виконає це повітря при його ізобаричному нагріванні на 17°С?
- В циліндрі під поршнем знаходиться 25г повітря. Для його нагрівання на 40ºС при постійному тиску витратили 1кДж теплоти. На скільки змінилась внутрішня енергія повітря. Молярна маса повітря 0,029кг/моль.
.
Лекційне заняття №19.
Тема: Теплові двигуни.
Історія термодинаміки нерозривно пов’язана з тепловими двигунами, тобто машинами які перетворюють внутрішню енергію палива (теплоту) в механічну роботу. Перший повністю автоматизований тепловий двигун (парову машину) було збудовано в 1774 році англійським винахідником Джеймсом Уаттом (Ваттом) *)(1736–1819). Парова машина Уатта швидко отримала широке практичне застосування. Але її енергетична ефективність (цю ефективність характеризує коефіцієнт корисної дії) була низькою і не перевищувала 4%.
*) Саме на честь Джеймса Уатта (англ. Watt) названо одиницю потужності – ват.
Ясно, що в такій ситуації інтереси виробництва вимагали створення більш економних машин. Очевидно і те, що створити максимально ефективну машину, без розуміння суті тих процесів які в ній відбуваються, практично неможливо. А це означало, що потреби виробництва вимагали від науки з’ясування закономірностей перетворення теплоти в механічну роботу та з’ясування тих умов за яких таке перетворення є максимально ефективним. В процесі вирішення цих практичних задач і було закладено основи термодинаміки.
Визначальний внесок у справу розбудови теорії теплових двигунів і термодинаміки загалом, зробив французький інженер Саді Карно (1796–1832). Розмірковуючи над будовою та принципом дії відомих на той час парових машин, Карно дійшов висновку: будь який тепловий двигун працює за схемою: 1. Нагрівник (джерело енергії) надає робочому тілу певну кількість теплоти (Q1). 2. Робоче тіло, частину цієї теплоти перетворює на механічну роботу (А), а частину (Q2= Q1–А) – передає холодильнику, яким по суті є навколишнє середовище. Іншими словами, принцип дії будь якого теплового двигуна можна представити у вигляді наступної схеми:

Мал.91. Схема принципу дії теплового двигуна.
Різноманіття сучасних теплових двигунів надзвичайно велике. За різними ознаками це різноманіття можна класифікувати по різному. Зазвичай за способом перетворення теплоти в механічну роботу, та за характерними конструктивними ознаками, теплові двигуни поділяють на поршневі, турбінні та реактивні. Не заглиблюючись в подробиці загального устрою та деталі принципу дії, про вище згадані різновидності теплових двигунів можна сказати наступне.
Поршневими, називають такі теплові двигуни, в яких виконання механічної роботи обумовлено тим, що високотемпературне робоче тіло, знаходячись в циліндрі двигуна, тисне на поршень та переміщує його. Поршневі двигуни поділяються на парові машини та двигуни внутрішнього згорання.
Паровими машинами, називають такі поршневі двигуни, в яких робочим тілом є нагрітий за межами циліндру пар. Парові машини були тими першими тепловими двигунами, які отримали надзвичайно широке практичне застосування. По суті, саме парова машина стала тією рушійною силою яка спричинила так звану промислову революцію, тобто перехід від мануфактурного ручного виробництва до виробництва машинного. Однак, якщо говорити про теперішній час, то в ньому парові машини не мають суттєвого застосування. Головний недолік парових машин полягає в тому, що в них робочим тілом є не продукти згорання палива, а нагріта цим паливом окрема речовина – пар. А це означає, що в робочому циклі парової машини є додаткова проміжна ланка – пар, як проміжне робоче тіло та паронагрівальний агрегат, як генератор цього пару. Ясно, що в такій ситуації к.к.д. парової машини є значно меншим за к.к.д. тих теплових двигунів в яких продукти згорання палива безпосередньо виконують корисну роботу. Зважаючи на ці обставини, парові машини практично повністю витіснені більш ефективними та компактними тепловими двигунами, зокрема двигунами внутрішнього згорання.
Двигунами внутрішнього згорання, називають такі поршневі двигуни, в яких робочим тілом є високотемпературний газ що утворюється в процесі згорання палива яке відбувається в середині робочого циліндру двигуна. Загальний устрій та етапи роботи типового двигуна внутрішнього згорання представлені на мал.92. Повний робочий цикл представленого на малюнку двигуна здійснюється за чотири етапи (такти). На першому етані відкривається вхідний клапан і циліндр заповнюється горючою сумішшю. На другому – ця суміш стискається. На третьому – горюча суміш підпалюється, згорає і виконує корисну роботу. На четвертому етапі, відкривається випускний клапан і відпрацьовані продукти згорання виштовхуються за межі робочого циліндра.
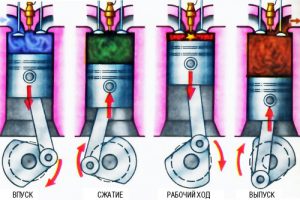
Мал.92. Загальний устрій та етапи роботи двигуна внутрішнього згорання.
На теперішній час, двигуни внутрішнього згорання є найбільш поширеними і конструктивно найбільш різноманітними тепловими двигунами. Різноманіття цих двигунів можна класифікувати за різними ознаками, зокрема:
– за способом утворення горючої суміші: двигуни з внутрішнім та зовнішнім сумішоутворенням;
– за організацією робочого циклу: двигуни двохтактні та чотирьохтактні;
– за швидкістю згорання палива: двигуни швидкого, повільного та змішаного згорання;
– за видом палива: двигуни газові та на рідкому паливі;
– за кількістю циліндрів: двигуни одноциліндрові, двоциліндрові, чотирьох циліндрові і т.д.
– за способом розташування циліндрів: двигуни з лінійним, V-подібним та круговим розташуванням циліндрів;
– за способом охолодження: двигуни з повітряним та водяним охолодженням;
– за іншими класифікаційними ознаками…
Зазвичай, за низкою ознак двигуни внутрішнього згорання поділяють на карбюраторні та дизельні. В карбюраторних (бензинових) двигунах, горюча суміш утворюється за межами робочого циліндра (в карбюраторі) і в потрібний момент запалюється електричною іскрою яку створює свічка запалювання. В дизельних двигунах нема карбюратора і нема свічки запалювання. Натомість є форсунка – прилад, який в момент гранично сильного стиснення повітря, впорскує в це розжарене повітря паливо яке самозаймається.
В побутовій практиці, ми майже завжди маємо справу з тими чи іншими різновидностями поршневих двигунів внутрішнього згорання. Адже саме такі двигуни стоять на наших автомобілях, мопедах, мотоциклах, моторних човнах, побутових електрогенераторах, тощо. Однак, якщо мова йде про більш потужні прилади, як то кораблі, підводні човни, літаки, генератори теплових електростанцій, тощо, то в них зазвичай застосовують так звані турбінні двигуни. Турбінними двигунами, називають такі теплові двигуни, в яких виконання механічної роботи обумовлено тим, що високотемпературне робоче тіло, направленим струменем викидається на спеціальне лопатчате колесо (ротор) і змушує його обертатись. Сучасні турбінні двигуни мають достатньо складну конструкцію. Однак принциповий устрій (мал.93) та принцип дії цих двигунів є гранично простими. І цей устрій та принцип дії мало чим відрізняється від устрою та принципу дії водяного колеса: потік води падає на лопатчате колесо і обертає його.
Мал.93. Що спільного між водяним колесом та турбінним двигуном?
Ще однією важливою різновидністю теплових двигунів є двигуни реактивні. Реактивними називають такі теплові двигуни, в яких виконання механічної роботи обумовлено тим, що високотемпературне робоче тіло з великою швидкістю вилітає назовню двигуна через так зване сопло. Зазвичай, сопло реактивного двигуна представляє собою певне звуження його камери згорання яке плавно переходить в характерне розширення. Така конструкція забезпечує вирішення двох задач: 1) створює умови за яких швидкість вильоту молекул робочого тіла стає максимально великою; 2) створює умови за яких рух молекул робочого тіла стає максимально упорядкованим (направленим вздовж осі сопла).
Поступальний рух реактивного двигуна та того тіла яке цей двигун переміщує, обумовлений тими ж силовими причинами що і рух гумової кульки з отвору якої витікає струмінь стиснутого повітря, або тіла гармати після вильоту з неї ядра, або рух човна з корми якого стрибає пірнальник. Просто з тіла реактивного двигуна вилітає не стиснуте повітря, не ядра, не кулі, не снаряди і не пірнальники, а молекули тієї речовини що згорає в двигуні. Реальний устрій реактивних двигунів може бути як гранично простим (двигуни некерованих реактивних снарядів), так і гранично складним (двигуни сучасних космічних ракет).
. .
.
Мал.94. Ілюстрація загального устрою та принципу дії реактивного двигуна.
Потрібно зауважити, що різноманіття сучасних теплових двигунів не обмежується класифікаційною схемою: двигуни поршневі, турбінні та реактивні. Натепер існує широке різноманіття комбінованих теплових двигунів, зокрема турбореактивні двигуни, роторно-поршневі двигуни, поршневі двигуни з турбонаддувом, тощо. Однак, в будь якому випадку, базовими видами сучасних теплових двигунів є двигуни поршневі, турбінні та реактивні.
Аналізуючи загальний устрій реактивних, турбінних та поршневих двигунів, важко віднайти бодай якісь конструктивні аналогії. Важко тому, що з точки зору технічних рішень, ці двигуни влаштовані по різному. І тим не менше, всі ці абсолютно не схожі двигуни, працюють за однією принциповою схемою. З’ясовуючи суть цієї схеми, задаймося питанням: «А які елементи теплового двигуна є найважливішими, тобто такими, без наявності яких не зможе працювати жоден тепловий двигун?» Відповідаючи на це запитання, ви неминуче прийдете до висновку, що найважливішими елементами теплового двигуна є не циліндри, не поршні, не колінчасті вали, не сопла і не турбінні колеса. Бо як би там не було, а всі ці деталі, це лише допоміжні технічні елементи які допомагають перетворити внутрішню енергію палива в механічну роботу. При цьому існують двигуни без поршнів, без циліндрів, без колінчастих валів, без сопел і без турбінних коліс.
А от без чого дійсно не може існувати будь який тепловий двигун, так це без сукупності трьох основних елементів: 1) нагрівника – джерела теплової енергії; 2) робочого тула – речовини, яка отримує від нагрівника теплову енергію та перетворює частину цієї енергії в механічну роботу; 3) холодильника – тієї «помийної ями» в яку викидається відпрацьоване робоче тіло, а разом з ним і та частина енергії, яка залишилась після виконання механічної роботи. І не важко збагнути що цією «помийною ямою» практично завжди є наше навколишнє середовище.
Таким чином, коли ми стверджуємо, що всі теплові двигуни працюють за єдиною принциповою схемою, то маємо на увазі факт того, що загальний принцип дії будь якого теплового двигуна полягає в наступному. 1. Нагрівник (джерело енергії) надає робочому тілу певну кількість теплоти (Q1). 2. Робоче тіло, частину цієї теплоти перетворює на механічну роботу (А), а решту (Q2= Q1–А) – передає холодильнику, яким по суті є навколишнє середовище.
Саді Карно не лише описав схему та принцип дії узагальненого теплового двигуна, а й теоретично довів, що максимально можливий к.к.д. такого двигуна визначається за формулою ηmax = (Т1 – Т2)/Т1, де Т1, Т2 – температура робочого тіла двигуна, відповідно на початку та вкінці робочого циклу.
Потрібно зауважити, що створюючи свою теорію, Карно виходив з того помилкового припущення, що теплота це певна речовина (теплець), яка в процесі переходу від більш нагрітого тіла до менш нагрітого, виконує певну механічну роботу. Виконує подібно до того, як падаюча з певної висоти вода обертає водяне колесо. Та не дивлячись на помилковість поглядів що до природи теплоти, Карно зумів зробити абсолютно правильний теоретичний висновок: енергетична ефективність ідеального теплового двигуна, визначальним чином залежить від тієї різниці температур яку має робоче тіло на початку (Т1) і вкінці (Т2) робочого циклу: ηmax=(Т1 – Т2)/Т1.
Із аналізу формули Карно, з усією очевидністю випливає практично важливий висновок: організовуючи роботу реального теплового двигуна, потрібно прагнути до того, щоб на початку робочого циклу, температура робочого тіла була максимально великою, а в кінці цього циклу – максимально низькою.
Ясно, що прагнучи максимально збільшити температуру робочого тіла, ми неминуче стикнемося з низкою технічних проблем. Наприклад, з проблемою того, що при високих температурах, конструктивні матеріали втрачають свої міцнісні властивості. З іншого боку, можливості максимального зниження температури робочого тіла також суттєво обмежені. Обмежені бодай тим, що робоче тіло не можна змусити виконувати корисну роботу, якщо температура цього тіла нижча за температуру навколишнього середовища.
Вище сказане означає, що к.к.д. найідеальнішого теплового двигуна не може бути гранично великим. Наприклад, якщо максимальна температура робочого тіла становить 2000К, а температура навколишнього середовища 300К, то к.к.д. найідеальнішого теплового двигуна не може перевищувати 85%: ηmax=(2000 – 300)/2000=0,85=85%. Якщо ж говорити про реальні теплові двигуни, з їх реальним перепадом температур та реальним рівнем інших енергетичних втрат, то їх к.к.д. практично завжди менший за 50%.
Таблиця. Коефіцієнти корисної дії сучасних теплових двигунів.
| Тип двигуна | к.к.д. (%) |
| Парова машина Уатта
Двигуни внутрішнього згорання: – карбюраторні – дизельні Турбінні двигуни Турбореактивні двигуни Реактивні двигуни |
3 – 4
25 – 35 30 – 40 25 – 35 25 – 35 30 – 35 |
Не важко бачити, що реальний коефіцієнт корисної дії теплового двигуна практично будь якої конструкції є надзвичайно низьким. Адже в процесі роботи теплового двигуна приблизно 70% тієї енергії що виділяється при згоранні палива, в буквальному сенсі викидається «на вітер». Чому ж енергетична ефективність навіть найсучасніших теплових двигунів є такою низькою? Чому к.к.д. електричного двигуна становить 97 – 99%, а теплового – лише 25 – 40%? Що ж, спробуємо відповісти і на ці слушні та важливі запитання.
Аналізуючи роботу реального теплового двигуна, наприклад двигуна внутрішнього згорання, не важко з’ясувати, що та теплова енергія (Q) яка виділяється в процесі згорання палива витрачається наступним чином:
– йде на виконання корисної механічної роботи (Амех);
– викидається в атмосферу разом з продуктами згорання (Qпр.гор);
– викидаються в атмосфера в процесі роботи системи охолодження (Qox);
– йде на інші неминучі втрати (Qiн).
Іншими словами: Q = Aмех + Qпр.гор + Qох + Qін .
Ми не будемо аналізувати всі джерела тих енергетичних втрат які супроводжують роботу будь якого теплового двигуна. Обмежимся лише стислим аналізом тих неминучих втрат, які пов’язані з фактом того, що велика частина тієї енергії яка виділяється при згоранні палива, викидається в атмосферу разом з продуктами згорання. Дійсно. В камері згорання сучасного карбюраторного двигуна, температура газу досягає 3000К. В процесі розширення, цей газ виконує механічну роботу і охолоджується. Однак, вже при температурі близькій до 1300К, газ викидається за межі циліндра. А разом з ним, викидається і величезна кількість нереалізованої енергії (≈ 43%). Виникає закономірне питання: «А чому теплова енергія газу використовується так неефективно?» Адже якби газ викидали не при 1300К, а скажімо при 400К, то рівень відповідних теплових втрат знизився б з 43% до 13%.
Сподіваюсь, ви не думаєте що ті інженери які проектують теплові двигуни не знають про вище згаданий факт? Звичайно знають. І безумовно працюють над тим, щоб максимально ефективно використати енергетичний потенціал палива. Але ця задача не є такою простою як може здатися на перший погляд. Дійсно. Припустимо, що ви хочете створити двигун в якому рівень теплових втрат є гранично низьким. З цією метою ви прагнете організувати робочий цикл двигуна таким чином, щоб його продукти згорання викидались не при 1300К, а при 400К. Проектуючи такий двигун, ви неодмінно з’ясуєте, що робочий хід його поршня потрібно збільшити в 3 рази. А це означає, що об’ємні розміри, а відповідно маса і ціна практично всіх деталей та вузлів двигуна починаючи від циліндрів, поршнів, шатунів та колінчастих валів і закінчуючи системою охолодження та амортизації, мають збільшитися у 33=27 разів. Крім цього, ви неодмінно з’ясуєте, що робочий цикл вашого «ідеального двигуна» стане більш тривалим. Що погіршяться динамічні параметри процесу. Зменшиться питома потужність двигуна. Збільшяться теплові втрати в системі охолодження. Виникнуть проблеми з організацією безпечного вихлопу продуктів згорання, тощо.
Таким чином, проектуючи реальний тепловий двигун, ви будете змушені вирішувати складний комплекс взаємопов’язаних проблем. Проблем такого ґатунку, що певний виграш в одному напрямку, неминуче призводить до відповідного програшу в інших напрямках. Кінцевим же рішенням цієї системи оптимізаційних задач буде висновок: для карбюраторних двигунів з максимальною температурою робочого тіла 3000К, оптимальна температура вихлопу продуктів згорання має бути близькою до 1300К.
Звичайно, ви можете спробувати підвищити максимальну температуру робочого тіла двигуна, скажімо до 4000К. Але і в цьому випадку, реалії життя неодмінно приготують вам нові сюрпризи. Наприклад вам знадобиться нова, більш дорога та енергетично більш затратна система охолодження. Вам неминуче знадобиться новий, більш дорогий вид палива. Вам знадобляться нові, більш дорогі конструктивні матеріали. Крім цього, ви неодмінно з’ясуєте, що для двигунів з максимальною температурою робочого тіла 4000К, оптимальною температурою вихлопу продуктів згорання є не 1300К, а 1500К. При цьому, ви знову переконаєтесь в тому, що намагаючись зменшити втрати в одному місці, ви будете створювати умови для їх появи в іншому.
Додайте до вище сказаного ті втрати які пов’язані з наявністю сил тертя, з роботою системи охолодження двигуна, з роботою гідравлічних, електричних, гальмівних та інших систем автомобіля, і ви зрозумієте чому к.к.д. навіть найсучасніших теплових двигунів не перевищує 50%.
Таким чином факт того, що сучасні теплові двигуни мають відносно низький к.к.д., зовсім не означає що ці двигуни недосконалі. Цей факт вказує лише на те, що процес перетворення теплоти в механічну роботу, неминуче супроводжується великими енергетичними втратами, і що величина цих втрат, зазвичай суттєво перевищує 50%. Власне факт того, що енергетична ефективність всього різноманіття сучасних теплових двигунів є відносно низькою, це прямий наслідок того, що ці двигуни перетворюють енергію безпорядку (теплоту) в енергію порядку (механічну роботу). А у відповідності з другим началом термодинаміки енергія безпорядку перетворюється в енергію порядку лише примусово і неповністю, тобто з певними енергетичними втратами.
Якщо ж говорити про двигун електричний, то він перетворює енергію одного порядку (енергію упорядкованого руху заряджених частинок), в енергію іншого порядку (механічну роботу). А таке перетворення, якщо і супроводжується певними енергетичними втратами, то лише такими які пов’язані з механічним або електричним тертям. А такі втрати відносно легко мінімізуються. Тому сучасні електричні двигуни мають високий к.к.д., величина якого досягає 99%.
Задача 1. Автомобіль, потужність двигуна якого 60кВт, а к.к.д. 30%, рухається зі швидкістю 72км/год. Визначити витрати бензину на кілометр шляху.
Дано:
N = 60кВт = 60∙103Вт
η = 30%ю
v = 72км/год = 20м/с
m/s = ?
Рішення. За визначенням η = (Акор/Азаг)100%. Оскільки потужність двигуна характеризує величину тієї корисної роботи яку виконує двигун за одиницю часу (N = Aкор/t), то Aкор = Nt. Оскільки в тепловому двигуні загальною енергією (роботою) є та теплова енергія яка виділяється при згоранні палива, то Азаг= Qгор = qm, де q(бензину) = 46∙106(Дж/кг). Таким чином η = (Акор/Азаг)100% = N∙t∙100%/q∙m. А враховуючи, що v = s/t, a отже t = s/v, можна записати η = N∙s∙100%/q∙m∙v. Звідси m/s = N∙100%/q∙v∙η.
Розрахунки: m/s = N∙100%/q∙v∙η = 60∙103Вт∙100%/46∙106(Дж/кг)∙20(м/с)∙30% = 0,00022(кг/м) = 0,22(кг/км).
Відповідь: m/s = 0,22(кг/км).
Задача 2. Одноатомний ідеальний газ здійснює зображений на малюнку цикл 1→2→3→4→1. Визначити ККД циклу.
Рішення. Оскільки за визначенням η=Акор/Азаг, та враховуючи що в умовах теплового двигуна, загальною енергією (роботою), є та енергія яку отримує робоче тіло від нагрівника Азаг=Qн, а корисною енергією (роботою) є різниця між тією теплотою яку робоче тіло отримало від нагрівника та тією теплотою яку воно віддало охолоджувачу Акор=Qн – Qох, можна записати η= (Qн–Qох)/Qн = 1–Qох/Qн.
Керуючись першим началом термодинаміки Q=ΔU+A, визначаємо кількість тієї теплоти яку отримує (+Q) або втрачає (–Q) робоче тіло на кожній ділянці заданого циклу.
Ділянка 1→2: V=const, p↑, оскільки pV/T=const, то T↑. А це означає:
1) А12=pΔV=0;
2) ΔU12=1,5VΔp=1,5V0 (2p0 – р0) = 1,5V0p0.
+Q12 = ΔU12 + A12 = 1,5p0V0.
Ділянка 2→3: V↑ p=const, оскільки pV/T=const, то T↑. А це означає:
1) А23=pΔV=2p0·2V0 = 4p0V0;
2) ΔU23=1,5pΔV=1,5·2p0·2V0= 6p0V0.
+Q23 = ΔU23 + A23 = 6p0V0 + 4p0V0 = 10p0V0.
Ділянка 3→4: V=const, p↓, оскільки pV/T=const, то T↓. А це означає:
1) А34=pΔV=0;
2) ΔU34=1,5VΔp=1,5·3V0(–1p0) = –4,5p0V0;
–Q12 = ΔU34 + A34 = 4,5p0V0.
Ділянка 4→1: V↓, p=const, оскільки pV/T=const, то T↓. А це означає:
1) А41=pΔV=p0·(–2)V0 = –2p0V0;
2) ΔU41=1,5pΔV=1,5·p0·(–2)V0= –3p0V0.
–Q41 = ΔU41 + A41 = 3p0V0 + 2p0V0 = 5p0V0.
Таким чином: Qн = +Q = 1,5p0V0 + 10p0V0 = 11,5p0V0.
Qох = –Q = 4,5p0V0 + 5p0V0 = 9,5p0V0.
η= 1–Qох/Qн = 1 – 9,5p0V0/11,5p0V0 = 1 – 0,83 = 0,17 = 17%.
Відповідь: η = 17%.
Контрольні запитання.
- Поясніть будову та принцип дії поршневого двигуна.
- Поясніть будову та принцип дії турбінного двигуна.
- Поясніть будову та принцип дії реактивного двигуна.
- Чим схожі та чим відрізняються дизельні і карбюраторні двигуни?
- Поясніть загальний принцип дії теплового двигуна.
- Що необхідно зробити для того щоб максимально збільшити ККД теплового двигуна? Чи легко це реалізувати на практиці? Чому?
- Чому в теплових двигунах продукти згорання палива викидають за межі двигуна при відносно великих температурах?
- Чому к.к.д. сучасних теплових двигунів значно менший за 50%, тоді як ККД сучасних електричних двигунів близький до 100%?
- В чому основна складність роботи інженера-конструктора?
Вправа 19.
- 1. На початку робочого циклу температура в камері згоранні поршневого двигуна 2500°С, а в кінці цього циклу 1000°С. Визначте максимально можливий ККД цього двигуна.
- ККД ідеального теплового двигуна 40%. Газ одержує від нагрівача 5кДж теплоти. Яка кількість теплоти віддана холодильнику?
- Визначити ККД теплового двигуна, який розвиває потужність 95кВт та витрачає за годину 25кг дизельного палива (q=42·106Дж/кг)?
- Потужність одного з найбільших дизельних двигуні становить 42000кВт. Скільки дизельного палива споживає цей двигун за годину роботи, якщо його к.к.д. 40%
- Яку кількість бензину витратили двигуни літака, що пролетів 500км з середньою швидкістю 250км/год, якщо середня потужність його двигунів 2000кВт? К.к.д. двигуна 25%.
- На скільки кілометрів шляху вистачить 8л бензину для двигуна мотоцикла, який маючи к.к.д. 25% при швидкості 72км/год розвиває потужність 9кВт? Густина бензину 0,7·103кг/м3.
- Визначити потужність двигуна автомобіля, який при швидкості 72км/год витрачає на кожний кілометр шляху 90г бензину. К.к.д. двигуна 30%
- За заданою р–V діаграмою двохатомного газу, визначте яку кількість теплоти отримав або віддав цей газ на кожній ділянці переходу 1→2→3→4→1. Якою є загальна кількість цієї теплоти? Визначити ККД циклу.
.