Сайт викладача фізики

          Лабораторна робота № 1.

Тема роботи. Визначення прискорення тіла при його рівноприскореному русі.

Мета роботи. Дослідним шляхом визначити прискорення тіла при його рівноприскореному русі.

Теоретичні відомості.

Прискорення (дотичне прискорення) – це фізична величина, яка характеризує зміну швидкості руху тіла і яка показує, на скільки змінюється ця швидкість за одиницю часу.

Позначається: а

Визначальне рівняння: а = (v_к – v₀)/t

Одиниця вимірювання: [а] = м/с².

Оскільки на практиці, виміряти миттєве значення кінцевої швидкості тіла, практично неможливо (v_к = ?), то ясно, що визначити прискорення тіла за формулою а = (v_к – v₀)/t , ми не можемо. Тому прискорення тіла ми визначимо на основі аналізу його рівняння руху, а точніше – рівняння пройденого шляху: s = v₀t + at²/2. Дійсно, в умовах нашого експерименту (v₀=0), це рівняння набуває вигляду s = at²/2. Звідси: a = 2s/t², де s, t – вимірюються.

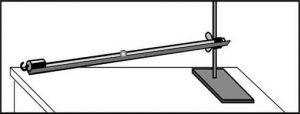
Обладнання. 1) Прямолінійний жолоб; 2) металева куля; 3) штатив; 4) лінійка (рулетка); 5) секундомір; 6) транспортир.

Результати вимірювань та обчислень.

Таблиця 1.

№  п/п	Пройдений  тілом шлях	Час руху тіла	Прискорення тіла	Кут нахилу жолоба
–	s	t	a	α
–	м	с	м/с2	град.
1	1,5	3,3		10
2	1,0	2,7		10
3	1,5	2,1		20
4	1,0	1,7		20

Розрахунки.

a₁ = 2s₁/t₁² =

a₂ = 2s₂/t₂² =

a₃ = 2s₃/t₃² =

a₄ = 2s₄/t₄² =

          Висновок.

          В даній лабораторній роботі я навчився визначати прискорення тіла при його рівноприскореному русі. При цьому, отримані мною результати підтверджують передбачення теорії. А це означає, що наша теорія є правильною.

Контрольні запитання.

1. Чому визначальне рівняння прискорення (а = (v_к – v₀)/t) не є придатним для практичного визначення цього прискорення?
2. Чи залежить в умовах даного експерименту, величина прискорення тіла, від величини пройденого ним шляху?
3. Як в умовах даного експерименту, прискорення тіла залежить від величини кута нахилу жолоба?
4. В умовах даного експерименту, точність вимірювання якої величини, найбільш впливає на точність визначення прискорення тіла? Поясніть, чому?

.

Лабораторна робота № 2.

Тема роботи. Визначення жорсткості пружини.

Мета роботи. Дослідним шляхом визначити жорсткість пружини.

Теоретичні відомості.

Жорсткість тіла – це фізична величина, яка характеризує пружні властивості даного тіла і яка дорівнює відношенню тієї сили (F) що деформує тіло, до величини тієї абсолютної деформації (∆ℓ) яку отримує тіло під дією відповідної  сили.

Позначається: k

Визначальне рівняння: k = F/∆ℓ

Одиниця вимірювання: [k] = Н/м.

Зважаючи на те, що в умовах нашого експерименту, тією силою яка деформує пружину, є сила тяжіння (F = mg), можна записати k = F/∆ℓ = mg/∆ℓ, де g ≈ 10м/с²;  m, ∆ℓ – вимірюються.

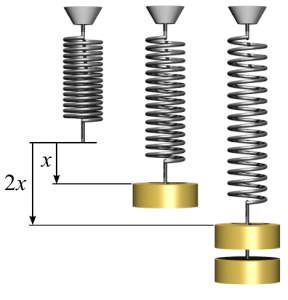
Обладнання.

1. Досліджувана пружина.
2. Набір тягарців.
3. Штатив.
4. Лінійка.

Результати вимірювань та обчислень.

Таблиця 2.

№     п/п	Маса тягарців	Деформуюча сила	Абсолютна деформація тіла	Жорсткість тіла
–	m	F	Δℓ	k
–	кг	Н	м	Н/м
1	0,1	1,0	0,025
2	0,2	2,0	0,050
3	0,3	3,0	0,075
4	0,4	4,0	0,100

Розрахунки.

k₁ = F₁/∆ℓ₁ =

k₂ = F₂/∆ℓ₂ =

k₃ = F₃/∆ℓ₃ =

k₄ = F₄/∆ℓ₄ =

 Висновок.

В даній лабораторній роботі, я навчився визначати жорсткість пружини. При цьому, отримані мною результати підтверджують передбачення теорії. А це означає, що наша теорія є правильною.

Контрольні запитання.

1. Чи залежить жорсткість тіла від величини його деформуючої сили?
2. Чи залежить жорсткість тіла від величини тієї абсолютної деформації, яку спричиняє деформуюча сила?
3. Від чого залежить жорсткість тіла?
4. Як зміниться жорсткість пружини, при зменшені її початкової довжини вдвічі?

.

 Лабораторна робота № 3.

Тема роботи.  Визначення прискорення вільного падіння тіла.

Мета роботи. За допомогою моделі математичного маятника, визначити прискорення вільного падіння тіл.

 Теоретичні відомості.

Загально відомо, що на Землі тіла вільно падають з прискоренням, усереднене значення якого g=9,81м/с². Однак, далеко не всі знають як визначається величина цього прискорення на практиці. Неважко збагнути, що з практичної точки зору визначальне рівняння прискорення а = (v_к – v₀)/t є мало придатним для визначення того прискорення з яким вільно падають тіла. (Малопридатним тому, що v_к=?) Тому на практиці прискорення вільного падіння визначають за допомогою моделі математичного маятника (нитяного маятника). Дійсно.

          Можна довести, що період коливання математичного маятника визначається за формулою: Т = 2π(ℓ/g)^1/2

де  ℓ – довжина маятника

g – прискорення вільного падіння

Враховуючи, що за визначенням Т=t/n, можна записати t²/n²=4π²ℓ/g, звідси

                                      g = 4π²ℓn²/t²

де  ℓ – довжина маятника (вимірюється)

n – кількість повних коливань маятника (задається)

t – тривалість цих коливань (вимірюється)

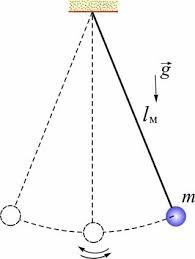
Обладнання.

1. Модель математичного маятника (нитяний маятник).
2. Лінійка (рулетка).
3. Секундомір.

Результати вимірювань та обчислень.

Таблиця 3.

№ п/п	Довжина маятника	Час коливань	Кількість коливань	Прискорен-ня вільного падіння	Табличне значення прискорення	Відносна похибка досліду
–	ℓ	t	n	g	gт	δ
–	м	с	–	м/с	м/с	%
1	0,39	25	20		9,81
2	0,46	20	15		9,81
3	1,20	22	10		9,81
4

 Розрахунки.

g₁ = 4π²ℓ₁n₁² / t₁² =

g₂ = 4π²ℓ₂n₂² / t₂² =

g₃ = 4π²ℓ₃n₃² / t₃² =

δ₁ = (g_т – g₁)100% / g_т =

δ₂ = (g_т – g₂)100% / g_т =

δ₃ = (g_т – g₃)100% / g_т =

 Висновок.

В даній лабораторній роботі, я навчився визначати прискорення вільного падіння тіл. При цьому, отримані мною результати достатньо точно співпадають з табличним значенням відповідного прискорення. А це означає, що наша теорія є правильною.

  Контрольні запитання.

1. Чому визначальне рівняння прискорення а=(v_к–v₀)/t практично не придатне для визначення прискорення вільного падіння тіл?
2. Чи залежить період коливань математичного маятника від маси вантажу?
3. Чи зміниться період коливань математичного маятника, якщо його перенести на місяць?
4. Чи залежить прискорення вільного падіння планети від періоду коливань математичного маятника?
5. Від чого залежить прискорення вільного падіння планети?
6. Які інші методи визначення прискорення вільного падіння ви можете запропонувати?

 .

Лабораторна робота №4.

Тема роботи.  Визначення відносної вологості повітря.

Мета роботи. Ознайомитись з будовою і принципом дії волосяного гігрометра, конденсаційного гігрометра та психрометра. Визначити вологість повітря в аудиторії.

Теоретичні відомості.

 Кількість водяного пару в повітрі характеризують двома величинами:

1) абсолютна вологість повітря;

2) відносна вологість повітря.

Абсолютна вологість повітря – це фізична величина, яка показує скільки водяної пари знаходиться в одиниці об’єму повітря. Іншими словами, абсолютна вологість повітря дорівнює реальній густині водяного пару в повітрі:

Позначається: ρ_а

Визначальне рівняння: ρ_а = m(H₂O)/V;

Одиниця вимірювання: [ρ_a] = кг/м³

Відносна вологість повітря – це фізична величина, яка дорівнює відношенню абсолютної вологості повітря до максимально можливої при даній температурі вологості.

Позначається: В

Визначальне рівняння: В =(ρ_a/ρ_н)100%;

Одиниця вимірювання: [B] = %

де ρ_н – густина насиченого пару (визначається за відповідною таблицею)

Точка роси – це температура при якій насичений пар (ρ_а<ρ_н) стає насиченим (ρ_а=ρ_н).

Відносну вологість повітря визначають за допомогою різних приладів, зокрема: 1) волосяного гігрометра, 2) конденсаційного гігрометра, 3) психрометра.

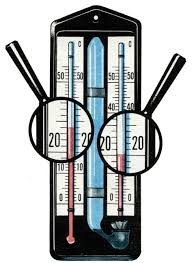
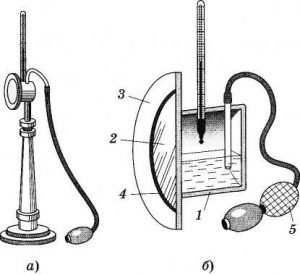
Обладнання.

1. Волосяний гігрометр.
2. Конденсаційний гігрометр.
3. Термометр.
4. Етиловий спирт.
5. Психрометр.

Результати вимірювань та обчислень.

1. Робота конденсаційним гігрометром .

Таблиця 4а.

№ п/п	Температура повітря	Точка роси	Абсолютна вологість повітря	Густина насиченої пари	Відносна вологість повітря
–	t	t0	ρа	ρн	B
	0С	0С	г/м	г/м	%
1	20	15	12,8	17,3	73
2	20	16	13,6	17,3	78

2. Робота з психрометром

Таблиця 4б.

Температура сухого термометра	Температура мокрого термометра	Різниця температур	Відносна вологість повітря
tс	tм	∆t	B
0С	0С	0C	%
20	17	3	74

Розрахунки.

В₁ = (ρ_а1/ρ_н1)100% =

В₂ = (ρ_а2/ρ_н2)100% =

Висновок.

В даній лабораторній роботі я навчився визначати відносну вологість повітря за допомогою різних приладів, зокрема волосяного гігрометра, конденсаційного гігрометра та психрометра. При цьому, отримані мною результати підтверджують передбачення теорії. А це означає, що наша теорія є правильною.

 Контрольні запитання.

1. Що характеризує абсолютна вологість повітря ?
2. Що характеризує відносна вологість повітря?
3. Будова і принцип дії волосяного гігрометра.
4. Будова і принцип дії конденсаційного гігрометра.
5. Що таке точка роси?
6. Будова і принцип дії психрометра.
7. Для чого в психрометрі вентилятор.

  .

Лабораторна робота № 5.

Тема роботи.  Визначення коефіцієнту поверхневого натягу рідини.

Мета роботи.  Дослідним шляхом визначити коефіцієнт поверхневого натягу води.

 Теоретичні відомості.

          Коефіцієнт поверхневого натягу рідини – це фізична величини, яка характеризує пружні властивості поверхневого шару рідини і яка дорівнює відношенню сили поверхневого натягу, до довжини периметру поверхні на якій ця сила виникає:

Позначається: σ

Визначальне рівняння: σ = F_пн/ℓ

Одиниця вимірювання: [σ] = Н/м

Коефіцієнт поверхневого натягу рідини визначається експериментально і записується у відповідну таблицю (дивись табл.11 ст.314). Наприклад для води σ=0,072Н/м.

Для визначення коефіцієнту поверхневого натягу застосовують різні методи, зокрема: 1) метод відриву крапель; 2) метод відриву тіла від поверхні рідини; 3) капілярний метод.

З практичної точки зору, найбільш простим та ефективним методом визначення коефіцієнту поверхневого натягу є капілярний метод. Його суть полягає в тому, що із умови рівноваги тих сил, що діють на рідину в капілярі, визначають величину коефіцієнту поверхневого натягу цієї рідини. Дійсно. Розглянемо ті сили, що діють на підняту в капілярі рідину. А на цю рідину діють дві рівні за величиною і протилежні за напрямком сили: тяжіння та сита поверхневого натягу.

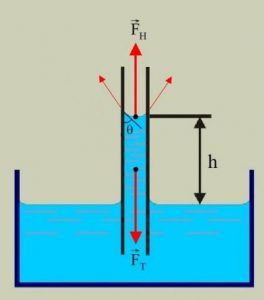
Оскільки F_т=mg=ρVg=ρhSg=ρhgπd²/4, а   F_пн=σℓ=σπd, то можна записати:

σπd  = ρhgπd²/4. Звідси  σ =  ρhgd/4.

Таким чином, коефіцієнт поверхневого натягу рідини можна визначити за формулою  σ = ρhdg/4

де   h – та висота на яку піднімається рідина в капілярі (вимірюється)

d – діаметр капіляру (вимірюється)

g = 9,8м/с² – прискорення вільного падіння

ρ – густина рідини (для води  ρ = 1∙10кг/м³).

Обладнання.

1. Посудина з водою.
2. Набір капілярних трубок.
3. Набір голок.
4. Штангенциркуль.
5. Лінійка.

Результати вимірювань та обчислень.

Таблиця 5.

№ п/п	Діаметр капіляру	Висота води в  капілярі	Коефіцієнт поверхневого натягу	Табличне значення коефіцієнту	Відносна похибка досліду
–	d	h	σ	σт	δ
–	м	м	Н/м	Н/м	%
1.	1∙10–3	3,0∙10–2		0,072
2.	1∙10–3	2,9∙10–2		0,072
3.

Розрахунки.

σ₁ = ρh₁dg/4 =

σ₂ = ρh₂dg/4 =

δ₁ = (σ_т – σ₁)100% / σ_т =

δ₂ = (σ_т – σ₂)100% / σ_т =

 Висновок.

          В даній лабораторній роботі, я навчився визначати коефіцієнт поверхневого натягу рідини (води). При цьому, отримані мною результати достатньо точно співпадають з табличним значенням відповідного коефіцієнту. А це означає, що наша теорія є правильною.

 Контрольні запитання.

1. Чим обумовлена поява сили поверхневого натягу?
2. Що показує коефіцієнт поверхневого натягу?
3. Якої форми намагається надати рідині сила поверхневого натягу? І чому ми говоримо, що рідини не мають певної стійкої форми?
4. Чим пояснити той факт, що вода змочує скло і не змочує парафін?
5. Чому вода піднімається в скляному капілярі?
6. Яка рідина має найбільший коефіцієнт поверхневого натягу?

.

Лабораторна робота № 6.

Тема роботи.  Визначення температурного коефіцієнту лінійного розширення.

Мета роботи. Дослідним шляхом визначити температурний коефіцієнт лінійного розширення алюмінію, сталі та скла.

Теоретичні відомості.

          Температурний коефіцієнт лінійного розширення –  це фізична величина яка характеризує теплове розширення даного матеріалу і яка показує на стільки деформується тіло довжиною один метр при його нагріванні на один градус Цельсія.

Позначається: α

Визначальне рівняння:  α = ∆ℓ/ℓ₀∆t

Одиниця вимірювання:  [α] = 1/⁰С

де  ℓ₀ – початкова довжина тіла (вимірюється)

∆ℓ – теплова деформація тіла (вимірюється)

∆t – різниця між кінцевою та початковою температурою тіла

Температурний коефіцієнт лінійного розширення визначається експериментально і записується у відповідну таблицю (дивись табл.12 ст.314). Наприклад, для алюмінію α=2,3∙10^–5(1/⁰С); для сталі α=1,2∙10^–5(1/⁰С); для скла α=0,9∙10^–5(1/⁰С).

Обладнання.

1. Стальний, алюмінієвий та скляний стержні.
2. Колба з водою.
3. Прилад для нагрівання води в колбі.
4. Термометр.
5. Індикатор видовження (мікрометр)
6. Джерело електричного струму.

Результати вимірювань та обчислень.

Таблиця 6.

Матеріал стержня	Початкова довжиня стержня	Зміна темп – ри стержня	Теплова деформ. стержня	Коефіц. лінійн. розшир.	Табличне значен. коефіц.	Відносна похибка досліду
–	ℓ0		Δℓ	α	αТ	δ
–	м	0С	м	1/0С	1/0С	%
алюміній	0,16	80	35∙10–5		2,3∙10–5
сталь	0,16	80	18∙10–5		1,2∙10–5
скло	0,16	80	14∙10–5		0,8∙10–5

 Розрахунки.

α₁ = ∆ℓ₁ /ℓ₀₁ ∆t₁ =

α₂ = ∆ℓ₂ /ℓ₀₂ ∆t₂ =

α₃ = ∆ℓ₃ /ℓ₀₃ ∆t₃ =

Висновок.

В даній лабораторній роботі я навчився визначати температурний коефіцієнт лінійного розширення алюмінію, сталі та скла. При цьому, отримані мною результати достатньо точно співпадають з табличними значеннями відповідних коефіцієнтів. А це означає, що наша теорія є правильною.

 Контрольні запитання.

1. Що показує температурний коефіцієнт лінійного розширення?
2. Чи залежить температурний коефіцієнт лінійного розширення від довжини тіла?
3. Чи залежить теплова деформація тіла від його довжини?
4. Чи залежить температурний коефіцієнт лінійного розширення від площі поперечного перерізу тіла?
5. Чи залежить температурний коефіцієнт лінійного розширення від матеріалу тіла?
6. Розкажіть про особливості теплового розширення води, і про те, яку роль відіграють ці особливості в природі.

 .

Лабораторна робота № 7.

Тема роботи.  Визначення питомого опору провідника.

Мета роботи.  Дослідним шляхом визначити питомий опір провідника (ніхрому).

Теоретичні відомості.

          Питомий опір провідника – це фізична величина, яка характеризує електропровідні властивості матеріалу провідника і яка чисельно дорівнює тому опору, який має виготовлений із даного матеріалу провідник, за умови, що його довжина 1м, а площа поперечного перерізу 1м (на практиці 1мм)

Позначається: ρ

Визначальне рівняння: ρ = RS/ℓ;

Одиниця вимірювання: [ρ] = Ом∙м

Питомий опір провідника визначається експериментально і записується у відповідну таблицю (дивись табл.15 ст.315). Наприклад для ніхрому ρ=1,05∙10^–6Ом∙м.

Оскільки R = U/I; S = πd²/4 , то визначальне рівняння ρ = RS/ℓ набуває вигляду  ρ = Uπd²/4Iℓ.

де   ℓ – довжина провідника  ( вимірюється)

d – діаметр провідника   (вимірюється)

I – сила струму в провіднику (вимірюється)

U – падіння напруги  (вимірюється)

π=3,14 – постійна величина

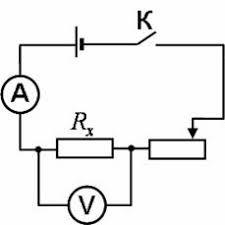
Для визначення опору провідника R=U/I, збираємо електричне коло за схемою:

  реостат

реохорд

.             

Обладнання.

1. Реохорд
2. Джерело струму.
3. Амперметр.
4. Вольтметр
5. Ключ.
6. Штангенциркуль.
7. З’єднувальні дроти.

Результати вимірювань та обчислень.

Таблиця 7.

№   п/п	Діаметр провідн.	Довжина провідн.	Напруга в провідн.	Сила струму в провідн.	Питомий опір провідн.	Табл. значен питом. опору	Відносна похибка досліду
–	d	ℓ	U	I	ρ	ρт	δ
–	м	м	В	А	Ом∙м	Ом∙м	%
1	5∙10–4	0,7	1,45	0,35		110∙10–8
2	5∙10–4	1,0	1,48	0,29		110∙10–8
3	5∙10–4	1,0	2,70	0,52		110∙10–8

Розрахунки.

ρ₁ = U₁πd² / 4I₁ℓ₁ =

ρ₂ = U₂πd² / 4I₂ℓ₂ =

ρ₃ = U₃πd² / 4I₃ℓ₃ =

δ₁ = (ρ_т – ρ₁)100% / ρ_т =

δ₂ = (ρ_т – ρ₂)100% / ρ_т =

δ₃ = (ρ_т – ρ₃)100% / ρ_т =

Висновок.

В даній лабораторній роботі, я навчився визначати питомий опір провідника. При цьому, отримані мною результати достатньо точно співпадають з табличним значенням відповідної величини. а це означає, що наша теорія є правильною.

        Контрольні запитання.

1. Що показує питомий опір провідника?
2. Чи залежить питомий опір провідника від його довжини?
3. Чи залежить опір провідника від його довжини?
4. Чи залежить питомий опір провідника від площі його поперечного перерізу?
5. Чи залежить питомий опір провідника від матеріалу провідника?
6. Чи залежить питомий опір провідника від його температури?
7. Для виготовлення реостатів використовують матеріали з великим чи малим питомим опором?

.

 Лабораторна робота № 8.

 Тема роботи.  Визначення е.р.с., внутрішнього опору та к.к.д. джерела струму.

Мета роботи.  Дослідним шляхом визначити е.р.с., внутрішній опір та к.к.д. джерела струму.

Теоретичні відомості.

          Е.р.с. джерела струму – це фізична величина яка є енергетичною характеристикою джерела струму і яка показує, яку роботу виконують сторонні (не електричні) сили в середині джерела струму, переміщуючи заряд в один кулон від одного полюса джерела до іншого:

Позначається: Ɛ

Визначальне рівняння:  Ɛ = А_ст/q

Одиниця вимірювання: [Ɛ] = Дж/Кл = В

По суті, е.р.с. джерела струму, чисельно дорівнює тій максимальній напрузі, яку здатне створити дане джерело: Ɛ = U_max

Оскільки, згідно з законом Ома для повного електричного кола:

I = Ɛ/(R+r),    то   r = (Ɛ – U)/I.

Оскільки, за визначенням к.к.д.: η = А_кор/А_заг)100%

та враховуючи, що  А_кор = А_ел = Е∙q;  A_заг = А_ст = Ɛ∙q ,

можна записати:    η = (U/Ɛ)100%

Таким чином: е.р.с., внутрішній опір та к.к.д. джерела струму, можна визначити за наступними формулами:  Ɛ= U_max;  r = (Ɛ – U)/I;  η = (U/Ɛ)100%.

Для визначення е.р.с, внутрішнього опору та к.к.д. джерела струму, збираємо електричне коло за схемою:

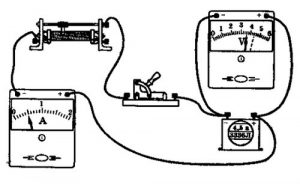
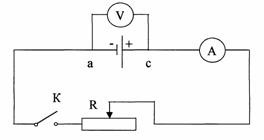
Обладнання.

1. Джерело струму.
2. Вольтметр.
3. Амперметр.
4. Реостат.
5. Ключ.
6. З’єднувальні дроти.

Результати вимірювань та обчислень.

Таблиця 9.

№ п/п	Е.Р.С. джерела струму	Падіння напруги на зовнішній ділянці кола	Сила струму в колі	Внутрішній опір джерела струму	К.к.д. джерела струму
–	Ɛ	U	I	r	η
–	В	В	А	Ом	%
1	1,59	1,44	0,35
2	1,59	1,41	0,33
3

Розрахунки.

r₁ = (Ɛ₁ – U₁) / I₁ =

η₁ = (U₁ /Ɛ₁)100% =

r₂ = (Ɛ₂ – U₂) / I₂ =

η₂ = (U₂ /Ɛ₂)100% =

Висновок.

В даній лабораторній роботі, я навчився визначати е.р.с, внутрішній опір та к.к.д. джерела струму. При цьому, отримані мною результати підтверджують передбачення теорії. А це означає, що наша теорія є правильною.

Контрольні запитання.

1. Що характеризує е.р.с. джерела струму?
2. Чим е.р.с. відрізняється від електричної напруги?
3. Що стверджується в законі Ома для повного електричного кола?
4. Чи можна за допомогою вольтметра безпосередньо виміряти точне значення е.р.с.? Чому?

 .

Лабораторна робота № 9.

Тема роботи.  Розширення вимірювальних меж вольтметра.

Мета роботи.  Навчитися розширювати вимірювальні межі наявного вольтметра.

Теоретичні відомості

Задача. На базі вольтметра розрахованого на вимірювання напруги до U вольт (наприклад до 6В) виготовили і протестували вольтметр розрахований на вимірювання напруги до Uвольт (наприклад до 60В)

 

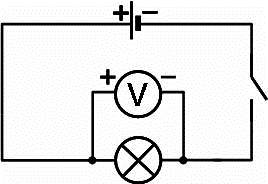
Рішення.  В процесі вимірювання напруги, вольтметр по суті реагує на той струм що по ньому проходить. Максимально допустиме значення цього струму (значення при якому вольтметр показує ту максимальну напругу на яку він розрахований)  визначається за формулою I_v = U_v/R_v,

де    U_v – та максимальна напруга на яку розраховано вольтметр

R_v – електричний опір вольтметра

В нашому випадку: U_v = U₁ = 6B.

Ясно, що в ситуації, коли на даний вольтметр подати напругу не 6В, а 60В, то по ньому пройде в 10 разів більший струм і вольтметр вийде з ладу. Для того, щоб цього не сталося, в коло вольтметра (послідовно з ним) потрібно включити певний додатковий опір (R_д). При цьому, включити таким чином, щоб виконувалось співвідношення  I_v = U₂/(R_v+R_д).

     

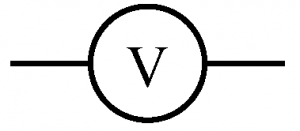
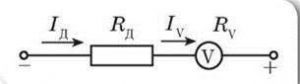
.            I_v = U₁/R_v                                                I_v = U₂/(R_v+R_д).

Величину додаткового опору можна визначити із умови: сила струму в вольтметрі при подачі напруги 6В (в першому випадку) і 60В (в другому випадку), має бути однаковою. А це означає, що має виконуватись співвідношення: U₁/R_v = U₂/(R_v+R_д). Звідси: R_v+R_д = R_v(U₂/U₁). Або

R_д = R_v(U₂/U₁) – R_v = R_v(U₂/U₁ – 1) = R_v(U₂ – U₁)/U₁.

Таким чином, включивши в коло вольтметра додатковий опір, величина якого визначається за формулою R_д = R_v(U₂ – U₁)/U₁, ми отримаємо прилад, який дозволяє вимірювати напругу в межах від 0(В)  до  U₂

 Обладнання.

1. Вольтметр, вимірювальні межі якого потрібно змінити.
2. Омметр.
3. Батарея опорів.
4. Контрольний вольтметр
5. Джерело струму.
6. З’єднувальні дроти.

Результати вимірювань та обчислень.

Таблиця 8.

№ п/п	Фактичний опір вольтметра	Напруга, на яку розраховано вольтметр	Напруга, на яку потрібно розра хувати вольтметр	Величина додаткового опору
–	Rv	U1	U2	Rд
–	Ом	В	В	Ом
1	5500	6	60
2	1000	3	15

Розрахунки.

R_д1 = R_v1 (U₂ – U₁) / U₁ =

R_д2 = R_v2 (U₂ – U₁) / U₁ =

Висновок.

В даній лабораторній роботі я навчився розширювати вимірювальні межі наявного вольтметра. При цьому, я отримав навички застосування теоретичних знань з фізики для вирішення практично важливих задач.

Контрольні запитання.

1. Що можна сказати про величини електричних опорів вольтметра та амперметра? З чим це пов’язано?
2. Чому при розширенні вимірювальних меж вольтметра, додатковий опір включають послідовно з ним, а не паралельно?
3. Як ви думаєте, чи можна амперметр перетворити на вольтметр? Якщо можна, то що для цього потрібно зробити?

.

Лабораторна робота № 10.

Тема роботи.  Визначення електрохімічного еквіваленту речовини.

Мета роботи.  Дослідним шляхом визначити електрохімічний еквівалент міді.

Теоретичні відомості.

          Електрохімічний еквівалент речовини – це фізична величина, яка характеризує електрохімічні властивості речовини і яка показує, скільки даної речовини виділиться на електроді при електролізі, якщо через електроліт пройде заряд в один кулон (тобто виділиться за одну секунду при силі струму в один ампер).

Позначається: k

Визначальне рівняння: k=∆m/It

Одиниця вимірювання: [k]=кг/А∙с

де   m – маса речовини що виділилась на катоді в процесі електролізу

(вимірюється)

І – сила струму в електроліті (вимірюється)

t – час проходження струму (вимірюється)

Електрохімічний еквівалент речовини визначається експериментально і записується у відповідну таблицю (дивись табл.17 ст. 316). Наприклад для міді k=3,3∙10^–7кг/А∙с.

Для визначення електрохімічного еквіваленту речовини збирається електричне коло за схемою:

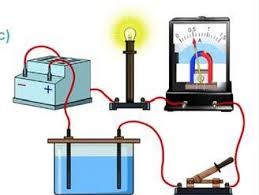
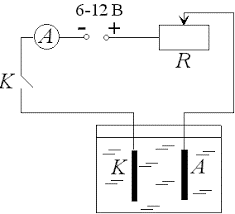
Обладнання.

1. Електроліт (розчин CuSO).
2. Мідні електроди.
3. Джерело постійного струму.
4. Амперметр.
5. Вольтметр.
6. Ключ.
7. Реостат.
8. З’єднувальні дроти.
9. Терези з рівновагами.
10. Секундомір.

Результати вимірювань та обчислень.

Таблиця 10.

Маса тієї міді, що виділилась на катоді	Сила струму в колі	Час проходження струму	Електрохімічний еквівалент міді	Табличне значення електрохім еквіваленту	Відносн похибка досліду
∆m	І	t	k	kт	δ
кг	А	с	кг/А∙с	кг/А∙с	%
1,4·10–3	5	900		3,3∙10–7

Розрахунки.

k = ∆m / It =

δ = (k_т – k)100% / k_т =

Висновок.

В даній лабораторній роботі, я навчився визначати електрохімічний еквівалент речовини (міді). При цьому, отримані мною результати достатньо точно співпадають з табличним значенням відповідного коефіцієнту. А це означає, що наша теорія є правильною.

 Контрольні запитання.

1. Що стверджується в законі Фарадея?
2. Що показує електрохімічний еквівалент речовини?
3. Чи залежить електрохімічний еквівалент речовини від сили струму в електроліті?
4. Чи залежить електрохімічний еквівалент речовини від маси і валентності її іонів?
5. Яка речовина має більший еквівалент, мідь чи срібло? Чому?
6. Які застосування має електроліз в сучасній електротехніці.

 .

Лабораторна робота № 11.

Тема роботи.  Дослідження електропровідних властивостей напівпровідникового діода.

Мета роботи. Дослідити електропровідні властивості напівпровідникового діода. Побудувати його воль-амперну характеристику.

Теоретичні відомості

Напівпровідниковий діод, це прилад з одним p-n переходом, який забезпечує односторонню електропровідність. Основною властивістю діода є здатність проводити струм в одному напрямку і не проводити в протилежному. Характер цієї односторонньої провідності можна представити у вигляді наступної вольт-амперної характеристики

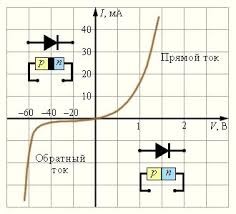
Для дослідження електропровідних властивостей діода, збираємо електричне коло за схемою:

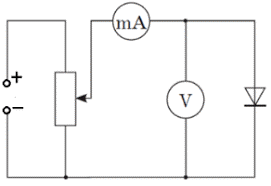
Обладнання.                                                             

1. Напівпровідниковий діод.
2. Джерело постійного струму.
3. Міліамперметр.
4. Вольтметр.
5. Реостат.
6. Ключ.
7. З’єднувальні дроти.

Результати вимірювань та обчислень.

Таблиця 11.

№ п/п	Включення	Напруга на діоді,  U	Сила струму в діоді,  І
	-.. . . П р я м е . . . . З в о р о т н е	В	мА
1		0,0	0,00
2		0,2	0,01
3		0,4	0,05
4		0,6	0,40
5		0,8	0,85
6		1,0	1,40
7		1,2	2,50
1		5	0,00
2		10	0,00
3		15	0,00
4		20	0,00

         За результатами вимірювань, будуємо відповідну вольт-амперну характеристику діода.

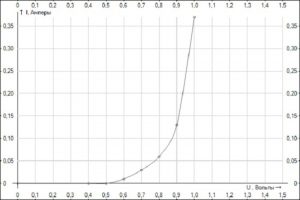
Висновок.

В даній лабораторній роботі я дослідив електропровідні властивості напівпровідникового діода та навчився будувати відповідну вольт-амперну характеристику. При цьому, я з’ясував, що отримані мною результати підтверджують передбачення теорії. А це означає, що наша теорія є правильною.

 Контрольні запитання.

1. Які матеріали називаються напівпровідниками?
2. Чому, в процесі нагрівання електричний опір напівпровідників не збільшується, як в металах, а зменшується?
3. Які частинки є носіями струму в напівпровідниках? Що представляють собою ці частинки ?
4. Що означає: даний напівпровідник має електропровідність n-типу?… електропровідність р-типу?
5. Відомо, що домішки погіршують електропровідність металів. А як впливають домішки на електропровідність напівпровідників ?

 .

Лабораторна робота №12.

Тема роботи. Визначення коефіцієнту трансформації та к.к.д. трансформатора.

Мета роботи. Дослідним шляхом визначити коефіцієнт трансформації та к.к.д. трансформатора.

 Теоретичні відомості.

Трансформатор, це прилад, який трансформує (змінює) напругу в колі змінного струму. До числа основних характеристик трансформатора відносяться: коефіцієнт трансформації (k), та коефіцієнт корисної дії (к.к.д.) трансформатора (η).

 Коефіцієнт трансформації – це фізична величина, яка чисельно дорівнює відношенню вихідної напруги трансформатора (U₂) до його вхідної напруги (U₁) виміряних в режимі холостого ходу трансформатора k = U₂/U₁.

Коефіцієнт корисної дії (к.к.д.) – це фізична величина, яка характеризує ефективність використання енергії в тому чи іншому приладі і яка визначається за формулою η = (А_кор/А_затр)100%

Не важко збагнути, що в трансформаторі корисною є та робота, яка виконується в колі вихідної (вторинної) обмотки (А_кор=А₂=U₂I₂t₂), а затраченою – та робота яка виконується в колі вхідної (первинної) обмотки (А_затр=А₁=U₁I₁t₁). Зважаючи на це, та враховуючи той факт, що час роботи вихідної та вхідної обмоток є однаковим (t₂=t₁), можна записати η=(U₂I₂/U₁I₁)100%.

Для визначення потрібних величин, збираємо електричне коло за схемою:

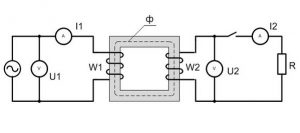
Обладнання.

1. Трансформатор.
2. Джерело змінного струму.
3. Амперметри (2 шт).
4. Вольтметри (2 шт) .
5. Реостати.
6. Ключ.
7. З’єднувальні дроти.

Результати вимірювань та обчислень.

Таблиця 12.

Режим роботи	Вхідна напруга	Вихідна напруга	Вхідний струм	Вихідний струм	Коефіц. тр – ції	К.к.д. тр – ра
–	U1	U2	I1	I2	k	η
не робочий	40	4	0,0	–		–
робочий	40	3,8	0,2	2,0	–

Розрахунки.

k = U₂/U₁ =

η=(U₂I₂/U₁I₁)100% =

Висновок.

 

Контрольні запитання.

1. Сформулюйте закон електромагнітної індукції.
2. Яке відношення має трансформатор до закону електромагнітної індукції?
3. Поясніть будову та принцип дії трансформатора.
4. Який трансформатор називають підвищувальним, а який понижуючим?
5. Чому в підвищувальному трансформаторі товщина дроту у вторинній обмотці менша аніж в первинній?
6. Чому сердечник (магнітопровід) трансформатора виготовляють пластинчатим, а не суцільним?

 .

Лабораторна робота № 13.

Тема роботи.  Визначення довжини світлової хвилі.

Мета роботи.  Дослідним шляхом визначити довжину світлової хвилі червоного та фіолетового випромінювання.

 Теоретичні відомості

         Видиме світло – це потік електромагнітних хвиль, довжини яких знаходяться в межах від 3,8∙10^–7м до 7,6∙10^–7м. Результатом інтерференції когерентних (узгоджених) світлових хвиль (джерелом таких хвиль є дифракційна решітка) є спектральна інтерференційна картинка , аналіз якої дозволяє визначити довжину світлової хвилі. Дійсно, розглянемо ті процеси які відбуваються в системі світло – дифракційна решітка – екран.

 

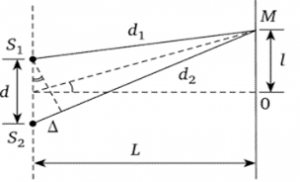
Із аналізу малюнку ясно, що ті світлові хвилі які виходять з точок S₁ і S₂, в точці M підсиляться тоді і тільки тоді, якщо на відрізку Δ = |S₂M| – |S₁M| поміститься ціле число довжин хвиль λ. Іншими словами, умову підсилення хвиль в точці А можна записати у вигляді Δ = n∙λ, де  n = 1; 2; 3; … n – ціле число. А це означає, що довжину максимально підсиленої в точці P світлової хвилі, можна визначити за формулою λ = Δ/n.

Із аналізу прямокутного трикутника S₁S₂S₂* випливає, що Δ = d∙sinφ, де φ – кут при вершині S₁. З іншого боку, із аналізу взаємоповязаних трикутників S₁S₂S₂* та MSO ясно, що кути φ та φʹ, де φ’ – кут при вершині S, є чисельно рівними (φ = φʹ). При цьому, виходячи з того, що величина кута φʹ є малою (а за умови L>>ℓ, цей кут дійсно малий φʹ ˂ 10º), можна стверджувати:  sinφ = sinφʹ ≈ tgφʹ = ℓ/L,  де ℓ – відстань від точки О до точки M; L – відстань від дифракційних граток до екрану. Зважаючи на вище сказане можна записати: λ = Δ/n = d∙sinφ/n = d∙sinφʹ/n ≈ d∙tgφʹ/n = d∙ℓ/L∙n.

Таким чином, довжину підсиленої в точці M світлової хвилі, можна визначити за формулою λ = d·ℓ/L·n,  де

d = 0,01 мм = 1∙10^–5м – шаг дифракційної решітки

L – відстань від дифракційної решітки до екрану (вимірюється)

ℓ – відстань від нулевої лінії екрану до лінії відповідного кольору спектру (вимірюється)

n – порядковий номер спектральної картинки (для першого спектру n = 1)

Обладнання.

1. Прилад для визначення довжини світлової хвилі.
2. Дифракційна решітка.
3. Джерело світла.

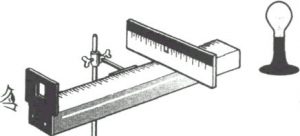
Результати вимірювань та обчислень.

Таблиця 13.

№ п/п	Шаг дифракц. гратки	Відстань до екрану	Відстань від нулевої .        лінії до		Довжина хвилі
			фіолетової	червоної	фіолетової	червоної
–	d	L	ℓф	ℓч	λф	λч
–	м	м	м	м	м	м
1	1∙10–5	0,3	1,2∙10–2	2,2∙10–2
2	1∙10–5	0,4	1,6∙10–2	3,0∙10–2

Розрахунки.

λ_ф1 = d∙ℓ_ф1 / L₁ = 1∙10^–5(м)∙ 1,2∙10^–2(м) /0,3(м) = (1,2/0,3)∙10^–7(м) = 4,0∙10^–7(м);

λ_ч1 = d∙ℓ_ч1 / L₁ =

λ_ф2 = d∙ℓ_ф2 / L₂ =

λ_ч2 = d∙ℓ_ч2 / L₂ =

          Висновок.

В даній лабораторній роботі, я навчився визначати довжину світлової хвилі червоного та фіолетового випромінювання. При цьому, отримані мною результати достатньо точно співпадають з табличними значеннями відповідних довжин. А це означає, що наша теорія є правильною.

 Контрольні запитання.

1. В чому суть інтерференції світла?
2. Які хвилі називаються когерентними?
3. При якій умові, результатом інтерференції світлових хвиль є стійка інтерференційна картинка? Назвіть приклади реалізації цієї умови.
4. Чи залежить довжина світлової хвилі від відстані між дифракційною решіткою і екраном?
5. Чому дифракційний спектр починається фіолетовим і закінчується червоним кольором?

   .       

Лабораторна робота № 14.

Тема роботи.  Спостереження та аналіз світлових спектрів.

Мета роботи.  За допомогою спектроскопа, провести спостереження суцільного та лінійчастого спектрів випромінювання, а також спектрів поглинання кольорових скелець. Отримані результати проаналізувати та замалювати.

Теоретичні відомості

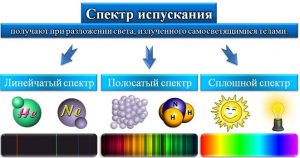
          Видиме світло – це потік електромагнітних хвиль, довжини яких знаходяться в межах від 3,8∙10^–7м до 7,6∙10^–7м. Результатом розкладання світла на його складові частини є кольорова картинка, яка називається спектром випрмін6ювання. Спектри бувають суцільними, лінійчастими та смугастими. Крім цього вони поділяються на спектри випромінювання та спектри поглинання.

Суцільний спектр, представляє собою суцільну кольорову картинку в якій містяться всі кольори видимого світла, а отже всі електромагнітні хвилі, довжини яких знаходяться в межах від 3,8∙10^–7м до 7,6∙10^–7м. Суцільний спектр є результатом інтенсивного теплового (хаотичного) руху частинок речовини. Такі спектри дають всі розжарені тверді та рідкі тіла, а також гази високої густини, наприклад зірки (Сонце).

Лінійчастий спектр, представляє собою певний набір тонких спектральних ліній. Лінійчастий спектр є результатом тих упорядкованих процесів, що відбуваються в енергетично збуджених атомах речовини. Тому кожна різновидність атомів дає свій неповторний лінійчастий спектр. Такі спектри дають нагріті розріджені гази атомарного складу.

Смугастий спектр це складна різновидність лінійчастого спектру. Смугастий спектр є результатом тих упорядкованих процесів, що відбуваються в енергетично збуджених молекулах речовини. При цьому кожна різновидність молекул, дає свій неповторний смугастий (складний лінійчастий) спектр.

Обладнання.

1. Спектроскоп прямого зору.
2. Джерело струму.
3. Денне сонячне світло.
4. Лампочка розжарювання.
5. Набір кольорових скелець.
6. Набір спектральних трубок.
7. Прилад для запалювання спектральних трубок.
8. Лампа денного світла
9. Набір кольорових олівців.

Результати вимірювань та обчислень.

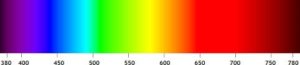
1. Суцільний спектр денного світла.

.    

2. Спектри поглинання кольорових скелець.

3. Лінійчасті спектри випромінювання розріджених газів.

Висновок.

В даній лабораторній роботі я, за допомогою спектроскопа прямого зору провів спостереження за суцільними та лінійчастими спектрами випромінювання, а також спектрами поглинання кольорових скелець. При цьому, отримані мною результати підтверджують передбачення теорії. А це означає, що наша теорія є правильною.

Контрольні запитання.

1. Які об’єкти дають суцільні спектри випромінювання і чим обумовлена поява таких спектрів?
2. Які об’єкти дають лінійчасті спектри випромінювання і чим обумовлена поява цих спектрів?
3. Чому лінійчаті спектри різних речовин – різні?
4. Чому хімічний елемент «гелій» має таку назву?
5. Що називають спектральним аналізом?
6. Які переваги має спектральний аналіз у порівнянні з хімічним аналізом?
7. Як ви думаєте, спектральний аналіз складних речовин проводять на основі аналізу їх спектрів випромінювання, чи спектрів поглинання? Чому?