
Розділ 1. Загальні основи ньютонівської механіки.
§7. Введеня в механіку.
§8. Основи математичної грамотності.
Тема 1.1. Основи кінематики поступального руху.
§9. Загальні відомості про механіку. Механічний рух.
§10. Відносність руху. Система відліку.
§11. Просторово-часові параметри поступального руху.
§12. Швидкість поступального руху. Середня швидкість.
§13. Загальні відомості про прискорення.
§14. Рівняння руху – основний закон кінематики.
§15. Розв’язування задач. Тема: Практичне застосування рівняння руху.
§16. Вільне падіння тіл. Прискорення вільного падіння.
§17. Розв’язування задач. Тема: Вільне падіння тіл.
§18. Рух матеріальної точки по колу. Доцентрове прискорення.
§19. Прості коливальні системи. Фізичний та пружинний маятники.
§20. Кінематика. Узагальнююче повторення.
.
Розділ 1. Загальні основи ньютонівської механіки.
§7. Введення в механіку.
Знати фізику визначальним чином означає, знати і розуміти мову цієї науки. Тобто знати і розуміти фізичну суть тих термінів (понять, об’єктів, явищ, величин, законів, приладів, тощо) які складають теоретично – термінологічну основу фізики. І це закономірно. Адже, якщо ви не знаєте фізичної суті того, що називається Природою, матерією, полем, швидкістю, силою, масою, густиною, температурою, термоелектронною емісією, законом електромагнітної індукції, принципом відносності, ідеальним газом, матеріальною точкою, напруженістю електричного поля, гравітаційною сталою, силою Ампера, законом Ампера, амперметром, ампером, та сотень інших фізичних термінів – то ви не знаєте і не можете знати фізики. Власне тому, вивченню термінологічних основ фізики ми приділяємо і будемо приділяти величезну увагу.
Однак якщо, навіть найдовершеніші теоретичні знання ви не вмієте застосовувати на практиці, то гріш ціна цим знанням. В фізиці ж, вміти застосовувати знання на практиці по суті означає, вміти розв’язувати задачі. А варто зауважити, що навчитися цьому вмінню, це те найскладніше що є у фізиці.
Малоприємна особливість фізики полягає в тому, що її вивчення починається і має починатися з того складного розділу, який називається «механіка». Складність же механіки в тому, що саме в механіці учні вчаться розв’язувати задачі. Задачі ж фізики суттєво відрізняються від тих задач, з якими ви маєте справу, наприклад в математиці.
Скажімо, коли в математиці вам говорять, що рівняння виду ах2 + bx + c = 0 називається квадратним рівнянням, і що в загальному випадку воно має два рішення: x1,2 = [–b ± √(b2 – 4ac)]/2a, то вчителю достатньо розв’язати два, три подібних рівнянь, щоб в подальшому ви могли самостійно розв’язати будь-яку їх кількість.
З задачами фізики ситуація інакша. Наприклад, ви розв’язуєте задачі на визначення середньої швидкості, тобто на застосування формули v = s/t. Не важко бачити, що ця формула надзвичайно проста. У всякому разі, значно простіша за x1,2 = [–b ± √(b2 – 4ac)]/2a. Та от парадокс. Ви скільки завгодно можете знати цю формулу і не вміти розв’язувати задачі на визначення середньої швидкості.
Навіть після того, як вчитель розв’яже вам п’ять, десять ба навіть сто подібних задач, нема гарантії того, що задана вам сто перша задача буде розв’язана. І справа не в тому що ви забули формулу v = s/t. Справа в іншому: в фізиці, головне не формули, а вміння логічно мислити. Ви можете скільки завгодно «зазубрювати» правильні формули і навіть зазубрити їх, але якщо за цими формулами ви не будете бачити реальних об’єктів і подій, то всі ваші зусилля будуть марними – ви не будете знати, розуміти і любити фізику.
Якщо ж ви дійсно хочете навчитися розв’язувати задачі фізики, а по суті навчитися логічно мислити, то маєте усвідомити: це не можливо зробити просто спостерігаючи за тим як розв’язує задачі вчитель. Скажімо, ви хочете навчитися грати в хокей. Для цього наймаєте тренера і він пояснює вам всі нюанси цієї гри. Пояснює день, два,…., місяць,….рік. Ви схвально киваєте головою і вам все зрозуміло. Але якщо ви думаєте, що через рік такого навчання, станете класним хокеїстом, то неминуче помиляєтеся.
Бо навчитися грати в хокей, просто спостерігаючи за тим як це роблять інші – неможливо. Для того, щоб стати хокеїстом, потрібно взувати ковзани, брати в руки ключку, виходити на лід і …. падати…, вставати…, знову падати і знову вставати, тобто вчитися грати в хокей. І якщо поруч буде фаховий тренер, то процес навчання буде успішним та ефективним.
Вчитель, це той же тренер. Без його допомоги навчитися розв’язувати задачі надзвичайно складно, але можливо. А от що дійсно неможливо, так це навчитися розв’язувати задачі не розв’язуючи їх самостійно. І якщо на шляху опанування мистецтвом розв’язування задач, вас будуть переслідувати труднощі і помилки, знайте, ще нікому не вдавалося пройти цей шлях без труднощів і помилок. Але якщо ви будете наполегливими і кмітливими, то вас неминуче очікує успіх. І ви не лише будете знати фізику, а й безумовно полюбите цю найвеличнішу і найпрекраснішу з наук.
Ситуація з задачами фізики кратно ускладнюється тим ганебним фактом, що той навчальний предмет, вивчення якого починається ще у дитячому садочку і який називається «арифметика-математика», на момент початку вивчення «фізики» не забезпечує учня належним рівнем математичних знань та вмінь. І мова ж йде не про якісь складні математичні витребеньки, а про елементарні математичні дії над числами представленими в стандартному вигляді, та про елементарні математичні трансформації формул на кшталт: якщо а/х = b, то х = a/b; якщо a – x = b, то x = a – b; якщо ах2 = b, то х = √(b/a).
А фізика влаштована таким чином, що в ній рішення будь якої найелементарніших задач передбачає вміння трансформувати формули. Скажімо, якщо v = s/t, то s = v∙t, a t = s/v. Бо в фізиці учень постійно має справу як з надзвичайно великими так і надзвичайно малими числами. При цьому учень повинен вміти записувати ці надвеликі і надмалі числа в зручному вигляді, та вміти виконувати над ними базові математичні дії: додавання, віднімання, множення, ділення, піднесення в степінь, визначення кореня квадратного, тощо.
Наприклад маса Землі 5 980 000 000 000 000 000 000 000 кг, а маса атома водню (гідрогену) 0,000 000 000 000 000 000 000 000 00166 кг. Ясно, що в подібних ситуаціях записувати відповідні числа в звичному для нас вигляді не зручно. А ще більше незручно, виконувати математичні дії над ними. Тому в фізиці та науці загалом, великі і малі числа зазвичай записують у так званому стандартному вигляді, тобто у вигляді певного малого числа помноженого на 10 у відповідній степені. Наприклад:
5 980 000 000 000 000 000 000 000 кг = 5,98·1024кг;
0,000 000 000 000 000 000 000 000 001 66 кг = 1,66·10–27кг.
На жаль, в системі вітчизняної освіти, математику вивчають за ради математики. І це при тому, що математика, а особливо математика шкільна, то лише той інструмент який потрібно надати учню для успішного вивчення тієї ж фізики, хімії, інформатики чи скажімо технічної механіки. І цей інструмент треба надати не коли попало, а коли треба.
Прямим же наслідком такого ганебного стану речей є факт того, що вчитель фізики, окрім самої фізики, має пояснювати учням, що 5∙105 = 500000, а 5∙10–5 = 0,00005. Що 5∙105∙5∙10–5 = 25∙100 = 25, і що 100 = 1. Пояснювати, що якщо а – x = b, то х = а – b; якщо a∙x = b, то x = b/a; якщо b = a/x, то x = a/b. При цьому як не старайся, як не викручуйся, а реалії життя такі, що не можна за один урок навчити тому, чого математика не навчила за десять років. Не можна не тому, що мова йде про щось складне, а тому, що подібне навчання потребує часу і практики.
Та як би там не було, а за наявності бажання і певних зусиль, кожен з вас цілком спроможний опанувати тим мінімально необхідним рівнем математичних знань, інформація про який надана в наступному параграфі. Цей параграф називається «Основи математичної грамотності», хоча чесно кажучи, його варто було б назвати «Математичний лікбез», що в буквальному перекладі означає «ліквідація математичної безграмотності».
Тепер коли ви знаєте про ті труднощі з якими неминуче стикнетеся в процесі вивчення фізики, прийшов час почати системне вивчення цієї самої фізики. А це вивчення починається з розділу, який називається «Механіка», а точніше – ньютонівська механіка.
Механіка (ньютонівська механіка) – це розділ фізики, в якому вивчають параметри, закономірності та причини механічного руху тіл в усіх його проявах, за умови, що швидкість цього руху значно менша за швидкість світла у вакуумі (300 000 км/с). Іншими словами, механіка – це наука про механічний рух.
Коли ми говоримо про механічний рух, то маємо на увазі такий процес (рух) при якому тіло, як єдине ціле, або певні цілісні фрагменти цього тіла, переміщуються відносно інших тіл. Човен пливе, автомобіль іде, вода тече, Земля обертається, колесо крутиться, газ розширюється, яблуко падає, собака біжить, дерево хитається, м’яч стрибає, стержень деформується – все це конкретні приклади механічного руху тих чи інших фізичних об’єктів (тіл). При цьому, однією з різновидностей механічного руху є такий рух, швидкість якого дорівнює нулю (v=0). Цю різновидність руху називають механічним спокоєм.
Крім цього, різновидністю механічного руху тіла є його механічна деформація, тобто та чи інша зміна форми (розмірів) тіла, що відбувається під дією певної деформуючої сили. А це означає, що в механіці вивчають не лише параметри, закономірності та причини власне самого механічного руху (спокою) тіла, а й параметри, закономірності та причини всіх видів його механічної деформації.
Теоретичною основою механіки є принцип відносності, три закони Ньютона та закон всесвітнього тяжіння. Це означає, що на базі цих законів, можна кількісно пояснити практично все різноманіття механічних явищ. Однак це зовсім не означає, що в механіці не діють і не мають широкого застосування інші закони. Просто ці закони, так чи інакше випливають із законів Ньютона та визначальних рівнянь відповідних фізичних величин.
Більше того, саме ці похідні закони, як то рівняння руху, умова механічної та динамічної рівноваги тіла, закон збереження механічної енергії, є тими базовими законами на основі яких ми в реальності і будемо пояснювати різноманіття механічних явищ. Стосовно ж законів Ньютона, то вони будуть сформульовані на завершальному етапі вивчення механіки.
Технологія вивчення механіки підпорядкована принципу «від простого до складного». Суть цього принципу полягає в тому, що складні процеси (явища) розкладаються на гранично прості складові. Ці прості складові досліджуються, вивчаються та пояснюються, а потім, на основі отриманих знань, пояснюється все різноманіття більш складних процесів.
Наприклад в механіці все різноманіття механічних рухів можна представити як певну комбінацію двох простих різновидностей: рух поступальний та рух обертальний. При цьому в механіці окремо вивчають параметри, закономірності та причини спочатку поступального руху, а потім – руху обертального. А знаючи параметри, закономірності та причини цих базових рухів, пояснюється все різноманіття комбінованих рухів.
І потрібно зауважити, що у відповідності з навчальною програмою для сьомого класу, ми по суті будемо вивчали основи механіки матеріальної точки, тобто тієї частини механіки, яка вивчає параметри, закономірності та причини поступального руху тіла.
На завершення додамо, що намагаючись певним чином систематизувати процес вивчення механіки, ми умовно розділимо її на чотири базових теми:
- Кінематика
- Статика
- Динаміка
- Механіка рідин та газів.
Контрольні запитання.
- Як ви розумієте твердження: знати фізику означає, знати мову цієї науки?
- Як ви розумієте твердження: знати фізику означає, вміти застосовувати отримані знання на практиці?
- В чому складність задач фізики?
- Що треба робити, щоб навчитися розв’язувати задачі фізики?
- Чи вмієте ви представляти числа в стандартному вигляді та виконувати математичні дії над ними?
- Чи маєте ви навички трансформації математичних формул?
- Що означає твердження: механіка – це наука про механічний рух?
- Чи є механічний спокій тіла (=0), його механічним рухом?
- Чи є деформація тіла, механічним рухом цього тіла?
- Що є теоретичною основою механіки?
- Що означає твердження: технологія вивчення механіки підпорядкована принципу «від простого до складного».
.
§8. Основи математичної грамотності.
Практика показує, що учні 7-х, 8-х класів мають дуже поверхові уявлення про представлення чисел в стандартному вигляді, та математичні дії над ними. Ще більш сумна історія з навичками трансформації математичних формул. А розв’язування навіть найпростіших задач фізики передбачає вміння певним чиним трансформувати (змінювати, перетворювати) загально відомі формули. Наприклад, якщо у відповідності з визначальним рівнянням густини ρ = m/V, то m = ρ∙V, a V = m/ρ. Якщо рівняння пройденого шляху s = at2/2, то a = 2s/t2, a t = √(2s/a). Якщо площа круга S = π∙R2, то R = √(S/π).
Зважаючи на ці малоприємні факти, ми просто змушені розглянути дану, по суті математичну, тему. Тему, яку варто було б назвати «Математичний лікбез», що в буквальному перекладі означає «ліквідація математичної безграмотності».
Звісно, одним параграфом та йому відповідною навчальною годиною не можливо замінити те, для повноцінного вивчення чого потрібно що найменше в десять разів більше часу. Втім, будемо виходити з того, що певний рівень математичних знань ви все ж маєте. І цей рівень безумовно дозволить вам, на основі конкретних прикладів, отримати ту мінімально необхідну кількість математичних знань, яка дозволить розв’язувати прості задачі фізики.
Однак ви маєте пам’ятати, що навчитися розв’язувати задачі, а в даному випадку математичні приклади, можливо лише в тому випадку, якщо ці задачі розв’язувати самостійно. А це означає, що на основі тих прикладів які наведені в даному параграфі, ви маєте самостійно розв’язати не меншу кількість аналогічних, бажано вами придуманих прикладів.
.
- Математичні трансформації (перетворення) формул.
В фізиці надзвичайно важливим вмінням, є вміння математично трансформувати (змінювати) задану формулу, а по суті, за заданою формулою визначати невідому величину. Загальне правило подібних трансформацій дуже просте: при перенесенні будь якої величини через знак дорівнює, пов’язана з цією величиною математична дія змінюється на протилежну: додавання змінюється на віднімання, віднімання змінюється на додавання, множення змінюється на ділення, а ділення змінюється на множення. При цьому відповідні величини переносять таким чином, щоб невідома величина (х) мала знак «+» і знаходилася в чисельнику.
Застосовуючи вище сформульоване правило, розглянемо низку конкретних ситуацій. А достовірність отриманого результату перевіримо на конкретних прикладах.
Загальні зауваження. Прагнучи максимально візуалізувати процес трансформації формули, цей процес на перших етапах бажано супроводжувати графічними ілюстраціями: та величина яка переноситься через знак « = », обводиться в кружечок і стрілкою вказується напрямок перенесення.
Зверніть увагу і на те, що в ситуаціях коли невідома величина має знак мінус (–х), або знаходиться в знаменнику (1/х), то трансформація формули здійснюється таким чином, щоб невідома величина була зі знаком плюс і в чисельнику.
Задача. За заданою формулою визначити невідому величину (х).
якщо х + а = b то x = b – a, дійсно, якщо х + 3 = 8, то x = 8 – 3 = 5;
якщо х – а = b то x = b + a, дійсно, якщо х – 3 = 8, то x = 8 + 3 = 11;
якщо а – х = b то x = a – b, дійсно, якщо 10 – х = 4, то x = 10 – 4 = 6;
якщо a = b – x то x = b – a, дійсно, якщо 5 = 20 – x, то x = 20 – 5 = 15;
якщо a·x = b то x = b/a, дійсно, якщо 5·x = 10, то x = 10/5 = 2;
якщо a/x = b то x = а/b, дійсно, якщо 20/x = 5, то x = 20/5 = 4;
якщо а = b/x то x = b/a, дійсно, якщо 5 = 10/x, то x = 10/5 = 2;
якщо ax/b = с то x = bc/a, дійсно, якщо 2·x/3 = 6, то x = 6·3/2 = 9;
якщо a/bx = с то x = a/bc, дійсно, якщо 6/3x = 2, то x = 6/3·2 =1;
якщо (a + x)/b = c, то 1) a+x = cb, 2) x = cb – a;
якщо a/(b – x) = c, то 1) b – x = a/c, 2) x = b – a/c;
якщо I = U/R, то U = I·R, R = U/I;
якщо v = s/t, то s =v·t, t = s/v;
якщо F = m∙a, m = F/a, a = F/m;
якщо x = x0 + vt, то vt = x – x0, звідси v = (x – x0)/t;
якщо s = at2/2, то a = 2s/t2,
якщо s = at2/2, то t2 = 2s/a, звідси t = √(2s/a);
якщо Q = I2Rt, то R = Q/I2t;
якщо Q = I2Rt, то I2 = Q/Rt, звідси I = √(Q/Rt).
.
- Представлення чисел в стандартному вигляді.
Оскільки: 103 = 10·10·10 = 1000; 105 = 10·10·10·10·10 = 100000 і т.д, то
4·105 = 400 000;
4,5·105 = 450 000;
28·104 = 280 000;
2,8·104 = 28 000.
І навпаки:
3 800 000 = 38·105 = 3,8·106;
125 000 000 = 125·106 = 12,5·107 = 1,25·108.
.
Оскільки: 10–3 = 1/103 = 0,001; 10–5 = 1/105 = 0,00001, то
4·10–3 = 0,004;
5·10–5 = 0,00005;
3,5·10–7 = 0,00000035.
І навпаки:
0,0002 = 2·10–4;
0,0000075 = 7,5·10–6 = 75·10–7;
0,000125 = 1,25·10–4 = 12,5·10–5 = 125·10–6.
.
- Математичні дії над числами представленими в стандартному вигляді.
Оскільки: 105·103 = (10·10·10·10·10)·(10·10·10) = 105+3 = 108,
105·10–3 = (10·10·10·10·10) / (10·10·10) = 105 –3 = 10–2,
то в загальному випадку 10х·10у = 10х+у. Наприклад:
2·104·4·106 = 2·4·104+6 = 8·1010;
5·106·3·103 = 5·3·106+3 = 15·109;
7·108·5·10–4 = 7·5·108–4 = 35·104;
4,4·10–5·2·10–3 = 4,4·2·10–5–3 = 8,8·10–8.
.
Оскільки: 1/103 = 1/1000 = 1·10–3; 1/10–3 = 1/0,001 =1·103, то в загальному випадку 1/10у = 10–у, 1/10–у = 10у (при перенесення степеню числа з чисельника до знаменники чи навпаки, знак степеню змінюється на протилежний). Наприклад:
2/10–5 = 2∙105 = 200000;
2/105 = 2∙10–5 = 0,00002;
2∙10– 5 = 2/105 = 0,00002.
.
В загальному випадку 10х/10у = 10х–у. Наприклад:
8·106/4·104 = (8/4)106–4 = 2·102;
12·105/3·10–4 = (12/3)105+4 = 4·109;
5·10–4/2·108 = (5/2)10–4–8 = 2,5·10–12;
15·103/3·108 = (15/3)103–8 = 5·10–5.
.
Оскільки (103)4 = (10·10·10)∙(10·10·10)∙(10·10·10)∙(10·10·10) = 103·4 = 1012, то в загальному випадку (10х)у = 10х·у. Наприклад:
(5·103)2 = 52·103·2 = 25·106;
(2·105)4 = 24·105·4 = 16·1020;
(4·10–3)2 = 42·10–3·2 = 16·10–6;
(3·10–4)3 = 33·10–4·3 = 27·10–12.
.
- Математичні дії над числами представленими у змішаному вигляді.
В науковій практиці загалом і в фізиці зокрема, виконуючи математичні дії над числами записаними в нестандартному або змішаному вигляді, ці числа спочатку представляють в стандартному вигляді, а вже потім виконують відповідні математичні дії. Наприклад:
500 000 · 0,003 = 5·105·3·10–3 = (5·3)·105–3 = 15·102;
0,00025·2·104 = 2,5·10–4·2·104 = (2,5·2)·10–4+4 = 5·100 = 5 (нагадаємо, будь яке число в нульовій степені дорівнює одиниці: 100 = 1);
12·104/0,0003 = 12·104/3·10–4 = (12/3)104+4 = 4·108;
0,00048/2·103 = 48·10–5/2·103 = (48/2)10–5–3 = 24·10–8.
.
- Визначення квадратного кореня числа.
Квадратним коренем числа а (позначається √а) називають таке число х, квадрат якого дорівнює числу а. Іншими словами: якщо х2 = а, то √а = х. Наприклад:
√4 = 2, бо 22 = 4;
√9 = 3, бо 33 = 9;
√16 = 4, бо 42 = 16;
√25 = 5, бо 52 = 25;
√100 = 10, бо 102 = 100;
√2 ≈ 1,41, бо 1,412 ≈ 2.
.
Можна довести: якщо мова йде про числа вигляду 10n, то √10n = 10n/2.
Наприклад: √104 = 104/2 = 102; √108 = 108/2 = 104; √10–6 = 10–6/2 = 10–3.
Можна довести, що √(а·b) = √а·√b. Наприклад:
√(25·106) = √25√106 = 5·103;
√(49·108) = √49√108 = 7·104;
√(16·10–4) = √16√10–4 = 4·10–2;
√(2,5·105) = √(25·104) = √25√104 = 5·102;
√(0,09·108) = √(9·106) = √9√106 = 3·103;
√(4,9·10–3) = √(49·10–4) = √49√10–4 = 7·10–2.
Задача. Маса однієї молекули води 3·10–20кг. Визначте масу 400 млн. молекул води.
Дано:
m1 = 3·10–20кг
N = 400 000 000 = 4∙108
m = ?
Рішення. Ясно, якщо маса однієї молекули m1, то загальна маса N таких молекул становитиме m = N∙m1.
Розрахунки: m = N∙m1 = 3·10–20кг∙4∙108 = (3∙4)∙10–20+8 = 12∙10–12кг.
Відповідь: m = 12∙10–12кг.
Вправа №8.
- За заданою формулою визначити невідому величину:
якщо V = S∙h, то h =
якщо a = F/m, то F =
якщо s = at2/2, то a =
якщо R = ρℓ/S, то S =
якщо R = ρℓ/S, то ℓ =
якщо Q = I2Rt, то R =
якщо S = πR2, то R =
якщо x = x0 – vt, то v =
якщо a = (v – v0)/t, то v =
- Задані числа представити в стандартному вигляді: 800000; 540000; 2540000; 0,000004; 0,00075; 0,00000128.
- Виконати математичні обчислення: 3·104·4·103; 6·10-5·3·104; 8·108·0,5·10–3; 2,8·10–4·2·10–3.
- Виконати математичні обчислення: 9·108/3·104; 45·10–3/5·105; 18·10–4/3·10–8; 3·106/2·10–4.
- Виконати математичні обчислення: (4·103)2; (2·10–4)4; (3·10–5)3; (8·106)2.
- Виконати математичні обчислення: 400000·3·105; 0,000025·2·10–5; 18·106/0,0006.
- Визначити корінь квадратний: √49; √81; √106; √(36·104); √(9·104); √(4·10– 4).
- Маса однієї бактерії 5·10–12кг. Визначте масу 400 млн. бактерій.
- Маса однієї кімнатної мухи 0,15г. Визначте масу 400 млн. мух.
.
Тема 1.1. Основи кінематики поступального руху.
§9. Загальні відомості про кінематику та механічний рух.
Кінематика (від грецького «kinematos» – рух) – це розділ механіки, в якому вивчають параметри та закономірності механічного руху тіл, без врахування їх мас та діючих на них сил. Іншими словами, в кінематиці вивчають параметри та закономірності механічного руху і не вивчають причини цього руху, а також не враховують фізичні властивості рухомого тіла.
До числа основних понять кінематики, тобто тих загальних термінів суть яких потрібно знати, відносяться: механічний рух, поступальний рух, обертальний рух, матеріальна точка, відносність руху, система відліку, траєкторія.
Механічний рух – це такий рух (процес), при якому тіло як єдине ціле, або певні цілісні фрагменти цього тіла, переміщується відносно інших тіл. Одним з часткових випадків механічного руху є такий рух, швидкість якого дорівнює нулю (v=0). Цей частковий випадок називають механічним спокоєм.
Розрізняють дві прості різновидності механічного руху: рух поступальний та рух обертальний. Поступальний рух – це такий механічний рух, при якому будь-яка приналежна тілу пряма залишається паралельною сама собі. Наприклад, якщо книга рухається поверхнею стола таким чином, що будь яка з її бічних сторін залишається паралельною самі собі, то рух книги є поступальним. Він буде поступальним навіть тоді, коли книга, не змінюючи своєї кутової орієнтації, рухається по колу, або будь-якій іншій складній кривій. Якщо в процесі руху будь-яка приналежна тілу пряма залишається паралельною сама собі, то це тіло рухається поступально.
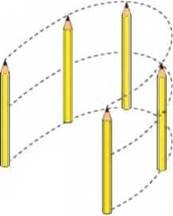
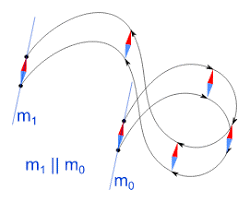
Мал.14. В процесі поступального руху тіла, будь-яка приналежна тілу пряма залишається паралельною сама собі.
Характерною та практично важливою особливістю поступального руху тіла є факт того, що при такому русі, всі точки тіла рухаються однаково. Однаково в тому сенсі, що мають однакові траєкторії руху, за однакові проміжки часу проходять однакові відстані, мають однакові миттєві і середні швидкості, однакові прискорення, тощо. А це означає, що описуючи поступальний рух тіла, нема потреби описувати рух кожної його окремої точки. Достатньо охарактеризувати рух будь-якої з цих точок, наприклад, центру маси тіла. Зважаючи на ці обставини, описуючи поступальний рух тіла, це тіло зазвичай замінюють його спрощеною (ідеалізованою) моделлю, яку прийняти називати матеріальною точкою.
Матеріальна точка, це така умовна точка, якою теоретично замінюють певне реальне тіло, в ситуаціях коли розмірами, формою та внутрішнім устроєм цього тіла можна знехтувати. Матеріальна точка зберігає лише одну механічну характеристику реального тіла – його масу. При цьому положення матеріальної точки практично завжди співпадає з положенням центру мас відповідного тіла.
Представляючи реальне тіло у вигляді матеріальної точки, ми абстрагуємося від несуттєвих в умовах даної задачі характеристик тіла і зосереджуємо свою увагу на його суттєво важливих характеристиках. В кінематиці такими характеристиками є час руху, траєкторія руху, швидкість руху, прискорення, пройдений шлях, тощо.
Потрібно підкреслити, що визначаючись з тим, можна чи не можна дане тіло вважати матеріальною точкою, в першу чергу враховують не реальні розміри тіла, а характер його руху та характер тих запитань які поставлені в даній задачі. Наприклад, якщо книга поступально рухається поверхнею стола і ми говоримо про швидкість її руху, її прискорення, пройдений шлях, то цю книгу можна вважати матеріальною точкою. Адже при поступальному русі всі точки книги проходять однаковий шлях, рухаються з однаковими швидкостями та з однаковими прискореннями. Якщо ж описуючи положення книги, ми говоримо про її координати, то скоріш за все цю книгу не можна вважати матеріальною точкою. Адже в масштабах стола, різні точки книги мають суттєво різні координати. Та як би там не було, а зазвичай в кінематиці поступального руху, тіла представляють у вигляді відповідних матеріальних точок.
Обертальний рух – це такий механічний рух, при якому всі точки тіла описують кола, центри яких знаходяться на одній прямій, яка називається віссю обертання. Наприклад, обертально рухаються стрілка годинника, колесо автомобіля, двері класної кімнати – звичайно за умови, що годинник «іде», колесо крутиться, двері відчиняються.

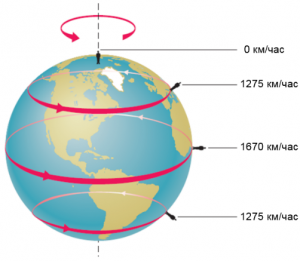
Мал.15. В процесі обертального руху тіла, всі його точки описують кола, центри яких знаходяться на одній прямій (осі обертання).
При обертальному русі різновіддалені від осі обертання точки тіла, рухаються суттєво по різному: мають різні траєкторії руху, різні пройдені шляхи, різні лінійні швидкості, різні прискорення, тощо. А це означає, що описуючи обертальний рух тіла, це тіло не можна замінювати матеріальною точкою.
В загальному випадку механічний рух тіла представляє собою певну комбінацію поступального і обертального рухів. Наприклад, коли ви кидаєте камінь, або б’єте футбольного м’яча, то скоріш за все рухи цих тіл будуть поступально-обертальними. Або наприклад, якщо автомобіль їде прямолінійною дорогою, то його корпус рухається поступально, колеса – поступально-обертально, а рух поршнів двигуна є певною комбінацією двох поступальних рухів. Якщо ж рельєф дороги складний, то всі ці руху стають набагато складнішими. Але яким би складним не був механічний рух тіла, його завжди можна представити як певну комбінацію двох простих рухів: поступального і обертального. А це означає, що вивчивши параметри та закономірності поступального і обертального руху можна описати та спрогнозувати будь-який найскладніший механічний рух.
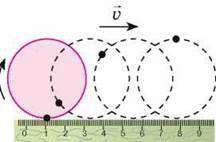
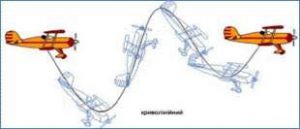
Мал.16. В загальному випадку рух тіла є поступально-обертальним.
Зважаючи на ці обставини та реалізуючи базовий методологічний принцип науки – від простого до складного, від часткового до загального, кінематику розділяють на дві частини кінематика поступального руху (кінематика матеріальної точки) та кінематика обертального руху. І потрібно зауважити, що у відповідності з навчальною програмою для 7-го класу ми по суті будемо вивчати основи кінематики поступального руху. Навіть в тих випадках коли ми будемо говорити про рух тіла по колу, то матимемо на увазі, що цей рух є поступальним, тобто таким, в процесі якого будь яка приналежна тілу пряма залишається паралельною сама собі.
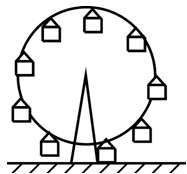
Мал.17. Рухаючись по колу, кабіна оглядового колеса рухається поступально.
Задача. Один велосипедист протягом 12с рухався зі швидкістю 6м/с, а другий – проїхав ту ж ділянку за 9с. Яка швидкість другого велосипедиста на цій ділянці шляху?
Дано:
t1 = 12c
v1 = 6м/c
s2 = s1
t2 = 9c
v2 =?
Рішення. Будемо виходити з того, що швидкість тіла визначається за формулою v = s/t, s – пройдений тілом шлях за час t. Для другого велосипедиста v2 = s2/t2, де s2 = ? Оскільки за умовою задачі s2 = s1, та враховуючи, що v1 = s1/t1, можна записати s2 = s1 = v1∙t1. Таким чином: v2 = s2/t2 = v1∙t1/t2,
Розрахунки: v2 = v1∙t1/t2 = 6(м/с)∙12с/9с = 8м/с.
Відповідь: v2 = 8м/с.
Контрольні запитання.
- Яка з наук, механіка чи кінематика, є більш загальною? Чому?
- Який рух називають механічним. Які різновидності механічного руху ви знаєте?
- Що називають механічною деформацією? Чи є механічна деформація різновидністю механічного руху?
- Який рух називають поступальним? Яка особливість цього руху?
- За яких умов рух тіла по колу буде поступальним. Чи є рух Землі навколо Сонця поступальним? Чому?
- Який рух називають обертальним? Чи можна описуючи обертальний рух тіла, представляти це тіло у вигляді матеріальної точки? Чому?
- Що називають матеріальною точкою? Чи є розміри тіла визначальними при відповіді на питання: можна чи не можна вважати дане тіло матеріальною точкою?
- Які критерії є визначальними при з’ясуванні того, можна чи не можна дане тіло вважати матеріальною точкою?
Вправа 9.
- Чи можна вважати м’яч матеріальною точкою:
а) описуючи його поступальний рух по футбольному полю?
б) описуючи його обертальний рух відносно власної осі обертання ?
в) визначаючи об’єм м’яча?
г) визначаючи його координати на футбольному полі?
- Які частини велосипеда під час руху прямолінійною дорогою рухаються поступально, які обертально, а які поступально-обертально?
- Яку траєкторію під час руху прямолінійною дорогою описує: а) вісь колеса велосипеда; б) точка на поверхні цього колеса?
- Страус бігає зі швидкістю 30м/с. Чи можливо його наздогнати рухаючись зі швидкістю 108км/год?
- Три тіла рухаються з швидкостями v1 = 36см/год, v2 = 0,01м/с, v3 = 10мм/с. Порівняйте ці швидкості.
- За 5год 30хв велосипедист проїхав шлях 99км. З якою середньою швидкістю рухався велосипедист?
- Протягом 30хв автомобіль рухався зі швидкістю 72км/год. Який шлях за цей час проїхав автомобіль?
- Протягом 30хв перший автомобіль рухався з середньою швидкістю 72км/год. При другий автомобіль проїхав ту ж ділянку шляху за 20хв. З якою середньою швидкістю рухався другий автомобіль?
.
§10. Відносність руху. Система відліку.
Напевно ви чули про те, що будь який механічний рух є відносним. Факт цієї відносності закарбовано в самому визначені механічного руху. Механічний рух, це такий рух при якому тіло переміщується відносно інших тіл. Автомобіль рухається відносно дороги. Поршень автомобільного двигуна рухається як відносно двигуна так і відносно тієї дороги якою їде автомобіль. Дорога разом з Землею рухається відносно Сонця, разом з Сонячною системою – відносно центру Галактики і т.д. При цьому рух поршня відносно двигуна автомобіля, суттєво відрізняється від руху того ж поршня відносно дороги.
По суті, твердження про те, що механічний рух є відносним означає, що різні спостерігачі, спостерігаючи за рухом одного і того ж тіла можуть бачити суттєво різні рухи. Дійсно. Уявіть собі велосипед, який з певною постійною швидкістю рухається прямолінійною дорогою. Уявіть, що за певним елементом цього велосипеда, наприклад за штуцером колеса (мал.18) спостерігають три спостерігачі. При цьому перший сидить на рамі велосипеда, другий – на землі, а третій – на самому колесі.
Кожен із спостерігачів дивиться на один і той же об’єкт (штуцер колеса) та описує його поведінку. Аналізуючи побачене, перший буде стверджувати, що штуцер рухається по колу. Другий, буде запевняти, що штуцер рухається певною кривою, яку прийнято називати циклоїдою. Третій – буде наполягати на тому, що штуцер не рухається. Не рухається тому, що розташування (положення) штуцера відносно елементів колеса велосипеда, а отже і відносно третього спостерігача, з плином часу залишається незмінним. І як це не дивно, але кожен з спостерігачів абсолютно правий. Адже відносно рами велосипеда штуцер дійсно рухається по колу, відносно дороги – по циклоїді, а відносно елементів колеса – не рухається взагалі.
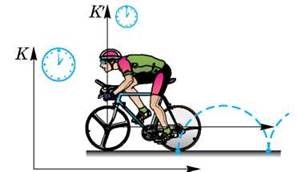
Мал.18. Різні спостерігачі, спостерігаючи за рухом одного і того ж об’єкту можуть бачити суттєво різні рухи.
Із вище сказаного ясно, що описуючи механічний рух тіла, необхідно чітко вказати, в якій системі відліку описується цей рух. Адже в різних системах відліку один і той же рух може виглядати по різному. Скажімо, якщо не вказати ту систему відліку в якій описується рух штуцера, то можна як завгодно довго та як завгодно запекло сперечатись стосовно того, як рухається штуцер – по колу, по циклоїді чи якось інакше. І кінця краю цій суперечці не буде.
Звичайно, якщо в тому чи іншому контексті, або в умові тієї чи іншої задачі не вказана система відліку, то скоріш за все, це означає що цією системою є та, що жорстко з’єднана з умовно нерухомою землею. Наприклад, коли ми говоримо, що будинок не рухається, то маємо на увазі що він не рухається відносно землі. Або, якщо ми стверджуємо, що автомобіль рухається з швидкістю 90км/год, то скоріш за все маємо на увазі його швидкість відносно дороги. При цьому відносно іншого автомобіля ця швидкість може бути іншою.
Говорячи про систему відліку мають на увазі взаємопов’язану сукупність (систему) трьох складових: точки відліку, системи координат та вимірювача часу (годинник, секундомір, тощо). Ця сукупність дозволяє однозначно описати просторово-часові параметри руху тіла. Це означає, що система відліку не лише визначає «адресу» (координати) рухомої точки, а й вказує на те в який момент часу ця «адреса» зафіксована.

Мал.19. Система відліку – це взаємопов’язана сукупність точки відліку, системи координат та вимірювача часу, яка застосовується для кількісної характеристики механічного руху матеріальної точки (тіла) в цій системі.
Система координат – це взаємопов’язана сукупність осей системи координат з вказаним на цих осях масштабом вимірювань. Точка відліку – це така умовно нерухома точка, яка є центром (нулевою точкою) відповідної системи координат. Задати систему координат означає: 1) вказати точку відліку даної системи; 2) задати просторову орієнтацію осей системи координат; 3) на кожній осі координат вказати масштаб вимірювань.
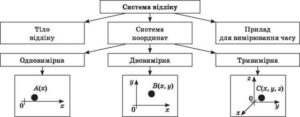
Місцезнаходження матеріальної точки в заданій системі координат, однозначно визначається її координатами. При цьому, якщо мова йде про одномірну (лінійну) систему координат (мал.20а), то в ній місцезнаходження матеріальної точки характеризується однією координатою М(х). В двомірній (плоскій) системі координат (мал.20б), розташування точки характеризується двома координатами М(х;y), а в тримірній (об’ємній, мал.20в) – трьома М(х;y;z).
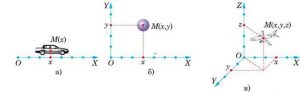
Мал.20. Системи відліку, це сукупність системи координат та вимірювача часу.
Лінію яку описує матеріальна точка в процесі руху у вибраній системі відліку називають траєкторією. В різних системах відліку траєкторія руху однієї і тієї ж матеріальної точки може бути суттєво різною. Наприклад, в системі відліку пов’язаною з землею, траєкторією руху велосипедного штуцера є сукупність послідовних циклоїд. В системі ж відліку пов’язаною з рамою велосипеда, цієї траєкторією буде сукупність співпадаючих кіл. А в системі відліку пов’язаній з колесом велосипеда – нерухома точка.
За формою траєкторії, механічні рухи поділяються на прямолінійні та криволінійні. Прямолінійним називають такий поступальний рух матеріальної точки, траєкторія якого представляє собою пряму лінію. Криволінійним називають такий поступальний рух матеріальної точки, траєкторія якого представляє собою криву лінію. Наприклад рух вертикально падаючого тіла (мал.21б) є прямолінійним, а рух тіла кинутого під кутом до горизонту (мал.21г) – криволінійним. Криволінійним є і рух тіла кинутого вертикально вгору (мал.21в). Його криволінійність полягає в тому, що відповідна траєкторія представляє собою ламану яка складається з двох прямолінійних відрізків.
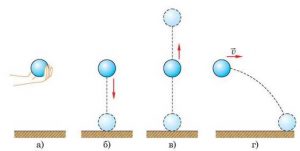
Мал.21. За формою траєкторії, поступальні рухи поділяються на прямолінійні (б) та криволінійні (в; г)
Та якою б криволінійною не була траєкторія руху тіла, а її завжди можна представити як певну сукупність послідовних прямолінійних відрізків. Це означає, що вивчивши параметри та закономірності прямолінійного руху, можна описати будь-який криволінійний рух. Виходячи з цього, вивченню параметрів та закономірностей прямолінійного руху матеріальної точки ми будемо приділяти особливу увагу.
Власне реалізуючи базовий методологічний принцип науки – від простого до складного, від часткового до загального, та зважаючи на факт того, що будь який криволінійний рух можна представити як певну сукупність прямолінійних рухів, ми перш за все будемо вивчати кінематику прямолінійного руху.
Задача 1. За заданими графіками руху тіл 1 і 2, визначити їх координати в момент часу 0с; 1с; 2с; 4с. Визначити де і коли ці тіла зустрінуться?
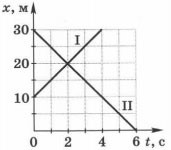
Рішення. На основі аналізу заданих графіків, можна стверджувати:
х1(0) = 10м; х2(0) = 30м;
х1(1) = 15м; х2(1) = 25м;
х1(2) = 20м; х2(2) = 20м;
х1(4) = 30м; х2(4) = 10м.
На основі аналізу заданих графіків, можна стверджувати, що задані тіла зустрінуться через 2с в точці з координатою 20м.
Задача 2. В заданій системі координат, визначити координати точок А, B, C, D, K, M.
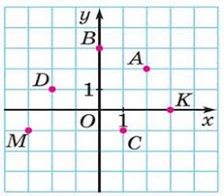
Рішення. На основі аналізу заданої системи координат та розтушування заданих точок в ній, можна записати: А(2; 2), B(0; 3), C(1; –1), D(1; –2), K(3; 0), M(–3; –1).
Задача 3. Задайте плоску прямокутну систему координат і побудуйте в ній точки з координатами А(–60; 20), В(–40; 60), С(20; 40), D(40; –20), Е(–40; –40).
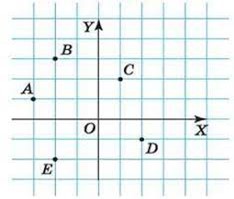
Рішення. Задаємо плоску прямокутну систему координат. (Нагадаємо, задати систему координат означає: 1) вказати точку відліку даної системи; 2) задати просторову орієнтацію осей системи координат; 3) на кожній осі координат вказати масштаб вимірювань). При цьому масштаб вимірювань вибираємо таким чином, щоб він відповідав умові конкретної задачі. Наприклад в умовах нашої задачі, довжині однієї клітинки малюнку відповідає 20 одиниць (на малюнку цифри масштабу не позначено). В заданій системі координат позначаємо відповідні точки.
Контрольні запитання.
- Що означає твердження: механічний рух є відносним? Наведіть приклади.
- Які частини велосипеда підчас рівномірного руху описують прямолінійні, а які криволінійні траєкторії відносно дороги?
- Що називають системою відліку?
- Що означає задати систему координат?
- Чим система відліку відрізняється від системи координат? Яка з цих систем є більш загальною?
- Що називають траєкторією і чи є траєкторія руху матеріальної точки відносною? Наведіть приклади.
- Траєкторії руху двох тіл перетинаються. Чи означає це що тіла зіштовхуються? Поясніть.
Вправа №10.
- Задайте плоску прямокутну систему координат і побудуйте в ній точки з координатами А(20;20); В(–20;40); С(20;0); Д(10;–30); К(0;20); М(–10;–20); N(0;0); Р(30;–20).
- Задайте лінійну систему координат і побудуйте в ній точки з координатами: А(200); В(–150); С(50); Д(250); К(–50); М(0); N(100).
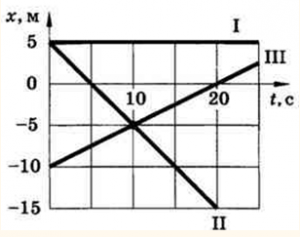
- За заданими графіками руху тіл 1, 2 і 3, визначити їх координати в момент часу 0; 5с; 10с; 20с. Визначити де і коли тіла 2 і 3 зустрінуться?
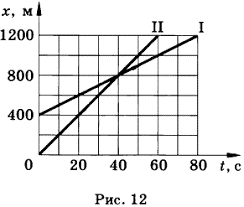
4. За заданими графіками руху тіл 1 і 2, визначити їх координати в момент часу 0с; 20с; 40с; 60с. Визначити де і коли ці тіла зустрінуться?
6. Хлопчик випустив з рук м’яч на висоті 1,5м, а коли м’яч відскочив від підлоги, спіймав його на висоті 1м. Який шлях пройшов м’яч? На якій відстані від вихідної точки було спіймано м’яч?
7. Пасажир потягу, що рухається з постійною швидкістю, підкидає вертикально вгору яблуко і ловить його. Намалюйте траєкторію руху яблука відносно: а) пасажира який сидить поруч; б) людини, яка стоїть на пероні вокзалу.
8. У змаганнях з бігу беруть участь 4 учні, які можуть бігти зі швидкостями 6м/с, 20км/год, 360м/хв, 0,35км/хв. Хто переможе і хто прибіжить останнім?
9. Відстань від Землі до Сонця 150млн. км. Скільки часу потрібно світлу, щоб подолати цю відстань? Швидкість світла 300 000км/с.
.
§11. Просторово-часові параметри поступального руху.
До числа основних фізичних величин кінематики поступального руху відносяться: час (t), координата (x), пройдений шлях (s) швидкість (v), прискорення (a).
Час – це фізична величина, яка характеризує тривалість подій (явищ, процесів, рухів, тощо) і яка дорівнює цій тривалості.
Позначається: t
Визначальне рівняння: нема
Одиниця вимірювання: [t] = с, (секунда).
Твердження про те, що час немає визначального рівняння по суті означає, що час належить до числа тих базових фізичних величин, одиниці вимірювання яких за домовленістю прийнято вважати основними. В механіці такими базовими величинами є час (t), довжина (ℓ) і маса (m).
Коли ми говоримо про координату матеріальної точки (тіла), то маємо на увазі певну величину, яка однозначно визначає місцезнаходження (положення) даної матеріальної точки в заданій системі координат. При цьому потрібно зауважити, що в фізиці координата, це не просто число яке визначає положення точки в вибраній системі координат. Координата, це відстань від точки відліку системи координат до даної точки, виміряній вздовж відповідної осі системи координат.
Наприклад, в зображеній на мал.22а лінійній системі координат, автобус має координату (300), а вантажний автомобіль (–100). Це означає, що відносно точки відліку системи координат, автобус знаходиться на відстані 300м в додатному напрямку осі х, а автомобіль – на відстані 100м у від’ємному напрямку цієї осі. Або наприклад, в зображеній на мал.22б плоскій системі координат, точка А має координати А(5;3). Це означає, що для потрапляння в точку А потрібно пройти 5м вздовж додатного напрямку осі х, а потім пройти 3м вздовж додатного напрямку осі y.
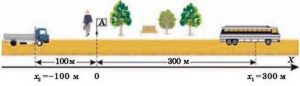
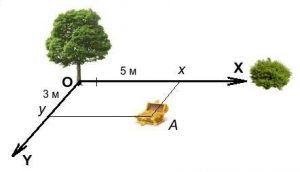
Мал.22. Координата точки дорівнює відстані від точки відліку системи координат до даної точки, виміряній вздовж відповідної осі системи координат.
Зважаючи на вище сказане можна дати наступне визначення.
Координата – це фізична величина, яка характеризує положення (місцезнаходження) матеріальної точки в заданій системі координат і яка дорівнює відстані від точки відліку цієї системи до проекції даної точки на відповідну вісь координат.
Позначається: х
Визначальне рівняння: х = ℓх
Одиниця вимірювання: [х] = м, (метр)
Оскільки координата, пройдений шлях, переміщення, висота, ширина, товщина, діаметр, радіус, периметр, діагональ, тощо, це різновидності тієї фізичної величини яка називається довжина, то буде не зайвим визначити і цю величину.
Довжина – це фізична величина, яка характеризує відстань між двома точками, виміряну вздовж певної лінії і яка дорівнює цій відстані.
Позначається: ℓ
Визначальне рівняння: нема
Одиниця вимірювання: [ℓ] = м, (метр).
Пройдений шлях – це фізична величина, яка характеризує пройдений матеріальною точкою (тілом) шлях і яка дорівнює довжині тієї траєкторії яку описує ця точка в процесі відповідного руху.
Позначається: s
Визначальне рівняння: s = ℓтр, для прямолінійного руху s = Δх
Одиниця вимірювання: [s] = м, (метр).
Зауваження. В науці загалом і в фізиці зокрема, символом ∆ – дельта (∆х, ∆t, ∆v, ∆m і т.д.) позначають різницю між кінцевим та початковим значенням відповідних величин:
∆х = хк – хп
∆t = tк – tп
∆v = vк – vп
∆m = mк – mп і т.д.
Ілюструючи можливості та межі застосуванні формули s = ∆х, розглянемо декілька простих ситуацій. Припустимо, що в заданій системі відліку точки А і В мають координати А(300); В(–100). Виходячи з цього, визначимо пройдений тілом шлях при його переміщенні: a) з точки А в точку В; б) з точки В в точку А; в) з точки А в точку В, а потім знову в точку А.

Із аналізу малюнка ясно, що при переміщенні А → В пройдений тілом шлях становить s1 = 400м, при переміщенні В → А: s2 = 400м, при переміщенні А → В → А: s3 = 400 + 400= 800м.
Тепер, застосуємо формулу s = ∆х та отримаємо відповідні результати так би мовити теоретичним шляхом:
якщо А → В, то s1 = ∆x = хк – хп = (–100) – (300) = –400м, де знак « – » вказує на те, що в заданій системі координат, переміщення за маршрутом А → В відбувалося у від’ємному напрямку;
якщо В → А, то s2 = ∆x= хк – хп = (300) – (–100) = 400м;
якщо А → В → А, то s3 = ∆x= хк – хп = (300) – (300) = 0м.
Не важко бачити, що останній результат явно суперечить реальному стану речей. Це пояснюється тим, що за визначенням, формула s = ∆x справедливою лише для прямолінійних ділянок руху. Рух же тіла за маршрутом А→В→А є криволінійним. І тому пройдений тілом шлях потрібно визначати не за формулою s = ∆х, а за формулою s = ℓтр = |s1| + |s2| + … + |sN| , де N – кількість тих послідовних прямолінійних відрізків які утворюють відповідну криволінійну траєкторію. Наприклад, в умовах нашої задачі s = |s1| + |s2| = |–400| + |400| = 800м. (Нагадаємо, запис |–400| означає модуль, тобто абсолютну величину відповідного числа, а модуль числа завжди додатний |–400| = 400).
Таким чином, застосовуючи визначальне рівняння s = ∆х потрібно пам’ятати, що воно є справедливим лише для прямолінійної ділянки руху. Втім, в котре наголошуємо, що будь-який криволінійний рух, завжди можна представити як певну сукупність прямолінійних відрізків.
Варто зауважити, що рівняння s = ∆х не лише визначає величину пройденого тілом прямолінійного шляху, а й вказує на той напрямок в якому цей шлях пройдено. Наприклад, при переміщенні з точки А в точку В тіло рухається у від’ємному напрямку і тому s1= –400м. Коли ж тіло переміщується з точки В в точку А, то воно рухається в додатному напрямку і тому s2 = +400м.
В механіці наряду з пройденим шляхом, часто застосовують величину яка називається переміщення (позначається s). На відміну від пройденого шляху (s), переміщення (s) є величиною векторною, тобто такою яка характеризується як величиною так і напрямком. Вектор переміщення (s) дорівнює тому направленому відрізку (вектору), який з’єднує точки початкового та кінцевого положення матеріальної точки.
Наприклад від свого будинку до школи ви можете йти різними шляхами. При цьому траєкторії вашого руху та їм відповідні пройдені шляхи, можуть бути різними. Натомість ваше переміщення від будинку до школи завжди буде однаковим і таким, що дорівнює виміряній по прямій відстані від будинку до школи.
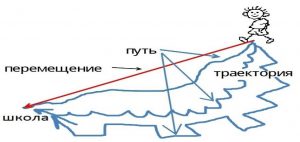
Мал.23. Пройдені шляхи різні, а переміщення – однакові.
Або якщо наприклад, ви вибігли поганяти з товаришами м’яча і через годину повернулися додому, то траєкторія вашого руху за цю годину буде дуже складною, а пройдений шлях – відповідно великим. При цьому ваше переміщення за вище вказану годину буде нульовим. Адже на початку і вкінці відповідної години, ваше місцезнаходження (координата) буде одним і тим же.
Задача 1. Турист пройшов 3км на північ, а потім 4км на схід. Визначити пройдений туристом шлях та величину (модуль) його переміщення. Задачу розв’язати графічно та алгебраїчно.
Графічне (геометричне) рішення. У вибраному масштабі (наприклад, 1см на малюнку відповідає 1км пройденого шляху), з дотриманням правил геометричних побудов та з застосуванням лінійки, виконуємо відповідні геометричні побудови. Вимірюємо довжину вектора переміщення |АС| та у відповідності з масштабом побудов, переводимо цю довжину у відповідне значення переміщення. В умовах нашої задачі |s| = |AC| ≈ 5км.
Відповідь: |АС| ≈ 5км.
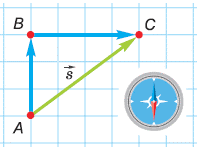
Головною перевагою графічного рішення задачі є простота та наочність цього рішення. А основним же недоліком графічного рішення є необхідність точних геометричних побудов та відсутність гарантованої точності результату. Адже точність цього результату залежить як від точності геометричних побудов так і від точності відповідних вимірювань.
Алгебраїчне рішення. Оскільки в умовах даної задачі (дивись мал.) відрізок АС є діагоналлю прямокутного трикутника АВС, де АВ=3км, ВС=4км, та враховуючи що у відповідності з теоремою Піфагора (АС)2 = (АВ)2 + (ВС)2, можна записати |АС| = √[(АВ)2 + (ВС)2]
Розрахунки: |АС| = √[(АВ)2 + (ВС)2] = √(32 + 42) = √(9+16) = √25 = 5км.
Відповідь: |АС| = 5км.
Основна перевага алгебраїчного рішення задачі полягає в гарантованій точності отриманого результату. А основний недолік – в тому, що алгебраїчне рішення потребує певного рівня теоретичних знань. В даному випадку потрібно знати теорему Піфагора та мати уявлення про те, що називають квадратним коренем числа.
Задача 2. Коло радіусом 50м велосипедист долає за 40с. Визначати пройдений велосипедистом шлях та модуль його переміщення за: а) 40с, б) 20с, в) 10с.
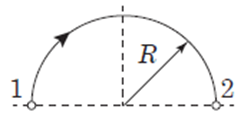
Дано:
R = 50м
T = 40c
t1 = 40c
t2 = 20c
t3 = 10c
s1 = ? s2 = ? s3 = ?
|s1| = ? |s2| = ? |s3| = ?
Рішення. Оскільки довжина кола ℓ залежить від його радіусу R і визначається за формулою ℓ = 2πR де π=3,14, та зважаючи на те, що повне коло велосипедист долає за T = 40c, можна стверджувати:
а) якщо t1 = 40c, то повне коло і тому s1 = ℓ = 2πR = 2∙3,14∙50м = 314м;
при цьому |s1| = 0м;
б) якщо t2 = 20c, то половина кола і тому s2 = ℓ/2 = 314м/2 = 157м;
при цьому |s2| = 2R = 2∙50м = 100м;
в) якщо t2 = 10c, то чверть кола і тому s3 = ℓ/4 = 314м/4 = 78,5м;
при цьому модуль переміщення |s3| дорівнює довжині гіпотенузи рівностороннього прямокутного трикутника, катети якого дорівнюють R, і яку можна визначити за теоремою Піфагора |s3|2 = R2 + R2 = 2R2, звідси |s3| = √2R2 = R√2 = 50м∙1,41 = 70,5м.
Контрольні запитання.
- Назвіть основні фізичні величини кінематики поступального руху.
- Дайте визначення термінам довжина, координата та пройдений шлях.
- Чому довжина не має визначального рівняння?
- Що в науці позначають символом Δ (дельта): Δх; Δt; Δm; тощо?
- В яких випадках пройдений шлях визначають за формулою s=ℓтр, а в яких s=Δх?
- Що означає твердження: переміщення – величина векторна?
- Чи може модуль переміщення бути більшим за відповідний пройдений шлях? Дорівнювати пройденому шляху?
- Пройдений тілом шлях становить 10км. При цьому його переміщення дорівнює нулю. Що це означає?
Вправа №11.
- М’яч упав з висоти 4м і відбившись від підлоги був пійманий на висоті 1м. Визначити пройдений м’ячем шлях та його переміщення?
- Відстань між пунктами А і В по прямій лінії 4км. Людина проходить цю відстань туди і назад за 2 години. Чому дорівнює шлях і модуль переміщення людини за 1 годину? За 2 години?
- На основі аналізу малюнку визначте пройдений матеріальною точкою шлях та її переміщення.
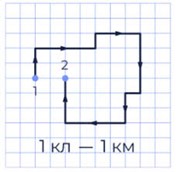
- Гвинтокрил, пролетівши в горизонтальному польоті по прямій 6км, повернув на 90º і пролетів ще 8км. Визначити шлях і модуль переміщення гвинтокрила. Задачу розв’язати графічно та алгебраїчно.
- Турист пройшов спочатку 400м на північний захід, потім 500м на схід і ще 300м на північ. Визначити графічно модуль переміщення туриста.
- Матеріальна точка переміщувалась за маршрутом А→В→С. Графічним методом визначте пройдений точкою шлях та її переміщення, якщо виражені в метрах координати точок: А(–30, 30), В(20, 20), С(–20, –20).
- Мотоцикліст, рухаючись ареною цирку, проїжджає коло радіусу 13м за 8с. Визначте шлях і модуль переміщення мотоцикліста: а) за 4с руху; б) за 8с руху.
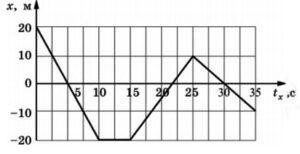
- На основі аналізу заданого графіку руху тіла, визначити пройдений ним шлях та переміщення за 35 секунд.
.
§12. Швидкість поступального руху. Середня швидкість.
Ви так часто чули слово «швидкість», що напевно без зайвих пояснень розумієте загальну суть цього терміну. І коли ви чуєте, що автомобіль рухається з швидкістю 20 метрів за секунду, то напевно розумієте, що за кожну секунду цей автомобіль проходить шлях 20 метрів. Розумієте і те, що за дві секунди, він проїде 40 метрів, за три секунди – 60 метрів і так далі. Звідси не важко збагнути, що для визначення швидкості автомобіля, потрібно пройдений ним шлях (s) поділити на той проміжок часу (t) за який цей шлях пройдено. А якщо швидкість позначити літерою v, то відповідна формула набуде вигляду v = s/t.
В загальних рисах такі уявлення про швидкість є правильними. Точніше, вони правильні в тому випадку, якщо швидкість руху тіла (матеріальної точки) є сталою (v = const), тобто такою величина і напрям якої з плином часу не змінюється. В загальному ж випадку, в процесі руху тіла, величина і напрям його швидкості можуть змінюватись. Скажімо, в процесі руху дорогами міста, автомобіль постійно здійснює певні маневри, які передбачають як певні зміни напрямку його руху, так і певні зміни величини швидкості руху. А це означає, що в кожній точці траєкторії руху, автомобіль може мати свою так звану миттєву швидкість, яка характеризується як певною величиною, так і певним напрямком.
Мал.24. В реальних ситуаціях, швидкість руху тіла може змінюватись як за величиною так і за напрямком.
Оскільки в загальному випадку швидкість руху тіла (матеріальної точки) може змінюватись як за величиною так і за напрямком, то визначаючи величину та напрям швидкості, в якості того проміжку часу за який визначається пройдений тілом шлях, беруть не годину, не хвилину і навіть не секунду, а гранично малу величину Δt→0. При цьому пройдений тілом шлях, а точніше – його переміщення Δх = хк – хп, також буде гранично малим і за будь якої траєкторії руху практично прямолінійним. В такому загальному випадку, та фізична величина яка називається швидкістю, має наступне визначення.
Швидкість – це фізична величина, яка характеризує швидкість поступального руху тіла (матеріальної точки), і яка дорівнює відношенню вектора того переміщення Δх яке здійснило тіло за гранично малий проміжок часу Δt, до величини цього проміжку часу.
Позначається: v
Визначальне рівняння: v = ∆x/∆t
Одиниця вимірювання: [v] = м/с, (метр на секунду).
Формула v = ∆x/∆t, є базовим визначальним рівнянням швидкості, яке справедливе для будь яких ситуацій, і яке за різних обставин може набувати різного вигляду. Наприклад, якщо мова йде про прямолінійний рух, тобто такий рух в процесі якого напрям швидкості не змінюється, то рівняння v=∆x/∆t, набуває вигляду v=∆x/∆t. Різниця між цими рівняннями в тому, що перше (v=∆x/∆t) дозволяє визначати як величину так і напрям швидкості, а друге (v=∆x/∆t) – лише величину швидкості. Втім, якщо мова йде про прямолінійний рух, то в цьому випадку напрям швидкості є визначеним і таким, що співпадає з напрямком руху тіла.
Оскільки в подальшому ми будемо говорити про прямолінійний рух матеріальної точки, то в якості визначального рівняння швидкості, будемо застосовувати формулу v=∆x/∆t. Фізичний зміст цієї формули полягає в наступному. Якщо в початковий момент часу t0 тіло знаходилось в точці з координатою х0, а в кінцевий момент часу t – в точці з координатою х, то це означає, що за час Δt = t – t0 тіло перемістилось на відстань Δх = х – х0 і тому швидкість цього тіла v=Δx/Δt.
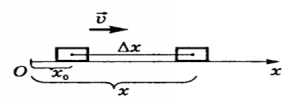
Мал.25. Якщо за час Δt тіло (матеріальна точка) переміщується на відстань Δх, то швидкість цього тіла v = Δx/Δt.
Задача 1. За заданим графіком руху автобусу (1) і легкового автомобіля (2), визначити величину і напрям їх швидкостей.
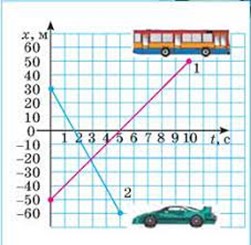
Рішення. За визначенням v = Δx/Δt. На основі аналізу малюнку (графіків руху) можна стверджувати.
Автобус (1): якщо Δt1 = 10с, то Δx1 = хк – хп = 50 – (–50) = 100м, отже v1 = Δx1/Δt1 = 100м/10с = 10м/с.
Автомобіль (2): якщо Δt2 = 5с, то Δx2 = хк – хп = – 60 – (30) = –90м, отже v2 = Δx2/Δt2 = –90м/5с = –18м/с, де знак « – » вказує на те, що рух легкового автомобіля відбувається у від’ємному напрямку осі х.
Відповідь: v1 = 10м/с; v2 = –18м/с.
Зазвичай в реальних ситуаціях швидкість руху тіла так чи інакше змінюється. Цю змінну швидкість характеризують певною усередненою величиною. Існує велике різноманіття усереднених швидкостей: середня шляхова швидкість, середня швидкість переміщення, середня арифметична швидкість, середня квадратична швидкість, тощо.
В кінематиці поступального руху ми будемо говорити лише про одну різновидність усередненої швидкості – середню шляхову швидкість, яку будемо називати просто: середня швидкість. Наприклад коли ми говоримо, що з Києва до Чернігова автомобіль рухався з швидкістю 60км/год, то маємо на увазі середню шляхову швидкість цього руху. Адже в залежності від ситуації на дорозі, на певних ділянках руху автомобіль прискорювався, на певних – пригальмовував, на одних ділянках рухався швидше, на інших – повільніше, а на деяких – взагалі зупинявся. Тому швидкість 60км/год є тією усередненою швидкістю, яка дорівнює відношенню пройденого автомобілем загального шляху (s), до того загального проміжку часу (t) за який цей шлях було пройдено (vс = s/t).
Середня швидкість (середня шляхова швидкість) – це та усереднена швидкість з якою тіло долає певну ділянку шляху і яка дорівнює відношенню пройденого тілом загального шляху s, до того загального проміжку часу t, за який цей шлях пройдено.
Позначається: vс
Визначальне рівняння: vс= s/t
Одиниця вимірювання: [vс] = м/с, (метр на секунду).
На відміну від швидкості тіла в даний момент часу (миттєвої швидкості), середня шляхова швидкість є величиною скалярною, тобто такою яка характеризується лише числовим значенням.
Задача 1. За представленим на малюнку графіком руху птаха, визначити його швидкість на кожній ділянці шляху, та середню швидкість на всьому шляху.
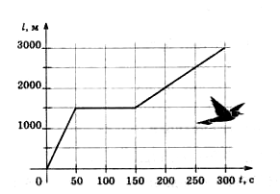
Рішення. На основі аналізу малюнку можна стверджувати, що рух птаха складається з трьох ділянок. При цьому:
Ділянка 1: t1 = Δt1 = 50c – 0c = 50c; ℓ1 = Δx1 = 1500м – 0м = 1500м;
v1 = ℓ1/t1 = 1500м/50с = 30м/с.
Ділянка 2: t2 = Δt2 = 150c – 50c = 100c; ℓ2 = Δx2 = 1500м – 1500м = 0м;
v2 = ℓ2/t2 = 0м/100с = 0м/с.
Ділянка 3: t3 = Δt3 = 300c – 150c =150c; ℓ3 = Δx3 = 3000м – 1500м = 1500м;
v3 = ℓ3/t3 = 1500м/150с = 10м/с.
Середня швидкість: vc = (ℓ1+ℓ2+ℓ3)/(t1+t2+t3) = 3000м/300с =10м/с
Задача 2. Велосипедист проїхав 40км зі швидкістю 20км/год, а потім ще 30км проїхав за 3год. Яка його середня швидкість на всьому шляху?
Загальні зауваження. Якщо в умові задачі одиниці вимірювання всіх фізичних величин гармонічно збалансовані, то переводити ці одиниці в міжнародну систему одиниць (СІ) не потрібно. Наприклад, в умовах нашої задачі, одиниці вимірювання всіх величин гармонічно (взаємопов’язано) збалансовані, тому переводити ці одиниці в СІ не потрібно.
Дано:
s1 = 40 км
v1 = 20 км/год
s2 = 30 км
t2 = 3 год
vc = ?
Рішення. За визначенням vc = s/t. В умовах нашої задачі s = s1 + s2 = 40км + 30км = 70км; t = t1 + t2, де t1 = ? Оскільки v1= s1/t1, то t1 = s1/v1 = 40км/20(км/год) = 2год.
Таким чином: t = t1 + t2 = 2год + 3год = 5год;
vc = s/t = 70км/5год = 14км/год.
Відповідь: vc = 14км/год.
Контрольні запитання.
- Що означає твердження: «швидкість – величина векторна»?
- Чим відрізняється формула v = ∆x/∆t від формули v = ∆x/∆t?
- Який рух називають прямолінійним
- Який рух називають прямолінійно-рівномірним?
- Чи відрізняються записи v = const і v = const? Якщо відрізняються то чим?
- За якої умови Δt = t?
- За яких умов, формула v = ∆x/∆t набуває вигляду v = s/t?
- Відстань від Києва до Черкас автомобіль проїхав зі швидкістю 60км/год. Про яку швидкість іде мова? Поясніть.
- Якщо тіло рухається прямолінійно і рівномірно, то чи відрізняються числові значення його миттєвої і середньої швидкостей?
Вправа №12.
- Антилопа розвиває швидкість 25м/с, лев – 80км/год, а зебра – 1км/хв. У кого з них швидкість найбільша.
- Який шлях проїде велосипедист за 2год, якщо його середня швидкість 15км/год?
- Турист пройшов 5км за 1,5год, а потім ще 2км за 0,5год. Яка середня швидкість туриста на всьому шляху?
- Один велосипедист протягом 12с рухався зі швидкістю 6м/с, а другий велосипедист проїхав ту саму ділянку шляху за 9с. Якою була швидкість другого велосипедиста?
- Коло радіусом 50м велосипедист долає за 40с. Визначати швидкість його руху.
- Автомобіль проїхав 72км зі швидкістю 20м/с, а потім ще 108км – за 3год. Яка середня швидкість автомобіля на всьому шляху?
- За заданими графіками руху (червона, синя, зелена прямі), визначити відповідні швидкості руху.
- За представленим на малюнку графіком руху, визначити швидкість руху на кожній ділянці шляху, та середню швидкість на всьому шляху.
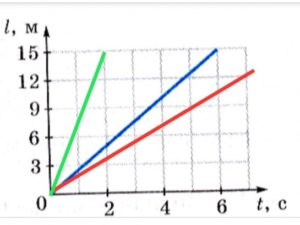
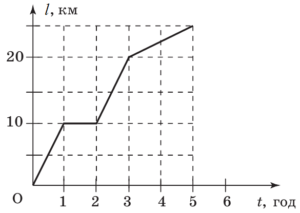
до задачі 7 до задачі 8
.
§13. Загальні відомості про прискорення.
Якщо швидкість тіла так чи інакше змінюється, то говорять що воно рухається з прискоренням. Прискорення – це фізична величина, яка характеризує зміну швидкості руху тіла, і яка дорівнює відношенню тієї зміни швидкості Δv, що відбулася за проміжок часу Δt, до величини цього проміжку часу.
Позначається: а
Визначальне рівняння: а = ∆v/∆t,
Одиниця вимірювання: [a] = м/с2, (метр на секунду в квадраті).
Оскільки швидкість, величина векторна, то вона може змінюватись як за величиною, так і за напрямком. Наприклад якщо рух тіла є прямолінійним, то його швидкість може змінюватись тільки за величиною (збільшуватись або зменшуватись). Якщо ж тіло рухається по колу, то його швидкість може змінюватись як за величиною так і за напрямком. При цьому, за напрямком вона змінюється обов’язково. Зважаючи на ці обставини, розрізняють дві різновидності прискорення:
1) Прискорення, яке характеризує зміну швидкості за величиною і яке визначається за формулою а = ∆v/∆t, або а = (vк–v0)/t. Це прискорення називають лінійним.
2) Прискорення, яке характеризує зміну швидкості за напрямком і яке визначається за формулою ад = v2/R. Це прискорення називають доцентровим. Про доцентрове прискорення ми поговоримо вивчаючи тему «Рух матеріальної точки по колу».
В подальшому терміном «прискорення» ми будемо позначати те прискорення яке характеризує зміну швидкості за величиною, і яке називається лінійним прискоренням, а частіше – просто прискоренням.
Лінійне прискорення (прискорення) – це таке прискорення, яке характеризує зміну швидкості за величиною.
Позначається: ал або а
Визначальне рівняння: а = ∆v/∆t
Одиниця вимірювання: [а] = м/с2
Лінійне прискорення завжди направлено вздовж лінії швидкості руху тіла. При цьому, якщо величина швидкості зростає (v↑), то вектори швидкості та прискорення співнаправлені, а якщо швидкість зменшується (v↓) – то ці напрямки протинаправлені.
Наприклад, коли автомобіль рушає з місця (мал.26а), то його швидкість збільшується (v↑) і тому напрям того прискорення з яким рухається автомобіль, співпадає з напрямком його руху (з напрямком швидкості). Якщо ж автомобіль гальмує (мал.26б), то його швидкість зменшується (v↓) і тому напрям того прискорення з яким рухається автомобіль, протилежний до напрямку його руху (протилежний до напрямку швидкості руху автомобіля).
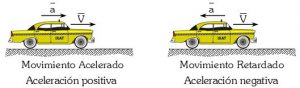
Мал.26. Якщо швидкість автомобіля збільшується (мал.а), то вектори a і v співнаправлені, а якщо зменшується (мал.б) – то протинаправлені.
Із визначального рівняння прискорення а = (vк–v0)/t, з усією очевидністю випливає, що при рівноприскореному русі (а=соnst) швидкість тіла можна визначити за формулою vк = v0 + at або v = v0+at, де v0 – початкова швидкість тіла. Дійсно, оскільки а = (vк – v0)/t, то розкривши дужки отримаємо а = vk/t – v0/t. Звідси випливає vк/t = v0/t + а, або vк = v0 + at. Зазвичай формулу v = v0 + at (точніше v = v0 ± at) називають рівнянням швидкості.
Варто зауважити, що коли рухаючись з постійним прискоренням (а = соnst), тіло збільшує свою швидкість (v↑), то відповідний рух називають рівноприскореним. При цьому говорять, що тіло має додатне прискорення (а > 0). Якщо ж швидкість тіла зменшується (v↓), то відповідний рух називають рівносповільненим, а відповідне прискорення – від’ємним (а < 0). А це означає, що рівняння v = v0 ± at для рівноприскореного руху набуває вигляду v = v0 + at, для руху рівносповільненого v = v0 – at.
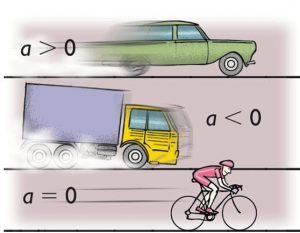
Мал.27. При рівноприскореному русі тіло має додатне прискорення (а > 0), а при рівносповільненому русі – від’ємне (а < 0).
Таким чином, на практиці швидкість прямолінійного руху тіла визначають за формулами:
1) при рівномірному русі (v = const), v = s/t;
2) при рівноприскореному русі (v↑), v = v0 + at;
3) при рівносповільненому русі (v↓), v = v0 – at.
В фізиці нема кращого способу засвоєння теоретичного матеріалу як той, що передбачає розв’язування відповідних задач, а по суті – застосування теорії на практиці.
Побутує думка ніби рішення задачі фізики полягає в тому, щоб серед незліченого різноманіття правильних формул вибрати потрібне розрахункове рівняння, тобто ту формулу підставивши в яку задані величини, можна визначити невідому величину. Така думка є абсолютно хибною. Хибною по перше тому, що в фізиці кожна задача індивідуальна. А це означає, що кожна з сотень, тисяч і мільйонів задач має своє розрахункове рівняння. І запам’ятовувати, зазубрювати чи заучувати різноманіття подібних рівнянь нема ані можливості ані сенсу.
По друге, рішення задачі фізики полягає не в тому, щоб із незліченного різноманіття правильних формул вибрати потрібну, а в тому щоб на основі аналізу умови конкретної задачі та певного обмеженого набору базових формул (базових законів та визначальних рівнянь фізичних величин), шляхом логічних міркувань та математичних дій вивести потрібне розрахункове рівняння.
Наприклад в умовах нашої теми, тими базовими формулами, на основі яких розв’язуються задачі кінематики матеріальної точки є: визначальні рівняння пройденого шляху s = Δx, швидкості v = Δx/Δt та прискорення a = Δv/Δt, а також основний закон кінематики, який називається рівнянням руху і про який ми поговоримо дещо пізніше. Інша справа, що в конкретних ситуаціях певні визначальні рівняння, можуть набувати більш конкретного вигляду. Наприклад рівняння a = Δv/Δt, в ситуації коли t0 = 0, набуває вигляду а = (vк – v0)/t, звідси v = v0 + at.
Таким чином, якщо для розв’язування задач кінематики вам потрібна шпаргалка (а така шпаргалка дійсно потрібна), то ось ця шпаргалка.
Базові формули: s = Δx; v = Δx/Δt; a = Δv/Δt. На практиці:
- s = Δx;
- якщо а = 0, то v= s/t;
- якщо а ≠ 0, то v = v0 + at;
- а = (vк – v0)/t.
Задача 1. Автомобіль що рухається зі швидкістю 108км/год, в процесі гальмування зупинився через 10с. З яким прискоренням рухався автомобіль?
Загальні зауваження. Дехто вважає, що задачі фізики є складними. Звичайно, якщо ви не знаєте, що час позначається t, швидкість – v, прискорення – а, якщо не знаєте, що визначальне рівняння прискорення а = (vк–v0)/t, якщо не розумієте, що твердження «автомобіль в процесі гальмування зупиняється» – означає, що кінцева швидкість автомобіля дорівнює нулю (vк = 0м/с), то задачі фізики дійсно складні. Однак якщо ви знаєте суть тих слів (термінів) які є азбукою фізики, якщо уважно читаєте умову задачі та бачите за цією умовою реальну ситуацію, то неминуче погодитесь з тим, що фізика, це зовсім нескладно, натомість цікаво, повчально і потрібно. Бо фізика, то ж не формули, а вміння творчо та логічно мислити.
Дано:
v0 = 108 км/год = 30м/с
vк = 0 м/с
t = 10 с
а = ?
Рішення. За визначенням а = (vк – v0)/t. В умовах нашої задачі а = (0м/с – 30м/с)/10с = –3м/с2, де знак «–» вказує на те, що рух автомобіля є рівносповільненим (швидкість зменшується).
Відповідь: а = –3м/с2.
Задача 2. За який час автомобіль рухаючись зі стану спокою з прискоренням 0,6м/с2 набуде швидкості 90км/год?
Дано:
v0 = 0м/с
vк = 90км/год = 25м/с
a = 0,6м/с2
t = ?
Рішення. Оскільки за визначенням а = (vк – v0)/t, то t = (vк – v0)/а = (25м/с – 0м/с)/0,6(м/с2) = 41,7с
Відповідь: t = 41,7с.
Задача 3. Автомобіль рухаючись з прискоренням 4м/с2, зупинився через 2с. Визначити швидкість автомобіля на початку гальмування.
Дано:
а = 4м/с2
vк = 0м/с
t = 2c
v0 = ?
Рішення. Оскільки при рівносповільненому русі (v↓), v = v0 – at, то v0 = v + at.
Розрахунки: v0 = v + at = 0м/с + 4(м/с2)∙2с = 8м/с.
Відповідь: v0 = 8м/с.
Задача 4. За заданим графіком швидкості руху тіла, визначити його прискорення на кожній ділянці шляху.
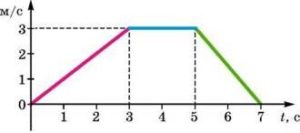
Рішення. На основі аналізу заданого графіку швидкості можна стверджувати, що даний рух складається з трьох ділянок. При цьому:
Ділянка 1: Δt1 = 3c – 0c = 3c; Δv1 = 3м/с – 0м/с = 3м/с;
а1 = Δv1/Δt1 = 3(м/с)/3с = 1м/с2.
Ділянка 2: Δt2 = 5c – 3c = 2c; Δv2 = 3м/с – 3м/с = 0м/с;
а2 = Δv2/Δt2 = 0(м/с)/2с = 0м/с2.
Ділянка 3: Δt3 = 7c – 5c = 2c; Δv3 = 0м/с – 3м/с = –3м/с;
а3 = Δv3/Δt3 = –3(м/с)/2с = –1,5м/с2, де знак «–» вказує на те, що рух тіла є рівносповільненим (швидкість руху зменшується).
Загальні зауваження. В рішенні задачі, ви повинні не лише записувати голі формули, а й робити відповідні письмові коментарі до них. Звичайно, ці коментарі мають бути максимально стислими, але такими, що чітко відображають логіку ваших міркувань. Наприклад: Виходячи з того, що …. та враховуючи, що…… можна записати ….Або: Оскільки … , то …
Контрольні запитання.
- Чому розрізняють дві різновидності прискорення?
- В якому випадку вектори швидкості і прискорення є співнаправленими, а в якому протинаправленими?
- Прискорення тіла дорівнює –2м/с2. Що це означає?
- Потяг відходить від станції. Як направлене його прискорення?
- Потяг починає гальмувати. Як направлене його прискорення?
- Прискорення тіла дорівнює 2м/с2. На скільки зміниться швидкість цього тіла за 1с?
Вправа №13.
- За 5с швидкість тіла зросла з 2м/с до 6м/с. Визначити прискорення тіла.
- Через 20 с після початку руху спідометр автомобіля показував 72 км/год. З яким середнім прискоренням рухався автомобіль
- Яку швидкість матиме тіло через 20с від початку руху, якщо воно рухається з прискоренням 0,2 м/с2?
- За який час автомобіль, рухаючись з прискореннями 0,2 м/с2 збільшить свою швидкість від 10м/с до 20м/с ?
- Автобус рухаючись з прискоренням 2м/с2, зупинився через 3с. Визначити швидкість автобуса на початку гальмування.
- Автомобіль рухається під ухил з прискоренням 0,4м/с2. Яку швидкість матиме автомобіль через 10с, якщо його початкова швидкість 36км/год?
- За заданим графіком швидкості руху тіла, визначити його прискорення на кожній ділянці шляху.
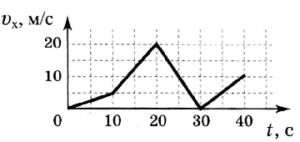
- За заданими графіками швидкості руху тіла, визначити його прискорення. Записати відповідні рівняння швидкості.
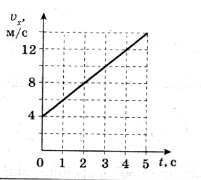
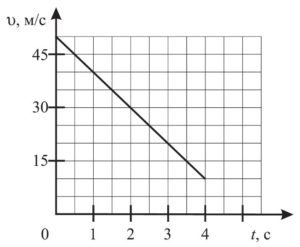
.
§14. Рівняння руху – основний закон кінематики.
Нагадаємо, до числа основних фізичних величин кінематики поступального руху відносяться: час (t), координата (х = ℓх), пройдений шлях (s = ∆x), швидкість (v = ∆x/∆t) та прискорення (а = ∆v/∆t). Якщо ж говорити про основний закон кінематики поступального руху, то він називається рівнянням руху.
Рівняння руху – це закон, в якому стверджується: в загальному випадку, прямолінійний рух матеріальної точки можна описати рівнянням:
х = х0 + v0t + (а/2)t2, де
х – координата матеріальної точки в момент часу t,
х0 – початкова координата точки, тобто її координата в момент часу t = 0,
v0 – початкова швидкість матеріальної точки,
а – прискорення матеріальної точки.
Потрібно зауважити, що в рівнянні х = х0 + v0t + (а/2)t2 арифметичний знак (плюс чи мінус) кожного доданку визначається із умов конкретної задачі. А це означає, що в загальному випадку рівняння руху має вигляд х = ± х0 ± v0t ± (а/2)t2.
Не буде перебільшенням сказати, що знаючи рівняння руху х = х0 + v0t + (a/2)t2 та визначальні рівняння базових фізичних величин кінематики (s = ∆x, v = ∆x/∆t, а = ∆v/∆t), можна розв’язати практично будь-яку задачу кінематики. У всякому разі ті задачі, складність яких не виходить за межі програми загальноосвітньої школи.
Втім, в фізиці не достатньо знати формули. В фізиці набагато важливіше бачити за цими формулами реальні події та їх параметри. Наприклад, в математиці рівняння х = 200 –10t + 0,2t2 це просто квадратне рівняння, яке в загальному випадку має два рішення і яке графічно можна представити у вигляді відповідної параболи. В фізиці, все те що вивчалося в математиці ви маєте знати та вміти застосовувати на практиці. Однак цього зовсім не достатньо для розв’язування задач фізики. Адже в фізиці за кожним рівнянням, за кожною цифрою, за кожною буквою та за кожним знаком, ви маєте бачити реальні події та їх характеристики.
Скажімо, просто поглянувши на рівняння х = 200 –10t + 0,2t2, та розуміючи що це рівняння руху, тобто рівняння вигляду х = х0 + v0t + (а/2)t2, ви відразу ж уявляєте наступну ситуацію. В момент часу t = 0с, дане тіло знаходиться в точці з координатою 200м і рухається у від’ємному напрямку з швидкістю 10м/с. При цьому величина цієї швидкості зменшується (зменшується тому, що знаки (напрямки) швидкості та прискорення є протилежними), а числове значення прискорення становить 0,4м/с2.
а = 0,4м/с2 тому, що (а/2) = 0,2, звідси а = 0,2·2= 0,4).
Таким чином, на основі порівняльного аналізу рівнянь
х = х0 + v0t + (а/2)t2,
х = 200 –10t + 0,2t2,
можна стверджувати:
х0 = 200м; v0 = –10м/с; а = 0,4м/с2; v↓
Загальні зауваження. Якщо в поясненнях до рівняння руху не вказані одиниці вимірювання відповідних величин, то потрібно вважати що цими одиницями є основні одиниці міжнародної системи (СІ): [x] = м; [v] = м/с; [a] = м/с2.
Задача 1. За заданим рівнянням руху x = –200 +15t – 0,4t2, дати загальну характеристику цього руху
Рішення. На основі порівняльного аналізу загального рівняння руху з конкретним рівнянням руху
х = х0 + v0t + (а/2)t2,
x = –200 +15t – 0,4t2,
можна записати:
х0 = –200м; v0 = 15м/с; а = –0,8м/с2; v↓.
Задача 2. За заданим рівнянням руху x = 100 – 8t – 0,1t2, дати загальну характеристику цього руху
Рішення. На основі порівняльного аналізу загального рівняння руху з конкретним рівнянням руху
х = х0 + v0t + (а/2)t2,
x = 100 – 8t – 0,1t2,
можна записати:
х0 = 100м; v0 = –8м/с; а = –0,2м/с2; v↑ (швидкість зростає тому, що знаки (напрямки) швидкості та прискорення є однаковими).
Задача 3. За заданим рівнянням руху х = 5 + 4t, дати загальну характеристику цього руху
Рішення. На основі порівняльного аналізу загального рівняння руху з конкретним рівнянням руху
х = х0 + v0t + (а/2)t2,
х = 5 + 4t,
можна записати:
х0 = 5м; v0 = 4м/с; а = 0м/с2; v = const.
Задача 4. За заданим рівнянням руху x = 200 – 0,5t2, дати загальну характеристику цього руху
Рішення. На основі порівняльного аналізу загального рівняння руху з конкретним рівнянням руху
х = х0 + v0t + (а/2)t2,
x = 200 – 0,5t2,
можна записати:
х0 = 200м; v0 = 0м/с; а = –1м/с2; v↑.
Задача 5. За заданим рівнянням руху x = 5t, дати загальну характеристику цього руху
Рішення. На основі порівняльного аналізу загального рівняння руху з конкретним рівнянням руху
х = х0 + v0t + (а/2)t2,
x = 5t,
можна записати:
х0 = 0м; v0 = –5м/с; а = 0м/с2; v = const.
Зверніть увагу, ми просто дивимося на рівняння руху і отримуємо з нього достатньо велику кількість інформації. Тепер уявіть, скільки інформації можна отримати на основі математичного та логічного аналізу цього рівняння. Втім, інформаційні можливості рівняння руху ми проілюструємо в наступному параграфі. На разі ж розв’яжемо декілька графічних задач.
Задача 6. За заданим малюнком записати рівняння руху автомобіля і автобуса. Визначити де і коли вони зустрінуться.

Загальні зауваження. Рівняння руху х = х0 + v0t + (а/2)t2 є справедливим і в тому випадку коли одиниці вимірювання відповідних величин не є основними одиницями СІ. Важливо лише те, щоб всі одиниці вимірювань були відповідними. Наприклад в умовах нашої задачі всі задані одиниці вимірювань є відповідними: [t] = год; [x] = км; [v] = км/год.
Рішення. На основі аналізу малюнку можна записати:
автомобіль: х1 = 0 + 80t;
автобус: х2 = 360 – 40t.
Оскільки в момент зустрічі х1 = х2, то можна записати 80t = 360 – 40t, звідси 80t + 40t = 360, звідси 120t = 360, звідси t = 3год = tзустр.
хзустр = х1(3) = 80(км/год)∙3год = 240км,
хзустр = х2(3) = 360км – 40(км/год)∙3год = 360км – 120км = 240км,
Відповідь: tзустр = 3год, хзустр = 240км.
В умовах переважної більшості задач, кінематична ситуація задається не певними рівняннями руху, а описується відповідними словами. Тому ви повинні не лише вміти за заданими рівняннями руху уявляти відповідну ситуацію, а й навпаки – за заданою ситуацією записувати відповідні рівняння руху. А це вміння формується в процесі розв’язування конкретних задач.
Задача 7. З пунктів А і В відстань між якими 6км, одночасно і в одному напрямку вийшли два пішоходи з швидкостями відповідно 5км/год та 3км/год. Визначити де і коли вони зустрінуться.
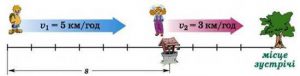
Загальні зауваження. Якщо в умові задачі фізичний зміст того чи іншого параметру чітко не визначений, то завжди обирають таке значення цього параметру яке є найпростішим і таким, що дозволяє розв’язати відповідну задачу. Наприклад, в умові даної задачі чітко не визначено якою (прямолінійною чи криволінійною) є та дорога що з’єднує пункти А і В. В подібних ситуаціях завжди обирають найбільш простий варіант. А цим варіантом є прямолінійна дорога. Крім цього, в умові даної задачі не визначена початкова координата жодного з пішоходів. Тому будемо вважати, що нульовою точкою нашої системи координат є точка А.
Дано:
s = 6км
v1 = 5км/год
v2 = 3км/год
xзустр=? tзустр=?
Рішення. На основі аналізу умови задачі виконуємо відповідний малюнок, на якому задаємо систему координат та відображаємо наявну ситуацію. У відповідності з малюнком і заданою системою координат, записуємо рівняння руху кожного пішохода: х1 = 5t; х2 = 6 + 3t. Оскільки в момент зустрічі х1 = х2, то 5tзустр= 6 + 3tзустр.
Звідси випливає, що 5tзустр – 3tзустр = 6, або tзустр(5 – 3) = 6, або tзустр= 6/2 = 3год.
Таким чином: хзустр= х1(3) = 5(км/год)·3год = 15км.
Відповідь: tзустр = 3год, хзустр = 15км.
Загальні зауваження. Звісно, дану задачу можна розв’язати й по-іншому, наприклад так. Оскільки перший пішохід з швидкістю 5км/год – 3км/год = 2км/год наздоганяє другого пішохода, то відстань 6км він здолає за 6км/2(км/год) = 3год. При цьому пройдений першим пішоходом шлях становитиме 5(км/год)∙3год = 15км. А це означає, що пішоходи зустрінуться через 3год на відстані 15км від точки А.
Таке рішення є правильним і має право на існування. Однак воно має ряд суттєвих недоліків. По-перше, його практично не можливо зробити органічною частиною більш-менш універсальної системи розв’язування задач. По-друге. Такий спосіб дозволяє розв’язувати лише очевидно прості задачі. Тому, якщо ви хочете кваліфіковано та системно розв’язувати задачі кінематики то повинні максимально широко застосовувати рівняння руху.
Контрольні запитання.
- Як змінюється швидкість руху тіла (збільшується чи зменшується), якщо в рівнянні руху:
а) як прискорення так і швидкість мають знак «+»;
б) як прискорення так і швидкість мають знак «–»;
в) прискорення має знак «+», а швидкість – знак «–»;
г) прискорення має знак «–», а швидкість – знак «+»?
- Якого вигляду набуває рівняння руху для рівномірного руху (а=0)?
- Якого вигляду набуває рівняння руху в ситуації коли х0=0?
- Якого вигляду набуває рівняння руху в ситуації коли v0=0 ?
- Якого вигляду набуває рівняння руху в ситуації коли х0=0; v0=0 ?
- Виходячи з того що s = ∆х = х – х0, запишіть рівняння пройденого шляху.
Вправа №14.
- За заданим рівнянням руху, дати загальну характеристику цього руху:
х1 = 100 + 10t + 0,5t2;
х2 = –100 + 5t – 0,2t2;
х3 = –10t – 0,3t2;
х4 = 150 – 0,25t2;
х5 = 8t;
х6 = t2;
х7 = –200.
- В заданій системі відліку рівняння руху тіл мають вигляд х1 = 15t, х2 = 200 + 10t. Де і коли зустрінуться ці тіла?
- В заданій системі відліку рівняння руху тіл мають вигляд х1 = – 200 + 15t, х2 = 10t, Де і коли зустрінуться ці тіла?
- На основі аналізу малюнку, записати рівняння руху мотоцикліста і пішохода.
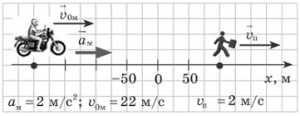
- На основі аналізу малюнку, записати рівняння руху мотоцикліста і велосипедиста.
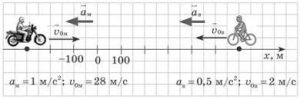
6. На основі аналізу малюнку, записати рівняння руху вантажного і легкового автомобілів, визначити де і коли вони зустрінуться.
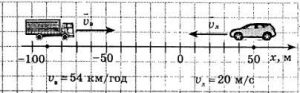
7. З пунктів А і В, відстань між якими 10км, одночасно і назустріч один одному вийшли два пішоходи з швидкостями відповідно 5км/год і 3км/год. Визначити де і коли вони зустрінуться.
8. Рушаючи з місця, автомобіль протягом 10с рухається з прискоренням 2м/с2. Яку швидкість встигає набрати автомобіль? Який шлях проходить при цьому?
9. Із станції вийшов товарний потяг зі швидкістю 36км/год. Через 0,5год, в тому ж напрямку вийшов пасажирський потяг, швидкість якого 72км/год. Через який час і на якій відстані від станції пасажирський потяг наздожене товарний.
.
§15. Розв’язування задач. Тема: Практичне застосування рівняння руху.
Ілюструючи лише незначну частину інформаційних можливостей рівняння руху (х = х0 + v0t + (а/2)t2), розглянемо ряд конкретних задач.
Задача 1. За заданим рівнянням руху х = 100 + 10t – 0,4t2:
1) дати загальну характеристику руху тіла;
2) визначити пройдений тілом шлях за десять секунд;
3) записати рівняння швидкості руху тіла та визначити цю швидкість через 10с;
- Визначити де і коли тіло зупиниться;
Рішення. Відповідаючи на кожне з поставлених запитань можна сказати наступне.
- Дати загальну характеристику руху тіла.
Із порівняльного аналізу рівнянь
х = х0 + v0t + (а/2)t2 та
х = 100 + 10t – 0,4t2, ясно:
х0 =100м; v0 = 10м/с; а = –0,8м/с2; v↓.
- Визначити пройдений тілом шлях за десять секунд: s(10) = ?
s = ∆х = хк – хп = х(10) – х0, де х(10) = ?
х(10) = 100 + 10(10) – 0,4(10)2 = 160м, отже
s(10) = х(10) – х0 = 160 – 100 = 60м.
- Записати рівняння швидкості руху та визначити цю швидкість через 10с.
Оскільки при рівноприскореному русі v = v0 + at, то в умовах нашої задачі (v0 = 10м/с, а = –0,8м/с2) можна записати v = 10 – 0,8t.
Якщо t = 10c, то v(10) = 10 – 0,8(10) = 2м/с.
- Визначити, де і коли тіло зупиниться: хзуп =? tзуп=?
Оскільки в момент зупинки швидкість тіла дорівнює нулю (v = 0), то можна записати: якщо t = tзуп, то v = 10 – 0,8tзуп = 0, звідси tзуп = 10/0,8 = 12,5c
А це означає, що хзуп = х(12,5) = 100 + 10(12,5) – 0,4(12,5)2 = 162,5м.
Задача 2. За заданим рівнянням руху х = 200 – 10t + 0,2t2:
1) дати загальну характеристику руху тіла: х0 = ?; v0 = ?; а = ?
2) визначити пройдений тілом шлях за десять секунд: s(10) = ?
3) визначити швидкість через 10с: v(10) = ?
- Визначити де і коли тіло зупиниться: хзуп = ? tзуп = ?
Рішення.
- Із порівняльного аналізу рівнянь
х = х0 + v0t + (а/2)t2 та
х = 200 – 10t + 0,2t2, ясно:
х0 =200м; v0 = –10м/с; а = 0,4м/с2; v↓.
- s(10) = ∆х = х(10) – х0, де х(10) = ?
х(10) = 200 – 10(10) + 0,2(10)2 = 120м, отже
s(10) = 120 – 200 = – 80м.
- Оскільки v = v0 + at, та враховуючи, що v0 = –10м/с, а = 0,4м/с2, можна записати v = –10 + 0,4t. Якщо t = 10c, то v(10) = –10 + 0,4(10) = –6м/с.
- Оскільки в момент зупинки v = 0, то для t = tзуп, v = –10 + 0,4tзуп = 0, звідси 0,4tзуп = 10, звідси tзуп = 10/0,4 = 25c
хзуп = х(25) = 200 – 10(25) + 0,2(25)2 = 75м.
Задача 3. Відходячи від станції, потяг протягом однієї хвилини рухається з прискоренням 0,4м/с2. Визначте той шлях який проїхав потяг за цей час, і швидкість наприкінці цього шляху.
Дано:
v0 = 0м/с
t = 1хв = 60с
a = 0,4м/с2
s = ? vк = ?
Рішення. Оскільки при рівноприскореному русі s = х – х0 = v0t + (a/2)t2, та зважаючи на те, що v0 = 0, можна записати s = (a/2)t2 = [(0,4м/с2)/2](60c)2 = 0,2(м/с2)3600с2 = 720м. Оскільки при рівноприскореному русі vк = v0 + at, то vк = 0(м/с) + 0,4(м/с2)60с = 24м/с.
Відповідь: s=720м; vк=24м/с.
Задача 4. Рушаючи з місця, автомобіль рухається з прискоренням 2м/с2 і набуває швидкості 20м/с. Визначити пройдений автомобілем шлях.
Дано:
а = 2м/с2
v0 = 0м/с
vк = 20м/с
s = ?
Рішення. В умовах нашої задачі (v0 = 0м/с), рівняння пройденого шляху s = v0t + (а/2)t2, набуває вигляду s = (а/2)t2, де t = ? Оскільки швидкість автомобіля змінюється за законом v = v0 + at, та зважаючи на те, що v0 = 0м/с, можна записати v = at, звідси t = v/a. Таким чином s = (а/2)t2 = (а/2)(v/a)2 = v2/2a.
Розрахунки: s = vк2/2a = (20м/с)2/2∙2м/с2 = 100м
Відповідь: s = 100м.
Загальні зауваження. На основі аналізу рівняння руху можна довести, що при рівноприскореному русі, між пройденим тілом шляхом s, його прискоренням а, та початковою v0 і кінцевою vk швидкостями, існує співвідношення s = (vk2 – v02)/2a. Дане співвідношення не є а ні визначальним рівнянням певної фізичної величини, а ні базовим законом кінематики. Однак зазвичай, при розв’язуванні задач формулу s = (vk2 – v02)/2a, використовують як базову. Тому запам’ятайте, що величину пройденого шляху можна визначити не лише за рівнянням пройденого шляху s = v0t + (а/2)t2, а й за формулою s = (vk2 – v02)/2a.
Задача 5. За заданими графіками руху, записати відповідні рівняння руху.
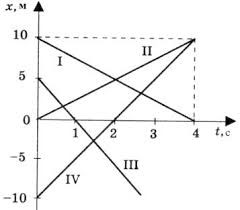
Загальні зауваження. Якщо графіком руху є пряма (відрізок прямої), то відповідний рух є рівномірним (v = const), тобто таким при якому а = 0. А це означає, що рівняння такого руху має вигляд х = х0 + vt.
Рішення. Оскільки представлені на малюнку графіки руху є прямими відрізками, то відповідні рівняння руху мають вигляд x = x0 + vt. Аналізуючи ці графіки можна записати:
- х01 = 10м; v1 = ∆x/∆t = (0м – 10м)/4с = – 2,5м/с, отже рівняння руху
х1 = 10 – 2,5t.
- х02 = 0м; v2 = ∆x/∆t = (10м – 0м)/4с = + 2,5м/с, отже рівняння руху
х2 = 2,5t.
- х03 = 5м; v3 = ∆x/∆t = (0м – 5м)/1с = – 5,0м/с, отже рівняння руху
х3 = 5 – 5,0t.
- х04 = – 10м; v4 = ∆x/∆t = (0м – (–10м)/2с = + 5,0м/с, отже рівняння руху
х4 = –10 + 5,0t.
Задача 6. За заданим графіком руху матеріальної точки визначити її швидкість на кожній ділянці шляху та записати відповідне рівняння руху.

Рішення. Оскільки на кожній ділянці графік руху представляє певну пряму, то відповідні рухи є рівномірними (v=const). А це означає, що швидкість такого руху визначається за формулою v=Δх/Δt. Тому, на основі кількісного аналізу графіку можна записати:
1) ділянка 1: Δt = 10c, х0 = 20м, Δx = –40м, v1=Δx/Δt= –20м/10с= –4м/с,
x1 =20 – 4t;
2) ділянка 2: Δt = 5c, х0 = –20м, Δx = 0м, v2=Δx/Δt= 0м/5с = 0м/с;
x2 = – 20;
3) ділянка 3: Δt = 10c, х0 = – 20м, Δx = 30м, v3=Δx/Δt= 30м/10с= 3м/с,
x3 = –20 + 4t;
4) ділянка 4: Δt = 10c, х0 = 10м, Δx = –20м, v4=Δx/Δt= –20м/10с= –2м/с,
x4 = 10 –2t.
Задача 7. За заданими графіками руху запишіть відповідні рівняння руху. Визначте де і коли тіла зустрінуться. Отриманий результат порівняти з результатом графічного рішення задачі.

Рішення. Оскільки графіки руху тіл є прямолінійними, то це означає, що тіла рухаються з постійною швидкістю (а = 0), і що тому їх рівняння руху мають вигляд х = х0 + vt.
На основі аналізу заданих графіків можна стверджувати.
Тіло 1: х0 = 400м, для Δt = 80c, Δx = 1200м – 400м = 800м, тому v1 = Δx/Δt = 800м/80с = 10м/с. Таким чиним х1 = 400 + 10t.
Тіло 2: х0 = 0м, для Δt = 60c, Δx = 1200м – 0м = 1200м, тому v1 = Δx/Δt = 1200м/60с = 20м/с. Таким чиним х2 = 20t.
Оскільки в момент зустрічі х1 = х2, то 400 + 10t = 20t, звідси 20t – 10t = 400, звідси t = tзустр = 400м/10(м/с) = 40с. При цьому хзустр = х1(40) = х2(40). Дійсно,
х1(40) = 400 + 10(40) = 800м,
х2(40) = 0 + 20(40) = 800м.
Задача 8. Із станції вийшов товарний потяг зі швидкістю 54км/год. Через 0,5год, в тому ж напрямку вийшов пасажирський потяг, швидкість якого 72км/год. Через який час і на якій відстані від станції пасажирський потяг наздожене товарний.
Дано:
v1 = 54км/год
Δt = 0,5год
v2 = 72км/год
tзустр = ?, xзустр = ?
Рішення. Через час Δt = 0,5год, товарний потяг буде на відстані х01 = 54(км/год)∙0,5год = 27км від станції. Виходячи з цього, запишемо рівняння руху товарного і пасажирського потягів на момент відходу пасажирського потягу від станції.
х1 = 27 + 54t,
x2 = 0 + 72t.
Оскільки в момент зустрічі х1 = х2, то 27 + 54t = 72t, звідси 72t – 54t = 27, звідси t = 27км/18(км/год) = 1,5год = tзустр.
хзустр = х1(1,5) = 27 + 54∙1,5 = 108км
хзустр = х2(1,5) = 72∙1,5 = 108км.
Відповідь: tзустр = 1,5год, хзустр = 108км.
Вправа №15.
- За заданим рівнянням руху х = 100 – 15t + 0,5t2:
1) дати загальну характеристику руху тіла;
2) визначити пройдений тілом шлях за 10с;
3) записати рівняння швидкості руху тіла;
4) визначити де і коли тіло зупиниться.
- За заданим рівнянням руху х = –200 + 12t – 0,3t2, визначити де і коли тіло зупиниться.
- За заданим рівнянням руху х = –200 – 12t + 0,3t2, визначити де і коли тіло зупиниться.
- В заданій системі відліку рівняння руху тіл мають вигляд х1 = 16t, х2 = 200 + 12t. Де і коли зустрінуться ці тіла?
- За заданими графіками руху, записати відповідні рівняння руху.
.
- За заданими графіками руху, записати відповідні рівняння руху. Визначити де і коли зустрінуться ці тіла. Отриманий результат порівняти з результатом графічного рішення задачі.

- За заданим графіком руху матеріальної точки визначити її швидкість на кожній ділянці шляху та записати відповідне рівняння руху.

- Із станції А вийшов товарний потяг зі швидкістю 36км/год. Через 0,5год, із станції В відстань до якої 108км назустріч товарному потягу вийшов пасажирський потяг швидкість якого 54км/год. Де і коли зустрінуться потяги?
.
§16. Вільне падіння тіл. Прискорення вільного падіння.
Вільним падінням називають такий рух тіла, який відбувається під дією сили тяжіння та за відсутності суттєвого впливу інших зовнішніх сил, зокрема сили опору повітря. В загальному випадку вільно падаючими вважають не лише ті тіла падіння яких починається з нулевою швидкістю (мал.28а), а й ті які з певною швидкістю кинули вертикально вниз, вертикально вгору, горизонтально або під кутом до горизонту (мал.28б,в,г,д). Адже в кожному з цих випадків, тіло після отримання певного початкового поштовху, рухається під дією лише однієї зовнішньої сили – сили тяжіння (звичайно за умови, що сила опору повітря є не суттєвою).
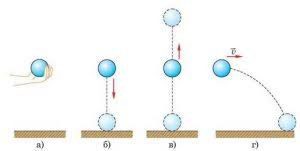
Мал.28. Рух тіла що відбувається під дією сили тяжіння та за відносності суттєвого впливу інших зовнішніх сил, називають вільним падінням тіла.
Характерною особливістю того руху який називається вільним падінням є те, що це падіння відбувається з певним постійним як за величиною так і за напрямком прискоренням, яке називається прискоренням сили тяжіння або прискоренням вільного падіння. Напрям прискорення вільного падіння співпадає з напрямком діючої на тіло сили тяжіння, тобто є направленим вертикально вниз. Просто коли тіло рухається вниз, діючи на нього сила тяжіння призводить до збільшення швидкості руху тіла. Коли ж тіло рухається вгору, то сила тяжіння призводить до зменшення його швидкості.
На перший погляд факт того, що важкі і легкі тіла падають з однаковим прискоренням, здається дивним. Адже та сила тяжіння з якою важкий камінь притягується до Землі в сотні разів перевищує ту силу тяжіння, з якою до Землі притягується легкий камінчик. І тим не менше, важкий камінь і легкий камінчик падають однаково швидко. Сьогодні ми не будемо говорити про те, чому важкі і легкі тіла падають однаково швидко, точніше – з однаковим прискоренням. Сьогодні ми просто констатуємо той експериментальний факт, що під дією сили тяжіння, та за відсутності суттєвого впливу опору повітря, всі тіла падають з однаковим прискоренням, яке називається прискоренням сили тяжіння або прискоренням вільного падіння.

Мал.29. Під дією сили тяжіння та за відсутності суттєвого впливу опору повітря, всі тіла падають з однаковим прискоренням – прискоренням вільного падіння (експериментальний факт).
Підкреслюючи важливість та значимість прискорення вільного падіння, його позначають окремою літерою g (від лат. gravitas – тяжіння). Для Землі, усереднена величина цього прискорення становить g = 9,8067 м/с2.
Прискорення вільного падіння визначальним чином залежить від маси та розмірів того космічного об’єкту який створює відповідну силу тяжіння. Наприклад, для Місяця g = 1,6 м/с2, для Марса g = 3,8 м/с2, для Венери g = 8,8 м/с2, для Юпітера g = 23,5 м/с2, а для Сонця g = 274,0 м/с2.
Зазвичай числове значення земного прискорення вільного падіння приймають рівним g = 9,8м/с2. Втім, зважаючи на те, що кількісне рішення переважної більшості задач на вільне падіння тіл є досить приблизним (приблизним бодай тому, що не враховує силу опору повітря), при наближених розрахунках величину прискорення вільного падіння часто округлюють до g = 10м/с2. Власне при розв’язуванні задач кінематики, з метою максимального спрощення розрахункової частини цих задач, ми будемо вважати, що g = 10м/с2.
Варто ще раз наголосити на тому, що величина і напрям прискорення вільного падіння не залежать від того в якому напрямку рухається тіло і з якою початковою швидкістю воно рухається. Наприклад, в незалежності від того чи вільно відпустили піднятий над землею камінь, чи з певною швидкістю кинули його вертикально вниз, вгору, горизонтально чи під кутом до горизонту, цей камінь рухається з прискоренням g = 9,8м/с2. В незалежності від того рухається камінь вгору чи падає вниз, він рухається з прискоренням g = 9,8м/с2 і це прискорення завжди направлено вертикально вниз. Навіть в точці максимального підйому тіла, де його швидкість дорівнює нулю, тіло має прискорення g = 9,8м/с2. Іншими словами, на всій траєкторії вільного польоту, тіло рухається з прискоренням вільного падіння.

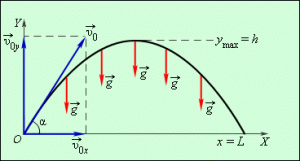
Мал.30. У всіх точках траєкторії вільного польоту, тіло рухається з прискоренням g = 9,8м/с2.
Як і будь-який рівноприскорений рух, вільне падіння тіла можна описати рівнянням виду х = х0 + v0t + (a/2)t2. Відмінність лише в тому, що говорячи про вільне падіння матеріальної точки, її вертикальну координату (висоту) зазвичай позначають літерою h, а прискорення – літерою g. Іншими словами, рух вільно падаючого тіла можна описати формулою h = h0 + v0t + (g/2)t2.
Ілюструючи закономірності того руху який називається вільним падінням тіла, а заодно ілюструючи практичну значимість того закону який називається рівнянням руху, розв’яжемо ряд конкретних задач.
Задача 1. Визначити глибину колодязя, якщо відомо, що випущений із руки камінь досягає води за 2с.
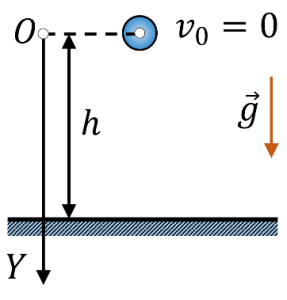
Дано :
v0 = 0 м/с
t = 2 с
h = ?
Рішення. Виконуємо малюнок який відображає фізичний зміст задачі. Задаємо систему координат та записуємо рівняння руху тіла в цій системі, тобто формулу яка має вигляд h = h0 + v0t + (g/2)t2. В умовах даної задачі h0 = 0м; v0 = 0м/с, це рівняння набуває вигляду: h = (g/2)t2, де g=10м/с2. Враховуючи, що t = 2c, виконуємо відповідні розрахунки.
Розрахунки: h = (10(м/с2)(2с)2/2 = 20м;
Відповідь: h = 20м.
Загальні зауваження. Конкретний вигляд рівняння руху, визначально залежить від того, як задана система координат. Наприклад, якщо в даній задачі за початок відліку взяти рівень дна колодязя, а вісь 0у направити вертикально вгору, то в цьому випадку рівняння руху h = h0 + v0t + (g/2)t2 набуде вигляду h = h0 – (g/2)t2, де h0 = ? Втім, рішення задачі та її відповідь, в обох випадках буде однаковим. Дійсно, в момент падіння тіла h = 0, тому h0 – (g/2)t2 = 0, звідси h0 = (g/2)t2 = 20м.
Задача 2. Тіло вільно падає з висоти 45м. Визначте час падіння тіла і його швидкість в момент падіння.

Дано:
h = 45м
tпад = ?
vпад = ?
Рішення. Виконуємо малюнок, задаємо систему координат та записуємо відповідне рівняння руху тіла, тобто формулу яка має вигляд h = h0 + v0t + (g/2)t2. В умовах даної задачі (h0 = 0м; v0 = 0м/с), це рівняння набуває вигляду: h = (g/2)t2. Звідси випливає t2 = 2h/g, звідси t = √(2h/g).
В загальному випадку рівняння швидкості рівноприскореного руху має вигляд v = v0 + at. В умовах нашої задачі (v0 = 0, a = g), це рівняння набуває вигляду v = gt.
Розрахунки: tпад = √(2h/g) = √(2·45м/10(м/с2))= √(9с2) = 3с,
vпад = gt = 10(м/с2)∙3с = 30м/с.
Відповідь: tпад= 3с, vпад = 10м/с.
Задача 3. Тіло кинули вертикально вгору з швидкістю 20м/с. На якій висоті буде тіло через: 1с; 2с; 3с; 4с польоту?
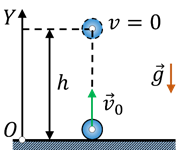
Дано :
v0 = 20 м/с
t1=1c; t2=2c
t3=2c; t4=4c
h1=?; h2=?
h3=?; h4=?
Рішення. Виконуємо малюнок, задаємо систему координат та записуємо відповідне рівняння руху тіла, тобто формулу яка має вигляд h = h0 + v0t + (g/2)t2. А оскільки в умовах нашої задачі h0 = 0м; g = 10м/с2, то рівняння руху набуває вигляду: h = v0t – (g/2)t2, або h = 20t – 5t2.
Розрахунки:
для t1 = 1c: h1=20(1) – 5(1)2 = 20 – 5 = 15м;
для t2 = 2c: h2=20(2) – 5(2)2 = 40 – 20 = 20м;
для t3 = 3c: h3=20(3) – 5(3)2 = 60 – 45 = 15м;
для t4 = 4c: h4=20(4) – 5(4)2 = 80 – 80 = 0м;
Відповідь: h1=15м; h2=20м; h3=15м; h4=0м.
Контрольні запитання.
- Що називають вільним падінням тіла?
- Чи можна стверджувати, що кинуте в горизонтальному напрямку тіло, знаходиться в стані вільного падіння? Чому?
- Чи залежить величина і напрям прискорення вільного падіння тіла від напрямку руху цього тіла?
- Чи залежить прискорення вільного падіння від маси падаючого тіла?
- Від чого залежить прискорення вільного падіння тіла?
- Одне тіло випустили з руки, а друге кинули вертикально вниз. Яке з цих тіл матиме більше прискорення вільного падіння?
- Тіло кинули вертикально вгору. Чому ми стверджуємо, що те прискорення з яким рухається тіло направлене вертикально вниз?
- Чи може тіло, маючи нульову швидкість, мати певне прискорення? Наведіть приклад.
Вправа 16.
- Визначити глибину ущелини, якщо камінь, падаючи без початкової швидкості досягає її дна за 4с.
- Тіло падає без початкової швидкості. Яка його швидкість після 2с падіння?
- Тіло подає з висоти 20м. Визначте час падіння тіла.
- 4. За який час тіло, що падає без початкової швидкості, пролетить шлях 10м?
- Тіло падає з початковою швидкістю 5м/с, якою буде ця швидкість через 1с падіння?
- Тіло кинули вертикально вгору з швидкістю 15м/с. На якій висоті буде це тіло через 1с польоту? Через 2с польоту?
- Камінь кинули вертикально вниз з початковою швидкістю 5м/с. З якої висоти кинули камінь якщо він падає 2с?
- Тіло падає без початкової швидкості з висоти 45м. Визначте середню швидкість падіння тіла.
.
§17. Розв’язування задач. Тема: Вільне падіння тіла.
Нагадаємо, вільним падінням називають такий рух тіла, який відбувається під дією сили тяжіння та за відсутності суттєвого впливу інших зовнішніх сил, зокрема сили опору повітря. На всій траєкторії вільного падіння, в незалежності від швидкості та напрямку руху тіла, воно рухається з постійним, направленим вертикально вниз прискоренням, яке називається прискоренням вільного падіння g = 9,8м/с2 (при наближених розрахунках g = 10м/с2). В загальному випадку, для того поступального руху який називається вільним падінням, рівняння руху х = х0 + v0t + (a/2)t2 набуває вигляду h = h0 + v0t + (g/2)t2.
Задача 1. На яку максимальну висоту підніметься тіло. Якщо його кинули вертикально вгору з швидкістю 20м/с?

Дано :
v0 = 20 м/с
hmax = ?
Рішення. Виконуємо малюнок, задаємо систему координат та записуємо відповідне рівняння руху тіла, тобто формулу яка має вигляд h = h0 + v0t + (g/2)t2. А оскільки в умовах даної задачі h0 = 0м; g =1 0м/с2, то рівняння руху набуває вигляду: h = v0t – (g/2)t2, або h=20t–5t2. Із аналізу рівняння руху ясно, що для визначення максимальної висоти підйому тіла (h = hmax) необхідно визначити час цього підйому t = tmax.
Оскільки на максимальній висоті, тобто в момент часу t = tmax, швидкість тіла дорівнює нулю, та зважаючи на те, що величина цієї швидкості визначається за формулою v = v0–gt, можна записати: v0–gtmax = 0. Звідси, tmax = v0/g = 20(м/с)/10(м/с2) = 2с.
Розрахунки: hmax = 20tmax – 5tmax2 = 20(м/с)2с – 5(м/с2)(2с)2 = 40м – 20м = 20м.
Відповідь: hmax = 20м.
Задача 2. З якою швидкістю тіло кинули вертикально вгору, якщо воно повернулося через дві секунди?

Дано :
tпол = 2с
v0 = ?
Рішення. Виконуємо малюнок, задаємо систему координат та записуємо відповідне рівняння руху тіла, тобто формулу яка має вигляд h = h0 + v0t + (g/2)t2. А оскільки в умовах даної задачі h0 = 0м; g = 10м/с2, то рівняння руху набуває вигляду: h = v0t – (g/2)t2. Виходячи з того, що 2с, це час польоту тіла, тобто той час за який тіло вилетівши з рівня h = 0 знову повертається на рівень h = 0, можна записати v0t – (g/2)t2 = 0, звідси v0t = (g/2)t2, звідси v0 = gt/2.
Розрахунки: v0 = gt/2 = 10(м/с2)2с/2 = 10м/с.
Відповідь: v0 = 10м/с.
Задача 3. Тіло, що знаходиться на висоті 10м кинули горизонтально з швидкістю 20 м/с. Визначити горизонтальну дальність польоту тіла.
Загальні зауваження. Рух тіла кинутого горизонтально є криволінійним, причому таким, який завжди можна розкласти на дві складові: горизонтальну та вертикальну. А це означає, що такий криволінійний рух описується системою двох рівнянь:
– рівняння руху по горизонталі;
– рівняння руху по вертикалі.
При цьому кожне з цих рівнянь є похідним від загального рівняння руху х = х0 + v0t + (a/2)t2.
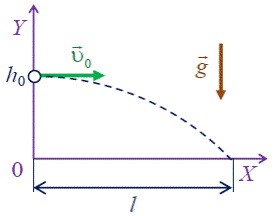
Дано:
h0 = 10 м
v0 = 20 м/с
ℓ = ?
Рішення. Виконуємо малюнок який відображає наявну ситуацію та задаємо відповідну систему координат. Криволінійний рух даного тіла по суті є результатом двох незалежних рухів: рівномірного горизонтального та рівноприскореного вертикального. Зважаючи на ці обставини, задаємо систему координат і записуємо рівняння кожного окремого руху, тобто формулу яка має вигляд х = х0 + v0t + (a/2)t2.
– горизонтальний рух: оскільки х = ℓ; х0 = ℓ0 = 0м; a = 0м/с2, то ℓ = v0t
– вертикальний рух: оскільки х=h; х0=h0; v0=0м/с; a=g=10м/с2, то h=h0 – gt2/2.
Таким чином даний рух описують два рівняння:
1) ℓ = v0t, або ℓ = 20t;
2) h = h0 – gt2/2, або h = 10 – 5t2.
Із аналізу рівнянь ясно, що для того щоб визначити дальність польоту тіла (ℓ = 20t), необхідно визначити тривалість цього польоту (t = tпол). А оскільки в момент падіння тіла, h = 0, то 10 – 5(tпол)2 = 0, звідси (tпол)2 = (10/5) = 2с2, звідси tпол=√2c2 = 1,4с.
Розрахунки: ℓ = 20tпол = 20(м/с)∙1,4с= 28м.
Відповідь: ℓ = 28м.
Задача 4. Тіло, що знаходиться на висоті 15м кинули горизонтально з швидкістю 20 м/с. Визначите координати цього тіла через 1с польоту.

Дано:
h0 = 15 м
v0 = 20 м/с
t1 = 1c
ℓ1=? h1=?
Рішення. Задаємо систему координат і записуємо рівняння кожного окремого руху, тобто формулу яка має вигляд х = х0 + v0t + (a/2)t2.
– горизонтальний рух: ℓ = v0t, або ℓ = 20t;
– вертикальний рух: h = h0 – gt2/2, або h = 15 – 5t2.
Якщо t1 = 1c, то ℓ1 = 20t1 = 20(м/с)∙1с = 20м;
h1 = 15 – 5t12 = 15м – 5(м/с2)∙(1с)2 = 10м.
Відповідь: ℓ1 = 20м; h1 = 10м.
Контрольні запитання.
- Як з плином часу змінюється модуль швидкості тіла, кинутого вертикально вгору?
- Чому дорівнює швидкість тіла, кинутого вертикально вгору, у найвищій точці його підйому?
- Чому дорівнює прискорення тіла, кинутого вертикально вгору, у найвищій точці його підйому?
- По якій траєкторії рухається тіло, кинуте горизонтально?
- З яким прискоренням рухається тіло, кинуте горизонтально?
- Чи залежить час польоту тіла, кинутого горизонтально, від величини його початкової швидкості?
Вправа 17.
- Тіло кинули вертикально вгору з швидкістю 25м/с. На якій висоті буде це тіло через 1с; 2с; 3с польоту?
- 2. Тіло кинули вертикально вгору з швидкістю 15м/с. Визначити максимальну висоту підйому тіла.
- Стрілу випустили з лука вертикально вгору. При цьому, вона впала на землю через 6с. Якою була початкова швидкість стріли?
4.Тіло кинули вертикально вниз швидкістю 10м/с. На якій висоті було тіло, якщо воно впало через 2с? Якою буде швидкість тіла в момент падіння?
- Тіло, що знаходиться на висоті 20м кинули горизонтально з швидкістю 15м/с. Визначити горизонтальну дальність польоту тіла.
- Тіло, що знаходиться на висоті 20м кинули горизонтально з швидкістю 20м/с. Визначите координати цього тіла через 1,5с польоту.
- З вікна кинуто м’яч у горизонтальному напрямку з швидкістю 12м/с. Він упав на землю через 2с. З якої висоти було кинуто м’яч і на якій відстані від будинку він упав.
.
§18. Рух матеріальної точки по колу. Доцентрове прискорення.
Довільний поступальний рух матеріальної точки (тіла) можна представити як певну сукупність прямолінійних та криволінійних ділянок. В загальному випадку, криволінійна траєкторія руху матеріальної точки може бути надзвичайно складною. Однак будь яку криволінійну траєкторію, можна представити як певну сукупність фрагментів кіл. А це означає, що знаючи закономірності руху матеріальної точки по колу, можна описати будь який криволінійний рух.
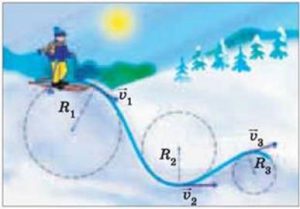
Мал.31. Довільний рух матеріальної точки, представляє собою певну сукупність прямолінійних та криволінійних ділянок.
Характерною особливістю руху матеріальної точки по колу є те, що в незалежності від швидкості руху, ця точка завжди рухається з певним прискоренням, яке характеризує зміну швидкості за напрямком. Дійсно, припустимо що матеріальна точка з певною незмінною за величиною (модулем) швидкістю (|v1| = |v2| = … = const), рухається по колу радіусу R (мал.32а). Не важко бачити, що в процесі такого руху, напрям швидкості постійно змінюється(v1 ≠ v2 ≠… ≠ const). А це означає, що відповідна точка рухається з певним прискоренням, яке характеризує зміну швидкості за напрямком. Це прискорення називають доцентровим (позн. ад). Така назва обумовлена фактом того, що в будь якій точці траєкторії, доцентрове прискорення направлено до центру того кола яке описує відповідна точка.
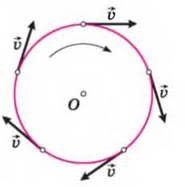
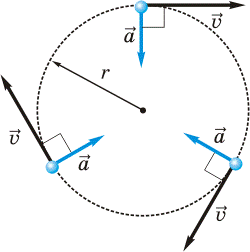
Мал.32. В процесі руху матеріальної точки по колу, напрям її швидкості постійно змінюється і тому вона рухається з відповідним прискоренням.
Виходячи з визначального рівняння прискорення (а = ∆v/∆t), можна довести, що величина доцентрового прискорення визначається за формулою ад = v2/R, де v – швидкість тіла в даній точці траєкторії; R – радіус кривизни цієї траєкторії.
Доцентрове прискорення – це таке прискорення, яке характеризує зміну швидкості за напрямком і яке дорівнює відношенню квадрату швидкості руху тіла (матеріальної точки) до радіусу кривизни його траєкторії у відповідній точці.
Позначається: ад
Визначальне рівняння: ад = v2/R
Одиниця вимірювання: [ад] = м/с2, (метр на секунду в квадраті).
Таким чином, якщо тіло рухається по колу, то в незалежності від того змінюється модуль його швидкості, чи не змінюється, це тіло має певне доцентрове прискорення, величина якого визначається за формулою ад = v2/R, і яке завжди направлено до центру відповідного кола.
Не важко збагнути, що на прямолінійних ділянках траєкторії, доцентрове прискорення неминуче дорівнює нулю. І це природньо. Адже на таких ділянках, напрям швидкості залишається незмінним і тому прискорення, яке характеризує зміну швидкості за напрямком має бути нульовим. Те, що на прямолінійних ділянках траєкторії, доцентрове прискорення дорівнює нулю, випливає не лише з визначення цього прискорення, а й з його визначального рівняння. Дійсно. Будь-яку прямолінійну ділянку траєкторії, можна вважати частиною кола з безкінечно великим радіусом (R = ∞). А це означає, що для таких ділянок aд = v2/R = v2/∞ = 0.
Рух по колу є надзвичайно поширеним як в природі загалом так і в штучно створеній техніці зокрема. По колу рухаються елементи коліс, шківів, валів та шестерень машин і механізмів. По колу рухаються точки секундних, хвилинних та годинникових стрілок годинників, лопатей вентиляторів, вітряків, турбін та корабельних двигунів. Практично по колу Місяць обертається навколо Землі, Земля – навколо Сонця, Сонце – навколо центру Галактики, тощо.
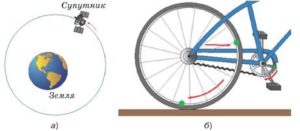
Мал. 33. Деякі приклади руху тіл та елементів тіл по колу.
Якщо в процесі руху по колу, модуль швидкості матеріальної точки залишається незмінним (v = const), то відповідний рух називають рівномірним рухом матеріальної точки по колу. Рівномірний рух матеріальної точки по колу характеризується не лише певною швидкістю (v) та певним доцентровим прискоренням (ад), а й певною повторюваністю (періодичністю). Цю повторюваність характеризують двома величинами: періодом обертання (Т) та частотою обертання (ν).
Наприклад, період обертання секундної стрілки годинника становить 60с, період обертання Землі навколо своєї осі – одна доба (Т = доба = 86400с); період обертання Місяця навколо Землі – 27,3доби (Т = 27,3доби = 2,36·106с); період обертання Землі навколо Сонця – один рік (Т = рік = 3,2·107с), а період обертання Сонячної системи навколо центру Галактики – 240 мільйонів земних років.

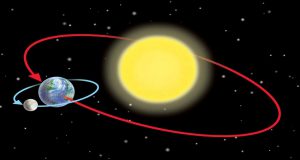
Мал.34. Рівномірний рух по колу, характеризується не лише певною швидкістю (v) та певним доцентровим прискоренням (ад), а й певною повторюваністю (періодичністю).
Період обертання (період) – це фізична величина, яка характеризує часову періодичність (повторюваність) обертального процесу і яка дорівнює тому проміжку часу за який система здійснює один повний оберт.
Позначається: Т
Визначальне рівняння: Т = t/n, де n – кількість обертів системи здійснених за час t;
Одиниця вимірювання: [Т] = с, (секунда).
Наприклад, якщо матеріальна точка в процесі рівномірного руху по колу за 5с здійснила 10 обертів, то період її обертання 0,5с: Т= t/n = 5с/10 = 0,5с.
Частота обертання (частота) – це фізична величина, яка характеризує частотну періодичність обертального процесу і яка дорівнює тій кількості обертів системи, яку вона здійснює за одиницю часу.
Позначається: ν (ню)
Визначальне рівняння: ν = n/t
Одиниця вимірювання: [ν] = 1/c = Гц, (герц).
Наприклад, якщо матеріальна точка в процесі рівномірного руху по колу за 5с здійснила 10 обертів, то частота її обертання 2Гц: ν = n/t = 10/5c = 2(1/с) = 2Гц.
Із визначальних рівнянь періоду і частоти (T = t/n; ν = n/t) з усією очевидністю випливає, що ці фізичні величини взаємопов’язані, і що цю взаємопов’язаність відображають співвідношення: T = 1/ν; ν = 1/T. Тому якщо, наприклад, за умовою задачі задано період обертання системи Т = 4с, то ви завжди можете визначити частоту цього обертання ν = 1/Т = 1/4с = 0,25Гц, і навпаки, якщо ν = 50Гц, то Т = 1/50Гц = 0,02с.
Вимірювання показують, що довжина тієї лінії яка називається колом (довжина кола), визначається за формулою ℓ=2πR, де R – радіус кола, π=3,14 постійна величина яка є однією з базових констант як фізики так і математики. Враховуючи даний факт, можна довести, що між періодом обертання Т, радіусом кола R та тією лінійною швидкістю v з якою матеріальна точка рухається по колу, існує співвідношення v = 2πR/T. Дійсно. Оскільки за визначенням v = s/t, та враховуючи, що за час t = Т (за один повний оберт) матеріальна точка рухаючись по колу проходить шлях s = 2πR, можна записати v = s/t = 2πR/T.
Задача 1. Визначити період та частоту обертання хвилинної стрілки годинника.
Рішення. Оскільки хвилинна стрілка годинника робить повний оберт (n=1) за одну годину (t = 1год = 60хв = 3600с), то період її обертання Т = t/n = 3600c. При цьому частота цього обертання: ν = n/ t= 1/3600 = 0,0002(7) = 2,(7)·10–4Гц.
Задача 2. За 10с колесо автомобіля зовнішній радіус якого 25см, здійснює 100 обертів. Визначте період та частоту обертання колеса. Визначте швидкість руху автомобіля.
Дано:
t = 10с
n = 100
R = 25см = 0,25м
T=? ν=? vавт = ?
Рішення. Оскільки за визначенням T = t/n; ν = n/t, то Т = 10с/100 = 0,1с; ν = 100/10с = 10Гц. Оскільки v = s/t, та зважаючи, що за один оберт колеса (за t = Т), автомобіль переміщується на s = 2πR, можна записати vавт = s/t = 2πR/T = 2·3,14·0,25м/0,1с = 15,7м/c.
Відповідь: Т = 0,1с; ν = 10Гц; vавт = 15,7м/с.
Задача 3. Відомо, що радіус Землі 6370км, а період її обертання навколо власної осі 1 доба. Визначити швидкість обертання тих тіл які знаходяться на екваторі Землі

Дано:
R = 6400км = 6,4·106м
T = 1доба = 8,64·104с
v = ?
Рішення. Оскільки за визначенням v = s/t, та враховуючи, що за один повний оберт Землі (t = T), ті тіла які знаходяться на її екваторі проходять шлях s = 2πR, можна записати v = s/t = 2πR/T.
Розрахунки: v = 2πR/T = 2·3,14·6,4·106м/8,64·104с = 465м/с = 1670км/год.
Відповідь: v = 1670км/год.
Контрольні запитання.
- Чому матеріальна точка, яка з постійною за модулем швидкістю рухається по колу, рухається з прискоренням? Як називається це прискорення? Чому воно має таку назву?
- Що характеризує доцентрове прискорення?
- Доведіть, що на прямолінійних ділянках траєкторії, доцентрове прискорення завжди дорівнює нулю.
- Які величини характеризують повторюваність обертального руху? Як пов’язані ці величини?
- Доведіть, що між періодом обертання Т, радіусом кола R та тією лінійною швидкістю v з якою матеріальна точка рухається по колу, існує співвідношення v = 2πR/T.
- Чому в процесі добового обертання Землі, лінійні швидкості різних за широтою точок її поверхні є різними? В яких місцях ця швидкість є найбільшою, а в яких – найменшою?
Вправа №18.
- Автомобіль рухається заокругленням дороги радіус якого 100м, зі швидкістю 36км/год. Чому дорівнює доцентрове прискорення автомобіля?
- З якою швидкістю має рухатися автомобіль заокругленням дороги радіусом 100м, щоб величина його доцентрового прискорення дорівнювала 2м/с2?
- Якого радіусу має бути заокруглення дороги, щоб при швидкості 72км/год доцентрове прискорення автомобіля становило 1м/с2?
- За 20 секунд колесо автомобіля здійснює 40 обертів. Визначити період та частоту обертання колеса.
- Визначити період і частоту обертання хвилинної та годинникової стрілок годинника.
- Вал діаметром 20см при обертанні робить один оберт за 0,4с. Визначте лінійну швидкість точок на поверхні вала.
- Частота обертання коліс автомобіля 15Гц. З якою швидкістю рухається автомобіль, якщо зовнішній радіус його коліс 30см?
- З якою лінійною швидкістю (в км/с) Земля обертається навколо Сонця, якщо радіус земної орбіти 1,5∙108км? Порівняйте цю швидкість зі швидкістю кулі 0,5км/с. Зробіть висновки.
.
§19. Коливання. Фізичний та математичний маятники.
В фізиці, процеси які так чи інакше повторюються називаються коливаннями. Коливається наприклад, збурена поверхня води та збурена землетрусом поверхня землі. В поривах вітру коливаються гілки дерев та листя на них. Під дією потягів та машин що рухаються, коливаються мости і дороги. Вібрують струни музичних інструментів та мембрани гучномовців. Коливальним чином рухаються маятники, стрілки та шестерні механічних годинників, поршні, клапани і колінчасті вали автомобільних двигунів. Періодично змінюються дні і ночі, пори року та їм відповідні життєві цикли рослин і тварин. Ритмічно б’ється серце і працюють легені вашого організму. Певним чином коливаються атоми, молекули і ті частинки з яких вони складаються. Звук який ви чуєте і світло яке бачите, це також результат певних коливальних процесів. Не буде перебільшенням сказати, що майже все що відбувається в Природі, так чи інакше пов’язано з тими чи іншими коливальними процесами.
Однією з найпростіших коливальних систем є так званий фізичний маятник. Фізичний маятник, це механічна коливальна система, яка представляє собою тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо осі, що не проходить через центр маси тіла. Наприклад, якщо ви візьмете будь яке тверде тіло, скажімо лінійку, виделку, ножиці чи молоток і закріпите його так щоб воно могло вільно обертатись навколо осі яка не проходить через центр маси тіла, то отримаєте відповідний фізичний маятник. Загально відомим прикладом фізичного маятника є дитяча гойдалка. Однією з різновидностей фізичного маятника є так званий нитяний маятник, який представляє собою масивне тіло що висить на тонкій нитці (мотузці, дротині, тощо).
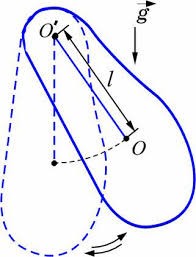


Мал.35. Приклади фізичних маятників.
Параметри коливального руху реального фізичного маятника, залежать від багатьох обставин: геометричних і вагових характеристик тіла, величини сили опору повітря, величини виникаючих в осі обертання тіла сили тертя, деформаційно-енергетичних втрат, тощо. Тому, при теоретичних дослідженнях, реальний фізичний маятник замінюють відповідною ідеалізованою моделлю, яка називається математичним маятником.
Математичний маятник – це ідеалізована модель фізичного маятника, яка представляє собою масивну матеріальну точку що висить на надтонкій, невагомій та нерозтяжній нитці і в процесі коливань якої відсутні будь які втрати енергії. Якщо нитка реального нитяного маятника достатньо тонка, міцна та легка, а прикріплене до неї тіло, достатньо масивне і таке що виготовлено з щільного матеріалу (залізо, мідь, свинець, тощо), то коливальні властивості цього реального маятника майже не відрізнятимуться від властивостей відповідного за довжиною математичного маятника.
По суті, основна відмінність фізичного маятника від відповідного математичного маятника полягає в тому, що вільні коливання реального фізичного маятника в тій чи іншій мірі згасаючі, а коливання математичного маятника – незгасаючі. Крім цього, нитяний маятник – це маятник реальний, а математичний маятник – це маятник віртуально-теоретичний.

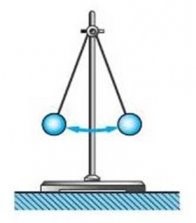
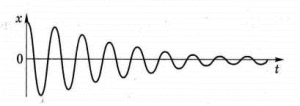
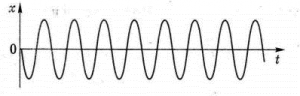
Мал.36. Коливання реального фізичного маятника є згасаючими, а коливання ідеального математичного маятника – незгасаючими.
Подібно до того як періодичність обертального руху характеризують періодом (T = t/n) та частотою (ν = n/t) обертання, періодичність всіх коливальних систем загалом і фізичного (математичного) маятника зокрема, характеризують періодом та частотою коливань.
Період коливань (період) – це фізична величина, яка характеризує часову періодичність (повторюваність) коливального процесу і яка дорівнює тому проміжку часу за який система здійснює одне повне коливання.
Позначається: Т
Визначальне рівняння: Т = t/n, де n – кількість коливань системи здійснених за час t;
Одиниця вимірювання: [Т] = с, секунда.
Наприклад, якщо нитяний маятник за 20 секунд здійснює 16 повних коливань, то період цих коливань 1,25с: Т= t/n = 20с/16 = 1,25с.
Частота коливань (частота) – це фізична величина, яка характеризує частотну періодичність коливального процесу і яка дорівнює тій кількості коливань системи, яку вона здійснює за одиницю часу.
Позначається: ν
Визначальне рівняння: ν = n/t
Одиниця вимірювання: [ν] = 1/c = Гц, герц.
Наприклад, якщо за 20 секунд нитяний маятник здійснює 16 коливань, то частота цих коливань 0,8Гц: ν = n/t = 16/20c = 0,8Гц.
По суті обертальний рух тіла (рух матеріальної точки по колу), є однією з різновидностей фізичних коливань – процесів, які так чи інакше повторюються. При цьому ті величини які ми називали періодом та частотою обертання, є частковими випадками більш загальних величин – періоду та частоти коливань.
Суттєва відмінність між обертальним рухом тіла та коливаннями фізичних, математичних, пружинних, крутильних та інших маятників, полягає лише в тому, що останні (маятники) характеризуються не лише періодом і частотою, а й амплітудою коливань.
Амплітуда коливань (амплітуда) – це фізична величина, яка характеризує максимальне за величиною (амплітудне) відхилення коливальної системи від нульового положення (положення рівноваги) і яка дорівнює цьому відхиленню. Позначається символом відповідної змінної величини з індексом «м»: хм, vм, Ім, Uм, тощо. Визначається як параметр конкретного коливального процесу. Вимірюється в одиницях відповідної фізичної величини: [xм] = м; [vм] = м/с; [Iм] = А; [Uм] = В і т.д.
Наприклад нитяний маятник здійснює механічні коливання, в процесі яких певним чином змінюється координата тієї матеріальної точки яка є тілом маятника. При цьому максимальне відхилення цієї точки від положення рівноваги (хм) і є амплітудою коливань маятника.
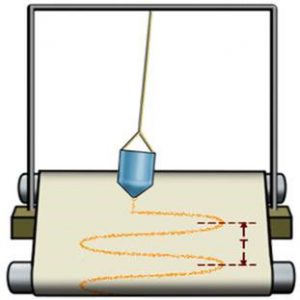
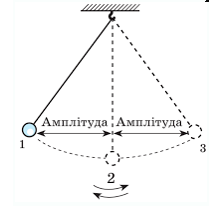
Мал.37. Амплітуда коливань – це максимальне відхилення коливальної системи від нульового положення (положення рівноваги)
Можна довести, що період коливань математичного маятника визначається за формулою Т = 2π·√(ℓ/g) де ℓ – довжина маятника, g – прискорення сили тяжіння. Із аналізу формули Т = 2π·√(ℓ/g) видно, що період коливань математичного маятника не залежить ні від маси тіла, ні від кута його відхилення (амплітуди коливань). Цей період визначальним чином залежить лише від довжини маятника та прискорення сили тяжіння.
Потрібно зауважити, що періоди коливань реального фізичного маятника та відповідного за довжиною ідеального математичного маятника є однаковими і такими, що визначаються за формулою Т = 2π√(ℓ/g). При цьому довжиною фізичного маятника (ℓ) називають відстань від осі обертання тіла фізичного маятника, до центру мас цього тіла.
Задача 1. Визначте період коливань математичного маятника, довжина якого 0,1м; 0,5м; 1,0м.
Дано:
ℓ1 = 0,1м
ℓ2 = 0,5м
ℓ1 = 1,0м
g = 10м/с2
Т1 = ? Т2 = ? Т3 = ?
Рішення. Оскільки період коливань математичного маятника визначається за формулою Т = 2π·√(ℓ/g), то:
Т1 = 2·3,14·√(0,1м/10м/с2) = 6,28·√(0,01с2) = 6,28·0,1с ≈ 0,6с;
Т2 = 2·3,14·√(0,5м/10м/с2) = 6,28·√(0,05с2) = 6,28·0,224с ≈ 1,4с;
Т3 = 2·3,14·√(1,0м/10м/с2) = 6,28·√(0,1с2) = 6,28·0,316с ≈ 2,0с.
Задача 2. Визначте періоди коливань математичного маятника довжиною 1м на Землі (g = 9,8м/с2), на Місяці (g = 1,6м/с2) та на Марсі (g = 3,7м/с2).
Дано:
ℓ = 1м
g1 = 9,8м/с2
g2 = 1,6м/с2
g3 = 3,7м/с2
T1=? T2=? T3=?
Рішення. Оскільки період коливань математичного маятника визначається за формулою Т = 2π·√(ℓ/g), то:
Т1 = 2·3,14·√(1м/9,8м/с2) = 6,28·√(0,102с2) = 2,0с;
Т2 = 2·3,14·√(1м/1,6м/с2) = 6,28·√(0,625с2) = 5,0с;
Т3 = 2·3,14·√(1м/3,7м/с2) = 6,28·√(0,270с2) = 3,3с.
Задача 3. Якої довжини має бути математичний маятник, щоб період його коливань дорівнював 10с?
Дано:
Т = 10с
g = 9,8м/с2
ℓ = ?
Рішення. Період коливань математичного маятника визначається за формулою Т = 2π·√(ℓ/g). Оскільки невідома величина (ℓ) знаходиться під знаком кореня квадратного, то щоб позбутися цього кореня, потрібно праву і ліву частини рівняння піднести в квадрат: (Т)2 = [2π·√(ℓ/g)]2 = 4π2ℓ/g, звідси ℓ = T2g/4π2.
Розрахунки: ℓ = T2g/4π2 = (10с)2·9,8(м/с2)/4·3,142 = 25м.
Відповідь: ℓ = 25м.
Контрольні запитання.
- Які процеси називаються коливальними? Наведіть приклади таких процесів.
- Що називають фізичним маятником? Наведіть приклади таких маятників.
- Що називають математичним маятником? Чи існують такі маятники в реальності?
- Чим відрізняється фізичний маятник від маятника математичного?
- Що називають амплітудою коливань?
- Чому дорівнює довжина фізичного маятника?
- Чи залежить період коливань нитяного (математичного) маятника від: маси тіла маятника; амплітуди коливань маятника; довжини маятника; параметрів гравітаційного поля Землі?
Вправа №19.
- За хвилину маятник здійснює 20 коливань. Визначити період та частоту цих коливань.
- Скільки коливань здійснює маятник за 3 хвилини, якщо частота його коливань 5Гц?
- Серце кита здійснює 7 скорочень за 1хв, а серце горобця за аналогічний час здійснює 1200 скорочень. Визначте частоту пульсу кита і горобця.
- Частота коливань крил комара 600Гц, а період коливань крил джмеля 5мс. Яка з комах і на скільки більше зробить помахів крил за 1хв?
- Визначити період і частоту коливань математичного маятника, якщо його довжина 2м, g=10м/с2.
- Скільки коливань здійснить за 1хв математичний маятник, довжина якого 20см?
- Період коливань математичного маятника 2с. Яка довжина цього маятника?
- Якої довжини має бути математичний маятник щоб на Місяці частота його коливань дорівнювала 2Гц?
.
§20. Кінематика. Узагальнююче повторення.
Важливою складовою процесу вивчення фізики є узагальнюючі повторення. Мета такого повторення полягає в тому, щоб із всього різноманіття попередньо отриманої інформації, виділити основну і представити її у вигляді гранично стислої системи знань.
Зазвичай узагальнення та систематизація вивченого в межах тієї чи іншої теми, відбувається за схемою: основні поняття – основні фізичні величини – основні закони – практичне застосування отриманих знань. Власне за такою схемою і будемо узагальнювати вивчене в кінематиці, статиці та динаміці.
Кінематика – це розділ механіки, в якому вивчають параметри та закономірності механічного руху тіл, без врахування їх мас і діючих на них сил. Іншими словами, в кінематиці вивчають параметри та закономірності механічного руху тіл і не вивчають причини цього руху.
Механічний рух – це такий рух (процес), при якому тіло як єдине ціле переміщується відносно інших тіл. Розрізняють дві прості різновидності механічного руху: рух поступальний та рух обертальний.
Поступальний рух – це такий механічний рух, при якому будь-яка приналежна тілу пряма залишається паралельною сама собі. При поступальному русі всі точки тіла рухаються однаково: мають однакові траєкторії руху, за однакові проміжки часу проходять однакові відстані, мають однакові швидкості, однакові прискорення, тощо. Зважаючи на ці обставини, описуючи поступальний рух тіла, це тіло зазвичай замінюють його спрощеною (ідеалізованою) моделлю, яку прийняти називати матеріальною точкою.
Матеріальна точка, це така умовна точка, якою теоретично замінюють певне реальне тіло, в ситуаціях коли розмірами, формою та внутрішнім устроєм цього тіла можна знехтувати. Матеріальна точка зберігає лише одну механічну характеристику реального тіла – його масу.
Обертальний рух – це такий механічний рух, при якому всі точки тіла описують кола, центри яких знаходяться на одній прямій, яка називається віссю обертання тіла. При обертальному русі різновіддалені від осі обертання точки, рухаються суттєво по різному: мають різні траєкторії руху, різні пройдені шляхи, різні лінійні швидкості, різні прискорення, тощо. А це означає, що описуючи обертальний рух тіла, представляти це тіло у вигляді матеріальної точки неможна.
В межах навчальної програми для 7-го класу, фактично вивчають основи кінематики поступального руху (кінематики матеріальної точки). Навіть в тому випадку коли мова йде про рух тіла по колу, мається на увазі, що цей рух відбувається без обертання тіла навколо власної осі обертання.
Будь який механічний рух є відносним. Це означає, що в різних системах відліку, один і той же механічний рух може виглядати по різному. Тому описуючи той чи інший рух, потрібно вказувати в якій системі відліку цей рух описується. Система відліку – це взаємопов’язана сукупність точки відліку, системи координат та вимірювача часу, яка застосовується для того, щоб кількісно описати механічний рух матеріальної точки (тіла) в цій систе
До числа основних фізичних величин кінематики поступального руху відносяться: час, координата, пройдений шлях, швидкість, прискорення.
Час – це фізична величина, яка характеризує тривалість подій ( явищ, процесів, рухів, тощо) і яка дорівнює цій тривалості.
Позначається: t
Визначальне рівняння: нема
Одиниця вимірювання: [t] = с, (секунда)
Координата – це фізична величина, яка характеризує положення (місцезнаходження) матеріальної точки в заданій системі координат і яка дорівнює відстані від точки відліку цієї системи до проекції даної точки на відповідну вісь координат.
Позначається: х
Визначальне рівняння: х = ℓх
Одиниця вимірювання: [х] = м, (метр)
Пройдений шлях – це фізична величина, яка характеризує пройдений матеріальною точкою (тілом) шлях і яка дорівнює довжині тієї траєкторії яку описує ця точка в процесі відповідного руху.
Позначається: s
Визначальне рівняння: s = ℓтр, для прямолінійного руху s =∆х
Одиниця вимірювання: [s] = м.
Швидкість – це фізична величина, яка характеризує швидкість поступального руху тіла (матеріальної точки), і яка дорівнює відношенню вектора того переміщення Δх яке здійснило тіло за гранично малий проміжок часу Δt, до величини цього проміжку часу.
Позначається: v
Визначальне рівняння: v = ∆x/∆t
Одиниця вимірювання: [v] = м/с, (метр на секунду).
На практиці швидкість прямолінійного руху тіла визначають за формулами:
1) при рівномірному русі (v = const), v = ∆x/∆t, або v = s/t;
2) при рівноприскореному русі (v↑), v = v0 + at;
3) при рівносповільненому русі (v↓), v = v0 – at, де а – прискорення тіла.
Прискорення – це фізична величина, яка характеризує зміну швидкості руху тіла, і яка дорівнює відношенню тієї зміни швидкості Δv, що відбулася за проміжок часу Δt, до величини цього проміжку часу.
Позначається: а
Визначальне рівняння: а=∆v/∆t
Одиниця вимірювання: [a] = м/с2, (метр на секунду в квадраті).
Оскільки швидкість, величина векторна, то вона може змінюватись як за величиною, так і за напрямком. Тому розрізняють дві різновидності прискорення:
Лінійне прискорення (прискорення) – це таке прискорення, яке характеризує зміну швидкості за величиною.
Позначається: ал або а
Визначальне рівняння: а = ∆v/∆t
Одиниця вимірювання: [а] = м/с2.
Лінійне прискорення завжди направлено вздовж лінії швидкості руху тіла. При цьому, якщо величина швидкості зростає (v↑), то вектори швидкості та прискорення співнаправлені, а якщо швидкість зменшується (v↓) – то ці напрямки протинаправлені.
Доцентрове прискорення – це таке прискорення, яке характеризує зміну швидкості за напрямком.
Позначається: ад
Визначальне рівняння: ад = v2/R
Одиниця вимірювання: [ад] = м/с2.
Доцентрового прискорення виникає лише при криволінійному русі тіла (при русі по колу) і завжди направлено до центру того кола яке опитує матеріальна точка в процесі свого руху.
Основний закон кінематики поступального руху називається рівнянням руху. Рівняння руху – це закон, в якому стверджується: в загальному випадку, прямолінійний рух матеріальної точки можна описати рівнянням:
х = х0 + v0t + (а/2)t2, де
х – координата матеріальної точки в момент часу t,
х0 – початкова координата точки, тобто її координата в момент часу t=0
v0 – початкова швидкість матеріальної точки
а – прискорення матеріальної точки.
Не буде перебільшенням сказати, що на основі аналізу заданого рівняння руху та базових фізичних величин кінематики (s = Δx; v = Δx/Δt; a = Δv/Δt) можна розв’язати практично будь яку задачу яка стосується кінематики відповідного руху.
Задача 1. За заданим рівнянням руху х = 100 а – 10t + 0,2t2:
1) дати загальну характеристику руху тіла: х0 = ?; v0 = ?; а = ?
2) визначити пройдений тілом шлях за десять секунд: s(10) = ?
3) визначити швидкість через 10с: v(10) = ?
- визначити де і коли тіло зупиниться: хзуп = ? tзуп = ?
Рішення.
- Із порівняльного аналізу рівнянь
х = х0 + v0t + (а/2)t2 та
х = 100 – 10t + 0,2t2, ясно:
х0 =100м; v0 = –10м/с; а = 0,4м/с2; v↓.
- s(10) = ∆х = х(10) – х0, де х(10) = ?
х(10) = 100 – 10(10) + 0,2(10)2 = 20м, отже
s(10) = 20 – 100 = – 80м.
- Оскільки v = v0 + at, та враховуючи, що v0 = –10м/с, а = 0,4м/с2, можна записати v = –10 + 0,4t. Якщо t = 10c, то v(10) = –10 + 0,4(10) = –6м/с.
- Оскільки в момент зупинки v = 0, то для t = tзуп, v = –10 + 0,4tзуп = 0, звідси 0,4tзуп = 10, звідси tзуп = 10/0,4 = 25c
хзуп = х(25) = 100 – 10(25) + 0,2(25)2 = – 25м.
Задача 2. За заданими графіками руху записати відповідні рівняння руху. Визначити де і коли тіла зустрінуться.
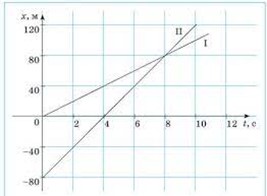
Рішення. На основі аналізу заданих графіків можна записати:
- х0 = 0м, для ∆t = 8c, ∆x = 80 – 0 = 80м,
отже v1 = ∆x/∆t = 80м/8с = 10м/с, отже x1 = 10t.
- х0 = – 80м, для ∆t = 4c, ∆x = 0 – (– 80) = 80м,
отже v1 = ∆x/∆t = 80м/4с = 20м/с, отже x2 = – 80 + 20t.
Оскільки в момент зустрічі х1 = х2, то можна записати 10t = – 80 + 20t, звідси 20t – 10t = 80, звідси t = 80м/10с = 8с = tзустр. хзустр = х1(8) = 10∙8 = 80м.
Відповідь: tзустр = 8с, хзустр = 80м.
Важливою різновидністю поступального руху є вільне падіння тіла. Вільним падінням називають такий рух тіла, який відбувається під дією сили тяжіння та за відсутності суттєвого впливу інших зовнішніх сил, зокрема сили опору повітря. Вільне падіння тіла відбувається з певним, направленим вертикально вниз прискоренням, яке називається прискоренням вільного падіння (прискоренням сили тяжіння) і позначається літерою g. На Землі, усереднена величина прискорення вільного падіння g = 9,8м/с2, при розв’язуванні задач кінематики g = 10м/с2.
Як і будь-який рівноприскорений рух, вільне падіння тіла можна описати рівнянням виду х = х0 + v0t + (a/2)t2. Відмінність лише в тому, що говорячи про вільне падіння матеріальної точки, її вертикальну координату (висоту) зазвичай позначають літерою h, а прискорення – літерою g. Іншими словами, рух вільно падаючого тіла можна описати формулою h = h0 + v0t + (g/2)t2.
Задача 3. Тіло, що знаходиться на висоті 20м кинули горизонтально з швидкістю 15 м/с. Визначити горизонтальну дальність польоту тіла.

Дано:
h0 = 20 м
v0 = 15 м/с
ℓ = ?
Рішення. Виконуємо малюнок який відображає наявну ситуацію та задаємо відповідну систему координат. Криволінійний рух даного тіла по суті є результатом двох незалежних рухів: рівномірного горизонтального та рівноприскореного вертикального. Зважаючи на ці обставини, задаємо систему координат і записуємо рівняння кожного окремого руху, тобто формулу яка має вигляд х = х0 + v0t + (a/2)t2.
– горизонтальний рух: оскільки х=ℓ; х0=ℓ0=0м; a=0м/с2, то ℓ = v0t
– вертикальний рух: оскільки х=h; х0=h0; v0=0м/с; a=g=10м/с2, то h = h0 – gt2/2.
Таким чином даний рух описують два рівняння:
1) ℓ = v0t, або ℓ = 15t;
2) h = h0 – gt2/2, або h = 20 – 5t2.
Із аналізу рівнянь ясно, що для того щоб визначити дальність польоту тіла (ℓ = 15t), необхідно визначити тривалість цього польоту (t = tпол). А оскільки в момент падіння тіла, h = 0, то 20 – 5(tпол)2 = 0, звідси (tпол)2 = (20/5) = 4с2, звідси tпол = √(4с2) = 2с.
Розрахунки: ℓ = 15tпол = 15(м/с)∙2с = 30м.
Відповідь: ℓ = 30м.
Узагальнюючі відомості про основні поняття, величини та закони кінематики поступального руху, можна представити у вигляді наступної таблиці.
| Основні поняття | Основні фізичні величини | Основні закони |
| Механіка
Кінематика Механічний рух Поступальний рух Матеріальна точка Відносність руху Система відліку Траєкторія |
час t (с)
координата x=ℓх (м) пройдений шлях s=∆x (м) швидкість v=∆x/∆t (м/с) прискорення: a=∆v/∆t (м/с2) лінійне a=∆v/∆t (м/с2) доцентрове aд=v2/R (м/с2) |
Рівняння руху
x = x0 + v0t + (a/2)t2 |
Вправа 20.
- За заданим рівнянням руху х = –100 + 20t – 0,2t2:
1) дати загальну характеристику руху тіла;
2) визначити пройдений тілом шлях за 10с;
3) визначити швидкість через 10с;
4) визначити де і коли тіло зупиниться.
- За заданими графіками руху записати відповідні рівняння руху.
- З пунктів 1 і 2 відстань між якими 6км, одночасно і в одному напрямку виїхали мотоцикліст і велосипедист з швидкостями відповідно 20м/с та 18км/год. Визначити де і коли вони зустрінуться.
- Рушаючи з місця, автомобіль протягом 5с рухається з прискоренням 3м/с2. Яку швидкість встигає набрати автомобіль? Який шлях проходить при цьому?
- Визначити глибину ущелини, якщо камінь падаючи без початкової швидкості досягає її дна за 3с.
- Тіло вільно падає з висоти 20м. Визначити час падіння тіла, швидкість в момент падіння та середню швидкість падіння.
- Стрілу випустили вертикально вгору з швидкістю 90км/год. Визначити максимальну висоту підйому стріли. Через який час стріла впаде на землю?
- За 12с колесо автомобіля зовнішній радіус якого 30см, здійснює 160 обертів. Визначте період та частоту обертання колеса. Визначте швидкість руху автомобіля.
.