Сайт викладача фізики

 

Модуль 1. Основи механіки.

Лекційне заняття №1. Тема: Основні поняття, величини та закони кінематики поступального руху.

Лекційне заняття №2. Тема: Вільне падіння тіл. Рух тіла кинутого вертикально, горизонтально та під кутом до горизонту.

Лекційне заняття №3. Тема: Кінематичний метод розв’язування задач.

Лекційне заняття №4. Тема: Основні поняття, величини та закони кінематики обертального руху.

Лекційне заняття №5. Тема: Основні поняття, величини та закони статики

матеріальної точки.

Лекційне заняття №6. Тема: Силовий метод розв’язування задач.

Лекційне заняття №7. Тема: Пара сил. Момент сили. Рівновага тіла що має вісь обертання. Важелі. Блоки.

Лекційне заняття №8. Тема: Рівновага тіла під дією довільної системи сил.

Лекційне заняття №9. Тема: Центр тяжіння тіла. Види механічної рівноваги та ступінь механічної стійкості тіла.

Лекційне заняття №10. Тема: Основні поняття, величини та закони динаміки матеріальної точки.

Лекційне заняття №11. Тема: Імпульсно-енергетичний метод розв’язування задач динаміки.

Лекційне заняття №12. Тема: Основні поняття, величини та закони динаміки обертального руху.

Лекційне заняття №13. Тема: Кінетична енергія тіла що обертається. Повна кінетична енергія тіла.

Лекційне заняття №14. Тема: Закони Ньютона в механіці обертального руху.

 

 

Лекційне заняття №1.

Тема: Основні поняття, величини та закони кінематики поступального руху.

Кінематика (від грецького “kinematos” – рух) – це розділ механіки, в якому вивчають параметри та закономірності механічного руху тіл, без врахування їх мас та діючих на них сил. Іншими словами, в кінематиці вивчають параметри та закономірності механічного руху і не вивчають причини цього руху, а також не враховують фізичні властивості рухомого тіла.

До числа основних понять кінематики, тобто тих загальних термінів суть яких потрібно знати, відносяться: механічний рух, поступальний рух, обертальний рух, матеріальна точка, відносність руху, система відліку, траєкторія.

Механічний рух – це такий рух (процес), при якому тіло як єдине ціле, або певні цілісні фрагменти цього тіла, переміщується відносно інших тіл. Поступальний рух – це такий механічний рух, при якому будь-яка приналежна тілу пряма залишається паралельною сама собі. Обертальний рух – це такий механічний рух, при якому всі точки тіла описують кола, центри яких знаходяться на одній прямій, яка називається віссю обертання. Матеріальна точка – це така умовна точка, якою теоретично замінюють певне реальне тіло, в ситуаціях коли розмірами, формою та внутрішнім устроєм цього тіла можна знехтувати. Матеріальна точка зберігає лише одну динамічну характеристику реального тіла – його масу. Відносність руху полягає в тому, що різні спостерігачі спостерігаючи за рухом одного і того ж тіла можуть бачити суттєво різні рухи. Система відліку – це взаємопов’язана сукупність системи координат та вимірювача часу, яка застосовується для того щоб кількісно описати механічний рух матеріальної точки (тіла) в цій системі. Система координат – це взаємопов’язана сукупність точки відліку та осей системи координат, яка застосовується для того щоб кількісно описати положення (розташування, місцезнаходження) матеріальної точки в цій системі. Траєкторія – це умовна лінія яку описує матеріальна точка в процесі свого руху в вибраній системі координат. Прямолінійним називають такий поступальний рух матеріальної точки траєкторія якого представляє собою пряму лінію. Криволінійним називають такий поступальний рух матеріальної точки, траєкторія якого представляє собою криву лінію.

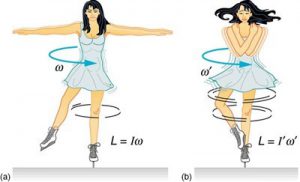
В загальному випадку механічний рух тіла представляє собою певну комбінацію поступального і обертального рухів. Але яким би складним не був механічний рух тіла, його завжди можна представити як певну комбінацію двох простих рухів: поступального і обертального. А це означає, що вивчивши параметри та закономірності поступального і обертального руху можна описати та спрогнозувати будь-який найскладніший механічний рух. Зважаючи на ці обставини та реалізуючи базовий методологічний принцип науки – від простого до складного, від часткового до загального, кінематику розділяють на дві частини  кінематика поступального руху (кінематика матеріальної точки) та кінематика обертального руху.

 

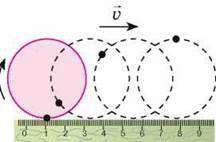
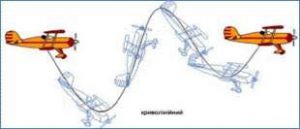
Мал.1. В загальному випадку рух тіла є поступально-обертальним.

До числа основних фізичних величин кінематики поступального руху відносяться: час (t), координата (x), пройдений шлях (s) швидкість (v), прискорення (a).

              Час – це фізична величина, яка характеризує тривалість подій (явищ, процесів, рухів, тощо) і яка дорівнює цій тривалості.

Позначається:  t

Визначальне рівняння:  нема

Одиниця вимірювання:  [t] = с, (секунда)

Твердження про те, що час немає визначального рівняння по суті означає, що час належить до числа тих базових фізичних величин одиниці вимірювання яких за домовленістю прийнято вважати основними. В механіці такими базовими величинами є час (t), довжина (ℓ) і маса (m).

Координата – це фізична величина, яка характеризує положення (місцезнаходження) матеріальної точки в заданій системі координат і яка дорівнює відстані від точки відліку цієї системи до проекції даної точки на відповідну вісь координат.

Позначається: х

Визначальне рівняння: х =ℓ_х

Одиниця вимірювання: [х] = м, (метр)

Мал.2. Координата точки дорівнює відстані від точки відліку системи координат до даної точки, виміряній вздовж відповідної осі системи координат.

Пройдений шлях – це фізична величина, яка характеризує пройдений матеріальною точкою (тілом) шлях і яка дорівнює довжині тієї траєкторії яку описує ця точка в процесі відповідного руху.

Позначається: s

Визначальне рівняння: s = ℓ_тр

Одиниця вимірювання: [s] = м, (метр).

Реалізуючи базовий методологічний принцип науки – від простого до складного, від часткового до загального, та зважаючи на факт того, що будь який криволінійний рух можна представити як певну сукупність прямолінійних рухів, ми перш за все будемо вивчати кінематику прямолінійного руху. А в цій кінематиці, рівняння s=ℓ_тр набуває вигляду s=∆х,  де ∆х = х_к– х_п.

Швидкість – це фізична величина, яка характеризує швидкість поступального руху тіла (матеріальної точки), і яка показує на скільки переміщується це тіло в заданій системі відліку, за одиницю часу.

Позначається: v

Визначальне рівняння: v =∆x/∆t,

Одиниця вимірювання: [v] = м/с,  (метр за секунду).

Швидкість – величина векторна, тобто така, що характеризується як певною величиною, так і певним напрямком. Напрям вектора швидкості співпадає з напрямком руху тіла (матеріальної точки) у відповідній точці траєкторії. А це означає, що вектор швидкості завжди направлений по дотичній до траєкторії руху тіла.

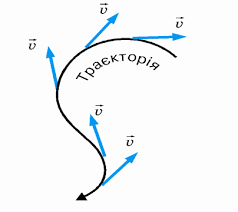
Мал.3. Напрям вектора швидкості завжди співпадає з напрямком руху тіла в заданій точці траєкторії, тобто направлений по дотичній до цієї траєкторії.

Якщо швидкість тіла так чи інакше змінюється, то говорять що воно рухається з прискоренням. Прискорення – це фізична величина, яка характеризує зміну швидкості руху тіла, і яка показує на скільки змінюється ця швидкість за одиницю часу.

Позначається: а

Визначальне рівняння: а=∆v/∆t,

Одиниця вимірювання: [a] = м/с²,  метр за секунду в квадраті

Оскільки швидкість, величина векторна, то вона може змінюватись як за величиною (модулем) так і за напрямком. Виходячи з цього розрізнюють дві різновидності прискорення:

1.Прискорення яке характеризує зміну швидкості за величиною (його називають тангенціальним прискоренням, або просто прискоренням);

2. Прискорення, яке характеризує зміну швидкості за напрямком (його називають доцентровим прискоренням).

Тангенціальне прискорення (прискорення) – це таке прискорення, яке характеризує зміну швидкості за величиною і яке дорівнює відношенню зміни швидкості руху тіла (Δv) до того проміжку часу (Δt) за який ця зміна відбулася.

Позначається: а_τ     або   а

Визначальне рівняння: а_τ=∆v/∆t

Одиниця вимірювання: [а_τ]= м/с².

Те прискорення яке характеризує зміну швидкості за величиною і яке зазвичай називають «прискоренням», завжди направлено вздовж лінії швидкості руху тіла. При цьому, якщо величина швидкості зростає (v↑), то вектори швидкості та прискорення співнаправлені, а якщо швидкість зменшується (v↓) – то ці напрямки протинаправлені. Наприклад, коли автомобіль рушає з місця (мал.4а), то його швидкість збільшується  (v↑) і тому напрям того прискорення з яким рухається автомобіль, співпадає з напрямком його руху (з напрямком швидкості). Якщо ж автомобіль гальмує (мал.4б), то його швидкість зменшується (v↓) і тому напрям того прискорення з яким рухається автомобіль, протилежний до напрямку його руху (протилежний до напрямку швидкості руху автомобіля).

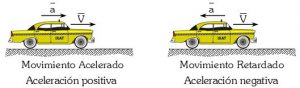
Мал.4. Якщо швидкість автомобіля збільшується (мал.а), то вектори a і v співнаправлені, а якщо зменшується (мал.б) – то протинаправлені.

Однак бувають ситуації, в яких величина швидкості залишається незмінною (v₁ = v₂ = … = const), а тіло рухається з певним прискоренням. Наприклад, якщо автомобіль з незмінною за модулем швидкістю рухається по колу (мал.5) то він неминуче рухається з певним прискоренням. Це прискорення називають доцентровим (позначається а_д). Його поява обумовлена не тим, що швидкість змінюється не за величиною (адже v=const), а тим, що вона змінюється за напрямком.

    

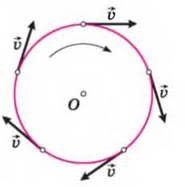
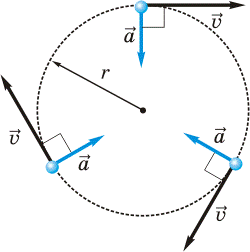
v₁ = v₂  = const

v₁ ≠ v₂  ≠ const

Мал.5. В процесі руху матеріальної точки по колу, напрям її швидкості постійно змінюється і тому вона рухається з відповідним прискоренням.

Виходячи з визначального рівняння прискорення (а=∆v/∆t), можна довести, що величина доцентрового прискорення визначається за формулою а_д =v²/R, де v – швидкість тіла в даній точці траєкторії; R – радіус кривизни в цій точці траєкторії.

Доцентрове прискорення – це таке прискорення, яке характеризує зміну швидкості за напрямком і яке дорівнює відношенню квадрату швидкості руху тіла (v²) в даній точці траєкторії, до радіусу кривизни (R) цієї траєкторії.

Позначається: а_д

Визначальне рівняння: а_д=v²/R

Одиниця вимірювання: [а_д]= м/с²,  метр за секунду в квадраті.

Доцентрове прискорення завжди направлено до центру кривизни в даній точці траєкторії, тобто по перпендикуляру (нормалі) до напрямку швидкості в цій точці. Зважаючи на ці обставини доцентрове прискорення іноді називають нормальним тобто перпендикулярним.

Таким чином, якщо тіло рухається криволінійною траєкторією, то в незалежності від того змінюється модуль його швидкості, чи не змінюється, це тіло має певне доцентрове прискорення, величина якого визначається за формулою  а_д=v²/R, і яке завжди направлено до центру кривизни в даній точці траєкторії.

          Основний закон кінематики поступального руху називається рівнянням руху. Рівняння руху – це закон, в якому стверджується: в загальному випадку, прямолінійний рух матеріальної точки можна описати рівнянням: х = х₀ + v₀t + (а/2)t²

де     х – координата матеріальної точки в момент часу t,

х₀  – початкова координата точки, тобто її координата в момент часу t=0,

v₀ – початкова швидкість матеріальної точки,

а – прискорення матеріальної точки.

Похідними від рівняння руху є рівняння пройденого шляху: s=v₀t+at²/2, та рівняння швидкості: v=v₀+at. Крім цього, в кінематиці поступального руху, важливе значення має похідна від рівняння руху формула s=(v_k²-v₀²)/2a

Не буде перебільшенням сказати, що знаючи рівняння руху х=х₀+v₀t+(a/2)t² та визначальні рівняння базових фізичних величин кінематики (s=∆x, v=∆x/∆t, а=∆v/∆t), можна розв’язати практично будь-яку задачу кінематики. У всякому разі ті задачі, складність яких не виходить за межі програми загальноосвітньої школи.

Втім, в фізиці не достатньо знати формули. В фізиці набагато важливіше бачити за цими формулами реальні події та їх параметри. Наприклад, в математиці рівняння х = 200 –10t + 0,2t² це просто квадратне рівняння, яке в загальному випадку має два рішення і яке графічно можна представити у вигляді відповідної параболи. В фізиці, все те що вивчалося в математиці ви маєте знати та вміти застосовувати на практиці. Однак цього зовсім не достатньо для розв’язування задач фізики. Адже в фізиці за кожним рівнянням, за кожною цифрою, за кожною буквою та за кожним знаком, ви маєте бачити реальні події та їх характеристики. Скажімо, просто поглянувши на рівняння х = 200 –10t + 0,2t², та розуміючи що це рівняння руху, тобто рівняння вигляду х=х₀+v₀t+(а/2)t², ви відразу ж уявляєте наступну ситуацію. В момент часу t=0, дане тіло знаходиться в точці з координатою 200м і рухається у від’ємному напрямку з швидкістю 10м/с. При цьому величина цієї швидкості зменшується (зменшується тому, що знаки (напрямки) швидкості та прискорення є протилежними), а числове значення прискорення становить 0,4м/с². (Сподіваюсь, ви розумієте, що з факту а/2=0,2 випливає а=0,4). Іншими словами, із аналізу заданого рівняння руху ясно:

х₀= 200м;   v₀= -10м/с;   а = 0,4м/с²;   v↓

Таким чином, вже першого погляду на рівняння руху, має бути достатньо для того, щоб дати загальну характеристику цього руху. Наприклад:

x₁ = -200 +15t – 0,4t²:    х₀ = -200м;  v₀ = 15м/с;  а = -0,8м/с²;  v↓

x₂ = 100 – 8t – 0,1t²:       х₀ = 100м;   v₀ = -8м/с;   а = -0,2м/с²;  v↑

x₃ = -5t:                           х₀ = 0м;       v₀ = -5м/с;   а = 0м/с²;  v = const

x₄ = 200 – t²:                   х₀ = 200м;   v₀ = -0м/с;   а = -2м/с²;   v↑

x₅ = -100:                        х₀ = -100м;  v₀ = 0м/с;  а = 0м/с²;  не рухається

Зауважимо. Якщо в поясненнях до рівняння руху не вказані одиниці вимірювання відповідних величин, то потрібно вважати що цими одиницями є основні одиниці міжнародної системи (СІ):  [x]=м;  [v]=м/с;  [a]=м/с².

Зверніть увагу, ми просто дивимося на рівняння руху і отримуємо з нього достатньо велику кількість інформації. Тепер же уявіть, скільки інформації можна отримати на основі математичного та логічного аналізу цього рівняння. Ілюструючи лише невеличку частину цих інформаційних можливостей, розглянемо конкретну задачу.

Задача 1. За заданим рівнянням руху  х = 100 + 10t – 0,4t²:

1) дати загальну характеристику руху тіла;

2) визначити пройдений тілом шлях за десять секунд;

3) записати  рівняння швидкості руху тіла та визначити цю швидкість через 10с;

4) Визначити де і коли тіло зупиниться;

Відповідаючи на кожне з поставлених запитань можна сказати наступне.

1.Дати загальну характеристику руху тіла: х₀ =? v₀=? а =? малюнок.

Із порівняльного аналізу рівнянь

х = х₀ + v₀t + (а/2)t² та

х=100 +10t – 0,4t²,  ясно:

х₀ =100м; v₀ = 10м/с; а = – 0,8м/с²;  v↓.

.                                a←——•——→  v↓                                                х(м)

0                                          100                                         200

2. Визначити пройдений тілом шлях за десять секунд: s(10)=?

Оскільки за визначенням s=∆х=х_к –х_п = х_к–х₀, та враховуючи що в умовах даної задачі    х_к = х(10) = 100 + 10(10) – 0,4(10)² = 160м, можна записати

s(10)= х(10) – х₀ = 160 – 100 = 60м.

3. Записати рівняння швидкості руху тіла та визначити цю швидкість через 10с

Оскільки при рівноприскореному русі v=v₀+at, то в умовах нашої задачі (v₀=10м/с, а = – 0,8м/с²) рівняння швидкості набуває вигляду v=10 – 0,8t

Зважаючи на ці обставини можна записати:

v(10)= 10 – 0,8(10) = 2м/с.

4. Визначити, де і коли тіло зупиниться: х_зуп =? t_зуп=?

Оскільки в момент зупинки швидкість тіла дорівнює нулю (v=0), то можна записати: якщо t=t_зуп, то  v = 10 – 0,8t_зуп = 0, звідси   t_зуп = 10/0,8=12,5c

А це означає, що  х_зуп =х(12,5)= 100+10(12,5) – 0,4(12,5)²  = 162,5м.

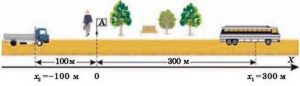
Задача 2. На основі аналізу малюнку, записати відповідні рівняння руху.

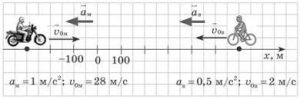
Рішення. Аналізуючи представлену на малюнку ситуацію, записуємо рівняння руху мотоцикліста та велосипедиста:

мотоцикліст: х = –300 + 28t – 0,5t²;

велосипедист: х = 600 – 2t – 0,25t².

Контрольні запитання.

1.Чи можна стверджувати, що рівняння х=х₀+v₀t+(a/2)t² описує не лише рівноприскорений (а =const), а й рівномірний рух (а=0) ?

2. Якого вигляду набуває рівняння руху для рівномірного руху?

3. Якого вигляду набуває рівняння руху в ситуації коли х₀=0; v₀=0 ?

4. Виходячи з того що s = ∆х = х – х₀, запишіть рівняння пройденого шляху.

5. Якого вигляду набуває рівняння пройденого шляху за умови v₀= 0м/с?

6. Який загальний вигляд рівняння швидкості?

7. Виходячи з того, що а=(v_k – v₀)/t, запишіть рівняння швидкості.

Вправа 1.

1.За рівнянням руху дати загальну характеристику відповідного руху:

х₁  = 100 + 10t + 0,5t²

х₂  = –100 + 5t – 0,2t²

х₃  = –10t – 0,3t²

х₄  = 150 – 0,25t²

х₅  = t²

2. За заданим рівнянням руху х = 100 – 15t + 0,5t²:

1) дати загальну характеристику руху тіла;

2) визначити пройдений тілом шлях за 10с;

3) записати рівняння швидкості руху тіла;

4) визначити де і коли тіло зупиниться.

3. За заданим рівнянням руху х = –200 + 12t – 0,3t², визначити де і коли тіло зупиниться.

4. Із пунктів А і В одночасно та в одному і тому ж напрямку виїхав автомобіль з швидкістю 22м/с та велосипедист з швидкістю 8м/с. Де і коли вони зустрінуться, якщо відстань між пунктами А і В 900м?

5. В заданій системі відліку рівняння руху тіл мають вигляд х₁=15t, х₂=200+10t. Де і коли зустрінуться ці тіла?

6. На основі аналізу малюнку, записати відповідні рівняння руху.

 

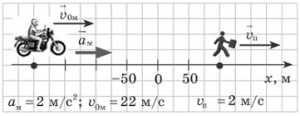
Лекційне заняття №2.

Тема: Вільне падіння тіл. Рух тіла кинутого вертикально, горизонтально та під кутом до горизонту.  

          Вільним падінням називають такий рух тіла, який відбувається під дією сили тяжіння та за відсутності суттєвого впливу інших зовнішніх сил, зокрема сили опору повітря. В загальному випадку вільно падаючими вважають не лише ті тіла падіння яких починається з нулевою швидкістю (мал.6а), а й ті які з певною швидкістю кинули вертикально вниз, вертикально вгору, горизонтально або під кутом до горизонту (мал.6 б,в,г,д). Адже в кожному з цих випадків, тіло після отримання певного початкового поштовху, рухається під дією лише однієї зовнішньої сили – сили тяжіння (звичайно за умови, що сила опору повітря є не суттєвою).

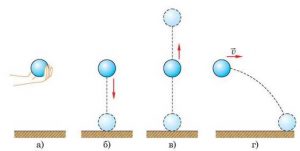
Мал.6. Рух тіла що відбувається під дією сили тяжіння та за відносності дії інших зовнішніх сил (зокрема суттєвого впливу опору повітря), називають вільним падінням тіла.

Характерною особливістю того руху який називається вільним падінням є те, що це падіння відбувається з певним постійним прискоренням, величина якого не залежить від маси тіла, а отже і від діючої на нього сили тяжіння. На перший погляд, така поведінка важкого і легкого тіл здається дивною. Адже та сила з якою важкий камінь притягується до Землі в сотні разів перевищує ту, з якою до Землі притягується легкий камінчик. І тим не менше, легкий камінчик і важкий камінь падають однаково швидко. Сьогодні ми не будемо говорити про те, чому важкі і легкі тіла падають однаково швидко. Сьогодні ми просто констатуємо той експериментальний факт, що під дією сили тяжіння, та за відсутності суттєвого впливу опору повітря, всі тіла падають з однаковим прискоренням яке називається прискоренням сили тяжіння або прискоренням вільного падіння.

Підкреслюючи важливість та значимість прискорення вільного падіння, його позначають окремою літерою g (від лат. gravitas – тяжіння). Напрям прискорення вільного падіння співпадає з напрямком діючої на тіло сили тяжіння, тобто є направленим вертикально вниз. Для Землі, усереднена величина прискорення вільного падіння становить g=9,8067 м/с². Зазвичай числове значення прискорення вільного падіння приймають рівним g=9,8м/с². А зважаючи на факт того, що числове рішення переважної більшості задач на вільне падіння тіл є досить приблизним (адже не враховує силу опору повітря), то при наближених розрахунках допускається g=10м/с².

Потрібно зауважити, що величина та напрям прискорення вільного падіння не залежать від того в якому напрямку рухається тіло і з якою початковою швидкістю воно рухається. Наприклад, в незалежності від того вільно відпустили піднятий над землею камінь (мал7а), чи з певною швидкістю кинули вертикально вниз (мал.7б), вгору (мал.7в) чи під кутом до горизонту (мал.7г), цей камінь буде падати з прискоренням g=9,8м/с². В незалежності від того рухається камінь вгору чи падає вниз, він рухається з прискоренням g=9,8м/с² і це прискорення завжди направлено вертикально вниз. Навіть в точці максимального підйому тіла, де його швидкість дорівнює нулю, тіло має прискорення g=9,8м/с². Іншими словами, на всій траєкторії вільного польоту тіла, це тіло рухається з прискоренням вільного падіння.

 

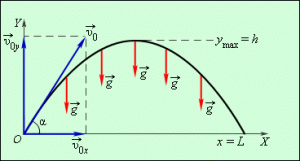
Мал.7. У всіх точках траєкторії вільного польоту, тіло рухається з прискоренням вільного падіння (g=9,8м/с²)

Як і будь-який рівноприскорений рух, вільне падіння тіла можна описати рівнянням виду х=х₀+v₀t+(a/2)t². Відмінність лише в тому, що говорячи про вільне падіння матеріальної точки, її вертикальну координату (висоту) позначають літерою h, а прискорення – літерою g. Іншими словами, рух вільно падаючого тіла можна описати формулою h=h₀+v₀t+(g/2)t².

Ілюструючи закономірності того руху який називається вільним падінням тіла, а заодно ілюструючи практичну значимість того закону який називається рівнянням руху, розв’яжемо ряд конкретних задач.

Задача 1. Визначити глибину колодязя, якщо відомо, що випущений із руки камінь досягає води за 2с.

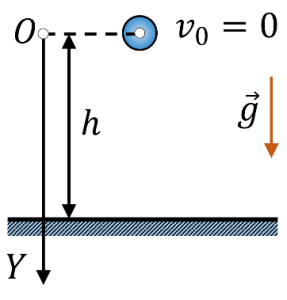
Дано :                                 Рішення:

v₀ = 0 м/с

 t = 2 с                                 Малюнок

h = ?

Задаємо систему координат та записуємо рівняння руху тіла в цій системі, тобто формулу яка має вигляд х=х₀+v₀t+(a/2)t². В умовах даної задачі х=h; х₀=h₀=0м; v₀=0м/с; а=g, це рівняння набуває вигляду: h=(g/2)t², де g=10м/с².

Враховуючи, що t=2c, виконуємо відповідні розрахунки.

Розрахунки:  h=(10(м/с²)(2с)²/2=20м;

Відповідь: h=20м.

Потрібно зауважити, що конкретний вигляд рівняння руху залежить не лише від самого руху, а й від вибору системи координат. Наприклад, якщо в умовах даної задачі за початок відліку обрати точку на дні колодязя, а вісь 0h направити вертикально вгору, то рівняння руху каменя матиме вигляд не h=(g/2)t², а h=h₀ – (g/2)t², де h₀ – висота каменя над поверхнею дна колодязі, а отже – глибина колодязі. Втім, результат розв’язку задачі буде одним і тим же. Дійсно, для рівняння h=h₀ – (g/2)t², в момент падіння каменя h=0. Тому h₀=(g/2)t²=(10(м/с²)(2с)²/2=20м.

Задача 2. Тіло впало з висоти 45м. Визначте час падіння тіла.

Дано:                 Рішення:

h = 45м       Виконуємо малюнок, задаємо систему координат

t_пад= ?         та записуємо відповідне рівняння руху тіла: h=(g/2)t².

Звідси випливає t² = 2h/g, t = √(2h/g).

Розрахунки: t = √(2·45м/10(м/с²))= √(9с²) = 3с

Відповідь t_пад= 3с.

Задача 3. Тіло падає без початкової швидкості. Яка його швидкість через 2с падіння?

Дано:                 Рішення:

v₀ = 0м/c       Виконуємо малюнок, задаємо систему координат

t = 2c            та записуємо відповідне рівняння швидкості тіла:

v = ?              v = gt

Розрахунки: v = 10(м/с²)2с = 20м/с.

Відповідь v = 20м/с.

Контрольні запитання.

1.Що називають вільним падінням тіла?

2.Чи можна стверджувати, що кинуте в горизонтальному напрямку тіло, знаходиться в стані вільного падіння? Чому?

3. Чи залежить величина і напрям прискорення вільного падіння тіла від напрямку руху цього тіла?

4. Чи залежить прискорення вільного падіння від маси падаючого тіла?

5. Чи залежить прискорення вільного падіння від маси Землі?

6. Одне тіло випустили з руки, а друге кинули вертикально вниз. Яке з цих тіл матиме більше прискорення вільного падіння?

7. Від чого залежить конкретний вигляд рівняння руху тіла?

                   Вправа 2.

1.Визначити глибину ущелини, якщо камінь, падаючи без початкової швидкості досягне її дна за 5с.

2. Тіло падає без початкової швидкості. Яка його швидкість після 2с падіння?

3. Тіло впало з висоти 20м. Визначте час падіння тіла.

4. Тіло падає з початковою швидкістю 5м/с, якою буде ця швидкість через 1с падіння?

5. Камінь кинули вертикально вниз з початковою швидкістю 5м/с. З якої висоти кинули камінь якщо він падає 2с?

6. Тіло падає без початкової швидкості з висоти 45м. Визначте середню швидкість падіння тіла.

 

 

Лекційне заняття №3.

Тема: Кінематичний метод розв’язування задач механіки.

Задачі кінематики є надзвичайно різноманітними та досить складними. Однак якщо говорити про алгоритм рішення більшості кінематичних задач, то він полягає в тому, що відповідне рішення отримують на основі аналізу рівняння відповідного руху, тобто формули вигляду х=х₀+v₀t+(a/2)t², та визначальних рівнянь відповідних фізичних величин (s=∆x, v=∆x/∆t, а=∆v/∆t). Суть та можливості кінематичного методу розглянемо на конкретних прикладах.

Задача 1. Тіло кинули вертикально вгору з швидкістю 20м/с. На якій висоті буде це тіло через 1,5с польоту? Через 2,5с польоту?

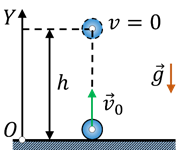
Дано :                                    Рішення:

v₀ = 20 м/с        Виконуємо малюнок, задаємо систему координат

t₁ = 1,5c            та записуємо відповідне рівняння руху тіла, тобто

t₂ = 2,5c             формулу вигляду х=х₀+v₀t+(a/2)t².

h₁=?; h₂=?         А оскільки в умовах даної задачі

х=h; х₀=h₀=0м; а=g=10м/с²,

то рівняння руху набуває вигляду: h = v₀t – (g/2)t², або h=20t–5t².

Розрахунки: для t₁=1,5c:    h₁=20(1,5) – 5(1,5)² = 30 – 11,25 = 18,75м;

для t₂=2,5c:    h₂=20(2,5) – 5(2,5)² = 50 – 31,25 = 18,75м.

Відповідь: h₁=18,75м;  h₂=18,75м.

Поясніть, чому кинуте вертикально вгору тіло, в різні моменти часу знаходилось на одній і тій же висоті?

          Задача 2. На яку максимальну висоту підніметься тіло. Якщо його кинули вертикально вгору з швидкістю 20м/с?

Дано :                                    Рішення:

v₀ = 20 м/с    Виконуємо малюнок, задаємо систему координат

h_max = ?          та записуємо відповідне рівняння руху тіла:

А оскільки в умовах даної задачі х=h; х₀=h₀=0м; а=g=10м/с²,

то рівняння руху набуває вигляду: h = v₀t – (g/2)t², або h=20t–5t².

Із аналізу рівняння руху ясно, що для визначення максимальної висоти підйому тіла (h=h_max) необхідно визначити час цього підйому t=t_max.

Оскільки на максимальній висоті, тобто в момент часу t=t_max, швидкість тіла дорівнює нулю, та зважаючи на те, що величина цієї швидкості визначається за формулою v=v₀–gt,  можна записати: v₀–gt_max=0. Звідси,  t_max=v₀/g=20(м/с)/10(м/с²)=2с

Таким чином: h_max=20t_max – 5t_max² = 20(м/с)2с – 5(м/с²)(2с)² = 40м – 20м =20м

Відповідь:  h_max=20м.

Задача 3. Тіло, що знаходиться на висоті 10м кинули горизонтально з швидкістю 20 м/с. Визначити горизонтальну дальність польоту тіла.

Загальне зауваження.  Рух тіла кинутого горизонтально є криволінійним, причому таким, який завжди можна розкласти на дві складові: рівномірний (v=const) горизонтальний та рівноприскорений (a=g=const) вертикальний. А це означає, що описуючи такий криволінійний рух, потрібно записати два незалежних рівняння, аналіз яких дозволяє відповісти на поставлені в задачі запитання.

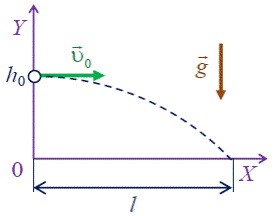
Дано:                                   Рішення:

h₀ = 10 м

v₀ = 20 м/с                         Малюнок

ℓ = ?

Криволінійний рух даного тіла по суті є результатом двох незалежних рухів: рівномірного горизонтального та рівноприскореного вертикального. Зважаючи на ці обставини, задаємо систему координат і записуємо рівняння кожного окремого руху, тобто формулу яка має вигляд х=х₀+v₀t+(a/2)t².

– горизонтальний рух: оскільки х=ℓ; х₀=ℓ₀=0м; a=0м/с², то  ℓ=v₀t

– вертикальний рух: оскільки х=h; х₀=h₀; v₀=0м/с; a=g=10м/с², то

h=h₀ – gt²/2.

Таким чином даний рух описують два рівняння:

1) ℓ = v₀t, або ℓ=20t;

2) h = h₀ – gt²/2, або h=10 – 5t².

Із аналізу рівнянь ясно, що для того щоб визначити дальність польоту тіла (ℓ=20t), необхідно визначити тривалість цього польоту (t=t_пол). А оскільки в момент падіння тіла, h=0, то: 10 – 5(t_пол)²= 0, звідси (t_пол)²=(10/5)=2с², звідси t_пол=√2=1,4с.

Розрахунки: ℓ=20t= 20(м/с)1,4с= 28м.

Відповідь: ℓ=28м.

Задача 4. Тіло, що знаходиться на висоті 15м кинули горизонтально з швидкістю 20 м/с. Визначите координати цього тіла через 1с польоту.

Дано:                                   Рішення:

h₀ = 15 м          Задаємо систему координат і записуємо і

v₀ = 20 м/с       записуємо рівняння кожного окремого руху,

t₁ = 1c               тобто формулу яка має вигляд

ℓ₁=? h₁=?                        х=х₀+v₀t+(a/2)t².

– горизонтальний рух: ℓ = v₀t, або ℓ=20t;

– вертикальний рух:     h = h₀ – gt²/2, або h=15 – 5t².

Якщо t₁ = 1c, то  ℓ₁=20t₁=20(м/с)1с=20м;

h₁=15 – 5t₁².= 15м – 5(м/с²)(1с)² = 10м.

Відповідь: ℓ₁=20м;  h₁=10м.

Тепер, коли ви ознайомились з закономірностями руху тіла кинутого вертикально та горизонтально, можна розглянути і більш загальний рух, рух тіла кинутого під кутом до горизонту.

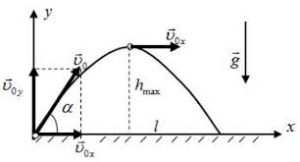
Мал.8. Кінематика руху тіла кинутого під кутом до горизонту.

На перший погляд, такий рух здається значно складнішим за рух тіла кинутого горизонтально. Насправді ж відмінності між цими рухами не такі вже й суттєві. Дійсно. Зважаючи на те, що вектор початкової швидкості (v₀) розкласти на дві складові:

– горизонтальну  v_x=v₀ cosα

– вертикальну      v_y=v₀ sinα,

даний криволінійний рух можна представити як результуючу двох лінійних рухів: рівномірного горизонтального та рівноприскореного вертикального. При цьому, кожен з цих рухів можна описати відповідним рівнянням. Наприклад, представлений на мал.8 рух, можна описати системою двох рівнянь:

ℓ=(v₀ cosα)t;

h=(v₀ sinα)t – gt²/2.

Доречно зауважити, що в процесі руху тіла кинутого під кутом до горизонту, горизонтальна складова його швидкості (v_x=v₀cosα) залишається незмінною (звичайно за умови не суттєвості опору повітря), а вертикальна складова цієї швидкості, змінюється за законом v_y=v₀sinα–gt (спочатку зменшується до нуля, а потім збільшується).

Задача 5. Снаряд вилетів з дула гармати під кутом 30° до горизонту, з швидкістю 800м/с. Визначити дальність польоту снаряду та максимальну висоту його підйому.

Дано:                                 Аналіз.

v₀ = 800м/с

α = 30°                             Малюнок

ℓ = ?

h_м = ?

В вибраній системі координат, вектор початкової швидкості розкладаємо на дві складові (v_x=v₀cosα, v_y=v₀sinα) та записуємо рівняння горизонтального і вертикального руху снаряду:

ℓ=(v₀cosα)t, або ℓ=(800·соs30°)t=800·0,87·t,  або ℓ=696t

h=(v₀sinα)t – gt²/2, або h=(800sin30°)t – 10t²/2= 8000·0,5t – 5t², або

h=400t – 5t².

Таким чином, в умовах даної задачі рух снаряду описують рівняння:

1) ℓ=696t;

2) h=400t – 5t².

Виходячи з того, що в момент падіння h=0м, визначаємо час польоту снаряду (t=t_пол): Оскільки h=400t – 5t²= t(400 – 5t)=0, то

1) t = 0

2) 400 – 5t=0, або 5t=400, звідси t=400/5=80c.

Отримані результати говорять про те, що на нулевій висоті (h=0) снаряд побував двічі: 1) в момент вильоту з дула гармати (t=0c); 2) в момент падіння на землю (t=80с).

Знаючи час польоту снаряду, не важко визначити дальність його польоту: ℓ = 696t = 696·80 ≈ 55000м = 55км.

Для того щоб визначити максимальну висоту підйому снаряду (h_м), потрібно знати час цього підйому(t_м). А оскільки рух снаряду є симетричним (тривалість підйому снаряду дорівнює тривалості його падіння), то можна стверджувати:  t_м= t_пол/2 = 80/2 = 40с. При цьому h_м = h(40) = 400·40 – 5·40² = 16000 – 8000 = 8000м = 8км.

Відповідь: ℓ ≈ 55 км; h_м ≈ 8 км.

Потрібно зауважити, що для тих швидкостей з якими рухаються кулі та снаряди, опір атмосферного повітря є дуже великим. Тому реальні параметри траєкторії руху снаряду, будуть суттєво відрізнятись від тих, які отримані без врахування опору повітря.

На завершення ще раз нагадаємо. Рішення задачі полягає не в тому, щоб в подібних задачах відшукати (а по суті списати) те розрахункове рівняння яке дозволяє визначити потрібну величину. Сенс цього рішення в тому, щоб на основі відомих базових формул та певних логічних міркувань, теоретично вивести (довести) потрібне розрахункове рівняння. А цими формулами є:

– рівняння руху, тобто формула вигляду х=х₀+v₀t+(a/2)t²,

– визначальні рівняння базових фізичних величин: s=∆x, v=∆x/∆t, а=∆v/∆t,

– похідні від рівняння руху та визначальних рівнянь формули:

v = v₀ + at,   s = (v_k²-v₀²)/2a.

Контрольні запитання.

1.Як змінюється модуль швидкості тіла, кинутого вертикально вгору?

2. Чому дорівнює швидкість тіла, кинутого вертикально вгору, у найвищій точці його підйому?

3. Чому дорівнює прискорення тіла, кинутого вертикально вгору, у найвищій точці його підйому?

4. По якій траєкторії рухається тіло, кинуте горизонтально?

5. З яким прискоренням рухається тіло, кинуте горизонтально?

6. Чи залежить час польоту тіла, кинутого горизонтально, від величини його початкової швидкості?

                   Вправа 3.

1.Тіло кинули вертикально вгору з швидкістю 15м/с. На якій висоті буде це тіло через 1с польоту? Через 2с польоту?

2.  Тіло кинули вертикально вгору з швидкістю 15м/с. Визначити максимальну висоту підйому цього тіла.

3. Стрілу випустили з лука вертикально вгору. При цьому, вона впала на землю через 6с. Яка початкова швидкість стріли і максимальна висота її підйому?

4. Тіло, що знаходиться на висоті 10м кинули горизонтально з швидкістю 15м/с. Визначити горизонтальну дальність польоту тіла.

5. Тіло, що знаходиться на висоті 20м кинули горизонтально з швидкістю 10 м/с. Визначите координати цього тіла через 1,5с польоту.

6. З вікна кинуто м’яч у горизонтальному напрямку з швидкістю 12м/с. Він упав на землю через 2с. З якої висоти було кинуто м’яч і на якій відстані від будинку він упав.

 

Лекційне заняття №4.

Тема: Основні поняття, величини та закони кінематики обертального руху.

Нагадаємо. Обертальний рух – це такий механічний рух, при якому всі точки тіла описують кола, центри яких знаходяться на одній прямій, яка називається віссю обертання. Оскільки при обертальному русі, різні точки тіла мають суттєво різні кінематичні характеристики (рухаються з різними швидкостями та прискореннями, описують різні траєкторії, проходять різні шляхи, тощо), то ясно, що описуючи такий рух, представляти тіло у вигляді матеріальної точки не припустимо. Як правило, в кінематиці обертального руху, реальне тіло представляють не у вигляді матеріальної точки, а у вигляді так званого абсолютно твердого тіла. Абсолютно тверде тіло – це таке умовне (ідеалізоване) тіло, яке в процесі механічних рухів та взаємодій не деформується.

До числа основних фізичних величин кінематики обертального руху відносяться: час (t), кутова координата (φ), кут повороту (Δφ), кутова швидкість (ω), кутове прискорення (ε).

Визначаючи базові величини кінематики обертального руху і перш за все ту, яка називається кутовою координатою (φ), або просто кутом, можна сказати наступне. В кінематиці поступального руху, розташування (місцезнаходження) матеріальної точки визначають її координатою (х). При цьому, в процесі поступального руху матеріальної точки, відповідно змінюється і її координата. Якщо ж говорити про обертальний рух тіла, то в процесі цього руху, координата тіла (тіла як матеріальної точки) по суті залишається незмінною. При обертальному русі, змінюється не координатне положення тіла, а його кутова орієнтація (мал.9). Цю орієнтацію характеризують величиною, яка називається кутом, а точніше – кутовою координатою.

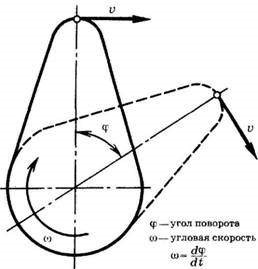
Мал.9. В процесі обертального руху тіла змінюється його кутова орієнтація.

Кутова координата (кут) – це фізична величина, яка характеризує просторову (кутову) орієнтацію тіла в вибраній системі координат і яка дорівнює відношенню довжини тієї дуги що обмежує даний центральний кут, до радіусу цієї дуги.

Позначається: φ

Визначальне рівняння: φ=ℓ/R

Одиниця вимірювання: [φ]=рад,   радіан.

Із визначального рівняння φ=ℓ/R ясно, що виміряти кут в радіанах, означає поділити довжину тієї дуги (ℓ) що обмежує даний кут, на радіус цієї дуги (R). При цьому, якщо довжина обмежуючої дуги дорівнює її радіусу (ℓ=R), то відповідний кут дорівнює одному радіану (від слова “радіус”).

Радіан – це одиниця вимірювання кутових величин, яка дорівнює такому центральному куту, довжина обмежуючої дуги якого дорівнює радіусу цієї дуги. По суті, радіан – величина безрозмірна [φ]=м/м=рад. Однак, щоб підкреслити, факт того, що ця безрозмірна величина характеризує саме кутову орієнтацію тіла, вона має спеціальну назву – радіан.

Вимірювання показують, що в повному колі міститься приблизно 6,28 радіан, а точніше 2π радіан, де π=3,141592653…≈ 3,14. Відображенням даного факту є та формула за якою визначають довжину кола: ℓ=2πR.

Напевно ви знаєте, що в математиці, геометрії та повсякденному житті, кутові величини зазвичай вимірюють не в радіанах, а в градусах. Градус – це одиниця вимірювання кутових величин, яка дорівнює такому центральному куту, що становить триста шістдесяту (1/360) частину повного кола. Іншими словами, якщо коло поділити на 360 рівних частин, то кутовий сектор в одну таку частину і є градусом.

Як ви думаєте, чому визначаючи одиницю кутових величин, люди з незапам’ятних часів, поділили коло на 360 частин? Не на 10, не на 100, чи скажімо на 250, а саме на 360? Правильно! З незапам’ятних часів, люди звернули увагу на те, що приблизно через 360 днів, все в цьому світі повторюється. Виходячи з цієї повторюваності, коло життя, а за ним і геометричне коло, поділили на 360 частин.

З практичної точки зору, градус є надзвичайно зручною одиницею. Тому в сфері геометричних побудов та повсякденного життя, кутові величини зазвичай вимірюють в градусах. Але, ця одиниця має один суттєвий недолік – вона жодним чином не пов’язана з параметрами того кола яке ми поділили на певну кількість кутових сегментів. А це означає, що градус не є органічною частиною цілісної системи взаємопов’язаних одиниць, а отже і цілісної системи знань про навколишній світ.

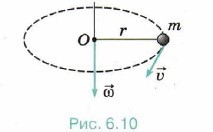
Для того щоб одиниця вимірювання кутових величин стала органічною частиною цілісної системи знань, коло потрібно поділити не так як нам подобається, чи здається зручним, а так щоб цей поділ відображав той реальний зв’язок який існує між кутовими та лінійними величинами. А цей зв’язок полягає в тому, що для будь якого кутового сегменту (φ) відношення його обмежуючої дуги (ℓ) до радіусу цієї дуги (R) є постійною величиною (мал.10). Власне це відношення і є тим кутом, величина якого виміряна в радіанах.

  

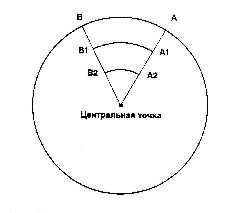
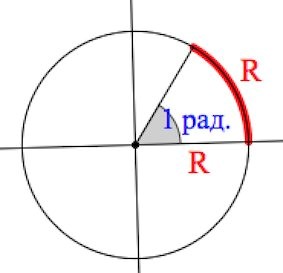
Мал.10.  Для будь якого кута φ відношення його обмежуючої дуги ℓ до радіусу R цієї дуги є постійною величиною.

Оскільки у повному колі, з одного боку міститься 360 градусів, а з іншого – 2π радіан, то між відповідними одиницями існує співвідношення 2π(рад)=360º. Звідси випливає, що 1рад=360º/2π ≈ 57º.

З побутово-практичної точки зору, вимірювати кутові величини в радіанах (1рад ≈ 57º) досить незручно. Тому в побутовій практиці та при геометричних побудовах, кутові величини зазвичай вимірюють в градусах. Однак якщо мова йде про фізику та сучасну науку загалом, то в ній основною одиницею вимірювання кутових величин є не градус, а радіан. Адже виміряний в радіанах кут є не лише мірою кутових величин, а й певним відображенням тих зв’язків, які об’єктивно існують між кутовими та лінійними величинами.

Тепер, коли ви знаєте що просторову орієнтацію тіла характеризують певним кутом і що величина цього кута вимірюється в радіанах, можна визначити й інші характеристики обертального руху тіла, зокрема його кут повороту, кутову швидкість та кутове прискорення.

Кут повороту – це фізична величина, яка характеризує кут повороту тіла і яка дорівнює цьому куту (тобто тому куту, на який повернулось тіло в процесі свого обертального руху).

Позначається: ∆φ

Визначальне рівняння: ∆φ=φ_к – φ₀,  або  ∆φ=s/R,

де s – довжина того шляху який пройшла певна точка тіла, рухаючись по колу радіусу R, при повороті тіла на кут ∆φ.

Одиниця вимірювання: [∆φ]=рад,  радіан.

Кутова швидкість – це фізична величина, яка характеризує кутову швидкість тіла (швидкість обертального руху тіла) і яка показує на який кут повертається тіло за одиницю часу.

Позначається: ω

Визначальне рівняння: ω=∆φ/∆t

Одиниця вимірювання: [ω]=рад/с,  радіан за секунду.

Кутове прискорення – це фізична величина, яка характеризує кутове прискорення тіла і яка показує на скільки змінюється кутова швидкість тіла за одиницю часу.

Позначається: ε

Визначальне рівняння: ε=∆ω/∆t

Одиниця вимірювання: [ε]=рад/с²,  радіан за секунду в квадраті.

По суті, кутова швидкість (ω) та кутове прискорення (ε) – величини векторні. Однак, зважаючи на факт того, що в межах програми загальноосвітньої школи, вивчають лише загальні основи механіки обертального руху, ми не будемо формулювати ті правила які визначають напрям цих векторів. Натомість будемо просто вважати, що кутова швидкість того тіла яке обертається за годинниковою стрілкою має знак “+”, а проти годинникової стрілки, знак «–». При цьому, якщо в процесі обертання, кутова швидкість збільшується, то знаки кутової швидкості та кутового прискорення є однаковими. А якщо ця швидкість зменшується, то відповідні знаки є різними.

Основний закон кінематики обертального руху називається рівнянням обертального руху. В цьому законі стверджується: в загальному випадку обертальний рух тіла можна описати рівнянням  φ = φ₀ + ω₀t + (ε/2)t²

де  φ – кутова координата тіла в момент часу t;

φ₀ – початкова кутова координата тіла;

ω₀ – початкова кутова швидкість тіла;

ε – кутове прискорення тіла.

В кінематиці обертального руху, рівняння φ=φ₀ + ω₀t + (ε/2)t² відіграє ту ж роль, що і рівняння х=х₀ + v₀t + (a/2)/t² в кінематиці поступального руху. А це означає, що на основі аналізу рівняння обертального руху тіла, можна розв’язати безліч задач які стосуються цього руху. Втім, програма загальноосвітньої школи не передбачає розв’язування подібних задач. Зважаючи на ці обставини, обмежимся лише тією загальною характеристикою обертального руху, яка з усією очевидністю випливає з аналізу рівняння цього руху.

Задача. За заданим рівнянням обертального руху φ = π/2+10t – 0,1t² дати загальну характеристику цього руху.

Із порівняльного аналізу рівнянь

φ=φ₀ + ω₀t + (ε/2)t²

φ=π/2 + 10t –  0,1t²

ясно: φ₀ = π/2 рад;  ω₀ = 10 рад/с;  ε = –0,2 рад/с²;  ω↓.

Це означає, що в заданій системі координат, початкова кутова координата тіла відповідає куту π/2 рад. При цьому тіло обертається в додатному напрямку (за годинниковою стрілкою) з початковою кутовою швидкістю 10 рад/с. Величина цієї швидкості зменшується, а числове значення кутового прискорення становить 0,2 рад/с² .

          Поділ механічних рухів на поступальні та обертальні, в значній мірі є умовним. Наприклад кабіна “оглядового колеса” (мал.11а), з одного боку, рухається поступально (в процесі руху будь яка приналежна тілу пряма залишається паралельною сама собі), а з іншого – обертально (в процесі руху, всі точки кабіни описують практично концентричні кола). Загалом, рух будь якої матеріальної точки по колу, з одного боку можна вважати обертальним, а з іншого – поступальним. А це означає, що описуючи такий рух, з одного боку говорять про кутову швидкість (ω), кутове прискорення (ε) і кут повороту (∆φ), а з іншого – про лінійну швидкість (v), лінійне прискорення (a) та пройдений шлях (s).

  

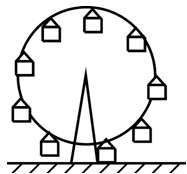
Мал.11. Рух кабіни “оглядового колеса” (а) та рух матеріальної точки по колу (б), одночасно є як поступальним так і обертальним.

Оскільки у вище наведених прикладах мова йде про один і той же поступально-обертальний рух, то між параметрами його поступальної та обертальної складових, існують певні кількісні співвідношення. Власне, ці співвідношення випливають із визначальних рівнянь відповідних фізичних величин. Дійсно. Якщо в процесі обертального руху матеріальна точка здійснює поворот на кут ∆φ=s/R, то її лінійне переміщення (пройдений шлях) становитиме s=∆φR. Якщо кутова швидкість матеріальної точки ω, то її лінійна швидкість v=ωR (за визначенням ω=∆φ/∆t=s/R∆t=v/R, звідси v=ωR). Якщо кутове прискорення матеріальної точки ε, то її лінійне прискорення а=εR (за визначенням ε=∆ω/∆t=∆v/R∆t=a/R, звідси а=εR).

Таким чином, якщо матеріальна точка рухається по колу радіусу R, то між параметрами її поступального (лінійного) та обертального руху існують співвідношення:

.                  s=∆φR;     v=ωR;    a=εR,  або

.                 ∆φ=s/R;    ω=v/R;    ε=a/R.

Характерною особливістю руху матеріальної точки по колу є те, що в незалежності від швидкості цього руху, ця точка завжди рухається з певним доцентровим прискоренням, яке характеризує зміну швидкості за напрямком і яке визначається за формулою а=v²/R. А зважаючи на те, що v=ωR, цю формулу можна записати у вигляді а_д=ω²R.

Аналізуючи параметри та закони поступального і обертального рухів, не важко бачити, що між цими параметрами та законами є певні очевидні аналогії. Ці аналогії можна представити у вигляді наступної узагальнюючої

таблиці.

 

 

Параметри та закони поступального руху	Параметри та закони обертального руху	Взаємопов’язаність цих параметрів
час                         t	час                                     t	t=t
координата           x=ℓ	кутова                           φ=ℓ/R координата	ℓ=φR
пройдений            s=∆x шлях	кут                               ∆φ=s/R повороту	s=∆φR
швидкість         v=∆x/∆t	кутова                          ω=∆φ/∆t швидкість	v=ωR
прискорення     a=∆v/∆t	кутове                          ε=∆ω/∆t прискорення	a=εR
доцентрове       aд=v2/R прискорення	_	ад=ω2R
рівняння поступального руху  x = x0 + v0t + (a/2)t2	рівняння обертального руху  φ = φ0 + ω0t +(ε/2)t2

Контрольні  запитання.

1.Чому, описуючи обертальний рух тіла, це тіло не можна представляти у вигляді матеріальної точки?

2.Чому, визначаючи кутовий градус, коло поділили на 360 частин?

3. Чому, в науковій практиці основною одиницею вимірювання кутових величин є не градус а радіан?

4. Якщо в будь якому повному колі міститься 2π радіан, то чому дорівнює довжина кола?

5. Чому дорівнює кут повороту хвилинної стрілки годинника за 15хв; за 30хв; за 2 години?

6. Визначте кутову швидкість секундної, хвилинної та годинної стрілок годинника.

7. За заданим рівнянням обертального руху, дати загальну характеристику цього руху: а) φ = –2π/3 +8t –0,1t²; б) φ = π – 10t – 0,2t²;в)  φ = –5t + 0,2t².

 

Лекційне заняття №5.

Тема: Основні поняття, величини та закони статики матеріальної точки.

          Статика (від грецького  statike – рівновага) – це розділ механіки в якому вивчають параметри, закономірності та причини стану механічної рівноваги тіла. Механічною рівновагою тіла (матеріальної точки) називають такий механічний стан тіла, при якому воно знаходиться в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v=const). Зазвичай в статиці розглядають ті ситуації коли тіло знаходиться в стані механічного спокою. Однак ви маєте знати, що з фізичної точки зору, між станом механічного  спокою тіла (v=0) та станом його прямолінійного рівномірного руху (v=const) нема суттєвої різниці. А якщо вам потрібні докази цьому на перший погляд парадоксальному факту, то запитайте себе та оточуючих, чи відчувають вони факт того, що Земля з швидкістю 30км/с обертається навколо Сонця, а навколо центру нашої Галактики – з швидкістю 250км/с?

Основною фізичною величиною статики є сила. Сила – це фізична величина, яка характеризує силову дію одного тіла на інше (є мірою взаємодії фізичних об’єктів) і яка дорівнює добутку маси тіла на величину того прискорення яке воно отримує під дією даної сили.

Позначається: F

Визначальне рівняння: F=ma

Одиниця вимірювання: [F]= кг∙м/с²= H,   ньютон.

Ньютон – це одиниця вимірювання сили, що дорівнює такій силі яка тілу масою 1кг надає прискорення 1м/с²:  1Н=1кг∙1м/с². Іншими словами, якщо тіло масою 1кг рухається з прискоренням 1м/с², то це означає, що на нього діє сила 1Н.

До числа основних сил статики і механіки загалом, відносяться:

– сила інерції                F_i = −ma

– сила тяжіння              F_т = mg

– реакція опори           N

– вага                              P = − N

– сила пружності         F_пр = −k(Δℓ)

– сила тертя                  F_тер = µN

– гравітаційна сила     F_гр = Gm₁m₂/ℓ²

– сила Архімеда           F_A= ρVg

Сила інерції – це та сила, поява якої обумовлена прискореним рухом тіла і яка завжди протидіє появі та зростанню цього прискорення.

Позначається: F_і

Визначальне рівняння: F_і = – ma

Одиниця вимірювання: [F_і] = Н

Сила тяжіння – це та сила,  з якою тіла притягуються до Землі і яка дорівнює добутку маси тіла на прискорення його вільного падіння.

Позначається: F_т

Визначальне рівняння: F_т= mg

Одиниця вимірювання: [F_т]= H .

Реакція опори – це та сила, з якою опора діє на тіло та жорстко протидіє його переміщенню.

Позначається: N

Визначальне рівняння: визначається з умов конкретної задачі.

Одиниця вимірювання: [N]=H .

Вага – це та сила з якою тіло діє на опору.

Позначається: Р

Визначальне рівняння: Р = – N, де N – реакція опори

Одиниця вимірювання: [P] = H,  ньютон.

Сила пружності – це та внутрішня сила, яка виникає в пружно деформованому тілі і яка завжди протидіє появі та зростанню цієї деформації.

Позначається: F_пр

Визначальне рівняння: F_пр = -k∆ℓ

Одиниця вимірювання: [F_пр] =H

Сила тертя (сила тертя ковзання) – це та сила, з якою поверхні взаємодіючих твердих тіл протидіють їх взаємному поступальному (ковзальному) переміщенню, або можливості такого переміщення.

Позначається: F_тер

Визначальне рівняння: F_тер =µN

Одиниця вимірювання: [F_тер] = Н

Сила гравітаційної взаємодії (гравітаційна сила) – це та сила, з якою тіла взаємодіють згідно з законом всесвітнього тяжіння.

Позначається: F_гр

Визначальне рівняння: F_гр =Gm₁m₂/r²

Одиниця вимірювання: [F_гр]=H.

          Сила Архімеда – це та сила, з якою тіла виштовхуються з рідин та газів і яка дорівнює вазі виштовхнутої тілом рідини або газу.

Позначається: F_a

Визначальне рівняння: F_a=ρVg ,

Одиниця вимірювання: [F_a] = H.

Зазвичай на тіло діє не одна сила, а їх певна сукупність. Сукупність тих сил що діють на дане тіло в даний момент часу називають системою сил. Наприклад, на представлене на мал.12а тіло, діє системи чотирьох сил: F₁; F₂; F₃; F₄. Систему сил, лінії дії яких перетинаються в одній точці, називають збіжною системою сил. Скажімо, зображена на мал.12а система сил є збіжною. Адже лінії дії всіх чотирьох сил перетинаються в одній точці – точці К.

  

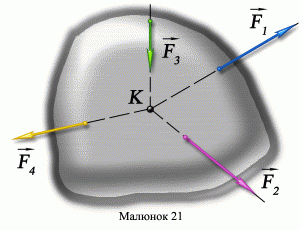
Мал.12. Систему діючих на тіло збіжних сил, можна замінити  їх рівнодійною силою.

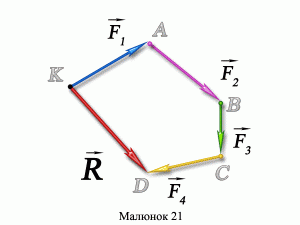
Якщо тверде тіло знаходиться під дією збіжної системи сил, то: по-перше, це тіло можна вважати матеріальною точкою, а по-друге, систему таких сил можна замінити однією рівнодійною силою (мал.12б). Рівнодійною силою (позначається R або F_р), називають таку силу, яка чинить на тіло (матеріальну точку) таку ж силову дію як і вся система реально діючих сил і яка дорівнює векторній сумі тих сил що реально діють на дане тіло, тобто R=F₁+F₂+ … +F_N. Це означає, що заміна системи реально діючих на тіло сил, відповідною рівнодійною силою, не змінить механічну поведінку тіла.

Механізм додавання векторів загалом і сил зокрема принципово простий і полягає в наступному. Від точки прикладання сил (точка К), з дотриманням обраного масштабу та відповідних напрямків, відкладають вектор F₁, з кінця вектора F₁ відкладають вектор F₂, з кінця F₂ відкладають F₃ і т.д. Вектор який з’єднує початок першого вектора (F₁) і кінець останнього (F_N) і є відповідною рівнодійною силою R. При цьому величина рівнодійної сили пропорційна довжині вектора R, а її напрямок – збігається з напрямком вектора R.

Геометричний метод додавання векторів виглядає досить простим та наочним. Однак, він має ряд суттєвих недоліків. Перший полягає в тому, що точність його результатів залежить від масштабу та точності геометричних побудов. При цьому, будь яка точність цих побудов, не гарантує безумовно точного результату. Другим суттєвим недоліком геометричного методу додавання векторів є факт того, що таке додавання погано поєднується з тими теоріями, в яких закони представляються у вигляді певних математичних формул. А переважна більшість фізичних теорій є саме такими.

Ці недоліки відсутні в алгебраїчному методі додавання векторів, тобто такому методі при якому результат додавання векторів визначають не шляхом геометричних побудов, а шляхом алгебраїчних розрахунків. Реалізуючи цю ідею, вектор F розкладають на дві складові: проекції цього вектора на осі системи координат F_x та F_y.

Проекції вектора на осі прямокутної системи координат можна визначити не лише шляхом геометричних побудов, а й шляхом алгебраїчних розрахунків. Ці розрахунки полягають в наступному. Якщо в заданій прямокутній системі координат (мал.13) вектор F має числову величину F та кутову орієнтацію α (де α – відкладено від осі 0х), то проекції цього вектора на осі системи координат визначаються за формулами: F_x=Fcosα; F_y=Fsinα.

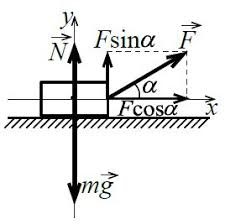
Мал.13. Будь який вектор F(F,α) можна представити у вигляді двох по суті скалярних величин: F_x=Fcosα;  F_y=Fsinα.

Практична реалізація алгебраїчного методу додавання векторів та розв’язування задач статики, не можуть бути успішними без розуміння фізичної суті того, що називають синусом і косинусом кута. В математиці ці функції зазвичай визначають наступним чином. Синусом гострого кута α прямокутного трикутника називають відношення протилежного катета b до гіпотенузи с: sinα=b/c. Косинусом гострого кута α прямокутного трикутника називають відношення прилеглого катета a до гіпотенузи с: cosα=a/c.

Мал.14. В математиці синус та косинус кута визначають як певні співвідношення між сторонами прямокутного трикутника: cosα=a/c; sinα=b/c.

З формальної точки зору, вище сформульовані визначення (cosα=a/c; sinα=b/c) є правильними. Однак вони мають ряд суттєвих недоліків. По-перше, дозволяють визначати синуси та косинуси лише гострих кутів, тоді як ці функції мають певні значення для будь яких кутів, будь-то 30°; 60°; 135° чи 5784°. По-друге, не пояснюють факту того, чому значення косинусів та синусів можуть бути як додатними так і від’ємними. По-третє, не пояснюють факту періодичності даних функцій. А головне, вище наведені визначення не розкривають фізичного змісту тих функцій які називаються синусом та косинусом кута. А цей зміст відображають наступні визначення.

Косинус кута α – це безрозмірна величина, яка дорівнює проекції відповідного цьому куту одиничного радіус-вектора на ту вісь від якої виміряно кут α. Синус кута α – це безрозмірна величина, яка дорівнює проекції відповідного цьому куту одиничного радіус-вектора на ту вісь, що є перпендикулярною до осі від якої виміряно кут α.

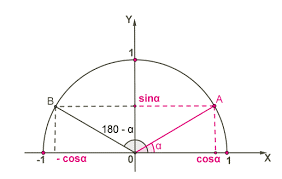
Мал.15. Синус та косинус довільного кута можна визначити як проекції відповідного цьому куту одиничного радіус-вектора на осі прямокутної системи координат.

Числові значення косинусів та синусів для найбільш поширених кутів можна представити у вигляді наступної таблиці.

α	0°	30°	45°	60°	90°	120°	135°	150°	180°
cosα	1,00	0,87	0,71	0,50	0,00	– 0,50	– 0,71	– 0,87	– 1,00
sinα	0,00	0,50	0,71	0,87	1,00	0,87	0,71	0,50	0,00

Доречно зауважити і те, що на практиці кутову орієнтацію вектора в заданій системі координат, задають кутом меншим за 90º. Наприклад в зображеній на мал.16д ситуації, положення вектора F характеризують не кутом α>90º, а йому відповідним кутом β=180º-α < 90º. Крім цього, проекції тих векторів, що є паралельними або перпендикулярними осям системи координат (мал.16.в,г), визначають із міркувань очевидності: наприклад, в ситуації мал.34в: F_x=F; F_y=0; мал.16г: F_x=0; F_y=−F.

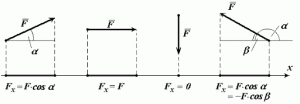
Мал.16. Визначаючи параметри проекцій вектора, потрібно враховувати від якої осі і в якому напрямку виміряно той кут, що характеризує положення відповідного вектора.

Основний закон статики називається умовою рівноваги тіла. В цьому законі стверджується: тіло (матеріальна точка) буде знаходитись в стані механічної рівноваги (v=0 або v=const ) тоді і тільки тоді, якщо векторна сума діючих на нього зовнішніх сил дорівнює нулю. Іншими словами: якщо ∑F_i=0 то v=0, або v=const  і навпаки: якщо v=0 або v=const,  то ∑F_i=0.

На практиці (при розв’язуванні задач), вектор сили (F) тобто тієї величини яка характеризується модулем (F) та кутовою орієнтацією (α), розкладають на дві по суті скалярні величини: проекції даного вектора на осі системи координат (F_x=Fcosα; F_y=Fsinα). При цьому, для плоскої системи сил умова рівноваги тіла набуває вигляду: ∑F_x ;  ∑F_y = 0

З формальної точки зору, ті ситуації в яких тіло рухається з певним прискоренням не є предметом вивчення статики. Однак з практичної точки зору, ситуація при якій тіло знаходиться в стані механічної рівноваги (v=0 або v=const), відрізняється від ситуації при якій воно рухається з певним прискоренням (a=const) лише тим, що в другому випадку на це тіло, окрім системи зовнішніх сил діє ще одна сила – сила інерції F_i = -mа.

Про тіло (матеріальну точку) яке під дією системи зовнішніх сил та сили інерції знаходиться в стані рівноприскореного руху (а=соnst) говорять, що воно перебуває в стані динамічної рівноваги. Цей стан характеризує закон, який називається умовою динамічної рівноваги тіла. В цьому законі стверджується: тіло (матеріальна точка) буде знаходитись в стані динамічної рівноваги (а =const) тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил та сили інерції дорівнює нулю. Іншими словами: якщо  а =const,  то  Σ F + F_i = 0 і навпаки.

                   Контрольні запитання.

1.Чим відрізняються векторні величини від скалярних?

2. В чому суть геометричного методу додавання векторів?

3. Які основні недоліки геометричного методу додавання векторів?

4. В чому суть векторно-проекційного способу визначення функцій sinα та cosα? Які переваги має цей спосіб?

5. З якої теореми випливає, що cos²α + sin²α = 1?

6. Шляхом геометричних міркувань виразіть задану тригонометричну функцію через відповідну функцію кута α.

cos(-α) =               ;      sin(-α) =                ;

cos(90º-α) =          ;      sin(90º-α) =          ;

cos(90º+α) =         ;      sin(90º+α) =         ;

cos(180º-α) =        ;      sin(180º-α) =        ;

cos(180º+α) =       ;      sin(180º+α) =        .

 

 

Лекційне заняття №6.

Тема: Силовий метод розв’язування задач.

Суть силового методу розв’язування задач полягає в тому, що невідомі величини визначають на основі векторного аналізу діючих на тіло сил та на базі умови його механічної рівноваги: якщо v=0, або v=const, то ∑F=0, або в проекціях на осі системи координат ΣF_x=0; ΣF_y=0.

Силовий метод розв’язування задач має ту перевагу, що порядок (алгоритм) їх розв’язку є чітко визначеним. І цей порядок наступний:

1.Уважно прочитати умову задачі та зробити стислий запис цієї умови.

2. Обов’язково виконати малюнок, на якому чітко вказати всі діючі на задане тіло (матеріальну точку) сили та напрямки цих сил.

3. Задати систему координат.

4. Записати умову рівноваги даної матеріальної точки, тобто систему рівнянь: ∑F_x=0; ∑F_y=0

5. Розв’язавши цю систему, визначити невідомі величини.

Загальне зауваження. В механіці матеріальної точки, а саме таку механіку ми і вивчаємо, прийнято вважати, що всі діючі на тіло сили, діють на його центр мас. Тому, якщо в умові задачі нема конкретних вказівок щодо точки прикладання конкретної сили, вважається що ця сила діє на цент мас відповідного тіла.

Дотримуючись вище наведеного алгоритму та зважаючи на зроблене зауваження, розв’яжемо декілька конкретних задач.

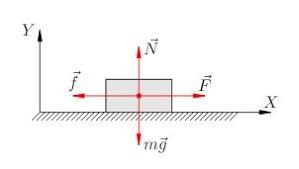
Задача 1. Дерев’яний брусок масою 2кг, за допомогою пружини жорсткістю 100Н/м рівномірно тягнуть горизонтальною поверхнею. Яким буде видовження пружини, якщо коефіцієнт тертя між бруском та поверхнею 0,3?

Дано:                                 Рішення:

m = 2кг              Виконуємо малюнок на якому вказуємо всі

k=100Н/м          діючі на тіло сили та задаємо відповідну

μ = 0,3                систему координат.

Δℓ =?

Записуємо умову рівноваги даного тіла:

ΣF_x = F – F_тер = kΔℓ – μN = 0;

ΣF_y = N – F_т = N – mg = 0.

Із рівняння (1) випливає kΔℓ = μN, звідси  Δℓ = μN/k, де N=?

Із рівняння (2) випливає N = mg = 2кг·10м/с² = 20Н.

Таким чином Δℓ = μN/k = 0,3·20Н/100(Н/м) = (6/100)м = 0,06м = 6см.

Відповідь: Δℓ = 6см.

Задача 2. Тіло масою 15кг знаходиться на горизонтальній поверхні. Яку горизонтальну силу треба прикласти до тіла щоб зрушити його змісця, якщо коефіцієнт тертя 0,4?

Дано:                                 Рішення:

m=15кг            Виконуємо малюнок на якому вказуємо всі діючі на

μ = 0,4             тіло сили та задаємо відповідну систему координат.

F = ?

Записуємо умову рівноваги даного тіла:

ΣF_x = F – F_тер = F – μN = 0;

ΣF_y = N – F_т = N – mg = 0.

Із рівняння (1) випливає F = μN, де N=?

Із рівняння (2) випливає N = mg = 15кг·10м/с² = 150Н.

Таким чином F = μN = 0,4·150Н =60Н.

Відповідь: F = 60Н.

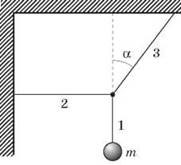
Задача 3. Тіло масою 20кг на дротах підвішено так, як показано на малюнку (α=30º). Визначити зусилля в дротах 2 і 3.

Дано:                     Рішення:

m = 20кг

α = 30º                 Малюнок

N₂=?

N₃=?

Виконуємо малюнок, на якому вказуємо діючі на точку рівноваги сили та задаємо систему координат. Записуємо умову рівноваги системи.

∑F_x = -N₂ + N₃sin30º= 0

∑F_y = -F_T + N₃cos30º= 0.

Розв’язавши систему рівнянь, визначаємо невідомі величини:

із (2) → N₃cos30º = F_T = mg; → N₃ = mg/cos30º = 20∙10/0,87= 230H;

із (1) → N₂ = N₃sin30º = 230∙0,5= 115H.

Відповідь: N₂ = 115H; N₃ = 230H.

          Задача 4. Тіло масою 10кг під дією сили тяжіння знаходиться в стані механічного спокою на похилій площині. Визначити величини діючих на тіло сил, якщо кут нахилу площини до лінії горизонту 30°.

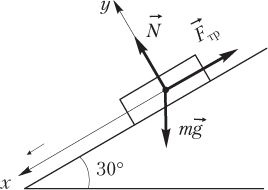
Зауваження. Рішення будь якої задачі механіки, в тій чи іншій мірі ідеалізоване. Наприклад в умовах нашої задачі, ті сили які ми називаємо реакцією опори та силою тертя, виникають в місті контакту тіла з відповідною поверхнею і є розподіленими по цій поверхні. Ми ж зображаємо ці сили такими, що сконцентровано прикладені до центру мас тіла. До речі, те ж стосується і сили тяжіння, дія якої фактично розподілена по всьому об’єму тіла і яку ми зображаємо такою, що діє в центрі мас цього тіла.

Дано:                     Аналіз:

m = 10кг

α =30°                    Малюнок

N = ?

F_тер = ?

Виконуємо малюнок на якому: вказуємо діючі на тіло (на центр мас тіла) сили; задаємо систему координат; вказуємо кутову орієнтацію сил. Записуємо умову рівноваги тіла і, розв’язавши систему відповідних рівнянь, визначаємо невідомі величини. ( F_т = mg = … =100H )

∑ F_x = – F_тер + F_т sinα = 0       (1)

∑ F_y = N – F_т cosα = 0            (2).

Із (1) → F_тер = F_т sinα .

Із (2) → N = F_т cosα .

Розрахунки:     F_тер = 100∙0,5 = 50Н

N = 100∙0,87 = 87H

Відповідь: N = 87H;  F_тер = 50H.

Задача 5. Автомобіль масою 900кг, маючи тягову силу 2кН, рухається з прискоренням 1м/с². Визначити загальну силу опору руху автомобіля (загальну силу тертя).

Дано:              СІ                            Рішення:

m = 900кг         –               Виконуємо малюнок на якому вказуємо

F_тяги = 2кН   2000Н           всі діючі на автомобіль сили в тому числі

a = 1м/с²           –                і направлену  в протилежну сторону від

F_тер = ?                                прискорення, силу інерції.

.                                           Задаємо відповідну систему координат.

(На жаль, малюнка на якому була б вказана сила інерції знайти практично не можливо. Тому наявність цієї сили просто уявіть)

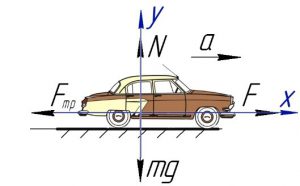
Записуємо умову рівноваги тіла вздовж осі 0х:

ΣF_x = F_тяги – F_тер – F_i = F_тяги – F_тер – mа = 0. Звідси випливає

F_тер = F_тяги – mа.

Розрахунки: F_тер = 2000Н – 900кг1м/с² = 2000Н – 900Н = 1100Н

Відповідь: F_тер = 1100Н.

Задача 6. З якою силою буде тиснути автомобіль масою 800кг на середину опуклого моста, якщо радіус моста 50м, а швидкість автомобіля 36км/год?

Дано:                СІ                        Рішення:

m = 800кг          –         Оскільки та сила з якою автомобіль тисне

R = 50м              –         на опору називається вагою автомобіля (Р),

v = 36км/год   10м/с       та зважаючи на те, що за визначенням

P = ?                                 Р=-N, а в числивих значеннях Р=N,

то рішення задачі зводиться до визначення діючої на автомобіль реакції опори. Визначаючи цю реакцію, виконуємо малюнок на якому вказуємо ті сили які діють на автомобіль у верхній точці моста. А враховуючи факт того, що автомобіль з швидкістю v рухається по колу, а отже рухається з доцентровим a=v²/R прискоренням, можна стверджувати, що на автомобіль окрім сили тяжіння та реакції опори діє сила інерції F_i=ma=mv²/R, і що у верхній точці моста вона направлена вертикально вгору.

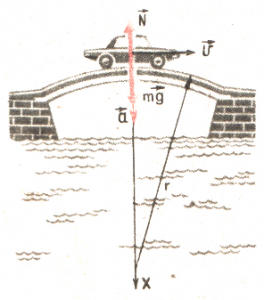
Записуємо умову рівноваги даного тіла в напрямку вертикальної осі (оскільки на малюнку ця вісь направлена вниз, то і знаки сил є відповідними):

ΣF_x = F_т – F_i – N = mg – mv²/R – N = 0. Звідси випливає:

N = mg – mv²/R = m(g – v²/R)

Розрахунки: N = 800кг(10м/с² – (10м/с)²/50м) = 800кг·8м/с² = 6400Н.

Відповідь: Р = 6400Н.

Вправа №4.

1.Тіло масою 8кг з постійною швидкістю рухається горизонтальною поверхнею. Під дією якої сили рухається тіло, якщо коефіцієнт тертя між тілом і поверхнею 0,3?

2. Тіло під дією горизонтальної сили 6Н рухається з постійною швидкістю. Яка маса тіла, якщо коефіцієнт тертя між тілом і поверхнею 0,4?

3. За допомогою пружини жорсткість якої 100Н/м тіло з постійною швидкістю тягнуть горизонтальною поверхнею. Яка маса тіла, якщо видовження пружини 4см, а коефіцієнт тертя між тілом та поверхнею 0,4?

4. В процесі аварійного гальмування автомобіль масою 4т рухається з прискоренням 2м/с². Визначити діючу на автомобіль силу тертя та коефіцієнт тертя.

5. З якою силою тисне автомобіль масою 2т на середину опуклого моста, якщо радіус моста 100м, а швидкість автомобіля 54км/год?

6. Автомобіль масою 900кг рухається заокругленням горизонтальної дороги з швидкістю 54км/год. Визначте величину діючої на шини автомобіля бічну силу тертя, та коефіцієнт тертя, якщо радіус заокруглення дороги 400м.

7. З якою швидкістю має рухатись автомобіль по опуклому мосту, радіус кривизни якого 90м, щоб у верхній точці моста, тиск автомобіля на поверхню моста дорівнював нулю?

 

Лекційне заняття №7.

Тема: Пара сил. Момент сили. Рівновага тіла, що має вісь обертання. Важелі. Блоки.

До сих пір, говорячи про механічну та динамічну рівновагу тіла, ми мали на увазі, що це тіло знаходиться під дією так званої збіжної системи сил, тобто такої сукупності одночасно діючих сил, лінії дії яких перетинаються в одній точці. По суті це означає, що ми вивчали статику матеріальної точки, тобто ту частину статики в якій тіло можна вважати матеріальною точкою, а діючу на це тіло систему сил, можна замінити однією рівнодіючою силою. Силою, яка надає тілу поступального руху.

Однак, далеко не всяка діюча на тіло система сил є збіжною і далеко не всяку систему сил можна замінити рівнодіючою. Наприклад, якщо на тіло діють дві рівні за величиною і протилежні за напрямком сили F₁ і F₂ які не лежать на одній прямій (мал.17), то замінити цю систему сил відповідною рівнодіючою, не можливо. Дійсно. Формально визначивши рівнодіючу сил F₁ і F₂ ми отримаємо нульову величину: F₁ + F₂= 0. Та чи означає це, що загальна механічна дія сил F₁ і F₂ є нульовою? Очевидно що ні. Адже дана система сил надає або намагається надати тілу певного обертального руху.

 

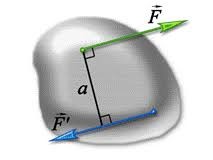
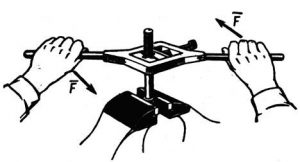
Мал.17.  Пару сил не можливо замінити  рівнодіючою силою.

Систему двох рівних за величиною і протилежних за напрямком сил, які не лежать на одній прямій і спільно діють на одне і те ж тіло, називають парою сил (або парою). Пара сил надає (або намагається надати) тілу обертального руху. Пару сил не можливо замінити або зрівноважити однією силою. Пару сил можна замінити чи зрівноважити лише іншою парою сил.

Ви можете заперечити в тому сенсі, що в певних випадках тіло може обертатись під дією лише однієї сили. Наприклад, відчиняючи двері, ми прикладаємо лише одну силу яка і надає їм обертального руху. Дійсно. На перший погляд здається, що двері обертаються під дією лише однієї сили. Насправді ж, одна сила не може змусити тіло обертатись. Це може зробити лише пара сил. І якщо двері обертаються, то це тільки тому, що на них діють дві сили які і утворюють відповідну пару. При цьому не важко збагнути, що другою силою пари є та реакція опори, яка виникає в петлях дверей. Петлях, які утворюють нерухому вісь обертання тіла.

Загалом, тіло яке має нерухому вісь обертання може рухатись лише обертально. І це обертання створює відповідна пара сил. Інша справа, що однією з цих сил може бути та реакція опори яка виникає в нерухомій осі обертання.

Мал.18.  Пара сил надає тілу (прагне надати) обертального руху.

Основною характеристикою пари сил, або тієї сили що діє на тіло з нерухомою віссю обертання, є фізична величина яка називається моментом сили або моментом пари сил.

          Момент сили – це фізична величина, яка характеризує обертальну дію сили (пари сил) і яка дорівнює добутку цієї сили F на плече її дії d.

Позначається: М

Визначальне рівняння: М=Fd ,  де  d – плече сили, тобто найкоротша відстань між лінією дії сили та віссю обертання тіла.

Одиниця вимірювання:  [М] = Н∙м,   (ньютон-метр).

Із аналізу рівняння М=F·d ясно, що момент сили залежить як від величини самої сили F, так і від величини плеча її дії d. При цьому величина плеча дії сили залежить як від точки прикладання сили, так і від напрямку її дії. Наприклад, прикладаючи одну і ту ж силу в різних точках руків’я гайкового ключа (мал.19а), ми отримаємо різні моменти сили: Fh₂>Fh₁. Різні тому, що плечі дії цих сил є різними h₂>h₁. З іншого боку, точки прикладання сили можуть бути однаковими, а моменти цих сил – різними. Наприклад в зображених на мал.19б,в ситуаціях, точки прикладання сили F є однаковими. А от створювані цими силами моменти є різними. Різними тому, що плечі дії сил різні. Бо плече дії сили, це не відстань від точки прикладання сили до осі обертання тіла. Плече сили – найкоротша відстань від лінії дії сили до осі обертання тіла.

  

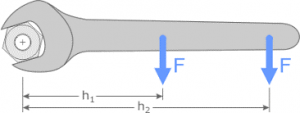
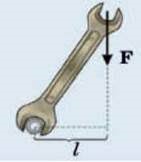
Мал.19. Плече сили, це найкоротша відстань від лінії дії сили до осі обертання тіла.

Потрібно зауважити, що момент сили – величина векторна. Однак, зважаючи на те, що в межах програми загальноосвітньої школи вивчають лише плоскі системи сил, момент сили можна вважати величиною скалярною, тобто такою яка характеризується абсолютною величиною та знаком. При цьому, знак моменту сили зазвичай визначають за правилом: якщо сила обертає (або намагається обертати) тіло за годинниковою стрілкою, то момент сили додатній (мал.20а), а якщо проти годинникової стрілки – від’ємний (мал.20б).

  

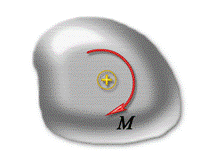
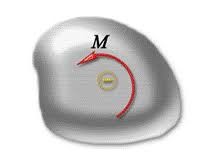
Мал.20. Якщо сила (пара сил) обертає тіло за годинниковою стрілкою, то момент сили додатній, а якщо проти годинникової стрілки – від’ємний.

Коли ми стверджували, що тіло буде знаходитись в стані механічної рівноваги тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил дорівнює нулю (∑F=0), то мали на увазі, що система діючих на тіло сил є збіжною, і що тому рівновага тіла є так би мовити поступальною. В загальному ж випадку, система діючих на тіло сил може бути довільною. І ця довільна система сил може надавати тілу не лише поступального руху, а й руху обертального. В такій ситуації основний закон статики  (загальна умова рівноваги тіла) набуває вигляду: тіло буде знаходитись в стані повної механічної рівноваги (спрощено кажучи, не буде рухатись ані поступально ані обертально) тоді і тільки тоді, коли векторна сума діючих на нього зовнішніх сил та моментів цих сил дорівнюють нулю, тобто за умови:

∑F =0; ∑M=0.

Оскільки те тіло яке має нерухому вісь обертання, поступально не рухається і рухатись не може, то векторна сума діючих на нього зовнішніх сил гарантовано дорівнює нулю. А це означає, що для такого тіла умова рівноваги набуває вигляду: тіло з нерухомою віссю обертання, буде знаходитись в стані обертальної рівноваги (обертального спокою), тоді і тільки тоді, коли сума діючих на нього моментів сил дорівнює нулю, тобто за умови: ∑М=0.

Потрібно зауважити, що формула ΣМ=0 є справедливою в незалежності від того, відносно якої точки тіла ви визначаєте діючі на нього моменти сил. Однак, якщо цією точкою буде не точка осі обертання тіла, то в цьому випадку потрібно враховувати і ту силу, яка виникає в осі обертання і яка називається реакцією опори. Зважаючи на ці обставини, застосовуючи формулу ΣМ=0, в якості тієї точки відносно якої визначаються моменти сил, ми будемо обирати точку осі обертання тіла. Адже в цьому випадку момент реакції опори дорівнює нулю (поясніть чому).

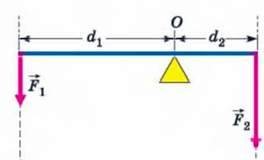
Одним з найпростіших і в той же час дуже важливих механічних приладів є важіль. Важіль – це прилад, який представляє собою довге тверде тіло яке має нерухому вісь обертання (одну точку опори) та застосовується для підсилення силової дії. Принцип дії важеля полягає в наступному. Якщо сила F₁ (мал.21) має плече d₁, а сила F₂ – плече d₂, то у відповідності з умовою рівноваги даного тіла (важеля) F₁d₁=F₂d₂. А це означає, що коли плече дії сили F₁ буде більшим за плече дії сили F₂ (d₁˃d₂) то у відповідну кількість разів сила F₂ буде більшою за силу F₁ : F₂=F₁(d₁/d₂) .

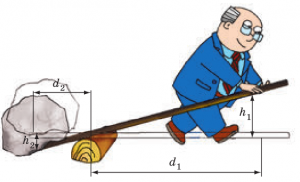
Мал.21.   Важіль – механізм який підсилює силову дію.

Було б дивним та неприроднім, якби за допомогою важеля ми отримували виграш в силі що називається “безкоштовно”, тобто не програючи в чомусь іншому. І очевидно, що цим “іншим” є програш в тому переміщенні яке здійснює підсилена сила. Можна довести, що виграючи в силі (F₂=nF₁ де n=d₁/d₂=s₁/s₂) ми в таку ж кількість разів програємо в тому переміщенні яке здійснює ця сила (s₂=s₁/n).

Про те, що “безкоштовних” виграшів в силі не буває, вчені знали ще з стародавніх часів. Приблизно дві тисячі років тому, давньогрецький механік Герон Олександрійський, сформулював правило, яке стосувалось всіх простих механізмів і в якому стверджувалось: у скільки разів виграєш в силі, у стільки ж разів програєш у відстані. Це правило прийнято називати золотим правилом механіки. По суті, золоте правило механіки є одним з перших формулювань базового закону сучасної науки – закону збереження енергії.

Певні важільні системи можна побачити в найрізноманітніших сучасних приладах, починаючи від дитячих гойдалок, весел, шлагбаумів та ножиць і закінчуючи елементами піднімально-транспортних механізмів, автомобілів, кораблів, літаків, тощо. Деякі приклади простих важільних систем представлені на мал.22.

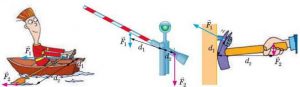
Мал.22. Деякі приклади простих важільних систем.

Задача 1. Відомо що маса слона 5т, а маса мухи 0,1г. Якої довжини має бути довше плече важіля, щоб муха зрівноважила слона. Довдина того плеча на якому стоїть слон 2м. Масу важеля не враховувати. На скільки має опуститися муха, щоб слон піднявся на 10см?

 

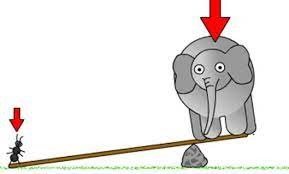
Дано:            СІ                              Рішення:

m₁ = 0,1г    1·10^-4кг      Виконуємо малюнок на якому вказуємо всі

m₂ = 5т       5·10³кг       діючі на тіло важеля сили та плече дії кожної

d₂ = 2м            –              з них. Записуємо умову

h₂ = 10см     0,1м           обертальної рівноваги важеля:

d₁ = ?                               ΣМ = F₂d₂ – F₁d₁ = m₂gd₂ – m₁gd₁ = 0.

h₁ = ?                               Звідси випливає m₁gd₁ – m₂gd₂, звідси

d₁ = d₂m₂/m₁ = 2м5·10³кг/1·10^-4кг = 10·10⁷м = 100·10⁶м.

Для порівняння: радіус Землі 6,37·10⁶м.

Із геометричних міркувань ясно: h₂/h₁ = d₂/d₁. Звідси випливає

h₁ = h₂d₁/d₂ = 0,1м100·10⁶м/2м = 5·10⁶м

Відповідь: d₁ = 100·10⁶м;  h₁ = 5·10⁶м.

Задача 2. На землі лежить труба довжиною 2м і масою 100кг. Яку силу треба прикласти, щоб підняти трубу за один з її кінців?

Дано:                                Рішення:

ℓ = 2м            Коли трубу починають піднімати за один кінець,

m = 100кг     то вона по суті перетворюється на важіль

F = ?              точкою опори якого є другий кінець труби.

При цьому на трубу (окрім реакції опори) діють дві вертикальні, протилежно направлені сили: сила тяжіння і та сила, що піннімає трубу. Зважаючи на вище сказане виконуємо відповідний малюнок та записуємо умову обертальної рівноваги труби:

ΣМ = F_т ℓ/2 – Fℓ = mgℓ/2 – Fℓ = 0. Звідси випливає Fℓ = mgℓ/2,

звідси F = mgℓ/2ℓ = mg/2.

Розрахунки F = 100кг10м/с²/2 = 500Н.

Відповідь: F = 500Н.

До числа найбільш розповсюджених простих механізмів, окрім важелів, відносяться різноманітні блоки. Блок – це прилад (механізм), який представляє собою круглий шків що має вісь обертання і по жолобу якого проходить елемент гнучкого зв’язку (канат, мотузка, трос, ланцюг, тощо). Якщо в процесі руху вантажу вісь блоку залишається нерухомою (мал.23а), то блок називається нерухомим. А якщо в процесі руху вантажу вісь блоку рухається разом з вантажем (мал.23б), то відповідний блок називають рухомим.

  

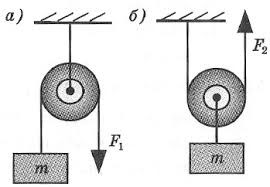
Мал.23.  Загальний устрій та найпростіші застосування блоку.

Оскільки шків блоку вільно обертається, то силовий натяг перекинутого через нього канату на вході та на виході шківа має бути однаковим. Власне ця однаковість випливає з умови обертальної рівноваги шківа. Дійсно. Під дією двох різнонаправлених сил F₁ і F₂ (мал.24а), шків буде знаходитись в стані обертальної рівноваги за умови, що момент тієї сили яка обертає  шків за годинниковою стрілкою (M₂=F₂R) дорівнює моменту тієї сили яка обертає його проти годинникової стрілки (M₁=F₁R), тобто за умови F₂R=F₁R, де R – радіус шківа. А це можливо лише тоді, якщо  F₂=F₁.

І потрібно зауважити, що натяг перекинутого через шків канату, не залежить від того, в якому напрямку цей канат натягують (мал.24б). А це означає, що нерухомий блок, не даючи виграшу в силі, дозволяє змінювати напрям цієї сили. Вже цей факт, робить подібні механізми потрібними та загальновживаними.

     

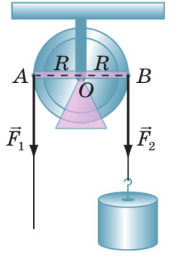
Мал.24. Нерухомий блок, не даючи виграшу в силі, дозволяє змінювати напрям цієї сили.

Але можливості блоків не вичерпуються лише зміною напрямку дії сили. В цьому не важко переконатись на прикладі системи яка складається з рухомого та нерухомого блоків (мал.25а). Не важко бачити, що в такій системі на рухомий блок, а отже і на те тіло яке він піднімає, діють дві рівні за величиною співнаправлені сили. А це означає, що натягуючи канат з силою F, на осі рухомого блоку ми отримаємо вдвічі більше тягове зусилля. Якщо ж в системі буде два рухомих блоки (мал.25б), то та загальна вага яку підніматиме ця система, буде у 4 рази більшою за величину тієї сили з якою натягують канат. Загалом же, додавання до системи кожного додаткового рухомого блоку, збільшує загальну вантажопід’ємність системи на 2F, де F – сила натягу канату.

  

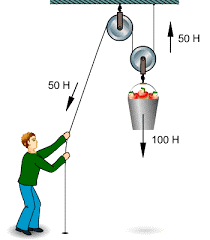
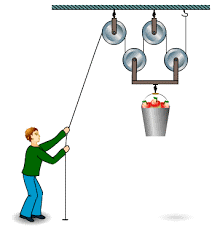
Мал.25. Кожний рухомий блок, збільшує вантажопід’ємність системи на 2F, де F – сила натягу канату.

Втім, потрібно мати на увазі, що загальна вантажопід’ємність системи рухомих та нерухомих блоків залежить не лише від числа рухомих блоків в ній, а й від місця закріплення нерухомого кінця канату. При цьому, якщо цей кінець кріпиться до нерухомої опори (26а), то загальна вантажопід’ємність системи n рухомих блоків дорівнює 2nF. Якщо ж нерухомий кінець канату кріпиться до рухомої опори, тобто тієї опори яка рухається разом з рухомими блоками (мал.26б), то в цьому випадку загальна вантажопід’ємність системи n блоків дорівнює (2n+1)F. Дійсно. Оскільки сила натягу канату в усіх його точках однакова, то в зображеній на мал.26в системі, на рухому опору діють п’ять рівних за величиною співнаправлених сил, кожна з яких дорівнює силі натягу канату. При цьому величина результуючої сили становить (2n+1)F.

   

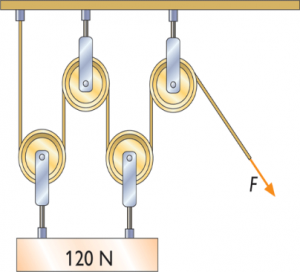
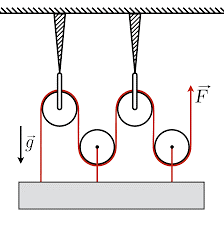
Мал.26. Загальна вантажопід’ємність системи блоків, залежить не лише від числа рухомих блоків в ній, а й від місця закріплення нерухомого кінця канату.

Ясно, що у вище наведених ситуаціях, отриманий виграш в силі не може бути «безкоштовним». Платою за цей виграш є неминучий програш в пройденому шляху. Дійсно. Для того, щоб за допомогою представленого на мал.25а рухомого блоку, підняти вантаж на ℓ метрів, потрібно на ℓ метрів зменшити довжину як правої так і лівої частин того канату який піднімає блок. А це означає, що той робітник який тягне канат з силою F, повинен прикладаючи цю силу протягнути 2ℓ метрів канату. Якщо ж система блоків дозволяє збільшити піднімальну силу в 4 рази (мал.25б), то відповідно в 4 рази зменшується та висота на яку піднімається вантаж (порівняно з довжиною переміщеного канату).

Таким чином, виграючи в тій силі яка піднімає вантаж, ми неминуче та у відповідну кількість разів програємо у тій висоті на яку піднімається вантаж. Що ж, Природу не можливо обманути: у скільки разів виграєш в силі, у стільки ж разів програєш в пройденому шляху (золоте правило механіки).

На завершення зауважимо, що визначаючи вантажопідйомність блоків та їх систем, треба враховувати не лише кількість рухомох блоків та місце закріплення нерухомого кінця канату, а й загальну вагу рухомих блоків. Крім цього, в реальних умовах між шківом та віссю його обертання діють певні сили тертя, які протидіють обертанню шківа, а отже певним чином зменшують вихідний натяг канату. Та якби там не було, а якщо в умовах задачі не наголошується на необхідності врахування ваги блоків та наявних сил тертя, то це означає, що враховувати цю вагу і ці сили не потрібно.

Задача 2. Який виграш у силі дає зображена на малюнку система блоків? Чому дорівнює сила натягу мотузки b, якщо маса вантажу 40кг?

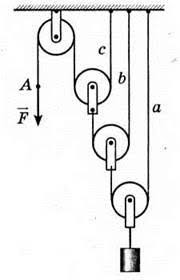
Рішення. Будемо виходити з того, що натяг суцільної мотузки в усіх її точках однаковий. Зважаючи на це, можна стверджувати:

1) Оскільки натяг мотузки с дорівнює силі F, то на рухомий блок с діє сила 2F.

2) Оскільки натяг мотузки b дорівнює силі 2F, то на рухомий блок b діє силa 2(2F)=4F.

3) Оскільки натяг мотузки a дорівнює силі 4F, то на рухомий блок a діє силa 2(4F)=8F.

Таким чином, дана система блоків забезпечує 8 разовий виграш в силі. А це означає, що ту силу тяжіння яка діє на вантаж масою 40кг і яка дорівнює 400Н, зрівноважить сила F=400H/8=50H. При цьому, враховуючи що напяг мотузки b дорівнює 2F, можна стверджувати що величина цього натягу 100Н.

Контрольні запитання.

1.Що називають парою сил?

2. Чи можна замінити пару сил рівнодійною силою? Чому?

3. Що називають моментом сили?

4. Чому ручки дверей ставлять на гранично великій відстані від осі їх обертання?

5. Поясніть загальний устрій та принцип дії важеля.

6. Що стверджується в золотому правелі механіки?

7. Який блок називають нерухомим, а який – рухомим?

8. Поясніть яким чином зображена на мал.25а система нерухомого та рухомого блоків, забезпечує подвійний виграш в силі?

9. Як працює золоте правило мехатіки, в зображеній на мал.25а системі блоків?

Вправа №5.

1.Щоб підняти один кінець труби що лежить на землі, потрібно прикласти силу 400Н. Яка маса труби

2. До точки 1 прикріплено вантаж масою 2кг. Якої маси вантаж треба закріпити в точці 2, щоб важіль був у рівновазі. Маса важеля 4кг.

3. Яка сила забезпечить рівномірне піднімання вантажів? На скільки піднімуться ці вантажі, при опусканні третього вантажу на 1м?

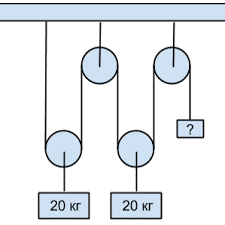
4. Який виграш у силі забезпечують зображені на малюнку системи блоків?

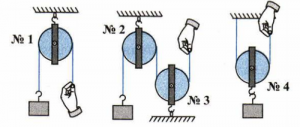
5. На основі аналізу малюнку визначте масу вантажу 2, якщо маса вантажу 1 дорівнює 20кг, а система перебуває в рівновазі.

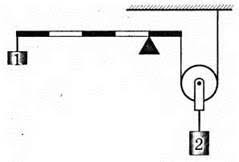
6. Стержень масою 9кг і довжиною 1м лежить на двох опорах. Одна з них підпирає лівий кінець стержня, а друга знаходиться на відстані 10см від правого кінця. Визначити реакції опор.

7. До країв важеля довжиною 2м підвісили вантажі масою 15кг і 10кг. На якій відстані від середини важеля треба встановити точку опори, щоб важіль перебував у рівновазі?

 

Лекційне заняття №8.

Тема: Рівновага тіла під дією довільної системи сил.

          В загальному випадку умову рівноваги тіла що знаходиться під дією плоскої системи довільних сил, можна записати у вигляді:

.                                              ∑ F_x = 0

.                                              ∑ F_y = 0

.                                              ∑ M = 0

Виходячи з цієї умови та дотримуючись загально прийнятого порядку розв’язку задач статики, розв’яжемо декілька з них. А загально прийнятий порядок розв’язку задач на рівновагу тіла під дією довільної системи сил, є наступним:

1.На основі аналізу умови задачі виконати малюнок (обов’язково), на якому чітко вказати всі діючі на задане тіло сили, їх кутові орієнтації та відстані між ними, а також діючі на тіло обертальні моменти.

2. Оптимальним чином задати систему координат.

3. Записати умову рівноваги даного тіла, тобто систему рівнянь:

.                                              ∑ F_x = 0

.                                              ∑ F_y = 0

.                                              ∑ M = 0

4. Розв’язавши цю систему, визначити невідомі величини.

Задача 1. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: q=100H/м, F=300H, α=60º, M=400Н∙м. Вагою балки знехтувати.

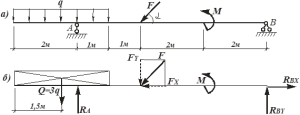
Рішення.

1.Виконуємо малюнок на якому вказуємо всі діючі на балку сили та відстані між ними. Задаємо систему координат. (Розподілене навантаження q=100H/м, замінюємо рівнодіючою силою Q=q∙ℓ=100Н/м∙3м=300Н).

2. Записуємо систему рівнянь які відповідають умові рівноваги даної балки.

∑ F_х = Fcosα – R_Bx = 0                                   (1)

∑ F_у = – Q + R_A – Fsinα + R_By = 0                  (2)

∑ M_B = – Q∙6,5 + R_A∙6 – Fsinα∙4 – M = 0       (3)

Зауваження.  1). Визначаючи момент сили F відносно точки B, доцільно розкладати цю силу на дві складові:  F_x = Fcosα;  F_y = Fsinα.  При цьому:  M(F_x) = 0,  (d=0);   M(F_y) = (Fsinα)4 ,  (d=4м). 2). Ту точку відносно якої визначаються моменти сил, обирається довільно. При цьому зазвичай її обирають таким чином, щоб максимальне число невідомих сил створювали нульові моменти.

3. Розв’язавши систему рівнянь, визначаємо невідомі величини:

Із (1) → R_Bx = Fcos60° = 300∙0,5=150H

Із (3) → R_A = [Q∙6,5 + Fsin60º∙4 + M]/6 = … = 406H

Із (2) → R_By = Q – R_A + Fsinα = … = 155H.

Відповідь: R_Bx=150H; R_By=155H; R_A= 406H.

Задача 2. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: q=100H/м, P₁=300H, P₂=400H. Вагою балки знехтувати.

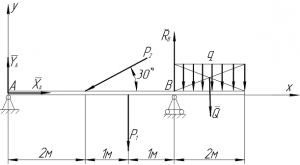
Зауваження. В науково-технічній практиці, діючі на тіло сили та реакції опор часто позначають по різному. Зважаючи на цей факт, при розв’язуванні задач будемо дотримуватись тих буквених позначок які зазначені на відповідному малюнку.

Рішення.

1. Виконуємо малюнок на якому вказуємо всі діючі на балку сили та відстані між ними. Задаємо систему координат.

2. Записуємо систему рівнянь які відповідають умові рівноваги даної балки.

∑ F_х = X_A – P₂cos30º = 0                                   (1)

∑ F_у = Y_A – P₂sin30º – P₁ + R_B – Q = 0             (2)

∑ M_A = (P₂sin30º)2 + P₁∙3 – R_B∙4 + Q∙5 = 0       (3)

де Q = q∙2 = 200H.

3. Розв’язавши систему рівнянь, визначаємо невідомі величини:

Із (1) → X_A =P₂cos30° = 400∙0,87=348H

Із (3) → R_B = [(P₂sin30º)∙2 + P₁∙3 + Q∙5]/4 = … = 575H

Із (2) → Y_A = P₂sin30º + P₁ – R_B + Q = … = 125H.

Відповідь: X_A=348H; Y_A=125H; R_B= 575H.

Задача 3. Під дією зображеної на малюнку системи сил жорстко закріплена балка знаходиться в стані механічної рівноваги. Визначити наявні в точці закріплення реакції опори. Вагою балки знехтувати.

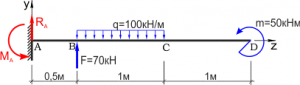
Зауваження. В загальному випадку реакція жорстко закріпленої опори має три складові: горизонтальну N_x (R_x, X_A,…), вертикальну N_у (R_у, Y_A,…) та протидіючий момент сили М. Однак в умовах нашої задачі, горизонтально діючі сили відсутні і тому горизонтальна складова реакції опори дорівнює нулю.

Рішення.

1.Виконуємо малюнок на якому вказуємо всі діючі на балку сили та відстані між ними. Задаємо систему координат.

2. Записуємо систему рівнянь які відповідають умові рівноваги даної балки.

∑ F_у = R_A + F – Q = 0                            (1)

∑ M_A = – M_A – F∙0,5 + Q∙1 – M = 0       (2)

де Q = q∙1 = 100кH.

3. Розв’язавши систему рівнянь, визначаємо невідомі величини:

Із (1) → R_A = – F + Q = -70+100 =30кH

Із (2) → M_A = – F∙0,5 + Q∙1 – M = … = 15кH∙м

Відповідь: R_A=30кН ; M=15кН∙м.

Задача 4. Труба масою 30кг і довжиною 4м приставлена до стіни під кутом 30° до поверхні стіни. З якою, прикладеною до центру труби горизонтальною силою F потрібно тягнути трубу, щоб відірвати її від стіни? Нижній кінець труби не ковзає.

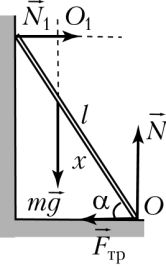
Дано:                             Аналіз:

m = 30кг

ℓ = 4м                        Малюнок

α = 30°

F = ?

Виконуємо малюнок, на якому вказуємо діючі на трубу сили і задаємо систему координат (вісь Ох направлена вздовж труби). При цьому враховуємо, що в момент відриву труби від вертикальної стіни, труба і стіна перестають взаємодіяти. В таких умовах на трубу діють чотири сили: F_т=mg, F, N, F_тер, при цьому три з них є невідомими. Визначаючи ці сили ми могли б записати три рівняння рівноваги і розв’язавши їх, визначити F, N, F_тер . Однак, за умовою задачі, нас цікавить лише одна величина – сила F. Тому ми запишемо і розв’яжемо лише одне рівняння ∑M_O=0 . (в цьому випадку моменти сил N_A і F_тер дорівнюють нулю).

∑ M_O = F∙d₁ – F_т∙d₂ = F(ℓ/2)cos30º – F_т(ℓ/2)sin30º = 0.   Звідси

F = [F_т(ℓ/2)sin30º]/[(ℓ/2)cos30º] = F_тtg30º = mgtg30º.

Розрахунки: F = mgtg30º = 30кг∙10м/с²∙0,577= 173H .

Відповідь: F = 173H.

Задача 5. Колесо радіусом R і масою m стоїть перед сходинкою висотою h. Яку горизонтальну силу F потрібно прикласти до осі колеса, щоб воно викотилось (піднялось) на сходинку?

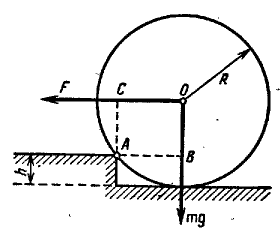
Рішення.

Виконуємо відповідний малюнок на якому вказуємо всі діючі на колесо сили. При цьому враховуємо, що в момент відриву колеса від горизонтальної поверхні, його взаємодія з цією поверхнею буде нулевою.

Для визначення невідомої сили F достатньо записати лише одне рівняння ∑M_A=0 . Адже відносно точки А силові моменти створюють лише сила тяжіння (F_т) і та зовнішня горизонтальна сила (F) яка і піднімає колесо на сходинку. При цьому плечі цих сил (відповідно АС і АВ) можна визначити із геометричних міркувань (див. мал.): 1) АС = R – h;  2) (АВ)² + (АС)² = R², або (АС)² + (R-h)² = R². Звідси  (АВ)² = R² – (R-h)² = 2Rh – h², або

АВ = (2Rh – h²)^1/2.

Враховуючи вище сказане, можна записати

∑ М_А= F(R – h) – F_т(2Rh-h²)^1/2 = 0 .

Звідси  F = [F (2Rh-h²)^1/2]/(R-h) = [mg(2Rh-h²)^1/2]/(R-h).

Відповідь: F = [mg(2Rh-h²)^1/2]/(R-h).

Вправа 6.

1.Балка масою 100кг під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опори.

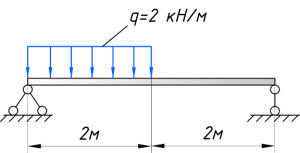
2. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: q=100H/м, F=300H, α=60º. Вагою балки знехтувати.

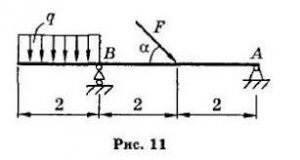
3. Балка АВ під дією зображеної на малюнку системи сил знаходиться в стані механічної рівноваги. Визначити діючі на балку реакції опор, якщо: q=75H/м, Р=300H, G=200H, M=400H∙м. Вагою балки знехтувати.

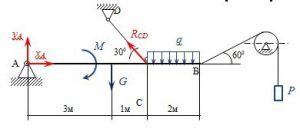
4. Під дією зображеної на малюнку системи сил жорстко закріплена балка знаходиться в стані механічної рівноваги. Визначити наявні в точці закріплення реакції опори. Вагою балки знехтувати.

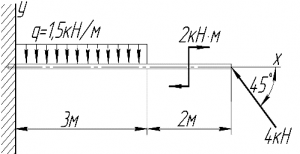
5. Однорідна балка лежить на платформі так, що одна четверта її довжини звисає з платформи. До звисаючого краю балки прикладають силу, направлену вертикально вниз. Коли ця сила досягає 2000Н протилежний край балки починає підніматись. Визначити масу балки.

6. Драбина довжиною 4м приставлена до гладенької стіни під кутом 30º. Коефіцієнт тертя між драбиною та підлогою 0,3. На яку відстань виміряну вздовж драбини може піднятись людина, перш ніж драбина почне зсковзувати підлогою.

 

Лекційне заняття №9.

Тема: Центр тяжіння тіла. Види механічної рівноваги та ступінь механічної стійкості тіла.

Коли ми говоримо, що на тіло діє певна сила тяжіння, то маємо на увазі ту результуючу силу, що є рівнодіючою величезної кількості співнаправлених елементарних сил, з якими окремі дрібні фрагменти тіла притягуються до Землі. Точку прикладання цієї результуючої сили, називають центром тяжіння тіла.

На практиці центр тяжіння будь якого (зазвичай плоского) тіла можна визначити наступним чином. Відповідне тіло, за допомогою нитки (мотузки, ланцюга чи іншої гнучкої опори) вільно підвішують за довільно обрану периферійну точку (мал.27а). При цьому, діючі на тіло сили, – сила тяжіння F та реакція опори N, зрівноважують одна одну. А це означає, що центр тяжіння даного тіла лежить на тій прямій яка є продовженням напрямку нитки. Уявно чи реально помічаємо цей напрям. Закріпивши нитку в іншій точці тіла, повторюємо експеримент і проводимо ще одну пряму (мал.27б). Точка перетину цих двох прямих і є центром тяжіння даного тіла. Закріплюючи нитку в різних місцях та багаторазово повторюючи експеримент, ви неодмінно переконаєтесь в тому, що за будь якого положення тіла, лінії дії результуючої сили тяжіння дійсно перетинаються в одній і тій же точці, яка і є центром тяжіння тіла.

Мал.27. Ілюстрація способів експериментального визначення центру тяжіння тіла.

Центром тяжіння тіла – називають ту пов’язану з цим тілом умовну геометричну точку, яка є точкою прикладання результуючої сили тяжіння і яка визначається як точка перетину ліній дій цієї результуючої сили, визначених при різних орієнтаціях тіла у просторі.

В науковій та побутовій практиці на ряду з поняттям центр тяжіння тіла застосовують більш загальне поняття – центр маси тіла. Центром мас (центром інерції) тіла – називають ту пов’язану з цим тілом умовну геометричну точку, яка характеризує розподіл мас в тілі і яка визначається як точка перетину ліній дій результуючої тих сил, які надають тілу поступального руху при різних орієнтаціях тіла у просторі.

Не заглиблюючись в деталі тих відмінностей які існують між центром тяжіння та центром мас тіла зауважимо, що за винятком певних, дуже специфічних умов, ці центри практично вточності співпадають. Тому на практиці терміни «центр тяжіння тіла» та «центр мас тіла» є тотожними.

Якщо ви думаєте, що центр тяжіння (центр мас) тіла, це реальна приналежна тілу точка, до якої прикладена реальна сила тяжіння, то помиляєтесь. Помиляєтесь по-перше тому, що центр тяжіння часто знаходиться за межами відповідного тіла. Скажімо, якщо ви визначите центри тяжіння кільця, чайника, каструлі чи будь якого іншого пустотілого предмету, то неодмінно переконаєтесь в тому, що ці центри знаходяться за межами відповідних тіл. По-друге, центр тяжіння, це лише певна умовна точка до якої прикладена умовна результуюча сила тяжіння. Втім, якщо реальне тіло дійсно зосередити в тій точці яка називається центром тяжіння, і якщо до цієї точки дійсно прикласти ту силу яка називається силою тяжіння, то механічна поведінка цієї точки і відповідного реального тіла будуть однаковими.

Можна довести: якщо однорідне тіло має вісь симетрії, то центр тяжіння цього тіла знаходиться на цій осі. Керуючись цим твердженням не важко визначити центри тяжіння тих однорідних тіл які мають дві і більше осей симетрії (прямокутники, паралелограми, куби, циліндри, стержні, кулі, тощо).

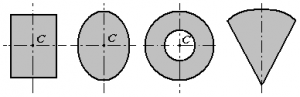
Мал.28. Якщо однорідне тіло має вісь (площину) симетрії, то центр тяжіння (центр мас) цього тіла знаходиться на цій осі (в цій площині).

Якщо ж мова йде про геометрично складні фігури, то їх завжди можна представити у вигляді певної сукупності геометрично простих фігур. Фігур, центри тяжінь яких легко визначаються. При цьому можна довести, що координати результуючого центру тяжіння складного тіла визначаються за формулами:

x_c = ∑m_ix_i/∑m_i;  y_c = ∑m_iy_i/∑m_i;  z_c = ∑m_iz_i/∑m_i ,     (1)

де   m_i – маса і-того тіла системи;  x_i , y_i , z_i  – координати  центру тяжіння і-того тіла системи.

Для однорідних плоских тіл (тіл постійної товщини) формули (1) набувають вигляду: х_с = ∑S_ix_i/∑S_i;  y_c = ∑S_iy_i/∑S_i ,   (2)

де  S_i – площа і-того тіла системи. Власне за системою формул (2) ми і будемо визначати центрів тяжіння складних геометричних фігур.

Задача 1. Визначити центр тяжіння плоского однорідного тіла, геометричні параметри якого представлені на малюнку.

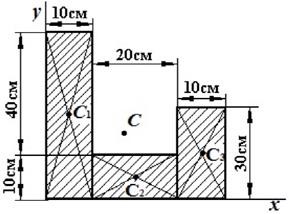
Рішення:

1.Задаємо систему координат і максимально зручним чином розбиваємо складну фігуру на геометрично прості.

2. Визначаємо площі і координати центрів тяжіння кожної окремої фігури.

1) S₁ = 50∙10 = 500см²;     x₁ = 5см;     y₁ = 25см

2) S₂ = 20∙10 = 200см²;     x₂ = 20см;    y₂ = 5см

3) S₃ = 10∙30 = 300см²;      x₃ = 35см;    y₃ =15см .

3. Визначаємо координати центру тяжіння всієї фігури.

х_с =(500∙5 + 200∙20 + 300∙35)/(500+200+300) = 17см

у_с =(500∙25 + 200∙5 + 300∙15)/(500+200+300) = 18см .

Відповідь:  х_с = 17см;   у_с = 18см .

Потрібно зауважити, що числові значення координат центру тяжіння тіла залежать від вибору системи координат. При цьому, за будь якого вибору цієї системи, фактичне розташування центру тяжіння тіла залишається незмінним.

Задача 2. Визначити центр тяжіння плоского однорідного тіла, геометричні параметри якого представлені на малюнку (розміри в мм)

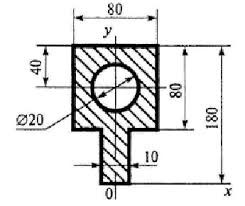
Загальне зауваження: якщо в однорідному тілі є отвори (пустоти), то визначаючи центр тяжіння цього тіла, в формулах (1) і (2), відповідно маси та площі отворів беруть зі знаком « – ».

Рішення:

1.Задаємо систему координат і максимально зручним чином розбиваємо складну фігуру на геометрично прості.

Оскільки дане тіло є однорідним та симетричним відносно осі 0у, то центр тяжіння цього тіла знаходиться на осі 0у. А це означає, що у вибраній системі координат, координата х_с є відомою (х_с = 0мм), і тому залишається визначити лише координату у_с.

2. Визначаємо площі і потрібну координату (у) кожної окремої фігури.

1) S₁ = 100∙10 = 1000мм²;                   y₁ = 50мм

2) S₂ = 80∙80 =6400мм²;                      y₂ = 140мм

3) S₃ = – πr² = – 3,14∙20² = -628мм²;     y₃ =140мм .

3. Визначаємо координати центру тяжіння всієї фігури.

у_с =(1000∙50 + 6400∙140 – 628∙140)/(1000+6400-628) = 126,7мм .

Відповідь:  х_с = 0,0мм;   у_с = 126,7мм .

Важливими складовими багатьох плоских тіл є прямокутні трикутники та напівсфери. І можна довести, що координати центрів тяжіння (центрів мас) цих геометричних фігур визначаються за представленими на малюнку формулами.

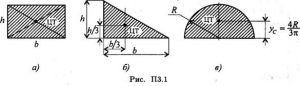
          Зазвичай механічною рівновагою називають такий стан тіла, при якому воно під дією зовнішніх сил знаходиться в стані механічного спокою (v=0; ω=0). Однак, сама по собі механічна рівновага тіла може бути суттєво різною. Наприклад, в зображених на мал.29 ситуаціях, під дією зовнішніх сил (сили тяжіння F_т та реакції опори N) куля знаходиться в стані механічної рівноваги. При цьому не важко бачити, що кожна з цих рівноваг є суттєво різною. Ця різність з усією очевидністю відображена у відповідних назвах:

– стійка рівновага (мал.29в)

– нестійка рівновага (мал.29б)

– байдужа рівновага (мал.29а)

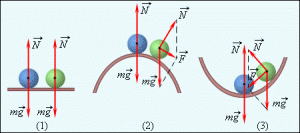
мал.29.  За характером поведінки тіла після виведення його із стану рівноваги, ця рівновага буває: стійкою (в), нестійкою (б) та байдужою (а).

Пояснюючи поведінку кулі при стійкій, нестійкій та байдужій рівновазі, розглянемо ситуацію в якій вона під дією випадкових зовнішніх чинників отримує незначне відхилення від положення рівноваги. Не важко бачити, що в незалежності від виду рівноваги, на кулю постійно діють дві зовнішні сили: сила тяжіння F_т і реакція опори N. Однак результат дії цих сил в кожному випадку буде суттєво різним. Дійсно. При стійкій рівновазі (мал.29в), результуюча сили тяжіння і реакції опори повертає кулю в початкове положення. При нестійкій рівновазі (мал.29б), результуюча сили тяжіння та реакції опори віддаляє кулю від початкового положення. При байдужій рівновазі (мал.29а), результуюча сили тяжіння та реакції опори дорівнює нулю, а отже є такою що не повертає і не віддаляє кулю від початкового положення.

Таким чиним, за характером поведінки тіла після відхилення його від заданого положення рівноваги, розрізняють три різновидності цієї рівноваги: стійка, нестійка та байдужа. При цьому:

1.Якщо, після незначного відхилення тіла від положення рівноваги, система діючі на нього зовнішніх сил повертає тіло до попереднього положення, то таку рівновагу називають стійкою.

2. Якщо, після незначного відхилення тіла від положення рівноваги, система діючих на нього зовнішніх сил, віддаляє тіло від попереднього положення, то таку рівновагу називають нестійкою.

3. Якщо, після незначного відхилення тіла від положення рівноваги, система діючих на нього зовнішніх сил, не повертає тіло до попереднього положення, але й не віддаляють від нього, то таку рівновагу називають байдужою.

Важливим прикладом стійкої, нестійкої та байдужої рівноваги, є рівновага тіла що має вісь обертання. Аналізуючи таку рівновагу (мал.30) не важко бачити, що її характер визначається розташуванням центру тяжіння тіла відносно його осі обертання. При цьому, якщо центр тяжіння знаходиться  нижче цієї осі, то рівновага є стійкою, якщо вище – нестійкою, а якщо на осі – байдужою.

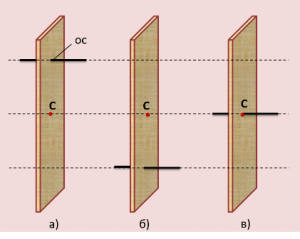
Мал.30. Характер рівноваги тіла що має вісь обертання залежить від розташування його центру тяжіння відносно осі обертання.

Вище розглянуті ситуації, наочно демонструють і пояснюють суть стійкої, нестійкої та байдужої рівноваги того тіла що має одну точку опори. Однак у повсякденному житті, ми зазвичай маємо справу з стійкістю тіл які спираються не на одну, а на велику кількість точок опори. Столи і стільці, телевізори і холодильники, книги і чайники, будинки і автомобілі, – всі вони певним чином спираються на велику кількість точок опор і мають певну механічну стійкість. Однак ступінь цієї стійкості може бути різною. При цьому, ми майже завжди зацікавлені в тому, щоб ступінь стійкості тіла була максимально великою.

З’ясовуючи ті фактори які так чи інакше впливають на ступінь стійкості тіла, розглянемо ряд простих ситуацій. Припустимо, що тіло в формі прямокутного паралепіпеда лежить на горизонтальній поверхні так, як це показано на мал.31. Не важко збагнути, що рівновага цього тіла в ситуації (б) є більш стійкою. Більш стійкою тому, що в цій ситуації центр тяжіння тіла знаходиться нижче, а площа його опори більша. Висновок очевидний: чим більша площа опори тіла і чим нижче центр його тяжіння, тим більша механічна стійкість тіла.

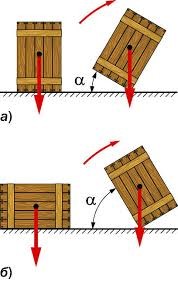
Мал.31.  Чим нижче центр тяжіння тіла і чим більша площа його опори, тим стійкіша рівновага.

Потрібно зауважити, що коли ми говоримо про площу опори того тіла яке спирається на декілька точок, то маємо на увазі не ту фактичну площу на яку спираються наприклад ніжки стола, а ту площу яка знаходиться в середині того чотирикутника, вершинами якого є ці ніжки.

Ступінь механічної стійкості тіла визначається не лише величиною його площі опори та висотою центру тяжіння над цією площею. Ця ступінь певним чином залежить і від того, як центр тяжіння тіла розташований відносно геометричного центру його опори. Дійсно. В зображених на мал.32 ситуаціях, тіла а, б, в, мають однакові площі опори, а їх центри тяжіння знаходяться на одній і тій же висоті. І тим не менше, ступінь стійкості цих тіл є очевидно різною. Різним тому, що центр тяжіння тіла по різному розташований відносно геометричного центру його опори. Власне одним з критеріїв стійкості тіла є так званий кут стійкості. Тобто той гранично великий кут, на який потрібно нахилити тіло до положення його нестійкої рівноваги.

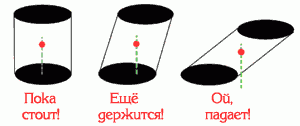
Мал.32.  Ступінь стійкості тіла, певним чином залежить від розташування вертикальної проекції його центру тяжіння відносно площі опори.

Загально відомим прикладом будівлі вісь симетрії якої суттєво нахилена до вертикалі, є Пізанська вежа (мал.33). Ця вежа має форму циліндра висотою 55м і радіусом опори 7м. При цьому вершина вежі відхилена від вертикалі на 4,5м. По суті це означає, що кут відхилення вежі від вертикалі становить α=arcsin(4,5/55)≈5º. Граничний же кут стійкості для подібної геометричної фігури, близький до 15º. Так що Пізанській вежі ще далеко до втрати механічної стійкості.

Втім, ми говоримо про певну ідеалізовану ситуацію, в якій суцільне абсолютно тверде тіло стоїть на абсолютно твердій та дещо нахиленій поверхні (або в якій тіло нахилене до поверхні). Реальні ж будівлі та їх опори не є суцільними та абсолютно твердими. Крім цього, вони знаходяться під постійним впливом величезної кількості силових навантажень, починаючи від вітрів, дощів та створюваних транспортом і людьми вібрацій, і закінчуючи ураганами, землетрусами, виверженнями вулканів, тощо.

Мал.33. Пізанська вежа – архітектурний, історичний та науковий пам’ятник.

Цікавим прикладом стійкої рівноваги є загально відома іграшка, яку називають по різному: в Росії «Ванька-встанька», в Америці «Bob of Toy», а в Україні «Іван-покиван»(мал.34). Пояснюючи принцип дії цієї іграшки, а заодно і їй подібних систем, можна сказати наступне. На твердій рівній поверхні, куля по суті представляє собою тіло яке має відносно нерухому (нерухому відносно кулі) точку обертання. І ця точка знаходиться в геометричному центрі відповідної кулі. Якщо куля однорідна(мал.34б), то її точка обертання співпадає з центром тяжіння. При цьому на рівній горизонтальній поверхні куля буде знаходитись в стані байдужої рівноваги. Це означає, що за будь якого відхилення, центр обертання кулі, її центр тяжіння та точка дотику з поверхнею будуть знаходитись на одній вертикальній прямій.

Якщо ж куля неоднорідна, наприклад така що має певні пустоти (мал.34в), то в цьому випадку точка обертання кулі не співпадає з її центром тяжіння. В такій ситуації куля може знаходитись як в стані нестійкої рівноваги (центр тяжіння знаходиться над точкою обертання), так і в стані стійкої рівноваги (центр тяжіння знаходиться під точкою обертання). По суті це означає, що куля центр тяжіння якої не співпадає з її геометричним центром, завжди прагне прийти до такого стану, при якому її геометричний центр, центр тяжіння та точка дотику з поверхнею, лежать на одній вертикальній прямій. І цей стан є станом стійкої рівноваги. Власне тому за будь якого відхилення Івана-покивана від положення рівноваги, він неминуче повертається до цього положення.

     

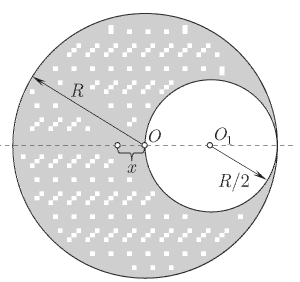
Мал.34. Іван-покиван, як приклад тіла, що знаходиться в стані стійкої рівноваги.

На практиці зовсім не обов’язково щоб вся іграшка була кулястої форми. Достатньо щоб кулястою була лише її нижня частина. При цьому, прагнучи до максимального віддалення геометричного центру кулі (центру кривизни кулі) від її центру тяжіння, нижню кулясту частину іграшки зазвичай заповнюють відносно важкою речовиною.

Принцип «ваньки-встаньки» застосовують не лише в іграшках, а й в техніці. Наприклад певні різновидності човнів виготовляють таким чином, що при перекиданні, вони відразу ж повертаються в початкове положення. Для цього на човні передбачені спеціальні заповнені легким пінопластом відсіки.

Контрольні запитання.

1.Чи може центр тяжіння тіла знаходитись за межами цього тіла?

2. Як експериментально визначити центр тяжіння тіла?

3. Чи залежать визначені за формулами (2) координати центру тяжіння тіла, від вибору системи координат?

4. Яку рівновагу називають стійкою; нестійкою; байдужою?

5. Від чого залежить вид рівноваги тіла що має нерухому вісь обертання?

6. Від чого залежить механічна стійкість того тіла яке має велику кількість точок опори?

7. Вантажний автомобіль перевозить вантажі однакової маси: в одному випадку – залізобетонні блоки, в іншому – дрова. В якому випадку автомобіль буде стійкішим?

8. В якій рівновазі буде перебувати куля на горизонтальній площині, якщо одна половина кулі дерев’яна, а інша – свинцева?

Вправа 7.

1.Визначити центр тяжіння плоского тіла, геометричні параметри якого представлені на малюнку (розміри задані в см).

     

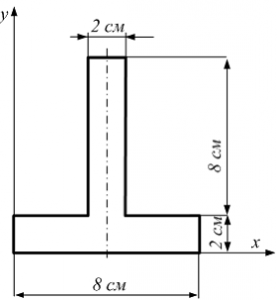
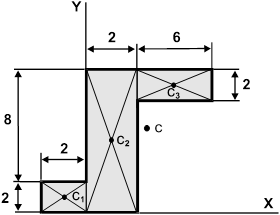
2. З однорідної круглої пластинки радіусом 10см, вирізали круг вдвічі меншого радіусу, так що виріз дотикається до нижнього краю пластинки. Визначити координати центру тяжіння пластинки з вирізом.

3. Дві однорідні кулі маси яких m₁=10кг і m₂=12кг та радіусами R₁=4см і R₂=6см з’єднані стержнем масою 4кг і довжиною 8см. Центри куль лежать на осі стержня. Визначити центр тяжіння цієї системи.

4. Визначити положення центру тяжіння квадратної пластинки зі стороною d, в якій вирізали круглий отвір радіусом d/4 так, що утворене коло торкається середини однієї з сторін квадрата.

5. Визначити центр тяжіння плоского тіла, геометричні параметри якого представлені на малюнку R=10см.

  

 

 

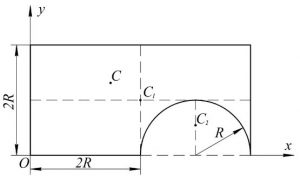
Лекційне заняття №10.

Тема: Основні поняття, величини та закони динаміки матеріальної точки.

          Динаміка – це розділ механіки, в якому вивчають параметри, закономірності та причини стану динамічної рівноваги тіла. Динаміка, це узагальнюючий розділ механіки, в якому ті знання які були отримані при вивченні кінематики та статики, доповнюються новими знаннями і узагальнюються. До числа основних фізичних величин динаміки, а точніше динаміки матеріальної точки, відносяться: маса (m), імпульс (р), енергія (Е), робота (А), потужність (Р) та коефіцієнт корисної дії (η). До числа основних законів динаміки і механіки загалом, відносяться: принцип відносності, перший, другий та третій закони Ньютона, закон збереження енергії та закон збереження імпульсу.

Основні поняття динаміки.

Динамічна рівновага тіла – це такий механічний стан тіла, при якому воно, під дією зовнішніх сил та сили інерції, знаходиться в стані рівноприскореного руху (а=соnst). Інерція, це універсальна властивість тіла, яка полягає в тому, що відповідне тіло протидіє будь якій зміні його швидкості. Кількісною мірою інерційних властивостей тіла є його маса. Гравітація, це універсальна властивість тіла, яка полягає в здатності цього тіла до тих взаємодій які описуються законом всесвітнього тяжіння. Кількісною мірою гравітаційних властивостей тіла є його маса.

Основні фізичні величини динаміки.

          Маса – це фізична величина яка є мірою :

1) інерціальних властивостей тіла;

2) гравітаційних властивостей тіла;

3) енергетичних властивостей тіла;

4) кількості речовини в тілі, виміряну в кілограмах.

Позначається: m

Визначальне рівняння: нема

Одиниця вимірювання: [m]= кг,  кілограм.

Імпульс (кількість руху) – це фізична величина, яка є мірою кількості механічного руху тіла (матеріальної точки) і яка дорівнює добутку маси тіла на вектор його швидкості.

Позначається: р

Визначальне рівняння: p=mv

Одиниця вимірювання: [p]=кг∙м/с,   кілограм-метр на секунду.

Енергія – це фізична величина, яка є загальною мірою всіх видів рухів та взаємодій і яка характеризує здатність тіла, частинки або поля виконати роботу.

Позначається: Е

Визначальне рівняння: 1) для загальної кількості енергії: Е=mс² ;

2) для конкретних видів енергії:  різні .

Одиниця вимірювання: [E] = Дж,  джоуль.

Кінетична енергія (енергія руху) – це та енергія, яку має тіло (фізичний об’єкт) за рахунок того що воно рухається і яка дорівнює половині добутку маси тіла на квадрат його швидкості.

Позначається: Е_к

Визначальне рівняння: Е_к=mv²/2 ,

Одиниця вимірювання: [Е_к] =Дж.

Потенціальна енергія (енергія взаємодії) – це та енергія яку має фізичний об’єкт за рахунок того, що він так чи інакше взаємодіяє з іншими об’єктами, або за рахунок тих взаємодій які відбуваються в середині цього об’єкту.

Позначається: Е_п

Визначальне рівняння: Е_п = ?

Одиниця вимірювання: [Е_п] = Дж.

Потенціальна енергія сили тяжіння (піднятого тіла) – це та енергія яку має підняте над землею тіло за рахунок його взаємодії з Землею.

Позначається: Е_п

Визначальне рівняння: Е_п = mgh

Одиниця вимірювання: [Е_п] = Дж.

Потенціальна енергія сили пружності (деформованого тіла) – це та енергія, яку має пружно деформоване тіло за рахунок тих міжмолекулярних взаємодій які відбуваються всередині цього тіла.

Позначається: Е_п

Визначальне рівняння: Е_п = kΔℓ²/2

Одиниця вимірювання: [Е_п] = Дж.

Робота – це фізична величина, яка характеризує затрати енергії на виконання роботи і яка дорівнює цим затратам.

Позначається: А

Визначальне рівняння: А=ΔЕ

Одиниця вимірювання: А=Дж,   джоуль.

Потужність – це фізична величина, яка характеризує роботу виконану за одиницю часу і яка дорівнює цій роботі (роботі виконаній за одиницю часу).

Позначається: Р

Визначальне рівняння: Р=А/t

Одиниця вимірювання: [Р]=Дж/с=Вт,  ват.

Коефіцієнт корисної дії (к.к.д) – це фізична величина, яка характеризує ефективність використання енергії в тому чи іншому приладі і яка дорівнює відношенню тієї енергії що йде на виконання корисної роботи (Е_кор=А_кор), до загальної кількості наданої приладу енергії (Е_заг=А_заг).

Позначається: η

Визначальне рівняння: η=(Е_кор/Е_заг)100%,  або   η=(А_кор/А_заг)100%

Одиниця вимірювання: [η] = % ,    відсотки.

Основні закони динаміки та механіки загалом.

Принцип відносності – це закон в якому стверджується: у всіх інерціальних системах відліку, тобто таких системах де виконується перший закон Ньютона (закон інерції) всі фізичні процеси відбуваються абсолютно однаково.

Перший закон Ньютона (закон інерції) – це закон, в якому стверджується: Будь-яке тіло, буде знаходитись в стані механічного спокою

(v = 0), або в стані прямолінійного рівномірного руху (v = const), до тих пір поки на нього не подіє зовнішня сила, яка і змусить тіло змінити цей стан.

Другий закон Ньютона – це закон, в якому стверджується: Під дією зовнішньої сили F, тіло масою  m отримує прискорення  а,  величина якого прямо пропорційна діючій на тіло силі і обернено пропорційна його масі, тобто:   F →  a = F/m .

Третій закон Ньютона – це закон, в якому стверджується: Діюча на тіло сила F, завжди породжує рівну їй за величиною і протилежну за напрямком протидіючу силу F′, тобто:  F → F′ = – F .

Закон збереження імпульсу – це закон, в якому стверджується: при будь яких процесах що відбуваються в замкнутій системі, загальна кількість імпульсу цієї системи залишається незмінною тобто зберігається. Іншими словами:   ∑ р_до=∑ р_після   або    ∑ р = соnst.

Закон збереження енергії – це закон, в якому стверджується: при будь яких процесах, що відбуваються в замкнутій (енергоізольованій) системі, загальна кількість енергії цієї системи залишається незмінною, тобто зберігається. Іншими словами: ∑Е_до = ∑Е_після  або   ∑Е = соnst.

Закон всесвітнього тяжіння – це закон, в якому стверджується: дві матеріальні точки масою m₁ і m₂ взаємно притягуються з гравітаційною силою (F_гр), величина якої прямо пропорційна добутку взаємодіючих мас (m₁m₂) і обернено пропорційна квадрату відстані між ними (r²). Іншими словами:

F_гр=Gm₁m₂/r², де  G = 6,6720∙10^-11Н∙м²/кг² – гравітаційна стала.

 

Лекційне заняття № 11.

Тема: Імпульсно-енергетичний метод розв’язування задач.

Складність динаміки визначається різноманіттям тих задач які в ній розв’язуються. А що ці задачі можуть бути надзвичайно різноманітними, випливає вже з факту того, що динаміка це той розділ механіки в якому кінематика, статика та власне динаміка, об’єднуються в єдине ціле. Чітко класифікувати задачі динаміки практично не можливо. Тим не менше, можна виділити два базових методи їх розв’язку: силовий та імпульсно-енергетичний.

Суть силового методу полягає в тому, що невідомі величини визначають на основі векторного аналізу діючих на тіло сил та на базі умови його динамічної рівноваги (∑F+F_i=0). При імпульсно-енергетичному методі, невідомі величини визначають на основі аналізу імпульсно-енергетичних параметрів тіл (імпульс, енергія, робота, потужність, к.к.д) та на базі відповідних визначальних рівнянь, закону збереження енергії (∑Е_до = ∑Е_після), та закону збереження імпульсу (∑р_до=∑р_після).

Звичайно, подібна класифікація є досить умовною. Умовною по-перше тому, що в багатьох випадках одну і ту ж задачу можна розв’язати як силовим так і імпульсно-енергетичним методом. А по-друге, рішення багатьох задач передбачає застосування певної комбінації обох методів. Втім, нема кращого способу розібратися в різноманітті динамічних задач та методах їх рішення, як практичне розв’язування максимально великої їх кількості.

Імпульсний метод розв’язування задач зазвичай застосовують в тих випадках, коли мова йде про короткотривалі взаємодії (поштовхи, удари, вибухи, тощо). Дане обмеження пояснюється фактом того, що в процесі відносно тривалих механічних взаємодій, значна частина імпульсу взаємодіючих тіл, передається їх атомам та перетворюється на енергію їх хаотичного руху (теплоту). При цьому розрізняють дві ідеалізовані різновидності короткотривалих взаємодій: абсолютно пружні та абсолютно не пружні удари. Абсолютно пружним ударом називають таку ідеалізовану, короткотривалу механічну взаємодію тіл, яка не супроводжується перетворенням механічної енергії в теплоту і після якої взаємодіючі тіла повністю відновлюючи свою попередню форму відокремлюються одне від одного. Абсолютно не пружним ударом називають таку короткотривалу механічну взаємодію тіл, яка не супроводжується перетворенням механічної енергії в теплоту і після якої взаємодіючі тіла не відновлюючи свою попередню форму рухаються як єдине ціле.

Розв’язуванні задач на застосування закону збереження імпульсу, дотримуються наступного порядку:

1.В вибраній системі координат зображають вектори імпульсів всіх взаємодіючих тіл, до та після їх взаємодії.

2.На базі векторної картини імпульсів, записують відповідне рівняння закону збереження імпульсу: ∑р_до=∑р_після. При цьому, якщо векторна картина імпульсів не лінійна, а плоска, то вектори імпульсів розкладають на відповідні проекції і записують систему двох рівнянь:

∑(р_до)_х = ∑(р_після)_х

∑(р_до)_у = ∑(р_після)_у

3.Математично розв’язуючи рівняння закону збереження імпульсу визначають невідомі величини.

Задача1. В платформу з піском що рухається зі швидкістю 2,0м/с влучає та застряє в піску снаряд який рухався назустріч платформі з швидкістю 400м/с. Визначте швидкість платформи після влучання снаряду. Маса платформи 10тон, а маса снаряду 10кг.

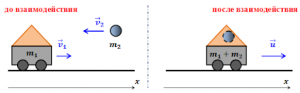
Дано:               СІ                     Аналіз

m₁ = 10т       10000кг

m₂ = 10кг          –                     Малюнок

v₁ = 2,0м/с         –

v₂ = 400м/с        –

u = ?                          У вибраній системі координат розглядаємо імпульсні характеристики складових системи платформа-снаряд, до та після взаємодії. Записуємо відповідне рівняння закону збереження імпульсу(∑р_до=∑р_після):

m₁v₁ – m₂v₂ = (m₁+m₂)u. Звідси u = (m₁v₁ – m₂v₂)/(m₁+m₂).

Розрахунки: u = … = 1,6м/с

Відповідь: u = 1,6м/с.

Задача 2. Снаряд вилітає з гармати під кутом 60º до горизонту з початковою швидкістю 800м/с. Визначити початкову швидкість відкату гармати, якщо маса снаряду 10кг, а маса гармати 500кг.

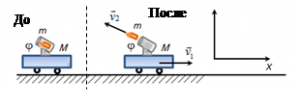
Дано:                            Аналіз:

m=10кг

M=500кг                       Малюнок

u₁₂=0м/с

v₂=800м/с

α=60°

v₁=?                 У вибраній системі координат, розглянемо імпульсні характеристики тіл системи гармата-снаряд до та після пострілу. Оскільки за умовою задачі нас цікавить швидкість відкату гармати, тобто горизонтальна складова швидкості гармати (v₁), то для її визначення закон, збереження імпульсу достатньо записати в проекціях на вісь 0х:

(M+m)u₁₂ = -mv_2x+Mv₁   де   u₁₂=0м/с ;    v_2x=v₂cosα.

Звідси         v₁ = mv₂ cosα/M

Розрахунки:  v₁ = … = 8м/с

Відповідь: v₁ =8м/с.

Задача 3. З якою початковою швидкістю v₀ потрібно кинути вниз м’яч з висоти h, щоб він підскочив на вдвічі більшу висоту H=2h? Удар об землю вважати абсолютно пружним.

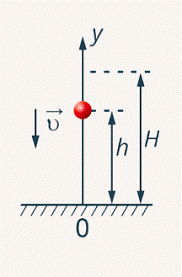
Дано:                          Аналіз:

h

 H=2h                         Малюнок

v₀=?

Оскільки абсолютно пружний удар не супроводжується втратами механічної енергії, то можна стверджувати, то згідно з законом збереження енергії, загальна кількість механічної енергії в момент вильоту м’яча Е = mgh + mv₀²/2, та в момент його максимального підйому (v₁=0м/с) Е = mgН + 0 = 2mgh; має бути однаковою. Тобто mgh + mv₀²/2 = 2mgh.

Звідси v₀ = (2gh)^1/2.

Відповідь: v₀ = (2gh)^1/2.

Задача 4. Тіло без тертя зісковзує з похилої площини, яка переходить у так звану «мертву петлю». З якої мінімальної висоти Н має зісковзувати тіло, щоб бути здатним описати «мертву петлю» радіусом R.

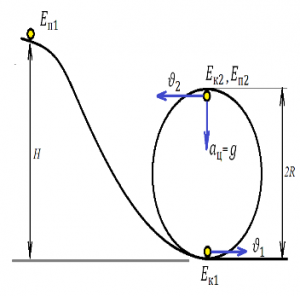
Рішення.

Оскільки за умовою задачі, в процесі руху тіла втратами енергії можна знехтувати, то та потенціальна енергія яку має тіло на висоті Н (Е_п1=mgH), в нижній точці спуску перетвориться на відповідну кількість кінетичної енергії Е_к1=Е_п1. При цьому, цієї енергії має вистачити на те, щоб по перше підняти тіло на висоту h=2R, тобто щоб надати тілу потенціальної енергії Е_п2=mg2R. А по друге, забезпечити таку швидкість руху тіла в верхній точці петлі, при якій діюча на нього сила тяжіння (F_т=mg), буде зрівноваженою відповідною силою інерції (F_i=ma_д=mv₂²/R). А це означає, що у верхній точці петлі, тіло повинно мати певний запас кінетичної енергії Е_к2=mv₂²/2, де v₂² визначається із співвідношення mv₂²/R = mg. Звідси v₂²=gR. При цьому Е_к2=mgR/2

Таким чином, для тієї мінімальної висоти Н, яка за відсутності енергетичних втрат забезпечує виконанням тілом «мертвої петлі», має виконуватись співвідношення mgH = 2mgR + mgR/2. Звідси H = 2R+R/2=2,5R.

Відповідь: H = 2,5R.

Задача 5.  Визначити швидкість вильоту кульки масою m з дула пружинного пістолета при горизонтальному пострілі, якщо жорсткість пружини k, а її деформація Δℓ. Чи зміниться ця швидкість при вертикальному пострілі?

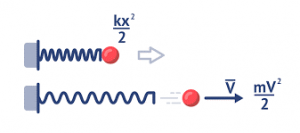
Дано:                                         Аналіз:

m

k                                           Малюнок

Δℓ

v= ?

v₁=?

Розглянемо енергетичні параметри об’єктів системи кулька-пружина до та після пострілу. Будемо виходити з того, що в процесі пострілу, потенціальна енергія пружно деформованого тіла Е^пр=kΔℓ²/2  йде на збільшення кінетичної енергії кульки Е_к=mv²/2. При цьому, згідно з законом збереження енергії можна записати:  kΔℓ²/2 = mv²/2, звідси v = (kΔℓ²/m)^1/2.

При вертикальному розташуванні пістолета, енергія деформованої пружини Е^пр=kΔℓ²/2  йде як на збільшення кінетичної енергії кульки Е_к=mv₁²/2, так і на збільшення її потенціальної енергії Е_п=mgΔℓ. При цьому, згідно з законом збереження енергії можна записати: kΔℓ²/2 = mv₁²/2 + mgΔℓ,  або  mv₁²/2 = kΔℓ²/2 – mgΔℓ, звідси v₁ = (kΔℓ²/m – 2gΔℓ)^1/2.

Відповідь: v = (kΔℓ²/m)^1/2; v₁ = (kΔℓ²/m – 2gΔℓ)^1/2.

Задача 6. Куля масою 7г летить в горизонтальному напрямку зі швидкістю 500м/с і влучає в брусок масою 2,0кг який висить на нитці, та застряє в ньому. На яку висоту підніметься брусок після удару кулі? Який відсоток кінетичної енергії кулі перетвориться на теплоту?

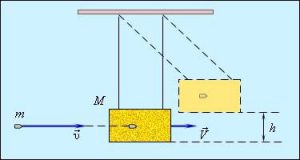
Дано:               СІ                                 Аналіз:

m=7г            7∙10^-3кг

v₁=500м/с          –                                 Малюнок

М=2,0кг            –

v₂=0м/с              –

h =

Q/E_к1=?

Керуючись законом збереження імпульсу визначаємо швидкість бруска (v₁₂) після взаємодії з кулею: mv₁ + Мv₂ = (m + М)v₁₂.   Враховуючи, що v₂=0  можна записати  v₁₂=mv₁(m₁+М).

Виходячи з того, що після взаємодії з кулею, брусок отримав певну кількість кінетичної енергії  Е_к=(m+М)v₁₂²/2  і що в процесі підйому бруска, ця енергія повністю перетворилась у відповідну кількість потенціальної енергії Е_п=(m+М)gh  можна записати:  (m+М)gh = (m+М)v₁₂²/2, звідси h=v₁₂²/2g. А враховуючи що  v₁₂=m₁v₁/(m₁+m₂), отримаємо

h = (1/2g)[mv₁/(m+М)]².

Кількість тієї енергії яка в процесі взаємодії з бруском перетворилась на теплоту, можна визначити як різницю між кінетичною енергією кулі до взаємодії та кінетичною енергією системи брусок-куля після взаємодії, тобто:

Q = mv₁²/2 – (m+М)v₁₂²/2,  або, враховуючи що v₁₂² = mv₁/(m+М):

Q = mv₁/2 – m²v₁²/2(m+М) = (mv₁²/2)[1 – m/(m+М)] = E_k1[1-m/(m+М)].

Таким чином:      Q/E_k1 = 1 – m/(m+М) = [1 – m/(m+М)]100%.

Розрахунки:   h = … = 0,156м = 15,6см

Q/E_k1 = … = 99,65%

Відповідь:   h = 15,6см;    Q/E_k1 = 99,65%.

Вправа 8.

1.З нерухомого човна загальна маса якого 155кг кидають на берег весло масою 5кг з горизонтальною швидкістю 10м/с. Якої швидкості при цьому набуває човен?

2. Якої швидкості набуває ракета масою 600г, якщо гази масою 25г вилітають з неї зі швидкістю 600м/с?

3. Ядро, що летіло горизонтально зі швидкістю 50м/с, розірвалось на два осколки масами 5кг і 10кг. При цьому, менший осколок з швидкістю 200м/с продовжував летіти в попередньому напрямку. Визначити напрям та швидкість руху більшого осколку.

4. З якою вертикальною швидкістю потрібно кинути тіло, щоб воно піднялось на висоту 10м?

5. В пружинному пістолеті жорсткість пружини 100Н/м. З якою швидкістю вилітатиме з нього кулька масою 3г, якщо пружина стиснута на 10см? На яку максимальну висоту може піднятись ця кулька?

6. Тіло масою 1кг рівномірно обертається в вертикальній площині. На скільки сила натягу нитки в нижній точці траєкторії більша аніж у верхній?

7. Тіло масою 0,5кг падає з деякої висоти на плиту масою 1кг укріплену на пружині жорсткістю 1кН/м. Визначте максимальне стиснення пружини, якщо в момент удару тіло мало швидкість 7м/с. Удар вважати непружним.

8. Кулька підвішена на невагомій нерозтяжній нитці довжиною 0,5м. Яку мінімальну швидкість потрібно надати кульці, щоб вона описала коло у вертикальній площині? Опором повітря знехтувати.

 

Лекційне заняття № 12.

Тема: Основні поняття, величини та закони динаміки обертального руху.

До тепер ми фактично вивчали ту частину динаміки яка називається динамікою матеріальної точки або динамікою поступального руху тіла.  Описуючи цей рух, ми говорили про швидкість руху (v) та його прискорення (a). Вказуючи на причини цього руху, а точніше на причини зміни його швидкості, ми говорили про діючу на тіло силу (F). Характеризуючи здатність тіла протидіяти зміні його швидкості, ми говорили про інерцію тіла, мірою якої є маса (m).

Однак, рух тіла може бути не лише поступальним а й обертальним. Про кінематичні та силові характеристики обертального руху ви вже знаєте. Зокрема знаєте про те, що обертальний рух тіла характеризують кутова швидкість (ω) та кутове прискорення (ɛ). Що причиною обертального руху тіла, а точніше причиною зміни його кутової швидкості є момент сили і що цей момент дорівнює добутку сили на плече її дії (M=Fd). Якщо ж говорити про основну обертально  динамічну властивість тіла та про ту фізичну величину яка є мірою цієї властивості, то ними є відповідно інерція обертального руху та момент інерції.

Нагадаємо, інерція – це універсальна властивість тіла, яка полягає в тому, що воно протидіє будь якій зміні його швидкості. Кількісною мірою інерції є маса тіла. Твердження про те, що маса є мірою інерціальних властивостей тіла потребує певного суттєвого уточнення. І це уточнення полягає в наступному. Коли ми стверджували: “маса є мірою інерціальних властивостей тіла, тобто мірою здатності тіла протидіяти зміні його швидкості”, то мали на увазі зміну швидкості поступального руху. Адже якщо мова йде про обертальний рух тіла, то в цьому випадку  маса не є безумовно об’єктивною мірою здатності тіла протидіяти зміні його кутової швидкості. Дійсно. Розглянемо три абсолютно однакових (однакових за масою, розмірами, формою, тощо) тіла, які можуть вільно обертатись навколо різних осей обертання (мал.35). Запитується. Чи відрізняються інерціальні властивості цих тіл при їх обертальному русі.

.                                             

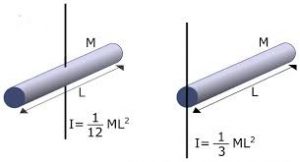
.    інерції мало                      інерції багато                    інерції дуже багато

мал.35.  Маси тіл однакові, а кількість інерції що до обертального руху, різна.

Напевно ви погодитесь з тим, що в першій ситуації (мал.35а) тіло легко розкрутити і відповідно легко зупинити його обертання. А це означає, що інерція обертального руху тіла в першій ситуації  є малою. В другій ситуації (мал.35б), тіло розкрутити значно важче, а відповідно важче зупинити його обертання. А це означає, що інерція обертального руху тіла в другій ситуації значно більша аніж в першій. Якщо ж говорити про третю ситуацію (мал.35в), то в ній інерція обертального руху тіла є найбільшою. (Застереження: експериментально перевіряти кількість інерціальних властивостей тіла при його обертальному русі, в ситуаціях подібних до тих що зображені на мал.35б,в, небезпечно.)

Оскільки в кожній із трьох вище наведених ситуацій маси тіл є однаковими, а їх інерціальні властивості щодо обертального руху – різні, то можна стверджувати: маса не є об’єктивною мірою інерціальних властивостей тіла при його обертальному русі. Звичайно, це не означає що інерція обертального руху тіла не залежить від його маси. Адже абсолютно очевидно, що легке дерев’яне і аналогічне за формою та розмірами важке залізне тіло мають різну кількість інерції обертального руху, і що ця різність обумовлена різницею їх мас. Однак не менш очевидно і те, що інерція обертального руху тіла залежить не лише від його маси, а й від того, наскільки віддаленими є його складові частини від осі обертання.

В науці об’єктивною мірою інерціальних властивостей тіла при його обертальному русі є не маса, а величина яку називають моментом інерції. Числове значення цієї величини визначають наступним чином .

1.Дане тіло представляють як сукупність достатньо великої кількості невеличких фрагментів, які можна вважати матеріальними точками.

2. Визначають добутки мас кожної з цих матеріальних точок на квадрат відстані до осі обертання тіла.

3. Визначають загальну суму цих добутків.

Ця сума і є моментом інерції даного тіла відносно відповідної осі обертання. Іншими словами, момент інерції тіла визначають за формулою:

J = ∑m_ir_i², ( і змінюється від i=1 до i=N),

де J – момент інерції тіла відносно певної осі обертання;

m_i – маса і-тої матеріальної точки;

r_i – відстань від цієї точки до осі обертання тіла;

N – та кількість матеріальних точок на яку умовно розділено дане тіло.

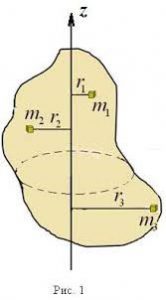
Мал.36 Момент інерції тіла визначають за формулою J = ∑m_ir_i².

Момент інерції – це фізична величина, яка характеризує інерціальні властивості тіла щодо його обертання навколо певної осі.

Позначається: J

Визначальне рівняння: J = ∑ m_ir_i²

Одиниця вимірювання: [J] = кг∙м²,   кілограм-метр квадратний.

Потрібно зауважити, що на відміну від маси тіла, величина його моменту інерції не є безумовно незмінною величиною. Адже одне і теж тіло, по відношенню до різних осей обертання може мати різні моменти інерції.

З практичної точки зору, визначальне рівняння моменту інерції (J=∑m_ir_i²) є незручним. Тому на практиці, момент інерції конкретного тіла визначають на основі певного набору відомих формул що є похідними від базового визначального рівняння,  але відрізняються від нього своєю практичною зручністю. Наведемо деякі з подібних формул, для однорідних геометрично простих тіл, осі обертання яких проходять через їх центри мас.

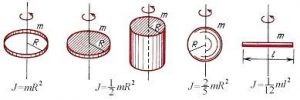
Мал.37. Моменти інерції деяких геометрично простих тіл.

1.Куля масою m і радіусом R: J₀ = (2/5)mR²

2. Тонкостінна сфера масою m і радіусом R: J₀ = (2/3)mR²

3. Стержень масою m і довжиною ℓ : J₀ = (1/12)mℓ²

4. Суцільний циліндр (вал, стержень) масою m і радіусом R: J₀ = (1/2)mR²

5. Порожнистий тонкостінний циліндр масою m і радіусом R: J₀ = mR².

          Динамічні параметри обертально рухомого тіла характеризують не лише його моментом інерції, а й моментом імпульсу. Момент імпульсу – це фізична величина, яка є мірою кількості обертального руху тіла і яка дорівнює добутку моменту інерції тіла J на його кутову швидкість ω.

Позначається: L

Визначальне рівняння: L=Jω

Одиниця вимірювання: [L]=кг∙м²/с,   кілограм-метр квадратний на секунду.

Фактично момент імпульсу є величиною векторною. Однак, зважаючи на те, що в межах програми загальноосвітньої школи вивчають лише ті обертальні рухи які відбуваються в певній визначеній площині, момент імпульсу можна вважати величиною скалярною.

Не важко бачити, що в динаміці обертального руху, момент імпульсу тіла (L=Jω) є певним аналогом тієї величини, яку в динаміці поступального руху називають імпульсом (p=mv). Різниця лише в тому, що при поступальному русі тіла, мірою його інерції є маса (m), а мірою швидкості руху – лінійна швидкість (v). При обертальному ж русі тіла, мірою його інерції є момент інерції (J), а мірою обертальної швидкості – кутова швидкість (ω).

Дослідження показують, що при будь яких процесах які відбуваються в замкнутій системі, зберігається не лише імпульс та енергія цієї системи, а й її момент імпульсу. Цей факт відображає закон який називається законом збереження моменту імпульсу. В цьому законі стверджується: При будь яких процесах які відбуваються в замкнутій системі, загальна кількість моменту імпульсу цієї системи залишається незмінною, тобто зберігається. Іншими словами ∑(Jω)_до = ∑(Jω)_після  або  ∑(Jω) = const.

Із закону збереження моменту імпульсу випливає, що при будь якій зміні моменту інерції замкнутої системи, автоматично змінюється швидкість її обертального руху (якщо J↓ то ω↑ , якщо J↑ то ω↓). Ілюструючи дію закону збереження моменту імпульсу, можна провести наступний експеримент. В центрі платформи виготовленої у вигляді легкого диску що може вільно обертатись, стоїть людина в руках якої знаходяться гантелі (мал.38а). Системі платформа-людина надають певного обертального руху. При цьому, коли людина притискає руки до тулуба, то швидкість обертального руху системи збільшується, а коли максимально розводить руки – зменшується. Подібні ситуації можна бачити коли наприклад фігуристи виконують вправу «дзиґа», або коли стрибуни у воду виконують багато обертальні сальто, або коли акробати виконують різноманітні кульбіти.

  

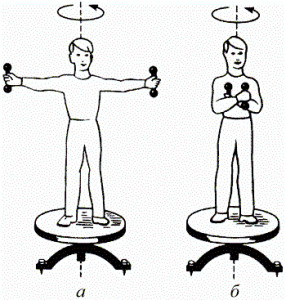
Мал.38. Якщо момент інерції системи зменшується, то швидкість її обертання збільшується. І навпаки.

Коментуючи результати даного експерименту можна сказати наступне. Коли людина притискає руки до тулуба (наближає до осі обертання системи), її момент інерції, а отже і момент інерції всієї системи, зменшується (J↓). При цьому, у повній відповідності з законом збереження моменту імпульсу (Jω=соnst) швидкість обертального руху системи збільшується (ω↑). Якщо ж людина знову розводить руки, то момент інерції системи збільшується (J↑), а швидкість її обертального руху відповідно зменшується (ω↓).

Закон збереження моменту імпульсу відіграє надзвичайно важливу роль в багатьох природних процесах. Зокрема під значним впливом цього закону формуються планетарні та зіркові системи. З’ясовуючи суть цього впливу розглянемо наступну задачу.

Задача 1.  Однорідна газоподібна куля радіусом R₁ обертається з кутовою швидкістю ω₁ . Під дією внутрішніх сил гравітаційної взаємодії куля стискається. При цьому її радіус зменшується в n разів. У скільки разів збільшиться швидкість обертального руху кулі.

Дано:                               Аналіз:

R₁/R₂=n            Згідно з законом збереження моменту імпульсу, момент

ω₂/ω₁=?         імпульсу системи до події J₁ω₁ (до зменшення розмірів кулі) і після події J₂ω₂ , має бути незмінним, тобто J₁ω₁ = J₂ω₂. Звідси ω₂/ω₁ = J₁/J₂.

Враховуючи що для однорідної кулі J=(2/5)mR², можна записати

ω₂/ω₁ = [(2/5)mR₁²]/(2/5)mR₂²]= (R₁/R₂)² = n² .

Відповідь: ω₂/ω₁ = n²

Таким чином, при зменшенні радіусу кулі в n разів, швидкість її обертального руху збільшується в n² разів. З іншого боку, в процесі збільшення швидкості обертання кулі, автоматично збільшується і величина тієї сили інерції, що діє на частинки цієї кулі. При цьому можна довести, що ця сила збільшується в n³ разів.

Аналізуючи та узагальнюючи результати вище розглянутої ситуації, можна сказати наступне. На частинки тієї кулі що обертається і в процесі обертання гравітаційно стискається, діють два силові фактори. 1) Об’ємні сили гравітаційної взаємодії які прагнуть зібрати всі частинки кулі в одну точку – центр мас системи. 2) Діючі в площині обертання тіла сили інерції, які протидіють гравітаційному стисненню системи (протидіють лише в тій площині що є перпендикулярною до осі обертання системи). А це означає, що в процесі гравітаційного стиснення, величезна газоподібна куля поступово перетвориться на дископодібну структуру в центральній частині якої буде зосереджена левова (понад 95%) частка її речовини.

Прикладом реалізації вище описаних подій є наша Сонячна система. Приблизно 5 мільярдів років тому на місці сучасної Сонячної системи була гігантська вихрова газопилова хмара. Під дією гравітаційних сил ця вихрова хмара поступово стискалась. А стискаючись – збільшувала швидкість свого обертання. Результатом цього тривалого процесу стало те, що через декілька мільйонів років, гігантська хмара перетворилась на величезний диск, в центрі якого було зосереджено близько 98% загальної маси системи. Поступово центральна частина цього диску перетворилась на те що ми називаємо Сонцем. А в його периферійній частині сформувались дрібніші космічні об’єкти які ми називаємо планетами (мал.39).

Мал.39. Сучасна Сонячна система, це результат тривалого еволюційного процесу, хід якого визначали сили гравітаційної взаємодії, сили інерції та закон збереження моменту імпульсу.

Потрібно зауважити, що вище описана картина космічних подій, буде реалізована лише в тому випадку, якщо швидкість обертання системи та її загальна маса знаходяться в певному інтервалі співвідношень. Загалом же, в залежності від величини цього співвідношення, можливі три варіанти кінцевого результату: а) зірка яка не має планетарної системи; б) зірка яка має планетарну систему; в) система двох або декількох зірок, що обертаються навколо спільного центру.

Втім, про те як утворюються планетарні та зіркові системи, як народжуються, живуть, старіють та помирають зірки, ми говорили в тому розділі фізики який називається “Космологією” – наукою про Всесвіт.

Контрольні запитання.

1.Що є причиною зміни швидкості: а) поступального руху тіла; б) обертального руху тіла.

2. Чому масу не можна вважати об’єктивною мірою інерціальних властивостей обертального руху тіла?

3. Яка фізична величина є об’єктивною мірою інерціальних властивостей тіла щодо його обертального руху?

4. Чому з практичної точки зору визначальне рівняння моменту інерції є незручним?

5. Чи є момент інерції тіла постійною величиною?

6. Аналогами яких фізичних величин є кутова швидкість; момент сили; момент інерції; момент імпульсу?

7. Наведіть приклади спортивних та інших вправ, які мають відношення до закону збереження моменту імпульсу.

 

Лекційне заняття № 13.

Тема: Кінетична енергія тіла що обертається.

Коли ми стверджуємо, що рухоме тіло має кінетичну енергію, величина якої визначається за формулою E_k=mv²/2, то маємо на увазі енергію його поступального руху. Але ж тіло може рухатись не лише поступально а й обертально. При цьому, абсолютно очевидно, що те тіло яке поступально не  рухається а лише обертається, здатне виконати певну роботу, а отже є таким що має певну кількість енергії. Величину цієї енергії можна визначити із наступних міркувань.

Припустимо, що деяке довільне тіло (мал.40б) обертається навколо нерухомої осі що проходить через його центр мас (т.О) і є перпендикулярною до площини малюнку. Розіб’ємо це тіло на N матеріальних точок маси яких m₁, m₂, m₃, …, m_N . Лінійні швидкості цих точок позначимо відповідно v₁, v₂, v₃, …, v_N , а їх відстані до осі обертання r₁, r₂, r₃, …, r_N.

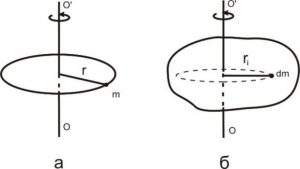
Мал.40.  Кожна точка тіла має певну кінетичну енергію: Е_кі=m_iv_i²/2, при цьому загальна кінетична енергія обертального руху тіла становить Е_к=J₀ω²/2 .

Оскільки кожна точка тіла рухається з певною лінійною швидкістю, то вона має певну кінетичну енергію, величина якої визначається за формулою Е_кі=m_iv_i²/2. При цьому загальна кінетична енергія тіла дорівнюватиме сумі кінетичних енергій всіх його матеріальних точок:

Е_к = m₁v₁²/2 + m₂v₂²/2 + … + m_Nv_N²/2 = ∑ m_iv_i²/2.

Зважаючи на те що при обертальному русі матеріальної точки, її лінійна (v) та кутова (ω) швидкості зв’язані співвідношенням v=ωr. І враховуючи що

ω₁ = ω₂ =  … =  ω_N, можна записати: E_k = m₁ω₁²r₁²/2 + m₂ω₂²r₂²/2 + … +

+ m_Nω_N²r_N²/2 = (ω²/2)(m₁r₁²+m₂r₂²+…+m_Nr_N²) = (ω²/2)∑m_ir_i² = J₀ω²/2 .

Таким чином, тіло що обертається навколо осі яка проходить через його центр мас, має кінетичну енергію (енергію обертального руху) величина якої визначається за формулою  Е_к=J₀ω²/2, де J₀ – момент інерції тіла відносно осі його обертання; ω – кутова швидкість тіла.

Не важко бачити, що формула Е_к=J₀ω²/2 в певному сенсі є аналогічною тій за якою визначають кінетичну енергію поступального руху тіла: Е_к=mv²/2. Різниця лише в тому, що при поступальному русі тіла, мірою інерції є маса (m), а при обертальному – момент інерції (J). При поступальному русі мірою швидкості руху є лінійна швидкість (v), а при обертальному русі – кутова швидкість (ω).

В багатьох практично важливих ситуаціях тіло одночасно рухається як поступально так і обертально (обертається навколо свого центру мас). Наприклад Земля, з певною лінійною швидкістю рухається навколо Сонця і з певною кутовою швидкістю обертається навколо своєї осі. Колесо рухомого автомобіля, куля що вилітає з дула нарізної зброї, акробат який виконує сальто, підкручений футбольний м’яч – в цих та їм подібних випадках, тіла рухаються як поступально так і обертально. При цьому їх загальна кінетична енергія визначається за формулою: Е_к = mv²/2 + J₀ω²/2, де  v – швидкість поступального руху центру мас тіла;  J₀ – момент інерції тіла відносно осі яка проходить через його центр мас і навколо якої обертається тіло.

Розглянемо декілька конкретних ситуацій в яких тіло рухається поступально-обертально та визначимо кількісні співвідношення між величинами їх кінетичної енергії поступального і обертального рухів.

Задача 1. Однорідний суцільний циліндр масою m котиться без ковзання горизонтальною площиною. Визначити кінетичну енергію циліндра, якщо швидкість його поступального руху v. Яку частину від цієї енергії становитиме кінетична енергія обертального руху?

Дано:                            Аналіз:

m

v                                Малюнок

Е_к

Е_к^об/Е_к=?            Оскільки даний циліндр рухається як поступально так і обертально, то його загальна кінетична енергія складається з двох частин: кінетичної енергії поступального руху Е_к=mv²/2 та кінетичної енергії обертального руху Е_к=J₀ω²/2 , тобто: E_k = mv²/2 + J₀ω²/2.

Враховуючи, що момент інерції однорідного циліндра при його обертанні навколо своєї осі симетрії визначається за формулою J₀=(1/2)mR², де R – радіус циліндра, та зважаючи на те що при обертальному русі циліндра його поступальна (v) і обертальна (ω) швидкості зв’язані співвідношенням ω=v/R , можна записати:  J₀ω²/2 =(1/2)(mR²/2)(v²/R²) = mv²/4.

Таким чинам:  1)  E_k = mv²/2 + mv²/4 = (3/4)mv² ;

.                                    2)  Е_к^об/Е_к = (mv²/4)/(3mv²/4) = 1/3 = 0,33 = 33%

Відповідь:  E_k = (3/4)mv²;   Е_к^об/Е_к=33%

Задача 2.  Однорідна суцільна куля що знаходиться на висоті h, скочується без ковзання похилою площиною. Визначити швидкість кулі в нижній точці похилої площини. Яка частина енергії кулі буде перетворена в кінетичну енергію її обертання? Втратами енергії на тертя та опір повітря знехтувати.

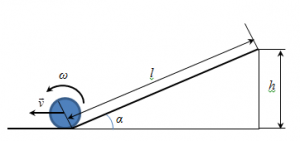
Дано:                              Аналіз:

h

v₀=0м/с                         Малюнок

v=?

E_k^об/Е_п=?        Розглянемо енергетичні параметри кулі перед та після спуску. Оскільки за умовою задачі втратами енергії можна знехтувати, то згідно з законом збереження енергії, потенціальна енергія кулі Е_п=mgh в процесі руху (скочування) перетворюється у відповідну кількість її кінетичної енергії. А зважаючи на те, що в процесі руху, куля набуває не лише лінійної а й кутової швидкості, можна записати: mgh =mv²/2 + J₀ω²/2.

Враховуючи, що для однорідної суцільної кулі J₀=(2/5)mR², а також що при обертальному русі кулі її поступальна (v) та кутова(ω) швидкості зв’язані співвідношенням ω=v/R, можна записати: J₀ω²/2 = 2mR²v²/2∙5R² = mR²/5 .

Таким чином: mgh = mv²/2 + mv²/5 = 7mv²/10,

звідси:  1)   v = (10gh/7)^1/2;

2)   E_к^об/E_п = (mv²/5)/(7mv²/10) = 10/35 = 0,29 = 29%

Відповідь:  v = (10gh/7)^1/2;

E_к^об/E_п = 29%.

Аналізуючи результати вище розв’язаних задач, не важко бачити, що значна частина кінетичної енергії тіла (в першому випадку 33%, в другому – 29%) може бути зосередженою у вигляді енергії його обертального руху. Тому, якщо за певних умов, оцінюючи кінетичну енергію тіла за формулою Е_к=mv²/2, ви з’ясуєте що цієї енергії виявилось значно менше за розрахункову величину, не поспішайте стверджувати, що закон збереження енергії не працює. Краще подивіться на те, чи не перетворилась частина вашої початкової енергії в енергію обертального руху. Або якщо, наприклад, в певній ситуації з’ясується, що величина виконаної тілом роботи більша за величину тієї початкової енергії яку ви визначили за формулою Е_к=mv²/2, то знову ж таки, не поспішайте звинувачувати закон збереження енергії. А краще зверніть увагу на те чи не мало ваше тіло енергії обертального руху.

Говорячи про енергію поступального та обертального руху, доречно зробити ще одне важливе зауваження. Коли ми стверджуємо, що кінетична енергія тіла складається з енергії його поступального та обертального руху, і що її загальна величина визначається за формулою Е_к = mv²/2 + J₀ω²/2, то під обертальним рухом розуміємо обертання тіла навколо свого центру мас, а не навколо певної сторонньої точки. Адже якщо, наприклад, тіло (матеріальна точка) з певною лінійною швидкістю (v) та відповідною кутовою швидкістю (ω) обертається навколо точки О (мал.41) і не обертається навколо власного центру мас, то повна кінетична енергію цього тіла має визначатись за формулою Е_к=mv²/2.

Мал.41. Якщо тіло обертається навколо т.О і не обертається навколо свого центру мас, то його кінетичну енергію потрібно визначати за формулою Е_к=mv²/2.

На перший погляд здається, що оскільки рух матеріальної точки по колу є як поступальним так і обертальним, то відповідна точка повинна мати як енергію поступального руху так і енергію обертального руху. Насправді ж ця точка має лише одну енергію. І цю енергію можна назвати як енергією поступального руху Е_к=mv²/2, так і енергією обертального руху Е_к=J₀ω²/2. При цьому, в незалежності від того, як ви назвете цю енергію і за якою формулою (Е_к=mv²/2 чи Е_к=J₀ω²/2) її визначатимете, результат буде абсолютно однаковим. Дійсно. Для будь якої матеріальної точки що рухається по колу радіусом R, справедливо:

J₀=mR²; ω=v/R   тому   E_k=J₀ω²/2=mR²v²/2R²=mv²/2.

По суті це означає, що описуючи обертальній рух матеріальної точки, її кінетичну енергію можна визначити як за формулою Е_к=mv²/2 так і за формулою Е_к=J₀ω²/2. Однак не можна одну і ту ж енергію враховувати двічі.

Таким чином, якщо визначаючи кінетичну енергію того тіла що поступально рухається круговою орбітою, ви застосовуєте формулу

Е_к= mv²/2 + J₀ω²/2 то вчиняєте не правильно. Не правильно тому, що двічі обчислюєте одну і ту ж енергію. Формула Е_к= mv²/2 + J₀ω²/2 справедлива лише в тих випадках коли тіло дійсно приймає участь в двох незалежних рухах: поступальному та обертальному. Наприклад Земля одночасно обертається як навколо Сонця так і навколо своєї осі. Тому її загальну кінетичну енергію потрібно визначати за формулою Е_к=mv²/2 + J₀ω²/2.

Втім, кінетична енергія тіла, як і швидкість його механічного руху, є величиною відносною. Тому визначаючи цю енергію, потрібно враховувати ті конкретні обставини по відношенню до яких ця енергія і визначається.

Контрольні запитання.

1.Коли ми говоримо, що кінетична енергія тіла визначається за формулою Е_к=mv²/2, то яку енергію маємо на увазі?

2. Наведіть приклади ситуацій в яких кінетична енергія тіла має як поступальну так і обертальну складову.

3. Чим схожі і чим відрізняються формули Е_к=mv²/2 і Е_к=J₀ω²/2?

4. В яких ситуаціях формули Е_к=mv²/2 і Е_к=J₀ω²/2 визначають одну і ту ж кінетичну енергію?

5. Чи може куля яка котиться вгору по похилій площині і має енергію поступального руху 100Дж, піднятись на висоту яка відповідає енергії 120Дж? Поясніть.

Вправа 9.

1.Однорідна суцільна куля масою 5кг і радіусом 20см обертається навколо своєї осі з кутовою швидкістю 10рад/с. Визначте кінетичну енергію кулі.

2. Однорідна суцільна куля масою 5кг і радіусом 20см котиться горизонтальною поверхнею, маючи при цьому кутову швидкість 10рад/с. Визначте кінетичну енергію кулі.

3. Суцільний однорідний циліндр скочується без ковзання похилою площиною з висоти 2м. визначити швидкість поступального руху циліндру в кінці спуску. Втратами енергії знехтувати.

4. Тонкостінний циліндр (труба) що знаходиться на висоті х, без ковзання скочується похилою площиною. Яка частина його потенціальної енергії перетворюється в енергію поступального руху, а яка – в енергію обертального руху?

5. Визначте повну кінетичну енергію планети Земля. Маса Землі 6∙10²⁴кг, її радіус 6,37∙10⁶м, відстань до Сонця 1,5∙10¹¹м. Порівняйте енергію поступального руху Землі з енергією її обертального руху.

 

Лекційне заняття № 14.

Тема: Закони Ньютона в механіці обертального руху.

          Вивчаючи механіку, важко не звернути увагу на очевидну симетричність тих величин і тих законів які фігурують в механіці поступального та механіці обертального руху. Дійсно.

Поступальний рух	Обертальний рух
Швидкість                            v=Δx/Δt	Кутова швидкість                  ω=Δφ/Δt
Прискорення                        a=Δv/Δt	Кутове прискорення              ɛ=Δω/Δt
Сила                                      F=ma	Момент сили                          M=Fd
Маса                                      m	Момент інерції                       J=∑miri2
Імпульс                                 p=mv	Момент імпульсу                   L=Jω
Кінетична енергія               Ek=mv2/2	Кінетична енергія                  Ek=Jω2/2
Рівняння руху              x=x0+v0t+at2/2	Рівняння руху              φ=φ0+ω0t+ɛt2/2
Умова рівноваги                  ∑ F=0	Умова рівноваги                     ∑ M=0
Закон збереження імпульсу                                      ∑mv=const	Закон збереження моменту імпульсу                           ∑Jω=const

 

Така симетричність характерна не лише для окремих величин та окремих законів механіки, а й для тих її базових тверджень які називаються законами Ньютона. Коли ми говорили про перший, другий та третій закони Ньютона, то згадували про те, що в механіці обертального руху кожен з них має свого “близнюка”. І от прийшов час познайомитись з цими “близнюками”. А щоб симетричність законів Ньютона була очевидною, давайте сформулюємо ці закони відповідними парами.

Перший закон Ньютона (в механіці поступального руху). Будь-яке тіло буде знаходитись в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v = const), до тих пір поки на нього не подіє зовнішня сила, яка і змусить тіло змінити цей стан.

Перший закон Ньютона (в механіці обертального руху). Будь яке тіло буде знаходитись в стані обертального спокою (ω=0), або в стані рівномірного обертального руху (ω=соnst) до тих пір, поки на нього не подіє зовнішній момент сили, який і змусить тіло змінити цей стан.

Другий закон Ньютона (в механіці поступального руху). Під дією зовнішньої сили F, тіло масою m отримує прискорення а, величина якого прямо пропорційна діючій на тіло силі і обернено пропорційна його масі, тобто:   F →   a = F/m.

Другий закон Ньютона (в механіці обертального руху). Під дією зовнішнього моменту сили М тіло з моментом інерції J, отримує кутове прискорення ɛ, величина якого прямо пропорційна діючому на тіло моменту сили і обернено пропорційна моменту інерції тіла, тобто: М → ɛ = М/J.

Третій закон Ньютона (в механіці поступального руху)  Діюча на тіло сила F, завжди  породжує рівну їй за величиною і протилежну за напрямком протидіючу силу F′, тобто:  F → F′ = – F .

Третій закон Ньютона (в механіці обертального руху). Діючий на тіло момент сили М, завжди породжує рівний йому за величиною і протилежний за напрямком протидіючий момент сили М´, тобто  М → М´= -М.

Не важко бачити, що закони Ньютона для обертального руху, відрізняються від аналогічних законів для поступального руху, лише тим, що в них замість сили F фігурує момент сили M, замість маси m – момент інерції J, замість прискорення а – кутове прискорення ɛ, а замість швидкості v – кутова швидкість ω. Втім, між законами Ньютона для механіки поступального руху і законами Ньютона для механіки обертального руху існують і певні принципові відмінності. Точніше, принципова відмінність стосується лише тієї частини першого закону Ньютона, яка відображає його зв’язок з принципом відносності.

Пояснюючи суть першого закону Ньютона ми наголошували на тому, що в цьому законі, окрім закону інерції, опосередковано сформульовано і принцип відносності. Дійсно. В першому законі Ньютона стверджується: будь-яке тіло буде знаходитись в стані механічного спокою (v=0), або в стані прямолінійного рівномірного руху (v = const), до тих пір поки на нього не подіє зовнішня сила, яка і змусить тіло змінити цей стан. По суті це означає, що з фізичної точки зору стан спокою (v=0) і стан прямолінійного рівномірного руху (v=const), це один і той же механічний стан системи (цей стан). Один і той же, в тому сенсі, що всі фізичні процеси які відбуваються в кабіні що стоїть і в кабіні що рівномірно рухається, відбуваються абсолютно однаково (Принцип відносності).

З іншого боку, в аналогічному за формою законі Ньютона для обертального руху стверджується: будь яке тіло буде знаходитись в стані обертального спокою (ω=0), або в стані рівномірного обертального руху (ω=соnst) до тих пір, поки на нього не подіє зовнішній момент сили, який і змусить тіло змінити цей стан.

На основі формального аналізу даного закону, можна зробити на перший погляд абсолютно логічний висновок: стан обертального спокою (ω=0) і стан рівномірного обертального руху (ω=const), це один і той же механічний стан системи (цей стан). Один і той же в тому сенсі, що всі фізичні процеси які відбуваються в кабіні що не обертається (ω=0) і в кабіні що рівномірно обертається (ω=const), відбуваються абсолютно однаково. Насправді ж такий висновок є хибним.  Хибним бодай тому, що суперечить експериментальним фактам. Адже якщо ви будете перебувати в закритій ізольованій кабіні і вона почне рівномірно обертатись, то ви неодмінно відчуєте факт цього обертання. Відчуєте тому, що на вас подіє певна сила інерції яка і вкаже на те що кабіна обертається. При цьому, чим більшою буде швидкість обертання кабіни, тим більшою буде відповідна сила інерції.

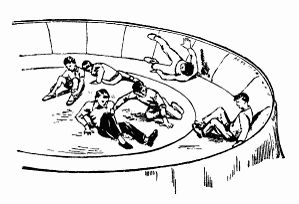
Мал.42. Перебуваючи в «кабіні» яка обертається, ви неодмінно відчуєте факт цього обертання.

Таким чином, принципова відмінність між поступальним та обертальним рухом полягає в тому, що ті події які відбуваються в кабіні яка стоїть (v=0) і в кабіні яка рівномірно поступально рухається (v=const) відбуваються абсолютно однаково. Натомість, ті події що відбуваються в кабіні яка не обертається (ω=0) і в кабіні яка рівномірно обертається (ω=const) відбуваються по різному. По різному тому, що в процесі обертального руху кабіни, всі її об’єкти рухаються з певним доцентровим прискоренням (а_д=v²/R=ω²R). А це означає, що на них неминуче діє відповідна сила інерція (F_i = –mа_д), яка і вказує на факт обертального руху системи.

Різниця між поступальним та обертальним рухом полягає не лише в тому, що тіла “відчувають” факт обертання кабіни, а й в тому що в процесі обертання змінюються параметри самих тіл. Адже якщо, наприклад, тіло кулястої форми (мал.43) почне обертатись навколо своєї осі, то воно в тій чи іншій мірі деформується. А це означає, що в ньому виникне певна сила пружності, певна механічна напруга, тощо.

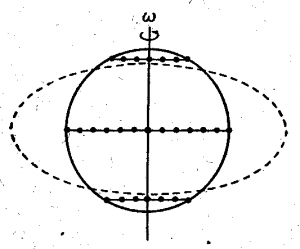
Мал.43. При рівномірному обертанні тіла, його геометричні та інші параметри певним чином змінюються.

До речі. З факту того, що в процесі обертального руху тіла, певним чином змінюються параметри самого тіла, зокрема його момент інерції, випливає ще одна суттєва відмінність між законами Ньютона для поступального та обертального рухів. І ця відмінність стосується другого закону Ньютона. Дійсно. В другому законі Ньютона для поступального руху стверджується:  F → a = F/m. При цьому, цілком обгрунтовано мається на увазі, що в процесі поступального руху тіла, його маса залишається незмінною (m=const). Якщо ж говорити про другий закон Ньютона для обертального руху: М → ɛ = М/J, то застосовуючи цей закон, потрібно мати на увазі, що в загальному випадку момент інерції тіла певним чином залежить від швидкості його обертання. Адже в процесі збільшення швидкості обертання тіла (ω↑), це тіло певним чином деформується (розтягується). При цьому момент інерції тіла збільшується (J↑), а відповідно зменшується величина його кутового прискорення (ε=M/J)↓.

Таким чином, порівнюючи закони Ньютона для поступального та обертального руху, можна виділити дві суттєві відмінності:

1. Перший закон Ньютона для обертального руху, не можна тлумачити як такий в якому опосередковано сформульовано принцип відносності. Не можна тому, що при переході від стану обертального спокою (ω=0) до стану рівномірного обертального руху (ω=const) ми по суті переходимо від інерціальної системи відліку до неінерціальної. В принципі ж відносності стверджується: “у всіх інерціальних системах відліку, всі фізичні процеси відбуваються абсолютно однаково”.

2. Застосовуючи другий закон Ньютона для обертального руху, потрібно мати на увазі, що момент інерції тіла (J) певним чином залежить від швидкості його обертання.

Контрольні запитання.

1.Назвіть величини які в механіці обертального руху є аналогами маси, сили, імпульсу, швидкості, пройденого шляху.

2. По парно сформулюйте закони Ньютона для поступального та обертального руху. Порівняйте ці закони.

3. Сформулюйте принцип відносності, (два формулювання).

4. Чому в процесі обертання тіла навколо свого центру мас, це тіло деформується? Як при цьому змінюється момент інерції тіла?

5. Чим перший закон Ньютона для обертального руху, принципово відрізняється від першого закону Ньютона для поступального руху?

6. Чим другий закон Ньютона для обертального руху суттєво відрізняється від аналогічного закону для поступального руху?