

Тема 5.1. Геометрична оптика.
Тема 5.1. Геометрична оптика.
§17. Основні поняття геометричної оптики.
§18. Закони геометричної оптики.
§19. Загальні відомості про дзеркала.
§20. Повне відбивання світла. Загальні відомості про
оптичні призми та оптичні волокна.
§21. Загальні відомості про лінзи.
§22. Оптичні прилади.
§23. Око як природний оптичний прилад. Дефекти зору.
§24. Оптичні ілюзії.
§17. Основні поняття геометричної оптики.
Геометрична оптика – це розділ оптики, в якому світло представляють як потік світлових променів і в якому вивчають ті явища які пояснюються виходячи з того, що світло це потік променів. Світловий промінь (промінь) – це умовна лінія, яка вказує на напрям розповсюдження тієї світлової енергії що випромінюється певним джерелом світла.
Наочні уявлення про світлові промені та їх властивості дають тонкі пучки світла які можна отримати за допомогою дрібних отворів, що знаходяться в потужному світловому потоці або спеціальних приладів (мал.45а). Однак, потрібно мати на увазі, що навіть найтонші світлові пучки, є лише грубими моделями світлового променя. Адже промінь, це фактично та умовна лінія яка вказує на напрям розповсюдження світла.


Мал.45. Наочні уявлення про світлові промені та їх поведінку, можна отримати за допомогою тонких світлових пучків.
Важливим поняттям оптики загалом та геометричної оптики зокрема, є джерело світла. Зазвичай, джерелом світла прийнято вважати будь який природний або штучний об’єкт в якому той чи інший вид енергії перетворюється на енергію видимого світла. Звідси ясно, що Сонце, зірки, блискавки, багаття, свічки, лампочки розжарювання та денного світла, кінескопи телевізорів та монітори комп’ютерів, є джерелами світла. А планети та їх супутники, дерева, столи, будинки, книги, люди – джерелами світла не являються. Однак, в багатьох галузях науки, в тому числі і в геометричній оптиці, джерелом світла вважають всі тіла що випромінюють світло. А це означає, що джерелами світла є не лише ті об’єкти які дійсно генерують світлову енергію, а й всі видимі тіла. Адже кожний фрагмент видимого тіла, по суті є джерелом світла, тільки світла не генерованого цим фрагментом, а відбитого ним. Таким чином, вивчаючи геометричну оптику, ми будемо виходити з того, що будь яке видиме тіло є джерелом світла.
В геометричній оптиці часто говорять про так звані точкові джерела світла, тобто такі джерела, розміри яких гранично малі порівняно з тією відстанню на якій оцінюють їх світлову дію. При цьому прийнято вважати, що інтенсивність того світла яке випромінюється точковим джерелом є однаковою в усіх напрямках. Зазвичай, видимі тіла не є точковими. Але будь яке з цих тіл можна представити у вигляді певної сукупності окремих точок.
Дослідження показують, що на межі двох оптично різних середовищ світловий потік частково відбивається, а частково проникає в нове середовище (мал.46). При цьому говорять про відбивання та заломлення світла. Відбивання світла – це явище, суть якого полягає в тому, що на межі двох оптично різних середовищ, частина світлового потоку відбивається від цієї межі і змінюючи напрям свого розповсюдження повертається в попереднє середовище. Заломлення світла – це явище, суть якого полягає в тому, що на межі двох оптично різних середовищ, частина світлового потоку проникає в нове середовище і змінюючи напрям свого руху (заломлюючись) продовжує розповсюджуватись в цьому новому середовищі.
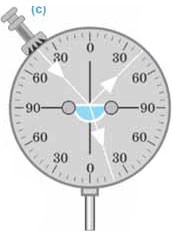
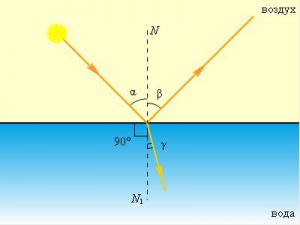
Мал.46. На межі двох оптично різних середовищ, світло частково відбивається, а частково проникає в нове середовище (заломлюється).
Потрібно зауважити, що про заломлення світла можна говорити лише в тому випадку, якщо те середовище в яке проникає світло є оптично прозорим, тобто таким, в якому процес розповсюдження світла не супроводжується значним перетворенням світлової енергії в енергію теплового руху частинок середовища. До числа оптично прозорих середовищ можна віднести повітря, скло, воду, лід, алмаз, переважну більшість газів та значну кількість рідин. Ідеально ж оптично прозорим “середовищем” є вакуум. Якщо ж мова йде про оптично непрозорі середовища, то в них світло не заломлюється, а поглинається, тобто перетворюється в енергію теплового руху частинок середовища. Крім цього, оптично не прозорими вважають і ті об’єкти, поверхні яких повністю відбивають світлову енергію.
Поділ речовин на оптично прозорі та оптично непрозорі є досить умовним. Наприклад метали, цілком обгрунтовано відносяться до оптично непрозорих об’єктів. Однак, якщо мова йде про надтонкі металеві плівки, то їх з не меншим обгрунтуванням можна вважати оптично прозорими.
В науці загалом і в геометричній оптиці зокрема, поверхні тіл, в залежності від величини їх мікронерівностей (шерсткостей), поділяють на оптично рівні та оптично нерівні. Оптично рівною називають таку поверхню, розміри мікронерівностей якої не перевищують довжини світлової хвилі (δ≤7,6·10-7м, на практиці δ≤1·10-6м=0,001мм). Зазвачай оптично рівні відбивні поверхні називають дзеркальними. Оптично не рівною називають таку поверхню, розміри мікронерівностей якої суттєво більші за довжину світлової хвилі. Зазвичай, оптично не рівні відбивні поверхні називають дифузійними або розсіювальними.
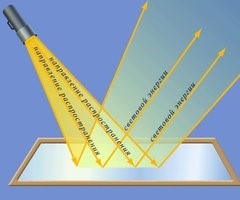
Дослідження показують, що оптично рівні та оптично не рівні поверхні, відбивають і заломлюють світло суттєво по різному. По різному в тому сенсі, що початково паралельні промені відбиваючись (заломлюючись) оптично рівною поверхнею залишаються паралельними (мал.47а), а відбиваючись (заломлюючись) оптично не рівною поверхнею – стають безладно розсіяними (мал.47б). Зазвичай, відбивання світла від оптично рівної поверхні називають дзеркальним, а відбивання від оптично не рівної поверхні – дифузійним або розсіяним.
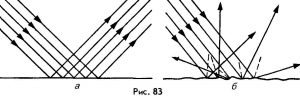
Мал.47. Оптично рівні (а) та оптично не рівні (б) поверхні відбивають (заломлюють) світло суттєво по різному.
Не важко бачити, що поведінка тих світлових променів які відбиваються (заломлюються) оптично рівною поверхнею є чітко визначеною, а отже прогнозованою. Цей факт корисно застосовують в різноманітних оптичних приладах, зокрема дзеркалах, лінзах та призмах. Робочі поверхні цих приладів завжди оптично рівні.
Потрібно заувавжити, що терміни “оптично рівна поверхня” та “геометрично рівна поверхня” є суттєво різними. Скажімо, поверхня стіни геометрично рівна, а оптично не рівна. Натомість поверхня опуклої лінзи – геометрично не рівна, а оптично рівна.
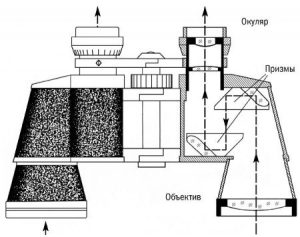
Мал.47а. Робочі поверхні будь якого оптичного приладу є оптично рівними.
Факт того, що кожен фрагмент оптично не рівної (дифузійної) поверхні відбиває світло у всіх можливих напрямках, по суті означає, що дифузійно відбите світло несе інформацію не про джерело первинного світла, а про той предмет від якого це світло відбивається. Власне тому, дивлячись на шерстку поверхню, ми бачимо саму поверхню, а не відбите в ній джерело світла. Якщо ж мова йде про дзеркальну поверхню, то відбите нею світло фактично несе інформацію не про саму поверхню, а про джерело первинного світла. Власне тому, дивлячись в дзеркало ми бачимо не його поверхню, а зображення тих предметів, світло яких відбивається в ньому.
Словник фізичних термінів.
Геометрична оптика – це розділ оптики, в якому світло представляють як потік світлових променів і в якому вивчають ті явища які пояснюються виходячи з того, що світло це потік променів. Світловий промінь (промінь) – це умовна лінія, яка вказує на напрям розповсюдження тієї світлової енергії що випромінюється певним джерелом світла.
Джерелом світла (в геометричній оптиці) називають будь який об’єкт що є джерелом генерованого або відбитого світла.
Оптично прозорим називають таке середовище, в якому процес розповсюдження світла не супроводжується значним перетворенням світлової енергії в енергію теплового руху частинок середовища.
Оптично не прозорим називають таке середовище, яке повністю поглинає ту світлову енергію що потрапляє в це середовище, або повністю відбиває цю енергію.
Оптично рівною називають таку поверхню, розміри мікронерівностей якої не перевищують довжини світлової хвилі. Зазвачай оптично рівні відбивні поверхні називають дзеркальними.
Оптично не рівною називають таку поверхню, розміри мікронерівностей якої суттєво більші за довжину світлової хвилі. Зазвичай, оптично не рівні відбивні поверхні називають дифузійними або розсіювальними.
Контрольні запитання.
1.На базі чого виникли уявлення про те, що світло, це потік променів?
2. Поясніть в яких випадках і чому за предметом утворюється певна комбінація тіні та напівтіні?
3. На якій підставі в геометричній оптиці всі видимі предмети називають джерелами світла?
4. Що називають заломленням світла?
5. Чи є поділ середовищ на оптично прозорі та оптично не прозорі безумовно чітким?
6. Чи є оптично рівна поверхня такою, що не має мікронерівностей?
7. Поясніть, чому робочі поверхні оптичних приладів (дзеркал, призм, лінз, тощо) мають бути оптично рівними? Чи означає це що вони мають бути геометрично рівними?
Вправа 7.
1.В сонячний день довжина тіні від вертикально поставленої метрової лінійки становить 40см, а від дерева 7м. Яка висота дерева?
2. Джерело світла діаметром 8см знаходиться на відстані 3м від екрану і освітлює непрозору кулю діаметром 20см, що знаходиться на відстані 2м від екрану. Визначити діаметр тіні та напівтіні на екрані.
3. Діаметр джерела світла 20см, а відстань від нього до екрану 2м. На якій найменшій відстані від екрану потрібно розташувати м’ячик діаметром 8см, щоб він давав лише напівтінь?
4. Визначити діаметр плями сонячного затемнення, якщо відомо, що радіус Сонця 7·105км, радіус Місяця 1,7·103км, відстань від Землі до Сонця 1,5·108км, а від Землі до Місяця 3,8·105км.
§18. Закони геометричної оптики.
Теоретичну основу геометричної оптики складають три експериментально встановлені факти, які сформульовані у вигляді відповідних законів геометричної оптики: закону прямолінійності розповсюдження світла, закону відбивання світла та закону заломлення світла. Про фізичну суть та особливості цих законів ми і поговоримо в даному параграфі.
Закон прямолінійності розповсюдження світла – це закон, в якому стверджується: в оптично однорідному середовищі, світлові промені розповсюджуються прямолінійно.
Коментуючи даний закон доречно зауважити, що світлові промені розповсюджуються прямолінійно не завжди, а лише в тих середовищах які є оптично однорідними, тобто такими, оптичні властивості яких в усіх точках одлнакові. Якщо ж середовище буде оптично неоднорідним, то відповідно не прямолінійним буде і хід світлових променів. Наприклад, в масштабах великих ділянок атмосфери Землі, оптичні властивості атмосферного повітря можуть суттєво змінюватись. Результатом цих змін можуть бути такі викривлення світлових променів які призводять до того що прийнято називати атмосферною рефракцією, міражами, тощо. Наприклад, якщо приповерхневий шар повітря є гарячим, а повітря над ним значно холоднішим, то можна спостерігати так званий нижній міраж (мал.48а). Загально відомим прикладом нижнього міражу є ілюзія того, що в спекотний день на горизонті автостради спостерігаються рясні калюжі води, які фактично є відображенням фрагментів неба. А це відображення обумовлене тим викривленням світлових променів, яке відбувається на межі холодного та теплого повітря. Якщо ж нижній шар повітря холодний, а верхній значно тепліший, то за певних додаткових умов, можна спостерігати так званий верхній міраж, який є відображенням тих об’єктів що знаходяться за лінією горизонту (мал.48б).

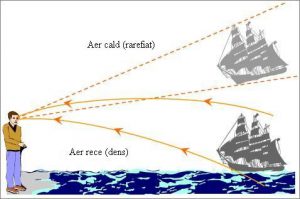
Мал.48. Якщо оптичні властивості середовища змінюються, то відповідно змінюється і напрям розповсюдження світлових променів.
Наступні два базові закони геометричної оптики (закони відбивання та заломлення світла) пов?язані з тими процесами які відбуваються на межі двох оптично різних середовищ. А на цій межі, світлові промені можуть як відбиватись так і заломлюватись (мал.46). Характеризуючи це відбивання та заломлення говорять про кут падіння (α), кут відбивання (β) та кут заломлення променя (γ). Тобто ті кути які характеризують відхилення падаючого, відбитого та заломленого променів від перпендикуляру (нормалі) до поверхні розділу середовищ, проведеного в точці падіння променя.
Закон відбивання світла – це закон, в якому стверджується: на межі двох оптично різних середовищ світлові промені відбиваються, при цьому: 1) проміннь падаючий, промінь відбитий і перпендикуляр до поверхні в точці падіння променя, лежать в одній площині; 2) кут відбивання променя (β) дорівнює куту його подіння (α): ∠β = ∠α.
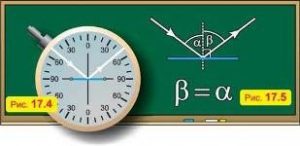

Мал.49. Кут відбивання променя дорівнює куту його падіння.
Іноді закон відбивання світла формулюють наступним чином. На межі двох оптично різних середовищ світлові промені відбиваються, при цьому, кут падіння променя дорівнює куту його відбивання: ∠α= ∠β. Таке формулювання закону є неправильним. Неправильним по перше тому, що з точки падіння променя можна провести безліч променів для яких виконується співвідношення ∠β = ∠α. Насправді ж реально відбитим буде лише один з цих променів. І цей єдино правильний промінь буде знаходитись в тій площині що є перпендикулярною відбивній поверхні. Власне цей факт і констатує перша частина закону відбивання світла: промінь падаючий, промінь відбитий і перпендикуляр до поверхні в точці падіння променя, лежать в одній площині.
Ще однією суттєвою помилкою вище наведеного неправильного формулювання закону є те, що в ньому стверджується: “при відбиванні світла, кут падіння променя дорівнює куту його відбивання: ∠α = ∠β “. По суті, в контексті того що називають законом, це означає що кут падіння променя залежить від кута його відбивання: α=ƒ(β). Насправді ж кут падіння променя залежить не від кута відбивання, а від взаємного розташування джерела світла, відбивної поверхні та точки падіння променя (мал.50). А от кут відбивання променя, дійсно залежить від куту його падіння. І цю залежність відображає формулювання: кут відбивання променя дорівнює куту його падіння: ∠β = ∠α.
мал.50. Кут падіння променя залежить не від кута його відбивання, а від взаємного розташування джерела світла, відбивної поверхні та точки падіння променя.
Говорячи про закон відбивання світла доречно додати. Прямим наслідком цього закону є твердження: падаючий та відбитий промені взаємообернені. Це означає, що направивши падаючий промінь шляхом відбитого, ми отримаємо такий відбитий промінь який розповсюджується шляхом відповідного падаючого променя.
Закон заломлення світла – це закон, в якому стверджується: на межі двох оптично різних та оптично прозорих середовищ, світлові промені заломлюються, тобто проникаючи в нове середовище змінюють напрям свого розповсюдження. При цьому: 1) промінь падаючий, промінь заломлений та перпиндикуляр до поверхні в точці падіння променя, лежать в одній площині; 2) відношення синуса кута падіння променя (sinα) до синусу кута його заломлення (sinγ) для даної пари середовищ є постійною величиною: sinα/sinγ = n12, де n12 – показник заломлення світла першого середовища відносно другого.

Мал.51. Потрапляючи в нове оптично порозоре середовище світлові промені заломлюються тобто змінюють напрям свого розповсюдження.
Дослідження показують, що причиною заломлення світла є факт того, що в різних середовищах швидкість розповсюдження світла є різною. При цьому, показник заломлення світла фактично показує, у скільки разів швидкість світла в першому середовищі (v1) більша за його швидкість в другому середовищі (v2), тобто n12 = v1/v2. Наприклад, якщо для пари повітря-вода n12=1,33, то це означає що швидкість світла у повітрі в 1,33 рази більша за швидкість світла у воді.
З іншого боку, показник заломлення світла констатує той факт, що падаючий та заломлений промінь взаємопов’язані таким чином, що кут падіння (α) та кут заломлення (γ) променя зв’язані співвідношенням: sinα/sinγ = n12. По суті це означає, що знаючи кут падіння променя завжди можна визначити кут його заломлення, тобто передбачити подальшу поведінку падаючого променя. Наприклад, якщо для пари вода–повітря α=30°, то γ=arcsin(sin30°/1,33)≅22°, якщо α=45°, то γ=arcsin(sin45°/1,33)≅32°; якщо α=60°, то γ=arcsin(sin60°/1,33)≅41°; і т.д.
Оскільки при переході світла із повітря у воду, показник заломленн визначається за формулою n12=v1/v2, то ясно, що при зворотньому переході ця формула набуватиме вигляду n21=v2/v1=1/n12=1/1,33=0,72. Тому якщо при переході із води в повітря α=30°, то γ=arcsin(sin30°/0,72)≅44°; якщо α=45°, то γ=arcsin(sin45°/0,72)≅79°; якщо α=60°, то γ=arcsin(sin60º/0,72)=arcsin1,2= не існує. А це означає, що при α=60° заломлення світла, тобо переходу світла із води в повітря, не відбувається.
Зверніть увагу на факт того, що при переході світла з води в повітря (з оптично більш густого середовища в оптично менш густе), кут залослення світла більший за кут його падіння (γ>α), і що тому, при певних кутах падіння, кут заломлення променів стає більшим за 90°. А це означає, що при певних кутах падіння (α ≥ αгр) світлові промені не переходять із води в повітря, а отже повністю відбиваються від межі вода-повітря. Це явище називають повним відбиванням світла. Про закономірності та прояви повного відбивання світла ми поговоримо дещо пізніше. А наразі додамо.
По суті, показник заломлення світла певним чином характеризує оптичні властивості даного середовища по відношенню до іншого оптично прозорого середовища. І якщо цим іншим середовищем є вакуум, то відповідний показник заломлення називають абсолютним.
Абсолютний показник заломлення світла, це фізична величина, яка характеризує оптичні властивості даного оптично прозорого середовища, і яка з одного боку дорівнює відношенню синусу кута падіння променя до синусу кута його заломлення (sin?/sin?),за умови переходу світла з вакууму в дане середовищеа, а з іншого – показує, у скільки разів швидкість світла в даному середовищі (v) менша за швидкість світла в вакуумі (с=3·108м/с).
Позначається: n
Визначальне рівняння: n =sinα/sinγ=c/v
Одиниця вимірювання: [n] = – , безрозмірна величина (рази).
Величина абсолютного показника заломлення світла визначається експериментально і записується у відповідну таблицю.
Таблиця 1.
Абсолютні показники заломлення світла деяких речовин.
| Речовина | n | Речовина | n |
| Повітря | 1,000292 | Скло: *) | |
| Вода | 1,33 | – легкий крон | 1,52 |
| Гліцерін | 1,47 | – крон | 1,56-1,60 |
| Олія кедрова | 1,52 | – флінт | 1,60-1,80 |
| Олія сонячникова | 1,47 | Сапфір, рубін | 1,77 |
| Лід | 1,31 | Алмаз | 2,42 |
*) Для більшості побутових сортів скла n=1,52. Тому за відсутності додаткових вказівок будемо вважати, що для скла n=1,52.
За відомими значеннями абсолютних показників заломлення двох середовищ (n1, n2) не важко визначити величини їх відносних показників заломлення n12 та n21. Дійсно. Оскільки n1=c/v1 , n2=c/v2 то n12=v1/v2=cn2/cn1=n2/n1, відповідно n21=n1/n2 . Наприклад, показник заломлення скла (n1=1,52) по відношенню до води (n2=1,33) становить n12=n2/n1=0,875. А води по відношенню до скла n21=n1/n2=1,143.
Оскільки абсолютні показники заломлення світла для повітря (n=1,000292) та вакууму (n=1,000000) є практично однаковими, то на практиці абсолютний показник заломлення даного середовища і його показник заломлення відносно повітря, прийнято вважати чисельно рівними.
Порівнюючи оптичні властивості двох прозорих середовищ говорять, що те з них яке має більше значення абсолютного показника заломлення є оптично більш густим, а те, яке має менше значення абсолютного показника заломлення – оптично менш густим. Наприклад скло (n=1,52) оптично густіше за воду (n=1,33), а алмаз (n=2,42) оптично густіший за скло.
Словник фізичних термінів
Закон прямолінійності розповсюдження світла – це закон, в якому стверджується: в оптично однорідному середовищі, світлові промені розповсюджуються прямолінійно.
Оптично однорідним, називають таке оптично прозоре середовище, оптичні властивості якого в усіх точках одлнакові.
Закон відбивання світла – це закон, в якому стверджується: на межі двох оптично різних середовищ світлові промені відбиваються, при цьому: 1) проміннь падаючий, промінь відбитий і перпендикуляр до поверхні в точці падіння променя, лежать в одній площині; 2) кут відбивання променя (β) дорівнює куту його подіння (α): ∠β = ∠α.
Закон заломлення світла – це закон, в якому стверджується: на межі двох оптично різних та оптично прозорих середовищ, світлові промені заломлюються, тобто проникаючи в нове середовище змінюють напрям свого розповсюдження. При цьому: 1) промінь падаючий, промінь заломлений та перпиндикуляр до поверхні в точці падіння променя, лежать в одній площині; 2) відношення синуса кута падіння променя (sinα) до синусу кута його заломлення (sinγ) для даної пари середовищ є постійною величиною: sinα/sinγ = n12, де n12 – показник заломлення світла першого середовища відносно другого.
Абсолютний показник заломлення світла, це фізична величина, яка характеризує оптичні властивості даного оптично прозорого середовища і яка з одного боку дорівнює відношенню синусу кута падіння променя до синусу кута його заломлення (sinα/sinγ), за умови переходу світла з вакууму в дане середовище, а з іншого – показує, у скільки разів швидкість світла в даному середовищі (v) менша за швидкість світла в вакуумі (с=3·108м/с).
Позначається: n
Визначальне рівняння: n =sinα/sinγ=c/v
Одиниця вимірювання: [n] = – , безрозмірна величина (рази).
Контрольні запитання.
1.Чи можуть світлові промені бути криволінійними?
2. Що називають кутом падіння кутом відбивання та кутом заломлення променя?
3. Чи є правильним формулювання закону: на межі двох оптично різних середовищ світлові промені відбиваються, при цьому кут падіння променя дорівнює куту його відбивання? Чому?
4. Від чого залежить кут падіння променя?
5. Чому світлові промені заломлюються?
6. Що означає твердження: промінь падаючий та промінь заломлений є взаємно оберненими?
7. Яке середовище є найбільш оптично густим?, найменш оптично густим?
Вправа 8.
1.Швидкість світла в рідині 240000км/с. З повітря на поверхню цієї рідини падають світлові промені під кутом 30°. Визначити кут заломлення променів.
2. Світловий промінь переходить з гліцерину в повітря. Яким буде кут заломлення променя, якщо кут його падіння 25°?
3. Під яким кутом має падати промінь на поверхню скла, щоб кут його заломлення був вдвічі меншим за кут падіння?
4. На дні водойми глибиною 60см лежить монета. Хлопчик тримаючи палицю під кутом 45° намагається влучити в монету. На якій відстані від монети палиця вткнеться в дно водойми?
5. Визначити швидкість поширення світла в скипідарі, якщо відомо що при куті падіння світла 45° кут його заломлення становить 30°?
6. В дно водойми глибиною 2м вбита свая яка на 0,5м виступає із води. Визначити довжину тіні від сваї на дні водойми, при куті падіння сонячного світла 40°
7. Якщо дивитися зверху на неглибоку водойму з чистою водою, то дно добре видно, проте глибина водойми здається меншою. У скільки разів?
§19. Загальні відомості про дзеркала.
Захоплюючись тими дивовижними речами які демонструють професійні ілюзіоністи, ми зазвичай не звертаємо увагу на ті не менш дивовижні речі, які оточують нас у повсякденному житті. Дійсно. Підійдіть до звичайного дзеркала і ви неодмінно побачите себе там де вас нема і бути неможе. Чи це не диво?
Говорячи про будову та принцип дії дзеркала можна сказати наступне. Дзеркало – це оптичний прилад, який представляє собою оптично рівну, відбивну (дзеркальну) поверхню, що має певну, геометрично правильну форму. Цією геометрично правильною формою може бути фрагмент площини, сфери, циліндра, тора, еліпсоїда, параболоїда, тощо. Принцип дії будь якого дзеркала базується на застосуванні закону відбивання світла. Це означає, що застосовуючи закон відбивання світла, можна передбачити параметри того зображення яке створює відповідне дзеркало в тій чи іншій ситуації.
Найпростішою та найбільш поширеною різновидністю дзеркал є дзеркала плоскі, тобто такі, робочою поверхнею яких є фрагмент площини. Пояснюючи принцип дії плоского дзеркала, розглянемо конкретну ситуацію. Припустимо, що відрізок МN – це поске дзеркало, а точка S – точкове джерело світла (мал.52). Візьмемо ряд довільних променів що виходять з точки S та застосовуючи закон відбивання світла, побудуємо відповідні відбиті промені.
Не важко бачити, що задзеркально відбиті промені певним чином розходяться. Але розходяться так, що їх уявні продовження перетинаються в одній і тій же точці – точці S1. По суті це означає, що будь який спостерігач, дивлячись в дзеркало, візуально зафіксує, що всі промені виходять з точки S1 і що тому точка S1 є точковим джерелом світла. Зауважимо, що фактично всі світлові промені виходять з точки S. Однак, дивлячись в дзеркало, спостерігач побачить цю точку не там де вона є насправді, а в іншому місці – у відповідній точці задзеркалля. При цьому, те що побачить спостерігач, буде певною ілюзією, тобто оптичним обманом (від лат. illusio – обман).
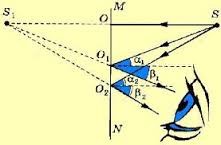
Мал.52. Дивлячись в дзеркало, спостерігач бачить точку S не там де вона є в реальності.
Можна довести, що реальна точка S та її дзеркальне відображення S1 є симетричними відносно площини дзеркала. Це означає, що точки S та S1 є рівновіддаленими від площини дзеркала і лежать на прямій яка перпендикулярна цій площині.
Знаючи закономірності побудови дзеркальних зображень окремих світлових точок, не важко визначити параметри зображення цілого тіла. Адже будь яке тіло завжди можна представити як певну сукупність окремих точок.
Характеризуючи те зображення яке створює плоске дзеркало, говорять що воно є уявним, дзеркально симетричним та геометрично рівним. Уявним, називають таке зображення яке є результатом уявного перетинання відбитих або заломлених променів. Наприклад, те зображення яке бачить спостерігач в плоскому дзеркалі є результатом уявного перетинання відбитих дзеркалом променів і тому є уявним.
Коли говорять, що зображення є дзеркально симетричним, то мають на увазі не лише те, що відповідні точки тіла та його зображення симетричні відносно площини дзеркала, а й факт того що дзеркальне зображення є оберненим. Оберненим в тому сенсі, що предмет та його зображення “дивляться” в протилежні сторони. А це означає, що ті елементи обличчя які для оригіналу є правими, для дзеркального зображення – лівими і навпаки.
В різноманітних оптичних системах, наряду з плоскими дзеркалами часто застосовують і дзеркала криві, тобто такі, відбивна поверхня яких є частиною тієї чи іншої викривленої поверхні, зокрема сфери, циліндра, тора, еліпсоїда, параболоїда, тощо. В загальному випадку криві дзеркала поділяються на увігнуті (вгнуті) або збиральні та опуклі або розсіювальні. Увігнуті дзеркала характеризуються тим, що їх робоча поверхня є увігнутою, і що вони збирають паралельні промені в близьких околицях певної точки, яку називають фокусом дзеркала. Опуклі дзеркала характеризуються тим, що їх робоча поверхня є опукою, і що вони розсюють падаючі на них паралельні промені, причому розсіюють так, що їх уявні продовження перетинаються в околицях певної точки, яку називають уявним фокусом дзеркала.
Найпростішою та найбільш поширеною різноводністю кривих дзеркал є дзеркала сферичні, тобто такі, відбивною поверхнею яких є певна частина сфери. Загальна інформація про основні характеристики сферичного дзеркала представлена на мал.53.
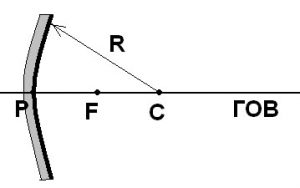
C – оптичний центр дзеркала; Р – полюс дзеркала; F – фокус дзеркала;
CР – головна оптична вісь дзеркала; R – радіус дзеркала
ƒ – фокусна відстань дзеркала
Мал.53. Сферичне дзеркало та його основні характеристики.
Досліджуючи властивості вгнутих та опуклих сферичних дзеркал, проведемо наступний експеримент. На відбивну поверхню вгнутого дзеркала (мал.54а) спрямуємо ряд співнаправлених променів (світлових пучків) що є паралельними головній оптичній осі дзеркала. Не важко бачити, що після відбивання, ці промені збираються в одній точці, яку прийнято називати фокусом (головним фокусом) вгнутого дзеркала. Якщо ж аналогічні промені направити на опукле дзеркало (мал.54б), то після відбивання вони будуть розсіюватись. При цьому розсіюватись таким чином, що їх уявні задзеркальні продовження будуть перетинатись в певній точці яку називають фокусом (головним фокусом) опуклого дзеркала.
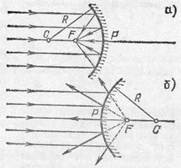
Мал.54. Вгнуті дзеркала збирають відбиті промені, а опуклі – розсіюють їх.
Не важко бачити, що фокус вгнутого дзеркала є дійсним, тобто таким в якому дзеркально відбиті промені дійсно перетинаються. Натомість фокус опуклого дзеркала є уявним, тобто таким, в якому перетинаються не дзеркально відбиті промені, а їх уявні задзеркальні продовження. Зауважимо також, що ті співнаправлені промені які не є паралельними головній оптичній осі дзеркала, після відбивання також перетинаються в дійсній або уявній точці (фокусі). Але ця точка знаходиться не на головній оптичній осі дзеркала, а належить тій площині що є перпендикулярною цій осі і проходить через головний фокус дзеркала (фокальна площина).
Можна довести, що відстань від головного фокуса сферичного дзеркала до його полюса (фокусна відстань) дорівнює половині радіуса цього дзеркала: ƒ=(1/2)R. Втім, дане твердження, рівно як і твердження про те, що всі паралельні промені після дзеркального відбивання перетинаються в дійсному або уявному фокусі сферичного дзеркала, не є безумовно правильними. Фактично ці твердження справедливі лише для так званих параксиальних (приосевих) променів, тобто таких променів які знаходяться на відносно невеликій відстані від головної оптичної осі дзеркала.
Збиральні властивості вгнутих та розсіювальні властивості опуклих дзеркал, є закономірним результатом їх геометричної форми та дії закону відбивання світла. В цьому не важко переконатись якщо, дотримуючись закону відбивання світла, визначити хід тих паралельних променів що відбиваються від поверхні вгнутого та опуклого дзеркал (мал.55). Виконуючи ці геометричні побудови не важко переконатись і в тому, що по мірі віддалення падаючих променів від головної оптичної осі сферичного дзеркала, точка перетинання відповідних відбитих променів, певним чином відхиляється від тієї точки яку називають фокусом дзеркала. По суті це означає, що те зображення яке утворює сферичне дзеркало буде певним чином викривленим.
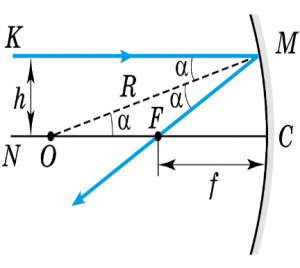
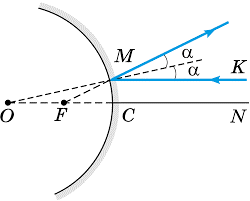
Мал.55. Оптичні властивості кривих дзеркал, є закономірним результатом їх геометричної форми та дії закону відбивання світла.
Оскільки падаючий та відбитий промені взаємно обернені, то ясно, що розташувавши точкове джерело світла в фокусі вгнутого дзеркала, на виході можна отримати направлений потік паралельних променів. Цю обставину застосовують в різноманітних прожекторах, ліхтарях, автомобільних фарах, тощо. Втім, потрібно мати на увазі, що сферичне дзеркало практично не може створити строго направлений світловий потік. Не може головним чином тому, що в сферичному дзеркалі паралельно направленими стають лише приосеві (параксиальні) промені. Крім цього, фокус сферичного дзеркала зазвичай знаходиться за межами геометричних обрисів тіла дзеркала. А це означає, що велика частина того світлового потоку який створює розміщене в фокусі дзеркала джерело світла, не буде потрапляти на тіло дзеркала, а відповідно не буде спрямовуватись в потрібному напрямку. Строго направлені світлові потоки створюють за допомогою спеціальних вгнутих дзеркал, які називаються параболічними (мал56б).
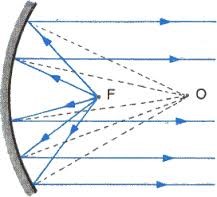
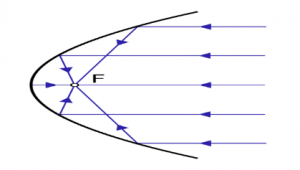
Мал.56. Строго направлені світлові потоки створюють за допомогою параболічних дзеркал.
Застосовуючи закон відбивання світла, можна побудувати дзеркальне забраження будь якої світлової точки, а отже і будь якого тіла. Однак, виконуючи подібні побудови, потрібно прагнути до того щоб вони були максимально ефективними. Скажімо, для того щоб отримати зображення будь якої точки, не обов’язково розглядати траєкторії всіх тих променів що виходіть з ціїє точки. Достатньо вибрати два з них, та виконавши відповідні геометричні побудови визначити точку дійсного чи уявного перетину відбитих променів. Ця точка і буде дзеркальним зображенням заданої точки. Впринципі, вихідні промені можуть бути довільними. Однак на практиці, із всього різноманіття можливих променів обирають ті, хід яких є загально відомим. Для сферичних дзеркал цими базовими променями є (мал.57):
1 – якщо падаючий промінь паралельний головній оптичній осі дзеркала, то промінь відбитий дійсно або уявно проходить через фокус дзеркала;
2 – якщо падаючий промінь дійсно або уявно проходить через фокус дзеркала, то промінь відбитий буде паралельним його головній оптичній осі;
3 – якщо падаючий промінь дійсно або уявно проходить через оптичний центр дзеркала, то відбитий промінь також проходить через цей центр.

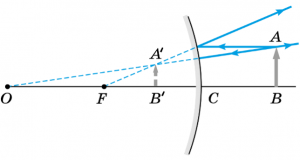
Мал.57. Хід тих базових променів які зазвичай застосовують для побудови зображень в сферичних дзеркалах.
Загальні уявлення про параметри тих зображень які дають сферичні дзеркала в тій чи іншій ситуації, можна отримати на основі аналізу мал.58.
|
F
дійсне, перевернуте, зменшене. |
F уявне, пряме, зменшене. |
|
F
дійсне, перевернуте, рівне. |
F уявне, пряме, зменшене. |
|
F
дійсне, перевернуте, збільшене. |
F уявне, пряме, зменшене. |
|
F
зображення відсутнє. |
F уявне, пряме, зменшене. |
|
F
уявне, пряме, збільшене. |
F уявне, пряме, зменшене |
Мал.58. Картина геометричних побудов та параметри тих зображень які дають сферичні дзеркала в тих чи інших ситуаціях.
На завершення додамо, що дійсні зображення знаходяться перед дзеркалом і мають певні ознаки реального джерела світла. Ці зображення чітко проектуються на розташовані у відповідному місці екрани та інші елементи оптичних систем. Однак дійсні дзеркальні зображення не є звичними та зручними для зорового сприйняття. Натомість уявні дзеркальні зображення, є звичними та зручними для наших зорових відчуттів.
Факт того, що вгнуті дзеркала, велику кількість світлової інформації збирають у відповідні дійсні зображення, широко застосовується в різноманітних оптичних системах, зокрема в потужних дзеркальних телескопах. Аналогічні збиральні функції виконують і різноманітні сферичниі та параболічні антени радіоприймальних приладів: телевізійні антени, антени радарів, радіотелескопів, тощо.
Словник фізичних термінів.
Дзеркало – це оптичний прилад, який представляє собою оптично рівну, відбивну (дзеркальну) поверхню, що має певну, геометрично правильну форму. Цією геометрично правильною формою може бути фрагмент площини (плоске дззеркало), або частина сфери, циліндра, тора, еліпсоїда, параболоїда, тощо (криве дзеркало).
Уявним, називають таке зображення яке є результатом уявного перетинання відбитих або заломлених променів.
Дійсним, називають таке зображення яке є результатом дійсного перетинання відбитих або заломлених променів.
Фокусом дзеркала (головним фокусом дзеркала) називають ту точку в якій дійсно або уявно перетинаються ті відбиті промені, які до відбивання були паралельними головній оптичній осі дзеркала.
Контрольні запитання.
1.Поясніть принцип дії плоского дзеркала.
2. Те зображення яке створює плоске дзеркало є уявним, дзеркально сисетричним та геометрично рівним. Поясніть, що це означає?
3. Чому фокус вгнутого дзеркала є дійсним, а опуклого – уявним?
4. Точкове джерело світла знаходиться в фокусі вгнутого сферичного дзеркала. Чи створить ця система строго направлений світловий потік? Чому?
5. Які промені є базовими при побудові зображень в сферичних дзеркалах?
6. За яких умов тіло немає зображення у вгнутому дзеркалі?
7. З якою метою на транспортних засобах встановлюють опуклі дзеркала?
8. На основі аналізу мал.18 зробіть узагальнюючі висновки стосовно того, як змінюються параметри зображення, в процесі наближення тіла до а) вгнутого дзеркала; б) опуклого дзеркала.
Вправа 9.
1.Людина йде в напрімку плоского дзеркала з швидкістю 2м/с. З якою швидкістю людина наближається до свого зображення?
2. Побудуйте зображення вектора АВ в плоскому дзеркалі та графічно визначте область бачення цього вектора в дзеркалі.
3. Побудуйте зображення трикутника АВС в плоскому дзеркалі та графічно визначте область його бачення в дзеркалі.
4. Геометричним шляхом визначити параметри зображення стержня у вгнутому сферичному дзеркалі радіус якого 10см. Висота стержня 2см, а відстань до полюса дзеркала а) 12см; б) 10см; в) 8см; г) 5см; д) 2см. Описати характер тих змін які відбуваються в процесі наближення стержня до дзеркала.
5. Розвязати попередню задачу для опуклого дзеркала.
6. У скільки разів збільшиться зображення предмету в сферичному вгнутому дзеркалі, якщо предмет знаходиться на відстані 15см від полюса дзеркала? Радіус дзеркала 60см. Задачу розв’язати графічно.
§20. Повне відбивання світла. Загальні відомості про оптичні призми та оптичні волокна.
Дослідження показують, що на межі двох оптично прозорих середовищ, частина світлового потоку відбивається, а частина проникає в нове середовище, тобто заломлюється. При цьому, при збільшенні кута падіння променів, кількість відбитого світла поступово збільшується, а кількість заломленого – відповідно зменшується.
Мал.59. При збільшенні кута падіння променів, кількість відбитого світла поступово збільшується, а кількість заломленого – відповідно зменшується.
Не важко довести, що для однієї і тієї ж пари оптично прозорих середовищ, співвідношення між кількістю відбитого та кількістю заломленого світла, залежить не лише від кута падіння променів, а й від напрямку переходу світлових променів. Дійсно. Якщо світлові промені переходять з оптично менш густого середовища в оптично більш густе, наприклад з повітря в скло, то для такого переходу n12 = sinα/sinγ = 1,52 > 1. А це означає що кут заломлення світла менший за кут його падіння (γ < α) і що тому, за будь якого кута падіння (0° ≤ α < 90°), певна частина світлового потоку потрапляє в нове середовище та розповсюджується в ньому.
Якщо ж світло переходить з оптично більш густого середовища в оптично менш густе, наприклад зі скла у повітря, то для такого переходу показник заломлення світла менший за одиницю: n21 = sinα/sinγ = 1/1,52 = 0,66 < 1. При цьому кут заломлення світла буде більшим за кут його падіння (γ > α). І не важко збагнути, що в такій ситуації при певному граничному куті падіння (α = αгр) кут заломлення світлових променів становитеме 90° і що при більших кутах падіння, величина кута заломлення має бути більшою за 90°. По суті це означає шо при певних кутах падіння (α ≥ αгр) увесь світловий потік, повністю відбиватиметься від межі двох оптично прозорих середовищ. Таке відбивання називають повним відбиванням світла.
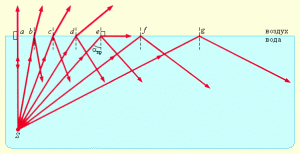
Мал.60. При певних кутах падіння (α ≥ αгр) те світло яке розповсюджується в оптично більш густому середовищі, повністю відбивається від межі з оптично менш густим середовищам.
Повне відбивання світла, це явище, суть якого полягає в тому, що при певних кутах падіння (α ≥ αгр) те світло яке розповсюджується в оптично більш густому середовищі, повністю відбивається від межі з оптично менш густим середовищем.
Той найменший кут падіння при якоку відбувається повне відбивання світла, називають граничним кутом повного відбивання (позначається αгр). Величину кута повного відбивання, визначають виходячи з того, що при цьому куті, кут заломлення світлових променів дорівнює 90° (γ=γгр=90°). Зважаючи на факт того, що sin90°=1, можна записати: sinαгр/sinγгр = sinαгр/sin90° = sinαгр = n21. Звідси αгр = arcsin n21, де n21 = n1/n2 – відносний показник заломлення світла оптично менш густого середовища (n1) відносно оптично більш густого середовища (n2).
Якщо граничний кут повного відбивання світла визначають по відношенню до повітря або вакууму (n1=1), то в цьому випадку n21 = 1/n і тому αгр = arcsin(1/n) де n – абсолютний показник заломлення того середовища в якому розповсюджується світло і яке межує з повітрям (вакуумом).
Зважаючи на вище сказане, можна довести, що по відношенню до повітря, кут повного відбивання світла становить:
– для води (n=1,33) αгр = 49°;
– для скла (n=1,52) αгр = 41°;
– для алмазу (n=2,42) αгр = 24°.
Повне відбивання світла, корисно застосовують в багатьох приладах, зокрема в оптичних призмах. Оптична призма, це прилад, який представляє собою оптично прозоре тіло, робочі поверхні якого геометрично та оптично рівні. Геометрична форма оптичної призми може бути різною (мал.61). При цьому, в залежності від цієї форми та відносної просторової орієнтації, призма може виконувати певний набір функцій.
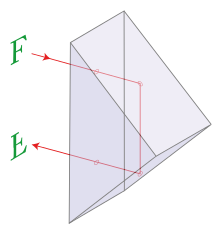
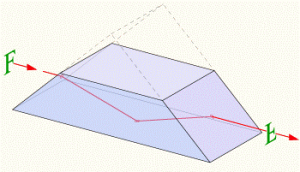
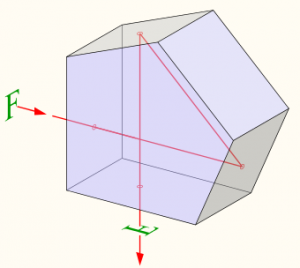
Мал.61. Геометрична форма та функціональні можливості оптичних призм можуть бути різними.
Принцип дії та функціональні можливості оптичної призми розглянемо на прикладі рівнобедреної прямокутно-трикутної призми (мал.62). В залежності від просторової орієнтації, ця призма може виконувати ряд оптичних функцій. Наприклад. Якщо призма розташована так як показано на мал.60а, то вона виконує функцію певним чином розташованого плоского дзеркала. Дійсно. За такого розташування призми, паралельні промені 1 і 2 падають на вертикальну поверхню під кутом 0°. При цьому, практично не відбиваючись і не заломлюючись (γ = (1/n)arcsin0° = 0°), прормені проникають в скляне тіло призми. Розповсюджуючись в склі, промені під кутом 45° падають на похилу поверхню. А оскільки кут падіння променів більший за граничний кут повного відбивання скла (45° > 41°), то ці промені дзеркально відбиваються і під кутом 0° падають на горизонтальну поверхню. Практично не відбиваючись і не заломлюючись цією поверхнею, промені виходять з скліного тіла призми. Виходять, зберігаючи свою паралельність. А це означає, що за заданого розташування, призма не змінюючи параметрів зображення, змінює хід променів на 90°. Іншими словами, призма виконує роль плоского дзеркала яке розташоване під кутом 45° до напрямку розповсюдження свтлових променів.
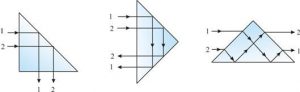
Мал.62. В залежності від просторової орієнтації, одна і та ж призма може виконуватии рід фупнкцій.
Аналогічним чином можна довести, що в ситуації 62б, дана призма виконує функції двох плоских дзеркал, які змінюють хід променів на 360° і перевертають вхідне зображення. Не важко довести і те, що в ситуації 62в, призма виконує функції двох заломлюючих поверхонь і одного плоского дзеркала та дозволяє, не змінюючи загального ходу променів, перевернати вхідне зображення.
Таким чином, в залежності від просторової орієнтації, одна і та ж рівнобедрена прямокутно-трикутна призма, може виконувати ряд функцій, зокрема: функцію певним чином розташованого плоского дзеркала, або функцію системи двох плоских дзеркал, або функцію дзеркала та двох заломлюючих поверхонь. При цьому, практично важливою особливістю призматичних дзеркал є факт того, що вони не мають спеціального шару відбивного матеріалу. А отже не потребують нанесення та захисту цього матеріалу, не бояться корозійного впливу навколишнього середовища, тощо. Крім цього, в залежності від просторової орієнтації, робоча поверхня оптичної призми може бути дзеркальною, напівдзеркальною чи оптичнор прозорою.
Із вище сказаного ясно, що оптична призма, це важливий багатофункціональний оптичний прилад. Прилад, який широко застосовується в багатьох більш складнох оптичних системах, зокрема біноклях, перескопах, мікроскопах, кутовимірювальних візирах, тощо.

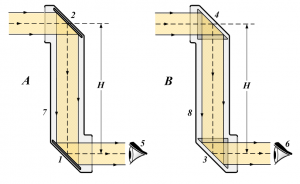
Мал.63. Призми є складовими елементами більш складних оптичних систем, зокрема: а)біноклів, б) пирескопів.
Однією з важливих та надзвичайно перспективних сфер застосування повного відбивання світла є так звана волоконна оптика. Оптичними волокнами називають тонкі оптично прозорі волокна, які дозволяють передавати світлові потоки та світлову інформацію криволінійними траєкторіями. Принцип дії оптичного волокна полягає в наступному. Те світло, яке на вході потрапляє всередину оптично прозорого волокна, багаторазово відбиваючись від його поверхневого шару (шару який контактує з оптично менш густим середовищем) досягає вихідного зрізу цього волокна.
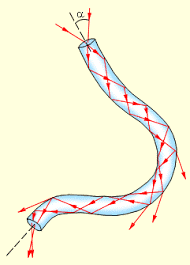

Мал.64. В оптичному волокні повне відбивання світла забезпечує рух світла за заданою траєкторією.
Зазвичай в волоконно-оптичних приладах застосовують не окремі оптичні волокна, а їх певну сукупність яку прийнято називати оптоволоконними кабелями. Оптоволоконний кабель (мал.64в), це прилад, який забезпечує криволінійний рух світлових потоків та світлової інформації і який представляє собою сукупність великої кількості щільно упакованих оптичних волокон.
Оптико-волоконні прилади мають широке застосування в багатьх галузях сучасної науки та тегніки. В медицині, за допомогою гнучких світловодів досліджують стан внутрішніх органів людини та лікують ці органи. В промисловості, за допомогою світловодів досліджують технічний стан важкодоступних частин складних технічних систем. В системах компютерних мереж та системах радіозвязку, за допомогою оптико-волоконних кабелів здійснюють передачу інформації. В військовій справі, світловоди застосовують для кодування інформації. За допомогою оптичних волокон вимірюють температуру, електричну напругу, тиск, тощо. Оптичні волокна застосовують в сейсмічних та гідролокаційних приладах. В лазерних гіроскопах та лазерних мікрофонах. Оптико-волоконне освітлення все частішевикористовують в комерційній рекламі, мистецтві та побутовій техніці.
Словник фізичних термінів
Повне відбивання світла, це явище, суть якого полягає в тому, що при певних кутах падіння (α > αгр) те світло яке розповсюджується в оптично більш густому середовищі, повністю відбивається від межі з оптично менш густим середовищем. Той найменший кут падіння при якоку відбувається повне відбивання світла, називають граничним кутом повного відбивання (позначається αгр).
Оптична призма, це прилад, який представляє собою оптично прозоре тіло, робочі поверхні якого геометрично та оптично рівні.
Контрольні запитання
1.Від чого залежить співвідношенні між кількістю відбитого та заломленого світла?
2. Яке середовище називають оптично більш густим, а яке – оптично менш густим?
3. Чому при переході з повітря в скло повного відбивання світла не відбувається а пи переході з скла в повітря – відбувається.
4. Поясніть поведінку світлових променів в ситуаціях зображених на мал. 22а; 22б; 22в.
5. Які переваги призматичного дзеркала над звичайним?
6. Поясніть принцип дії оптичного волокна.
Вправа 10.
1.Відомо, що абсолютний показник заломлення світла: льоду – 1,31; цукру – 1,56; рубіну – 1,76. Визначте граничні кути повного відбивання світла для відповідної речовини по відношенню до вакууму.
2. Граничний кут повного відбивання світла для гліцерину становить 43°. Яка швидкість світла в гліцерині?
3. Промінь переходить із скла в воду. Визначте кут заломлення променя, якщо його кут падіння 35°. Визначте граничний кут повного відбивання.
4. Під яким кутом промінь падає на поверхню скла, якщо його кут заломлення, в два рази менший за кут падіння?
5. Під яким кутом має падати промінь на скло, щоб заломлений промінь був перпендикулярним до відбитого?
§21. Загальні відомості про лінзи.
Лінза (оптична лінза), це прилад, який представляє собою оптично прозоре тіло обмежене двома оптично рівними криволінійними або криволінійною та плоскою, поверхнями і який визначеним чином формує відповідне оптичне зображеня. В залежності від форми обмежуючої поверхні, лінзи поділяються на сферичні, циліндричні, тороїдальні та інші. При цьому, найбільш розповсюдженою різновидністю лінз є лінзи сферичні. Власне, про такі лінзи ми і будемо говорити в подальшому. Характерною властивістю будь якої лінзи є здатність заломлювати світлові промені та формувати відповідне оптичне зображення. За зовнішніми ознаками та характером поведінки заломлених лінзою променів, лінзи поділяються на збиральні або опуклі та розсіювальні або вгнуті.
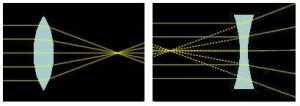
Мал.65. За зовнішніми ознаками та характером поведінки заломлених променів, лінзи поділяються на: а) збиральні (опуклі); б) розсіювальні (вгнуті).
Збиральними (опуклими) називають такі лінзи, які будучи розташованими в оптично менш густому серидовищі, збирають початково паралельні промені в околицях певної точки, яку називають фокусом лінзи. Характерною зовнішньою ознакою збиральних лінз є їх опуклість, тобто факт того, що центральна частина лінзи, товща за краєву. В залежності від особливостей геометричної форми, збиральні лінзи (мал.64а) поділяються на: подвійноопуклі, плоскоопуклі та вгнутоопуклі.
Розсіювальними (вгнутими) називають такі лінзи, які будучи розташованими в оптично менш густому середовищі, розсіюють початково паралельні промені, причому розсіюють таким чином, що їх уявні продовження перетинаються в околицях певної точки, яку називають фокусом розсіювальної лінзи. Характерною зовнішньою ознакою розсіювальних лінз є їх вгнутість, яка проявляється в тому, що центральна частина розсіювальної лінзи тонша за краєву. В залежності від особливостей геометричної форми, розсіювальні лінзи (мал.66б) поділяються на: подвійновгнуті, плосковгнуті та опукловгнуті.
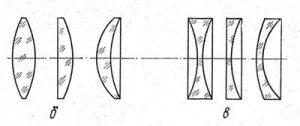
Мал.66. Різновидності збиральних (а) та розсіювальних (б) лінз.
Потрібно зауважити, що опуклі лінзи є збиральними, а вгнуті – розсіювальними, лише в тому випадку, якщо показник заломлення матеріалу лінзи більший за показник заломлення навколишнього середовища. В зворотній же ситуації, властивості лінз будуть зворотніми. Наприклад, якщо розташованій у воді повітряній бульбашці надати форму опуклої лінзи, то ця лінза буде розсіювальною, а відповідна вгнута лінза – збиральною. Втім, враховуючи факт того, що в реальних ситуаціях лінзи практично завжди оточені менш густим середовищем, прийнято вважати, що опуклі лінзи є збиральними, а вгнуті – розсіювальними.
До числа основних геометричних характеристик оптичної лінзи відносяться: центри кривизни поверхонь лінзи (О1 , О2), радіуси кривизни поверхонь лінзи (R1 , R2), головна оптична вісь лінзи (O1O2), оптичний центр лінзи (O), товщина лінзи (d), фокус (F) та фокусна відстань (ƒ) лінзи, оптична сила лінзи (D=1/ƒ). Загальні відомості про більшість з вище названих характеристик, можна отримати на основі аналізу мал.65.
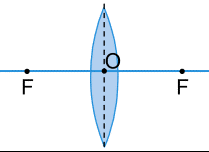

Мал.67. Основні геометричні характеристики лінзи.
Серед різноманіття геометричних характеристик лінзи, найважливішими є її фокус та фокусна відстань. Фокусом (головним фокусом) лінзи, називають ту точку, в якій дійсно або уявно перетинаються ті заломлені лінзою промені, які до проходження через лінзу були паралельними її головній оптичній осі. Відстань від фокусу лінзи до її оптичного центру називають фокусною відстанню лінзи (позн. ƒ).
Зважаючи на факт того, що світлові промені можуть падати на лінзу з двох сторін, будь яка лінза має два фокуси та дві фокусні відстані. При цьому, той фокус який знаходиться збоку падаючих променів називають переднім фокусом, а той, який знаходиться збоку заломлених променів називають заднім фокусом.
На практиці, заломлювальні властивості оптичної лінзи характеризують величиною яка називається оптичною силою лінзи. Оптична сила лінзи, це фізична величина, яка характеризує заломлювальні властивості опричної лінзи і яка обернена до її фокусної відстані.
Позначається: D
Визначальне рівняння: D = 1/
Одиниця вимірювання: [D] = 1/м = дп , діоптрія.
Прийнято вважати, що оптична сила збиральної лінзи є дадатньою (D>0), а оптична сила розсіювальної лінзи – від’ємною (D<0).
Застосовуючи закон заломлення світла, можна визначити хід будь якого променя в будь якій лінзі. Однак, практичне застосування цього закону є надзвичайно складним. Адже для того щоб передбачити поведінку лише одного заломленого лінзою променя, потрібно виконати цілу низку точних побудов, вимірювань та розрахунків. Зважаючи на ці обставини, параметри того зображення яке створює лінза, визначають на основі певного набору базових променів, поведінка яких є загальновідомою. Цими базовими променями є:
1 – якщо падаючий промінь проходить через оптичний центр лінзи, то промінь заломлений є прямим продовженням падаючого променя;
2 – якщо падаючий промінь паралельний головній оптичній осі лінзи, то промінь заломлений дійсно або уявно проходить через: а) задній фокус збиральної лінзи; б) передній фокус розсіювальної лінзи;
3 – якщо падаючий промінь дійсно або уявно проходить через: а) передній фокус збиральної лінзи; б) задній фокус розсіювальної лінзи, то заломлений промінь є паралельним головній оптичній осі відповідної лінзи.
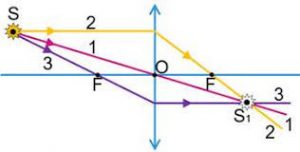
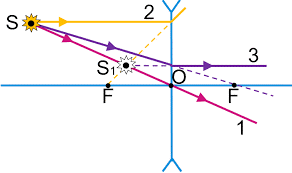
Мал.68. Виконуючи геометричні побудови тих зображень які утворюють збиральні (а) та розсіювальні (б) лінзи, застосовують певний набір базових променів.
Потрібно зауважити, що вище описаний метод геометричного визначення параметрів зображень, є задовільно точним лише для так званих тонких лінз. Тонкою називають таку лінзу, товщана якої набагато менша за кожен з радіусів кривизни її поверхонь (d << R1; d << R2). В межах програми загальноосвітньої школи по суті вивчають лише ті лінзи які є тонкими.
Знаючи поведінку базовох променів, не вожко визначити параметри того зображення, яке створює відповідна лінза. Ілюструючи дане твердження розвяжемо дві конкрктні задачі.
Задача 1. Шляхом геометричних побудов, визначити параметри зображення предмету (вертикильного відрізку), яке дає збиральна лінза фокусна відстань якої 30см. Висота предмету 15см. Відстань від предмету до оптичного центру лінзи: а) 80см; б) 60см; в) 40см; г) 30см; д) 20см.
Рішення. Дотримуючись певного масштабу (М 1:10), виконуємо відповідні геометричні побудови та вимірювання.
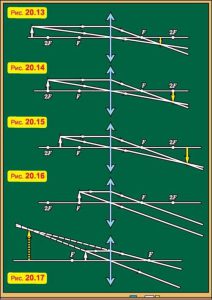
Результати побудов та вимірювань:
а) зображення: дійсне, зменшене, перевернуте, h1‘ ≅10см, l1‘ ≅50см;
б) зображення: дійсне, рівне, перевернуте, h2‘ ≅ 15см, l2‘ ≅ 80см;
в) зображення: дійсне, збільшене, перевернуте, h3‘ ≅ 45см, l3‘ ≅120см;
г) предмет не має зображення;
д) зображення: уявне, збільшене пряме, h5‘ ≅ 45см, l5‘ ≅ − 60см.
Не важко бачити, що в залежності від розташування тіла, його зображення в збиральній лінзі може бути як дійсним так і уявним, як збільшеним так і зменшеним, як прямим так і перевернутим. Крім цього, якщо тіло знаходиться в фокальній площині збиральної лінзи, то воно не має певного зображення, а точніше, це зображення розчиняється в безкінечності (h4‘→∞, l4‘→∞).
Задача 2. Шляхом геометричних побудов, визначити параметри зображення предмету (вертикильного відрізку), яке дає розсіювальна лінза фокусна відстань якої 40см. Висота предмету 15см. Відстань від предмету до оптичного центру лінзи: а) 100см; б) 80см; в) 60см; г) 40см; д) 20см.
Рішення. Дотримуючись певного масштабу (М 1:10), виконуємо відповідні геометричні побудови та вимірювання.
а) F
б) F
в) F
г) F
д) F
Не важко бачити, що за будь якого розташування тіла, його зображення в розсіювальній лінзі є уявним, прямим та зменшеним.
Задача 3. Знаючи фокусну відстань (ƒ) збиральної лінзи та координати заданої точки (l, h), визначити координати зображення ції точки (l‘, h‘).
Рішення. Розв’яжемо дану задачу шляхом відповідних геометричних побудов.
Аналізуючи геометричне рішення задачі, з’ясуємо ті кількісні співвідношення що існують між заданими величинами (ƒ, l, h) та невідомими координатами зображення точки (l‘, h‘). З цією метою розглянемо дві пари подібних трикутників: 1) ?ΔАОВ та ΔА‘ОВ‘; 2) ΔNOF та ΔА‘В‘F.
Виходячи з того, що в кожній виділеній парі трикутників є однакові кути, представимо тангенси цих кутів через співвідношення відповідних сторін:
для ΔАОВ: tgα = h/l (1)
для ΔА‘ОВ‘: tgα = h‘/l‘ (2)
для ΔNОF: tgβ = h/l (3)
для ΔА‘В‘F: tgβ = h‘/(l‘−ƒ) (4).
Не важко бачити, що з (1) та (2) випливає: h/l = h‘/l‘ або h = h‘l/l‘ (5).
Із (3) та (4) випливає: h/l = h‘/(l‘−ƒ) або h = h‘l/(l‘−ƒ) (6).
Із (5) та (6) випливає: h‘l/l‘ = h‘ƒ/(l‘−ƒ), або l/l‘ = ƒ/(l‘-ƒ), або l(l‘-ƒ) = l‘ƒ, або ll‘−lƒ−l‘ƒ = 0. Розділивши всі доданки останнього рівняння на ll‘ƒ, отримаємо: 1/ƒ – 1/l‘ – 1/l = 0 або 1/l + 1/l‘ = 1/ƒ.
Таким чином, поздовжня координата заданої точки (l) та її зображення (l‘), зв’язані з фокусною відстань лінзи (ƒ) співвідношенням 1/l + 1/l‘ = 1/ƒ. Це співвідношення називають формулою лінзи, а точніше – формулою тонкої лінзи.
Із формули лінзи випливає, що l‘ = lƒ/(l−ƒ) (7). А о скільки згідно з рівнянням (5) h‘ = hl‘/l, то з урахуванням (7), можна записати: h‘ = hƒ/(l-ƒ). А це означає: якщо відома фокусна відстань лінзи (ƒ) та координати заданої точки (l, h), то застосовуючи рівняння l‘ = lƒ/(l−ƒ) та h‘ = hƒ/(l-ƒ), можна визначити координати зображення відповідної точки. При цьому, застосовуючи дані рівняння дотримуються наступних правил знаків:
1.Фокусна відстань збиральної лінзи є додатньою (ƒ > 0), а фокусна відстань розсіювальної лінзи – відємною (ƒ < 0).
2. Якщо l‘ > 0, то зображення дійсне, а якщо l‘ < 0 – уявне.
3. Якщо h i h‘ мають однакові знаки, то зображення перевернуте, а якщо ці знаки є різними – то пряме.
Потрібно зауважити, що з урахуванням вище сформульованих правил, формули l‘ = lƒ/(l−ƒ); h‘ = hƒ/(l−ƒ) є справедливим не лише для збиральних, а й для розсіювальних лінз. Однак, потрібно пам’ятати, що ці формули є наближено правильними і що з достатньою точністю їх можна застосовувати лише для тонких лінз.
Ілюструючи можливості та перевіряючи достовірність формул l‘ = lƒ/(l−ƒ); h‘ = hƒ/(l−ƒ) розв’яжемо задачу 1 і задачу 2 алгебраїчним методом.
Задача 1. (алгебраїчне рішення).
Дано: ƒ=30см; h=15см; l1=80см; l2=60см; l3=40см; l4=30см; l5=20см.
Визначити та охарактеризувати параметри зображення.
1) l1‘=80·30/(80-30)=48см; h1‘=15·30/(80-30)=9см.
Зображення: дійсне, зменшене, перевернуте.
2) l2‘=60·30/(60-30)=60см; h2‘=15·30/(60-30)=15см.
Зображення: дійсне, рівне, перевернуте.
3) l3‘=40·30/(40-30)=120см; h3‘=15·30/(40-30)=45см.
Зображення: дійсне, збільшене, перевернуте.
4) l4‘=30·30/(30-30)=∞см; h4‘=15·30/(30-30)=∞см.
Предмет не має зображення (зображення розчиняється в безкінечності).
5) l5‘=20·30/(20-30)= -60см; h5‘=15·30/(20-30)= -45см.
Зображення: уявне, збільшене, пряме.
Задача 2. (алгебраїчне рішення).
Дано: ƒ=-40см; h=15см; l1=100см; l2=80см; l3=60см; l4=40см; l5=20см.
Визначити та охарактеризувати параметри зображення.
1) l1‘=100(-40)/(100+40)= -28,6см; h1‘=15(-40)/(100+40)= -4,3см.
Зображення: уявне, зменшене, пряме.
2) l2‘=80(-40)/(80+40)= -26,7см; h2‘=15(-40)/(80+40)= -5,0см.
Зображення: уявне, зменшене, пряме.
3) l3‘=60(-40)/(60+40)= -24,0см; h3‘=15(-40)/(60+40)= -6,0см.
Зображення: уявне, зменшене, пряме.
4) l4‘=40(-40)/(40+40)= -20,0см; h4?=15(-40)/(40+40)= -7,5см.
Зображення: уявне, зменшене, пряме.
5) l5‘=20(-40)/(20+40)= -13,3см; h5‘=15(-40)/(20+40)= -10,0см.
Зображення: уявне, зменшене, пряме.
Не важко бачити, що ті результати які ми отримали шляхом алгебраїчних розрахунків як кількісно так і якісно співпадають з тими результатами які були отримані шляхом геометричних побудов. Однак, не варто забувати, що точність геометричного рішення задачі, значною мірою залежить від масштабу та точності геометричних побудов. І в цьому сенсі, результати алгебраїчного рішення є гарантовано точнішими.
Словник фізичних термінів.
Лінза (оптична лінза), це прилад, який представляє собою оптично прозоре тіло обмежене двома оптично рівними криволінійними або криволінійною та плоскою, поверхнями і який визначеним чином формує відповідне оптичне зображеня.
Збиральними (опуклими) називають такі лінзи, які будучи розташованими в оптично менш густому серидовищі, збирають початково паралельні промені в околицях певної точки, яку називають фокусом лінзи. Розсіювальними (вгнутими) називають такі лінзи, які будучи розташованими в оптично менш густому середовищі, розсіюють початково паралельні промені, причому розсіюють таким чином, що їх уявні продовження перетинаються в околицях певної точки, яку називають фокусом розсіювальної лінзи.
Фокусом (головним фокусом) лінзи, називають ту точку, в якій дійсно або уявно перетинаються ті заломлені лінзою промені, які до проходження через лінзу були паралельними її головній оптичній осі. Відстань від фокусу лінзи до її оптичного центру називають фокусною відстанню лінзи (позн. ƒ).
Оптична сила лінзи, це фізична величина, яка характеризує заломлювальні властивості опричної лінзи і яка обернена до її фокусної відстані.
Позначається: D
Визначальне рівняння: D = 1/ƒ
Одиниця вимірювання: [D] = 1/м = дп , діоптрія.
Контрольні запитання.
1.Чи може опукла лінза бути розсіювальною, а вгнута – збиральною? Якщо може, то за яких умов?
2. Опишіть поведінку базових променів при їх проходженні через збиральну лінзу.
3. Опишіть поведінку базових променів при їх проходженні через розсіювальну лінзу.
4. Чи є загально прийнята поведінка базових променів такою, що вточності відображає їх реальну поведінку? Наведіть докази.
5. Сформулюйте правила знаків, які застосовують при алгебраїчному методі визначення параметрів того зображення що створює лінза.
6. Назвіть переваги та недоліки геометричного і алгебраїчного методів розв’язування задач геометричної оптики.
Вправа11.
1.Визначити параметри зображення вертикального відрізки висотою 10см в збиральній лінзі, фокусна відстань якої 20см. Відстань від підніжжя відрізку до оптичного центру лінзи: а) 60см; б) 40см; в) 30см; г) 20см д) 10см.
2. Задачу 1 розв’язати для аналогічної розсіювальної лінзи.
3. Відстань від уявного зображення предмету до збиральної лінзи, оптична сила якої 3дпр, становить 50см. Визначте відстань від лінзи до предмету.
4. Предмет знаходиться на відстані 80см від лінзи, оптична сила якої 2,5дпр. Як зміниться висота зображення предмету, якщо його наблизити до лінзи на 40см?
5. Якщо відстань від предмету до збиральної лінзи 36см, то висота його зображення 10см. Якщо ж відстань від предмету до лінзи 24см, то висота зображення 20см. Визначте фокусну відстань лінзи.
6. Визначте оптичну силу розсіювальної лінзи, якщо вона дає зображення предмету на відстані 6см від самого предмету. Висота предмету 8см, висота зображення 4см.
§22. Оптичні прилади.
Лінзи, призми та дзеркала є основними елементами більш складних оптичних приладів, зокрема мікроскопів, телескопів, біноклів, фотооб’єктивів, тощо.
Мікроскоп (від грец. mikros – маленький, skopeo – дивитись), це прилад, призначений для візуального спостереження за мікрооб’єктами, тобто тими об’єктами що є невидимими для “неозброєного” ока людини. По суті, мікроскоп представляє собою систему двох збиральних лінз, одна з яких називається об’єктивом (від лат. objectus – предмет, об’єкт), інша окуляром (від лат. oculus – око). Ці лінзи розташовані таким чином, що коли дрібний предмет (об’єкт досліджень) знаходиться перед фокусом об’єктива, то збільшене дійсне зображення предмету, буде знаходитись за фокусом окуляра. А це означає, що спостерігач чепрез окуляр буде бачити уявне, подвійно збільшене зображення предмету. Іншими словами, система двох, певним чином розташованих збиральних лінз, дозволяє подвійно збільшувати зображення дрібних предметів. При цьому, якщо об’єктив збільшує видимі розміри предмету в 20 разів, а окуляр – в 10 разів, то загальне збільшення мікрооб’єкту становитиме 20·10=200 разів. Загалом же, сучасні оптичні мікроскопи забезпечують збільшення досліджуваних об’єктів до 2500 разів. Потрібно зауважити, що збільшувальні можливості оптичних мікроскопів обмежені хвильовими властивостями світла. А ці властивості такі, що не дозволяють бачити ті об’єкти, лінійні розміри яких менші за половину довжини світлової хвилі (λmin=4·10-7м). Дрібніші об’єкти досліджують за допомогою так званих електронних мікроскопів.
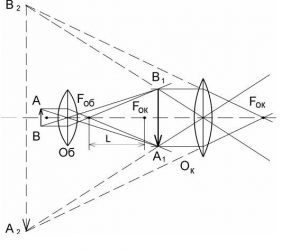
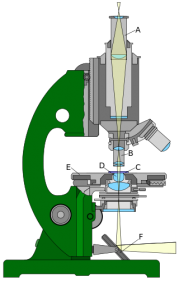
Мал.69. Принципова схема (а) та загальний устрій (б) оптичного мікроскопа. Загальний устрій об’єктиву мікроскопа (в).
Як це зазвичай буває, реальний устрій приладу значно складніший за ту принципову схему що пояснює принцип його дії. І в цьому сенсі мікроскопи не виняток. Сучасні оптичні мікроскопи, це надзвичайно складні системи, елементами яких є складні багатофункціональні об’єктиви та окуляри, складні системи освітлення досліджуваних об’єктів, складні системи регулювання та налаштування приладу, тощо. Ілюструючи складність сучасного мікроскопа, достатньо подивитись на загальний устрій його типового об’єктиву (мал.69в). Втім, яким би складним не був сучасний мікроскоп, а його принципова схема залишається незмінною і такою що зображена на мал.69а.
Оптичні прилади дозволяють спостерігати не лише за невидимими об’єктами мікросвіту, а й за невидимими мега об’єктами космосу. Прилад, який видимі та невидимі космічні об’єкти робить візуально більш близькими, та більш яскравими називають телескопом. Телескоп (від грец. tele – далеко, skopeo – дивитись), це прилад, призначений для візуального спостереження за далекими космічними об’єктами: планетами, кометами, зірками, галактиками, тощо. Завдання будь якого телескопу, по суті полягає в тому, щоб зібрати максимально велику кількість світлової інформації про певний космічний об’єкт, перетворити цю інформацію у відповідне зображення та направити його в око спостерігача або інший світлочутливий прилад.
Перші телескопи (зорові труби) з’явились на початку 17-го століття. При цьому, майже одночасно було створено дві різновидності подібних приладів: телескоп Галілея (1609) та телескоп Кеплера (1611).
В певному сенсі, телескоп Кеплера (мал.70а) схожий на мікроскоп. Як і мікроскоп, він складається з двох, певним чином розташованих збиральних лінз. Відмінність лише в тому, що в телескопі, ці лінзи розташовані так би мовити навпаки: велика (довгофокусна) лінза розташована з боку досліджуваного об’єкту і виконує роль об’єктива, а мала (короткофокусна) лінза, розташована з боку спостерігача і виконує роль окуляра. Принцип дії цієї системи полягає в наступному. Об’єктив телескопа збирає максимально велику кількість світлової інформації та створює відповідне дійсне зображення. А оскільки це зображення розташоване за фокусом окуляра, то через окуляр спостерігач бачитиме його уявним, збільшеним та перевернутим.
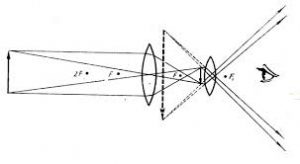
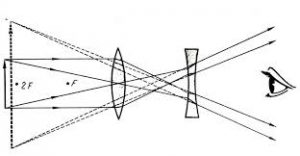
Мал.70. Схема принципового устрою а) телескопа Кеплера; б) телескопа Галілея.
На відміну від телескопа Кеплера, в телескопі Галілея окуляром є не збиральна лінза, а лінза розсіювальна (мал.70б). Ця лінза розташована таким чином, що створюване об’єктивом дійсне зображення знаходиться за цією лінзою. За такого розташування, окуляр телескопа розсіює світлові промені таким чином, що спостерігач бачить пряме уявне та збільшене зображення відповідного об’єкту.
Існують й інші різновидності телескопів, зокрема телескопи дзеркальні (мал.72). В таких телескопах об’єктивом є не збиральна лінза, а вгнуте дзеркало, яке збирає падаючі на нього промені та формує відповідне дійсне зображення. Це зображення за допомогою невеликого плоского (мал.72а) чи вгнутого (мал.72б) дзеркала спрямовується в окуляр телескопа, який і створює те зображення яке бачить спостерігач. Дзеркальні об’єктиви, а особливо об’єктиви великих розмірів, мають відносно малу питому масу та є відносно дешевшими. Тому більшість сучасних потужних телескопів є дзеркальними.
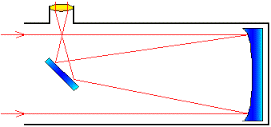
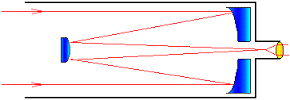
Мал.72. Схема принципового устрою дзеркального телескопа.
Застосовуючи сучасні телескопи, можна розгледіти деталі багатьох космічних об’єктів, зокрема Сонці, Місяця, комет, планет Сонячної системи, тощо. Однак телескопи не дозволяють побачити деталі тих зірок та планет які знаходяться за межами Сонячної системи. Не дозволяють тому, що відстані до таких об’єктів є фантастично великими. Великими настільки, що навіть в найпотужніших телескопах далекі зірки виглядають як певні світлові точки. Втім, це зовсім не означає, що телескопи не дозволяють отримувати нову інформацію про зірки та інші наддалекі космічні об’єкти. Адже телескоп в сотні, тисячі і мільйони разів посилює видиму яскравість зірок. Посилює тому, що через телескоп в наше око потрапляє у стільки разів більше світлової енергії, у скільки разів площа його об’єктиву більша за площу зрачка. А це означає, що в телескопі ми можемо побачити не лише ті зірки які видно неозброєним оком, а й ті, які зазвичай є невидимими. Крім цього, телескоп в десятки і сотні разів збільшує видимі відстані між окремими космічними об’єктами. При цьому з’ясовується, що велика кількість тих об’єктів які виглядають як окремі світлові точки, насправді представляють собою скупчення величезної кількості окремих зірок.
Ще одним важливим та загально відомим оптичним приладом є бінокль (від лат. bini – два, oculus – око). Бінокль, це прилад складений з двох паралельно з’єднаних зорових труб та призначений для візуального спостереження за віддаленими земними об’єктами.
Біноклі поділяються на театральні та польові (або призмові). Театральний бінокль (мал.73а) по суті представляє собою систему двох невеликих, паралельно з’єднаних зорових труб Галілея. Такі біноклі мають просту будову, малі габарити, малі втрати світлового потоку та великий кут огляду. Однак кутове збільшення театральних біноклів є відносно малим і зазвичай становить від 2 до 4 одиниць.
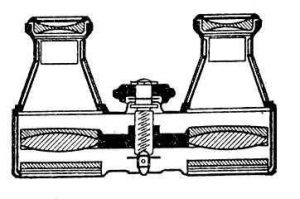

Мал.73. Загальний устрій театрального (а) та польового (б) біноклів.
Значно більше кутове збільшення (до 22 одиниць), забезпечують так звані польові або призмові біноклі (мал.73б). Такі біноклі по суті представляють собою систему двох, паралельно з’єднаних зорових труб Кеплера. Зорова труба Кеплера має той недолік, що створюване нею зображення є перевернутим. Звичайно, коли мова йде про далекі космічні об’єкти, то факт перевернутості їх зображень не має суттєвого значення. Однак для земних об’єктів, цей факт є суттєво негативним. Зважаючи на ці обставини, в польовому біноклі застосовують певну систему скляних призм, яка не лише забезпечує формування прямого зображення, а й практично вдвічі зменшує довжину бінокля. Крім цього, застосування призм дозволяє значно збільшити відстань між об’єктивами польового бінокля. А це суттєво покращує об’ємне (стереоскопічне) бачення та дозволяє застосовувати об’єктиви більших діаметрів.
Потрібно зауважити, що візуальне сприйняття величини предмету, залежить не від його реальних розмірів, а від величини його зображення на сітківці ока. А це зображення залежить від величини того кута зору під яким спостерігач бачить відповідний предмет. Зважаючи на ці обставини, мірою збільшуваних (наближувальних) властивостей оптичних приладів, є величина яку називають кутовим збільшенням оптичної системи. Це збільшення дорівнює відношенню тангенсу того кута зору (?) під яким спостерігач бачить предмет через оптичний прилад, до тангенсу того кута зору (?0) під яким він бачить цей же предмет без оптичного приладу (? = tg?/tg?0).

Мал.74. Видимі розміри предмету, залежать від величини того кута зору під яким цей предмет (або його зображення) видно.
До числа безумовно важливих оптичних приладів можна віднести і найрізноманітніші фотооб’єктиви. Фотооб’єктив, це оптичний прилад, який є складовою частиною іншого, більш складного приладу (фотоапарат, кінокамера, телекамера, тощо) і який призначений для того, щоб максимально чітко сфокусувати зображення об’єкту фотографування на світлочутливий елемент основного приладу (фотоплівка, кіноплівка, напівпровідниковий фотоелемент, тощо).
В гранично простому випадку, фотооб’єктивом може бути будь яка короткофокусна збиральна лінза (мал.75а). Однак, застосувавши таку лінзу на практиці, ви неодмінно з’ясуєте, що вона має ряд суттєвих недоліків, зокрема той, що створюване нею зображення має велику кількість оптичних спотворень (аберацій). Тому на практиці, навіть найпростіший фотооб’єктив представляє собою достатньо складну оптичну систему (мал.75б,в). Систему, до якої висувається ціла низка вимог. По перше, те зображення яке створює фотооб’єктив не повинно мати суттєвих оптичних спотворень (аберацій). По друге, те зображення яке створює фотооб’єктив, має бути максимально чітким та сфокусованим. По третє, фотооб’єктив за певний короткий проміжок часу повинен пропускати певну, визначену кількість світлового потоку. На кінець, фотооб’єктив має бути достатньо універсальним, тобто таким, що якісно виконує свої функції за різних умов: за різної відстані до об’єкту фотографування; за різної освітленості цього об’єкту; за різної чутливості фотоплівки, тощо. Ясно, що оптична система яка забезпечує виконання всього спектру подібних вимог не може бути надто простою.
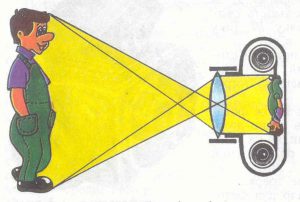

Мал.75. Схема принципу дії (а) та реальний устрій (б, в) фотооб’єктиву.
Різноманіття оптичних приладів не вичерпується різноманіттям мікроскопів, телескопів, біноклів та фотооб’єктивів. Окуляри, лупи, фото-, діа-, кіно-, проектори, спектроскопи, оптиметри, профілографи, сферометри, теодоліти, військові приціли, – ось далеко не повний перелік тих приладів, які з повним правом називають оптичними. Крім цього, оптичні прилади та їх елементи є складовими частинами безлічі інших приладів, які не вважаються оптичними. Ми не будемо розглядати будову та принцип дії кожного відомого оптичного приладу. Зауважимо тільки, що базовими елементами практично всіх оптичних приладів є лінзи, дзеркала та призми. І що принцип дії переважної більшості оптичних приладів базується на застосуванні законів геометричної оптики.
Словник фізичних термінів.
Мікроскоп, це прилад, призначений для візуального спостереження за тими мікрооб’єктами, що є невидимими для “неозброєного” ока людини.
Телескоп, це прилад, призначений для візуального спостереження за далекими космічними об’єктами.
Бінокль, це прилад складений з двох паралельно з’єднаних зорових труб та призначений для візуального спостереження за віддаленими земними об’єктами.
Фотооб’єктив, це оптичний прилад, який є складовою частиною іншого, більш складного приладу і який призначений для того, щоб максимально чітко сфокусувати зображення об’єкту фотографування на світлочутливий елемент основного приладу.
Контрольні запитання
1.Поясніть принцип дії мікроскопа (мал.69а).
2. Поясніть чому, навіть в найпотужнішому оптичному мікроскопі, об’єкти лінійні розміри яких менші за 2·10-7м, є невидимими?
3. Поясніть принцип дії телескопа Кеплера (мал.70).
4. Поясніть принцип дії телескопа Галілея (мал.71).
5. Поясніть принцип дії фотооб’єктива (мал.75).
6.Поясніть, чому далекі предмети здаються маленькими, тоді як аналогічні близькі предмети виглядають великими?
7. Поясніть буквальне значення слів: мікроскоп, телескоп, об’єктив, окуляр, бінокль.
Вправа 12.
1.Під яким кутом зору спостерігач бачить стовп висотою 6м, якщо цей стовп знаходиться на відстані: 50м; 100м; 300м?
2. Людина знаходиться на відстані 200м від будинку і бачить його під кутом зору 10?. Яка висота будинку?
§23. Око як природний оптичний прилад. Дефекти зору.
Важливість наших зорових відчуттів важко переоцінити. Достатньо сказати, що близько 90% інформації про навколишній світ, ми отримуємо через зорові відчуття, а отже через ту систему яка ці відчуття створює. В загальних рисах принцип дії цієї системи полягає в наступному. Світлова інформація, через оптичну систему ока фокусується на його сітківці, яка представляє собою складну систему світлочутливих рецепторів (колбочок та паличок), з’єднаних з клітинами (нейронами) центральної нервової системи. В світлочутливих рецепторах сітківки, енергія світлових імпульсів трансформується у відповідні біоелектричні сигнали, які через клітини центральної нервової системи передаються у відповідні відділи кори головного мозку, де аналізуються та перетворюються у відповідні зорові образи.
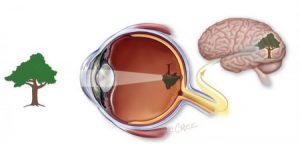
Мал.76 Схема загального устрою та принципу дії системи зорових відчуттів людини.
Ясно, що в межах даної теми, ми не будемо заглиблюватись в деталі тих надскладних нейрофізіологічних та психологічних процесів, результатом яких є наші зорові відчуття. Ми просто опишемо загальний устрій та принцип дії тієї складової зорової системи людини, яка називається оком.
В цілому, око людини складається з власне самого ока або очного яблука та допоміжних елементів, основними з яких є повіки, окорухові м’язи та слізні органи. Якщо ж говорити про основні складові самого ока (мал.77), то до їх числа відносяться: склера – зовнішня оболонка ока; рогівка – передня прозора частина склери; судинна оболонка – внутрішня частина склери; райдужна оболонка – передня забарвлена частина судинної оболонки; зіниця ока – круглий отвір в центрі райдужної оболонки; передня камера ока – заповнений прозорою рідиною простір між рогівкою та райдужною оболонкою; кришталик – оптично прозоре, хрящоподібне тіло, яке виконує функції збиральної лінзи, оптична сила якої може змінюватись; зв’язки кришталика – м’язи які утримує кришталик в певному положенні, та за необхідності, деформують його; скловидне тіло – желеподібна, оптично прозора речовина, що заповнює внутрішню частину ока; сітківка ока – світлочутлива внутрішня оболонка ока, яка представляє собою складну систему світлочутливих рецепторів та нервових клітин; зоровий нерв – сукупність великої кількості нервових клітин (нейронів) які поєднують око з певними частинами кори головного мозку.
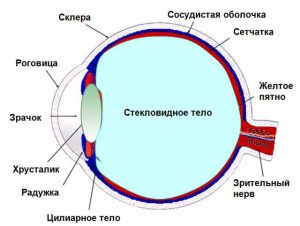
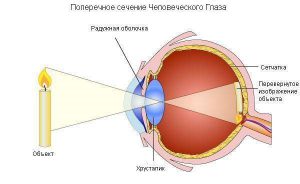
Мал.77. Схема загального устрою та принципу дії ока людини.
В певному сенсі, оптична система ока схожа на об’єктив фотоапарату. Як і фотооб’єктив, ця система сприймає світлову інформацію, певним чином дозує цю інформацію та фокусує її на фоточутливий елемент системи, яким в фотоапараті є фотоплівка, а в оці – сітківка. Однак оптична система ока значно досконаліша за будь який фотооб’єктив. І ця досконалість забезпечується не кількістю лінз, призм та дзеркал, а універсальністю та саморегульованістю тих небагатьох елементів системи, які забезпечують ефективне виконання поставлених завдань. Ілюструючи цю універсальність та саморегульованість, розглянемо лише декілька показових прикладів.
Найочевидніший з них полягає в тому, що в залежності від інтенсивності зовнішнього освітлення, автоматично змінюється діаметр зіниці ока, а отже і кількість того світла, що проникає всередину очного яблука. Це означає, що в залежності від інтенсивності зовнішнього освітлення, райдужна оболонка ока рефлекторно скорочується або розширюється і відповідно регулює величину того світлового потоку, що потрапляє в око людини. Іншими словами, автоматично працююча райдужна оболонка, виконує функції діафрагми фотоапарату.
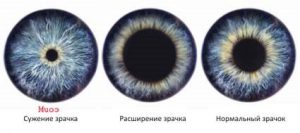

Мал.78. Райдужна оболонка ока виконує функції діафрагми фотоапарату.
Крім цього, подібно до того як в залежності від інтенсивності освітлення, досвідчений фотограф може застосовувати фотоплівки різної чутливості, в оці людини також застосовуються різночутливі “фотоплівки”. Одна з них складається з світлочутливих рецепторів які називаються паличками, інша – з світлочутливих рецепторів які називаються колбочками. Палички є фоторецепторами присмеркового зору. Вони пристосовані для сприйняття слабкого світла, однак не дозволяють розрізняти кольори та формувати чітке зображення. Колбочки, це фоторецептори денного зору. Вони пристосовані для сприйняття яскравого денного світла, сприйняття різних кольорів та формування чіткого зображення. Втім, говорячи про певні функції паличок та колбочок, не потрібно забувати, що система зорових відчуттів, це надзвичайно складний біологічний організм, кожний елемент якого є універсальним та багатофункціональним. Тому, коли ми стверджуємо, що в потоці слабкого світла, палички здатні реагувати практично на кожний світловий фотон, то це зовсім не означає, що аналогічним чином вони будуть вести себе і в потоці інтенсивного денного світла.
Ще одним прикладом універсальності оптичної системи ока, є її здатність автоматично (рефлекторно) фокусуватися на різновіддалених предметах. Механізм реалізації цієї здатності полягає в наступному. Око влаштоване таким чином, що коли ви дивитесь на суттєво віддалені предмети, то його кришталик знаходиться в недеформованому стані. При цьому, зображення віддаленого предмету є чітко сфокусованим на сітківці ока. Якби оптичні властивості кришталика залишались незмінними, то при наближенні предмету, його зображення поступово віддалялось би від сітківки ока (мал.79а). А це означає, що візуальне сприйняття того предмету який наближається до спостерігача, ставало б все більш і більш розмитим (не чітким).
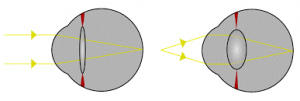
Мал.79. В процесі наближення предмету, кришталик деформується. При цьому зображення предмету виявляється постійно сфокусованим на сітківці ока.
Однак в дійсності нічого подібного не відбувається. Не відбувається тому, що оптичні властивості кришталика можуть певним чином змінюватись. Механізм цих змін полягає в тому, що по мірі наближення предмету до спостерігача, ті м’язи які утримують кришталик скорочуються і певним чином деформують його. При цьому кришталик стає все більш і більш опуклим, а зображення предмету виявляється постійно сфокусованим на сітківці ока. (мал.79б). Здатність ока пристосовуватись до сфокусованого сприйняття різновіддалених предметів називають акомодацією ока (від лат. accommodation – пристосовуватись).
Потрібно зауважити, що оптична система ока складається не лише з райдужної оболонки та кришталика. Складовими елементами цієї системи є рогівка, передня камера ока, райдужна оболонка ока, кришталик та скловидне тіло. Кожен з цих елементів так чи інакше заломлює світлові промені та приймає участь в їх фокусуванні на сітківку ока. Кожен з цих елементів в тій чи іншій мірі універсальний та багатофункціональний оптичний прилад. При цьому лише взаємопов’язана сукупність цих приладів і утворюють той досконалий та універсальний фотооб’єктив, який називається оптичною системою ока.
Однак око, це не лише складна оптична система, а й не менш складна трансформаційно-аналітична система. Адже око не лише сприймає світлову інформацію, дозує та фокусує її на світлочутливий екран, а й перетворює цю інформацію на відповідні біоелектричні імпульси та здійснює первинний аналіз цих імпульсів. І як ви розумієте, основою трансформаційно-аналітичної системи ока є його сітківка. Саме в світлочутливих рецепторах сітківки (паличках та колбочках) відбуваються ті фотохімічні реакції в результаті яких енергія світлових фотонів трансформується в енергію певних біоелектричних імпульсів. Імпульсів, які через клітини центральної нервової системи передаються у відповідну частину кори головного мозку. При цьому той суперкомп’ютер який називається головним мозком людини, аналізує всі ці біоелектричні імпульси та формує відповідний візуальний образ.
Та якою б досконалою не була оптична система ока, але і вона може мати певні дефекти. Скажімо з віком, еластичність кришталика зменшується. А отже зменшується і його здатність до тієї пружної деформованості яка забезпечує чітке фокусування зображень близько розташованих об’єктів на сітківку ока. При цьому говорять, що у людини розвивається далекозорість. “Далекозорість” – не надто вдала назва. Адже вона ніби натякає на те, що далекозора людина, далекі об’єкти бачить краще аніж людина з нормальним зором. Насправді ж суть того що називають далекозорістю та короткозорістю полягає в наступному.
Дослідження показують, що в людини з нормальним зором, недеформований кришталик забезпечує чітке фокусування віддалених предметів на сітківку ока (мал.80а). Однак, якщо ті чи інші елементи оптичної системи ока мають певні вади, то недеформований кришталик не забезпечує чіткого фокусування зображень віддалених об’єктів. При цьому, якщо зображення фокусується перед сітківкою (мал.80в), то око називають короткозорим, а якщо за сітківкою (мал.80б) – далекозорим.
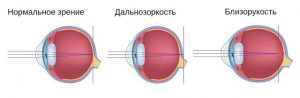
Мал.80. У своєму ненапруженому стані, нормальне око (а) фокусує зображення віддалених предметів на сітківці; далекозоре (б) – за сітківкою; короткозоре (в) – перед сітківкою.
Ясно, що як при короткозорості так і при далекозорості, зображення віддалених предметів будуть не чіткими (не сфокусованими). При цьому, якщо далекозорість не надто велика, то завдяки механізму акомодації, тобто рефлекторно-примусового деформування кришталика, око здатне рефлекторно компенсувати шкідливі прояви далекозорості. А це означає, що віддалені предмети далекозора людина бачить практично так же добре як і людина з нормальним зором. Однак, акомодаційні можливості ока не безмежні. Тому, починаючи з певної відстані, акомодаційний механізм не може компенсувати шкідливі прояви далекозорості. А це означає, що починаючи з певної відстані, далекозора людина не може чітко бачити близько розташовані об’єкти.
При короткозорості, зображення віддаленого предмету також на сфокусоване на сітківці ока. Але в цьому випадку, воно знаходиться не за сітківкою, а перед нею. В такій ситуації, механізм акомодації не може компенсувати даний дефект зору. Не може тому, що цей механізм дозволяє переносити на сітківку лише ті зображення які знаходяться за нею. Єдина природня можливість короткозорої людини чітко побачити віддалений предмет, полягає в тому, щоб наблизитись до цього предмету. Адже при такому наближенні, зображення предмету природнім шляхом зміщується вбік сітківки і за певної, відстані опиняється на ній. По суті це означає, що короткозора людина здатна чітко бачити лише ті предмети, які знаходяться ближче за певну відстань.
Потрібно зауважити, що далекозорість є практично неминучим наслідком тих чи інших вікових змін. Натомість короткозорість в більшості випадків є дефектом набутим. Не буде перебільшенням сказати, що короткозорість – це хвороба цивілізованої людини. Людини, яка постійно знаходиться в приміщенні, постійно бачить близькі предмети, годинами дивиться телевізор, сидить за комп’ютером, читає, пише, тощо. В таких умовах, погляд людини постійно зосереджений на близько розташованих предметах. А це означає, що оптична система ока знаходиться в постійному напруженні. Поступово це напруження трансформується в незворотні, залишкові деформації кришталика та інших елементів оптичної системи ока. Результатом цих незворотних деформацій і є короткозорість. Зважаючи на ці малоприємні обставини, ви маєте розуміти, що відпочиваючи на свіжому повітрі, ви не лише дихаєте цим повітрям, не лише насолоджуєтесь мальовничими краєвидами, а й даєте відпочинок своїм постійно напруженим очам та запобігаєте ймовірній короткозорості.
Цивілізація не лише створила умови для появи певних дефектів зору, а й винайшла ефективні методи боротьби з ними. Найпоширенішим з цих методів є застосування окулярів та контактних лінз. Принцип дії окулярів, а відповідно і контактних лінз очевидно простий. Для того щоб компенсувати короткозорість, перед оком розташовують відповідну розсіювальну лінзу (мал.81а). Ця лінза заломлює промені таким чином, щоб потрапляючи в оптичну систему ока, вони фокусувались на його сітківці. Для запобігання далекозорості, перед оком ставлять відповідну збиральну лінзу (мал.81б), яка заломлює промені таким чином, щоб потрапляючи в оптичну систему ока, вони фокусувались на його сітківці.
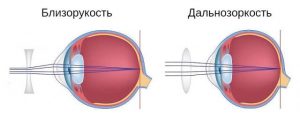
Мал.81. Короткозорість (а) та далекозорість (б) можна виправити шляхом застосування відповідних лінз (окулярів).
Про короткозорість та далекозорість знають майже всі. Однак не всі знають про ще один достатньо поширений дефект зору. Цей дефект називають астигматизмом (від лат. astigma – не точка). Така назва обумовлена тим, що в астигматичному оці, ті промені які йдуть від точкового джерела світла, зазвичай не збираються в чітко вираженій точці. При астигматизмі предмети виглядають певним чином роздвоєними (мал.80). Пояснюючи даний факт, можна сказати наступне. Зазвичай, робочі поверхні рогівки та кришталика є фрагментами певних сфер. Але іноді, ці поверхні виявляються деформованими таким чином, що в різних площинах, радіуси кривизни однієї і тієї ж поверхні є суттєво різними. В такій ситуації, те зображення яке створює відповідна оптична система, в одному напрямку виявляється сфокусованим на сітківці ока (чітким), а в іншому – не сфокусованим на ній (не чітким).
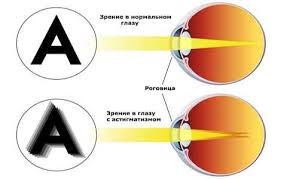
Мал.82. Астигматизм, це дефект зору, результатом якого є характерна роздвоєність зображень або викривлення їх форми.
Потрібно зауважити, що астигматизм може проявлятися не лише в тому, що зображення предметів є певним чином роздвоєним, а й в тому, що це зображення може бути геометрично викривленим. Наприклад коло може виглядати як еліпс, квадрат – як викривлений прямокутник, тощо.
Прояви астигматизму є досить індивідуальними та характеризуються широким різноманіттям причин. Тому не існує такої універсальної лінзи, яка б вирішувала проблему астигматизму в будь якій ситуації. Прості форми астигматизму зазвичай виправляють за допомогою циліндричних розсіювальних лінз. В більш складних випадках застосовують лінзи індивідуальних форм.
На завершення зауважимо, що короткозорість, далекозорість та астигматизм, це не хвороби зору, а його дефекти. Або, якщо хочете, малоприємні індивідуальні особливості системи зору конкретної людини. При цьому, ці особливості можуть бути як вродженими так і набутими.
Контрольні запитання.
1.Які функції виконує око?
2. Яке призначення та принцип дії райдужної оболонки?
3. Яке призначення та принцип дії кришталика?
4. Поясніть загальну схему формування зорових відчуттів.
5. Поясніть фізичну суть акомодації ока.
6. Поясніть фізичну суть далекозорості.
7. Поясніть фізичну суть короткозорості.
8. Чому короткозорість називають хворобою цивілізованих людей?
9. Яким чином виправляють а) короткозорість ока; б) далекозорість ока?
§24*. Оптичні ілюзії.
Дивлячись на навколишній світ, ми переконані в тому, що наші зорові відчуття вточності відображають реальність. Однак, в деяких ситуаціях (зазвичай ситуаціях штучно створених), те що ми бачимо та візуально відчуваємо, певним чином відрізняється від реальності. В подібних ситуаціях говорять про оптичні ілюзії (від. лат. illusion – обман). Наприклад дивлячись на малюнок 83 практично не можливо повірити в те, що перед вами не спіральна крива, а набір концентричних кіл. Навіть після того, як обвівши всі лінії, ви переконаєтесь в тому, що вони дійсно утворюють систему окремих концентричних кіл, вам все рівно буде здаватись, що перед вами неперервна спіральна лінія яка йде в глибину малюнку. І тим не менше, те що ви явно бачите, це оптична ілюзія, а простіше кажучи – оптичний обман.
Відразу ж зауважимо, що оптична ілюзія це не галюцинація, не прояви хворобливої уяви чи певних психічних збуджень. Оптична ілюзія, це цілком природня та закономірна реакція системи зору нормальної здорової людини на певні не стандартні ситуації.


Мал.83. Чи співпадають ваші зорові відчуття з фактом того, що зображені на малюнку криві є системою окремих концентричних кіл (кілець)?
Відповідаючи на питання як та чому виникають оптичні ілюзії, ми повинні розуміти, що наші зорові відчуття, тобто ті візуальні картинки які ми бачимо дивлячись на навколишній світ, це результат роботи надскладної системи, основними елементами якої є очі, зорові нерви та півкулі головного мозку (див.мал.76). Ми маємо розуміти, що та візуальна картинка яку ми бачимо, створюється не в наших очах, а в наших мізках. Ми маємо розуміти, що наші органи зору не просто дзеркально фіксують об’єкти та події, а здійснюють певний аналіз цих об’єктів та подій. Аналіз, який враховує не лише дзеркально зафіксовані факти, а й той генетично-індивідуальний досвід людини, який закарбовано в її підсвідомості.
Оптичні ілюзії характеризуються надзвичайним різноманіттям. Це різноманіття складно систематизувати, а тим більше пояснити. І тим не менше, ми все ж спробуємо виділити певним чином пов’язані групи ілюзій та стисло пояснити їх походження. Звісно, наші пояснення будуть гранично спрощеними. Адже мова йде не лише про таку надскладну біологічну систему як організм людини, а й про те, що прийнято називати свідомістю.
Чисельну групу оптичних ілюзій складають ті, що виникають на фоні певного графічного контексту. Деякі з подібних ілюзій представлені на мал.84. Це і зображені на фоні певного графічного контексту фігурки, серед яких фактично найменша (фігурка чоловіка) здається найбільшою, а фактично найбільша (фігурка дівчинки) – найменшою. Це і абсолютно однакові фігурки монстрів, які виглядають різновеликими. Це і паралельні прямі, які здаються не паралельними. Це і прямі відрізки які виглядають ломаними, тощо.


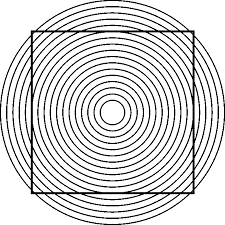
Мал.84. Ілюзії які виникають на фоні певного графічного контексту.
Аналізуючи ці та їм подібні ілюзії не важко збагнути, що їх поява обумовлена наявністю певного графічного контексту, на фоні якого відповідні об’єкти здаються візуально більшими або візуально меншими, візуально викривленими, непаралельними, нерівними, несуцільними, тощо.
Ясно, що в межах одного параграфу не можливо розглянути, проаналізувати та пояснити кожну окремо взяту ілюзійну ситуацію. Тому пояснимо лише одну, але узагальнююче типову контекстову ілюзію, наприклад таку, що представлена на мал.84а. Аналізуючи цю ілюзію можна сказати наступне. В підсвідомості кожного з нас закарбовані певні аксіоми, достовірність яких підтверджена не лише нашим повсякденним досвідом, а й досвідом всіх попередніх поколінь. Ці аксіоми стверджують: 1. По мірі того, як об’єкти віддаляються від спостерігача, їх візуальні розміри поступово зменшуються, поступово зменшуються візуальні відстані між різними об’єктами, певним чином змінюється їх колір, характер освітлення, тощо.
2.Чим більше елементів навколишнього фону закриває об’єкт, тим більші його реальні розміри.
Ці, тисячоліттями перевірені постулати (аксіоми), практично завжди об’єктивно відображають реальність та дозволяють нам безпомилково орієнтуватись в ній. Власне завдяки цим постулатам, ми в значній мірі і відчуваємо глибину та об’ємність навколишнього простору.
А що ж ми бачимо на спеціально створеному малюнку (мал.84а). А бачимо наступне. На дорозі що йде в далечінь, зображено три приблизно однакові силуети. При цьому кожен з них закриває різну кількість елементів одного й того ж навколишнього фону: дальній силует закриває найбільшу кількість цих елементів, ближній – найменшу. Аналізуючи ці факти, наша система зору робить абсолютно природній висновок: дальній силует є найбільшим, ближній – найменшим. Цей висновок здається тим більш обгрунтованим, якщо врахувати ту психологічно вагому обставину, що мова йде не просто про предмети, а про зображення маленької дівчинки та дорослого чоловіка.
Таким чином, прагнучи максимально об’єктивно відобразити реальні властивості навколишнього світу, та керуючись віками перевіреними та генетично закарбованими правилами, система зору дає абсолютно адекватну оцінку того що бачить. Інша справа, що в даному випадку система зору реагує не на реальний навколишній світ, а на певну, штучно створену графічну провокацію. В такій ситуації, звинувачувати систему зору в тому, що вона когось обманює, – що найменше некоректно. Адже ця система створена не для розгадування штучно створених графічних ребусів, а для того щоб об’єктивно відображати реалії навколишнього світу.
Цікаво, коли ви дивитесь на картину художника, наприклад на майстерно виконаний пейзаж, то чи усвідомлюєте факт того, що перед вами суцільна оптична ілюзія. Адже те що знаходиться перед вашими очима, не що інше як плоский шматок паперу, тканини чи стіни, на якому щось намальовано. І це намальоване є безумовно плоским. Тим не менше, ви бачите певну об’ємну картину. Бачите тому, що наш зір здатний певним чином реагувати на графічні провокації та створювати відповідні оптичні ілюзії. Не будь цієї здатності, ми б не мали задоволення захоплюватись шедеврами художнього мистецтва. А художники були б позбавлені роботи. Адже все що вони роблять, так це створюють майстерні оптичні ілюзії.

Мал.85. Чи усвідомлюєте ви факт того, що перед вами суцільна оптична ілюзія?
Особливо ефектну групу ілюзій складають ті, в яких елементи основного малюнку певним чином зливаються з елементами фонового контексту. Класичним прикладом такої ефектної ілюзії є зображена на мал.83 система концентричних кіл, які на відповідному фоні утворюють ілюзорну спіраль. Характерною особливістю подібних фонових ілюзій є те, що в них фоновий контекст є практично невід’ємною складовою основного малюнку. Втім, особлива ефектність цих ілюзій, визначальним чином обумовлена не структурою самого малюнка, а тим, як людський зір цей малюнок сприймає.
Справа в тому, що наше око не є тим фотографічним апаратом який беземоційно фіксує все те що потрапляє в його об’єктив. Дослідження показують, що будучи сфокусованим на певному предметі, наш зір не фотографує цей предмет, а певним чином сканує його. Це означає, що коли ми зосереджено (сфокусовано) дивимось на певний об’єкт, то наше око в процесі надзвичайно швидких рефлекторних рухів, багаторазово оглядає відповідний об’єкт та фіксує його характерні деталі. Власне ці деталі і визначають параметри того візуального образу, який формується в нашій свідомості.
Зважаючи на ці обставини, наш зір в тих провокаційних ситуаціях де основний та фоновий контексти по суті утворюють єдине ціле, одночасно реагує як на елементи основного малюнка, так і на елементи фонового контексту. Результатом такого реагування є факт того, що система окремих концентричних кіл, виглядає як неперервна спіральна лінія (мал.83а), система нерухомих кілець стає динамічно рухливою (мал83б), фактично вертикальні та паралельні контури літер, стають явно не паралельними і явно не вертикальними (мал.86а); білі цятки перетинів світлих смужок, на чорному фоні, ілюзорно сприймаються як періодично зникаючі та виникаючі чорні цятки (мал86б), тощо.
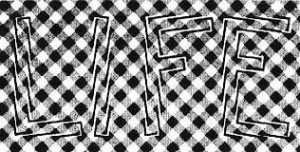

Мал.86. Порівняйте ваші зорові відчуття з реально намальованим.
Оптичні ілюзії можуть виникати не лише на фоні певного графічного контексту, а й завдяки його відсутності. Адже в багатьох ситуаціях, за відсутності пояснювального графічного контексту, системі зору важко однозначно ідентифікувати об’єкт. І якщо цей об’єкт так чи інакше схожий на декілька об’єктів одночасно, то виникають так звані ілюзії “перевертні”. Це означає, що дивлячись на один і той же малюнок, спостерігач почергово бачить то один то інший образ. Ілюзії такого гатунку представлені на мал.87.



Мал.87. Ілюзії “перевертні”.
Пояснюючи механізм появи ілюзій перевертнів, можна сказати наступне. Наша зорова свідомість влаштована таким чином, що завжди прагне ідентифікувати будь який побачений об’єкт. І якщо цей об’єкт виявляється схожим на декілька відомих об’єктів, а зовнішній фон не підказує правильного рішення, то свідомість почергово “висвітлює” кожен з можливих варіантів.
Певними різновидностями ілюзій перевертнів є велике різноманіття художніх картин, в яких загальне ілюзорне зображення, представляє собою певну сукупність, сюжетно пов’язаних самостійних картинок. Наприклад на мал.88а фактично зображено певний сільський пейзаж, елементами якого є захмарене небо, сільські хати, пастушок, вівці, стовбури дерев, тощо. При цьому, у своїй сукупності цей пейзаж утворює ілюзорний образ Т.Г. Шевченка. На мал.88б, ви можете побачити обриси дівочого обличчя, яке утворене системою квіток, стебел, листків та метелика. На мал.88в, ви безумовно побачите жіноче обличчя, яке утворено обрисами двох грайливих коней та певної кількості пташок.



Мал.88. Ілюзії перевертні, як витвори художнього мистецтва.
Факт того, що наша система зору певним чином сканує об’єкт спостережень, аналізує цей об’єкт та, враховуючи свій попередній досвід, намагається певним чином ідентифікувати його, наочно проявляється в тих ефектних ілюзіях, які називаються ілюзіями післядії. Ілюзії післядії виникають наприклад при розглядувані негативів світлин чи їм подібних малюнків. Намагаючись ідентифікувати об’єкт спостережень та представити його у звичному вигляді, система зору прагне представити негатив світлини у вигляді відповідного позитиву. Дійсно. На протязі 20-30 секунд, сконцентровано подивіться на негатив світлини (мал.89). Потім переведіть свій погляд на білу частину даної сторінки. При цьому, скоріш за все ви побачите, як негатив світлини дивовижним чином перетворюється на її позитив.


Мал.89. Ілюзії післядії, є результатом прагнень системи зору людини представити об’єкт спостережень у звичному та реально існуючому вигляді.
Ілюзії післядії є наочною ілюстрацією факту того, що наша система зору не просто фіксує ту світлову інформацію яка потрапляє в око спостерігача, а певним чином аналізує об’єкт спостережень, та прагне представити його у звичному для візуального сприйняття вигляді. Власне це прагнення сприяє тому, що те неприроднє зображення яке в реальності бачить спостерігач і яке представляє собою негатив світлини, система зору прагне представити у звичному та реально існуючому вигляді, тобто у вигляді позитивного зображення відповідної світлини.
До числа оптичних ілюзій можна віднести і так звані неможливі фігури. Втім, в даному випадку система зору нікого не обманює. Вона просто констатує той факт, що такого об’єкту який зображений на відповідному малюнку не існує і не може існувати. Не може тому, що зображене на малюнку, порушує певні просторово-геометричні принципи. Скажімо не можливо рухаючись замкнутою траєкторією, постійно підніматись вгору, або постійно опускатись вниз. А саме така можливість і допускається малюнком 90а.
Характерна особливість неможливих фігур полягає в тому, що їх окремі фрагменти є цілком реальними. Однак, у своєму поєднанні, ці реальні фрагменти створюють нереальну фігуру. Дійсно, уважно придивимся до тієї загально відомої неможливої фігури, яку прийнято називати «неможливим тризубом» (мал.90б). Окремі фрагменти цього тризуба, зокрема його передня частина – зубці тризуба, та задня частина – основа тризуба, самі по собі є цілком нормальними і такими, що не суперечать жодним законам графічного відображення реальності.
Однак, у своєму поєднанні, ці на перший погляд цілком нормальні фрагменти, утворюють тризуб якого в реальності бути не може. Дійсно, простежимо хід тих ліній що є контурами середнього зубця тризуба. Не важко бачити, що волею художника, одна з цих ліній стає нижньою частиною правого бічного зубця, а друга – верхньою частиною лівого зубця. В результаті, по мірі того як зір спостерігача рухається від краю тризуба до його основи, середній зубець зникає: кінець зубця – є, а його початок – відсутній. При зворотному ж русі погляду, навпаки – середній зубець тризуба дивним чином з’являється невідомо звідки. Загально відомим прикладом неможливої фігури є так званий «неможливий трикутник». Його неможливість полягає в тому, що кожна сторона цього трикутника, одночасно знаходиться в двох різних площинах. А саме такий трикутник і зображено на мал.90в.
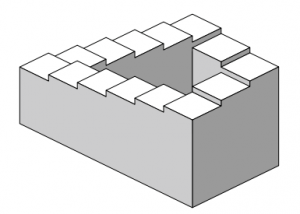
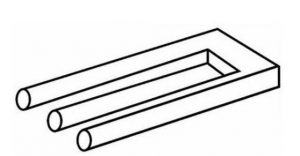

Мал.90. Неможливі фігури.
Потрібно зауважити, що неможливі фігури, це результат творчої фантазії художників. Саме вони, маніпулюючи певними законами графічного відображення дійсності, створюють ті малюнки які суперечать цій дійсності та намагаються обдурити наші відчуття. Втім, система зору людини влаштована таким чином, що можливе називає можливим, а неможливе – неможливим.
Факт того, що система зору людини спроможна відрізняти можливе від неможливого, безумовно вказує на те, що ця система не просто фіксує об’єкти та події, а й здійснює певний аналіз цих об’єктів і подій. Аналіз, який враховує не лише дзеркально зафіксовані факти, а й ту генетичну інформацію яка закарбовано в підсвідомості спостерігача. А в цій підсвідомості закарбовано, що не можливо рухаючись замкнутою траєкторією постійно підніматись вгору, або постійно опускатись вниз. Не можливо, щоб одна частина цілого мала два зубці, а друга – три. Не можливо, щоб певний прямолінійний відрізок одночасно знаходився в двох різних площинах. І якщо те, що ми бачимо суперечить тим базовим принципам які закарбовані в нашій генетичній пам’яті, то система зору безпомилково вказує на те, що побачене в реальності є неможливим.
Новомодніми різновидностями неможливих фігур і в той же час – ілюзій перевертнів, є різноманітні комп’ютерно фотографічні провокації, зокрема ті, в яких певний фрагмент обличчя, з одного боку виглядає як його профіль, а з іншого – як анфас.


Мал.90* Комп’ютерно фотографічні ілюзії, які певною мірою є як ілюзіями перевертнями так і неможливими фігурами.
На завершення згадаємо ще одну цікаву та важливу групу ілюзій, які відрізняються тим, що є ілюзіями динамічними, тобто такими, поява яких обумовлена певною послідовною зміною тих картинок які ми бачимо. Такі динамічні ілюзії пов’язані з інертністю нашого зору, тобто з його здатністю зберігати зорове враження навіть після того, коли джерело цього враження зникає. Простіше кажучи, якщо ви дивитесь на певний предмет і цей предмет раптово зникає, то на протязі певного проміжку часу (приблизно 0,1с), ви продовжуватимете бачити цей предмет.
Факт того, що наш зір має певні інерційні властивості, корисно застосовується в таких невід’ємних атрибутах сучасного життя як кіно та телебачення (телебачення, мобільний відеозв’язок, тощо). Адже те що вам фактично показують на кіно- та теле- екрані, це нерухомі фрагменти (кадри) певних подій. Фрагменти, які розташовані в тій послідовності, що відображає динаміку цих подій. А оскільки ці нерухомі картинки з достатньо високою частотою змінюють одна одну (24 або 25 кадрів за секунду), то завдяки інерційності зору, візуальне враження від кожного наступного кадру, накладається на враження від кадру попереднього. При цьому створюється ілюзія неперервності подій.
Певними проявами динамічних ілюзій є ті, що пов’язані з так званим стробоскопічним ефектом. Скажімо, коли дивлячись кінофільм, ви бачите, що лопаті гвинтокрила обертаються повільно, або не обертаються взагалі то це певна ілюзія. Адже фактично лопаті гвинтокрила обертаються з шалено великою швидкістю. Або наприклад, коли ви бачите що колеса автомобіля обертаються в напрямку протилежному від напрямку його руху, то це ілюзія, яка є прямим наслідком стробоскопічного ефекту.
Стробоскопічний ефект, це зорова ілюзія, поява якої обумовлена фактом того, що фіксація положення певного об’єкту, здійснюється не безперервно, а в певні послідовні проміжки часу. Скажімо, ілюзія з лопатями гвинтокрила виникає тому, що частота обертань цих лопатей співпадає з частотою спрацювань затвору кінокамери, або є кратною цій частоті. А це означає, що лопаті гвинтокрила фотографувалися саме в ті моменти коли вони знаходились в одному і тому ж положенні.
Узагальнюючи вище сказане, вкотре наголосимо: оптичні ілюзії, це цілком природня та закономірна реакція системи зору нормальної людини на певні нестандартні, зазвичай штучно створені, ситуації. Оптичні ілюзії безумовно вказують на те, що наші зорові відчуття, це не фотографічне відображення навколишньої дійсності, а результат надскладного біопсихологічного процесу. Процесу, який враховує не лише дзеркально зафіксовані факти, а й той генетичний та індивідуальний досвід який закарбовано в підсвідомості людини. Процесу, при якому отримана світлова інформація певним чином аналізується, систематизується та узагальнюється.
Оптичні ілюзії, невід’ємна складова нашого життя. Ці ілюзії допомагають нам відчувати об’ємність та глибину простору. Завдяки цим ілюзіям ми можемо насолоджуватись шедеврами художнього мистецтва. Завдяки опричним ілюзіям існує кіно, телебачення та сучасні мобільні засоби відеозв’язку. І як це не парадоксально, а оптичні ілюзії допомагають вченим об’єктивно досліджувати навколишній світ.